1 Introduction
In 1980, Siu [Reference Siu20] studied the strong rigidity of compact Kähler manifolds by using the theory of harmonic maps. The basic discovery by Siu was a new Bochner-type formula for harmonic maps between Kähler manifolds, which does not involve the Ricci curvature tensor of the domains. Using the modified Bochner formula, he proved that all harmonic maps from a compact Kähler manifold to a Kähler manifold with strongly seminegative curvature are actually pluriharmonic and some curvature expressions vanish. When the target manifolds are Kähler manifolds with strongly negative curvature or compact quotients of irreducible bounded symmetric domains, the vanishing curvature terms, under the assumption of sufficiently high rank, force the maps to be either holomorphic or antiholomorphic. Later, Sampson [Reference Sampson19] showed that all harmonic maps from compact Kähler manifolds into Riemannian manifolds with nonpositive Hermitian curvature are also pluriharmonic, which generalized the pluriharmonicity result of Siu to more general targets. Pluriharmonic maps, holomorphic maps and Siu–Sampson type results have many important applications in geometry and topology of Kähler manifolds. The readers are referred to [Reference Toledo23] for details.
In 2002, Petit [Reference Petit16] established some rigidity results for harmonic maps from strictly pseudoconvex CR manifolds, endowed with a positively oriented contact form, to Kähler manifolds and Riemannian manifolds by using tools of spinorial geometry. First, he proved that any harmonic map
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
from a compact Sasakian manifold to a Riemannian manifold with nonpositive sectional curvature satisfies that
$\unicode[STIX]{x1D719}:M\rightarrow N$
from a compact Sasakian manifold to a Riemannian manifold with nonpositive sectional curvature satisfies that
![]() $d\unicode[STIX]{x1D719}(T)=0$
, where
$d\unicode[STIX]{x1D719}(T)=0$
, where
![]() $T$
is the characteristic direction of
$T$
is the characteristic direction of
![]() $(M,\unicode[STIX]{x1D703})$
. A map with this property will be called foliated. Next he proved that under suitable rank conditions the harmonic map from a compact Sasakian manifold to a Kähler manifold with strongly negative curvature is
$(M,\unicode[STIX]{x1D703})$
. A map with this property will be called foliated. Next he proved that under suitable rank conditions the harmonic map from a compact Sasakian manifold to a Kähler manifold with strongly negative curvature is
![]() $(J,J^{N})$
-holomorphic or anti-
$(J,J^{N})$
-holomorphic or anti-
![]() $(J,J^{N})$
-holomorphic. However, Petit [Reference Petit16] did not specifically discuss the relevant notions of pluriharmonicity. On the other hand, Barletta et al. in [Reference Barletta, Dragomir and Urakawa1] introduced the so-called pseudoharmonic maps from nondegenerate CR manifolds which are a natural generalization of harmonic maps. In his thesis [Reference Chang4], Chang discussed some fundamental properties of pseudoharmonic maps.
$(J,J^{N})$
-holomorphic. However, Petit [Reference Petit16] did not specifically discuss the relevant notions of pluriharmonicity. On the other hand, Barletta et al. in [Reference Barletta, Dragomir and Urakawa1] introduced the so-called pseudoharmonic maps from nondegenerate CR manifolds which are a natural generalization of harmonic maps. In his thesis [Reference Chang4], Chang discussed some fundamental properties of pseudoharmonic maps.
In this paper, we establish some rigidity results for both harmonic maps and pseudoharmonic maps from pseudo-Hermitian manifolds by using the moving frame method. First, we find a result about the relationship between harmonic maps and pseudoharmonic maps from pseudo-Hermitian manifolds, which claims that these two kinds of maps are actually equivalent if the maps are foliated. By the moving frame method, we not only recapture Petit’s result about harmonic maps from compact Sasakian manifolds to Riemannian manifolds with nonpositive curvature (Theorem 5.2), but also show that the result is still valid for pseudoharmonic maps (Theorem 5.1).
The usual Bochner-type formula for the energy density of harmonic maps was given in [Reference Eells and Lemaire10]. In [Reference Chang4], Chang derived the CR Bochner-type formula for the horizontal energy density of a pseudoharmonic map
![]() $\unicode[STIX]{x1D719}$
. Unlike the Bochner formula of harmonic maps, there is a mixed term
$\unicode[STIX]{x1D719}$
. Unlike the Bochner formula of harmonic maps, there is a mixed term
![]() $\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})$
appearing in the CR Bochner formula for the pseudoharmonic map (cf. Lemma 4.1). When
$\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})$
appearing in the CR Bochner formula for the pseudoharmonic map (cf. Lemma 4.1). When
![]() $\unicode[STIX]{x1D719}$
is a function, it is known that the CR Paneitz operator, which is a divergence of a third order differential operator
$\unicode[STIX]{x1D719}$
is a function, it is known that the CR Paneitz operator, which is a divergence of a third order differential operator
![]() $P$
, is a useful tool to treat such kind of term. One important property of the CR Paneitz operator is its nonnegativity when the dimension of the CR manifold
$P$
, is a useful tool to treat such kind of term. One important property of the CR Paneitz operator is its nonnegativity when the dimension of the CR manifold
![]() ${\geqslant}5$
(cf. [Reference Chang and Chiu5]). We generalize the operator
${\geqslant}5$
(cf. [Reference Chang and Chiu5]). We generalize the operator
![]() $P$
to a differential operator, still denoted by
$P$
to a differential operator, still denoted by
![]() $P$
, acting on maps from a pseudo-Hermitian manifolds into a Riemannian manifold, and establish similar nonnegativity under the assumptions that the domain manifold has dimension
$P$
, acting on maps from a pseudo-Hermitian manifolds into a Riemannian manifold, and establish similar nonnegativity under the assumptions that the domain manifold has dimension
![]() ${\geqslant}5$
and the target manifold is of nonpositive Hermitian curvature (Theorem 4.1). This enables us to establish a CR Bochner-type result for pseudoharmonic maps (Theorem 4.2).
${\geqslant}5$
and the target manifold is of nonpositive Hermitian curvature (Theorem 4.1). This enables us to establish a CR Bochner-type result for pseudoharmonic maps (Theorem 4.2).
As mentioned previously, the notion of “pluriharmonicity” is important for Siu–Sampson type results and other potential applications. We shall discuss suitable notion of pluriharmonic maps from pseudo-Hermitian manifolds. On a pseudo-Hermitian manifold, we have two canonical connections, that is, the Levi-Civita connection of the Webster metric and the Tanaka–Webster connection of the pseudo-Hermitian structure. As a result, there are two kinds of second fundamental forms for a map from a pseudo-Hermitian manifold to a Riemannian manifold: the usual second fundamental form
![]() $B$
and a new second fundamental form
$B$
and a new second fundamental form
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
. The later one is defined with respect to the Tanaka–Webster connection of the domain pseudo-Hermitian manifold and the Levi-Civita connection of the target Riemannian manifold (see Section 2). Using
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
. The later one is defined with respect to the Tanaka–Webster connection of the domain pseudo-Hermitian manifold and the Levi-Civita connection of the target Riemannian manifold (see Section 2). Using
![]() $B$
, Ianus and Pastore [Reference Ianus and Pastore13] defined two kinds of pluriharmonic notions. In [Reference Dragomir and Kamishima8], Dragomir and Kamishima introduced the notion of
$B$
, Ianus and Pastore [Reference Ianus and Pastore13] defined two kinds of pluriharmonic notions. In [Reference Dragomir and Kamishima8], Dragomir and Kamishima introduced the notion of
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map by means of
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map by means of
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
. It turns out that a
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
. It turns out that a
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is pseudoharmonic and foliated, and thus it is harmonic too. In addition, when the target manifold is Kähler, the
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is pseudoharmonic and foliated, and thus it is harmonic too. In addition, when the target manifold is Kähler, the
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic maps in [Reference Dragomir and Kamishima8] are more compatible with the
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic maps in [Reference Dragomir and Kamishima8] are more compatible with the
![]() $(J,J^{N})$
-holomorphic maps in the sense that all
$(J,J^{N})$
-holomorphic maps in the sense that all
![]() $(J,J^{N})$
-holomorphic maps are automatically
$(J,J^{N})$
-holomorphic maps are automatically
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic. Next, using the Siu–Sampson technique, we prove that all harmonic maps or pseudoharmonic maps from compact Sasakian manifolds to Riemannian manifolds with nonpositive Hermitian curvature or Kähler manifolds with strong seminegative curvature are
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic. Next, using the Siu–Sampson technique, we prove that all harmonic maps or pseudoharmonic maps from compact Sasakian manifolds to Riemannian manifolds with nonpositive Hermitian curvature or Kähler manifolds with strong seminegative curvature are
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic (Theorems 6.1, 6.2). If the target is a Kähler manifold with strongly negative curvature and the rank of the map
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic (Theorems 6.1, 6.2). If the target is a Kähler manifold with strongly negative curvature and the rank of the map
![]() ${\geqslant}3$
at some point, then the harmonic map or the pseudoharmonic map is
${\geqslant}3$
at some point, then the harmonic map or the pseudoharmonic map is
![]() $(J,J^{N})$
-holomorphic or anti-
$(J,J^{N})$
-holomorphic or anti-
![]() $(J,J^{N})$
-holomorphic (Theorem 7.3). In [Reference Petit16], Petit proved a similar result for harmonic maps using different technique. When the target is a locally Hermitian symmetric space of noncompact type whose universal cover does not contain the hyperbolic plane as a factor, we show that the harmonic or pseudoharmonic maps are
$(J,J^{N})$
-holomorphic (Theorem 7.3). In [Reference Petit16], Petit proved a similar result for harmonic maps using different technique. When the target is a locally Hermitian symmetric space of noncompact type whose universal cover does not contain the hyperbolic plane as a factor, we show that the harmonic or pseudoharmonic maps are
![]() $(J,J^{N})$
-holomorphic under some explicit rank conditions (Theorem 7.1). These generalize some similar results in [Reference Carlson and Toledo3] to the pseudo-Hermitian case. To derive the above results, we also investigate the conic extensions of harmonic maps,
$(J,J^{N})$
-holomorphic under some explicit rank conditions (Theorem 7.1). These generalize some similar results in [Reference Carlson and Toledo3] to the pseudo-Hermitian case. To derive the above results, we also investigate the conic extensions of harmonic maps,
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic maps and
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic maps and
![]() $(J,J^{N})$
-holomorphic maps from Sasakian manifolds respectively, and establish also a unique continuation theorem for
$(J,J^{N})$
-holomorphic maps from Sasakian manifolds respectively, and establish also a unique continuation theorem for
![]() $(J,J^{N})$
-holomorphicity (Proposition 7.2). Using a technique in [Reference Pigola, Rigoli and Setti17], we consider harmonic maps and pseudoharmonic maps from complete noncompact pseudo-Hermitian manifolds too. Under some decay conditions, some foliated results and
$(J,J^{N})$
-holomorphicity (Proposition 7.2). Using a technique in [Reference Pigola, Rigoli and Setti17], we consider harmonic maps and pseudoharmonic maps from complete noncompact pseudo-Hermitian manifolds too. Under some decay conditions, some foliated results and
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity results are given.
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity results are given.
Finally, we would like to mention that Yuxin Dong in [Reference Dong7] has established similar rigidity results including Siu type results for pseudoharmonic maps between pseudo-Hermitian manifolds.
2 Preliminaries
2.1 Pseudo-Hermitian structures
A smooth manifold
![]() $M$
of real
$M$
of real
![]() $(2m+1)$
-dimension is said to be a CR manifold (of type
$(2m+1)$
-dimension is said to be a CR manifold (of type
![]() $(m,1)$
) if there exists a smooth
$(m,1)$
) if there exists a smooth
![]() $m$
-dimensional complex subbundle
$m$
-dimensional complex subbundle
![]() $T_{1,0}(M)$
of the complexifed tangent bundle
$T_{1,0}(M)$
of the complexifed tangent bundle
![]() $T^{\mathbb{C}}(M)=T(M)\otimes \mathbb{C}$
, such that
$T^{\mathbb{C}}(M)=T(M)\otimes \mathbb{C}$
, such that
and
for any open subset
![]() $U\subset M$
. Here
$U\subset M$
. Here
![]() $T_{0,1}(M)=\overline{T_{1,0}(M)}$
denotes the complex conjugate of
$T_{0,1}(M)=\overline{T_{1,0}(M)}$
denotes the complex conjugate of
![]() $T_{1,0}(M)$
. The subbundle
$T_{1,0}(M)$
. The subbundle
![]() $T_{1,0}(M)$
is called a CR structure on
$T_{1,0}(M)$
is called a CR structure on
![]() $M$
. Equivalently, the CR structure may also be described by the Levi distribution
$M$
. Equivalently, the CR structure may also be described by the Levi distribution
![]() $H(M)=\text{Re}\{T_{1,0}(M)\oplus T_{0,1}(M)\}$
, which carries a complex structure
$H(M)=\text{Re}\{T_{1,0}(M)\oplus T_{0,1}(M)\}$
, which carries a complex structure
![]() $J:H(M)\rightarrow H(M)$
given by
$J:H(M)\rightarrow H(M)$
given by
for any
![]() $Z\in T_{1,0}(M)$
.
$Z\in T_{1,0}(M)$
.
Hereafter we assume
![]() $M$
is orientable. Let us set
$M$
is orientable. Let us set
for any
![]() $x\in M$
. Then
$x\in M$
. Then
![]() $E\rightarrow M$
becomes an orientable real line subbundle of the cotangent bundle
$E\rightarrow M$
becomes an orientable real line subbundle of the cotangent bundle
![]() $T^{\ast }(M)$
, and thus there exist globally defined nonvanishing sections
$T^{\ast }(M)$
, and thus there exist globally defined nonvanishing sections
![]() $\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E4}^{\infty }(E)$
. Any such a section
$\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E4}^{\infty }(E)$
. Any such a section
![]() $\unicode[STIX]{x1D703}$
is called a pseudo-Hermitian structure on
$\unicode[STIX]{x1D703}$
is called a pseudo-Hermitian structure on
![]() $M$
. The Levi form
$M$
. The Levi form
![]() $G_{\unicode[STIX]{x1D703}}$
of
$G_{\unicode[STIX]{x1D703}}$
of
![]() $\unicode[STIX]{x1D703}$
is defined by
$\unicode[STIX]{x1D703}$
is defined by
for any
![]() $X,Y\in H(M)$
. A CR manifold
$X,Y\in H(M)$
. A CR manifold
![]() $(M,T_{1,0}(M))$
is said to be a strictly pseudoconvex CR manifold if the Levi form
$(M,T_{1,0}(M))$
is said to be a strictly pseudoconvex CR manifold if the Levi form
![]() $G_{\unicode[STIX]{x1D703}}$
is positive definite for some pseudo-Hermitian structure
$G_{\unicode[STIX]{x1D703}}$
is positive definite for some pseudo-Hermitian structure
![]() $\unicode[STIX]{x1D703}$
on
$\unicode[STIX]{x1D703}$
on
![]() $M$
. Standard examples of strictly pseudoconvex CR manifolds are the odd-dimensional spheres and the Heisenberg groups.
$M$
. Standard examples of strictly pseudoconvex CR manifolds are the odd-dimensional spheres and the Heisenberg groups.
When
![]() $(M,T_{1,0}(M))$
is strictly pseudoconvex, it is natural to orient
$(M,T_{1,0}(M))$
is strictly pseudoconvex, it is natural to orient
![]() $E$
by declaring a pseudo-Hermitian structure
$E$
by declaring a pseudo-Hermitian structure
![]() $\unicode[STIX]{x1D703}$
to be positive if
$\unicode[STIX]{x1D703}$
to be positive if
![]() $G_{\unicode[STIX]{x1D703}}$
is positive definite. Henceforth we shall assume that
$G_{\unicode[STIX]{x1D703}}$
is positive definite. Henceforth we shall assume that
![]() $(M,T_{1,0}(M))$
is strictly pseudoconvex and
$(M,T_{1,0}(M))$
is strictly pseudoconvex and
![]() $\unicode[STIX]{x1D703}$
is a positive pseudo-Hermitian structure. The triple
$\unicode[STIX]{x1D703}$
is a positive pseudo-Hermitian structure. The triple
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is called a pseudo-Hermitian manifold.
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is called a pseudo-Hermitian manifold.
Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Then there exists a unique nonvanishing vector field
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Then there exists a unique nonvanishing vector field
![]() $T$
on
$T$
on
![]() $M$
, transverse to
$M$
, transverse to
![]() $H(M)$
, satisfying
$H(M)$
, satisfying
![]() $\unicode[STIX]{x1D703}(T)=1$
and
$\unicode[STIX]{x1D703}(T)=1$
and
![]() $T\lrcorner \,d\unicode[STIX]{x1D703}=0$
. The vector field
$T\lrcorner \,d\unicode[STIX]{x1D703}=0$
. The vector field
![]() $T$
is referred to as the characteristic direction or the Reeb vector field of
$T$
is referred to as the characteristic direction or the Reeb vector field of
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
. Then we can extend
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
. Then we can extend
![]() $G_{\unicode[STIX]{x1D703}}$
to a Riemannian metric
$G_{\unicode[STIX]{x1D703}}$
to a Riemannian metric
![]() $g_{\unicode[STIX]{x1D703}}$
, called the Webster metric, on
$g_{\unicode[STIX]{x1D703}}$
, called the Webster metric, on
![]() $M$
as follows:
$M$
as follows:
for any
![]() $X,Y\in T(M)$
, where
$X,Y\in T(M)$
, where
![]() $\unicode[STIX]{x1D70B}_{H}:T(M)\rightarrow H(M)$
is the projection associated to the direct sum decomposition
$\unicode[STIX]{x1D70B}_{H}:T(M)\rightarrow H(M)$
is the projection associated to the direct sum decomposition
![]() $T(M)=H(M)\oplus \mathbb{R}T$
. Let us extend
$T(M)=H(M)\oplus \mathbb{R}T$
. Let us extend
![]() $J$
to a
$J$
to a
![]() $(1,1)$
tensor field on
$(1,1)$
tensor field on
![]() $M$
by requesting that
$M$
by requesting that
![]() $JT=0$
. Then the two-form
$JT=0$
. Then the two-form
![]() $\unicode[STIX]{x1D6FA}$
defined by
$\unicode[STIX]{x1D6FA}$
defined by
![]() $\unicode[STIX]{x1D6FA}(X,Y)=g_{\unicode[STIX]{x1D703}}(X,JY)$
coincides with the two-form
$\unicode[STIX]{x1D6FA}(X,Y)=g_{\unicode[STIX]{x1D703}}(X,JY)$
coincides with the two-form
![]() $-d\unicode[STIX]{x1D703}$
. Thus the pseudo-Hermitian manifold
$-d\unicode[STIX]{x1D703}$
. Thus the pseudo-Hermitian manifold
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
carries a contact metric structure
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
carries a contact metric structure
![]() $(J,-T,-\unicode[STIX]{x1D703},g_{\unicode[STIX]{x1D703}})$
(cf. [Reference Dragomir and Tomassini9]).
$(J,-T,-\unicode[STIX]{x1D703},g_{\unicode[STIX]{x1D703}})$
(cf. [Reference Dragomir and Tomassini9]).
On a pseudo-Hermitian manifold, there exists a canonical linear connection preserving both the CR structure and the Webster metric.
Lemma 2.1. (cf. [Reference Dragomir and Tomassini9, Reference Tanaka22, Reference Webster26])
Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
![]() $g_{\unicode[STIX]{x1D703}}$
the Webster metric of
$g_{\unicode[STIX]{x1D703}}$
the Webster metric of
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
. Then there exists a unique linear connection
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
. Then there exists a unique linear connection
![]() $\unicode[STIX]{x1D6FB}$
on
$\unicode[STIX]{x1D6FB}$
on
![]() $M$
, called the Tanaka–Webster connection, such that:
$M$
, called the Tanaka–Webster connection, such that:
(1) the Levi distribution
 $H(M)$
is parallel with respect to
$H(M)$
is parallel with respect to
 $\unicode[STIX]{x1D6FB}$
;
$\unicode[STIX]{x1D6FB}$
;(2)
 $\unicode[STIX]{x1D6FB}g_{\unicode[STIX]{x1D703}}=0$
,
$\unicode[STIX]{x1D6FB}g_{\unicode[STIX]{x1D703}}=0$
,
 $\unicode[STIX]{x1D6FB}J=0$
,
$\unicode[STIX]{x1D6FB}J=0$
,
 $\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D703}=0$
(hence
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D703}=0$
(hence
 $\unicode[STIX]{x1D6FB}T=0$
);
$\unicode[STIX]{x1D6FB}T=0$
);(3) the torsion
 $T_{\unicode[STIX]{x1D6FB}}$
of
$T_{\unicode[STIX]{x1D6FB}}$
of
 $\unicode[STIX]{x1D6FB}$
satisfies
$\unicode[STIX]{x1D6FB}$
satisfies
 $T_{\unicode[STIX]{x1D6FB}}(X,Y)=-2\unicode[STIX]{x1D6FA}(X,Y)T$
and
$T_{\unicode[STIX]{x1D6FB}}(X,Y)=-2\unicode[STIX]{x1D6FA}(X,Y)T$
and
 $T_{\unicode[STIX]{x1D6FB}}(T,JX)=-JT_{\unicode[STIX]{x1D6FB}}(T,X)$
, for any
$T_{\unicode[STIX]{x1D6FB}}(T,JX)=-JT_{\unicode[STIX]{x1D6FB}}(T,X)$
, for any
 $X,Y\in H(M)$
.
$X,Y\in H(M)$
.
Unlike the Levi-Civita connection, the torsion
![]() $T_{\unicode[STIX]{x1D6FB}}$
of the Tanaka–Webster connection
$T_{\unicode[STIX]{x1D6FB}}$
of the Tanaka–Webster connection
![]() $\unicode[STIX]{x1D6FB}$
is always nonzero. The pseudo-Hermitian torsion of
$\unicode[STIX]{x1D6FB}$
is always nonzero. The pseudo-Hermitian torsion of
![]() $\unicode[STIX]{x1D6FB}$
, denoted by
$\unicode[STIX]{x1D6FB}$
, denoted by
![]() $\unicode[STIX]{x1D70F}$
, is defined by
$\unicode[STIX]{x1D70F}$
, is defined by
![]() $\unicode[STIX]{x1D70F}(X)=T_{\unicode[STIX]{x1D6FB}}(T,X)$
, for any
$\unicode[STIX]{x1D70F}(X)=T_{\unicode[STIX]{x1D6FB}}(T,X)$
, for any
![]() $X\in T(M)$
. Note that
$X\in T(M)$
. Note that
![]() $\unicode[STIX]{x1D70F}$
is trace-free and self-adjoint with respect to the Webster metric
$\unicode[STIX]{x1D70F}$
is trace-free and self-adjoint with respect to the Webster metric
![]() $g_{\unicode[STIX]{x1D703}}$
(cf. [Reference Dragomir and Tomassini9]). Let us set
$g_{\unicode[STIX]{x1D703}}$
(cf. [Reference Dragomir and Tomassini9]). Let us set
for any
![]() $X,Y\in T(M)$
. Then we have
$X,Y\in T(M)$
. Then we have
![]() $A(X,Y)=A(Y,X)$
.
$A(X,Y)=A(Y,X)$
.
Theorem 2.1. (cf. [Reference Dragomir and Tomassini9])
Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Then the Webster metric
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Then the Webster metric
![]() $g_{\unicode[STIX]{x1D703}}$
is Sasakian if and only if the Tanaka–Webster connection of
$g_{\unicode[STIX]{x1D703}}$
is Sasakian if and only if the Tanaka–Webster connection of
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
has vanishing pseudo-Hermitian torsion, that is,
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
has vanishing pseudo-Hermitian torsion, that is,
![]() $\unicode[STIX]{x1D70F}=0$
.
$\unicode[STIX]{x1D70F}=0$
.
Remark 2.1. In the following of this paper, a pseudo-Hermitian manifold
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is said to be a Sasakian manifold, if the Webster metric
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is said to be a Sasakian manifold, if the Webster metric
![]() $g_{\unicode[STIX]{x1D703}}$
is Sasakian. The quadruple
$g_{\unicode[STIX]{x1D703}}$
is Sasakian. The quadruple
![]() $(J,-T,-\unicode[STIX]{x1D703},g_{\unicode[STIX]{x1D703}})$
is referred to as a Sasakian structure on
$(J,-T,-\unicode[STIX]{x1D703},g_{\unicode[STIX]{x1D703}})$
is referred to as a Sasakian structure on
![]() $M$
. The readers are referred to [Reference Boyer and Galicki2] for the original definition of Sasakian metrics.
$M$
. The readers are referred to [Reference Boyer and Galicki2] for the original definition of Sasakian metrics.
Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Let
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Let
![]() $\{T_{\unicode[STIX]{x1D6FC}}:1\leqslant \unicode[STIX]{x1D6FC}\leqslant m\}$
be a local frame of
$\{T_{\unicode[STIX]{x1D6FC}}:1\leqslant \unicode[STIX]{x1D6FC}\leqslant m\}$
be a local frame of
![]() $T_{1,0}(M)$
defined on an open set
$T_{1,0}(M)$
defined on an open set
![]() $U\subset M$
and
$U\subset M$
and
![]() $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}:1\leqslant \unicode[STIX]{x1D6FC}\leqslant m\}$
the corresponding admissible local coframe, that is,
$\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}:1\leqslant \unicode[STIX]{x1D6FC}\leqslant m\}$
the corresponding admissible local coframe, that is,
![]() $\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FD}})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FD}})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}$
,
![]() $\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T_{\bar{\unicode[STIX]{x1D6FD}}})=0$
,
$\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T_{\bar{\unicode[STIX]{x1D6FD}}})=0$
,
![]() $\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T)=0$
. Clearly Lemma 2.1 implies that there exist unique locally defined complex 1-forms
$\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T)=0$
. Clearly Lemma 2.1 implies that there exist unique locally defined complex 1-forms
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\ast }(M)\otimes \mathbb{C})$
such that
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\ast }(M)\otimes \mathbb{C})$
such that
where
![]() $T_{\bar{\unicode[STIX]{x1D6FC}}}=\overline{T_{\unicode[STIX]{x1D6FC}}}$
and
$T_{\bar{\unicode[STIX]{x1D6FC}}}=\overline{T_{\unicode[STIX]{x1D6FC}}}$
and
![]() $\unicode[STIX]{x1D714}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FC}}}=\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}}$
. These are the connection 1-forms of the Tanaka–Webster connection
$\unicode[STIX]{x1D714}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FC}}}=\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}}$
. These are the connection 1-forms of the Tanaka–Webster connection
![]() $\unicode[STIX]{x1D6FB}$
. Since
$\unicode[STIX]{x1D6FB}$
. Since
![]() $\unicode[STIX]{x1D70F}(T_{1,0}(M))\subset T_{0,1}(M)$
, there are uniquely defined smooth functions
$\unicode[STIX]{x1D70F}(T_{1,0}(M))\subset T_{0,1}(M)$
, there are uniquely defined smooth functions
![]() $A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FD}}}:U\rightarrow \mathbb{C}$
such that
$A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FD}}}:U\rightarrow \mathbb{C}$
such that
Writing
![]() $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=A(T_{\unicode[STIX]{x1D6FC}},T_{\unicode[STIX]{x1D6FD}})$
and
$A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=A(T_{\unicode[STIX]{x1D6FC}},T_{\unicode[STIX]{x1D6FD}})$
and
![]() $h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=g_{\unicode[STIX]{x1D703}}(T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FD}}})$
, we have
$h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=g_{\unicode[STIX]{x1D703}}(T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FD}}})$
, we have
![]() $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FE}}}h_{\bar{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FD}}$
. Let us define the local 1-forms
$A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FE}}}h_{\bar{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FD}}$
. Let us define the local 1-forms
![]() $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\ast }(M)\otimes \mathbb{C})$
by setting
$\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\ast }(M)\otimes \mathbb{C})$
by setting
![]() $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}=A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}$
. Then
$\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}=A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}$
. Then
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}\otimes T_{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D70F}^{\bar{\unicode[STIX]{x1D6FC}}}\otimes T_{\bar{\unicode[STIX]{x1D6FC}}}$
, where
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}\otimes T_{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D70F}^{\bar{\unicode[STIX]{x1D6FC}}}\otimes T_{\bar{\unicode[STIX]{x1D6FC}}}$
, where
![]() $\unicode[STIX]{x1D70F}^{\bar{\unicode[STIX]{x1D6FC}}}=\overline{\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}}$
.
$\unicode[STIX]{x1D70F}^{\bar{\unicode[STIX]{x1D6FC}}}=\overline{\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}}$
.
The Tanaka–Webster connection induces a covariant differential operator
![]() $\unicode[STIX]{x1D6FB}$
on tensors on
$\unicode[STIX]{x1D6FB}$
on tensors on
![]() $M$
. We denote components of covariant derivatives with indices preceded by a comma; for instance,
$M$
. We denote components of covariant derivatives with indices preceded by a comma; for instance,
![]() $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6FE}}}=(\unicode[STIX]{x1D6FB}_{T_{\bar{\unicode[STIX]{x1D6FE}}}}A)(T_{\unicode[STIX]{x1D6FC}},T_{\unicode[STIX]{x1D6FD}})$
and
$A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6FE}}}=(\unicode[STIX]{x1D6FB}_{T_{\bar{\unicode[STIX]{x1D6FE}}}}A)(T_{\unicode[STIX]{x1D6FC}},T_{\unicode[STIX]{x1D6FD}})$
and
![]() $A_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}^{\bar{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}[(\unicode[STIX]{x1D6FB}_{T_{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D70F})(T_{\unicode[STIX]{x1D6FC}})]$
. The indices
$A_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}^{\bar{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}[(\unicode[STIX]{x1D6FB}_{T_{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D70F})(T_{\unicode[STIX]{x1D6FC}})]$
. The indices
![]() $\{0,\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}\}$
indicate derivatives with respect to
$\{0,\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}\}$
indicate derivatives with respect to
![]() $\{T,T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FC}}}\}$
. For derivatives of a scalar function, we omit the comma; for example,
$\{T,T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FC}}}\}$
. For derivatives of a scalar function, we omit the comma; for example,
![]() $u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=\overline{\bar{u}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}}=T_{\bar{\unicode[STIX]{x1D6FD}}}T_{\unicode[STIX]{x1D6FC}}u-\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}(T_{\bar{\unicode[STIX]{x1D6FD}}})T_{\unicode[STIX]{x1D6FE}}u$
and
$u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=\overline{\bar{u}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}}=T_{\bar{\unicode[STIX]{x1D6FD}}}T_{\unicode[STIX]{x1D6FC}}u-\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}(T_{\bar{\unicode[STIX]{x1D6FD}}})T_{\unicode[STIX]{x1D6FE}}u$
and
![]() $u_{00}=TTu$
. Then we have the following structure equations for the Tanaka–Webster connection
$u_{00}=TTu$
. Then we have the following structure equations for the Tanaka–Webster connection
![]() $\unicode[STIX]{x1D6FB}$
.
$\unicode[STIX]{x1D6FB}$
.
Lemma 2.2. (cf. [Reference Dragomir and Tomassini9, Reference Webster26])
The structure equations for the Tanaka–Webster connection of
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
in terms of local coframe
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
in terms of local coframe
![]() $\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\}$
are
$\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\}$
are
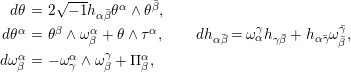 $$\begin{eqnarray}\qquad \begin{array}{@{}rcl@{}}d\unicode[STIX]{x1D703}\ & =\ & 2\sqrt{-1}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}},\\ d\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\ & =\ & \unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D703}\wedge \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}},\qquad dh_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}h_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}+h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D714}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FE}}},\\ d\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\ & =\ & -\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}},\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\qquad \begin{array}{@{}rcl@{}}d\unicode[STIX]{x1D703}\ & =\ & 2\sqrt{-1}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}},\\ d\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\ & =\ & \unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D703}\wedge \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}},\qquad dh_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}h_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}+h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D714}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FE}}},\\ d\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\ & =\ & -\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}},\end{array}\end{eqnarray}$$
where
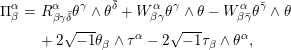 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}} & = & \displaystyle R_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FF}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FE}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FF}}}+W_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FE}}\wedge \unicode[STIX]{x1D703}-W_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FE}}}\wedge \unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}-2\sqrt{-1}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}} & = & \displaystyle R_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FF}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FE}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FF}}}+W_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FE}}\wedge \unicode[STIX]{x1D703}-W_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FE}}}\wedge \unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}-2\sqrt{-1}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
with
and
![]() $(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}})$
is the inverse matrix of the matrix
$(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}})$
is the inverse matrix of the matrix
![]() $(h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}})$
.
$(h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}})$
.
Let us set by definition
![]() $R_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=g_{\unicode[STIX]{x1D703}}(R(T_{\unicode[STIX]{x1D706}},T_{\bar{\unicode[STIX]{x1D707}}})T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FD}}})=h_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FE}}$
, where
$R_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=g_{\unicode[STIX]{x1D703}}(R(T_{\unicode[STIX]{x1D706}},T_{\bar{\unicode[STIX]{x1D707}}})T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FD}}})=h_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FE}}$
, where
![]() $R$
is the curvature tensor of
$R$
is the curvature tensor of
![]() $\unicode[STIX]{x1D6FB}$
. From (2.1), one may derive that (cf. [Reference Webster26]):
$\unicode[STIX]{x1D6FB}$
. From (2.1), one may derive that (cf. [Reference Webster26]):
![]() $R_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D707}}}$
. The pseudo-Hermitian Ricci tensor is given by
$R_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D707}}}$
. The pseudo-Hermitian Ricci tensor is given by
![]() $R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FC}}=R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FC}}$
, which satisfies
$R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FC}}=R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FC}}$
, which satisfies
![]() $R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\bar{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D706}}$
. Since the Tanaka–Webster connection can be viewed as a connection in
$R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\bar{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D706}}$
. Since the Tanaka–Webster connection can be viewed as a connection in
![]() $T_{1,0}(M)$
, the pseudo-Hermitian Ricci tensor and the torsion tensor on
$T_{1,0}(M)$
, the pseudo-Hermitian Ricci tensor and the torsion tensor on
![]() $T_{1,0}(M)$
are also denoted by
$T_{1,0}(M)$
are also denoted by
and
for any
![]() $X=X^{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$
,
$X=X^{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$
,
![]() $Y=Y^{\unicode[STIX]{x1D6FD}}T_{\unicode[STIX]{x1D6FD}}\in T_{1,0}(M)$
.
$Y=Y^{\unicode[STIX]{x1D6FD}}T_{\unicode[STIX]{x1D6FD}}\in T_{1,0}(M)$
.
The divergence of a vector field
![]() $X$
on
$X$
on
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is defined by
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is defined by
where
![]() $\mathscr{L}_{X}$
denotes the Lie derivative and
$\mathscr{L}_{X}$
denotes the Lie derivative and
![]() $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D703}\wedge (d\unicode[STIX]{x1D703})^{m}$
is, up to a constant, the volume form on
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D703}\wedge (d\unicode[STIX]{x1D703})^{m}$
is, up to a constant, the volume form on
![]() $(M,g_{\unicode[STIX]{x1D703}})$
. The divergence
$(M,g_{\unicode[STIX]{x1D703}})$
. The divergence
![]() $\text{div}(X)$
can be computed in another way, that is,
$\text{div}(X)$
can be computed in another way, that is,
If
![]() $Z=Z^{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$
, then
$Z=Z^{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$
, then
![]() $\text{div}(Z)=T_{\unicode[STIX]{x1D6FC}}(Z^{\unicode[STIX]{x1D6FC}})+Z^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FC}})$
. For a 1-form
$\text{div}(Z)=T_{\unicode[STIX]{x1D6FC}}(Z^{\unicode[STIX]{x1D6FC}})+Z^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FC}})$
. For a 1-form
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $M$
, we denote by
$M$
, we denote by
![]() $X_{\unicode[STIX]{x1D70E}}$
its dual vector field, that is,
$X_{\unicode[STIX]{x1D70E}}$
its dual vector field, that is,
![]() $g_{\unicode[STIX]{x1D703}}(X_{\unicode[STIX]{x1D70E}},Y)=\unicode[STIX]{x1D70E}(Y)$
for any
$g_{\unicode[STIX]{x1D703}}(X_{\unicode[STIX]{x1D70E}},Y)=\unicode[STIX]{x1D70E}(Y)$
for any
![]() $Y\in T(M)$
. The divergence of
$Y\in T(M)$
. The divergence of
![]() $\unicode[STIX]{x1D70E}$
denoted by
$\unicode[STIX]{x1D70E}$
denoted by
![]() $\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})$
is defined by
$\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})$
is defined by
![]() $\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})=\text{div}(X_{\unicode[STIX]{x1D70E}})$
. If
$\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})=\text{div}(X_{\unicode[STIX]{x1D70E}})$
. If
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}$
, then
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}$
, then
![]() $\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FD}}}h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}$
. The sublaplacian of
$\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FD}}}h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}$
. The sublaplacian of
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is the differential operator
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is the differential operator
![]() $\unicode[STIX]{x1D6E5}_{b}$
on functions defined by
$\unicode[STIX]{x1D6E5}_{b}$
on functions defined by
for any
![]() $u\in C^{2}(M)$
. Here
$u\in C^{2}(M)$
. Here
![]() $\unicode[STIX]{x1D6FB}^{H}u=\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D6FB}u$
is the horizontal gradient, and
$\unicode[STIX]{x1D6FB}^{H}u=\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D6FB}u$
is the horizontal gradient, and
![]() $\unicode[STIX]{x1D6FB}u$
is the ordinary gradient of
$\unicode[STIX]{x1D6FB}u$
is the ordinary gradient of
![]() $u$
with respect to the Webster metric
$u$
with respect to the Webster metric
![]() $g_{\unicode[STIX]{x1D703}}$
, that is,
$g_{\unicode[STIX]{x1D703}}$
, that is,
![]() $g_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FB}u,X)=X(u)$
for any
$g_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FB}u,X)=X(u)$
for any
![]() $X\in T(M)$
. With respect to the local frame
$X\in T(M)$
. With respect to the local frame
![]() $\{T,T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FC}}}\}$
, the sublaplacian
$\{T,T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FC}}}\}$
, the sublaplacian
![]() $\unicode[STIX]{x1D6E5}_{b}$
can be expressed as
$\unicode[STIX]{x1D6E5}_{b}$
can be expressed as
![]() $\unicode[STIX]{x1D6E5}_{b}u=-(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}u_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}})$
.
$\unicode[STIX]{x1D6E5}_{b}u=-(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}u_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}})$
.
We denote by
![]() $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$
the Levi-Civita connection of
$\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$
the Levi-Civita connection of
![]() $(M,g_{\unicode[STIX]{x1D703}})$
. From [Reference Dragomir and Tomassini9, Lemma 1.3], we know that the Levi-Civita connection
$(M,g_{\unicode[STIX]{x1D703}})$
. From [Reference Dragomir and Tomassini9, Lemma 1.3], we know that the Levi-Civita connection
![]() $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$
is related to the Tanaka–Webster connection
$\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$
is related to the Tanaka–Webster connection
![]() $\unicode[STIX]{x1D6FB}$
by
$\unicode[STIX]{x1D6FB}$
by
where
![]() $2(\unicode[STIX]{x1D703}\odot J)(X,Y)=\unicode[STIX]{x1D703}(X)JY+\unicode[STIX]{x1D703}(Y)JX$
. By (2.4), we have
$2(\unicode[STIX]{x1D703}\odot J)(X,Y)=\unicode[STIX]{x1D703}(X)JY+\unicode[STIX]{x1D703}(Y)JX$
. By (2.4), we have
![]() $\unicode[STIX]{x1D6FB}_{X}^{\unicode[STIX]{x1D703}}T=\unicode[STIX]{x1D70F}(X)+JX$
. In particular,
$\unicode[STIX]{x1D6FB}_{X}^{\unicode[STIX]{x1D703}}T=\unicode[STIX]{x1D70F}(X)+JX$
. In particular,
![]() $\unicode[STIX]{x1D6FB}_{T}^{\unicode[STIX]{x1D703}}T=0$
. If
$\unicode[STIX]{x1D6FB}_{T}^{\unicode[STIX]{x1D703}}T=0$
. If
![]() $X,Y\in H(M)$
, then
$X,Y\in H(M)$
, then
Since
![]() $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D6FB}$
is a
$\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D6FB}$
is a
![]() $(1,2)$
tensor field on
$(1,2)$
tensor field on
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D6FB}_{T}^{\unicode[STIX]{x1D703}}T=\unicode[STIX]{x1D6FB}_{T}T=0$
, we can define a vector field
$\unicode[STIX]{x1D6FB}_{T}^{\unicode[STIX]{x1D703}}T=\unicode[STIX]{x1D6FB}_{T}T=0$
, we can define a vector field
![]() $V$
on
$V$
on
![]() $M$
given by
$M$
given by
Actually we have
![]() $V=-\text{trace}_{g_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70F})T=0$
. On the Riemannian manifold
$V=-\text{trace}_{g_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70F})T=0$
. On the Riemannian manifold
![]() $(M,g_{\unicode[STIX]{x1D703}})$
, the Laplace–Beltrami operator is given by
$(M,g_{\unicode[STIX]{x1D703}})$
, the Laplace–Beltrami operator is given by
![]() $\unicode[STIX]{x1D6E5}u=-\text{trace}_{g_{\unicode[STIX]{x1D703}}}\{Y\in T(M)\mapsto \unicode[STIX]{x1D6FB}_{Y}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FB}u)\}$
for any
$\unicode[STIX]{x1D6E5}u=-\text{trace}_{g_{\unicode[STIX]{x1D703}}}\{Y\in T(M)\mapsto \unicode[STIX]{x1D6FB}_{Y}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FB}u)\}$
for any
![]() $u\in C^{2}(M)$
. Since
$u\in C^{2}(M)$
. Since
![]() $V=0$
, we have
$V=0$
, we have
![]() $\unicode[STIX]{x1D6E5}u=-\text{div}(\unicode[STIX]{x1D6FB}u)$
and
$\unicode[STIX]{x1D6E5}u=-\text{div}(\unicode[STIX]{x1D6FB}u)$
and
![]() $\unicode[STIX]{x1D6E5}u=-(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}u_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}+u_{00})$
.
$\unicode[STIX]{x1D6E5}u=-(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}u_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}+u_{00})$
.
2.2 Harmonic maps and pseudoharmonic maps
Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold (
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold (
![]() $g_{\unicode[STIX]{x1D703}}$
is positive definite). Let us denote by
$g_{\unicode[STIX]{x1D703}}$
is positive definite). Let us denote by
![]() $\unicode[STIX]{x1D6FB}$
and
$\unicode[STIX]{x1D6FB}$
and
![]() $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$
the Tanaka–Webster connection of
$\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$
the Tanaka–Webster connection of
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
and the Levi-Civita connection of the Webster metric
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
and the Levi-Civita connection of the Webster metric
![]() $g_{\unicode[STIX]{x1D703}}$
, respectively. Let
$g_{\unicode[STIX]{x1D703}}$
, respectively. Let
![]() $(N,h)$
be a Riemannian manifold with the Levi-Civita connection
$(N,h)$
be a Riemannian manifold with the Levi-Civita connection
![]() $\unicode[STIX]{x1D6FB}^{h}$
. For a smooth map
$\unicode[STIX]{x1D6FB}^{h}$
. For a smooth map
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
, there are two induced connections
$\unicode[STIX]{x1D719}:M\rightarrow N$
, there are two induced connections
![]() $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}\otimes \unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$
and
$\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}\otimes \unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$
and
![]() $\unicode[STIX]{x1D6FB}\otimes \unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$
on
$\unicode[STIX]{x1D6FB}\otimes \unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$
on
![]() $T^{\ast }(M)\otimes \unicode[STIX]{x1D719}^{-1}T(N)$
. Using these two connections, one may define the usual second fundamental form
$T^{\ast }(M)\otimes \unicode[STIX]{x1D719}^{-1}T(N)$
. Using these two connections, one may define the usual second fundamental form
![]() $B(\unicode[STIX]{x1D719})$
and a new second fundamental form
$B(\unicode[STIX]{x1D719})$
and a new second fundamental form
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
(cf. [Reference Petit16]) for the map
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
(cf. [Reference Petit16]) for the map
![]() $\unicode[STIX]{x1D719}$
as follows:
$\unicode[STIX]{x1D719}$
as follows:
and
for any
![]() $X,Y\in T(M)$
, where
$X,Y\in T(M)$
, where
![]() $\unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$
is written as
$\unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$
is written as
![]() $\unicode[STIX]{x1D6FB}^{h}$
for simplicity. While
$\unicode[STIX]{x1D6FB}^{h}$
for simplicity. While
![]() $B(\unicode[STIX]{x1D719})$
is symmetric on
$B(\unicode[STIX]{x1D719})$
is symmetric on
![]() $T(M)\otimes T(M)$
,
$T(M)\otimes T(M)$
,
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
is, in general, nonsymmetric.
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
is, in general, nonsymmetric.
For any bilinear form
![]() $C$
on
$C$
on
![]() $T(M)$
, we denote by
$T(M)$
, we denote by
![]() $\unicode[STIX]{x1D70B}_{H}C$
the restriction of
$\unicode[STIX]{x1D70B}_{H}C$
the restriction of
![]() $C$
to
$C$
to
![]() $H(M)\otimes H(M)$
. Recall that
$H(M)\otimes H(M)$
. Recall that
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
is pseudoharmonic if the vector field along
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
is pseudoharmonic if the vector field along
![]() $\unicode[STIX]{x1D719}$
given by
$\unicode[STIX]{x1D719}$
given by
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719}))$
vanishes. In [Reference Barletta, Dragomir and Urakawa1], the pseudoharmonic map is the critical point of the horizontal energy functional
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719}))$
vanishes. In [Reference Barletta, Dragomir and Urakawa1], the pseudoharmonic map is the critical point of the horizontal energy functional
for any
![]() $\unicode[STIX]{x1D6FA}\subset \subset M$
, where
$\unicode[STIX]{x1D6FA}\subset \subset M$
, where
![]() $e_{H}(\unicode[STIX]{x1D719})=(1/2)\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D719}^{\ast }h)$
is the horizontal energy density and
$e_{H}(\unicode[STIX]{x1D719})=(1/2)\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D719}^{\ast }h)$
is the horizontal energy density and
![]() $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D703}\wedge (d\unicode[STIX]{x1D703})^{m}$
. Let
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D703}\wedge (d\unicode[STIX]{x1D703})^{m}$
. Let
![]() $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})$
be the usual tension field of
$\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})$
be the usual tension field of
![]() $\unicode[STIX]{x1D719}$
given by
$\unicode[STIX]{x1D719}$
given by
![]() $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=\text{trace}_{g_{\unicode[STIX]{x1D703}}}B(\unicode[STIX]{x1D719})$
. Then
$\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=\text{trace}_{g_{\unicode[STIX]{x1D703}}}B(\unicode[STIX]{x1D719})$
. Then
![]() $\unicode[STIX]{x1D719}:(M,g_{\unicode[STIX]{x1D703}})\rightarrow (N,h)$
is harmonic if and only if
$\unicode[STIX]{x1D719}:(M,g_{\unicode[STIX]{x1D703}})\rightarrow (N,h)$
is harmonic if and only if
![]() $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=0$
(cf. [Reference Eells and Lemaire10]). Due to
$\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=0$
(cf. [Reference Eells and Lemaire10]). Due to
![]() $V=0$
, we have
$V=0$
, we have
and
A smooth map
![]() $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
is said to be a foliated map if
$\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
is said to be a foliated map if
![]() $d\unicode[STIX]{x1D719}(T)=0$
.
$d\unicode[STIX]{x1D719}(T)=0$
.
Proposition 2.1. (cf. [Reference Urakawa, Gu, Hu and Xin25])
Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
![]() $(N,h)$
a Riemannian manifold. Let
$(N,h)$
a Riemannian manifold. Let
![]() $\unicode[STIX]{x1D719}:M\rightarrow (N,h)$
be a smooth map. Then
$\unicode[STIX]{x1D719}:M\rightarrow (N,h)$
be a smooth map. Then
If in addition
![]() $\unicode[STIX]{x1D719}$
is foliated, then
$\unicode[STIX]{x1D719}$
is foliated, then
![]() $\unicode[STIX]{x1D719}$
is harmonic if and only if it is pseudoharmonic.
$\unicode[STIX]{x1D719}$
is harmonic if and only if it is pseudoharmonic.
Definition 2.1. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
![]() $(N,h)$
a Riemannian manifold. Let
$(N,h)$
a Riemannian manifold. Let
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. We say that:
$\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. We say that:
(i) [Reference Ianus and Pastore13]
 $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
 $J$
-pluriharmonic, if
$J$
-pluriharmonic, if
 $B(\unicode[STIX]{x1D719})(X,Y)+B(\unicode[STIX]{x1D719})(JX,JY)=0$
, for any
$B(\unicode[STIX]{x1D719})(X,Y)+B(\unicode[STIX]{x1D719})(JX,JY)=0$
, for any
 $X,Y\in T(M)$
;
$X,Y\in T(M)$
;(ii) [Reference Ianus and Pastore13]
 $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
 $H(M)$
-pluriharmonic, if
$H(M)$
-pluriharmonic, if
 $B(\unicode[STIX]{x1D719})(X,Y)+B(\unicode[STIX]{x1D719})(JX,JY)=0$
, for any
$B(\unicode[STIX]{x1D719})(X,Y)+B(\unicode[STIX]{x1D719})(JX,JY)=0$
, for any
 $X,Y\in H(M)$
;
$X,Y\in H(M)$
;(iii) [Reference Dragomir and Kamishima8]
 $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
 $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, if
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, if
 $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y)+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,JY)=0$
, for any
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y)+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,JY)=0$
, for any
 $X,Y\in H(M)$
;
$X,Y\in H(M)$
;(iv) [Reference Gherghe, Ianus and Pastore11] when
 $(N,h)$
is a Kähler manifold with complex structure
$(N,h)$
is a Kähler manifold with complex structure
 $J^{N}$
,
$J^{N}$
,
 $\unicode[STIX]{x1D719}$
is called a
$\unicode[STIX]{x1D719}$
is called a
 $(J,J^{N})$
-holomorphic (resp. anti-
$(J,J^{N})$
-holomorphic (resp. anti-
 $(J,J^{N})$
-holomorphic) map, if (2.11)
$(J,J^{N})$
-holomorphic) map, if (2.11) $$\begin{eqnarray}d\unicode[STIX]{x1D719}\circ J=J^{N}\circ d\unicode[STIX]{x1D719},\quad (\text{resp.}~d\unicode[STIX]{x1D719}\circ J=-J^{N}\circ d\unicode[STIX]{x1D719}).\end{eqnarray}$$
$$\begin{eqnarray}d\unicode[STIX]{x1D719}\circ J=J^{N}\circ d\unicode[STIX]{x1D719},\quad (\text{resp.}~d\unicode[STIX]{x1D719}\circ J=-J^{N}\circ d\unicode[STIX]{x1D719}).\end{eqnarray}$$
Obviously, both the
![]() $J$
-pluriharmonic map and the
$J$
-pluriharmonic map and the
![]() $(J,J^{N})$
-holomorphic map are harmonic (cf. [Reference Gherghe, Ianus and Pastore11, Reference Ianus and Pastore13]). By (2.9), the
$(J,J^{N})$
-holomorphic map are harmonic (cf. [Reference Gherghe, Ianus and Pastore11, Reference Ianus and Pastore13]). By (2.9), the
![]() $H(M)$
-pluriharmonic map is pseudoharmonic. Dragomir and Kamishima in [Reference Dragomir and Kamishima8] proved that every
$H(M)$
-pluriharmonic map is pseudoharmonic. Dragomir and Kamishima in [Reference Dragomir and Kamishima8] proved that every
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is a pseudoharmonic map. Actually, we get that any
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is a pseudoharmonic map. Actually, we get that any
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is foliated.
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is foliated.
Proposition 2.2. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
![]() $(N,h)$
a Riemannian manifold. If
$(N,h)$
a Riemannian manifold. If
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is
$\unicode[STIX]{x1D719}:M\rightarrow N$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then
![]() $\unicode[STIX]{x1D719}$
is a foliated map.
$\unicode[STIX]{x1D719}$
is a foliated map.
Proof. For any
![]() $Z=X-\sqrt{-1}JX$
,
$Z=X-\sqrt{-1}JX$
,
![]() $W=Y-\sqrt{-1}JY\in T_{1,0}(M)$
, we have
$W=Y-\sqrt{-1}JY\in T_{1,0}(M)$
, we have
and
Thus we get that
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic if and only if
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic if and only if
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Z,\overline{W})=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(\overline{Z},W)=0$
for any
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Z,\overline{W})=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(\overline{Z},W)=0$
for any
![]() $Z,W\in T_{1,0}(M)$
. Therefore, any
$Z,W\in T_{1,0}(M)$
. Therefore, any
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is pseudoharmonic.
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map is pseudoharmonic.
If
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is
$\unicode[STIX]{x1D719}:M\rightarrow N$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then we have
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then we have
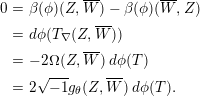 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Z,\overline{W})-\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(\overline{W},Z)\nonumber\\ \displaystyle & = & \displaystyle d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FB}}(Z,\overline{W}))\nonumber\\ \displaystyle & = & \displaystyle -2\unicode[STIX]{x1D6FA}(Z,\overline{W})\,d\unicode[STIX]{x1D719}(T)\nonumber\\ \displaystyle & = & \displaystyle 2\sqrt{-1}g_{\unicode[STIX]{x1D703}}(Z,\overline{W})\,d\unicode[STIX]{x1D719}(T).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Z,\overline{W})-\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(\overline{W},Z)\nonumber\\ \displaystyle & = & \displaystyle d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FB}}(Z,\overline{W}))\nonumber\\ \displaystyle & = & \displaystyle -2\unicode[STIX]{x1D6FA}(Z,\overline{W})\,d\unicode[STIX]{x1D719}(T)\nonumber\\ \displaystyle & = & \displaystyle 2\sqrt{-1}g_{\unicode[STIX]{x1D703}}(Z,\overline{W})\,d\unicode[STIX]{x1D719}(T).\end{eqnarray}$$
If we take
![]() $Z=W\neq 0$
, then
$Z=W\neq 0$
, then
![]() $g_{\unicode[STIX]{x1D703}}(Z,\overline{W})\neq 0$
, thus we have
$g_{\unicode[STIX]{x1D703}}(Z,\overline{W})\neq 0$
, thus we have
![]() $d\unicode[STIX]{x1D719}(T)=0$
.◻
$d\unicode[STIX]{x1D719}(T)=0$
.◻
Proposition 2.3. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
![]() $(N,h)$
a Kähler manifold with complex structure
$(N,h)$
a Kähler manifold with complex structure
![]() $J^{N}$
. Suppose
$J^{N}$
. Suppose
![]() $\unicode[STIX]{x1D719}:\rightarrow N$
is a
$\unicode[STIX]{x1D719}:\rightarrow N$
is a
![]() $\pm (J,J^{N})$
-holomorphic map. Then
$\pm (J,J^{N})$
-holomorphic map. Then
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.
Proof. Without loss of generality, we assume that
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic. Since
$(J,J^{N})$
-holomorphic. Since
![]() $J^{N}\,d\unicode[STIX]{x1D719}(T)=d\unicode[STIX]{x1D719}(JT)=0$
, we get that
$J^{N}\,d\unicode[STIX]{x1D719}(T)=d\unicode[STIX]{x1D719}(JT)=0$
, we get that
![]() $\unicode[STIX]{x1D719}$
is foliated. Because of the following identity
$\unicode[STIX]{x1D719}$
is foliated. Because of the following identity
for any
![]() $X,Y\in H(M)$
, we get that
$X,Y\in H(M)$
, we get that
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
is symmetric on
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
is symmetric on
![]() $H(M)\otimes H(M)$
. On the other hand, we have
$H(M)\otimes H(M)$
. On the other hand, we have
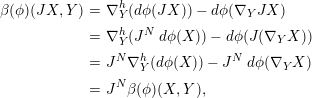 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,Y) & = & \displaystyle \unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(JX))-d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}JX)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{Y}^{h}(J^{N}\,d\unicode[STIX]{x1D719}(X))-d\unicode[STIX]{x1D719}(J(\unicode[STIX]{x1D6FB}_{Y}X))\nonumber\\ \displaystyle & = & \displaystyle J^{N}\unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(X))-J^{N}\,d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}X)\nonumber\\ \displaystyle & = & \displaystyle J^{N}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,Y) & = & \displaystyle \unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(JX))-d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}JX)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{Y}^{h}(J^{N}\,d\unicode[STIX]{x1D719}(X))-d\unicode[STIX]{x1D719}(J(\unicode[STIX]{x1D6FB}_{Y}X))\nonumber\\ \displaystyle & = & \displaystyle J^{N}\unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(X))-J^{N}\,d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}X)\nonumber\\ \displaystyle & = & \displaystyle J^{N}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y),\end{eqnarray}$$
for any
![]() $X,Y\in H(M)$
. Thus we have
$X,Y\in H(M)$
. Thus we have
Therefore, the
![]() $(J,J^{N})$
-holomorphic map
$(J,J^{N})$
-holomorphic map
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.◻
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.◻
3 Commutation relations
Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Let
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold. Let
![]() $(N,h)$
be a Riemannian manifold with the Levi-Civita connection
$(N,h)$
be a Riemannian manifold with the Levi-Civita connection
![]() $\unicode[STIX]{x1D6FB}^{h}$
. Let
$\unicode[STIX]{x1D6FB}^{h}$
. Let
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. Choose a local admissible coframe
$\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. Choose a local admissible coframe
![]() $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
$\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
![]() $M$
and a local orthonormal coframe field
$M$
and a local orthonormal coframe field
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
on
$\{\unicode[STIX]{x1D70E}^{i}\}$
on
![]() $N$
. Throughout this paper we employ the index conventions
$N$
. Throughout this paper we employ the index conventions
 $$\begin{eqnarray}\displaystyle & A,B,C=0,1,\ldots ,m,\bar{1},\ldots ,\bar{m}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}=1,\ldots ,m, & \displaystyle \nonumber\\ \displaystyle & i,j,k=1,\ldots ,n, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & A,B,C=0,1,\ldots ,m,\bar{1},\ldots ,\bar{m}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}=1,\ldots ,m, & \displaystyle \nonumber\\ \displaystyle & i,j,k=1,\ldots ,n, & \displaystyle \nonumber\end{eqnarray}$$
and use the summation convention on repeating indices. The structure equations for the Levi-Civita connection
![]() $\unicode[STIX]{x1D6FB}^{h}$
of
$\unicode[STIX]{x1D6FB}^{h}$
of
![]() $(N,h)$
in terms of local orthonormal coframe field
$(N,h)$
in terms of local orthonormal coframe field
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
are
$\{\unicode[STIX]{x1D70E}^{i}\}$
are
where
![]() $\unicode[STIX]{x1D6FA}_{j}^{i}=(1/2)\widehat{R}_{jkl}^{i}\unicode[STIX]{x1D70E}^{k}\wedge \unicode[STIX]{x1D70E}^{l}$
are the curvature forms of
$\unicode[STIX]{x1D6FA}_{j}^{i}=(1/2)\widehat{R}_{jkl}^{i}\unicode[STIX]{x1D70E}^{k}\wedge \unicode[STIX]{x1D70E}^{l}$
are the curvature forms of
![]() $\unicode[STIX]{x1D6FB}^{h}$
.
$\unicode[STIX]{x1D6FB}^{h}$
.
Under the map
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
, we denote the components of
$\unicode[STIX]{x1D719}:M\rightarrow N$
, we denote the components of
![]() $d\unicode[STIX]{x1D719}$
, the covariant derivatives
$d\unicode[STIX]{x1D719}$
, the covariant derivatives
![]() $\unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719}$
with respect to the local frames
$\unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719}$
with respect to the local frames
![]() $\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\}$
and
$\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\}$
and
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
by
$\{\unicode[STIX]{x1D70E}^{i}\}$
by
![]() $\unicode[STIX]{x1D719}_{A}^{i}$
,
$\unicode[STIX]{x1D719}_{A}^{i}$
,
![]() $\unicode[STIX]{x1D719}_{AB}^{i}$
and
$\unicode[STIX]{x1D719}_{AB}^{i}$
and
![]() $\unicode[STIX]{x1D719}_{ABC}^{i}$
respectively, that is,
$\unicode[STIX]{x1D719}_{ABC}^{i}$
respectively, that is,
 $$\begin{eqnarray}\displaystyle d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{A}^{i}\unicode[STIX]{x1D703}^{A}\otimes E_{i},\nonumber\\ \displaystyle \unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{AB}^{i}\unicode[STIX]{x1D703}^{A}\otimes \unicode[STIX]{x1D703}^{B}\otimes E_{i},\nonumber\\ \displaystyle \unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{ABC}^{i}\unicode[STIX]{x1D703}^{A}\otimes \unicode[STIX]{x1D703}^{B}\otimes \unicode[STIX]{x1D703}^{C}\otimes E_{i},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{A}^{i}\unicode[STIX]{x1D703}^{A}\otimes E_{i},\nonumber\\ \displaystyle \unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{AB}^{i}\unicode[STIX]{x1D703}^{A}\otimes \unicode[STIX]{x1D703}^{B}\otimes E_{i},\nonumber\\ \displaystyle \unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{ABC}^{i}\unicode[STIX]{x1D703}^{A}\otimes \unicode[STIX]{x1D703}^{B}\otimes \unicode[STIX]{x1D703}^{C}\otimes E_{i},\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D703}^{0}=\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}^{0}=\unicode[STIX]{x1D703}$
and
![]() $\{E_{i}\}$
is the dual vector field of
$\{E_{i}\}$
is the dual vector field of
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
. Thus we have
$\{\unicode[STIX]{x1D70E}^{i}\}$
. Thus we have
Hereafter we drop
![]() $\unicode[STIX]{x1D719}^{\ast }$
in such formulas when their meaning is clear from the context.
$\unicode[STIX]{x1D719}^{\ast }$
in such formulas when their meaning is clear from the context.
By taking the exterior derivative of (3.2) and making use of the structure equations (2.1) and (3.1), we get
where
Then (3.3) gives
Then the map
![]() $\unicode[STIX]{x1D719}$
is harmonic if and only if
$\unicode[STIX]{x1D719}$
is harmonic if and only if
and
![]() $\unicode[STIX]{x1D719}$
is pseudoharmonic if and only if
$\unicode[STIX]{x1D719}$
is pseudoharmonic if and only if
Differentiating the equation (3.4) and using the structure equations in
![]() $M$
and
$M$
and
![]() $N$
, we have
$N$
, we have
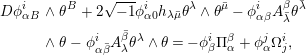 $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}B}^{i} & \wedge & \displaystyle \unicode[STIX]{x1D703}^{B}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}h_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D706}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D707}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D706}}}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & \wedge & \displaystyle \unicode[STIX]{x1D703}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D706}}^{\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D706}}\wedge \unicode[STIX]{x1D703}=-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D6FA}_{j}^{i},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}B}^{i} & \wedge & \displaystyle \unicode[STIX]{x1D703}^{B}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}h_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D706}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D707}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D706}}}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & \wedge & \displaystyle \unicode[STIX]{x1D703}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D706}}^{\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D706}}\wedge \unicode[STIX]{x1D703}=-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D6FA}_{j}^{i},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FE}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}^{i}\unicode[STIX]{x1D703}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FE}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}0}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0B}^{i}\unicode[STIX]{x1D703}^{B}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FE}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}^{i}\unicode[STIX]{x1D703}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FE}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}0}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0B}^{i}\unicode[STIX]{x1D703}^{B}.\nonumber\end{eqnarray}$$
From (3.8), we get the following commutation relations
Similarly the exterior derivative of (3.6) yields
where
 $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D703}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{00}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{00}^{i}+\unicode[STIX]{x1D719}_{00}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{00B}^{i}\unicode[STIX]{x1D703}^{B}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D703}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{00}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{00}^{i}+\unicode[STIX]{x1D719}_{00}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{00B}^{i}\unicode[STIX]{x1D703}^{B}.\nonumber\end{eqnarray}$$
We get from (3.14) the commutation relations
From (3.7), we can derive:
If
![]() $(N,h)$
is a Kähler manifold, we choose a local orthonormal coframe field
$(N,h)$
is a Kähler manifold, we choose a local orthonormal coframe field
![]() $\{\widetilde{\unicode[STIX]{x1D714}}^{i},\widetilde{\unicode[STIX]{x1D714}}^{\bar{i}}=\overline{\widetilde{\unicode[STIX]{x1D714}}^{i}}\}$
on
$\{\widetilde{\unicode[STIX]{x1D714}}^{i},\widetilde{\unicode[STIX]{x1D714}}^{\bar{i}}=\overline{\widetilde{\unicode[STIX]{x1D714}}^{i}}\}$
on
![]() $N$
. The structure equations for the Levi-Civita connection of
$N$
. The structure equations for the Levi-Civita connection of
![]() $(N,h)$
in terms of local orthonormal frame
$(N,h)$
in terms of local orthonormal frame
![]() $\{\widetilde{\unicode[STIX]{x1D714}}^{i},\widetilde{\unicode[STIX]{x1D714}}^{\bar{i}}\}$
are
$\{\widetilde{\unicode[STIX]{x1D714}}^{i},\widetilde{\unicode[STIX]{x1D714}}^{\bar{i}}\}$
are
where
![]() $\widetilde{\unicode[STIX]{x1D6FA}}_{j}^{i}=\widetilde{R}_{jk\overline{l}}^{i}\widetilde{\unicode[STIX]{x1D714}}^{k}\wedge \widetilde{\unicode[STIX]{x1D714}}^{\bar{l}}$
. Similar to the above discussions, we may obtain the following commutation formula:
$\widetilde{\unicode[STIX]{x1D6FA}}_{j}^{i}=\widetilde{R}_{jk\overline{l}}^{i}\widetilde{\unicode[STIX]{x1D714}}^{k}\wedge \widetilde{\unicode[STIX]{x1D714}}^{\bar{l}}$
. Similar to the above discussions, we may obtain the following commutation formula:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FE}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{\bar{l}}\widetilde{R}_{jk\bar{l}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{l}}\widetilde{R}_{jk\bar{l}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}A_{\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D706}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FE}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{\bar{l}}\widetilde{R}_{jk\bar{l}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{l}}\widetilde{R}_{jk\bar{l}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}A_{\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D706}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
4 CR Bochner-type result
Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold and
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold and
![]() $(N,h)$
a Riemannian manifold. Let
$(N,h)$
a Riemannian manifold. Let
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map. We choose a local orthonormal admissible coframe
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map. We choose a local orthonormal admissible coframe
![]() $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
$\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
![]() $M$
, a local orthonormal coframe field
$M$
, a local orthonormal coframe field
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
on
$\{\unicode[STIX]{x1D70E}^{i}\}$
on
![]() $N$
. We still use the notations of the last section. Denote
$N$
. We still use the notations of the last section. Denote
 $$\begin{eqnarray}\displaystyle & d_{b}\unicode[STIX]{x1D719}=d\unicode[STIX]{x1D719}|_{H(M)}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\otimes E_{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\otimes E_{i}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|_{H(M)}=(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i})\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\otimes E_{i}+(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i})\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}\otimes E_{i}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & d_{b}\unicode[STIX]{x1D719}=d\unicode[STIX]{x1D719}|_{H(M)}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\otimes E_{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\otimes E_{i}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|_{H(M)}=(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i})\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\otimes E_{i}+(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i})\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}\otimes E_{i}, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $\{E_{i}\}$
is the dual vector field of
$\{E_{i}\}$
is the dual vector field of
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
.
$\{\unicode[STIX]{x1D70E}^{i}\}$
.
We first derive the following CR Bochner formula.
Lemma 4.1. Set
![]() $\widehat{R}_{ijkl}=h_{jp}\widehat{R}_{ikl}^{p}=\unicode[STIX]{x1D6FF}_{jp}\widehat{R}_{ikl}^{p}=\widehat{R}_{ikl}^{j}$
. Then
$\widehat{R}_{ijkl}=h_{jp}\widehat{R}_{ikl}^{p}=\unicode[STIX]{x1D6FF}_{jp}\widehat{R}_{ikl}^{p}=\widehat{R}_{ikl}^{j}$
. Then
 $$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})+\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})-4\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})+\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})-4\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}),\end{eqnarray}$$
where
![]() $\langle \langle \cdot ,\cdot \rangle \rangle$
is the metric in
$\langle \langle \cdot ,\cdot \rangle \rangle$
is the metric in
![]() $T^{\ast }(M)\otimes \unicode[STIX]{x1D719}^{-1}T(N)$
induced by
$T^{\ast }(M)\otimes \unicode[STIX]{x1D719}^{-1}T(N)$
induced by
![]() $g_{\unicode[STIX]{x1D703}}$
and
$g_{\unicode[STIX]{x1D703}}$
and
![]() $h$
.
$h$
.
Proof. From the definition of the components of
![]() $\unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719}$
, it is easy to get that
$\unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719}$
, it is easy to get that
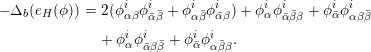 $$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}.\nonumber\end{eqnarray}$$
By the commutation relations of Section 3, we have
 $$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}-2\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}R_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{\bar{\unicode[STIX]{x1D706}}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}R_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jkl}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}}-2m\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jkl}^{i}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}}+2m\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}})\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}})-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}}))\nonumber\\ \displaystyle & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D6FC}}}}^{i}-2m\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D706}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & & \displaystyle -\,4\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}-2\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}R_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{\bar{\unicode[STIX]{x1D706}}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}R_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jkl}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}}-2m\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jkl}^{i}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}}+2m\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}})\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}})-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}}))\nonumber\\ \displaystyle & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D6FC}}}}^{i}-2m\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D706}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & & \displaystyle -\,4\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}).\nonumber\end{eqnarray}$$
The main difficulty in applications of Lemma 4.1 comes from the mixed term
![]() $\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})$
. It is known that the CR Paneitz operator is a useful tool to deal with such a term. In [Reference Graham and Lee12, Reference Lee14] the authors introduced the following differential operator acting on functions
$\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})$
. It is known that the CR Paneitz operator is a useful tool to deal with such a term. In [Reference Graham and Lee12, Reference Lee14] the authors introduced the following differential operator acting on functions
which characterizes CR pluriharmonic functions on
![]() $M$
(cf. also [Reference Dragomir and Tomassini9, Chapter 5]). In [Reference Chang and Chiu5] Chang and Chiu discussed the CR Paneitz operator
$M$
(cf. also [Reference Dragomir and Tomassini9, Chapter 5]). In [Reference Chang and Chiu5] Chang and Chiu discussed the CR Paneitz operator
where
![]() $\unicode[STIX]{x1D6FF}_{b}$
is the divergence operator that takes 1-forms to functions, and they proved that when
$\unicode[STIX]{x1D6FF}_{b}$
is the divergence operator that takes 1-forms to functions, and they proved that when
![]() $m\geqslant 2$
, the corresponding CR Paneitz operator is always nonnegative, that is
$m\geqslant 2$
, the corresponding CR Paneitz operator is always nonnegative, that is
We generalize the operator
![]() $P$
to an operator, still denoted by
$P$
to an operator, still denoted by
![]() $P$
, acting on maps from compact pseudo-Hermitian manifolds into Riemannian manifolds. Define
$P$
, acting on maps from compact pseudo-Hermitian manifolds into Riemannian manifolds. Define
where
![]() $P_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{j}+2\sqrt{-1}mA_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}$
. From the definition of
$P_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{j}+2\sqrt{-1}mA_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}$
. From the definition of
![]() $\unicode[STIX]{x1D719}_{A}^{i}$
,
$\unicode[STIX]{x1D719}_{A}^{i}$
,
![]() $\unicode[STIX]{x1D719}_{AB}^{i}$
and
$\unicode[STIX]{x1D719}_{AB}^{i}$
and
![]() $\unicode[STIX]{x1D719}_{ABC}^{i}$
, we can see that the definition of the operator
$\unicode[STIX]{x1D719}_{ABC}^{i}$
, we can see that the definition of the operator
![]() $P$
is independent of the choice of the local admissible coframe
$P$
is independent of the choice of the local admissible coframe
![]() $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
and local frame field
$\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
and local frame field
![]() $\{E_{i}\}$
, thus the operator
$\{E_{i}\}$
, thus the operator
![]() $P$
is well-defined.
$P$
is well-defined.
Lemma 4.2.
 $$\begin{eqnarray}\displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}) & = & \displaystyle \frac{1}{m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle -\frac{1}{2m}\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}) & = & \displaystyle \frac{1}{m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle -\frac{1}{2m}\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
Proof. From (3.19), we have
 $$\begin{eqnarray}\displaystyle \sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i} & = & \displaystyle \sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i})-\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\overline{P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}}\cdot \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}-\frac{1}{2m}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i} & = & \displaystyle \sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i})-\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\overline{P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}}\cdot \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}-\frac{1}{2m}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}.\nonumber\end{eqnarray}$$
After taking the conjugation of the above formula, we obtain
Consequently, we get
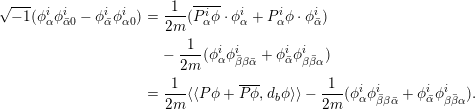 $$\begin{eqnarray}\displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}) & = & \displaystyle \frac{1}{2m}(\overline{P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}}\cdot \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}+P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2m}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle -\frac{1}{2m}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}) & = & \displaystyle \frac{1}{2m}(\overline{P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}}\cdot \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}+P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2m}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle -\frac{1}{2m}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}).\end{eqnarray}$$
On the other hand, one can derive the following:
 $$\begin{eqnarray}\displaystyle \langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i})+\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i})+\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$
Therefore, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i} & = & \displaystyle \langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle -\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i} & = & \displaystyle \langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle -\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$
We complete the proof by substituting the above formula into (4.4).◻
Thus the CR Bochner formula could be refreshed by the following corollary.
Corollary 4.1.
 $$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\nonumber\\ \displaystyle & & \displaystyle +\left(1+\frac{2}{m}\right)\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m+2)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{4}{m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{ijkl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{ijkl}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\nonumber\\ \displaystyle & & \displaystyle +\left(1+\frac{2}{m}\right)\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m+2)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{4}{m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{ijkl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{ijkl}).\end{eqnarray}$$
In order to apply the above CR Bochner formula, we want to investigate the sign of the integral of the term
![]() $\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}\rangle \rangle$
. We now state two lemmas.
$\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}\rangle \rangle$
. We now state two lemmas.
Lemma 4.3.
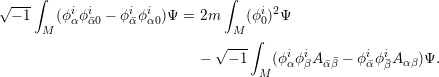 $$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle 2m\int _{M}(\unicode[STIX]{x1D719}_{0}^{i})^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle 2m\int _{M}(\unicode[STIX]{x1D719}_{0}^{i})^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
Proof. From (3.7) we can derive the following equality:
Integrating both sides of the above formula and using the divergence theorem, we obtain
 $$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
By (3.7), we have
The proof is completed by combining the above two formulas. ◻
Lemma 4.4.
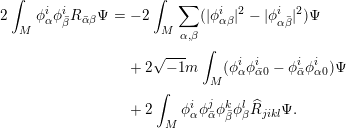 $$\begin{eqnarray}\displaystyle 2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6F9} & = & \displaystyle -2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}m\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6F9} & = & \displaystyle -2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}m\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
Proof. From (3.11), we have
Hence
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle \quad =2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle \quad =2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}).\nonumber\end{eqnarray}$$
Using the divergence theorem, we derive
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle \quad =-2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle \quad =-2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
Consequently
 $$\begin{eqnarray}\displaystyle -2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9} & = & \displaystyle 2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6F9}-2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9} & = & \displaystyle 2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6F9}-2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
This completes the proof of Lemma 4.4. ◻
We can establish the nonnegative property of the generalized operator
![]() $P$
under suitable conditions. Recall that a Riemannian manifold
$P$
under suitable conditions. Recall that a Riemannian manifold
![]() $(N^{n},h)$
is said to have nonpositive Hermitian curvature if
$(N^{n},h)$
is said to have nonpositive Hermitian curvature if
for any
![]() $X,Y\in T(N)\otimes \mathbb{C}$
(cf. [Reference Sampson19]).
$X,Y\in T(N)\otimes \mathbb{C}$
(cf. [Reference Sampson19]).
Theorem 4.1. Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold with
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold with
![]() $m\geqslant 2$
and
$m\geqslant 2$
and
![]() $(N,h)$
a Riemannian manifold with nonpositive Hermitian curvature. Suppose
$(N,h)$
a Riemannian manifold with nonpositive Hermitian curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is a smooth map, then
$\unicode[STIX]{x1D719}:M\rightarrow N$
is a smooth map, then
Proof. Integrating (4.1) on
![]() $M$
and substituting (4.7) into it, we have
$M$
and substituting (4.7) into it, we have
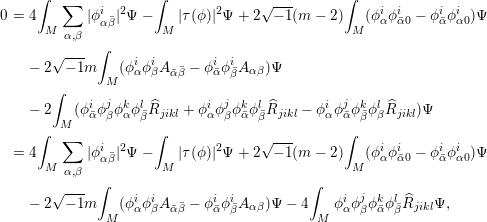 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 4\!\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\!\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}+2\sqrt{-1}(m-2)\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\!\int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle 4\!\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\!\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}+2\sqrt{-1}(m-2)\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}-4\!\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 4\!\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\!\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}+2\sqrt{-1}(m-2)\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\!\int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle 4\!\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\!\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}+2\sqrt{-1}(m-2)\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}-4\!\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the second equality follows from the Bianchi identity. Integrating both sides of (4.2) and using the divergence theorem, we get
 $$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle \frac{1}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}+\frac{1}{2m}\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle \frac{1}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}+\frac{1}{2m}\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
Calculating (4.10) ×
![]() $2(m-1)$
- (4.6) × 2 and substituting the result into (4.9), we have
$2(m-1)$
- (4.6) × 2 and substituting the result into (4.9), we have
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 4\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\frac{1}{m}\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}-4m\int _{M}(\unicode[STIX]{x1D719}_{0}^{i})^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2(m-1)}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}-4\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 4\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\frac{1}{m}\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}-4m\int _{M}(\unicode[STIX]{x1D719}_{0}^{i})^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2(m-1)}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}-4\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$
Since
we conclude
Combing this theorem with Corollary 4.1, we obtain the following CR Bochner-type result.
Theorem 4.2. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold with
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold with
![]() $m\geqslant 2$
and
$m\geqslant 2$
and
![]() $(N,h)$
a Riemannian manifold with nonpositive Hermitian curvature. Let
$(N,h)$
a Riemannian manifold with nonpositive Hermitian curvature. Let
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
be a pseudoharmonic map. Suppose that
$\unicode[STIX]{x1D719}:M\rightarrow N$
be a pseudoharmonic map. Suppose that
for any
![]() $Z\in \unicode[STIX]{x1D6E4}^{\infty }(T_{1,0}M)$
, then
$Z\in \unicode[STIX]{x1D6E4}^{\infty }(T_{1,0}M)$
, then
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$
for any
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$
for any
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. In particular,
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. In particular,
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.
Proof. From (4.5), we have
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}-\left(1+\frac{2}{m}\right)\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{4}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{M}(\text{Ric}-(m+2)\text{Tor})((\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}},(\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl})\unicode[STIX]{x1D6F9},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}-\left(1+\frac{2}{m}\right)\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{4}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{M}(\text{Ric}-(m+2)\text{Tor})((\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}},(\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl})\unicode[STIX]{x1D6F9},\nonumber\end{eqnarray}$$
where
![]() $(\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}T_{\unicode[STIX]{x1D6FC}}$
. By Theorem 4.1, the third term on the right-hand side of the preceding equation is nonnegative. Because of the curvature condition of
$(\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}T_{\unicode[STIX]{x1D6FC}}$
. By Theorem 4.1, the third term on the right-hand side of the preceding equation is nonnegative. Because of the curvature condition of
![]() $N$
, the last term on the right-hand side is nonnegative. Since
$N$
, the last term on the right-hand side is nonnegative. Since
![]() $\unicode[STIX]{x1D719}$
is pseudoharmonic, from (4.13) we get
$\unicode[STIX]{x1D719}$
is pseudoharmonic, from (4.13) we get
Hence
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$
. From
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$
. From
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$
, we see that
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$
, we see that
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.◻
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic.◻
Corollary 4.2. If the manifold
![]() $M$
in Theorem 4.2 is Sasakian and
$M$
in Theorem 4.2 is Sasakian and
![]() $\text{Ric}(Z,Z)\geqslant 0$
, then we have
$\text{Ric}(Z,Z)\geqslant 0$
, then we have
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})\equiv 0$
.
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})\equiv 0$
.
5 Foliated results of harmonic and pseudoharmonic maps
Let
![]() $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map from a pseudo-Hermitian manifold into a Riemannian manifold. To obtain the foliated results for the map
$\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map from a pseudo-Hermitian manifold into a Riemannian manifold. To obtain the foliated results for the map
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
, we consider the sublaplacian and the Laplacian of the square norm of
$\unicode[STIX]{x1D719}:M\rightarrow N$
, we consider the sublaplacian and the Laplacian of the square norm of
![]() $d\unicode[STIX]{x1D719}(T)$
, respectively.
$d\unicode[STIX]{x1D719}(T)$
, respectively.
We choose a local orthonormal admissible coframe
![]() $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
$\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
![]() $M$
and a local orthonormal coframe field
$M$
and a local orthonormal coframe field
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
on
$\{\unicode[STIX]{x1D70E}^{i}\}$
on
![]() $N$
. By the commutation relations of Section 3, we have
$N$
. By the commutation relations of Section 3, we have
Lemma 5.1.
 $$\begin{eqnarray}\displaystyle -\frac{1}{2}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+\langle \langle d\unicode[STIX]{x1D719}(T),\unicode[STIX]{x1D6FB}_{T}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}});\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\frac{1}{2}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+\langle \langle d\unicode[STIX]{x1D719}(T),\unicode[STIX]{x1D6FB}_{T}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}});\end{eqnarray}$$
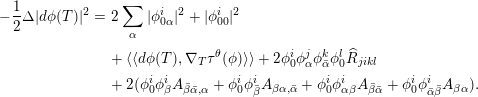 $$\begin{eqnarray}\displaystyle -\frac{1}{2}\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\langle \langle d\unicode[STIX]{x1D719}(T),\unicode[STIX]{x1D6FB}_{T}\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\frac{1}{2}\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\langle \langle d\unicode[STIX]{x1D719}(T),\unicode[STIX]{x1D6FB}_{T}\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}).\end{eqnarray}$$
Proof. Using (3.21), (3.13), (3.7) and their complex conjugate, we compute
 $$\begin{eqnarray}\displaystyle -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle (\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}),_{\bar{\unicode[STIX]{x1D6FC}}}+(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}),_{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{i}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}0}^{i})+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle (\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}),_{\bar{\unicode[STIX]{x1D6FC}}}+(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}),_{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{i}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}0}^{i})+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$
Since the formula for
![]() $-(1/2)\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2}$
can be derived similarly, we omit the details.◻
$-(1/2)\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2}$
can be derived similarly, we omit the details.◻
Lemma 5.2. Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold and
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact pseudo-Hermitian manifold and
![]() $(N,h)$
a Riemannian manifold. Let
$(N,h)$
a Riemannian manifold. Let
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. If the second fundamental form satisfies
$\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. If the second fundamental form satisfies
then
![]() $\unicode[STIX]{x1D719}$
is foliated.
$\unicode[STIX]{x1D719}$
is foliated.
Proof. By the integration by parts and the commutation formulas (3.7), we have
 $$\begin{eqnarray}\displaystyle 0=\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle m\int _{M}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle m\int _{M}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$
Thus we have
![]() $\unicode[STIX]{x1D719}_{0}^{i}=0$
, that is,
$\unicode[STIX]{x1D719}_{0}^{i}=0$
, that is,
![]() $d\unicode[STIX]{x1D719}(T)=0$
.◻
$d\unicode[STIX]{x1D719}(T)=0$
.◻
First, we prove the following result by the moving frame method.
Theorem 5.1. Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
![]() $(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is a pseudoharmonic map. Then
$\unicode[STIX]{x1D719}:M\rightarrow N$
is a pseudoharmonic map. Then
![]() $\unicode[STIX]{x1D719}$
is foliated.
$\unicode[STIX]{x1D719}$
is foliated.
Proof. Since
![]() $\unicode[STIX]{x1D719}$
is pseudoharmonic, we have
$\unicode[STIX]{x1D719}$
is pseudoharmonic, we have
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=0$
. The Sasakian condition for
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=0$
. The Sasakian condition for
![]() $M$
implies that
$M$
implies that
![]() $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=0$
, for any
$A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=0$
, for any
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. Thus (5.1) becomes
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. Thus (5.1) becomes
Since the sectional curvature of
![]() $N$
is nonpositive, we take
$N$
is nonpositive, we take
![]() $T_{\unicode[STIX]{x1D6FC}}=(1/\sqrt{2})(e_{\unicode[STIX]{x1D6FC}}-iJe_{\unicode[STIX]{x1D6FC}})$
and
$T_{\unicode[STIX]{x1D6FC}}=(1/\sqrt{2})(e_{\unicode[STIX]{x1D6FC}}-iJe_{\unicode[STIX]{x1D6FC}})$
and
![]() $T_{\bar{\unicode[STIX]{x1D6FC}}}=(1/\sqrt{2})(e_{\unicode[STIX]{x1D6FC}}+iJe_{\unicode[STIX]{x1D6FC}})$
and compute the following curvature term to find
$T_{\bar{\unicode[STIX]{x1D6FC}}}=(1/\sqrt{2})(e_{\unicode[STIX]{x1D6FC}}+iJe_{\unicode[STIX]{x1D6FC}})$
and compute the following curvature term to find
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl} & = & \displaystyle h(\widehat{R}(d\unicode[STIX]{x1D719}(T_{\bar{\unicode[STIX]{x1D6FC}}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}h(\widehat{R}(d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}+iJe_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}-iJe_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}\! [h(\widehat{R}(d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & & \displaystyle +\,h(\widehat{R}(d\unicode[STIX]{x1D719}(Je_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(Je_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl} & = & \displaystyle h(\widehat{R}(d\unicode[STIX]{x1D719}(T_{\bar{\unicode[STIX]{x1D6FC}}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}h(\widehat{R}(d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}+iJe_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}-iJe_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}\! [h(\widehat{R}(d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & & \displaystyle +\,h(\widehat{R}(d\unicode[STIX]{x1D719}(Je_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(Je_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 0.\end{eqnarray}$$
Hence we have
The divergence theorem yields
The fact that
![]() $\unicode[STIX]{x1D719}$
is foliated can be easily obtained by Lemma 5.2.◻
$\unicode[STIX]{x1D719}$
is foliated can be easily obtained by Lemma 5.2.◻
The next result gives another proof of Petit’s result.
Theorem 5.2. (cf. [Reference Petit16])
Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
![]() $(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is a harmonic map. Then
$\unicode[STIX]{x1D719}:M\rightarrow N$
is a harmonic map. Then
![]() $\unicode[STIX]{x1D719}$
is foliated.
$\unicode[STIX]{x1D719}$
is foliated.
Proof. Since
![]() $\unicode[STIX]{x1D719}$
is harmonic, we have
$\unicode[STIX]{x1D719}$
is harmonic, we have
![]() $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=0$
. By (5.2), we get
$\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=0$
. By (5.2), we get
Using the divergence theorem, we derive
![]() $\unicode[STIX]{x1D719}_{00}^{i}=\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}=\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}=0$
. By Lemma 5.2 again, we find that the map
$\unicode[STIX]{x1D719}_{00}^{i}=\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}=\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}=0$
. By Lemma 5.2 again, we find that the map
![]() $\unicode[STIX]{x1D719}$
is foliated.◻
$\unicode[STIX]{x1D719}$
is foliated.◻
Remark 5.1. From Theorems 5.1 and 5.2, we get that if
![]() $M$
is a compact Sasakian manifold and
$M$
is a compact Sasakian manifold and
![]() $N$
is a Riemannian manifold with nonpositive curvature, then the map
$N$
is a Riemannian manifold with nonpositive curvature, then the map
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is harmonic if and only if it is pseudoharmonic.
$\unicode[STIX]{x1D719}:M\rightarrow N$
is harmonic if and only if it is pseudoharmonic.
Now we use a technique in [Reference Pigola, Rigoli and Setti17] to treat harmonic maps or pseudoharmonic maps from complete noncompact pseudo-Hermitian manifolds. Here the completeness of a pseudo-Hermitian manifold is with respect to the Webster metric. Let
![]() $r$
be the Riemannian distance on the complete noncompact pseudo-Hermitian manifold
$r$
be the Riemannian distance on the complete noncompact pseudo-Hermitian manifold
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
from a fixed point
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
from a fixed point
![]() $x_{0}\in M$
. Set
$x_{0}\in M$
. Set
![]() $B_{R}=\{x\in M:r(x)<R\}$
.
$B_{R}=\{x\in M:r(x)<R\}$
.
For a measurable function
![]() $u$
defined on
$u$
defined on
![]() $\mathbb{R}$
, we use the notation
$\mathbb{R}$
, we use the notation
![]() $u\notin L^{1}(+\infty )$
to mean that
$u\notin L^{1}(+\infty )$
to mean that
![]() $|u|\notin L^{1}((K,+\infty ))$
for any positive number
$|u|\notin L^{1}((K,+\infty ))$
for any positive number
![]() $K$
.
$K$
.
Proposition 5.1. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold of dimension
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold of dimension
![]() $2m+1$
and
$2m+1$
and
![]() $(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
where
![]() ${\mathcal{H}}$
is the
${\mathcal{H}}$
is the
![]() $2m$
-dimensional Hausdorff measure on
$2m$
-dimensional Hausdorff measure on
![]() $\unicode[STIX]{x2202}B_{r}$
, which coincides with the Riemannian measure induced on the regular part of
$\unicode[STIX]{x2202}B_{r}$
, which coincides with the Riemannian measure induced on the regular part of
![]() $\unicode[STIX]{x2202}B_{r}$
, then the second fundamental form satisfies
$\unicode[STIX]{x2202}B_{r}$
, then the second fundamental form satisfies
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$
for any
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$
for any
![]() $X\in H(M)$
.
$X\in H(M)$
.
Proof. We consider only the case
![]() $\unicode[STIX]{x1D719}$
is a harmonic map, because the other case is analogous. By the divergence theorem, (5.5) gives
$\unicode[STIX]{x1D719}$
is a harmonic map, because the other case is analogous. By the divergence theorem, (5.5) gives
 $$\begin{eqnarray}\displaystyle \int _{B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right)\unicode[STIX]{x1D6F9} & {\leqslant} & \displaystyle -\frac{1}{2}\int _{B_{r}}\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{\unicode[STIX]{x2202}B_{r}}g_{\unicode[STIX]{x1D703}}\left(\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right)\unicode[STIX]{x1D6F9} & {\leqslant} & \displaystyle -\frac{1}{2}\int _{B_{r}}\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{\unicode[STIX]{x2202}B_{r}}g_{\unicode[STIX]{x1D703}}\left(\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}.\end{eqnarray}$$
Here the quantity
![]() $\sum _{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}$
is well-defined, since it is independent of the choice of the local frame fields on
$\sum _{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}$
is well-defined, since it is independent of the choice of the local frame fields on
![]() $M$
and
$M$
and
![]() $N$
. Recalling
$N$
. Recalling
![]() $\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2}=2\sum _{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}T_{\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}T_{\unicode[STIX]{x1D6FC}})+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{00}^{i}T$
we have
$\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2}=2\sum _{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}T_{\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}T_{\unicode[STIX]{x1D6FC}})+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{00}^{i}T$
we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\int _{\unicode[STIX]{x2202}B_{r}}g_{\unicode[STIX]{x1D703}}\left(\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left\{\int _{\unicode[STIX]{x2202}B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\int _{\unicode[STIX]{x2202}B_{r}}g_{\unicode[STIX]{x1D703}}\left(\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left\{\int _{\unicode[STIX]{x2202}B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$
Let
Then by the co-area formula, we get
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(r) & = & \displaystyle \frac{d}{dr}\left\{\int _{0}^{r}\int _{\unicode[STIX]{x2202}B_{t}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}\,dt\right\}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x2202}B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(r) & = & \displaystyle \frac{d}{dr}\left\{\int _{0}^{r}\int _{\unicode[STIX]{x2202}B_{t}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}\,dt\right\}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x2202}B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}.\nonumber\end{eqnarray}$$
Putting together (5.7) and (5.8) and squaring we finally get
Next, we reason by contradiction and we suppose
![]() $\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\neq 0$
for some
$\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\neq 0$
for some
![]() $\unicode[STIX]{x1D6FC}$
. It follows that there exists a
$\unicode[STIX]{x1D6FC}$
. It follows that there exists a
![]() $R>0$
sufficiently large such that
$R>0$
sufficiently large such that
![]() $\unicode[STIX]{x1D701}(r)>0$
, for every
$\unicode[STIX]{x1D701}(r)>0$
, for every
![]() $r\geqslant R$
. Fix such an
$r\geqslant R$
. Fix such an
![]() $R$
. From (5.9) we then derive
$R$
. From (5.9) we then derive
and letting
![]() $r\rightarrow +\infty$
we contradict (5.6).◻
$r\rightarrow +\infty$
we contradict (5.6).◻
Corollary 5.1. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
![]() $(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
then the second fundamental form satisfies
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$
for any
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$
for any
![]() $X\in H(M)$
.
$X\in H(M)$
.
Proof. Set
So, by the co-area formula, we have
From of [Reference Rigoli and Setti18, Proposition 3.1], we know that
Suppose that
![]() $\unicode[STIX]{x1D719}$
satisfies (5.10), this implies
$\unicode[STIX]{x1D719}$
satisfies (5.10), this implies
Thus we deduce
![]() $1/h^{\prime }(r)\notin L^{1}(+\infty )$
, that is,
$1/h^{\prime }(r)\notin L^{1}(+\infty )$
, that is,
![]() $\unicode[STIX]{x1D719}$
satisfies (5.6). Hence we prove the corollary.◻
$\unicode[STIX]{x1D719}$
satisfies (5.6). Hence we prove the corollary.◻
Proposition 5.2. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact pseudo-Hermitian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact pseudo-Hermitian manifold and
![]() $(N,h)$
a Riemannian manifold. Let
$(N,h)$
a Riemannian manifold. Let
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. If the second fundamental form satisfies
$\unicode[STIX]{x1D719}:M\rightarrow N$
be a smooth map. If the second fundamental form satisfies
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$
for any
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$
for any
![]() $X\in H(M)$
and
$X\in H(M)$
and
then
![]() $\unicode[STIX]{x1D719}$
is foliated.
$\unicode[STIX]{x1D719}$
is foliated.
Proof. By the property of
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
and the divergence theorem, we have
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$
and the divergence theorem, we have
 $$\begin{eqnarray}\displaystyle m\int _{B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{B_{r}}\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m\int _{B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{B_{r}}\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\nonumber\end{eqnarray}$$
Set
![]() $\unicode[STIX]{x1D702}(r)=\int _{B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9}$
. Then we have
$\unicode[STIX]{x1D702}(r)=\int _{B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9}$
. Then we have
If
![]() $\unicode[STIX]{x1D719}$
is not foliated, then for
$\unicode[STIX]{x1D719}$
is not foliated, then for
![]() $r>R$
,
$r>R$
,
where
![]() $R$
is large enough such that
$R$
is large enough such that
![]() $\unicode[STIX]{x1D702}(R)>0$
, and letting
$\unicode[STIX]{x1D702}(R)>0$
, and letting
![]() $r\rightarrow +\infty$
we contradict (5.11).◻
$r\rightarrow +\infty$
we contradict (5.11).◻
Theorem 5.3. Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
![]() $(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
where
![]() $e(\unicode[STIX]{x1D719})=(1/2)\text{trace}_{g_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D719}^{\ast }h)$
is the energy density of
$e(\unicode[STIX]{x1D719})=(1/2)\text{trace}_{g_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D719}^{\ast }h)$
is the energy density of
![]() $\unicode[STIX]{x1D719}$
, then
$\unicode[STIX]{x1D719}$
, then
![]() $\unicode[STIX]{x1D719}$
is a foliated map.
$\unicode[STIX]{x1D719}$
is a foliated map.
Proof. Since
![]() $e(\unicode[STIX]{x1D719})=e_{H}(\unicode[STIX]{x1D719})+(1/2)|d\unicode[STIX]{x1D719}(T)|^{2}$
, the condition (5.12) implies both (5.6) and (5.11). It follows from Propositions 5.1 and 5.2 that
$e(\unicode[STIX]{x1D719})=e_{H}(\unicode[STIX]{x1D719})+(1/2)|d\unicode[STIX]{x1D719}(T)|^{2}$
, the condition (5.12) implies both (5.6) and (5.11). It follows from Propositions 5.1 and 5.2 that
![]() $\unicode[STIX]{x1D719}$
is foliated.◻
$\unicode[STIX]{x1D719}$
is foliated.◻
Corollary 5.2. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
![]() $(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
then
![]() $\unicode[STIX]{x1D719}$
is foliated.
$\unicode[STIX]{x1D719}$
is foliated.
6
 $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity results
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity results
In this section, we give some conditions to ensure the
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity for both harmonic and pseudoharmonic maps from either a compact Sasakian manifold or a complete Sasakian manifold. Recall that Petit [Reference Petit16] gave similar results for harmonic maps from a compact Sasakian manifold by using tools of spinorial geometry, although he did not mention the notion of
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity for both harmonic and pseudoharmonic maps from either a compact Sasakian manifold or a complete Sasakian manifold. Recall that Petit [Reference Petit16] gave similar results for harmonic maps from a compact Sasakian manifold by using tools of spinorial geometry, although he did not mention the notion of
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity. The moving frame method, which enables us to treat both cases of harmonic maps and pseudoharmonic maps, seems closer to the classical methods in differential geometry. Let
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity. The moving frame method, which enables us to treat both cases of harmonic maps and pseudoharmonic maps, seems closer to the classical methods in differential geometry. Let
![]() $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map from a pseudo-Hermitian manifold
$\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map from a pseudo-Hermitian manifold
![]() $M$
into a Riemannian manifold
$M$
into a Riemannian manifold
![]() $N$
. Inspired by Sampson’s technique (cf. [Reference Dong6, Reference Sampson19]), we introduce a global 1-form on
$N$
. Inspired by Sampson’s technique (cf. [Reference Dong6, Reference Sampson19]), we introduce a global 1-form on
![]() $M$
given by
$M$
given by
in terms of the local orthonormal admissible coframe
![]() $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
$\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
![]() $M$
and the local orthonormal coframe field
$M$
and the local orthonormal coframe field
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
on
$\{\unicode[STIX]{x1D70E}^{i}\}$
on
![]() $N$
.
$N$
.
Lemma 6.1.
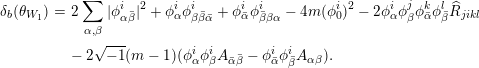 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-4m(\unicode[STIX]{x1D719}_{0}^{i})^{2}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-4m(\unicode[STIX]{x1D719}_{0}^{i})^{2}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
Proof. By the definition of the divergence of 1-forms on
![]() $M$
, we have
$M$
, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}),_{\bar{\unicode[STIX]{x1D6FD}}}+(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}),_{\bar{\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}),_{\bar{\unicode[STIX]{x1D6FD}}}+(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}),_{\bar{\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}.\nonumber\end{eqnarray}$$
Using (3.7), (3.10) and their complex conjugate, we get
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}-2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FD}}}-2m\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}}+2m\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & & \displaystyle -\,2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}-4m(\unicode[STIX]{x1D719}_{0}^{i})^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}-2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FD}}}-2m\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}}+2m\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & & \displaystyle -\,2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}-4m(\unicode[STIX]{x1D719}_{0}^{i})^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$
Theorem 6.1. Let
![]() $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold of and
$(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold of and
![]() $(N^{n},h)$
be a Riemannian manifold with nonpositive Hermitian curvature. Suppose
$(N^{n},h)$
be a Riemannian manifold with nonpositive Hermitian curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. Then
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. Then
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
Proof. The fact that
![]() $N$
has a nonpositive Hermitian curvature implies that the sectional curvature of
$N$
has a nonpositive Hermitian curvature implies that the sectional curvature of
![]() $N$
is nonpositive. According to Theorems 5.1 and 5.2, we know that the condition that
$N$
is nonpositive. According to Theorems 5.1 and 5.2, we know that the condition that
![]() $\unicode[STIX]{x1D719}$
is harmonic is equivalent to that
$\unicode[STIX]{x1D719}$
is harmonic is equivalent to that
![]() $\unicode[STIX]{x1D719}$
is pseudoharmonic. Besides, we get that the map is foliated in this circumstance. By (3.7), we have
$\unicode[STIX]{x1D719}$
is pseudoharmonic. Besides, we get that the map is foliated in this circumstance. By (3.7), we have
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$
for any
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$
for any
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. Thus we have
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. Thus we have
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}E_{i}$
, where
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}E_{i}$
, where
![]() $\{E_{i}\}$
is the dual vector field of
$\{E_{i}\}$
is the dual vector field of
![]() $\{\unicode[STIX]{x1D70E}^{i}\}$
.
$\{\unicode[STIX]{x1D70E}^{i}\}$
.
From (6.2), we get
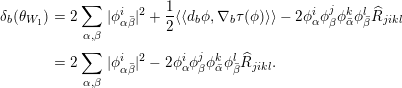 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\frac{1}{2}\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle -2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\frac{1}{2}\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle -2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}.\end{eqnarray}$$
Since
![]() $N$
has nonpositive Hermitian curvature, we have
$N$
has nonpositive Hermitian curvature, we have
By the divergence theorem, we derive from (6.4) that
![]() $\unicode[STIX]{x1D719}$
is a
$\unicode[STIX]{x1D719}$
is a
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with property (6.3).◻
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with property (6.3).◻
Then consider the case that the target manifold
![]() $(N,h)$
is a Kähler manifold. The curvature operator
$(N,h)$
is a Kähler manifold. The curvature operator
![]() $\widetilde{Q}$
of
$\widetilde{Q}$
of
![]() $N$
is defined by
$N$
is defined by
for any
![]() $X,Y,Z,W\in T(N)$
. The complex extension of
$X,Y,Z,W\in T(N)$
. The complex extension of
![]() $\widetilde{Q}$
to
$\widetilde{Q}$
to
![]() $\wedge ^{2}T^{\mathbb{C}}(N)$
is also denoted by
$\wedge ^{2}T^{\mathbb{C}}(N)$
is also denoted by
![]() $\widetilde{Q}$
. Let us set
$\widetilde{Q}$
. Let us set
The Kähler identity of
![]() $N$
yields
$N$
yields
Set
Definition 6.1. (cf. [Reference Siu20])
Let
![]() $(N,h)$
be a Kähler manifold. The curvature tensor of
$(N,h)$
be a Kähler manifold. The curvature tensor of
![]() $N$
is said to be strongly negative (resp. strongly seminegative) if
$N$
is said to be strongly negative (resp. strongly seminegative) if
for any
![]() $\unicode[STIX]{x1D709}=(Z\wedge W)^{(1,1)}\neq 0$
,
$\unicode[STIX]{x1D709}=(Z\wedge W)^{(1,1)}\neq 0$
,
![]() $Z,W\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\mathbb{C}}(N))$
.
$Z,W\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\mathbb{C}}(N))$
.
Let
![]() $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map from a pseudo-Hermitian manifold
$\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$
be a smooth map from a pseudo-Hermitian manifold
![]() $M$
into a Kähler manifold
$M$
into a Kähler manifold
![]() $N$
. Similar to (6.1) (cf. [Reference Sampson19] and [Reference Dong6]), we introduce a global 1-form on
$N$
. Similar to (6.1) (cf. [Reference Sampson19] and [Reference Dong6]), we introduce a global 1-form on
![]() $M$
defined as
$M$
defined as
in terms of the local orthonormal admissible coframe
![]() $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
$\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$
on
![]() $M$
and the local orthonormal frame field
$M$
and the local orthonormal frame field
![]() $\{\widetilde{E}_{i}\}$
on
$\{\widetilde{E}_{i}\}$
on
![]() $N$
. By (3.7), (3.23) and their complex conjugate, we have
$N$
. By (3.7), (3.23) and their complex conjugate, we have
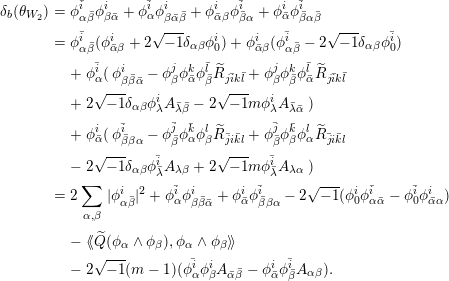 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{2}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{\bar{i}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{0}^{i})+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}-2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{0}^{\bar{i}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\! (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{l}}\widetilde{R}_{j\bar{i}k\bar{l}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{l}}\widetilde{R}_{j\bar{i}k\bar{l}}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FD}}}-2\sqrt{-1}m\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}} )\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\! (\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{\bar{i}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{j}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{k}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widetilde{R}_{\bar{j}i\bar{k}l}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{j}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{\bar{k}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{l}\widetilde{R}_{\bar{j}i\bar{k}l}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{\bar{i}}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}}+2\sqrt{-1}m\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{\bar{i}}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{\bar{i}}-2\sqrt{-1}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{\bar{i}}-\unicode[STIX]{x1D719}_{0}^{\bar{i}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,\langle \!\langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \!\rangle \nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{2}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{\bar{i}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{0}^{i})+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}-2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{0}^{\bar{i}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\! (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{l}}\widetilde{R}_{j\bar{i}k\bar{l}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{l}}\widetilde{R}_{j\bar{i}k\bar{l}}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FD}}}-2\sqrt{-1}m\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}} )\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\! (\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{\bar{i}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{j}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{k}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widetilde{R}_{\bar{j}i\bar{k}l}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{j}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{\bar{k}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{l}\widetilde{R}_{\bar{j}i\bar{k}l}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{\bar{i}}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}}+2\sqrt{-1}m\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{\bar{i}}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{\bar{i}}-2\sqrt{-1}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{\bar{i}}-\unicode[STIX]{x1D719}_{0}^{\bar{i}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,\langle \!\langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \!\rangle \nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
Theorem 6.2. Let
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic or pseudoharmonic map from a compact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. Then
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic or pseudoharmonic map from a compact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. Then
![]() $\unicode[STIX]{x1D719}$
is a
$\unicode[STIX]{x1D719}$
is a
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map and
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map and
where
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}=d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FC}})$
.
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}=d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FC}})$
.
Proof. Since strongly seminegative curvature implies nonpositive sectional curvature, we get that
![]() $\unicode[STIX]{x1D719}$
must be pseudoharmonic and foliated. Then we have
$\unicode[STIX]{x1D719}$
must be pseudoharmonic and foliated. Then we have
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$
and
![]() $\unicode[STIX]{x1D719}_{0}^{i}=0$
. So we get
$\unicode[STIX]{x1D719}_{0}^{i}=0$
. So we get
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\widetilde{E}_{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\widetilde{E}_{\bar{i}})=0$
, that is,
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\widetilde{E}_{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\widetilde{E}_{\bar{i}})=0$
, that is,
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}=0$
. As
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}=0$
. As
![]() $M$
is Sasakian, by (6.7) we have
$M$
is Sasakian, by (6.7) we have
The divergence theorem and the curvature condition of
![]() $N$
imply that
$N$
imply that
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
![]() $\langle \langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \rangle =0$
, for any
$\langle \langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \rangle =0$
, for any
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
.◻
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
.◻
Now we attempt to give some conditions to ensure
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity for harmonic and pseudoharmonic maps from complete noncompact Sasakian manifolds.
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonicity for harmonic and pseudoharmonic maps from complete noncompact Sasakian manifolds.
Theorem 6.3. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
![]() $(N,h)$
be a Riemannian manifold with nonpositive Hermitian curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive Hermitian curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
then
![]() $\unicode[STIX]{x1D719}$
is a
$\unicode[STIX]{x1D719}$
is a
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.3).
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.3).
Proof. By Theorem 5.3, we get that
![]() $\unicode[STIX]{x1D719}$
is foliated and pseudoharmonic. From (6.4) and (6.5), we have
$\unicode[STIX]{x1D719}$
is foliated and pseudoharmonic. From (6.4) and (6.5), we have
Using the divergence theorem, we get
On the other hand, by the definition of
![]() $\unicode[STIX]{x1D703}_{W_{1}}$
, we have
$\unicode[STIX]{x1D703}_{W_{1}}$
, we have
 $$\begin{eqnarray}\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{1}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\leqslant 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{1}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\leqslant 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$
Putting together (6.11) and (6.12) and squaring we finally get
where we have set
Next suppose that
![]() $\unicode[STIX]{x1D719}$
is not
$\unicode[STIX]{x1D719}$
is not
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic. Then there exists a
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic. Then there exists a
![]() $R>0$
sufficiently large such that
$R>0$
sufficiently large such that
![]() $\unicode[STIX]{x1D6FE}(R)>0$
. For any
$\unicode[STIX]{x1D6FE}(R)>0$
. For any
![]() $r\geqslant R$
, from (6.13) we can deduce
$r\geqslant R$
, from (6.13) we can deduce
and letting
![]() $r\rightarrow +\infty$
we contradict (6.10). Hence
$r\rightarrow +\infty$
we contradict (6.10). Hence
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
![]() $\unicode[STIX]{x1D703}_{W_{1}}\equiv 0$
. Then (6.2) implies that
$\unicode[STIX]{x1D703}_{W_{1}}\equiv 0$
. Then (6.2) implies that
![]() $\unicode[STIX]{x1D719}$
satisfies (6.3).◻
$\unicode[STIX]{x1D719}$
satisfies (6.3).◻
Corollary 6.1. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a complete noncompact Sasakian manifold and
![]() $(N,h)$
be a Riemannian manifold with nonpositive Hermitian curvature. Suppose
$(N,h)$
be a Riemannian manifold with nonpositive Hermitian curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
then
![]() $\unicode[STIX]{x1D719}$
is a
$\unicode[STIX]{x1D719}$
is a
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.3).
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.3).
Theorem 6.4. Let
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic or pseudoharmonic map from a complete noncompact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. If
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic or pseudoharmonic map from a complete noncompact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
then
![]() $\unicode[STIX]{x1D719}$
is a
$\unicode[STIX]{x1D719}$
is a
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.8).
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.8).
Proof. Obviously, the map
![]() $\unicode[STIX]{x1D719}$
is foliated, and hence
$\unicode[STIX]{x1D719}$
is foliated, and hence
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$
. It follows from (6.7) that
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$
. It follows from (6.7) that
By the definition of
![]() $\unicode[STIX]{x1D703}_{W_{2}}$
, we have
$\unicode[STIX]{x1D703}_{W_{2}}$
, we have
 $$\begin{eqnarray}\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{2}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\leqslant 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{2}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\leqslant 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$
Set
Then
Suppose that
![]() $\unicode[STIX]{x1D719}$
is not
$\unicode[STIX]{x1D719}$
is not
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then there exists a
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then there exists a
![]() $R>0$
sufficiently large such that
$R>0$
sufficiently large such that
![]() $\unicode[STIX]{x1D70C}(r)>0$
for any
$\unicode[STIX]{x1D70C}(r)>0$
for any
![]() $r>R$
. Fix such a
$r>R$
. Fix such a
![]() $R$
. From (6.15) we deduce the following
$R$
. From (6.15) we deduce the following
and letting
![]() $r\rightarrow +\infty$
we contradict (6.14). Hence
$r\rightarrow +\infty$
we contradict (6.14). Hence
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and
![]() $\unicode[STIX]{x1D703}_{W_{2}}\equiv 0$
. Then (6.7) implies that
$\unicode[STIX]{x1D703}_{W_{2}}\equiv 0$
. Then (6.7) implies that
![]() $\unicode[STIX]{x1D719}$
satisfies (6.8).◻
$\unicode[STIX]{x1D719}$
satisfies (6.8).◻
Corollary 6.2. Let
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic or pseudoharmonic map from a complete noncompact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. If
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic or pseudoharmonic map from a complete noncompact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. If
![]() $\unicode[STIX]{x1D719}$
satisfies
$\unicode[STIX]{x1D719}$
satisfies
then
![]() $\unicode[STIX]{x1D719}$
is a
$\unicode[STIX]{x1D719}$
is a
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.8).
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map with the property (6.8).
7 Siu–Sampson type results
In this section, we establish some results of Siu–Sampson type for both harmonic maps and pseudoharmonic maps from compact Sasakian manifolds. Similar to the results for harmonic maps from Kähler manifolds in [Reference Carlson and Toledo3, Reference Sampson19, Reference Siu20], we may derive
![]() $(J,J^{N})$
-holomorphicity under rank conditions for harmonic and pseudoharmonic maps from compact Sasakian manifolds by analysing the curvature equations (6.8). Note that Petit [Reference Petit16] also gave the
$(J,J^{N})$
-holomorphicity under rank conditions for harmonic and pseudoharmonic maps from compact Sasakian manifolds by analysing the curvature equations (6.8). Note that Petit [Reference Petit16] also gave the
![]() $(J,J^{N})$
-holomorphicity results for harmonic maps from Sasakian manifolds using spinorial geometry. As mentioned previously, our method is different from his. Besides recapturing Petit’s results by using the moving frame method, we also add some new results which include the results for pseudoharmonic maps, the conic extension of harmonic maps from Sasakian manifolds and a unique continuation theorem for
$(J,J^{N})$
-holomorphicity results for harmonic maps from Sasakian manifolds using spinorial geometry. As mentioned previously, our method is different from his. Besides recapturing Petit’s results by using the moving frame method, we also add some new results which include the results for pseudoharmonic maps, the conic extension of harmonic maps from Sasakian manifolds and a unique continuation theorem for
![]() $(J,J^{N})$
-holomorphicity.
$(J,J^{N})$
-holomorphicity.
First, we consider the case where the target manifold
![]() $N$
is a locally symmetric space of noncompact type (cf. [Reference Carlson and Toledo3, Reference Sampson19]). The universal covering manifold of
$N$
is a locally symmetric space of noncompact type (cf. [Reference Carlson and Toledo3, Reference Sampson19]). The universal covering manifold of
![]() $N$
is a symmetric space
$N$
is a symmetric space
![]() $G/K$
, where
$G/K$
, where
![]() $K$
is a connected and closed subgroup of the noncompact connected Lie group
$K$
is a connected and closed subgroup of the noncompact connected Lie group
![]() $G$
, and
$G$
, and
![]() $G/K$
is given the invariant metric determined by the Killing form
$G/K$
is given the invariant metric determined by the Killing form
![]() $\langle ,\rangle$
on
$\langle ,\rangle$
on
![]() $\mathfrak{g}$
. If the corresponding Cartan decomposition of the Lie algebra of
$\mathfrak{g}$
. If the corresponding Cartan decomposition of the Lie algebra of
![]() $G$
is
$G$
is
![]() $\mathfrak{g}=\mathfrak{k}+\mathfrak{p}$
, then the real tangent space of
$\mathfrak{g}=\mathfrak{k}+\mathfrak{p}$
, then the real tangent space of
![]() $N$
at any point can be identified with
$N$
at any point can be identified with
![]() $\mathfrak{p}$
. The Killing form
$\mathfrak{p}$
. The Killing form
![]() $\langle ,\rangle$
is positive definite on
$\langle ,\rangle$
is positive definite on
![]() $\mathfrak{p}$
and negative definite on
$\mathfrak{p}$
and negative definite on
![]() $\mathfrak{k}$
. The curvature tensor of
$\mathfrak{k}$
. The curvature tensor of
![]() $N$
is given by
$N$
is given by
for any
![]() $X,Y,Z\in \mathfrak{p}$
, and the Hermitian curvature of
$X,Y,Z\in \mathfrak{p}$
, and the Hermitian curvature of
![]() $N$
is given by
$N$
is given by
which is nonpositive, and zero if and only if
![]() $[X,Y]=0$
, because of
$[X,Y]=0$
, because of
![]() $[\mathfrak{p},\mathfrak{p}]\subset \mathfrak{k}$
. By Theorem 6.1, we get
$[\mathfrak{p},\mathfrak{p}]\subset \mathfrak{k}$
. By Theorem 6.1, we get
for any
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. Thus we have
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. Thus we have
Proposition 7.1. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
![]() $N$
a locally symmetric space of noncompact type. If
$N$
a locally symmetric space of noncompact type. If
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map, then
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map, then
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and for any
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic and for any
![]() $x\in M$
,
$x\in M$
,
![]() $d\unicode[STIX]{x1D719}_{x}$
maps
$d\unicode[STIX]{x1D719}_{x}$
maps
![]() $T_{1,0}(M)_{x}$
onto an abelian subspace
$T_{1,0}(M)_{x}$
onto an abelian subspace
![]() $W$
of
$W$
of
![]() $\mathfrak{p}\otimes \mathbb{C}$
.
$\mathfrak{p}\otimes \mathbb{C}$
.
Under the assumption of Proposition 7.1, the image under
![]() $d\unicode[STIX]{x1D719}_{x}$
of real tangent space
$d\unicode[STIX]{x1D719}_{x}$
of real tangent space
![]() $T_{x}(M)$
is the subspace of real points of space
$T_{x}(M)$
is the subspace of real points of space
![]() $W+\overline{W}\subset T_{\unicode[STIX]{x1D719}(x)}^{\mathbb{C}}(N)$
, so that
$W+\overline{W}\subset T_{\unicode[STIX]{x1D719}(x)}^{\mathbb{C}}(N)$
, so that
If
![]() $G/K$
is a Hermitian symmetric space, then corresponding to any invariant complex structure on
$G/K$
is a Hermitian symmetric space, then corresponding to any invariant complex structure on
![]() $G/K$
we have the decomposition
$G/K$
we have the decomposition
and the integrability condition
![]() $[\mathfrak{p}^{1,0},\mathfrak{p}^{1,0}]\subset \mathfrak{p}^{1,0}$
is equivalent, in view of
$[\mathfrak{p}^{1,0},\mathfrak{p}^{1,0}]\subset \mathfrak{p}^{1,0}$
is equivalent, in view of
![]() $[\mathfrak{p},\mathfrak{p}]\subset \mathfrak{k}$
, to
$[\mathfrak{p},\mathfrak{p}]\subset \mathfrak{k}$
, to
![]() $[\mathfrak{p}^{1,0},\mathfrak{p}^{1,0}]=0$
, thus
$[\mathfrak{p}^{1,0},\mathfrak{p}^{1,0}]=0$
, thus
![]() $\mathfrak{p}^{1,0}$
is an abelian subalgebra of
$\mathfrak{p}^{1,0}$
is an abelian subalgebra of
![]() $\mathfrak{p}\otimes \mathbb{C}$
.
$\mathfrak{p}\otimes \mathbb{C}$
.
Lemma 7.1. (cf. [Reference Carlson and Toledo3])
Let
![]() $G/K$
be a symmetric space of noncompact type. Let
$G/K$
be a symmetric space of noncompact type. Let
![]() $W\subset \mathfrak{p}\otimes \mathbb{C}$
be an abelian subspace. Then
$W\subset \mathfrak{p}\otimes \mathbb{C}$
be an abelian subspace. Then
![]() $\dim W\leqslant (1/2)\dim \mathfrak{p}\otimes \mathbb{C}$
. Equality holds in this inequality if and only if
$\dim W\leqslant (1/2)\dim \mathfrak{p}\otimes \mathbb{C}$
. Equality holds in this inequality if and only if
![]() $G/K$
is Hermitian symmetric and
$G/K$
is Hermitian symmetric and
![]() $W=\mathfrak{p}^{1,0}$
for an invariant complex structure on
$W=\mathfrak{p}^{1,0}$
for an invariant complex structure on
![]() $G/K$
.
$G/K$
.
From Lemma 7.1, we get immediately the following result.
Corollary 7.1. Let
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
be as in Proposition 7.1 and suppose that
$\unicode[STIX]{x1D719}:M\rightarrow N$
be as in Proposition 7.1 and suppose that
![]() $N$
is not locally Hermitian symmetric. Then
$N$
is not locally Hermitian symmetric. Then
![]() $\text{rank}\,d\unicode[STIX]{x1D719}<\dim N$
.
$\text{rank}\,d\unicode[STIX]{x1D719}<\dim N$
.
The above corollary use only the case of strict inequality in Lemma 7.1. We have treated the case of equality in such detail in order to obtain the following theorem.
Theorem 7.1. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
![]() $N$
a locally Hermitian symmetric space of noncompact type whose universal cover does not contain the hyperbolic plane as a factor. If
$N$
a locally Hermitian symmetric space of noncompact type whose universal cover does not contain the hyperbolic plane as a factor. If
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map, and there is a point
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map, and there is a point
![]() $x\in M$
such that
$x\in M$
such that
![]() $d\unicode[STIX]{x1D719}(T_{x}(M))=T_{\unicode[STIX]{x1D719}(x)}(N)$
, then
$d\unicode[STIX]{x1D719}(T_{x}(M))=T_{\unicode[STIX]{x1D719}(x)}(N)$
, then
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic.
$(J,J^{N})$
-holomorphic.
Proof. Since
![]() $d\unicode[STIX]{x1D719}(T_{1,0}(M))$
is an abelian subspace of half the dimension, it must be
$d\unicode[STIX]{x1D719}(T_{1,0}(M))$
is an abelian subspace of half the dimension, it must be
![]() $\mathfrak{p}^{1,0}$
for an invariant complex structure on
$\mathfrak{p}^{1,0}$
for an invariant complex structure on
![]() $N$
, that is,
$N$
, that is,
![]() $d\unicode[STIX]{x1D719}_{x}(T_{1,0}(M)_{x})=\mathfrak{p}^{1,0}$
. Consequently this property must hold on a neighborhood
$d\unicode[STIX]{x1D719}_{x}(T_{1,0}(M)_{x})=\mathfrak{p}^{1,0}$
. Consequently this property must hold on a neighborhood
![]() $U$
of
$U$
of
![]() $x$
. By Proposition 7.1 and Proposition 2.2, we have
$x$
. By Proposition 7.1 and Proposition 2.2, we have
![]() $d\unicode[STIX]{x1D719}(T)=0$
. Therefore, the map
$d\unicode[STIX]{x1D719}(T)=0$
. Therefore, the map
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic on
$(J,J^{N})$
-holomorphic on
![]() $U$
. We get that the map
$U$
. We get that the map
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic on
$(J,J^{N})$
-holomorphic on
![]() $M$
by the following unique continuation Proposition 7.2.◻
$M$
by the following unique continuation Proposition 7.2.◻
Then, we give some fundamental knowledge about the warped product. Let
![]() $(B,g_{B})$
and
$(B,g_{B})$
and
![]() $(S,g_{S})$
be two Riemannian manifolds and
$(S,g_{S})$
be two Riemannian manifolds and
![]() $f$
be a positive smooth function on
$f$
be a positive smooth function on
![]() $B$
. Consider the product manifold
$B$
. Consider the product manifold
![]() $B\times S$
with its natural projections
$B\times S$
with its natural projections
![]() $\unicode[STIX]{x1D70B}_{B}:B\times S\rightarrow B$
and
$\unicode[STIX]{x1D70B}_{B}:B\times S\rightarrow B$
and
![]() $\unicode[STIX]{x1D70B}_{S}:B\times S\rightarrow S$
. The warped product
$\unicode[STIX]{x1D70B}_{S}:B\times S\rightarrow S$
. The warped product
![]() $B\times _{f}S$
is the manifold
$B\times _{f}S$
is the manifold
![]() $B\times S$
furnished with the following Riemannian metric
$B\times S$
furnished with the following Riemannian metric
The Levi-Civita connection of
![]() $B\times _{f}S$
can now be related to those of
$B\times _{f}S$
can now be related to those of
![]() $B$
and
$B$
and
![]() $S$
as follows.
$S$
as follows.
Lemma 7.2. (cf. [Reference O’Neill15, p. 206])
Let
![]() $\widetilde{\unicode[STIX]{x1D6FB}}$
,
$\widetilde{\unicode[STIX]{x1D6FB}}$
,
![]() $^{B}\unicode[STIX]{x1D6FB}$
and
$^{B}\unicode[STIX]{x1D6FB}$
and
![]() $^{S}\unicode[STIX]{x1D6FB}$
be the Levi-Civita connections on
$^{S}\unicode[STIX]{x1D6FB}$
be the Levi-Civita connections on
![]() $B\times _{f}S$
,
$B\times _{f}S$
,
![]() $B$
and
$B$
and
![]() $S$
respectively. If
$S$
respectively. If
![]() $V$
,
$V$
,
![]() $W$
are vector fields on
$W$
are vector fields on
![]() $B$
, and
$B$
, and
![]() $X$
,
$X$
,
![]() $Y$
are vector fields on
$Y$
are vector fields on
![]() $S$
, the lift of
$S$
, the lift of
![]() $X,Y,V,W$
to
$X,Y,V,W$
to
![]() $B\times _{f}S$
are also denoted by the same notations, then
$B\times _{f}S$
are also denoted by the same notations, then
(i)
 $\widetilde{\unicode[STIX]{x1D6FB}}_{V}W$
is the lift of
$\widetilde{\unicode[STIX]{x1D6FB}}_{V}W$
is the lift of
 $^{B}\unicode[STIX]{x1D6FB}_{V}W$
;
$^{B}\unicode[STIX]{x1D6FB}_{V}W$
;(ii)
 $\widetilde{\unicode[STIX]{x1D6FB}}_{V}X=\widetilde{\unicode[STIX]{x1D6FB}}_{X}V=(Vf/f)X$
;
$\widetilde{\unicode[STIX]{x1D6FB}}_{V}X=\widetilde{\unicode[STIX]{x1D6FB}}_{X}V=(Vf/f)X$
;(iii)
 $(\widetilde{\unicode[STIX]{x1D6FB}}_{X}Y)_{B}=-(\tilde{g}(X,Y)/f)\,\text{grad}\,f$
;
$(\widetilde{\unicode[STIX]{x1D6FB}}_{X}Y)_{B}=-(\tilde{g}(X,Y)/f)\,\text{grad}\,f$
;(iv)
 $(\widetilde{\unicode[STIX]{x1D6FB}}_{X}Y)_{S}$
is the lift of
$(\widetilde{\unicode[STIX]{x1D6FB}}_{X}Y)_{S}$
is the lift of
 $^{S}\unicode[STIX]{x1D6FB}_{X}Y$
on
$^{S}\unicode[STIX]{x1D6FB}_{X}Y$
on
 $S$
.
$S$
.
We consider the special case: let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold and
![]() $C(M)$
be the manifold
$C(M)$
be the manifold
![]() $\mathbb{R}^{+}\times _{r}M$
endowed with the metric
$\mathbb{R}^{+}\times _{r}M$
endowed with the metric
![]() $\widetilde{g}=dr^{2}+r^{2}g_{\unicode[STIX]{x1D703}}$
. Therefore, by Lemma 7.2, we have
$\widetilde{g}=dr^{2}+r^{2}g_{\unicode[STIX]{x1D703}}$
. Therefore, by Lemma 7.2, we have
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \widetilde{\unicode[STIX]{x1D6FB}}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}=0,\qquad \widetilde{\unicode[STIX]{x1D6FB}}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r}X=\widetilde{\unicode[STIX]{x1D6FB}}_{X}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}=\frac{1}{r}X,\\ \displaystyle \widetilde{\unicode[STIX]{x1D6FB}}_{X}Y=\unicode[STIX]{x1D6FB}_{X}^{\unicode[STIX]{x1D703}}Y-rg_{\unicode[STIX]{x1D703}}(X,Y)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \widetilde{\unicode[STIX]{x1D6FB}}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}=0,\qquad \widetilde{\unicode[STIX]{x1D6FB}}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r}X=\widetilde{\unicode[STIX]{x1D6FB}}_{X}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}=\frac{1}{r}X,\\ \displaystyle \widetilde{\unicode[STIX]{x1D6FB}}_{X}Y=\unicode[STIX]{x1D6FB}_{X}^{\unicode[STIX]{x1D703}}Y-rg_{\unicode[STIX]{x1D703}}(X,Y)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}.\end{array}\end{eqnarray}$$
Theorem 7.2. (cf. [Reference Boyer and Galicki2])
If
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is a Sasakian manifold, then
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
is a Sasakian manifold, then
![]() $(C(M),\tilde{g})$
is Kähler.
$(C(M),\tilde{g})$
is Kähler.
Proof. Set
![]() $\unicode[STIX]{x1D701}=r(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)$
and define smooth section of
$\unicode[STIX]{x1D701}=r(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)$
and define smooth section of
![]() $\text{End}\,TC(M)$
by the formula
$\text{End}\,TC(M)$
by the formula
It is easy to see that
![]() $\widetilde{J}$
is an almost complex structure on
$\widetilde{J}$
is an almost complex structure on
![]() $C(M)$
and the metric
$C(M)$
and the metric
![]() $\widetilde{g}$
is Hermitian. From (7.4) and (7.5) we can show that
$\widetilde{g}$
is Hermitian. From (7.4) and (7.5) we can show that
![]() $\widetilde{\unicode[STIX]{x1D6FB}}\widetilde{J}=0$
. Thus
$\widetilde{\unicode[STIX]{x1D6FB}}\widetilde{J}=0$
. Thus
![]() $C(M)$
is Kähler.◻
$C(M)$
is Kähler.◻
Lemma 7.3. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold,
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a pseudo-Hermitian manifold,
![]() $(C(M),\widetilde{g})$
its cone manifold,
$(C(M),\widetilde{g})$
its cone manifold,
![]() $(N^{n},h)$
a Riemannian manifold. If
$(N^{n},h)$
a Riemannian manifold. If
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is a harmonic map, then the conic extension
$\unicode[STIX]{x1D719}:M\rightarrow N$
is a harmonic map, then the conic extension
![]() $\widetilde{\unicode[STIX]{x1D719}}:C(M)\rightarrow N$
defined by
$\widetilde{\unicode[STIX]{x1D719}}:C(M)\rightarrow N$
defined by
is also harmonic.
Proof. We take a local orthonormal frame field
![]() $\{T,e_{\unicode[STIX]{x1D6FC}},Je_{\unicode[STIX]{x1D6FC}}\}$
on
$\{T,e_{\unicode[STIX]{x1D6FC}},Je_{\unicode[STIX]{x1D6FC}}\}$
on
![]() $T(M)$
, then
$T(M)$
, then
![]() $\{(1/r)T,(1/r)e_{\unicode[STIX]{x1D6FC}},(1/r)Je_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\}$
is an orthonormal local frame field on
$\{(1/r)T,(1/r)e_{\unicode[STIX]{x1D6FC}},(1/r)Je_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\}$
is an orthonormal local frame field on
![]() $T(C(M))$
. By (7.4), we get that the usual tension field of
$T(C(M))$
. By (7.4), we get that the usual tension field of
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is equivalent to
$\widetilde{\unicode[STIX]{x1D719}}$
is equivalent to
![]() $(1/r^{2})\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})$
. Thus, the harmonicity of
$(1/r^{2})\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})$
. Thus, the harmonicity of
![]() $\widetilde{\unicode[STIX]{x1D719}}$
follows that of
$\widetilde{\unicode[STIX]{x1D719}}$
follows that of
![]() $\unicode[STIX]{x1D719}$
.◻
$\unicode[STIX]{x1D719}$
.◻
Lemma 7.4. Let
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h,J^{N})$
be a smooth map from a Sasakian manifold to a Kähler manifold,
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h,J^{N})$
be a smooth map from a Sasakian manifold to a Kähler manifold,
![]() $(C(M),\widetilde{g})$
the cone manifold of
$(C(M),\widetilde{g})$
the cone manifold of
![]() $M$
. Then:
$M$
. Then:
(i)
 $\unicode[STIX]{x1D719}$
is a
$\unicode[STIX]{x1D719}$
is a
 $(J,J^{N})$
-holomorphic (resp. anti-
$(J,J^{N})$
-holomorphic (resp. anti-
 $(J,J^{N})$
-holomorphic) map if and only if the conic extension
$(J,J^{N})$
-holomorphic) map if and only if the conic extension
 $\widetilde{\unicode[STIX]{x1D719}}$
is holomorphic (resp. antiholomorphic);
$\widetilde{\unicode[STIX]{x1D719}}$
is holomorphic (resp. antiholomorphic);(ii) if
 $\unicode[STIX]{x1D719}:M\rightarrow N$
is a
$\unicode[STIX]{x1D719}:M\rightarrow N$
is a
 $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map, then the conic extension
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map, then the conic extension
 $\widetilde{\unicode[STIX]{x1D719}}$
is a pluriharmonic map.
$\widetilde{\unicode[STIX]{x1D719}}$
is a pluriharmonic map.
Proof. (i) It can be proved by (7.5). We omit the details.
(ii) If
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then by Proposition 2.2 we have
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic, then by Proposition 2.2 we have
![]() $d\unicode[STIX]{x1D719}(T)=0$
. Let
$d\unicode[STIX]{x1D719}(T)=0$
. Let
![]() $B(\widetilde{\unicode[STIX]{x1D719}})$
be the usual second fundamental form for
$B(\widetilde{\unicode[STIX]{x1D719}})$
be the usual second fundamental form for
![]() $\widetilde{\unicode[STIX]{x1D719}}$
. From (7.5), (7.4) and (2.4) we get
$\widetilde{\unicode[STIX]{x1D719}}$
. From (7.5), (7.4) and (2.4) we get
for any
![]() $\widetilde{X},\widetilde{Y}\in T(C(M))$
. Therefore, the map
$\widetilde{X},\widetilde{Y}\in T(C(M))$
. Therefore, the map
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is pluriharmonic.◻
$\widetilde{\unicode[STIX]{x1D719}}$
is pluriharmonic.◻
In [Reference Siu20], Siu derived the following unique continuation theorem for holomorphicity.
Lemma 7.5. (cf. [Reference Siu20])
Suppose
![]() $M,N$
are two Kähler manifolds (
$M,N$
are two Kähler manifolds (
![]() $M$
is connected) and
$M$
is connected) and
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is a harmonic map. Let
$\unicode[STIX]{x1D719}:M\rightarrow N$
is a harmonic map. Let
![]() $U$
be a nonempty open subset of
$U$
be a nonempty open subset of
![]() $M$
. If
$M$
. If
![]() $\unicode[STIX]{x1D719}$
is holomorphic (resp. antiholomorphic) on
$\unicode[STIX]{x1D719}$
is holomorphic (resp. antiholomorphic) on
![]() $U$
, then
$U$
, then
![]() $\unicode[STIX]{x1D719}$
is holomorphic (resp. antiholomorphic) on
$\unicode[STIX]{x1D719}$
is holomorphic (resp. antiholomorphic) on
![]() $M$
.
$M$
.
From the Lemmas 7.3–7.5, we get the following unique continuation theorem.
Proposition 7.2. Let
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic map from a connected Sasakian manifold to a Kähler manifold. Let
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
be a harmonic map from a connected Sasakian manifold to a Kähler manifold. Let
![]() $U$
be a nonempty open subset of
$U$
be a nonempty open subset of
![]() $M$
. If
$M$
. If
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic (resp. anti-
$(J,J^{N})$
-holomorphic (resp. anti-
![]() $(J,J^{N})$
-holomorphic) on
$(J,J^{N})$
-holomorphic) on
![]() $U$
, then
$U$
, then
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic (resp. anti-
$(J,J^{N})$
-holomorphic (resp. anti-
![]() $(J,J^{N})$
-holomorphic) on
$(J,J^{N})$
-holomorphic) on
![]() $M$
.
$M$
.
Proof. From Lemma 7.3, we get that
![]() $\widetilde{\unicode[STIX]{x1D719}}:C(M)\rightarrow N$
is harmonic. Suppose
$\widetilde{\unicode[STIX]{x1D719}}:C(M)\rightarrow N$
is harmonic. Suppose
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic on
$(J,J^{N})$
-holomorphic on
![]() $U$
. It follows from Lemma 7.4 that
$U$
. It follows from Lemma 7.4 that
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is holomorphic on
$\widetilde{\unicode[STIX]{x1D719}}$
is holomorphic on
![]() $\mathbb{R}_{+}\times _{r}U$
. By Lemma 7.5, we have that
$\mathbb{R}_{+}\times _{r}U$
. By Lemma 7.5, we have that
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is holomorphic on
$\widetilde{\unicode[STIX]{x1D719}}$
is holomorphic on
![]() $C(M)$
and thus, from Lemma 7.4,
$C(M)$
and thus, from Lemma 7.4,
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic on
$(J,J^{N})$
-holomorphic on
![]() $M$
.◻
$M$
.◻
Now we may establish the following Siu type results.
Theorem 7.3. Let
![]() $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
$(M,T_{1,0}(M),\unicode[STIX]{x1D703})$
be a compact Sasakian manifold and
![]() $N$
be a Kähler manifold with strongly negative curvature. Suppose
$N$
be a Kähler manifold with strongly negative curvature. Suppose
![]() $\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map, and
$\unicode[STIX]{x1D719}:M\rightarrow N$
is either a harmonic map or a pseudoharmonic map, and
![]() $\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 3$
at some point of
$\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 3$
at some point of
![]() $M$
, then
$M$
, then
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $(J,J^{N})$
-holomorphic or anti-
$(J,J^{N})$
-holomorphic or anti-
![]() $(J,J^{N})$
-holomorphic on
$(J,J^{N})$
-holomorphic on
![]() $M$
.
$M$
.
Proof. From Theorem 6.2 and Lemma 7.3, we know that
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is harmonic. By Siu’s results, we have
$\widetilde{\unicode[STIX]{x1D719}}$
is harmonic. By Siu’s results, we have
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is
$\widetilde{\unicode[STIX]{x1D719}}$
is
![]() $\pm$
holomorphic on
$\pm$
holomorphic on
![]() $C(M)$
. By Lemma 7.4, we conclude that
$C(M)$
. By Lemma 7.4, we conclude that
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\pm (J,J^{N})$
-holomorphic on
$\pm (J,J^{N})$
-holomorphic on
![]() $M$
.◻
$M$
.◻
Keeping in mind Udagawa’s proof to Theorem 4 of [Reference Udagawa24] the following result is relevant.
Theorem 7.4. Every
![]() $\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map
$\bar{\unicode[STIX]{x2202}}_{b}$
-pluriharmonic map
![]() $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
from a Sasakian manifold
$\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$
from a Sasakian manifold
![]() $M$
into an irreducible Hermitian symmetric space
$M$
into an irreducible Hermitian symmetric space
![]() $N$
of compact or noncompact type is
$N$
of compact or noncompact type is
![]() $\pm (J,J^{N})$
holomorphic if
$\pm (J,J^{N})$
holomorphic if
![]() $\text{Max}_{M}\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 2P(N)+1$
, where
$\text{Max}_{M}\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 2P(N)+1$
, where
![]() $P(N)$
is the degree of strong nondegenerate of the bisectional curvature of
$P(N)$
is the degree of strong nondegenerate of the bisectional curvature of
![]() $N$
(cf. [Reference Siu21] for the definition of the degree of strong nondegenerate of the bisectional curvature of
$N$
(cf. [Reference Siu21] for the definition of the degree of strong nondegenerate of the bisectional curvature of
![]() $N$
).
$N$
).
Proof. By Lemma 7.4, we get that
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is pluriharmonic. Since
$\widetilde{\unicode[STIX]{x1D719}}$
is pluriharmonic. Since
![]() $\text{Max}_{M}\,\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 2P(N)+1$
implies that
$\text{Max}_{M}\,\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 2P(N)+1$
implies that
![]() $\text{Max}_{C(M)}\text{rank}_{\mathbb{R}}\,d\widetilde{\unicode[STIX]{x1D719}}\geqslant 2P(N)+1$
, it follows from [Reference Udagawa24, Theorem 4] that
$\text{Max}_{C(M)}\text{rank}_{\mathbb{R}}\,d\widetilde{\unicode[STIX]{x1D719}}\geqslant 2P(N)+1$
, it follows from [Reference Udagawa24, Theorem 4] that
![]() $\widetilde{\unicode[STIX]{x1D719}}$
is
$\widetilde{\unicode[STIX]{x1D719}}$
is
![]() $\pm$
holomorphic. From Lemma 7.4, we have that
$\pm$
holomorphic. From Lemma 7.4, we have that
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\pm (J,J^{N})$
-holomorphic.◻
$\pm (J,J^{N})$
-holomorphic.◻
Acknowledgments
This work was partially supported by the National Natural Science Foundation of China [grant number 11271071] and Laboratory of Mathematics for Nonlinear Science, Fudan; Yibin Ren was supported by NSFC Tianyuan fund for Mathematics Grant No. 11626217 and Guilin Yang was partially supported by HUST Innovation Research Grant 0118011034. The authors are grateful to the referee for comments leading to improvements of the present paper.


