Introduction
The possibility of air movement through snow due to wind action has been discussed for a long time. It has potential consequences for important processes like heat transfer through snow and crystal growth in snow. Without air movement, heat and vapor flow in snow are limited by diffusion, which tends to be very slow compared to the heat and vapor transfer that can take place if air moves. While heat conduction is important in snow, the transfer of heat by vapor movement down the temperature gradient must also be considered, and even thermal convection can take place (Powers and others, 1985). Thermal convection does not seem to be common in snow, but the variable nature of wind and atmospheric pressure does suggest the possibility that forced air movement could be significant in snow for several reasons. First, normal barometric pressure changes induce air movement in response to surface pressure changes. Secondly, turbulent winds over a snow surface induce rapid pressure changes due to the deceleration of downward air currents at the surface. Thirdly, the geometry of the snow surface induces a pressure distribution on the surface that causes movement through the permeable snow. I will try to show that the latter mechanism is most important, although Reference Clarke, Fisher and WaddingtonClarke and others (1987) have already concluded that windpumping by the dissipation of turbulent energy is important.
If the pressure field on the surface can be established, the flow of air through snow can be calculated as Darcian flow through a porous medium. In the case of slow pressure changes associated with synoptic systems, however, the adjustment of the air in the pore space can take place rapidly enough so that it is not necessary to consider the dynamics but only the mass balance. Thus, 1 begin by examining the effect of slow pressure changes where air movements occur essentially as fast as the rate of pressure change.
Slow Pressure Changes
Barometric changes are commonly in the range of ±2% of the total barometric pressure and occur over large areas, so flow into or out of the snow should be uniform. For isothermal conditions and increasing pressure, the original volume of air in the snow would be compressed to an equal mass whose new volume would be reduced by the ratio of the pressure change divided by the original pressure, a factor of generally less than 0.04. When the pressure increases, the original air mass would be compressed towards the bottom of the snow as the new air enters the top of the snow. For a total of 4% change in atmospheric pressure, the thickness of the layer of new air would be about 4% of the thickness of the snow. With slow changes in atmospheric pressure, the air cycles in and out of the snow in phase with the pressure changes and mostly affects the upper layer.
If the atmosphere is unsaturated with respect to ice at the temperature of the isothermal snow, the upper layer of snow, which is exchanging air with the atmosphere, should lose mass each time atmospheric air is cycled in and back out. Mass loss in the upper 50–100 mm of deep glacial firn has been observed by Reference AlleyAlley (1988) but only to a much shallower depth than is suggested by the above arguments. This discrepancy probably indicates that the dominant mechanism of air pumping in that location is not long-term pressure changes.
If air flows into the snow from above due to increasing atmospheric pressure, the existing air in the pore space would move downward and the air in the upper layer would be replaced by atmospheric air of a different heat content. Compared to the existing heat content of the ventilated layer, the sensible heat of the air has very little effect on the snow over just one cycle. Furthermore, the effect probably does not accumulate in the snow because the cycling is too slow. Thus, it appears that many rapid cycles of air infiltration or continuous infiltration over a long period are necessary to affect the snow temperature in any significant way. Likewise, air infiltration due to barometric pressure changes cannot move enough vapor into the snow to affect crystal growth. Temperature changes could complement the pressure changes, but the effect would still be small.
Fast Pressure Changes
When the surface pressure changes rapidly enough, the air flow cannot keep up with the surface change, so the flow must be calculated from the surface boundary condition. On the air–snow boundary at the height I above the snow-soil or snow–ice boundary, I assume a sinusoidal perturbation p’ about the mean air pressure p.
where l is the snow thickness, P is the amplitude of the pressure perturbation, ω is its frequency, and t is time. At the lower boundary — soil underlying snow or ice underlying firn — the flow vanishes.
Ignoring the slight hydrostatic pressure gradient, air moves through snow according to Darcy’s law
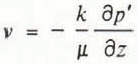
where ν is volume flux of air in the vertical direction, µ is permeability, z is dynamic viscosity, and ζ is the vertical coordinate with its origin at the base of the snow and is positive upwards. The air mass is conserved when
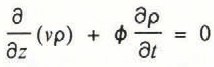
where ϕ is porosity and ρ is air density. The air also obeys the ideal gas law:
where R is the gas constant for air, or the universal gas constant divided by the average molecular weight for air, and T is the temperature. When the mean air pressure ρ is constant and is much greater than the perturbation ρ’, these equations show that the air diffuses through the pore space according to
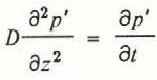
where D is kp/μϕ. Although this is the linear approximation to the actual diffusion equation for gas flow in porous media, it is the approach normally taken for gas flow.
The solution for diffusion in a medium of thickness 21 with a sinusoidal boundary condition on the two boundaries (±l) has been given by Reference Carslaw and JaegerCarslaw and Jaeger (1959, p. 105). Here, 1 take the solution for one-half of that thickness so that the flux across one boundary is zero, although the pressure varies on both boundaries, z = 0 and l. The non-transient part of this solution is
where A is given by
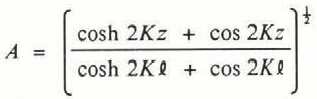
and the phase is given by the complex term
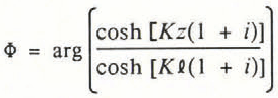
where K is (ω/20)*. Taking the average air speed (V) in the vertical direction as ν/Φ, from Equations (2) and (6),

An example of the air flow into and out of a 1 m snow cover over one cycle is shown in Figure I, The distribution of the flow is symmetrical about zero with an equal amount of flow into and out of the snow over one cycle. In this example, the flow is phase-lagged behind the pressure by π/4. Because of the limited depth in this example, the entire snow cover “breathes” as a unit. This would not be the case for a much deeper snow cover, which would respond to a surface forcing with waves of air moving up and down simultaneously at different levels, just as waves of heat are known to do (Reference ColbeckColbeck, 1989). For large depths or high frequencies, the movement of air is much lower at the base of the snow cover than at the surface as shown in Figure 1.
The effects of depth of the snow and frequency of the pressure perturbation can be seen in Figures 2 and 3, where the maximum value of the flow during one cycle is shown versus depth. The magnitude of the flow is greater for deeper snow covers because of the greater compressibility of the larger amount of air, but the phase shift does not change with snow depth. Likewise, the phase shift is constant for different frequencies, although the magnitude of the flow increases significantly with the frequency of the surface forcing. The higher flow rates result from higher pressure gradients in the snow at the higher frequencies. For these particular parameters, the flow ceases to be in phase throughout the depth if either the thickness of the snow or the frequency is increased very much beyond the values shown in these two figures. For greater depths or more rapid surface forcing, the air flow throughout the snow would no longer respond as a unit.

Fig.1. Air flow in and out of the snow cover for a1s cycle and a 1m snow depth (k = 4 × 10−9 m2, ρ = 10bNZmi. ϕ = 0.6).

Fig.2. Maximum value of V/P versus normalized height for various snow depths (same snow parameters as Figure 1).

Fig.3. Maximum value of V/P versus height in the snow for various frequencies (same snow parameters as Figure 1).
It is clear that snow will breathe with periodic changes in surface pressure, but the magnitudes of the pressure variations arising out of turbulent flow over a surface have to be considered. Reference ElliottElliott (1972) showed the spectral density versus frequency of the static pressures at frequencies greater than 0.01 Hz as measured at the surface in a flat grassy area. The strongest pressure fluctuations arising from the turbulent flow were measured over the range of frequencies given in Figure 3, 0.01–10 Hz. Elliott’s data suggest a relationship between 5 m wind speed and P:
where U is the wind speed in m/s. Thus, for a wind speed of 10 m/s, the peak of the pressure fluctuations would be about 1.5 N/m2, not a very strong pressure fluctuation when compared to atmospheric or stagnation pressure fluctuations.
For the example given in Figure 3, the greatest displacement of the air in the pore space would equal only about 14 µm at a wind speed of 10 m/s. This small displacement arises because the air flow in the snow increases with frequency but, at high frequencies, the time for displacement is short. Since the speed shown in Figure 3 increases faster than the frequency, the displacement of the air parcel increases with frequency but only up to a small value. Thus, it appears that the pressure fluctuations at the surface arising from turbulence cause air movement over very short distances in the snow cover.
Reference Schols and WartenaSchols and Wartena (1986) observed another spectral peak at a lower frequency where the flow into the snow could occur over a longer period of time. However, snow without fine-grained, high-density crusts is sufficiently permeable that, even at the upper limit of the frequencies considered in Figure 3, the pressure perturbations reach the base of the snow cover with nearly their entire amplitude because the value of A from Equation (7) is always nearly equal to one for this example. Thus, even at a frequency of 10 Hz in a 1m snow cover, the entire snow cover “breathes” as a unit. At a mean wind speed of 5.8 m/s, Schols and Wartena observed static pressure fluctuations of around 7 N/m2. If these perturbations fully penetrated the 1 m snow cover, the atmospheric air would enter only to a depth of about 70 µm, so again there is little mass flow from turbulent pressure fluctuation because it is inherently a high-frequency phenomenon. Thus, it appears that air movement caused by turbulence over the snow cover will not affect crystal growth.
Reference Clarke, Fisher and WaddingtonClarke and others (1987) had a more extensive look at windpumping due to turbulent fluctuations and concluded that the viscous dissipation of energy could be a significant heat source at depth in snow. With the small displacements quoted above, it is tempting to dismiss this notion intuitively, but these small displacements arise in part because I use a lower value for the permeability and expect the amplitude of the pressure perturbation to be lower than their value. Clearly, this requires more careful consideration and probably measurements to test these ideas. Neither Reference Clarke, Fisher and WaddingtonClarke and others (1987) nor I have considered the possibility of two-dimensional surface flows arising from the pressure distribution on the surface from turbulence bursts. These flows appear to occur on a sufficient time-scale to develop with the turbulence bursts and may limit most of the flow to a surface layer. Regardless of the effects of turbulence, it is shown next that on a snow surface of normal roughness the surface topography should generate large flow fields.
Surface Roughness
There are variations over a rough surface at a constant wind speed that could be strong enough to induce large air motions in the snow. Certainly, the stagnation pressure, 0.5ρU 2, is large enough to cause flow through snow structures. The variation in the stagnation pressure, about 0.15ρU 2 at a turbulence level of 25% (Reference Schols and WartenaSchols and Wartena, 1986), is somewhat larger than the turbulent pressure fluctuations on a flat surface described above. It is, however, the steady flow of air over surface features such as wind-deposited dunes that seems most likely to cause significant air movement below the surface. Reference Vanoni and HwangVanoni and Hwang (1967) measured pressure distributions over typical ripples in streams. The high pressures are on the up-stream side of the ripples, and the low pressures, on the lee faces, with a variation in pressure that is approximately sinusoidal with distance along the bed. The magnitude of the pressure variation P decreased as the water depth increased in their experiments but, at the greatest depth, the boundary layer is sufficiently well developed to assume that a similar amplitude would be found for an infinite depth.
Reference ChepilChepil (1958) measured the pressure distribution around hemispheres subjected to air flow in a wind tunnel. The pattern of the pressure distribution was independent of sphere size and wind speed, but the magnitude of the pressure drop increased with wind speed. As expected, the pressure was greater on the up-stream side of the obstacle. From those data, the pressure drop across the hemisphere increases as about 16U 2 N/m2 where U is in m/s. This pressure drop is about 50 times greater than would be expected from the pressure drop measured over ripples by Reference Vanoni and HwangVanoni and Hwang (1967), presumably because of the streamlined nature of the ripples in Vanoni and Hwang’s experiments. Nevertheless, from these two data sets, it is clear that the pressure drop scales as U 2 and that it is reasonable to take the pressure distribution over an undulating snow surface as
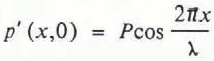
where λ is the wavelength of the ripples and x is the coordinate along the surface. P is still the magnitude of the pressure fluctuation, although p’ is no longer due to turbulent fluctuations. For a steady wind, Equation (5) is reduced to the harmonic equation:
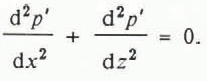
By inspection, for this boundary condition, Equation (12) has the solution
which specifies the pressure field within a surface dune of wavelength λ. For the purposes of using this solution, I am assuming that the aspect ratio of the surface features is sufficiently small that the flow field can reasonably be calculated as if this pressure distribution exists beneath a flat surface.

Fig.4. Spatial variation of the pressure perturbation normalized to P (same snow parameters as Figure 1).
An example is shown in Figure 4, where it can be seen that both the pressure perturbation and the gradients decrease with depth and that there is no flow across the vertical lines at 0, λ/2, and λ. The air flow is cyclic in nature, with the flow in the two cells being in opposite directions. The air enters the snow at the high-pressure, up-stream area and exits at the low-pressure area. The strength of the flow decreases rapidly with depth according to the horizontal u and vertical v components of flux,
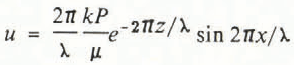
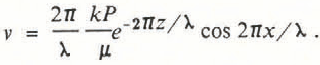
The magnitude of the total flux q at any position is given by
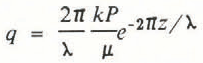
which is independent of position along the surface but decays rapidly with depth such that the 1/e decay in flux is reached at λ/2π. This rapid decay rate with depth suggests that the majority of the flow may be within the surface ripples themselves, although the air flux there could be quite strong. This may explain why mass loss is observed only in the upper 50–100 mm (Reference AlleyAlley, 1988) in polar snow.
Taking the pressure drop as proportional to the ratio of the dune height to the wavelength (personal communication from G. Ashton), from Reference Vanoni and HwangVanoni and Hwang’s (1967) data for flow over dunes, the amplitude of the pressure variation along the dune is
where H is the height of the dune. This is close to the potential solution for a wavy boundary, πρU 2 H/λ (personal communication from G. Ashton). Equations (16) and (17) can be combined to show that the total flux of air decays rapidly with depth in the snow and decreases as the wavelength of the topography but increases as the aspect ratio of the surface topography and the square of the wind speed at the top of the logarithmic boundary layer.
On the scale of 0.05–10 m, there are a variety of surface features due to drift on snow surfaces (Reference CornishCornish, 1914). These tend to have H/λ ratios of 0.15 for smaller features and ratios of 0.025 for larger features. Because the flow increase as H/λ 2, the flow near the surface would be much stronger for the smaller features, although the flow at depth can be greater for the larger features. This occurs because the 1/e decay depth for 10 m features is 1.6 m, whereas for a wavelength of 0.05 m it is only at a depth of about eight grain diameters.
Discussion
There are two obvious applications of the information generated here about air movement in snow: I want to know how air movement will influence crystal growth and heat flow. For these purposes, I will divide the problem into two parts: low-density seasonal snow and higher-density glacial firn. In seasonal snow there are surface features on the scale of centimeters to about 10 m (Reference CornishCornish, 1914), whereas for glacial firn the important scales range up to 5–7 km with amplitudes of 15–20 m (Reference Holzapfel and KirschHolzapfel and Kirsch, 1934).
Combining Equations (16) and (17), air flux is
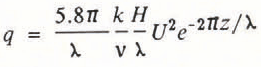
where ν is the kinematic viscosity. For a wind speed of 10 m/s, a permeability of 4 × 10−9 m2, wavelength of 1 m, and H of 0.1 m, the air-flow rate at the 1/e decay depth is 0.021 m3/m2s, which corresponds to an air speed of about 35 mm/s. This flow rate is much greater than what was predicted for natural convection by Powers and others (1985) and the mass transfer due to forced vapor movement should be greater too. The Peclet number for this flow rate is 1.6, which corresponds to only about a 20Ψο increase in the Sherwood number (Reference Clift, Grace and WeberClift and others, 1978, fig. 3.10), which is a direct measure of the increase in mass transfer. Accordingly, it seems reasonable to conclude that the increase in air-flow rate will not have a great effect on crystal growth.
Air movement through snow carries thermal energy at the rate qρc p δΤ, where c p is the specific heat of air and δΤ is the local temperature difference between the air and the snow. The heat necessary to raise a unit volume of snow to the temperature of the air is ρ s c i δΤ, where ρ s is the snow density, and c i is the specific heat of ice. To construct a simple model, I assume that the snow above the level ζ has all been chilled to the ambient air temperature, whereas the snow below the level ξ is at the undisturbed snow temperature given by the temperature gradient T’ before the onset of wind. Then, the rate of downward propagation of the chilled layer in the absence of heat conduction is
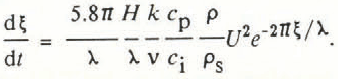
For a snow density of 0.3 Mg/m3 and a wind speed of 10 m/s, I use this equation to show how long the wind would have to blow to chill the snow to the 1/e decay depth. At a wavelength of 10 m and an amplitude of 0.25 m, where the 1/e decay is 1.59 m, the wind would have to blow for about 4 d. For the same conditions, the response would be much quicker close to the surface where the air currents are stronger. Therefore, thermal disruption of the snow cover by winds is entirely possible. The effect would be much stronger for shorter wavelengths and smaller amplitudes, which are more common. For 1 m wavelengths, the depth of penetration to the 1/e level of 0.16 m is only 15 min, because of its shallow depth and the stronger air movement associated with the shorter wavelengths. Thus, thermal disruption due to commonly occurring surface features may be normal.
Although I have assumed a flat surface for the air-flow analysis from a given pressure distribution, the two-dimensional character of the surface would affect the nature of the flow. In the example just given, 1/e depth is not much greater than the amplitude, so the assumption of a flat surface for the purpose of a flow calculation clearly indicates that the results are only qualitatively correct. For the larger wavelengths and lesser aspect ratios, this approximation would be less important. It is also important to note that for the IOrn example, the heat advected by air flow at the 1/e depth is greater than would normally occur from conduction. Thus, windpumping can completely disrupt the normal temperature profile.
For the very long wavelengths of glacial firn, 5–7 km with amplitudes of 15–20 m (Reference Holzapfel and KirschHolzapfel and Kirsch, 1934), the magnitude of the driving pressure gradient is certain to be lower but the 1/e depth is greater than the standard 10 m reference depth. Thus, the cumulative effect of even a small amount of air flow taken over an annual cycle may affect the thermal regime. In fact, for these long wavelengths, the 1/e depth equals about the entire depth of firn, so flow through the whole profile might be expected unless there were significant icy layers that would restrict the flow to upper levels. From Equation (18), I find that the flow rate in homogeneous firn of permeability 4 × 10−9 m2 would equal 11.4m3/m2 a at the 20 m depth. The amount of thermal energy advected by this air flow appears to be small compared to the heat conducted through firn, even below 10 m where the temperature gradients are affected little by the annual cycle. Thus, only shorter wavelengths could affect the thermal regime and then only closer to the surface.
Conclusion
Air flow through snow occurs in response to pressure gradients at the surface that arise from the surface topography. Other possible mechanisms for air flow include turbulent pressure fluctuations and barometric pressure changes, but neither one appears to induce a significant amount of flow. However, Reference Clarke, Fisher and WaddingtonClarke and others (1987) have concluded that turbulent pressure fluctuations could dissipate a significant amount of energy at depth.
The strength of the flow through the surface decreases rapidly with increasing wavelength, so the smaller surface features generate stronger flows. However, the depth at which the flow decays to 1/e of its surface value is greater for longer wavelengths because the flow decays more rapidly with depth at shorter wavelengths. Nevertheless, the flow due to wavelengths on the scale of kilometers is too weak to disrupt the thermal regime at the 10 m level, whereas the flow due to wavelengths on the scale of meters can disrupt the thermal regime in snow during strong winds.
AcknowledgementS
This work was supported at U.S. Army CRREL by Mechanical Processes in a Snow Cover, DA Project 4A161102. Very useful comments and information were provided by Dr E. Andreas, Dr G. Ashton, Dr G. Clarke, and J. Wuebben.






