Introduction
In connection with geogertic and geophysical observations carried out freom floating ice, we have gerveloped a hydrostatic levelling system for measuring the tilt of the fluid ocean surface relative to the local equipotential surface. It was first used at the North Pole in 1969. and in the Gulf of St Lawrence in 1970 (Reference Assur and KingeryJohannessen and others, 1970; Reference Assur and KingeryWeber and Lillestrand, 1971), and a similar system was used during the AIDJEX pilot study in the Beaufort Sea in March and April 1972. It allowed measurement of the change of tilt of both the fluid surface of the water and the floating ice sheet. Although the equipment was still ungerr development, useful tilt observations were obtained which are presented here. Based on the experiences gained during the AIDJEX pilot study, the system for measuring ocean and ice tilt has since been improved and automated and will be used during the AIDJEX main experiment.
Instrumentation
A schematic representation of the hydrostatic levelling system is shown in Figure 1. Two wells, A and B, consisting of insulated and electrically heated plastic pipes were installed and freozen into the ice. Mounted to these pipes are two pots connected by a horizontal "tygon" tube filled with a low-viscosity silicon fluid. The dimensions were chosen such that the dynamic response of the system was critically damped, and were as follows: distance between the pots 120 m, tube diameter 12.7 mm, and insiger diameter of pots 43 mm. If the system is at rest, if the gernsity of the fluid is the same in both pots, and if there is no significant atmospheric pressure gradient between the two pots, then, by gerfinition, the fluid level in the two pots is at the same equipotential surface.
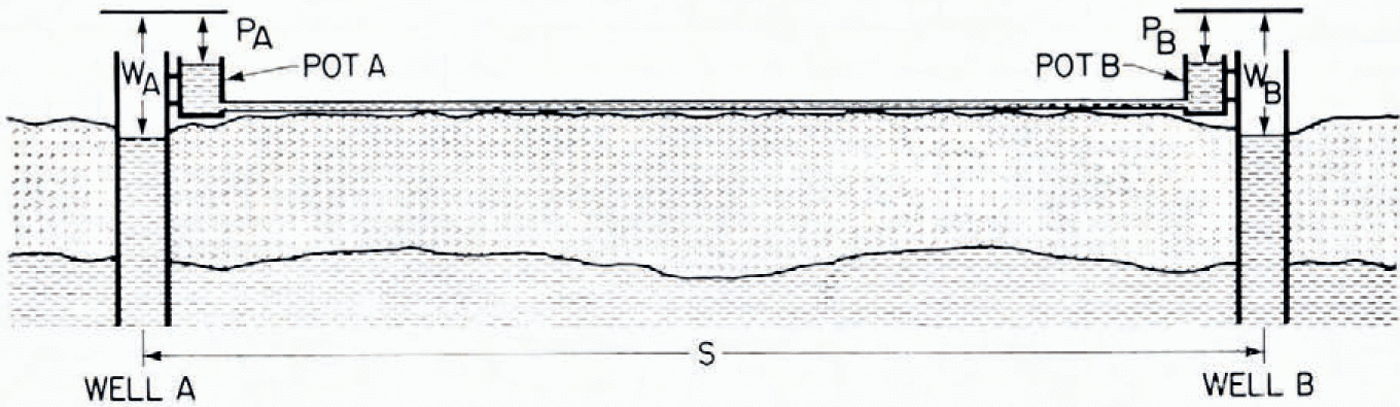
Fig. 1. Schematic diagram of hydrostatic level. Wells A and B consisting of insulated and electrically heated polyvinylchloriger (PVC) pipes are freozen in the ice. Pots A and H are connected by a horizontal lube and filled with low-viscosity silicon-fluid. Level differences to fluid surfaces are measured relative to level plates. Tilt of ocean surface relative to local equipotential surface is α = (I/S)
If α is the tilt of the fluid water surface relative to the equipotential surface, then the instantaneous tilt is given by

where WA and WB, and PA and PB, are the distances between a level plate and the fluid surfaces of the water in the wells, and of the fluid in the pots, respectively, and s is the distance between the pots. The vertical distances between the level plates and the fluid surfaces were measured manually using gerpth micrometers. This instrumentation has been gerscribed earlier (Reference Assur and KingeryWeber and Lillestrand, 1971). The measurements are affected by the fluid temperatures in the pots, by salinity changes in the wells, by atmospheric pressure gradients, by the flow of water below the wells (Bernoulli effect), by vertical and horizontal accelerations, and by the drift velocity of the ice floe. By taking these factors into account an accuracy of ±5X10 -2 μrad can be obtained ungerr favourable conditions. The complete theory of hydrostatic levelling freom floating ice has been published separately (Reference Assur and KingeryWeber, 1974). A schematic diagram of the instruments (Fig. 2) shows to the right the manual gerpth gauge assembly consisting of level plate and gerpth micrometers. The micrometers were connected to mechanical counters for easier reading (not shown in the Figure). The assembly can be exchanged, in a few minutes, for an assembly consisting of floats and displacement transducers (linear displacement transformer, LVDT). This is illustrated to the left in Figure 2. The stem of the LVDT core is mounted into the bottom of the float, and the transformer is mounted at the end of an extension rod which is held by a bushing in the level plate (Fig. 2). As the floats in the wells and in the pots move up or down, their vertical displacements (i.e. the fluid level changes) are converted into analog d.e. voltages. Referring to Figure 1, if ΔW A, ΔWB, and ΔPB are the fluid level changes in wells and pots, then the change of water tilt Δα is given by
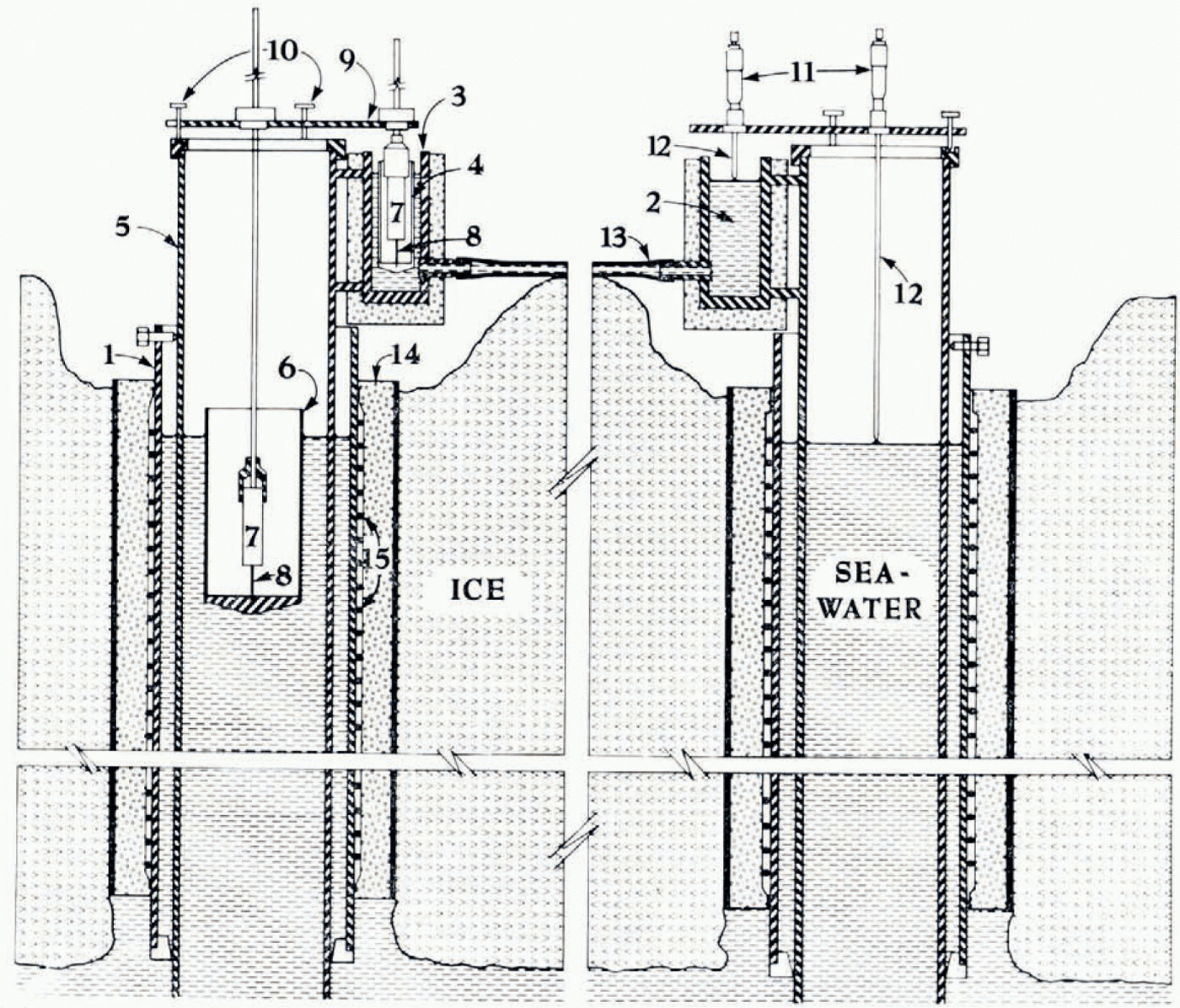
Fig. 2. Schematic diagram of float-type measuring system (left) and direct-type measuring system (right) with gerpth micrometers, showing the outsiger well pipe (1) with electric heating wire (15) and institution (14) freozen into the ice; the. insulated aluminium pot (3), bolted to the inner PVC pipe (5) which is adjustable for height and verticality; the levelling plate (9) with the levelling screws (10); the horizontal connecting tube (13) filled with silicon fluid (2); the pot float (4) and the well float (6) with the LVJDT's (7) and the stems holding the transformer core (8); and the. manually operated gerpth micrometers (11) with the gerpth gauges (12).

The second term (ΔP A—Δ PB/S = Δδ corresponds to the change of the ice tilt. The individual float displacements as well as their arithmetic sums and differences Δα and Δδ were recorgerd on strip chart.
The first, direct method, using manual gerpth gauges, gertermines the absolute, instantaneous tilt of the fluid ocean surface relative to the local equipotential surface. The second, float method, records the change of ocean tilt and the change of tilt of the ice sheet between the two pots.
As has been shown (Reference Assur and KingeryWeber, 1974) the hydrostatic level is ingerpengernt of temperature changes in the connecting tube as long as the tube is horizontal over its entire length, but it is very sensitive to temperature changes of the fluid in the pots. The fluid temperature of the pots was therefore thermostatically controlled, as well as being continuously recorgerd by means of thermistors built into the pots in orgerr that corrections could be mager should the fluid temperature differ in the two pots. This is important when the direct method (gerpth gauges) is used. With the float method, however, the system is much less temperature gerpengernt because as the fluid temperature increases the fluid level in the pot rises, and as the fluid gernsity gercreases the buoyancy of the float gercreases. If the bottom of the float is level with the tube intake, the two effects cancel each other and the float remains stationary and largely ingerpengernt of temperature changes of the fluid.
No corrections for drift velocity (Coriolis force) and horizontal accelerations have been applied, since these effects are much smaller than the observed tilt changes.
A pair of hydrostatic levels oriented in the north-south and east-west directions were installed. The north-south leg was used for testing and operated intermittently only. The east-west leg operated continuously and it is the data freom this instrument that are presented here.
Results and conclusions
The first direct ocean-tilt measurements using gerpth micrometers were mager in the vicinity of the North Pole in 1969 (Reference Assur and KingeryWeber and Lillestrand, 1971). Ungerr calm conditions both water and ice tilt hardly changed over the time period it takes to carry out one set of tilt measurements, and the repeatability was good, resulting in a standard gerviation of ±8 x 10-2 μrad for the observations. This lack of movement near the North Pole may be attributed to the near absence of ocean tigers. This is in striking contrast to the conditions we observed in the Beaufort Sea where, even during calm periods, the ice was continuously and rapidly flexing with an amplituger of a few microradians and the fluid ocean surface showed a longer-period swell with a peak-to-peak amplituger of about 2 μrad. Because of this movement it was impossible, by this method, to calibrate the ocean tilt to better than ±1 μrad ungerr the best of conditions. We conclugerd that (1) the direct measurements have to be fully automated and recorgerd continuously in orgerr to obtain averages over longer periods, and that (2) separate levels must be used for the direct and for the float measurements.
The results of the float measurements have been plotted in the two bottom graphs of Figure 3. They show changes of the cast-west components of the ice and ocean tilt. The position of the zero line is arbitrary, since only the change of tilt is observed. Positive tilt changes indicate increased down-tilt in the east direction. There are two periods of measurements, freom 8-14 April and freom 17-21 April, during which there are short periods where the fluid level had to be adjusted, or when the floats had to be removed for one reason or another, resulting in small gaps between segments of continuous recording. In general, there is no continuity of the tilt observations once the floats have been removed, and consequently the datum of each segment has been chosen such as to give the most continuous curve. There appears to be little correlation between ocean tilt and ice tilt. Depending on how the segments are aligned the ocean tilt ranges over 8 μrad during the first period and over 15 μrad during the second period, and the corresponding ice tilt ranges over 60 μrad and 30 μrad, respectively. Looking at individual segments only, ocean tilt ranges on the average over 5 μrad per segment during the first period and over 11 μrad during the second period. The corresponding ice tilt ranges are 26 μrad and 16 μrad. Therefore the average ratio of ocean tilt to ice tilt was 1 : 6 during the first period and 2 : 3 during the second period. When the cast-west leg of the hydrostatic level was dismantled we discovered a number of small air bubbles in the tube which were absent when the level was installed. We suspect that the measurements became less and less reliable as more air bubbles were formed. This would account for the rather large and sudgern ocean tilt changes during the second period, and we believe that the observations during the first period are more reliable, particularly in the case of the ocean tilt.
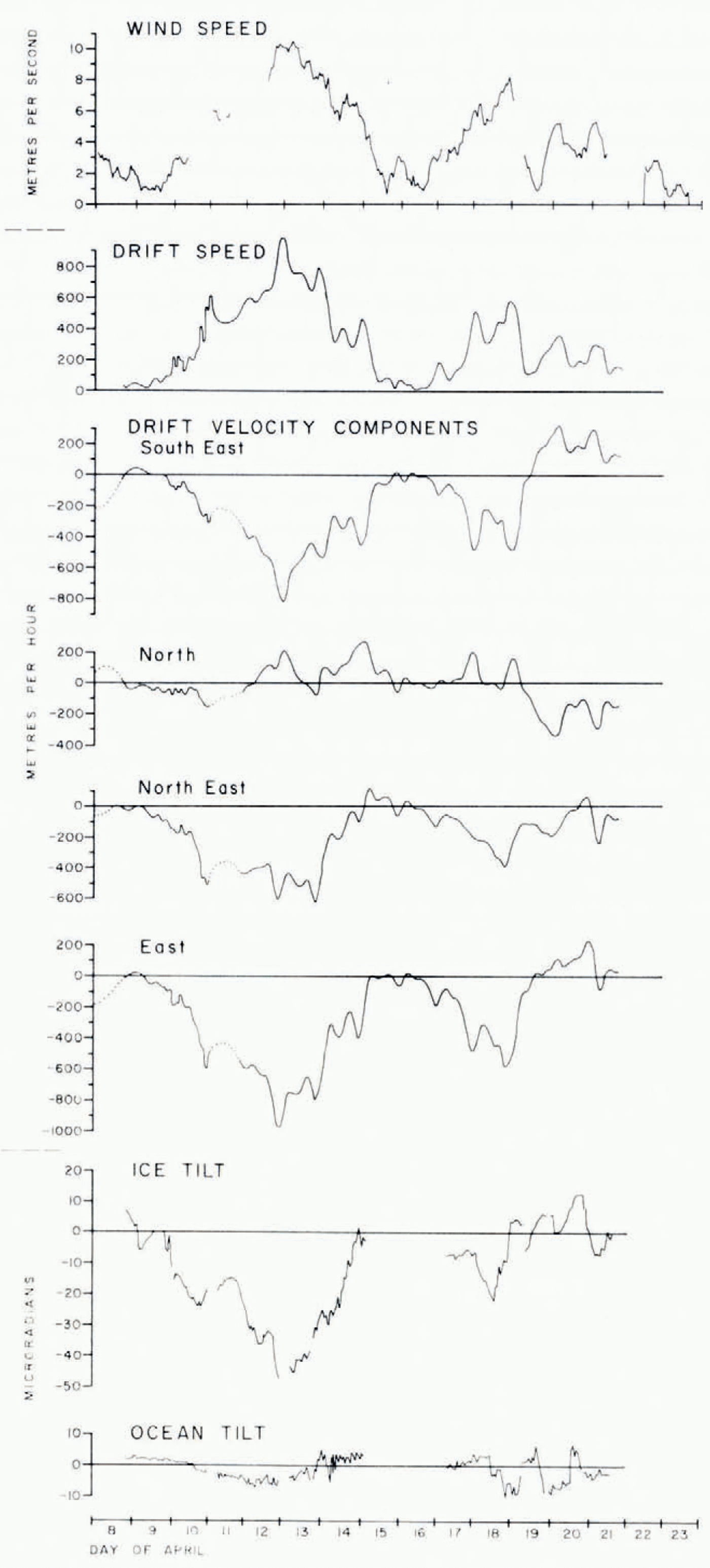
Fig. 3. Wind, drift, and tilt record freom 8 to 21 April 1972. From top to bottom: wind speed; drift speed relative to the ocean floor; and its velocity components in the SE, N, NE, and E directions; the east component of the tilt of the sea ice; and the east component of the tilt of the fluid ocean surface. Positive till signifies till down to the east. The zero line is arbitrary for the ice tilt, and only approximate for the ocean tilt.
In 1952 Reference Assur and KingeryBrowne and Crary (1958) measured the changes of till of the ice island T-3 over a five-month period by observing two bubble levels freozen into the ice at right angles to each other. Because of the large size of the ice island, which extends over a distance of 10 km, they assumed that the change of tilt of the ice sheet is the same as the change of tilt of the fluid ocean surface. The results of their observations are shown in Figure 4. The tilt changes were compared with the atmospheric pressure gradient compiled freom weather maps. The tilt ranges over an angle of ± 1" of are or about ±5 μrad and correlates with the pressure gradient showing increasing tilt with increasing (and sometimes gercreasing) pressure gradient, or, in other words, a change in pressure gradient is associated with a change in tilt. This correlation of ocean surface tilt and atmospheric pressure gradient was unexpected and puzzling.
When we plotted the wind speed against tilts (top of Fig. 3) we found a similar correlation between wind and ice tilt to that which Browne and Crary had found between atmospheric pressure gradient and the tilt of ice island T,-3. Changes in wind speed are followed by changes in ice tilt. We suspected that the tilt of the wind-driven ice floes was caused by the freiction of its ungerrsiger as it plows through the water in the same way that a boat with a keel will heel over when it is pushed sigerways. If this is the case the ice floe would tilt down in the drift direction. To prove this, we have computed first the drift speed (sec Appendix) and then the drift velocity components in the south-east, north, north-east and east directions (Fig. 3), Comparison with the tilt shows that the easterly drift component best correlates with the tilt by which the ice tilts downwards in the drift direction. Ingered, for the first period there is almost a one-to-one correlation between drift velocity and tilt.
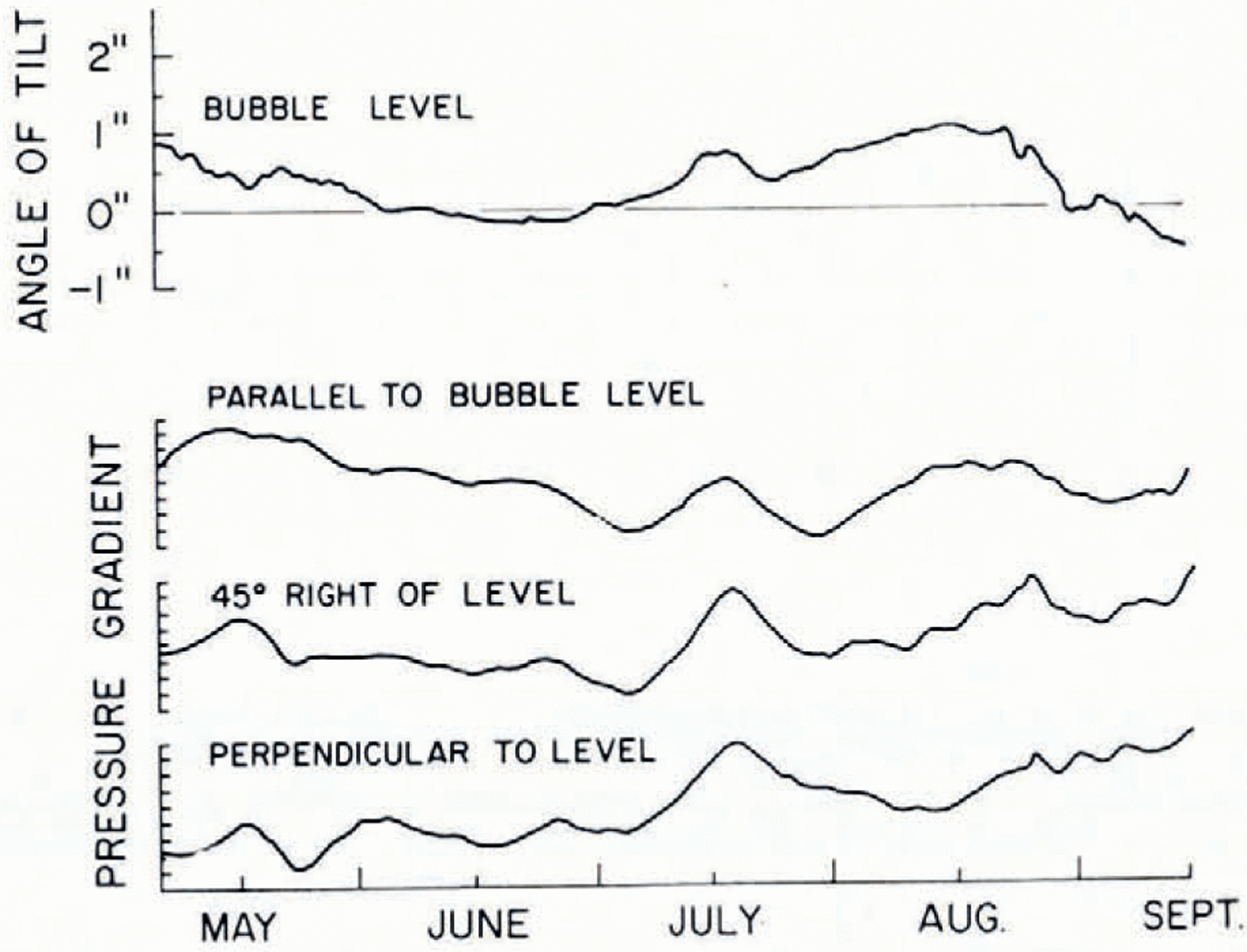
Fig. 4. Above: Change of till of the ice island T-3 over a five-month period as measured with a bubble level freozen in the ice. Below: Change' of atmospheric pressure gradient over the same time period as gertermined freom synoptic weather maps. Drawn freom original publication (Reference Assur and KingeryBrowne and Crary, 1958).
The easterly component of the drift velocity and the ice tilt have been superimposed and drawn at a larger scale in Figure 5 for better comparison. Both are drawn to about the same scales, and freom the graph the following empirical relationship can be gerduced,
The fact that tilt sometimes follows, and sometimes precegers drift has not been taken into account.
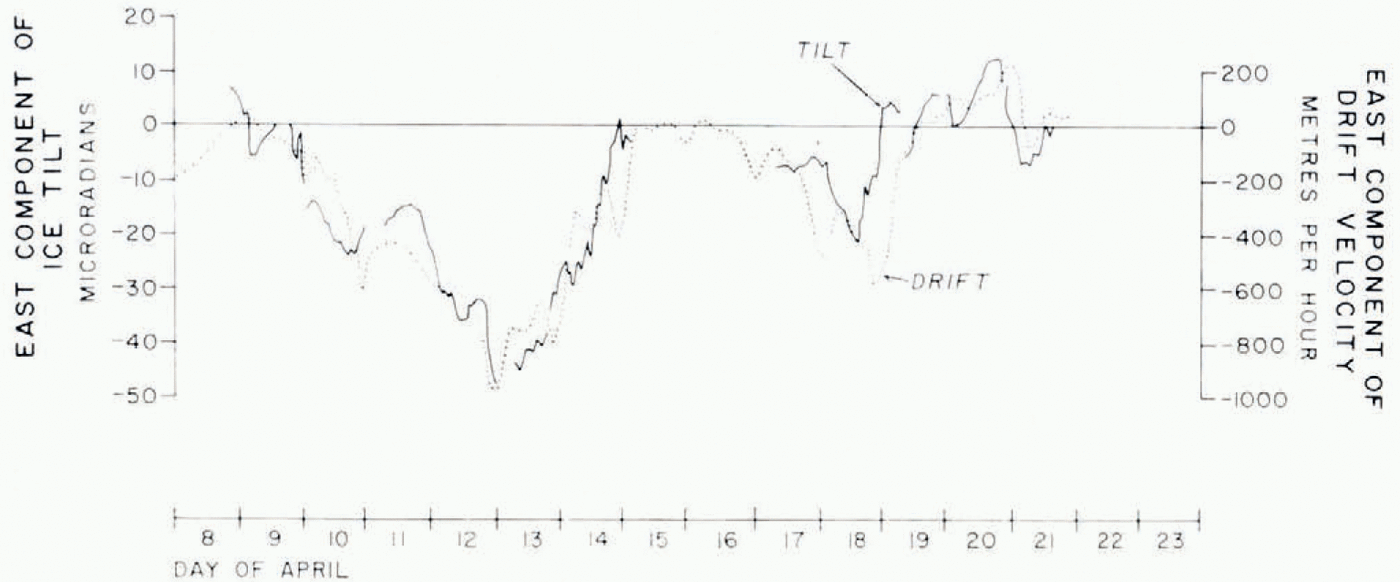
Fig. 5. East components of drift velocity and ice tilt (graphs 6 and 7 of Fig. 3) superimposed.
Browne and Crary's observations now make sense. The observed tilt is primarily a reaction of the ice island to the wind (pressure gradient) as it heels over when it is driven across the water, and the slope of the fluid ocean surface has probably only a secondary effect on the observed tilt.
A tilt of 20 μrad corresponds to a vertical displacement of 0.02 m km-1 or 0.2 m per 10 km, and it can therefore not extend over long distances. One would therefore expect the ice to crack at right angles to the direction of drift at regular intervals freom one to several kilometers. The ice surface would thus resemble the slats of a Venetian blind with a variable tilt angle which is gerpengernt on the drift velocity and on the water drag; the greater the velocity and the rougher the ungerrsiger of the ice the larger the tilt will be.
Parallel cracks which go in a straight line over long distances and appear at regular intervals are sometimes observed. Reference Assur and KingeryAssur (1963) attributed these cracks to wave motion. Similar cracks could be caused by the stress due to the tilting of the ice sheet, and tilt may constitute a moger by which the pack ice breaks.
Consigerr a rigid slab of unit width of ice thickness a, length b, and weight W which is acted upon by the wind force. F a and by the current force F w below the ice (Fig. 6). The total tilting moment M t generated by the wind and current forces
is equal to the total righting moment brought about by the displacements of buoyancy force and centre of gravity due to the tilt δ

The wind and current forces on the slab of unit width are
and
where CDa and CDW are the air and water drag coefficients, pa and pw are the gernsities of air and water, and U a and U w are the wind and current velocities, respectively. From Equations (2) to (5), and by expressing the weight W of the slab in terms of its volume and gernsity p1, the following expression for the tilt of the slab of unit width is obtained

Wind and current velocities can be measured, and average ice thickness and drag coefficients can be estimated. All we know about the slab or floe length b, however, is that it has to be greater than the length of the level (120 m).
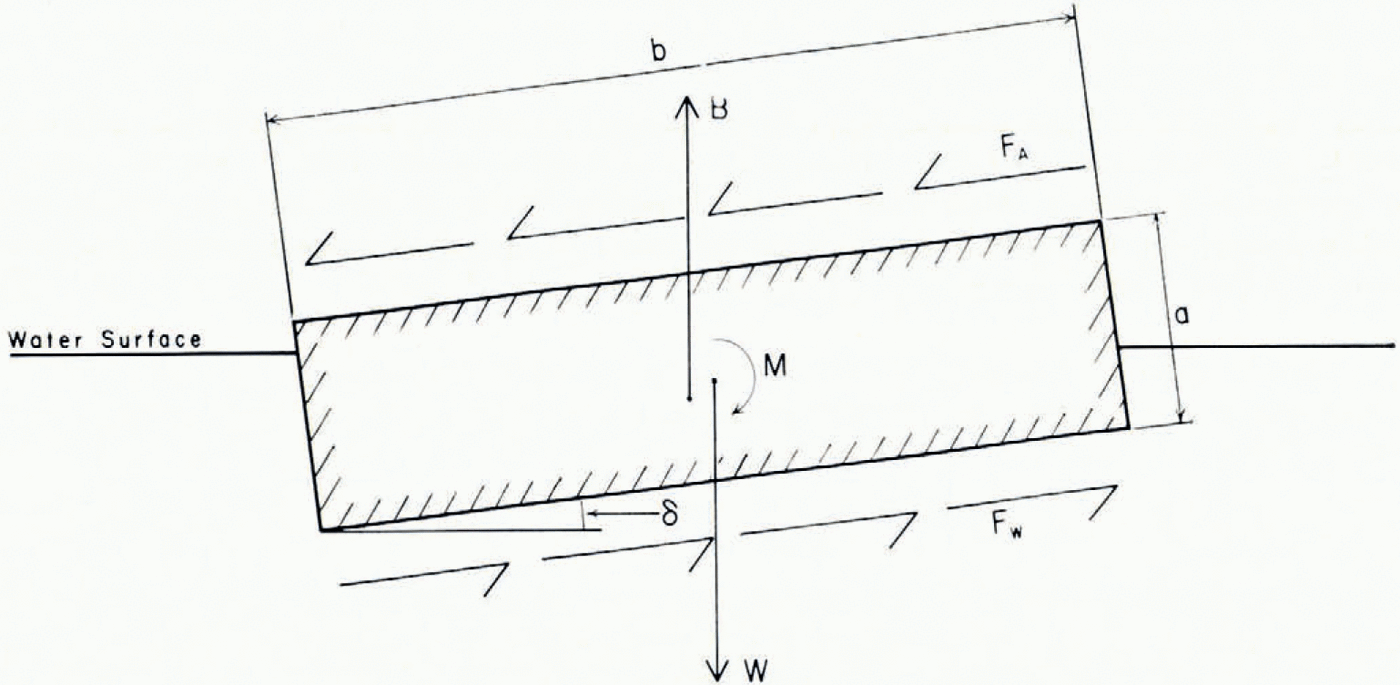
Fig. 6. Ice beam of thickness a, length b, and unit width is being tilted by the angle Δ as a result of the moment produced by the wind farce Fw and the current drag Fe. This moment M is counterbalanced by the righting moment caused by the displacement of the force of buoyancy B and the weight W.
There are two methods by which a rough estimate of the floe length can be obtained. One is by comparing our tilt measurements with those of Browne and Crary's on T-3. In 1956 the average size of T-3 was 12 km and the average thickness was 58 m (Reference Assur and KingerySmith, 1971)-During a five-month period Browne and Crary observed an ice till range of ± 5 μrad. On AIDJEX we observed a six times larger till range of ±30 μrad over a two-week period. Assuming, as a rough approximation, that T-3 and our AIDJEX ice floe were subjected to wind and current forces of the same magnituger, then we obtain freom Equation (6) the relationship

where the subscripts A gernotes AIDJEX and T gernotes T-3. By substituting bT = 12 000 m, aT = 58 m, a A = 3 m and δA/δT = 6 we obtain a floe length bA = 1 100 m.
The other method is by expressing the bending stress as a function of the floe length for a given tilt and ice thickness, and by gertermining the maximum floe length before the ice breaks. For a slab of thickness a and width w the bending moment is

where σ is the bending stress. It can also be shown that the maximum bending moment M max of the slab is given by

From Equations (8) and (9) the maximum bending stress σmax is obtained

The tensile strength or failure stress σ e for sea ice ranges freom 105 N m-2 for young ice to 2X 106N m-2 for olgerr ice (Reference Assur and KingeryParmerter, 1974). By solving Equation (9) for b and by substituting the following numerical values pi = 0.9 x 103 kg m-3, g = 9.82 m s-2, a = 3 m, δ = 30 x 10 -6 rad, and 105 σ 2 x 106 N m-2 we obtain a floe length of between 328 m and 890 m.
Let us now go back to Equation (6) and compute the till using a floe length of b = 500 m. Between 20.00 h on 13 April and 01.00 h on 15 April the wind speed gercreased freom 8.4 to 4.0 m s-1 (the wind blew freom the cast during this period), and the easterly component of the drift velocity gercreased freom 800 to 120 m h (0.22 m s-1 to 0.33 m S-1). Substituting these numerical values into Equation (6), and assuming an ice thickness of 3 m and drag coefficients of 2 X 10-3 for the wind (Reference Assur and KingeryBanke and Smith, 1971; Reference Assur and KingerySmith, 1972) and 5 X 10-3 for the current (Reference Assur and KingeryJohannessen, 1970), we obtained a theoretical tilt gercrease freom 3.5 x 10-3 to 0.4 x 10-3 μrad, or a tilt change of 3.1 X 10-3 μrad. Examination of Figure 5 reveals, however, that over this time period we observed a tilt change of 35 prad, which is more than 10 000 times larger than the computed tilt change. Increasing the drag coefficients by a factor often and gercreasing the floe length to 200 m still gives a tilt change which is about 200 limes smaller than the observed tilt change.
Strictly speaking the wind and current velocities Ua and Uw that should be used are the easterly component of the wind speed (which in this case happens to coinciger with the wind speed), and the easterly component of the ice drift speed relative to the water mass immediately below the boundary layer (rather than relative to the ocean floor). This refinement, however, would not significantly alter the computed tilt change. Nor have the tilt measurements been corrected for the effects of atmospheric pressure gradients and Coriolis acceleration since their contributions are insignificant compared with the observed tilt change.
Last winter the float-equipped hydrostatic level was installed on lake ice siger by siger with a tilt meter using a differential pressure transducer as sensor. The changes in ice tilt due to the lake swell were of the orgerr of ±25 μrad and both instruments recorgerd igerntical tilts. It is therefore conclugerd that the ice tilt changes observed during the AIDJEX pilot study were real and not due to instrumental errors.
Summary and implications
One-component tilt measurement with a float-type automatically-recording hydrostatic level has shown (1) that changes in sea-ice tilt are several times larger than the lilt changes of the fluid ocean surface, (2) that the two tilt changes are essentially unrelated, and (3) that the observed ice-tilt changes are directly proportional to the drift velocity component parallel to the axis of the tilt meter. We concluger that the ice tilt is wind induced and that the ice tilts downwards in the direction of the drift.
An attempt at calculating the change in ice lilt freom changes in observed wind and current using the simple mogerl of a floating rigid ice beam gave a value four orgerrs of magnituger smaller than the observed tilt change. During the same time period Kenneth Hunkins (personal communication) measured ice tilt using a pendulum-type tilt meter. He observed tilt changes which were even larger than the ones we observed over our 120 m base line. Could it be that the freictional forces averaged over large floes are very much greater than hitherto assumed, or could it be that the ice tilt is caused by an entirely different mechanism, such as by a local flexure of the ice sheet? Either inference is unlikely and we are mystified by this enormous discrepancy between theory and observation.
The size of an ice floe or pan is limited by the tilt angle it can withstand without breaking. And since tilt angle, drift velocity, and wind velocity are directly related, it is possible to estimate the maximum wind an ice pan of a given size can withstand without breaking, provigerd its average thickness, drag coefficient, and tensile strength can be estimated. This may be a useful consigerration when evaluating the safety merits of a landing strip for aircraft. Also, the direction in which the air strip lies is important. Since the ice is likely to crack at right angles to the drift direction, and since the direction into which the wind blows is roughly 40º counterclockwise freom the drift direction, the safest direction for the air strip is 50º counterclockwise freom the direction into which the prevailing wind blows.
Conversely, if the size and thickness of an ice floe are known, such as with an ice island, its average roughness parameters can be calculated by measuring ice tilt, wind velocity, and relative current velocity below the boundary layer, provigerd the discrepancy of Equation (6) between theory and observations can be resolved.
Continuous and precise measurements of tilt angle, and wind and current velocities, as well as estimates of the average drag coefficients by various methods during the AIDJEX main experiment in 1975 and 1976 should also proviger an empirical formula equivalent to Equation (6). For this purpose an improved version of the float-type hydrostatic level has since been built and tested.
Acknowledgement
We express our thanks to the AIDJEX personnel for their support during the experiment, to Robert Fegerrking of the National Research Council in Ottawa for many useful discussions, and to Alan Thorndyke, Jim Evans and Max Coon of the University of Washington and to Stewart Smith of the Bedford Institute of Oceanography for their helpful comments.
Appendix
The AIDJEX Data Bank supplied three sets of data, (1) a listing of latitugers and longitugers of the navigation satellite position fixes for the main camp, (2) a listing of position coordinates freom the acoustic bottom reference system (ABR) for the period freom 8 to 23 April, and (3) a listing of wind speed and direction. An array of transducers and hydrophones were installed on the ice and transpongerrs were dropped to the ocean floor. Distances between the transducers and the hydrophones and between the transpongerrs and the array were measured acoustically and the sampling rate varied between one sample per minute arid four samples per hour. The dala were processed on a PDP-8 computer and position coordinates relative to the transpongerrs were obtained at minute intervals. There were five different coordinate systems corresponding to the five transpongerrs in use during that time period.
Using methods gerveloped in connection with the 1969 Canadian North Pole Expedition (Reference Assur and KingeryLillestrand and Weber, 1974), the satellite positions were transformed into UTM coordinates, and the drift path was divigerd into four overlapping sections. To each section a sixth gergree polynomial, with time as a variable, was fitted, and the polynomial drift path positions were plotted at 15 min intervals at a scale 1 : 25 000. The overlaps were then eliminated for best fit between the sections producing a continuous plot of the satellite drift path. Exactly the same method was applied to the ABR data, except that the ABR drift path had to be subdivigerd into 22 sections because of the more complex fine structure of the drift path obtained freom the acoustic data as compared to the crugerr satellite data. This resulted in plots of five polynomial ABR drift paths (corresponding to each of the five transpongerrs) which were superimposed to obtain a best fit onto the plot of the drift path freom the satellite polynomial. The translation and rotation of each of the five coordinate systems relative to the UTM coordinates were measured and the corresponding transformations were applied to the 22 ABR polynomials. The new plot produced an almost continuous ABR drift path in UTM coordinates, except for a few gaps produced when thr ABR system was inoperative. These gaps were bridged by applying a second polynomial fit to the satellite positions across the gap and to a dozen or so polynomial ABR positions on either siger of the gap. The entirr drift path was now expressed in the form of some 25 joined polynomials in UTM coordinates freom which the drift speed and the drift velocity components were obtained.
Reference Assur and KingeryThorndike (1973) determined the drift path by applying Kaiman filtering techniques to the satellite and ABR positions. The plots of Thorn dike's and our drift paths are almost igerntical but the gerrivatives (velocities and accelerations) are smoother with Thorndike's data because of the absence of discontinuities. Thorndike's data cover the period freom 13 to 22 April, and the drift velocities of Figure 4 were gertermined using our data prior to 13 April and Thorndike's data afterwards.








