Article contents
Commonality and difference in the eigenfunctions of various types of acoustic trapped modes
Published online by Cambridge University Press: 26 January 2024
Abstract
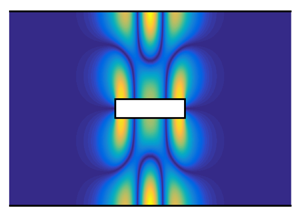
We investigate and compare various types of acoustic trapped modes (TMs) in resonator–waveguide systems. The goal is to understand the commonality and difference between the mechanisms of common (symmetry protected, invisibility protected and symmetry–periodicity protected) and accidental TMs, occurring continuously and discretely in the resonator length–frequency two-parameter space. The latter type cannot yet be explained via an operator decomposition. Here, all TMs are explained in the same way by analysing why and how the propagating-wave loops in the eigenfunctions can satisfy the eigenmode condition (loop magnitude and phase constraints for closure) and the wave-trapping condition (loop zero-radiation condition) simultaneously. Firstly, the unified analysis reveals the commonality that one or multiple coupled propagating-wave loops satisfy TM conditions, and the difference. In common TMs, the loop zero radiation is independent of the single loop phase constraint that selects the TM frequency as a continuous function of resonator length. On the other hand, loop zero radiation in accidental TMs depends on the loop phase constraints and there are two phase constraints. Only at the crossing points of the two phase constraints can zero-radiation loops be ensured. Secondly, in contrast to previous studies, it suggests that modal degeneracy, avoided crossing and resonance-width bifurcation are not the mechanisms of accidental TMs.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by



