No CrossRef data available.
Article contents
NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS
Published online by Cambridge University Press: 03 June 2024
Abstract
We consider the existence problem of meromorphic solutions of the Fermat-type difference equation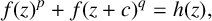 
$$ \begin{align*} f(z)^p+f(z+c)^q=h(z), \end{align*} $$
where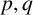 
$p,q$ are positive integers, and h has few zeros and poles in the sense that 
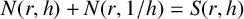$N(r,h) + N(r,1/h) = S(r,h)$. As a particular case, we consider 
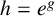$h=e^g$, where g is an entire function. Additionally, we briefly discuss the case where h is small with respect to f in the standard sense 
$T(r,h)=S(r,f)$.
MSC classification
Secondary:
39B32: Equations for complex functions
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Bergweiler, W. and Langley, J. K., ‘Zeros of differences of meromorphic functions’, Math. Proc. Cambridge Philos. Soc. 142(1) (2007), 133–147.CrossRefGoogle Scholar
Bi, W. and Lü, F., ‘On meromorphic solutions of the Fermat-type functional equations
$f{(z)}^3+f{\left(z+c\right)}^3={e}^P$
’, Anal. Math. Phys. 13 (2023), Article no. 24.CrossRefGoogle Scholar
$f{(z)}^3+f{\left(z+c\right)}^3={e}^P$
’, Anal. Math. Phys. 13 (2023), Article no. 24.CrossRefGoogle ScholarChen, Z. X., Complex Differences and Difference Equations (Science Press, Beijing, 2013).Google Scholar
Gundersen, G., ‘Finite order solutions of second order linear differential equations’, Trans. Amer. Math. Soc. 305 (1988), 415–429.CrossRefGoogle Scholar
Guo, Y. and Liu, K., ‘Meromophic solutions of Fermat type differential and difference equations of certain types’, Ann. Polon. Math. 131 (2023), 1–19.CrossRefGoogle Scholar
Halburd, R. G., Korhonen, R. and Tohge, K., ‘Holomorphic curves with shift-invariant hyper-plane preimages’, Trans. Amer. Math. Soc. 366 (2014), 4267–4298.CrossRefGoogle Scholar
Korhonen, R. and Zhang, Y. Y., ‘Existence of meromorphic solutions of first-order difference equations’, Constr. Approx. 51 (2020), 465–504.CrossRefGoogle Scholar
Laine, I. and Latreuch, Z., ‘Remarks on meromorphic solutions of some delay-differential equations’, Anal. Math. 48 (2022), 1081–1104.CrossRefGoogle Scholar
Laine, I. and Yang, C. C., ‘Clunie theorems for difference and
$q$
-difference polynomials’, J. Lond. Math. Soc. (2) 76 (2007), 556–566.CrossRefGoogle Scholar
$q$
-difference polynomials’, J. Lond. Math. Soc. (2) 76 (2007), 556–566.CrossRefGoogle ScholarLi, B. Q., ‘On Fermat-type functional and partial differential equations’, in: The Mathematical Legacy of Leon Ehrenpreis, Springer Proceedings in Mathematics, 16 (eds. Sabadini, I. and Struppa, D. C.) (Springer, Milan, 2012), 209–222.CrossRefGoogle Scholar
Liu, K., Laine, I. and Yang, L. Z., Complex Delay-Differential Equations (Walter de Gruyter, Berlin–Boston, 2021).CrossRefGoogle Scholar
Lü, F. and Guo, H. X., ‘On meromorphic solutions of the Fermat-type functional equation
$f{(z)}^n+f{\left(z+c\right)}^m={e}^{\alpha z+\beta }$
’, Mediterr. J. Math. 19 (2022), Article no. 118.CrossRefGoogle Scholar
$f{(z)}^n+f{\left(z+c\right)}^m={e}^{\alpha z+\beta }$
’, Mediterr. J. Math. 19 (2022), Article no. 118.CrossRefGoogle ScholarLü, F. and Han, Q., ‘On the Fermat-type equation
$f{(z)}^3+f{\left(z+c\right)}^3=1$
’, Aequationes Math. 91 (2017), 129–136.CrossRefGoogle Scholar
$f{(z)}^3+f{\left(z+c\right)}^3=1$
’, Aequationes Math. 91 (2017), 129–136.CrossRefGoogle ScholarYang, C. C., ‘A generalization of a theorem of P. Montel on entire functions’, Proc. Amer. Math. Soc. 26 (1970), 332–334.CrossRefGoogle Scholar
Yang, C. C. and Yi, H. X., Uniqueness Theory of Meromorphic Functions (Kluwer Academic Publishers, London, 2003).CrossRefGoogle Scholar
Zemirni, M. A., Laine, I. and Latreuch, Z., ‘New findings on the periodicity of entire functions and their differential polynomials’, Mediterr. J. Math. 20 (2023), Article no. 136.CrossRefGoogle Scholar