No CrossRef data available.
Article contents
The structure of pointwise recurrent expansive homeomorphisms
Part of:
Topological dynamics
Published online by Cambridge University Press: 03 November 2022
Abstract
Let X be a compact metric space and let 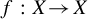 $f: X\!\rightarrow \! X$ be a homeomorphism on X. We show that if f is both pointwise recurrent and expansive, then the dynamical system
$f: X\!\rightarrow \! X$ be a homeomorphism on X. We show that if f is both pointwise recurrent and expansive, then the dynamical system 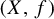 $(X, f)$ is topologically conjugate to a subshift of some symbolic system. Moreover, if f is pointwise positively recurrent, then the subshift is semisimple; a counterexample is given to show the necessity of positive recurrence to ensure the semisimplicity.
$(X, f)$ is topologically conjugate to a subshift of some symbolic system. Moreover, if f is pointwise positively recurrent, then the subshift is semisimple; a counterexample is given to show the necessity of positive recurrence to ensure the semisimplicity.
MSC classification
Secondary:
37B20: Notions of recurrence
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Aoki, N.. Topological dynamics. Topics in General Topology. Eds. Morita, K. and Nagata, J.. North-Holland, Amsterdam, 1989.Google Scholar
Artigue, A.. On continuum-wise minimality. Fund. Math. 258(3) (2022), 265–289.CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and Their Extensions (North-Holland Mathematics Studies, 153). North-Holland, Amsterdam, 1988.Google Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
Downarowicz, T. and Ye, X.. When every point is either transitive or periodic. Colloq. Math. 93(1) (2002), 137–150.CrossRefGoogle Scholar
Furstenberg, H.. The structure of distal flows. Amer. J. Math. 85 (1963), 477–515.CrossRefGoogle Scholar
Glasner, S. and Maon, D.. Rigidity in topological dynamics. Ergod. Th. & Dynam. Sys. 9 (1989), 309–320.CrossRefGoogle Scholar
Gottschalk, W., Powers of homeomorphisms with almost periodic properties. Bull. Amer. Math. Soc. (N.S.) 50 (1944), 222–227.CrossRefGoogle Scholar
Hiraide, K.. Expansive homeomorphisms of compact surfaces are pseudo-Anosov. Osaka J. Math. 27(1) (1990), 117–162.Google Scholar
Katznelson, Y. and Weiss, B..
When all points are recurrent/generic
. Ergodic Theory and Dynamical Systems, I (College Park, MD, 1979–1980) (Progress in Mathematics, 10). Ed. A. Katok. Birkhäuser, Boston, MA, 1981, pp. 195–210.Google Scholar
Kolev, B. and Pérouème, M.. Recurrent surface homeomorphisms. Math. Proc. Cambridge Philos. Soc. 124 (1998), 161–168.CrossRefGoogle Scholar
Lewowicz, J.. Expansive homeomorphisms on surfaces. Bol. Soc. Bras. Mat. 20(1) (1989), 113–133.CrossRefGoogle Scholar
Liang, B., Shi, E., Xie, Z. and Xu, H.. The non-coexistence of distality and expansivity for group actions on infinite compacta. Preprint, 2021, arXiv:2110.00341.Google Scholar
Mai, J. and Ye, X.. The structure of pointwise recurrent maps having the pseudo orbit tracing property. Nagoya Math. J. 166 (2002), 83–92.CrossRefGoogle Scholar
Mañé, R.. Expansive homeomorphisms and topological dimension. Trans. Amer. Math. Soc. 252 (1979), 313–319.CrossRefGoogle Scholar
Montgomery, D.. Pointwise periodic homeomorphisms. Amer. J. Math. 59(1) (1937), 118–120.CrossRefGoogle Scholar
Nadler, S. Jr. Continuum Theory: An Introduction (Monographs and Textbooks in Pure and Applied Mathematics, 158). Marcel Dekker, Inc., New York, 1992.Google Scholar
O’Brien, T. and Reddy, W.. Each compact orientable surface of positive genus admits an expansive homeomorphism. Pacific J. Math. 35 (1970), 737–741.CrossRefGoogle Scholar
Oversteegen, L. and Tymchatyn, E.. Recurrent homeomorphisms on
 ${\mathbb{R}}^2$
are periodic. Proc. Amer. Math. Soc. 110(4) (1990), 1083–1088.Google Scholar
${\mathbb{R}}^2$
are periodic. Proc. Amer. Math. Soc. 110(4) (1990), 1083–1088.Google Scholar
Reddy, W.. Expansive canonical coordinates are hyperbolic. Topology Appl. 15 (1983), 205–210.CrossRefGoogle Scholar



