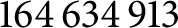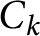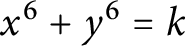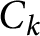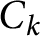1 Introduction and statement of results
Fermat’s classification of which integers are the sum of two integer squares allows one to prove that if k is a positive integer and there are
![]() $a, b \in \mathbb {Q}$
with
$a, b \in \mathbb {Q}$
with
![]() $a^{2} + b^{2} = k$
, then there are
$a^{2} + b^{2} = k$
, then there are
![]() $c, d \in \mathbb {Z}$
with
$c, d \in \mathbb {Z}$
with
![]() $c^{2} + d^{2} = k$
. (For more detail, see Proposition 5.4.9 of [Reference Cohen5].)
$c^{2} + d^{2} = k$
. (For more detail, see Proposition 5.4.9 of [Reference Cohen5].)
However, when considering higher powers, the analogous result is no longer true. In particular,
 $6 = \left (\frac {17}{21}\right )^{3} + \left (\frac {37}{21}\right )^{3}$
despite the fact that there are no integers x and y so that
$6 = \left (\frac {17}{21}\right )^{3} + \left (\frac {37}{21}\right )^{3}$
despite the fact that there are no integers x and y so that
![]() $x^{3} + y^{3} = 6$
. In [Reference Bremner and Morton3], Bremner and Morton prove that
$x^{3} + y^{3} = 6$
. In [Reference Bremner and Morton3], Bremner and Morton prove that
 $5\,906 = \left (\frac {25}{17}\right )^{4} + \left (\frac {149}{17}\right )^{4}$
is the smallest positive integer which is a sum of two rational fourth powers, but not a sum of two integer fourth powers. Their proof involves a number of explicit calculations involving class numbers and units in rings of integers of number fields.
$5\,906 = \left (\frac {25}{17}\right )^{4} + \left (\frac {149}{17}\right )^{4}$
is the smallest positive integer which is a sum of two rational fourth powers, but not a sum of two integer fourth powers. Their proof involves a number of explicit calculations involving class numbers and units in rings of integers of number fields.
It is natural to ask what can be said about values of
![]() $n> 4$
. In particular, is there always an integer k that is a sum of two rational nth powers, but not a sum of two integer nth powers? In John Byrum’s unpublished undergraduate thesis (conducted under the direction of the second author), he proves that if there is a prime
$n> 4$
. In particular, is there always an integer k that is a sum of two rational nth powers, but not a sum of two integer nth powers? In John Byrum’s unpublished undergraduate thesis (conducted under the direction of the second author), he proves that if there is a prime
![]() $p \equiv 1 \pmod {2n}$
with
$p \equiv 1 \pmod {2n}$
with
![]() $p \leq 2n^{2} - n + 1$
, then there is a positive integer k that is a sum of two rational nth powers, but not a sum of two integer nth powers. It is not known that one can find such a prime p. Even assuming the generalized Riemann hypothesis (GRH), the strongest known result at this time is that the smallest prime
$p \leq 2n^{2} - n + 1$
, then there is a positive integer k that is a sum of two rational nth powers, but not a sum of two integer nth powers. It is not known that one can find such a prime p. Even assuming the generalized Riemann hypothesis (GRH), the strongest known result at this time is that the smallest prime
![]() $p \equiv 1 \ \pmod {2n}$
is less than or equal to
$p \equiv 1 \ \pmod {2n}$
is less than or equal to
![]() $(\phi (2n) \log (2n))^{2}$
(by Corollary 1.2 of [Reference Lamzouri, Li and Soundararajan15]), which is not sufficiently small unless
$(\phi (2n) \log (2n))^{2}$
(by Corollary 1.2 of [Reference Lamzouri, Li and Soundararajan15]), which is not sufficiently small unless
![]() $n = 3$
. It is conjectured that the smallest prime
$n = 3$
. It is conjectured that the smallest prime
![]() $p \equiv a \ \pmod {q}$
satisfies
$p \equiv a \ \pmod {q}$
satisfies
![]() $p \ll q^{1+\epsilon }$
, which would be sufficient.
$p \ll q^{1+\epsilon }$
, which would be sufficient.
The goal of the present paper is to handle the case
![]() $n = 6$
and prove an analogous result to that of Bremner and Morton. Our main result is the following.
$n = 6$
and prove an analogous result to that of Bremner and Morton. Our main result is the following.
Theorem 1 The smallest positive integer which is a sum of two rational sixth powers but not a sum of two integer sixth powers is
 $$ \begin{align*} 164\,634\,913 = \left(\frac{44}{5}\right)^{6} + \left(\frac{117}{5}\right)^{6}\!. \end{align*} $$
$$ \begin{align*} 164\,634\,913 = \left(\frac{44}{5}\right)^{6} + \left(\frac{117}{5}\right)^{6}\!. \end{align*} $$
To prove the main result, we must show that if an integer
![]() $k < 164\,634\,913$
is sixth-power free and is not a sum of two integer sixth powers, then it is not a sum of two rational sixth powers either. We proceed by studying when
$k < 164\,634\,913$
is sixth-power free and is not a sum of two integer sixth powers, then it is not a sum of two rational sixth powers either. We proceed by studying when
![]() $C_{k} : x^{6} + y^{6} = kz^{6}$
has a solution in
$C_{k} : x^{6} + y^{6} = kz^{6}$
has a solution in
![]() $\mathbb {Q}_{p}$
for all primes p, which reduces the number of necessary k to consider to
$\mathbb {Q}_{p}$
for all primes p, which reduces the number of necessary k to consider to
![]() $111\,625$
. To handle these, we decompose the Jacobian of
$111\,625$
. To handle these, we decompose the Jacobian of
![]() $C_{k}$
(up to isogeny) as a product of 10 elliptic curves, each with j-invariant zero. If
$C_{k}$
(up to isogeny) as a product of 10 elliptic curves, each with j-invariant zero. If
![]() $k \not \in \{ 1, 2 \}$
is sixth-power free and one of these elliptic curves has rank zero, it follows that
$k \not \in \{ 1, 2 \}$
is sixth-power free and one of these elliptic curves has rank zero, it follows that
![]() $C_{k}(\mathbb {Q})$
is empty (via Theorem 6). If we are able to determine a finite-index subgroup of the Mordell–Weil group of one of the elliptic curves, we use the Mordell–Weil sieve to prove that
$C_{k}(\mathbb {Q})$
is empty (via Theorem 6). If we are able to determine a finite-index subgroup of the Mordell–Weil group of one of the elliptic curves, we use the Mordell–Weil sieve to prove that
![]() $C_{k}(\mathbb {Q})$
is empty.
$C_{k}(\mathbb {Q})$
is empty.
We note that there are infinitely many integers that are sums of two rational sixth powers, but not sums of two integer sixth powers.
Theorem 2 Let t be an integer and
![]() $f_{1} = (2\,863 + 10\,764t)/13$
and
$f_{1} = (2\,863 + 10\,764t)/13$
and
![]() $f_{2} = (1\,207 + 26\,455t)/13$
. Then
$f_{2} = (1\,207 + 26\,455t)/13$
. Then
![]() $f_{1}^{6} + f_{2}^{6}$
is an integer that is a sum of two rational sixth powers, but not a sum of two integer sixth powers.
$f_{1}^{6} + f_{2}^{6}$
is an integer that is a sum of two rational sixth powers, but not a sum of two integer sixth powers.
The polynomial
![]() $f_{1}^{6} + f_{2}^{6}$
is constructed so that the coefficients of
$f_{1}^{6} + f_{2}^{6}$
is constructed so that the coefficients of
![]() $t, t^2, \ldots , t^6$
are all multiples of
$t, t^2, \ldots , t^6$
are all multiples of
![]() $13$
, whereas the constant coefficient is equivalent to
$13$
, whereas the constant coefficient is equivalent to
![]() $5 \ \pmod {13}.$
Since it is impossible to have an integer equivalent to
$5 \ \pmod {13}.$
Since it is impossible to have an integer equivalent to
![]() $5 \ \pmod {13}$
be a sum of two integer sixth powers, we have our result.
$5 \ \pmod {13}$
be a sum of two integer sixth powers, we have our result.
Remark It seems likely that no positive integer can be written as a sum of two rational sixth powers in more than one way. In [Reference Ekl9], Ekl searched for integer solutions to
![]() $a^{6} + b^{6} = c^{6} + d^{6}$
with
$a^{6} + b^{6} = c^{6} + d^{6}$
with
![]() $a \ne c$
and
$a \ne c$
and
![]() $a \ne d$
and found none for which
$a \ne d$
and found none for which
![]() $a^{6} + b^{6} < 7.25 \times 10^{24}$
. The surface
$a^{6} + b^{6} < 7.25 \times 10^{24}$
. The surface
![]() $X : a^{6} + b^{6} = c^{6} + d^{6}$
is a surface of general type, and the Bombieri–Lang conjecture predicts that there are only finitely many rational points on X that do not lie on a genus
$X : a^{6} + b^{6} = c^{6} + d^{6}$
is a surface of general type, and the Bombieri–Lang conjecture predicts that there are only finitely many rational points on X that do not lie on a genus
![]() $0$
or
$0$
or
![]() $1$
curve.
$1$
curve.
2 Background
We let
![]() $\mathbb {Q}_{p}$
denote the field of p-adic numbers. We say a curve C is locally solvable if
$\mathbb {Q}_{p}$
denote the field of p-adic numbers. We say a curve C is locally solvable if
![]() $C(\mathbb {R}) \ne \emptyset $
and
$C(\mathbb {R}) \ne \emptyset $
and
![]() $C(\mathbb {Q}_{p}) \ne \emptyset $
for all primes p.
$C(\mathbb {Q}_{p}) \ne \emptyset $
for all primes p.
For our purposes, an elliptic curve is a smooth cubic curve of the form
There is a natural abelian group structure on
![]() $E(\mathbb {Q})$
, the set of rational points on E.
$E(\mathbb {Q})$
, the set of rational points on E.
Theorem 3 [Reference Silverman17, Theorem VIII.4.1]
The group
![]() $E(\mathbb {Q})$
is finitely generated. That is, there is a finite group
$E(\mathbb {Q})$
is finitely generated. That is, there is a finite group
![]() $E(\mathbb {Q})_{\textrm {tors}}$
so that
$E(\mathbb {Q})_{\textrm {tors}}$
so that
![]() $E(\mathbb {Q}) \cong E(\mathbb {Q})_{\textrm {tors}} \times \mathbb {Z}^{r}$
for some nonnegative integer r.
$E(\mathbb {Q}) \cong E(\mathbb {Q})_{\textrm {tors}} \times \mathbb {Z}^{r}$
for some nonnegative integer r.
The nonnegative integer r is called the rank of
![]() $E(\mathbb {Q})$
. The Birch and Swinnerton-Dyer conjecture predicts that if
$E(\mathbb {Q})$
. The Birch and Swinnerton-Dyer conjecture predicts that if
![]() $L(E,s)$
is the L-function of E, the
$L(E,s)$
is the L-function of E, the
![]() ${\textrm {ord}}_{s=1} L(E,s) = r$
. This is proved in the case that
${\textrm {ord}}_{s=1} L(E,s) = r$
. This is proved in the case that
![]() $r = 0$
or
$r = 0$
or
![]() $1$
by Gross and Zagier [Reference Gross and Zagier13] and Kolyvagin [Reference Kolyvagin14].
$1$
by Gross and Zagier [Reference Gross and Zagier13] and Kolyvagin [Reference Kolyvagin14].
For
![]() $k \ne 0$
, the curve
$k \ne 0$
, the curve
![]() $C_{k} : x^{6} + y^{6} = kz^{6}$
is a curve of genus
$C_{k} : x^{6} + y^{6} = kz^{6}$
is a curve of genus
![]() $10$
. For
$10$
. For
![]() $k = 1$
, the decomposition of the Jacobian is worked out in [Reference Aoki1], and it follows that each factor of
$k = 1$
, the decomposition of the Jacobian is worked out in [Reference Aoki1], and it follows that each factor of
![]() $J(C_{1})$
is an elliptic curve with j-invariant zero. We will show in Section 5 that there are nonconstant morphisms from
$J(C_{1})$
is an elliptic curve with j-invariant zero. We will show in Section 5 that there are nonconstant morphisms from
![]() $C_{k}$
to six different elliptic curves of the form
$C_{k}$
to six different elliptic curves of the form
![]() $E_{a} : y^{2} = x^{3} + a$
. The torsion subgroup of an elliptic curve of the form
$E_{a} : y^{2} = x^{3} + a$
. The torsion subgroup of an elliptic curve of the form
![]() $E_{a}$
has been known for some time.
$E_{a}$
has been known for some time.
Theorem 4 [Reference Fueter11]
If
![]() $E_{a} : y^{2} = x^{3} + a$
, then
$E_{a} : y^{2} = x^{3} + a$
, then
 $$ \begin{align*} E_{a}(\mathbb{Q})_{\textrm{tors}} \cong \begin{cases} \mathbb{Z}/6\mathbb{Z} & \text{ if } a \text{ is a sixth power, } \\ \mathbb{Z}/3\mathbb{Z} & \text{ if } a \text{ is a square but not a sixth power or }\\ &\qquad a \text{ is } -432 \text{ times a sixth power, }\\ \mathbb{Z}/2\mathbb{Z} & \text{ if } a \text{ is a cube but not a sixth power, }\\ \mathbb{Z}/1\mathbb{Z} & \text{ otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*} E_{a}(\mathbb{Q})_{\textrm{tors}} \cong \begin{cases} \mathbb{Z}/6\mathbb{Z} & \text{ if } a \text{ is a sixth power, } \\ \mathbb{Z}/3\mathbb{Z} & \text{ if } a \text{ is a square but not a sixth power or }\\ &\qquad a \text{ is } -432 \text{ times a sixth power, }\\ \mathbb{Z}/2\mathbb{Z} & \text{ if } a \text{ is a cube but not a sixth power, }\\ \mathbb{Z}/1\mathbb{Z} & \text{ otherwise. } \end{cases} \end{align*} $$
There is a torsion point on
![]() $y^{2} = x^{3} + a$
for which x and y are both nonzero only when
$y^{2} = x^{3} + a$
for which x and y are both nonzero only when
![]() $a = -432k^{6}$
(namely
$a = -432k^{6}$
(namely
![]() $(12k^{2} : \pm 36k^{3} : 1)$
) or
$(12k^{2} : \pm 36k^{3} : 1)$
) or
![]() $a = k^{6}$
(namely
$a = k^{6}$
(namely
![]() $(2k^{2} : \pm 3k^{3} : 1)$
).
$(2k^{2} : \pm 3k^{3} : 1)$
).
The Mordell–Weil sieve is a technique for proving that a curve C has no rational points. For a thorough treatment of this subject, see the paper of Bruin and Stoll [Reference Bruin and Stoll4].
Let J be the Jacobian of C, and assume that we have in hand a
![]() $\mathbb {Q}$
-rational divisor D of degree
$\mathbb {Q}$
-rational divisor D of degree
![]() $1$
on C. Let
$1$
on C. Let
![]() $\iota \colon C \to J$
be the map
$\iota \colon C \to J$
be the map
![]() $\iota (P) = P-D$
. Fix a positive integer N and a finite set S of primes. We then have the following commutative diagram:
$\iota (P) = P-D$
. Fix a positive integer N and a finite set S of primes. We then have the following commutative diagram:

If
![]() $C(\mathbb {Q})$
is nonempty, then there will be an element in
$C(\mathbb {Q})$
is nonempty, then there will be an element in
![]() $\prod _{p \in S} J(\mathbb {F}_{p})/NJ(\mathbb {F}_{p})$
that is in the image of both
$\prod _{p \in S} J(\mathbb {F}_{p})/NJ(\mathbb {F}_{p})$
that is in the image of both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Therefore, if we can find an N and a finite set S for which the image of
$\beta $
. Therefore, if we can find an N and a finite set S for which the image of
![]() $\alpha $
and the image of
$\alpha $
and the image of
![]() $\beta $
are disjoint, then
$\beta $
are disjoint, then
![]() $C(\mathbb {Q})$
is empty.
$C(\mathbb {Q})$
is empty.
The curve
![]() $C_{k}$
has maps to six different elliptic curves:
$C_{k}$
has maps to six different elliptic curves:
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
,
$E_{4k}$
,
![]() $E_{-k^{2}}$
,
$E_{-k^{2}}$
,
![]() $E_{16k^{2}}$
,
$E_{16k^{2}}$
,
![]() $E_{k^{3}}$
, and
$E_{k^{3}}$
, and
![]() $E_{-4k^{4}}$
. As a consequence, we will replace J with one of these six curves in our applications. Computing the Mordell–Weil group (or a finite index subgroup thereof) for one of these six elliptic curves allows us to apply the Mordell–Weil sieve to
$E_{-4k^{4}}$
. As a consequence, we will replace J with one of these six curves in our applications. Computing the Mordell–Weil group (or a finite index subgroup thereof) for one of these six elliptic curves allows us to apply the Mordell–Weil sieve to
![]() $C_{k}$
.
$C_{k}$
.
3 Finding an integer that is a sum of two rational sixth powers
We will describe briefly how the representation of
![]() $164\,634\,913 = (44/5)^{6} + (117/5)^{6}$
was generated by the authors. We seek integers x, y, and m for which
$164\,634\,913 = (44/5)^{6} + (117/5)^{6}$
was generated by the authors. We seek integers x, y, and m for which
![]() $x^{6} + y^{6} \equiv 0 \pmod {m^{6}}$
with
$x^{6} + y^{6} \equiv 0 \pmod {m^{6}}$
with
![]() $\gcd (x,m) = \gcd (y,m) = 1$
. This equation implies that
$\gcd (x,m) = \gcd (y,m) = 1$
. This equation implies that
![]() $xy^{-1}$
must have order
$xy^{-1}$
must have order
![]() $4$
or
$4$
or
![]() $12$
in
$12$
in
![]() $(\mathbb {Z}/m^{6} \mathbb {Z})^{\times }$
, which implies that all the prime factors of m must be
$(\mathbb {Z}/m^{6} \mathbb {Z})^{\times }$
, which implies that all the prime factors of m must be
![]() $\equiv 1 \ \pmod {4}$
. The smallest such m is
$\equiv 1 \ \pmod {4}$
. The smallest such m is
![]() $m = 5$
.
$m = 5$
.
We let
![]() $q = 1\,068$
be an element of order
$q = 1\,068$
be an element of order
![]() $4$
in
$4$
in
![]() $(\mathbb {Z}/5^{6} \mathbb {Z})^{\times }$
. Then
$(\mathbb {Z}/5^{6} \mathbb {Z})^{\times }$
. Then
![]() $1^{6} + q^{6} \equiv 0 \ \pmod {5^{6}}$
. We wish to find an integer a so that
$1^{6} + q^{6} \equiv 0 \ \pmod {5^{6}}$
. We wish to find an integer a so that
![]() $\pm a \bmod 5^{6}$
and
$\pm a \bmod 5^{6}$
and
![]() $\pm aq \bmod 5^{6}$
are both small. We consider the lattice
$\pm aq \bmod 5^{6}$
are both small. We consider the lattice
![]() $L \subseteq \mathbb {R}^{2}$
consisting of all vectors
$L \subseteq \mathbb {R}^{2}$
consisting of all vectors
 $\left \{ \begin {bmatrix} x \\ y \end {bmatrix} : y \equiv qx \ \pmod {5^{6}} \right \}$
. We find that an
$\left \{ \begin {bmatrix} x \\ y \end {bmatrix} : y \equiv qx \ \pmod {5^{6}} \right \}$
. We find that an
![]() $LLL$
-reduced basis for this lattice consists of
$LLL$
-reduced basis for this lattice consists of
 $\begin {bmatrix} 117 \\ 44 \end {bmatrix}$
and
$\begin {bmatrix} 117 \\ 44 \end {bmatrix}$
and
 $\begin {bmatrix} 44 \\ -117 \end {bmatrix}$
from which we obtain
$\begin {bmatrix} 44 \\ -117 \end {bmatrix}$
from which we obtain
 $164\,634\,913 = \left (\frac {44}{5}\right )^{6} + \left (\frac {117}{5}\right )^{6}$
.
$164\,634\,913 = \left (\frac {44}{5}\right )^{6} + \left (\frac {117}{5}\right )^{6}$
.
We wish to note that this representation was found at least twice previouoeisly. First, it is given by Gandhi on page 1 001 of [Reference Gandhi12]. Second, it was noted by John W. Layman on October 20, 2005 in connection with Online Encyclopedia of Integer Sequences (OEIS) sequence A111152 (the smallest integers that are a sum of two rational nth powers, but not a sum of two integer nth powers).
For integers of the form
![]() $x^{n} + y^{n}$
with n odd, there are no local restrictions, and setting
$x^{n} + y^{n}$
with n odd, there are no local restrictions, and setting
 $x = \frac {2^{n-1} - 1}{2}$
and
$x = \frac {2^{n-1} - 1}{2}$
and
 $y = \frac {2^{n-1} + 1}{2}$
leads to a fairly small integer that is a sum of two rational nth powers. For
$y = \frac {2^{n-1} + 1}{2}$
leads to a fairly small integer that is a sum of two rational nth powers. For
![]() $n = 5$
, this leads to
$n = 5$
, this leads to
 $68\,101 = \left (\frac {15}{2}\right )^{5} + \left (\frac {17}{2}\right )^{5}$
. At present, it is not known if
$68\,101 = \left (\frac {15}{2}\right )^{5} + \left (\frac {17}{2}\right )^{5}$
. At present, it is not known if
![]() $68\,101$
is the smallest positive integer that is a sum of two rational fifth powers, but not a sum of two integer fifth powers.
$68\,101$
is the smallest positive integer that is a sum of two rational fifth powers, but not a sum of two integer fifth powers.
4 Local solvability
In this section, we study the question of when
![]() $C_{k} : x^{6} + y^{6} = k$
is locally solvable.
$C_{k} : x^{6} + y^{6} = k$
is locally solvable.
Theorem 5 Let k be a positive integer which is sixth-power free. Then
![]() $C_{k}$
is locally solvable if and only if
$C_{k}$
is locally solvable if and only if
![]() $C_{k}$
has points over
$C_{k}$
has points over
![]() $\mathbb {Q}_{p}$
for all primes
$\mathbb {Q}_{p}$
for all primes
![]() $p < 400$
and all odd prime factors
$p < 400$
and all odd prime factors
![]() $p \mid k$
have
$p \mid k$
have
![]() $p \equiv 1 \ \pmod {4}$
.
$p \equiv 1 \ \pmod {4}$
.
Proof The curve
![]() $C_{k}$
is smooth over
$C_{k}$
is smooth over
![]() $\mathbb {F}_{p}$
for all primes p other than
$\mathbb {F}_{p}$
for all primes p other than
![]() $2$
,
$2$
,
![]() $3$
and those dividing k. Since
$3$
and those dividing k. Since
![]() $C_{k}$
has genus
$C_{k}$
has genus
![]() $10$
, Hasse’s theorem gives that
$10$
, Hasse’s theorem gives that
![]() $|C_{k}(\mathbb {F}_{p})|> p+1 - 20 \sqrt {p}$
provided
$|C_{k}(\mathbb {F}_{p})|> p+1 - 20 \sqrt {p}$
provided
![]() $C_{k}/\mathbb {F}_{p}$
is smooth. The latter quantity is positive if
$C_{k}/\mathbb {F}_{p}$
is smooth. The latter quantity is positive if
![]() $p> 400$
. Furthermore, Hensel’s lemma implies that if
$p> 400$
. Furthermore, Hensel’s lemma implies that if
![]() $C_{k}(\mathbb {F}_{p})$
has a nonsingular point, then it lifts to a nonsingular point of
$C_{k}(\mathbb {F}_{p})$
has a nonsingular point, then it lifts to a nonsingular point of
![]() $C_{k}(\mathbb {Q}_{p})$
and hence
$C_{k}(\mathbb {Q}_{p})$
and hence
![]() $C_{k}(\mathbb {Q}_{p}) \ne \emptyset $
.
$C_{k}(\mathbb {Q}_{p}) \ne \emptyset $
.
If
![]() $p \mid k$
and
$p \mid k$
and
![]() $p \equiv 1 \ \pmod {4}$
, then
$p \equiv 1 \ \pmod {4}$
, then
![]() $p = a^{2} + b^{2}$
for some
$p = a^{2} + b^{2}$
for some
![]() $a, b \in \mathbb {Z}$
. Since
$a, b \in \mathbb {Z}$
. Since
![]() ${a^{2} + b^{2} \mid a^{6} + b^{6}}$
, we have that
${a^{2} + b^{2} \mid a^{6} + b^{6}}$
, we have that
![]() $(a : b : 1)$
is a smooth point on
$(a : b : 1)$
is a smooth point on
![]() $C_{k}/\mathbb {F}_{p}$
and therefore
$C_{k}/\mathbb {F}_{p}$
and therefore
![]() $C_{k}(\mathbb {Q}_{p}) \ne \emptyset $
.
$C_{k}(\mathbb {Q}_{p}) \ne \emptyset $
.
Suppose that
![]() $p \mid k$
,
$p \mid k$
,
![]() $p \equiv 3 \ \pmod {4}$
and
$p \equiv 3 \ \pmod {4}$
and
![]() $(x_{0} : y_{0} : z_{0}) \in C_{k}(\mathbb {Q}_{p})$
with
$(x_{0} : y_{0} : z_{0}) \in C_{k}(\mathbb {Q}_{p})$
with
![]() $x_{0}, y_{0}, z_{0} \in \mathbb {Z}_{p}$
, not all of which are multiples of p. It follows that p divides one of
$x_{0}, y_{0}, z_{0} \in \mathbb {Z}_{p}$
, not all of which are multiples of p. It follows that p divides one of
![]() $x_{0}^{2} + y_{0}^{2}$
or
$x_{0}^{2} + y_{0}^{2}$
or
![]() $x_{0}^{4} - x_{0}^{2} y_{0}^{2} + y_{0}^{4}$
, and both of these imply that
$x_{0}^{4} - x_{0}^{2} y_{0}^{2} + y_{0}^{4}$
, and both of these imply that
![]() $x_{0} \equiv y_{0} \equiv 0 \ \pmod {p}$
. It follows that
$x_{0} \equiv y_{0} \equiv 0 \ \pmod {p}$
. It follows that
![]() $x_{0}^{6} + y_{0}^{6} = kz_{0}^{6}$
is a multiple of
$x_{0}^{6} + y_{0}^{6} = kz_{0}^{6}$
is a multiple of
![]() $p^{6}$
. Since k is sixth-power free, it follows that
$p^{6}$
. Since k is sixth-power free, it follows that
![]() $p \mid z_{0}$
, which is a contradiction. Thus,
$p \mid z_{0}$
, which is a contradiction. Thus,
![]() $C_{k}(\mathbb {Q}_{p}) = \emptyset $
. ▪
$C_{k}(\mathbb {Q}_{p}) = \emptyset $
. ▪
We note that the smallest positive integer k that is not a sum of two integer sixth powers for which
![]() $C_{k}$
is locally solvable is
$C_{k}$
is locally solvable is
![]() $k = 2\,017$
.
$k = 2\,017$
.
To enumerate the
![]() $k < 164\,634\,913$
for which
$k < 164\,634\,913$
for which
![]() $C_{k}$
is locally solvable, we note that if
$C_{k}$
is locally solvable, we note that if
![]() $C_{k}$
is locally solvable, then
$C_{k}$
is locally solvable, then
![]() $k \equiv 1, 2 \ \pmod {7}$
,
$k \equiv 1, 2 \ \pmod {7}$
,
![]() $k \equiv 1, 2 \ \pmod {8}$
, and
$k \equiv 1, 2 \ \pmod {8}$
, and
![]() $k \equiv 1, 2 \ \pmod {9}$
. Moreover, for each
$k \equiv 1, 2 \ \pmod {9}$
. Moreover, for each
![]() $p \equiv 1 \ \pmod {6}$
with
$p \equiv 1 \ \pmod {6}$
with
![]() $13 \leq p \leq 400$
, we enumerate and cache the integers which are sums of two sixth powers modulo p. Now, we test integers less than or equal to
$13 \leq p \leq 400$
, we enumerate and cache the integers which are sums of two sixth powers modulo p. Now, we test integers less than or equal to
![]() $164\,634\,913$
in each of the eight residue classes modulo
$164\,634\,913$
in each of the eight residue classes modulo
![]() $504 = 7 \times 8 \times 9$
. We remove the values of k that are not sixth-power free, that are divisible by a prime
$504 = 7 \times 8 \times 9$
. We remove the values of k that are not sixth-power free, that are divisible by a prime
![]() $\equiv 3 \ \pmod {4}$
, that are sums of two integer sixth powers, and that reduce modulo some
$\equiv 3 \ \pmod {4}$
, that are sums of two integer sixth powers, and that reduce modulo some
![]() $p \equiv 1 \ \pmod {6}$
to an element of
$p \equiv 1 \ \pmod {6}$
to an element of
![]() $\mathbb {F}_{p}$
that is not a sum of two sixth powers. The result is a list of
$\mathbb {F}_{p}$
that is not a sum of two sixth powers. The result is a list of
![]() $111\,625$
values of
$111\,625$
values of
![]() $k < 164\,634\,913$
which are not sums of two integer sixth powers and for which
$k < 164\,634\,913$
which are not sums of two integer sixth powers and for which
![]() $C_{k}$
is locally solvable. The computation runs in 46.29 seconds, and the code can be found in the script
step1-localtest.txt
.
$C_{k}$
is locally solvable. The computation runs in 46.29 seconds, and the code can be found in the script
step1-localtest.txt
.
5 Maps from
 $C_{k}$
to elliptic curves
$C_{k}$
to elliptic curves
The curve
![]() $C_{k} : x^{6} + y^{6} = kz^{6}$
has at least
$C_{k} : x^{6} + y^{6} = kz^{6}$
has at least
![]() $72$
automorphisms defined over
$72$
automorphisms defined over
![]() $\mathbb {Q}(\zeta _{6})$
, generated by the maps
$\mathbb {Q}(\zeta _{6})$
, generated by the maps
![]() $\mu _{1}(x : y : z) = (\zeta _{6} x : y : z)$
,
$\mu _{1}(x : y : z) = (\zeta _{6} x : y : z)$
,
![]() $\mu _{2}(x : y : z) = (x : \zeta _{6} y : z)$
, and
$\mu _{2}(x : y : z) = (x : \zeta _{6} y : z)$
, and
![]() $\mu _{3}(x : y : z) = (y : x : z)$
. Magma can work out the action of each of these maps on the
$\mu _{3}(x : y : z) = (y : x : z)$
. Magma can work out the action of each of these maps on the
![]() $10$
-dimensional space of holomorphic
$10$
-dimensional space of holomorphic
![]() $1$
-forms on
$1$
-forms on
![]() $C_{k}$
. We find eight subgroups H of
$C_{k}$
. We find eight subgroups H of
![]() ${\textrm {Aut}}(C_{k})$
for which the quotient curve
${\textrm {Aut}}(C_{k})$
for which the quotient curve
![]() $C_{k}/H$
has genus
$C_{k}/H$
has genus
![]() $1$
and the corresponding one-dimensional subspaces of holomorphic
$1$
and the corresponding one-dimensional subspaces of holomorphic
![]() $1$
-forms are distinct. From these, it is not difficult to compute the corresponding map to an elliptic curve.
$1$
-forms are distinct. From these, it is not difficult to compute the corresponding map to an elliptic curve.
For example, one such subgroup is
![]() $\langle \mu _{1}^{5} \mu _{2}, \mu _{2}^{3} \mu _{3} \rangle $
. The monomials
$\langle \mu _{1}^{5} \mu _{2}, \mu _{2}^{3} \mu _{3} \rangle $
. The monomials
![]() $x^{3} y^{3}$
,
$x^{3} y^{3}$
,
![]() $xyz^{4}$
, and
$xyz^{4}$
, and
![]() $x^{6} - y^{6}$
are all fixed by
$x^{6} - y^{6}$
are all fixed by
![]() $\mu _{1}^{5} \mu _{2}$
, and each is sent to their negative by
$\mu _{1}^{5} \mu _{2}$
, and each is sent to their negative by
![]() $\mu _{2}^{3} \mu _{3}$
. If
$\mu _{2}^{3} \mu _{3}$
. If
![]() $\phi : C_{k} \to \mathbb {P}^{2}$
is given by
$\phi : C_{k} \to \mathbb {P}^{2}$
is given by
![]() $\phi ((x : y : z)) = (x^{3} y^{3} : xyz^{4} : x^{6} - y^{6})$
, then we have
$\phi ((x : y : z)) = (x^{3} y^{3} : xyz^{4} : x^{6} - y^{6})$
, then we have
![]() $\phi (P) = \phi (\alpha (P))$
for all points P on
$\phi (P) = \phi (\alpha (P))$
for all points P on
![]() $C_{k}$
and all
$C_{k}$
and all
![]() $\alpha \in \langle \mu _{1}^{5} \mu _{2}, \mu _{2}^{3} \mu _{3} \rangle $
. Letting
$\alpha \in \langle \mu _{1}^{5} \mu _{2}, \mu _{2}^{3} \mu _{3} \rangle $
. Letting
![]() $a = x^{3}y^{3}$
,
$a = x^{3}y^{3}$
,
![]() $b = xyz^{4}$
, and
$b = xyz^{4}$
, and
![]() $c = x^{6} - y^{6}$
, the image of
$c = x^{6} - y^{6}$
, the image of
![]() $\phi $
is the curve
$\phi $
is the curve
 $$ \begin{align*} a^{3} - \frac{k^{2}}{4} b^{3} + \frac{1}{4} ac^{2} = 0. \end{align*} $$
$$ \begin{align*} a^{3} - \frac{k^{2}}{4} b^{3} + \frac{1}{4} ac^{2} = 0. \end{align*} $$
This curve has genus
![]() $1$
, and thus is the quotient curve
$1$
, and thus is the quotient curve
![]() $C_{k}/\langle \mu _{1}^{5} \mu _{2}, \mu _{2}^{3} \mu _{3} \rangle $
. This curve has the point
$C_{k}/\langle \mu _{1}^{5} \mu _{2}, \mu _{2}^{3} \mu _{3} \rangle $
. This curve has the point
![]() $(0 : 0 : 1)$
on it, and a change of variables turns this into the elliptic curve
$(0 : 0 : 1)$
on it, and a change of variables turns this into the elliptic curve
![]() $E_{-4k^{4}}$
. Composing these maps gives the map
$E_{-4k^{4}}$
. Composing these maps gives the map
![]() $\phi : C_{k} \to E_{-4k^{4}}$
given by
$\phi : C_{k} \to E_{-4k^{4}}$
given by
![]() $\phi (x : y : z) = (k^{2} xyz^{4} : -k^{2} x^{6} + k^{2} y^{6} : x^{3} y^{3})$
.
$\phi (x : y : z) = (k^{2} xyz^{4} : -k^{2} x^{6} + k^{2} y^{6} : x^{3} y^{3})$
.
The table below lists all 10 independent maps from
![]() $C_{k}$
to elliptic curves.
$C_{k}$
to elliptic curves.

We wish to note that for the maps from
![]() $C_{k} \to E_{4k}$
, the quotient curve by the subgroup indicated (either
$C_{k} \to E_{4k}$
, the quotient curve by the subgroup indicated (either
![]() $\langle \mu _{1} \mu _{2}^{2} \rangle $
or
$\langle \mu _{1} \mu _{2}^{2} \rangle $
or
![]() $\langle \mu _{1}^{2} \mu _{2} \rangle $
) is the genus two hyperelliptic curve given by
$\langle \mu _{1}^{2} \mu _{2} \rangle $
) is the genus two hyperelliptic curve given by
 $D_{k} : y^{2} = \frac {1}{k} x^{6} + \frac {1}{4k^{2}}$
. This equation may be rewritten as
$D_{k} : y^{2} = \frac {1}{k} x^{6} + \frac {1}{4k^{2}}$
. This equation may be rewritten as
 $$ \begin{align*} \left(\frac{2ky}{x^{3}}\right)^{2} = \left(\frac{1}{x^{2}}\right)^{3} + 4k. \end{align*} $$
$$ \begin{align*} \left(\frac{2ky}{x^{3}}\right)^{2} = \left(\frac{1}{x^{2}}\right)^{3} + 4k. \end{align*} $$
As a consequence, we have the map
 $\phi (x,y) = \left (\frac {1}{x^{2}},\frac {2ky}{x^{3}}\right )$
from
$\phi (x,y) = \left (\frac {1}{x^{2}},\frac {2ky}{x^{3}}\right )$
from
![]() $D_{k} \to E_{4k}$
. (The authors did not find a subgroup of
$D_{k} \to E_{4k}$
. (The authors did not find a subgroup of
![]() ${\textrm {Aut}}(C_{k})$
that fixed a one-dimensional space of differentials corresponding to these maps.)
${\textrm {Aut}}(C_{k})$
that fixed a one-dimensional space of differentials corresponding to these maps.)
Theorem 6 Suppose that k is a sixth-power-free integer and
![]() $P = (x,y)$
is a rational point on
$P = (x,y)$
is a rational point on
![]() $C_{k}$
, and the image of P under one of the 10 maps given above is a torsion point. Then
$C_{k}$
, and the image of P under one of the 10 maps given above is a torsion point. Then
![]() $k = 1$
or
$k = 1$
or
![]() $k = 2$
.
$k = 2$
.
Proof Apart from the cases of
![]() $E_{a^{6}}$
and
$E_{a^{6}}$
and
![]() $E_{-432a^{6}}$
, every torsion point on
$E_{-432a^{6}}$
, every torsion point on
![]() $E_{a}$
has the x or y coordinate zero. Inspecting the 10 maps above, we find that if
$E_{a}$
has the x or y coordinate zero. Inspecting the 10 maps above, we find that if
![]() $P \in C_{k}(\mathbb {Q})$
and its image on
$P \in C_{k}(\mathbb {Q})$
and its image on
![]() $E_{a}$
has the x or y coordinate zero, then
$E_{a}$
has the x or y coordinate zero, then
![]() $x = 0$
or
$x = 0$
or
![]() $y = 0$
or (for the 7th or 10th maps) that
$y = 0$
or (for the 7th or 10th maps) that
![]() $x^{6} = y^{6} = k/2$
. This implies that
$x^{6} = y^{6} = k/2$
. This implies that
![]() $k/2$
is a sixth power, but since k is sixth-power free,
$k/2$
is a sixth power, but since k is sixth-power free,
![]() $k = 2$
.
$k = 2$
.
Now, we consider the case that
![]() $E_{a} = E_{\alpha ^{6}}$
or
$E_{a} = E_{\alpha ^{6}}$
or
![]() $E_{a} = E_{-432 \alpha ^{6}}$
for
$E_{a} = E_{-432 \alpha ^{6}}$
for
![]() $a \in \{k, 4k, -k^{2}, 16k^{2}, k^{3}, -4k^{4} \}$
. If
$a \in \{k, 4k, -k^{2}, 16k^{2}, k^{3}, -4k^{4} \}$
. If
![]() $\alpha $
is a rational number and
$\alpha $
is a rational number and
![]() $k = \alpha ^{6}$
is a sixth power, this forces
$k = \alpha ^{6}$
is a sixth power, this forces
![]() $k = 1$
. If
$k = 1$
. If
![]() $4k = \alpha ^{6}$
and k is sixth-power free, then
$4k = \alpha ^{6}$
and k is sixth-power free, then
![]() $k = 16$
, but
$k = 16$
, but
![]() $x^{6} + y^{6} = 16$
has no points in
$x^{6} + y^{6} = 16$
has no points in
![]() $\mathbb {Q}_{2}$
. The cases
$\mathbb {Q}_{2}$
. The cases
![]() $-k^{2} = -432\alpha ^{6}$
and
$-k^{2} = -432\alpha ^{6}$
and
![]() $-4k^{4} = -432\alpha ^{6}$
never occur. If
$-4k^{4} = -432\alpha ^{6}$
never occur. If
![]() $16k^{2} = \alpha ^{6}$
, then
$16k^{2} = \alpha ^{6}$
, then
![]() $k = 2$
. Finally, if
$k = 2$
. Finally, if
![]() $k^{3} = \alpha ^{6}$
, then k is a perfect square. In this case,
$k^{3} = \alpha ^{6}$
, then k is a perfect square. In this case,
![]() $E_{k^{3}}$
has the torsion points
$E_{k^{3}}$
has the torsion points
![]() $(2 \alpha ^{2}, \pm 3 \alpha ^{3})$
. However, we have that
$(2 \alpha ^{2}, \pm 3 \alpha ^{3})$
. However, we have that
 $2 \alpha ^{2} = \frac {\alpha ^{2} x^{2}}{y^{2}}$
or
$2 \alpha ^{2} = \frac {\alpha ^{2} x^{2}}{y^{2}}$
or
 $\frac {\alpha ^{2} y^{2}}{x^{2}}$
, which implies that
$\frac {\alpha ^{2} y^{2}}{x^{2}}$
, which implies that
 $2 = \frac {x^{2}}{y^{2}}$
or
$2 = \frac {x^{2}}{y^{2}}$
or
![]() $\frac {y^{2}}{x^{2}}$
, contradicting the irrationality of
$\frac {y^{2}}{x^{2}}$
, contradicting the irrationality of
![]() $\sqrt {2}$
. ▪
$\sqrt {2}$
. ▪
As a consequence of the above result, if
![]() $k \not \in \{ 1, 2 \}$
is sixth-power free and the rank of one of the six elliptic curves
$k \not \in \{ 1, 2 \}$
is sixth-power free and the rank of one of the six elliptic curves
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
,
$E_{4k}$
,
![]() $E_{-k^{2}}$
,
$E_{-k^{2}}$
,
![]() $E_{16k^{2}}$
,
$E_{16k^{2}}$
,
![]() $E_{k^{3}}$
, or
$E_{k^{3}}$
, or
![]() $E_{-4k^{4}}$
is zero, then k is not a sum of two rational sixth powers. For each of the
$E_{-4k^{4}}$
is zero, then k is not a sum of two rational sixth powers. For each of the
![]() $111\,625$
values of k found in the previous section, we need to determine the Mordell–Weil group (or a finite index subgroup thereof) of one of these six curves. The most straightforward approach to this problem is to conduct a
$111\,625$
values of k found in the previous section, we need to determine the Mordell–Weil group (or a finite index subgroup thereof) of one of these six curves. The most straightforward approach to this problem is to conduct a
![]() $2$
-descent. However, a
$2$
-descent. However, a
![]() $2$
-descent on
$2$
-descent on
![]() $E_{k}$
requires computing the class group of
$E_{k}$
requires computing the class group of
![]() $\mathbb {Q}(\sqrt [3]{-k})$
, and this is time-consuming to do unconditionally if k is large. We proceed to apply a number of other techniques specific to our situation and resort to an unconditional
$\mathbb {Q}(\sqrt [3]{-k})$
, and this is time-consuming to do unconditionally if k is large. We proceed to apply a number of other techniques specific to our situation and resort to an unconditional
![]() $2$
-descent only when absolutely necessary.
$2$
-descent only when absolutely necessary.
6 Checking if
 $L(E_{k^{3}},1) = 0$
$L(E_{k^{3}},1) = 0$
The elliptic curve
![]() $E_{k^{3}} : y^{2} = x^{3} + k^{3}$
is a quadratic twist of
$E_{k^{3}} : y^{2} = x^{3} + k^{3}$
is a quadratic twist of
![]() $E_{1} : y^{2} = x^{3} + 1$
. If
$E_{1} : y^{2} = x^{3} + 1$
. If
![]() $k \equiv 1 \pmod {8}$
, the sign of the functional equation for
$k \equiv 1 \pmod {8}$
, the sign of the functional equation for
![]() $E_{k^{3}}$
is
$E_{k^{3}}$
is
![]() $1$
, whereas if
$1$
, whereas if
![]() $k \equiv 2 \ \pmod {8}$
, the sign of the functional equation is
$k \equiv 2 \ \pmod {8}$
, the sign of the functional equation is
![]() $-1$
. We are able to rule out most odd values of k by showing that
$-1$
. We are able to rule out most odd values of k by showing that
![]() $L(E_{k^{3}},1) \ne 0$
.
$L(E_{k^{3}},1) \ne 0$
.
Waldspurger’s theorem [Reference Waldspurger18] says, very roughly speaking, that
 $$ \begin{align*} \sum_{k} k^{1/4} \sqrt{L(E_{k^{3}},1)} q^{k} \end{align*} $$
$$ \begin{align*} \sum_{k} k^{1/4} \sqrt{L(E_{k^{3}},1)} q^{k} \end{align*} $$
is a weight
![]() $3/2$
modular form of a particular level. In Theorem 11 of [Reference Purkait16], Purkait works out the predictions of Waldspurger’s theorem, showing that there is a modular form
$3/2$
modular form of a particular level. In Theorem 11 of [Reference Purkait16], Purkait works out the predictions of Waldspurger’s theorem, showing that there is a modular form
![]() $f = \sum b(k) q^{k}$
of level
$f = \sum b(k) q^{k}$
of level
![]() $576$
and trivial character whose Fourier coefficients encode the L-values of
$576$
and trivial character whose Fourier coefficients encode the L-values of
![]() $L(E_{k^{3}},1)$
under the assumption that
$L(E_{k^{3}},1)$
under the assumption that
![]() $3 \nmid k$
. In Example 2 of [Reference Purkait16], Purkait gives a complicated formula for this modular form f in terms of ternary theta series. We are able to find a formula more amenable to computation using the theta series for the six ternary quadratic forms:
$3 \nmid k$
. In Example 2 of [Reference Purkait16], Purkait gives a complicated formula for this modular form f in terms of ternary theta series. We are able to find a formula more amenable to computation using the theta series for the six ternary quadratic forms:
 $$ \begin{align*} Q_{1} &= x^{2} + 4y^{2} + 144z^{2},\\ Q_{2} &= 4x^{2} - 4xy + 5y^{2} + 36z^{2},\\ Q_{3} &= 4x^{2} + 9y^{2} + 16z^{2},\\ Q_{4} &= x^{2} + 16y^{2} + 36z^{2},\\ Q_{5} &= 4x^{2} + 13y^{2} + 10yz + 13z^{2}, \text{ and }\\ Q_{6} &= 4x^{2} + 4y^{2} + 4yz + 37z^{2}. \end{align*} $$
$$ \begin{align*} Q_{1} &= x^{2} + 4y^{2} + 144z^{2},\\ Q_{2} &= 4x^{2} - 4xy + 5y^{2} + 36z^{2},\\ Q_{3} &= 4x^{2} + 9y^{2} + 16z^{2},\\ Q_{4} &= x^{2} + 16y^{2} + 36z^{2},\\ Q_{5} &= 4x^{2} + 13y^{2} + 10yz + 13z^{2}, \text{ and }\\ Q_{6} &= 4x^{2} + 4y^{2} + 4yz + 37z^{2}. \end{align*} $$
These six quadratic forms constitute a single genus. Let
 $$ \begin{align*} h = \frac{5}{16} \theta_{Q_{1}} - \frac{3}{16} \theta_{Q_{2}} - \frac{7}{16} \theta_{Q_{3}} + \frac{5}{16} \theta_{Q_{4}} + \frac{9}{16} \theta_{Q_{5}} - \frac{3}{16} \theta_{Q_{6}} = \sum c(n) q^{n}. \end{align*} $$
$$ \begin{align*} h = \frac{5}{16} \theta_{Q_{1}} - \frac{3}{16} \theta_{Q_{2}} - \frac{7}{16} \theta_{Q_{3}} + \frac{5}{16} \theta_{Q_{4}} + \frac{9}{16} \theta_{Q_{5}} - \frac{3}{16} \theta_{Q_{6}} = \sum c(n) q^{n}. \end{align*} $$
Then, for
![]() $k \equiv 1 \ \pmod {24}$
, we have
$k \equiv 1 \ \pmod {24}$
, we have
![]() $c(k) = b(k)$
, and if
$c(k) = b(k)$
, and if
![]() $k \equiv 17 \ \pmod {24}$
, we have
$k \equiv 17 \ \pmod {24}$
, we have
![]() $c(k) = 6b(k)$
. It follows that if
$c(k) = 6b(k)$
. It follows that if
![]() $k \equiv 1 \ \pmod {8}$
is a fundamental discriminant and
$k \equiv 1 \ \pmod {8}$
is a fundamental discriminant and
![]() $c(k) \ne 0$
, then
$c(k) \ne 0$
, then
![]() $L(E_{k^{3}},1) \ne 0$
. Hence,
$L(E_{k^{3}},1) \ne 0$
. Hence,
![]() $E_{k^{3}}$
has rank zero, and if
$E_{k^{3}}$
has rank zero, and if
![]() $k> 1$
, this implies that k is not the sum of two rational sixth powers. (If k is not square-free, we can simply replace k with
$k> 1$
, this implies that k is not the sum of two rational sixth powers. (If k is not square-free, we can simply replace k with
![]() $k/m^{2}$
in the above calculation.)
$k/m^{2}$
in the above calculation.)
Each theta series above can be computed by multiplying a binary theta series by a unary theta series. In this way, it is possible to compute the first
![]() $165$
million coefficients of h and among these determine the odd values of k for which
$165$
million coefficients of h and among these determine the odd values of k for which
![]() $L(E_{k^{3}},1) \ne 0$
. Of the
$L(E_{k^{3}},1) \ne 0$
. Of the
![]() $111\,625$
values of k for which
$111\,625$
values of k for which
![]() $C_{k}$
is locally solvable,
$C_{k}$
is locally solvable,
![]() $55\,284$
are odd, whereas
$55\,284$
are odd, whereas
![]() $56\,341$
are even. The computation just described rules out all but
$56\,341$
are even. The computation just described rules out all but
![]() $2\,753$
odd values of k. The computation takes 559.20 seconds, and the code run can be found in the script
step2-wald.txt
.
$2\,753$
odd values of k. The computation takes 559.20 seconds, and the code run can be found in the script
step2-wald.txt
.
7 Computing Mordell–Weil groups
Here and elsewhere, we rely on the procedure for explicit n-descent developed by Cremona et al. in [Reference Cremona, Fisher, O’Neil, Simon and Stoll6–Reference Cremona, Fisher, O’Neil, Simon and Stoll8] and implemented in Magma with much of the code written by Michael Stoll, Tom Fisher, and Steve Donnelly.
First, we use that each elliptic curve
![]() $E_{a}$
has a cyclic
$E_{a}$
has a cyclic
![]() $3$
-isogeny. We take the remaining
$3$
-isogeny. We take the remaining
![]() $59\,094$
values of k and compute the
$59\,094$
values of k and compute the
![]() $3$
-isogeny Selmer groups to bound the rank for the elliptic curves in the set
$3$
-isogeny Selmer groups to bound the rank for the elliptic curves in the set
![]() $\{ E_{k}, E_{4k}, E_{-k^{2}}, E_{16k^{2}}, E_{-4k^{4}} \}$
. We hope to rule out k’s for which one of these curves has rank zero and so we only test elliptic curves with root number equal to
$\{ E_{k}, E_{4k}, E_{-k^{2}}, E_{16k^{2}}, E_{-4k^{4}} \}$
. We hope to rule out k’s for which one of these curves has rank zero and so we only test elliptic curves with root number equal to
![]() $1$
. This test is run in
step3-3isog.txt
and takes a bit under 6 hours (namely 20 551.4 seconds). This step rules out
$1$
. This test is run in
step3-3isog.txt
and takes a bit under 6 hours (namely 20 551.4 seconds). This step rules out
![]() $39\,586$
values of k, and
$39\,586$
values of k, and
![]() $19\,508$
values remain.
$19\,508$
values remain.
Second, for each of the
![]() $19\,508$
remaining k’s, we perform a full
$19\,508$
remaining k’s, we perform a full
![]() $3$
-descent by doing a first and second
$3$
-descent by doing a first and second
![]() $3$
-isogeny descent (via the Magma command
$3$
-isogeny descent (via the Magma command
) on
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
, and
$E_{4k}$
, and
![]() $E_{k^{3}}$
. For these curves, this command requires class group computations of low-discriminant quadratic and cubic fields. We search for points on the resulting
$E_{k^{3}}$
. For these curves, this command requires class group computations of low-discriminant quadratic and cubic fields. We search for points on the resulting
![]() $3$
-covers in the hope that we can provably compute the rank of
$3$
-covers in the hope that we can provably compute the rank of
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
, or
$E_{4k}$
, or
![]() $E_{k^{3}}$
. This test is run in
step4-findMW.txt
. Once the
$E_{k^{3}}$
. This test is run in
step4-findMW.txt
. Once the
![]() $3$
-covers are found, we sort the curves in increasing order of the upper bound on the rank and search for points on the associated
$3$
-covers are found, we sort the curves in increasing order of the upper bound on the rank and search for points on the associated
![]() $3$
-covers with a height bound of
$3$
-covers with a height bound of
![]() $10\,000$
. If we are not successful, we double the height bound and search again. If we are not successful at a height bound of
$10\,000$
. If we are not successful, we double the height bound and search again. If we are not successful at a height bound of
![]() $320\,000$
, we give up. This is the most time-consuming step of the process, taking about 26 hours. This step finds
$320\,000$
, we give up. This is the most time-consuming step of the process, taking about 26 hours. This step finds
![]() $864$
additional values of k for which one of
$864$
additional values of k for which one of
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
, or
$E_{4k}$
, or
![]() $E_{k^{3}}$
has rank zero. In the end, we succeed in computing the Mordell–Weil groups of one of
$E_{k^{3}}$
has rank zero. In the end, we succeed in computing the Mordell–Weil groups of one of
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
, or
$E_{4k}$
, or
![]() $E_{k^{3}}$
for all but
$E_{k^{3}}$
for all but
![]() $196$
values of k. There are also 34 cases where the elliptic curve in question has rank 5, and one case (
$196$
values of k. There are also 34 cases where the elliptic curve in question has rank 5, and one case (
![]() $k = 123\,975\,217$
) for which the rank of
$k = 123\,975\,217$
) for which the rank of
![]() $E_{k}$
is 6. For these k’s, we seek to find the Mordell–Weil group of a different elliptic curve.
$E_{k}$
is 6. For these k’s, we seek to find the Mordell–Weil group of a different elliptic curve.
Third, for each of the
![]() $196+35 = 231$
remaining k’s, we obtain as much unconditional information as possible about the ranks of the six elliptic curves using descent by
$196+35 = 231$
remaining k’s, we obtain as much unconditional information as possible about the ranks of the six elliptic curves using descent by
![]() $3$
-isogeny, as well as a
$3$
-isogeny, as well as a
![]() $2$
-descent on
$2$
-descent on
![]() $E_{k^{3}}$
(combined with the Cassels–Tate pairing to identify
$E_{k^{3}}$
(combined with the Cassels–Tate pairing to identify
![]() $2$
-covers as corresponding to a nontrivial element of the Shafarevich–Tate group of
$2$
-covers as corresponding to a nontrivial element of the Shafarevich–Tate group of
![]() $E_{k^{3}}$
). Once these unconditional upper bounds on ranks have been obtained, we search for points on these curves by assuming GRH and performing
$E_{k^{3}}$
). Once these unconditional upper bounds on ranks have been obtained, we search for points on these curves by assuming GRH and performing
![]() $2$
-descents and
$2$
-descents and
![]() $4$
-descents on all six curves and searching for points on the
$4$
-descents on all six curves and searching for points on the
![]() $2$
-covers and
$2$
-covers and
![]() $4$
-covers to see if enough independent points are found to match the unconditional rank upper bound. This takes about 22 minutes (1 292.52 seconds). The code that runs these computations is available in the scripts
step5-24descent.txt
and
step5-highrank.txt
. Of the
$4$
-covers to see if enough independent points are found to match the unconditional rank upper bound. This takes about 22 minutes (1 292.52 seconds). The code that runs these computations is available in the scripts
step5-24descent.txt
and
step5-highrank.txt
. Of the
![]() $196 k$
’s for which generators were not found, this step is unsuccessful for
$196 k$
’s for which generators were not found, this step is unsuccessful for
![]() $26$
, and of the
$26$
, and of the
![]() $35 k$
’s for which one of
$35 k$
’s for which one of
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
, or
$E_{4k}$
, or
![]() $E_{k^{3}}$
has rank
$E_{k^{3}}$
has rank
![]() $5$
or
$5$
or
![]() $6$
, this is unsuccessful for four values of k.
$6$
, this is unsuccessful for four values of k.
Fourth, for each of the 30 remaining values of k, we use the method of Fisher [Reference Fisher10] to search for points using
![]() $12$
-descent. For each of the remaining k’s, there is at least one elliptic curve
$12$
-descent. For each of the remaining k’s, there is at least one elliptic curve
![]() $E_{a}$
for which we have an unconditional upper bound on the rank of
$E_{a}$
for which we have an unconditional upper bound on the rank of
![]() $1$
, and for which the root number is
$1$
, and for which the root number is
![]() $-1$
. For each such k, we choose a minimal subject to these conditions and perform a conditional
$-1$
. For each such k, we choose a minimal subject to these conditions and perform a conditional
![]() $12$
-descent and search for points. We succeed in finding a generator in
$12$
-descent and search for points. We succeed in finding a generator in
![]() $23$
cases. We fail to find a generator for the following seven values of k:
$23$
cases. We fail to find a generator for the following seven values of k:
![]() $49\,897\,450$
;
$49\,897\,450$
;
![]() $117\,092\,530$
;
$117\,092\,530$
;
![]() $120\,813\,050$
;
$120\,813\,050$
;
![]() $128\,327\,978$
;
$128\,327\,978$
;
![]() $130\,187\,450$
;
$130\,187\,450$
;
![]() $149\,477\,050$
; and
$149\,477\,050$
; and
![]() $160\,631\,290$
. (For
$160\,631\,290$
. (For
![]() $k = 128\,327\,978$
,
$k = 128\,327\,978$
,
![]() $E_{k^{3}}$
has rank
$E_{k^{3}}$
has rank
![]() $5$
with easily found generators.) This is performed with the script
step6-12desc.txt
, and the running time is just over 3 hours (11 180.99 seconds).
$5$
with easily found generators.) This is performed with the script
step6-12desc.txt
, and the running time is just over 3 hours (11 180.99 seconds).
So far, we have avoided doing an unconditional
![]() $2$
-descent on any elliptic curve other than
$2$
-descent on any elliptic curve other than
![]() $E_{k^{3}}$
because of the cost of computing the class group of a (potentially high discriminant) cubic field. We now do this for the remaining seven values of k. For each k, we choose the elliptic curve for which the corresponding Minkowski bound is the smallest. For
$E_{k^{3}}$
because of the cost of computing the class group of a (potentially high discriminant) cubic field. We now do this for the remaining seven values of k. For each k, we choose the elliptic curve for which the corresponding Minkowski bound is the smallest. For
![]() $k = 49\,897\,450$
and
$k = 49\,897\,450$
and
![]() $k = 149\,477\,050$
, this shows that
$k = 149\,477\,050$
, this shows that
![]() $E_{k}$
has rank zero. For
$E_{k}$
has rank zero. For
![]() $k = 120\,813\,050$
and
$k = 120\,813\,050$
and
![]() $k = 130\,187\,450$
this shows that
$k = 130\,187\,450$
this shows that
![]() $E_{4k}$
has rank zero. For
$E_{4k}$
has rank zero. For
![]() $k = 128\,327\,978$
, the computation shows that
$k = 128\,327\,978$
, the computation shows that
![]() $E_{16k^{2}}$
has rank zero (using both a
$E_{16k^{2}}$
has rank zero (using both a
![]() $2$
-descent and the Cassels–Tate pairing). For
$2$
-descent and the Cassels–Tate pairing). For
![]() $k = 117\,092\,530$
and
$k = 117\,092\,530$
and
![]() $k = 160\,631\,290$
, a
$k = 160\,631\,290$
, a
![]() $2$
-descent shows that
$2$
-descent shows that
![]() $E_{k}$
has rank
$E_{k}$
has rank
![]() $1$
(whereas previously our unconditional bound on the rank had been
$1$
(whereas previously our unconditional bound on the rank had been
![]() $3$
). This is performed with the script
step7-2descents.txt
, and the running time is just under 2 hours (7 153.69 seconds). For
$3$
). This is performed with the script
step7-2descents.txt
, and the running time is just under 2 hours (7 153.69 seconds). For
![]() $k = 117\,092\,530$
, the Minkowski bound for
$k = 117\,092\,530$
, the Minkowski bound for
![]() $\mathbb {Q}(\sqrt [3]{-k})$
is
$\mathbb {Q}(\sqrt [3]{-k})$
is
![]() $57\,383\,551$
, and the time needed for the proof phase of the class group computation is
$57\,383\,551$
, and the time needed for the proof phase of the class group computation is
![]() $3\,327.08$
seconds.
$3\,327.08$
seconds.
Of the
![]() $19\,508$
values of k that remained after Step
$19\,508$
values of k that remained after Step
![]() $3$
$3$
![]() $864$
were removed in Step
$864$
were removed in Step
![]() $4$
and 5 more were removed in Step
$4$
and 5 more were removed in Step
![]() $7$
. For each of the remaining
$7$
. For each of the remaining
![]() $18\,639$
values of k, we know a finite-index subgroup of the Mordell–Weil group of one of the six corresponding elliptic curves, and moreover that curve has rank less than or equal to
$18\,639$
values of k, we know a finite-index subgroup of the Mordell–Weil group of one of the six corresponding elliptic curves, and moreover that curve has rank less than or equal to
![]() $4$
. In fact, of the
$4$
. In fact, of the
![]() $18\,639$
values of k, the chosen elliptic curve has rank
$18\,639$
values of k, the chosen elliptic curve has rank
![]() $1$
in
$1$
in
![]() $16\,032$
cases, rank
$16\,032$
cases, rank
![]() $2$
in
$2$
in
![]() $1\,172$
cases, rank
$1\,172$
cases, rank
![]() $3$
in
$3$
in
![]() $1\,371$
cases, and rank
$1\,371$
cases, and rank
![]() $4$
in only
$4$
in only
![]() $64$
cases.
$64$
cases.
8 Using the Mordell–Weil sieve
As indicated in Section 2, the goal of the Mordell–Weil sieve is to choose an integer N and a finite set S of primes p of good reduction for E and consider the diagram:

If one finds that
![]() ${\textrm {im}}~ \alpha \cap {\textrm {im}}~ \beta = \emptyset $
, then
${\textrm {im}}~ \alpha \cap {\textrm {im}}~ \beta = \emptyset $
, then
![]() $C_{k}(\mathbb {Q})$
must be empty. Here, E can be any of the six elliptic curves
$C_{k}(\mathbb {Q})$
must be empty. Here, E can be any of the six elliptic curves
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{4k}$
,
$E_{4k}$
,
![]() $E_{-k^{2}}$
,
$E_{-k^{2}}$
,
![]() $E_{16k^{2}}$
,
$E_{16k^{2}}$
,
![]() $E_{k^{3}}$
, or
$E_{k^{3}}$
, or
![]() $E_{-4k^{4}}$
. In practice, we are not always able to provably find
$E_{-4k^{4}}$
. In practice, we are not always able to provably find
![]() $E(\mathbb {Q})$
. Instead, we have used the Saturation command in Magma to compute a finite index subgroup
$E(\mathbb {Q})$
. Instead, we have used the Saturation command in Magma to compute a finite index subgroup
![]() $A \subseteq E(\mathbb {Q})$
with the property that
$A \subseteq E(\mathbb {Q})$
with the property that
![]() $[E(\mathbb {Q}) : A]$
is not divisible by any primes
$[E(\mathbb {Q}) : A]$
is not divisible by any primes
![]() $p \leq 100$
. It follows that if there is no prime
$p \leq 100$
. It follows that if there is no prime
![]() $\ell> 100$
for which
$\ell> 100$
for which
![]() $\ell \mid N$
, then
$\ell \mid N$
, then
![]() $A/NA \cong E(\mathbb {Q})/NE(\mathbb {Q})$
, and we may use A in place of
$A/NA \cong E(\mathbb {Q})/NE(\mathbb {Q})$
, and we may use A in place of
![]() $E(\mathbb {Q})$
in the diagram above. In practice, the largest N we need to use is
$E(\mathbb {Q})$
in the diagram above. In practice, the largest N we need to use is
![]() $N = 84$
.
$N = 84$
.
Before discussing the method and the results, we begin with a simple example. Let
![]() $k = 138\,826$
. We have
$k = 138\,826$
. We have
![]() $E_{4k}(\mathbb {Q}) \cong \mathbb {Z}$
, and a generator is
$E_{4k}(\mathbb {Q}) \cong \mathbb {Z}$
, and a generator is
 $$ \begin{align*} P = \left(\frac{605\,879\,737}{2\,358^{2}}, \frac{-17\,828\,809\,046\,227}{2\,358^{3}}\right). \end{align*} $$
$$ \begin{align*} P = \left(\frac{605\,879\,737}{2\,358^{2}}, \frac{-17\,828\,809\,046\,227}{2\,358^{3}}\right). \end{align*} $$
We use the map
![]() $\phi : C_{k} \to E_{4k}$
given by
$\phi : C_{k} \to E_{4k}$
given by
 $\phi (x,y) = \left (\frac {x^{4}}{y^{2}}, \frac {x^{6} + 2y^{6}}{y^{3}}\right )$
. We find that
$\phi (x,y) = \left (\frac {x^{4}}{y^{2}}, \frac {x^{6} + 2y^{6}}{y^{3}}\right )$
. We find that
![]() $C_{k}(\mathbb {F}_{5})$
contains six points,
$C_{k}(\mathbb {F}_{5})$
contains six points,
![]() $E_{4k}(\mathbb {F}_{5}) \cong \mathbb {Z}/6\mathbb {Z}$
, but that the image of
$E_{4k}(\mathbb {F}_{5}) \cong \mathbb {Z}/6\mathbb {Z}$
, but that the image of
![]() $C_{k}(\mathbb {F}_{5}) \to E_{4k}(\mathbb {F}_{5})$
consists of three points. The reduction
$C_{k}(\mathbb {F}_{5}) \to E_{4k}(\mathbb {F}_{5})$
consists of three points. The reduction
![]() $\tilde {P} \in E_{4k}(\mathbb {F}_{5})$
has order
$\tilde {P} \in E_{4k}(\mathbb {F}_{5})$
has order
![]() $6$
, and if n is an integer, then
$6$
, and if n is an integer, then
![]() $nP$
reduces to a point in
$nP$
reduces to a point in
![]() $E_{4k}(\mathbb {F}_{5})$
that is in the image of
$E_{4k}(\mathbb {F}_{5})$
that is in the image of
![]() $C_{k}(\mathbb {F}_{5}) \to E_{4k}(\mathbb {F}_{5})$
if and only if n is even. It follows that if
$C_{k}(\mathbb {F}_{5}) \to E_{4k}(\mathbb {F}_{5})$
if and only if n is even. It follows that if
![]() $Q \in C_{k}(\mathbb {Q})$
, then
$Q \in C_{k}(\mathbb {Q})$
, then
![]() $\phi (Q) = nP$
for some even n.
$\phi (Q) = nP$
for some even n.
Now, we consider reduction modulo
![]() $7$
. In this case,
$7$
. In this case,
![]() $C_{k}(\mathbb {F}_{7})$
has
$C_{k}(\mathbb {F}_{7})$
has
![]() $36$
points and the image of
$36$
points and the image of
![]() $C_{k}(\mathbb {F}_{7}) \to E_{4k}(\mathbb {F}_{7})$
consists of
$C_{k}(\mathbb {F}_{7}) \to E_{4k}(\mathbb {F}_{7})$
consists of
![]() $6$
points. We have
$6$
points. We have
![]() $E_{4k}(\mathbb {F}_{7}) \cong \mathbb {Z}/2\mathbb {Z} \times \mathbb {Z}/6\mathbb {Z}$
, and the reduction
$E_{4k}(\mathbb {F}_{7}) \cong \mathbb {Z}/2\mathbb {Z} \times \mathbb {Z}/6\mathbb {Z}$
, and the reduction
![]() $\tilde {P} \in E_{4k}(\mathbb {F}_{7})$
again has order
$\tilde {P} \in E_{4k}(\mathbb {F}_{7})$
again has order
![]() $6$
. This time, we find that
$6$
. This time, we find that
![]() $nP$
reduces to a point in
$nP$
reduces to a point in
![]() $E_{4k}(\mathbb {F}_{7})$
that is in the image of
$E_{4k}(\mathbb {F}_{7})$
that is in the image of
![]() $C_{k}(\mathbb {F}_{7}) \to E_{4k}(\mathbb {F}_{7})$
if and only if
$C_{k}(\mathbb {F}_{7}) \to E_{4k}(\mathbb {F}_{7})$
if and only if
![]() $n \equiv 1 \text { or } 5 \ \pmod {6}$
. It follows that if
$n \equiv 1 \text { or } 5 \ \pmod {6}$
. It follows that if
![]() $Q \in C_{k}(\mathbb {Q})$
, then
$Q \in C_{k}(\mathbb {Q})$
, then
![]() $\phi (Q) = nP$
for some odd n, and this contradicts the previous paragraph. Thus,
$\phi (Q) = nP$
for some odd n, and this contradicts the previous paragraph. Thus,
![]() $C_{k}(\mathbb {Q}) = \emptyset $
.
$C_{k}(\mathbb {Q}) = \emptyset $
.
As explained in Section 3.2 of [Reference Bruin and Stoll4], the sets
![]() $A/NA$
can be very large if N is large or if the rank of E is high. For this reason, we follow their suggestion of successively raising N one prime factor at a time. Suppose that we have already computed the admissible elements of
$A/NA$
can be very large if N is large or if the rank of E is high. For this reason, we follow their suggestion of successively raising N one prime factor at a time. Suppose that we have already computed the admissible elements of
![]() $A/NA$
(i.e., those that could possibly occur as the image of a point from
$A/NA$
(i.e., those that could possibly occur as the image of a point from
![]() $C_{k}(\mathbb {Q})$
) by sieving using a collection of small primes S. We then choose a small prime r and set
$C_{k}(\mathbb {Q})$
) by sieving using a collection of small primes S. We then choose a small prime r and set
![]() $N' = rN$
. Then we find the full preimage of the admissible elements in
$N' = rN$
. Then we find the full preimage of the admissible elements in
![]() $A/N'A$
, retest their admissibility for primes in S, and possibly test a further set of primes. Unlike the case of [Reference Bruin and Stoll4], the maximum N needed to prove that
$A/N'A$
, retest their admissibility for primes in S, and possibly test a further set of primes. Unlike the case of [Reference Bruin and Stoll4], the maximum N needed to prove that
![]() $C_{k}(\mathbb {Q})$
is empty is never more than
$C_{k}(\mathbb {Q})$
is empty is never more than
![]() $84$
(whereas Bruin and Stoll report occasionally needing to have N as large as
$84$
(whereas Bruin and Stoll report occasionally needing to have N as large as
![]() $10^{100}$
).
$10^{100}$
).
As an example, consider the case of
![]() $k = 3\,506\,050$
. The elliptic curve
$k = 3\,506\,050$
. The elliptic curve
![]() $E_{k}$
has rank
$E_{k}$
has rank
![]() $4$
and trivial torsion subgroup. First, we let
$4$
and trivial torsion subgroup. First, we let
![]() $N = 2$
and test the primes p of good reduction less than or equal to
$N = 2$
and test the primes p of good reduction less than or equal to
![]() $311$
. We find that of the 16 elements of
$311$
. We find that of the 16 elements of
![]() $A/2A$
,
$A/2A$
,
![]() $9$
are admissible. We then increase N to
$9$
are admissible. We then increase N to
![]() $4$
and begin with
$4$
and begin with
![]() $9 \times 16 = 144$
elements of
$9 \times 16 = 144$
elements of
![]() $A/4A$
. We retest their admissibility for primes less than or equal to
$A/4A$
. We retest their admissibility for primes less than or equal to
![]() $311$
and find that all of them are admissible. We then increase N from
$311$
and find that all of them are admissible. We then increase N from
![]() $4$
to
$4$
to
![]() $12$
and test primes
$12$
and test primes
![]() $p \leq 479$
. Initially, we had
$p \leq 479$
. Initially, we had
![]() $11\,664$
elements of
$11\,664$
elements of
![]() $A/12A$
, but this is reduced to
$A/12A$
, but this is reduced to
![]() $1\,296$
. Next, we increase N from
$1\,296$
. Next, we increase N from
![]() $12$
to
$12$
to
![]() $84$
and start with
$84$
and start with
![]() $3\,111\,696$
elements of
$3\,111\,696$
elements of
![]() $A/84A$
. Testing for
$A/84A$
. Testing for
![]() $p \leq 229$
reduces this to
$p \leq 229$
reduces this to
![]() $1\,204$
elements, and by the time we test
$1\,204$
elements, and by the time we test
![]() $p = 1021$
, no admissible elements remain. Hence,
$p = 1021$
, no admissible elements remain. Hence,
![]() $C_{3\,506\,050}(\mathbb {Q}) = \emptyset $
. The total time required for this k was
$C_{3\,506\,050}(\mathbb {Q}) = \emptyset $
. The total time required for this k was
![]() $508$
seconds, and this is the most time-consuming of all the k’s we test.
$508$
seconds, and this is the most time-consuming of all the k’s we test.
Compared with the previous steps, the Mordell–Weil sieve step is comparatively fast, taking about 35 minutes (2 107.69 seconds) to show that
![]() $C_{k}(\mathbb {Q}) = \emptyset $
for all
$C_{k}(\mathbb {Q}) = \emptyset $
for all
![]() $18\,639$
remaining k’s with
$18\,639$
remaining k’s with
![]() $k < 164\,634\,913$
. This computation is performed by the script
step8-MWsieve.txt
. This concludes the proof of Theorem 1. Below is a table summarizing the steps in the computation and the time required for each.
$k < 164\,634\,913$
. This computation is performed by the script
step8-MWsieve.txt
. This concludes the proof of Theorem 1. Below is a table summarizing the steps in the computation and the time required for each.

9 Concluding remarks
As mentioned in the introduction, it is natural to consider the problem of finding the smallest positive integer which is a sum of two rational nth powers but not a sum of two integer nth powers. If
![]() $n = 5$
, the curve
$n = 5$
, the curve
![]() $D_{k} : x^{5} + y^{5} = k$
admits no map to an elliptic curve, and the projective closure of
$D_{k} : x^{5} + y^{5} = k$
admits no map to an elliptic curve, and the projective closure of
![]() $D_{k}$
always has a rational point (namely (
$D_{k}$
always has a rational point (namely (
![]() $-1 : 1 : 0$
)). This precludes the possibility of ruling out rational points on
$-1 : 1 : 0$
)). This precludes the possibility of ruling out rational points on
![]() $D_{k}$
using local methods or the Mordell–Weil sieve. For these reasons, the
$D_{k}$
using local methods or the Mordell–Weil sieve. For these reasons, the
![]() $n = 5$
case appears to be more challenging than the
$n = 5$
case appears to be more challenging than the
![]() $n = 4$
or
$n = 4$
or
![]() $n = 6$
cases.
$n = 6$
cases.
Similar techniques should allow one to approach the cases of
![]() $n = 8$
and
$n = 8$
and
![]() $n = 12$
where there are maps from
$n = 12$
where there are maps from
![]() $x^{n} + y^{n} = k$
to elliptic curves, but the smallest known values of k for which these curves are known to have rational noninteger points are
$x^{n} + y^{n} = k$
to elliptic curves, but the smallest known values of k for which these curves are known to have rational noninteger points are
![]() $8\,000\,587\,738\,704\,025\,541\,501\,346\,146$
and
$8\,000\,587\,738\,704\,025\,541\,501\,346\,146$
and
![]() $873\,135\,263\,681\,497\,645\,296\,811\,652\,793\,869\,145\,886\,016\,236\,198\,018\,083\,488\,332\,176\,234\,017$
, respectively. The size of these numbers would make an exhaustive search prohibitively time-consuming.
$873\,135\,263\,681\,497\,645\,296\,811\,652\,793\,869\,145\,886\,016\,236\,198\,018\,083\,488\,332\,176\,234\,017$
, respectively. The size of these numbers would make an exhaustive search prohibitively time-consuming.
Acknowledgment
This work represents joint work done when the first author was a master’s student at Wake Forest University. Computations were done in Magma [Reference Bosma, Cannon and Playoust2] version 2.26-9 on a desktop with an Intel i9-11900K CPU and 128 GB of RAM. The authors thank the referees for the detailed suggestions including the decomposition of the Jacobian of
![]() $x^{6}+y^{6}=kz^{6}$
and computational suggestions that led to an unconditional main result.
$x^{6}+y^{6}=kz^{6}$
and computational suggestions that led to an unconditional main result.