Nomenclature

D stagnation depth

g acceleration due to gravity

h snow depth measured vertically

p dynamic component of pressure

u component of creep velocity parallel to the slope

u_A component of creep velocity parallel to the slope, at the top of the snow-pack

u₀ glide velocity at the ground

v component of velocity perpendicular to the slope

x coordinate axis parallel to the slope

x' back-pressure zone length

z coordinate axis perpendicular to the slope

α slope angle

ß creep angle

η effective bulk viscosity

μ effective shear viscosity

p snow density

σ_x longitudinal stress

Σ_ι first invariant of the stress tensor

<τ> average shear stress at the base of the snow-pack

T_xz shear stress

Creep of Well-Settled Isothermal Snow

Neutral-zone measurements on well-settled isothermal snow which is assumed to obey a viscous flow law show that both the shear and vertical strain-rates are independent of depth (Reference Bader, Bader, Haefeli, Bucher, Neher, Eckel, Thams and NiggliBader and others, 1939; McClung, in press, unpublished). McClung has pointed out that the simplest constitutive law for isotropic creep which is consistent with these observations is a two-parameter law with the effective shear viscosity μ and bulk viscosity η proportional to Σ_ι, the first invariant of the stress tensor (the bulk stress). Such a formalism provides relationships which are invariant with respect to proper orthogonal coordinate transformations as required by continuum mechanics. The precise relationship between the stress and the viscous strain-rate has not been formulated as yet. Several relationships have been proposed, for example by Reference Brown, G.B., Evans and McClungBrown and others (1973), McClung (in press, unpublished) and Reference SalmSalm (in press). However, neutral-zone measurements of creep strongly indicate that, when a two-parameter constitutive law is considered, it is likely that the effective shear and bulk viscosities may be considered to be proportional to the bulk stress. Accordingly, the calculations presented below are based on that assumption. The ratio μ/η is assumed to be constant in the calculations since the precise form of the constitutive law is unknown. Such an assumption is not expected to cause a large error in the magnitude of the calculated pressures.

Formulation of the Glide-Boundary Condition in the Zone of Influence of a Structure on a Slope

It is unlikely that the distribution of glide velocity or shear stress at the snow-earth interface will ever be known sufficiently well for a formulation to be made of a velocity or stress boundary condition in the zone of influence of a structure on a slope. The proper boundary condition is a relationship between the glide velocity and the shear stress at the base of the snow pack. The distribution of glide velocity and shear stress are then to be calculated from a constitutive equation for glide.

McClung (in press) has suggested a relationship of the form

(1)

for the glide constitutive equation in the case where the glide mechanism is that of creep over rough obstacles at the base of the snow-pack. τ is the average basal shear-stress, μ is the shear viscosity, u₀ is the glide velocity, and D is the stagnation depth defined as in Figure 1 (Reference NyeNye, 1969). For the case where the snow is modeled as a linear, incompressible Newtonian fluid, μ is a constant. In that case, Equation (1) is a continuum mechanical formulation of the assumptions made by Haefeli in his formulation of snow pressure. McClung (in press) has also given an approximate equation in an attempt to account for the observed non-linearity in the constitutive law for creep

(2)

where k is a constant and Σ_ι is the first invariant of the stress tensor. The stagnation depth depends upon the bed topography and the degree of wetness of the interface; this has been discussed in detail by McClung (in press).

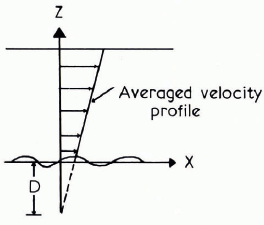
Fig. 1. A definition of stagnation depth following Reference NyeNye (1969).

Calculations of Snow Pressure

Figure 2 shows the geometry used in the two-dimensional calculations of snow pressure on a rigid retaining structure on a slope. The calculations of dynamic component described here are made using the finite-element method. We assume a situation where a plane strain-rate exists and we also assume that the calculation is made over a time interval short enough that overall geometry changes may be ignored. The snow-pack is assumed to be isothermal and have a uniform density. This is typical of the conditions which obtain during the late winter or early spring in the Cascade Mountains, U.S.A. when maximum snow pressures usually occur. Figure 3 shows the finite-element mesh (Reference Zienkiewicz and CheungZienkiewicz and Cheung, 1967). The calculations presented here assume non-linearity in both the creep and glide constitutive equations because we treat the effective shear and bulk viscosities as being proportional to the bulk stress. The ratio of the shear and bulk viscosity is assumed to be constant and has been defined by some field measurements made by McClung (in press, unpublished).

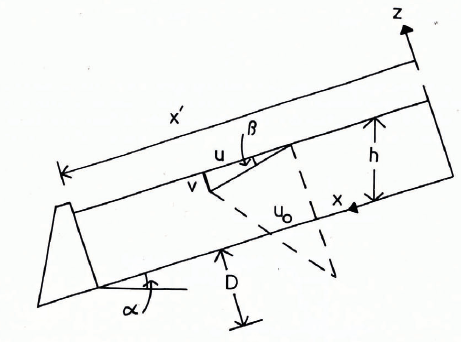
Fig. 2. A diagram which shows the nomenclature used in this paper. D is the stagnation depth; h, the snow depth; u, the creep velocity parallel to the slope; u_o, the glide velocity; v, the creep velocity perpendicular to the slope; x', the back-pressure zone length; α, the slope angle; and β. the creep angle.

Fig. 3. Fig. 3. The finite-element grid.

Figures 4-7 show the results of some calculations of the dynamic component of pressure for conditions which might be expected to occur during the early spring in the Cascade Mountains, U.S.A. Snow density is taken as 550 kg m^-3, the slope angle is assumed to be 45° and the effective viscous analog of Poisson's ratio is taken to be 0.3 (this corresponds to a creep angle β of 16°).

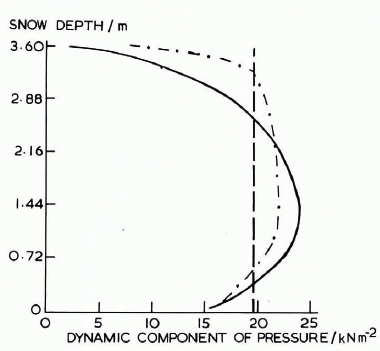
Fig. 4. Snow depth plotted against the dynamic component of pressure. The solid line gives the results of a numerical calculation (the back-pressure zone length is 28 m). The broken line gives the result of calculations involving the equations of Haefeli (back-pressure zone length equals 15.5m). The dot-dash line indicates the calculation for constant viscosity. For all calculations α = 45°, ß = 16°, and the stagnation depth 1.13 m. The boundary condition on the structure is: u = v = 0.

Fig. 5. Snow depth plotted against the dynamic component of pressure. The solid line gives the results of the numerical calculation. The broken line gives the result of calculations involving the equations of Haefeli. The parameters used in the calculations are the same as those used in Figure 4 except for the boundary condition on the structure which is; u = τ_xz = 0.

Fig. 6. Snow depth plotted against the dynamic component of pressure. The solid line gives the results of the numerical calculation (the back-pressure zone length is 21 m). The broken line gives the results of calculations involving the equations of Haefeli (back-pressure zone length equals 14 m). For both calculations α = 45°, β = 16°, and the stagnation depth = 0.215m. The boundary condition on the structure is: u = v = 0.

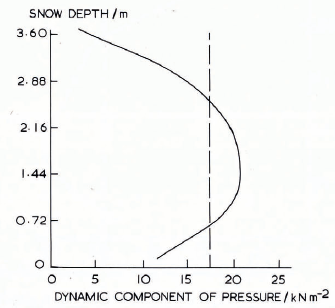
Fig. 7. Snow depth plotted against the dynamic component of pressure. The solid-line gives the. results of the numerical calculation. The broken line goes the results of calculations involving the equations of Haefeli. The parameters used in the calculations are the same as those used in Figure 6 except for the boundary condition on the structure which is: u = τ_xz = 0.

These calculations were made with a computer program called PLANE 2 whose algorithms assume a condition of plane strain. The program allows the values of viscosity to be different for each element. In addition the program has the ability to incorporate the boundary condition of non-linear slip by allowing input of the ratio of load to glide velocity on the boundary nodes of the snow-earth interface. The calculations were made by an iteration procedure which calculated the shear and bulk velocities during each step and used the calculated values in each successive iteration until convergence was obtained. This convergence condition was usually obtained within three or Tour iterations for each calculation.

The calculations are given for two different boundary conditions for glide which correspond to stagnation depths of D = 1.13 m (Figs 4 and 5) and D = 0.215 m (Figs 6 and 7). The first of these might correspond to a glide condition in which rain and melt water wets the interface whereas the second might correspond to a normal steady-glide condition on a slope of moderate roughness (McClung, in press, unpublished). For both boundary conditions for glide, the calculations were made for two boundary conditions at the structure. If a structure has a perfectly rough surface, this condition is

(3)

(corresponding to no slip), For a perfectly smooth structure the condition is

(4)

(corresponding to no friction on the structure). The boundary condition at the snow-air interface is assumed to be a free surface. The boundary condition up-slope of the barrier is assumed to be the neutral-zone distribution of creep velocity.

The static component of pressure may be taken as the neutral-zone longitudinal stress perpendicular to the barrier σ_x. Under the assumption of a constant ratio of shear to bulk viscosity the relationship is:

(5)

where K ₀ = 0.43 and is defined by the field measurements of McClung (in press, unpublished). In this case, the static component of pressure varies linearly with depth from zero at the snow-air interface to 5.9 kN m^-2 at the snow-earth interface. These values must be added to the calculated dynamic components of pressure in each case to yield the total snow pressure.

Comparison with the Equations of Haefeli

It is instructive to compare the results presented here with those given by Haefeli (Bader and others, 1939). Haefeli's equations may be re-stated in terms of the two fundamental neutral-zone measurements given by continuum mechanics: the creep angle β (Perla, unpublished) and the stagnation depth D.

Haefeli gives the following relationship for the up-slope zone of influence (back-pressure zone):

(6)

where u>₀ is the creep velocity at the ground, U_A is the creep velocity at the top of the snow pack and A is the snow depth. The equation may be restated in terms of the geometry given in Figure 1 as

(7)

Haefeli gives the dynamic component of pressure as

(8)

where p is the snow density. Figures 4-7 show comparisons of Haefeli's estimates of the dynamic component of pressure and back-pressure zone lengths with the present results, Figure 4 also shows a comparison with the case where the linear creep and glide constitutive equations are used.

The results of such calculations indicate that the estimates of the dynamic component of pressure made by Haefeli are in reasonable agreement with the formulation presented here. Thus, Haefeli's estimates are very useful when an estimate of the snow pressure is needed quickly. On the other hand, when we need to know the distribution of pressure on the structure, or when complicated geometries are involved, the numerical method may be needed.

The estimates of back-pressure zone lengths given by the equations of Haefeli do not agree very closely with the present formulation. The apparent reason is that Haefeli arbitrarily assumed a parabolic distribution of glide velocity and shear stress in the back-pressure zone. The glide velocity and shear stress calculated by the finite clement method lead to a function which approaches the estimates of the neutral zone more slowly and thus produces longer back-pressure zones.

Figure 8 shows the calculated distribution of glide velocity in the back-pressure zone for the creep and glide constitutive equations in both the linear and non-linear cases when the stagnation depth D is taken as 1.13 m. There is no difference between the linear and nonlinear formulation for the zone of influence for glide in this case, because the constant viscosities chosen for the linear calculation were for the estimates at the bottom of the snow-pack in the neutral zone.

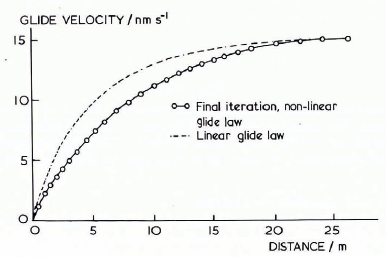
Fig. 8. The distribution of glide velocity in the back-pressure zone length for a stagnation depth of 1.13 m and a boundary condition on the structure of u = v = 0.

Summary

A method has been given for the calculation of snow pressure. This method stems from a continuum-mechanical formulation of the problem. The static component of pressure is equivalent to that given by Haefeli (Bader and others, 1939). The dynamic component of pressure is calculated by the finite element method with the assumption of non-linear viscous creep and glide constitutive equations. The technique proposed here is potentially very powerful. Any slope geometry, barrier geometry, distribution of density and distribution of ground roughness are easily incorporated into the calculations. The method gives, in addition, the distribution of pressure on the structure.

The numerical calculations presented here show a reasonable agreement with the estimates of Haefeli for the magnitude of the dynamic component of pressure. There is, however, some disagreement in the prediction of the length of the back-pressure zone. The calculations indicate that the pressure is not very sensitive to the boundary condition on the structure, and that the dynamic component of pressure is sensitive to the snow-earth boundary condition. This agrees with field observations which suggest that fast glide is an important determining factor for snow pressure. With regard to the calculations in which the larger stagnation depth was used, it was assumed that increased amounts of water from melting or rainfall affects glide by increasing the stagnation depth. Clearly, the properties of the snow will also be affected by the presence of water. It is then better to regard the calculations as a study into the sensitivity with which the chosen model for the glide boundary condition affects the dynamic component of pressure.

Non-linearity in the constitutive equations has the effect of increasing the snow viscosity in the vicinity of the structure. Increase in the viscosity causes a decrease in the glide velocity near the structure as shown in Figure 8. The model chosen here shows that the non-linearity in creep tends to increase the pressure and shift the force resultant toward the bottom of the structure. Since the exact form of the constitutive equation for viscous creep is, at present, unknown, these results are derived from the assumption of a constant ratio of shear to bulk viscosity.

Acknowledgements

This study was made as part of my doctoral research in geophysics at the University of Washington. I am indebted to Professors C. B. Brown and R. J. Evans for their useful discussions with me regarding this work and to Professor E. R. LaChapelle for his provision of financial support and encouragement. This research was funded by the Washington Slate Highway Department under Contract Y-1301. Norges Geotekniske Institutt provided support during the preparation of the manuscript.