Article contents
Non-uniform ergodic properties of Hamiltonian flows with impacts
Published online by Cambridge University Press: 20 October 2021
Abstract
The ergodic properties of two uncoupled oscillators, one horizontal and one vertical, residing in a class of non-rectangular star-shaped polygons with only vertical and horizontal boundaries and impacting elastically from its boundaries are studied. We prove that the iso-energy level sets topology changes non-trivially; the flow on level sets is always conjugated to a translation flow on a translation surface, yet, for some segments of partial energies the genus of the surface is strictly greater than
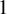 $1$
. When at least one of the oscillators is unharmonic, or when both are harmonic and non-resonant, we prove that for almost all partial energies, including the impacting ones, the flow on level sets is uniquely ergodic. When both oscillators are harmonic and resonant, we prove that there exist intervals of partial energies on which periodic ribbons and additional ergodic components coexist. We prove that for almost all partial energies in such segments the motion is uniquely ergodic on the part of the level set that is not occupied by the periodic ribbons. This implies that ergodic averages project to piecewise smooth weighted averages in the configuration space.
$1$
. When at least one of the oscillators is unharmonic, or when both are harmonic and non-resonant, we prove that for almost all partial energies, including the impacting ones, the flow on level sets is uniquely ergodic. When both oscillators are harmonic and resonant, we prove that there exist intervals of partial energies on which periodic ribbons and additional ergodic components coexist. We prove that for almost all partial energies in such segments the motion is uniquely ergodic on the part of the level set that is not occupied by the periodic ribbons. This implies that ergodic averages project to piecewise smooth weighted averages in the configuration space.
Keywords
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by



