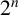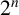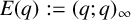1 Introduction
For any complex number a, we define
 $$ \begin{align*} \displaystyle(a;q)_k:=\prod_{n=1}^{k}(1-aq^{n-1}) \end{align*} $$
$$ \begin{align*} \displaystyle(a;q)_k:=\prod_{n=1}^{k}(1-aq^{n-1}) \end{align*} $$
and
 $$ \begin{align*} \displaystyle(a;q)_\infty := \lim_{k\rightarrow\infty}(a;q)_k = \prod_{n=1}^{\infty}(1-aq^{n-1}),\quad |q|<1. \end{align*} $$
$$ \begin{align*} \displaystyle(a;q)_\infty := \lim_{k\rightarrow\infty}(a;q)_k = \prod_{n=1}^{\infty}(1-aq^{n-1}),\quad |q|<1. \end{align*} $$
We set
![]() $E(q):=(q;q)_\infty =\prod _{n=1}^{\infty }(1-q^n)$
;
$E(q):=(q;q)_\infty =\prod _{n=1}^{\infty }(1-q^n)$
;
![]() $E(q)$
is known as Euler’s product. We can view
$E(q)$
is known as Euler’s product. We can view
![]() $E(q)$
as a particular case of Ramanujan’s theta function (see [Reference Berndt1, page 34]): that is,
$E(q)$
as a particular case of Ramanujan’s theta function (see [Reference Berndt1, page 34]): that is,
 $$ \begin{align*} f(a,b):=\displaystyle\sum_{n=-\infty}^{\infty}a^{n(n+1)/2}b^{n(n-1)/2},\quad|ab|<1. \end{align*} $$
$$ \begin{align*} f(a,b):=\displaystyle\sum_{n=-\infty}^{\infty}a^{n(n+1)/2}b^{n(n-1)/2},\quad|ab|<1. \end{align*} $$
Jacobi’s triple product identity (see [Reference Hirschhorn5, page 5]) is
 $$ \begin{align*} \sum_{n=-\infty}^{\infty}q^{n^2}z^n=(-qz;q^2)_\infty(-q/z;q^2)_\infty(q^2;q^2)_\infty,\quad|q|<1. \end{align*} $$
$$ \begin{align*} \sum_{n=-\infty}^{\infty}q^{n^2}z^n=(-qz;q^2)_\infty(-q/z;q^2)_\infty(q^2;q^2)_\infty,\quad|q|<1. \end{align*} $$
Replacing
![]() $qz$
by a and
$qz$
by a and
![]() $q/z$
by b in Jacobi’s triple product identity, yields
$q/z$
by b in Jacobi’s triple product identity, yields
In particular,
A t-dissection of a power series
![]() $A(q)$
is given by
$A(q)$
is given by
![]() $A(q)=\sum _{k=0}^{t-1}q^kA_k(q^t)$
, where the
$A(q)=\sum _{k=0}^{t-1}q^kA_k(q^t)$
, where the
![]() $A_k(q^t)$
are power series in
$A_k(q^t)$
are power series in
![]() $q^t$
. The
$q^t$
. The
![]() $3$
-dissection of
$3$
-dissection of
![]() $E(q)$
(see [Reference Berndt1, entry 31, page 48]) is
$E(q)$
(see [Reference Berndt1, entry 31, page 48]) is
We also have
 $$ \begin{align*} E(q) &=E(q^{25})\bigg[\frac{f(-q^{10},-q^{15})}{f(-q^{5},-q^{20})} -q-q^2\frac{f(-q^{5},-q^{20})}{f(-q^{10},-q^{15})}\bigg], \\ E(q) &=E(q^{49})\bigg[\frac{f(-q^{14},-q^{35})}{f(-q^{7},-q^{42})} -q\frac{f(-q^{21},-q^{28})} {f(-q^{14},-q^{35})}-q^2+q^3\frac{f(-q^{7},-q^{42})}{f(-q^{21},-q^{28})}\bigg],\\ E(q) &=E(q^{121})\bigg[\frac{f(-q^{44},-q^{77})}{f(-q^{22},-q^{99})} -q\frac{f(-q^{22},-q^{99})}{f(-q^{11},-q^{110})}-q^2\frac{f(-q^{55},-q^{66})}{f(-q^{33},-q^{88})}\notag\\ &\qquad\qquad\quad +q^5+q^7\frac{f(-q^{33},-q^{88})}{f(-q^{44},-q^{77})}-q^{15}\frac{f(-q^{11},-q^{110})}{f(-q^{55},-q^{66})}\bigg], \end{align*} $$
$$ \begin{align*} E(q) &=E(q^{25})\bigg[\frac{f(-q^{10},-q^{15})}{f(-q^{5},-q^{20})} -q-q^2\frac{f(-q^{5},-q^{20})}{f(-q^{10},-q^{15})}\bigg], \\ E(q) &=E(q^{49})\bigg[\frac{f(-q^{14},-q^{35})}{f(-q^{7},-q^{42})} -q\frac{f(-q^{21},-q^{28})} {f(-q^{14},-q^{35})}-q^2+q^3\frac{f(-q^{7},-q^{42})}{f(-q^{21},-q^{28})}\bigg],\\ E(q) &=E(q^{121})\bigg[\frac{f(-q^{44},-q^{77})}{f(-q^{22},-q^{99})} -q\frac{f(-q^{22},-q^{99})}{f(-q^{11},-q^{110})}-q^2\frac{f(-q^{55},-q^{66})}{f(-q^{33},-q^{88})}\notag\\ &\qquad\qquad\quad +q^5+q^7\frac{f(-q^{33},-q^{88})}{f(-q^{44},-q^{77})}-q^{15}\frac{f(-q^{11},-q^{110})}{f(-q^{55},-q^{66})}\bigg], \end{align*} $$
which are, respectively, 5-, 7- and 11- dissections of
![]() $E(q)$
(see [Reference Berndt1, pages 82, 303 and 363]. A generalised form of these dissections is given in the following theorem.
$E(q)$
(see [Reference Berndt1, pages 82, 303 and 363]. A generalised form of these dissections is given in the following theorem.
Theorem 1.1 [Reference Berndt1, Theorem 12.1, page 274].
Suppose m is a positive integer with
![]() $m\equiv 1 \ (\text {mod}~6)$
. If
$m\equiv 1 \ (\text {mod}~6)$
. If
![]() $m=6t+1$
with t positive, then
$m=6t+1$
with t positive, then
 $$ \begin{align*} \frac{E(q^{1/m})}{E(q^m)} & =(-1)^tq^{(m^2-1)/{(24m)}} +\sum_{k=1}^{(m-1)/2}(-1)^{k+t}q^{(k-t)(3k-3t-1)/(2n)}\frac{f(-q^{2k},-q^{n-2k})}{f(-q^{k},-q^{n-k})}. \end{align*} $$
$$ \begin{align*} \frac{E(q^{1/m})}{E(q^m)} & =(-1)^tq^{(m^2-1)/{(24m)}} +\sum_{k=1}^{(m-1)/2}(-1)^{k+t}q^{(k-t)(3k-3t-1)/(2n)}\frac{f(-q^{2k},-q^{n-2k})}{f(-q^{k},-q^{n-k})}. \end{align*} $$
If
![]() $m=6t-1$
with t positive, then
$m=6t-1$
with t positive, then
 $$ \begin{align*} \frac{E(q^{1/m})}{E(q^m)} =(-1)^tq^{(m^2-1)/{(24m)}} +\sum_{k=1}^{(m-1)/2}(-1)^{k+t}q^{(k-t)(3k-3t+1)/(2n)}\frac{f(-q^{2k},-q^{n-2k})}{f(-q^{k},-q^{n-k})}. \end{align*} $$
$$ \begin{align*} \frac{E(q^{1/m})}{E(q^m)} =(-1)^tq^{(m^2-1)/{(24m)}} +\sum_{k=1}^{(m-1)/2}(-1)^{k+t}q^{(k-t)(3k-3t+1)/(2n)}\frac{f(-q^{2k},-q^{n-2k})}{f(-q^{k},-q^{n-k})}. \end{align*} $$
Theorem 1.1 was found independently by Ramanathan [Reference Ramanathan7] and Evans [Reference Evans4]. Recently, it was reproved by McLaughlin [Reference McLaughlin6] while establishing some other general dissections involving infinite products.
Hirschhorn [Reference Hirschhorn5, page 332] gave the 2- and 4- dissections of
![]() $E(q)$
as
$E(q)$
as
 $$ \begin{align} \hspace{-5pt}E(q) & =-q(q^4,q^{28};q^{32})_\infty(q^6,q^{10},q^{16};q^{16})_\infty+(q^{12},q^{20};q^{32})_\infty(q^2,q^{14},q^{16};q^{16})_\infty,\\\hspace{-5pt}E(q) & =q^7(q^{8},q^{120};q^{128})_\infty\!(q^{28},q^{36},q^{64};q^{64})_\infty\!-q^2(q^{24},q^{104}; q^{128})_\infty(q^{20},q^{44},q^{64};q^{64})_\infty\notag \end{align} $$
$$ \begin{align} \hspace{-5pt}E(q) & =-q(q^4,q^{28};q^{32})_\infty(q^6,q^{10},q^{16};q^{16})_\infty+(q^{12},q^{20};q^{32})_\infty(q^2,q^{14},q^{16};q^{16})_\infty,\\\hspace{-5pt}E(q) & =q^7(q^{8},q^{120};q^{128})_\infty\!(q^{28},q^{36},q^{64};q^{64})_\infty\!-q^2(q^{24},q^{104}; q^{128})_\infty(q^{20},q^{44},q^{64};q^{64})_\infty\notag \end{align} $$
 $$ \begin{align} E(q) & =q^7(q^{8},q^{120};q^{128})_\infty\!(q^{28},q^{36},q^{64};q^{64})_\infty\!-q^2(q^{24},q^{104}; q^{128})_\infty(q^{20},q^{44},q^{64};q^{64})_\infty,\notag\\ &\quad+(q^{40},q^{88};q^{128})_\infty(q^{12},q^{52},q^{64};q^{64})_\infty-q(q^{56},q^{72}; q^{128})_\infty(q^{4},q^{60},q^{64};q^{64})_\infty, \end{align} $$
$$ \begin{align} E(q) & =q^7(q^{8},q^{120};q^{128})_\infty\!(q^{28},q^{36},q^{64};q^{64})_\infty\!-q^2(q^{24},q^{104}; q^{128})_\infty(q^{20},q^{44},q^{64};q^{64})_\infty,\notag\\ &\quad+(q^{40},q^{88};q^{128})_\infty(q^{12},q^{52},q^{64};q^{64})_\infty-q(q^{56},q^{72}; q^{128})_\infty(q^{4},q^{60},q^{64};q^{64})_\infty, \end{align} $$
where
![]() $(a_1, a_2,\ldots ,a_n;q)_\infty :=(a_1;q)_\infty (a_2;q)_\infty \cdots (a_n;q)_\infty $
.
$(a_1, a_2,\ldots ,a_n;q)_\infty :=(a_1;q)_\infty (a_2;q)_\infty \cdots (a_n;q)_\infty $
.
Identity (1.2) was obtained by 4-dissecting the products
![]() $(q^6,q^{10},q^{16};q^{16})_\infty $
and
$(q^6,q^{10},q^{16};q^{16})_\infty $
and
![]() $(q^2,q^{14},q^{16};q^{16})_\infty $
in (1.1). Hirschhorn also remarked that we can continue in the same manner and find the 8-dissection, the 16-dissection and so on. He concluded by noting the following conjecture on the
$(q^2,q^{14},q^{16};q^{16})_\infty $
in (1.1). Hirschhorn also remarked that we can continue in the same manner and find the 8-dissection, the 16-dissection and so on. He concluded by noting the following conjecture on the
![]() $2^n$
-dissection of
$2^n$
-dissection of
![]() $E(q)$
.
$E(q)$
.
Conjecture 1.2.
 $$ \begin{align*} E(q)&=\sum_{k=1}^{2^n} (-1)^{n+k+1} q^{c_k}(q^{(2k-1)2^{n+1}},q^{2^{2n+3}-(2k-1)2^{n+1}};q^{2^{2n+3}})_\infty\notag\\ &\quad \times (q^{2^{2n+1}+(2k-1)2^{n}},q^{2^{2n+1}-(2k-1)2^{n}},q^{2^{2n+2}};q^{2^{2n+2}})_\infty, \end{align*} $$
$$ \begin{align*} E(q)&=\sum_{k=1}^{2^n} (-1)^{n+k+1} q^{c_k}(q^{(2k-1)2^{n+1}},q^{2^{2n+3}-(2k-1)2^{n+1}};q^{2^{2n+3}})_\infty\notag\\ &\quad \times (q^{2^{2n+1}+(2k-1)2^{n}},q^{2^{2n+1}-(2k-1)2^{n}},q^{2^{2n+2}};q^{2^{2n+2}})_\infty, \end{align*} $$
where
and
Cao [Reference Cao3] discussed product identities for theta functions using integer matrix exact covering systems. In particular, he gave the following result involving the product of two theta functions.
Theorem 1.3 [Reference Cao3, Corollary 2.2].
If
![]() $|ab|<1$
and
$|ab|<1$
and
![]() $cd=(ab)^{k_1k_2}$
, where both
$cd=(ab)^{k_1k_2}$
, where both
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are positive integers, then
$k_2$
are positive integers, then
 $$ \begin{align} & f(a,b)f(c,d) \notag\\ &\quad =\sum_{r=0}^{k_1+k_2-1}a^{{r(r+1)}/{2}}b^{{r(r-1)}/{2}}f (a^{{(k_1^2+k_1)}/{2}+k_1r}b^{{(k_1^2-k_1)}/{2}+k_1r}d, a^{{(k_1^2-k_1)}/{2}-k_1r}b^{{(k_1^2+k_1)}/{2}-k_1r}c)\notag\\ &\qquad\times f(a^{{(k_2^2+k_2)}/{2}+k_2r}b^{{(k_2^2-k_2)}/{2}+k_2r}c,a^{{(k_2^2-k_2)}/{2}-k_2r}b^{{(k_2^2+k_2)}/{2}-k_2r}d). \end{align} $$
$$ \begin{align} & f(a,b)f(c,d) \notag\\ &\quad =\sum_{r=0}^{k_1+k_2-1}a^{{r(r+1)}/{2}}b^{{r(r-1)}/{2}}f (a^{{(k_1^2+k_1)}/{2}+k_1r}b^{{(k_1^2-k_1)}/{2}+k_1r}d, a^{{(k_1^2-k_1)}/{2}-k_1r}b^{{(k_1^2+k_1)}/{2}-k_1r}c)\notag\\ &\qquad\times f(a^{{(k_2^2+k_2)}/{2}+k_2r}b^{{(k_2^2-k_2)}/{2}+k_2r}c,a^{{(k_2^2-k_2)}/{2}-k_2r}b^{{(k_2^2+k_2)}/{2}-k_2r}d). \end{align} $$
Finally, we give the following version of the quintuple product identity.
Theorem 1.4 (Quintuple product identity [Reference Berndt2, page 19]).
For
![]() $a\neq 0$
,
$a\neq 0$
,
 $$ \begin{align} &(-aq;q)_\infty(-a^{-1};q)_\infty(a^2q;q^2)_\infty(a^{-2}q;q^2)_\infty(q;q)_\infty\notag\\ &\quad =(a^3q^2;q^3)_\infty(a^{-3}q;q^3)_\infty(q^3;q^3)_\infty+a^{-1}(a^3q;q^3)_\infty(a^{-3}q^2;q^3)_\infty(q^3;q^3)_\infty\notag\\ &\quad =f(-a^3q^2,-a^{-3}q)+a^{-1}f(-a^3q,-a^{-3}q^2). \end{align} $$
$$ \begin{align} &(-aq;q)_\infty(-a^{-1};q)_\infty(a^2q;q^2)_\infty(a^{-2}q;q^2)_\infty(q;q)_\infty\notag\\ &\quad =(a^3q^2;q^3)_\infty(a^{-3}q;q^3)_\infty(q^3;q^3)_\infty+a^{-1}(a^3q;q^3)_\infty(a^{-3}q^2;q^3)_\infty(q^3;q^3)_\infty\notag\\ &\quad =f(-a^3q^2,-a^{-3}q)+a^{-1}f(-a^3q,-a^{-3}q^2). \end{align} $$
We use (1.6), (1.7) and other properties of Ramanujan’s theta function to prove Conjecture 1.2. In Section 2, we mention some preliminary results involving Ramanujan’s theta function and the pentagonal numbers
![]() $P(n)$
. In Section 3, we provide the proof of Conjecture 1.2.
$P(n)$
. In Section 3, we provide the proof of Conjecture 1.2.
2 Preliminaries
Lemma 2.1. If
![]() $ab=cd$
, then
$ab=cd$
, then
Proof. Set
![]() $k_1=k_2=1$
in (1.6).
$k_1=k_2=1$
in (1.6).
Lemma 2.2 [Reference Berndt1, Entry 18, page 34].
For any integer n,
Lemma 2.3. We have
Proof. Set
![]() $n=1$
in (2.2).
$n=1$
in (2.2).
Lemma 2.4. Let
![]() $P(n)$
be as in (1.5). For positive integers n and k,
$P(n)$
be as in (1.5). For positive integers n and k,
Proof. We have
Replacing s and t by
![]() $2^{n+1}+k-1$
and
$2^{n+1}+k-1$
and
![]() $k-1$
, respectively, in (2.5), we find that
$k-1$
, respectively, in (2.5), we find that
Lemma 2.5. If n is even and
![]() $c_k=P(-{(2^{n+1}-2)}/{3}+(k-1))$
, then
$c_k=P(-{(2^{n+1}-2)}/{3}+(k-1))$
, then
Proof. We have
![]() $c_k=P(((3k-2^{n+1})-1)/{3})$
, so
$c_k=P(((3k-2^{n+1})-1)/{3})$
, so
 $$ \begin{align} & P\bigg(\frac{2^{n+2}+2}{3} -k\bigg)-c_k =P\bigg(\frac{2^{n+2}-3k+2}{3}\bigg)-P\bigg(\frac{3k-2^{n+1}-1}{3}\bigg)\notag\\ & \quad=\frac{1}{2}\bigg(\frac{2^{n+2}-3k+2}{3}-\frac{3k-2^{n+1}-1}{3}\bigg) \times(2^{n+2}-3k+2+3k-2^{n+1}-1-1)\notag\\ &\quad=2^n (2^{n+1}-2k+1) =2^{2n+1}-2^n(2k-1). \end{align} $$
$$ \begin{align} & P\bigg(\frac{2^{n+2}+2}{3} -k\bigg)-c_k =P\bigg(\frac{2^{n+2}-3k+2}{3}\bigg)-P\bigg(\frac{3k-2^{n+1}-1}{3}\bigg)\notag\\ & \quad=\frac{1}{2}\bigg(\frac{2^{n+2}-3k+2}{3}-\frac{3k-2^{n+1}-1}{3}\bigg) \times(2^{n+2}-3k+2+3k-2^{n+1}-1-1)\notag\\ &\quad=2^n (2^{n+1}-2k+1) =2^{2n+1}-2^n(2k-1). \end{align} $$
Similar calculations give the formulas in the following three lemmas.
Lemma 2.6. If n is even and
![]() $c_k=P(-{(2^{n+1}-2)}/{3}+(k-1))$
, then
$c_k=P(-{(2^{n+1}-2)}/{3}+(k-1))$
, then
Lemma 2.7. If n is odd and
![]() $c_k=P({(2^{n+1}-1)}/{3}-(k-1))$
, then
$c_k=P({(2^{n+1}-1)}/{3}-(k-1))$
, then
Lemma 2.8. If n odd is and
![]() $c_k=P({(2^{n+1}-1)}/{3}-(k-1))$
, then
$c_k=P({(2^{n+1}-1)}/{3}-(k-1))$
, then
3 Proof of the main result
Theorem 3.1. Conjecture 1.2 is true.
Proof. We set
![]() $a=-q$
,
$a=-q$
,
![]() $b=-q^2$
,
$b=-q^2$
,
![]() $c=-q^{2^{2n+2}} d=-q^{2^{2n+3}}$
,
$c=-q^{2^{2n+2}} d=-q^{2^{2n+3}}$
,
![]() $k_1=k_2=2^{n+1}$
and
$k_1=k_2=2^{n+1}$
and
![]() $r=k-1$
in (1.6) to obtain
$r=k-1$
in (1.6) to obtain
 $$ \begin{align} &f(-q,-q^2)f(-q^{2^{2n+2}},-q^{2^{2n+3}}) \notag\\ &\quad =\sum_{k=1}^{2^{n+2}}(-1)^{k+1}q^{{(k-1)(3k-4)}/{2}} f (-q^{7\times2^{2n+1}+2^n(6k-7)},-q^{5\times2^{2n+1}-2^n(6k-7)})\notag\\ &\qquad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)}). \end{align} $$
$$ \begin{align} &f(-q,-q^2)f(-q^{2^{2n+2}},-q^{2^{2n+3}}) \notag\\ &\quad =\sum_{k=1}^{2^{n+2}}(-1)^{k+1}q^{{(k-1)(3k-4)}/{2}} f (-q^{7\times2^{2n+1}+2^n(6k-7)},-q^{5\times2^{2n+1}-2^n(6k-7)})\notag\\ &\qquad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)}). \end{align} $$
Since
![]() $f(-q,-q^2)=E(q)$
,
$f(-q,-q^2)=E(q)$
,
![]() $f(-q^{2^{2n+2}},-q^{2^{2n+3}})=E(q^{2^{2n+2}})$
,
$f(-q^{2^{2n+2}},-q^{2^{2n+3}})=E(q^{2^{2n+2}})$
,
![]() $P(k-1)={(k-1)(3k-4)}/{2}$
, we can rewrite (3.1) as
$P(k-1)={(k-1)(3k-4)}/{2}$
, we can rewrite (3.1) as
 $$ \begin{align} E(q)E(q^{2^{2n+2}})&= \sum_{k=1}^{2^{n+2}}T_k =\sum_{k=1}^{2^{n+2}}(-1)^{k+1} q^{P(k-1)}f(-q^{7\times2^{2n+1}+2^n(6k-7)}, -q^{5\times2^{2n+1}-2^n(6k-7)}),\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)}), \end{align} $$
$$ \begin{align} E(q)E(q^{2^{2n+2}})&= \sum_{k=1}^{2^{n+2}}T_k =\sum_{k=1}^{2^{n+2}}(-1)^{k+1} q^{P(k-1)}f(-q^{7\times2^{2n+1}+2^n(6k-7)}, -q^{5\times2^{2n+1}-2^n(6k-7)}),\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)}), \end{align} $$
where
 $$ \begin{align} T_k&=(-1)^{k+1}q^{P(k-1)}f(-q^{7\times2^{2n+1}+2^n(6k-7)},-q^{5\times2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)}). \end{align} $$
$$ \begin{align} T_k&=(-1)^{k+1}q^{P(k-1)}f(-q^{7\times2^{2n+1}+2^n(6k-7)},-q^{5\times2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)}). \end{align} $$
Now
 $$ \begin{align} T_{2^{n+1}+k}&=(-1)^{2^{n+1}+k+1}q^{P(2^{n+1}+k-1)}f(-q^{7\times2^{2n+1}+2^n(6(2^{n+1}+k)-7)},-q^{5\times2^{2n+1}-2^n(6(2^{n+1}+k)-7)})\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6(2^{n+1}+k)-7)},-q^{7\times2^{2n+1}-2^n(6(2^{n+1}+k)-7)}). \end{align} $$
$$ \begin{align} T_{2^{n+1}+k}&=(-1)^{2^{n+1}+k+1}q^{P(2^{n+1}+k-1)}f(-q^{7\times2^{2n+1}+2^n(6(2^{n+1}+k)-7)},-q^{5\times2^{2n+1}-2^n(6(2^{n+1}+k)-7)})\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6(2^{n+1}+k)-7)},-q^{7\times2^{2n+1}-2^n(6(2^{n+1}+k)-7)}). \end{align} $$
Employing (2.4) and simplifying the exponents of the arguments of the theta functions, we can rewrite (3.4) as
 $$ \begin{align} T_{2^{n+1}+k}&=(-1)^{k+1}q^{P(k-1)}q^{3\times2^{2n+1}+2^n(6k-7)}f(-q^{13\times2^{2n+1}+2^n(6k-7)},-q^{-2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{11\times2^{2n+1}+2^n(6k-7)},-q^{2^{2n+1}-2^n(6k-7)}). \end{align} $$
$$ \begin{align} T_{2^{n+1}+k}&=(-1)^{k+1}q^{P(k-1)}q^{3\times2^{2n+1}+2^n(6k-7)}f(-q^{13\times2^{2n+1}+2^n(6k-7)},-q^{-2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{11\times2^{2n+1}+2^n(6k-7)},-q^{2^{2n+1}-2^n(6k-7)}). \end{align} $$
 $$ \begin{align} T_k+ T_{2^{n+1}+k}&=(-1)^{k+1}q^{P(k-1)}(f(-q^{7\times2^{2n+1}+2^n(6k-7)},-q^{5\times2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)})\notag\\ &\quad +q^{3\times2^{2n+1}+2^n(6k-7)}f(-q^{13\times2^{2n+1}+2^n(6k-7)},-q^{-2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{11\times2^{2n+1}+2^n(6k-7)},-q^{2^{2n+1}-2^n(6k-7)})). \end{align} $$
$$ \begin{align} T_k+ T_{2^{n+1}+k}&=(-1)^{k+1}q^{P(k-1)}(f(-q^{7\times2^{2n+1}+2^n(6k-7)},-q^{5\times2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{5\times2^{2n+1}+2^n(6k-7)},-q^{7\times2^{2n+1}-2^n(6k-7)})\notag\\ &\quad +q^{3\times2^{2n+1}+2^n(6k-7)}f(-q^{13\times2^{2n+1}+2^n(6k-7)},-q^{-2^{2n+1}-2^n(6k-7)})\notag\\ &\quad\times f(-q^{11\times2^{2n+1}+2^n(6k-7)},-q^{2^{2n+1}-2^n(6k-7)})). \end{align} $$
Setting
![]() $a=q^{3\times 2^{2n+1}+2^n(6k-7)}$
,
$a=q^{3\times 2^{2n+1}+2^n(6k-7)}$
,
![]() $b=q^{3\times 2^{2n+1}-2^n(6k-7)}$
,
$b=q^{3\times 2^{2n+1}-2^n(6k-7)}$
,
![]() $c=-q^{2^{2n+2}}$
and
$c=-q^{2^{2n+2}}$
and
![]() $d=-q^{2^{2n+3}}$
in (3.6) gives
$d=-q^{2^{2n+3}}$
in (3.6) gives
 $$ \begin{align} T_k+ T_{2^{n+1}+k}&=(-1)^{k+1}q^{P(k-1)}f(a,b)f(c,d)\notag\\ &=(-1)^{k+1}q^{P(k-1)}f(q^{3\times2^{2n+1}+2^n(6k-7)},q^{3\times2^{2n+1}-2^n(6k-7)})f(-q^{2^{2n+2}},-q^{2^{2n+3}})\notag\\ &=(-1)^{k+1}q^{P(k-1)}f(q^{3\times2^{2n+1}+2^n(6k-7)},q^{3\times2^{2n+1}-2^n(6k-7)})E(q^{2^{2n+2}}). \end{align} $$
$$ \begin{align} T_k+ T_{2^{n+1}+k}&=(-1)^{k+1}q^{P(k-1)}f(a,b)f(c,d)\notag\\ &=(-1)^{k+1}q^{P(k-1)}f(q^{3\times2^{2n+1}+2^n(6k-7)},q^{3\times2^{2n+1}-2^n(6k-7)})f(-q^{2^{2n+2}},-q^{2^{2n+3}})\notag\\ &=(-1)^{k+1}q^{P(k-1)}f(q^{3\times2^{2n+1}+2^n(6k-7)},q^{3\times2^{2n+1}-2^n(6k-7)})E(q^{2^{2n+2}}). \end{align} $$
From (3.2),
 $$ \begin{align} E(q)E(q^{2^{2n+2}})=\sum_{k=1}^{2^{n+1}}(T_k+T_{2^{n+1}+k}). \end{align} $$
$$ \begin{align} E(q)E(q^{2^{2n+2}})=\sum_{k=1}^{2^{n+1}}(T_k+T_{2^{n+1}+k}). \end{align} $$
 $$ \begin{align*} E(q)=\sum_{k=1}^{2^{n+1}}(-1)^{k+1}q^{P(k-1)}f(q^{3\times2^{2n+1}+2^n(6k-7)},q^{3\times2^{2n+1}-2^n(6k-7)}) =\sum_{k=1}^{2^{n+1}}H_k, \end{align*} $$
$$ \begin{align*} E(q)=\sum_{k=1}^{2^{n+1}}(-1)^{k+1}q^{P(k-1)}f(q^{3\times2^{2n+1}+2^n(6k-7)},q^{3\times2^{2n+1}-2^n(6k-7)}) =\sum_{k=1}^{2^{n+1}}H_k, \end{align*} $$
where
![]() $H_k=(-1)^{k+1}q^{P(k-1)}f(q^{3\times 2^{2n+1}+2^n(6k-7)},q^{3\times 2^{2n+1}-2^n(6k-7)})$
. We now arrange the
$H_k=(-1)^{k+1}q^{P(k-1)}f(q^{3\times 2^{2n+1}+2^n(6k-7)},q^{3\times 2^{2n+1}-2^n(6k-7)})$
. We now arrange the
![]() $H_k$
in pairs so that each of these pairs can be reduced to quintuple products. For this purpose, we consider two separate cases according to whether n is even or odd.
$H_k$
in pairs so that each of these pairs can be reduced to quintuple products. For this purpose, we consider two separate cases according to whether n is even or odd.
Case I: n is even. We consider
 $$ \begin{align} S_1&=\sum_{k=1}^{{(2^{n+1}-2)}/{3}}(H_{{(2^{n+2}+2)}/{3}-k+1}+H_{{(2^{n+2}+5)}/{3}+k-1}), \end{align} $$
$$ \begin{align} S_1&=\sum_{k=1}^{{(2^{n+1}-2)}/{3}}(H_{{(2^{n+2}+2)}/{3}-k+1}+H_{{(2^{n+2}+5)}/{3}+k-1}), \end{align} $$
 $$ \begin{align} S_2 &=\sum_{k={(2^{n+1}+1)}/{3}}^{2^n}(H_{k+1-{(2^{n+1}+1)}/{3}}+H_{{(2^{n+2}+5)}/{3}-k}). \end{align} $$
$$ \begin{align} S_2 &=\sum_{k={(2^{n+1}+1)}/{3}}^{2^n}(H_{k+1-{(2^{n+1}+1)}/{3}}+H_{{(2^{n+2}+5)}/{3}-k}). \end{align} $$
Note that
![]() $S_2$
is the sum of
$S_2$
is the sum of
![]() $H_1,H_2,\ldots ,H_{{(2^{n+1}+4)}/{3}}$
and
$H_1,H_2,\ldots ,H_{{(2^{n+1}+4)}/{3}}$
and
![]() $S_1$
is the sum of
$S_1$
is the sum of
![]() $H_{{(2^{n+1}+7)}/{3}}$
,
$H_{{(2^{n+1}+7)}/{3}}$
,
![]() $H_{{(2^{n+1}+10)}/{3}},\ldots ,H_{2^{n+1}}$
and so
$H_{{(2^{n+1}+10)}/{3}},\ldots ,H_{2^{n+1}}$
and so
We also note that
![]() $c_k$
is given by (1.4).
$c_k$
is given by (1.4).
Now
 $$ \begin{align} H_{{(2^{n+2}+2)}/{3}-k+1} & = (-1)^{{(2^{n+2}+2)}/{3}-k}q^{P({(2^{n+2}+2)}/{3}-k)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+2}+2)}/{3}-k+1)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+2}+2)}/{3}-k+1)-7)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+2}+2)}/{3}-k+1} & = (-1)^{{(2^{n+2}+2)}/{3}-k}q^{P({(2^{n+2}+2)}/{3}-k)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+2}+2)}/{3}-k+1)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+2}+2)}/{3}-k+1)-7)}). \end{align} $$
Employing Lemma 2.5 in (3.13) and simplifying the exponents of the arguments of the theta functions, we find that
Also
 $$ \begin{align} H_{{(2^{n+2}+5)}/{3}+k-1} & = (-1)^{{(2^{n+2}+5)}/{3}+k}q^{P({(2^{n+2}+2)}/{3}+k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+2}+2)}/{3}+k)-7)}, q^{3\times2^{2n+1}-2^n(6({(2^{n+2}+2)}/{3}+k)-7)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+2}+5)}/{3}+k-1} & = (-1)^{{(2^{n+2}+5)}/{3}+k}q^{P({(2^{n+2}+2)}/{3}+k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+2}+2)}/{3}+k)-7)}, q^{3\times2^{2n+1}-2^n(6({(2^{n+2}+2)}/{3}+k)-7)}). \end{align} $$
Employing Lemma 2.6 in (3.15) and simplifying the exponents,
Substituting the expressions for
![]() $H_{{(2^{n+2}+2)}/{3}-k+1}$
and
$H_{{(2^{n+2}+2)}/{3}-k+1}$
and
![]() $H_{{(2^{n+2}+5)}/{3}+k-1}$
from (3.14) and (3.17), respectively, in (3.10), we find that
$H_{{(2^{n+2}+5)}/{3}+k-1}$
from (3.14) and (3.17), respectively, in (3.10), we find that
 $$ \begin{align} S_1&=\sum_{k=1}^{{(2^{n+1}-2)}/{3}}(-1)^{k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)},q^{-2^{2n+1}+3\times2^n(2k-1)})). \end{align} $$
$$ \begin{align} S_1&=\sum_{k=1}^{{(2^{n+1}-2)}/{3}}(-1)^{k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)},q^{-2^{2n+1}+3\times2^n(2k-1)})). \end{align} $$
Further,
 $$ \begin{align} H_{k+1-{(2^{n+1}+1)}/{3}} & = (-1)^{k-{(2^{n+1}+1)}/{3}}q^{P(k-{(2^{n+1}+1)}/{3})}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6(k+1-{(2^{n+1}+1)}/{3})-7)},q^{3\times2^{2n+1}-2^n(6(k+1-{(2^{n+1}+1)}/{3})-7)})\notag\\ & = (-1)^{k+1}q^{c_k}f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
$$ \begin{align} H_{k+1-{(2^{n+1}+1)}/{3}} & = (-1)^{k-{(2^{n+1}+1)}/{3}}q^{P(k-{(2^{n+1}+1)}/{3})}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6(k+1-{(2^{n+1}+1)}/{3})-7)},q^{3\times2^{2n+1}-2^n(6(k+1-{(2^{n+1}+1)}/{3})-7)})\notag\\ & = (-1)^{k+1}q^{c_k}f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
Also,
 $$ \begin{align} H_{{(2^{n+2}+5)}/{3}-k} & = (-1)^{{(2^{n+2}+5)}/{3}-k+1}q^{P({(2^{n+2}+5)}/{3}-k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+2}+5)}/{3}-k)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+2}+5)}/{3}-k)-7)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+2}+5)}/{3}-k} & = (-1)^{{(2^{n+2}+5)}/{3}-k+1}q^{P({(2^{n+2}+5)}/{3}-k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+2}+5)}/{3}-k)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+2}+5)}/{3}-k)-7)}). \end{align} $$
Employing Lemma 2.5 in (3.20) and simplifying the exponents,
Using (3.19) and (3.21) in (3.11),
 $$ \begin{align} S_2 &=\sum_{k={(2^{n+1}+1)}/{3}}^{2^n} (-1)^{k+1} q^{c_k}(f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-(2k-1)2^n}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)}, q^{-2^{2n+1}+3\times2^n(2k-1)})). \end{align} $$
$$ \begin{align} S_2 &=\sum_{k={(2^{n+1}+1)}/{3}}^{2^n} (-1)^{k+1} q^{c_k}(f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-(2k-1)2^n}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)}, q^{-2^{2n+1}+3\times2^n(2k-1)})). \end{align} $$
From (3.12), (3.18) and (3.22),
 $$ \begin{align} E(q) & =\bigg(\sum_{k=1}^{{(2^{n+1}-2)}/{3}}+\sum_{k={(2^{n+1}+1)}/{3}}^{2^n}\bigg)(-1)^{k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n (2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)}) \notag\\ &\quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)},q^{-2^{2n+1}+3\times2^n(2k-1)}))\notag\\ & =\sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-2^n(2k-1)}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)},q^{-2^{2n+1}+3\times2^n(2k-1)})). \end{align} $$
$$ \begin{align} E(q) & =\bigg(\sum_{k=1}^{{(2^{n+1}-2)}/{3}}+\sum_{k={(2^{n+1}+1)}/{3}}^{2^n}\bigg)(-1)^{k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n (2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)}) \notag\\ &\quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)},q^{-2^{2n+1}+3\times2^n(2k-1)}))\notag\\ & =\sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-2^n(2k-1)}f(q^{7\times2^{2n+1}-3\times2^n(2k-1)},q^{-2^{2n+1}+3\times2^n(2k-1)})). \end{align} $$
Case II: n is odd. In this case, we consider the sums
 $$ \begin{align} S_3&=\sum_{k=1}^{{(2^{n+1}+2)}/{3}}(H_{{(2^{n+1}+2)}/{3}-k+1}+H_{{(2^{n+1}+5)}/{3}+k-1}), \end{align} $$
$$ \begin{align} S_3&=\sum_{k=1}^{{(2^{n+1}+2)}/{3}}(H_{{(2^{n+1}+2)}/{3}-k+1}+H_{{(2^{n+1}+5)}/{3}+k-1}), \end{align} $$
 $$ \begin{align} S_4 &=\sum_{k={(2^{n+1}+5)}/{3}}^{2^n}(H_{{(2^{n+1}+2)}/{3}+k}+H_{{(2^{n+3}+5)}/{3}-k}). \end{align} $$
$$ \begin{align} S_4 &=\sum_{k={(2^{n+1}+5)}/{3}}^{2^n}(H_{{(2^{n+1}+2)}/{3}+k}+H_{{(2^{n+3}+5)}/{3}-k}). \end{align} $$
Note that
![]() $S_3$
is the sum of
$S_3$
is the sum of
![]() $H_1,H_2,\ldots ,H_{{(2^{n+2}+4)}/{3}}$
and
$H_1,H_2,\ldots ,H_{{(2^{n+2}+4)}/{3}}$
and
![]() $S_4$
is the sum of
$S_4$
is the sum of
![]() $H_{{(2^{n+2}+7)}/{3}}$
,
$H_{{(2^{n+2}+7)}/{3}}$
,
![]() $H_{{(2^{n+2}+10)}/{3}},\ldots ,H_{2^{n+1}}$
and so
$H_{{(2^{n+2}+10)}/{3}},\ldots ,H_{2^{n+1}}$
and so
We also note that
![]() $c_k$
is given by (1.3).
$c_k$
is given by (1.3).
We have
 $$ \begin{align} H_{{(2^{n+1}+2)}/{3}-k+1}&=(-1)^{{(2^{n+1}+2)}/{3}-k}q^{P({(2^{n+1}+2)}/{3}-k)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+1}+2)}/{3}-k+1)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+1}+2)}/{3}-k+1)-7)})\notag\\ &=(-1)^{k}q^{c_k}f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+1}+2)}/{3}-k+1}&=(-1)^{{(2^{n+1}+2)}/{3}-k}q^{P({(2^{n+1}+2)}/{3}-k)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+1}+2)}/{3}-k+1)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+1}+2)}/{3}-k+1)-7)})\notag\\ &=(-1)^{k}q^{c_k}f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
Similarly,
 $$ \begin{align} H_{{(2^{n+1}+5)}/{3}+k-1} & =(-1)^{{(2^{n+1}+5)}/{3}+k}q^{P({(2^{n+1}+5)}/{3}+k-2)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+1}+5)}/{3}+k-1)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+1}+5)}/{3}+k-1)-7)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+1}+5)}/{3}+k-1} & =(-1)^{{(2^{n+1}+5)}/{3}+k}q^{P({(2^{n+1}+5)}/{3}+k-2)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+1}+5)}/{3}+k-1)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+1}+5)}/{3}+k-1)-7)}). \end{align} $$
Using Lemma 2.7 in (3.28) and simplifying the exponents,
Now we employ (2.3) in (3.29) to obtain
 $$ \begin{align} H_{{(2^{n+1}+5)}/{3}+k-1} & =(-1)^{k+1}q^{c_k+(2k-1)2^{n+1}}q^{2^{2n+1}-3\times2^n(2k-1)} \notag\\ & \quad\times f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ & =(-1)^{k+1}q^{c_k+2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+1}+5)}/{3}+k-1} & =(-1)^{k+1}q^{c_k+(2k-1)2^{n+1}}q^{2^{2n+1}-3\times2^n(2k-1)} \notag\\ & \quad\times f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ & =(-1)^{k+1}q^{c_k+2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
Using (3.27) and (3.30) in (3.24),
 $$ \begin{align} S_3&=\sum_{k=1}^{{(2^{n+1}+2)}/{3}}(-1)^{k}q^{c_k}(f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ &\quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})). \end{align} $$
$$ \begin{align} S_3&=\sum_{k=1}^{{(2^{n+1}+2)}/{3}}(-1)^{k}q^{c_k}(f(q^{2^{2n+1}+3\times2^n(2k-1)},q^{5\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ &\quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})). \end{align} $$
Also,
 $$ \begin{align} H_{{(2^{n+1}+2)}/{3}+k} & =(-1)^{{(2^{n+1}+2)}/{3}+k+1}q^{P({(2^{n+1}+2)}/{3}+k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+1}+2)}/{3}+k)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+1}+2)}/{3}+k)-7)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+1}+2)}/{3}+k} & =(-1)^{{(2^{n+1}+2)}/{3}+k+1}q^{P({(2^{n+1}+2)}/{3}+k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+1}+2)}/{3}+k)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+1}+2)}/{3}+k)-7)}). \end{align} $$
Using Lemma 2.7 in (3.32) and simplifying the exponents,
Employing (2.2) in (3.33), we find that
 $$ \begin{align} H_{{(2^{n+1}+2)}/{3}+k} & =(-1)^{k+1}q^{c_k+2^{n+1}(2k-1)}q^{2^{2n+1}-3\times2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ &=(-1)^{k+1}q^{c_k}q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+1}+2)}/{3}+k} & =(-1)^{k+1}q^{c_k+2^{n+1}(2k-1)}q^{2^{2n+1}-3\times2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})\notag\\ &=(-1)^{k+1}q^{c_k}q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)}). \end{align} $$
Further,
 $$ \begin{align} H_{{(2^{n+3}+5)}/{3}-k} & =(-1)^{{(2^{n+3}+5)}/{3}-k+1}q^{P({(2^{n+3}+5)}/{3}-k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+3}+5)}/{3}-k)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+3}+5)}/{3}-k)-7)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+3}+5)}/{3}-k} & =(-1)^{{(2^{n+3}+5)}/{3}-k+1}q^{P({(2^{n+3}+5)}/{3}-k-1)}\notag\\ &\quad\times f(q^{3\times2^{2n+1}+2^n(6({(2^{n+3}+5)}/{3}-k)-7)},q^{3\times2^{2n+1}-2^n(6({(2^{n+3}+5)}/{3}-k)-7)}). \end{align} $$
Using Lemma 2.8 in (3.35), we find that
 $$ \begin{align} H_{{(2^{n+3}+5)}/{3}-k} & =(-1)^{k}q^{c_k+5\times2^{2n+1}-3\times2^n(2k-1)}q^{-5\times2^{2n+1}+3\times2^n(2k-1)} \notag\\ &\quad\times f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ & =(-1)^{k}q^{c_k}f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)}). \end{align} $$
$$ \begin{align} H_{{(2^{n+3}+5)}/{3}-k} & =(-1)^{k}q^{c_k+5\times2^{2n+1}-3\times2^n(2k-1)}q^{-5\times2^{2n+1}+3\times2^n(2k-1)} \notag\\ &\quad\times f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ & =(-1)^{k}q^{c_k}f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)}). \end{align} $$
From (3.34), (3.37) and (3.25),
 $$ \begin{align} S_4 & =\sum_{k={(2^{n+1}+5)}/{3}}^{2^n}(-1)^{k}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})). \end{align} $$
$$ \begin{align} S_4 & =\sum_{k={(2^{n+1}+5)}/{3}}^{2^n}(-1)^{k}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})). \end{align} $$
Substituting the expressions for
![]() $S_3$
and
$S_3$
and
![]() $S_4$
from (3.31) and (3.38), respectively, in (3.26),
$S_4$
from (3.31) and (3.38), respectively, in (3.26),
 $$ \begin{align} E(q)&= \bigg(\sum_{k=1}^{{(2^{n+1}+2)}/{3}}+\sum_{k={(2^{n+1}+5)}/{3}}^{2^n}\bigg)(-1)^{k}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)}, q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ & \quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)}))\notag\\ &=\sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ & \quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})). \end{align} $$
$$ \begin{align} E(q)&= \bigg(\sum_{k=1}^{{(2^{n+1}+2)}/{3}}+\sum_{k={(2^{n+1}+5)}/{3}}^{2^n}\bigg)(-1)^{k}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)}, q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ & \quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)}))\notag\\ &=\sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ & \quad-q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})). \end{align} $$
From (3.23) and (3.39) we find that, for any positive integer n,
 $$ \begin{align} E(q)&= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})), \end{align} $$
$$ \begin{align} E(q)&= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(q^{5\times2^{2n+1}-3\times2^n(2k-1)},q^{2^{2n+1}+3\times2^n(2k-1)})\notag\\ &\quad -q^{2^{2n+1}-2^n(2k-1)}f(q^{-2^{2n+1}+3\times2^n(2k-1)},q^{7\times2^{2n+1}-3\times2^n(2k-1)})), \end{align} $$
where the appropriate expression for
![]() $c_k$
is chosen according to whether n is even or odd.
$c_k$
is chosen according to whether n is even or odd.
Setting
![]() $A=-q^{-2^{2n+1}+2^n(2k-1)}$
and
$A=-q^{-2^{2n+1}+2^n(2k-1)}$
and
![]() $Q=q^{2^{2n+2}}$
in (3.40), we obtain
$Q=q^{2^{2n+2}}$
in (3.40), we obtain
 $$ \begin{align} E(q)&= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(-A^3Q^2,-A^{-3}Q)+A^{-1}f(-A^3Q,-A^{-3}Q^2)). \end{align} $$
$$ \begin{align} E(q)&= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(f(-A^3Q^2,-A^{-3}Q)+A^{-1}f(-A^3Q,-A^{-3}Q^2)). \end{align} $$
Employing the quintuple product identity in (3.41),
 $$ \begin{align*} E(q)&= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(-AQ;Q)_\infty(-A^{-1};Q)_\infty(A^2Q;Q^2)_\infty(A^{-2}Q;Q^2)_\infty(Q;Q)_\infty\\ &= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(A^2Q,A^{-2}Q;Q^2)_\infty(-AQ,-A^{-1},Q;Q)_\infty\\ &= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(q^{2^{n+1}(2k-1)},q^{2^{2n+3}-2^{n+1}(2k-1)};q^{2^{2n+3}})_\infty\\ &\quad\times (q^{2^{2n+1}+2^{n}(2k-1)},q^{2^{2n+1}-2^{n}(2k-1)},q^{2^{2n+2}};q^{2^{2n+2}})_\infty. \end{align*} $$
$$ \begin{align*} E(q)&= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(-AQ;Q)_\infty(-A^{-1};Q)_\infty(A^2Q;Q^2)_\infty(A^{-2}Q;Q^2)_\infty(Q;Q)_\infty\\ &= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(A^2Q,A^{-2}Q;Q^2)_\infty(-AQ,-A^{-1},Q;Q)_\infty\\ &= \sum_{k=1}^{2^n}(-1)^{n+k+1}q^{c_k}(q^{2^{n+1}(2k-1)},q^{2^{2n+3}-2^{n+1}(2k-1)};q^{2^{2n+3}})_\infty\\ &\quad\times (q^{2^{2n+1}+2^{n}(2k-1)},q^{2^{2n+1}-2^{n}(2k-1)},q^{2^{2n+2}};q^{2^{2n+2}})_\infty. \end{align*} $$
Thus we have completed the proof of Conjecture 1.2.