Equation (2.10) in Costa, Brandt & Picano (Reference Costa, Brandt and Picano2020) for the lift force model used in the point-particle direct numerical simulations (DNS), and which is derived from the classical lift force of Saffman (Reference Saffman1965),
 $$\begin{eqnarray}\boldsymbol{F}_{l}=1.615J\unicode[STIX]{x1D707}D|\boldsymbol{U}_{s}|\sqrt{\frac{D^{2}|\unicode[STIX]{x1D74E}|}{\unicode[STIX]{x1D708}}}\frac{\unicode[STIX]{x1D74E}\times \boldsymbol{U}_{s}}{|\unicode[STIX]{x1D74E}|\,|\boldsymbol{U}_{s}|},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{F}_{l}=1.615J\unicode[STIX]{x1D707}D|\boldsymbol{U}_{s}|\sqrt{\frac{D^{2}|\unicode[STIX]{x1D74E}|}{\unicode[STIX]{x1D708}}}\frac{\unicode[STIX]{x1D74E}\times \boldsymbol{U}_{s}}{|\unicode[STIX]{x1D74E}|\,|\boldsymbol{U}_{s}|},\end{eqnarray}$$does not correspond to the force model actually used in the point-particle DNS with lift force presented in the manuscript. Instead, the following equation was used:
 $$\begin{eqnarray}\boldsymbol{F}_{l}=1.615J\unicode[STIX]{x1D707}|\unicode[STIX]{x1D74E}|D^{2}\sqrt{\frac{D^{2}|\unicode[STIX]{x1D74E}|}{\unicode[STIX]{x1D708}}}\frac{\unicode[STIX]{x1D74E}\times \boldsymbol{U}_{s}}{|\unicode[STIX]{x1D74E}|\,|\boldsymbol{U}_{s}|},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{F}_{l}=1.615J\unicode[STIX]{x1D707}|\unicode[STIX]{x1D74E}|D^{2}\sqrt{\frac{D^{2}|\unicode[STIX]{x1D74E}|}{\unicode[STIX]{x1D708}}}\frac{\unicode[STIX]{x1D74E}\times \boldsymbol{U}_{s}}{|\unicode[STIX]{x1D74E}|\,|\boldsymbol{U}_{s}|},\end{eqnarray}$$ which replaces the first occurrence of the term  $|\boldsymbol{U}_{s}|$ on the right-hand-side of (1) with
$|\boldsymbol{U}_{s}|$ on the right-hand-side of (1) with  $|\unicode[STIX]{x1D74E}|D$. We recall that two cases were considered in the manuscript depending on the value of
$|\unicode[STIX]{x1D74E}|D$. We recall that two cases were considered in the manuscript depending on the value of  $J$ in the lift force equation:
$J$ in the lift force equation:  $J=1$ in the case denoted PP-Saffman; and
$J=1$ in the case denoted PP-Saffman; and  $J$ given by
$J$ given by
 $$\begin{eqnarray}J=0.3\left(1+\tanh \left[{\textstyle \frac{5}{2}}\left(\log _{10}\unicode[STIX]{x1D700}+0.191\right)\right]\right)\left({\textstyle \frac{2}{3}}+\tanh (6\unicode[STIX]{x1D700}-1.92)\right),\end{eqnarray}$$
$$\begin{eqnarray}J=0.3\left(1+\tanh \left[{\textstyle \frac{5}{2}}\left(\log _{10}\unicode[STIX]{x1D700}+0.191\right)\right]\right)\left({\textstyle \frac{2}{3}}+\tanh (6\unicode[STIX]{x1D700}-1.92)\right),\end{eqnarray}$$ with  $\unicode[STIX]{x1D700}=\sqrt{|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D708}}/|\boldsymbol{U}_{s}|$, in the case denoted PP-McLaughlin.
$\unicode[STIX]{x1D700}=\sqrt{|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D708}}/|\boldsymbol{U}_{s}|$, in the case denoted PP-McLaughlin.
Also, equation (2.13) of the manuscript – describing the perfectly elastic hard-sphere rebound – is incorrect; the term  $D/2$ should be
$D/2$ should be  $D$:
$D$:
 $$\begin{eqnarray}Y=V\unicode[STIX]{x0394}t_{s}-(Y_{in}-D).\end{eqnarray}$$
$$\begin{eqnarray}Y=V\unicode[STIX]{x0394}t_{s}-(Y_{in}-D).\end{eqnarray}$$Despite the lapse in the manuscript, equation (4) was implemented correctly (Costa et al. Reference Costa, Brandt and Picano2020).
The results from the point-particle DNS with the model reported in (2.10) of Costa et al. (Reference Costa, Brandt and Picano2020) ((1) above) differ from those reported in the manuscript, and are shown in figure 1 (cf. figures 7 and 8 of Costa et al. (Reference Costa, Brandt and Picano2020)). The statistics presented here have been collected in the fully developed state from 600 samples over a time interval of  $250h/U_{b}$, which ensured statistical convergence of the results. The results from the point-particle cases presented in the original manuscript are also reproduced here with this (higher) statistical sampling, and show very minor differences with respect to figures 7 and 8 of Costa et al. (Reference Costa, Brandt and Picano2020).
$250h/U_{b}$, which ensured statistical convergence of the results. The results from the point-particle cases presented in the original manuscript are also reproduced here with this (higher) statistical sampling, and show very minor differences with respect to figures 7 and 8 of Costa et al. (Reference Costa, Brandt and Picano2020).
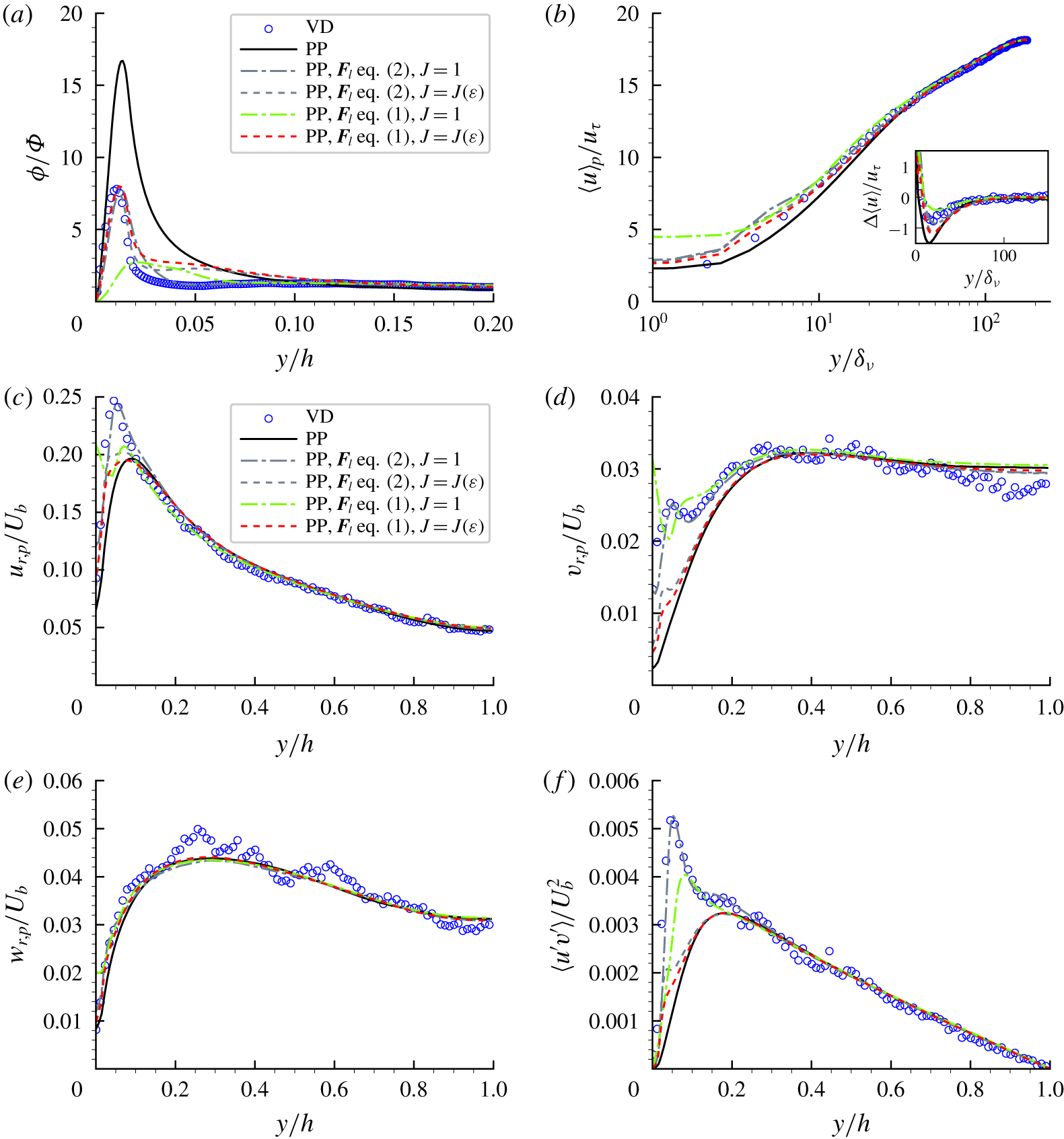
Figure 1. Same as figure 7 (panels a and b) and figure 8 (panels c to e) of Costa et al. (Reference Costa, Brandt and Picano2020), where (1) is correctly used for the point-particle DNS with lift force models. As indicated in the legend, the grey lines correspond to the data shown in the paper, where (2) is used to compute the lift force, and the green and red lines correspond to the results when (1) is used instead.
In light of these results, the conclusions drawn from the results in the last section of § 3 of the manuscript must be therefore reformulated:
(i) The Saffman lift model does not correctly predict the near-wall statistics of the interface-resolved DNS very close to the wall, including the near-wall concentration peak.
(ii) The equation proposed by Mei (Reference Mei1992) that fits the model of McLaughlin (Reference McLaughlin1991) shows results similar to those reported in the original manuscript for this model. That is, it predicts well the near-wall concentration peak, and fails to predict the other observables near the wall.
(iii) Equation (2) for
 $\boldsymbol{F}_{l}$ presented above, with
$\boldsymbol{F}_{l}$ presented above, with  $J=1$, predicts very well all the observables in figure 1.
$J=1$, predicts very well all the observables in figure 1.
We have therefore accidentally discovered that the expression (2) for  $\boldsymbol{F}_{l}$ predicts the observed particle statistics very well. Still, the reason for the strikingly good agreement remains elusive to us. We hope that this result can be further exploited for the improvement lift force models for point-particle simulations of wall-bounded turbulent flows.
$\boldsymbol{F}_{l}$ predicts the observed particle statistics very well. Still, the reason for the strikingly good agreement remains elusive to us. We hope that this result can be further exploited for the improvement lift force models for point-particle simulations of wall-bounded turbulent flows.
Acknowledgement
We kindly thank Z. Cui from Tsinghua University for the feedback that led to the discovery of this issue.





