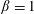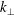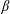1 Introduction
Plasma turbulence is ubiquitous in the universe. In near-Earth collisionless plasmas – such as the solar corona, the solar wind and the Earth’s magnetosphere – turbulence plays a fundamental role in the transport of energy from large fluid scales to small kinetic scales. This cascade of turbulence energy across scales is usually characterized by a power law in the energy spectrum of fluctuating quantities. A spectral break (change of the power law index) in the energy spectrum near the proton scale defines the transition into the dissipation range where the turbulence energy is converted into plasma heat and/or particle energization. How this process occurs remains a key subject of current kinetic plasma research in space observations (He et al. Reference He, Tu, Marsch and Yao2012; Alexandrova et al. Reference Alexandrova, Chen, Sorriso-Valvo, Horbury and Bale2013; Chen et al. Reference Chen, Boldyrev, Xia and Perez2013; Narita et al. Reference Narita, Nakamura, Baumjohann, Glassmeier, Motschmann, Giles, Magnes, Fischer, Torbert and Russell2016; Perrone et al. Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016; Roberts et al. Reference Roberts, Alexandrova, Kajdi, Turc, Perrone, Escoubet and Walsh2017; Vech, Klein & Kasper Reference Vech, Klein and Kasper2017; Wang et al. Reference Wang, Tu, He and Wang2018), numerical simulations (Howes et al. Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008b ; Parashar et al. Reference Parashar, Shay, Cassak and Matthaeus2009; Karimabadi et al. Reference Karimabadi, Roytershteyn, Wan, Matthaeus, Daughton, Wu, Shay, Loring, Borovsky and Leonardis2013; TenBarge, Howes & Dorland Reference TenBarge, Howes and Dorland2013; Chang, Peter Gary & Wang Reference Chang, Peter Gary and Wang2014; Vásconez et al. Reference Vásconez, Valentini, Camporeale and Veltri2014; Franci et al. Reference Franci, Landi, Matteini, Verdini and Hellinger2015; Told et al. Reference Told, Jenko, TenBarge, Howes and Hammett2015; Li et al. Reference Li, Howes, Klein and TenBarge2016; Navarro et al. Reference Navarro, Teaca, Told, Groselj, Crandall and Jenko2016; Parashar & Matthaeus Reference Parashar and Matthaeus2016; Wan et al. Reference Wan, Matthaeus, Roytershteyn, Parashar, Wu and Karimabadi2016; Grośelj et al. Reference Grośelj, Cerri, Navarro, Willmott, Told, Loureiro, Califano and Jenko2017; Hughes et al. Reference Hughes, Gary, Wang and Parashar2017; Yang et al. Reference Yang, Matthaeus, Parashar, Haggerty, Roytershteyn, Daughton, Wan, Shi and Chen2017; Cerri, Kunz & Califano Reference Cerri, Kunz and Califano2018; Grośelj et al. Reference Grośelj, Chen, Mallet, Samtaney, Schneider and Jenko2018; Arzamasskiy et al. Reference Arzamasskiy, Kunz, Chandran and Quataert2019; Kawazura, Barnes & Schekochihin Reference Kawazura, Barnes and Schekochihin2019) and theoretical efforts (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a ; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Boldyrev et al. Reference Boldyrev, Horaites, Xia and Perez2013; Howes Reference Howes2015; Passot & Sulem Reference Passot and Sulem2015; Schekochihin et al. Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016; Adkins & Schekochihin Reference Adkins and Schekochihin2018; Schekochihin, Kawazura & Barnes Reference Schekochihin, Kawazura and Barnes2019).
Recent advances in temporal and phase-space resolution in spacecraft observations (Servidio et al. Reference Servidio, Chasapis, Matthaeus, Perrone, Valentini, Parashar, Veltri, Gershman, Russell and Giles2017; Chen, Klein & Howes Reference Chen, Klein and Howes2019) and numerical simulations (Li et al. Reference Li, Howes, Klein and TenBarge2016; Klein, Howes & TenBarge Reference Klein, Howes and TenBarge2017; Cerri et al. Reference Cerri, Kunz and Califano2018) have opened up new pathways for characterizing turbulence: using the velocity distribution functions (VDFs) to investigate non-thermal structures in the velocity space arising from the dissipation mechanisms. These velocity-space structures contain important information about the transfer of energy to particles from turbulent fields, ultimately leading to the thermodynamic heating of the plasma. Indeed, information in the VDFs underlying the nature of dissipation has been explored and identified in recent three-dimensional (3-D) kinetic turbulence simulations (Li et al. Reference Li, Howes, Klein and TenBarge2016; Klein et al. Reference Klein, Howes and TenBarge2017; Cerri et al. Reference Cerri, Kunz and Califano2018). Current space missions such as the Multiscale Magnetosphere Mission (MMS) (Burch et al. Reference Burch, Moore, Torbert and Giles2016) have the capability to sample well-resolved VDFs at high time cadence. Utilizing and understanding the crucial information contained in the phase space represents a new avenue in kinetic turbulence research (Howes Reference Howes2017).
Recently, an innovative technique tracking the net energy transfer between turbulent fields and plasma particles in velocity space was developed, the field–particle correlation technique, (Klein & Howes Reference Klein and Howes2016; Howes, Klein & Li Reference Howes, Klein and Li2017), and first illustrated in a nonlinear one-dimensional-one-velocity (1D–1V) Vlasov–Poisson plasma. Clear velocity-space signatures of direct energy exchange between the electric field and the particles was demonstrated. The 3-D implementation of this technique and application to single-point data sets was performed in gyrokinetic turbulence simulations, which showed velocity-space structures associated with ion Landau resonance (Klein et al. Reference Klein, Howes and TenBarge2017). It was also applied to diagnose the particle energization in current sheets arising self-consistently from Alfvén wave collisions (Howes Reference Howes2016), showing spatially localized energization by Landau damping (Howes, McCubbin & Klein Reference Howes, McCubbin and Klein2018). It has recently been applied to well-resolved data from the MMS, which has provided evidence for electron Landau damping in the turbulent magnetosheath (Chen et al. Reference Chen, Klein and Howes2019).
Both of these previous numerical studies sampled the 3-D electromagnetic turbulence simulation at single spatial points. Here we apply this technique in Fourier space for the first time. Sampling in Fourier space is a complementary approach to sampling in spatial space in numerical simulations, but it requires full spatial information of the system and therefore cannot be applied to spacecraft data that often make in situ measurements from only one or a few spatial locations at a given time. Nevertheless, application of the field–particle correlation technique in Fourier space can be advantageous. It can be particularly useful in revealing information on the length scale dependence of the energy transfer mechanisms. In Alfvénic turbulence, the nonlinear turbulent cascade of Alfvén waves may undergo significant collisionless damping when it reaches the kinetic regime
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gtrsim 1$
(where
$k_{\bot }$
is the perpendicular wavenumber and
$\unicode[STIX]{x1D70C}_{i}$
the ion gyroradius), where the kinetic Alfvén wave becomes dispersive. In this dispersive regime, the resonant velocity
$v_{p\Vert }$
associated with the collisionless damping of kinetic Alfvén waves depends on
$k_{\bot }$
linearly. Sampling at a single point will measure contributions from a broad range of
$k_{\bot }$
modes, each with a different resonant velocity, potentially smearing out any resonant signatures of the energy transfer in velocity space. Analysing in Fourier space, however, each turbulent wave mode specified by
$\boldsymbol{k}=(k_{x},k_{y},k_{z})$
has
$v_{p\Vert }$
that directly depends on
$k_{\bot }$
, producing a relatively clean resonant signature at that
$v_{p\Vert }$
even in a turbulent plasma containing a broadband spectrum of modes.
In this work, we study the properties of energy transfer in a
$\unicode[STIX]{x1D6FD}=1$
, gyrokinetic turbulence simulation. Resonant signatures associated with Landau resonances are observed in particle velocity space in all diagnosed Fourier modes spanning the dissipation range of the simulation. The energy transfer signatures also show a clear
$k_{\bot }$
dependence of the resonant velocity (moving to higher resonant velocities with increasing
$k_{\bot }$
), reflecting the characteristic of phase velocity of kinetic Alfvén waves. Remarkable agreement with the
$\unicode[STIX]{x1D6FD}$
dependence of the resonant velocity is observed in the energy transfer signatures in identical simulations with lower
$\unicode[STIX]{x1D6FD}$
. Our results demonstrate the resonant nature of field–particle energy transfer by collisionless wave–particle interactions with Alfvén waves.
This paper is organized as follows: the theory of nonlinear field–particle energy transfer in collisionless plasmas in three dimensions and in Fourier space is outlined in § 2.1; field–particle correlations are defined and constructed in the gyrokinetic framework in § 2.2; the form of field–particle correlations in Fourier space is derived in § 2.3; the sampled spectrum in Fourier space is illustrated in § 2.4; the simulation set-up and parameters are described in § 2.5; the results on energy evolution of the systems are presented in § 3; field–particle correlations in gyrotropic velocity space
$(v_{\Vert },v_{\bot })$
are examined in § 4.1; primary results of this work including (i) examples of
$v_{\bot }$
-integrated, reduced correlations of individual Fourier modes for electrons and ions, (ii) correlations summing over a range of
$k_{z}$
modes for all diagnosed
$(k_{x},k_{y})$
Fourier modes, (iii)
$k_{\bot }$
dependence in summed-
$k_{z}$
modes and (iv)
$\unicode[STIX]{x1D6FD}_{i}$
dependence of energy transfer signatures are presented and discussed in § 4.2; we further discuss and summarize our results in § 5.
2 Techniques and simulation set-up
Here we describe the field–particle correlation technique in terms of its formulation in physical and Fourier space, its implementation within the gyrokinetic framework, and provide the set-up of the simulation.
2.1 Rate of energy transfer between fields and particles in a collisionless plasma
Dissipation in weakly collisional plasmas consists of a two-step process (Howes Reference Howes2017). First, energy is transferred from the electromagnetic fields to plasma particles, appearing as non-thermal energy in the particle velocity distributions. This collisionless process is reversible. Then, the non-thermal energy is cascaded in phase space, generating fine structures in the velocity space that are eventually smoothed out as thermal energy in the particle distributions via the action of collisions, and hence realizing irreversible heating of the plasma (Howes Reference Howes2008; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). The energy transfer directly measured by the field–particle correlation technique is the net energy transferred between the electromagnetic fields and plasma particles in the first step.
The theory describing the energy transfer between fields and plasma particles, which is directly measured in field–particle correlations, was first derived for a 1D–1V Vlasov–Poisson plasma (Klein & Howes Reference Klein and Howes2016; Howes et al.
Reference Howes, Klein and Li2017), and subsequently for a 3D–3V electromagnetic plasma (Klein et al.
Reference Klein, Howes and TenBarge2017). Here we briefly summarize the key points of the theory in 3D–3V, using insights from the 1D–1V model. Consider the Boltzmann’s equation for species
$s(=i,e)$
in a proton–electron plasma
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{s}+\frac{q_{s}}{m_{s}}\left(\boldsymbol{E}+\frac{\boldsymbol{v}\times \boldsymbol{B}}{c}\right)\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}=\left(\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}\right)_{c}.\end{eqnarray}$$
Focusing on the net collisionless energy transfer in the first step of dissipation, we neglect the collision term,
$(\unicode[STIX]{x2202}f_{s}/\unicode[STIX]{x2202}t)_{c}$
, on the right. We then multiply the whole equation by
$m_{s}v^{2}/2$
to obtain an equation for the rate of change of phase-space energy density,
$w_{s}\equiv (m_{s}v^{2}/2)f_{s}$
,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}w_{s}}{\unicode[STIX]{x2202}t}=-\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}w_{s}-q_{s}\frac{v^{2}}{2}\boldsymbol{E}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}-\frac{q_{s}}{c}\frac{v^{2}}{2}(\boldsymbol{v}\times \boldsymbol{B})\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}.\end{eqnarray}$$
When integrating over all space and velocity,
$w_{s}$
gives the microscopic kinetic energy
$W_{s}$
$$\begin{eqnarray}W_{s}\equiv \int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{v}\frac{1}{2}m_{s}v^{2}f_{s}.\end{eqnarray}$$
When integrating (2.2) over all space, the first term on the right vanishes for periodic or infinite spatial boundaries. When integrating over velocity space, the magnetic force term involves
$\boldsymbol{v}\boldsymbol{\cdot }(\boldsymbol{v}\times \boldsymbol{B})=0$
and therefore does not contribute to the change of the microscopic kinetic energy
$W_{s}$
, as expected. The change of the microscopic kinetic energy, or equivalently, the energy transfer to species
$s$
, comes from the electric field term. We can further separate the
$E_{\Vert }$
and
$\boldsymbol{E}_{\bot }$
contributions to the rate of change of the microscopic kinetic energy as
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}W_{s}}{\unicode[STIX]{x2202}t}=-\frac{q_{s}}{2}\int \text{d}^{3}\boldsymbol{x}\int \,\text{d}^{3}\boldsymbol{v}\,v^{2}\left(E_{\Vert }\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}v_{\Vert }}+\boldsymbol{E}_{\bot }\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}_{\bot }}\right),\end{eqnarray}$$
where ‘
$\Vert$
’ is with respect to the local magnetic field. The first and second terms on the right represent energy transfer mediated by
$E_{\Vert }$
and
$\boldsymbol{E}_{\bot }$
, respectively. Note that this rate of energy density transfer, when integrated over velocity, simply yields the rate the work done by the electric field,
$\boldsymbol{J}_{s}\boldsymbol{\cdot }\boldsymbol{E}=J_{s\Vert }\boldsymbol{\cdot }E_{\Vert }+\boldsymbol{J}_{s\bot }\boldsymbol{\cdot }\boldsymbol{E}_{\bot }$
(Klein & Howes Reference Klein and Howes2016; Howes et al.
Reference Howes, Klein and Li2017; Klein et al.
Reference Klein, Howes and TenBarge2017).
2.2 Field–particle correlations and gyrokinetics
We can now construct the field–particle correlations based on (2.4). Without integrating over space or velocity, the transfer rate of phase-space energy density can be directly computed by correlating
$E_{\Vert }$
or
$\boldsymbol{E}_{\bot }$
with the corresponding velocity derivative of
$f_{s}$
at a point
$\boldsymbol{x}$
and time
$t$
over a correlation interval
$\unicode[STIX]{x1D70F}$
as
$$\begin{eqnarray}C_{E_{\Vert }}(\boldsymbol{x},\boldsymbol{v},t,\unicode[STIX]{x1D70F})=C\left(-q_{s}\frac{v_{\Vert }^{2}}{2}\frac{\unicode[STIX]{x2202}f_{s}(\boldsymbol{x},\boldsymbol{v},t)}{\unicode[STIX]{x2202}v_{\Vert }},E_{\Vert }(\boldsymbol{x},t)\right)\end{eqnarray}$$
$$\begin{eqnarray}C_{E_{\bot }}(\boldsymbol{x},\boldsymbol{v},t,\unicode[STIX]{x1D70F})=C\left(-q_{s}\frac{v_{\bot 1}^{2}}{2}\frac{\unicode[STIX]{x2202}f_{s}(\boldsymbol{x},\boldsymbol{v},t)}{\unicode[STIX]{x2202}v_{\bot 1}},E_{\bot 1}(\boldsymbol{x},t)\right)+C\left(\!-q_{s}\frac{v_{\bot 2}^{2}}{2}\frac{\unicode[STIX]{x2202}f_{s}(\boldsymbol{x},\boldsymbol{v},t)}{\unicode[STIX]{x2202}v_{\bot 2}},E_{\bot 2}(\boldsymbol{x},t)\!\right),\end{eqnarray}$$
where the unnormalized correlation on the right is defined as
$$\begin{eqnarray}C(A,B)=\frac{1}{N}\mathop{\sum }_{j=i+1}^{i+N}A_{j}B_{j}\end{eqnarray}$$
for real quantities
$A_{j}$
and
$B_{j}$
measured at discrete times
$t_{j}=j\unicode[STIX]{x0394}t$
over a correlation interval
$\unicode[STIX]{x1D70F}=N\unicode[STIX]{x0394}t$
that starts from an initial time
$t_{i+1}$
. The factor
$v^{2}=v_{\Vert }^{2}+v_{\bot }^{2}$
in (2.4) is reduced to
$v_{\Vert }^{2}$
in (2.5) upon integration
$\int \text{d}\boldsymbol{v}_{\bot }$
as it can be separated from
$\int \text{d}v_{\Vert }$
. The correlation interval
$\unicode[STIX]{x1D70F}$
is an important parameter in the unnormalized correlation. When
$\unicode[STIX]{x1D70F}$
is set to zero, the unnormalized correlation measures the instantaneous energy transfer at each time
$t$
, which often contains a large oscillatory component due to undamped wave motions To measure the net secular or long-term energy transfer,
$\unicode[STIX]{x1D70F}$
is chosen to be sufficiently long such that the oscillatory component in the instantaneous energy transfer, which is often large but does not contribute to the net energy transfer, can be averaged out. Normally, one wave period of the outer-scale mode is sufficient (Howes et al.
Reference Howes, Klein and Li2017). The parallel correlation
$C_{E_{\Vert }}(\boldsymbol{x},\boldsymbol{v},t,\unicode[STIX]{x1D70F})$
measures the net energy transfer rate mediated by the parallel electric field, and is therefore a suitable measure for Landau damping (Landau Reference Landau1946), or mechanisms like strong-guide-field magnetic reconnection that may be dominated by
$E_{\Vert }$
(Dahlin, Drake & Swisdak Reference Dahlin, Drake and Swisdak2016); it, however, does not capture transit time damping (Barnes Reference Barnes1966; Quataert Reference Quataert1998) that arises from the change in the magnetic field strength. Similarly, the perpendicular correlation
$C_{E_{\bot }}(\boldsymbol{x},\boldsymbol{v},t,\unicode[STIX]{x1D70F})$
captures the net transfer rate mediated by the perpendicular electric field, and is therefore suitable for determining cyclotron damping (Coleman Reference Coleman1968; Isenberg & Hollweg Reference Isenberg and Hollweg1983) or stochastic ion heating (Chen, Lin & White Reference Chen, Lin and White2001; Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). In this study using gyrokinetic simulations, we cannot explore perpendicular energization due to the conservation of the magnetic moment in gyrokinetic theory, so we focus here on the net energy transfer rate accomplished by
$E_{\Vert }$
.
In gyrokinetics, the system evolves in a three-spatial and two-velocity dimension (3D–2V) phase space, where the two velocity coordinates are
$v_{\Vert }$
and
$v_{\bot }$
. The distribution function to the first order in gyrokinetics (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006) is given by
$$\begin{eqnarray}f_{s}(v_{\Vert },v_{\bot })=\left(1-\frac{q_{s}\unicode[STIX]{x1D711}}{T_{0s}}\right)F_{0s}(v)+h_{s}(v_{\Vert },v_{\bot }),\end{eqnarray}$$
where
$F_{0s}=(n_{0s}/\unicode[STIX]{x03C0}^{3/2}v_{ts}^{3})\exp (-v^{2}/v_{ts}^{2})$
is the equilibrium Maxwellian distribution,
$q_{s}\unicode[STIX]{x1D711}/T_{0s}$
is the Boltzmann term (
$q_{s}$
the species charge and
$\unicode[STIX]{x1D711}$
the electric potential),
$h_{s}$
is the first-order gyroaveraged part of the perturbed distribution. When substituting
$f_{s}(v_{\Vert },v_{\bot })$
into the first term in (2.4), we see that
$\unicode[STIX]{x2202}F_{0s}(v)/\unicode[STIX]{x2202}v_{\Vert }$
is odd in
$v_{\Vert }$
, and is multiplied by an even power
$v_{\Vert }^{2}$
. Thus, this term vanishes upon integration over all
$v_{\Vert }$
(again,
$\int \text{d}\boldsymbol{v}_{\bot }$
can be separated from
$\int \text{d}v_{\Vert }$
here). Hence, the equilibrium Maxwellian distribution and the Boltzmann term in (2.8) do not contribute to the net energy transfer in the field–particle correlation in (2.5). The perturbed, gyroaveraged contribution
$h_{s}$
can be used in place of
$f_{s}$
for the purpose of calculating field–particle correlations.
Another convenient transformation used is the complementary distribution function
$g_{s}$
(Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009)
$$\begin{eqnarray}g_{s}(v_{\Vert },v_{\bot })=h_{s}(v_{\Vert },v_{\bot })-\frac{q_{s}F_{0s}}{T_{0s}}\left\langle \unicode[STIX]{x1D711}-\frac{\boldsymbol{v}_{\bot }\boldsymbol{\cdot }\boldsymbol{A}_{\bot }}{c}\right\rangle _{\boldsymbol{R}_{s}},\end{eqnarray}$$
where
$\langle \cdots \!\,\rangle$
represents gyroaveraging at constant guiding centre
$\boldsymbol{R}_{s}$
, capturing the perturbations to the Maxwellian distribution in the moving frame of Alfvén waves. It retains the parallel perturbations of
$\unicode[STIX]{x1D6FF}f_{s}(\equiv f_{s}-F_{0s})$
in (2.8), and is therefore appropriate for calculating the net energy transfer. Note that the term
$\langle \unicode[STIX]{x1D711}-\boldsymbol{v}_{\bot }\boldsymbol{\cdot }\boldsymbol{A}_{\bot }/c\rangle _{\boldsymbol{R}_{s}}$
is independent of
$v_{\Vert }$
, and therefore yields zero upon integration
$\int \text{d}v_{\Vert }$
when substituted into the first term in (2.4). Therefore, this term is the same, whether evaluated with
$h_{s}$
or
$g_{s}$
. As a result, the correlation
$C_{E_{\Vert }}$
in (2.5), which is based on this term, is quantitatively similar using
$h_{s}$
or
$g_{s}$
, but
$g_{s}$
contains less additional terms and can more clearly reveal structures near the resonant velocity in the distribution functions themselves.
Here we will use
$g_{s}$
in the calculation of field–particle correlations, so the specific parallel field–particle correlation used to analyse the gyrokinetic turbulence simulations here takes the form
$$\begin{eqnarray}C_{E_{\Vert }}(\boldsymbol{x},v_{\Vert },v_{\bot },t,\unicode[STIX]{x1D70F})=C\left(-q_{s}\frac{v_{\Vert }^{2}}{2}\frac{\unicode[STIX]{x2202}g_{s}(\boldsymbol{x},v_{\Vert },v_{\bot },t)}{\unicode[STIX]{x2202}v_{\Vert }},E_{\Vert }(\boldsymbol{x},t)\right),\end{eqnarray}$$
where
$E_{\Vert }$
is gyroaveraged. For simplicity, we refer to this form of parallel correlation that depends on gyrotropic velocity space
$(v_{\Vert },v_{\bot })$
as
$C_{E_{\Vert }}(v_{\Vert },v_{\bot },t)$
. The parallel reduced correlation
$C_{E_{\Vert }}(v_{\Vert },t)$
, defined by integrating
$C_{E_{\Vert }}(v_{\Vert },v_{\bot },t)$
over all
$v_{\bot }$
, is given by
$$\begin{eqnarray}C_{E_{\Vert }}(v_{\Vert },t,\unicode[STIX]{x1D70F})=\int v_{\bot }\,\text{d}v_{\bot }C_{E_{\Vert }}(v_{\Vert },v_{\bot },t,\unicode[STIX]{x1D70F}).\end{eqnarray}$$
2.3 Field–particle correlations in Fourier space
To derive the appropriate form of the field–particle correlation in Fourier space, we first express the electric field at a single position
$\boldsymbol{x}$
by a Fourier series
$$\begin{eqnarray}\boldsymbol{E}(\boldsymbol{x})=\mathop{\sum }_{\boldsymbol{k}}\boldsymbol{E}_{\boldsymbol{k}}\text{e}^{\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}},\end{eqnarray}$$
summed over all Fourier modes
$\boldsymbol{k}$
in a 3-D domain of volume
$L^{3}$
. The particle velocity distribution function
$f_{s}(\boldsymbol{x})$
is expressed similarly in terms of its Fourier coefficients
$f_{s\boldsymbol{k}}$
. The product of two real quantities
$A(\boldsymbol{x})$
and
$B(\boldsymbol{x})$
integrated over a volume
$L^{3}$
can be converted to a sum over the product of the Fourier coefficients
$$\begin{eqnarray}\int \text{d}^{3}\boldsymbol{x}\,A(\boldsymbol{x})B(\boldsymbol{x})=L^{3}\mathop{\sum }_{\boldsymbol{k}}A_{\boldsymbol{k}}^{\ast }B_{\boldsymbol{ k}}=L^{3}\mathop{\sum }_{\boldsymbol{k}}A_{\boldsymbol{k}}B_{\boldsymbol{k}}^{\ast },\end{eqnarray}$$
where the complex Fourier coefficients
$A_{\boldsymbol{k}}$
and
$B_{\boldsymbol{k}}$
both satisfy the reality condition
$A_{\boldsymbol{k}}=A_{-\boldsymbol{k}}^{\ast }$
. Substituting these Fourier series into (2.4) and using this relation, we obtain the rate of change of microscopic kinetic energy in terms of the Fourier coefficients of the electric field and particle distribution function,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}W_{s}}{\unicode[STIX]{x2202}t}=\mathop{\sum }_{\boldsymbol{k}}\left(-\frac{q_{s}}{2}\right)L^{3}\int \text{d}^{3}\boldsymbol{v}\,v^{2}\left(E_{\Vert \boldsymbol{k}}\frac{\unicode[STIX]{x2202}f_{s\boldsymbol{k}}^{\ast }}{\unicode[STIX]{x2202}v_{\Vert }}+\boldsymbol{E}_{\bot \boldsymbol{k}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s\boldsymbol{k}}^{\ast }}{\unicode[STIX]{x2202}\boldsymbol{v}_{\bot }}\right).\end{eqnarray}$$
Without summing over all Fourier modes, the contribution to the change of particle energy from each Fourier mode
$\boldsymbol{k}$
is given by the summand, leading to the following forms of the field–particle correlations in Fourier space corresponding to (2.5) and (2.6):
$$\begin{eqnarray}\displaystyle & \displaystyle C_{E_{\Vert }}(\boldsymbol{k},\boldsymbol{v},t,\unicode[STIX]{x1D70F})=C\left(-q_{s}\frac{v_{\Vert }^{2}}{2}\frac{\unicode[STIX]{x2202}f_{s\boldsymbol{k}}^{\ast }(\boldsymbol{v},t)}{\unicode[STIX]{x2202}v_{\Vert }},E_{\Vert \boldsymbol{k}}(t)\right) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{E_{\bot }}(\boldsymbol{k},\boldsymbol{v},t,\unicode[STIX]{x1D70F})=C\left(-q_{s}\frac{v_{\bot 1}^{2}}{2}\frac{\unicode[STIX]{x2202}f_{s\boldsymbol{k}}^{\ast }(\boldsymbol{v},t)}{\unicode[STIX]{x2202}v_{\bot 1}},E_{\bot 1\boldsymbol{k}}(t)\right)+C\left(-q_{s}\frac{v_{\bot 2}^{2}}{2}\frac{\unicode[STIX]{x2202}f_{s\boldsymbol{k}}^{\ast }(\boldsymbol{v},t)}{\unicode[STIX]{x2202}v_{\bot 2}},E_{\bot 2\boldsymbol{k}}(t)\right). & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The discussion on using
$g_{s}$
in gyrokinetics in place of
$f_{s}$
, which is based on velocity integrals, applies also to the correlations in Fourier space (with the gyroaveraging operation
$\langle \cdots \!\,\rangle$
in (2.9) reduced to multiplications by Bessel functions (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Numata et al.
Reference Numata, Howes, Tatsuno, Barnes and Dorland2010)). The parallel correlation in (2.10) then becomes
$$\begin{eqnarray}C_{E_{\Vert }}(\boldsymbol{k},v_{\Vert },v_{\bot },t,\unicode[STIX]{x1D70F})=C\left(-q_{s}\frac{v_{\Vert }^{2}}{2}\frac{\unicode[STIX]{x2202}g_{s\boldsymbol{k}}^{\ast }(v_{\Vert },v_{\bot },t)}{\unicode[STIX]{x2202}v_{\Vert }},E_{\Vert \boldsymbol{k}}(t)\right).\end{eqnarray}$$
This represents the net energy transfer rate in Fourier and gyrotropic velocity space. Together with the parallel reduced correlation in (2.11), it is the form of field–particle correlations we use in this work.
2.4 Diagnosing energy transfer in Fourier space
Previous studies have used the field–particle correlation technique at a single point in physical space to evaluate the energy transfer between fields and particles (Klein & Howes Reference Klein and Howes2016; Howes Reference Howes2017; Howes et al.
Reference Howes, Klein and Li2017, Reference Howes, McCubbin and Klein2018; Klein Reference Klein2017; Klein et al.
Reference Klein, Howes and TenBarge2017; Chen et al.
Reference Chen, Klein and Howes2019). Here we diagnose the particle energization in Fourier space, where each Fourier mode
$\boldsymbol{k}$
is specified by a normalized wavevector
$(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i},k_{z}L_{z}/2\unicode[STIX]{x03C0})$
, where
$L_{z}$
is the system size in
$z$
. There are a number of advantages when applying field–particle correlations in Fourier space compared to physical space. First, by utilizing full spatial information of the whole domain as opposed to a single point, we can determine how the length scale of fluctuations, within the broadband turbulent spectrum, influences the collisionless field–particle energy transfer. Second, in the gyrokinetic limit
$k_{\Vert }\ll k_{\bot }$
, well justified for the anisotropic turbulence observed in the solar wind at kinetic scales (Sahraoui et al.
Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010; Narita et al.
Reference Narita, Gary, Saito, Glassmeier and Motschmann2011; Roberts, Li & Li Reference Roberts, Li and Li2013; Roberts, Li & Jeska Reference Roberts, Li and Jeska2015), the parallel phase velocity
$v_{p\Vert }=\unicode[STIX]{x1D714}/k_{\Vert }$
of the linear wave modes depends only on the perpendicular wavenumber and the plasma parameters,
$\overline{\unicode[STIX]{x1D714}}\equiv \unicode[STIX]{x1D714}/(k_{\Vert }v_{A})=v_{p\Vert }/v_{A}=\overline{\unicode[STIX]{x1D714}}(k_{\bot }\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). Therefore, the parallel phase velocity that governs resonant collisionless interactions is well defined for each mode
$\boldsymbol{k}$
in Fourier space. In contrast, at a single point in physical space, the dispersive nature of kinetic Alfvén waves (see figure 1) would lead to a range of resonant velocities, broadening the energy transfer signal and potentially smearing out any resonant energy transfer signatures in velocity space. Third, the broadband turbulent fluctuations have decreasing amplitudes with increasing perpendicular wavenumber
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
, but in Fourier space one can isolate the fluctuations at higher
$k_{\bot }$
from the rest of the fluctuations containing much larger amplitude fluctuations at lower
$k_{\bot }$
.
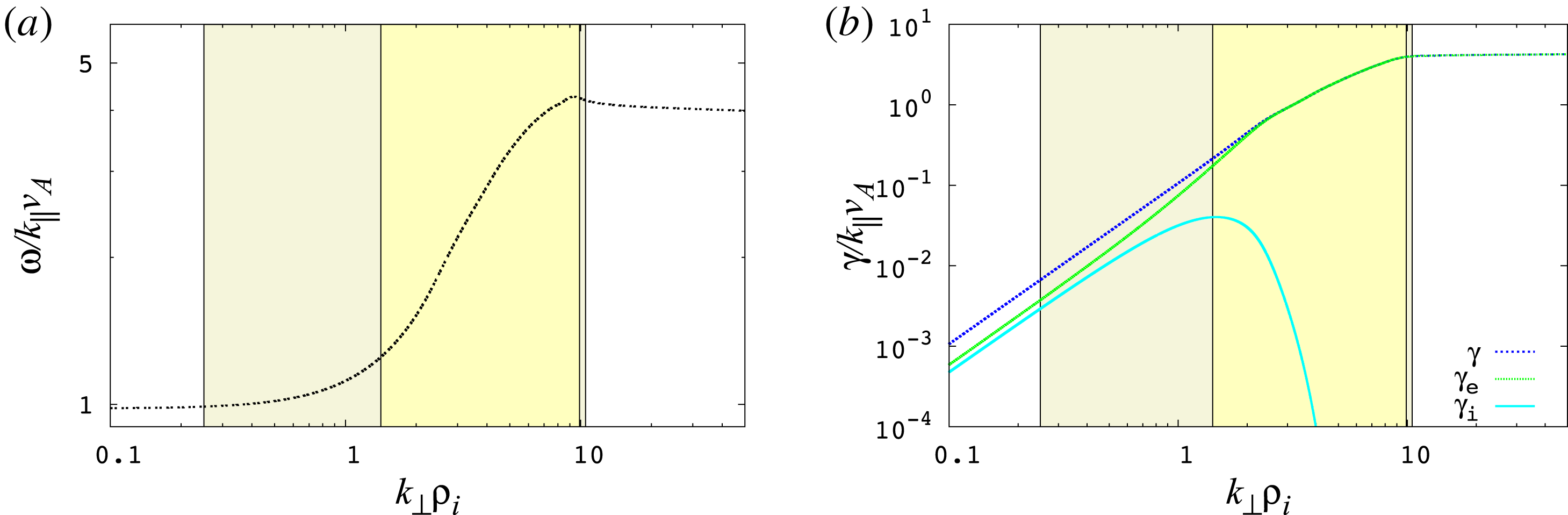
Figure 1. The linear gyrokinetic dispersion relation for a
$\unicode[STIX]{x1D6FD}_{i}=1$
and
$T_{i}/T_{e}=1$
plasma, showing (a) the normalized real frequency or phase velocity
$\unicode[STIX]{x1D714}/k_{\Vert }v_{A}$
(dashed black) and (b) damping rates
$\unicode[STIX]{x1D6FE}/k_{\Vert }v_{A}$
for the electrons (green), ions (cyan) and the total damping rate (blue). The total shaded region represents the resolved dynamic range
$0.25\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 10.5$
. The inner yellow shaded region indicates the range of the sampled
$k_{\bot }$
spectrum given in table 1,
$1.4\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 9.9$
.
In figure 1, we plot (a) the normalized frequency
$\unicode[STIX]{x1D714}/k_{\Vert }v_{A}$
and (b) the normalized damping rate
$\unicode[STIX]{x1D6FE}/k_{\Vert }v_{A}$
as a function of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
from the linear gyrokinetic dispersion relation (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006) for a plasma with parameters
$\unicode[STIX]{x1D6FD}_{i}\equiv 8\unicode[STIX]{x03C0}n_{i}T_{i}/B^{2}=v_{ti}^{2}/v_{A}^{2}=1$
,
$T_{i}/T_{e}=1$
, and
$m_{i}/m_{e}=25$
. The total shaded region represents the resolved dynamic range of
$k_{\bot }$
in the simulation,
$0.25\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 10.5$
. Table 1 lists the perpendicular wavevectors
$(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i})$
of Fourier modes that are sampled in the simulation, along with the corresponding normalized perpendicular wavenumber
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
, where
$k_{\bot }\equiv \sqrt{k_{x}^{2}+k_{y}^{2}}$
. The range of these sampled perpendicular wavenumbers
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
is indicated in figure 1 by the inner yellow shaded region, covering
$1.4\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 9.9$
or 0.3
${\leqslant}k_{\bot }\unicode[STIX]{x1D70C}_{e}\leqslant$
2.0. For each
$(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i})$
mode, seven
$k_{z}L_{z}/2\unicode[STIX]{x03C0}\in$
[
$-3$
,3] modes are selected, for a total sampling of 42 modes in
$(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i},k_{z}L_{z}/2\unicode[STIX]{x03C0})$
Fourier space. Also tabulated in table 1 are the parallel phase velocities normalized to the ion thermal velocity,
$v_{p\Vert }/v_{ti}=\unicode[STIX]{x1D714}/k_{\Vert }v_{A}$
(valid for a
$\unicode[STIX]{x1D6FD}_{i}=1$
plasma) and
$v_{p\Vert }/v_{te}$
. The last column gives the linear wave period
$\unicode[STIX]{x1D70F}_{k}$
of a kinetic Alfvén wave specified by
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
.
Table 1. List of diagnosed
$(k_{x},k_{y})$
modes in Fourier space.
The dispersion relation plot in figure 1(a) shows the characteristic dispersion of kinetic Alfvén waves, where the parallel phase velocity begins increasing at the transition of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$
. Given the energy transfer from fields to particles due to resonant collisionless wave damping is governed by the parallel phase velocity, one would expect to observe that the region of velocity space in which the particles exchange energy with the fields, known as the velocity-space signature of the particle energization, will shift to higher parallel velocities, tracking the increased parallel phase velocity as the perpendicular wavenumber
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
increases. Our analysis in §§ 4.1 and 4.2 confirms this expectation.
Finally, the collisionless damping rates for ions (cyan) and electrons (green) and the total damping rate (blue) are plotted in figure 1(b). The total damping of the waves is primarily attributed to electron damping for
$k_{\bot }\unicode[STIX]{x1D70C}_{i}>$
2 while both ion and electron damping contribute for
$k_{\bot }\unicode[STIX]{x1D70C}_{i}<$
2. Particularly, ion collisionless damping becomes significant and peaks around
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim$
1, but drops off very rapidly for
$k_{\bot }\unicode[STIX]{x1D70C}_{i}>2$
.
2.5 Simulation set-up
The simulation was performed with the gyrokinetic code AstroGK (Numata et al.
Reference Numata, Howes, Tatsuno, Barnes and Dorland2010). It has been extensively used to investigate turbulence in weakly collisional space plasmas (Howes et al.
Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008b
; Tatsuno et al.
Reference Tatsuno, Schekochihin, Dorland, Plunk, Barnes, Cowley and Howes2009; Howes et al.
Reference Howes, TenBarge, Dorland, Quataert, Schekochihin, Numata and Tatsuno2011; TenBarge & Howes Reference TenBarge and Howes2012; Nielson, Howes & Dorland Reference Nielson, Howes and Dorland2013; TenBarge & Howes Reference TenBarge and Howes2013; Kobayashi, Rogers & Numata Reference Kobayashi, Rogers and Numata2014; Howes Reference Howes2016; Li et al.
Reference Li, Howes, Klein and TenBarge2016; Howes et al.
Reference Howes, McCubbin and Klein2018) as well as collisionless magnetic reconnection in the strong-guide-field limit (Numata et al.
Reference Numata, Dorland, Howes, Loureiro, Rogers and Tatsuno2011; TenBarge et al.
Reference TenBarge, Daughton, Karimabadi, Howes and Dorland2014; Numata & Loureiro Reference Numata and Loureiro2015). AstroGK is an Eulerian continuum code with triply periodic boundary conditions. It has a slab geometry elongated along the straight, uniform background magnetic field,
$\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
. The code evolves the perturbed gyroaveraged Vlasov–Maxwell equations in five-dimensional phase space (3D–2V) (Frieman & Chen Reference Frieman and Chen1982; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). The evolved quantities are the electromagnetic gyroaveraged complementary distribution function
$g_{s}(x,y,z,\unicode[STIX]{x1D706},\unicode[STIX]{x1D700})$
for each species
$s$
, the scalar potential
$\unicode[STIX]{x1D711}$
, parallel vector potential
$A_{\Vert }$
and the parallel magnetic field perturbation
$\unicode[STIX]{x1D6FF}B_{\Vert }$
, where
$\Vert$
is along the total local magnetic field
$\boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
. Note that the total and background magnetic fields are the same to first-order accuracy, which is retained for perturbed fields in gyrokinetics. The 2V velocity grid is specified by pitch angle
$\unicode[STIX]{x1D706}=v_{\bot }^{2}/v^{2}$
and energy
$\unicode[STIX]{x1D700}=v^{2}/2$
. The background distribution functions for both species are stationary uniform Maxwellians. Collisions are incorporated using a fully conservative, linearized gyroaveraged Landau collision operator consisting of energy diffusion and pitch-angle scattering between like particles, electrons and ions and inter-species scattering of electrons off ions (Abel et al.
Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008; Barnes et al.
Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009).
The same simulation set-up as Li et al. (Reference Li, Howes, Klein and TenBarge2016) is used, a 3-D generalization of the classic 2-D Orszag–Tang Vortex (OTV) problem (Orszag & Tang Reference Orszag and Tang1979). The 2-D problem was widely used in fluid and MHD turbulence simulations; various 3-D generalizations have also been used for studying turbulence (Dahlburg & Picone Reference Dahlburg and Picone1989; Politano, Pouquet & Sulem Reference Politano, Pouquet and Sulem1989; Picone & Dahlburg Reference Picone and Dahlburg1991; Politano, Pouquet & Sulem Reference Politano, Pouquet and Sulem1995; Grauer & Marliani Reference Grauer and Marliani2000; Mininni, Pouquet & Montgomery Reference Mininni, Pouquet and Montgomery2006; Parashar et al.
Reference Parashar, Shay, Cassak and Matthaeus2009; Parashar, Vasquez & Markovskii Reference Parashar, Vasquez and Markovskii2014). This 3-D OTV set-up consists of counterpropagating Alfvén waves along
$\boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}$
such that on the
$z=0$
plane, its initial condition reduces to that of the 2-D OTV problem. An initial amplitude
$z_{0}$
of Elsässer variables in the OTV set-up (Li et al.
Reference Li, Howes, Klein and TenBarge2016) is chosen to yield a nonlinearity parameter
$\unicode[STIX]{x1D712}=k_{\bot }z_{0}/(k_{\Vert }v_{A})=1$
(where
$v_{A}=B_{0}/\sqrt{4\unicode[STIX]{x03C0}m_{i}n_{0}}$
is a characteristic Alfvén speed), corresponding to critical balance (Goldreich & Sridhar Reference Goldreich and Sridhar1995), or a state of strong turbulence. Note that previous studies using AstroGK have shown consistency with the prediction of a critically balanced cascade in the dissipation range (TenBarge & Howes Reference TenBarge and Howes2012; TenBarge et al.
Reference TenBarge, Howes and Dorland2013).
To resolve the turbulent cascade from the inertial range to the dissipation range for both ions and electrons, a reduced mass ratio of
$m_{i}/m_{e}=25$
is used. The simulation domain is
$L_{\bot }=8\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{i}$
and dimensions are
$(n_{x},n_{y},n_{z},n_{\unicode[STIX]{x1D706}},n_{\unicode[STIX]{x1D700}},n_{s})=(128,128,32,64,32,2)$
, which resolves a dynamic range of
$0.25\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 10.5$
, or
$0.05\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{e}\leqslant 2.1$
, covering both the inertial and dissipation ranges of the system. Typical conditions of solar wind turbulence are considered with ion plasma beta
$\unicode[STIX]{x1D6FD}_{i}=8\unicode[STIX]{x03C0}n_{i}T_{0i}/B_{0}^{2}=1$
, where
$T_{0i}$
is the constant background ion temperature, and equal temperatures are used for ions and electrons (
$T_{0i}/T_{0e}=1$
).
To realize collisional dissipation of turbulent energy in particle velocity space, weak finite collision frequencies are required (Howes Reference Howes2008; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Low collision frequencies
$\unicode[STIX]{x1D708}_{s}/\unicode[STIX]{x1D714}_{A0}\ll 1$
are chosen to avoid altering the weakly collisional dynamics, where collision frequencies of
$\unicode[STIX]{x1D708}_{i}=3\times 10^{-3}\unicode[STIX]{x1D714}_{A0}$
and
$\unicode[STIX]{x1D708}_{e}=0.06\unicode[STIX]{x1D714}_{A0}$
(where
$\unicode[STIX]{x1D714}_{A0}\equiv k_{\Vert }v_{A}$
is a characteristic Alfvén wave frequency) are used. We also employ a constant ion hypercollision frequency of
$\unicode[STIX]{x1D708}_{Hi}=6\times 10^{-3}\unicode[STIX]{x1D714}_{A0}$
and adaptive electron hypercollision frequency of
$\unicode[STIX]{x1D708}_{He}=0.12\unicode[STIX]{x1D714}_{A0}$
to ensure fluctuations in velocity space remain well resolved (Howes Reference Howes2008; Howes et al.
Reference Howes, TenBarge, Dorland, Quataert, Schekochihin, Numata and Tatsuno2011). The electron hypercollisional coefficient is adjusted based on nonlinear estimations of the total collisional damping rate (including hypercollisions)
$\unicode[STIX]{x1D6FE}_{nl}$
and of the energy transfer frequency
$\unicode[STIX]{x1D714}_{nl}$
(that is given by the cascade model (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a
) and dependent on the magnitude of the magnetic field fluctuations) such that a value of
$\unicode[STIX]{x1D6FE}_{nl}/\unicode[STIX]{x1D714}_{nl}\simeq 1/2\unicode[STIX]{x03C0}$
is achieved within some tolerance. The hypercollisionality chosen has the form of a pitch-angle-scattering operator with a wavenumber-dependent collision rate
$\unicode[STIX]{x1D708}_{Hs}(k_{\bot }/k_{\bot \max })^{p_{s}}$
, where
$k_{\bot \max }$
is a grid-scale wavenumber with
$p_{i}=4$
and
$p_{e}=8$
. It produces positive–definite heating close to the grid scale and is sufficient to terminate the turbulent cascade at the smallest resolved scales.
3 Energy evolution and current density
Here we present an overview of the evolution of the 3-D OTV simulation in terms of the evolution of the energy and the self-consistent development of current sheets in the simulation.
Under weakly collisional conditions, the removal of energy from turbulent fluctuations and the eventual conversion of that energy into plasma heat, unlike in the more familiar fluid limit, is a two-step process (Howes Reference Howes2017): first, the turbulent fluctuations are damped through reversible, collisionless interactions between the electromagnetic fields and the plasma particles, leading to energization of the particles; and second, this non-thermal energization of the particle velocity distributions is subsequently thermalized by arbitrarily weak collisions, thereby accomplishing the ultimate conversion of the turbulent energy into particle heat.
In a gyrokinetic system, the total fluctuating energy
$\unicode[STIX]{x1D6FF}W$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Brizard & Hahm Reference Brizard and Hahm2007; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009) is given byFootnote
1
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}W=\int \text{d}^{3}\boldsymbol{r}\left[\frac{|\unicode[STIX]{x1D6FF}\boldsymbol{B}|^{2}+|\unicode[STIX]{x1D6FF}\boldsymbol{E}|^{2}}{8\unicode[STIX]{x03C0}}+\mathop{\sum }_{s}\int \text{d}^{3}\boldsymbol{v}~\frac{T_{0s}\unicode[STIX]{x1D6FF}f_{s}^{2}}{2F_{0s}}\right],\end{eqnarray}$$
where the index
$s$
indicates the plasma species and
$T_{0s}$
is the temperature of each species’ Maxwellian equilibrium. The left term represents the electromagnetic energy and the right term represents that microscopic fluctuating kinetic energy of the particles of each plasma species
$s$
. As explained in Howes et al. (Reference Howes, McCubbin and Klein2018), in the standard form of gyrokinetic theory the appropriate conserved quadratic quantity in gyrokinetics is the Kruskal–Obermann energy,
$E_{s}^{(\unicode[STIX]{x1D6FF}f)}\equiv \int \text{d}^{3}\boldsymbol{r}\int \text{d}^{3}\boldsymbol{v}~T_{0s}\unicode[STIX]{x1D6FF}f_{s}^{2}/2F_{0s}$
(Kruskal & Oberman Reference Kruskal and Oberman1958; Morrison Reference Morrison1994), in contrast to the usual kinetic theory definition of microscopic kinetic energy,
$\int \text{d}^{3}\boldsymbol{r}\int \text{d}^{3}\boldsymbol{v}~(m_{s}v^{2}/2)f_{s}$
. Note also that
$\unicode[STIX]{x1D6FF}W$
includes neither the equilibrium thermal energy,
$\int \text{d}^{3}\boldsymbol{r}(3/2)n_{0s}T_{0s}=\int \text{d}^{3}\boldsymbol{r}\int \text{d}^{3}\boldsymbol{v}1/2m_{s}v^{2}F_{0s}$
, nor the equilibrium magnetic field energy,
$\int \text{d}^{3}\boldsymbol{r}~B_{0}^{2}/8\unicode[STIX]{x03C0}$
. Thus, the terms of
$\unicode[STIX]{x1D6FF}W$
in (3.1) represent the perturbed electromagnetic field energies and the microscopic kinetic energy of the deviations from the Maxwellian velocity distribution for each species.
A more intuitive form of the total fluctuating energy
$\unicode[STIX]{x1D6FF}W$
can be obtained by separating out the kinetic energy of the bulk motion of the plasma species from the non-thermal energy in the distribution function that is not associated with bulk flows (Li et al.
Reference Li, Howes, Klein and TenBarge2016),
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}W=\int \,\text{d}^{3}\boldsymbol{r}\left[\frac{|\unicode[STIX]{x1D6FF}\boldsymbol{B}|^{2}+|\unicode[STIX]{x1D6FF}\boldsymbol{E}|^{2}}{8\unicode[STIX]{x03C0}}+\mathop{\sum }_{s}\left(\frac{1}{2}n_{0s}m_{s}|\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\boldsymbol{s}}|^{2}+\frac{3}{2}\unicode[STIX]{x1D6FF}P_{s}\right)\right],\end{eqnarray}$$
where
$n_{0s}$
is the equilibrium density,
$m_{s}$
is mass and
$\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\boldsymbol{s}}$
is the fluctuating bulk flow velocity, which includes the parallel and perpendicular bulk flows. The non-thermal energy in the distribution function (not including the bulk kinetic energy) is defined by TenBarge et al. (Reference TenBarge, Daughton, Karimabadi, Howes and Dorland2014)
$$\begin{eqnarray}E_{s}^{(nt)}\equiv \int \text{d}^{3}\boldsymbol{r}\frac{3}{2}\unicode[STIX]{x1D6FF}P_{s}\equiv \int \text{d}^{3}\boldsymbol{r}\left[\int \text{d}^{3}\boldsymbol{v}\left(\frac{T_{0s}\unicode[STIX]{x1D6FF}f_{s}^{2}}{2F_{0s}}\right)-\frac{1}{2}n_{0s}m_{s}|\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\boldsymbol{s}}|^{2}\right].\end{eqnarray}$$
The turbulent energy is defined as the sum of the electromagnetic field and the bulk flow kinetic energies (Howes Reference Howes2015; Li et al. Reference Li, Howes, Klein and TenBarge2016; Howes et al. Reference Howes, McCubbin and Klein2018),
$$\begin{eqnarray}E^{(turb)}\equiv \int \text{d}^{3}\boldsymbol{r}\left[\frac{|\unicode[STIX]{x1D6FF}\boldsymbol{B}|^{2}+|\unicode[STIX]{x1D6FF}\boldsymbol{E}|^{2}}{8\unicode[STIX]{x03C0}}+\mathop{\sum }_{s}\frac{1}{2}n_{0s}m_{s}|\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\boldsymbol{s}}|^{2}\right].\end{eqnarray}$$
Therefore the total fluctuating energy is simply the sum of the turbulent energy and species non-thermal energies,
$\unicode[STIX]{x1D6FF}W=E^{(turb)}+E_{i}^{(nt)}+E_{e}^{(nt)}$
.
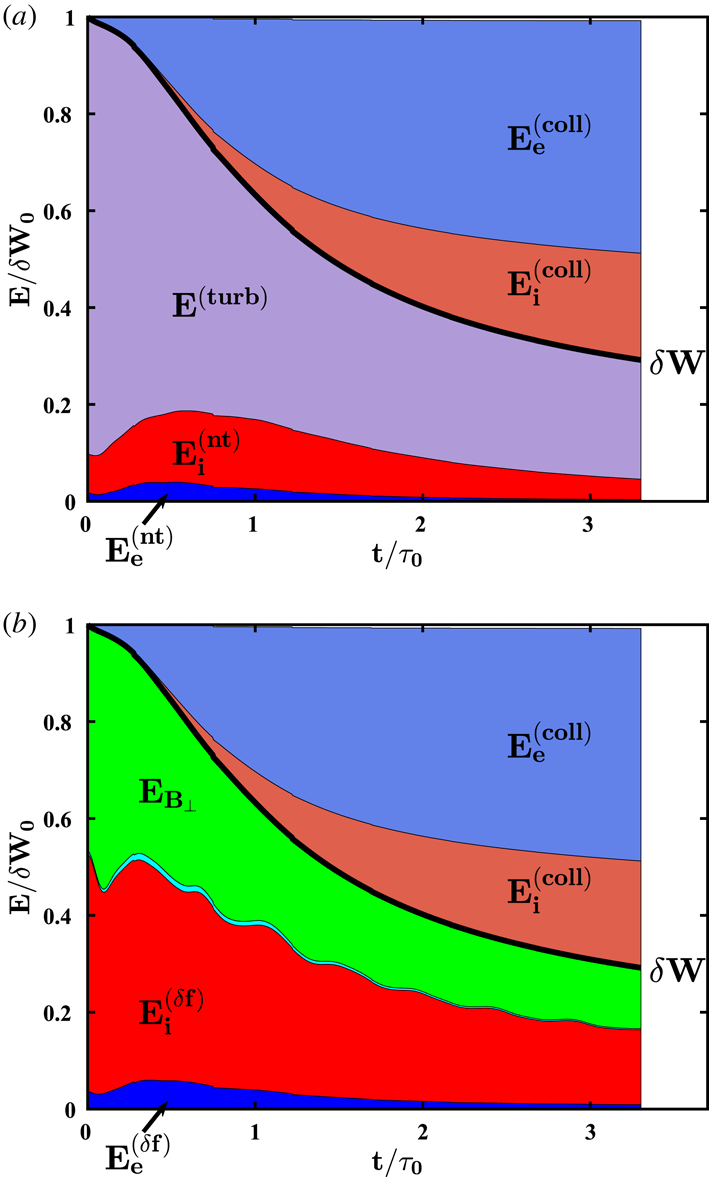
Figure 2. (a) The energy budget of the simulation versus time, showing the turbulent energy
$E^{(turb)}$
, non-thermal ion energy
$E_{i}^{(nt)}$
, non-thermal electron energy
$E_{e}^{(nt)}$
, ion heat
$E_{i}^{(\text{coll})}$
and electron heat
$E_{e}^{(\text{coll})}$
. (b) The same energy budget decomposed according to (3.1), showing the perpendicular magnetic field energy
$E_{B_{\bot }}$
, parallel magnetic field energy
$E_{B_{\Vert }}$
(cyan, not labelled, appearing between
$E_{B_{\bot }}$
and
$E_{i}^{(\unicode[STIX]{x1D6FF}f)}$
), total fluctuating ion kinetic energy
$E_{i}^{(\unicode[STIX]{x1D6FF}f)}$
, total fluctuating electron kinetic energy
$E_{e}^{(\unicode[STIX]{x1D6FF}f)}$
, ion heat
$E_{i}^{(\text{coll})}$
and electron heat
$E_{e}^{(\text{coll})}$
. The total fluctuating energy
$\unicode[STIX]{x1D6FF}W$
is shown in both panels (thick black line).
In figure 2, we present area plots of the components of the energy in the simulation as a function of normalized time
$t/\unicode[STIX]{x1D70F}_{0}$
, where
$\unicode[STIX]{x1D70F}_{0}$
is the period of Alfvén waves at the domain scale. Note that collisions in AstroGK, as well as in real plasma systems, convert non-thermal to thermal energy, representing irreversible plasma heating with an associated increase of entropy. The energy lost from
$\unicode[STIX]{x1D6FF}W$
by collisions is tracked by AstroGK and represents thermal heating of the plasma species, but this energy is not fed back into the code to evolve the equilibrium thermal temperature,
$T_{0s}$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Numata et al.
Reference Numata, Howes, Tatsuno, Barnes and Dorland2010; Li et al.
Reference Li, Howes, Klein and TenBarge2016). We account for the energy lost from
$\unicode[STIX]{x1D6FF}W$
in the AstroGK simulation to collisional plasma heating by accumulating the thermalized energy in each species over time,
$E_{s}^{(\text{coll})}(t)=\int _{0}^{t}\text{d}t^{\prime }Q_{s}(t^{\prime })$
, where AstroGK computes the collisional heating rate per unit volume for ions
$Q_{i}$
and electrons
$Q_{e}$
.
In figure 2(a), we plot the evolution of the energy budget over the course of the simulation, showing that turbulent energy
$E^{(turb)}$
, which dominates at the beginning of the simulation, is largely converted to electron heat
$E_{e}^{(\text{coll})}$
and ion heat
$E_{i}^{(\text{coll})}$
and by the end of the simulation, with approximately 70 % of the initial total fluctuating energy
$\unicode[STIX]{x1D6FF}W_{0}$
lost by
$t/\unicode[STIX]{x1D70F}_{0}=3$
. Approximately one third of the energy dissipated is channelled to ions and two thirds to electrons. This is in close agreement with a recent gyrokinetic turbulent simulation using a realistic mass ratio of
$m_{i}/m_{e}=1836$
in which approximately 70 % of the total dissipated energy is channelled through electrons (Told et al.
Reference Told, Jenko, TenBarge, Howes and Hammett2015). Total energy
$E$
is conserved over the course of the simulation to less than 1 %.
Another view of the energy budget, based on (3.1), is presented in figure 2(b), where we plot the perpendicular magnetic field energy
$E_{B_{\bot }}$
(green) and parallel magnetic field energy
$E_{B_{\Vert }}$
(cyan) along with the total fluctuating kinetic energy of the ions and electrons
$E_{s}^{(\unicode[STIX]{x1D6FF}f)}$
. An interesting feature of the evolution of the energy budget, seen in both panels (a,b), is that although the electrons gain the bulk of the thermal energy, the total fluctuating kinetic energy
$E_{e}^{(\unicode[STIX]{x1D6FF}f)}$
and total non-thermal energy
$E_{e}^{(nt)}$
in the electrons remains small. Thus, electrons do not contain much of the non-thermal energy at any given time, and are an effective conduit for channelling the turbulent energy into electron thermal energy.
The field–particle correlation technique diagnoses the collisionless, reversible transfer of energy between the electromagnetic fields and the particles. This first step of the two-step process in converting turbulent energy into particle thermal energy is not easily discerned in the energy budget plots shown in figure 2. To more directly evaluate this rate of energy transfer, we compute the net rate of energy transfer due to field–particle interactions using
$$\begin{eqnarray}{\dot{E}}_{s}^{(fp)}={\dot{E}}_{s}^{(nt)}+Q_{s},\end{eqnarray}$$
where
${\dot{E}}_{s}^{(nt)}$
is the rate of change of non-thermal species energy and
$Q_{s}$
is the collisional heating of the species. To check the energy conservation in the simulation, we can plot
$$\begin{eqnarray}-{\dot{E}}^{(turb)}={\dot{E}}_{i}^{(fp)}+{\dot{E}}_{e}^{(fp)},\end{eqnarray}$$
because the rate of change of turbulent energy must be the sum of the collisionless field–particle energy transfer for each species.
In figure 3, we plot these energy transfer rates, normalized to the characteristic heating rate per unit volume,
$Q_{0}=(n_{0i}T_{0i}v_{ti}/L_{\Vert })(\unicode[STIX]{x03C0}/8)(L_{\bot }/L_{\Vert })^{2}$
, for (a) ions (red) and (b) electrons (blue), as well as (c) the total energy transfer rate balance given by (3.6). Several features of these energy transfer rate curves are notable. First, with the exception of a brief large energy transfer to ions within the first
$0.2\unicode[STIX]{x1D70F}_{0}$
, the field–particle energy transfer rate to electrons is about twice of that to ions on average. Second, the time lag between field–particle energy transfer to electrons and the collisional thermalization of that energy is very short, a delay of approximately
$0.1\unicode[STIX]{x1D70F}_{0}$
. Thus, energy transferred to electron non-thermal energy is rapidly converted to electron heat by collisions. In contrast, for the ions, the time lag between the peaks of the field–particle energization of the ions and the collisional thermalization of that energy is much longer, approximately
$1.0\unicode[STIX]{x1D70F}_{0}$
. This longer time lag for ions is consistent with the need for the ion entropy cascade (Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Tatsuno et al.
Reference Tatsuno, Schekochihin, Dorland, Plunk, Barnes, Cowley and Howes2009; Cerri et al.
Reference Cerri, Kunz and Califano2018) to transfer non-thermal energy to sufficient small scales in velocity space before collisions can effectively thermalize that energy. Finally, (c) the sum of the field–particle energy transfer to ions and electrons is in quantitative agreement with the loss of turbulent energy.
Figure 3. The rate of energy transfer by field–particle interactions
${\dot{E}}_{s}^{(fp)}$
(solid), the rate of change of non-thermal energy
${\dot{E}}_{s}^{(nt)}$
(dotted) and the collisional heating rate
$Q_{s}$
(dashed) for (a) ions (red) and (b) electrons (blue). (c) The energy balance between the loss of turbulent energy
$-{\dot{E}}^{(turb)}$
(purple solid) and the summed transfer of energy to both ions and electrons,
${\dot{E}}_{i}^{(fp)}+{\dot{E}}_{e}^{(fp)}$
(black dashed).
Figure 4. Spatial profile of (a)
$J_{\Vert }$
(colour) and
$A_{\Vert }$
(contour), (b)
$J_{\Vert }E_{\Vert }$
and (c)
$E_{\Vert }$
on the
$z=0$
plane at
$t/\unicode[STIX]{x1D70F}_{0}=0.5$
. Contours represent positive (white) and negative (black) values of
$A_{\Vert }$
.
In figure 4, we plot the spatial profiles on the
$z=0$
plane at
$t/\unicode[STIX]{x1D70F}_{0}=0.5$
of (a) the parallel current
$J_{\Vert }$
(colour) and vector potential
$A_{\Vert }$
(contour), (b)
$J_{\Vert }E_{\Vert }$
and (c)
$E_{\Vert }$
. The topology of the initial double-vortex pattern, representative of the Orzag–Tang vortex, is traceable by the central white contours. Multiscale features in
$J_{\Vert }$
, including self-consistently generated current sheets, are seen over the entire
$(x,y)$
plane, representing a turbulent state containing a spectrum of nonlinearly generated modes.
$J_{\Vert }E_{\Vert }$
represents the net energy density transfer rate mediated by the parallel electric field (the first term on the right-hand side of (2.4) when integrated over velocity). In (b), strong energy transfer density (red) occurs in sub-ion- or ion-scale regions. Two particularly strong
$J_{\Vert }E_{\Vert }$
regions are centred at
$(x,y)\sim$
(3,14) and (20,10). They co-locate with thin sheet-like currents and share similar shapes with them, but not necessarily with the strongest
$J_{\Vert }$
regions. They, however, are seen at the strongest
$E_{\Vert }$
in (c), which also occurs in localized ion-scale regions. Otherwise,
$E_{\Vert }$
has generally broad features.
4 Field–particle correlations
Here we present results on identifying the collisionless energy transfer in the simulation using field–particle correlations.
4.1 Field–particle correlations in gyrotropic velocity space
To identify the regions of gyrotropic velocity space
$(v_{\Vert },v_{\bot })$
where particles play a role in the collisionless transfer of energy density from the parallel electric field to the plasma ions and electrons, we employ the field–particle correlation technique to compute
$C_{E_{\Vert }}(\boldsymbol{k},v_{\Vert },v_{\bot },t,\unicode[STIX]{x1D70F})$
, given by (2.17).
Figure 5. Electron gyrotropic correlation
$C_{E_{\Vert }}(v_{\Vert },v_{\bot },t)$
for the
$(2,2,-1)$
Fourier mode using (a)
$\unicode[STIX]{x1D70F}=0$
and (c)
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
, plotted at
$t_{c}/\unicode[STIX]{x1D70F}_{0}=0.86$
, corresponding to
$t/\unicode[STIX]{x1D70F}_{k}=0.81$
for
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
. Also plotted are
$C_{E_{\Vert }}(v_{\Vert },v_{\bot },t)$
for the
$(6,6,+3)$
Fourier mode using (b)
$\unicode[STIX]{x1D70F}=0$
and (d)
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
at
$t_{c}/\unicode[STIX]{x1D70F}_{0}=0.34$
, corresponding to
$t/\unicode[STIX]{x1D70F}_{k}=0.42$
for
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
. Dashed lines denote Landau resonant velocities:
$v_{p\Vert }/v_{te}=\pm 0.42$
for the
$(2,2,-1)$
Fourier mode and
$v_{p\Vert }/v_{te}=\pm 0.84$
for the
$(6,6,+3)$
Fourier mode. Arbitrary units are used in the colour bars while the relative amplitudes between the
$\unicode[STIX]{x1D70F}=0$
and
$2\unicode[STIX]{x1D70F}_{k}$
correlations are preserved for each Fourier mode.
4.1.1 Electron gyrotropic correlations
Here we explore the net energy transfer rate to the electrons by the parallel electric field as a function of particle velocity in gyrotropic velocity space
$(v_{\Vert },v_{\bot })$
for particular Fourier modes, each denoted by their normalized wavevector
$(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i},k_{z}L_{z}/2\unicode[STIX]{x03C0})$
. On the top row of figure 5, we plot the instantaneous correlation
$C_{E_{\Vert }}(\boldsymbol{k},v_{\Vert },v_{\bot },t,\unicode[STIX]{x1D70F}=0)$
for modes (a)
$(2,2,-1)$
and (b)
$(6,6,+3)$
. The instantaneous energy transfer is spread over a wide range of
$v_{\Vert }$
relative to
$v_{p\Vert }$
of each Fourier mode of the kinetic Alfvén wave, given by (a)
$\unicode[STIX]{x1D714}/(k_{\Vert }v_{te})=\pm 0.42$
and (b)
$\unicode[STIX]{x1D714}/(k_{\Vert }v_{te})=\pm 0.84$
, indicated by the vertical dashed black lines. This shows that particles over a relatively broad range of
$v_{\Vert }$
participate in energy exchange with the parallel electric field.
In order to eliminate the often large contribution to the instantaneous energy transfer given by the oscillating energy transfer associated with undamped wave motions (which is measured in a kinetic Alfvén wave (Gershman et al.
Reference Gershman, F-Viñas, Dorelli, Boardsen, Avanov, Bellan, Schwartz, Lavraud, Coffey and Chandler2017)), the field–particle correlation technique performs a time average of the correlation product (in the unnormalized correlation) over a suitably long time period (Klein & Howes Reference Klein and Howes2016; Howes et al.
Reference Howes, Klein and Li2017). This effectively removes the oscillating component of the energy transfer, isolating the often smaller net secular energy transfer from fields to particles. In both of these cases, we choose a correlation interval
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
where
$\unicode[STIX]{x1D70F}_{k}$
is the linear wave period of a kinetic Alfvén wave specified by the normalized wavevector, given by the final column in table 1. The correlation interval is chosen such that the time evolution of the parallel reduced correlation qualitatively converges, which corresponds to
$\unicode[STIX]{x1D70F}\geqslant \unicode[STIX]{x1D70F}_{k}$
(see Appendix). The resulting time-averaged field–particle correlations are plotted in figure 5 for Fourier modes (c)
$(2,2,-1)$
and (d)
$(6,6,+3)$
.
For the time-averaged correlations, time
$t$
is defined at the beginning of the correlation interval
$\unicode[STIX]{x1D70F}$
. Another convenient way to specify time is at the centre of the correlation interval, giving a centred time of
$t_{c}=t+\unicode[STIX]{x1D70F}/2$
. Both
$t$
and
$t_{c}$
are given in figure 5 for reference.
Several key features of the net energy transfer over the correlation interval
$\unicode[STIX]{x1D70F}$
are observed in figure 5(c,d). First, the region in velocity space of largest net transfer of energy between
$E_{\Vert }$
and the electrons is closely connected to
$v_{p\Vert }$
. This contrasts with the broader spread over
$v_{\Vert }$
of instantaneous energy transfer when taking
$\unicode[STIX]{x1D70F}=0$
in panels (a,b). The resulting velocity-space characteristic of the energy transfer is consistent with the velocity-space signature of Landau damping of the turbulent fluctuations, as found in previous studies (Klein & Howes Reference Klein and Howes2016; Klein et al.
Reference Klein, Howes and TenBarge2017; Howes et al.
Reference Howes, Klein and Li2017, Reference Howes, McCubbin and Klein2018; Chen et al.
Reference Chen, Klein and Howes2019). The contrast in the energy transfer signals between the instantaneous and long-time-averaged correlations shows that while electrons over a broad range of parallel velocities participate in instantaneous energy transfer, the net secular energy transfer is largely contributed by ‘near-resonance’ electrons that are closely connected to
$v_{p\Vert }$
. This reflects the resonant nature of secular net energy transfer in Landau damping of the turbulent fluctuations. Second, the variation in the energy transfer is largely a function of
$v_{\Vert }$
, with weak
$v_{\bot }$
dependence other than the monotonic drop off as
$v_{\bot }$
increases. For the
$(6,6,+3)$
mode in (d) which has
$k_{\bot }\unicode[STIX]{x1D70C}_{e}\approx 1.7>1$
, however, there is weak
$v_{\bot }$
dependence near
$v_{\Vert }/v_{te}\sim 1$
, which lasts very briefly, for
${\sim}0.2\unicode[STIX]{x1D70F}_{k}$
. This
$v_{\bot }$
dependence in the energy transfer reveals structuring of the distribution in
$v_{\bot }$
as
$E_{\Vert }$
does not depend on velocity. This qualitative feature is consistent with the expectation of the electron entropy cascade (Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Tatsuno et al.
Reference Tatsuno, Schekochihin, Dorland, Plunk, Barnes, Cowley and Howes2009; Schoeffler et al.
Reference Schoeffler, Loureiro, Fonseca and Silva2014), which predicts some structuring of the distribution in
$v_{\bot }$
due to nonlinear phase mixing for
$k_{\bot }\unicode[STIX]{x1D70C}_{e}>1$
.
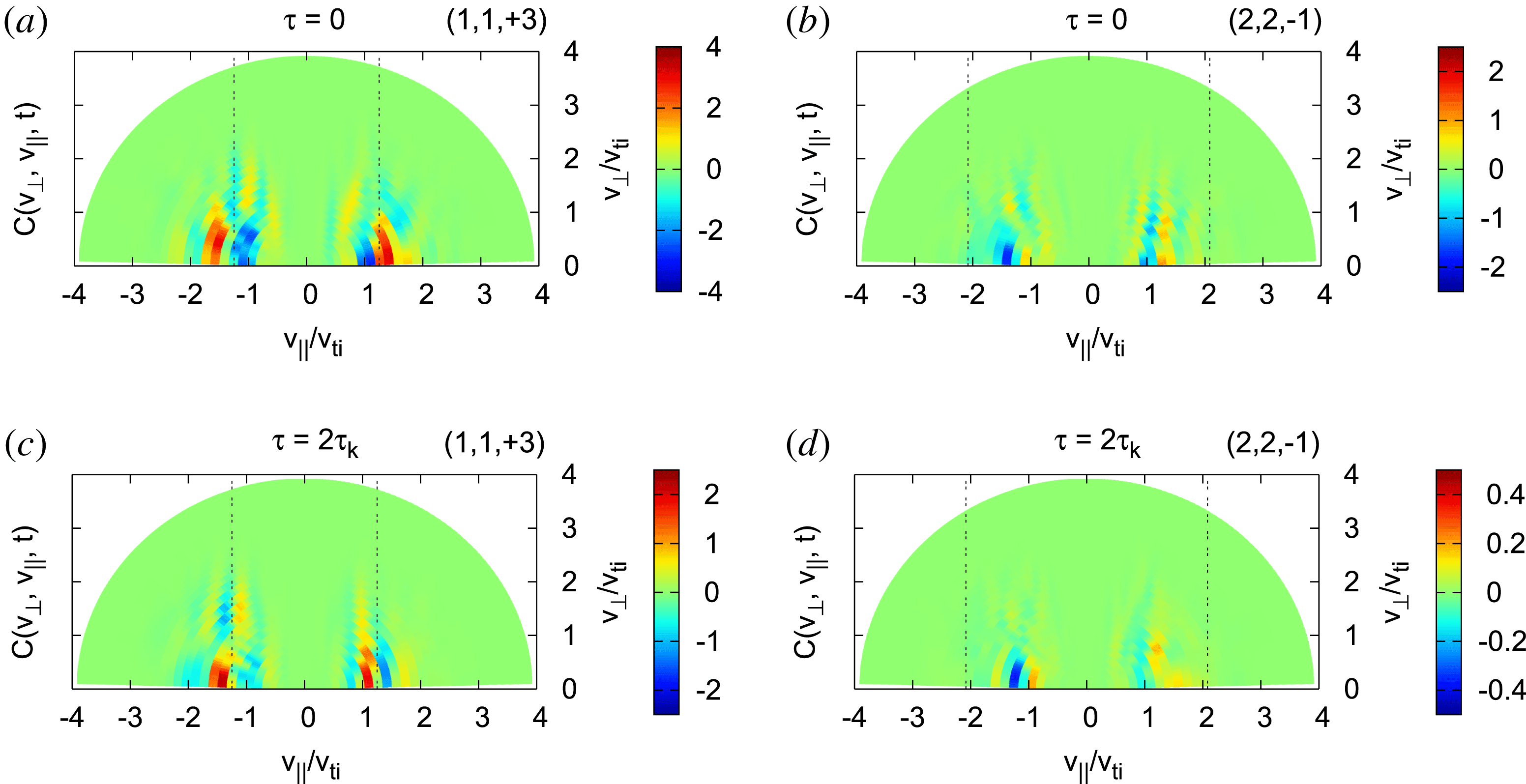
Figure 6. Ion gyrotropic correlation
$C_{E_{\Vert }}(v_{\Vert },v_{\bot },t)$
for the
$(1,1,+3)$
Fourier mode using (a)
$\unicode[STIX]{x1D70F}=0$
and (c)
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
, plotted at
$t_{c}/\unicode[STIX]{x1D70F}_{0}=1.2$
, corresponding to
$t/\unicode[STIX]{x1D70F}_{k}=0.48$
for
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
. (c) Shows observable weak
$v_{\bot }$
variations at
$v_{\Vert }<0$
in addition to more prominent
$v_{\Vert }$
dependence. Also plotted are
$C_{E_{\Vert }}(v_{\Vert },v_{\bot },t)$
for the
$(2,2,-1)$
Fourier mode using (b)
$\unicode[STIX]{x1D70F}=0$
and (d)
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
at
$t_{c}/\unicode[STIX]{x1D70F}_{0}=0.90$
, corresponding to
$t/\unicode[STIX]{x1D70F}_{k}=0.90$
for
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
. Dashed lines denote Landau resonant velocities:
$v_{p\Vert }/v_{ti}=\pm 1.3$
and
$\pm 2.1$
for the
$(1,1,+3)$
and
$(2,2,-1)$
Fourier modes, respectively. The same format is used as figure 5.
4.1.2 Ion gyrotropic correlations
In figure 6, we plot the instantaneous correlation
$C_{E_{\Vert }}(\boldsymbol{k},v_{\Vert },v_{\bot },t,\unicode[STIX]{x1D70F}=0)$
for ions for modes (a)
$(1,1,+3)$
and (b)
$(2,2,-1)$
. As with the instantaneous correlations for the electrons in figure 5, we see that the energy transfer is not tightly constrained in
$v_{\Vert }$
to the resonant parallel phase velocities for these modes ((a)
$\unicode[STIX]{x1D714}/(k_{\Vert }v_{ti})=\pm 1.2$
and (b)
$\unicode[STIX]{x1D714}/(k_{\Vert }v_{ti})=\pm 2.1$
(vertical dashed black lines)). For the
$(2,2,-1)$
mode, having resonant parallel phase velocities much higher than the ion thermal speed, there is only very weak energy transfer.
Computing the unnormalized correlation (time average) over the correlation interval
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
for each mode, we obtain the ion energization rate in gyrotropic velocity space shown in figure 6 for Fourier modes (c)
$(1,1,+3)$
and (d)
$(2,2,-1)$
. The ion energy transfer rate results for (c)
$(1,1,+3)$
have similar characteristics to the findings for the electrons: (i) the secular energy transfer rate is closely connected to the parallel resonant velocity; and (ii) the energy transfer rate varies strongly as a function of
$v_{\Vert }$
, again consistent with the velocity-space signature expected of Landau damping. One notable difference is that there is significantly more variation of the energy transfer rate in the
$v_{\bot }$
direction than for the electrons. This is qualitatively consistent with the action of the ion entropy cascade (Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Tatsuno et al.
Reference Tatsuno, Schekochihin, Dorland, Plunk, Barnes, Cowley and Howes2009) which leads to structuring of the perturbed distribution function in the
$v_{\bot }$
direction (Howes Reference Howes2008).
Another notable difference from the electron case is that the energy transfer rates are significantly weaker, with nearly no resonant energy transfer signatures near
$v_{p\Vert }/v_{ti}$
, for the (d)
$(2,2,-1)$
Fourier mode. In fact, the
$(1,1)$
Fourier modes are the only
$k_{\bot }$
value in the sampled spectrum (table 1) displaying resonant signatures in the resolved range of
$v_{\Vert }/v_{ti}$
plotted. The
$(1,1)$
Fourier modes also sit near the peak of the ion collisionless damping rate (
$\unicode[STIX]{x1D6FE}_{i}$
in figure 1). At
$k_{\bot }\unicode[STIX]{x1D70C}_{i}>$
2,
$\unicode[STIX]{x1D6FE}_{i}$
drops off rapidly. This is because
$v_{p\Vert }/v_{ti}$
moves to the tail of the ion distribution (at greater than twice the ion thermal speed) where there are very few particles to interact with the waves. For instance, the
$(2,2)$
and
$(3,4)$
Fourier modes have
$v_{p\Vert }/v_{ti}=\pm 2.1$
and
$\pm 3.3$
, respectively, which are in the tail of the distribution. Indeed, resonant energy transfer signatures are not observed for the
$(2,2)$
to
$(7,7)$
Fourier modes.
4.2 Parallel reduced correlations
Because the variation of the rate of energy density transfer, shown in figures 5 and 6, is largely a function of
$v_{\Vert }$
with little variation in
$v_{\bot }$
, we may integrate over
$v_{\bot }$
to obtain reduced parallel correlations
$C_{E_{\Vert }}(v_{\Vert },t,\unicode[STIX]{x1D70F})$
, given by (2.11). These reduced correlations can conveniently be plotted, for a given correlation interval
$\unicode[STIX]{x1D70F}$
, as timestack plots of
$C_{E_{\Vert }}(v_{\Vert },t)$
as a function of
$v_{\Vert }$
and time
$t$
to illustrate the evolution of the field–particle energy transfer due to a single Fourier mode over the course of the entire simulation.
4.2.1 Electron parallel reduced correlations
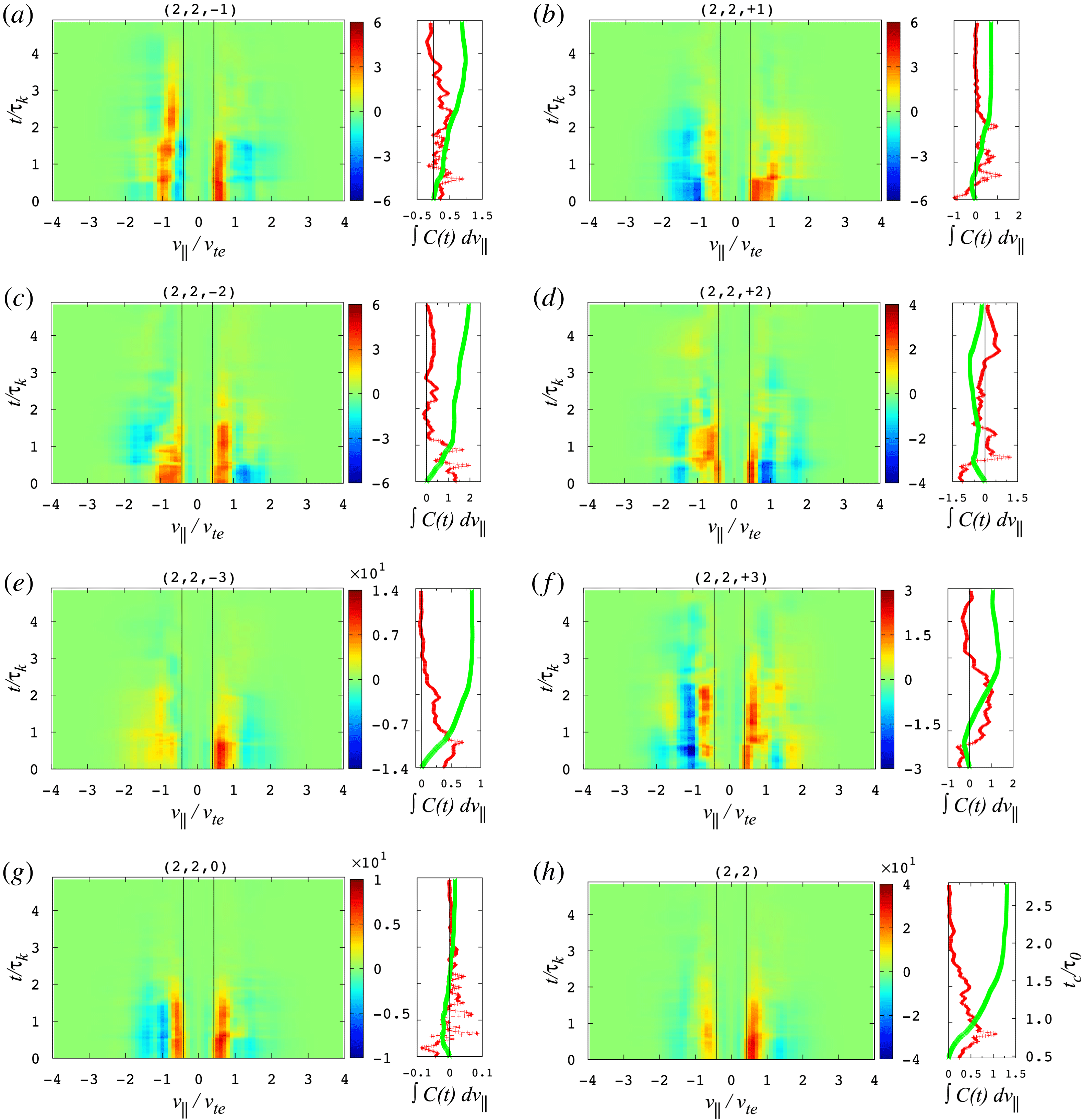
Figure 7. Electron parallel reduced correlations
$C_{E_{\Vert }}(v_{\Vert },t)$
for seven
$k_{z}$
modes and summed
$C_{E_{\Vert }}(v_{\Vert },t)$
for the
$(2,2)$
Fourier mode. Correlation interval of
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
is chosen. Time
$t$
is defined at the beginning of the correlation interval. Vertical black lines indicate Landau resonant velocities:
$v_{p\Vert }/v_{te}=\pm 0.42$
. An arbitrary unit is used. Line plots on the right of each correlation are the
$v_{\Vert }$
-integrated correlation as a function of time (red curve) and accumulated over time (green curve). The
$\times 10^{n}$
factor above each colour bar applies also to the
$x$
-axis of the line plots. Also plotted on the right of panel (h) is an axis for the normalized centred time
$t_{c}/\unicode[STIX]{x1D70F}_{0}$
.
Plotted in figure 7 are timestack plots of the parallel reduced correlations
$C_{E_{\Vert }}(v_{\Vert },t)$
for the electrons for the
$(2,2)$
Fourier mode, separately for each of the seven
$k_{z}\in [-3,+3]$
modes in panels (a–g) and the sum of these seven
$k_{z}$
modes in panel (h), labelled
$(2,2)$
. The correlation interval chosen for all panels is
$\unicode[STIX]{x1D70F}$
=
$2\unicode[STIX]{x1D70F}_{k}$
. Plotted to the right of each timestack plot is the
$v_{\Vert }$
-integrated correlation, giving the net transfer rate of energy density for that Fourier mode
$\int C_{E_{\Vert }}(v_{\Vert },t)\,\text{d}v_{\Vert }$
as a function of time (red curve) and the accumulated energy transferred
$\int _{0}^{t}\text{d}t\int C_{E_{\Vert }}(v_{\Vert },t)\,\text{d}v_{\Vert }$
over time (green curve). The Landau resonant parallel phase velocity of each Fourier mode is indicated by vertical black lines. We note that, for a given value of
$k_{\bot }$
, the normalized phase velocity
$\overline{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}/k_{\Vert }v_{A}$
is independent of
$k_{\Vert }$
, so the phase velocity (
$\unicode[STIX]{x1D714}/k_{\Vert }$
) is constant for all
$k_{z}$
(note that
$k_{\Vert }$
and
$k_{z}$
are the same in the linear dispersion relation by which
$\overline{\unicode[STIX]{x1D714}}$
is given). This leads to a constant Landau resonant velocity,
$v_{p\Vert }/v_{te}$
=
$\pm$
0.42, for all
$(2,2,k_{z})$
Fourier modes in figure 7. Also plotted on the right of the
$v_{\Vert }$
-integrated correlation for (h) the sum of the seven
$k_{z}$
mode is an axis for the normalized centred time
$t_{c}/\unicode[STIX]{x1D70F}_{0}$
.
A key characteristic of the parallel reduced correlations for all
$(2,2,k_{z})$
Fourier modes is that the energy transfer is largely dominated by particles connected to
$v_{p\Vert }$
, with an increase in electron energy (red) just above
$v_{p\Vert }$
. This reduced parallel velocity-space signature is consistent with previous results showing Landau damping (Klein & Howes Reference Klein and Howes2016; Klein et al.
Reference Klein, Howes and TenBarge2017; Howes et al.
Reference Howes, Klein and Li2017, Reference Howes, McCubbin and Klein2018; Chen et al.
Reference Chen, Klein and Howes2019). This localization of the energy transfer in parallel velocity indicates that collisionless damping by Landau resonant electrons is the dominant mechanism for transferring energy from the turbulent electromagnetic fluctuations to the electrons, a primary result of this study.
Furthermore, the timestack plots show clearly that this resonant energization of the electrons by the parallel electric field is sustained over the course of the simulation, although the amplitude of this rate of energization decreases in time as the initial fluctuations (the total turbulence energy) damp in time. In fact, the decrease in the rate of electron energization by the electric field over the course of the simulation is qualitatively consistent with the decrease in the spatially integrated rate of electron energization
${\dot{E}}_{e}^{(fp)}$
(solid blue) in figure 3(b). Additionally, the characteristic time scale of the energy transfer in the parallel reduced correlations is approximately
$\unicode[STIX]{x1D70F}_{k}$
of this
$(2,2)$
Fourier mode. This time scale is consistent with the linear wave period of this Fourier mode, as naturally expected.
The panels (a–g) for the seven different
$(2,2,k_{z})$
Fourier modes in figure 7 show that most of the different
$k_{z}$
modes yield a net energy gain (green curve) at the end of the run. The (h) sum of these seven
$k_{z}$
components of the
$(2,2)$
Fourier mode indeed demonstrates a net heating of electrons over the course of the simulation.
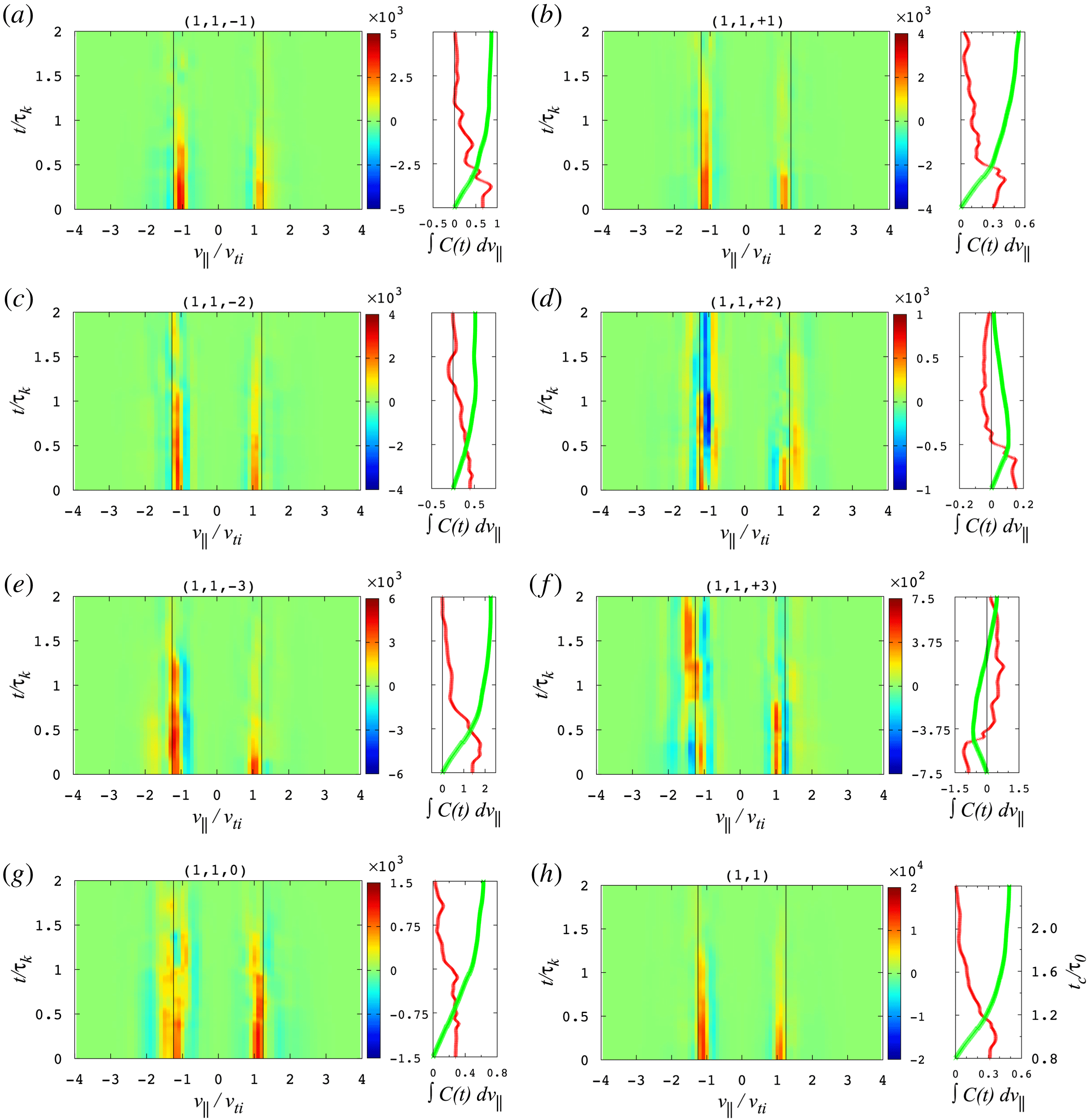
Figure 8. Ion parallel reduced correlations
$C_{E_{\Vert }}(v_{\Vert },t)$
for seven
$k_{z}$
modes and summed
$C_{E_{\Vert }}(v_{\Vert },t)$
for the
$(1,1)$
Fourier mode. Correlation interval of
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
is used.
$C_{E_{\Vert }}(v_{\Vert },t)$
for each individual
$k_{z}$
mode shows resonant signatures associated with Landau resonances,
$v_{p\Vert }/v_{ti}=\pm 1.3$
, indicated by vertical black lines. Highly localized energy transfer signals are observed for all seven Fourier modes. The same format is used as figure 7. Arbitrary unit is used.
4.2.2 Ion parallel reduced correlations
In figure 8, we plot timestack plots of the parallel reduced correlations
$C_{E_{\Vert }}(v_{\Vert },t)$
for the ions for the
$(1,1)$
Fourier mode, in the same format as for the electrons in figure 7. Again, a correlation interval of
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
is used for all plots. The Landau resonant parallel phase velocity for these modes, normalized in terms of the ion thermal velocity, is given by
$v_{p\Vert }/v_{ti}=\pm 1.3$
.
The ion reduced parallel correlations for the
$(1,1,k_{z})$
modes also show that the energy transfer is largely dominated by particles near the resonant velocity, indicating that collisionless damping by Landau resonant ions is the dominant mechanism for transferring energy from the parallel electric field to the ions. Although there is significantly more variation of the accumulated energy transfer to the ions among the different
$k_{z}$
modes in panels (a–g), the summed
$k_{z}$
result in (h) is also qualitatively consistent with the gradual decrease in time of the spatially integrated rate of ion energization
${\dot{E}}_{i}^{(fp)}$
(solid red) in figure 3(a). Furthermore, in the same way as the characteristic time scale of the electron energization rate being consistent with
$\unicode[STIX]{x1D70F}_{k}$
of the Fourier mode in figure 7, the characteristic time scale of the ion energization rate for the different
$k_{z}$
modes is also approximately
$\unicode[STIX]{x1D70F}_{k}$
of this
$(1,1)$
Fourier mode.
Consistent with the rapid decrease of the ion collisionless damping rate
$\unicode[STIX]{x1D6FE}_{i}/k_{\Vert }v_{A}$
(cyan) in figure 2 at perpendicular wavenumbers
$k_{\bot }\unicode[STIX]{x1D70C}_{i}>2$
, the reduced parallel correlations (not shown) for all Fourier modes other than
$(1,1)$
do not exhibit clear resonant energy transfer velocity-space signatures.
4.2.3 Reduced parallel correlations:
$k_{\bot }$
dependence and
$\unicode[STIX]{x1D6FD}_{i}$
dependence
Previous applications of the field–particle correlation have analysed the energy transfer at a single point in space (Klein & Howes Reference Klein and Howes2016; Klein et al.
Reference Klein, Howes and TenBarge2017; Howes et al.
Reference Howes, Klein and Li2017, Reference Howes, McCubbin and Klein2018; Chen et al.
Reference Chen, Klein and Howes2019). Although this has the advantage of enabling the spatial localization of the energy transfer between fields and particles to be studied, it cannot provide any information about how that energy transfer is mediated by fluctuations at different scales. By performing the field–particle correlation analysis in Fourier space, we can examine how the energy transfer as a function of the scale of the Fourier modes plays a role in the energy transfer. In the gyrokinetic limit
$k_{\Vert }\ll k_{\bot }$
, the resonant parallel phase velocity
$\unicode[STIX]{x1D714}/k_{\Vert }$
of the kinetic Alfvén wave modes is strictly a function of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
(as shown in figure 1
a), so the reduced parallel correlation for a single perpendicular wavevector
$(k_{x},k_{y})$
summed over
$k_{z}$
has a single resonant velocity. We may obtain a clean velocity-space signature for each distinct
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
mode.
In figure 9, we present timestack plots of the reduced parallel correlations for the electrons summed over the seven
$k_{z}$
modes for each diagnosed
$k_{\bot }$
case spanning
$1.4\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 9.9$
, or
$0.3\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{e}\leqslant 2$
. The same format as the summed-
$k_{z}$
results in figure 7(h) is used. The results clearly show the distinct advantages of the Fourier implementation of the field–particle correlation technique. First, the energy transfer signal for different
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
modes follows closely the increasing Landau resonant velocity (vertical black lines) as
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
increases from (a) through (f). A net energy energization of the electrons is obtained in all of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
modes, as shown in the accumulated energy transferred (green curve). Clearly, Landau resonant interactions with the electrons must play a key role in the damping of fluctuations across the sampled range of scales, consistent with expectations for a significant rate of collisionless damping by the electrons,
$\unicode[STIX]{x1D6FE}_{e}/\unicode[STIX]{x1D714}_{A0}\gtrsim O(0.1)$
, as shown in figure 1(b). Second, the magnitude of energy transfer drops by approximately 3 orders of magnitude from
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=1.4$
to
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=9.9$
. Of course, the number of perpendicular Fourier modes increases linearly with
$k_{\bot }$
, so the decrease in amplitude with
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
is partly compensated by the larger number of Fourier modes at higher
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
. Nonetheless, the first one or two
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
modes that we diagnosed here (specifically
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=1.4$
and
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=2.8$
) would dominate the signals in a single-point diagnostic, so one would not be able to identify the energy transfer mediated by higher
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
modes without Fourier decomposition. Finally, the characteristic time scale of the energy transfer is consistent with
$\unicode[STIX]{x1D70F}_{k}$
of each
$(k_{x},k_{y})$
Fourier mode, even though
$\unicode[STIX]{x1D70F}_{k}$
decreases with increasing
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
. As seen in the accumulated energy transferred (green curve), most of the electron energization occurs before a normalized centred time of
$t_{c}/\unicode[STIX]{x1D70F}_{0}\sim 1.5$
. This is consistent with the spatially integrated rate of electron energization
${\dot{E}}_{e}^{(fp)}$
(solid blue) in figure 3(b) being the most significant by
$1.5\unicode[STIX]{x1D70F}_{0}$
.
In order to illustrate more clearly how the energy transfer to the electrons closely tracks that Landau resonant velocity of kinetic Alfvén waves with a given perpendicular wavenumber
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
, we zoom into the central part of the
$v_{\Vert }$
range in figure 10(a–c). The localized region dominating electron energization moves to higher
$v_{\Vert }$
with higher
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
, consistent with the increasing resonant parallel phase velocity of kinetic Alfvén waves as
$k_{\bot }$
increases. This analysis strongly suggests that collisionless damping via the Landau resonance with electrons plays a key role in the removal of energy from the turbulence and consequent energization of the electrons.
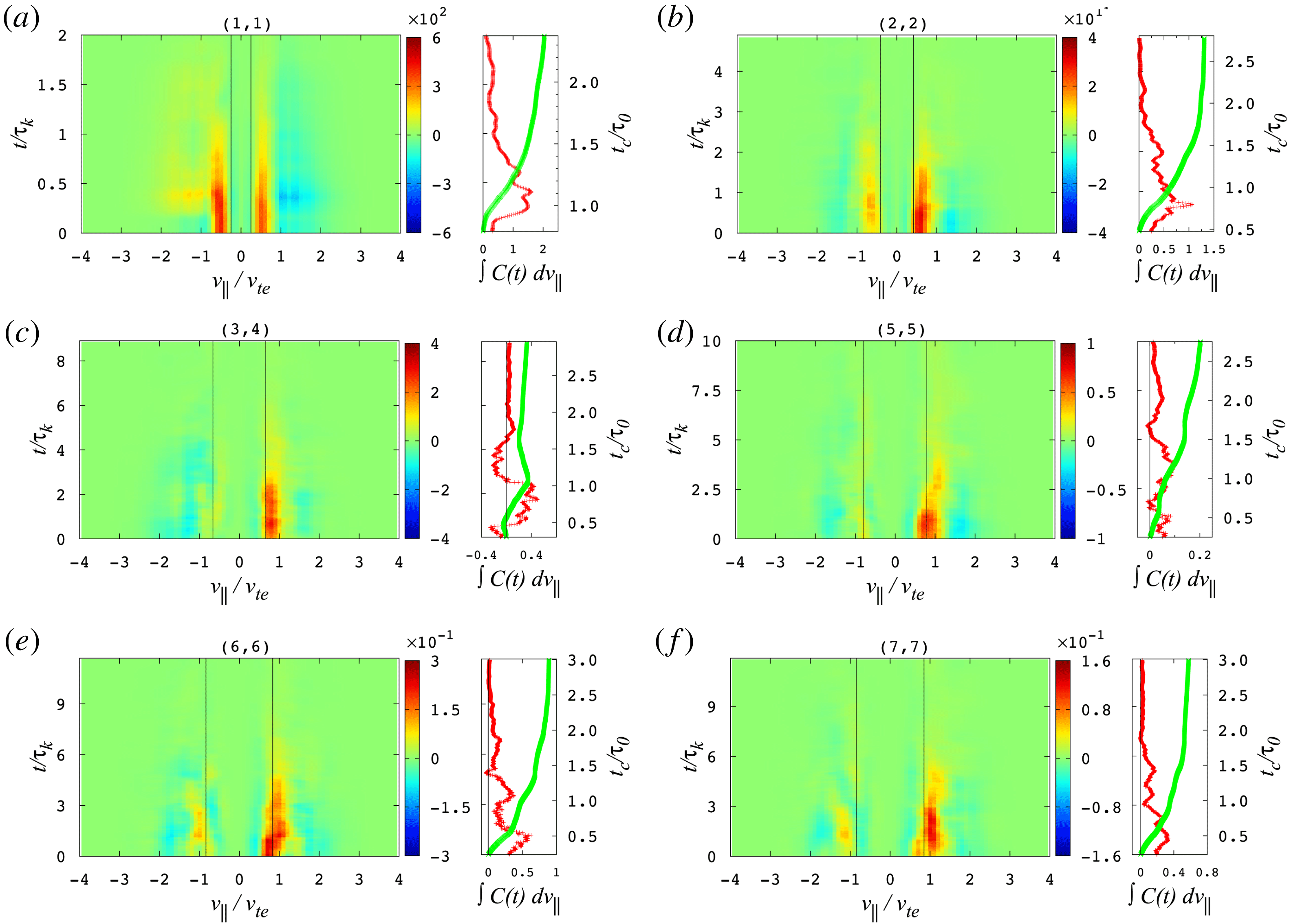
Figure 9. Parallel reduced correlations summed over seven
$k_{z}$
modes
$\sum _{k_{z}=-3}^{+3}C_{E_{\Vert }}(v_{\Vert },t)$
for
$6(k_{x},k_{y})$
values:
$(1,1)$
,
$(2,2)$
,
$(3,4)$
,
$(5,5)$
,
$(6,6)$
and
$(7,7)$
, representing a total of 42 Fourier modes of electron parallel reduced correlations. Their Landau resonant velocities are:
$v_{p\Vert }/v_{te}=\pm (0.25,0.42,0.66,0.79,0.84,0.85)$
respectively. The same format is used as figure 7(h).
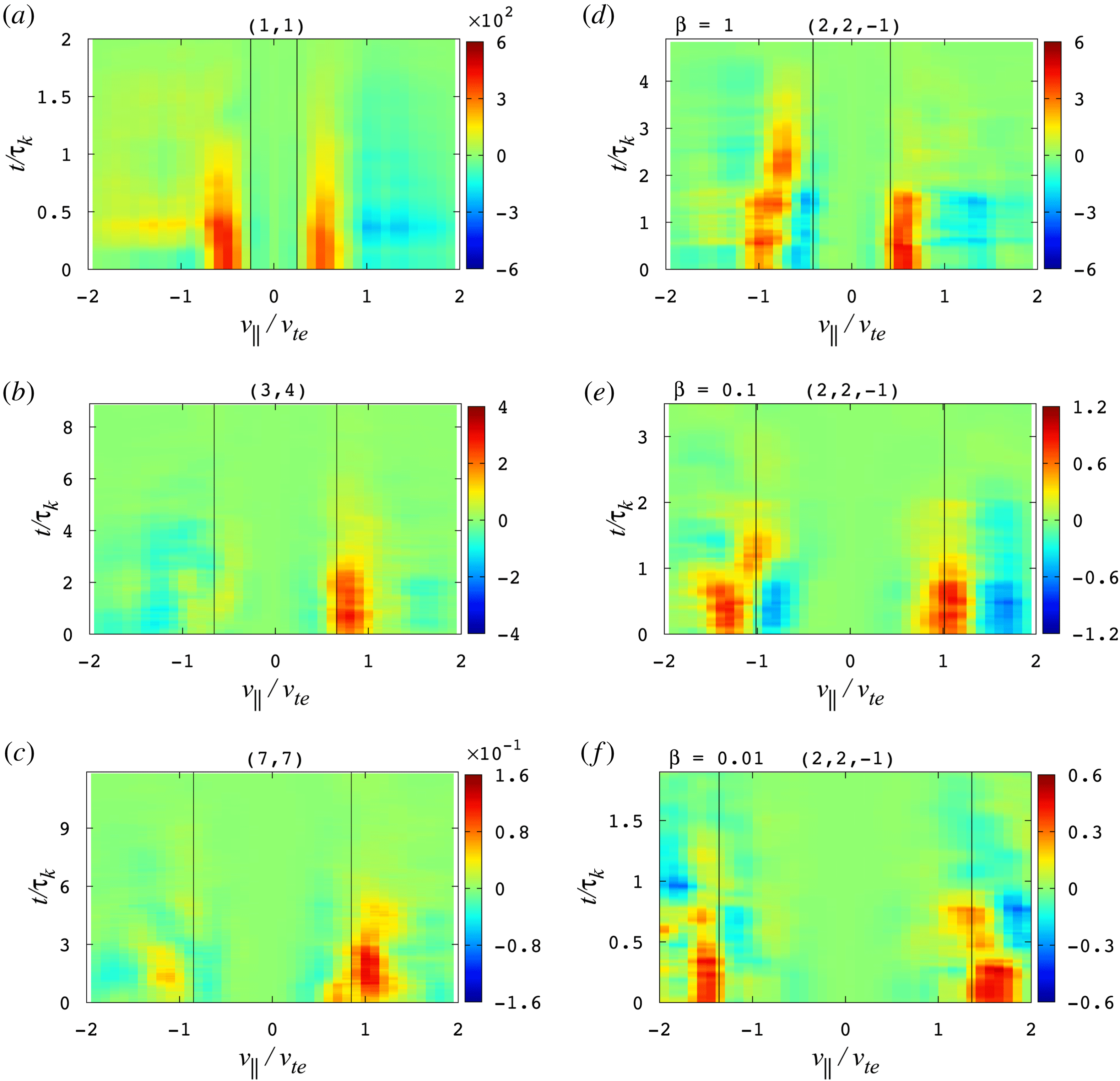
Figure 10. (a–c) Zoomed-in plot of summed-
$k_{z}$
correlations from figure 9 for 3
$(k_{x},k_{y})$
values –
$(1,1)$
,
$(3,4)$
and
$(7,7)$
with the corresponding Landau resonant velocities being
$v_{p\Vert }/v_{te}=\pm (0.25,0.66,0.85)$
, respectively – showing how the field–particle energy transfer rate closely tracks the resonant parallel phase velocities as
$(k_{x},k_{y})$
increases. (d–f) Electron parallel reduced correlations
$C_{E_{\Vert }}(v_{\Vert },t)$
for the
$(2,2,-1)$
Fourier mode from simulations with
$\unicode[STIX]{x1D6FD}_{i}=1$
(current run), 0.1 and 0.01 in which the Landau resonant velocity,
$v_{p\Vert }/v_{te}=\pm (0.42,1.0,1.4)$
, respectively, increases with decreasing
$\unicode[STIX]{x1D6FD}_{i}$
. The energy transfer signals from all three simulations show remarkable agreement with the increasing parallel resonant velocity.
Another plasma parameter that has a strong impact on the resonant parallel phase velocity of kinetic Alfvén waves is the plasma
$\unicode[STIX]{x1D6FD}_{i}$
. We performed simulations with an identical set-up as the
$\unicode[STIX]{x1D6FD}_{i}=1$
simulation described in § 2.5, but with values
$\unicode[STIX]{x1D6FD}_{i}=0.1$
and
$\unicode[STIX]{x1D6FD}_{i}=0.01$
. To analyse both of these additional simulations, we take a correlation interval
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{k}$
for the
$(2,2,-1)$
mode analysed here. In figure 10(d–f), we present timestack plots of the reduced parallel correlation
$C_{E_{\Vert }}(v_{\Vert },t,\unicode[STIX]{x1D70F})$
for electrons for Fourier mode
$(2,2,-1)$
. The resonant parallel phase velocity
$v_{p\Vert }$
for the
$(2,2)$
Fourier mode, when normalized to
$v_{te}$
, increases with values
$\unicode[STIX]{x1D714}/(k_{\Vert }v_{te})=\pm 0.42,\pm 1.0,\pm 1.4$
(vertical black lines) as the values of
$\unicode[STIX]{x1D6FD}_{i}$
decreases for these three simulations
$\unicode[STIX]{x1D6FD}_{i}=1,0.1,0.01$
. We indeed find a remarkably close association between
$v_{p\Vert }$
and the region of velocity space where the electrons participate in energy exchange with the parallel electric field
$E_{\Vert }$
. This close quantitative agreement with the
$\unicode[STIX]{x1D6FD}_{i}$
dependence of phase velocities observed in the simulations again suggests the dominant role that the Landau resonance plays in the field–particle energy transfer for electrons in the turbulence systems.
4.2.4 Accumulated particle energization:
$k_{\bot }$
dependence
The collisionless field–particle energy transfer rate is directly measured by the field–particle correlations. With the sampled Fourier spectrum, we can see how the accumulated particle energization varies as a function of the length scales of the fluctuations. In figure 11, we plot this accumulated particle energization at the end of the simulation
$\unicode[STIX]{x0394}E_{s}^{(fp)}$
as a function of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
. Each point represents the accumulated energization in each
$(k_{x},k_{y})$
Fourier mode summed over
$k_{z}$
for ions (blue) and electrons (green). The electron energization
$\unicode[STIX]{x0394}E_{e}^{(fp)}$
is then the value of the green curve at the end of the simulation for each
$(k_{x},k_{y})$
mode in figure 9. The same normalization is used for both ion and electron energization,
$\unicode[STIX]{x0394}E_{i}^{(fp)}$
and
$\unicode[STIX]{x0394}E_{e}^{(fp)}$
.
Figure 11. Accumulated particle energization
$\unicode[STIX]{x0394}E_{s}^{(fp)}$
at the end of the simulation for the sampled
$(k_{x},k_{y})$
modes (summed over
$k_{z}$
) as a function of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
. Each
$(k_{x},k_{y})$
mode is represented by a point and all points are connected by lines. The same normalization is used for both ion
$\unicode[STIX]{x0394}E_{i}^{(fp)}$
(blue) and electron
$\unicode[STIX]{x0394}E_{e}^{(fp)}$
(green) energization.
Several features of
$\unicode[STIX]{x0394}E_{s}^{(fp)}$
are notable. First, the particle energization is dominated by the lowest
$k_{\bot }$
mode that has the strongest amplitude, as expected. Second, the total ion and electron energization over the sampled spectrum are comparable given that both species are nearly equally energized at this dominant, lowest
$k_{\bot }$
mode. This is consistent with the comparable species heating rates due to field–particle interactions
${\dot{E}}_{s}^{(fp)}$
(solid) in figure 3 in the turbulence systemFootnote
2
. This is also consistent with the ion and electron collisionless damping rates,
$\unicode[STIX]{x1D6FE}_{i}$
and
$\unicode[STIX]{x1D6FE}_{e}$
, being of the same order of magnitude at
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$
, represented by the lowest
$k_{\bot }$
mode, in figure 1. Third, when plotted as a function of
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
,
$\unicode[STIX]{x0394}E_{s}^{(fp)}$
here can represent the energy transfer spectra; for electrons,
$\unicode[STIX]{x0394}E_{e}^{(fp)}$
indicates a spectral rollover at the electron gyroradius scale of
$k_{\bot }\unicode[STIX]{x1D70C}_{e}=1$
(
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=5$
), becoming less steep at
$k_{\bot }\unicode[STIX]{x1D70C}_{e}>1$
. Lastly, ion energization shows a dip at
$k_{\bot }\unicode[STIX]{x1D70C}_{i}=7$
, rather than a monotonic drop for all
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\geqslant 7$
modes as would be expected from the ion collisionless damping rate, suggesting that collisionless damping cannot completely explain ion energization. These interesting features deserve further investigation in the future.
5 Conclusions
The field–particle correlation technique is a new method both for determining the rate of transfer of energy between electromagnetic fields and plasma particles and for identifying the physical mechanisms responsible for that energy transfer through their velocity-space signatures. Previous implementations of this novel technique employ a time series of the particle velocity distribution and electromagnetic field measurements performed at a single point in space. Here, we present an alternative Fourier implementation of the field–particle correlation technique that determines the energy transfer for a single wavevector in Fourier space instead of at a single point in physical space.
The Fourier implementation has the capability to explore the energy transfer between fields and particles as a function of the length scale of the fluctuations, information that cannot be obtained through single-point measurements in physical space. Furthermore, in a broadband turbulent spectrum, the resonant parallel phase velocity
$\unicode[STIX]{x1D714}/k_{\Vert }$
is generally a function of the wavevector, resonant collisionless interactions analysed in terms of Fourier wavevector modes are expected to yield a clean velocity-space signature at the resonant velocity. This contrasts the single-point implementation in which all wave modes will contribute to the energy transfer at a given point, potentially smearing out the velocity-space signals over the range of resonant velocities for all contributing wave modes. Furthermore, the Fourier decomposition separates the contributions to the energy transfer from each scale, enabling the energy transfer for small amplitude modes at high wavenumber to be observed even in the presence of much larger amplitude modes at lower wavenumbers. This contrasts with the single-point implementation in which the much larger amplitude modes at lower wavenumbers will dominate the energy transfer. Finally, in the Fourier implementation, the correlation intervals need only extend over a few periods of the mode under investigation, even in the presence of larger amplitude, lower-frequency modes.
The Fourier implementation employs information throughout the spatial domain to decompose fluctuations as a function of scale, so it cannot be applied to analyse spacecraft observations that provide measurements at only one, or possibly a few, points in space. Nonetheless, it can be used in numerical simulations in which full spatial information is accessible. The key advantage of the Fourier implementation to investigate the particle energization as a function of the length scale of the electromagnetic fluctuations provides insights that are complementary to the spatial information of particle energization provided by the more standard, single-point implementation. In fact, dual implementation of the field–particle correlation technique in both physical and Fourier space in simulations can take the advantages of both approaches in identifying collisionless energy transfer in simulations supporting spacecraft missions.
Here we apply the Fourier implementation of the field–particle correlation technique to investigate the energization of the ions and electrons in strong electromagnetic turbulence. We simulate a 3-D extension of the standard Orzsag–Tang vortex (3-D OTV) problem, a set-up previously used to explore the differences between 2-D and 3-D turbulence (Li et al.
Reference Li, Howes, Klein and TenBarge2016). We follow the flow of energy in the simulation from turbulent energy that is first collisionlessly transferred to particles as non-thermal energy in the velocity distribution functions of the ions and electrons, and later is collisionally thermalized to ion and electron heat. For the
$\unicode[STIX]{x1D6FD}_{i}=1$
conditions of the simulation, we find that the electrons are heated about twice as much as the ions. We show that the particle energization in the simulation, equal to
$\boldsymbol{J}\boldsymbol{\cdot }\boldsymbol{E}$
integrated over the simulation volume, occurs in a spatially non-uniform manner, with the dominant heating confined to narrow current sheet layers associated with strong parallel electric fields.
Applying the Fourier implementation of the field–particle correlation technique to the simulation, we find that the velocity-space signature of electron and ion energization for a particular Fourier mode is consistent with Landau damping at the resonant parallel phase velocity of the kinetic Alfvén wave for that mode. Timestack plots of the electron and ion energization by the parallel electric field
$E_{\Vert }$
also show a net energization of the plasma particles at the expense of the turbulent energy.
The regions of velocity space in which particles exchange energy with the electric field closely follow the resonant parallel phase velocity for kinetic Alfvén waves as the perpendicular wavenumber
$k_{\bot }$
and plasma
$\unicode[STIX]{x1D6FD}_{i}$
are varied (figure 10). This shows that collisionless damping via the Landau resonance with ions and electrons is an important channel of particle energization in strong electromagnetic turbulence, relevant to space plasmas, such as the solar corona, solar wind and planetary magnetospheres.
Acknowledgements
T.C.L. is grateful to T. Parashar, N. Loureiro, K. Schoeffler and A. Mallet for valuable discussions. Supported by NSF CAREER Award AGS-1054061, NASA grants 80NSSC18K0754, 80NSSC18K0289, 80NSSC18K0643, 80NSSC18K1217 and 80NSSC18K1371, NASA HSR grant NNX16AM23G, and NSF SHINE award AGS-1622306. Computations used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF grant ACI-1053575.
Appendix. Determination and significance of correlation interval
Here we illustrate how a sufficiently long correlation interval is determined and its significance using electron parallel reduced correlations, which conveniently depict the energy transfer rate as a function of
$v_{\Vert }$
and time
$t$
. Plotted in figure 12 are electron parallel reduced correlations for a correlation interval
$\unicode[STIX]{x1D70F}=0,0.5\unicode[STIX]{x1D70F}_{k}$
,
$\unicode[STIX]{x1D70F}_{k}$
and
$2\unicode[STIX]{x1D70F}_{k}$
for the
$(2,2,-1)$
Fourier mode in (a)–(d).
Figure 12. Electron parallel reduced correlations
$C_{E_{\Vert }}(v_{\Vert },t)$
using a correlation interval (a)
$\unicode[STIX]{x1D70F}=0$
, (b)
$\unicode[STIX]{x1D70F}=0.5\unicode[STIX]{x1D70F}_{k}$
, (c)
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{k}$
and (d)
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
for the
$(2,2,-1)$
Fourier mode. The Landau resonant velocities:
$v_{p\Vert }/v_{te}=\pm 0.42$
, are indicated by vertical black lines. Time
$t$
is defined at the beginning of the correlation interval.
Using
$\unicode[STIX]{x1D70F}=0$
, (a) the instantaneous energy transfer between
$E_{\Vert }$
and electrons manifests as alternating red and blue signals over short time scales as they exchange energy back and forth many times throughout the course of the simulation. As
$\unicode[STIX]{x1D70F}$
increases in (b) through (d), the time evolution of the energy transfer becomes increasing concentrated to
$v_{p\Vert }$
. In (c,d), the time evolution of the energy transfer begins to be qualitatively consistent, with mostly red signals just above
$v_{p\Vert }$
. The maximum amplitude of energy transfer for
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{k}$
and
$2\unicode[STIX]{x1D70F}_{k}$
in (c,d) becomes comparable, whereas it is reduced by over twice from (a)
$\unicode[STIX]{x1D70F}=0$
to (b)
$\unicode[STIX]{x1D70F}=0.5\unicode[STIX]{x1D70F}_{k}$
. This indicates that a correlation interval of
$\unicode[STIX]{x1D70F}\geqslant \unicode[STIX]{x1D70F}_{k}$
leads to a qualitative convergence of the time evolution of the energy transfer rate as a function of
$v_{\Vert }$
. Hence,
$\unicode[STIX]{x1D70F}\geqslant \unicode[STIX]{x1D70F}_{k}$
represents a sufficiently long correlation interval. The choice of
$\unicode[STIX]{x1D70F}=2\unicode[STIX]{x1D70F}_{k}$
used in this work is suitable for capturing the net secular energy transfer signals in velocity space.
An important feature again illustrated in figure 12 is that while electrons over a broad range of
$v_{\Vert }$
participate in (a) the instantaneous energy transfer, the secular net energy transfer identified by correlating over a suitably long time period in (c,d) is dominated by ‘near-resonance’ electrons that are close to the parallel resonant velocity
$v_{p\Vert }$
.
