Hostname: page-component-f554764f5-fnl2l Total loading time: 0 Render date: 2025-04-20T11:36:46.588Z Has data issue: false hasContentIssue false
  • English
  • Français

A revisit to “On BMO and Carleson measures on Riemannian manifolds”

Part of: Abstract harmonic analysis Higher-dimensional theory Harmonic analysis in several variables

Published online by Cambridge University Press:  18 July 2023

Bo Li ,
Jinxia Li ,
Qingze Lin ,
Bolin Ma  and
Tianjun Shen
Bo Li
Affiliation:
College of Data Science, Jiaxing University, Jiaxing 314001, China ([email protected])
Jinxia Li
Affiliation:
School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo, 454003, China ([email protected])
Qingze Lin
Affiliation:
School of Mathematics, Sun Yat-sen University, Guangzhou 510275, China ([email protected])
Bolin Ma
Affiliation:
College of Data Science, Jiaxing University, Jiaxing 314001, China ([email protected])
Tianjun Shen*
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, China ([email protected])
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\mathcal {M}$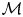 be an Ahlfors $n$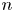-regular Riemannian manifold such that either the Ricci curvature is non-negative or the Ricci curvature is bounded from below together with a bound on the gradient of the heat kernel. In the paper [IMRN, 2022, no. 2, 1245-1269] of Brazke–Schikorra–Sire, the authors characterised the BMO function $u : \mathcal {M} \to \mathbb {R}$ 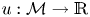by a Carleson measure condition of its $\sigma$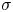-harmonic extension $U:\mathcal {M}\times \mathbb {R}_+ \to \mathbb {R}$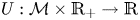. This paper is concerned with the similar problem under a more general Dirichlet metric measure space setting, and the limiting behaviours of BMO & Carleson measure, where the heat kernel admits only the so-called diagonal upper estimate. More significantly, without the Ricci curvature condition, we relax the Ahlfors regularity to a doubling property, and remove the pointwise bound on the gradient of the heat kernel. Some similar results for the Lipschitz function are also given, and two open problems related to our main result are considered.

Keywords

Harmonic functionmetric measure spaceBMOCarleson measure

MSC classification

Primary: 31B25: Boundary behavior
Secondary: 43A85: Analysis on homogeneous spaces 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 4 , August 2024 , pp. 1281 - 1307
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baudoin, F., Lang, Q. and Sire, Y., Powers of generators on Dirichlet spaces and applications to Harnack principles, arXiv: 2010.01036.Google Scholar
Brazke, D., Schikorra, A. and Sire, Y.. On BMO and Carleson measures on Riemannian manifolds. Int. Math. Res. Not. IMRN 2022 (2022), 1245–1269.10.1093/imrn/rnaa140CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Comm. Partial Differ. Equ. 32 (2007), 1245–1260.10.1080/03605300600987306CrossRefGoogle Scholar
Carron, G.. Riesz transform on manifolds with quadratic curvature decay. Rev. Mat. Iberoam. 33 (2017), 749–788.10.4171/rmi/954CrossRefGoogle Scholar
Chen, J.. A representation theorem of harmonic functions and its application to BMO on manifolds. Appl. Math. J. Chinese Univ. Ser. B 16 (2001), 279–284.Google Scholar
Chen, P., Duong, X., Li, J., Song, L. and Yan, L.. Carleson measures, BMO spaces and balayages associated to Schrödinger operators. Sci. China Math. 60 (2017), 2077–2092.10.1007/s11425-016-9147-yCrossRefGoogle Scholar
Coifman, R. and Weiss, G.. Extensions of Hardy spaces and their use in analysis. Bull. Amer. Math. Soc. 83 (1977), 569–645.10.1090/S0002-9904-1977-14325-5CrossRefGoogle Scholar
Coulhon, T., Jiang, R., Koskela, P. and Sikora, A.. Gradient estimates for heat kernels and harmonic functions. J. Funct. Anal. 278 (2020), 108398.10.1016/j.jfa.2019.108398CrossRefGoogle Scholar
Coulhon, T. and Sikora, A.. Gaussian heat kernel upper bounds via the Phragmén-Lindelöf theorem. Proc. Lond. Math. Soc. (3) 96 (2008), 507–544.10.1112/plms/pdm050CrossRefGoogle Scholar
Ding, Y., Lee, M. and Lin, C.. Carleson measure characterization of weighted BMO associated with a family of general sets. J. Geom. Anal. 27 (2017), 842–867.10.1007/s12220-016-9700-4CrossRefGoogle Scholar
Duong, X., Yan, L. and Zhang, C.. On characterization of Poisson integrals of Schrödinger operators with BMO traces. J. Funct. Anal. 266 (2014), 2053–2085.10.1016/j.jfa.2013.09.008CrossRefGoogle Scholar
Fabes, E., Johnson, R. and Neri, U.. Spaces of harmonic functions representable by Poisson integrals of functions in BMO and $L_{p,\lambda}$. Indiana Univ. Math. J. 25 (1976), 159–170.10.1512/iumj.1976.25.25012CrossRefGoogle Scholar
Fabes, E. and Neri, U.. Characterization of temperatures with initial data in BMO. Duke Math. J. 42 (1975), 725–734.10.1215/S0012-7094-75-04260-XCrossRefGoogle Scholar
Fefferman, C.. Characterizations of bounded mean oscillation. Bull. Amer. Math. Soc. 77 (1971), 587–588.10.1090/S0002-9904-1971-12763-5CrossRefGoogle Scholar
Fukushima, M., Oshima, Y. and Takeda, M., Dirichlet Forms and Symmetric Markov Processes, in: de Gruyter Studies in Mathematics, Vol. 19 (Walter de Gruyter & Co., Berlin, 1994).10.1515/9783110889741CrossRefGoogle Scholar
Galé, J., Miana, P. and Stinga, P.. Extension problem and fractional operators: semigroups and wave equations. J. Evol. Equ. 13 (2013), 343–368.10.1007/s00028-013-0182-6CrossRefGoogle Scholar
Grigor'yan, A.. Gaussian upper bounds for the heat kernel on arbitrary manifolds. J. Differ. Geom. 45 (1997), 33–52.Google Scholar
Grigor'yan, A.. The heat equation on noncompact Riemannian manifolds. (Russian) Mat. Sb. 182 (1991), 55–87. translation in Math. USSR-Sb. 72 (1992), 47–77.Google Scholar
Gyrya, P., Saloff-Coste, L.: Neumann and Dirichlet heat kernels in inner uniform domains, Astérisque, 33 (2011), Soc. Math. France.Google Scholar
Hartzstein, S. and Salinas, O.. Weighted BMO and Carleson measures on spaces of homogeneous type. J. Math. Anal. Appl. 342 (2008), 950–969.10.1016/j.jmaa.2007.12.065CrossRefGoogle Scholar
Heinonen, J., Koskela, P., Shanmugalingam, N. and Tyson, T., Sobolev spaces on metric measure spaces. An approach based on upper gradients, New Mathematical Monographs, Vol. 27 (Cambridge University Press, Cambridge, 2015).10.1017/CBO9781316135914CrossRefGoogle Scholar
Jiang, R. and Li, B.. Dirichlet problem for Schrödinger equation with the boundary value in the BMO space. Sci. China Math. 65 (2022), 1431–1468.10.1007/s11425-020-1834-1CrossRefGoogle Scholar
Jiang, R. and Lin, F.. Riesz transform under perturbations via heat kernel regularity. J. Math. Pures Appl. (9) 133 (2020), 39–65.10.1016/j.matpur.2019.02.009CrossRefGoogle Scholar
Jiang, R., Xiao, J. and Yang, D.. Towards spaces of harmonic functions with traces in square Campanato spaces and their scaling invariants. Anal. Appl. (Singap.) 14 (2016), 679–703.10.1142/S0219530515500190CrossRefGoogle Scholar
Jin, Y., Li, B. and Shen, T., Harmonic functions with BMO traces and their limiting behaviors on metric measure spaces, preprint.Google Scholar
Li, B., Ma, B., Shen, T., Wu, X. and Zhang, C.. On the caloric functions with BMO traces and their limiting behaviors. J. Geom. Anal. 33 (2023), 215, 42 pp.10.1007/s12220-023-01245-6CrossRefGoogle Scholar
Lin, C. and Liu, H.. $\mathrm {BMO}_L(\mathbb {H}^n)$ spaces and Carleson measures for Schrödinger operators. Adv. Math. 228 (2011), 1631–1688.10.1016/j.aim.2011.06.024CrossRefGoogle Scholar
Song, L., Tian, X. and Yan, L.. On characterization of Poisson integrals of Schrödinger operators with Morrey traces. Acta Math. Sin. (Engl. Ser.) 34 (2018), 787–800.10.1007/s10114-018-7368-3CrossRefGoogle Scholar
Song, L. and Wu, L.. The CMO-Dirichlet problem for the Schrödinger equation in the upper half-space and characterizations of CMO. J. Geom. Anal. 32 (2022), 130, 37 pp.10.1007/s12220-022-00875-6CrossRefGoogle Scholar
Stinga, P. and Torrea, J.. Extension problem and Harnack's inequality for some fractional operators. Comm. Partial Differ. Equ. 35 (2010), 2092–2122.10.1080/03605301003735680CrossRefGoogle Scholar
Sturm, K.. Analysis on local Dirichlet spaces. III. The parabolic Harnack inequality. J. Math. Pures Appl. (9) 75 (1996), 273–297.Google Scholar
Trong, N. and Tung, N.. Weighted BMO type spaces associated to admissible functions and applications. Acta Math. Vietnam. 41 (2016), 209–241.10.1007/s40306-014-0109-5CrossRefGoogle Scholar
Wang, Y. and Xiao, J.. Homogeneous Campanato–Sobolev classes. Appl. Comput. Harmon. Anal. 39 (2015), 214–247.10.1016/j.acha.2014.09.002CrossRefGoogle Scholar