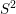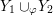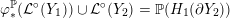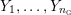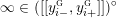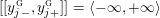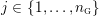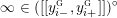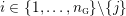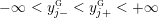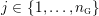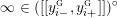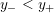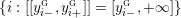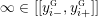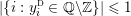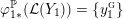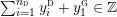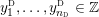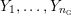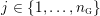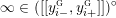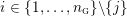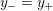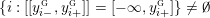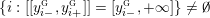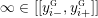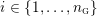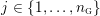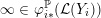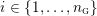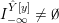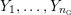1 Introduction
In the late 1990s, Thurston showed [Reference Calegari and DunfieldCD03] that any taut foliation on an atoroidal three-manifold
![]() $M$
makes
$M$
makes
![]() $\unicode[STIX]{x1D70B}_{1}(M)$
act faithfully on the circle. This result came almost two decades after Eisenbud, Hirsch, and Neumann [Reference Eisenbud, Hirsch and NeumannEHN81] encountered a complementary phenomenon: they proved that an oriented three-manifold
$\unicode[STIX]{x1D70B}_{1}(M)$
act faithfully on the circle. This result came almost two decades after Eisenbud, Hirsch, and Neumann [Reference Eisenbud, Hirsch and NeumannEHN81] encountered a complementary phenomenon: they proved that an oriented three-manifold
![]() $M$
Seifert fibered over
$M$
Seifert fibered over
![]() $S^{2}$
admits a co-oriented foliation transverse to the fiber if and only if
$S^{2}$
admits a co-oriented foliation transverse to the fiber if and only if
![]() $\unicode[STIX]{x1D70B}_{1}(M)$
admits a representation in
$\unicode[STIX]{x1D70B}_{1}(M)$
admits a representation in
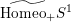 $\widetilde{\text{Homeo}_{+}}S^{1}$
sending
$\widetilde{\text{Homeo}_{+}}S^{1}$
sending
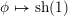 $\unicode[STIX]{x1D719}\mapsto \text{sh}(1)$
, where
$\unicode[STIX]{x1D719}\mapsto \text{sh}(1)$
, where
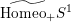 $\widetilde{\text{Homeo}_{+}}S^{1}$
is the universal cover of the group of orientation-preserving homeomorphisms of the circle,
$\widetilde{\text{Homeo}_{+}}S^{1}$
is the universal cover of the group of orientation-preserving homeomorphisms of the circle,
![]() $\unicode[STIX]{x1D719}$
is the regular fiber class, and
$\unicode[STIX]{x1D719}$
is the regular fiber class, and
 $\text{sh}(s):t\mapsto t+s$
for any
$\text{sh}(s):t\mapsto t+s$
for any
![]() $s\in \mathbb{R}$
, making
$s\in \mathbb{R}$
, making
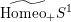 $\widetilde{\text{Homeo}_{+}}S^{1}$
the centralizer of
$\widetilde{\text{Homeo}_{+}}S^{1}$
the centralizer of
![]() $\text{sh}(1)$
in
$\text{sh}(1)$
in
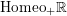 $\text{Homeo}_{+}\mathbb{R}$
.
$\text{Homeo}_{+}\mathbb{R}$
.
1.1 Jankins–Neumann classification
Inspired by this observation, Jankins and Neumann used Poincaré’s ‘rotation number’ invariant to generalize the criterion of [Reference Eisenbud, Hirsch and NeumannEHN81] to a more local representation-theoretic condition in terms of meridians of exceptional fibers. This new formulation of the problem, in addition to a correct conjecture that the necessary representation-theoretic conditions could be met in
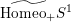 $\widetilde{\text{Homeo}_{+}}S^{1}$
if and only if they could also be met in a smooth Lie subgroup thereof, allowed them to work out a complete, explicit classification [Reference Jankins and NeumannJN85], which they proved in all but one special case, later proven by Naimi [Reference NaimiNai94].
$\widetilde{\text{Homeo}_{+}}S^{1}$
if and only if they could also be met in a smooth Lie subgroup thereof, allowed them to work out a complete, explicit classification [Reference Jankins and NeumannJN85], which they proved in all but one special case, later proven by Naimi [Reference NaimiNai94].
Theorem 1.1 [Reference Jankins and NeumannJN85, Reference NaimiNai94].
For
![]() $n>1$
, the manifold
$n>1$
, the manifold
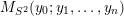 $M_{S^{2}}(y_{0};y_{1},\ldots ,y_{n})$
Seifert fibered over
$M_{S^{2}}(y_{0};y_{1},\ldots ,y_{n})$
Seifert fibered over
![]() $S^{2}$
admits a co-oriented taut foliation if and only if
$S^{2}$
admits a co-oriented taut foliation if and only if
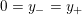 $0=y_{-}=y_{+}$
or
$0=y_{-}=y_{+}$
or
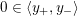 $0\in \langle y_{+},y_{-}\rangle$
, where
$0\in \langle y_{+},y_{-}\rangle$
, where
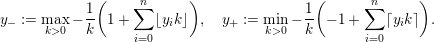 $$\begin{eqnarray}y_{-}:=\max _{k>0}-\frac{1}{k}\biggl(1+\mathop{\sum }_{i=0}^{n}\lfloor y_{i}k\rfloor \biggr),\quad y_{+}:=\min _{k>0}-\frac{1}{k}\biggl(-1+\mathop{\sum }_{i=0}^{n}\lceil y_{i}k\rceil \biggr).\end{eqnarray}$$
$$\begin{eqnarray}y_{-}:=\max _{k>0}-\frac{1}{k}\biggl(1+\mathop{\sum }_{i=0}^{n}\lfloor y_{i}k\rfloor \biggr),\quad y_{+}:=\min _{k>0}-\frac{1}{k}\biggl(-1+\mathop{\sum }_{i=0}^{n}\lceil y_{i}k\rceil \biggr).\end{eqnarray}$$
(In the above, and henceforth in this paper, we always regard
![]() $k$
as an integer, writing
$k$
as an integer, writing
![]() $k>0$
as shorthand for the restriction
$k>0$
as shorthand for the restriction
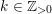 $k\in \mathbb{Z}_{{>}0}$
.)
$k\in \mathbb{Z}_{{>}0}$
.)
Since then, the Jankins–Neumann–Naimi classification has served as a Rosetta stone for certain a priori unrelated properties.
Theorem 1.2 [Reference Eisenbud, Hirsch and NeumannEHN81, Reference Jankins and NeumannJN85, Reference NaimiNai94, Reference Calegari and WalkerCW11, Reference Ozsváth and SzabóOS04, Reference Lisca and MatićLM04, Reference Lisca and StipsiczLS07, Reference Boyer, Gordon and WatsonBGW13, Reference Rasmussen and RasmussenRR15].
If
![]() $M$
is a closed oriented Seifert fibered space, then the following are equivalent:
$M$
is a closed oriented Seifert fibered space, then the following are equivalent:
- (1a)
-
 $\unicode[STIX]{x1D70B}_{1}(M)$
admits a non-trivial representation in
$\unicode[STIX]{x1D70B}_{1}(M)$
admits a non-trivial representation in
 $\text{Homeo}_{+}\mathbb{R}$
;
$\text{Homeo}_{+}\mathbb{R}$
; - (1b)
-
 $\unicode[STIX]{x1D70B}_{1}(M)$
is left-orderable;
$\unicode[STIX]{x1D70B}_{1}(M)$
is left-orderable; - (2)
-
 $M$
admits a co-oriented
$M$
admits a co-oriented
 $C^{0}$
taut foliation;
$C^{0}$
taut foliation; - (3)
-
 $M$
has non-trivial Heegaard Floer homology, i.e.
$M$
has non-trivial Heegaard Floer homology, i.e.
 $M$
fails to be an L-space.
$M$
fails to be an L-space.
One often uses
![]() $(1\text{a})$
as a proxy for
$(1\text{a})$
as a proxy for
![]() $(1\text{b})$
, since a result of Boyer, Rolfsen, and Wiest [Reference Boyer, Rolfsen and WiestBRW05, Theorem 1.1.1], combined with the well-known fact [Reference LinnellLin99] that the set of countable left-orderable groups coincides with the set of countable non-trivial subgroups of
$(1\text{b})$
, since a result of Boyer, Rolfsen, and Wiest [Reference Boyer, Rolfsen and WiestBRW05, Theorem 1.1.1], combined with the well-known fact [Reference LinnellLin99] that the set of countable left-orderable groups coincides with the set of countable non-trivial subgroups of
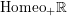 $\text{Homeo}_{+}\mathbb{R}$
, shows that
$\text{Homeo}_{+}\mathbb{R}$
, shows that
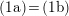 $(1\text{a})\!=\!(1\text{b})$
for every prime compact oriented three-manifold. Boyer, Gordon, and Watson have conjectured that
$(1\text{a})\!=\!(1\text{b})$
for every prime compact oriented three-manifold. Boyer, Gordon, and Watson have conjectured that
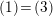 $(1)\!=\!(3)$
for any prime compact oriented three-manifold [Reference Boyer, Gordon and WatsonBGW13], and quite recently, Kazez and Roberts [Reference Kazez and RobertsKR15], and independently Bowden [Reference BowdenBow15], have extended a
$(1)\!=\!(3)$
for any prime compact oriented three-manifold [Reference Boyer, Gordon and WatsonBGW13], and quite recently, Kazez and Roberts [Reference Kazez and RobertsKR15], and independently Bowden [Reference BowdenBow15], have extended a
![]() $C^{2}$
foliations result of Ozsváth and Szabó [Reference Ozsváth and SzabóOS04] to show that
$C^{2}$
foliations result of Ozsváth and Szabó [Reference Ozsváth and SzabóOS04] to show that
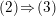 $(2)\!\Rightarrow \!(3)$
for any compact oriented three-manifold. (For this reason, all foliations in this paper are assumed to be
$(2)\!\Rightarrow \!(3)$
for any compact oriented three-manifold. (For this reason, all foliations in this paper are assumed to be
![]() $C^{0}$
unless otherwise stated.)
$C^{0}$
unless otherwise stated.)
The implication
 $(3)\!\Rightarrow \!(2)$
, however, is entirely more mysterious. In particular, all known proofs [Reference Lisca and MatićLM04, Reference Lisca and StipsiczLS07, Reference Rasmussen and RasmussenRR15] that non-L-space oriented Seifert fibered spaces admit co-oriented taut foliations rely on an explicit comparison of sets of manifolds: one works out the classification of Seifert fibered manifolds over
$(3)\!\Rightarrow \!(2)$
, however, is entirely more mysterious. In particular, all known proofs [Reference Lisca and MatićLM04, Reference Lisca and StipsiczLS07, Reference Rasmussen and RasmussenRR15] that non-L-space oriented Seifert fibered spaces admit co-oriented taut foliations rely on an explicit comparison of sets of manifolds: one works out the classification of Seifert fibered manifolds over
![]() $S^{2}\!$
with non-trivial Heegaard Floer homology, and observes that this classification coincides with the Jankins–Neumann–Naimi classification of oriented Seifert fibered spaces over
$S^{2}\!$
with non-trivial Heegaard Floer homology, and observes that this classification coincides with the Jankins–Neumann–Naimi classification of oriented Seifert fibered spaces over
![]() $S^{2}$
admitting co-oriented taut foliations. (The implication
$S^{2}$
admitting co-oriented taut foliations. (The implication
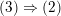 $(3)\Rightarrow (2)$
holds vacuously for closed oriented Seifert fibered spaces with
$(3)\Rightarrow (2)$
holds vacuously for closed oriented Seifert fibered spaces with
![]() $b_{1}>0$
, all of which admit co-oriented taut foliations [Reference GabaiGab83], and for oriented Seifert fibered spaces over
$b_{1}>0$
, all of which admit co-oriented taut foliations [Reference GabaiGab83], and for oriented Seifert fibered spaces over
![]() $\mathbb{R}\mathbb{P}^{2}\!$
, all of which are L-spaces [Reference Boyer, Gordon and WatsonBGW13].)
$\mathbb{R}\mathbb{P}^{2}\!$
, all of which are L-spaces [Reference Boyer, Gordon and WatsonBGW13].)
1.2 Graph manifolds
Boyer and Clay recently brought insight to this question by introducing a relative version of the problem, studying the gluing behavior of properties (1a), (1b), and (2) along the incompressible tori separating Seifert fibered components of graph manifolds. By showing that these three properties glue in an identical manner along boundaries of JSJ components of rational homology sphere graph manifolds, they were able to prove the equivalence of these three properties for any closed graph manifold [Reference Boyer and ClayBC14]. Boyer and Clay also conjectured that property (3) should obey the same gluing behavior.
In answer, Hanselman and Watson [Reference Hanselman and WatsonHW15], and independently Rasmussen and the author [Reference Rasmussen and RasmussenRR15], were able to confirm this gluing conjecture for a larger class of three-manifolds with torus boundary, but subject to certain hypotheses, which one can show are safe to remove in the case of graph manifolds. The four of us [Reference Hanselman, Rasmussen, Rasmussen and WatsonHR15] were therefore able to prove the following.
Theorem 1.3 [Reference Hanselman, Rasmussen, Rasmussen and WatsonHR15].
A graph manifold is an L-space if and only if it fails to admit a co-oriented taut foliation.
The current paper follows an independent trajectory from the work of [Reference Hanselman, Rasmussen, Rasmussen and WatsonHR15], launched before the author joined the other collaboration. Although the two papers overlap in one or two results, including slightly variant proofs of Theorem 1.3 and the below gluing criterion, the main result of the current paper is the generalization of the Jankins–Neumann classification formula to graph manifolds, for which we now introduce some notation.
Definition 1.4. If
![]() $Y\!$
is a compact oriented three-manifold with torus boundary, then the L-space interval of
$Y\!$
is a compact oriented three-manifold with torus boundary, then the L-space interval of
![]() $Y$
is the space
$Y$
is the space
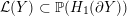 ${\mathcal{L}}(Y)\subset \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
of L-space Dehn-filling slopes of
${\mathcal{L}}(Y)\subset \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
of L-space Dehn-filling slopes of
![]() $Y\!$
.
$Y\!$
.
We call
![]() ${\mathcal{L}}(Y)$
an interval because if it contains more than one point, then it is the intersection of
${\mathcal{L}}(Y)$
an interval because if it contains more than one point, then it is the intersection of
 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
with either a closed interval in
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
with either a closed interval in
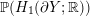 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y;\mathbb{R}))$
or the complement of a single point in
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y;\mathbb{R}))$
or the complement of a single point in
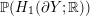 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y;\mathbb{R}))$
. It therefore makes sense to speak of the interior
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y;\mathbb{R}))$
. It therefore makes sense to speak of the interior
![]() ${\mathcal{L}}^{\circ }(Y)$
of
${\mathcal{L}}^{\circ }(Y)$
of
![]() ${\mathcal{L}}(Y)$
. If
${\mathcal{L}}(Y)$
. If
![]() ${\mathcal{L}}^{\circ }(Y)$
is non-empty, we call
${\mathcal{L}}^{\circ }(Y)$
is non-empty, we call
![]() $Y$
Floer simple.
$Y$
Floer simple.
Proposition 1.5. If
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
are non-solid-torus graph manifolds with torus boundary, then the union
$Y_{2}$
are non-solid-torus graph manifolds with torus boundary, then the union
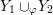 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
, with gluing map
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
, with gluing map
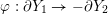 $\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
, is an L-space if and only if
$\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
, is an L-space if and only if
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2})).\end{eqnarray}$$
In particular, Floer simplicity is not required.
A graph manifold
![]() $Y$
with torus boundary and
$Y$
with torus boundary and
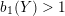 $b_{1}(Y)>1$
has
$b_{1}(Y)>1$
has
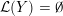 ${\mathcal{L}}(Y)=\emptyset$
. If
${\mathcal{L}}(Y)=\emptyset$
. If
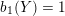 $b_{1}(Y)=1$
, then the graph for
$b_{1}(Y)=1$
, then the graph for
![]() $Y$
is a tree, and we choose to root this tree at the JSJ component
$Y$
is a tree, and we choose to root this tree at the JSJ component
![]() ${\hat{Y}}$
containing
${\hat{Y}}$
containing
![]() $\unicode[STIX]{x2202}Y$
. Writing
$\unicode[STIX]{x2202}Y$
. Writing
 $Y_{1},\ldots ,Y_{n_{{\rm \small{G}}}}$
for the
$Y_{1},\ldots ,Y_{n_{{\rm \small{G}}}}$
for the
![]() $n_{{\rm \small{G}}}$
components of
$n_{{\rm \small{G}}}$
components of
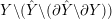 $Y\setminus ({\hat{Y}}\setminus (\unicode[STIX]{x2202}{\hat{Y}}\setminus \unicode[STIX]{x2202}Y))$
, we then regard
$Y\setminus ({\hat{Y}}\setminus (\unicode[STIX]{x2202}{\hat{Y}}\setminus \unicode[STIX]{x2202}Y))$
, we then regard
![]() $Y$
as the union
$Y$
as the union
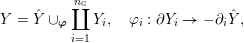 $$\begin{eqnarray}Y={\hat{Y}}\cup _{\boldsymbol{\unicode[STIX]{x1D711}}}\coprod _{i=1}^{n_{{\rm \small{g}}}}Y_{i},\quad \unicode[STIX]{x1D711}_{i}:\unicode[STIX]{x2202}Y_{i}\rightarrow -\unicode[STIX]{x2202}_{i}{\hat{Y}},\end{eqnarray}$$
$$\begin{eqnarray}Y={\hat{Y}}\cup _{\boldsymbol{\unicode[STIX]{x1D711}}}\coprod _{i=1}^{n_{{\rm \small{g}}}}Y_{i},\quad \unicode[STIX]{x1D711}_{i}:\unicode[STIX]{x2202}Y_{i}\rightarrow -\unicode[STIX]{x2202}_{i}{\hat{Y}},\end{eqnarray}$$
with
![]() ${\hat{Y}}$
Seifert fibered over an (
${\hat{Y}}$
Seifert fibered over an (
![]() $n_{{\rm \small{g}}}+1$
)-punctured
$n_{{\rm \small{g}}}+1$
)-punctured
![]() $S^{2}$
or
$S^{2}$
or
![]() $\mathbb{R}\mathbb{P}^{2}$
. Note that each
$\mathbb{R}\mathbb{P}^{2}$
. Note that each
![]() $Y_{i}$
is again a graph manifold with torus boundary and
$Y_{i}$
is again a graph manifold with torus boundary and
![]() $b_{1}\!=\!1$
, hence is endowed with its own tree graph rooted at the JSJ component containing
$b_{1}\!=\!1$
, hence is endowed with its own tree graph rooted at the JSJ component containing
![]() $\unicode[STIX]{x2202}Y_{i}$
, but with the height of this tree strictly less than the height of the tree for
$\unicode[STIX]{x2202}Y_{i}$
, but with the height of this tree strictly less than the height of the tree for
![]() $Y$
, so that a recursive computation of
$Y$
, so that a recursive computation of
![]() ${\mathcal{L}}(Y)$
in terms of the
${\mathcal{L}}(Y)$
in terms of the
![]() ${\mathcal{L}}(Y_{i})$
is a finite process.
${\mathcal{L}}(Y_{i})$
is a finite process.
For any (necessarily toroidal) boundary component of an oriented Seifert fibered space, we fix the reverse-oriented homology basis
![]() $(\tilde{f},-\tilde{h})$
, where
$(\tilde{f},-\tilde{h})$
, where
![]() $\tilde{h}$
is the meridian of the excised regular fiber, and
$\tilde{h}$
is the meridian of the excised regular fiber, and
![]() $\tilde{f}$
is the lift dual to
$\tilde{f}$
is the lift dual to
![]() $\tilde{h}$
of the regular fiber class, so that we can express any slope
$\tilde{h}$
of the regular fiber class, so that we can express any slope
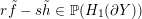 $r\tilde{f}-s\tilde{h}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
as
$r\tilde{f}-s\tilde{h}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
as
 $r/s\in \mathbb{Q}\cup \{\infty \}$
. For any
$r/s\in \mathbb{Q}\cup \{\infty \}$
. For any
![]() $Y_{i}$
with non-empty
$Y_{i}$
with non-empty
![]() ${\mathcal{L}}(Y_{i})$
, we then write
${\mathcal{L}}(Y_{i})$
, we then write
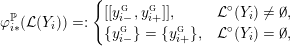 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i}))=:\left\{\begin{array}{@{}ll@{}}[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]],\quad & {\mathcal{L}}^{\circ }(Y_{i})\neq \emptyset ,\\ \{y_{i-}^{{\rm \small{g}}}\}=\{y_{i+}^{{\rm \small{g}}}\},\quad & {\mathcal{L}}^{\circ }(Y_{i})=\emptyset ,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i}))=:\left\{\begin{array}{@{}ll@{}}[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]],\quad & {\mathcal{L}}^{\circ }(Y_{i})\neq \emptyset ,\\ \{y_{i-}^{{\rm \small{g}}}\}=\{y_{i+}^{{\rm \small{g}}}\},\quad & {\mathcal{L}}^{\circ }(Y_{i})=\emptyset ,\end{array}\right.\end{eqnarray}$$
where we use the notation
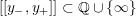 $[[y_{-},y_{+}]]\subset \mathbb{Q}\cup \{\infty \}$
to denote the L-space interval with left-hand endpoint
$[[y_{-},y_{+}]]\subset \mathbb{Q}\cup \{\infty \}$
to denote the L-space interval with left-hand endpoint
![]() $y_{-}$
and right-hand endpoint
$y_{-}$
and right-hand endpoint
![]() $y_{+}$
, since any L-space interval with non-empty interior is uniquely specified by its endpoints.
$y_{+}$
, since any L-space interval with non-empty interior is uniquely specified by its endpoints.
We also write
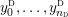 $y_{0}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}$
for the Seifert data of
$y_{0}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}$
for the Seifert data of
![]() ${\hat{Y}}$
, so that
${\hat{Y}}$
, so that
![]() ${\hat{Y}}$
is the complement of
${\hat{Y}}$
is the complement of
![]() $n_{{\rm \small{g}}}\!+\!1$
regular fibers in either
$n_{{\rm \small{g}}}\!+\!1$
regular fibers in either
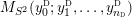 $M_{S^{2}}(y_{0}^{{\rm \small{d}}};y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
or
$M_{S^{2}}(y_{0}^{{\rm \small{d}}};y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
or
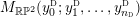 $M_{\mathbb{R}\mathbb{P}^{2}}(y_{0}^{{\rm \small{d}}};y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
, depending on whether
$M_{\mathbb{R}\mathbb{P}^{2}}(y_{0}^{{\rm \small{d}}};y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
, depending on whether
![]() ${\hat{Y}}$
has orientable or non-orientable base. (These
${\hat{Y}}$
has orientable or non-orientable base. (These
![]() $y_{i}^{{\rm \small{d}}}$
can also be regarded as Dehn-filling slopes in terms of the basis
$y_{i}^{{\rm \small{d}}}$
can also be regarded as Dehn-filling slopes in terms of the basis
 $(\tilde{f}_{i}^{{\rm \small{d}}},-\tilde{h}_{i}^{{\rm \small{d}}})$
described above. See § 2.2 for notation and homology conventions for Seifert fibered spaces.) We can now state our main result.
$(\tilde{f}_{i}^{{\rm \small{d}}},-\tilde{h}_{i}^{{\rm \small{d}}})$
described above. See § 2.2 for notation and homology conventions for Seifert fibered spaces.) We can now state our main result.
Theorem 1.6. Suppose that
![]() $Y$
is not a solid torus and that
$Y$
is not a solid torus and that
![]() ${\mathcal{L}}(Y)$
is non-empty. Then
${\mathcal{L}}(Y)$
is non-empty. Then
 $$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}\langle -\infty ,+\infty \rangle ,\quad & {\hat{Y}}\;\text{has non-orientable base},\\ \text{}[[y_{-},y_{+}]],\quad & {\hat{Y}}\;\text{has orientable base},\;{\mathcal{L}}^{\circ }(Y)\neq \emptyset ,\\ \{y_{-}\}=\{y_{+}\},\quad & {\hat{Y}}\;\text{has orientable base},\;{\mathcal{L}}^{\circ }(Y)=\emptyset ,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}\langle -\infty ,+\infty \rangle ,\quad & {\hat{Y}}\;\text{has non-orientable base},\\ \text{}[[y_{-},y_{+}]],\quad & {\hat{Y}}\;\text{has orientable base},\;{\mathcal{L}}^{\circ }(Y)\neq \emptyset ,\\ \{y_{-}\}=\{y_{+}\},\quad & {\hat{Y}}\;\text{has orientable base},\;{\mathcal{L}}^{\circ }(Y)=\emptyset ,\end{array}\right.\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle y_{-} & := & \displaystyle \max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=0}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\nonumber\\ \displaystyle y_{+} & := & \displaystyle \min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=0}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{-} & := & \displaystyle \max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=0}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\nonumber\\ \displaystyle y_{+} & := & \displaystyle \min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=0}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\nonumber\end{eqnarray}$$
(In the above, we define
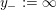 $y_{-}:=\infty$
or
$y_{-}:=\infty$
or
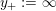 $y_{+}:=\infty$
, respectively, if any infinite terms appear as summands of
$y_{+}:=\infty$
, respectively, if any infinite terms appear as summands of
![]() $y_{-}$
or
$y_{-}$
or
![]() $y_{+}$
, respectively.)
$y_{+}$
, respectively.)
Whereas every oriented Seifert fibered space over the disk or Möbius strip is Floer simple, i.e. has
![]() ${\mathcal{L}}^{\circ }\neq \emptyset$
, the story for graph manifolds is more complicated. Consider the following examples, for all of which we take
${\mathcal{L}}^{\circ }\neq \emptyset$
, the story for graph manifolds is more complicated. Consider the following examples, for all of which we take
![]() ${\hat{Y}}$
to have orientable base:
${\hat{Y}}$
to have orientable base:
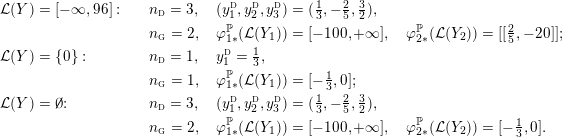 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle {\mathcal{L}}(Y)=[-\infty ,96]: & \displaystyle \quad n_{{\rm \small{d}}}=3,\quad (y_{1}^{{\rm \small{d}}},y_{2}^{{\rm \small{d}}},y_{3}^{{\rm \small{d}}})=({\textstyle \frac{1}{3}},-{\textstyle \frac{2}{5}},{\textstyle \frac{3}{2}}),\\ & \quad \displaystyle n_{{\rm \small{g}}}=2,\quad \displaystyle \unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=[-100,+\infty ],\quad \unicode[STIX]{x1D711}_{2\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{2}))=[[{\textstyle \frac{2}{5}},-20]];\\ \displaystyle {\mathcal{L}}(Y)=\{0\}: & \quad n_{{\rm \small{d}}}=1,\quad \displaystyle y_{1}^{{\rm \small{d}}}={\textstyle \frac{1}{3}},\\ & \displaystyle \quad n_{{\rm \small{g}}}=1,\quad \unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=[-{\textstyle \frac{1}{3}},0];\\ \displaystyle {\mathcal{L}}(Y)=\emptyset : & \quad n_{{\rm \small{d}}}=3,\quad \displaystyle (y_{1}^{{\rm \small{d}}},y_{2}^{{\rm \small{d}}},y_{3}^{{\rm \small{d}}})=({\textstyle \frac{1}{3}},-{\textstyle \frac{2}{5}},{\textstyle \frac{3}{2}}),\\ & \displaystyle \quad n_{{\rm \small{g}}}=2,\quad \displaystyle \unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=[-100,+\infty ],\quad \unicode[STIX]{x1D711}_{2\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{2}))=[-{\textstyle \frac{1}{3}},0].\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle {\mathcal{L}}(Y)=[-\infty ,96]: & \displaystyle \quad n_{{\rm \small{d}}}=3,\quad (y_{1}^{{\rm \small{d}}},y_{2}^{{\rm \small{d}}},y_{3}^{{\rm \small{d}}})=({\textstyle \frac{1}{3}},-{\textstyle \frac{2}{5}},{\textstyle \frac{3}{2}}),\\ & \quad \displaystyle n_{{\rm \small{g}}}=2,\quad \displaystyle \unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=[-100,+\infty ],\quad \unicode[STIX]{x1D711}_{2\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{2}))=[[{\textstyle \frac{2}{5}},-20]];\\ \displaystyle {\mathcal{L}}(Y)=\{0\}: & \quad n_{{\rm \small{d}}}=1,\quad \displaystyle y_{1}^{{\rm \small{d}}}={\textstyle \frac{1}{3}},\\ & \displaystyle \quad n_{{\rm \small{g}}}=1,\quad \unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=[-{\textstyle \frac{1}{3}},0];\\ \displaystyle {\mathcal{L}}(Y)=\emptyset : & \quad n_{{\rm \small{d}}}=3,\quad \displaystyle (y_{1}^{{\rm \small{d}}},y_{2}^{{\rm \small{d}}},y_{3}^{{\rm \small{d}}})=({\textstyle \frac{1}{3}},-{\textstyle \frac{2}{5}},{\textstyle \frac{3}{2}}),\\ & \displaystyle \quad n_{{\rm \small{g}}}=2,\quad \displaystyle \unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=[-100,+\infty ],\quad \unicode[STIX]{x1D711}_{2\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{2}))=[-{\textstyle \frac{1}{3}},0].\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Above, we see examples in which
![]() $Y$
is Floer simple, has an isolated L-space filling, or has empty L-space interval. One cannot use Theorem 1.6 without first knowing which of these three cases occurs for
$Y$
is Floer simple, has an isolated L-space filling, or has empty L-space interval. One cannot use Theorem 1.6 without first knowing which of these three cases occurs for
![]() $Y$
. We therefore provide Proposition 4.7, which lists explicit criteria for the multiple mutually exclusive cases in which
$Y$
. We therefore provide Proposition 4.7, which lists explicit criteria for the multiple mutually exclusive cases in which
![]() $Y$
is Floer simple or in which
$Y$
is Floer simple or in which
![]() $Y$
has an isolated L-space filling. In the complement of these criteria,
$Y$
has an isolated L-space filling. In the complement of these criteria,
![]() ${\mathcal{L}}(Y)$
is empty.
${\mathcal{L}}(Y)$
is empty.
In fact, the validity of Theorem 4.6 extends beyond the realm of graph manifolds.
Proposition 1.7. Theorem 1.6 holds for any boundary incompressible Floer simple three-manifolds
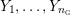 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
, provided that
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
, provided that
![]() $Y$
satisfies the criteria in Proposition 4.7 for
$Y$
satisfies the criteria in Proposition 4.7 for
![]() ${\mathcal{L}}(Y)$
to be non-empty.
${\mathcal{L}}(Y)$
to be non-empty.
One immediate application of this generalization is the computation of L-space intervals for cables of Floer simple knot complements.
1.3 Cables
The
![]() $(p,q)$
-cable
$(p,q)$
-cable
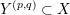 $Y^{(p,q)}\subset X$
of a knot complement
$Y^{(p,q)}\subset X$
of a knot complement
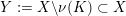 $Y:=X\setminus \unicode[STIX]{x1D708}(K)\subset X$
is given by the knot complement
$Y:=X\setminus \unicode[STIX]{x1D708}(K)\subset X$
is given by the knot complement
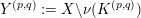 $Y^{(p,q)}:=X\setminus \unicode[STIX]{x1D708}(K^{(p,q)})$
, where
$Y^{(p,q)}:=X\setminus \unicode[STIX]{x1D708}(K^{(p,q)})$
, where
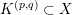 $K^{(p,q)}\subset X$
is the image of the
$K^{(p,q)}\subset X$
is the image of the
![]() $(p,q)$
-torus knot embedded in the boundary of
$(p,q)$
-torus knot embedded in the boundary of
![]() $Y\!$
. Since one can realize any cable of
$Y\!$
. Since one can realize any cable of
![]() $Y\subset X$
by gluing an appropriate Seifert fibered space onto
$Y\subset X$
by gluing an appropriate Seifert fibered space onto
![]() $Y\!$
, we can use the above generalization of Theorem 1.6 to prove the following result.
$Y\!$
, we can use the above generalization of Theorem 1.6 to prove the following result.
Theorem 1.8. Suppose that
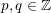 $p,q\in \mathbb{Z}$
with
$p,q\in \mathbb{Z}$
with
![]() $p>1$
and
$p>1$
and
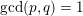 $\gcd (p,q)=1$
, and that
$\gcd (p,q)=1$
, and that
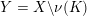 $Y=X\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple knot complement in an L-space
$Y=X\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple knot complement in an L-space
![]() $X$
, with L-space interval
$X$
, with L-space interval
 ${\mathcal{L}}(Y)=[[a_{-}/b_{-},a_{+}/b_{+}]]$
, written in terms of the surgery basis
${\mathcal{L}}(Y)=[[a_{-}/b_{-},a_{+}/b_{+}]]$
, written in terms of the surgery basis
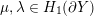 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
for
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
for
![]() $K$
, with
$K$
, with
![]() $\unicode[STIX]{x1D707}$
the meridian of
$\unicode[STIX]{x1D707}$
the meridian of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D706}$
a choice of longitude. Then in terms of the surgery basis produced by cabling, the
$\unicode[STIX]{x1D706}$
a choice of longitude. Then in terms of the surgery basis produced by cabling, the
![]() $(p,q)$
-cable
$(p,q)$
-cable
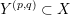 $Y^{(p,q)}\subset X$
of
$Y^{(p,q)}\subset X$
of
![]() $Y\subset X$
has L-space interval
$Y\subset X$
has L-space interval
 $$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & {\displaystyle \frac{a_{-}}{b_{-}}}\in \biggl[{\displaystyle \frac{p^{\ast }}{q^{\ast }}},\infty \biggr],\;{\displaystyle \frac{a_{+}}{b_{+}}}\in \biggl[{\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}},{\displaystyle \frac{q}{p}}\rangle \cup \{\infty \},\\ \text{}[[1/y_{+},1/y_{-}]]\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & {\displaystyle \frac{a_{-}}{b_{-}}}\in \biggl[{\displaystyle \frac{p^{\ast }}{q^{\ast }}},\infty \biggr],\;{\displaystyle \frac{a_{+}}{b_{+}}}\in \biggl[{\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}},{\displaystyle \frac{q}{p}}\rangle \cup \{\infty \},\\ \text{}[[1/y_{+},1/y_{-}]]\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
where
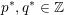 $p^{\ast },q^{\ast }\in \mathbb{Z}$
are defined to satisfy
$p^{\ast },q^{\ast }\in \mathbb{Z}$
are defined to satisfy
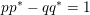 $pp^{\ast }-qq^{\ast }=1$
with
$pp^{\ast }-qq^{\ast }=1$
with
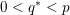 $0<q^{\ast }<p$
, and where we define
$0<q^{\ast }<p$
, and where we define
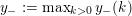 $y_{-}:=\max _{k>0}y_{-}(k)$
and
$y_{-}:=\max _{k>0}y_{-}(k)$
and
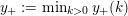 $y_{+}:=\min _{k>0}y_{+}(k)$
, with
$y_{+}:=\min _{k>0}y_{+}(k)$
, with
 $$\begin{eqnarray}\displaystyle y_{-}(k):={\displaystyle \frac{1}{k}}\biggl(\lceil {\displaystyle \frac{q^{\ast }}{p}}k\rceil -\lceil y_{1+}k\rceil \biggr),\quad y_{+}(k):={\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\lfloor y_{1-}k\rfloor \biggr), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{-}(k):={\displaystyle \frac{1}{k}}\biggl(\lceil {\displaystyle \frac{q^{\ast }}{p}}k\rceil -\lceil y_{1+}k\rceil \biggr),\quad y_{+}(k):={\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\lfloor y_{1-}k\rfloor \biggr), & & \displaystyle \nonumber\end{eqnarray}$$
and
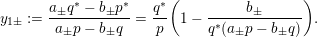 $$\begin{eqnarray}\displaystyle y_{1\pm }:=\frac{a_{\pm }q^{\ast }-b_{\pm }p^{\ast }}{a_{\pm }p-b_{\pm }q}=\frac{q^{\ast }}{p}\biggl(1-\frac{b_{\pm }}{q^{\ast }(a_{\pm }p-b_{\pm }q)}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{1\pm }:=\frac{a_{\pm }q^{\ast }-b_{\pm }p^{\ast }}{a_{\pm }p-b_{\pm }q}=\frac{q^{\ast }}{p}\biggl(1-\frac{b_{\pm }}{q^{\ast }(a_{\pm }p-b_{\pm }q)}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
We also prove a slightly more general version of Theorem 1.8 which does not require that
![]() $X$
be an L-space, and which holds for any
$X$
be an L-space, and which holds for any
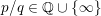 $p/q\in \mathbb{Q}\cup \{\infty \}$
.
$p/q\in \mathbb{Q}\cup \{\infty \}$
.
A brief application of the theorem, followed by an appropriate change of basis, recovers the following result of Hedden [Reference HeddenHed09] and Hom [Reference HomHom11].
Corollary 1.9. Suppose
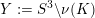 $Y:=S^{3}\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple positive knot complement in
$Y:=S^{3}\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple positive knot complement in
![]() $S^{3}$
. If
$S^{3}$
. If
![]() $p>0$
and
$p>0$
and
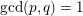 $\gcd (p,q)=1$
, then in terms of the conventional basis for knot complements in
$\gcd (p,q)=1$
, then in terms of the conventional basis for knot complements in
![]() $S^{3}$
,
$S^{3}$
,
![]() $Y^{(p,q)}$
has L-space interval
$Y^{(p,q)}$
has L-space interval
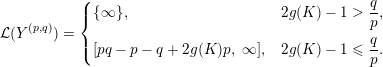 $$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & 2g(K)-1>{\displaystyle \frac{q}{p}},\\ \text{}[pq-p-q+2g(K)p,\;\infty ],\quad & 2g(K)-1\leqslant {\displaystyle \frac{q}{p}}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & 2g(K)-1>{\displaystyle \frac{q}{p}},\\ \text{}[pq-p-q+2g(K)p,\;\infty ],\quad & 2g(K)-1\leqslant {\displaystyle \frac{q}{p}}.\end{array}\right.\end{eqnarray}$$
By positive, we simply mean that
![]() $Y$
has an L-space Dehn filling
$Y$
has an L-space Dehn filling
![]() $Y(N)$
for some
$Y(N)$
for some
![]() $N>0$
.
$N>0$
.
Note that equating
 $pq-p-q+2g(K)p$
with
$pq-p-q+2g(K)p$
with
 $2g(K^{(p,q)})-1$
recovers the formula for the genus of the
$2g(K^{(p,q)})-1$
recovers the formula for the genus of the
![]() $(p,q)$
-cable of
$(p,q)$
-cable of
 $K\subset S^{3}$
. Note also that since
$K\subset S^{3}$
. Note also that since
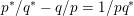 $p^{\ast }/q^{\ast }-q/p=1/pq^{\ast }$
, with
$p^{\ast }/q^{\ast }-q/p=1/pq^{\ast }$
, with
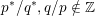 $p^{\ast }/q^{\ast },q/p\notin \mathbb{Z}$
, the domain specified for Floer simple cables in the above corollary is equivalent to the condition
$p^{\ast }/q^{\ast },q/p\notin \mathbb{Z}$
, the domain specified for Floer simple cables in the above corollary is equivalent to the condition
 $2g(K)-1\notin [p^{\ast }/q^{\ast },\infty ]$
, matching Theorem 1.8.
$2g(K)-1\notin [p^{\ast }/q^{\ast },\infty ]$
, matching Theorem 1.8.
1.4 Generalized solid tori
A recent result of Gillespie [Reference GillespieGil16] states that a compact oriented three-manifold
![]() $Y$
with torus boundary satisfies
$Y$
with torus boundary satisfies
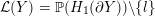 ${\mathcal{L}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus \{l\}$
if and only if
${\mathcal{L}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus \{l\}$
if and only if
![]() $Y$
has genus 0 and an L-space filling, where
$Y$
has genus 0 and an L-space filling, where
![]() $l$
denotes the rational longitude of
$l$
denotes the rational longitude of
![]() $Y$
. Such manifolds are called generalized solid tori in [Reference Rasmussen and RasmussenRR15] and are of independent interest [Reference BergeBer91, Reference GabaiGab89, Reference CebanuCeb13, Reference Baker, Buck and LecuonaBBL16, Reference Hanselman and WatsonHW15].
$Y$
. Such manifolds are called generalized solid tori in [Reference Rasmussen and RasmussenRR15] and are of independent interest [Reference BergeBer91, Reference GabaiGab89, Reference CebanuCeb13, Reference Baker, Buck and LecuonaBBL16, Reference Hanselman and WatsonHW15].
Using the version of Theorem 1.8 that does not require
![]() $X$
to be an L-space, along with some incremental results from the proof of Theorem 1.6, we are able to show the following.
$X$
to be an L-space, along with some incremental results from the proof of Theorem 1.6, we are able to show the following.
Theorem 1.10. If
![]() $Y$
is a generalized solid torus, then any cable of
$Y$
is a generalized solid torus, then any cable of
 $Y\subset Y(l)$
is a generalized solid torus. If
$Y\subset Y(l)$
is a generalized solid torus. If
![]() $Y\!$
is a graph manifold with torus boundary,
$Y\!$
is a graph manifold with torus boundary,
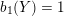 $b_{1}(Y)=1$
, and rational longitude other than the regular fiber, then
$b_{1}(Y)=1$
, and rational longitude other than the regular fiber, then
![]() $Y$
is a generalized solid torus if and only if it is homeomorphic to an iterated cable of the regular fiber complement in
$Y$
is a generalized solid torus if and only if it is homeomorphic to an iterated cable of the regular fiber complement in
 $S^{1}\times S^{2}$
.
$S^{1}\times S^{2}$
.
Similarly, for any class of manifolds for which the gluing result in Proposition 1.5 holds without the requirement of Floer simplicity—such as graph manifolds—one has the result that if
![]() $Y$
has an isolated L-space filling, i.e. if
$Y$
has an isolated L-space filling, i.e. if
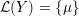 ${\mathcal{L}}(Y)=\{\unicode[STIX]{x1D707}\}$
for some
${\mathcal{L}}(Y)=\{\unicode[STIX]{x1D707}\}$
for some
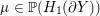 $\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
, then any cable of
$\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
, then any cable of
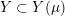 $Y\subset Y(\unicode[STIX]{x1D707})$
has
$Y\subset Y(\unicode[STIX]{x1D707})$
has
![]() $Y(\unicode[STIX]{x1D707})$
as an isolated L-space filling.
$Y(\unicode[STIX]{x1D707})$
as an isolated L-space filling.
1.5 Floer simple knot complements
Whereas the regular fiber complement in a rational homology sphere Seifert fibered space could arguably be called the prototypical Floer simple manifold, not every regular fiber complement in an L-space graph manifold is Floer simple, due to the existence of isolated L-space fillings. However, the next best thing is true.
Given a closed graph manifold
![]() $X$
, call an exceptional fiber
$X$
, call an exceptional fiber
![]() $f_{{\rm \small{e}}}\subset X$
invariantly exceptional if the JSJ component
$f_{{\rm \small{e}}}\subset X$
invariantly exceptional if the JSJ component
![]() ${\hat{Y}}\subset X$
containing
${\hat{Y}}\subset X$
containing
![]() $f_{{\rm \small{e}}}$
has more than one exceptional fiber. Note that if
$f_{{\rm \small{e}}}$
has more than one exceptional fiber. Note that if
![]() ${\hat{Y}}$
has only one exceptional fiber, then
${\hat{Y}}$
has only one exceptional fiber, then
![]() ${\hat{Y}}$
is either a lens space (if
${\hat{Y}}$
is either a lens space (if
![]() $X$
is Seifert fibered) or a punctured solid torus. Since the solid torus has non-unique Seifert structure, one can show that if
$X$
is Seifert fibered) or a punctured solid torus. Since the solid torus has non-unique Seifert structure, one can show that if
![]() $X$
is not a lens space, it is homeomorphic to a graph manifold
$X$
is not a lens space, it is homeomorphic to a graph manifold
![]() $X^{\prime }$
in which the image
$X^{\prime }$
in which the image
![]() $f_{{\rm \small{e}}}^{\prime }$
of
$f_{{\rm \small{e}}}^{\prime }$
of
![]() $f_{{\rm \small{e}}}$
is a regular fiber. Excluding this scenario allows us to show the following.
$f_{{\rm \small{e}}}$
is a regular fiber. Excluding this scenario allows us to show the following.
Theorem 1.11. Every invariantly exceptional fiber complement in an L-space graph manifold is Floer simple.
There are also Floer simple knot complements traversing the graph structure of
![]() $X$
.
$X$
.
Proposition 1.12. If
![]() $X$
is an L-space graph manifold, then for every incompressible torus
$X$
is an L-space graph manifold, then for every incompressible torus
![]() $T\subset X$
, there is a knot
$T\subset X$
, there is a knot
![]() $K\subset X$
transversely intersecting
$K\subset X$
transversely intersecting
![]() $T$
for which the complement
$T$
for which the complement
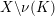 $X\setminus \unicode[STIX]{x1D708}(K)$
is Floer simple.
$X\setminus \unicode[STIX]{x1D708}(K)$
is Floer simple.
The same occurs for an arbitrary L-space
![]() $X$
, provided that
$X$
, provided that
![]() $X$
decomposes as a union of Floer simple manifolds along
$X$
decomposes as a union of Floer simple manifolds along
![]() $T$
(see Proposition 6.6).
$T$
(see Proposition 6.6).
The above results, together with the evidence of various other classes of L-spaces, and a certain degree of optimism, motivate the following.
Conjecture 1.13. Every L-space admits a Floer simple knot complement.
1.6 Organization
In § 2 we introduce our conventions for Seifert fibered spaces and provide a lengthy discussion of the Jankins–Neumann problem, since we cannot hope for Theorem 1.6 to provide insight if the original theorem of Jankins, Neumann and Naimi is opaque to the reader.
Section 3 reviews some basic facts about L-space intervals, including the independent results of Hanselman and Watson [Reference Hanselman and WatsonHW15] and Rasmussen and the author [Reference Rasmussen and RasmussenRR15] about L-space criteria for unions of Floer simple manifolds.
Section 4 is where we prove our main graph manifold results, including Theorems 1.3 and 1.6 in the forms of Theorems 4.5 and 4.6. This section also derives the classification in Proposition 4.7 of single-boundary-component graph manifolds with non-empty L-space intervals.
Our main cabling results reside in § 5, although the proof of Theorem 1.10, for generalized solid tori, is relegated to § 6.
Lastly, § 6 justifies the generalization in Proposition 1.7 of our Jankins–Neumann graph manifold result to the union of a Seifert fibered space with Floer simple manifolds. This final section also lists an array of applications of the paper’s main results, including the aforementioned generalized solid torus cabling result and proofs of the Floer simple knot complement results from Theorem 1.11 and Proposition 1.12.
2 Foliations on Seifert fibered spaces
A graph manifold is a prime compact oriented three-manifold which admits a JSJ decomposition—which in this case, we take to be a minimal cutting apart along incompressible tori into disjoint pieces—such that each JSJ component is an oriented Seifert fibered space. The data for reassembling these components into the original manifold are encoded in a labeled graph, where each vertex corresponds to a Seifert fibered JSJ component, and each edge corresponds to a gluing of two Seifert fibered pieces along an incompressible torus.
2.1 Restricting taut foliations to JSJ components
Questions about taut foliations on graph manifolds can often be reduced to questions about taut foliations on Seifert fibered spaces, due in part to the following result.
Proposition 2.1 [Reference RoussarieRou74, Reference ThurstonThu80, Reference Brittenham and RobertsBR99].
If
![]() $Y$
is a compact oriented three-manifold admitting a taut foliation
$Y$
is a compact oriented three-manifold admitting a taut foliation
![]() $F$
transverse to
$F$
transverse to
![]() $\unicode[STIX]{x2202}Y$
, then every incompressible separating torus in
$\unicode[STIX]{x2202}Y$
, then every incompressible separating torus in
![]() $Y$
can be isotoped to be everywhere transverse to
$Y$
can be isotoped to be everywhere transverse to
![]() $F$
.
$F$
.
Proof. Roussarie [Reference RoussarieRou74] showed that if
![]() $F$
is
$F$
is
![]() $C^{2}$
, then each incompressible torus
$C^{2}$
, then each incompressible torus
![]() $T\subset Y$
can be isotoped to be either everywhere transverse to
$T\subset Y$
can be isotoped to be either everywhere transverse to
![]() $F$
or a leaf of
$F$
or a leaf of
![]() $F$
. A later theorem of Brittenham and Roberts [Reference Brittenham and RobertsBR99] extends the validity of this proposition to
$F$
. A later theorem of Brittenham and Roberts [Reference Brittenham and RobertsBR99] extends the validity of this proposition to
![]() $C^{0}$
foliations. Thus, since a taut foliation has no compact separating leaves, an incompressible separating torus cannot be isotoped to be a leaf of
$C^{0}$
foliations. Thus, since a taut foliation has no compact separating leaves, an incompressible separating torus cannot be isotoped to be a leaf of
![]() $F$
, and so it must be possible to isotop any incompressible separating torus to be everywhere transverse to
$F$
, and so it must be possible to isotop any incompressible separating torus to be everywhere transverse to
![]() $F$
. This is also believed to have been known by Thurston [Reference ThurstonThu80].◻
$F$
. This is also believed to have been known by Thurston [Reference ThurstonThu80].◻
As noted by Brittenham, Naimi, and Roberts [Reference Brittenham, Naimi and RobertsBNR97], this result has major consequences for graph manifolds.
Corollary 2.2. If
![]() $Y\!$
is a graph manifold with tree graph and
$Y\!$
is a graph manifold with tree graph and
![]() $F$
is a taut foliation on
$F$
is a taut foliation on
![]() $Y$
transverse to
$Y$
transverse to
![]() $\unicode[STIX]{x2202}Y$
, then
$\unicode[STIX]{x2202}Y$
, then
![]() $F$
can be isotoped so that it restricts to boundary-transverse taut foliations on the Seifert fibered JSJ components of
$F$
can be isotoped so that it restricts to boundary-transverse taut foliations on the Seifert fibered JSJ components of
![]() $Y$
.
$Y$
.
When a closed graph manifold has positive first Betti number, the question of existence of taut foliations becomes trivial, since a result of Gabai states that any such manifold admits a co-oriented taut foliation [Reference GabaiGab83]. Correspondingly, any closed oriented three-manifold with
![]() $b_{1}>0$
has non-trivial Heegaard Floer homology, hence is not an L-space. We therefore restrict attention to rational homology sphere graph manifolds, hence to oriented Seifert fibered spaces over
$b_{1}>0$
has non-trivial Heegaard Floer homology, hence is not an L-space. We therefore restrict attention to rational homology sphere graph manifolds, hence to oriented Seifert fibered spaces over
![]() $S^{2}$
or
$S^{2}$
or
![]() $\mathbb{R}\mathbb{P}^{2}\!$
, and regular fiber complements thereof.
$\mathbb{R}\mathbb{P}^{2}\!$
, and regular fiber complements thereof.
2.2 Conventions for Seifert fibered spaces
If
![]() $\hat{M}$
denotes the trivial circle fibration over the (
$\hat{M}$
denotes the trivial circle fibration over the (
![]() $n+1$
)-punctured two-sphere,
$n+1$
)-punctured two-sphere,
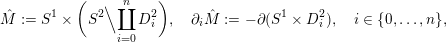 $$\begin{eqnarray}\hat{M}:=S^{1}\times \biggl(S^{2}\Big\backslash\coprod _{i=0}^{n}D_{i}^{2}\biggr),\quad \unicode[STIX]{x2202}_{i}\hat{M}:=-\unicode[STIX]{x2202}(S^{1}\times D_{i}^{2}),\quad i\in \{0,\ldots ,n\},\end{eqnarray}$$
$$\begin{eqnarray}\hat{M}:=S^{1}\times \biggl(S^{2}\Big\backslash\coprod _{i=0}^{n}D_{i}^{2}\biggr),\quad \unicode[STIX]{x2202}_{i}\hat{M}:=-\unicode[STIX]{x2202}(S^{1}\times D_{i}^{2}),\quad i\in \{0,\ldots ,n\},\end{eqnarray}$$
then writing
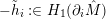 $-\tilde{h}_{i}:\in H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})$
for the meridian of each excised solid torus
$-\tilde{h}_{i}:\in H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})$
for the meridian of each excised solid torus
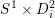 $S^{1}\times D_{i}^{2}$
, we have
$S^{1}\times D_{i}^{2}$
, we have
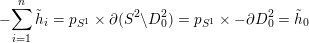 $$\begin{eqnarray}-\mathop{\sum }_{i=1}^{n}\tilde{h}_{i}=p_{S^{1}}\times \unicode[STIX]{x2202}(S^{2}\setminus D_{0}^{2})=p_{S^{1}}\times -\unicode[STIX]{x2202}D_{0}^{2}=\tilde{h}_{0}\end{eqnarray}$$
$$\begin{eqnarray}-\mathop{\sum }_{i=1}^{n}\tilde{h}_{i}=p_{S^{1}}\times \unicode[STIX]{x2202}(S^{2}\setminus D_{0}^{2})=p_{S^{1}}\times -\unicode[STIX]{x2202}D_{0}^{2}=\tilde{h}_{0}\end{eqnarray}$$
for any point class
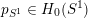 $p_{S^{1}}\in H_{0}(S^{1})$
of the circle fiber. For each
$p_{S^{1}}\in H_{0}(S^{1})$
of the circle fiber. For each
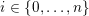 $i\in \{0,\ldots ,n\}$
, if we write
$i\in \{0,\ldots ,n\}$
, if we write
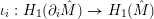 $\unicode[STIX]{x1D704}_{i}:H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\rightarrow H_{1}(\hat{M})$
for the map induced by inclusion, then there is a lift
$\unicode[STIX]{x1D704}_{i}:H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\rightarrow H_{1}(\hat{M})$
for the map induced by inclusion, then there is a lift
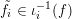 $\tilde{f}_{i}\in \unicode[STIX]{x1D704}_{i}^{-1}(f)$
of the regular fiber class
$\tilde{f}_{i}\in \unicode[STIX]{x1D704}_{i}^{-1}(f)$
of the regular fiber class
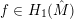 $f\in H_{1}(\hat{M})$
satisfying
$f\in H_{1}(\hat{M})$
satisfying
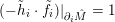 $(-\tilde{h}_{i}\cdot \tilde{f}_{i})|_{\unicode[STIX]{x2202}_{i}\hat{M}}=1$
. The reverse-oriented basis
$(-\tilde{h}_{i}\cdot \tilde{f}_{i})|_{\unicode[STIX]{x2202}_{i}\hat{M}}=1$
. The reverse-oriented basis
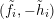 $(\tilde{f}_{i},-\tilde{h}_{i})$
for
$(\tilde{f}_{i},-\tilde{h}_{i})$
for
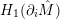 $H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})$
induces a projectivization map
$H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})$
induces a projectivization map
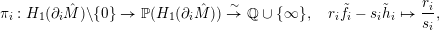 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{i}:H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\setminus \{0\}\rightarrow \mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}\hat{M}))\stackrel{{\sim}}{\rightarrow }\mathbb{Q}\cup \{\infty \},\quad r_{i}\tilde{f}_{i}-s_{i}\tilde{h}_{i}\mapsto \frac{r_{i}}{s_{i}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{i}:H_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\setminus \{0\}\rightarrow \mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}\hat{M}))\stackrel{{\sim}}{\rightarrow }\mathbb{Q}\cup \{\infty \},\quad r_{i}\tilde{f}_{i}-s_{i}\tilde{h}_{i}\mapsto \frac{r_{i}}{s_{i}},\end{eqnarray}$$
by which we identify Seifert invariants with slopes, and slopes with
 $\mathbb{Q}\cup \{\infty \}$
.
$\mathbb{Q}\cup \{\infty \}$
.
The Seifert fibered space
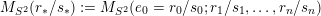 $M_{S^{2}}(r_{\ast }/s_{\ast }):=M_{S^{2}}(e_{0}=r_{0}/s_{0};r_{1}/s_{1},\ldots ,r_{n}/s_{n})$
over
$M_{S^{2}}(r_{\ast }/s_{\ast }):=M_{S^{2}}(e_{0}=r_{0}/s_{0};r_{1}/s_{1},\ldots ,r_{n}/s_{n})$
over
![]() $S^{2}$
is the Dehn filling of
$S^{2}$
is the Dehn filling of
![]() $\hat{M}$
along the slopes
$\hat{M}$
along the slopes
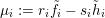 $\unicode[STIX]{x1D707}_{i}:=r_{i}\tilde{f}_{i}-s_{i}\tilde{h}_{i}$
, with
$\unicode[STIX]{x1D707}_{i}:=r_{i}\tilde{f}_{i}-s_{i}\tilde{h}_{i}$
, with
 $\unicode[STIX]{x1D70B}_{i}(\unicode[STIX]{x1D707}_{i})=r_{i}/s_{i}$
, subject to the convention that
$\unicode[STIX]{x1D70B}_{i}(\unicode[STIX]{x1D707}_{i})=r_{i}/s_{i}$
, subject to the convention that
 $e_{0}=r_{0}/s_{0}\in \mathbb{Z}$
and
$e_{0}=r_{0}/s_{0}\in \mathbb{Z}$
and
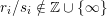 $r_{i}/s_{i}\notin \mathbb{Z}\cup \{\infty \}$
. Setting each
$r_{i}/s_{i}\notin \mathbb{Z}\cup \{\infty \}$
. Setting each
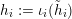 $h_{i}:=\unicode[STIX]{x1D704}_{i}(\tilde{h}_{i})$
then gives the presentation
$h_{i}:=\unicode[STIX]{x1D704}_{i}(\tilde{h}_{i})$
then gives the presentation
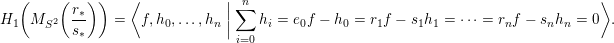 $$\begin{eqnarray}H_{1}\biggl(M_{S^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\biggr)=\langle f,h_{0},\ldots ,h_{n}\biggm\vert\mathop{\sum }_{i=0}^{n}h_{i}=e_{0}f-h_{0}=r_{1}f-s_{1}h_{1}=\cdots =r_{n}f-s_{n}h_{n}=0\rangle .\end{eqnarray}$$
$$\begin{eqnarray}H_{1}\biggl(M_{S^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\biggr)=\langle f,h_{0},\ldots ,h_{n}\biggm\vert\mathop{\sum }_{i=0}^{n}h_{i}=e_{0}f-h_{0}=r_{1}f-s_{1}h_{1}=\cdots =r_{n}f-s_{n}h_{n}=0\rangle .\end{eqnarray}$$
Likewise, if we respectively lift
![]() $f$
and each
$f$
and each
![]() $h_{i}$
to generators
$h_{i}$
to generators
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D702}_{i}$
for
$\unicode[STIX]{x1D702}_{i}$
for
 $\unicode[STIX]{x1D70B}_{1}(M_{S^{2}}(r_{\ast }/s_{\ast }))$
and substitute
$\unicode[STIX]{x1D70B}_{1}(M_{S^{2}}(r_{\ast }/s_{\ast }))$
and substitute
![]() $\unicode[STIX]{x1D719}^{e_{0}}$
for
$\unicode[STIX]{x1D719}^{e_{0}}$
for
![]() $\unicode[STIX]{x1D702}_{0}$
, then we obtain the fundamental group presentation
$\unicode[STIX]{x1D702}_{0}$
, then we obtain the fundamental group presentation
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}\biggl(M_{S^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\biggr)=\langle \unicode[STIX]{x1D719},\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}\biggm\vert\unicode[STIX]{x1D719}~\text{central, }\mathop{\prod }_{i=1}^{n}\!\unicode[STIX]{x1D702}_{i}\!=\!\unicode[STIX]{x1D719}^{-e_{0}},\,\unicode[STIX]{x1D702}_{1}^{s_{1}}\!=\!\unicode[STIX]{x1D719}^{r_{1}},\,\ldots ,\,\unicode[STIX]{x1D702}_{n}^{s_{n}}\!=\!\unicode[STIX]{x1D719}^{r_{n}}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}\biggl(M_{S^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\biggr)=\langle \unicode[STIX]{x1D719},\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}\biggm\vert\unicode[STIX]{x1D719}~\text{central, }\mathop{\prod }_{i=1}^{n}\!\unicode[STIX]{x1D702}_{i}\!=\!\unicode[STIX]{x1D719}^{-e_{0}},\,\unicode[STIX]{x1D702}_{1}^{s_{1}}\!=\!\unicode[STIX]{x1D719}^{r_{1}},\,\ldots ,\,\unicode[STIX]{x1D702}_{n}^{s_{n}}\!=\!\unicode[STIX]{x1D719}^{r_{n}}\rangle .\end{eqnarray}$$
For a manifold
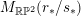 $M_{\mathbb{R}\mathbb{P}^{2}}(r_{\ast }/s_{\ast })$
Seifert fibered over
$M_{\mathbb{R}\mathbb{P}^{2}}(r_{\ast }/s_{\ast })$
Seifert fibered over
![]() $\mathbb{R}\mathbb{P}^{2}$
, we adopt the same homology and slope conventions for the boundary of a regular fiber complement, but the global homology is slightly different. Since, this time,
$\mathbb{R}\mathbb{P}^{2}$
, we adopt the same homology and slope conventions for the boundary of a regular fiber complement, but the global homology is slightly different. Since, this time,
![]() $\hat{M}$
is the twisted circle bundle over a punctured
$\hat{M}$
is the twisted circle bundle over a punctured
![]() $\mathbb{R}\mathbb{P}^{2}$
, the fiber class
$\mathbb{R}\mathbb{P}^{2}$
, the fiber class
![]() $f$
is now 2-torsion. Also, since puncturing
$f$
is now 2-torsion. Also, since puncturing
![]() $\mathbb{R}\mathbb{P}^{2}$
once gives a Möbius strip instead of a disk, the sum
$\mathbb{R}\mathbb{P}^{2}$
once gives a Möbius strip instead of a disk, the sum
 $\sum _{i=1}^{n}\tilde{h}_{i}$
differs from
$\sum _{i=1}^{n}\tilde{h}_{i}$
differs from
 $p_{\mathbb{R}\mathbb{P}^{2}}\times \unicode[STIX]{x2202}(\mathbb{R}\mathbb{P}^{2}\setminus D_{0}^{2})$
by twice the one-cell
$p_{\mathbb{R}\mathbb{P}^{2}}\times \unicode[STIX]{x2202}(\mathbb{R}\mathbb{P}^{2}\setminus D_{0}^{2})$
by twice the one-cell
![]() $c$
glued to the disk to make
$c$
glued to the disk to make
![]() $\mathbb{R}\mathbb{P}^{2}$
, yielding a homology presentation of the form
$\mathbb{R}\mathbb{P}^{2}$
, yielding a homology presentation of the form
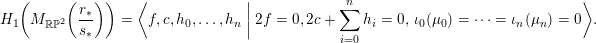 $$\begin{eqnarray}H_{1}\biggl(M_{\mathbb{R}\mathbb{P}^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\biggr)=\langle f,c,h_{0},\ldots ,h_{n}\biggm\vert2f=0,2c+\mathop{\sum }_{i=0}^{n}h_{i}=0,\,\unicode[STIX]{x1D704}_{0}(\unicode[STIX]{x1D707}_{0})=\cdots =\unicode[STIX]{x1D704}_{n}(\unicode[STIX]{x1D707}_{n})=0\rangle .\end{eqnarray}$$
$$\begin{eqnarray}H_{1}\biggl(M_{\mathbb{R}\mathbb{P}^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\biggr)=\langle f,c,h_{0},\ldots ,h_{n}\biggm\vert2f=0,2c+\mathop{\sum }_{i=0}^{n}h_{i}=0,\,\unicode[STIX]{x1D704}_{0}(\unicode[STIX]{x1D707}_{0})=\cdots =\unicode[STIX]{x1D704}_{n}(\unicode[STIX]{x1D707}_{n})=0\rangle .\end{eqnarray}$$
For either type of base, the Seifert fibration is invariant under any reparameterization
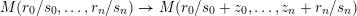 $M(r_{0}/s_{0},\ldots ,r_{n}/s_{n})\rightarrow M(r_{0}/s_{0}+z_{0},\ldots ,z_{n}+r_{n}/s_{n})$
with
$M(r_{0}/s_{0},\ldots ,r_{n}/s_{n})\rightarrow M(r_{0}/s_{0}+z_{0},\ldots ,z_{n}+r_{n}/s_{n})$
with
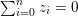 $\sum _{i=0}^{n}z_{i}=0$
and each
$\sum _{i=0}^{n}z_{i}=0$
and each
![]() $z_{i}\in \mathbb{Z}$
. The manifold also admits orientation-reversing homeomorphism,
$z_{i}\in \mathbb{Z}$
. The manifold also admits orientation-reversing homeomorphism,
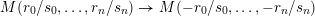 $M(r_{0}/s_{0},\ldots ,r_{n}/s_{n})\rightarrow M(-r_{0}/s_{0},\ldots ,-r_{n}/s_{n})$
.
$M(r_{0}/s_{0},\ldots ,r_{n}/s_{n})\rightarrow M(-r_{0}/s_{0},\ldots ,-r_{n}/s_{n})$
.
A regular fiber complement
 $Y:=M\setminus \unicode[STIX]{x1D708}(f)$
in a rational homology sphere Seifert fibered space has
$Y:=M\setminus \unicode[STIX]{x1D708}(f)$
in a rational homology sphere Seifert fibered space has
 $b_{1}(Y)=1$
, hence has a well-defined rational longitude.
$b_{1}(Y)=1$
, hence has a well-defined rational longitude.
Definition 2.3. Any compact oriented three-manifold
![]() $Y\!$
with torus boundary and
$Y\!$
with torus boundary and
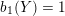 $b_{1}(Y)=1$
has a rational longitude, a unique class
$b_{1}(Y)=1$
has a rational longitude, a unique class
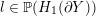 $l\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
such that representatives in
$l\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
such that representatives in
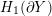 $H_{1}(\unicode[STIX]{x2202}Y)$
have torsion image in
$H_{1}(\unicode[STIX]{x2202}Y)$
have torsion image in
![]() $H_{1}(Y)$
under the homomorphism induced by inclusion of the boundary.
$H_{1}(Y)$
under the homomorphism induced by inclusion of the boundary.
It is straightforward to show (see, for example, [Reference Rasmussen and RasmussenRR15]) that
 $$\begin{eqnarray}M_{S^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\setminus \unicode[STIX]{x1D708}(f)\text{ has rational longitude }l=-\mathop{\sum }_{i=0}^{n}\frac{r_{i}}{s_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}M_{S^{2}}\biggl(\frac{r_{\ast }}{s_{\ast }}\biggr)\setminus \unicode[STIX]{x1D708}(f)\text{ has rational longitude }l=-\mathop{\sum }_{i=0}^{n}\frac{r_{i}}{s_{i}}.\end{eqnarray}$$
A mild generalization of the calculation in [Reference Rasmussen and RasmussenRR15] shows that the above result also holds if each solid torus
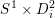 $S^{1}\times D_{i}^{2}$
is replaced with an arbitrary compact oriented three-manifold
$S^{1}\times D_{i}^{2}$
is replaced with an arbitrary compact oriented three-manifold
![]() $Y_{i}$
with torus boundary and
$Y_{i}$
with torus boundary and
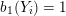 $b_{1}(Y_{i})=1$
, with
$b_{1}(Y_{i})=1$
, with
![]() $r_{i}/s_{i}$
the image of the rational longitude of
$r_{i}/s_{i}$
the image of the rational longitude of
![]() $Y_{i}$
. By contrast, if the JSJ component containing
$Y_{i}$
. By contrast, if the JSJ component containing
![]() $\unicode[STIX]{x2202}Y$
has non-orientable base, then
$\unicode[STIX]{x2202}Y$
has non-orientable base, then
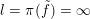 $l=\unicode[STIX]{x1D70B}(\tilde{f})=\infty$
.
$l=\unicode[STIX]{x1D70B}(\tilde{f})=\infty$
.
Remark.
The requirement that
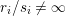 $r_{i}/s_{i}\neq \infty$
for
$r_{i}/s_{i}\neq \infty$
for
 $i\in \{0,\ldots ,n\}$
is a necessary (assuming
$i\in \{0,\ldots ,n\}$
is a necessary (assuming
![]() $n>1$
) and sufficient condition for the resulting Seifert fibered space to be prime—an important property for manifolds serving as building blocks in combinatorial constructions. To understand necessity, let
$n>1$
) and sufficient condition for the resulting Seifert fibered space to be prime—an important property for manifolds serving as building blocks in combinatorial constructions. To understand necessity, let
![]() $\hat{M}^{\infty }$
denote the result of Dehn filling
$\hat{M}^{\infty }$
denote the result of Dehn filling
![]() $\hat{M}$
with slope
$\hat{M}$
with slope
![]() $\infty$
along
$\infty$
along
![]() $\unicode[STIX]{x2202}_{0}\hat{M}$
. If
$\unicode[STIX]{x2202}_{0}\hat{M}$
. If
![]() $\hat{M}$
is fibered over a punctured
$\hat{M}$
is fibered over a punctured
![]() $S^{2}$
, then
$S^{2}$
, then
![]() $\hat{M}^{\infty }$
is a connected sum of
$\hat{M}^{\infty }$
is a connected sum of
![]() $n$
solid tori, each with longitude of slope
$n$
solid tori, each with longitude of slope
![]() $\infty$
. Similarly, if
$\infty$
. Similarly, if
![]() $\hat{M}$
is fibered over a punctured
$\hat{M}$
is fibered over a punctured
![]() $\mathbb{R}\mathbb{P}^{2}$
, then
$\mathbb{R}\mathbb{P}^{2}$
, then
![]() $\hat{M}^{\infty }$
is the connected sum of an
$\hat{M}^{\infty }$
is the connected sum of an
 $S^{1}\times S^{2}$
with
$S^{1}\times S^{2}$
with
![]() $n$
solid tori, each with longitude of slope
$n$
solid tori, each with longitude of slope
![]() $\infty$
.
$\infty$
.
Primality is especially important in the context of foliations, since, by Novikov [Reference NovikovNov65], no reducible manifold except
 $S^{1}\times S^{2}$
admits a co-oriented taut foliation. On the other hand, not all connected sums are L-spaces, so any correspondence between being an L-space and failing to admit a co-oriented taut foliation breaks down beyond the realm of prime manifolds.
$S^{1}\times S^{2}$
admits a co-oriented taut foliation. On the other hand, not all connected sums are L-spaces, so any correspondence between being an L-space and failing to admit a co-oriented taut foliation breaks down beyond the realm of prime manifolds.
2.3 Rotation number, shift, and foliation slope
One of the key insights of Jankins and Neumann into the work of Eisenbud, Hirsch, and Neumann on taut foliations on Seifert fibered spaces was the need for a better invariant on
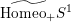 $\widetilde{\text{Homeo}_{+}}S^{1}$
. Whereas the latter group relied on the invariants
$\widetilde{\text{Homeo}_{+}}S^{1}$
. Whereas the latter group relied on the invariants
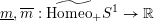 $\text{}\underline{m},\overline{m}:\widetilde{\text{Homeo}_{+}}S^{1}\rightarrow \mathbb{R}$
, with
$\text{}\underline{m},\overline{m}:\widetilde{\text{Homeo}_{+}}S^{1}\rightarrow \mathbb{R}$
, with
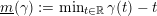 $\text{}\underline{m}(\unicode[STIX]{x1D6FE}):=\min _{t\in \mathbb{R}}\unicode[STIX]{x1D6FE}(t)-t$
and
$\text{}\underline{m}(\unicode[STIX]{x1D6FE}):=\min _{t\in \mathbb{R}}\unicode[STIX]{x1D6FE}(t)-t$
and
 $\overline{m}(\unicode[STIX]{x1D6FE}):=\max _{t\in \mathbb{R}}\unicode[STIX]{x1D6FE}(t)-t$
, Jankins and Neumann introduced the problem to a more precise invariant of circle actions: a conjugacy invariant called the (Poincaré) rotation number,
$\overline{m}(\unicode[STIX]{x1D6FE}):=\max _{t\in \mathbb{R}}\unicode[STIX]{x1D6FE}(t)-t$
, Jankins and Neumann introduced the problem to a more precise invariant of circle actions: a conjugacy invariant called the (Poincaré) rotation number,
 $$\begin{eqnarray}\text{rot}:\widetilde{\text{Homeo}_{+}}(S^{1})\rightarrow \mathbb{R},\quad \text{rot}(\unicode[STIX]{x1D6FE})=\lim _{k\rightarrow \infty }{\displaystyle \frac{1}{k}}(\unicode[STIX]{x1D6FE}^{k}(t)-t),\end{eqnarray}$$
$$\begin{eqnarray}\text{rot}:\widetilde{\text{Homeo}_{+}}(S^{1})\rightarrow \mathbb{R},\quad \text{rot}(\unicode[STIX]{x1D6FE})=\lim _{k\rightarrow \infty }{\displaystyle \frac{1}{k}}(\unicode[STIX]{x1D6FE}^{k}(t)-t),\end{eqnarray}$$
which is independent of
![]() $t\in \mathbb{R}$
, and rational if and only if
$t\in \mathbb{R}$
, and rational if and only if
![]() $\unicode[STIX]{x1D6FE}$
has some closed orbit [Reference GhysGhy01]. The rotation number is not, in general, a homomorphism. However, it restricts to a homomorphism on any amenable, hence any abelian, subgroup [Reference GhysGhy01]. In particular, it restricts to a homomorphism on any representation of the fundamental group of a torus.
$\unicode[STIX]{x1D6FE}$
has some closed orbit [Reference GhysGhy01]. The rotation number is not, in general, a homomorphism. However, it restricts to a homomorphism on any amenable, hence any abelian, subgroup [Reference GhysGhy01]. In particular, it restricts to a homomorphism on any representation of the fundamental group of a torus.
The simplest element of
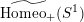 $\widetilde{\text{Homeo}_{+}}(S^{1})$
is a rotation, or shift,
$\widetilde{\text{Homeo}_{+}}(S^{1})$
is a rotation, or shift,
 $$\begin{eqnarray}\text{sh}(s):t\mapsto t+s,\quad t\in \mathbb{R}.\end{eqnarray}$$
$$\begin{eqnarray}\text{sh}(s):t\mapsto t+s,\quad t\in \mathbb{R}.\end{eqnarray}$$
Whereas
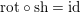 $\text{rot}\circ \text{sh}=\text{id}$
, not every element of
$\text{rot}\circ \text{sh}=\text{id}$
, not every element of
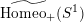 $\widetilde{\text{Homeo}_{+}}(S^{1})$
is conjugate to a rotation. It is a classic result, however, that every element of
$\widetilde{\text{Homeo}_{+}}(S^{1})$
is conjugate to a rotation. It is a classic result, however, that every element of
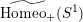 $\widetilde{\text{Homeo}_{+}}(S^{1})$
with irrational rotation number is left and right semiconjugate to a shift of the same rotation number [Reference GhysGhy01].
$\widetilde{\text{Homeo}_{+}}(S^{1})$
with irrational rotation number is left and right semiconjugate to a shift of the same rotation number [Reference GhysGhy01].
Rotation numbers can also be used to associate slopes to taut foliations on tori.
Definition 2.4. For the two-torus
![]() $T$
, there is a canonical map
$T$
, there is a canonical map
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:\{C^{0}\text{ codimension-one foliations on }T\}\rightarrow \mathbb{P}(H_{1}(T;\mathbb{R})),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:\{C^{0}\text{ codimension-one foliations on }T\}\rightarrow \mathbb{P}(H_{1}(T;\mathbb{R})),\end{eqnarray}$$
constructed below, which respects isotopy. We call
![]() $\unicode[STIX]{x1D6FC}(F)$
the slope of
$\unicode[STIX]{x1D6FC}(F)$
the slope of
![]() $F$
.
$F$
.
If
![]() $F$
has Reeb components, then
$F$
has Reeb components, then
![]() $\unicode[STIX]{x1D6FC}(F)$
is given by the class of any closed leaf of
$\unicode[STIX]{x1D6FC}(F)$
is given by the class of any closed leaf of
![]() $F$
. All Reebless foliations on tori are taut. Thus, if
$F$
. All Reebless foliations on tori are taut. Thus, if
![]() $F$
is Reebless, then there is a curve, say
$F$
is Reebless, then there is a curve, say
![]() $C_{\unicode[STIX]{x1D706}}$
of primitive class
$C_{\unicode[STIX]{x1D706}}$
of primitive class
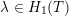 $\unicode[STIX]{x1D706}\in H_{1}(T)$
, which intersects every leaf transversely, and
$\unicode[STIX]{x1D706}\in H_{1}(T)$
, which intersects every leaf transversely, and
![]() $F$
can be realized as the suspension of a circle homeomorphism
$F$
can be realized as the suspension of a circle homeomorphism
 $\unicode[STIX]{x1D6FE}_{F,\unicode[STIX]{x1D706}}\in \text{Homeo}_{+}S^{1}$
from
$\unicode[STIX]{x1D6FE}_{F,\unicode[STIX]{x1D706}}\in \text{Homeo}_{+}S^{1}$
from
![]() $C_{\unicode[STIX]{x1D706}}$
to itself [Reference Hector and HirschHH81]. A choice of
$C_{\unicode[STIX]{x1D706}}$
to itself [Reference Hector and HirschHH81]. A choice of
 $\unicode[STIX]{x1D707}\in H_{1}(T)$
with
$\unicode[STIX]{x1D707}\in H_{1}(T)$
with
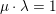 $\unicode[STIX]{x1D707}\cdot \unicode[STIX]{x1D706}=1$
induces a lift of this suspension to a suspension from a universal cover
$\unicode[STIX]{x1D707}\cdot \unicode[STIX]{x1D706}=1$
induces a lift of this suspension to a suspension from a universal cover
![]() $\tilde{C}_{\unicode[STIX]{x1D706}}$
of
$\tilde{C}_{\unicode[STIX]{x1D706}}$
of
![]() $C_{\unicode[STIX]{x1D706}}$
to its translate by
$C_{\unicode[STIX]{x1D706}}$
to its translate by
![]() $\unicode[STIX]{x1D707}$
in the universal cover of
$\unicode[STIX]{x1D707}$
in the universal cover of
![]() $T$
. That is, if we regard
$T$
. That is, if we regard
![]() $\tilde{C}_{\unicode[STIX]{x1D706}}$
as the real vector space
$\tilde{C}_{\unicode[STIX]{x1D706}}$
as the real vector space
![]() $\{t\unicode[STIX]{x1D706}\}_{t\in \mathbb{R}}$
spanned by
$\{t\unicode[STIX]{x1D706}\}_{t\in \mathbb{R}}$
spanned by
![]() $\unicode[STIX]{x1D706}$
, with
$\unicode[STIX]{x1D706}$
, with
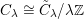 $C_{\unicode[STIX]{x1D706}}\cong \tilde{C}_{\unicode[STIX]{x1D706}}/\unicode[STIX]{x1D706}\mathbb{Z}$
, then we can lift the foliation
$C_{\unicode[STIX]{x1D706}}\cong \tilde{C}_{\unicode[STIX]{x1D706}}/\unicode[STIX]{x1D706}\mathbb{Z}$
, then we can lift the foliation
![]() $F$
to the universal cover of
$F$
to the universal cover of
![]() $T$
by iteratively suspending the map
$T$
by iteratively suspending the map
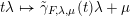 $t\unicode[STIX]{x1D706}\mapsto \tilde{\unicode[STIX]{x1D6FE}}_{F,\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}(t)\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}$
, for an appropriate lift
$t\unicode[STIX]{x1D706}\mapsto \tilde{\unicode[STIX]{x1D6FE}}_{F,\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}(t)\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}$
, for an appropriate lift
 $\tilde{\unicode[STIX]{x1D6FE}}_{F,\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}\in \widetilde{\text{Homeo}}_{+}S^{1}\subset \text{Homeo}_{+}\mathbb{R}$
of
$\tilde{\unicode[STIX]{x1D6FE}}_{F,\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}\in \widetilde{\text{Homeo}}_{+}S^{1}\subset \text{Homeo}_{+}\mathbb{R}$
of
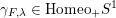 $\unicode[STIX]{x1D6FE}_{F,\unicode[STIX]{x1D706}}\in \text{Homeo}_{+}S^{1}$
.
$\unicode[STIX]{x1D6FE}_{F,\unicode[STIX]{x1D706}}\in \text{Homeo}_{+}S^{1}$
.
This lifted suspension, in turn, induces a representation
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}:\unicode[STIX]{x1D70B}_{1}(T)\rightarrow \widetilde{\text{Homeo}}_{+}S^{1},\quad [\unicode[STIX]{x1D706}]\mapsto \text{sh}(1),\quad [-\unicode[STIX]{x1D707}]\mapsto \tilde{\unicode[STIX]{x1D6FE}}_{F,\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}:\unicode[STIX]{x1D70B}_{1}(T)\rightarrow \widetilde{\text{Homeo}}_{+}S^{1},\quad [\unicode[STIX]{x1D706}]\mapsto \text{sh}(1),\quad [-\unicode[STIX]{x1D707}]\mapsto \tilde{\unicode[STIX]{x1D6FE}}_{F,\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}},\end{eqnarray}$$
where
![]() $[\unicode[STIX]{x1D706}]$
and
$[\unicode[STIX]{x1D706}]$
and
![]() $[\unicode[STIX]{x1D707}]$
denote the lifts of
$[\unicode[STIX]{x1D707}]$
denote the lifts of
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D707}$
to
$\unicode[STIX]{x1D707}$
to
![]() $\unicode[STIX]{x1D70B}_{1}(T)$
. One can regard
$\unicode[STIX]{x1D70B}_{1}(T)$
. One can regard
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}$
as describing how to traverse the line
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}$
as describing how to traverse the line
 $\{t\unicode[STIX]{x1D706}\}_{t\in \mathbb{R}}\subset \langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\rangle _{\mathbb{R}}$
by traveling only along foliation leaves or integer multiples of
$\{t\unicode[STIX]{x1D706}\}_{t\in \mathbb{R}}\subset \langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\rangle _{\mathbb{R}}$
by traveling only along foliation leaves or integer multiples of
![]() $\unicode[STIX]{x1D706}$
or
$\unicode[STIX]{x1D706}$
or
![]() $\unicode[STIX]{x1D707}$
. That is, if one starts at some
$\unicode[STIX]{x1D707}$
. That is, if one starts at some
![]() $t_{0}\unicode[STIX]{x1D706}$
, hops by
$t_{0}\unicode[STIX]{x1D706}$
, hops by
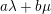 $a\unicode[STIX]{x1D706}+b\unicode[STIX]{x1D707}$
for some
$a\unicode[STIX]{x1D706}+b\unicode[STIX]{x1D707}$
for some
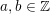 $a,b\in \mathbb{Z}$
, takes the foliation leaf intersecting this new point, and follows this leaf back to the line
$a,b\in \mathbb{Z}$
, takes the foliation leaf intersecting this new point, and follows this leaf back to the line
![]() $\{t\unicode[STIX]{x1D706}\}_{t\in \mathbb{R}}$
, then one will arrive at
$\{t\unicode[STIX]{x1D706}\}_{t\in \mathbb{R}}$
, then one will arrive at
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}(a\unicode[STIX]{x1D706}+b\unicode[STIX]{x1D707})(t_{0})\unicode[STIX]{x1D706}$
. Note that while
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}(a\unicode[STIX]{x1D706}+b\unicode[STIX]{x1D707})(t_{0})\unicode[STIX]{x1D706}$
. Note that while
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}$
is independent of the choice of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}$
is independent of the choice of
![]() $\unicode[STIX]{x1D707}$
, and is determined up to conjugacy by a choice of
$\unicode[STIX]{x1D707}$
, and is determined up to conjugacy by a choice of
![]() $\unicode[STIX]{x1D706}$
, it still depends on
$\unicode[STIX]{x1D706}$
, it still depends on
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
On the other hand, when we define the slope
![]() $\unicode[STIX]{x1D6FC}(F)$
of
$\unicode[STIX]{x1D6FC}(F)$
of
![]() $F$
to be
$F$
to be
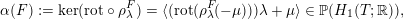 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(F):=\ker (\text{rot}\circ \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F})=\langle (\text{rot}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}\!(-\unicode[STIX]{x1D707})))\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}\rangle \in \mathbb{P}(H_{1}(T;\mathbb{R})),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(F):=\ker (\text{rot}\circ \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F})=\langle (\text{rot}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}\!(-\unicode[STIX]{x1D707})))\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}\rangle \in \mathbb{P}(H_{1}(T;\mathbb{R})),\end{eqnarray}$$
then the rotation number washes out all dependence on
![]() $\unicode[STIX]{x1D706}$
and choice of suspension. That is, one can use the definition of rotation number to compute
$\unicode[STIX]{x1D706}$
and choice of suspension. That is, one can use the definition of rotation number to compute
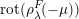 $\text{rot}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}\!(-\unicode[STIX]{x1D707}))$
in terms of the rotation number associated to a different choice of basis and suspension for
$\text{rot}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}^{F}\!(-\unicode[STIX]{x1D707}))$
in terms of the rotation number associated to a different choice of basis and suspension for
![]() $F$
, and obtain the same answer for
$F$
, and obtain the same answer for
![]() $\unicode[STIX]{x1D6FC}(F)$
in both cases. Alternatively, any suspension homeomorphism with rational rotation number has a periodic orbit, hence realizes a foliation with a compact leaf of slope
$\unicode[STIX]{x1D6FC}(F)$
in both cases. Alternatively, any suspension homeomorphism with rational rotation number has a periodic orbit, hence realizes a foliation with a compact leaf of slope
![]() $\unicode[STIX]{x1D6FC}(F)$
. If the suspension homeomorphism has irrational rotation number, then it is semiconjugate to a shift of matching rotation number [Reference GhysGhy01], giving rise to a linear foliation of slope
$\unicode[STIX]{x1D6FC}(F)$
. If the suspension homeomorphism has irrational rotation number, then it is semiconjugate to a shift of matching rotation number [Reference GhysGhy01], giving rise to a linear foliation of slope
![]() $\unicode[STIX]{x1D6FC}(F)$
.
$\unicode[STIX]{x1D6FC}(F)$
.
2.4 Restricting Seifert fibered space foliations to torus foliations
If a compact oriented three-manifold
![]() $Y$
admits a co-oriented taut foliation transverse to
$Y$
admits a co-oriented taut foliation transverse to
![]() $\unicode[STIX]{x2202}Y$
, then Gabai tells us that
$\unicode[STIX]{x2202}Y$
, then Gabai tells us that
![]() $\unicode[STIX]{x2202}Y$
can only have toroidal components [Reference GabaiGab83]. Thus, we often encounter foliations on tori as boundary restrictions of foliations on three-manifolds. Moreover, on a Seifert fibered space, any taut foliation transverse to the boundary restricts to taut foliations on boundary components.
$\unicode[STIX]{x2202}Y$
can only have toroidal components [Reference GabaiGab83]. Thus, we often encounter foliations on tori as boundary restrictions of foliations on three-manifolds. Moreover, on a Seifert fibered space, any taut foliation transverse to the boundary restricts to taut foliations on boundary components.
Suppose
![]() $F$
is a co-oriented taut foliation transverse to the fibration of the Seifert fibered Dehn filling
$F$
is a co-oriented taut foliation transverse to the fibration of the Seifert fibered Dehn filling
 $M_{S^{2}}(r_{\ast }/s_{\ast })$
along the slopes
$M_{S^{2}}(r_{\ast }/s_{\ast })$
along the slopes
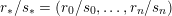 $r_{\ast }/s_{\ast }=(r_{0}/s_{0},\ldots ,r_{n}/s_{n})$
of the trivial circle fibration
$r_{\ast }/s_{\ast }=(r_{0}/s_{0},\ldots ,r_{n}/s_{n})$
of the trivial circle fibration
![]() $\hat{M}$
over an (
$\hat{M}$
over an (
![]() $n+1$
)-punctured
$n+1$
)-punctured
![]() $S^{2}$
, according to the conventions of § 2.2. For each boundary component
$S^{2}$
, according to the conventions of § 2.2. For each boundary component
![]() $\unicode[STIX]{x2202}_{i}\hat{M}$
, we regard the foliation
$\unicode[STIX]{x2202}_{i}\hat{M}$
, we regard the foliation
 $F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
as a suspension of a homeomorphism of the curve of class
$F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
as a suspension of a homeomorphism of the curve of class
![]() $\tilde{f}_{i}$
to itself, and since the class
$\tilde{f}_{i}$
to itself, and since the class
![]() $-\tilde{h}_{i}$
satisfies
$-\tilde{h}_{i}$
satisfies
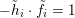 $-\tilde{h}_{i}\cdot \tilde{f}_{i}=1$
, it specifies a lift of this suspension to a suspension of an element
$-\tilde{h}_{i}\cdot \tilde{f}_{i}=1$
, it specifies a lift of this suspension to a suspension of an element
 $\unicode[STIX]{x1D6FE}_{F,\tilde{f}_{i},-\tilde{h}_{i}}\in \widetilde{\text{Homeo}_{+}}S^{1}$
. To this suspension we associate the representation
$\unicode[STIX]{x1D6FE}_{F,\tilde{f}_{i},-\tilde{h}_{i}}\in \widetilde{\text{Homeo}_{+}}S^{1}$
. To this suspension we associate the representation
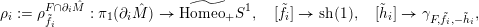 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{i}:=\unicode[STIX]{x1D70C}_{\tilde{f}_{i}}^{F\cap \unicode[STIX]{x2202}_{i}\hat{M}}:\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\rightarrow \widetilde{\text{Homeo}_{+}}S^{1},\quad [\tilde{f}_{i}]\rightarrow \text{sh}(1),\quad [\tilde{h}_{i}]\rightarrow \unicode[STIX]{x1D6FE}_{F,\tilde{f}_{i},-\tilde{h}_{i}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{i}:=\unicode[STIX]{x1D70C}_{\tilde{f}_{i}}^{F\cap \unicode[STIX]{x2202}_{i}\hat{M}}:\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\rightarrow \widetilde{\text{Homeo}_{+}}S^{1},\quad [\tilde{f}_{i}]\rightarrow \text{sh}(1),\quad [\tilde{h}_{i}]\rightarrow \unicode[STIX]{x1D6FE}_{F,\tilde{f}_{i},-\tilde{h}_{i}},\end{eqnarray}$$
allowing us to express the slope
 $\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})$
of
$\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})$
of
 $F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
as
$F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
as
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=\unicode[STIX]{x1D70B}_{i}(\text{rot}(\unicode[STIX]{x1D70C}_{i}([\tilde{h}_{i}]))\tilde{f}_{i}-\tilde{h}_{i})=\text{rot}(\unicode[STIX]{x1D70C}_{i}([\tilde{h}_{i}])).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=\unicode[STIX]{x1D70B}_{i}(\text{rot}(\unicode[STIX]{x1D70C}_{i}([\tilde{h}_{i}]))\tilde{f}_{i}-\tilde{h}_{i})=\text{rot}(\unicode[STIX]{x1D70C}_{i}([\tilde{h}_{i}])).\end{eqnarray}$$
The construction of Eisenbud, Hirsch, and Neumann [Reference Eisenbud, Hirsch and NeumannEHN81] associating a representation
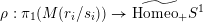 $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(M(r_{i}/s_{i}))\rightarrow \widetilde{\text{Homeo}_{+}}S^{1}$
to
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(M(r_{i}/s_{i}))\rightarrow \widetilde{\text{Homeo}_{+}}S^{1}$
to
![]() $F$
, sending the fiber class
$F$
, sending the fiber class
![]() $\unicode[STIX]{x1D719}=[f]$
to
$\unicode[STIX]{x1D719}=[f]$
to
![]() $\text{sh}(1)$
, is sufficiently compatible with the construction of each
$\text{sh}(1)$
, is sufficiently compatible with the construction of each
![]() $\unicode[STIX]{x1D70C}_{i}$
above that, possibly after conjugation of each
$\unicode[STIX]{x1D70C}_{i}$
above that, possibly after conjugation of each
![]() $\unicode[STIX]{x1D70C}_{i}$
,
$\unicode[STIX]{x1D70C}_{i}$
,
![]() $\unicode[STIX]{x1D70C}$
can be chosen to satisfy
$\unicode[STIX]{x1D70C}$
can be chosen to satisfy
 $\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D70C}\,\circ \,\unicode[STIX]{x1D704}_{i}^{\unicode[STIX]{x1D70B}_{1}}$
, with
$\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D70C}\,\circ \,\unicode[STIX]{x1D704}_{i}^{\unicode[STIX]{x1D70B}_{1}}$
, with
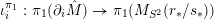 $\unicode[STIX]{x1D704}_{i}^{\unicode[STIX]{x1D70B}_{1}}:\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\rightarrow \unicode[STIX]{x1D70B}_{1}(M_{S^{2}}(r_{\ast }/s_{\ast }))$
the homomorphism induced by inclusion. The presentation (6) for
$\unicode[STIX]{x1D704}_{i}^{\unicode[STIX]{x1D70B}_{1}}:\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x2202}_{i}\hat{M})\rightarrow \unicode[STIX]{x1D70B}_{1}(M_{S^{2}}(r_{\ast }/s_{\ast }))$
the homomorphism induced by inclusion. The presentation (6) for
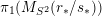 $\unicode[STIX]{x1D70B}_{1}(M_{S^{2}}(r_{\ast }/s_{\ast }))$
then places the following restrictions on
$\unicode[STIX]{x1D70B}_{1}(M_{S^{2}}(r_{\ast }/s_{\ast }))$
then places the following restrictions on
![]() $\unicode[STIX]{x1D70C}$
, as observed by Jankins and Neumann [Reference Jankins and NeumannJN85]:
$\unicode[STIX]{x1D70C}$
, as observed by Jankins and Neumann [Reference Jankins and NeumannJN85]:
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D702}_{i}=\unicode[STIX]{x1D719}^{-e_{0}} & \;\Longrightarrow \; & \displaystyle \bullet \;\text{rot}\biggl(\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})\biggr)=-e_{0}=-\frac{r_{0}}{s_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D702}_{i}=\unicode[STIX]{x1D719}^{-e_{0}} & \;\Longrightarrow \; & \displaystyle \bullet \;\text{rot}\biggl(\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})\biggr)=-e_{0}=-\frac{r_{0}}{s_{0}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle i\in \{0,\ldots ,n\}\!:\quad \unicode[STIX]{x1D702}_{i}^{s_{i}}=\unicode[STIX]{x1D719}^{r_{i}} & \;\Longrightarrow \; & \displaystyle \left\{\begin{array}{@{}l@{}}\bullet \;\text{rot}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))={\displaystyle \frac{r_{i}}{s_{i}}},\quad \\ \bullet \;\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})\text{ is conjugate to }\text{sh}\biggl({\displaystyle \frac{r_{i}}{s_{i}}}\biggr).\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i\in \{0,\ldots ,n\}\!:\quad \unicode[STIX]{x1D702}_{i}^{s_{i}}=\unicode[STIX]{x1D719}^{r_{i}} & \;\Longrightarrow \; & \displaystyle \left\{\begin{array}{@{}l@{}}\bullet \;\text{rot}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))={\displaystyle \frac{r_{i}}{s_{i}}},\quad \\ \bullet \;\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})\text{ is conjugate to }\text{sh}\biggl({\displaystyle \frac{r_{i}}{s_{i}}}\biggr).\quad \end{array}\right.\end{eqnarray}$$
Jankins and Neumann mostly focused on the case of
![]() $n=3$
,
$n=3$
,
 $e_{0}=-1$
, and
$e_{0}=-1$
, and
 $0<r_{1}/s_{1},r_{2}/s_{2},r_{3}/s_{3}<1$
, but their above observation holds in general.
$0<r_{1}/s_{1},r_{2}/s_{2},r_{3}/s_{3}<1$
, but their above observation holds in general.
Whereas the first condition enforces a global restriction on
![]() $F$
, the latter two conditions provide local restrictions at each
$F$
, the latter two conditions provide local restrictions at each
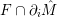 $F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
, which we could recover simply by considering Dehn fillings. The solid torus admits only one taut foliation, namely, the product foliation with slope given by the rational longitude. As a consequence, the co-oriented taut foliation
$F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
, which we could recover simply by considering Dehn fillings. The solid torus admits only one taut foliation, namely, the product foliation with slope given by the rational longitude. As a consequence, the co-oriented taut foliation
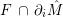 $F\,\cap \,\unicode[STIX]{x2202}_{i}\hat{M}$
extends to a co-oriented taut foliation on the Dehn filling
$F\,\cap \,\unicode[STIX]{x2202}_{i}\hat{M}$
extends to a co-oriented taut foliation on the Dehn filling
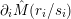 $\unicode[STIX]{x2202}_{i}\hat{M}(r_{i}/s_{i})$
if and only if
$\unicode[STIX]{x2202}_{i}\hat{M}(r_{i}/s_{i})$
if and only if
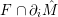 $F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
is the product foliation of slope
$F\cap \unicode[STIX]{x2202}_{i}\hat{M}$
is the product foliation of slope
![]() $r_{i}/s_{i}$
, which occurs if and only if
$r_{i}/s_{i}$
, which occurs if and only if
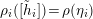 $\unicode[STIX]{x1D70C}_{i}([\tilde{h}_{i}])\!=\!\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})$
is conjugate to
$\unicode[STIX]{x1D70C}_{i}([\tilde{h}_{i}])\!=\!\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})$
is conjugate to
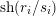 $\text{sh}(r_{i}/s_{i})$
, a condition which requires
$\text{sh}(r_{i}/s_{i})$
, a condition which requires
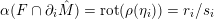 $\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=\text{rot}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))=r_{i}/s_{i}$
. In particular, the
$\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=\text{rot}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))=r_{i}/s_{i}$
. In particular, the
![]() $j\text{th}$
shift conjugacy condition, that
$j\text{th}$
shift conjugacy condition, that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{j})$
be conjugate to
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{j})$
be conjugate to
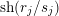 $\text{sh}(r_{j}/s_{j})$
, is due solely to the fact that
$\text{sh}(r_{j}/s_{j})$
, is due solely to the fact that
![]() $\unicode[STIX]{x2202}_{j}\hat{M}$
is glued to a solid torus. As emphasized by Boyer and Clay [Reference Boyer and ClayBC14], when one relaxes the
$\unicode[STIX]{x2202}_{j}\hat{M}$
is glued to a solid torus. As emphasized by Boyer and Clay [Reference Boyer and ClayBC14], when one relaxes the
![]() $j\text{th}$
shift conjugacy condition, one can still find manifolds
$j\text{th}$
shift conjugacy condition, one can still find manifolds
![]() $Y$
with torus boundary for which
$Y$
with torus boundary for which
![]() $F$
extends to a taut foliation on
$F$
extends to a taut foliation on
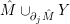 $\hat{M}\cup _{\unicode[STIX]{x2202}_{j}\hat{M}}Y\!$
, for a suitable choice of gluing map.
$\hat{M}\cup _{\unicode[STIX]{x2202}_{j}\hat{M}}Y\!$
, for a suitable choice of gluing map.
It is presumably for this reason that Jankins and Neumann focused on the more general condition of
![]() $J$
-realizability for an (
$J$
-realizability for an (
![]() $n+1$
)-tuple
$n+1$
)-tuple
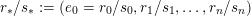 $r_{\ast }/s_{\ast }:=(e_{0}=r_{0}/s_{0},r_{1}/s_{1},\ldots ,r_{n}/s_{n})$
, given a subset
$r_{\ast }/s_{\ast }:=(e_{0}=r_{0}/s_{0},r_{1}/s_{1},\ldots ,r_{n}/s_{n})$
, given a subset
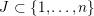 $J\subset \{1,\ldots ,n\}$
. They deem
$J\subset \{1,\ldots ,n\}$
. They deem
![]() $r_{\ast }/s_{\ast }$
$r_{\ast }/s_{\ast }$
![]() $J$
-realizable if there is a representation
$J$
-realizable if there is a representation
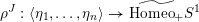 $\unicode[STIX]{x1D70C}^{J}:\langle \unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}\rangle \rightarrow \widetilde{\text{Homeo}_{+}}S^{1}$
such that
$\unicode[STIX]{x1D70C}^{J}:\langle \unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}\rangle \rightarrow \widetilde{\text{Homeo}_{+}}S^{1}$
such that
![]() $\unicode[STIX]{x1D70C}^{J}$
meets the
$\unicode[STIX]{x1D70C}^{J}$
meets the
![]() $r_{\ast }/s_{\ast }$
rotation number condition, that
$r_{\ast }/s_{\ast }$
rotation number condition, that
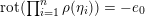 $\text{rot}(\prod _{i=1}^{n}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))=-e_{0}$
with
$\text{rot}(\prod _{i=1}^{n}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))=-e_{0}$
with
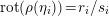 $\text{rot}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))\!=\!r_{i}/s_{i}$
for each
$\text{rot}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i}))\!=\!r_{i}/s_{i}$
for each
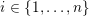 $i\in \{1,\ldots ,n\}$
, and such that
$i\in \{1,\ldots ,n\}$
, and such that
![]() $\unicode[STIX]{x1D70C}^{J}$
meets the
$\unicode[STIX]{x1D70C}^{J}$
meets the
![]() $j\text{th}$
shift conjugacy condition for each
$j\text{th}$
shift conjugacy condition for each
![]() $j\in J$
. We have already shown that
$j\in J$
. We have already shown that
![]() $J$
-realizability is a necessary condition for
$J$
-realizability is a necessary condition for
![]() $\hat{M}$
to admit a taut foliation
$\hat{M}$
to admit a taut foliation
![]() $F$
of slopes
$F$
of slopes
 $\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=r_{i}/s_{i}$
which extends to a taut foliation on the partial Dehn filling of
$\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=r_{i}/s_{i}$
which extends to a taut foliation on the partial Dehn filling of
![]() $\hat{M}$
along the slopes
$\hat{M}$
along the slopes
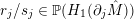 $r_{j}/s_{j}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{j}\hat{M}))$
for all
$r_{j}/s_{j}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{j}\hat{M}))$
for all
 $j\in \{0\}\cup J$
. With the help of Naimi, Jankins and Neumann showed that the condition is also sufficient [Reference Jankins and NeumannJN85, Reference NaimiNai94].
$j\in \{0\}\cup J$
. With the help of Naimi, Jankins and Neumann showed that the condition is also sufficient [Reference Jankins and NeumannJN85, Reference NaimiNai94].
2.5 Solutions for
 $J$
-realizability
$J$
-realizability
Jankins and Neumann conjectured that a slope
![]() $r_{\ast }/s_{\ast }$
is
$r_{\ast }/s_{\ast }$
is
![]() $J$
-realizable in
$J$
-realizable in
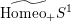 $\widetilde{\text{Homeo}_{+}}S^{1}$
if and only if it is
$\widetilde{\text{Homeo}_{+}}S^{1}$
if and only if it is
![]() $J$
-realizable in a smooth Lie subgroup of
$J$
-realizable in a smooth Lie subgroup of
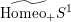 $\widetilde{\text{Homeo}_{+}}S^{1}$
. Observing that any smooth Lie subgroup of
$\widetilde{\text{Homeo}_{+}}S^{1}$
. Observing that any smooth Lie subgroup of
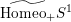 $\widetilde{\text{Homeo}_{+}}S^{1}$
is conjugate to
$\widetilde{\text{Homeo}_{+}}S^{1}$
is conjugate to
 $\widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
for some
$\widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
for some
![]() $k\!\in \!\mathbb{Z}_{{>}0}$
, where
$k\!\in \!\mathbb{Z}_{{>}0}$
, where
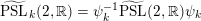 $\widetilde{\text{PSL}}_{k}(2,\mathbb{R})=\unicode[STIX]{x1D713}_{k}^{-1}\widetilde{\text{PSL}}(2,\mathbb{R})\unicode[STIX]{x1D713}_{k}$
for
$\widetilde{\text{PSL}}_{k}(2,\mathbb{R})=\unicode[STIX]{x1D713}_{k}^{-1}\widetilde{\text{PSL}}(2,\mathbb{R})\unicode[STIX]{x1D713}_{k}$
for
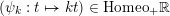 $(\unicode[STIX]{x1D713}_{k}:t\mapsto kt)\in \text{Homeo}_{+}\mathbb{R}$
, they computed
$(\unicode[STIX]{x1D713}_{k}:t\mapsto kt)\in \text{Homeo}_{+}\mathbb{R}$
, they computed
 $$\begin{eqnarray}\max \;\text{rot}\biggl(\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D6FE}_{i}\biggr)=\frac{1}{k}\biggl(-1+\mathop{\sum }_{i=1}^{n}\biggl(\biggl\lfloor\frac{r_{i}k}{s_{i}}\biggr\rfloor+1\biggr)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\max \;\text{rot}\biggl(\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D6FE}_{i}\biggr)=\frac{1}{k}\biggl(-1+\mathop{\sum }_{i=1}^{n}\biggl(\biggl\lfloor\frac{r_{i}k}{s_{i}}\biggr\rfloor+1\biggr)\biggr)\end{eqnarray}$$
for the maximum rotation number of a product of elements
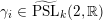 $\unicode[STIX]{x1D6FE}_{i}\in \widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
with each
$\unicode[STIX]{x1D6FE}_{i}\in \widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
with each
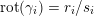 $\text{rot}(\unicode[STIX]{x1D6FE}_{i})=r_{i}/s_{i}$
. They then proved the above conjecture in all but one case, later proven by Naimi [Reference NaimiNai94]. More recently, in [Reference Calegari and WalkerCW11, Theorem 3.9] (appropriately generalized from 2 to
$\text{rot}(\unicode[STIX]{x1D6FE}_{i})=r_{i}/s_{i}$
. They then proved the above conjecture in all but one case, later proven by Naimi [Reference NaimiNai94]. More recently, in [Reference Calegari and WalkerCW11, Theorem 3.9] (appropriately generalized from 2 to
![]() $n$
), Calegari and Walker rederived (18) (with the maximum taken over
$n$
), Calegari and Walker rederived (18) (with the maximum taken over
![]() $k\!\in \!\mathbb{Z}_{{>}0}$
) for
$k\!\in \!\mathbb{Z}_{{>}0}$
) for
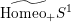 $\widetilde{\text{Homeo}_{+}}S^{1}$
, without appealing to
$\widetilde{\text{Homeo}_{+}}S^{1}$
, without appealing to
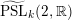 $\widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
, by using dynamical techniques similar to those of Naimi.
$\widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
, by using dynamical techniques similar to those of Naimi.
One obtains the analogous minimum rotation number of a product by sending
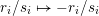 $r_{i}/s_{i}\mapsto -r_{i}/s_{i}$
in (18). Demanding that
$r_{i}/s_{i}\mapsto -r_{i}/s_{i}$
in (18). Demanding that
![]() $-e_{0}$
lie between the minimum and maximum rotation numbers for
$-e_{0}$
lie between the minimum and maximum rotation numbers for
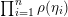 $\prod _{i=1}^{n}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})$
, and multiplying the resulting inequality by
$\prod _{i=1}^{n}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D702}_{i})$
, and multiplying the resulting inequality by
![]() $-1$
, implies that a representation in
$-1$
, implies that a representation in
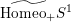 $\widetilde{\text{Homeo}_{+}}S^{1}$
can only satisfy the rotation number condition for
$\widetilde{\text{Homeo}_{+}}S^{1}$
can only satisfy the rotation number condition for
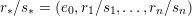 $r_{\ast }/s_{\ast }=(e_{0},r_{1}/s_{1},\ldots ,r_{n}/s_{n})$
if
$r_{\ast }/s_{\ast }=(e_{0},r_{1}/s_{1},\ldots ,r_{n}/s_{n})$
if
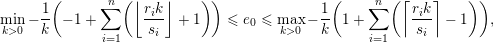 $$\begin{eqnarray}\min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n}\biggl(\biggl\lfloor{\displaystyle \frac{r_{i}k}{s_{i}}}\biggr\rfloor+1\biggr)\biggr)\leqslant e_{0}\leqslant \max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n}\biggl(\lceil {\displaystyle \frac{r_{i}k}{s_{i}}}\rceil -1\biggr)\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n}\biggl(\biggl\lfloor{\displaystyle \frac{r_{i}k}{s_{i}}}\biggr\rfloor+1\biggr)\biggr)\leqslant e_{0}\leqslant \max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n}\biggl(\lceil {\displaystyle \frac{r_{i}k}{s_{i}}}\rceil -1\biggr)\biggr),\end{eqnarray}$$
a criterion which Jankins and Neumann prove is also sufficient [Reference Jankins and NeumannJN85]. Moreover,
![]() $r_{\ast }/s_{\ast }$
is
$r_{\ast }/s_{\ast }$
is
![]() $J$
-realizable in
$J$
-realizable in
 $\widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
, for some
$\widetilde{\text{PSL}}_{k}(2,\mathbb{R})$
, for some
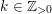 $k\in \mathbb{Z}_{{>}0}$
, if and only if
$k\in \mathbb{Z}_{{>}0}$
, if and only if
 $$\begin{eqnarray}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=0}^{n}\biggl(\biggl\lfloor{\displaystyle \frac{r_{i}k}{s_{i}}}\biggr\rfloor+1\biggr)\biggr)\leqslant 0\leqslant -\mathop{\sum }_{i=0}^{n}{\displaystyle \frac{r_{i}}{s_{i}}}\text{ or }-\mathop{\sum }_{i=0}^{n}{\displaystyle \frac{r_{i}}{s_{i}}}\leqslant 0\leqslant -{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=0}^{n}\biggl(\lceil {\displaystyle \frac{r_{i}k}{s_{i}}}\rceil -1\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=0}^{n}\biggl(\biggl\lfloor{\displaystyle \frac{r_{i}k}{s_{i}}}\biggr\rfloor+1\biggr)\biggr)\leqslant 0\leqslant -\mathop{\sum }_{i=0}^{n}{\displaystyle \frac{r_{i}}{s_{i}}}\text{ or }-\mathop{\sum }_{i=0}^{n}{\displaystyle \frac{r_{i}}{s_{i}}}\leqslant 0\leqslant -{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=0}^{n}\biggl(\lceil {\displaystyle \frac{r_{i}k}{s_{i}}}\rceil -1\biggr)\biggr).\end{eqnarray}$$
The shift conjugacy condition is easier to apply: one can approximate an element of
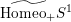 $\widetilde{\text{Homeo}_{+}}S^{1}$
with a shift-conjugate element of arbitrarily close rotation number. Jankins and Neumann used this fact to show that if one fixes all
$\widetilde{\text{Homeo}_{+}}S^{1}$
with a shift-conjugate element of arbitrarily close rotation number. Jankins and Neumann used this fact to show that if one fixes all
![]() $r_{i}/s_{i}$
with
$r_{i}/s_{i}$
with
![]() $i\neq j$
, for some fixed
$i\neq j$
, for some fixed
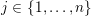 $j\in \{1,\ldots ,n\}$
, then imposing the
$j\in \{1,\ldots ,n\}$
, then imposing the
![]() $j\text{th}$
shift conjugacy condition is equivalent to restricting to the interior of the interval of
$j\text{th}$
shift conjugacy condition is equivalent to restricting to the interior of the interval of
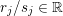 $r_{j}/s_{j}\in \mathbb{R}$
for which the
$r_{j}/s_{j}\in \mathbb{R}$
for which the
![]() $r_{\ast }/s_{\ast }$
rotation number condition is satisfied. More generally, Calegari and Walker have shown that the same principle holds for the rotation number condition associated to any fixed positive word [Reference Calegari and WalkerCW11, Lemma 3.31].
$r_{\ast }/s_{\ast }$
rotation number condition is satisfied. More generally, Calegari and Walker have shown that the same principle holds for the rotation number condition associated to any fixed positive word [Reference Calegari and WalkerCW11, Lemma 3.31].
Since for any
![]() $r\in \mathbb{R}$
and
$r\in \mathbb{R}$
and
![]() $z\in \mathbb{Z}$
, we have
$z\in \mathbb{Z}$
, we have
 $$\begin{eqnarray}z\leqslant \lfloor r\rfloor ~\;\Longleftrightarrow \;~z\leqslant r,\quad \lceil r\rceil \leqslant z~\;\Longleftrightarrow \;~r\leqslant z,\end{eqnarray}$$
$$\begin{eqnarray}z\leqslant \lfloor r\rfloor ~\;\Longleftrightarrow \;~z\leqslant r,\quad \lceil r\rceil \leqslant z~\;\Longleftrightarrow \;~r\leqslant z,\end{eqnarray}$$
it follows, for any
 $j\in \{1,\ldots ,n\}$
, that if we fix all
$j\in \{1,\ldots ,n\}$
, that if we fix all
![]() $r_{i}/s_{i}$
with
$r_{i}/s_{i}$
with
![]() $i\neq j$
, then the interval of
$i\neq j$
, then the interval of
 $r_{j}/s_{j}\in \mathbb{R}$
satisfying (19) is closed. On the other hand, for any
$r_{j}/s_{j}\in \mathbb{R}$
satisfying (19) is closed. On the other hand, for any
![]() $r\in \mathbb{R}$
and
$r\in \mathbb{R}$
and
![]() $z\in \mathbb{Z}$
, we know that
$z\in \mathbb{Z}$
, we know that
 $$\begin{eqnarray}z\leqslant \lceil r\rceil -1~\;\Longleftrightarrow \;~z<r,\quad \lfloor r\rfloor +1\leqslant z~\;\Longleftrightarrow \;~r<z.\end{eqnarray}$$
$$\begin{eqnarray}z\leqslant \lceil r\rceil -1~\;\Longleftrightarrow \;~z<r,\quad \lfloor r\rfloor +1\leqslant z~\;\Longleftrightarrow \;~r<z.\end{eqnarray}$$
These identities led Jankins and Neumann to produce the formulas in the following result.
[JN85] and Naimi [Nai94];
Theorem 2.5 (Jankins and Neumann [Reference Jankins and NeumannJN85] and Naimi [Reference NaimiNai94]; cf. Calegari and Walker [Reference Calegari and WalkerCW11]).
For any
![]() $n\geqslant 2$
, partition
$n\geqslant 2$
, partition
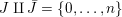 $J\amalg \bar{J}=\{0,\ldots ,n\}$
with
$J\amalg \bar{J}=\{0,\ldots ,n\}$
with
![]() $0\in J$
, and
$0\in J$
, and
![]() $(n+1)$
-tuple
$(n+1)$
-tuple
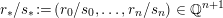 $r_{\ast }/s_{\ast }\!:=\!(r_{0}/s_{0},\ldots ,r_{n}/s_{n})\in \mathbb{Q}^{n+1}$
with
$r_{\ast }/s_{\ast }\!:=\!(r_{0}/s_{0},\ldots ,r_{n}/s_{n})\in \mathbb{Q}^{n+1}$
with
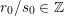 $r_{0}/s_{0}\in \mathbb{Z}$
and
$r_{0}/s_{0}\in \mathbb{Z}$
and
 $r_{i}/s_{i}\notin \mathbb{Z}$
for
$r_{i}/s_{i}\notin \mathbb{Z}$
for
![]() $i>0$
, the trivial circle fibration
$i>0$
, the trivial circle fibration
![]() $\hat{M}$
over an
$\hat{M}$
over an
![]() $(n+1)$
-punctured
$(n+1)$
-punctured
![]() $S^{2}\!$
admits a co-oriented taut foliation
$S^{2}\!$
admits a co-oriented taut foliation
![]() $F$
transverse to the boundary, with slopes
$F$
transverse to the boundary, with slopes
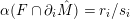 $\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=r_{i}/s_{i}$
for
$\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}\hat{M})=r_{i}/s_{i}$
for
 $i\in \{0,\ldots ,n\}$
, and with
$i\in \{0,\ldots ,n\}$
, and with
![]() $F$
extending to a co-oriented taut foliation on the Dehn filling of
$F$
extending to a co-oriented taut foliation on the Dehn filling of
![]() $\unicode[STIX]{x2202}_{j}\hat{M}$
of slope
$\unicode[STIX]{x2202}_{j}\hat{M}$
of slope
![]() $r_{j}/s_{j}$
for each
$r_{j}/s_{j}$
for each
![]() $j\in J$
, if and only if
$j\in J$
, if and only if
 $0=y_{-}=y_{+}$
or
$0=y_{-}=y_{+}$
or
 $0\in \langle y_{+},y_{-}\rangle$
, with
$0\in \langle y_{+},y_{-}\rangle$
, with
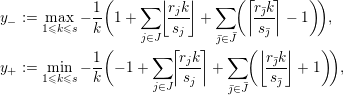 $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle y_{-}:=\max _{1\leqslant k\leqslant s}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{j\in J}\!\biggl\lfloor\!{\displaystyle \frac{r_{j}k}{s_{j}}}\!\biggr\rfloor+\mathop{\sum }_{\bar{\jmath }\in \bar{J}}\!\biggl(\lceil \!{\displaystyle \frac{r_{\bar{\jmath }}k}{s_{\bar{\jmath }}}}\!\rceil -1\biggr)\!\biggr),\\ \displaystyle y_{+}:=\min _{1\leqslant k\leqslant s}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{j\in J}\!\lceil \!{\displaystyle \frac{r_{j}k}{s_{j}}}\!\rceil +\mathop{\sum }_{\bar{\jmath }\in \bar{J}}\!\biggl(\biggl\lfloor\!{\displaystyle \frac{r_{\bar{\jmath }}k}{s_{\bar{\jmath }}}}\!\biggr\rfloor+1\biggr)\!\biggr),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle y_{-}:=\max _{1\leqslant k\leqslant s}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{j\in J}\!\biggl\lfloor\!{\displaystyle \frac{r_{j}k}{s_{j}}}\!\biggr\rfloor+\mathop{\sum }_{\bar{\jmath }\in \bar{J}}\!\biggl(\lceil \!{\displaystyle \frac{r_{\bar{\jmath }}k}{s_{\bar{\jmath }}}}\!\rceil -1\biggr)\!\biggr),\\ \displaystyle y_{+}:=\min _{1\leqslant k\leqslant s}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{j\in J}\!\lceil \!{\displaystyle \frac{r_{j}k}{s_{j}}}\!\rceil +\mathop{\sum }_{\bar{\jmath }\in \bar{J}}\!\biggl(\biggl\lfloor\!{\displaystyle \frac{r_{\bar{\jmath }}k}{s_{\bar{\jmath }}}}\!\biggr\rfloor+1\biggr)\!\biggr),\end{array}\end{eqnarray}$$
where
![]() $s$
is the least common positive multiple of the
$s$
is the least common positive multiple of the
![]() $s_{i}$
.
$s_{i}$
.
2.6 Dehn fillings and
 $\bar{N}$
-fillings
$\bar{N}$
-fillings
For any particular
 $i\in \{1,\ldots ,n\}$
in the above theorem, if one fixes the remaining slopes, one finds that the space of slopes in
$i\in \{1,\ldots ,n\}$
in the above theorem, if one fixes the remaining slopes, one finds that the space of slopes in
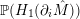 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}\hat{M}))$
for which the desired taut foliation exists is often an interval. We now introduce some notation to describe such spaces of slopes in general.
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}\hat{M}))$
for which the desired taut foliation exists is often an interval. We now introduce some notation to describe such spaces of slopes in general.
Definition 2.6. If
![]() $Y$
is a compact oriented three-manifold with torus boundary, then we define the sets
$Y$
is a compact oriented three-manifold with torus boundary, then we define the sets
 ${\mathcal{F}}^{L}(Y)\subset {\mathcal{F}}^{D}(Y)\subset {\mathcal{F}}(Y)\subset \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y;\mathbb{Z}))$
of rational foliation slopes as follows:
${\mathcal{F}}^{L}(Y)\subset {\mathcal{F}}^{D}(Y)\subset {\mathcal{F}}(Y)\subset \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y;\mathbb{Z}))$
of rational foliation slopes as follows:
 $$\begin{eqnarray}\displaystyle {\mathcal{F}}^{L}(Y) & := & \displaystyle \left\{\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}Y)\biggm\vert\begin{array}{@{}c@{}}\displaystyle F\text{ is a co-oriented taut foliation on }Y\!\text{ transverse to }\unicode[STIX]{x2202}Y,\\ \displaystyle \text{restricting to a rational co-oriented }linear\text{foliation on }\unicode[STIX]{x2202}Y\end{array}\right\},\nonumber\\ \displaystyle \displaystyle {\mathcal{F}}^{D}(Y) & := & \displaystyle \{\unicode[STIX]{x1D707}\mid \text{The Dehn filling }Y(\unicode[STIX]{x1D707})\text{ admits a co-oriented taut foliation}\},\nonumber\\ \displaystyle \displaystyle {\mathcal{F}}(Y) & := & \displaystyle \{\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}Y)\mid F\text{ is a co-oriented taut foliation on }Y\!\text{ transverse to }\unicode[STIX]{x2202}Y\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}^{L}(Y) & := & \displaystyle \left\{\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}Y)\biggm\vert\begin{array}{@{}c@{}}\displaystyle F\text{ is a co-oriented taut foliation on }Y\!\text{ transverse to }\unicode[STIX]{x2202}Y,\\ \displaystyle \text{restricting to a rational co-oriented }linear\text{foliation on }\unicode[STIX]{x2202}Y\end{array}\right\},\nonumber\\ \displaystyle \displaystyle {\mathcal{F}}^{D}(Y) & := & \displaystyle \{\unicode[STIX]{x1D707}\mid \text{The Dehn filling }Y(\unicode[STIX]{x1D707})\text{ admits a co-oriented taut foliation}\},\nonumber\\ \displaystyle \displaystyle {\mathcal{F}}(Y) & := & \displaystyle \{\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}Y)\mid F\text{ is a co-oriented taut foliation on }Y\!\text{ transverse to }\unicode[STIX]{x2202}Y\}.\nonumber\end{eqnarray}$$
All linear foliations, even irrational ones, are taut, but rational linear foliations are product foliations, hence extend to co-oriented taut foliations on Dehn fillings of matching slope, implying
 ${\mathcal{F}}^{L}(Y)\subset {\mathcal{F}}^{D}(Y)\subset {\mathcal{F}}(Y)$
. In fact, the work of Jankins and Neumann tells us that
${\mathcal{F}}^{L}(Y)\subset {\mathcal{F}}^{D}(Y)\subset {\mathcal{F}}(Y)$
. In fact, the work of Jankins and Neumann tells us that
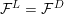 ${\mathcal{F}}^{L}={\mathcal{F}}^{D}$
for manifolds Seifert fibered over the disk, and that the analogous result holds for manifolds Seifert fibered over a punctured
${\mathcal{F}}^{L}={\mathcal{F}}^{D}$
for manifolds Seifert fibered over the disk, and that the analogous result holds for manifolds Seifert fibered over a punctured
![]() $S^{2}$
. Since the same also holds for manifolds Seifert fibered over a punctured
$S^{2}$
. Since the same also holds for manifolds Seifert fibered over a punctured
![]() $\mathbb{R}\mathbb{P}^{2}$
[Reference Boyer and ClayBC14], and since Corollary 2.2 tells us that taut foliations on homology sphere graph manifolds isotop to restrict to taut foliations transverse to boundaries on Seifert fibered JSJ components, we additionally have
$\mathbb{R}\mathbb{P}^{2}$
[Reference Boyer and ClayBC14], and since Corollary 2.2 tells us that taut foliations on homology sphere graph manifolds isotop to restrict to taut foliations transverse to boundaries on Seifert fibered JSJ components, we additionally have
 ${\mathcal{F}}^{L}={\mathcal{F}}^{D}$
for any graph manifold with torus boundary and
${\mathcal{F}}^{L}={\mathcal{F}}^{D}$
for any graph manifold with torus boundary and
![]() $b_{1}=1$
.
$b_{1}=1$
.
In this latter case, it is natural to ask whether
![]() ${\mathcal{F}}(Y)$
admits a description analogous to the Dehn filling characterization for
${\mathcal{F}}(Y)$
admits a description analogous to the Dehn filling characterization for
![]() ${\mathcal{F}}^{L}(Y)$
. That is, can
${\mathcal{F}}^{L}(Y)$
. That is, can
![]() ${\mathcal{F}}(Y)$
be characterized in terms of taut foliations on some closed union of
${\mathcal{F}}(Y)$
be characterized in terms of taut foliations on some closed union of
![]() $Y$
with some other manifold? Boyer and Clay answer this question affirmatively [Reference Boyer and ClayBC14], as we shall see.
$Y$
with some other manifold? Boyer and Clay answer this question affirmatively [Reference Boyer and ClayBC14], as we shall see.
Let
![]() $\bar{N}$
denote the regular fiber complement
$\bar{N}$
denote the regular fiber complement
 $$\begin{eqnarray}\bar{N}:=M_{S^{2}}(0,-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}})\setminus (S^{1}\!\times \!D_{0}^{2}),\end{eqnarray}$$
$$\begin{eqnarray}\bar{N}:=M_{S^{2}}(0,-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}})\setminus (S^{1}\!\times \!D_{0}^{2}),\end{eqnarray}$$
which Boyer and Clay call the ‘twisted
![]() $I$
-bundle over the Klein bottle’, or
$I$
-bundle over the Klein bottle’, or
![]() $N_{2}$
. The manifold
$N_{2}$
. The manifold
![]() $\bar{N}$
can play a role analogous to that of the solid torus for Dehn fillings.
$\bar{N}$
can play a role analogous to that of the solid torus for Dehn fillings.
Definition 2.7. Suppose
![]() $Y$
is an oriented three-manifold with toroidal boundary component
$Y$
is an oriented three-manifold with toroidal boundary component
![]() $\unicode[STIX]{x2202}_{i}Y$
. We call any union
$\unicode[STIX]{x2202}_{i}Y$
. We call any union
 $Y\cup _{\unicode[STIX]{x1D711}}\bar{N}$
with gluing map
$Y\cup _{\unicode[STIX]{x1D711}}\bar{N}$
with gluing map
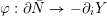 $\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}\bar{N}\rightarrow -\unicode[STIX]{x2202}_{i}Y$
an
$\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}\bar{N}\rightarrow -\unicode[STIX]{x2202}_{i}Y$
an
![]() $\bar{N}$
-filling of
$\bar{N}$
-filling of
![]() $Y\!$
along
$Y\!$
along
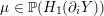 $\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}Y))$
, where
$\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}Y))$
, where
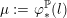 $\unicode[STIX]{x1D707}:=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(l)$
is the image of the rational longitude
$\unicode[STIX]{x1D707}:=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(l)$
is the image of the rational longitude
![]() $l$
of
$l$
of
![]() $\bar{N}$
. If
$\bar{N}$
. If
![]() $Y$
has (single) torus boundary, we denote an
$Y$
has (single) torus boundary, we denote an
![]() $\bar{N}$
-filling of
$\bar{N}$
-filling of
![]() $Y$
along
$Y$
along
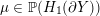 $\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
by
$\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
by
![]() $Y^{\bar{N}}(\unicode[STIX]{x1D707})$
.
$Y^{\bar{N}}(\unicode[STIX]{x1D707})$
.
More generally, if
 $\unicode[STIX]{x2202}Y=\coprod _{i=1}^{n}\unicode[STIX]{x2202}_{i}Y$
is a disjoint union of tori, then given a slope
$\unicode[STIX]{x2202}Y=\coprod _{i=1}^{n}\unicode[STIX]{x2202}_{i}Y$
is a disjoint union of tori, then given a slope
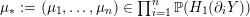 $\unicode[STIX]{x1D707}_{\ast }:=(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{n})\in \prod _{i=1}^{n}\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}Y))$
and subset
$\unicode[STIX]{x1D707}_{\ast }:=(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{n})\in \prod _{i=1}^{n}\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}Y))$
and subset
 $\bar{J}\subset \{1,\ldots ,n\}$
, we denote by
$\bar{J}\subset \{1,\ldots ,n\}$
, we denote by
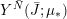 $Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
any manifold resulting from
$Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
any manifold resulting from
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
![]() $Y\!$
along
$Y\!$
along
![]() $\unicode[STIX]{x1D707}_{\bar{\jmath }}$
in
$\unicode[STIX]{x1D707}_{\bar{\jmath }}$
in
![]() $\unicode[STIX]{x2202}_{\bar{\jmath }}Y$
for each
$\unicode[STIX]{x2202}_{\bar{\jmath }}Y$
for each
![]() $\bar{\jmath }\in \bar{J}$
.
$\bar{\jmath }\in \bar{J}$
.
We then have the following result for
![]() $\bar{N}$
-fillings.
$\bar{N}$
-fillings.
Proposition 2.8. Suppose
![]() $Y\!$
is a prime compact oriented manifold with boundary a disjoint union
$Y\!$
is a prime compact oriented manifold with boundary a disjoint union
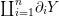 $\coprod _{i=1}^{n}\unicode[STIX]{x2202}_{i}Y\!$
of tori, with some given slope
$\coprod _{i=1}^{n}\unicode[STIX]{x2202}_{i}Y\!$
of tori, with some given slope
 $\unicode[STIX]{x1D707}_{\ast }:=(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{n})\in \prod _{i=1}^{n}\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}Y))$
. Moreover, suppose either that
$\unicode[STIX]{x1D707}_{\ast }:=(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{n})\in \prod _{i=1}^{n}\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{i}Y))$
. Moreover, suppose either that
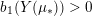 $b_{1}(Y(\unicode[STIX]{x1D707}_{\ast }))>0$
for the Dehn filling
$b_{1}(Y(\unicode[STIX]{x1D707}_{\ast }))>0$
for the Dehn filling
![]() $Y(\unicode[STIX]{x1D707}_{\ast })$
, or that
$Y(\unicode[STIX]{x1D707}_{\ast })$
, or that
![]() $Y\!$
is a graph manifold, and there is some (possibly empty)
$Y\!$
is a graph manifold, and there is some (possibly empty)
 $\bar{J}\subset \{1,\ldots ,n\}$
, and
$\bar{J}\subset \{1,\ldots ,n\}$
, and
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
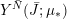 $Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
of
$Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
of
![]() $Y\!$
along
$Y\!$
along
![]() $\unicode[STIX]{x1D707}_{\bar{\jmath }}$
in
$\unicode[STIX]{x1D707}_{\bar{\jmath }}$
in
![]() $\unicode[STIX]{x2202}_{\bar{\jmath }}Y$
for each
$\unicode[STIX]{x2202}_{\bar{\jmath }}Y$
for each
![]() $\bar{\jmath }\in \bar{J}$
, such that
$\bar{\jmath }\in \bar{J}$
, such that
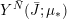 $Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
admits a co-oriented taut foliation
$Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
admits a co-oriented taut foliation
![]() $F$
transverse to the boundary, with
$F$
transverse to the boundary, with
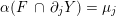 $\unicode[STIX]{x1D6FC}(F\,\cap \,\unicode[STIX]{x2202}_{j}Y)=\unicode[STIX]{x1D707}_{j}$
for each
$\unicode[STIX]{x1D6FC}(F\,\cap \,\unicode[STIX]{x2202}_{j}Y)=\unicode[STIX]{x1D707}_{j}$
for each
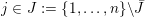 $j\in J:=\{1,\ldots ,n\}\setminus \bar{J}$
.
$j\in J:=\{1,\ldots ,n\}\setminus \bar{J}$
.
Then, for every
 $\bar{J}\subset \{1,\ldots ,n\}$
, every
$\bar{J}\subset \{1,\ldots ,n\}$
, every
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
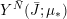 $Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
(including
$Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
(including
 $Y:=Y^{\bar{N}}(\emptyset ;\unicode[STIX]{x1D707}_{\ast })$
) admits a co-oriented taut foliation
$Y:=Y^{\bar{N}}(\emptyset ;\unicode[STIX]{x1D707}_{\ast })$
) admits a co-oriented taut foliation
![]() $F$
transverse to the boundary, with
$F$
transverse to the boundary, with
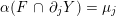 $\unicode[STIX]{x1D6FC}(F\,\cap \,\unicode[STIX]{x2202}_{j}Y)=\unicode[STIX]{x1D707}_{j}$
for each
$\unicode[STIX]{x1D6FC}(F\,\cap \,\unicode[STIX]{x2202}_{j}Y)=\unicode[STIX]{x1D707}_{j}$
for each
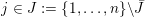 $j\in J:=\{1,\ldots ,n\}\setminus \bar{J}$
.
$j\in J:=\{1,\ldots ,n\}\setminus \bar{J}$
.
Proof. Part (2) of Gabai’s main theorem in [Reference GabaiGab83] tells us that any prime oriented three-manifold with
![]() $b_{1}>0$
and boundary a (possibly empty) union of tori admits a co-oriented taut foliation transverse to the boundary. Thus, if
$b_{1}>0$
and boundary a (possibly empty) union of tori admits a co-oriented taut foliation transverse to the boundary. Thus, if
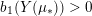 $b_{1}(Y(\unicode[STIX]{x1D707}_{\ast }))>0$
, then any
$b_{1}(Y(\unicode[STIX]{x1D707}_{\ast }))>0$
, then any
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
 $Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast }):=Y^{\bar{N}}(\{1,\ldots ,n\};\unicode[STIX]{x1D707}_{\ast })$
has
$Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast }):=Y^{\bar{N}}(\{1,\ldots ,n\};\unicode[STIX]{x1D707}_{\ast })$
has
![]() $b_{1}>0$
, hence admits a co-oriented taut foliation
$b_{1}>0$
, hence admits a co-oriented taut foliation
![]() $F$
. Since each
$F$
. Since each
![]() $\unicode[STIX]{x2202}_{i}Y$
is an incompressible separating torus in this
$\unicode[STIX]{x2202}_{i}Y$
is an incompressible separating torus in this
![]() $\bar{N}$
-filling, Proposition 2.1 allows us to isotop these separating tori so that they are everywhere transverse to
$\bar{N}$
-filling, Proposition 2.1 allows us to isotop these separating tori so that they are everywhere transverse to
![]() $F$
. Restricting
$F$
. Restricting
![]() $F$
to any sub-
$F$
to any sub-
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
 $Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })\subset Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast })$
then gives the desired taut foliation on
$Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })\subset Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast })$
then gives the desired taut foliation on
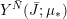 $Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
.
$Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
.
If, instead,
![]() $Y$
is a graph manifold with
$Y$
is a graph manifold with
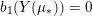 $b_{1}(Y(\unicode[STIX]{x1D707}_{\ast }))=0$
, and we are given
$b_{1}(Y(\unicode[STIX]{x1D707}_{\ast }))=0$
, and we are given
 $\bar{J}\subset \{1,\ldots ,n\}$
and a co-oriented taut foliation
$\bar{J}\subset \{1,\ldots ,n\}$
and a co-oriented taut foliation
![]() $F$
on some
$F$
on some
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
 $Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
, with
$Y^{\bar{N}}(\bar{J};\unicode[STIX]{x1D707}_{\ast })$
, with
![]() $F$
transverse to the boundary and with
$F$
transverse to the boundary and with
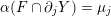 $\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{j}Y)=\unicode[STIX]{x1D707}_{j}$
for each
$\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{j}Y)=\unicode[STIX]{x1D707}_{j}$
for each
 $j\in J:=\{1,\ldots ,n\}\setminus \bar{J}$
, then Proposition 2.1 again allows us to isotop each separating torus
$j\in J:=\{1,\ldots ,n\}\setminus \bar{J}$
, then Proposition 2.1 again allows us to isotop each separating torus
![]() $\unicode[STIX]{x2202}_{\bar{\jmath }}Y$
so that
$\unicode[STIX]{x2202}_{\bar{\jmath }}Y$
so that
![]() $F$
restricts to a co-oriented taut foliation on
$F$
restricts to a co-oriented taut foliation on
![]() $Y$
, transverse to
$Y$
, transverse to
![]() $\unicode[STIX]{x2202}Y$
, with
$\unicode[STIX]{x2202}Y$
, with
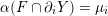 $\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}Y)=\unicode[STIX]{x1D707}_{i}$
for each
$\unicode[STIX]{x1D6FC}(F\cap \unicode[STIX]{x2202}_{i}Y)=\unicode[STIX]{x1D707}_{i}$
for each
 $i\in \{1,\ldots ,n\}$
.
$i\in \{1,\ldots ,n\}$
.
We then apply the foliation gluing theorem of Boyer and Clay [Reference Boyer and ClayBC14, Theorem 9.5.2]. That is, for each
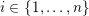 $i\in \{1,\ldots ,n\}$
, Theorem 2.5 computes that
$i\in \{1,\ldots ,n\}$
, Theorem 2.5 computes that
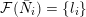 ${\mathcal{F}}(\bar{N}_{i})=\{l_{i}\}$
, with
${\mathcal{F}}(\bar{N}_{i})=\{l_{i}\}$
, with
![]() $l_{i}$
(of slope
$l_{i}$
(of slope
![]() $0$
) the rational longitude of the
$0$
) the rational longitude of the
![]() $i\text{th}$
copy
$i\text{th}$
copy
![]() $\bar{N}_{i}$
of
$\bar{N}_{i}$
of
![]() $\bar{N}$
. Thus, for any gluing maps
$\bar{N}$
. Thus, for any gluing maps
 $\unicode[STIX]{x1D711}_{i}:\bar{N}_{i}\rightarrow -\unicode[STIX]{x2202}_{i}Y$
sending
$\unicode[STIX]{x1D711}_{i}:\bar{N}_{i}\rightarrow -\unicode[STIX]{x2202}_{i}Y$
sending
![]() $l_{i}\mapsto \unicode[STIX]{x1D707}_{i}$
in homology, Boyer and Clay’s gluing theorem tells us that there exist co-oriented taut foliations
$l_{i}\mapsto \unicode[STIX]{x1D707}_{i}$
in homology, Boyer and Clay’s gluing theorem tells us that there exist co-oriented taut foliations
![]() $F^{\prime }$
on
$F^{\prime }$
on
![]() $Y$
and
$Y$
and
![]() $F_{i}$
on
$F_{i}$
on
![]() $\bar{N}_{i}$
, transverse to respective boundaries, with
$\bar{N}_{i}$
, transverse to respective boundaries, with
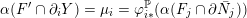 $\unicode[STIX]{x1D6FC}(F^{\prime }\cap \unicode[STIX]{x2202}_{i}Y)=\unicode[STIX]{x1D707}_{i}=\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}(\unicode[STIX]{x1D6FC}(F_{j}\cap \unicode[STIX]{x2202}\bar{N}_{j}))$
for each
$\unicode[STIX]{x1D6FC}(F^{\prime }\cap \unicode[STIX]{x2202}_{i}Y)=\unicode[STIX]{x1D707}_{i}=\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}(\unicode[STIX]{x1D6FC}(F_{j}\cap \unicode[STIX]{x2202}\bar{N}_{j}))$
for each
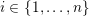 $i\in \{1,\ldots ,n\}$
, such that the
$i\in \{1,\ldots ,n\}$
, such that the
![]() $F_{i}$
and
$F_{i}$
and
![]() $F^{\prime }$
glue together to form a co-oriented taut foliation on the
$F^{\prime }$
glue together to form a co-oriented taut foliation on the
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
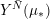 $Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast })$
specified by the
$Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast })$
specified by the
![]() $\unicode[STIX]{x1D711}_{i}$
. After isotoping the
$\unicode[STIX]{x1D711}_{i}$
. After isotoping the
![]() $\unicode[STIX]{x2202}_{i}Y$
to be transverse to this foliation, we can restrict this foliation to any sub-
$\unicode[STIX]{x2202}_{i}Y$
to be transverse to this foliation, we can restrict this foliation to any sub-
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
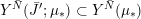 $Y^{\bar{N}}(\bar{J}^{\prime };\unicode[STIX]{x1D707}_{\ast })\subset Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast })$
.◻
$Y^{\bar{N}}(\bar{J}^{\prime };\unicode[STIX]{x1D707}_{\ast })\subset Y^{\bar{N}}(\unicode[STIX]{x1D707}_{\ast })$
.◻
In particular, for a graph manifold
![]() $Y$
with torus boundary, we have
$Y$
with torus boundary, we have
 $\unicode[STIX]{x1D707}\in {\mathcal{F}}(Y)$
if and only if an
$\unicode[STIX]{x1D707}\in {\mathcal{F}}(Y)$
if and only if an
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
![]() $Y^{\bar{N}}(\unicode[STIX]{x1D707})$
admits a co-oriented taut foliation.
$Y^{\bar{N}}(\unicode[STIX]{x1D707})$
admits a co-oriented taut foliation.
3 L-space intervals
An L-space is a closed oriented three-manifold whose Heegaard Floer homology is trivial, in the sense that for each
![]() $\text{Spin}^{c}$
structure, the hat Heegaard Floer homology looks like the singular homology of a point. The reader unfamiliar with L-spaces could consult [Reference Ozsváth and SzabóOS06a, Reference Ozsváth and SzabóOS06b] for an introduction to Heegaard Floer homology, or [Reference Rasmussen and RasmussenRR15] for a treatment of L-space Dehn fillings. For present purposes, we shall only need the classification of Seifert fibered L-spaces, some formal properties of sets of L-space Dehn-filling slopes, and some basic gluing results, all of which we catalog below.
$\text{Spin}^{c}$
structure, the hat Heegaard Floer homology looks like the singular homology of a point. The reader unfamiliar with L-spaces could consult [Reference Ozsváth and SzabóOS06a, Reference Ozsváth and SzabóOS06b] for an introduction to Heegaard Floer homology, or [Reference Rasmussen and RasmussenRR15] for a treatment of L-space Dehn fillings. For present purposes, we shall only need the classification of Seifert fibered L-spaces, some formal properties of sets of L-space Dehn-filling slopes, and some basic gluing results, all of which we catalog below.
3.1 L-space Dehn fillings and
 $\bar{N}$
-fillings
$\bar{N}$
-fillings
Definition 3.1. If
![]() $Y$
is a compact oriented three-manifold with torus boundary, then we define the L-space interval of
$Y$
is a compact oriented three-manifold with torus boundary, then we define the L-space interval of
![]() $Y$
to be
$Y$
to be
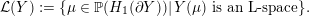 $$\begin{eqnarray}{\mathcal{L}}(Y):=\{\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))|\,Y(\unicode[STIX]{x1D707})\text{ is an L-space}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y):=\{\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))|\,Y(\unicode[STIX]{x1D707})\text{ is an L-space}\}.\end{eqnarray}$$
We shall write
![]() ${\mathcal{L}}^{\circ }(Y)$
for the interior of
${\mathcal{L}}^{\circ }(Y)$
for the interior of
![]() ${\mathcal{L}}(Y)$
in
${\mathcal{L}}(Y)$
in
 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
Thus,
![]() ${\mathcal{L}}(Y)$
is analogous to, and often complementary to,
${\mathcal{L}}(Y)$
is analogous to, and often complementary to,
![]() ${\mathcal{F}}^{D}(Y)$
, especially when
${\mathcal{F}}^{D}(Y)$
, especially when
![]() $Y$
has no reducible non-L-space Dehn fillings. Moreover, since the set of slopes of co-oriented taut foliations meeting a generalized rotation number condition is often the closure of the set of product foliation slopes meeting that condition [Reference Calegari and WalkerCW11, Lemma 3.31], it is natural to ask if
$Y$
has no reducible non-L-space Dehn fillings. Moreover, since the set of slopes of co-oriented taut foliations meeting a generalized rotation number condition is often the closure of the set of product foliation slopes meeting that condition [Reference Calegari and WalkerCW11, Lemma 3.31], it is natural to ask if
![]() ${\mathcal{F}}(Y)$
bears any relation to the complement of
${\mathcal{F}}(Y)$
bears any relation to the complement of
![]() ${\mathcal{L}}^{\circ }(Y)$
. In fact, we have the following result.
${\mathcal{L}}^{\circ }(Y)$
. In fact, we have the following result.
Proposition 3.2 [Reference Rasmussen and RasmussenRR15].
If
![]() $Y$
is a compact oriented three-manifold with torus boundary, then an
$Y$
is a compact oriented three-manifold with torus boundary, then an
![]() $\bar{N}$
-filling
$\bar{N}$
-filling
![]() $Y^{\bar{N}}(\unicode[STIX]{x1D707})$
is an L-space if and only if
$Y^{\bar{N}}(\unicode[STIX]{x1D707})$
is an L-space if and only if
 $\unicode[STIX]{x1D707}\in {\mathcal{L}}^{\circ }(Y)$
.
$\unicode[STIX]{x1D707}\in {\mathcal{L}}^{\circ }(Y)$
.
Proof. In [Reference Rasmussen and RasmussenRR15, Proposition 7.9], Rasmussen and the author prove the above result with
![]() $\bar{N}$
replaced by any member of a more general class of manifolds dubbed generalized solid tori. Since
$\bar{N}$
replaced by any member of a more general class of manifolds dubbed generalized solid tori. Since
![]() $\bar{N}$
is a generalized solid torus as defined in [Reference Rasmussen and RasmussenRR15], the result follows.◻
$\bar{N}$
is a generalized solid torus as defined in [Reference Rasmussen and RasmussenRR15], the result follows.◻
Thus
![]() ${\mathcal{L}}^{\circ }(Y)$
can be regarded as the L-space
${\mathcal{L}}^{\circ }(Y)$
can be regarded as the L-space
![]() $\bar{N}$
-filling interval of
$\bar{N}$
-filling interval of
![]() $Y$
.
$Y$
.
3.2 L-space gluing
Our primary tool for characterizing when a union of three-manifolds along a torus boundary gives an L-space is the following joint result of Rasmussen and the author [Reference Rasmussen and RasmussenRR15]. Hanselman and Watson have proven a similar result in [Reference Hanselman and WatsonHW15].
Proposition 3.3 [Reference Rasmussen and RasmussenRR15].
If each of
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
is a compact oriented three-manifold with torus boundary, then for any gluing map
$Y_{2}$
is a compact oriented three-manifold with torus boundary, then for any gluing map
 $\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
with
$\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
with
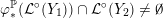 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})\neq \emptyset$
, the union
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})\neq \emptyset$
, the union
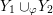 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space if and only if
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space if and only if
 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})$
if both
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})$
if both
![]() $Y_{i}$
are boundary incompressible, and if and only if
$Y_{i}$
are boundary incompressible, and if and only if
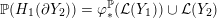 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))\cup {\mathcal{L}}(Y_{2})$
otherwise.
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))\cup {\mathcal{L}}(Y_{2})$
otherwise.
Proof. Recall that a compact three-manifold with torus boundary is boundary incompressible if and only if it is not a connected sum of a solid torus with a (possibly empty) closed three-manifold. The above proposition replicates from [Reference Rasmussen and RasmussenRR15, Theorem 6.2], except with the hypothesis of boundary incompressibility of each
![]() $Y_{i}$
replacing an a priori more technical condition that certain subsets
$Y_{i}$
replacing an a priori more technical condition that certain subsets
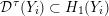 ${\mathcal{D}}^{\unicode[STIX]{x1D70F}}(Y_{i})\subset H_{1}(Y_{i})$
be non-empty. Thomas Gillespie has recently shown [Reference GillespieGil16] these two conditions to be equivalent. None of our gluing arguments involving graph manifolds actually make use of his result, but our later cabling results, which in principle require unions with non-graph manifolds, do require Gillespie’s result.◻
${\mathcal{D}}^{\unicode[STIX]{x1D70F}}(Y_{i})\subset H_{1}(Y_{i})$
be non-empty. Thomas Gillespie has recently shown [Reference GillespieGil16] these two conditions to be equivalent. None of our gluing arguments involving graph manifolds actually make use of his result, but our later cabling results, which in principle require unions with non-graph manifolds, do require Gillespie’s result.◻
We shall later show that in the case of non-solid-torus graph manifolds
![]() $Y_{i}$
with torus boundary, various foliation results allow us to drop some of the above hypotheses, so that one obtains an L-space if and only if
$Y_{i}$
with torus boundary, various foliation results allow us to drop some of the above hypotheses, so that one obtains an L-space if and only if
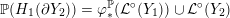 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})$
.
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})$
.
In rather the opposite direction, if
![]() $Y$
is Seifert fibered over a punctured
$Y$
is Seifert fibered over a punctured
![]() $S^{2}$
or
$S^{2}$
or
![]() $\mathbb{R}\mathbb{P}^{2}$
, then a Dehn filling
$\mathbb{R}\mathbb{P}^{2}$
, then a Dehn filling
![]() $Y^{\prime }$
of
$Y^{\prime }$
of
![]() $Y$
fails to be a graph manifold if and only if
$Y$
fails to be a graph manifold if and only if
![]() $Y^{\prime }$
fails to be prime, if and only if
$Y^{\prime }$
fails to be prime, if and only if
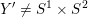 $Y^{\prime }\neq S^{1}\times S^{2}$
and the Dehn filling, in some
$Y^{\prime }\neq S^{1}\times S^{2}$
and the Dehn filling, in some
![]() $\unicode[STIX]{x2202}_{i}Y$
, was along the fiber lift
$\unicode[STIX]{x2202}_{i}Y$
, was along the fiber lift
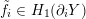 $\tilde{f}_{i}\in H_{1}(\unicode[STIX]{x2202}_{i}Y)$
of slope
$\tilde{f}_{i}\in H_{1}(\unicode[STIX]{x2202}_{i}Y)$
of slope
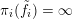 $\unicode[STIX]{x1D70B}_{i}(\tilde{f}_{i})=\infty$
(see the remark near the end of § 2.2). In this case,
$\unicode[STIX]{x1D70B}_{i}(\tilde{f}_{i})=\infty$
(see the remark near the end of § 2.2). In this case,
![]() $Y^{\prime }$
is neither a graph manifold nor a habitat for taut foliations, but since it has compressible boundary, its L-space gluing properties simplify, due to the following result.
$Y^{\prime }$
is neither a graph manifold nor a habitat for taut foliations, but since it has compressible boundary, its L-space gluing properties simplify, due to the following result.
Proposition 3.4. Suppose that each of
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
is a compact oriented three-manifold with torus boundary, and that
$Y_{2}$
is a compact oriented three-manifold with torus boundary, and that
![]() $Y_{1}$
has compressible boundary. Then the union
$Y_{1}$
has compressible boundary. Then the union
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space if and only if
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space if and only if
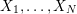 $X_{1},\ldots ,X_{N}$
are all L-spaces and
$X_{1},\ldots ,X_{N}$
are all L-spaces and
 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(l_{1})\in {\mathcal{L}}(Y_{2})$
, where
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(l_{1})\in {\mathcal{L}}(Y_{2})$
, where
![]() $l_{1}$
is the rational longitude of
$l_{1}$
is the rational longitude of
![]() $Y_{1}$
, and where
$Y_{1}$
, and where
![]() $Y_{1}$
decomposes as
$Y_{1}$
decomposes as
 $Y_{1}=(S^{1}\times D^{2})\#(X_{1}\#\cdots \#X_{N})$
.
$Y_{1}=(S^{1}\times D^{2})\#(X_{1}\#\cdots \#X_{N})$
.
Proof. A union along toroidal boundaries with a solid torus is just a Dehn filling, so we have
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}=Y_{2}(\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(l_{1}))\#X_{1}\#\cdots \#X_{N}$
, and a connected sum of closed manifolds is an L-space if and only if each summand is an L-space.◻
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}=Y_{2}(\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(l_{1}))\#X_{1}\#\cdots \#X_{N}$
, and a connected sum of closed manifolds is an L-space if and only if each summand is an L-space.◻
The above result explains why not every graph manifold
![]() $Y$
with torus boundary satisfies
$Y$
with torus boundary satisfies
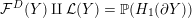 ${\mathcal{F}}^{D}(Y)\amalg {\mathcal{L}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. That is, no reducible manifold (besides
${\mathcal{F}}^{D}(Y)\amalg {\mathcal{L}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. That is, no reducible manifold (besides
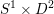 $S^{1}\times D^{2}$
) admits a co-oriented taut foliation, but there exist graph manifolds with reducible Dehn fillings which are not
$S^{1}\times D^{2}$
) admits a co-oriented taut foliation, but there exist graph manifolds with reducible Dehn fillings which are not
 $S^{1}\times D^{2}$
or an L-space.
$S^{1}\times D^{2}$
or an L-space.
3.3 Floer simple manifolds and L-space intervals
It is not known, in general, what forms the sets
![]() ${\mathcal{F}}(Y)$
or
${\mathcal{F}}(Y)$
or
![]() ${\mathcal{F}}^{D}(Y)$
can take for an arbitrary compact oriented three-manifold
${\mathcal{F}}^{D}(Y)$
can take for an arbitrary compact oriented three-manifold
![]() $Y$
with torus boundary, but the situation for L-spaces is better understood. As shown in [Reference Rasmussen and RasmussenRR15] by Rasmussen and the author,
$Y$
with torus boundary, but the situation for L-spaces is better understood. As shown in [Reference Rasmussen and RasmussenRR15] by Rasmussen and the author,
![]() ${\mathcal{L}}(Y)$
can only be empty, the set of a single point, a closed interval, or the complement of the rational longitude in
${\mathcal{L}}(Y)$
can only be empty, the set of a single point, a closed interval, or the complement of the rational longitude in
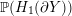 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. For historical reasons, we call
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. For historical reasons, we call
![]() $Y$
Floer simple in the latter two cases. Equivalently, we could define Floer simple manifolds as follows.
$Y$
Floer simple in the latter two cases. Equivalently, we could define Floer simple manifolds as follows.
Definition 3.5. A compact oriented three-manifold
![]() $Y$
with torus boundary is Floer simple if
$Y$
with torus boundary is Floer simple if
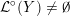 ${\mathcal{L}}^{\circ }(Y)\neq \emptyset$
.
${\mathcal{L}}^{\circ }(Y)\neq \emptyset$
.
In particular, if
![]() $Y$
is Floer simple, then its space
$Y$
is Floer simple, then its space
![]() ${\mathcal{L}}(Y)$
of L-space Dehn filling slopes can be specified entirely in terms of the left-hand and right-hand endpoints of
${\mathcal{L}}(Y)$
of L-space Dehn filling slopes can be specified entirely in terms of the left-hand and right-hand endpoints of
![]() ${\mathcal{L}}(Y)$
, in a sense we can make precise, prefaced with the introduction of an abbreviative notation for the closed interval with infinite endpoint.
${\mathcal{L}}(Y)$
, in a sense we can make precise, prefaced with the introduction of an abbreviative notation for the closed interval with infinite endpoint.
Definition 3.6. For
![]() $y\in \mathbb{Q}$
, we shall write
$y\in \mathbb{Q}$
, we shall write
![]() $[-\infty ,y]$
,
$[-\infty ,y]$
,
![]() $[y,+\infty ]$
,
$[y,+\infty ]$
,
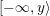 $[-\infty ,y\rangle$
, and
$[-\infty ,y\rangle$
, and
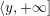 $\langle y,+\infty ]$
for the following intervals in
$\langle y,+\infty ]$
for the following intervals in
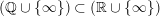 $(\mathbb{Q}\cup \{\infty \})\subset (\mathbb{R}\cup \{\infty \})$
:
$(\mathbb{Q}\cup \{\infty \})\subset (\mathbb{R}\cup \{\infty \})$
:
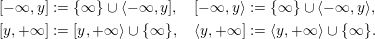 $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle \,[-\infty ,y]:=\{\infty \}\cup \langle -\infty ,y],\quad [-\infty ,y\rangle :=\{\infty \}\cup \langle -\infty ,y\rangle ,\\ \displaystyle \,[y,+\infty ]:=[y,+\infty \rangle \cup \{\infty \},\quad \langle y,+\infty ]:=\langle y,+\infty \rangle \cup \{\infty \}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle \,[-\infty ,y]:=\{\infty \}\cup \langle -\infty ,y],\quad [-\infty ,y\rangle :=\{\infty \}\cup \langle -\infty ,y\rangle ,\\ \displaystyle \,[y,+\infty ]:=[y,+\infty \rangle \cup \{\infty \},\quad \langle y,+\infty ]:=\langle y,+\infty \rangle \cup \{\infty \}.\end{array}\end{eqnarray}$$
Definition 3.7. If
 $y_{-},y_{+}\!\in \mathbb{Q}\cup \{\infty \}$
, then we define the L-space interval from
$y_{-},y_{+}\!\in \mathbb{Q}\cup \{\infty \}$
, then we define the L-space interval from
![]() $y_{-}$
to
$y_{-}$
to
![]() $y_{+}$
, denoted
$y_{+}$
, denoted
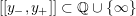 $[[y_{-},y_{+}]]\subset \mathbb{Q}\cup \{\infty \}$
, as follows:
$[[y_{-},y_{+}]]\subset \mathbb{Q}\cup \{\infty \}$
, as follows:
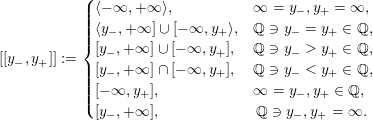 $$\begin{eqnarray}[[y_{-},y_{+}]]:=\left\{\begin{array}{@{}ll@{}}\langle -\infty ,+\infty \rangle ,\quad & \infty =y_{-},y_{+}=\infty ,\\ \langle y_{-},+\infty ]\cup [-\infty ,y_{+}\rangle ,\quad & \mathbb{Q}\ni y_{-}=y_{+}\in \mathbb{Q},\\ \text{}[y_{-},+\infty ]\cup [-\infty ,y_{+}],\quad & \mathbb{Q}\ni y_{-}>y_{+}\in \mathbb{Q},\\ \text{}[y_{-},+\infty ]\cap [-\infty ,y_{+}],\quad & \mathbb{Q}\ni y_{-}<y_{+}\in \mathbb{Q},\\ \text{}[-\infty ,y_{+}],\quad & \infty =y_{-},y_{+}\in \mathbb{Q},\\ \text{}[y_{-},+\infty ],\quad & \,\mathbb{Q}\ni y_{-},y_{+}=\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}[[y_{-},y_{+}]]:=\left\{\begin{array}{@{}ll@{}}\langle -\infty ,+\infty \rangle ,\quad & \infty =y_{-},y_{+}=\infty ,\\ \langle y_{-},+\infty ]\cup [-\infty ,y_{+}\rangle ,\quad & \mathbb{Q}\ni y_{-}=y_{+}\in \mathbb{Q},\\ \text{}[y_{-},+\infty ]\cup [-\infty ,y_{+}],\quad & \mathbb{Q}\ni y_{-}>y_{+}\in \mathbb{Q},\\ \text{}[y_{-},+\infty ]\cap [-\infty ,y_{+}],\quad & \mathbb{Q}\ni y_{-}<y_{+}\in \mathbb{Q},\\ \text{}[-\infty ,y_{+}],\quad & \infty =y_{-},y_{+}\in \mathbb{Q},\\ \text{}[y_{-},+\infty ],\quad & \,\mathbb{Q}\ni y_{-},y_{+}=\infty .\end{array}\right.\end{eqnarray}$$
In other words,
 $[[y_{-},y_{+}]]$
is the unique interval with left-hand endpoint
$[[y_{-},y_{+}]]$
is the unique interval with left-hand endpoint
![]() $y_{-}$
and right-hand endpoint
$y_{-}$
and right-hand endpoint
![]() $y_{+}$
which is closed if
$y_{+}$
which is closed if
 $y_{-}\neq y_{+}$
and open otherwise.
$y_{-}\neq y_{+}$
and open otherwise.
Remark.
In practice, we extend the above definition to allow
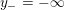 $y_{-}=-\infty$
or
$y_{-}=-\infty$
or
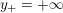 $y_{+}=+\infty$
, which we treat as identical to the respective cases of
$y_{+}=+\infty$
, which we treat as identical to the respective cases of
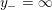 $y_{-}=\infty$
or
$y_{-}=\infty$
or
 $y_{+}=\infty$
.
$y_{+}=\infty$
.
Proposition 3.8. Suppose, for some compact oriented three-manifold
![]() $Y$
with torus boundary, that we are given an identification
$Y$
with torus boundary, that we are given an identification
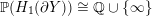 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\cong \mathbb{Q}\cup \{\infty \}$
. If
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\cong \mathbb{Q}\cup \{\infty \}$
. If
![]() $Y$
is Floer simple, then there are unique
$Y$
is Floer simple, then there are unique
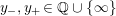 $y_{-},y_{+}\!\in \mathbb{Q}\cup \{\infty \}$
such that
$y_{-},y_{+}\!\in \mathbb{Q}\cup \{\infty \}$
such that
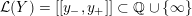 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]\subset \mathbb{Q}\cup \{\infty \}$
. Conversely, if there are
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]\subset \mathbb{Q}\cup \{\infty \}$
. Conversely, if there are
 $y_{-},y_{+}\!\in \mathbb{Q}\cup \{\infty \}$
for which
$y_{-},y_{+}\!\in \mathbb{Q}\cup \{\infty \}$
for which
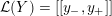 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, then
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, then
![]() $Y$
is Floer simple.
$Y$
is Floer simple.
The above follows from the aforementioned result, proven in [Reference Rasmussen and RasmussenRR15], that if
![]() ${\mathcal{L}}(Y)$
contains more than one point, then
${\mathcal{L}}(Y)$
contains more than one point, then
![]() ${\mathcal{L}}(Y)$
is either a closed interval or the complement of a point in
${\mathcal{L}}(Y)$
is either a closed interval or the complement of a point in
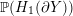 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. The following computation of L-space intervals for Seifert fibered spaces demonstrates one use of this ‘
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. The following computation of L-space intervals for Seifert fibered spaces demonstrates one use of this ‘
![]() $[[\cdot ,\cdot ]]$
’ notation.
$[[\cdot ,\cdot ]]$
’ notation.
Proposition 3.9. If
![]() $Y$
is a regular fiber complement in a Seifert fibered rational homology sphere, then
$Y$
is a regular fiber complement in a Seifert fibered rational homology sphere, then
 ${\mathcal{L}}^{\circ }(Y)\amalg {\mathcal{F}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. If
${\mathcal{L}}^{\circ }(Y)\amalg {\mathcal{F}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. If
![]() $Y$
has non-orientable base, we have
$Y$
has non-orientable base, we have
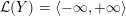 ${\mathcal{L}}(Y)=\langle -\infty ,+\infty \rangle$
and
${\mathcal{L}}(Y)=\langle -\infty ,+\infty \rangle$
and
 ${\mathcal{F}}^{D}(Y)=\emptyset$
(unless
${\mathcal{F}}^{D}(Y)=\emptyset$
(unless
![]() $Y$
is the twisted
$Y$
is the twisted
![]() $S^{2}$
-bundle over the Möbius strip, in which case
$S^{2}$
-bundle over the Möbius strip, in which case
 ${\mathcal{F}}^{D}(Y)=\{\infty \}$
). If
${\mathcal{F}}^{D}(Y)=\{\infty \}$
). If
![]() $Y$
is a regular fiber complement in
$Y$
is a regular fiber complement in
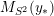 $M_{S^{2}}(y_{\ast })$
, for some
$M_{S^{2}}(y_{\ast })$
, for some
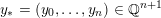 $y_{\ast }=(y_{0},\ldots ,y_{n})\in \mathbb{Q}^{n+1}$
, then
$y_{\ast }=(y_{0},\ldots ,y_{n})\in \mathbb{Q}^{n+1}$
, then
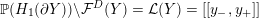 $\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus {\mathcal{F}}^{D}(Y)={\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, where
$\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus {\mathcal{F}}^{D}(Y)={\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, where
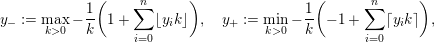 $$\begin{eqnarray}y_{-}:=\max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=0}^{n}\lfloor y_{i}k\rfloor \biggr),\quad y_{+}:=\min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=0}^{n}\lceil y_{i}k\rceil \biggr),\end{eqnarray}$$
$$\begin{eqnarray}y_{-}:=\max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=0}^{n}\lfloor y_{i}k\rfloor \biggr),\quad y_{+}:=\min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=0}^{n}\lceil y_{i}k\rceil \biggr),\end{eqnarray}$$
unless
![]() $Y$
is a solid torus, in which case
$Y$
is a solid torus, in which case
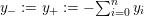 $y_{-}:=y_{+}:=-\!\sum _{i=0}^{n}y_{i}$
is the rational longitude of
$y_{-}:=y_{+}:=-\!\sum _{i=0}^{n}y_{i}$
is the rational longitude of
![]() $Y$
.
$Y$
.
Proof. For the case of
![]() $Y$
with non-orientable base, see the work of Boyer, Gordon, and Watson [Reference Boyer, Gordon and WatsonBGW13] and Boyer and Clay [Reference Boyer and ClayBC14]. For
$Y$
with non-orientable base, see the work of Boyer, Gordon, and Watson [Reference Boyer, Gordon and WatsonBGW13] and Boyer and Clay [Reference Boyer and ClayBC14]. For
![]() $Y$
with orientable base, the foliations result is due to Jankins, Neumann, and Naimi [Reference Jankins and NeumannJN85, Reference NaimiNai94], and the L-space result is originally due to the combined work of Jankins, Neumann, and Naimi [Reference Jankins and NeumannJN85, Reference NaimiNai94], Eliashberg and Thurston [Reference Eliashberg and ThurstonET98], Ozsváth and Szabó [Reference Ozsváth and SzabóOS04], Lisca and Matić [Reference Lisca and MatićLM04], and Lisca and Stipsicz [Reference Lisca and StipsiczLS07]. Alternatively, Rasmussen and the author offer a recent stand-alone proof of the L-space result [Reference Rasmussen and RasmussenRR15].◻
$Y$
with orientable base, the foliations result is due to Jankins, Neumann, and Naimi [Reference Jankins and NeumannJN85, Reference NaimiNai94], and the L-space result is originally due to the combined work of Jankins, Neumann, and Naimi [Reference Jankins and NeumannJN85, Reference NaimiNai94], Eliashberg and Thurston [Reference Eliashberg and ThurstonET98], Ozsváth and Szabó [Reference Ozsváth and SzabóOS04], Lisca and Matić [Reference Lisca and MatićLM04], and Lisca and Stipsicz [Reference Lisca and StipsiczLS07]. Alternatively, Rasmussen and the author offer a recent stand-alone proof of the L-space result [Reference Rasmussen and RasmussenRR15].◻
4 L-space intervals and foliation slopes for graph manifolds
This is the section in which we prove most of our main results. We begin, however, by introducing the notion of L/NTF-equivalence, the presence of which makes gluing easier. We further pause in § 4.2 to establish some conventions for graph manifolds with torus boundary and
![]() $b_{1}=1$
.
$b_{1}=1$
.
4.1 L/NTF-equivalence and gluing
For a pair of manifolds spliced together along torus boundaries, we can often prove stronger gluing results about the existence of co-oriented taut foliations or non-trivial Heegaard Floer homology if we are able to use gluing theorems from both areas of mathematics. In general, however, this strategy only works if we know that each manifold behaves in a suitably complementary manner with respect to co-oriented taut foliations and L-space Dehn fillings, a notion which we now make precise.
Definition 4.1. If
![]() $Y\!$
is a prime compact oriented three-manifold with torus boundary, then we say that
$Y\!$
is a prime compact oriented three-manifold with torus boundary, then we say that
![]() $Y$
is L/NTF-equivalent if
$Y$
is L/NTF-equivalent if
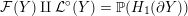 ${\mathcal{F}}(Y)\amalg {\mathcal{L}}^{\circ }(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
${\mathcal{F}}(Y)\amalg {\mathcal{L}}^{\circ }(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
In certain circumstances, one can characterize L/NTF-equivalence in terms of
![]() $\bar{N}$
-fillings.
$\bar{N}$
-fillings.
Proposition 4.2. Suppose
![]() $Y\!$
is a prime compact oriented three-manifold with torus boundary. If
$Y\!$
is a prime compact oriented three-manifold with torus boundary. If
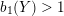 $b_{1}(Y)>1$
or
$b_{1}(Y)>1$
or
![]() $Y$
is a graph manifold, then
$Y$
is a graph manifold, then
![]() $Y\!$
is L/NTF-equivalent if and only if each
$Y\!$
is L/NTF-equivalent if and only if each
![]() $\bar{N}$
-filling of
$\bar{N}$
-filling of
![]() $Y\!$
is an L-space precisely when it fails to admit a co-oriented taut foliation.
$Y\!$
is an L-space precisely when it fails to admit a co-oriented taut foliation.
There are some classes of manifold which we already know to be L/NTF-equivalent.
Proposition 4.3. Suppose
![]() $Y$
is a prime compact oriented three-manifold with torus boundary. If
$Y$
is a prime compact oriented three-manifold with torus boundary. If
 $b_{1}(Y)>1$
, or if
$b_{1}(Y)>1$
, or if
![]() $Y$
is the union of a Seifert fibered space with zero or more copies of
$Y$
is the union of a Seifert fibered space with zero or more copies of
![]() $\bar{N}$
, then
$\bar{N}$
, then
![]() $Y$
is L/NTF-equivalent.
$Y$
is L/NTF-equivalent.
Proof. If
 $b_{1}(Y)>1$
, then since no Dehn filling of
$b_{1}(Y)>1$
, then since no Dehn filling of
![]() $Y$
is a rational homology sphere, we have
$Y$
is a rational homology sphere, we have
 ${\mathcal{L}}(Y)=\emptyset$
, implying
${\mathcal{L}}(Y)=\emptyset$
, implying
 ${\mathcal{L}}^{\circ }(Y)=\emptyset$
. Correspondingly, Proposition 2.8 implies
${\mathcal{L}}^{\circ }(Y)=\emptyset$
. Correspondingly, Proposition 2.8 implies
 ${\mathcal{F}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
${\mathcal{F}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
Suppose
![]() $Y$
has
$Y$
has
 $b_{1}(Y)=1$
and is the union of a Seifert fibered space with zero or more copies of
$b_{1}(Y)=1$
and is the union of a Seifert fibered space with zero or more copies of
![]() $\bar{N}$
. Then, using [Reference Rasmussen and RasmussenRR15, Proposition 7.9] of Rasmussen and the author to replace Boyer’s and Clay’s ‘
$\bar{N}$
. Then, using [Reference Rasmussen and RasmussenRR15, Proposition 7.9] of Rasmussen and the author to replace Boyer’s and Clay’s ‘
![]() $N_{t}$
’ manifolds with
$N_{t}$
’ manifolds with
![]() $\bar{N}$
, we invoke the ‘slope detection’ theorem of Boyer and Clay [Reference Boyer and ClayBC14, Theorem 8.1] to deduce L/NTF-equivalence for
$\bar{N}$
, we invoke the ‘slope detection’ theorem of Boyer and Clay [Reference Boyer and ClayBC14, Theorem 8.1] to deduce L/NTF-equivalence for
![]() $Y$
.
$Y$
.
Alternatively, one could prove the same result by inductively performing
![]() $\bar{N}$
-fillings in regular fiber complements, starting with Proposition 3.9 for the Seifert fibered base case, and using the gluing result in Proposition 4.4 below, together with (21) and (22), to evolve (27) to match (23). Similar inductive arguments appear in the proof of Theorem 4.6.◻
$\bar{N}$
-fillings in regular fiber complements, starting with Proposition 3.9 for the Seifert fibered base case, and using the gluing result in Proposition 4.4 below, together with (21) and (22), to evolve (27) to match (23). Similar inductive arguments appear in the proof of Theorem 4.6.◻
Remark.
We later prove L/NTF-equivalence for all graph manifolds with torus boundary.
We are now ready to state our main gluing result.
Proposition 4.4. Suppose
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
are non-solid-torus L/NTF-equivalent graph manifolds with torus boundary. Then for any union
$Y_{2}$
are non-solid-torus L/NTF-equivalent graph manifolds with torus boundary. Then for any union
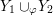 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
,
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
,
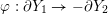 $\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
, the following are equivalent:
$\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
, the following are equivalent:
-
(i)
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space;
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space; -
(ii)
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
does not admit a co-oriented taut foliation;
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
does not admit a co-oriented taut foliation; -
(iii)
 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))$
.
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2}))$
.
Proof. Suppose (iii) holds, so that Proposition 3.3 implies
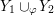 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space. Ozsváth and Szabó have shown [Reference Ozsváth and SzabóOS04] that an L-space does not admit
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is an L-space. Ozsváth and Szabó have shown [Reference Ozsváth and SzabóOS04] that an L-space does not admit
![]() $C^{2}$
co-oriented taut foliations, and this result has been improved to
$C^{2}$
co-oriented taut foliations, and this result has been improved to
![]() $C^{0}$
co-oriented taut foliations by Bowden [Reference BowdenBow15] and independently by Kazez and Roberts [Reference Kazez and RobertsKR15].
$C^{0}$
co-oriented taut foliations by Bowden [Reference BowdenBow15] and independently by Kazez and Roberts [Reference Kazez and RobertsKR15].
Suppose (iii) fails to hold. If
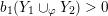 $b_{1}(Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2})>0$
, then Gabai [Reference GabaiGab83] tells us there is a co-oriented taut foliation on
$b_{1}(Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2})>0$
, then Gabai [Reference GabaiGab83] tells us there is a co-oriented taut foliation on
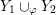 $Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
, and we also know that
$Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
, and we also know that
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
is not an L-space. Suppose instead that
$Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
is not an L-space. Suppose instead that
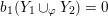 $b_{1}(Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2})=0$
. Then L/NTF-equivalence implies
$b_{1}(Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2})=0$
. Then L/NTF-equivalence implies
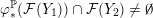 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{F}}(Y_{1}))\cap {\mathcal{F}}(Y_{2})\neq \emptyset$
, and so there are co-oriented taut foliations
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{F}}(Y_{1}))\cap {\mathcal{F}}(Y_{2})\neq \emptyset$
, and so there are co-oriented taut foliations
![]() $F_{i}$
on
$F_{i}$
on
![]() $Y_{i}$
transverse to
$Y_{i}$
transverse to
![]() $\unicode[STIX]{x2202}Y_{i}$
such that
$\unicode[STIX]{x2202}Y_{i}$
such that
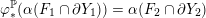 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(\unicode[STIX]{x1D6FC}(F_{1}\cap \unicode[STIX]{x2202}Y_{1}))=\unicode[STIX]{x1D6FC}(F_{2}\cap \unicode[STIX]{x2202}Y_{2})$
. By Corollary 2.2, we can isotop the incompressible tori in
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}(\unicode[STIX]{x1D6FC}(F_{1}\cap \unicode[STIX]{x2202}Y_{1}))=\unicode[STIX]{x1D6FC}(F_{2}\cap \unicode[STIX]{x2202}Y_{2})$
. By Corollary 2.2, we can isotop the incompressible tori in
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
so that each
$Y_{2}$
so that each
![]() $F_{i}$
restricts to boundary-transverse co-oriented taut foliations on each of the JSJ components of each
$F_{i}$
restricts to boundary-transverse co-oriented taut foliations on each of the JSJ components of each
![]() $Y_{i}$
. This means that the JSJ components of
$Y_{i}$
. This means that the JSJ components of
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
each admit boundary-transverse co-oriented taut foliations which restrict to boundary foliations of matching slopes with respect to boundary-gluing maps. We can therefore invoke the foliation gluing theorem of Boyer and Clay [Reference Boyer and ClayBC14, Theorem 9.5.2] to assert the existence of a co-oriented taut foliation on all of
$Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
each admit boundary-transverse co-oriented taut foliations which restrict to boundary foliations of matching slopes with respect to boundary-gluing maps. We can therefore invoke the foliation gluing theorem of Boyer and Clay [Reference Boyer and ClayBC14, Theorem 9.5.2] to assert the existence of a co-oriented taut foliation on all of
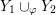 $Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
. Again, this co-oriented taut foliation implies that
$Y_{1}\cup _{\unicode[STIX]{x1D711}}Y_{2}$
. Again, this co-oriented taut foliation implies that
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is not an L-space.◻
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
is not an L-space.◻
4.2 Graph manifold conventions
Any closed graph manifold can be regarded as a Dehn filling of a graph manifold
![]() $Y$
with torus boundary. If
$Y$
with torus boundary. If
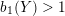 $b_{1}(Y)>1$
, then
$b_{1}(Y)>1$
, then
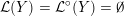 ${\mathcal{L}}(Y)={\mathcal{L}}^{\circ }(Y)=\emptyset$
and
${\mathcal{L}}(Y)={\mathcal{L}}^{\circ }(Y)=\emptyset$
and
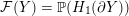 ${\mathcal{F}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
(see Proposition 4.3), which is not very interesting.
${\mathcal{F}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
(see Proposition 4.3), which is not very interesting.
If
 $b_{1}(Y)=1$
, then we call
$b_{1}(Y)=1$
, then we call
![]() $Y$
a tree manifold, since
$Y$
a tree manifold, since
![]() $Y$
admits a rational homology sphere Dehn filling, corresponding to a tree graph. Rooting the tree graph for
$Y$
admits a rational homology sphere Dehn filling, corresponding to a tree graph. Rooting the tree graph for
![]() $Y$
at the Seifert fibered piece containing
$Y$
at the Seifert fibered piece containing
![]() $\unicode[STIX]{x2202}Y$
provides a recursive construction for
$\unicode[STIX]{x2202}Y$
provides a recursive construction for
![]() $Y$
,
$Y$
,
 $$\begin{eqnarray}Y=\hat{M}\cup \biggl(\coprod _{i=1}^{n_{{\rm \small{d}}}}(S^{1}\times D_{i}^{2})\;\amalg \;\coprod _{i=1}^{n_{{\rm \small{g}}}}Y_{i}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}Y=\hat{M}\cup \biggl(\coprod _{i=1}^{n_{{\rm \small{d}}}}(S^{1}\times D_{i}^{2})\;\amalg \;\coprod _{i=1}^{n_{{\rm \small{g}}}}Y_{i}\biggr),\end{eqnarray}$$
where each of
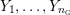 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
is a non-solid-torus tree manifold with torus boundary. Since
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
is a non-solid-torus tree manifold with torus boundary. Since
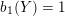 $b_{1}(Y)=1$
,
$b_{1}(Y)=1$
,
![]() $\hat{M}$
is the trivial circle fibration over an (
$\hat{M}$
is the trivial circle fibration over an (
![]() $n+1$
)-punctured
$n+1$
)-punctured
![]() $S^{2}$
or the twisted circle fibration over an (
$S^{2}$
or the twisted circle fibration over an (
![]() $n+1$
)-punctured
$n+1$
)-punctured
![]() $\mathbb{R}\mathbb{P}^{2}\!$
, with boundary components
$\mathbb{R}\mathbb{P}^{2}\!$
, with boundary components
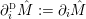 $\unicode[STIX]{x2202}_{i}^{{\rm \small{d}}}\hat{M}:=\unicode[STIX]{x2202}_{i}\hat{M}$
for
$\unicode[STIX]{x2202}_{i}^{{\rm \small{d}}}\hat{M}:=\unicode[STIX]{x2202}_{i}\hat{M}$
for
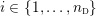 $i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
,
$i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
,
 $\unicode[STIX]{x2202}_{i}^{{\rm \small{g}}}\hat{M}:=\unicode[STIX]{x2202}_{n_{{\rm \small{d}}}+i}\hat{M}$
for
$\unicode[STIX]{x2202}_{i}^{{\rm \small{g}}}\hat{M}:=\unicode[STIX]{x2202}_{n_{{\rm \small{d}}}+i}\hat{M}$
for
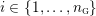 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, and
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, and
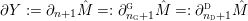 $\unicode[STIX]{x2202}Y:=\unicode[STIX]{x2202}_{n+1}\hat{M}=:\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}+1}^{{\rm \small{g}}}\hat{M}=:\unicode[STIX]{x2202}_{n_{{\rm \small{d}}}+1}^{{\rm \small{d}}}\hat{M}$
, with
$\unicode[STIX]{x2202}Y:=\unicode[STIX]{x2202}_{n+1}\hat{M}=:\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}+1}^{{\rm \small{g}}}\hat{M}=:\unicode[STIX]{x2202}_{n_{{\rm \small{d}}}+1}^{{\rm \small{d}}}\hat{M}$
, with
 $n:=n_{{\rm \small{d}}}+n_{{\rm \small{g}}}$
. We shall sometimes call
$n:=n_{{\rm \small{d}}}+n_{{\rm \small{g}}}$
. We shall sometimes call
![]() $\hat{M}$
the ‘foundation’ for
$\hat{M}$
the ‘foundation’ for
![]() $Y$
.
$Y$
.
Since edges in the graph for
![]() $Y$
correspond to gluings along incompressible tori, each gluing map
$Y$
correspond to gluings along incompressible tori, each gluing map
 $\unicode[STIX]{x1D711}_{i}:\unicode[STIX]{x2202}Y_{i}\rightarrow -\unicode[STIX]{x2202}_{i}^{{\rm \small{g}}}\hat{M}$
, for
$\unicode[STIX]{x1D711}_{i}:\unicode[STIX]{x2202}Y_{i}\rightarrow -\unicode[STIX]{x2202}_{i}^{{\rm \small{g}}}\hat{M}$
, for
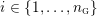 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, labels one of the
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, labels one of the
![]() $n_{{\rm \small{g}}}$
edges descending from the root of the graph for
$n_{{\rm \small{g}}}$
edges descending from the root of the graph for
![]() $Y$
. We call
$Y$
. We call
 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
the daughter subtrees of
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
the daughter subtrees of
![]() $Y$
. Each
$Y$
. Each
![]() $Y_{i}$
is a tree manifold with torus boundary and
$Y_{i}$
is a tree manifold with torus boundary and
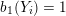 $b_{1}(Y_{i})=1$
, with tree rooted at the Seifert fibered piece containing
$b_{1}(Y_{i})=1$
, with tree rooted at the Seifert fibered piece containing
![]() $\unicode[STIX]{x2202}Y_{i}$
, giving rise to a recursive description for
$\unicode[STIX]{x2202}Y_{i}$
, giving rise to a recursive description for
![]() $Y_{i}$
analogous to that for
$Y_{i}$
analogous to that for
![]() $Y$
in (28). For any
$Y$
in (28). For any
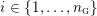 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
for which
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
for which
![]() $Y_{i}$
is Floer simple, i.e. for which
$Y_{i}$
is Floer simple, i.e. for which
 ${\mathcal{L}}^{\circ }(Y_{i})\neq \emptyset$
, we invoke Proposition 3.8 to write
${\mathcal{L}}^{\circ }(Y_{i})\neq \emptyset$
, we invoke Proposition 3.8 to write
 $$\begin{eqnarray}[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]:=\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i})).\end{eqnarray}$$
$$\begin{eqnarray}[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]:=\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i})).\end{eqnarray}$$
If, instead,
 ${\mathcal{L}}(Y_{i})\neq \emptyset$
for some non-Floer-simple
${\mathcal{L}}(Y_{i})\neq \emptyset$
for some non-Floer-simple
![]() $Y_{i}$
, then we write
$Y_{i}$
, then we write
 $$\begin{eqnarray}\{y_{i-}^{{\rm \small{g}}}\}:=\{y_{i+}^{{\rm \small{g}}}\}:=\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i})).\end{eqnarray}$$
$$\begin{eqnarray}\{y_{i-}^{{\rm \small{g}}}\}:=\{y_{i+}^{{\rm \small{g}}}\}:=\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i})).\end{eqnarray}$$
Since the
![]() $n_{{\rm \small{d}}}$
solid tori glued to
$n_{{\rm \small{d}}}$
solid tori glued to
![]() $\hat{M}$
create the exceptional fibers of the Seifert fibered ‘root’
$\hat{M}$
create the exceptional fibers of the Seifert fibered ‘root’
 $\hat{M}\cup \coprod _{i=1}^{n_{{\rm \small{d}}}}(S^{1}\times D_{i}^{2})$
of our tree, we record the Seifert data of this Seifert fibered space by labeling the root vertex with the Dehn filling slopes
$\hat{M}\cup \coprod _{i=1}^{n_{{\rm \small{d}}}}(S^{1}\times D_{i}^{2})$
of our tree, we record the Seifert data of this Seifert fibered space by labeling the root vertex with the Dehn filling slopes
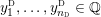 $y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\in \mathbb{Q}$
. More explicitly, to each solid torus
$y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\in \mathbb{Q}$
. More explicitly, to each solid torus
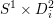 $S^{1}\times D_{i}^{2}$
in (28) we associate the gluing map
$S^{1}\times D_{i}^{2}$
in (28) we associate the gluing map
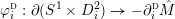 $\unicode[STIX]{x1D711}_{i}^{{\rm \small{d}}}:\unicode[STIX]{x2202}(S^{1}\times D_{i}^{2})\rightarrow -\unicode[STIX]{x2202}_{i}^{{\rm \small{d}}}\hat{M}$
, and set
$\unicode[STIX]{x1D711}_{i}^{{\rm \small{d}}}:\unicode[STIX]{x2202}(S^{1}\times D_{i}^{2})\rightarrow -\unicode[STIX]{x2202}_{i}^{{\rm \small{d}}}\hat{M}$
, and set
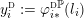 $y_{i}^{{\rm \small{d}}}:=\unicode[STIX]{x1D711}_{i\ast }^{{\rm \small{d}}\mathbb{P}}(l_{i})$
, for
$y_{i}^{{\rm \small{d}}}:=\unicode[STIX]{x1D711}_{i\ast }^{{\rm \small{d}}\mathbb{P}}(l_{i})$
, for
![]() $l_{i}$
the rational longitude of
$l_{i}$
the rational longitude of
 $S^{1}\times D_{i}^{2}$
. As usual, we demand that each
$S^{1}\times D_{i}^{2}$
. As usual, we demand that each
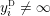 $y_{i}^{{\rm \small{d}}}\neq \infty$
. We stray slightly from our earlier convention by allowing
$y_{i}^{{\rm \small{d}}}\neq \infty$
. We stray slightly from our earlier convention by allowing
![]() $y_{i}^{{\rm \small{d}}}\in \mathbb{Z}$
, but this allows us to fix
$y_{i}^{{\rm \small{d}}}\in \mathbb{Z}$
, but this allows us to fix
 $e_{0}:=y_{0}^{{\rm \small{d}}}:=0$
and then forget the zeroth fiber complement altogether, without loss of generality.
$e_{0}:=y_{0}^{{\rm \small{d}}}:=0$
and then forget the zeroth fiber complement altogether, without loss of generality.
4.3 Statement of main results
We first show that all graph manifolds with torus boundary are L/NTF-equivalent, making our main gluing tool, Proposition 4.4, applicable for all such non-solid-torus graph manifolds. We then can make the inductive gluing arguments necessary to calculate L-space intervals for graph manifolds with torus boundary.
Theorem 4.5. Every graph manifold
![]() $Y$
with torus boundary is L/NTF equivalent, i.e. satisfies
$Y$
with torus boundary is L/NTF equivalent, i.e. satisfies
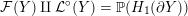 ${\mathcal{F}}(Y)\amalg {\mathcal{L}}^{\circ }(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. Moreover, if we let
${\mathcal{F}}(Y)\amalg {\mathcal{L}}^{\circ }(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. Moreover, if we let
![]() ${\mathcal{R}}(Y)\!$
denote the set of slopes of reducible (and not
${\mathcal{R}}(Y)\!$
denote the set of slopes of reducible (and not
 $S^{1}\times D^{2}$
) Dehn fillings of
$S^{1}\times D^{2}$
) Dehn fillings of
![]() $Y\!$
, then
$Y\!$
, then
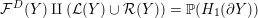 ${\mathcal{F}}^{D}(Y)\amalg ({\mathcal{L}}(Y)\cup {\mathcal{R}}(Y))=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
${\mathcal{F}}^{D}(Y)\amalg ({\mathcal{L}}(Y)\cup {\mathcal{R}}(Y))=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
.
The above also implies that the following calculation of
![]() ${\mathcal{L}}(Y)$
for graph manifolds
${\mathcal{L}}(Y)$
for graph manifolds
![]() $Y\!$
with torus boundary completely determines both
$Y\!$
with torus boundary completely determines both
![]() ${\mathcal{F}}(Y)$
and
${\mathcal{F}}(Y)$
and
![]() ${\mathcal{F}}^{D}(Y)$
.
${\mathcal{F}}^{D}(Y)$
.
Theorem 4.6. Suppose
![]() $Y$
is a graph manifold with torus boundary and non-empty
$Y$
is a graph manifold with torus boundary and non-empty
![]() ${\mathcal{L}}(Y)$
. If the Seifert fibered component of
${\mathcal{L}}(Y)$
. If the Seifert fibered component of
![]() $Y$
containing
$Y$
containing
![]() $\unicode[STIX]{x2202}Y$
has non-orientable base, then
$\unicode[STIX]{x2202}Y$
has non-orientable base, then
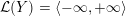 ${\mathcal{L}}(Y)=\langle -\infty ,+\infty \rangle$
. Otherwise, we have
${\mathcal{L}}(Y)=\langle -\infty ,+\infty \rangle$
. Otherwise, we have
 $$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}[[y_{-},y_{+}]],\quad & \quad Y\,\text{Floer simple},\\ \{y_{-}\}=\{y_{+}\},\quad & \quad Y\text{ not Floer simple},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}[[y_{-},y_{+}]],\quad & \quad Y\,\text{Floer simple},\\ \{y_{-}\}=\{y_{+}\},\quad & \quad Y\text{ not Floer simple},\end{array}\right.\end{eqnarray}$$
where, for
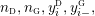 $n_{{\rm \small{d}}},n_{{\rm \small{g}}},y_{i}^{{\rm \small{d}}},y_{i-}^{{\rm \small{g}}},$
and
$n_{{\rm \small{d}}},n_{{\rm \small{g}}},y_{i}^{{\rm \small{d}}},y_{i-}^{{\rm \small{g}}},$
and
![]() $y_{i+}^{{\rm \small{g}}}$
as defined in § 4.2, we define
$y_{i+}^{{\rm \small{g}}}$
as defined in § 4.2, we define
 $y_{-},y_{+}\in \mathbb{Q}\cup \{\infty \}$
as
$y_{-},y_{+}\in \mathbb{Q}\cup \{\infty \}$
as
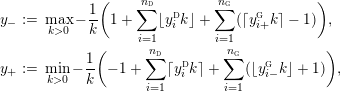 $$\begin{eqnarray}\displaystyle y_{-} & := & \displaystyle \,\max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\nonumber\\ \displaystyle y_{+} & := & \displaystyle \,\min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{-} & := & \displaystyle \,\max _{k>0}-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\nonumber\\ \displaystyle y_{+} & := & \displaystyle \,\min _{k>0}-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr),\nonumber\end{eqnarray}$$
unless
![]() $Y\!$
is a solid torus, in which case
$Y\!$
is a solid torus, in which case
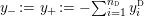 $y_{-}\!:=y_{+}\!:=-\!\sum _{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}$
.
$y_{-}\!:=y_{+}\!:=-\!\sum _{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}$
.
Remark.
The above formulas for
![]() $y_{\mp }$
are finitely computable. In particular, the maximum (respectively, minimum) is realized for
$y_{\mp }$
are finitely computable. In particular, the maximum (respectively, minimum) is realized for
![]() $k\leqslant s_{\pm }$
, where
$k\leqslant s_{\pm }$
, where
![]() $s_{\pm }$
is the least common positive multiple of the denominators of
$s_{\pm }$
is the least common positive multiple of the denominators of
 $y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}$
and
$y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}$
and
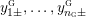 $y_{1\pm }^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}\pm }^{{\rm \small{g}}}$
, with
$y_{1\pm }^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}\pm }^{{\rm \small{g}}}$
, with
![]() $\mp$
and
$\mp$
and
![]() $\pm$
cases taken respectively from top to bottom. If computation is not the goal, then one can avoid treating the solid torus case separately by replacing ‘
$\pm$
cases taken respectively from top to bottom. If computation is not the goal, then one can avoid treating the solid torus case separately by replacing ‘
![]() $\max$
’ with ‘
$\max$
’ with ‘
![]() $\sup$
’ and ‘
$\sup$
’ and ‘
![]() $\min$
’ with ‘
$\min$
’ with ‘
![]() $\inf$
’.
$\inf$
’.
Unlike the case of oriented Seifert fibered spaces over the Möbius strip or disk, not all graph manifolds with torus boundary are Floer simple. We therefore need a companion result to characterize precisely when
![]() ${\mathcal{L}}^{\circ }$
or
${\mathcal{L}}^{\circ }$
or
![]() ${\mathcal{L}}$
is non-empty.
${\mathcal{L}}$
is non-empty.
Proposition 4.7. Suppose
![]() $Y\!$
is a graph manifold with torus boundary. If
$Y\!$
is a graph manifold with torus boundary. If
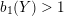 $b_{1}(Y)>1$
, then
$b_{1}(Y)>1$
, then
 ${\mathcal{L}}(Y)=\emptyset$
. Suppose
${\mathcal{L}}(Y)=\emptyset$
. Suppose
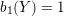 $b_{1}(Y)=1$
, so that
$b_{1}(Y)=1$
, so that
![]() $Y\!$
admits the recursive description in § 4.2.
$Y\!$
admits the recursive description in § 4.2.
If the JSJ component containing
![]() $\unicode[STIX]{x2202}Y$
has non-orientable base, then
$\unicode[STIX]{x2202}Y$
has non-orientable base, then
 ${\mathcal{L}}(Y)\neq \emptyset$
if and only if
${\mathcal{L}}(Y)\neq \emptyset$
if and only if
![]() $Y\!$
is Floer simple, if and only if the following holds:
$Y\!$
is Floer simple, if and only if the following holds:
- (fs0)
-
All daughter subtrees
 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple;
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple;
 $\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
$\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
.
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
.
If the JSJ component containing
![]() $\unicode[STIX]{x2202}Y$
has orientable base, then
$\unicode[STIX]{x2202}Y$
has orientable base, then
![]() $Y$
is Floer simple if and only if the daughter subtrees
$Y$
is Floer simple if and only if the daughter subtrees
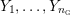 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are each Floer simple and one of the following holds:
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are each Floer simple and one of the following holds:
- (fs1)
-
 $[[y_{j-}^{{\rm \small{g}}},y_{j+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle$
for some
$[[y_{j-}^{{\rm \small{g}}},y_{j+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle$
for some
 $j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
$j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
 $\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
$\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}\setminus \{j\}$
.
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}\setminus \{j\}$
. - (fs2)
-
 $-\infty <y_{j-}^{{\rm \small{g}}}<y_{j+}^{{\rm \small{g}}}<+\infty$
, for some
$-\infty <y_{j-}^{{\rm \small{g}}}<y_{j+}^{{\rm \small{g}}}<+\infty$
, for some
 $j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
$j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
 $\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
$\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}\setminus \{j\}$
;
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}\setminus \{j\}$
;
 $y_{-}<y_{+}$
.
$y_{-}<y_{+}$
. - (fs3)
-
At least one of
 $\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[-\infty ,y_{i+}^{{\rm \small{g}}}]\}$
and
$\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[-\infty ,y_{i+}^{{\rm \small{g}}}]\}$
and
 $\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\}$
is the empty set;
$\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\}$
is the empty set;
 $\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]$
for all
$\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
.
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
.
If the JSJ component containing
![]() $\unicode[STIX]{x2202}Y$
has orientable base, then
$\unicode[STIX]{x2202}Y$
has orientable base, then
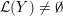 ${\mathcal{L}}(Y)\neq \emptyset$
with
${\mathcal{L}}(Y)\neq \emptyset$
with
![]() $Y$
not Floer simple if and only if one of the following holds:
$Y$
not Floer simple if and only if one of the following holds:
- (nfs1)
-
 $n_{{\rm \small{g}}}=1$
,
$n_{{\rm \small{g}}}=1$
,
 $|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|\leqslant 1$
;
$|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|\leqslant 1$
;
 $\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=\{y_{1}^{{\rm \small{g}}}\}$
for some
$\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=\{y_{1}^{{\rm \small{g}}}\}$
for some
 $y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
;
$y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
;
 $\sum _{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
or all
$\sum _{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
or all
 $y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\in \mathbb{Z}$
.
$y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\in \mathbb{Z}$
. - (nfs2)
-
All daughter subtrees
 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple;
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple;
 $-\infty <y_{j-}^{{\rm \small{g}}}<y_{j+}^{{\rm \small{g}}}<+\infty$
, for some
$-\infty <y_{j-}^{{\rm \small{g}}}<y_{j+}^{{\rm \small{g}}}<+\infty$
, for some
 $j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
$j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
 $\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
$\infty \in ([[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]])^{\circ }$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}\setminus \{j\}$
;
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}\setminus \{j\}$
;
 $y_{-}=y_{+}$
.
$y_{-}=y_{+}$
. - (nfs3)
-
All daughter subtrees
 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple;
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple;
 $\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[-\infty ,y_{i+}^{{\rm \small{g}}}]\}\neq \emptyset$
and
$\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[-\infty ,y_{i+}^{{\rm \small{g}}}]\}\neq \emptyset$
and
 $\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\}\neq \emptyset$
;
$\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\}\neq \emptyset$
;
 $\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]$
for all
$\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
.
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. - (nfs4)
-
 $\unicode[STIX]{x1D711}_{j\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{j}))=\{\infty \}$
for some
$\unicode[STIX]{x1D711}_{j\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{j}))=\{\infty \}$
for some
 $j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
$j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
;
 $\infty \in \unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i}))$
for all
$\infty \in \unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i}))$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
.
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
.
Note that all eight
![]() $({\rm \small{fs}})$
and
$({\rm \small{fs}})$
and
![]() $({\rm \small{nfs}})$
conditions are mutually exclusive. Note also that the isolated L-space fillings described in
$({\rm \small{nfs}})$
conditions are mutually exclusive. Note also that the isolated L-space fillings described in
![]() $({\rm \small{nfs3}})$
and
$({\rm \small{nfs3}})$
and
![]() $({\rm \small{nfs4}})$
are not graph manifolds.
$({\rm \small{nfs4}})$
are not graph manifolds.
We now proceed to prove our main results, starting with that of L/NTF-equivalence.
4.4 Proof of Theorem 4.5
Proposition 4.3 gives the desired result for
 $b_{1}(Y)>1$
.
$b_{1}(Y)>1$
.
We therefore restrict attention to graph manifolds
![]() $Y$
with
$Y$
with
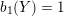 $b_{1}(Y)=1$
and torus boundary
$b_{1}(Y)=1$
and torus boundary
![]() $\unicode[STIX]{x2202}Y$
, so that
$\unicode[STIX]{x2202}Y$
, so that
![]() $Y$
admits the recursive description in (28), with tree graph rooted at the Seifert fibered piece containing
$Y$
admits the recursive description in (28), with tree graph rooted at the Seifert fibered piece containing
![]() $\unicode[STIX]{x2202}Y$
. Inductively assume that any such
$\unicode[STIX]{x2202}Y$
. Inductively assume that any such
![]() $Y\!$
with tree height less than or equal to
$Y\!$
with tree height less than or equal to
![]() $k-1$
is L/NTF-equivalent and satisfies
$k-1$
is L/NTF-equivalent and satisfies
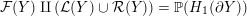 ${\mathcal{F}}(Y)\amalg ({\mathcal{L}}(Y)\cup {\mathcal{R}}(Y))=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
, noting that Proposition 3.9 covers the case of trees of height zero. Fix an arbitrary tree manifold
${\mathcal{F}}(Y)\amalg ({\mathcal{L}}(Y)\cup {\mathcal{R}}(Y))=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
, noting that Proposition 3.9 covers the case of trees of height zero. Fix an arbitrary tree manifold
![]() $Y$
with
$Y$
with
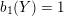 $b_{1}(Y)=1$
, torus boundary, and tree height
$b_{1}(Y)=1$
, torus boundary, and tree height
![]() $k>0$
, and parameterize its data as in § 4.2.
$k>0$
, and parameterize its data as in § 4.2.
To each
 $j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
,
$j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
,
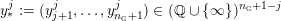 $y_{\ast }^{j}:=(y_{j+1}^{j},\ldots ,y_{n_{{\rm \small{g}}}+1}^{j})\in (\mathbb{Q}\cup \{\infty \})^{n_{{\rm \small{g}}}+1-j}$
, and
$y_{\ast }^{j}:=(y_{j+1}^{j},\ldots ,y_{n_{{\rm \small{g}}}+1}^{j})\in (\mathbb{Q}\cup \{\infty \})^{n_{{\rm \small{g}}}+1-j}$
, and
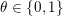 $\unicode[STIX]{x1D703}\in \{0,1\}$
we associate a manifold
$\unicode[STIX]{x1D703}\in \{0,1\}$
we associate a manifold
![]() $Y_{\unicode[STIX]{x1D703}}^{j}[y_{\ast }^{j}]$
, constructed as follows. Starting with
$Y_{\unicode[STIX]{x1D703}}^{j}[y_{\ast }^{j}]$
, constructed as follows. Starting with
![]() $\hat{M}$
, first perform Dehn fillings of slopes
$\hat{M}$
, first perform Dehn fillings of slopes
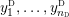 $y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}$
along the respective boundary components
$y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}$
along the respective boundary components
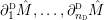 $\unicode[STIX]{x2202}_{1}^{{\rm \small{d}}}\hat{M},\ldots ,\unicode[STIX]{x2202}_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\hat{M}$
in
$\unicode[STIX]{x2202}_{1}^{{\rm \small{d}}}\hat{M},\ldots ,\unicode[STIX]{x2202}_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\hat{M}$
in
![]() $\hat{M}$
. Next, attach the graph manifolds
$\hat{M}$
. Next, attach the graph manifolds
 $Y_{1},\ldots ,Y_{j-1}$
, via the respective gluing maps
$Y_{1},\ldots ,Y_{j-1}$
, via the respective gluing maps
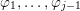 $\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{j-1}$
, to the resulting manifold. Leaving the boundary component
$\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{j-1}$
, to the resulting manifold. Leaving the boundary component
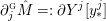 $\unicode[STIX]{x2202}_{j}^{{\rm \small{g}}}\hat{M}=:\unicode[STIX]{x2202}Y^{j}[y_{\ast }^{j}]$
unfilled, lastly perform
$\unicode[STIX]{x2202}_{j}^{{\rm \small{g}}}\hat{M}=:\unicode[STIX]{x2202}Y^{j}[y_{\ast }^{j}]$
unfilled, lastly perform
![]() $\bar{N}$
-fillings of slopes
$\bar{N}$
-fillings of slopes
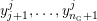 $y_{j+1}^{j},\ldots ,y_{n_{{\rm \small{g}}}+1}^{j}$
along the respective boundary components
$y_{j+1}^{j},\ldots ,y_{n_{{\rm \small{g}}}+1}^{j}$
along the respective boundary components
 $\unicode[STIX]{x2202}_{j+1}^{{\rm \small{g}}}\hat{M},\ldots ,\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}+1}^{{\rm \small{g}}}\hat{M}$
of the resulting manifold, and call the result
$\unicode[STIX]{x2202}_{j+1}^{{\rm \small{g}}}\hat{M},\ldots ,\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}+1}^{{\rm \small{g}}}\hat{M}$
of the resulting manifold, and call the result
![]() $Y_{0}^{j}[y_{\ast }^{j}]$
. To form
$Y_{0}^{j}[y_{\ast }^{j}]$
. To form
![]() $Y_{1}^{j}[y_{\ast }^{j}]$
, replace the
$Y_{1}^{j}[y_{\ast }^{j}]$
, replace the
![]() $\bar{N}$
-filling of slope
$\bar{N}$
-filling of slope
![]() $y_{n_{{\rm \small{g}}}+1}^{j}$
in
$y_{n_{{\rm \small{g}}}+1}^{j}$
in
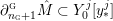 $\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}+1}^{{\rm \small{g}}}\hat{M}\subset Y_{0}^{j}[y_{\ast }^{j}]$
with the Dehn filling of slope
$\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}+1}^{{\rm \small{g}}}\hat{M}\subset Y_{0}^{j}[y_{\ast }^{j}]$
with the Dehn filling of slope
![]() $y_{n_{{\rm \small{g}}}+1}^{j}$
. In addition, set
$y_{n_{{\rm \small{g}}}+1}^{j}$
. In addition, set
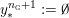 $y_{\ast }^{n_{{\rm \small{g}}}+1}:=\emptyset$
and
$y_{\ast }^{n_{{\rm \small{g}}}+1}:=\emptyset$
and
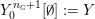 $Y_{0}^{n_{{\rm \small{g}}}+1}[\emptyset ]:=Y$
.
$Y_{0}^{n_{{\rm \small{g}}}+1}[\emptyset ]:=Y$
.
For positive
![]() $j\leqslant n_{{\rm \small{g}}}$
, inductively assume that for any
$j\leqslant n_{{\rm \small{g}}}$
, inductively assume that for any
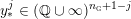 $y_{\ast }^{j}\in (\mathbb{Q}\cup \infty )^{n_{{\rm \small{g}}}+1-j}$
and
$y_{\ast }^{j}\in (\mathbb{Q}\cup \infty )^{n_{{\rm \small{g}}}+1-j}$
and
 $\unicode[STIX]{x1D703}\in \{0,1\}$
, any manifold of the form
$\unicode[STIX]{x1D703}\in \{0,1\}$
, any manifold of the form
![]() $Y_{\unicode[STIX]{x1D703}}^{j}[y_{\ast }^{j}]$
is L/NTF-equivalent if it is prime, noting that Proposition 4.3 covers the base case of
$Y_{\unicode[STIX]{x1D703}}^{j}[y_{\ast }^{j}]$
is L/NTF-equivalent if it is prime, noting that Proposition 4.3 covers the base case of
![]() $j=1$
. For any
$j=1$
. For any
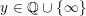 $y\in \mathbb{Q}\cup \{\infty \}$
,
$y\in \mathbb{Q}\cup \{\infty \}$
,
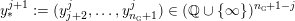 $y_{\ast }^{j+1}:=(y_{j+2}^{j},\ldots ,y_{n_{{\rm \small{g}}}+1}^{j})\in (\mathbb{Q}\cup \{\infty \})^{n_{{\rm \small{g}}}+1-j}$
,
$y_{\ast }^{j+1}:=(y_{j+2}^{j},\ldots ,y_{n_{{\rm \small{g}}}+1}^{j})\in (\mathbb{Q}\cup \{\infty \})^{n_{{\rm \small{g}}}+1-j}$
,
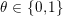 $\unicode[STIX]{x1D703}\in \{0,1\}$
, and manifold of the form
$\unicode[STIX]{x1D703}\in \{0,1\}$
, and manifold of the form
 $Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]$
, we can make matching choices of
$Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]$
, we can make matching choices of
![]() $\bar{N}$
-filling gluing maps to obtain
$\bar{N}$
-filling gluing maps to obtain
 $$\begin{eqnarray}Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]^{\bar{N}}(y)=Y_{j}\cup Y_{\unicode[STIX]{x1D703}}^{j}[(y,y_{\ast }^{j+1})].\end{eqnarray}$$
$$\begin{eqnarray}Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]^{\bar{N}}(y)=Y_{j}\cup Y_{\unicode[STIX]{x1D703}}^{j}[(y,y_{\ast }^{j+1})].\end{eqnarray}$$
Suppose
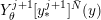 $Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]^{\bar{N}}(y)$
is prime, implying
$Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]^{\bar{N}}(y)$
is prime, implying
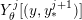 $Y_{\unicode[STIX]{x1D703}}^{j}[(y,y_{\ast }^{j+1})]$
is prime and hence L/NTF-equivalent by inductive assumption. Since
$Y_{\unicode[STIX]{x1D703}}^{j}[(y,y_{\ast }^{j+1})]$
is prime and hence L/NTF-equivalent by inductive assumption. Since
 $Y_{\unicode[STIX]{x1D703}}^{j}[(y,y_{\ast }^{j+1})]$
and
$Y_{\unicode[STIX]{x1D703}}^{j}[(y,y_{\ast }^{j+1})]$
and
![]() $Y_{j}$
are L/NTF-equivalent non-solid-torus graph manifolds with torus boundary, Proposition 4.4 makes
$Y_{j}$
are L/NTF-equivalent non-solid-torus graph manifolds with torus boundary, Proposition 4.4 makes
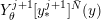 $Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]^{\bar{N}}(y)$
an L-space if and only if it fails to admit a co-oriented taut foliation. Since this holds for arbitrary
$Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]^{\bar{N}}(y)$
an L-space if and only if it fails to admit a co-oriented taut foliation. Since this holds for arbitrary
 $y\in \mathbb{Q}\cup \{\infty \}$
, Proposition 4.2 tells us
$y\in \mathbb{Q}\cup \{\infty \}$
, Proposition 4.2 tells us
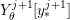 $Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]$
is L/NTF-equivalent.
$Y_{\unicode[STIX]{x1D703}}^{j+1}[y_{\ast }^{j+1}]$
is L/NTF-equivalent.
Completing our induction on
![]() $j$
, we conclude that
$j$
, we conclude that
 $Y:=Y_{0}^{n_{{\rm \small{g}}}+1}[\emptyset ]$
is L/NTF-equivalent, and that
$Y:=Y_{0}^{n_{{\rm \small{g}}}+1}[\emptyset ]$
is L/NTF-equivalent, and that
![]() $Y_{1}^{n_{{\rm \small{g}}}}[y]$
is L/NTF-equivalent for any
$Y_{1}^{n_{{\rm \small{g}}}}[y]$
is L/NTF-equivalent for any
 $y\in \mathbb{Q}\cup \{\infty \}$
for which
$y\in \mathbb{Q}\cup \{\infty \}$
for which
![]() $Y_{1}^{n_{{\rm \small{g}}}}[y]$
is prime. Thus, for any prime Dehn filling
$Y_{1}^{n_{{\rm \small{g}}}}[y]$
is prime. Thus, for any prime Dehn filling
![]() $Y(y)$
, Proposition 4.4 tells us that the union
$Y(y)$
, Proposition 4.4 tells us that the union
 $$\begin{eqnarray}Y(y)=Y_{n_{{\rm \small{g}}}}\cup _{\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}}}Y_{1}^{n_{{\rm \small{g}}}}[y]\end{eqnarray}$$
$$\begin{eqnarray}Y(y)=Y_{n_{{\rm \small{g}}}}\cup _{\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}}}Y_{1}^{n_{{\rm \small{g}}}}[y]\end{eqnarray}$$
is an L-space if and only if it fails to admit a co-oriented taut foliation, and so
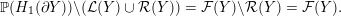 $$\begin{eqnarray}\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus ({\mathcal{L}}(Y)\cup {\mathcal{R}}(Y))={\mathcal{F}}(Y)\setminus {\mathcal{R}}(Y)={\mathcal{F}}(Y).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus ({\mathcal{L}}(Y)\cup {\mathcal{R}}(Y))={\mathcal{F}}(Y)\setminus {\mathcal{R}}(Y)={\mathcal{F}}(Y).\end{eqnarray}$$
Inducting on tree height
![]() $k$
then completes the proof.◻
$k$
then completes the proof.◻
We next prove Theorem 4.6 and Proposition 4.7 in tandem over the course of §§ 4.5–4.8. The inductive program laid out in § 4.5 spans all three of the subsequent subsections.
4.5 Inductive set-up for proof of Theorem 4.6 and Proposition 4.7
Both results hold automatically when
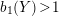 $b_{1}(Y)\!>\!1$
. This leaves the case of
$b_{1}(Y)\!>\!1$
. This leaves the case of
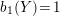 $b_{1}(Y)\!=\!1$
, so that
$b_{1}(Y)\!=\!1$
, so that
![]() $Y$
admits the recursive description in (28), with tree rooted at the Seifert fibered piece containing
$Y$
admits the recursive description in (28), with tree rooted at the Seifert fibered piece containing
![]() $\unicode[STIX]{x2202}Y$
.
$\unicode[STIX]{x2202}Y$
.
Inductively assume that both Theorem 4.6 and Proposition 4.7 hold for all tree manifolds with torus boundary,
![]() $b_{1}=1$
, and tree height less than or equal to
$b_{1}=1$
, and tree height less than or equal to
![]() $k-1$
, noting that Proposition 3.9 covers the height zero case. In addition, inductively assume that Theorem 4.6 and Proposition 4.7 hold for any tree manifold with torus boundary,
$k-1$
, noting that Proposition 3.9 covers the height zero case. In addition, inductively assume that Theorem 4.6 and Proposition 4.7 hold for any tree manifold with torus boundary,
![]() $b_{1}=1$
, tree height less than or equal to
$b_{1}=1$
, tree height less than or equal to
![]() $k$
, and up to
$k$
, and up to
![]() $n_{{\rm \small{g}}}-1$
daughter subtrees, noting that Proposition 3.9 also covers the case of zero daughter subtrees.
$n_{{\rm \small{g}}}-1$
daughter subtrees, noting that Proposition 3.9 also covers the case of zero daughter subtrees.
For the remainder of the proof, we fix an arbitrary height
![]() $k$
tree manifold
$k$
tree manifold
![]() $Y$
with torus boundary and
$Y$
with torus boundary and
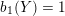 $b_{1}(Y)=1$
, as described in § 4.2. Thus,
$b_{1}(Y)=1$
, as described in § 4.2. Thus,
![]() $Y$
has
$Y$
has
![]() $n_{{\rm \small{g}}}$
daughter subtrees
$n_{{\rm \small{g}}}$
daughter subtrees
 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
, attached via respective gluing maps
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
, attached via respective gluing maps
 $\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}}$
, and the Seifert fibered piece containing
$\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}}$
, and the Seifert fibered piece containing
![]() $\unicode[STIX]{x2202}Y$
, at which we root the tree for
$\unicode[STIX]{x2202}Y$
, at which we root the tree for
![]() $Y$
, is the Dehn filling of slope
$Y$
, is the Dehn filling of slope
 $y_{\ast }^{{\rm \small{d}}}=(y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
of the ‘foundation’
$y_{\ast }^{{\rm \small{d}}}=(y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
of the ‘foundation’
![]() $\hat{M}$
of
$\hat{M}$
of
![]() $Y,$
where
$Y,$
where
![]() $\hat{M}$
is either the trivial
$\hat{M}$
is either the trivial
![]() $S^{1}$
-fibration over an (
$S^{1}$
-fibration over an (
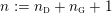 $n:=n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1$
)-punctured
$n:=n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1$
)-punctured
![]() $S^{2}$
or the twisted
$S^{2}$
or the twisted
![]() $S^{1}$
-fibration over an
$S^{1}$
-fibration over an
![]() $n$
-punctured
$n$
-punctured
![]() $\mathbb{R}\mathbb{P}^{2}$
. For any
$\mathbb{R}\mathbb{P}^{2}$
. For any
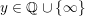 $y\in \mathbb{Q}\cup \{\infty \}$
, let
$y\in \mathbb{Q}\cup \{\infty \}$
, let
![]() ${\hat{Y}}[y]$
denote the complement of
${\hat{Y}}[y]$
denote the complement of
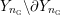 $Y_{n_{{\rm \small{g}}}}\setminus \unicode[STIX]{x2202}Y_{n_{{\rm \small{g}}}}$
in the Dehn filling
$Y_{n_{{\rm \small{g}}}}\setminus \unicode[STIX]{x2202}Y_{n_{{\rm \small{g}}}}$
in the Dehn filling
![]() $Y(y)$
, so that we regard
$Y(y)$
, so that we regard
![]() $Y(y)$
as the union
$Y(y)$
as the union
 $$\begin{eqnarray}Y(y)={\hat{Y}}[y]\cup _{\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}}}Y_{n_{{\rm \small{g}}}}.\end{eqnarray}$$
$$\begin{eqnarray}Y(y)={\hat{Y}}[y]\cup _{\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}}}Y_{n_{{\rm \small{g}}}}.\end{eqnarray}$$
For any
![]() $y\in \mathbb{Q}$
, our inductive assumptions make Theorem 4.6 and Proposition 4.7 hold for
$y\in \mathbb{Q}$
, our inductive assumptions make Theorem 4.6 and Proposition 4.7 hold for
![]() ${\hat{Y}}[y]$
and
${\hat{Y}}[y]$
and
![]() $Y_{n_{{\rm \small{g}}}}$
, since
$Y_{n_{{\rm \small{g}}}}$
, since
![]() $Y_{n_{{\rm \small{g}}}}$
has tree height less than or equal to
$Y_{n_{{\rm \small{g}}}}$
has tree height less than or equal to
![]() $k-1$
, and since for
$k-1$
, and since for
![]() $y\neq \infty$
,
$y\neq \infty$
,
![]() ${\hat{Y}}[y]$
is a
${\hat{Y}}[y]$
is a
![]() $b_{1}=1$
tree manifold with torus boundary,
$b_{1}=1$
tree manifold with torus boundary,
![]() $n_{{\rm \small{g}}}-1$
daughter subtrees, and tree height less than or equal to
$n_{{\rm \small{g}}}-1$
daughter subtrees, and tree height less than or equal to
![]() $k$
.
$k$
.
4.6 Non-orientable base
Consider the case in which
![]() $\hat{M}$
is
$\hat{M}$
is
![]() $S^{1}$
-fibered over a punctured
$S^{1}$
-fibered over a punctured
![]() $\mathbb{R}\mathbb{P}^{2}$
. First note that since the regular fiber class is torsion, its primitive lift
$\mathbb{R}\mathbb{P}^{2}$
. First note that since the regular fiber class is torsion, its primitive lift
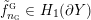 $\tilde{f}_{n_{{\rm \small{g}}}}^{{\rm \small{g}}}\in H_{1}(\unicode[STIX]{x2202}Y)$
, of slope
$\tilde{f}_{n_{{\rm \small{g}}}}^{{\rm \small{g}}}\in H_{1}(\unicode[STIX]{x2202}Y)$
, of slope
![]() $\infty$
, is the rational longitude, which means that
$\infty$
, is the rational longitude, which means that
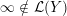 $\infty \notin {\mathcal{L}}(Y)$
.
$\infty \notin {\mathcal{L}}(Y)$
.
Suppose there is some
![]() $y\neq \infty$
for which
$y\neq \infty$
for which
 ${\mathcal{L}}({\hat{Y}}[y])\neq \emptyset$
. Then, by inductive assumption, Proposition 4.7 tells us that the daughter subtrees
${\mathcal{L}}({\hat{Y}}[y])\neq \emptyset$
. Then, by inductive assumption, Proposition 4.7 tells us that the daughter subtrees
 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}-1}$
are Floer simple, with
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}-1}$
are Floer simple, with
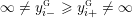 $\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
for all
$\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
for all
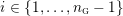 $i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, where
$i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, where
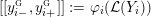 $[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]:=\unicode[STIX]{x1D711}_{i}({\mathcal{L}}(Y_{i}))$
. This conversely implies that
$[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]:=\unicode[STIX]{x1D711}_{i}({\mathcal{L}}(Y_{i}))$
. This conversely implies that
![]() ${\hat{Y}}[y]$
is Floer simple for all
${\hat{Y}}[y]$
is Floer simple for all
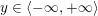 $y\in \langle -\infty ,+\infty \rangle$
. Now, for each
$y\in \langle -\infty ,+\infty \rangle$
. Now, for each
 $y\in \langle -\infty ,+\infty \rangle$
,
$y\in \langle -\infty ,+\infty \rangle$
,
![]() ${\hat{Y}}[y]$
is a non-solid-torus graph manifold, and so Proposition 4.4 tells us that the union
${\hat{Y}}[y]$
is a non-solid-torus graph manifold, and so Proposition 4.4 tells us that the union
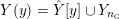 $Y(y)={\hat{Y}}[y]\cup Y_{n_{{\rm \small{g}}}}$
in (34) is an L-space if and only if
$Y(y)={\hat{Y}}[y]\cup Y_{n_{{\rm \small{g}}}}$
in (34) is an L-space if and only if
 $$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}}^{{\rm \small{ g}}}\hat{M})).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}_{n_{{\rm \small{g}}}}^{{\rm \small{ g}}}\hat{M})).\end{eqnarray}$$
Since, by inductive assumption, Theorem 4.6 implies
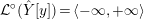 ${\mathcal{L}}^{\circ }({\hat{Y}}[y])\!=\!\langle -\infty ,+\infty \rangle$
for all
${\mathcal{L}}^{\circ }({\hat{Y}}[y])\!=\!\langle -\infty ,+\infty \rangle$
for all
 $y\!\in \!\langle -\infty ,+\infty \rangle$
, (35) holds if and only if
$y\!\in \!\langle -\infty ,+\infty \rangle$
, (35) holds if and only if
![]() $Y_{n_{{\rm \small{g}}}}$
is Floer simple and has
$Y_{n_{{\rm \small{g}}}}$
is Floer simple and has
 $\infty \neq y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}\geqslant y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\neq \infty$
, in which case we consequently have
$\infty \neq y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}\geqslant y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\neq \infty$
, in which case we consequently have
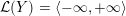 ${\mathcal{L}}(Y)=\langle -\infty ,+\infty \rangle$
.
${\mathcal{L}}(Y)=\langle -\infty ,+\infty \rangle$
.
Conversely, suppose that
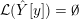 ${\mathcal{L}}({\hat{Y}}[y])=\emptyset$
for all
${\mathcal{L}}({\hat{Y}}[y])=\emptyset$
for all
![]() $y\in \mathbb{Q}$
. Then for all
$y\in \mathbb{Q}$
. Then for all
![]() $y\in \mathbb{Q}$
, Proposition 4.4 implies that
$y\in \mathbb{Q}$
, Proposition 4.4 implies that
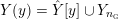 $Y(y)={\hat{Y}}[y]\cup Y_{n_{{\rm \small{g}}}}$
is not an L-space, and so
$Y(y)={\hat{Y}}[y]\cup Y_{n_{{\rm \small{g}}}}$
is not an L-space, and so
 ${\mathcal{L}}(Y)=\emptyset$
. Moreover, since there is
${\mathcal{L}}(Y)=\emptyset$
. Moreover, since there is
![]() $y\in \mathbb{Q}$
with
$y\in \mathbb{Q}$
with
 ${\mathcal{L}}({\hat{Y}}[y])=\emptyset$
, our inductive assumption for Proposition 4.7 tells us that either there is some
${\mathcal{L}}({\hat{Y}}[y])=\emptyset$
, our inductive assumption for Proposition 4.7 tells us that either there is some
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
for which
$i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
for which
![]() $Y_{i}$
is not Floer simple, or there is some Floer simple
$Y_{i}$
is not Floer simple, or there is some Floer simple
![]() $Y_{i}$
failing to satisfy
$Y_{i}$
failing to satisfy
 $\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
.
$\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
.
Thus, in either case, both Theorem 4.6 and Proposition 4.7 hold for
![]() $Y$
.
$Y$
.
4.7 Orientable base: cases in which
 ${\hat{Y}}[y]$
is never a solid torus
${\hat{Y}}[y]$
is never a solid torus
From now on, we assume that the JSJ component of
![]() $Y$
containing
$Y$
containing
![]() $\unicode[STIX]{x2202}Y$
has orientable base.
$\unicode[STIX]{x2202}Y$
has orientable base.
In this subsection of the proof, we consider the case in which
![]() ${\hat{Y}}[y]$
is not a solid torus for any
${\hat{Y}}[y]$
is not a solid torus for any
 $y\in \mathbb{Q}\cup \{\infty \}$
. More precisely, we consider the case of a fixed tree manifold
$y\in \mathbb{Q}\cup \{\infty \}$
. More precisely, we consider the case of a fixed tree manifold
![]() $Y$
with torus boundary and
$Y$
with torus boundary and
 $b_{1}(Y)=1$
, parameterized as in § 4.2, with tree height
$b_{1}(Y)=1$
, parameterized as in § 4.2, with tree height
![]() $k>0$
and
$k>0$
and
![]() $n_{{\rm \small{g}}}>0$
daughter subtrees, where we demand that if
$n_{{\rm \small{g}}}>0$
daughter subtrees, where we demand that if
 $n_{{\rm \small{g}}}-1=0$
, then
$n_{{\rm \small{g}}}-1=0$
, then
![]() $y_{i}^{{\rm \small{d}}}\notin \mathbb{Z}$
for at least two distinct values of
$y_{i}^{{\rm \small{d}}}\notin \mathbb{Z}$
for at least two distinct values of
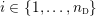 $i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
.
$i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
.
We begin by fixing some notation. For all
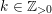 $k\in \mathbb{Z}_{{>}0}$
, define
$k\in \mathbb{Z}_{{>}0}$
, define
 ${\hat{y}}_{-}^{0}(k),{\hat{y}}_{+}^{0}(k)\in \mathbb{Q}\cup \{\infty \}$
by
${\hat{y}}_{-}^{0}(k),{\hat{y}}_{+}^{0}(k)\in \mathbb{Q}\cup \{\infty \}$
by
 $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle {\hat{y}}_{-}^{0}(k):=-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\\ \displaystyle {\hat{y}}_{+}^{0}(k):=-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle {\hat{y}}_{-}^{0}(k):=-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\\ \displaystyle {\hat{y}}_{+}^{0}(k):=-{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\end{array}\end{eqnarray}$$
The endpoints
 $y_{-},y_{+}\in \mathbb{Q}\cup \{\infty \}$
defined in Theorem 4.6 are then given by
$y_{-},y_{+}\in \mathbb{Q}\cup \{\infty \}$
defined in Theorem 4.6 are then given by
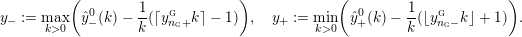 $$\begin{eqnarray}y_{-}:=\max _{k>0}\biggl({\hat{y}}_{-}^{0}(k)-\frac{1}{k}(\lceil y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\rceil -1)\biggr),\quad y_{+}:=\min _{k>0}\biggl({\hat{y}}_{+}^{0}(k)-\frac{1}{k}(\lfloor y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}y_{-}:=\max _{k>0}\biggl({\hat{y}}_{-}^{0}(k)-\frac{1}{k}(\lceil y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\rceil -1)\biggr),\quad y_{+}:=\min _{k>0}\biggl({\hat{y}}_{+}^{0}(k)-\frac{1}{k}(\lfloor y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\end{eqnarray}$$
Moreover, if we define the functions
 ${\hat{y}}_{-},{\hat{y}}_{+}\in \mathbb{Q}\cup \{\infty \}$
of
${\hat{y}}_{-},{\hat{y}}_{+}\in \mathbb{Q}\cup \{\infty \}$
of
 $y\in \mathbb{Q}\cup \{\infty \}$
by
$y\in \mathbb{Q}\cup \{\infty \}$
by
 $$\begin{eqnarray}{\hat{y}}_{-}:=\max _{k>0}\biggl(-\frac{1}{k}\lfloor yk\rfloor +{\hat{y}}_{-}^{0}(k)\biggr),\quad {\hat{y}}_{+}:=\min _{k>0}\biggl(-\frac{1}{k}\lceil yk\rceil +{\hat{y}}_{+}^{0}(k)\biggr),\end{eqnarray}$$
$$\begin{eqnarray}{\hat{y}}_{-}:=\max _{k>0}\biggl(-\frac{1}{k}\lfloor yk\rfloor +{\hat{y}}_{-}^{0}(k)\biggr),\quad {\hat{y}}_{+}:=\min _{k>0}\biggl(-\frac{1}{k}\lceil yk\rceil +{\hat{y}}_{+}^{0}(k)\biggr),\end{eqnarray}$$
then by inductive assumption, we have
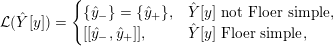 $$\begin{eqnarray}{\mathcal{L}}({\hat{Y}}[y])=\left\{\begin{array}{@{}ll@{}}\{{\hat{y}}_{-}\}=\{{\hat{y}}_{+}\},\quad & {\hat{Y}}[y]\text{ not Floer simple},\\ \text{}[[{\hat{y}}_{-},{\hat{y}}_{+}]],\quad & {\hat{Y}}[y]\;\text{Floer simple},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}({\hat{Y}}[y])=\left\{\begin{array}{@{}ll@{}}\{{\hat{y}}_{-}\}=\{{\hat{y}}_{+}\},\quad & {\hat{Y}}[y]\text{ not Floer simple},\\ \text{}[[{\hat{y}}_{-},{\hat{y}}_{+}]],\quad & {\hat{Y}}[y]\;\text{Floer simple},\end{array}\right.\end{eqnarray}$$
for all
![]() $y\in \mathbb{Q}$
for which
$y\in \mathbb{Q}$
for which
 ${\mathcal{L}}({\hat{Y}}[y])\neq \emptyset$
. Since
${\mathcal{L}}({\hat{Y}}[y])\neq \emptyset$
. Since
![]() ${\hat{Y}}[y]$
and
${\hat{Y}}[y]$
and
![]() $Y_{n_{{\rm \small{g}}}}$
are each non-solid-torus graph manifolds for all
$Y_{n_{{\rm \small{g}}}}$
are each non-solid-torus graph manifolds for all
![]() $y\in \mathbb{Q}$
, Proposition 4.4 then implies, for each
$y\in \mathbb{Q}$
, Proposition 4.4 then implies, for each
![]() $y\in \mathbb{Q}$
, that
$y\in \mathbb{Q}$
, that
 $$\begin{eqnarray}y\in {\mathcal{L}}(Y)\quad \;\Longleftrightarrow \;\quad {\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=\mathbb{Q}\cup \{\infty \}\end{eqnarray}$$
$$\begin{eqnarray}y\in {\mathcal{L}}(Y)\quad \;\Longleftrightarrow \;\quad {\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=\mathbb{Q}\cup \{\infty \}\end{eqnarray}$$
for all
![]() $y\in \mathbb{Q}$
. Note that
$y\in \mathbb{Q}$
. Note that
![]() ${\hat{Y}}[\infty ]$
is not a graph manifold, being a non-solid-torus with compressible boundary, hence not prime.
${\hat{Y}}[\infty ]$
is not a graph manifold, being a non-solid-torus with compressible boundary, hence not prime.
We next prove some basic rules about the behavior of
![]() $y_{-}$
and
$y_{-}$
and
![]() $y_{+}$
.
$y_{+}$
.
Claim 1. If
 $y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}},{\hat{y}}_{-},y_{-},y\in \mathbb{Q}$
, then
$y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}},{\hat{y}}_{-},y_{-},y\in \mathbb{Q}$
, then
 $$\begin{eqnarray}y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}\quad \;\Longleftrightarrow \;\quad y\in [y_{-},+\infty ].\end{eqnarray}$$
$$\begin{eqnarray}y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}\quad \;\Longleftrightarrow \;\quad y\in [y_{-},+\infty ].\end{eqnarray}$$
If
 $y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},{\hat{y}}_{+},y_{+},y\in \mathbb{Q}$
, then
$y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},{\hat{y}}_{+},y_{+},y\in \mathbb{Q}$
, then
 $$\begin{eqnarray}y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}<{\hat{y}}_{+}\quad \;\Longleftrightarrow \;\quad y\in [-\infty ,y_{+}].\end{eqnarray}$$
$$\begin{eqnarray}y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}<{\hat{y}}_{+}\quad \;\Longleftrightarrow \;\quad y\in [-\infty ,y_{+}].\end{eqnarray}$$
Proof of Claim 1.
Suppose that
 $y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}},{\hat{y}}_{-},y_{-},y\in \mathbb{Q}$
. Then
$y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}},{\hat{y}}_{-},y_{-},y\in \mathbb{Q}$
. Then
 $$\begin{eqnarray}\displaystyle & \displaystyle y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-} & \displaystyle \nonumber\\ \displaystyle \displaystyle \;\Longleftrightarrow \; & y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>-\frac{1}{k}\lfloor yk\rfloor +{\hat{y}}_{-}^{0}(k) & \displaystyle \forall k\in \mathbb{Z}_{{>}0}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-} & \displaystyle \nonumber\\ \displaystyle \displaystyle \;\Longleftrightarrow \; & y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>-\frac{1}{k}\lfloor yk\rfloor +{\hat{y}}_{-}^{0}(k) & \displaystyle \forall k\in \mathbb{Z}_{{>}0}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \;\Longleftrightarrow \; & \lceil y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\rceil -1\geqslant -\lfloor yk\rfloor +{\hat{y}}_{-}^{0}(k)k & \displaystyle \forall k\in \mathbb{Z}_{{>}0}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \;\Longleftrightarrow \; & \lceil y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\rceil -1\geqslant -\lfloor yk\rfloor +{\hat{y}}_{-}^{0}(k)k & \displaystyle \forall k\in \mathbb{Z}_{{>}0}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \;\Longleftrightarrow \; & yk\geqslant {\hat{y}}_{-}^{0}(k)k-(\lceil y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\rceil -1) & \displaystyle \forall k\in \mathbb{Z}_{{>}0}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \;\Longleftrightarrow \; & yk\geqslant {\hat{y}}_{-}^{0}(k)k-(\lceil y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\rceil -1) & \displaystyle \forall k\in \mathbb{Z}_{{>}0}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \;\Longleftrightarrow \; & y\geqslant y_{-}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \;\Longleftrightarrow \; & y\geqslant y_{-}, & \displaystyle\end{eqnarray}$$
where (37) implies (43), (22) implies (44), (21) implies (45), and (38) implies (46). The proof of (42) is nearly identical, but with signs reversed.◻
Claim 2. If
 $y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\in \mathbb{Q},$
then
$y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\in \mathbb{Q},$
then
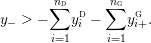 $$\begin{eqnarray}y_{-}>-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}y_{i+}^{{\rm \small{g}}}.\end{eqnarray}$$
$$\begin{eqnarray}y_{-}>-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}y_{i+}^{{\rm \small{g}}}.\end{eqnarray}$$
If
 $y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}},y_{1-}^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}\in \mathbb{Q},$
then
$y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}},y_{1-}^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}\in \mathbb{Q},$
then
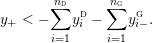 $$\begin{eqnarray}y_{+}<-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}y_{i-}^{{\rm \small{g}}}.\end{eqnarray}$$
$$\begin{eqnarray}y_{+}<-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}y_{i-}^{{\rm \small{g}}}.\end{eqnarray}$$
Proof of Claim 2.
Writing
 $[\cdot ]:\mathbb{Q}\rightarrow [0,1\rangle$
for the map sending
$[\cdot ]:\mathbb{Q}\rightarrow [0,1\rangle$
for the map sending
 $q\mapsto [q]:=q-\lfloor q\rfloor$
, define
$q\mapsto [q]:=q-\lfloor q\rfloor$
, define
 $$\begin{eqnarray}y_{-}^{\prime }(k):={\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}[y_{i}^{{\rm \small{d}}}k]+\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(1-[-y_{i+}^{{\rm \small{g}}}k])\biggr)\end{eqnarray}$$
$$\begin{eqnarray}y_{-}^{\prime }(k):={\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}[y_{i}^{{\rm \small{d}}}k]+\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(1-[-y_{i+}^{{\rm \small{g}}}k])\biggr)\end{eqnarray}$$
for each
 $k\in \mathbb{Z}_{{>}0}$
, so that
$k\in \mathbb{Z}_{{>}0}$
, so that
 $$\begin{eqnarray}y_{-}=-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}y_{i+}^{{\rm \small{g}}}+\max _{k>0}y_{-}^{\prime }(k).\end{eqnarray}$$
$$\begin{eqnarray}y_{-}=-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\!\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}y_{i+}^{{\rm \small{g}}}+\max _{k>0}y_{-}^{\prime }(k).\end{eqnarray}$$
In addition, let
 $$\begin{eqnarray}s_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{1}^{{\rm \small{d}}}k,\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{ d}}}k,y_{1+}^{{\rm \small{g}}}k,\ldots ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\in \mathbb{Z}\}\end{eqnarray}$$
$$\begin{eqnarray}s_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{1}^{{\rm \small{d}}}k,\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{ d}}}k,y_{1+}^{{\rm \small{g}}}k,\ldots ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}k\in \mathbb{Z}\}\end{eqnarray}$$
denote the least common positive multiple of the denominators of the
![]() $\{y_{i}^{{\rm \small{d}}}\}$
and
$\{y_{i}^{{\rm \small{d}}}\}$
and
![]() $\{y_{i+}^{{\rm \small{g}}}\}$
.
$\{y_{i+}^{{\rm \small{g}}}\}$
.
Suppose (47) fails to hold. Then since
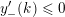 $y_{-}^{\prime }(k)\leqslant 0$
for all
$y_{-}^{\prime }(k)\leqslant 0$
for all
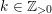 $k\in \mathbb{Z}_{{>}0}$
, we have
$k\in \mathbb{Z}_{{>}0}$
, we have
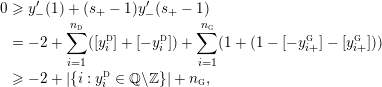 $$\begin{eqnarray}\displaystyle 0 & {\geqslant} & \displaystyle y_{-}^{\prime }(1)+(s_{+}-1)y_{-}^{\prime }(s_{+}-1)\nonumber\\ \displaystyle & = & \displaystyle -2+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}([y_{i}^{{\rm \small{d}}}]+[-y_{i}^{{\rm \small{d}}}])+\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(1+(1-[-y_{i+}^{{\rm \small{g}}}]-[y_{i+}^{{\rm \small{g}}}]))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle -2+|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|+n_{{\rm \small{g}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & {\geqslant} & \displaystyle y_{-}^{\prime }(1)+(s_{+}-1)y_{-}^{\prime }(s_{+}-1)\nonumber\\ \displaystyle & = & \displaystyle -2+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}([y_{i}^{{\rm \small{d}}}]+[-y_{i}^{{\rm \small{d}}}])+\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(1+(1-[-y_{i+}^{{\rm \small{g}}}]-[y_{i+}^{{\rm \small{g}}}]))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle -2+|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|+n_{{\rm \small{g}}},\end{eqnarray}$$
and likewise, we have
 $$\begin{eqnarray}0\geqslant s_{+}y_{-}^{\prime }(s_{+})=-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}1=n_{{\rm \small{g}}}-1.\end{eqnarray}$$
$$\begin{eqnarray}0\geqslant s_{+}y_{-}^{\prime }(s_{+})=-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}1=n_{{\rm \small{g}}}-1.\end{eqnarray}$$
The hypotheses of § 4.7, however, demand that either
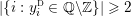 $|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|\geqslant 2$
and
$|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|\geqslant 2$
and
![]() $n_{{\rm \small{g}}}=1$
, contradicting (52), or
$n_{{\rm \small{g}}}=1$
, contradicting (52), or
![]() $n_{{\rm \small{g}}}\!>\!1$
, contradicting (53). Thus (47) holds, and a similar argument proves (48).◻
$n_{{\rm \small{g}}}\!>\!1$
, contradicting (53). Thus (47) holds, and a similar argument proves (48).◻
For the proof that Theorem 4.6 and Proposition 4.7 hold for
![]() $Y$
, we divide our argument into two main cases, depending on whether or not
$Y$
, we divide our argument into two main cases, depending on whether or not
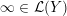 $\infty \in {\mathcal{L}}(Y)$
.
$\infty \in {\mathcal{L}}(Y)$
.
Proposition 4.8.
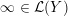 $\infty \in {\mathcal{L}}(Y)$
if and only if either condition
$\infty \in {\mathcal{L}}(Y)$
if and only if either condition
![]() $({\rm \small{fs3}})$
from Proposition 4.7 holds, in which case
$({\rm \small{fs3}})$
from Proposition 4.7 holds, in which case
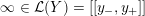 $\infty \in {\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, or condition
$\infty \in {\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, or condition
![]() $({\rm \small{nfs3}})$
or
$({\rm \small{nfs3}})$
or
![]() $({\rm \small{nfs4}})$
from Proposition 4.7 holds, in which case
$({\rm \small{nfs4}})$
from Proposition 4.7 holds, in which case
 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}=\{\infty \}$
.
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}=\{\infty \}$
.
Proof. Since
![]() ${\hat{Y}}[\infty ]$
is not a graph manifold, our inductive assumptions fail to hold for
${\hat{Y}}[\infty ]$
is not a graph manifold, our inductive assumptions fail to hold for
![]() ${\hat{Y}}[\infty ]$
, but fortunately,
${\hat{Y}}[\infty ]$
, but fortunately,
![]() $Y(\infty )$
has a simple structure. The remark in § 2.2 implies
$Y(\infty )$
has a simple structure. The remark in § 2.2 implies
 $$\begin{eqnarray}Y(\infty )=\biggl(\#_{i=1}^{n_{{\rm \small{d}}}}L(s_{i}^{{\rm \small{d}}},r_{i}^{{\rm \small{d}}})\biggr)\#\biggl(\#_{i=1}^{n_{{\rm \small{g}}}}Y_{i}((\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}})^{-1}(\infty ))\biggr),\end{eqnarray}$$
$$\begin{eqnarray}Y(\infty )=\biggl(\#_{i=1}^{n_{{\rm \small{d}}}}L(s_{i}^{{\rm \small{d}}},r_{i}^{{\rm \small{d}}})\biggr)\#\biggl(\#_{i=1}^{n_{{\rm \small{g}}}}Y_{i}((\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}})^{-1}(\infty ))\biggr),\end{eqnarray}$$
where we have written
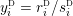 $y_{i}^{{\rm \small{d}}}=r_{i}^{{\rm \small{d}}}/s_{i}^{{\rm \small{d}}}$
,
$y_{i}^{{\rm \small{d}}}=r_{i}^{{\rm \small{d}}}/s_{i}^{{\rm \small{d}}}$
,
 $L(s_{i}^{{\rm \small{d}}},r_{i}^{{\rm \small{d}}})$
denotes the lens space of slope
$L(s_{i}^{{\rm \small{d}}},r_{i}^{{\rm \small{d}}})$
denotes the lens space of slope
![]() $s_{i}^{{\rm \small{d}}}/r_{i}^{{\rm \small{d}}}$
, and
$s_{i}^{{\rm \small{d}}}/r_{i}^{{\rm \small{d}}}$
, and
 $Y_{i}((\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}})^{-1}(\infty ))$
is the Dehn filling of the inverse image of the slope
$Y_{i}((\unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}})^{-1}(\infty ))$
is the Dehn filling of the inverse image of the slope
![]() $\infty$
. Thus,
$\infty$
. Thus,
 $$\begin{eqnarray}\infty \in {\mathcal{L}}(Y)~\;\Longleftrightarrow \;~\infty \in \unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i}))\quad \text{for all }i\in \{1,\ldots ,n_{{\rm \small{g}}}\}.\end{eqnarray}$$
$$\begin{eqnarray}\infty \in {\mathcal{L}}(Y)~\;\Longleftrightarrow \;~\infty \in \unicode[STIX]{x1D711}_{i\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{i}))\quad \text{for all }i\in \{1,\ldots ,n_{{\rm \small{g}}}\}.\end{eqnarray}$$
Conditions
![]() $({\rm \small{nfs3}})$
and
$({\rm \small{nfs3}})$
and
![]() $({\rm \small{fs3}})$
jointly exhaust the cases in which the right-hand condition of (55) holds and all daughter subtrees
$({\rm \small{fs3}})$
jointly exhaust the cases in which the right-hand condition of (55) holds and all daughter subtrees
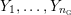 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple. Condition
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
are Floer simple. Condition
![]() $({\rm \small{nfs4}})$
, on the other hand, describes all cases in which the right-hand condition of (55) holds and at least one
$({\rm \small{nfs4}})$
, on the other hand, describes all cases in which the right-hand condition of (55) holds and at least one
![]() $Y_{j}$
is not Floer simple.
$Y_{j}$
is not Floer simple.
If
![]() $({\rm \small{nfs4}})$
holds, then, permuting the daughter subtrees without loss of generality so that
$({\rm \small{nfs4}})$
holds, then, permuting the daughter subtrees without loss of generality so that
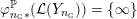 $\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{n_{{\rm \small{g}}}}))=\{\infty \}$
, we have
$\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{n_{{\rm \small{g}}}}))=\{\infty \}$
, we have
 ${\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}})=\emptyset$
, which, by (40), implies
${\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}})=\emptyset$
, which, by (40), implies
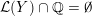 ${\mathcal{L}}(Y)\cap \mathbb{Q}=\emptyset$
, so that
${\mathcal{L}}(Y)\cap \mathbb{Q}=\emptyset$
, so that
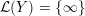 ${\mathcal{L}}(Y)=\{\infty \}$
. Moreover, the fact that
${\mathcal{L}}(Y)=\{\infty \}$
. Moreover, the fact that
 $\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{n_{{\rm \small{g}}}}))=\{\infty \}$
implies, by inductive assumption, that
$\unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{n_{{\rm \small{g}}}}))=\{\infty \}$
implies, by inductive assumption, that
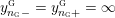 $y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}=y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}=\infty$
. Thus
$y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}=y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}=\infty$
. Thus
![]() $y_{-}$
and
$y_{-}$
and
![]() $y_{+}$
each have infinite summands, and so
$y_{+}$
each have infinite summands, and so
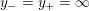 $y_{-}=y_{+}=\infty$
.
$y_{-}=y_{+}=\infty$
.
Next suppose that
![]() $({\rm \small{nfs3}})$
holds, and set
$({\rm \small{nfs3}})$
holds, and set
 $$\begin{eqnarray}I_{-\infty }:=\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[-\infty ,y_{i+}^{{\rm \small{g}}}]\},\quad I_{+\infty }:=\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\}.\end{eqnarray}$$
$$\begin{eqnarray}I_{-\infty }:=\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[-\infty ,y_{i+}^{{\rm \small{g}}}]\},\quad I_{+\infty }:=\{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\}.\end{eqnarray}$$
We can also define the analogous sets for
![]() ${\hat{Y}}[y]$
:
${\hat{Y}}[y]$
:
 $$\begin{eqnarray}I_{-\infty }^{{\hat{Y}}[y]}:=I_{-\infty }\cap \{1,\ldots ,n_{{\rm \small{g}}}-1\},\quad I_{+\infty }^{{\hat{Y}}[y]}:=I_{+\infty }\cap \{1,\ldots ,n_{{\rm \small{g}}}-1\}.\end{eqnarray}$$
$$\begin{eqnarray}I_{-\infty }^{{\hat{Y}}[y]}:=I_{-\infty }\cap \{1,\ldots ,n_{{\rm \small{g}}}-1\},\quad I_{+\infty }^{{\hat{Y}}[y]}:=I_{+\infty }\cap \{1,\ldots ,n_{{\rm \small{g}}}-1\}.\end{eqnarray}$$
Since
![]() $I_{-\infty }$
and
$I_{-\infty }$
and
![]() $I_{+\infty }$
are non-empty for
$I_{+\infty }$
are non-empty for
![]() $({\rm \small{nfs3}})$
, we know that
$({\rm \small{nfs3}})$
, we know that
![]() $y_{-}$
and
$y_{-}$
and
![]() $y_{+}$
each have infinite summands, implying
$y_{+}$
each have infinite summands, implying
 $y_{-}=y_{+}=\infty$
. Assume without loss of generality that
$y_{-}=y_{+}=\infty$
. Assume without loss of generality that
 $n_{{\rm \small{g}}}\in I_{+\infty }$
. Thus
$n_{{\rm \small{g}}}\in I_{+\infty }$
. Thus
 $I_{-\infty }^{{\hat{Y}}[y]}\neq \emptyset$
, and
$I_{-\infty }^{{\hat{Y}}[y]}\neq \emptyset$
, and
![]() $I_{+\infty }^{{\hat{Y}}[y]}$
is either empty or not. By inductive assumption, Proposition 4.7 holds for
$I_{+\infty }^{{\hat{Y}}[y]}$
is either empty or not. By inductive assumption, Proposition 4.7 holds for
![]() ${\hat{Y}}[y]$
for all
${\hat{Y}}[y]$
for all
![]() $y\in \mathbb{Q}$
. Thus, for each
$y\in \mathbb{Q}$
. Thus, for each
![]() $y\in \mathbb{Q}$
, either
$y\in \mathbb{Q}$
, either
![]() $I_{-\infty }^{{\hat{Y}}[y]}$
and
$I_{-\infty }^{{\hat{Y}}[y]}$
and
![]() $I_{+\infty }^{{\hat{Y}}[y]}$
are both non-empty, making
$I_{+\infty }^{{\hat{Y}}[y]}$
are both non-empty, making
![]() $({\rm \small{nfs3}})$
hold for
$({\rm \small{nfs3}})$
hold for
![]() ${\hat{Y}}[y]$
, so that
${\hat{Y}}[y]$
, so that
 ${\mathcal{L}}({\hat{Y}}[y])=\{\infty \}$
; or
${\mathcal{L}}({\hat{Y}}[y])=\{\infty \}$
; or
 $I_{-\infty }^{{\hat{Y}}[y]}\neq \emptyset$
and
$I_{-\infty }^{{\hat{Y}}[y]}\neq \emptyset$
and
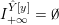 $I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
, making
$I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
, making
![]() $({\rm \small{fs3}})$
hold for
$({\rm \small{fs3}})$
hold for
![]() ${\hat{Y}}[y]$
, so that
${\hat{Y}}[y]$
, so that
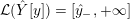 ${\mathcal{L}}({\hat{Y}}[y])=[{\hat{y}}_{-},+\infty ]$
. In both cases, the right-hand side of (40) fails to hold for all
${\mathcal{L}}({\hat{Y}}[y])=[{\hat{y}}_{-},+\infty ]$
. In both cases, the right-hand side of (40) fails to hold for all
![]() $y\in \mathbb{Q}$
, and we are left with
$y\in \mathbb{Q}$
, and we are left with
 ${\mathcal{L}}(Y)=\{\infty \}=\{y_{-}\}=\{y_{+}\}$
.
${\mathcal{L}}(Y)=\{\infty \}=\{y_{-}\}=\{y_{+}\}$
.
This leaves us with the case in which
![]() $({\rm \small{fs3}})$
holds, for which we first consider the subcase
$({\rm \small{fs3}})$
holds, for which we first consider the subcase
 $I_{+\infty }=\emptyset$
and
$I_{+\infty }=\emptyset$
and
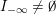 $I_{-\infty }\neq \emptyset$
, implying
$I_{-\infty }\neq \emptyset$
, implying
 $[[y_{-},y_{+}]]=[y_{-},+\infty ]$
. Without loss of generality, assume
$[[y_{-},y_{+}]]=[y_{-},+\infty ]$
. Without loss of generality, assume
 $n_{{\rm \small{g}}}\in I_{-\infty }$
, so that
$n_{{\rm \small{g}}}\in I_{-\infty }$
, so that
 $[[y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}]]=[-\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}]$
. Since
$[[y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}]]=[-\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}]$
. Since
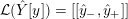 ${\mathcal{L}}({\hat{Y}}[y])=[[{\hat{y}}_{-},{\hat{y}}_{+}]]$
for all
${\mathcal{L}}({\hat{Y}}[y])=[[{\hat{y}}_{-},{\hat{y}}_{+}]]$
for all
![]() $y\in \mathbb{Q}$
by inductive assumption, we know that either:
$y\in \mathbb{Q}$
by inductive assumption, we know that either:
-
(a)
 $I_{-\infty }^{{\hat{Y}}[y]}=I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
; or
$I_{-\infty }^{{\hat{Y}}[y]}=I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
; or -
(b)
 $I_{-\infty }^{{\hat{Y}}[y]}\neq \emptyset$
, with
$I_{-\infty }^{{\hat{Y}}[y]}\neq \emptyset$
, with
 ${\mathcal{L}}({\hat{Y}}[y])=[{\hat{y}}_{-},+\infty ]$
.
${\mathcal{L}}({\hat{Y}}[y])=[{\hat{y}}_{-},+\infty ]$
.
In case (a), the condition
 $I_{-\infty }^{{\hat{Y}}[y]}=I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
, together with (55), implies
$I_{-\infty }^{{\hat{Y}}[y]}=I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
, together with (55), implies
 $$\begin{eqnarray}\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty \quad \text{for all }i\in \{1,\ldots ,n_{{\rm \small{ g}}}-1\}.\end{eqnarray}$$
$$\begin{eqnarray}\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty \quad \text{for all }i\in \{1,\ldots ,n_{{\rm \small{ g}}}-1\}.\end{eqnarray}$$
Thus, if we apply Claim 2 to (38), respectively substituting
![]() ${\hat{y}}_{-}$
,
${\hat{y}}_{-}$
,
![]() ${\hat{y}}_{+}$
,
${\hat{y}}_{+}$
,
![]() $n_{{\rm \small{d}}}+1$
,
$n_{{\rm \small{d}}}+1$
,
![]() $n_{{\rm \small{g}}}-1$
, and
$n_{{\rm \small{g}}}-1$
, and
 $(y,y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
for
$(y,y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
for
![]() $y_{-}$
,
$y_{-}$
,
![]() $y_{+}$
,
$y_{+}$
,
![]() $n_{{\rm \small{d}}}$
,
$n_{{\rm \small{d}}}$
,
![]() $n_{{\rm \small{g}}}$
and
$n_{{\rm \small{g}}}$
and
 $(y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
in the statement of the claim, then we obtain
$(y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})$
in the statement of the claim, then we obtain
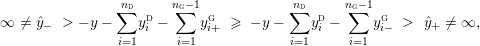 $$\begin{eqnarray}\infty \neq {\hat{y}}_{-}~>-y-\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}y_{i+}^{{\rm \small{g}}}\;\geqslant \;-y-\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}y_{i-}^{{\rm \small{g}}}\;>~{\hat{y}}_{+}\neq \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\infty \neq {\hat{y}}_{-}~>-y-\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}y_{i+}^{{\rm \small{g}}}\;\geqslant \;-y-\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}y_{i}^{{\rm \small{d}}}-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}-1}y_{i-}^{{\rm \small{g}}}\;>~{\hat{y}}_{+}\neq \infty ,\end{eqnarray}$$
with the outer, strict, inequalities resulting from Claim 2, and the middle, non-strict, inequality resulting from (58). Thus, for any
![]() $y\in \mathbb{Q}$
, we have
$y\in \mathbb{Q}$
, we have
 $$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=(\langle {\hat{y}}_{-},+\infty ]\cup [-\infty ,{\hat{y}}_{+}\rangle )\cup \langle -\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\rangle\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=(\langle {\hat{y}}_{-},+\infty ]\cup [-\infty ,{\hat{y}}_{+}\rangle )\cup \langle -\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\rangle\end{eqnarray}$$
by inductive assumption, and so (40) implies that
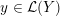 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
 $y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
, which, by Claim 1, occurs if and only if
$y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
, which, by Claim 1, occurs if and only if
 $y\in [y_{-},+\infty ]$
. On the other hand, in case (b), with
$y\in [y_{-},+\infty ]$
. On the other hand, in case (b), with
 ${\mathcal{L}}^{\circ }({\hat{Y}}[y])=\langle {\hat{y}}_{-},+\infty \rangle$
, (40) again implies, for any
${\mathcal{L}}^{\circ }({\hat{Y}}[y])=\langle {\hat{y}}_{-},+\infty \rangle$
, (40) again implies, for any
![]() $y\in \mathbb{Q}$
, that
$y\in \mathbb{Q}$
, that
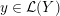 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
 $y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
, which again occurs if and only if
$y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
, which again occurs if and only if
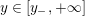 $y\in [y_{-},+\infty ]$
. Thus, whether case (a) or (b) holds, we always have
$y\in [y_{-},+\infty ]$
. Thus, whether case (a) or (b) holds, we always have
 $\infty \in {\mathcal{L}}(Y)=[y_{-},+\infty ]=[[y_{-},y_{+}]]$
.
$\infty \in {\mathcal{L}}(Y)=[y_{-},+\infty ]=[[y_{-},y_{+}]]$
.
If
![]() $({\rm \small{fs3}})$
holds with
$({\rm \small{fs3}})$
holds with
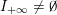 $I_{+\infty }\neq \emptyset$
and
$I_{+\infty }\neq \emptyset$
and
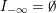 $I_{-\infty }=\emptyset$
, then an argument precisely analogous to that in the preceding paragraph shows that
$I_{-\infty }=\emptyset$
, then an argument precisely analogous to that in the preceding paragraph shows that
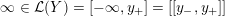 $\infty \in {\mathcal{L}}(Y)=[-\infty ,y_{+}]=[[y_{-},y_{+}]]$
.
$\infty \in {\mathcal{L}}(Y)=[-\infty ,y_{+}]=[[y_{-},y_{+}]]$
.
Lastly, suppose that
![]() $({\rm \small{fs3}})$
holds with
$({\rm \small{fs3}})$
holds with
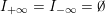 $I_{+\infty }=I_{-\infty }=\emptyset$
. This, as well as the fact that
$I_{+\infty }=I_{-\infty }=\emptyset$
. This, as well as the fact that
![]() $\infty \in$
$\infty \in$
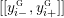 $[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]$
for each
$[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]$
for each
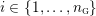 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, implies that
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, implies that
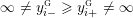 $\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
for all
$\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, which, by Claim 2, implies that
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
, which, by Claim 2, implies that
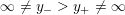 $\infty \neq y_{-}>y_{+}\neq \infty$
. Moreover, applying Claim 2 to (38) as in case (a) above yields (59), so that we also have
$\infty \neq y_{-}>y_{+}\neq \infty$
. Moreover, applying Claim 2 to (38) as in case (a) above yields (59), so that we also have
 $\infty \neq {\hat{y}}_{-}>{\hat{y}}_{+}\neq \infty$
. By inductive assumption, we then have
$\infty \neq {\hat{y}}_{-}>{\hat{y}}_{+}\neq \infty$
. By inductive assumption, we then have
 $$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=(\langle {\hat{y}}_{-},+\infty ]\cup [-\infty ,{\hat{y}}_{+}\rangle )\cup (\langle y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},+\infty ]\cup [-\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\rangle )\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \unicode[STIX]{x1D711}_{n_{{\rm \small{g}}}\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}}))=(\langle {\hat{y}}_{-},+\infty ]\cup [-\infty ,{\hat{y}}_{+}\rangle )\cup (\langle y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},+\infty ]\cup [-\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\rangle )\end{eqnarray}$$
for any
![]() $y\in \mathbb{Q}$
, and so (40) implies that
$y\in \mathbb{Q}$
, and so (40) implies that
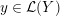 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
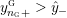 $y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
or
$y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
or
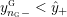 $y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}<{\hat{y}}_{+}$
which, by Claim 1, occurs if and only if
$y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}<{\hat{y}}_{+}$
which, by Claim 1, occurs if and only if
 $y\in [y_{-},+\infty ]\cup [-\infty ,y_{+}]$
. We therefore have
$y\in [y_{-},+\infty ]\cup [-\infty ,y_{+}]$
. We therefore have
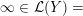 $\infty \in {\mathcal{L}}(Y)=$
$\infty \in {\mathcal{L}}(Y)=$
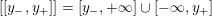 $[[y_{-},y_{+}]]=[y_{-},+\infty ]\cup [-\infty ,y_{+}]$
, completing our proof.◻
$[[y_{-},y_{+}]]=[y_{-},+\infty ]\cup [-\infty ,y_{+}]$
, completing our proof.◻
Proposition 4.9. Suppose
 $\infty \notin {\mathcal{L}}(Y)$
. Then
$\infty \notin {\mathcal{L}}(Y)$
. Then
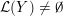 ${\mathcal{L}}(Y)\neq \emptyset$
if and only if either
${\mathcal{L}}(Y)\neq \emptyset$
if and only if either
![]() $({\rm \small{nfs2}})$
holds for
$({\rm \small{nfs2}})$
holds for
![]() $Y$
, in which case
$Y$
, in which case
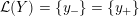 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
, or
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
, or
![]() $({\rm \small{fs1}})$
or
$({\rm \small{fs1}})$
or
![]() $({\rm \small{fs2}})$
holds for
$({\rm \small{fs2}})$
holds for
![]() $Y$
, in which case
$Y$
, in which case
 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
Proof. We first observe that if any daughter subtree of
![]() $Y$
fails to be Floer simple, then
$Y$
fails to be Floer simple, then
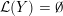 ${\mathcal{L}}(Y)=\emptyset$
. That if we choose
${\mathcal{L}}(Y)=\emptyset$
. That if we choose
![]() $Y_{n_{{\rm \small{g}}}}$
to be non-Floer-simple, then by (40),
$Y_{n_{{\rm \small{g}}}}$
to be non-Floer-simple, then by (40),
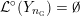 ${\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}})=\emptyset$
implies
${\mathcal{L}}^{\circ }(Y_{n_{{\rm \small{g}}}})=\emptyset$
implies
 ${\mathcal{L}}(Y)\cap \mathbb{Q}=\emptyset$
, which, since
${\mathcal{L}}(Y)\cap \mathbb{Q}=\emptyset$
, which, since
 $\infty \notin {\mathcal{L}}(Y)$
, implies
$\infty \notin {\mathcal{L}}(Y)$
, implies
 ${\mathcal{L}}(Y)=\emptyset$
. Thus, we henceforth assume the daughter subtrees
${\mathcal{L}}(Y)=\emptyset$
. Thus, we henceforth assume the daughter subtrees
![]() $Y_{1}$
, …,
$Y_{1}$
, …,
![]() $Y_{n_{{\rm \small{g}}}}$
are all Floer simple.
$Y_{n_{{\rm \small{g}}}}$
are all Floer simple.
Let
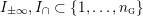 $I_{\pm \infty },I_{\cap }\subset \{1,\ldots ,n_{{\rm \small{g}}}\}$
denote the sets
$I_{\pm \infty },I_{\cap }\subset \{1,\ldots ,n_{{\rm \small{g}}}\}$
denote the sets
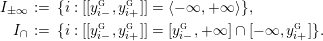 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}\displaystyle I_{\pm \infty } & \!\!\!:=\!\!\!\! & \{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle \},\\ \displaystyle I_{\cap } & \!\!\!:=\!\!\!\! & \{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\cap [-\infty ,y_{i+}^{{\rm \small{g}}}]\}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\displaystyle I_{\pm \infty } & \!\!\!:=\!\!\!\! & \{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle \},\\ \displaystyle I_{\cap } & \!\!\!:=\!\!\!\! & \{i:[[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]=[y_{i-}^{{\rm \small{g}}},+\infty ]\cap [-\infty ,y_{i+}^{{\rm \small{g}}}]\}.\end{array}\end{eqnarray}$$
Then by (55) from the proof of Proposition 4.8, we know that
 $$\begin{eqnarray}I_{\pm \infty }\cup I_{\cap }\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}I_{\pm \infty }\cup I_{\cap }\neq \emptyset .\end{eqnarray}$$
Suppose
 $I_{\pm \infty }\neq \emptyset$
. We claim that in this case,
$I_{\pm \infty }\neq \emptyset$
. We claim that in this case,
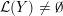 ${\mathcal{L}}(Y)\neq \emptyset$
if and only if
${\mathcal{L}}(Y)\neq \emptyset$
if and only if
![]() $({\rm \small{fs1}})$
holds for
$({\rm \small{fs1}})$
holds for
![]() $Y$
, in which case
$Y$
, in which case
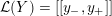 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
. First note that
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
. First note that
![]() $Y$
fails to satisfy any of the conditions for non-empty
$Y$
fails to satisfy any of the conditions for non-empty
![]() ${\mathcal{L}}(Y)$
in Proposition 4.7, except possibly
${\mathcal{L}}(Y)$
in Proposition 4.7, except possibly
![]() $({\rm \small{fs1}})$
. Suppose that
$({\rm \small{fs1}})$
. Suppose that
![]() $Y$
satisfies
$Y$
satisfies
![]() $({\rm \small{fs1}})$
. Then for each
$({\rm \small{fs1}})$
. Then for each
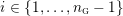 $i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, we have
$i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, we have
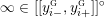 $\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]^{\circ }$
, implying
$\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]^{\circ }$
, implying
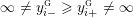 $\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
, which by Claim 2 implies
$\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
, which by Claim 2 implies
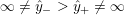 $\infty \neq {\hat{y}}_{-}>{\hat{y}}_{+}\neq \infty$
for all
$\infty \neq {\hat{y}}_{-}>{\hat{y}}_{+}\neq \infty$
for all
![]() $y\in \mathbb{Q}$
. By inductive assumption, we then have
$y\in \mathbb{Q}$
. By inductive assumption, we then have
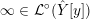 $\infty \in {\mathcal{L}}^{\circ }({\hat{Y}}[y])$
for all
$\infty \in {\mathcal{L}}^{\circ }({\hat{Y}}[y])$
for all
![]() $y\in \mathbb{Q}$
. Thus, since (40) tells us that
$y\in \mathbb{Q}$
. Thus, since (40) tells us that
 $$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \langle -\infty ,+\infty \rangle =\mathbb{Q}\cup \{\infty \}\quad \;\Longleftrightarrow \;\quad y\in {\mathcal{L}}(Y),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}^{\circ }({\hat{Y}}[y])\cup \langle -\infty ,+\infty \rangle =\mathbb{Q}\cup \{\infty \}\quad \;\Longleftrightarrow \;\quad y\in {\mathcal{L}}(Y),\end{eqnarray}$$
we have
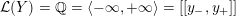 ${\mathcal{L}}(Y)=\mathbb{Q}=\langle -\infty ,+\infty \rangle =[[y_{-},y_{+}]]$
. Suppose instead we are given that
${\mathcal{L}}(Y)=\mathbb{Q}=\langle -\infty ,+\infty \rangle =[[y_{-},y_{+}]]$
. Suppose instead we are given that
 ${\mathcal{L}}(Y)\neq \emptyset$
. Then (64) tells us that
${\mathcal{L}}(Y)\neq \emptyset$
. Then (64) tells us that
 $\infty \in {\mathcal{L}}^{\circ }({\hat{Y}}[y])$
for all
$\infty \in {\mathcal{L}}^{\circ }({\hat{Y}}[y])$
for all
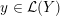 $y\in {\mathcal{L}}(Y)$
. By inductive assumption this implies, for each
$y\in {\mathcal{L}}(Y)$
. By inductive assumption this implies, for each
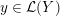 $y\in {\mathcal{L}}(Y)$
, that
$y\in {\mathcal{L}}(Y)$
, that
![]() $({\rm \small{fs3}})$
holds for
$({\rm \small{fs3}})$
holds for
![]() ${\hat{Y}}[y]$
, with
${\hat{Y}}[y]$
, with
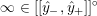 $\infty \in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }$
. Since
$\infty \in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }$
. Since
 $\infty \neq \{{\hat{y}}_{-},{\hat{y}}_{+}\}$
, we know that
$\infty \neq \{{\hat{y}}_{-},{\hat{y}}_{+}\}$
, we know that
![]() ${\hat{y}}_{-}$
and
${\hat{y}}_{-}$
and
![]() ${\hat{y}}_{+}$
cannot have infinite summands, and so
${\hat{y}}_{+}$
cannot have infinite summands, and so
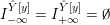 $I_{-\infty }^{{\hat{Y}}[y]}=I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
. This, in addition to the fact that
$I_{-\infty }^{{\hat{Y}}[y]}=I_{+\infty }^{{\hat{Y}}[y]}=\emptyset$
. This, in addition to the fact that
![]() $({\rm \small{fs3}})$
holds for
$({\rm \small{fs3}})$
holds for
![]() ${\hat{Y}}[y]$
, implies that
${\hat{Y}}[y]$
, implies that
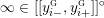 $\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]^{\circ }$
for all
$\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]^{\circ }$
for all
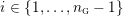 $i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, and thus
$i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, and thus
![]() $({\rm \small{fs1}})$
holds for
$({\rm \small{fs1}})$
holds for
![]() $Y$
.
$Y$
.
Next, consider the case in which
 $I_{\pm \infty }=\emptyset$
, so that by (63), we have
$I_{\pm \infty }=\emptyset$
, so that by (63), we have
![]() $I_{\cap }\neq \emptyset$
. Assume, without loss of generality, that
$I_{\cap }\neq \emptyset$
. Assume, without loss of generality, that
![]() $n_{{\rm \small{g}}}\in I_{\cap }$
. Then since
$n_{{\rm \small{g}}}\in I_{\cap }$
. Then since
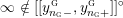 $\infty \notin [[y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}]]^{\circ }$
, the L-space gluing condition in (40) again tells us that
$\infty \notin [[y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}]]^{\circ }$
, the L-space gluing condition in (40) again tells us that
 $\infty \in {\mathcal{L}}^{\circ }({\hat{Y}}[y])$
for all
$\infty \in {\mathcal{L}}^{\circ }({\hat{Y}}[y])$
for all
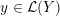 $y\in {\mathcal{L}}(Y)$
. Just as in the preceding paragraph, we deduce from this that
$y\in {\mathcal{L}}(Y)$
. Just as in the preceding paragraph, we deduce from this that
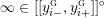 $\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]^{\circ }$
for all
$\infty \in [[y_{i-}^{{\rm \small{g}}},y_{i+}^{{\rm \small{g}}}]]^{\circ }$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, and that this implies that
$i\in \{1,\ldots ,n_{{\rm \small{g}}}-1\}$
, and that this implies that
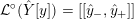 ${\mathcal{L}}^{\circ }({\hat{Y}}[y])=[[{\hat{y}}_{-},{\hat{y}}_{+}]]$
, with
${\mathcal{L}}^{\circ }({\hat{Y}}[y])=[[{\hat{y}}_{-},{\hat{y}}_{+}]]$
, with
 $\infty \neq {\hat{y}}_{-}>{\hat{y}}_{+}\neq \infty$
, for all
$\infty \neq {\hat{y}}_{-}>{\hat{y}}_{+}\neq \infty$
, for all
![]() $y\in \mathbb{Q}$
. Since
$y\in \mathbb{Q}$
. Since
![]() $y_{-}$
and
$y_{-}$
and
![]() $y_{+}$
have only finite summands, we also know that
$y_{+}$
have only finite summands, we also know that
 $y_{-},y_{+}\in \mathbb{Q}$
. We therefore have
$y_{-},y_{+}\in \mathbb{Q}$
. We therefore have
 $$\begin{eqnarray}\displaystyle y\in {\mathcal{L}}(Y) & \;\Longleftrightarrow \; & \displaystyle (\langle {\hat{y}}_{-},+\infty ]\cup [-\infty ,{\hat{y}}_{+}\rangle )\cup (\langle y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},+\infty ]\cap [-\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\rangle )=\mathbb{Q}\cup \{\infty \}\nonumber\\ \displaystyle & \;\Longleftrightarrow \; & \displaystyle y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}\quad \text{and}\quad y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}<{\hat{y}}_{+}\nonumber\\ \displaystyle & \;\Longleftrightarrow \; & \displaystyle y\in [y_{-},+\infty ]\cap [-\infty ,y_{+}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y\in {\mathcal{L}}(Y) & \;\Longleftrightarrow \; & \displaystyle (\langle {\hat{y}}_{-},+\infty ]\cup [-\infty ,{\hat{y}}_{+}\rangle )\cup (\langle y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}},+\infty ]\cap [-\infty ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}\rangle )=\mathbb{Q}\cup \{\infty \}\nonumber\\ \displaystyle & \;\Longleftrightarrow \; & \displaystyle y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}}>{\hat{y}}_{-}\quad \text{and}\quad y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}}<{\hat{y}}_{+}\nonumber\\ \displaystyle & \;\Longleftrightarrow \; & \displaystyle y\in [y_{-},+\infty ]\cap [-\infty ,y_{+}],\end{eqnarray}$$
where the first line is due to (40), and the third line is due to Claim 1. Thus, if
 $y_{-}>y_{+}$
, then
$y_{-}>y_{+}$
, then
 ${\mathcal{L}}(Y)=\emptyset$
; if
${\mathcal{L}}(Y)=\emptyset$
; if
 $y_{-}=y_{+}$
, then
$y_{-}=y_{+}$
, then
![]() $({\rm \small{nfs2}})$
holds for
$({\rm \small{nfs2}})$
holds for
![]() $Y$
, with
$Y$
, with
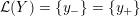 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
; and if
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
; and if
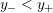 $y_{-}<y_{+}$
, then
$y_{-}<y_{+}$
, then
![]() $({\rm \small{fs2}})$
holds for
$({\rm \small{fs2}})$
holds for
![]() $Y$
, with
$Y$
, with
 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]=[y_{-},y_{+}]$
.◻
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]=[y_{-},y_{+}]$
.◻
4.8 Orientable base: cases involving solid tori
 ${\hat{Y}}[y]$
${\hat{Y}}[y]$
In this final subsection of the proof of Theorem 4.6 and Proposition 4.7, we consider all cases of
![]() $Y$
for which
$Y$
for which
![]() ${\hat{Y}}[y]$
, defined in (34), is a solid torus for some
${\hat{Y}}[y]$
, defined in (34), is a solid torus for some
 $y\in \mathbb{Q}\cup \{\infty \}$
. Recall that we have fixed a tree manifold
$y\in \mathbb{Q}\cup \{\infty \}$
. Recall that we have fixed a tree manifold
![]() $Y$
with torus boundary,
$Y$
with torus boundary,
 $b_{1}(Y)=1$
, tree height
$b_{1}(Y)=1$
, tree height
![]() $k>0$
, and
$k>0$
, and
![]() $n_{{\rm \small{g}}}>0$
daughter subtrees, as parameterized in § 4.2. Since
$n_{{\rm \small{g}}}>0$
daughter subtrees, as parameterized in § 4.2. Since
![]() ${\hat{Y}}[y]$
contains no incompressible tori, we must have
${\hat{Y}}[y]$
contains no incompressible tori, we must have
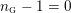 $n_{{\rm \small{g}}}-1=0$
. Thus, for any
$n_{{\rm \small{g}}}-1=0$
. Thus, for any
![]() $y\in \mathbb{Q}$
,
$y\in \mathbb{Q}$
,
![]() ${\hat{Y}}[y]$
is Seifert fibered over the disk, and is a solid torus if and only if it has one or fewer exceptional fibers. This occurs for
${\hat{Y}}[y]$
is Seifert fibered over the disk, and is a solid torus if and only if it has one or fewer exceptional fibers. This occurs for
![]() $y\in \mathbb{Z}$
if and only if the set
$y\in \mathbb{Z}$
if and only if the set
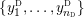 $\{y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\}$
contains one or fewer non-integers. Since
$\{y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}\}$
contains one or fewer non-integers. Since
![]() ${\hat{Y}}[y]$
and
${\hat{Y}}[y]$
and
![]() $Y\!$
are invariant under reparameterizations
$Y\!$
are invariant under reparameterizations
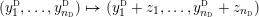 $(y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})\mapsto (y_{1}^{{\rm \small{d}}}+z_{1},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}+z_{n_{{\rm \small{d}}}})$
with
$(y_{1}^{{\rm \small{d}}},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}})\mapsto (y_{1}^{{\rm \small{d}}}+z_{1},\ldots ,y_{n_{{\rm \small{d}}}}^{{\rm \small{d}}}+z_{n_{{\rm \small{d}}}})$
with
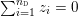 $\sum _{i=1}^{n_{{\rm \small{d}}}}z_{i}=0$
and each
$\sum _{i=1}^{n_{{\rm \small{d}}}}z_{i}=0$
and each
![]() $z_{i}\in \mathbb{Z}$
, or under the operation of forgetting a fiber complement with Dehn filling of slope
$z_{i}\in \mathbb{Z}$
, or under the operation of forgetting a fiber complement with Dehn filling of slope
 $\unicode[STIX]{x1D70B}_{i}(-\tilde{h}_{i})=0$
, we may assume, without loss of generality, that
$\unicode[STIX]{x1D70B}_{i}(-\tilde{h}_{i})=0$
, we may assume, without loss of generality, that
![]() $n_{{\rm \small{d}}}=1$
. Thus
$n_{{\rm \small{d}}}=1$
. Thus
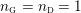 $n_{{\rm \small{g}}}=n_{{\rm \small{d}}}=1$
.
$n_{{\rm \small{g}}}=n_{{\rm \small{d}}}=1$
.
If the unique daughter subtree
![]() $Y_{1}$
satisfies
$Y_{1}$
satisfies
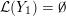 ${\mathcal{L}}(Y_{1})=\emptyset$
, then the gluing Propositions 4.4 and 3.4 imply that
${\mathcal{L}}(Y_{1})=\emptyset$
, then the gluing Propositions 4.4 and 3.4 imply that
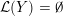 ${\mathcal{L}}(Y)=\emptyset$
, as predicted for
${\mathcal{L}}(Y)=\emptyset$
, as predicted for
![]() $Y$
by Proposition 4.7.
$Y$
by Proposition 4.7.
We therefore henceforth assume
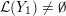 ${\mathcal{L}}(Y_{1})\neq \emptyset$
. Since
${\mathcal{L}}(Y_{1})\neq \emptyset$
. Since
![]() $Y$
has tree height
$Y$
has tree height
![]() $k$
,
$k$
,
![]() $Y_{1}$
has tree height
$Y_{1}$
has tree height
![]() $k-1$
. Thus, by inductive assumption as laid out in § 4.5,
$k-1$
. Thus, by inductive assumption as laid out in § 4.5,
![]() $Y_{1}$
satisfies Theorem 4.6 and Proposition 4.7, with
$Y_{1}$
satisfies Theorem 4.6 and Proposition 4.7, with
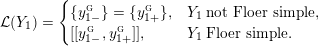 $$\begin{eqnarray}{\mathcal{L}}(Y_{1})=\left\{\begin{array}{@{}ll@{}}\{y_{1-}^{{\rm \small{g}}}\}=\{y_{1+}^{{\rm \small{g}}}\},\quad & Y_{1}\;\text{not Floer simple},\\ \text{}[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]],\quad & Y_{1}\;\text{Floer simple}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y_{1})=\left\{\begin{array}{@{}ll@{}}\{y_{1-}^{{\rm \small{g}}}\}=\{y_{1+}^{{\rm \small{g}}}\},\quad & Y_{1}\;\text{not Floer simple},\\ \text{}[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]],\quad & Y_{1}\;\text{Floer simple}.\end{array}\right.\end{eqnarray}$$
We proceed, once again, by fixing some notation. Recall the definitions of
![]() $y_{-}$
and
$y_{-}$
and
![]() $y_{+}$
:
$y_{+}$
:
 $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle y_{-}:=\max _{k>0}-\frac{1}{k}(1+\lfloor y_{1}^{{\rm \small{d}}}k\rfloor +(\lceil y_{1+}^{{\rm \small{g}}}k\rceil -1)),\\ \displaystyle y_{+}:=\min _{k>0}-{\displaystyle \frac{1}{k}}(-1+\lceil y_{1}^{{\rm \small{d}}}k\rceil +(\lfloor y_{1-}^{{\rm \small{g}}}k\rfloor +1)),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle y_{-}:=\max _{k>0}-\frac{1}{k}(1+\lfloor y_{1}^{{\rm \small{d}}}k\rfloor +(\lceil y_{1+}^{{\rm \small{g}}}k\rceil -1)),\\ \displaystyle y_{+}:=\min _{k>0}-{\displaystyle \frac{1}{k}}(-1+\lceil y_{1}^{{\rm \small{d}}}k\rceil +(\lfloor y_{1-}^{{\rm \small{g}}}k\rfloor +1)),\end{array}\end{eqnarray}$$
where, as always, we define
![]() $y_{-}$
or
$y_{-}$
or
![]() $y_{+}$
to be infinite if any of its summands is infinite.
$y_{+}$
to be infinite if any of its summands is infinite.
For any
![]() $y\neq \infty$
,
$y\neq \infty$
,
![]() ${\hat{Y}}[y]$
is Seifert fibred over the disk, hence is Floer simple, allowing us to write
${\hat{Y}}[y]$
is Seifert fibred over the disk, hence is Floer simple, allowing us to write
 $[[{\hat{y}}_{-},{\hat{y}}_{+}]]:={\mathcal{L}}({\hat{Y}}[y])$
. Moreover, when
$[[{\hat{y}}_{-},{\hat{y}}_{+}]]:={\mathcal{L}}({\hat{Y}}[y])$
. Moreover, when
![]() ${\hat{Y}}[y]$
is not a solid torus, we have
${\hat{Y}}[y]$
is not a solid torus, we have
 $$\begin{eqnarray}\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset ;\quad \begin{array}{@{}l@{}}\displaystyle {\hat{y}}_{-}=\max _{k>0}-\frac{1}{k}(1+\lfloor yk\rfloor +\lfloor y_{1}^{{\rm \small{d}}}k\rfloor ),\\ \displaystyle {\hat{y}}_{+}=\min _{k>0}-\frac{1}{k}(-1+\lceil yk\rceil +\lceil y_{1}^{{\rm \small{d}}}k\rceil ),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset ;\quad \begin{array}{@{}l@{}}\displaystyle {\hat{y}}_{-}=\max _{k>0}-\frac{1}{k}(1+\lfloor yk\rfloor +\lfloor y_{1}^{{\rm \small{d}}}k\rfloor ),\\ \displaystyle {\hat{y}}_{+}=\min _{k>0}-\frac{1}{k}(-1+\lceil yk\rceil +\lceil y_{1}^{{\rm \small{d}}}k\rceil ),\end{array}\end{eqnarray}$$
but when
![]() ${\hat{Y}}[y]$
is a solid torus, we have
${\hat{Y}}[y]$
is a solid torus, we have
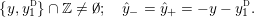 $$\begin{eqnarray}\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset ;\quad {\hat{y}}_{-}={\hat{y}}_{+}=-y-y_{1}^{{\rm \small{d}}}.\end{eqnarray}$$
$$\begin{eqnarray}\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset ;\quad {\hat{y}}_{-}={\hat{y}}_{+}=-y-y_{1}^{{\rm \small{d}}}.\end{eqnarray}$$
We next prove the analogs of Claims 1 and 2 from § 4.7.
Claim 3. For any
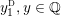 $y_{1}^{{\rm \small{d}}},y\in \mathbb{Q}$
, we have
$y_{1}^{{\rm \small{d}}},y\in \mathbb{Q}$
, we have
 $$\begin{eqnarray}\displaystyle y\in [y_{-},+\infty ] & \;\Longleftrightarrow \; & \displaystyle \left\{\begin{array}{@{}ll@{}}y_{1+}^{{\rm \small{g}}}>\,{\hat{y}}_{-}\quad & \quad \text{if }\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset \\ y_{1+}^{{\rm \small{g}}}\geqslant \,{\hat{y}}_{-}\quad & \quad \text{if }\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset \end{array}\right.\quad \text{if }y_{1+}^{{\rm \small{g}}}\in \mathbb{Q};\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y\in [y_{-},+\infty ] & \;\Longleftrightarrow \; & \displaystyle \left\{\begin{array}{@{}ll@{}}y_{1+}^{{\rm \small{g}}}>\,{\hat{y}}_{-}\quad & \quad \text{if }\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset \\ y_{1+}^{{\rm \small{g}}}\geqslant \,{\hat{y}}_{-}\quad & \quad \text{if }\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset \end{array}\right.\quad \text{if }y_{1+}^{{\rm \small{g}}}\in \mathbb{Q};\end{eqnarray}$$
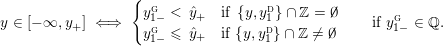 $$\begin{eqnarray}\displaystyle y\in [-\infty ,y_{+}] & \;\Longleftrightarrow \; & \displaystyle \left\{\begin{array}{@{}l@{}}y_{1-}^{{\rm \small{g}}}<\,{\hat{y}}_{+}\quad \text{if}\;\,\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset \quad \\ y_{1-}^{{\rm \small{g}}}\leqslant \,{\hat{y}}_{+}\quad \text{if }\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset \quad \end{array}\right.\quad \text{if }y_{1-}^{{\rm \small{g}}}\in \mathbb{Q}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y\in [-\infty ,y_{+}] & \;\Longleftrightarrow \; & \displaystyle \left\{\begin{array}{@{}l@{}}y_{1-}^{{\rm \small{g}}}<\,{\hat{y}}_{+}\quad \text{if}\;\,\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset \quad \\ y_{1-}^{{\rm \small{g}}}\leqslant \,{\hat{y}}_{+}\quad \text{if }\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset \quad \end{array}\right.\quad \text{if }y_{1-}^{{\rm \small{g}}}\in \mathbb{Q}.\end{eqnarray}$$
Proof of Claim 3.
To understand (70), note that due to (21), we have
![]() $y\geqslant y_{-}$
if and only if
$y\geqslant y_{-}$
if and only if
 $$\begin{eqnarray}\lfloor yk\rfloor \geqslant -(\lfloor y_{1}^{{\rm \small{d}}}k\rfloor +\lceil y_{1+}^{{\rm \small{g}}}k\rceil ),\quad \text{ for all }k>0.\end{eqnarray}$$
$$\begin{eqnarray}\lfloor yk\rfloor \geqslant -(\lfloor y_{1}^{{\rm \small{d}}}k\rfloor +\lceil y_{1+}^{{\rm \small{g}}}k\rceil ),\quad \text{ for all }k>0.\end{eqnarray}$$
When
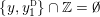 $\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset$
, (22) implies that (72) holds if and only if
$\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}=\emptyset$
, (22) implies that (72) holds if and only if
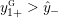 $y_{1+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
. On the other hand, if
$y_{1+}^{{\rm \small{g}}}>{\hat{y}}_{-}$
. On the other hand, if
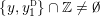 $\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset$
, then
$\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset$
, then
 $\lfloor yk\rfloor +\lfloor y_{1}^{{\rm \small{d}}}k\rfloor =\lfloor (y+y_{1}^{{\rm \small{d}}})k\rfloor$
, and so applying (21) to (72) yields
$\lfloor yk\rfloor +\lfloor y_{1}^{{\rm \small{d}}}k\rfloor =\lfloor (y+y_{1}^{{\rm \small{d}}})k\rfloor$
, and so applying (21) to (72) yields
 $$\begin{eqnarray}y+y_{1}^{{\rm \small{d}}}\geqslant \max _{k>0}-\frac{1}{k}\lceil y_{1+}^{{\rm \small{g}}}k\rceil =-y_{1+}^{{\rm \small{g}}},\end{eqnarray}$$
$$\begin{eqnarray}y+y_{1}^{{\rm \small{d}}}\geqslant \max _{k>0}-\frac{1}{k}\lceil y_{1+}^{{\rm \small{g}}}k\rceil =-y_{1+}^{{\rm \small{g}}},\end{eqnarray}$$
which is equivalent to the inequality
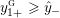 $y_{1+}^{{\rm \small{g}}}\geqslant {\hat{y}}_{-}$
, completing the proof of (70). One can then obtain (71) by replacing
$y_{1+}^{{\rm \small{g}}}\geqslant {\hat{y}}_{-}$
, completing the proof of (70). One can then obtain (71) by replacing
![]() $y$
,
$y$
,
![]() $y_{1+}^{{\rm \small{g}}}$
, and
$y_{1+}^{{\rm \small{g}}}$
, and
![]() $y_{1}^{{\rm \small{d}}}$
in (70) with
$y_{1}^{{\rm \small{d}}}$
in (70) with
![]() $-y$
,
$-y$
,
![]() $-y_{1-}^{{\rm \small{g}}}$
, and
$-y_{1-}^{{\rm \small{g}}}$
, and
![]() $-y_{1}^{{\rm \small{d}}}$
, respectively.◻
$-y_{1}^{{\rm \small{d}}}$
, respectively.◻
Claim 4. If
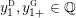 $y_{1}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}}\in \mathbb{Q}$
, then
$y_{1}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}}\in \mathbb{Q}$
, then
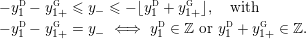 $$\begin{eqnarray}\displaystyle -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}} & {\leqslant} & \displaystyle y_{-}\leqslant -\lfloor y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\rfloor ,\quad \text{with}\nonumber\\ \displaystyle -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}} & = & \displaystyle y_{-}\;\Longleftrightarrow \;y_{1}^{{\rm \small{d}}}\in \mathbb{Z}\text{ or }y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}} & {\leqslant} & \displaystyle y_{-}\leqslant -\lfloor y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\rfloor ,\quad \text{with}\nonumber\\ \displaystyle -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}} & = & \displaystyle y_{-}\;\Longleftrightarrow \;y_{1}^{{\rm \small{d}}}\in \mathbb{Z}\text{ or }y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}.\nonumber\end{eqnarray}$$
If
 $y_{1}^{{\rm \small{d}}},y_{1-}^{{\rm \small{g}}}\in \mathbb{Q}$
, then
$y_{1}^{{\rm \small{d}}},y_{1-}^{{\rm \small{g}}}\in \mathbb{Q}$
, then
 $$\begin{eqnarray}\displaystyle -\lceil y_{1}^{{\rm \small{d}}}+y_{1-}^{{\rm \small{g}}}\rceil \leqslant y_{+} & {\leqslant} & \displaystyle -y_{1}^{{\rm \small{d}}}-y_{1-}^{{\rm \small{g}}},\quad \text{with}\nonumber\\ \displaystyle y_{+} & = & \displaystyle -y_{1}^{{\rm \small{d}}}-y_{1-}^{{\rm \small{g}}}\;\Longleftrightarrow \;y_{1}^{{\rm \small{d}}}\in \mathbb{Z}\text{ or }y_{1}^{{\rm \small{d}}}+y_{1-}^{{\rm \small{g}}}\in \mathbb{Z}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\lceil y_{1}^{{\rm \small{d}}}+y_{1-}^{{\rm \small{g}}}\rceil \leqslant y_{+} & {\leqslant} & \displaystyle -y_{1}^{{\rm \small{d}}}-y_{1-}^{{\rm \small{g}}},\quad \text{with}\nonumber\\ \displaystyle y_{+} & = & \displaystyle -y_{1}^{{\rm \small{d}}}-y_{1-}^{{\rm \small{g}}}\;\Longleftrightarrow \;y_{1}^{{\rm \small{d}}}\in \mathbb{Z}\text{ or }y_{1}^{{\rm \small{d}}}+y_{1-}^{{\rm \small{g}}}\in \mathbb{Z}.\nonumber\end{eqnarray}$$
Proof of Claim 4.
Just as in the proof of Claim 2, we define
 $$\begin{eqnarray}y_{-}^{\prime }(k):={\displaystyle \frac{1}{k}}([y_{1}^{{\rm \small{d}}}k]-[-y_{1+}^{{\rm \small{g}}}k])\end{eqnarray}$$
$$\begin{eqnarray}y_{-}^{\prime }(k):={\displaystyle \frac{1}{k}}([y_{1}^{{\rm \small{d}}}k]-[-y_{1+}^{{\rm \small{g}}}k])\end{eqnarray}$$
for each
 $k\in \mathbb{Z}_{{>}0}$
, so that
$k\in \mathbb{Z}_{{>}0}$
, so that
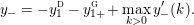 $$\begin{eqnarray}y_{-}=-y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}\!+\max _{k>0}y_{-}^{\prime }(k).\end{eqnarray}$$
$$\begin{eqnarray}y_{-}=-y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}\!+\max _{k>0}y_{-}^{\prime }(k).\end{eqnarray}$$
Demanding
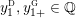 $y_{1}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}}\in \mathbb{Q}$
, we again set
$y_{1}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}}\in \mathbb{Q}$
, we again set
 $s_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{1}^{{\rm \small{d}}}k,y_{1+}^{{\rm \small{g}}}k\in \mathbb{Z}\}$
.
$s_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{1}^{{\rm \small{d}}}k,y_{1+}^{{\rm \small{g}}}k\in \mathbb{Z}\}$
.
Since
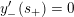 $y_{-}^{\prime }(s_{+})=0$
, we already know that
$y_{-}^{\prime }(s_{+})=0$
, we already know that
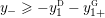 $y_{-}\geqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
for all
$y_{-}\geqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
for all
 $y_{1}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}}\in \mathbb{Q}$
. If
$y_{1}^{{\rm \small{d}}},y_{1+}^{{\rm \small{g}}}\in \mathbb{Q}$
. If
![]() $y_{i}^{{\rm \small{d}}}\in \mathbb{Z}$
, then
$y_{i}^{{\rm \small{d}}}\in \mathbb{Z}$
, then
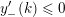 $y_{-}^{\prime }(k)\leqslant 0$
for all
$y_{-}^{\prime }(k)\leqslant 0$
for all
 $k\in \mathbb{Z}_{{>}0}$
, implying
$k\in \mathbb{Z}_{{>}0}$
, implying
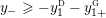 $y_{-}\geqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
. Suppose that
$y_{-}\geqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
. Suppose that
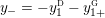 $y_{-}=-y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
for some
$y_{-}=-y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
for some
 $y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}$
. Then since
$y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}$
. Then since
 $y_{-}^{\prime }(k)\leqslant 0$
for all
$y_{-}^{\prime }(k)\leqslant 0$
for all
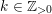 $k\in \mathbb{Z}_{{>}0}$
, we have
$k\in \mathbb{Z}_{{>}0}$
, we have
 $$\begin{eqnarray}\displaystyle 0 & {\geqslant} & \displaystyle y_{-}^{\prime }(1)+(s_{+}-1)y_{-}^{\prime }(s_{+}-1)\nonumber\\ \displaystyle & = & \displaystyle ([y_{1}^{{\rm \small{d}}}]+[-y_{1}^{{\rm \small{d}}}])-([-y_{1+}^{{\rm \small{g}}}]+[y_{1+}^{{\rm \small{g}}}])\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & {\geqslant} & \displaystyle y_{-}^{\prime }(1)+(s_{+}-1)y_{-}^{\prime }(s_{+}-1)\nonumber\\ \displaystyle & = & \displaystyle ([y_{1}^{{\rm \small{d}}}]+[-y_{1}^{{\rm \small{d}}}])-([-y_{1+}^{{\rm \small{g}}}]+[y_{1+}^{{\rm \small{g}}}])\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 0.\end{eqnarray}$$
Thus, the top line of (76) must be an equality, which, since
 $y_{-}^{\prime }(k)\leqslant 0$
for all
$y_{-}^{\prime }(k)\leqslant 0$
for all
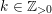 $k\in \mathbb{Z}_{{>}0}$
, implies
$k\in \mathbb{Z}_{{>}0}$
, implies
 $y_{-}^{\prime }(1)=y_{-}^{\prime }(s_{+}-1)=0$
. In particular, the fact that
$y_{-}^{\prime }(1)=y_{-}^{\prime }(s_{+}-1)=0$
. In particular, the fact that
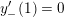 $y_{-}^{\prime }(1)=0$
implies that
$y_{-}^{\prime }(1)=0$
implies that
 $y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
. Conversely, if
$y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
. Conversely, if
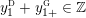 $y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
, then
$y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
, then
 $y_{-}^{\prime }(k)\equiv 0$
for all
$y_{-}^{\prime }(k)\equiv 0$
for all
 $k\in \mathbb{Z}_{{>}0}$
, implying
$k\in \mathbb{Z}_{{>}0}$
, implying
 $y_{-}=-y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
.
$y_{-}=-y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
.
We have shown that
 $y_{-}\geqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
, with equality if and only if
$y_{-}\geqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}$
, with equality if and only if
![]() $y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
or
$y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
or
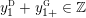 $y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
, and so it remains to show that
$y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
, and so it remains to show that
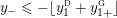 $y_{-}\leqslant -\lfloor y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\rfloor$
. Note that for each
$y_{-}\leqslant -\lfloor y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\rfloor$
. Note that for each
 $k\in \mathbb{Z}_{{>}0}$
, we have
$k\in \mathbb{Z}_{{>}0}$
, we have
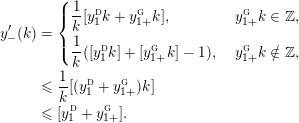 $$\begin{eqnarray}\displaystyle y_{-}^{\prime }(k) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{k}}[y_{1}^{{\rm \small{d}}}k+y_{1+}^{{\rm \small{g}}}k],\quad & \;y_{1+}^{{\rm \small{g}}}k\in \mathbb{Z},\\ {\displaystyle \frac{1}{k}}([y_{1}^{{\rm \small{d}}}k]+[y_{1+}^{{\rm \small{g}}}k]-1),\quad & \;y_{1+}^{{\rm \small{g}}}k\notin \mathbb{Z},\end{array}\right.\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {\displaystyle \frac{1}{k}}[(y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}})k]\nonumber\\ \displaystyle & {\leqslant} & \displaystyle [y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{-}^{\prime }(k) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{k}}[y_{1}^{{\rm \small{d}}}k+y_{1+}^{{\rm \small{g}}}k],\quad & \;y_{1+}^{{\rm \small{g}}}k\in \mathbb{Z},\\ {\displaystyle \frac{1}{k}}([y_{1}^{{\rm \small{d}}}k]+[y_{1+}^{{\rm \small{g}}}k]-1),\quad & \;y_{1+}^{{\rm \small{g}}}k\notin \mathbb{Z},\end{array}\right.\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {\displaystyle \frac{1}{k}}[(y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}})k]\nonumber\\ \displaystyle & {\leqslant} & \displaystyle [y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}].\end{eqnarray}$$
Thus, by (75), we have
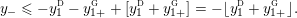 $$\begin{eqnarray}y_{-}\leqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}+[y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}]=-\lfloor y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\rfloor .\end{eqnarray}$$
$$\begin{eqnarray}y_{-}\leqslant -y_{1}^{{\rm \small{d}}}-y_{1+}^{{\rm \small{g}}}+[y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}]=-\lfloor y_{1}^{{\rm \small{d}}}+y_{1+}^{{\rm \small{g}}}\rfloor .\end{eqnarray}$$
A similar argument proves all of the analogous results for
![]() $y_{+}$
.◻
$y_{+}$
.◻
For the proof that Theorem 4.6 and Proposition 4.7 hold for
![]() $Y$
, we divide our argument into three main cases, first according to whether or not
$Y$
, we divide our argument into three main cases, first according to whether or not
![]() $Y_{1}$
is Floer simple, and then according to whether
$Y_{1}$
is Floer simple, and then according to whether
 $\infty \in {\mathcal{L}}(Y)$
.
$\infty \in {\mathcal{L}}(Y)$
.
Proposition 4.10. Suppose
 ${\mathcal{L}}(Y_{1})\neq \emptyset$
with
${\mathcal{L}}(Y_{1})\neq \emptyset$
with
![]() $Y_{1}$
not Floer simple. Then
$Y_{1}$
not Floer simple. Then
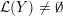 ${\mathcal{L}}(Y)\neq \emptyset$
if and only if condition
${\mathcal{L}}(Y)\neq \emptyset$
if and only if condition
![]() $({\rm \small{nfs1}})$
or
$({\rm \small{nfs1}})$
or
![]() $({\rm \small{nfs4}})$
from Proposition 4.7 holds, in which case
$({\rm \small{nfs4}})$
from Proposition 4.7 holds, in which case
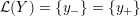 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
.
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
.
Proof. For brevity, set
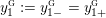 $y_{1}^{{\rm \small{g}}}:=y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}$
, so that
$y_{1}^{{\rm \small{g}}}:=y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}$
, so that
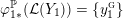 $\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=\{y_{1}^{{\rm \small{g}}}\}$
. We first note that if
$\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}({\mathcal{L}}(Y_{1}))=\{y_{1}^{{\rm \small{g}}}\}$
. We first note that if
![]() ${\hat{Y}}[y]$
has incompressible boundary, in which case
${\hat{Y}}[y]$
has incompressible boundary, in which case
![]() ${\hat{Y}}[y]$
is a non-solid-torus graph manifold, then Proposition 4.4 implies that the union
${\hat{Y}}[y]$
is a non-solid-torus graph manifold, then Proposition 4.4 implies that the union
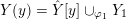 $Y(y)={\hat{Y}}[y]\cup _{\unicode[STIX]{x1D711}_{1}}Y_{1}$
is not an L-space.
$Y(y)={\hat{Y}}[y]\cup _{\unicode[STIX]{x1D711}_{1}}Y_{1}$
is not an L-space.
![]() ${\hat{Y}}[y]$
has compressible boundary if and only if
${\hat{Y}}[y]$
has compressible boundary if and only if
![]() $y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
or
$y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
or
 $y\in \mathbb{Z}\cup \{\infty \}$
. Thus, for any
$y\in \mathbb{Z}\cup \{\infty \}$
. Thus, for any
 $y\in \mathbb{Q}\cup \{\infty \}$
, Proposition 3.4 implies
$y\in \mathbb{Q}\cup \{\infty \}$
, Proposition 3.4 implies
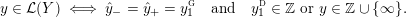 $$\begin{eqnarray}y\in {\mathcal{L}}(Y)\;\Longleftrightarrow \;{\hat{y}}_{-}={\hat{y}}_{+}=y_{1}^{{\rm \small{g}}}\quad \text{and}\quad y_{1}^{{\rm \small{d}}}\in \mathbb{Z}\text{ or }y\in \mathbb{Z}\cup \{\infty \}.\end{eqnarray}$$
$$\begin{eqnarray}y\in {\mathcal{L}}(Y)\;\Longleftrightarrow \;{\hat{y}}_{-}={\hat{y}}_{+}=y_{1}^{{\rm \small{g}}}\quad \text{and}\quad y_{1}^{{\rm \small{d}}}\in \mathbb{Z}\text{ or }y\in \mathbb{Z}\cup \{\infty \}.\end{eqnarray}$$
Condition
![]() $({\rm \small{nfs4}})$
holds if and only if
$({\rm \small{nfs4}})$
holds if and only if
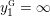 $y_{1}^{{\rm \small{g}}}=\infty$
. Since
$y_{1}^{{\rm \small{g}}}=\infty$
. Since
 ${\hat{y}}_{-}={\hat{y}}_{+}=\infty$
if and only if
${\hat{y}}_{-}={\hat{y}}_{+}=\infty$
if and only if
![]() $y=\infty$
, we then have
$y=\infty$
, we then have
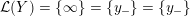 ${\mathcal{L}}(Y)=\{\infty \}=\{y_{-}\}=\{y_{-}\}$
when
${\mathcal{L}}(Y)=\{\infty \}=\{y_{-}\}=\{y_{-}\}$
when
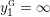 $y_{1}^{{\rm \small{g}}}=\infty$
.
$y_{1}^{{\rm \small{g}}}=\infty$
.
We henceforth demand
![]() $y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
. If
$y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
. If
![]() $y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
, then
$y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
, then
![]() $({\rm \small{nfs1}})$
holds, and we have
$({\rm \small{nfs1}})$
holds, and we have
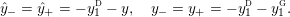 $$\begin{eqnarray}{\hat{y}}_{-}={\hat{y}}_{+}=-y_{1}^{{\rm \small{d}}}-y,\quad y_{-}=y_{+}=-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}.\end{eqnarray}$$
$$\begin{eqnarray}{\hat{y}}_{-}={\hat{y}}_{+}=-y_{1}^{{\rm \small{d}}}-y,\quad y_{-}=y_{+}=-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}.\end{eqnarray}$$
Statement (79) then tells us that
 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
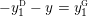 $-y_{1}^{{\rm \small{d}}}-y=y_{1}^{{\rm \small{g}}}$
, which occurs if and only if
$-y_{1}^{{\rm \small{d}}}-y=y_{1}^{{\rm \small{g}}}$
, which occurs if and only if
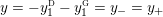 $y=-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}=y_{-}=y_{+}$
, which means that
$y=-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}=y_{-}=y_{+}$
, which means that
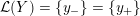 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
.
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
.
Lastly, suppose that
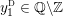 $y_{1}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}$
, with
$y_{1}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}$
, with
![]() $y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
. Since
$y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
. Since
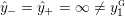 ${\hat{y}}_{-}={\hat{y}}_{+}=\infty \neq y_{1}^{{\rm \small{g}}}$
when
${\hat{y}}_{-}={\hat{y}}_{+}=\infty \neq y_{1}^{{\rm \small{g}}}$
when
![]() $y=\infty$
, (79) tells us that
$y=\infty$
, (79) tells us that
 $\infty \notin {\mathcal{L}}(Y)$
. Thus
$\infty \notin {\mathcal{L}}(Y)$
. Thus
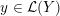 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
![]() $y\in \mathbb{Z}$
and
$y\in \mathbb{Z}$
and
 ${\hat{y}}_{-}={\hat{y}}_{+}=y_{1}^{{\rm \small{g}}}$
. Since
${\hat{y}}_{-}={\hat{y}}_{+}=y_{1}^{{\rm \small{g}}}$
. Since
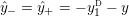 ${\hat{y}}_{-}={\hat{y}}_{+}=-y_{1}^{{\rm \small{d}}}-y$
when
${\hat{y}}_{-}={\hat{y}}_{+}=-y_{1}^{{\rm \small{d}}}-y$
when
![]() $y\in \mathbb{Z}$
, this means
$y\in \mathbb{Z}$
, this means
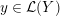 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
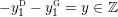 $-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}=y\in \mathbb{Z}$
. That is,
$-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}=y\in \mathbb{Z}$
. That is,
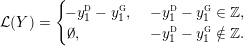 $$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}\!-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}},\quad & \;-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\in \mathbb{Z},\\ \emptyset ,\quad & \;-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\notin \mathbb{Z}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}\!-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}},\quad & \;-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\in \mathbb{Z},\\ \emptyset ,\quad & \;-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\notin \mathbb{Z}.\end{array}\right.\end{eqnarray}$$
Thus, if
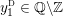 $y_{1}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}$
and
$y_{1}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}$
and
![]() $y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
, then
$y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
, then
![]() ${\mathcal{L}}(Y)$
is non-empty if and only if
${\mathcal{L}}(Y)$
is non-empty if and only if
![]() $({\rm \small{nfs1}})$
holds, in which case, since
$({\rm \small{nfs1}})$
holds, in which case, since
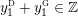 $y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
, Claim 4 implies
$y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
, Claim 4 implies
 $y_{-}=y_{+}=-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}$
, so that
$y_{-}=y_{+}=-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}$
, so that
 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
.◻
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
.◻
We henceforth demand that
![]() $Y_{1}$
be Floer simple, in which case Propositions 4.4 and 3.4 tell us that for any
$Y_{1}$
be Floer simple, in which case Propositions 4.4 and 3.4 tell us that for any
 $y\in \mathbb{Q}\cup \{\infty \}$
, the union
$y\in \mathbb{Q}\cup \{\infty \}$
, the union
 $Y(y)={\hat{Y}}[y]\cup _{\unicode[STIX]{x1D711}_{1}}Y_{1}$
is an L-space if and only if
$Y(y)={\hat{Y}}[y]\cup _{\unicode[STIX]{x1D711}_{1}}Y_{1}$
is an L-space if and only if
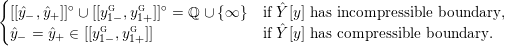 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}[[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }\cup [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]^{\circ }=\mathbb{Q}\cup \{\infty \}\quad & \text{if }{\hat{Y}}[y]\text{ has incompressible boundary},\\ {\hat{y}}_{-}={\hat{y}}_{+}\in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]\quad & \text{if }{\hat{Y}}[y]\text{ has compressible boundary}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}[[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }\cup [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]^{\circ }=\mathbb{Q}\cup \{\infty \}\quad & \text{if }{\hat{Y}}[y]\text{ has incompressible boundary},\\ {\hat{y}}_{-}={\hat{y}}_{+}\in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]\quad & \text{if }{\hat{Y}}[y]\text{ has compressible boundary}.\end{array}\right.\end{eqnarray}$$
Note that
![]() ${\hat{Y}}[y]$
has compressible boundary if and only if
${\hat{Y}}[y]$
has compressible boundary if and only if
 $\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset$
or
$\{y,y_{1}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset$
or
![]() $y=\infty$
, with the former condition accounting for the case of solid torus
$y=\infty$
, with the former condition accounting for the case of solid torus
![]() ${\hat{Y}}[y]$
, and the latter condition accounting for the case in which
${\hat{Y}}[y]$
, and the latter condition accounting for the case in which
![]() ${\hat{Y}}[\infty ]$
is either a solid torus (when
${\hat{Y}}[\infty ]$
is either a solid torus (when
![]() $y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
) or the connected sum of a solid torus with a lens space (when
$y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
) or the connected sum of a solid torus with a lens space (when
![]() $y_{1}^{{\rm \small{d}}}\notin \mathbb{Z}$
).
$y_{1}^{{\rm \small{d}}}\notin \mathbb{Z}$
).
Proposition 4.11. Suppose
![]() $Y_{1}$
is Floer simple. Then
$Y_{1}$
is Floer simple. Then
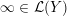 $\infty \in {\mathcal{L}}(Y)$
if and only if condition
$\infty \in {\mathcal{L}}(Y)$
if and only if condition
![]() $({\rm \small{fs3}})$
from Proposition 4.7 holds, in which case
$({\rm \small{fs3}})$
from Proposition 4.7 holds, in which case
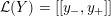 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
Proof. The first part of the statement is immediate. That is, since
![]() ${\hat{Y}}[\infty ]$
has compressible boundary, with
${\hat{Y}}[\infty ]$
has compressible boundary, with
 ${\hat{y}}_{-}={\hat{y}}_{+}=\infty$
, we have
${\hat{y}}_{-}={\hat{y}}_{+}=\infty$
, we have
 $\infty \in {\mathcal{L}}(Y)$
if and only if
$\infty \in {\mathcal{L}}(Y)$
if and only if
 $\infty \in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
, which occurs if and only if
$\infty \in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
, which occurs if and only if
![]() $({\rm \small{fs3}})$
holds. For the remainder of the proof, we assume
$({\rm \small{fs3}})$
holds. For the remainder of the proof, we assume
![]() $({\rm \small{fs3}})$
holds.
$({\rm \small{fs3}})$
holds.
Consider the case in which
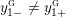 $y_{1-}^{{\rm \small{g}}}\neq y_{1+}^{{\rm \small{g}}}$
. Since
$y_{1-}^{{\rm \small{g}}}\neq y_{1+}^{{\rm \small{g}}}$
. Since
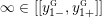 $\infty \in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
,
$\infty \in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
,
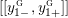 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
takes one of the forms (a)
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
takes one of the forms (a)
 $[y_{1-}^{{\rm \small{g}}},+\infty ]$
, (b)
$[y_{1-}^{{\rm \small{g}}},+\infty ]$
, (b)
 $[-\infty ,y_{1+}^{{\rm \small{g}}}]$
, or (c)
$[-\infty ,y_{1+}^{{\rm \small{g}}}]$
, or (c)
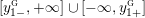 $[y_{1-}^{{\rm \small{g}}},+\infty ]\cup [-\infty ,y_{1+}^{{\rm \small{g}}}]$
, in which cases
$[y_{1-}^{{\rm \small{g}}},+\infty ]\cup [-\infty ,y_{1+}^{{\rm \small{g}}}]$
, in which cases
 $[[y_{-},y_{+}]]$
takes the respective forms (a)
$[[y_{-},y_{+}]]$
takes the respective forms (a)
 $[-\infty ,y_{+}]$
, (b)
$[-\infty ,y_{+}]$
, (b)
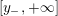 $[y_{-},+\infty ]$
, (c)
$[y_{-},+\infty ]$
, (c)
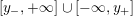 $[y_{-},+\infty ]\cup [-\infty ,y_{+}]$
, with case (c) due to the fact that
$[y_{-},+\infty ]\cup [-\infty ,y_{+}]$
, with case (c) due to the fact that
 $\infty \neq y_{1-}^{{\rm \small{g}}}>y_{1+}^{{\rm \small{g}}}\neq \infty$
implies
$\infty \neq y_{1-}^{{\rm \small{g}}}>y_{1+}^{{\rm \small{g}}}\neq \infty$
implies
 $\infty \neq y_{-}>y_{+}\neq \infty$
by Claim 4. Thus, for
$\infty \neq y_{-}>y_{+}\neq \infty$
by Claim 4. Thus, for
![]() $y\in \mathbb{Q}$
, the condition
$y\in \mathbb{Q}$
, the condition
 $y\in [[y_{-},y_{+}]]$
is respectively equivalent to the right-hand conditions of (a) (70), (b) (71), or (c) (70) or (71) from Claim 3, each of which conditions, given the respective form of
$y\in [[y_{-},y_{+}]]$
is respectively equivalent to the right-hand conditions of (a) (70), (b) (71), or (c) (70) or (71) from Claim 3, each of which conditions, given the respective form of
 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
, is equivalent to (82), which holds if and only if
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
, is equivalent to (82), which holds if and only if
![]() $Y(y)$
is an L-space, and we conclude that
$Y(y)$
is an L-space, and we conclude that
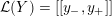 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
Next, suppose that
![]() $({\rm \small{fs3}})$
holds with
$({\rm \small{fs3}})$
holds with
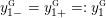 $y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}=:y_{1}^{{\rm \small{g}}}$
. Since
$y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}=:y_{1}^{{\rm \small{g}}}$
. Since
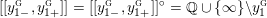 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]^{\circ }=\mathbb{Q}\cup \{\infty \}\setminus y_{1}^{{\rm \small{g}}}$
, the L-space condition in (82) takes the following form. For any
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]^{\circ }=\mathbb{Q}\cup \{\infty \}\setminus y_{1}^{{\rm \small{g}}}$
, the L-space condition in (82) takes the following form. For any
![]() $y\in \mathbb{Q}$
,
$y\in \mathbb{Q}$
,
 $$\begin{eqnarray}y\in {\mathcal{L}}(Y)\quad \;\Longleftrightarrow \;\quad \left\{\begin{array}{@{}ll@{}}y_{1}^{{\rm \small{g}}}\in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ },\quad & \{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}=\emptyset ,\\ y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}},\quad & \{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}\neq \emptyset .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}y\in {\mathcal{L}}(Y)\quad \;\Longleftrightarrow \;\quad \left\{\begin{array}{@{}ll@{}}y_{1}^{{\rm \small{g}}}\in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ },\quad & \{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}=\emptyset ,\\ y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}},\quad & \{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}\neq \emptyset .\end{array}\right.\end{eqnarray}$$
The derivation of the
 $\{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}=\emptyset$
case from (82) is immediate. In the
$\{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}=\emptyset$
case from (82) is immediate. In the
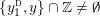 $\{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}\neq \emptyset$
case, (82) tells us that
$\{y_{1}^{{\rm \small{d}}},y\}\cap \mathbb{Z}\neq \emptyset$
case, (82) tells us that
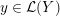 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
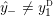 ${\hat{y}}_{-}\neq y_{1}^{{\rm \small{d}}}$
. Since
${\hat{y}}_{-}\neq y_{1}^{{\rm \small{d}}}$
. Since
 ${\hat{y}}_{-}={\hat{y}}_{+}=-y_{1}^{{\rm \small{d}}}-y$
, this occurs if and only if
${\hat{y}}_{-}={\hat{y}}_{+}=-y_{1}^{{\rm \small{d}}}-y$
, this occurs if and only if
 $y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}$
, completing the proof of (83).
$y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}$
, completing the proof of (83).
Now, since
![]() $({\rm \small{fs3}})$
demands that
$({\rm \small{fs3}})$
demands that
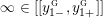 $\infty \in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
, implying
$\infty \in [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
, implying
![]() $y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
, Claim 4 tells us that
$y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
, Claim 4 tells us that
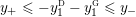 $y_{+}\leqslant -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\leqslant y_{-}$
, with
$y_{+}\leqslant -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\leqslant y_{-}$
, with
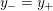 $y_{-}=y_{+}$
if and only if
$y_{-}=y_{+}$
if and only if
![]() $y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
or
$y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
or
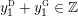 $y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
. If
$y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
. If
![]() $y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
, then (83) implies
$y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
, then (83) implies
 ${\mathcal{L}}(Y)=\mathbb{Q}\cup \{\infty \}\setminus \{-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\}=[[y_{-},y_{+}]]$
. Suppose instead that
${\mathcal{L}}(Y)=\mathbb{Q}\cup \{\infty \}\setminus \{-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}\}=[[y_{-},y_{+}]]$
. Suppose instead that
![]() $y_{1}^{{\rm \small{d}}}\notin \mathbb{Z}$
. If
$y_{1}^{{\rm \small{d}}}\notin \mathbb{Z}$
. If
 $y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
, then for each
$y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
, then for each
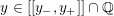 $y\in [[y_{-},y_{+}]]\cap \mathbb{Q}$
, either
$y\in [[y_{-},y_{+}]]\cap \mathbb{Q}$
, either
![]() $y\notin \mathbb{Z}$
, in which case, the fact that
$y\notin \mathbb{Z}$
, in which case, the fact that
 $y\in [y_{-},+\infty ]\cup [-\infty ,y_{+}]$
makes Claim 3 tell us that
$y\in [y_{-},+\infty ]\cup [-\infty ,y_{+}]$
makes Claim 3 tell us that
 $y_{1}^{{\rm \small{g}}}\in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }$
, so that (83) implies
$y_{1}^{{\rm \small{g}}}\in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }$
, so that (83) implies
 $y\in {\mathcal{L}}(Y)$
; or
$y\in {\mathcal{L}}(Y)$
; or
![]() $y\in \mathbb{Z}$
, in which case (83) tells us that
$y\in \mathbb{Z}$
, in which case (83) tells us that
 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
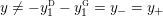 $y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}=y_{-}=y_{+}$
. Combining these two results makes
$y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}=y_{-}=y_{+}$
. Combining these two results makes
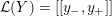 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
Lastly, consider the case in which
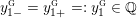 $y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}=:y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
,
$y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}=:y_{1}^{{\rm \small{g}}}\in \mathbb{Q}$
,
![]() $y_{1}^{{\rm \small{d}}}\notin \mathbb{Z}$
, and
$y_{1}^{{\rm \small{d}}}\notin \mathbb{Z}$
, and
 $y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\notin \mathbb{Z}$
. Since in this case
$y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\notin \mathbb{Z}$
. Since in this case
![]() $y\in \mathbb{Z}$
automatically implies
$y\in \mathbb{Z}$
automatically implies
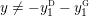 $y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}$
, we deduce that the second line of (83) is vacuous. That is,
$y\neq -y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}$
, we deduce that the second line of (83) is vacuous. That is,
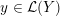 $y\in {\mathcal{L}}(Y)$
for all
$y\in {\mathcal{L}}(Y)$
for all
![]() $y\in \mathbb{Z}$
. Accordingly, since Claim 4 tells us that
$y\in \mathbb{Z}$
. Accordingly, since Claim 4 tells us that
 $$\begin{eqnarray}-\!\lceil y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\rceil \leqslant y_{+}<-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}<y_{-}\leqslant -\lfloor y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\rfloor ,\end{eqnarray}$$
$$\begin{eqnarray}-\!\lceil y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\rceil \leqslant y_{+}<-y_{1}^{{\rm \small{d}}}-y_{1}^{{\rm \small{g}}}<y_{-}\leqslant -\lfloor y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\rfloor ,\end{eqnarray}$$
we observe that the complement of
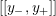 $[[y_{-},y_{+}]]$
contains no integers, and so
$[[y_{-},y_{+}]]$
contains no integers, and so
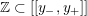 $\mathbb{Z}\subset [[y_{-},y_{+}]]$
. On the other hand, for any
$\mathbb{Z}\subset [[y_{-},y_{+}]]$
. On the other hand, for any
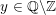 $y\in \mathbb{Q}\setminus \mathbb{Z}$
, (83) tells us that
$y\in \mathbb{Q}\setminus \mathbb{Z}$
, (83) tells us that
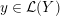 $y\in {\mathcal{L}}(Y)$
if and only if
$y\in {\mathcal{L}}(Y)$
if and only if
 $y_{1}^{{\rm \small{g}}}\in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }$
, which, by Claim 3, occurs if and only if
$y_{1}^{{\rm \small{g}}}\in [[{\hat{y}}_{-},{\hat{y}}_{+}]]^{\circ }$
, which, by Claim 3, occurs if and only if
 $y\in [y_{-},+\infty ]\cup [-\infty ,y_{+}]=[[y_{-},y_{+}]]$
. Thus, once again,
$y\in [y_{-},+\infty ]\cup [-\infty ,y_{+}]=[[y_{-},y_{+}]]$
. Thus, once again,
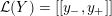 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, completing the proof of the proposition.◻
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, completing the proof of the proposition.◻
Proposition 4.12. Suppose
![]() $Y_{1}$
is Floer simple and
$Y_{1}$
is Floer simple and
 $\infty \notin {\mathcal{L}}(Y)$
. Then
$\infty \notin {\mathcal{L}}(Y)$
. Then
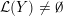 ${\mathcal{L}}(Y)\neq \emptyset$
if and only if either condition
${\mathcal{L}}(Y)\neq \emptyset$
if and only if either condition
![]() $({\rm \small{nfs2}})$
from Proposition 4.7 holds, in which case
$({\rm \small{nfs2}})$
from Proposition 4.7 holds, in which case
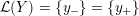 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
, or condition
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
, or condition
![]() $({\rm \small{fs1}})$
or
$({\rm \small{fs1}})$
or
![]() $({\rm \small{fs2}})$
holds, in which case
$({\rm \small{fs2}})$
holds, in which case
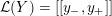 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
.
Proof. Since
![]() $Y_{1}$
is Floer simple, and since
$Y_{1}$
is Floer simple, and since
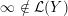 $\infty \notin {\mathcal{L}}(Y)$
implies that
$\infty \notin {\mathcal{L}}(Y)$
implies that
![]() $({\rm \small{fs3}})$
fails to hold, we know that
$({\rm \small{fs3}})$
fails to hold, we know that
 $\infty \notin [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
. Thus,
$\infty \notin [[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]$
. Thus,
 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle$
or
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle$
or
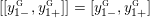 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]$
.
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]$
.
Suppose that
 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle$
, which occurs if and only if condition
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=\langle -\infty ,+\infty \rangle$
, which occurs if and only if condition
![]() $({\rm \small{fs1}})$
holds. For any
$({\rm \small{fs1}})$
holds. For any
![]() $y\in \mathbb{Q}$
, we have
$y\in \mathbb{Q}$
, we have
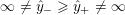 $\infty \neq {\hat{y}}_{-}\geqslant {\hat{y}}_{+}\neq \infty$
, implying condition (82) holds, making
$\infty \neq {\hat{y}}_{-}\geqslant {\hat{y}}_{+}\neq \infty$
, implying condition (82) holds, making
![]() $Y(y)$
an L-space. Thus, since
$Y(y)$
an L-space. Thus, since
 $y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}=\infty$
implies
$y_{1-}^{{\rm \small{g}}}=y_{1+}^{{\rm \small{g}}}=\infty$
implies
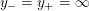 $y_{-}=y_{+}=\infty$
, we have
$y_{-}=y_{+}=\infty$
, we have
 ${\mathcal{L}}(Y)=\mathbb{Q}=\langle -\infty ,+\infty \rangle =[[y_{-},y_{+}]]$
.
${\mathcal{L}}(Y)=\mathbb{Q}=\langle -\infty ,+\infty \rangle =[[y_{-},y_{+}]]$
.
Lastly, suppose
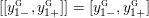 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]$
. For any
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]$
. For any
![]() $y\in \mathbb{Q}$
, we have
$y\in \mathbb{Q}$
, we have
 $y\in [y_{-},+\infty ]\cap [-\infty ,y_{+}]$
if and only if the right-hand conditions of (70) and (71) from Claim 3 hold, which, since
$y\in [y_{-},+\infty ]\cap [-\infty ,y_{+}]$
if and only if the right-hand conditions of (70) and (71) from Claim 3 hold, which, since
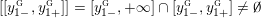 $[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[y_{1-}^{{\rm \small{g}}},+\infty ]\cap [y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]\neq \emptyset$
, occurs if and only if (82) holds, which happens precisely when
$[[y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]]=[y_{1-}^{{\rm \small{g}}},+\infty ]\cap [y_{1-}^{{\rm \small{g}}},y_{1+}^{{\rm \small{g}}}]\neq \emptyset$
, occurs if and only if (82) holds, which happens precisely when
![]() $Y(y)$
is an L-space. Thus,
$Y(y)$
is an L-space. Thus,
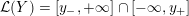 ${\mathcal{L}}(Y)=[y_{-},+\infty ]\cap [-\infty ,y_{+}]$
, or in other words,
${\mathcal{L}}(Y)=[y_{-},+\infty ]\cap [-\infty ,y_{+}]$
, or in other words,
 $$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}[[y_{-},y_{+}]],\quad & y_{-}<y_{+},\\ \{y_{-}\}=\{y_{+}\},\quad & y_{-}=y_{+},\\ \emptyset ,\quad & y_{-}>y_{+}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y)=\left\{\begin{array}{@{}ll@{}}[[y_{-},y_{+}]],\quad & y_{-}<y_{+},\\ \{y_{-}\}=\{y_{+}\},\quad & y_{-}=y_{+},\\ \emptyset ,\quad & y_{-}>y_{+}.\end{array}\right.\end{eqnarray}$$
That is,
![]() ${\mathcal{L}}(Y)$
is non-empty if and only if either
${\mathcal{L}}(Y)$
is non-empty if and only if either
![]() $({\rm \small{fs2}})$
holds, in which case
$({\rm \small{fs2}})$
holds, in which case
 ${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, or
${\mathcal{L}}(Y)=[[y_{-},y_{+}]]$
, or
![]() $({\rm \small{nfs2}})$
holds, in which case
$({\rm \small{nfs2}})$
holds, in which case
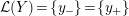 ${\mathcal{L}}(Y)\!=\!\{y_{-}\}\!=\!\{y_{+}\}$
.◻
${\mathcal{L}}(Y)\!=\!\{y_{-}\}\!=\!\{y_{+}\}$
.◻
The combined results of §§ 4.6, 4.7, and 4.8 prove that Theorem 4.6 and Proposition 4.7 hold for any graph manifold
![]() $Y$
with torus boundary,
$Y$
with torus boundary,
![]() $b_{1}=1$
, tree height
$b_{1}=1$
, tree height
![]() $k>0$
, and
$k>0$
, and
![]() $n_{{\rm \small{g}}}>0$
daughter subtrees, given the inductive assumptions, laid out in § 4.5, that Theorem 4.6 and Proposition 4.7 hold for any graph manifold with torus boundary,
$n_{{\rm \small{g}}}>0$
daughter subtrees, given the inductive assumptions, laid out in § 4.5, that Theorem 4.6 and Proposition 4.7 hold for any graph manifold with torus boundary,
![]() $b_{1}=1$
, and either tree height
$b_{1}=1$
, and either tree height
![]() $k$
and up to
$k$
and up to
![]() $n_{{\rm \small{g}}}-1$
daughter subtrees, or tree height less than or equal to
$n_{{\rm \small{g}}}-1$
daughter subtrees, or tree height less than or equal to
![]() $k-1$
.
$k-1$
.
For graph manifolds
![]() $Y$
with torus boundary,
$Y$
with torus boundary,
![]() $b_{1}=1$
, and tree height
$b_{1}=1$
, and tree height
![]() $k$
, inducting on the number of daughter subtrees
$k$
, inducting on the number of daughter subtrees
![]() $n_{{\rm \small{g}}}$
yields the result that any graph manifold with torus boundary,
$n_{{\rm \small{g}}}$
yields the result that any graph manifold with torus boundary,
![]() $b_{1}=1$
, and tree height
$b_{1}=1$
, and tree height
![]() $k$
satisfies Theorem 4.6 and Proposition 4.7. Inducting on tree height
$k$
satisfies Theorem 4.6 and Proposition 4.7. Inducting on tree height
![]() $k$
then completes the proof of Theorem 4.6 and Proposition 4.7.◻
$k$
then completes the proof of Theorem 4.6 and Proposition 4.7.◻
4.9 Some technical results for
 $y_{-}$
and
$y_{-}$
and
 $y_{+}$
$y_{+}$
We conclude this section with the proof of some basic facts about
![]() $y_{-}$
and
$y_{-}$
and
![]() $y_{+}$
for later use.
$y_{+}$
for later use.
Recall that
![]() $y_{-}$
and
$y_{-}$
and
![]() $y_{+}$
are defined by
$y_{+}$
are defined by
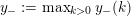 $y_{-}:=\max _{k>0}y_{-}(k)$
and
$y_{-}:=\max _{k>0}y_{-}(k)$
and
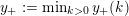 $y_{+}:=\min _{k>0}y_{+}(k)$
, where
$y_{+}:=\min _{k>0}y_{+}(k)$
, where
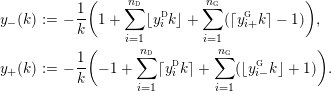 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}\displaystyle y_{-}(k)\ & :=\ & \displaystyle -{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\\ \displaystyle y_{+}(k)\ & :=\ & \displaystyle -{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\displaystyle y_{-}(k)\ & :=\ & \displaystyle -{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr),\\ \displaystyle y_{+}(k)\ & :=\ & \displaystyle -{\displaystyle \frac{1}{k}}\biggl(-1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lceil y_{i}^{{\rm \small{d}}}k\rceil +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lfloor y_{i-}^{{\rm \small{g}}}k\rfloor +1)\biggr).\end{array}\end{eqnarray}$$
Let
 $k_{-},k_{+}\in \mathbb{Z}_{{>}0}$
denote the lowest values of
$k_{-},k_{+}\in \mathbb{Z}_{{>}0}$
denote the lowest values of
![]() $k$
for which these extrema occur. That is, set
$k$
for which these extrema occur. That is, set
 $$\begin{eqnarray}k_{-}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{-}(k)=y_{-}\},\quad k_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{+}(k)=y_{+}\}.\end{eqnarray}$$
$$\begin{eqnarray}k_{-}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{-}(k)=y_{-}\},\quad k_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{+}(k)=y_{+}\}.\end{eqnarray}$$
We then have the following result.
Proposition 4.13. If
![]() $Y$
is not a solid torus, and
$Y$
is not a solid torus, and
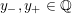 $y_{-},y_{+}\in \mathbb{Q}$
, then
$y_{-},y_{+}\in \mathbb{Q}$
, then
![]() $k_{-}\!$
and
$k_{-}\!$
and
![]() $k_{+}$
are the respective denominators of
$k_{+}$
are the respective denominators of
![]() $y_{-}\!$
and
$y_{-}\!$
and
![]() $y_{+}$
. That is,
$y_{+}$
. That is,
 $$\begin{eqnarray}k_{-}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{-}k\in \mathbb{Z}\},\quad k_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{+}k\in \mathbb{Z}\}.\end{eqnarray}$$
$$\begin{eqnarray}k_{-}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{-}k\in \mathbb{Z}\},\quad k_{+}:=\min \{k\in \mathbb{Z}_{{>}0}\mid y_{+}k\in \mathbb{Z}\}.\end{eqnarray}$$
Proof. Since this question is unaffected by an overall translation of
![]() $y_{-}$
by an integer, we assume without loss of generality that
$y_{-}$
by an integer, we assume without loss of generality that
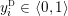 $y_{i}^{{\rm \small{d}}}\in \langle 0,1\rangle$
for all
$y_{i}^{{\rm \small{d}}}\in \langle 0,1\rangle$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
and that
$i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
and that
 $y_{i+}^{{\rm \small{g}}}\in [0,1\rangle$
for all
$y_{i+}^{{\rm \small{g}}}\in [0,1\rangle$
for all
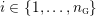 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. In addition, we permute the daughter subtrees
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. In addition, we permute the daughter subtrees
 $Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
so that
$Y_{1},\ldots ,Y_{n_{{\rm \small{g}}}}$
so that
 $y_{i+}^{{\rm \small{g}}}\in \langle 0,1\rangle$
for all
$y_{i+}^{{\rm \small{g}}}\in \langle 0,1\rangle$
for all
 $i\in \{1,\ldots ,\bar{n}_{{\rm \small{g}}}\}$
, and
$i\in \{1,\ldots ,\bar{n}_{{\rm \small{g}}}\}$
, and
![]() $y_{i+}^{{\rm \small{g}}}=0$
for all
$y_{i+}^{{\rm \small{g}}}=0$
for all
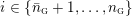 $i\in \{\bar{n}_{{\rm \small{g}}}+1,\ldots ,n_{{\rm \small{g}}}\}$
, for some
$i\in \{\bar{n}_{{\rm \small{g}}}+1,\ldots ,n_{{\rm \small{g}}}\}$
, for some
 $\bar{n}_{{\rm \small{g}}}\leqslant n_{{\rm \small{g}}}$
.
$\bar{n}_{{\rm \small{g}}}\leqslant n_{{\rm \small{g}}}$
.
Setting
 $N_{{\rm \small{g}}}:=n_{{\rm \small{g}}}-\bar{n}_{{\rm \small{g}}}$
, we note that if
$N_{{\rm \small{g}}}:=n_{{\rm \small{g}}}-\bar{n}_{{\rm \small{g}}}$
, we note that if
![]() $N_{{\rm \small{g}}}>0$
, then we obtain
$N_{{\rm \small{g}}}>0$
, then we obtain
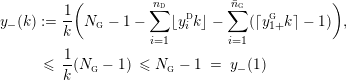 $$\begin{eqnarray}\displaystyle y_{-}(k) & := & \displaystyle {\displaystyle \frac{1}{k}}\biggl(N_{{\rm \small{g}}}-1-\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor -\mathop{\sum }_{i=1}^{\bar{n}_{{\rm \small{g}}}}(\lceil y_{1+}^{{\rm \small{g}}}k\rceil -1)\biggr),\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {\displaystyle \frac{1}{k}}(N_{{\rm \small{g}}}-1)\;\leqslant N_{{\rm \small{g}}}-1\;=\;y_{-}(1)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{-}(k) & := & \displaystyle {\displaystyle \frac{1}{k}}\biggl(N_{{\rm \small{g}}}-1-\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor -\mathop{\sum }_{i=1}^{\bar{n}_{{\rm \small{g}}}}(\lceil y_{1+}^{{\rm \small{g}}}k\rceil -1)\biggr),\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {\displaystyle \frac{1}{k}}(N_{{\rm \small{g}}}-1)\;\leqslant N_{{\rm \small{g}}}-1\;=\;y_{-}(1)\end{eqnarray}$$
for all
![]() $k>0$
, making
$k>0$
, making
 $y_{-}=y_{-}(1)$
. On the other hand, if
$y_{-}=y_{-}(1)$
. On the other hand, if
![]() $N_{{\rm \small{g}}}=0$
, then the top line of (89) implies
$N_{{\rm \small{g}}}=0$
, then the top line of (89) implies
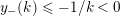 $y_{-}(k)\leqslant -1/k<0$
for all
$y_{-}(k)\leqslant -1/k<0$
for all
![]() $k>0$
, which, since
$k>0$
, which, since
![]() $y_{-}\in \mathbb{Z}$
, implies
$y_{-}\in \mathbb{Z}$
, implies
 $y_{-}\leqslant -1=y_{-}(1)$
. Thus, in either case, we have
$y_{-}\leqslant -1=y_{-}(1)$
. Thus, in either case, we have
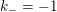 $k_{-}=-1$
, and a similar argument shows
$k_{-}=-1$
, and a similar argument shows
![]() $k_{+}=1$
when
$k_{+}=1$
when
![]() $y_{+}\in \mathbb{Z}$
.
$y_{+}\in \mathbb{Z}$
.
If
![]() $n_{{\rm \small{g}}}=0$
and
$n_{{\rm \small{g}}}=0$
and
![]() $n_{{\rm \small{d}}}\leqslant 1$
, then
$n_{{\rm \small{d}}}\leqslant 1$
, then
![]() $Y$
is a solid torus, a case excluded by hypothesis. Suppose
$Y$
is a solid torus, a case excluded by hypothesis. Suppose
![]() $n_{{\rm \small{d}}}=0$
and
$n_{{\rm \small{d}}}=0$
and
![]() $n_{{\rm \small{g}}}=1$
. If
$n_{{\rm \small{g}}}=1$
. If
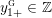 $y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
, then the above argument shows
$y_{1+}^{{\rm \small{g}}}\in \mathbb{Z}$
, then the above argument shows
![]() $y_{-}\in \mathbb{Z}$
and
$y_{-}\in \mathbb{Z}$
and
![]() $k_{-}=1$
. If
$k_{-}=1$
. If
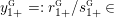 $y_{1+}^{{\rm \small{g}}}=:r_{1+}^{{\rm \small{g}}}/s_{1+}^{{\rm \small{g}}}\in$
$y_{1+}^{{\rm \small{g}}}=:r_{1+}^{{\rm \small{g}}}/s_{1+}^{{\rm \small{g}}}\in$
![]() $\langle 0,1\rangle$
with
$\langle 0,1\rangle$
with
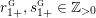 $r_{1+}^{{\rm \small{g}}},s_{1+}^{{\rm \small{g}}}\in \mathbb{Z}_{{>}0}$
relatively prime, then for all
$r_{1+}^{{\rm \small{g}}},s_{1+}^{{\rm \small{g}}}\in \mathbb{Z}_{{>}0}$
relatively prime, then for all
![]() $k>0$
, we have
$k>0$
, we have
 $$\begin{eqnarray}y_{-}(k)=-y_{1+}^{{\rm \small{g}}}-{\displaystyle \frac{1}{k}}[-y_{1+}^{{\rm \small{g}}}]\leqslant -y_{1+}^{{\rm \small{g}}}=y_{-}(s_{1+}^{{\rm \small{g}}}).\end{eqnarray}$$
$$\begin{eqnarray}y_{-}(k)=-y_{1+}^{{\rm \small{g}}}-{\displaystyle \frac{1}{k}}[-y_{1+}^{{\rm \small{g}}}]\leqslant -y_{1+}^{{\rm \small{g}}}=y_{-}(s_{1+}^{{\rm \small{g}}}).\end{eqnarray}$$
Thus
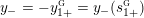 $y_{-}=-y_{1+}^{{\rm \small{g}}}=y_{-}(s_{1+}^{{\rm \small{g}}})$
, and since
$y_{-}=-y_{1+}^{{\rm \small{g}}}=y_{-}(s_{1+}^{{\rm \small{g}}})$
, and since
 $y_{-}(k)<y_{-}$
for all
$y_{-}(k)<y_{-}$
for all
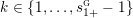 $k\in \{1,\ldots ,s_{1+}^{{\rm \small{g}}}-1\}$
, we also have
$k\in \{1,\ldots ,s_{1+}^{{\rm \small{g}}}-1\}$
, we also have
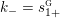 $k_{-}=s_{1+}^{{\rm \small{g}}}$
, which is the denominator of
$k_{-}=s_{1+}^{{\rm \small{g}}}$
, which is the denominator of
![]() $y_{-}$
. A similar argument shows that (88) also holds for
$y_{-}$
. A similar argument shows that (88) also holds for
![]() $k_{+}$
when
$k_{+}$
when
![]() $n_{{\rm \small{d}}}=0$
and
$n_{{\rm \small{d}}}=0$
and
![]() $n_{{\rm \small{g}}}=1$
.
$n_{{\rm \small{g}}}=1$
.
Finally, suppose we exclude all cases considered in the preceding paragraph, and all cases in which
![]() $y_{-}\in \mathbb{Z}$
. Since
$y_{-}\in \mathbb{Z}$
. Since
![]() $y_{-}\in \mathbb{Q}$
by hypothesis, the second paragraph implies we also have
$y_{-}\in \mathbb{Q}$
by hypothesis, the second paragraph implies we also have
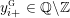 $y_{i+}^{{\rm \small{g}}}\in \mathbb{Q}\setminus \mathbb{Z}$
for all
$y_{i+}^{{\rm \small{g}}}\in \mathbb{Q}\setminus \mathbb{Z}$
for all
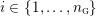 $i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. Since the problem is still unaffected by an overall integer translation of
$i\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. Since the problem is still unaffected by an overall integer translation of
![]() $y_{-}$
, we demand without loss of generality that
$y_{-}$
, we demand without loss of generality that
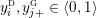 $y_{i}^{{\rm \small{d}}},y_{j+}^{{\rm \small{g}}}\in \langle 0,1\rangle$
for all
$y_{i}^{{\rm \small{d}}},y_{j+}^{{\rm \small{g}}}\in \langle 0,1\rangle$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
and
$i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
and
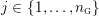 $j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. Thus, after removing one more regular fiber neighborhood
$j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. Thus, after removing one more regular fiber neighborhood
![]() $\unicode[STIX]{x1D708}(f_{0})$
from the JSJ component containing
$\unicode[STIX]{x1D708}(f_{0})$
from the JSJ component containing
![]() $\unicode[STIX]{x2202}Y$
, and Dehn-filling this complement with slope
$\unicode[STIX]{x2202}Y$
, and Dehn-filling this complement with slope
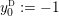 $y_{0}^{{\rm \small{d}}}:=-1$
, we may appeal to Theorem 3 from Jankins and Neumann [Reference Jankins and NeumannJN85], which is equivalent to the following statement.
$y_{0}^{{\rm \small{d}}}:=-1$
, we may appeal to Theorem 3 from Jankins and Neumann [Reference Jankins and NeumannJN85], which is equivalent to the following statement.
If
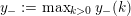 $y_{-}:=\max _{k>0}y_{-}(k)$
, where
$y_{-}:=\max _{k>0}y_{-}(k)$
, where
 $$\begin{eqnarray}y_{-}(k):=1-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}y_{-}(k):=1-{\displaystyle \frac{1}{k}}\biggl(1+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}\lfloor y_{i}^{{\rm \small{d}}}k\rfloor +\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1)\biggr)\end{eqnarray}$$
(with the initial
![]() $1$
coming from
$1$
coming from
![]() $-y_{0}^{{\rm \small{d}}}$
), and if
$-y_{0}^{{\rm \small{d}}}$
), and if
![]() $k_{-}$
is defined as in (87), then there is a positive integer
$k_{-}$
is defined as in (87), then there is a positive integer
![]() $c<k_{-}$
with
$c<k_{-}$
with
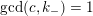 $\gcd (c,k_{-})=1$
, a permutation
$\gcd (c,k_{-})=1$
, a permutation
![]() $\unicode[STIX]{x1D70B}$
on
$\unicode[STIX]{x1D70B}$
on
 $n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1$
elements, and an (
$n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1$
elements, and an (
 $n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1$
)-tuple
$n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1$
)-tuple
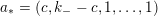 $a_{\ast }=(c,k_{-}-c,1,\ldots ,1)$
, such that
$a_{\ast }=(c,k_{-}-c,1,\ldots ,1)$
, such that
 $$\begin{eqnarray}\lfloor y_{i}^{{\rm \small{d}}}k_{-}\rfloor +1=a_{\unicode[STIX]{x1D70B}(i)},\quad \lceil y_{j+}^{{\rm \small{g}}}k_{-}\rceil =a_{\unicode[STIX]{x1D70B}(n_{{\rm \small{d}}}+j)},\quad y_{-}=\frac{a_{\unicode[STIX]{x1D70B}(n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1)}}{k_{-}}\end{eqnarray}$$
$$\begin{eqnarray}\lfloor y_{i}^{{\rm \small{d}}}k_{-}\rfloor +1=a_{\unicode[STIX]{x1D70B}(i)},\quad \lceil y_{j+}^{{\rm \small{g}}}k_{-}\rceil =a_{\unicode[STIX]{x1D70B}(n_{{\rm \small{d}}}+j)},\quad y_{-}=\frac{a_{\unicode[STIX]{x1D70B}(n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1)}}{k_{-}}\end{eqnarray}$$
for all
 $i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
and
$i\in \{1,\ldots ,n_{{\rm \small{d}}}\}$
and
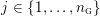 $j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. In particular,
$j\in \{1,\ldots ,n_{{\rm \small{g}}}\}$
. In particular,
 $\gcd (a_{\unicode[STIX]{x1D70B}(n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1)},k_{-})=1$
, making
$\gcd (a_{\unicode[STIX]{x1D70B}(n_{{\rm \small{d}}}+n_{{\rm \small{g}}}+1)},k_{-})=1$
, making
![]() $k_{-}$
satisfy (88). A similar argument shows that (88) holds for
$k_{-}$
satisfy (88). A similar argument shows that (88) holds for
![]() $k_{+}$
, completing the proof.◻
$k_{+}$
, completing the proof.◻
The above result is useful for proving the following proposition, but first, we define
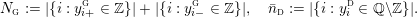 $$\begin{eqnarray}N_{{\rm \small{g}}}:=|\{i:y_{i+}^{{\rm \small{g}}}\in \mathbb{Z}\}|+|\{i:y_{i-}^{{\rm \small{g}}}\in \mathbb{Z}\}|,\quad \bar{n}_{{\rm \small{ d}}}:=|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|.\end{eqnarray}$$
$$\begin{eqnarray}N_{{\rm \small{g}}}:=|\{i:y_{i+}^{{\rm \small{g}}}\in \mathbb{Z}\}|+|\{i:y_{i-}^{{\rm \small{g}}}\in \mathbb{Z}\}|,\quad \bar{n}_{{\rm \small{ d}}}:=|\{i:y_{i}^{{\rm \small{d}}}\in \mathbb{Q}\setminus \mathbb{Z}\}|.\end{eqnarray}$$
Proposition 4.14. Suppose that
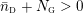 $\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}>0$
, with
$\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}>0$
, with
![]() $Y\!$
not a solid torus. If
$Y\!$
not a solid torus. If
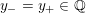 $y_{-}=y_{+}\in \mathbb{Q}$
, then
$y_{-}=y_{+}\in \mathbb{Q}$
, then
 $y_{-}=y_{-}(1)=y_{+}(1)=y_{+}\in \mathbb{Z}$
.
$y_{-}=y_{-}(1)=y_{+}(1)=y_{+}\in \mathbb{Z}$
.
Proof. Since
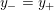 $y_{-}=y_{+}$
, we have
$y_{-}=y_{+}$
, we have
 $$\begin{eqnarray}0=y_{-}-y_{+}=\max _{k_{1}>0}y_{-}(k_{1})-\min _{k_{2}>0}y_{+}(k_{2})=\max _{k_{1},k_{2}>0}\!(y_{-}(k_{1})-y_{+}(k_{2})),\end{eqnarray}$$
$$\begin{eqnarray}0=y_{-}-y_{+}=\max _{k_{1}>0}y_{-}(k_{1})-\min _{k_{2}>0}y_{+}(k_{2})=\max _{k_{1},k_{2}>0}\!(y_{-}(k_{1})-y_{+}(k_{2})),\end{eqnarray}$$
with
![]() $y_{-}(k)$
and
$y_{-}(k)$
and
![]() $y_{+}(k)$
as defined in (86). Defining
$y_{+}(k)$
as defined in (86). Defining
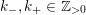 $k_{-},k_{+}\in \mathbb{Z}_{{>}0}$
as in (87), we observe that since
$k_{-},k_{+}\in \mathbb{Z}_{{>}0}$
as in (87), we observe that since
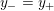 $y_{-}=y_{+}$
, Proposition 4.13 implies
$y_{-}=y_{+}$
, Proposition 4.13 implies
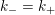 $k_{-}=k_{+}$
. In particular, the set of
$k_{-}=k_{+}$
. In particular, the set of
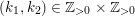 $(k_{1},k_{2})\in \mathbb{Z}_{{>}0}\times \mathbb{Z}_{{>}0}$
for which
$(k_{1},k_{2})\in \mathbb{Z}_{{>}0}\times \mathbb{Z}_{{>}0}$
for which
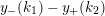 $y_{-}(k_{1})-y_{+}(k_{2})$
is maximized has non-trivial intersection with the set of
$y_{-}(k_{1})-y_{+}(k_{2})$
is maximized has non-trivial intersection with the set of
 $(k_{1},k_{2})\in \mathbb{Z}_{{>}0}\times \mathbb{Z}_{{>}0}$
for which
$(k_{1},k_{2})\in \mathbb{Z}_{{>}0}\times \mathbb{Z}_{{>}0}$
for which
![]() $k_{1}=k_{2}$
. We therefore have
$k_{1}=k_{2}$
. We therefore have
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \max _{k>0}(y_{-}(k)+y_{+}(k))\nonumber\\ \displaystyle & = & \displaystyle \max _{k>0}{\displaystyle \frac{1}{k}}\biggl(-2+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}(\lceil y_{i}^{{\rm \small{d}}}k\rceil -\lfloor y_{i}^{{\rm \small{d}}}k\rfloor )-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1+\lceil -y_{i-}^{{\rm \small{g}}}k\rceil -1)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}\lfloor {\tilde{y}}_{i}^{{\rm \small{g}}}\rfloor +\max _{k>0}{\displaystyle \frac{1}{k}}\biggl(N_{{\rm \small{g}}}-2+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}(\lceil y_{i}^{{\rm \small{d}}}k\rceil -\lfloor y_{i}^{{\rm \small{d}}}k\rfloor )-\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}(\lceil [{\tilde{y}}_{i}^{{\rm \small{g}}}]k\rceil -1)\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \max _{k>0}(y_{-}(k)+y_{+}(k))\nonumber\\ \displaystyle & = & \displaystyle \max _{k>0}{\displaystyle \frac{1}{k}}\biggl(-2+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}(\lceil y_{i}^{{\rm \small{d}}}k\rceil -\lfloor y_{i}^{{\rm \small{d}}}k\rfloor )-\mathop{\sum }_{i=1}^{n_{{\rm \small{g}}}}(\lceil y_{i+}^{{\rm \small{g}}}k\rceil -1+\lceil -y_{i-}^{{\rm \small{g}}}k\rceil -1)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}\lfloor {\tilde{y}}_{i}^{{\rm \small{g}}}\rfloor +\max _{k>0}{\displaystyle \frac{1}{k}}\biggl(N_{{\rm \small{g}}}-2+\mathop{\sum }_{i=1}^{n_{{\rm \small{d}}}}(\lceil y_{i}^{{\rm \small{d}}}k\rceil -\lfloor y_{i}^{{\rm \small{d}}}k\rfloor )-\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}(\lceil [{\tilde{y}}_{i}^{{\rm \small{g}}}]k\rceil -1)\biggr),\end{eqnarray}$$
where the second line uses the fact that
 $-\lfloor q\rfloor =\lceil -q\rceil$
for all
$-\lfloor q\rfloor =\lceil -q\rceil$
for all
![]() $q\in \mathbb{Q}$
, and where in the third line, if we set
$q\in \mathbb{Q}$
, and where in the third line, if we set
 ${\tilde{n}}_{{\rm \small{g}}}:=2n_{{\rm \small{g}}}-N_{{\rm \small{g}}}$
, then
${\tilde{n}}_{{\rm \small{g}}}:=2n_{{\rm \small{g}}}-N_{{\rm \small{g}}}$
, then
 ${\tilde{y}}_{\ast }^{{\rm \small{g}}}\in \mathbb{Q}^{{\tilde{n}}_{{\rm \small{g}}}}$
is the
${\tilde{y}}_{\ast }^{{\rm \small{g}}}\in \mathbb{Q}^{{\tilde{n}}_{{\rm \small{g}}}}$
is the
![]() ${\tilde{n}}_{{\rm \small{g}}}$
-tuple obtained from deleting the
${\tilde{n}}_{{\rm \small{g}}}$
-tuple obtained from deleting the
![]() $N_{{\rm \small{g}}}$
integer-valued entries from the
$N_{{\rm \small{g}}}$
integer-valued entries from the
![]() $2n_{{\rm \small{g}}}$
-tuple
$2n_{{\rm \small{g}}}$
-tuple
 $(y_{1+}^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}},-y_{1-}^{{\rm \small{g}}},\ldots ,-y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}})$
. The third line also makes use of the notation
$(y_{1+}^{{\rm \small{g}}},\ldots ,y_{n_{{\rm \small{g}}}+}^{{\rm \small{g}}},-y_{1-}^{{\rm \small{g}}},\ldots ,-y_{n_{{\rm \small{g}}}-}^{{\rm \small{g}}})$
. The third line also makes use of the notation
 $[\cdot ]:\mathbb{Q}\rightarrow [0,1\rangle$
,
$[\cdot ]:\mathbb{Q}\rightarrow [0,1\rangle$
,
 $q\mapsto [q]:=q-\lfloor q\rfloor$
.
$q\mapsto [q]:=q-\lfloor q\rfloor$
.
Since
 $\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}>0$
, we know that
$\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}>0$
, we know that
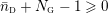 $\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}-1\geqslant 0$
. Thus for all
$\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}-1\geqslant 0$
. Thus for all
![]() $k>0$
, we have
$k>0$
, we have
 $$\begin{eqnarray}\displaystyle y_{-}(k)+y_{+}(k) & {<} & \displaystyle -\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}\lfloor {\tilde{y}}_{i}^{{\rm \small{g}}}\rfloor +{\displaystyle \frac{1}{k}}(\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}-1)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle -\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}\lfloor {\tilde{y}}_{i}^{{\rm \small{g}}}\rfloor +\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}-1\nonumber\\ \displaystyle & = & \displaystyle y_{-}(1)+y_{+}(1)+1\in \mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{-}(k)+y_{+}(k) & {<} & \displaystyle -\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}\lfloor {\tilde{y}}_{i}^{{\rm \small{g}}}\rfloor +{\displaystyle \frac{1}{k}}(\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}-1)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle -\mathop{\sum }_{i=1}^{{\tilde{n}}_{{\rm \small{g}}}}\lfloor {\tilde{y}}_{i}^{{\rm \small{g}}}\rfloor +\bar{n}_{{\rm \small{d}}}+N_{{\rm \small{g}}}-1\nonumber\\ \displaystyle & = & \displaystyle y_{-}(1)+y_{+}(1)+1\in \mathbb{Z},\end{eqnarray}$$
which, since
 $\max _{k>0}(y_{-}(k)+y_{+}(k))\in \mathbb{Z}$
, implies that
$\max _{k>0}(y_{-}(k)+y_{+}(k))\in \mathbb{Z}$
, implies that
 $y_{-}(k)+y_{+}(k)$
is maximized at
$y_{-}(k)+y_{+}(k)$
is maximized at
![]() $k=1$
. Thus,
$k=1$
. Thus,
![]() $y_{-}(k_{1})$
and
$y_{-}(k_{1})$
and
![]() $y_{+}(k_{2})$
are respectively maximized and minimized at
$y_{+}(k_{2})$
are respectively maximized and minimized at
![]() $k_{1}=1$
and
$k_{1}=1$
and
![]() $k_{2}=1$
, completing the proof of the proposition.◻
$k_{2}=1$
, completing the proof of the proposition.◻
5 Cabling
The
![]() $(p,q)$
-cable
$(p,q)$
-cable
 $Y^{(p,q)}\subset k$
of a knot complement
$Y^{(p,q)}\subset k$
of a knot complement
 $Y:=X\setminus \unicode[STIX]{x1D708}(K)\subset X$
is given by the knot complement
$Y:=X\setminus \unicode[STIX]{x1D708}(K)\subset X$
is given by the knot complement
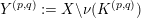 $Y^{(p,q)}:=X\setminus \unicode[STIX]{x1D708}(K^{(p,q)})$
, where
$Y^{(p,q)}:=X\setminus \unicode[STIX]{x1D708}(K^{(p,q)})$
, where
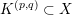 $K^{(p,q)}\subset X$
is the image of the
$K^{(p,q)}\subset X$
is the image of the
![]() $(p,q)$
-torus knot embedded in the boundary of
$(p,q)$
-torus knot embedded in the boundary of
![]() $Y\!$
. I recently made the mundane, and almost certainly not novel, observation that one can realize any cable of
$Y\!$
. I recently made the mundane, and almost certainly not novel, observation that one can realize any cable of
![]() $Y\subset X$
by gluing on an appropriate Seifert fibered space.
$Y\subset X$
by gluing on an appropriate Seifert fibered space.
5.1 Cabling via gluing
Suppose
 $Y:=X\setminus \unicode[STIX]{x1D708}(K)$
is the knot complement of an arbitrary knot
$Y:=X\setminus \unicode[STIX]{x1D708}(K)$
is the knot complement of an arbitrary knot
![]() $K\subset X$
in an arbitrary closed oriented three-manifold
$K\subset X$
in an arbitrary closed oriented three-manifold
![]() $X$
. We construct the
$X$
. We construct the
![]() $(p,q)$
-cable
$(p,q)$
-cable
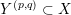 $Y^{(p,q)}\subset X$
of
$Y^{(p,q)}\subset X$
of
![]() $Y\subset X$
as follows.
$Y\subset X$
as follows.
Let
 $\unicode[STIX]{x1D707}\in H_{1}(\unicode[STIX]{x2202}Y)$
denote the meridian of
$\unicode[STIX]{x1D707}\in H_{1}(\unicode[STIX]{x2202}Y)$
denote the meridian of
![]() $K$
, and let
$K$
, and let
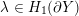 $\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
denote a choice of longitude, so that
$\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
denote a choice of longitude, so that
 $X=Y(\unicode[STIX]{x1D707})$
and
$X=Y(\unicode[STIX]{x1D707})$
and
 $\unicode[STIX]{x1D707}\cdot \unicode[STIX]{x1D706}=1$
. Choosing
$\unicode[STIX]{x1D707}\cdot \unicode[STIX]{x1D706}=1$
. Choosing
 $p^{\ast },q^{\ast }\in Z$
such that
$p^{\ast },q^{\ast }\in Z$
such that
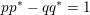 $pp^{\ast }-qq^{\ast }=1$
, let
$pp^{\ast }-qq^{\ast }=1$
, let
![]() $Y_{(-q^{\ast },p)}$
denote the regular fiber complement
$Y_{(-q^{\ast },p)}$
denote the regular fiber complement
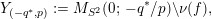 $$\begin{eqnarray}Y_{(-q^{\ast },p)}:=M_{S^{2}}(0;\,-q^{\ast }/p)\setminus \unicode[STIX]{x1D708}(f),\end{eqnarray}$$
$$\begin{eqnarray}Y_{(-q^{\ast },p)}:=M_{S^{2}}(0;\,-q^{\ast }/p)\setminus \unicode[STIX]{x1D708}(f),\end{eqnarray}$$
so that
![]() $Y_{(-q^{\ast },p)}$
is a solid torus whose compressing disk has boundary of slope
$Y_{(-q^{\ast },p)}$
is a solid torus whose compressing disk has boundary of slope
![]() $q^{\ast }/p$
.
$q^{\ast }/p$
.
To construct the
![]() $(p,q)$
-cable
$(p,q)$
-cable
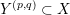 $Y^{(p,q)}\subset X$
, we form the union
$Y^{(p,q)}\subset X$
, we form the union
 $$\begin{eqnarray}Y^{(p,q)}:={\hat{Y}}_{(-q^{\ast },p)}\cup _{\unicode[STIX]{x1D711}}Y,\quad \unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y\rightarrow -\unicode[STIX]{x2202}_{1}{\hat{Y}}_{(-q^{\ast },p)},\end{eqnarray}$$
$$\begin{eqnarray}Y^{(p,q)}:={\hat{Y}}_{(-q^{\ast },p)}\cup _{\unicode[STIX]{x1D711}}Y,\quad \unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y\rightarrow -\unicode[STIX]{x2202}_{1}{\hat{Y}}_{(-q^{\ast },p)},\end{eqnarray}$$
where
![]() ${\hat{Y}}_{(-q^{\ast },p)}$
is a regular fiber complement in
${\hat{Y}}_{(-q^{\ast },p)}$
is a regular fiber complement in
![]() $Y_{(-q^{\ast },p)}$
, with
$Y_{(-q^{\ast },p)}$
, with
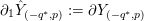 $\unicode[STIX]{x2202}_{1}{\hat{Y}}_{(-q^{\ast },p)}:=\unicode[STIX]{x2202}Y_{(-q^{\ast },p)}$
, and where
$\unicode[STIX]{x2202}_{1}{\hat{Y}}_{(-q^{\ast },p)}:=\unicode[STIX]{x2202}Y_{(-q^{\ast },p)}$
, and where
![]() $\unicode[STIX]{x1D711}$
is chosen to induce the map
$\unicode[STIX]{x1D711}$
is chosen to induce the map
![]() $\unicode[STIX]{x1D711}_{\ast }$
on homology defined by
$\unicode[STIX]{x1D711}_{\ast }$
on homology defined by
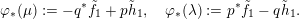 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D707}):=-q^{\ast }\tilde{f}_{1}+p\tilde{h}_{1},\quad \unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D706}):=p^{\ast }\tilde{f}_{1}-q\tilde{h}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D707}):=-q^{\ast }\tilde{f}_{1}+p\tilde{h}_{1},\quad \unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D706}):=p^{\ast }\tilde{f}_{1}-q\tilde{h}_{1}.\end{eqnarray}$$
Proposition 5.1.
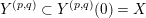 $Y^{(p,q)}\subset Y^{(p,q)}(0)=X$
is the
$Y^{(p,q)}\subset Y^{(p,q)}(0)=X$
is the
![]() $(p,q)$
-cable of the knot complement
$(p,q)$
-cable of the knot complement
![]() $Y\subset X$
.
$Y\subset X$
.
Proof. To verify that
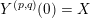 $Y^{(p,q)}(0)=X$
, note that
$Y^{(p,q)}(0)=X$
, note that
 $Y^{(p,q)}(0)$
is a union of
$Y^{(p,q)}(0)$
is a union of
![]() $Y$
with the solid torus
$Y$
with the solid torus
![]() $Y_{(-q^{\ast },p)}$
, such that
$Y_{(-q^{\ast },p)}$
, such that
![]() $\unicode[STIX]{x1D707}$
is sent to the slope
$\unicode[STIX]{x1D707}$
is sent to the slope
![]() $q^{\ast }/p$
bounding the compressing disk of
$q^{\ast }/p$
bounding the compressing disk of
![]() $Y_{(-q^{\ast },p)}$
. In other words,
$Y_{(-q^{\ast },p)}$
. In other words,
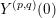 $Y^{(p,q)}(0)$
is the Dehn filling
$Y^{(p,q)}(0)$
is the Dehn filling
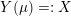 $Y(\unicode[STIX]{x1D707})=:X$
.
$Y(\unicode[STIX]{x1D707})=:X$
.
Since
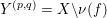 $Y^{(p,q)}=X\setminus \unicode[STIX]{x1D708}(f)$
is the complement of the regular fiber
$Y^{(p,q)}=X\setminus \unicode[STIX]{x1D708}(f)$
is the complement of the regular fiber
![]() $f$
, we next must verify that, in the boundary of the solid torus (
$f$
, we next must verify that, in the boundary of the solid torus (
![]() ${\rm \small{st}}$
) to which
${\rm \small{st}}$
) to which
![]() $Y$
is glued, the regular fiber is of class
$Y$
is glued, the regular fiber is of class
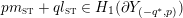 $pm_{{\rm \small{st}}}+ql_{{\rm \small{st}}}\in H_{1}(\unicode[STIX]{x2202}Y_{(-q^{\ast },p)})$
in terms of the basis
$pm_{{\rm \small{st}}}+ql_{{\rm \small{st}}}\in H_{1}(\unicode[STIX]{x2202}Y_{(-q^{\ast },p)})$
in terms of the basis
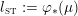 $l_{{\rm \small{st}}}:=\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D707})$
,
$l_{{\rm \small{st}}}:=\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D707})$
,
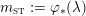 $m_{{\rm \small{st}}}:=\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D706})$
specified by the meridian
$m_{{\rm \small{st}}}:=\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D706})$
specified by the meridian
![]() $\unicode[STIX]{x1D707}$
and longitude
$\unicode[STIX]{x1D707}$
and longitude
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $K$
. Indeed, we have
$K$
. Indeed, we have
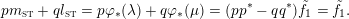 $$\begin{eqnarray}pm_{{\rm \small{st}}}+ql_{{\rm \small{st}}}=p\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D706})+q\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D707})=(pp^{\ast }-qq^{\ast })\tilde{f}_{1}=\tilde{f}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}pm_{{\rm \small{st}}}+ql_{{\rm \small{st}}}=p\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D706})+q\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D707})=(pp^{\ast }-qq^{\ast })\tilde{f}_{1}=\tilde{f}_{1}.\end{eqnarray}$$
◻
5.2 L-space intervals for cables
Supposing
![]() $Y\subset X$
is Floer simple and boundary incompressible, write
$Y\subset X$
is Floer simple and boundary incompressible, write
 $a_{-}\unicode[STIX]{x1D707}+b_{-}\unicode[STIX]{x1D706}$
and
$a_{-}\unicode[STIX]{x1D707}+b_{-}\unicode[STIX]{x1D706}$
and
 $a_{+}\unicode[STIX]{x1D707}+b_{+}\unicode[STIX]{x1D706}$
for respective representatives in
$a_{+}\unicode[STIX]{x1D707}+b_{+}\unicode[STIX]{x1D706}$
for respective representatives in
 $H_{1}(\unicode[STIX]{x2202}Y)$
of the left-hand and right-hand endpoints of the L-space interval
$H_{1}(\unicode[STIX]{x2202}Y)$
of the left-hand and right-hand endpoints of the L-space interval
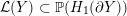 ${\mathcal{L}}(Y)\subset \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. Now,
${\mathcal{L}}(Y)\subset \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
. Now,
![]() $\unicode[STIX]{x1D711}$
is an orientation-reversing map, but since we change from a positively-oriented basis to a negatively-oriented basis, the induced map
$\unicode[STIX]{x1D711}$
is an orientation-reversing map, but since we change from a positively-oriented basis to a negatively-oriented basis, the induced map
![]() $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}$
is orientation-preserving. We therefore have
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}$
is orientation-preserving. We therefore have
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}(Y))=[[y_{1-},y_{1+}]],\quad y_{1\pm }:=\frac{a_{\pm }q^{\ast }-b_{\pm }p^{\ast }}{a_{\pm }p-b_{\pm }q}=\frac{q^{\ast }}{p}\biggl(1-\frac{b_{\pm }}{q^{\ast }(a_{\pm }p-b_{\pm }q)}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}(Y))=[[y_{1-},y_{1+}]],\quad y_{1\pm }:=\frac{a_{\pm }q^{\ast }-b_{\pm }p^{\ast }}{a_{\pm }p-b_{\pm }q}=\frac{q^{\ast }}{p}\biggl(1-\frac{b_{\pm }}{q^{\ast }(a_{\pm }p-b_{\pm }q)}\biggr).\end{eqnarray}$$
For
 $k\in \mathbb{Z}_{{>}0}$
, define
$k\in \mathbb{Z}_{{>}0}$
, define
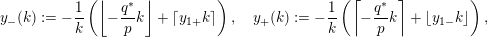 $$\begin{eqnarray}y_{-}(k):=-{\displaystyle \frac{1}{k}}\left(\left\lfloor -{\displaystyle \frac{q^{\ast }}{p}}k\right\rfloor +\lceil y_{1+}k\rceil \right),\quad y_{+}(k):=-{\displaystyle \frac{1}{k}}\left(\left\lceil -{\displaystyle \frac{q^{\ast }}{p}}k\right\rceil +\lfloor y_{1-}k\rfloor \right),\end{eqnarray}$$
$$\begin{eqnarray}y_{-}(k):=-{\displaystyle \frac{1}{k}}\left(\left\lfloor -{\displaystyle \frac{q^{\ast }}{p}}k\right\rfloor +\lceil y_{1+}k\rceil \right),\quad y_{+}(k):=-{\displaystyle \frac{1}{k}}\left(\left\lceil -{\displaystyle \frac{q^{\ast }}{p}}k\right\rceil +\lfloor y_{1-}k\rfloor \right),\end{eqnarray}$$
which simplifies to
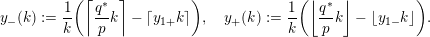 $$\begin{eqnarray}y_{-}(k):={\displaystyle \frac{1}{k}}\biggl(\bigg\lceil{\displaystyle \frac{q^{\ast }}{p}}k\bigg\rceil-\lceil y_{1+}k\rceil \biggr),\quad y_{+}(k):={\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\lfloor y_{1-}k\rfloor \biggr).\end{eqnarray}$$
$$\begin{eqnarray}y_{-}(k):={\displaystyle \frac{1}{k}}\biggl(\bigg\lceil{\displaystyle \frac{q^{\ast }}{p}}k\bigg\rceil-\lceil y_{1+}k\rceil \biggr),\quad y_{+}(k):={\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\lfloor y_{1-}k\rfloor \biggr).\end{eqnarray}$$
As usual, we also define
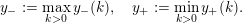 $$\begin{eqnarray}y_{-}:=\max _{k>0}y_{-}(k),\quad y_{+}:=\min _{k>0}y_{+}(k).\end{eqnarray}$$
$$\begin{eqnarray}y_{-}:=\max _{k>0}y_{-}(k),\quad y_{+}:=\min _{k>0}y_{+}(k).\end{eqnarray}$$
Since
![]() $Y$
is Floer simple and boundary incompressible, and since every Dehn filling of
$Y$
is Floer simple and boundary incompressible, and since every Dehn filling of
![]() ${\hat{Y}}_{(-q^{\ast },p)}$
along
${\hat{Y}}_{(-q^{\ast },p)}$
along
![]() $\unicode[STIX]{x2202}Y^{(p,q)}$
is Floer simple, we can still invoke Theorem 4.6 and Proposition 4.7 to compute the L-space interval for
$\unicode[STIX]{x2202}Y^{(p,q)}$
is Floer simple, we can still invoke Theorem 4.6 and Proposition 4.7 to compute the L-space interval for
![]() $Y^{(p,q)}$
(see Corollary 6.2 for justification of this generalization). Thus, in terms of the Seifert basis
$Y^{(p,q)}$
(see Corollary 6.2 for justification of this generalization). Thus, in terms of the Seifert basis
![]() $(\tilde{f},-\tilde{h})$
,
$(\tilde{f},-\tilde{h})$
,
![]() ${\hat{Y}}_{(-q^{\ast },p)}$
has L-space interval
${\hat{Y}}_{(-q^{\ast },p)}$
has L-space interval
 $[[y_{-},y_{+}]]$
if it is Floer simple, and
$[[y_{-},y_{+}]]$
if it is Floer simple, and
 $\{y_{-}\}=\{y_{+}\}$
if it has an isolated L-space filling.
$\{y_{-}\}=\{y_{+}\}$
if it has an isolated L-space filling.
It is often more natural, however, to express this L-space interval in terms of the surgery basis for the cabled knot. Recall that
 ${\hat{Y}}_{(-q^{\ast },p)}=X\setminus \unicode[STIX]{x1D708}(f)$
. The natural surgery basis associated to the complement of the regular fiber is given by the meridian
${\hat{Y}}_{(-q^{\ast },p)}=X\setminus \unicode[STIX]{x1D708}(f)$
. The natural surgery basis associated to the complement of the regular fiber is given by the meridian
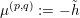 $\unicode[STIX]{x1D707}^{(p,q)}:=-\tilde{h}$
and longitude
$\unicode[STIX]{x1D707}^{(p,q)}:=-\tilde{h}$
and longitude
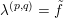 $\unicode[STIX]{x1D706}^{(p,q)}=\tilde{f}$
, yielding the following result.
$\unicode[STIX]{x1D706}^{(p,q)}=\tilde{f}$
, yielding the following result.
Theorem 5.2. Suppose
 $Y\,=\,X\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple knot complement with L-space interval
$Y\,=\,X\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple knot complement with L-space interval
 ${\mathcal{L}}(Y)\,=\,[[a_{-}/b_{-},a_{+}/b_{+}]]$
in terms of the surgery basis
${\mathcal{L}}(Y)\,=\,[[a_{-}/b_{-},a_{+}/b_{+}]]$
in terms of the surgery basis
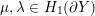 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
for
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
for
![]() $K$
, with
$K$
, with
![]() $\unicode[STIX]{x1D707}$
the meridian of
$\unicode[STIX]{x1D707}$
the meridian of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D706}$
a choice of longitude. Then in terms of the surgery basis produced by cabling, the
$\unicode[STIX]{x1D706}$
a choice of longitude. Then in terms of the surgery basis produced by cabling, the
![]() $(p,q)$
-cable
$(p,q)$
-cable
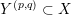 $Y^{(p,q)}\subset X$
of
$Y^{(p,q)}\subset X$
of
![]() $Y\subset X$
has L-space interval
$Y\subset X$
has L-space interval
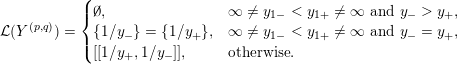 $$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\emptyset ,\quad & \infty \neq y_{1-}<y_{1+}\neq \infty \text{and }y_{-}>y_{+},\\ \{1/y_{-}\}=\{1/y_{+}\},\quad & \infty \neq y_{1-}<y_{1+}\neq \infty \text{and }y_{-}=y_{+},\\ \text{}[[1/y_{+},1/y_{-}]],\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\emptyset ,\quad & \infty \neq y_{1-}<y_{1+}\neq \infty \text{and }y_{-}>y_{+},\\ \{1/y_{-}\}=\{1/y_{+}\},\quad & \infty \neq y_{1-}<y_{1+}\neq \infty \text{and }y_{-}=y_{+},\\ \text{}[[1/y_{+},1/y_{-}]],\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
5.3 Knots in
 $S^{3}$
$S^{3}$
As an illustration, we apply the above result to an arbitrary boundary incompressible Floer simple knot complement
 $Y:=S^{3}\setminus \unicode[STIX]{x1D708}(K)$
in
$Y:=S^{3}\setminus \unicode[STIX]{x1D708}(K)$
in
![]() $S^{3}\!$
. The surgery basis for a knot complement in
$S^{3}\!$
. The surgery basis for a knot complement in
![]() $S^{3}$
conventionally takes
$S^{3}$
conventionally takes
![]() $\unicode[STIX]{x1D706}$
to be the rational longitude, which in
$\unicode[STIX]{x1D706}$
to be the rational longitude, which in
![]() $S^{3}$
is Seifert framed. The meridian
$S^{3}$
is Seifert framed. The meridian
![]() $\unicode[STIX]{x1D707}$
of
$\unicode[STIX]{x1D707}$
of
![]() $K$
is automatically dual to this
$K$
is automatically dual to this
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Without loss of generality (up to replacing
![]() $K$
with its mirror image), we demand that
$K$
with its mirror image), we demand that
![]() $K$
be positive, by which we mean that there exist positive
$K$
be positive, by which we mean that there exist positive
 $u,v\in \mathbb{Z}$
such that the Dehn filling
$u,v\in \mathbb{Z}$
such that the Dehn filling
 $Y(u\unicode[STIX]{x1D707}+v\unicode[STIX]{x1D706})$
is an L-space. In terms of the projectivization map
$Y(u\unicode[STIX]{x1D707}+v\unicode[STIX]{x1D706})$
is an L-space. In terms of the projectivization map
 $x\unicode[STIX]{x1D707}+y\unicode[STIX]{x1D706}\mapsto x/y\in \mathbb{Q}\cup \{\infty \}$
, it is easy to show (see ‘example’ in [Reference Rasmussen and RasmussenRR15, §4]) that
$x\unicode[STIX]{x1D707}+y\unicode[STIX]{x1D706}\mapsto x/y\in \mathbb{Q}\cup \{\infty \}$
, it is easy to show (see ‘example’ in [Reference Rasmussen and RasmussenRR15, §4]) that
![]() $Y$
has L-space interval
$Y$
has L-space interval
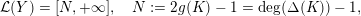 $$\begin{eqnarray}{\mathcal{L}}(Y)=[N,+\infty ],\quad N:=2g(K)-1=\deg (\unicode[STIX]{x1D6E5}(K))-1,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y)=[N,+\infty ],\quad N:=2g(K)-1=\deg (\unicode[STIX]{x1D6E5}(K))-1,\end{eqnarray}$$
where
![]() $g(K)$
and
$g(K)$
and
![]() $\unicode[STIX]{x1D6E5}(K)$
are the genus and Alexander polynomial of
$\unicode[STIX]{x1D6E5}(K)$
are the genus and Alexander polynomial of
![]() $K$
.
$K$
.
Choosing
 $q^{\ast },p^{\ast }\in \mathbb{Z}$
such that
$q^{\ast },p^{\ast }\in \mathbb{Z}$
such that
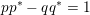 $pp^{\ast }-qq^{\ast }=1$
, and demanding
$pp^{\ast }-qq^{\ast }=1$
, and demanding
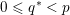 $0\leqslant q^{\ast }<p$
, we then have
$0\leqslant q^{\ast }<p$
, we then have
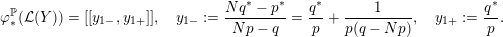 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}(Y))=[[y_{1-},y_{1+}]],\quad y_{1-}:={\displaystyle \frac{Nq^{\ast }-p^{\ast }}{Np-q}}={\displaystyle \frac{q^{\ast }}{p}}+{\displaystyle \frac{1}{p(q-Np)}},\quad y_{1+}:={\displaystyle \frac{q^{\ast }}{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}(Y))=[[y_{1-},y_{1+}]],\quad y_{1-}:={\displaystyle \frac{Nq^{\ast }-p^{\ast }}{Np-q}}={\displaystyle \frac{q^{\ast }}{p}}+{\displaystyle \frac{1}{p(q-Np)}},\quad y_{1+}:={\displaystyle \frac{q^{\ast }}{p}}.\end{eqnarray}$$
From (103) and (104), we immediately compute that
![]() $y_{-}=0$
. For
$y_{-}=0$
. For
![]() $y_{+}$
, we have
$y_{+}$
, we have
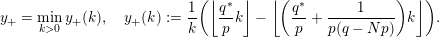 $$\begin{eqnarray}y_{+}=\min _{k>0}y_{+}(k),\quad y_{+}(k):={\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\biggl\lfloor\biggl({\displaystyle \frac{q^{\ast }}{p}}+{\displaystyle \frac{1}{p(q-Np)}}\biggr)k\biggr\rfloor\biggr).\end{eqnarray}$$
$$\begin{eqnarray}y_{+}=\min _{k>0}y_{+}(k),\quad y_{+}(k):={\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\biggl\lfloor\biggl({\displaystyle \frac{q^{\ast }}{p}}+{\displaystyle \frac{1}{p(q-Np)}}\biggr)k\biggr\rfloor\biggr).\end{eqnarray}$$
If
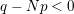 $q-Np<0$
, then
$q-Np<0$
, then
 $y_{+}(k)\geqslant 0$
for all
$y_{+}(k)\geqslant 0$
for all
![]() $k>0$
, and so
$k>0$
, and so
![]() $y_{+}(k)$
is minimized at
$y_{+}(k)$
is minimized at
 $y_{+}=y_{+}(1)=0$
. Since
$y_{+}=y_{+}(1)=0$
. Since
 $\infty \neq y_{1-}<y_{1+}\neq \infty$
in this case, we then have
$\infty \neq y_{1-}<y_{1+}\neq \infty$
in this case, we then have
 ${\mathcal{L}}(Y^{(p,q)})=\{0\}$
. If
${\mathcal{L}}(Y^{(p,q)})=\{0\}$
. If
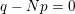 $q-Np=0$
, then
$q-Np=0$
, then
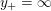 $y_{+}=\infty$
, yielding
$y_{+}=\infty$
, yielding
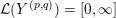 ${\mathcal{L}}(Y^{(p,q)})=[0,\infty ]$
. If
${\mathcal{L}}(Y^{(p,q)})=[0,\infty ]$
. If
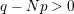 $q-Np>0$
, then
$q-Np>0$
, then
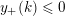 $y_{+}(k)\leqslant 0$
for all
$y_{+}(k)\leqslant 0$
for all
![]() $k>0$
, and it is straightforward to show that
$k>0$
, and it is straightforward to show that
![]() $y_{+}(k)$
is minimized at the lowest value of
$y_{+}(k)$
is minimized at the lowest value of
![]() $k_{+}>0$
for which
$k_{+}>0$
for which
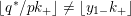 $\lfloor q^{\ast }/pk_{+}\rfloor \neq \lfloor y_{1-}k_{+}\rfloor$
. Since
$\lfloor q^{\ast }/pk_{+}\rfloor \neq \lfloor y_{1-}k_{+}\rfloor$
. Since
 $y_{1-}-q^{\ast }/p<1/p$
, a necessary condition for this to occur is to have
$y_{1-}-q^{\ast }/p<1/p$
, a necessary condition for this to occur is to have
 $$\begin{eqnarray}\biggl(y_{1-}-{\displaystyle \frac{q^{\ast }}{p}}\biggr)k_{+}\geqslant {\displaystyle \frac{1}{p}},\quad \text{which implies }k_{+}\geqslant q-Np.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(y_{1-}-{\displaystyle \frac{q^{\ast }}{p}}\biggr)k_{+}\geqslant {\displaystyle \frac{1}{p}},\quad \text{which implies }k_{+}\geqslant q-Np.\end{eqnarray}$$
Since
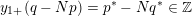 $y_{1+}(q-Np)=p^{\ast }-Nq^{\ast }\in \mathbb{Z}$
, setting
$y_{1+}(q-Np)=p^{\ast }-Nq^{\ast }\in \mathbb{Z}$
, setting
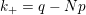 $k_{+}=q-Np$
is also sufficient:
$k_{+}=q-Np$
is also sufficient:
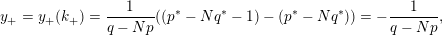 $$\begin{eqnarray}y_{+}=y_{+}(k_{+})={\displaystyle \frac{1}{q-Np}}((p^{\ast }-Nq^{\ast }-1)-(p^{\ast }-Nq^{\ast }))=-{\displaystyle \frac{1}{q-Np}},\end{eqnarray}$$
$$\begin{eqnarray}y_{+}=y_{+}(k_{+})={\displaystyle \frac{1}{q-Np}}((p^{\ast }-Nq^{\ast }-1)-(p^{\ast }-Nq^{\ast }))=-{\displaystyle \frac{1}{q-Np}},\end{eqnarray}$$
and we have
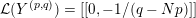 ${\mathcal{L}}(Y^{(p,q)})=[[0,-1/(q-Np)]]$
.
${\mathcal{L}}(Y^{(p,q)})=[[0,-1/(q-Np)]]$
.
As a final step, we re-express
 ${\mathcal{L}}(Y^{(p,q)})$
in terms of the conventional basis for knot complements in
${\mathcal{L}}(Y^{(p,q)})$
in terms of the conventional basis for knot complements in
![]() $S^{3}$
. We again use the meridian
$S^{3}$
. We again use the meridian
 $\unicode[STIX]{x1D707}^{(p,q)}:=-\tilde{h}$
, but the rational longitude is
$\unicode[STIX]{x1D707}^{(p,q)}:=-\tilde{h}$
, but the rational longitude is
 $$\begin{eqnarray}l^{(p,q)}=-\biggl(-{\displaystyle \frac{q^{\ast }}{p}}+\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}([\unicode[STIX]{x1D706}])\biggr)=-\biggl(-{\displaystyle \frac{q^{\ast }}{p}}+{\displaystyle \frac{p^{\ast }}{q}}\biggr)=-{\displaystyle \frac{1}{pq}},\end{eqnarray}$$
$$\begin{eqnarray}l^{(p,q)}=-\biggl(-{\displaystyle \frac{q^{\ast }}{p}}+\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}([\unicode[STIX]{x1D706}])\biggr)=-\biggl(-{\displaystyle \frac{q^{\ast }}{p}}+{\displaystyle \frac{p^{\ast }}{q}}\biggr)=-{\displaystyle \frac{1}{pq}},\end{eqnarray}$$
for which we choose the representative
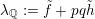 $\unicode[STIX]{x1D706}_{\mathbb{Q}}:=\tilde{f}+pq\tilde{h}$
to achieve
$\unicode[STIX]{x1D706}_{\mathbb{Q}}:=\tilde{f}+pq\tilde{h}$
to achieve
 $\unicode[STIX]{x1D707}^{(p,q)}\cdot \unicode[STIX]{x1D706}_{\mathbb{Q}}=1$
. Performing the requisite change of basis on
$\unicode[STIX]{x1D707}^{(p,q)}\cdot \unicode[STIX]{x1D706}_{\mathbb{Q}}=1$
. Performing the requisite change of basis on
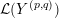 ${\mathcal{L}}(Y^{(p,q)})$
for the three cases described in the preceding paragraph then recovers the following result of Hedden [Reference HeddenHed09] and Hom [Reference HomHom11].
${\mathcal{L}}(Y^{(p,q)})$
for the three cases described in the preceding paragraph then recovers the following result of Hedden [Reference HeddenHed09] and Hom [Reference HomHom11].
Corollary 5.3.
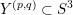 $Y^{(p,q)}\subset S^{3}$
has L-space interval
$Y^{(p,q)}\subset S^{3}$
has L-space interval
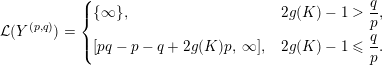 $$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & 2g(K)-1>{\displaystyle \frac{q}{p}},\\ \text{}[pq-p-q+2g(K)p,\;\infty ],\quad & 2g(K)-1\leqslant {\displaystyle \frac{q}{p}}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & 2g(K)-1>{\displaystyle \frac{q}{p}},\\ \text{}[pq-p-q+2g(K)p,\;\infty ],\quad & 2g(K)-1\leqslant {\displaystyle \frac{q}{p}}.\end{array}\right.\end{eqnarray}$$
5.4 Knots in L-spaces
It is possible to prove an analogous result for boundary incompressible Floer simple knot complements in arbitrary L-spaces.
To simplify the statement of such a result, we discard cables with
![]() $p=0$
,
$p=0$
,
![]() $p=1$
, or
$p=1$
, or
![]() $q=0$
, since the zero-cable of a knot complement
$q=0$
, since the zero-cable of a knot complement
![]() $Y\subset X$
is just the connected sum of
$Y\subset X$
is just the connected sum of
![]() $X$
with the unknot complement in
$X$
with the unknot complement in
![]() $S^{3}$
; the
$S^{3}$
; the
![]() $1/q$
-cable is just a change of framing; and the
$1/q$
-cable is just a change of framing; and the
![]() $1/0$
-cable, which changes the framing by zero, is the identity cable. We then have the following.
$1/0$
-cable, which changes the framing by zero, is the identity cable. We then have the following.
Theorem 5.4. Suppose that
 $p,q\in \mathbb{Z}$
with
$p,q\in \mathbb{Z}$
with
![]() $p>1$
and
$p>1$
and
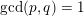 $\gcd (p,q)=1$
, and that
$\gcd (p,q)=1$
, and that
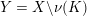 $Y=X\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple knot complement in an L-space
$Y=X\setminus \unicode[STIX]{x1D708}(K)$
is a boundary incompressible Floer simple knot complement in an L-space
![]() $X$
, with L-space interval
$X$
, with L-space interval
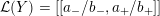 ${\mathcal{L}}(Y)=[[a_{-}/b_{-},a_{+}/b_{+}]]$
, written in terms of the surgery basis
${\mathcal{L}}(Y)=[[a_{-}/b_{-},a_{+}/b_{+}]]$
, written in terms of the surgery basis
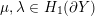 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
for
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in H_{1}(\unicode[STIX]{x2202}Y)$
for
![]() $K$
, with
$K$
, with
![]() $\unicode[STIX]{x1D707}$
the meridian of
$\unicode[STIX]{x1D707}$
the meridian of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D706}$
a choice of longitude. Then in terms of the surgery basis produced by cabling, the
$\unicode[STIX]{x1D706}$
a choice of longitude. Then in terms of the surgery basis produced by cabling, the
![]() $(p,q)$
-cable
$(p,q)$
-cable
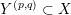 $Y^{(p,q)}\subset X$
of
$Y^{(p,q)}\subset X$
of
![]() $Y\subset X$
has L-space interval
$Y\subset X$
has L-space interval
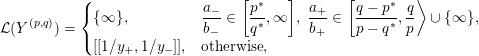 $$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & {\displaystyle \frac{a_{-}}{b_{-}}}\in \biggl[{\displaystyle \frac{p^{\ast }}{q^{\ast }}},\infty \biggr],\;{\displaystyle \frac{a_{+}}{b_{+}}}\in \biggl[{\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}},{\displaystyle \frac{q}{p}}\rangle \cup \{\infty \},\\ \text{}[[1/y_{+},1/y_{-}]],\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(Y^{(p,q)})=\left\{\begin{array}{@{}ll@{}}\{\infty \},\quad & {\displaystyle \frac{a_{-}}{b_{-}}}\in \biggl[{\displaystyle \frac{p^{\ast }}{q^{\ast }}},\infty \biggr],\;{\displaystyle \frac{a_{+}}{b_{+}}}\in \biggl[{\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}},{\displaystyle \frac{q}{p}}\rangle \cup \{\infty \},\\ \text{}[[1/y_{+},1/y_{-}]],\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
where
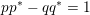 $pp^{\ast }-qq^{\ast }=1$
with
$pp^{\ast }-qq^{\ast }=1$
with
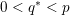 $0<q^{\ast }<p$
.
$0<q^{\ast }<p$
.
Proof. If
![]() $Y^{(p,q)}$
is Floer simple, then Theorem 5.2 implies
$Y^{(p,q)}$
is Floer simple, then Theorem 5.2 implies
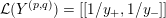 ${\mathcal{L}}(Y^{(p,q)})=[[1/y_{+},1/y_{-}]]$
in terms of the surgery basis produced by cabling.
${\mathcal{L}}(Y^{(p,q)})=[[1/y_{+},1/y_{-}]]$
in terms of the surgery basis produced by cabling.
Observe that
![]() $Y^{(p,q)}$
is not Floer simple if and only if
$Y^{(p,q)}$
is not Floer simple if and only if
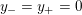 $y_{-}=y_{+}=0$
. That is, if
$y_{-}=y_{+}=0$
. That is, if
![]() $Y^{(p,q)}$
is not Floer simple, then the meridional filling
$Y^{(p,q)}$
is not Floer simple, then the meridional filling
![]() $X$
is the only L-space filling, and conversely if
$X$
is the only L-space filling, and conversely if
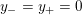 $y_{-}=y_{+}=0$
, then since
$y_{-}=y_{+}=0$
, then since
 $0\notin [[0,0]]$
, we know that
$0\notin [[0,0]]$
, we know that
![]() $Y^{(p,q)}$
is not Floer simple.
$Y^{(p,q)}$
is not Floer simple.
Choose
 $p^{\ast },q^{\ast }\in \mathbb{Z}$
so that
$p^{\ast },q^{\ast }\in \mathbb{Z}$
so that
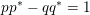 $pp^{\ast }-qq^{\ast }=1$
with
$pp^{\ast }-qq^{\ast }=1$
with
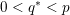 $0<q^{\ast }<p$
. Then for
$0<q^{\ast }<p$
. Then for
 $y_{1\pm }\neq \infty$
, one has
$y_{1\pm }\neq \infty$
, one has
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}y_{-}=-\lceil y_{1+}\rceil +1,\quad & 1-[-y_{1+}]\geqslant {\displaystyle \frac{q^{\ast }}{p}},\\ y_{-}\notin \mathbb{Z},\quad & 1-[-y_{1+}]<{\displaystyle \frac{q^{\ast }}{p}},\end{array}\right.\quad \left\{\begin{array}{@{}ll@{}}y_{+}=-\lfloor y_{1-}\rfloor ,\quad & [y_{1-}]\leqslant {\displaystyle \frac{q^{\ast }}{p}},\\ y_{+}\notin \mathbb{Z},\quad & [y_{1-}]>{\displaystyle \frac{q^{\ast }}{p}}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}y_{-}=-\lceil y_{1+}\rceil +1,\quad & 1-[-y_{1+}]\geqslant {\displaystyle \frac{q^{\ast }}{p}},\\ y_{-}\notin \mathbb{Z},\quad & 1-[-y_{1+}]<{\displaystyle \frac{q^{\ast }}{p}},\end{array}\right.\quad \left\{\begin{array}{@{}ll@{}}y_{+}=-\lfloor y_{1-}\rfloor ,\quad & [y_{1-}]\leqslant {\displaystyle \frac{q^{\ast }}{p}},\\ y_{+}\notin \mathbb{Z},\quad & [y_{1-}]>{\displaystyle \frac{q^{\ast }}{p}}.\end{array}\right.\end{eqnarray}$$
That is, since
 $$\begin{eqnarray}y_{+}=-\lfloor y_{1-}\rfloor +\min _{k>0}{\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\lfloor [y_{1-}]k\rfloor \biggr),\end{eqnarray}$$
$$\begin{eqnarray}y_{+}=-\lfloor y_{1-}\rfloor +\min _{k>0}{\displaystyle \frac{1}{k}}\biggl(\biggl\lfloor{\displaystyle \frac{q^{\ast }}{p}}k\biggr\rfloor-\lfloor [y_{1-}]k\rfloor \biggr),\end{eqnarray}$$
the right-hand summand vanishes when
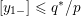 $[y_{1-}]\leqslant q^{\ast }/p$
, but when
$[y_{1-}]\leqslant q^{\ast }/p$
, but when
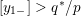 $[y_{1-}]>q^{\ast }/p$
, the right-hand summand is not minimized at
$[y_{1-}]>q^{\ast }/p$
, the right-hand summand is not minimized at
![]() $k=1$
. Thus
$k=1$
. Thus
 $y_{+}\neq y_{+}(1)$
, and Proposition 4.13 tells us that
$y_{+}\neq y_{+}(1)$
, and Proposition 4.13 tells us that
![]() $y_{+}\notin \mathbb{Z}$
. A similar argument holds for
$y_{+}\notin \mathbb{Z}$
. A similar argument holds for
![]() $y_{-}$
.
$y_{-}$
.
We therefore have
 $$\begin{eqnarray}y_{-}=0\quad \;\Longleftrightarrow \;\quad {\displaystyle \frac{q^{\ast }}{p}}\leqslant y_{1+}\leqslant 1\quad \;\Longleftrightarrow \;\quad {\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}}\leqslant {\displaystyle \frac{a_{+}}{b_{+}}}<{\displaystyle \frac{q}{p}}\text{ or }{\displaystyle \frac{a_{+}}{b_{+}}}=\infty ,\end{eqnarray}$$
$$\begin{eqnarray}y_{-}=0\quad \;\Longleftrightarrow \;\quad {\displaystyle \frac{q^{\ast }}{p}}\leqslant y_{1+}\leqslant 1\quad \;\Longleftrightarrow \;\quad {\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}}\leqslant {\displaystyle \frac{a_{+}}{b_{+}}}<{\displaystyle \frac{q}{p}}\text{ or }{\displaystyle \frac{a_{+}}{b_{+}}}=\infty ,\end{eqnarray}$$
and similarly,
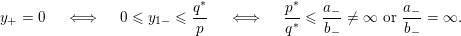 $$\begin{eqnarray}y_{+}=0\quad \;\Longleftrightarrow \;\quad 0\leqslant y_{1-}\leqslant {\displaystyle \frac{q^{\ast }}{p}}\quad \;\Longleftrightarrow \;\quad {\displaystyle \frac{p^{\ast }}{q^{\ast }}}\leqslant {\displaystyle \frac{a_{-}}{b_{-}}}\neq \infty \text{or }{\displaystyle \frac{a_{-}}{b_{-}}}=\infty .\end{eqnarray}$$
$$\begin{eqnarray}y_{+}=0\quad \;\Longleftrightarrow \;\quad 0\leqslant y_{1-}\leqslant {\displaystyle \frac{q^{\ast }}{p}}\quad \;\Longleftrightarrow \;\quad {\displaystyle \frac{p^{\ast }}{q^{\ast }}}\leqslant {\displaystyle \frac{a_{-}}{b_{-}}}\neq \infty \text{or }{\displaystyle \frac{a_{-}}{b_{-}}}=\infty .\end{eqnarray}$$
Thus
 $y_{-}=y_{+}=0$
if and only if
$y_{-}=y_{+}=0$
if and only if
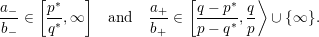 $$\begin{eqnarray}{\displaystyle \frac{a_{-}}{b_{-}}}\in \biggl[{\displaystyle \frac{p^{\ast }}{q^{\ast }}},\infty \biggr]\quad \text{and}\quad {\displaystyle \frac{a_{+}}{b_{+}}}\in \biggl[{\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}},{\displaystyle \frac{q}{p}}\rangle \cup \{\infty \}.\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{a_{-}}{b_{-}}}\in \biggl[{\displaystyle \frac{p^{\ast }}{q^{\ast }}},\infty \biggr]\quad \text{and}\quad {\displaystyle \frac{a_{+}}{b_{+}}}\in \biggl[{\displaystyle \frac{q-p^{\ast }}{p-q^{\ast }}},{\displaystyle \frac{q}{p}}\rangle \cup \{\infty \}.\end{eqnarray}$$
◻
6 Observations
Our demonstration of extended L/NTF-equivalence for graph manifolds in Theorem 4.5 gives a (mildly) alternate proof of the Theorem 1.3 statement that a graph manifold is an L-space if and only if it fails to admit a co-oriented taut foliation.
From a practical standpoint, however, the main utility of Theorem 4.5 for us was its implication that the gluing result in Proposition 4.4 holds for all graph manifolds:
Corollary 6.1. If
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
are non-solid-torus graph manifolds with torus boundary, then the union
$Y_{2}$
are non-solid-torus graph manifolds with torus boundary, then the union
 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
, with gluing map
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
, with gluing map
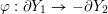 $\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
, is an L-space if and only if
$\unicode[STIX]{x1D711}:\unicode[STIX]{x2202}Y_{1}\rightarrow -\unicode[STIX]{x2202}Y_{2}$
, is an L-space if and only if
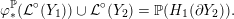 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2})).\end{eqnarray}$$
Corollary 6.1 has two advantages over the more general L-space gluing criterion of Proposition 3.3: it removes the condition that
 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
be non-empty, and it allows one to prove that
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
be non-empty, and it allows one to prove that
![]() $Y_{1}\cup Y_{2}$
is not an L-space in cases in which boundary incompressible
$Y_{1}\cup Y_{2}$
is not an L-space in cases in which boundary incompressible
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
are not Floer simple.
$Y_{2}$
are not Floer simple.
6.1 Generalization of Theorem 4.6
Nevertheless, while the L-space gluing result analogous to Proposition 3.3 proved by Hanselman and Watson in [Reference Hanselman and WatsonHW15] replaces the hypothesis of Floer simplicity by a more technical condition, their gluing result does not impose the hypothesis of non-empty
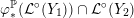 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
required by the gluing result of Rasmussen and the author in [Reference Rasmussen and RasmussenRR15]. In [Reference Hanselman, Rasmussen, Rasmussen and WatsonHR15], the four authors discuss how these two gluing results can be combined to prove a gluing result analogous to Proposition 3.3 which requires Floer simplicity but not non-empty
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
required by the gluing result of Rasmussen and the author in [Reference Rasmussen and RasmussenRR15]. In [Reference Hanselman, Rasmussen, Rasmussen and WatsonHR15], the four authors discuss how these two gluing results can be combined to prove a gluing result analogous to Proposition 3.3 which requires Floer simplicity but not non-empty
 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
. Thus, the only real hypothesis we have circumvented is that of Floer simplicity. If we replace the condition that the
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
. Thus, the only real hypothesis we have circumvented is that of Floer simplicity. If we replace the condition that the
![]() $Y_{i}$
glued to
$Y_{i}$
glued to
![]() $\hat{M}$
be graph manifolds with the condition that they be Floer simple, then we can extend the domain of validity of Proposition 4.7 and Theorem 4.6 as follows.
$\hat{M}$
be graph manifolds with the condition that they be Floer simple, then we can extend the domain of validity of Proposition 4.7 and Theorem 4.6 as follows.
6.2 Generalized solid tori
A recent result of Gillespie [Reference GillespieGil16] states that a compact oriented three-manifold
![]() $Y$
with torus boundary satisfies
$Y$
with torus boundary satisfies
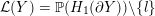 ${\mathcal{L}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus \{l\}$
if and only if
${\mathcal{L}}(Y)=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))\setminus \{l\}$
if and only if
![]() $Y\!$
has genus 0 and an L-space filling. Such manifolds, called generalized solid tori in [Reference Rasmussen and RasmussenRR15], are of independent interest.
$Y\!$
has genus 0 and an L-space filling. Such manifolds, called generalized solid tori in [Reference Rasmussen and RasmussenRR15], are of independent interest.
In the proof of Theorem 4.6 and Proposition 4.7, we find many generalized solid tori with the regular fiber class as rational longitude, but there are limited circumstances in which other generalized solid tori appear. In fact, we can prove the following.
Theorem 6.3. If
![]() $Y\!$
is a graph manifold with torus boundary,
$Y\!$
is a graph manifold with torus boundary,
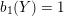 $b_{1}(Y)=1$
, and rational longitude other than the regular fiber, then
$b_{1}(Y)=1$
, and rational longitude other than the regular fiber, then
![]() $Y$
is a generalized solid torus if and only if it is homeomorphic to an iterated cable of the regular fiber complement in
$Y$
is a generalized solid torus if and only if it is homeomorphic to an iterated cable of the regular fiber complement in
 $S^{1}\times S^{2}$
.
$S^{1}\times S^{2}$
.
Proof. Suppose
![]() $Y$
is a generalized solid torus graph manifold, with rational longitude
$Y$
is a generalized solid torus graph manifold, with rational longitude
![]() $l$
not coinciding with the regular fiber. Since
$l$
not coinciding with the regular fiber. Since
![]() $Y$
is Floer simple with
$Y$
is Floer simple with
 $\infty \in {\mathcal{L}}^{\circ }(Y)$
,
$\infty \in {\mathcal{L}}^{\circ }(Y)$
,
![]() $Y$
must satisfy
$Y$
must satisfy
![]() $({\rm \small{fs3}})$
from Proposition 4.7, and since
$({\rm \small{fs3}})$
from Proposition 4.7, and since
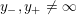 $y_{-},y_{+}\neq \infty$
, we must have
$y_{-},y_{+}\neq \infty$
, we must have
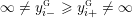 $\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
. Claim 2 from § 4.7 then implies
$\infty \neq y_{i-}^{{\rm \small{g}}}\geqslant y_{i+}^{{\rm \small{g}}}\neq \infty$
. Claim 2 from § 4.7 then implies
 $y_{-}>y_{+}$
unless
$y_{-}>y_{+}$
unless
![]() $n_{{\rm \small{g}}}=1$
with
$n_{{\rm \small{g}}}=1$
with
![]() $n_{{\rm \small{d}}}\leqslant 1$
or
$n_{{\rm \small{d}}}\leqslant 1$
or
![]() $n_{{\rm \small{g}}}=0$
with
$n_{{\rm \small{g}}}=0$
with
![]() $n_{{\rm \small{d}}}\leqslant 2$
.
$n_{{\rm \small{d}}}\leqslant 2$
.
If
![]() $n_{{\rm \small{g}}}=1$
, then according to Claim 4 from § 4.8, either
$n_{{\rm \small{g}}}=1$
, then according to Claim 4 from § 4.8, either
![]() $y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
, in which case
$y_{1}^{{\rm \small{d}}}\in \mathbb{Z}$
, in which case
![]() $Y$
is homeomorphic to
$Y$
is homeomorphic to
![]() $Y_{1}$
and we should replace
$Y_{1}$
and we should replace
![]() $Y$
with
$Y$
with
![]() $Y_{1}$
and begin again; or
$Y_{1}$
and begin again; or
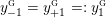 $y_{-1}^{{\rm \small{g}}}=y_{+1}^{{\rm \small{g}}}=:y_{1}^{{\rm \small{g}}}$
with
$y_{-1}^{{\rm \small{g}}}=y_{+1}^{{\rm \small{g}}}=:y_{1}^{{\rm \small{g}}}$
with
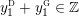 $y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
, in which case
$y_{1}^{{\rm \small{d}}}+y_{1}^{{\rm \small{g}}}\in \mathbb{Z}$
, in which case
![]() $Y_{1}$
is a generalized solid torus, and Proposition 5.1 implies
$Y_{1}$
is a generalized solid torus, and Proposition 5.1 implies
 $Y\subset Y(l)$
is a cable of
$Y\subset Y(l)$
is a cable of
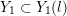 $Y_{1}\subset Y_{1}(l)$
.
$Y_{1}\subset Y_{1}(l)$
.
If
![]() $n_{{\rm \small{g}}}=0$
, then
$n_{{\rm \small{g}}}=0$
, then
![]() $Y$
is Seifert fibered with
$Y$
is Seifert fibered with
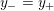 $y_{-}=y_{+}$
, and so either from [Reference Rasmussen and RasmussenRR15] or from a mildly modified version of Claim 4, we deduce that either
$y_{-}=y_{+}$
, and so either from [Reference Rasmussen and RasmussenRR15] or from a mildly modified version of Claim 4, we deduce that either
 $y_{1}^{{\rm \small{d}}}+y_{2}^{{\rm \small{d}}}\in \mathbb{Z}$
, in which case Proposition 5.1 implies
$y_{1}^{{\rm \small{d}}}+y_{2}^{{\rm \small{d}}}\in \mathbb{Z}$
, in which case Proposition 5.1 implies
![]() $Y\!$
is a cable of the regular fiber complement in
$Y\!$
is a cable of the regular fiber complement in
![]() $S^{1}\times \!S^{2}$
; or
$S^{1}\times \!S^{2}$
; or
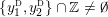 $\{y_{1}^{{\rm \small{d}}},y_{2}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset$
, in which case
$\{y_{1}^{{\rm \small{d}}},y_{2}^{{\rm \small{d}}}\}\cap \mathbb{Z}\neq \emptyset$
, in which case
![]() $Y$
is a solid torus, hence homeomorphic to the regular fiber complement in
$Y$
is a solid torus, hence homeomorphic to the regular fiber complement in
 $S^{1}\times S^{2}\!\!$
.
$S^{1}\times S^{2}\!\!$
.
The converse is an immediate corollary of Proposition 5.1 and Theorem 4.6.◻
We also have the following result for arbitrary generalized solid tori.
Proposition 6.4. If
![]() $Y$
is a generalized solid torus, then any cable of
$Y$
is a generalized solid torus, then any cable of
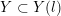 $Y\subset Y(l)$
is a generalized solid torus.
$Y\subset Y(l)$
is a generalized solid torus.
Proof. If
![]() $Y$
is boundary compressible, then it is the connected sum of a solid torus with lens spaces, and Theorem 6.3 implies that any cable of a solid torus within its longitudinal filling is a generalized solid torus. If
$Y$
is boundary compressible, then it is the connected sum of a solid torus with lens spaces, and Theorem 6.3 implies that any cable of a solid torus within its longitudinal filling is a generalized solid torus. If
![]() $Y$
is boundary incompressible, then the result is an immediate corollary of Theorem 5.2.◻
$Y$
is boundary incompressible, then the result is an immediate corollary of Theorem 5.2.◻
Similarly, for any class of manifolds for which the gluing result in Proposition 1.5 holds without the requirement of Floer simplicity—such as graph manifolds—one has the result that if
![]() $Y$
has an isolated L-space filling, i.e. if
$Y$
has an isolated L-space filling, i.e. if
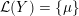 ${\mathcal{L}}(Y)=\{\unicode[STIX]{x1D707}\}$
for some
${\mathcal{L}}(Y)=\{\unicode[STIX]{x1D707}\}$
for some
 $\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
, then any cable of
$\unicode[STIX]{x1D707}\in \mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y))$
, then any cable of
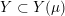 $Y\subset Y(\unicode[STIX]{x1D707})$
has
$Y\subset Y(\unicode[STIX]{x1D707})$
has
![]() $Y(\unicode[STIX]{x1D707})$
as an isolated L-space filling.
$Y(\unicode[STIX]{x1D707})$
as an isolated L-space filling.
6.3 Isolated L-space fillings
A Seifert fiber complement in an L-space Seifert fibered manifold could justifiably be called the prototypical Floer simple manifold, just as a lens space is the prototypical L-space. It is therefore striking that we encounter isolated L-space fillings as regular fiber complements in graph manifolds. Fortunately, this still does not prevent L-space graph manifolds from admitting Floer simple Seifert fiber complements.
Given a closed graph manifold
![]() $X$
, we shall call an exceptional fiber
$X$
, we shall call an exceptional fiber
![]() $f_{{\rm \small{e}}}\subset X$
invariantly exceptional if the JSJ component
$f_{{\rm \small{e}}}\subset X$
invariantly exceptional if the JSJ component
![]() ${\hat{Y}}\subset X$
containing
${\hat{Y}}\subset X$
containing
![]() $f_{{\rm \small{e}}}$
has more than one exceptional fiber. To motivate this name, note that if
$f_{{\rm \small{e}}}$
has more than one exceptional fiber. To motivate this name, note that if
![]() $X$
has more than one JSJ component and
$X$
has more than one JSJ component and
![]() ${\hat{Y}}$
has only one exceptional fiber, say, of slope
${\hat{Y}}$
has only one exceptional fiber, say, of slope
![]() $y_{1}^{{\rm \small{d}}}=y_{0}$
, then since the punctured solid torus has non-unique Seifert structure,
$y_{1}^{{\rm \small{d}}}=y_{0}$
, then since the punctured solid torus has non-unique Seifert structure,
![]() $X$
is homeomorphic to a graph manifold in which
$X$
is homeomorphic to a graph manifold in which
![]() $y_{1}^{{\rm \small{d}}}$
is replaced with
$y_{1}^{{\rm \small{d}}}$
is replaced with
![]() $0$
and
$0$
and
![]() $\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}$
is replaced with
$\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}$
is replaced with
 $\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}\!+y_{0}$
.
$\unicode[STIX]{x1D711}_{1\ast }^{\mathbb{P}}\!+y_{0}$
.
Theorem 6.5. Every invariantly exceptional fiber complement in an L-space graph manifold is Floer simple.
Proof. Suppose
![]() $X$
is an L-space graph manifold. If
$X$
is an L-space graph manifold. If
![]() $X$
is Seifert fibered, then every Seifert fiber complement, regular or otherwise, is Floer simple.
$X$
is Seifert fibered, then every Seifert fiber complement, regular or otherwise, is Floer simple.
Suppose
![]() $X$
has more than one JSJ component, and let
$X$
has more than one JSJ component, and let
![]() $Y$
denote a non-Floer-simple complement of an invariantly exceptional fiber. Since
$Y$
denote a non-Floer-simple complement of an invariantly exceptional fiber. Since
 ${\mathcal{L}}(Y)\neq \emptyset$
,
${\mathcal{L}}(Y)\neq \emptyset$
,
![]() $Y$
non-Floer-simple implies
$Y$
non-Floer-simple implies
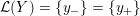 ${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
, with
${\mathcal{L}}(Y)=\{y_{-}\}=\{y_{+}\}$
, with
![]() $y_{\pm }\in \mathbb{Q}$
. However, since
$y_{\pm }\in \mathbb{Q}$
. However, since
![]() $Y$
has at least one exceptional fiber, Proposition 4.14 tells us that
$Y$
has at least one exceptional fiber, Proposition 4.14 tells us that
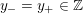 $y_{-}=y_{+}\in \mathbb{Z}$
, contradicting the hypothesis that
$y_{-}=y_{+}\in \mathbb{Z}$
, contradicting the hypothesis that
![]() $Y$
is an exceptional fiber complement of
$Y$
is an exceptional fiber complement of
![]() $X$
. Thus the theorem holds.◻
$X$
. Thus the theorem holds.◻
On the other hand, for a graph manifold with more than one JSJ component, Seifert fibers are not the only knots yielding Floer simple knot complements, due to the following result for arbitrary L-spaces.
Proposition 6.6. If an L-space
![]() $X$
decomposes as a union
$X$
decomposes as a union
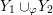 $Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
of Floer simple manifolds
$Y_{1}\cup _{\unicode[STIX]{x1D711}}\!Y_{2}$
of Floer simple manifolds
![]() $Y_{i}$
along an incompressible torus
$Y_{i}$
along an incompressible torus
![]() $T\subset X$
, then there is a knot
$T\subset X$
, then there is a knot
![]() $K\subset X$
transversely intersecting
$K\subset X$
transversely intersecting
![]() $T$
for which knot the complement
$T$
for which knot the complement
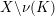 $X\setminus \unicode[STIX]{x1D708}(K)$
is Floer simple.
$X\setminus \unicode[STIX]{x1D708}(K)$
is Floer simple.
Proof. In fact, an analogous result holds for any toroidal L-space.
Suppose the above hypotheses hold. Then since
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
are Floer simple with incompressible boundary, Proposition 3.3 implies
$Y_{2}$
are Floer simple with incompressible boundary, Proposition 3.3 implies
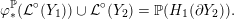 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cup {\mathcal{L}}^{\circ }(Y_{2})=\mathbb{P}(H_{1}(\unicode[STIX]{x2202}Y_{2})).\end{eqnarray}$$
Since
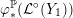 $\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))$
and
$\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))$
and
![]() ${\mathcal{L}}^{\circ }(Y_{2})$
are open, (119) implies they intersect. Choosing any
${\mathcal{L}}^{\circ }(Y_{2})$
are open, (119) implies they intersect. Choosing any
 $\unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
, set
$\unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}}({\mathcal{L}}^{\circ }(Y_{1}))\cap {\mathcal{L}}^{\circ }(Y_{2})$
, set
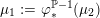 $\unicode[STIX]{x1D707}_{1}:=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}-1}(\unicode[STIX]{x1D707}_{2})$
, and let
$\unicode[STIX]{x1D707}_{1}:=\unicode[STIX]{x1D711}_{\ast }^{\mathbb{P}-1}(\unicode[STIX]{x1D707}_{2})$
, and let
![]() $K_{i}$
denote the knot core of
$K_{i}$
denote the knot core of
 $Y_{i}(\unicode[STIX]{x1D707}_{i})\setminus Y_{i}$
. As explained in more detail in the proof of [Reference Rasmussen and RasmussenRR15, Theorem 6.2],
$Y_{i}(\unicode[STIX]{x1D707}_{i})\setminus Y_{i}$
. As explained in more detail in the proof of [Reference Rasmussen and RasmussenRR15, Theorem 6.2],
![]() $X$
can be regarded as zero-surgery on the knot
$X$
can be regarded as zero-surgery on the knot
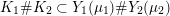 $K_{1}\#K_{2}\subset Y_{1}(\unicode[STIX]{x1D707}_{1})\#Y_{2}(\unicode[STIX]{x1D707}_{2})$
. Thus, if we set
$K_{1}\#K_{2}\subset Y_{1}(\unicode[STIX]{x1D707}_{1})\#Y_{2}(\unicode[STIX]{x1D707}_{2})$
. Thus, if we set
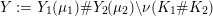 $Y:=Y_{1}(\unicode[STIX]{x1D707}_{1})\#Y_{2}(\unicode[STIX]{x1D707}_{2})\setminus \unicode[STIX]{x1D708}(K_{1}\#K_{2})$
and let
$Y:=Y_{1}(\unicode[STIX]{x1D707}_{1})\#Y_{2}(\unicode[STIX]{x1D707}_{2})\setminus \unicode[STIX]{x1D708}(K_{1}\#K_{2})$
and let
![]() $K$
denote the knot core of
$K$
denote the knot core of
![]() $X\setminus Y$
, then the knot complement
$X\setminus Y$
, then the knot complement
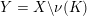 $Y=X\setminus \unicode[STIX]{x1D708}(K)$
has at least two distinct L-space fillings, hence is Floer simple. Moreover, since
$Y=X\setminus \unicode[STIX]{x1D708}(K)$
has at least two distinct L-space fillings, hence is Floer simple. Moreover, since
![]() $K$
is dual to
$K$
is dual to
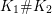 $K_{1}\#K_{2}$
under surgery,
$K_{1}\#K_{2}$
under surgery,
![]() $K$
intersects the separating torus transversely.◻
$K$
intersects the separating torus transversely.◻
Corollary 6.7. If
![]() $X$
is an L-space graph manifold, then for every incompressible torus
$X$
is an L-space graph manifold, then for every incompressible torus
![]() $T\subset X$
, there is a knot
$T\subset X$
, there is a knot
![]() $K\subset X$
transversely intersecting
$K\subset X$
transversely intersecting
![]() $T$
for which knot the complement
$T$
for which knot the complement
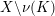 $X\setminus \unicode[STIX]{x1D708}(K)$
is Floer simple.
$X\setminus \unicode[STIX]{x1D708}(K)$
is Floer simple.
Proof. Choose an arbitrary incompressible torus
![]() $T\subset X$
, not necessarily one used in the minimal JSJ decomposition for
$T\subset X$
, not necessarily one used in the minimal JSJ decomposition for
![]() $X$
, and write
$X$
, and write
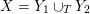 $X=Y_{1}\cup _{T}Y_{2}$
. Since
$X=Y_{1}\cup _{T}Y_{2}$
. Since
![]() $X$
is an L-space, Corollary 6.1 implies each
$X$
is an L-space, Corollary 6.1 implies each
![]() $Y_{i}$
has non-empty
$Y_{i}$
has non-empty
![]() ${\mathcal{L}}^{\circ }(Y_{i})$
, hence is Floer simple. Thus, we can apply Proposition 6.6.◻
${\mathcal{L}}^{\circ }(Y_{i})$
, hence is Floer simple. Thus, we can apply Proposition 6.6.◻
This section has only cataloged the most obvious corollaries of the paper’s main results. We invite the reader to find more.
Acknowledgements
I would like to thank Jonathan Bowden, Thomas Gillespie, Jake Rasmussen, and Rachel Roberts for helpful conversations, Liam Watson and Jonathan Hanselman for comments on an earlier draft, and the referee for helpful suggestions. The author was supported by EPSRC grant EP/M000648/1.