Introduction
Understanding the energy balance is crucial to quantifying the melt rate of snow and ice surfaces. Broadly, the energy balance can be divided into two components: radiative and turbulent energy fluxes. Predominantly, melt occurs in response to radiative energy, which may account for >70% of the net energy (Reference HockHock, 2005); however, in maritime settings (Reference Moore and OwensMoore and Owens, 1984; Reference Ishikawa, Owens and SturmanIshikawa and others, 1992) turbulent fluxes may be more significant, contributing up to ~ 80% of the melt energy (Reference Willis, Arnold and BrockWillis and others, 2002). Critically, melt energy available from the two energy components can be strongly influenced by the micro-topography or roughness of the melting surface itself.
Impurities at the ice/atmosphere interface contribute to the development of surface roughness at metre to sub-metre scales. Mineral dust content and associated biological consortia can significantly increase the shortwave incident radiation contributing to melt on snow (Reference Warren, Warren, Brandt and HintonWarren, 1984; Reference Kohshima, Yoshimura, Seko and OhataKohshima and others, 1994; Reference Thomas and DuvalThomas and Duval, 1995; Reference Conway, Gades and RaymondConway and others, 1996; Reference PainterPainter and others, 2007) and glacier ice (Reference Kohshima, Seko and YoshimuraKohshima and others, 1993; Reference Adhikary, Nakawo, Seko and ShakyaAdhikary and others, 2000; Takeuchi, 2002) where water content is similarly influential (Reference Cutler and MunroCutler and Munro, 1996). Consequently, topography can become exaggerated or inverted as the relative proportions of radiative and turbulent energies vary, particularly at synoptic timescales (MReference Müller and Keelerüller and Keeler, 1969; Reference IntyreMcIntyre, 1984; Reference Rhodes, Armstrong and WarrenRhodes and others, 1987; Reference Fassnacht, Velasco, Meiman and WhittFassnacht and others, 2010). Such dynamics of snow/ice surface roughness modulates the response of remote satellite-mounted sensors, particularly those utilizing microwave wavelengths whose data products relate to signal backscatter and surface dielectric properties (Reference Jin and SimpsonJin and Simpson, 1999; Reference König, Winther and IsakssonKönig and others, 2001; Reference Nolin, Fetter and ScambosNolin and others, 2002). Moreover, varying roughness influences radiative incidence angles and surface albedo (Reference Cutler and MunroCutler and Munro, 1996; Reference Warren, Warren, Brandt and HintonWarren and others, 1998), and defines turbulent energy fluxes at the ice/atmosphere boundary layer (Reference Munro and DaviesMunro and Davies, 1977).
At Haut Glacier d’Arolla, Switzerland, Reference Brock, Willis and SharpBrock and others (2006) suggested that variation to within one standard deviation from the mean surface aerodynamic roughness length resulted in turbulent energy flux changes of up to 20%. The temporal evolution of snow surface roughness appears progressive, as described by independent meteorological variables (e.g. Reference Brock, Willis and SharpBrock and others, 2006; Reference FassnachtFassnacht, 2010); however, results for small-scale glacier ice surface roughness are contradictory, with evidence both for and against similar systematic change in space and/or time (cf. Dunykerke and Van den Broeke, 1994; Reference Smeets, Duynkerke and VugtsSmeets and others, 1999; Reference Brock, Willis and SharpBrock and others, 2006; Reference Smeets and Van den BroekeSmeets and Van den Broeke, 2008). Consequently, because of the logistical challenges in monitoring melting ice surfaces, the dynamical values of glacier surface roughness remain poorly constrained and surprisingly sparse (Reference Brock, Willis and SharpBrock and others, 2006).
The absence of well-described surface roughness parameters, especially for changing ice surfaces over time and space, is critical to predictive, numerical runoff models (Reference HockHock, 2005). Many spatially distributed ice melt models have ignored variations in roughness, opting for a constant value (Reference Arnold, Rees, Hodson and KohlerArnold and others, 2006) or empirical derivations of turbulent fluxes (Reference Klok and OerlemansKlok and Oerlemans, 2002), while others have employed statistical roughness distributions (Reference Brock, Willis, Sharp and ArnoldBrock and others, 2000). Yet, to study and forecast ice melt more accurately, it is necessary to know the detailed site-specific variation of the surface roughness over time, highlighting the research necessity to develop a reproducible method to derive such empirical relationships (Reference AndreasAndreas, 2011). With increasing research into the use of low-cost photogrammetry for environmental applications (e.g. Reference ChandlerChandler, 1999; Reference Lascelles, Mortlock, Parsons and BoardmanLascelles and others, 2002; Reference Smith, Chandler and RoseSmith and others, 2009; Reference James and RobsonJames and Robson, 2012; Reference Westoby, Brasington, Glasser, Hambrey and ReynoldsWestoby and others, 2012; Reference Whitehead, Moorman and HugenholtzWhitehead and others, 2013), the aim of this paper is to evaluate the use of close-range digital photogrammetry as a rapid, cost-effective method to quantify and characterize the dynamics of glacier ice surface roughness. In particular, we build upon our earlier work (Reference Sanz-Ablanedo, Chandler and FynnSanz-Ablanedo and other, 2012a) and look to describe spatial and temporal variability of the ice surface, assessing the validity and reproducibility of the method at the plot scale.
Photogrammetry And Glacier Surface Characterization
Over the past 15 years, the slow and manual data acquisition phase of photogrammetry has become fully and digitally automated (Reference ChandlerChandler, 1999; Reference Baltsavias, Favey, Bauder, Boesch and PaterakiBaltsavias and others, 2001; Reference Fox and GoochFox and Gooch, 2001; Reference Westoby, Brasington, Glasser, Hambrey and ReynoldsWestoby and others, 2012; Reference Whitehead, Moorman and HugenholtzWhitehead and others, 2013; Javenick and others, 2014), allowing high-resolution datasets or digital surface models (DSMs) to be generated. This has resulted in the use of cheaper, consumer-grade digital cameras, of ever-increasing resolution (Reference Chandler, Fryer and JackChandler and others, 2005; Reference Rieke-Zapp, Nearing, Romkens and WangRieke-Zapp and Nearing, 2005; Taconet and Ciarletti, 2007; Reference Heng, Chandler and ArmstrongHeng and others, 2010). The digital revolution has also provided opportunities to relax strict geometric constraints, allowing greater freedom during initial data acquisition (Reference Heng, Chandler and ArmstrongHeng and others, 2010). Automated camera calibration software has simplified the extraction of relevant parameters describing internal camera geometries, as necessary for accurate data acquisition (Reference BrownBrown, 1971; Reference Fryer, Mitchell and ChandlerFryer and others, 2007; Reference Sanz-Ablanedo, Chandler and WackrowSanz-Ablanedo and others, 2012b), and continues to advance rapidly. Prior to these developments, close-range plot-scale photogrammetry had played a leading role in deriving roughness of soil surfaces (Reference Welch, Jordan and ThomasWelch and others, 1984) and water-worked gravel beds (Reference Butler, Lane and ChandlerButler and others, 1998). However, more recently, scientists have made increasing use of high-resolution DSMs derived from digital images and pixel-matching algorithms to represent soil surfaces and derive measures of roughness without necessitating the direct measurement of specific transects (e.g. Reference Rieke-Zapp, Nearing, Romkens and WangRieke-Zapp and Nearing, 2005; Taconet and Ciarletti, 2007). A review of parameterizations of soil surface roughness from high-resolution DSMs at plot scales reveals a wide variety of roughness metrics including: elevation standard deviation (e.g. Reference KuipersKuipers, 1957), slope angle and tortuosity index (e.g. Reference BoiffinBoiffin, 1984) and elevation auto-covariance (e.g. Taconet and Ciarletti, 2007).
In glaciological contexts, there is a long history of measuring ice surfaces using photogrammetry, particularly over large areas where aircraft mounted cameras offer many logistical advantages (Reference Kääb, Pellikka and ReesKääb, 2010). Reference Baltsavias, Favey, Bauder, Boesch and PaterakiBaltsavias and others (2001) provide a useful historical review and used automated DSM extraction tools based upon photogrammetric area correlation to generate DSMs of Unteraargletscher, Switzerland, which achieved good results compared to airborne laser scanning data, except in areas where image texture (the spatial contrasts and variations in colour and/or light intensity) was low. At closer range, Reference Kaufmann and LadstädterKaufmann and Ladstädter (2004) used terrestrial photogrammetry to monitor glacier ablation at Goessnitzkees, Austria, with decimetre uncertainties using imagery sources extending over 15 years. For close-range applications, DSMs of ice surface areas of ~ 100 m2 using similar methods have been produced but exhibit similar vertical uncertainties (e.g. Reference Pitkänen and KajuuttiPitkänen and Kajutti, 2004). Difficulties in DSM creation generally arise from areas exhibiting strong shadows or, conversely, large expanses of white ice/snow (see Reference Fox and GoochFox and Gooch, 2001; Reference Hopkinson, Ottawa Hopkinson, Hayashi and PeddleHopkinson and others, 2009). Consequently, airborne laser scanning (ALS) of glacier surfaces has been used more frequently to retrieve glacier surface DSMs (e.g. Reference Kennett and EikenKennett and Eiken, 1997; Reference Bamber, Krabill, Raper, Dowdeswell and OerlemansBamber and others, 2005; Reference Hopkinson, Ottawa Hopkinson, Hayashi and PeddleHopkinson and others, 2009) and large-scale ice surface roughness metrics (e.g. Reference Van der Veen, Ahn, Csatho, Thompson and KrabillVan der Veen and others, 1998, 2009; Reference Rees and ArnoldRees and Arnold, 2006). However, the sampling interval and vertical accuracy for ALS are typically of the order of ~ 1 m and 0.05 m, respectively, and accordingly inappropriate for energy balance and some remote-sensing applications.
Mirroring successful use of portable laser scanners (Reference Huang and BradfordHuang and Bradford, 1992; Reference Flanagan, Huang, Norton and ParkerFlanagan and others, 1995) and terrestrial laser scanning (TLS) (Reference Schmid, Kirchner and HildebrandSchmid and others, 2004; Reference Perez-Gutierrez, Martinez-Fernandez, Sanchez and MozosPerez-Gutierrez and others, 2007) for soil roughness applications, TLS has been trialled for snow and glacier surfaces (e.g. Reference Hopkinson, Ottawa Hopkinson, Hayashi and PeddleHopkinson, 2004; Reference Avian and BauerAvian and Bauer, 2006; Reference Kerr, Owens, Rack and GardnerKerr and others, 2009; Kassalainen and others, 2011; Reference Nield, Chiverrell, Darby, Leyland, Vircavs and JacobsNield and others, 2013). From such data, DSMs and surface profiles can be retrieved at sub-centimetre horizontal and vertical resolution over intermediate (<200 m) scan distances. Nonetheless, plot-scale TLS point clouds exhibit a number of errors related to scanner hardware, data acquisition, scan and surface geometries, and point-cloud processing (Reference Hodge, Brasington and RichardsHodge and others, 2009). The success of TLS on icy surfaces can be influenced by factors including the specific laser wavelength, scan repeatability and the associated signal loss on the varied surface materials and textures in supraglacial environments (Reference Hopkinson, Ottawa Hopkinson, Hayashi and PeddleHopkinson, 2004; Reference Kerr, Owens, Rack and GardnerKerr and others, 2009). Moreover, for a melting ice surface, it may also be necessary to consider through-water correction where the laser pulse penetrates a film of sediment-free surface water (e.g. Reference Smith, Vericat and GibbinsSmith and others, 2012).
To date, plot-scale (<10 m) ice surface roughness has principally been quantified using manual surveying methods (Reference MunroMunro, 1989; Reference Brock, Willis and SharpBrock and others, 2006) or using close-range two-dimensional (2-D) digital photogrammetry. Reference Arnold and ReesArnold and Rees (2003) derived surface roughness metrics for both snow and glacier ice at ≤ 1 m horizontal length scales, and subcentimetre horizontal and vertical resolution, using predefined planes marked by a black board inserted directly into the snow or ice surface. Similarly, high-resolution work on snow surface roughness has employed such a technique (e.g. Reference Fassnacht, Williams and CorraoFassnacht and others, 2009a; Reference Manninen, Anttila, Karjalainen and LahtinenManninen and others, 2012). However, these examples focus on singular, site-specific, 2-D digital profiles, and fail to retrieve three-dimensional (3-D) data at the plot scale. Therefore, in field settings, application of close-range photogrammetry with modern consumer-grade digital cameras offers a potentially rapid, useful and complementary research tool for deriving surface roughness metrics over space and time at scales critical to both energy-balance modelling and remote-sensing research.
Methodology
Field site and image acquisition
This study was conducted during 2010 on Midtre Lovénbreen, Svalbard (78°52’ N, 12°05’ E; Fig. 1a). The glacier’s surface topography is critical to its energy balance and seasonal ablation (Reference Arnold, Rees, Hodson and KohlerArnold and others, 2006), with previous estimates of the supraglacial aerodynamic roughness length (z 0) between 0.29 and 2.68 mm (Reference Rees and ArnoldRees and Arnold, 2006). At site RC3 (Fig. 1a), a location ~ 200 m a.s.l. on Midtre Lovénbreen’s centre line, a 2.5 m polyethylene pole was drilled and secured on 16 July such that the base of the pole froze into the ice for the duration of observations reported here (Fig. 1b). The pole provided a fixed reference point relative to the glacial surface for all surveys at the site.

Fig. 1. (a) Oblique aerial view of Midtre Lovénbreen indicating site RC3 (arrow). (b) Illustration of image acquisition at RC3; note the glacier orientation, and the horizontal reference strings and vertical reference pole (photograph courtesy of Jon Bridge). (c) Example visualization of 3-D ice surface reconstruction using PhotoModeler ScannerTM for an area approximately 3 m × 3 m, with stereo-pair images acquired on 28 July. The polyethylene marker pole for RC3 is evident.
Digital images of the glacier surface were acquired at the RC3 plot on 21 and 28 July and 4 and 18 August. The ice surface for both the first and last surveys was partially snow-covered: initially as the transient snowline retreated, and latterly due to a summer snowfall event in mid-August. Surface roughness elements were preferentially oriented down-glacier, aligned with the dominant katabatic wind direction. For each imaging survey, during periods of low wind speed, two taut 5 m nylon survey strings were tied from the reference pole to temporary vertical poles secured with ice screws to provide a horizontal reference plane (Fig. 1b); to maximize the string tautness, a taut-line hitch was used. The strings, marked at 0.5 m intervals, were oriented at 90° defined by a set-square, with one perpendicular to the ice surface slope and prevailing wind direction, and the second aligned down-glacier. Imagery was acquired obliquely from eye level (~1.6 m; Fig. 1b). One or two pairs of convergent photographs were taken using a 5 Mpix Nikon 5400 consumer-grade digital camera, which had been calibrated at infinity focus (see below). Photo pairs were captured at three distances, allowing coverage of the RC3 area of interest at differing scales: plots of 25, 4 and 1 m2 were imaged, using an approximate separation-to-distance ratio of 1: 5 to create a suitable stereo-pair with the same image centre point. In addition to image capture, a coincident manual roughness survey was conducted, following Reference Brock, Willis and SharpBrock and others (2006): measurements of distance between the ice surface and horizontal marker string to an accuracy of ± 2.5 mm were taken at 100 mm intervals along the single 5 m profile across-glacier.
Photogrammetric processing
Contemporary photogrammetry is a technique that allows the extraction of the 3-D coordinates of any identifiable point appearing in two (or more) photos taken from different viewpoints (Reference Mikhail, Bethel and GoneMikhail and others, 2001; Reference Fox and GoochFryer and others, 2007). Here we provide a brief synopsis for this particular study.
When an object is photographed, each visible 3-D point of the object corresponds to a point on the 2-D image plane, according to the principles of central projection. The ideal straight path of the light connecting the object point, the centre of projection and the point on the image is affected by real elements in camera. These modified paths need to be calculated and mathematically modelled; this is achieved by a procedure called ’self-calibration’. For this study, self-calibration was realized with 15 specific and convergent photographs taken at distances 3–6 m from a calibration surface, which included 132 distinct target points, all visible on all frames. This target design allowed all targets to be measured fully (Reference Sanz-Ablanedo, Chandler and WackrowSanz-Ablanedo and others, 2012b).
A second stage of photogrammetric processing involved calculating the position and orientation of the camera at the time of image acquisition. This is achieved by marking homologous points in the pictures. Although strictly just four points are required, a far higher number of such ‘homologous’ points are normally used to help isolate inaccurate or erroneous points. Automated detection algorithms typically facilitate the measurement of several hundred points, thereby allowing reliable determination of the relative position and orientation of the camera at the time of image acquisition, within an initial arbitrary coordinate reference system which can then be redefined. In this project, we manually defined the coordinates of the marks on the taut survey strings and the polyethylene anchor pole. This then allowed translation, rotation and scaling such that each point was related to the reference datum defined by the pole and strings. Once the absolute position and orientation of the two cameras is known in the desired coordinate system, it is possible to calculate the 3-D coordinates of any point visible on both photographs, using an intersection process.
The final part of photogrammetric processing therefore involves generating a high-resolution point cloud to capture and represent all features. This process is generally known as ‘dense surfacing’ and is a well-established and automated procedure (Reference ChandlerChandler, 1999), which extracts 3-D information from homologous points appearing on a pair of images with a regular grid pattern. Although 5 Mpix images were acquired, only a portion of these data relate to the specific plot area of interest. Moreover, given the different viewshed of both images, there are areas that appear in only one of the photographs. Additionally, the procedure relies upon identifying common texture appearing within small patches of pixels, so not all pixels can be recognized reliably (Reference ChandlerChandler, 1999). Such areas will not generate reliable 3-D information and will result in holes in the point cloud, as can be identified by the gaps in Figure 1c. In this study, the procedure was particularly influenced by the viewing angle and texture of the surface of the glacier. For the photographic stereo-pairs of areas of 25 m2, only a few tens of points were recovered (see Reference Sanz-Ablanedo, Chandler and FynnSanz-Ablanedo and others, 2012a), while in the areas of 4 m2 and 1 m2 the improved texture due to greater contrast and reduced topographic shadowing yielded point clouds consisting of 2500 points m–2 and 100 000 points m–2, respectively. Due to the low point-cloud recovery (typically <10 points m–2), data from the 25 m2 plot areas were excluded from these analyses. Finally, to facilitate comparisons between the four individual image acquisition dates, or with manual measurements, the point clouds were converted to regular gridded meshes using a kriging interpolation routine (e.g. Reference Stein, Taconet, Ciarletti and TakeuchiStein, 1999). Reference Sanz-Ablanedo, Chandler and FynnSanz-Ablanedo and others (2012a) provide further details of the photogrammetric procedures adopted.
To quicken the photogrammetric processing, which involves many measurement and iterative computational operations, the use of software tools is preferable. Currently, there is a rapidly increasing and varied range of software packages for photogrammetric applications, although many have been developed for conventional mapping using vertical aerial images. Photomodeler ScannerTM is a commercial package marketed by Eos Systems Inc., which implements all stages of photogrammetric processing. This package was chosen for several reasons: it is specifically designed for convergent imagery and close-range ground-based imaging; includes tools for automatic measurement and recognition of points required for all stages of data processing; facilitates and implements camera calibration; and finally, provides the user with a high degree of control in processing steps and parameters when automatically generating high-resolution DSMs.
Roughness metric extraction
As in soil science, there is a range of definitions of surface roughness used for glaciological applications (Reference Van der Veen, Ahn, Csatho, Thompson and KrabillVan der Veen and others, 2009). Owing to the large number of potential roughness metrics, the choice of roughness parameter should be informed by the specific process or feature under investigation (Reference Smith, Cox and BrackenSmith and others, 2011). Of specific interest for energy-balance considerations is the aerodynamic roughness length parameter (z 0), which can be estimated by the eddy correlation method, using detailed observations of near-surface wind speed profiles and temperature gradients (Reference Munro and DaviesMunro and Davies, 1978; Reference Smeets and Van den BroekeSmeets and Van den Broeke, 2008). However, such detailed and sensitive boundary layer measurements are logistically challenging in the context of the hydrometeorological conditions in glacial settings, and Reference MunroMunro (1989) suggested that using micro-topographic data (i.e. high-resolution surface profiles) was the most robust approximation to the surface roughness problem, especially where installation of the necessarily responsive instrumentation may be unfeasible.
Conventional, spatially discrete, micro-topographical techniques to estimate z 0 are based on Reference LettauLettau (1969): along a profile of length L, perpendicular to the prevailing wind direction, distances to the ice surface (h) are taken from a local horizontal reference datum, and the roughness parameter z 0 is given as
where σh is half the effective roughness element height, s is the typical roughness element silhouette area and S is the density of roughness elements (Reference MunroMunro, 1989; Reference Brock, Willis and SharpBrock and others, 2006). To estimate the effective roughness height, the data series for h is rescaled with a mean equal to zero (h 0), where σh is the standard deviation of h 0 and is equivalent to the ‘random roughness’ detailed by Reference KuipersKuipers (1957). Both approximations for s and S are dependent on the typical roughness element width, defined as L divided by the number of groups of positive deviations above the zero mean across the profile (f). Consequently, to approximate the aerodynamic roughness length, Eqn (1) can be rewritten
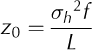
The sampling interval of h needed for adequate representation of z 0 varies, from ≤ 10 cm for aerodynamic roughness estimates over metre scales, to ≤ 1 cm over sub-metre scales for remote-sensing applications (Reference Rees and ArnoldRees and Arnold, 2006).
From the photogrammetric DSMs, surface elevation data were extracted along profiles from the DSMs at 10 and 20 mm intervals, respectively, for the 1 and 4 m2 plot areas. A total of 95 profiles were employed in both across- and down-glacier directions for each DSM (after Reference Fassnacht, Stednick, Deems and CorraoFassnacht and others, 2009b). This sampling approach, although reducing the source data available, significantly improves on any previously published work assessing plot-scale ice roughness, as a much greater density of topographic data is available. The surface elevation (h) data were then detrended. Linear detrending over the profile length was necessary to eliminate the bias introduced by the influence of larger-scale surface slope within the area of interest and, in light of the non-stationarity of the surface, to allow direct comparison of calculated bidirectional roughness metrics. In addition to estimating z 0 from the detrended profile data using Eqn (2), derived roughness metrics included
(i) effective roughness height (σh ) described above, (ii) the sum of absolute slopes (∑S) between each observation point over a profile window of length L (Reference Currence and LovelyCurrence and Lovely, 1970), and (iii) a dimensionless micro-topography index (MI; Romkens and Wang, 1987):

for which n is the number of observations within the profile analysed. Comparable roughness values were also derived from the four discrete ice-surface profiles manually recorded coincident with the dates of image acquisition.
Analytical Results
Uncertainty and validation
Based upon the scale and geometry defined by the imagery acquired, it is possible to quantify the precision of data generated using photogrammetry. Here this was achieved internally by the PhotoModeler software using variance propagation methods and is conveyed by the ‘point quality’ output table. By using the average of achieved precisions for all points used for geo-referencing the surveys (18 points in 1 m2 surveys and 17 points in 4 m2 surveys), global precision can be estimated in three dimensions. In this configuration, the horizontal x –axis is approximately parallel to the camera lens whilst both the y – and vertical axes are at an oblique angle relative to the plane of the camera lens. For the 1 m2 surveys, average precisions for these axes were approximately 2.5, 5.0 and 3.4 mm. For the 4 m2 surveys, imagery was acquired less steeply and the associated precisions were 3.8, 6.4 and 2.6 mm respectively. As expected, the axis approximately orthogonal to the plane of the camera lens exhibited the lowest precision, while the axis most closely aligned with the camera lens plane yields the highest precision. Consequently, the best precision is obtained along the vertical axis in the 4 m2 test area, where the degree of convergence of imagery is lower. Note that point precision varies spatially: optimum precision is achieved for those points located closest to the camera, but precision gradually degrades with increasing distance.
The scale of the DSMs created is defined by the control markers located upon the two string lines established at the RC3 supraglacial plot. Attempts were made to make these as taut as possible, but inevitably these string lines did exhibit a small degree of sag. It is possible to quantify the degree of sag using a catenary equation, generally used for correcting survey measurements acquired using a steel band (Reference Uren, Price, Van der Veen, Krabill, Csathó and BolzanUren and Price, 2005):
where D is the string line length, w is weight per unit length of tape, θ is the vertical angle between end-points and T is the applied tension. Assuming a modest tension of 10 N, for the 5 m string line length with a weight per unit length of 0.15 N m−1, the appropriate correction would be just 1.1 mm for the horizontal string lines used in this study. This correction is comparatively minor and it must be remembered that such a small-scale discrepancy would have negligible effect on the vertical precision of the derived DSMs or measures of roughness generated here.
In view of these potential sources of error uncertainty, the horizontal resolutions achieved in the gridded DSMs used here were sub-centimetre: 5 mm for the 1 m2 plot, and 10 mm for the 4 m2 plot. The vertical precisions of ~ 3 mm in the DSMs approach the scale of measurement noise.
To validate the reconstructed DSMs, data from the manually measured, concurrent surface profiles at 100 mm horizontal intervals were used for comparison with the surface profiles derived from the DSMs (Fig. 2). Because the DSM and manually collected datasets are independent, and both contain uncertainty, total least-squares regression was used to appropriately quantify the ‘degree of fit’ between the datasets. Where edge effects were noted, data were removed from the regression. Given the known importance of image texture and shadowing in stereo-pair photogrammetry (Reference ChandlerChandler, 1999; Reference Fox and GoochFox and Gooch, 2001; Reference Hopkinson, Ottawa Hopkinson, Hayashi and PeddleHopkinson and others, 2009), the regressions were re-run following removal of manually measured data points noted as being snow or small-scale (< 3 cm diameter) debris holes. Table 1 presents the measures of error retrieved from the residuals. Both the root-mean-square error (RMSE) and mean absolute error (MAE) were typically ≤16 mm, and this reduced to sub-centimetre uncertainties when accounting for surface characteristics likely to result in greater uncertainty in the final DSM (e.g. textureless snow, or isolated debris holes). Such uncertainties improve on the 5 mm reported for singular 2-D surveys of ice surface profiles by Reference Arnold and ReesArnold and Rees (2003). Critically, our photogrammetric uncertainties compare particularly well to real-time-kinematic differential GPS systems, whose vertical accuracy may only be of the order of >17 mm (Reference Wheaton, Brasington, Darby and SearWheaton and others, 2010). Appreciably, this validation is limited to the cross-glacier direction, but provides reasonable confidence in the data retrieved by the close-range photogrammetry.
Table 1. Detail of uncertainty in DSM compared to manual surface measurements based on residuals from total least-squares regression analysis. Uncertainty includes root-mean-square error (RMSE) and mean absolute error (MAE). Values in parentheses relate to regressions with data from points classified as snow or debris holes removed
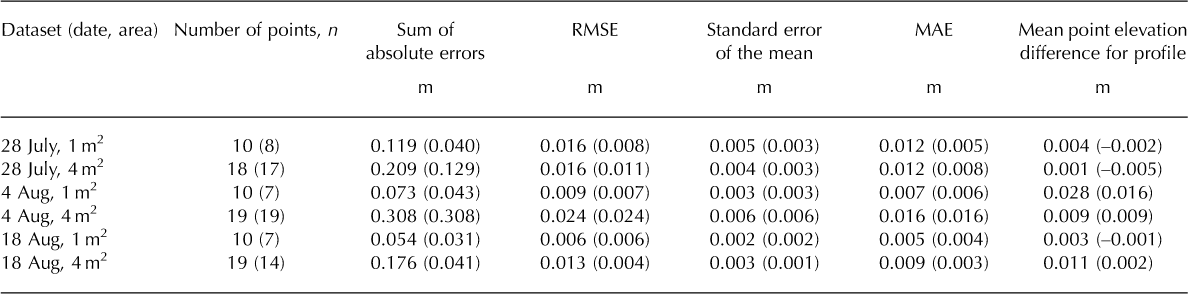
Fig. 2. Plot illustrating similarity between manually measured and photogrammetrically derived surface profiles for data collected on 4 August.
Plot-scale datasets
Figure 3 shows an example of the DSMs created for the 1 and 4 m2 plot areas, and the corresponding roughness metrics for the sampled profiles. Plots of the four roughness metrics showed a clear contrast between the down- and cross-glacier directions. Table 2 and Figure 4 summarize data for the four roughness metrics retrieved from the DSMs. Despite approximately linear standard-deviation–inter-quartile-range (IQR) relationships for the data in the down-glacier direction (Fig. 5), the profiles’ surface elevation data deviated from the pattern expected for normally distributed data. This observation was more marked for the across-glacier dataset. With consistently low or negative kurtosis (less than 3), the surface elevation in all four surveys was non-normally distributed in both directions. The roughness metrics similarly exhibited non-normal distributions, thus requiring non-parametric methods of comparison.
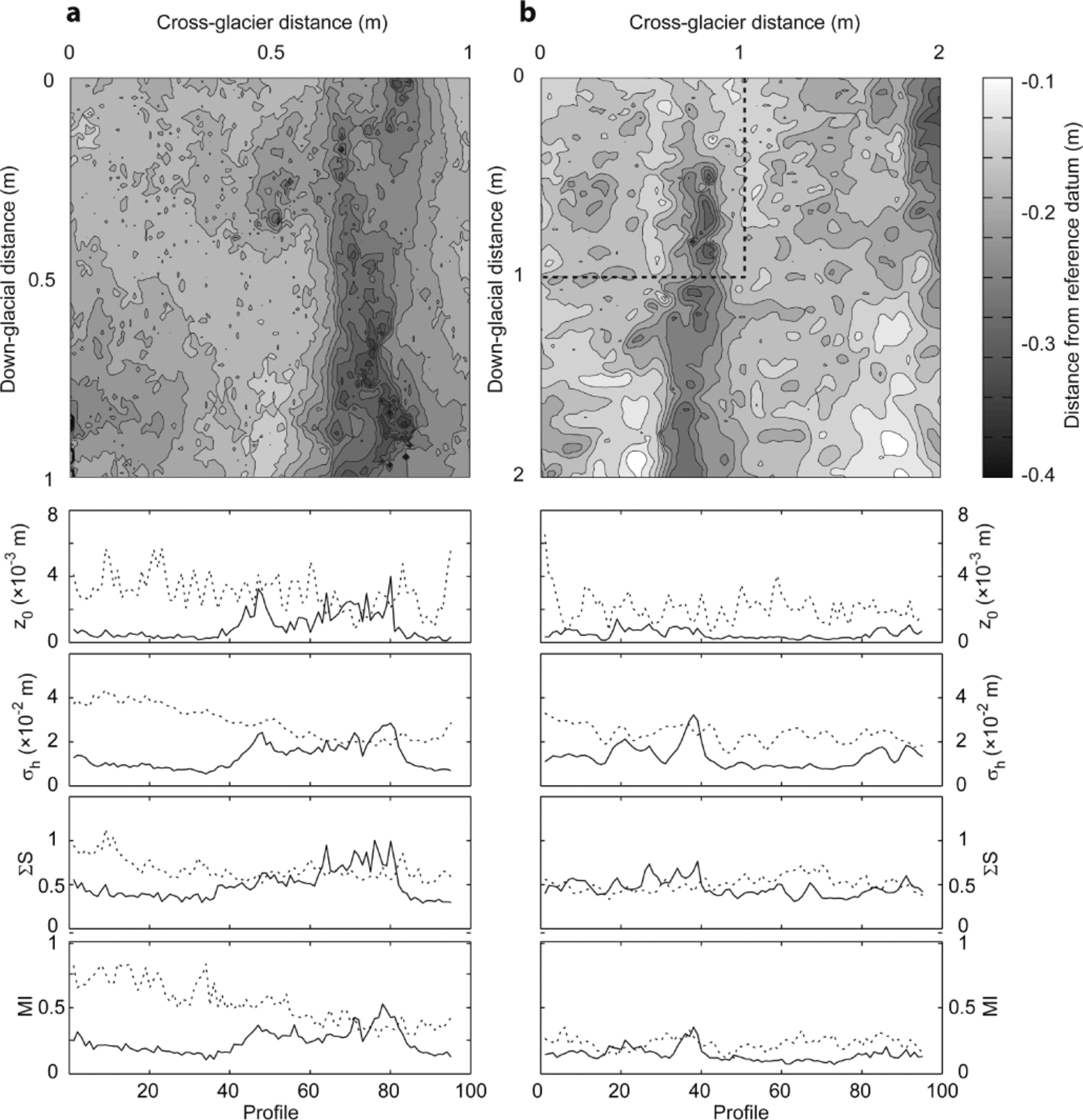
Fig. 3. Shaded contour maps for (a) 1 m2 and (b) 4 m2 plot areas for 28 July plotting distance from the reference datum; contours at 0.0015 m intervals. Corresponding graphs below each DSM illustrate values for roughness metrics (z 0, σh , ∑S and MI) for the respective plot areas for each of the 95 cross-glacier (dashed) and down-glacier (solid) profiles. The co-location of the two plot areas is indicated by the dashed outline on the 4 m2 plot (b).
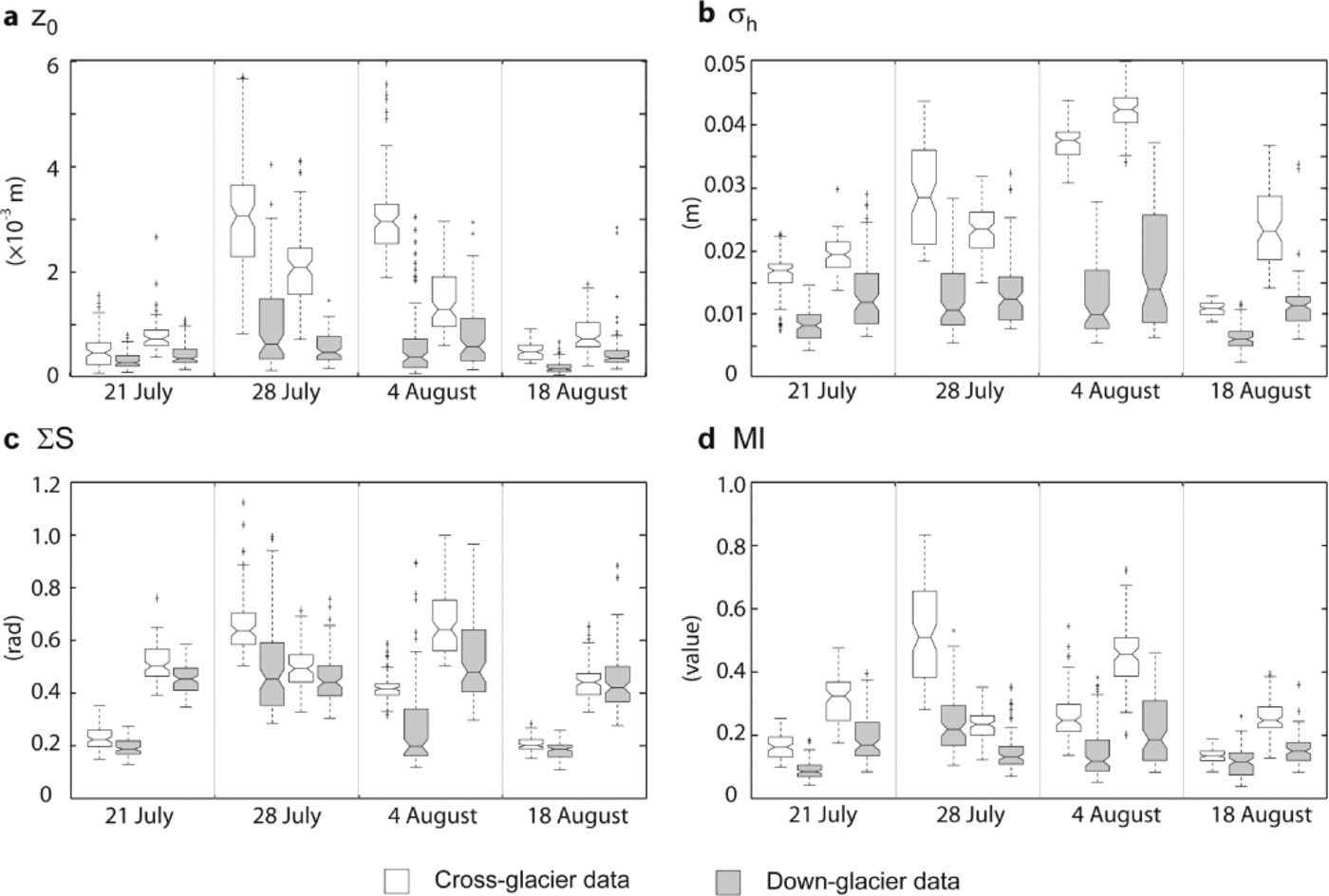
Fig. 4. Box-and-whisker plots describing the distribution of four roughness metrics, (a) z 0, (b) σh , (c) ∑S and (d) MI, for the four image acquisition dates for both 1 and 4 m2 plots. Clear plots indicate the across-glacier direction, and greyed plots indicate down-glacier. For each survey date, the first box-plot pair represent the 1 m2 area.
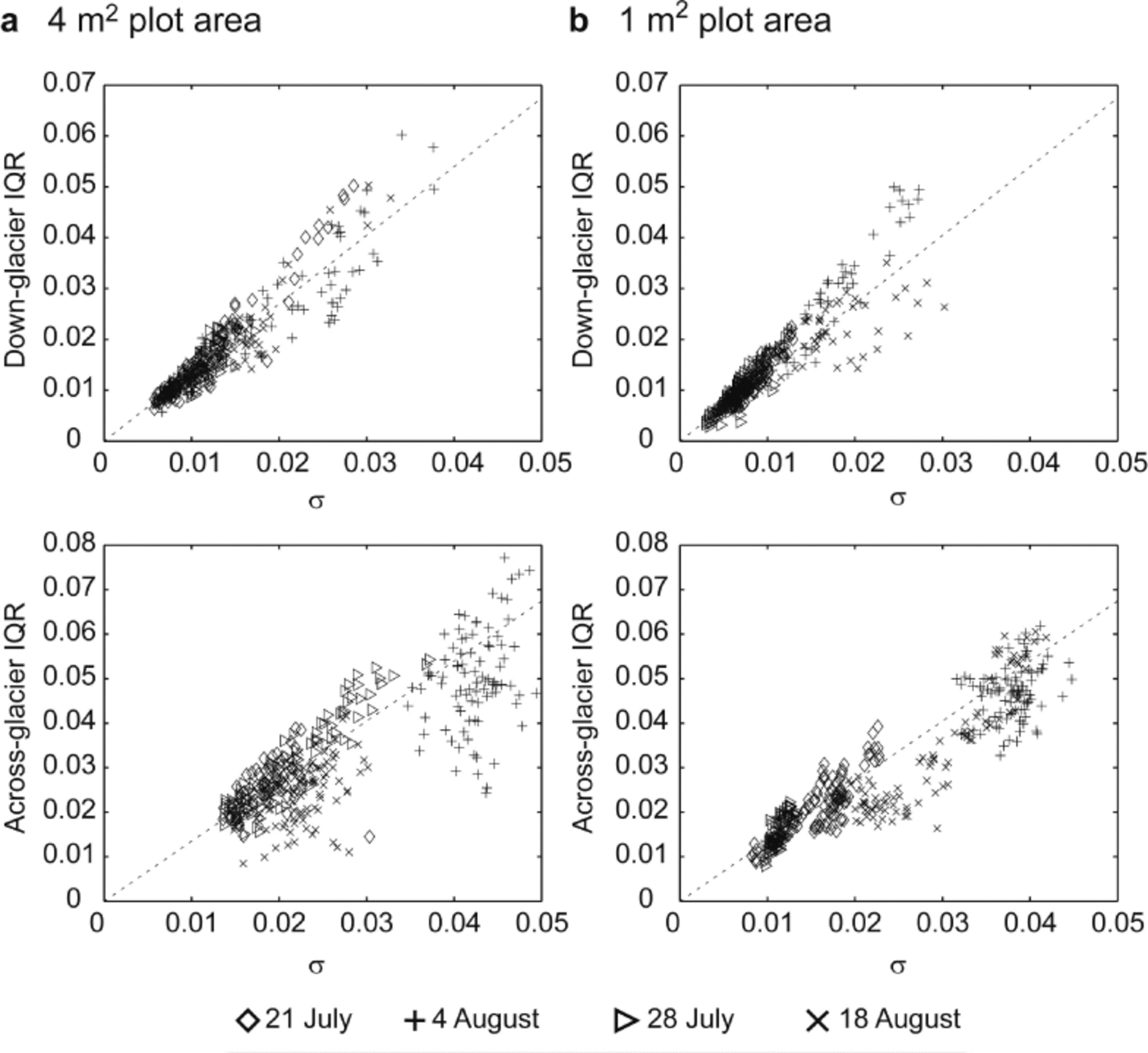
Fig. 5. Plots of standard deviation vs IQR for the raw surface elevation profile data for (a) the 4 m2 plot areas and (b) the 1 m2 plot areas. The dashed lines represent the distribution expected for a normal (Gaussian) dataset.
Figure 4 presents box-and-whisker plots of the distribution of the cross- and down-glacier roughness metrics for the four discrete DSMs. To explore ice surface anisotropy, Wilcoxon rank sum tests were used to examine whether the roughness metric distributions in cross- and down-glacier directions exhibited statistically similar median values. For the 1 m2 area, a significant difference was evident between all cross-and down-glacier roughness measures (p < 0.00021); for the 4 m2 plot, all metrics showed a significant directional contrast (p < 0.00016) with the exception of ∑S on 18 August (p = 0.42). Similarly, comparison between 1 m2 and 4 m2 plot area scales through application of rank tests demonstrated that with the exception of down-glacier σh and ∑S on 18 August (p > 0: 46), no similarity between the roughness measures at the two contrasting length scales was observed for each of the four surveys.
The plots of surface elevation descriptors for the four surveys (Figs 4 and 5) suggested that, particularly for the cross-glacier direction, there were differences over time. Difference models of the DSMs for 28 July and 4 August (Fig. 6a) emphasized spatial variation in surface change (equivalent to melt rates), with a maximum of ~ 0.19 m ice ablation or 0.028 m d−1. Over this period, mean ice surface lowering over the plot areas was 0.044 ± 0.035 m and 0.044 ± 0.033 m for 4 and 1 m2, respectively. Critically, there was spatial variability in ice ablation: heightened melt was observed in elongated areas oriented parallel with ice flow direction (down-glacier) at ~ 0.8 and 1.9 m, and in areas that were initially at lower elevations. Kruskal–Wallis tests were used to examine differences between the four discrete surveys, revealing statistically significant (p < 0.05) contrast for all roughness metrics at both length scales and both orientations (Fig. 4). Of interest in Figure 4 is the asynchronous variation in temporal trends of roughness metrics; for example, cross-glacier σh appears to increase between 21 July and 4 August, while cross-glacier MI peaks on 28 July and decreases thereafter. The down-glacier metrics exhibited the least variation over time, as reflected in the ice ablation patterns on the surface.

Fig. 6. Spatial difference plots showing surface elevation change between 28 July and 4 August for (a) the 1 m2 and (b) 4 m2 plot areas, and between DSMs generated using two independent stereo-pairs acquired on 28 July for (c) the 1 m2 and (d) 4 m2 plot areas. Contours in (a–d) are at 0.025 m intervals. Note that in (c) and (d) sites of significant difference are associated with topographic lows and as discrete point locations are suggestive of the impact of isolated debris holes which experience topographic or self-shadowing, thereby influencing the vertical precision of the photogrammetrically derived DSM data in these locations.
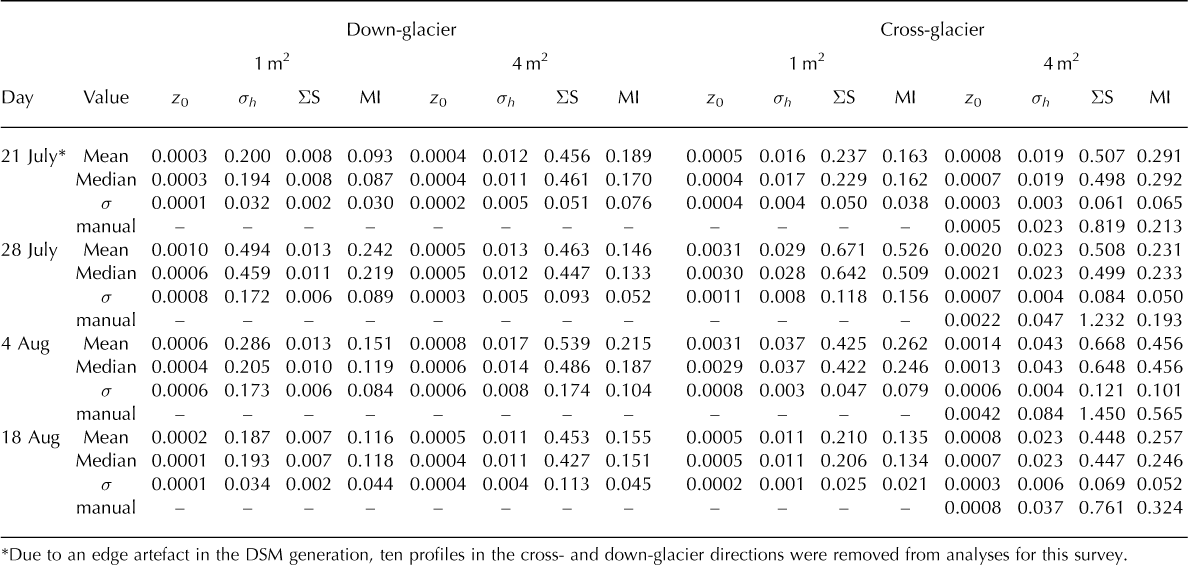
Simple comparison of the spatially discrete manual roughness survey against the data derived from the 95 cross-glacier profiles for the 4 m2 plot (Table 2) highlighted that, with the exception of 4 August, the estimates for z0 lie within one standard deviation of the mean value. However, the 0.003 mm difference between the two values retrieved for 4 August suggested that while discrete measurements represent an invaluable estimate of roughness descriptors, at the length scales of 1–5 m these may not necessarily reveal appropriate or representative values.
Table 2. Summary statistics for roughness metrics z 0, σh , ∑S, and MI for the 1 and 4 m2 areas over the four observation dates: data are reported as mean, median and standard deviation () for the n = 95 observation sets in cross- and down-glacier directions. Results from the manual survey are shown for comparison
Repeatability
To examine the repeatability of the digital surface reconstruction process, DSMs derived for both the 1 and 4 m2 plots on 28 July were compared to data derived from a second image stereo-pair acquired at the same time by examining the surface difference (Fig. 6b). The mean elevation difference across the plot area was relatively small in both instances: for 1 m2, –0.005 ± 0.013 m and for 4 m2, –0.003 ± 0.015 m. Such differences lie remarkably close to the sub-centimetre uncertainties estimated for each of the DSMs, and provide confidence in the method, particularly for the 4 m2 plot. Areas indicating greatest uncertainty in ice surface topography were observed at the domain edge, in discrete topographic lows where topographic shadowing occurred (e.g. debris or cryoconite holes) and where point
cloud returns were absent (cf. Figs 1c, 3a and 6a). Comparison of all the roughness metrics with a Wilcoxon rank sum test revealed that at the 4 m2 scale, with the exception of cross-glacier z 0, all metrics exhibited statistically similar medians at the 99% confidence level for the two paired surveys. The results for the paired 1 m2 plots were different: all metrics exhibited significantly different medians (p ≪ 0: 01), with the exception of down-glacier σh (p = 0.034).
Discussion And Conclusion
This paper provides the first assessment of close-range digital photogrammetry as a tool to retrieve data relating to glacier surface topography at the plot scale. Here, using a commercially available software package and a consumer-grade 5 Mpix camera, we demonstrate successful DSM generation to describe a glacier surface from stereo-pair imagery. Horizontal resolution of the 1 m2 ice surface DSM was subcentimetre, with 3.4 mm vertical precision, while for the 4 m2 plot area, comparable horizontal resolution and vertical precision of 10 and 2.6 mm, respectively, was achieved.
Validation of the DSMs against manual, across-glacier surveys of the ice surface suggested mean vertical uncertainties were <16 mm, being the same order or less than those associated with traditional 2-D profiling methods (e.g. Reference Arnold and ReesArnold and Rees, 2003) and real-time-kinematic differential GPS (Reference Wheaton, Brasington, Darby and SearWheaton and others, 2010). Comparison of DSMs created from two concurrent but independent stereo-pairs indicated surface elevation differences were broadly comparable to the uncertainties associated with the DSMs themselves. The effectiveness of this photogrammetric method is dependent on the ice surface texture; improved results are achieved where there is increased rugosity and distributed, fine debris or cryoconite deposits, two inextricably linked properties of an ablating ice surface (Reference IntyreMcIntyre, 1984; Reference Irvine-Fynn, Bridge and HodsonIrvine-Fynn and others, 2011). Critically, there has been increasing recognition of dust and cryoconite as a characteristic feature on glacier ablation zones worldwide (Reference HodsonHodson and others, 2008), suggesting the photogrammetric method to characterize glacier surfaces could be widely adopted.
The maximum and mean plot-scale ice surface lowering, 28 and 6.3 mm d–1, respectively, exceeds the sub-centimetre uncertainties in our DSM data, and compares well to the seasonally averaged ablation rate of 15.5 ± 2.8 mm d–1 observed at Midtre Lovénbreen during 2010. The greatest variability in surface lowering was seen in the cross-slope direction, corresponding to the existing topographic lows, and indicating the role that meltwater drainage at the rill (centimetre to decimetre) scale has in changing ice topography. Variability in the glacier surface, and its ablation rates over the four measurement dates, influenced by the partial cover from summer snow, suggested temporal change in roughness metrics could be expected. The estimates of mean supraglacial σh between 0.007 and 0.043 m correspond well with equivalent metrics for rough snow of ~ 0.01 m (Reference Fassnacht, Williams and CorraoFassnacht and others, 2009a,Reference Fassnacht, Stednick, Deems and Corraob), while the order-of-magnitude range of mean z0 values 0.0002–0.002 m agrees with existing estimates for supraglacial aerodynamic roughness values (Reference Brock, Willis and SharpBrock and others, 2006), and even matches those for the same glacier (Reference Rees and ArnoldRees and Arnold, 2006). The contrast between the metrics and their median values for the two plot scales, using the photogrammetry-derived data and manual measurements, may be related to the fact this study bridged the scale-independent (<1 m) and scale-dependent (>1 m) length scales (Reference Rees and ArnoldRees and Arnold, 2006).
One key pattern found with all four roughness metrics reported here was the contrast between down- and cross-glacier directions. In all cases, the down-glacier metrics were consistently lower than across-glacier. The use of detrending prior to calculating roughness metrics lends weight to this result. Interestingly, this bidirectional roughness variation was found at both the scale-dependent and scale-independent length scales. Such surface anisotropy has been recorded for glaciers, both at the large scale (Reference Smith, Raymond and ScambosSmith and others, 2006) and the small to micro-scale (Reference Rees and ArnoldRees and Arnold, 2006), and is well known for sea ice as an important variation to account for in remote-sensing applications (Reference Jin and SimpsonJin and Simpson, 1999).
There was variability in the surface roughness measures; however, the apparent temporal trends over the four survey dates between 21 July and 18 August were neither progressive nor synchronous across the four metrics considered. This subtle difference highlights a question that is currently an active area of research (see Reference SmithSmith, 2014), particularly in consideration of remotely sensed data: which roughness metric is the most appropriate to use? Nonetheless, as could be expected, the roughness for times of partial snow cover (21 July and 18 August) was significantly lower than for the glacier ice. This was demonstrated by the lowered standard deviation and IQR (Fig. 5), implying that the presence of residual snow smoothed the surface and removed extremes in the micro-topography at the 1 and 4 m2 plot scales. While there was no evidence of longer-term systematic change in roughness (e.g. Reference Smeets, Duynkerke and VugtsSmeets and others, 1999; Reference Smeets and Van den BroekeSmeets and Van den Broeke, 2008), with only four snapshots considered here, we suggest the method presented, and the ability to test similarity of roughness metrics, provides a route by which temporal (and spatial) variation in roughness parameters and aerodynamic roughness approximations can be explored quantitatively. More detailed surface analyses could include utilization of semivariance (Reference Arnold and ReesArnold and Rees, 2003) or spectral (Reference Hubbard, Siegert and CarrollHubbard and others, 2000; Reference Rees and ArnoldRees and Arnold, 2006) analyses of plot areas. However, the implication that, for the ice surface, significant difference in roughness can be observed at a single plot suggests that Reference Brock, Willis and SharpBrock and others’ (2006) assertion that a single, distributed micro-topographic survey of the glacier surface would be sufficient to describe spatial variation in roughness (z0) may demand further assessment.
A limitation of the photogrammetric method described here was associated with the varying obliquity associated with capturing plot areas of >4 m2 with an image acquisition height of 1.6 m. The increasingly shallow viewing angle for larger plot-scales increases areas of shaded, or self-shadowed, ice surface behind micro- and meso-topographic ridges or features. For the specific camera and stereo-pair input used here, more detailed analyses demonstrated that for an improved representation of the 4 m2 area, the image capture height should be increased by 28 cm, to ~ 1.9 m, while at a height of ~ 3 m photogrammetric solutions of 9– 25 m2 ice surface plots would be possible (Reference Sanz-Ablanedo, Chandler and FynnSanz-Ablanedo and others, 2012a). This could be readily achieved using inspection poles designed to elevate cameras up to 10 m above the surface and allow the method presented here to be scaled up to larger plot areas. However, since the initiation of this work, photogrammetric software packages (e.g. Eos Systems’ PhotoModeler Scanner, Agisoft’s PhotoScan) and their algorithms have advanced markedly, and it is now possible to use multiple images over larger areas and with varied viewpoints to capture and reconstruct topography (e.g. Reference Javernick, Brasington and CarusoJavernick and others, 2014). While incorporating additional uncertainty, this technical advance reduces the limitations afforded by stereo-pair imagery; additional images can capture otherwise self-shaded locations. Similarly, incorporation of additional images increases the size of the plot area that can be reconstructed using a photogram-metric approach. Nonetheless, the resolution of DSMs produced using this method is dependent on the camera resolution and camera-to-surface distance. For example, imagery from 300 m above a glacier surface with a 10 Mpix camera yields a horizontal surface resolution of only 0.12 m per pixel (Reference Whitehead, Moorman and HugenholtzWhitehead and others, 2013). However, subcentimetre resolutions across the range of length scales reported here may be readily achieved using ground-based image capture with contemporary consumer-grade cameras which now typically capture >12 Mpix images. However, the successful DSM creation for the 1 and 4 m2 plots demonstrates that a photogrammetric approach, with appropriate image settings and acquisition geometry, can provide a powerful technique to examine glacier surfaces, and variability thereof, at the plot scale in high spatial resolution.
The roughness of ice surfaces demands continued investigation, addressing problems with backscatter to satellite-mounted sensors as well as resolving appropriate aerodynamic roughness representations. Specifically, on glaciers, researchers have yet to resolve questions over assumed spatial and scale similarity (Reference Rees and ArnoldRees and Arnold, 2006), persistence of spatial patterns (Reference Brock, Willis and SharpBrock and others, 2006) and progressive temporal variations (Reference Smeets and Van den BroekeSmeets and Van den Broeke, 2008) in roughness. Recent research has even suggested that ice surface microbiology can be strongly influenced by local hydrology which is explicitly related to plot-scale topography (e.g. Reference EdwardsEdwards and others, 2011). Consequently, the ability to retrieve data to construct detailed DSMs of a glacier surface and derive roughness metrics at the resolutions and length scales reported here is a step-change from previously published 2-D datasets, and is an important technique to develop further. Close-range digital photogrammetry has advantages in the form of low-cost and rapid data acquisition, and is well suited to surveys across a wide range of spatial scales or utilizing autonomous time-lapse image acquisition modes, with retrospective data processing to retrieve the desired variable(s). The method opens new possibilities for interrogating and constraining supraglacial processes, in particular offering the potential to feed high-density topographic datasets into studies of ice surface characteristics at the glacier scale, which are important for both remote-sensing applications and glacier ablation. Given the rapidly advancing area of less constrained photogrammetry methods for environmental monitoring (e.g. Reference James and RobsonJames and Robson, 2012; Reference Westoby, Brasington, Glasser, Hambrey and ReynoldsWestoby and others, 2012; Reference Javernick, Brasington and CarusoJavernick and others, 2014), this assessment of a more conventional use of the technique provides a benchmark for the anticipated increase in these types of studies in glacial environments.
Acknowledgements
T.D.I.-F. acknowledges UK Natural Environment Research Council (NERC) Standard Grant NE/G006253/1 (principal investigator A.J. Hodson, University of Sheffield) for enabling data collection at Midtre Lovénbreen, and the Climate Change Consortium of Wales (C3W) for facilitating the completion of this work. Logistical support in Svalbard from Nick Cox (NERC Arctic Research Station), and field assistance from Aga Nowak and Jon Bridge, was gratefully received. E S.-A. and J.H.C. thank Eos Systems Inc. for providing access to PhotoModeler software at reduced academic rates. Helpful comments from Tim James, Arwyn Edwards and Tom Holt are appreciated. Informative input from Duncan Quincey, and constructive and detailed insights from two anonymous reviewers significantly improved this paper.










