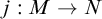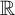1 Introduction
The notion of an elementary embedding between transitive models of set theory is central to the investigation of principles of high consistency strength. A typical situation involves an elementary
![]() $j : M \to N$
, where M and N are models of ZFC sharing the same ordinals, and j is not the identity map. Such a map cannot be the identity on ordinals, and the least ordinal moved is called the critical point. Postulating more agreement between M and N, and with the “real” universe V, usually results in a stronger hypothesis. Kunen established an upper bound to this collection of ideas, showing that there is no nontrivial elementary
$j : M \to N$
, where M and N are models of ZFC sharing the same ordinals, and j is not the identity map. Such a map cannot be the identity on ordinals, and the least ordinal moved is called the critical point. Postulating more agreement between M and N, and with the “real” universe V, usually results in a stronger hypothesis. Kunen established an upper bound to this collection of ideas, showing that there is no nontrivial elementary
![]() $j : V \to V$
.
$j : V \to V$
.
The question is how exactly to formalize Kunen’s result, which is not on its face equivalent to a first-order statement. Indeed, it cannot be about an arbitrary elementary embedding which may exist in some outer universe, as the relatively low-strength assumption of
![]() $0^{\sharp }$
gives a nontrivial elementary
$0^{\sharp }$
gives a nontrivial elementary
![]() $j : L \to L$
. Furthermore, requiring j to be definable from parameters in V yields an impossibility using more elementary considerations and not requiring the Axiom of Choice [Reference Suzuki16]. One way to express the content of Kunen’s Theorem is to require that V satisfies the expansion of ZFC to include Replacement and Comprehension for formulas that use j as a predicate. Another way is to localize its combinatorial content, which shows that there cannot be a cardinal
$j : L \to L$
. Furthermore, requiring j to be definable from parameters in V yields an impossibility using more elementary considerations and not requiring the Axiom of Choice [Reference Suzuki16]. One way to express the content of Kunen’s Theorem is to require that V satisfies the expansion of ZFC to include Replacement and Comprehension for formulas that use j as a predicate. Another way is to localize its combinatorial content, which shows that there cannot be a cardinal
![]() $\lambda $
and a nontrivial elementary
$\lambda $
and a nontrivial elementary
![]() $j : V_{\lambda +2} \to V_{\lambda +2}$
.
$j : V_{\lambda +2} \to V_{\lambda +2}$
.
We begin with an elaboration on Kunen’s theorem in a slightly different direction. Using the main idea of Woodin’s proof of Kunen’s theorem (see [Reference Kanamori11, Theorem 23.12]), we show that whenever one model of ZFC is embedded into another with the same ordinals, there are some general constraints on what the models can know about the embedding and about each other.
Theorem 1.1. Suppose
![]() $j : M \to N$
is a nontrivial elementary embedding between transitive models of
$j : M \to N$
is a nontrivial elementary embedding between transitive models of
![]() $\mathrm {ZFC} $
with the same class of ordinals
$\mathrm {ZFC} $
with the same class of ordinals
![]() $\Omega $
. Then at least one of the following holds:
$\Omega $
. Then at least one of the following holds:
-
(1) The critical sequence
 $\langle j^n(\operatorname {\mathrm {crit}}(j)) : n \in \omega \rangle $
is cofinal in
$\langle j^n(\operatorname {\mathrm {crit}}(j)) : n \in \omega \rangle $
is cofinal in
 $\Omega $
.
$\Omega $
. -
(2) For some
 $\alpha \in \Omega $
,
$\alpha \in \Omega $
,
 $j[\alpha ] \notin N$
.
$j[\alpha ] \notin N$
. -
(3) For some
 $\alpha \in \Omega $
,
$\alpha \in \Omega $
,
 $\alpha $
is regular in M and singular in N.
$\alpha $
is regular in M and singular in N.
Proof We will suppose that all of the alternatives fail and derive a contradiction. Let
![]() $\lambda \in \Omega $
be the supremum of the critical sequence. Since
$\lambda \in \Omega $
be the supremum of the critical sequence. Since
![]() $j[\lambda ] \in N$
, the critical sequence is a member of N, and thus
$j[\lambda ] \in N$
, the critical sequence is a member of N, and thus
![]() $N \models \operatorname {\mathrm {cf}}(\lambda ) = \omega $
. Since
$N \models \operatorname {\mathrm {cf}}(\lambda ) = \omega $
. Since
![]() $\operatorname {\mathrm {cf}}(\lambda )^M$
is regular in M, it is also regular in N, and so
$\operatorname {\mathrm {cf}}(\lambda )^M$
is regular in M, it is also regular in N, and so
![]() $M \models \operatorname {\mathrm {cf}}(\lambda ) = \omega $
as well. Thus
$M \models \operatorname {\mathrm {cf}}(\lambda ) = \omega $
as well. Thus
![]() $j(\lambda ) = \lambda $
. Since
$j(\lambda ) = \lambda $
. Since
![]() $(\lambda ^+)^M$
is regular in N, we must have that
$(\lambda ^+)^M$
is regular in N, we must have that
![]() $(\lambda ^+)^M$
is also a fixed point.
$(\lambda ^+)^M$
is also a fixed point.
Let
![]() $\kappa = \operatorname {\mathrm {crit}}(j)$
, and choose in M a pairwise-disjoint sequence of stationary subsets of
$\kappa = \operatorname {\mathrm {crit}}(j)$
, and choose in M a pairwise-disjoint sequence of stationary subsets of
![]() $\lambda ^+ \cap \operatorname {\mathrm {cof}}(\omega )$
,
$\lambda ^+ \cap \operatorname {\mathrm {cof}}(\omega )$
,
![]() $\langle S_{\alpha } : \alpha < \kappa \rangle $
. Let
$\langle S_{\alpha } : \alpha < \kappa \rangle $
. Let
![]() $\langle S^{\prime }_{\alpha } : \alpha < j(\kappa ) \rangle = j(\langle S_{\alpha } : \alpha < \kappa \rangle )$
. Let
$\langle S^{\prime }_{\alpha } : \alpha < j(\kappa ) \rangle = j(\langle S_{\alpha } : \alpha < \kappa \rangle )$
. Let
![]() $C = \{ \alpha < \lambda ^+ : j[\alpha ] \subseteq \alpha \}$
. C is a member of N and a club in
$C = \{ \alpha < \lambda ^+ : j[\alpha ] \subseteq \alpha \}$
. C is a member of N and a club in
![]() $\lambda ^+$
, so let
$\lambda ^+$
, so let
![]() $\alpha \in C \cap S^{\prime }_{\kappa }$
. Since
$\alpha \in C \cap S^{\prime }_{\kappa }$
. Since
![]() $N \models \operatorname {\mathrm {cf}}(\alpha ) = \omega $
, there is a sequence
$N \models \operatorname {\mathrm {cf}}(\alpha ) = \omega $
, there is a sequence
![]() $\langle \alpha _n : n < \omega \rangle \in M$
cofinal in
$\langle \alpha _n : n < \omega \rangle \in M$
cofinal in
![]() $\alpha $
. Since
$\alpha $
. Since
![]() $\alpha $
is closed under j,
$\alpha $
is closed under j,
![]() $j(\alpha ) = \sup _{n<\omega } j(\alpha _n) = \alpha $
. By elementarity, there is some
$j(\alpha ) = \sup _{n<\omega } j(\alpha _n) = \alpha $
. By elementarity, there is some
![]() $\beta < \kappa $
such that
$\beta < \kappa $
such that
![]() $\alpha \in S_{\beta }$
. But then
$\alpha \in S_{\beta }$
. But then
![]() $\alpha \in S^{\prime }_{\beta } \cap S^{\prime }_{\kappa } = \emptyset $
, a contradiction.
$\alpha \in S^{\prime }_{\beta } \cap S^{\prime }_{\kappa } = \emptyset $
, a contradiction.
Let us list some key examples of embeddings between transitive models of ZFC with the same ordinals, in which exactly one of the above alternatives holds:
-
(1) Axiom I3 asserts the existence of a nontrivial elementary embedding
 $j : V_{\lambda } \to V_{\lambda }$
, where
$j : V_{\lambda } \to V_{\lambda }$
, where
 $\lambda $
is a limit ordinal. (2) and (3) must both fail for such j, so (1) must hold.
$\lambda $
is a limit ordinal. (2) and (3) must both fail for such j, so (1) must hold. -
(2) Suppose
 ${\mathcal U}$
is a countably complete ultrafilter over some set. If
${\mathcal U}$
is a countably complete ultrafilter over some set. If
 $j : V \to M \cong \operatorname {\mathrm {Ult}}(V,{\mathcal U})$
is the ultrapower embedding, then (1) fails by the Replacement axiom, and (3) fails since
$j : V \to M \cong \operatorname {\mathrm {Ult}}(V,{\mathcal U})$
is the ultrapower embedding, then (1) fails by the Replacement axiom, and (3) fails since
 $M \subseteq V$
. Thus (2) holds.
$M \subseteq V$
. Thus (2) holds. -
(3) Situations in which (1) and (2) both fail will be considered in Sections 3 and 4 of the present paper.
We will say that an elementary embedding
![]() $j : M \to N$
is (target-)amenable if
$j : M \to N$
is (target-)amenable if
![]() $j[x] \in N$
for all
$j[x] \in N$
for all
![]() $x \in M$
, or in other words that alternative (2) fails. For ZFC models, this is equivalent to saying that
$x \in M$
, or in other words that alternative (2) fails. For ZFC models, this is equivalent to saying that
![]() $j \cap \alpha ^2 \in N$
for all ordinals
$j \cap \alpha ^2 \in N$
for all ordinals
![]() $\alpha \in N$
. It is easy to see that
$\alpha \in N$
. It is easy to see that
![]() $M \subseteq N$
in such a situation. It is an immediate consequence of Theorem 1.1 that if M and N are transitive models of ZFC with the same ordinals
$M \subseteq N$
in such a situation. It is an immediate consequence of Theorem 1.1 that if M and N are transitive models of ZFC with the same ordinals
![]() $\Omega $
, and
$\Omega $
, and
![]() $j : M \to N$
is an amenable elementary embedding such that its critical sequence is not cofinal in
$j : M \to N$
is an amenable elementary embedding such that its critical sequence is not cofinal in
![]() $\Omega $
, then M and N do not agree on cofinalities. The proof actually shows that M and N cannot agree on both the class of cardinals and the class
$\Omega $
, then M and N do not agree on cofinalities. The proof actually shows that M and N cannot agree on both the class of cardinals and the class
![]() $\{ \alpha : \operatorname {\mathrm {cf}}(\alpha ) = \omega \}$
.
$\{ \alpha : \operatorname {\mathrm {cf}}(\alpha ) = \omega \}$
.
When the domain and target of an elementary embedding are the same, alternative (3) cannot hold. If
![]() $j : M \to M$
is definable from parameters in some larger universe V, then alternatives (1) and (2) show that the closure of M, as measured by V, must run out at some point. In contrast to the I3 examples that achieve amenability at the cost of countable closure, we show it is possible for such M to be as near to V as desired, and find in this motif a characterization of supercompactness:
$j : M \to M$
is definable from parameters in some larger universe V, then alternatives (1) and (2) show that the closure of M, as measured by V, must run out at some point. In contrast to the I3 examples that achieve amenability at the cost of countable closure, we show it is possible for such M to be as near to V as desired, and find in this motif a characterization of supercompactness:
Theorem 1.2. Suppose
![]() $\kappa \leq \lambda $
are regular.
$\kappa \leq \lambda $
are regular.
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-supercompact if and only if there is a
$\lambda $
-supercompact if and only if there is a
![]() $\lambda $
-closed transitive class M and a nontrivial elementary
$\lambda $
-closed transitive class M and a nontrivial elementary
![]() $j : M \to M$
with critical point
$j : M \to M$
with critical point
![]() $\kappa $
.
$\kappa $
.
Finally, we consider amenable embeddings for which alternative (1) does not hold. Because of the importance of regular fixed points in the proof of Theorem 1.1, we first explore the possible behaviors of cardinal fixed points of amenable embeddings, showing that essentially anything can happen. Then we explore the possible structural configurations of commuting systems of amenable embeddings.
Given an ordinal
![]() $\delta $
, let
$\delta $
, let
![]() $\mathcal E_{\delta }$
be the category whose objects are all transitive models of ZFC of height
$\mathcal E_{\delta }$
be the category whose objects are all transitive models of ZFC of height
![]() $\delta $
and whose arrows are all elementary embeddings between these models. Let
$\delta $
and whose arrows are all elementary embeddings between these models. Let
![]() ${\mathcal A}_{\delta }$
be the subcategory where we take only amenable embeddings as arrows. (It is easy to see that amenable embeddings are closed under composition.)
${\mathcal A}_{\delta }$
be the subcategory where we take only amenable embeddings as arrows. (It is easy to see that amenable embeddings are closed under composition.)
Partial orders are naturally represented as categories where between any two objects there is at most one arrow, which we take to point from the lesser object to the greater. We would like to know what kinds of partial orders can appear in a reasonable way as subcategories of an
![]() ${\mathcal A}_{\delta }$
. Let us say that a subcategory
${\mathcal A}_{\delta }$
. Let us say that a subcategory
![]() $\mathcal D$
of a category
$\mathcal D$
of a category
![]() $\mathcal C$
is honest if whenever x and y are objects of
$\mathcal C$
is honest if whenever x and y are objects of
![]() $\mathcal D$
and there is an arrow
$\mathcal D$
and there is an arrow
![]() $f : x \to y$
in
$f : x \to y$
in
![]() $\mathcal C$
, then there is one in
$\mathcal C$
, then there is one in
![]() $\mathcal D$
as well.
$\mathcal D$
as well.
Theorem 1.3. If there is a transitive model of ZFC plus sufficiently many large cardinals,Footnote
1
then there is a countable ordinal
![]() $\delta $
such that
$\delta $
such that
![]() ${\mathcal A}_{\delta }$
contains honest subcategories isomorphic to:
${\mathcal A}_{\delta }$
contains honest subcategories isomorphic to:
-
(1) The real numbers.
-
(2) The complete binary tree of any countable height.
-
(3) The reverse-ordered complete binary tree of height
 $\omega $
.
$\omega $
. -
(4) An Aronszajn tree.
-
(5) Every countable pseudotree.
A pseudotree is a partial order that is linear below any given element, which generalizes both linear orders and trees. These have been considered by several authors, for example in [Reference Alós-Ferrer and Ritzberger1, Reference Koppelberg and Monk12, Reference Kurepa13]. In order to show the last item, we develop the model theory of pseudotrees. We show that there is a countable pseudotree that has the same kind of universal property that the rationals have with respect to linear orders: It is characterized up to isomorphism by some first-order axioms, and every other countable pseudotree appears as a substructure. We prove that for suitable
![]() $\delta $
, the category
$\delta $
, the category
![]() ${\mathcal A}_{\delta }$
contains a copy of this universal countable pseudotree.
${\mathcal A}_{\delta }$
contains a copy of this universal countable pseudotree.
We also rule out some kinds of subcategories. For example, if
![]() $\delta $
is countable, then
$\delta $
is countable, then
![]() ${\mathcal A}_{\delta }$
cannot contain a copy of
${\mathcal A}_{\delta }$
cannot contain a copy of
![]() $\omega _1$
or a Suslin tree. There are many natural questions about the possible structure of these categories, and we list some of them at the end.
$\omega _1$
or a Suslin tree. There are many natural questions about the possible structure of these categories, and we list some of them at the end.
2 Self-embeddings of highly closed classes
In this section, we will prove Theorem 1.2. First let us show that if
![]() $\lambda $
is regular, M is a
$\lambda $
is regular, M is a
![]() $\lambda $
-closed transitive class, and
$\lambda $
-closed transitive class, and
![]() $j : M \to M$
is a nontrivial elementary embedding with critical point
$j : M \to M$
is a nontrivial elementary embedding with critical point
![]() $\kappa $
, then
$\kappa $
, then
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-supercompact. First note that we may assume
$\lambda $
-supercompact. First note that we may assume
![]() $j(\kappa )> \lambda $
: The proof of Theorem 1.1 shows that the critical sequence eventually must overtake
$j(\kappa )> \lambda $
: The proof of Theorem 1.1 shows that the critical sequence eventually must overtake
![]() $\lambda $
. For if not, then
$\lambda $
. For if not, then
![]() $\lambda \geq \eta ^+$
, where
$\lambda \geq \eta ^+$
, where
![]() $\eta = \sup _{n<\omega } j^n(\kappa )$
, and we can derive a contradiction from the assumption that
$\eta = \sup _{n<\omega } j^n(\kappa )$
, and we can derive a contradiction from the assumption that
![]() $j[\eta ^+] \in M$
. So composing j with itself finitely many times yields an embedding that sends
$j[\eta ^+] \in M$
. So composing j with itself finitely many times yields an embedding that sends
![]() $\kappa $
above
$\kappa $
above
![]() $\lambda $
.
$\lambda $
.
Next we claim that
![]() $\lambda ^{<\kappa } = \lambda $
, using a well-known argument (see [Reference Cummings3]). Let
$\lambda ^{<\kappa } = \lambda $
, using a well-known argument (see [Reference Cummings3]). Let
![]() $\vec C = \langle C_{\alpha } : \alpha < \lambda \rangle $
be such that
$\vec C = \langle C_{\alpha } : \alpha < \lambda \rangle $
be such that
![]() $C_{\alpha }$
is a club in
$C_{\alpha }$
is a club in
![]() $\alpha $
of ordertype
$\alpha $
of ordertype
![]() $\operatorname {\mathrm {cf}}(\alpha )$
. Since
$\operatorname {\mathrm {cf}}(\alpha )$
. Since
![]() $j[\lambda ] \in M$
and
$j[\lambda ] \in M$
and
![]() $j(\lambda )$
is regular in M,
$j(\lambda )$
is regular in M,
![]() $\gamma := \sup j[\lambda ] < j(\lambda )$
. Let
$\gamma := \sup j[\lambda ] < j(\lambda )$
. Let
![]() $C^* = j(\vec C)(\gamma )$
. Let
$C^* = j(\vec C)(\gamma )$
. Let
![]() $D = j^{-1}[C^*]$
. Since
$D = j^{-1}[C^*]$
. Since
![]() $j[\lambda ]$
is
$j[\lambda ]$
is
![]() ${<}\kappa $
-closed,
${<}\kappa $
-closed,
![]() $|D| = \lambda $
. If
$|D| = \lambda $
. If
![]() $x \in [D]^{<\kappa }$
, then
$x \in [D]^{<\kappa }$
, then
![]() $j(x) = j[x]$
, and by elementarity,
$j(x) = j[x]$
, and by elementarity,
![]() $x \subseteq C_{\alpha }$
for some
$x \subseteq C_{\alpha }$
for some
![]() $\alpha < \lambda $
such that
$\alpha < \lambda $
such that
![]() $\operatorname {\mathrm {cf}}(\alpha )<\kappa $
. Since
$\operatorname {\mathrm {cf}}(\alpha )<\kappa $
. Since
![]() $\kappa $
is inaccessible,
$\kappa $
is inaccessible,
![]() $|\mathcal {P}(C_{\alpha })| < \kappa $
when
$|\mathcal {P}(C_{\alpha })| < \kappa $
when
![]() $|C_{\alpha }|<\kappa $
. Thus
$|C_{\alpha }|<\kappa $
. Thus
![]() $\lambda ^{<\kappa } \leq \lambda \cdot \kappa = \lambda $
.
$\lambda ^{<\kappa } \leq \lambda \cdot \kappa = \lambda $
.
Thus, all subsets of
![]() $\mathcal {P}_{\kappa }\lambda $
are in M. From j we may define a
$\mathcal {P}_{\kappa }\lambda $
are in M. From j we may define a
![]() $\lambda $
-supercompactness measure in the usual way:
$\lambda $
-supercompactness measure in the usual way:
![]() ${\mathcal U} = \{ X \subseteq \mathcal {P}_{\kappa }\lambda : j[\lambda ] \in j(X) \}$
.
${\mathcal U} = \{ X \subseteq \mathcal {P}_{\kappa }\lambda : j[\lambda ] \in j(X) \}$
.
For the other direction, we use an iterated ultrapower. Let
![]() ${\mathcal U}$
be a normal, fine,
${\mathcal U}$
be a normal, fine,
![]() $\kappa $
-complete ultrafilter on
$\kappa $
-complete ultrafilter on
![]() $\mathcal {P}_{\kappa }\lambda $
. Let
$\mathcal {P}_{\kappa }\lambda $
. Let
![]() $V = M_0$
and for
$V = M_0$
and for
![]() $n<\omega $
, let
$n<\omega $
, let
![]() $j_{n,n+1} : M_n \to M_{n+1} = \operatorname {\mathrm {Ult}}(M_n,j_{0,n}({\mathcal U}))$
be the ultrapower embedding, and let
$j_{n,n+1} : M_n \to M_{n+1} = \operatorname {\mathrm {Ult}}(M_n,j_{0,n}({\mathcal U}))$
be the ultrapower embedding, and let
![]() $j_{m,n+1} = j_{n,n+1} \circ j_{m,n}$
for
$j_{m,n+1} = j_{n,n+1} \circ j_{m,n}$
for
![]() $m < n$
. Let
$m < n$
. Let
![]() $M_{\omega }$
the direct limit, and for
$M_{\omega }$
the direct limit, and for
![]() $n<\omega $
, let
$n<\omega $
, let
![]() $j_{n,\omega }$
be the direct limit embedding. Note that each
$j_{n,\omega }$
be the direct limit embedding. Note that each
![]() $M_n$
is
$M_n$
is
![]() $\lambda $
-closed, but the limit
$\lambda $
-closed, but the limit
![]() $M_{\omega }$
is not even countably closed.
$M_{\omega }$
is not even countably closed.
![]() $j_{0,\omega }(\kappa ) = \sup _{n<\omega } j_{0,n}(\kappa )$
, yet this ordinal is inaccessible in
$j_{0,\omega }(\kappa ) = \sup _{n<\omega } j_{0,n}(\kappa )$
, yet this ordinal is inaccessible in
![]() $M_{\omega }$
.
$M_{\omega }$
.
To construct the desired model M, we find a generic for a Prikry forcing over
![]() $M_{\omega }$
, which will restore
$M_{\omega }$
, which will restore
![]() $\lambda $
-closure when adjoined. The sequences of classes
$\lambda $
-closure when adjoined. The sequences of classes
![]() $\langle M_n : n < \omega \rangle $
and embeddings
$\langle M_n : n < \omega \rangle $
and embeddings
![]() $\langle j_{m,n} : m < n < \omega \rangle $
are definable in V from
$\langle j_{m,n} : m < n < \omega \rangle $
are definable in V from
![]() ${\mathcal U}$
. Applying
${\mathcal U}$
. Applying
![]() $j_{{\mathcal U}}$
to the sequences yields
$j_{{\mathcal U}}$
to the sequences yields
![]() $\langle M_n : 1 \leq n < \omega \rangle $
and
$\langle M_n : 1 \leq n < \omega \rangle $
and
![]() $\langle j_{m,n} : 1\leq m < n < \omega \rangle $
, which has the same direct limit,
$\langle j_{m,n} : 1\leq m < n < \omega \rangle $
, which has the same direct limit,
![]() $M_{\omega }$
. For any formula
$M_{\omega }$
. For any formula
![]() $\varphi (v_0,\dots ,v_n)$
and parameters
$\varphi (v_0,\dots ,v_n)$
and parameters
![]() $a_0,\dots ,a_n \in M_{\omega }$
,
$a_0,\dots ,a_n \in M_{\omega }$
,
![]() $\varphi ^{M_{\omega }}(a_0,\dots ,a_n) \Leftrightarrow \varphi ^{M_{\omega }}(j_{{\mathcal U}}(a_0),\dots ,j_{{\mathcal U}}(a_n))$
. Hence,
$\varphi ^{M_{\omega }}(a_0,\dots ,a_n) \Leftrightarrow \varphi ^{M_{\omega }}(j_{{\mathcal U}}(a_0),\dots ,j_{{\mathcal U}}(a_n))$
. Hence,
![]() $j_{{\mathcal U}} \ M_{\omega }$
is an elementary embedding into
$j_{{\mathcal U}} \ M_{\omega }$
is an elementary embedding into
![]() $M_{\omega }$
.
$M_{\omega }$
.
Let us define the Prikry forcing
![]() $\mathbb P_{{\mathcal U}}$
, which is standard. Conditions take the form
$\mathbb P_{{\mathcal U}}$
, which is standard. Conditions take the form
![]() $\langle x_0,\dots ,x_n,A \rangle $
, where:
$\langle x_0,\dots ,x_n,A \rangle $
, where:
-
(1) Each
 $x_i \in \mathcal {P}_{\kappa }\lambda $
, and
$x_i \in \mathcal {P}_{\kappa }\lambda $
, and
 $\kappa _i := x_i \cap \kappa $
is inaccessible.
$\kappa _i := x_i \cap \kappa $
is inaccessible. -
(2)
 $x_i \subseteq x_{i+1}$
, and
$x_i \subseteq x_{i+1}$
, and
 $|x_i| < \kappa _{i+1}$
.
$|x_i| < \kappa _{i+1}$
. -
(3)
 $A \in {\mathcal U}$
.
$A \in {\mathcal U}$
.
Suppose
![]() $p = \langle x_0,\dots ,x_n,A \rangle $
and
$p = \langle x_0,\dots ,x_n,A \rangle $
and
![]() $q = \langle x^{\prime }_0,\dots ,x^{\prime }_m,B \rangle $
. We say
$q = \langle x^{\prime }_0,\dots ,x^{\prime }_m,B \rangle $
. We say
![]() $q \leq p$
when:
$q \leq p$
when:
-
(1)
 $m \geq n$
, and for
$m \geq n$
, and for
 $i \leq n$
,
$i \leq n$
,
 $x_i = x^{\prime }_i$
.
$x_i = x^{\prime }_i$
. -
(2) For
 $n < i \leq m$
,
$n < i \leq m$
,
 $x^{\prime }_i \in A$
.
$x^{\prime }_i \in A$
. -
(3)
 $B \subseteq A$
.
$B \subseteq A$
.
Proof of the following can be found in [Reference Gitik9]:
Lemma 2.1.
![]() $\mathbb P_{{\mathcal U}}$
adds no bounded subsets of
$\mathbb P_{{\mathcal U}}$
adds no bounded subsets of
![]() $\kappa $
, collapses
$\kappa $
, collapses
![]() $\lambda $
to
$\lambda $
to
![]() $\kappa $
, and is
$\kappa $
, and is
![]() $\lambda ^+$
-c.c.
$\lambda ^+$
-c.c.
We now argue that there exists an
![]() $M_{\omega }$
-generic filter
$M_{\omega }$
-generic filter
![]() $G \subseteq j_{0,\omega }(\mathbb P_{{\mathcal U}})$
in V. Furthermore,
$G \subseteq j_{0,\omega }(\mathbb P_{{\mathcal U}})$
in V. Furthermore,
![]() $M_{\omega }[G]$
is
$M_{\omega }[G]$
is
![]() $\lambda $
-closed. The idea for
$\lambda $
-closed. The idea for
![]() $\kappa = \lambda $
is due to Dehornoy [Reference Dehornoy4].
$\kappa = \lambda $
is due to Dehornoy [Reference Dehornoy4].
For
![]() $n < \omega $
, let
$n < \omega $
, let
![]() $z_n = j_{n,\omega }[j_{0,n}(\lambda )]$
. Since
$z_n = j_{n,\omega }[j_{0,n}(\lambda )]$
. Since
![]() $\operatorname {\mathrm {crit}}(j_{n+1,\omega }) = j_{0,n+1}(\kappa )> j_{0,n}(\lambda )$
,
$\operatorname {\mathrm {crit}}(j_{n+1,\omega }) = j_{0,n+1}(\kappa )> j_{0,n}(\lambda )$
,
![]() $z_n = j_{n+1,\omega }(j_{n,n+1}[j_{0,n}(\lambda )])\in \mathcal {P}_{j_{0,\omega }(\kappa )} (j_{0,\omega }(\lambda ))^{M_{\omega }}$
. We define G as the collection of
$z_n = j_{n+1,\omega }(j_{n,n+1}[j_{0,n}(\lambda )])\in \mathcal {P}_{j_{0,\omega }(\kappa )} (j_{0,\omega }(\lambda ))^{M_{\omega }}$
. We define G as the collection of
![]() $\langle x_0,\dots ,x_n,A \rangle \in j_{0,\omega }(\mathbb P_{{\mathcal U}})$
such that
$\langle x_0,\dots ,x_n,A \rangle \in j_{0,\omega }(\mathbb P_{{\mathcal U}})$
such that
![]() $\langle x_0,\dots ,x_n\rangle $
is an initial segment of
$\langle x_0,\dots ,x_n\rangle $
is an initial segment of
![]() $\langle z_i : i < \omega \rangle $
and
$\langle z_i : i < \omega \rangle $
and
![]() $\{ z_i : n < i < \omega \} \subseteq A$
.
$\{ z_i : n < i < \omega \} \subseteq A$
.
Lemma 2.2.
G is generic over
![]() $M_{\omega }$
.
$M_{\omega }$
.
Proof We use an analogue of Rowbottom’s Theorem [Reference Rowbottom15]: If
![]() $F : [\mathcal {P}_{\kappa }\lambda ]^{<\omega } \to 2$
, then there is a set
$F : [\mathcal {P}_{\kappa }\lambda ]^{<\omega } \to 2$
, then there is a set
![]() $A \in {\mathcal U}$
and a sequence
$A \in {\mathcal U}$
and a sequence
![]() $r \in {{}^{\omega }}2$
such that whenever
$r \in {{}^{\omega }}2$
such that whenever
![]() $\langle x_i,\dots ,x_n \rangle \subseteq A$
is such that
$\langle x_i,\dots ,x_n \rangle \subseteq A$
is such that
![]() $x_i \subseteq x_{i+1}$
and
$x_i \subseteq x_{i+1}$
and
![]() $|x_i| < x_{i+1} \cap \kappa \in \kappa $
, then
$|x_i| < x_{i+1} \cap \kappa \in \kappa $
, then
![]() $F(\{x_0,\dots ,x_{n-1}\}) = r(n)$
. Let D be a dense open subset of
$F(\{x_0,\dots ,x_{n-1}\}) = r(n)$
. Let D be a dense open subset of
![]() $j_{0,\omega }(\mathbb P_{{\mathcal U}})$
in
$j_{0,\omega }(\mathbb P_{{\mathcal U}})$
in
![]() $M_{\omega }$
. For each s such that
$M_{\omega }$
. For each s such that
![]() $s^{\frown } \langle j_{0,\omega }(\mathcal {P}_{\kappa }\lambda )\rangle \in j_{0,\omega }(\mathbb P_{{\mathcal U}})$
, let
$s^{\frown } \langle j_{0,\omega }(\mathcal {P}_{\kappa }\lambda )\rangle \in j_{0,\omega }(\mathbb P_{{\mathcal U}})$
, let
![]() $F_s : [\mathcal {P}_{\kappa }\lambda ]^{<\omega } \to 2$
be defined by
$F_s : [\mathcal {P}_{\kappa }\lambda ]^{<\omega } \to 2$
be defined by
![]() $F_s(t) = 1$
if there is
$F_s(t) = 1$
if there is
![]() $B_{s,t}$
such that
$B_{s,t}$
such that
![]() $s^{\frown } t^{\frown } \langle B_{s,t} \rangle \in D$
, and
$s^{\frown } t^{\frown } \langle B_{s,t} \rangle \in D$
, and
![]() $F_s(t) = 0$
otherwise. If
$F_s(t) = 0$
otherwise. If
![]() $F_s(t) = 0$
, define
$F_s(t) = 0$
, define
![]() $B_{s,t} = j_{0,\omega }(\mathcal {P}_{\kappa }\lambda )$
. For each s, let
$B_{s,t} = j_{0,\omega }(\mathcal {P}_{\kappa }\lambda )$
. For each s, let
![]() $B_s$
be the diagonal intersection
$B_s$
be the diagonal intersection
![]() $\Delta _t B_{s,t} \in j_{0,\omega }({\mathcal U})$
. For each s, let
$\Delta _t B_{s,t} \in j_{0,\omega }({\mathcal U})$
. For each s, let
![]() $A_s$
and
$A_s$
and
![]() $r_s$
be given by the analogue of Rowbottom’s Theorem. Let
$r_s$
be given by the analogue of Rowbottom’s Theorem. Let
![]() $A^*$
be the diagonal intersection
$A^*$
be the diagonal intersection
![]() $\Delta _s A_s \cap B_s$
.
$\Delta _s A_s \cap B_s$
.
We claim that for each s, whether a condition
![]() $s^{\frown } t ^{\frown } \langle B\rangle \leq s^{\frown } \langle A^* \rangle $
is in D depends only on the length of t. Let s be given and let
$s^{\frown } t ^{\frown } \langle B\rangle \leq s^{\frown } \langle A^* \rangle $
is in D depends only on the length of t. Let s be given and let
![]() $t,t'$
be of the same length n, such that
$t,t'$
be of the same length n, such that
![]() $s^{\frown } t ^{\frown } \langle B\rangle $
and
$s^{\frown } t ^{\frown } \langle B\rangle $
and
![]() $s^{\frown } t' \!^{\frown } \langle B' \rangle $
are both
$s^{\frown } t' \!^{\frown } \langle B' \rangle $
are both
![]() $\leq s^{\frown } \langle A^* \rangle $
. Then
$\leq s^{\frown } \langle A^* \rangle $
. Then
![]() $t,t' \subseteq A_s$
and
$t,t' \subseteq A_s$
and
![]() $B,B' \subseteq B_s$
, so
$B,B' \subseteq B_s$
, so
![]() $B \subseteq B_{s,t}$
and
$B \subseteq B_{s,t}$
and
![]() $B' \subseteq B_{s,t'}$
. Thus
$B' \subseteq B_{s,t'}$
. Thus
![]() $F_s(t) = F_s(t') = r_s(n)$
, so either both
$F_s(t) = F_s(t') = r_s(n)$
, so either both
![]() $s^{\frown } t ^{\frown } \langle B\rangle $
and
$s^{\frown } t ^{\frown } \langle B\rangle $
and
![]() $s^{\frown } t' \!^{\frown } \langle B' \rangle $
are in D, or they are both are not in D.
$s^{\frown } t' \!^{\frown } \langle B' \rangle $
are in D, or they are both are not in D.
Now if D is a dense open subset of
![]() $j_{0,\omega }(\mathbb P_{{\mathcal U}})$
in
$j_{0,\omega }(\mathbb P_{{\mathcal U}})$
in
![]() $M_{\omega }$
, there is some
$M_{\omega }$
, there is some
![]() $n <\omega $
and
$n <\omega $
and
![]() $\bar D \in M_n$
such that
$\bar D \in M_n$
such that
![]() $j_{n,\omega }(\bar D) = D$
. Let
$j_{n,\omega }(\bar D) = D$
. Let
![]() $A^*$
be as above, and let
$A^*$
be as above, and let
![]() $m \geq n$
be such that
$m \geq n$
be such that
![]() $A^* = j_{m,\omega }(\bar A^*)$
for some
$A^* = j_{m,\omega }(\bar A^*)$
for some
![]() $\bar A^* \in j_{0,m}({\mathcal U})$
. Let
$\bar A^* \in j_{0,m}({\mathcal U})$
. Let
![]() $l <\omega $
be such that for all sequences t of length
$l <\omega $
be such that for all sequences t of length
![]() $\geq l$
and all B such that
$\geq l$
and all B such that
![]() $\langle z_0,\dots ,z_{m-1} \rangle ^{\frown } t ^{\frown } \langle B \rangle \leq \langle z_0,\dots ,z_{m-1} \rangle ^{\frown } \langle A^* \rangle $
, we have
$\langle z_0,\dots ,z_{m-1} \rangle ^{\frown } t ^{\frown } \langle B \rangle \leq \langle z_0,\dots ,z_{m-1} \rangle ^{\frown } \langle A^* \rangle $
, we have
![]() $\langle z_0,\dots ,z_{m-1} \rangle ^{\frown } t ^{\frown } \langle B \rangle \in D$
. Since
$\langle z_0,\dots ,z_{m-1} \rangle ^{\frown } t ^{\frown } \langle B \rangle \in D$
. Since
![]() $z_k \in A^*$
for all
$z_k \in A^*$
for all
![]() $k \geq m$
,
$k \geq m$
,
![]() $D \cap G \not = \emptyset $
.
$D \cap G \not = \emptyset $
.
Lemma 2.3. The map
![]() $j_{{\mathcal U}} \restriction M_{\omega }$
can be extended to a map
$j_{{\mathcal U}} \restriction M_{\omega }$
can be extended to a map
![]() $j : M_{\omega }[G] \to M_{\omega }[G]$
.
$j : M_{\omega }[G] \to M_{\omega }[G]$
.
Proof Note that for each
![]() $z_n$
,
$z_n$
,
Let
![]() $G'$
be the generic filter generated by
$G'$
be the generic filter generated by
![]() $\langle z_n : 1 \leq n < \omega \rangle $
. Then
$\langle z_n : 1 \leq n < \omega \rangle $
. Then
![]() $j_{{\mathcal U}}[G] \subseteq G'$
. Thus by Silver’s criterion, we may extend the map to
$j_{{\mathcal U}}[G] \subseteq G'$
. Thus by Silver’s criterion, we may extend the map to
![]() $j : M_{\omega }[G] \to M_{\omega }[G']$
by putting
$j : M_{\omega }[G] \to M_{\omega }[G']$
by putting
![]() $j(\tau ^G) = j_{{\mathcal U}}(\tau )^{G'}$
for every
$j(\tau ^G) = j_{{\mathcal U}}(\tau )^{G'}$
for every
![]() $j_{0,\omega }(\mathbb P_{{\mathcal U}})$
-name
$j_{0,\omega }(\mathbb P_{{\mathcal U}})$
-name
![]() $\tau $
. But clearly,
$\tau $
. But clearly,
![]() $M_{\omega }[G'] = M_{\omega }[G]$
.
$M_{\omega }[G'] = M_{\omega }[G]$
.
Lemma 2.4.
![]() $M_{\omega }[G]$
is
$M_{\omega }[G]$
is
![]() $\lambda $
-closed.
$\lambda $
-closed.
Proof It suffices to show that
![]() $M_{\omega }[G]$
contains all
$M_{\omega }[G]$
contains all
![]() $\lambda $
-sequences of ordinals. Suppose
$\lambda $
-sequences of ordinals. Suppose
![]() $\langle \xi _{\alpha } : \alpha < \lambda \rangle \subseteq \operatorname {\mathrm {Ord}}$
. For each
$\langle \xi _{\alpha } : \alpha < \lambda \rangle \subseteq \operatorname {\mathrm {Ord}}$
. For each
![]() $\alpha $
, there is
$\alpha $
, there is
![]() $n < \omega $
and a function
$n < \omega $
and a function
![]() $f_{\alpha } : (\mathcal {P}_{\kappa }\lambda )^n \to \operatorname {\mathrm {Ord}}$
such that
$f_{\alpha } : (\mathcal {P}_{\kappa }\lambda )^n \to \operatorname {\mathrm {Ord}}$
such that
![]() $\xi _{\alpha } = j_{0,\omega }(f_{\alpha })(z_0,\dots ,z_{n-1})$
. The sequence
$\xi _{\alpha } = j_{0,\omega }(f_{\alpha })(z_0,\dots ,z_{n-1})$
. The sequence
![]() $\langle j_{0,\omega }(f_{\alpha }) : \alpha < \lambda \rangle $
can be computed from
$\langle j_{0,\omega }(f_{\alpha }) : \alpha < \lambda \rangle $
can be computed from
![]() $j_{0,\omega }(\langle f_{\alpha } : \alpha < \lambda \rangle )$
and
$j_{0,\omega }(\langle f_{\alpha } : \alpha < \lambda \rangle )$
and
![]() $j_{0,\omega }[\lambda ]$
, both of which are in
$j_{0,\omega }[\lambda ]$
, both of which are in
![]() $M_{\omega }$
. The sequence
$M_{\omega }$
. The sequence
![]() $\langle \xi _{\alpha } : \alpha < \lambda \rangle $
can be computed from
$\langle \xi _{\alpha } : \alpha < \lambda \rangle $
can be computed from
![]() $\langle j_{0,\omega }(f_{\alpha }) : \alpha < \lambda \rangle $
and
$\langle j_{0,\omega }(f_{\alpha }) : \alpha < \lambda \rangle $
and
![]() $\langle z_n : n < \omega \rangle $
, and is thus in
$\langle z_n : n < \omega \rangle $
, and is thus in
![]() $M_{\omega }[G]$
.
$M_{\omega }[G]$
.
This concludes the proof of Theorem 1.2.
3 Fixed point behavior of amenable embeddings
One way to produce elementary embeddings is with indiscernibles, like the embeddings derived from
![]() $0^{\sharp }$
. If we want the embedding to be amenable to the target model, more consistency strength is required. Vickers and Welch [Reference Vickers and Welch17] showed a near-equiconsistency between the existence of an elementary
$0^{\sharp }$
. If we want the embedding to be amenable to the target model, more consistency strength is required. Vickers and Welch [Reference Vickers and Welch17] showed a near-equiconsistency between the existence of an elementary
![]() $j : M \to V$
, where M is a transitive class and V satisfies ZFC for formulas involving j, and the existence of a Ramsey cardinal. In this section, we begin with the argument for constructing nontrivial amenable embeddings from a Ramsey cardinal, and then we elaborate on this idea using measurable cardinals to control the behavior of the embedding more precisely.
$j : M \to V$
, where M is a transitive class and V satisfies ZFC for formulas involving j, and the existence of a Ramsey cardinal. In this section, we begin with the argument for constructing nontrivial amenable embeddings from a Ramsey cardinal, and then we elaborate on this idea using measurable cardinals to control the behavior of the embedding more precisely.
Recall that a cardinal
![]() $\kappa $
is Ramsey when for every coloring of its finite subsets in
$\kappa $
is Ramsey when for every coloring of its finite subsets in
![]() $<\kappa $
colors,
$<\kappa $
colors,
![]() $c : [\kappa ]^{<\omega } \to \delta < \kappa $
, there is
$c : [\kappa ]^{<\omega } \to \delta < \kappa $
, there is
![]() $X \in [\kappa ]^{\kappa }$
such that
$X \in [\kappa ]^{\kappa }$
such that
![]() $c \restriction [X]^n$
is constant for all
$c \restriction [X]^n$
is constant for all
![]() $n<\omega $
(X is homogeneous). Rowbottom [Reference Rowbottom15] showed that if
$n<\omega $
(X is homogeneous). Rowbottom [Reference Rowbottom15] showed that if
![]() $\kappa $
is measurable and
$\kappa $
is measurable and
![]() ${\mathcal U}$
is a normal measure on
${\mathcal U}$
is a normal measure on
![]() $\kappa $
, then for any coloring
$\kappa $
, then for any coloring
![]() $c : [\kappa ]^{<\omega } \to \delta < \kappa $
, there is a homogeneous
$c : [\kappa ]^{<\omega } \to \delta < \kappa $
, there is a homogeneous
![]() $X \in {\mathcal U}$
.
$X \in {\mathcal U}$
.
Suppose
![]() $\kappa $
is Ramsey. Let
$\kappa $
is Ramsey. Let
![]() $\frak A$
be a structure on
$\frak A$
be a structure on
![]() $V_{\kappa }$
in a language of size
$V_{\kappa }$
in a language of size
![]() $\delta <\kappa $
, that includes a well-order of
$\delta <\kappa $
, that includes a well-order of
![]() $V_{\kappa }$
so that the structure has definable Skolem functions. For
$V_{\kappa }$
so that the structure has definable Skolem functions. For
![]() $X \subseteq \frak A$
, we write
$X \subseteq \frak A$
, we write
![]() $\operatorname {\mathrm {Hull}}^{\frak A}(X)$
for the set
$\operatorname {\mathrm {Hull}}^{\frak A}(X)$
for the set
![]() $\{ f(z) : z \in X^{<\omega }$
and f is a definable Skolem function for
$\{ f(z) : z \in X^{<\omega }$
and f is a definable Skolem function for
![]() $\frak A \}$
. For
$\frak A \}$
. For
![]() $\alpha _0<\dots <\alpha _n<\kappa $
, let
$\alpha _0<\dots <\alpha _n<\kappa $
, let
![]() $c(\alpha _0,\dots ,\alpha _n) = \{ \varphi (v_0,\dots ,v_n) : \frak A \models \varphi (\alpha _0,\dots ,\alpha _n) \}$
. The number of colors is at most
$c(\alpha _0,\dots ,\alpha _n) = \{ \varphi (v_0,\dots ,v_n) : \frak A \models \varphi (\alpha _0,\dots ,\alpha _n) \}$
. The number of colors is at most
![]() $2^{\delta }$
, so let
$2^{\delta }$
, so let
![]() $X \in [\kappa ]^{\kappa }$
be homogeneous for c. If
$X \in [\kappa ]^{\kappa }$
be homogeneous for c. If
![]() $Y \subseteq X$
and
$Y \subseteq X$
and
![]() $\xi \in X \setminus Y$
, then
$\xi \in X \setminus Y$
, then
![]() $\xi \notin \operatorname {\mathrm {Hull}}^{\frak A}(Y)$
: For if not, let
$\xi \notin \operatorname {\mathrm {Hull}}^{\frak A}(Y)$
: For if not, let
![]() $f(v_0,\dots ,v_n)$
be a definable Skolem function, and let
$f(v_0,\dots ,v_n)$
be a definable Skolem function, and let
![]() $\{\alpha _0,\dots ,\alpha _n\} \subseteq Y$
be such that
$\{\alpha _0,\dots ,\alpha _n\} \subseteq Y$
be such that
![]() $\xi = f(\alpha _0,\dots ,\alpha _n)$
. Let
$\xi = f(\alpha _0,\dots ,\alpha _n)$
. Let
![]() $m\leq n$
be the maximum such that
$m\leq n$
be the maximum such that
![]() $\alpha _m < \xi $
. Suppose first that
$\alpha _m < \xi $
. Suppose first that
![]() $m<n$
. Let
$m<n$
. Let
![]() $\alpha _{n+1}> \alpha _n$
be in X. By homogeneity,
$\alpha _{n+1}> \alpha _n$
be in X. By homogeneity,
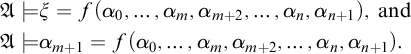 $$ \begin{align*} \frak A \models & \xi = f(\alpha_0,\dots,\alpha_m,\alpha_{m+2},\dots,\alpha_n,\alpha_{n+1}), \text{ and } \\ \frak A \models & \alpha_{m+1} = f(\alpha_0,\dots,\alpha_m,\alpha_{m+2},\dots,\alpha_n,\alpha_{n+1}). \end{align*} $$
$$ \begin{align*} \frak A \models & \xi = f(\alpha_0,\dots,\alpha_m,\alpha_{m+2},\dots,\alpha_n,\alpha_{n+1}), \text{ and } \\ \frak A \models & \alpha_{m+1} = f(\alpha_0,\dots,\alpha_m,\alpha_{m+2},\dots,\alpha_n,\alpha_{n+1}). \end{align*} $$
This contradicts that f is a function. If
![]() $\xi> \alpha _n$
, then similarly,
$\xi> \alpha _n$
, then similarly,
![]() $A \models \xi = \xi ' = f(\alpha _0,\dots ,\alpha _n)$
, for some
$A \models \xi = \xi ' = f(\alpha _0,\dots ,\alpha _n)$
, for some
![]() $\xi '>\xi $
in X, again a contradiction. Furthermore, for every infinite
$\xi '>\xi $
in X, again a contradiction. Furthermore, for every infinite
![]() $\mu \in [\delta ,\kappa )$
,
$\mu \in [\delta ,\kappa )$
,
![]() $|\mathcal {P}(\mu ) \cap \operatorname {\mathrm {Hull}}^{\frak A}(X)| \leq \mu $
[Reference Rowbottom15].
$|\mathcal {P}(\mu ) \cap \operatorname {\mathrm {Hull}}^{\frak A}(X)| \leq \mu $
[Reference Rowbottom15].
Therefore, if
![]() $Y \subseteq X$
has size
$Y \subseteq X$
has size
![]() $\kappa $
, and M is the transitive collapse of
$\kappa $
, and M is the transitive collapse of
![]() $\operatorname {\mathrm {Hull}}^{\frak A}(Y)$
, then M is a proper transitive subset of
$\operatorname {\mathrm {Hull}}^{\frak A}(Y)$
, then M is a proper transitive subset of
![]() $V_{\kappa }$
of size
$V_{\kappa }$
of size
![]() $\kappa $
, and there is an elementary
$\kappa $
, and there is an elementary
![]() $j : M \to V_{\kappa }$
. j is amenable simply because
$j : M \to V_{\kappa }$
. j is amenable simply because
![]() $V_{\kappa }$
has all sets of rank
$V_{\kappa }$
has all sets of rank
![]() $<\kappa $
, so in particular
$<\kappa $
, so in particular
![]() $j[x] \in V_{\kappa }$
for all
$j[x] \in V_{\kappa }$
for all
![]() $x \in M$
. Furthermore, if
$x \in M$
. Furthermore, if
![]() $Y_0,Y_1 \in [X]^{\kappa }$
, then the order-preserving bijection
$Y_0,Y_1 \in [X]^{\kappa }$
, then the order-preserving bijection
![]() $f : Y_0 \to Y_1$
induces an isomorphism
$f : Y_0 \to Y_1$
induces an isomorphism
![]() $\pi : \operatorname {\mathrm {Hull}}^{\frak A}(Y_0) \to \operatorname {\mathrm {Hull}}^{\frak A}(Y_1)$
, and thus these two hulls have the same transitive collapse M. So given the structure
$\pi : \operatorname {\mathrm {Hull}}^{\frak A}(Y_0) \to \operatorname {\mathrm {Hull}}^{\frak A}(Y_1)$
, and thus these two hulls have the same transitive collapse M. So given the structure
![]() $\frak A$
, this process produces one proper transitive subset
$\frak A$
, this process produces one proper transitive subset
![]() $M \subseteq V_{\kappa }$
of size
$M \subseteq V_{\kappa }$
of size
![]() $\kappa $
, which can be amenably embedded into
$\kappa $
, which can be amenably embedded into
![]() $V_{\kappa }$
in many different ways. Let us examine the ways in which these embeddings may differ with regard to fixed points.
$V_{\kappa }$
in many different ways. Let us examine the ways in which these embeddings may differ with regard to fixed points.
Theorem 3.1. Suppose
![]() $\kappa $
is measurable. There is a transitive
$\kappa $
is measurable. There is a transitive
![]() $M \subseteq V_{\kappa }$
of size
$M \subseteq V_{\kappa }$
of size
![]() $\kappa $
such that for every
$\kappa $
such that for every
![]() $\delta \leq \kappa $
, there is an elementary embedding
$\delta \leq \kappa $
, there is an elementary embedding
![]() $j : M \to V_{\kappa }$
such that the set of M-cardinals fixed by j above
$j : M \to V_{\kappa }$
such that the set of M-cardinals fixed by j above
![]() $\operatorname {\mathrm {crit}}(j)$
has ordertype
$\operatorname {\mathrm {crit}}(j)$
has ordertype
![]() $\delta $
.
$\delta $
.
Proof Fix a normal ultrafilter
![]() ${\mathcal U}$
on
${\mathcal U}$
on
![]() $\kappa $
and some cardinal
$\kappa $
and some cardinal
![]() $\theta> 2^{\kappa }$
. Let
$\theta> 2^{\kappa }$
. Let
![]() $\frak A$
be a structure in a countable language expanding
$\frak A$
be a structure in a countable language expanding
![]() $(H_{\theta },\in ,{\mathcal U})$
with definable Skolem functions. Let
$(H_{\theta },\in ,{\mathcal U})$
with definable Skolem functions. Let
![]() $\frak A_0 \prec \frak A$
be such that
$\frak A_0 \prec \frak A$
be such that
![]() $|\frak A_0| = |\frak A_0 \cap \kappa | < \kappa $
. We show something a little stronger than the claimed result; namely, for every
$|\frak A_0| = |\frak A_0 \cap \kappa | < \kappa $
. We show something a little stronger than the claimed result; namely, for every
![]() $\delta \leq \kappa $
, there is a set of indiscernibles
$\delta \leq \kappa $
, there is a set of indiscernibles
![]() $B \subseteq \kappa $
of size
$B \subseteq \kappa $
of size
![]() $\kappa $
such that if
$\kappa $
such that if
![]() $\frak B = \operatorname {\mathrm {Hull}}(\frak A_0 \cup B)$
, then
$\frak B = \operatorname {\mathrm {Hull}}(\frak A_0 \cup B)$
, then
![]() $\frak B \cap \sup (\frak A_0 \cap \kappa ) = \frak A_0 \cap \kappa $
, and the set of cardinals in the interval
$\frak B \cap \sup (\frak A_0 \cap \kappa ) = \frak A_0 \cap \kappa $
, and the set of cardinals in the interval
![]() $[\sup (\frak A_0 \cap \kappa ),\kappa )$
that are fixed by the transitive collapse of
$[\sup (\frak A_0 \cap \kappa ),\kappa )$
that are fixed by the transitive collapse of
![]() $\frak B$
has ordertype
$\frak B$
has ordertype
![]() $\delta $
. Thus if the inverse of the transitive collapse map of
$\delta $
. Thus if the inverse of the transitive collapse map of
![]() $\frak A_0$
has no fixed points above its critical point, for example if
$\frak A_0$
has no fixed points above its critical point, for example if
![]() $\frak A_0$
is countable, then the result follows.
$\frak A_0$
is countable, then the result follows.
Let
![]() $\alpha _0 \in \bigcap ({\mathcal U} \cap \frak A_0)$
be strictly greater than
$\alpha _0 \in \bigcap ({\mathcal U} \cap \frak A_0)$
be strictly greater than
![]() $\sup (\frak A_0 \cap \kappa )$
, and let
$\sup (\frak A_0 \cap \kappa )$
, and let
![]() $\frak A_1 = \operatorname {\mathrm {Hull}}(\frak A_0 \cup \{ \alpha _0 \})$
. We claim that
$\frak A_1 = \operatorname {\mathrm {Hull}}(\frak A_0 \cup \{ \alpha _0 \})$
. We claim that
![]() $\frak A_0 \cap \kappa = \frak A_1 \cap \alpha _0$
. If
$\frak A_0 \cap \kappa = \frak A_1 \cap \alpha _0$
. If
![]() $\gamma \in \frak A_1 \cap \kappa $
, then there is a function
$\gamma \in \frak A_1 \cap \kappa $
, then there is a function
![]() $f : \kappa \to \kappa $
in
$f : \kappa \to \kappa $
in
![]() $\frak A_0$
such that
$\frak A_0$
such that
![]() $f(\alpha _0) = \gamma $
. If
$f(\alpha _0) = \gamma $
. If
![]() $\gamma < \alpha _0$
, then f is regressive on a set in
$\gamma < \alpha _0$
, then f is regressive on a set in
![]() ${\mathcal U}$
, and therefore constant on a set in
${\mathcal U}$
, and therefore constant on a set in
![]() ${\mathcal U}$
, and thus
${\mathcal U}$
, and thus
![]() $\gamma \in \frak A_0$
. Continue in this way, producing a continuous increasing sequence of elementary substructures of
$\gamma \in \frak A_0$
. Continue in this way, producing a continuous increasing sequence of elementary substructures of
![]() $\frak A$
,
$\frak A$
,
![]() $\langle \frak A_i : i < \kappa \rangle $
, and an increasing sequence of ordinals
$\langle \frak A_i : i < \kappa \rangle $
, and an increasing sequence of ordinals
![]() $\langle \alpha _i : i < \kappa \rangle $
, such that for
$\langle \alpha _i : i < \kappa \rangle $
, such that for
![]() $0<i<\kappa $
,
$0<i<\kappa $
,
![]() $\alpha _i = \min \bigcap ({\mathcal U} \cap \frak A_i)$
, and
$\alpha _i = \min \bigcap ({\mathcal U} \cap \frak A_i)$
, and
![]() $\frak A_{i+1} = \operatorname {\mathrm {Hull}} (\frak A_i \cup \{ \alpha _i \})$
.
$\frak A_{i+1} = \operatorname {\mathrm {Hull}} (\frak A_i \cup \{ \alpha _i \})$
.
Claim 3.2.
![]() $\{ \alpha _i : i < \kappa \} \in {\mathcal U} $
.
$\{ \alpha _i : i < \kappa \} \in {\mathcal U} $
.
Proof Let
![]() $\frak A_{\kappa } = \bigcup _{i<\kappa } \frak A_i$
, and let
$\frak A_{\kappa } = \bigcup _{i<\kappa } \frak A_i$
, and let
![]() $\langle X_i : i < \kappa \rangle $
enumerate
$\langle X_i : i < \kappa \rangle $
enumerate
![]() ${\mathcal U} \cap \frak A_{\kappa }$
. There is a club
${\mathcal U} \cap \frak A_{\kappa }$
. There is a club
![]() $C\subseteq \kappa $
such that for all
$C\subseteq \kappa $
such that for all
![]() $\beta \in C$
,
$\beta \in C$
,
![]() ${\mathcal U} \cap \frak A_{\beta } = \{ X_i : i < \beta \}$
, and
${\mathcal U} \cap \frak A_{\beta } = \{ X_i : i < \beta \}$
, and
![]() $\beta = \sup (\frak A_{\beta } \cap \kappa )$
. If
$\beta = \sup (\frak A_{\beta } \cap \kappa )$
. If
![]() $\beta \in \bigcap _{i<\beta } X_i$
, then
$\beta \in \bigcap _{i<\beta } X_i$
, then
![]() $\alpha _{\beta } = \beta $
. This means that
$\alpha _{\beta } = \beta $
. This means that
![]() $C \cap \Delta _{i<\kappa } X_i \subseteq \{ \alpha _i : i < \kappa \}$
. Since
$C \cap \Delta _{i<\kappa } X_i \subseteq \{ \alpha _i : i < \kappa \}$
. Since
![]() ${\mathcal U}$
is normal, the claim follows.
${\mathcal U}$
is normal, the claim follows.
Let
![]() $A = \{ \alpha _i : i < \kappa \}$
. Under a mild assumption on
$A = \{ \alpha _i : i < \kappa \}$
. Under a mild assumption on
![]() $\frak A_0$
, A is a set of order-indiscernibles for
$\frak A_0$
, A is a set of order-indiscernibles for
![]() $\frak A$
. For let
$\frak A$
. For let
![]() $\varphi $
be a formula in n free variables in the language of
$\varphi $
be a formula in n free variables in the language of
![]() $\frak A$
. Let
$\frak A$
. Let
![]() $c_{\varphi } : [\kappa ]^n \to 2$
be the coloring defined by
$c_{\varphi } : [\kappa ]^n \to 2$
be the coloring defined by
![]() $c_{\varphi }(a_1,\dots ,a_n) = 1$
if
$c_{\varphi }(a_1,\dots ,a_n) = 1$
if
![]() $\frak A \models \varphi (a_1,\dots ,a_n)$
, and 0 otherwise. Since
$\frak A \models \varphi (a_1,\dots ,a_n)$
, and 0 otherwise. Since
![]() $c_{\varphi } \in \frak A$
, Rowbottom’s Theorem implies that there is a set
$c_{\varphi } \in \frak A$
, Rowbottom’s Theorem implies that there is a set
![]() $X_{\varphi } \in {\mathcal U}$
such that
$X_{\varphi } \in {\mathcal U}$
such that
![]() $\frak A \models \varphi (a_1,\dots ,a_n) \leftrightarrow \varphi (b_1,\dots ,b_n)$
whenever
$\frak A \models \varphi (a_1,\dots ,a_n) \leftrightarrow \varphi (b_1,\dots ,b_n)$
whenever
![]() $\langle a_1,\dots ,a_n \rangle ,\langle b_1,\dots ,b_n \rangle $
are increasing sequences from
$\langle a_1,\dots ,a_n \rangle ,\langle b_1,\dots ,b_n \rangle $
are increasing sequences from
![]() $X_{\varphi }$
. By slightly enlarging
$X_{\varphi }$
. By slightly enlarging
![]() $\frak A_0$
at the beginning if necessary, we may assume
$\frak A_0$
at the beginning if necessary, we may assume
![]() $c_{\varphi } \in \frak A_0$
for each
$c_{\varphi } \in \frak A_0$
for each
![]() $\varphi $
. By elementarity, we may assume
$\varphi $
. By elementarity, we may assume
![]() $X_{\varphi } \in \frak A_0$
. Thus
$X_{\varphi } \in \frak A_0$
. Thus
![]() $A \subseteq X_{\varphi }$
for each such
$A \subseteq X_{\varphi }$
for each such
![]() $\varphi $
.
$\varphi $
.
Let
![]() $\langle \beta _i : i < \kappa \rangle $
be the increasing enumeration of the closure of
$\langle \beta _i : i < \kappa \rangle $
be the increasing enumeration of the closure of
![]() $A \cup \{ \sup (\frak A_0 \cap \kappa ) \}$
.
$A \cup \{ \sup (\frak A_0 \cap \kappa ) \}$
.
Claim 3.3. For every
![]() $X \subseteq A$
and
$X \subseteq A$
and
![]() $\gamma <\kappa $
, if
$\gamma <\kappa $
, if
![]() $\beta _{\gamma } \notin X$
, then
$\beta _{\gamma } \notin X$
, then
![]() $\operatorname {\mathrm {Hull}}(\frak A_0 \cup X)$
is disjoint from the interval
$\operatorname {\mathrm {Hull}}(\frak A_0 \cup X)$
is disjoint from the interval
![]() $[\beta _{\gamma },\beta _{\gamma +1})$
.
$[\beta _{\gamma },\beta _{\gamma +1})$
.
Proof Suppose
![]() $\beta _{\gamma } \notin X$
,
$\beta _{\gamma } \notin X$
,
![]() $\xi \in [\beta _{\gamma },\beta _{\gamma +1})$
, but there are elements
$\xi \in [\beta _{\gamma },\beta _{\gamma +1})$
, but there are elements
![]() $c_1,\dots ,c_k \in \frak A_0$
, ordinals
$c_1,\dots ,c_k \in \frak A_0$
, ordinals
![]() $i_1 < \cdots < i_n$
, and a Skolem function f such that
$i_1 < \cdots < i_n$
, and a Skolem function f such that
![]() $\xi = f(c_1,\dots ,c_k,\alpha _{i_1},\dots ,\alpha _{i_n})$
, with
$\xi = f(c_1,\dots ,c_k,\alpha _{i_1},\dots ,\alpha _{i_n})$
, with
![]() $\{ \alpha _{i_1},\dots ,\alpha _{i_n} \} \subseteq X$
. Let us assume that we have chosen f and
$\{ \alpha _{i_1},\dots ,\alpha _{i_n} \} \subseteq X$
. Let us assume that we have chosen f and
![]() $c_1,\dots ,c_k$
to output
$c_1,\dots ,c_k$
to output
![]() $\xi $
with the least number n of parameters from X. Since
$\xi $
with the least number n of parameters from X. Since
![]() $\alpha _{i_n+1}> \sup (\frak A_{i_n+1} \cap \kappa )$
, we have
$\alpha _{i_n+1}> \sup (\frak A_{i_n+1} \cap \kappa )$
, we have
![]() $\xi < \alpha _{i_n}$
. Working in
$\xi < \alpha _{i_n}$
. Working in
![]() $N = \operatorname {\mathrm {Hull}}(\frak A_0 \cup \{ \alpha _{i_1},\dots ,\alpha _{i_{n-1}} \})$
, let
$N = \operatorname {\mathrm {Hull}}(\frak A_0 \cup \{ \alpha _{i_1},\dots ,\alpha _{i_{n-1}} \})$
, let
Since
![]() $\alpha _{i_n} \in Y \in {\mathcal U}$
and
$\alpha _{i_n} \in Y \in {\mathcal U}$
and
![]() ${\mathcal U}$
is normal, there is
${\mathcal U}$
is normal, there is
![]() $\zeta < \kappa $
and
$\zeta < \kappa $
and
![]() $Z \in {\mathcal U} \cap N$
such that
$Z \in {\mathcal U} \cap N$
such that
![]() $f(c_1,\dots ,c_k, \alpha _{i_1},\dots ,\alpha _{i_{n-1}},\eta ) = \zeta $
for all
$f(c_1,\dots ,c_k, \alpha _{i_1},\dots ,\alpha _{i_{n-1}},\eta ) = \zeta $
for all
![]() $\eta \in Z$
. Thus,
$\eta \in Z$
. Thus,
![]() $\zeta = \xi \in N$
, and
$\zeta = \xi \in N$
, and
![]() $\xi $
is the output of a Skolem function with only
$\xi $
is the output of a Skolem function with only
![]() $n-1$
inputs from X, contrary to the minimality assumption.
$n-1$
inputs from X, contrary to the minimality assumption.
Now let
![]() $D \subseteq A \cap \lim A$
have ordertype
$D \subseteq A \cap \lim A$
have ordertype
![]() $\delta $
. Let
$\delta $
. Let
![]() $B = (A \setminus \lim A) \cup D$
. Let
$B = (A \setminus \lim A) \cup D$
. Let
![]() $\frak B = \operatorname {\mathrm {Hull}}(\frak A_0 \cup B)$
, let H be the transitive collapse of
$\frak B = \operatorname {\mathrm {Hull}}(\frak A_0 \cup B)$
, let H be the transitive collapse of
![]() $\frak B$
, let
$\frak B$
, let
![]() $M = H \cap V_{\kappa }$
, and let
$M = H \cap V_{\kappa }$
, and let
![]() $j : M \to V_{\kappa }$
be the inverse of the collapse map.
$j : M \to V_{\kappa }$
be the inverse of the collapse map.
Let
![]() $C = j^{-1}[B]$
, and let
$C = j^{-1}[B]$
, and let
![]() $\langle B(i) : i < \kappa \rangle $
and
$\langle B(i) : i < \kappa \rangle $
and
![]() $\langle C(i) : i < \kappa \rangle $
denote the respective increasing enumerations of these sets. Let
$\langle C(i) : i < \kappa \rangle $
denote the respective increasing enumerations of these sets. Let
![]() $\lambda \in \lim C$
. By Claim 3.3, there is some
$\lambda \in \lim C$
. By Claim 3.3, there is some
![]() $i<\kappa $
such that
$i<\kappa $
such that
![]() $j(\lambda ) = \beta _i$
, and
$j(\lambda ) = \beta _i$
, and
![]() $\beta _i \in B$
. Thus C is closed. Since
$\beta _i \in B$
. Thus C is closed. Since
![]() $|C(i)| = |C(i+1)|$
for all i, every cardinal of
$|C(i)| = |C(i+1)|$
for all i, every cardinal of
![]() $V_{\kappa }$
above
$V_{\kappa }$
above
![]() $C(0)$
is a limit point of C.
$C(0)$
is a limit point of C.
Let
![]() $\kappa _0 = \operatorname {\mathrm {ot}}(\frak A_0 \cap \kappa )$
. Since
$\kappa _0 = \operatorname {\mathrm {ot}}(\frak A_0 \cap \kappa )$
. Since
![]() $\frak B \cap \alpha _0 = \frak A_0 \cap \kappa $
,
$\frak B \cap \alpha _0 = \frak A_0 \cap \kappa $
,
![]() $j(\kappa _0) = \alpha _0> \kappa _0$
. Define an increasing continuous sequence
$j(\kappa _0) = \alpha _0> \kappa _0$
. Define an increasing continuous sequence
![]() $\langle \kappa _i : i < \kappa \rangle $
as follows. Given
$\langle \kappa _i : i < \kappa \rangle $
as follows. Given
![]() $\kappa _i$
, if
$\kappa _i$
, if
![]() $j(\kappa _i)> \kappa _i$
, let
$j(\kappa _i)> \kappa _i$
, let
![]() $\kappa _{i+1} = j(\kappa _i)$
, and if
$\kappa _{i+1} = j(\kappa _i)$
, and if
![]() $j(\kappa _i) = \kappa _i$
, let
$j(\kappa _i) = \kappa _i$
, let
![]() $\kappa _{i+1} = (\kappa _i^+)^M$
. For limit
$\kappa _{i+1} = (\kappa _i^+)^M$
. For limit
![]() $\lambda $
, let
$\lambda $
, let
![]() $\kappa _{\lambda } = \sup _{i<\lambda }\kappa _i$
.
$\kappa _{\lambda } = \sup _{i<\lambda }\kappa _i$
.
We claim that D is the set of points above
![]() $\kappa _0$
that are fixed by j. To show each point in D is fixed, note that if
$\kappa _0$
that are fixed by j. To show each point in D is fixed, note that if
![]() $\xi \in D$
, then
$\xi \in D$
, then
![]() $\xi $
is closed under j, because
$\xi $
is closed under j, because
![]() $\operatorname {\mathrm {ot}}(B \cap \xi ) = \xi $
. Thus
$\operatorname {\mathrm {ot}}(B \cap \xi ) = \xi $
. Thus
![]() $\xi = \kappa _{\xi }$
, and
$\xi = \kappa _{\xi }$
, and
![]() $j(\xi ) = \xi $
. To show no other points are fixed, we argue by induction that if
$j(\xi ) = \xi $
. To show no other points are fixed, we argue by induction that if
![]() $\xi \notin D$
, then
$\xi \notin D$
, then
![]() $j(\kappa _{\xi }) = \kappa _{\xi +1}$
. Assume that this holds for all
$j(\kappa _{\xi }) = \kappa _{\xi +1}$
. Assume that this holds for all
![]() $i<\xi $
, and
$i<\xi $
, and
![]() $\xi \notin D$
.
$\xi \notin D$
.
-
•
 ${\textrm{Case}\ 1{:}}\ \ \xi $
is a limit. Then
${\textrm{Case}\ 1{:}}\ \ \xi $
is a limit. Then
 $\kappa _{\xi } = \sup _{i<\xi } \kappa _{\xi }$
. By the inductive assumption,
$\kappa _{\xi } = \sup _{i<\xi } \kappa _{\xi }$
. By the inductive assumption,
 $\kappa _i \in \operatorname {\mathrm {ran}}(j)$
for unboundedly many
$\kappa _i \in \operatorname {\mathrm {ran}}(j)$
for unboundedly many
 $i <\xi $
, so
$i <\xi $
, so
 $\kappa _{\xi }$
is a cardinal in V, and thus
$\kappa _{\xi }$
is a cardinal in V, and thus
 $\kappa _{\xi } = C(\kappa _{\xi })$
. Therefore,
$\kappa _{\xi } = C(\kappa _{\xi })$
. Therefore,
 $j(\kappa _{\xi }) = B(\kappa _{\xi })$
. If
$j(\kappa _{\xi }) = B(\kappa _{\xi })$
. If
 $\xi < \kappa _{\xi }$
, then
$\xi < \kappa _{\xi }$
, then
 $\kappa _{\xi } \notin A$
since it is singular, so
$\kappa _{\xi } \notin A$
since it is singular, so
 $B(\kappa _{\xi })> \kappa _{\xi }$
. If
$B(\kappa _{\xi })> \kappa _{\xi }$
. If
 $\xi = \kappa _{\xi }$
, then
$\xi = \kappa _{\xi }$
, then
 $B(\xi )> \xi $
since
$B(\xi )> \xi $
since
 $\xi \notin D$
. In either case, the definition of the sequence gives that
$\xi \notin D$
. In either case, the definition of the sequence gives that
 $\kappa _{\xi +1} = j(\kappa _{\xi })$
.
$\kappa _{\xi +1} = j(\kappa _{\xi })$
. -
•
 ${\textrm{Case}\ 2{:}} \ \ \xi = \eta +1$
, and
${\textrm{Case}\ 2{:}} \ \ \xi = \eta +1$
, and
 $\eta \in D$
. Then
$\eta \in D$
. Then
 $\kappa _{\xi } = (\kappa _{\eta }^+)^M$
. Since
$\kappa _{\xi } = (\kappa _{\eta }^+)^M$
. Since
 $|\frak A_{\eta +1}| = \eta $
,
$|\frak A_{\eta +1}| = \eta $
,
 $(\kappa _{\eta }^+)^M < (\kappa _{\eta }^+)^V$
. Thus
$(\kappa _{\eta }^+)^M < (\kappa _{\eta }^+)^V$
. Thus
 $j(\kappa _{\xi }) = (\kappa _{\eta }^+)^V = \kappa _{\xi +1}$
.
$j(\kappa _{\xi }) = (\kappa _{\eta }^+)^V = \kappa _{\xi +1}$
. -
•
 ${\textrm{Case}\ 3{:}}\ \ \xi = \eta +1$
, and
${\textrm{Case}\ 3{:}}\ \ \xi = \eta +1$
, and
 $\eta \notin D$
. Then by induction,
$\eta \notin D$
. Then by induction,
 $\kappa _{\eta } < j(\kappa _{\eta }) = \kappa _{\xi }$
. By elementarity,
$\kappa _{\eta } < j(\kappa _{\eta }) = \kappa _{\xi }$
. By elementarity,
 $\kappa _{\xi } = j(\kappa _{\eta }) < j(\kappa _{\xi })$
, so by definition,
$\kappa _{\xi } = j(\kappa _{\eta }) < j(\kappa _{\xi })$
, so by definition,
 $\kappa _{\xi +1} = j(\kappa _{\xi })$
.
$\kappa _{\xi +1} = j(\kappa _{\xi })$
.
To conclude, if
![]() $\xi \in D$
, then the interval
$\xi \in D$
, then the interval
![]() $[\kappa _{\xi },\kappa _{\xi +1})$
contains only one M-cardinal, and it is fixed. If
$[\kappa _{\xi },\kappa _{\xi +1})$
contains only one M-cardinal, and it is fixed. If
![]() $\xi \notin D$
, then the interval
$\xi \notin D$
, then the interval
![]() $[\kappa _{\xi },\kappa _{\xi +1})$
is moved into the interval
$[\kappa _{\xi },\kappa _{\xi +1})$
is moved into the interval
![]() $[\kappa _{\xi +1},\kappa _{\xi +2})$
.
$[\kappa _{\xi +1},\kappa _{\xi +2})$
.
Theorem 3.4. Suppose
![]() $\kappa $
is a measurable limit of measurables,
$\kappa $
is a measurable limit of measurables,
![]() $\delta \leq \kappa $
, and
$\delta \leq \kappa $
, and
![]() $f : \delta \to 2$
. Then there is a transitive
$f : \delta \to 2$
. Then there is a transitive
![]() $M \subseteq V_{\kappa }$
of size
$M \subseteq V_{\kappa }$
of size
![]() $\kappa $
and an elementary embedding
$\kappa $
and an elementary embedding
![]() $j : M \to V_{\kappa }$
such that the set of M-cardinals fixed by j above
$j : M \to V_{\kappa }$
such that the set of M-cardinals fixed by j above
![]() $\operatorname {\mathrm {crit}}(j)$
has ordertype
$\operatorname {\mathrm {crit}}(j)$
has ordertype
![]() $\delta $
, and for all
$\delta $
, and for all
![]() $\alpha < \delta $
, the
$\alpha < \delta $
, the
![]() $\alpha ^{th}$
fixed point is regular iff
$\alpha ^{th}$
fixed point is regular iff
![]() $f(\alpha ) = 1$
.
$f(\alpha ) = 1$
.
Proof Let
![]() ${\mathcal U}$
be a normal measure on
${\mathcal U}$
be a normal measure on
![]() $\kappa $
, let
$\kappa $
, let
![]() $\theta> 2^{\kappa }$
, and let
$\theta> 2^{\kappa }$
, and let
![]() $\frak A$
be a structure in a countable language expanding
$\frak A$
be a structure in a countable language expanding
![]() $(H_{\theta },\in ,{\mathcal U})$
with definable Skolem functions. Let us first show how to get isolated singular fixed points. Suppose
$(H_{\theta },\in ,{\mathcal U})$
with definable Skolem functions. Let us first show how to get isolated singular fixed points. Suppose
![]() $\frak A_0 \prec \frak A$
and there is a cardinal
$\frak A_0 \prec \frak A$
and there is a cardinal
![]() $\mu \in \frak A_0 \cap \kappa $
such that
$\mu \in \frak A_0 \cap \kappa $
such that
![]() $|\frak A_0|<\mu $
. Let
$|\frak A_0|<\mu $
. Let
![]() $\langle \delta _n : n < \omega \rangle $
enumerate the first
$\langle \delta _n : n < \omega \rangle $
enumerate the first
![]() $\omega $
measurable cardinals in
$\omega $
measurable cardinals in
![]() $\frak A_0 \cap \kappa $
above
$\frak A_0 \cap \kappa $
above
![]() $\mu $
. By the previous construction, we may make a series of elementary extensions
$\mu $
. By the previous construction, we may make a series of elementary extensions
![]() $\frak A_0 \prec \frak A_1 \prec \frak A_2 \prec \cdots $
such that:
$\frak A_0 \prec \frak A_1 \prec \frak A_2 \prec \cdots $
such that:
-
(1) For all n,
 $\frak A_n \cap \delta _n = \frak A_{n+1} \cap \delta _n$
.
$\frak A_n \cap \delta _n = \frak A_{n+1} \cap \delta _n$
. -
(2)
 $\operatorname {\mathrm {ot}}(\frak A_1 \cap \delta _0) = | \frak A_1 | = \mu $
.
$\operatorname {\mathrm {ot}}(\frak A_1 \cap \delta _0) = | \frak A_1 | = \mu $
. -
(3) For
 $n \geq 1$
,
$n \geq 1$
,
 $\operatorname {\mathrm {ot}}(\frak A_n \cap \delta _n) = |\frak A_n | = \delta _{n-1}$
.
$\operatorname {\mathrm {ot}}(\frak A_n \cap \delta _n) = |\frak A_n | = \delta _{n-1}$
.
Then let
![]() $\frak A_{\omega } = \bigcup _{n<\omega } \frak A_n$
. Let
$\frak A_{\omega } = \bigcup _{n<\omega } \frak A_n$
. Let
![]() $j : H \to \frak A_{\omega }$
be the inverse of the transitive collapse. It is easy to see that
$j : H \to \frak A_{\omega }$
be the inverse of the transitive collapse. It is easy to see that
![]() $j(\mu ) = \delta _0$
, and for all
$j(\mu ) = \delta _0$
, and for all
![]() $n<\omega $
,
$n<\omega $
,
![]() $j(\delta _n) = \delta _{n+1}$
. Let
$j(\delta _n) = \delta _{n+1}$
. Let
![]() $\delta _{\omega } = \sup _n \delta _n$
, which is in
$\delta _{\omega } = \sup _n \delta _n$
, which is in
![]() $\frak A_0$
. Since
$\frak A_0$
. Since
![]() $\operatorname {\mathrm {ot}}(\frak A_{\omega } \cap \delta _{\omega }) = \delta _{\omega }$
,
$\operatorname {\mathrm {ot}}(\frak A_{\omega } \cap \delta _{\omega }) = \delta _{\omega }$
,
![]() $j(\delta _{\omega }) = \delta _{\omega }$
. Since
$j(\delta _{\omega }) = \delta _{\omega }$
. Since
![]() $|\frak A_{\omega }| = \delta _{\omega }$
, all cardinals of H above
$|\frak A_{\omega }| = \delta _{\omega }$
, all cardinals of H above
![]() $\delta _{\omega }$
are below
$\delta _{\omega }$
are below
![]() $(\delta _{\omega }^+)^V$
, so j has no cardinal fixed points greater than
$(\delta _{\omega }^+)^V$
, so j has no cardinal fixed points greater than
![]() $\delta _{\omega }$
.
$\delta _{\omega }$
.
To prove the theorem, we build a continuous chain of elementary submodels of
![]() $\frak A$
,
$\frak A$
,
![]() $\langle \frak A_{\alpha } : \alpha < \kappa \rangle $
, along with an increasing sequence of cardinals
$\langle \frak A_{\alpha } : \alpha < \kappa \rangle $
, along with an increasing sequence of cardinals
![]() $\langle \delta _{\alpha } : \alpha < \delta \rangle \subseteq \kappa $
, such that:
$\langle \delta _{\alpha } : \alpha < \delta \rangle \subseteq \kappa $
, such that:
-
(1) If
 $\alpha < \beta $
, then
$\alpha < \beta $
, then
 $\frak A_{\beta } \cap \sup (\frak A_{\alpha } \cap \kappa )= \frak A_{\alpha } \cap \kappa $
.
$\frak A_{\beta } \cap \sup (\frak A_{\alpha } \cap \kappa )= \frak A_{\alpha } \cap \kappa $
. -
(2) For each
 $\alpha $
,
$\alpha $
,
 $\delta _{\alpha } \in \frak A_{\alpha +1} \setminus \sup (\frak A_{\alpha } \cap \kappa )$
.
$\delta _{\alpha } \in \frak A_{\alpha +1} \setminus \sup (\frak A_{\alpha } \cap \kappa )$
. -
(3) If
 $\alpha < \delta $
, then
$\alpha < \delta $
, then
 $\delta _{\alpha }$
is the unique cardinal fixed point of the transitive collapse of
$\delta _{\alpha }$
is the unique cardinal fixed point of the transitive collapse of
 $\frak A_{\alpha +1}$
that is
$\frak A_{\alpha +1}$
that is
 $\geq \sup (\frak A_{\alpha } \cap \kappa )$
, and
$\geq \sup (\frak A_{\alpha } \cap \kappa )$
, and
 $\delta _{\alpha }$
is regular iff
$\delta _{\alpha }$
is regular iff
 $f(\alpha ) = 1$
.
$f(\alpha ) = 1$
. -
(4) If
 $\alpha \geq \delta $
, then there are no fixed points in the transitive collapse of
$\alpha \geq \delta $
, then there are no fixed points in the transitive collapse of
 $\frak A_{\alpha +1}$
that are
$\frak A_{\alpha +1}$
that are
 $\geq \sup (\frak A_{\alpha } \cap \kappa )$
.
$\geq \sup (\frak A_{\alpha } \cap \kappa )$
.
Given
![]() $\frak A_{\alpha }$
, first adjoin an ordinal
$\frak A_{\alpha }$
, first adjoin an ordinal
![]() $\gamma _{\alpha } \in \bigcap (\frak A_{\alpha } \cap {\mathcal U})$
that is strictly above
$\gamma _{\alpha } \in \bigcap (\frak A_{\alpha } \cap {\mathcal U})$
that is strictly above
![]() $\sup (\frak A_{\alpha } \cap \kappa )$
, to form a model
$\sup (\frak A_{\alpha } \cap \kappa )$
, to form a model
![]() $\frak A_{\alpha }'$
with the same ordinals below
$\frak A_{\alpha }'$
with the same ordinals below
![]() $\gamma _{\alpha }$
, so that if
$\gamma _{\alpha }$
, so that if
![]() $\pi $
is the transitive collapse of
$\pi $
is the transitive collapse of
![]() $\frak A_{\alpha }'$
, then
$\frak A_{\alpha }'$
, then
![]() $\pi (\gamma _{\alpha })<\gamma _{\alpha }$
. If
$\pi (\gamma _{\alpha })<\gamma _{\alpha }$
. If
![]() $\alpha <\delta $
and
$\alpha <\delta $
and
![]() $f(\alpha ) = 0$
, let
$f(\alpha ) = 0$
, let
![]() $\delta _{\alpha }$
be the supremum of the first
$\delta _{\alpha }$
be the supremum of the first
![]() $\omega $
measurable cardinals in
$\omega $
measurable cardinals in
![]() $\frak A_{\alpha }'$
above
$\frak A_{\alpha }'$
above
![]() $\gamma _{\alpha }$
. If
$\gamma _{\alpha }$
. If
![]() $\alpha < \delta $
and
$\alpha < \delta $
and
![]() $f(\alpha ) = 1$
, let
$f(\alpha ) = 1$
, let
![]() $\delta _{\alpha }$
be the least measurable cardinal in
$\delta _{\alpha }$
be the least measurable cardinal in
![]() $\frak A_{\alpha }'$
above
$\frak A_{\alpha }'$
above
![]() $\gamma _{\alpha }$
. Depending on
$\gamma _{\alpha }$
. Depending on
![]() $f(\alpha )$
, use either the above construction or that of Theorem 3.1 to build an extension
$f(\alpha )$
, use either the above construction or that of Theorem 3.1 to build an extension
![]() $\frak A_{\alpha +1}$
of
$\frak A_{\alpha +1}$
of
![]() $\frak A_{\alpha }'$
with size
$\frak A_{\alpha }'$
with size
![]() $\delta _{\alpha }$
, so that
$\delta _{\alpha }$
, so that
![]() $\delta _{\alpha }$
is the unique cardinal fixed point of its transitive collapse above
$\delta _{\alpha }$
is the unique cardinal fixed point of its transitive collapse above
![]() $\sup (\frak A_{\alpha } \cap \kappa )$
, and
$\sup (\frak A_{\alpha } \cap \kappa )$
, and
![]() $\frak A_{\alpha +1} \cap \gamma _{\alpha } = \frak A_{\alpha } \cap \kappa $
.
$\frak A_{\alpha +1} \cap \gamma _{\alpha } = \frak A_{\alpha } \cap \kappa $
.
If
![]() $\delta = \kappa $
, we continue the same process for
$\delta = \kappa $
, we continue the same process for
![]() $\kappa $
-many steps. If
$\kappa $
-many steps. If
![]() $\delta < \kappa $
, then once we have
$\delta < \kappa $
, then once we have
![]() $\frak A_{\delta }$
, we can apply Theorem 3.1 to extend to a
$\frak A_{\delta }$
, we can apply Theorem 3.1 to extend to a
![]() $\kappa $
-sized model
$\kappa $
-sized model
![]() $\frak A_{\kappa }$
, such that
$\frak A_{\kappa }$
, such that
![]() $\frak A_{\kappa } \cap \sup (\frak A_{\delta } \cap \kappa ) = \frak A_{\delta } \cap \kappa $
, and the transitive collapse of
$\frak A_{\kappa } \cap \sup (\frak A_{\delta } \cap \kappa ) = \frak A_{\delta } \cap \kappa $
, and the transitive collapse of
![]() $\frak A_{\kappa }$
has no fixed points in the interval
$\frak A_{\kappa }$
has no fixed points in the interval
![]() $[\sup (\frak A_{\delta } \cap \kappa ),\kappa )$
.
$[\sup (\frak A_{\delta } \cap \kappa ),\kappa )$
.
4 Categories of amenable embeddings
In this section, we explore the structure of the categories
![]() ${\mathcal A}_{\delta }$
of models of ZFC of height
${\mathcal A}_{\delta }$
of models of ZFC of height
![]() $\delta $
and amenable embeddings between them. We attempt to determine, as comprehensively as we can, what kinds of linear and partial orders can appear as honest subcategories of
$\delta $
and amenable embeddings between them. We attempt to determine, as comprehensively as we can, what kinds of linear and partial orders can appear as honest subcategories of
![]() ${\mathcal A}_{\delta }$
, for a countable ordinal
${\mathcal A}_{\delta }$
, for a countable ordinal
![]() $\delta $
. We start by applying the methods of the previous section to build patterns of “amalgamation” and then use stationary tower forcing to build transfinite chains and patterns of “splitting.” Then we pass to ill-founded models that are well-founded up to
$\delta $
. We start by applying the methods of the previous section to build patterns of “amalgamation” and then use stationary tower forcing to build transfinite chains and patterns of “splitting.” Then we pass to ill-founded models that are well-founded up to
![]() $\delta $
to find subcategories of
$\delta $
to find subcategories of
![]() ${\mathcal A}_{\delta }$
that are isomorphic to certain canonical ill-founded structures.
${\mathcal A}_{\delta }$
that are isomorphic to certain canonical ill-founded structures.
The following large cardinal notion will be important for this section:
Definition [Reference Larson14]
A cardinal
![]() $\kappa $
is called completely Jónsson if it is inaccessible and for every
$\kappa $
is called completely Jónsson if it is inaccessible and for every
![]() $a \in V_{\kappa }$
which is stationary in
$a \in V_{\kappa }$
which is stationary in
![]() $\bigcup a$
, the set
$\bigcup a$
, the set
![]() $\{ M \subseteq V_{\kappa } : M \cap \bigcup a \in a \text { and } |M \cap \kappa | = \kappa \}$
is stationary in
$\{ M \subseteq V_{\kappa } : M \cap \bigcup a \in a \text { and } |M \cap \kappa | = \kappa \}$
is stationary in
![]() $\mathcal {P}(V_{\kappa })$
.
$\mathcal {P}(V_{\kappa })$
.
The construction of the previous section shows that measurable cardinals are completely Jónsson. For let
![]() $\kappa $
be measurable and let
$\kappa $
be measurable and let
![]() $a \in V_{\kappa }$
be stationary. For any function
$a \in V_{\kappa }$
be stationary. For any function
![]() $F : V_{\kappa }^{<\omega } \to V_{\kappa }$
, we can take a well-order
$F : V_{\kappa }^{<\omega } \to V_{\kappa }$
, we can take a well-order
![]() $\lhd $
on
$\lhd $
on
![]() $H_{\theta }$
, where
$H_{\theta }$
, where
![]() $\theta> 2^{\kappa }$
, and find an elementary substructure
$\theta> 2^{\kappa }$
, and find an elementary substructure
![]() $\frak A \prec (H_{\theta },\in ,\lhd ,F)$
of size
$\frak A \prec (H_{\theta },\in ,\lhd ,F)$
of size
![]() $<\kappa $
, and such that
$<\kappa $
, and such that
![]() $\frak A \cap \bigcup a \in a$
. By repeated end-extension, we get
$\frak A \cap \bigcup a \in a$
. By repeated end-extension, we get
![]() $\frak B \prec (H_{\theta },\in ,\lhd ,F)$
such that
$\frak B \prec (H_{\theta },\in ,\lhd ,F)$
such that
![]() $|\frak B \cap \kappa | = \kappa $
and
$|\frak B \cap \kappa | = \kappa $
and
![]() $\frak B \cap \bigcup a = \frak A \cap \bigcup a$
. Since
$\frak B \cap \bigcup a = \frak A \cap \bigcup a$
. Since
![]() $\frak B \cap V_{\kappa }$
is closed under F, the claim follows. An easy reflection argument shows that if
$\frak B \cap V_{\kappa }$
is closed under F, the claim follows. An easy reflection argument shows that if
![]() $\kappa $
is measurable and
$\kappa $
is measurable and
![]() ${\mathcal U}$
is a normal measure on
${\mathcal U}$
is a normal measure on
![]() $\kappa $
, then the set of completely Jónsson cardinals below
$\kappa $
, then the set of completely Jónsson cardinals below
![]() $\kappa $
is in
$\kappa $
is in
![]() ${\mathcal U}$
.
${\mathcal U}$
.
Similar arguments show the following: If
![]() $\langle \kappa _i : i < \delta \rangle $
is an increasing sequence of measurable cardinals with supremum
$\langle \kappa _i : i < \delta \rangle $
is an increasing sequence of measurable cardinals with supremum
![]() $\theta $
, and
$\theta $
, and
![]() $\langle \mu _i : i < \delta \rangle $
is a nondecreasing sequence of cardinals with
$\langle \mu _i : i < \delta \rangle $
is a nondecreasing sequence of cardinals with
![]() $\mu _i \leq \kappa _i$
for all i, then the set
$\mu _i \leq \kappa _i$
for all i, then the set
![]() $\{ X \subseteq \theta : |X \cap \kappa _i| = \mu _i$
for all
$\{ X \subseteq \theta : |X \cap \kappa _i| = \mu _i$
for all
![]() $i \}$
is stationary.
$i \}$
is stationary.
4.1 Collapsing inward
Following [Reference Jech10], let us say that a sequential tree is a collection of functions
![]() $p : n \to \omega $
for
$p : n \to \omega $
for
![]() $n<\omega $
closed under initial segments, ordered by
$n<\omega $
closed under initial segments, ordered by
![]() $p \leq q$
iff
$p \leq q$
iff
![]() $p \supseteq q$
. If T is a well-founded sequential tree, then it has a rank function
$p \supseteq q$
. If T is a well-founded sequential tree, then it has a rank function
![]() $\rho _T : T \to \omega _1$
, defined inductively by putting
$\rho _T : T \to \omega _1$
, defined inductively by putting
![]() $\rho _T(p) = 0$
for minimal nodes p, and
$\rho _T(p) = 0$
for minimal nodes p, and
![]() $\rho _T(p) = \sup \{ \rho _T(q) + 1 : q < p \}$
. The rank of T is
$\rho _T(p) = \sup \{ \rho _T(q) + 1 : q < p \}$
. The rank of T is
![]() $\rho _T(\emptyset )$
.
$\rho _T(\emptyset )$
.
Theorem 4.1. Suppose there is a countable transitive model N of ZFC containing a completely Jónsson cardinal
![]() $\delta $
that has infinitely many measurables below it,
$\delta $
that has infinitely many measurables below it,
![]() $\alpha \in N$
is an ordinal, and T is a well-founded sequential tree of rank
$\alpha \in N$
is an ordinal, and T is a well-founded sequential tree of rank
![]() $\alpha $
. Then there is an honest subcategory of
$\alpha $
. Then there is an honest subcategory of
![]() ${\mathcal A}_{\delta }$
isomorphic to T.
${\mathcal A}_{\delta }$
isomorphic to T.
Proof For the purposes of this argument, for a natural number n and a model M in the language of set theory, let
![]() $\kappa _n^M$
denote the
$\kappa _n^M$
denote the
![]() $n^{th}$
measurable cardinal in M, if it exists. We show the following claim by induction on
$n^{th}$
measurable cardinal in M, if it exists. We show the following claim by induction on
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\Phi (T,\alpha ,M,\delta ,f)$
stand for the assertion that:
$\Phi (T,\alpha ,M,\delta ,f)$
stand for the assertion that:
-
(1) T is a well-founded sequential tree of rank
 $\alpha $
.
$\alpha $
. -
(2)
 $M \in N$
is a transitive model of
$M \in N$
is a transitive model of
 $\mathrm {ZF} -$
Powerset + “Every set has a well-ordering” + “
$\mathrm {ZF} -$
Powerset + “Every set has a well-ordering” + “
 $\delta $
is a completely Jónsson cardinal with infinitely many measurables below it”
$\delta $
is a completely Jónsson cardinal with infinitely many measurables below it”
 $+$
“
$+$
“
 $V_{\delta +\alpha +1}$
exists.”
$V_{\delta +\alpha +1}$
exists.” -
(3)
 $f : \omega ^2 \to \omega $
is an injection in M.
$f : \omega ^2 \to \omega $
is an injection in M.
We claim that if
![]() $\Phi (T,\alpha ,M,\delta ,f)$
holds, then there is an assignment
$\Phi (T,\alpha ,M,\delta ,f)$
holds, then there is an assignment
![]() $p \mapsto M_p$
for
$p \mapsto M_p$
for
![]() $p \in T$
such that:
$p \in T$
such that:
-
(1) Each
 $M_p$
is a transitive set of rank
$M_p$
is a transitive set of rank
 $\delta $
in M, with
$\delta $
in M, with
 $M_{\emptyset } = V^M_{\delta }$
.
$M_{\emptyset } = V^M_{\delta }$
. -
(2) If
 $p \leq q$
, then there is an amenable
$p \leq q$
, then there is an amenable
 $j : M_p \to M_q$
in M.
$j : M_p \to M_q$
in M. -
(3) For all
 $p \in T$
,
$p \in T$
,
 $\kappa _{f(i,p(i))}^{M_p} < \kappa _{f(i,p(i))}^M$
for
$\kappa _{f(i,p(i))}^{M_p} < \kappa _{f(i,p(i))}^M$
for
 $i < \operatorname {\mathrm {len}}(p)$
, and
$i < \operatorname {\mathrm {len}}(p)$
, and
 $\kappa _{f(i,i')}^{M_p} = \kappa _{f(i,i')}^M$
for
$\kappa _{f(i,i')}^{M_p} = \kappa _{f(i,i')}^M$
for
 $(i,i') \notin p$
.
$(i,i') \notin p$
.
Let us first show why the claim implies that the generated subcategory is honest. Suppose
![]() $p(i) \not = q(i)$
, and let
$p(i) \not = q(i)$
, and let
![]() $n = f(i,q(i))$
. If there were an elementary embedding
$n = f(i,q(i))$
. If there were an elementary embedding
![]() $j : M_p \to M_q$
, then
$j : M_p \to M_q$
, then
which is impossible since embeddings are monotonic on ordinals.
Suppose
![]() $\Phi (T,\alpha ,M,\delta ,f)$
holds, and the claim holds below
$\Phi (T,\alpha ,M,\delta ,f)$
holds, and the claim holds below
![]() $\alpha $
. Without loss of generality,
$\alpha $
. Without loss of generality,
![]() $\langle n \rangle \in T$
for each
$\langle n \rangle \in T$
for each
![]() $n<\omega $
, since every sequential tree of rank
$n<\omega $
, since every sequential tree of rank
![]() $\alpha $
can be embedded into one of this form. For each n, let
$\alpha $
can be embedded into one of this form. For each n, let
![]() $T_n = \{ \langle p(1),\dots ,p(\operatorname {\mathrm {len}}(p) -1) \rangle : p \in T$
and
$T_n = \{ \langle p(1),\dots ,p(\operatorname {\mathrm {len}}(p) -1) \rangle : p \in T$
and
![]() $p(0) = n \}$
. Note that each
$p(0) = n \}$
. Note that each
![]() $T_n$
is a well-founded sequential tree, and
$T_n$
is a well-founded sequential tree, and
![]() $\alpha = \sup _n (\operatorname {\mathrm {rank}}(T_n)+1)$
. Let
$\alpha = \sup _n (\operatorname {\mathrm {rank}}(T_n)+1)$
. Let
![]() $\alpha _n = \operatorname {\mathrm {rank}}(T_n)$
.
$\alpha _n = \operatorname {\mathrm {rank}}(T_n)$
.
Working in M, let
![]() $\theta = |V_{\delta +\alpha }|^+$
. We can take for each
$\theta = |V_{\delta +\alpha }|^+$
. We can take for each
![]() $n<\omega $
, an elementary substructure
$n<\omega $
, an elementary substructure
![]() $\frak A_n \prec H_{\theta }$
such that:
$\frak A_n \prec H_{\theta }$
such that:
-
(1)
 $| \frak A_n \cap \kappa _{f(0,n)}^M | < \kappa _{f(0,n)}^M$
.
$| \frak A_n \cap \kappa _{f(0,n)}^M | < \kappa _{f(0,n)}^M$
. -
(2)
 $| \frak A_n \cap \kappa _{f(i,i')}^M | = \kappa _{f(i,i')}^M$
for
$| \frak A_n \cap \kappa _{f(i,i')}^M | = \kappa _{f(i,i')}^M$
for
 $(i,i') \not = (0,n)$
.
$(i,i') \not = (0,n)$
. -
(3)
 $\delta \in \frak A_n$
and
$\delta \in \frak A_n$
and
 $| \frak A_n \cap \delta | = \delta $
.
$| \frak A_n \cap \delta | = \delta $
.
Let
![]() $M_n$
be the transitive collapse of
$M_n$
be the transitive collapse of
![]() $\frak A_n$
. Let
$\frak A_n$
. Let
![]() $M_{\emptyset } = V_{\delta }^M$
and
$M_{\emptyset } = V_{\delta }^M$
and
![]() $M_{\langle n \rangle } = (V_{\delta })^{M_n}$
. (Note that
$M_{\langle n \rangle } = (V_{\delta })^{M_n}$
. (Note that
![]() $M_{\langle n \rangle }$
is a rank initial segment of
$M_{\langle n \rangle }$
is a rank initial segment of
![]() $M_n$
, and the larger model does not satisfy the powerset axiom.) Each
$M_n$
, and the larger model does not satisfy the powerset axiom.) Each
![]() $M_{\langle n \rangle }$
amenably embeds into
$M_{\langle n \rangle }$
amenably embeds into
![]() $M_{\emptyset }$
. For each n,
$M_{\emptyset }$
. For each n,
![]() $\kappa _{f(0,n)}^{M_n} < \kappa _{f(0,n)}^M$
and
$\kappa _{f(0,n)}^{M_n} < \kappa _{f(0,n)}^M$
and
![]() $\kappa _{f(i,i')}^{M_n} = \kappa _{f(i,i')}^M$
for
$\kappa _{f(i,i')}^{M_n} = \kappa _{f(i,i')}^M$
for
![]() $(i,i') \not = (0,n)$
.
$(i,i') \not = (0,n)$
.
Let
![]() $g : \omega ^2 \to \omega $
be defined by
$g : \omega ^2 \to \omega $
be defined by
![]() $g(i,i') = f(i+1,i')$
. Then
$g(i,i') = f(i+1,i')$
. Then
![]() $\Phi (T_n,\alpha _n,M_n,\delta ,g)$
holds for each n. By the induction hypothesis, there is an assignment
$\Phi (T_n,\alpha _n,M_n,\delta ,g)$
holds for each n. By the induction hypothesis, there is an assignment
![]() $p \mapsto M_p$
, for
$p \mapsto M_p$
, for
![]() $p \in T \setminus \{ \emptyset \}$
, such that whenever
$p \in T \setminus \{ \emptyset \}$
, such that whenever
![]() $p(0) = n$
,
$p(0) = n$
,
-
(1)
 $M_p$
is a transitive set of rank
$M_p$
is a transitive set of rank
 $\delta $
in
$\delta $
in
 $M_n$
.
$M_n$
. -
(2) If
 $q \leq p$
, then there is an amenable
$q \leq p$
, then there is an amenable
 $j : M_q \to M_p$
in
$j : M_q \to M_p$
in
 $M_n$
.
$M_n$
. -
(3) For
 $1 \leq i < \operatorname {\mathrm {len}}(p)$
, and for a pair
$1 \leq i < \operatorname {\mathrm {len}}(p)$
, and for a pair $$ \begin{align*} \kappa_{g(i-1,p(i))}^{M_p} = \kappa_{f(i,p(i))}^{M_p} < \kappa_{f(i,p(i))}^{M_{n}} = \kappa_{f(i,p(i))}^M, \end{align*} $$
$$ \begin{align*} \kappa_{g(i-1,p(i))}^{M_p} = \kappa_{f(i,p(i))}^{M_p} < \kappa_{f(i,p(i))}^{M_{n}} = \kappa_{f(i,p(i))}^M, \end{align*} $$
 $(i,i') \notin p$
, with
$(i,i') \notin p$
, with
 $i \geq 1$
,
$i \geq 1$
,  $$ \begin{align*} \kappa_{g(i-1,i')}^{M_p} = \kappa_{f(i,i')}^{M_p} = \kappa_{f(i,i')}^{M_{n}} = \kappa_{f(i,i')}^M. \end{align*} $$
$$ \begin{align*} \kappa_{g(i-1,i')}^{M_p} = \kappa_{f(i,i')}^{M_p} = \kappa_{f(i,i')}^{M_{n}} = \kappa_{f(i,i')}^M. \end{align*} $$
-
(4) For all
 $m<\omega $
,
$m<\omega $
,
 $\kappa _{f(0,m)}^{M_p} = \kappa _{f(0,m)}^{M_n}$
.
$\kappa _{f(0,m)}^{M_p} = \kappa _{f(0,m)}^{M_n}$
.
Therefore, the induction hypothesis holds for
![]() $\alpha $
.
$\alpha $
.
4.2 Forcing outward
The background material for this subsection can be found in [Reference Larson14].
Definition (Woodin)
The (proper class) stationary tower forcing
![]() $\mathbb P_{\infty }$
is the class of stationary sets ordered by
$\mathbb P_{\infty }$
is the class of stationary sets ordered by
![]() $a \leq b$
if
$a \leq b$
if
![]() $\bigcup a \supseteq \bigcup b$
and
$\bigcup a \supseteq \bigcup b$
and
![]() $\{ x \cap \bigcup b : x \in a \} \subseteq b$
. If
$\{ x \cap \bigcup b : x \in a \} \subseteq b$
. If
![]() $\kappa $
is a strong limit cardinal, then
$\kappa $
is a strong limit cardinal, then
![]() $\mathbb P_{<\kappa } = \mathbb P_{\infty } \cap V_{\kappa }$
.
$\mathbb P_{<\kappa } = \mathbb P_{\infty } \cap V_{\kappa }$
.
Theorem 4.2 (Woodin)
Suppose there is a proper class of completely Jónsson cardinals, and
![]() $G \subseteq \mathbb P_{\infty }$
is generic over V. Then there is an amenable elementary embedding
$G \subseteq \mathbb P_{\infty }$
is generic over V. Then there is an amenable elementary embedding
![]() $j : V \to V[G]$
with unboundedly many regular fixed points.
$j : V \to V[G]$
with unboundedly many regular fixed points.
The above theorem immediately implies that if there is a countable transitive model
![]() $M_0$
of height
$M_0$
of height
![]() $\delta $
with a proper class of completely Jónsson cardinals, then
$\delta $
with a proper class of completely Jónsson cardinals, then
![]() ${\mathcal A}_{\delta }$
contains a subcategory isomorphic to the linear order
${\mathcal A}_{\delta }$
contains a subcategory isomorphic to the linear order
![]() $\omega $
. Given
$\omega $
. Given
![]() $M_n$
, we can take a
$M_n$
, we can take a
![]() $\mathbb P_{\infty }$
-generic
$\mathbb P_{\infty }$
-generic
![]() $G_n$
over
$G_n$
over
![]() $M_n$
, which gives us an amenable
$M_n$
, which gives us an amenable
![]() $j : M_n \to M_{n+1} = M_n[G_n]$
. In order to construct more complicated subcategories, we use the following to determine the action of the maps:
$j : M_n \to M_{n+1} = M_n[G_n]$
. In order to construct more complicated subcategories, we use the following to determine the action of the maps:
Fact 4.3. Suppose
![]() $G \subseteq \mathbb P_{\infty }$
and
$G \subseteq \mathbb P_{\infty }$
and
![]() $j : V \to V[G]$
are as above. Suppose
$j : V \to V[G]$
are as above. Suppose
![]() $\varphi (x_0,\dots ,x_n,y)$
is a formula,
$\varphi (x_0,\dots ,x_n,y)$
is a formula,
![]() $a_0,\dots ,a_n,b \in V$
, and b is transitive. Then
$a_0,\dots ,a_n,b \in V$
, and b is transitive. Then
Consequently,
![]() $\kappa = \operatorname {\mathrm {crit}}(j) \Leftrightarrow \{ z \subseteq \kappa : z \cap \kappa \in \kappa \} \in G$
.
$\kappa = \operatorname {\mathrm {crit}}(j) \Leftrightarrow \{ z \subseteq \kappa : z \cap \kappa \in \kappa \} \in G$
.
To construct subcategories containing transfinite chains, we use our latitude in determining critical points so that the equivalence classes that make up the ordinals of the direct limit are all eventually “frozen.”
Lemma 4.4. Suppose the following:
-
(1)
 $\langle \delta _n : n < \omega \rangle $
is an increasing sequence of ordinals.
$\langle \delta _n : n < \omega \rangle $
is an increasing sequence of ordinals. -
(2)
 $\langle M_n : n <\omega \rangle $
is a sequence of transitive ZFC models, each of height
$\langle M_n : n <\omega \rangle $
is a sequence of transitive ZFC models, each of height
 $\delta = \sup _{n<\omega } \delta _n$
.
$\delta = \sup _{n<\omega } \delta _n$
. -
(3)
 $\langle j_{m,n} : M_m \to M_n : m \leq n < \omega \rangle $
is a commuting system of elementary embeddings.
$\langle j_{m,n} : M_m \to M_n : m \leq n < \omega \rangle $
is a commuting system of elementary embeddings. -
(4) For all
 $m \leq n$
,
$m \leq n$
,
 $j_{m,n}(\delta _n)<\operatorname {\mathrm {crit}}(j_{n,n+1}) $
.
$j_{m,n}(\delta _n)<\operatorname {\mathrm {crit}}(j_{n,n+1}) $
.
Then the direct limit is isomorphic to a transitive model
![]() $M_{\omega } \subseteq \bigcup _{n<\omega } M_n$
. If each
$M_{\omega } \subseteq \bigcup _{n<\omega } M_n$
. If each
![]() $j_{m,n}$
is amenable, then so is each direct limit map
$j_{m,n}$
is amenable, then so is each direct limit map
![]() $j_{n,\omega }$
, and thus
$j_{n,\omega }$
, and thus
![]() $M_{\omega } = \bigcup _{n<\omega } M_n$
.
$M_{\omega } = \bigcup _{n<\omega } M_n$
.
Proof Recall that the direct limit is defined as the set of equivalence classes
![]() $[n,x]$
, where
$[n,x]$
, where
![]() $x \in M_n$
, and we put
$x \in M_n$
, and we put
![]() $[n,x] \sim [m,y]$
for
$[n,x] \sim [m,y]$
for
![]() $n \leq m$
when
$n \leq m$
when
![]() $j_{n,m}(x) = y$
. The membership relation is defined similarly: for
$j_{n,m}(x) = y$
. The membership relation is defined similarly: for
![]() $n\leq m$
,
$n\leq m$
,
![]() $[n,x]$
“
$[n,x]$
“
![]() $\in $
”
$\in $
”
![]() $[m,y]$
when
$[m,y]$
when
![]() $j_{n,m}(x) \in y$
. Suppose
$j_{n,m}(x) \in y$
. Suppose
![]() $\alpha < \delta $
and
$\alpha < \delta $
and
![]() $n<\omega $
. Let
$n<\omega $
. Let
![]() $m \geq n$
be such that
$m \geq n$
be such that
![]() $\delta _m \geq \alpha $
, and let
$\delta _m \geq \alpha $
, and let
![]() $\beta = j_{n,m}(\alpha )$
. Then for all
$\beta = j_{n,m}(\alpha )$
. Then for all
![]() $k> m$
,
$k> m$
,
![]() $\operatorname {\mathrm {crit}}(j_{m,k})>\beta $
. Thus if
$\operatorname {\mathrm {crit}}(j_{m,k})>\beta $
. Thus if
![]() $[k,\gamma ] < [n,\alpha ]$
in the direct limit, then there is some
$[k,\gamma ] < [n,\alpha ]$
in the direct limit, then there is some
![]() $\xi <\beta $
such that
$\xi <\beta $
such that
![]() $[k,\gamma ] \sim [m,\xi ]$
. Thus the set of predecessors of any ordinal in the direct limit is isomorphic to an ordinal below
$[k,\gamma ] \sim [m,\xi ]$
. Thus the set of predecessors of any ordinal in the direct limit is isomorphic to an ordinal below
![]() $\delta $
, so the direct limit can be identified with a transitive model
$\delta $
, so the direct limit can be identified with a transitive model
![]() $M_{\omega }$
of height
$M_{\omega }$
of height
![]() $\delta $
. To show
$\delta $
. To show
![]() $M_{\omega } \subseteq \bigcup _n M_n$
, let
$M_{\omega } \subseteq \bigcup _n M_n$
, let
![]() $x \in M_{\omega }$
and let
$x \in M_{\omega }$
and let
![]() $n,y$
be such that
$n,y$
be such that
![]() $x = j_{n,\omega }(y)$
. Let
$x = j_{n,\omega }(y)$
. Let
![]() $m\geq n$
be such that
$m\geq n$
be such that
![]() $\operatorname {\mathrm {rank}}(y) <\delta _m$
.
$\operatorname {\mathrm {rank}}(y) <\delta _m$
.
![]() $\operatorname {\mathrm {crit}}(j_{m,\omega })> \operatorname {\mathrm {rank}}(j_{n,m}(y))$
, so
$\operatorname {\mathrm {crit}}(j_{m,\omega })> \operatorname {\mathrm {rank}}(j_{n,m}(y))$
, so
![]() $x = j_{m,\omega } \circ j_{n,m}(y) = j_{n,m}(y) \in M_m$
.
$x = j_{m,\omega } \circ j_{n,m}(y) = j_{n,m}(y) \in M_m$
.
Now suppose each
![]() $j_{m,n}$
is amenable. Let
$j_{m,n}$
is amenable. Let
![]() $x \in M_n$
. Let
$x \in M_n$
. Let
![]() $m\geq n$
be such that
$m\geq n$
be such that
![]() $\operatorname {\mathrm {rank}}(x) <\delta _m$
. The critical point of
$\operatorname {\mathrm {rank}}(x) <\delta _m$
. The critical point of
![]() $j_{m,k}$
is greater than
$j_{m,k}$
is greater than
![]() $j_{n,m}(\delta _m)$
for all
$j_{n,m}(\delta _m)$
for all
![]() $k>m$
. By amenability,
$k>m$
. By amenability,
![]() $j_{n,m}[x] \in (V_{j_{n,m}(\delta _m)})^{M_m}$
. But
$j_{n,m}[x] \in (V_{j_{n,m}(\delta _m)})^{M_m}$
. But
![]() $j_{n,\omega }[x] = j_{m,\omega }[j_{n,m}[x]] = j_{m,\omega }(j_{n,m}[x]) \in M_{\omega }$
.
$j_{n,\omega }[x] = j_{m,\omega }[j_{n,m}[x]] = j_{m,\omega }(j_{n,m}[x]) \in M_{\omega }$
.
Corollary 4.5. Suppose M is a countable transitive model of ZFC of height
![]() $\delta $
satisfying that there is a proper class of completely Jónsson cardinals. Let
$\delta $
satisfying that there is a proper class of completely Jónsson cardinals. Let
![]() $\xi $
be any countable ordinal. Then there is a subcategory of
$\xi $
be any countable ordinal. Then there is a subcategory of
![]() ${\mathcal A}_{\delta }$
isomorphic to
${\mathcal A}_{\delta }$
isomorphic to
![]() $\xi $
.
$\xi $
.
Proof We argue by induction on
![]() $\xi $
, using the following stronger hypothesis: If
$\xi $
, using the following stronger hypothesis: If
![]() $M_0$
is a countable transitive model of ZFC + “There is a proper class of completely Jónsson cardinals” of height
$M_0$
is a countable transitive model of ZFC + “There is a proper class of completely Jónsson cardinals” of height
![]() $\delta $
, and
$\delta $
, and
![]() $\gamma <\delta $
, then there is a linear system of amenable embeddings
$\gamma <\delta $
, then there is a linear system of amenable embeddings
![]() $\langle j_{\alpha ,\beta } : M_{\alpha } \to M_{\beta } : \alpha \leq \beta \leq \xi \rangle $
with
$\langle j_{\alpha ,\beta } : M_{\alpha } \to M_{\beta } : \alpha \leq \beta \leq \xi \rangle $
with
![]() $\operatorname {\mathrm {crit}}(j_{0,\xi })> \gamma $
, each
$\operatorname {\mathrm {crit}}(j_{0,\xi })> \gamma $
, each
![]() $M_{\alpha }$
having the same ordinals
$M_{\alpha }$
having the same ordinals
![]() $\delta $
. Suppose this is true for all
$\delta $
. Suppose this is true for all
![]() $\xi ' < \xi $
. If
$\xi ' < \xi $
. If
![]() $\xi =\xi '+1$
, then we may continue to
$\xi =\xi '+1$
, then we may continue to
![]() $\xi $
by taking the final embedding
$\xi $
by taking the final embedding
![]() $j_{\xi ',\xi }$
to be a stationary tower embedding with large enough critical point. Suppose
$j_{\xi ',\xi }$
to be a stationary tower embedding with large enough critical point. Suppose
![]() $\xi $
is a limit ordinal, and let
$\xi $
is a limit ordinal, and let
![]() $\xi = \sup _{n<\omega } \xi _n$
and
$\xi = \sup _{n<\omega } \xi _n$
and
![]() $\delta = \sup _{n<\omega } \delta _n$
, where the
$\delta = \sup _{n<\omega } \delta _n$
, where the
![]() $\xi _n$
and
$\xi _n$
and
![]() $\delta _n$
are increasing. Let
$\delta _n$
are increasing. Let
![]() $\gamma <\delta $
. Inductively choose for each
$\gamma <\delta $
. Inductively choose for each
![]() $n<\omega $
, a chain of amenable embeddings
$n<\omega $
, a chain of amenable embeddings
![]() $\langle j_{\alpha ,\beta } : M_{\alpha } \to M_{\beta } : \xi _n \leq \alpha \leq \beta \leq \xi _{n+1} \rangle $
, such that for all
$\langle j_{\alpha ,\beta } : M_{\alpha } \to M_{\beta } : \xi _n \leq \alpha \leq \beta \leq \xi _{n+1} \rangle $
, such that for all
![]() $m\leq n <\omega $
,
$m\leq n <\omega $
,
![]() $\operatorname {\mathrm {crit}}(j_{\xi _n,\xi _{n+1}})> j_{\xi _m,\xi _n}(\delta _n)+\gamma $
. Then by Lemma 4.4, the direct limit
$\operatorname {\mathrm {crit}}(j_{\xi _n,\xi _{n+1}})> j_{\xi _m,\xi _n}(\delta _n)+\gamma $
. Then by Lemma 4.4, the direct limit
![]() $M_{\xi }$
is well-founded of height
$M_{\xi }$
is well-founded of height
![]() $\delta $
, and each direct limit map
$\delta $
, and each direct limit map
![]() $j_{\xi _n,\xi } : M_{\xi _n} \to M_{\xi }$
is amenable. For
$j_{\xi _n,\xi } : M_{\xi _n} \to M_{\xi }$
is amenable. For
![]() $\alpha <\xi $
, let
$\alpha <\xi $
, let
![]() $j_{\alpha ,\xi } : M_{\alpha } \to M_{\xi }$
be
$j_{\alpha ,\xi } : M_{\alpha } \to M_{\xi }$
be
![]() $j_{\xi _n,\xi } \circ j_{\alpha ,\xi _n}$
, where n is least such that
$j_{\xi _n,\xi } \circ j_{\alpha ,\xi _n}$
, where n is least such that
![]() $\xi _n \geq \alpha $
. For
$\xi _n \geq \alpha $
. For
![]() $\alpha <\beta <\xi $
coming from different intervals, let
$\alpha <\beta <\xi $
coming from different intervals, let
![]() $j_{\alpha ,\beta } = j_{\xi _m,\beta } \circ j_{\xi _{m-1},\xi _m} \circ \cdots \circ j_{\xi _n,\xi _{n+1}} \circ j_{\alpha ,\xi _n}$
, where n is least such
$j_{\alpha ,\beta } = j_{\xi _m,\beta } \circ j_{\xi _{m-1},\xi _m} \circ \cdots \circ j_{\xi _n,\xi _{n+1}} \circ j_{\alpha ,\xi _n}$
, where n is least such
![]() $\xi _n \geq \alpha $
and m is greatest such that
$\xi _n \geq \alpha $
and m is greatest such that
![]() $\xi _m \leq \beta $
. These are amenable since they are the composition of amenable maps. It is easy to check that
$\xi _m \leq \beta $
. These are amenable since they are the composition of amenable maps. It is easy to check that
![]() $\operatorname {\mathrm {crit}}(j_{0,\xi })> \gamma $
.
$\operatorname {\mathrm {crit}}(j_{0,\xi })> \gamma $
.
The countability of
![]() $\xi $
above is optimal:
$\xi $
above is optimal:
Theorem 4.6. For any ordinal
![]() $\delta $
,
$\delta $
,
![]() $\mathcal E_{\delta }$
contains no subcategory isomorphic to
$\mathcal E_{\delta }$
contains no subcategory isomorphic to
![]() $\delta ^+$
. Moreover, if T is a tree of height
$\delta ^+$
. Moreover, if T is a tree of height
![]() $\delta ^+$
such that for every
$\delta ^+$
such that for every
![]() $t \in T$
and every
$t \in T$
and every
![]() $\alpha <\delta ^+$
, there is
$\alpha <\delta ^+$
, there is
![]() $s \geq t$
of height
$s \geq t$
of height
![]() $\geq \alpha $
, and T is isomorphic to a subcategory of
$\geq \alpha $
, and T is isomorphic to a subcategory of
![]() $\mathcal E_{\delta }$
, then forcing with T collapses
$\mathcal E_{\delta }$
, then forcing with T collapses
![]() $\delta ^+$
.
$\delta ^+$
.
Proof Suppose
![]() $\{ M_{\alpha } : \alpha < \delta ^+ \}$
is set of objects in
$\{ M_{\alpha } : \alpha < \delta ^+ \}$
is set of objects in
![]() $\mathcal E_{\delta }$
, and each pair
$\mathcal E_{\delta }$
, and each pair
![]() $\alpha < \beta $
is assigned an embedding
$\alpha < \beta $
is assigned an embedding
![]() $j_{\alpha ,\beta } : M_{\alpha } \to M_{\beta }$
, such that for
$j_{\alpha ,\beta } : M_{\alpha } \to M_{\beta }$
, such that for
![]() $\alpha < \beta < \gamma $
,
$\alpha < \beta < \gamma $
,
![]() $j_{\alpha ,\gamma } = j_{\beta ,\gamma } \circ j_{\alpha ,\beta }$
.
$j_{\alpha ,\gamma } = j_{\beta ,\gamma } \circ j_{\alpha ,\beta }$
.
We select continuous increasing sequences of ordinals,
![]() $\langle \xi _i : i <\delta ^+ \rangle $
, and subsets of
$\langle \xi _i : i <\delta ^+ \rangle $
, and subsets of
![]() $\delta $
,
$\delta $
,
![]() $\langle F_i : i < \delta ^+\rangle $
. Let
$\langle F_i : i < \delta ^+\rangle $
. Let
![]() $\xi _0 = 0$
and let
$\xi _0 = 0$
and let
![]() $F_0$
be the set of ordinals that are fixed by every map
$F_0$
be the set of ordinals that are fixed by every map
![]() $j_{\alpha ,\beta }$
. Given
$j_{\alpha ,\beta }$
. Given
![]() $\xi _i$
, the sequence
$\xi _i$
, the sequence
![]() $\langle j_{\xi _i,\beta }(\alpha ) : \beta < \delta ^+ \rangle $
is nondecreasing. Thus there is
$\langle j_{\xi _i,\beta }(\alpha ) : \beta < \delta ^+ \rangle $
is nondecreasing. Thus there is
![]() $\xi _{i+1}<\delta ^+$
such that
$\xi _{i+1}<\delta ^+$
such that
![]() $j_{\xi _i,\xi _{i+1}}(\alpha ) = j_{\xi _i,\beta }(\alpha )$
for all
$j_{\xi _i,\xi _{i+1}}(\alpha ) = j_{\xi _i,\beta }(\alpha )$
for all
![]() $\beta \geq \xi _{i+1}$
, and all
$\beta \geq \xi _{i+1}$
, and all
![]() $\alpha <\delta $
. Let
$\alpha <\delta $
. Let
![]() $F_{i+1} = j_{\xi _i,\xi _{i+1}}[\delta ]$
. Take unions at limits. By induction, the sets
$F_{i+1} = j_{\xi _i,\xi _{i+1}}[\delta ]$
. Take unions at limits. By induction, the sets
![]() $F_i$
are increasing, and for all
$F_i$
are increasing, and for all
![]() $i<\delta ^+$
,
$i<\delta ^+$
,
![]() $j_{\xi _i,\beta }(\alpha ) = \alpha $
for
$j_{\xi _i,\beta }(\alpha ) = \alpha $
for
![]() $\alpha \in F_i$
and
$\alpha \in F_i$
and
![]() $\beta \geq \xi _i$
.
$\beta \geq \xi _i$
.
Let
![]() $\gamma < \delta ^+$
be the point at which the sets
$\gamma < \delta ^+$
be the point at which the sets
![]() $F_i$
stabilize. We claim that for all
$F_i$
stabilize. We claim that for all
![]() $i> \gamma $
,
$i> \gamma $
,
![]() $j_{\xi _{\gamma },i}$
is the identity map and thus
$j_{\xi _{\gamma },i}$
is the identity map and thus
![]() $M_i = M_{\xi _{\gamma }}$
. Otherwise, let
$M_i = M_{\xi _{\gamma }}$
. Otherwise, let
![]() $\alpha $
and
$\alpha $
and
![]() $\eta $
be such that
$\eta $
be such that
![]() $j_{\xi _{\gamma },\eta }(\alpha )> \alpha $
. But then
$j_{\xi _{\gamma },\eta }(\alpha )> \alpha $
. But then
![]() $j_{\xi _{\gamma },\xi _{\gamma +1}}(\alpha ) \in F_{\gamma +1} \setminus F_{\gamma }$
, a contradiction.
$j_{\xi _{\gamma },\xi _{\gamma +1}}(\alpha ) \in F_{\gamma +1} \setminus F_{\gamma }$
, a contradiction.
To show the claim about
![]() $\delta ^+$
-trees, suppose on the contrary T is a tree satisfying the hypothesis. If b is T-generic branch over V, then b has length
$\delta ^+$
-trees, suppose on the contrary T is a tree satisfying the hypothesis. If b is T-generic branch over V, then b has length
![]() $(\delta ^+)^V$
. If
$(\delta ^+)^V$
. If
![]() $\delta ^+$
is preserved, then in the extension, b gives a chain of length
$\delta ^+$
is preserved, then in the extension, b gives a chain of length
![]() $\delta ^+$
in
$\delta ^+$
in
![]() $\mathcal E_{\delta }$
, contradicting what we have shown.
$\mathcal E_{\delta }$
, contradicting what we have shown.
To further explore the structure of these categories, we use countable transitive models
![]() $M \models \mathrm {ZFC} $
of some height
$M \models \mathrm {ZFC} $
of some height
![]() $\delta $
which is the supremum of an increasing sequence
$\delta $
which is the supremum of an increasing sequence
![]() $\langle \delta _n : n<\omega \rangle $
such that:
$\langle \delta _n : n<\omega \rangle $
such that:
-
(1) Each
 $\delta _n$
is a completely Jónsson cardinal in M.
$\delta _n$
is a completely Jónsson cardinal in M. -
(2) For each n,
 $V_{\delta _n}^M \prec M$
.
$V_{\delta _n}^M \prec M$
.
Let us call these good models, and let us say an ordinal
![]() $\delta $
is good if there exists a good model of height
$\delta $
is good if there exists a good model of height
![]() $\delta $
. The existence of a good model follows from the existence a measurable cardinal. Note that if M is good, N has the same ordinals, and
$\delta $
. The existence of a good model follows from the existence a measurable cardinal. Note that if M is good, N has the same ordinals, and
![]() $j : M \to N$
is elementary, then
$j : M \to N$
is elementary, then
![]() $\langle j(\delta _n) : n <\omega \rangle $
witnesses that N is good. Over good models, we can build generics for
$\langle j(\delta _n) : n <\omega \rangle $
witnesses that N is good. Over good models, we can build generics for
![]() $\mathbb P_{\infty }$
in a way that allows precise control over what happens to the cardinals
$\mathbb P_{\infty }$
in a way that allows precise control over what happens to the cardinals
![]() $\delta _n$
:
$\delta _n$
:
Lemma 4.7. Let
![]() $f : \omega \to \omega $
be any increasing function, let M be good with witnessing sequence
$f : \omega \to \omega $
be any increasing function, let M be good with witnessing sequence
![]() $\langle \delta _n : n < \omega \rangle $
, and let
$\langle \delta _n : n < \omega \rangle $
, and let
![]() $\kappa _0<\kappa _1$
be regular cardinals of M below
$\kappa _0<\kappa _1$
be regular cardinals of M below
![]() $\delta _{f(0)}$
. There is
$\delta _{f(0)}$
. There is
![]() $G \subseteq \mathbb P_{\infty }^M$
generic over M such that if j is the associated generic embedding, then:
$G \subseteq \mathbb P_{\infty }^M$
generic over M such that if j is the associated generic embedding, then:
-
(1)
 $\kappa _0 = \operatorname {\mathrm {crit}}(j)$
and
$\kappa _0 = \operatorname {\mathrm {crit}}(j)$
and
 $j(\kappa _0) \geq \kappa _1$
.
$j(\kappa _0) \geq \kappa _1$
. -
(2) For all n,
 $\delta _{f(n)}$
is a fixed point of j.
$\delta _{f(n)}$
is a fixed point of j. -
(3) For all n, if
 $f(n) < m < f(n+1)$
, then
$f(n) < m < f(n+1)$
, then
 $\delta _m$
has cardinality
$\delta _m$
has cardinality
 $\delta _{f(n)}$
in
$\delta _{f(n)}$
in
 $M[G]$
.
$M[G]$
.
Proof Let
![]() $\langle p_i : i < \omega \rangle $
enumerate M, such that for all n,
$\langle p_i : i < \omega \rangle $
enumerate M, such that for all n,
![]() $p_n \in V_{\delta _n}$
. For each dense class
$p_n \in V_{\delta _n}$
. For each dense class
![]() $D \subseteq {\mathbb P}_{\infty }^M$
definable in M from a parameter p, if
$D \subseteq {\mathbb P}_{\infty }^M$
definable in M from a parameter p, if
![]() $p \in V_{\delta _n}$
, then by elementarity,
$p \in V_{\delta _n}$
, then by elementarity,
![]() $D \cap V_{\delta _n}$
is dense in
$D \cap V_{\delta _n}$
is dense in
![]() ${\mathbb P}_{<\delta _n}$
. Let
${\mathbb P}_{<\delta _n}$
. Let
![]() $n \mapsto \langle n_0,n_1 \rangle $
be the Gödel pairing function, and let
$n \mapsto \langle n_0,n_1 \rangle $
be the Gödel pairing function, and let
![]() $\langle \varphi _n(x,y) : n < \omega \rangle $
enumerate the formulas in two free variables. Now enumerate the dense subclasses of
$\langle \varphi _n(x,y) : n < \omega \rangle $
enumerate the formulas in two free variables. Now enumerate the dense subclasses of
![]() ${\mathbb P}_{\infty }$
as follows. For
${\mathbb P}_{\infty }$
as follows. For
![]() $n< \omega $
, if
$n< \omega $
, if
![]() $\{ x : \varphi _{n_0}(x,p_{n_1}) \}$
is dense, let
$\{ x : \varphi _{n_0}(x,p_{n_1}) \}$
is dense, let
![]() $D_n$
be this class, and otherwise let
$D_n$
be this class, and otherwise let
![]() $D_n = {\mathbb P}_{\infty }$
.
$D_n = {\mathbb P}_{\infty }$
.
Let
![]() $b = \{ z \subseteq \kappa _1 : z \cap \kappa _0 \in \kappa _0, \operatorname {\mathrm {ot}}(z) \leq \kappa _0 \},$
which by Fact 4.3 forces that
$b = \{ z \subseteq \kappa _1 : z \cap \kappa _0 \in \kappa _0, \operatorname {\mathrm {ot}}(z) \leq \kappa _0 \},$
which by Fact 4.3 forces that
![]() $\kappa _1 = \operatorname {\mathrm {ot}}(j[\kappa _1]) \leq j(\kappa _0)$
. Then take
$\kappa _1 = \operatorname {\mathrm {ot}}(j[\kappa _1]) \leq j(\kappa _0)$
. Then take
![]() $b' \leq b$
in
$b' \leq b$
in
![]() $D_0 \cap V_{\delta _{f(0)}}$
. Let
$D_0 \cap V_{\delta _{f(0)}}$
. Let
![]() $a_0 = \{ z \subseteq V_{\delta _{f(0)}} : z \cap \bigcup b' \in b', \operatorname {\mathrm {ot}}(z \cap \delta _{f(0)} )= \delta _{f(0)} \}$
, which forces
$a_0 = \{ z \subseteq V_{\delta _{f(0)}} : z \cap \bigcup b' \in b', \operatorname {\mathrm {ot}}(z \cap \delta _{f(0)} )= \delta _{f(0)} \}$
, which forces
![]() $\delta _{f(0)}$
to be fixed.
$\delta _{f(0)}$
to be fixed.
We choose inductively a sequence
![]() $a_0 \geq a_1 \geq a_2 \geq \cdots $
such that for all n:
$a_0 \geq a_1 \geq a_2 \geq \cdots $
such that for all n:
-
(1)
 $a_{n}$
is below something in
$a_{n}$
is below something in
 $D_{n}$
.
$D_{n}$
. -
(2)
 $a_{n} \subseteq \{ z \subseteq V_{\delta _{f(n)}} : \operatorname {\mathrm {ot}}(z) = \delta _{f(n)} \}$
.
$a_{n} \subseteq \{ z \subseteq V_{\delta _{f(n)}} : \operatorname {\mathrm {ot}}(z) = \delta _{f(n)} \}$
. -
(3)
 $a_{n+1}$
forces
$a_{n+1}$
forces
 $\delta _{f(n+1)-1}< j(\delta _{f(n)}^+)<\delta _{f(n+1)}$
.
$\delta _{f(n+1)-1}< j(\delta _{f(n)}^+)<\delta _{f(n+1)}$
.
The last condition ensures that if
![]() $f(n)<m<f(n+1)$
, then
$f(n)<m<f(n+1)$
, then
![]() $\delta _m$
is collapsed to
$\delta _m$
is collapsed to
![]() $\delta _{f(n)}$
in
$\delta _{f(n)}$
in
![]() $M[G]$
. Given
$M[G]$
. Given
![]() $a_n$
, take a cardinal
$a_n$
, take a cardinal
![]() $\kappa $
,
$\kappa $
,
![]() $\delta _{f(n+1)-1}< \kappa <\delta _{f(n+1)}$
, and let
$\delta _{f(n+1)-1}< \kappa <\delta _{f(n+1)}$
, and let
![]() $a_n'$
be the stationary set
$a_n'$
be the stationary set
![]() $\{ z \subseteq V_{\kappa } : z \cap \bigcup a_n \in a_n, |z| = \delta _{f(n)} \}$
. By Fact 4.3, this forces that
$\{ z \subseteq V_{\kappa } : z \cap \bigcup a_n \in a_n, |z| = \delta _{f(n)} \}$
. By Fact 4.3, this forces that
![]() $\kappa = \operatorname {\mathrm {ot}}(j[\kappa ]) < j(\delta _{f(n)}^+)$
. Then extend to
$\kappa = \operatorname {\mathrm {ot}}(j[\kappa ]) < j(\delta _{f(n)}^+)$
. Then extend to
![]() $a_n" \in D_{n+1} \cap V_{\delta _{f(n+1)}}$
. Then let
$a_n" \in D_{n+1} \cap V_{\delta _{f(n+1)}}$
. Then let
![]() $a_{n+1} = \{ z \subseteq V_{\delta _{f(n+1)}} : z \cap \bigcup a_n" \in a_n", \operatorname {\mathrm {ot}}(z \cap \delta _{f(n+1)}) = \delta _{f(n+1)}\}$
.
$a_{n+1} = \{ z \subseteq V_{\delta _{f(n+1)}} : z \cap \bigcup a_n" \in a_n", \operatorname {\mathrm {ot}}(z \cap \delta _{f(n+1)}) = \delta _{f(n+1)}\}$
.
Theorem 4.8. If
![]() $\delta $
is good, then
$\delta $
is good, then
![]() ${\mathcal A}_{\delta }$
contains an honest subcategory isomorphic to an Aronszajn tree.
${\mathcal A}_{\delta }$
contains an honest subcategory isomorphic to an Aronszajn tree.
Proof Let us first describe our mechanism for splitting into incompatible nodes. Suppose M is a good model of height
![]() $\delta $
with witnessing sequence
$\delta $
with witnessing sequence
![]() $\langle \delta _n : n < \omega \rangle $
. Let us partition the natural numbers into blocks
$\langle \delta _n : n < \omega \rangle $
. Let us partition the natural numbers into blocks
![]() $B_0,B_1,B_2,\dots $
as follows. Let
$B_0,B_1,B_2,\dots $
as follows. Let
![]() $B_0 = \emptyset $
, and given
$B_0 = \emptyset $
, and given
![]() $B_{n-1}$
, let
$B_{n-1}$
, let
![]() $B_n$
be the next n numbers above
$B_n$
be the next n numbers above
![]() $B_{n-1}$
. In other words,
$B_{n-1}$
. In other words,
![]() $B_n = \{ \frac {n(n-1)}{2},\frac {n(n-1)}{2} + 1, \dots ,\frac {n(n-1)}{2} + n -1 \}$
for
$B_n = \{ \frac {n(n-1)}{2},\frac {n(n-1)}{2} + 1, \dots ,\frac {n(n-1)}{2} + n -1 \}$
for
![]() $n>0$
. Let
$n>0$
. Let
![]() $\langle B_n(i) : i < n \rangle $
enumerate block
$\langle B_n(i) : i < n \rangle $
enumerate block
![]() $B_n$
in increasing order. Using Lemma 4.7, for each n, we can take a
$B_n$
in increasing order. Using Lemma 4.7, for each n, we can take a
![]() $\mathbb P_{\infty }$
-generic
$\mathbb P_{\infty }$
-generic
![]() $G_n$
over M with associated embedding
$G_n$
over M with associated embedding
![]() $j_n$
such that:
$j_n$
such that:
-
(1)
 $\operatorname {\mathrm {crit}}(j_n) \geq \delta _n$
.
$\operatorname {\mathrm {crit}}(j_n) \geq \delta _n$
. -
(2) For sufficiently large m,
 $\delta _{B_m(n)}$
is fixed by
$\delta _{B_m(n)}$
is fixed by
 $j_n$
.
$j_n$
. -
(3) For sufficiently large m, if
 $B_{m}(n)<i<B_{m+1}(n)$
, then
$B_{m}(n)<i<B_{m+1}(n)$
, then
 $\delta _i$
has cardinality
$\delta _i$
has cardinality
 $\delta _{B_{m}(n)}$
in
$\delta _{B_{m}(n)}$
in
 $M[G_n]$
.
$M[G_n]$
.
This ensures that if
![]() $n_0 < n_1$
, then there is no model N of ZF with the same class of ordinals
$n_0 < n_1$
, then there is no model N of ZF with the same class of ordinals
![]() $\delta $
containing both
$\delta $
containing both
![]() $M[G_{n_0}]$
and
$M[G_{n_0}]$
and
![]() $M[G_{n_1}]$
. For if there were such an N, then in N, for sufficiently large m,
$M[G_{n_1}]$
. For if there were such an N, then in N, for sufficiently large m,
![]() $|\delta _{B_m(n_0)}| = |\delta _{B_m(n_1)}| = |\delta _{B_{m+1}(n_0)}|$
, and so N would have a largest cardinal.
$|\delta _{B_m(n_0)}| = |\delta _{B_m(n_1)}| = |\delta _{B_{m+1}(n_0)}|$
, and so N would have a largest cardinal.
Let
![]() $M_0$
be a good model of height
$M_0$
be a good model of height
![]() $\delta $
, with witnessing sequence
$\delta $
, with witnessing sequence
![]() $\langle \delta _n : n <\omega \rangle $
. We will build an
$\langle \delta _n : n <\omega \rangle $
. We will build an
![]() $\omega _1$
-tree
$\omega _1$
-tree
![]() $T \subseteq \,^{<\omega _1}\omega $
by induction. Each
$T \subseteq \,^{<\omega _1}\omega $
by induction. Each
![]() $\sigma \in T$
will be assigned a good model
$\sigma \in T$
will be assigned a good model
![]() $M_{\sigma }$
of height
$M_{\sigma }$
of height
![]() $\delta $
, and for pairs
$\delta $
, and for pairs
![]() $\sigma \subseteq \tau $
in T, we will assign an amenable embedding
$\sigma \subseteq \tau $
in T, we will assign an amenable embedding
![]() $j_{\sigma ,\tau } : M_{\sigma } \to M_{\tau }$
, such that if
$j_{\sigma ,\tau } : M_{\sigma } \to M_{\tau }$
, such that if
![]() $\sigma \subseteq \tau \subseteq \upsilon $
, then
$\sigma \subseteq \tau \subseteq \upsilon $
, then
![]() $j_{\sigma ,\upsilon } = j_{\tau ,\upsilon }\circ j_{\sigma ,\tau }$
. When
$j_{\sigma ,\upsilon } = j_{\tau ,\upsilon }\circ j_{\sigma ,\tau }$
. When
![]() $\sigma \perp \tau $
, we will arrange that there is not any ZF model N of height
$\sigma \perp \tau $
, we will arrange that there is not any ZF model N of height
![]() $\delta $
such that
$\delta $
such that
![]() $M_{\sigma },M_{\tau } \subseteq N$
, which guarantees that there is no arrow between
$M_{\sigma },M_{\tau } \subseteq N$
, which guarantees that there is no arrow between
![]() $M_{\sigma }$
and
$M_{\sigma }$
and
![]() $M_{\tau }$
in the category
$M_{\tau }$
in the category
![]() ${\mathcal A}_{\delta }$
. This makes the tree of models an honest subcategory. Theorem 4.6 will ensure that T is Aronszajn.
${\mathcal A}_{\delta }$
. This makes the tree of models an honest subcategory. Theorem 4.6 will ensure that T is Aronszajn.
We build T as a union of trees
![]() $T_{\alpha }$
for
$T_{\alpha }$
for
![]() $\alpha < \omega _1$
, where
$\alpha < \omega _1$
, where
![]() $T_{\alpha }$
has height
$T_{\alpha }$
has height
![]() $\alpha +1$
, and
$\alpha +1$
, and
![]() $T_{\beta }$
end-extends
$T_{\beta }$
end-extends
![]() $T_{\beta }$
for
$T_{\beta }$
for
![]() $\beta>\alpha $
. Along the way, we build an increasing sequence of injective functors
$\beta>\alpha $
. Along the way, we build an increasing sequence of injective functors
![]() $F_{\alpha } : T_{\alpha } \to {\mathcal A}_{\delta }$
. Put
$F_{\alpha } : T_{\alpha } \to {\mathcal A}_{\delta }$
. Put
![]() $T_0 = \{\emptyset \}$
and
$T_0 = \{\emptyset \}$
and
![]() $F_0(\emptyset ) = M_0$
. Given
$F_0(\emptyset ) = M_0$
. Given
![]() $T_{\alpha }$
and
$T_{\alpha }$
and
![]() $F_{\alpha }$
, form
$F_{\alpha }$
, form
![]() $T_{\alpha +1}$
by adding
$T_{\alpha +1}$
by adding
![]() $\sigma ^{\smallfrown } \langle n \rangle $
for each top node
$\sigma ^{\smallfrown } \langle n \rangle $
for each top node
![]() $\sigma $
and each
$\sigma $
and each
![]() $n < \omega $
. For such top nodes
$n < \omega $
. For such top nodes
![]() $\sigma $
, take an embedding
$\sigma $
, take an embedding
![]() $j_{\sigma ,\sigma ^{\smallfrown }\langle n\rangle } : M_{\sigma } \to M_{\sigma ,\sigma ^{\smallfrown }\langle n\rangle } = M_{\sigma }[G_n]$
as above, so that no two of them amalgamate. For
$j_{\sigma ,\sigma ^{\smallfrown }\langle n\rangle } : M_{\sigma } \to M_{\sigma ,\sigma ^{\smallfrown }\langle n\rangle } = M_{\sigma }[G_n]$
as above, so that no two of them amalgamate. For
![]() $\tau \subseteq \sigma $
, let
$\tau \subseteq \sigma $
, let
![]() $j_{\tau ,\sigma ^{\smallfrown }\langle n\rangle } = j_{\sigma ,\sigma ^{\smallfrown }\langle n\rangle } \circ j_{\tau ,\sigma }$
.
$j_{\tau ,\sigma ^{\smallfrown }\langle n\rangle } = j_{\sigma ,\sigma ^{\smallfrown }\langle n\rangle } \circ j_{\tau ,\sigma }$
.
Suppose
![]() $\lambda $
is a countable limit ordinal and we have constructed
$\lambda $
is a countable limit ordinal and we have constructed
![]() $T_{\alpha }$
and
$T_{\alpha }$
and
![]() $F_{\alpha }$
for
$F_{\alpha }$
for
![]() $\alpha <\lambda $
. Let
$\alpha <\lambda $
. Let
![]() $T_{\lambda }'$
and
$T_{\lambda }'$
and
![]() $F_{\lambda }'$
be the unions of the previously constructed trees and functors. We must build the top level. Let us assume the following inductive hypothesis: for each
$F_{\lambda }'$
be the unions of the previously constructed trees and functors. We must build the top level. Let us assume the following inductive hypothesis: for each
![]() $\alpha <\lambda $
, each
$\alpha <\lambda $
, each
![]() $\sigma \in T_{\alpha }$
, and each
$\sigma \in T_{\alpha }$
, and each
![]() $n<\omega $
, there is
$n<\omega $
, there is
![]() $\tau \supseteq \sigma $
at the top level of
$\tau \supseteq \sigma $
at the top level of
![]() $T_{\alpha }$
such that
$T_{\alpha }$
such that
![]() $\operatorname {\mathrm {crit}}(j_{\sigma ,\tau }) \geq \delta _n$
. To construct
$\operatorname {\mathrm {crit}}(j_{\sigma ,\tau }) \geq \delta _n$
. To construct
![]() $T_{\lambda }$
, use the induction hypothesis to choose for each node
$T_{\lambda }$
, use the induction hypothesis to choose for each node
![]() $\sigma \in T_{\lambda }'$
and each
$\sigma \in T_{\lambda }'$
and each
![]() $n<\omega $
, an increasing sequence
$n<\omega $
, an increasing sequence
![]() $\langle \tau _i : i < \omega \rangle \subseteq T_{\lambda }'$
such that
$\langle \tau _i : i < \omega \rangle \subseteq T_{\lambda }'$
such that
![]() $\tau _0 = \sigma $
,
$\tau _0 = \sigma $
,
![]() $\sup _i \operatorname {\mathrm {len}}(\tau _i) = \lambda $
, and for each
$\sup _i \operatorname {\mathrm {len}}(\tau _i) = \lambda $
, and for each
![]() $i < \omega $
,
$i < \omega $
,
Let
![]() $\tau (\sigma ,n) = \bigcup _i \tau _i$
. By Lemma 4.4, the direct limit of the system
$\tau (\sigma ,n) = \bigcup _i \tau _i$
. By Lemma 4.4, the direct limit of the system
![]() $\langle j_{\tau _i,\tau _m} : M_{\tau _i} \to M_{\tau _m} : i \leq m < \omega \rangle $
yields a model
$\langle j_{\tau _i,\tau _m} : M_{\tau _i} \to M_{\tau _m} : i \leq m < \omega \rangle $
yields a model
![]() $M_{\tau (\sigma ,n)}$
of height
$M_{\tau (\sigma ,n)}$
of height
![]() $\delta $
such that the direct limit maps
$\delta $
such that the direct limit maps
![]() $j_{\tau _i, \tau (\sigma ,n)} : M_{\tau _i} \to M_{\tau (\sigma ,n)}$
are amenable. If
$j_{\tau _i, \tau (\sigma ,n)} : M_{\tau _i} \to M_{\tau (\sigma ,n)}$
are amenable. If
![]() $\sigma \subseteq \upsilon \subseteq \tau (\sigma ,n)$
, then the map
$\sigma \subseteq \upsilon \subseteq \tau (\sigma ,n)$
, then the map
![]() $j_{\upsilon ,\tau (\sigma ,n)}$
is given by
$j_{\upsilon ,\tau (\sigma ,n)}$
is given by
![]() $j_{\tau _i,\tau (\sigma ,n)} \circ j_{\upsilon ,\tau _i}$
for any i such that
$j_{\tau _i,\tau (\sigma ,n)} \circ j_{\upsilon ,\tau _i}$
for any i such that
![]() $\tau _i \supseteq \upsilon $
. Let the top level of
$\tau _i \supseteq \upsilon $
. Let the top level of
![]() $T_{\lambda }$
consist of all such
$T_{\lambda }$
consist of all such
![]() $\tau (\sigma ,n)$
, and let the functor
$\tau (\sigma ,n)$
, and let the functor
![]() $F_{\lambda }$
be defined as above. By construction, the inductive hypothesis is preserved.
$F_{\lambda }$
be defined as above. By construction, the inductive hypothesis is preserved.
Similar constructions yield other kinds of uncountable trees as honest subcategories of
![]() ${\mathcal A}_{\delta }$
. For example, we can build a copy of
${\mathcal A}_{\delta }$
. For example, we can build a copy of
![]() $^{<\omega }\omega $
where we also require that if
$^{<\omega }\omega $
where we also require that if
![]() $\sigma $
has length n, then for every initial segment
$\sigma $
has length n, then for every initial segment
![]() $\tau \subseteq \sigma $
and every
$\tau \subseteq \sigma $
and every
![]() $m<\omega $
,
$m<\omega $
,
![]() $\operatorname {\mathrm {crit}}(j_{\sigma ,\sigma ^{\smallfrown } \langle m \rangle })> j_{\tau ,\sigma }(\delta _n)$
. Then every branch yields a nice direct limit. An induction as in Corollary 4.5 allows this to be extended to any countable height. Let us record this as:
$\operatorname {\mathrm {crit}}(j_{\sigma ,\sigma ^{\smallfrown } \langle m \rangle })> j_{\tau ,\sigma }(\delta _n)$
. Then every branch yields a nice direct limit. An induction as in Corollary 4.5 allows this to be extended to any countable height. Let us record this as:
Proposition 4.9. If
![]() $\delta $
is good, then for every countable ordinal
$\delta $
is good, then for every countable ordinal
![]() $\alpha $
, there is an honest subcategory of
$\alpha $
, there is an honest subcategory of
![]() ${\mathcal A}_{\delta }$
isomorphic to the complete binary tree of height
${\mathcal A}_{\delta }$
isomorphic to the complete binary tree of height
![]() $\alpha $
.
$\alpha $
.
4.3 Ill-founded subcategories
In order to construct ill-founded subcategories of
![]() ${\mathcal A}_{\delta }$
, we pass to models of enough set theory that are well-founded beyond
${\mathcal A}_{\delta }$
, we pass to models of enough set theory that are well-founded beyond
![]() $\delta $
and contain some chosen member of
$\delta $
and contain some chosen member of
![]() ${\mathcal A}_{\delta }$
, but ultimately have ill-founded
${\mathcal A}_{\delta }$
, but ultimately have ill-founded
![]() $\omega _1$
. One way of achieving this is via Barwise compactness [Reference Barwise2]. Another is via the following:
$\omega _1$
. One way of achieving this is via Barwise compactness [Reference Barwise2]. Another is via the following:
Fact 4.10 (See [Reference Foreman6, Section 2.6])
Suppose r is a real. Let G be generic for
![]() $\mathcal {P}(\omega _1)/\operatorname {\mathrm {NS}}$
over
$\mathcal {P}(\omega _1)/\operatorname {\mathrm {NS}}$
over
![]() $L[r]$
. Let
$L[r]$
. Let
![]() $j : L[r] \to N = \operatorname {\mathrm {Ult}}(L[r],G)$
be the ultrapower embedding. Then N is well-founded up to
$j : L[r] \to N = \operatorname {\mathrm {Ult}}(L[r],G)$
be the ultrapower embedding. Then N is well-founded up to
![]() $\omega _2^{L[r]}$
, but
$\omega _2^{L[r]}$
, but
![]() $\omega _1^N$
is ill-founded.
$\omega _1^N$
is ill-founded.
We can decompose each ordinal in such a model into a sum of purely ill-founded and a purely well-founded part. Let N be any countable ill-founded model of
![]() $\mathrm { ZF} -$
Powerset that has standard
$\mathrm { ZF} -$
Powerset that has standard
![]() $\omega $
. Let
$\omega $
. Let
![]() $\xi $
be the ordertype of the set of well-founded ordinals of N. Friedman [Reference Friedman7] showed that the ordertype of the ordinals of N is
$\xi $
be the ordertype of the set of well-founded ordinals of N. Friedman [Reference Friedman7] showed that the ordertype of the ordinals of N is
![]() $\xi + ({\mathbb Q} \times \xi )$
. Thus every N-ordinal
$\xi + ({\mathbb Q} \times \xi )$
. Thus every N-ordinal
![]() $\alpha $
can be written as
$\alpha $
can be written as
![]() $\alpha = i(\alpha ) + w(\alpha )$
, where
$\alpha = i(\alpha ) + w(\alpha )$
, where
![]() $w(\alpha ) <\xi $
, and
$w(\alpha ) <\xi $
, and
![]() $i(\alpha )$
is either 0 or is represented in the isomorphism as
$i(\alpha )$
is either 0 or is represented in the isomorphism as
![]() $(q,0)$
, where
$(q,0)$
, where
![]() $q \in {\mathbb Q}$
.
$q \in {\mathbb Q}$
.
We apply this trick to construct honest subcategories of
![]() ${\mathcal A}_{\delta }$
isomorphic to three canonical ill-founded partial orders: the real numbers, the universal countable pseudotree (to be defined below), and the reverse-ordered complete binary tree. We present them in increasing order of the consistency strength of the hypothesis employed.
${\mathcal A}_{\delta }$
isomorphic to three canonical ill-founded partial orders: the real numbers, the universal countable pseudotree (to be defined below), and the reverse-ordered complete binary tree. We present them in increasing order of the consistency strength of the hypothesis employed.
Theorem 4.11. Suppose there is a countable transitive model of height
![]() $\delta $
of ZFC + “There is a proper class of completely Jónsson cardinals.” Then there is a subcategory of
$\delta $
of ZFC + “There is a proper class of completely Jónsson cardinals.” Then there is a subcategory of
![]() ${\mathcal A}_{\delta }$
isomorphic to the linear order
${\mathcal A}_{\delta }$
isomorphic to the linear order
![]() $\mathbb R$
.
$\mathbb R$
.
Proof Suppose M is a countable transitive model of height
![]() $\delta $
of ZFC + “There is a proper class of completely Jónsson cardinals” and
$\delta $
of ZFC + “There is a proper class of completely Jónsson cardinals” and
![]() $r_M$
is a real coding M. Let N be a countable model of
$r_M$
is a real coding M. Let N be a countable model of
![]() $\mathrm {ZFC} -$
Powerset with standard
$\mathrm {ZFC} -$
Powerset with standard
![]() $\omega $
and ill-founded
$\omega $
and ill-founded
![]() $\omega _1$
, such that
$\omega _1$
, such that
![]() $r_M \in N$
and the conclusion of Corollary 4.5 holds in N.
$r_M \in N$
and the conclusion of Corollary 4.5 holds in N.
Fix some
![]() $\zeta $
that N thinks is a countable ordinal but is really ill-founded. There is a subcategory of
$\zeta $
that N thinks is a countable ordinal but is really ill-founded. There is a subcategory of
![]() ${\mathcal A}_{\delta }$
isomorphic to the linear order
${\mathcal A}_{\delta }$
isomorphic to the linear order
![]() $\{ \alpha : N \models \alpha < \zeta \}$
. If we fix an increasing sequence
$\{ \alpha : N \models \alpha < \zeta \}$
. If we fix an increasing sequence
![]() $\langle \delta _n : n < \omega \rangle $
cofinal in
$\langle \delta _n : n < \omega \rangle $
cofinal in
![]() $\delta $
, then we can modify the construction in Corollary 4.5 slightly to require that if
$\delta $
, then we can modify the construction in Corollary 4.5 slightly to require that if
![]() $\kappa = \operatorname {\mathrm {crit}}(j_{\alpha ,\alpha +1})$
and
$\kappa = \operatorname {\mathrm {crit}}(j_{\alpha ,\alpha +1})$
and
![]() $\delta _n \leq \kappa <\delta _{n+1}$
, then
$\delta _n \leq \kappa <\delta _{n+1}$
, then
![]() $j_{\alpha ,\alpha +1}(\kappa ) \geq \delta _{n+1}$
.
$j_{\alpha ,\alpha +1}(\kappa ) \geq \delta _{n+1}$
.
Thus there is a subcategory of
![]() ${\mathcal A}_{\delta }$
isomorphic to the rationals, which has as its objects all models indexed by
${\mathcal A}_{\delta }$
isomorphic to the rationals, which has as its objects all models indexed by
![]() $i(\alpha )$
for
$i(\alpha )$
for
![]() $0<i(\alpha )<\zeta $
. Let us write this as
$0<i(\alpha )<\zeta $
. Let us write this as
![]() $\langle j_{a,b} : M_a \to M_b : a \leq b \in {\mathbb Q} \rangle $
. We have that for rationals
$\langle j_{a,b} : M_a \to M_b : a \leq b \in {\mathbb Q} \rangle $
. We have that for rationals
![]() $a<b$
, if
$a<b$
, if
![]() $\kappa = \operatorname {\mathrm {crit}}(j_{a,b})$
and
$\kappa = \operatorname {\mathrm {crit}}(j_{a,b})$
and
![]() $\delta _n \leq \kappa < \delta _{n+1}$
, then
$\delta _n \leq \kappa < \delta _{n+1}$
, then
![]() $j_{a,b}(\kappa ) \geq \delta _{n+1}$
. Now we argue that we can fill in the Dedekind cuts with direct limits and get a larger subcategory of
$j_{a,b}(\kappa ) \geq \delta _{n+1}$
. Now we argue that we can fill in the Dedekind cuts with direct limits and get a larger subcategory of
![]() ${\mathcal A}_{\delta }$
.
${\mathcal A}_{\delta }$
.
Suppose
![]() $r \in \mathbb R \setminus {\mathbb Q}$
. Let
$r \in \mathbb R \setminus {\mathbb Q}$
. Let
![]() $M_r$
be the direct limit and let
$M_r$
be the direct limit and let
![]() $j_{a,r}$
be the direct limit map for rationals
$j_{a,r}$
be the direct limit map for rationals
![]() $a<r$
. Let
$a<r$
. Let
![]() $b> r$
be rational. For
$b> r$
be rational. For
![]() $x \in M_r$
, there is a rational
$x \in M_r$
, there is a rational
![]() $a<r$
and
$a<r$
and
![]() $y \in M_a$
such that
$y \in M_a$
such that
![]() $x = j_{a,r}(y)$
. Let
$x = j_{a,r}(y)$
. Let
![]() $j_{r,b}(x) = j_{a,b}(y)$
for any such
$j_{r,b}(x) = j_{a,b}(y)$
for any such
![]() $a,y$
. The choice of
$a,y$
. The choice of
![]() $a,y$
does not matter, since if
$a,y$
does not matter, since if
![]() $x = j_{a,r}(y) = j_{a',r}(y')$
for
$x = j_{a,r}(y) = j_{a',r}(y')$
for
![]() $a < a'$
, then
$a < a'$
, then
![]() $y' = j_{a,a'}(y)$
, and
$y' = j_{a,a'}(y)$
, and
![]() $j_{a,b}(y) = j_{a',b}(y')$
. Furthermore, if
$j_{a,b}(y) = j_{a',b}(y')$
. Furthermore, if
![]() $b,b'$
are rational such that
$b,b'$
are rational such that
![]() $r<b<b'$
, then
$r<b<b'$
, then
![]() $j_{r,b'} = j_{b,b'} \circ j_{r,b}$
. This is because if
$j_{r,b'} = j_{b,b'} \circ j_{r,b}$
. This is because if
![]() $x \in M_r$
and
$x \in M_r$
and
![]() $a,y$
are such that
$a,y$
are such that
![]() $j_{a,r}(y) = x$
, then
$j_{a,r}(y) = x$
, then
If
![]() $M_r \models \varphi (x_0,\dots ,x_{n-1})$
, then there are a rational
$M_r \models \varphi (x_0,\dots ,x_{n-1})$
, then there are a rational
![]() $a<r$
and
$a<r$
and
![]() $y_0,\dots ,y_{n-1} \in M_a$
such that
$y_0,\dots ,y_{n-1} \in M_a$
such that
![]() $j_{a,r}(y_m) = x_m$
for
$j_{a,r}(y_m) = x_m$
for
![]() $m<n$
, and so
$m<n$
, and so
![]() $M_b \models \varphi (j_{a,b}(y_0),\dots ,j_{a,b}(y_{n-1}))$
. Thus
$M_b \models \varphi (j_{a,b}(y_0),\dots ,j_{a,b}(y_{n-1}))$
. Thus
![]() $j_{r,b}$
is elementary, and so
$j_{r,b}$
is elementary, and so
![]() $M_r$
is well-founded and has height
$M_r$
is well-founded and has height
![]() $\delta $
. For irrational numbers
$\delta $
. For irrational numbers
![]() $r<s$
, let
$r<s$
, let
![]() $j_{r,s} = j_{b,s} \circ j_{r,b}$
for any rational
$j_{r,s} = j_{b,s} \circ j_{r,b}$
for any rational
![]() $b \in (r,s)$
. The choice of b does not matter, since for
$b \in (r,s)$
. The choice of b does not matter, since for
![]() $b,b'$
rational such that
$b,b'$
rational such that
![]() $r < b < b' < s$
, we have
$r < b < b' < s$
, we have
To verify the commutativity of the system, let
![]() $r<s<t$
be reals and let
$r<s<t$
be reals and let
![]() $x \in M_r$
. Let
$x \in M_r$
. Let
![]() $b,c$
be rational such that
$b,c$
be rational such that
![]() $r<b<s<c<t$
. Then
$r<b<s<c<t$
. Then
But by definition,
![]() $j_{b,c}(z) = j_{s,c} \circ j_{b,s}(z)$
for any
$j_{b,c}(z) = j_{s,c} \circ j_{b,s}(z)$
for any
![]() $z \in M_b$
. Thus
$z \in M_b$
. Thus
To show that the maps are amenable, first suppose r is irrational,
![]() $a<r$
is rational, and
$a<r$
is rational, and
![]() $\gamma < \delta $
. Let
$\gamma < \delta $
. Let
![]() $\langle a_n : n < \omega \rangle $
be an increasing sequence of rationals converging to r, with
$\langle a_n : n < \omega \rangle $
be an increasing sequence of rationals converging to r, with
![]() $a_0 = a$
. For
$a_0 = a$
. For
![]() $n<\omega $
, let
$n<\omega $
, let
![]() $\kappa _n = \min \{ \operatorname {\mathrm {crit}}(j_{a_n,a_m}) : n<m < \omega \}$
. By passing to a subsequence if necessary, we may assume that for all n,
$\kappa _n = \min \{ \operatorname {\mathrm {crit}}(j_{a_n,a_m}) : n<m < \omega \}$
. By passing to a subsequence if necessary, we may assume that for all n,
![]() $\kappa _n = \operatorname {\mathrm {crit}}(j_{a_n,a_{n+1}})$
, and
$\kappa _n = \operatorname {\mathrm {crit}}(j_{a_n,a_{n+1}})$
, and
![]() $\kappa _n \leq \kappa _{n+1}$
. Now it cannot happen that for infinitely many n and all
$\kappa _n \leq \kappa _{n+1}$
. Now it cannot happen that for infinitely many n and all
![]() $m> n$
,
$m> n$
,
![]() $j_{a_n,a_m}(\kappa _n)> \kappa _m$
, because then the direct limit would be ill-founded. Thus there is some
$j_{a_n,a_m}(\kappa _n)> \kappa _m$
, because then the direct limit would be ill-founded. Thus there is some
![]() $n^*$
such that for all
$n^*$
such that for all
![]() $n \geq n^*$
, there is
$n \geq n^*$
, there is
![]() $m>n$
such that
$m>n$
such that
![]() $j_{a_n,a_m}(\kappa _n) \leq \kappa _m$
. By our extra requirement on how high the critical points are sent, this means that for large enough n,
$j_{a_n,a_m}(\kappa _n) \leq \kappa _m$
. By our extra requirement on how high the critical points are sent, this means that for large enough n,
![]() $\kappa _n> \gamma $
. Therefore, for a large enough n,
$\kappa _n> \gamma $
. Therefore, for a large enough n,
![]() $j_{a,r}[\gamma ] = j_{a_n,r}(j_{a,a_n}[\gamma ]) \in M_r$
.
$j_{a,r}[\gamma ] = j_{a_n,r}(j_{a,a_n}[\gamma ]) \in M_r$
.
Now suppose r is irrational,
![]() $b>r$
is rational, and
$b>r$
is rational, and
![]() $\gamma <\delta $
. By the previous paragraph, there is some rational
$\gamma <\delta $
. By the previous paragraph, there is some rational
![]() $a<r$
such that
$a<r$
such that
![]() $\operatorname {\mathrm {crit}}(j_{a,r})> \gamma $
. Thus
$\operatorname {\mathrm {crit}}(j_{a,r})> \gamma $
. Thus
![]() $j_{r,b}[\gamma ] = j_{a,b}[\gamma ] \in M_b$
. Finally, if
$j_{r,b}[\gamma ] = j_{a,b}[\gamma ] \in M_b$
. Finally, if
![]() $r<s$
are irrational, the map
$r<s$
are irrational, the map
![]() $j_{r,s}$
is amenable since it is the composition of two amenable maps
$j_{r,s}$
is amenable since it is the composition of two amenable maps
![]() $j_{b,s} \circ j_{r,b}$
, for any rational
$j_{b,s} \circ j_{r,b}$
, for any rational
![]() $b \in (r,s)$
.
$b \in (r,s)$
.
We note also that
![]() $M_r = \bigcup _{a<r} M_a$
for any r. This is true for rational r by the construction in the proof of Lemma 4.5, since all limit models are direct limits. If r is irrational and
$M_r = \bigcup _{a<r} M_a$
for any r. This is true for rational r by the construction in the proof of Lemma 4.5, since all limit models are direct limits. If r is irrational and
![]() $x \in M_r$
, then
$x \in M_r$
, then
![]() $x \in M_b$
for all rational
$x \in M_b$
for all rational
![]() $b> r$
. If
$b> r$
. If
![]() $x \notin \bigcup _{a<r} M_a$
, then N thinks there is some least ordinal
$x \notin \bigcup _{a<r} M_a$
, then N thinks there is some least ordinal
![]() $\gamma $
such that
$\gamma $
such that
![]() $x \in M_{\gamma }$
, which must be a successor ordinal of N. Thus
$x \in M_{\gamma }$
, which must be a successor ordinal of N. Thus
![]() $x \notin M_{i(\gamma )}$
, and
$x \notin M_{i(\gamma )}$
, and
![]() $i(\gamma )$
corresponds to a rational number greater than r. This contradiction shows that
$i(\gamma )$
corresponds to a rational number greater than r. This contradiction shows that
![]() $x \in M_a$
for some
$x \in M_a$
for some
![]() $a<r$
.
$a<r$
.
Using stationary tower forcing as the basic building block, we have constructed various (well-founded) trees and linear orders as honest subcategories of
![]() ${\mathcal A}_{\delta }$
. A natural generalization of these two kinds of partial orders is the notion of a pseudotree, which is simply a partial order which is linear below any given element. By the well-known universality of
${\mathcal A}_{\delta }$
. A natural generalization of these two kinds of partial orders is the notion of a pseudotree, which is simply a partial order which is linear below any given element. By the well-known universality of
![]() ${\mathbb Q}$
, all countable linear orders appear in
${\mathbb Q}$
, all countable linear orders appear in
![]() ${\mathcal A}_{\delta }$
for appropriate
${\mathcal A}_{\delta }$
for appropriate
![]() $\delta $
. In fact, this generalizes to pseudotrees:
$\delta $
. In fact, this generalizes to pseudotrees:
Theorem 4.12. If
![]() $\delta $
is good, then every countable pseudotree is isomorphic to an honest subcategory of
$\delta $
is good, then every countable pseudotree is isomorphic to an honest subcategory of
![]() ${\mathcal A}_{\delta }$
.
${\mathcal A}_{\delta }$
.
To prove this, we first construct a certain countable pseudotree which contains every other countable pseudotree as a substructure. Let
![]() $T_{{\mathbb Q}}$
be the collection of all partial functions
$T_{{\mathbb Q}}$
be the collection of all partial functions
![]() $f : {\mathbb Q} \to \omega $
such that:
$f : {\mathbb Q} \to \omega $
such that:
-
(1)
 $\operatorname {\mathrm {dom}} f$
is a proper initial segment of
$\operatorname {\mathrm {dom}} f$
is a proper initial segment of
 ${\mathbb Q}$
.
${\mathbb Q}$
. -
(2) If
 $f \not = \emptyset $
, then there is a finite sequence
$f \not = \emptyset $
, then there is a finite sequence
 $-\infty = q_0 < q_1 < \cdots < q_n = \max (\operatorname {\mathrm {dom}} f)$
such that for
$-\infty = q_0 < q_1 < \cdots < q_n = \max (\operatorname {\mathrm {dom}} f)$
such that for
 $i <n$
,
$i <n$
,
 $f \restriction (q_i,q_{i+1}]$
is constant.
$f \restriction (q_i,q_{i+1}]$
is constant.
We put
![]() $f \leq g$
when
$f \leq g$
when
![]() $f \subseteq g$
. Notice that
$f \subseteq g$
. Notice that
![]() $T_{{\mathbb Q}}$
satisfies the following axiom set, which we call DPM for “Dense Pseudotrees with Meets”:
$T_{{\mathbb Q}}$
satisfies the following axiom set, which we call DPM for “Dense Pseudotrees with Meets”:
-
(1) It’s a pseudotree with a least element 0.
-
(2) Every two elements
 $f,g$
have an infimum
$f,g$
have an infimum
 $f \wedge g$
.
$f \wedge g$
. -
(3) Infinite Splitting: For all
 $g,f_0,\dots ,f_{n-1}$
such that
$g,f_0,\dots ,f_{n-1}$
such that
 $f_i \wedge f_j = g$
for
$f_i \wedge f_j = g$
for
 $i<j < n$
, there is
$i<j < n$
, there is
 $f_n> g$
such that
$f_n> g$
such that
 $f_i \wedge f_n = g$
for
$f_i \wedge f_n = g$
for
 $i< n$
.
$i< n$
. -
(4) Density: If
 $g<f$
, there is h such that
$g<f$
, there is h such that
 $g<h<f$
.
$g<h<f$
.
To be more precise, we take the language to be
![]() $\{ 0, \wedge , \leq \}$
, where 0 is a constant,
$\{ 0, \wedge , \leq \}$
, where 0 is a constant,
![]() $\wedge $
is a binary function, and
$\wedge $
is a binary function, and
![]() $a<b$
means
$a<b$
means
![]() $a \leq b$
and
$a \leq b$
and
![]() $a \not = b$
. The third axiom is actually an infinite scheme. Let PM be the system consisting of only the first two axioms. Note that in the theory PM,
$a \not = b$
. The third axiom is actually an infinite scheme. Let PM be the system consisting of only the first two axioms. Note that in the theory PM,
![]() $\leq $
is definable in terms of
$\leq $
is definable in terms of
![]() $\wedge $
:
$\wedge $
:
![]() $p \leq q$
iff
$p \leq q$
iff
![]() $p \wedge q = p$
. Thus to verify that a map from one model of PM to another is an embedding, it suffices to show that it is an injection that is a homomorphism in the restricted language
$p \wedge q = p$
. Thus to verify that a map from one model of PM to another is an embedding, it suffices to show that it is an injection that is a homomorphism in the restricted language
![]() $\{0,\wedge \}$
.
$\{0,\wedge \}$
.
Lemma 4.13. Suppose T satisfies PM, Q satisfies DPM,
![]() $a \in T$
, S is a finite substructure of T, and
$a \in T$
, S is a finite substructure of T, and
![]() $\pi : S \to Q$
is an embedding. Then there is a finite substructure
$\pi : S \to Q$
is an embedding. Then there is a finite substructure
![]() $S'$
of T containing
$S'$
of T containing
![]() $S \cup \{ a \}$
and an embedding
$S \cup \{ a \}$
and an embedding
![]() $\pi ' : S' \to Q$
extending
$\pi ' : S' \to Q$
extending
![]() $\pi $
.
$\pi $
.
Proof Let us assume
![]() $a \notin S$
. Let
$a \notin S$
. Let
![]() $b = \max \{ a \wedge s : s \in S \}$
. Note that
$b = \max \{ a \wedge s : s \in S \}$
. Note that
![]() $a \wedge s = b \wedge s$
for all
$a \wedge s = b \wedge s$
for all
![]() $s \in S$
by the maximality of b. First we claim that
$s \in S$
by the maximality of b. First we claim that
![]() $S \cup \{ b \}$
and
$S \cup \{ b \}$
and
![]() $S \cup \{ a,b \}$
are both closed under the operation
$S \cup \{ a,b \}$
are both closed under the operation
![]() $\wedge $
. Let
$\wedge $
. Let
![]() $s_0 = \inf \{ s \in S : s \geq b \}$
. Since T is linearly ordered below
$s_0 = \inf \{ s \in S : s \geq b \}$
. Since T is linearly ordered below
![]() $s_0$
, for all
$s_0$
, for all
![]() $s \in S$
,
$s \in S$
,
 $$ \begin{align*}b \wedge s = \begin{cases} b, &\text{ if } b \leq s_0 \wedge s, \\ s_0 \wedge s, &\text{ if } s_0 \wedge s \leq b. \\ \end{cases}\end{align*} $$
$$ \begin{align*}b \wedge s = \begin{cases} b, &\text{ if } b \leq s_0 \wedge s, \\ s_0 \wedge s, &\text{ if } s_0 \wedge s \leq b. \\ \end{cases}\end{align*} $$
Thus for all
![]() $s \in S$
,
$s \in S$
,
![]() $b \wedge s \in S \cup \{ b \}$
. Further, if
$b \wedge s \in S \cup \{ b \}$
. Further, if
![]() $b \leq s \wedge s_0$
, then
$b \leq s \wedge s_0$
, then
![]() $b \leq a \wedge s$
. Thus for all
$b \leq a \wedge s$
. Thus for all
![]() $s \in S$
, either
$s \in S$
, either
![]() $a \wedge s = b$
, or
$a \wedge s = b$
, or
![]() $b> a \wedge s$
and so
$b> a \wedge s$
and so
![]() $b> s \wedge s_0$
, which implies
$b> s \wedge s_0$
, which implies
![]() $a \wedge s = b \wedge s = s \wedge s_0 \in S$
. Therefore,
$a \wedge s = b \wedge s = s \wedge s_0 \in S$
. Therefore,
![]() $S \cup \{ a,b \}$
is also closed under
$S \cup \{ a,b \}$
is also closed under
![]() $\wedge $
.
$\wedge $
.
Let us first extend
![]() $\pi $
to an embedding
$\pi $
to an embedding
![]() $\pi ' : S \cup \{b \} \to Q$
. If
$\pi ' : S \cup \{b \} \to Q$
. If
![]() $b \notin S$
, let
$b \notin S$
, let
![]() $s_1 \in S$
be the maximum element below b. Use Density to pick some
$s_1 \in S$
be the maximum element below b. Use Density to pick some
![]() $b^* \in Q$
such that
$b^* \in Q$
such that
![]() $\pi (s_1)<b^*<\pi (s_0)$
, and let
$\pi (s_1)<b^*<\pi (s_0)$
, and let
![]() $\pi '(b) = b^*$
. Suppose
$\pi '(b) = b^*$
. Suppose
![]() $s \in S$
. If
$s \in S$
. If
![]() $s_0 \leq s$
, then
$s_0 \leq s$
, then
![]() $\pi '(b \wedge s) = \pi '(b) = b^* = b^* \wedge \pi (s)$
, since
$\pi '(b \wedge s) = \pi '(b) = b^* = b^* \wedge \pi (s)$
, since
![]() $\pi (s) \geq \pi (s_0)> b^*$
. If
$\pi (s) \geq \pi (s_0)> b^*$
. If
![]() $s_0 \nleq s$
, then
$s_0 \nleq s$
, then
![]() $s_0 \wedge s \leq s_1$
by the minimality of
$s_0 \wedge s \leq s_1$
by the minimality of
![]() $s_0$
, and
$s_0$
, and
![]() $\pi '(b \wedge s) = \pi (s_0 \wedge s) = \pi (s_0) \wedge \pi (s) = b^* \wedge \pi (s_0) \wedge \pi (s) = b^* \wedge \pi (s)$
, since
$\pi '(b \wedge s) = \pi (s_0 \wedge s) = \pi (s_0) \wedge \pi (s) = b^* \wedge \pi (s_0) \wedge \pi (s) = b^* \wedge \pi (s)$
, since
![]() $\pi (s) \wedge \pi (s_0) \leq \pi (s_1) < b^*$
.
$\pi (s) \wedge \pi (s_0) \leq \pi (s_1) < b^*$
.
Now if b is not maximal in
![]() $S \cup \{b \}$
, let
$S \cup \{b \}$
, let
![]() $\{ c_0,\dots ,c_{n-1} \}$
be the set of minimal elements above b in S, which implies that
$\{ c_0,\dots ,c_{n-1} \}$
be the set of minimal elements above b in S, which implies that
![]() $c_i \wedge c_j = b$
for
$c_i \wedge c_j = b$
for
![]() $i < j < n$
. Use Infinite Splitting to find
$i < j < n$
. Use Infinite Splitting to find
![]() $a^* \in Q$
such that
$a^* \in Q$
such that
![]() $a^*> b^*$
and, if the
$a^*> b^*$
and, if the
![]() $c_i$
are defined,
$c_i$
are defined,
![]() $a^* \wedge \pi (c_i) = b^*$
for
$a^* \wedge \pi (c_i) = b^*$
for
![]() $i< n$
. We claim that for all
$i< n$
. We claim that for all
![]() $s \in S$
,
$s \in S$
,
![]() $a^* \wedge \pi (s) = b^* \wedge \pi (s)$
. For if
$a^* \wedge \pi (s) = b^* \wedge \pi (s)$
. For if
![]() $s = b$
,
$s = b$
,
![]() $a^* \wedge \pi (b) = a^* \wedge b^* = b^* = b^* \wedge b^*$
. If
$a^* \wedge \pi (b) = a^* \wedge b^* = b^* = b^* \wedge b^*$
. If
![]() $s> b$
, then
$s> b$
, then
![]() $s \geq c_i$
for some
$s \geq c_i$
for some
![]() $i < n$
, so
$i < n$
, so
![]() $a^* \wedge \pi (s) = b^*$
. If
$a^* \wedge \pi (s) = b^*$
. If
![]() $s \ngeq b$
, then
$s \ngeq b$
, then
![]() $\pi (s) \wedge b^* < b^* < a^*$
, so also
$\pi (s) \wedge b^* < b^* < a^*$
, so also
![]() $\pi (s) \wedge a^* < b^*$
, and thus
$\pi (s) \wedge a^* < b^*$
, and thus
![]() $a^* \wedge \pi (s) = b^* \wedge \pi (s)$
. Thus for all
$a^* \wedge \pi (s) = b^* \wedge \pi (s)$
. Thus for all
![]() $s \in S$
,
$s \in S$
,
![]() $\pi '(a \wedge s) = \pi '(b \wedge s) = b^* \wedge \pi (s) = a^* \wedge \pi (s)$
. Therefore, we may define the desired extension
$\pi '(a \wedge s) = \pi '(b \wedge s) = b^* \wedge \pi (s) = a^* \wedge \pi (s)$
. Therefore, we may define the desired extension
![]() $\pi "$
of
$\pi "$
of
![]() $\pi '$
by putting
$\pi '$
by putting
![]() $\pi "(a) = a^*$
.
$\pi "(a) = a^*$
.
Corollary 4.14. Any countable model of PM can be embedded into any model of DPM, and any two countable models of DPM are isomorphic.
Proof Suppose
![]() $S \models $
PM,
$S \models $
PM,
![]() $T \models $
DPM, and S is countable. Let
$T \models $
DPM, and S is countable. Let
![]() $\langle s_i : i < \omega \rangle $
enumerate S. Using Lemma 4.13, we can build increasing sequences of finite substructures
$\langle s_i : i < \omega \rangle $
enumerate S. Using Lemma 4.13, we can build increasing sequences of finite substructures
![]() $S_n \subseteq S$
and embeddings
$S_n \subseteq S$
and embeddings
![]() $\pi _n : S_n \to T$
for
$\pi _n : S_n \to T$
for
![]() $n<\omega $
, such that
$n<\omega $
, such that
![]() $S_n \supseteq \{ s_i : i < n \}$
. Then
$S_n \supseteq \{ s_i : i < n \}$
. Then
![]() $\pi = \bigcup _{n<\omega } \pi _n$
is an embedding of S into T. If we additionally assume that
$\pi = \bigcup _{n<\omega } \pi _n$
is an embedding of S into T. If we additionally assume that
![]() $T = \{ t_i : i < \omega \}$
and
$T = \{ t_i : i < \omega \}$
and
![]() $S \models $
DPM, then given
$S \models $
DPM, then given
![]() $\pi _n : S_n \to T$
, we can find a finite substructure
$\pi _n : S_n \to T$
, we can find a finite substructure
![]() $T_n \supseteq \operatorname {\mathrm {ran}} \pi _n \cup \{ t_n \}$
and an embedding
$T_n \supseteq \operatorname {\mathrm {ran}} \pi _n \cup \{ t_n \}$
and an embedding
![]() $\sigma _n : T_n \to S$
extending
$\sigma _n : T_n \to S$
extending
![]() $\pi _n^{-1}$
. We then take
$\pi _n^{-1}$
. We then take
![]() $S_{n+1} \supseteq \operatorname {\mathrm {ran}} \sigma _n \cup \{ s_n \}$
and
$S_{n+1} \supseteq \operatorname {\mathrm {ran}} \sigma _n \cup \{ s_n \}$
and
![]() $\pi _{n+1}$
extending
$\pi _{n+1}$
extending
![]() $\sigma _n^{-1}$
. Then
$\sigma _n^{-1}$
. Then
![]() $\pi = \bigcup _{n<\omega } \pi _n$
is an isomorphism.
$\pi = \bigcup _{n<\omega } \pi _n$
is an isomorphism.
Lemma 4.15. Every pseudotree is a substructure of a model of PM.
Proof Let T be a pseudotree. T is isomorphic to the collection of its subsets of the form
![]() $S_t = \{ x \in T : x \leq t \}$
, ordered by inclusion. Extend this to a collection
$S_t = \{ x \in T : x \leq t \}$
, ordered by inclusion. Extend this to a collection
![]() $T^*$
by adding
$T^*$
by adding
![]() $S_{t_0} \cap S_{t_1}$
for every two
$S_{t_0} \cap S_{t_1}$
for every two
![]() $t_0,t_1\in T$
, and
$t_0,t_1\in T$
, and
![]() $\emptyset $
if T does not already have a minimal element. We claim that
$\emptyset $
if T does not already have a minimal element. We claim that
![]() $T^*$
is closed under finite intersection. Let
$T^*$
is closed under finite intersection. Let
![]() $t_0,t_1,t_2,t_3 \in T$
. The sets
$t_0,t_1,t_2,t_3 \in T$
. The sets
![]() $S_{t_0} \cap S_{t_i}$
for
$S_{t_0} \cap S_{t_i}$
for
![]() $i < 4$
are initial segments of the linearly ordered set
$i < 4$
are initial segments of the linearly ordered set
![]() $S_{t_0}$
, and so are
$S_{t_0}$
, and so are
![]() $\subseteq $
-comparable. If j is such that
$\subseteq $
-comparable. If j is such that
![]() $S_{t_0} \cap S_{t_j}$
is smallest, then
$S_{t_0} \cap S_{t_j}$
is smallest, then
![]() $S_{t_0} \cap S_{t_j} \subseteq S_{t_i}$
for all
$S_{t_0} \cap S_{t_j} \subseteq S_{t_i}$
for all
![]() $i<4$
. To check that
$i<4$
. To check that
![]() $T^*$
is a pseudotree, suppose
$T^*$
is a pseudotree, suppose
![]() $S_0,S_1,S_2 \in T^*$
and
$S_0,S_1,S_2 \in T^*$
and
![]() $S_0,S_1 \subseteq S_2$
. Again,
$S_0,S_1 \subseteq S_2$
. Again,
![]() $S_0$
and
$S_0$
and
![]() $S_1$
are initial segments of a linear order, so one is contained in the other.
$S_1$
are initial segments of a linear order, so one is contained in the other.
Corollary 4.16. Every countable pseudotree can be embedded into
![]() $T_{{\mathbb Q}}$
.
$T_{{\mathbb Q}}$
.
Now we argue that if
![]() $\delta $
is a good ordinal, there is a countable honest subcategory of
$\delta $
is a good ordinal, there is a countable honest subcategory of
![]() ${\mathcal A}_{\delta }$
that is a partial order satisfying DPM. Suppose M is a good model of height
${\mathcal A}_{\delta }$
that is a partial order satisfying DPM. Suppose M is a good model of height
![]() $\delta $
and
$\delta $
and
![]() $r_M$
is a real coding M. Let N be a countable model of
$r_M$
is a real coding M. Let N be a countable model of
![]() $\mathrm {ZFC} -$
Powerset with standard
$\mathrm {ZFC} -$
Powerset with standard
![]() $\omega $
and ill-founded
$\omega $
and ill-founded
![]() $\omega _1$
, such that
$\omega _1$
, such that
![]() $r_M \in N$
and N satisfies the conclusion of Theorem 4.8. In the real universe, the object T that N thinks is an Aronszajn tree isomorphic to an honest subcategory of
$r_M \in N$
and N satisfies the conclusion of Theorem 4.8. In the real universe, the object T that N thinks is an Aronszajn tree isomorphic to an honest subcategory of
![]() ${\mathcal A}_{\delta }^N$
is actually a countable pseudotree isomorphic to an honest subcategory of
${\mathcal A}_{\delta }^N$
is actually a countable pseudotree isomorphic to an honest subcategory of
![]() ${\mathcal A}_{\delta }$
, since
${\mathcal A}_{\delta }$
, since
![]() $\delta $
is in the well-founded part of N, and because the non-amalgamability of models corresponding to incompatible nodes is witnessed in an absolute way. We will find a substructure of T that satisfies DPM.
$\delta $
is in the well-founded part of N, and because the non-amalgamability of models corresponding to incompatible nodes is witnessed in an absolute way. We will find a substructure of T that satisfies DPM.
As before, each N-ordinal
![]() $\alpha $
has a decomposition into ill-founded and well-founded parts,
$\alpha $
has a decomposition into ill-founded and well-founded parts,
![]() $\alpha = i(\alpha )+w(\alpha )$
, and the collection
$\alpha = i(\alpha )+w(\alpha )$
, and the collection
![]() $\{ i(\alpha ) : \alpha < \omega _1^N \}$
is a dense linear order with a left endpoint. Let
$\{ i(\alpha ) : \alpha < \omega _1^N \}$
is a dense linear order with a left endpoint. Let
![]() $S \subseteq T$
be the collection of nodes at levels
$S \subseteq T$
be the collection of nodes at levels
![]() $i(\alpha )$
for
$i(\alpha )$
for
![]() $\alpha < \omega _1^N$
. Let us verify each axiom of DPM. We have already argued that it’s a pseudotree, and we keep the root node. For infima, if
$\alpha < \omega _1^N$
. Let us verify each axiom of DPM. We have already argued that it’s a pseudotree, and we keep the root node. For infima, if
![]() $s,t \in S$
are incomparable, then N thinks that there is a least ordinal
$s,t \in S$
are incomparable, then N thinks that there is a least ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $s(\alpha ) \not = t(\alpha )$
. Then
$s(\alpha ) \not = t(\alpha )$
. Then
![]() $s \restriction i(\alpha ) = t \restriction i(\alpha )$
is the infimum of s and t in S, since
$s \restriction i(\alpha ) = t \restriction i(\alpha )$
is the infimum of s and t in S, since
![]() $i(\alpha )<i(\beta )$
implies
$i(\alpha )<i(\beta )$
implies
![]() $\alpha <\beta $
. To verify Density, just use the fact that the collection of levels of S is a dense linear order. To verify Infinite Splitting, let
$\alpha <\beta $
. To verify Density, just use the fact that the collection of levels of S is a dense linear order. To verify Infinite Splitting, let
![]() $g,f_0,\dots ,f_{n-1}$
be as in the hypothesis, so that
$g,f_0,\dots ,f_{n-1}$
be as in the hypothesis, so that
![]() $g = f_k \wedge _S f_m$
for
$g = f_k \wedge _S f_m$
for
![]() $k<m<n$
. Let
$k<m<n$
. Let
![]() $\gamma = \operatorname {\mathrm {dom}} g$
. We may select any
$\gamma = \operatorname {\mathrm {dom}} g$
. We may select any
![]() $f_n\in S$
such that
$f_n\in S$
such that
![]() $f_n \restriction \gamma = g$
and
$f_n \restriction \gamma = g$
and
![]() $f_n(\gamma ) \not = f_m(\gamma )$
for all
$f_n(\gamma ) \not = f_m(\gamma )$
for all
![]() $m<n$
. This completes the proof of Theorem 4.12.
$m<n$
. This completes the proof of Theorem 4.12.
Remark. As pointed out by the referee, Theorem 4.12 has the following generalization. If we construct the tree of models and embeddings in the proof of Theorem 4.8 with the additional requirement that the critical points are always sent sufficiently high, as in the proof of Theorem 4.11, then we can take a Dedekind completion of our universal countable pseudotree and obtain an isomorphic honest subcategory of
![]() ${\mathcal A}_{\delta }$
. Such a pseudotree will be universal for the class of pseudotrees possessing a countable dense subset.
${\mathcal A}_{\delta }$
. Such a pseudotree will be universal for the class of pseudotrees possessing a countable dense subset.
Theorem 4.17. If there is a set of measurable cardinals of ordertype
![]() $\omega +1$
, then there is a countable ordinal
$\omega +1$
, then there is a countable ordinal
![]() $\delta $
such that
$\delta $
such that
![]() ${\mathcal A}_{\delta }$
contains an honest subcategory isomorphic to the reverse-ordered complete binary tree of height
${\mathcal A}_{\delta }$
contains an honest subcategory isomorphic to the reverse-ordered complete binary tree of height
![]() $\omega $
.
$\omega $
.
Proof Let
![]() $\kappa $
be the
$\kappa $
be the
![]() $\omega +1^{st}$
measurable cardinal, with normal measure
$\omega +1^{st}$
measurable cardinal, with normal measure
![]() ${\mathcal U}$
. Let M be a countable transitive set such that there is an elementary embedding
${\mathcal U}$
. Let M be a countable transitive set such that there is an elementary embedding
![]() $\sigma : M \to (H_{\theta },\in ,{\mathcal U})$
, for
$\sigma : M \to (H_{\theta },\in ,{\mathcal U})$
, for
![]() $\theta>2^{\kappa }$
regular. Let
$\theta>2^{\kappa }$
regular. Let
![]() $\kappa ^*,{\mathcal U}^* \in M$
be such that
$\kappa ^*,{\mathcal U}^* \in M$
be such that
![]() $\sigma (\kappa ^*) = \kappa $
and
$\sigma (\kappa ^*) = \kappa $
and
![]() $\sigma ({\mathcal U}^*)={\mathcal U}$
. Then
$\sigma ({\mathcal U}^*)={\mathcal U}$
. Then
![]() $(M,{\mathcal U}^*)$
is iterable. (See, for example, Lemma 19.11 of [Reference Kanamori11].)
$(M,{\mathcal U}^*)$
is iterable. (See, for example, Lemma 19.11 of [Reference Kanamori11].)
Let
![]() $r_M$
be a real coding
$r_M$
be a real coding
![]() $(M,{\mathcal U}^*)$
, and let N be a countable model of
$(M,{\mathcal U}^*)$
, and let N be a countable model of
![]() $\mathrm {ZFC} - $
Powerset with standard
$\mathrm {ZFC} - $
Powerset with standard
![]() $\omega $
and ill-founded
$\omega $
and ill-founded
![]() $\omega _1$
, such that
$\omega _1$
, such that
![]() $r_M \in N$
, and satisfying that
$r_M \in N$
, and satisfying that
![]() $(M,{\mathcal U}^*)$
is iterable. Let
$(M,{\mathcal U}^*)$
is iterable. Let
![]() $\delta < \kappa ^*$
be completely Jónsson in M and above the first
$\delta < \kappa ^*$
be completely Jónsson in M and above the first
![]() $\omega $
measurables of M. Working in N, iterate
$\omega $
measurables of M. Working in N, iterate
![]() $(M,{\mathcal U}^*) \ \omega _1^N$
-many times, and let
$(M,{\mathcal U}^*) \ \omega _1^N$
-many times, and let
![]() $j : M \to M_{\omega _1^N}$
be the iterated ultrapower map. Then j is the identity below
$j : M \to M_{\omega _1^N}$
be the iterated ultrapower map. Then j is the identity below
![]() $\kappa ^*$
, and
$\kappa ^*$
, and
![]() $j(\kappa ^*) = \omega _1^N$
. Then take in N an elementary substructure
$j(\kappa ^*) = \omega _1^N$
. Then take in N an elementary substructure
![]() $M^*$
of
$M^*$
of
![]() $(V_{j(\kappa ^*)})^{M_{\omega _1^N}}$
that N thinks is countable and transitive, containing some N-ordinal
$(V_{j(\kappa ^*)})^{M_{\omega _1^N}}$
that N thinks is countable and transitive, containing some N-ordinal
![]() $\zeta $
which is really ill-founded.
$\zeta $
which is really ill-founded.
Now we apply Theorem 4.1 in N. Let
![]() $T \in N$
be a sequential tree such that N thinks T is well-founded and of rank
$T \in N$
be a sequential tree such that N thinks T is well-founded and of rank
![]() $\zeta $
. In N, there is an honest subcategory of
$\zeta $
. In N, there is an honest subcategory of
![]() ${\mathcal A}_{\delta }$
isomorphic to T. The honesty is absolute to our universe, since the incomparability is just witnessed by inequalities among the ordertypes of the first
${\mathcal A}_{\delta }$
isomorphic to T. The honesty is absolute to our universe, since the incomparability is just witnessed by inequalities among the ordertypes of the first
![]() $\omega $
measurable cardinals of the various models corresponding to the nodes of T.
$\omega $
measurable cardinals of the various models corresponding to the nodes of T.
To complete the argument, we show that in our universe, there is a subtree of T isomorphic to the complete binary tree of height
![]() $\omega $
. It suffices to show that if
$\omega $
. It suffices to show that if
![]() $S \in N$
is a sequential tree such that
$S \in N$
is a sequential tree such that
![]() $N \models \rho _S(\emptyset ) = \zeta $
, where
$N \models \rho _S(\emptyset ) = \zeta $
, where
![]() $\zeta $
is really ill-founded, then there are incomparable nodes
$\zeta $
is really ill-founded, then there are incomparable nodes
![]() $p,q \in S$
such that
$p,q \in S$
such that
![]() $\rho _S(p)$
and
$\rho _S(p)$
and
![]() $\rho _S(q)$
are both ill-founded ordinals, for then the conclusion follows by a simple induction. Now since
$\rho _S(q)$
are both ill-founded ordinals, for then the conclusion follows by a simple induction. Now since
![]() $N \models \rho _S(t) = \sup _{s < t}(\rho _S(s) + 1)$
for all
$N \models \rho _S(t) = \sup _{s < t}(\rho _S(s) + 1)$
for all
![]() $t \in S$
, there is
$t \in S$
, there is
![]() $p \in S$
of rank
$p \in S$
of rank
![]() $i(\zeta )$
. Since
$i(\zeta )$
. Since
![]() $i(\zeta )$
is a limit ordinal, p must have infinitely many nodes immediately below it, call them
$i(\zeta )$
is a limit ordinal, p must have infinitely many nodes immediately below it, call them
![]() $\{ q_i : i <\omega \}$
, and
$\{ q_i : i <\omega \}$
, and
![]() $N \models \rho _S(p) = \sup _i(\rho _S(q_i) + 1)$
. Thus there are
$N \models \rho _S(p) = \sup _i(\rho _S(q_i) + 1)$
. Thus there are
![]() $n<m$
such that
$n<m$
such that
![]() $\rho _S(q_n)$
and
$\rho _S(q_n)$
and
![]() $\rho _S(q_m)$
are both ill-founded, as there is no least ill-founded ordinal.
$\rho _S(q_m)$
are both ill-founded, as there is no least ill-founded ordinal.
5 Questions
In an earlier version of this manuscript, we asked whether there can be two models of ZFC with the same ordinals such that each is elementarily embeddable into the other. This was answered in [Reference Eskew, Friedman, Hayut and Schlutzenberg5].
If M is a self-embeddable inner model, then in light of Theorems 1.1 and 1.2, it is interesting to ask how close M can be to V. The second author [Reference Friedman8] showed under some mild large cardinal assumptions that V can be a class-generic forcing extension of such an M. Some related questions include:
Question 1. Suppose M is a transitive proper class definable from parameters.
-
(1) Can M be self-embeddable and correct about cardinals?
-
(2) Can M be self-embeddable and correct about cofinalities?
-
(3) Can M be embeddable into V and be correct about either cardinals or cofinality
 $\omega $
?
$\omega $
?
Our direct-limit constructions in Section 4 were particular to countable models. Thus it is natural to ask:
Question 2. Is it consistent that there is an ordinal
![]() $\delta $
of uncountable cofinality such that
$\delta $
of uncountable cofinality such that
![]() ${\mathcal A}_{\delta }$
contains a copy of the linear order
${\mathcal A}_{\delta }$
contains a copy of the linear order
![]() $\omega +1$
?
$\omega +1$
?
Although we ruled out the possibility of a Suslin tree being isomorphic to a subcategory of
![]() ${\mathcal A}_{\delta }$
for a countable
${\mathcal A}_{\delta }$
for a countable
![]() $\delta $
, we don’t know much else about the combinatorial properties of the Aronszajn tree constructed in Theorem 4.8.
$\delta $
, we don’t know much else about the combinatorial properties of the Aronszajn tree constructed in Theorem 4.8.
Question 3. Characterize the class of Aronszajn trees that can be isomorphic to an honest subcategory of
![]() ${\mathcal A}_{\delta }$
for a countable
${\mathcal A}_{\delta }$
for a countable
![]() $\delta $
. Can it contain non-special trees?
$\delta $
. Can it contain non-special trees?
Our methods for building upward-growing and downward-growing trees as honest subcategories of
![]() ${\mathcal A}_{\delta }$
are quite different, and we don’t know if they can be combined in any interesting way. We would like to know if there is any structural asymmetry in this category, or rather:
${\mathcal A}_{\delta }$
are quite different, and we don’t know if they can be combined in any interesting way. We would like to know if there is any structural asymmetry in this category, or rather:
Question 4. Can an
![]() ${\mathcal A}_{\delta }$
contain an honest subcategory isomorphic to a “diamond,” i.e., the standard partial order on the four-element Boolean algebra?
${\mathcal A}_{\delta }$
contain an honest subcategory isomorphic to a “diamond,” i.e., the standard partial order on the four-element Boolean algebra?
Question 5. If
![]() $\mathbb P$
is a partial order isomorphic to an honest subcategory of
$\mathbb P$
is a partial order isomorphic to an honest subcategory of
![]() ${\mathcal A}_{\delta }$
, does this hold for the reverse of
${\mathcal A}_{\delta }$
, does this hold for the reverse of
![]() $\mathbb P$
?
$\mathbb P$
?
Acknowledgment
The authors wish to acknowledge the support of the Austrian Science Fund (FWF) through Research Project P28420.