1. Introduction
The addition of a small amount of flexible polymers in turbulent flows of Newtonian fluids can alter the flow properties significantly. The most notable effect is a significant reduction in the friction drag. The phenomenon of turbulent drag reduction by polymers was discovered approximately 75 years ago by Toms, who observed a substantial reduction in drag by adding only 10 parts per million by weight of polymethyl methacrylate in a turbulent flow of chlorobenzene down a pipe while studying the degradation of polymers (Toms Reference Toms1949). Similar effects have been observed in turbulent pipe or channel flows of water with polyethylene oxide or polyacrylamide (see, e.g. Virk Reference Virk1975). This effect has since been used to reduce energy losses in the transportation of crude oil in the Trans Alaska pipeline system (Burger, Munk & Wahl Reference Burger, Munk and Wahl1982). Thus, understanding the polymer-flow interactions and the mechanisms leading to drag reduction is not only a fundamental scientific challenge but also important for technological applications.
Numerical simulations play a crucial role in advancing our understanding of polymer drag reduction. A reasonably realistic model for flexible polymer chains is the Kuhn chain, which is a freely jointed chain of 
$N$ beads and $N-1$ rod-like links with the length $l$ of each link taken as the Kuhn length $l_K \equiv r_{eq}^2/L$, where $r_{eq}$ is the root-mean-square end-to-end distance and $L$ the contour length of the polymer (Doi & Edwards Reference Doi and Edwards1988). Coarse-grained models, known as bead-spring models, are obtained by replacing the rods of a freely jointed chain with one or more entropic springs. The bead-spring model with $N=2$ beads connected by a finitely extensible nonlinear elastic (FENE) spring (Bird et al. Reference Bird, Hassager, Armstrong and Curtiss1987) is called the FENE dumbbell model. Using the FENE dumbbell model and kinetic theory, continuum models of dilute polymer solutions can be obtained (Bird, Dotson & Johnson Reference Bird, Dotson and Johnson1980). Specifically, the constitutive equation relating the polymer stress tensor to the polymer conformation tensor and the evolution equation of the polymer conformation tensor have been derived using Peterlin's approximation (Peterlin Reference Peterlin1966). The resulting FENE-P model has been widely used in numerical studies and has captured the qualitative behaviour of polymer drag reduction found in experiments although quantitative agreement requires unphysical parameters such as unrealistically high polymer concentrations (Sureshkumar, Beris & Handler Reference Sureshkumar, Beris and Handler1997; De Angelis, Casciola & Piva Reference De Angelis, Casciola and Piva2002). Moreover, various numerical difficulties of the continuum FENE-P model have been known (Vaithianathan & Collins Reference Vaithianathan and Collins2003) and the Peterlin approximation has been shown to give rise to artifacts in turbulent flows when the Weissenberg number (the ratio of polymer relaxation time to fluid time scale), $Wi$, is large (Vincenzi et al. Reference Vincenzi, Perlekar, Biferale and Toschi2015). Lagrangian simulations of FENE dumbbells coupled with the turbulent flow of a Newtonian solvent (carrier fluid), generated by direct numerical simulation of incompressible Navier–Stokes equations, can overcome these numerical difficulties and problems (Peters & Schumacher Reference Peters and Schumacher2007; Watanabe & Gotoh Reference Watanabe and Gotoh2013). Such a hybrid Eulerian–Lagrangian numerical simulation (Serafini et al. Reference Serafini, Battista, Gualtieri and Casciola2022) of a turbulent flow coupled with DNA macromolecules modelled by FENE dumbbells with realistic parameters indeed shows significant drag reduction at sufficiently large $Wi$.
2. Overview
Real polymers have many internal degrees of freedom and a broad spectrum of relaxation time scales whereas the FENE dumbbell model is a highly simplified coarse-grained model and can only represent the longest relaxation time of the polymer. Extra degrees of freedom can be introduced by adding beads and springs, and this gives rise to a multibead FENE chain of $N$ beads connected by $N-1$ FENE springs (which reduces to the FENE dumbbell when $N=2$). Using Eulerian–Lagrangian simulations, Serafini et al. (Reference Serafini, Battista, Gualtieri and Casciola2024) have studied the dynamics of polymers, described by different models, in a turbulent pipe flow at a moderate friction Reynolds number and different $Wi = \tau /(r/U_b)$. The different models of polymers used are the Kuhn chain, FENE dumbbells and multibead FENE chain with $N > 2$, and freely jointed chain with $N \leqslant 101$. Here, $\tau$ is the polymer relaxation time, $r=0.5$ mm is the radius of the pipe, $U_b=Q/({\rm \pi} r^2)$ is the bulk velocity, and $Q$ is the volumetric flow rate. A small population of $10^5$ polymers has been used and the back reaction of the polymers to the flow is ignored. In their simulations, they chose $L=0.04 r$ and $l_K=2 \times 10^{-4} r$ to mimic a double-stranded DNA macromolecule with $\tau \approx 1$ s (Harnau & Reineker Reference Harnau and Reineker1999), which match those used in an experimental study of turbulent drag reduction (Choi et al. Reference Choi, Lim, Lai and Chan2002). With these values, it can be found that $N=201$ for the Kuhn chains. The maximum extension of the spring for the multibead FENE chains and the constant rod length for the freely jointed chains with general $N$ are chosen to maintain the same contour length $L$.
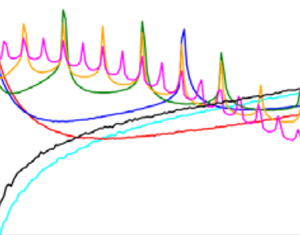
Figure 1 shows the distributions $p(R/L)$ of the end-to-end distance $R$ normalized by $L$ for the different models at $Wi=10^4$. The distribution for the FENE dumbbell ($N=2$) is close to that for the realistic Kuhn chain. Increasing the number of beads in a FENE chain worsens its accuracy in characterizing polymer spatial conformations. A multibead FENE chain with $N>2$ has a larger chance of folding up compared with the reference Kuhn chain thus overestimates the probability of folded configurations leading to spurious peaks in $p(R/L)$ (see figure 1a). Together with earlier findings that the polymer extension and polymer stresses statistics are insensitive to the number of beads of a multibead FENE chain (Jin & Collins Reference Jin and Collins2007; Watanabe & Gotoh Reference Watanabe and Gotoh2010; Vincenzi et al. Reference Vincenzi, Watanabe, Ray and Picardo2020) in isotropic turbulence at moderate $Wi$, these results for turbulent pipe flows at large $Wi$ establish that the FENE dumbbell is a better model than a multibead FENE chain with $N>2$ for studying polymer drag reduction. For the freely jointed chains, $p(R/L)$ converges as $N$ is increased and the results for $N \geqslant 21$ are almost indistinguishable (see figure 1b). Thus, a 21-bead freely jointed chain model would be a good choice for probing internal configurations of polymers at large $Wi$.
Figure 1. Distribution $p(R/L)$ of the normalized end-to-end distance for (a) multibead FENE chain with $N\,{\geqslant}\,2$ and the Kuhn chain (solid black line) and (b) freely jointed chain ($N=201$ for the Kuhn chain). Compilation from figures 2(a) and 5 in Serafini et al. (Reference Serafini, Battista, Gualtieri and Casciola2024).
3. Relevance and outlook
Understanding polymer–turbulence interactions and polymer drag reduction is highly challenging because of the wide range of length and time scales involved. Numerical simulation has been a major and important tool for addressing this challenge. The choice of what polymer model to use in numerical studies of polymer drag reduction depends on the balance between the accuracy of the model in capturing the essential details of real polymers and computational cost and feasibility. The work of Serafini et al. (Reference Serafini, Battista, Gualtieri and Casciola2024) has provided strong support that the highly simplified FENE dumbbell model is a reasonable choice. With this relatively simple model, efforts can then be focused to fully understand polymer–turbulence interactions.
In a recent Eulerian–Lagrangian simulation of a turbulent pipe flow of a dilute solution of polymers, modelled by FENE dumbbells with realistic physical parameters, the same authors (Serafini et al. Reference Serafini, Battista, Gualtieri and Casciola2022), showed that at $Wi = 10^4$, there is a significant drag reduction, and the drag reduction is due entirely to the back-reaction of fully stretched polymers. Moreover, the polymer stress resulted from this back-reaction force can be expressed in terms of some effective viscosity that depends on the local concentration of the polymers. It is important to check the generality of this physical picture by expanding the range of $Wi$ in numerical investigations since the relaxation time of drag reducing polymers varies a great deal depending on the molecular weights and specific types of polymers. Another interesting problem is to study the flow-dependent and thus space-dependent effective viscosity of the polymers, extracted from the polymer back-reaction force, and test whether it can explain the drag reducing effects of polymers in the same spirit as previously proposed in a phenomenological theory (Benzi et al. Reference Benzi, De Angelis, L'vov, Procaccia and Tiberkevich2006; Procaccia, L'vov & Benzi Reference Procaccia, L'vov and Benzi2008).
$p(R/L)$ of the normalized end-to-end distance for (a) multibead FENE chain with 
$N\,{\geqslant}\,2$ and the Kuhn chain (solid black line) and (b) freely jointed chain (
$N=201$ for the Kuhn chain). Compilation from figures 2(a) and 5 in Serafini et al. (2024).
You have
Access
Open access
1. Introduction
The addition of a small amount of flexible polymers in turbulent flows of Newtonian fluids can alter the flow properties significantly. The most notable effect is a significant reduction in the friction drag. The phenomenon of turbulent drag reduction by polymers was discovered approximately 75 years ago by Toms, who observed a substantial reduction in drag by adding only 10 parts per million by weight of polymethyl methacrylate in a turbulent flow of chlorobenzene down a pipe while studying the degradation of polymers (Toms Reference Toms1949). Similar effects have been observed in turbulent pipe or channel flows of water with polyethylene oxide or polyacrylamide (see, e.g. Virk Reference Virk1975). This effect has since been used to reduce energy losses in the transportation of crude oil in the Trans Alaska pipeline system (Burger, Munk & Wahl Reference Burger, Munk and Wahl1982). Thus, understanding the polymer-flow interactions and the mechanisms leading to drag reduction is not only a fundamental scientific challenge but also important for technological applications.
Numerical simulations play a crucial role in advancing our understanding of polymer drag reduction. A reasonably realistic model for flexible polymer chains is the Kuhn chain, which is a freely jointed chain of
$N$ beads and 
$N-1$ rod-like links with the length 
$l$ of each link taken as the Kuhn length 
$l_K \equiv r_{eq}^2/L$, where 
$r_{eq}$ is the root-mean-square end-to-end distance and 
$L$ the contour length of the polymer (Doi & Edwards Reference Doi and Edwards1988). Coarse-grained models, known as bead-spring models, are obtained by replacing the rods of a freely jointed chain with one or more entropic springs. The bead-spring model with 
$N=2$ beads connected by a finitely extensible nonlinear elastic (FENE) spring (Bird et al. Reference Bird, Hassager, Armstrong and Curtiss1987) is called the FENE dumbbell model. Using the FENE dumbbell model and kinetic theory, continuum models of dilute polymer solutions can be obtained (Bird, Dotson & Johnson Reference Bird, Dotson and Johnson1980). Specifically, the constitutive equation relating the polymer stress tensor to the polymer conformation tensor and the evolution equation of the polymer conformation tensor have been derived using Peterlin's approximation (Peterlin Reference Peterlin1966). The resulting FENE-P model has been widely used in numerical studies and has captured the qualitative behaviour of polymer drag reduction found in experiments although quantitative agreement requires unphysical parameters such as unrealistically high polymer concentrations (Sureshkumar, Beris & Handler Reference Sureshkumar, Beris and Handler1997; De Angelis, Casciola & Piva Reference De Angelis, Casciola and Piva2002). Moreover, various numerical difficulties of the continuum FENE-P model have been known (Vaithianathan & Collins Reference Vaithianathan and Collins2003) and the Peterlin approximation has been shown to give rise to artifacts in turbulent flows when the Weissenberg number (the ratio of polymer relaxation time to fluid time scale), 
$Wi$, is large (Vincenzi et al. Reference Vincenzi, Perlekar, Biferale and Toschi2015). Lagrangian simulations of FENE dumbbells coupled with the turbulent flow of a Newtonian solvent (carrier fluid), generated by direct numerical simulation of incompressible Navier–Stokes equations, can overcome these numerical difficulties and problems (Peters & Schumacher Reference Peters and Schumacher2007; Watanabe & Gotoh Reference Watanabe and Gotoh2013). Such a hybrid Eulerian–Lagrangian numerical simulation (Serafini et al. Reference Serafini, Battista, Gualtieri and Casciola2022) of a turbulent flow coupled with DNA macromolecules modelled by FENE dumbbells with realistic parameters indeed shows significant drag reduction at sufficiently large 
$Wi$.
2. Overview
Real polymers have many internal degrees of freedom and a broad spectrum of relaxation time scales whereas the FENE dumbbell model is a highly simplified coarse-grained model and can only represent the longest relaxation time of the polymer. Extra degrees of freedom can be introduced by adding beads and springs, and this gives rise to a multibead FENE chain of
$N$ beads connected by 
$N-1$ FENE springs (which reduces to the FENE dumbbell when 
$N=2$). Using Eulerian–Lagrangian simulations, Serafini et al. (Reference Serafini, Battista, Gualtieri and Casciola2024) have studied the dynamics of polymers, described by different models, in a turbulent pipe flow at a moderate friction Reynolds number and different 
$Wi = \tau /(r/U_b)$. The different models of polymers used are the Kuhn chain, FENE dumbbells and multibead FENE chain with 
$N > 2$, and freely jointed chain with 
$N \leqslant 101$. Here, 
$\tau$ is the polymer relaxation time, 
$r=0.5$ mm is the radius of the pipe, 
$U_b=Q/({\rm \pi} r^2)$ is the bulk velocity, and 
$Q$ is the volumetric flow rate. A small population of 
$10^5$ polymers has been used and the back reaction of the polymers to the flow is ignored. In their simulations, they chose 
$L=0.04 r$ and 
$l_K=2 \times 10^{-4} r$ to mimic a double-stranded DNA macromolecule with 
$\tau \approx 1$ s (Harnau & Reineker Reference Harnau and Reineker1999), which match those used in an experimental study of turbulent drag reduction (Choi et al. Reference Choi, Lim, Lai and Chan2002). With these values, it can be found that 
$N=201$ for the Kuhn chains. The maximum extension of the spring for the multibead FENE chains and the constant rod length for the freely jointed chains with general 
$N$ are chosen to maintain the same contour length 
$L$.
Figure 1 shows the distributions
$p(R/L)$ of the end-to-end distance 
$R$ normalized by 
$L$ for the different models at 
$Wi=10^4$. The distribution for the FENE dumbbell (
$N=2$) is close to that for the realistic Kuhn chain. Increasing the number of beads in a FENE chain worsens its accuracy in characterizing polymer spatial conformations. A multibead FENE chain with 
$N>2$ has a larger chance of folding up compared with the reference Kuhn chain thus overestimates the probability of folded configurations leading to spurious peaks in 
$p(R/L)$ (see figure 1a). Together with earlier findings that the polymer extension and polymer stresses statistics are insensitive to the number of beads of a multibead FENE chain (Jin & Collins Reference Jin and Collins2007; Watanabe & Gotoh Reference Watanabe and Gotoh2010; Vincenzi et al. Reference Vincenzi, Watanabe, Ray and Picardo2020) in isotropic turbulence at moderate 
$Wi$, these results for turbulent pipe flows at large 
$Wi$ establish that the FENE dumbbell is a better model than a multibead FENE chain with 
$N>2$ for studying polymer drag reduction. For the freely jointed chains, 
$p(R/L)$ converges as 
$N$ is increased and the results for 
$N \geqslant 21$ are almost indistinguishable (see figure 1b). Thus, a 21-bead freely jointed chain model would be a good choice for probing internal configurations of polymers at large 
$Wi$.
Figure 1. Distribution
$p(R/L)$ of the normalized end-to-end distance for (a) multibead FENE chain with 
$N\,{\geqslant}\,2$ and the Kuhn chain (solid black line) and (b) freely jointed chain (
$N=201$ for the Kuhn chain). Compilation from figures 2(a) and 5 in Serafini et al. (Reference Serafini, Battista, Gualtieri and Casciola2024).
3. Relevance and outlook
Understanding polymer–turbulence interactions and polymer drag reduction is highly challenging because of the wide range of length and time scales involved. Numerical simulation has been a major and important tool for addressing this challenge. The choice of what polymer model to use in numerical studies of polymer drag reduction depends on the balance between the accuracy of the model in capturing the essential details of real polymers and computational cost and feasibility. The work of Serafini et al. (Reference Serafini, Battista, Gualtieri and Casciola2024) has provided strong support that the highly simplified FENE dumbbell model is a reasonable choice. With this relatively simple model, efforts can then be focused to fully understand polymer–turbulence interactions.
In a recent Eulerian–Lagrangian simulation of a turbulent pipe flow of a dilute solution of polymers, modelled by FENE dumbbells with realistic physical parameters, the same authors (Serafini et al. Reference Serafini, Battista, Gualtieri and Casciola2022), showed that at
$Wi = 10^4$, there is a significant drag reduction, and the drag reduction is due entirely to the back-reaction of fully stretched polymers. Moreover, the polymer stress resulted from this back-reaction force can be expressed in terms of some effective viscosity that depends on the local concentration of the polymers. It is important to check the generality of this physical picture by expanding the range of 
$Wi$ in numerical investigations since the relaxation time of drag reducing polymers varies a great deal depending on the molecular weights and specific types of polymers. Another interesting problem is to study the flow-dependent and thus space-dependent effective viscosity of the polymers, extracted from the polymer back-reaction force, and test whether it can explain the drag reducing effects of polymers in the same spirit as previously proposed in a phenomenological theory (Benzi et al. Reference Benzi, De Angelis, L'vov, Procaccia and Tiberkevich2006; Procaccia, L'vov & Benzi Reference Procaccia, L'vov and Benzi2008).
Declaration of interest
The author reports no conflict of interest.