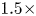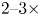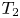1 Introduction
1.1 Motivation
Quantum computers may eventually become indispensable to scientific computing due to their ability to accelerate many calculations of interest. Because the physics of plasmas crucially relies on understanding how the motion of charged particles responds to electromagnetic fields and how the fields, in turn, respond to the particles, understanding how quantum computers can be used to accelerate the simulation of complex nonlinear dynamics is of great importance to the field. Plasma transport strongly depends on whether the particle motion possesses adiabatic invariants, such as the magnetic moment, or whether the invariants are destroyed and the motion is chaotic. While the former is the basis for particle confinement, the latter is used for heating plasmas to fusion relevant temperatures. In many situations of interest, the dynamics of the fields are often chaotic or even turbulent, which enhances the transport of particles, heat and momentum through the plasma. Thus, a key research direction for quantum algorithms for plasma physics is to accelerate the simulation of the nonlinear, chaotic and turbulent dynamics of plasmas (Joseph et al. Reference Joseph, Shi, Porter, Castelli, Geyko, Graziani, Libby and DuBois2023).
Interactions between particles and fields in a plasma are often classified into wave–particle and wave–wave interactions. Wave–particle interactions refer to the change in the trajectories of particles due to the electromagnetic fields, the change in the trajectories of wave packets due to scattering from particles and the resulting exchanges of energy and momentum (Nicholson Reference Nicholson1983; Davidson Reference Davidson2012). The electromagnetic forces generate evolution of the particle distribution function (p.d.f.) in phase space, and there are analogous processes that cause wave packets to evolve in wavenumber, ${\boldsymbol k}$![]() , and frequency, $\omega$
, and frequency, $\omega$![]() , space. Wave–particle interactions such as Landau damping, quasilinear theory, plasma echos and induced scattering are ubiquitous. Wave–wave interactions refer to nonlinear interactions between wave packets of different types, which can, in fact, be mediated through the particles. This includes calculations of the wave–wave scattering process, as well as both strong and weak turbulence theory (Nazarenko Reference Nazarenko2011; Zakharov, L'vov & Falkovich Reference Zakharov, L'vov and Falkovich2012). At a fundamental level, all of these processes can be viewed as the evolution of a plasma as a nonlinear dynamical system.
, space. Wave–particle interactions such as Landau damping, quasilinear theory, plasma echos and induced scattering are ubiquitous. Wave–wave interactions refer to nonlinear interactions between wave packets of different types, which can, in fact, be mediated through the particles. This includes calculations of the wave–wave scattering process, as well as both strong and weak turbulence theory (Nazarenko Reference Nazarenko2011; Zakharov, L'vov & Falkovich Reference Zakharov, L'vov and Falkovich2012). At a fundamental level, all of these processes can be viewed as the evolution of a plasma as a nonlinear dynamical system.
For small amplitude waves, the effects of nonlinear interactions can be understood through an expansion in wave amplitude. The linear response for wave–particle interactions is largest at a resonance between the particle velocity and the phase velocity of the wave, $\omega ={\boldsymbol k}\boldsymbol {\cdot }{\boldsymbol v}$![]() , where the phase velocity, $\omega /k$
, where the phase velocity, $\omega /k$![]() , matches the particle velocity ${\boldsymbol v}$
, matches the particle velocity ${\boldsymbol v}$![]() . If the p.d.f. decays in velocity at the location of the resonance relative to the bulk, then the waves experience Landau damping. The opposite case is unstable and inverse Landau damping causes the wave amplitude to grow. For a finite wave amplitude, $E$
. If the p.d.f. decays in velocity at the location of the resonance relative to the bulk, then the waves experience Landau damping. The opposite case is unstable and inverse Landau damping causes the wave amplitude to grow. For a finite wave amplitude, $E$![]() , particles are trapped in an island in phase space of finite width, $\delta v=\sqrt {2 E }$
, particles are trapped in an island in phase space of finite width, $\delta v=\sqrt {2 E }$![]() , for a particle of unit charge and mass. When multiple waves are present with different frequencies and wavenumbers, resonances can occur at the phase velocity of the nonlinear beat wave, $\sum _i \omega _i=\sum _i {\boldsymbol k}_i \boldsymbol {\cdot } {\boldsymbol v}$
, for a particle of unit charge and mass. When multiple waves are present with different frequencies and wavenumbers, resonances can occur at the phase velocity of the nonlinear beat wave, $\sum _i \omega _i=\sum _i {\boldsymbol k}_i \boldsymbol {\cdot } {\boldsymbol v}$![]() , which generalizes the resonance condition for wave–wave interactions. Once the islands generated by waves at different phase velocities begin to overlap, i.e. above the Chirikov criterion (Chirikov Reference Chirikov1979), there is a transition to chaotic particle motion, where particles effectively diffuse in momentum space. Quasilinear theory derives the effective diffusion that particles experience due to the wave power spectrum and the transfer of energy and momentum between waves and particles. In fact, this transition to chaos is generic for any dynamical system. However, in the chaotic regions of phase space, the true motion is rather complex and accurate numerical simulations are required to determine the evolution of the p.d.f.
, which generalizes the resonance condition for wave–wave interactions. Once the islands generated by waves at different phase velocities begin to overlap, i.e. above the Chirikov criterion (Chirikov Reference Chirikov1979), there is a transition to chaotic particle motion, where particles effectively diffuse in momentum space. Quasilinear theory derives the effective diffusion that particles experience due to the wave power spectrum and the transfer of energy and momentum between waves and particles. In fact, this transition to chaos is generic for any dynamical system. However, in the chaotic regions of phase space, the true motion is rather complex and accurate numerical simulations are required to determine the evolution of the p.d.f.
In general, plasma simulations must be addressed with computational approaches for solving the relevant partial differential equations (PDEs), e.g. the Vlasov–Poisson or Vlasov–Maxwell system. This requires both an accurate calculation of the particle orbits in the force field generated by the waves and an accurate calculation of the response of the waves to the charge and current density of the particles. Due to the high-dimensional phase space, solving for the motion of the particle p.d.f. is computationally demanding and is the largest computational overhead in today's kinetic codes, both for Lagrangian (particle-in-cell) and Eulerian (e.g. finite volume or finite element) approaches. Moreover, self-consistent calculations are highly demanding precisely because plasma evolution often leads to chaotic and turbulent dynamics that require extremely high spatial resolution for accurate results.
The power of quantum computers to apply useful operations to high-dimensional Hilbert spaces, essentially in parallel, implies that it may one day be possible to accelerate calculations of wave–particle interactions. In fact, we recently proposed the Koopman–von Neumann approach (Joseph Reference Joseph2020; Joseph et al. Reference Joseph, Shi, Porter, Castelli, Geyko, Graziani, Libby and DuBois2023) for using quantum computers to evolve all trajectories at once in an efficient manner, potentially leading to exponential speedup for the evolution of the p.d.f. In this work we shift focus from designing algorithms for future fault-tolerant quantum computers to understanding how such algorithms perform in practice on one of today's hardware platforms. In order to make the problem more tractable, we consider simulating a toy model of wave–particle interactions by simulating the evolution of the p.d.f. in a fixed electrostatic potential. Another paper in this special issue (Shi et al. Reference Shi, Evert, Brown, Tripathi, Sete, Geyko, Cho, Joseph, Lidar and DuBois2024) tests the ability of present day quantum computers to simulate a toy model of the chaotic dynamics of wave–wave interactions as a proxy for nonlinear PDEs of interest to plasma physics.
However, the present era of quantum computing has been dubbed the noisy intermediate-scale quantum (NISQ) era because present day quantum computers are limited in the fidelity of the basic gate operations as well as in the overall number of gates (gate depth) that can be applied coherently. The presence of errors in the calculation requires some type of error characterization and mitigation strategy, and, without error correction, it is not yet possible to perform the high-precision calculations necessary for plasma simulation. Our conclusion is that it is important to control the type and strength of various noise processes in order to obtain accurate results.
1.2 Quantum maps
The first step in simulating wave–particle interactions is to compute how the particle trajectories changes in response to the fields. In the early days of plasma research, physicists explored the chaotic dynamics of the particle motion through the study of discrete time dynamical systems called nonlinear maps (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1992). Relatively simple nonlinear maps, such as the Chirikov standard map (Chirikov Reference Chirikov1979), generate chaotic motion by breaking time invariance with a series of periodic kicks in time. Nonlinear maps are both simpler and more accurate to study than nonlinear differential equations because they avoid numerical integration in time. Hence, they have no truncation errors associated with the discrete approximation of the integrals and, perhaps more importantly, they require far fewer operations per time step, so that numerical errors associated with finite precision arithmetic are kept to a minimum. Thus, nonlinear maps can be computed very efficiently and allow one to explore the rich structure of the chaotic dynamics of natural plasma processes such as the heating of magnetized plasmas by cyclotron waves (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1992). Although the dynamics is controlled by a small set of parameters, it usually displays rich structural properties due to the multitude of bifurcations in the number and types of fixed points of the mapping as the parameters are varied (Guckenheimer & Holmes Reference Guckenheimer and Holmes2013).
While there are formally exact methods for developing quantum algorithms that simulate classical dynamics (Joseph Reference Joseph2020; Liu et al. Reference Liu, Kolden, Krovi, Loureiro, Trivisa and Childs2021; Joseph et al. Reference Joseph, Shi, Porter, Castelli, Geyko, Graziani, Libby and DuBois2023), for small system sizes the method of quantization is cheaper in terms of resource requirements, i.e. number of qubits and quantum gates. A symplectic nonlinear map can be quantized by embedding the dynamics within a unitary transformation in a manner that reproduces the classical dynamics in the semiclassical limit (Benenti, Casati & Montangero Reference Benenti, Casati and Montangero2004). While achieving the semiclassical limit is challenging classically, the exponential memory resources of a quantum computer and the ability to simulate superpositions efficiently make this approach feasible quantumly. For example, the quantized version of the Chirikov standard map, the prototypical example of chaotic particle motion in response to a nonlinear wave, is shown in figure 1. The map is run starting from an initial condition localized in momentum space that then explores the accessible phase space over time. One can clearly see a large-scale island in the centre of the figure, whose width scales as $K^{1/2}$![]() , as expected. The fact that the map is kicked periodically in time also generates islands at other phase velocities and chaotic motion occurs near the regions where islands overlap. As the map parameter $K$
, as expected. The fact that the map is kicked periodically in time also generates islands at other phase velocities and chaotic motion occurs near the regions where islands overlap. As the map parameter $K$![]() varies across the point at which the last Kolmogorov–Arnold–Moser (KAM) surface is destroyed (estimated as $K\simeq 0.971635406$
varies across the point at which the last Kolmogorov–Arnold–Moser (KAM) surface is destroyed (estimated as $K\simeq 0.971635406$![]() using Greene's method Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1992), the wavefunction begins to diffuse over the entire phase space. Thus, simulating the quantized evolution can be thought of as a quantum walk algorithm that accelerates the exploration of and averaging over the accessible chaotic region (Di Molfetta & Debbasch Reference Di Molfetta and Debbasch2016; Joseph et al. Reference Joseph, Shi, Porter, Castelli, Geyko, Graziani, Libby and DuBois2023).
using Greene's method Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1992), the wavefunction begins to diffuse over the entire phase space. Thus, simulating the quantized evolution can be thought of as a quantum walk algorithm that accelerates the exploration of and averaging over the accessible chaotic region (Di Molfetta & Debbasch Reference Di Molfetta and Debbasch2016; Joseph et al. Reference Joseph, Shi, Porter, Castelli, Geyko, Graziani, Libby and DuBois2023).

Figure 1. Husimi-Q quasiprobability distribution for the quantum standard map (same decomposition as (2.2)), but with the potential in (2.1) modified to $K(1-\cos \hat {\theta })$![]() starting from the initial condition $p=3N/8$
starting from the initial condition $p=3N/8$![]() ($J=3{\rm \pi} /4$
($J=3{\rm \pi} /4$![]() ) for 10 qubits. The map is evolved for 1000 time steps and then the final probability distribution is averaged over the last 50 time steps. Parameters: $L=1$
) for 10 qubits. The map is evolved for 1000 time steps and then the final probability distribution is averaged over the last 50 time steps. Parameters: $L=1$![]() and (a,b) $K=0.95$
and (a,b) $K=0.95$![]() below the destruction of the last KAM surface, (c,d) $K=1.0$
below the destruction of the last KAM surface, (c,d) $K=1.0$![]() above the destruction of the last KAM surface, (e, f) $K=1.5$
above the destruction of the last KAM surface, (e, f) $K=1.5$![]() chaotic diffusive regime. Calculations performed on a classical computer without noise.
chaotic diffusive regime. Calculations performed on a classical computer without noise.
Simulation of the exact quantum dynamics (Brodin & Zamanian Reference Brodin and Zamanian2022), including quantum wave–particle interactions (Misra & Brodin Reference Misra and Brodin2022), is of great scientific interest, but challenging using classical computers due to the memory and time required to directly simulate the exponentially large Hilbert space for the fully quantized system. Hence, quantum simulation using quantum computers is one of the main applications of interest for achieving a near term quantum advantage (Babbush et al. Reference Babbush, McClean, Newman, Gidney, Boixo and Neven2021). Simulating chaotic dynamics is of particular interest due to the provable difficulty of simulating chaos. Recent claims of quantum supremacy relied on the difficulty of simulating chaotic quantum circuits (Boixo et al. Reference Boixo, Isakov, Smelyanskiy, Babbush, Ding, Jiang, Bremner, Martinis and Neven2018; Arute et al. Reference Arute, Arya, Babbush, Bacon, Bardin, Barends, Biswas, Boixo, Brandao and Buell2019) and, among paths to quantum advantage, simulating chaotic dynamics may be the most qubit efficient (Babbush Reference Babbush2021). Thus, direct simulation of the quantized system opens the pathway both for simulating the intrinsically quantum dynamics as well as for accelerating the simulation of classical dynamics.
This work explores the quantum sawtooth map (QSM) as a prototypical point example of both the classical and quantum plasma physics simulations that quantum computers may one day accelerate. The QSM is one of the cheapest possible maps to simulate (Benenti et al. Reference Benenti, Casati, Montangero and Shepelyansky2001) because it only depends quadratically on the momentum and the position, which significantly reduces the number of arithmetic operations per time step, both classically and quantumly. This has led to a proposal to use the QSM as a benchmark problem to measure the ability of quantum algorithms to accelerate the simulation of dynamical systems (Benenti et al. Reference Benenti, Casati and Montangero2004). The result of evolving the QSM from a localized initial momentum state is shown in figure 2. Again, one can clearly see a transition to the regime of chaotic diffusion as the map parameter increases (compare with the standard map in figure 1).

Figure 2. Husimi-Q quasiprobability distribution for the QSM (2.2) for $n=10$![]() qubits, starting from the initial condition $p=3N/8$
qubits, starting from the initial condition $p=3N/8$![]() ($J=3{\rm \pi} /4$
($J=3{\rm \pi} /4$![]() ). The map is evolved for 1000 time steps and then the final probability distribution is averaged over the last 50 time steps. Parameters: $L=1$
). The map is evolved for 1000 time steps and then the final probability distribution is averaged over the last 50 time steps. Parameters: $L=1$![]() and (a,b) $K=-0.1$
and (a,b) $K=-0.1$![]() regular motion, (c,d) $K=0.1$
regular motion, (c,d) $K=0.1$![]() anomalous diffusion, (e, f) $K=1.5$
anomalous diffusion, (e, f) $K=1.5$![]() chaotic diffusive regime. Calculations performed on a classical computer without noise.
chaotic diffusive regime. Calculations performed on a classical computer without noise.
Both chaotic/diffusive dynamics and dynamical localization, which is an intrinsically quantum effect, can be observed in the QSM. (Here, we use the term diffusive rather than chaotic because the dynamics is not clearly chaotic until a sufficient number of qubits is used (Porter & Joseph Reference Porter and Joseph2022).) The transition from diffusion to localization occurs when the ratio of diffusion strength to effective Planck's constant ($\hbar$![]() ) is small and quantum interference dominates.
) is small and quantum interference dominates.
1.3 Leveraging noise
The NISQ devices that are available today provide a unique platform for exploring the dynamics of many-body quantum systems. However, the ubiquitous presence of interactions with the environment generates noise that adds complexity to the interpretation of the results. Depending on context, noise can affect the simulation dynamics in different ways. It may completely wash out the dynamics of interest or it can potentially be used to measure key signatures of the dynamics (Porter & Joseph Reference Porter and Joseph2022).
An important feature of quantum transport simulations is that they can be performed in the presence of noise. In fact, the algorithm for calculating the Lyapunov exponent measures the fidelity decay rate of a Loschmidt echo experiment that crucially relies on noise being present as part of the calculation. On future error-corrected quantum computers, one can carefully introduce effective noise sources into the calculation by design. For today's NISQ computers, one might utilize specific types of hardware noise that may already be present to one's advantage, as long as the strength of the noise and the strength of the Lyapunov exponent can be chosen to reside within a certain window in parameter space (Porter & Joseph Reference Porter and Joseph2022). The ability to characterize and control the types of noise present could enable this by leveraging tailored noise (Guimarães et al. Reference Guimarães, Lim, Vasilevskiy, Huelga and Plenio2023; Van Den Berg et al. Reference Van Den Berg, Minev, Kandala and Temme2023). Quantum hardware platforms with enough qubits and with the right magnitude of noise to perform such calculations may be available in the near future.
Measuring the decay of fidelity can provide an exponentially efficient measure of the classical Lyapunov exponent (Benenti & Casati Reference Benenti and Casati2002; Benenti et al. Reference Benenti, Casati and Montangero2004) and chaotic decoherence (Poulin et al. Reference Poulin, Blume-Kohout, Laflamme and Ollivier2004). Measuring dynamical localization of classically chaotic systems may yield a similar speedup (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001). The fidelities of quantized versions of classically chaotic Hamiltonian systems can decay differently (often faster) than for integrable dynamics (Peres Reference Peres1984; Lysne et al. Reference Lysne, Kuper, Poggi, Deutsch and Jessen2020; Porter & Joseph Reference Porter and Joseph2022). Quantum chaos can magnify the effect of Trotter errors (Sieberer et al. Reference Sieberer, Olsacher, Elben, Heyl, Hauke, Haake and Zoller2019) while quantum localization can reduce the upper bound on their impact (Heyl, Hauke & Zoller Reference Heyl, Hauke and Zoller2019).
1.4 Summary of results
In this work we ask the question: How do dynamics, entanglement and noise impact the fidelity of the results? We show experimentally that varying the dynamics of the QSM alters the fidelity decay rate. Henry et al. (Reference Henry, Emerson, Martinez and Cory2006) and Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021) initiated the use of the QSM to characterize experimental noise by using the degree of localization as a test of device fidelity. We extend previous work by studying the phase transition from localization to diffusion and the Loschmidt echo fidelity throughout this transition, opening the door to probing the interaction between quantum map dynamics and experimental noise.
The main results are as follows. (1) We report on the first experimental evidence demonstrating that the Loschmidt echo fidelity of a digital quantum simulation decreases as the dynamics transitions from integrable to chaotic even as the gate count remains constant. (2) While this behaviour was anticipated by previous studies, we found that the parametric noise models that others had explored cannot explain the experimental results. (3) Instead, this behaviour can be phenomenologically explained by the fact that chaotic evolution creates randomly entangled states, defined as having significant amplitude on all basis states with random relative phases on each, that are more sensitive to dephasing and similarly sensitive to relaxation as localized states. This can be attributed to an increase both in superposition, which increases the effect of pure dephasing and reduces the effect of relaxation, and in entanglement with random phases, which increases the effect of relaxation. (4) Three noise models that we explore agree on a common value of the effective $T_2$![]() time during gate operation that, as is to be expected, is far shorter than IBM-Q's reported value for $T_{2E}$
time during gate operation that, as is to be expected, is far shorter than IBM-Q's reported value for $T_{2E}$![]() from a Hahn echo experiment.
from a Hahn echo experiment.
We introduce a gate-based Lindblad model that both captures the effect of dynamics on fidelity in a minimal physically motivated model and results in an effective $T_2$![]() time similar to that from a Qiskit Aer model fit. In contrast, the parametric noise model often used by other authors in the quantum maps literature does not capture the correct form of the fidelity decay, and randomized benchmarking (RB) with depolarizing noise does not have the minimum two parameters required to describe a fidelity that depends on more than gate count.
time similar to that from a Qiskit Aer model fit. In contrast, the parametric noise model often used by other authors in the quantum maps literature does not capture the correct form of the fidelity decay, and randomized benchmarking (RB) with depolarizing noise does not have the minimum two parameters required to describe a fidelity that depends on more than gate count.
1.5 Overview of contents
In § 2 the QSM is introduced, its conditions for dynamical localization are described and its gate decomposition is given. In § 3 the experimental results are presented and compared with IBM-Q reported metrics. In § 4 noise models are described and fit to experimental data to extract effective decoherence times. Appendix E provides background rationale for the gate-based Lindblad model that is a primary tool in this section. Sections 4.2 and 4.3 consider single-qubit Lindblad noise models, § 4.4 considers the qiskit Aer noise model and § 4.5 fits the three resulting models to the data. Lastly § 5 provides a summary of our results. Discussion of the parametric noise model considered in previous work is relegated to Appendix D.
2 Quantum sawtooth map
2.1 Definition
The QSM is defined by the dimensionless time-periodic Hamiltonian

which is derived in Porter & Joseph (Reference Porter and Joseph2022) from the classical Hamiltonian by quantizing in dimensionless $\hbar$![]() to get $\hat {J} = \hbar \hat {p}$
to get $\hat {J} = \hbar \hat {p}$![]() and discretizing to get $\hat {\theta } = 2 {\rm \pi}\hat {q}/N$
and discretizing to get $\hat {\theta } = 2 {\rm \pi}\hat {q}/N$![]() to yield momentum and position operators $\hat p$
to yield momentum and position operators $\hat p$![]() and $\hat q$
and $\hat q$![]() , respectively, with eigenvalues $-N/2 \le p, q < N/2$
, respectively, with eigenvalues $-N/2 \le p, q < N/2$![]() . The quantum evolution propagator over one period is then
. The quantum evolution propagator over one period is then

where $\hat {\mathcal {T}}$![]() is the time-ordering operator, $k \equiv K/\hbar$
is the time-ordering operator, $k \equiv K/\hbar$![]() is the quantum kicking parameter and $\beta \equiv 2{\rm \pi} /N$
is the quantum kicking parameter and $\beta \equiv 2{\rm \pi} /N$![]() for $N$
for $N$![]() basis states. In the context of quantum computing $N=2^n$
basis states. In the context of quantum computing $N=2^n$![]() for $n$
for $n$![]() qubits. Equation (2.2) is exact with no Trotter error due to the delta-function potential that is kicked periodically in time. In this instant the potential energy overwhelms the kinetic energy and so can be considered to occur at the beginning of each time step, entirely before the kinetic evolution. The whole single-period propagator is often called a Floquet operator with periodicity one (Rudner & Lindner Reference Rudner and Lindner2020) since it uses a time-periodic Hamiltonian, but since it corresponds to a classical map it is also known as a quantum map. (See the conclusions and outlook section of Mori (Reference Mori2023) for a review of Floquet theory in the context of open quantum systems.) Periodicity matching between the classical and quantum systems gives $\hbar = 2{\rm \pi} L /N$
qubits. Equation (2.2) is exact with no Trotter error due to the delta-function potential that is kicked periodically in time. In this instant the potential energy overwhelms the kinetic energy and so can be considered to occur at the beginning of each time step, entirely before the kinetic evolution. The whole single-period propagator is often called a Floquet operator with periodicity one (Rudner & Lindner Reference Rudner and Lindner2020) since it uses a time-periodic Hamiltonian, but since it corresponds to a classical map it is also known as a quantum map. (See the conclusions and outlook section of Mori (Reference Mori2023) for a review of Floquet theory in the context of open quantum systems.) Periodicity matching between the classical and quantum systems gives $\hbar = 2{\rm \pi} L /N$![]() for positive integer $L$
for positive integer $L$![]() (Porter & Joseph Reference Porter and Joseph2022).
(Porter & Joseph Reference Porter and Joseph2022).
Note a partial symmetry between the phases of ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}$![]() and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$
and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$![]() : $\hbar =L* 2{\rm \pi} /N$
: $\hbar =L* 2{\rm \pi} /N$![]() while $-k \beta ^2 = -K/L* 2{\rm \pi} /N$
while $-k \beta ^2 = -K/L* 2{\rm \pi} /N$![]() . Typically, the qubits are mapped to the $p$
. Typically, the qubits are mapped to the $p$![]() basis, but mapping instead to the $q$
basis, but mapping instead to the $q$![]() basis would swap the roles of $L$
basis would swap the roles of $L$![]() and $-K/L$
and $-K/L$![]() .
.
2.2 Localization and initial conditions
The QSM is integrable when $K=-4,-3,-2,-1, 0$![]() and, hence, the wavefunctions are localized for these cases. For the intermediate region, $K\in (-4,0)$
and, hence, the wavefunctions are localized for these cases. For the intermediate region, $K\in (-4,0)$![]() , the dynamics is not localized, but has a zero Lyapunov exponent. The dynamics of the QSM are chaotic for $K<-4$
, the dynamics is not localized, but has a zero Lyapunov exponent. The dynamics of the QSM are chaotic for $K<-4$![]() and $K>0$
and $K>0$![]() . For $0< K<1$
. For $0< K<1$![]() , the wavefunction is chaotic, but it is in a regime of anomalously slow diffusion. Figure 2 illustrates the difference in QSM dynamics between the zero Lyapunov case, $K=-0.1$
, the wavefunction is chaotic, but it is in a regime of anomalously slow diffusion. Figure 2 illustrates the difference in QSM dynamics between the zero Lyapunov case, $K=-0.1$![]() , the anomalous slow diffusion case, $K=+0.1$
, the anomalous slow diffusion case, $K=+0.1$![]() , and the standard chaotic case, $K=1.5$
, and the standard chaotic case, $K=1.5$![]() . Since the focus of this paper is on chaotic dynamics, from now on only $K>0$
. Since the focus of this paper is on chaotic dynamics, from now on only $K>0$![]() will be considered.
will be considered.
The presence of broken cantori in the classical system can slow diffusion at small $K$![]() , so there are two regimes given by the classical diffusion coefficient
, so there are two regimes given by the classical diffusion coefficient

which measures the rate of trajectories diffusing through the phase space (Benenti et al. Reference Benenti, Casati, Montangero and Shepelyansky2001). When $D_{K}$![]() is small compared with $\hbar ^2$
is small compared with $\hbar ^2$![]() , the QSM is predicted to reach a steady state after the Heisenberg time that is exponentially localized around an initial momentum state $\left |p_0\right \rangle$
, the QSM is predicted to reach a steady state after the Heisenberg time that is exponentially localized around an initial momentum state $\left |p_0\right \rangle$![]() as
as
with localization length (Benenti et al. Reference Benenti, Casati and Montangero2004)
The Heisenberg time or ‘break’ time (Benenti et al. Reference Benenti, Casati and Montangero2004) is the time to resolve the energy levels, defined as the inverse mean energy level spacing (Shepelyansky Reference Shepelyansky2020; Šuntajs et al. Reference Šuntajs, Bonča, Prosen and Vidmar2020).
Due to the periodicity and finite size of the system, localization only occurs if the localization length is small enough to have a global maximum at its central peak. This occurs when (Porter & Joseph Reference Porter and Joseph2022)

with diffusion occurring otherwise. These two dynamical regimes are demonstrated in figure 3.

Figure 3. Exact noiseless simulations of the QSM, showing the localized case $k=0.1$![]() (blue) and the diffusive case $k=4.55$
(blue) and the diffusive case $k=4.55$![]() (red) for $t=1,2,4,8$
(red) for $t=1,2,4,8$![]() . Initial state prepared in $\left |p=-2\right \rangle$
. Initial state prepared in $\left |p=-2\right \rangle$![]() . Parameters: $n=3\, (N=8), L=1; k=4K/{\rm \pi}, k_\textrm {loc} \approx 1.87$
. Parameters: $n=3\, (N=8), L=1; k=4K/{\rm \pi}, k_\textrm {loc} \approx 1.87$![]() . The horizontal axis corresponds to the vertical axis of figure 2, but at different $N$
. The horizontal axis corresponds to the vertical axis of figure 2, but at different $N$![]() .
.
When localization is strong ($\ell \ll N$![]() ), the above formula for average $\ell$
), the above formula for average $\ell$![]() does not uniformly apply to all initial conditions, with $\ell$
does not uniformly apply to all initial conditions, with $\ell$![]() instead depending on the initial condition in a manner dependent on $L$
instead depending on the initial condition in a manner dependent on $L$![]() . Less localized clusters of momentum eigenstates appear at $L$
. Less localized clusters of momentum eigenstates appear at $L$![]() equally spaced locations in momentum space, reducing $\ell$
equally spaced locations in momentum space, reducing $\ell$![]() for initial momentum states in the vicinity of these groups. Once $L \sim N$
for initial momentum states in the vicinity of these groups. Once $L \sim N$![]() this transitions to more uniform $\ell$
this transitions to more uniform $\ell$![]() with just $\left |p=0\right \rangle$
with just $\left |p=0\right \rangle$![]() strongly localized. This is how Henry et al. (Reference Henry, Emerson, Martinez and Cory2006) and Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021) used $N=8, L=7$
strongly localized. This is how Henry et al. (Reference Henry, Emerson, Martinez and Cory2006) and Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021) used $N=8, L=7$![]() to obtain strong localization at $\left |p=0\right \rangle$
to obtain strong localization at $\left |p=0\right \rangle$![]() , despite other states being less localized. In this study we fix $L=1$
, despite other states being less localized. In this study we fix $L=1$![]() to keep the state-dependent effect on localization length constant. When demonstrating strong localization in figure 3 we show a single initial condition $\left |p\right \rangle$
to keep the state-dependent effect on localization length constant. When demonstrating strong localization in figure 3 we show a single initial condition $\left |p\right \rangle$![]() with $p \neq 0$
with $p \neq 0$![]() to avoid early delocalization. But in other figures the fidelity is averaged over all initial conditions to average out state-dependent effects. This averaging of fidelity is motivated by the standard approach to observing the Lyapunov exponent in the fidelity decay rate (Benenti & Casati Reference Benenti and Casati2002).
to avoid early delocalization. But in other figures the fidelity is averaged over all initial conditions to average out state-dependent effects. This averaging of fidelity is motivated by the standard approach to observing the Lyapunov exponent in the fidelity decay rate (Benenti & Casati Reference Benenti and Casati2002).
It is also worth noting that the initial conditions are chosen to be momentum eigenstates, which in the strongly localized limit are not perfectly localized since they are not quantum map eigenstates. Rather, in this limit the map eigenstates are complex superpositions of $\left |p\right \rangle$![]() and $\left |-p\right \rangle$
and $\left |-p\right \rangle$![]() . As the quantum map causes the phase of each map eigenstate to evolve at a rate proportional to its quasienergy, pairs of states will fall out of phase, causing an initial state $\left |p\right \rangle$
. As the quantum map causes the phase of each map eigenstate to evolve at a rate proportional to its quasienergy, pairs of states will fall out of phase, causing an initial state $\left |p\right \rangle$![]() to evolve to $\left |-p\right \rangle$
to evolve to $\left |-p\right \rangle$![]() after a phase difference ${\rm \pi}$
after a phase difference ${\rm \pi}$![]() . However, in the localized limit the quasienergies of these map eigenstate pairs are close together, making this process long and irrelevant for the short-time scales discussed in this paper. The fact that we reverse the map to calculate fidelity further reduces the relevance of this effect.
. However, in the localized limit the quasienergies of these map eigenstate pairs are close together, making this process long and irrelevant for the short-time scales discussed in this paper. The fact that we reverse the map to calculate fidelity further reduces the relevance of this effect.
2.3 The QSM algorithm
There is a natural mapping of the QSM to a qubit-based quantum computer. The $N$![]() momentum eigenstates can be mapped to the $2^{n}$
momentum eigenstates can be mapped to the $2^{n}$![]() qubit states when $N=2^n$
qubit states when $N=2^n$![]() . The unitary ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$
. The unitary ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$![]() can then be implemented exactly in four steps (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001; Benenti et al. Reference Benenti, Casati and Montangero2004; Porter & Joseph Reference Porter and Joseph2022), written compactly as
can then be implemented exactly in four steps (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001; Benenti et al. Reference Benenti, Casati and Montangero2004; Porter & Joseph Reference Porter and Joseph2022), written compactly as
where the operators ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}={{{\boldsymbol{\mathsf{U}}}}}_\textrm {phase}(\hbar )$![]() and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}={{{\boldsymbol{\mathsf{U}}}}}_\textrm {phase}(-k\beta ^2)$
and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}={{{\boldsymbol{\mathsf{U}}}}}_\textrm {phase}(-k\beta ^2)$![]() are many-qubit diagonal phase operators in the position and momentum bases, respectively, defined in (2.2), and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$
are many-qubit diagonal phase operators in the position and momentum bases, respectively, defined in (2.2), and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$![]() is the quantum Fourier transform (QFT) used to alternate between the momentum and position bases. The diagonal phase operators can be implemented exactly due to a method for decomposing order-$P$
is the quantum Fourier transform (QFT) used to alternate between the momentum and position bases. The diagonal phase operators can be implemented exactly due to a method for decomposing order-$P$![]() polynomial terms in the Hamiltonian into polynomially many $P$
polynomial terms in the Hamiltonian into polynomially many $P$![]() -qubit gates, given in Appendix B (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001). A similar yet approximate algorithm exists for any quantum map whose Hamiltonian has separable kinetic and potential energy terms each with a convergent power series expansion, such as the standard map (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001) or kicked Harper model (Lévi & Georgeot Reference Lévi and Georgeot2004). An exact representation of trigonometric terms requires ancilla qubits. Compared with these trigonometic potentials, the QSM algorithm has a particularly efficient algorithm due to its quadratic potential requiring only quadratically many two-qubit gates. While any polynomial length algorithm may be considered ‘efficient’, the QSM is the second-most efficient among quantum maps when using the Georgeot algorithm (Porter & Joseph Reference Porter and Joseph2022). For the ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$
-qubit gates, given in Appendix B (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001). A similar yet approximate algorithm exists for any quantum map whose Hamiltonian has separable kinetic and potential energy terms each with a convergent power series expansion, such as the standard map (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001) or kicked Harper model (Lévi & Georgeot Reference Lévi and Georgeot2004). An exact representation of trigonometric terms requires ancilla qubits. Compared with these trigonometic potentials, the QSM algorithm has a particularly efficient algorithm due to its quadratic potential requiring only quadratically many two-qubit gates. While any polynomial length algorithm may be considered ‘efficient’, the QSM is the second-most efficient among quantum maps when using the Georgeot algorithm (Porter & Joseph Reference Porter and Joseph2022). For the ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$![]() steps, we use the standard algorithm from IBM's library, which is exact, efficient and requires no ancilla qubits (Nielsen & Chuang Reference Nielsen and Chuang2010; IBM 2021b).
steps, we use the standard algorithm from IBM's library, which is exact, efficient and requires no ancilla qubits (Nielsen & Chuang Reference Nielsen and Chuang2010; IBM 2021b).
Using the derivation in Appendix B, the efficient circuit decomposition for the QSM is

where H is a Hadamard gate, P and CP are one-qubit phase and two-qubit controlled-phase gates, respectively, and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$![]() follows the Qiskit reverse-ordering convention. The second term in the argument of each P gate translates the domain to $p \in [-N/2, (N-1)/2]$
follows the Qiskit reverse-ordering convention. The second term in the argument of each P gate translates the domain to $p \in [-N/2, (N-1)/2]$![]() , as described in Appendix B. This algorithm is shown for three qubits in figure 4, with the SWAP gates from ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$
, as described in Appendix B. This algorithm is shown for three qubits in figure 4, with the SWAP gates from ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$![]() having been eliminated by reversing the order of qubits during ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$
having been eliminated by reversing the order of qubits during ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$![]() .
.

Figure 4. Circuit for a single forward map iteration of the three-qubit QSM algorithm from (2.8), both in block form and in algorithmic form before conversion to hardware connectivity and transpilation to native gates. Two-qubit CPHASE gates are used. Here ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$![]() and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}$
and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}$![]() steps use PHASE and CPHASE gates, while ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$
steps use PHASE and CPHASE gates, while ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QFT}$![]() steps use CPHASE and H gates. We use $k=4.55$
steps use CPHASE and H gates. We use $k=4.55$![]() here.
here.
Since our algorithm is exact while maintaining polynomial gate scaling, there is no clear benefit to methods that scale near optimally with error such as quantum signal processing (QSP) (Low & Chuang Reference Low and Chuang2017). Moreover, QSP has a large constant overhead cost and requires ancilla qubits that make it inappropriate for few-qubit applications. Another approach, a decomposition of diagonal unitaries to Walsh functions provided by Welch et al. (Reference Welch, Greenbaum, Mostame and Aspuru-Guzik2014), is also an approximation and so unnecessary here. Furthermore, it is only efficient if the diagonal Hamiltonian is smooth enough that the number of Walsh functions $k$![]() is independent of the qubits $n$
is independent of the qubits $n$![]() at any fixed approximation error. However, as one reduces the error tolerance, the number of required gates would grow as $2^k$
at any fixed approximation error. However, as one reduces the error tolerance, the number of required gates would grow as $2^k$![]() .
.
The initial conditions used in this work will vary between figures, as specified in their captions. However, all basis states are valid initial conditions for exploring the dynamics of the QSM.
3 Experimental results
3.1 Fidelity definition
This section discusses the core experimental results. The main result concerns the Loschmidt echo fidelity, which is defined as the probability of evolving a state and then reversing that evolution perfectly in the presence of noise. In an experiment noise is naturally present in both the ‘forward’ and ‘backward’ steps. For the QSM, an initial pure state $\left |\psi \right \rangle$![]() is evolved under the unitary ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$
is evolved under the unitary ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$![]() in the presence of noise for $t/2$
in the presence of noise for $t/2$![]() time steps, followed by its inverse ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}^{-1}$
time steps, followed by its inverse ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}^{-1}$![]() with the same noise processes for $t/2$
with the same noise processes for $t/2$![]() time steps, resulting in the total noisy evolution $\varPhi _{t}$
time steps, resulting in the total noisy evolution $\varPhi _{t}$![]() and the final mixed state ${\boldsymbol \sigma }(t) = \varPhi _{t}(\left |\psi \right \rangle \left \langle \psi \right |)$
and the final mixed state ${\boldsymbol \sigma }(t) = \varPhi _{t}(\left |\psi \right \rangle \left \langle \psi \right |)$![]() . Then for an initial computational basis state $\left |\psi \right \rangle = \left |p\right \rangle$
. Then for an initial computational basis state $\left |\psi \right \rangle = \left |p\right \rangle$![]() , the Loschmidt echo fidelity is
, the Loschmidt echo fidelity is
For simulations and experiments, we use $t \equiv 2*t_\textrm {fb}$![]() to define $t_\textrm {fb}$
to define $t_\textrm {fb}$![]() , the number of forward-and-back pairs of steps. Hence, the fidelity is given by $f(t) \equiv f(2*t_\textrm {fb})$
, the number of forward-and-back pairs of steps. Hence, the fidelity is given by $f(t) \equiv f(2*t_\textrm {fb})$![]() and plotted with respect to $t_\textrm {fb}$
and plotted with respect to $t_\textrm {fb}$![]() . For a more thorough description of the Loschmidt echo, see § 4. The main experimental result is that the rates of fidelity decay in figure 6 increase as the QSM increases its quantum kick parameter $k$
. For a more thorough description of the Loschmidt echo, see § 4. The main experimental result is that the rates of fidelity decay in figure 6 increase as the QSM increases its quantum kick parameter $k$![]() . This only alters the phases of transpiled RZ gates in ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$
. This only alters the phases of transpiled RZ gates in ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$![]() (see Appendix A), and does not change the CNOT gate count. Note, however, that the change in fidelity is correlated with the transition between localized and diffusive dynamics and saturates to limiting values at both low and high values of $k$
(see Appendix A), and does not change the CNOT gate count. Note, however, that the change in fidelity is correlated with the transition between localized and diffusive dynamics and saturates to limiting values at both low and high values of $k$![]() . This behaviour resembles but is distinct from the semiclassical regime (Porter & Joseph Reference Porter and Joseph2022) where the fidelity decay rate can be controlled by the Lyapunov exponent and, hence, the strength of chaos in the system. This regime it not yet experimentally accessible on IBM-Q.
. This behaviour resembles but is distinct from the semiclassical regime (Porter & Joseph Reference Porter and Joseph2022) where the fidelity decay rate can be controlled by the Lyapunov exponent and, hence, the strength of chaos in the system. This regime it not yet experimentally accessible on IBM-Q.
The phrase ‘diffusive dynamics’ above refers to dynamics that, taken in the classical limit of infinite qubits, would recover the chaotic classical diffusion discussed in § 2.2. However, in the context of small quantum systems, diffused quantum states fully explore the Hilbert space and have essentially random phases on each basis state. These states will be referred to as ‘randomly entangled’ states in § 4.2.
3.2 Dynamical localization
One goal of simulating the QSM on present day hardware is to assess the hardware's ability to execute complex dynamical simulations. Figure 5 shows the results of simulating the QSM ‘forward only’ (ideally ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$![]() ) on the ibmq_manila device in both the localized and diffusive regimes. The effect of dynamics is clearly apparent, and the localized state's probability is an informal metric of the fidelity of the quantum hardware. The raw data shows the localized state retains the maximum probability among the eight states through $t=7$
) on the ibmq_manila device in both the localized and diffusive regimes. The effect of dynamics is clearly apparent, and the localized state's probability is an informal metric of the fidelity of the quantum hardware. The raw data shows the localized state retains the maximum probability among the eight states through $t=7$![]() . However, the results of figure 6 for simulating ‘forward and back’ (ideally ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}^{-1} {{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$
. However, the results of figure 6 for simulating ‘forward and back’ (ideally ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}^{-1} {{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$![]() ) retain fidelity through at least $t_\textrm {fb}=5$
) retain fidelity through at least $t_\textrm {fb}=5$![]() , suggesting the forward-only localized case may retain information about its initial state through at least $t=10$
, suggesting the forward-only localized case may retain information about its initial state through at least $t=10$![]() .
.

Figure 5. Dynamics of the QSM for three qubits on the ibmq_manila device, showing localization ($k=0.1$![]() ) and diffusion ($k=4.55$
) and diffusion ($k=4.55$![]() ) for $t=1,2,4,8$
) for $t=1,2,4,8$![]() and the initial condition $\left |p=-2\right \rangle$
and the initial condition $\left |p=-2\right \rangle$![]() $(\left |\psi \right \rangle = \left |010\right \rangle )$
$(\left |\psi \right \rangle = \left |010\right \rangle )$![]() for best localization. Compare to figure 3. Hereafter 8192 experimental shots were taken for each $k$
for best localization. Compare to figure 3. Hereafter 8192 experimental shots were taken for each $k$![]() , $t$
, $t$![]() and initial condition, giving statistical uncertainty $1/\sqrt {N_\textrm {shots}} \approx 1.1\,\%$
and initial condition, giving statistical uncertainty $1/\sqrt {N_\textrm {shots}} \approx 1.1\,\%$![]() . The experiment was performed on April 11, 2022 at 10:19 pm EST. Here ibmq_manila is recalibrated every 1–2 h to adjust for drift that can increase error.
. The experiment was performed on April 11, 2022 at 10:19 pm EST. Here ibmq_manila is recalibrated every 1–2 h to adjust for drift that can increase error.

Figure 6. Average Loschmidt echo fidelity of the QSM on the ibmq_manila device for three qubits and varying $k$![]() . Localization occurs below $k_\textrm {loc} \approx 1.87$
. Localization occurs below $k_\textrm {loc} \approx 1.87$![]() . Data are averaged over all eight initial computational basis states. Statistical uncertainty per data point is $1/\sqrt {8192*8} \approx 0.4\,\%$
. Data are averaged over all eight initial computational basis states. Statistical uncertainty per data point is $1/\sqrt {8192*8} \approx 0.4\,\%$![]() . The number of CNOT gates per forward-and-back step is $M_\textrm {CNOT}=66$
. The number of CNOT gates per forward-and-back step is $M_\textrm {CNOT}=66$![]() . The absolute fidelity gap at $t_\textrm {fb}=1$
. The absolute fidelity gap at $t_\textrm {fb}=1$![]() between the most localized and most diffusive cases is 10.6 %. The experiment was performed on January 28, 2022 at 2:44 pm EST.
between the most localized and most diffusive cases is 10.6 %. The experiment was performed on January 28, 2022 at 2:44 pm EST.
The metric of the localized state's probability was used more thoroughly in Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021). Figure 5 does not easily compare to Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021) because different map parameters were used, namely $L=1$![]() in this work and $L=7$
in this work and $L=7$![]() in Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021). This significantly changes the eigenstates, independently of $k$
in Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021). This significantly changes the eigenstates, independently of $k$![]() , and therefore, changes the degree of localization. Different parameters were used in the present work to achieve more strongly localized dynamics, as explained in § 2.2.
, and therefore, changes the degree of localization. Different parameters were used in the present work to achieve more strongly localized dynamics, as explained in § 2.2.
3.3 Fidelity and dynamics
The Loschmidt echo fidelity is a more quantitative metric of hardware ability for exploring the effect of dynamics on the fidelity. It is described in §§ 3.1 and 4.1.
By varying the parameter $k$![]() of the QSM the interaction between experimental noise and dynamics can be measured, as shown in figure 6. As predicted by the single-qubit Lindblad noise models in §§ 4.2 and 4.3, localized and diffusive dynamics have different fidelity decay rates during the various substeps of the simulation. The experiment shows a continuous transition in the fidelity decay rate as the dynamics change from localized to diffusive. The noise models are used in § 4.5 to fit the data and extract effective decoherence parameters.
of the QSM the interaction between experimental noise and dynamics can be measured, as shown in figure 6. As predicted by the single-qubit Lindblad noise models in §§ 4.2 and 4.3, localized and diffusive dynamics have different fidelity decay rates during the various substeps of the simulation. The experiment shows a continuous transition in the fidelity decay rate as the dynamics change from localized to diffusive. The noise models are used in § 4.5 to fit the data and extract effective decoherence parameters.
Note that for $n=3, L=1$![]() as used here, the predicted transition to full diffusion should occur at $k_\textrm {loc} \approx 1.87$
as used here, the predicted transition to full diffusion should occur at $k_\textrm {loc} \approx 1.87$![]() . In the experiment, the largest three $k$
. In the experiment, the largest three $k$![]() values have indistinguishable fidelities up to a $1.5\,\%$
values have indistinguishable fidelities up to a $1.5\,\%$![]() absolute difference despite $k=1.0$
absolute difference despite $k=1.0$![]() being below the transition threshold. Further resolution of the observed transition value $k_\textrm {loc}$
being below the transition threshold. Further resolution of the observed transition value $k_\textrm {loc}$![]() requires greater statistics and a larger system size. The smallest three $k$
requires greater statistics and a larger system size. The smallest three $k$![]() values show a gradual transition from the strongly localized $k=0.1$
values show a gradual transition from the strongly localized $k=0.1$![]() to the weakly localized $k=0.45$
to the weakly localized $k=0.45$![]() .
.
3.4 Gate error
The most direct metric for comparing our simulation results to reported metrics from IBM-Q is the CNOT gate error. This does not rely on any noise model, as it is a single-parameter fit (gate error) for each $k$![]() . In table 2, error fits are reported using just the first time step $f(1)$
. In table 2, error fits are reported using just the first time step $f(1)$![]() and the state preparation and measurement (SPAM) error $f(0)$
and the state preparation and measurement (SPAM) error $f(0)$![]() . The fidelity dependence on dynamics is codified here as gate error dependence on dynamics, with a factor of $1.5\times$
. The fidelity dependence on dynamics is codified here as gate error dependence on dynamics, with a factor of $1.5\times$![]() in gate error between the extreme dynamical cases.
in gate error between the extreme dynamical cases.
Table 1. Native gate counts and fidelity for executing each forward-and-back iteration of the QSM experimentally on IBM-Q devices. We include ibmq_5_yorktown to compare the effect of higher connectivity. To calculate forward-only gate counts as for figure 5, divide by two. (a) The CNOT gate count when Qiskit transpiler attempts direct gate decomposition of the QSM unitary. (b) The CNOT gate count when using the efficient algorithm (2.8) plus transpiler optimization on linear qubit connectivity. (c) Physical single-qubit gate count, not including virtual RZ gates. Range is over initial condition and dynamical map parameter $k$![]() . (d) Fidelity as measured by the one-step Loschmidt echo, partly from figure 6. The range is over $k$
. (d) Fidelity as measured by the one-step Loschmidt echo, partly from figure 6. The range is over $k$![]() , varied from diffusive to localizing dynamics, after averaging over initial conditions. The experiment on ibmq_5_yorktown was performed on October 22, 2020 at 4:41pm EST and experiments on ibmq_manila were performed on the date and time in figure 6. Fidelities include measurement error and are at full decoherence reach $1/N$
, varied from diffusive to localizing dynamics, after averaging over initial conditions. The experiment on ibmq_5_yorktown was performed on October 22, 2020 at 4:41pm EST and experiments on ibmq_manila were performed on the date and time in figure 6. Fidelities include measurement error and are at full decoherence reach $1/N$![]() .
.

Table 2. Comparison of IBM-Q's reported RB gate error to error extracted from a three-qubit experiment with localized ($k=0.1$![]() ) or diffusive ($k=4.55$
) or diffusive ($k=4.55$![]() ) dynamics. The experimental error $\epsilon$
) dynamics. The experimental error $\epsilon$![]() is calculated from fidelity decay $f(t)$
is calculated from fidelity decay $f(t)$![]() via $f(1) = (f(0)-1/2^n) (1-\epsilon )^{66} +1/2^n$
via $f(1) = (f(0)-1/2^n) (1-\epsilon )^{66} +1/2^n$![]() .
.

More interestingly, this range of observed errors is $3.0{-}4.5{\times }$![]() worse than the error reported by IBM-Q on their online ‘Systems’ screen at the time the experiment was performed (IBM 2022). Their reported error comes from standard two-qubit RB with a depolarizing noise model (McKay et al. Reference McKay, Sheldon, Smolin, Chow and Gambetta2019). The nature of RB circuits makes this difference in observed error unsurprising. However, it is worth describing several possible contributors.
worse than the error reported by IBM-Q on their online ‘Systems’ screen at the time the experiment was performed (IBM 2022). Their reported error comes from standard two-qubit RB with a depolarizing noise model (McKay et al. Reference McKay, Sheldon, Smolin, Chow and Gambetta2019). The nature of RB circuits makes this difference in observed error unsurprising. However, it is worth describing several possible contributors.
There are two main ways in which RB circuits reduce their observed error: the uniformly randomized Clifford gates effectively depolarize the error, reducing the effect of coherent errors relative to general circuits; and the same randomization causes low-frequency noise to ‘echo’ and partially cancel, similar to a dynamical decoupling protocol. While these do simplify the interpretation of RB, they also make it an overly optimistic metric for predicting the performance of general circuits.
Another cause of the error difference is the extra crosstalk from adding a third qubit relative to two-qubit RB. The role of third qubit crosstalk has been investigated with simultaneous RB (McKay et al. Reference McKay, Sheldon, Smolin, Chow and Gambetta2019), where the average CNOT error per gate was found to increase from $1.63\times 10^{-2}$![]() for two-qubit RB to $2.70\times 10^{-2}$
for two-qubit RB to $2.70\times 10^{-2}$![]() for (2+1)-qubit simultaneous RB, a factor increase due to a crosstalk of $1.66$
for (2+1)-qubit simultaneous RB, a factor increase due to a crosstalk of $1.66$![]() . How this factor varies across devices and between experiments is however less clear.
. How this factor varies across devices and between experiments is however less clear.
There are also differences between the dynamics of the QSM circuit and RB Clifford gates that may contribute. Recent research suggests Clifford gates have different quantum scrambling properties than general unitary dynamics: out-of-time-order correlators (OTOCs), which are measures of quantum chaos and scrambling and close relatives of the Loschmidt echo fidelity, reach very different asymptotic values under Clifford and non-Clifford unitary evolution (Roberts & Yoshida Reference Roberts and Yoshida2017; Leone, Oliviero & Hamma Reference Leone, Oliviero and Hamma2021). This may relate to the Clifford group being a 2-design on qudits (and a 3-design on qubits) (Webb Reference Webb2015; Roberts & Yoshida Reference Roberts and Yoshida2017; Zhu Reference Zhu2017). Since OTOCs for quantum chaotic systems only grow exponentially until the Ehrenfest time $\tau _E$![]() (Hashimoto, Murata & Yoshii Reference Hashimoto, Murata and Yoshii2017), the QSM that has $\tau _E \sim 1$
(Hashimoto, Murata & Yoshii Reference Hashimoto, Murata and Yoshii2017), the QSM that has $\tau _E \sim 1$![]() (see Appendix C) saturates OTOCs quickly. While this faster, more thorough quantum scrambling may influence the fidelity, we leave the quantification of such an effect to future work.
(see Appendix C) saturates OTOCs quickly. While this faster, more thorough quantum scrambling may influence the fidelity, we leave the quantification of such an effect to future work.
Most of these effects could be captured in a process matrix picture, in which certain elements of the CNOT process matrix are more strongly enacted in the QSM circuit relative to an average over RB circuits. However, the effect of crosstalk goes beyond a static process matrix, as it causes the process matrix to depend on the number of qubits. This is because even spectator qubits can increase error (McKay et al. Reference McKay, Sheldon, Smolin, Chow and Gambetta2019). The limited connectivity of IBM-Q devices becomes desirable here, as it reduces the number of neighbours per qubit that should limit the magnitude of crosstalk when scaling to many-qubit algorithms.
Lastly, the depolarizing noise model determined through RB is clearly unable to capture or explain the fidelity dependence on dynamics. Its single parameter $\alpha _{2Q}$![]() of two-qubit gate error measures an average tendency towards the state ${\boldsymbol \rho }=I/N$
of two-qubit gate error measures an average tendency towards the state ${\boldsymbol \rho }=I/N$![]() , rather than capturing important details of how different density matrix elements contribute different rates of decay. Additionally, its focus on averaging over unitary errors, while mathematically convenient, is perhaps less appropriate than decoherence for describing present day superconducting quantum devices.
, rather than capturing important details of how different density matrix elements contribute different rates of decay. Additionally, its focus on averaging over unitary errors, while mathematically convenient, is perhaps less appropriate than decoherence for describing present day superconducting quantum devices.
4 Noise models
4.1 Types of noise and fidelities
Present day quantum devices are impacted by many different types of noise. This motivates studies of the types of noise that are present and how the errors impact algorithms of interest. On the IBM-Q platform errors occur primarily during two-qubit gates that in the QSM algorithm contribute about $10$![]() times more to the total error over single-qubit gates, as discussed in Appendix A. The types of error that occur may be incoherent Markovian relaxation and dephasing error ($T_1$
times more to the total error over single-qubit gates, as discussed in Appendix A. The types of error that occur may be incoherent Markovian relaxation and dephasing error ($T_1$![]() and $T_2$
and $T_2$![]() , respectively), coherent error, multi-qubit incoherent errors or something else. Here three models of noise based on Lindblad master equations are considered for understanding the effects of errors: (1) an approximate analytic theory of the effects of relaxation and dephasing, (2) a Lindblad master equation simulation using single-qubit Lindblad errors with the four substeps of ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$
, respectively), coherent error, multi-qubit incoherent errors or something else. Here three models of noise based on Lindblad master equations are considered for understanding the effects of errors: (1) an approximate analytic theory of the effects of relaxation and dephasing, (2) a Lindblad master equation simulation using single-qubit Lindblad errors with the four substeps of ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$![]() in (2.7) rather than the actual gate decomposition, and (3) the IBM-Q Aer simulator that uses the exact gate decomposition and a Kraus noise process model based on single-qubit relaxation and dephasing. In Appendix D we prove that a stochastic Hamiltonian parametric noise model cannot explain the experimental results.
in (2.7) rather than the actual gate decomposition, and (3) the IBM-Q Aer simulator that uses the exact gate decomposition and a Kraus noise process model based on single-qubit relaxation and dephasing. In Appendix D we prove that a stochastic Hamiltonian parametric noise model cannot explain the experimental results.
The overall impact of noise can be studied by its effect on the rate of fidelity decay of our quantum system. When the noise is unitary, such as parametric noise (see Appendix D), with total evolution ${{{\boldsymbol{\mathsf{U}}}}}_\epsilon$![]() and noise amplitude $\epsilon$
and noise amplitude $\epsilon$![]() , and a pure state $\left |\psi \right \rangle$
, and a pure state $\left |\psi \right \rangle$![]() is used as an initial condition, the fidelity of the evolution can be measured by
is used as an initial condition, the fidelity of the evolution can be measured by
which is also known as the Loschmidt echo. Here $\epsilon '$![]() indicates the same magnitude as $\epsilon$
indicates the same magnitude as $\epsilon$![]() while being statistically independent. For non-unitary noise, such as Lindblad noise, one must use the more general density matrix formulation
while being statistically independent. For non-unitary noise, such as Lindblad noise, one must use the more general density matrix formulation
for ideal (initial) and noisy (final) density matrices ${\boldsymbol \rho }$![]() and ${\boldsymbol \sigma }$
and ${\boldsymbol \sigma }$![]() , respectively. In the noiseless case, ${\boldsymbol \sigma }$
, respectively. In the noiseless case, ${\boldsymbol \sigma }$![]() should again return to its initial state ${\boldsymbol \rho }$
should again return to its initial state ${\boldsymbol \rho }$![]() due to the forward-and-back evolution. For an initial pure state ${\boldsymbol \rho }= |\psi \rangle \langle \psi |$
due to the forward-and-back evolution. For an initial pure state ${\boldsymbol \rho }= |\psi \rangle \langle \psi |$![]() , this simplifies to
, this simplifies to

which is used in §§ 3.1 and 4.2.
Contrary to previous studies, noise here occurs during both forward-and-backward evolution to connect simulation to experiment. This increases the total time relative to the number of forward map steps by a factor of two, and therefore, the observed fidelity decay rate by the same factor. In all cases we average the fidelity over the $N$![]() initial conditions $\left |p\right \rangle$
initial conditions $\left |p\right \rangle$![]() of the computational basis in order to study the average dynamics (Benenti & Casati Reference Benenti and Casati2002).
of the computational basis in order to study the average dynamics (Benenti & Casati Reference Benenti and Casati2002).
4.2 Effects of dynamics on Lindblad noise
The Lindblad master equation is the most general type of completely positive trace-preserving Markovian master equation (Gorini, Kossakowski & Sudarshan Reference Gorini, Kossakowski and Sudarshan1976; Lindblad Reference Lindblad1976; Gardiner & Zoller Reference Gardiner and Zoller2004; Stéphane, Joye & Pillet Reference Stéphane, Joye and Pillet2006; Pearle Reference Pearle2012; Manzano Reference Manzano2020). It can be written in dimensionless form as

for general Lindblad operators $\{{{{\boldsymbol{\mathsf{L}}}}}_i\}$![]() , where $t = t_\textrm {phys}/T_\textrm {step}$
, where $t = t_\textrm {phys}/T_\textrm {step}$![]() has units in the number of map steps, $T_\textrm {step}$
has units in the number of map steps, $T_\textrm {step}$![]() is the dimensioned time to execute ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$
is the dimensioned time to execute ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$![]() on hardware, ${{{\boldsymbol{\mathsf{H}}}}}={{{\boldsymbol{\mathsf{H}}}}}_\textrm {phys} T_\textrm {step}/\hbar$
on hardware, ${{{\boldsymbol{\mathsf{H}}}}}={{{\boldsymbol{\mathsf{H}}}}}_\textrm {phys} T_\textrm {step}/\hbar$![]() with the forms of ${{{\boldsymbol{\mathsf{H}}}}}$
with the forms of ${{{\boldsymbol{\mathsf{H}}}}}$![]() and ${{{\boldsymbol{\mathsf{H}}}}}_\textrm {phys}$
and ${{{\boldsymbol{\mathsf{H}}}}}_\textrm {phys}$![]() depending on the substep of the algorithm and $\nu _i = \nu _{i, \textrm {phys}} T_\textrm {step}$
depending on the substep of the algorithm and $\nu _i = \nu _{i, \textrm {phys}} T_\textrm {step}$![]() . The Loschmidt echo fidelity $f(t)$
. The Loschmidt echo fidelity $f(t)$![]() comes from reversing the unitary evolution from ${{{\boldsymbol{\mathsf{H}}}}}$
comes from reversing the unitary evolution from ${{{\boldsymbol{\mathsf{H}}}}}$![]() without inverting the noise processes ${{{\boldsymbol{\mathsf{L}}}}}_i$
without inverting the noise processes ${{{\boldsymbol{\mathsf{L}}}}}_i$![]() . This is modified in the case of parametric noise; see Appendix D for details.
. This is modified in the case of parametric noise; see Appendix D for details.
As for the Lindblad operators in (4.4), we use $2n$![]() single-qubit operators $\{{{{\boldsymbol{\mathsf{L}}}}}_{1,j}, {{{\boldsymbol{\mathsf{L}}}}}_{2,j}\}$
single-qubit operators $\{{{{\boldsymbol{\mathsf{L}}}}}_{1,j}, {{{\boldsymbol{\mathsf{L}}}}}_{2,j}\}$![]() , defined as
, defined as
causing relaxation to the ground state at rate $\nu _1$![]() and pure dephasing at rate $\nu _2$
and pure dephasing at rate $\nu _2$![]() for each qubit $j$
for each qubit $j$![]() , as described in Appendix C. These relate to the relaxation time $T_1$
, as described in Appendix C. These relate to the relaxation time $T_1$![]() and total dephasing time $T_2$
and total dephasing time $T_2$![]() via
via
as can be seen by comparing Appendix C to Krantz et al. (Reference Krantz, Kjaergaard, Yan, Orlando, Gustavsson and Oliver2019). For calculating the fidelity, the ideal expected density matrix, which is also the initial density matrix, will be denoted ${\boldsymbol \rho }$![]() , and the noisy evolving density matrix will be denoted ${\boldsymbol \sigma }$
, and the noisy evolving density matrix will be denoted ${\boldsymbol \sigma }$![]() .
.
The main interaction between dynamics and Lindblad noise is that different types of dynamics have different typical density matrices that are influenced by each decoherence effect to different degrees. These include on-diagonal relaxation (of computational basis states), off-diagonal relaxation (of superpositions of basis states) and off-diagonal dephasing. In Appendix C we analytically determine the decay of fidelity for pure states in the two dynamical limits of being highly localized and highly diffusive, as well as the case of uniform superposition, all three of which are summarized in this section. Briefly, the fidelity of localized pure states is affected only by on-diagonal relaxation due to their lack of off-diagonal terms, while the fidelity of diffusive pure states is affected only by off-diagonal relaxation and dephasing due to a cancellation of on-diagonal effects. The key findings here are that the $\nu _1$![]() dependence is the same for both despite differing origins while the $\nu _2$
dependence is the same for both despite differing origins while the $\nu _2$![]() dependence is greater in the diffusive case.
dependence is greater in the diffusive case.
Starting with the fully localized case that has $k=0$![]() , initial conditions $\left |\psi \right \rangle =\left |p\right \rangle$
, initial conditions $\left |\psi \right \rangle =\left |p\right \rangle$![]() of computational basis states and fidelity $f=\sigma _{p,p}$
of computational basis states and fidelity $f=\sigma _{p,p}$![]() , the evolution of $\left |\psi \right \rangle$
, the evolution of $\left |\psi \right \rangle$![]() due to the diagonal Hamiltonian has no effect on the density matrix ${\boldsymbol \sigma }$
due to the diagonal Hamiltonian has no effect on the density matrix ${\boldsymbol \sigma }$![]() and, therefore, on the fidelity. The Lindblad evolution acts alone, causing relaxation of each qubit towards the ground state at rate $\nu _1$
and, therefore, on the fidelity. The Lindblad evolution acts alone, causing relaxation of each qubit towards the ground state at rate $\nu _1$![]() . If one averages the fidelity over all possible initial states $\left |p\right \rangle$
. If one averages the fidelity over all possible initial states $\left |p\right \rangle$![]() , the result is
, the result is
so that the initial effective decay rate is

where
for the localized case. The factor of $1/2$![]() derives from the average $1/2$
derives from the average $1/2$![]() chance of each qubit starting in the excited state. The factor of $n$
chance of each qubit starting in the excited state. The factor of $n$![]() due to $n$
due to $n$![]() qubits decaying is an important aspect of interpreting measured $T_1$
qubits decaying is an important aspect of interpreting measured $T_1$![]() and $T_2$
and $T_2$![]() times. Dynamics that are less than fully localized will start to show effects of the diffusive case described below.
times. Dynamics that are less than fully localized will start to show effects of the diffusive case described below.
Between the localized and diffusive cases, another interesting case is the decay of a uniform superposition state, where all $n$![]() qubits are in $\left |+\right \rangle$
qubits are in $\left |+\right \rangle$![]() states that are unentangled relative to the computational basis. The fidelity is a product of the single-qubit fidelities. This may look like a simple model of a diffused state since the probability has spread to all states equally, but a general diffused state would also be entangled with random, independent phases on each of the $2^n$
states that are unentangled relative to the computational basis. The fidelity is a product of the single-qubit fidelities. This may look like a simple model of a diffused state since the probability has spread to all states equally, but a general diffused state would also be entangled with random, independent phases on each of the $2^n$![]() states. The uniform superposition state is then a useful test of the relative roles of spreading probability versus entanglement in quantum state diffusion. Only half of the single-qubit fidelity decays, similar to the averaging factor of one half in the localized case. The same (4.8) and (4.9) apply with
states. The uniform superposition state is then a useful test of the relative roles of spreading probability versus entanglement in quantum state diffusion. Only half of the single-qubit fidelity decays, similar to the averaging factor of one half in the localized case. The same (4.8) and (4.9) apply with
In the diffusive case the Hamiltonian evolution becomes important, but for the QSM, we have found it can be abstracted away to simplify the problem and still produce predictions that agree well with simulation, as we describe here. To simplify, note that chaotic mixing occurs on faster time scales than Lindblad decay. Then the density matrix can be expected to quickly reach a randomly entangled pure state, having (approximately) uniformly spread probability and random relative phases, after which the Hamiltonian evolution has little qualitative effect aside from rapidly changing the precise values of the phases; see (C14) for a model of a randomly entangled state. Fidelity decay during diffusive dynamics can then be approximated as the decay of this random pure state under Lindblad evolution. Averaging over initial conditions (basis states) allows this random state to be analysed via the average behaviour of the statistical ensemble it belongs to. For a chaotic system, this corresponds to averaging over the entire accessible phase space. Such averaging contributes to an averaging over these random phases, causing the phase-dependent terms in $f$![]() to vanish. Inspecting $f=\sum _{i,j} \sigma _{i,j} \rho _{i,j}^*$
to vanish. Inspecting $f=\sum _{i,j} \sigma _{i,j} \rho _{i,j}^*$![]() shows that only $\sigma _{i,j}$
shows that only $\sigma _{i,j}$![]() terms that retain their initial phase from $\rho _{i,j}$
terms that retain their initial phase from $\rho _{i,j}$![]() survive due to phase cancellation in $f$
survive due to phase cancellation in $f$![]() . Surprisingly, this causes the qubits to effectively disentangle for off-diagonal terms $\sigma _{i,j} \rho _{i,j}^*$
. Surprisingly, this causes the qubits to effectively disentangle for off-diagonal terms $\sigma _{i,j} \rho _{i,j}^*$![]() , in a manner describable by two pieces: a non-trace-preserving single-qubit decay and a trace-preserving correction. Along the $n$
, in a manner describable by two pieces: a non-trace-preserving single-qubit decay and a trace-preserving correction. Along the $n$![]() -qubit diagonal the flat $\rho _{i,i}=1/2^n$
-qubit diagonal the flat $\rho _{i,i}=1/2^n$![]() causes relaxation effects across $\sigma _{i,i} \rho _{i,i}^*$
causes relaxation effects across $\sigma _{i,i} \rho _{i,i}^*$![]() to cancel out. This leaves only effects from dephasing and off-diagonal relaxation, where the random phase averaging removes the gain to lower states but not the loss from higher states. The exact fidelity expression for the diffusive case is provided in (C26) in Appendix C, but its initial decay rate using (4.9) is simply
to cancel out. This leaves only effects from dephasing and off-diagonal relaxation, where the random phase averaging removes the gain to lower states but not the loss from higher states. The exact fidelity expression for the diffusive case is provided in (C26) in Appendix C, but its initial decay rate using (4.9) is simply
which is strictly faster than both the localized and superposition cases, and any unentangled case, when $\nu _1, \nu _2 > 0$![]() . Random entanglement has the same dephasing rate as unentangled superposition, but it has an additional relaxation effect due to the average over random phases between the excited and decaying states.
. Random entanglement has the same dephasing rate as unentangled superposition, but it has an additional relaxation effect due to the average over random phases between the excited and decaying states.
Figure 7 compares the full analytic fidelity evolution for each dynamical case. Each fidelity has the expected feature of starting with an exponential decay that gradually relaxes to the uniformly mixed value of $1/N$![]() . In superconducting qubits the $\nu _2$
. In superconducting qubits the $\nu _2$![]() rate often dominates, so three types of dynamics are compared for that case in figure 7(b). These fidelity decay rates do not account for the gate implementation used in the experiment, which is partly rectified in the next section.
rate often dominates, so three types of dynamics are compared for that case in figure 7(b). These fidelity decay rates do not account for the gate implementation used in the experiment, which is partly rectified in the next section.

Figure 7. Theoretical Lindblad fidelity evolution from forward-and-back noise for $\nu _1=0.1$![]() and $\nu _2=0.2$
and $\nu _2=0.2$![]() : (a) comparing the decay of a diffusive state for three, six and nine qubits; (b) comparing the decay of localized, superposition and diffusive states for six qubits. The average fidelity plateaus at the uniformly mixed limit $1/N$
: (a) comparing the decay of a diffusive state for three, six and nine qubits; (b) comparing the decay of localized, superposition and diffusive states for six qubits. The average fidelity plateaus at the uniformly mixed limit $1/N$![]() when no information about the original state remains.
when no information about the original state remains.
4.3 Gate-based Lindblad model
The theoretical expressions for the localized and diffusive dynamical cases can now be modified to a gate-based form to better match experimental observations in which the majority of errors occur during certain specific gates. Since two-qubit gates are the dominant source of error on IBM-Q, one can model circuit error to lowest order as solely being due to the two-qubit gates causing an enhanced Lindblad decay for each of the target qubits. Further rationale for this model is provided in Appendix E. Averaged over the possible two-qubit subsystems on which the gates act during a circuit, this is approximately described by the dynamics-dependent expressions previously derived, with the number of qubits set to two. If the gates are performed serially then the serial gate-based fidelity $f_{\textrm {GB, S}}(t,n)$![]() can be given in terms of the dynamics-dependent expressions for the Lindblad fidelity $f_{L}(t',n')$
can be given in terms of the dynamics-dependent expressions for the Lindblad fidelity $f_{L}(t',n')$![]() of (4.9) as
of (4.9) as
where $M$![]() is the number of gates per map step, $t=1$
is the number of gates per map step, $t=1$![]() is the time to complete a map step, $n$
is the time to complete a map step, $n$![]() is the total number of qubits in the circuit, $n'=2$
is the total number of qubits in the circuit, $n'=2$![]() is the number of decaying qubits per gate duration and $t'=1/M$
is the number of decaying qubits per gate duration and $t'=1/M$![]() is the time per gate duration as a fraction of a map step. Note the late-time (average) fidelity should always approach $1/2^n=1/N$
is the time per gate duration as a fraction of a map step. Note the late-time (average) fidelity should always approach $1/2^n=1/N$![]() . For large $M$
. For large $M$![]() , the Lindblad expression simplifies to $f_{L}(t \ll 1,n) \approx \textrm {e}^{-n \nu _\textrm {single} t}$
, the Lindblad expression simplifies to $f_{L}(t \ll 1,n) \approx \textrm {e}^{-n \nu _\textrm {single} t}$![]() , so
, so
This model will be seen in § 4.5 to qualitatively match experimental results for $n=3$![]() . Compared with a model that assumes all three qubits are decaying at equal rates, when fitted to the experimental data this gate-based model measures $\nu _1$
. Compared with a model that assumes all three qubits are decaying at equal rates, when fitted to the experimental data this gate-based model measures $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() that are about $3/2$
that are about $3/2$![]() larger.
larger.
Performing some gates in parallel would increase the average number of simultaneously targeted qubits from two to $n_\textrm {eff} \equiv 2*\lfloor n/2 \rfloor \leq n$![]() and decrease gate depth from $M$
and decrease gate depth from $M$![]() to $D=2M/n_\textrm {eff}$
to $D=2M/n_\textrm {eff}$![]() . Then the fidelity would be
. Then the fidelity would be
For large $M$![]() , this simplifies to
, this simplifies to
Since $\nu _\textrm {single} = \nu _\textrm {single,phys} T_\textrm {step}$![]() depends on the physical map step time $T_\textrm {step}$
depends on the physical map step time $T_\textrm {step}$![]() , which is $n_\textrm {eff}/2$
, which is $n_\textrm {eff}/2$![]() times shorter for the parallel case compared with the serial case, the two cases yield the same fidelity as a function of map step $t$
times shorter for the parallel case compared with the serial case, the two cases yield the same fidelity as a function of map step $t$![]() . This just reflects the fact that total fidelity is the product of gate fidelities when gate error is much greater than idle error. As gate error approaches idle error and the number of idle qubits increases, idle errors complicate this analysis and a benefit to parallelization appears.
. This just reflects the fact that total fidelity is the product of gate fidelities when gate error is much greater than idle error. As gate error approaches idle error and the number of idle qubits increases, idle errors complicate this analysis and a benefit to parallelization appears.
To test the theoretical predictions of (4.13) and (4.15), we use QuTiP's (Johansson, Nation & Nori Reference Johansson, Nation and Nori2012) master equation solver. To partially mimic a circuit model, we simulate the four unitary steps of (2.7) sequentially, rather than simulating the whole Hamiltonian at once. This turns out to be especially important for the localized case, as described below. For the three-qubit simulation, we also mimic two-qubit gates by only applying Lindblad operators to two qubits at a time, alternating the qubit pairs $[0,1]$![]() and $[1,2]$
and $[1,2]$![]() to mimic the near-linear connectivity on many IBM-Q devices. This matches the effective two-qubit decay rate from theory.
to mimic the near-linear connectivity on many IBM-Q devices. This matches the effective two-qubit decay rate from theory.
The simulation results in figure 8 require a modified interpretation of the theory, as shown for three qubits with serial gates and six qubits with parallel gates. In the localized case, a straightforward Hamiltonian simulation would keep the state localized during the whole map step and would fit well to the theoretical localized decay. But decomposing the evolution to substeps (or further to gates) reveals that the QFTs take the localized state to and from a delocalized state during half of each map step. This delocalized state has phases that are even spaced around the unit circle and, thus, will usually average to zero. This effect is similar to the derivation of the diffusive fidelity decay rate in Appendix C, suggesting that the diffusive decay rate could be appropriate here. This is empirically supported by the simulation results in figure 8 for $k=0.1$![]() , which fit better to a half-localized, half-diffusive model as shown than to a half-localized, half-superposition model that would decrease $\nu _\textrm {single}$
, which fit better to a half-localized, half-diffusive model as shown than to a half-localized, half-superposition model that would decrease $\nu _\textrm {single}$![]() by $\nu _1/8$
by $\nu _1/8$![]() . Therefore, we model the map step fidelity as $f_\textrm {semi-loc} \approx f_\textrm {loc}(t/2) f_\textrm {dif}(t/2) \approx (f_\textrm {loc} f_\textrm {dif})^{1/2}$
. Therefore, we model the map step fidelity as $f_\textrm {semi-loc} \approx f_\textrm {loc}(t/2) f_\textrm {dif}(t/2) \approx (f_\textrm {loc} f_\textrm {dif})^{1/2}$![]() . Using (4.9) with (4.10) for $f_{loc}$
. Using (4.9) with (4.10) for $f_{loc}$![]() and (4.12) for $f_{\textrm {dif}}$
and (4.12) for $f_{\textrm {dif}}$![]() implies a ‘semi-localized’ decay rate given by
implies a ‘semi-localized’ decay rate given by
With this modified theoretical prediction, the difference between localized simulation and semi-localized theory is small. One cause of the remaining difference in figure 8 is the small non-zero $k$![]() allows small, random amplitudes on other states. This creates some random entanglement that enhances the decay rate during the localized part of the algorithm. This explains some but not all of the difference, with the unexplained portion growing with increasing $n$
allows small, random amplitudes on other states. This creates some random entanglement that enhances the decay rate during the localized part of the algorithm. This explains some but not all of the difference, with the unexplained portion growing with increasing $n$![]() and $t_\textrm {fb}$
and $t_\textrm {fb}$![]() . For example, at $n=3$
. For example, at $n=3$![]() the effect of non-zero $k$
the effect of non-zero $k$![]() accounts for $\ge 50\,\%$
accounts for $\ge 50\,\%$![]() of the difference for $t_\textrm {fb} \geq 5$
of the difference for $t_\textrm {fb} \geq 5$![]() , but at $n=6$
, but at $n=6$![]() it explains only $12\,\%$
it explains only $12\,\%$![]() of the difference at $t_\textrm {fb} = 5$
of the difference at $t_\textrm {fb} = 5$![]() (note that simulations of this are not shown). The remaining difference between theory and numerics is attributable to equating between a randomly diffused state and the QFT of a localized state in deriving (4.17).
(note that simulations of this are not shown). The remaining difference between theory and numerics is attributable to equating between a randomly diffused state and the QFT of a localized state in deriving (4.17).

Figure 8. Comparing Lindblad evolutions from full simulation (solid) to the theoretical steady-state approximation (dashed) for the fully localized (blue), semi-localized (purple, $k=0.1$![]() ) and fully diffusive (red, $k=10.0$
) and fully diffusive (red, $k=10.0$![]() ) cases. Using $\nu _1=0.1$
) cases. Using $\nu _1=0.1$![]() and $\nu _2=0.2$
and $\nu _2=0.2$![]() . Results are shown for (a) $n=3$
. Results are shown for (a) $n=3$![]() ($n_\textrm {eff}=2$
($n_\textrm {eff}=2$![]() ) and (b) $n=6$
) and (b) $n=6$![]() ($n_\textrm {eff}=6$
($n_\textrm {eff}=6$![]() ).
).
In the diffusive case the difference between theory and numerics is generally smaller despite neglect of the exact Hamiltonian evolution. This suggests that the effect of the precise Hamiltonian evolution on the fidelity is subdominant.
While this model only includes error from two-qubit gates, it could be modified to include other gates. The largest correction would come from idle gates for idling qubits, which have their own decay rates $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() . Idle gates are important because CNOT gate error comes primarily from the duration of the gate, implying that any qubit idling in parallel with a CNOT gate is experiencing a significant fraction of the error. For more details, see Appendix A.1.2 for gate specifics and table 3 for experimental fits.
. Idle gates are important because CNOT gate error comes primarily from the duration of the gate, implying that any qubit idling in parallel with a CNOT gate is experiencing a significant fraction of the error. For more details, see Appendix A.1.2 for gate specifics and table 3 for experimental fits.
Table 3. Parameter fits from figure 9. All values are averaged over three qubits connected in a line on ibmq_manila. Here $T_{1,\textrm {phys}}$![]() and $T_{2,\textrm {phys}}$
and $T_{2,\textrm {phys}}$![]() values are converted from simulations using $T_{1,\textrm {phys}} = T_\textrm {step} / \nu _1$
values are converted from simulations using $T_{1,\textrm {phys}} = T_\textrm {step} / \nu _1$![]() and $T_{2,\textrm {phys}} = T_\textrm {step}*2 / (\nu _1+\nu _2)$
and $T_{2,\textrm {phys}} = T_\textrm {step}*2 / (\nu _1+\nu _2)$![]() , where $T_\textrm {step}=33*350 ns$
, where $T_\textrm {step}=33*350 ns$![]() . Errors are propagated by assuming zero covariance of $\nu _1$
. Errors are propagated by assuming zero covariance of $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() , as the Lindblad model stipulates. Relaxation $\nu _1$
, as the Lindblad model stipulates. Relaxation $\nu _1$![]() and pure dephasing $\nu _2$
and pure dephasing $\nu _2$![]() are dimensionless decay rates per single-direction map step forwards or backwards in time. The analytic theory applies continuous Lindblad decay for two qubits for each of the $66$
are dimensionless decay rates per single-direction map step forwards or backwards in time. The analytic theory applies continuous Lindblad decay for two qubits for each of the $66$![]() gates per map step. The Lindblad simulation continuously applies Lindblad operators to two qubits in alternating pairs during the eight algorithm substeps. The modified Aer simulator applies Lindblad decay to one and two qubits as Kraus operators after each gate.
gates per map step. The Lindblad simulation continuously applies Lindblad operators to two qubits in alternating pairs during the eight algorithm substeps. The modified Aer simulator applies Lindblad decay to one and two qubits as Kraus operators after each gate.


Figure 9. Numerical fits of several models to the data in figure 6 for the extreme conditions of localized (purple, $k=0.1$![]() ) and diffusive (red, $k=4.55$
) and diffusive (red, $k=4.55$![]() ) dynamics. Models are described in the main text. Note that, for both values of $k$
) dynamics. Models are described in the main text. Note that, for both values of $k$![]() , the plots for the theory fit and Aer simulation fit overlap and resemble a solid line.
, the plots for the theory fit and Aer simulation fit overlap and resemble a solid line.
4.4 The IBM Aer gate-based Lindblad simulator
For artificial noisy simulators, IBM offers several options. One option is their device-specific noise models (IBM 2021a) that are calibrated to each device's reported errors. Reported $T_1$![]() and $T_2$
and $T_2$![]() times and per gate error rates from RB are used as input for a combined relaxation, dephasing and depolarization error model. However, because these models are not customizable they cannot be fit to experimental data.
times and per gate error rates from RB are used as input for a combined relaxation, dephasing and depolarization error model. However, because these models are not customizable they cannot be fit to experimental data.
We instead use a custom IBM Aer noise model. Closest to our gate-based Linblad model is a simple Aer model based on the function thermal_relaxation_error with parameters $T_1$![]() and $T_2$
and $T_2$![]() and an effective temperature that we set to zero (the default option) (IBM 2021c). This function applies a single-qubit Lindblad decay to each qubit targeted by a gate based on the duration of the gate, after the gate is done. When $T_2>T_1$
and an effective temperature that we set to zero (the default option) (IBM 2021c). This function applies a single-qubit Lindblad decay to each qubit targeted by a gate based on the duration of the gate, after the gate is done. When $T_2>T_1$![]() , it applies Kraus operators, but when $T_2< T_1$
, it applies Kraus operators, but when $T_2< T_1$![]() , as is common, it probabilistically applies single-qubit gates instead. We modify this function to always apply Kraus operators. This model will be used in figure 9 to compare the relative importance of specifying the full gate dynamics as in Aer versus simplifying to the four unitary substeps (2.7) as in the gate-based Lindblad model.
, as is common, it probabilistically applies single-qubit gates instead. We modify this function to always apply Kraus operators. This model will be used in figure 9 to compare the relative importance of specifying the full gate dynamics as in Aer versus simplifying to the four unitary substeps (2.7) as in the gate-based Lindblad model.
4.5 Fitting theory to experiment
Having now described our noise models and performed derivations and simulations that qualitatively agree with experiment, it is interesting to fit these models to experiment to extract phenomenological decoherence parameters. The computational models can be fit through standard variational methods. The analytic gate-based Lindblad model from (4.14) has a fidelity that decays as
where $n_\textrm {eff}=2$![]() for the two active qubits per gate, $t \equiv 2 t_\textrm {fb}$
for the two active qubits per gate, $t \equiv 2 t_\textrm {fb}$![]() with $t_\textrm {fb}$
with $t_\textrm {fb}$![]() as the number of forward-and-back pairs of map steps and $\nu _\textrm {single}$
as the number of forward-and-back pairs of map steps and $\nu _\textrm {single}$![]() depends on the dynamics of the map. After adjusting for the dynamics of the full QSM algorithm, the effect of localized dynamics is that
depends on the dynamics of the map. After adjusting for the dynamics of the full QSM algorithm, the effect of localized dynamics is that
while the effect of diffusive dynamics is that
as explained in §§ 4.2 and 4.3, with further details in Appendix C.
To compare the experiment of figure 6 to this theory, it is convenient to focus on the extreme cases of $k=0.1$![]() and $k=4.55$
and $k=4.55$![]() . An account of continuously changing $k$
. An account of continuously changing $k$![]() in a Lindblad model and its effect on fidelity would require a careful application of localization length to the Lindblad model, which is beyond the scope of this paper.
in a Lindblad model and its effect on fidelity would require a careful application of localization length to the Lindblad model, which is beyond the scope of this paper.
Figure 9 shows numerical fits to experimental fidelity of extreme $k$![]() for the gate-based Lindblad theory, the gate-based Lindblad simulations and an IBM-Q Aer simulator model, all described in § 4. Also included is the default Aer model from the function AerSimulator.from_backend(FakeManila()), which is designed to fit the error measured by RB.
for the gate-based Lindblad theory, the gate-based Lindblad simulations and an IBM-Q Aer simulator model, all described in § 4. Also included is the default Aer model from the function AerSimulator.from_backend(FakeManila()), which is designed to fit the error measured by RB.
The default Aer model underestimates error, but it only underestimates it by a factor of $1.5$![]() instead of $3.0{-}4.5$
instead of $3.0{-}4.5$![]() from table 2. This is because it draws from a previous device calibration when the relevant gates were $2.0{-}3.0\times$
from table 2. This is because it draws from a previous device calibration when the relevant gates were $2.0{-}3.0\times$![]() worse, artificially improving its accuracy. On average it is likely to be less accurate for the three-qubit QSM than shown here.
worse, artificially improving its accuracy. On average it is likely to be less accurate for the three-qubit QSM than shown here.
The three higher accuracy model fits demonstrate different approaches. The Lindblad theory fit uses the gate-based model (4.14) with rates (4.17) for localized dynamics and (4.12) for diffusive dynamics. The Lindblad simulation fit applies single-qubit relaxation and dephasing of uniform rates $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() continuously to two out of three qubits, alternating between qubits 0 and 1 or 1 and 2. This is applied during the four unitary steps per (2.7) evolved forward and back with QuTiP's mesolve function. The Aer simulator fit applies two-qubit and single-qubit gates followed by Kraus operators on the targeted qubits that are determined from decoherence parameters $T_{1,\textrm {phys}}$
continuously to two out of three qubits, alternating between qubits 0 and 1 or 1 and 2. This is applied during the four unitary steps per (2.7) evolved forward and back with QuTiP's mesolve function. The Aer simulator fit applies two-qubit and single-qubit gates followed by Kraus operators on the targeted qubits that are determined from decoherence parameters $T_{1,\textrm {phys}}$![]() and $T_{2,\textrm {phys}}$
and $T_{2,\textrm {phys}}$![]() .
.
These models of fidelity all have just two parameters: $\nu _1$![]() for relaxation and $\nu _2$
for relaxation and $\nu _2$![]() for dephasing, which relate to the physical decoherence times through (4.7) and $T_1 = T_{1,\textrm {phys}}/T_\textrm {step}, T_2 = T_{2,\textrm {phys}}/T_\textrm {step}$
for dephasing, which relate to the physical decoherence times through (4.7) and $T_1 = T_{1,\textrm {phys}}/T_\textrm {step}, T_2 = T_{2,\textrm {phys}}/T_\textrm {step}$![]() . Here $T_\textrm {step}$
. Here $T_\textrm {step}$![]() is the time to complete a single forward or backward map step on hardware, with $T_\textrm {step}=33*350 ns$
is the time to complete a single forward or backward map step on hardware, with $T_\textrm {step}=33*350 ns$![]() to match $33$
to match $33$![]() CNOT gates of average duration $\approx 350 ns$
CNOT gates of average duration $\approx 350 ns$![]() on each of the forward-and-backward simulation steps. (This was an accurate average gate time when these experiments were performed, though since then IBM's two-qubit gates have changed in type and duration. (IBM 2022).) This only considers time spent in CNOT gates, in accordance with the single-gate-based Lindblad model. The Aer simulator model uses the same $T_\textrm {step}$
on each of the forward-and-backward simulation steps. (This was an accurate average gate time when these experiments were performed, though since then IBM's two-qubit gates have changed in type and duration. (IBM 2022).) This only considers time spent in CNOT gates, in accordance with the single-gate-based Lindblad model. The Aer simulator model uses the same $T_\textrm {step}$![]() to convert between parameters, despite including single-qubit gates decaying at the same rate as the CNOT gates, since the single-qubit gates contribute $<5\,\%$
to convert between parameters, despite including single-qubit gates decaying at the same rate as the CNOT gates, since the single-qubit gates contribute $<5\,\%$![]() to the total duration of gates ($1/10$
to the total duration of gates ($1/10$![]() the duration of a CNOT gate and $< 1/2$
the duration of a CNOT gate and $< 1/2$![]() as many gates). Since it directly fits $T_{1,\textrm {phys}}$
as many gates). Since it directly fits $T_{1,\textrm {phys}}$![]() and $T_{2,\textrm {phys}}$
and $T_{2,\textrm {phys}}$![]() , this extra error is in the converted $\nu _1$
, this extra error is in the converted $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() values. Measurement error is neglected in all models, which requires additional parameters to describe the probability of each state being misclassified, and which has a small effect on the large exponential decay rates measured here.
values. Measurement error is neglected in all models, which requires additional parameters to describe the probability of each state being misclassified, and which has a small effect on the large exponential decay rates measured here.
The fit of all three models in figure 9 is qualitatively quite good. The Lindblad simulation is a slightly worse fit than the others, which is surprising since it should be more accurate than the corresponding simplified theoretical model. The late time fit may appear to have higher error, but this is only an illusion of plotting the log of fidelity that accentuates the errors when the fidelity is small.
Table 3 provides the quantitative parameter fits. The most striking result is the consistent values of $T_2$![]() across models, as it is also the dominant error source. Here $T_2$
across models, as it is also the dominant error source. Here $T_2$![]() measures the dephasing of states that are in superposition, and the QSM with diffusive dynamics produces randomly entangled states that dephase similarly to superposition states (see Appendix C), so it is well suited to benchmark an effective version of this noise process. The agreement between models suggests the analytical model might be usable for lightweight extraction of the effective circuit $T_2$
measures the dephasing of states that are in superposition, and the QSM with diffusive dynamics produces randomly entangled states that dephase similarly to superposition states (see Appendix C), so it is well suited to benchmark an effective version of this noise process. The agreement between models suggests the analytical model might be usable for lightweight extraction of the effective circuit $T_2$![]() time.
time.
The variance across the fit $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() values suggests differing effective weights on each across the three models. The analytic model suggests that $\nu _2$
values suggests differing effective weights on each across the three models. The analytic model suggests that $\nu _2$![]() is the sole cause of a difference between localized and diffusive fidelity decay rates. However, three qubits is a small system and has poor random phase averaging for the diffusive case, which could alter the relative roles of $\nu _1$
is the sole cause of a difference between localized and diffusive fidelity decay rates. However, three qubits is a small system and has poor random phase averaging for the diffusive case, which could alter the relative roles of $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() . For larger system sizes, the simplified theoretical model should have better agreement with the simulation results.
. For larger system sizes, the simplified theoretical model should have better agreement with the simulation results.
The average $T_2$![]() fit of the three models is $14.0 \,\mathrm {\mu } \textrm {s}$
fit of the three models is $14.0 \,\mathrm {\mu } \textrm {s}$![]() , which is $2.7\times$
, which is $2.7\times$![]() smaller than the reported single-qubit idle $T_2$
smaller than the reported single-qubit idle $T_2$![]() time from IBM-Q. It is no surprise that a complex circuit decoheres more quickly than idle qubits. The experimental $T_1$
time from IBM-Q. It is no surprise that a complex circuit decoheres more quickly than idle qubits. The experimental $T_1$![]() fit values are less consistent, though this is due mostly to the small values of $\nu _1$
fit values are less consistent, though this is due mostly to the small values of $\nu _1$![]() being close to zero and therefore being similar in magnitude to the error bars, making them difficult to resolve. In particular, the observed $T_1$
being close to zero and therefore being similar in magnitude to the error bars, making them difficult to resolve. In particular, the observed $T_1$![]() from the Aer simulator fit is larger than the reported idle value, casting some doubt on the model's accuracy with respect to $T_1$
from the Aer simulator fit is larger than the reported idle value, casting some doubt on the model's accuracy with respect to $T_1$![]() .
.
The ratio of idle $T_2$![]() to circuit CNOT $T_2$
to circuit CNOT $T_2$![]() is also a useful test of the question posed in Appendix A.1.2: How does the error of a CNOT gate $\epsilon _\textrm {CNOT}$
is also a useful test of the question posed in Appendix A.1.2: How does the error of a CNOT gate $\epsilon _\textrm {CNOT}$![]() compare to the error of an idle gate of the same duration $\epsilon _\textrm {IDLE}$
compare to the error of an idle gate of the same duration $\epsilon _\textrm {IDLE}$![]() ? This test is hampered somewhat by IBM-Q reporting a $T_2$
? This test is hampered somewhat by IBM-Q reporting a $T_2$![]() value measured by the Hahn echo $T_{2E}$
value measured by the Hahn echo $T_{2E}$![]() . That experiment is less sensitive to ‘inhomogeneous broadening’, that is, low-frequency fluctuations that can cause large differences from trial to trial (Krantz et al. Reference Krantz, Kjaergaard, Yan, Orlando, Gustavsson and Oliver2019). Since $T_{2E} \ge T_2$
. That experiment is less sensitive to ‘inhomogeneous broadening’, that is, low-frequency fluctuations that can cause large differences from trial to trial (Krantz et al. Reference Krantz, Kjaergaard, Yan, Orlando, Gustavsson and Oliver2019). Since $T_{2E} \ge T_2$![]() , this only provides an upper bound, $\epsilon _\textrm {CNOT} / \epsilon _\textrm {IDLE} \lesssim T_{2E,\textrm {IDLE}} / T_{2,\textrm {CNOT}} \approx 3$
, this only provides an upper bound, $\epsilon _\textrm {CNOT} / \epsilon _\textrm {IDLE} \lesssim T_{2E,\textrm {IDLE}} / T_{2,\textrm {CNOT}} \approx 3$![]() , when the effective $T_1$
, when the effective $T_1$![]() is negligible. This bound is right in between the limits of $\epsilon _\textrm {CNOT} = \epsilon _\textrm {IDLE}$
is negligible. This bound is right in between the limits of $\epsilon _\textrm {CNOT} = \epsilon _\textrm {IDLE}$![]() and $\epsilon _\textrm {CNOT} \gg \epsilon _\textrm {IDLE}$
and $\epsilon _\textrm {CNOT} \gg \epsilon _\textrm {IDLE}$![]() , suggesting that the benefit of gate parallelization must be treated carefully. In particular, the approximation of negligible idle error in § 4.3, which was reasonable to first order here, will become poor for serially executed circuits if even a few more idle qubits are added.
, suggesting that the benefit of gate parallelization must be treated carefully. In particular, the approximation of negligible idle error in § 4.3, which was reasonable to first order here, will become poor for serially executed circuits if even a few more idle qubits are added.
5 Conclusion
We performed digital quantum simulations of the QSM, a toy model of wave–particle interactions in plasmas, in order to understand the interaction between chaotic dynamics and noise on quantum hardware platforms. We chose to simulate the QSM, a quantized analog of the classical sawtooth map, because it is one of the simplest possible such maps with one of the shortest possible gate sequences and could be used to test the Lyapunov algorithm on future NISQ devices. The resulting dynamics can be tuned from integrable and localized to chaotic and diffusive and leverages the noise that is naturally present on NISQ quantum hardware platforms to benchmark quantum computations that are relevant to particle transport in plasmas. An important conclusion of our work is that the dynamics of a simulation can strongly influence the fidelity decay rate by changing the relative impact of different noise processes on the fidelity.
In this study the important relationship between dynamics and noise in a quantum simulation and the resulting effect on fidelity were examined in a minimal and experimentally accessible context. A gate- and qubit-efficient digital quantum simulation of the QSM was performed on the open-access IBM-Q platform, and then simulated with a gate-based Lindblad noise model that was shown to qualitatively capture the intended effect. Experiment, numerics and analytic theory all demonstrated that as this quantum map is varied from near-integrable localized dynamics to diffusive and randomly entangled dynamics the corresponding fidelities decay at an effective multi-qubit $T_1$![]() rate and a rate that is faster than the multi-qubit $T_1$
rate and a rate that is faster than the multi-qubit $T_1$![]() or $T_2$
or $T_2$![]() alone, respectively. In numerics, the substep decomposition of the algorithm caused these rates to partially mix, though the further effect of decomposing to native gates was smaller. In analytics, the intermediate case of diffusive but unentangled dynamics was used to clarify that the difference between the effects of dephasing and of random entanglement on fidelity decay is, in our simple model, due only to the greater influence from relaxation in the latter.
alone, respectively. In numerics, the substep decomposition of the algorithm caused these rates to partially mix, though the further effect of decomposing to native gates was smaller. In analytics, the intermediate case of diffusive but unentangled dynamics was used to clarify that the difference between the effects of dephasing and of random entanglement on fidelity decay is, in our simple model, due only to the greater influence from relaxation in the latter.
The gate-based Lindblad model was used with only single-qubit $T_1$![]() and $T_2$
and $T_2$![]() noise for the single gate with the largest error, CNOT. When fit to experimental data, this model extracts far less information than full process tomography, but more than fitting a depolarizing noise model. A natural next extension of this model would be to consider multiple gates, such as by including the identity gate that can have high error due to its long duration in some circuits. The physical motivation behind the gate-based Lindblad model makes it ideal for capturing the effects of dynamics at minimal experimental cost.
noise for the single gate with the largest error, CNOT. When fit to experimental data, this model extracts far less information than full process tomography, but more than fitting a depolarizing noise model. A natural next extension of this model would be to consider multiple gates, such as by including the identity gate that can have high error due to its long duration in some circuits. The physical motivation behind the gate-based Lindblad model makes it ideal for capturing the effects of dynamics at minimal experimental cost.
Treating the experiment as a benchmarking exercise, first the average error per CNOT gate was estimated. Due to the fidelity dependence on dynamics, the average error varies by a factor of $1.5\times$![]() over the dynamics. The observed error is $3.0{-}4.5\times$
over the dynamics. The observed error is $3.0{-}4.5\times$![]() greater than reported by IBM-Q's method of RB with a depolarizing noise model. This discrepancy is largely explainable by RB being less sensitive to certain noise sources such as coherent error and low-frequency noise, and by an increase in crosstalk error when using three qubits rather than two. However, how much the different dynamics between RB and the QSM also contribute is not yet clear.
greater than reported by IBM-Q's method of RB with a depolarizing noise model. This discrepancy is largely explainable by RB being less sensitive to certain noise sources such as coherent error and low-frequency noise, and by an increase in crosstalk error when using three qubits rather than two. However, how much the different dynamics between RB and the QSM also contribute is not yet clear.
The noise models were also fit to experiment to extract effective $T_1$![]() and $T_2$
and $T_2$![]() times for the CNOT gate. All models agree well on the effective $T_2$
times for the CNOT gate. All models agree well on the effective $T_2$![]() time, which is dominant, but diverge on the $T_1$
time, which is dominant, but diverge on the $T_1$![]() time, which has a weaker effect and is difficult to resolve. The effective CNOT $T_2$
time, which has a weaker effect and is difficult to resolve. The effective CNOT $T_2$![]() time is $2.7\times$
time is $2.7\times$![]() shorter than the $T_{2 \textrm {Echo}}$
shorter than the $T_{2 \textrm {Echo}}$![]() of an idle qubit, suggesting CNOT error is no more than $\sim 3\times$
of an idle qubit, suggesting CNOT error is no more than $\sim 3\times$![]() larger than idle gate error when the noise is dominated by $T_2$
larger than idle gate error when the noise is dominated by $T_2$![]() .
.
Retrieving useful experimental fidelities for complex Hamiltonian simulation was enabled by the highly efficient gate decomposition of the QSM. It combines the exactness of quantum maps, which do not require Trotterization due to the exact decomposition of the delta-kicked potential, with a polynomial length algorithm for low-order polynomial Hamiltonians (see Appendix B). On IBM-Q the QSM required only 33 CNOT gates per evolution time step and 66 CNOT gates per Loschmidt echo time step. This enabled seven time steps of clearly localized dynamics and five time steps of Loschmidt echo fidelity decay.
A model of low-frequency parametric noise is also studied in Appendix D, which is relevant to future experiments on more qubits. This model was previously used to show that a minimum of six qubits is required to observe the Lyapunov exponent in the QSM. Here it was combined with Lindblad noise to show that the Lyapunov exponent can still be observed, but will require seven or more qubits depending on the strength of the Lindblad noise. The parametric noise model can be applied to determine the Lyapunov exponent on future fault-tolerant error-corrected quantum computers. However, ensuring that the Lyapunov algorithm works on NISQ hardware will require the ability to control and tune the magnitude of the various types of noise processes appropriately.
The existence of a large fidelity gap between different dynamics in digital quantum simulations also raises the question of whether arbitrary algorithms may have dynamics that affect their fidelity. In particular, the degrees of entanglement, superposition and randomness during an algorithm could suggest particular fidelity dependence on the effective $T_1$![]() and $T_2$
and $T_2$![]() . This could be crucial for anticipating quantum advantage by better extrapolating limited device characterization to predict the fidelities of NISQ algorithms.
. This could be crucial for anticipating quantum advantage by better extrapolating limited device characterization to predict the fidelities of NISQ algorithms.
Acknowledgements
The authors thank the Quantum Leap group at LLNL for stimulating discussions and ideas that improved the paper, including V. Geyko, F. R. Graziani, S. B. Libby and Y. Shi. We also thank J. L. DuBois, K.M. Beck, A. R. Castelli and Y. J. Rosen of the Quantum Coherent Device Physics group at LLNL, K.A. Wendt of the Nuclear Data and Theory group at LLNL and R. T. Sutherland at Oxford Ionics for their insights into quantum hardware and noise processes.
Editor N. Loureiro thanks the referees for their advice in evaluating this article.
Funding
This work was performed by LLNL under the auspices of the U.S.DOE under Contract DE-AC52-07NA27344 and was supported by the DOE Office of Fusion Energy Sciences ‘Quantum Leap for Fusion Energy Sciences’ project FWP-SCW1680 and by LLNL Laboratory Directed Research and Development project 19-FS-078.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Implementation
A.1 IBM-Q Implementation
A.1.1 Circuit optimization
Despite the relative simplicity of the QSM algorithm, executing the circuit in (2.8) on IBM-Q's state-of-the-art hardware quickly accumulates error. Optimizing the circuit to reduce error can greatly improve the results.
We only attempt to reduce error by decreasing the gate count of the two-qubit CNOT gate, the largest error gate. This is motivated by the goal of benchmarking, which would be complicated by the use of other noise mitigation techniques such as dynamical decoupling. The focus on CNOT gates is motivated by the small total contribution of single-qubit gate errors. According to IBM-Q's reported RB error estimates, each CNOT gate produces about $30\times$![]() more error than physical single-qubit gates, namely SX (square-root-of-not) and X gates. (Note that Z gates are virtual with presumably even smaller error (McKay et al. Reference McKay, Wood, Sheldon, Chow and Gambetta2017).) This can partially be attributed to the gate duration, with a CNOT gate taking on average about $10$
more error than physical single-qubit gates, namely SX (square-root-of-not) and X gates. (Note that Z gates are virtual with presumably even smaller error (McKay et al. Reference McKay, Wood, Sheldon, Chow and Gambetta2017).) This can partially be attributed to the gate duration, with a CNOT gate taking on average about $10$![]() times longer to execute than SX and X gates, which have identical durations. Combining the observations that single-qubit gate error is $1/30$
times longer to execute than SX and X gates, which have identical durations. Combining the observations that single-qubit gate error is $1/30$![]() of the CNOT gate error and that from table 1 single-qubit gates appear $1/2$
of the CNOT gate error and that from table 1 single-qubit gates appear $1/2$![]() as often in the circuit for ibmq_manila $n=3$
as often in the circuit for ibmq_manila $n=3$![]() , it appears that single-qubit gates contribute no more than $2\,\%$
, it appears that single-qubit gates contribute no more than $2\,\%$![]() of the total error in this context. This remains true for increasing qubit count $n$
of the total error in this context. This remains true for increasing qubit count $n$![]() per the faster scaling of two-qubit gates in (2.8) and the gate decomposition in the next paragraph.
per the faster scaling of two-qubit gates in (2.8) and the gate decomposition in the next paragraph.
To determine the base CNOT gate count of the circuit (2.8) on IBM-Q, first logic gates are decomposed to native hardware gates. The simple relations for decomposing are: $\textrm {PHASE}(\phi ) = \textrm {RZ}(\phi$![]() ) up to an unimportant global phase, where $\textrm {RZ}(\phi )$
) up to an unimportant global phase, where $\textrm {RZ}(\phi )$![]() is a Z rotation by angle $\phi$
is a Z rotation by angle $\phi$![]() ; $\textrm {H} = \textrm {RZ}({\rm \pi} /2) \textrm {SX RZ}({\rm \pi} /2$
; $\textrm {H} = \textrm {RZ}({\rm \pi} /2) \textrm {SX RZ}({\rm \pi} /2$![]() ); $\textrm {SWAP}_{01} = \textrm {CNOT}_{01} \textrm {CNOT}_{10} \textrm {CNOT}_{01}$
); $\textrm {SWAP}_{01} = \textrm {CNOT}_{01} \textrm {CNOT}_{10} \textrm {CNOT}_{01}$![]() ; and lastly the $\textrm {CPHASE}$
; and lastly the $\textrm {CPHASE}$![]() gate is given by $\textrm {CPHASE}_{01}(\phi ) = \textrm {RZ}_1(\phi /2) \textrm {CNOT}_{01} \textrm {RZ}_1(2{\rm \pi} -\phi /2) \textrm {CNOT}_{01} \textrm {RZ}_0(\phi /2)$
gate is given by $\textrm {CPHASE}_{01}(\phi ) = \textrm {RZ}_1(\phi /2) \textrm {CNOT}_{01} \textrm {RZ}_1(2{\rm \pi} -\phi /2) \textrm {CNOT}_{01} \textrm {RZ}_0(\phi /2)$![]() . These decompositions are performed automatically by Qiskit's transpile function.
. These decompositions are performed automatically by Qiskit's transpile function.
Reducing the CNOT gate count is done with the gate count optimizer that is automatically applied by the transpile function. This does not guarantee optimal results but provides a useful improvement. For this, the barriers in figure 4 are removed, though barriers between map steps are retained for scalability with the number of map steps. Using the above decompositions of each gate on figure 4, the base CNOT count on three fully connected qubits is $12 \times 2 = 24$![]() CNOT gates. Using transpile per Appendix A applies gate transformations stochastically to search for gate reductions. Out of 100 attempts the best optimization reduces the gate count from $24 \rightarrow 19$
CNOT gates. Using transpile per Appendix A applies gate transformations stochastically to search for gate reductions. Out of 100 attempts the best optimization reduces the gate count from $24 \rightarrow 19$![]() CNOTs, for a $21\,\%$
CNOTs, for a $21\,\%$![]() reduction. Smaller gate counts were found, but were for incorrect circuits due to a bug described in Appendix A or used approximations that did not generalize to other values of $k$
reduction. Smaller gate counts were found, but were for incorrect circuits due to a bug described in Appendix A or used approximations that did not generalize to other values of $k$![]() .
.
Retaining a consistent gate count across $k$![]() is crucial to isolating the effect of dynamics on fidelity decay. This required avoiding specific values of $k$
is crucial to isolating the effect of dynamics on fidelity decay. This required avoiding specific values of $k$![]() , such as $2.0$
, such as $2.0$![]() and $4.5$
and $4.5$![]() , and avoiding $k \ll 2{\rm \pi} /\beta ^2$
, and avoiding $k \ll 2{\rm \pi} /\beta ^2$![]() where some CP gates in $U_\textrm {pot}$
where some CP gates in $U_\textrm {pot}$![]() approach identity and the transpiler may eliminate them from the circuit.
approach identity and the transpiler may eliminate them from the circuit.
Sparse device connectivity increases gate counts, which allows for further gate count optimization. For two unconnected qubits, a $\textrm {CNOT}_{02}$![]() gate is replaced with $\textrm {SWAP}_{01} \textrm {CNOT}_{12} \textrm {SWAP}_{01}$
gate is replaced with $\textrm {SWAP}_{01} \textrm {CNOT}_{12} \textrm {SWAP}_{01}$![]() , transforming one gate to seven. However, each $\textrm {CPHASE}_{02}$
, transforming one gate to seven. However, each $\textrm {CPHASE}_{02}$![]() gate only needs one pair of SWAPs despite its base decomposition to two CNOT gates. So figure 4 before optimization transforms due to linear connectivity from $24 \rightarrow 48$
gate only needs one pair of SWAPs despite its base decomposition to two CNOT gates. So figure 4 before optimization transforms due to linear connectivity from $24 \rightarrow 48$![]() CNOT gates. Gate optimization over 100 transpile attempts reduces the gate count from $48 \rightarrow 33$
CNOT gates. Gate optimization over 100 transpile attempts reduces the gate count from $48 \rightarrow 33$![]() CNOTs, a $31\,\%$
CNOTs, a $31\,\%$![]() reduction. The connectivity-caused CNOTs have partially cancelled with algorithmic CNOTs, reducing the cost of sparse connectivity.
reduction. The connectivity-caused CNOTs have partially cancelled with algorithmic CNOTs, reducing the cost of sparse connectivity.
A.1.2 Circuit scaling
The scaling of circuit error is not very relevant to the three-qubit experiments in this paper, but it is useful for estimating the feasibility of larger simulations, e.g. that could be used to observe the Lyapunov exponent (Porter & Joseph Reference Porter and Joseph2022). It is discussed here for completeness in understanding the QSM system as a future benchmarking tool. Gate error is assumed constant for an increasing number of qubits, without accounting for error sources like crosstalk that are known to increase the average error per CNOT gate (McKay et al. Reference McKay, Sheldon, Smolin, Chow and Gambetta2019). Moreover, additional scaling may depend on the device under consideration.
When scaling to more than three qubits, performing CNOT gates in parallel becomes a crucial tool in reducing total error. The degree to which the total circuit error depends on gate count versus gate depth of parallel gates depends on how the error of a single CNOT gate $\epsilon _\textrm {CNOT}$![]() compares to idle error of the same duration $\epsilon _\textrm {IDLE}$
compares to idle error of the same duration $\epsilon _\textrm {IDLE}$![]() . If $\epsilon _\textrm {CNOT} = \epsilon _\textrm {IDLE}$
. If $\epsilon _\textrm {CNOT} = \epsilon _\textrm {IDLE}$![]() then performing two CNOTs in parallel gives the same error as performing a single CNOT gate with the other qubits idle, meaning performing gates in parallel is a big gain and gate depth determines circuit error. If $\epsilon _\textrm {CNOT} \gg \epsilon _\textrm {IDLE}$
then performing two CNOTs in parallel gives the same error as performing a single CNOT gate with the other qubits idle, meaning performing gates in parallel is a big gain and gate depth determines circuit error. If $\epsilon _\textrm {CNOT} \gg \epsilon _\textrm {IDLE}$![]() then two CNOTs in parallel have a similar error as two in series, meaning parallelization does little and gate count determines circuit error. The model in § 4.3 assumed $\epsilon _\textrm {CNOT} \gg \epsilon _\textrm {IDLE}$
then two CNOTs in parallel have a similar error as two in series, meaning parallelization does little and gate count determines circuit error. The model in § 4.3 assumed $\epsilon _\textrm {CNOT} \gg \epsilon _\textrm {IDLE}$![]() to determine gate-specific error to lowest order. When analysing circuit scaling, different hypotheses about this relation can lead to a range of results. This combines with uncertainty about how parallelized a circuit is for a total effectiveness of parallelization. This effectiveness reduces error relative to a serial circuit by a factor between one and $n/2$
to determine gate-specific error to lowest order. When analysing circuit scaling, different hypotheses about this relation can lead to a range of results. This combines with uncertainty about how parallelized a circuit is for a total effectiveness of parallelization. This effectiveness reduces error relative to a serial circuit by a factor between one and $n/2$![]() . The relationship between $\epsilon _\textrm {CNOT}$
. The relationship between $\epsilon _\textrm {CNOT}$![]() and $\epsilon _\textrm {IDLE}$
and $\epsilon _\textrm {IDLE}$![]() is experimentally estimated in § 4.5.
is experimentally estimated in § 4.5.
To predict the scaling of circuit error due to CNOT gate count and gate depth to many qubits, the previous insights can be combined. The base CNOT gate count from (2.8) scales as $O(n^2)$![]() for $n$
for $n$![]() qubits. Worse-case device connectivity (linear) increases this, as the average single CNOT gate between two arbitrary qubits requires an extra $O(n)$
qubits. Worse-case device connectivity (linear) increases this, as the average single CNOT gate between two arbitrary qubits requires an extra $O(n)$![]() SWAPs, each requiring three CNOTs, to connect qubits separated by an average of $O(n)$
SWAPs, each requiring three CNOTs, to connect qubits separated by an average of $O(n)$![]() connections. Gate count optimization, e.g. using the transpile function or similar, may reduce this by up to $O(n)$
connections. Gate count optimization, e.g. using the transpile function or similar, may reduce this by up to $O(n)$![]() . Parallelization effectiveness decreases circuit error by between $O(1)$
. Parallelization effectiveness decreases circuit error by between $O(1)$![]() and $O(n)$
and $O(n)$![]() regardless of connectivity. In summary, a circuit with all-to-all connectivity has between $O(n)$
regardless of connectivity. In summary, a circuit with all-to-all connectivity has between $O(n)$![]() and $O(n^2)$
and $O(n^2)$![]() circuit error scaling due to CNOT gates, and one with linear connectivity has between $O(n)$
circuit error scaling due to CNOT gates, and one with linear connectivity has between $O(n)$![]() and $O(n^3)$
and $O(n^3)$![]() scaling. These ranges depend on the effectiveness of gate count optimization and parallelization. They could be refined by using IBM's transpiler to see how well CNOT gates parallelize in the QSM across different topologies.
scaling. These ranges depend on the effectiveness of gate count optimization and parallelization. They could be refined by using IBM's transpiler to see how well CNOT gates parallelize in the QSM across different topologies.
For the gate count optimization performed by transpile, it is unknown whether an optimal solution can be found in a scalable fashion. Finding an optimal gate reduction on all-to-all qubit connectivity is an NP-complete problem (Botea, Kishimoto & Marinescu Reference Botea, Kishimoto and Marinescu2018). In fact, even for few qubits with linear connectivity transpile struggles to find optimal results. In table 1 this is demonstrated by comparing the CNOT gate count from the known algorithm (2.8) plus optimization in column (b) to a naive approach of compiling the raw unitary ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {QSM}$![]() directly in column (a). In each case about one hundred iterations of transpile is attempted. For $n = 3$
directly in column (a). In each case about one hundred iterations of transpile is attempted. For $n = 3$![]() , the naive approach yields over twice the gate count. Whether this suboptimal optimization can provide a scalable benefit is unclear, though focusing on optimizing few-qubit subcircuits in large algorithms may be the most practical use case.
, the naive approach yields over twice the gate count. Whether this suboptimal optimization can provide a scalable benefit is unclear, though focusing on optimizing few-qubit subcircuits in large algorithms may be the most practical use case.
Since these scalings are all polynomial, they would all achieve an exponential speedup relative to the $O(n 2^n)$![]() operations required by a classical computer using the fast Fourier transform (Benenti et al. Reference Benenti, Casati and Montangero2004). However, one should keep in mind the scaling of the measurement step, since measuring the entire final state would take an exponential number of runs and destroy the speedup. The speedup is preserved only for measuring collective properties like the Lyapunov exponent (Porter & Joseph Reference Porter and Joseph2022), localization length or anamolous diffusion exponent (Benenti et al. Reference Benenti, Casati and Montangero2004).
operations required by a classical computer using the fast Fourier transform (Benenti et al. Reference Benenti, Casati and Montangero2004). However, one should keep in mind the scaling of the measurement step, since measuring the entire final state would take an exponential number of runs and destroy the speedup. The speedup is preserved only for measuring collective properties like the Lyapunov exponent (Porter & Joseph Reference Porter and Joseph2022), localization length or anamolous diffusion exponent (Benenti et al. Reference Benenti, Casati and Montangero2004).
A.1.3 Choosing a device
At the time of writing IBM-Q freely provides six five-qubit devices, each containing only linear three-qubit sublattices. Among these we choose to test ibmq_manila based on its small reported gate error (often $<6.5\times 10^{-3}$![]() on some three-qubit sublattice) and large quantum volume (32). The now-retired five-qubit device (ibmq_5_yorktown) had a bow-tie shape with two triangular sublattices but much larger gate error ($>2.0\times 10^{-2}$
on some three-qubit sublattice) and large quantum volume (32). The now-retired five-qubit device (ibmq_5_yorktown) had a bow-tie shape with two triangular sublattices but much larger gate error ($>2.0\times 10^{-2}$![]() ), so we performed experiments on it to explore the trade off between connectivity and gate error. In table 1, ibmq_5_yorktown and ibmq_manila are compared, albeit 1.5 years apart, with the latter giving much better performance. Our experiments on ibmq_santiago contemporary to the ibmq_5_yorktown experiments gave similar results as the more recent ibmq_manila, indicating that the time lapse has not had a large effect. A similar result comparing ibmq_5_yorktown and ibmq_santiago was also found in Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021).
), so we performed experiments on it to explore the trade off between connectivity and gate error. In table 1, ibmq_5_yorktown and ibmq_manila are compared, albeit 1.5 years apart, with the latter giving much better performance. Our experiments on ibmq_santiago contemporary to the ibmq_5_yorktown experiments gave similar results as the more recent ibmq_manila, indicating that the time lapse has not had a large effect. A similar result comparing ibmq_5_yorktown and ibmq_santiago was also found in Pizzamiglio et al. (Reference Pizzamiglio, Chang, Bondani, Montangero, Gerace and Benenti2021).
A.2 Optimizing performance on IBM-Q
Despite using an efficient algorithm, various difficulties can harm performance. Some insights for avoiding pitfalls are as follows.
(i) Optimize for qubit connectivity: circuits that are transpiled to devices with sparse connectivity will add SWAP gates to connect distant qubits. This allows for partial cancellation between the algorithm CNOT gates and the swapping CNOT gates. The automated approach to this is to use a stochastic transpiler as offered by Qiskit. To enable this level of optimization, first set the transpile function's option optimization_level from =1 (the default) to =3 (the maximum). Next perform a trial-and-error optimization over the transpiler seed by iterating over the option seed_transpiler=seed and looking for the lowest resulting gate count of CNOTs using circ.count_ops() on the transpiled circuit. Check that the transpiled circuit produces the expected outcome in a noiseless Aer simulator, due to the bug discussed below. Consider saving the result as seed behaviour may change. This procedure does not directly scale to many qubits, but on few-qubit subspaces it may be useful at NISQ scales, and may eventually be automated for real applications.
(ii) Optimize algorithms: look for small optimizations that can be done by hand. For example, the QFT algorithm and its inverse require SWAP gates to reverse the qubit ordering. But this can be cancelled with the argument do_swaps=False and replaced with a free, manual reversal of qubit ordering for gates in between the QFT pair.
(iii) Optimize coherence times: noise properties of backend devices can drift and worsen from their reported values. The IBM-Q routinely recalibrates their systems, adjusting qubit and gate pulse properties to reduce error. Each device is currently recalibrated between hourly and weekly, with the time since the last calibration reported on each device's status screen online. Timing experiments to occur soon after calibration can help achieve optimal performance for devices that calibrate less than hourly. Choosing the connected set of qubits with the lowest-error gates is also important and should be repeated after a calibration that recharacterizes them, though these occur less often.
(iv) Watch out for unexpected changes when concatenating circuits: a hidden pitfall (at the time of this publication) can occur when a circuit without the final measurement step is transpiled. The final qubit identities can be automatically swapped, despite the fact that no measurement is present to absorb this change (Porter Reference Porter2021). An unsuspecting user may want to repeat an algorithm step, as done in this paper, and hope to get high gate efficiency at low cost by transpiling one step and repeating it. However, one should check whether qubit swapping has occurred and either try a new seed or undo the swaps manually to ensure there are none between steps.
Appendix B. Gate decomposition of polynomial Hamiltonian evolution
The first step in converting the operators of (2.2) into a series of common two-qubit gates is knowing how to implement $\hat p$![]() or $\hat q$
or $\hat q$![]() (which have an identical form in their respective bases). Representing a single-body state of quantum number $p=0,\ldots,N-1$
(which have an identical form in their respective bases). Representing a single-body state of quantum number $p=0,\ldots,N-1$![]() on $n=\log (N)$
on $n=\log (N)$![]() qubits can be accomplished via the binary representation (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001)
qubits can be accomplished via the binary representation (Georgeot & Shepelyansky Reference Georgeot and Shepelyansky2001)

where $\alpha _j=0$![]() or $1$
or $1$![]() for each qubit $j$
for each qubit $j$![]() depending on the value of $p$
depending on the value of $p$![]() . One can express diagonal operators similarly. The operator ${{{\boldsymbol{\mathsf{U}}}}}_{p}=\exp ({-\textrm {i}\, \hbar \hat p^2/2})$
. One can express diagonal operators similarly. The operator ${{{\boldsymbol{\mathsf{U}}}}}_{p}=\exp ({-\textrm {i}\, \hbar \hat p^2/2})$![]() can be expressed in the $p$
can be expressed in the $p$![]() basis by noting that
basis by noting that


This describes PHASE gates on every qubit $j_1$![]() and CPHASE gates on every pair of qubits $j_1 < j_2$
and CPHASE gates on every pair of qubits $j_1 < j_2$![]() with phase $-\hbar 2^{j_1 + j_2 }$
with phase $-\hbar 2^{j_1 + j_2 }$![]() (after merging $j_1>j_2$
(after merging $j_1>j_2$![]() into $j_1< j_2$
into $j_1< j_2$![]() ). Since the desired operator ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}$
). Since the desired operator ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}$![]() is shifted by $N/2$
is shifted by $N/2$![]() from ${{{\boldsymbol{\mathsf{U}}}}}_{p}$
from ${{{\boldsymbol{\mathsf{U}}}}}_{p}$![]() , because the correct range is $p'=-N/2,\ldots, (N-1)/2$
, because the correct range is $p'=-N/2,\ldots, (N-1)/2$![]() , it gets modified to
, it gets modified to

with the unobservable global phase neglected. This contributes further PHASE gates described by
This describes the ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}$![]() gate, but the ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$
gate, but the ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$![]() gate is identical in its own basis with $\hbar$
gate is identical in its own basis with $\hbar$![]() replaced by $-k \beta ^2$
replaced by $-k \beta ^2$![]() and $\hat p$
and $\hat p$![]() by $\hat q$
by $\hat q$![]() with the same $q=0,\ldots,N-1$
with the same $q=0,\ldots,N-1$![]() :
:

Switching between bases as in (2.7) is needed to execute both ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {kin}$![]() and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$
and ${{{\boldsymbol{\mathsf{U}}}}}_\textrm {pot}$![]() with this efficient decomposition. The full algorithm is converted to gates in (2.8).
with this efficient decomposition. The full algorithm is converted to gates in (2.8).
Appendix C. Fidelity decay of localized and diffusive dynamics under single-qubit Lindblad noise
C.1 Fidelity of pure states
The QSM exhibits dynamics that range from localized to diffusive (chaotic). To study its interaction with single-qubit Lindblad noise from a theoretical standpoint, we can make some reasonable simplifying assumptions. The main assumption is that decay of an evolving density matrix is approximately the decay of a pure state with distribution and entanglement typical of the evolving state. In the localized limit this is exactly true. In the diffusive case this requires that the initial evolution to a typical diffusive state is fast relative to Lindblad decay and that after a typical diffusive state is reached the ongoing Hamiltonian evolution can be neglected. The goal is to calculate the fidelity of the decaying state relative to the initial pure state over time. The pure state assumption allows a simplified form. First, the general fidelity of corrupted density matrix ${\boldsymbol \sigma }$![]() relative to pure state density matrix ${\boldsymbol \rho }$
relative to pure state density matrix ${\boldsymbol \rho }$![]() is
is
But a pure state has the nice property that
which simplifies the fidelity to

the Frobenius inner product of the density matrices. It will be useful to consider the elements of the Hadamard elementwise product
which has elements that sum to the fidelity.
C.2 Localized dynamics
The QSM has a limit of localized dynamics at $k \rightarrow 0$![]() . In this limit the Hamiltonian becomes a diagonal phase matrix ${{{\boldsymbol{\mathsf{H}}}}} = \textrm {diag}(H_0 \, H_1)$
. In this limit the Hamiltonian becomes a diagonal phase matrix ${{{\boldsymbol{\mathsf{H}}}}} = \textrm {diag}(H_0 \, H_1)$![]() . This only evolves the off-diagonal elements $\rho _{i,j}$
. This only evolves the off-diagonal elements $\rho _{i,j}$![]() of the density matrix ${\boldsymbol \rho }$
of the density matrix ${\boldsymbol \rho }$![]() , as seen on a single-qubit example
, as seen on a single-qubit example
If we assume an initial state in the computational basis ${\boldsymbol \rho } = \textrm {diag}(0 \cdots 1 \cdots 0)$![]() then the Hamiltonian evolution has no effect on ${\boldsymbol \rho }$
then the Hamiltonian evolution has no effect on ${\boldsymbol \rho }$![]() .
.
C.2.1 Single-qubit decomposition
The effect of Lindblad noise on the localized state can be trivially decomposed into single-qubit effects, since both the Lindblad operators and density matrix decompose.
The Lindblad equation (4.4) in the main text describes the noisy time evolution of initial state ${\boldsymbol \rho }$![]() . Here we consider only single-qubit Lindblad collapse operators
. Here we consider only single-qubit Lindblad collapse operators
which describe relaxation at a rate $\nu _1$![]() and pure dephasing (Krantz et al. Reference Krantz, Kjaergaard, Yan, Orlando, Gustavsson and Oliver2019) at a rate $\nu _2$
and pure dephasing (Krantz et al. Reference Krantz, Kjaergaard, Yan, Orlando, Gustavsson and Oliver2019) at a rate $\nu _2$![]() , respectively, on each qubit $j$
, respectively, on each qubit $j$![]() . For a single unentangled qubit, the solution ${\boldsymbol \sigma }$
. For a single unentangled qubit, the solution ${\boldsymbol \sigma }$![]() to the Lindblad equation when $H$
to the Lindblad equation when $H$![]() has no effect evolves as
has no effect evolves as

with decay rates that obey $\nu _1 \equiv 1/T_1$![]() , $\nu _2 \equiv 1/T_\varphi$
, $\nu _2 \equiv 1/T_\varphi$![]() and $\nu _1/2+\nu _2/2 = 1/T_2$
and $\nu _1/2+\nu _2/2 = 1/T_2$![]() . Solving this differential equation is simple, as three of the elements depend only on themselves, yielding exponential decays, and the $\sigma _{00}$
. Solving this differential equation is simple, as three of the elements depend only on themselves, yielding exponential decays, and the $\sigma _{00}$![]() element is determined by trace preservation $\mathrm {Tr}({\boldsymbol \sigma }) = 1$
element is determined by trace preservation $\mathrm {Tr}({\boldsymbol \sigma }) = 1$![]() . Trace preservation is equivalent to the conservation of probability.
. Trace preservation is equivalent to the conservation of probability.
Localization simplifies both ${\boldsymbol \sigma }$![]() and the fidelity calculation. If the qubit starts in $\left |\psi \right \rangle =\left |1\right \rangle$
and the fidelity calculation. If the qubit starts in $\left |\psi \right \rangle =\left |1\right \rangle$![]() then
then
and $f = \sigma _{11} = \textrm {e}^{-\nu _1 t}$![]() . If it starts in $\left |\psi \right \rangle =\left |0\right \rangle$
. If it starts in $\left |\psi \right \rangle =\left |0\right \rangle$![]() then $f=1$
then $f=1$![]() . No off-diagonal terms means no $\nu _2$
. No off-diagonal terms means no $\nu _2$![]() dependence.
dependence.
C.2.2 Average fidelity
It is useful to average the localized fidelity over all initial conditions for comparison to the diffusive case later. The fidelity for $n$![]() qubits decomposes into the product of single-qubit fidelities since both ${\boldsymbol \rho }$
qubits decomposes into the product of single-qubit fidelities since both ${\boldsymbol \rho }$![]() and ${{{\boldsymbol{\mathsf{L}}}}}_{i,j}$
and ${{{\boldsymbol{\mathsf{L}}}}}_{i,j}$![]() decompose. Here $j$
decompose. Here $j$![]() excited qubits then decay at an exponential rate $-j \nu _1$
excited qubits then decay at an exponential rate $-j \nu _1$![]() . Averaging over initial conditions includes $n$
. Averaging over initial conditions includes $n$![]() states decaying at $-\nu _1$
states decaying at $-\nu _1$![]() , ($n$
, ($n$![]() choose 2) states decaying at $-2\nu _1$
choose 2) states decaying at $-2\nu _1$![]() and so on. These sum to
and so on. These sum to

The single-qubit decay rate is seen to be $-\nu _1/2$![]() , as expected.
, as expected.
C.3 Diffusive dynamics
In the other limit of the QSM, large $k$![]() leads to chaotic, diffusive dynamics. Hamiltonian evolution now has an effect, but will be simplified by two assumptions.
leads to chaotic, diffusive dynamics. Hamiltonian evolution now has an effect, but will be simplified by two assumptions.
The first assumption is that the fast Hamiltonian evolution reaches a fully diffused state quickly enough to be considered immediate, so that the analysis begins with a randomly entangled state. To justify this, there are two relevant time scales for the initial wavefunction spreading: the Ehrenfest time $\tau _E$![]() and the Heisenberg time $\tau _H$
and the Heisenberg time $\tau _H$![]() (see § 2.2). The Ehrenfest time is how long the quantum dynamics closely match the classical dynamics (Shepelyansky Reference Shepelyansky2020). For a chaotic system, this implies rapid spreading at the rate $\textrm {e}^{\lambda t}$
(see § 2.2). The Ehrenfest time is how long the quantum dynamics closely match the classical dynamics (Shepelyansky Reference Shepelyansky2020). For a chaotic system, this implies rapid spreading at the rate $\textrm {e}^{\lambda t}$![]() . This must end after reaching the finite system size $N$
. This must end after reaching the finite system size $N$![]() . This implies an Ehrenfest time of $\tau _E \sim \ln (N)/\lambda$
. This implies an Ehrenfest time of $\tau _E \sim \ln (N)/\lambda$![]() . To avoid localization, $K \gtrsim N^{-2/5}$
. To avoid localization, $K \gtrsim N^{-2/5}$![]() when $L=1$
when $L=1$![]() , implying that $\lambda \gtrsim N^{-1/5}$
, implying that $\lambda \gtrsim N^{-1/5}$![]() and a bound on Ehrenfest time of $\tau _E \lesssim \ln (N) N^{1/5}$
and a bound on Ehrenfest time of $\tau _E \lesssim \ln (N) N^{1/5}$![]() . For small system sizes, this is clearly small and simulations suggest that $\tau _E \sim 1$
. For small system sizes, this is clearly small and simulations suggest that $\tau _E \sim 1$![]() .
.
Between the Ehrenfest time and Heisenberg time a much slower diffusion occurs. But after the Heisenberg time the effects of quantum interference are fully realized and dynamical localization occurs, halting diffusion. The Heisenberg time for localization is $\tau _H \sim \ell$![]() (Benenti et al. Reference Benenti, Casati and Montangero2004; Shepelyansky Reference Shepelyansky2020), which if extended to the diffusive regime suggests that $\tau _H \gtrsim N$
(Benenti et al. Reference Benenti, Casati and Montangero2004; Shepelyansky Reference Shepelyansky2020), which if extended to the diffusive regime suggests that $\tau _H \gtrsim N$![]() . Since the Ehrenfest time represents the bulk of the spreading and occurs on a short-time scale, this justifies the assumption of an immediate fully diffused state.
. Since the Ehrenfest time represents the bulk of the spreading and occurs on a short-time scale, this justifies the assumption of an immediate fully diffused state.
The second assumption is that Hamiltonian evolution after full diffusion has little effect on the fidelity decay and can be neglected to simplify the Lindblad evolution. This assumption is supported by numerical simulation results in figure 8.
A ‘typical’ diffused state will be considered, with random features to be averaged over. This diffused state is statistically independent of the initial state before Hamiltonian evolution, so an explicit averaging over initial conditions will not be needed. While both amplitudes and phases should be random, a further simplification is to assume that the amplitudes are nearly uniform after the diffusive process occurs, leaving only random phases. This assumption is justified by ergodicity of the dynamics.
After these simplifications, a diffusive state is characterized by two features: statistically uniform probability distribution and random entanglement.
C.3.1 Unentangled state
To test uniform probability and random entanglement independently, first consider a uniform state that is not entangled. Such a state is constructed by initializing in the ground state and applying a Hadmard gate to each qubit. In this case one can again decompose to single-qubit evolution (C8), but acting on the initial state
The Lindblad solution for initial condition ${\boldsymbol \rho }$![]() is
is
The fidelity is again the product of single-qubit fidelities, with each qubit contributing $f = \tfrac {1}{2} \sum _{i,j} \sigma _{i,j} = \frac {1}{2}(1 + \textrm {e}^{-(({\nu _1 + \nu _2})/{2}) t})$![]() where exponentials on the diagonal cancel. The $n$
where exponentials on the diagonal cancel. The $n$![]() -qubit fidelity for any initial condition is
-qubit fidelity for any initial condition is
which is the same form as the averaged localized case (C10), but with $\nu _1 \rightarrow ({\nu _1 + \nu _2})/{2}$![]() .
.
C.3.2 Entangled states
In a randomly entangled diffusive state, the phases of each $n$![]() -qubit basis state would be random, preventing decomposition to single qubits. This means that
-qubit basis state would be random, preventing decomposition to single qubits. This means that

The fidelity $f = \sum _{i,j} \sigma _{i,j} \rho _{i,j}^*$![]() shows these phases cancel out at $t=0$
shows these phases cancel out at $t=0$![]() when ${\boldsymbol \sigma }(t=0)={\boldsymbol \rho }$
when ${\boldsymbol \sigma }(t=0)={\boldsymbol \rho }$![]() , giving $f=4^n/4^n=1$
, giving $f=4^n/4^n=1$![]() . But how does an $n$
. But how does an $n$![]() -qubit ${\boldsymbol \sigma }$
-qubit ${\boldsymbol \sigma }$![]() evolve?
evolve?
Similarly to (C8), the equation for a given $\dot \sigma _{i,j}$![]() will have a relaxation term $-\nu _1 \sigma _{i,j}$
will have a relaxation term $-\nu _1 \sigma _{i,j}$![]() for each qubit that is 1 in both states $i$
for each qubit that is 1 in both states $i$![]() and $j$
and $j$![]() , a gain term $\nu _1 \sigma _{i+2^k,j+2^k}$
, a gain term $\nu _1 \sigma _{i+2^k,j+2^k}$![]() for each qubit that is 0 in both states $i$
for each qubit that is 0 in both states $i$![]() and $j$
and $j$![]() where $k$
where $k$![]() is that qubit's index in the list of qubits, and a dephasing term $-({\nu _1 + \nu _2})/{2} \sigma _{i,j}$
is that qubit's index in the list of qubits, and a dephasing term $-({\nu _1 + \nu _2})/{2} \sigma _{i,j}$![]() for each qubit that is 0 in $i$
for each qubit that is 0 in $i$![]() or $j$
or $j$![]() but 1 in the other. With only the gain term coupling the matrix elements, and only along the same diagonal, it is straightforward if time consuming to solve the set of equations on each diagonal of ${\boldsymbol \sigma }$
but 1 in the other. With only the gain term coupling the matrix elements, and only along the same diagonal, it is straightforward if time consuming to solve the set of equations on each diagonal of ${\boldsymbol \sigma }$![]() . Then the elements of ${\boldsymbol \sigma } \circ {\boldsymbol \rho }^*$
. Then the elements of ${\boldsymbol \sigma } \circ {\boldsymbol \rho }^*$![]() can be summed to calculate the fidelity.
can be summed to calculate the fidelity.
C.3.3 Two qubits
It is instructive to work out the fidelity for two qubits. The main diagonal terms have the simplest contribution, since $\sum \sigma _{i,i} \rho _{i,i} = \sum \sigma _{i,i}/2^n = 1/2^n$![]() due to trace preservation $\mathrm {Tr}({\boldsymbol \sigma })=1$
due to trace preservation $\mathrm {Tr}({\boldsymbol \sigma })=1$![]() . The precise dynamics on the diagonal are irrelevant for the diffusive fidelity, as was seen even in the unentangled state.
. The precise dynamics on the diagonal are irrelevant for the diffusive fidelity, as was seen even in the unentangled state.
For off-diagonal terms, many high-index elements of ${\boldsymbol \sigma }$![]() do not have gain terms, making them simple exponential decays. For two qubits,
do not have gain terms, making them simple exponential decays. For two qubits,

where the indices correspond to binary states, i.e. $2=10_2, 3=11_2$![]() . This matrix element describes qubit 0 in superposition and qubit 1 in state 1, producing the first and second terms above, respectively. In contrast, a low-index state depends on decay from high-index states:
. This matrix element describes qubit 0 in superposition and qubit 1 in state 1, producing the first and second terms above, respectively. In contrast, a low-index state depends on decay from high-index states:
If we insert the ansatz $\sigma _{0,1} = A \,\textrm {e}^{at} + B \,\textrm {e}^{bt}$![]() into the equation, then we find that
into the equation, then we find that

with initial condition

giving the solution
In the unentangled limit where all $\phi _i \rightarrow 0$![]() , the fidelity contributions of the two elements $\sigma _{2,3}$
, the fidelity contributions of the two elements $\sigma _{2,3}$![]() and $\sigma _{0,1}$
and $\sigma _{0,1}$![]() partially cancel, eliminating the faster decay. But with random phase entanglement their combined contribution generally does not cancel, instead giving
partially cancel, eliminating the faster decay. But with random phase entanglement their combined contribution generally does not cancel, instead giving

In the fidelity this is further combined with its complex conjugate, resulting in cosines of the phases.
So the effect of random phases from diffusive entanglement does not change which fidelity decay rates are possible, but rather changes the relative weight of each term. This lesson will generalize to $n$![]() qubits.
qubits.
Since (C3) says fidelity is a sum over matrix elements of ${\boldsymbol \sigma } \circ {\boldsymbol \rho }^*$![]() (C4), it is helpful to show this full matrix for two qubits:
(C4), it is helpful to show this full matrix for two qubits:

Here $\phi _{123} \equiv ( \phi _1 + \phi _2 - \phi _3)$![]() . The diagonal matrix elements only have terms for relaxation to lower states and gain from higher states. Off-diagonal terms also have dephasing due to superposition qubits. The number of superposition qubits for an element can be counted from its indices, i.e. element $({\boldsymbol \sigma } \circ {\boldsymbol \rho }^*)_{2,3}$
. The diagonal matrix elements only have terms for relaxation to lower states and gain from higher states. Off-diagonal terms also have dephasing due to superposition qubits. The number of superposition qubits for an element can be counted from its indices, i.e. element $({\boldsymbol \sigma } \circ {\boldsymbol \rho }^*)_{2,3}$![]() measures the superposition between states $2 = 10_2$
measures the superposition between states $2 = 10_2$![]() and $3 = 11_2$
and $3 = 11_2$![]() , so only qubit 0 is in superposition between $0$
, so only qubit 0 is in superposition between $0$![]() and $1$
and $1$![]() . This contributes one factor of $\textrm {e}^{-(({\nu _1 + \nu _2})/{2}) t}$
. This contributes one factor of $\textrm {e}^{-(({\nu _1 + \nu _2})/{2}) t}$![]() , which combines with the decay term $\textrm {e}^{-\nu _1 t}$
, which combines with the decay term $\textrm {e}^{-\nu _1 t}$![]() from qubit 1. Off-diagonal gain terms are the only terms for which the random phase factors of ${\boldsymbol \sigma }$
from qubit 1. Off-diagonal gain terms are the only terms for which the random phase factors of ${\boldsymbol \sigma }$![]() and ${\boldsymbol \rho }^*$
and ${\boldsymbol \rho }^*$![]() do not cancel, making them the only way phase dependence enters the fidelity.
do not cancel, making them the only way phase dependence enters the fidelity.
C.3.4 $n$ qubits
qubits
An $n$![]() -qubit average fidelity can be found based on this two-qubit example. First, when $\nu _1=0$
-qubit average fidelity can be found based on this two-qubit example. First, when $\nu _1=0$![]() , the coupling between elements disappears, eliminating the phase-dependent terms in fidelity. This is just the unentangled case with the solution (C13).
, the coupling between elements disappears, eliminating the phase-dependent terms in fidelity. This is just the unentangled case with the solution (C13).
When $\nu _1 \neq 0$![]() , the fidelity $f = \sum _{i,j} \sigma _{i,j} \rho _{i,j}^*$
, the fidelity $f = \sum _{i,j} \sigma _{i,j} \rho _{i,j}^*$![]() generally depends on the phases. However, we can calculate the average fidelity over random phases $\phi _i$
generally depends on the phases. However, we can calculate the average fidelity over random phases $\phi _i$![]() . The motivation for this phase averaging is twofold. First, the $2^n$
. The motivation for this phase averaging is twofold. First, the $2^n$![]() initial conditions of basis states $\{\left |p\right \rangle \}$
initial conditions of basis states $\{\left |p\right \rangle \}$![]() are averaged over, with each producing statistically independent phases. Second, even if the phases have some probability distribution with finite variance and zero mean, the number of independent phases that sum in the fidelity grows quickly with the number of qubits. Two-qubit fidelity has only one independent phase $\phi _{123}$
are averaged over, with each producing statistically independent phases. Second, even if the phases have some probability distribution with finite variance and zero mean, the number of independent phases that sum in the fidelity grows quickly with the number of qubits. Two-qubit fidelity has only one independent phase $\phi _{123}$![]() per initial condition and time step, but three-qubit fidelity has four, each appearing with multiple decay rates. As the number of qubits grows, most decay rate coefficients sum over many independent phases, producing an additional effective averaging. Between these two averaging effects over the uniform distribution of phases, the variance of the mean should quickly shrink towards zero.
per initial condition and time step, but three-qubit fidelity has four, each appearing with multiple decay rates. As the number of qubits grows, most decay rate coefficients sum over many independent phases, producing an additional effective averaging. Between these two averaging effects over the uniform distribution of phases, the variance of the mean should quickly shrink towards zero.
Some phase-dependent terms will always be controlled by just a few phases, specifically $\sim n$![]() phases rather than one due to $n$
phases rather than one due to $n$![]() -fold symmetry in permuting qubit identities. This could break the assumption of phase averaging. However, in the worst case a single such poorly averaged decay rate coefficient will have fidelity contribution $\sim n/4^n$
-fold symmetry in permuting qubit identities. This could break the assumption of phase averaging. However, in the worst case a single such poorly averaged decay rate coefficient will have fidelity contribution $\sim n/4^n$![]() , so the effect of each will be small, as well as independent.
, so the effect of each will be small, as well as independent.
Assuming then that averaging over each phase gives an approximately correct total fidelity, one can use $\langle \textrm {e}^{\textrm {i} \phi _i} \rangle = 0$![]() to eliminate phase dependence in the fidelity. This does not reduce to the unentangled case. Off-diagonal elements of ${\boldsymbol \sigma } \circ {\boldsymbol \rho }^*$
to eliminate phase dependence in the fidelity. This does not reduce to the unentangled case. Off-diagonal elements of ${\boldsymbol \sigma } \circ {\boldsymbol \rho }^*$![]() lose their gain terms but not their relaxation and dephasing terms. This means probability flow from high to low states retains the loss from high but not the gain to low. Equivalently, all coupling terms in the differential equations for ${\boldsymbol \sigma }$
lose their gain terms but not their relaxation and dephasing terms. This means probability flow from high to low states retains the loss from high but not the gain to low. Equivalently, all coupling terms in the differential equations for ${\boldsymbol \sigma }$![]() can be dropped, greatly simplifying each matrix element to a single term each. Diagonal elements are not changed by phase averaging since they have no phase dependence, so they retain their gain terms.
can be dropped, greatly simplifying each matrix element to a single term each. Diagonal elements are not changed by phase averaging since they have no phase dependence, so they retain their gain terms.
The general $n$![]() -qubit average fidelity can be constructed from this understanding. The fidelity is
-qubit average fidelity can be constructed from this understanding. The fidelity is

This construction goes as follows. First, count the diagonal terms as the sum ${1}/{2^n}$![]() due to trace preservation. Then for each off-diagonal term $\sigma _{i,j}$
due to trace preservation. Then for each off-diagonal term $\sigma _{i,j}$![]() , count the number of qubits $k$
, count the number of qubits $k$![]() in superposition between states $i$
in superposition between states $i$![]() and $j$
and $j$![]() . For $k$
. For $k$![]() qubits in superposition, the effects of dephasing combine for a decay rate contribution of $-k (({\nu _1 +\nu _2})/{2})$
qubits in superposition, the effects of dephasing combine for a decay rate contribution of $-k (({\nu _1 +\nu _2})/{2})$![]() . The number of qubit permutations with $k$
. The number of qubit permutations with $k$![]() qubits in superposition is ($n$
qubits in superposition is ($n$![]() choose $k$
choose $k$![]() ), and there are $2^k$
), and there are $2^k$![]() ways the superposition qubits can be flipped between matrix index contribution ordering $0,1$
ways the superposition qubits can be flipped between matrix index contribution ordering $0,1$![]() and $1,0$
and $1,0$![]() , i.e. matrix element $0,3 = 000_2, 011_2$
, i.e. matrix element $0,3 = 000_2, 011_2$![]() and $2,1 = 010_2, 001_2$
and $2,1 = 010_2, 001_2$![]() have the same dephasing rate. These two factors count the number of matrix elements with that dephasing rate. The non-superposition qubits can each be in state 0 or 1, but phase averaging has eliminated gain to 0 while preserving relaxation from 1. This requires a sum over the number of excited qubits. Elements with $l$
have the same dephasing rate. These two factors count the number of matrix elements with that dephasing rate. The non-superposition qubits can each be in state 0 or 1, but phase averaging has eliminated gain to 0 while preserving relaxation from 1. This requires a sum over the number of excited qubits. Elements with $l$![]() excited qubits have additional exponential fidelity decay at a rate $-l \nu _1$
excited qubits have additional exponential fidelity decay at a rate $-l \nu _1$![]() , and there are ($(n-k)$
, and there are ($(n-k)$![]() choose $l$
choose $l$![]() ) permutations of these excited qubits. Lastly, since the diagonal elements must be excluded from these sums for not following the same rules after averaging, the index $k=0$
) permutations of these excited qubits. Lastly, since the diagonal elements must be excluded from these sums for not following the same rules after averaging, the index $k=0$![]() for zero superposition qubits must be removed. It is helpful to subtract this term after the fact.
for zero superposition qubits must be removed. It is helpful to subtract this term after the fact.
One validation of (C23) is that it can be easily modified to describe the unentangled case of (C13). When all phases $\phi _i$![]() are zero, instead of the gain terms averaging to zero they perfectly cancel the decay terms. To reflect this, remove the effect of decay in (C23) via the replacement $\textrm {e}^{-l \nu _1 t} \rightarrow 1$
are zero, instead of the gain terms averaging to zero they perfectly cancel the decay terms. To reflect this, remove the effect of decay in (C23) via the replacement $\textrm {e}^{-l \nu _1 t} \rightarrow 1$![]() . The sum over $l$
. The sum over $l$![]() then evaluates to $2^{n-k}$
then evaluates to $2^{n-k}$![]() and simplifying recovers (C13).
and simplifying recovers (C13).
The full (C23) simplifies to
where both approximations assume early time $t \ll 1/\nu _1, 1/\nu _2$![]() . Comparing this averaged diffusive randomly entangled decay to the diffusive unentangled decay (C13), the effect of $\nu _1$
. Comparing this averaged diffusive randomly entangled decay to the diffusive unentangled decay (C13), the effect of $\nu _1$![]() on the initial rate approximately doubled but the effect of $\nu _2$
on the initial rate approximately doubled but the effect of $\nu _2$![]() remains the same. The extra $\nu _1$
remains the same. The extra $\nu _1$![]() contribution comes from relaxation terms that no longer cancel with gain terms.
contribution comes from relaxation terms that no longer cancel with gain terms.
The diffusive fidelity (C26) can be understood more intuitively by noting that the phase averaging decouples all matrix elements except the $n$![]() -qubit diagonal. A single decoupled, phase-averaged qubit within the $n$
-qubit diagonal. A single decoupled, phase-averaged qubit within the $n$![]() -qubit system, ignoring the trace preservation from the $n$
-qubit system, ignoring the trace preservation from the $n$![]() -qubit diagonal, can be considered as having a fidelity matrix ${\boldsymbol \sigma } \circ {\boldsymbol \rho }^*$
-qubit diagonal, can be considered as having a fidelity matrix ${\boldsymbol \sigma } \circ {\boldsymbol \rho }^*$![]() of
of
where the gain term has been removed relative to (C12). The fidelity $f = \sum _{i,j} \sigma _{i,j} \rho _{i,j}^*$![]() of this to the $n$
of this to the $n$![]() th power for $n$
th power for $n$![]() qubits forms the first term in (C26). The latter two terms are corrections for the $n$
qubits forms the first term in (C26). The latter two terms are corrections for the $n$![]() -qubit diagonal, since the diagonal has no phases to average as is clear from initial state (C15). The second term removes the erroneous diagonal term and the third replaces it with the appropriate $1/2^n$
-qubit diagonal, since the diagonal has no phases to average as is clear from initial state (C15). The second term removes the erroneous diagonal term and the third replaces it with the appropriate $1/2^n$![]() from trace preservation.
from trace preservation.
Appendix D. Parametric noise
D.1 Effects of parametric noise
It is worth comparing Lindblad noise models to a parametric noise model that is more common in the study of dynamics in quantum maps. This section demonstrates that the forms of the fidelity decay are very different, making this parametric noise model a poor fit to the experimental results of § 3. However, the simulations of this and the following section may be useful for explaining future experiments where low-frequency or coherent noise may dominate.
Hamiltonian noise models have been studied widely in the quantum maps literature (Benenti et al. Reference Benenti, Casati, Montangero and Shepelyansky2001; Jacquod, Silvestrov & Beenakker Reference Jacquod, Silvestrov and Beenakker2001; Benenti & Casati Reference Benenti and Casati2002; Benenti et al. Reference Benenti, Casati, Montangero and Shepelyansky2002, Reference Benenti, Casati, Montangero and Shepelyansky2003, Reference Benenti, Casati and Montangero2004; Frahm, Fleckinger & Shepelyansky Reference Frahm, Fleckinger and Shepelyansky2004; Wang, Casati & Li Reference Wang, Casati and Li2004; Gorin et al. Reference Gorin, Prosen, Seligman and Žnidarič2006; Jacquod & Petitjean Reference Jacquod and Petitjean2009), with noise in a parameter being a common variant. Hamiltonian noise models use unitary Markovian errors representing low-frequency or coherent noise. In this section we study the model of Benenti & Casati (Reference Benenti and Casati2002) and Benenti et al. (Reference Benenti, Casati, Montangero and Shepelyansky2003, Reference Benenti, Casati and Montangero2004) in which Hamiltonian evolution is perturbed stochastically at each discrete map step by $k \rightarrow k + \Delta k$![]() . The noise $\Delta k$
. The noise $\Delta k$![]() is drawn from a normal distribution with standard deviation $\sigma$
is drawn from a normal distribution with standard deviation $\sigma$![]() , where the p.d.f. is given by
, where the p.d.f. is given by
This model is discussed more thoroughly in Porter & Joseph (Reference Porter and Joseph2022). This produces a similar effect as the fixed Hamiltonian perturbation discussed in Jacquod & Petitjean (Reference Jacquod and Petitjean2009), which itself resembles static coherent noise. Coherent noise can be divided into a component that is consistent over many gates, which can often be fixed through calibration, and a component that varies, which is more difficult to address. The latter resembles parametric noise.
When this parametric noise model is used, the initial conditions $\left |p\right \rangle =\left |0\right \rangle,\left |-N/2\right \rangle$![]() are excluded from simulations because their symmetry with respect to the map causes their noise-averaged fidelity to asymptotically approach $2/N$
are excluded from simulations because their symmetry with respect to the map causes their noise-averaged fidelity to asymptotically approach $2/N$![]() rather than $1/N$
rather than $1/N$![]() . This effect can be misleading on small systems so is avoided here for clarity.
. This effect can be misleading on small systems so is avoided here for clarity.
In the presence of random parametric noise, the fidelity of a chaotic map initially decays as $\textrm {e}^{-A n_g t}$![]() with Fermi golden rule $A \sim \sigma ^2$
with Fermi golden rule $A \sim \sigma ^2$![]() for noise magnitude $\sigma$
for noise magnitude $\sigma$![]() and $n_g$
and $n_g$![]() gates (Frahm et al. Reference Frahm, Fleckinger and Shepelyansky2004), until the golden rule breaks down for large $\sigma$
gates (Frahm et al. Reference Frahm, Fleckinger and Shepelyansky2004), until the golden rule breaks down for large $\sigma$![]() (Porter & Joseph Reference Porter and Joseph2022). In the presence of static unitary noise the fidelity initially decays tangent to $\exp ({-A n_q n_g^2 t})$
(Porter & Joseph Reference Porter and Joseph2022). In the presence of static unitary noise the fidelity initially decays tangent to $\exp ({-A n_q n_g^2 t})$![]() with $A \sim \sigma ^2$
with $A \sim \sigma ^2$![]() for $n_q$
for $n_q$![]() qubits, but at some fraction of the Heisenberg time this transitions to a faster Gaussian decay of $\ln (f) \sim -t^2$
qubits, but at some fraction of the Heisenberg time this transitions to a faster Gaussian decay of $\ln (f) \sim -t^2$![]() (Frahm et al. Reference Frahm, Fleckinger and Shepelyansky2004). Quantum dynamical effects, such as Lyapunov and algebraic decay described below, do not immediately set in, so they do not affect the above initial decay rates.
(Frahm et al. Reference Frahm, Fleckinger and Shepelyansky2004). Quantum dynamical effects, such as Lyapunov and algebraic decay described below, do not immediately set in, so they do not affect the above initial decay rates.
It was previously shown that in the diffusive regime a minimum of six qubits is needed to observe the fidelity decaying at the Lyapunov exponent rate (Porter & Joseph Reference Porter and Joseph2022). However, in the localized regime an algebraic decay rate is predicted instead (Cucchietti Reference Cucchietti2004; Jacquod & Petitjean Reference Jacquod and Petitjean2009; Porter & Joseph Reference Porter and Joseph2022). This effect is shown in the QSM in figure 10(b), close to the predicted $f \propto 1/t$![]() at intermediate times for dimension $d=1$
at intermediate times for dimension $d=1$![]() and no time autocorrelation of the noise. Since algebraic decay has less stringent constraints than Lyapunov rate decay, it might be observable on fewer than six qubits, though no fewer than four as discussed below.
and no time autocorrelation of the noise. Since algebraic decay has less stringent constraints than Lyapunov rate decay, it might be observable on fewer than six qubits, though no fewer than four as discussed below.

Figure 10. Parametric noise simulations for (a) $n=3$![]() and (b) $n=6$
and (b) $n=6$![]() on log–log plots to show the algebraic decay rate for localized dynamics. Values of the kick $k$
on log–log plots to show the algebraic decay rate for localized dynamics. Values of the kick $k$![]() and Gaussian noise $\sigma$
and Gaussian noise $\sigma$![]() are chosen to avoid $k_\textrm {eff}=k+\Delta k<0$
are chosen to avoid $k_\textrm {eff}=k+\Delta k<0$![]() while keeping the number of map steps small. The resulting localized values of $k$
while keeping the number of map steps small. The resulting localized values of $k$![]() are further from zero due to this. Using 1000 and 100 realizations of the stochastic noise plus 6 and 62 initial conditions for (a) and (b), respectively.
are further from zero due to this. Using 1000 and 100 realizations of the stochastic noise plus 6 and 62 initial conditions for (a) and (b), respectively.
For parametric noise, $f(t=2 t_\textrm {fb})$![]() still indicates the fidelity during forward-and-back noise for $t_\textrm {fb}$
still indicates the fidelity during forward-and-back noise for $t_\textrm {fb}$![]() map step pairs, and its Fermi golden rule decay has double the decay rate relative to forward-only noise decay, that is, $f_\textrm {FGR,fb}(t) \approx f_{\textrm {FGR},f}(2t)$
map step pairs, and its Fermi golden rule decay has double the decay rate relative to forward-only noise decay, that is, $f_\textrm {FGR,fb}(t) \approx f_{\textrm {FGR},f}(2t)$![]() , where $t$
, where $t$![]() is the total forward-and-back time regardless of noise. But its Lyapunov rate decay depends only on the number of forward steps, so that $f_\textrm {Lyap,fb}(t) \approx f_{\textrm {Lyap},f}(t) \approx \textrm {e}^{- \lambda t/2}$
is the total forward-and-back time regardless of noise. But its Lyapunov rate decay depends only on the number of forward steps, so that $f_\textrm {Lyap,fb}(t) \approx f_{\textrm {Lyap},f}(t) \approx \textrm {e}^{- \lambda t/2}$![]() for semiclassical Lyapunov exponent $\lambda$
for semiclassical Lyapunov exponent $\lambda$![]() , showing no increased rate (Porter & Joseph Reference Porter and Joseph2022). A similar effect cannot be tested for in algebraic decay, since after fitting the initial fidelities, $f_\textrm {alg}(t \gg 1) = f_0 t_0 / t$
, showing no increased rate (Porter & Joseph Reference Porter and Joseph2022). A similar effect cannot be tested for in algebraic decay, since after fitting the initial fidelities, $f_\textrm {alg}(t \gg 1) = f_0 t_0 / t$![]() and $f_\textrm {alg}(2 t \gg 1) = f_0\, 2 t_0 / 2 t$
and $f_\textrm {alg}(2 t \gg 1) = f_0\, 2 t_0 / 2 t$![]() are equivalent.
are equivalent.
Since the diffusive and localized cases have different qualitative behaviour under parametric noise, a fidelity gap between the two should appear. This might be confused with the effect of Lindblad noise in a sufficiently noisy experiment, so it is important to check when algebraic decay might occur. Simulations with only parametric noise show a gap that is only observed on four or more qubits. On three qubits the gap is in fact reversed, with diffusive fidelity decaying slightly more slowly than localized fidelity. This is demonstrated in figure 10(a) where a reversed gap of about $3\,\%$![]() (absolute) appears. Interpreting this is complicated by the use of a Guassian parametric noise distribution that in the case shown causes $2\,\%$
(absolute) appears. Interpreting this is complicated by the use of a Guassian parametric noise distribution that in the case shown causes $2\,\%$![]() of map steps to have $k_\textrm {eff}=k+\Delta k<0$
of map steps to have $k_\textrm {eff}=k+\Delta k<0$![]() , where anomalous diffusion occurs. However, the reversed gap persists when anomalous diffusion is avoided with small noise $\sigma \ll k$
, where anomalous diffusion occurs. However, the reversed gap persists when anomalous diffusion is avoided with small noise $\sigma \ll k$![]() , so that is not the main cause. A reversed gap or no gap is observed consistently when comparing $0 \leq k \leq 1.9 \approx k_\textrm {loc}$
, so that is not the main cause. A reversed gap or no gap is observed consistently when comparing $0 \leq k \leq 1.9 \approx k_\textrm {loc}$![]() to $k=20$
to $k=20$![]() at noise values $0 \leq \sigma \leq 1.0$
at noise values $0 \leq \sigma \leq 1.0$![]() . Comparing the decay rates to $1/t$
. Comparing the decay rates to $1/t$![]() suggests that the localized case is still close to algebraic decay, but the diffusive case is limited by the system size to an even slower decay. This result for three qubits suggests the predictions of Lindblad noise are more relevant than parametric noise in present day experiments.
suggests that the localized case is still close to algebraic decay, but the diffusive case is limited by the system size to an even slower decay. This result for three qubits suggests the predictions of Lindblad noise are more relevant than parametric noise in present day experiments.
Dynamical localization displays Poisson-like energy spacing statistics, and so indicates locally integrable quantum dynamics, which is the source of the algebraic fidelity decay (Jacquod & Petitjean Reference Jacquod and Petitjean2009). But a dynamical fidelity gap can also occur in locally integrable quantum systems such as Lysne et al. (Reference Lysne, Kuper, Poggi, Deutsch and Jessen2020) (see their figure 3).
D.2 Combining Lindblad and parametric noise
The theory of Appendix C demonstrates that Lindblad noise by itself does not cause the same qualitative behaviour as the parametric noise model; e.g. algebraic decay or exponential decay at the Lyapunov rate. Combining Lindblad and parametric noise can generate these effects, but if the parametric noise is small relative to the Lindblad noise the effects may be difficult to observe.
If the noise processes are statistically independent, then Lindblad and parametric noise fidelities should multiply together. The simulations of the combined noise model in figure 11 support this conclusion for both localized and chaotic dynamics. In the chaotic case the rate slows for $1 \leq t_\textrm {fb} \leq 4$![]() to the product of the Lindblad diffusive rate and the Lyapunov rate, matching pure parametric noise simulations. If the two fidelities instead summed then the slowest exponential rate, namely the Lindblad rate, would dominate by outlasting the others, but that would predict a $3\times$
to the product of the Lindblad diffusive rate and the Lyapunov rate, matching pure parametric noise simulations. If the two fidelities instead summed then the slowest exponential rate, namely the Lindblad rate, would dominate by outlasting the others, but that would predict a $3\times$![]() slower decay than observed. The localized case also supports multiplying fidelities, as during $4 \leq t_\textrm {fb} \leq 7$
slower decay than observed. The localized case also supports multiplying fidelities, as during $4 \leq t_\textrm {fb} \leq 7$![]() , near the start of $1/t$
, near the start of $1/t$![]() decay in figure 10, the decay remains faster than either the $1/t$
decay in figure 10, the decay remains faster than either the $1/t$![]() or semi-localized ((4.16) and (4.17)) analytic decays, rather than one rate dominating. By $t_\textrm {fb}=8$
or semi-localized ((4.16) and (4.17)) analytic decays, rather than one rate dominating. By $t_\textrm {fb}=8$![]() the $1/N$
the $1/N$![]() term begins to dominate and slow the decay.
term begins to dominate and slow the decay.

Figure 11. Comparing combined Lindblad and parametric noise simulations (solid) to theory (dashed) for the semi-localized (purple, $k=1.8$![]() ) and diffusive (red, $k=10.0$
) and diffusive (red, $k=10.0$![]() ) cases. Theory (dashed) includes $1/t$
) cases. Theory (dashed) includes $1/t$![]() (blue), Lindblad semi-localized (purple) and the product of Lindblad diffusive and Lyapunov rate decays (red). Simulations average over all 128 initial conditions at one random realization each. All results use $n=7, \nu _1=0.025, \nu _2=0.05, \textrm { and } \sigma =0.9$
(blue), Lindblad semi-localized (purple) and the product of Lindblad diffusive and Lyapunov rate decays (red). Simulations average over all 128 initial conditions at one random realization each. All results use $n=7, \nu _1=0.025, \nu _2=0.05, \textrm { and } \sigma =0.9$![]() . For Lyapunov rate decay, theory assumes that $f_{\textrm {fb},\textrm {Lyap}}(t_\textrm {fb}) = \textrm {e}^{- \lambda t_\textrm {fb}}$
. For Lyapunov rate decay, theory assumes that $f_{\textrm {fb},\textrm {Lyap}}(t_\textrm {fb}) = \textrm {e}^{- \lambda t_\textrm {fb}}$![]() as observed.
as observed.
In Porter & Joseph (Reference Porter and Joseph2022) three bounds were derived on the observability of Lyapunov decay under parametric noise. However, if dynamical and Lindblad noise do have multiplicative effects on the fidelity decay, then one can predict how this noise combination would cause these bounds to change. Bound (1) should remain unchanged, as Lindblad noise likely affects both Fermi golden rule decay and Lyapunov decay equally, causing no change in their competition. Bound (2) should also remain unchanged, as the transition to localization likely occurs at the same parameter value. But bound (3) would tighten, since it describes the limited time steps available to observe Lyapunov decay, which the addition of Lindblad noise would certainly reduce.
Appendix E. Rationale for gate-based Lindblad model
Working with a complete decoherence model of quantum gates is quite challenging because there are many terms that are potentially active (Breuer et al. Reference Breuer and Petruccione2002). For a linear trace-preserving quantum process model, the number of terms is $N^4{-}N^2$![]() , where $N$
, where $N$![]() is the number of states. Clearly, for all-to-all connectivity, a complete characterization is not scalable to many qubits.
is the number of states. Clearly, for all-to-all connectivity, a complete characterization is not scalable to many qubits.
Performing quantum process tomography (Chuang & Nielsen Reference Chuang and Nielsen1997) for a single entangling gate already requires a relatively large number of measurements. While there are software packages such as pyGSTi (Nielsen et al. Reference Nielsen, Rudinger, Proctor, Russo, Young and Blume-Kohout2020, Reference Nielsen, Gamble, Rudinger, Scholten, Young and Blume-Kohout2021) that allow one to automatically characterize a complete set of two-qubit gates, many of the commercial quantum hardware platforms available today do not allow enough run time to perform a complete characterization of even a single entangling gate. Moreover, because the complete protocol takes so long to run, the hardware characteristics may drift significantly over the duration of the experiments.
To make headway under such circumstances, one must attempt to utilize plausible simplifications of the number and types of decoherence processes under consideration. Assume that for each gate, one can identify a simplified set of decoherence processes that are dominant. One could then perform a restricted form of process tomography to characterize each gate. One could even characterize an entire gate set – assuming that the number of independent decoherence processes is small enough that this procedure is scalable.
Presumably, a detailed understanding of the physical processes that mediate decoherence mechanisms would yield a relatively concise mathematical description of the dominant decoherence processes. However, this could still potentially be quite complicated, for instance, including non-Markovian processes, and would require custom experiments to diagnose and verify. Moreover, this could potentially require a physical model for the environment as well as for the quantum computing hardware, making the model non-Markovian and more complex than the process tomography paradigm typically admits.
Yet simply understanding the way that the physical system imposes a mathematical structure on the decoherence processes is potentially quite valuable. For example, theoretical studies have proven that the Lindblad master equation (Breuer et al. Reference Breuer and Petruccione2002) is the appropriate infinitesimal generator of the temporal evolution of a quantum system coupled to an incoherent process that is both trace preserving and completely positive. Hence, this implies that the Lindbladian form should be considered primary and that integrating the master equation over a finite-time interval should be used to determine the associated process matrix. Clearly, a sparse representation in terms of Lindblad operators will typically yield a rather dense process matrix. Thus, from the physical perspective, it is much more likely for the Lindblad representation to be sparse than it is for the associated process matrix.
Another plausible physical assumption is that the dominant noise processes are from one- and two-qubit interactions. This reduces the number of processes exponentially, from $O(N^4)$![]() (the elements of the infinitesimal process matrix) when including up to all-qubit processes to just $O(\log ^2(N))$
(the elements of the infinitesimal process matrix) when including up to all-qubit processes to just $O(\log ^2(N))$![]() (the number of qubit pairs) for up to two-qubit processes. In the infinitesimal process matrix this corresponds to an exponential reduction in the number of elements. This can be seen by considering the relationship between the Lindblad equation, which describes the time evolution of the density matrix, and the infinitesimal process matrix, which describes the coupling of density matrix elements. Most process matrix elements of a large system couple density matrix elements between which more than two qubits have differing states. So limiting to one- and two-qubit processes treats most process matrix elements as zero, leaving an exponentially small number of elements active.
(the number of qubit pairs) for up to two-qubit processes. In the infinitesimal process matrix this corresponds to an exponential reduction in the number of elements. This can be seen by considering the relationship between the Lindblad equation, which describes the time evolution of the density matrix, and the infinitesimal process matrix, which describes the coupling of density matrix elements. Most process matrix elements of a large system couple density matrix elements between which more than two qubits have differing states. So limiting to one- and two-qubit processes treats most process matrix elements as zero, leaving an exponentially small number of elements active.
Two-qubit processes could be further limited to fewer physically plausible channels. For instance, photon exchange between qubits mediated by the environment could be an important channel, since it requires only one photon and is an extension of single-qubit relaxation and excitation processes (K. Wendt, private communication, 2022). A stronger restriction is limiting interactions to nearest neighbours in a sparsely connected device, reducing the number of processes to $O(\log (N))$![]() . This also strengthens the assumption that no more than two-qubit processes need to be considered.
. This also strengthens the assumption that no more than two-qubit processes need to be considered.
Two-qubit dephasing is a physically plausible channel that we found in our numerical studies to have very similar qualitative effects as the standard single-qubit dephasing. Presumably, the reason is that each multi-qubit dephasing process can be understood as single-qubit dephasing in an alternate basis. Understanding whether or not such non-standard dephasing terms are important for describing actual quantum hardware performance could be an interesting subject for future work.
The greatest physical simplification that can plausibly be applied to a Lindblad model is that only the single-qubit relaxation and dephasing processes are important, averaged over all qubits for simplicity, but that they are enhanced over their measured values during gate operation. (For typical quantum hardware platforms, the temperature is so far below the excitation energy that excitation processes can be considered subdominant.) While this may be a vast oversimplification, these processes are clearly important because they are universally required to model experimental data in practice. The physical meaning of this model is simple: the physical processes that actuate the gate renormalize the interaction between the qubit and the environment and, hence, renormalize the characteristic single-qubit relaxation and dephasing rates. Note, however, that the predictions are non-trivial because the associated time-integrated process matrix has a relatively dense form that depends on the products of the rates with the overall gate time.
While many other decoherence processes are likely needed for a truly accurate description of the quantum hardware evolution, we have found that this simplest Lindblad model is sufficient for modelling the experimental data described in this work. Our work here has the restricted goal of attempting to determine the single-qubit decoherence enhancement for the CNOT gates that clearly dominate the IBM-Q error budget. Moreover, given the limited experimental data that one is able to obtain using today's platforms, the data may not contain enough information to robustly determine additional free parameters over and above those contained in this simple model. In the future, it could be interesting to explore a more comprehensive approach to the determination of the relevant decoherence processes. Perhaps one could even attempt a version of gate set tomography (Nielsen et al. Reference Nielsen, Gamble, Rudinger, Scholten, Young and Blume-Kohout2021) that deduces the relevant relaxation and dephasing enhancements for every qubit and every gate in the set.