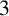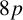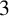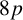1 Introduction
All graphs considered in this paper are undirected finite graphs with no loops, possibly with multiple edges. Let
$\Gamma $
be a graph with vertex set
$V(\Gamma )$
and edge set
$E(\Gamma )$
. An orientation
$\mathrm {D}$
of
$\Gamma $
is an assignment of a direction to each edge of
$\Gamma $
. Given an orientation,
$\mathrm {D}^{+}(v)$
(respectively
$\mathrm {D}^{-}(v)$
) denotes the set of all edges with tail (respectively head) at v for every
$v\in V(\Gamma )$
. Let
$\varphi $
be an integer-valued function on
$E(\Gamma )$
and k a positive integer. We call the ordered pair
$(\mathrm {D}, \varphi )$
a k-flow of
$\Gamma $
if
$\sum _{e\in \mathrm {D}^{+}(v)} \varphi (e) = \sum _{e\in \mathrm {D}^{-}(v)} \varphi (e)$
and
$|\varphi (e)| < k$
for all
$v\in V(\Gamma )$
. If in addition
$\varphi (e)\neq 0$
for every edge
$e\in E(\Gamma )$
, then
$(\mathrm {D}, \varphi )$
is called a nowhere-zero k-flow.
In the middle of the last century, Tutte [Reference Tutte11, Reference Tutte12] initiated the study of nowhere-zero integer flows in graphs. He observed that every nowhere-zero k-flow on a planar graph gives rise to a k-face-colouring of this graph, and vice versa. This implies that every planar graph admits a nowhere-zero
$4$
-flow if and only if the four colour conjecture holds. He also proposed three conjectures, namely the
$5$
-flow,
$4$
-flow and
$3$
-flow conjectures. This paper focus on Tutte’s
$3$
-flow conjecture which is stated now.
Conjecture 1.1. Every
$4$
-edge-connected graph admits a nowhere-zero
$3$
-flow.
Despite a great deal of research on this conjecture, it remains open. Jaeger [Reference Jaeger3] proposed the following so-called weak
$3$
-flow conjecture: there is a positive integer k such that every k-edge-connected graph admits a nowhere-zero
$3$
-flow. Kochol [Reference Kochol4] proved that Conjecture 1.1 is equivalent to the conjecture that every
$5$
-edge-connected graph admits a nowhere-zero
$3$
-flow. Jaeger’s conjecture was confirmed by Thomassen [Reference Thomassen10] who proved that the statement is true when
$k = 8$
. This breakthrough was further improved by Lovász et al. [Reference Lovász, Thomassen, Wu and Zhang6] who proved that every
$6$
-edge-connected graph admits a nowhere-zero
$3$
-flow.
In the past two decades, nowhere-zero
$3$
-flows in Cayley graphs have received considerable attention. Potočnik et al. [Reference Potočnik, Škoviera and Škrekovski8] proved that every Cayley graph of valency at least four on an abelian group admits a nowhere-zero
$3$
-flow. This was improved by Nánásiová and Škoviera [Reference Nánásiová and Škoviera7] who proved that Conjecture 1.1 is true for Cayley graphs on groups whose Sylow
$2$
-subgroup is a direct factor of the group. In particular, it is true for Cayley graphs on nilpotent groups. Subsequently, Conjecture 1.1 was proved to be true for Cayley graphs on more classes of groups, including dihedral groups [Reference Yang and Li13], generalised dihedral groups [Reference Li and Li5], generalised quaternion groups [Reference Li and Li5], generalised dicyclic groups [Reference Ahanjideh and Iranmanesh1], groups of order
$pq^2$
where p and q are two primes [Reference Zhang and Zhang14], supersolvable groups with a noncyclic Sylow
$2$
-subgroup and groups with square-free order derived subgroup [Reference Zhang and Zhou15].
At present, it seems impossible to verify Conjecture 1.1 for all Cayley graphs. As an attempt, it is reasonable to consider Cayley graphs on groups of order a product of a few primes. This has been done for groups of order
$pq^2$
by the first author and Zhang [Reference Zhang and Zhang14]. In this paper, we deal with a further step by proving that Conjecture 1.1 is true for Cayley graphs on groups of order
$8p$
where p is an odd prime.
Theorem 1.2. Let p be an odd prime. Then every Cayley graph of valency at least four on a group of order
$8p$
admits a nowhere-zero
$3$
-flow.
The paper is structured as follows. After this introductory section, we introduce some preparatory results in Section 2. In Section 3, we give the proof of Theorem 1.2.
2 Preliminaries
Groups considered in this paper are finite groups with identity element denoted by
$1$
. For a set S, we use
$|S|$
to denote the number of elements contained in S. Let G be a group. Then
$|G|$
is the order of G. If S is a subset of G, then we use
$\langle S\rangle $
to denote the subgroup of G generated by S. Let H be a subgroup of G. Then
$N_{G}(H)$
and
$C_{G}(H)$
denote the normaliser and centraliser of H in G, respectively. It is well known that
$|H|$
is a divisor of
$|G|$
and
$|G:H|:=|G|/|H|$
is called the index of H in G. An element of G is called an involution if it is of order
$2$
. An involution c of G is called a central involution if
$cg = gc$
for all
$g\in G$
. Let P be a subgroup of G and p a prime divisor of
$|G|$
. If
$|P|$
is a power of p and
$|G:H|$
is not divisible by p, then P is called a Sylow p-subgroup of G. The derived subgroup of G, denoted by
$G'$
, is the subgroup generated by all commutators
$[x,y]:=x^{-1}y^{-1}xy$
of G for
$x, y\in G$
.
Let X be a subset of G satisfying
$1\notin X$
and
$X^{-1} = X$
. The Cayley graph
$\mathrm {Cay}(G, X)$
on G with connection set X is the graph with vertex set G in which two vertices g and h are adjacent if and only if
$g^{-1}h\in X$
. If X is a multiset with elements in
$G\setminus \{1\}$
such that
$X = X^{-1}$
and the multiplicity of x is equal to that of
$x^{-1}$
for every
$x \in X$
, then the Cayley multigraph
$\mathrm {Cay}(G, X)$
is defined to be the multigraph with vertex set G such that the number of edges joining g and h is equal to the multiplicity of
$g^{-1}h\in X$
. It is obvious that the valency of the Cayley graph (multigraph)
$\mathrm {Cay}(G, X)$
is equal to the cardinality of X, and
$\mathrm {Cay}(G, X)$
is connected if and only if
$G = \langle X\rangle $
.
Let
$\mathrm {Cay}(G, X)$
be a Cayley graph (multigraph) on G and N a normal subgroup of G such that every element of N is of multiplicity
$0$
in X. Then the Cayley graph (multigraph)
$\mathrm {Cay}(G/N, X/N)$
is called the quotient graph of
$\mathrm {Cay}(G, X)$
induced by N. Note that
$\mathrm {Cay}(G/N,X/N)$
may be a multigraph even if
$\mathrm {Cay}(G,X)$
is not.
Lemma 2.1 [Reference Nánásiová and Škoviera7, Proposition 4.1].
Let G be a group having a normal subgroup N. Let
$\mathrm {Cay}(G,X)$
be a Cayley graph on G such that
$N\cap X = \emptyset $
. If
$\mathrm {Cay}(G/N,X/N)$
admits a nowhere-zero k-flow, then so does
$\mathrm { Cay}(G,X)$
.
A graph is said to be even if each of its vertices is of even valency. It is well known that a graph admits a nowhere-zero
$2$
-flow if and only if it is even [Reference Bondy and Murty2, Theorem 21.4]. Therefore, every even graph admits a nowhere-zero k-flow for any
$k\geq 2$
. It is also well known (see [Reference Bondy and Murty2, Theorem 21.5]) that a
$2$
-edge-connected cubic graph admits a nowhere-zero
$3$
-flow if and only if it is bipartite. Combining these two results gives the following lemma.
Lemma 2.2. Let
$\Gamma $
be a regular graph of odd valency. If
$\Gamma $
has a cubic bipartite spanning subgraph, then
$\Gamma $
admits a nowhere-zero 3-flow.
A group G is said to be supersolvable if it has a normal series
$\{1\} = G_{0}\leq G_{1} \leq \cdots \leq G_{n} = G$
such that the quotient group
$G_{i}/G_{i-1}$
is cyclic for
$1 \leq i \leq n$
. It is obvious that a group of order
$8p$
is supersolvable provided it has a normal Sylow p-subgroup. The following lemma is a direct corollary of the main results in [Reference Zhang and Zhou15].
Lemma 2.3. Let G be a group of order
$8p$
where p is an odd prime and let
$\Gamma = \mathrm {Cay}(G,X)$
be a Cayley graph of valency at least
$4$
. If G has a normal Sylow p-subgroup, then
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Proof. Assume that G has a normal Sylow p-subgroup P. Then G is supersolvable. Let Q be a Sylow
$2$
-subgroup of G. Then
$G/P \cong Q$
. By [Reference Potočnik, Škoviera and Škrekovski8, Theorem 1.1],
$\Gamma $
admits a nowhere-zero
$3$
-flow if G is abelian. Now we assume that G is nonabelian. Then
$G' = P$
provided Q is cyclic. Therefore, either Q is noncyclic or
$G'$
is of square-free order. By [Reference Zhang and Zhou15, Theorems 1.2 and 1.3],
$\Gamma $
admits a nowhere-zero
$3$
-flow.
3 Proof of Theorem 1.2
Let G be a group of order
$8p$
where p is an odd prime and let
$\Gamma =\mathrm {Cay}(G,X)$
be a Cayley graph of valency at least
$4$
. Since every even graph admits a nowhere-zero
$3$
-flow, we may assume that
$\Gamma $
is of odd valency at least
$5$
. Moreover, since every
$6$
-edge-connected graph admits a nowhere-zero
$3$
-flow [Reference Lovász, Thomassen, Wu and Zhang6] and the edge connectivity of a Cayley graph is equal to its valency, it suffices to deal with the case that
$\Gamma $
is of valency
$5$
. If
$\Gamma $
is disconnected, then
$\langle X\rangle $
is a proper subgroup of G. Therefore, the order of
$\langle X\rangle $
is a proper divisor of
$8p$
and it follows that
$\mathrm {Cay}(\langle X\rangle ,X)$
admits a nowhere-zero
$3$
-flow. Since every connected component of
$\Gamma $
is isomorphic to
$\mathrm {Cay}(\langle X\rangle ,X)$
, we conclude that
$\Gamma $
admits a nowhere-zero
$3$
-flow.
From now on, we assume that
$\Gamma $
is a connected graph of valency
$5$
. Then
$G = \langle X \rangle $
and
$|X| = 5$
.
Let
$n_{p}$
be the number of Sylow p-subgroups of G. By Sylow’s theorem (see [Reference Robinson9, 4.12]), we have
$n_{p}=|G:N_{G}(P)|\equiv 1\pmod p$
, where P is an arbitrary Sylow p-subgroup of G. In particular,
$n_p\mid 8$
. If
$n_p=1$
, then the unique Sylow p-subgroup of G is normal in G. By Lemma 2.3,
$\Gamma $
admits a nowhere-zero
$3$
-flow. In what follows, we assume
$n_{p}\neq 1$
. Then
$n_{p}=4~\mbox {or}~8$
. Furthermore, every minimal normal subgroup of G is an elementary abelian group of order
$2$
,
$4$
or
$8$
. Based on this, we divide the rest of the proof into three lemmas.
Lemma 3.1. If there is a minimal normal subgroup N of G of order
$2$
, then
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Proof. Since
$|N|=2$
and
$|G|=8p$
, the quotient group
$G/N$
is of order
$4p$
. Set
${N=\langle c\rangle }$
. Then c is a central involution of G. Since a Cayley graph of valency
$5$
admits a nowhere-zero
$3$
-flow provided its connection set contains a central involution [Reference Nánásiová and Škoviera7, Theorem 3.3],
$\Gamma $
admits a nowhere-zero
$3$
-flow if
$c\in X$
.
Now we assume that X contains no central involutions, so that
$c\notin X$
. Then N induces a quotient graph
$\Gamma _{N}:=\mathrm {Cay}(G/N,X/N)$
of
$\Gamma $
. Since every simple Cayley graph of order
$4p$
and valency
$5$
admits a nowhere-zero
$3$
-flow [Reference Zhang and Zhang14, Theorem 1.2], it follows from Lemma 2.1 that
$\Gamma $
admits a nowhere-zero
$3$
-flow if
$\Gamma _{N}$
is simple. In what follows, we assume that
$\Gamma _{N}$
is a multigraph. Then there exists an element
$x\in X$
such that
$xc\in X$
. We proceed with the proof in the following three cases.
Case 1: x (or
$xc$
) is an involution. Since c is a central involution of G, both x and
$xc$
are involutions. Since X is of cardinality
$5$
and inverse closed, there exists an involution
$a\in X\setminus \{x,xc\}$
. Then the Cayley graph
$\mathrm {Cay}(\langle \{x,c,a\}\rangle ,\{x,xc,a\})$
is a bipartite graph with the bipartition
$\{\langle xa,c\rangle , x\langle xa,c\rangle \}$
. It follows that the Cayley graph
$\mathrm {Cay}(G,\{x,xc,a\})$
is a cubic bipartite spanning subgraph of
$\Gamma $
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Case 2: x and
$xc$
are both of even order greater than
$2$
. In this case, the Cayley graph
$\mathrm {Cay}(\langle x,c\rangle , \{x,x^{-1},xc,cx^{-1}\})$
is a bipartite graph with the bipartition
$\{\langle x^2,c\rangle , x\langle x^2,c\rangle \}$
. It follows that
$\mathrm {Cay}(G, \{x,x^{-1},xc,cx^{-1}\})$
is a bipartite spanning subgraph of
$\Gamma $
. Let
$\Gamma '$
be a graph obtained from
$\mathrm { Cay}(G, \{x,x^{-1},xc,cx^{-1}\})$
by removing a perfect matching. Then
$\Gamma '$
is a cubic bipartite spanning subgraph of
$\Gamma $
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Case 3: x or
$xc$
is of odd order. Without loss of generality, we assume that x is of odd order. Since G is of order
$8p$
, it follows that x is of order p. Then
$xc$
is of order
$2p$
. In particular,
$\langle x\rangle $
is a Sylow p-subgroup of G and a normal subgroup of the cyclic group
$\langle xc\rangle $
. Thus,
$|G:N_{G}(\langle x\rangle )|\leq ~4$
. Recall that
$n_p\equiv 1\pmod p$
and
$n_p=|G:N_{G}(P)|\neq 1$
for any Sylow p-subgroup P of G. It follows that
$n_p=4$
and
$p=3$
. Therefore, G is of order
$24$
and
$N_{G}(P)$
is of order
$6$
. In particular,
$N_{G}(\langle x\rangle )=\langle xc\rangle =C_{G}(\langle x\rangle )$
. By Burnside’s normal complement theorem [Reference Robinson9, Theorem 7.50],
$\langle x\rangle $
has a normal complement Q in G. Indeed, Q is the unique Sylow
$2$
-subgroup of G.
Set
$X=\{x,x^{-1},cx,cx^{-1},a\}$
, where a is an involution. Since
$c\notin X$
, then
$c\ne a$
. Set
$x^{-1}ax=b$
and
$x^{-1}bx=d$
. Since x is of order
$3$
, we get
$x^{-1}dx=a$
. Note that
$a,b,c,d\in Q$
and
$|Q|=8$
. Since c is a central involution,
$a,b,c,d,ac,bc,dc$
are pairwise distinct involutions. It follows that Q is an elementary abelian group. Since
$x^{-1}(ac)x=bc$
,
$x^{-1}(bc)x=dc$
and
$x^{-1}(dc)x=ac$
, we see that c is the unique involution in Q such that
$x^{-1}cx=c$
. Since
$x^{-1}(abd)x=bda=abd$
, we have
$abd=c$
or
$1$
.
If
$abd=c$
, then it is straightforward to check that
$\langle ac,bc\rangle $
is normal in G and therefore
$\Gamma $
has a cubic bipartite spanning subgraph
$\mathrm {Cay}(G,\{cx,cx^{-1},a\})$
with the bipartition
$\{\langle ac,bc\rangle \langle x\rangle , \langle ac,bc\rangle \langle x\rangle a\}$
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Now we assume that
$abd=1$
. Then
$d=ab$
and therefore
$\langle a,b\rangle $
is normal in G. Moreover, it is straightforward to check that
$\langle a,b\rangle \langle x\rangle \cong A_{4}$
and
$G=\langle a,b\rangle \langle x\rangle \times \langle c\rangle $
. In particular, the Cayley graph
$\mathrm {Cay}(G,\{a,x,x^{-1}\})$
has two connected components which are the first two graphs depicted in Figure 1. Let
$\Sigma $
be the graph obtained from
$\mathrm {Cay}(G,\{a,x,x^{-1}\})$
by removing the four edges
$\{1,a\}$
,
$\{b,ab\}$
,
$\{c,ca\}$
and
$\{cb,cab\}$
. Then
$\Sigma $
has two connected components which are the third and fourth graphs depicted in Figure 1. Let
$\Lambda $
be the graph obtained from
$\Gamma $
by removing all the edges of
$\Sigma $
. Then
$\Lambda $
is a graph with two connected components depicted in Figure 2. It is obvious that both
$\Sigma $
and
$\Lambda $
admit a nowhere-zero
$3$
-flow. Since
$\Gamma $
is the edge-disjoint union of
$\Sigma $
and
$\Lambda $
, it follows that
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Figure 1
$\mathrm {Cay}(G,\{a,x,x^{-1}\})$
and some of its subgraphs.
Figure 2 The graph
$\Lambda $
.
Lemma 3.2. If there is a minimal normal subgroup N of G of order
$4$
, then
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Proof. By Lemma 3.1, we can assume that G has no minimal normal subgroups of order
$2$
. Let P be a Sylow p-subgroup of G. Then
$NP$
is a subgroup of G of order
$4p$
. Moreover,
$NP$
is normal in G as it is of index
$2$
in G. Since P is not normal in G, it follows that P is not a characteristic subgroup of
$NP$
and therefore not normal in
$NP$
. By Sylow’s theorem,
$|G:N_{G}(P)|\equiv |NP:N_{NP}(P)|\equiv 1\pmod p$
. It follows that
$p=3$
and
$|G:N_{G}(P)|=|NP:N_{NP}(P)|=4$
. In particular,
$|N_{G}(P)|=6$
and
$|G|=24$
. Since G has no minimal normal subgroups of order
$2$
,
$N_{G}(P)$
is core-free in G. Therefore, G is isomorphic to
$S_4$
. Since N is of order
$4$
,
$|N\cap X|\le 3$
. We proceed with the proof in four cases.
Case 1:
$|N\cap X|=3$
. In this case, it can be proved that all elements in X are involutions. Otherwise,
$X=(N\setminus \{1\})\cup \{y,y^{-1}\}$
and
$\langle X\rangle =N\langle y \rangle $
, where y is of order greater than
$2$
. Since
$G\cong S_4$
, y is of order
$4$
or
$3$
. Therefore,
$\langle X\rangle $
is of order
$8$
or
$12$
, which is a contradiction since
$G=\langle X\rangle $
.
Take
$z\in X\setminus N$
. Then
$\langle (N\setminus \{1\})\cup \{z\}\rangle =N\langle z\rangle $
. Since z is an involution,
$N\langle z\rangle $
is of order
$8$
and therefore a Sylow
$2$
-subgroup of G. In particular,
$N\langle z\rangle $
is a dihedral group, which contains exactly one central involution. Let Z be the subset of X obtained from
$(N\setminus \{1\})\cup \{z\}$
by removing the unique central involution of
$N\langle z\rangle $
. Then
$|Z|=3$
,
$\langle Z\rangle =N\langle z\rangle $
and all elements in Z are involutions outside the index
$2$
cyclic subgroup A of
$\langle Z\rangle $
. Therefore, the Cayley graph
$\mathrm {Cay}(\langle Z\rangle ,Z)$
is a bipartite graph with the bipartition
$\{A,Az\}$
. Thus,
$\mathrm {Cay}(G,Z)$
is a cubic bipartite spanning subgraph of
$\Gamma $
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Case 2:
$N\cap X=\emptyset $
. In this case, N induces a quotient graph
$\Gamma _{N}:=\mathrm {Cay}(G/N,X/N)$
of
$\Gamma $
. Note that
$G/N$
is a dihedral group. By [Reference Yang and Li13, Theorems 1.3 and 4.1],
$\Gamma _{N}$
admits a nowhere-zero
$3$
-flow. By Lemma 2.1,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Case 3:
$|N\cap X|=1~\mbox {or}~2$
and X contains no elements of order
$3$
. Set
$Y=X\setminus N$
. Then all elements in Y are of even order and
$Y\cap NP=\emptyset $
. Therefore, the Cayley graph
$\mathrm {Cay}(G,Y)$
is a bipartite graph with the bipartition
$\{NP,G\setminus NP\}$
. Since
$|N\cap X|=1~\mbox {or}~2$
, we conclude that
$\mathrm {Cay}(G,Y)$
is of valency
$4~\mbox {or}~3$
. Therefore,
$\mathrm { Cay}(G,Y)$
has a cubic bipartite spanning subgraph which is also a spanning subgraph of
$\Gamma $
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Case 4:
$|N\cap X|=1~\mbox {or}~2$
and X contains an element x of order
$3$
. Note that
$N\langle x\rangle $
is a subgroup of G of index
$2$
. In particular,
$N\langle x\rangle \cong A_4$
. Let a be an involution in
$N\cap X$
. Since
$G=\langle X\rangle $
, there exists
$c\in X$
such that
$c\notin N\langle x\rangle $
but
$c^2\in N\langle x\rangle $
. In particular, c is of order
$2$
or
$4$
. Set
$x^{-1}ax=b$
. Then
$x^{-1}bx=ab$
and the Cayley graph
$\mathrm {Cay}(G,\{a,x,x^{-1}\})$
has two connected components which are the first two graphs depicted in Figure 1. The remainder of the proof is divided into three subcases.
Subcase 4.1:
$X=\{a,c,z,x,x^{-1}\}$
where
$z\in N$
. In this subcase, both c and z are involutions. Note that
$N\langle c\rangle $
is a Sylow
$2$
-subgroup of G which is a dihedral group of order
$8$
. Therefore, either
$ac\ne ca$
or
$zc\ne cz$
. Without loss of generality, assume
$zc\ne cz$
. Set
$y=cz$
. Then y is of order
$4$
. If
$a\ne y^2$
, then the Cayley graph
$\mathrm {Cay}(\langle a,c,z\rangle ,\{a,c,z\})$
is a bipartite graph with the bipartition
$\{\langle y\rangle ,\langle y\rangle c\}$
. Thus,
$\mathrm {Cay}(G,\{a,c,z\})$
is a cubic bipartite spanning subgraph of
$\Gamma $
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow. If
$a=y^2$
, then
$\mathrm {Cay}(G,\{a,c,z\})$
is the disconnected graph depicted in Figure 3. It is obvious that the graph
$\Sigma $
obtained from
$\mathrm {Cay}(G,\{a,c,z\})$
by removing the three edges
$\{yc,yca\}$
,
$\{x,xa\}$
,
$\{x^2,x^2a\}$
admits a nowhere-zero
$3$
-flow. Moreover, the last graph depicted in Figure 1 is a connected component of
$\Gamma -E(\Sigma )$
and the other connected components of
$\Gamma -E(\Sigma )$
are triangles. Therefore,
$\Gamma -E(\Sigma )$
admits a nowhere-zero
$3$
-flow. It follows that
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Figure 3
$\mathrm {Cay}(G,\{a,c,z\})$
.
Subcase 4.2:
$X=\{a,c,z,x,x^{-1}\}$
where
$z\notin N$
and
$Nc\ne Nz$
. We first prove that both c and z are involutions. Otherwise,
$c=z^{-1}$
and z is of order
$3$
or
$4$
. If z is of order
$3$
, then
$c,z\in N\langle x\rangle $
, which is a contradiction since
$G=\langle X\rangle $
. If z is of order
$4$
, then
$z^2\in N$
, which contradicts
$Nc\ne Nz$
.
Since c and z are involutions outside N, we have
$c,z\notin N\langle x\rangle $
. Recall that
$N\langle x\rangle $
is of index
$2$
in G. Therefore,
$cz\in N\langle x\rangle $
. Set
$y=cz$
. Since
$Nc\ne Nz$
, we have
$y\in N\langle x\rangle \setminus N$
and hence y is of order
$3$
.
Let
$\Sigma $
be the graph obtained from the Cayley graph
$\mathrm {Cay}(G,\{a,x,x^{-1}\})$
by removing the four edges
$\{1,a\}$
,
$\{b,ab\}$
,
$\{c,ca\}$
and
$\{cb,cab\}$
. Then
$\Sigma $
has two connected components which are the third and fourth graphs depicted in Figure 1. It is obvious that
$\Sigma $
admits a nowhere-zero
$3$
-flow.
Set
$\Theta =\Gamma -E(\Sigma )$
. If
$ac=ca$
, then
$\Theta $
has two connected components which are the first two graphs depicted in Figure 4. If
$ac\ne ca$
, then
$c^{-1}ac=b~\mbox {or}~ab$
. Without loss of generality, assume
$c^{-1}ac=b$
. Then
$\Theta $
is the third graph depicted in Figure 4. Therefore,
$\Theta $
admits a nowhere-zero
$3$
-flow for either
$ac=ca$
or
$ac\ne ca$
.
Figure 4 The graph
$\Theta $
.
Now we have proved that both
$\Sigma $
and
$\Theta $
admit a nowhere-zero
$3$
-flow. Since
$\Gamma $
is the edge-disjoint union of
$\Sigma $
and
$\Theta $
, we see that
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Subcase 4.3:
$X=\{a,c,z,x,x^{-1}\}$
where
$z\notin N$
and
$Nc=Nz$
. Since
$G=\langle X\rangle $
and
$Nc=Nz$
, neither c nor z is of order
$3$
. Set
$Y=\{c,z,x,x^{-1}\}$
. Then
$N\cap Y=\emptyset $
. It is straightforward to check that the quotient graph
$\mathrm {Cay}(G/N,Y/N)$
of
$\mathrm {Cay}(G,Y)$
induced by N is isomorphic to the first graph depicted in Figure 5. Note that
$\mathrm {Cay}(G/N,Y/N)$
has a cubic bipartite spanning subgraph which is isomorphic to the second graph depicted in Figure 5. Therefore,
$\mathrm {Cay}(G,Y)$
has a cubic bipartite spanning subgraph which is also a cubic bipartite spanning subgraph of
$\Gamma $
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Figure 5
$\mathrm {Cay}(G/N,Y/N)$
and one of its subgraphs.
Lemma 3.3. If there is a minimal normal subgroup N of G of order
$8$
, then
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Proof. Assume that G has a minimal normal subgroup N of order
$8$
. Then N is an elementary abelian
$2$
-group. Moreover, N is a Sylow
$2$
-subgroup of G and a maximal group of G. Since N is normal in G, every involution of G is contained in N. Since
$\Gamma =\mathrm {Cay}(G,X)$
is of valency
$5$
, X contains an odd number of involutions. Let a be an involution contained in X, then
$a\in N$
. Since
$G=\langle X\rangle $
, there exists
$x\in X\setminus N$
. It is obvious that
$G=\langle N,x\rangle =N\langle x\rangle $
. Thus,
$N\cap \langle x\rangle $
is normal in G. Since N is a minimal normal subgroup of G, we have
$N\cap \langle x\rangle =\{1\}$
. Therefore, x is of order p. Moreover, the orbit of every nonidentity element under the conjugate action of
$\langle x\rangle $
on N is of length p and generates N. Since N contains exactly
$7$
nonidentity elements,
$p=7$
. It is straightforward to check that
$N=\langle a\rangle \times \langle x^{-1}ax\rangle \times \langle x^{-2}ax^2\rangle $
and
$x^{-3}ax^3=ax^{-2}ax^2$
or
$x^{-3}ax^3=ax^{-1}ax$
. If
$x^{-3}ax^3=ax^{-1}ax$
, then
$x^{3}ax^{-3}=ax^{2}ax^{-2}$
. Therefore, without loss of generality, we assume
$x^{-3}ax^3=ax^{-2}ax^2$
(as we can replace x by
$x^{-1}$
). Set
$x^{-1}ax=b$
and
$x^{-1}bx=c$
. Then
$N=\langle a\rangle \times \langle b\rangle \times \langle c\rangle $
and
$x^{-1}cx=ac$
.
Case 1: X contains three involutions. Set
$Y=X\setminus \{x,x^{-1}\}$
. Then Y consists of the three involutions of X. In particular, Y is a subset of N. If
$N=\langle Y\rangle $
, then every connected component of the Cayley graph
$\mathrm {Cay}(G,Y)$
is isomorphic to the cube. Therefore,
$\mathrm {Cay}(G,Y)$
is a cubic bipartite spanning subgraph of
$\Gamma $
. By Lemma 2.2,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
In what follows, we assume
$N\ne \langle Y\rangle $
so that
$\langle Y\rangle $
is of order
$4$
.
If
$x^{-1}Yx\cap Y\ne \emptyset $
, then there exists
$y\in Y$
such that
$x^{-1}yx\in Y$
. Since
$\langle Y\rangle $
is of order
$4$
,
$Y=\{y,x^{-1}yx,yx^{-1}yx\}$
. Without loss of generality, let
$y=a$
. Then
$Y=\{a,b,ab\}$
. Let
$\Sigma _1$
be the subgraph of the Cayley graph
$\mathrm {Cay}(G,\{a,x,x^{-1}\})$
depicted in Figure 6. Then
$\Sigma _1$
can be contracted to a cubic bipartite graph and therefore admits a nowhere-zero
$3$
-flow. It is straightforward to check that every connected component of
$\Gamma -E(\Sigma _1)$
is either a
$4$
-cycle or a graph obtained from the complete graph of order
$4$
by removing an edge. Therefore,
$\Gamma -E(\Sigma _1)$
admits a nowhere-zero
$3$
-flow and so does
$\Gamma $
.
Figure 6 The graph
$\Sigma _1$
.
If
$x^{-1}Yx\cap Y=\emptyset $
, then
$x^{-2}Yx^2\cap Y\ne \emptyset $
. Therefore, there exists
$y\in Y$
such that
$Y=\{y,x^{-2}yx^2,yx^{-2}yx^2\}$
. Without loss of generality, let
$y=a$
. Then
$Y=\{a,c,ac\}$
. Note that the subgraph
$\Sigma _2$
of
$\mathrm {Cay}(G,\{a,x,x^{-1}\})$
depicted in Figure 7 can be contracted to a cubic bipartite graph. Note also that every connected component of
$\Gamma -E(\Sigma _1)$
is either a
$4$
-cycle or a graph obtained from the complete graph of order
$4$
by removing an edge. Therefore,
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Figure 7 The graph
$\Sigma _2$
.
Case 2: X contains a unique involution. Set
$X=\{a,x,x^{-1},y,y^{-1}\}$
where y is not an involution. As for x, we see that y is of order
$7$
and
$G=\langle a,y\rangle $
. Since
$G=\bigcup _{i=0}^{6}Nx^i$
and
$N\cap Ny=\emptyset $
, either
$(Nx\cup Nx^2\cup Nx^3)\cap Ny\ne \emptyset $
or
$(Nx^4\cup Nx^5\cup Nx^6)\cap Ny\ne \emptyset $
. Without loss of generality, assume
$(Nx\cup Nx^2\cup Nx^3)\cap Ny\ne \emptyset $
. Then
$Ny=Nx, Nx^2~\mbox {or}~Nx^3$
. Since
$Nx^{-1}=Ny^2$
if
$Ny=Nx^3$
, the case
$Ny=Nx^3$
reduces to the case
$Ny=Nx^2$
by replacing the pair of elements
$(x^{-1},y)$
by
$(y,x)$
. Therefore, it suffices to consider the two cases
$Ny=Nx$
and
$Ny=Nx^2$
. Now assume
$Ny=Nx~\mbox {or}~Nx^2$
. Let
$\Lambda $
be the graph obtained from the Cayley graph
$\mathrm {Cay}(G,\{x,x^{-1},y,y^{-1})$
by removing all the edges in
$\{\{h,hx\}:h\in N\cup Nx^2\cup Nx^4\cup Nx^6\}$
. Then the quotient graph
$\Lambda _N$
of
$\Lambda $
induced by N is isomorphic to the first or second graph in Figure 8 according as
$Ny=Nx$
or
$Ny=Nx^2$
. Since
$\Lambda _N$
can be contracted to a cubic bipartite graph, so can
$\Lambda $
. Therefore,
$\Lambda $
admits a nowhere-zero
$3$
-flow. It is straightforward to check that every component of
$\Gamma -E(\Lambda )$
is either the third graph depicted in Figure 8 or an
$8$
-cycle. Since the third graph depicted in Figure 8 can be contracted to a cubic bipartite graph, we conclude that
$\Gamma -E(\Lambda )$
admits a nowhere-zero
$3$
-flow. It follows that
$\Gamma $
admits a nowhere-zero
$3$
-flow.
Figure 8
$\Lambda _{N}$
and one connected component of
$\Gamma -E(\Lambda )$
.
