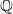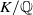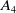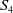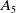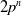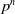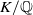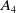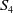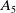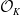1. Introduction
Let
![]() $K/F$
be a finite Galois extension of number fields or
$K/F$
be a finite Galois extension of number fields or
![]() $p$
-adic fields and let
$p$
-adic fields and let
![]() $G=\textrm{Gal}(K/F)$
. The classical normal basis theorem says that
$G=\textrm{Gal}(K/F)$
. The classical normal basis theorem says that
![]() $K$
is free of rank
$K$
is free of rank
![]() $1$
as a module over the group algebra
$1$
as a module over the group algebra
![]() $F[G]$
. A much more difficult problem is that of determining whether the ring of integers
$F[G]$
. A much more difficult problem is that of determining whether the ring of integers
![]() $\mathcal{O}_{K}$
is free of rank
$\mathcal{O}_{K}$
is free of rank
![]() $1$
over an appropriate
$1$
over an appropriate
![]() $\mathcal{O}_{F}$
-order in
$\mathcal{O}_{F}$
-order in
![]() $F[G]$
. The natural choice of such an order is the so-called associated order
$F[G]$
. The natural choice of such an order is the so-called associated order
since this is the only
![]() $\mathcal{O}_{F}$
-order in
$\mathcal{O}_{F}$
-order in
![]() $F[G]$
over which
$F[G]$
over which
![]() $\mathcal{O}_{K}$
can possibly be free.
$\mathcal{O}_{K}$
can possibly be free.
It is clear that the group ring
![]() $\mathcal{O}_{F}[G]$
is contained in
$\mathcal{O}_{F}[G]$
is contained in
![]() $\mathfrak{A}_{K/F}$
. In fact,
$\mathfrak{A}_{K/F}$
. In fact,
![]() $\mathfrak{A}_{K/F}=\mathcal{O}_{F}[G]$
if and only if
$\mathfrak{A}_{K/F}=\mathcal{O}_{F}[G]$
if and only if
![]() $K/F$
is at most tamely ramified. It is in this setting that by far the most progress has been made and we say that
$K/F$
is at most tamely ramified. It is in this setting that by far the most progress has been made and we say that
![]() $K/F$
has a normal integral basis if
$K/F$
has a normal integral basis if
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathcal{O}_{F}[G]$
. The celebrated Hilbert-Speiser theorem says that if
$\mathcal{O}_{F}[G]$
. The celebrated Hilbert-Speiser theorem says that if
![]() $K/\mathbb{Q}$
is a tamely ramified finite abelian extension, then it has a normal integral basis. Leopoldt removed the assumption on ramification to obtain the following generalisation of this result.
$K/\mathbb{Q}$
is a tamely ramified finite abelian extension, then it has a normal integral basis. Leopoldt removed the assumption on ramification to obtain the following generalisation of this result.
Theorem 1.1. [Reference Leopoldt27] Let
![]() $K/\mathbb{Q}$
be a finite abelian extension. Then,
$K/\mathbb{Q}$
be a finite abelian extension. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
Leopoldt also specified a generator and the associated order; Lettl [Reference Lettl28] gave a simplified and more explicit proof of the same result. We also have the following result of Bergé.
Theorem 1.2. [Reference Bergé2] Let
![]() $p$
be a prime and let
$p$
be a prime and let
![]() $K/\mathbb{Q}$
be a dihedral extension of degree
$K/\mathbb{Q}$
be a dihedral extension of degree
![]() $2p$
. Then,
$2p$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
Now let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q})\cong Q_{8}$
, the quaternion group of order
$\textrm{Gal}(K/\mathbb{Q})\cong Q_{8}$
, the quaternion group of order
![]() $8$
. Suppose that
$8$
. Suppose that
![]() $K/\mathbb{Q}$
is tamely ramified. Martinet [Reference Martinet31] gave three examples of such extensions, one with and two without normal integral bases. Moreover, Fröhlich [Reference Fröhlich14] showed that both possibilities occur infinitely often. By contrast, in the case that
$K/\mathbb{Q}$
is tamely ramified. Martinet [Reference Martinet31] gave three examples of such extensions, one with and two without normal integral bases. Moreover, Fröhlich [Reference Fröhlich14] showed that both possibilities occur infinitely often. By contrast, in the case that
![]() $K/\mathbb{Q}$
is wildly ramified, we have the following result of Martinet.
$K/\mathbb{Q}$
is wildly ramified, we have the following result of Martinet.
Theorem 1.3. [Reference Martinet and Sci32] Let
![]() $K/\mathbb{Q}$
be a wildly ramified Galois extension with
$K/\mathbb{Q}$
be a wildly ramified Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q})\cong Q_{8}$
. Then,
$\textrm{Gal}(K/\mathbb{Q})\cong Q_{8}$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
In the present article, we prove other Leopoldt-type theorems for non-abelian extensions of
![]() $\mathbb{Q}$
. An important notion is that of local freeness, which we now review.
$\mathbb{Q}$
. An important notion is that of local freeness, which we now review.
For the rest of the introduction, let
![]() $K/\mathbb{Q}$
be a finite Galois extension and let
$K/\mathbb{Q}$
be a finite Galois extension and let
![]() $G=\textrm{Gal}(K/\mathbb{Q})$
. We recall that
$G=\textrm{Gal}(K/\mathbb{Q})$
. We recall that
![]() $\mathcal{O}_{K}$
is said to be locally free over
$\mathcal{O}_{K}$
is said to be locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
at a rational prime
$\mathfrak{A}_{K/\mathbb{Q}}$
at a rational prime
![]() $p$
if
$p$
if
![]() $\mathcal{O}_{K,p}\;:\!=\;\mathbb{Z}_p\otimes _{\mathbb{Z}}\mathcal{O}_K$
is free as an
$\mathcal{O}_{K,p}\;:\!=\;\mathbb{Z}_p\otimes _{\mathbb{Z}}\mathcal{O}_K$
is free as an
![]() $\mathfrak{A}_{K/\mathbb{Q},p}\;:\!=\;\mathbb{Z}_p\otimes _{\mathbb{Z}}\mathfrak{A}_{K/\mathbb{Q}}$
-module. We say that
$\mathfrak{A}_{K/\mathbb{Q},p}\;:\!=\;\mathbb{Z}_p\otimes _{\mathbb{Z}}\mathfrak{A}_{K/\mathbb{Q}}$
-module. We say that
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if this holds for all rational primes
$\mathfrak{A}_{K/\mathbb{Q}}$
if this holds for all rational primes
![]() $p$
. Of course, this condition is necessary for
$p$
. Of course, this condition is necessary for
![]() $\mathcal{O}_K$
to be free over
$\mathcal{O}_K$
to be free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
If
![]() $K/\mathbb{Q}$
is tamely ramified, then
$K/\mathbb{Q}$
is tamely ramified, then
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}=\mathbb{Z}[G]$
(see Theorem 3.14). By contrast, if
$\mathfrak{A}_{K/\mathbb{Q}}=\mathbb{Z}[G]$
(see Theorem 3.14). By contrast, if
![]() $K/\mathbb{Q}$
is wildly ramified then
$K/\mathbb{Q}$
is wildly ramified then
![]() $\mathbb{Z}[G]$
is strictly contained in
$\mathbb{Z}[G]$
is strictly contained in
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
and
$\mathfrak{A}_{K/\mathbb{Q}}$
and
![]() $\mathcal{O}_{K}$
is not necessarily locally free over
$\mathcal{O}_{K}$
is not necessarily locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
. For instance, Bergé [Reference Bergé4] gave examples of wildly ramified dihedral extensions of
$\mathfrak{A}_{K/\mathbb{Q}}$
. For instance, Bergé [Reference Bergé4] gave examples of wildly ramified dihedral extensions of
![]() $\mathbb{Q}$
without the local freeness property (see Theorem 3.18 for a complete classification).
$\mathbb{Q}$
without the local freeness property (see Theorem 3.18 for a complete classification).
Now let
![]() $N/M$
be a finite Galois extension of
$N/M$
be a finite Galois extension of
![]() $p$
-adic fields. One can consider the analogous problem of whether
$p$
-adic fields. One can consider the analogous problem of whether
![]() $\mathcal{O}_{N}$
is free over
$\mathcal{O}_{N}$
is free over
![]() $\mathfrak{A}_{N/M}$
. Indeed, this is the case when
$\mathfrak{A}_{N/M}$
. Indeed, this is the case when
![]() $N/M$
is unramified, tamely ramified or weakly ramified, or
$N/M$
is unramified, tamely ramified or weakly ramified, or
![]() $M=\mathbb{Q}_{p}$
and
$M=\mathbb{Q}_{p}$
and
![]() $N/\mathbb{Q}_{p}$
is abelian or dihedral of order
$N/\mathbb{Q}_{p}$
is abelian or dihedral of order
![]() $2\ell$
for some prime
$2\ell$
for some prime
![]() $\ell$
(see Section 3.1 for a detailed overview of such results). However, freeness in this situation does not relate to the aforementioned notion of local freeness in the way one might expect.
$\ell$
(see Section 3.1 for a detailed overview of such results). However, freeness in this situation does not relate to the aforementioned notion of local freeness in the way one might expect.
Definition 1.4.
A rational prime
![]() $p$
is said to be a decomposition obstruction for
$p$
is said to be a decomposition obstruction for
![]() $K$
if
$K$
if
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
for one (indeed, every) prime
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
for one (indeed, every) prime
![]() $\mathfrak{P}$
of
$\mathfrak{P}$
of
![]() $K$
above
$K$
above
![]() $p$
, but
$p$
, but
![]() $\mathcal{O}_{K,p}$
is not free over
$\mathcal{O}_{K,p}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
(here
$\mathfrak{A}_{K/\mathbb{Q},p}$
(here
![]() $K_{\mathfrak{P}}$
denotes the completion of
$K_{\mathfrak{P}}$
denotes the completion of
![]() $K$
at
$K$
at
![]() $\mathfrak{P}$
).
$\mathfrak{P}$
).
Note that decomposition obstructions do exist. This is an important obstacle that can arise when the decomposition group is a proper non-trivial subgroup of the Galois group, and it needs to be overcome in the proofs of the main results of the present article. In Sections 6 and 7, we will present a detailed algebraic interpretation of such a property: we will start from the results of Bergé [Reference Bergé4] on the induction of associated orders and then prove new results that will be crucial for our purpose.
We now return to the problem of whether
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
. If
$\mathfrak{A}_{K/\mathbb{Q}}$
. If
![]() $K/\mathbb{Q}$
is (at most) tamely ramified, then the problem of determining whether it has a normal integral basis is well understood, thanks to Taylor’s proof of Fröhlich’s conjecture [Reference Taylor39]: he determined the class of
$K/\mathbb{Q}$
is (at most) tamely ramified, then the problem of determining whether it has a normal integral basis is well understood, thanks to Taylor’s proof of Fröhlich’s conjecture [Reference Taylor39]: he determined the class of
![]() $\mathcal{O}_{K}$
in the so-called locally free class group
$\mathcal{O}_{K}$
in the so-called locally free class group
![]() $\text{Cl}(\mathbb{Z}[G])$
(see Definition 2.4) in terms of Artin root numbers of the irreducible symplectic characters of
$\text{Cl}(\mathbb{Z}[G])$
(see Definition 2.4) in terms of Artin root numbers of the irreducible symplectic characters of
![]() $G$
(see [Reference Fröhlich15, I] for an overview). In particular, if
$G$
(see [Reference Fröhlich15, I] for an overview). In particular, if
![]() $G$
has no irreducible symplectic characters (this is the case, for instance, if
$G$
has no irreducible symplectic characters (this is the case, for instance, if
![]() $G$
is abelian, dihedral or of odd order), then
$G$
is abelian, dihedral or of odd order), then
![]() $K/\mathbb{Q}$
has a normal integral basis.
$K/\mathbb{Q}$
has a normal integral basis.
In the present article, we consider the question of whether
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
in certain cases where the locally free class group
$\mathfrak{A}_{K/\mathbb{Q}}$
in certain cases where the locally free class group
![]() $\text{Cl}(\mathbb{Z}[G])$
is trivial. In this situation, it is also the case that
$\text{Cl}(\mathbb{Z}[G])$
is trivial. In this situation, it is also the case that
![]() $\text{Cl}(\mathfrak{A}_{K/\mathbb{Q}})$
is trivial and the question reduces to whether
$\text{Cl}(\mathfrak{A}_{K/\mathbb{Q}})$
is trivial and the question reduces to whether
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
. A result of Endô and Hironaka [Reference Endô and Hironaka12] shows that if
$\mathfrak{A}_{K/\mathbb{Q}}$
. A result of Endô and Hironaka [Reference Endô and Hironaka12] shows that if
![]() $G$
is non-abelian and non-dihedral then
$G$
is non-abelian and non-dihedral then
![]() $\text{Cl}(\mathbb{Z}[G])$
is trivial if and only if
$\text{Cl}(\mathbb{Z}[G])$
is trivial if and only if
![]() $G$
is isomorphic to
$G$
is isomorphic to
![]() $A_4$
,
$A_4$
,
![]() $S_4$
or
$S_4$
or
![]() $A_5$
.
$A_5$
.
In the case that
![]() $G$
is dihedral of order
$G$
is dihedral of order
![]() $2p^{n}$
for a prime number
$2p^{n}$
for a prime number
![]() $p$
and a positive integer
$p$
and a positive integer
![]() $n$
, Keating [Reference Keating26] gave sufficient conditions for
$n$
, Keating [Reference Keating26] gave sufficient conditions for
![]() $\text{Cl}(\mathbb{Z}[G])$
to be trivial and Bergé [Reference Bergé4] gave necessary and sufficient conditions for
$\text{Cl}(\mathbb{Z}[G])$
to be trivial and Bergé [Reference Bergé4] gave necessary and sufficient conditions for
![]() $\mathcal{O}_{K}$
to be locally free over
$\mathcal{O}_{K}$
to be locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
. Despite being a straightforward application of these existing results, the following result does not appear to have been known until now.
$\mathfrak{A}_{K/\mathbb{Q}}$
. Despite being a straightforward application of these existing results, the following result does not appear to have been known until now.
Theorem 1.5.
Let
![]() $n$
be a positive integer and let
$n$
be a positive integer and let
![]() $p\geq 5$
be a regular prime number such that the class number of
$p\geq 5$
be a regular prime number such that the class number of
![]() $\mathbb{Q}(\zeta _{p^{n}})^+$
is
$\mathbb{Q}(\zeta _{p^{n}})^+$
is
![]() $1$
. Let
$1$
. Let
![]() $K/\mathbb{Q}$
be a dihedral extension of degree
$K/\mathbb{Q}$
be a dihedral extension of degree
![]() $2p^{n}$
. Then,
$2p^{n}$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if the ramification index of
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if the ramification index of
![]() $p$
in
$p$
in
![]() $K/\mathbb{Q}$
either is coprime to
$K/\mathbb{Q}$
either is coprime to
![]() $p$
or is a power of
$p$
or is a power of
![]() $p$
.
$p$
.
Here
![]() $\mathbb{Q}(\zeta _{p^{n}})^+$
denotes the maximal totally real subfield
$\mathbb{Q}(\zeta _{p^{n}})^+$
denotes the maximal totally real subfield
![]() $\mathbb{Q}(\zeta _{p^{n}})$
. Using the class number computations of Miller [Reference Miller33], we obtain the following corollary.
$\mathbb{Q}(\zeta _{p^{n}})$
. Using the class number computations of Miller [Reference Miller33], we obtain the following corollary.
Corollary 1.6.
Let
![]() $K/\mathbb{Q}$
be a dihedral extension of degree
$K/\mathbb{Q}$
be a dihedral extension of degree
![]() $2p^{n}$
where
$2p^{n}$
where
![]() $(p,n)$
is
$(p,n)$
is
![]() $(5,2)$
,
$(5,2)$
,
![]() $(5,3)$
,
$(5,3)$
,
![]() $(7,2)$
or
$(7,2)$
or
![]() $(11,2)$
. Then,
$(11,2)$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if the ramification index of
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if the ramification index of
![]() $p$
in
$p$
in
![]() $K/\mathbb{Q}$
either is coprime to
$K/\mathbb{Q}$
either is coprime to
![]() $p$
or is a power of
$p$
or is a power of
![]() $p$
.
$p$
.
Similar but more complicated results hold when
![]() $p=2$
or
$p=2$
or
![]() $3$
(see Theorem 5.2 for the full statement and proof).
$3$
(see Theorem 5.2 for the full statement and proof).
The main results of the present article will be necessary and sufficient conditions for
![]() $\mathcal{O}_{K}$
to be free over
$\mathcal{O}_{K}$
to be free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
when
$\mathfrak{A}_{K/\mathbb{Q}}$
when
![]() $G$
is isomorphic to
$G$
is isomorphic to
![]() $A_{4}$
,
$A_{4}$
,
![]() $S_{4}$
or
$S_{4}$
or
![]() $A_{5}$
. The discussion above shows that the main work is in determining when
$A_{5}$
. The discussion above shows that the main work is in determining when
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
. A key ingredient is the notion of hybrid
$\mathfrak{A}_{K/\mathbb{Q}}$
. A key ingredient is the notion of hybrid
![]() $p$
-adic group rings, introduced by Johnston and Nickel [Reference Johnston and Nickel21]; using this tool, it is straightforward to show that
$p$
-adic group rings, introduced by Johnston and Nickel [Reference Johnston and Nickel21]; using this tool, it is straightforward to show that
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
at
$\mathfrak{A}_{K/\mathbb{Q}}$
at
![]() $p=3$
when
$p=3$
when
![]() $G$
is isomorphic to
$G$
is isomorphic to
![]() $A_{4}$
or
$A_{4}$
or
![]() $S_{4}$
.
$S_{4}$
.
The statements of the following theorems will depend on certain primes of
![]() $K$
having given decomposition or inertia subgroups up to conjugation. We remark that such properties will not depend on which prime of
$K$
having given decomposition or inertia subgroups up to conjugation. We remark that such properties will not depend on which prime of
![]() $K$
we choose above a given rational prime. For example, saying that a prime
$K$
we choose above a given rational prime. For example, saying that a prime
![]() $p$
is tamely ramified will mean that some, and hence every, prime of
$p$
is tamely ramified will mean that some, and hence every, prime of
![]() $K$
above
$K$
above
![]() $p$
is (at most) tamely ramified in
$p$
is (at most) tamely ramified in
![]() $K/\mathbb{Q}$
. We shall henceforth abbreviate ‘at most tamely ramified’ to ‘tamely ramified’. We will say that a rational prime
$K/\mathbb{Q}$
. We shall henceforth abbreviate ‘at most tamely ramified’ to ‘tamely ramified’. We will say that a rational prime
![]() $p$
has full decomposition group if there is only one prime in
$p$
has full decomposition group if there is only one prime in
![]() $K$
above
$K$
above
![]() $p$
, with decomposition group equal to
$p$
, with decomposition group equal to
![]() $\textrm{Gal}(K/\mathbb{Q})$
.
$\textrm{Gal}(K/\mathbb{Q})$
.
The following result is Theorem 8.1.
Theorem 1.7.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}) \cong A_{4}$
. Then,
$\textrm{Gal}(K/\mathbb{Q}) \cong A_{4}$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $2$
is tamely ramified or has full decomposition group.
$2$
is tamely ramified or has full decomposition group.
The proof of the ‘if’ direction of this result involves the aforementioned tools. To prove the converse, we show that if
![]() $2$
is wildly ramified and has decomposition group of order
$2$
is wildly ramified and has decomposition group of order
![]() $2$
or
$2$
or
![]() $4$
then
$4$
then
![]() $\mathcal{O}_{K}$
is not locally free over
$\mathcal{O}_{K}$
is not locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
at
$\mathfrak{A}_{K/\mathbb{Q}}$
at
![]() $p=2$
. This reduces to showing that the lattice
$p=2$
. This reduces to showing that the lattice
![]() $\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}\;:\!=\;\mathbb{Z}_{2}[G]\otimes _{\mathbb{Z}_{2}[D]}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
is not free over
$\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}\;:\!=\;\mathbb{Z}_{2}[G]\otimes _{\mathbb{Z}_{2}[D]}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
, where
$\mathfrak{A}_{K/\mathbb{Q},2}$
, where
![]() $\mathfrak{P}$
is a fixed prime above
$\mathfrak{P}$
is a fixed prime above
![]() $2$
and
$2$
and
![]() $D$
is its decomposition group. The main theorem used here is Hattori’s result [Reference Hattori17] that commutative orders are ‘clean’ (see Section 6.2).
$D$
is its decomposition group. The main theorem used here is Hattori’s result [Reference Hattori17] that commutative orders are ‘clean’ (see Section 6.2).
The following two results are Theorem 8.3 and Theorem 8.6, respectively.
Theorem 1.8.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})\cong S_4$
. Then,
$G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})\cong S_4$
. Then,
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if one of the following conditions on
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if one of the following conditions on
![]() $K/\mathbb{Q}$
holds:
$K/\mathbb{Q}$
holds:
-
(i)
 $2$
is tamely ramified;
$2$
is tamely ramified; -
(ii)
 $2$
has decomposition group equal to the unique subgroup of
$2$
has decomposition group equal to the unique subgroup of
 $G$
of order
$G$
of order
 $12$
;
$12$
; -
(iii)
 $2$
is wildly and weakly ramified and has full decomposition group; or
$2$
is wildly and weakly ramified and has full decomposition group; or -
(iv)
 $2$
is wildly and weakly ramified, has decomposition group of order
$2$
is wildly and weakly ramified, has decomposition group of order
 $8$
in
$8$
in
 $G$
, and has inertia subgroup equal to the unique normal subgroup of order
$G$
, and has inertia subgroup equal to the unique normal subgroup of order
 $4$
in
$4$
in
 $G$
.
$G$
.
Theorem 1.9.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}) \cong A_{5}$
. Then,
$\textrm{Gal}(K/\mathbb{Q}) \cong A_{5}$
. Then,
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if all three of the following conditions on
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if all three of the following conditions on
![]() $K/\mathbb{Q}$
hold:
$K/\mathbb{Q}$
hold:
-
(i)
 $2$
is tamely ramified;
$2$
is tamely ramified; -
(ii)
 $3$
is tamely ramified or is weakly ramified with ramification index
$3$
is tamely ramified or is weakly ramified with ramification index
 $6$
; and
$6$
; and -
(iii)
 $5$
is tamely ramified or is weakly ramified with ramification index
$5$
is tamely ramified or is weakly ramified with ramification index
 $10$
.
$10$
.
In contrast to the proof of Theorem 1.7, the proofs of Theorems 1.8 and 1.9 use the (updated) implementations in Magma [Reference Bosma, Cannon and Playoust1] of the algorithms developed by Bley and Johnston [Reference Bley and Johnston5] and by Hofmann and Johnston [Reference Hofmann and Johnston18].
Notation and conventions. All rings are assumed to have an identity element, and all modules are assumed to be left modules unless otherwise stated. We denote certain finite groups as follows:
-
•
 $D_{2n}$
is the dihedral group of order
$D_{2n}$
is the dihedral group of order
 $2n$
;
$2n$
; -
•
 $Q_{8}$
is the quaternion group of order
$Q_{8}$
is the quaternion group of order
 $8$
;
$8$
; -
•
 $A_{n}$
is the alternating group on
$A_{n}$
is the alternating group on
 $n$
letters;
$n$
letters; -
•
 $S_{n}$
is the symmetric group on
$S_{n}$
is the symmetric group on
 $n$
letters.
$n$
letters.
Let
![]() $K$
be a number field. By a prime of
$K$
be a number field. By a prime of
![]() $K$
, we mean a non-zero prime ideal of
$K$
, we mean a non-zero prime ideal of
![]() $\mathcal{O}_{K}$
. If
$\mathcal{O}_{K}$
. If
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $K$
, we let
$K$
, we let
![]() $K_{\mathfrak{P}}$
denote the completion of
$K_{\mathfrak{P}}$
denote the completion of
![]() $K$
at
$K$
at
![]() $\mathfrak{P}$
. We say that a prime is tamely ramified if it is at most tamely ramified.
$\mathfrak{P}$
. We say that a prime is tamely ramified if it is at most tamely ramified.
Let
![]() $H$
be a subgroup of a finite group
$H$
be a subgroup of a finite group
![]() $G$
. We denote by
$G$
. We denote by
![]() $\textrm{ncl}_G(H)$
the normal closure of
$\textrm{ncl}_G(H)$
the normal closure of
![]() $H$
in
$H$
in
![]() $G$
, defined as the smallest normal subgroup of
$G$
, defined as the smallest normal subgroup of
![]() $G$
containing
$G$
containing
![]() $H$
or, equivalently, the subgroup generated by all the conjugates of
$H$
or, equivalently, the subgroup generated by all the conjugates of
![]() $H$
in
$H$
in
![]() $G$
.
$G$
.
For a positive integer
![]() $n$
, we let
$n$
, we let
![]() $\zeta _n$
denote a primitive
$\zeta _n$
denote a primitive
![]() $n$
th root of unity.
$n$
th root of unity.
2. Associated orders and local freeness
2.1. Lattices and orders
For further background, we refer the reader to [Reference Reiner35] or [Reference Curtis and Reiner9]. Let
![]() $R$
be a Dedekind domain with field of fractions
$R$
be a Dedekind domain with field of fractions
![]() $F$
. An
$F$
. An
![]() $R$
-lattice
$R$
-lattice
![]() $M$
is a finitely generated torsion-free
$M$
is a finitely generated torsion-free
![]() $R$
-module, or equivalently, a finitely generated projective
$R$
-module, or equivalently, a finitely generated projective
![]() $R$
-module. Note that any
$R$
-module. Note that any
![]() $R$
-submodule of an
$R$
-submodule of an
![]() $R$
-lattice is again an
$R$
-lattice is again an
![]() $R$
-lattice. For any finite-dimensional
$R$
-lattice. For any finite-dimensional
![]() $F$
-vector space
$F$
-vector space
![]() $V$
, an
$V$
, an
![]() $R$
-lattice in
$R$
-lattice in
![]() $V$
is a finitely generated
$V$
is a finitely generated
![]() $R$
-submodule
$R$
-submodule
![]() $M$
in
$M$
in
![]() $V$
. We define a
$V$
. We define a
![]() $F$
-vector subspace of
$F$
-vector subspace of
![]() $V$
by
$V$
by
and say that
![]() $M$
is a full
$M$
is a full
![]() $R$
-lattice in
$R$
-lattice in
![]() $V$
if
$V$
if
![]() $FM=V$
. We may identify
$FM=V$
. We may identify
![]() $FM$
with
$FM$
with
![]() $F \otimes _{R} M$
.
$F \otimes _{R} M$
.
Let
![]() $A$
be a finite-dimensional
$A$
be a finite-dimensional
![]() $F$
-algebra. An
$F$
-algebra. An
![]() $R$
-order in
$R$
-order in
![]() $A$
is a subring
$A$
is a subring
![]() $\Lambda$
of
$\Lambda$
of
![]() $A$
(so in particular has the same unity element as
$A$
(so in particular has the same unity element as
![]() $A$
) such that
$A$
) such that
![]() $\Lambda$
is a full
$\Lambda$
is a full
![]() $R$
-lattice in
$R$
-lattice in
![]() $A$
. A
$A$
. A
![]() $\Lambda$
-lattice is a
$\Lambda$
-lattice is a
![]() $\Lambda$
-module which is also an
$\Lambda$
-module which is also an
![]() $R$
-lattice. For
$R$
-lattice. For
![]() $\Lambda$
-lattices
$\Lambda$
-lattices
![]() $M$
and
$M$
and
![]() $N$
, a homomorphism of
$N$
, a homomorphism of
![]() $\Lambda$
-modules
$\Lambda$
-modules
![]() $f\;:\; M \rightarrow N$
is called a homomorphism of
$f\;:\; M \rightarrow N$
is called a homomorphism of
![]() $\Lambda$
-lattices.
$\Lambda$
-lattices.
The following well-known lemma follows from [Reference Curtis and Reiner9, Exercise 23.2].
Lemma 2.1.
Let
![]() $\Lambda \subseteq \Gamma$
be two
$\Lambda \subseteq \Gamma$
be two
![]() $R$
-orders in
$R$
-orders in
![]() $A$
. Let
$A$
. Let
![]() $M$
and
$M$
and
![]() $N$
be
$N$
be
![]() $\Gamma$
-lattices and let
$\Gamma$
-lattices and let
![]() $f\; :\; M\rightarrow N$
be a homomorphism of
$f\; :\; M\rightarrow N$
be a homomorphism of
![]() $\Lambda$
-lattices. Then,
$\Lambda$
-lattices. Then,
![]() $f$
is a homomorphism of
$f$
is a homomorphism of
![]() $\Gamma$
-lattices.
$\Gamma$
-lattices.
2.2. Associated orders
Let
![]() $\Lambda$
be an
$\Lambda$
be an
![]() $R$
-order in a finite-dimensional
$R$
-order in a finite-dimensional
![]() $F$
-algebra
$F$
-algebra
![]() $A$
. Let
$A$
. Let
![]() $M$
be a full
$M$
be a full
![]() $R$
-lattice in a free
$R$
-lattice in a free
![]() $A$
-module of rank
$A$
-module of rank
![]() $1$
(thus
$1$
(thus
![]() $FM \cong A$
as
$FM \cong A$
as
![]() $A$
-modules). The associated order of
$A$
-modules). The associated order of
![]() $M$
is defined to be
$M$
is defined to be
Note that
![]() $\mathfrak{A}(A, M)$
is an
$\mathfrak{A}(A, M)$
is an
![]() $R$
-order (see [Reference Reiner35, §8]). In particular, it is the largest order
$R$
-order (see [Reference Reiner35, §8]). In particular, it is the largest order
![]() $\Lambda$
over which
$\Lambda$
over which
![]() $M$
has a structure of
$M$
has a structure of
![]() $\Lambda$
-module. The following well-known result says that
$\Lambda$
-module. The following well-known result says that
![]() $\mathfrak{A}(A, M)$
is the only
$\mathfrak{A}(A, M)$
is the only
![]() $R$
-order in
$R$
-order in
![]() $A$
over which
$A$
over which
![]() $M$
can possibly be free.
$M$
can possibly be free.
Proposition 2.2.
Let
![]() $\Lambda$
be an
$\Lambda$
be an
![]() $R$
-order in
$R$
-order in
![]() $A$
and let
$A$
and let
![]() $M$
be a free
$M$
be a free
![]() $\Lambda$
-lattice of rank
$\Lambda$
-lattice of rank
![]() $1$
. Then,
$1$
. Then,
![]() $FM$
is a free
$FM$
is a free
![]() $A$
-module of rank
$A$
-module of rank
![]() $1$
and
$1$
and
![]() $\Lambda =\mathfrak{A}(A, M)$
.
$\Lambda =\mathfrak{A}(A, M)$
.
Proof. By hypothesis there exists
![]() $\alpha \in M$
such that
$\alpha \in M$
such that
![]() $M=\Lambda \alpha$
is a free
$M=\Lambda \alpha$
is a free
![]() $\Lambda$
-module. Thus,
$\Lambda$
-module. Thus,
![]() $FM=A\alpha$
is free over
$FM=A\alpha$
is free over
![]() $A$
. Let
$A$
. Let
![]() $x \in \mathfrak{A}(A, M)$
. Then,
$x \in \mathfrak{A}(A, M)$
. Then,
![]() $x \alpha \in M = \Lambda \alpha$
, so
$x \alpha \in M = \Lambda \alpha$
, so
![]() $x\alpha = y\alpha$
for some
$x\alpha = y\alpha$
for some
![]() $y \in \Lambda$
. Since
$y \in \Lambda$
. Since
![]() $FM$
is freely generated by
$FM$
is freely generated by
![]() $\alpha$
, we must have
$\alpha$
, we must have
![]() $x=y$
. Hence,
$x=y$
. Hence,
![]() $\mathfrak{A}(A, M) \subseteq \Lambda$
. The reverse inclusion is trivial and therefore
$\mathfrak{A}(A, M) \subseteq \Lambda$
. The reverse inclusion is trivial and therefore
![]() $\Lambda = \mathfrak{A}(A, M)$
.
$\Lambda = \mathfrak{A}(A, M)$
.
Remark 2.3.
Suppose
![]() $\Lambda$
is an
$\Lambda$
is an
![]() $R$
-order in
$R$
-order in
![]() $A$
. Then, clearly
$A$
. Then, clearly
![]() $\Lambda \subseteq \mathfrak{A}(A, \Lambda )$
. Moreover,
$\Lambda \subseteq \mathfrak{A}(A, \Lambda )$
. Moreover,
![]() $\mathfrak{A}(A, \Lambda ) 1_{A} \subseteq \Lambda$
and so
$\mathfrak{A}(A, \Lambda ) 1_{A} \subseteq \Lambda$
and so
![]() $\mathfrak{A}(A, \Lambda ) \subseteq \Lambda$
. Therefore,
$\mathfrak{A}(A, \Lambda ) \subseteq \Lambda$
. Therefore,
![]() $\mathfrak{A}(A, \Lambda ) = \Lambda$
.
$\mathfrak{A}(A, \Lambda ) = \Lambda$
.
2.3. Completion and local freeness
Let
![]() $\mathfrak{p}$
be any maximal ideal of
$\mathfrak{p}$
be any maximal ideal of
![]() $R$
. Let
$R$
. Let
![]() $F_{\mathfrak{p}}$
denote the completion of
$F_{\mathfrak{p}}$
denote the completion of
![]() $F$
with respect to a valuation defined by
$F$
with respect to a valuation defined by
![]() $\mathfrak{p}$
and let
$\mathfrak{p}$
and let
![]() $R_{\mathfrak{p}}$
be the corresponding valuation ring. For any
$R_{\mathfrak{p}}$
be the corresponding valuation ring. For any
![]() $R$
-module
$R$
-module
![]() $M$
we write
$M$
we write
![]() $M_{\mathfrak{p}}$
for
$M_{\mathfrak{p}}$
for
![]() $R_{\mathfrak{p}} \otimes _{R} M$
and
$R_{\mathfrak{p}} \otimes _{R} M$
and
![]() $V_{\mathfrak{p}}= F_{\mathfrak{p}} \otimes _{F} V$
for any
$V_{\mathfrak{p}}= F_{\mathfrak{p}} \otimes _{F} V$
for any
![]() $F$
-vector space
$F$
-vector space
![]() $V$
. These two notations are consistent as the map
$V$
. These two notations are consistent as the map
![]() $\lambda \otimes _{\mathcal{O}_{F}} v \mapsto \lambda \otimes _{F} v$
(
$\lambda \otimes _{\mathcal{O}_{F}} v \mapsto \lambda \otimes _{F} v$
(
![]() $v \in V$
,
$v \in V$
,
![]() $\lambda \in \mathcal{O}_{F_{\mathfrak{p}}}$
) is an isomorphism (see [Reference Fröhlich and Taylor16, p. 93]).
$\lambda \in \mathcal{O}_{F_{\mathfrak{p}}}$
) is an isomorphism (see [Reference Fröhlich and Taylor16, p. 93]).
Let
![]() $\Lambda$
be an
$\Lambda$
be an
![]() $R$
-order and let
$R$
-order and let
![]() $M$
be a
$M$
be a
![]() $\Lambda$
-lattice in some
$\Lambda$
-lattice in some
![]() $A$
-module
$A$
-module
![]() $V$
. Then,
$V$
. Then,
![]() $\Lambda _{\mathfrak{p}}$
is an
$\Lambda _{\mathfrak{p}}$
is an
![]() $R_{\mathfrak{p}}$
-order in
$R_{\mathfrak{p}}$
-order in
![]() $A_{\mathfrak{p}}$
and
$A_{\mathfrak{p}}$
and
![]() $M_{\mathfrak{p}}$
is a
$M_{\mathfrak{p}}$
is a
![]() $\Lambda _{\mathfrak{p}}$
-lattice in
$\Lambda _{\mathfrak{p}}$
-lattice in
![]() $V_{\mathfrak{p}}$
. We say that
$V_{\mathfrak{p}}$
. We say that
![]() $M$
is locally free over
$M$
is locally free over
![]() $\Lambda$
if
$\Lambda$
if
![]() $M_{\mathfrak{p}}$
is free over
$M_{\mathfrak{p}}$
is free over
![]() $\Lambda _{\mathfrak{p}}$
for every
$\Lambda _{\mathfrak{p}}$
for every
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
Let
![]() $G$
be a finite group and let
$G$
be a finite group and let
![]() $M$
be a full
$M$
be a full
![]() $R[G]$
-lattice in a free
$R[G]$
-lattice in a free
![]() $A$
-module of rank
$A$
-module of rank
![]() $1$
. Then,
$1$
. Then,
![]() $R[G] \subseteq \mathfrak{A}(F[G], M)$
and
$R[G] \subseteq \mathfrak{A}(F[G], M)$
and
![]() $R_{\mathfrak{p}}[G] \subseteq \mathfrak{A}(F_{\mathfrak{p}}[G], M_{\mathfrak{p}}) \cong \mathfrak{A}(F[G], M)_{\mathfrak{p}}$
. Moreover,
$R_{\mathfrak{p}}[G] \subseteq \mathfrak{A}(F_{\mathfrak{p}}[G], M_{\mathfrak{p}}) \cong \mathfrak{A}(F[G], M)_{\mathfrak{p}}$
. Moreover,
![]() $M$
is locally free over
$M$
is locally free over
![]() $\mathfrak{A}(F[G], M)$
if
$\mathfrak{A}(F[G], M)$
if
![]() $M_{\mathfrak{p}}$
is free over
$M_{\mathfrak{p}}$
is free over
![]() $\mathfrak{A}(F_{\mathfrak{p}}[G], M_{\mathfrak{p}})$
for every
$\mathfrak{A}(F_{\mathfrak{p}}[G], M_{\mathfrak{p}})$
for every
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
2.4. Associated orders of rings of integers and decomposition obstructions
Let
![]() $K/F$
be a finite Galois extension of number fields and let
$K/F$
be a finite Galois extension of number fields and let
![]() $G=\textrm{Gal}(K/F)$
. We consider the behaviour of the associated order
$G=\textrm{Gal}(K/F)$
. We consider the behaviour of the associated order
![]() $\mathfrak{A}_{K/F}\;:\!=\;\mathfrak{A}(F[G],\mathcal{O}_{K})$
with respect to localisation and induction.
$\mathfrak{A}_{K/F}\;:\!=\;\mathfrak{A}(F[G],\mathcal{O}_{K})$
with respect to localisation and induction.
Let
![]() $\mathfrak{p}$
be a maximal ideal of
$\mathfrak{p}$
be a maximal ideal of
![]() $\mathcal{O}_{F}$
. Then, we have decompositions
$\mathcal{O}_{F}$
. Then, we have decompositions
where
![]() $\{ \mathfrak{P}' \mid \mathfrak{p} \}$
consists of the primes of
$\{ \mathfrak{P}' \mid \mathfrak{p} \}$
consists of the primes of
![]() $\mathcal{O}_{K}$
above
$\mathcal{O}_{K}$
above
![]() $\mathfrak{p}$
(see [Reference Fröhlich and Taylor16, p. 109]). Fix a prime
$\mathfrak{p}$
(see [Reference Fröhlich and Taylor16, p. 109]). Fix a prime
![]() $\mathfrak{P}$
above
$\mathfrak{P}$
above
![]() $\mathfrak{p}$
and let
$\mathfrak{p}$
and let
![]() $D$
be its decomposition group in
$D$
be its decomposition group in
![]() $G$
. Then, as
$G$
. Then, as
![]() $G$
acts transitively on
$G$
acts transitively on
![]() $\{ \mathfrak{P}' \mid \mathfrak{p} \}$
we have
$\{ \mathfrak{P}' \mid \mathfrak{p} \}$
we have
where the products run over a system of representatives of the left cosets
![]() $G/D$
. Hence,
$G/D$
. Hence,
and
where the last isomorphism follows from [Reference Curtis and Reiner9, Exercise 24.2], for instance. Thus,
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/F}$
at
$\mathfrak{A}_{K/F}$
at
![]() $\mathfrak{p}$
if and only if
$\mathfrak{p}$
if and only if
![]() $\textrm{Ind}_{D}^{G}\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\textrm{Ind}_{D}^{G}\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}(F_{\mathfrak{p}}[G],\textrm{Ind}_{D}^{G}\mathcal{O}_{K_{\mathfrak{P}}})$
.
$\mathfrak{A}(F_{\mathfrak{p}}[G],\textrm{Ind}_{D}^{G}\mathcal{O}_{K_{\mathfrak{P}}})$
.
We recall from the introduction that it may be the case that we encounter a prime
![]() $\mathfrak{p}$
that is a decomposition obstruction for
$\mathfrak{p}$
that is a decomposition obstruction for
![]() $K$
, i.e. such that
$K$
, i.e. such that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/F_{\mathfrak{p}}}$
but
$\mathfrak{A}_{K_{\mathfrak{P}}/F_{\mathfrak{p}}}$
but
![]() $\mathcal{O}_{K}$
is not locally free over
$\mathcal{O}_{K}$
is not locally free over
![]() $\mathfrak{A}_{K/F}$
at
$\mathfrak{A}_{K/F}$
at
![]() $\mathfrak{p}$
(indeed, Definition 1.4 can be easily generalised to base fields other than
$\mathfrak{p}$
(indeed, Definition 1.4 can be easily generalised to base fields other than
![]() $\mathbb{Q}$
). In Section 6, we will consider the relationship between
$\mathbb{Q}$
). In Section 6, we will consider the relationship between
![]() $\mathfrak{A}(F_{\mathfrak{p}}[G],\textrm{Ind}_{D}^{G}\mathcal{O}_{K_{\mathfrak{P}}})$
and
$\mathfrak{A}(F_{\mathfrak{p}}[G],\textrm{Ind}_{D}^{G}\mathcal{O}_{K_{\mathfrak{P}}})$
and
![]() $\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/F_{\mathfrak{p}}}$
, as well as conditions under which the implication ‘if
$\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/F_{\mathfrak{p}}}$
, as well as conditions under which the implication ‘if
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/F_{\mathfrak{p}}}$
then
$\mathfrak{A}_{K_{\mathfrak{P}}/F_{\mathfrak{p}}}$
then
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/F}$
at
$\mathfrak{A}_{K/F}$
at
![]() $\mathfrak{p}$
’ holds.
$\mathfrak{p}$
’ holds.
Notation. We henceforth consider the isomorphism
![]() $\mathfrak{A}_{K/F,\mathfrak{p}}\cong \mathfrak{A}(F_{\mathfrak{p}}[G],\mathcal{O}_{K,\mathfrak{p}})$
as an identification. In particular, we consider
$\mathfrak{A}_{K/F,\mathfrak{p}}\cong \mathfrak{A}(F_{\mathfrak{p}}[G],\mathcal{O}_{K,\mathfrak{p}})$
as an identification. In particular, we consider
![]() $\mathfrak{A}_{K/F,\mathfrak{p}}$
as an
$\mathfrak{A}_{K/F,\mathfrak{p}}$
as an
![]() $\mathcal{O}_{F,\mathfrak{p}}$
-order in
$\mathcal{O}_{F,\mathfrak{p}}$
-order in
![]() $F_{\mathfrak{p}}[G]$
.
$F_{\mathfrak{p}}[G]$
.
2.5. Reduction to the study of local freeness
We define locally free class groups. Background material on locally free class groups, including a discussion of equivalent definitions, can be found in [Reference Curtis and Reiners10, §49].
Definition 2.4.
Let
![]() $F$
be a number field with ring of integers
$F$
be a number field with ring of integers
![]() $\mathcal{O}_{F}$
and let
$\mathcal{O}_{F}$
and let
![]() $\Lambda$
be an
$\Lambda$
be an
![]() $\mathcal{O}_{F}$
-order in a finite-dimensional semisimple
$\mathcal{O}_{F}$
-order in a finite-dimensional semisimple
![]() $F$
-algebra
$F$
-algebra
![]() $A$
. Let
$A$
. Let
![]() $P(\Lambda )$
be the free abelian group generated by symbols
$P(\Lambda )$
be the free abelian group generated by symbols
![]() $[X]$
, one for each isomorphism class of locally free
$[X]$
, one for each isomorphism class of locally free
![]() $\Lambda$
-lattices
$\Lambda$
-lattices
![]() $X$
, modulo relations
$X$
, modulo relations
![]() $[X] = [X_{1}] + [X_{2}]$
whenever
$[X] = [X_{1}] + [X_{2}]$
whenever
![]() $X \cong X_{1} \oplus X_{2}$
. We define the locally free class group
$X \cong X_{1} \oplus X_{2}$
. We define the locally free class group
![]() $\text{Cl}(\Lambda )$
of
$\text{Cl}(\Lambda )$
of
![]() $\Lambda$
to be the subgroup of
$\Lambda$
to be the subgroup of
![]() $P(\Lambda )$
consisting of all expressions
$P(\Lambda )$
consisting of all expressions
![]() $[X]-[Y]$
, with
$[X]-[Y]$
, with
![]() $X,Y$
locally free and
$X,Y$
locally free and
![]() $FX \cong FY$
. If
$FX \cong FY$
. If
![]() $X$
is a
$X$
is a
![]() $\Lambda$
-lattice such that
$\Lambda$
-lattice such that
![]() $FX\cong A$
, we will refer to
$FX\cong A$
, we will refer to
![]() $[X]-[\Lambda ]$
as the class of
$[X]-[\Lambda ]$
as the class of
![]() $X$
in
$X$
in
![]() $\textrm{Cl}(\Lambda )$
.
$\textrm{Cl}(\Lambda )$
.
Remark 2.5.
By [
Reference Curtis and Reiner9, Corollary (31.7)], each element of
![]() $\text{Cl}(\Lambda )$
can be written in the form
$\text{Cl}(\Lambda )$
can be written in the form
![]() $[M]-[\Lambda ]$
for some locally free
$[M]-[\Lambda ]$
for some locally free
![]() $\Lambda$
-lattice
$\Lambda$
-lattice
![]() $M$
of rank
$M$
of rank
![]() $1$
. As a consequence, the Jordan-Zassenhaus Theorem [
Reference Curtis and Reiner9, Theorem (24.1)] implies that the locally free class group
$1$
. As a consequence, the Jordan-Zassenhaus Theorem [
Reference Curtis and Reiner9, Theorem (24.1)] implies that the locally free class group
![]() $\text{Cl}(\Lambda )$
is always finite.
$\text{Cl}(\Lambda )$
is always finite.
The following proposition underpins the proofs of all the new theorems stated in the introduction.
Proposition 2.6.
Let
![]() $G$
be a finite group such that
$G$
be a finite group such that
![]() $\textrm{Cl}(\mathbb{Z}[G])$
is trivial and let
$\textrm{Cl}(\mathbb{Z}[G])$
is trivial and let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}) \cong G$
. Then,
$\textrm{Gal}(K/\mathbb{Q}) \cong G$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
Proof. One implication is trivial. By [Reference Curtis and Reiners10, Theorem (49.25)], the inclusion
![]() $\mathbb{Z}[G]\subseteq \mathfrak{A}_{K/\mathbb{Q}}$
induces a surjection
$\mathbb{Z}[G]\subseteq \mathfrak{A}_{K/\mathbb{Q}}$
induces a surjection
![]() $\text{Cl}(\mathbb{Z}[G]) \twoheadrightarrow \text{Cl}(\mathfrak{A}_{K/\mathbb{Q}})$
, and so
$\text{Cl}(\mathbb{Z}[G]) \twoheadrightarrow \text{Cl}(\mathfrak{A}_{K/\mathbb{Q}})$
, and so
![]() $\text{Cl}(\mathfrak{A}_{K/\mathbb{Q}})$
is also trivial. Moreover, by [Reference Endô and Hironaka12] the triviality of
$\text{Cl}(\mathfrak{A}_{K/\mathbb{Q}})$
is also trivial. Moreover, by [Reference Endô and Hironaka12] the triviality of
![]() $\textrm{Cl}(\mathbb{Z}[G])$
implies that
$\textrm{Cl}(\mathbb{Z}[G])$
implies that
![]() $G$
must be abelian, dihedral, or isomorphic to
$G$
must be abelian, dihedral, or isomorphic to
![]() $A_{4}$
,
$A_{4}$
,
![]() $S_{4}$
or
$S_{4}$
or
![]() $A_{5}$
(see also [Reference Curtis and Reiners10, Theorem (50.29)]). In each of these cases,
$A_{5}$
(see also [Reference Curtis and Reiners10, Theorem (50.29)]). In each of these cases,
![]() $\mathbb{Q}[G]$
is isomorphic to a finite direct product of matrix rings over number fields. Hence by [Reference Curtis and Reiners10, Proposition (51.2)]
$\mathbb{Q}[G]$
is isomorphic to a finite direct product of matrix rings over number fields. Hence by [Reference Curtis and Reiners10, Proposition (51.2)]
![]() $\mathbb{Q}[G]$
satisfies the Eichler condition (see [Reference Curtis and Reiners10, Definitions (45.4) or §51A]). Thus the Jacobinski cancellation theorem [Reference Jacobinski19] (see also [Reference Curtis and Reiners10, Theorem (51.24)]) implies that
$\mathbb{Q}[G]$
satisfies the Eichler condition (see [Reference Curtis and Reiners10, Definitions (45.4) or §51A]). Thus the Jacobinski cancellation theorem [Reference Jacobinski19] (see also [Reference Curtis and Reiners10, Theorem (51.24)]) implies that
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
has the locally free cancellation property. The non-trivial implication now follows easily.
$\mathfrak{A}_{K/\mathbb{Q}}$
has the locally free cancellation property. The non-trivial implication now follows easily.
Corollary 2.7.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}) \cong A_{4},S_{4}$
or
$\textrm{Gal}(K/\mathbb{Q}) \cong A_{4},S_{4}$
or
![]() $A_{5}$
. Then,
$A_{5}$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
Proof. Let
![]() $G=\textrm{Gal}(K/\mathbb{Q})$
. In each case
$G=\textrm{Gal}(K/\mathbb{Q})$
. In each case
![]() $\text{Cl}(\mathbb{Z}[G])$
is trivial, as shown in [Reference Reiner and Ullom37].
$\text{Cl}(\mathbb{Z}[G])$
is trivial, as shown in [Reference Reiner and Ullom37].
3. Review of results relating to local freeness in field extensions
3.1. Freeness results for Galois extensions of
 $p$
-adic fields
$p$
-adic fields
Many of the results and definitions of this subsection also hold for local fields of positive characteristic, but for simplicity we restrict to the case of
![]() $p$
-adic fields. We fix a prime number
$p$
-adic fields. We fix a prime number
![]() $p$
.
$p$
.
Theorem 3.1.
Let
![]() $K/F$
be a tamely ramified finite Galois extension of
$K/F$
be a tamely ramified finite Galois extension of
![]() $p$
-adic fields and let
$p$
-adic fields and let
![]() $G=\textrm{Gal}(K/F)$
. Then,
$G=\textrm{Gal}(K/F)$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/F}=\mathcal{O}_{F}[G]$
.
$\mathfrak{A}_{K/F}=\mathcal{O}_{F}[G]$
.
Remark 3.2.
Theorem 3.1 is usually attributed to Emmy Noether [Reference Noether34]. In fact, as noted in [Reference Chapman8], she only stated and proved the result in the case that
![]() $p \nmid |G|$
. Complete proofs can be found in [Reference Fröhlich15], [Reference Kawamoto25] and [Reference Chapman8].
$p \nmid |G|$
. Complete proofs can be found in [Reference Fröhlich15], [Reference Kawamoto25] and [Reference Chapman8].
Theorem 3.3. [Reference Lettl29] Let
![]() $K/F$
be an extension of
$K/F$
be an extension of
![]() $p$
-adic fields such that
$p$
-adic fields such that
![]() $K/\mathbb{Q}_{p}$
is a finite abelian extension. Then,
$K/\mathbb{Q}_{p}$
is a finite abelian extension. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/F}$
.
$\mathfrak{A}_{K/F}$
.
Theorem 3.4. [Reference Bergé2] Let
![]() $K/\mathbb{Q}_p$
be a Galois extension with
$K/\mathbb{Q}_p$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}_p)\cong D_{2\ell }$
, where
$\textrm{Gal}(K/\mathbb{Q}_p)\cong D_{2\ell }$
, where
![]() $\ell$
is a prime number. Then,
$\ell$
is a prime number. Then,
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}_p}$
.
$\mathfrak{A}_{K/\mathbb{Q}_p}$
.
Theorem 3.5. [Reference Martinet and Sci32] Let
![]() $K/\mathbb{Q}_{p}$
be a Galois extension with
$K/\mathbb{Q}_{p}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}_p)\cong Q_{8}$
. Then,
$\textrm{Gal}(K/\mathbb{Q}_p)\cong Q_{8}$
. Then,
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}_p}$
.
$\mathfrak{A}_{K/\mathbb{Q}_p}$
.
Remark 3.6. Theorem 3.5 is not explicitly stated in [Reference Martinet and Sci32]. However, the proof of Theorem 1.3 given in loc. cit. also works essentially unchanged in the setting of Theorem 3.5.
Theorem 3.7. [Reference Jaulent20] Let
![]() $p,n$
and
$p,n$
and
![]() $r$
be positive integers such that
$r$
be positive integers such that
![]() $p$
is an odd prime,
$p$
is an odd prime,
![]() $n$
divides
$n$
divides
![]() $p-1$
and
$p-1$
and
![]() $r$
is a primitive
$r$
is a primitive
![]() $n$
th root modulo
$n$
th root modulo
![]() $p$
. Let
$p$
. Let
![]() $G$
be the metacyclic group with the following structure:
$G$
be the metacyclic group with the following structure:
Let
![]() $K/\mathbb{Q}_{p}$
be a Galois extension with
$K/\mathbb{Q}_{p}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}_p) \cong G$
. Then,
$\textrm{Gal}(K/\mathbb{Q}_p) \cong G$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}_p}$
.
$\mathfrak{A}_{K/\mathbb{Q}_p}$
.
Remark 3.8.
In the special case
![]() $n=2$
, the group
$n=2$
, the group
![]() $G$
of (3.1) is dihedral of order
$G$
of (3.1) is dihedral of order
![]() $2p$
.
$2p$
.
Let
![]() $K/F$
be a Galois extension of
$K/F$
be a Galois extension of
![]() $p$
-adic fields and let
$p$
-adic fields and let
![]() $G=\textrm{Gal}(K/F)$
. We recall that for an integer
$G=\textrm{Gal}(K/F)$
. We recall that for an integer
![]() $t \geq -1$
the
$t \geq -1$
the
![]() $t$
th ramification group is defined to be
$t$
th ramification group is defined to be
where
![]() $v_{K}$
is the normalised valuation on
$v_{K}$
is the normalised valuation on
![]() $K$
(i.e. with image
$K$
(i.e. with image
![]() $\mathbb{Z}$
). When it is not obvious which extension we are referring to we will use the notation ‘
$\mathbb{Z}$
). When it is not obvious which extension we are referring to we will use the notation ‘
![]() $G_t(K/F)$
’ or similar. Thus,
$G_t(K/F)$
’ or similar. Thus,
![]() $K/F$
is unramified if and only if
$K/F$
is unramified if and only if
![]() $G_{0}$
is trivial and is tamely ramified if and only if
$G_{0}$
is trivial and is tamely ramified if and only if
![]() $G_{1}$
is trivial. We say that the extension is weakly ramified if
$G_{1}$
is trivial. We say that the extension is weakly ramified if
![]() $G_{2}$
is trivial.
$G_{2}$
is trivial.
Theorem 3.9. [Reference Johnston23] Let
![]() $K/F$
be a weakly ramified finite Galois extension of
$K/F$
be a weakly ramified finite Galois extension of
![]() $p$
-adic fields and let
$p$
-adic fields and let
![]() $G=\textrm{Gal}(K/F)$
. Then,
$G=\textrm{Gal}(K/F)$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/F}$
. Moreover, if
$\mathfrak{A}_{K/F}$
. Moreover, if
![]() $K/F$
is both wildly and weakly ramified then
$K/F$
is both wildly and weakly ramified then
![]() $\mathfrak{A}_{K/F}=\mathcal{O}_F[G][\pi _{F}^{-1}\textrm{Tr}_{G_0}]$
(i.e. the
$\mathfrak{A}_{K/F}=\mathcal{O}_F[G][\pi _{F}^{-1}\textrm{Tr}_{G_0}]$
(i.e. the
![]() $\mathcal{O}_ F[G]$
-algebra generated by
$\mathcal{O}_ F[G]$
-algebra generated by
![]() $\pi _{F}^{-1}\textrm{Tr}_{G_0}$
, which is an
$\pi _{F}^{-1}\textrm{Tr}_{G_0}$
, which is an
![]() $\mathcal{O}_F$
-order), where
$\mathcal{O}_F$
-order), where
![]() $\pi _{F}$
is a uniformiser of
$\pi _{F}$
is a uniformiser of
![]() $\mathcal{O}_{F}$
and
$\mathcal{O}_{F}$
and
![]() $\textrm{Tr}_{G_0}=\sum _{\gamma \in G_{0}}\gamma$
is the sum of the elements of the inertia group
$\textrm{Tr}_{G_0}=\sum _{\gamma \in G_{0}}\gamma$
is the sum of the elements of the inertia group
![]() $G_{0}$
.
$G_{0}$
.
For a subgroup
![]() $H$
of
$H$
of
![]() $G$
define
$G$
define
![]() $\textrm{Tr}_{H}=\sum _{h\in H}h \in F[G]$
and
$\textrm{Tr}_{H}=\sum _{h\in H}h \in F[G]$
and
![]() $e_{H}=\frac{1}{|H|}\textrm{Tr}_{H} \in F[G]$
. Note that
$e_{H}=\frac{1}{|H|}\textrm{Tr}_{H} \in F[G]$
. Note that
![]() $e_{H}$
is an idempotent. We say that
$e_{H}$
is an idempotent. We say that
![]() $K/F$
is almost-maximally ramified if
$K/F$
is almost-maximally ramified if
![]() $e_{H} \in \mathfrak{A}_{K/F}$
for every subgroup
$e_{H} \in \mathfrak{A}_{K/F}$
for every subgroup
![]() $H$
of
$H$
of
![]() $G$
such that
$G$
such that
![]() $G_{t+1} \subseteq H \subseteq G_{t}$
for some
$G_{t+1} \subseteq H \subseteq G_{t}$
for some
![]() $t \geq 1$
.
$t \geq 1$
.
Theorem 3.10 ([Reference Bergé4, Proposition 7]). Let
![]() $K/F$
be a finite dihedral extension of
$K/F$
be a finite dihedral extension of
![]() $p$
-adic fields such that
$p$
-adic fields such that
![]() $F/\mathbb{Q}_{p}$
is unramified. Let
$F/\mathbb{Q}_{p}$
is unramified. Let
![]() $G=\textrm{Gal}(K/F)$
. Then,
$G=\textrm{Gal}(K/F)$
. Then,
![]() $\mathcal{O}_{K}$
is projective over
$\mathcal{O}_{K}$
is projective over
![]() $\mathfrak{A}_{K/F}$
if and only if
$\mathfrak{A}_{K/F}$
if and only if
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/F}$
if and only if either
$\mathfrak{A}_{K/F}$
if and only if either
-
(i)
 $K/F$
is almost-maximally ramified, in which case
$K/F$
is almost-maximally ramified, in which case
 $\mathfrak{A}_{K/F}=\mathcal{O}_F[G][\{e_{G_t}\}_{t\geq 1}]$
, or
$\mathfrak{A}_{K/F}=\mathcal{O}_F[G][\{e_{G_t}\}_{t\geq 1}]$
, or -
(ii)
 $K/F$
is not almost-maximally ramified, and the inertia subgroup
$K/F$
is not almost-maximally ramified, and the inertia subgroup
 $G_0$
is dihedral of order
$G_0$
is dihedral of order
 $2p$
, in which case
$2p$
, in which case
 $\mathfrak{A}_{K/F}=\mathcal{O}_F[G][2e_{G_0}]$
.
$\mathfrak{A}_{K/F}=\mathcal{O}_F[G][2e_{G_0}]$
.
Remark 3.11.
Throughout the article, and in particular in Theorem 3.10, the group
![]() $C_2\times C_2$
is considered to be dihedral of order
$C_2\times C_2$
is considered to be dihedral of order
![]() $2\cdot 2$
.
$2\cdot 2$
.
Remark 3.12.
Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
and let
$G$
and let
![]() $r$
be a positive integer. We now show how to determine whether
$r$
be a positive integer. We now show how to determine whether
![]() $\frac{1}{r}\textrm{Tr}_{H}\in \mathfrak{A}_{K/F}$
. For example, when
$\frac{1}{r}\textrm{Tr}_{H}\in \mathfrak{A}_{K/F}$
. For example, when
![]() $r=|H|$
this can be used to check for almost-maximal ramification. Let
$r=|H|$
this can be used to check for almost-maximal ramification. Let
![]() $M$
be the subfield of
$M$
be the subfield of
![]() $K$
fixed by
$K$
fixed by
![]() $H$
. We denote by
$H$
. We denote by
![]() $\mathfrak{D}_{K/M}$
the different of the extension
$\mathfrak{D}_{K/M}$
the different of the extension
![]() $K/M$
(see [
Reference Serre38, III§3]) and by
$K/M$
(see [
Reference Serre38, III§3]) and by
![]() $v_{p}(x)$
the
$v_{p}(x)$
the
![]() $p$
-adic valuation of an integer
$p$
-adic valuation of an integer
![]() $x$
(thus,
$x$
(thus,
![]() $v_{p}$
is the restriction of
$v_{p}$
is the restriction of
![]() $v_{\mathbb{Q}_p}$
to
$v_{\mathbb{Q}_p}$
to
![]() $\mathbb{Z}$
).
$\mathbb{Z}$
).
 \begin{align*} \begin{split} \frac{1}{r}\text{Tr}_H\in \mathfrak{A}_{K/F} & \Longleftrightarrow \frac{1}{r}\text{Tr}_{K/M}(\mathcal{O}_K)\subseteq \mathcal{O}_M\\[5pt] &\Longleftrightarrow \text{Tr}_{K/M}(\mathcal{O}_{K})\subseteq r\mathcal{O}_{M} \\[5pt] &\Longleftrightarrow \mathcal{O}_K \subseteq r\mathcal{O}_M \mathfrak{D}_{K/M}^{-1}\text{ by [Ser79, III Proposition 7]}\\[5pt] &\Longleftrightarrow \mathfrak{D}_{K/M} \subseteq r\mathcal{O}_K \\[5pt] &\Longleftrightarrow v_K(\mathfrak{D}_{K/M})\geq e(K/\mathbb{Q}_p)v_p(r)\\[5pt] &\Longleftrightarrow \sum _{i=0}^\infty (|G_i(K/M)|-1)\geq e(K/\mathbb{Q}_p) v_p(r)\text{ by [Ser79, IV Proposition 4]}. \end{split} \end{align*}
\begin{align*} \begin{split} \frac{1}{r}\text{Tr}_H\in \mathfrak{A}_{K/F} & \Longleftrightarrow \frac{1}{r}\text{Tr}_{K/M}(\mathcal{O}_K)\subseteq \mathcal{O}_M\\[5pt] &\Longleftrightarrow \text{Tr}_{K/M}(\mathcal{O}_{K})\subseteq r\mathcal{O}_{M} \\[5pt] &\Longleftrightarrow \mathcal{O}_K \subseteq r\mathcal{O}_M \mathfrak{D}_{K/M}^{-1}\text{ by [Ser79, III Proposition 7]}\\[5pt] &\Longleftrightarrow \mathfrak{D}_{K/M} \subseteq r\mathcal{O}_K \\[5pt] &\Longleftrightarrow v_K(\mathfrak{D}_{K/M})\geq e(K/\mathbb{Q}_p)v_p(r)\\[5pt] &\Longleftrightarrow \sum _{i=0}^\infty (|G_i(K/M)|-1)\geq e(K/\mathbb{Q}_p) v_p(r)\text{ by [Ser79, IV Proposition 4]}. \end{split} \end{align*}
Remark 3.13.
From Theorem 3.4, Theorem 3.10, and Remark 3.12 (also see [
Reference Bergé3, Corollaire to Proposition 3]), we deduce that a dihedral extension
![]() $K/\mathbb{Q}_p$
of degree
$K/\mathbb{Q}_p$
of degree
![]() $2p$
either is almost-maximally ramified or is weakly and totally ramified.
$2p$
either is almost-maximally ramified or is weakly and totally ramified.
3.2. Local freeness results for Galois extensions of number fields
Let
![]() $K/F$
be a finite Galois extension of number fields. If
$K/F$
be a finite Galois extension of number fields. If
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{F/K}$
, then it is clear that
$\mathfrak{A}_{F/K}$
, then it is clear that
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{F/K}$
. In particular, the analogues of Theorems 1.1, 1.2 and 1.3 all hold, with ‘locally free’ in place of ‘free’. Theorems 3.15 and 3.17 below are generalisations of the first two of these analogues.
$\mathfrak{A}_{F/K}$
. In particular, the analogues of Theorems 1.1, 1.2 and 1.3 all hold, with ‘locally free’ in place of ‘free’. Theorems 3.15 and 3.17 below are generalisations of the first two of these analogues.
Theorem 3.14.
Let
![]() $K/F$
be a finite Galois extension of number fields. Let
$K/F$
be a finite Galois extension of number fields. Let
![]() $G=\textrm{Gal}(K/F)$
and let
$G=\textrm{Gal}(K/F)$
and let
![]() $\mathfrak{p}$
be a prime of
$\mathfrak{p}$
be a prime of
![]() $F$
that is tamely ramified in
$F$
that is tamely ramified in
![]() $K/F$
. Then,
$K/F$
. Then,
![]() $\mathcal{O}_{K, \mathfrak{p}}$
is free over
$\mathcal{O}_{K, \mathfrak{p}}$
is free over
![]() $\mathfrak{A}_{K/F,\mathfrak{p}} = \mathcal{O}_{F_{\mathfrak{p}}}[G]$
.
$\mathfrak{A}_{K/F,\mathfrak{p}} = \mathcal{O}_{F_{\mathfrak{p}}}[G]$
.
Theorem 3.15. [Reference Lettl29] Let
![]() $K/F$
be an extension of number fields such that
$K/F$
be an extension of number fields such that
![]() $K/\mathbb{Q}$
is a finite abelian extension. Then,
$K/\mathbb{Q}$
is a finite abelian extension. Then,
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/F}$
.
$\mathfrak{A}_{K/F}$
.
Remark 3.16. Theorems 3.14 and 3.15 are well-known consequences of Theorems 3.1 and 3.3, respectively. For a proof see Remark 6.3 and Corollary 6.6 , for instance.
Theorem 3.17. [Reference Jaulent20] Let
![]() $K/\mathbb{Q}$
be a Galois extension such that
$K/\mathbb{Q}$
be a Galois extension such that
![]() $\textrm{Gal}(K/\mathbb{Q})$
is metacyclic of type (
3.1
). Then,
$\textrm{Gal}(K/\mathbb{Q})$
is metacyclic of type (
3.1
). Then,
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
Theorem 3.18 ([Reference Bergé4, Théorème]). Let
![]() $K/\mathbb{Q}$
be a finite dihedral extension and let
$K/\mathbb{Q}$
be a finite dihedral extension and let
![]() $G=\textrm{Gal}(K/\mathbb{Q})$
. Let
$G=\textrm{Gal}(K/\mathbb{Q})$
. Let
![]() $p$
be an odd prime number that is wildly ramified in
$p$
be an odd prime number that is wildly ramified in
![]() $K/\mathbb{Q}$
and let
$K/\mathbb{Q}$
and let
![]() $N$
be the unique cyclic subgroup of
$N$
be the unique cyclic subgroup of
![]() $G$
of index
$G$
of index
![]() $2$
. Then,
$2$
. Then,
![]() $\mathcal{O}_{K,p}$
is projective over
$\mathcal{O}_{K,p}$
is projective over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q},p}$
if and only if
![]() $\mathcal{O}_{K,p}$
is free over
$\mathcal{O}_{K,p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
if and only if one of the following conditions holds:
$\mathfrak{A}_{K/\mathbb{Q},p}$
if and only if one of the following conditions holds:
-
(i)
 $p$
is almost-maximally ramified in
$p$
is almost-maximally ramified in
 $K/\mathbb{Q}$
, in which case
$K/\mathbb{Q}$
, in which case \begin{equation*} \mathfrak {A}_{K/\mathbb {Q},p}=\mathbb {Z}_p[G][\{e_{G_t}\}_{t\geq 1}],\text { }or \end{equation*}
\begin{equation*} \mathfrak {A}_{K/\mathbb {Q},p}=\mathbb {Z}_p[G][\{e_{G_t}\}_{t\geq 1}],\text { }or \end{equation*}
-
(ii)
 $p$
is not almost-maximally ramified,
$p$
is not almost-maximally ramified,
 $|G_{0}|=2p$
and
$|G_{0}|=2p$
and
 $[G\;:\;G_0] \mid 2$
, in which case
$[G\;:\;G_0] \mid 2$
, in which case \begin{equation*} \mathfrak {A}_{K/\mathbb {Q},p}=\mathbb {Z}_p[G][e_{G_0}]. \end{equation*}
\begin{equation*} \mathfrak {A}_{K/\mathbb {Q},p}=\mathbb {Z}_p[G][e_{G_0}]. \end{equation*}
Remark 3.19.
In fact, Theorem 3.18 is [
Reference Bergé4, Théorème] specialised to the case that
![]() $p$
is odd and the base field is
$p$
is odd and the base field is
![]() $\mathbb{Q}$
; the more general statement is somewhat more complicated.
$\mathbb{Q}$
; the more general statement is somewhat more complicated.
4. Hybrid group rings and applications to local freeness
4.1. Hybrid group rings
Let
![]() $R$
be a discrete valuation ring with fraction field
$R$
be a discrete valuation ring with fraction field
![]() $F$
and let
$F$
and let
![]() $G$
be a finite group. Let
$G$
be a finite group. Let
![]() $M$
be a full
$M$
be a full
![]() $R[G]$
-lattice in
$R[G]$
-lattice in
![]() $F[G]$
. Note that
$F[G]$
. Note that
![]() $R[G]\subseteq \mathfrak{A}(F[G], M)$
.
$R[G]\subseteq \mathfrak{A}(F[G], M)$
.
For a normal subgroup
![]() $N$
of
$N$
of
![]() $G$
define
$G$
define
![]() $e_{N}=\frac{1}{|N|}\sum _{n\in N}n \in F[G]$
to be the central idempotent associated with
$e_{N}=\frac{1}{|N|}\sum _{n\in N}n \in F[G]$
to be the central idempotent associated with
![]() $N$
.
$N$
.
Proposition 4.1.
If
![]() $N$
is a normal subgroup of
$N$
is a normal subgroup of
![]() $G$
such that
$G$
such that
![]() $|N| \in R^{\times }$
, then
$|N| \in R^{\times }$
, then
-
(i)
 $R[G] = e_{N} R[G] \times (1-e_{N})R[G]\cong R[G/N] \times (1-e_N)R[G]$
,
$R[G] = e_{N} R[G] \times (1-e_{N})R[G]\cong R[G/N] \times (1-e_N)R[G]$
, -
(ii)
 $e_{N}M$
has the structure of a
$e_{N}M$
has the structure of a
 $e_{N}R[G]\cong R[G/N]$
-lattice, and
$e_{N}R[G]\cong R[G/N]$
-lattice, and -
(iii)
 $e_{N}\mathfrak{A}(F[G],M)=\mathfrak{A}(F[G],M)\cap e_{N}F[G]=\mathfrak{A}(e_NF[G],e_{N}M)\cong \mathfrak{A}(F[G/N],e_{N}M)$
.
$e_{N}\mathfrak{A}(F[G],M)=\mathfrak{A}(F[G],M)\cap e_{N}F[G]=\mathfrak{A}(e_NF[G],e_{N}M)\cong \mathfrak{A}(F[G/N],e_{N}M)$
.
Proof. Since
![]() $|N| \in R^{\times }$
we have
$|N| \in R^{\times }$
we have
![]() $e_{N} \in R[G]$
. Moreover, it is straightforward to show that
$e_{N} \in R[G]$
. Moreover, it is straightforward to show that
![]() $e_{N}R[G] \cong R[G/N]$
. Thus, we have established (i) and (ii), and it remains to prove (iii).
$e_{N}R[G] \cong R[G/N]$
. Thus, we have established (i) and (ii), and it remains to prove (iii).
The last isomorphism of (iii) is immediate from (ii). We now prove the first equality, that is,
![]() $e_{N}\mathfrak{A}(F[G],M)=\mathfrak{A}(F[G],M)\cap e_{N}F[G]$
. Since
$e_{N}\mathfrak{A}(F[G],M)=\mathfrak{A}(F[G],M)\cap e_{N}F[G]$
. Since
![]() $e_{N}\in R[G]\subseteq \mathfrak{A}(F[G],M)$
, we easily have that
$e_{N}\in R[G]\subseteq \mathfrak{A}(F[G],M)$
, we easily have that
![]() $e_{N}\mathfrak{A}(F[G],M)\subseteq \mathfrak{A}(F[G],M)\cap e_{N}F[G]$
. The other containment follows from the fact that
$e_{N}\mathfrak{A}(F[G],M)\subseteq \mathfrak{A}(F[G],M)\cap e_{N}F[G]$
. The other containment follows from the fact that
![]() $e_{N}^{2}=e_{N}$
; hence, any element in
$e_{N}^{2}=e_{N}$
; hence, any element in
![]() $\mathfrak{A}(F[G],M)\cap e_{N}F[G]$
, with the harmless multiplication by
$\mathfrak{A}(F[G],M)\cap e_{N}F[G]$
, with the harmless multiplication by
![]() $e_{N}$
, can be written as an element in
$e_{N}$
, can be written as an element in
![]() $e_{N}\mathfrak{A}(F[G],M)$
.
$e_{N}\mathfrak{A}(F[G],M)$
.
We now prove that
![]() $\mathfrak{A}(F[G],M)\cap e_{N}F[G]=\mathfrak{A}(e_NF[G],e_{N}M)$
. Consider
$\mathfrak{A}(F[G],M)\cap e_{N}F[G]=\mathfrak{A}(e_NF[G],e_{N}M)$
. Consider
![]() $e_Nx\in \mathfrak{A}(F[G],M)\cap e_NF[G]$
for a certain
$e_Nx\in \mathfrak{A}(F[G],M)\cap e_NF[G]$
for a certain
![]() $x\in F[G]$
; we have to prove that
$x\in F[G]$
; we have to prove that
![]() $e_{N}x$
preserves
$e_{N}x$
preserves
![]() $e_{N}M$
. Since
$e_{N}M$
. Since
![]() $e_{N}M\subseteq M$
and
$e_{N}M\subseteq M$
and
![]() $e_{N}x\in \mathfrak{A}(F[G],M)$
, we have that
$e_{N}x\in \mathfrak{A}(F[G],M)$
, we have that
![]() $e_{N}xe_{N}M\subseteq M$
. Hence,
$e_{N}xe_{N}M\subseteq M$
. Hence,
![]() $e_{N}xe_{N}M=e_{N}e_{N}xe_{N}M\subseteq e_{N}M$
. Conversely, let us consider an element
$e_{N}xe_{N}M=e_{N}e_{N}xe_{N}M\subseteq e_{N}M$
. Conversely, let us consider an element
![]() $e_{N}x\in \mathfrak{A}(e_NF[G],e_NM)$
, thus such that
$e_{N}x\in \mathfrak{A}(e_NF[G],e_NM)$
, thus such that
![]() $e_{N}xe_{N}M\subseteq e_{N}M$
. We must prove that
$e_{N}xe_{N}M\subseteq e_{N}M$
. We must prove that
![]() $e_{N}x\in \mathfrak{A}(F[G],M)$
, which is automatic since
$e_{N}x\in \mathfrak{A}(F[G],M)$
, which is automatic since
![]() $e_{N}xM=e_{N}e_{N}xM=e_{N}xe_{N}M\subseteq e_{N}M\subseteq M$
.
$e_{N}xM=e_{N}e_{N}xM=e_{N}xe_{N}M\subseteq e_{N}M\subseteq M$
.
We now recall the notion of hybrid group ring introduced in [Reference Johnston and Nickel21, §2] and further developed in [Reference Johnston and Nickel22, §2].
Definition 4.2.
Let
![]() $N$
be a normal subgroup of
$N$
be a normal subgroup of
![]() $G$
. We say that
$G$
. We say that
![]() $R[G]$
is
$R[G]$
is
![]() $N$
-hybrid if
$N$
-hybrid if
![]() $|N| \in R^{\times }$
and
$|N| \in R^{\times }$
and
![]() $(1-e_N)R[G]$
is a maximal
$(1-e_N)R[G]$
is a maximal
![]() $R$
-order in
$R$
-order in
![]() $(1-e_{N})F[G]$
.
$(1-e_{N})F[G]$
.
Remark 4.3.
The group ring
![]() $R[G]$
is a maximal
$R[G]$
is a maximal
![]() $R$
-order if and only if
$R$
-order if and only if
![]() $|G| \in R^{\times }$
if and only if
$|G| \in R^{\times }$
if and only if
![]() $R[G]$
is
$R[G]$
is
![]() $G$
-hybrid, where the first equivalence is given by [
Reference Curtis and Reiner9, Proposition (27.1)]. In this situation,
$G$
-hybrid, where the first equivalence is given by [
Reference Curtis and Reiner9, Proposition (27.1)]. In this situation,
![]() $\mathfrak{A}(F[G], M)=R[G]$
, and thus,
$\mathfrak{A}(F[G], M)=R[G]$
, and thus,
![]() $M$
is free over
$M$
is free over
![]() $\mathfrak{A}(F[G], M)$
by [
Reference Reiner35, Theorem (18.10)].
$\mathfrak{A}(F[G], M)$
by [
Reference Reiner35, Theorem (18.10)].
Example 4.4.
Let
![]() $G=A_{4}$
or
$G=A_{4}$
or
![]() $S_{4}$
and let
$S_{4}$
and let
![]() $N$
be its unique normal subgroup of order
$N$
be its unique normal subgroup of order
![]() $4$
. Then,
$4$
. Then,
![]() $\mathbb{Z}_{3}[G]$
is
$\mathbb{Z}_{3}[G]$
is
![]() $N$
-hybrid as shown in [
Reference Johnston and Nickel21, Examples 2.16 and 2.18]. Indeed, we have
$N$
-hybrid as shown in [
Reference Johnston and Nickel21, Examples 2.16 and 2.18]. Indeed, we have
where
![]() $M_{3 \times 3}(\mathbb{Z}_{p})$
is a maximal
$M_{3 \times 3}(\mathbb{Z}_{p})$
is a maximal
![]() $\mathbb{Z}_{p}$
-order by [
Reference Reiner35, Theorem (8.7)].
$\mathbb{Z}_{p}$
-order by [
Reference Reiner35, Theorem (8.7)].
Example 4.5.
Let
![]() $n$
be an odd positive integer and let
$n$
be an odd positive integer and let
![]() $N_{n}$
be the unique subgroup of index
$N_{n}$
be the unique subgroup of index
![]() $2$
in
$2$
in
![]() $D_{2n}$
. Then,
$D_{2n}$
. Then,
![]() $\mathbb{Z}_{2}[D_{2n}]$
is
$\mathbb{Z}_{2}[D_{2n}]$
is
![]() $N_{n}$
-hybrid as shown in [
Reference Johnston and Nickel21, Example 2.14].
$N_{n}$
-hybrid as shown in [
Reference Johnston and Nickel21, Example 2.14].
Proposition 4.6.
Suppose
![]() $R[G]$
is
$R[G]$
is
![]() $N$
-hybrid. Then,
$N$
-hybrid. Then,
Moreover,
![]() $M$
is free over
$M$
is free over
![]() $\mathfrak{A}(F[G],M)$
if and only if
$\mathfrak{A}(F[G],M)$
if and only if
![]() $e_{N}M$
is free over
$e_{N}M$
is free over
![]() $\mathfrak{A}(F[G/N],e_{N}M)$
.
$\mathfrak{A}(F[G/N],e_{N}M)$
.
Proof. The first claim follows from Proposition 4.1, Definition 4.2, and the fact that
![]() $R[G] \subseteq \mathfrak{A}(F[G],M)$
. Since
$R[G] \subseteq \mathfrak{A}(F[G],M)$
. Since
![]() $(1-e_{N})R[G]$
is a maximal
$(1-e_{N})R[G]$
is a maximal
![]() $R$
-order,
$R$
-order,
![]() $(1-e_{N})M$
is free over
$(1-e_{N})M$
is free over
![]() $(1-e_{N})R[G]$
by [Reference Reiner35, Theorem (18.10)]. The second claim now follows from the decomposition
$(1-e_{N})R[G]$
by [Reference Reiner35, Theorem (18.10)]. The second claim now follows from the decomposition
![]() $M \cong e_{N} M \oplus (1-e_{N})M$
.
$M \cong e_{N} M \oplus (1-e_{N})M$
.
4.2. Applications to local freeness for extensions of number fields
Proposition 4.7.
Let
![]() $K/F$
be a finite Galois extension of number fields and let
$K/F$
be a finite Galois extension of number fields and let
![]() $G=\textrm{Gal}(K/F)$
. Let
$G=\textrm{Gal}(K/F)$
. Let
![]() $p$
be a rational prime and let
$p$
be a rational prime and let
![]() $\mathfrak{p}$
be a prime of
$\mathfrak{p}$
be a prime of
![]() $F$
above
$F$
above
![]() $p$
. Let
$p$
. Let
![]() $N$
be a normal subgroup of
$N$
be a normal subgroup of
![]() $G$
such that
$G$
such that
![]() $p \nmid |N|$
and let
$p \nmid |N|$
and let
![]() $M$
be the subfield of
$M$
be the subfield of
![]() $K$
fixed by
$K$
fixed by
![]() $N$
. Then, we have an identification
$N$
. Then, we have an identification
![]() $e_{N}\mathcal{O}_{K,\mathfrak{p}}=\mathcal{O}_{M,\mathfrak{p}}$
. Moreover, via this identification, the structure of
$e_{N}\mathcal{O}_{K,\mathfrak{p}}=\mathcal{O}_{M,\mathfrak{p}}$
. Moreover, via this identification, the structure of
![]() $e_{N}\mathcal{O}_{K,\mathfrak{p}}$
as an
$e_{N}\mathcal{O}_{K,\mathfrak{p}}$
as an
![]() $e_{N}\mathcal{O}_{F_{\mathfrak{p}}}[G]$
-module coincides with the structure of
$e_{N}\mathcal{O}_{F_{\mathfrak{p}}}[G]$
-module coincides with the structure of
![]() $\mathcal{O}_{M,\mathfrak{p}}$
as an
$\mathcal{O}_{M,\mathfrak{p}}$
as an
![]() $\mathcal{O}_{F_{\mathfrak{p}}}[G/N]$
-module under the canonical identification
$\mathcal{O}_{F_{\mathfrak{p}}}[G/N]$
-module under the canonical identification
![]() $G/N \cong \textrm{Gal}(M/F)$
. In particular,
$G/N \cong \textrm{Gal}(M/F)$
. In particular,
Now further suppose that
![]() $\mathcal{O}_{F_{\mathfrak{p}}}[G]$
is
$\mathcal{O}_{F_{\mathfrak{p}}}[G]$
is
![]() $N$
-hybrid. Then,
$N$
-hybrid. Then,
and
![]() $\mathcal{O}_{K,\mathfrak{p}}$
is free over
$\mathcal{O}_{K,\mathfrak{p}}$
is free over
![]() $\mathfrak{A}_{K/F,\mathfrak{p}}$
if and only if
$\mathfrak{A}_{K/F,\mathfrak{p}}$
if and only if
![]() $\mathcal{O}_{M,\mathfrak{p}}$
is free over
$\mathcal{O}_{M,\mathfrak{p}}$
is free over
![]() $\mathfrak{A}_{M/F,\mathfrak{p}}$
.
$\mathfrak{A}_{M/F,\mathfrak{p}}$
.
Proof. The claims regarding the identifications are clear. The remaining claims are then specialisations of Propositions 4.1 and 4.6.
Corollary 4.8.
Let
![]() $K/\mathbb{Q}$
be a finite Galois extension and let
$K/\mathbb{Q}$
be a finite Galois extension and let
![]() $G=\textrm{Gal}(K/\mathbb{Q})$
. Let
$G=\textrm{Gal}(K/\mathbb{Q})$
. Let
![]() $N$
be a normal subgroup of
$N$
be a normal subgroup of
![]() $G$
and such that
$G$
and such that
![]() $G/N$
is abelian or metacyclic of type (
3.1
). Let
$G/N$
is abelian or metacyclic of type (
3.1
). Let
![]() $p$
be a rational prime. If
$p$
be a rational prime. If
![]() $\mathbb{Z}_{p}[G]$
is
$\mathbb{Z}_{p}[G]$
is
![]() $N$
-hybrid, then
$N$
-hybrid, then
![]() $\mathcal{O}_{K,p}$
is free over
$\mathcal{O}_{K,p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
.
$\mathfrak{A}_{K/\mathbb{Q},p}$
.
Proof. Let
![]() $M$
be the subfield of
$M$
be the subfield of
![]() $K$
fixed by
$K$
fixed by
![]() $N$
. Then,
$N$
. Then,
![]() $\mathcal{O}_{M,p}$
is free over
$\mathcal{O}_{M,p}$
is free over
![]() $\mathfrak{A}_{M/\mathbb{Q},p}$
by Theorem 1.1 or Theorem 3.17. The result now follows from Proposition 4.7.
$\mathfrak{A}_{M/\mathbb{Q},p}$
by Theorem 1.1 or Theorem 3.17. The result now follows from Proposition 4.7.
Remark 4.9.
Jaulent [Reference Jaulent20] developed similar arguments to Corollary 4.8
, but restricted to the case that
![]() $G$
is metacyclic of type (
3.1
).
$G$
is metacyclic of type (
3.1
).
4.3. Preliminary results on
 $A_{4}$
and
$A_{4}$
and
 $S_{4}$
-extensions of
$S_{4}$
-extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
Proposition 4.10.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q})\cong A_{4}$
or
$\textrm{Gal}(K/\mathbb{Q})\cong A_{4}$
or
![]() $S_{4}$
. Then,
$S_{4}$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $\mathcal{O}_{K,2}$
is free over
$\mathcal{O}_{K,2}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
.
$\mathfrak{A}_{K/\mathbb{Q},2}$
.
Proof. By Corollary 2.7, it suffices to show that
![]() $\mathcal{O}_{K,p}$
is free over
$\mathcal{O}_{K,p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
for each rational prime
$\mathfrak{A}_{K/\mathbb{Q},p}$
for each rational prime
![]() $p \geq 3$
. For
$p \geq 3$
. For
![]() $p \geq 5$
, this follows from Theorem 3.14. Let
$p \geq 5$
, this follows from Theorem 3.14. Let
![]() $G=\textrm{Gal}(K/\mathbb{Q})$
and let
$G=\textrm{Gal}(K/\mathbb{Q})$
and let
![]() $N$
be its unique normal subgroup of order
$N$
be its unique normal subgroup of order
![]() $4$
. By Example 4.4, the group ring
$4$
. By Example 4.4, the group ring
![]() $\mathbb{Z}_{3}[G]$
is
$\mathbb{Z}_{3}[G]$
is
![]() $N$
-hybrid. Moreover,
$N$
-hybrid. Moreover,
![]() $G/N \cong C_{3}$
or
$G/N \cong C_{3}$
or
![]() $S_{3}$
(note that
$S_{3}$
(note that
![]() $S_{3} \cong D_{6}$
is metacyclic of type (3.1)). Thus by Corollary 4.8, we have that
$S_{3} \cong D_{6}$
is metacyclic of type (3.1)). Thus by Corollary 4.8, we have that
![]() $\mathcal{O}_{K,3}$
is free over
$\mathcal{O}_{K,3}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},3}$
.
$\mathfrak{A}_{K/\mathbb{Q},3}$
.
Lemma 4.11.
There is a unique Galois extension
![]() $L/\mathbb{Q}_{2}$
with
$L/\mathbb{Q}_{2}$
with
![]() $\textrm{Gal}(L/\mathbb{Q}_{2}) \cong A_{4}$
. Moreover, this extension is wildly and weakly ramified, and the inertia subgroup is equal to the unique (normal) subgroup of order
$\textrm{Gal}(L/\mathbb{Q}_{2}) \cong A_{4}$
. Moreover, this extension is wildly and weakly ramified, and the inertia subgroup is equal to the unique (normal) subgroup of order
![]() $4$
.
$4$
.
Proof. This can easily be checked by, for instance, using the database of
![]() $p$
-adic fields [Reference Jones and Roberts24] (which is now accessible via the database [30]). Indeed,
$p$
-adic fields [Reference Jones and Roberts24] (which is now accessible via the database [30]). Indeed,
![]() $L$
is the Galois closure of the extension of
$L$
is the Galois closure of the extension of
![]() $\mathbb{Q}_{2}$
generated by the polynomial
$\mathbb{Q}_{2}$
generated by the polynomial
![]() $x^{4}+2x^{3}+2x^{2}+2$
.
$x^{4}+2x^{3}+2x^{2}+2$
.
Proposition 4.12.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}) \cong A_{4}$
. If
$\textrm{Gal}(K/\mathbb{Q}) \cong A_{4}$
. If
![]() $2$
either is tamely ramified in
$2$
either is tamely ramified in
![]() $K/\mathbb{Q}$
or has full decomposition group in
$K/\mathbb{Q}$
or has full decomposition group in
![]() $\textrm{Gal}(K/\mathbb{Q})$
, then
$\textrm{Gal}(K/\mathbb{Q})$
, then
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
Proof. By Proposition 4.10, it suffices to show that
![]() $\mathcal{O}_{K,2}$
is free over
$\mathcal{O}_{K,2}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. If
$\mathfrak{A}_{K/\mathbb{Q},2}$
. If
![]() $2$
is tamely ramified in
$2$
is tamely ramified in
![]() $K/\mathbb{Q}$
, then this follows from Theorem 3.14. Now suppose that
$K/\mathbb{Q}$
, then this follows from Theorem 3.14. Now suppose that
![]() $2$
has full decomposition group in
$2$
has full decomposition group in
![]() $G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})$
. Then,
$G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})$
. Then,
![]() $2$
is weakly ramified in
$2$
is weakly ramified in
![]() $K/\mathbb{Q}$
by Lemma 4.11. Let
$K/\mathbb{Q}$
by Lemma 4.11. Let
![]() $\mathfrak{P}$
be the unique prime of
$\mathfrak{P}$
be the unique prime of
![]() $K$
above
$K$
above
![]() $2$
. Then,
$2$
. Then,
so the result now follows from Theorem 3.9.
5. Leopoldt-type theorems for certain dihedral extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
We first recall the following theorem of Bergé stated in the introduction.
Theorem 5.1. [Reference Bergé2] Let
![]() $p$
be a prime number and let
$p$
be a prime number and let
![]() $K/\mathbb{Q}$
be a dihedral extension of degree
$K/\mathbb{Q}$
be a dihedral extension of degree
![]() $2p$
. Then,
$2p$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
In the following theorem and corollaries, we consider other dihedral extensions of
![]() $\mathbb{Q}$
. For a positive integer
$\mathbb{Q}$
. For a positive integer
![]() $m$
, let
$m$
, let
![]() $\mathbb{Q}(\zeta _{m})^+$
denote the maximal totally real subfield of the
$\mathbb{Q}(\zeta _{m})^+$
denote the maximal totally real subfield of the
![]() $m$
th cyclotomic field
$m$
th cyclotomic field
![]() $\mathbb{Q}(\zeta _{m})$
. If
$\mathbb{Q}(\zeta _{m})$
. If
![]() $m$
is odd, then
$m$
is odd, then
![]() $\mathbb{Q}(\zeta _{2m})= \mathbb{Q}(\zeta _{m})$
and so
$\mathbb{Q}(\zeta _{2m})= \mathbb{Q}(\zeta _{m})$
and so
![]() $\mathbb{Q}(\zeta _{2m})^{+}= \mathbb{Q}(\zeta _{m})^{+}$
. We recall that we abbreviate ‘at most tamely ramified’ to ‘tamely ramified’.
$\mathbb{Q}(\zeta _{2m})^{+}= \mathbb{Q}(\zeta _{m})^{+}$
. We recall that we abbreviate ‘at most tamely ramified’ to ‘tamely ramified’.
Theorem 5.2.
Let
![]() $p$
be a prime and let
$p$
be a prime and let
![]() $n\geq 2$
be an integer. Let
$n\geq 2$
be an integer. Let
![]() $K/\mathbb{Q}$
be a dihedral extension of degree
$K/\mathbb{Q}$
be a dihedral extension of degree
![]() $2p^{n}$
. Suppose that
$2p^{n}$
. Suppose that
![]() $p$
is a regular prime such that the class number of
$p$
is a regular prime such that the class number of
![]() $\mathbb{Q}(\zeta _{2p^{n}})^{+}$
is
$\mathbb{Q}(\zeta _{2p^{n}})^{+}$
is
![]() $1$
. Consider the following assertions:
$1$
. Consider the following assertions:
-
(i)
 $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
 $\mathfrak{A}_{K/\mathbb{Q}}$
;
$\mathfrak{A}_{K/\mathbb{Q}}$
; -
(ii)
 $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
 $\mathfrak{A}_{K/\mathbb{Q}}$
at
$\mathfrak{A}_{K/\mathbb{Q}}$
at
 $p$
;
$p$
; -
(iii)
 $p$
tamely ramified or is almost-maximally ramified in the extension
$p$
tamely ramified or is almost-maximally ramified in the extension
 $K/\mathbb{Q}$
;
$K/\mathbb{Q}$
; -
(iv) the ramification index of
 $p$
in
$p$
in
 $K/\mathbb{Q}$
either is coprime to
$K/\mathbb{Q}$
either is coprime to
 $p$
or is a power of
$p$
or is a power of
 $p$
.
$p$
.
Then, we have the following conclusions:
-
(i) (i) and (ii) are equivalent;
-
(ii) if
 $p$
is odd, then (i), (ii) and (iii) are equivalent;
$p$
is odd, then (i), (ii) and (iii) are equivalent; -
(iii) if
 $p$
is odd, then (iv) implies (i), (ii) and (iii);
$p$
is odd, then (iv) implies (i), (ii) and (iii); -
(iv) if
 $p\geq 5$
, then (i), (ii), (iii) and (iv) are equivalent.
$p\geq 5$
, then (i), (ii), (iii) and (iv) are equivalent.
Proof. Let
![]() $G=\textrm{Gal} (K/\mathbb{Q})$
. By [Reference Washington40, Theorem 10.1] the condition on the class number of
$G=\textrm{Gal} (K/\mathbb{Q})$
. By [Reference Washington40, Theorem 10.1] the condition on the class number of
![]() $\mathbb{Q}(\zeta _{2p^{n}})^{+}$
implies that the class number of
$\mathbb{Q}(\zeta _{2p^{n}})^{+}$
implies that the class number of
![]() $\mathbb{Q}(\zeta _{2p^d})^+$
is
$\mathbb{Q}(\zeta _{2p^d})^+$
is
![]() $1$
for every
$1$
for every
![]() $d\leq n$
. This together with the regularity of
$d\leq n$
. This together with the regularity of
![]() $p$
implies that the locally free class group
$p$
implies that the locally free class group
![]() $\text{Cl}(\mathbb{Z}[G])$
is trivial: if
$\text{Cl}(\mathbb{Z}[G])$
is trivial: if
![]() $p$
is odd this follows from a special case of the main result of [Reference Keating26, Theorem 1] (also see [Reference Curtis and Reiners10, (50.28)]), if
$p$
is odd this follows from a special case of the main result of [Reference Keating26, Theorem 1] (also see [Reference Curtis and Reiners10, (50.28)]), if
![]() $p=2$
this follows from the results of [Reference Fröhlich, Keating and Wilson13] (also see [Reference Curtis and Reiners10, Theorem (50.31)] and [Reference Curtis and Reiner9, Example (7.39)]). Therefore,
$p=2$
this follows from the results of [Reference Fröhlich, Keating and Wilson13] (also see [Reference Curtis and Reiners10, Theorem (50.31)] and [Reference Curtis and Reiner9, Example (7.39)]). Therefore,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
by Proposition 2.6. Note that
$\mathfrak{A}_{K/\mathbb{Q}}$
by Proposition 2.6. Note that
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
at
$\mathfrak{A}_{K/\mathbb{Q}}$
at
![]() $\ell$
for every rational prime
$\ell$
for every rational prime
![]() $\ell \neq 2,p$
by Theorem 3.14. Moreover, if
$\ell \neq 2,p$
by Theorem 3.14. Moreover, if
![]() $p$
is odd then Example 4.5 implies that
$p$
is odd then Example 4.5 implies that
![]() $\mathbb{Z}_{2}[G]$
is
$\mathbb{Z}_{2}[G]$
is
![]() $N$
-hybrid where
$N$
-hybrid where
![]() $N$
is the unique subgroup of
$N$
is the unique subgroup of
![]() $G$
of index
$G$
of index
![]() $2$
, and so
$2$
, and so
![]() $\mathcal{O}_{K}$
is locally free over
$\mathcal{O}_{K}$
is locally free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
at
$\mathfrak{A}_{K/\mathbb{Q}}$
at
![]() $\ell =2$
by Corollary 4.8. Thus we have proven claim (a).
$\ell =2$
by Corollary 4.8. Thus we have proven claim (a).
Claim (b) now follows from Theorems 3.14 and 3.18 (note that case (ii) of Theorem 3.18 cannot occur when
![]() $p$
is odd and
$p$
is odd and
![]() $n \geq 2$
). Finally, claims (c) and (d) follow from the definition of tame ramification and the characterisation of almost-maximal ramification in dihedral extensions given in [Reference Bergé4, Corollaire to Proposition 6].
$n \geq 2$
). Finally, claims (c) and (d) follow from the definition of tame ramification and the characterisation of almost-maximal ramification in dihedral extensions given in [Reference Bergé4, Corollaire to Proposition 6].
Remark 5.3.
Let
![]() $p$
be a prime and let
$p$
be a prime and let
![]() $n$
be a positive integer. It is well known that
$n$
be a positive integer. It is well known that
![]() $p$
is regular if
$p$
is regular if
![]() $p \lt 37$
. Moreover, by the results of [Reference Miller33] the class number of
$p \lt 37$
. Moreover, by the results of [Reference Miller33] the class number of
![]() $\mathbb{Q}(\zeta _{2p^{n}})^{+}$
is
$\mathbb{Q}(\zeta _{2p^{n}})^{+}$
is
![]() $1$
whenever
$1$
whenever
![]() $(p,n)$
is
$(p,n)$
is
![]() $(2,6)$
,
$(2,6)$
,
![]() $(3,4)$
,
$(3,4)$
,
![]() $(5,3)$
,
$(5,3)$
,
![]() $(7,2)$
,
$(7,2)$
,
![]() $(11,2)$
, or the same pairs with a smaller choice of
$(11,2)$
, or the same pairs with a smaller choice of
![]() $n \geq 2$
. Hence, the hypotheses of Theorem 5.2 hold for these values. In particular, we obtain the following corollaries.
$n \geq 2$
. Hence, the hypotheses of Theorem 5.2 hold for these values. In particular, we obtain the following corollaries.
Corollary 5.4.
Let
![]() $K/\mathbb{Q}$
be a dihedral extension of degree
$K/\mathbb{Q}$
be a dihedral extension of degree
![]() $2 \cdot 3^{n}$
where
$2 \cdot 3^{n}$
where
![]() $n=2,3$
or
$n=2,3$
or
![]() $4$
. If the ramification index of
$4$
. If the ramification index of
![]() $3$
in
$3$
in
![]() $K/\mathbb{Q}$
either is coprime to
$K/\mathbb{Q}$
either is coprime to
![]() $3$
or is a power of
$3$
or is a power of
![]() $3$
then
$3$
then
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
.
$\mathfrak{A}_{K/\mathbb{Q}}$
.
Corollary 5.5.
Let
![]() $K/\mathbb{Q}$
be a dihedral extension of degree
$K/\mathbb{Q}$
be a dihedral extension of degree
![]() $2p^{n}$
where
$2p^{n}$
where
![]() $(p,n)$
is
$(p,n)$
is
![]() $(5,2)$
,
$(5,2)$
,
![]() $(5,3)$
,
$(5,3)$
,
![]() $(7,2)$
or
$(7,2)$
or
![]() $(11,2)$
. Then,
$(11,2)$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if the ramification index of
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if the ramification index of
![]() $p$
in
$p$
in
![]() $K/\mathbb{Q}$
either is coprime to
$K/\mathbb{Q}$
either is coprime to
![]() $p$
or is a power of
$p$
or is a power of
![]() $p$
.
$p$
.
Remark 5.6.
In the proof of Theorem 5.2, we could have used [
Reference Bergé4, Théorème] to establish local freeness at
![]() $\ell =2$
instead of Example 4.5 and Corollary 4.8
.
$\ell =2$
instead of Example 4.5 and Corollary 4.8
.
6. Review of results on induction of lattices and associated orders
In this section, we shall give an exposition of Bergé’s results contained in [Reference Bergé4, §I]. We include some of the proofs for the convenience of the reader. The motivation for this section comes from Section 2.4.
6.1. Associated orders and induction
Let
![]() $R$
be a Dedekind domain with field of fractions
$R$
be a Dedekind domain with field of fractions
![]() $F$
. Let
$F$
. Let
![]() $H$
be a subgroup of a finite group
$H$
be a subgroup of a finite group
![]() $G$
and let
$G$
and let
![]() $M$
be an
$M$
be an
![]() $R[H]$
-lattice such that
$R[H]$
-lattice such that
![]() $FM$
is free of rank
$FM$
is free of rank
![]() $1$
over
$1$
over
![]() $F[H]$
.
$F[H]$
.
We recall that
![]() $\textrm{Ind}_{H}^{G} M$
is the induced module
$\textrm{Ind}_{H}^{G} M$
is the induced module
![]() $R[G] \otimes _{R[H]} M \cong \bigoplus _{s\in G/H} sM$
, where on the right-hand side we choose a system of representatives in
$R[G] \otimes _{R[H]} M \cong \bigoplus _{s\in G/H} sM$
, where on the right-hand side we choose a system of representatives in
![]() $G$
of the left cosets
$G$
of the left cosets
![]() $G/H$
and the left
$G/H$
and the left
![]() $R[G]$
-module structure is given by the relation
$R[G]$
-module structure is given by the relation
![]() $gs=th$
for some coset representative
$gs=th$
for some coset representative
![]() $t$
and
$t$
and
![]() $h\in H$
. We wish to understand the relationship between
$h\in H$
. We wish to understand the relationship between
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
and
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
and
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
. Note that these both contain the group ring
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
. Note that these both contain the group ring
![]() $R[G]$
.
$R[G]$
.
Proposition 6.1 ([Reference Bergé4, §1.3]). We have
Corollary 6.2.
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if it is equal to
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if it is equal to
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
.
Proof. If
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring, then
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring, then
![]() $g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1} = \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
for all
$g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1} = \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
for all
![]() $g \in G$
and thus
$g \in G$
and thus
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
by Proposition 6.1. Conversely, if
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
by Proposition 6.1. Conversely, if
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
then the left-hand side is a ring since the right-hand side is an associated order and thus a ring.
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
then the left-hand side is a ring since the right-hand side is an associated order and thus a ring.
Remark 6.3.
In general,
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
need not be a ring. However, it is straightforward to deduce from the above that
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
need not be a ring. However, it is straightforward to deduce from the above that
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring in the following cases:
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring in the following cases:
-
(i) there exists a subgroup
 $K\leq G$
such that
$K\leq G$
such that
 $G\cong H\times K$
,
$G\cong H\times K$
, -
(ii)
 $H$
is contained in the centre of
$H$
is contained in the centre of
 $G$
, or
$G$
, or -
(iii)
 $\mathfrak{A}(F[H], N) = R[H]$
.
$\mathfrak{A}(F[H], N) = R[H]$
.
Remark 6.4.
Proposition 6.1 implies that
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)\subseteq \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
. Hence
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)\subseteq \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
. Hence
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is an
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is an
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattice.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattice.
Proposition 6.5.
If
![]() $M$
is free over
$M$
is free over
![]() $\mathfrak{A}(F[H], M)$
, then
$\mathfrak{A}(F[H], M)$
, then
![]() $\textrm{Ind}_{H}^{G} M \cong \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
as
$\textrm{Ind}_{H}^{G} M \cong \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
as
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattices.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattices.
Proof. Since
![]() $R[H] \subseteq \mathfrak{A}(F[H], M)$
and
$R[H] \subseteq \mathfrak{A}(F[H], M)$
and
![]() $M$
is free (necessarily of rank
$M$
is free (necessarily of rank
![]() $1$
) over
$1$
) over
![]() $\mathfrak{A}(F[H], M)$
, we see that
$\mathfrak{A}(F[H], M)$
, we see that
![]() $M$
and
$M$
and
![]() $\mathfrak{A}(F[H], M)$
are isomorphic as
$\mathfrak{A}(F[H], M)$
are isomorphic as
![]() $R[H]$
-lattices. Extension of scalars gives an isomorphism
$R[H]$
-lattices. Extension of scalars gives an isomorphism
![]() $\textrm{Ind}_{H}^{G}M \cong \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
of
$\textrm{Ind}_{H}^{G}M \cong \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
of
![]() $R[G]$
-lattices. By Lemma 2.1, this is also an isomorphism of
$R[G]$
-lattices. By Lemma 2.1, this is also an isomorphism of
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattices.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattices.
Corollary 6.6.
Suppose that
![]() $M$
is free over
$M$
is free over
![]() $\mathfrak{A}(F[H], M)$
. If
$\mathfrak{A}(F[H], M)$
. If
-
(i)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is free over
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is free over
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
,
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, -
(ii)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, or
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, or -
(iii)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring,
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring,
then
![]() $\textrm{Ind}_{H}^{G} M$
is free over
$\textrm{Ind}_{H}^{G} M$
is free over
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
.
Proof. In case (i) this follows immediately from Proposition 6.5. Clearly, (ii)
![]() $\Rightarrow$
(i). Moreover, (ii)
$\Rightarrow$
(i). Moreover, (ii)
![]() $\Leftrightarrow$
(iii) by Corollary 6.2.
$\Leftrightarrow$
(iii) by Corollary 6.2.
Remark 6.7. In the proofs of the main theorems of the present article, Corollary 6.6 will be used to show that certain primes are not decomposition obstructions (see Definition 1.4).
The following is a partial converse to Corollary 6.6(i).
Proposition 6.8 ([Reference Bergé4, Proposition 2]). If
![]() $\textrm{Ind}_{H}^{G} M$
is a projective
$\textrm{Ind}_{H}^{G} M$
is a projective
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} N)$
-lattice, then
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} N)$
-lattice, then
![]() $M$
is a projective
$M$
is a projective
![]() $\mathfrak{A}(F[H], M)$
-lattice.
$\mathfrak{A}(F[H], M)$
-lattice.
If
![]() $H$
is normal in
$H$
is normal in
![]() $G$
, then we define
$G$
, then we define
![]() $\mathfrak{A}^{*}(M)=\bigcap _{g\in G}g\mathfrak{A}(F[H], M)g^{-1}$
.
$\mathfrak{A}^{*}(M)=\bigcap _{g\in G}g\mathfrak{A}(F[H], M)g^{-1}$
.
Proposition 6.9 ([Reference Bergé4, Proposition 3]). Suppose that
![]() $H$
is normal in
$H$
is normal in
![]() $G$
. Then,
$G$
. Then,
-
(i)
 $\mathfrak{A}^{*}(M)$
is an
$\mathfrak{A}^{*}(M)$
is an
 $R$
-order in
$R$
-order in
 $F[H]$
,
$F[H]$
, -
(ii)
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)=\textrm{Ind}_{H}^{G}\mathfrak{A}^{*}(M)$
, and
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)=\textrm{Ind}_{H}^{G}\mathfrak{A}^{*}(M)$
, and -
(iii)
 $\textrm{Ind}_{H}^{G} M$
is a projective
$\textrm{Ind}_{H}^{G} M$
is a projective
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattice if and only if
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
-lattice if and only if
 $M$
is a projective
$M$
is a projective
 $\mathfrak{A}^{*}(M)$
-lattice.
$\mathfrak{A}^{*}(M)$
-lattice.
6.2. Clean orders and induction
Let
![]() $R$
be a discrete valuation ring with field of fractions
$R$
be a discrete valuation ring with field of fractions
![]() $F$
of characteristic zero and suppose that the residue field of
$F$
of characteristic zero and suppose that the residue field of
![]() $R$
is finite.
$R$
is finite.
Definition 6.10.
Let
![]() $\Lambda$
be an
$\Lambda$
be an
![]() $R$
-order in a finite-dimensional semisimple
$R$
-order in a finite-dimensional semisimple
![]() $F$
-algebra
$F$
-algebra
![]() $A$
. Then,
$A$
. Then,
![]() $\Lambda$
is said to be clean if it has the following property: if
$\Lambda$
is said to be clean if it has the following property: if
![]() $M$
is a projective
$M$
is a projective
![]() $\Lambda$
-lattice such that
$\Lambda$
-lattice such that
![]() $FM$
is free over
$FM$
is free over
![]() $A$
then
$A$
then
![]() $M$
is free over
$M$
is free over
![]() $\Lambda$
.
$\Lambda$
.
Theorem 6.11 (Hattori). Commutative
![]() $R$
-orders in finite-dimensional semisimple
$R$
-orders in finite-dimensional semisimple
![]() $F$
-algebras are clean.
$F$
-algebras are clean.
Proof. See [Reference Hattori17] or [Reference Roggenkamp36, IX Corollary 1.5].
Proposition 6.12 ([Reference Bergé4, Corollaire to Proposition 3]). Let
![]() $H$
be a normal abelian subgroup of a finite group
$H$
be a normal abelian subgroup of a finite group
![]() $G$
and let
$G$
and let
![]() $M$
be an
$M$
be an
![]() $R[H]$
-lattice such that
$R[H]$
-lattice such that
![]() $FM$
is free of rank
$FM$
is free of rank
![]() $1$
over
$1$
over
![]() $F[H]$
. Then, the following are equivalent:
$F[H]$
. Then, the following are equivalent:
-
(i)
 $\textrm{Ind}_{H}^{G}M$
is projective over
$\textrm{Ind}_{H}^{G}M$
is projective over
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
;
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
; -
(ii)
 $\textrm{Ind}_{H}^{G}M$
is free over
$\textrm{Ind}_{H}^{G}M$
is free over
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
;
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
; -
(iii)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring and
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring and
 $\textrm{Ind}_{H}^{G}M$
is free over
$\textrm{Ind}_{H}^{G}M$
is free over
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
;
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
; -
(iv)
 $M$
is free over
$M$
is free over
 $\mathfrak{A}(F[H], M)$
and
$\mathfrak{A}(F[H], M)$
and
 $\mathfrak{A}^{*}(M)=\mathfrak{A}(F[H], M)$
.
$\mathfrak{A}^{*}(M)=\mathfrak{A}(F[H], M)$
.
Proof. (i)
![]() $\Rightarrow$
(iv). By Proposition 6.9(iii),
$\Rightarrow$
(iv). By Proposition 6.9(iii),
![]() $M$
is projective over
$M$
is projective over
![]() $\mathfrak{A}^{*}(M)$
. Moreover,
$\mathfrak{A}^{*}(M)$
. Moreover,
![]() $\mathfrak{A}^{*}(M)$
is a clean order by Theorem 6.11 and thus
$\mathfrak{A}^{*}(M)$
is a clean order by Theorem 6.11 and thus
![]() $M$
is in fact free over
$M$
is in fact free over
![]() $\mathfrak{A}^{*}(M)$
. Hence
$\mathfrak{A}^{*}(M)$
. Hence
![]() $\mathfrak{A}^{*}(M)=\mathfrak{A}(F[H], M)$
by Proposition 2.2.
$\mathfrak{A}^{*}(M)=\mathfrak{A}(F[H], M)$
by Proposition 2.2.
(iv)
![]() $\Rightarrow$
(iii). We have
$\Rightarrow$
(iii). We have
![]() $\textrm{Ind}^{G}_{H}\mathfrak{A}(F[H], M)=\textrm{Ind}^{G}_{H}\mathfrak{A}^{*}(M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, where the second equality is Proposition 6.9(ii). Thus,
$\textrm{Ind}^{G}_{H}\mathfrak{A}(F[H], M)=\textrm{Ind}^{G}_{H}\mathfrak{A}^{*}(M)=\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, where the second equality is Proposition 6.9(ii). Thus,
![]() $\textrm{Ind}^{G}_{H}\mathfrak{A}(F[H], M)$
is a ring by Corollary 6.2. Hence,
$\textrm{Ind}^{G}_{H}\mathfrak{A}(F[H], M)$
is a ring by Corollary 6.2. Hence,
![]() $\textrm{Ind}_{H}^{G}M$
is free over
$\textrm{Ind}_{H}^{G}M$
is free over
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
by Corollary 6.6(iii).
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
by Corollary 6.6(iii).
(iii)
![]() $\Rightarrow$
(ii). This follows from Corollary 6.2.
$\Rightarrow$
(ii). This follows from Corollary 6.2.
(ii)
![]() $\Rightarrow$
(i). This follows from the general fact that every free module is projective.
$\Rightarrow$
(i). This follows from the general fact that every free module is projective.
Remark 6.13.
Let
![]() $K/\mathbb{Q}$
be a finite Galois extension, let
$K/\mathbb{Q}$
be a finite Galois extension, let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $K$
above the rational prime
$K$
above the rational prime
![]() $p$
, let
$p$
, let
![]() $M=\mathcal{O}_{K_{\mathfrak{P}}}$
, let
$M=\mathcal{O}_{K_{\mathfrak{P}}}$
, let
![]() $H=D(\mathfrak{P}|p)$
be the decomposition group and let
$H=D(\mathfrak{P}|p)$
be the decomposition group and let
![]() $R=\mathbb{Z}_p$
. If
$R=\mathbb{Z}_p$
. If
![]() $H$
is normal and abelian in
$H$
is normal and abelian in
![]() $G$
and
$G$
and
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
, Proposition 6.12 tells us that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
, Proposition 6.12 tells us that
![]() $p$
is a decomposition obstruction for
$p$
is a decomposition obstruction for
![]() $K$
unless
$K$
unless
![]() $\textrm{Ind}_H^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\mathfrak{A}_{K/\mathbb{Q},p}$
. This observation is crucial in the proofs in Section
8
.
$\textrm{Ind}_H^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\mathfrak{A}_{K/\mathbb{Q},p}$
. This observation is crucial in the proofs in Section
8
.
7. Induction for orders of a certain structure
Let
![]() $R$
be a discrete valuation ring with field of fractions
$R$
be a discrete valuation ring with field of fractions
![]() $F$
of characteristic zero and suppose that the residue field of
$F$
of characteristic zero and suppose that the residue field of
![]() $R$
is finite. Let
$R$
is finite. Let
![]() $G$
be a finite group and let
$G$
be a finite group and let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
. In Section 6, we reviewed some general induction properties of the associated order
$G$
. In Section 6, we reviewed some general induction properties of the associated order
![]() $\mathfrak{A}(F[H], M)$
(with weaker hypotheses on
$\mathfrak{A}(F[H], M)$
(with weaker hypotheses on
![]() $R$
for some results). In this section, we prove new results concerning inductions of orders of a certain form and then consider arithmetic applications such as the study of weakly ramified extensions.
$R$
for some results). In this section, we prove new results concerning inductions of orders of a certain form and then consider arithmetic applications such as the study of weakly ramified extensions.
Let
![]() $\pi$
be a uniformiser of
$\pi$
be a uniformiser of
![]() $R$
. For a subgroup
$R$
. For a subgroup
![]() $P$
of
$P$
of
![]() $G$
, let
$G$
, let
![]() $\textrm{ncl}_G(P)$
denote the normal closure of
$\textrm{ncl}_G(P)$
denote the normal closure of
![]() $P$
in
$P$
in
![]() $G$
and let
$G$
and let
![]() $\textrm{Tr}_{P} = \sum _{k\in P}k \in R[G]$
.
$\textrm{Tr}_{P} = \sum _{k\in P}k \in R[G]$
.
Theorem 7.1.
Let
![]() $M$
be an
$M$
be an
![]() $R[H]$
-lattice such that
$R[H]$
-lattice such that
![]() $FM$
is free of rank
$FM$
is free of rank
![]() $1$
over
$1$
over
![]() $F[H]$
. Suppose that there exists a positive integer
$F[H]$
. Suppose that there exists a positive integer
![]() $n$
and a subgroup
$n$
and a subgroup
![]() $P$
of
$P$
of
![]() $H$
such that
$H$
such that
Then, the following statements hold:
-
(i)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=R[G]+\pi ^{-n}R[G]\textrm{Tr}_P$
.
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=R[G]+\pi ^{-n}R[G]\textrm{Tr}_P$
. -
(ii)
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)=R[G]+\pi ^{-n}R[G]\textrm{Tr}_{\textrm{ncl}_G(P)}$
.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)=R[G]+\pi ^{-n}R[G]\textrm{Tr}_{\textrm{ncl}_G(P)}$
. -
(iii)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if
 $P$
is normal in
$P$
is normal in
 $G$
.
$G$
. -
(iv) If
 $P$
is normal in
$P$
is normal in
 $G$
and
$G$
and
 $M$
is free over
$M$
is free over
 $\mathfrak{A}(F[H], M)$
, then
$\mathfrak{A}(F[H], M)$
, then
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is free over
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is free over
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
. -
(v) If
 $H$
is abelian and normal in
$H$
is abelian and normal in
 $G$
and
$G$
and
 $\textrm{Ind}_{H}^{G} M$
is projective over
$\textrm{Ind}_{H}^{G} M$
is projective over
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, then
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, then
 $P$
is normal in
$P$
is normal in
 $G$
.
$G$
.
Proof. Note that if
![]() $h$
runs through a set of coset representatives of
$h$
runs through a set of coset representatives of
![]() $G/H$
and
$G/H$
and
![]() $k$
runs through a set of coset representatives of
$k$
runs through a set of coset representatives of
![]() $H/P$
, then
$H/P$
, then
![]() $hk$
runs through a set of left coset representatives of
$hk$
runs through a set of left coset representatives of
![]() $G/P$
. Thus, we have
$G/P$
. Thus, we have
 \begin{align*} \begin{split} \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)&=\textrm{Ind}_{H}^{G}\left (R[H]+\left \{{\pi ^{-n}}\left (\sum _{k\in H/P}a_{k}k\right ):a_{k}\in R\right \}\cdot \textrm{Tr}_{P}\right )\\[5pt] &=R[G]+\left \{\sum _{h\in G/H}{\pi ^{-n}}h\left (\sum _{k\in H/P}a_{h,k}k\right )\;:\; a_{h,k}\in R\right \}\cdot \textrm{Tr}_{P}\\[5pt] &=R[G]+\left \{{\pi ^{-n}}\left (\sum _{h\in G/H}\sum _{k\in H/P}a_{h,k}hk\right ):a_{h,k}\in R\right \}\cdot \textrm{Tr}_{P}\\[5pt] &=R[G]+{\pi ^{-n}}R[G]\textrm{Tr}_{P}, \end{split} \end{align*}
\begin{align*} \begin{split} \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)&=\textrm{Ind}_{H}^{G}\left (R[H]+\left \{{\pi ^{-n}}\left (\sum _{k\in H/P}a_{k}k\right ):a_{k}\in R\right \}\cdot \textrm{Tr}_{P}\right )\\[5pt] &=R[G]+\left \{\sum _{h\in G/H}{\pi ^{-n}}h\left (\sum _{k\in H/P}a_{h,k}k\right )\;:\; a_{h,k}\in R\right \}\cdot \textrm{Tr}_{P}\\[5pt] &=R[G]+\left \{{\pi ^{-n}}\left (\sum _{h\in G/H}\sum _{k\in H/P}a_{h,k}hk\right ):a_{h,k}\in R\right \}\cdot \textrm{Tr}_{P}\\[5pt] &=R[G]+{\pi ^{-n}}R[G]\textrm{Tr}_{P}, \end{split} \end{align*}
which proves (i). Moreover, we have
 \begin{align*} \begin{split} \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)&=R[G]+{\pi ^{-n}}R[G/P]\textrm{Tr}_{P}\\[5pt] &=R[G]+\left \{{\pi ^{-n}}\left (\sum _{h\in G/P}a_hh\right ) \;:\; a_h\textrm{ is a representative of }R/(\pi ^{n})\right \}\cdot \textrm{Tr}_{P}\\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G}a_\gamma \gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2} \in P\Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})}\right \}. \end{split} \end{align*}
\begin{align*} \begin{split} \textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)&=R[G]+{\pi ^{-n}}R[G/P]\textrm{Tr}_{P}\\[5pt] &=R[G]+\left \{{\pi ^{-n}}\left (\sum _{h\in G/P}a_hh\right ) \;:\; a_h\textrm{ is a representative of }R/(\pi ^{n})\right \}\cdot \textrm{Tr}_{P}\\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G}a_\gamma \gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2} \in P\Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})}\right \}. \end{split} \end{align*}
Thus for every
![]() $g\in G$
, we have
$g\in G$
, we have
 \begin{align*} \begin{split} g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1} &= R[G]+{\pi ^{-n}}R[G/gPg^{-1}]\textrm{Tr}_{gPg^{-1}}\\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G} a_{\gamma }\gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2}\in gPg^{-1}\Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})}\right \}. \end{split} \end{align*}
\begin{align*} \begin{split} g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1} &= R[G]+{\pi ^{-n}}R[G/gPg^{-1}]\textrm{Tr}_{gPg^{-1}}\\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G} a_{\gamma }\gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2}\in gPg^{-1}\Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})}\right \}. \end{split} \end{align*}
We will now use the following general fact. Let
![]() $G$
be a group, let
$G$
be a group, let
![]() $B$
be any set, let
$B$
be any set, let
![]() $A$
be a subset of
$A$
be a subset of
![]() $G$
and let
$G$
and let
![]() $A'$
be the subgroup of
$A'$
be the subgroup of
![]() $G$
generated by
$G$
generated by
![]() $A$
. Then from the description of the elements of
$A$
. Then from the description of the elements of
![]() $A'$
in terms of products of elements of
$A'$
in terms of products of elements of
![]() $A$
and their inverses, we have
$A$
and their inverses, we have
 \begin{multline*} \left \{\{a_\gamma \}_{\gamma \in G}\in \textstyle{\prod _{\gamma \in G}} \, B\;:\;\gamma _1^{-1}\gamma _2\in A\Rightarrow a_{\gamma _1}=a_{\gamma _2}\right \} \\[5pt] =\left \{\{a_\gamma \}_{\gamma \in G}\in \textstyle{\prod _{\gamma \in G}} B \;:\; \gamma _1^{-1}\gamma _2\in A'\Rightarrow a_{\gamma _1}=a_{\gamma _2}\right \}. \end{multline*}
\begin{multline*} \left \{\{a_\gamma \}_{\gamma \in G}\in \textstyle{\prod _{\gamma \in G}} \, B\;:\;\gamma _1^{-1}\gamma _2\in A\Rightarrow a_{\gamma _1}=a_{\gamma _2}\right \} \\[5pt] =\left \{\{a_\gamma \}_{\gamma \in G}\in \textstyle{\prod _{\gamma \in G}} B \;:\; \gamma _1^{-1}\gamma _2\in A'\Rightarrow a_{\gamma _1}=a_{\gamma _2}\right \}. \end{multline*}
This said, by Proposition 6.1, we have that
 \begin{align*} \begin{split} \mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M) &= \bigcap _{g \in G} g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1}\\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G}a_\gamma \gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2}\in \bigcup _{g \in G} gPg^{-1} \Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})} \right \} \\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G}a_\gamma \gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2}\in \textrm{ncl}_G(P) \Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})} \right \} \\[5pt] &=R[G]+{\pi ^{-n}}R[G/\textrm{ncl}_G(P)]\textrm{Tr}_{\textrm{ncl}_G(P)},\\[5pt] &=R[G]+{\pi ^{-n}}R[G]\textrm{Tr}_{\textrm{ncl}_G(P)}, \end{split} \end{align*}
\begin{align*} \begin{split} \mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M) &= \bigcap _{g \in G} g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1}\\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G}a_\gamma \gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2}\in \bigcup _{g \in G} gPg^{-1} \Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})} \right \} \\[5pt] &={\pi ^{-n}}\left \{\sum _{\gamma \in G}a_\gamma \gamma \in R[G] \;:\; \gamma _{1}^{-1}\gamma _{2}\in \textrm{ncl}_G(P) \Rightarrow a_{\gamma _{1}}\equiv a_{\gamma _{2}}\bmod{(\pi ^{n})} \right \} \\[5pt] &=R[G]+{\pi ^{-n}}R[G/\textrm{ncl}_G(P)]\textrm{Tr}_{\textrm{ncl}_G(P)},\\[5pt] &=R[G]+{\pi ^{-n}}R[G]\textrm{Tr}_{\textrm{ncl}_G(P)}, \end{split} \end{align*}
which proves (ii).
By Corollary 6.2,
![]() $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if it is equal to
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if it is equal to
![]() $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, which by (i) and (ii) is true if and only if
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, which by (i) and (ii) is true if and only if
![]() $P=\textrm{ncl}(P)$
. This proves (iii). Part (iv) follows from (iii) and Corollary 6.6(iii). Part (v) follows from (iii) and Proposition 6.12(i)
$P=\textrm{ncl}(P)$
. This proves (iii). Part (iv) follows from (iii) and Corollary 6.6(iii). Part (v) follows from (iii) and Proposition 6.12(i)
![]() $\Rightarrow$
(iii).
$\Rightarrow$
(iii).
We have the following application to the understanding of local freeness in weakly ramified extensions of number fields.
Corollary 7.2.
Let
![]() $K/F$
be a finite Galois extension of number fields with Galois group
$K/F$
be a finite Galois extension of number fields with Galois group
![]() $G$
and let
$G$
and let
![]() $\mathfrak{P}|\mathfrak{p}$
be two primes of
$\mathfrak{P}|\mathfrak{p}$
be two primes of
![]() $K/F$
such that
$K/F$
such that
![]() $K_{\mathfrak{P}}/F_{\mathfrak{p}}$
is wildly and weakly ramified.
$K_{\mathfrak{P}}/F_{\mathfrak{p}}$
is wildly and weakly ramified.
-
(i) If the inertia group
 $G_{0}=G_{0}(\mathfrak{P}|\mathfrak{p})$
is normal in
$G_{0}=G_{0}(\mathfrak{P}|\mathfrak{p})$
is normal in
 $G$
, then
$G$
, then
 $\mathcal{O}_{K,\mathfrak{p}}$
is free over
$\mathcal{O}_{K,\mathfrak{p}}$
is free over
 $\mathfrak{A}_{K/F,\mathfrak{p}}$
.
$\mathfrak{A}_{K/F,\mathfrak{p}}$
. -
(ii) Suppose that the decomposition group
 $D=D(\mathfrak{P}|\mathfrak{p})$
is abelian and normal in
$D=D(\mathfrak{P}|\mathfrak{p})$
is abelian and normal in
 $G$
. Then,
$G$
. Then,
 $\mathcal{O}_{K,\mathfrak{p}}$
is free over
$\mathcal{O}_{K,\mathfrak{p}}$
is free over
 $\mathfrak{A}_{K/F,\mathfrak{p}}$
if and only if
$\mathfrak{A}_{K/F,\mathfrak{p}}$
if and only if
 $G_{0}$
is normal in
$G_{0}$
is normal in
 $ G$
.
$ G$
.
Proof. Let
![]() $\pi$
be any uniformiser of
$\pi$
be any uniformiser of
![]() $\mathcal{O}_{F_{\mathfrak{p}}}$
. Then by Theorem 3.9, we have
$\mathcal{O}_{F_{\mathfrak{p}}}$
. Then by Theorem 3.9, we have
and
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}(F_{\mathfrak p}[D],\mathcal{O}_{K_{\mathfrak{P}}})$
. Hence claim (i) follows from Theorem 7.1(iv). Claim (ii) follows from Theorem 7.1(v) for one direction and from claim (i) for the other direction.
$\mathfrak{A}(F_{\mathfrak p}[D],\mathcal{O}_{K_{\mathfrak{P}}})$
. Hence claim (i) follows from Theorem 7.1(iv). Claim (ii) follows from Theorem 7.1(v) for one direction and from claim (i) for the other direction.
Remark 7.3.
Note that by using Corollary 7.2(ii), databases such as [30], and a computational algebra system such as Magma to determine whether certain subgroups are normal, we can easily read off examples of number fields
![]() $K$
and decomposition obstructions for
$K$
and decomposition obstructions for
![]() $K$
. For instance, let
$K$
. For instance, let
![]() $K$
be the splitting field of
$K$
be the splitting field of
![]() $x^4-x^2-4x-11$
over
$x^4-x^2-4x-11$
over
![]() $\mathbb{Q}$
. Then,
$\mathbb{Q}$
. Then,
![]() $K$
is an
$K$
is an
![]() $S_4$
-extension of
$S_4$
-extension of
![]() $\mathbb{Q}$
, for which the prime
$\mathbb{Q}$
, for which the prime
![]() $2$
is weakly ramified, has normal decomposition group isomorphic to
$2$
is weakly ramified, has normal decomposition group isomorphic to
![]() $C_2^2$
and (non-normal) inertia group isomorphic to
$C_2^2$
and (non-normal) inertia group isomorphic to
![]() $C_2$
: in other words,
$C_2$
: in other words,
![]() $2$
is a decomposition obstruction for
$2$
is a decomposition obstruction for
![]() $K$
(this case is in fact covered in the proof of Theorem 8.3
: it lies on the entry (5) of Table
1
).
$K$
(this case is in fact covered in the proof of Theorem 8.3
: it lies on the entry (5) of Table
1
).
We now prove the following generalisation of Theorem 7.1.
Theorem 7.4.
Let
![]() $M$
be an
$M$
be an
![]() $R[H]$
-lattice such that
$R[H]$
-lattice such that
![]() $FM$
is free of rank
$FM$
is free of rank
![]() $1$
over
$1$
over
![]() $F[H]$
. Suppose that there exist integers
$F[H]$
. Suppose that there exist integers
![]() $0=n_0\lt n_1\lt \cdots \lt n_r$
and subgroups
$0=n_0\lt n_1\lt \cdots \lt n_r$
and subgroups
such that
Then, the following statements hold:
-
(i)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\sum _{i=0}^r\pi ^{-n_i}R[G]\textrm{Tr}_{P_i}$
.
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)=\sum _{i=0}^r\pi ^{-n_i}R[G]\textrm{Tr}_{P_i}$
. -
(ii)
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)=\sum _{i=0}^r\pi ^{-n_i}R[G]\textrm{Tr}_{\textrm{ncl}_G(P_i)}$
.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)=\sum _{i=0}^r\pi ^{-n_i}R[G]\textrm{Tr}_{\textrm{ncl}_G(P_i)}$
. -
(iii)
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is a ring if and only if
 $P_i$
is normal in
$P_i$
is normal in
 $ G$
for every
$ G$
for every
 $i$
.
$i$
. -
(iv) If
 $P_i$
is normal in
$P_i$
is normal in
 $ G$
for every
$ G$
for every
 $i$
and
$i$
and
 $M$
is free over
$M$
is free over
 $\mathfrak{A}(F[H], M)$
, then
$\mathfrak{A}(F[H], M)$
, then
 $\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is free over
$\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)$
is free over
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
.
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
. -
(v) If
 $H$
is abelian and normal in
$H$
is abelian and normal in
 $G$
and
$G$
and
 $\textrm{Ind}_{H}^{G} M$
is projective over
$\textrm{Ind}_{H}^{G} M$
is projective over
 $\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, then
$\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
, then
 $P_i$
is normal in
$P_i$
is normal in
 $ G$
for every
$ G$
for every
 $i$
.
$i$
.
Proof. The proof of part (i) is exactly as for Theorem 7.1(i).
We already know from Theorem 7.1 that (ii) holds if
![]() $r=1$
. So suppose that
$r=1$
. So suppose that
![]() $r\gt 1$
. Note that, since each
$r\gt 1$
. Note that, since each
![]() $\textrm{ncl}_G(P_i)$
is normal in
$\textrm{ncl}_G(P_i)$
is normal in
![]() $G$
, for each
$G$
, for each
![]() $g \in G$
we have that
$g \in G$
we have that
where
![]() $\textrm{Tr}_{\textrm{ncl}_G(P_i)/P_i}$
is the sum over any fixed choice of coset representatives of
$\textrm{Tr}_{\textrm{ncl}_G(P_i)/P_i}$
is the sum over any fixed choice of coset representatives of
![]() $\textrm{ncl}_{G}(P_{i})/P_{i}$
. Hence for each
$\textrm{ncl}_{G}(P_{i})/P_{i}$
. Hence for each
![]() $g\in G$
we have
$g\in G$
we have
![]() $\pi ^{-n_i}\textrm{Tr}_{\textrm{ncl}_G(P_i)}\in g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1}$
. Together with Proposition 6.1, this implies that
$\pi ^{-n_i}\textrm{Tr}_{\textrm{ncl}_G(P_i)}\in g\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)g^{-1}$
. Together with Proposition 6.1, this implies that
![]() $\pi ^{-n_i}\textrm{Tr}_{\textrm{ncl}_G(P_i)}\in \mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
. Therefore
$\pi ^{-n_i}\textrm{Tr}_{\textrm{ncl}_G(P_i)}\in \mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
. Therefore
It remains to show the reverse containment. First note that
where the containment follows from Remark 6.4 and the equality is part (i). Let
![]() $\theta \in \mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
. Then, we can write
$\theta \in \mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)$
. Then, we can write
![]() $\theta =\sum _{i=0}^{r} \pi ^{-n_i}\theta _{i}\textrm{Tr}_{P_i}$
, where
$\theta =\sum _{i=0}^{r} \pi ^{-n_i}\theta _{i}\textrm{Tr}_{P_i}$
, where
![]() $\theta _{i} \in R[G]$
for each
$\theta _{i} \in R[G]$
for each
![]() $i$
. For each integer
$i$
. For each integer
![]() $j$
with
$j$
with
![]() $0 \leq j \leq r$
, we shall prove that
$0 \leq j \leq r$
, we shall prove that
 \begin{equation*} \theta \in \sum _{i=0}^{r-j-1}\pi ^{-n_i}R[G]\textrm {Tr}_{P_i} +\sum _{i=r-j}^r\pi ^{-n_i}R[G]\textrm {Tr}_{\mathrm {ncl}_G(P_i)}. \end{equation*}
\begin{equation*} \theta \in \sum _{i=0}^{r-j-1}\pi ^{-n_i}R[G]\textrm {Tr}_{P_i} +\sum _{i=r-j}^r\pi ^{-n_i}R[G]\textrm {Tr}_{\mathrm {ncl}_G(P_i)}. \end{equation*}
We proceed by induction on
![]() $j$
and first consider the base case
$j$
and first consider the base case
![]() $j=0$
. We have that
$j=0$
. We have that
Also note that for each
![]() $g \in G$
, we have
$g \in G$
, we have
 \begin{align*} g^{-1}\pi ^{n_{r-1}}\theta g & \in g^{-1}\pi ^{n_{r-1}}\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)g\\[5pt] &= \pi ^{n_{r-1}}\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)\\[5pt] &\subseteq \pi ^{n_{r-1}}\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)\\[5pt] &\subseteq R[G]+\pi ^{n_{r-1}-n_r}R[G]\textrm{Tr}_{P_r}. \end{align*}
\begin{align*} g^{-1}\pi ^{n_{r-1}}\theta g & \in g^{-1}\pi ^{n_{r-1}}\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)g\\[5pt] &= \pi ^{n_{r-1}}\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)\\[5pt] &\subseteq \pi ^{n_{r-1}}\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)\\[5pt] &\subseteq R[G]+\pi ^{n_{r-1}-n_r}R[G]\textrm{Tr}_{P_r}. \end{align*}
Hence,
where the equality follows from the case
![]() $r=1$
. Thus there exists
$r=1$
. Thus there exists
![]() $\alpha \in R[G]$
such that
$\alpha \in R[G]$
such that
where the equality follows from (7.2) and the containment
![]() $R[G]\textrm{Tr}_{P_r}\subseteq R[G]\textrm{Tr}_{P_{r-1}}$
, which holds since
$R[G]\textrm{Tr}_{P_r}\subseteq R[G]\textrm{Tr}_{P_{r-1}}$
, which holds since
![]() $\textrm{Tr}_{P_r}=\textrm{Tr}_{P_r/P_{r-1}}\textrm{Tr}_{P_{r-1}}$
. This completes the base case
$\textrm{Tr}_{P_r}=\textrm{Tr}_{P_r/P_{r-1}}\textrm{Tr}_{P_{r-1}}$
. This completes the base case
![]() $j=0$
.
$j=0$
.
We now proceed with the induction step. Suppose our claim is valid for
![]() $j-1$
, and let us prove it for
$j-1$
, and let us prove it for
![]() $j$
. Using the inductive hypothesis and subtracting an appropriate element of
$j$
. Using the inductive hypothesis and subtracting an appropriate element of
![]() $\sum _{i=j+1}^{r} \pi ^{-n_i}R[G]\textrm{Tr}_{\textrm{ncl}_G(P_i)}$
, we can and do assume without loss of generality that
$\sum _{i=j+1}^{r} \pi ^{-n_i}R[G]\textrm{Tr}_{\textrm{ncl}_G(P_i)}$
, we can and do assume without loss of generality that
for some
![]() $\theta _{i} \in R[G]$
. Hence, it remains to show that
$\theta _{i} \in R[G]$
. Hence, it remains to show that
As in the base case, for each
![]() $g\in G$
we have
$g\in G$
we have
 \begin{align*} \begin{split} g^{-1}\pi ^{n_{r-j-1}}\theta g &\in \pi ^{n_{r-j-1}-n_{r-j}}R[G]\cap \pi ^{n_{r-j-1}}\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)\\[5pt] &\subseteq \pi ^{n_{r-j-1}-n_{r-j}}R[G]\cap \pi ^{n_{r-j-1}}\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)\\[5pt] &\subseteq R[G]+\pi ^{n_{r-j-1}-n_{r-j}}R[G]\textrm{Tr}_{P_{r-j}}, \end{split} \end{align*}
\begin{align*} \begin{split} g^{-1}\pi ^{n_{r-j-1}}\theta g &\in \pi ^{n_{r-j-1}-n_{r-j}}R[G]\cap \pi ^{n_{r-j-1}}\mathfrak{A}(F[G], \textrm{Ind}_{H}^{G} M)\\[5pt] &\subseteq \pi ^{n_{r-j-1}-n_{r-j}}R[G]\cap \pi ^{n_{r-j-1}}\textrm{Ind}_{H}^{G} \mathfrak{A}(F[H], M)\\[5pt] &\subseteq R[G]+\pi ^{n_{r-j-1}-n_{r-j}}R[G]\textrm{Tr}_{P_{r-j}}, \end{split} \end{align*}
so, by the result for
![]() $r=1$
, we have
$r=1$
, we have
Thus, there exists
![]() $\alpha \in R[G]$
such that
$\alpha \in R[G]$
such that
 \begin{equation*} \theta -\pi ^{-n_{r-j}}\alpha \mathrm {Tr}_{\mathrm {ncl}_G(P_{r-j})}\in \pi ^{-n_{r-j-1}}R[G]\cap \left ( \sum _{i=0}^{r-j} \pi ^{-n_i}\theta _i\mathrm {Tr}_{P_i}\right )=\sum _{i=0}^{r-j-1}\pi ^{-n_i}R[G]\textrm {Tr}_{P_i}. \end{equation*}
\begin{equation*} \theta -\pi ^{-n_{r-j}}\alpha \mathrm {Tr}_{\mathrm {ncl}_G(P_{r-j})}\in \pi ^{-n_{r-j-1}}R[G]\cap \left ( \sum _{i=0}^{r-j} \pi ^{-n_i}\theta _i\mathrm {Tr}_{P_i}\right )=\sum _{i=0}^{r-j-1}\pi ^{-n_i}R[G]\textrm {Tr}_{P_i}. \end{equation*}
This concludes the induction step. Therefore, we deduce that
which concludes the proof of part (ii).
We easily see with the same methods that
precisely when
![]() $P_i=\textrm{ncl}_G(P_i)$
for every
$P_i=\textrm{ncl}_G(P_i)$
for every
![]() $i$
, establishing part (iii). Part (iv) follows from part (iii) and Corollary 6.6(iii). Part (v) follows from Proposition 6.12(i)
$i$
, establishing part (iii). Part (iv) follows from part (iii) and Corollary 6.6(iii). Part (v) follows from Proposition 6.12(i)
![]() $\Rightarrow$
(iii).
$\Rightarrow$
(iii).
Remark 7.5.
It follows from the proof of Theorem 7.4 that the subgroups
![]() $P_i$
and the numbers
$P_i$
and the numbers
![]() $n_i$
are uniquely determined by
$n_i$
are uniquely determined by
![]() $\mathfrak{A}(F[H],M)$
. Moreover,
$\mathfrak{A}(F[H],M)$
. Moreover,
![]() $P_i$
is normal in
$P_i$
is normal in
![]() $H$
(a way to see this from what we already proved is the following:
$H$
(a way to see this from what we already proved is the following:
![]() $\textrm{Ind}_H^H\mathfrak{A}(F[H], M)=\mathfrak{A}(F[H], M)$
is a ring, so that we can apply (iii) with
$\textrm{Ind}_H^H\mathfrak{A}(F[H], M)=\mathfrak{A}(F[H], M)$
is a ring, so that we can apply (iii) with
![]() $G=H$
) and
$G=H$
) and
![]() $\pi ^{n_i}$
divides the order of
$\pi ^{n_i}$
divides the order of
![]() $P_{i}$
for all
$P_{i}$
for all
![]() $i$
.
$i$
.
8. Leopoldt-type theorems for
 $A_4$
,
$A_4$
,
 $S_4$
and
$S_4$
and
 $A_5$
-extensions of
$A_5$
-extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
In this section, we prove Theorems 1.7, 1.8 and 1.9 from the introduction. We first give an overview of our methods. Let
![]() $K/\mathbb{Q}$
be a finite Galois extension, let
$K/\mathbb{Q}$
be a finite Galois extension, let
![]() $G=\textrm{Gal}(K/\mathbb{Q})$
, and suppose that
$G=\textrm{Gal}(K/\mathbb{Q})$
, and suppose that
![]() $G \cong A_4$
,
$G \cong A_4$
,
![]() $S_4$
or
$S_4$
or
![]() $A_5$
. As proven in Corollary 2.7, the only property to check is local freeness. By Proposition 4.10, if
$A_5$
. As proven in Corollary 2.7, the only property to check is local freeness. By Proposition 4.10, if
![]() $G$
is isomorphic to
$G$
is isomorphic to
![]() $A_4$
or
$A_4$
or
![]() $S_4$
then we only have to check for local freeness at
$S_4$
then we only have to check for local freeness at
![]() $2$
, while freeness in the
$2$
, while freeness in the
![]() $G\cong A_5$
-case only happens if we have local freeness simultaneously at
$G\cong A_5$
-case only happens if we have local freeness simultaneously at
![]() $2$
,
$2$
,
![]() $3$
and
$3$
and
![]() $5$
.
$5$
.
If
![]() $G\cong A_4$
or
$G\cong A_4$
or
![]() $S_4$
, let
$S_4$
, let
![]() $p=2$
. If
$p=2$
. If
![]() $G\cong A_5$
, let
$G\cong A_5$
, let
![]() $p\in \{2,3,5\}$
. Let
$p\in \{2,3,5\}$
. Let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $K$
above
$K$
above
![]() $p$
, with decomposition group
$p$
, with decomposition group
![]() $D=D(\mathfrak{P}|p)$
. We will first apply the techniques of the previous sections to compute
$D=D(\mathfrak{P}|p)$
. We will first apply the techniques of the previous sections to compute
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and determine whether
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and determine whether
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
.
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
.
When
![]() $G\cong A_4$
or
$G\cong A_4$
or
![]() $S_4$
, in some cases it will suffice to directly apply results such as Theorem 3.14, Lemma 4.11, Proposition 4.12 or Corollary 7.2(i). We will study these cases at the beginning of each of the proofs. In the remaining cases, the analysis will be somewhat more complicated.
$S_4$
, in some cases it will suffice to directly apply results such as Theorem 3.14, Lemma 4.11, Proposition 4.12 or Corollary 7.2(i). We will study these cases at the beginning of each of the proofs. In the remaining cases, the analysis will be somewhat more complicated.
It could be the case that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is not even free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not even free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
. In general, this does not necessarily imply that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
. In general, this does not necessarily imply that
![]() $\mathcal{O}_{K,p}$
is not free over
$\mathcal{O}_{K,p}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
. However, this will occur only when
$\mathfrak{A}_{K/\mathbb{Q},p}$
. However, this will occur only when
![]() $G\cong S_4$
and in two specific cases:
$G\cong S_4$
and in two specific cases:
-
•
 $D=G$
, which guarantees that
$D=G$
, which guarantees that
 $\mathcal{O}_{K,p}=\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
$\mathcal{O}_{K,p}=\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
 $\mathfrak{A}_{K/\mathbb{Q},p}=\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
: we will use [Reference Bley and Johnston5, Algorithm 3.1(6)] to verify that in four specific
$\mathfrak{A}_{K/\mathbb{Q},p}=\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
: we will use [Reference Bley and Johnston5, Algorithm 3.1(6)] to verify that in four specific
 $S_{4}$
-extensions of
$S_{4}$
-extensions of
 $\mathbb{Q}_{2}$
the ring of integers is not free over its associated order;
$\mathbb{Q}_{2}$
the ring of integers is not free over its associated order; -
•
 $D$
is dihedral of order
$D$
is dihedral of order
 $8$
, in which case, by Theorem 3.10,
$8$
, in which case, by Theorem 3.10,
 $\mathcal{O}_{K_{\mathfrak{P}}}$
is not even projective over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not even projective over
 $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
, which allows us to conclude that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
, which allows us to conclude that
 $\mathcal{O}_{K,p}$
cannot be free over
$\mathcal{O}_{K,p}$
cannot be free over
 $\mathfrak{A}_{K/\mathbb{Q},p}$
by Proposition 6.8.
$\mathfrak{A}_{K/\mathbb{Q},p}$
by Proposition 6.8.
We call this method ‘the non-freeness method’.
In all the remaining cases, we have that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
. We will see that the structure of
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
. We will see that the structure of
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
will always satisfy the hypotheses of Theorem 7.4 (in some cases its simpler version, i.e. Theorem 7.1). We can then apply Theorem 7.4(i) and (ii) to compute
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
will always satisfy the hypotheses of Theorem 7.4 (in some cases its simpler version, i.e. Theorem 7.1). We can then apply Theorem 7.4(i) and (ii) to compute
![]() $\textrm{Ind}_D^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and
$\textrm{Ind}_D^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
. By Proposition 6.5, we are reduced to verifying whether
$\mathfrak{A}_{K/\mathbb{Q},p}$
. By Proposition 6.5, we are reduced to verifying whether
![]() $\textrm{Ind}_{D}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
$\textrm{Ind}_{D}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
. In all cases of
$\mathfrak{A}_{K/\mathbb{Q},p}$
. In all cases of
![]() $G\cong A_4$
with predicted non-freeness of
$G\cong A_4$
with predicted non-freeness of
![]() $\mathcal{O}_K$
over
$\mathcal{O}_K$
over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
, we can reduce to the case in which
$\mathfrak{A}_{K/\mathbb{Q}}$
, we can reduce to the case in which
![]() $D$
is normal in
$D$
is normal in
![]() $G$
and abelian, hence apply Theorem 7.4(v). We call this method ‘the theoretical freeness method’; this can also be applied to some cases when
$G$
and abelian, hence apply Theorem 7.4(v). We call this method ‘the theoretical freeness method’; this can also be applied to some cases when
![]() $G\cong S_4$
.
$G\cong S_4$
.
When the above strategy cannot be followed, the structure of
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
allows us to construct both
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
allows us to construct both
![]() $\textrm{Ind}_{D}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and
$\textrm{Ind}_{D}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
in Magma. Hofmann and Johnston [Reference Hofmann and Johnston18, §8.5] described the implementation of an algorithm in Magma that, given a finite group
$\mathfrak{A}_{K/\mathbb{Q},p}$
in Magma. Hofmann and Johnston [Reference Hofmann and Johnston18, §8.5] described the implementation of an algorithm in Magma that, given a finite group
![]() $\Gamma$
, a rational prime
$\Gamma$
, a rational prime
![]() $p$
, and
$p$
, and
![]() $\mathbb{Z}[\Gamma ]$
-lattices
$\mathbb{Z}[\Gamma ]$
-lattices
![]() $X$
and
$X$
and
![]() $Y$
contained in
$Y$
contained in
![]() $\mathbb{Q}[\Gamma ]$
, determines whether the localisations
$\mathbb{Q}[\Gamma ]$
, determines whether the localisations
![]() $X_{p}$
and
$X_{p}$
and
![]() $Y_{p}$
are isomorphic over
$Y_{p}$
are isomorphic over
![]() $\mathbb{Z}_{(p)}[\Gamma ]$
. Note that by [Reference Curtis and Reiner9, Proposition (30.17)], this is equivalent to checking whether the
$\mathbb{Z}_{(p)}[\Gamma ]$
. Note that by [Reference Curtis and Reiner9, Proposition (30.17)], this is equivalent to checking whether the
![]() $p$
-adic completions are isomorphic over
$p$
-adic completions are isomorphic over
![]() $\mathbb{Z}_{p}[\Gamma ]$
. In present situation, we are interested in understanding whether
$\mathbb{Z}_{p}[\Gamma ]$
. In present situation, we are interested in understanding whether
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over its associated order
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over its associated order
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
. By Lemma 2.1 this condition is equivalent to
$\mathfrak{A}_{K/\mathbb{Q},p}$
. By Lemma 2.1 this condition is equivalent to
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
being isomorphic to
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
being isomorphic to
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
as
$\mathfrak{A}_{K/\mathbb{Q},p}$
as
![]() $\mathbb{Z}_p[G]$
-lattices. Since both lattices will be of the form
$\mathbb{Z}_p[G]$
-lattices. Since both lattices will be of the form
![]() $\mathbb{Z}_p[G]+\frac{1}{p^{n_1}}\mathbb{Z}_p[G]\textrm{Tr}_{H_1}+\cdots +\frac{1}{p^{n_k}}\mathbb{Z}_p[G]\textrm{Tr}_{H_k}$
, which is the completion of
$\mathbb{Z}_p[G]+\frac{1}{p^{n_1}}\mathbb{Z}_p[G]\textrm{Tr}_{H_1}+\cdots +\frac{1}{p^{n_k}}\mathbb{Z}_p[G]\textrm{Tr}_{H_k}$
, which is the completion of
![]() $\mathbb{Z}[G]+\frac{1}{p^{n_1}}\mathbb{Z}[G]\textrm{Tr}_{H_1}+\cdots +\frac{1}{p^{n_k}}\mathbb{Z}[G]\textrm{Tr}_{H_k}$
, the aforementioned algorithm will tell us if
$\mathbb{Z}[G]+\frac{1}{p^{n_1}}\mathbb{Z}[G]\textrm{Tr}_{H_1}+\cdots +\frac{1}{p^{n_k}}\mathbb{Z}[G]\textrm{Tr}_{H_k}$
, the aforementioned algorithm will tell us if
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
. We call this method ‘the algorithmic freeness method’.
$\mathfrak{A}_{K/\mathbb{Q},p}$
. We call this method ‘the algorithmic freeness method’.
With both freeness methods we will mostly find that
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is not free over
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
, that is,
$\mathfrak{A}_{K/\mathbb{Q},p}$
, that is,
![]() $p$
is a decomposition obstruction for
$p$
is a decomposition obstruction for
![]() $K$
.
$K$
.
Notation. Let
![]() $G$
be a finite group, let
$G$
be a finite group, let
![]() $H_1,\dots, H_k$
be subgroups of
$H_1,\dots, H_k$
be subgroups of
![]() $G$
and let
$G$
and let
![]() $n_1,\cdots, n_k$
be integers. We will denote by
$n_1,\cdots, n_k$
be integers. We will denote by
![]() $\langle 1,\frac{1}{p^{n_1}}\textrm{Tr}_{H_1},\cdots,\frac{1}{p^{n_k}}\textrm{Tr}_{H_k}\rangle _G^p$
the lattice
$\langle 1,\frac{1}{p^{n_1}}\textrm{Tr}_{H_1},\cdots,\frac{1}{p^{n_k}}\textrm{Tr}_{H_k}\rangle _G^p$
the lattice
8.1. Galois module structure of
 $A_4$
-extensions of
$A_4$
-extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
In this subsection, we shall prove the following result, which is Theorem 1.7 stated in the introduction.
Theorem 8.1.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q})\cong A_4$
. Then,
$\textrm{Gal}(K/\mathbb{Q})\cong A_4$
. Then,
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $2$
is tamely ramified or has full decomposition group.
$2$
is tamely ramified or has full decomposition group.
Remark 8.2.
After considering computational evidence, in [
Reference Bley and Johnston5, §8] the authors raised the question of whether it is always the case that
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
for every
$\mathfrak{A}_{K/\mathbb{Q}}$
for every
![]() $A_{4}$
-extension
$A_{4}$
-extension
![]() $K/\mathbb{Q}$
. Theorem 8.1 shows that this is false. Indeed, one can use the database of number fields [30] to verify that every possible decomposition group of
$K/\mathbb{Q}$
. Theorem 8.1 shows that this is false. Indeed, one can use the database of number fields [30] to verify that every possible decomposition group of
![]() $2$
of even order can be realised by an
$2$
of even order can be realised by an
![]() $A_4$
-extension
$A_4$
-extension
![]() $K/\mathbb{Q}$
in which
$K/\mathbb{Q}$
in which
![]() $2$
is wildly ramified.
$2$
is wildly ramified.
Proof of Theorem 8.1. We already showed the ‘if’ direction in Proposition 4.12. Now we prove that if
![]() $2$
is wildly ramified in
$2$
is wildly ramified in
![]() $K/\mathbb{Q}$
and does not have full decomposition group then
$K/\mathbb{Q}$
and does not have full decomposition group then
![]() $\mathcal{O}_{K}$
is not (locally) free (at
$\mathcal{O}_{K}$
is not (locally) free (at
![]() $2$
) over
$2$
) over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
. Let
$\mathfrak{A}_{K/\mathbb{Q}}$
. Let
![]() $V_4$
denote the unique normal subgroup of
$V_4$
denote the unique normal subgroup of
![]() $G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})\cong A_{4}$
of order
$G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})\cong A_{4}$
of order
![]() $4$
, which is isomorphic to
$4$
, which is isomorphic to
![]() $C_{2} \times C_{2}$
. Recall that
$C_{2} \times C_{2}$
. Recall that
![]() $A_{4} \cong V_{4} \rtimes C_{3}$
and we have the following lattice of the subgroups of
$A_{4} \cong V_{4} \rtimes C_{3}$
and we have the following lattice of the subgroups of
![]() $A_4$
up to conjugacy (see, for instance, the GroupNames database [Reference Dokchitser11]).
$A_4$
up to conjugacy (see, for instance, the GroupNames database [Reference Dokchitser11]).

Here the subscript on the left denotes the number of conjugate subgroups and is taken to be
![]() $1$
when omitted (so that the subgroup is normal).
$1$
when omitted (so that the subgroup is normal).
Let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $K$
above
$K$
above
![]() $2$
, let
$2$
, let
![]() $D=D(\mathfrak{P}|2)$
be the decomposition group and let
$D=D(\mathfrak{P}|2)$
be the decomposition group and let
![]() $G_0=G_0(\mathfrak{P}|2)$
be the inertia group of
$G_0=G_0(\mathfrak{P}|2)$
be the inertia group of
![]() $K/\mathbb{Q}$
. Since
$K/\mathbb{Q}$
. Since
![]() $2$
is wildly ramified,
$2$
is wildly ramified,
![]() $D$
has even order. Thus, since
$D$
has even order. Thus, since
![]() $D$
is a proper subgroup of
$D$
is a proper subgroup of
![]() $G$
, the subgroup lattice implies that either
$G$
, the subgroup lattice implies that either
![]() $D=V_4$
or
$D=V_4$
or
![]() $D \cong C_2$
. More precisely, there are three possibilities for the pair
$D \cong C_2$
. More precisely, there are three possibilities for the pair
![]() $(D,G_0)$
up to isomorphism:
$(D,G_0)$
up to isomorphism:
![]() $(V_{4},V_{4})$
,
$(V_{4},V_{4})$
,
![]() $(V_{4},C_{2})$
and
$(V_{4},C_{2})$
and
![]() $(C_{2},C_{2})$
. Since
$(C_{2},C_{2})$
. Since
![]() $D$
is abelian in each of these cases, we have that
$D$
is abelian in each of these cases, we have that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
by Theorem 3.3. Thus by Proposition 6.5 we have that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
by Theorem 3.3. Thus by Proposition 6.5 we have that
![]() $\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2} \cong \textrm{Ind}_{D}^{G} \mathcal{O}_{K_{\mathfrak{P}}} \cong \mathcal{O}_{K,2}$
as
$\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2} \cong \textrm{Ind}_{D}^{G} \mathcal{O}_{K_{\mathfrak{P}}} \cong \mathcal{O}_{K,2}$
as
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
-lattices. Therefore, it suffices to show that
$\mathfrak{A}_{K/\mathbb{Q},2}$
-lattices. Therefore, it suffices to show that
![]() $\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
$\textrm{Ind}_{D}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
in each of the three cases; in other words, we will show that
$\mathfrak{A}_{K/\mathbb{Q},2}$
in each of the three cases; in other words, we will show that
![]() $2$
is a decomposition obstruction for
$2$
is a decomposition obstruction for
![]() $K$
. We will apply the ‘theoretical freeness method’ in all cases.
$K$
. We will apply the ‘theoretical freeness method’ in all cases.
First suppose that
![]() $D=G_{0}=V_{4}$
. Then from the database of
$D=G_{0}=V_{4}$
. Then from the database of
![]() $p$
-adic fields [Reference Jones and Roberts24], we see that there are four possible extensions
$p$
-adic fields [Reference Jones and Roberts24], we see that there are four possible extensions
![]() $K_{\mathfrak{P}}/\mathbb{Q}_{2}$
, each of which has
$K_{\mathfrak{P}}/\mathbb{Q}_{2}$
, each of which has
![]() $1$
and
$1$
and
![]() $3$
as (lower) ramification jumps. Let
$3$
as (lower) ramification jumps. Let
![]() $F$
denote the subfield of
$F$
denote the subfield of
![]() $K_{\mathfrak{P}}$
fixed by
$K_{\mathfrak{P}}$
fixed by
![]() $G_{2}$
. Then by Remark 3.12, we have
$G_{2}$
. Then by Remark 3.12, we have
![]() $e_{G_2} \in \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
since
$e_{G_2} \in \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
since
Similarly, we have
![]() $e_{V_4}=e_{G_1} \in \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
since
$e_{V_4}=e_{G_1} \in \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_{2}}$
since
Thus,
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified, and so by Theorem 3.10(i) we have that
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified, and so by Theorem 3.10(i) we have that
Since
![]() $G_2\cong C_2$
is not normal in
$G_2\cong C_2$
is not normal in
![]() $G$
and
$G$
and
![]() $D$
is both abelian and normal in
$D$
is both abelian and normal in
![]() $G$
, Theorem 7.4(v) implies that
$G$
, Theorem 7.4(v) implies that
![]() $\textrm{Ind}_D^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
$\textrm{Ind}_D^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. Hence
$\mathfrak{A}_{K/\mathbb{Q},2}$
. Hence
![]() $\mathcal{O}_{K,2}$
is not free over
$\mathcal{O}_{K,2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. As an aside, using Theorem 7.4(i) and (ii) and the fact that
$\mathfrak{A}_{K/\mathbb{Q},2}$
. As an aside, using Theorem 7.4(i) and (ii) and the fact that
![]() $\textrm{ncl}_G(G_2)=V_4$
, we note that in this case we have
$\textrm{ncl}_G(G_2)=V_4$
, we note that in this case we have
Now suppose that
![]() $D=V_4$
and
$D=V_4$
and
![]() $G_{0} \cong C_{2}$
. Since
$G_{0} \cong C_{2}$
. Since
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
![]() $G_{0}=G_{1}$
is not dihedral of order
$G_{0}=G_{1}$
is not dihedral of order
![]() $4$
, Theorem 3.10 implies that
$4$
, Theorem 3.10 implies that
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\mathbb{Z}_2[D][e_{G_0}]=\langle 1,\frac{1}{2}\textrm{Tr}_{G_0}\rangle _D^2$
. (Alternatively, we can use the database of
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\mathbb{Z}_2[D][e_{G_0}]=\langle 1,\frac{1}{2}\textrm{Tr}_{G_0}\rangle _D^2$
. (Alternatively, we can use the database of
![]() $p$
-adic fields [Reference Jones and Roberts24] to check for almost-maximal ramification as in the previous case; the ramification jump turns out to be
$p$
-adic fields [Reference Jones and Roberts24] to check for almost-maximal ramification as in the previous case; the ramification jump turns out to be
![]() $1$
or
$1$
or
![]() $2$
). Since
$2$
). Since
![]() $D$
is both abelian and normal in
$D$
is both abelian and normal in
![]() $G$
and
$G$
and
![]() $G_{0}$
is not normal in
$G_{0}$
is not normal in
![]() $G$
, Theorem 7.1(v) implies that
$G$
, Theorem 7.1(v) implies that
![]() $\textrm{Ind}_D^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
$\textrm{Ind}_D^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. Hence,
$\mathfrak{A}_{K/\mathbb{Q},2}$
. Hence,
![]() $\mathcal{O}_{K,2}$
is not free over
$\mathcal{O}_{K,2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. Note that in the next paragraph, we shall use that
$\mathfrak{A}_{K/\mathbb{Q},2}$
. Note that in the next paragraph, we shall use that
which follows from Theorem 7.1(i) and (ii).
Finally, suppose
![]() $D=G_{0} \cong C_{2}$
. Then,
$D=G_{0} \cong C_{2}$
. Then,
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is a
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is a
![]() $\mathbb{Z}_2$
-order in
$\mathbb{Z}_2$
-order in
![]() $\mathbb{Q}_2[D]\cong \mathbb{Q}_2[C_2]$
strictly containing
$\mathbb{Q}_2[D]\cong \mathbb{Q}_2[C_2]$
strictly containing
![]() $\mathbb{Z}_2[D]$
. As there is only one such order, we must have
$\mathbb{Z}_2[D]$
. As there is only one such order, we must have
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_D\rangle _D^2$
. Since
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_D\rangle _D^2$
. Since
![]() $D$
is not normal in
$D$
is not normal in
![]() $G$
, we cannot directly apply Theorem 7.1(v) as in the previous cases. Instead, Theorem 7.1(i) and (ii) implies that
$G$
, we cannot directly apply Theorem 7.1(v) as in the previous cases. Instead, Theorem 7.1(i) and (ii) implies that
Once we fix a copy of
![]() $C_2$
inside
$C_2$
inside
![]() $G$
, note that
$G$
, note that
![]() $\textrm{Ind}_{D}^{G} \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
$\textrm{Ind}_{D}^{G} \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
are exactly the same as in the
$\mathfrak{A}_{K/\mathbb{Q},2}$
are exactly the same as in the
![]() $(V_{4},C_2)$
-case of the previous paragraph, where we already showed that
$(V_{4},C_2)$
-case of the previous paragraph, where we already showed that
![]() $\textrm{Ind}_{D}^{G} \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
$\textrm{Ind}_{D}^{G} \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. Therefore
$\mathfrak{A}_{K/\mathbb{Q},2}$
. Therefore
![]() $\mathcal{O}_{K,2}$
is not free over
$\mathcal{O}_{K,2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
.
$\mathfrak{A}_{K/\mathbb{Q},2}$
.
8.2. Galois module structure of
 $S_4$
-extensions of
$S_4$
-extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
In this subsection, we shall prove the following result, which is Theorem 1.8 stated in the introduction.
Theorem 8.3.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})\cong S_4$
. Then,
$G\;:\!=\;\textrm{Gal}(K/\mathbb{Q})\cong S_4$
. Then,
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if one of the following conditions on
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if one of the following conditions on
![]() $K/\mathbb{Q}$
holds:
$K/\mathbb{Q}$
holds:
-
(i)
 $2$
is tamely ramified;
$2$
is tamely ramified; -
(ii)
 $2$
has decomposition group equal to the unique subgroup of
$2$
has decomposition group equal to the unique subgroup of
 $G$
of order
$G$
of order
 $12$
;
$12$
; -
(iii)
 $2$
is wildly and weakly ramified and has full decomposition group; or
$2$
is wildly and weakly ramified and has full decomposition group; or -
(iv)
 $2$
is wildly and weakly ramified, has decomposition group of order
$2$
is wildly and weakly ramified, has decomposition group of order
 $8$
in
$8$
in
 $G$
, and has inertia subgroup equal to the unique normal subgroup of order
$G$
, and has inertia subgroup equal to the unique normal subgroup of order
 $4$
in
$4$
in
 $G$
.
$G$
.
Proof. By Proposition 4.10,
![]() $\mathcal{O}_K$
is free over
$\mathcal{O}_K$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $\mathcal{O}_{K,2}$
is free over
$\mathcal{O}_{K,2}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
.
$\mathfrak{A}_{K/\mathbb{Q},2}$
.
We first show that if any of conditions (i)–(iv) hold then
![]() $\mathcal{O}_{K,2}$
is free over
$\mathcal{O}_{K,2}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. In case (i), this follows from Theorem 3.14. In case (ii), Lemma 4.11 shows that
$\mathfrak{A}_{K/\mathbb{Q},2}$
. In case (i), this follows from Theorem 3.14. In case (ii), Lemma 4.11 shows that
![]() $2$
is wildly and weakly ramified in
$2$
is wildly and weakly ramified in
![]() $K/\mathbb{Q}$
and has inertia group equal to the unique normal subgroup of order
$K/\mathbb{Q}$
and has inertia group equal to the unique normal subgroup of order
![]() $4$
in
$4$
in
![]() $G$
(note that
$G$
(note that
![]() $A_{4}$
is the unique subgroup of
$A_{4}$
is the unique subgroup of
![]() $S_{4}$
of order
$S_{4}$
of order
![]() $12$
). Therefore in cases (ii), (iii) and (iv),
$12$
). Therefore in cases (ii), (iii) and (iv),
![]() $2$
is wildly and weakly ramified in
$2$
is wildly and weakly ramified in
![]() $K/\mathbb{Q}$
and its inertia group is normal in
$K/\mathbb{Q}$
and its inertia group is normal in
![]() $G$
, and so the desired result follows from Corollary 7.2(i).
$G$
, and so the desired result follows from Corollary 7.2(i).
It now remains to show that if we are not in any of the cases (i)–(iv) then
![]() $\mathcal{O}_{K,2}$
is not free over
$\mathcal{O}_{K,2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. We have the following lattice of the subgroups of
$\mathfrak{A}_{K/\mathbb{Q},2}$
. We have the following lattice of the subgroups of
![]() $S_4$
up to conjugacy (see, for instance, the GroupNames database [Reference Dokchitser11]).
$S_4$
up to conjugacy (see, for instance, the GroupNames database [Reference Dokchitser11]).

Here the subscript on the left denotes the number of conjugate subgroups and is taken to be
![]() $1$
when omitted (so that the subgroup is normal). In particular, the only normal subgroups are
$1$
when omitted (so that the subgroup is normal). In particular, the only normal subgroups are
![]() $C_{1}$
,
$C_{1}$
,
![]() $V_{4}$
,
$V_{4}$
,
![]() $A_{4}$
and
$A_{4}$
and
![]() $S_{4}$
. (Recall that
$S_{4}$
. (Recall that
![]() $V_{4} \cong C_{2} \times C_{2}$
.)
$V_{4} \cong C_{2} \times C_{2}$
.)
We fix an isomorphism
![]() $G\;:\!=\;\textrm{Gal}(K/\mathbb{Q}) \cong S_{4}$
and denote by
$G\;:\!=\;\textrm{Gal}(K/\mathbb{Q}) \cong S_{4}$
and denote by
![]() $A_4$
,
$A_4$
,
![]() $D_{8}$
,
$D_{8}$
,
![]() $S_{3}$
,
$S_{3}$
,
![]() $C_{2}^{2}$
,
$C_{2}^{2}$
,
![]() $V_{4}$
,
$V_{4}$
,
![]() $C_{4}$
a choice of subgroups of
$C_{4}$
a choice of subgroups of
![]() $G$
in such a way that whenever there is a containment between choices of conjugates of two such subgroups, one of the subgroups is in fact contained in the other.
$G$
in such a way that whenever there is a containment between choices of conjugates of two such subgroups, one of the subgroups is in fact contained in the other.
Suppose that
![]() $K/\mathbb{Q}$
does not satisfy any of the conditions (i)–(iv). Let
$K/\mathbb{Q}$
does not satisfy any of the conditions (i)–(iv). Let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $K$
above
$K$
above
![]() $2$
and let
$2$
and let
![]() $D=D(\mathfrak{P}|2)$
be the decomposition group. In particular,
$D=D(\mathfrak{P}|2)$
be the decomposition group. In particular,
![]() $2$
is wildly ramified in
$2$
is wildly ramified in
![]() $K/\mathbb{Q}$
and so
$K/\mathbb{Q}$
and so
![]() $D$
must be of even order. We cannot have
$D$
must be of even order. We cannot have
![]() $D=A_{4}$
as this corresponds to case (ii). Moreover, we cannot have
$D=A_{4}$
as this corresponds to case (ii). Moreover, we cannot have
![]() $D=S_{3}$
since the subgroups of
$D=S_{3}$
since the subgroups of
![]() $D$
of order
$D$
of order
![]() $2$
are not normal, but the wild inertia subgroup
$2$
are not normal, but the wild inertia subgroup
![]() $G_{1}$
must be normal in
$G_{1}$
must be normal in
![]() $D$
.
$D$
.
We will start by applying the ‘non-freeness method’ in those cases in which
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
. By Theorem 3.3, we are in the case in which
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
. By Theorem 3.3, we are in the case in which
![]() $D$
is not abelian. Suppose that
$D$
is not abelian. Suppose that
![]() $D=S_{4}$
. Since we are not in case (iii), this implies that
$D=S_{4}$
. Since we are not in case (iii), this implies that
![]() $2$
is wildly but not weakly ramified in
$2$
is wildly but not weakly ramified in
![]() $K/\mathbb{Q}$
. From the database of
$K/\mathbb{Q}$
. From the database of
![]() $p$
-adic fields [Reference Jones and Roberts24], we see that there are four possibilities for the completed extension
$p$
-adic fields [Reference Jones and Roberts24], we see that there are four possibilities for the completed extension
![]() $K_{\mathfrak{P}}/\mathbb{Q}_{2}$
. By using the updated Magma implementation of [Reference Bley and Johnston5, Algorithm 3.1(6)], which is based on that of [Reference Bley and Wilson7, §4.2], we can verify that
$K_{\mathfrak{P}}/\mathbb{Q}_{2}$
. By using the updated Magma implementation of [Reference Bley and Johnston5, Algorithm 3.1(6)], which is based on that of [Reference Bley and Wilson7, §4.2], we can verify that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in any of these cases (for the details on the implementation see Section A.1). Since the decomposition group is full, this immediately implies that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in any of these cases (for the details on the implementation see Section A.1). Since the decomposition group is full, this immediately implies that
![]() $\mathcal{O}_{K,2}$
is not free over
$\mathcal{O}_{K,2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
.
$\mathfrak{A}_{K/\mathbb{Q},2}$
.
Now suppose that
![]() $D\cong D_8$
; without loss of generality, we can and do assume that
$D\cong D_8$
; without loss of generality, we can and do assume that
![]() $D=D_8$
. Since we are assuming
$D=D_8$
. Since we are assuming
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, we have that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, we have that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is not projective over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not projective over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
by Theorem 3.10, and so
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
by Theorem 3.10, and so
![]() $\mathcal{O}_{K,2}$
is not free over
$\mathcal{O}_{K,2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
by Proposition 6.8. As an aside, by using the database [Reference Jones and Roberts24], Theorem 3.10 and Remark 3.12, it is straightforward to check that
$\mathfrak{A}_{K/\mathbb{Q},2}$
by Proposition 6.8. As an aside, by using the database [Reference Jones and Roberts24], Theorem 3.10 and Remark 3.12, it is straightforward to check that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
if and only if the ramification jumps of
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
if and only if the ramification jumps of
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
are
$K_{\mathfrak{P}}/\mathbb{Q}_2$
are
![]() $1$
,
$1$
,
![]() $3$
and
$3$
and
![]() $5$
.
$5$
.
Therefore in the remaining cases, we can and do assume that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, since either
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, since either
![]() $D$
is abelian (in which case we can apply Theorem 3.3) or
$D$
is abelian (in which case we can apply Theorem 3.3) or
![]() $D=D_{8}$
(in which case the situation in which
$D=D_{8}$
(in which case the situation in which
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is not free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
has already been considered in the previous paragraph). For these cases, we will apply the ‘algorithmic freeness method’. As we wish to show that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
has already been considered in the previous paragraph). For these cases, we will apply the ‘algorithmic freeness method’. As we wish to show that
![]() $\mathcal{O}_{K,2}$
is not free over
$\mathcal{O}_{K,2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
(so that
$\mathfrak{A}_{K/\mathbb{Q},2}$
(so that
![]() $2$
is a decomposition obstruction for
$2$
is a decomposition obstruction for
![]() $K$
), by Proposition 6.5 it suffices to show that
$K$
), by Proposition 6.5 it suffices to show that
![]() $\textrm{Ind}_D^G \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
$\textrm{Ind}_D^G \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. Our strategy will be to determine the possible ramification groups, use this to derive the explicit structure of
$\mathfrak{A}_{K/\mathbb{Q},2}$
. Our strategy will be to determine the possible ramification groups, use this to derive the explicit structure of
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and then apply Theorem 7.4(i) and (ii) to obtain explicit descriptions of
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and then apply Theorem 7.4(i) and (ii) to obtain explicit descriptions of
![]() $\textrm{Ind}_D^G \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
$\textrm{Ind}_D^G \mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
, which will be listed in Table 1 below. For instance, if
$\mathfrak{A}_{K/\mathbb{Q},2}$
, which will be listed in Table 1 below. For instance, if
![]() $D=D_8$
and
$D=D_8$
and
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{V_2},\frac{1}{4}\textrm{Tr}_{C_4},\frac{1}{8}\textrm{Tr}_{D_8}\rangle _{D_8}^2$
(where
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{V_2},\frac{1}{4}\textrm{Tr}_{C_4},\frac{1}{8}\textrm{Tr}_{D_8}\rangle _{D_8}^2$
(where
![]() $V_2$
is the subgroup of
$V_2$
is the subgroup of
![]() $C_4$
of order
$C_4$
of order
![]() $2$
), then by Theorem 7.4(i) the same groups will appear in
$2$
), then by Theorem 7.4(i) the same groups will appear in
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, so that
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, so that
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{V_2},\frac{1}{4}\textrm{Tr}_{C_4},\frac{1}{8}\textrm{Tr}_{D_8}\rangle _{G}^2$
. The normal closure of
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{V_2},\frac{1}{4}\textrm{Tr}_{C_4},\frac{1}{8}\textrm{Tr}_{D_8}\rangle _{G}^2$
. The normal closure of
![]() $C_4$
and
$C_4$
and
![]() $D_8$
in
$D_8$
in
![]() $G$
is
$G$
is
![]() $G$
, while the normal closure of
$G$
, while the normal closure of
![]() $V_2$
is
$V_2$
is
![]() $V_4$
; by Theorem 7.4(ii), this tells us that
$V_4$
; by Theorem 7.4(ii), this tells us that
![]() $\mathfrak{A}_{K/\mathbb{Q},2}=\langle 1,\frac{1}{2}\textrm{Tr}_{V_4},\frac{1}{8}\textrm{Tr}_{G}\rangle _G^2$
(in fact, this will be entry (1) of Table 1).
$\mathfrak{A}_{K/\mathbb{Q},2}=\langle 1,\frac{1}{2}\textrm{Tr}_{V_4},\frac{1}{8}\textrm{Tr}_{G}\rangle _G^2$
(in fact, this will be entry (1) of Table 1).
We first consider the case
![]() $D=D_{8}$
. We have the following subgroup lattice.
$D=D_{8}$
. We have the following subgroup lattice.

Note that
![]() $D_{8}$
has a unique normal subgroup of order
$D_{8}$
has a unique normal subgroup of order
![]() $2$
, which we denoted by
$2$
, which we denoted by
![]() $V_{2}$
, and, as a subgroup of
$V_{2}$
, and, as a subgroup of
![]() $S_{4}$
, this is generated by a double transposition and contained in
$S_{4}$
, this is generated by a double transposition and contained in
![]() $C_4$
. (Also note that under
$C_4$
. (Also note that under
![]() $D_8$
-conjugation we have three conjugacy classes of subgroups of order
$D_8$
-conjugation we have three conjugacy classes of subgroups of order
![]() $2$
compared to two in the
$2$
compared to two in the
![]() $S_4$
-lattice).
$S_4$
-lattice).
We now find
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
using Theorem 3.10, which determines the structure of the associated order depending upon whether
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
using Theorem 3.10, which determines the structure of the associated order depending upon whether
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified or not. We recall we are assuming
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified or not. We recall we are assuming
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
. Suppose that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
. Suppose that
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified. Then by Theorem 3.10(i), we have
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified. Then by Theorem 3.10(i), we have
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\mathbb{Z}_2[D]+\sum _{t\geq 1}\frac{1}{|G_t|}\mathbb{Z}_2[D]\textrm{Tr}_{G_t}$
and all quotients of two consecutive different ramification groups are of order
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\mathbb{Z}_2[D]+\sum _{t\geq 1}\frac{1}{|G_t|}\mathbb{Z}_2[D]\textrm{Tr}_{G_t}$
and all quotients of two consecutive different ramification groups are of order
![]() $2$
(see the database [Reference Jones and Roberts24], for example). We have that
$2$
(see the database [Reference Jones and Roberts24], for example). We have that
![]() $V_2$
must be among the ramification groups since they are all normal in
$V_2$
must be among the ramification groups since they are all normal in
![]() $D_{8}$
. Thus if the ramification index of
$D_{8}$
. Thus if the ramification index of
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is 2, then
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is 2, then
![]() $V_2$
is the unique ramification group. Otherwise, there is a ramification group of order
$V_2$
is the unique ramification group. Otherwise, there is a ramification group of order
![]() $4$
, which must be one of
$4$
, which must be one of
![]() $V_4$
,
$V_4$
,
![]() $C_2^2$
or
$C_2^2$
or
![]() $C_4$
. Moreover,
$C_4$
. Moreover,
![]() $D_8$
is a ramification group if and only if the ramification index of
$D_8$
is a ramification group if and only if the ramification index of
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is
![]() $8$
. This case contributes to entries (1), (2), (3), (4), (5), (6) and (9) of Table 1.
$8$
. This case contributes to entries (1), (2), (3), (4), (5), (6) and (9) of Table 1.
Suppose that
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is not almost-maximally ramified. Then by Theorem 3.10(ii), we deduce that
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is not almost-maximally ramified. Then by Theorem 3.10(ii), we deduce that
![]() $G_0\cong C_2^2$
and
$G_0\cong C_2^2$
and
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{G_0}\rangle _G^2$
. Moreover, by Remark 3.12 we must have that
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{G_0}\rangle _G^2$
. Moreover, by Remark 3.12 we must have that
![]() $G_2=\{1\}$
or
$G_2=\{1\}$
or
![]() $G_2\cong C_2$
and
$G_2\cong C_2$
and
![]() $G_3=\{1\}$
, but in the latter case the upper ramification jumps are not integral, which is not possible by Hasse-Arf theorem (alternatively, just use the database [Reference Jones and Roberts24]); hence,
$G_3=\{1\}$
, but in the latter case the upper ramification jumps are not integral, which is not possible by Hasse-Arf theorem (alternatively, just use the database [Reference Jones and Roberts24]); hence,
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is weakly ramified. Note that
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is weakly ramified. Note that
![]() $G_0$
is not equal to
$G_0$
is not equal to
![]() $V_4$
; otherwise, we are in case (iv) of the statement of Theorem 8.3; hence, we can assume
$V_4$
; otherwise, we are in case (iv) of the statement of Theorem 8.3; hence, we can assume
![]() $G_0=C_2^2$
. This contributes to entry (8) of Table 1.
$G_0=C_2^2$
. This contributes to entry (8) of Table 1.
Now suppose that
![]() $D\cong C_4$
; without loss of generality, we can and do assume that
$D\cong C_4$
; without loss of generality, we can and do assume that
![]() $D=C_{4}$
. If the ramification index of
$D=C_{4}$
. If the ramification index of
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is
![]() $2$
, then
$2$
, then
![]() $G_0=V_2$
and by Remark 3.12
$G_0=V_2$
and by Remark 3.12
![]() $K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified, and hence
$K_{\mathfrak{P}}/\mathbb{Q}_2$
is almost-maximally ramified, and hence
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{G_0}\rangle _D^2$
(see [Reference Bergé3, Corollaire 3 to Théorème 1], for example), which contributes to entry (9) of Table 1. If the ramification index is
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}=\langle 1,\frac{1}{2}\textrm{Tr}_{G_0}\rangle _D^2$
(see [Reference Bergé3, Corollaire 3 to Théorème 1], for example), which contributes to entry (9) of Table 1. If the ramification index is
![]() $4$
, then there must be two ramification jumps; since the upper ramification jumps are integral, Remark 3.12 implies that the extension is almost-maximally ramified and so
$4$
, then there must be two ramification jumps; since the upper ramification jumps are integral, Remark 3.12 implies that the extension is almost-maximally ramified and so
![]() $\frac{1}{2}\textrm{Tr}_{V_2}$
and
$\frac{1}{2}\textrm{Tr}_{V_2}$
and
![]() $\frac{1}{4}\textrm{Tr}_{D}$
belong to
$\frac{1}{4}\textrm{Tr}_{D}$
belong to
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
. Hence
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
. Hence
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2} = \langle 1,\frac{1}{2}\textrm{Tr}_{V_2},\frac{1}{4}\textrm{Tr}_{D}\rangle _D^2$
, where the containment ‘
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2} = \langle 1,\frac{1}{2}\textrm{Tr}_{V_2},\frac{1}{4}\textrm{Tr}_{D}\rangle _D^2$
, where the containment ‘
![]() $\subseteq$
’ follows from the fact that the right-hand side is the unique maximal order in
$\subseteq$
’ follows from the fact that the right-hand side is the unique maximal order in
![]() $\mathbb{Q}_2[D]$
(see [Reference Bergé3, Proposition 5], for example). This corresponds to entry (4) of Table 1.
$\mathbb{Q}_2[D]$
(see [Reference Bergé3, Proposition 5], for example). This corresponds to entry (4) of Table 1.
Finally, in the cases
![]() $D\cong C_2^2$
or
$D\cong C_2^2$
or
![]() $D\cong C_2$
, we already computed
$D\cong C_2$
, we already computed
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in the proof of Theorem 8.1. Note that in the present proof and notation the case
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in the proof of Theorem 8.1. Note that in the present proof and notation the case
![]() $D\cong C_2^2$
corresponds to either
$D\cong C_2^2$
corresponds to either
![]() $D=V_4$
(which contributes to entry (5) of Table 1) or
$D=V_4$
(which contributes to entry (5) of Table 1) or
![]() $D=C_2^2$
(entries (6) and (7), where we denote by
$D=C_2^2$
(entries (6) and (7), where we denote by
![]() $W_2$
a choice of a subgroup of
$W_2$
a choice of a subgroup of
![]() $S_4$
generated by a transposition and contained in
$S_4$
generated by a transposition and contained in
![]() $D_8$
). The case
$D_8$
). The case
![]() $D\cong C_2$
corresponds to
$D\cong C_2$
corresponds to
![]() $D=V_2$
(entry (9)) or
$D=V_2$
(entry (9)) or
![]() $D=W_2$
(entry (10)).
$D=W_2$
(entry (10)).
Table 1. Local freeness at 2 in
![]() $S_4$
-extensions.
$S_4$
-extensions.

As anticipated, all the possible values of
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
are listed in Table 1.
$\mathfrak{A}_{K/\mathbb{Q},2}$
are listed in Table 1.
We conclude the application of the ‘algorithmic freeness method’ by using the algorithm [Reference Hofmann and Johnston18, §8.5], as explained in the overview at the beginning of this section. We find that
![]() $\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
$\textrm{Ind}_D^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is not free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
in each of the ten cases in Table 1 (for the implementation see Section A.2).
$\mathfrak{A}_{K/\mathbb{Q},2}$
in each of the ten cases in Table 1 (for the implementation see Section A.2).
Remark 8.4. In some of the cases, we can apply the ‘theoretical freeness method’: cases (5) and (9) from Table 1 can be tackled using Theorem 7.4 (v) and cases (7) and (10) using Theorem 7.4 (v) combined with Proposition 6.8 . More precisely:
-
• for (5) we apply Theorem 7.4 (v) with
 $H=V_4$
and
$H=V_4$
and
 $G=S_4$
;
$G=S_4$
; -
• for (7) we apply Theorem 7.4 (v) with
 $H=C_2^2$
and
$H=C_2^2$
and
 $G=D_8$
and Proposition 6.8 inducing from
$G=D_8$
and Proposition 6.8 inducing from
 $D_8$
to
$D_8$
to
 $\textrm{Gal}(K/\mathbb{Q})\cong S_4$
;
$\textrm{Gal}(K/\mathbb{Q})\cong S_4$
; -
• for (9) we apply Theorem 7.4 (v) with
 $H=V_4$
and
$H=V_4$
and
 $G=S_4$
;
$G=S_4$
; -
• for (10) we apply Theorem 7.4 (v) with
 $H=W_2$
and
$H=W_2$
and
 $G=D_8$
and Proposition 6.8 inducing from
$G=D_8$
and Proposition 6.8 inducing from
 $D_8$
to
$D_8$
to
 $\textrm{Gal}(K/\mathbb{Q})\cong S_4$
.
$\textrm{Gal}(K/\mathbb{Q})\cong S_4$
.
Note that here
![]() $G$
is not necessarily the Galois group and
$G$
is not necessarily the Galois group and
![]() $H$
is not necessarily one of the decomposition groups.
$H$
is not necessarily one of the decomposition groups.
Remark 8.5.
The computations in the proof of Theorem 8.3 show that each of the lattices considered is free over its associated order if and only if the lattice is a ring if and only if the lattice is equal to its associated order. However, with the algorithm of [
Reference Hofmann and Johnston18, §8.5] we found that
![]() $\langle 1,\frac{1}{4}\textrm{Tr}_{V_4},\frac{1}{8}\textrm{Tr}_{D_8}\rangle _G^2$
is free over
$\langle 1,\frac{1}{4}\textrm{Tr}_{V_4},\frac{1}{8}\textrm{Tr}_{D_8}\rangle _G^2$
is free over
![]() $\langle 1,\frac{1}{4}\textrm{Tr}_{V_4},\frac{1}{8}\textrm{Tr}_{G}\rangle _G^2$
(see Section A.2 for the implementation).
$\langle 1,\frac{1}{4}\textrm{Tr}_{V_4},\frac{1}{8}\textrm{Tr}_{G}\rangle _G^2$
(see Section A.2 for the implementation).
8.3. Galois module structure of
 $A_5$
-extensions of
$A_5$
-extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
In this subsection, we shall prove the following result, which is Theorem 1.9 stated in the introduction.
Theorem 8.6.
Let
![]() $K/\mathbb{Q}$
be a Galois extension with
$K/\mathbb{Q}$
be a Galois extension with
![]() $\textrm{Gal}(K/\mathbb{Q}) \cong A_{5}$
. Then,
$\textrm{Gal}(K/\mathbb{Q}) \cong A_{5}$
. Then,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if all three of the following conditions on
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if all three of the following conditions on
![]() $K/\mathbb{Q}$
hold:
$K/\mathbb{Q}$
hold:
-
(i)
 $2$
is tamely ramified;
$2$
is tamely ramified; -
(ii)
 $3$
is tamely ramified or is weakly ramified with ramification index
$3$
is tamely ramified or is weakly ramified with ramification index
 $6$
; and
$6$
; and -
(iii)
 $5$
is tamely ramified or is weakly ramified with ramification index
$5$
is tamely ramified or is weakly ramified with ramification index
 $10$
.
$10$
.
Proof of Theorem 8.6. By Corollary 2.7,
![]() $\mathcal{O}_{K}$
is free over
$\mathcal{O}_{K}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
$\mathfrak{A}_{K/\mathbb{Q}}$
if and only if
![]() $\mathcal{O}_{K,p}$
is free over
$\mathcal{O}_{K,p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
for every rational prime
$\mathfrak{A}_{K/\mathbb{Q},p}$
for every rational prime
![]() $p$
. If
$p$
. If
![]() $p$
is tamely ramified in
$p$
is tamely ramified in
![]() $K/\mathbb{Q}$
then
$K/\mathbb{Q}$
then
![]() $\mathcal{O}_{K,p}$
is indeed free over
$\mathcal{O}_{K,p}$
is indeed free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
by Theorem 3.14. Thus, it remains to consider the situation in which at least one of the primes
$\mathfrak{A}_{K/\mathbb{Q},p}$
by Theorem 3.14. Thus, it remains to consider the situation in which at least one of the primes
![]() $p=2,3,5$
is wildly ramified in
$p=2,3,5$
is wildly ramified in
![]() $K/\mathbb{Q}$
.
$K/\mathbb{Q}$
.
We have the following lattice of the subgroups of
![]() $A_{5}$
up to conjugacy (see, for instance, the GroupNames database [Reference Dokchitser11]).
$A_{5}$
up to conjugacy (see, for instance, the GroupNames database [Reference Dokchitser11]).

Here the subscript on the left denotes the number of conjugate subgroups. Recall that
![]() $A_{5}$
is simple and note that the subgroup lattice shows that isomorphic subgroups must be conjugate. Moreover, since
$A_{5}$
is simple and note that the subgroup lattice shows that isomorphic subgroups must be conjugate. Moreover, since
![]() $A_5$
is not soluble, no prime can have full decomposition group. We fix an isomorphism
$A_5$
is not soluble, no prime can have full decomposition group. We fix an isomorphism
![]() $G\;:\!=\;\textrm{Gal}(K/\mathbb{Q}) \cong A_{5}$
and denote by
$G\;:\!=\;\textrm{Gal}(K/\mathbb{Q}) \cong A_{5}$
and denote by
![]() $A_4$
,
$A_4$
,
![]() $D_{10}$
etc. a choice of subgroups of
$D_{10}$
etc. a choice of subgroups of
![]() $G$
in such a way that whenever there is a containment between choices of conjugates of two such subgroups, one of the subgroups is in fact contained in the other.
$G$
in such a way that whenever there is a containment between choices of conjugates of two such subgroups, one of the subgroups is in fact contained in the other.
Suppose that
![]() $p=2$
is wildly ramified in
$p=2$
is wildly ramified in
![]() $K/\mathbb{Q}$
. Let
$K/\mathbb{Q}$
. Let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $K$
above
$K$
above
![]() $2$
and let
$2$
and let
![]() $D(2)$
be its decomposition group. Then,
$D(2)$
be its decomposition group. Then,
![]() $D(2)$
must be isomorphic to
$D(2)$
must be isomorphic to
![]() $A_{4}$
,
$A_{4}$
,
![]() $C_{2}^{2}$
or
$C_{2}^{2}$
or
![]() $C_{2}$
, since for every other subgroup
$C_{2}$
, since for every other subgroup
![]() $H$
of
$H$
of
![]() $A_5$
there is no normal non-trivial
$A_5$
there is no normal non-trivial
![]() $2$
-subgroup in
$2$
-subgroup in
![]() $H$
. Hence in each of these cases
$H$
. Hence in each of these cases
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
(if
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
(if
![]() $D(2)=A_4$
, this follows from Lemma 4.11 and Theorem 3.9; otherwise, this follows from Theorem 3.3). We will apply the ‘algorithmic freeness method’ for every such case. By Proposition 6.5,
$D(2)=A_4$
, this follows from Lemma 4.11 and Theorem 3.9; otherwise, this follows from Theorem 3.3). We will apply the ‘algorithmic freeness method’ for every such case. By Proposition 6.5,
![]() $\textrm{Ind}_{D(2)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2} \cong \textrm{Ind}_{D(2)}^{G} \mathcal{O}_{K_{\mathfrak{P}}} \cong \mathcal{O}_{K,2}$
as
$\textrm{Ind}_{D(2)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2} \cong \textrm{Ind}_{D(2)}^{G} \mathcal{O}_{K_{\mathfrak{P}}} \cong \mathcal{O}_{K,2}$
as
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
-lattices. Thus we need to analyse when
$\mathfrak{A}_{K/\mathbb{Q},2}$
-lattices. Thus we need to analyse when
![]() $\textrm{Ind}_{D(2)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is free over
$\textrm{Ind}_{D(2)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
. Note that, by Lemma 4.11, Theorem 3.9 and Theorem 7.1(i), the structure of
$\mathfrak{A}_{K/\mathbb{Q},2}$
. Note that, by Lemma 4.11, Theorem 3.9 and Theorem 7.1(i), the structure of
![]() $\textrm{Ind}_{D(2)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in the case
$\textrm{Ind}_{D(2)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in the case
![]() $D(2)=A_4$
is covered by the proof of Theorem 8.1. Hence, in each of the aforementioned possibilities for
$D(2)=A_4$
is covered by the proof of Theorem 8.1. Hence, in each of the aforementioned possibilities for
![]() $D(2)$
, we already know
$D(2)$
, we already know
![]() $\textrm{Ind}_{D(2)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
$\textrm{Ind}_{D(2)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
and
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
from the proof of Theorem 8.1, using Theorem 7.4(i) and (ii). The results are shown in Table 2.
$\mathfrak{A}_{K/\mathbb{Q},2}$
from the proof of Theorem 8.1, using Theorem 7.4(i) and (ii). The results are shown in Table 2.
Table 2. Local freeness at 2 in
![]() $A_5$
-extensions.
$A_5$
-extensions.

We now use the Magma implementation of the algorithm described in [Reference Hofmann and Johnston18, §8.5]. We can hence verify that in none of the above cases
![]() $\textrm{Ind}_{D(2)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}\cong \mathcal{O}_{K,2}$
is free over
$\textrm{Ind}_{D(2)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}\cong \mathcal{O}_{K,2}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},2}$
(see Section A.3 for the implementation).
$\mathfrak{A}_{K/\mathbb{Q},2}$
(see Section A.3 for the implementation).
Now suppose that
![]() $p=3$
or
$p=3$
or
![]() $5$
and that
$5$
and that
![]() $p$
is wildly ramified in
$p$
is wildly ramified in
![]() $K/\mathbb{Q}$
. Let
$K/\mathbb{Q}$
. Let
![]() $\mathfrak{P}$
be a choice of a prime of
$\mathfrak{P}$
be a choice of a prime of
![]() $K$
above
$K$
above
![]() $p$
and let
$p$
and let
![]() $D(p)$
be its decomposition group. There is no Galois extension
$D(p)$
be its decomposition group. There is no Galois extension
![]() $L/\mathbb{Q}_{3}$
such that
$L/\mathbb{Q}_{3}$
such that
![]() $\textrm{Gal}(L/\mathbb{Q}_{3}) \cong A_{4}$
(since the subgroups of
$\textrm{Gal}(L/\mathbb{Q}_{3}) \cong A_{4}$
(since the subgroups of
![]() $A_4$
of order
$A_4$
of order
![]() $3$
are not normal). Hence,
$3$
are not normal). Hence,
![]() $D(p)$
must be isomorphic to either
$D(p)$
must be isomorphic to either
![]() $D_{2p}$
or
$D_{2p}$
or
![]() $C_{p}$
, which implies that
$C_{p}$
, which implies that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
by Theorems 3.3 and 3.4. Again we can use the ‘algorithmic freeness method’, so that our goal is to analyse when
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
by Theorems 3.3 and 3.4. Again we can use the ‘algorithmic freeness method’, so that our goal is to analyse when
![]() $\textrm{Ind}_{D(p)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
$\textrm{Ind}_{D(p)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
. If
$\mathfrak{A}_{K/\mathbb{Q},p}$
. If
![]() $D(p)\cong C_p$
(in which case we can and do assume that
$D(p)\cong C_p$
(in which case we can and do assume that
![]() $D(p)=C_{p}$
), then as
$D(p)=C_{p}$
), then as
![]() $K_{\mathfrak{P}}/\mathbb{Q}_p$
is wildly ramified this implies that
$K_{\mathfrak{P}}/\mathbb{Q}_p$
is wildly ramified this implies that
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\langle 1,\frac{1}{p}\textrm{Tr}_{D(p)}\rangle _{D(p)}^p$
, which is the unique maximal order in
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\langle 1,\frac{1}{p}\textrm{Tr}_{D(p)}\rangle _{D(p)}^p$
, which is the unique maximal order in
![]() $\mathbb{Q}_{p}[D(p)]$
. If
$\mathbb{Q}_{p}[D(p)]$
. If
![]() $D(p)\cong D_{2p}$
(in which case we can and do assume that
$D(p)\cong D_{2p}$
(in which case we can and do assume that
![]() $D=D_{2p}$
), we can use Theorem 3.10: in case of almost-maximal ramification,
$D=D_{2p}$
), we can use Theorem 3.10: in case of almost-maximal ramification,
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\langle 1,\frac{1}{p}\textrm{Tr}_{C_p}\rangle _{D(p)}^p$
(which gives the same structure for
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\langle 1,\frac{1}{p}\textrm{Tr}_{C_p}\rangle _{D(p)}^p$
(which gives the same structure for
![]() $\textrm{Ind}_{D(p)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
as when
$\textrm{Ind}_{D(p)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
as when
![]() $D(p)=C_p$
); otherwise, by Remark 3.13,
$D(p)=C_p$
); otherwise, by Remark 3.13,
![]() $K_{\mathfrak{P}}/\mathbb{Q}_p$
is weakly and totally ramified and
$K_{\mathfrak{P}}/\mathbb{Q}_p$
is weakly and totally ramified and
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\langle 1,\frac{1}{p}\textrm{Tr}_{D(p)}\rangle _{D(p)}^p$
. Hence there are two possibilities for
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}=\langle 1,\frac{1}{p}\textrm{Tr}_{D(p)}\rangle _{D(p)}^p$
. Hence there are two possibilities for
![]() $\textrm{Ind}_{D(p)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and
$\textrm{Ind}_{D(p)}^G\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
and
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
, shown in Table 3.
$\mathfrak{A}_{K/\mathbb{Q},p}$
, shown in Table 3.
Table 3. Local freeness at 3 and 5 in
![]() $A_5$
-extensions.
$A_5$
-extensions.

We used the Magma implementation of the algorithm from [Reference Hofmann and Johnston18, §8.5] to verify that
![]() $\textrm{Ind}_{D(p)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
$\textrm{Ind}_{D(p)}^{G}\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_p}$
is free over
![]() $\mathfrak{A}_{K/\mathbb{Q},p}$
if and only if we are in case (2), that is, precisely when
$\mathfrak{A}_{K/\mathbb{Q},p}$
if and only if we are in case (2), that is, precisely when
![]() $K_{\mathfrak{P}}/\mathbb{Q}_p$
is weakly ramified or, equivalently, when it is not almost-maximally ramified (see Section A.3).
$K_{\mathfrak{P}}/\mathbb{Q}_p$
is weakly ramified or, equivalently, when it is not almost-maximally ramified (see Section A.3).
Remark 8.7.
Note that from the proof of Theorem 8.1, we already knew that neither
![]() $\langle 1,\frac{1}{2}\textrm{Tr}_{C_2}\rangle _{A_4}^2$
nor
$\langle 1,\frac{1}{2}\textrm{Tr}_{C_2}\rangle _{A_4}^2$
nor
![]() $\langle 1,\frac{1}{2}\textrm{Tr}_{C_2},\frac{1}{4}\textrm{Tr}_{C_2^2}\rangle _{A_4}^2$
are even projective over their associated orders; induction from
$\langle 1,\frac{1}{2}\textrm{Tr}_{C_2},\frac{1}{4}\textrm{Tr}_{C_2^2}\rangle _{A_4}^2$
are even projective over their associated orders; induction from
![]() $A_4$
to
$A_4$
to
![]() $S_4$
and Proposition 6.8 permit us to conclude that
$S_4$
and Proposition 6.8 permit us to conclude that
![]() $\langle 1,\frac{1}{2}\textrm{Tr}_{C_2}\rangle _G^2$
and
$\langle 1,\frac{1}{2}\textrm{Tr}_{C_2}\rangle _G^2$
and
![]() $\langle 1,\frac{1}{2}\textrm{Tr}_{C_2},\frac{1}{4}\textrm{Tr}_{C_2^2}\rangle _G^2$
are not projective over their associated orders. Thus we can treat cases (1) and (2) from Table
2
without using the algorithm.
$\langle 1,\frac{1}{2}\textrm{Tr}_{C_2},\frac{1}{4}\textrm{Tr}_{C_2^2}\rangle _G^2$
are not projective over their associated orders. Thus we can treat cases (1) and (2) from Table
2
without using the algorithm.
Remark 8.8.
Note that for
![]() $p=3$
and
$p=3$
and
![]() $p=5$
we found that
$p=5$
we found that
![]() $\langle 1,\frac{1}{p}\textrm{Tr}_{D_{2p}}\rangle _G^p$
is free over
$\langle 1,\frac{1}{p}\textrm{Tr}_{D_{2p}}\rangle _G^p$
is free over
![]() $\langle 1,\frac{1}{p}\textrm{Tr}_{G}\rangle _G^p$
without the two being equal. We also found with the algorithm from [Reference Hofmann and Johnston18] that
$\langle 1,\frac{1}{p}\textrm{Tr}_{G}\rangle _G^p$
without the two being equal. We also found with the algorithm from [Reference Hofmann and Johnston18] that
![]() $\langle 1,\frac{1}{2}\textrm{Tr}_{A_4}\rangle _G^p$
, which does not come from a ring of integers, is free over
$\langle 1,\frac{1}{2}\textrm{Tr}_{A_4}\rangle _G^p$
, which does not come from a ring of integers, is free over
![]() $\langle 1,\frac{1}{2}\textrm{Tr}_G\rangle _G^p$
(see Section A.3).
$\langle 1,\frac{1}{2}\textrm{Tr}_G\rangle _G^p$
(see Section A.3).
Acknowledgments
This work is part of the author’s PhD thesis at the University of Exeter. The author wishes to thank his PhD supervisor, Henri Johnston, for his encouragement and valuable comments, Nigel Byott and Christian Wuthrich for helpful comments and discussions, and Werner Bley and Tommy Hofmann for their help with the computer calculations in Appendix A. Finally, the author is grateful to the anonymous referee for a number of helpful comments, which led to an improved exposition.
The author is grateful to the University of Exeter for funding his PhD scholarship; he was subsequently supported by an LMS Early Career Fellowship and then by EPSRC grant EP/W52265X/1.
Data availability statement
Data sharing is not applicable to this article, as no datasets were generated or analysed during the present work.
Appendix A: Computer calculations
A.1. Determining freeness for
 $S_4$
-extensions of
$S_4$
-extensions of
 $\mathbb{Q}_2$
$\mathbb{Q}_2$
Let
![]() $K/\mathbb{Q}$
be an
$K/\mathbb{Q}$
be an
![]() $S_4$
-extension with full decomposition group that is wildly ramified. Here we describe how to use the Magma implementation of [Reference Bley and Johnston5, Algorithm 3.1(6)] to check whether or not
$S_4$
-extension with full decomposition group that is wildly ramified. Here we describe how to use the Magma implementation of [Reference Bley and Johnston5, Algorithm 3.1(6)] to check whether or not
![]() $\mathcal{O}_K$
is locally free at
$\mathcal{O}_K$
is locally free at
![]() $2$
over
$2$
over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
, or equivalently, whether
$\mathfrak{A}_{K/\mathbb{Q}}$
, or equivalently, whether
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, where
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, where
![]() $\mathfrak{P}$
is the unique prime of
$\mathfrak{P}$
is the unique prime of
![]() $K$
above
$K$
above
![]() $2$
. We used the database [30] to find six number fields, each of which has a completion at
$2$
. We used the database [30] to find six number fields, each of which has a completion at
![]() $2$
equal to one of the six wildly ramified
$2$
equal to one of the six wildly ramified
![]() $S_4$
-extensions of
$S_4$
-extensions of
![]() $\mathbb{Q}_2$
listed in the database of
$\mathbb{Q}_2$
listed in the database of
![]() $p$
-adic fields [Reference Jones and Roberts24]. Note that two of these extensions of
$p$
-adic fields [Reference Jones and Roberts24]. Note that two of these extensions of
![]() $\mathbb{Q}_{2}$
are weakly ramified, and so Corollary 7.2(ii) already shows that
$\mathbb{Q}_{2}$
are weakly ramified, and so Corollary 7.2(ii) already shows that
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in both cases, but we include them anyway as an additional check. The files RelAlgKTheory.m and INB.m referred to below are available on Werner Bley’s website https://www.mathematik.uni-muenchen.de/~bley/pub.php
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
in both cases, but we include them anyway as an additional check. The files RelAlgKTheory.m and INB.m referred to below are available on Werner Bley’s website https://www.mathematik.uni-muenchen.de/~bley/pub.php
We refer to the sample file sample.m from the article [Reference Bley and Johnston5]. Note that here we use the updated file INB.m from [Reference Bley and Johnston6] rather than the original file ao.m.

A.2. Determining local freeness at
 $2$
for
$2$
for
 $S_4$
-extensions of
$S_4$
-extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
Here we describe how to use the Magma implementation of [Reference Hofmann and Johnston18, §8.5] to show that for an
![]() $S_{4}$
-extension
$S_{4}$
-extension
![]() $K/\mathbb{Q}$
we have that
$K/\mathbb{Q}$
we have that
![]() $\mathcal{O}_K$
is not locally free at
$\mathcal{O}_K$
is not locally free at
![]() $2$
over
$2$
over
![]() $\mathfrak{A}_{K/\mathbb{Q}}$
if
$\mathfrak{A}_{K/\mathbb{Q}}$
if
![]() $K/\mathbb{Q}$
does not satisfy any of the conditions (i)–(iv) of Theorem 8.3 and
$K/\mathbb{Q}$
does not satisfy any of the conditions (i)–(iv) of Theorem 8.3 and
![]() $\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
$\mathcal{O}_{K_{\mathfrak{P}}}$
is free over
![]() $\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, where
$\mathfrak{A}_{K_{\mathfrak{P}}/\mathbb{Q}_2}$
, where
![]() $\mathfrak{P}$
is a prime of
$\mathfrak{P}$
is a prime of
![]() $K$
above
$K$
above
![]() $2$
(see Table 1). Moreover, we also prove the freeness claim of Remark 8.5. The files Iso.m, Lattices.m and Iso.spec referred to below are contained in Iso.zip, available in the link to [Reference Hofmann and Johnston18] on Tommy Hofmann’s website https://www.thofma.com
$2$
(see Table 1). Moreover, we also prove the freeness claim of Remark 8.5. The files Iso.m, Lattices.m and Iso.spec referred to below are contained in Iso.zip, available in the link to [Reference Hofmann and Johnston18] on Tommy Hofmann’s website https://www.thofma.com

A.3. Determining local freeness for
 $A_5$
-extensions of
$A_5$
-extensions of
 $\mathbb{Q}$
$\mathbb{Q}$
Here we describe how to use the Magma implementation of [Reference Hofmann and Johnston18, §8.5] to check local freeness in
![]() $A_5$
-extensions of
$A_5$
-extensions of
![]() $\mathbb{Q}$
at the wildly ramified primes (see Tables 2 and 3). Moreover, we also prove the second freeness claim of Remark 8.8. The files Iso.m, Lattices.m and Iso.spec referred to below are contained in Iso.zip, available in the link to [Reference Hofmann and Johnston18] on Tommy Hofmann’s website https://www.thofma.com
$\mathbb{Q}$
at the wildly ramified primes (see Tables 2 and 3). Moreover, we also prove the second freeness claim of Remark 8.8. The files Iso.m, Lattices.m and Iso.spec referred to below are contained in Iso.zip, available in the link to [Reference Hofmann and Johnston18] on Tommy Hofmann’s website https://www.thofma.com
When IsLocallyIsomorphic(QG, BasisMatrix(M), BasisMatrix(A), 2) is ‘true’, we suppress the full output, which includes an element
![]() $x\in \mathbb{Q}[G]$
such that
$x\in \mathbb{Q}[G]$
such that
![]() $x(\mathbb{Z}_2\otimes _{\mathbb{Z}}M)=\mathbb{Z}_2\otimes _{\mathbb{Z}} A$
(whose existence is in our case equivalent to
$x(\mathbb{Z}_2\otimes _{\mathbb{Z}}M)=\mathbb{Z}_2\otimes _{\mathbb{Z}} A$
(whose existence is in our case equivalent to
![]() $\mathbb{Z}_2\otimes _{\mathbb{Z}}M$
being free over
$\mathbb{Z}_2\otimes _{\mathbb{Z}}M$
being free over
![]() $\mathbb{Z}_2\otimes _{\mathbb{Z}} A$
).
$\mathbb{Z}_2\otimes _{\mathbb{Z}} A$
).