Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-12T08:39:21.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbations of graphs for Newton maps I: bounded hyperbolic components

Part of: Complex dynamical systems

Published online by Cambridge University Press:  31 August 2022

YAN GAO  and
HONGMING NIE
YAN GAO
Affiliation:
College of Mathematics and Statistics, Shenzhen University, Shenzhen 518061, China (e-mail: [email protected])
HONGMING NIE*
Affiliation:
Institute for Mathematical Sciences, Stony Brook University, Stony Brook, NY 11794, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider graphs consisting of finitely many internal rays for degenerating Newton maps and state a convergence result. As an application, we prove that a hyperbolic component in the moduli space of quartic Newton maps is bounded if and only if every element has degree 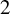$2$ on the immediate basin of each root. This provides the first complete description of bounded hyperbolic components in a complex two-dimensional moduli space.

Keywords

Newton mapsinternal rayshyperbolic componentsNewton graphs

MSC classification

Primary: 37F20: Combinatorics and topology
Secondary: 37F10: Polynomials; rational maps; entire and meromorphic functions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 9 , September 2023 , pp. 2997 - 3025
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Buff, X. and Tan, L.. Dynamical convergence and polynomial vector fields. J. Differential Geom. 77 (2007), 1–41.CrossRefGoogle Scholar
DeMarco, L.. Iteration at the boundary of the space of rational maps. Duke Math. J. 130 (2005), 169–197.CrossRefGoogle Scholar
Douady, A.. Does a Julia set depend continuously on the polynomial? Complex Dynamical Systems (Cincinnati, OH, 1994) (Proceedings of Symposia in Applied Mathematics, 49). Ed. R. Devaney. American Mathematical Society, Providence, RI, 1994, pp. 91–138.Google Scholar
Drach, K., Mikukich, Y., Rückert, J. and Schleicher, D.. A combinatorial classification of postcritically fixed Newton maps. Ergod. Th. & Dynam. Sys. 39 (2019), 2983–3014.10.1017/etds.2018.2CrossRefGoogle Scholar
Drach, K. and Schleicher, D.. Rigidity of Newton dynamics. Adv. Math. 408 (2022), 108591.10.1016/j.aim.2022.108591CrossRefGoogle Scholar
Epstein, A. L.. Bounded hyperbolic components of quadratic rational maps. Ergod. Th. & Dynam. Sys. 20 (2000), 727–748.CrossRefGoogle Scholar
Gamelin, T. W.. Complex Analysis (Undergraduate Texts in Mathematics). Springer-Verlag, New York, 2001.10.1007/978-0-387-21607-2CrossRefGoogle Scholar
Gao, Y.. Density of hyperbolicity of real Newton maps. Preprint, 2019, arXiv:1906.03556.Google Scholar
Gao, Y.. On the core entropy of Newton maps. Sci. China Math., to appear.Google Scholar
Gao, Y. and Giulio, T.. The core entropy for polynomials of higher degree. J. Eur. Math. Soc. (JEMS), published online first 2021.10.4171/JEMS/1154CrossRefGoogle Scholar
Gao, Y. and Nie, H.. Perturbations of graphs for Newton maps II: unbounded hyperbolic components, in preparation.Google Scholar
Goldberg, L. and Milnor, J.. Fixed point portraits of polynomial maps, Part II: fixed point portraits. Exp. Math. 26 (1993), 51–98.Google Scholar
Lodge, R., Mikulich, Y. and Schleicher, D.. Combinatorial properties of Newton maps. Indiana Univ. Math. J. 70 (2021), 1833–1867.CrossRefGoogle Scholar
Lodge, R., Mikulich, Y. and Schleicher, D.. A classification of postcritically finite Newton maps. In the Tradition of Thurston. Vol. II. Eds. K. Ohshika and A. Papadopoulos. Springer, Cham, 2022.Google Scholar
McMullen, C.. Automorphisms of rational maps. Holomorphic Functions and Moduli, Volume I (Berkeley, CA, 1986) (Mathematical Sciences Research Institute Publications, 10). Eds. D. Drasin, C. J. Earle, F. W. Gehring, I. Kra and A. Marden. Springer, New York, 1988, pp. 31–60.CrossRefGoogle Scholar
McMullen, C. T.. Complex Dynamics and Renormalization (Annals of Mathematics Studies, 135). Princeton University Press, Princeton, NJ, 1994.Google Scholar
Milnor, J.. Geometry and dynamics of quadratic rational maps. Exp. Math. 2 (1993), 37–83, with an appendix by the author and Lei Tan.10.1080/10586458.1993.10504267CrossRefGoogle Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160), 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Milnor, J.. Cubic polynomial maps with periodic critical orbit. I. Complex Dynamics. Ed. D. Schleicher. A K Peters, Wellesley, MA, 2009, pp. 333–411.CrossRefGoogle Scholar
Milnor, J.. Hyperbolic component boundaries. http://www.math.stonybrook.edu/jack/HCBkoreaPrint.pdf.Google Scholar
Nie, H.. Iteration at the boundary of Newton maps. PhD Thesis, Indiana University, ProQuest LLC, Ann Arbor, MI, 2018.Google Scholar
Nie, H. and Pilgrim, K. M.. Boundedness of hyperbolic components of Newton maps. Israel J. Math. 238 (2020), 837–869.CrossRefGoogle Scholar
Nie, H. and Pilgrim, K. M.. Bounded hyperbolic components of bicritical rational maps. J. Mod. Dyn., to appear.Google Scholar
Roesch, P.. Holomorphic motions and puzzles (following M. Shishikura). The Mandelbrot Set, Theme and Variations (London Mathematical Society Lecture Note Series, 274). Ed. L. Tan. Cambridge University Press, Cambridge, 2000, pp. 117–132.CrossRefGoogle Scholar
Roesch, P.. On local connectivity for the Julia set of rational maps: Newton’s famous example. Ann. of Math. (2) 168 (2008), 127–174.10.4007/annals.2008.168.127CrossRefGoogle Scholar
Shishikura, M.. On the quasiconformal surgery of rational functions. Ann. Sci. Éc. Norm. Supér. (4) 20 (1987), 1–29.CrossRefGoogle Scholar
Shishikura, M.. The connectivity of the Julia set and fixed points. Complex Dynamics. Ed. D. Schleicher. A K Peters, Wellesley, MA, 2009, pp. 257–276.10.1201/b10617-9CrossRefGoogle Scholar
Thurston, W. P.. Hyperbolic structures on $3$ -manifolds. I. Deformation of acylindrical manifolds. Ann. of Math. (2) 124 (1986), pp. 203–246.CrossRefGoogle Scholar
Wang, X., Yin, Y. and Zeng, J.. Dynamics of newton maps. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2021.168. Published online 15 February 2022.CrossRefGoogle Scholar