No CrossRef data available.
Published online by Cambridge University Press: 02 December 2024
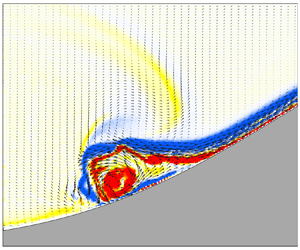
The breaking and energy distribution of mode-1 depression internal solitary wave interactions with Gaussian ridges are examined through laboratory experiments. A series of processes, such as shoaling, breaking, transmission and reflection, are captured completely by measuring the velocity field in a large region. It is found that the maximum interface descent ( $a_{max}$) during wave shoaling is an important parameter for diagnosing the type of wave–ridge interaction and energy distribution. The wave breaking on the ridge depends on the modified blockage parameter
$a_{max}$) during wave shoaling is an important parameter for diagnosing the type of wave–ridge interaction and energy distribution. The wave breaking on the ridge depends on the modified blockage parameter  $\zeta _m$, the ratio of the sum of the upper layer depth and
$\zeta _m$, the ratio of the sum of the upper layer depth and  $a_{max}$ to the water depth at the top of the ridge. As
$a_{max}$ to the water depth at the top of the ridge. As  $\zeta _m$ increases, the interaction type transitions from no breaking to plunging and mixed plunging–collapsing breaking. Within the scope of this experiment, the energy distribution can be characterized solely by
$\zeta _m$ increases, the interaction type transitions from no breaking to plunging and mixed plunging–collapsing breaking. Within the scope of this experiment, the energy distribution can be characterized solely by  $\zeta _m$. The transmission energy decreases monotonically with increasing
$\zeta _m$. The transmission energy decreases monotonically with increasing  $\zeta _m$, and there is a linear relationship between
$\zeta _m$, and there is a linear relationship between  $\zeta _m^2$ and the reflection coefficient. The value of
$\zeta _m^2$ and the reflection coefficient. The value of  $a_{max}$ can be determined from the basic initial parameters of the experiment. Based on the incident wave parameters, the depth of the upper and lower layers, and the topographic parameters, two new simple methods for predicting
$a_{max}$ can be determined from the basic initial parameters of the experiment. Based on the incident wave parameters, the depth of the upper and lower layers, and the topographic parameters, two new simple methods for predicting  $a_{max}$ on the ridge are proposed.
$a_{max}$ on the ridge are proposed.