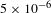2 Leak rate specification

In order to expedite the manufacture of these assemblies, we need to derive a leakage specification that we believe will not impact the performance of the target. To do so we consider several factors below. It is useful to note that the typical amount of gas in the hohlraum at fielding temperature of about 18.3 K is given by:

(1) $$\begin{eqnarray}n_{t}=\frac{PV}{RT}=1.007\times 10^{-4}~\text{mol},\end{eqnarray}$$

where $n_{t}=\text{moles}$ of gas; $P=\text{pressure}=0.5$  atm; $V=\text{volume}=\unicode[STIX]{x1D70B}(0.3~\text{cm})^{\text{2}}~(1.07~\text{cm})\times 10^{-3}~\text{L}/\text{cm}^{3}=3.03\times 10^{-4}$  L; $R=0.082~\text{L}\cdot \text{atms}/(\text{mol}\cdot \text{K})$ ; $T=\text{temperature}=18.3~\text{K}$ , and one standard cc (scc) is $4.47\times 10^{-5}$  mol.

At RT, we expect to observe small amounts of He gas flow out of hohlraum assemblies due to permeation through the various polymer elements used in the target (primarily windows and glue bonds). But as the target is cooled to deep cryogenic conditions, permeation is completely cut out and any He loss occurs only through small leaks in the many glue joints in these systems. We now consider the impact of this leak on the thermal performance of the system.

1. (1) Heat load on the hohlraum due to warm gas flowing in to hold the pressure constant

   We estimate that the incoming He gas is cooled to about 60 K by the first stage of the cryocooler, and that its remaining enthalpy goes into the hohlraum. The heat capacity of He at constant pressure is $(5/2)R$ . This works out to 39 mW/sccs, where sccs is scc per second. The heat dissipation due to the beta decay of DT is about $30~\unicode[STIX]{x03BC}\text{W}$ ^{[Reference Sangster, Betti and Craxton5]}, so if we require that the heat load introduced by the make-up He gas be less than 1% of the DT power, we come up with a limiting value of $8\times 10^{-6}$  sccs.

2. (2) Change in the flow velocity of the gas in the hohlraum

   Finite element modeling shows that the peak velocity of the convecting He gas is about 0.4 mm/s^{[Reference Klingmann, Atherton and Bernat11]}. The cold hohlraum has about 2 scc of He, so a leak rate of 1 sccs will lead to decay time on the order of 10 s. The length scale is 10 mm, so this will lead to an average velocity of about 1 mm/s. Even if we require that the velocity not exceed 0.01% of the convection velocity, this only gets us down to about $1\times 10^{-4}$  sccs.

3. (3) Limit on the amount of He that can be leaked into the target chamber

   NIF is designed such that the target chamber pumping system should be able to handle a leak rate from a cryogenic target of $2.5\times 10^{-4}~\text{torr}\cdot \text{L}/\text{s}$ , or $3.3\times 10^{-4}$  sccs. This is also weaker than the limit for 1 discussed above.

4. (4) Conduction from the clamshell shroud to the target

   The inner surface of the clamshell shroud can have a measured temperature of up to 150 K. Any gas leaking from the target assembly will cause heat transfer from the shroud surface to the 18.3 K target assembly. This extra heat load carried by the leaking gas to the hohlraum surface has to be removed by Si cooling arms on each end of the hohlraum. Of particular interest is the effect during the process of shimming where a specific axial temperature profile is generated by putting heat into two heaters placed on the hohlraum over and under the capsule position. Shimming allows the axial nature of the cylindrical hohlraum to be made closer to the spherical symmetry required around the capsule. Hence, the disturbance temperature profile created by heat transfer by the leaking gas must be negligible in comparison to the desired shim temperature profile.

A rough estimate of the temperature drop as a function of target assembly leak rate computed using a finite element model is shown below. The temperature drop is a function of the gas heat conduction to the hohlraum surface, the heat conductance between the hohlraum surface and the cooling rings. The gas heat conduction is determined by the pressure and species of the gas. The pressure is a function of the leak rate and the combined conductance of the ‘escape’ paths that allow for the gas to be released from the shroud enclosure. It is assumed that the only significant escape path is via the ${\sim}5$  mm gap between the blast shield that is placed to protect against the plasma plume after the shot, and the shroud. The resulting temperature, $\unicode[STIX]{x1D6E5}T$ , drop between the hohlraum midplane and the Si cooling arm caused by gas heat conduction is:

(2) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}T=4.5\frac{\text{K}}{\text{sccs}}.\end{eqnarray}$$

Therefore, leak rates below $1\times 10^{-5}$  sccs for an impact of no more than 0.05 mK or a tenth of the desired temperature control authority.

It is useful to mention here that radiative heating of the target is controlled using cold shields and reflective windows. The clamshell shroud that surrounds the target is made of two sections: an outer shell which is not cooled and an inner shell that is maintained at about 125 K. Windows on the shroud are gold coated such that virtually all the IR radiation is reflected while still permitting transmission of visible radiation to enable alignment of the target. In this design, the radiative load on the target is negligible.

Considering all of these perspectives together, the limiting factor is the heat load on the hohlraum brought in by the warm gas to hold He pressure constant. Hence, we propose that the upper limit for leak rate specification is $5\times 10^{-6}$  sccs for doing a successful layering operation.

It must be noted that the fuel is transported into the capsule through a $5~\unicode[STIX]{x03BC}\text{m}$ ID glass capillary filltube that enters the capsule at a small laser drilled hole and leakage of fuel due to failure at the joint to the capillary filltube is also a major concern. The considerations for the maximum allowed rate in that case are different and ultimately amount to a requirement of a rate smaller than $1\times 10^{-8}$  sccs. Since the discussion below is limited to the problems with integrity of the hohlraum, we do not delve into details of the capsule leak rate limit.

The upper limit of $5\times 10^{-6}$  sccs is a stringent requirement and it is helpful to put the rate in context. This is done below. Assuming a single point of leak such as an orifice, we can estimate the size of the channel required to cause this leak. The equation for flow of a compressible fluid through an orifice^{[Reference Reader-Harris17]} is expressed as

(3) $$\begin{eqnarray}q=CA\sqrt{\frac{2zRT}{MW}X\left(\frac{k}{k-1}\right)},\end{eqnarray}$$

and the term $X$ is

(4) $$\begin{eqnarray}X=\left[\left(\frac{P_{2}}{P_{1}}\right)^{2/k}-\left(\frac{P_{2}}{P_{1}}\right)^{(k+1)/k}\right],\end{eqnarray}$$

where $q=\text{volumetric}$ flow rate; $C=\text{orifice}$ coefficient of discharge; $A=\text{cross-sectional}$ area of the channel; $z=\text{gas}$ compressibility factor; $k=\text{specific}$ heat ratio ( $C_{\text{P}}/C_{\text{V}}$ ); $MW=\text{molecular}$ weight of the gas; $P_{1}=\text{upstream}$ pressure; $P_{2}=\text{downstream}$ pressure; while the upstream pressure is often known as the pressure in the hohlraum in our case, the downstream pressure is the pressure immediately outside the orifice. The pressure recorded is often far away from the orifice and so the magnitude of the local downstream pressure on the other side of the orifice is not obvious. Using a disk with a laser cut circular $25~\unicode[STIX]{x03BC}\text{m}$ diameter orifice as a known leak source, we determined that the ratio of $P_{2}/P_{1}$ needs to be 0.03 (Figure 4).

Figure 4. Matching the model and the data using a $25~\unicode[STIX]{x03BC}\text{m}$ diameter orifice.

This now allows us to get a measure of the computed orifice size as a function of any leak rate (Figure 5). The above specification of $5\times 10^{-6}$  sccs corresponds to an orifice diameter of only $0.4~\unicode[STIX]{x03BC}\text{m}$ at typical conditions of 18 K and 450 torr.

Figure 5. Relationship between an orifice diameter and the corresponding flow rate at 18 K and 450 torr upstream pressure.

This demonstrates how challenging it is to find the source an unacceptably high leak.

3 Target failures

As NIF has become fully operational as a national user facility, experiments are scheduled as frequently as possible^{[Reference Edwards1]}. On average, one cryogenic target is required per week day. Some of these are not used for DT ice layering but instead for studies that aid the understanding of the fusion reaction. As stated above, targets are held together using adhesives. Some of these bonds are made with the help of a micromanipulator but majority are done by hand due to the small volumes that need to be dispensed in hard to reach geometries.

For a successful target, all of the pores in those bonds that hold the TMPs and associated components together need to have a cumulative area smaller than that of a $0.5~\unicode[STIX]{x03BC}\text{m}$ hole. These are often due to incomplete application of the adhesive, which went unnoticed because the open channel size of concern is too small to be detected using optical microscopy techniques. To ensure that the ultimate target fielded for a shot on NIF is trouble-free, each target is ‘proofed’. During this process, the hohlraum and the capsule are both pressurized to at least the final pressure called for in the experiment and any leaks are quantified using an He leak detector both at RT and at the cryogenic shot temperature. Incomplete bond lines or pinholes in windows can often be spotted early in the proofing procedure during RT leak check, even though permeation through polymer windows imposes a lower bound.

Of greater concern, however, are stresses caused by mismatch in contraction of the different materials at these joints upon cooling to cryogenic temperatures that can cause mechanical failure of the adhesive and a resultant leak. Through careful selection of adhesives, we have achieved requisite high proofing yield ( ${>}98\%$ ) over multiple years of operation. But failures do occur and they can either render a target useless or require time-consuming repairs.

Failures can be binned into two broad categories: recurring ones and sporadic ones. The latter type are often due to a mishap or an extenuating circumstance during assembly and by definition, do not repeat over time. It is the former that requires serious attention. Often these failures assume epidemic proportions as they occur due to subtle process drifts and are challenging to unravel.

4 Example of a recurring leak problem on NIF targets

In this section, we describe the investigation of failures due to hohlraum leaks to illustrate the type of in-depth analysis that is frequently called for. After a prolonged period of high yield production, as is the norm, there was a sudden onset of a specific type of leak which then continued to occur with alarming regularity. An immediate review of the assembly processes showed that there was nothing notably different and needed rectification. Since targets are produced at the rate of one per day, an event such as this tends to cripple the output with no end in sight till the right root cause is identified and resolved.

Identification of the location of a leak is often the first major hurdle, especially as it is not possible to put the whole target in an electron microscope without stressing the many membranes used within. Thus, we needed try to use other clues and methods to help hone in onto probable locations. In this case, the leaks had this characteristic behavior: initially, at RT, the hohlraum behaved normally showing nominal He permeation, then failure at cryogenic temperatures upon cooling with very high leak rates ( ${>}5\times 10^{-5}$  sccs), followed by normal behavior at RT upon warming up. This mode of leakage that was seen solely at cryogenic temperatures with recovery upon warming is not uncommon when adhesive bonds fail due to the thermal stresses [i.e., due the coefficient of thermal expansion (CTE) mismatch].

The question, of course, is at what location? One possibility is using the concept of a sniffer test with a capillary where a local area is puffed briefly with He. But the facts that the target cannot handle high pressure differential and that the leak effectively disappears at RT make that practically impossible. Thorough inspection of the target with an optical microscope revealed nothing specific, which is not surprising.

But there was one peculiar feature to this leak behavior that provided a further clue. We can see this in Figure 6, which shows the pressure testing of the hohlraum at 18 K.

Figure 6. Results from the cryogenic proofing of the hohlraum at cryogenic temperature. The solid blue line is the supply line pressure while the dotted blue line is that of the return line. The red dots are the corresponding leak rate. Both lines are open to the hohlraum after 1000 s.

In order to understand the plot, it is necessary to briefly describe the proofing algorithm for the hohlraum. Starting with the target at vacuum at ${\sim}18$  K, we confirm the arrival of He in the hohlraum by doing a flow through whereby only one of the two fill lines (i.e., supply line) into the hohlraum is pressurized. As the pressure in the second (return) line starts to increase, it serves to ascertain that there is flow into and through the hohlraum. This avoids pitfalls such as fill lines being plugged due to formation of ice from any residual gases at 18 K that can mask a leak in the hohlraum. Once the openness to the hohlraum is established, both lines can be used to pressurize the hohlraum.

As seen in Figure 6, the hohlraum was leak-tight till a threshold pressure was reached, in this case 406 torr, when it sprung the leak. This suggests that there are two causes for the failure: change in the temperature (and the resultant thermal stresses) and a threshold pressure. The fact that pressure plays a role implies that the failing component ought to have a large area so that the resultant force on the bond is amplified (in contrast to say a filltube joint with a small cross-sectional area). One component that has a large area is a sealing window as it spans across a large hole in the TMP. There are, of course, two types of windows: the LEH windows and the diagnostic windows. While we cannot differentiate between them with this reasoning, it helps narrow down the number of possibilities and makes it possible to focus the efforts. It turned out that making a new bondline on the outer perimeter of the LEH windows alone noticeably affected the leak rate, sometimes making it smaller and other times greater. But there was no effect of doing the same to the diagnostic windows. That can been inferred as strong evidence that the source of the leak was on the periphery of the LEH window.

It is helpful to review the essential steps in assembling the window to the TMP. Recall that the functional portion of the LEH window is the 500 nm polyimide membrane with a 25 nm of Al on top. The Al helps to restrict the entrance of IR radiation into the hohlraum chamber as it can interfere with the layering process. These windows are fabricated by Luxel Corporation and supplied on a $120~\unicode[STIX]{x03BC}\text{m}$ thick Al washer. As the last step of the target assembly process, these washers are placed on a circular lip machined on the inside of the TMP near the top so that there is a gap, per design, between the TMP and the washer. This is seen in Figure 7.

Figure 7. Schematic of the TMP window washer to Al TMP bonding design. The picture on the right is an image of the typical LEH bonding operation.

The gap can then be filled with a low viscosity UV cured adhesive through capillary action. This provides a deterministic method for generating a well-controlled circular fillet of adhesive that can be exposed to light. Given that this process was successfully used to make over 1400 window assemblies before failures appeared, it naturally begs the question as to what triggered these failures?

5 Failure analysis

When one such failed LEH window region was inspected in the SEM, a small section of the circular bondline showed the presence of dark bands (Figure 8).

Figure 8. SEM images of features seen in the LEH to TMP bondline of a failed target. The red circle highlights the arc where dark bands, like the one seen in the lower left, were seen. These bands were seen to be linear holes in the bondline (image on the right).

They were not seen in the windows that did not leak. Upon high-resolution imaging, it was seen that these bands were linear holes in a glue fillet, but it was not clear how deep these holes were and as such, exactly what the leak path was. In order to determine that, we needed to cross section the region of interest in such a manner that the procedure itself would not obscure the evidence in any way. One method that is custom-made for this procedure is localized etching with a focused gallium ion beam (FIB). Figure 9 shows the electron microscopy results after FIB etching.

Figure 9. SEM image of the FIB etched section showing the internal cross-section of the region under the band seen in Figure 8.

Interestingly, the image reveals a gap running along the Al TMP wall over almost the entire height of the fillet.

One obvious cause for this gap is the generation of tensile stresses in the fillet. The CTE of Al at RT is 23 ppm/K whereas that of the adhesive is about 70 ppm/K. Even though CTE value drops with decreasing temperature, the RT CTE value is a good indicator of the disparity between any two materials in this respect. Curiously, the specific configuration encountered in this case leads to different behavior on each of the two Al surfaces. Due to its greater propensity to shrink relative to Al, the circular glue fillet exerts a compressive stress at the inner interface (i.e., the LEH washer) and simultaneously a tensile stress on the outer one (i.e., the TMP surface). The magnitude of this stress $\unicode[STIX]{x1D70E}$ is closely approximated by this simple equation:

(5) $$\begin{eqnarray}\unicode[STIX]{x1D70E}=\int _{295}^{18}E(T)\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6FC}(T)\,\text{d}T,\end{eqnarray}$$

where $E=\text{biaxial}$ elastic modulus; $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6FC}=\text{difference}$ in CTE between the two materials at any given temperature.

This yields a tensile stress of 11 MPa exerted during cool down. If this were to exceed the interfacial strength of the bond, we would see delamination failure. Since interfacial strengths are extremely dependent on the surface energy of the substrate which can be easily altered by the exact processing history or invisible contamination, this is a viable mechanism. It is certainly consistent with the gap seen only on the side facing the TMP wall. The implication of this would be that greater attention would need to be paid to the surface preparation for return to high yield.

Whereas the above argument is seemingly convincing and often true, it is imperative to look carefully at the details seen in the image. In particular, we see that the width of the gap is about $1.2~\unicode[STIX]{x03BC}\text{m}$ . If a delamination were to occur due the tensile stresses as detailed above, it would create a gap of only 300 nm at cryogenic temperatures that would then go back to near zero at RT. In other words, we should have seen evidence of fine cracks but not a large gap. So, looking at this issue from the standpoint of strain, the argument that stress in the underlying cause fails.

Re-examining what else can create a gap, the only other mechanism that can be invoked is shrinkage during curing. Typical acrylic adhesives shrink 3% to 4% linearly^{[Reference Moeck, Bianchi, Petry, Weder and Helsby18]}. The thickness of the adhesive layer is about $35~\unicode[STIX]{x03BC}\text{m}$ , so a gap of $1.2~\unicode[STIX]{x03BC}\text{m}$ is consistent with being a result of shrinkage upon curing. However, the question that comes up is what would have triggered this new onset of shrinkage at this specific location. It is possible to come up with various scenarios. But for the efforts not to diverge, it is necessary to do a careful scrutiny for all-around validity of any proposed mechanism. Our ultimate hypothesis for this was as follows (Figure 10). When the glue layer is exposed to UV light from the vertical direction, the free surface moves to accommodate the shrinkage. But if exposure occurs at an angle, then there is shadowing along some portion of the wall, leading to a region that cures late, and more importantly after the free surface has solidified.

Figure 10. Schematic of the hypothesis used to account for the FIB-SEM results.

In effect, the curing of free surface prior to full internal solidification imposes a constraint on where the shrinkage can occur. Shrinkage now has to happen internally and it does so along the shadowed wall. Upon inquiry, it turned out that the operation had indeed been modified recently to occasionally include a top down viewing of the exposure process with a microscope that forced the UV curing beam to be incident from the side and hence at an angle the TMP. The procedure had not formally called out for a vertical exposure, though it was the practiced norm for several years. A new operator presumed the tilting to be a benign enough modification and as a result, it was completely overlooked as a change during process review.

The final check was to correct the problem and validate the hypothesis. We installed a fixture that allowed the wand to be placed only at an orthogonal angle and at the right distance. Figure 11 shows the instantaneous and sustained improvement in the yield.

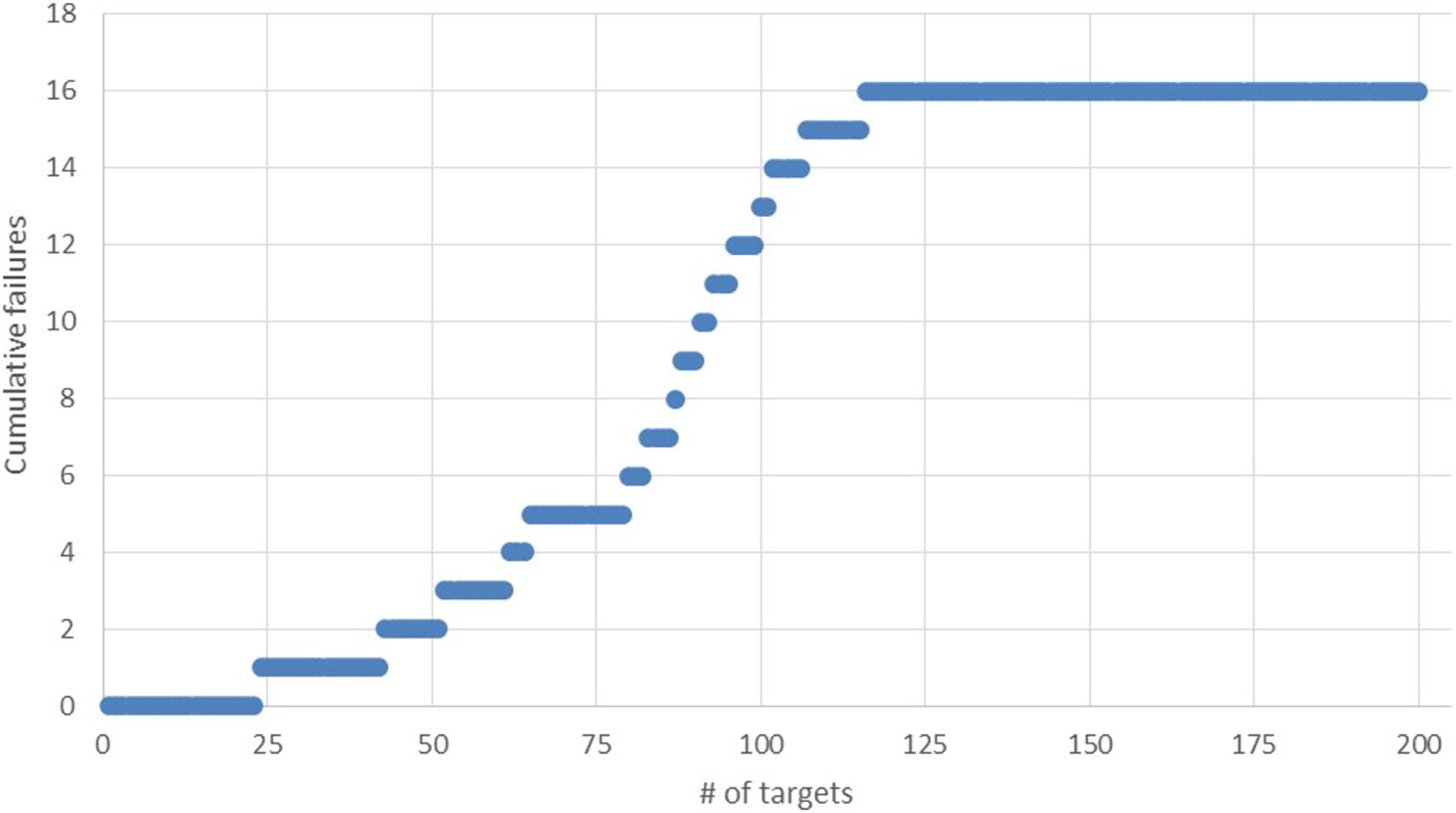
Figure 11. Plot showing the cumulative failures as a function of number of the targets built, representing a snapshot in time in target production. Note that the first instance of failure was around target 25. The installation of the fixture for vertical curing was implemented at target # 119, after which the failures stopped.

This served as the ultimate verification of the hypothesis.

Our goal of documenting this is to underline the subtlety involved in coming up with the exact cause for failure in this case. This has been equally true for other cases not mentioned here. This entire episode played out over about 4 months. About 30 days from the first failure, we had statistical data to say that the failure mode was not random fluctuation. Off-line testing and analysis took about 2 more months. While the implementation of solution was done quickly, to establish its sustained success meant another month of testing.

An important lesson to be learned from this is importance of any complex, multi-step production process to stay completely true to the established protocols. Corporations such as Intel have been known to espouse this principle when increasing throughput through expansion of production lines (replicate-everything-exactly motto). Likewise, it is equally important to specify the range of tolerance of the various steps when the process is being defined early on, particularly if it involves human operation. Drifts in procedures can cumulatively become a significant change over time. Designing fixtures to standardize is a great solution to this issue but can also be prohibitively expensive. When this is the case and failures happen, process reviews need to be rigorous and exacting.

6 Summary

ICF targets present interesting material challenges, one of the biggest of which is making sure that the thermal stresses that develop due the mismatch in coefficients of thermal expansion do not lead to failures in the numerous bonds. In this paper, we discuss the different factors that need to be considered to be able to specify the maximum flow rate allowed if a failure were to result in a leak at the operating temperature of ${\sim}18$  K. This maximum flow rate turns out to be $5\times 10^{-6}$  sccs, which is a very stringent requirement. Producing leak-tight targets everyday with nanoliter bond volumes to meet this requirement is a formidable task as the source of the leak is almost invariably too small to be detected via examination. This is exemplified by the analysis of a recurring failure mode that struck target production suddenly causing significant loss of time and labor. We describe our reasoning for the identification of the location as well as the in-depth failure analysis to identify the cause. The cause was far removed from the usual suspect of thermal stresses overcoming the bond strength. Here, it was due to a change in the angle of radiation curing of the adhesive that was presumed to be an insignificant change. The hall-mark of all problem-solving efforts for target leaks has been the consistent need for looking at all the minute details lest the efforts diverge in the wrong directions.