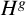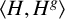1 Introduction
Let G be a group. A subgroup X of G is said to be pronormal in G if X is conjugate to
![]() $X^g$
in
$X^g$
in
![]() $\langle X,X^g\rangle $
for all
$\langle X,X^g\rangle $
for all
![]() $g\in G$
. Pronormal subgroups were introduced by P. Hall in his lectures in Cambridge with the aim of introducing a class of subgroups containing all normal and maximal subgroups of a group; actually, it is clear that for finite groups, all Sylow p-subgroups are pronormal and for soluble finite groups, all Hall
$g\in G$
. Pronormal subgroups were introduced by P. Hall in his lectures in Cambridge with the aim of introducing a class of subgroups containing all normal and maximal subgroups of a group; actually, it is clear that for finite groups, all Sylow p-subgroups are pronormal and for soluble finite groups, all Hall
![]() $\pi $
-subgroups are pronormal as well. It is also very easy to see that any subnormal subgroup which is pronormal must actually be normal. The first relevant results on pronormality were obtained by Rose [Reference Rose24], who proved, among other things, that two pronormal subgroups, one of which normalises the other, have a pronormal product. Later, Peng [Reference Peng22] showed that a finite group having only pronormal subgroups is soluble, but the consideration of the alternating group of degree
$\pi $
-subgroups are pronormal as well. It is also very easy to see that any subnormal subgroup which is pronormal must actually be normal. The first relevant results on pronormality were obtained by Rose [Reference Rose24], who proved, among other things, that two pronormal subgroups, one of which normalises the other, have a pronormal product. Later, Peng [Reference Peng22] showed that a finite group having only pronormal subgroups is soluble, but the consideration of the alternating group of degree
![]() $5$
shows that finite simple groups may have pronormal subgroups. Recently, Revin and Vdovin [Reference Revin and Vdovin23] proved that every Hall
$5$
shows that finite simple groups may have pronormal subgroups. Recently, Revin and Vdovin [Reference Revin and Vdovin23] proved that every Hall
![]() $\pi $
-subgroup of a finite simple group is pronormal; moreover, in [Reference Kondrat’ev, Maslova and Revin18], they investigated the pronormality of subgroups of odd index in finite simple groups (see also [Reference Kondrat’ev, Maslova and Revin19]). Based on this work, finite simple groups whose nonpronormal subgroups are abelian have been classified in [Reference Brescia and Trombetti3]. Actually, finite soluble groups whose nonabelian subgroups are pronormal began to be studied in [Reference Brescia, Ferrara and Trombetti2, Reference Ferrara and Trombetti12] with the aim of expanding well-known structural theorems concerning metahamiltonian groups (that is, groups whose proper subgroups are either abelian or normal) to larger classes of groups (see also [Reference De Falco, de Giovanni, Musella and Schmidt8, Reference Ferrara and Trombetti10, Reference Ferrara and Trombetti11] for other generalisations of this type) and these results were applied to obtain the results in [Reference Brescia and Trombetti3]. Here, we propose a different approach which does not rely on the complex study of the structure of finite soluble groups with only abelian or pronormal subgroups and makes it possible to characterise which finite simple groups have only pronormal or nilpotent subgroups.
$\pi $
-subgroup of a finite simple group is pronormal; moreover, in [Reference Kondrat’ev, Maslova and Revin18], they investigated the pronormality of subgroups of odd index in finite simple groups (see also [Reference Kondrat’ev, Maslova and Revin19]). Based on this work, finite simple groups whose nonpronormal subgroups are abelian have been classified in [Reference Brescia and Trombetti3]. Actually, finite soluble groups whose nonabelian subgroups are pronormal began to be studied in [Reference Brescia, Ferrara and Trombetti2, Reference Ferrara and Trombetti12] with the aim of expanding well-known structural theorems concerning metahamiltonian groups (that is, groups whose proper subgroups are either abelian or normal) to larger classes of groups (see also [Reference De Falco, de Giovanni, Musella and Schmidt8, Reference Ferrara and Trombetti10, Reference Ferrara and Trombetti11] for other generalisations of this type) and these results were applied to obtain the results in [Reference Brescia and Trombetti3]. Here, we propose a different approach which does not rely on the complex study of the structure of finite soluble groups with only abelian or pronormal subgroups and makes it possible to characterise which finite simple groups have only pronormal or nilpotent subgroups.
Theorem 1.1. Let G be a nonabelian finite simple group. Then G has only pronormal or nilpotent subgroups if and only if it is isomorphic to one of the following groups.
-
•
 $\operatorname {PSL}(2,q)$
, where q satisfies one of the following properties:
$\operatorname {PSL}(2,q)$
, where q satisfies one of the following properties:-
(i)
 $q=2^d$
and d is prime;
$q=2^d$
and d is prime; -
(ii)
 $q=3^d$
and d is an odd prime;
$q=3^d$
and d is an odd prime; -
(iii) q is prime and if
 $q\equiv _8\pm 1$
, then either
$q\equiv _8\pm 1$
, then either
 $q-1$
or
$q-1$
or
 $q+1$
is a power of
$q+1$
is a power of
 $2$
.
$2$
.
-
-
•
 $\operatorname {J}_1$
.
$\operatorname {J}_1$
. -
•
 $\operatorname {Sz}(q)$
, where
$\operatorname {Sz}(q)$
, where
 $q=2^{2n+1}$
where
$q=2^{2n+1}$
where
 $2n+1$
is a prime number.
$2n+1$
is a prime number.
Theorem 1.2. No infinite locally finite simple group has only nilpotent or pronormal subgroups.
Finally, it should be noted that in Section 3 (by comparison with the main theorem of [Reference Brescia and Trombetti3]), our results actually classify (locally) finite simple groups whose subgroups are either nilpotent of class
![]() $\leq c$
or pronormal.
$\leq c$
or pronormal.
2 Preliminaries
In our discussion, we will need the following easy facts on pronormality which are essential to prove that given subgroups are pronormal.
Lemma 2.1 [Reference Revin and Vdovin23, Lemma 5].
Let H be a subgroup of a group G. If H contains a subgroup P which is pronormal in G, then H is pronormal in G if and only if H is conjugate to
![]() $H^g$
in
$H^g$
in
![]() $\langle H,H^g\rangle $
for all
$\langle H,H^g\rangle $
for all
![]() $g\in N_G(P)$
.
$g\in N_G(P)$
.
Proof. The necessity of the condition being obvious, we prove the sufficiency. Let
![]() $g\in G$
. Since P is pronormal in G, there exists an element
$g\in G$
. Since P is pronormal in G, there exists an element
![]() $x\in \langle P,P^g\rangle \leq \langle H,H^g\rangle $
such that
$x\in \langle P,P^g\rangle \leq \langle H,H^g\rangle $
such that
![]() $P^x=P^g$
. Thus,
$P^x=P^g$
. Thus,
![]() $gx^{-1}$
belongs to
$gx^{-1}$
belongs to
![]() $N_G(P)$
and, by hypothesis, there is an element
$N_G(P)$
and, by hypothesis, there is an element
![]() $y\in \langle H,H^{gx^{-1}}\rangle \leq \langle H,H^g\rangle $
such that
$y\in \langle H,H^{gx^{-1}}\rangle \leq \langle H,H^g\rangle $
such that
![]() $H^y=H^{gx^{-1}}$
. Therefore,
$H^y=H^{gx^{-1}}$
. Therefore,
![]() $H^{yx}=H^g$
and
$H^{yx}=H^g$
and
![]() $yx$
belongs to
$yx$
belongs to
![]() $\langle H,H^g\rangle $
. The arbitrariness of g in G shows that H is pronormal in G.
$\langle H,H^g\rangle $
. The arbitrariness of g in G shows that H is pronormal in G.
Lemma 2.2. Let p be a prime and let A be a normal abelian p-subgroup of a group G having only pronormal or nilpotent subgroups. Let
![]() $B\leq A$
and suppose there is
$B\leq A$
and suppose there is
![]() ${1\neq x\in N_G(B)\setminus C_G(B)}$
having order prime to p. Then,
${1\neq x\in N_G(B)\setminus C_G(B)}$
having order prime to p. Then,
![]() $N_G(\langle x\rangle )\leq N_G(B)$
.
$N_G(\langle x\rangle )\leq N_G(B)$
.
Proof. Let
![]() $y\in N_G(\langle x\rangle )$
. Since the subgroup
$y\in N_G(\langle x\rangle )$
. Since the subgroup
![]() $\langle x\rangle B$
is nonnilpotent, it is pronormal in G and hence
$\langle x\rangle B$
is nonnilpotent, it is pronormal in G and hence
![]() $\langle x\rangle B$
is conjugate to
$\langle x\rangle B$
is conjugate to
![]() $\langle x\rangle B^y$
in
$\langle x\rangle B^y$
in
![]() $X=\langle x,B,B^y\rangle $
through an element
$X=\langle x,B,B^y\rangle $
through an element
![]() $x_1\in X$
. However,
$x_1\in X$
. However,
![]() $B^y\leq A$
centralises B showing that B is normal in X. Thus,
$B^y\leq A$
centralises B showing that B is normal in X. Thus,
![]() $B=B^{x_1}=B^y$
and the statement is proved.
$B=B^{x_1}=B^y$
and the statement is proved.
The following is a well-known result by John Rose, but since we will use it several times, we state it here as a lemma.
Lemma 2.3. Let p be a prime and let P be a p-subgroup of a finite group G. Then, P is pronormal in G if and only if P is normal in the normaliser of any Sylow p-subgroup containing it.
Since all subgroups of a cyclic Sylow p-subgroup S are normal in the normaliser of S, the above lemma has the following immediate consequence.
Corollary 2.4. Let G be a finite group with a cyclic Sylow p-subgroup S. Then, all subgroups of S are pronormal in G.
The following lemma is crucial in showing that many finite simple groups have nonnilpotent, nonpronormal subgroups: in fact, if a group G has a subquotient containing a nonnilpotent, nonpronormal subgroup, then G also contains such a subgroup.
Lemma 2.5. The following statements hold.
-
(i) The alternating group
 $\operatorname {Alt}(6)$
has a nonnilpotent, nonpronormal subgroup.
$\operatorname {Alt}(6)$
has a nonnilpotent, nonpronormal subgroup. -
(ii) A dihedral group
 $G=\operatorname {Dih}(2^nd)$
with
$G=\operatorname {Dih}(2^nd)$
with
 $(2,d)=1$
and
$(2,d)=1$
and
 $n\geq 1$
has only nilpotent or pronormal subgroups if and only if either
$n\geq 1$
has only nilpotent or pronormal subgroups if and only if either
 $d=1$
or
$d=1$
or
 $n\leq 2$
.
$n\leq 2$
. -
(iii) Let
 $n>3$
. The Weyl group
$n>3$
. The Weyl group
 $W_n$
for type
$W_n$
for type
 $\operatorname {D}_n$
contains a nonnilpotent, nonpronormal subgroup.
$\operatorname {D}_n$
contains a nonnilpotent, nonpronormal subgroup. -
(iv) The Weyl group W for type
 $\operatorname {F}_4$
contains a nonnilpotent, nonpronormal subgroup.
$\operatorname {F}_4$
contains a nonnilpotent, nonpronormal subgroup. -
(v) If
 $n\geq 4$
, the Weyl group W for type
$n\geq 4$
, the Weyl group W for type
 $\operatorname {B}_n/\operatorname {C}_n$
contains a nonnilpotent, nonpronormal subgroup.
$\operatorname {B}_n/\operatorname {C}_n$
contains a nonnilpotent, nonpronormal subgroup.
Proof. (i) Let
![]() $X=\langle (1,2,3),(1,2)(4,5)\rangle $
; in particular,
$X=\langle (1,2,3),(1,2)(4,5)\rangle $
; in particular,
![]() $X\simeq \operatorname {Sym}(3)$
. Let g be the permutation
$X\simeq \operatorname {Sym}(3)$
. Let g be the permutation
![]() $(1,4)(2,5,3,6)$
. The subgroup
$(1,4)(2,5,3,6)$
. The subgroup
 $$ \begin{align*} \langle X,X^g\rangle & =\langle (1,2,3),\, (1,2)(4,5),\, (4,5,6),\,(4,5)(1,3)\rangle\\ & =\langle (1,2)(4,5)\rangle\ltimes(\langle (1,2,3)\rangle\times\langle (4,5,6)\rangle) \end{align*} $$
$$ \begin{align*} \langle X,X^g\rangle & =\langle (1,2,3),\, (1,2)(4,5),\, (4,5,6),\,(4,5)(1,3)\rangle\\ & =\langle (1,2)(4,5)\rangle\ltimes(\langle (1,2,3)\rangle\times\langle (4,5,6)\rangle) \end{align*} $$
contains
![]() $\langle (1,2,3)\rangle $
as a normal subgroup. Thus, X cannot be conjugate to
$\langle (1,2,3)\rangle $
as a normal subgroup. Thus, X cannot be conjugate to
![]() $X^g$
in
$X^g$
in
![]() $\langle X,X^g\rangle $
; in particular, X is not pronormal in G. Since it is not even nilpotent, the statement is proved.
$\langle X,X^g\rangle $
; in particular, X is not pronormal in G. Since it is not even nilpotent, the statement is proved.
(ii) Of course, if
![]() $d=1$
, then G is a
$d=1$
, then G is a
![]() $2$
-group and so even nilpotent. However, if
$2$
-group and so even nilpotent. However, if
![]() $n\leq 2$
, then all nonnilpotent subgroups of G are products of a pronormal subgroup of order
$n\leq 2$
, then all nonnilpotent subgroups of G are products of a pronormal subgroup of order
![]() $2$
, a normal
$2$
, a normal
![]() $2'$
-subgroup and possibly also of a central subgroup of order
$2'$
-subgroup and possibly also of a central subgroup of order
![]() $2$
, so they are pronormal by Lemma 2.3.
$2$
, so they are pronormal by Lemma 2.3.
Conversely, suppose
![]() $d\neq 1$
and
$d\neq 1$
and
![]() $n\geq 3$
. Write
$n\geq 3$
. Write
![]() $G=\langle a\rangle \ltimes \langle b\rangle $
, where a has order
$G=\langle a\rangle \ltimes \langle b\rangle $
, where a has order
![]() $2$
and b has order
$2$
and b has order
![]() $2^{n-1}d$
. In this case, it is easy to see that the nonnilpotent subgroup
$2^{n-1}d$
. In this case, it is easy to see that the nonnilpotent subgroup
![]() $\langle a,b^{2^{n-1}}\rangle $
is subnormal but not normal in G, so it cannot be pronormal.
$\langle a,b^{2^{n-1}}\rangle $
is subnormal but not normal in G, so it cannot be pronormal.
(iii) It is well known that the group in question is of the form
![]() $\operatorname {Sym}(n)\ltimes \mathbb {Z}_2^{n-1}$
, so the case
$\operatorname {Sym}(n)\ltimes \mathbb {Z}_2^{n-1}$
, so the case
![]() $n\geq 6$
follows at once from proof (i). The other cases are straightforward.
$n\geq 6$
follows at once from proof (i). The other cases are straightforward.
(iv) It is evident by an inspection of the Dynkin diagram for type
![]() $\operatorname {F}_4$
that W contains a subgroup which is isomorphic with the Weyl group for type
$\operatorname {F}_4$
that W contains a subgroup which is isomorphic with the Weyl group for type
![]() $\operatorname {D}_4$
(see, for instance, [Reference Carter5, page 47]). Thus, the result follows from proof (iii).
$\operatorname {D}_4$
(see, for instance, [Reference Carter5, page 47]). Thus, the result follows from proof (iii).
(v) It is well known that the Weyl group for type
![]() $\operatorname {B}_4$
is isomorphic to the semi-direct product
$\operatorname {B}_4$
is isomorphic to the semi-direct product
![]() $\operatorname {Sym}(4)\ltimes (\langle a_1\rangle \times \langle a_2\rangle \times \langle a_3\rangle \times \langle a_4\rangle )$
, where each
$\operatorname {Sym}(4)\ltimes (\langle a_1\rangle \times \langle a_2\rangle \times \langle a_3\rangle \times \langle a_4\rangle )$
, where each
![]() $a_i$
has order
$a_i$
has order
![]() $2$
and
$2$
and
![]() $\operatorname {Sym}(4)$
acts on the
$\operatorname {Sym}(4)$
acts on the
![]() $a_i$
permuting the indexes in a natural way. Now, it is easy to check that the subgroup
$a_i$
permuting the indexes in a natural way. Now, it is easy to check that the subgroup
![]() $X=\langle (1,2,3),a_1a_2\rangle $
is isomorphic to
$X=\langle (1,2,3),a_1a_2\rangle $
is isomorphic to
![]() $\operatorname {Alt}(4)$
, so it is not nilpotent. Conjugation by
$\operatorname {Alt}(4)$
, so it is not nilpotent. Conjugation by
![]() $g=(1,2)$
shows that X is not conjugate to
$g=(1,2)$
shows that X is not conjugate to
![]() $X^g$
in
$X^g$
in
![]() $\langle X,X^g\rangle $
. In fact, the Sylow
$\langle X,X^g\rangle $
. In fact, the Sylow
![]() $2$
-subgroup S of X is normal in
$2$
-subgroup S of X is normal in
![]() $\langle X,X^g\rangle $
, but
$\langle X,X^g\rangle $
, but
![]() $S^g\neq S$
.
$S^g\neq S$
.
Finally, the result follows from the observation that the Weyl group for type
![]() $\operatorname {B}_4$
embeds in that for type
$\operatorname {B}_4$
embeds in that for type
![]() $\operatorname {B}_n$
when
$\operatorname {B}_n$
when
![]() $n\geq 4$
, and that the Weyl group for type
$n\geq 4$
, and that the Weyl group for type
![]() $\operatorname {C}_n$
coincides with that for type
$\operatorname {C}_n$
coincides with that for type
![]() $\operatorname {B}_n$
.
$\operatorname {B}_n$
.
3 Proof of the main theorems
To prove Theorem 1.1, we proceed along the following lines: first we show that
![]() $\operatorname {J}_1$
is the only sporadic group to have only pronormal or nilpotent subgroups (see Theorem 3.1); then we show that the only finite simple groups of untwisted Lie type with only pronormal or nilpotent subgroups are to be found in those of type
$\operatorname {J}_1$
is the only sporadic group to have only pronormal or nilpotent subgroups (see Theorem 3.1); then we show that the only finite simple groups of untwisted Lie type with only pronormal or nilpotent subgroups are to be found in those of type
![]() $\operatorname {A}_n$
(see Theorems 3.2 and 3.3); finally, Theorem 3.4 shows that for finite simple groups of twisted Lie type, we must look at Suzuki groups and then Theorem 3.5 shows that the Suzuki groups we are looking for are precisely the minimal nonsimple ones. Theorem 1.1 clearly follows from a combination of these theorems.
$\operatorname {A}_n$
(see Theorems 3.2 and 3.3); finally, Theorem 3.4 shows that for finite simple groups of twisted Lie type, we must look at Suzuki groups and then Theorem 3.5 shows that the Suzuki groups we are looking for are precisely the minimal nonsimple ones. Theorem 1.1 clearly follows from a combination of these theorems.
Theorem 3.1.
![]() $\operatorname {J}_1$
is the only sporadic group whose subgroups are either pronormal or nilpotent.
$\operatorname {J}_1$
is the only sporadic group whose subgroups are either pronormal or nilpotent.
Proof. It follows from [Reference Conway, Curtis, Norton, Parker and Wilson6] that, apart from
![]() $\operatorname {J}_1$
, all sporadic groups contain a subquotient isomorphic to
$\operatorname {J}_1$
, all sporadic groups contain a subquotient isomorphic to
![]() $\operatorname {Alt}(6)$
; thus by Lemma 2.5, no sporadic group, apart from possibly
$\operatorname {Alt}(6)$
; thus by Lemma 2.5, no sporadic group, apart from possibly
![]() $\operatorname {J}_1$
, has only pronormal or nilpotent subgroups. Finally, it follows from [Reference Brescia and Trombetti3, Proposition 5] that all subgroups of
$\operatorname {J}_1$
, has only pronormal or nilpotent subgroups. Finally, it follows from [Reference Brescia and Trombetti3, Proposition 5] that all subgroups of
![]() $\operatorname {J}_1$
are either pronormal or abelian, so in particular they are either pronormal or nilpotent. The proof is complete.
$\operatorname {J}_1$
are either pronormal or abelian, so in particular they are either pronormal or nilpotent. The proof is complete.
We refer to [Reference Dickson9] for a detailed list of all isomorphism classes of subgroups of
![]() $\operatorname {PSL}(2,F)$
for a finite field F.
$\operatorname {PSL}(2,F)$
for a finite field F.
Theorem 3.2. Let G be a projective special linear simple group over a finite field (and let
![]() $c\geq 1$
). Then, G has only nilpotent (of class
$c\geq 1$
). Then, G has only nilpotent (of class
![]() $\leq c$
) or pronormal subgroups if and only if it is isomorphic with
$\leq c$
) or pronormal subgroups if and only if it is isomorphic with
![]() $\operatorname {PSL}(2,q)$
, where q satisfies one of the following properties:
$\operatorname {PSL}(2,q)$
, where q satisfies one of the following properties:
-
(i)
 $q=2^d$
and d is prime;
$q=2^d$
and d is prime; -
(ii)
 $q=3^d$
and d is an odd prime;
$q=3^d$
and d is an odd prime; -
(iii) q is prime and if
 $q\equiv _8\pm 1$
, then either
$q\equiv _8\pm 1$
, then either
 $q-1$
or
$q-1$
or
 $q+1$
is a power
$q+1$
is a power
 $2^m$
of
$2^m$
of
 $2$
(and
$2$
(and
 $m-3\leq c$
).
$m-3\leq c$
).
Proof. Suppose G is isomorphic to
![]() $\operatorname {PSL}(n,F)$
for a finite field F of order
$\operatorname {PSL}(n,F)$
for a finite field F of order
![]() $q=p^d$
for a prime p, and has only pronormal or nilpotent subgroups. Since the alternating group on n elements can always be embedded into
$q=p^d$
for a prime p, and has only pronormal or nilpotent subgroups. Since the alternating group on n elements can always be embedded into
![]() $\operatorname {PSL}(n,F)$
through the consideration of the permutation matrices, it follows from Lemma 2.5 that
$\operatorname {PSL}(n,F)$
through the consideration of the permutation matrices, it follows from Lemma 2.5 that
![]() $n<6$
.
$n<6$
.
Assume now
![]() $n\geq 3$
. If p is odd, then the subgroup
$n\geq 3$
. If p is odd, then the subgroup
![]() $X=\langle a,b\rangle $
of
$X=\langle a,b\rangle $
of
![]() $\operatorname {SL}(2,F)$
, where
$\operatorname {SL}(2,F)$
, where
 $$ \begin{align*}a=\begin{pmatrix} 1 & 1 & 0\\[0.2cm] 0 & 1 & 1\\[0.2cm] 0 & 0 &1\end{pmatrix}\quad\mathrm{and}\quad b=\begin{pmatrix} -1 & 0 & 0\\[0.2cm] 0 & 1 & -1\\[0.2cm] 0 & 0 & -1\end{pmatrix},\end{align*} $$
$$ \begin{align*}a=\begin{pmatrix} 1 & 1 & 0\\[0.2cm] 0 & 1 & 1\\[0.2cm] 0 & 0 &1\end{pmatrix}\quad\mathrm{and}\quad b=\begin{pmatrix} -1 & 0 & 0\\[0.2cm] 0 & 1 & -1\\[0.2cm] 0 & 0 & -1\end{pmatrix},\end{align*} $$
is easily seen to be dihedral of order
![]() $2p$
, so nonnilpotent. If
$2p$
, so nonnilpotent. If
 $$ \begin{align*}g=\begin{pmatrix} 1 & 0 & 0\\[0.2cm] 0 & -1 & 0\\[0.2cm] 0 & 0 & -1\end{pmatrix},\end{align*} $$
$$ \begin{align*}g=\begin{pmatrix} 1 & 0 & 0\\[0.2cm] 0 & -1 & 0\\[0.2cm] 0 & 0 & -1\end{pmatrix},\end{align*} $$
then
![]() $g\in C_G(b)$
and
$g\in C_G(b)$
and
![]() $H=\langle X,X^g\rangle =\langle b\rangle \ltimes Y$
, where
$H=\langle X,X^g\rangle =\langle b\rangle \ltimes Y$
, where
![]() $Y=\operatorname {UT}(3,p)$
; in particular, Y is nonabelian of order
$Y=\operatorname {UT}(3,p)$
; in particular, Y is nonabelian of order
![]() $p^3$
and exponent p. Since
$p^3$
and exponent p. Since
![]() $a^g\not \in \langle a,Y'\rangle \trianglelefteq H$
, it follows that X is not conjugate to
$a^g\not \in \langle a,Y'\rangle \trianglelefteq H$
, it follows that X is not conjugate to
![]() $X^g$
in H. Since X embeds isomorphically in
$X^g$
in H. Since X embeds isomorphically in
![]() $\operatorname {PSL}(2,F)$
, we have a contradiction. Thus,
$\operatorname {PSL}(2,F)$
, we have a contradiction. Thus,
![]() $p=2$
. Since it is well known that
$p=2$
. Since it is well known that
![]() $\operatorname {PSL}(3,4)$
contains a subgroup isomorphic to
$\operatorname {PSL}(3,4)$
contains a subgroup isomorphic to
![]() $\operatorname {Alt}(6)$
, we are left with
$\operatorname {Alt}(6)$
, we are left with
![]() $q=2$
by Lemma 2.5. Now,
$q=2$
by Lemma 2.5. Now,
![]() $\operatorname {PSL}(4,2)\simeq \operatorname {Alt}(8)$
is contained in
$\operatorname {PSL}(4,2)\simeq \operatorname {Alt}(8)$
is contained in
![]() $\operatorname {PSL}(5,2)$
as a subgroup. Again by Lemma 2.5, the only possibility left is
$\operatorname {PSL}(5,2)$
as a subgroup. Again by Lemma 2.5, the only possibility left is
![]() $\operatorname {PSL}(3,2)$
, but this is isomorphic to
$\operatorname {PSL}(3,2)$
, but this is isomorphic to
![]() $\operatorname {PSL}(2,7)$
which has only pronormal or abelian subgroups (see [Reference Brescia and Trombetti3, Proposition 4]).
$\operatorname {PSL}(2,7)$
which has only pronormal or abelian subgroups (see [Reference Brescia and Trombetti3, Proposition 4]).
Suppose now
![]() $n=2$
, so
$n=2$
, so
![]() $q\geq 4$
. Let X be the image of
$q\geq 4$
. Let X be the image of
![]() $\operatorname {UT}(2,q)$
in G; in particular, X is an elementary abelian p-group of order q. It is well known that
$\operatorname {UT}(2,q)$
in G; in particular, X is an elementary abelian p-group of order q. It is well known that
![]() $N_G(X)/X$
is a cyclic group of order
$N_G(X)/X$
is a cyclic group of order
![]() $(p^d-1)/\operatorname {gcd}(2,p^d-1)$
irreducibly acting on X. Since
$(p^d-1)/\operatorname {gcd}(2,p^d-1)$
irreducibly acting on X. Since
![]() $X=C_G(X)$
, it follows from Lemma 2.2 that all elements of
$X=C_G(X)$
, it follows from Lemma 2.2 that all elements of
![]() $N_G(X)/X$
must act irreducibly on X. This immediately yields that
$N_G(X)/X$
must act irreducibly on X. This immediately yields that
![]() $N_G(X)/X$
is odd when
$N_G(X)/X$
is odd when
![]() $d>1$
; in particular,
$d>1$
; in particular,
![]() $q=9$
is impossible. Moreover, if
$q=9$
is impossible. Moreover, if
![]() $d=ab$
for some
$d=ab$
for some
![]() $a,b>1$
, then
$a,b>1$
, then
and so
![]() $p^a-1=1$
, which is a contradiction. Thus, d is prime when
$p^a-1=1$
, which is a contradiction. Thus, d is prime when
![]() $d>1$
.
$d>1$
.
Suppose
![]() $p>3$
. In this case,
$p>3$
. In this case,
![]() $N_G(X)/X$
contains a nontrivial subgroup of order
$N_G(X)/X$
contains a nontrivial subgroup of order
![]() ${(p-1)/2}$
and so
${(p-1)/2}$
and so
![]() $p=q$
. If
$p=q$
. If
![]() $q\equiv _8\pm 1$
and
$q\equiv _8\pm 1$
and
![]() $q\neq 7$
, then
$q\neq 7$
, then
![]() $q>13$
and hence G contains dihedral groups of order
$q>13$
and hence G contains dihedral groups of order
![]() $q-1$
and
$q-1$
and
![]() $q+1$
. By Lemma 2.5, either
$q+1$
. By Lemma 2.5, either
![]() $q-1$
or
$q-1$
or
![]() $q+1$
is a power of
$q+1$
is a power of
![]() $2$
. Now, the result follows easily from the fact that a dihedral group of order
$2$
. Now, the result follows easily from the fact that a dihedral group of order
![]() $2^m$
with
$2^m$
with
![]() $m\geq 4$
has a subgroup of order
$m\geq 4$
has a subgroup of order
![]() $2^{m-2}$
with nilpotency class
$2^{m-2}$
with nilpotency class
![]() $m-3$
which is not pronormal.
$m-3$
which is not pronormal.
Conversely, suppose G is isomorphic to one of the groups described in the statement. It follows from [Reference Brescia and Trombetti3, Proposition 4] that we may assume
![]() $p>3$
,
$p>3$
,
![]() $p=q$
and either
$p=q$
and either
![]() $q+1$
or
$q+1$
or
![]() $q-1$
being equal to
$q-1$
being equal to
![]() $2^m$
for some m with
$2^m$
for some m with
![]() $3\leq m$
(
$3\leq m$
(
![]() $\leq c+3$
,
$\leq c+3$
,
![]() $c\geq 2$
). Let X be a nonnilpotent (of class
$c\geq 2$
). Let X be a nonnilpotent (of class
![]() $\leq c$
) and nonpronormal subgroup of G; in particular, X is not a maximal subgroup of G. Let
$\leq c$
) and nonpronormal subgroup of G; in particular, X is not a maximal subgroup of G. Let
![]() $g\in G$
be such that X is not conjugate to
$g\in G$
be such that X is not conjugate to
![]() $X^g$
in
$X^g$
in
![]() $\langle X,X^g\rangle $
, so
$\langle X,X^g\rangle $
, so
![]() $X<\langle X,X^g\rangle <G$
.
$X<\langle X,X^g\rangle <G$
.
If X is isomorphic to
![]() $\operatorname {Alt}(4)$
, then
$\operatorname {Alt}(4)$
, then
![]() $\langle X,X^g\rangle $
is either
$\langle X,X^g\rangle $
is either
![]() $\operatorname {Sym}(4)$
or
$\operatorname {Sym}(4)$
or
![]() $\operatorname {Alt}(5)$
, and both these groups have only one conjugacy class of subgroups isomorphic to
$\operatorname {Alt}(5)$
, and both these groups have only one conjugacy class of subgroups isomorphic to
![]() $\operatorname {Alt}(4)$
. Thus, X is pronormal in these cases and this is a contradiction. A similar argument applies if
$\operatorname {Alt}(4)$
. Thus, X is pronormal in these cases and this is a contradiction. A similar argument applies if
![]() $\langle X,X^g\rangle $
is contained in a maximal subgroup M isomorphic to
$\langle X,X^g\rangle $
is contained in a maximal subgroup M isomorphic to
![]() $\operatorname {Alt}(5)$
and
$\operatorname {Alt}(5)$
and
![]() $X\simeq \operatorname {Sym}(3),\operatorname {Dih}(10)$
: just note that in these cases, X is maximal in M.
$X\simeq \operatorname {Sym}(3),\operatorname {Dih}(10)$
: just note that in these cases, X is maximal in M.
Suppose X is isomorphic to a subgroup of the normaliser of a Sylow p-subgroup of G. Then, since it is nonabelian, it must contain the Sylow p-subgroup of G and so it is pronormal by Lemma 2.1, which is a contradiction. (If X is contained in a Sylow
![]() $2$
-subgroup S, then it must be a normal subgroup of
$2$
-subgroup S, then it must be a normal subgroup of
![]() $S=N_G(S)$
and hence Lemma 2.3 gives a contradiction.)
$S=N_G(S)$
and hence Lemma 2.3 gives a contradiction.)
The only case left is that in which X is contained in a maximal dihedral subgroup of G and X has order
![]() $2r$
for some odd number r dividing either
$2r$
for some odd number r dividing either
![]() $q-1$
or
$q-1$
or
![]() $q+1$
. Since the Sylow d-subgroups of G are cyclic for any divisor d of r, it follows from Lemma 2.3 that the
$q+1$
. Since the Sylow d-subgroups of G are cyclic for any divisor d of r, it follows from Lemma 2.3 that the
![]() $2'$
-component of X is pronormal in G. Now, Lemma 2.1 shows that also in this case, X is pronormal in G, which is the final contradiction.
$2'$
-component of X is pronormal in G. Now, Lemma 2.1 shows that also in this case, X is pronormal in G, which is the final contradiction.
Theorem 3.3. Every finite simple group G of untwisted Lie type
![]() $\neq \operatorname {A}_n$
has a nonnilpotent, nonpronormal subgroup.
$\neq \operatorname {A}_n$
has a nonnilpotent, nonpronormal subgroup.
Proof. By Lemma 2.5, it is enough to look at finite simple groups of types
![]() $\operatorname {B}_n, \operatorname {C}_n,\operatorname {E}_6$
,
$\operatorname {B}_n, \operatorname {C}_n,\operatorname {E}_6$
,
![]() $\operatorname {E}_7,\operatorname {E}_8,\operatorname {G}_2$
with
$\operatorname {E}_7,\operatorname {E}_8,\operatorname {G}_2$
with
![]() $n\leq 3$
.
$n\leq 3$
.
Suppose G is of type
![]() $\operatorname {B}_n$
,
$\operatorname {B}_n$
,
![]() $n>1$
. Since
$n>1$
. Since
![]() $\operatorname {B}_2(2)$
is isomorphic to
$\operatorname {B}_2(2)$
is isomorphic to
![]() $\operatorname {Sym}(6)$
, we may assume by Lemma 2.5 that the characteristic of the ground field is odd. In this case, the subgroup X of
$\operatorname {Sym}(6)$
, we may assume by Lemma 2.5 that the characteristic of the ground field is odd. In this case, the subgroup X of
![]() $\operatorname {B}_2$
generated by
$\operatorname {B}_2$
generated by
 $$ \begin{align*}\begin{pmatrix} 0 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0& 0 & 0 & 0 & 1 \end{pmatrix} \quad\mbox{and}\quad \begin{pmatrix} 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 & 0\\ 0& 0 & 0 & 0 & 1 \end{pmatrix} \end{align*} $$
$$ \begin{align*}\begin{pmatrix} 0 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0& 0 & 0 & 0 & 1 \end{pmatrix} \quad\mbox{and}\quad \begin{pmatrix} 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 & 0\\ 0& 0 & 0 & 0 & 1 \end{pmatrix} \end{align*} $$
is isomorphic to
![]() $\operatorname {SL}(2,3)$
, so it is not nilpotent. Conjugation by
$\operatorname {SL}(2,3)$
, so it is not nilpotent. Conjugation by
 $$ \begin{align*}g:=\begin{pmatrix} -1 & 0 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 & 0\\ 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0& 0 & 0 & 0 & -1 \end{pmatrix}\end{align*} $$
$$ \begin{align*}g:=\begin{pmatrix} -1 & 0 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 & 0\\ 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0& 0 & 0 & 0 & -1 \end{pmatrix}\end{align*} $$
yields that X is not pronormal in W: indeed,
![]() $O=\operatorname {O}_2(X)$
is normal in
$O=\operatorname {O}_2(X)$
is normal in
![]() $\langle X,X^g\rangle $
but
$\langle X,X^g\rangle $
but
![]() ${O^g\neq O}$
.
${O^g\neq O}$
.
Suppose now G is a finite simple group of type
![]() $\operatorname {C}_n$
(
$\operatorname {C}_n$
(
![]() $n\geq 3$
). If the characteristic of the ground field is even, then G is isomorphic to the corresponding group of type
$n\geq 3$
). If the characteristic of the ground field is even, then G is isomorphic to the corresponding group of type
![]() $\operatorname {B}_n$
. Assume the characteristic of the ground field is odd. It is well known that
$\operatorname {B}_n$
. Assume the characteristic of the ground field is odd. It is well known that
![]() $\operatorname {C}_n$
contains a subgroup isomorphic to the general linear group of degree n over the same field. Thus, the result in this case follows from Theorem 3.2.
$\operatorname {C}_n$
contains a subgroup isomorphic to the general linear group of degree n over the same field. Thus, the result in this case follows from Theorem 3.2.
For the following discussion concerning finite simple groups of types
![]() $\operatorname {E}_6$
,
$\operatorname {E}_6$
,
![]() $\operatorname {E}_7$
and
$\operatorname {E}_7$
and
![]() $\operatorname {E}_8$
, we refer to [Reference Humphreys14, Section 2.12]. The Weyl group for type
$\operatorname {E}_8$
, we refer to [Reference Humphreys14, Section 2.12]. The Weyl group for type
![]() $\operatorname {E}_6$
has a subgroup which is isomorphic to
$\operatorname {E}_6$
has a subgroup which is isomorphic to
![]() $\operatorname {B}_2(3)$
, so it has some nonnilpotent, nonpronormal subgroup; note here that the Weyl group for type
$\operatorname {B}_2(3)$
, so it has some nonnilpotent, nonpronormal subgroup; note here that the Weyl group for type
![]() $\operatorname {E}_6$
embeds in the one for type
$\operatorname {E}_6$
embeds in the one for type
![]() $\operatorname {E}_7$
. Finally, the Weyl group for type
$\operatorname {E}_7$
. Finally, the Weyl group for type
![]() $\operatorname {E}_8$
has a homomorphic image isomorphic to
$\operatorname {E}_8$
has a homomorphic image isomorphic to
![]() $\operatorname {D}_4(2)$
and so Lemma 2.5 completes the discussion in these cases.
$\operatorname {D}_4(2)$
and so Lemma 2.5 completes the discussion in these cases.
Finally, suppose G is of type
![]() $\operatorname {G}_2$
. If the characteristic is even, then G contains a subgroup isomorphic to
$\operatorname {G}_2$
. If the characteristic is even, then G contains a subgroup isomorphic to
![]() $\operatorname {Sym}(3)\times \operatorname {Sym}(3)$
(see [Reference Cooperstein7]) which is easily checked to contain a nonnilpotent, nonpronormal subgroup. Suppose therefore the characteristic is odd. In this case, G contains a subgroup isomorphic to
$\operatorname {Sym}(3)\times \operatorname {Sym}(3)$
(see [Reference Cooperstein7]) which is easily checked to contain a nonnilpotent, nonpronormal subgroup. Suppose therefore the characteristic is odd. In this case, G contains a subgroup isomorphic to
![]() $\operatorname {SL}_3$
over the same field (see for instance [Reference Kleidman16]) and so Theorem 3.2 yields that G contains a nonnilpotent, nonpronormal subgroup.
$\operatorname {SL}_3$
over the same field (see for instance [Reference Kleidman16]) and so Theorem 3.2 yields that G contains a nonnilpotent, nonpronormal subgroup.
Theorem 3.4. All finite simple groups of twisted Lie type except possibly from type
![]() $^2\!\operatorname {B}_2$
have a nonnilpotent, nonpronormal subgroup.
$^2\!\operatorname {B}_2$
have a nonnilpotent, nonpronormal subgroup.
Proof. Suppose first that G is of type
![]() $^2\!\operatorname {A}_n$
. We can rule out this case precisely as in [Reference Brescia and Trombetti3]. Here, we describe an alternative approach. If
$^2\!\operatorname {A}_n$
. We can rule out this case precisely as in [Reference Brescia and Trombetti3]. Here, we describe an alternative approach. If
![]() $n=3$
and
$n=3$
and
![]() $p=q=5$
, then a look at [Reference Bray, Holt and Roney-Dougal1, Table 8.6] shows that G involves an alternating group of degree
$p=q=5$
, then a look at [Reference Bray, Holt and Roney-Dougal1, Table 8.6] shows that G involves an alternating group of degree
![]() $6$
and the conclusion is reached by Lemma 2.5. Assume
$6$
and the conclusion is reached by Lemma 2.5. Assume
![]() $n=3$
and
$n=3$
and
![]() $q\neq 5$
, and let B be a Borel subgroup of G and X a Levi complement of B, so
$q\neq 5$
, and let B be a Borel subgroup of G and X a Levi complement of B, so
![]() $B=XS$
, where S is a Sylow p-subgroup of G. In particular, X is cyclic and
$B=XS$
, where S is a Sylow p-subgroup of G. In particular, X is cyclic and
![]() $|X|=(q^2-1)/d$
, where
$|X|=(q^2-1)/d$
, where
![]() $d=(q+1,3)$
(see [Reference Bray, Holt and Roney-Dougal1, Table 8.5]). Put
$d=(q+1,3)$
(see [Reference Bray, Holt and Roney-Dougal1, Table 8.5]). Put
![]() $\overline B=B/Z(S)$
. Now it is not difficult to see (using also [Reference Simpson and Frame25, Table 2]) that there exist a subgroup
$\overline B=B/Z(S)$
. Now it is not difficult to see (using also [Reference Simpson and Frame25, Table 2]) that there exist a subgroup
![]() $\overline {H}$
of
$\overline {H}$
of
![]() $\overline S=S/Z(S)$
and elements
$\overline S=S/Z(S)$
and elements
![]() $\overline x$
and
$\overline x$
and
![]() $\overline y$
of
$\overline y$
of
![]() $\overline X=XZ(S)/Z(S)$
, such that
$\overline X=XZ(S)/Z(S)$
, such that
![]() $\overline {x}$
normalises
$\overline {x}$
normalises
![]() $\overline {H}$
, while
$\overline {H}$
, while
![]() $\langle \overline {x},\overline {H}\rangle $
and
$\langle \overline {x},\overline {H}\rangle $
and
![]() $\langle \overline {x},\overline {H}\rangle ^{\overline {y}}$
are not conjugate in the subgroup they generate. Therefore, we may assume
$\langle \overline {x},\overline {H}\rangle ^{\overline {y}}$
are not conjugate in the subgroup they generate. Therefore, we may assume
![]() $n>3$
. Now, the discussion follows the notation in [Reference Burgoyne, Griess and Lyons4]. Let H be the simple adjoint algebraic group over
$n>3$
. Now, the discussion follows the notation in [Reference Burgoyne, Griess and Lyons4]. Let H be the simple adjoint algebraic group over
![]() $\overline {\mathbb {F}}_q$
with associated Dynkin diagram of type
$\overline {\mathbb {F}}_q$
with associated Dynkin diagram of type
![]() $\operatorname {A}_n$
,
$\operatorname {A}_n$
,
![]() $\lambda =\sigma _q$
and
$\lambda =\sigma _q$
and
![]() $\mu =\,^2\sigma _q$
. Then
$\mu =\,^2\sigma _q$
. Then
![]() $H_\lambda =\operatorname {PGL}_n(q)$
,
$H_\lambda =\operatorname {PGL}_n(q)$
,
![]() $H_\mu =PGU_{n+1}(q)$
,
$H_\mu =PGU_{n+1}(q)$
,
![]() $\operatorname {O}^{p'}(H_\lambda )=\operatorname {L}_{n+1}(q)$
,
$\operatorname {O}^{p'}(H_\lambda )=\operatorname {L}_{n+1}(q)$
,
![]() $\operatorname {O}^{p'}(H_\mu )=\operatorname {U}_{n+1}(q)=G$
,
$\operatorname {O}^{p'}(H_\mu )=\operatorname {U}_{n+1}(q)=G$
,
 $$ \begin{align*} X=O^{p'}(H_\mu\cap H_\lambda)= \begin{cases} \operatorname{PSp}_{n+1}(q) & \text{if }n\text{ is odd}\\ \Omega_{n+1}(q) & \text{if }n\text{ is even and }q\text{ is odd}\\ \operatorname{Sp}_{n}(q) & \text{if }n\text{ and }q\text{ are even.} \end{cases} \end{align*} $$
$$ \begin{align*} X=O^{p'}(H_\mu\cap H_\lambda)= \begin{cases} \operatorname{PSp}_{n+1}(q) & \text{if }n\text{ is odd}\\ \Omega_{n+1}(q) & \text{if }n\text{ is even and }q\text{ is odd}\\ \operatorname{Sp}_{n}(q) & \text{if }n\text{ and }q\text{ are even.} \end{cases} \end{align*} $$
Since
![]() $n>3$
, X is either simple of type B or C (and we apply Theorem 3.3) or it is
$n>3$
, X is either simple of type B or C (and we apply Theorem 3.3) or it is
![]() $\operatorname {Sp}_4(2)\simeq \operatorname {Sym}(6)$
(and we apply Lemma 2.5).
$\operatorname {Sp}_4(2)\simeq \operatorname {Sym}(6)$
(and we apply Lemma 2.5).
Assume now
![]() $G\simeq \,^2\!\operatorname {G}_2(q)$
for
$G\simeq \,^2\!\operatorname {G}_2(q)$
for
![]() $q=3^{2n+1}\geq 27$
. It follows from [Reference Kleidman16] that G has a subgroup X of type
$q=3^{2n+1}\geq 27$
. It follows from [Reference Kleidman16] that G has a subgroup X of type
![]() $\mathbb {Z}_3\ltimes (V\times D)$
, where D is dihedral of order
$\mathbb {Z}_3\ltimes (V\times D)$
, where D is dihedral of order
![]() $(1/2)(q+1)$
and the elements of order
$(1/2)(q+1)$
and the elements of order
![]() $3$
normalise but do not centralise the four-group
$3$
normalise but do not centralise the four-group
![]() $V\simeq \mathbb {Z}_2\times \mathbb {Z}_2$
. Since a Sylow
$V\simeq \mathbb {Z}_2\times \mathbb {Z}_2$
. Since a Sylow
![]() $2$
-subgroup of G is elementary abelian of order
$2$
-subgroup of G is elementary abelian of order
![]() $8$
, it follows that D is nonnilpotent; but it can be easily seen that X contains a subgroup isomorphic to D which is not even pronormal in X.
$8$
, it follows that D is nonnilpotent; but it can be easily seen that X contains a subgroup isomorphic to D which is not even pronormal in X.
If G is of type
![]() $^2\!\operatorname {F}_4$
, then it contains a subgroup isomorphic to a finite simple group of type
$^2\!\operatorname {F}_4$
, then it contains a subgroup isomorphic to a finite simple group of type
![]() $\operatorname {B}_2$
(see [Reference Malle21]) and Theorem 3.3 shows that G contains a nonnilpotent, nonpronormal subgroup.
$\operatorname {B}_2$
(see [Reference Malle21]) and Theorem 3.3 shows that G contains a nonnilpotent, nonpronormal subgroup.
If
![]() $G\simeq \,^3D_4(q^3)$
, then it contains a subgroup X isomorphic to
$G\simeq \,^3D_4(q^3)$
, then it contains a subgroup X isomorphic to
![]() $\operatorname {G}_2(q)$
(see [Reference Kleidman17]) and so again Theorem 3.3 shows that G contains a nonnilpotent, nonpronormal subgroup in the case where
$\operatorname {G}_2(q)$
(see [Reference Kleidman17]) and so again Theorem 3.3 shows that G contains a nonnilpotent, nonpronormal subgroup in the case where
![]() $q>2$
. If
$q>2$
. If
![]() $q=2$
, then
$q=2$
, then
![]() $G'\simeq \,^2\!\operatorname {A}_2(3^2)$
and we are done in any case.
$G'\simeq \,^2\!\operatorname {A}_2(3^2)$
and we are done in any case.
The case
![]() $^2\!\operatorname {E}_6$
can be easily handled noticing that it contains as a subgroup a finite simple group of type
$^2\!\operatorname {E}_6$
can be easily handled noticing that it contains as a subgroup a finite simple group of type
![]() $\operatorname {F}_4$
(see [Reference Liebeck and Saxl20, Table 1]).
$\operatorname {F}_4$
(see [Reference Liebeck and Saxl20, Table 1]).
Assume G is of type
![]() $^2\!\operatorname {D}_n$
for
$^2\!\operatorname {D}_n$
for
![]() $n\geq 4$
: the discussion here follows again the notation in [Reference Burgoyne, Griess and Lyons4]. Let H be the simple adjoint algebraic group over
$n\geq 4$
: the discussion here follows again the notation in [Reference Burgoyne, Griess and Lyons4]. Let H be the simple adjoint algebraic group over
![]() $\overline {\mathbb {F}}_q$
with associated Dynkin diagram of type
$\overline {\mathbb {F}}_q$
with associated Dynkin diagram of type
![]() $\operatorname {D}_n$
,
$\operatorname {D}_n$
,
![]() $\lambda =\sigma _q$
and
$\lambda =\sigma _q$
and
![]() $\mu =\,^2\sigma _q$
. Then,
$\mu =\,^2\sigma _q$
. Then,
![]() $O^{p'}(H_\lambda )=P\Omega _{2n}^+(q)$
,
$O^{p'}(H_\lambda )=P\Omega _{2n}^+(q)$
,
![]() $O^{p'}(H_\mu )=P\Omega _{2n}^-(q)=G$
and
$O^{p'}(H_\mu )=P\Omega _{2n}^-(q)=G$
and
 $$ \begin{align*} X=O^{p'}(H_\mu\cap H_\lambda)= \begin{cases} \Omega_{2n-1}(q) & q\text{ odd,}\\ \operatorname{Sp}_{2n-2}(q) & q\text{ even.} \end{cases} \end{align*} $$
$$ \begin{align*} X=O^{p'}(H_\mu\cap H_\lambda)= \begin{cases} \Omega_{2n-1}(q) & q\text{ odd,}\\ \operatorname{Sp}_{2n-2}(q) & q\text{ even.} \end{cases} \end{align*} $$
Since
![]() $n\geq 4$
, X is a finite simple group of type
$n\geq 4$
, X is a finite simple group of type
![]() $\operatorname {B}_{n-1}$
or of type
$\operatorname {B}_{n-1}$
or of type
![]() $\operatorname {C}_{n-1}$
, Theorem 3.3 completes the proof in this case.
$\operatorname {C}_{n-1}$
, Theorem 3.3 completes the proof in this case.
Theorem 3.5. Let
![]() $q=2^{2n+1}$
for some positive integer n. Then
$q=2^{2n+1}$
for some positive integer n. Then
![]() $\operatorname {Sz}(q)$
has only nilpotent (of class
$\operatorname {Sz}(q)$
has only nilpotent (of class
![]() $\leq 2$
) or pronormal subgroups if and only if
$\leq 2$
) or pronormal subgroups if and only if
![]() $2n+1$
is a prime.
$2n+1$
is a prime.
Proof. It is well known that a subgroup of G is either isomorphic to
![]() $\operatorname {Sz}(s)$
with q a power of s, or conjugate to a subgroup of one of the following groups.
$\operatorname {Sz}(s)$
with q a power of s, or conjugate to a subgroup of one of the following groups.
-
(1) A solvable Frobenius group F of cardinality
 $q^2(q-1)$
; note that
$q^2(q-1)$
; note that
 $F=D\ltimes S$
, where D is cyclic of order
$F=D\ltimes S$
, where D is cyclic of order
 $q-1$
and S is a Sylow
$q-1$
and S is a Sylow
 $2$
-subgroup of G.
$2$
-subgroup of G. -
(2)
 $\operatorname {Dih}(2(q-1))$
; this is actually the normaliser of the diagonal subgroup of order
$\operatorname {Dih}(2(q-1))$
; this is actually the normaliser of the diagonal subgroup of order
 $q-1$
.
$q-1$
. -
(3) The normaliser N of a cyclic group A of cardinality
 $q\pm r+1$
with
$q\pm r+1$
with
 $r^2=2q$
; in this case, N has order
$r^2=2q$
; in this case, N has order
 $4(q\pm r+1)$
.
$4(q\pm r+1)$
.
We also remark that the order of G is
![]() $q^2(q^2+1)(q-1)$
and that the numbers
$q^2(q^2+1)(q-1)$
and that the numbers
![]() ${q-1}$
,
${q-1}$
,
![]() $q+r+1$
and
$q+r+1$
and
![]() $q-r+1$
are odd and pairwise relatively prime. Moreover, a Sylow p-subgroup S of G is such that
$q-r+1$
are odd and pairwise relatively prime. Moreover, a Sylow p-subgroup S of G is such that
![]() $S'=\Omega _1(S)\leq Z(S)$
,
$S'=\Omega _1(S)\leq Z(S)$
,
![]() $S/S'$
is elementary abelian of order q; a cyclic subgroup
$S/S'$
is elementary abelian of order q; a cyclic subgroup
![]() $D\leq N_G(S)$
of order
$D\leq N_G(S)$
of order
![]() $q-1$
acts on
$q-1$
acts on
![]() $S'\setminus \{1\}$
transitively. It is therefore clear that if
$S'\setminus \{1\}$
transitively. It is therefore clear that if
![]() $d\in D$
normalises some proper nontrivial subgroup L of
$d\in D$
normalises some proper nontrivial subgroup L of
![]() $S'$
, then
$S'$
, then
![]() $\langle d\rangle L$
is nonpronormal and not even nilpotent; since the former condition is equivalent to the requirement that
$\langle d\rangle L$
is nonpronormal and not even nilpotent; since the former condition is equivalent to the requirement that
![]() $2n+1$
is a prime, the necessity of the condition is proved.
$2n+1$
is a prime, the necessity of the condition is proved.
Suppose now that
![]() $2n+1$
is a prime and let H be a nonnilpotent, nonpronormal subgroup of G. It follows from Lemma 2.1 and Corollary 2.4 that H cannot be contained in a subgroup of type (2) or (3). The only possibility left is that H is contained in a subgroup
$2n+1$
is a prime and let H be a nonnilpotent, nonpronormal subgroup of G. It follows from Lemma 2.1 and Corollary 2.4 that H cannot be contained in a subgroup of type (2) or (3). The only possibility left is that H is contained in a subgroup
![]() $F=D\ltimes S$
of type (1). In such circumstances,
$F=D\ltimes S$
of type (1). In such circumstances,
![]() $H\geq S'$
. Since H is not a maximal subgroup of G, we may also assume that
$H\geq S'$
. Since H is not a maximal subgroup of G, we may also assume that
![]() $H\cap S=S'$
. Let
$H\cap S=S'$
. Let
![]() $g\in G$
be such that H is not conjugate to
$g\in G$
be such that H is not conjugate to
![]() $H^g$
in
$H^g$
in
![]() $J=\langle H,H^g\rangle $
. Since
$J=\langle H,H^g\rangle $
. Since
![]() $G>J>H$
, it is easy to see that
$G>J>H$
, it is easy to see that
![]() $J\leq S$
; moreover, since
$J\leq S$
; moreover, since
![]() $S'=\Omega _1(S)$
, it follows that
$S'=\Omega _1(S)$
, it follows that
![]() $g\in N_G(S')$
and
$g\in N_G(S')$
and
![]() $S'$
is normal in J. Finally, since all subgroups of S of order dividing
$S'$
is normal in J. Finally, since all subgroups of S of order dividing
![]() $q-1$
are conjugate in S, it follows that H is conjugate to
$q-1$
are conjugate in S, it follows that H is conjugate to
![]() $H^g$
in J, which is a contradiction.
$H^g$
in J, which is a contradiction.
Proof of Theorem 1.2.
Let G be an infinite locally finite simple group with only nilpotent or pronormal subgroups. Using [Reference Kegel and Wehrfritz15, Theorem 4.4], we may assume that G is countably infinite. Let
![]() $\mathcal {K}$
be a Kegel cover of G; using Theorem 1.1, we may certainly arrange this in such a way that the Kegel factors are either all of type
$\mathcal {K}$
be a Kegel cover of G; using Theorem 1.1, we may certainly arrange this in such a way that the Kegel factors are either all of type
![]() $\operatorname {A}_n$
or all of type
$\operatorname {A}_n$
or all of type
![]() $^2\!\operatorname {B}_2$
.
$^2\!\operatorname {B}_2$
.
Since every finite subgroup of G is isomorphic to a subgroup of some Kegel factor, [Reference Hall and Hartley13, Theorem 1] and Malcev’s representation theorem yield that G is linear over some field. Now, it follows from [Reference Kegel and Wehrfritz15, Proposition 4.6] that G is the union of an ascending chain of finite simple groups and this is impossible by Theorem 1.1.