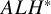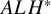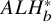1 Introduction
Gravitational instantons were introduced by Hawking [Reference Hawking11] as certain solutions to the classical Einstein equations. They are the building blocks of Euclidean quantum gravity and are analogous to self-dual Yang-Mills instantons arising from Yang-Mills theory. Mathematically, gravitational instantons are noncompact, complete hyperKähler manifolds with
![]() $L^2$
-integrable curvature tensor. Depending on the volume growth of the geometry at infinity, there are a few known classes of gravitational instantons discovered first:
$L^2$
-integrable curvature tensor. Depending on the volume growth of the geometry at infinity, there are a few known classes of gravitational instantons discovered first:
![]() $ALE$
,
$ALE$
,
![]() $ALF$
,
$ALF$
,
![]() $ALG$
,
$ALG$
,
![]() $ALH$
. Here
$ALH$
. Here
![]() $ALE$
is the abbreviation for asymptotically locally Euclidean,
$ALE$
is the abbreviation for asymptotically locally Euclidean,
![]() $ALF$
is for asymptotically locally flat, and the latter two were simply named by induction. Later, Hein [Reference Hein12] constructed new gravitational instantons with different curvature decay and volume growth on the complement of a fibre in a rational elliptic surface, named
$ALF$
is for asymptotically locally flat, and the latter two were simply named by induction. Later, Hein [Reference Hein12] constructed new gravitational instantons with different curvature decay and volume growth on the complement of a fibre in a rational elliptic surface, named
![]() $ALG^*$
(corresponding to Kodaira type
$ALG^*$
(corresponding to Kodaira type
![]() $I^*_b$
-fibre) and
$I^*_b$
-fibre) and
![]() $ALH^*$
(corresponding to Kodaira type
$ALH^*$
(corresponding to Kodaira type
![]() $I_b$
-fibre). The first class has the same volume growth as
$I_b$
-fibre). The first class has the same volume growth as
![]() $ALG$
but with different curvature decay, while the latter has a volume growth of
$ALG$
but with different curvature decay, while the latter has a volume growth of
![]() $r^{4/3}$
.
$r^{4/3}$
.
Gravitational instantons also play an important role in differential geometry, as they arise as the blow-up limits of hyperKähler metrics [Reference Hein, Sun, Viaclovsky and Zhang14, Reference Chen, Viaclovsky and Zhang6]. Recently, Sun-Zhang [Reference Song and Zhang27] made use of the Cheeger-Fukaya-Gromov theory of
![]() $\mathcal {N}$
-structures to prove that any nonflat gravitational instanton has a unique asymptotic cone and indeed falls into one of the families in the above list. Thus, it remains to classify the gravitational instantons in each class.
$\mathcal {N}$
-structures to prove that any nonflat gravitational instanton has a unique asymptotic cone and indeed falls into one of the families in the above list. Thus, it remains to classify the gravitational instantons in each class.
The classification of the gravitational instantons has a long history. By work of Kronheimer [Reference Kronheimer17],
![]() $ALE$
gravitational instantons always have the underlying geometry of a minimal resolution of the quotient of
$ALE$
gravitational instantons always have the underlying geometry of a minimal resolution of the quotient of
![]() $\mathbb {C}^2$
by a finite subgroup of
$\mathbb {C}^2$
by a finite subgroup of
![]() $SU(2)$
. Moreover, Kronheimer established a Torelli-type theorem for ALE gravitational instantons. More recently, building on work of Minerbe [Reference Minerbe21], Chen-Chen [Reference Chen and Chen3] studied gravitational instantons with curvature decay
$SU(2)$
. Moreover, Kronheimer established a Torelli-type theorem for ALE gravitational instantons. More recently, building on work of Minerbe [Reference Minerbe21], Chen-Chen [Reference Chen and Chen3] studied gravitational instantons with curvature decay
![]() $|Rm|\leqslant r^{-2-\varepsilon }$
for some
$|Rm|\leqslant r^{-2-\varepsilon }$
for some
![]() $\varepsilon>0$
. They proved such gravitational instantons must be of the class
$\varepsilon>0$
. They proved such gravitational instantons must be of the class
![]() $ALE$
,
$ALE$
,
![]() $ALF$
,
$ALF$
,
![]() $ALG$
or
$ALG$
or
![]() $ALH$
. Moreover, Chen-Chen proved that up to hyperKähler rotation,
$ALH$
. Moreover, Chen-Chen proved that up to hyperKähler rotation,
![]() $ALH$
(or
$ALH$
(or
![]() $ALG$
) gravitational instantons are isomorphic to the complement of a fibre with zero (or finite) monodromy in a rational elliptic surface. Very recently, Chen-Viaclovsky [Reference Chen, Viaclovsky and Zhang6] studied the Hodge theory of
$ALG$
) gravitational instantons are isomorphic to the complement of a fibre with zero (or finite) monodromy in a rational elliptic surface. Very recently, Chen-Viaclovsky [Reference Chen, Viaclovsky and Zhang6] studied the Hodge theory of
![]() $ALG^*$
-gravitational instantons, and then Chen-Viaclovsky-Zhang [Reference Chen, Viaclovsky and Zhang7] proved the Torelli-type theorem for the
$ALG^*$
-gravitational instantons, and then Chen-Viaclovsky-Zhang [Reference Chen, Viaclovsky and Zhang7] proved the Torelli-type theorem for the
![]() $ALG,ALG^*$
gravitational instantons. So the remaining case is the classification of the gravitational instantons of type
$ALG,ALG^*$
gravitational instantons. So the remaining case is the classification of the gravitational instantons of type
![]() $ALH^*$
.
$ALH^*$
.
Examples of
![]() $ALH^*$
gravitational instantons are constructed from del Pezzo surfaces by Tian-Yau [Reference Tian and Yau28] and from rational elliptic surfaces by Hein [Reference Hein12]. Hein observed that these two examples have the same curvature decay, injectivity radius and volume growth. The relation between the two examples was made precise by the authors [Reference Collins, Jacob and Lin4, Reference Collins, Jacob and Lin5] as a by-product of their work on the Strominger-Yau-Zaslow mirror symmetry of log Calabi-Yau surfaces; in particular, it was shown that these two examples are related by a global hyperKähler rotation.
$ALH^*$
gravitational instantons are constructed from del Pezzo surfaces by Tian-Yau [Reference Tian and Yau28] and from rational elliptic surfaces by Hein [Reference Hein12]. Hein observed that these two examples have the same curvature decay, injectivity radius and volume growth. The relation between the two examples was made precise by the authors [Reference Collins, Jacob and Lin4, Reference Collins, Jacob and Lin5] as a by-product of their work on the Strominger-Yau-Zaslow mirror symmetry of log Calabi-Yau surfaces; in particular, it was shown that these two examples are related by a global hyperKähler rotation.
The goal is this paper is to give a short proof of a Torelli theorem for
![]() $ALH^*$
gravitational instantons using the earlier results in [Reference Collins, Jacob and Lin4, Reference Collins, Jacob and Lin5], together with the recent work of Sun-Zhang [Reference Song and Zhang27]. Below, we give an informal statement of the main theorem and refer the reader to Theorem 3.9 for a precise version.
$ALH^*$
gravitational instantons using the earlier results in [Reference Collins, Jacob and Lin4, Reference Collins, Jacob and Lin5], together with the recent work of Sun-Zhang [Reference Song and Zhang27]. Below, we give an informal statement of the main theorem and refer the reader to Theorem 3.9 for a precise version.
Theorem 1.1.
![]() $ALH^*$
gravitational instantons are classified by the cohomology classes of their hyperKähler triple.
$ALH^*$
gravitational instantons are classified by the cohomology classes of their hyperKähler triple.
The proof of the above theorem is similar to the Torelli theorem for K3 surfaces, which is a consequence of the results from [Reference Piatetskii-Shapiro and Shafarevich26, Reference Burns and Rapoport2, Reference Looijenga and Peters20] and the Calabi conjecture [Reference Yau29]. The proof goes as follows; using the exponential decay result of
![]() $ALH^*$
gravitational instantons to the Calabi ansatz by Sun-Zhang [Reference Song and Zhang27], an earlier argument of the authors from [Reference Collins, Jacob and Lin4] implies that up to hyperKähler rotation, any
$ALH^*$
gravitational instantons to the Calabi ansatz by Sun-Zhang [Reference Song and Zhang27], an earlier argument of the authors from [Reference Collins, Jacob and Lin4] implies that up to hyperKähler rotation, any
![]() $ALH^*$
gravitational instanton can be compactified to a rational elliptic surface. The complex structure of such a rational elliptic surface is determined by Gross-Hacking-Keel’s [Reference Gross, Hacking and Keel9] Torelli theorem for log Calabi-Yau surfaces. Theorem 3.9 then follows from a local model calculation in combination with the essentially optimal uniqueness theorem for solutions of the complex Monge-Ampère equations established by the authors in [Reference Collins, Jacob and Lin5].
$ALH^*$
gravitational instanton can be compactified to a rational elliptic surface. The complex structure of such a rational elliptic surface is determined by Gross-Hacking-Keel’s [Reference Gross, Hacking and Keel9] Torelli theorem for log Calabi-Yau surfaces. Theorem 3.9 then follows from a local model calculation in combination with the essentially optimal uniqueness theorem for solutions of the complex Monge-Ampère equations established by the authors in [Reference Collins, Jacob and Lin5].
The paper is organised as follows. In Section 2, we review the earlier work of the authors. This includes the construction of special Lagrangian tori via the mean curvature flow in the geometry asymptotic to the Calabi ansatz and the hyperKähler rotation of the Calabi ansatz, as well as a uniqueness theorem for Ricci-flat metrics on the complement of an
![]() $I_b$
-fibre in a rational elliptic surface. In Section 3, we first recall the result of Sun-Zhang [Reference Song and Zhang27] on
$I_b$
-fibre in a rational elliptic surface. In Section 3, we first recall the result of Sun-Zhang [Reference Song and Zhang27] on
![]() $ALH^*$
gravitational instantons and provide a short proof of the Torelli theorem based on the results reviewed in Section 2.
$ALH^*$
gravitational instantons and provide a short proof of the Torelli theorem based on the results reviewed in Section 2.
2 Previous results
2.1 Ansatz special Lagrangians and their hyperKähler rotations
We begin by reviewing the Calabi ansatz. Let
![]() $D=\mathbb {C}/(\mathbb {Z}\oplus \mathbb {Z}\tau )$
be an elliptic curve with
$D=\mathbb {C}/(\mathbb {Z}\oplus \mathbb {Z}\tau )$
be an elliptic curve with
![]() $\mbox {Im}\tau>0$
and
$\mbox {Im}\tau>0$
and
![]() $\omega _D$
a flat metric on D. For a fixed
$\omega _D$
a flat metric on D. For a fixed
![]() $b\in \mathbb {N}$
, let L be a degree b line bundle over D, and denote by
$b\in \mathbb {N}$
, let L be a degree b line bundle over D, and denote by
![]() $Y_{\mathcal {C}}$
the total space of L with projection
$Y_{\mathcal {C}}$
the total space of L with projection
![]() $\pi _{\mathcal {C}}:Y_{\mathcal {C}}\rightarrow D$
. Let
$\pi _{\mathcal {C}}:Y_{\mathcal {C}}\rightarrow D$
. Let
![]() $X_{\mathcal {C}}$
be the complement of the zero section in
$X_{\mathcal {C}}$
be the complement of the zero section in
![]() $Y_{\mathcal {C}}$
. Choose h to be the unique hermitian metric on L with curvature given by
$Y_{\mathcal {C}}$
. Choose h to be the unique hermitian metric on L with curvature given by
![]() $\omega _D$
with
$\omega _D$
with
![]() $\int _D \omega _D=2\pi b$
. If we let z be the coordinate on D and
$\int _D \omega _D=2\pi b$
. If we let z be the coordinate on D and
![]() $\xi $
a local trivialisation of L, we get coordinates on L via
$\xi $
a local trivialisation of L, we get coordinates on L via
![]() $(z,w)\mapsto (z,w\xi )$
. The Calabi ansatz is then given by
$(z,w)\mapsto (z,w\xi )$
. The Calabi ansatz is then given by
for a given holomorphic function
![]() $f(z)$
such that
$f(z)$
such that
 $$ \begin{align*} \frac{i}{2}\int_{D} \frac{Res_{D}\Omega_{\mathcal{C}}}{2\pi i}\wedge \overline{\bigg(\frac{Res_D{\Omega}_{\mathcal{C}}}{2\pi i}\bigg)}=2\pi b. \end{align*} $$
$$ \begin{align*} \frac{i}{2}\int_{D} \frac{Res_{D}\Omega_{\mathcal{C}}}{2\pi i}\wedge \overline{\bigg(\frac{Res_D{\Omega}_{\mathcal{C}}}{2\pi i}\bigg)}=2\pi b. \end{align*} $$
It is straightforward to check that
![]() $(\omega _{\mathcal {C}},\Omega _{\mathcal {C}})$
is a hyperKähler triple: that is,
$(\omega _{\mathcal {C}},\Omega _{\mathcal {C}})$
is a hyperKähler triple: that is,
![]() $2\omega _{\mathcal {C}}^2=\Omega _{\mathcal {C}}\wedge \bar {\Omega }_{\mathcal {C}}$
. The induced Riemannian metric is complete but not of bounded geometry. Specifically, if r denotes the distance function to a fixed point, then as one travels towards the zero section, the curvature and injectivity radius have the following behaviour:
$2\omega _{\mathcal {C}}^2=\Omega _{\mathcal {C}}\wedge \bar {\Omega }_{\mathcal {C}}$
. The induced Riemannian metric is complete but not of bounded geometry. Specifically, if r denotes the distance function to a fixed point, then as one travels towards the zero section, the curvature and injectivity radius have the following behaviour:
Let
![]() $\underline {L}$
be a special Lagrangian in D with respect to
$\underline {L}$
be a special Lagrangian in D with respect to
![]() $(\omega _D,\Omega _D)$
, where
$(\omega _D,\Omega _D)$
, where
![]() $\Omega _D$
is a holomorphic volume form on D such that
$\Omega _D$
is a holomorphic volume form on D such that
![]() $\omega _D=\frac {i}{2}\Omega _D\wedge \bar {\Omega }_D$
. A straightforward calculation shows that
$\omega _D=\frac {i}{2}\Omega _D\wedge \bar {\Omega }_D$
. A straightforward calculation shows that
is a special Lagrangian submanifold of
![]() $(X_{\mathcal {C}},\omega _{\mathcal {C}},\Omega _{\mathcal {C}})$
. We call
$(X_{\mathcal {C}},\omega _{\mathcal {C}},\Omega _{\mathcal {C}})$
. We call
![]() $L_{\mathcal {C}}$
an ansatz special Lagrangian. In particular, a special Lagrangian fibration in D induces a special Lagrangian fibration in
$L_{\mathcal {C}}$
an ansatz special Lagrangian. In particular, a special Lagrangian fibration in D induces a special Lagrangian fibration in
![]() $X_{\mathcal {C}}$
, and by direct calculation, the monodromy of such fibration is conjugate to
$X_{\mathcal {C}}$
, and by direct calculation, the monodromy of such fibration is conjugate to
![]() $\begin {pmatrix} 1 & b \\ 0 & 1 \end {pmatrix}$
. The middle homology
$\begin {pmatrix} 1 & b \\ 0 & 1 \end {pmatrix}$
. The middle homology
![]() $H_2(X_{\mathcal {C}},\mathbb {Z})\cong \mathbb {Z}^2$
is generated by
$H_2(X_{\mathcal {C}},\mathbb {Z})\cong \mathbb {Z}^2$
is generated by
![]() $[L_{\mathcal {C}}],[L^{\prime }_{\mathcal {C}}]$
, where
$[L_{\mathcal {C}}],[L^{\prime }_{\mathcal {C}}]$
, where
![]() $\underline {L},\underline {L}'$
are any pair such that
$\underline {L},\underline {L}'$
are any pair such that
![]() $[\underline {L}],[\underline {L}']$
generates
$[\underline {L}],[\underline {L}']$
generates
![]() $H_1(D,\mathbb {Z})$
.
$H_1(D,\mathbb {Z})$
.
Since in complex dimension two, all Ricci-flat Kähler metrics are hyperKähler, one can perform a hyperKähler rotation and arrive at
![]() $\check {X}_{mod}$
with a Kähler form
$\check {X}_{mod}$
with a Kähler form
![]() $\check {\omega }_{\mathcal C}$
and holomorphic volume form
$\check {\omega }_{\mathcal C}$
and holomorphic volume form
![]() $\check {\Omega }_{\mathcal C}$
that has the same underlying space as
$\check {\Omega }_{\mathcal C}$
that has the same underlying space as
![]() $X_{\mathcal {C}}$
. By choosing the hyperKähler rotation appropriately, the special Lagrangian fibration near infinity in
$X_{\mathcal {C}}$
. By choosing the hyperKähler rotation appropriately, the special Lagrangian fibration near infinity in
![]() $X_{\mathcal {C}}$
becomes an elliptic fibration
$X_{\mathcal {C}}$
becomes an elliptic fibration
![]() $\check {X}_{mod}\rightarrow \Delta ^*$
over a punctured disc
$\check {X}_{mod}\rightarrow \Delta ^*$
over a punctured disc
![]() $\Delta ^*$
. The monodromy of the fibration implies that after a choice of section
$\Delta ^*$
. The monodromy of the fibration implies that after a choice of section
![]() $\sigma :\Delta ^*\rightarrow \check {X}_{mod}$
, the space
$\sigma :\Delta ^*\rightarrow \check {X}_{mod}$
, the space
![]() $X_{mod}$
is biholomorphic to
$X_{mod}$
is biholomorphic to
Here we will use u for the complex coordinate of the disc and v for the fibre. See [Reference Collins, Jacob and Lin5, Appendix A]. There is a natural partial compactification
![]() $\check {Y}_{mod}\rightarrow \Delta $
by adding an
$\check {Y}_{mod}\rightarrow \Delta $
by adding an
![]() $I_b$
fibre over the origin of
$I_b$
fibre over the origin of
![]() $\Delta $
.
$\Delta $
.
Before we identify
![]() $\check {\omega }_{\mathcal C}$
and
$\check {\omega }_{\mathcal C}$
and
![]() $\check {\Omega }_{\mathcal C}$
, we recall the standard semi-flat metric on
$\check {\Omega }_{\mathcal C}$
, we recall the standard semi-flat metric on
![]() $\check {X}_{mod}$
, written down in [Reference Greene, Shapere, Vafa and Yau10]:
$\check {X}_{mod}$
, written down in [Reference Greene, Shapere, Vafa and Yau10]:
 $$ \begin{align*} \omega_{sf,\varepsilon} &:= \sqrt{-1}|\kappa(u)|^2 \frac{k|\log|u||}{2\pi\varepsilon}\frac{du\wedge d\bar{u}}{|u|^2} \\ &\quad + \frac{\sqrt{-1}}{2} \frac{2\pi\varepsilon}{k|\log|u||} \left(dv+B(u,v)du\right)\wedge \overline{\left(dv+B(u,v)du\right)}, \end{align*} $$
$$ \begin{align*} \omega_{sf,\varepsilon} &:= \sqrt{-1}|\kappa(u)|^2 \frac{k|\log|u||}{2\pi\varepsilon}\frac{du\wedge d\bar{u}}{|u|^2} \\ &\quad + \frac{\sqrt{-1}}{2} \frac{2\pi\varepsilon}{k|\log|u||} \left(dv+B(u,v)du\right)\wedge \overline{\left(dv+B(u,v)du\right)}, \end{align*} $$
where
![]() $B(u,v) = -\frac {\mathrm {Im}(v)}{\sqrt {-1}u|\log |u||}$
. A straightforward calculation shows that
$B(u,v) = -\frac {\mathrm {Im}(v)}{\sqrt {-1}u|\log |u||}$
. A straightforward calculation shows that
-
1.
 $\varepsilon $
is the size of the fibre with respect to
$\varepsilon $
is the size of the fibre with respect to
 $\omega _{sf}$
.
$\omega _{sf}$
. -
2.
 $\omega _{sf}$
is flat along the fibres.
$\omega _{sf}$
is flat along the fibres. -
3.
 $(\omega _{sf},\Omega _{sf})$
form a hyperKähler triple, where
$(\omega _{sf},\Omega _{sf})$
form a hyperKähler triple, where
 $\Omega _{sf}=\frac {\kappa (u)}{u}dv\wedge du$
is the unique volume form such that
$\Omega _{sf}=\frac {\kappa (u)}{u}dv\wedge du$
is the unique volume form such that
 $\int _{C}\Omega _{sf}=1$
, and C is the
$\int _{C}\Omega _{sf}=1$
, and C is the
 $2$
-cycle represented by
$2$
-cycle represented by
 $\{|u|=const, \mbox {Im}(v)=0 \}$
.
$\{|u|=const, \mbox {Im}(v)=0 \}$
.
The cycle C is called a ‘bad cycle’ by Hein [Reference Hein12],Footnote 1 and this notion is refined by the authors in [Reference Collins, Jacob and Lin5]. It is easy to see that
![]() $H_2(\check {X}_{mod},\mathbb {Z})$
is freely generated by the fibre class and C; we therefore define
$H_2(\check {X}_{mod},\mathbb {Z})$
is freely generated by the fibre class and C; we therefore define
Definition 2.1. A cycle
![]() $C' \subset X_{mod}$
is called a quasi-bad cycle if the homology class
$C' \subset X_{mod}$
is called a quasi-bad cycle if the homology class
![]() $[C'] \in H_2(\check {X}_{mod},\mathbb {Z})$
can be written as
$[C'] \in H_2(\check {X}_{mod},\mathbb {Z})$
can be written as
![]() $m[C]+[F]$
, where
$m[C]+[F]$
, where
![]() $[F]$
is the fibre class.
$[F]$
is the fibre class.
It was observed by Hein that the semi-flat metric has the same asymptotic behaviour for
![]() $|Rm|$
and
$|Rm|$
and
![]() $inj$
as the Calabi ansatz [Reference Hein12]. This motivates the natural guess that the hyperKähler rotation of the Calabi ansatz would give the semi-flat metric. However, there is a certain subtle discrepancy, and one must first introduce a class of nonstandard semi-flat metrics, as defined in [Reference Collins, Jacob and Lin5]. For any
$inj$
as the Calabi ansatz [Reference Hein12]. This motivates the natural guess that the hyperKähler rotation of the Calabi ansatz would give the semi-flat metric. However, there is a certain subtle discrepancy, and one must first introduce a class of nonstandard semi-flat metrics, as defined in [Reference Collins, Jacob and Lin5]. For any
![]() $b_0\in \mathbb {R}$
, we define the nonstandard semi-flat metric as
$b_0\in \mathbb {R}$
, we define the nonstandard semi-flat metric as
 $$ \begin{align*} \omega_{sf, b_0, \varepsilon} &:= \sqrt{-1}\frac{|\kappa(u)|^2}{\varepsilon} W^{-1}\frac{du\wedge d\bar{u}}{|u|^2}\\ &\quad + \frac{\sqrt{-1}}{2} W \varepsilon \left(dv+\widetilde{\Gamma}(v,u,b_0) du\right) \wedge \overline{\left(dv+\widetilde{\Gamma}(u,v,b_0) du\right)}, \end{align*} $$
$$ \begin{align*} \omega_{sf, b_0, \varepsilon} &:= \sqrt{-1}\frac{|\kappa(u)|^2}{\varepsilon} W^{-1}\frac{du\wedge d\bar{u}}{|u|^2}\\ &\quad + \frac{\sqrt{-1}}{2} W \varepsilon \left(dv+\widetilde{\Gamma}(v,u,b_0) du\right) \wedge \overline{\left(dv+\widetilde{\Gamma}(u,v,b_0) du\right)}, \end{align*} $$
where
![]() $W= \frac {2\pi }{k|\log |u||}$
and
$W= \frac {2\pi }{k|\log |u||}$
and
![]() $ \widetilde {\Gamma }(u,v,b_0) = B(u,v)+ \frac {b_0}{2\pi ^2}\frac {|\log |u||}{u}$
. An appealing way to think of nonstandard semi-flat metrics is that they are obtained from standard semi-flat metrics by pulling back along the fibrewise translation map defined by a multi-valued (possibly uncountably valued) section
$ \widetilde {\Gamma }(u,v,b_0) = B(u,v)+ \frac {b_0}{2\pi ^2}\frac {|\log |u||}{u}$
. An appealing way to think of nonstandard semi-flat metrics is that they are obtained from standard semi-flat metrics by pulling back along the fibrewise translation map defined by a multi-valued (possibly uncountably valued) section
![]() $\sigma :\Delta ^*\rightarrow \check {X}_{mod}$
; see [Reference Collins, Jacob and Lin5]. A nonstandard semi-flat metric has the same curvature and injectivity radius decay as a standard semi-flat metric. However, if
$\sigma :\Delta ^*\rightarrow \check {X}_{mod}$
; see [Reference Collins, Jacob and Lin5]. A nonstandard semi-flat metric has the same curvature and injectivity radius decay as a standard semi-flat metric. However, if
![]() $\frac {2b_0}{b}\notin \mathbb {Z}$
, then the cohomology class of the nonstandard semi-flat metric cannot be realised by a standard semi-flat metric. We now state the following result.
$\frac {2b_0}{b}\notin \mathbb {Z}$
, then the cohomology class of the nonstandard semi-flat metric cannot be realised by a standard semi-flat metric. We now state the following result.
Theorem 2.2 [Reference Collins, Jacob and Lin5, Appendix A]
Assume that
![]() $D\cong \mathbb {C}/\mathbb {Z}\oplus \mathbb {Z}\tau $
is an elliptic curve, with
$D\cong \mathbb {C}/\mathbb {Z}\oplus \mathbb {Z}\tau $
is an elliptic curve, with
![]() $\tau $
in the upper half-plane. Let
$\tau $
in the upper half-plane. Let
![]() $Y_{\mathcal {C}}$
be the total space of a degree b line bundle L over D and
$Y_{\mathcal {C}}$
be the total space of a degree b line bundle L over D and
![]() $X_{\mathcal {C}}$
the complement of the zero section. Let
$X_{\mathcal {C}}$
the complement of the zero section. Let
![]() $\omega _{\mathcal {C}}$
and
$\omega _{\mathcal {C}}$
and
![]() $\Omega _{\mathcal {C}}$
be the forms arising from the Calabi ansatz on
$\Omega _{\mathcal {C}}$
be the forms arising from the Calabi ansatz on
![]() $X_{\mathcal {C}}$
, as above. Consider the hyperKähler rotation of
$X_{\mathcal {C}}$
, as above. Consider the hyperKähler rotation of
![]() $X_{\mathcal {C}}$
with Kähler form
$X_{\mathcal {C}}$
with Kähler form
![]() $\check {\omega }_{\mathcal {C}}$
and holomorphic volume form
$\check {\omega }_{\mathcal {C}}$
and holomorphic volume form
![]() $\check {\Omega }_{\mathcal {C}}$
such that the ansatz special Lagrangian corresponding to
$\check {\Omega }_{\mathcal {C}}$
such that the ansatz special Lagrangian corresponding to
![]() $1\in \mathbb {Z}\oplus \mathbb {Z}\tau $
is of phase zero. Then with a suitable choice of coordinates, one has
$1\in \mathbb {Z}\oplus \mathbb {Z}\tau $
is of phase zero. Then with a suitable choice of coordinates, one has
where
![]() $b_0=-\frac {1}{2}\mbox {Re}(\tau )b$
,
$b_0=-\frac {1}{2}\mbox {Re}(\tau )b$
,
![]() $\varepsilon =\frac {2\sqrt {2}\pi }{\mbox {Im}(\tau )}$
and
$\varepsilon =\frac {2\sqrt {2}\pi }{\mbox {Im}(\tau )}$
and
![]() $\alpha =\sqrt {b\pi \mbox {Im}(\tau )}$
. In particular, there exists a bijection between
$\alpha =\sqrt {b\pi \mbox {Im}(\tau )}$
. In particular, there exists a bijection between
![]() $\tau \leftrightarrow (b_0,\varepsilon )$
: that is, every (possibly nonstandard) semi-flat metric can be realised as some hyperKähler rotation of certain Calabi ansatz up to a scaling.
$\tau \leftrightarrow (b_0,\varepsilon )$
: that is, every (possibly nonstandard) semi-flat metric can be realised as some hyperKähler rotation of certain Calabi ansatz up to a scaling.
As a direct consequence, we get the following special Lagrangian fibrations in
![]() $\check {X}_{mod}$
via hyperKähler rotations from the Calabi ansatz:
$\check {X}_{mod}$
via hyperKähler rotations from the Calabi ansatz:
Lemma 2.3. Fix an m-quasi bad cycle class
![]() $[L]\in H_2(\check {X}_{mod},\mathbb {Z})$
that is primitive. There exists a special Lagrangian fibration in
$[L]\in H_2(\check {X}_{mod},\mathbb {Z})$
that is primitive. There exists a special Lagrangian fibration in
![]() $\check {X}_{mod}$
with respect to the semi-flat hyperKähler triple
$\check {X}_{mod}$
with respect to the semi-flat hyperKähler triple
![]() $(\omega _{sf,b_0,\varepsilon },\Omega _{sf})$
if and only if
$(\omega _{sf,b_0,\varepsilon },\Omega _{sf})$
if and only if
![]() $\int _{[L]}\omega _{sf,b_0,\varepsilon }=0$
.
$\int _{[L]}\omega _{sf,b_0,\varepsilon }=0$
.
2.2 A uniqueness theorem for Ricci-flat metrics on noncompact Calabi-Yau surfaces
Recall that a rational elliptic surface is a rational surface with an elliptic fibration structure. Using the standard semi-flat metric as an asymptotic model, Hein [Reference Hein12] constructed many Ricci-flat metrics on the complement of a fibre in a rational elliptic surface. In the case that the removed fibre is of Kodaira type
![]() $I_b$
, the authors established the uniqueness of these metrics as well as the existence of a parameter space. We recall the setup here.
$I_b$
, the authors established the uniqueness of these metrics as well as the existence of a parameter space. We recall the setup here.
Let
![]() $\check {Y}$
be a rational elliptic surface and
$\check {Y}$
be a rational elliptic surface and
![]() $\check {D}$
an
$\check {D}$
an
![]() $I_b$
-fibre. Fix a meromorphic form
$I_b$
-fibre. Fix a meromorphic form
![]() $\check {\Omega }$
with a simple pole along
$\check {\Omega }$
with a simple pole along
![]() $\check {D}$
. Denote
$\check {D}$
. Denote
![]() $\check {X}=\check {Y}\setminus \check {D}$
, and let
$\check {X}=\check {Y}\setminus \check {D}$
, and let
![]() $\mathcal {K}_{dR,\check {X}}$
be the set of de Rham cohomology classes that can be represented by Kähler forms on
$\mathcal {K}_{dR,\check {X}}$
be the set of de Rham cohomology classes that can be represented by Kähler forms on
![]() $\check {X}$
. Then
$\check {X}$
. Then
![]() $\mathcal {K}_{dR,\check {X}}$
is a cone in
$\mathcal {K}_{dR,\check {X}}$
is a cone in
![]() $H^2(\check {X},\mathbb {R})$
. With a slight modification of the work of Hein [Reference Hein12], the authors generalised the existence theorem:
$H^2(\check {X},\mathbb {R})$
. With a slight modification of the work of Hein [Reference Hein12], the authors generalised the existence theorem:
Theorem 2.4 [Reference Collins, Jacob and Lin5, Theorem 2.16]
Given any
![]() $[\check {\omega }]\in \mathcal {K}_{dR,\check {X}}$
, there exists
$[\check {\omega }]\in \mathcal {K}_{dR,\check {X}}$
, there exists
![]() $\alpha _0$
such that for
$\alpha _0$
such that for
![]() $\alpha>\alpha _0$
, there exists a Ricci-flat metric
$\alpha>\alpha _0$
, there exists a Ricci-flat metric
![]() $\check {\omega }\in [\check {\omega }]$
on
$\check {\omega }\in [\check {\omega }]$
on
![]() $\check {X}$
with a suitable choice of section and a semi-flat metric
$\check {X}$
with a suitable choice of section and a semi-flat metric
![]() $\omega _{sf,b_0,\varepsilon }$
such that
$\omega _{sf,b_0,\varepsilon }$
such that
-
1.
 $\check {\omega }^2=\alpha \check {\Omega }\wedge \bar {\check {\Omega }}$
: that is,
$\check {\omega }^2=\alpha \check {\Omega }\wedge \bar {\check {\Omega }}$
: that is,
 $\check {\omega }$
solves the Monge-Ampére equation.
$\check {\omega }$
solves the Monge-Ampére equation. -
2. The curvature
 $\check {\omega }$
satisfies
$\check {\omega }$
satisfies
 $|\nabla ^kRm|_{\check {\omega }} \lesssim r^{-2-k}$
for every
$|\nabla ^kRm|_{\check {\omega }} \lesssim r^{-2-k}$
for every
 $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
. -
3.
 $\check {\omega }$
is asymptotic to the semi-flat metric in the following sense: there exists
$\check {\omega }$
is asymptotic to the semi-flat metric in the following sense: there exists
 $C>0$
such that for every
$C>0$
such that for every
 $k\in \mathbb {N}$
, one has
$k\in \mathbb {N}$
, one has  $$ \begin{align*} |\nabla^k (\check{\omega}-\omega_{sf,b_0,\varepsilon})|_{\check{\omega}}\sim O(e^{-Cr^{2/3}}). \end{align*} $$
$$ \begin{align*} |\nabla^k (\check{\omega}-\omega_{sf,b_0,\varepsilon})|_{\check{\omega}}\sim O(e^{-Cr^{2/3}}). \end{align*} $$
We refer the reader to [Reference Collins, Jacob and Lin5, Remark 2.17] for a description of some (minor) differences between Theorem 2.4 and the work of Hein. The authors then proved an essentially optimal uniqueness theorem for Ricci-flat metrics with polynomial decay to a (possibly nonstandard) semiflat metrics on
![]() $\check {X}$
.
$\check {X}$
.
Theorem 2.5 [Reference Collins, Jacob and Lin5, Proposition 4.8]
Suppose
![]() $\check {\omega }_1, \check {\omega }_2$
are two complete Calabi-Yau metrics on
$\check {\omega }_1, \check {\omega }_2$
are two complete Calabi-Yau metrics on
![]() $\check {X}= \check {Y}\setminus \check {D}$
with the following properties:
$\check {X}= \check {Y}\setminus \check {D}$
with the following properties:
-
(i)
 $\check {\omega }_i^2= \alpha ^2 \check {\Omega } \wedge \overline {\check {\Omega }}$
, for
$\check {\omega }_i^2= \alpha ^2 \check {\Omega } \wedge \overline {\check {\Omega }}$
, for
 $i=1,2$
.
$i=1,2$
. -
(ii)
 $[\check {\omega }_1]_{dR} = [\check {\omega }_2]_{dR} \in H^{2}_{dR}(\check {X},\mathbb {R})$
.
$[\check {\omega }_1]_{dR} = [\check {\omega }_2]_{dR} \in H^{2}_{dR}(\check {X},\mathbb {R})$
. -
(iii) There are (possibly nonstandard) semi-flat metrics
 $\omega _{sf, \sigma _i, b_{0,i}, \varepsilon _i}$
such that and
$\omega _{sf, \sigma _i, b_{0,i}, \varepsilon _i}$
such that and $$\begin{align*}[\omega_{sf, \sigma_i, b_{0,i}, \varepsilon_i}]_{BC}=[\check{\omega}_i]_{BC} \in H^{1,1}_{BC}(\check{X}_{\Delta^*}, \mathbb{R}) \end{align*}$$
where
$$\begin{align*}[\omega_{sf, \sigma_i, b_{0,i}, \varepsilon_i}]_{BC}=[\check{\omega}_i]_{BC} \in H^{1,1}_{BC}(\check{X}_{\Delta^*}, \mathbb{R}) \end{align*}$$
where $$\begin{align*}|\check{\omega}_i-\alpha \omega_{sf, \sigma_i, b_{0,i}, \frac{\varepsilon_i}{\alpha}}| \leqslant Cr_i^{-4/3}, \end{align*}$$
$$\begin{align*}|\check{\omega}_i-\alpha \omega_{sf, \sigma_i, b_{0,i}, \frac{\varepsilon_i}{\alpha}}| \leqslant Cr_i^{-4/3}, \end{align*}$$
 $r_i$
is the distance from a fixed point with respect to
$r_i$
is the distance from a fixed point with respect to
 $\check {\omega }_i$
.
$\check {\omega }_i$
.
Then there is a fibre preserving holomorphic map
![]() $\Phi \in \mathrm {Aut}_0(X,\mathbb {C})$
such that
$\Phi \in \mathrm {Aut}_0(X,\mathbb {C})$
such that
![]() $\Phi ^*\check {\omega }_2=\check {\omega }_1$
.
$\Phi ^*\check {\omega }_2=\check {\omega }_1$
.
2.3 Perturbations of the model special Lagrangians
Let
![]() $(X,\omega )$
be a Kähler manifold such that the corresponding Riemannian metric is Ricci-flat. Given a Lagrangian submanifold
$(X,\omega )$
be a Kähler manifold such that the corresponding Riemannian metric is Ricci-flat. Given a Lagrangian submanifold
![]() $L\subseteq X$
, we can deform L via its mean curvature
$L\subseteq X$
, we can deform L via its mean curvature
![]() $\vec {H}$
, defining a family of Lagrangians
$\vec {H}$
, defining a family of Lagrangians
![]() $L_t$
such that
$L_t$
such that
It is proved by Smoczyk [Reference Smoczyk25] that the Maslov zero Lagrangian condition is preserved under the flow; thus the name Lagrangian mean curvature flow (LMCF). If X admits a covariant holomorphic volume form
![]() $\Omega $
, then there exists a phase function
$\Omega $
, then there exists a phase function
![]() $\theta :L\rightarrow S^1$
defined by
$\theta :L\rightarrow S^1$
defined by
![]() $\Omega |_L=e^{i\theta }\mbox {Vol}_L$
. If
$\Omega |_L=e^{i\theta }\mbox {Vol}_L$
. If
![]() $\theta $
is constant, then L is a special Lagrangian. Since we are working on a Calabi-Yau manifold, the mean curvature of L can be computed by
$\theta $
is constant, then L is a special Lagrangian. Since we are working on a Calabi-Yau manifold, the mean curvature of L can be computed by
![]() $\vec {H}=\nabla \theta $
. In particular, if the LMCF converges smoothly, it converges to a special Lagrangian.
$\vec {H}=\nabla \theta $
. In particular, if the LMCF converges smoothly, it converges to a special Lagrangian.
Now, in general, the LMCF may develop a finite time singularity [Reference Neves23], which is expected to be related to the Harder-Narasimhan filtration of the Fukaya category [Reference Joyce16]. However, using a quantitative version of the machinery of Li [Reference Li18], the authors proved a quantitative local regularity theorem for the LMCF in the present setting; see [Reference Collins, Jacob and Lin4, Theorem 4.23].
Theorem 2.6 (Theorem 4.23, [Reference Collins, Jacob and Lin4])
Let X be a noncompact Calabi-Yau surface with Ricci-flat metric
![]() $\omega $
and holomorphic volume form
$\omega $
and holomorphic volume form
![]() $\Omega $
. Fix a point in X, and let r denote the distance function to this fixed point. Assume that there exists a diffeomorphism F from the end of
$\Omega $
. Fix a point in X, and let r denote the distance function to this fixed point. Assume that there exists a diffeomorphism F from the end of
![]() $\mathcal {C}$
to X such that for all
$\mathcal {C}$
to X such that for all
![]() $k\in \mathbb {N}$
, one has
$k\in \mathbb {N}$
, one has
for some constant
![]() $C_k>0$
. Then given an ansatz special Lagrangian (from Section 2.1) mapped to X via F, if it is sufficiently close to infinity along the end of X, it can be deformed to a genuine special Lagrangian with respect to
$C_k>0$
. Then given an ansatz special Lagrangian (from Section 2.1) mapped to X via F, if it is sufficiently close to infinity along the end of X, it can be deformed to a genuine special Lagrangian with respect to
![]() $(\omega ,\Omega )$
.
$(\omega ,\Omega )$
.
Specifically, in [Reference Collins, Jacob and Lin4], the authors argue that an ansatz special Lagrangian can be deformed via Moser’s trick to a Lagrangian with respect to the Ricci flat metric
![]() $\omega $
. After proving this deformation preserves several geometric bounds (including exponential decay of the mean curvature vector along the end of X), the authors show that the mean curvature flow converges exponentially fast to a special Lagrangian. We direct the reader to [Reference Collins, Jacob and Lin4] for further details.
$\omega $
. After proving this deformation preserves several geometric bounds (including exponential decay of the mean curvature vector along the end of X), the authors show that the mean curvature flow converges exponentially fast to a special Lagrangian. We direct the reader to [Reference Collins, Jacob and Lin4] for further details.
3 The Torelli theorem
First we recall the definition of
![]() $ALH^*$
gravitational instantons following Sun-Zhang [Reference Song and Zhang27]:
$ALH^*$
gravitational instantons following Sun-Zhang [Reference Song and Zhang27]:
Definition 3.1.
-
1. Given
 $b\in \mathbb {N}$
, an
$b\in \mathbb {N}$
, an
 $ALH^*_b$
model end is the hyperKähler triple from the Gibbons-Hawking ansatz on
$ALH^*_b$
model end is the hyperKähler triple from the Gibbons-Hawking ansatz on
 $\mathbb {T}^2\times [0,\infty )$
with the harmonic function
$\mathbb {T}^2\times [0,\infty )$
with the harmonic function
 $b\rho $
, where
$b\rho $
, where
 $T^2$
is the flat two-torus and
$T^2$
is the flat two-torus and
 $\rho $
is the coordinate on
$\rho $
is the coordinate on
 $[0,\infty )$
$[0,\infty )$
-
2. A gravitational instanton
 $(X,g)$
is of type
$(X,g)$
is of type
 $ALH^*$
if there exists a diffeomorphism F from
$ALH^*$
if there exists a diffeomorphism F from
 $\mathcal {C}$
to X such that for all
$\mathcal {C}$
to X such that for all
 $k\in \mathbb {N}$
, one has for some
$k\in \mathbb {N}$
, one has for some $$ \begin{align*} \parallel \nabla^k_{g_{\mathcal{C}}}(F^*g-g_{\mathcal{C}}) \parallel_g\, = O(r^{-k-\varepsilon}) \end{align*} $$
$$ \begin{align*} \parallel \nabla^k_{g_{\mathcal{C}}}(F^*g-g_{\mathcal{C}}) \parallel_g\, = O(r^{-k-\varepsilon}) \end{align*} $$
 $\varepsilon>0$
.
$\varepsilon>0$
.
Remark 3.2. It is explained in [Reference Hein, Sun, Viaclovsky and Zhang14, Section 2.2] that the Calabi ansatz is actually an
![]() $ALH^*_b$
model end for some b.
$ALH^*_b$
model end for some b.
Let
![]() $(X,g)$
be an
$(X,g)$
be an
![]() $ALH^*_b$
gravitational instanton, and fix a choice of hyperKähler triple
$ALH^*_b$
gravitational instanton, and fix a choice of hyperKähler triple
![]() $(\omega ,\Omega )$
such that
$(\omega ,\Omega )$
such that
![]() $\omega $
is the Kähler form with respect to the complex structure determined by
$\omega $
is the Kähler form with respect to the complex structure determined by
![]() $\Omega $
. Sun-Zhang proved that the geometry at infinity has exponential decay to the model end.
$\Omega $
. Sun-Zhang proved that the geometry at infinity has exponential decay to the model end.
Theorem 3.3 [Reference Song and Zhang27, Theorem 6.19]
There exist
![]() $\delta>0$
and a diffeomorphism F from the end of
$\delta>0$
and a diffeomorphism F from the end of
![]() $\mathcal {C}$
to X such that for all
$\mathcal {C}$
to X such that for all
![]() $k\in \mathbb {N}$
, one has
$k\in \mathbb {N}$
, one has
![]() $F^*\omega = \omega _{\mathcal {C}} + d\sigma $
for some
$F^*\omega = \omega _{\mathcal {C}} + d\sigma $
for some
![]() $1$
-form
$1$
-form
![]() $\sigma $
and
$\sigma $
and
for some constant
![]() $C_k>0$
.
$C_k>0$
.
Consider
![]() $L_{\mathcal {C}}\in X_{\mathcal {C}}$
for any primitive class
$L_{\mathcal {C}}\in X_{\mathcal {C}}$
for any primitive class
![]() $[L_{\mathcal {C}}]\in H_2(X_{\mathcal {C}},\mathbb {Z})$
with
$[L_{\mathcal {C}}]\in H_2(X_{\mathcal {C}},\mathbb {Z})$
with
![]() $\varepsilon $
small enough. Then as above, one can use Moser’s trick to modify
$\varepsilon $
small enough. Then as above, one can use Moser’s trick to modify
![]() $F(L_{\mathcal {C}})$
to a Lagrangian
$F(L_{\mathcal {C}})$
to a Lagrangian
![]() $L\subseteq X$
. The LMCF starting at L will then converge smoothly to a special Lagrangian tori by Theorem 3.3 and Theorem 2.6. Notice that from [Reference Collins, Jacob and Lin4, Proposition 5.24], the LMCF flows the ansatz special Lagrangian fibration near infinity to a genuine special Lagrangian fibration on
$L\subseteq X$
. The LMCF starting at L will then converge smoothly to a special Lagrangian tori by Theorem 3.3 and Theorem 2.6. Notice that from [Reference Collins, Jacob and Lin4, Proposition 5.24], the LMCF flows the ansatz special Lagrangian fibration near infinity to a genuine special Lagrangian fibration on
![]() $X\setminus K$
for some compact set K.
$X\setminus K$
for some compact set K.
Now consider the hyperKähler rotation
![]() $\check {X}$
equipped with Kähler form
$\check {X}$
equipped with Kähler form
![]() $\check {\omega }$
and holomorphic volume form
$\check {\omega }$
and holomorphic volume form
![]() $\check {\Omega }$
such that
$\check {\Omega }$
such that
Then
![]() $\check {X}\setminus K$
admits an elliptic fibration to a noncompact Riemann surface
$\check {X}\setminus K$
admits an elliptic fibration to a noncompact Riemann surface
![]() $\check {B}$
, which is diffeomorphic to an annuli. From the uniformisation theorem,
$\check {B}$
, which is diffeomorphic to an annuli. From the uniformisation theorem,
![]() $\check {B}$
is either biholomorphic to a punctured disc or a holomorphic annulus. Notice that the j-invariants of the elliptic fibres converge to infinity at the end from Theorem 2.2 and Theorem 3.3. Since the j-invariant is a holomorphic function on
$\check {B}$
is either biholomorphic to a punctured disc or a holomorphic annulus. Notice that the j-invariants of the elliptic fibres converge to infinity at the end from Theorem 2.2 and Theorem 3.3. Since the j-invariant is a holomorphic function on
![]() $\check {B}$
, one has
$\check {B}$
, one has
![]() $\check {B}$
must be biholomorphic to a punctured disc.
$\check {B}$
must be biholomorphic to a punctured disc.
Again from [Reference Collins, Jacob and Lin4, Proposition 5.24], the monodromy of the fibration
![]() $\check {X}\setminus K\rightarrow \check {B}$
near infinity is the same as the explicit model special Lagrangian fibration. There are two consequences. Firstly, there is no sequence of multiple fibres converging to infinity. Secondly, the monodromy is conjugate to
$\check {X}\setminus K\rightarrow \check {B}$
near infinity is the same as the explicit model special Lagrangian fibration. There are two consequences. Firstly, there is no sequence of multiple fibres converging to infinity. Secondly, the monodromy is conjugate to
![]() $\begin {pmatrix} 1 & b \\ 0 & 1 \end {pmatrix}$
from direct calculation. Then one can compactify
$\begin {pmatrix} 1 & b \\ 0 & 1 \end {pmatrix}$
from direct calculation. Then one can compactify
![]() $\check {X}$
to a compact complex surface
$\check {X}$
to a compact complex surface
![]() $\check {X}$
by adding an
$\check {X}$
by adding an
![]() $I_b$
-fibre
$I_b$
-fibre
![]() $\check {D}$
at infinity by [Reference Collins, Jacob and Lin4, Corollary 6.3]. Now we can use to the classification of surfaces to deduce the following:
$\check {D}$
at infinity by [Reference Collins, Jacob and Lin4, Corollary 6.3]. Now we can use to the classification of surfaces to deduce the following:
Proposition 3.4.
![]() $\check {Y}$
is a rational elliptic surface.Footnote 2
$\check {Y}$
is a rational elliptic surface.Footnote 2
Proof. From Appendix [Reference Collins, Jacob and Lin5, Appendix A], the form
![]() $\check {\Omega }$
is meromorphic with a simple pole along
$\check {\Omega }$
is meromorphic with a simple pole along
![]() $\check {D}$
. Therefore, we have
$\check {D}$
. Therefore, we have
![]() $K_{\check {Y}}=\mathcal {O}_{\check {Y}}(-\check {D})$
. From the elliptic fibration on
$K_{\check {Y}}=\mathcal {O}_{\check {Y}}(-\check {D})$
. From the elliptic fibration on
![]() $\check {Y}\setminus K$
, we have
$\check {Y}\setminus K$
, we have
![]() $c_1(\check {Y})^2=0$
. There are no
$c_1(\check {Y})^2=0$
. There are no
![]() $(-1)$
curves in the fibre by the adjunction formula. Since
$(-1)$
curves in the fibre by the adjunction formula. Since
![]() $b_1(\check {X})=0$
by [Reference Song and Zhang27, Corollary 7.6],Footnote 3 we also have
$b_1(\check {X})=0$
by [Reference Song and Zhang27, Corollary 7.6],Footnote 3 we also have
![]() $b_1(Y)=0$
from the Mayer-Vietoris sequence. Assume that
$b_1(Y)=0$
from the Mayer-Vietoris sequence. Assume that
![]() $\check {Y}$
is minimal. Since
$\check {Y}$
is minimal. Since
![]() $c_1(\check {Y})^2=0$
and
$c_1(\check {Y})^2=0$
and
![]() $b_1(\check {Y})=0$
, by the Enriques-Kodaira classification (see, for example, [Reference Barth, Peters and Van de Ven1, Chapter VI, Table 10]), it follows that
$b_1(\check {Y})=0$
, by the Enriques-Kodaira classification (see, for example, [Reference Barth, Peters and Van de Ven1, Chapter VI, Table 10]), it follows that
![]() $\check {Y}$
can only be an Enriques surface, a K3 surface or a minimal properly elliptic surface.
$\check {Y}$
can only be an Enriques surface, a K3 surface or a minimal properly elliptic surface.
![]() $K_{\check {Y}}=\mathcal {O}_{\check {Y}}(-\check {D})$
obviously excludes the first two possibilities. Furthermore, recall that a properly elliptic surface has Kodaira dimension
$K_{\check {Y}}=\mathcal {O}_{\check {Y}}(-\check {D})$
obviously excludes the first two possibilities. Furthermore, recall that a properly elliptic surface has Kodaira dimension
![]() $1$
. This is again impossible because
$1$
. This is again impossible because
![]() $K_{\check {Y}}=\mathcal {O}_{\check {Y}}(-\check {D})$
. To sum up, it must be the case that
$K_{\check {Y}}=\mathcal {O}_{\check {Y}}(-\check {D})$
. To sum up, it must be the case that
![]() $\check {Y}$
is not minimal.
$\check {Y}$
is not minimal.
Now, any
![]() $(-1)$
curve E in
$(-1)$
curve E in
![]() $\check {Y}$
has intersection one with
$\check {Y}$
has intersection one with
![]() $\check {D}$
, so
$\check {D}$
, so
![]() $(\check {D}+E)^2>0$
. Therefore,
$(\check {D}+E)^2>0$
. Therefore,
![]() $\check {Y}$
is projective by [Reference Barth, Peters and Van de Ven1, Chapter IV, Theorem 5.2]. Then
$\check {Y}$
is projective by [Reference Barth, Peters and Van de Ven1, Chapter IV, Theorem 5.2]. Then
![]() $h^1(\check {Y},\mathcal {O}_{\check {Y}})=0$
from Hodge theory and
$h^1(\check {Y},\mathcal {O}_{\check {Y}})=0$
from Hodge theory and
![]() $h^0(\check {Y},K_{\check {Y}}^2)=0$
since
$h^0(\check {Y},K_{\check {Y}}^2)=0$
since
![]() $-K_{\check {Y}}$
is effective. Finally, Castelnuovo’s rationality criterion implies that
$-K_{\check {Y}}$
is effective. Finally, Castelnuovo’s rationality criterion implies that
![]() $\check {Y}$
is rational. Thus the local elliptic fibration near
$\check {Y}$
is rational. Thus the local elliptic fibration near
![]() $\check {D}$
in
$\check {D}$
in
![]() $\check {Y}$
actually extends to an elliptic fibration. Indeed, one has
$\check {Y}$
actually extends to an elliptic fibration. Indeed, one has
![]() $\mbox {Pic}(\check {Y})\cong H^2(\check {Y},\mathbb {Z})$
since
$\mbox {Pic}(\check {Y})\cong H^2(\check {Y},\mathbb {Z})$
since
![]() $H^1(\check {Y},\mathcal {O}_{\check {Y}})=H^2(\check {Y},\mathcal {O}_{\check {Y}})=0$
. Thus,
$H^1(\check {Y},\mathcal {O}_{\check {Y}})=H^2(\check {Y},\mathcal {O}_{\check {Y}})=0$
. Thus,
![]() $\check {Y}$
is a rational elliptic surface.
$\check {Y}$
is a rational elliptic surface.
To sum up, we proved the following uniformisation theorem:
Theorem 3.5. Any
![]() $ALH^*_b$
gravitational instanton (up to hyperKähler rotation) can be compactified to a rational elliptic surface.
$ALH^*_b$
gravitational instanton (up to hyperKähler rotation) can be compactified to a rational elliptic surface.
Remark 3.6. An analogue result of Hein-Sun-Viaclovsky-Zhang [Reference Hein, Sun, Viaclovsky and Zhang15] proves that up to hyperKähler rotation, any
![]() $ALH^*_b$
gravitational instanton can be compactified to a weak del Pezzo surface.
$ALH^*_b$
gravitational instanton can be compactified to a weak del Pezzo surface.
The possible singular fibres of a rational elliptic surface are classified by Persson [Reference Persson24]. The rational elliptic surface
![]() $\check {Y}$
can only admit an
$\check {Y}$
can only admit an
![]() $I_b$
-fibre for
$I_b$
-fibre for
![]() $b\leqslant 9$
, which gives a constraint on b. From the work of Persson [Reference Persson24] (see also [Reference Heckman and Looijenga13, Section 3.3], or Proposition 9.15, Proposition 9.16 of [Reference Friedman8]), there exists a single deformation family of pairs of rational elliptic surfaces with an
$b\leqslant 9$
, which gives a constraint on b. From the work of Persson [Reference Persson24] (see also [Reference Heckman and Looijenga13, Section 3.3], or Proposition 9.15, Proposition 9.16 of [Reference Friedman8]), there exists a single deformation family of pairs of rational elliptic surfaces with an
![]() $I_b$
fibre for
$I_b$
fibre for
![]() $b\neq 8$
, and there are two deformation families for
$b\neq 8$
, and there are two deformation families for
![]() $b=8$
. Different families have different Betti numbers. In particular, there exist
$b=8$
. Different families have different Betti numbers. In particular, there exist
![]() $ALH^*_b$
gravitational instantons for every
$ALH^*_b$
gravitational instantons for every
![]() $1\leqslant b\leqslant 9$
from the work of Hein [Reference Hein12]. Thus, we have the following consequence:
$1\leqslant b\leqslant 9$
from the work of Hein [Reference Hein12]. Thus, we have the following consequence:
Corollary 3.7.
-
1. There are only
 $ALH^*_b$
gravitational instantons for
$ALH^*_b$
gravitational instantons for
 $b\leqslant 9$
.
$b\leqslant 9$
. -
2. There are only
 $10$
diffeomorphism types of
$10$
diffeomorphism types of
 $ALH^*_b$
gravitation instantons.
$ALH^*_b$
gravitation instantons.
Before we prove the Torelli theorem of
![]() $ALH^*_b$
-gravitational instantons, we first recall the Torelli theorem of log Calabi-Yau surfaces [Reference Gross, Hacking and Keel9]. Let
$ALH^*_b$
-gravitational instantons, we first recall the Torelli theorem of log Calabi-Yau surfaces [Reference Gross, Hacking and Keel9]. Let
![]() $(Y,D)$
be a Looijenga pair: that is, Y is a rational surface, and
$(Y,D)$
be a Looijenga pair: that is, Y is a rational surface, and
![]() $D\in |-K_Y|$
is an anti-canonical cycle. Consider the homology long exact sequence of pairs
$D\in |-K_Y|$
is an anti-canonical cycle. Consider the homology long exact sequence of pairs
![]() $(Y,D)$
with coefficients in
$(Y,D)$
with coefficients in
![]() $\mathbb {Z}$
:
$\mathbb {Z}$
:
Here we identify
![]() $H_k(Y,Y\setminus D)$
with
$H_k(Y,Y\setminus D)$
with
![]() $H^{4-k}(D)$
by Poincare duality. Let
$H^{4-k}(D)$
by Poincare duality. Let
![]() $\varepsilon \in H^1(D)$
denote a generator, which determines its orientation. There exists a unique meromorphic volume form
$\varepsilon \in H^1(D)$
denote a generator, which determines its orientation. There exists a unique meromorphic volume form
![]() $\Omega _{Y}$
with a simple pole along D and normalisation
$\Omega _{Y}$
with a simple pole along D and normalisation
![]() $\int _{\partial _*(\varepsilon )}\Omega _Y=1$
. Denote by
$\int _{\partial _*(\varepsilon )}\Omega _Y=1$
. Denote by
![]() $C_Y^{++}$
the subcone of
$C_Y^{++}$
the subcone of
![]() $\mbox {Pic}(Y)$
that consists of element
$\mbox {Pic}(Y)$
that consists of element
![]() $\beta $
satisfying
$\beta $
satisfying
-
1.
 $\beta ^2>0$
: that is,
$\beta ^2>0$
: that is,
 $\beta $
is in the positive cone.
$\beta $
is in the positive cone. -
2.
 $\beta. [E]\geqslant 0$
for any
$\beta. [E]\geqslant 0$
for any
 $(-1)$
-curve E in Y.
$(-1)$
-curve E in Y.
By [Reference Gross, Hacking and Keel9, Lemma 2.13],
![]() $C_Y^{++}$
is invariant under parallel transport. We denote by
$C_Y^{++}$
is invariant under parallel transport. We denote by
![]() $\Delta _{Y}$
the set of nodal classes of Y: that is,
$\Delta _{Y}$
the set of nodal classes of Y: that is,
For each element
![]() $\alpha \in \Delta _Y$
, there is an associate reflection as an automorphism on
$\alpha \in \Delta _Y$
, there is an associate reflection as an automorphism on
![]() $\mbox {Pic}(Y)$
given by
$\mbox {Pic}(Y)$
given by
The Weyl group
![]() $W_{Y}$
is then the group generated by
$W_{Y}$
is then the group generated by
![]() $s_{\alpha },\alpha \in \Delta _Y$
.
$s_{\alpha },\alpha \in \Delta _Y$
.
With the above notations, the Gross-Hacking-Keel weak Torelli theorem for Looijenga pairs is stated as follows:
Theorem 3.8 (Theorem 1.8, [Reference Gross, Hacking and Keel9])
Let
![]() $(Y_1,D),(Y_2,D)$
be two Looijenga pairs and
$(Y_1,D),(Y_2,D)$
be two Looijenga pairs and
![]() $\mu :\mbox {Pic}(Y_1)\rightarrow \mbox {Pic}(Y_2)$
be an isomorphism of lattices. Assume that
$\mu :\mbox {Pic}(Y_1)\rightarrow \mbox {Pic}(Y_2)$
be an isomorphism of lattices. Assume that
-
1.
 $\mu ([D_i])=([D_i])$
for all i.
$\mu ([D_i])=([D_i])$
for all i. -
2.
 $\mu (C_{Y_1}^{++})=C_{Y_2}^{++}$
.
$\mu (C_{Y_1}^{++})=C_{Y_2}^{++}$
. -
3.
 $\mu ([\Omega _{Y_1}])=[\Omega _{Y_2}]$
, where
$\mu ([\Omega _{Y_1}])=[\Omega _{Y_2}]$
, where
 $\Omega _i$
is the meromorphic form on
$\Omega _i$
is the meromorphic form on
 $Y_i$
with a simple pole along
$Y_i$
with a simple pole along
 $D_i$
and the normalisation described above.Footnote 4
$D_i$
and the normalisation described above.Footnote 4
Then there exists a unique
![]() $g\in W_{Y_1}$
such that
$g\in W_{Y_1}$
such that
![]() $\mu \circ g=f^*$
for an isomorphism of pairs
$\mu \circ g=f^*$
for an isomorphism of pairs
![]() $f:(Y_2,D)\rightarrow (Y_1,D)$
.
$f:(Y_2,D)\rightarrow (Y_1,D)$
.
We are now ready to prove our Torelli theorem.
Theorem 3.9. Let
![]() $(X_i,\omega _i,\Omega _i)$
be
$(X_i,\omega _i,\Omega _i)$
be
![]() $ALH^*_b$
gravitational instantons such that there exists a diffeomorphism
$ALH^*_b$
gravitational instantons such that there exists a diffeomorphism
![]() $F:X_2\cong X_1$
with
$F:X_2\cong X_1$
with
Then there exists a diffeomorphism
![]() $f:X_2\rightarrow X_1$
such that
$f:X_2\rightarrow X_1$
such that
![]() $f^*\omega _1=\omega _2$
and
$f^*\omega _1=\omega _2$
and
![]() $f^*\Omega _1=\Omega _2$
.
$f^*\Omega _1=\Omega _2$
.
Proof. Assume that
![]() $(\check {Y}_2,\check {D}_2)$
are the pair of a rational elliptic surface and an
$(\check {Y}_2,\check {D}_2)$
are the pair of a rational elliptic surface and an
![]() $I_b$
fibre such that
$I_b$
fibre such that
![]() $\check {X}_2=\check {Y}_2\setminus \check {D}_2$
is a hyperKähler rotation of
$\check {X}_2=\check {Y}_2\setminus \check {D}_2$
is a hyperKähler rotation of
![]() $(X_2,\omega _2,\Omega _2)$
with elliptic fibration and fibre class
$(X_2,\omega _2,\Omega _2)$
with elliptic fibration and fibre class
![]() $[L]\in H_2(X_2,\mathbb {Z})$
. Thanks to the assumption
$[L]\in H_2(X_2,\mathbb {Z})$
. Thanks to the assumption
![]() $F^*[\Omega _1]=[\Omega _2]$
, there exists a special Lagrangian fibration on
$F^*[\Omega _1]=[\Omega _2]$
, there exists a special Lagrangian fibration on
![]() $(X_1,\omega _1,\Omega _1)$
with fibre class
$(X_1,\omega _1,\Omega _1)$
with fibre class
![]() $F_*[L]$
. Let
$F_*[L]$
. Let
![]() $(\check {Y}_1,\check {D}_1)$
be the pair of rational elliptic surface and
$(\check {Y}_1,\check {D}_1)$
be the pair of rational elliptic surface and
![]() $I_b$
fibre such that
$I_b$
fibre such that
![]() $\check {X}_1=\check {Y}_1\setminus \check {D}_{1}$
is a hyperKähler rotation of
$\check {X}_1=\check {Y}_1\setminus \check {D}_{1}$
is a hyperKähler rotation of
![]() $X_1$
with elliptic fibration with fibre class
$X_1$
with elliptic fibration with fibre class
![]() $F_*[L]$
. Denote
$F_*[L]$
. Denote
![]() $(\check {\omega }_i,\check {\Omega }_i)$
for the hyperKähler triple on
$(\check {\omega }_i,\check {\Omega }_i)$
for the hyperKähler triple on
![]() $\check {X}_i$
. From Theorem 2.2 and Theorem 3.3, the resulting holomorphic volume form
$\check {X}_i$
. From Theorem 2.2 and Theorem 3.3, the resulting holomorphic volume form
![]() $\check {\Omega }_i$
on
$\check {\Omega }_i$
on
![]() $\check {X}_i$
is meromorphic on
$\check {X}_i$
is meromorphic on
![]() $\check {Y}_i$
and has a simple pole along
$\check {Y}_i$
and has a simple pole along
![]() $\check {D}_i$
.
$\check {D}_i$
.
We will first use the weak Torelli theorem of Looijenga pairs (Theorem 3.8) to show that there exists a biholomorphism
![]() $\check {Y}_2\rightarrow \check {Y}_1$
such that the induced map on
$\check {Y}_2\rightarrow \check {Y}_1$
such that the induced map on
![]() $H^2(\check {X}_2,\mathbb {Z})$
is the same as
$H^2(\check {X}_2,\mathbb {Z})$
is the same as
![]() $F^*$
. To achieve that, we will construct an isomorphism of lattices
$F^*$
. To achieve that, we will construct an isomorphism of lattices
![]() $\tilde {F}^*:H^2(\check {Y}_1,\mathbb {Z})\rightarrow H^2(\check {Y}_2,\mathbb {Z})$
from the diffeomorphism F such that
$\tilde {F}^*:H^2(\check {Y}_1,\mathbb {Z})\rightarrow H^2(\check {Y}_2,\mathbb {Z})$
from the diffeomorphism F such that
![]() $\tilde {F}^*([\check {D}_{1,i}])=[\check {D}_{2,i}]$
.
$\tilde {F}^*([\check {D}_{1,i}])=[\check {D}_{2,i}]$
.
Lemma 3.10. There exists a diffeomorphism
![]() $F':X_2\rightarrow X_1$
such that
$F':X_2\rightarrow X_1$
such that
-
1.
 $F'$
is homotopic to F and
$F'$
is homotopic to F and -
2. if
 $C\subseteq \check {Y}_2$
is a
$C\subseteq \check {Y}_2$
is a
 $2$
-cycle that is a local section of the fibration
$2$
-cycle that is a local section of the fibration
 $\check {Y}_2\rightarrow \mathbb {P}^1$
near infinity and intersects
$\check {Y}_2\rightarrow \mathbb {P}^1$
near infinity and intersects
 $\check {D}_{i,2}$
transversally for some i, then the closure of
$\check {D}_{i,2}$
transversally for some i, then the closure of
 $F'(C\cap X_2)$
intersects
$F'(C\cap X_2)$
intersects
 $\check {D}_{i,1}$
transversally and is again a local section of
$\check {D}_{i,1}$
transversally and is again a local section of
 $\check {Y}_1\rightarrow \mathbb {P}^1$
near infinity.
$\check {Y}_1\rightarrow \mathbb {P}^1$
near infinity.
Proof. There exist compact sets
![]() $K_i\subset X_i$
such that
$K_i\subset X_i$
such that
![]() $g_i:X_i\setminus K_i\cong X_{\mathcal {C}}$
. Recall that F sends a neighbourhood of infinity of
$g_i:X_i\setminus K_i\cong X_{\mathcal {C}}$
. Recall that F sends a neighbourhood of infinity of
![]() $X_2$
to a neighbourhood of infinity of
$X_2$
to a neighbourhood of infinity of
![]() $X_1$
; and for each
$X_1$
; and for each
![]() $i=1,2$
, there exists a special Lagrangian fibration on
$i=1,2$
, there exists a special Lagrangian fibration on
![]() $X_i\setminus K_i\rightarrow \Delta ^*$
, where
$X_i\setminus K_i\rightarrow \Delta ^*$
, where
![]() $\Delta ^*$
is the punctured disc. We may choose
$\Delta ^*$
is the punctured disc. We may choose
![]() $K_1,K_2$
such that
$K_1,K_2$
such that
![]() $F(X_2\setminus K_2)\subseteq X_1\setminus K_1$
and
$F(X_2\setminus K_2)\subseteq X_1\setminus K_1$
and
![]() $\partial K_i$
is the preimage of a loop in
$\partial K_i$
is the preimage of a loop in
![]() $\Delta ^*$
under the special Lagrangian fibration; that is, there exists
$\Delta ^*$
under the special Lagrangian fibration; that is, there exists
![]() $\nu _i:\partial K_i\rightarrow S^1$
. Since both
$\nu _i:\partial K_i\rightarrow S^1$
. Since both
![]() $\partial K_1,F(\partial K_2)$
are the boundary of a neighbourhood of infinity of
$\partial K_1,F(\partial K_2)$
are the boundary of a neighbourhood of infinity of
![]() $X_1$
and
$X_1$
and
![]() $X_1\setminus K_1\cong X_{\mathcal {C}}\cong \check {X}_{mod}\cong \partial K_1 \times (0,1)$
, there exists a vector field on
$X_1\setminus K_1\cong X_{\mathcal {C}}\cong \check {X}_{mod}\cong \partial K_1 \times (0,1)$
, there exists a vector field on
![]() $X_1\setminus K_1$
such that the induced flow takes
$X_1\setminus K_1$
such that the induced flow takes
![]() $\partial K_1$
to
$\partial K_1$
to
![]() $F(\partial K_2)$
. We will denote such a diffeomorphism by
$F(\partial K_2)$
. We will denote such a diffeomorphism by
![]() $v:\partial K_1\cong F(\partial K_2)$
.
$v:\partial K_1\cong F(\partial K_2)$
.
Since
![]() $S^1$
is the Eilenberg-MacLane space
$S^1$
is the Eilenberg-MacLane space
![]() $K(\mathbb {Z},1)$
, we have
$K(\mathbb {Z},1)$
, we have
![]() $[\partial K_1, S^1]=H^1(\partial K_1,\mathbb {Z})\cong \mathbb {Z}^2$
. Restricting the model special Lagrangian fibrations in
$[\partial K_1, S^1]=H^1(\partial K_1,\mathbb {Z})\cong \mathbb {Z}^2$
. Restricting the model special Lagrangian fibrations in
![]() $g_1^{-1}(X_{\mathcal {C}})$
and possibly composing with multiple cover
$g_1^{-1}(X_{\mathcal {C}})$
and possibly composing with multiple cover
![]() $S^1\rightarrow S^1$
gives
$S^1\rightarrow S^1$
gives
![]() $\mathbb {Z}^2$
nonhomotopic maps from
$\mathbb {Z}^2$
nonhomotopic maps from
![]() $\partial K_1$
to
$\partial K_1$
to
![]() $S^1$
. Notice that they all have different fibre homology classes. Therefore, two maps from
$S^1$
. Notice that they all have different fibre homology classes. Therefore, two maps from
![]() $\partial K_1$
to
$\partial K_1$
to
![]() $S^1$
are homotopic if and only if the corresponding fibre classes are homologous. Therefore, we have
$S^1$
are homotopic if and only if the corresponding fibre classes are homologous. Therefore, we have
![]() $\nu _1\sim \nu _2 \circ F^{-1}\circ v$
, and we can modify v such that v sends fibres of
$\nu _1\sim \nu _2 \circ F^{-1}\circ v$
, and we can modify v such that v sends fibres of
![]() $\nu _1$
to fibres of
$\nu _1$
to fibres of
![]() $\nu _2 \circ F^{-1}$
, which are
$\nu _2 \circ F^{-1}$
, which are
![]() $2$
-tori. Let
$2$
-tori. Let
![]() $T^2$
be a fibre of
$T^2$
be a fibre of
![]() $\nu _1(\partial K_1)$
; then
$\nu _1(\partial K_1)$
; then
![]() $\varphi =\nu _2\circ F^{-1}\circ v\circ \nu _1^{-1}$
induces an element in the mapping class group
$\varphi =\nu _2\circ F^{-1}\circ v\circ \nu _1^{-1}$
induces an element in the mapping class group
![]() $MCG(T^2)\cong SL(2,\mathbb {Z})$
. The monodromy M of
$MCG(T^2)\cong SL(2,\mathbb {Z})$
. The monodromy M of
![]() $\partial K\rightarrow S^1$
is conjugate to
$\partial K\rightarrow S^1$
is conjugate to
![]() $\begin {pmatrix} 1 & b\\ 0 & 1 \end {pmatrix}$
and commutes with
$\begin {pmatrix} 1 & b\\ 0 & 1 \end {pmatrix}$
and commutes with
![]() $\varphi $
. Thus,
$\varphi $
. Thus,
![]() $\varphi $
is also of the form
$\varphi $
is also of the form
 $\pm \begin {pmatrix} 1 & m\\ 0 & 1 \end {pmatrix}$
for some
$\pm \begin {pmatrix} 1 & m\\ 0 & 1 \end {pmatrix}$
for some
![]() $m\in \mathbb {Z}$
. Therefore, we may modify F such that fibrewise, it is given by
$m\in \mathbb {Z}$
. Therefore, we may modify F such that fibrewise, it is given by
![]() $\varphi $
on
$\varphi $
on
![]() $X_2\setminus K^{\prime }_2$
for large enough compact set
$X_2\setminus K^{\prime }_2$
for large enough compact set
![]() $K_2'$
. In terms of the coordinates in Section 2.1,
$K_2'$
. In terms of the coordinates in Section 2.1,
![]() $F'$
(after the identification
$F'$
(after the identification
![]() $X_{\mathcal {C}}\cong \check {X}_{mod}$
) is given by
$X_{\mathcal {C}}\cong \check {X}_{mod}$
) is given by
Now every continuous section of
![]() $\check {X}_{mod}$
that extends to
$\check {X}_{mod}$
that extends to
![]() $\check {Y}_{mod}$
is of the form
$\check {Y}_{mod}$
is of the form
where
![]() $h(u)$
is a continuous function over
$h(u)$
is a continuous function over
![]() $\Delta $
and
$\Delta $
and
![]() $a\in \mathbb {Z}$
. A straightforward calculation shows that equation (3.3) maps sections of
$a\in \mathbb {Z}$
. A straightforward calculation shows that equation (3.3) maps sections of
![]() $\check {Y}_{mod}$
to sections
$\check {Y}_{mod}$
to sections
![]() $\check {Y}_{mod}$
; this finishes the proof of the lemma.
$\check {Y}_{mod}$
; this finishes the proof of the lemma.
From now on, we will replace F by
![]() $F'$
in Lemma 3.10 and still denote it by F. Recall that the second homology group of a rational elliptic surface is generated by the components of fibres and sections. The lemma implies that there exists a map
$F'$
in Lemma 3.10 and still denote it by F. Recall that the second homology group of a rational elliptic surface is generated by the components of fibres and sections. The lemma implies that there exists a map
![]() $\tilde {F}^*:H^2(\check {Y}_1,\mathbb {Z})\rightarrow H^2(\check {Y}_2,\mathbb {Z})$
such that the following diagram commutes
$\tilde {F}^*:H^2(\check {Y}_1,\mathbb {Z})\rightarrow H^2(\check {Y}_2,\mathbb {Z})$
such that the following diagram commutes

and the intersection pairing is preserved. Here the vertical maps are the natural ones induced from the restriction. From Poincare duality,
![]() $\tilde {F}^*$
must be an isometry of lattices.
$\tilde {F}^*$
must be an isometry of lattices.
From [Reference Gross, Hacking and Keel9, Construction 5.7], there exists a universal family
![]() $(\mathcal {Y},\mathcal {D})$
over
$(\mathcal {Y},\mathcal {D})$
over
![]() $\mbox {Hom}(\mbox {Pic}(\check {Y}_1),\mathbb {C}^*)$
such that
$\mbox {Hom}(\mbox {Pic}(\check {Y}_1),\mathbb {C}^*)$
such that
![]() $(\check {Y}_1,\check {D}_1)=(\mathcal {Y}_{1},\mathcal {D}_1)$
is the reference fibre and there exists an isomorphism of pairs
$(\check {Y}_1,\check {D}_1)=(\mathcal {Y}_{1},\mathcal {D}_1)$
is the reference fibre and there exists an isomorphism of pairs
![]() $\rho :(\check {Y}_2,\check {D}_2)\cong (\mathcal {Y}_2,\mathcal {D}_2)$
with some fibre
$\rho :(\check {Y}_2,\check {D}_2)\cong (\mathcal {Y}_2,\mathcal {D}_2)$
with some fibre
![]() $(\mathcal {Y}_2,\mathcal {D}_2)$
. Now
$(\mathcal {Y}_2,\mathcal {D}_2)$
. Now
![]() $\tilde {F}^*$
can be decomposed as
$\tilde {F}^*$
can be decomposed as
where
![]() $\mbox {Par}$
denotes a choice of the parallel transport via the universal family. Since
$\mbox {Par}$
denotes a choice of the parallel transport via the universal family. Since
![]() $\rho :\check {Y}_2\cong \mathcal {Y}_2$
is a biholomorphism, it preserves the set of exceptional curves and positive cones. Together with the fact that
$\rho :\check {Y}_2\cong \mathcal {Y}_2$
is a biholomorphism, it preserves the set of exceptional curves and positive cones. Together with the fact that
![]() $C^{++}$
is preserved under the parallel transport, we have
$C^{++}$
is preserved under the parallel transport, we have
![]() $\tilde {F}^*(C^{++}_{\check {Y}_1})=C^{++}_{\check {Y}_2}$
. Now, from Theorem 3.8, there exists an isomorphism of pairs
$\tilde {F}^*(C^{++}_{\check {Y}_1})=C^{++}_{\check {Y}_2}$
. Now, from Theorem 3.8, there exists an isomorphism of pairs
![]() $h:(\check {Y}_2,\check {D})\rightarrow (\check {Y}_1,\check {D})$
such that
$h:(\check {Y}_2,\check {D})\rightarrow (\check {Y}_1,\check {D})$
such that
![]() $\tilde {F}^*\circ g=h^*$
for some
$\tilde {F}^*\circ g=h^*$
for some
![]() $g\in W_{\check {Y}_1}$
.
$g\in W_{\check {Y}_1}$
.
Next, we will show that g is the identity. From [Reference Gross, Hacking and Keel9, Theorem 3.2], the hyperplanes
![]() $\alpha ^{\perp }, \alpha \in W_{\check {Y}_1}\cdot \Delta _{\check {Y}_1}$
divide
$\alpha ^{\perp }, \alpha \in W_{\check {Y}_1}\cdot \Delta _{\check {Y}_1}$
divide
![]() $C^{++}_{\check {D}}$
into chambers, and the Weyl group
$C^{++}_{\check {D}}$
into chambers, and the Weyl group
![]() $W_{\check {Y}_1}$
simply acts transitively on the chambers. Moreover, there exists a unique chamber containing the nef cone and thus the ample cone. Chambers divided by
$W_{\check {Y}_1}$
simply acts transitively on the chambers. Moreover, there exists a unique chamber containing the nef cone and thus the ample cone. Chambers divided by
![]() $\alpha ^{\perp }$
in
$\alpha ^{\perp }$
in
![]() $H^2(\check {Y}_1)$
have disjoint image under the restriction map
$H^2(\check {Y}_1)$
have disjoint image under the restriction map
![]() $\iota ^*:H^2(\check {Y}_1)\rightarrow H^2(\check {X}_1)$
. Indeed, if
$\iota ^*:H^2(\check {Y}_1)\rightarrow H^2(\check {X}_1)$
. Indeed, if
![]() $\delta _1,\delta _2\in H^2(\check {Y}_1)$
and
$\delta _1,\delta _2\in H^2(\check {Y}_1)$
and
![]() $\iota ^*\delta _1=\iota ^*\delta _2$
, then from the dual of the long exact sequence of equation (3.2), we have
$\iota ^*\delta _1=\iota ^*\delta _2$
, then from the dual of the long exact sequence of equation (3.2), we have
Thus
![]() $\delta _1,\delta _2$
fall in the same chamber because
$\delta _1,\delta _2$
fall in the same chamber because
![]() $\alpha \cdot [D_i]=0$
for all
$\alpha \cdot [D_i]=0$
for all
![]() $\alpha \in W_{\check {Y}_1}\cdot \Delta _{\check {Y}_1}$
. Again from the long exact sequence in equation (3.2), the image of
$\alpha \in W_{\check {Y}_1}\cdot \Delta _{\check {Y}_1}$
. Again from the long exact sequence in equation (3.2), the image of
![]() $\iota ^*$
is a hyperplane in
$\iota ^*$
is a hyperplane in
![]() $H^2(\check {X}_1)$
. For each
$H^2(\check {X}_1)$
. For each
![]() $\alpha \in \Delta _{\check {Y}_1}$
, there is a corresponding
$\alpha \in \Delta _{\check {Y}_1}$
, there is a corresponding
![]() $(-2)$
-curve
$(-2)$
-curve
![]() $C_{\alpha }$
of
$C_{\alpha }$
of
![]() $\check {Y}_1$
that completely falls in
$\check {Y}_1$
that completely falls in
![]() $\check {X}_1$
. Given a compact
$\check {X}_1$
. Given a compact
![]() $2$
-cycle C of
$2$
-cycle C of
![]() $\check {X}$
, we can associate a hyperplane
$\check {X}$
, we can associate a hyperplane
![]() $[C]^{\perp _{\check {X}_1}}$
of
$[C]^{\perp _{\check {X}_1}}$
of
![]() $H^2(\check {X}_1)$
given by
$H^2(\check {X}_1)$
given by
Then
![]() $\iota ^*(\alpha ^{\perp })$
is the intersection of the hyperplanes
$\iota ^*(\alpha ^{\perp })$
is the intersection of the hyperplanes
![]() $[C_{\alpha }]^{\perp _{\check {X}_1}}$
and
$[C_{\alpha }]^{\perp _{\check {X}_1}}$
and
![]() $[\partial _*(\varepsilon )]^{\perp _{\check {X}_1}}$
. Again, the hyperplanes
$[\partial _*(\varepsilon )]^{\perp _{\check {X}_1}}$
. Again, the hyperplanes
![]() $[C_{\alpha }]^{\perp _{\check {X}_1}}$
,
$[C_{\alpha }]^{\perp _{\check {X}_1}}$
,
![]() $\alpha \in W_{\check {Y}_1}\cdot \Delta _{\check {Y}_1}$
divide
$\alpha \in W_{\check {Y}_1}\cdot \Delta _{\check {Y}_1}$
divide
![]() $H^2(\check {X}_1)$
into chambers. There exists a unique one that contains the image of the Kähler cone of
$H^2(\check {X}_1)$
into chambers. There exists a unique one that contains the image of the Kähler cone of
![]() $\check {Y}_1$
, which consists of
$\check {Y}_1$
, which consists of
![]() $2$
-forms integrating positively on
$2$
-forms integrating positively on
![]() $C_{\alpha }$
for all
$C_{\alpha }$
for all
![]() $\alpha \in \Delta _{\check {Y}_1}$
. Since
$\alpha \in \Delta _{\check {Y}_1}$
. Since
![]() $F^*$
sends
$F^*$
sends
![]() $[\omega _1]$
to
$[\omega _1]$
to
![]() $[\omega _2]$
and
$[\omega _2]$
and
![]() $h^*$
preserves the Kähler classes of
$h^*$
preserves the Kähler classes of
![]() $\check {Y}_1$
, one must have that g is the identity and
$\check {Y}_1$
, one must have that g is the identity and
![]() $\tilde {F}^*=h^*$
.
$\tilde {F}^*=h^*$
.
When restricting to
![]() $\check {X}_1$
, we have
$\check {X}_1$
, we have
![]() $h^*=\tilde {F}^*=F^*$
. Since
$h^*=\tilde {F}^*=F^*$
. Since
![]() $F^*[\check {\Omega }_1]=[\check {\Omega }_2]$
from the assumption and
$F^*[\check {\Omega }_1]=[\check {\Omega }_2]$
from the assumption and
![]() $h^*\check {\Omega }_1=c\check {\Omega }_2$
for some constant
$h^*\check {\Omega }_1=c\check {\Omega }_2$
for some constant
![]() $c\in \mathbb {C}^*$
, we then have
$c\in \mathbb {C}^*$
, we then have
![]() $h^*\check {\Omega }_1=\check {\Omega }_2$
. From Theorem 2.2 and Theorem 3.3, the resulting Kähler form
$h^*\check {\Omega }_1=\check {\Omega }_2$
. From Theorem 2.2 and Theorem 3.3, the resulting Kähler form
![]() $\check {\omega }_i$
is exponentially decaying to a possibly nonstandard semi-flat metric. Then Theorem 2.5 implies that
$\check {\omega }_i$
is exponentially decaying to a possibly nonstandard semi-flat metric. Then Theorem 2.5 implies that
![]() $T_{\sigma }^*h^*\check {\omega }_1=\check {\omega }_2$
, where
$T_{\sigma }^*h^*\check {\omega }_1=\check {\omega }_2$
, where
![]() $T_{\sigma }$
is a translation by a global section of
$T_{\sigma }$
is a translation by a global section of
![]() $\check {X}_2$
, which doesn’t alter the
$\check {X}_2$
, which doesn’t alter the
![]() $(2,0)$
-forms. We may take
$(2,0)$
-forms. We may take
![]() $f=h\circ T_{\sigma }$
, and this finishes the proof of the Torelli theorem.
$f=h\circ T_{\sigma }$
, and this finishes the proof of the Torelli theorem.
Remark 3.11. Ongoing work by Mazzeo and Zhu [Reference Mazzeo and Zhu22] studies the Fredholm mapping properties of the Laplace operator on ALH* space with applications to Hodge theory and perturbation theory.
Acknowledgements
The third author would like to thank X. Zhu for some related discussions. The authors are grateful to S.-T. Yau for his interest and encouragement and the AIM workshop on Stability in Mirror Symmetry for providing a good (virtual) environment for discussion. The authors also thank the anonymous reviewer for the helpful comments. T. Collins is supported in part by NSF CAREER grant DMS-1944952 and an Alfred P. Sloan Fellowship. A. Jacob is supported in part by a Simons collaboration grant. Y.-S. Lin is supported by Simons collaboration grant # 635846 and NSF grant DMS-2204109.
Conflicts of Interests
None.