1. Introduction
An individual is said to be inbred if its parents are genetically related to each other. The degree to which an individual is inbred can be summarized by that individual's inbreeding coefficient, f, which can be defined as the probability that the individual's two alleles at a random autosomal locus will both be copies of a single allele present in one of the individual's ancestors. In other words, f is the probability that an individual's two alleles will be identical by descent (IBD) from some ancestor.
There has been recent interest in the estimation of inbreeding coefficients or the related topic of estimating relatedness between individuals in the presence of inbreeding (Anderson & Weir, Reference Anderson and Weir2007; Purcell et al., Reference Purcell, Neale, Todd-Brown, Thomas, Ferreira, Bender, Maller, Sklar, de Bakker, Daly and Sham2007; Chybicki & Burczyk, Reference Chybicki and Burczyk2009; Wang, Reference Wang2011a , Reference Wang b ; Yang et al., Reference Yang, Lee, Goddard and Visscher2011). The main topic of this paper is the development of maximum likelihood estimators for estimating inbreeding coefficients from molecular marker data.
The presence of null alleles complicates the estimation of inbreeding coefficients. A null allele is an allele that cannot be directly observed during genotyping. An individual homozygous for a null allele will not produce any readable alleles at that marker and so will be recorded as having a missing genotype. An individual heterozygous for the null allele and another allele will be recorded as being homozygous for that other allele. The uncertainty in genotypes caused by the presence of null alleles can cause difficulty in interpreting the results of a number of kinds of population genetic studies (Chapuis & Estoup, Reference Chapuis and Estoup2007; Chybicki & Burczyk, Reference Chybicki and Burczyk2009) and there has been recent interest in detecting null alleles and/or estimating their frequencies (Kalinowski & Taper, Reference Kalinowski and Taper2006; Van Oosterhout et al., Reference Van Oosterhout, Weetman and Hutchinson2006; Chybicki & Burczyk, Reference Chybicki and Burczyk2009; Girard, Reference Girard2011). In developing a method that could estimate inbreeding coefficients in the presence of null alleles, we noted that both null alleles and inbreeding cause an increase in observed homozygosity. If used effectively, though, a dataset consisting of genotypes of multiple individuals genotyped at several markers can be used to distinguish between null alleles and inbreeding because the two sources of excess homozygosity leave somewhat different footprints in the data. For example, markers with common null alleles will tend to have more missing data than other markers, especially among individuals who are more inbred. In contrast, at loci with no null alleles (or rare null alleles), inbred and non-inbred individuals should show similar rates of missingness. In addition, more highly inbred individuals will tend to have more missing genotypes (because such individuals are more likely to be homozygous for the null allele), particularly at markers with higher null allele frequencies. By looking at inbreeding and null alleles together, one can take advantage of these types of patterns in the data.
In this paper, we will compare new and previously existing methods that either (1) estimate individual inbreeding coefficients assuming known allele frequencies and no null alleles, (2) jointly estimate inbreeding coefficients and allele frequencies, again assuming no null alleles, or (3) jointly estimate individual inbreeding coefficients and allele frequencies in the presence of null alleles.
2. Theory and methods
(i) Existing methods for estimating inbreeding coefficients when there are no null alleles
Perhaps the most sophisticated method in this category is Leutenegger's method (Leutenegger et al., Reference Leutenegger, Prum, Génin, Verny, Lemainque, Clerget-Darpoux and Thompson2003), which performs maximum likelihood estimation of inbreeding coefficients using (potentially) linked genetic markers. Leutenegger's method is the only method to be mentioned in this paper that models linkage between loci. Since we are concerned with unlinked markers, we did not include Leutenegger's method directly in our calculations. However, Leutenegger's method applied to unlinked markers (with no genotyping error) should be equivalent to our Method 1 described below. The only difference between the two is the algorithm used to numerically maximize the likelihood function.
Another estimator, which we call the ‘Simple’ estimator, is
where HO is the total number of loci at which the individual is heterozygous and HE is the expected number of loci at which the individual is heterozygous, given the known allele frequencies. If pjk is the relative frequency of allele k at marker j, m is the number of genotyped markers and nj is the number of possible alleles at marker j, then
Note that this estimator is slightly different than Wright's population inbreeding coefficient estimator because Wright's estimator deals with genotypes from multiple individuals at a single marker, whereas this estimator deals with genotypes from a single individual at multiple markers. This estimator is similar in spirit to the one presented in Carothers et al. (Reference Carothers, Ruden, Kolcic, Polasek, Hayward, Wright, Campbell, Teague, Hastie and Weber2006), but differs in the details of the calculations. In the case in which there are only two possible alleles at a marker and allele frequencies are known (not estimated from the dataset), this estimator is the same as the estimator calculated by the PLINK program (Purcell et al., Reference Purcell, Neale, Todd-Brown, Thomas, Ferreira, Bender, Maller, Sklar, de Bakker, Daly and Sham2007).
Another popular moment estimator, due to Ritland (specifically, eqn (5) in Ritland, Reference Ritland1996), is
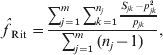
where Sjk is 1 if the individual is homozygous for allele k at marker j and 0 otherwise. This estimator can be viewed as a variant of eqn (5) in Li & Horvitz (Reference Li and Horvitz1953), except that Li's version assumes multiple individuals have been genotyped at a single locus, while Ritland's version applies to a single individual genotyped at multiple loci and, additionally, Li's version assumes allele frequencies have been estimated from the dataset by allele counting.
Both the Simple and Ritland estimators have the property that they do not constrain their estimated inbreeding coefficients to be between 0 and 1. If one considers only inbreeding coefficients between 0 and 1, one might replace any negative estimate by 0 and any estimate greater than 1 by 1 itself. The versions of the Simple and Ritland estimators for which we made these adjustments are called the adjusted Simple and adjusted Ritland estimators.
The above estimators do not take uncertainty in allele frequencies into account. Vogl et al. (Reference Vogl, Karhu, Moran and Savolainen2002)developed a Bayesian method to jointly estimate allele frequencies and inbreeding coefficients using a dataset containing multiple individuals genotyped at multiple markers. The Vogl model assumes that the inbreeding coefficients in the dataset are random values from a beta distribution. The final estimated inbreeding coefficients take both the beta prior distribution and the observed data into account. We ran Vogl's algorithm with the prior recommendation by Vogl et al. (a beta prior with α1=α2=0·001) and also using a uniform prior (a beta prior with α1=α2=1·0).
(ii) Existing method for estimating null allele frequencies, assuming no inbreeding
Kalinowski & Taper (Reference Kalinowski and Taper2006) produced an expectation–maximization (EM) algorithm to estimate allele frequencies and showed that it produced smaller root mean square errors (RMSE) than other estimators. The Kalinowski and Taper method considers one marker at a time and estimates the frequencies of all alleles at the marker (including a null allele) as well as a parameter, β, that measures the rate at which genotypes are randomly missing for reasons unrelated to null alleles. The β parameter is essential – without it, a marker with many missing genotypes but no other sign of excess homozygosity would produce a high estimated null allele frequency since, without β, the estimator would assume that any missing genotype is in fact homozygous for the null allele.
(iii) Existing method for jointly estimating null allele frequencies and inbreeding coefficients
Vogl et al. (Reference Vogl, Karhu, Moran and Savolainen2002), in their paper on estimating inbreeding coefficients, also described how their Bayesian method could be adapted to the case of null alleles.
(iv) New Method 1: an EM algorithm for maximum likelihood estimation of inbreeding coefficients when allele frequencies are known
When allele frequencies are known, individuals in the dataset can be considered one at a time. Since we are considering unlinked markers, the likelihood (the probability of the data, viewed as a function of the parameter f) is the product of the single-marker likelihoods. Let gj
be the genotype of the individual at marker j, let ![]() and let
and let ![]() be the possible alleles at marker j. Then the likelihood function is
be the possible alleles at marker j. Then the likelihood function is
where, letting ![]() denote the matrix of allele frequencies at the various markers, with pjk
denoting the relative frequency of allele k at marker j,
denote the matrix of allele frequencies at the various markers, with pjk
denoting the relative frequency of allele k at marker j,
The maximum likelihood estimate for f is found by maximizing the likelihood, L(f), with respect to f.
We will perform this maximization via an EM algorithm. For each marker, j, define a random variable Xj as follows:
If the Xj
values were known, then the maximum likelihood estimator (MLE) for f would be ![]() . If the Xj
values were unknown but we could calculate their expected values (noting that
. If the Xj
values were unknown but we could calculate their expected values (noting that ![]() is the probability that an individual's 2 alleles at marker j are IBD, given the individual's genotypes and inbreeding coefficient), the MLE for f would still be easy to find (
is the probability that an individual's 2 alleles at marker j are IBD, given the individual's genotypes and inbreeding coefficient), the MLE for f would still be easy to find (![]() ). Unfortunately, the probabilities
). Unfortunately, the probabilities ![]() depend on f and hence cannot be calculated without first knowing f. That leaves us with the following: if we knew f, we could estimate the
depend on f and hence cannot be calculated without first knowing f. That leaves us with the following: if we knew f, we could estimate the ![]() values and, if we knew the
values and, if we knew the ![]() values, we could estimate f. The EM algorithm proceeds by alternating between steps in which we estimate the
values, we could estimate f. The EM algorithm proceeds by alternating between steps in which we estimate the ![]() values based on our current estimate for f, and steps in which we update our estimate for f based on our current values for
values based on our current estimate for f, and steps in which we update our estimate for f based on our current values for ![]() . The algorithm begins with an initial guess for f, call it f
(0). Let f
(z) denote our estimate for f at the start of the zth iteration of our algorithm. The steps for the (z+1)st iterations are:
. The algorithm begins with an initial guess for f, call it f
(0). Let f
(z) denote our estimate for f at the start of the zth iteration of our algorithm. The steps for the (z+1)st iterations are:
-
(1) Given f (z), estimate the value for Xj for every marker j using the following equation:
(7)![\eqalign{E_{z} \left[ {X_{j} \vert\hskip2pt f^{\hskip1pt\lpar z\rpar } \comma \vec{g}} \right]\!\equals\! \tab \left\{ {\matrix{ {{\textstyle{{f^{\hskip2pt\lpar z\rpar } p_{jk} } \over {f^{\hskip1pt\lpar z\rpar } p_{jk} \plus \left( {1 \minus f^{\hskip1pt\lpar z\rpar } } \right)p_{jk}^{\setnum{2}} }}}\comma } \hfill \tab\hskip-3pt {{\rm if}\,g_{j} \equals A_{jk} A_{jk} \comma \tab } \hfill \cr {0\comma } \hfill \tab\hskip-3pt {{\rm if}\, g_{j} \equals A_{jk} A_{jl} \ \lpar k \ne l\rpar .} \hfill \cr} } \right.](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
-
(2) Given the
![E_{z} \left[ {X_{j} \vert\hskip2pt f^{\hskip2pt\lpar z\rpar } \comma \vec{g}} \right]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) estimates, update the estimate for f using the following equation:(8)
estimates, update the estimate for f using the following equation:(8)![f^{\hskip2pt\lpar z \plus \setnum{1}\rpar } \tab \equals {{\sum\nolimits_{j} \,E_{z} \left[ {X_{j} \vert\hskip2pt f^{\hskip2pt\lpar z\rpar } \comma \vec{g}} \right]} \over m}.](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
Maximization is accomplished by iterating eqns (7) and (8) until convergence is reached. Note that the algorithm should be repeated using several different starting values for f because an EM algorithm can converge to a local rather than a global maximum (see, for example, Wu, Reference Wu1983). A more formal derivation of this algorithm is included in the online Supplementary Material at http://journals.cambridge.org/GRH.
New Method 2: an EM algorithm for joint maximum likelihood estimation of inbreeding coefficients and allele frequencies
We consider a dataset with N individuals genotyped at m markers. Let fi
denote the inbreeding coefficient of individual i (i=1, …,N) and gij
be the genotype of individual i at marker j. Letting ![]() and
and ![]() be the matrix of allele frequencies, the likelihood equation now becomes
be the matrix of allele frequencies, the likelihood equation now becomes
where the ![]() values are still calculated as in eqn (5). The maximization of the likelihood is now taken with respect to
values are still calculated as in eqn (5). The maximization of the likelihood is now taken with respect to ![]() and all the allele frequencies (
and all the allele frequencies (![]() ) jointly. Let δ
ijkl
=1 if individual i's genotype at marker j is AjkAjl
and δ
ijkl
=0 otherwise and let Xij
be defined such that Xij
=1 if individual i's two alleles at marker j are IBD and Xij
=0 otherwise. Using Ez
[Xij
] as a shorthand notation for E[Xij
|fi
(z), gij
], the equations for the EM algorithm are
) jointly. Let δ
ijkl
=1 if individual i's genotype at marker j is AjkAjl
and δ
ijkl
=0 otherwise and let Xij
be defined such that Xij
=1 if individual i's two alleles at marker j are IBD and Xij
=0 otherwise. Using Ez
[Xij
] as a shorthand notation for E[Xij
|fi
(z), gij
], the equations for the EM algorithm are
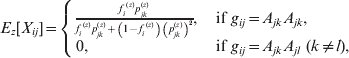
![\eqalign{\tab p_{jk}^{\lpar z \plus \setnum{1}\rpar } \equals\cr\tab\quad {{{\sum\nolimits_{i \equals \setnum{1}}^{N} \,\left[ {\delta _{ijkk} \left( {E_{z} \lsqb X_{ij} \rsqb \plus 2\left( {1 \minus E_{z} \lsqb X_{ij} \rsqb } \right)} \right) \plus \sum\nolimits_{l \ne k} \,\delta _{ijkl} } \right]} \over {\sum\nolimits_{l \equals \setnum{1}}^{n_{j} } \,\sum\nolimits_{i \equals \setnum{1}}^{N} \,\left[ {\delta _{ijll} \left( {E_{z} \lsqb X_{ij} \rsqb \plus 2\left( {1 \minus E_{z} \lsqb X_{ij} \rsqb } \right)} \right) \plus \sum\nolimits_{h \ne l} \,\delta _{ijhl} } \right]}}} \comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235928737-0299:S0016672312000341:S0016672312000341_eqn11.gif?pub-status=live)
Here, eqns (10) and (12) are analogous to eqns (7) and (8) in the previous method. Equation (11) provides updated estimates of the allele frequencies, given the estimated Xij values. In spirit, the numerator in eqn (11) represents a calculation in which we go through the list of all individuals genotyped at marker j and, for each individual homozygous for allele Ak , we count 1 allele if the individual's 2 alleles are IBD and 2 distinct alleles otherwise. For each individual heterozygous for allele Ak , we count one allele. Since we cannot see whether a homozygous genotype contains two IBD alleles or not, we do not know precisely whether to count 1 or 2 distinct alleles so, in the numerator of eqn (12), we take a weighted average between 1 and 2, weighted by the probability that the two alleles are IBD. That gives us the (expected) total number of distinct Ak alleles in the dataset based on our current estimates for the Xij values. In the denominator we count the total (expected) number of distinct alleles at marker j in the dataset. The updated estimate for pjk is the estimated proportion of distinct alleles in the dataset that are of type Ajk . A more formal derivation of this algorithm is presented in the online Supplementary Material at http://journals.cambridge.org/GRH.
(vi) New Method 3: an EM algorithm for joint estimation of inbreeding coefficients and allele frequencies including null alleles
For this algorithm, we generalize our Method 2 algorithm by adding the possibility of null alleles. This algorithm can also be viewed as a generalization of Kalinowski and Taper's method in which we allow their model to include the possibility of inbreeding. We take the convention that there are now nj
+1 possible alleles at marker j (j=1, …, m), where A
j
1,= ![]() are the visible alleles and Aj,n
is the null allele. We adopt Kalinowski and Taper's model for missing data: that each genotype at marker j (j=1, 2 …, m) has a probability β
j
of being missing, independent of the genotype at that marker.
are the visible alleles and Aj,n
is the null allele. We adopt Kalinowski and Taper's model for missing data: that each genotype at marker j (j=1, 2 …, m) has a probability β
j
of being missing, independent of the genotype at that marker.
The presence of null alleles, as well as the fact that a genotype may be randomly missing, may cause a difference between the observed and true genotypes. Define gij
* to be individual i's true genotype at marker j and gij
to be the observed genotype, with the convention that gij
=M denotes a missing genotype. Define Θ to be the values of all the parameters, so Θ=(![]() ). As before, let Xij
be 0 or 1 depending on whether individual i's 2 alleles at marker j are IBD. Define Bij
(i=1, …,N, j=1, …, m) such that Bij
=1 if individual i's genotype at marker j is missing at random and Bij
=0 otherwise. The variable Bij
is unobserved because a missing genotype may be missing randomly or missing because the genotype is homozygous for a null allele.
). As before, let Xij
be 0 or 1 depending on whether individual i's 2 alleles at marker j are IBD. Define Bij
(i=1, …,N, j=1, …, m) such that Bij
=1 if individual i's genotype at marker j is missing at random and Bij
=0 otherwise. The variable Bij
is unobserved because a missing genotype may be missing randomly or missing because the genotype is homozygous for a null allele.
The equations for the EM algorithm depend on two critical quantities, Pr(gij *|gij , Xij , Θ), and E[Xij|gij , Θ], i=1, …, N, j=1, …, m. Values for the first of these can be found in Table 1. Note that there are no formulae given for Pr(gij *|gij =AkAl , Xij =1, Θ) in Table 1, since, if Xij =1 (and so the 2 alleles are IBD), it is impossible to observe a heterozygous genotype under this model. The values for E[Xij|gij , Θ] are given in the following equation.
![\eqalign{ \tab E\hskip2pt\lsqb X_{ij} \vert g_{ij} \comma \rmTheta \rsqb\equals\cr \tab \hskip8pt \left\{ {\matrix{ {{\displaystyle{{f_{i} p_{jk} } \over {f_{i} p_{jk} \plus \lpar 1 \minus f_{i} \rpar \lpar p_{jk}^{\setnum{2}} \plus 2p_{jn} p_{jk} \rpar }}}\comma } \hfill \tab {g_{ij} \equals A_{jk} A_{jk} \comma } \hfill \cr {0\comma } \hfill \tab {g_{ij} \equals A_{jk} A_{jl} \comma \ \lpar k \ne l\rpar \comma }\hskip-6pt \hfill \cr {{\displaystyle{{f_{i} \lpar \beta _{j} \plus \lpar 1 \minus \beta _{j} \rpar p_{jn} \rpar } \over {\beta _{j} \plus \lpar 1 \minus \beta _{j} \rpar \left[ {fp_{jn} \plus \lpar 1 \minus f\rpar p_{jn}^{\setnum{2}} } \right]}}}\comma } \hfill \tab {g_{ij} \equals M.}\hfill \cr} } \right. \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235928737-0299:S0016672312000341:S0016672312000341_eqn13.gif?pub-status=live)
The likelihood is now
Given the estimated parameter values after the zth iteration, namely ![]() , the EM algorithm proceeds as follows (as before, using the notation E[Xij|gij
, Θ(z)]=Ez
[Xij
] when convenient):
, the EM algorithm proceeds as follows (as before, using the notation E[Xij|gij
, Θ(z)]=Ez
[Xij
] when convenient):
-
(1) Update the values of E[Xij|gij , Θ(z)] for all i and j using eqn (13). Call these updated values Ez [Xij ].
-
(2) The updated estimates for the inbreeding coefficients are:
(15)
-
(3) Update the allele frequency estimates using the following equations:
(16)where![\hskip-12pt\eqalign{ p_{jk}^{\lpar z \plus \setnum{1}\rpar }\equals \tab \mathop\sum\limits_{i \equals \setnum{1}}^{N} \,\left[ {2P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{k} A_{k} \vert g_{ij} \comma X_{ij} \equals 0\comma \rmTheta ^{\lpar z\rpar } } \right)} \right. \cr \tab\times\left( {1 \minus E_{z} \lsqb X_{ij} \rsqb } \right) \plus P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{k} A_{k} \vert g_{ij} \comma X_{ij} \equals 1\comma \rmTheta ^{\lpar z\rpar } } \right)\hskip-58pt \cr \tab \times E_{z} \lsqb X_{ij} \rsqb \plus \mathop\sum\limits_{l \ne k} \,P\left( {g_{ij}{ \hskip-4pt\ast } \equals A_{k} A_{l} \vert g_{ij} \comma X_{ij}{\hskip-4pt \ast } \equals 0\comma \rmTheta ^{\lpar z\rpar } } \right)\hskip-58pt\cr \tab\times( 1 \minus E_{z} \lsqb X_{ij} \rsqb) \right]\sol C_{j}^{\lpar z \plus \setnum{1}\rpar }{ \comma \cr](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) (17)
(17)![\eqalign{ C_{j}^{\hskip2pt\lpar z \plus \setnum{1}\rpar } \tab \equals \mathop\sum\limits_{i \equals \setnum{1}}^{N} \,\mathop\sum\limits_{l \equals \setnum{1}}^{n_{j} } \,\left[ {2P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{l} A_{l} \vert g_{ij} \comma X_{ij} \equals 0\comma \rmTheta ^{\lpar z\rpar } } \right)} \right.\hskip-82pt \cr \tab\times {\left( {1 \minus E_{z} \lsqb X_{ij} \rsqb } \right)\plus P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{l} A_{l} \vert g_{ij} \comma X_{ij} \equals 1\comma \rmTheta ^{\lpar z\rpar } } \right)}\hskip-82pt \cr \tab\times \left. E_{z} \lsqb X_{ij} \rsqb \plus 2\mathop\sum\limits_{h \lt l} \,P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{l} A_{h} \vert g_{ij} \comma X_{ij} \equals 0\comma \rmTheta ^{\lpar z\rpar }}\right)\right.\hskip-82pt\cr\tab\times\left.( 1 \minus E_{z} \lsqb X_{ij} \rsqb) \right]. \cr](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
The values for quantities of the form P(gij *|gij,Xij, Θ) can be calculated according to Table 1.
-
(4) Update the probability that a genotype will be randomly missing:
(18)![\hskip-12pt\eqalign{p_{miss}^{\lpar z\rpar } \tab \equals \beta _{j}^{\lpar z\rpar } \plus \left( {1 \minus \beta _{j}^{\lpar z\rpar } } \right)\left[ {f_{i}^{\hskip2pt\lpar z\rpar } p_{j\comma n }^{\lpar z\rpar } \!\plus \!\left( {1 \minus f_{i}^{\hskip2pt\lpar z\rpar } } \right)\mathop {\left( {p_{j\comma n }^{\lpar z\rpar } } \right)}\nolimits^{\setnum{2}} } \right].](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
-
(5) The updated estimates for β j (j=1, …, m) are
(19)A detailed derivation of this algorithm can be found in the online Supplementary Material at http://journals.cambridge.org/GRH.
Table 1. Conditional genotype probabilities of the form Pr(gij*|gij, Xij, Θ) for each combination of gij, gij* and Xij

(vii) Simulations without null alleles
We performed a number of simulations in order to evaluate the performance of our estimators and compare them with other estimators. We varied the number of genotyped markers (m=5, 10, 20, 50 and 100), number of alleles per marker (a=2, 5 and 10) and number of individuals in the simulated datasets (N=20 and 100). In all cases the allele frequencies at a marker with m alleles were (1c, 2c, …, mc), where c=2/(m(m+1)). The markers were simulated to be unlinked and not in linkage disequilibrium with each other. A simulated dataset consisted of equal numbers of individuals with the following inbreeding coefficients: f=0·00, 0·02, 0·05, 0·10, 0·20, 0·30, 0·4, 0·5, 0·7 and 0·9. Once an individual was assigned an inbreeding coefficient, its genotypes were simulated independently at each locus according to the probabilities given in eqn (5). For each dataset, we recorded the estimated inbreeding coefficient for 10 individuals – one with each of the possible inbreeding coefficients. One thousand datasets were generated for each combination of m, a and N.
For these simulations, we compared the behaviour of our Method 1 MLE with that of the Simple estimator and Ritland's estimator (and versions of these adjusted to give estimated values of f that lie between 0 and 1). Since these methods assume known allele frequencies, we assumed the true allele frequencies (the allele frequencies used to generate the data) when we used these algorithms to estimate the inbreeding coefficients.
Considering the case in which allele frequencies were not assumed to be known, we also looked at the behaviour of our Method 2 MLE and the version of Vogl's estimators that did not account for null alleles. These were also compared with our Method 1 MLE, Ritland's estimator, and the Simple estimator where these methods were given allele frequencies naively estimated from the data using simple allele-counting methods.
Two criteria for judging the performance of an estimator are the bias and the mean-square-error (MSE). The bias of an estimator is the average amount by which it overestimates or underestimates a parameter. Let ![]() be the estimated inbreeding coefficient for the ith individual analysed of those 1000. Then our estimate for the bias is the average value by which the estimator missed the true value f,
be the estimated inbreeding coefficient for the ith individual analysed of those 1000. Then our estimate for the bias is the average value by which the estimator missed the true value f,
Since, within each dataset, we recorded the estimated inbreeding coefficient for one individual with each true inbreeding coefficient (f=0·00, 0·02, 0·05, 0·10, 0·20, 0·30, 0·4, 0·5, 0·7 and 0·9), we could use eqn (20) to estimate the bias for each true inbreeding coefficient. We knew that the estimated inbreeding coefficients would be biased upward when f was quite small, and looking at bias separately for different degrees of inbreeding would allow us to see how this bias decreases with increasing sample size.
The MSE of an estimator is the average squared distance between the value of the estimator and the parameter it is supposed to estimate. An estimate for the MSE of the estimators was found by taking
In our summaries, we reported the RMSE, which is the square root of the MSE.
(viii) Simulations with null alleles
Each simulated dataset had loci with null alleles. The null alleles had variable frequencies as follows: the first simulated marker had p null=0, the second had p null=0·1, the third had p null=0·2, and this pattern was repeated (i.e. every third marker had a frequency of 0, etc.). At each marker the frequencies of the non-null alleles were given by
where p jk is the allele frequency of the kth observable allele at marker j, p null is the frequency of the null allele and n j is the number of observable alleles. The rate at which a genotype would be missing at random was β=0·05 at all loci.
Other than the addition of null alleles and randomly missing data, these simulations were performed similarly to the simulations without null alleles with the following exceptions: (1) We did not simulate the case in which the number of (visible) alleles at a marker was a=2, (2) 400 datasets were generated for each combination of m, a and N, (3) we used the version of Vogl's algorithm that allows for the presence of null alleles.
(ix) Real datasets
To evaluate the performance of the estimators on real data, we looked at two datasets: the Mouse dataset (Laurie et al., Reference Laurie, Nickerson, Anderson, Weir, Livingston, Dean, Smith, Schadt and Nachman2007) contained 94 wild-caught mice (M. musculus domesticus) captured in Arizona. We chose to use 757 single nucleotide polymorphism (SNP) loci with an average inter-marker spacing of 2 Mb. At this spacing, we expect that there is no linkage disequilibrium between the loci. We chose this dataset because mice are generally known to practice inbreeding (Ihe et al., Reference Ihe, Ravaoarimanana, Thomas and Tautz2006). There was some missing data in this dataset; however, all 94 mice were genotyped at at least 714 of these markers.
The Deer dataset (Shaw et al., Reference Shaw, Lancia, Conner and Rosenberry2006) consisted of 740 white-tailed deer (Odocoileus virginianus) genotyped at 15 microsatellite loci. The number of observed alleles at each locus ranged from 5 to 17. This dataset was of interest to us because DeYoung et al. (Reference DeYoung, Demarais, Honeycutt, Gonzales, Gee and Anderson2003)had found null alleles at a number of these loci in another population of white-tailed deer, so this was a dataset for which we expected both inbreeding and null alleles.
3. Results
(i) Simulation results
Our first simulations were designed to investigate the behaviour of the estimators that analyse data from a single individual and assume known allele frequencies. Tables showing the estimated bias and RMSE values for the MLE, Ritland, Simple, adjusted Ritland and adjusted Simple estimators are included in the online Supplementary Material at http://journals.cambridge.org/GRH. It should be noted that, because allele frequencies were the same for all loci in our simulations, the Simple estimator is identical to the unweighted version of the estimator given in Carothers et al. (Reference Carothers, Ruden, Kolcic, Polasek, Hayward, Wright, Campbell, Teague, Hastie and Weber2006)for these simulations. Although the MLE and adjusted Simple estimators gave quite different estimates of f in many instances, both estimators yielded nearly identical estimates for RMSE and bias for all sample sizes and all values of f that we examined. The adjusted Ritland estimator performed similarly to the others with the exception that it tended to have a larger RMSE when f was large.
We next turned our attention to the situation in which allele frequencies were not known and had to be estimated from the dataset. In this case, we compared our Method 2 MLE and Vogl's estimators. We also included the Method 1 MLE, as well as the adjusted Ritland and Simple estimators, with the provision that these estimators would use allele frequencies estimated by simple allele counting from the dataset. Table 2 shows the estimated RMSE values for these estimators for the situation in which there were 20 individuals in each simulated dataset. More results appear in the online Supplementary Materials. Even with just 20 individuals in the sample, these estimators performed similarly to the case in which allele frequencies were known. It did not seem to matter much whether allele frequencies were estimated using sophisticated methods (e.g. our Method 2 MLE or Vogl's methods) or by simple allele counting. Also apparent from the table is that Vogl's method that used a strongly informative prior (V2, which begins with a strong assumption that the values of f will be close to 0 or 1) gives an inflated RMSE compared with the other estimators when f is moderately large and the number of markers is not large. The other side of this phenomenon is that this estimator did very well when f was small, which is not surprising since the estimator is based on a strong prior assumption that f will be close to 0.
Table 2. RMSE, allele frequencies unknown, 10 possible alleles at each marker
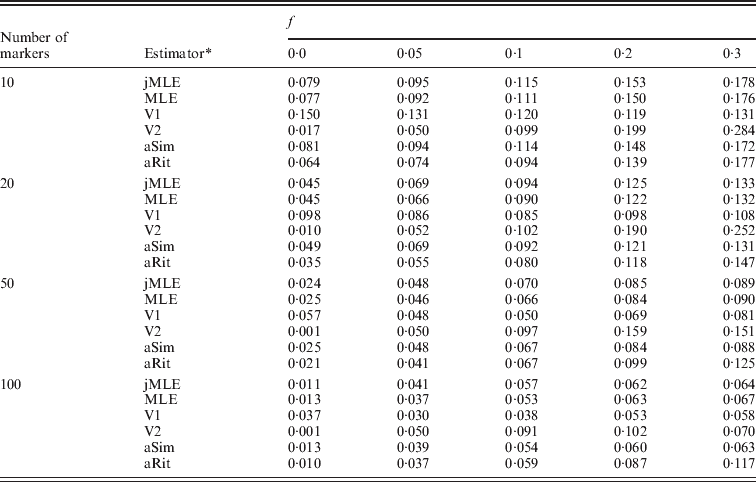
* The estimators are denoted as follows: jMLE is our Method 2 MLE (which jointly estimates allele frequencies and inbreeding coefficients), MLE is the Method 1 MLE, V1 is Vogl's Bayesian estimator (assuming a uniform prior), V2 is Vogl's Bayesian estimator (assuming the prior suggested in Vogl et al., Reference Vogl, Karhu, Moran and Savolainen2002), aSim and aRit are the adjusted Simple and Ritland estimators, respectively. The MLE, aSim and aRit estimators all used allele frequencies estimated from the data by allele counting.
Next, we considered the case in which null alleles were present in the data. Table 3 shows the mean bias observed among 400 datasets for each of several inbreeding coefficients when the simulated datasets each consisted of 20 individuals. Tables showing RMSE are included in the online Supplementary Materials. Three things are apparent from Table 3: (1) the estimators that ignored the presence of null alleles (the adjusted Ritland and Simple estimators and the Method 2 MLE) tended to over-estimate inbreeding coefficients when null alleles are present. (2) The Method 3 MLE was able to dramatically reduce the bias compared with the estimators that ignore null alleles. (3) For the Vogl algorithm, neither prior used in our analyses was entirely satisfactory. Under the uniform prior, the Vogl algorithm systematically over-estimated the degree of inbreeding for individuals that had low-inbreeding coefficients. The Vogl algorithm with the prior suggested in Vogl et al. (Reference Vogl, Karhu, Moran and Savolainen2002)resulted in inbreeding coefficients being substantially under-estimated for highly inbred individuals. In fact, this algorithm tended to assign inbreeding coefficients close to 0 even for individuals whose true inbreeding coefficients were as high as 0·5 when there were up to 50 markers genotyped (results not shown).
Table 3. Estimated bias in the presence of null alleles, 10 alleles per marker
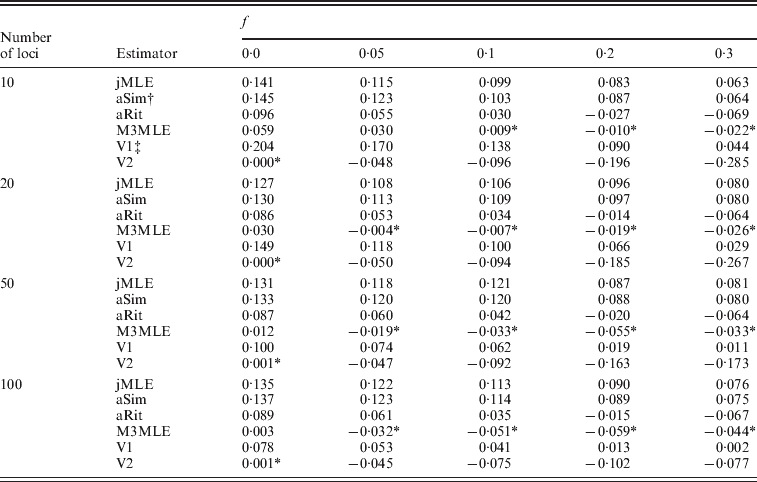
* Indicates a value that is not significantly different than 0 at a significance level of α=0·05.
† The adjusted Simple and Ritland algorithms used in these analyses used allele frequencies estimated for each dataset by allele counting.
‡ The Vogl algorithms used in these analyses were the versions of the Vogl algorithm that account for null alleles.
The Method 3 MLE, Vogl's method and the algorithm of Kalinowski and Taper were all constructed with the ability to estimate null allele frequencies. To examine each algorithm's ability to give accurate estimates of the null allele frequently, we looked at the estimated null allele frequency for just three markers from each simulated dataset: one marker for each of the three possible null allele frequencies that were present in the simulations. Table 4 shows the average estimated null allele frequency over 400 datasets when there were 20 individuals in each dataset and 10 observable alleles at each marker. As might be expected, the Kalinowski and Taper algorithm, which was developed for use on datasets with non-inbred individuals, tends to over-estimate the frequencies of null alleles considerably. The Vogl estimator that assumes the beta (0·001, 0·001) prior performs similarly. Both of these algorithms assume lower inbreeding coefficients than actually exist in the dataset: the Kalinowski and Taper algorithm assumes that f=0 for all individuals and the Vogl algorithm with this prior begins with a strong assumption that the inbreeding coefficients will be close to 0 and so tends to produce under-estimates of f for individuals with larger inbreeding coefficients. When inbreeding coefficients are under-estimated, the excess homozygosity observed in the data results in inflated null allele frequencies. The Vogl estimator with the uniform prior and the Method 3 MLE, which do better at estimating the inbreeding coefficients, consequently give more accurate estimated null allele frequencies.
Table 4. Mean estimated null allele frequencies, 10 alleles per locus
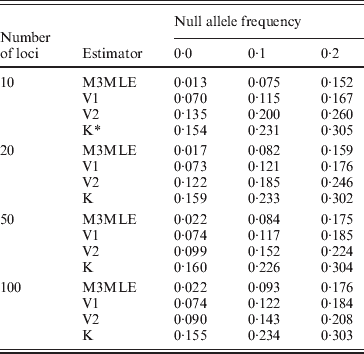
* K denotes the Kalinowski and Taper estimator.
(ii) Real data results
For both the mouse and deer datasets, we compared the behaviour of the Method 3 MLE and the Vogl estimator that assumed a uniform prior. The top row of Fig. 1 shows some results from the analysis of the mouse data. For this dataset, the Vogl estimator nearly always gave considerably smaller estimated inbreeding coefficients than the MLE. Consequently (because excess homozygosity must be due to either null alleles or inbreeding), Vogl gave higher estimates for the frequency of null alleles than did the MLE. Interestingly, there were many markers for which the Vogl and MLE estimators were in sharp disagreement regarding the frequency of null alleles. Specifically, there were 148 (out of the 757) markers for which the MLE gave null allele frequencies below 0·01 and the Vogl estimator gave null allele frequencies above 0·05. This type of behaviour can be explained as follows: in the version of Vogl's estimator that we used (the version explicitly described in Vogl et al., Reference Vogl, Karhu, Moran and Savolainen2002), the model assumes that any missing genotype is homozygous for a null allele. Hence, Vogl's algorithm will assign a high null allele frequency to any marker with a substantial number of missing genotypes. The model used in calculating our MLE, however, following Kalinowski & Taper (Reference Kalinowski and Taper2006), has a parameter that allows genotypes to be missing at random at a marker. With this parameter in the model, the MLE will not assign a high null allele frequency to markers that have missing data but no other sign of excess homozygosity beyond that accounted for by the inbreeding coefficients of the individuals in the dataset.
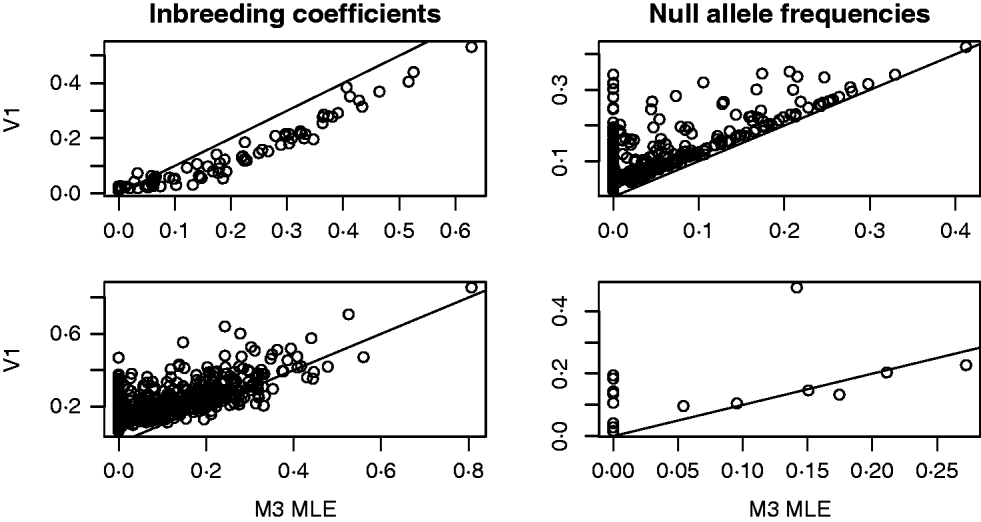
Fig. 1. Results from the analyses of the Arizona Mice (top row) and Deer (bottom row) datasets. The plots on the left contain a point for each individual (mouse or deer) in the dataset. The x- and y-coordinates of each point are the estimated inbreeding coefficients for that individual from the Method 3 MLE (M3) and the Vogl estimator with the uniform prior (V1), respectively. In the plots on the right, each point represents a marker in the dataset and the coordinates are the estimated frequencies of the null allele at that marker.
The second row of Fig. 1 shows some results from the analysis of the deer data. As with the mouse data, we focused on the behaviour of the Method 3 MLE and the Vogl estimator that assumed a uniform prior. The estimators are in rough agreement about the estimated inbreeding coefficients for each deer in the dataset, with the MLE tending to give lower estimates than Vogl's estimator. When estimating null allele frequencies, the two estimators tended to give similar results except for markers with a high degree of missing data, in which case the Vogl estimator yielded much higher estimates.
4. Discussion
In our analyses, we found that the MLE algorithms presented in the paper work generally well. We found weaknesses in most of the other estimators we examined. For example, Ritland's estimator had problems when the true inbreeding coefficients were large and Vogl's estimator was sensitive to the choice of parameters of the prior distribution and tended to over-estimate null allele frequencies when confronted with missing data. As pointed out in Vogel et al. (Reference Vogl, Karhu, Moran and Savolainen2002), however, Vogl's algorithm could be easily adjusted to handle missing data more effectively. The Simple estimator, which is similar to Carother's estimator, was the only estimator examined that seemed to perform as well as the MLE. Unfortunately, it is not obvious how to adjust the Simple estimator to account for null alleles.
The bias of the MLE is virtually identical to the bias of the adjusted versions of the moment estimators (see the online Supplementary Materials). The conclusion to be drawn is that the bias of the MLE is completely inconsequential for most purposes as it seems to be primarily the result of assigning an inbreeding coefficient of 0 rather than a negative value to individuals that show less homozygosity than expected. There is one situation in which the moment estimators might be preferred to the MLE, namely, if a researcher is interested in showing that individuals in a population are showing less heterozygosity than would occur by random mating (e.g. this might occur if the population is showing an avoidance of matings between relatives). The moment estimators we looked at are capable of giving the negative inbreeding coefficients that could indicate that sort of scenario. As the MLEs are based on a model that views f as a probability rather than a correlation coefficient, they cannot give negative values.
In order to investigate the robustness of the estimators to various strange situations or violations of model assumptions, we performed additional simulations, the details of which are included in the online Supplementary Materials. The first set of these simulations looked at the performance of the estimators on datasets consisting of sets of closely related individuals. In our simulations, all estimators performed poorly under these circumstances. The second question was whether the estimators that allow for null alleles would have trouble if there were no null alleles or if all markers had the same null allele frequencies. In our simulations, this seemed to pose no difficulty. Finally, the third set of additional simulations was designed to see the effect of having certain individuals for which many genotypes were missing due to degradation. This common situation is different from that modelled by the Method 3 MLE (in which genotypes are missing at random for all individuals, or are missing because they are homozygous for null alleles) or by Vogl's algorithms (which assume missing genotypes are homozygous for null alleles). In our simulations, this type of missingness was disastrous. All three estimators greatly overestimated the inbreeding coefficients for these individuals. In our simulations, these individuals consisted of just 10 out of the 100 individuals in the simulated datasets. Their inclusion did not seem to have a great effect on the estimated inbreeding coefficients of the other individuals in the datasets.
An estimator that was not included in this study is that of Wang (Reference Wang2011a ). Wang's estimator is a Bayesian estimator that accounts for null alleles and allelic dropout. Wang uses an exponential distribution as the prior distribution for inbreeding coefficients. In Wang's paper, the likelihood equation was written out for a single individual. Allele frequencies (including the null allele frequency) and the dropout rate were required to be known values. As written, then, Wang's estimator is not directly comparable to any of our MLEs. To make our Method 3 estimator comparable to Wang's estimator would involve treating the allele frequencies and error rates in our model as known constants rather than values that are estimated using our EM algorithm. Similarly, Wang's method could be modified to estimate null allele frequencies and/or error rates as follows: the likelihood for a set of individuals would be the product of Wang's likelihood for single individual. Using this new likelihood function (and, presumably, a prior distribution for the inbreeding coefficients that would be the product of exponential distributions), the allele frequencies and dropout rates could be estimated along with the inbreeding coefficients. The difference in which parameters are considered known and which are estimated constitutes a minor difference between our Method 3 estimator and Wang's estimator. Apart from this, there are three actual differences between the estimators: (1) Wang begins by assuming a prior distribution for the inbreeding coefficient that will tend to gently push his estimated inbreeding coefficients towards zero, (2) Wang's model includes the possibility of allelic dropout (but only for genotypes that are heterozygous for non-null alleles), which is a source of excess homozygosity that is ignored in our model and (3) Wang's model uses only non-missing data, and hence, does not make use of the fact that, when null alleles exist, missing data itself provide some evidence of homozygosity.
A key point that is apparent from our simulations is that the variability of all the estimators we examined will be substantial unless a large number of markers is used (see the RMSE values in the tables in the online Supplementary Materials). For example, when there are unknown allele frequencies and no null alleles, and 50 markers have been genotyped, each with 10 alleles, the Method 2 MLE yields a RMSE of 0·048 for individuals with f=0·05. Since the bias is small, the RMSE will be close to the standard deviation. A margin of error for an estimator will be roughly twice its standard deviation, so, in this case, even with 50 markers, the margin of error for the estimate will be close to 0·10. Hence, even with 50 highly variable markers, the estimated inbreeding coefficients will be quite imprecise.
Researchers intending to use an estimated inbreeding coefficient in a subsequent linear regression against, for example, a fitness-related trait, should be aware of how uncertainty in estimates of f may affect their results. There is a body of literature on the effects of measurement error on regression analyses (e.g. Frost & Thompson, 2000) and it can be shown that variability in the predictor variable (estimated inbreeding coefficients) will result in a systematic tendency to under-estimate the strength of the relationship between the predictor and response variables (inbreeding and fitness). This will reduce the power of studies looking for evidence of inbreeding depression.
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Declaration of interests
None.


![\eqalign{E_{z} \left[ {X_{j} \vert\hskip2pt f^{\hskip1pt\lpar z\rpar } \comma \vec{g}} \right]\!\equals\! \tab \left\{ {\matrix{ {{\textstyle{{f^{\hskip2pt\lpar z\rpar } p_{jk} } \over {f^{\hskip1pt\lpar z\rpar } p_{jk} \plus \left( {1 \minus f^{\hskip1pt\lpar z\rpar } } \right)p_{jk}^{\setnum{2}} }}}\comma } \hfill \tab\hskip-3pt {{\rm if}\,g_{j} \equals A_{jk} A_{jk} \comma \tab } \hfill \cr {0\comma } \hfill \tab\hskip-3pt {{\rm if}\, g_{j} \equals A_{jk} A_{jl} \ \lpar k \ne l\rpar .} \hfill \cr} } \right.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235928737-0299:S0016672312000341:S0016672312000341_eqn7.gif?pub-status=live)
![\hskip-12pt\eqalign{ p_{jk}^{\lpar z \plus \setnum{1}\rpar }\equals \tab \mathop\sum\limits_{i \equals \setnum{1}}^{N} \,\left[ {2P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{k} A_{k} \vert g_{ij} \comma X_{ij} \equals 0\comma \rmTheta ^{\lpar z\rpar } } \right)} \right. \cr \tab\times\left( {1 \minus E_{z} \lsqb X_{ij} \rsqb } \right) \plus P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{k} A_{k} \vert g_{ij} \comma X_{ij} \equals 1\comma \rmTheta ^{\lpar z\rpar } } \right)\hskip-58pt \cr \tab \times E_{z} \lsqb X_{ij} \rsqb \plus \mathop\sum\limits_{l \ne k} \,P\left( {g_{ij}{ \hskip-4pt\ast } \equals A_{k} A_{l} \vert g_{ij} \comma X_{ij}{\hskip-4pt \ast } \equals 0\comma \rmTheta ^{\lpar z\rpar } } \right)\hskip-58pt\cr \tab\times( 1 \minus E_{z} \lsqb X_{ij} \rsqb) \right]\sol C_{j}^{\lpar z \plus \setnum{1}\rpar }{ \comma \cr](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235928737-0299:S0016672312000341:S0016672312000341_eqn16.gif?pub-status=live)
![\eqalign{ C_{j}^{\hskip2pt\lpar z \plus \setnum{1}\rpar } \tab \equals \mathop\sum\limits_{i \equals \setnum{1}}^{N} \,\mathop\sum\limits_{l \equals \setnum{1}}^{n_{j} } \,\left[ {2P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{l} A_{l} \vert g_{ij} \comma X_{ij} \equals 0\comma \rmTheta ^{\lpar z\rpar } } \right)} \right.\hskip-82pt \cr \tab\times {\left( {1 \minus E_{z} \lsqb X_{ij} \rsqb } \right)\plus P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{l} A_{l} \vert g_{ij} \comma X_{ij} \equals 1\comma \rmTheta ^{\lpar z\rpar } } \right)}\hskip-82pt \cr \tab\times \left. E_{z} \lsqb X_{ij} \rsqb \plus 2\mathop\sum\limits_{h \lt l} \,P\left( {g_{ij}{\hskip-4pt \ast } \equals A_{l} A_{h} \vert g_{ij} \comma X_{ij} \equals 0\comma \rmTheta ^{\lpar z\rpar }}\right)\right.\hskip-82pt\cr\tab\times\left.( 1 \minus E_{z} \lsqb X_{ij} \rsqb) \right]. \cr](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235928737-0299:S0016672312000341:S0016672312000341_eqn17.gif?pub-status=live)





