1. Introduction
Hydrodynamic flow in finely structured porous media is important in a wide variety of contemporary applications, particularly those in which soft nanostructured materials, such as synthetic hydrogels, membranes and biological tissue, are central. For example, in a purely hydrodynamic context, the permeability of such media has recently been identified as controlling the rate of energy dissipation in shock absorbers for protecting against traumatic sports injuries (Sokoloff Reference Sokoloff2022). Moreover, flow in hydrogel phantoms of neural tissues is pertinent to the perfusion of drugs in the brain and spine (Gillies et al. Reference Gillies, Wilhelm, Humphrey, Fillmore, Holloway and Broaddus2002; Pomfret, Miranpuri & Sillay Reference Pomfret, Miranpuri and Sillay2013a). Manipulating the microstructure of agarose gels, in particular, has been proposed as a means to mimic ion transport in brain tissue (Williams et al. Reference Williams, Hippensteel, Dilgen, Shain and Kipke2007; Lempka et al. Reference Lempka, Miocinovic, Johnson, Vitek and McIntyre2009; Pomfret, Sillay & Miranpuri Reference Pomfret, Sillay and Miranpuri2013b).
Polyelectrolytes bearing a nanoscale structure are central to batteries (Harris Reference Harris2018), fuel cells (Matos Reference Matos2020), polymeric/soft electronics and sensors (Pan et al. Reference Pan2012) and biomaterials (Brown et al. Reference Brown, Helena, Damen and Thambyah2020; Zimmerman et al. Reference Zimmerman, Nims, Chen, Hung and Ateshian2021). To explore these from a theoretical perspective, Hill (Reference Hill2022) recently proposed a theory for steady ionic transport in multi-porous charged media. The theory couples disturbances to the electrostatic potential, ion concentrations and electro-osmotic flow arising from a microstructure with heterogeneous charge- and hydrodynamic permeability. These were computed for a single spherical cavity embedded in an unbounded continuous medium, and their far-field asymptotic decays were used to report the effective conductivity. The averaging neglected electrostatic, ion-concentration and hydrodynamic interactions, and so is accurate to ![]() $O(\phi )$ in the cavity volume fraction
$O(\phi )$ in the cavity volume fraction ![]() $\phi$. Hydrodynamic aspects of the problem advanced those of Davis & Stone (Reference Davis and Stone1993) for the permeability of chromatography columns, bringing additional physics from electrokinetic phenomena, along the lines of Saville (Reference Saville1979) and O'Brien & Perrins (Reference O'Brien and Perrins1984). Vortical flows arising from such ‘multiphysics’, albeit on larger scales than Hill's theory, have been demonstrated to enhance convective mixing in disordered porous media (Mirzadeh et al. Reference Mirzadeh, Zhou, Amooie, Fraggedakis, Ferguson and Bazant2020).
$\phi$. Hydrodynamic aspects of the problem advanced those of Davis & Stone (Reference Davis and Stone1993) for the permeability of chromatography columns, bringing additional physics from electrokinetic phenomena, along the lines of Saville (Reference Saville1979) and O'Brien & Perrins (Reference O'Brien and Perrins1984). Vortical flows arising from such ‘multiphysics’, albeit on larger scales than Hill's theory, have been demonstrated to enhance convective mixing in disordered porous media (Mirzadeh et al. Reference Mirzadeh, Zhou, Amooie, Fraggedakis, Ferguson and Bazant2020).
In composites for which contrast in the properties of the dispersed and continuous phases is step-like, it is customary to express averaging for dilute media in terms of an integral over the internal volume of a single inclusion embedded in an unbounded continuous phase, as exemplified by Jeffrey (Reference Jeffrey1973) in the context of scalar diffusion in random suspensions of spheres. However, when the dispersed phase is more complex, it is oftentimes preferable to express the averaging in terms of the asymptotic far-field disturbances of a dispersed particle, as exemplified by Delacey & White (Reference Delacey and White1981) in the context of the conductivity of colloidal dispersions. Merits of computing electrical and hydrodynamic forces on nanoparticle spheres decorated with charge-regulating polyelectrolyte layers, in the context of nanoparticle electrophoresis, are demonstrated by Hill (Reference Hill2015). These motivate, in part, subsequent efforts to circumvent cumbersome volume integrations (for complex dispersed particulates) by drawing on the asymptotic decay of far-field disturbances.
Along these lines, Hill (Reference Hill2022) employed the ensemble averaging of Koch & Brady (Reference Koch and Brady1985) to derive an averaged momentum transport equation for dilute cavity-doped polyelectrolyte hydrogels in which coupled mass and ion fluxes are driven by an external pressure gradient and electric field. The averaged fluid velocity in a charged/polyelectrolyte porous medium that is doped with spherical inclusions (having an arbitrary, contrasting permeability) was expressed in terms of the dipole pressure disturbance of a single inclusion. No direct verification of this theory has been undertaken, e.g. to test that the underlying integral is unconditionally convergent (Jeffrey Reference Jeffrey1973). Moreover, even if the theory is validated in the dilute limit, it remains to establish how accurate the approximation might be at higher concentrations. Significant computational challenges are anticipated from coupled viscoelastic, hydrodynamic and ion-transport physics in complex, three-dimensional geometries. For example, recent two-dimensional direct computations of thermal convection in porous media (comprising square arrays of solid cylinders) have been prompted by (i) the prohibitive challenge of performing well-resolved three-dimensional simulations and (ii) reasonable grounds that a two-dimensional approximation may still furnish robust physical insights and quantitative analysis in the dimensionless parameter space (Liu et al. Reference Liu, Jiang, Chong, Zhu, Wan, Verzicco, Stevens, Lohse and Sun2020).
This paper seeks to test Hill's ensemble averaging and assess the importance of hydrodynamic interactions, albeit in a simpler but more transparent two-dimensional, hydrodynamic framework. This may still provide valuable insights to guide future computational studies of coupled, time-dependent physics in three dimensions. In the broader context of the present work, the frequency-dependent electrical impedance of structured polyelectrolytes, within which viscoelastic coupling of a charged polyelectrolyte skeleton to electroosmotic flow is pertinent, will be reported elsewhere.
The present work is informed, in part, by literatures addressing scalar diffusion and hydrodynamic drag in composites. This stems from Brinkman's model (Brinkman Reference Brinkman1947; Durlofsky & Brady Reference Durlofsky and Brady1987) bridging the Darcy- and Stokes-flow regimes. The Darcy limit in which the volume flux ![]() $\boldsymbol {u} = - (\ell ^2 / \eta ) \boldsymbol{\nabla } p$ brings an obvious parallel with scalar diffusion (
$\boldsymbol {u} = - (\ell ^2 / \eta ) \boldsymbol{\nabla } p$ brings an obvious parallel with scalar diffusion (![]() $\ell ^2 / \eta$ is the Darcy permeability and
$\ell ^2 / \eta$ is the Darcy permeability and ![]() $p$ is the pressure with
$p$ is the pressure with ![]() $\ell$ the Brinkman screening length and
$\ell$ the Brinkman screening length and ![]() $\eta$ the shear viscosity).
$\eta$ the shear viscosity).
For scalar diffusion, Jeffrey (Reference Jeffrey1973) highlighted the difference between the effective diffusivities for ordered and random arrays of spheres as manifesting at ![]() $O(\phi ^2)$, where
$O(\phi ^2)$, where ![]() $\phi$ is the sphere volume fraction. For random arrays, Jeffrey calculated the
$\phi$ is the sphere volume fraction. For random arrays, Jeffrey calculated the ![]() $O(\phi ^2)$ contribution to an effective diffusivity (relative to the continuous-phase diffusivity) having the form
$O(\phi ^2)$ contribution to an effective diffusivity (relative to the continuous-phase diffusivity) having the form ![]() $D_e / D \approx 1 - 3 \phi (1 - \alpha )/(2 + \alpha ) + O(\phi ^2)$, where
$D_e / D \approx 1 - 3 \phi (1 - \alpha )/(2 + \alpha ) + O(\phi ^2)$, where ![]() $\alpha$ is the ratio of the dispersed- and continuous-phase diffusivities. Figure 1 compares the coefficient of the
$\alpha$ is the ratio of the dispersed- and continuous-phase diffusivities. Figure 1 compares the coefficient of the ![]() $O(\phi ^2)$ expansion of Maxwell's self-consistent formula (Bird, Stewart & Lightfoot Reference Bird, Stewart and Lightfoot2002, (9.6-1)) (also termed the Clausius–Mosotti equation (Bonnecaze & Brady Reference Bonnecaze and Brady1991)) with the coefficient from Jeffrey (Reference Jeffrey1973, table 1). Arguably, the self-consistent formula furnishes an at least qualitative approximation of the effective diffusivity to
$O(\phi ^2)$ expansion of Maxwell's self-consistent formula (Bird, Stewart & Lightfoot Reference Bird, Stewart and Lightfoot2002, (9.6-1)) (also termed the Clausius–Mosotti equation (Bonnecaze & Brady Reference Bonnecaze and Brady1991)) with the coefficient from Jeffrey (Reference Jeffrey1973, table 1). Arguably, the self-consistent formula furnishes an at least qualitative approximation of the effective diffusivity to ![]() $O(\phi ^2)$ as long as the contrast
$O(\phi ^2)$ as long as the contrast ![]() $\alpha$ is not too large or small. According to Jeffrey's analysis, the coefficient of
$\alpha$ is not too large or small. According to Jeffrey's analysis, the coefficient of ![]() $\phi ^2$ spans the range
$\phi ^2$ spans the range ![]() $\approx$0.588–4.51 (according to
$\approx$0.588–4.51 (according to ![]() $\alpha$), whereas the self-consistent Maxwell formula spans the range 0.75–3.
$\alpha$), whereas the self-consistent Maxwell formula spans the range 0.75–3.

Figure 1. The coefficients of the ![]() $O(\phi )$ and
$O(\phi )$ and ![]() $O(\phi ^2)$ terms in the expansion of Maxwell's self-consistent effective diffusivity plotted vs the ratio of the dispersed- (spheres) and continuous-phase diffusivities. The
$O(\phi ^2)$ terms in the expansion of Maxwell's self-consistent effective diffusivity plotted vs the ratio of the dispersed- (spheres) and continuous-phase diffusivities. The ![]() $O(\phi ^2)$ term is compared with the
$O(\phi ^2)$ term is compared with the ![]() $O(\phi ^2)$ theory of Jeffrey (Reference Jeffrey1973, table 1).
$O(\phi ^2)$ theory of Jeffrey (Reference Jeffrey1973, table 1).
In the other extreme limit of the Brinkman model, i.e. of Stokes flow through ordered and random arrays of impenetrable spheres, the drag forces are distinguished by their leading orders in ![]() $\phi$: for simple-cubic arrays, the drag coefficient (force scaled by the Stokes drag force based on the superficial fluid velocity) in the dilute limit is
$\phi$: for simple-cubic arrays, the drag coefficient (force scaled by the Stokes drag force based on the superficial fluid velocity) in the dilute limit is ![]() $F \approx 1 + 1.7601 \phi ^{1/3}$ (Hasimoto Reference Hasimoto1959), whereas the counterpart for random arrays is
$F \approx 1 + 1.7601 \phi ^{1/3}$ (Hasimoto Reference Hasimoto1959), whereas the counterpart for random arrays is ![]() $F \approx 1 + (3 / \sqrt {2})\phi ^{1/2}$ (Brinkman Reference Brinkman1947). However, by analogy with scalar diffusion, the hydrodynamic interactions of spheres (radius
$F \approx 1 + (3 / \sqrt {2})\phi ^{1/2}$ (Brinkman Reference Brinkman1947). However, by analogy with scalar diffusion, the hydrodynamic interactions of spheres (radius ![]() $a$) embedded in a Brinkman medium (with Brinkman length
$a$) embedded in a Brinkman medium (with Brinkman length ![]() $\ell$) are expected to be weak when particles are well separated and intervened by Darcy flow. In three dimensions, these conditions demand
$\ell$) are expected to be weak when particles are well separated and intervened by Darcy flow. In three dimensions, these conditions demand ![]() $\phi \lesssim 4 {\rm \pi}/ 3^4 \approx 0.16$ with
$\phi \lesssim 4 {\rm \pi}/ 3^4 \approx 0.16$ with ![]() $\ell / a \lesssim 1$. If the Brinkman medium is itself comprised spheres with radius
$\ell / a \lesssim 1$. If the Brinkman medium is itself comprised spheres with radius ![]() $a$, then (to leading order in
$a$, then (to leading order in ![]() $\phi$)
$\phi$) ![]() $\ell / a \sim \sqrt {2 / (3 \phi )}$, so the condition
$\ell / a \sim \sqrt {2 / (3 \phi )}$, so the condition ![]() $\ell / a \lesssim 1$ demands
$\ell / a \lesssim 1$ demands ![]() $\phi \gtrsim 2/9 \approx 0.22$, suggesting a very narrow window
$\phi \gtrsim 2/9 \approx 0.22$, suggesting a very narrow window ![]() $0.16\lesssim \phi \lesssim 0.22$ where both the foregoing conditions may be met. More generally, however,
$0.16\lesssim \phi \lesssim 0.22$ where both the foregoing conditions may be met. More generally, however, ![]() $\ell / a$ is an independent parameter that, when sufficiently small, may furnish
$\ell / a$ is an independent parameter that, when sufficiently small, may furnish ![]() $\phi \lesssim 0.16$ so that, by analogy with scalar diffusion, the effective permeability of the composite may be expected independent of the type of sphere packing (to leading order in
$\phi \lesssim 0.16$ so that, by analogy with scalar diffusion, the effective permeability of the composite may be expected independent of the type of sphere packing (to leading order in ![]() $\phi$). This is born out for diffusion by the computations of Bonnecaze & Brady (Reference Bonnecaze and Brady1990, Reference Bonnecaze and Brady1991), which furnished reduced effective diffusivities for
$\phi$). This is born out for diffusion by the computations of Bonnecaze & Brady (Reference Bonnecaze and Brady1990, Reference Bonnecaze and Brady1991), which furnished reduced effective diffusivities for ![]() $\phi = 0.1$ and
$\phi = 0.1$ and ![]() $\alpha = D_s / D = 10$:
$\alpha = D_s / D = 10$: ![]() $D_e / D \approx 1.247 \pm 0.011$ (random hard sphere),
$D_e / D \approx 1.247 \pm 0.011$ (random hard sphere), ![]() $1.243$ (simple cubic),
$1.243$ (simple cubic), ![]() $1.243$ (body-centred cubic),
$1.243$ (body-centred cubic), ![]() $1.243$ (face-centred cubic). Expectations for the effective Brinkman permeability are tested in the present study, albeit in a two-dimensional context for which the analogue of the foregoing condition becomes (for the cylinder area fraction)
$1.243$ (face-centred cubic). Expectations for the effective Brinkman permeability are tested in the present study, albeit in a two-dimensional context for which the analogue of the foregoing condition becomes (for the cylinder area fraction) ![]() $\phi \lesssim {\rm \pi}/ 9 \approx 0.3$ with
$\phi \lesssim {\rm \pi}/ 9 \approx 0.3$ with ![]() $\ell / a \lesssim 1$.
$\ell / a \lesssim 1$.
The theory § 2 presents the hydrodynamic model in a form by which the dependent variables (pressure and velocity) are computed using a direct numerical computation on a periodic unit cell, for any discrete-phase area fraction, and discrete- and continuous-phase permeabilities. Next, an analytical solution is presented for the dilute limit in which the discrete-phase area fraction is small. In the results § 3, this analytical model is compared with the direct computations (solving Brinkman's equations), establishing the parameter space in which the analytical theory is accurate, also testing the computations in dilute and almost-touching regimes. Comparisons of the dilute theory and extensions to finite area fractions – drawing on the Rayleigh self-consistent approximation – are motivated, in part, by the analogy of Darcy hydrodynamics and scalar diffusion. Finally, a cursory examination of the velocity fluctuations arising from shear-viscosity contrasts in media with uniform Brinkman screening length is undertaken. The paper concludes in § 4 with a brief summary.
2. Theory
As illustrated in figure 2, the porous media under investigation in this work have continuous and discrete phases, each modelled as uniform Brinkman media with contrasting Brinkman permeabilities. For the analytical model, the disturbance of a single cylindrical inclusion in an unbounded continuous phase is used to derive the effective permeability of a composite with inclusion area fraction ![]() $\phi \ll 1$. For the computations, a periodic unit cell with finite
$\phi \ll 1$. For the computations, a periodic unit cell with finite ![]() $\phi$ is subjected to a uniform pressure gradient
$\phi$ is subjected to a uniform pressure gradient ![]() $\boldsymbol {P}$, and the volume average of the steady fluid velocity
$\boldsymbol {P}$, and the volume average of the steady fluid velocity ![]() $\langle \boldsymbol {u} \rangle$ furnishes the effective permeability. For a square unit cell (area
$\langle \boldsymbol {u} \rangle$ furnishes the effective permeability. For a square unit cell (area ![]() $L^2$) containing a single cylindrical inclusion (radius
$L^2$) containing a single cylindrical inclusion (radius ![]() $a$) and
$a$) and ![]() $\boldsymbol {P}$ perpendicular to the cylinder axes, the effective permeability (of the simple-square array) is isotropic. For random configurations, averaging over an ensemble furnishes an effective permeability that is isotropic, even though the permeability of each member of the ensemble is not.
$\boldsymbol {P}$ perpendicular to the cylinder axes, the effective permeability (of the simple-square array) is isotropic. For random configurations, averaging over an ensemble furnishes an effective permeability that is isotropic, even though the permeability of each member of the ensemble is not.

Figure 2. (a) A periodic array of parallel cylindrical inclusions, each with Brinkman screening length ![]() $\ell _c^2$ and radius
$\ell _c^2$ and radius ![]() $a$, embedded in a continuous Brinkman medium with screening length
$a$, embedded in a continuous Brinkman medium with screening length ![]() $\ell$, subjected to a mean pressure gradient
$\ell$, subjected to a mean pressure gradient ![]() $\boldsymbol {P} = - \langle \boldsymbol{\nabla } p \rangle$ (perpendicular to the cylinder axes). The Newtonian fluid is considered to have a uniform shear viscosity
$\boldsymbol {P} = - \langle \boldsymbol{\nabla } p \rangle$ (perpendicular to the cylinder axes). The Newtonian fluid is considered to have a uniform shear viscosity ![]() $\eta$, but, more generally, fluid within the inclusions may be prescribed a shear viscosity
$\eta$, but, more generally, fluid within the inclusions may be prescribed a shear viscosity ![]() $\eta _c = \chi \eta$. (b) Finite-element computations of Brinkman flow (with
$\eta _c = \chi \eta$. (b) Finite-element computations of Brinkman flow (with ![]() $\boldsymbol {P} = P \boldsymbol {e}_1$) in a simple-square array (top) is compared with a random counterpart (bottom) (with the same inclusion area fraction
$\boldsymbol {P} = P \boldsymbol {e}_1$) in a simple-square array (top) is compared with a random counterpart (bottom) (with the same inclusion area fraction ![]() $\phi$).
$\phi$).
2.1. Computational model
The steady, incompressible, inertialess flows in this work are modelled by the Brinkman equations (Brinkman Reference Brinkman1947; Durlofsky & Brady Reference Durlofsky and Brady1987)
where the fluid shear viscosity ![]() $\eta$ is predominantly assumed uniform (unless explicitly stated otherwise), and the Brinkman screening length
$\eta$ is predominantly assumed uniform (unless explicitly stated otherwise), and the Brinkman screening length ![]() $\ell (\boldsymbol {x})$ is prescribed a (uniform) value
$\ell (\boldsymbol {x})$ is prescribed a (uniform) value ![]() $\ell$ in the continuous phase and
$\ell$ in the continuous phase and ![]() $\ell _c$ in the discrete (cylinder) phase of a periodic unit cell (see figure 2). Using Stokesian-dynamics simulations, Durlofsky & Brady (Reference Durlofsky and Brady1987) have shown that Brinkman's model accurately describes the conditionally averaged velocity disturbance in porous media comprising randomly positioned, non-overlapping impenetrable spheres (radius
$\ell _c$ in the discrete (cylinder) phase of a periodic unit cell (see figure 2). Using Stokesian-dynamics simulations, Durlofsky & Brady (Reference Durlofsky and Brady1987) have shown that Brinkman's model accurately describes the conditionally averaged velocity disturbance in porous media comprising randomly positioned, non-overlapping impenetrable spheres (radius ![]() $a$) when the sphere volume fraction
$a$) when the sphere volume fraction ![]() ${\lesssim }0.05$, thus corresponding to
${\lesssim }0.05$, thus corresponding to ![]() $\ell \gtrsim 2.1 a$ with characteristic sphere separation
$\ell \gtrsim 2.1 a$ with characteristic sphere separation ![]() ${\gtrsim }4.4 a$. In the present work, the Brinkman media are envisioned – without loss of generality – to represent hydrogel networks for which the solid volume fraction (crudely considered an assembly of Stokes-resistance centres) is often
${\gtrsim }4.4 a$. In the present work, the Brinkman media are envisioned – without loss of generality – to represent hydrogel networks for which the solid volume fraction (crudely considered an assembly of Stokes-resistance centres) is often ![]() ${\lesssim }0.1$ with
${\lesssim }0.1$ with ![]() $\ell \sim 0.1\unicode{x2013}100$ nm.
$\ell \sim 0.1\unicode{x2013}100$ nm.
The response of Brinkman's model to forcing by a first-order tensor ![]() $\boldsymbol {X}$, e.g.
$\boldsymbol {X}$, e.g. ![]() $\boldsymbol {X} = \boldsymbol {P}$ (average pressure gradient) or
$\boldsymbol {X} = \boldsymbol {P}$ (average pressure gradient) or ![]() $\boldsymbol {U}$ (average velocity), furnishes the pressure (to within an arbitrary constant) and velocity of the form (linear in
$\boldsymbol {U}$ (average velocity), furnishes the pressure (to within an arbitrary constant) and velocity of the form (linear in ![]() $\boldsymbol {X}$)
$\boldsymbol {X}$)
where ![]() $\hat {\boldsymbol {p}}$ and
$\hat {\boldsymbol {p}}$ and ![]() $\hat {\boldsymbol {u}}$ are periodic first- and second-order tensors, respectively. Accordingly, the model to be solved for
$\hat {\boldsymbol {u}}$ are periodic first- and second-order tensors, respectively. Accordingly, the model to be solved for ![]() $\hat {\boldsymbol {p}}$ and
$\hat {\boldsymbol {p}}$ and ![]() $\hat {\boldsymbol {u}}$ on a periodic domain is
$\hat {\boldsymbol {u}}$ on a periodic domain is
In this paper, the periodic unit cells are square, enclosing either a single circular inclusion or randomly positioned, non-overlapping inclusions (with doubly periodic boundary conditions). The accompanying deterministic or statistical isotropy reduces the model to one for which ![]() $\boldsymbol {X} = X \boldsymbol {e}_i$ (
$\boldsymbol {X} = X \boldsymbol {e}_i$ (![]() $i = 1, 2$), where
$i = 1, 2$), where ![]() $\boldsymbol {e}_i$ is a unit vector. It follows that
$\boldsymbol {e}_i$ is a unit vector. It follows that ![]() $\boldsymbol {X} \boldsymbol{\cdot} \hat {\boldsymbol {p}} \rightarrow P \hat {p}$ and
$\boldsymbol {X} \boldsymbol{\cdot} \hat {\boldsymbol {p}} \rightarrow P \hat {p}$ and ![]() $\boldsymbol {X} \boldsymbol{\cdot} \hat {\boldsymbol {u}} \rightarrow P \hat {\boldsymbol {u}}$, where
$\boldsymbol {X} \boldsymbol{\cdot} \hat {\boldsymbol {u}} \rightarrow P \hat {\boldsymbol {u}}$, where ![]() $\hat {p}$ and
$\hat {p}$ and ![]() $\hat {\boldsymbol {u}}$ become periodic scalar and vector fields, respectively.
$\hat {\boldsymbol {u}}$ become periodic scalar and vector fields, respectively.
When ![]() $\hat {\boldsymbol {u}}$ is an isotropic second-order tensor (so
$\hat {\boldsymbol {u}}$ is an isotropic second-order tensor (so ![]() $\boldsymbol {X} \boldsymbol{\cdot} \hat {\boldsymbol {u}}$ is a first-order tensor), the volume-average velocity
$\boldsymbol {X} \boldsymbol{\cdot} \hat {\boldsymbol {u}}$ is a first-order tensor), the volume-average velocity
where ![]() $\ell _e^2 / \eta$ is the effective permeability with
$\ell _e^2 / \eta$ is the effective permeability with ![]() $\ell _e$ the effective Brinkman screening length. This may be written as
$\ell _e$ the effective Brinkman screening length. This may be written as
where, for small dispersed-phase volume fractions ![]() $\phi$, the permeability increment
$\phi$, the permeability increment ![]() $\alpha _{UP}$ is independent of
$\alpha _{UP}$ is independent of ![]() $\phi$. Note that
$\phi$. Note that ![]() $\alpha _{UP}$ is defined by analogy with the ionic conductivity increment for colloidal dispersions being the limiting slope of the conductivity–volume fraction relation (Zukoski & Saville Reference Zukoski and Saville1985), as expected based on considerations of linearity, isotropy and a neglect of particle interactions (to leading order in
$\alpha _{UP}$ is defined by analogy with the ionic conductivity increment for colloidal dispersions being the limiting slope of the conductivity–volume fraction relation (Zukoski & Saville Reference Zukoski and Saville1985), as expected based on considerations of linearity, isotropy and a neglect of particle interactions (to leading order in ![]() $\phi$).
$\phi$).
The Brinkman model comprising (2.3) and (2.4) with periodic boundary conditions was solved as a coupled triplet of scalar partial-differential equations using the COMSOL Multiphysics (versions 5.1.0.145 and 6.1) finite-element software. Direct evaluation of ![]() $\langle \boldsymbol {u} \rangle$ furnishes
$\langle \boldsymbol {u} \rangle$ furnishes ![]() $\ell _e^2 / \eta$ and thus
$\ell _e^2 / \eta$ and thus ![]() $\alpha _{UP} / (\ell ^2 / \eta )$, which are compared with analytical theory based on the averaging methodology of Hill (Reference Hill2022) for random media when the inclusion area fraction
$\alpha _{UP} / (\ell ^2 / \eta )$, which are compared with analytical theory based on the averaging methodology of Hill (Reference Hill2022) for random media when the inclusion area fraction ![]() $\phi \ll 1$. In this dilute limit (which also requires the continuous-phase Brinkman screening length
$\phi \ll 1$. In this dilute limit (which also requires the continuous-phase Brinkman screening length ![]() $\ell$ to be small compared with the characteristic inclusion separation),
$\ell$ to be small compared with the characteristic inclusion separation), ![]() $\alpha _{UP}$ becomes independent of
$\alpha _{UP}$ becomes independent of ![]() $\phi$, as demonstrated below by direct numerical calculations and comparison with analytical theory. Accordingly, the next section presents an analytical solution of the Brinkman model in two dimensions for a dilute discrete phase. In the results section, this is used to test the analytical averaging methodology of Hill (Reference Hill2022), which is hereunto unverified by any independent analysis. Moreover, a thin-gap approximation is undertaken for the close-packing limit in which
$\phi$, as demonstrated below by direct numerical calculations and comparison with analytical theory. Accordingly, the next section presents an analytical solution of the Brinkman model in two dimensions for a dilute discrete phase. In the results section, this is used to test the analytical averaging methodology of Hill (Reference Hill2022), which is hereunto unverified by any independent analysis. Moreover, a thin-gap approximation is undertaken for the close-packing limit in which ![]() $\ell$ is kept small compared with the vanishing gap
$\ell$ is kept small compared with the vanishing gap ![]() $\epsilon$ between almost-touching circular inclusions.
$\epsilon$ between almost-touching circular inclusions.
2.2. Analytical model
Consider a single cylindrical domain (centred at the origin, radius ![]() $a$) with Brinkman screening length
$a$) with Brinkman screening length ![]() $\ell _c$ and shear viscosity
$\ell _c$ and shear viscosity ![]() $\chi \eta$ (
$\chi \eta$ (![]() $\chi$ is the viscosity ratio, which will be set to one as prescribed in the foregoing computational model) in an unbounded continuous medium with Brinkman screening length
$\chi$ is the viscosity ratio, which will be set to one as prescribed in the foregoing computational model) in an unbounded continuous medium with Brinkman screening length ![]() $\ell$ and shear viscosity
$\ell$ and shear viscosity ![]() $\eta$. Defining
$\eta$. Defining ![]() $\beta = a / \ell$ and
$\beta = a / \ell$ and ![]() $\beta _c = a / \ell _c$, scaling position with
$\beta _c = a / \ell _c$, scaling position with ![]() $a$, velocity with the Darcy velocity
$a$, velocity with the Darcy velocity ![]() $u_c = P \ell ^2 / \eta$ and pressure with
$u_c = P \ell ^2 / \eta$ and pressure with ![]() $p_c = \eta u_c / a = P \ell ^2 / a$, the (scaled) velocity and pressure have the forms (inside and outside the cylinder)
$p_c = \eta u_c / a = P \ell ^2 / a$, the (scaled) velocity and pressure have the forms (inside and outside the cylinder)
 \begin{align} \boldsymbol{u}(r<1) &= \left\{ U/X - b_1 - b_2 \left[ {\rm I}_0(\beta_c r) - \frac{{\rm I}_1(\beta_c r)}{\beta_c r} \right] \right\} \boldsymbol{X}\nonumber\\ &\quad + b_2 \left[ {\rm I}_0(\beta_c r) - 2 \frac{{\rm I}_1(\beta_c r)}{\beta_c r} \right] \boldsymbol{X} \boldsymbol{\cdot} \boldsymbol{e}_r \boldsymbol{e}_r, \end{align}
\begin{align} \boldsymbol{u}(r<1) &= \left\{ U/X - b_1 - b_2 \left[ {\rm I}_0(\beta_c r) - \frac{{\rm I}_1(\beta_c r)}{\beta_c r} \right] \right\} \boldsymbol{X}\nonumber\\ &\quad + b_2 \left[ {\rm I}_0(\beta_c r) - 2 \frac{{\rm I}_1(\beta_c r)}{\beta_c r} \right] \boldsymbol{X} \boldsymbol{\cdot} \boldsymbol{e}_r \boldsymbol{e}_r, \end{align}and
 \begin{align} \boldsymbol{u}(r>1) &= \left\{ U/X + c_1 \beta \left[{\rm K}_0(\beta r) + \frac{{\rm K}_1(\beta r)}{\beta r}\right] - \frac{\lambda}{r^2}\right\} \boldsymbol{X} \nonumber\\ &\quad+ \left\{2 \frac{\lambda}{r^2} - c_1 \beta \left[{\rm K}_0(\beta r) + 2 \frac{{\rm K}_1(\beta r)}{\beta r}\right] \right\} \boldsymbol{X} \boldsymbol{\cdot} \boldsymbol{e}_r \boldsymbol{e}_r, \end{align}
\begin{align} \boldsymbol{u}(r>1) &= \left\{ U/X + c_1 \beta \left[{\rm K}_0(\beta r) + \frac{{\rm K}_1(\beta r)}{\beta r}\right] - \frac{\lambda}{r^2}\right\} \boldsymbol{X} \nonumber\\ &\quad+ \left\{2 \frac{\lambda}{r^2} - c_1 \beta \left[{\rm K}_0(\beta r) + 2 \frac{{\rm K}_1(\beta r)}{\beta r}\right] \right\} \boldsymbol{X} \boldsymbol{\cdot} \boldsymbol{e}_r \boldsymbol{e}_r, \end{align}
where ![]() $\boldsymbol {e}_r = \boldsymbol {x} / r$. These forms of the velocity and pressure are deduced by considerations of linearity (with respect to
$\boldsymbol {e}_r = \boldsymbol {x} / r$. These forms of the velocity and pressure are deduced by considerations of linearity (with respect to ![]() $\boldsymbol {X}$), symmetry and fluid incompressibility (Batchelor Reference Batchelor1967). Substitution into Brinkman's momentum- and mass-conservation equations furnishes ordinary differential equations for the unknown scalar functions of radial position. These furnish the modified Bessel functions (
$\boldsymbol {X}$), symmetry and fluid incompressibility (Batchelor Reference Batchelor1967). Substitution into Brinkman's momentum- and mass-conservation equations furnishes ordinary differential equations for the unknown scalar functions of radial position. These furnish the modified Bessel functions (![]() ${\rm I}_0$,
${\rm I}_0$, ![]() ${\rm I}_1$,
${\rm I}_1$, ![]() ${\rm K}_0$ and
${\rm K}_0$ and ![]() ${\rm K}_1$) and integration constants (
${\rm K}_1$) and integration constants (![]() $b_1$,
$b_1$, ![]() $b_2$,
$b_2$, ![]() $c_1$ and
$c_1$ and ![]() $\lambda$). Accordingly, four independent linear algebraic relations are required to prescribe a continuous velocity and stress at
$\lambda$). Accordingly, four independent linear algebraic relations are required to prescribe a continuous velocity and stress at ![]() $r = 1$
$r = 1$
 \begin{gather} \chi \left\{ b_2 \left[ \beta_c {\rm I}_1(\beta_c) - 5 {\rm I}_0(\beta_c) + 10 \frac{{\rm I}_1(\beta_c)}{\beta_c} \right] - \beta_c^2 (b_1 - 1) \right\} \nonumber\\ \quad = c_1 \beta \left[\beta {\rm K}_1(\beta) + 5 {\rm K}_0(\beta) + 8 \frac{{\rm K}_1(\beta)}{\beta} \right] - 10 \lambda - \beta^2\left(\lambda - 1\right). \end{gather}
\begin{gather} \chi \left\{ b_2 \left[ \beta_c {\rm I}_1(\beta_c) - 5 {\rm I}_0(\beta_c) + 10 \frac{{\rm I}_1(\beta_c)}{\beta_c} \right] - \beta_c^2 (b_1 - 1) \right\} \nonumber\\ \quad = c_1 \beta \left[\beta {\rm K}_1(\beta) + 5 {\rm K}_0(\beta) + 8 \frac{{\rm K}_1(\beta)}{\beta} \right] - 10 \lambda - \beta^2\left(\lambda - 1\right). \end{gather} Integrating the (Newtonian) stress traction over the cylinder surface (![]() $r = 1$) furnishes a (dimensional) force (per unit length)
$r = 1$) furnishes a (dimensional) force (per unit length)
where ![]() $\boldsymbol {U} = - \boldsymbol {P} \ell ^2 / \eta$ is the far-field (undisturbed) fluid velocity, and
$\boldsymbol {U} = - \boldsymbol {P} \ell ^2 / \eta$ is the far-field (undisturbed) fluid velocity, and ![]() $c_1$ and
$c_1$ and ![]() $\lambda$ are from (2.11)–(2.14). This solution of Brinkman's model for a permeable inclusion may now be compared with prior solutions in more restricted regions of the parameter space.
$\lambda$ are from (2.11)–(2.14). This solution of Brinkman's model for a permeable inclusion may now be compared with prior solutions in more restricted regions of the parameter space.
For an impenetrable cylinder (![]() $\beta _c \gg 1$), it can be shown that (2.15) reduces to
$\beta _c \gg 1$), it can be shown that (2.15) reduces to
which is the same as derived by Spielman & Goren (Reference Spielman and Goren1968, (26)) using a streamfunction. Note that ![]() $\beta \rightarrow 0$ corresponds to viscous flow past a cylinder, which becomes subject to the well-known Stokes’ paradox and inertial effects (Spielman & Goren Reference Spielman and Goren1968; Koch & Ladd Reference Koch and Ladd1997). For a large impenetrable cylinder (
$\beta \rightarrow 0$ corresponds to viscous flow past a cylinder, which becomes subject to the well-known Stokes’ paradox and inertial effects (Spielman & Goren Reference Spielman and Goren1968; Koch & Ladd Reference Koch and Ladd1997). For a large impenetrable cylinder (![]() $\beta _c \gg \beta \gg 1$), we find
$\beta _c \gg \beta \gg 1$), we find
which is the force from a Darcy flow
The analogy between scalar diffusion and Darcy flow, which arises from the Brinkman model when ![]() $\beta \gg 1$ and
$\beta \gg 1$ and ![]() $\beta _c \gg 1$, will be drawn upon to assess the degree to which theories for tracer diffusion may be applied to approximate the more general Brinkman model.
$\beta _c \gg 1$, will be drawn upon to assess the degree to which theories for tracer diffusion may be applied to approximate the more general Brinkman model.
Next, similarly to the averaging undertaken by Hill (Reference Hill2022) for dilute arrays of spherical inclusions, the averaged momentum counterpart for dilute arrays of cylindrical inclusions (accurate only to leading order in ![]() $\phi$) is furnished by evaluating a surface integral of the far-field pressure disturbance (dimensional) (the counterpart of the pressure dipole
$\phi$) is furnished by evaluating a surface integral of the far-field pressure disturbance (dimensional) (the counterpart of the pressure dipole ![]() $\eta A^X = \eta \lambda \beta ^2$ in Hill's paper is
$\eta A^X = \eta \lambda \beta ^2$ in Hill's paper is ![]() $C^X \eta / \ell ^2$. Moreover, in all of Hill's formulas for the averaged fluxes (not Hill's equations (19) and (20)),
$C^X \eta / \ell ^2$. Moreover, in all of Hill's formulas for the averaged fluxes (not Hill's equations (19) and (20)), ![]() $C^X$ is signed as minus that of the pressure-dipole strength, whereas in Hill's equations (19) and (20),
$C^X$ is signed as minus that of the pressure-dipole strength, whereas in Hill's equations (19) and (20), ![]() $C^X$ is signed as the pressure dipole strength)
$C^X$ is signed as the pressure dipole strength)
where ![]() $A^X$ is a constant (dimensioned according to
$A^X$ is a constant (dimensioned according to ![]() $\boldsymbol {X}$).
$\boldsymbol {X}$).
For the cylindrical inclusions in the present two-dimensional geometry, Hill's integral (now on a per unit length basis) is
thus furnishing an averaged momentum equation (Hill Reference Hill2022)
where ![]() $\phi = n {\rm \pi}a^2 \ll 1$ (
$\phi = n {\rm \pi}a^2 \ll 1$ (![]() $n$ is the cylinder number density) and (dimensionless)
$n$ is the cylinder number density) and (dimensionless) ![]() $\lambda$ is from (2.11)–(2.14). The (dimensionless) permeability increment (from (2.6)) is therefore
$\lambda$ is from (2.11)–(2.14). The (dimensionless) permeability increment (from (2.6)) is therefore
Note that (2.21) is the two-dimensional counterpart of Hill's averaged momentum equation for dilute arrays of spherical inclusions. The factor ![]() $2$ in (2.22) is the counterpart of Hill's factor
$2$ in (2.22) is the counterpart of Hill's factor ![]() $3$ for three dimensions. Comparing this analytical approximation with direct numerical solutions of (2.3) and (2.4) on ordered and random periodic domains (in the dilute limit), as undertaken in the next section, serves to validate the averaging methodology (albeit in a two-dimensional framework) and provide insights into the hydrodynamic interactions when
$3$ for three dimensions. Comparing this analytical approximation with direct numerical solutions of (2.3) and (2.4) on ordered and random periodic domains (in the dilute limit), as undertaken in the next section, serves to validate the averaging methodology (albeit in a two-dimensional framework) and provide insights into the hydrodynamic interactions when ![]() $\phi$ is not sufficiently small.
$\phi$ is not sufficiently small.
3. Results
The analytical model, evaluated by solving (2.11)–(2.14) and substituting ![]() $c_1$ and
$c_1$ and ![]() $\lambda$ into (2.15) and (2.22), is plotted in figure 3. Panel (a) shows the scaled drag force (per unit length) according to (2.15) for several values of
$\lambda$ into (2.15) and (2.22), is plotted in figure 3. Panel (a) shows the scaled drag force (per unit length) according to (2.15) for several values of ![]() $\beta _c = a / \ell _c$. The upper limit is bounded by the Brinkman drag (for impenetrable inclusions, (2.16)), which approaches the Darcy drag (large, impenetrable inclusions, (2.17)) when
$\beta _c = a / \ell _c$. The upper limit is bounded by the Brinkman drag (for impenetrable inclusions, (2.16)), which approaches the Darcy drag (large, impenetrable inclusions, (2.17)) when ![]() $\beta \gtrsim 10$. Panel (b) shows the dimensionless permeability increment, which vanishes at values for which there is zero permeability contrast between the discrete and continuous phases. As expected, for inclusions that are more permeable than the continuous phase, the increment is positive, reflecting an increase in the permeability of the composite relative to its continuous phase, and vice versa.
$\beta \gtrsim 10$. Panel (b) shows the dimensionless permeability increment, which vanishes at values for which there is zero permeability contrast between the discrete and continuous phases. As expected, for inclusions that are more permeable than the continuous phase, the increment is positive, reflecting an increase in the permeability of the composite relative to its continuous phase, and vice versa.

Figure 3. Theoretical predictions of the Brinkman theory equation (2.21) for dilute arrays of permeable cylindrical inclusions with ![]() $\beta _c = a / \ell _c= 0.01$ (blue, bottom in (a) and top in (b)),
$\beta _c = a / \ell _c= 0.01$ (blue, bottom in (a) and top in (b)), ![]() $0.7$ (red),
$0.7$ (red), ![]() $1$,
$1$, ![]() $2$,
$2$, ![]() $4$,
$4$, ![]() $8$,
$8$, ![]() $16$,
$16$, ![]() $32$,
$32$, ![]() $64$,
$64$, ![]() $128$ (solid lines),
$128$ (solid lines), ![]() $\infty$ (impenetrable cylinders, dashed lines, (2.16)) in a continuous Brinkman medium with
$\infty$ (impenetrable cylinders, dashed lines, (2.16)) in a continuous Brinkman medium with ![]() $\beta = a / \ell$. (a) Scaled drag force (per unit length) according to (2.15) and (b) scaled hydrodynamic permeability increment according to (2.22). Dash-dotted line in (a) is the Darcy drag force for an impenetrable cylinder according to (2.17).
$\beta = a / \ell$. (a) Scaled drag force (per unit length) according to (2.15) and (b) scaled hydrodynamic permeability increment according to (2.22). Dash-dotted line in (a) is the Darcy drag force for an impenetrable cylinder according to (2.17).
Comparing direct numerical computations (for simple-square arrays of cylindrical inclusions) with the forgoing analytical model in the dilute-inclusion limit tests the averaging methodology underlying the theory of Hill (Reference Hill2022), albeit in a two-dimensional context. As shown in figure 4(a), the analytical theory (solid lines) agrees well with the direct numerical solutions (circles) when ![]() $\beta \gtrsim 1$. Here, the numerical solutions in panel (a) are undertaken with a small cylinder area fraction
$\beta \gtrsim 1$. Here, the numerical solutions in panel (a) are undertaken with a small cylinder area fraction ![]() $\phi = {\rm \pi}/ 100$. Under these conditions, the agreement is excellent when
$\phi = {\rm \pi}/ 100$. Under these conditions, the agreement is excellent when ![]() $\beta \gtrsim 1$. This is because the hydrodynamic interactions of the cylinders are screened by the intervening Brinkman medium. This is expected when the characteristic distance between the cylinders
$\beta \gtrsim 1$. This is because the hydrodynamic interactions of the cylinders are screened by the intervening Brinkman medium. This is expected when the characteristic distance between the cylinders ![]() $L - 2a = L( 1 - \sqrt {4 \phi / {\rm \pi}})\gtrsim a$ with
$L - 2a = L( 1 - \sqrt {4 \phi / {\rm \pi}})\gtrsim a$ with ![]() $\beta = a / \ell \gtrsim 1$. Thus, with
$\beta = a / \ell \gtrsim 1$. Thus, with ![]() $\phi = {\rm \pi}(a / L)^2$ we find
$\phi = {\rm \pi}(a / L)^2$ we find
which is in reasonable accord with figure 4. Otherwise, when ![]() $\beta \lesssim 1$, the permeability is subject to hydrodynamic interactions that are not addressed by the analytical theory. Here, the accuracy of the finite-element computations may be tested, in part, by comparing the permeability based on slow viscous flow through dilute simple-square arrays of impenetrable cylinders.
$\beta \lesssim 1$, the permeability is subject to hydrodynamic interactions that are not addressed by the analytical theory. Here, the accuracy of the finite-element computations may be tested, in part, by comparing the permeability based on slow viscous flow through dilute simple-square arrays of impenetrable cylinders.
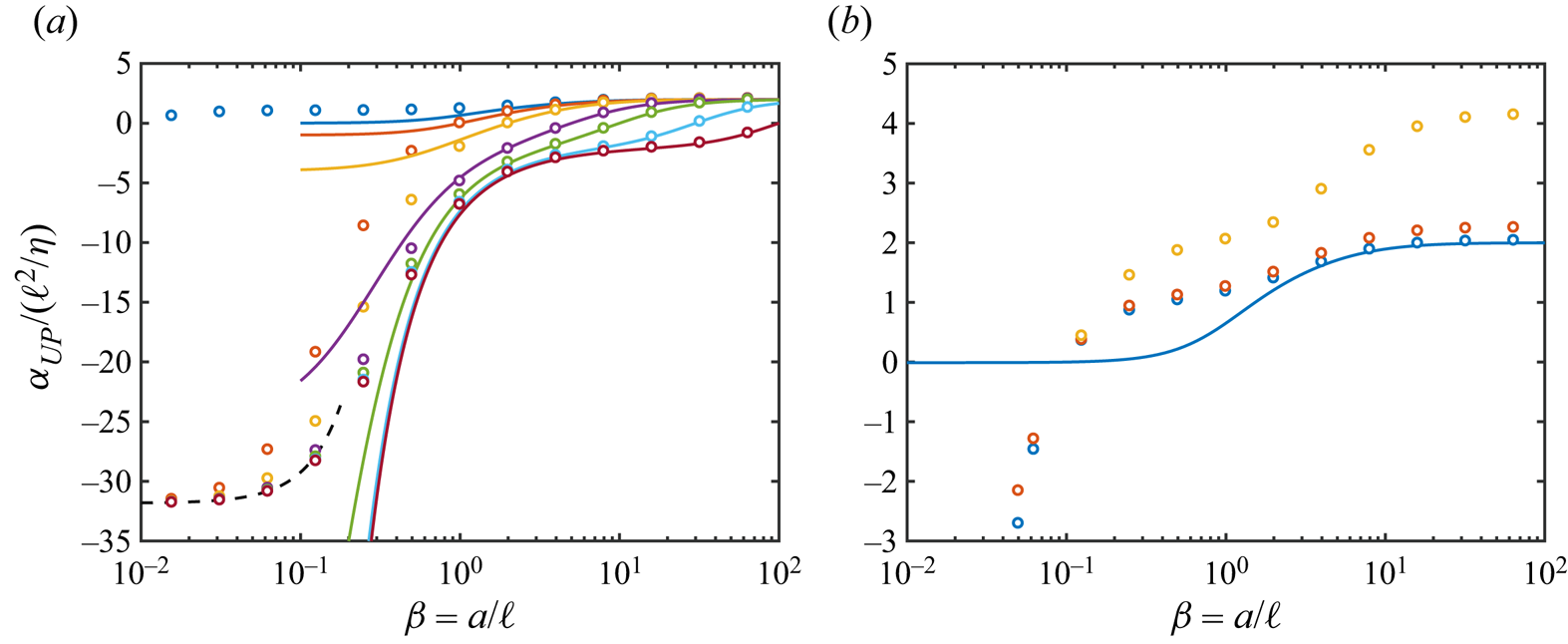
Figure 4. Scaled hydrodynamic permeability increment for simple-square arrays of porous cylinders. Circles are from finite-element computations, and solid lines are the Brinkman theory equation (2.22) for ![]() $\phi \rightarrow 0$. Panel (a) shows
$\phi \rightarrow 0$. Panel (a) shows ![]() $\beta _c = a / \ell _c = 0.01$ (blue),
$\beta _c = a / \ell _c = 0.01$ (blue), ![]() $1$ (red),
$1$ (red), ![]() $2$,
$2$, ![]() $5$,
$5$, ![]() $10$,
$10$, ![]() $30$ (cyan),
$30$ (cyan), ![]() $100$ with
$100$ with ![]() $L / a = 10$ corresponding to
$L / a = 10$ corresponding to ![]() $\phi \approx 0.0314$. Dashed line is (3.4) for Stokes flow in dilute simple-square arrays of impenetrable cylinders. Panel (b) shows
$\phi \approx 0.0314$. Dashed line is (3.4) for Stokes flow in dilute simple-square arrays of impenetrable cylinders. Panel (b) shows ![]() $L / a = 10$ (blue),
$L / a = 10$ (blue), ![]() $5$ (red),
$5$ (red), ![]() $2.5$ (yellow) correspond to
$2.5$ (yellow) correspond to ![]() $\phi = 0.0314$,
$\phi = 0.0314$, ![]() $0.1257$,
$0.1257$, ![]() $0.5027$, respectively, with
$0.5027$, respectively, with ![]() $\beta _c = 0.1$ (highly permeable inclusions).
$\beta _c = 0.1$ (highly permeable inclusions).
Note that Koch & Ladd (Reference Koch and Ladd1997) provide an analytical formula from the multipole expansion of Sangani & Acrivos (Reference Sangani and Acrivos1982) for the Stokes drag force per unit length on simple-square arrays of aligned cylinders (flow parallel to the cylinder axes). Writing the average pressure gradient in terms of the cylinder number density and drag force per unit length gives
thus furnishing
and
where the drag coefficient (Koch & Ladd Reference Koch and Ladd1997)
Equation (3.4), which is clearly not independent of ![]() $\phi$ as
$\phi$ as ![]() $\phi \rightarrow 0$, is plotted in figure 4(a) as the dashed line to which the finite-element computations for impenetrable cylinders (
$\phi \rightarrow 0$, is plotted in figure 4(a) as the dashed line to which the finite-element computations for impenetrable cylinders (![]() $\beta _c \gtrsim 30$) agree when
$\beta _c \gtrsim 30$) agree when ![]() $\beta \lesssim 0.1$. These conditions correspond to a highly permeable continuous phase, thus mimicking the viscous flow underlying (3.4). Figure 4(b) compares the finite-element computations for several cylinder area fractions, spanning the dilute to concentrated range, when
$\beta \lesssim 0.1$. These conditions correspond to a highly permeable continuous phase, thus mimicking the viscous flow underlying (3.4). Figure 4(b) compares the finite-element computations for several cylinder area fractions, spanning the dilute to concentrated range, when ![]() $\beta _c = 0.1$, corresponding to highly permeable inclusions. For reference, the line is (2.22) for the dilute limit. These results are consistent with (3.1), also showing that the permeability is significantly enhanced by hydrodynamic interactions when
$\beta _c = 0.1$, corresponding to highly permeable inclusions. For reference, the line is (2.22) for the dilute limit. These results are consistent with (3.1), also showing that the permeability is significantly enhanced by hydrodynamic interactions when ![]() $\phi \gtrsim 0.3$. This is explored in the section below by reference to finite-element computations for random, non-overlapping-inclusion arrays.
$\phi \gtrsim 0.3$. This is explored in the section below by reference to finite-element computations for random, non-overlapping-inclusion arrays.
Figure 5 shows streamlines for more permeable inclusions (![]() $\beta _c = 1/100$), at three cylinder area fractions spanning the dilute to almost-touching limits with two continuous-phase permeabilities. The close resemblance of the streamlines in panel (a) to their counterparts in panel (b) reflects hydrodynamic screening by the intervening Brinkman medium. This screening is seen to break down in panel (c), where the streamlines are increasingly aligned with the primary flow (i.e. less tortuous) throughout the periodic unit cell.
$\beta _c = 1/100$), at three cylinder area fractions spanning the dilute to almost-touching limits with two continuous-phase permeabilities. The close resemblance of the streamlines in panel (a) to their counterparts in panel (b) reflects hydrodynamic screening by the intervening Brinkman medium. This screening is seen to break down in panel (c), where the streamlines are increasingly aligned with the primary flow (i.e. less tortuous) throughout the periodic unit cell.
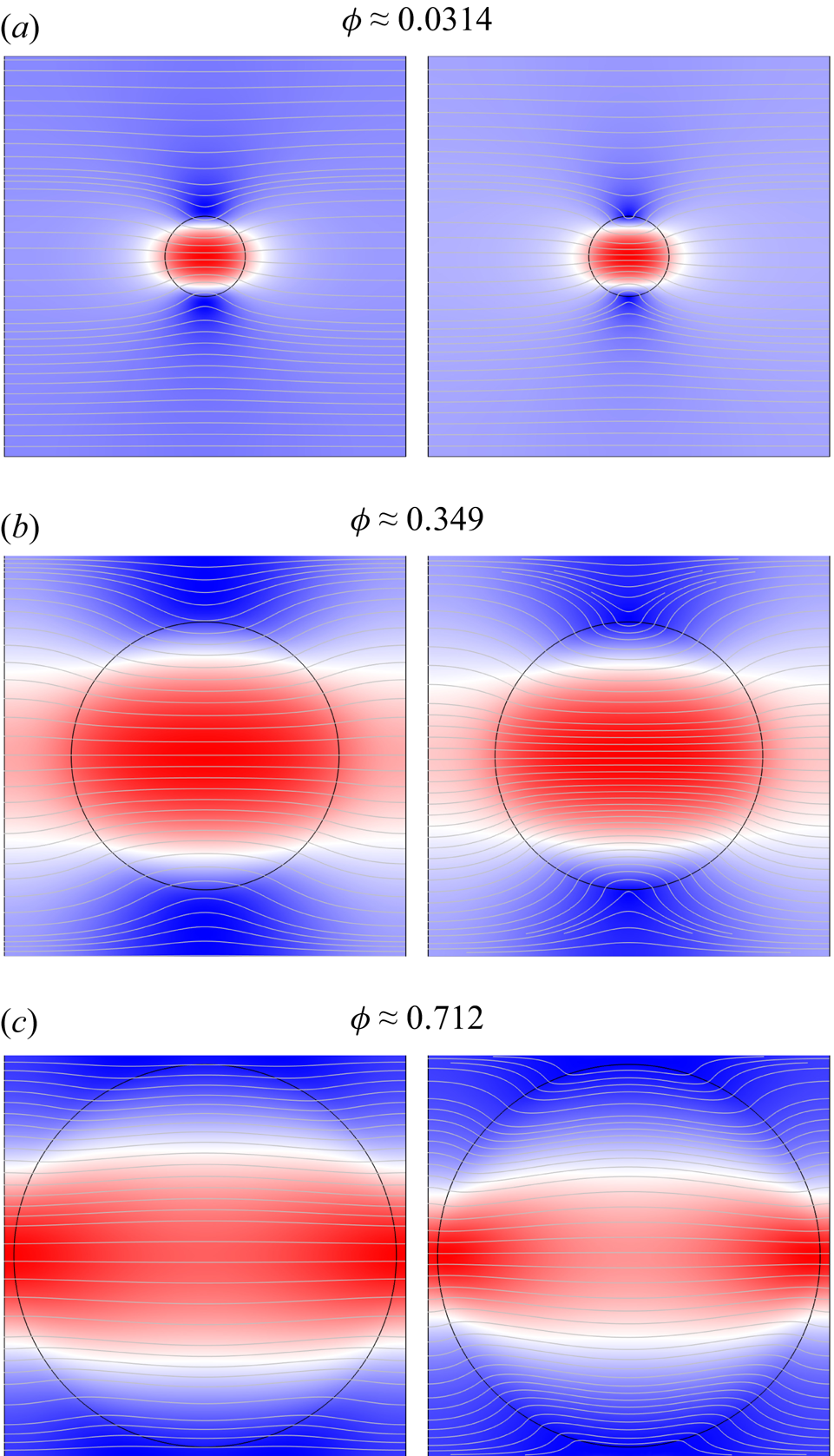
Figure 5. Streamlines and ![]() $|\boldsymbol {u}|$ (colour map) for pressure-driven flows through simple-square arrays of cylindrical inclusions in continuous Brinkman media:
$|\boldsymbol {u}|$ (colour map) for pressure-driven flows through simple-square arrays of cylindrical inclusions in continuous Brinkman media: ![]() $\phi = {\rm \pi}/ 10^2$ (a),
$\phi = {\rm \pi}/ 10^2$ (a), ![]() ${\rm \pi} / 3^2$ (b),
${\rm \pi} / 3^2$ (b), ![]() ${\rm \pi} / 2.1^2$ (c);
${\rm \pi} / 2.1^2$ (c); ![]() $\beta = 8$ (left),
$\beta = 8$ (left), ![]() $64$ (right);
$64$ (right); ![]() $\beta _c = 1/100$.
$\beta _c = 1/100$.
Figure 6 focuses on the permeability increment with finite cavity area fractions spanning the dilute to almost-touching limits. In both panels, the finite-element solutions are in good agreement with the analytical model when ![]() $\phi \lesssim 0.1$ and
$\phi \lesssim 0.1$ and ![]() $\beta \gtrsim 1$. The close-packing limit is amenable to a thin-gap approximation (Batchelor & O'Brien Reference Batchelor and O'Brien1977), furnishing the dashed line in figure 6(b). As shown below, this approximation is valid in the limit where the smallest gap between the cylinders
$\beta \gtrsim 1$. The close-packing limit is amenable to a thin-gap approximation (Batchelor & O'Brien Reference Batchelor and O'Brien1977), furnishing the dashed line in figure 6(b). As shown below, this approximation is valid in the limit where the smallest gap between the cylinders ![]() $\epsilon$ is large compared with
$\epsilon$ is large compared with ![]() $\ell$ as
$\ell$ as ![]() $\epsilon \rightarrow 0$.
$\epsilon \rightarrow 0$.

Figure 6. Scaled hydrodynamic permeability increment for simple-square arrays of cylindrical inclusions (![]() $\beta _c = a / \ell _c = 1/100$). Circles are finite-element computations, and solid lines are the Brinkman theory for the dilute limit
$\beta _c = a / \ell _c = 1/100$). Circles are finite-element computations, and solid lines are the Brinkman theory for the dilute limit ![]() $\phi \rightarrow 0$. Panel (a) shows
$\phi \rightarrow 0$. Panel (a) shows ![]() $L / a = 10$ (blue),
$L / a = 10$ (blue), ![]() $5$ (red),
$5$ (red), ![]() $2.5$ (yellow),
$2.5$ (yellow), ![]() $4$,
$4$, ![]() $3$,
$3$, ![]() $2.2$ (cyan),
$2.2$ (cyan), ![]() $2.1$ (red). Panel (b) shows
$2.1$ (red). Panel (b) shows ![]() $\beta = a / \ell = 64$ (blue),
$\beta = a / \ell = 64$ (blue), ![]() $8$ (red),
$8$ (red), ![]() $4$ (orange),
$4$ (orange), ![]() $1$,
$1$, ![]() $1/32$,
$1/32$, ![]() $1/64$ (cyan). Dashed line is the thin-wall approximation, (3.8), for the closed-packed limit, as detailed further in figure 7.
$1/64$ (cyan). Dashed line is the thin-wall approximation, (3.8), for the closed-packed limit, as detailed further in figure 7.
In the close-packing limit where ![]() $L \rightarrow 2 a$ and
$L \rightarrow 2 a$ and ![]() $\phi \rightarrow {\rm \pi}/ 4$, the smallest gap between the inclusions is
$\phi \rightarrow {\rm \pi}/ 4$, the smallest gap between the inclusions is ![]() $\epsilon = L - 2 a = L (1 - \sqrt {4 \phi / {\rm \pi}})$, and so the average volume flux through this thin gap may be approximated as
$\epsilon = L - 2 a = L (1 - \sqrt {4 \phi / {\rm \pi}})$, and so the average volume flux through this thin gap may be approximated as
where ![]() $\Delta p \approx P L$ is the pressure differential across the gap, and
$\Delta p \approx P L$ is the pressure differential across the gap, and ![]() $\alpha \sim L / 2 \approx a$. This formula is derived similarly to Batchelor & O'Brien (Reference Batchelor and O'Brien1977) for perfectly conducting, random spheres; here, the volume flux across the gap is taken to be a unidirectional Darcy flow with local pressure gradient
$\alpha \sim L / 2 \approx a$. This formula is derived similarly to Batchelor & O'Brien (Reference Batchelor and O'Brien1977) for perfectly conducting, random spheres; here, the volume flux across the gap is taken to be a unidirectional Darcy flow with local pressure gradient ![]() $\Delta p / y(x)$, where
$\Delta p / y(x)$, where ![]() $y(x) \ge \epsilon$ is the gap thickness. In addition to the cavity being highly permeable (
$y(x) \ge \epsilon$ is the gap thickness. In addition to the cavity being highly permeable (![]() $\beta _i \ll 1$), the gap must be larger than the Brinkman screening length for this approximation to hold, i.e.
$\beta _i \ll 1$), the gap must be larger than the Brinkman screening length for this approximation to hold, i.e. ![]() $\epsilon / \ell = \beta \epsilon / a \gg 1$. Expanding the denominator of the integrand for small gaps, i.e.
$\epsilon / \ell = \beta \epsilon / a \gg 1$. Expanding the denominator of the integrand for small gaps, i.e. ![]() $\epsilon / a \ll 1$, gives a thin-wall approximation
$\epsilon / a \ll 1$, gives a thin-wall approximation
which, upon integrating, and taking ![]() $\alpha / \sqrt {a \epsilon } = L / \sqrt {4 a \epsilon } \gg 1$, furnishes
$\alpha / \sqrt {a \epsilon } = L / \sqrt {4 a \epsilon } \gg 1$, furnishes
As shown in figure 6(b), this provides a compelling upper bound on the permeability in the close-packing limit. As expected by the quadratic approximation of the gap under-estimating the gap, (3.8) over-predicts the permeability. Note that the requirement for ![]() $\beta \epsilon / a \gg 1$ with
$\beta \epsilon / a \gg 1$ with ![]() $\epsilon / a \ll 1$ places an increasingly stringent limit on the validity of (3.8) as
$\epsilon / a \ll 1$ places an increasingly stringent limit on the validity of (3.8) as ![]() $\epsilon / a \rightarrow 0$.
$\epsilon / a \rightarrow 0$.
The accuracy of (3.8) is explored more rigorously in figure 7, where the permeability increment is plotted versus the scaled gap ![]() $\epsilon / a$ for three values of
$\epsilon / a$ for three values of ![]() $\beta \gtrsim 1$. The vertical lines identify the area fractions at which
$\beta \gtrsim 1$. The vertical lines identify the area fractions at which ![]() $\epsilon = a / \beta = \ell$. Thus, the parameter space where
$\epsilon = a / \beta = \ell$. Thus, the parameter space where ![]() $\epsilon \lesssim a$ and
$\epsilon \lesssim a$ and ![]() $\ell \lesssim \epsilon$ is confined to the narrow windows where the abscissa
$\ell \lesssim \epsilon$ is confined to the narrow windows where the abscissa ![]() $\epsilon / a \lesssim 1$, but with
$\epsilon / a \lesssim 1$, but with ![]() $\epsilon / a$ still well to the right of the vertical lines. This is clearly best achieved in the close-packing limit with
$\epsilon / a$ still well to the right of the vertical lines. This is clearly best achieved in the close-packing limit with ![]() $\beta = 256$ (blue). Such calculations demand highly refined finite-element meshes. An example of the streamlines and velocity magnitude in such an array is shown in figure 8. Here, the fastest flowing fluid is ostensibly localized to the small almost-touching regions at poles that are aligned along the primary flow direction.
$\beta = 256$ (blue). Such calculations demand highly refined finite-element meshes. An example of the streamlines and velocity magnitude in such an array is shown in figure 8. Here, the fastest flowing fluid is ostensibly localized to the small almost-touching regions at poles that are aligned along the primary flow direction.

Figure 7. Scaled hydrodynamic permeability increment for simple-square arrays of cylindrical inclusions (![]() $\beta _c = 1/100$) in the close-packing limit, testing the validity of the thin-wall approximation, (3.8). Circles are finite-element computations, and the solid line is (3.8), valid for
$\beta _c = 1/100$) in the close-packing limit, testing the validity of the thin-wall approximation, (3.8). Circles are finite-element computations, and the solid line is (3.8), valid for ![]() $1 /\beta \ll \epsilon / a \ll 1$:
$1 /\beta \ll \epsilon / a \ll 1$: ![]() $\beta = 256$ (blue),
$\beta = 256$ (blue), ![]() $64$ (red)
$64$ (red) ![]() $32$ (yellow). Vertical lines identify
$32$ (yellow). Vertical lines identify ![]() $\epsilon / a = 1 / \beta = \ell / a$ (colours matched to the respective values of
$\epsilon / a = 1 / \beta = \ell / a$ (colours matched to the respective values of ![]() $\beta$).
$\beta$).

Figure 8. Streamlines and ![]() $|\boldsymbol {u}|$ (colour map from blue to red identifies increasing fluid speed) for pressure-driven flow through a simple-square array of highly permeable cylindrical inclusions in a low-permeability, continuous Brinkman medium:
$|\boldsymbol {u}|$ (colour map from blue to red identifies increasing fluid speed) for pressure-driven flow through a simple-square array of highly permeable cylindrical inclusions in a low-permeability, continuous Brinkman medium: ![]() $\phi = {\rm \pi}/ 2.005^2 \approx 0.7815$,
$\phi = {\rm \pi}/ 2.005^2 \approx 0.7815$, ![]() $\beta = 256$,
$\beta = 256$, ![]() $\beta _c = 1/100$.
$\beta _c = 1/100$.
Finite-element meshes for the simple-square arrays above were explicitly refined in the interfacial regions. In general, calculations in the dilute- and close-packing limits were most demanding. Inadequately refined meshes in the dilute limit failed to produce convergence, or converged to an ostensibly incorrect solution. Bounds on the element sizes, particularly in the interfacial regions, were prescribed according to the specific values of ![]() $\beta$ and
$\beta$ and ![]() $a / L$. Accuracy was assessed by ensuring that numerical results were invariant to at least three significant figures upon doubling the mesh resolution. Numerical integration to furnish the volume-averaged velocity underlying the permeability calculations was undertaken using standard integration functions within the COMSOL finite-element framework. It was necessary to adopt linear basis functions for the pressure to mitigate spurious, large-amplitude spatial oscillations at the mesh length scale.
$a / L$. Accuracy was assessed by ensuring that numerical results were invariant to at least three significant figures upon doubling the mesh resolution. Numerical integration to furnish the volume-averaged velocity underlying the permeability calculations was undertaken using standard integration functions within the COMSOL finite-element framework. It was necessary to adopt linear basis functions for the pressure to mitigate spurious, large-amplitude spatial oscillations at the mesh length scale.
3.1. Random arrays
To address hydrodynamic interactions in more detail, computations of flows in simple-square arrays of cylindrical inclusions and ensembles of their periodic, non-overlapping random counterparts were undertaken. Ensembles with cylinder area fractions ![]() $\phi \lesssim 0.55$ were generated using a random-insertion Monte–Carlo algorithm with periodic boundary conditions and hard-sphere interaction potential. A summary of these computations with statistical hypothesis tests against theoretical formulas and computations for their periodic, ordered counterparts is provided in table 1. The random-insertion approach fails at higher area fractions, since the probability of accepting trail insertions becomes vanishing small. This motivates the swelling and displacement trials undertaken in a code provided by Dr A. Zinchenko (modified from its three-dimensional counterpart of Zinchenko & Davis (Reference Zinchenko and Davis2008)) applied here for the ensemble with
$\phi \lesssim 0.55$ were generated using a random-insertion Monte–Carlo algorithm with periodic boundary conditions and hard-sphere interaction potential. A summary of these computations with statistical hypothesis tests against theoretical formulas and computations for their periodic, ordered counterparts is provided in table 1. The random-insertion approach fails at higher area fractions, since the probability of accepting trail insertions becomes vanishing small. This motivates the swelling and displacement trials undertaken in a code provided by Dr A. Zinchenko (modified from its three-dimensional counterpart of Zinchenko & Davis (Reference Zinchenko and Davis2008)) applied here for the ensemble with ![]() $\phi \approx 0.621$.
$\phi \approx 0.621$.
Table 1. Statistical analysis of the average fluid velocity ![]() $\langle u_x \rangle$ (scaled with
$\langle u_x \rangle$ (scaled with ![]() $-P a^2 / \eta$) in ordered (simple square, SS) and random arrays (square periodic unit cell, size
$-P a^2 / \eta$) in ordered (simple square, SS) and random arrays (square periodic unit cell, size ![]() $L$,
$L$, ![]() $N$ cylindrical inclusions) with inclusion area fraction
$N$ cylindrical inclusions) with inclusion area fraction ![]() $\phi$: ensemble mean (m), ensemble standard deviation (s.d.), Student's
$\phi$: ensemble mean (m), ensemble standard deviation (s.d.), Student's ![]() $t$ distribution
$t$ distribution ![]() $95$% confidence interval (c.i.) for
$95$% confidence interval (c.i.) for ![]() $\nu = n - 1$ degrees of freedom;
$\nu = n - 1$ degrees of freedom; ![]() $p$-values in parentheses reference the null hypothesis that the ensemble mean equals the SS or dilute-theory counterpart.
$p$-values in parentheses reference the null hypothesis that the ensemble mean equals the SS or dilute-theory counterpart.

To mitigate periodic artefacts, square domains containing ![]() $N = 16$ cylinders with area fractions in the range
$N = 16$ cylinders with area fractions in the range ![]() $\phi = N {\rm \pi}(a/L)^2 \approx 0.104$–
$\phi = N {\rm \pi}(a/L)^2 \approx 0.104$–![]() $0.621$ were adopted to target a domain size
$0.621$ were adopted to target a domain size ![]() $L \approx 4$ times the characteristic cylinder separation
$L \approx 4$ times the characteristic cylinder separation ![]() $a \sqrt {{\rm \pi} / \phi }$. For reference, in their Stokesian-dynamics inspired calculations of the effective conductivity of random suspensions of spherical particles, Bonnecaze & Brady (Reference Bonnecaze and Brady1990) reported that
$a \sqrt {{\rm \pi} / \phi }$. For reference, in their Stokesian-dynamics inspired calculations of the effective conductivity of random suspensions of spherical particles, Bonnecaze & Brady (Reference Bonnecaze and Brady1990) reported that ![]() $N = 20$ spheres (in a cubic domain) were required (at a volume fraction
$N = 20$ spheres (in a cubic domain) were required (at a volume fraction ![]() $\phi = 0.4$) to furnish domain-size-independent results; this corresponds to a domain size
$\phi = 0.4$) to furnish domain-size-independent results; this corresponds to a domain size ![]() $L$ that is only approximately
$L$ that is only approximately ![]() $20^{1/3} \approx 2.7$ times the characteristic sphere separation
$20^{1/3} \approx 2.7$ times the characteristic sphere separation ![]() $a [4 {\rm \pi}/ (3 \phi )]^{1/3}$. Representative flows are shown in figure 9 for highly permeable inclusions (
$a [4 {\rm \pi}/ (3 \phi )]^{1/3}$. Representative flows are shown in figure 9 for highly permeable inclusions (![]() $\beta _c = a / \ell _c = 1/10$) in a low-permeability continuous phase (
$\beta _c = a / \ell _c = 1/10$) in a low-permeability continuous phase (![]() $\beta = a / \ell = 10$) with
$\beta = a / \ell = 10$) with ![]() $\eta _c = \eta$. These highlight an increasing propensity of the flow with increasing inclusion concentration to connect inclusions in the principal flow direction (co-linear with
$\eta _c = \eta$. These highlight an increasing propensity of the flow with increasing inclusion concentration to connect inclusions in the principal flow direction (co-linear with ![]() $\boldsymbol {P}$ along the
$\boldsymbol {P}$ along the ![]() $x$-axis).
$x$-axis).
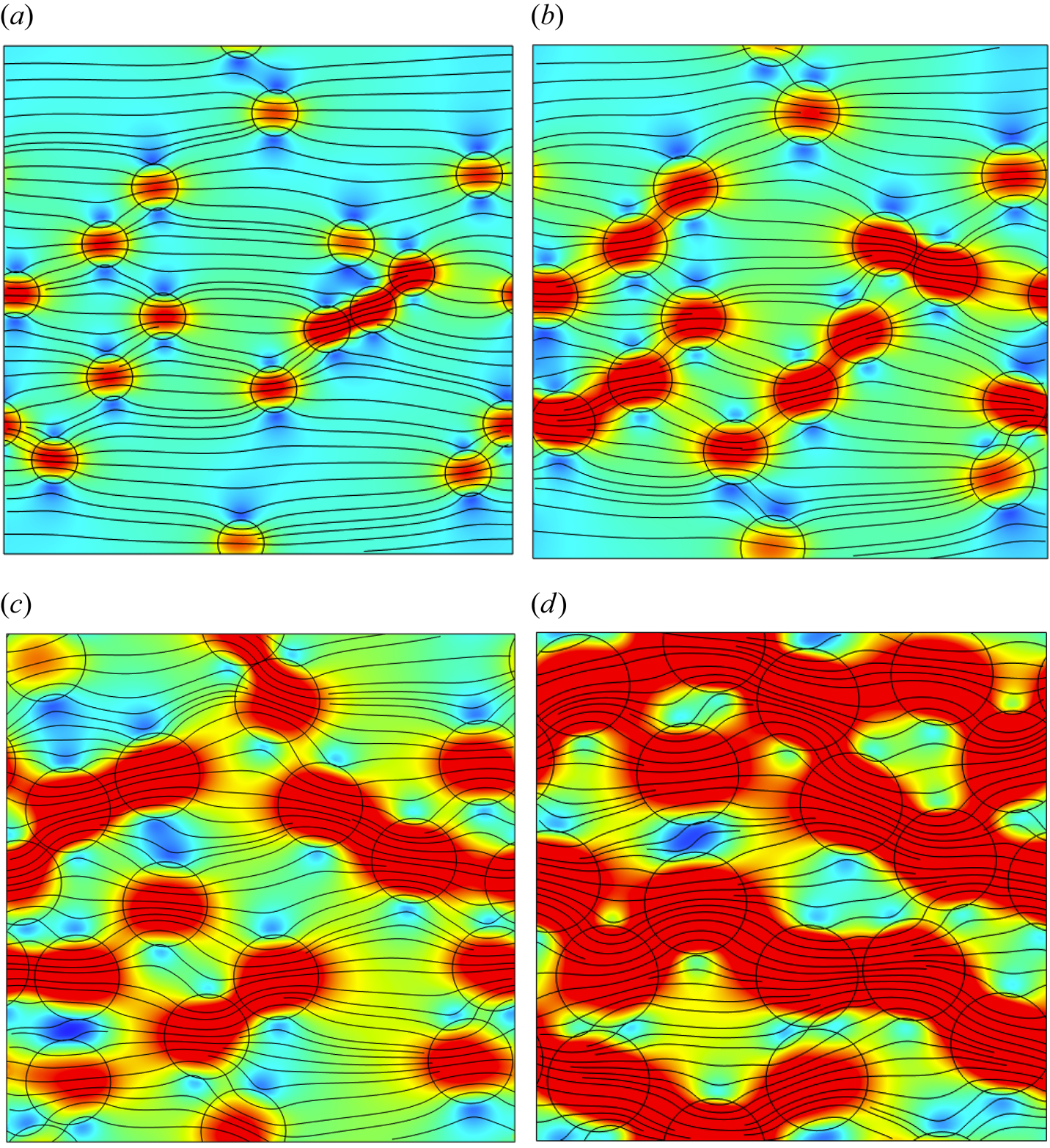
Figure 9. Streamlines and ![]() $|\boldsymbol {u}|$ (colour map from blue to red identifies increasing fluid speed) for pressure-driven flow through periodic, random arrays of highly permeable cylindrical inclusions in low-permeability, continuous Brinkman media:
$|\boldsymbol {u}|$ (colour map from blue to red identifies increasing fluid speed) for pressure-driven flow through periodic, random arrays of highly permeable cylindrical inclusions in low-permeability, continuous Brinkman media: ![]() $\beta = a / \ell = 10$,
$\beta = a / \ell = 10$, ![]() $\beta _c = a / \ell _c = 1 / 10$ (Darcy-like flow in the continuous phase);
$\beta _c = a / \ell _c = 1 / 10$ (Darcy-like flow in the continuous phase); ![]() $\phi \approx 0.104$ (a),
$\phi \approx 0.104$ (a), ![]() $0.196$ (b),
$0.196$ (b), ![]() $0.349$ (c) and
$0.349$ (c) and ![]() $0.503$ (d).
$0.503$ (d).
The statistical hypothesis testing in table 1 indicates negligible differences (![]() $p \gtrsim 0.05$) between the permeabilities for ordered arrays and their random counterparts, as might be expected based on differences between the self-consistent random and simple-square Rayleigh formulas being
$p \gtrsim 0.05$) between the permeabilities for ordered arrays and their random counterparts, as might be expected based on differences between the self-consistent random and simple-square Rayleigh formulas being ![]() $O(\phi ^5)$. On the other hand, there are significant differences (
$O(\phi ^5)$. On the other hand, there are significant differences (![]() $p \lesssim 0.05$) revealed between the computations for random arrays and the dilute theory. Note that this does not reflect a failure of the dilute theory, but is rather evidence of the statistical testing being able to discriminate
$p \lesssim 0.05$) revealed between the computations for random arrays and the dilute theory. Note that this does not reflect a failure of the dilute theory, but is rather evidence of the statistical testing being able to discriminate ![]() $O(\phi ^2)$ differences between the computations and
$O(\phi ^2)$ differences between the computations and ![]() $O(\phi )$ dilute theory.
$O(\phi )$ dilute theory.
The ensemble-averaged fluid velocity (scaled with the Darcy velocity ![]() $- P \ell ^2 / \eta$) is plotted as a function of the cylinder area fraction in figure 11(a) (circles). Error bars are the Student's
$- P \ell ^2 / \eta$) is plotted as a function of the cylinder area fraction in figure 11(a) (circles). Error bars are the Student's ![]() $t$ distribution 95 % confidence interval on each estimate of the ensemble mean from
$t$ distribution 95 % confidence interval on each estimate of the ensemble mean from ![]() $n = 3$ random configurations. The notably larger fluctuations when
$n = 3$ random configurations. The notably larger fluctuations when ![]() $\phi \gtrsim 0.3$ appear to reflect channelling (through the network of permeable inclusions), percolating the periodic unit cells. These fluctuations are much weaker when there is smaller permeability contrast, as demonstrated by the cases in panels (b,c). When the inclusion permeability is low, there are notably larger fluctuations at intermediate area fractions, as demonstrated in panel (d) with
$\phi \gtrsim 0.3$ appear to reflect channelling (through the network of permeable inclusions), percolating the periodic unit cells. These fluctuations are much weaker when there is smaller permeability contrast, as demonstrated by the cases in panels (b,c). When the inclusion permeability is low, there are notably larger fluctuations at intermediate area fractions, as demonstrated in panel (d) with ![]() $\beta _c = 100$. As revealed in figure 10, this reflects tortuous channelling through the continuous phase, as highlighted in panel (c) with
$\beta _c = 100$. As revealed in figure 10, this reflects tortuous channelling through the continuous phase, as highlighted in panel (c) with ![]() $\phi \approx 0.349$.
$\phi \approx 0.349$.

Figure 10. The same as figure 9 but with ![]() $\beta = a / \ell = 10$,
$\beta = a / \ell = 10$, ![]() $\beta _c = a / \ell _c = 100$ (Darcy-like flow in the continuous and discrete phases). Here,
$\beta _c = a / \ell _c = 100$ (Darcy-like flow in the continuous and discrete phases). Here, ![]() $\phi \approx 0.104$ (a),
$\phi \approx 0.104$ (a), ![]() $0.196$ (b),
$0.196$ (b), ![]() $0.349$ (c) and
$0.349$ (c) and ![]() $0.503$ (d).
$0.503$ (d).
Figure 11(a) demonstrates that the effective permeabilities for media with ![]() $\ell / a = 0.1 \ll 1$ are well approximated by the self-consistent Rayleigh model (blue line) for which the reduced effective scalar diffusivity
$\ell / a = 0.1 \ll 1$ are well approximated by the self-consistent Rayleigh model (blue line) for which the reduced effective scalar diffusivity ![]() $D_e / D$ is readily modified to furnish a reduced effective permeability
$D_e / D$ is readily modified to furnish a reduced effective permeability
where
is the conductivity/diffusivity ratio modified for Darcy hydrodynamics. Recall, the analogy between Darcy flow and scalar diffusion reflects the mass and tracer fluxes being proportional to gradients of pressure and concentration, respectively.

Figure 11. Average streamwise component of the velocity (scaled with ![]() $-P \ell ^2 / \eta$) in simple-square (squares) and random (circles) arrays vs the cylindrical-inclusion area fraction: (a)
$-P \ell ^2 / \eta$) in simple-square (squares) and random (circles) arrays vs the cylindrical-inclusion area fraction: (a) ![]() $\beta = a / \ell = 10$,
$\beta = a / \ell = 10$, ![]() $\beta _c = a / \ell _c = 1 / 10$; (b)
$\beta _c = a / \ell _c = 1 / 10$; (b) ![]() $\beta = a / \ell = 2$,
$\beta = a / \ell = 2$, ![]() $\beta _c = a / \ell _c = 1 / 10$; (c)
$\beta _c = a / \ell _c = 1 / 10$; (c) ![]() $\beta = a / \ell = 2$,
$\beta = a / \ell = 2$, ![]() $\beta _c = a / \ell _c = 1 / 2$; (d)
$\beta _c = a / \ell _c = 1 / 2$; (d) ![]() $\beta = a / \ell = 10$,
$\beta = a / \ell = 10$, ![]() $\beta _c = a / \ell _c = 100$. Error bars identify the Student's
$\beta _c = a / \ell _c = 100$. Error bars identify the Student's ![]() $t$ distribution 95 % confidence interval on each estimate of the ensemble mean (see table 1). Red lines are Rayleigh formulas evaluated with the Darcy permeability ratio equation (3.10); blue lines are the Rayleigh formulas evaluated with an effective permeability ratio according to (3.11). Black lines are the dilute Brinkman theory equation (2.21).
$t$ distribution 95 % confidence interval on each estimate of the ensemble mean (see table 1). Red lines are Rayleigh formulas evaluated with the Darcy permeability ratio equation (3.10); blue lines are the Rayleigh formulas evaluated with an effective permeability ratio according to (3.11). Black lines are the dilute Brinkman theory equation (2.21).
The lines referenced in figure 11 with the descriptor ‘Brinkman’ are calculated by enforcing an equality of the dilute limits (![]() $\phi \rightarrow 0$) for the effective hydrodynamic (‘Brinkman’, (2.21)) and conduction/diffusion (‘Rayleigh’, (3.9)) theories, thus furnishing
$\phi \rightarrow 0$) for the effective hydrodynamic (‘Brinkman’, (2.21)) and conduction/diffusion (‘Rayleigh’, (3.9)) theories, thus furnishing
Figure 11 also shows Rayleigh's calculation of the effective conductivity/diffusivity for square arrays, as reported in Bird et al. (Reference Bird, Stewart and Lightfoot2002, (9.6-4)), here with ![]() $\alpha = (\ell _c / \ell )^2$ (‘Rayleigh’) and according to (3.11) (‘Brinkman’). As expected,
$\alpha = (\ell _c / \ell )^2$ (‘Rayleigh’) and according to (3.11) (‘Brinkman’). As expected, ![]() $\alpha = (\ell _c / \ell )^2$ furnishes a reasonable approximation when flow in the continuous phase may be approximated as Darcy flow, i.e.
$\alpha = (\ell _c / \ell )^2$ furnishes a reasonable approximation when flow in the continuous phase may be approximated as Darcy flow, i.e. ![]() $\beta = a / \ell \gg 1$, as illustrated in figure 11(a) and the respective flows in figure 9. Panels (b,c) demonstrate a breakdown of the scalar-diffusion analogy. Here, the self-consistent and square-array formulas based on (3.11) are much improved over their (‘Darcy’ flow) counterparts with
$\beta = a / \ell \gg 1$, as illustrated in figure 11(a) and the respective flows in figure 9. Panels (b,c) demonstrate a breakdown of the scalar-diffusion analogy. Here, the self-consistent and square-array formulas based on (3.11) are much improved over their (‘Darcy’ flow) counterparts with ![]() $\alpha = (\ell _c / \ell )^2$, but still depart significantly from the computations when
$\alpha = (\ell _c / \ell )^2$, but still depart significantly from the computations when ![]() $\phi \gtrsim 0.1$. As already noted, the differences between the computations for ordered and random arrays are qualitatively similar to those between the Rayleigh formulas for simple-square and random arrays. This echoes inferences above that Brinkman screening of the hydrodynamic interactions (when
$\phi \gtrsim 0.1$. As already noted, the differences between the computations for ordered and random arrays are qualitatively similar to those between the Rayleigh formulas for simple-square and random arrays. This echoes inferences above that Brinkman screening of the hydrodynamic interactions (when ![]() $\beta = a / \ell \gg 1$ and
$\beta = a / \ell \gg 1$ and ![]() $\phi \lesssim 0.3$) makes the effective hydrodynamic permeability relatively insensitive to microstructural order, perhaps also explaining why the confidence intervals in table 1 and figure 9 are generally small.
$\phi \lesssim 0.3$) makes the effective hydrodynamic permeability relatively insensitive to microstructural order, perhaps also explaining why the confidence intervals in table 1 and figure 9 are generally small.
Finally, figure 12 shows flows in a dilute (![]() $\phi \approx 0.104$) random array, computed with four combinations (cases a–d) of shear viscosities and uniform permeability, i.e.
$\phi \approx 0.104$) random array, computed with four combinations (cases a–d) of shear viscosities and uniform permeability, i.e. ![]() $\ell = \ell _c$, as detailed in the caption. Here, the non-uniform fluid viscosity imparts notable fluid-velocity fluctuations, some statistics of which are compared in figure 13. Note that it is not presently clear if or how such model predictions – in this perhaps obscure region of the parameter space – should be applied to physical systems. Nevertheless, the fluid velocity and its fluctuations might inform, e.g., on the initial stage of displacing a dispersed/segregated fluid through a uniform porous medium. Circular domains must serve as two-dimensional approximations of spherical drops or bubbles having a low/vanishing surface tension, or as Hele-Shaw flow with appropriate prescription of the shear viscosities and permeabilities (Batchelor Reference Batchelor1967). Note that the drops or bubbles in this context are envisioned to wet/permeate the porous medium in the same manner as the continuous phase, thus demanding
$\ell = \ell _c$, as detailed in the caption. Here, the non-uniform fluid viscosity imparts notable fluid-velocity fluctuations, some statistics of which are compared in figure 13. Note that it is not presently clear if or how such model predictions – in this perhaps obscure region of the parameter space – should be applied to physical systems. Nevertheless, the fluid velocity and its fluctuations might inform, e.g., on the initial stage of displacing a dispersed/segregated fluid through a uniform porous medium. Circular domains must serve as two-dimensional approximations of spherical drops or bubbles having a low/vanishing surface tension, or as Hele-Shaw flow with appropriate prescription of the shear viscosities and permeabilities (Batchelor Reference Batchelor1967). Note that the drops or bubbles in this context are envisioned to wet/permeate the porous medium in the same manner as the continuous phase, thus demanding ![]() $a \gtrsim \ell$, i.e.
$a \gtrsim \ell$, i.e. ![]() $\beta _c = \beta \gtrsim 1$, as might be achieved by micro- or macro-scale bubbles or drops in a hydrogel (Haudin et al. Reference Haudin, Noblin, Bouret, Argentina and Raufaste2016). Circular and spherical phases are expected from nucleation and growth, upon which a pressure gradient may initiate flow, thus inducing translation and deformation. If such a flow were sufficiently slow, then the velocity fields from the Brinkman model might be considered quasi-static snapshots of the dispersed phase translating through the porous medium. The contrasting viscosities then control the relative velocity of the discrete and continuous phases, inducing hydrodynamic dispersion. The underlying forces and velocities may also inform how susceptible the dispersed phase is to flow-induced deformation and dispersion.
$\beta _c = \beta \gtrsim 1$, as might be achieved by micro- or macro-scale bubbles or drops in a hydrogel (Haudin et al. Reference Haudin, Noblin, Bouret, Argentina and Raufaste2016). Circular and spherical phases are expected from nucleation and growth, upon which a pressure gradient may initiate flow, thus inducing translation and deformation. If such a flow were sufficiently slow, then the velocity fields from the Brinkman model might be considered quasi-static snapshots of the dispersed phase translating through the porous medium. The contrasting viscosities then control the relative velocity of the discrete and continuous phases, inducing hydrodynamic dispersion. The underlying forces and velocities may also inform how susceptible the dispersed phase is to flow-induced deformation and dispersion.

Figure 12. Streamlines and ![]() $|\boldsymbol {u}|$ (colour map from blue to red identifies increasing fluid speed) for pressure-driven flow of a dilute (
$|\boldsymbol {u}|$ (colour map from blue to red identifies increasing fluid speed) for pressure-driven flow of a dilute (![]() $\phi = 0.104$) random array of cylindrical inclusions with shear-viscosity contrast in uniform Brinkman media: (a)
$\phi = 0.104$) random array of cylindrical inclusions with shear-viscosity contrast in uniform Brinkman media: (a) ![]() $\eta _c / \eta = 0.1$,
$\eta _c / \eta = 0.1$, ![]() $\beta _c = \beta = 10$; (b)
$\beta _c = \beta = 10$; (b) ![]() $\eta _c / \eta = 10$,
$\eta _c / \eta = 10$, ![]() $\beta _c = \beta = 10$; (c)
$\beta _c = \beta = 10$; (c) ![]() $\eta _c / \eta = 0.1$,
$\eta _c / \eta = 0.1$, ![]() $\beta _c = \beta = 1$; (d)
$\beta _c = \beta = 1$; (d) ![]() $\eta _c / \eta = 10$,
$\eta _c / \eta = 10$, ![]() $\beta _c = \beta = 1$. Statistics from these flows are summarized in figure 13.
$\beta _c = \beta = 1$. Statistics from these flows are summarized in figure 13.

Figure 13. Statistics of the streamwise velocity (scaled with ![]() $-P \ell ^2 / \eta$) for pressure-driven flow of a dilute (
$-P \ell ^2 / \eta$) for pressure-driven flow of a dilute (![]() $\phi = 0.104$) random array of cylindrical inclusions with shear-viscosity contrast in uniform Brinkman media. Parameters: (a)
$\phi = 0.104$) random array of cylindrical inclusions with shear-viscosity contrast in uniform Brinkman media. Parameters: (a) ![]() $\eta _c / \eta = 0.1$,
$\eta _c / \eta = 0.1$, ![]() $\beta _c = \beta = 10$; (b)
$\beta _c = \beta = 10$; (b) ![]() $\eta _c / \eta = 10$,
$\eta _c / \eta = 10$, ![]() $\beta _c = \beta = 10$; (c)
$\beta _c = \beta = 10$; (c) ![]() $\eta _c / \eta = 0.1$,
$\eta _c / \eta = 0.1$, ![]() $\beta _c = \beta = 1$; (d)
$\beta _c = \beta = 1$; (d) ![]() $\eta _c / \eta = 10$,
$\eta _c / \eta = 10$, ![]() $\beta _c = \beta = 1$. Here,
$\beta _c = \beta = 1$. Here, ![]() $\langle {\cdot } \rangle$ and
$\langle {\cdot } \rangle$ and ![]() $\langle {\cdot } \rangle _c$ denote area averages over the entire domain and over the cylinder/discrete phase, respectively.
$\langle {\cdot } \rangle _c$ denote area averages over the entire domain and over the cylinder/discrete phase, respectively.
Note that the average velocities ![]() $\langle u_x \rangle$ in figure 13 are scaled with the continuous-phase Darcy velocity (
$\langle u_x \rangle$ in figure 13 are scaled with the continuous-phase Darcy velocity (![]() $- P \ell ^2 / \eta$), the magnitude of which varies considerably with the large changes in the permeability (
$- P \ell ^2 / \eta$), the magnitude of which varies considerably with the large changes in the permeability (![]() $\beta ^2 = \beta _c^2 = 10^2$ and
$\beta ^2 = \beta _c^2 = 10^2$ and ![]() $1$). The averaged streamwise velocities from the direct computations (blue bars) are in good agreement with the dilute Brinkman theory (2.21) (red bars), as to be expected based on the low dispersed-phase area fraction. The average velocity of the dispersed phase relative to the medium average
$1$). The averaged streamwise velocities from the direct computations (blue bars) are in good agreement with the dilute Brinkman theory (2.21) (red bars), as to be expected based on the low dispersed-phase area fraction. The average velocity of the dispersed phase relative to the medium average ![]() $\langle u_x \rangle _c - \langle u_x \rangle$ (orange bars) has a direction/sign and magnitude that varies considerably with the shear-viscosity contrast and medium permeability; low permeability (cases a,b) clearly accentuates the magnitudes, which are significant. As expected from the flows visualized in figure 12, the (root mean squared) velocity fluctuations within the medium as a whole (violet) have respectable magnitudes. Further analysis, perhaps in a three-dimensional context with consideration of interfacial tension, should be undertaken in a future study.
$\langle u_x \rangle _c - \langle u_x \rangle$ (orange bars) has a direction/sign and magnitude that varies considerably with the shear-viscosity contrast and medium permeability; low permeability (cases a,b) clearly accentuates the magnitudes, which are significant. As expected from the flows visualized in figure 12, the (root mean squared) velocity fluctuations within the medium as a whole (violet) have respectable magnitudes. Further analysis, perhaps in a three-dimensional context with consideration of interfacial tension, should be undertaken in a future study.
4. Summary
The momentum averaging proposed by Hill (Reference Hill2022) for pressure- and electric-field-driven flows in electrolyte-saturated cavity-doped hydrogels has been tested in a two-dimensional hydrodynamic computational framework. Whereas Hill's theory for spherical inclusions furnished a pre-factor of the pressure dipole equal to ![]() $3$ for spherical inclusions, by a similar analytical calculation, this factor was shown to be
$3$ for spherical inclusions, by a similar analytical calculation, this factor was shown to be ![]() $2$ for cylindrical inclusions (two-dimensional counterpart). The analytical averaging of the momentum in two dimensions was verified by comparison with direct numerical calculations of the flow in periodic unit cells when the cavity area fraction
$2$ for cylindrical inclusions (two-dimensional counterpart). The analytical averaging of the momentum in two dimensions was verified by comparison with direct numerical calculations of the flow in periodic unit cells when the cavity area fraction ![]() $\phi \ll 1$. Such comparisons identified the parameter space (
$\phi \ll 1$. Such comparisons identified the parameter space (![]() $\phi, \beta _c = a / \ell _c, \beta = a/ \ell$) in which the analytical averaging breaks down due to hydrodynamic interactions at finite cavity area fractions. However, even for highly permeable inclusions (
$\phi, \beta _c = a / \ell _c, \beta = a/ \ell$) in which the analytical averaging breaks down due to hydrodynamic interactions at finite cavity area fractions. However, even for highly permeable inclusions (![]() $\beta _c \ll 1$) with continuous-phase permeabilities that are representative of real porous solids (
$\beta _c \ll 1$) with continuous-phase permeabilities that are representative of real porous solids (![]() $\beta \gg 1$), the hydrodynamic interactions are weak due to Brinkman screening, so the analytical theory (for two dimensions, and, by inference/speculation, for the three-dimensional counterpart) provides a reasonable approximation of the effective permeability when
$\beta \gg 1$), the hydrodynamic interactions are weak due to Brinkman screening, so the analytical theory (for two dimensions, and, by inference/speculation, for the three-dimensional counterpart) provides a reasonable approximation of the effective permeability when ![]() $\phi \lesssim 0.3$ and
$\phi \lesssim 0.3$ and ![]() $\beta \gtrsim 1$. Computations were undertaken for random ensembles, systematically varying the inclusion area fraction, comparing with computations for ordered arrays and Rayleigh's self-consistent approximation evaluated using the single-inclusion disturbances for Darcy and Brinkman flows. The self-consistent Rayleigh approximations based on the Brinkman disturbance improved correspondence with computations, but still failed to adequately capture the hydrodynamic interactions when
$\beta \gtrsim 1$. Computations were undertaken for random ensembles, systematically varying the inclusion area fraction, comparing with computations for ordered arrays and Rayleigh's self-consistent approximation evaluated using the single-inclusion disturbances for Darcy and Brinkman flows. The self-consistent Rayleigh approximations based on the Brinkman disturbance improved correspondence with computations, but still failed to adequately capture the hydrodynamic interactions when ![]() $\beta = a / \ell \lesssim 10$ and
$\beta = a / \ell \lesssim 10$ and ![]() $\phi \gtrsim 0.3$. The random velocity fields arising from shear-viscosity contrast in Brinkman media with uniform permeability
$\phi \gtrsim 0.3$. The random velocity fields arising from shear-viscosity contrast in Brinkman media with uniform permeability ![]() $\ell ^2$ were considered very briefly. These might inspire future studies of dispersion in three dimensions, accounting for interfacial tension between the phases with contrasting viscosity. The present study, which was conducted in a purely hydrodynamic context, sets the stage for computations of electrokinetic transport in such media (structured polyelectrolytes). These will be reported elsewhere in the context of ion conduction, as probed experimentally, and interpreted empirically, using impedance spectroscopy at frequencies into the megahertz range.
$\ell ^2$ were considered very briefly. These might inspire future studies of dispersion in three dimensions, accounting for interfacial tension between the phases with contrasting viscosity. The present study, which was conducted in a purely hydrodynamic context, sets the stage for computations of electrokinetic transport in such media (structured polyelectrolytes). These will be reported elsewhere in the context of ion conduction, as probed experimentally, and interpreted empirically, using impedance spectroscopy at frequencies into the megahertz range.
Funding
Financial support from an NSERC Discovery Grant is gratefully acknowledged. The author is grateful to Dr A. Zinchenko (University of Colorado, Boulder) for providing the Monte Carlo code for dense cylinder packings, and to several anonymous referees for constructive suggestions on improving the manuscript.
Declaration of interests
The author reports no conflict of interest.