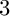1 Introduction
Cluster algebras, introduced by Fomin and Zelevinsky [Reference Fomin and Zelevinsky19], are combinatorially defined algebras with applications to many areas of mathematics, and have been the subject of intense study (see [Reference Keller33] for a survey of connections between cluster algebras and the representation theory of associative algebras, and the references therein for applications to other fields).
A cluster algebra is typically defined using a generating set of cluster variables, which is constructed iteratively from the data of an initial seed via a process of mutation. Here, we consider cluster algebras of geometric type coming from quivers (equivalently, skew-symmetric matrices), so that a seed is given by the data of a quiver together with a collection of rational functions (which are some of the aforementioned cluster variables) in bijection with its vertices. Mutating at one of the quiver vertices modifies the quiver according to Fomin–Zelevinsky’s mutation rule (see, e.g., [Reference Keller33, §3.2]) and exchanges the cluster variable attached to this vertex for a new one. A subset of the quiver vertices may be frozen (giving the quiver the structure of an ice quiver; see Definition 2.1), indicating that mutation at these vertices is not permitted, and thus the corresponding cluster variables, also called frozen, appear in every seed.
Categorification provides an effective tool for studying this combinatorics via the representation theory of quivers. Cluster algebras without frozen variables have been successfully categorified in large generality, beginning with Buan–Marsh–Reineke–Reiten–Todorov’s construction [Reference Buan, Marsh, Reineke, Reiten and Todorov10] of cluster categories of acyclic quivers, later generalized by Amiot [Reference Amiot1] to allow for the existence of cycles. In these categories, certain maximal rigid objects, called cluster-tilting objects, play the role of seeds—in particular, they can be mutated at their indecomposable summands [Reference Iyama and Yoshino31]. Cluster algebras categorified in this way have seeds in bijection with cluster-tilting objects (within a fixed mutation class) in the category, and cluster variables in bijection with indecomposable rigid objects (appearing as indecomposable summands of cluster-tilting objects in the fixed mutation class). Cluster categories of acyclic quivers have only a single mutation class of cluster-tilting objects (see [Reference Buan, Marsh, Reiten and Todorov11, Th. A.1]), and so the caveats in the preceding sentence may be dropped.
These results have led to clean, conceptual proofs of many key statements for those cluster algebras without frozen variables admitting such a categorification, including cluster determines seed [Reference Buan, Marsh, Reiten and Todorov11], linear independence of cluster monomials [Reference Cerulli Irelli, Keller, Labardini-Fragoso and Plamondon14], sign coherence of c-vectors [Reference Speyer and Thomas49], and so on. However, most cluster algebras appearing in nature, such as the cluster structures on the coordinate rings of partial flag varieties [Reference Geiß, Leclerc and Schröer24], their double Bruhat cells [Reference Berenstein, Fomin and Zelevinsky4], and Grassmannian positroid strata [Reference Galashin and Lam23], do have frozen variables, which we would also like to capture in a categorification.
This has been achieved for a number of families of cluster algebras [Reference Demonet and Iyama16], [Reference Demonet and Luo17], [Reference Geiß, Leclerc and Schröer24], [Reference Jensen, King and Su32], [Reference Nájera Chávez39] using suitable stably
![]() $2$
-Calabi–Yau Frobenius categories in place of the
$2$
-Calabi–Yau Frobenius categories in place of the
![]() $2$
-Calabi–Yau triangulated cluster categories appearing in the case of no frozen variables. A Frobenius category is, by definition, an exact category with enough projective objects and enough injective objects, such that these two classes of objects coincide. It is the indecomposable projective–injective objects, which necessarily appear as summands of any cluster-tilting object, that will correspond to the frozen variables. The fact that specializing all frozen variables to
$2$
-Calabi–Yau triangulated cluster categories appearing in the case of no frozen variables. A Frobenius category is, by definition, an exact category with enough projective objects and enough injective objects, such that these two classes of objects coincide. It is the indecomposable projective–injective objects, which necessarily appear as summands of any cluster-tilting object, that will correspond to the frozen variables. The fact that specializing all frozen variables to
![]() $1$
in a cluster algebra produces a new cluster algebra without frozen variables (which we call the principal part) corresponds to the fact that the stable category of a Frobenius category, defined as the quotient by the ideal of morphisms factoring through a projective object (so that these objects are isomorphic to the zero object in the quotient), is a triangulated category (see [Reference Happel29, §I.2]). We require this stable category to be
$1$
in a cluster algebra produces a new cluster algebra without frozen variables (which we call the principal part) corresponds to the fact that the stable category of a Frobenius category, defined as the quotient by the ideal of morphisms factoring through a projective object (so that these objects are isomorphic to the zero object in the quotient), is a triangulated category (see [Reference Happel29, §I.2]). We require this stable category to be
![]() $2$
-Calabi–Yau so that cluster-tilting objects may be mutated in the appropriate way.
$2$
-Calabi–Yau so that cluster-tilting objects may be mutated in the appropriate way.
In this paper, we will primarily consider the cluster algebra
![]() $\widetilde {\mathscr {A}}_{Q}$
with polarized principal coefficients associated with a quiver Q. We define this cluster algebra precisely in §2, but for now note that each of its seeds has
$\widetilde {\mathscr {A}}_{Q}$
with polarized principal coefficients associated with a quiver Q. We define this cluster algebra precisely in §2, but for now note that each of its seeds has
![]() $3n$
cluster variables, of which
$3n$
cluster variables, of which
![]() $2n$
are frozen, when Q has n vertices. Specializing half of these frozen variables to
$2n$
are frozen, when Q has n vertices. Specializing half of these frozen variables to
![]() $1$
, we obtain the principal coefficient cluster algebra
$1$
, we obtain the principal coefficient cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
attached to Q by Fomin–Zelevinsky. They used this cluster algebra to study the combinatorics of other cluster algebras having the same principal part; for example, their expansion formula [Reference Fomin and Zelevinsky20, Cor. 6.3] for cluster variables in such a cluster algebra involves F-polynomials, defined as specializations of cluster variables in
$\mathscr {A}_{Q}^{\bullet }$
attached to Q by Fomin–Zelevinsky. They used this cluster algebra to study the combinatorics of other cluster algebras having the same principal part; for example, their expansion formula [Reference Fomin and Zelevinsky20, Cor. 6.3] for cluster variables in such a cluster algebra involves F-polynomials, defined as specializations of cluster variables in
![]() $\mathscr {A}_{Q}^{\bullet }$
[Reference Fomin and Zelevinsky20, (3.3)], and hence also obtained as specializations of cluster variables in
$\mathscr {A}_{Q}^{\bullet }$
[Reference Fomin and Zelevinsky20, (3.3)], and hence also obtained as specializations of cluster variables in
![]() $\widetilde {\mathscr {A}}_{Q}$
. Many of the results of Gross–Hacking–Keel–Kontsevich [Reference Gross, Hacking, Keel and Kontsevich28] on canonical bases are proved by first reducing to the case of principal coefficients. Further applications of principal coefficient cluster algebras include Lee–Schiffler’s realization [Reference Lee and Schiffler38] of Jones polynomials of
$\widetilde {\mathscr {A}}_{Q}$
. Many of the results of Gross–Hacking–Keel–Kontsevich [Reference Gross, Hacking, Keel and Kontsevich28] on canonical bases are proved by first reducing to the case of principal coefficients. Further applications of principal coefficient cluster algebras include Lee–Schiffler’s realization [Reference Lee and Schiffler38] of Jones polynomials of
![]() $2$
-bridge links as specializations of their cluster variables. The polarized principal coefficient cluster algebra
$2$
-bridge links as specializations of their cluster variables. The polarized principal coefficient cluster algebra
![]() $\widetilde {\mathscr {A}}_{Q}$
, in the case that Q is a Dynkin quiver, has itself appeared in recent work of Borges and Pierin [Reference Borges and Pierin5], who define a modified cluster character on the ordinary triangulated cluster category of Q, taking values in
$\widetilde {\mathscr {A}}_{Q}$
, in the case that Q is a Dynkin quiver, has itself appeared in recent work of Borges and Pierin [Reference Borges and Pierin5], who define a modified cluster character on the ordinary triangulated cluster category of Q, taking values in
![]() $\widetilde {\mathscr {A}}_{Q}$
. (A more general version of this final result is a consequence of our considerations here, as explained in Remark 9.8.)
$\widetilde {\mathscr {A}}_{Q}$
. (A more general version of this final result is a consequence of our considerations here, as explained in Remark 9.8.)
Our main result is to construct a Frobenius categorification of the cluster algebra
![]() $\widetilde {\mathscr {A}}_{Q}$
in the case that Q is acyclic.
$\widetilde {\mathscr {A}}_{Q}$
in the case that Q is acyclic.
Theorem 1 (Categorification for polarized principal coefficients).
Let Q be an acyclic quiver. Then the category
![]() $\mathcal {E}_Q$
(Definition 5.3):
$\mathcal {E}_Q$
(Definition 5.3):
-
(a) is a Hom-finite Frobenius cluster category (Definition 2.7),
-
(b) has stable category
 $\underline {\mathcal {E}}_Q$
equivalent to the cluster category
$\underline {\mathcal {E}}_Q$
equivalent to the cluster category
 $\mathcal {C}_{Q}$
,
$\mathcal {C}_{Q}$
, -
(c) carries a Fu–Keller cluster character [Reference Fu and Keller21], inducing a bijection between isomorphism classes of indecomposable rigid objects of
 $\mathcal {E}_Q$
and cluster variables of
$\mathcal {E}_Q$
and cluster variables of
 $\widetilde {\mathscr {A}}_{Q}$
, and
$\widetilde {\mathscr {A}}_{Q}$
, and -
(d) the previous bijection induces a further bijection between isomorphism classes of cluster-tilting objects of
 $\mathcal {E}_Q$
and seeds of the polarized principal coefficient cluster algebra
$\mathcal {E}_Q$
and seeds of the polarized principal coefficient cluster algebra
 $\widetilde {\mathscr {A}}_{Q}$
, commuting with mutation, such that the ice quiver of the endomorphism algebraFootnote
1
of each cluster-tilting object agrees, up to arrows between frozen vertices, with the ice quiver of the corresponding seed.
$\widetilde {\mathscr {A}}_{Q}$
, commuting with mutation, such that the ice quiver of the endomorphism algebraFootnote
1
of each cluster-tilting object agrees, up to arrows between frozen vertices, with the ice quiver of the corresponding seed.
In addition to providing categorifications for a new family of cluster algebras, the proof of Theorem 1 demonstrates the effectiveness of a new and general methodology for making such constructions, based on prior work of the author [Reference Pressland42]. Earlier work providing Frobenius categorifications of cluster algebras has typically depended on having some insight into the cluster algebra in its totality, rather than just the data of an initial seed, before constructing the categorification. For example, Geiß–Leclerc–Schröer [Reference Geiß, Leclerc and Schröer24], Demonet–Luo [Reference Demonet and Luo17], Jensen–King–Su [Reference Jensen, King and Su32], and Demonet–Iyama [Reference Demonet and Iyama16] construct Frobenius categorifications for cluster algebra structures on coordinate rings of partial flag varieties by exploiting the fact that these rings are well understood geometrically. The Frobenius categorifications of universal coefficient cluster algebras by Nájera Chávez [Reference Nájera Chávez39] are restricted to finite type, again making the global combinatorics of the cluster algebra (such as its exchange graph and cluster complex) more tractable. By contrast, our approach is more akin to the work of Buan–Marsh–Reineke–Reiten–Todorov [Reference Buan, Marsh, Reineke, Reiten and Todorov10] and Amiot [Reference Amiot1], in which categorifications are constructed from the local data defining the cluster algebra, namely the initial seed (enhanced in Amiot’s case by choosing the extra data of a potential on the quiver).
Indeed, our construction begins with the definition of an algebra A as a particular quotient of the (complete) path algebra of a quiver
![]() $\widetilde {Q}$
agreeing with that of the initial seed of
$\widetilde {Q}$
agreeing with that of the initial seed of
![]() $\widetilde {\mathscr {A}}_{Q}$
up to the addition of arrows between frozen vertices. The algebra A is finite-dimensional and has a strong homological symmetry property—it is bimodule internally
$\widetilde {\mathscr {A}}_{Q}$
up to the addition of arrows between frozen vertices. The algebra A is finite-dimensional and has a strong homological symmetry property—it is bimodule internally
![]() $3$
-Calabi–Yau with respect to the frozen vertices (see [Reference Pressland42, Def. 2.4]). We then construct the category
$3$
-Calabi–Yau with respect to the frozen vertices (see [Reference Pressland42, Def. 2.4]). We then construct the category
![]() $\mathcal {E}_Q$
from A by applying earlier results of the author (see [Reference Pressland42, Ths. 4.1 and 4.10]). The main step in the proof of Theorem 1, taking up §2–5 of the paper, is to define A and show that it satisfies the assumptions of these theorems.
$\mathcal {E}_Q$
from A by applying earlier results of the author (see [Reference Pressland42, Ths. 4.1 and 4.10]). The main step in the proof of Theorem 1, taking up §2–5 of the paper, is to define A and show that it satisfies the assumptions of these theorems.
As a consequence of this approach, we obtain the following surprising result, which is not specific to acyclic quivers, and which we expect to be of independent interest. For the definitions of ordinary and frozen Jacobian algebras, see Definition 2.1.
Theorem 2 (Corollary of Theorem 4.14).
Let
![]() $(Q,W)$
be a quiver with potential, and let
$(Q,W)$
be a quiver with potential, and let
![]() $\underline {A}=J(Q,W)$
be its Jacobian algebra. Then there is a frozen Jacobian algebra
$\underline {A}=J(Q,W)$
be its Jacobian algebra. Then there is a frozen Jacobian algebra
![]() $A=A_{Q,W}$
(Definition 3.1), internally bimodule
$A=A_{Q,W}$
(Definition 3.1), internally bimodule
![]() $3$
-Calabi–Yau with respect to its frozen idempotent e, such that
$3$
-Calabi–Yau with respect to its frozen idempotent e, such that
![]() $\underline {A}=A/\langle e\rangle $
.
$\underline {A}=A/\langle e\rangle $
.
We see this statement as analogous to a result of Van den Bergh [Reference Keller34, Th. A.12], implying that the Jacobian algebra of a quiver with potential may be realized as the zeroth homology of a bimodule
![]() $3$
-Calabi–Yau dg-algebra constructed by Ginzburg [Reference Ginzburg25]. Indeed, the construction of
$3$
-Calabi–Yau dg-algebra constructed by Ginzburg [Reference Ginzburg25]. Indeed, the construction of
![]() $A_{Q,W}$
has some features in common with that of the Ginzburg dg-algebra
$A_{Q,W}$
has some features in common with that of the Ginzburg dg-algebra
![]() $\Gamma _{Q,W}$
of
$\Gamma _{Q,W}$
of
![]() $(Q,W)$
(see Remark 4.16), but at present we do not know a precise recipe for constructing
$(Q,W)$
(see Remark 4.16), but at present we do not know a precise recipe for constructing
![]() $A_{Q,W}$
from
$A_{Q,W}$
from
![]() $\Gamma _{Q,W}$
.
$\Gamma _{Q,W}$
.
It is necessary to pass from the more familiar system of principal coefficients to some larger collection of frozen variables in order for a result like Theorem 1 to be possible, since a Frobenius categorification of the principal coefficient cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
cannot exist (see Proposition 2.3). However, by taking a suitable quotient of
$\mathscr {A}_{Q}^{\bullet }$
cannot exist (see Proposition 2.3). However, by taking a suitable quotient of
![]() $\mathcal {E}_Q$
, we also define a second category
$\mathcal {E}_Q$
, we also define a second category
![]() $\mathcal {E}^+_Q$
, which is extriangulated in the sense of Nakaoka and Palu [Reference Nakaoka and Palu40]. This second category is the categorification of
$\mathcal {E}^+_Q$
, which is extriangulated in the sense of Nakaoka and Palu [Reference Nakaoka and Palu40]. This second category is the categorification of
![]() $\mathscr {A}_{Q}^{\bullet }$
referred to in the title. Our construction allows the desired properties of
$\mathscr {A}_{Q}^{\bullet }$
referred to in the title. Our construction allows the desired properties of
![]() $\mathcal {E}^+_Q$
to be deduced directly from the corresponding properties of
$\mathcal {E}^+_Q$
to be deduced directly from the corresponding properties of
![]() $\mathcal {E}_Q$
appearing in Theorem 1, via [Reference Nakaoka and Palu40, Prop. 3.30].
$\mathcal {E}_Q$
appearing in Theorem 1, via [Reference Nakaoka and Palu40, Prop. 3.30].
Corollary 1 (Categorification for principal coefficients).
Let Q be an acyclic quiver. Then the category
![]() $\mathcal {E}^+_Q$
(Definition 7.1) has the properties that:
$\mathcal {E}^+_Q$
(Definition 7.1) has the properties that:
-
(a) The stable category
 $\underline {\mathcal {E}}^+_Q$
is equivalent to the cluster category
$\underline {\mathcal {E}}^+_Q$
is equivalent to the cluster category
 $\mathcal {C}_{Q}$
.
$\mathcal {C}_{Q}$
. -
(b) The cluster character on
 $\mathcal {E}_Q$
(see Theorem 1
(c)) induces a bijection between isomorphism classes of indecomposable rigid objects of
$\mathcal {E}_Q$
(see Theorem 1
(c)) induces a bijection between isomorphism classes of indecomposable rigid objects of
 $\mathcal {E}^+_Q$
and cluster variables of
$\mathcal {E}^+_Q$
and cluster variables of
 $\mathscr {A}_{Q}^{\bullet }$
.
$\mathscr {A}_{Q}^{\bullet }$
. -
(c) This induces a further bijection between isomorphism classes of cluster-tilting objects of
 $\mathcal {E}_Q$
and seeds of the principal coefficient cluster algebra
$\mathcal {E}_Q$
and seeds of the principal coefficient cluster algebra
 $\widetilde {\mathscr {A}}_{Q}$
, commuting with mutation, such that the ice quiver of the endomorphism algebra of each cluster-tilting object agrees, up to arrows between frozen vertices, with the ice quiver of the corresponding seed.
$\widetilde {\mathscr {A}}_{Q}$
, commuting with mutation, such that the ice quiver of the endomorphism algebra of each cluster-tilting object agrees, up to arrows between frozen vertices, with the ice quiver of the corresponding seed.
We note that Fu and Keller [Reference Fu and Keller21] have a different approach to categorifying
![]() $\mathscr {A}_{Q}^{\bullet }$
, via a full subcategory
$\mathscr {A}_{Q}^{\bullet }$
, via a full subcategory
![]() $\mathcal {U}_Q$
of the cluster category
$\mathcal {U}_Q$
of the cluster category
![]() $\mathcal {C}_{Q^{\bullet }}$
attached to the quiver
$\mathcal {C}_{Q^{\bullet }}$
attached to the quiver
![]() $Q^{\bullet }$
of the standard initial seed of
$Q^{\bullet }$
of the standard initial seed of
![]() $\mathscr {A}_{Q}^{\bullet }$
. Since it is extension-closed as a subcategory of the triangulated category
$\mathscr {A}_{Q}^{\bullet }$
. Since it is extension-closed as a subcategory of the triangulated category
![]() $\mathcal {C}_{Q^{\bullet }}$
, the category
$\mathcal {C}_{Q^{\bullet }}$
, the category
![]() $\mathcal {U}_Q$
is naturally extriangulated (see [Reference Nakaoka and Palu40, Rem. 2.18]).
$\mathcal {U}_Q$
is naturally extriangulated (see [Reference Nakaoka and Palu40, Rem. 2.18]).
Conjecture 1. The category
![]() $\mathcal {E}^+_Q$
from Corollary 1 is equivalent, as an extriangulated category, to Fu–Keller’s category
$\mathcal {E}^+_Q$
from Corollary 1 is equivalent, as an extriangulated category, to Fu–Keller’s category
![]() $\mathcal {U}_Q$
.
$\mathcal {U}_Q$
.
Producing equivalences between cluster-like categories is known to be a hard problem, although there are some results of this kind for triangulated categories, due to Keller–Reiten [Reference Keller and Reiten36] and Amiot–Reiten–Todorov [Reference Amiot, Reiten and Todorov2]. At present, we are not aware of any general result constructing such equivalences between extriangulated categories. Even if Conjecture 1 is true, the fact that we describe the categorification via a partial stabilization of the Frobenius category
![]() $\mathcal {E}_Q$
instead of as an extension-closed subcategory of
$\mathcal {E}_Q$
instead of as an extension-closed subcategory of
![]() $\mathcal {C}_{Q^{\bullet }}$
gives us access to different techniques for studying it, as we demonstrate in §9. Indeed, cluster theory is at present better developed for exact categories than for extriangulated categories such as
$\mathcal {C}_{Q^{\bullet }}$
gives us access to different techniques for studying it, as we demonstrate in §9. Indeed, cluster theory is at present better developed for exact categories than for extriangulated categories such as
![]() $\mathcal {E}_Q^+$
and
$\mathcal {E}_Q^+$
and
![]() $\mathcal {U}_Q$
, and it is useful to be able to exploit this.
$\mathcal {U}_Q$
, and it is useful to be able to exploit this.
The main results of the paper are contained in §2–7. In §2, we describe the cluster algebras with polarized principal coefficients that we will categorify, and recall the results of [Reference Pressland42], which we will use to construct the category
![]() $\mathcal {E}_Q$
appearing in Theorem 1. The algebra
$\mathcal {E}_Q$
appearing in Theorem 1. The algebra
![]() $A=A_{Q,W}$
needed as input for this construction is defined in §3, from the data of a quiver with potential
$A=A_{Q,W}$
needed as input for this construction is defined in §3, from the data of a quiver with potential
![]() $(Q,W)$
. In §4, we explain results from [Reference Pressland42], which allow us to establish the bimodule internally
$(Q,W)$
. In §4, we explain results from [Reference Pressland42], which allow us to establish the bimodule internally
![]() $3$
-Calabi–Yau property for a frozen Jacobian algebra, and apply these results to A, thus proving Theorem 2. We first restrict to acyclic quivers in §5, where we show that A is finite-dimensional, and hence Noetherian, under this assumption—this is why we require Q to be acyclic in Theorem 1. All of these ingredients are combined in §6 to give a proof of Theorem 1. The proof of Corollary 1 then follows in §7.
$3$
-Calabi–Yau property for a frozen Jacobian algebra, and apply these results to A, thus proving Theorem 2. We first restrict to acyclic quivers in §5, where we show that A is finite-dimensional, and hence Noetherian, under this assumption—this is why we require Q to be acyclic in Theorem 1. All of these ingredients are combined in §6 to give a proof of Theorem 1. The proof of Corollary 1 then follows in §7.
In the remaining sections, we investigate some of the features of the category
![]() $\mathcal {E}_Q$
appearing in Theorem 1. This category is defined as the category of Gorenstein projective modules over an Iwanaga–Gorenstein algebra
$\mathcal {E}_Q$
appearing in Theorem 1. This category is defined as the category of Gorenstein projective modules over an Iwanaga–Gorenstein algebra
![]() $B_Q$
, which we describe explicitly via a quiver with relations in §8. In §9, we explain how to use the category
$B_Q$
, which we describe explicitly via a quiver with relations in §8. In §9, we explain how to use the category
![]() $\mathcal {E}_Q$
to recover cluster-algebraic information about
$\mathcal {E}_Q$
to recover cluster-algebraic information about
![]() $\widetilde {\mathscr {A}}_{Q}$
and
$\widetilde {\mathscr {A}}_{Q}$
and
![]() $\mathscr {A}_{Q}^{\bullet }$
. We close in §10 with examples, in particular observing that Theorem 1 remains true when Q is a
$\mathscr {A}_{Q}^{\bullet }$
. We close in §10 with examples, in particular observing that Theorem 1 remains true when Q is a
![]() $3$
-cycle, provided we replace
$3$
-cycle, provided we replace
![]() $\mathcal {C}_{Q}$
by Amiot’s cluster category
$\mathcal {C}_{Q}$
by Amiot’s cluster category
![]() $\mathcal {C}_{Q,W}$
for a particular potential W.
$\mathcal {C}_{Q,W}$
for a particular potential W.
Throughout, algebras are assumed to be associative and unital. All modules are left modules, the composition of maps
![]() $f\colon X\to Y$
and
$f\colon X\to Y$
and
![]() $g\colon Y\to Z$
is denoted by
$g\colon Y\to Z$
is denoted by
![]() $gf$
, and we use the same convention for compositions of arrows in quivers. The Jacobson radical of a module X is denoted by
$gf$
, and we use the same convention for compositions of arrows in quivers. The Jacobson radical of a module X is denoted by
![]() $\operatorname {rad}{X}$
. If p is a path in a quiver, we denote its head by
$\operatorname {rad}{X}$
. If p is a path in a quiver, we denote its head by
![]() $h{p}$
and its tail by
$h{p}$
and its tail by
![]() $t{p}$
. We fix an algebraically closed field
$t{p}$
. We fix an algebraically closed field
![]() $\mathbb {K}$
, over which all our algebras and categories will be defined unless specified otherwise. For a
$\mathbb {K}$
, over which all our algebras and categories will be defined unless specified otherwise. For a
![]() $\mathbb {K}$
-algebra A, we denote the module category of A by
$\mathbb {K}$
-algebra A, we denote the module category of A by
![]() $\operatorname{Mod}A$
and the subcategory of finitely generated A-modules by
$\operatorname{Mod}A$
and the subcategory of finitely generated A-modules by
![]() $\operatorname{mod}A$
.
$\operatorname{mod}A$
.
2 Coefficient systems and cluster categories
In this section, we introduce our main definitions. We will not give the full definition of a cluster algebra, since this is somewhat lengthy and can be found easily in many other sources; we recommend Keller’s survey [Reference Keller33]. For concreteness, our cluster algebras will be defined over
![]() $\mathbb {Q}$
, and we do not assume frozen variables to be invertible; that is, the cluster algebra
$\mathbb {Q}$
, and we do not assume frozen variables to be invertible; that is, the cluster algebra
![]() $\mathscr {A}_{}$
generated by an initial seed with cluster
$\mathscr {A}_{}$
generated by an initial seed with cluster
![]() $(x_1,\dotsc ,x_n,x_{n+1},\dotsc ,x_m)$
, in which the mutable variables are
$(x_1,\dotsc ,x_n,x_{n+1},\dotsc ,x_m)$
, in which the mutable variables are
![]() $x_1,\dotsc ,x_n$
, is defined to be a subalgebra of
$x_1,\dotsc ,x_n$
, is defined to be a subalgebra of
![]() $\mathbb {Q}(x_1,\dotsc ,x_n)[x_{n+1},\dotsc ,x_m]$
. However, since our results are concerned with the set of cluster variables of
$\mathbb {Q}(x_1,\dotsc ,x_n)[x_{n+1},\dotsc ,x_m]$
. However, since our results are concerned with the set of cluster variables of
![]() $\mathscr {A}_{}$
, their grouping into clusters, and the exchange graph on these clusters, they are insensitive to changing these conventions by replacing
$\mathscr {A}_{}$
, their grouping into clusters, and the exchange graph on these clusters, they are insensitive to changing these conventions by replacing
![]() $\mathbb {Q}$
by a field extension or inverting the frozen variables. As such, we de-emphasize these conventions below, and simply refer to the cluster algebra generated by a seed.
$\mathbb {Q}$
by a field extension or inverting the frozen variables. As such, we de-emphasize these conventions below, and simply refer to the cluster algebra generated by a seed.
Let
![]() $\mathscr {A}_{}$
be a cluster algebra of geometric type without frozen variables, and let
$\mathscr {A}_{}$
be a cluster algebra of geometric type without frozen variables, and let
![]() $s_0$
be a seed of
$s_0$
be a seed of
![]() $\mathscr {A}_{}$
, with quiver Q and cluster variables
$\mathscr {A}_{}$
, with quiver Q and cluster variables
![]() $(x_1,\dotsc ,x_n)$
. By definition, the quiver Q has no loops or
$(x_1,\dotsc ,x_n)$
. By definition, the quiver Q has no loops or
![]() $2$
-cycles. The principal coefficient cluster algebra
$2$
-cycles. The principal coefficient cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
corresponding to these data is defined by the following initial seed. The mutable cluster variables are again
$\mathscr {A}_{Q}^{\bullet }$
corresponding to these data is defined by the following initial seed. The mutable cluster variables are again
![]() $(x_1,\dotsc ,x_n)$
, and the frozen variables are
$(x_1,\dotsc ,x_n)$
, and the frozen variables are
![]() $(x_1^+,\dotsc ,x_n^+)$
, where the indexing reveals a preferred bijection between the mutable and frozen variables. The ice quiver
$(x_1^+,\dotsc ,x_n^+)$
, where the indexing reveals a preferred bijection between the mutable and frozen variables. The ice quiver
![]() $Q^{\bullet }$
of this seed contains Q as a full subquiver, with mutable vertices, and for each vertex
$Q^{\bullet }$
of this seed contains Q as a full subquiver, with mutable vertices, and for each vertex
![]() $i\in Q_0$
(corresponding to the variable
$i\in Q_0$
(corresponding to the variable
![]() $x_i$
),
$x_i$
),
![]() $Q^{\bullet }$
has a frozen vertex
$Q^{\bullet }$
has a frozen vertex
![]() $i^+$
(corresponding to
$i^+$
(corresponding to
![]() $x_i^+$
) and an arrow
$x_i^+$
) and an arrow
![]() $i\to i^+$
. While
$i\to i^+$
. While
![]() $\mathscr {A}_{}$
is isomorphic (as a cluster algebra) to the cluster algebra determined by any quiver mutation equivalent to Q, this is not true of
$\mathscr {A}_{}$
is isomorphic (as a cluster algebra) to the cluster algebra determined by any quiver mutation equivalent to Q, this is not true of
![]() $\mathscr {A}_{Q}^{\bullet }$
.
$\mathscr {A}_{Q}^{\bullet }$
.
Specializing all frozen variables of
![]() $\mathscr {A}_{Q}^{\bullet }$
to
$\mathscr {A}_{Q}^{\bullet }$
to
![]() $1$
to obtain a cluster algebra without frozen variables (which we refer to as taking the principal part) recovers
$1$
to obtain a cluster algebra without frozen variables (which we refer to as taking the principal part) recovers
![]() $\mathscr {A}_{}$
, and gives a bijection between the seeds of
$\mathscr {A}_{}$
, and gives a bijection between the seeds of
![]() $\mathscr {A}_{Q}^{\bullet }$
and those of
$\mathscr {A}_{Q}^{\bullet }$
and those of
![]() $\mathscr {A}_{}$
[Reference Cerulli Irelli, Keller, Labardini-Fragoso and Plamondon14]; we write
$\mathscr {A}_{}$
[Reference Cerulli Irelli, Keller, Labardini-Fragoso and Plamondon14]; we write
![]() $s^{\bullet }$
for the seed of
$s^{\bullet }$
for the seed of
![]() $\mathscr {A}_{Q}^{\bullet }$
corresponding to a seed s of
$\mathscr {A}_{Q}^{\bullet }$
corresponding to a seed s of
![]() $\mathscr {A}_{}$
. Precisely, if
$\mathscr {A}_{}$
. Precisely, if
![]() $s^{\bullet }$
has cluster
$s^{\bullet }$
has cluster
![]() $(v_1,\dotsc ,v_n,x_1^+,\dotsc ,x_n^+)$
, then s has cluster
$(v_1,\dotsc ,v_n,x_1^+,\dotsc ,x_n^+)$
, then s has cluster
![]() $(v_1,\dotsc ,v_n)|_{x_i^+=1,1\leq i\leq n}$
, and the quiver of s is the full subquiver of that of
$(v_1,\dotsc ,v_n)|_{x_i^+=1,1\leq i\leq n}$
, and the quiver of s is the full subquiver of that of
![]() $s^{\bullet }$
on the mutable vertices. Principal coefficients are important since knowledge of the cluster algebra
$s^{\bullet }$
on the mutable vertices. Principal coefficients are important since knowledge of the cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
can be used to study any cluster algebra
$\mathscr {A}_{Q}^{\bullet }$
can be used to study any cluster algebra
![]() $\mathscr {A}'$
with principal part
$\mathscr {A}'$
with principal part
![]() $\mathscr {A}$
, via the theory of g-vectors and F-polynomials [Reference Fomin and Zelevinsky20].
$\mathscr {A}$
, via the theory of g-vectors and F-polynomials [Reference Fomin and Zelevinsky20].
By choosing some extra data on Q, Amiot [Reference Amiot1] constructs a categorification of
![]() $\mathscr {A}_{}$
. The construction uses Jacobian algebras, so we recall some relevant definitions, at the level of generality needed later in the paper.
$\mathscr {A}_{}$
. The construction uses Jacobian algebras, so we recall some relevant definitions, at the level of generality needed later in the paper.
Definition 2.1. An ice quiver
![]() $(Q,F)$
consists of a finite quiver Q without loops and a subquiver F of Q. Denote by
$(Q,F)$
consists of a finite quiver Q without loops and a subquiver F of Q. Denote by
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
the completion of the path algebra of Q over our fixed algebraically closed field
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
the completion of the path algebra of Q over our fixed algebraically closed field
![]() $\mathbb {K}$
with respect to the ideal
$\mathbb {K}$
with respect to the ideal
![]() $J_Q$
generated by arrows, treated as a topological algebra with the
$J_Q$
generated by arrows, treated as a topological algebra with the
![]() $J_Q$
-adic topology. A potential on Q is an element W of the vector space quotient
$J_Q$
-adic topology. A potential on Q is an element W of the vector space quotient
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /\overline {\{\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle ,\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \}}$
, of
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /\overline {\{\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle ,\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \}}$
, of
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
by the closure of the subspace spanned by commutators, such that W lies in the image of the natural map from
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
by the closure of the subspace spanned by commutators, such that W lies in the image of the natural map from
![]() $J_Q$
to this vector space. (More informally, W is a possibly infinite linear combination of cyclic equivalence classes of cycles of positive length in Q.)
$J_Q$
to this vector space. (More informally, W is a possibly infinite linear combination of cyclic equivalence classes of cycles of positive length in Q.)
A vertex or arrow of Q is called frozen if it is a vertex or arrow of F, and mutable or unfrozen otherwise. For brevity, we write
![]() $Q_0^\circ =Q_0\setminus F_0$
and
$Q_0^\circ =Q_0\setminus F_0$
and
![]() $Q_1^\circ =Q_1\setminus F_1$
for the sets of mutable vertices and unfrozen arrows, respectively. For
$Q_1^\circ =Q_1\setminus F_1$
for the sets of mutable vertices and unfrozen arrows, respectively. For
![]() $\alpha \in Q_1$
and
$\alpha \in Q_1$
and
![]() $\alpha _k\dotsm \alpha _1$
a cycle in Q, write
$\alpha _k\dotsm \alpha _1$
a cycle in Q, write
 $$\begin{align*}\partial_{\alpha}{\alpha_k\dotsm\alpha_1}=\sum_{\alpha_i=\alpha}\alpha_{i-1}\dotsm\alpha_1\alpha_k\dotsm\alpha_{i+1}.\end{align*}$$
$$\begin{align*}\partial_{\alpha}{\alpha_k\dotsm\alpha_1}=\sum_{\alpha_i=\alpha}\alpha_{i-1}\dotsm\alpha_1\alpha_k\dotsm\alpha_{i+1}.\end{align*}$$
Extending the map
![]() $\partial _{\alpha }$
linearly and continuously, and noting that it vanishes on commutators, allows us to define
$\partial _{\alpha }$
linearly and continuously, and noting that it vanishes on commutators, allows us to define
![]() $\partial _{\alpha }{W}$
. The ideal
$\partial _{\alpha }{W}$
. The ideal
![]() $\langle \partial _{\alpha }{W}:\alpha \in Q_1^\circ \rangle $
of
$\langle \partial _{\alpha }{W}:\alpha \in Q_1^\circ \rangle $
of
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is called the Jacobian ideal, and we define the frozen Jacobian algebra associated with
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is called the Jacobian ideal, and we define the frozen Jacobian algebra associated with
![]() $(Q,F,W)$
by
$(Q,F,W)$
by
Write
![]() $A=J(Q,F,W)$
. The above presentation of A suggests a preferred idempotent
$A=J(Q,F,W)$
. The above presentation of A suggests a preferred idempotent
 $$\begin{align*}e=\sum_{v\in F_0}e_{v},\end{align*}$$
$$\begin{align*}e=\sum_{v\in F_0}e_{v},\end{align*}$$
which we call the frozen idempotent. We will call the subalgebra
![]() $B=eAe$
the boundary algebra of A. If
$B=eAe$
the boundary algebra of A. If
![]() $F=\varnothing $
, then we refer to the pair
$F=\varnothing $
, then we refer to the pair
![]() $(Q,W)$
as a quiver with potential, and call
$(Q,W)$
as a quiver with potential, and call
![]() $J(Q,W)=J(Q,\varnothing ,W)$
simply the Jacobian algebra of
$J(Q,W)=J(Q,\varnothing ,W)$
simply the Jacobian algebra of
![]() $(Q,W)$
. If
$(Q,W)$
. If
![]() $J(Q,W)$
is finite-dimensional, we call both W and the pair
$J(Q,W)$
is finite-dimensional, we call both W and the pair
![]() $(Q,W)$
Jacobi-finite.
$(Q,W)$
Jacobi-finite.
Remark 2.2. In much of the paper, we will consider algebras defined by a quiver Q together with a set of relations R, in the ordinary path algebra
![]() $\mathbb {K} Q$
, having the property that the natural map
$\mathbb {K} Q$
, having the property that the natural map
![]() $\mathbb {K} Q/\langle R\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /\overline {\langle R\rangle }$
is an isomorphism—for example, this happens when the domain is finite-dimensional. However, we take complete path algebras in the general theory since we want the categories we construct to be Krull–Schmidt [Reference Krause37, §4] (cf. [Reference Jensen, King and Su32, Rem. 3.3]). Furthermore, we note that the Jacobson radical
$\mathbb {K} Q/\langle R\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /\overline {\langle R\rangle }$
is an isomorphism—for example, this happens when the domain is finite-dimensional. However, we take complete path algebras in the general theory since we want the categories we construct to be Krull–Schmidt [Reference Krause37, §4] (cf. [Reference Jensen, King and Su32, Rem. 3.3]). Furthermore, we note that the Jacobson radical
![]() $J_Q$
of
$J_Q$
of
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is generated by the arrows (unlike the Jacobson radical of
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is generated by the arrows (unlike the Jacobson radical of
![]() $\mathbb {K} Q$
when Q has cycles). Since the Jacobian ideal defining
$\mathbb {K} Q$
when Q has cycles). Since the Jacobian ideal defining
![]() $A=J(Q,F,W)$
is contained in
$A=J(Q,F,W)$
is contained in
![]() $J_Q$
, it follows that A has Jacobson radical
$J_Q$
, it follows that A has Jacobson radical
![]() $J(A)$
generated by the arrows of Q, and so
$J(A)$
generated by the arrows of Q, and so
![]() $A/J(A)\cong \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /J_Q\cong \mathbb {K}^{Q_0}$
is a semisimple algebra. We use this fact in §4.
$A/J(A)\cong \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /J_Q\cong \mathbb {K}^{Q_0}$
is a semisimple algebra. We use this fact in §4.
The terminology boundary algebra is inspired by and compatible with [Reference Baur, King and Marsh3] (see also [Reference Pressland45]), although in the general case Q need not admit any embedding into a manifold so that F is embedded into the boundary.
Assume that Q is a quiver admitting a Jacobi-finite potential W. Then, by work of Amiot [Reference Amiot1], there is a
![]() $2$
-Calabi–Yau triangulated category
$2$
-Calabi–Yau triangulated category
![]() $\mathcal {C}_{Q,W}$
categorifying
$\mathcal {C}_{Q,W}$
categorifying
![]() $\mathscr {A}_{Q}$
. If W is additionally nondegenerate [Reference Derksen, Weyman and Zelevinsky18, Def. 7.2], then the seeds of
$\mathscr {A}_{Q}$
. If W is additionally nondegenerate [Reference Derksen, Weyman and Zelevinsky18, Def. 7.2], then the seeds of
![]() $\mathscr {A}_{}$
correspond bijectively to additive equivalence classes of cluster-tilting objects of
$\mathscr {A}_{}$
correspond bijectively to additive equivalence classes of cluster-tilting objects of
![]() $\mathcal {C}_{Q,W}$
related by a finite sequence of mutations to an initial cluster-tilting object
$\mathcal {C}_{Q,W}$
related by a finite sequence of mutations to an initial cluster-tilting object
![]() $T_0$
with
$T_0$
with
![]() $\operatorname {End}_{\mathcal {C}_{Q,W}}(T_0)^{\mathrm {op}}=J(Q,W)$
; such cluster-tilting objects are called reachable, and we denote the seed corresponding to such an object T by
$\operatorname {End}_{\mathcal {C}_{Q,W}}(T_0)^{\mathrm {op}}=J(Q,W)$
; such cluster-tilting objects are called reachable, and we denote the seed corresponding to such an object T by
![]() $s_T$
. Nondegeneracy is needed here to see, using results of Buan–Iyama–Reiten–Smith [Reference Buan, Iyama, Reiten and Smith9], that mutation of cluster-tilting objects in the mutation class of
$s_T$
. Nondegeneracy is needed here to see, using results of Buan–Iyama–Reiten–Smith [Reference Buan, Iyama, Reiten and Smith9], that mutation of cluster-tilting objects in the mutation class of
![]() $T_0$
corresponds to Fomin–Zelevinsky mutation at the level of quivers of endomorphism algebras, and so in particular mutation is well defined at any indecomposable summand of any reachable cluster-tilting object.
$T_0$
corresponds to Fomin–Zelevinsky mutation at the level of quivers of endomorphism algebras, and so in particular mutation is well defined at any indecomposable summand of any reachable cluster-tilting object.
A priori, to categorify the principal coefficient cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
, we would like to find a Frobenius category
$\mathscr {A}_{Q}^{\bullet }$
, we would like to find a Frobenius category
![]() $\mathcal {E}$
such that:
$\mathcal {E}$
such that:
-
(a) The stable category
 $\underline {\mathcal {E}}$
is triangle equivalent to
$\underline {\mathcal {E}}$
is triangle equivalent to
 $\mathcal {C}_{Q,W}$
(so that cluster-tilting objects of
$\mathcal {C}_{Q,W}$
(so that cluster-tilting objects of
 $\underline {\mathcal {E}}$
may be identified with those of
$\underline {\mathcal {E}}$
may be identified with those of
 $\mathcal {C}_{Q,W}$
, and hence cluster-tilting objects in
$\mathcal {C}_{Q,W}$
, and hence cluster-tilting objects in
 $\mathcal {E}$
can be mutated at their nonprojective indecomposable summands).
$\mathcal {E}$
can be mutated at their nonprojective indecomposable summands). -
(b) For any reachable cluster-tilting object T, there is an isomorphism
 $\mathbb {K}\langle \hspace {-0.1em}\langle Q'\rangle \hspace {-0.1em}\rangle /\overline {I}\stackrel {\sim }{\to }\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}$
, for some ideal
$\mathbb {K}\langle \hspace {-0.1em}\langle Q'\rangle \hspace {-0.1em}\rangle /\overline {I}\stackrel {\sim }{\to }\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}$
, for some ideal
 $I\subseteq J_{Q'}^2$
, where
$I\subseteq J_{Q'}^2$
, where
 $Q'$
is, up to arrows between frozen vertices, the quiver of the seed
$Q'$
is, up to arrows between frozen vertices, the quiver of the seed
 $s_T^{\bullet }$
of
$s_T^{\bullet }$
of
 $\mathscr {A}_{Q}^{\bullet }$
. (As always, we define the frozen vertices of
$\mathscr {A}_{Q}^{\bullet }$
. (As always, we define the frozen vertices of
 $Q'$
to be those whose image under the given isomorphism to
$Q'$
to be those whose image under the given isomorphism to
 $\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}$
is a projection onto an indecomposable projective summand.)
$\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}$
is a projection onto an indecomposable projective summand.)
Unfortunately, this is not possible.
Proposition 2.3. There does not exist a Frobenius category
![]() $\mathcal {E}$
satisfying conditions (a) and (b) above.
$\mathcal {E}$
satisfying conditions (a) and (b) above.
Proof. Assume that
![]() $\mathcal {E}$
were such a Frobenius category, and let
$\mathcal {E}$
were such a Frobenius category, and let
![]() $\hat {T}_0$
be the cluster-tilting object in
$\hat {T}_0$
be the cluster-tilting object in
![]() $\mathcal {E}$
which, when viewed as an object of
$\mathcal {E}$
which, when viewed as an object of
![]() $\underline {\mathcal {E}}$
, is identified with
$\underline {\mathcal {E}}$
, is identified with
![]() $T_0$
under the equivalence in (a). By (b), we have an isomorphism
$T_0$
under the equivalence in (a). By (b), we have an isomorphism
![]() $\operatorname {End}_{\mathcal {E}}(\hat {T}_0)^{\mathrm {op}}\stackrel {\sim }{\to }\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /\overline {I}$
for
$\operatorname {End}_{\mathcal {E}}(\hat {T}_0)^{\mathrm {op}}\stackrel {\sim }{\to }\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /\overline {I}$
for
![]() $I\subseteq J_Q^2$
and Q a quiver differing from
$I\subseteq J_Q^2$
and Q a quiver differing from
![]() $Q^{\bullet }$
only by the possible addition of arrows between frozen vertices. This latter property means that there is no path in Q from a frozen vertex to a mutable one, and hence there are no nonzero maps in
$Q^{\bullet }$
only by the possible addition of arrows between frozen vertices. This latter property means that there is no path in Q from a frozen vertex to a mutable one, and hence there are no nonzero maps in
![]() $\mathcal {E}$
from an indecomposable nonprojective summand of
$\mathcal {E}$
from an indecomposable nonprojective summand of
![]() $\hat {T}_0$
to an injective object in
$\hat {T}_0$
to an injective object in
![]() $\mathcal {E}$
, contradicting the assumption that
$\mathcal {E}$
, contradicting the assumption that
![]() $\mathcal {E}$
has enough injective objects.
$\mathcal {E}$
has enough injective objects.
For this reason, we will first consider, and categorify, a different cluster algebra
![]() $\widetilde {\mathscr {A}}_{Q}$
with initial seed obtained from that of
$\widetilde {\mathscr {A}}_{Q}$
with initial seed obtained from that of
![]() $\mathscr {A}_{Q}^{\bullet }$
by adding more frozen variables. Starting from our seed
$\mathscr {A}_{Q}^{\bullet }$
by adding more frozen variables. Starting from our seed
![]() $s_0$
of
$s_0$
of
![]() $\mathscr {A}_{}$
, with quiver Q and cluster variables
$\mathscr {A}_{}$
, with quiver Q and cluster variables
![]() $(x_1,\dotsc ,x_n)$
, we construct an initial seed
$(x_1,\dotsc ,x_n)$
, we construct an initial seed
![]() $\widetilde {s}_0$
of
$\widetilde {s}_0$
of
![]() $\widetilde {\mathscr {A}}_{Q}$
as follows: the seed
$\widetilde {\mathscr {A}}_{Q}$
as follows: the seed
![]() $\widetilde {s}_0$
has mutable variables
$\widetilde {s}_0$
has mutable variables
![]() $(x_1,\dotsc ,x_n)$
, and frozen variables
$(x_1,\dotsc ,x_n)$
, and frozen variables
![]() $(x_1^+,\dotsc ,x_n^+,x_1^-,\dotsc ,x_n^-)$
. Its ice quiver
$(x_1^+,\dotsc ,x_n^+,x_1^-,\dotsc ,x_n^-)$
. Its ice quiver
![]() $\widetilde {Q}$
is described fully in Definition 3.1; the relevant features for defining the cluster algebra are that
$\widetilde {Q}$
is described fully in Definition 3.1; the relevant features for defining the cluster algebra are that
![]() $\widetilde {Q}$
contains Q as a full subquiver, with mutable vertices, and has two frozen vertices
$\widetilde {Q}$
contains Q as a full subquiver, with mutable vertices, and has two frozen vertices
![]() $i^+$
(corresponding to
$i^+$
(corresponding to
![]() $x_i^+$
) and
$x_i^+$
) and
![]() $i^-$
(corresponding to
$i^-$
(corresponding to
![]() $x_i^-)$
for each mutable vertex
$x_i^-)$
for each mutable vertex
![]() $i\in Q_0$
, with arrows
$i\in Q_0$
, with arrows
![]() $i\to i^+$
and
$i\to i^+$
and
![]() $i^-\to i$
. (In Definition 3.1, we also describe arrows between the frozen vertices that will play a role in our categorification, but are not important for defining
$i^-\to i$
. (In Definition 3.1, we also describe arrows between the frozen vertices that will play a role in our categorification, but are not important for defining
![]() $\widetilde {\mathscr {A}}_{Q}$
.) We call
$\widetilde {\mathscr {A}}_{Q}$
.) We call
![]() $\widetilde {\mathscr {A}}_{Q}$
the polarized principal coefficient cluster algebra associated with Q.
$\widetilde {\mathscr {A}}_{Q}$
the polarized principal coefficient cluster algebra associated with Q.
We adopt the word polarised, referring to the partitioning of the frozen variables into two sets, to differentiate this coefficient system from the double principal coefficients studied by Rupel, Stella, and Williams [Reference Rupel, Stella and Williams46]. Since one encounters the same issues categorifying cluster algebras with double principal coefficients as in the case of ordinary principal coefficients, namely that no categorification may have enough injective objects, our preference here is for the polarized version.
As discussed in the introduction, we will construct a categorification of
![]() $\widetilde {\mathscr {A}}_{Q}$
using methodology introduced by the author in [Reference Pressland42]. We now recall the key definitions and results needed to explain this construction. Given a
$\widetilde {\mathscr {A}}_{Q}$
using methodology introduced by the author in [Reference Pressland42]. We now recall the key definitions and results needed to explain this construction. Given a
![]() $\mathbb {K}$
-algebra A, we write
$\mathbb {K}$
-algebra A, we write
![]() ${\mathcal {D}}(A)$
for its derived category and
${\mathcal {D}}(A)$
for its derived category and
![]() ${A}^{\varepsilon }=A\mathbin {\otimes }_{\mathbb {K}} A^{\mathrm {op}}$
for its enveloping algebra, modules of which are precisely A-bimodules. We denote by
${A}^{\varepsilon }=A\mathbin {\otimes }_{\mathbb {K}} A^{\mathrm {op}}$
for its enveloping algebra, modules of which are precisely A-bimodules. We denote by
![]() $\operatorname {per}{A}$
the perfect derived category of A, that is, the thick subcategory of
$\operatorname {per}{A}$
the perfect derived category of A, that is, the thick subcategory of
![]() ${\mathcal {D}}(A)$
generated by A, and write
${\mathcal {D}}(A)$
generated by A, and write
![]() $\Omega _{A}=\operatorname {\mathbf {R}Hom}_{{A}^{\varepsilon }}(A,{A}^{\varepsilon })$
.
$\Omega _{A}=\operatorname {\mathbf {R}Hom}_{{A}^{\varepsilon }}(A,{A}^{\varepsilon })$
.
Definition 2.4 [Reference Pressland42, Def. 2.4].
Given an algebra A and idempotent
![]() $e\in A$
, we say A is bimodule internally
$e\in A$
, we say A is bimodule internally
![]() $3$
-Calabi–Yau with respect to e if:
$3$
-Calabi–Yau with respect to e if:
-
(a)
 $\operatorname {p.dim}_{{A}^{\varepsilon }}{A}\leq 3$
,
$\operatorname {p.dim}_{{A}^{\varepsilon }}{A}\leq 3$
, -
(b)
 $A\in \operatorname {per}{{A}^{\varepsilon }}$
, and
$A\in \operatorname {per}{{A}^{\varepsilon }}$
, and -
(c) there exists a triangle
 $A\stackrel {\psi }{\longrightarrow }\Omega _{A}[3]\stackrel {}{\longrightarrow }C\stackrel {}{\longrightarrow }A[1]$
in
$A\stackrel {\psi }{\longrightarrow }\Omega _{A}[3]\stackrel {}{\longrightarrow }C\stackrel {}{\longrightarrow }A[1]$
in
 ${\mathcal {D}}({A}^{\varepsilon })$
such that
${\mathcal {D}}({A}^{\varepsilon })$
such that  $$\begin{align*}\operatorname{\mathbf{R}Hom}_A(C,M)=0=\operatorname{\mathbf{R}Hom}_{A^{\mathrm{op}}}(C,N) \end{align*}$$
$$\begin{align*}\operatorname{\mathbf{R}Hom}_A(C,M)=0=\operatorname{\mathbf{R}Hom}_{A^{\mathrm{op}}}(C,N) \end{align*}$$
for any
 $M\in {\mathcal {D}}(A)$
whose total cohomology is a finite-dimensional
$M\in {\mathcal {D}}(A)$
whose total cohomology is a finite-dimensional
 $A/AeA$
-module, and any
$A/AeA$
-module, and any
 $N\in {\mathcal {D}}(A^{\mathrm {op}})$
satisfying the analogous condition.
$N\in {\mathcal {D}}(A^{\mathrm {op}})$
satisfying the analogous condition.
Remark 2.5. Assume that A is bimodule internally
![]() $3$
-Calabi–Yau with respect to e. Then
$3$
-Calabi–Yau with respect to e. Then
![]() $\operatorname {gl.dim}{A}\leq 3$
, and there is a functorial duality
$\operatorname {gl.dim}{A}\leq 3$
, and there is a functorial duality
for any finite-dimensional
![]() $A/AeA$
-module M and any A-module N (see [Reference Pressland42, Cor. 2.9]). Moreover,
$A/AeA$
-module M and any A-module N (see [Reference Pressland42, Cor. 2.9]). Moreover,
![]() $A^{\mathrm {op}}$
has the same properties (see [Reference Pressland42, Rem. 2.6]).
$A^{\mathrm {op}}$
has the same properties (see [Reference Pressland42, Rem. 2.6]).
To construct our Frobenius categories, we will use the following theorem.
Theorem 2.6 [Reference Pressland42, Ths. 4.1 and 4.10].
Let A be an algebra, and let
![]() $e\in A$
be an idempotent. If A is Noetherian,
$e\in A$
be an idempotent. If A is Noetherian,
![]() $\underline {A}=A/AeA$
is finite-dimensional, and A is bimodule internally
$\underline {A}=A/AeA$
is finite-dimensional, and A is bimodule internally
![]() $3$
-Calabi–Yau with respect to e, then:
$3$
-Calabi–Yau with respect to e, then:
-
(a)
 $B=eAe$
is Iwanaga–Gorenstein (of injective dimension at most
$B=eAe$
is Iwanaga–Gorenstein (of injective dimension at most
 $3$
), so the category
$3$
), so the category  $$\begin{align*}\operatorname{GP}(B)=\{X\in\operatorname{mod}\ {B}: \operatorname{Ext}^i_B(X,B)=0 \text{ for all } i>0\} \end{align*}$$
$$\begin{align*}\operatorname{GP}(B)=\{X\in\operatorname{mod}\ {B}: \operatorname{Ext}^i_B(X,B)=0 \text{ for all } i>0\} \end{align*}$$
of Gorenstein projective B-modules is a Frobenius category.
-
(b)
 $eA\in \operatorname {GP}(B)$
is cluster-tilting.
$eA\in \operatorname {GP}(B)$
is cluster-tilting. -
(c) There are natural isomorphisms
 $\operatorname {End}_{B}(eA)^{\mathrm {op}}\stackrel {\sim }{\to } A$
and
$\operatorname {End}_{B}(eA)^{\mathrm {op}}\stackrel {\sim }{\to } A$
and
 $\underline {\operatorname {End}}_{B}(eA)^{\mathrm {op}}\stackrel {\sim }{\to }\underline {A}$
.
$\underline {\operatorname {End}}_{B}(eA)^{\mathrm {op}}\stackrel {\sim }{\to }\underline {A}$
. -
(d) The stable category
 $\underline {\operatorname {GP}}(B)$
is
$\underline {\operatorname {GP}}(B)$
is
 $2$
-Calabi–Yau.
$2$
-Calabi–Yau.
In many cases—in particular in our application in the proof of Theorem 1—the Frobenius category
![]() $\operatorname {GP}(B)$
appearing in Theorem 2.6 is a Frobenius cluster category, as studied in [Reference Pressland42], and defined as follows.
$\operatorname {GP}(B)$
appearing in Theorem 2.6 is a Frobenius cluster category, as studied in [Reference Pressland42], and defined as follows.
Definition 2.7 (cf. [Reference Pressland42, Def. 3.3]).
A Frobenius category
![]() $\mathcal {E}$
is called a Frobenius cluster category if it is Krull–Schmidt, stably
$\mathcal {E}$
is called a Frobenius cluster category if it is Krull–Schmidt, stably
![]() $2$
-Calabi–Yau, and
$2$
-Calabi–Yau, and
![]() $\operatorname {gl.dim}{\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}}\leq 3$
for any cluster-tilting object
$\operatorname {gl.dim}{\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}}\leq 3$
for any cluster-tilting object
![]() $T\in \mathcal {E}$
, of which there is at least one.
$T\in \mathcal {E}$
, of which there is at least one.
Proposition 2.8. In the context of Theorem 2.6, if A is additionally finite-dimensional, then
![]() $\operatorname {GP}(B)$
is a Frobenius cluster category.
$\operatorname {GP}(B)$
is a Frobenius cluster category.
Proof. The category
![]() $\operatorname {GP}(B)$
is idempotent complete for any algebra B, Frobenius by Theorem 2.6
(a), and stably
$\operatorname {GP}(B)$
is idempotent complete for any algebra B, Frobenius by Theorem 2.6
(a), and stably
![]() $2$
-Calabi–Yau by Theorem 2.6
(d). Now, we use the extra assumption that A is finite-dimensional. First, by [Reference Pressland42, Prop. 3.7], the endomorphism algebra of a cluster-tilting object in
$2$
-Calabi–Yau by Theorem 2.6
(d). Now, we use the extra assumption that A is finite-dimensional. First, by [Reference Pressland42, Prop. 3.7], the endomorphism algebra of a cluster-tilting object in
![]() $\operatorname {GP}(B)$
has global dimension at most
$\operatorname {GP}(B)$
has global dimension at most
![]() $3$
provided it is Noetherian; when A is finite-dimensional, the category
$3$
provided it is Noetherian; when A is finite-dimensional, the category
![]() $\operatorname {GP}(B)$
is Hom-finite, so this condition certainly holds. Moreover, finite-dimensional algebras are semiperfect, which together with the earlier observation that
$\operatorname {GP}(B)$
is Hom-finite, so this condition certainly holds. Moreover, finite-dimensional algebras are semiperfect, which together with the earlier observation that
![]() $\operatorname {GP}(B)$
is idempotent complete implies that it is a Krull–Schmidt category by [Reference Krause37, Cor. 4.4].
$\operatorname {GP}(B)$
is idempotent complete implies that it is a Krull–Schmidt category by [Reference Krause37, Cor. 4.4].
Remark 2.9. As suggested by the proof, the assumption that A is finite-dimensional is likely to be much stronger than needed for the conclusion of Proposition 2.8. For example, it may already be true under the assumptions of Theorem 2.6 that all cluster-tilting objects in
![]() $\operatorname {GP}(B)$
have Noetherian endomorphism algebra—this is true for the cluster-tilting object
$\operatorname {GP}(B)$
have Noetherian endomorphism algebra—this is true for the cluster-tilting object
![]() $eA$
by the theorem, but we do not currently know how to deduce it for other cluster-tilting objects. Moreover, there are many infinite-dimensional semiperfect algebras, such as complete path algebras of finite quivers with cycles.
$eA$
by the theorem, but we do not currently know how to deduce it for other cluster-tilting objects. Moreover, there are many infinite-dimensional semiperfect algebras, such as complete path algebras of finite quivers with cycles.
Returning to the problem of categorifying the cluster algebra
![]() $\widetilde {\mathscr {A}}_{Q}$
, our aim now is to construct an algebra A satisfying the conditions of Theorem 2.6, defined as a quotient of the complete path algebra of the quiver
$\widetilde {\mathscr {A}}_{Q}$
, our aim now is to construct an algebra A satisfying the conditions of Theorem 2.6, defined as a quotient of the complete path algebra of the quiver
![]() $\widetilde {Q}$
used to define
$\widetilde {Q}$
used to define
![]() $\widetilde {\mathscr {A}}_{Q}$
.
$\widetilde {\mathscr {A}}_{Q}$
.
3 An ice quiver with potential
Consider again our initial seed
![]() $s_0$
for
$s_0$
for
![]() $\mathscr {A}_{}$
, with quiver Q, and choose a potential W on Q. In this section, we will construct from
$\mathscr {A}_{}$
, with quiver Q, and choose a potential W on Q. In this section, we will construct from
![]() $(Q,W)$
an ice quiver with potential
$(Q,W)$
an ice quiver with potential
![]() $(\widetilde {Q},\widetilde {F},\widetilde {W})$
, and thus a frozen Jacobian algebra
$(\widetilde {Q},\widetilde {F},\widetilde {W})$
, and thus a frozen Jacobian algebra
![]() $J(\widetilde {Q},\widetilde {F},\widetilde {W})$
. It is this algebra that we intend to use as the input for the construction of a Frobenius category by Theorem 2.6; to apply this theorem, we will require that
$J(\widetilde {Q},\widetilde {F},\widetilde {W})$
. It is this algebra that we intend to use as the input for the construction of a Frobenius category by Theorem 2.6; to apply this theorem, we will require that
![]() $J(Q,W)$
is finite-dimensional, but we do not assume this yet.
$J(Q,W)$
is finite-dimensional, but we do not assume this yet.
Definition 3.1. Let
![]() $(Q,W)$
be a quiver with potential. We define
$(Q,W)$
be a quiver with potential. We define
![]() $\widetilde {Q}$
to be the quiver with vertex set given by
$\widetilde {Q}$
to be the quiver with vertex set given by
where
![]() $Q_0^+=\{i^+:i\in Q_0\}$
is a set of formal symbols in bijection with
$Q_0^+=\{i^+:i\in Q_0\}$
is a set of formal symbols in bijection with
![]() $Q_0$
, and similarly for
$Q_0$
, and similarly for
![]() $Q_0^-=\{i^-:i\in Q_0\}$
. The set of arrows is given by
$Q_0^-=\{i^-:i\in Q_0\}$
. The set of arrows is given by
and the head and tail functions
![]() $h,t\colon \widetilde {Q}_1\to \widetilde {Q}_0$
are extended from those of Q by defining
$h,t\colon \widetilde {Q}_1\to \widetilde {Q}_0$
are extended from those of Q by defining
 $$ \begin{align*} h{\alpha_i}&=i^+,&h{\beta_i}&=i,&h{\delta_i}&=i^-,&h{\delta_a}&=(t{a})^-,\\ t{\alpha_i}&=i,&t{\beta_i}&=i^-,&t{\delta_i}&=i^+,&t{\delta_a}&=(h{a})^+. \end{align*} $$
$$ \begin{align*} h{\alpha_i}&=i^+,&h{\beta_i}&=i,&h{\delta_i}&=i^-,&h{\delta_a}&=(t{a})^-,\\ t{\alpha_i}&=i,&t{\beta_i}&=i^-,&t{\delta_i}&=i^+,&t{\delta_a}&=(h{a})^+. \end{align*} $$
The frozen subquiver
![]() $\widetilde {F}$
is defined by
$\widetilde {F}$
is defined by
Note that the head and tail of any arrow in
![]() $\widetilde {F}_1$
lie in
$\widetilde {F}_1$
lie in
![]() $\widetilde {F}_0$
, so these subsets describe a valid subquiver of
$\widetilde {F}_0$
, so these subsets describe a valid subquiver of
![]() $\widetilde {Q}$
, which is even full. The quiver
$\widetilde {Q}$
, which is even full. The quiver
![]() $\widetilde {F}$
is also bipartite, meaning that every vertex is either a source or a sink, and so it has no paths of length greater than
$\widetilde {F}$
is also bipartite, meaning that every vertex is either a source or a sink, and so it has no paths of length greater than
![]() $1$
; precisely, the vertices in
$1$
; precisely, the vertices in
![]() $Q_0^+$
are sources in
$Q_0^+$
are sources in
![]() $\widetilde {F}$
, and those in
$\widetilde {F}$
, and those in
![]() $Q_0^-$
are sinks. As a vertex of
$Q_0^-$
are sinks. As a vertex of
![]() $\widetilde {Q}$
, each
$\widetilde {Q}$
, each
![]() $i^+$
has unique incoming arrow
$i^+$
has unique incoming arrow
![]() $\alpha _i$
and each
$\alpha _i$
and each
![]() $i^-$
has unique outgoing arrow
$i^-$
has unique outgoing arrow
![]() $\beta _i$
.
$\beta _i$
.
Finally, we define a potential
![]() $\widetilde {W}$
on
$\widetilde {W}$
on
![]() $\widetilde {Q}$
by
$\widetilde {Q}$
by
 $$\begin{align*}\widetilde{W}=W+\sum_{i\in Q_0}\beta_i\delta_i\alpha_i-\sum_{a\in Q_1}a\beta_{t{a}}\delta_a\alpha_{h{a}},\end{align*}$$
$$\begin{align*}\widetilde{W}=W+\sum_{i\in Q_0}\beta_i\delta_i\alpha_i-\sum_{a\in Q_1}a\beta_{t{a}}\delta_a\alpha_{h{a}},\end{align*}$$
and let
be the frozen Jacobian algebra determined by
![]() $(\widetilde {Q},\widetilde {F},\widetilde {W})$
. We denote the boundary algebra of
$(\widetilde {Q},\widetilde {F},\widetilde {W})$
. We denote the boundary algebra of
![]() $A_{Q,W}$
by
$A_{Q,W}$
by
![]() $B_{Q,W}=eA_{Q,W}e$
, where
$B_{Q,W}=eA_{Q,W}e$
, where
![]() $e=\sum _{i\in Q_0}(e_i^++e_i^-)$
is the frozen idempotent of
$e=\sum _{i\in Q_0}(e_i^++e_i^-)$
is the frozen idempotent of
![]() $A_{Q,W}$
.
$A_{Q,W}$
.
Note. To aid legibility, if the vertices
![]() $i^+$
and
$i^+$
and
![]() $i^-$
appear as subscripts, we will usually move the sign into a superscript, as in the above expression for the frozen idempotent. When
$i^-$
appear as subscripts, we will usually move the sign into a superscript, as in the above expression for the frozen idempotent. When
![]() $W=0$
, we will typically drop it from the notation; for example, we write
$W=0$
, we will typically drop it from the notation; for example, we write
![]() $A_Q=A_{Q,0}$
. The reader is warned that
$A_Q=A_{Q,0}$
. The reader is warned that
![]() $\widetilde {0}$
is not the zero potential on
$\widetilde {0}$
is not the zero potential on
![]() $\widetilde {Q}$
.
$\widetilde {Q}$
.
Since
![]() $\widetilde {W}$
has a straightforward description in terms of W, so do the defining relations of
$\widetilde {W}$
has a straightforward description in terms of W, so do the defining relations of
![]() $A_{Q,W}$
; these form the set R consisting of
$A_{Q,W}$
; these form the set R consisting of
 $$ \begin{align} \partial_{a}{\widetilde{W}}=\partial_{a}{W}-\beta_{t{a}}\delta_a\alpha_{h{a}},\quad \partial_{\alpha_i}{\widetilde{W}}=\beta_i\delta_i-\sum_{\substack{\gamma\in Q_1\\h{\gamma}=i}}\gamma\beta_{t{\gamma}}\delta_{\gamma},\quad \partial_{\beta_i}{\widetilde{W}}=\delta_i\alpha_i-\sum_{\substack{\gamma\in Q_1\\t{\gamma}=i}}\delta_{\gamma}\alpha_{h{\gamma}}\gamma, \end{align} $$
$$ \begin{align} \partial_{a}{\widetilde{W}}=\partial_{a}{W}-\beta_{t{a}}\delta_a\alpha_{h{a}},\quad \partial_{\alpha_i}{\widetilde{W}}=\beta_i\delta_i-\sum_{\substack{\gamma\in Q_1\\h{\gamma}=i}}\gamma\beta_{t{\gamma}}\delta_{\gamma},\quad \partial_{\beta_i}{\widetilde{W}}=\delta_i\alpha_i-\sum_{\substack{\gamma\in Q_1\\t{\gamma}=i}}\delta_{\gamma}\alpha_{h{\gamma}}\gamma, \end{align} $$
for
![]() $a\in Q_1$
and
$a\in Q_1$
and
![]() $i\in Q_0$
. Having such an explicit generating set of relations will prove to be extremely useful later in the paper.
$i\in Q_0$
. Having such an explicit generating set of relations will prove to be extremely useful later in the paper.
To be able to apply Theorem 2.6, we wish to show that
![]() $A_{Q,W}$
is bimodule internally
$A_{Q,W}$
is bimodule internally
![]() $3$
-Calabi–Yau with respect to its frozen idempotent e, in the sense of Definition 2.4. We will do this, under a mild assumption on
$3$
-Calabi–Yau with respect to its frozen idempotent e, in the sense of Definition 2.4. We will do this, under a mild assumption on
![]() $(Q,W)$
, in §4, but first we give some examples.
$(Q,W)$
, in §4, but first we give some examples.
Example 3.2. The quiver with potential
![]() $(Q,0)$
, for Q an
$(Q,0)$
, for Q an
![]() $\mathsf {A}_2$
quiver, provides the most basic example revealing all of the combinatorial features of the construction. In this case, we have
$\mathsf {A}_2$
quiver, provides the most basic example revealing all of the combinatorial features of the construction. In this case, we have

with
![]() $\widetilde {F}$
indicated by the boxed vertices and dashed arrows. The potential on this ice quiver is
$\widetilde {F}$
indicated by the boxed vertices and dashed arrows. The potential on this ice quiver is
One can check that the frozen Jacobian algebra
![]() $A_Q$
attached to these data is isomorphic to the endomorphism algebra of a cluster-tilting object in the Frobenius cluster category consisting of those modules for the preprojective algebra of type
$A_Q$
attached to these data is isomorphic to the endomorphism algebra of a cluster-tilting object in the Frobenius cluster category consisting of those modules for the preprojective algebra of type
![]() $\mathsf {A}_4$
with socle supported at a fixed bivalent vertex [Reference Geiß, Leclerc and Schröer24]. For an explanation of why the categories arising in [Reference Geiß, Leclerc and Schröer24] are Frobenius cluster categories, see [Reference Pressland42, Exam. 3.11].
$\mathsf {A}_4$
with socle supported at a fixed bivalent vertex [Reference Geiß, Leclerc and Schröer24]. For an explanation of why the categories arising in [Reference Geiß, Leclerc and Schröer24] are Frobenius cluster categories, see [Reference Pressland42, Exam. 3.11].
Example 3.3. Now, let
![]() $(Q,W)$
be the quiver with potential in which
$(Q,W)$
be the quiver with potential in which

and
![]() $W=cba$
. The Jacobian algebra is a cluster-tilted algebra of type
$W=cba$
. The Jacobian algebra is a cluster-tilted algebra of type
![]() $\mathsf {A}_3$
, and has infinite global dimension (like any nonhereditary cluster-tilted algebra [Reference Keller and Reiten35, Cor. 2.1]). In this case,
$\mathsf {A}_3$
, and has infinite global dimension (like any nonhereditary cluster-tilted algebra [Reference Keller and Reiten35, Cor. 2.1]). In this case,

with
![]() $\widetilde {F}$
again indicated by boxed vertices and dashed arrows. The potential is
$\widetilde {F}$
again indicated by boxed vertices and dashed arrows. The potential is
The associated frozen Jacobian algebra
![]() $A_{Q,W}$
also arises from a dimer model on a disk with six marked points on its boundary [Reference Baur, King and Marsh3], and is isomorphic to the endomorphism algebra of a cluster-tilting object in Jensen–King–Su’s categorification of the cluster algebra structure on the Grassmannian
$A_{Q,W}$
also arises from a dimer model on a disk with six marked points on its boundary [Reference Baur, King and Marsh3], and is isomorphic to the endomorphism algebra of a cluster-tilting object in Jensen–King–Su’s categorification of the cluster algebra structure on the Grassmannian
![]() $\mathrm {Gr}_{2}^{6}$
[Reference Jensen, King and Su32]. This category is again a Frobenius cluster category (see [Reference Pressland42, Exam. 3.12]). Unlike the first example, this algebra is infinite-dimensional. However, it is Noetherian, so Theorem 2.6 still applies.
$\mathrm {Gr}_{2}^{6}$
[Reference Jensen, King and Su32]. This category is again a Frobenius cluster category (see [Reference Pressland42, Exam. 3.12]). Unlike the first example, this algebra is infinite-dimensional. However, it is Noetherian, so Theorem 2.6 still applies.
Since, in Examples 3.2 and 3.3, the algebra
![]() $A_{Q,W}$
is the endomorphism algebra of a cluster-tilting object in a Frobenius cluster category, it is internally
$A_{Q,W}$
is the endomorphism algebra of a cluster-tilting object in a Frobenius cluster category, it is internally
![]() $3$
-Calabi–Yau with respect to its frozen idempotent—that is, it has the properties in Remark 2.5—by a result of Keller–Reiten [Reference Keller and Reiten35, §5.4] (see also [Reference Pressland42, Cor. 3.10]). This foreshadows Theorem 4.14, which states that under mild assumptions on
$3$
-Calabi–Yau with respect to its frozen idempotent—that is, it has the properties in Remark 2.5—by a result of Keller–Reiten [Reference Keller and Reiten35, §5.4] (see also [Reference Pressland42, Cor. 3.10]). This foreshadows Theorem 4.14, which states that under mild assumptions on
![]() $(Q,W)$
, the algebra
$(Q,W)$
, the algebra
![]() $A_{Q,W}$
has the (a priori stronger) bimodule internal Calabi–Yau property from Definition 2.4.
$A_{Q,W}$
has the (a priori stronger) bimodule internal Calabi–Yau property from Definition 2.4.
4 Calabi–Yau properties for frozen Jacobian algebras
In this section, we will recall from [Reference Pressland42, §5] a bimodule complex
![]() $0\to \mathbf {P}(A)\to A\to 0$
for a frozen Jacobian algebra A, exactness of which implies that A is bimodule internally
$0\to \mathbf {P}(A)\to A\to 0$
for a frozen Jacobian algebra A, exactness of which implies that A is bimodule internally
![]() $3$
-Calabi–Yau with respect to its frozen idempotent. We show that this complex is exact when
$3$
-Calabi–Yau with respect to its frozen idempotent. We show that this complex is exact when
![]() $A=A_{Q,W}$
is as in Definition 3.1. Thus, these frozen Jacobian algebras satisfy the most complicated condition in Theorem 2.6. This constitutes the main step in the proof of Theorem 1.
$A=A_{Q,W}$
is as in Definition 3.1. Thus, these frozen Jacobian algebras satisfy the most complicated condition in Theorem 2.6. This constitutes the main step in the proof of Theorem 1.
Our arguments exploit the fact that the algebras we consider are pseudocompact, and so we begin with some useful generalities on such algebras. Further background can be found in [Reference Brumer7], [Reference Gabriel22], [Reference Iusenko and MacQuarrie30], [Reference Simson47], [Reference Van den Bergh51], for example.
Definition 4.1. Let A be a topological
![]() $\mathbb {K}$
-algebra. We say that A is pseudocompact if there is a system
$\mathbb {K}$
-algebra. We say that A is pseudocompact if there is a system
![]() $\mathcal {I}=\{I\}$
of neighborhoods of
$\mathcal {I}=\{I\}$
of neighborhoods of
![]() $0\in A$
consisting of (open) ideals such that
$0\in A$
consisting of (open) ideals such that
![]() $A/I$
is finite-dimensional for all
$A/I$
is finite-dimensional for all
![]() $I\in \mathcal {I}$
and the natural map
$I\in \mathcal {I}$
and the natural map
is an isomorphism. The Jacobson radical of A, denoted by J, is the intersection of maximal closed left ideals of A, and we say that A is J-adically complete if the natural map
![]() $A\to \varprojlim _nA/J^n$
is an isomorphism.
$A\to \varprojlim _nA/J^n$
is an isomorphism.
Proposition 4.2. If Q is a finite quiver, the complete path algebra
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is pseudocompact and J-adically complete, where J is the Jacobson radical.
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is pseudocompact and J-adically complete, where J is the Jacobson radical.
Proof. The algebra
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
may be identified with the continuous dual of the path coalgebra of
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
may be identified with the continuous dual of the path coalgebra of
![]() $Q^{\mathrm {op}}$
, that is, the space of continuous functionals on this coalgebra (see, e.g., [Reference Simson47, Prop. 8.1(c)]). The continuous dual of any coalgebra is pseudocompact (see [Reference Simson48]).
$Q^{\mathrm {op}}$
, that is, the space of continuous functionals on this coalgebra (see, e.g., [Reference Simson47, Prop. 8.1(c)]). The continuous dual of any coalgebra is pseudocompact (see [Reference Simson48]).
The Jacobson radical of
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is generated by the arrows. In particular,
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is generated by the arrows. In particular,
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /J^2$
is finite-dimensional, since Q is a finite quiver, and so
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /J^2$
is finite-dimensional, since Q is a finite quiver, and so
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is J-adically complete by [Reference Iusenko and MacQuarrie30, Prop. 2.7].
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
is J-adically complete by [Reference Iusenko and MacQuarrie30, Prop. 2.7].
Proposition 4.3. Let Q be a finite quiver. Then, for any ideal
![]() $I\leq \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
which is closed in the J-adic topology, for J the Jacobson radical, the quotient algebra
$I\leq \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
which is closed in the J-adic topology, for J the Jacobson radical, the quotient algebra
![]() $A=\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /I$
is pseudocompact.
$A=\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /I$
is pseudocompact.
Proof. This statement (in a more general form) can be found in The Stacks Project §00M9Footnote
2
, but we give a direct argument. For each
![]() $n\in \mathbb {Z}$
, there is a short exact sequence
$n\in \mathbb {Z}$
, there is a short exact sequence
where
![]() $\pi \colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to A=\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /I$
is the projection. In particular, it follows that
$\pi \colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to A=\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle /I$
is the projection. In particular, it follows that
![]() $A/\pi J^n$
is finite-dimensional. Note that the ideals
$A/\pi J^n$
is finite-dimensional. Note that the ideals
![]() $\pi J^n$
form a system of open neighborhoods of
$\pi J^n$
form a system of open neighborhoods of
![]() $0$
in A, since
$0$
in A, since
![]() $\pi ^{-1}(\pi J^n)=I+J^n$
is open in
$\pi ^{-1}(\pi J^n)=I+J^n$
is open in
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
.
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
.
The sequence (4.1) is the nth component of a short exact sequence of inverse systems, each of which has only surjective morphisms and so satisfies (in a trivial way) the Mittag-Leffler condition. Thus, we obtain a short exact sequence of inverse limits
The left-hand term of this sequence may be naturally identified with
![]() $\bigcap _{n\geq 1}(I+J^n)$
, which is the closure of I in the J-adic topology, and is thus equal to I since I is closed. Moreover, the middle term is
$\bigcap _{n\geq 1}(I+J^n)$
, which is the closure of I in the J-adic topology, and is thus equal to I since I is closed. Moreover, the middle term is
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
since this algebra is J-adically complete by Proposition 4.2. Hence, the right-hand term is A, which is therefore pseudocompact.
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
since this algebra is J-adically complete by Proposition 4.2. Hence, the right-hand term is A, which is therefore pseudocompact.
Corollary 4.4. For any ice quiver with potential
![]() $(Q,F,W)$
, the frozen Jacobian algebra
$(Q,F,W)$
, the frozen Jacobian algebra
![]() $J(Q,F,W)$
is pseudocompact.
$J(Q,F,W)$
is pseudocompact.
Proof. By definition,
![]() $J(Q,F,W)$
is the quotient of
$J(Q,F,W)$
is the quotient of
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
by a closed ideal. Thus, the result follows by Proposition 4.3.
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
by a closed ideal. Thus, the result follows by Proposition 4.3.
We now return to the setting of ice quivers with potential. Let
![]() $(Q,F,W)$
be an ice quiver with potential and write
$(Q,F,W)$
be an ice quiver with potential and write
![]() $A=J(Q,F,W)$
. Recall that
$A=J(Q,F,W)$
. Recall that
![]() $Q_0^\circ =Q_0\setminus F_0$
and
$Q_0^\circ =Q_0\setminus F_0$
and
![]() $Q_1^\circ =Q_1\setminus F_1$
denote the sets of mutable vertices and unfrozen arrows of Q, respectively. For
$Q_1^\circ =Q_1\setminus F_1$
denote the sets of mutable vertices and unfrozen arrows of Q, respectively. For
![]() $i\in Q_0$
, we write
$i\in Q_0$
, we write
![]() ${\mathrm {H}_{i}}$
for the set of arrows of Q with head i, and
${\mathrm {H}_{i}}$
for the set of arrows of Q with head i, and
![]() ${\mathrm {T}_{i}}$
for the set of arrows of Q with tail i. We denote by
${\mathrm {T}_{i}}$
for the set of arrows of Q with tail i. We denote by
![]() $\mathrm {H}_{i}^{\circ }$
and
$\mathrm {H}_{i}^{\circ }$
and
![]() $\mathrm {T}_{i}^{\circ }$
the intersection of
$\mathrm {T}_{i}^{\circ }$
the intersection of
![]() $Q_1^\circ $
with
$Q_1^\circ $
with
![]() ${\mathrm {H}_{i}}$
and
${\mathrm {H}_{i}}$
and
![]() ${\mathrm {T}_{i}}$
, respectively. Recall from Remark 2.2 that the quotient
${\mathrm {T}_{i}}$
, respectively. Recall from Remark 2.2 that the quotient
![]() $S:=A/J(A)$
of A by its Jacobson radical is a semisimple algebra, isomorphic as a left A-module to the direct sum of the vertex simple A-modules. (This property is sometimes [Reference Iusenko and MacQuarrie30, §3.2] called pointedness.) Thus, S has a basis given by the vertex idempotents
$S:=A/J(A)$
of A by its Jacobson radical is a semisimple algebra, isomorphic as a left A-module to the direct sum of the vertex simple A-modules. (This property is sometimes [Reference Iusenko and MacQuarrie30, §3.2] called pointedness.) Thus, S has a basis given by the vertex idempotents
![]() $e_i$
for
$e_i$
for
![]() $i\in Q_0$
. For the remainder of this section, we write
$i\in Q_0$
. For the remainder of this section, we write
![]() $\mathbin {\otimes }=\mathbin {\otimes }_S$
.
$\mathbin {\otimes }=\mathbin {\otimes }_S$
.
Introduce formal symbols
![]() $\rho _{\alpha }$
for each
$\rho _{\alpha }$
for each
![]() $\alpha \in Q_1$
and
$\alpha \in Q_1$
and
![]() $\omega _v$
for each
$\omega _v$
for each
![]() $v\in Q_0$
, and define S-bimodule structures on the vector spaces
$v\in Q_0$
, and define S-bimodule structures on the vector spaces
 $$ \begin{align*} V_0&=\bigoplus_{i\in Q_0}\mathbb{K}e_{i},& V_1&=\bigoplus_{\alpha\in Q_1}\mathbb{K}\alpha,& V_2&=\bigoplus_{\alpha\in Q_1^\circ}\mathbb{K}\rho_{\alpha},& V_3&=\bigoplus_{i\in Q_0^\circ}\mathbb{K}\omega_i, \end{align*} $$
$$ \begin{align*} V_0&=\bigoplus_{i\in Q_0}\mathbb{K}e_{i},& V_1&=\bigoplus_{\alpha\in Q_1}\mathbb{K}\alpha,& V_2&=\bigoplus_{\alpha\in Q_1^\circ}\mathbb{K}\rho_{\alpha},& V_3&=\bigoplus_{i\in Q_0^\circ}\mathbb{K}\omega_i, \end{align*} $$
via the formulae
Next, we describe various morphisms
![]() $\mu _k$
of A-bimodules. Since
$\mu _k$
of A-bimodules. Since
![]() $V_0\cong S$
, the A-bimodule
$V_0\cong S$
, the A-bimodule
![]() $A\mathbin {\otimes } V_0\mathbin {\otimes } A$
is canonically isomorphic to
$A\mathbin {\otimes } V_0\mathbin {\otimes } A$
is canonically isomorphic to
![]() $A\mathbin {\otimes } A$
. Composing this isomorphism with the multiplication map for A, we obtain a map
$A\mathbin {\otimes } A$
. Composing this isomorphism with the multiplication map for A, we obtain a map
![]() $\mu _0\colon A\mathbin {\otimes } V_0\mathbin {\otimes } A\to A$
. Define
$\mu _0\colon A\mathbin {\otimes } V_0\mathbin {\otimes } A\to A$
. Define
![]() $\mu _1\colon A\mathbin {\otimes } V_1\mathbin {\otimes } A\to A\mathbin {\otimes } V_0\mathbin {\otimes } A$
by
$\mu _1\colon A\mathbin {\otimes } V_1\mathbin {\otimes } A\to A\mathbin {\otimes } V_0\mathbin {\otimes } A$
by
For any path
![]() $p=\alpha _m\dotsm \alpha _1$
of
$p=\alpha _m\dotsm \alpha _1$
of
![]() $\mathbb {K} Q$
, we may define
$\mathbb {K} Q$
, we may define
 $$\begin{align*}\Delta_{\alpha}(p)=\sum_{\alpha_i=\alpha}\alpha_m\dotsm\alpha_{i+1}\mathbin{\otimes}\alpha_i\mathbin{\otimes}\alpha_{i-1}\dotsm\alpha_1,\end{align*}$$
$$\begin{align*}\Delta_{\alpha}(p)=\sum_{\alpha_i=\alpha}\alpha_m\dotsm\alpha_{i+1}\mathbin{\otimes}\alpha_i\mathbin{\otimes}\alpha_{i-1}\dotsm\alpha_1,\end{align*}$$
and extend by linearity and continuity to obtain a map
![]() $\Delta _{\alpha }\colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to A\mathbin {\otimes } V_1\mathbin {\otimes } A$
. We then define
$\Delta _{\alpha }\colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to A\mathbin {\otimes } V_1\mathbin {\otimes } A$
. We then define
![]() $\mu _2\colon A\mathbin {\otimes } V_2\mathbin {\otimes } A\to A\mathbin {\otimes } V_1\mathbin {\otimes } A$
by
$\mu _2\colon A\mathbin {\otimes } V_2\mathbin {\otimes } A\to A\mathbin {\otimes } V_1\mathbin {\otimes } A$
by
 $$\begin{align*}\mu_2(x\mathbin{\otimes}\rho_{\alpha}\mathbin{\otimes} y)=\sum_{\beta\in Q_1}x\Delta_{\beta}(\partial_{\alpha}{W})y.\end{align*}$$
$$\begin{align*}\mu_2(x\mathbin{\otimes}\rho_{\alpha}\mathbin{\otimes} y)=\sum_{\beta\in Q_1}x\Delta_{\beta}(\partial_{\alpha}{W})y.\end{align*}$$
Finally, define
![]() $\mu _3\colon A\mathbin {\otimes } V_3\mathbin {\otimes } A\to A\mathbin {\otimes } V_2\mathbin {\otimes } A$
by
$\mu _3\colon A\mathbin {\otimes } V_3\mathbin {\otimes } A\to A\mathbin {\otimes } V_2\mathbin {\otimes } A$
by
 $$\begin{align*}\mu_3(x\mathbin{\otimes}\omega_v\mathbin{\otimes} y)=\sum_{\alpha\in{\mathrm{T}_{v}}}x\mathbin{\otimes}\rho_{\alpha}\mathbin{\otimes}\alpha y-\sum_{\beta\in{\mathrm{H}_{v}}}x\beta\mathbin{\otimes}\rho_{\beta}\mathbin{\otimes} y.\end{align*}$$
$$\begin{align*}\mu_3(x\mathbin{\otimes}\omega_v\mathbin{\otimes} y)=\sum_{\alpha\in{\mathrm{T}_{v}}}x\mathbin{\otimes}\rho_{\alpha}\mathbin{\otimes}\alpha y-\sum_{\beta\in{\mathrm{H}_{v}}}x\beta\mathbin{\otimes}\rho_{\beta}\mathbin{\otimes} y.\end{align*}$$
Note that we have
![]() $A\otimes V_k\otimes A\otimes _AS=A\otimes V_k\otimes S=A\otimes V_k$
for
$A\otimes V_k\otimes A\otimes _AS=A\otimes V_k\otimes S=A\otimes V_k$
for
![]() $0\leq k\leq 3$
. Thus, for each
$0\leq k\leq 3$
. Thus, for each
![]() $1\leq k\leq 3$
, we obtain a map
$1\leq k\leq 3$
, we obtain a map
![]() $\bar {\mu }_k:=(\mu _k\otimes _AS)\colon A\otimes V_k\to A\otimes V_{k-1}$
.
$\bar {\mu }_k:=(\mu _k\otimes _AS)\colon A\otimes V_k\to A\otimes V_{k-1}$
.
Lemma 4.5. Let
![]() $1\leq k\leq 3$
and consider
$1\leq k\leq 3$
and consider
![]() $x\otimes v\otimes y\in A\otimes V_k\otimes A$
, where
$x\otimes v\otimes y\in A\otimes V_k\otimes A$
, where
![]() $x,y\in A$
and
$x,y\in A$
and
![]() $v\in V_k$
. Then
$v\in V_k$
. Then
where
![]() $r\in A\otimes V_{k-1}\otimes Jy$
.
$r\in A\otimes V_{k-1}\otimes Jy$
.
Proof. This follows directly from the definition of the maps
![]() $\mu _k$
, recalling that the Jacobson radical J is generated by the arrows of Q and that
$\mu _k$
, recalling that the Jacobson radical J is generated by the arrows of Q and that
![]() $A/J=S$
.
$A/J=S$
.
Definition 4.6. For an ice quiver with potential
![]() $(Q,F,W)$
with frozen Jacobian algebra A, denote by
$(Q,F,W)$
with frozen Jacobian algebra A, denote by
![]() $\mathbf {P}(A)$
the complex of A-bimodules with nonzero terms
$\mathbf {P}(A)$
the complex of A-bimodules with nonzero terms
and
![]() $A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A$
in degree
$A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A$
in degree
![]() $0$
. That this sequence is indeed a complex is [Reference Pressland42, Lem. 5.5].
$0$
. That this sequence is indeed a complex is [Reference Pressland42, Lem. 5.5].
By [Reference Pressland42, Th. 5.7], if A is a frozen Jacobian algebra such that
is exact, then A is bimodule internally
![]() $3$
-Calabi–Yau with respect to the idempotent
$3$
-Calabi–Yau with respect to the idempotent
![]() $e=\sum _{i\in F_0}e_{i}$
. Our goal for the remainder of the section is to check exactness of (4.2) when
$e=\sum _{i\in F_0}e_{i}$
. Our goal for the remainder of the section is to check exactness of (4.2) when
![]() $A=A_{Q,W}$
is the algebra from Definition 3.1. The following lemma allows us to simplify this calculation; its proof is based on [Reference Broomhead6, Prop. 7.5], but adapted to exploit pseudocompactness of A in place of a suitable grading.
$A=A_{Q,W}$
is the algebra from Definition 3.1. The following lemma allows us to simplify this calculation; its proof is based on [Reference Broomhead6, Prop. 7.5], but adapted to exploit pseudocompactness of A in place of a suitable grading.
Proof. The forward implication holds since
![]() $\mathbf {P}(A)\stackrel {\mu _0}{\longrightarrow }A$
is perfect as a complex of right A-modules, and so remains exact under
$\mathbf {P}(A)\stackrel {\mu _0}{\longrightarrow }A$
is perfect as a complex of right A-modules, and so remains exact under
![]() $-\mathbin {\otimes }_AM$
for any
$-\mathbin {\otimes }_AM$
for any
![]() $M\in \operatorname{Mod}{A}$
.
$M\in \operatorname{Mod}{A}$
.
For the converse implication, we use pseudocompactness. Abbreviate
![]() $\bar {\mu }_{k,n}=\mu _k\otimes _AA/J^n$
(so that
$\bar {\mu }_{k,n}=\mu _k\otimes _AA/J^n$
(so that
![]() $\bar {\mu }_{k,1}=\bar {\mu }_k$
as defined above). We will show inductively that
$\bar {\mu }_{k,1}=\bar {\mu }_k$
as defined above). We will show inductively that
is exact for all n; the assumed exactness of (4.3) gives the base case
![]() $n=1$
of this induction. Then the result will follow as in the proof of Proposition 4.3 from the fact that (4.4) remains exact under taking inverse limits, noting again that the relevant inverse systems satisfy the Mittag-Leffler condition since all their morphisms are surjective.
$n=1$
of this induction. Then the result will follow as in the proof of Proposition 4.3 from the fact that (4.4) remains exact under taking inverse limits, noting again that the relevant inverse systems satisfy the Mittag-Leffler condition since all their morphisms are surjective.
That (4.4) is exact at
![]() $A/J^n$
(and indeed, that (4.2) is exact at A) follows since
$A/J^n$
(and indeed, that (4.2) is exact at A) follows since
![]() $\mu _0$
is multiplication in the unital algebra A, so we concentrate on the other terms, each of which has the form
$\mu _0$
is multiplication in the unital algebra A, so we concentrate on the other terms, each of which has the form
![]() $A\otimes V_k\otimes A/J^n$
for some S-bimodule
$A\otimes V_k\otimes A/J^n$
for some S-bimodule
![]() $V_k$
, adopting the convention that
$V_k$
, adopting the convention that
![]() $V_k=0$
for
$V_k=0$
for
![]() $k>3$
.
$k>3$
.
Choose
![]() $k\geq 0$
, let
$k\geq 0$
, let
![]() $\phi _0\in A\otimes V_k\otimes A/J^n$
for some
$\phi _0\in A\otimes V_k\otimes A/J^n$
for some
![]() $n\geq 2$
, and write
$n\geq 2$
, and write
![]() $\phi _0^{\prime }$
for the projection of
$\phi _0^{\prime }$
for the projection of
![]() $\phi _0$
to
$\phi _0$
to
![]() $A\otimes V_k\otimes A/J^{n-1}$
. If
$A\otimes V_k\otimes A/J^{n-1}$
. If
![]() $\phi _0$
is closed, that is, if
$\phi _0$
is closed, that is, if
![]() $\bar {\mu }_{k,n}(\phi _0)=0$
, then
$\bar {\mu }_{k,n}(\phi _0)=0$
, then
![]() $\phi ^{\prime }_0$
is also closed, and so by induction there is
$\phi ^{\prime }_0$
is also closed, and so by induction there is
![]() $\psi _0^{\prime }\in A\otimes V_{k+1}\otimes A/J^{n-1}$
with
$\psi _0^{\prime }\in A\otimes V_{k+1}\otimes A/J^{n-1}$
with
![]() $\bar {\mu }_{k+1,n-1}(\psi ')=\phi '$
. Choose any
$\bar {\mu }_{k+1,n-1}(\psi ')=\phi '$
. Choose any
![]() $\psi _0\in A\otimes V_{k+1}\otimes A/J^n$
projecting to
$\psi _0\in A\otimes V_{k+1}\otimes A/J^n$
projecting to
![]() $\psi ^{\prime }_0$
. Then
$\psi ^{\prime }_0$
. Then
![]() $\phi _1:=\phi _0-\bar {\mu }_{k+1,n}(\psi _0)$
projects to
$\phi _1:=\phi _0-\bar {\mu }_{k+1,n}(\psi _0)$
projects to
![]() $\phi _0^{\prime }-\bar {\mu }_{k,n-1}(\psi _0^{\prime })=0$
, and hence
$\phi _0^{\prime }-\bar {\mu }_{k,n-1}(\psi _0^{\prime })=0$
, and hence
![]() $\phi _1\in A\otimes V_k\otimes J^{n-1}/J^n$
. Moreover,
$\phi _1\in A\otimes V_k\otimes J^{n-1}/J^n$
. Moreover,
![]() $\phi _1$
is closed.
$\phi _1$
is closed.
Now, let Y be a basis of the finite-dimensional vector space
![]() $J^{n-1}/J^n$
, so that we may write
$J^{n-1}/J^n$
, so that we may write
 $$\begin{align*}\phi_1=\sum_{y\in Y}u_y\otimes y\end{align*}$$
$$\begin{align*}\phi_1=\sum_{y\in Y}u_y\otimes y\end{align*}$$
for some
![]() $u_y\in A\otimes V_k$
. Since each
$u_y\in A\otimes V_k$
. Since each
![]() $y\in J^{n-1}/J^n$
and
$y\in J^{n-1}/J^n$
and
![]() $\phi _1$
is closed, we have
$\phi _1$
is closed, we have
 $$\begin{align*}0=\sum_{y\in Y}\bar{\mu}_{k,n}(u_y\otimes y)=\sum_{y\in Y}\bar{\mu}_k(u_y)\otimes y\end{align*}$$
$$\begin{align*}0=\sum_{y\in Y}\bar{\mu}_{k,n}(u_y\otimes y)=\sum_{y\in Y}\bar{\mu}_k(u_y)\otimes y\end{align*}$$
by Lemma 4.5. It then follows by linear independence of the set Y that
![]() $\bar {\mu }_k(u_y)=0$
for all
$\bar {\mu }_k(u_y)=0$
for all
![]() $y\in Y$
. By the assumed exactness of (4.3), there are therefore
$y\in Y$
. By the assumed exactness of (4.3), there are therefore
![]() $v_y\in A\otimes V_{k+1}$
with
$v_y\in A\otimes V_{k+1}$
with
![]() $\bar {\mu }_{k+1}(v_y)=u_y$
.
$\bar {\mu }_{k+1}(v_y)=u_y$
.
Now, let
 $$\begin{align*}\psi_1=\sum_{y\in Y}v_y\otimes y\in A\otimes V_{k+1}\otimes A/J^n.\end{align*}$$
$$\begin{align*}\psi_1=\sum_{y\in Y}v_y\otimes y\in A\otimes V_{k+1}\otimes A/J^n.\end{align*}$$
Using Lemma 4.5 again, we may calculate
 $$\begin{align*}\bar{\mu}_{k+1,n}(\psi_1)=\sum_{y\in Y}\bar{\mu}_{k+1}(v_y)\otimes y=\sum_{y\in Y}u_y\otimes y=\phi_1,\end{align*}$$
$$\begin{align*}\bar{\mu}_{k+1,n}(\psi_1)=\sum_{y\in Y}\bar{\mu}_{k+1}(v_y)\otimes y=\sum_{y\in Y}u_y\otimes y=\phi_1,\end{align*}$$
and so
![]() $\phi _0=\bar {\mu }_{k+1,n}(\psi _0+\psi _1)$
is exact. Thus, each sequence (4.4), and hence the limit (4.2), is exact as required.
$\phi _0=\bar {\mu }_{k+1,n}(\psi _0+\psi _1)$
is exact. Thus, each sequence (4.4), and hence the limit (4.2), is exact as required.
Thus, it suffices for us to show that (4.3) is exact. This complex decomposes along with S, so that its exactness is equivalent to the exactness of
for each
![]() $i\in \widetilde {Q}_0$
, where
$i\in \widetilde {Q}_0$
, where
![]() $S_{i}$
denotes the vertex simple left A-module at i. We may calculate the terms in this complex as
$S_{i}$
denotes the vertex simple left A-module at i. We may calculate the terms in this complex as
 $$ \begin{align} \begin{aligned} A\mathbin{\otimes}\mathbb{K} Q_1\mathbin{\otimes} A\mathbin{\otimes}_AS_{i}&\cong\bigoplus_{b\in{\mathrm{T}_{i}}}Ae_{h{b}}, \\ A\mathbin{\otimes}\mathbb{K} Q_2^\circ\mathbin{\otimes} A\mathbin{\otimes}_AS_{i}&\cong\bigoplus_{a\in\mathrm{H}_{i}^{\circ}}Ae_{t{a}}, \\ A\mathbin{\otimes}\mathbb{K} Q_3^\circ\mathbin{\otimes} A\mathbin{\otimes}_AS_{i}&\cong{\begin{cases}Ae_{i},&i\in Q_0^\circ,\\ 0,&i\in F_0.\end{cases}} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} A\mathbin{\otimes}\mathbb{K} Q_1\mathbin{\otimes} A\mathbin{\otimes}_AS_{i}&\cong\bigoplus_{b\in{\mathrm{T}_{i}}}Ae_{h{b}}, \\ A\mathbin{\otimes}\mathbb{K} Q_2^\circ\mathbin{\otimes} A\mathbin{\otimes}_AS_{i}&\cong\bigoplus_{a\in\mathrm{H}_{i}^{\circ}}Ae_{t{a}}, \\ A\mathbin{\otimes}\mathbb{K} Q_3^\circ\mathbin{\otimes} A\mathbin{\otimes}_AS_{i}&\cong{\begin{cases}Ae_{i},&i\in Q_0^\circ,\\ 0,&i\in F_0.\end{cases}} \end{aligned} \end{align} $$
In the first two cases, the right-hand sides are of the form
![]() $\bigoplus _{a\in X}Ae_{v(a)}$
, where X is a set of arrows, and
$\bigoplus _{a\in X}Ae_{v(a)}$
, where X is a set of arrows, and
![]() $v\colon X\to Q_0$
. We will denote by
$v\colon X\to Q_0$
. We will denote by
![]() $x\mapsto x\otimes [a]$
the inclusion
$x\mapsto x\otimes [a]$
the inclusion
![]() $Ae_{v(a)}\to \bigoplus _{a\in X}Ae_{v(a)}$
mapping the domain to the summand indexed by a; this helps us to distinguish these various inclusions when v is not injective. As a consequence, a general element of the direct sum is
$Ae_{v(a)}\to \bigoplus _{a\in X}Ae_{v(a)}$
mapping the domain to the summand indexed by a; this helps us to distinguish these various inclusions when v is not injective. As a consequence, a general element of the direct sum is
![]() $x=\sum _{a\in X}x_a\otimes [a]$
for
$x=\sum _{a\in X}x_a\otimes [a]$
for
![]() $x_a\in Ae_{v(a)}$
.
$x_a\in Ae_{v(a)}$
.
Each arrow
![]() $b\in Q_1$
has an associated right derivative
$b\in Q_1$
has an associated right derivative
![]() $\partial ^r_{b}\colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
, which is linear and continuous and given by
$\partial ^r_{b}\colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
, which is linear and continuous and given by
 $$ \begin{align} \partial^r_{b}(\alpha_{\ell}\dotsm\alpha_1)=\begin{cases}\alpha_{\ell}\dotsm\alpha_2,&\alpha_1=b,\\ 0,&\alpha_1\ne b\end{cases} \end{align} $$
$$ \begin{align} \partial^r_{b}(\alpha_{\ell}\dotsm\alpha_1)=\begin{cases}\alpha_{\ell}\dotsm\alpha_2,&\alpha_1=b,\\ 0,&\alpha_1\ne b\end{cases} \end{align} $$
on paths. Using this map, we may write
 $$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{i})(x)=\sum_{b\in{\mathrm{T}_{i}}}\bigg(\sum_{a\in\mathrm{H}_{i}^{\circ}}x_a\partial^r_{b}{\partial_{a}{W}}\bigg)\mathbin{\otimes}[b].\end{align*}$$
$$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{i})(x)=\sum_{b\in{\mathrm{T}_{i}}}\bigg(\sum_{a\in\mathrm{H}_{i}^{\circ}}x_a\partial^r_{b}{\partial_{a}{W}}\bigg)\mathbin{\otimes}[b].\end{align*}$$
Calculating
![]() $\mu _k\otimes _A S_i$
for the other values of k is similar, and more straightforward.
$\mu _k\otimes _A S_i$
for the other values of k is similar, and more straightforward.
Remark 4.8. By standard results on presentations of algebras (see, e.g., [Reference Butler and King12]), the complex (4.2) is always exact in degrees
![]() $-1$
,
$-1$
,
![]() $0$
, and
$0$
, and
![]() $1$
, and hence the same is true for each complex (4.5). Thus, in the following argument, we need only check the exactness of (4.5) at
$1$
, and hence the same is true for each complex (4.5). Thus, in the following argument, we need only check the exactness of (4.5) at
![]() $A\otimes V_3\otimes S_i$
and
$A\otimes V_3\otimes S_i$
and
![]() $A\otimes V_2\otimes S_i$
.
$A\otimes V_2\otimes S_i$
.
Now, let
![]() $(Q,W)$
be a quiver with potential, and let
$(Q,W)$
be a quiver with potential, and let
![]() $A=A_{Q,W}=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
. The following series of results will establish exactness of the complex (4.3) for A for each vertex
$A=A_{Q,W}=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
. The following series of results will establish exactness of the complex (4.3) for A for each vertex
![]() $i\in \widetilde {Q}_0$
, using heavily the explicit set R of defining relations for A given in (3.1).
$i\in \widetilde {Q}_0$
, using heavily the explicit set R of defining relations for A given in (3.1).
Lemma 4.9. Let
![]() $i\in \widetilde {Q}_0^\circ =Q_0$
. If
$i\in \widetilde {Q}_0^\circ =Q_0$
. If
![]() $y\in Ae_i$
satisfies
$y\in Ae_i$
satisfies
![]() $y\beta _i=0$
, then
$y\beta _i=0$
, then
![]() $y=0$
.
$y=0$
.
Proof. Let
![]() $\widetilde {y}$
be an arbitrary lift of y to
$\widetilde {y}$
be an arbitrary lift of y to
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_i$
. Now, assume
$\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_i$
. Now, assume
![]() $y\beta _i=0$
, so
$y\beta _i=0$
, so
![]() $\widetilde {y}\beta _i\in \overline {\langle R\rangle }$
. Since every term of
$\widetilde {y}\beta _i\in \overline {\langle R\rangle }$
. Since every term of
![]() $\widetilde {y}\beta _i$
, when written in the basis of paths of
$\widetilde {y}\beta _i$
, when written in the basis of paths of
![]() $\widetilde {Q}$
, ends with the arrow
$\widetilde {Q}$
, ends with the arrow
![]() $\beta _i$
, but no term of any element of R has a term ending with
$\beta _i$
, but no term of any element of R has a term ending with
![]() $\beta _i$
, we must be able to write
$\beta _i$
, we must be able to write
![]() $\widetilde {y}\beta _i=z\beta _i$
for some
$\widetilde {y}\beta _i=z\beta _i$
for some
![]() $z\in \overline {\langle R\rangle }e_i$
. Comparing terms, we see that
$z\in \overline {\langle R\rangle }e_i$
. Comparing terms, we see that
![]() $\widetilde {y}=z\in \overline {\langle R\rangle }$
, and so
$\widetilde {y}=z\in \overline {\langle R\rangle }$
, and so
![]() $y=0$
in A.
$y=0$
in A.
Proposition 4.10. For
![]() $i\in \widetilde {Q}_0^\circ $
, the map
$i\in \widetilde {Q}_0^\circ $
, the map
 $\mu _3\mathbin {\otimes }_AS_{i}\colon Ae_{i}\to \displaystyle \bigoplus _{a\in \mathrm {H}_{i}^{\circ }} Ae_{t{a}}$
is injective.
$\mu _3\mathbin {\otimes }_AS_{i}\colon Ae_{i}\to \displaystyle \bigoplus _{a\in \mathrm {H}_{i}^{\circ }} Ae_{t{a}}$
is injective.
Proof. We have
![]() $(\mu _3\mathbin {\otimes }_AS_{i})(y)=\sum _{a\in \mathrm {H}_{i}^{\circ }}-ya\otimes [a]$
. Since i is mutable,
$(\mu _3\mathbin {\otimes }_AS_{i})(y)=\sum _{a\in \mathrm {H}_{i}^{\circ }}-ya\otimes [a]$
. Since i is mutable,
![]() $\mathrm {H}_{i}^{\circ }={\mathrm {H}_{i}}$
contains
$\mathrm {H}_{i}^{\circ }={\mathrm {H}_{i}}$
contains
![]() $\beta _i$
by the construction of
$\beta _i$
by the construction of
![]() $(\widetilde {Q},\widetilde {F})$
. Thus, if
$(\widetilde {Q},\widetilde {F})$
. Thus, if
![]() $(\mu _3\mathbin {\otimes }_AS_{i})(y)=0$
, it follows that
$(\mu _3\mathbin {\otimes }_AS_{i})(y)=0$
, it follows that
![]() $-y\beta _i\mathbin {\otimes }[\beta _i]=0$
, hence
$-y\beta _i\mathbin {\otimes }[\beta _i]=0$
, hence
![]() $y\beta _i=0$
, and so
$y\beta _i=0$
, and so
![]() $y=0$
by Lemma 4.9.
$y=0$
by Lemma 4.9.
Lemma 4.11. Let
![]() $i\in \widetilde {Q}_0^\circ $
. For each
$i\in \widetilde {Q}_0^\circ $
. For each
![]() $a\in \mathrm {H}_{i}^{\circ }$
, pick
$a\in \mathrm {H}_{i}^{\circ }$
, pick
![]() $x_a\in Ae_{t a}$
. If
$x_a\in Ae_{t a}$
. If
![]() $x_{\beta _i}\delta _i=\sum _{a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}}x_a\beta _{t{a}}\delta _a$
, then there exists
$x_{\beta _i}\delta _i=\sum _{a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}}x_a\beta _{t{a}}\delta _a$
, then there exists
![]() $y\in Ae_i$
such that
$y\in Ae_i$
such that
![]() $x_a=ya$
for each
$x_a=ya$
for each
![]() $a\in \mathrm {H}_{i}^{\circ }$
.
$a\in \mathrm {H}_{i}^{\circ }$
.
Proof. Pick a lift
![]() $\widetilde {x}_a\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle $
of each
$\widetilde {x}_a\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle $
of each
![]() $x_a$
. Writing
$x_a$
. Writing
![]() $p=\widetilde {x}_{\beta _i}\delta _i-\sum _{a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}}\widetilde {x}_a\beta _{t{a}}\delta _a$
, our assumption on the
$p=\widetilde {x}_{\beta _i}\delta _i-\sum _{a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}}\widetilde {x}_a\beta _{t{a}}\delta _a$
, our assumption on the
![]() $x_a$
is equivalent to
$x_a$
is equivalent to
![]() $p\in \overline {\langle R\rangle }$
. Since every term of p ends with either
$p\in \overline {\langle R\rangle }$
. Since every term of p ends with either
![]() $\delta _i$
or
$\delta _i$
or
![]() $\beta _{t{a}}\delta _a$
for some
$\beta _{t{a}}\delta _a$
for some
![]() $a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}$
, and the only element of R including terms ending with these arrows is
$a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}$
, and the only element of R including terms ending with these arrows is
![]() $\beta _i\delta _i-\sum _{a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}}a\beta _{t{a}}\delta _a$
, we can write
$\beta _i\delta _i-\sum _{a\in \mathrm {H}_{i}^{\circ }\setminus \{\beta _i\}}a\beta _{t{a}}\delta _a$
, we can write
 $$\begin{align*}p=z_i\delta_i+\sum_{a\in\mathrm{H}_{i}^{\circ}\setminus\{\beta_i\}}z_a\beta_{t{a}}\delta_a+y\Big(\beta_i\delta_i-\sum_{a\in\mathrm{H}_{i}^{\circ}\setminus\{\beta_i\}}a\beta_{t{a}}\delta_a\Big),\end{align*}$$
$$\begin{align*}p=z_i\delta_i+\sum_{a\in\mathrm{H}_{i}^{\circ}\setminus\{\beta_i\}}z_a\beta_{t{a}}\delta_a+y\Big(\beta_i\delta_i-\sum_{a\in\mathrm{H}_{i}^{\circ}\setminus\{\beta_i\}}a\beta_{t{a}}\delta_a\Big),\end{align*}$$
where
![]() $z_i\in \overline {\langle R\rangle }e_i^-$
,
$z_i\in \overline {\langle R\rangle }e_i^-$
,
![]() $z_a\in \overline {\langle R\rangle }e_{t{a}}$
, and
$z_a\in \overline {\langle R\rangle }e_{t{a}}$
, and
![]() $y\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_i$
. Comparing terms in our two expressions for p, we see that
$y\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_i$
. Comparing terms in our two expressions for p, we see that
![]() $\widetilde {x}_{\beta _i}=y\beta _i+z_i$
and
$\widetilde {x}_{\beta _i}=y\beta _i+z_i$
and
![]() $\widetilde {x}_{a}=ya-z_a$
. Since
$\widetilde {x}_{a}=ya-z_a$
. Since
![]() $z_i,z_a\in \overline {\langle R\rangle }$
, when we pass to the quotient algebra A, we see that
$z_i,z_a\in \overline {\langle R\rangle }$
, when we pass to the quotient algebra A, we see that
![]() $x_{\beta _i}=y\beta _i$
and
$x_{\beta _i}=y\beta _i$
and
![]() $x_a=ya$
, as required.
$x_a=ya$
, as required.
Proposition 4.12. For
![]() $i\in \widetilde {Q}_0^\circ $
, we have
$i\in \widetilde {Q}_0^\circ $
, we have
![]() $\ker (\mu _2\mathbin {\otimes }_AS_{i})=\operatorname {im}(\mu _3\mathbin {\otimes }_AS_{i})$
.
$\ker (\mu _2\mathbin {\otimes }_AS_{i})=\operatorname {im}(\mu _3\mathbin {\otimes }_AS_{i})$
.
Proof. Since
![]() $\mathbf {P}(A)$
is a complex, it is enough to show that
$\mathbf {P}(A)$
is a complex, it is enough to show that
![]() $\ker (\mu _2\mathbin {\otimes }_AS_{i})\subseteq \operatorname {im}(\mu _3\mathbin {\otimes }_AS_{i})$
. Let
$\ker (\mu _2\mathbin {\otimes }_AS_{i})\subseteq \operatorname {im}(\mu _3\mathbin {\otimes }_AS_{i})$
. Let
![]() $x=\sum _{a\in \mathrm {H}_{i}^{\circ }}x_a\mathbin {\otimes }[a]\in \bigoplus _{a\in \mathrm {H}_{i}^{\circ }}Ae_{t{a}}$
. Then
$x=\sum _{a\in \mathrm {H}_{i}^{\circ }}x_a\mathbin {\otimes }[a]\in \bigoplus _{a\in \mathrm {H}_{i}^{\circ }}Ae_{t{a}}$
. Then
 $$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{i})(x)=\sum_{b\in{\mathrm{T}_{i}}}\bigg(\sum_{a\in\mathrm{H}_{i}^{\circ}}x_a\partial^r_{b}{\partial_{a}{\widetilde{W}}}\bigg)\mathbin{\otimes}[b]\in\bigoplus_{b\in{\mathrm{T}_{i}}}Ae_{h{b}}.\end{align*}$$
$$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{i})(x)=\sum_{b\in{\mathrm{T}_{i}}}\bigg(\sum_{a\in\mathrm{H}_{i}^{\circ}}x_a\partial^r_{b}{\partial_{a}{\widetilde{W}}}\bigg)\mathbin{\otimes}[b]\in\bigoplus_{b\in{\mathrm{T}_{i}}}Ae_{h{b}}.\end{align*}$$
In particular,
![]() $\alpha _i\in {\mathrm {T}_{i}}$
, so if
$\alpha _i\in {\mathrm {T}_{i}}$
, so if
![]() $x\in \ker (\mu _2\otimes _AS_{i})$
, we have
$x\in \ker (\mu _2\otimes _AS_{i})$
, we have
![]() $\left (\sum _{a\in \mathrm {H}_{i}^{\circ }}x_a\partial ^r_{\alpha _i}{\partial _{a}{\widetilde {W}}}\right )\otimes [\alpha _i]=0$
. Using the explicit expressions for the relations
$\left (\sum _{a\in \mathrm {H}_{i}^{\circ }}x_a\partial ^r_{\alpha _i}{\partial _{a}{\widetilde {W}}}\right )\otimes [\alpha _i]=0$
. Using the explicit expressions for the relations
![]() $\partial _{a}{\widetilde {W}}$
computed in (3.1), we see that
$\partial _{a}{\widetilde {W}}$
computed in (3.1), we see that
 $$\begin{align*}\sum_{a\in\mathrm{H}_{i}^{\circ}}x_a\partial^r_{\alpha_i}\partial_{a}{\widetilde{W}}=x_{\beta_i}\delta_i-\sum_{a\in\mathrm{H}_{i}^{\circ}\setminus\{\beta_i\}}x_a\beta_{t{a}}\delta_a=0,\end{align*}$$
$$\begin{align*}\sum_{a\in\mathrm{H}_{i}^{\circ}}x_a\partial^r_{\alpha_i}\partial_{a}{\widetilde{W}}=x_{\beta_i}\delta_i-\sum_{a\in\mathrm{H}_{i}^{\circ}\setminus\{\beta_i\}}x_a\beta_{t{a}}\delta_a=0,\end{align*}$$
and so by Lemma 4.11 there exists
![]() $y\in Ae_{i}$
such that
$y\in Ae_{i}$
such that
![]() $x_a=ya$
for each a. It follows that
$x_a=ya$
for each a. It follows that
![]() $x=(\mu _3\mathbin {\otimes }_AS_{i})(y)$
, as required.
$x=(\mu _3\mathbin {\otimes }_AS_{i})(y)$
, as required.
Proposition 4.13. If
![]() $i^{\pm }\in \widetilde {F}_0$
, then the complex
$i^{\pm }\in \widetilde {F}_0$
, then the complex
is exact.
Proof. Since
![]() $i^{\pm }\in \widetilde {F}_0$
, our complex is zero in degree
$i^{\pm }\in \widetilde {F}_0$
, our complex is zero in degree
![]() $-3$
. By Remark 4.8, we need only check that
$-3$
. By Remark 4.8, we need only check that
![]() $\mu _2\mathbin {\otimes }_AS_{i}^{\pm }$
is injective. Since
$\mu _2\mathbin {\otimes }_AS_{i}^{\pm }$
is injective. Since
![]() $\mathrm {H}_{i^-}^{\circ }=\varnothing $
, the complex
$\mathrm {H}_{i^-}^{\circ }=\varnothing $
, the complex
![]() $\mathbf {P}(A)\mathbin {\otimes }_AS_{i}^-$
is also zero in degree
$\mathbf {P}(A)\mathbin {\otimes }_AS_{i}^-$
is also zero in degree
![]() $-2$
, so we are left to consider
$-2$
, so we are left to consider
![]() $\mu _2\mathbin {\otimes }_AS_{i}^+$
.
$\mu _2\mathbin {\otimes }_AS_{i}^+$
.
Since
![]() $\mathrm {H}_{i^+}^{\circ }=\{\alpha _i\}$
, we have
$\mathrm {H}_{i^+}^{\circ }=\{\alpha _i\}$
, we have
![]() $\mu _2\mathbin {\otimes }_AS_{i}^+\colon Ae_i\to \bigoplus _{b\in {\mathrm {T}_{i}}^+}Ae_{h{b}}$
. Let
$\mu _2\mathbin {\otimes }_AS_{i}^+\colon Ae_i\to \bigoplus _{b\in {\mathrm {T}_{i}}^+}Ae_{h{b}}$
. Let
![]() $x\in Ae_i$
, for which we calculate
$x\in Ae_i$
, for which we calculate
 $$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{i}^+)(x)=\sum_{b\in{\mathrm{T}_{i}}^+}x\partial^r_{b}{\partial_{\alpha_i}{\widetilde{W}}}\otimes[b].\end{align*}$$
$$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{i}^+)(x)=\sum_{b\in{\mathrm{T}_{i}}^+}x\partial^r_{b}{\partial_{\alpha_i}{\widetilde{W}}}\otimes[b].\end{align*}$$
Assume that this is
![]() $0$
. Considering
$0$
. Considering
![]() $\delta _i\in {\mathrm {T}_{i}}^+$
, we see that we must have
$\delta _i\in {\mathrm {T}_{i}}^+$
, we see that we must have
![]() $0=x\partial ^r_{\delta _i}{\partial _{\alpha _i}{\widetilde {W}}}=x\beta _i$
. By Lemma 4.9, it follows that
$0=x\partial ^r_{\delta _i}{\partial _{\alpha _i}{\widetilde {W}}}=x\beta _i$
. By Lemma 4.9, it follows that
![]() $x=0$
, and
$x=0$
, and
![]() $\mu _2\mathbin {\otimes }_AS_{i}^+$
is injective as required.
$\mu _2\mathbin {\otimes }_AS_{i}^+$
is injective as required.
Summarizing the discussion above, we are able to establish the desired internal Calabi–Yau property for
![]() $A_{Q,W}$
.
$A_{Q,W}$
.
Theorem 4.14. For any quiver with potential
![]() $(Q,W)$
, the algebra
$(Q,W)$
, the algebra
![]() $A_{Q,W}=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
is bimodule internally
$A_{Q,W}=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
is bimodule internally
![]() $3$
-Calabi–Yau with respect to the frozen idempotent
$3$
-Calabi–Yau with respect to the frozen idempotent
![]() $e=\sum _{i\in Q_0}(e_i^++e_i^-)$
.
$e=\sum _{i\in Q_0}(e_i^++e_i^-)$
.
Proof. Given Remark 4.8, Propositions 4.10 and 4.12 show that (4.5) is exact when i is a mutable vertex, whereas Proposition 4.13 deals with the case that i is frozen. Thus, (4.3) is exact and so, since
![]() $A_{Q,W}$
is pseudocompact by Corollary 4.4, it follows from Lemma 4.7 that (4.2) is also exact. Hence, we obtain the result by [Reference Pressland42, Th. 5.7].
$A_{Q,W}$
is pseudocompact by Corollary 4.4, it follows from Lemma 4.7 that (4.2) is also exact. Hence, we obtain the result by [Reference Pressland42, Th. 5.7].
Since for
![]() $A=A_{Q,W}$
we have
$A=A_{Q,W}$
we have
![]() $A/AeA=J(Q,W)$
by construction, Theorem 2 from the introduction is an immediate consequence. We record a further corollary, obtained by combining Theorem 4.14 with Theorem 2.6.
$A/AeA=J(Q,W)$
by construction, Theorem 2 from the introduction is an immediate consequence. We record a further corollary, obtained by combining Theorem 4.14 with Theorem 2.6.
Corollary 4.15. Let
![]() $(Q,W)$
be a Jacobi-finite quiver with potential. Assume that
$(Q,W)$
be a Jacobi-finite quiver with potential. Assume that
![]() $A=A_{Q,W}$
is Noetherian, let
$A=A_{Q,W}$
is Noetherian, let
![]() $e=\sum _{i\in Q_0}(e_i^++e_i^-)$
be the frozen idempotent of A, let
$e=\sum _{i\in Q_0}(e_i^++e_i^-)$
be the frozen idempotent of A, let
![]() $B=eAe$
be its boundary algebra, and let
$B=eAe$
be its boundary algebra, and let
![]() $T=eA$
. Then T is a cluster-tilting object of the stably
$T=eA$
. Then T is a cluster-tilting object of the stably
![]() $2$
-Calabi–Yau Frobenius category
$2$
-Calabi–Yau Frobenius category
![]() $\operatorname {GP}(B)$
, with
$\operatorname {GP}(B)$
, with
![]() $\operatorname {End}_{B}(T)^{\mathrm {op}}\cong A$
and
$\operatorname {End}_{B}(T)^{\mathrm {op}}\cong A$
and
![]() $\underline {\operatorname {End}}_{B}(T)^{\mathrm {op}}\cong J(Q,W)$
.
$\underline {\operatorname {End}}_{B}(T)^{\mathrm {op}}\cong J(Q,W)$
.
![]() $\Box $
$\Box $
It is this corollary that we will use to define the Frobenius category
![]() $\mathcal {E}_Q$
appearing in Theorem 1 for an acyclic quiver Q; to be able to do so, it only remains to check that
$\mathcal {E}_Q$
appearing in Theorem 1 for an acyclic quiver Q; to be able to do so, it only remains to check that
![]() $A_Q$
is Noetherian in this case, and we will show in §5 that it is even finite-dimensional. Unfortunately, at the moment, we lack methods for showing that
$A_Q$
is Noetherian in this case, and we will show in §5 that it is even finite-dimensional. Unfortunately, at the moment, we lack methods for showing that
![]() $A_{Q,W}$
is Noetherian in more cases (and expect that
$A_{Q,W}$
is Noetherian in more cases (and expect that
![]() $A_{Q,W}$
is not Noetherian general), preventing us from extending Theorem 1 to the case of quivers with cycles. We already observed in Example 3.3 that
$A_{Q,W}$
is not Noetherian general), preventing us from extending Theorem 1 to the case of quivers with cycles. We already observed in Example 3.3 that
![]() $A_{Q,W}$
is Noetherian (but not finite-dimensional) when
$A_{Q,W}$
is Noetherian (but not finite-dimensional) when
![]() $(Q,W)$
is the
$(Q,W)$
is the
![]() $3$
-cycle with its natural potential. This quiver with potential is Jacobi-finite, so Corollary 4.15 also applies in this case.
$3$
-cycle with its natural potential. This quiver with potential is Jacobi-finite, so Corollary 4.15 also applies in this case.
Remark 4.16. Combinatorially, the algebra
![]() $A_{Q,W}$
seems to be related the dg-algebra
$A_{Q,W}$
seems to be related the dg-algebra
![]() $\Gamma _{Q,W}$
associated with
$\Gamma _{Q,W}$
associated with
![]() $(Q,W)$
by Ginzburg [Reference Ginzburg25, §4.2]; the loops in cohomological degree
$(Q,W)$
by Ginzburg [Reference Ginzburg25, §4.2]; the loops in cohomological degree
![]() $-2$
in
$-2$
in
![]() $\Gamma _{Q,W}$
are replaced by the cycles
$\Gamma _{Q,W}$
are replaced by the cycles
![]() $i\to i^+\to i^-\to i$
, and the degree
$i\to i^+\to i^-\to i$
, and the degree
![]() $-1$
arrows are replaced by the paths
$-1$
arrows are replaced by the paths
![]() $h{a}\to h{a}^+\to t{a}^-\to t{a}$
. Here, we use Amiot’s sign conventions [Reference Amiot1, Def. 3.1], which are opposite to Ginzburg’s. By a result of Van den Bergh [Reference Keller34, Th. A.12], the dg-algebra
$h{a}\to h{a}^+\to t{a}^-\to t{a}$
. Here, we use Amiot’s sign conventions [Reference Amiot1, Def. 3.1], which are opposite to Ginzburg’s. By a result of Van den Bergh [Reference Keller34, Th. A.12], the dg-algebra
![]() $\Gamma _{Q,W}$
is bimodule
$\Gamma _{Q,W}$
is bimodule
![]() $3$
-Calabi–Yau, and we expect this to be related to the fact that
$3$
-Calabi–Yau, and we expect this to be related to the fact that
![]() $A_{Q,W}$
is bimodule internally
$A_{Q,W}$
is bimodule internally
![]() $3$
-Calabi–Yau with respect to the idempotent determined by the vertices not appearing in Ginzburg’s construction. We will show in proving Theorem 1
(b) that, when Q is acyclic, the two constructions are also related via a triangle equivalence
$3$
-Calabi–Yau with respect to the idempotent determined by the vertices not appearing in Ginzburg’s construction. We will show in proving Theorem 1
(b) that, when Q is acyclic, the two constructions are also related via a triangle equivalence
By a result of Wu [Reference Wu52, Lem. 5.10], it follows from exactness of (4.2) that the relative Ginzburg algebra
![]() $\Gamma _{\widetilde {Q},\widetilde {F},\widetilde {W}}$
[Reference Wu52, Def. 4.20] is concentrated in degree
$\Gamma _{\widetilde {Q},\widetilde {F},\widetilde {W}}$
[Reference Wu52, Def. 4.20] is concentrated in degree
![]() $0$
, its zeroth cohomology being the algebra
$0$
, its zeroth cohomology being the algebra
![]() $A_{Q,W}$
. There is thus [Reference Wu53, Prop. 3.19] a homotopy pushout diagram
$A_{Q,W}$
. There is thus [Reference Wu53, Prop. 3.19] a homotopy pushout diagram

taken in the category of k-linear dg-categories with Tabuada’s model structure [Reference Tabuada50], where the functor G is the deformed relative
![]() $3$
-Calabi–Yau completion, with respect to
$3$
-Calabi–Yau completion, with respect to
![]() $\widetilde {W}$
, of the natural map
$\widetilde {W}$
, of the natural map
![]() $\mathbb {K}\widetilde {F}\to \mathbb {K}\widetilde {Q}$
. In particular, this makes
$\mathbb {K}\widetilde {F}\to \mathbb {K}\widetilde {Q}$
. In particular, this makes
![]() $\mathbf {\Pi }_{\widetilde {F}}$
the
$\mathbf {\Pi }_{\widetilde {F}}$
the
![]() $2$
-Calabi–Yau completion of
$2$
-Calabi–Yau completion of
![]() $\mathbb {K}\widetilde {F}$
(a dg version of the preprojective algebra of
$\mathbb {K}\widetilde {F}$
(a dg version of the preprojective algebra of
![]() $\widetilde {F}$
). Thus, we can reconstruct the Ginzburg dg-algebra
$\widetilde {F}$
). Thus, we can reconstruct the Ginzburg dg-algebra
![]() $\Gamma _{Q,W}$
from
$\Gamma _{Q,W}$
from
![]() $A_{Q,W}$
(plus enough additional data to recover the dg-functor G). It is also possible to obtain the triangle equivalence (4.8) using this style of argument (see Remark 5.4).
$A_{Q,W}$
(plus enough additional data to recover the dg-functor G). It is also possible to obtain the triangle equivalence (4.8) using this style of argument (see Remark 5.4).
However, the only properties of the ice quiver with potential
![]() $(\widetilde {Q},\widetilde {F},\widetilde {W})$
that we use here are that
$(\widetilde {Q},\widetilde {F},\widetilde {W})$
that we use here are that
![]() $\Gamma _{\widetilde {Q},\widetilde {F},\widetilde {W}}$
is concentrated in degree
$\Gamma _{\widetilde {Q},\widetilde {F},\widetilde {W}}$
is concentrated in degree
![]() $0$
, and that removing the frozen vertices recovers
$0$
, and that removing the frozen vertices recovers
![]() $(Q,W)$
; typically, there are many ice quivers with potential with these two properties. At present, we do not know a natural construction of the specific frozen Jacobian algebra
$(Q,W)$
; typically, there are many ice quivers with potential with these two properties. At present, we do not know a natural construction of the specific frozen Jacobian algebra
![]() $A_{Q,W}$
from
$A_{Q,W}$
from
![]() $\Gamma _{Q,W}$
, despite the combinatorial similarity of their definitions.
$\Gamma _{Q,W}$
, despite the combinatorial similarity of their definitions.
5 The acyclic case
Let
![]() $(Q,W)$
be a Jacobi-finite quiver with potential, so that the algebra
$(Q,W)$
be a Jacobi-finite quiver with potential, so that the algebra
![]() $A_{Q,W}$
from Definition 3.1 satisfies all of the assumptions of Corollary 4.15 except possibly Noetherianity. Our goal in this section is to show that if Q is an acyclic quiver, then the algebra
$A_{Q,W}$
from Definition 3.1 satisfies all of the assumptions of Corollary 4.15 except possibly Noetherianity. Our goal in this section is to show that if Q is an acyclic quiver, then the algebra
![]() $A=A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
is even finite-dimensional, so that this result does indeed apply.
$A=A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
is even finite-dimensional, so that this result does indeed apply.
Lemma 5.1. Let Q be a finite quiver, and let p be a path in
![]() $\widetilde {Q}$
containing at least one arrow not in
$\widetilde {Q}$
containing at least one arrow not in
![]() $Q_1$
, and with
$Q_1$
, and with
![]() $h{p},t{p}\in Q_0$
. Then p is in the kernel of the projection
$h{p},t{p}\in Q_0$
. Then p is in the kernel of the projection
![]() $\pi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle \to A=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
. Moreover, if q is a path of length at least
$\pi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle \to A=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
. Moreover, if q is a path of length at least
![]() $5$
containing no arrows of
$5$
containing no arrows of
![]() $Q_1$
, then
$Q_1$
, then
![]() $q\in \ker {\pi }$
.
$q\in \ker {\pi }$
.
Proof. Let
![]() $\gamma $
be the first arrow of p in
$\gamma $
be the first arrow of p in
![]() $\widetilde {Q}_1\setminus Q_1$
. If
$\widetilde {Q}_1\setminus Q_1$
. If
![]() $\gamma $
has a predecessor in p, then this arrow is in
$\gamma $
has a predecessor in p, then this arrow is in
![]() $Q_1$
, and so
$Q_1$
, and so
![]() $t{\gamma }\in Q_0$
. On the other hand, if
$t{\gamma }\in Q_0$
. On the other hand, if
![]() $\gamma $
is the first arrow of p, then
$\gamma $
is the first arrow of p, then
![]() $t{\gamma }=t{p}\in Q_0$
by assumption. By the construction of
$t{\gamma }=t{p}\in Q_0$
by assumption. By the construction of
![]() $\widetilde {Q}$
, it follows that
$\widetilde {Q}$
, it follows that
![]() $\gamma =\alpha _i$
for some
$\gamma =\alpha _i$
for some
![]() $i\in Q_0$
. Since
$i\in Q_0$
. Since
![]() $h{p}\in Q_0$
, the path p cannot terminate with
$h{p}\in Q_0$
, the path p cannot terminate with
![]() $\alpha _i$
, so this arrow has a successor. Looking again at the definition of
$\alpha _i$
, so this arrow has a successor. Looking again at the definition of
![]() $\widetilde {Q}$
, the only options are
$\widetilde {Q}$
, the only options are
![]() $\delta _a$
for some
$\delta _a$
for some
![]() $a\in Q_1$
with
$a\in Q_1$
with
![]() $h{a}=i$
, or
$h{a}=i$
, or
![]() $\delta _i$
. We break into two cases.
$\delta _i$
. We break into two cases.
First, assume
![]() $\alpha _i$
is followed in p by
$\alpha _i$
is followed in p by
![]() $\delta _a$
for some
$\delta _a$
for some
![]() $a\in Q_0$
. This again cannot be the final arrow of p, since
$a\in Q_0$
. This again cannot be the final arrow of p, since
![]() $h{p}\in Q_0$
. The only arrow leaving
$h{p}\in Q_0$
. The only arrow leaving
![]() $h{\delta _a}=i_{t{a}}^-$
is
$h{\delta _a}=i_{t{a}}^-$
is
![]() $\beta _{t{a}}$
, so this must be the next arrow of p. But after projection to A by
$\beta _{t{a}}$
, so this must be the next arrow of p. But after projection to A by
![]() $\pi $
, we have
$\pi $
, we have
![]() $\beta _{t{a}}\delta _a\alpha _{h{a}}=\partial _{a}{W}=0$
since
$\beta _{t{a}}\delta _a\alpha _{h{a}}=\partial _{a}{W}=0$
since
![]() $W=0$
, so
$W=0$
, so
![]() $p\in \ker {\pi }$
.
$p\in \ker {\pi }$
.
In the second case,
![]() $\alpha _i$
is followed by
$\alpha _i$
is followed by
![]() $\delta _i$
. As above,
$\delta _i$
. As above,
![]() $\delta _i$
must be followed in p by
$\delta _i$
must be followed in p by
![]() $\beta _i$
, and projecting to A yields
$\beta _i$
, and projecting to A yields
 $$\begin{align*}\beta_i\delta_i\alpha_i=\bigg(\sum_{\substack{a\in Q_1\\ h{a}=i}}a\beta_{t{a}}\delta_a\bigg)\alpha_i=\sum_{\substack{a\in Q_1\\ h{a}=i}}a\beta_{t{a}}\delta_a\alpha_{h{a}}=0,\end{align*}$$
$$\begin{align*}\beta_i\delta_i\alpha_i=\bigg(\sum_{\substack{a\in Q_1\\ h{a}=i}}a\beta_{t{a}}\delta_a\bigg)\alpha_i=\sum_{\substack{a\in Q_1\\ h{a}=i}}a\beta_{t{a}}\delta_a\alpha_{h{a}}=0,\end{align*}$$
so that again
![]() $p\in \ker {\pi }$
.
$p\in \ker {\pi }$
.
For the second statement, we have already shown that
![]() $\beta _{t{a}}\delta _a\alpha _{h{a}}\in \ker {\pi }$
for any
$\beta _{t{a}}\delta _a\alpha _{h{a}}\in \ker {\pi }$
for any
![]() $a\in Q_1$
and
$a\in Q_1$
and
![]() $\beta _i\delta _i\alpha _i\in \ker {\pi }$
for any
$\beta _i\delta _i\alpha _i\in \ker {\pi }$
for any
![]() $i\in Q_0$
. It then follows from the bipartite property of
$i\in Q_0$
. It then follows from the bipartite property of
![]() $\widetilde {F}$
that any path which is not in
$\widetilde {F}$
that any path which is not in
![]() $\ker {\pi }$
and involves only arrows not in
$\ker {\pi }$
and involves only arrows not in
![]() $Q_1$
must be a subpath of
$Q_1$
must be a subpath of
![]() $\delta _x\alpha _i\beta _i\delta _y$
for some
$\delta _x\alpha _i\beta _i\delta _y$
for some
![]() $x,y\in Q_0\cup Q_1$
and
$x,y\in Q_0\cup Q_1$
and
![]() $i\in Q_0$
with
$i\in Q_0$
with
![]() $h{x}=i=t{y}$
. In particular, such a path has length at most
$h{x}=i=t{y}$
. In particular, such a path has length at most
![]() $4$
.
$4$
.
Theorem 5.2. Let Q be an acyclic quiver. Then
![]() $A=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
is finite-dimensional.
$A=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
is finite-dimensional.
Proof. We show that there are finitely many paths of
![]() $\widetilde {Q}$
determining nonzero elements of A. By Lemma 5.1, any path p of
$\widetilde {Q}$
determining nonzero elements of A. By Lemma 5.1, any path p of
![]() $\widetilde {Q}$
determining a nonzero element of A may not have any subpath with endpoints in
$\widetilde {Q}$
determining a nonzero element of A may not have any subpath with endpoints in
![]() $Q_0$
and containing an arrow outside
$Q_0$
and containing an arrow outside
![]() $Q_1$
. Thus, we must have
$Q_1$
. Thus, we must have
![]() $p=q_2p'q_1$
, where
$p=q_2p'q_1$
, where
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are (possibly empty) paths not involving arrows of
$q_2$
are (possibly empty) paths not involving arrows of
![]() $Q_1$
, and
$Q_1$
, and
![]() $p'$
is a path in Q. Since Q is acyclic, there are only finitely many possibilities for
$p'$
is a path in Q. Since Q is acyclic, there are only finitely many possibilities for
![]() $p'$
. By Lemma 5.1 again,
$p'$
. By Lemma 5.1 again,
![]() $q_1$
and
$q_1$
and
![]() $q_2$
have length at most
$q_2$
have length at most
![]() $4$
for p to be nonzero in A, and so there are again only finitely many possibilities.
$4$
for p to be nonzero in A, and so there are again only finitely many possibilities.
We have now established everything we need in order to construct the Frobenius cluster category required by Theorem 1, and to prove the first two parts of this theorem.
Definition 5.3. Let Q be an acyclic quiver, let
![]() $A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
be the frozen Jacobian algebra defined from Q in Definition 3.1, and let
$A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
be the frozen Jacobian algebra defined from Q in Definition 3.1, and let
![]() $B_Q=eA_Qe$
be its boundary algebra. We define
$B_Q=eA_Qe$
be its boundary algebra. We define
![]() $\mathcal {E}_Q=\operatorname {GP}(B_Q)$
to be the category of Gorenstein projective
$\mathcal {E}_Q=\operatorname {GP}(B_Q)$
to be the category of Gorenstein projective
![]() $B_Q$
-modules.
$B_Q$
-modules.
Proof of Theorem 1 (a)
Since Q is an acyclic quiver,
![]() $J(Q,0)=\mathbb {K} Q$
is finite-dimensional. By Theorem 5.2, the algebra
$J(Q,0)=\mathbb {K} Q$
is finite-dimensional. By Theorem 5.2, the algebra
![]() $A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
is also finite-dimensional, and hence Noetherian.
$A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {0})$
is also finite-dimensional, and hence Noetherian.
Since the boundary algebra
![]() $B_Q=eA_Qe$
is finite-dimensional, Corollary 4.15 and Proposition 2.8 combine to show that
$B_Q=eA_Qe$
is finite-dimensional, Corollary 4.15 and Proposition 2.8 combine to show that
![]() $\mathcal {E}_Q=\operatorname {GP}(B_Q)$
is a Hom-finite Frobenius cluster category, as required.
$\mathcal {E}_Q=\operatorname {GP}(B_Q)$
is a Hom-finite Frobenius cluster category, as required.
Proof of Theorem 1(b)
We use Keller–Reiten’s recognition theorem [Reference Keller and Reiten36, Th. 2.1]; by Corollary 4.15,
![]() $\underline {\mathcal {E}}_Q$
is a
$\underline {\mathcal {E}}_Q$
is a
![]() $2$
-Calabi–Yau triangulated category admitting a cluster-tilting object
$2$
-Calabi–Yau triangulated category admitting a cluster-tilting object
![]() $T=eA_Q$
with endomorphism algebra
$T=eA_Q$
with endomorphism algebra
![]() $\mathbb {K} Q$
, so
$\mathbb {K} Q$
, so
![]() $\underline {\mathcal {E}}_Q$
is triangle equivalent to the cluster category
$\underline {\mathcal {E}}_Q$
is triangle equivalent to the cluster category
![]() $\mathcal {C}_{Q}$
as required.
$\mathcal {C}_{Q}$
as required.
We already observed after stating Corollary 4.15 that our construction applies to
![]() $(Q,W)$
given by the
$(Q,W)$
given by the
![]() $3$
-cycle with natural potential to produce a stably
$3$
-cycle with natural potential to produce a stably
![]() $2$
-Calabi–Yau Frobenius cluster category
$2$
-Calabi–Yau Frobenius cluster category
![]() $\mathcal {E}_{Q,W}=\operatorname {GP}(B_{Q,W})$
. We claim that the analogous statement to Theorem 1
(b) also holds here, namely that
$\mathcal {E}_{Q,W}=\operatorname {GP}(B_{Q,W})$
. We claim that the analogous statement to Theorem 1
(b) also holds here, namely that
![]() $\underline {\mathcal {E}}_{Q,W}$
is triangle equivalent to Amiot’s cluster category
$\underline {\mathcal {E}}_{Q,W}$
is triangle equivalent to Amiot’s cluster category
![]() $\mathcal {C}_{Q,W}$
. While Keller–Reiten’s recognition theorem no longer applies to the cluster-tilting object T provided by Corollary 4.15, since its stable endomorphism algebra is not hereditary, one can in this case find another cluster-tilting object
$\mathcal {C}_{Q,W}$
. While Keller–Reiten’s recognition theorem no longer applies to the cluster-tilting object T provided by Corollary 4.15, since its stable endomorphism algebra is not hereditary, one can in this case find another cluster-tilting object
![]() $T'\in \mathcal {E}_{Q,W}$
with
$T'\in \mathcal {E}_{Q,W}$
with
![]() $\underline {\operatorname {End}}_{\mathcal {E}_{Q,W}}(T')^{\mathrm {op}}\cong \mathbb {K} Q'$
, for
$\underline {\operatorname {End}}_{\mathcal {E}_{Q,W}}(T')^{\mathrm {op}}\cong \mathbb {K} Q'$
, for
![]() $Q'$
an orientation of the Dynkin diagram
$Q'$
an orientation of the Dynkin diagram
![]() $\mathsf {A}_{3}$
. Thus, the recognition theorem shows that
$\mathsf {A}_{3}$
. Thus, the recognition theorem shows that
![]() $\underline {\mathcal {E}}_{Q,W}\simeq \mathcal {C}_{Q'}$
, and
$\underline {\mathcal {E}}_{Q,W}\simeq \mathcal {C}_{Q'}$
, and
![]() $\mathcal {C}_{Q'}\simeq \mathcal {C}_{Q,W}$
either by the recognition theorem again or by [Reference Amiot1, Cor. 3.11].
$\mathcal {C}_{Q'}\simeq \mathcal {C}_{Q,W}$
either by the recognition theorem again or by [Reference Amiot1, Cor. 3.11].
We note that while Amiot, Reiten, and Todorov have a recognition theorem [Reference Amiot, Reiten and Todorov2, Th. 3.1], which identifies certain stable categories of Frobenius categories admitting a cluster-tilting object with frozen Jacobian endomorphism algebra as generalized cluster categories, this theorem does not apply to our object T when
![]() $W\ne 0$
, because then
$W\ne 0$
, because then
![]() $(\widetilde {Q},\widetilde {F},\widetilde {W})$
cannot satisfy their assumptions (H3) and (H4). Assumption (H3) requires a nonnegative degree function on the arrows of
$(\widetilde {Q},\widetilde {F},\widetilde {W})$
cannot satisfy their assumptions (H3) and (H4). Assumption (H3) requires a nonnegative degree function on the arrows of
![]() $\widetilde {Q}$
giving
$\widetilde {Q}$
giving
![]() $\widetilde {W}$
degree
$\widetilde {W}$
degree
![]() $1$
, and (H4) requires that the arrows
$1$
, and (H4) requires that the arrows
![]() $\alpha _i$
, for
$\alpha _i$
, for
![]() $i\in Q_0$
, all have degree
$i\in Q_0$
, all have degree
![]() $1$
. But if
$1$
. But if
![]() $W\ne 0$
, then (H3) forces some arrow
$W\ne 0$
, then (H3) forces some arrow
![]() $a\in Q_1$
to have degree
$a\in Q_1$
to have degree
![]() $1$
, and then (H4) implies that the potential term
$1$
, and then (H4) implies that the potential term
![]() $a\beta _{t{a}}\delta _a\alpha _{h{a}}$
has degree at least
$a\beta _{t{a}}\delta _a\alpha _{h{a}}$
has degree at least
![]() $2$
, so (H3) does not hold.
$2$
, so (H3) does not hold.
Remark 5.4. We could also prove Theorem 1
(b) by using further results of Wu [Reference Wu53, Ths. 6.2 and 7.9], exploiting in particular the fact that
![]() $A_{Q,W}$
is quasi-isomorphic to the relative Ginzburg dg-algebra
$A_{Q,W}$
is quasi-isomorphic to the relative Ginzburg dg-algebra
![]() $\Gamma _{\widetilde {Q},\widetilde {F},\widetilde {W}}$
(cf. Remark 4.16). This does not increase the generality of the result, since this approach requires
$\Gamma _{\widetilde {Q},\widetilde {F},\widetilde {W}}$
(cf. Remark 4.16). This does not increase the generality of the result, since this approach requires
![]() $A_{Q,W}$
to be finite-dimensional, a fact we only establish in the acyclic case (and which is false in general). However, it seems more realistic to generalize Wu’s results to infinite-dimensional Jacobian algebras than to remove the acyclicity assumption from Keller–Reiten’s theorem.
$A_{Q,W}$
to be finite-dimensional, a fact we only establish in the acyclic case (and which is false in general). However, it seems more realistic to generalize Wu’s results to infinite-dimensional Jacobian algebras than to remove the acyclicity assumption from Keller–Reiten’s theorem.
6 Mutation and the cluster character
To complete the proof of Theorem 1, we need to understand the relationship between mutation of cluster-tilting objects in
![]() $\operatorname {GP}(B_Q)$
and Fomin–Zelevinsky mutation of their quivers. These operations turn out to be compatible, in a much larger class of Frobenius cluster categories, in the sense of the following theorem.
$\operatorname {GP}(B_Q)$
and Fomin–Zelevinsky mutation of their quivers. These operations turn out to be compatible, in a much larger class of Frobenius cluster categories, in the sense of the following theorem.
Theorem 6.1. Let
![]() $\mathcal {E}$
be a Hom-finite Frobenius cluster category, and assume that there is a cluster-tilting object
$\mathcal {E}$
be a Hom-finite Frobenius cluster category, and assume that there is a cluster-tilting object
![]() $T\in \mathcal {E}$
such that
$T\in \mathcal {E}$
such that
![]() $\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong J(Q,F,W)$
, where Q is the Gabriel quiver of this algebra. Then:
$\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong J(Q,F,W)$
, where Q is the Gabriel quiver of this algebra. Then:
-
(a) Q has no loops or
 $2$
-cycles incident with any mutable vertex, so the Iyama–Yoshino mutation of T at any indecomposable nonprojective summand is well defined.
$2$
-cycles incident with any mutable vertex, so the Iyama–Yoshino mutation of T at any indecomposable nonprojective summand is well defined. -
(b) If
 $T'$
is obtained from T by mutation at such a summand, then
$T'$
is obtained from T by mutation at such a summand, then
 $\operatorname {End}_{\mathcal {E}}(T')^{\mathrm {op}}\cong J(Q',F',W')$
, where
$\operatorname {End}_{\mathcal {E}}(T')^{\mathrm {op}}\cong J(Q',F',W')$
, where
 $(Q',F',W')$
is the mutation of
$(Q',F',W')$
is the mutation of
 $(Q,F,W)$
at the vertex corresponding to this summand.
$(Q,F,W)$
at the vertex corresponding to this summand. -
(c) The quiver
 $Q'$
is both the Gabriel quiver of
$Q'$
is both the Gabriel quiver of
 $\operatorname {End}_{\mathcal {E}}(T')^{\mathrm {op}}$
and, up to arrows between frozen vertices, the Fomin–Zelevinsky mutation of Q at the appropriate vertex. In particular, it also has no loops or
$\operatorname {End}_{\mathcal {E}}(T')^{\mathrm {op}}$
and, up to arrows between frozen vertices, the Fomin–Zelevinsky mutation of Q at the appropriate vertex. In particular, it also has no loops or
 $2$
-cycles incident with mutable vertices.
$2$
-cycles incident with mutable vertices.
These results then extend inductively to any cluster-tilting object in the mutation class of T.
Proof. This combines [Reference Pressland43, Th. 5.15] and [Reference Pressland44, Prop. 3] (which corrects [Reference Pressland43, Prop. 5.16]).
The proof of [Reference Pressland43, Th. 5.15] referred to in that of Theorem 6.1 is similar to an analogous result of Buan–Iyama–Reiten–Smith for triangulated categories [Reference Buan, Iyama, Reiten and Smith9]. The definition of mutation for an ice quiver with potential is given in [Reference Pressland43, Def. 4.1], and is similar to that for ordinary quivers with potential [Reference Buan, Iyama, Reiten and Smith9, §1.2]. We also explain in [Reference Pressland43] how to extend the definition of Fomin–Zelevinsky mutation to ice quivers which may have arrows between their frozen vertices. Thus, the same argument proves a stronger version of Theorem 6.1 (c) in which these arrows are still considered, but we will not use this here.
A consequence of Theorem 6.1 is that the Frobenius category
![]() $\mathcal {E}_Q$
we attach to an acyclic quiver has a cluster structure in the sense of Buan–Iyama–Reiten–Scott [Reference Buan, Iyama, Reiten and Scott8, §II.1], which will allow us to use results of Fu and Keller [Reference Fu and Keller21] to complete the proof of Theorem 1.
$\mathcal {E}_Q$
we attach to an acyclic quiver has a cluster structure in the sense of Buan–Iyama–Reiten–Scott [Reference Buan, Iyama, Reiten and Scott8, §II.1], which will allow us to use results of Fu and Keller [Reference Fu and Keller21] to complete the proof of Theorem 1.
Proposition 6.2. The Frobenius category
![]() $\mathcal {E}_Q$
from Definition 5.3 has a cluster structure.
$\mathcal {E}_Q$
from Definition 5.3 has a cluster structure.
Proof. By [Reference Buan, Iyama, Reiten and Scott8, Th. II.1.6], it is enough to check that endomorphism algebras of cluster-tilting objects in
![]() $\mathcal {E}_Q$
have no loops or
$\mathcal {E}_Q$
have no loops or
![]() $2$
-cycles in their quivers. Because
$2$
-cycles in their quivers. Because
![]() $\mathcal {E}_Q$
is a Hom-finite Frobenius cluster category, this holds for those cluster-tilting objects in the mutation class of
$\mathcal {E}_Q$
is a Hom-finite Frobenius cluster category, this holds for those cluster-tilting objects in the mutation class of
![]() $T=eA_Q$
by Theorem 6.1. But since
$T=eA_Q$
by Theorem 6.1. But since
![]() $\underline {\mathcal {E}}_Q\simeq \mathcal {C}_{Q}$
by Theorem 1
(b), every cluster-tilting object of
$\underline {\mathcal {E}}_Q\simeq \mathcal {C}_{Q}$
by Theorem 1
(b), every cluster-tilting object of
![]() $\mathcal {E}_Q$
is in this mutation class [Reference Buan, Marsh, Reiten and Todorov11, Th. A.1].
$\mathcal {E}_Q$
is in this mutation class [Reference Buan, Marsh, Reiten and Todorov11, Th. A.1].
Proof of Theorem 1(c) and (d)
Since
![]() $\mathcal {E}_Q$
is a Hom-finite stably
$\mathcal {E}_Q$
is a Hom-finite stably
![]() $2$
-Calabi–Yau Frobenius category, with cluster-tilting object
$2$
-Calabi–Yau Frobenius category, with cluster-tilting object
![]() $T=eA_Q$
, it has a cluster character
$T=eA_Q$
, it has a cluster character
![]() $\varphi ^{T}\colon \operatorname {Ob}(\mathcal {E}_Q)\to \widetilde {\mathscr {A}}_{Q}$
relative to T, as defined by Fu and Keller (see [Reference Fu and Keller21, §3], or (9.8), for an explicit formula for
$\varphi ^{T}\colon \operatorname {Ob}(\mathcal {E}_Q)\to \widetilde {\mathscr {A}}_{Q}$
relative to T, as defined by Fu and Keller (see [Reference Fu and Keller21, §3], or (9.8), for an explicit formula for
![]() $\varphi ^{T}$
).
$\varphi ^{T}$
).
Moreover, in Fu–Keller’s terminology [Reference Fu and Keller21, Def. 5.1], the pair
![]() $(\mathcal {E}_Q,T)$
is a Frobenius
$(\mathcal {E}_Q,T)$
is a Frobenius
![]() $2$
-Calabi–Yau realization of the polarized principal coefficient cluster algebra
$2$
-Calabi–Yau realization of the polarized principal coefficient cluster algebra
![]() $\widetilde {\mathscr {A}}_{Q}$
; this follows from Proposition 6.2 and by using Theorem 2.6
(c) to see that
$\widetilde {\mathscr {A}}_{Q}$
; this follows from Proposition 6.2 and by using Theorem 2.6
(c) to see that
![]() $\operatorname {End}_{\mathcal {E}_Q}(T)^{\mathrm {op}}\cong A_Q$
has ice quiver
$\operatorname {End}_{\mathcal {E}_Q}(T)^{\mathrm {op}}\cong A_Q$
has ice quiver
![]() $\widetilde {Q}$
.
$\widetilde {Q}$
.
Both Theorem 1
(c) and Theorem 1
(d) now follow from [Reference Fu and Keller21, Th. 5.4(a)]. Note that references to reachable objects in this theorem may be dropped since every indecomposable rigid object and every cluster-tilting object in
![]() $\mathcal {E}_Q$
is reachable by [Reference Buan, Marsh, Reiten and Todorov11, Th. A.1], as in the proof of Proposition 6.2. Note also that, unlike us, Fu and Keller do not consider the frozen variables of
$\mathcal {E}_Q$
is reachable by [Reference Buan, Marsh, Reiten and Todorov11, Th. A.1], as in the proof of Proposition 6.2. Note also that, unlike us, Fu and Keller do not consider the frozen variables of
![]() $\widetilde {\mathscr {A}}_{Q}$
to be cluster variables, which leads them to exclude the indecomposable projective objects from their statement. However, it is straightforward to check (see [Reference Fu and Keller21, Th. 3.3(a)]) that
$\widetilde {\mathscr {A}}_{Q}$
to be cluster variables, which leads them to exclude the indecomposable projective objects from their statement. However, it is straightforward to check (see [Reference Fu and Keller21, Th. 3.3(a)]) that
![]() $\varphi ^{T}$
also gives a bijection between the indecomposable projectives in
$\varphi ^{T}$
also gives a bijection between the indecomposable projectives in
![]() $\mathcal {E}_Q$
, which are summands of T, and the frozen variables of
$\mathcal {E}_Q$
, which are summands of T, and the frozen variables of
![]() $\widetilde {\mathscr {A}}_{Q}$
.
$\widetilde {\mathscr {A}}_{Q}$
.
Just as for Theorem 1
(b), the conclusions of Theorem 1
(c) and (d) still hold when Q is a
![]() $3$
-cycle, replacing
$3$
-cycle, replacing
![]() $B_Q$
by
$B_Q$
by
![]() $B_{Q,W}$
for W the natural potential on Q. In this case,
$B_{Q,W}$
for W the natural potential on Q. In this case,
![]() $\widetilde {\mathscr {A}}_{Q}$
is the cluster algebra of the Grassmannian
$\widetilde {\mathscr {A}}_{Q}$
is the cluster algebra of the Grassmannian
![]() $G_2^6$
, and
$G_2^6$
, and
![]() $\operatorname {GP}(B_{Q,W})$
is the Grassmannian cluster category constructed by Jensen–King–Su [Reference Jensen, King and Su32] (see Example 3.3). The analogue of Theorem 6.1 holds for Grassmannian cluster categories, despite them being Hom-infinite (see [Reference Pressland43, Prop. 5.17] and its preceding discussion).
$\operatorname {GP}(B_{Q,W})$
is the Grassmannian cluster category constructed by Jensen–King–Su [Reference Jensen, King and Su32] (see Example 3.3). The analogue of Theorem 6.1 holds for Grassmannian cluster categories, despite them being Hom-infinite (see [Reference Pressland43, Prop. 5.17] and its preceding discussion).
For a general quiver with potential
![]() $(Q,W)$
, even assuming that
$(Q,W)$
, even assuming that
![]() $A_{Q,W}$
is Noetherian so that the category
$A_{Q,W}$
is Noetherian so that the category
![]() $\mathcal {E}_{Q,W}$
is well defined, it may still be the case that the cluster-tilting objects in this category form several different mutation classes. However, this would not significantly affect our arguments here: while we can only rule out loops and
$\mathcal {E}_{Q,W}$
is well defined, it may still be the case that the cluster-tilting objects in this category form several different mutation classes. However, this would not significantly affect our arguments here: while we can only rule out loops and
![]() $2$
-cycles in the mutation class of
$2$
-cycles in the mutation class of
![]() $T=eA_{Q,W}$
via our methods, and so we cannot show that
$T=eA_{Q,W}$
via our methods, and so we cannot show that
![]() $\mathcal {E}_{Q,W}$
has a cluster structure in the strict sense, Fu–Keller’s bijections (with the word reachable reinstated) are still valid in this situation. A more detailed discussion of this issue can be found in [Reference Pressland45, §6].
$\mathcal {E}_{Q,W}$
has a cluster structure in the strict sense, Fu–Keller’s bijections (with the word reachable reinstated) are still valid in this situation. A more detailed discussion of this issue can be found in [Reference Pressland45, §6].
7 An extriangulated categorification
In this section, we will prove Corollary 1, but first we need to define the extriangulated category appearing in the statement. To keep our discussion brief, and since we only deal with very particular examples, we will not define extriangulated categories fully here, and instead refer the reader to [Reference Nakaoka and Palu40]. The most important piece of data for us will be that of the extension group
![]() $\mathbb {E}(X,Y)$
for any two objects X and Y in the extriangulated category; in our context, the objects of the category will be the same as those of the exact category
$\mathbb {E}(X,Y)$
for any two objects X and Y in the extriangulated category; in our context, the objects of the category will be the same as those of the exact category
![]() $\mathcal {E}_Q$
, and we will have
$\mathcal {E}_Q$
, and we will have
![]() $\mathbb {E}(X,Y)=\operatorname {Ext}^1_{\mathcal {E}_Q}(X,Y)$
.
$\mathbb {E}(X,Y)=\operatorname {Ext}^1_{\mathcal {E}_Q}(X,Y)$
.
Definition 7.1. Let Q be an acyclic quiver, with associated Frobenius category
![]() $\mathcal {E}_Q=\operatorname {GP}(B_Q)$
as in Definition 5.3. Write
$\mathcal {E}_Q=\operatorname {GP}(B_Q)$
as in Definition 5.3. Write
![]() $e^-=\sum _{i\in Q_0}e_i^-$
, and
$e^-=\sum _{i\in Q_0}e_i^-$
, and
![]() $P^-=B_{Q}e^-$
. Define
$P^-=B_{Q}e^-$
. Define
![]() $\mathcal {E}^+_{Q}=\mathcal {E}_{Q}/[P^-]$
to be the quotient of
$\mathcal {E}^+_{Q}=\mathcal {E}_{Q}/[P^-]$
to be the quotient of
![]() $\mathcal {E}_{Q}$
by the ideal of morphisms factoring through an object of
$\mathcal {E}_{Q}$
by the ideal of morphisms factoring through an object of
![]() $\operatorname {add}{P^-}$
.
$\operatorname {add}{P^-}$
.
Proposition 7.2. The category
![]() $\mathcal {E}^+_{Q}$
carries the structure of an extriangulated category. Moreover, it is a Frobenius extriangulated category [Reference Nakaoka and Palu40, Def. 7.1], and its stable category
$\mathcal {E}^+_{Q}$
carries the structure of an extriangulated category. Moreover, it is a Frobenius extriangulated category [Reference Nakaoka and Palu40, Def. 7.1], and its stable category
![]() $\underline {\mathcal {E}}^+_{Q}$
coincides with
$\underline {\mathcal {E}}^+_{Q}$
coincides with
![]() $\underline {\mathcal {E}}_{Q}$
, meaning in particular that it is triangulated and
$\underline {\mathcal {E}}_{Q}$
, meaning in particular that it is triangulated and
![]() $2$
-Calabi–Yau.
$2$
-Calabi–Yau.
Proof. Since
![]() $P^-$
is a projective–injective object of
$P^-$
is a projective–injective object of
![]() $\operatorname {GP}(B_{Q})$
, the extriangulated structure on
$\operatorname {GP}(B_{Q})$
, the extriangulated structure on
![]() $\mathcal {E}_{Q}^+$
is induced from the exact structure on
$\mathcal {E}_{Q}^+$
is induced from the exact structure on
![]() $\mathcal {E}_{Q}$
as in [Reference Nakaoka and Palu40, Prop. 3.30]. Since the extension groups
$\mathcal {E}_{Q}$
as in [Reference Nakaoka and Palu40, Prop. 3.30]. Since the extension groups
![]() $\mathbb {E}_{\mathcal {E}^+_{Q}}(X,Y)$
in this extriangulated category coincide with the extension groups
$\mathbb {E}_{\mathcal {E}^+_{Q}}(X,Y)$
in this extriangulated category coincide with the extension groups
![]() $\operatorname {Ext}^1_{\mathcal {E}_{Q}}(X,Y)$
in the exact category
$\operatorname {Ext}^1_{\mathcal {E}_{Q}}(X,Y)$
in the exact category
![]() $\mathcal {E}_{Q}$
, we see that an object is projective in
$\mathcal {E}_{Q}$
, we see that an object is projective in
![]() $\mathcal {E}^+_Q$
if and only if it is projective in
$\mathcal {E}^+_Q$
if and only if it is projective in
![]() $\mathcal {E}_{Q}$
, if and only if it is injective in
$\mathcal {E}_{Q}$
, if and only if it is injective in
![]() $\mathcal {E}_{Q}$
, and if and only if it is injective in
$\mathcal {E}_{Q}$
, and if and only if it is injective in
![]() $\mathcal {E}^+_{Q}$
. This agreement of extension groups also allows us to deduce the fact that
$\mathcal {E}^+_{Q}$
. This agreement of extension groups also allows us to deduce the fact that
![]() $\mathcal {E}^+_{Q}$
has enough projective and injective objects [Reference Nakaoka and Palu40, Def. 3.25] from this fact for
$\mathcal {E}^+_{Q}$
has enough projective and injective objects [Reference Nakaoka and Palu40, Def. 3.25] from this fact for
![]() $\operatorname {GP}(B_{Q})$
, and thus conclude that
$\operatorname {GP}(B_{Q})$
, and thus conclude that
![]() $\mathcal {E}^+_Q$
is Frobenius. It also follows from the agreement of projective–injective objects in
$\mathcal {E}^+_Q$
is Frobenius. It also follows from the agreement of projective–injective objects in
![]() $\mathcal {E}^+_{Q}$
and
$\mathcal {E}^+_{Q}$
and
![]() $\mathcal {E}_{Q}$
that
$\mathcal {E}_{Q}$
that
![]() $\underline {\mathcal {E}}^+_{Q}=\underline {\mathcal {E}}_{Q}$
, the latter being a
$\underline {\mathcal {E}}^+_{Q}=\underline {\mathcal {E}}_{Q}$
, the latter being a
![]() $2$
-Calabi–Yau triangulated category by Corollary 4.15.
$2$
-Calabi–Yau triangulated category by Corollary 4.15.
Note that if
![]() $(Q,W)$
is a Jacobi-finite quiver with potential such that
$(Q,W)$
is a Jacobi-finite quiver with potential such that
![]() $A_{Q,W}$
is Noetherian and internally Calabi–Yau with respect to e (such as the
$A_{Q,W}$
is Noetherian and internally Calabi–Yau with respect to e (such as the
![]() $3$
-cycle with its usual potential), so that we have a stably
$3$
-cycle with its usual potential), so that we have a stably
![]() $2$
-Calabi–Yau Frobenius category
$2$
-Calabi–Yau Frobenius category
![]() $\mathcal {E}_{Q,W}$
, we can define
$\mathcal {E}_{Q,W}$
, we can define
![]() $\mathcal {E}_{Q,W}^+=\mathcal {E}_{Q,W}/[B_{Q,W}e^-]$
. The statement of Proposition 7.2 also holds for this category, with the same proof.
$\mathcal {E}_{Q,W}^+=\mathcal {E}_{Q,W}/[B_{Q,W}e^-]$
. The statement of Proposition 7.2 also holds for this category, with the same proof.
Proof of Corollary 1
Statement (a) follows from Proposition 7.2, using Theorem 1
(b) to see that
![]() $\underline {\mathcal {E}}_Q^+=\underline {\mathcal {E}}_Q$
is equivalent to the cluster category
$\underline {\mathcal {E}}_Q^+=\underline {\mathcal {E}}_Q$
is equivalent to the cluster category
![]() $\mathcal {C}_{Q}$
.
$\mathcal {C}_{Q}$
.
To deduce the remaining statements from Theorem 1, first note that
for any X and Y in the common set of objects of the three categories
![]() $\mathcal {E}_Q$
,
$\mathcal {E}_Q$
,
![]() $\mathcal {E}^+_Q$
, and
$\mathcal {E}^+_Q$
, and
![]() $\underline {\mathcal {E}}_Q$
. This means that a set of representatives of isomorphism classes of cluster-tilting objects in
$\underline {\mathcal {E}}_Q$
. This means that a set of representatives of isomorphism classes of cluster-tilting objects in
![]() $\mathcal {E}_Q$
is also such a set for
$\mathcal {E}_Q$
is also such a set for
![]() $\mathcal {E}_Q^+$
and for
$\mathcal {E}_Q^+$
and for
![]() $\underline {\mathcal {E}}_Q$
. Moreover, since
$\underline {\mathcal {E}}_Q$
. Moreover, since
![]() $\mathcal {E}^+_Q$
and
$\mathcal {E}^+_Q$
and
![]() $\mathcal {E}_Q$
have the same projective–injective objects, a direct summand of one of these cluster-tilting objects is indecomposable nonprojective in one of these subcategories if and only if this is the case in all three. Thus, two of these cluster-tilting objects are related by mutation at an indecomposable summand in one of the categories if and only if they are related by mutation at the same summand in all three. Consequently, the identity map is a bijection from the set of cluster-tilting objects of
$\mathcal {E}_Q$
have the same projective–injective objects, a direct summand of one of these cluster-tilting objects is indecomposable nonprojective in one of these subcategories if and only if this is the case in all three. Thus, two of these cluster-tilting objects are related by mutation at an indecomposable summand in one of the categories if and only if they are related by mutation at the same summand in all three. Consequently, the identity map is a bijection from the set of cluster-tilting objects of
![]() $\mathcal {E}_Q$
to the set of cluster-tilting objects of
$\mathcal {E}_Q$
to the set of cluster-tilting objects of
![]() $\mathcal {E}^+_Q$
, commuting with mutation. A more detailed discussion of mutation of cluster-tilting objects in extriangulated categories can be found in [Reference Chang, Zhou and Zhu15] (see also [Reference Zhou and Zhu54]).
$\mathcal {E}^+_Q$
, commuting with mutation. A more detailed discussion of mutation of cluster-tilting objects in extriangulated categories can be found in [Reference Chang, Zhou and Zhu15] (see also [Reference Zhou and Zhu54]).
Finally, the indecomposable rigid objects of
![]() $\mathcal {E}_Q^+$
are, up to isomorphism, precisely the indecomposable rigid objects of
$\mathcal {E}_Q^+$
are, up to isomorphism, precisely the indecomposable rigid objects of
![]() $\mathcal {E}_Q$
which are not summands of
$\mathcal {E}_Q$
which are not summands of
![]() $P^-$
.
$P^-$
.
It now follows from Theorem 1
(c) and (d) that composing Fu–Keller’s cluster character
![]() $\operatorname {Ob}(\mathcal {E}_Q)\to \widetilde {\mathscr {A}}_{Q}$
with the map
$\operatorname {Ob}(\mathcal {E}_Q)\to \widetilde {\mathscr {A}}_{Q}$
with the map
![]() $\widetilde {\mathscr {A}}_{Q}\to \mathscr {A}_{Q}^{\bullet }$
evaluating the frozen variables
$\widetilde {\mathscr {A}}_{Q}\to \mathscr {A}_{Q}^{\bullet }$
evaluating the frozen variables
![]() $x_i^-$
at
$x_i^-$
at
![]() $1$
provides the required bijections. To see Corollary 1
(c), note additionally that each seed of
$1$
provides the required bijections. To see Corollary 1
(c), note additionally that each seed of
![]() $\mathscr {A}_{Q}^{\bullet }$
is obtained from one of
$\mathscr {A}_{Q}^{\bullet }$
is obtained from one of
![]() $\widetilde {\mathscr {A}}_{Q}$
by removing the frozen variables
$\widetilde {\mathscr {A}}_{Q}$
by removing the frozen variables
![]() $x_i^-$
and deleting the corresponding vertices (together with any incident arrows) from the quiver. Similarly, one obtains the quiver of
$x_i^-$
and deleting the corresponding vertices (together with any incident arrows) from the quiver. Similarly, one obtains the quiver of
![]() $\operatorname {End}_{\mathcal {E}_Q^+}(T)^{\mathrm {op}}$
from that of
$\operatorname {End}_{\mathcal {E}_Q^+}(T)^{\mathrm {op}}$
from that of
![]() $\operatorname {End}_{\mathcal {E}_Q}(T)^{\mathrm {op}}$
by removing the vertices corresponding to summands of
$\operatorname {End}_{\mathcal {E}_Q}(T)^{\mathrm {op}}$
by removing the vertices corresponding to summands of
![]() $P^-$
.
$P^-$
.
8 Boundary algebras
Since the objects of the Frobenius category
![]() $\mathcal {E}_Q$
in Theorem 1 are modules for the idempotent subalgebra
$\mathcal {E}_Q$
in Theorem 1 are modules for the idempotent subalgebra
![]() $B_Q=eA_Qe$
determined by the frozen vertices of
$B_Q=eA_Qe$
determined by the frozen vertices of
![]() $\widetilde {Q}$
, we wish to describe this subalgebra more explicitly. In this section, we will give a presentation of
$\widetilde {Q}$
, we wish to describe this subalgebra more explicitly. In this section, we will give a presentation of
![]() $B_Q$
via a quiver with relations.
$B_Q$
via a quiver with relations.
Recall that the double quiver
![]() $\overline {Q}$
of a quiver Q has vertex set
$\overline {Q}$
of a quiver Q has vertex set
![]() $Q_0$
and arrows
$Q_0$
and arrows
![]() $Q_1\cup Q^*_1$
, where
$Q_1\cup Q^*_1$
, where
![]() $Q^*_1=\{\alpha ^*:\alpha \in Q_1\}$
. The head and tail maps agree with those of Q on
$Q^*_1=\{\alpha ^*:\alpha \in Q_1\}$
. The head and tail maps agree with those of Q on
![]() $Q_1$
, and are defined by
$Q_1$
, and are defined by
![]() $h{\alpha ^*}=t{\alpha }$
and
$h{\alpha ^*}=t{\alpha }$
and
![]() $t{\alpha ^*}=h{\alpha }$
on
$t{\alpha ^*}=h{\alpha }$
on
![]() $Q^*_1$
. The complete preprojective algebra of Q is
$Q^*_1$
. The complete preprojective algebra of Q is
and, up to isomorphism, depends only on the underlying graph of Q. We begin with the following general statement for frozen Jacobian algebras, which reveals some of the relations of
![]() $B_{Q,W}$
for an arbitrary quiver with potential
$B_{Q,W}$
for an arbitrary quiver with potential
![]() $(Q,W)$
.
$(Q,W)$
.
Proposition 8.1. Let
![]() $(Q,F,W)$
be an ice quiver with potential, let
$(Q,F,W)$
be an ice quiver with potential, let
![]() $A=J(Q,F,W)$
, and let
$A=J(Q,F,W)$
, and let
![]() $B=eAe$
be the boundary algebra of A. Then there is an algebra homomorphism
$B=eAe$
be the boundary algebra of A. Then there is an algebra homomorphism
![]() $\pi \colon \Pi _{F}\to B$
given by
$\pi \colon \Pi _{F}\to B$
given by
![]() $\pi (e_{i})=e_{i}$
for
$\pi (e_{i})=e_{i}$
for
![]() $i\in F_0$
, and
$i\in F_0$
, and
![]() $\pi (\alpha )=\alpha $
,
$\pi (\alpha )=\alpha $
,
![]() $\pi (\alpha ^*)=\partial _{\alpha }{W}$
for
$\pi (\alpha ^*)=\partial _{\alpha }{W}$
for
![]() $\alpha \in F_1$
.
$\alpha \in F_1$
.
Proof. It suffices to check that
![]() $\pi (\sum _{\alpha \in F_1}[\alpha ,\alpha ^*])=0$
, that is,
$\pi (\sum _{\alpha \in F_1}[\alpha ,\alpha ^*])=0$
, that is,
![]() $\sum _{\alpha \in F_1}[\alpha ,\partial _{\alpha }{W}]=0$
. By construction, for any
$\sum _{\alpha \in F_1}[\alpha ,\partial _{\alpha }{W}]=0$
. By construction, for any
![]() $i\in Q_0$
, we have
$i\in Q_0$
, we have
 $$\begin{align*}\sum_{\alpha\in\mathrm{H}_v}\alpha\partial_{\alpha}{W}-\sum_{\beta\in\mathrm{T}_v}\partial_{\beta}{W}\beta=0\end{align*}$$
$$\begin{align*}\sum_{\alpha\in\mathrm{H}_v}\alpha\partial_{\alpha}{W}-\sum_{\beta\in\mathrm{T}_v}\partial_{\beta}{W}\beta=0\end{align*}$$
in
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
. Projecting to A and summing over vertices, we see that
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
. Projecting to A and summing over vertices, we see that
 $$\begin{align*}0=\sum_{\alpha\in Q_1}[\alpha,\partial_{\alpha}{W}]=\sum_{\alpha\in Q_1^\circ}[\alpha,\partial_{\alpha}{W}]+\sum_{\alpha\in F_1}[\alpha,\partial_{\alpha}{W}]=\sum_{\alpha\in F_1}[\alpha,\partial_{\alpha}{W}],\end{align*}$$
$$\begin{align*}0=\sum_{\alpha\in Q_1}[\alpha,\partial_{\alpha}{W}]=\sum_{\alpha\in Q_1^\circ}[\alpha,\partial_{\alpha}{W}]+\sum_{\alpha\in F_1}[\alpha,\partial_{\alpha}{W}]=\sum_{\alpha\in F_1}[\alpha,\partial_{\alpha}{W}],\end{align*}$$
where the final equality holds since
![]() $\partial _{\alpha }{W}=0$
in A whenever
$\partial _{\alpha }{W}=0$
in A whenever
![]() $\alpha \in Q_1^\circ $
.
$\alpha \in Q_1^\circ $
.
Remark 8.2. Familiarity with the constructions of [Reference Buan, Iyama, Reiten and Scott8, Reference Geiß, Leclerc and Schröer24, Reference Jensen, King and Su32] may make it tempting to conjecture that the map
![]() $\pi $
in Proposition 8.1 is surjective, at least when
$\pi $
in Proposition 8.1 is surjective, at least when
![]() $J(Q,F,W)$
is bimodule internally
$J(Q,F,W)$
is bimodule internally
![]() $3$
-Calabi–Yau, but this is in fact rarely the case. Indeed, we will see in this section that
$3$
-Calabi–Yau, but this is in fact rarely the case. Indeed, we will see in this section that
![]() $\pi $
fails to be surjective for our frozen Jacobian algebras
$\pi $
fails to be surjective for our frozen Jacobian algebras
![]() $J(\widetilde {Q},\widetilde {F},\widetilde {W})$
whenever Q is acyclic with a path of length
$J(\widetilde {Q},\widetilde {F},\widetilde {W})$
whenever Q is acyclic with a path of length
![]() $2$
(see Example 8.4).
$2$
(see Example 8.4).
We now turn to our description of
![]() $B_Q$
, beginning with what will turn out to be its Gabriel quiver.
$B_Q$
, beginning with what will turn out to be its Gabriel quiver.
Definition 8.3. Let Q be an acyclic quiver, and consider the frozen subquiver
![]() $\widetilde {F}$
of
$\widetilde {F}$
of
![]() $\widetilde {Q}$
, which has vertex set
$\widetilde {Q}$
, which has vertex set
![]() $\widetilde {F}_0=\{i^+,i^-:i\in Q_0\}$
and arrows
$\widetilde {F}_0=\{i^+,i^-:i\in Q_0\}$
and arrows
for each
![]() $i\in Q_0$
and
$i\in Q_0$
and
![]() $a\in Q_1$
. We define a quiver
$a\in Q_1$
. We define a quiver
![]() $\Lambda _Q$
by adjoining to
$\Lambda _Q$
by adjoining to
![]() $\widetilde {F}$
an arrow
$\widetilde {F}$
an arrow
for each path p of Q. Since Q is acyclic, it has finitely many paths, and so
![]() $\Lambda _Q$
is a finite quiver.
$\Lambda _Q$
is a finite quiver.
If
![]() $p=e_{i}$
is the trivial path at
$p=e_{i}$
is the trivial path at
![]() $i\in Q_0$
, we write
$i\in Q_0$
, we write
![]() $\delta ^*_p=\delta ^*_i$
to avoid a double subscript. The double quiver of
$\delta ^*_p=\delta ^*_i$
to avoid a double subscript. The double quiver of
![]() $\widetilde {F}$
appears as the subquiver of
$\widetilde {F}$
appears as the subquiver of
![]() $\Lambda _Q$
obtained by excluding the arrows
$\Lambda _Q$
obtained by excluding the arrows
![]() $\delta ^*_p$
for p of length 2 or more; the notation for the arrows of
$\delta ^*_p$
for p of length 2 or more; the notation for the arrows of
![]() $\Lambda _Q$
is chosen to be consistent with that used earlier for the arrows of this double quiver.
$\Lambda _Q$
is chosen to be consistent with that used earlier for the arrows of this double quiver.
Example 8.4. Let
be a linearly oriented quiver of type
![]() $\mathsf {A}_3$
. Then
$\mathsf {A}_3$
. Then
![]() $\Lambda _Q$
is the following quiver.
$\Lambda _Q$
is the following quiver.

Definition 8.5. Let Q be a quiver. A zigzag in Q is a triple
![]() $(q,a,p)$
, where p and q are paths in Q, and
$(q,a,p)$
, where p and q are paths in Q, and
![]() $a\in Q_1$
is an arrow such that
$a\in Q_1$
is an arrow such that
![]() $h{p}=h{a}$
and
$h{p}=h{a}$
and
![]() $t{q}=t{a}$
. Thus, if
$t{q}=t{a}$
. Thus, if
![]() $a\colon v\to w$
is an arrow of Q, a zigzag involving a is some configuration
$a\colon v\to w$
is an arrow of Q, a zigzag involving a is some configuration

where the dotted arrows denote paths. We call the zigzag strict if
![]() $p\ne ap'$
for any path
$p\ne ap'$
for any path
![]() $p'$
and
$p'$
and
![]() $q\ne q'a$
for any path
$q\ne q'a$
for any path
![]() $q'$
, but do not exclude these possibilities in general. If
$q'$
, but do not exclude these possibilities in general. If
![]() $z=(q,a,p)$
is a zigzag, then we define
$z=(q,a,p)$
is a zigzag, then we define
![]() $h{z}=h{q}$
and
$h{z}=h{q}$
and
![]() $t{z}=t{p}$
.
$t{z}=t{p}$
.
We now write down elements of
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
that will turn out to be a set of generating relations for
$\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
that will turn out to be a set of generating relations for
![]() $B_Q$
, having three flavors, as follows:
$B_Q$
, having three flavors, as follows:
-
(R1) For each path p of Q, let
 $$\begin{align*}r_1(p)=\delta^*_p\delta_{t{p}}-\sum_{\substack{a\in Q_1\\h{a}=t{p}}}\delta^*_{pa}\delta_a.\end{align*}$$
$$\begin{align*}r_1(p)=\delta^*_p\delta_{t{p}}-\sum_{\substack{a\in Q_1\\h{a}=t{p}}}\delta^*_{pa}\delta_a.\end{align*}$$
-
(R2) For each path p of Q, let
 $$\begin{align*}r_2(p)=\delta_{h{p}}\delta^*_p-\sum_{\substack{a\in Q_1\\t{a}=h{p}}}\delta_a\delta_{ap}^*.\end{align*}$$
$$\begin{align*}r_2(p)=\delta_{h{p}}\delta^*_p-\sum_{\substack{a\in Q_1\\t{a}=h{p}}}\delta_a\delta_{ap}^*.\end{align*}$$
-
(R3) For each zigzag
 $(q,a,p)$
of Q, let
$(q,a,p)$
of Q, let  $$\begin{align*}r_3(q,a,p)=\delta^*_{q}\delta_a\delta^*_{p}.\end{align*}$$
$$\begin{align*}r_3(q,a,p)=\delta^*_{q}\delta_a\delta^*_{p}.\end{align*}$$
We write I for the ideal of
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
generated by the union of these three sets of relations. This generating set is usually not minimal, as for certain zigzags
$\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
generated by the union of these three sets of relations. This generating set is usually not minimal, as for certain zigzags
![]() $(q,a,p)$
, the relation
$(q,a,p)$
, the relation
![]() $r_3(q,a,p)$
may already lie in the ideal generated by relations of the forms
$r_3(q,a,p)$
may already lie in the ideal generated by relations of the forms
![]() $r_1$
and
$r_1$
and
![]() $r_2$
. For example, if
$r_2$
. For example, if
![]() $a\in Q_1$
is an arrow such that
$a\in Q_1$
is an arrow such that
![]() $i=t{a}$
is not incident with any other arrows of Q, then
$i=t{a}$
is not incident with any other arrows of Q, then
so in
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {\langle r_1(a),r_2(e_i)\rangle }$
we already have
$\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {\langle r_1(a),r_2(e_i)\rangle }$
we already have
One can check that if
![]() $(q,a,p)$
is a strict zigzag, then
$(q,a,p)$
is a strict zigzag, then
![]() $r_3(q,a,p)$
is not redundant, but this condition is not necessary; if Q is a linearly oriented quiver of type
$r_3(q,a,p)$
is not redundant, but this condition is not necessary; if Q is a linearly oriented quiver of type
![]() $\mathsf {A}_4$
and a is the middle arrow, then the nonstrict zigzag
$\mathsf {A}_4$
and a is the middle arrow, then the nonstrict zigzag
![]() $(a,a,a)$
yields an irredundant relation.
$(a,a,a)$
yields an irredundant relation.
Remark 8.6. When
![]() $p=e_i$
is a vertex idempotent, the relations
$p=e_i$
is a vertex idempotent, the relations
![]() $r_1(e_i)$
and
$r_1(e_i)$
and
![]() $r_2(e_i)$
reduce to the preprojective relations on the double quiver of
$r_2(e_i)$
reduce to the preprojective relations on the double quiver of
![]() $\widetilde {F}$
, of the form predicted by Proposition 8.1. Each arrow
$\widetilde {F}$
, of the form predicted by Proposition 8.1. Each arrow
![]() $a\in Q_1$
is part of the trivial strict zigzag
$a\in Q_1$
is part of the trivial strict zigzag
![]() $(e_{t{a}},a,e_{h{a}})$
, and so contributes an irredundant relation
$(e_{t{a}},a,e_{h{a}})$
, and so contributes an irredundant relation
![]() $r_3(e_{t{a}},a,e_{h{a}})=\delta ^*_{t{a}}\delta _a\delta ^*_{h{a}}$
.
$r_3(e_{t{a}},a,e_{h{a}})=\delta ^*_{t{a}}\delta _a\delta ^*_{h{a}}$
.
Let
![]() $\Phi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle \to A_Q$
be the map given by the identity on the vertices of
$\Phi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle \to A_Q$
be the map given by the identity on the vertices of
![]() $\Lambda _Q$
and the arrows
$\Lambda _Q$
and the arrows
![]() $\delta _i$
and
$\delta _i$
and
![]() $\delta _a$
for
$\delta _a$
for
![]() $i\in Q_0$
and
$i\in Q_0$
and
![]() $a\in Q_1$
; this makes sense as these are subsets of the vertices and arrows of
$a\in Q_1$
; this makes sense as these are subsets of the vertices and arrows of
![]() $\widetilde {Q}$
. On the remaining arrows
$\widetilde {Q}$
. On the remaining arrows
![]() $\delta ^*_p$
of
$\delta ^*_p$
of
![]() $\Lambda _Q$
, we define
$\Lambda _Q$
, we define
![]() $\Phi (\delta ^*_p)=\alpha _{h{p}}p\beta _{t{p}}$
.
$\Phi (\delta ^*_p)=\alpha _{h{p}}p\beta _{t{p}}$
.
Proposition 8.7. The map
![]() $\Phi $
above induces a well-defined map
$\Phi $
above induces a well-defined map
![]() $\Phi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {I}\to B_Q$
.
$\Phi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {I}\to B_Q$
.
Proof. Since
![]() $\Phi $
sends every vertex or arrow of
$\Phi $
sends every vertex or arrow of
![]() $\Lambda _Q$
to the image in
$\Lambda _Q$
to the image in
![]() $A_Q$
of a path in
$A_Q$
of a path in
![]() $\widetilde {Q}$
with frozen head and tail, it takes values in
$\widetilde {Q}$
with frozen head and tail, it takes values in
![]() $B_Q$
. It remains to check that it is zero on each of the generating relations of I, which we do by explicit calculation. Let p be a path in Q. Then
$B_Q$
. It remains to check that it is zero on each of the generating relations of I, which we do by explicit calculation. Let p be a path in Q. Then
 $$ \begin{align*} \Phi(r_1(p))&=\alpha_{h p}p\beta_{t{p}}\delta_{t{p}}-\sum_{\substack{a\in Q_1\\h{a}=t{p}}}\alpha_{h p}pa\beta_{t{a}}\delta_a=\alpha_{h{p}}p(\partial_{\alpha_{t{p}}}{\widetilde{W}})=0,\\ \Phi(r_2(p))&=\delta_{h{p}}\alpha_{h p}p\beta_{t{p}}-\sum_{\substack{a\in Q_1\\t{a}=h{p}}}\delta_a\alpha_{h{a}}ap\beta_{t{p}}=(\partial_{\beta_{h{p}}}{\widetilde{W}})p\beta_{t{p}}=0. \end{align*} $$
$$ \begin{align*} \Phi(r_1(p))&=\alpha_{h p}p\beta_{t{p}}\delta_{t{p}}-\sum_{\substack{a\in Q_1\\h{a}=t{p}}}\alpha_{h p}pa\beta_{t{a}}\delta_a=\alpha_{h{p}}p(\partial_{\alpha_{t{p}}}{\widetilde{W}})=0,\\ \Phi(r_2(p))&=\delta_{h{p}}\alpha_{h p}p\beta_{t{p}}-\sum_{\substack{a\in Q_1\\t{a}=h{p}}}\delta_a\alpha_{h{a}}ap\beta_{t{p}}=(\partial_{\beta_{h{p}}}{\widetilde{W}})p\beta_{t{p}}=0. \end{align*} $$
If
![]() $(q,a,p)$
is a zigzag, then
$(q,a,p)$
is a zigzag, then
since
![]() $0=\partial _{a}{\widetilde {W}}=\partial _{a}{W}-\beta _{t{a}}\delta _a\alpha _{h{a}}=-\beta _{t{a}}\delta _a\alpha _{h{a}}$
by acyclicity of Q.
$0=\partial _{a}{\widetilde {W}}=\partial _{a}{W}-\beta _{t{a}}\delta _a\alpha _{h{a}}=-\beta _{t{a}}\delta _a\alpha _{h{a}}$
by acyclicity of Q.
Theorem 8.8. Let Q be an acyclic quiver. Then the map
![]() $\Phi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {I}\to B_Q$
, where
$\Phi \colon \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {I}\to B_Q$
, where
![]() $\Phi $
,
$\Phi $
,
![]() $\Lambda _Q$
, and I are all defined as above, is an isomorphism.
$\Lambda _Q$
, and I are all defined as above, is an isomorphism.
Proof. We begin by showing surjectivity. As in the proof of Theorem 5.2, we may use Lemma 5.1 to see that any path in
![]() $\widetilde {Q}$
determining a nonzero element of A has the form
$\widetilde {Q}$
determining a nonzero element of A has the form
![]() $p=q_1p'q_2$
where
$p=q_1p'q_2$
where
![]() $q_1$
and
$q_1$
and
![]() $q_2$
contain no arrows of
$q_2$
contain no arrows of
![]() $Q_1$
, and
$Q_1$
, and
![]() $p'$
is a path of Q. If p has frozen head and tail, then
$p'$
is a path of Q. If p has frozen head and tail, then
![]() $q_1$
and
$q_1$
and
![]() $q_2$
must be nonzero, so we even have
$q_2$
must be nonzero, so we even have
Now,
![]() $q_1^{\prime }$
and
$q_1^{\prime }$
and
![]() $q_2^{\prime }$
are, like p, paths of
$q_2^{\prime }$
are, like p, paths of
![]() $\widetilde {Q}$
with frozen head and tail, but with the additional property that they include no arrows of
$\widetilde {Q}$
with frozen head and tail, but with the additional property that they include no arrows of
![]() $Q_1$
. Let q be such a path. If q contains the arrow
$Q_1$
. Let q be such a path. If q contains the arrow
![]() $\beta _i$
for some
$\beta _i$
for some
![]() $i\in Q_0$
, then this arrow must have a successor in q, since its head is unfrozen. Moreover, this successor must be
$i\in Q_0$
, then this arrow must have a successor in q, since its head is unfrozen. Moreover, this successor must be
![]() $\alpha _i$
, since this is the only arrow outside of
$\alpha _i$
, since this is the only arrow outside of
![]() $Q_1$
that may follow
$Q_1$
that may follow
![]() $\beta _i$
. Similarly, any occurrence of
$\beta _i$
. Similarly, any occurrence of
![]() $\alpha _i$
in q must be preceded by
$\alpha _i$
in q must be preceded by
![]() $\beta _i$
. It follows that q is either a vertex idempotent
$\beta _i$
. It follows that q is either a vertex idempotent
![]() $e_i^\pm =\Phi (e_i^\pm )$
, or is formed by composing paths of the form
$e_i^\pm =\Phi (e_i^\pm )$
, or is formed by composing paths of the form
![]() $\delta _i=\Phi (\delta _i)$
for
$\delta _i=\Phi (\delta _i)$
for
![]() $i\in Q_0$
,
$i\in Q_0$
,
![]() $\delta _a=\Phi (\delta _a)$
for
$\delta _a=\Phi (\delta _a)$
for
![]() $a\in Q_1$
, or
$a\in Q_1$
, or
![]() $\alpha _i\beta _i=\Phi (\delta ^*_i)$
for
$\alpha _i\beta _i=\Phi (\delta ^*_i)$
for
![]() $i\in Q_0$
, and so is in the image of
$i\in Q_0$
, and so is in the image of
![]() $\Phi $
. We conclude that the projection to
$\Phi $
. We conclude that the projection to
![]() $A_Q$
of any path in
$A_Q$
of any path in
![]() $\widetilde {Q}$
with frozen head and tail lies in the image of
$\widetilde {Q}$
with frozen head and tail lies in the image of
![]() $\Phi $
. Since these projections span
$\Phi $
. Since these projections span
![]() $B_Q$
, we see that
$B_Q$
, we see that
![]() $\Phi $
is surjective.
$\Phi $
is surjective.
From now on, we abbreviate
![]() $B=B_Q$
. To complete the proof, we will use [Reference Buan, Iyama, Reiten and Smith9, Prop. 3.3], which in this context states that
$B=B_Q$
. To complete the proof, we will use [Reference Buan, Iyama, Reiten and Smith9, Prop. 3.3], which in this context states that
![]() $\Phi $
is an isomorphism if and only if
$\Phi $
is an isomorphism if and only if

and

are exact sequences for all
![]() $i\in Q_0$
. Here, the left-most maps in each sequence are obtained from our generators for the ideal I by right-differentiation (4.7) and the application of
$i\in Q_0$
. Here, the left-most maps in each sequence are obtained from our generators for the ideal I by right-differentiation (4.7) and the application of
![]() $\Phi $
, as prescribed in [Reference Buan, Iyama, Reiten and Smith9], so they act on components by
$\Phi $
, as prescribed in [Reference Buan, Iyama, Reiten and Smith9], so they act on components by
 $$ \begin{align} \begin{aligned} f(ye_{h{p}}^+)&=y\Phi(\delta^*_p)\mathbin{\otimes}[i]-\sum_{\substack{a\in Q_1\\h{a}=i}}y\Phi(\delta^*_{pa})\mathbin{\otimes}[a],\\ g(ye_{h{p}}^-)&=y\delta_{h{p}}\mathbin{\otimes}[p]-\sum_{\substack{a\in Q_1\\t{a}=h{p}}}y\delta_a\mathbin{\otimes}[ap],\\ g(ye_{h{z}}^+)&=y\Phi(\delta^*_{q})\delta_a\otimes[p],\ \text{where } z=(q,a,p). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} f(ye_{h{p}}^+)&=y\Phi(\delta^*_p)\mathbin{\otimes}[i]-\sum_{\substack{a\in Q_1\\h{a}=i}}y\Phi(\delta^*_{pa})\mathbin{\otimes}[a],\\ g(ye_{h{p}}^-)&=y\delta_{h{p}}\mathbin{\otimes}[p]-\sum_{\substack{a\in Q_1\\t{a}=h{p}}}y\delta_a\mathbin{\otimes}[ap],\\ g(ye_{h{z}}^+)&=y\Phi(\delta^*_{q})\delta_a\otimes[p],\ \text{where } z=(q,a,p). \end{aligned} \end{align} $$
Here, we have dealt with the ambiguity about which summand contains each term as in §4, denoting elements of
![]() $\bigoplus _{a\in X}Be_{v(a)}$
by
$\bigoplus _{a\in X}Be_{v(a)}$
by
![]() $\sum _{a\in X}x_a\otimes [a]$
, with
$\sum _{a\in X}x_a\otimes [a]$
, with
![]() $x_a\in Be_{v(x)}$
and
$x_a\in Be_{v(x)}$
and
![]() $x_a\otimes [a]$
denoting its inclusion into the summand of
$x_a\otimes [a]$
denoting its inclusion into the summand of
![]() $\bigoplus _{a\in X}Be_{v(a)}$
indexed by a. We adopt the convention here that the summand
$\bigoplus _{a\in X}Be_{v(a)}$
indexed by a. We adopt the convention here that the summand
![]() $Be_{i}^-$
appearing in the middle term of (8.1) is indexed by the vertex i.
$Be_{i}^-$
appearing in the middle term of (8.1) is indexed by the vertex i.
Since
![]() $\Phi $
is well defined and surjective, sequences (8.1) and (8.2) are complexes and exact at
$\Phi $
is well defined and surjective, sequences (8.1) and (8.2) are complexes and exact at
![]() $\operatorname {rad}{Be_i^+}$
and
$\operatorname {rad}{Be_i^+}$
and
![]() $\operatorname {rad}{Be_i^-}$
, respectively, so we need only check exactness at the middle term in each case. We proceed as in §4, using the explicit set R of relations for
$\operatorname {rad}{Be_i^-}$
, respectively, so we need only check exactness at the middle term in each case. We proceed as in §4, using the explicit set R of relations for
![]() $A_Q$
from (3.1), and begin with (8.1). Let
$A_Q$
from (3.1), and begin with (8.1). Let
![]() $x_i\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_i^-$
and
$x_i\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_i^-$
and
![]() $x_a\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{t{a}}^-$
for each
$x_a\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{t{a}}^-$
for each
![]() $a\in Q_1$
with
$a\in Q_1$
with
![]() $h{a}=i$
, determining the element
$h{a}=i$
, determining the element
 $$\begin{align*}x=x_i\otimes[i]+\sum_{\substack{a\in Q_1\\h{a}=i}}x_a\otimes[a]\end{align*}$$
$$\begin{align*}x=x_i\otimes[i]+\sum_{\substack{a\in Q_1\\h{a}=i}}x_a\otimes[a]\end{align*}$$
of the middle term of (8.1). Assume that x is a cycle for this complex, that is,
 $$\begin{align*}x_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}x_a\delta_a\in\overline{\langle R\rangle}.\end{align*}$$
$$\begin{align*}x_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}x_a\delta_a\in\overline{\langle R\rangle}.\end{align*}$$
Since the only generating relation for
![]() $A_Q$
with terms ending in
$A_Q$
with terms ending in
![]() $\delta _i$
or
$\delta _i$
or
![]() $\delta _a$
for
$\delta _a$
for
![]() $a\in Q_1$
with
$a\in Q_1$
with
![]() $h{a}=i$
is
$h{a}=i$
is
![]() $\partial _{\alpha _i}{W}$
, it follows that in
$\partial _{\alpha _i}{W}$
, it follows that in
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle $
we have
$\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle $
we have
 $$ \begin{align*} x_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}x_a\delta_a&=z_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}z_a\delta_a+y\partial_{\alpha_i}{W}\\ &=z_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}z_a\delta_a+y\bigg(\beta_i\delta_i-\sum_{\substack{a\in Q_1\\h{a}=i}}a\beta_{t{a}}\delta_a\bigg)\end{align*} $$
$$ \begin{align*} x_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}x_a\delta_a&=z_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}z_a\delta_a+y\partial_{\alpha_i}{W}\\ &=z_i\delta_i+\sum_{\substack{a\in Q_1\\h{a}=i}}z_a\delta_a+y\bigg(\beta_i\delta_i-\sum_{\substack{a\in Q_1\\h{a}=i}}a\beta_{t{a}}\delta_a\bigg)\end{align*} $$
for
![]() $z_i,z_a\in \overline {\langle R\rangle }$
and
$z_i,z_a\in \overline {\langle R\rangle }$
and
![]() $y\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{i}$
. Comparing terms, we see that
$y\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{i}$
. Comparing terms, we see that
![]() $x_i=z_i+y\beta _i$
and
$x_i=z_i+y\beta _i$
and
![]() $x_a=z_a-ya\beta _{t{a}}$
. Since
$x_a=z_a-ya\beta _{t{a}}$
. Since
![]() $h{x_i}$
and
$h{x_i}$
and
![]() $h{x_a}$
are frozen, but
$h{x_a}$
are frozen, but
![]() $h{\beta _j}$
is unfrozen for all
$h{\beta _j}$
is unfrozen for all
![]() $j\in Q_0$
, we must have
$j\in Q_0$
, we must have
 $$\begin{align*}y=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\alpha_{h p}p\end{align*}$$
$$\begin{align*}y=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\alpha_{h p}p\end{align*}$$
for some
![]() $y_p\in Be_{h{p}}^+$
. Projecting to B, we have
$y_p\in Be_{h{p}}^+$
. Projecting to B, we have
 $$\begin{align*}x_i=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\Phi(\delta^*_p),\qquad x_a=\sum_{\substack{p \text{ path in} Q\\t{p}=i}}-y_p\Phi(\delta^*_{pa}). \end{align*}$$
$$\begin{align*}x_i=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\Phi(\delta^*_p),\qquad x_a=\sum_{\substack{p \text{ path in} Q\\t{p}=i}}-y_p\Phi(\delta^*_{pa}). \end{align*}$$
Thus,
 $$\begin{align*}y=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\otimes p\end{align*}$$
$$\begin{align*}y=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\otimes p\end{align*}$$
satisfies
![]() $f(y)=x$
, and so sequence (8.1) is exact.
$f(y)=x$
, and so sequence (8.1) is exact.
Now, we turn to (8.2). For each path p in Q with
![]() $t{p}=i$
, pick
$t{p}=i$
, pick
![]() $x_p\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{h{p}}^+$
, and assume that
$x_p\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{h{p}}^+$
, and assume that
 $$\begin{align*}\sum_{\substack{p \text{ path in } Q\\t{q}=i}}x_p\alpha_{h{p}}p\beta_i\in\overline{\langle R\rangle},\end{align*}$$
$$\begin{align*}\sum_{\substack{p \text{ path in } Q\\t{q}=i}}x_p\alpha_{h{p}}p\beta_i\in\overline{\langle R\rangle},\end{align*}$$
so that
 $$\begin{align*}x=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}x_p\otimes[p]\end{align*}$$
$$\begin{align*}x=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}x_p\otimes[p]\end{align*}$$
is a cycle in the middle term of (8.2). By comparison with the generating relations, we see that we may write
 $$\begin{align*}&\sum_{\substack{p \text{ path in } Q\\t{p}=i}}x_p\alpha_{h{p}}p\beta_i\\&\quad=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}\Bigg(z_p\alpha_{h{p}}p\beta_i+y_p\bigg(\delta_{h{p}}\alpha_{h{p}}-\sum_{\substack{b\in Q_1\\t{b}=h{p}}}\delta_b\alpha_{h{b}}b\bigg)p\beta_i-\sum_{\substack{a\in Q_1\\h{a}=h{p}}}y_{a,p}(\beta_{t{a}}\delta_a\alpha_{h{a}})p\beta_i\Bigg)\end{align*}$$
$$\begin{align*}&\sum_{\substack{p \text{ path in } Q\\t{p}=i}}x_p\alpha_{h{p}}p\beta_i\\&\quad=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}\Bigg(z_p\alpha_{h{p}}p\beta_i+y_p\bigg(\delta_{h{p}}\alpha_{h{p}}-\sum_{\substack{b\in Q_1\\t{b}=h{p}}}\delta_b\alpha_{h{b}}b\bigg)p\beta_i-\sum_{\substack{a\in Q_1\\h{a}=h{p}}}y_{a,p}(\beta_{t{a}}\delta_a\alpha_{h{a}})p\beta_i\Bigg)\end{align*}$$
for some
![]() $z_p\in \overline {\langle R\rangle }$
,
$z_p\in \overline {\langle R\rangle }$
,
![]() $y_p\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{h{p}}^-$
and
$y_p\in \mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{h{p}}^-$
and
![]() $y_{a,p}\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{t{a}}$
. Each path p in the sum is either the trivial path
$y_{a,p}\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{t{a}}$
. Each path p in the sum is either the trivial path
![]() $e_i$
or of the form
$e_i$
or of the form
![]() $p=br$
for some arrow b and path r. By comparing terms, we deduce that after projection to B we have
$p=br$
for some arrow b and path r. By comparing terms, we deduce that after projection to B we have
 $$\begin{align*}x_i=y_i\delta_i-\sum_{\substack{a\in Q_1\\h{a}=i}}y_{a,e_i}\beta_{t{a}}\delta_a,\qquad x_{br}=y_{br}\delta_{h{b}}-y_{r}\delta_b-\sum_{\substack{a\in Q_1\\h{a}=h{b}}}y_{a,br}\beta_{t{a}}\delta_a. \end{align*}$$
$$\begin{align*}x_i=y_i\delta_i-\sum_{\substack{a\in Q_1\\h{a}=i}}y_{a,e_i}\beta_{t{a}}\delta_a,\qquad x_{br}=y_{br}\delta_{h{b}}-y_{r}\delta_b-\sum_{\substack{a\in Q_1\\h{a}=h{b}}}y_{a,br}\beta_{t{a}}\delta_a. \end{align*}$$
Since
![]() $y_{a,p}\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{t{a}}$
, we must have
$y_{a,p}\in e\mathbb {K}\langle \hspace {-0.1em}\langle \widetilde {Q}\rangle \hspace {-0.1em}\rangle e_{t{a}}$
, we must have
 $$\begin{align*}y_{a,p}=\sum_{\substack{q \text{ path in } Q\\t{q}=t{a}}}y_{q,a,p}\alpha_{h{q}}q\end{align*}$$
$$\begin{align*}y_{a,p}=\sum_{\substack{q \text{ path in } Q\\t{q}=t{a}}}y_{q,a,p}\alpha_{h{q}}q\end{align*}$$
for some
![]() $y_{q,a,p}\in e\mathbb {K} \widetilde {Q}e_{h{q}}^+$
. The triple
$y_{q,a,p}\in e\mathbb {K} \widetilde {Q}e_{h{q}}^+$
. The triple
![]() $z=(q,a,p)$
occurring in a subscript here satisfies
$z=(q,a,p)$
occurring in a subscript here satisfies
![]() $h{a}=h{q}$
and
$h{a}=h{q}$
and
![]() $t{a}=t{p}$
, so it is a zigzag. One may then calculate explicitly using (8.3) that the
$t{a}=t{p}$
, so it is a zigzag. One may then calculate explicitly using (8.3) that the
![]() $y_p$
and
$y_p$
and
![]() $y_z=y_{q,a,p}$
give a preimage
$y_z=y_{q,a,p}$
give a preimage
 $$\begin{align*}y=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\otimes[p]+\sum_{\substack{z \text{ zig-zag}\\t{z}=i}}y_z\otimes[z]\end{align*}$$
$$\begin{align*}y=\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\otimes[p]+\sum_{\substack{z \text{ zig-zag}\\t{z}=i}}y_z\otimes[z]\end{align*}$$
of x under g.
We close this section with the following curious property of the category
![]() $\mathcal {E}_Q=\operatorname {GP}(B_Q)$
. Recall that
$\mathcal {E}_Q=\operatorname {GP}(B_Q)$
. Recall that
![]() $\operatorname {Sub}(X)$
, for
$\operatorname {Sub}(X)$
, for
![]() $X\in \operatorname {mod}{B_Q}$
, denotes the full subcategory of
$X\in \operatorname {mod}{B_Q}$
, denotes the full subcategory of
![]() $\operatorname {mod}{B_Q}$
on objects M admitting a monomorphism
$\operatorname {mod}{B_Q}$
on objects M admitting a monomorphism
![]() $M\to X^n$
for some n.
$M\to X^n$
for some n.
Proposition 8.9. Write
![]() $P^+=\bigoplus _{i\in Q_0}B_Qe_k^+$
. If Q is acyclic and has no isolated vertices, then
$P^+=\bigoplus _{i\in Q_0}B_Qe_k^+$
. If Q is acyclic and has no isolated vertices, then
![]() $\operatorname {GP}(B_Q)\subseteq \operatorname {Sub}(P^+)$
.
$\operatorname {GP}(B_Q)\subseteq \operatorname {Sub}(P^+)$
.
Proof. Write
![]() $B=B_Q$
. Since
$B=B_Q$
. Since
![]() $\operatorname {GP}(B)$
is a Frobenius category with injective objects those in
$\operatorname {GP}(B)$
is a Frobenius category with injective objects those in
![]() $\operatorname {add}{B}$
, it suffices to show that
$\operatorname {add}{B}$
, it suffices to show that
![]() $B\in \operatorname {Sub}(P^+)$
, or that
$B\in \operatorname {Sub}(P^+)$
, or that
![]() $Be_i^\pm \in \operatorname {Sub}(P^+)$
for each i. Since this is true of
$Be_i^\pm \in \operatorname {Sub}(P^+)$
for each i. Since this is true of
![]() $Be_i^+$
by definition of
$Be_i^+$
by definition of
![]() $P^+$
, it remains to show that
$P^+$
, it remains to show that
![]() $Be_i^-\in \operatorname {Sub}(P^+)$
for each
$Be_i^-\in \operatorname {Sub}(P^+)$
for each
![]() $i\in Q_0$
. Since Q has no isolated vertices, i cannot be both a source and a sink.
$i\in Q_0$
. Since Q has no isolated vertices, i cannot be both a source and a sink.
First, assume that i is not a source in Q. Then the map
![]() $Be_i^-\to Be_i^+$
given by right multiplication by
$Be_i^-\to Be_i^+$
given by right multiplication by
![]() $\delta _i$
is injective, as follows. If
$\delta _i$
is injective, as follows. If
![]() $x\in Be_i^-$
satisfies
$x\in Be_i^-$
satisfies
![]() $x\delta _i=0$
in
$x\delta _i=0$
in
![]() $Be_i^+$
, then lifting to
$Be_i^+$
, then lifting to
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
and using the explicit generating set of I, we have
$\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
and using the explicit generating set of I, we have
 $$\begin{align*}x\delta_i=z\delta_i+\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\bigg(\delta^*_p\delta_i-\sum_{\substack{a\in Q_1\\h{a}=i}}\delta_{pa}^*\delta_a\bigg)\end{align*}$$
$$\begin{align*}x\delta_i=z\delta_i+\sum_{\substack{p \text{ path in } Q\\t{p}=i}}y_p\bigg(\delta^*_p\delta_i-\sum_{\substack{a\in Q_1\\h{a}=i}}\delta_{pa}^*\delta_a\bigg)\end{align*}$$
for some
![]() $z\in I$
and
$z\in I$
and
![]() $y_p\in e\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle e_{h{p}}^+$
. Since i is not a source, the sum over arrows on the right-hand side is nonempty. By comparing coefficients, we see that
$y_p\in e\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle e_{h{p}}^+$
. Since i is not a source, the sum over arrows on the right-hand side is nonempty. By comparing coefficients, we see that
![]() $y_p=0$
for all p, and hence
$y_p=0$
for all p, and hence
![]() $x=z=0$
in A.
$x=z=0$
in A.
Now, assume that i is not a sink. Pick
![]() $a\in Q_1$
with
$a\in Q_1$
with
![]() $t{a}=i$
. Then the map
$t{a}=i$
. Then the map
![]() $Be_i^-\to Be_{h{a}}^+$
given by right multiplication by
$Be_i^-\to Be_{h{a}}^+$
given by right multiplication by
![]() $\delta _a$
is injective as follows. If
$\delta _a$
is injective as follows. If
![]() $x\in Be_i^-$
satisfies
$x\in Be_i^-$
satisfies
![]() $x\delta _a=0$
in
$x\delta _a=0$
in
![]() $Be_{h{a}}^+$
, then lifting to
$Be_{h{a}}^+$
, then lifting to
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
and using our explicit relations, we have
$\mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle $
and using our explicit relations, we have
 $$\begin{align*}x\delta_a=z+\sum_{\substack{p \text{ path in } Q\\ t{p}=h{a}}}y_p\bigg(\delta_p^*\delta_{h{a}}-\sum_{\substack{b\in Q_1\\h{b}= h{a}}}\delta^*_{pa}\delta_a\bigg),\end{align*}$$
$$\begin{align*}x\delta_a=z+\sum_{\substack{p \text{ path in } Q\\ t{p}=h{a}}}y_p\bigg(\delta_p^*\delta_{h{a}}-\sum_{\substack{b\in Q_1\\h{b}= h{a}}}\delta^*_{pa}\delta_a\bigg),\end{align*}$$
for
![]() $z\in I$
, and it follows by comparing coefficients that
$z\in I$
, and it follows by comparing coefficients that
![]() $y_p=0$
for all p, so
$y_p=0$
for all p, so
![]() $x=0$
.
$x=0$
.
Example 10.2 shows that we may have
![]() $\mathcal {E}_Q\subsetneq \operatorname {Sub}(P^+)$
. The assumption on isolated vertices is necessary, since such a vertex i of Q results in a direct summand of
$\mathcal {E}_Q\subsetneq \operatorname {Sub}(P^+)$
. The assumption on isolated vertices is necessary, since such a vertex i of Q results in a direct summand of
![]() $\mathcal {E}_Q$
equivalent to
$\mathcal {E}_Q$
equivalent to
![]() $\operatorname {mod}\ {\Pi }$
for
$\operatorname {mod}\ {\Pi }$
for
![]() $\Pi $
the preprojective algebra of type
$\Pi $
the preprojective algebra of type
![]() $\mathsf {A}_2$
, with indecomposable objects
$\mathsf {A}_2$
, with indecomposable objects
![]() $S_i^\pm $
and
$S_i^\pm $
and
![]() $P_i^\pm $
, and
$P_i^\pm $
, and
![]() $S_i^-,P_i^-\notin \operatorname {Sub}(P^+)=\operatorname {Sub}(P_i^+)$
.
$S_i^-,P_i^-\notin \operatorname {Sub}(P^+)=\operatorname {Sub}(P_i^+)$
.
9 g-vectors, indices, and dimension vectors
In this section, we show how representation-theoretic information about the category
![]() $\mathcal {E}_Q$
from Theorem 1 can be used to recover information about the principal coefficient cluster algebra
$\mathcal {E}_Q$
from Theorem 1 can be used to recover information about the principal coefficient cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
. These are not new results (unsurprisingly, since this cluster algebra is very well-studied), but the style of proofs is different and demonstrates how the categorification given here can be used. Our results are also not restricted to the acyclic case, but hold whenever an appropriate Frobenius categorification can be constructed, for example, in the context of Corollary 4.15.
$\mathscr {A}_{Q}^{\bullet }$
. These are not new results (unsurprisingly, since this cluster algebra is very well-studied), but the style of proofs is different and demonstrates how the categorification given here can be used. Our results are also not restricted to the acyclic case, but hold whenever an appropriate Frobenius categorification can be constructed, for example, in the context of Corollary 4.15.
Let
![]() $(Q,W)$
be a Jacobi-finite quiver with potential such that the frozen Jacobian algebra
$(Q,W)$
be a Jacobi-finite quiver with potential such that the frozen Jacobian algebra
![]() $A=A_{Q,W}$
is Noetherian; for example, one can take Q to be an acyclic quiver. Then, by Corollary 4.15, the category
$A=A_{Q,W}$
is Noetherian; for example, one can take Q to be an acyclic quiver. Then, by Corollary 4.15, the category
![]() $\mathcal {E}=\operatorname {GP}(eAe)$
is a stably
$\mathcal {E}=\operatorname {GP}(eAe)$
is a stably
![]() $2$
-Calabi–Yau category with a cluster-tilting object
$2$
-Calabi–Yau category with a cluster-tilting object
![]() $T=eA$
, and there are compatible isomorphisms
$T=eA$
, and there are compatible isomorphisms
![]() $\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A$
and
$\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A$
and
![]() $\underline {\operatorname {End}}_{\mathcal {E}}(T)^{\mathrm {op}}\cong J(Q,W)$
. We keep the abbreviated notation A, T, and
$\underline {\operatorname {End}}_{\mathcal {E}}(T)^{\mathrm {op}}\cong J(Q,W)$
. We keep the abbreviated notation A, T, and
![]() $\mathcal {E}$
for the rest of the section.
$\mathcal {E}$
for the rest of the section.
The isomorphism
![]() $\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A$
allows us to write the indecomposable summands of T as
$\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A$
allows us to write the indecomposable summands of T as
![]() $T_i$
, for
$T_i$
, for
![]() $i\in Q_0$
, where
$i\in Q_0$
, where
![]() $T_i$
corresponds to
$T_i$
corresponds to
![]() $Ae_i$
under the isomorphism. We write
$Ae_i$
under the isomorphism. We write
![]() $P_i^\pm $
instead of
$P_i^\pm $
instead of
![]() $T_i^\pm $
, noting that these are the indecomposable projective–injective objects of
$T_i^\pm $
, noting that these are the indecomposable projective–injective objects of
![]() $\mathcal {E}$
, and write
$\mathcal {E}$
, and write
![]() $P^\pm =\bigoplus _{i\in Q_0}P_i^\pm $
, which is compatible with the notation in §8. We abbreviate
$P^\pm =\bigoplus _{i\in Q_0}P_i^\pm $
, which is compatible with the notation in §8. We abbreviate
![]() and
and
![]() , these being functors
, these being functors
![]() $\mathcal {E}\to \operatorname {mod}\ {A}$
via the isomorphism
$\mathcal {E}\to \operatorname {mod}\ {A}$
via the isomorphism
![]() $\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A$
. Finally, we write
$\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A$
. Finally, we write
![]() $[M:N]$
for the multiplicity of N as an indecomposable summand of M (for M and N objects in any category in which this makes sense).
$[M:N]$
for the multiplicity of N as an indecomposable summand of M (for M and N objects in any category in which this makes sense).
Lemma 9.1. Let
![]() $X\in \mathcal {E}$
. Then the minimal projective resolution
$X\in \mathcal {E}$
. Then the minimal projective resolution
of
![]() $GX$
has the property that, for each
$GX$
has the property that, for each
![]() $j\in Q_0$
,
$j\in Q_0$
,
 $$ \begin{align*} [P^k:Ae_j^+]&={\begin{cases}\dim_{\mathbb{K}}(e_jGX),&k=1,\\0,&\text{otherwise},\end{cases}}\\ [P^k:Ae_j^-]&={\begin{cases}\dim_{\mathbb{K}}(e_jGX),&k=2,\\0,&\text{otherwise}.\end{cases}} \end{align*} $$
$$ \begin{align*} [P^k:Ae_j^+]&={\begin{cases}\dim_{\mathbb{K}}(e_jGX),&k=1,\\0,&\text{otherwise},\end{cases}}\\ [P^k:Ae_j^-]&={\begin{cases}\dim_{\mathbb{K}}(e_jGX),&k=2,\\0,&\text{otherwise}.\end{cases}} \end{align*} $$
Proof. Note that
![]() $eGX=\operatorname {Ext}^1_{\mathcal {E}}(P^+\oplus P^-,X)=0$
, so the composition series of
$eGX=\operatorname {Ext}^1_{\mathcal {E}}(P^+\oplus P^-,X)=0$
, so the composition series of
![]() $GX$
includes only the simple modules
$GX$
includes only the simple modules
![]() $S_i$
for
$S_i$
for
![]() $i\in Q_0$
a mutable vertex. In this case, the sequence (4.5), which is exact by Propositions 4.10 and 4.12, is a projective resolution of the simple A-module
$i\in Q_0$
a mutable vertex. In this case, the sequence (4.5), which is exact by Propositions 4.10 and 4.12, is a projective resolution of the simple A-module
![]() $S_{i}$
. We write this resolution as
$S_{i}$
. We write this resolution as
for projective A-modules
![]() $P_i^k$
which can be described explicitly using (4.6). In particular, one sees using this description that the only appearances of the projective A-modules
$P_i^k$
which can be described explicitly using (4.6). In particular, one sees using this description that the only appearances of the projective A-modules
![]() $Ae_j^\pm $
in (9.2) are one copy of
$Ae_j^\pm $
in (9.2) are one copy of
![]() $Ae_i^+$
in
$Ae_i^+$
in
![]() $P_i^1$
, and one copy of
$P_i^1$
, and one copy of
![]() $Ae_i^-$
in
$Ae_i^-$
in
![]() $P_i^2$
.
$P_i^2$
.
By the horseshoe lemma, we can thus construct a (possibly nonminimal) projective resolution of
![]() $GX$
in which the degree k term
$GX$
in which the degree k term
![]() $\hat {P}^k$
is a direct sum of the
$\hat {P}^k$
is a direct sum of the
![]() $P_i^k$
over composition factors
$P_i^k$
over composition factors
![]() $S_i$
of
$S_i$
of
![]() $GX$
. As a consequence, this resolution includes
$GX$
. As a consequence, this resolution includes
![]() $\dim _{\mathbb {K}}(e_jGX)$
copies of
$\dim _{\mathbb {K}}(e_jGX)$
copies of
![]() $Ae_j^+$
, all summands of
$Ae_j^+$
, all summands of
![]() $\hat {P}^1$
, and
$\hat {P}^1$
, and
![]() $\dim _{\mathbb {K}}(e_jGX)$
copies of
$\dim _{\mathbb {K}}(e_jGX)$
copies of
![]() $Ae_j^-$
, all summands of
$Ae_j^-$
, all summands of
![]() $\hat {P}^2$
. Since each
$\hat {P}^2$
. Since each
![]() $Ae_j^\pm $
appears in only one homological degree in this resolution, it cannot be part of an acyclic summand, and so it appears with the same multiplicity and degree in the minimal projective resolution (9.1) of
$Ae_j^\pm $
appears in only one homological degree in this resolution, it cannot be part of an acyclic summand, and so it appears with the same multiplicity and degree in the minimal projective resolution (9.1) of
![]() $GX$
, as required.
$GX$
, as required.
Recall that any
![]() $X\in \mathcal {E}$
fits into an exact sequence
$X\in \mathcal {E}$
fits into an exact sequence
with
![]() $K_X,R_X\in \operatorname {add}{T}$
. Indeed, this holds for any Frobenius cluster category and cluster-tilting object, and the choice of sequence (9.3) is equivalent to the choice of the map
$K_X,R_X\in \operatorname {add}{T}$
. Indeed, this holds for any Frobenius cluster category and cluster-tilting object, and the choice of sequence (9.3) is equivalent to the choice of the map
![]() $R_X\to X$
, subject to the condition that this map is a right
$R_X\to X$
, subject to the condition that this map is a right
![]() $\operatorname {add}{T}$
-approximation. Dually, X fits into an exact sequence
$\operatorname {add}{T}$
-approximation. Dually, X fits into an exact sequence
with
![]() $L_X,C_X\in \operatorname {add}{T}$
, with the choice of sequence being equivalent to the choice of left
$L_X,C_X\in \operatorname {add}{T}$
, with the choice of sequence being equivalent to the choice of left
![]() $\operatorname {add}{T}$
-approximation
$\operatorname {add}{T}$
-approximation
![]() $X\to L_X$
. We say that the sequence (9.3) is minimal if the map
$X\to L_X$
. We say that the sequence (9.3) is minimal if the map
![]() ${R_X\to X}$
is a minimal right
${R_X\to X}$
is a minimal right
![]() $\operatorname {add}{T}$
-approximation of X, or equivalently if no nonzero component of the map
$\operatorname {add}{T}$
-approximation of X, or equivalently if no nonzero component of the map
![]() $K_X\to R_X$
is an isomorphism, and define minimality for (9.4) dually.
$K_X\to R_X$
is an isomorphism, and define minimality for (9.4) dually.
Lemma 9.2. For any
![]() $X\in \mathcal {E}$
, choose minimal sequences of the forms (9.3) and (9.4), and let
$X\in \mathcal {E}$
, choose minimal sequences of the forms (9.3) and (9.4), and let
![]() $i\in Q_0$
. Then
$i\in Q_0$
. Then
 $$ \begin{align*} [K_X:P_i^\pm]=[C_X:P_i^\pm]&=0,\\ [R_X:P_i^+]=[L_X:P_i^-]&=0,\\ [R_X:P_i^-]=[L_X:P_i^+]&=\dim_{\mathbb{K}}(e_iGX). \end{align*} $$
$$ \begin{align*} [K_X:P_i^\pm]=[C_X:P_i^\pm]&=0,\\ [R_X:P_i^+]=[L_X:P_i^-]&=0,\\ [R_X:P_i^-]=[L_X:P_i^+]&=\dim_{\mathbb{K}}(e_iGX). \end{align*} $$
Proof. The first line of equalities follows immediately from minimality, using that
![]() $P_i^\pm $
is projective–injective. For the remaining equalities, recall that F restricts to an equivalence
$P_i^\pm $
is projective–injective. For the remaining equalities, recall that F restricts to an equivalence
![]() $\operatorname {add}{T}\stackrel {\sim }{\to }\operatorname {proj}{A}$
by the Yoneda lemma. Applying F to (9.3) yields the exact sequence
$\operatorname {add}{T}\stackrel {\sim }{\to }\operatorname {proj}{A}$
by the Yoneda lemma. Applying F to (9.3) yields the exact sequence
which is a projective resolution of
![]() $FX$
. Applying F to (9.3) yields
$FX$
. Applying F to (9.3) yields
and taking the cup product with (9.5) yields
which is a projective resolution of
![]() $GX$
. Furthermore, since the
$GX$
. Furthermore, since the
![]() $\operatorname {add}{T}$
-approximations
$\operatorname {add}{T}$
-approximations
![]() $R_X\to X$
and
$R_X\to X$
and
![]() $X\to L_X$
were chosen to be minimal, the projective resolutions (9.5) and (9.6) are also minimal. Noting that
$X\to L_X$
were chosen to be minimal, the projective resolutions (9.5) and (9.6) are also minimal. Noting that
![]() $[R_X:P_i^\pm ]=[FR_X:FP_i^\pm ]$
and
$[R_X:P_i^\pm ]=[FR_X:FP_i^\pm ]$
and
![]() $[L_X:P_i^\pm ]=[FL_X:FP_i^\pm ]$
, and that
$[L_X:P_i^\pm ]=[FL_X:FP_i^\pm ]$
, and that
![]() $FP_i^\pm =Ae_i^\pm $
by Corollary 4.15, the result follows from Lemma 9.1.
$FP_i^\pm =Ae_i^\pm $
by Corollary 4.15, the result follows from Lemma 9.1.
These observations will allow us to compute the g-vectors of any cluster algebra arising from a seed with principal part Q in terms of in terms of the category
![]() $\mathcal {E}=\mathcal {E}_Q$
. We define g-vectors via a grading on the principal coefficient cluster algebra
$\mathcal {E}=\mathcal {E}_Q$
. We define g-vectors via a grading on the principal coefficient cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
, as in [Reference Fomin and Zelevinsky20, §6]. Write the initial cluster variables of this cluster algebra as
$\mathscr {A}_{Q}^{\bullet }$
, as in [Reference Fomin and Zelevinsky20, §6]. Write the initial cluster variables of this cluster algebra as
![]() $x_i$
and
$x_i$
and
![]() $x_i^+$
for
$x_i^+$
for
![]() $i\in Q_0$
, where the
$i\in Q_0$
, where the
![]() $x_i^+$
are frozen. We then give these variables
$x_i^+$
are frozen. We then give these variables
![]() $\mathbb {Z}^{Q_0}$
-degrees
$\mathbb {Z}^{Q_0}$
-degrees
where
![]() $\varepsilon _i$
is the ith standard basis vector (named to avoid confusion with idempotents) and
$\varepsilon _i$
is the ith standard basis vector (named to avoid confusion with idempotents) and
![]() $b_i$
is the ith row of the exchange matrix b of Q. We extend this to the initial cluster variables of
$b_i$
is the ith row of the exchange matrix b of Q. We extend this to the initial cluster variables of
![]() $\widetilde {\mathscr {A}}_{Q}$
by setting
$\widetilde {\mathscr {A}}_{Q}$
by setting
![]() $\deg {x_i^-}=0$
. This assignment puts a grading on the Laurent polynomial ring in variables
$\deg {x_i^-}=0$
. This assignment puts a grading on the Laurent polynomial ring in variables
![]() $x_i$
,
$x_i$
,
![]() $x_i^+$
, and
$x_i^+$
, and
![]() $x_i^-$
, and thus on its subalgebra
$x_i^-$
, and thus on its subalgebra
![]() $\widetilde {\mathscr {A}}_{Q}$
; note that the specialization
$\widetilde {\mathscr {A}}_{Q}$
; note that the specialization
![]() $x_i^-=1$
, which restricts to a map
$x_i^-=1$
, which restricts to a map
![]() $\widetilde {\mathscr {A}}_{Q}\to \mathscr {A}_{Q}^{\bullet }$
, preserves degrees. We refer to the degree of any homogeneous element of the Laurent polynomial ring in
$\widetilde {\mathscr {A}}_{Q}\to \mathscr {A}_{Q}^{\bullet }$
, preserves degrees. We refer to the degree of any homogeneous element of the Laurent polynomial ring in
![]() $x_i$
and
$x_i$
and
![]() $x_i^+$
as the g-vector of the element.
$x_i^+$
as the g-vector of the element.
All cluster variables of
![]() $\widetilde {\mathscr {A}}_{Q}$
are homogeneous in the above grading; by work of Grabowski [Reference Grabowski26, Prop. 3.2], this follows from the matrix identity
$\widetilde {\mathscr {A}}_{Q}$
are homogeneous in the above grading; by work of Grabowski [Reference Grabowski26, Prop. 3.2], this follows from the matrix identity
 $$ \begin{align} \begin{pmatrix}-b&1_n&-1_n\end{pmatrix}\begin{pmatrix}1_n\\b\\0_n\end{pmatrix}, \end{align} $$
$$ \begin{align} \begin{pmatrix}-b&1_n&-1_n\end{pmatrix}\begin{pmatrix}1_n\\b\\0_n\end{pmatrix}, \end{align} $$
where
![]() $1_n$
is the
$1_n$
is the
![]() $n\times n$
identity matrix and
$n\times n$
identity matrix and
![]() $0_n$
is the
$0_n$
is the
![]() $n\times n$
zero matrix, by observing that the first matrix in the product is the transposed exchange matrix of the initial seed of
$n\times n$
zero matrix, by observing that the first matrix in the product is the transposed exchange matrix of the initial seed of
![]() $\widetilde {\mathscr {A}}_{Q}$
, and the second has rows given by the degrees of the cluster variables in this seed. Thus, the cluster variables of
$\widetilde {\mathscr {A}}_{Q}$
, and the second has rows given by the degrees of the cluster variables in this seed. Thus, the cluster variables of
![]() $\mathscr {A}_{Q}^{\bullet }$
are also homogeneous and hence have well-defined g-vectors.
$\mathscr {A}_{Q}^{\bullet }$
are also homogeneous and hence have well-defined g-vectors.
Given any seed s with principal part Q, the mutable cluster variables of
![]() $\mathscr {A}_{Q}^{\bullet }$
are in natural bijection with those of the cluster algebra
$\mathscr {A}_{Q}^{\bullet }$
are in natural bijection with those of the cluster algebra
![]() $\mathscr {A}_{s}$
with initial seed s, and so we define the g-vector of a cluster variable in
$\mathscr {A}_{s}$
with initial seed s, and so we define the g-vector of a cluster variable in
![]() $\mathscr {A}_{s}$
to be the g-vector of the corresponding cluster variable in
$\mathscr {A}_{s}$
to be the g-vector of the corresponding cluster variable in
![]() $\mathscr {A}_{Q}^{\bullet }$
. This applies in particular to the coefficient-free cluster algebra
$\mathscr {A}_{Q}^{\bullet }$
. This applies in particular to the coefficient-free cluster algebra
![]() $\mathscr {A}_{Q}$
.
$\mathscr {A}_{Q}$
.
The main results of this section involve the Fu–Keller cluster character
![]() $\varphi ^{T}$
as in [Reference Fu and Keller21] and §6. While we are only assuming that
$\varphi ^{T}$
as in [Reference Fu and Keller21] and §6. While we are only assuming that
![]() $A=\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}$
is Noetherian, and not necessarily finite-dimensional, this is sufficient for the cluster character to be well defined (cf. [Reference Grabowski and Pressland27, §3] and [Reference Pressland45, §6]).
$A=\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}$
is Noetherian, and not necessarily finite-dimensional, this is sufficient for the cluster character to be well defined (cf. [Reference Grabowski and Pressland27, §3] and [Reference Pressland45, §6]).
Theorem 9.3. Assume that
![]() $A=A_{Q,W}$
is Noetherian, and consider the corresponding Frobenius category
$A=A_{Q,W}$
is Noetherian, and consider the corresponding Frobenius category
![]() $\mathcal {E}=\mathcal {E}_{Q,W}$
and cluster-tilting object
$\mathcal {E}=\mathcal {E}_{Q,W}$
and cluster-tilting object
![]() $T=eA$
. Let
$T=eA$
. Let
![]() $X\in \mathcal {E}$
, and choose a minimal short exact sequence of the form (9.3). Write
$X\in \mathcal {E}$
, and choose a minimal short exact sequence of the form (9.3). Write
 $$\begin{align*}R_X=P\mathbin{\oplus}\bigoplus_{i\in Q_0}T_i^{r_i},\qquad K_X=\bigoplus_{i\in Q_0}T_i^{k_i}, \end{align*}$$
$$\begin{align*}R_X=P\mathbin{\oplus}\bigoplus_{i\in Q_0}T_i^{r_i},\qquad K_X=\bigoplus_{i\in Q_0}T_i^{k_i}, \end{align*}$$
where
![]() $P\in \mathcal {E}$
is projective and
$P\in \mathcal {E}$
is projective and
![]() $T_i=eAe_i$
. Then
$T_i=eAe_i$
. Then
![]() $\varphi ^{T}(X)$
is homogeneous, and its g-vector is
$\varphi ^{T}(X)$
is homogeneous, and its g-vector is
![]() $\sum _{i\in Q_0}(r_i-k_i)\varepsilon _i$
.
$\sum _{i\in Q_0}(r_i-k_i)\varepsilon _i$
.
Proof. We first observe that
![]() $K_X$
has no projective summands, since this would violate minimality, and so
$K_X$
has no projective summands, since this would violate minimality, and so
![]() $R_X$
and
$R_X$
and
![]() $K_X$
have expressions of the required form. The element
$K_X$
have expressions of the required form. The element
 $$\begin{align*}G=\sum_{i\in Q_0}[S_i]\otimes \varepsilon_i+\sum_{i\in Q_0}[S_i^+]\otimes b_i\in\mathrm{K}_0(\operatorname{fd}{A})\otimes\mathbb{Z}^{Q_0},\end{align*}$$
$$\begin{align*}G=\sum_{i\in Q_0}[S_i]\otimes \varepsilon_i+\sum_{i\in Q_0}[S_i^+]\otimes b_i\in\mathrm{K}_0(\operatorname{fd}{A})\otimes\mathbb{Z}^{Q_0},\end{align*}$$
where
![]() $S_j$
denotes the simple A-module at vertex
$S_j$
denotes the simple A-module at vertex
![]() $j\in \widetilde {Q}_0$
, is a grading of
$j\in \widetilde {Q}_0$
, is a grading of
![]() $\mathcal {E}$
in the sense of [Reference Grabowski and Pressland27, Def. 3.7]; this follows again from the matrix identity (9.7), as in [Reference Grabowski and Pressland27, Rem. 3.9(ii)]. We write this grading of
$\mathcal {E}$
in the sense of [Reference Grabowski and Pressland27, Def. 3.7]; this follows again from the matrix identity (9.7), as in [Reference Grabowski and Pressland27, Rem. 3.9(ii)]. We write this grading of
![]() $\mathcal {E}$
as
$\mathcal {E}$
as
![]() $\deg _G$
. It then follows from [Reference Grabowski and Pressland27, Prop. 3.11(i)] that
$\deg _G$
. It then follows from [Reference Grabowski and Pressland27, Prop. 3.11(i)] that
![]() $\varphi ^{T}(X)$
is homogeneous and its g-vector is equal to
$\varphi ^{T}(X)$
is homogeneous and its g-vector is equal to
![]() $\deg _G(X)$
.
$\deg _G(X)$
.
Now, by [Reference Grabowski and Pressland27, Prop. 3.11(ii)], we have
By construction, we have
 $$ \begin{align*} \deg_G(R_X)&=\deg_G(P)+\sum_{i\in Q_0}r_i\deg_G(T_i)=\deg_G(P)+\sum_{i\in Q_0}r_i\varepsilon_i,\\ \deg_G(K_X)&=\sum_{i\in Q_0}k_i\deg_G(T_i)=\sum_{i\in Q_0}k_i\varepsilon_i, \end{align*} $$
$$ \begin{align*} \deg_G(R_X)&=\deg_G(P)+\sum_{i\in Q_0}r_i\deg_G(T_i)=\deg_G(P)+\sum_{i\in Q_0}r_i\varepsilon_i,\\ \deg_G(K_X)&=\sum_{i\in Q_0}k_i\deg_G(T_i)=\sum_{i\in Q_0}k_i\varepsilon_i, \end{align*} $$
so that
 $$\begin{align*}\deg_G(X)=\deg_G(P)+\sum_{i\in Q_0}(r_i-k_i)\varepsilon_i.\end{align*}$$
$$\begin{align*}\deg_G(X)=\deg_G(P)+\sum_{i\in Q_0}(r_i-k_i)\varepsilon_i.\end{align*}$$
But, by Lemma 9.2, we have
![]() $P\in \operatorname {add}{P^-}$
, so
$P\in \operatorname {add}{P^-}$
, so
![]() $\deg _G(P)=0$
and the result follows.
$\deg _G(P)=0$
and the result follows.
Remark 9.4. The quantity
![]() $\sum _{i\in Q_0}(r_i-k_i)\varepsilon _i$
is by definition (cf. [Reference Palu41, §2.1]) the index of X with respect to T. Thus, Theorem 9.3 recovers the well-known result [Reference Fu and Keller21, Prop. 4.3] that the g-vector is categorified by the index, at least for those cluster algebras admitting appropriate additive categorifications (e.g., those defined by acyclic quivers).
$\sum _{i\in Q_0}(r_i-k_i)\varepsilon _i$
is by definition (cf. [Reference Palu41, §2.1]) the index of X with respect to T. Thus, Theorem 9.3 recovers the well-known result [Reference Fu and Keller21, Prop. 4.3] that the g-vector is categorified by the index, at least for those cluster algebras admitting appropriate additive categorifications (e.g., those defined by acyclic quivers).
We may use similar methods to show how the cluster character
![]() $\varphi ^{T}$
on
$\varphi ^{T}$
on
![]() $\mathcal {E}$
may be computed solely in terms of the representation theory of the stable category
$\mathcal {E}$
may be computed solely in terms of the representation theory of the stable category
![]() $\underline {\mathcal {E}}$
, and of the finite-dimensional algebra
$\underline {\mathcal {E}}$
, and of the finite-dimensional algebra
![]() $J(Q,W)$
. This is the first point at which we use an explicit formula for
$J(Q,W)$
. This is the first point at which we use an explicit formula for
![]() $\varphi ^{T}$
, and so we recall this from [Reference Fu and Keller21].
$\varphi ^{T}$
, and so we recall this from [Reference Fu and Keller21].
Recall that we are assuming
![]() $\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A=A_{Q,W}$
is Noetherian. A consequence of Theorem 4.14 is that
$\operatorname {End}_{\mathcal {E}}(T)^{\mathrm {op}}\cong A=A_{Q,W}$
is Noetherian. A consequence of Theorem 4.14 is that
![]() $\operatorname {gl.dim}{A}\leq 3$
, and so the Euler form
$\operatorname {gl.dim}{A}\leq 3$
, and so the Euler form
 $$\begin{align*}\langle M,N\rangle=\sum_{i=0}^3(-1)^i\dim\operatorname{Ext}^i_A(M,N)\end{align*}$$
$$\begin{align*}\langle M,N\rangle=\sum_{i=0}^3(-1)^i\dim\operatorname{Ext}^i_A(M,N)\end{align*}$$
is well defined when
![]() $M\in \operatorname {mod}{A}$
is finitely generated and
$M\in \operatorname {mod}{A}$
is finitely generated and
![]() $N\in \operatorname {mod}{A}$
is finite-dimensional. Since A has finite global dimension, the value of
$N\in \operatorname {mod}{A}$
is finite-dimensional. Since A has finite global dimension, the value of
![]() $\langle M,N\rangle $
depends only on the dimension vector of the finite-dimensional module N by the horseshoe lemma, and so we may write
$\langle M,N\rangle $
depends only on the dimension vector of the finite-dimensional module N by the horseshoe lemma, and so we may write
![]() $\langle M,d\rangle :=\langle M,N\rangle $
for an arbitrary A-module N with dimension vector
$\langle M,d\rangle :=\langle M,N\rangle $
for an arbitrary A-module N with dimension vector
![]() $d\in \mathbb {Z}^{\widetilde {Q}_0}$
. Theorem 4.14 also implies that
$d\in \mathbb {Z}^{\widetilde {Q}_0}$
. Theorem 4.14 also implies that
![]() $\langle M,N\rangle =-\langle N,M\rangle $
if both modules are finite-dimensional and
$\langle M,N\rangle =-\langle N,M\rangle $
if both modules are finite-dimensional and
![]() $eN=0$
, so we may analogously define
$eN=0$
, so we may analogously define
![]() $\langle d,M\rangle $
for
$\langle d,M\rangle $
for
![]() $d\in \mathbb {Z}^{\widetilde {Q}_0}$
supported only on the set
$d\in \mathbb {Z}^{\widetilde {Q}_0}$
supported only on the set
![]() $Q_0$
of mutable vertices and M a finite-dimensional A-module.
$Q_0$
of mutable vertices and M a finite-dimensional A-module.
Recall further that we write
![]() and
and
![]() . Now, Fu–Keller’s cluster character for
. Now, Fu–Keller’s cluster character for
![]() $X\in \mathcal {E}$
can be written
$X\in \mathcal {E}$
can be written
 $$ \begin{align} \varphi^{T}(X)=x^{\hat{g}_X}\sum_{d\in\mathbb{Z}^{Q_0}}\lambda_dx^{\hat{v}_d}, \end{align} $$
$$ \begin{align} \varphi^{T}(X)=x^{\hat{g}_X}\sum_{d\in\mathbb{Z}^{Q_0}}\lambda_dx^{\hat{v}_d}, \end{align} $$
with notation as follows. The vector
![]() $\hat {g}_X\in \mathbb {Z}^{\widetilde {Q}_0}$
has ith coordinate
$\hat {g}_X\in \mathbb {Z}^{\widetilde {Q}_0}$
has ith coordinate
![]() $\langle FX,S_i\rangle $
, where
$\langle FX,S_i\rangle $
, where
![]() $FX=\operatorname {Hom}_{\mathcal {E}}(T,X)$
as above and
$FX=\operatorname {Hom}_{\mathcal {E}}(T,X)$
as above and
![]() $S_i$
denotes the simple A-module at vertex
$S_i$
denotes the simple A-module at vertex
![]() $i\in \widetilde {Q}_0$
. Similarly, the vector
$i\in \widetilde {Q}_0$
. Similarly, the vector
![]() $\hat {v}_d\in \mathbb {Z}^{\widetilde {Q}_0}$
has ith coordinate
$\hat {v}_d\in \mathbb {Z}^{\widetilde {Q}_0}$
has ith coordinate
![]() $\langle d,S_i\rangle =-\langle S_i,d\rangle $
. We use the standard monomial notation
$\langle d,S_i\rangle =-\langle S_i,d\rangle $
. We use the standard monomial notation
![]() $x^u:=\prod _{i\in \widetilde {Q}_0}x_i^{u_i}$
for
$x^u:=\prod _{i\in \widetilde {Q}_0}x_i^{u_i}$
for
![]() $u\in \mathbb {Z}^{\widetilde {Q}_0}$
. Finally,
$u\in \mathbb {Z}^{\widetilde {Q}_0}$
. Finally,
![]() $\lambda _d\in \mathbb {Z}$
is the Euler characteristic of the quiver Grassmannian of d-dimensional submodules of the A-module
$\lambda _d\in \mathbb {Z}$
is the Euler characteristic of the quiver Grassmannian of d-dimensional submodules of the A-module
![]() $GX=\operatorname {Ext}^1_{\mathcal {E}}(T,X)$
. Note that
$GX=\operatorname {Ext}^1_{\mathcal {E}}(T,X)$
. Note that
![]() $GX$
is a finite-dimensional
$GX$
is a finite-dimensional
![]() $\underline {\operatorname {End}}_{\mathcal {E}}(T)^{\mathrm {op}}\cong J(Q,W)$
-module, hence the restriction to
$\underline {\operatorname {End}}_{\mathcal {E}}(T)^{\mathrm {op}}\cong J(Q,W)$
-module, hence the restriction to
![]() $d\in \mathbb {Z}^{Q_0}$
in the summation. Thus,
$d\in \mathbb {Z}^{Q_0}$
in the summation. Thus,
![]() $\lambda _d$
can be nonzero only for the finite set of
$\lambda _d$
can be nonzero only for the finite set of
![]() $d\in \mathbb {Z}^{Q_0}$
satisfying
$d\in \mathbb {Z}^{Q_0}$
satisfying
![]() $0\leq d\leq \operatorname {\underline{dim}}{GX}$
coordinatewise.
$0\leq d\leq \operatorname {\underline{dim}}{GX}$
coordinatewise.
For each
![]() $X\in \mathcal {E}$
and
$X\in \mathcal {E}$
and
![]() $d\in \mathbb {Z}^{\widetilde {Q}_0}$
, let
$d\in \mathbb {Z}^{\widetilde {Q}_0}$
, let
![]() $g_X,v_d\in \mathbb {Z}^{Q_0}$
be the restrictions of
$g_X,v_d\in \mathbb {Z}^{Q_0}$
be the restrictions of
![]() $\hat {g}_X$
and
$\hat {g}_X$
and
![]() $\hat {v}_d$
, respectively, to the mutable vertices
$\hat {v}_d$
, respectively, to the mutable vertices
![]() $Q_0$
. Furthermore, write
$Q_0$
. Furthermore, write
By [Reference Fu and Keller21, Th. 3.3(b)], this function coincides with Palu’s cluster character [Reference Palu41] for the stable category
![]() $\underline {\mathcal {E}}$
, evaluated on the shifted object
$\underline {\mathcal {E}}$
, evaluated on the shifted object
![]() $\Sigma X$
. Consequently, the data of
$\Sigma X$
. Consequently, the data of
![]() $g_X$
,
$g_X$
,
![]() $v_d$
and
$v_d$
and
![]() $\lambda _d$
may be computed entirely from
$\lambda _d$
may be computed entirely from
![]() $\underline {\mathcal {E}}$
and the algebra
$\underline {\mathcal {E}}$
and the algebra
![]() $J(Q,W)$
.
$J(Q,W)$
.
The next result shows that this is in fact also true of the extended vectors
![]() $\hat {g}_X$
and
$\hat {g}_X$
and
![]() $\hat {v}_d$
, and hence of the cluster character
$\hat {v}_d$
, and hence of the cluster character
![]() $\varphi ^{T}(X)$
. To state it, we extend our monomial notation to write
$\varphi ^{T}(X)$
. To state it, we extend our monomial notation to write
![]() $(x^+)^u=\prod _{i\in Q_0}(x_i^+)^{u_i}$
when
$(x^+)^u=\prod _{i\in Q_0}(x_i^+)^{u_i}$
when
![]() $u\in \mathbb {Z}^{Q_0}$
, and define
$u\in \mathbb {Z}^{Q_0}$
, and define
![]() $(x^-)^u$
similarly. We treat
$(x^-)^u$
similarly. We treat
![]() $\mathbb {Z}^{Q_0}$
as a subset of
$\mathbb {Z}^{Q_0}$
as a subset of
![]() $\mathbb {Z}^{\widetilde {Q}_0}$
in the natural way, so that a monomial
$\mathbb {Z}^{\widetilde {Q}_0}$
in the natural way, so that a monomial
![]() $x^u$
for
$x^u$
for
![]() $u\in \mathbb {Z}^{Q_0}$
lies in the same ring as a monomial
$u\in \mathbb {Z}^{Q_0}$
lies in the same ring as a monomial
![]() $x^v$
for
$x^v$
for
![]() $v\in \mathbb {Z}^{\widetilde {Q}_0}$
(cf., e.g., (9.11)).
$v\in \mathbb {Z}^{\widetilde {Q}_0}$
(cf., e.g., (9.11)).
Theorem 9.5. Assume that
![]() $A_{Q,W}$
is Noetherian, and let
$A_{Q,W}$
is Noetherian, and let
![]() $\mathcal {E}=\mathcal {E}_{Q,W}$
with cluster-tilting object
$\mathcal {E}=\mathcal {E}_{Q,W}$
with cluster-tilting object
![]() $T=eA_{Q,W}$
. Then, for any
$T=eA_{Q,W}$
. Then, for any
![]() $X\in \mathcal {E}$
, the cluster character of X with respect to T is
$X\in \mathcal {E}$
, the cluster character of X with respect to T is
 $$ \begin{align} \varphi^{T}(X)=x^{g_X}\sum_{d\in\mathbb{Z}^{Q_0}}\lambda_dx^{v_d}(x^+)^{d}(x^-)^{\underline{\operatorname{dim}}(GX)-d}, \end{align} $$
$$ \begin{align} \varphi^{T}(X)=x^{g_X}\sum_{d\in\mathbb{Z}^{Q_0}}\lambda_dx^{v_d}(x^+)^{d}(x^-)^{\underline{\operatorname{dim}}(GX)-d}, \end{align} $$
for
![]() $g_X$
,
$g_X$
,
![]() $v_d$
, and
$v_d$
, and
![]() $\lambda _d$
as above.
$\lambda _d$
as above.
Proof. Bearing in mind the identity (9.9) (cf. [Reference Fu and Keller21, Th. 3.3(b)]), it is sufficient to compute the power of
![]() $x_i^\pm $
appearing in each term of the formula (9.8) for
$x_i^\pm $
appearing in each term of the formula (9.8) for
![]() $\varphi ^{T}(X)$
.
$\varphi ^{T}(X)$
.
First, we deal with the leading term
![]() $x^{\hat {g}_X}$
. For
$x^{\hat {g}_X}$
. For
![]() $i\in Q_0$
, the
$i\in Q_0$
, the
![]() $i^\pm $
-component of
$i^\pm $
-component of
![]() $\hat {g}_X$
is by definition
$\hat {g}_X$
is by definition
![]() $\langle FX,S_i^\pm \rangle $
. This can be computed using the projective resolution (9.5) of
$\langle FX,S_i^\pm \rangle $
. This can be computed using the projective resolution (9.5) of
![]() $FX$
, which shows that
$FX$
, which shows that
 $$ \begin{align*} \langle FX,S_i^\pm\rangle&=\dim\operatorname{Hom}_A(FR_X,S_i^\pm)-\dim\operatorname{Hom}_A(FK_X,S_i^\pm)\\ &=[R_X:P_i^\pm]-[K_X:P_i^\pm] \end{align*} $$
$$ \begin{align*} \langle FX,S_i^\pm\rangle&=\dim\operatorname{Hom}_A(FR_X,S_i^\pm)-\dim\operatorname{Hom}_A(FK_X,S_i^\pm)\\ &=[R_X:P_i^\pm]-[K_X:P_i^\pm] \end{align*} $$
for
![]() $R_X,K_X\in \operatorname {add}{T}$
as in (9.3); the second equality uses that
$R_X,K_X\in \operatorname {add}{T}$
as in (9.3); the second equality uses that
![]() $\dim \operatorname {Hom}_A(FR_X,S_i^\pm )$
counts the multiplicity of the projective
$\dim \operatorname {Hom}_A(FR_X,S_i^\pm )$
counts the multiplicity of the projective
![]() $FP_i^\pm $
as a summand of the projective
$FP_i^\pm $
as a summand of the projective
![]() $FR_X$
(and similarly for
$FR_X$
(and similarly for
![]() $K_X$
), and also the Yoneda lemma as in the proof of Lemma 9.2. We may then use this lemma to see that
$K_X$
), and also the Yoneda lemma as in the proof of Lemma 9.2. We may then use this lemma to see that
 $$ \begin{align*} \langle FX,S_i^+\rangle&=0,\\ \langle FX,S_i^-\rangle&=\dim_{\mathbb{K}}(e_iGX), \end{align*} $$
$$ \begin{align*} \langle FX,S_i^+\rangle&=0,\\ \langle FX,S_i^-\rangle&=\dim_{\mathbb{K}}(e_iGX), \end{align*} $$
so that
We calculate
![]() $x^{\hat {v}_d}$
, for
$x^{\hat {v}_d}$
, for
![]() $d\in \mathbb {Z}^{\widetilde {Q}_0}$
, similarly. The
$d\in \mathbb {Z}^{\widetilde {Q}_0}$
, similarly. The
![]() $i^\pm $
-component is
$i^\pm $
-component is
 $$\begin{align*}\langle d,S_i^\pm\rangle=\sum_{j\in Q_0}d_j\langle S_j,S_i^\pm\rangle.\end{align*}$$
$$\begin{align*}\langle d,S_i^\pm\rangle=\sum_{j\in Q_0}d_j\langle S_j,S_i^\pm\rangle.\end{align*}$$
Now, arguing as for
![]() $\hat {g}_X$
, we may use (9.2) to compute that
$\hat {g}_X$
, we may use (9.2) to compute that
 $$ \begin{align*} \langle S_j,S_i^+\rangle&=\begin{cases}1,&i=j,\\0,&\text{otherwise},\end{cases}\\ \langle S_j,S_i^-\rangle&=\begin{cases}-1,&i=j,\\0,&\text{otherwise}.\end{cases} \end{align*} $$
$$ \begin{align*} \langle S_j,S_i^+\rangle&=\begin{cases}1,&i=j,\\0,&\text{otherwise},\end{cases}\\ \langle S_j,S_i^-\rangle&=\begin{cases}-1,&i=j,\\0,&\text{otherwise}.\end{cases} \end{align*} $$
It then follows that
and we obtain the desired result by substituting (9.11) and (9.12) back into (9.8).
Remark 9.6. Using the interpretation of
![]() $\lambda _d$
as the Euler characteristic of a quiver Grassmannian, the nonzero terms of the sum in (9.10) are indexed by (dimension vectors of) submodules of the
$\lambda _d$
as the Euler characteristic of a quiver Grassmannian, the nonzero terms of the sum in (9.10) are indexed by (dimension vectors of) submodules of the
![]() $J(Q,W)$
-module
$J(Q,W)$
-module
![]() $GX$
. In the term indexed by such a submodule N, the exponent of
$GX$
. In the term indexed by such a submodule N, the exponent of
![]() $x^+$
is
$x^+$
is
![]() $\underline {\operatorname {dim}}(N)$
, and that of
$\underline {\operatorname {dim}}(N)$
, and that of
![]() $x^-$
is
$x^-$
is
![]() $\underline {\operatorname {dim}}(GX/N)$
.
$\underline {\operatorname {dim}}(GX/N)$
.
Corollary 9.7. The bijection between rigid indecomposable objects of
![]() $\mathcal {E}_Q^+$
and cluster variables of the principal coefficient cluster algebra
$\mathcal {E}_Q^+$
and cluster variables of the principal coefficient cluster algebra
![]() $\mathscr {A}_{Q}^{\bullet }$
, as in Corollary 1
(b), is given by
$\mathscr {A}_{Q}^{\bullet }$
, as in Corollary 1
(b), is given by
![]() $X\mapsto \varphi ^{T}_+(X)$
where
$X\mapsto \varphi ^{T}_+(X)$
where
 $$\begin{align*}\varphi^{T}_+(X)=x^{g_X}\sum_{d\in\mathbb{Z}^{Q_0}}\lambda_dx^{v_d}(x^+)^{d}. \end{align*}$$
$$\begin{align*}\varphi^{T}_+(X)=x^{g_X}\sum_{d\in\mathbb{Z}^{Q_0}}\lambda_dx^{v_d}(x^+)^{d}. \end{align*}$$
Proof. As in the proof of Corollary 1, the bijection is given by specializing Fu–Keller’s cluster character on
![]() $\mathcal {E}_Q$
(where X is also an object) at
$\mathcal {E}_Q$
(where X is also an object) at
![]() $x_i^-=1$
for all
$x_i^-=1$
for all
![]() $i\in Q_0$
. The result is then immediate from Theorem 9.5.
$i\in Q_0$
. The result is then immediate from Theorem 9.5.
Remark 9.8. The right-hand side of (9.10) is precisely the cluster character with coefficients considered by Borges and Pierin [Reference Borges and Pierin5, Def. 3.1] for the cluster category of a Dynkin quiver. As a consequence, their expression satisfies the cluster character multiplication formula (see, e.g., [Reference Caldero and Keller13, Th. 2]), even after extending the setting to cluster categories of arbitrary acyclic quivers.
10 Examples
Example 10.1. Let Q be an
![]() $\mathsf {A}_2$
quiver, so, as computed in Example 3.2,
$\mathsf {A}_2$
quiver, so, as computed in Example 3.2,

and
![]() $\widetilde {W}=\beta _1\delta _1\alpha _1+\beta _2\delta _2\alpha _2-a\beta _1\delta _a\alpha _2$
. Then
$\widetilde {W}=\beta _1\delta _1\alpha _1+\beta _2\delta _2\alpha _2-a\beta _1\delta _a\alpha _2$
. Then
![]() $A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
, and its boundary algebra is
$A_Q=J(\widetilde {Q},\widetilde {F},\widetilde {W})$
, and its boundary algebra is
![]() $B_Q\cong \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {I}$
for
$B_Q\cong \mathbb {K}\langle \hspace {-0.1em}\langle \Lambda _Q\rangle \hspace {-0.1em}\rangle /\overline {I}$
for

and
![]() $I=\langle \alpha ^*\alpha ,\ \alpha \alpha ^*-\beta ^*\beta ,\ \beta \beta ^*-\gamma ^*\gamma ,\ \gamma \gamma ^*,\ \beta \alpha ,\ \gamma \beta ,\ \alpha ^*\beta ^*\gamma ^*\rangle $
. Here, we have relabeled the vertices by identifying the ordered sets
$I=\langle \alpha ^*\alpha ,\ \alpha \alpha ^*-\beta ^*\beta ,\ \beta \beta ^*-\gamma ^*\gamma ,\ \gamma \gamma ^*,\ \beta \alpha ,\ \gamma \beta ,\ \alpha ^*\beta ^*\gamma ^*\rangle $
. Here, we have relabeled the vertices by identifying the ordered sets
![]() $(1^+,1^-,2^+,2^-)$
and
$(1^+,1^-,2^+,2^-)$
and
![]() $(1,2,3,4)$
. The Auslander–Reiten quiver of
$(1,2,3,4)$
. The Auslander–Reiten quiver of
![]() $\operatorname {GP}(B)$
is shown in Figure 1, where we identify the left and right sides of the picture so that the quiver is drawn on a Möbius band. To calculate the objects of
$\operatorname {GP}(B)$
is shown in Figure 1, where we identify the left and right sides of the picture so that the quiver is drawn on a Möbius band. To calculate the objects of
![]() $\operatorname {GP}(B_Q)$
, it is useful to observe that, in this example,
$\operatorname {GP}(B_Q)$
, it is useful to observe that, in this example,
![]() $B_Q$
is
$B_Q$
is
![]() $1$
-Iwanaga–Gorenstein, and so
$1$
-Iwanaga–Gorenstein, and so
![]() $\operatorname {GP}(B_Q)=\operatorname {Sub}(B_Q)$
. The stable category
$\operatorname {GP}(B_Q)=\operatorname {Sub}(B_Q)$
. The stable category
![]() $\underline {\operatorname {GP}}(B_Q)$
is the cluster category of type
$\underline {\operatorname {GP}}(B_Q)$
is the cluster category of type
![]() $\mathsf {A}_2$
, as expected. The cluster-tilting object
$\mathsf {A}_2$
, as expected. The cluster-tilting object
of
![]() $\operatorname {GP}(B_Q)$
has endomorphism algebra
$\operatorname {GP}(B_Q)$
has endomorphism algebra
![]() $A_Q$
, and corresponds to the initial seed of the cluster algebra with polarized principal coefficients associated with our initial
$A_Q$
, and corresponds to the initial seed of the cluster algebra with polarized principal coefficients associated with our initial
![]() $\mathsf {A}_2$
quiver Q.
$\mathsf {A}_2$
quiver Q.

Figure 1 The Auslander–Reiten quiver of
![]() $\operatorname {GP}(B_Q)$
for Q of type
$\operatorname {GP}(B_Q)$
for Q of type
![]() $\mathsf {A}_2$
.
$\mathsf {A}_2$
.
Example 10.2. Let Q be a linearly oriented quiver of type
![]() $\mathsf {A}_3$
. We may then compute
$\mathsf {A}_3$
. We may then compute

Relabeling vertices similarly to Example 10.1, the boundary algebra
![]() $B_Q$
has quiver
$B_Q$
has quiver

as computed before in Example 8.4. Explicit relations can be written down as in §8, but here we will simply give radical filtrations for the projective modules. Note that despite the geographical separation of
![]() $2$
and
$2$
and
![]() $5$
in these filtrations, the arrow
$5$
in these filtrations, the arrow
![]() $2\to 5$
always acts as a vector space isomorphism from the one-dimensional subspace of
$2\to 5$
always acts as a vector space isomorphism from the one-dimensional subspace of
![]() $e_2B_Q$
indicated by a
$e_2B_Q$
indicated by a
![]() $2$
in the filtration to the one-dimensional subspace of
$2$
in the filtration to the one-dimensional subspace of
![]() $e_5B_Q$
indicated by a
$e_5B_Q$
indicated by a
![]() $5$
in the row below, when this configuration occurs.
$5$
in the row below, when this configuration occurs.

In this case, the Gorenstein dimension of
![]() $B_Q$
is
$B_Q$
is
![]() $2$
; the indecomposable projective
$2$
; the indecomposable projective
![]() $P_2$
has injective dimension
$P_2$
has injective dimension
![]() $2$
, whereas all others have injective dimension
$2$
, whereas all others have injective dimension
![]() $1$
. The Auslander–Reiten quiver of
$1$
. The Auslander–Reiten quiver of
![]() $\operatorname {GP}(B_Q)$
is shown, again on a Möbius band, in Figure 2.
$\operatorname {GP}(B_Q)$
is shown, again on a Möbius band, in Figure 2.

Figure 2 The Auslander–Reiten quiver of
![]() $\operatorname {GP}(B_Q)$
for Q linearly oriented of type
$\operatorname {GP}(B_Q)$
for Q linearly oriented of type
![]() $\mathsf {A}_3$
. In addition to the usual mesh relations coming from Auslander–Reiten sequences, the length 2 path from
$\mathsf {A}_3$
. In addition to the usual mesh relations coming from Auslander–Reiten sequences, the length 2 path from
![]() $P_2$
to
$P_2$
to
![]() $P_5$
represents the zero map.
$P_5$
represents the zero map.
The initial cluster-tilting object from Corollary 4.15 is
Example 10.3. Applying our construction to the quiver with potential
![]() $(Q,W)$
from Example 3.3 in which Q is a
$(Q,W)$
from Example 3.3 in which Q is a
![]() $3$
-cycle (which we may do, since while A is not finite-dimensional in this case, it is still Noetherian) yields, as observed in Example 3.3, the Grassmannian cluster category for the Grassmannian
$3$
-cycle (which we may do, since while A is not finite-dimensional in this case, it is still Noetherian) yields, as observed in Example 3.3, the Grassmannian cluster category for the Grassmannian
![]() $\mathrm {Gr}_{2}^{6}$
[Reference Jensen, King and Su32]. This is a Hom-infinite category, and the Gorenstein projective B-modules are all infinite-dimensional. Representing these modules by Plücker labels as in [Reference Jensen, King and Su32], the Auslander–Reiten quiver of
$\mathrm {Gr}_{2}^{6}$
[Reference Jensen, King and Su32]. This is a Hom-infinite category, and the Gorenstein projective B-modules are all infinite-dimensional. Representing these modules by Plücker labels as in [Reference Jensen, King and Su32], the Auslander–Reiten quiver of
![]() $\operatorname {GP}(B_{Q,W})$
is shown, on the now familiar Möbius band, in Figure 3.
$\operatorname {GP}(B_{Q,W})$
is shown, on the now familiar Möbius band, in Figure 3.

Figure 3 The Auslander–Reiten quiver of
![]() $\operatorname {GP}(B_{Q,W})$
, where
$\operatorname {GP}(B_{Q,W})$
, where
![]() $(Q,W)$
is a
$(Q,W)$
is a
![]() $3$
-cycle and its usual potential, shown as the Grassmannian cluster category
$3$
-cycle and its usual potential, shown as the Grassmannian cluster category
![]() $\operatorname {CM}(B_{2,6})$
.
$\operatorname {CM}(B_{2,6})$
.
In this case, the quiver of the endomorphism algebra of the object
is
![]() $\widetilde {Q}$
, as is the quiver of the (isomorphic) endomorphism algebra of
$\widetilde {Q}$
, as is the quiver of the (isomorphic) endomorphism algebra of
![]() $24\mathbin {\oplus } 26\mathbin {\oplus } 46\mathbin {\oplus } B_{Q,W}$
. We note that the stable category
$24\mathbin {\oplus } 26\mathbin {\oplus } 46\mathbin {\oplus } B_{Q,W}$
. We note that the stable category
![]() $\underline {\operatorname {GP}}(B_{Q,W})$
is equivalent to the cluster category
$\underline {\operatorname {GP}}(B_{Q,W})$
is equivalent to the cluster category
![]() $\mathcal {C}_{Q,W}\simeq \mathcal {C}_{Q'}$
where
$\mathcal {C}_{Q,W}\simeq \mathcal {C}_{Q'}$
where
![]() $Q'$
is any orientation of the Dynkin diagram
$Q'$
is any orientation of the Dynkin diagram
![]() $\mathsf {A}_3$
. Thus, all of the conclusions of Theorem 1 (replacing
$\mathsf {A}_3$
. Thus, all of the conclusions of Theorem 1 (replacing
![]() $\mathcal {E}_Q$
by
$\mathcal {E}_Q$
by
![]() $\mathcal {E}_{Q,W}$
and
$\mathcal {E}_{Q,W}$
and
![]() $\mathcal {C}_{Q}$
by
$\mathcal {C}_{Q}$
by
![]() $\mathcal {C}_{Q,W}$
) still hold in this case, despite the failure of acyclicity.
$\mathcal {C}_{Q,W}$
) still hold in this case, despite the failure of acyclicity.
Acknowledgments
We thank Mikhail Gorsky, Alfredo Nájera Chávez, Hiroyuki Nakaoka, Yann Palu, and Salvatore Stella for useful conversations and for providing references. We are particularly grateful to Bernhard Keller for pointing out the role of pseudocompactness in the results of §4, and also thank the anonymous referee for suggesting various improvements.