Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-16T22:48:28.866Z Has data issue: false hasContentIssue false
  • English
  • Français

Tangent cones to generalised theta divisors and generic injectivity of the theta map

Part of: Cycles and subschemes Curves Commutative algebra: Homological methods Special varieties Local theory

Published online by Cambridge University Press:  13 September 2017

George H. Hitching  and
Michael Hoff
George H. Hitching
Affiliation:
Høgskolen i Oslo og Akershus, Postboks 4, St. Olavs plass, 0130 Oslo, Norway email [email protected]
Michael Hoff
Affiliation:
Universität des Saarlandes, Campus E2 4, D-66123 Saarbrücken, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 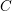$C$ be a Petri general curve of genus 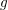$g$ and 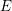$E$ a general stable vector bundle of rank $r$ and slope 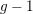$g-1$ over 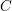$C$ with 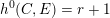$h^{0}(C,E)=r+1$. For 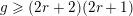$g\geqslant (2r+2)(2r+1)$, we show how the bundle 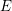$E$ can be recovered from the tangent cone to the generalised theta divisor 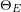$\unicode[STIX]{x1D6E9}_{E}$ at 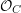${\mathcal{O}}_{C}$. We use this to give a constructive proof and a sharpening of Brivio and Verra’s theorem that the theta map 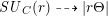$\mathit{SU}_{C}(r){\dashrightarrow}|r\unicode[STIX]{x1D6E9}|$ is generically injective for large values of 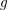$g$.

Keywords

vector bundlesgeneralised theta divisorsBrill–Noether theory

MSC classification

Primary: 14H60: Vector bundles on curves and their moduli 14H51: Special divisors (gonality, Brill-Noether theory) 14M12: Determinantal varieties 14B10: Infinitesimal methods 13D10: Deformations and infinitesimal methods
Secondary: 14C34: Torelli problem
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 12 , December 2017 , pp. 2643 - 2657
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J., Geometry of algebraic curves, Vol. I, Grundlehren der Mathematischen Wissenschaften, vol. 267 [Fundamental Principles of Mathematical Sciences] (Springer, New York, 1985).CrossRefGoogle Scholar
Beauville, A., Fibrés de rang 2 sur une courbe, fibré déterminant et fonctions thêta. (Rank 2 fiber bundles on a curve, determinant bundle and theta functions) , Bull. Soc. Math. France 116 (1988), 431–448.CrossRefGoogle Scholar
Beauville, A., Vector bundles on curves and theta functions , in Moduli spaces and arithmetic geometry. Papers of the 13th International Research Institute of the Mathematical Society of Japan, Kyoto, Japan, September 8–15, 2004 (Mathematical Society of Japan, Tokyo, 2006), 145–156.Google Scholar
Bhosle, U. N., Brambila-Paz, L. and Newstead, P. E., On coherent systems of type (n, d, n + 1) on Petri curves , Manuscripta Math. 126 (2008), 409–441.CrossRefGoogle Scholar
Bhosle, U. N., Brambila-Paz, L. and Newstead, P. E., On linear series and a conjecture of D. C. Butler , Internat. J. Math. 26 (2015), 1550007, 18.CrossRefGoogle Scholar
Bradlow, S. B., García-Prada, O., Muñoz, V. and Newstead, P. E., Coherent systems and Brill-Noether theory , Internat. J. Math. 14 (2003), 683–733.CrossRefGoogle Scholar
Brivio, S. and Verra, A., Plücker forms and the theta map , Amer. J. Math. 134 (2012), 1247–1273.CrossRefGoogle Scholar
Bruno, A. and Sernesi, E., A note on the Petri loci , Manuscripta Math. 136 (2011), 439–443.CrossRefGoogle Scholar
Casalaina-Martin, S. and Teixidor i Bigas, M., Singularities of Brill-Noether loci for vector bundles on a curve , Math. Nachr. 284 (2011), 1846–1871.CrossRefGoogle Scholar
Ciliberto, C. and Sernesi, E., Singularities of the theta divisor and congruences of planes , J. Algebr. Geom. 1 (1992), 231–250.Google Scholar
Dieudonné, J., Sur une généralisation du groupe orthogonal à quatre variables , Arch. Math. 1 (1949), 282–287.CrossRefGoogle Scholar
Drezet, J.-M. and Narasimhan, M. S., Groupe de Picard des variétés de modules de fibrés semi-stables sur les courbes algébriques , Invent. Math. 97 (1989), 53–94.CrossRefGoogle Scholar
Eisenbud, D., Linear sections of determinantal varieties , Amer. J. Math. 110 (1988), 541–575.CrossRefGoogle Scholar
Farkas, G., Gaussian maps, Gieseker–Petri loci and large theta-characteristics , J. Reine Angew. Math. 581 (2005), 151–173.CrossRefGoogle Scholar
Frobenius, G. F., Über die Darstellung der endlichen Gruppe durch lineare Substitutionen , Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin 2 (1897), 994–1015.Google Scholar
Gieseker, D., Stable curves and special divisors: Petri’s conjecture , Invent. Math. 66 (1982), 251–275.CrossRefGoogle Scholar
Green, M. L., Quadrics of rank four in the ideal of a canonical curve , Invent. Math. 75 (1984), 85–104.CrossRefGoogle Scholar
Grzegorczyk, I. and Teixidor i Bigas, M., Brill–Noether theory for stable vector bundles , in Moduli spaces and vector bundles, London Mathematical Society Lecture Note Series, vol. 359 (Cambridge University Press, Cambridge, 2009), 29–50.CrossRefGoogle Scholar
Kempf, G. R., On the geometry of a theorem of Riemann , Ann. of Math. (2) 98 (1973), 178–185.CrossRefGoogle Scholar
Kempf, G. R., Abelian integrals, Monografías del Instituto de Matemáticas, vol. 13 [Monographs of the Institute of Mathematics] (Universidad Nacional Autónoma de México, México, 1983).Google Scholar
Kempf, G. R. and Schreyer, F.-O., A Torelli theorem for osculating cones to the theta divisor , Compos. Math. 67 (1988), 343–353.Google Scholar
Narasimhan, M. S. and Ramanan, S., Moduli of vector bundles on a compact Riemann surface , Ann. of Math. (2) 89 (1969), 14–51.CrossRefGoogle Scholar
Pauly, C., On cubics and quartics through a canonical curve , Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 2 (2003), 803–822.Google Scholar
Pauly, C., Rank four vector bundles without theta divisor over a curve of genus two , Adv. Geom. 10 (2010), 647–657.CrossRefGoogle Scholar
Popa, M., On the base locus of the generalized theta divisor , C. R. Acad. Sci., Paris, Sér. I, Math. 329 (1999), 507–512.CrossRefGoogle Scholar
Raynaud, M., Sections des fibrés vectoriels sur une courbe , Bull. Soc. Math. France 110 (1982), 103–125.CrossRefGoogle Scholar
Teixidor i Bigas, M., The divisor of curves with a vanishing theta-null , Compos. Math. 66 (1988), 15–22.Google Scholar
Teixidor i Bigas, M., Injectivity of the Petri map for twisted Brill–Noether loci , Manuscripta Math. 145 (2014), 389–397.CrossRefGoogle Scholar
van Geemen, B. and Izadi, E., The tangent space to the moduli space of vector bundles on a curve and the singular locus of the theta divisor of the Jacobian , J. Algebraic Geom. 10 (2001), 133–177.Google Scholar
Waterhouse, W. C., Automorphisms of det(X ij ): the group scheme approach , Adv. Math. 65 (1987), 171–203.CrossRefGoogle Scholar