I. INTRODUCTION
Cognitive radio is seen as a solution for the spectrum scarcity problem that arises with the increased number of users and applications that require higher data rates such as video and Internet and it is expected to recognize different wireless networks and has the capability to interact with them. Multicarrier techniques, especially orthogonal frequency division multiplex (OFDM) system is a special cognitive radio system, which has been widely used in military and civilian applications [Reference Weinstein1]. One crucial aspect of spectrum monitoring and electronic countermeasures reconnaissance is the identification for OFDM signal [Reference Shahriar, Clancy and Mcgwier2]. In order to recognize the transmitted OFDM signal parameters, the identification of OFDM signal must be achieved first. However, there are substantial technical challenges to overcome in sensing and identifying OFDM signal due to many different transmission technologies and standards [Reference Eldemerdash and Dobre3]. Therefore, studies have attracted many researchers and given rise to many contributions dealing with the identification of OFDM signal.
Concerning the OFDM identification, various blind identification of OFDM system parameter estimation schemes have been studied recently for signal identification. The most commonly used conventional methods for OFDM signal identification rely on the fact that the cyclic prefix is identical to a portion of the useful part of the autocorrelation of the receiver signal introduced by the cyclic prefix. For instance, some authors suggested identifying the OFDM signal in the AWGN channel by searching the peak of the autocorrelation which may occur at a time lag equal to the useful part duration [Reference Chaudhari, Koivunen and Poor4–Reference Cao, Peng, Dong and Wang6]. However, these methods' computational load is comparatively high because of the requirement of the exploration for the starting and ending position among entire OFDM symbol. In addition, when the power of the autocorrelation of the received signal is weak or the ratio between the cyclic prefix duration and the useful part is small, the performance of such algorithms is very poor. In the works of [Reference Punchihewa, Zhang, Dobre, Spooner, Rajan and Inkol7–Reference Sun, Chen, Liu and Wang10], cyclostationary signal analysis has been extensively examined as a technique of identification for OFDM signal. Due to its reasonable accuracy for various types of air interface signal, cyclostationary is an important feature of wireless communication signal which can be used to determine the existence of the OFDM signal. But the method needs computationally complex receiver design which leads to overly long processing and detection time. In addition, the cyclostationary detecting OFDM signal methods require the exploration of a wide range of cyclic frequencies and a long observation time in order to obtain reliable analysis. Other identification methods could be also achieved in multipath channel circumstance, but these methods all have their own drawbacks. The author of [Reference Guo and Yu11] achieved the identification for OFDM signal based on high-order cumulants, and the method constructed multiple characteristic values to classify the OFDM signal and single carrier (SC) signal. However, the computation load of this method is very high. Panayirci et al. [Reference Panayirci, Senol and Poor12] and Aboutorab et al. [Reference Aboutorab, Hardjawana and Vucetic13] developed a joint iterative algorithm to realize the blind recognition of the OFDM signal by taking advantage of every channel's estimation information. However, this method needs to know the basic model of the channel environment and does not consider the iterative model error; thus, the identification performance of the algorithm is not good and the convergence speed is slow. In general, none of the method mentioned above has provided a performance evaluation under poor transmission environment where the propagation behavior is more complex and thus the system may fail to maintain performance due to considerable interference.
In this paper, a blind identification design is proposed to detect the OFDM signal among SC and noise. Firstly, by theoretically analyzing the fractal box dimension of OFDM signal and SC signal, we conclude that the fractal box dimension of OFDM signal and SC signal has obvious differences. Thus, we use the fractal box dimension of the two types of signal to discriminate OFDM signal and SC signal. But the fractal box dimension of OFDM signal and Gaussian noise is nearly close, thus we could not identify the OFDM signal under low signal-to-noise ratio (SNR). So, we construct a novel feature called pseudo-inverse spectrum (PIS) of an OFDM signal according to the characteristics of the OFDM signal. Through theoretical analysis and the experimental simulation, it illustrates that the classification feature could be extracted by detecting the periodical peak of OFDM signal's PIS and it could be used for identifying OFDM signal when the SNR is not high. Test results are made to evaluate the performance of the proposed approach under various scenarios of system interference. Simulation results demonstrate that the proposed algorithm has better performance than the conventional algorithm based on autocorrelation.
The rest of the paper is structured as follows. In Section II, we briefly introduce the system model of an oversampled OFDM signal. In Section III, we analyze the fractal box dimension of OFDM signal and SC signal, and demonstrate that the classification of OFDM signal and SC signal could be achieved by setting a reasonable threshold. In addition, we propose a new method based on PIS of an OFDM signal to supplement the prior algorithm that cannot detect an OFDM signal in the Gaussian noise when the SNR is relatively low. In Section IV, we conduct experimental simulation to evaluate the performance of the identification for OFDM signal in various scenarios, and finally, the paper is concluded in Section V.
II. SYSTEM MODEL
OFDM converts a serial data stream into parallel blocks and modulates these blocks using inverse discrete Fourier transform and the continuous-time OFDM signal in the baseband can be written as:
 $$\eqalign{s(t)& = \displaystyle{{1}\over{\sqrt {N_S}}}\sum\limits_{l=0}^L \,\sum\limits_{k=0}^{N_s -1} d_{k,l} \cr & \quad \times exp\left( {-j2\pi \displaystyle{{k}\over{T_S}}(t-LT_S )} \right)e^{j\displaystyle{{2\pi \varepsilon t}\over{N_s}}}u(t),}$$
$$\eqalign{s(t)& = \displaystyle{{1}\over{\sqrt {N_S}}}\sum\limits_{l=0}^L \,\sum\limits_{k=0}^{N_s -1} d_{k,l} \cr & \quad \times exp\left( {-j2\pi \displaystyle{{k}\over{T_S}}(t-LT_S )} \right)e^{j\displaystyle{{2\pi \varepsilon t}\over{N_s}}}u(t),}$$where d k,l is the transmitted data symbol at lth subcarrier of kth OFDM symbol, these data symbols are assumed to be independent and identically distributed (i.i.d). T S is the OFDM symbol period, N S is the number of subcarriers, L is the number of OFDM symbols, ε is the carrier frequency offset (normalized by the subcarrier spacing), and u(t) is a Nyquist pulse. A raised cosine waveform is taken into consideration in this paper due to its ability to minimize inter-symbol interference and smooth the sharp edges of baseband signal, which is defined on (0, T S) and expressed as:
where α stands for the roll-off factor. Denoting h(t) to be frequency-selective multipath channel function, the received time-domain signal is defined as:
 $$x(t)=\sum_{m=1}^M {h(m)s(t-mT_s )+w(t)},$$
$$x(t)=\sum_{m=1}^M {h(m)s(t-mT_s )+w(t)},$$
where M is the number of multipath channel, w(t) denotes the additive Gaussian noise with zero mean and variance ![]() $\sigma _w^2 $. Assuming that the sampling period at the receiver side is T b and T b < T S, the oversampling factor q is defined as q = T b/T S and the corresponding oversampled OFDM signal can be consequently denoted by:
$\sigma _w^2 $. Assuming that the sampling period at the receiver side is T b and T b < T S, the oversampling factor q is defined as q = T b/T S and the corresponding oversampled OFDM signal can be consequently denoted by:
 $$x(n)=\sum_{m=1}^M {h(m)s(n-qm)+w(n)}.$$
$$x(n)=\sum_{m=1}^M {h(m)s(n-qm)+w(n)}.$$III. IDENTIFICATION ALGORITHM
A) OFDM and SC signal classification algorithm
Considering an OFDM signal with N S transmission subcarriers be denoted by ![]() $\{ {s(t_1 ),s(t_2 ),\ldots ,s({t_{N_S } })}\}$, according to the definition of fractal box dimension of digital communication signal, the fractal box dimension of the OFDM signal D(s) can be defined as [Reference Li, Li and Lin14]:
$\{ {s(t_1 ),s(t_2 ),\ldots ,s({t_{N_S } })}\}$, according to the definition of fractal box dimension of digital communication signal, the fractal box dimension of the OFDM signal D(s) can be defined as [Reference Li, Li and Lin14]:
with
 $$d(\Delta )=\sum\limits_{i=1}^{N_S } {\left\vert {s(t_i )-s(t_{i+1} )} \right\vert}=LE\vert s_i -s_{i+1} \vert,$$
$$d(\Delta )=\sum\limits_{i=1}^{N_S } {\left\vert {s(t_i )-s(t_{i+1} )} \right\vert}=LE\vert s_i -s_{i+1} \vert,$$ $$d(2\Delta )=\sum\limits_{i=1}^{N_S /2} {\{s_{max} (t_{2i} )-s_{min} (t_{2i})\}},$$
$$d(2\Delta )=\sum\limits_{i=1}^{N_S /2} {\{s_{max} (t_{2i} )-s_{min} (t_{2i})\}},$$and
The modulation of OFDM signal's every carrier is different and these carriers are assumed to be independent and orthogonal. According to the central limit theorem, the instantaneous amplitude of OFDM signal can be assumed to have a Gaussian distribution when the number of OFDM carrier is large enough. So, when N S → ∞, the probability density function of the OFDM signal can be written as:
where σ and η are the variance and mean value of the OFDM signal. Let F s (s) be the distribution function of OFDM signal, P = s max (t 2i), Q = s min (t 2i), and the distribution function of P and Q is ![]() $F_P (p)=F^3_S (p)$, F Q (q) = 1 − (1 − F S (q))3, then we can get the first-order derivative with respect to P and Q, so the probability density function of P and Q is
$F_P (p)=F^3_S (p)$, F Q (q) = 1 − (1 − F S (q))3, then we can get the first-order derivative with respect to P and Q, so the probability density function of P and Q is ![]() $f_P (p)=3F^2_s (p)f_s (p)$,
$f_P (p)=3F^2_s (p)f_s (p)$, ![]() $f_Q (q)=3f_s (q)-6F_S (q)f_s (q)+3F^2_s (q)f_s (q)$. Then the expectation of P and Q can be expressed as follows:
$f_Q (q)=3f_s (q)-6F_S (q)f_s (q)+3F^2_s (q)f_s (q)$. Then the expectation of P and Q can be expressed as follows:
 $$\eqalign{E(Q) & = \int_{-\infty }^{+\infty } {qf_Q (q)dq}, \cr & = \int_{-\infty }^{+\infty } {q[3f_s (q)} -6F_S (q)f_s (q) \cr & \quad + 3F^2_s (q)f_s(q)]dq}$$
$$\eqalign{E(Q) & = \int_{-\infty }^{+\infty } {qf_Q (q)dq}, \cr & = \int_{-\infty }^{+\infty } {q[3f_s (q)} -6F_S (q)f_s (q) \cr & \quad + 3F^2_s (q)f_s(q)]dq}$$and
 $$\eqalign{& E(P)-E(Q) \cr & \quad = 6\int_{-\infty }^{+\infty } {nF_S (n)f_s (n)}dn-3\int_{-\infty }^{+\infty } {nf_s (n)} dn \cr & \quad = 3E(max(s_i ,s_{i+1} ))-3E(s_i) \cr & \quad =\displaystyle{{3}\over{2}}(E(s_i )+E(s_{i+1} )+E(\vert s_i -s_{i+1} \vert ))-3E(s_i )\cr & \quad =\displaystyle{{3}\over{2}}E(\vert s_i -s_{i+1} \vert)}$$
$$\eqalign{& E(P)-E(Q) \cr & \quad = 6\int_{-\infty }^{+\infty } {nF_S (n)f_s (n)}dn-3\int_{-\infty }^{+\infty } {nf_s (n)} dn \cr & \quad = 3E(max(s_i ,s_{i+1} ))-3E(s_i) \cr & \quad =\displaystyle{{3}\over{2}}(E(s_i )+E(s_{i+1} )+E(\vert s_i -s_{i+1} \vert ))-3E(s_i )\cr & \quad =\displaystyle{{3}\over{2}}E(\vert s_i -s_{i+1} \vert)}$$this leads to
By replacing equations (6) and (14) into equation (5), we can get:
 $$\eqalign{D(s) & = 1+\displaystyle{{lg(d(\Delta )/d(2\Delta ))}\over{lg2}} \cr & = 1+\displaystyle{{1}\over{lg2}}lg \displaystyle{{LE\vert s_i -s_{i-1} \vert }\over{(3L/4)E\vert s_i-s_{i-1}\vert}} \cr & =1+\displaystyle{{lg(4/3)}\over{lg2}}=1.415.}$$
$$\eqalign{D(s) & = 1+\displaystyle{{lg(d(\Delta )/d(2\Delta ))}\over{lg2}} \cr & = 1+\displaystyle{{1}\over{lg2}}lg \displaystyle{{LE\vert s_i -s_{i-1} \vert }\over{(3L/4)E\vert s_i-s_{i-1}\vert}} \cr & =1+\displaystyle{{lg(4/3)}\over{lg2}}=1.415.}$$By analyzing the fractal box dimension of the OFDM signal, we get the fractal box dimension of OFDM signal's amplitude as 1.415. For a SC signal, the shaping filter of every symbol has no difference, the instantaneous amplitude of samples is restricted by each other; thus, the fractal box dimension of a SC signal is smaller than the OFDM signal. Next, we will demonstrate that the fractal box dimension of SC signal's amplitude among adjacent three samples. We are considering the three adjacent samples can be divided into two cases based on the monotonicity of the samples.
(a) When the samples of a SC signal are monotonic, the maximum value and minimum value located in the two endpoints of samples spacing, so, |s(t 2i−1) − s(t 2i)| + |s(t 2i) − s(t 2i+1)| and |s(t 2i−1) − s(t 2i+1)| are equal, in this case, d(Δ) = 2d(2Δ), and the fractal box dimension of SC signal is D(s) = 1.
(b) When the samples of a SC signal are not monotonic, according to the relation of three points in the same plane, we can get P − Q < |s(t 2i−1) − s(t 2i)| + |s(t 2i) − s(t 2i+1)| ≤ 2(P − Q) and the equality holds for one particular condition that s(t 2i−1) = s(t 2i+1). Similarly, in this case, d(2Δ) ≤ d(Δ) < 2d(2Δ), so the fractal box dimension of a SC signal is 1 < D(s) ≤ 2.
Under normal circumstances, when the oversampling ratio q is large enough, the number of SC signal's samples in case (a) is more than the samples in case (b); thus, the fractal box dimension of SC signal could be assumed to be a little larger than 1. So, the fractal box dimension of a SC signal and OFDM signal has an apparent difference, it could be used for the classification of a signal as a SC or OFDM signal. We set the classification threshold of the fractal box dimension D J as 1.4 to discriminate OFDM signal and SC signal. By comparing the fractal box dimension of income signal ς to the threshold D J, the received signal is classified as OFDM signal if ![]() $\varsigma >D_J $ or SC signal if
$\varsigma >D_J $ or SC signal if ![]() $\varsigma <D_J $. The performance of the algorithm depends on the SNR. If SNR is relatively high, the algorithm will have a good performance. However, if SNR is very low, the Gaussian noise power is large enough, and the Gaussian noise distribution is random, its fractal box dimension is close to OFDM signal, thus we cannot identify OFDM signal in the Gaussian noise using this algorithm. In such a case, a new method to detect an OFDM signal in the Gaussian noise with a wide range of SNR value is proposed.
$\varsigma <D_J $. The performance of the algorithm depends on the SNR. If SNR is relatively high, the algorithm will have a good performance. However, if SNR is very low, the Gaussian noise power is large enough, and the Gaussian noise distribution is random, its fractal box dimension is close to OFDM signal, thus we cannot identify OFDM signal in the Gaussian noise using this algorithm. In such a case, a new method to detect an OFDM signal in the Gaussian noise with a wide range of SNR value is proposed.
B) Detect OFDM signal in the Gaussian noise
Now we assume the transmitted OFDM signal to be s(t), and P OFDM (w) is the power spectrum of an OFDM signal. In order to detect an OFDM signal in the Gaussian noise, we use a novel feature named PIS, which is defined as the power spectrum of an OFDM signal's power spectrum. The technique fully uses quasi-period characteristics in the signal frequency domain and tests OFDM signal components submerged in the Gaussian noise, thus realize OFDM signal detection. The PISPIS of OFDM is given as:
The autocorrelation function of the OFDM signal can be obtained by inverse Fourier transformation of the power spectrum, so the PIS of OFDM can be rewritten as:
where K is a constant, R OFDM (τ) is the autocorrelation function of an OFDM signal under the given time delay and has even symmetry. The autocorrelation function of an OFDM signal would appear as a periodical peak induced by cyclic prefix, and the PIS of an OFDM signal represents modulus square of autocorrelation function and has higher periodic characteristics than the autocorrelation function.
When OFDM signal is mixed with Gaussian noise, the received OFDM signal can be expressed as:
The power spectrum of the Gaussian noise w(t) is P n (w) = N 0, and the noise and signal are assumed to be independent, thus the power spectrum of the received signal is:
By replacing equation (19) into equation (16), we can get the PIS of the received signal:
 $$\eqalign{S(t\prime) & = \vert FFT[P_x (w)]\vert ^2=\vert FFT[P_{OFDM} (w)+N_0 ]\vert^2 \cr & = \vert FFT[N_0 ]\vert ^2+\vert FFT[P_{OFDM} (w)]\vert ^2 \cr & \quad +2\vert FFT[N_0]FFT[P_{OFDM} (w)]\vert \cr & = \vert N_0 2\pi \delta (t\prime )\vert ^2+K\vert R_{OFDM} (t\prime)\vert ^2 \cr & \quad +\vert 2N_0 2\pi R_{OFDM} (0)\delta (t\prime )\vert.}$$
$$\eqalign{S(t\prime) & = \vert FFT[P_x (w)]\vert ^2=\vert FFT[P_{OFDM} (w)+N_0 ]\vert^2 \cr & = \vert FFT[N_0 ]\vert ^2+\vert FFT[P_{OFDM} (w)]\vert ^2 \cr & \quad +2\vert FFT[N_0]FFT[P_{OFDM} (w)]\vert \cr & = \vert N_0 2\pi \delta (t\prime )\vert ^2+K\vert R_{OFDM} (t\prime)\vert ^2 \cr & \quad +\vert 2N_0 2\pi R_{OFDM} (0)\delta (t\prime )\vert.}$$From equation (20), it is known that the signal additive noise PIS result is linked with autocorrelation function of signal and average power of noise. For OFDM signal, its autocorrelation function contains narrow pulse periodically appearing. Narrow pulse is a Sa function compressed from an OFDM signal with T S width and its width is about 1/B, B is the bandwidth of OFDM signal, then it has T S B times of gain. But the noise after spectrum reprocessing has not processed gain except for zero point. Therefore, the PIS-based detecting method improves the output SNR, and has higher detecting capability. So the PIS can add the non-linear operation to the power spectrum (such as logarithm, evolution, etc.) to suppress multiplicative interference and strengthen the characteristic of the spectrum line, and extract signal feature parameters more accurately. Then we can definite a new detection characteristic to detect OFDM signal in the Gaussian noise according to the periodical peak of OFDM signal's PIS:
where {J 1, J 2, …, J Y} represents the periodical peak sequence of OFDM signal's PIS, {J 12, J 23, …, J Y−1 J Y} is the mean value sequence between adjacent periodical peak. Through the theory analysis, we could know that the detection characteristic of OFDM signal is much larger than the noise's, then we could set a reasonable detection threshold J D to detect OFDM signal in the Gaussian noise by comparing the detection characteristic of incoming signal γ to the threshold J D. If γ > J D, we could conclude that the received signal exists OFDM signal. Otherwise, the received signal is considered as Gaussian noise.
C) OFDM signal detection algorithm flow
This section describes the algorithm flow of the identification for OFDM signal as below.
(1) Replacing the received signal into equations (6) and (14), we can get d(Δ) and d(2Δ), then according to equation (5), we compute the fractal box dimension of the received signal using d(Δ) and d(2Δ).
(2) Setting the classification threshold D J to discriminate the OFDM signal and SC signal. By comparing the fractal box dimension of incoming signal ς to the threshold D J, the received signal is classified as OFDM signal if
 $\varsigma >D_J $ or SC signal if
$\varsigma >D_J $ or SC signal if  $\varsigma <D_J $.
$\varsigma <D_J $.(3) Judging the received signal as OFDM signal with Gaussian noise, we could substitute the received OFDM signal into equation (20) to calculate the PIS of an OFDM signal.
(4) Detecting the location of periodical peak of the received signal first and then compute the periodical peak sequence of OFDM signal's PIS thanks to the peak location. Replacing the sequence into equation (21), we can get the classification feature J.
(5) Setting the detection threshold J D to detect OFDM signal with Gaussian noise by comparing the detection characteristic of incoming signal γ to the threshold J D. If γ > J D, we could conclude that the received signal exists OFDM signal. Otherwise, the received signal is considered as Gaussian noise.
IV. RESULTS AND DISCUSSION
In this section, we will evaluate the proposed algorithm by means of numerical simulation. We here simulate OFDM system equivalent to IEEE 802.11a-based WLAN [Reference Tekbıyık, Tuğrel, Kurt and Ayyıldız15]. The parameters of the OFDM system used in the simulation are: the number of subcarriers is N S = 64, the cyclic prefix rate is 1/4, the transmission bandwidth is 20 MHz, and cyclic prefix and total symbol duration corresponding to 0.8 and 4-μs, respectively. The oversampling rate ratio is assumed to be 4, the factor of raised cosine filter at the transmitter is 0.5 and the number of existing OFDM symbols at the receiver is 20. The transmit signal passes through a multipath fading channel (the number of paths is 10), where each path delay uniformly distributed between [0, τ max] and τ max is chosen to be equal to half length of cyclic prefix, and the SNR is defined as ![]() $SNR(dB)=10log_{10} (E_S/\sigma _w^{2})$. The performance evaluation has been done thanks to Monte Carlo simulation with 500 trials for every point.
$SNR(dB)=10log_{10} (E_S/\sigma _w^{2})$. The performance evaluation has been done thanks to Monte Carlo simulation with 500 trials for every point.
A) The fractal box dimension of OFDM and SC signal
In this section, in order to demonstrate the difference between the fractal box dimension of OFDM and SC signal, we compare the fractal box dimension of OFDM with six modulation types of SC, including BPSK, QPSK, 8PSK, 16QAM, 64QAM, and 256QAM. The range of SNR is [ − 20, 20]dB, step is 5 dB, we consider a perfect time and frequency synchronization context, and the fractal box dimension of OFDM and SC (SC) is presented in Fig. 1.
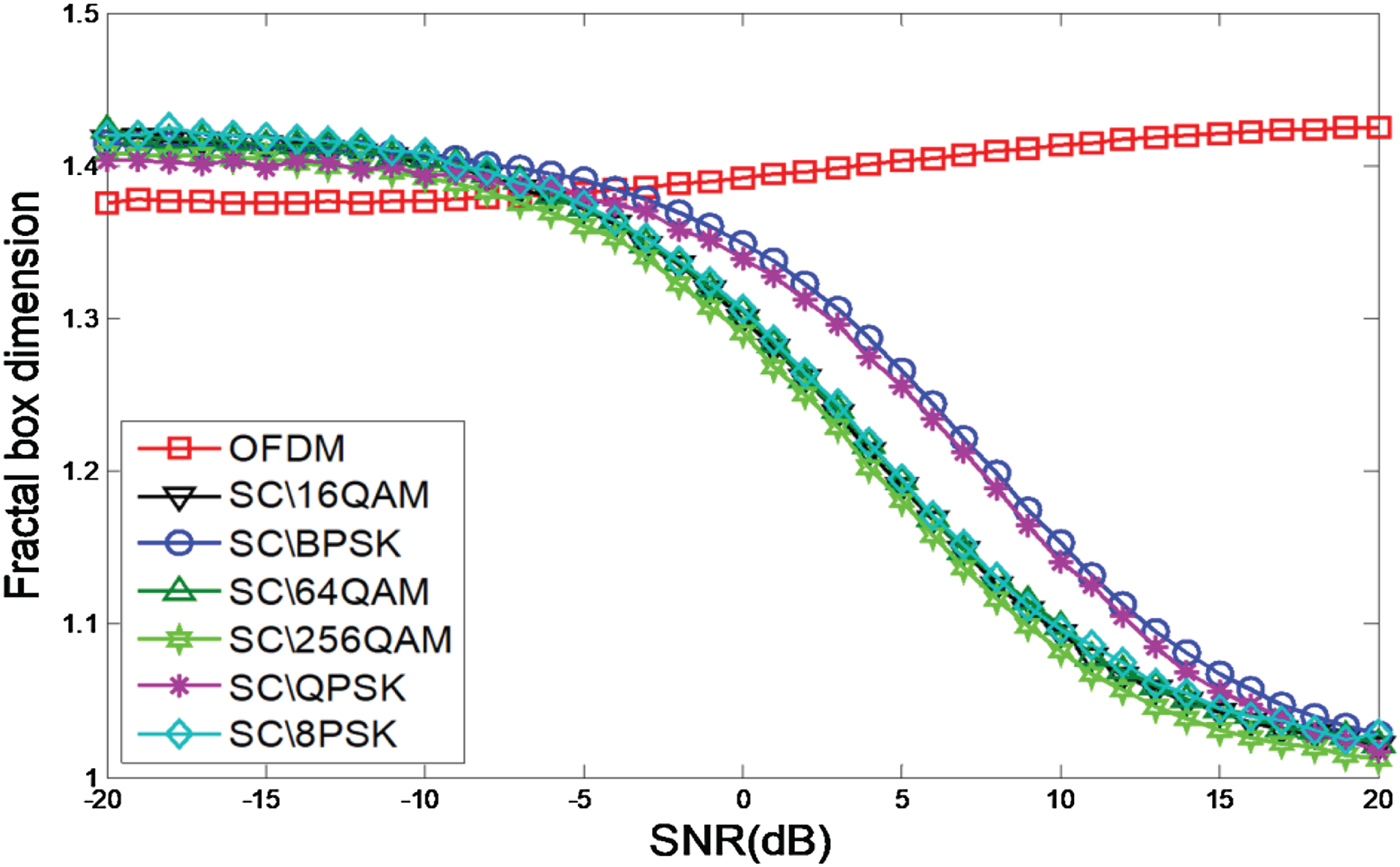
Fig. 1. The fractal box dimension of OFDM and SC.
Figure 1 illustrates the fractal box dimension of OFDM and SC. As shown in the figure, the fractal box dimension of the two types of signal is easy to be affected by noise, and the fractal box dimension of OFDM and SC is aliasing together and not easy to distinguish when the SNR is lower than −5 dB, this result was caused by Gaussian noise. High Gaussian noise in the signal would lead to the fractal box dimension of the received signal to be close to that of the Gaussian noise, and the fractal box dimension of the Gaussian noise is close to OFDM's fractal box dimension. Thus, in this scenario, it is difficult to classify the OFDM signal and SC signal. When the SNR rises to 5 dB, the two types of signal have obvious difference. With the SNR rising up, the fractal box dimension of the two types of signal is settled out, the fractal box dimension of OFDM signal is nearly close to 1.415, and the fractal box dimension of SC signal is nearly close to 1, and the experimental result is in accordance with the theoretical analysis.
B) Performance of classification method for OFDM and SC signal
In order to test the robustness of our identification method based on fractal box dimension (denoted by FDB) to short cyclic prefix OFDM signal and the performance under different SNR, we present the correct detection probability for the autocorrelation-based method (denoted by AC) versus SNR when short cyclic prefix OFDM lengths have been employed ![]() $(\hbox {CP ratio}=\{1/8, /16, 1/32\})$ and the average correct probability under different CP ratio been evaluated as the number of correct detection. The range of SNR is [ − 10, 10] dB, step is 2 dB.
$(\hbox {CP ratio}=\{1/8, /16, 1/32\})$ and the average correct probability under different CP ratio been evaluated as the number of correct detection. The range of SNR is [ − 10, 10] dB, step is 2 dB.
Figure 2 illustrates the detection probability versus SNR for short CP of two algorithms. From the figure, we can remark that the FDB algorithm provides a better performance under ![]() $\hbox {CP ratio}={\{}1/8, /16, 1/32{\}}$. The correct detection probability of the FDB algorithm is nearly reached 100% at SNR equal to 2 dB. In contrast, the correct detection probability of AC algorithm under
$\hbox {CP ratio}={\{}1/8, /16, 1/32{\}}$. The correct detection probability of the FDB algorithm is nearly reached 100% at SNR equal to 2 dB. In contrast, the correct detection probability of AC algorithm under ![]() $\hbox {CP ratio} = {\{}1/8, /16, 1/32{\}}$ is lower than 60, 40, and 10%, respectively. So, the FDB algorithm is more robust than short cyclic prefix OFDM identification algorithm. Actually, this can be easily explained as follows: the identification method for OFDM is based on the correlation of signal symbol induced by cyclic prefix, when the cyclic prefix becomes short, the correlation between OFDM symbols is degrading, and the performance of AC algorithm based on correlation fails down while the FDB algorithm still works well. Notice that standard CP differs from 1/32 (DVB-T in France) to 1/4 (WiFi); consequently, the FDB algorithm is more appropriate for the cognitive radio than the autocorrelation-based method.
$\hbox {CP ratio} = {\{}1/8, /16, 1/32{\}}$ is lower than 60, 40, and 10%, respectively. So, the FDB algorithm is more robust than short cyclic prefix OFDM identification algorithm. Actually, this can be easily explained as follows: the identification method for OFDM is based on the correlation of signal symbol induced by cyclic prefix, when the cyclic prefix becomes short, the correlation between OFDM symbols is degrading, and the performance of AC algorithm based on correlation fails down while the FDB algorithm still works well. Notice that standard CP differs from 1/32 (DVB-T in France) to 1/4 (WiFi); consequently, the FDB algorithm is more appropriate for the cognitive radio than the autocorrelation-based method.
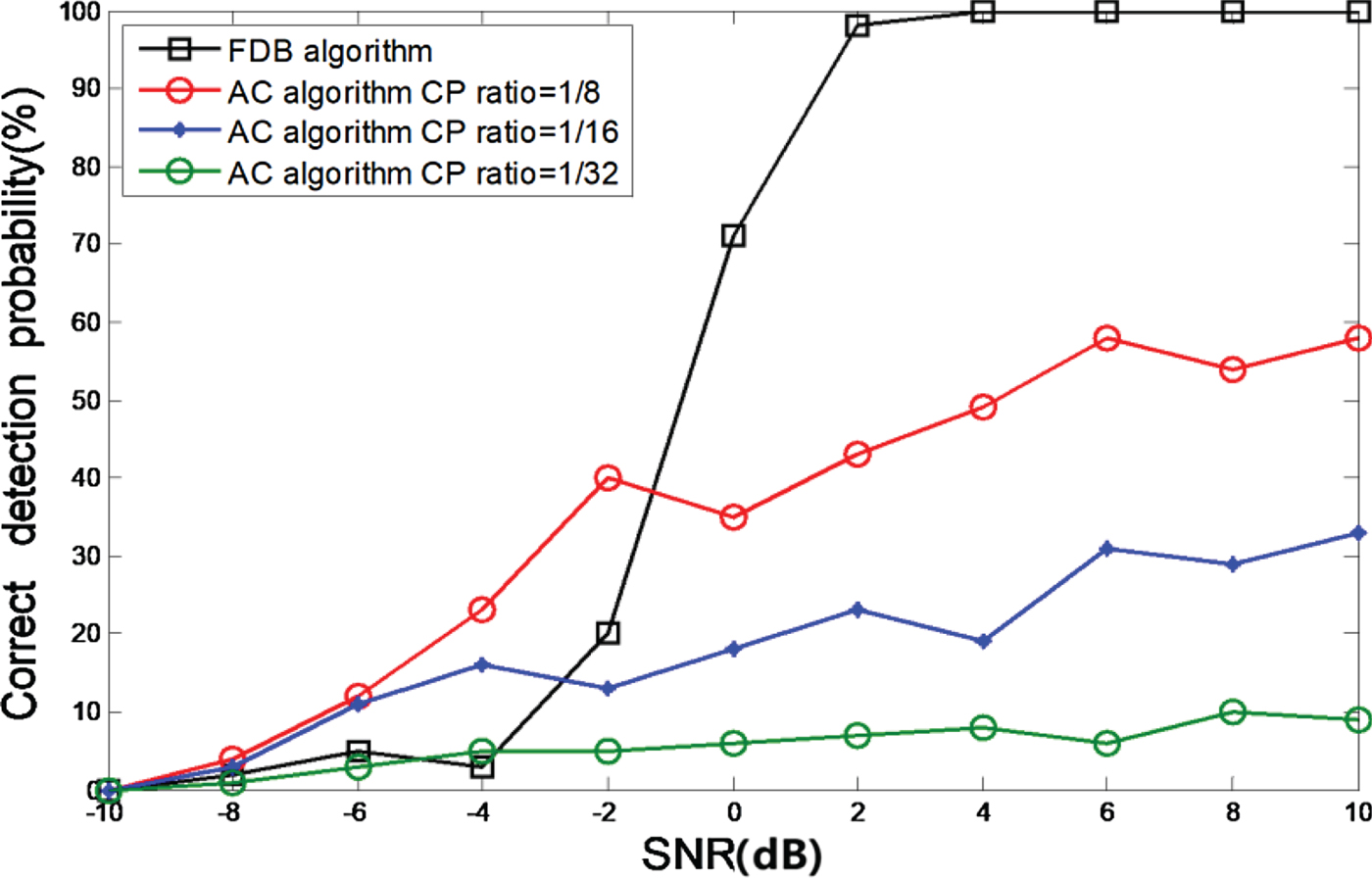
Fig. 2. The correct detection probability versus SNR for short CP of two algorithms.
C) Complexity analysis of the FDB algorithm
In this section, the computation reduction of the proposed algorithm is shown in detail. Let L be the total number of OFDM signal samples, the computational load needed for the FDB algorithm and the other two identification algorithms are shown in Table 1.
Table 1. Computational load of three algorithms.

The comparison of the computational complexity between the proposed algorithm and the other two identification algorithms is listed in Table 1; we can remark from Table 1 that the cyclostationary detecting OFDM signal method (the method of [Reference Cao, Peng, Dong and Wang6]) requires the exploration of a wide range of time delay and computational load is a little high. The method of [Reference Guo and Yu11] used the high-order cumulants of OFDM signal and SC signal to achieve the classification. But the method brings in the eighth cumulants, whose mathematics model is very complex. By analyzing the complexity of above mentioned algorithms, we can discover that the proposed algorithm has lower computational complexity than the other two algorithms.
D) The PIS classification feature of OFDM signal and the Gaussian noise
In this section, we present the PIS classification feature of OFDM signal and the Gaussian noise. The range of SNR is [ − 20, 20] dB, step is 5 dB.
Figure 3 describes the classification feature of OFDM signal and the Gaussian noise at different SNR, from the figure we can know that the classification feature of OFDM signal and Gaussian noise show subtler difference when the SNR is below −15 dB, in this case, it is hard to detect OFDM signal in the Gaussian noise. With the improvement of SNR, the difference between the classification feature of OFDM signal and the Gaussian noise becomes larger. When the SNR rise to −5 dB, the classification feature of OFDM signal and the Gaussian noise can be separated from each other, at this time we can detect OFDM signal in the Gaussian noise.
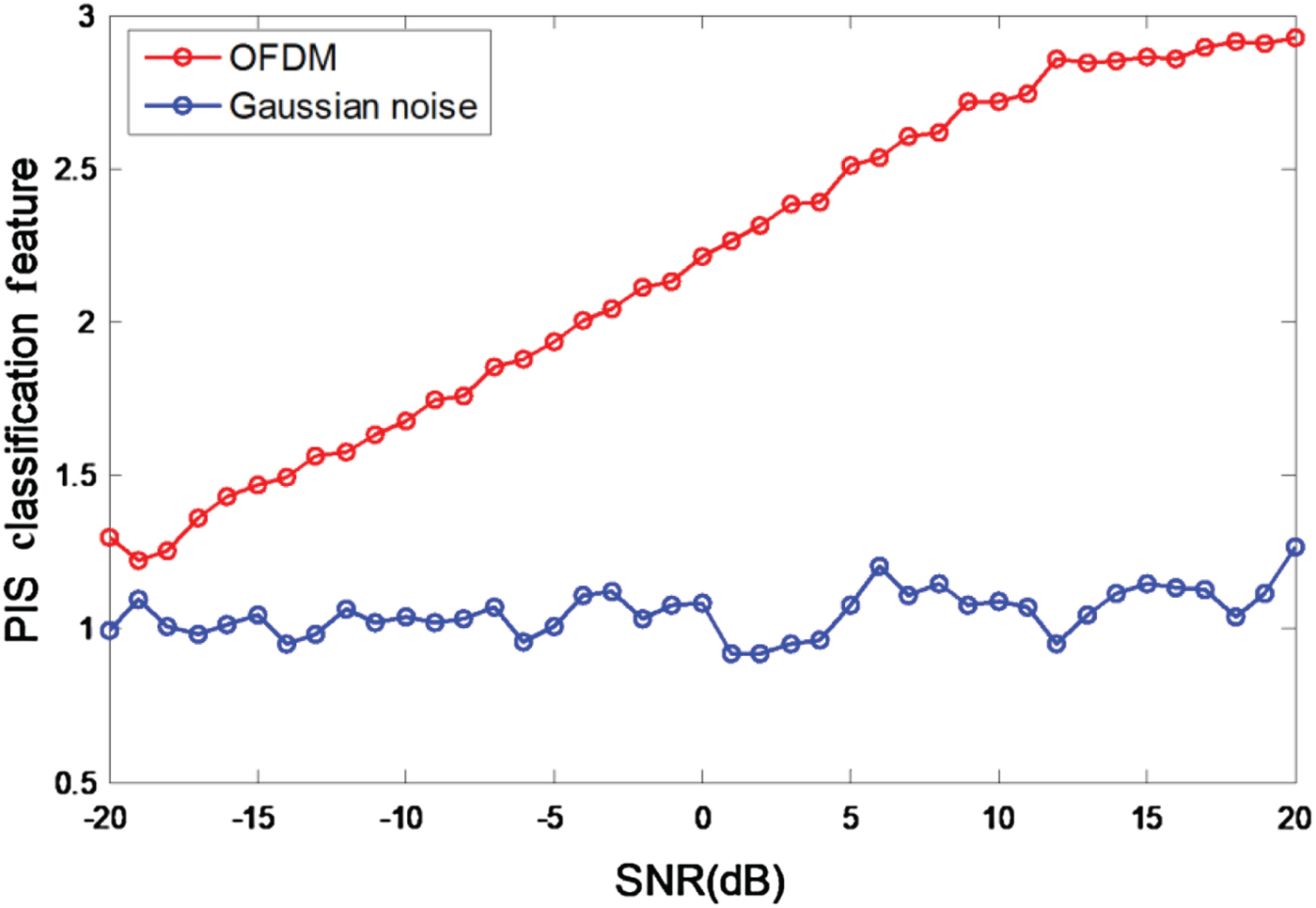
Fig. 3. The classification feature of OFDM signal and the Gaussian noise.
E) Recognition probability of classification method for OFDM signal in the Gaussian noise
In this section, we present the recognition probability of the proposed algorithm for OFDM signal in the Gaussian noise and compare the result with the algorithm proposed in [Reference Punchihewa, Zhang, Dobre, Spooner, Rajan and Inkol7]. The range of SNR is [0, 10]dB, step is 2 dB.
Table 2 illustrates the recognition probability of the proposed algorithm and the algorithm proposed in [Reference Punchihewa, Zhang, Dobre, Spooner, Rajan and Inkol7]. It is clear that under the SNR given in Table 2, the proposed algorithm can correctly detect OFDM signal in the Gaussian noise, and the recognition probability almost reached 100% when ![]() $\hbox {SNR}=0\,\hbox {dB}$. If we compare these results with the algorithm proposed in [Reference Cao, Peng, Dong and Wang6], we could find that the recognition probability of the algorithm proposed by [Reference Punchihewa, Zhang, Dobre, Spooner, Rajan and Inkol7] is lower than the proposed algorithm at every SNR. Thus, it can be concluded that the proposed algorithm is more suitable for detecting OFDM signal in the Gaussian noise than the conventional method.
$\hbox {SNR}=0\,\hbox {dB}$. If we compare these results with the algorithm proposed in [Reference Cao, Peng, Dong and Wang6], we could find that the recognition probability of the algorithm proposed by [Reference Punchihewa, Zhang, Dobre, Spooner, Rajan and Inkol7] is lower than the proposed algorithm at every SNR. Thus, it can be concluded that the proposed algorithm is more suitable for detecting OFDM signal in the Gaussian noise than the conventional method.
Table 2. Recognition probabilities under different SNR.

V. CONCLUSION
In this paper, we introduce a new OFDM signal identification method to classify the OFDM signal with a SC and detect OFDM signal in the Gaussian noise. Firstly, the method identifies the OFDM signal and SC signal based on the fractal box dimension of the two types of signal. The method has the main advantage of not limiting to the cyclic prefix length ratio and showing robustness to the short cyclic prefix, but it could not detect an OFDM signal in the Gaussian noise when the SNR is relatively low. Thus, we construct the PIS of an OFDM signal and present a novel classification feature to detect OFDM signal in the Gaussian noise. Simulation results confirm the efficiency of the proposed algorithm and show that the proposed algorithm has much better performance than the state of art methods. However, the effect of Rayleigh and Rice wireless channels on the threshold is not considered, which also an affecting factor for the performance of the proposed algorithm. Therefore, it will be explored in the future.
ACKNOWLEDGEMENT
This work was supported by the National Natural Science Foundation of China (grant number 41405009).
Wenlong Tang received a degree in signal and information processing from Electronic Engineering Institute in 2016. He is currently pursuing the Ph.D. degree at the Naval University of Engineering. His main research interests are radio wave propagation theory and refractivity estimation techniques.
Hao Cha received his Ph.D. degree in electrical and computer engineering from College of Electronic Engineering, Nanjing University of Aeronautics in 2004. He is currently a full professor with the College of Electronic Engineering, Naval University of Engineering, and director of the Institute of Electromagnetic Environment. His main research interests are radio wave propagation theory and general radar technology.
Min Wei received his B.Sc. degree in signal and information processing from Electronic Engineering Institute in 2016. He is currently an assistant engineer at the unit 31003 of PLA, Beijing, China. His current research interests include radio wave propagation theory and radar sea clutter modeling.
Bin Tian received his Ph.D. degree in communication and information system from the Naval University of Engineering in 2010. He is currently an associate professor with the College of Electronic Engineering, Naval University of Engineering, and director of the Institute of Electromagnetic Environment. His main research interest is radar engineering.
Xichuang Ren received his Ph.D. degree in communication and information system from the Naval University of Engineering in 2011. He is currently an engineer at the unit 91469 of PLA, Beijing, China. His main research interest is wireless communication.







