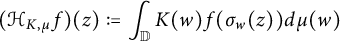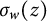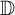1 Introduction
Denote by
$\mathbb {D}$
the open unit disk in the complex plane, and let
$\partial \mathbb {D}=\{z:|z|=1\}$
be the unit circle. Define
$H(\mathbb {D})$
as the space of all analytic function on
$\mathbb {D}$
.
The set of all conformal automorphisms of
$\mathbb {D}$
forms a group which is called the Möbius group and is denoted by Aut
$(\mathbb {D})$
. It is well known that
$\varphi $
belongs to Aut
$(\mathbb {D})$
if and only if there exists a real number
$\theta $
and a point
$a\in \mathbb {D}$
such that
$$ \begin{align*} \varphi(z)=e^{i\theta}\sigma_{a}(z) \,, \end{align*} $$
where
$\sigma _{a}(z)=\frac {a-z}{1-\overline {a}z}\,, \forall z\in \mathbb {D}$
.
Let
$\mu $
be a positive Radon measure, and let K be a
$\mu $
-measurable function on
$\mathbb {D}$
, the Hausdorff operator
$\mathcal {H}_{K,\,\mu }$
is defined by
$$ \begin{align*} (\mathcal{H}_{K,\,\mu}f)(z):=\int_{\mathbb{D}}K(w)f(\sigma_w(z))d\mu(w). \end{align*} $$
The original Hausdorff operator on the real line
$\mathbb {R}$
was introduced by Georgakis in [Reference Georgakis10]. Since then, the boundedness of such operators had attracted lots of attentions of analysts from harmonic analysis (see the survey article [Reference Chen, Fan and Wang2] for some developments in the theory of Hausdorff operators). In [Reference Lerner and Liflyand18, Reference Liflyand19], Lerner and Liflyand investigated the boundedness of the multidimensional Hausdorff operators on real Hardy spaces over
$\mathbb {R}^n$
(see [Reference Liflyand20–Reference Liflyand and Miyachi22] for more research on this line). Some of the above results were generalized to locally compact groups by Mirotin [Reference Mirotin28]. Among them, Mirotin found that for the circle group
$\mathbb {T}$
, this definition leads to Hausdorff operators being almost trivial due to the almost triviality of Aut(
$\mathbb {T}$
). Therefore, Mirotin [Reference Mirotin29] introduced a new definition of the Hausdorff operator (it is such operator we study here) on the unit disk and discussed the boundedness of this operator on some classical function spaces, including Hardy spaces, Bergman spaces, and Bloch spaces. Quickly later, the boundedness of such Hausdorff operator on all Möbius invariant spaces in the unit disk was investigated in [Reference Mirotin30]. Later, Karapetyants and Mirotin [Reference Karapetyants and Mirotin16] continued to study the Hausdorff operators and presented the boundedness, compactness, and nuclearity of these operators on some Banach spaces of analytic functions on the unit disk. In addition, they called these operators “Hausdorff–Zhu operators” because their definitions are similar to those of the Hausdorff–Berezin operators introduced by Karapetyants, Samko, and Zhu [Reference Karapetyants, Samko and Zhu17]. Following the works of them, Bonet [Reference Bonet1] discussed the continuity of Hausdorff operators on weighted Banach spaces of holomorphic functions of type
$H^{\infty }$
. For some applications of the Hausdorff–Zhu operators, we refer the readers to the interesting paper [Reference Grudsky, Karapetyants and Mirotin14].
Motivated by the works mentioned above, we mainly investigate the boundedness of the Hausdorff operators on some important function spaces in this paper, which is a continuation of the works of Mirotin et al. The content structure of this article is as follows.
In Section 2, we give some definitions of function spaces and collect some lemmas that will be used throughout the paper.
In Section 3, we explore the boundedness of the Hausdorff operators on weighted Dirichlet spaces (see Theorem 3.1). Meanwhile, we also show sufficient conditions for the boundedness of such operators between different weighted Dirichlet spaces (see Theorem 3.3).
In Section 4, we consider the Hausdorff operators on derivative Hardy spaces. The boundedness of such operators on derivative Hardy spaces and between different derivative Hardy spaces will be shown in Theorems 4.1 and 4.3.
In Section 5, we discuss the boundedness of the Hausdorff operators on Bloch type spaces. We consider two cases for the spaces
$\mathcal {B}^{\alpha }$
:
$0<\alpha <1$
and
$1<\alpha $
(see Theorem 5.1). For boundedness of Hausdorff operators between different Bloch type spaces, see Theorem 5.2.
Throughout this paper, for any two positive functions
$f(x)$
and
$g(x)$
, we write
$f\lesssim g$
if
$f\leq Cg$
holds, where C is a positive constant independent of the variable x. We write
$f\approx g$
whenever
$f\lesssim g\lesssim f$
. Moreover, the value of C may vary from line to line but will remain independent of the main variables.
2 Preliminaries
For
$0<p<\infty $
, the Hardy space
$H^p$
is the space consisting of all analytic functions
$f\in H(\mathbb {D})$
such that
$$ \begin{align*}\|f\|^p_{H^p}=\sup_{0<r<1}\frac{1}{2\pi}\int^{2\pi}_{0}|f(re^{i\theta})|^pd\theta<\infty.\end{align*} $$
If
$p=\infty $
,
$H^{\infty }$
is the space of bounded analytic functions f in
$H(\mathbb {D})$
with
$$ \begin{align*}\|f\|_{\infty}=\sup\{|f(z)|:z\in \mathbb{D}\}.\end{align*} $$
The derivative Hardy space
$S^p$
is defined by
$$ \begin{align*}S^p=\{f\in H(\mathbb{D}):\|f\|_{S^p}:=|f(0)|+\|f'\|_{H^p}<\infty\}.\end{align*} $$
For more results about the derivative Hardy spaces, we refer the readers to [Reference Cowen and MacCluer3–Reference Čučković and Paudyal5, Reference Duren7, Reference Gu and Luo15, Reference Lin23, Reference Lin, Liu and Wu25, Reference MacCluer27, Reference Roan32] and the references therein.
For
$0<p<\infty $
and
$-1<\alpha <\infty $
, the weighted Bergman space
$A^p_{\alpha }$
consists of all functions f analytic in
$\mathbb {D}$
such that
$$ \begin{align*}\|f\|^p_{A^p_{\alpha}}=\int_{\mathbb{D}}|f(w)|^pdA_{\alpha}(w)<\infty,\end{align*} $$
where
$dA(w)=(1/\pi )dxdy$
is the normalized Lebesgue area measure on
$\mathbb {D}$
and
$dA_{\alpha }(w)=(1+\alpha )(1-|w|^2)^{\alpha }dA(w)$
is the weighted Lebesgue measure (see [Reference Duren and Schuster8] for more information about Bergman spaces).
For
$0<p<\infty $
and
$-1<\alpha <\infty $
, the weighted Dirichlet space
$\mathcal {D}^p_{\alpha }$
consists of those functions f analytic on
$\mathbb {D}$
that satisfy
$$ \begin{align*}\|f\|_{\mathcal{D}^p_{\alpha}}=\left(|f(0)|^p+\int_{\mathbb{D}}|f'(w)|^pdA_{\alpha}(w) \right) ^{1/p}<\infty.\end{align*} $$
It is clearly that
$f\in \mathcal {D}^p_{\alpha }$
if and only if
$f'\in A^p_{\alpha }$
. When
$p<\alpha +1$
, the weighted Dirichlet space
$\mathcal {D}^p_{\alpha }$
coincides with the weighted Bergman space
$A^{p}_{\alpha -p}$
with equivalence of norms. If
$p>\alpha +2$
, then the weighted Dirichlet space
$\mathcal {D}^p_{\alpha }$
is contained in the space
$H^{\infty }$
(see [Reference Wu33, Theorem 4.2]). Readers who interested in weighted Dirichlet spaces are referred to [Reference Galanopoulos, Girela and Peláez9, Reference Girela and Peláez11–Reference Girela and Peláez13] .
For
$\alpha>0$
, the Bloch type space
$\mathcal {B}^{\alpha }$
is defined to be the space of analytic functions f on
$\mathbb {D}$
such that
$$ \begin{align*}\|f\|^{\prime}_{\mathcal{B}^{\alpha}}=\sup\{(1-|z|^2)^{\alpha}|f'(z)|:z\in\mathbb{D}\}<+\infty.\end{align*} $$
It can be easily verified that
$\|\cdot \|^{\prime }_{\mathcal {B}^{\alpha }}$
is a complete semi-norm on
$\mathcal {B}^{\alpha }$
, and
$\mathcal {B}^{\alpha }$
can be made into a Banach space by introducing the norm
$$ \begin{align*}\|f\|_{\mathcal{B}^{\alpha}}=|f(0)|+\|f\|^{\prime}_{\mathcal{B}^{\alpha}}.\end{align*} $$
When
$\alpha =1$
,
$\mathcal {B}^1=\mathcal {B}$
is the classic Bloch space. Readers who interested in Bloch type spaces are referred to [Reference Zhu35].
First, we state the following lemma, which is one of the key tools to prove the boundedness of the Hausdorff operators.
Lemma 2.1 [Reference Mirotin28, Lemma 2]
Let
$(X,m)$
be a measure space,
$\mathcal {F}(X)$
be some Banach space of m-measurable functions on X, let
$(\Omega ,\mu )$
be a
$\sigma $
-compact quasi-metric space with positive Radon measure
$\mu $
, and let
$F(w,z)$
be a function on
$\Omega \times X$
. Assume that:
-
(i) the convergence of a sequence in norm in
$\mathcal {F}(X)$
yields the convergence of some subsequence to the same function for m-a.e.
$z\in X$
; -
(ii)
$F(w,\cdot )\in \mathcal {F}(X)$
for
$\mu $
-a.e.
$w\in \Omega $
; -
(iii) the map
$w\mapsto F(w,\cdot ):\Omega \rightarrow \mathcal {F}(X)$
is Bochner integrable with respect to
$\mu $
.
Then for m-a.e.
$z\in X$
, one has
$$ \begin{align*}\left((B)\int_{\Omega} F(w,\cdot)d\mu(w)\right)(z)=\int_{\Omega}F(w,z) d\mu(w).\end{align*} $$
Remark 2.2 Indeed, by examining the proof of [Reference Mirotin28, Lemma 2] carefully, we can see that [Reference Mirotin28, Lemma 2] is also true for quasi-Banach spaces (see [Reference Yosida34, p. 31] for related definitions). In particular, when
$p\in (0,1)$
, it is easy to verify that
$\|\cdot \|^p_{S^p}$
is a quasi-norm, so does for the case of weighted Dirichlet spaces.
Next, the estimations of the growth rates of functions on
$\mathcal {D}^p_{\alpha }$
,
$S^p$
and
$\mathcal {B}^{\alpha }$
are given in the following lemmas, respectively, which are needed in the later proofs of the main results.
Lemma 2.3 [Reference Lin24, Lemma 4.1]
Let
$0<p< \infty $
and
$\alpha>-1$
. If
$f\in \mathcal {D}^p_{\alpha }$
, then:
-
(1)
$|f(z)|\lesssim \frac {\|f\|_{\mathcal {D}^p_{\alpha }}}{(1-|z|^2)^{\frac {\alpha +2-p}{p}}}$
, whenever
$p<\alpha +2$
; -
(2)
$|f(z)|\lesssim \left ( \log \frac {2}{1-|z|^2}\right ) ^{\frac {p-1}{p}}\|f\|_{\mathcal {D}^p_{\alpha }}$
, whenever
$p=\alpha +2 $
; -
(3)
$|f(z)|\leq \|f\|_{\mathcal {D}^p_{\alpha }}$
, whenever
$p>\alpha +2$
.
Lemma 2.4 [Reference Lin, Liu and Wu25, Reference Lin, Liu and Wu26]
Let
$1\leq p<\infty $
. For any
$f\in S^p$
, then
$|f(z)|\leq \pi \|f\|_{S^p}, ~z\in \mathbb {D}.$
If
$0<p<1$
, then
$$ \begin{align*}|f(z)|\lesssim\frac{\|f\|_{S^p}}{(1-|z|^2)^{1/p-1}}.\end{align*} $$
Lemma 2.5 [Reference Ohno, Stroethoff and Zhao31]
Let
$0<\alpha <\infty $
. If
$f\in \mathcal {B}^{\alpha }$
, then:
-
(1) if
$\kern1pt 0<\alpha <1$
,
$|f(z)|\lesssim \|f\|_{\mathcal {B}^{\alpha }}$
; -
(2) if
$\alpha =1 $
,
$|f(z)|\lesssim \|f\|_{\mathcal {B}^{\alpha }} \log \frac {2}{1-|z|^2} $
; -
(3) if
$\alpha>1$
,
$|f(z)|\lesssim \frac {\|f\|_{\mathcal {B}^{\alpha }}}{(1-|z|^2)^{\alpha -1}}$
.
We need two more lemmas which are concerned with the boundedness of the composition operators on Hardy spaces and Bergman spaces.
Lemma 2.6 [Reference Zhu36, Theorem 11.6, p. 308]
If
$\varphi :\mathbb {D}\rightarrow \mathbb {D}$
is analytic and
$p>0$
, then
$$ \begin{align*}\int_{\mathbb{D}}|f(\varphi(z))|^pdA_{\alpha}(z)\leq\left( \frac{1+|\varphi(0)|}{1-|\varphi(0)|}\right)^{2+\alpha} \int_{\mathbb{D}}|f(z)|^pdA_{\alpha}(z)\end{align*} $$
for all analytic functions f on
$\mathbb {D}$
.
Lemma 2.7 [Reference Zhu36, Theorem 11.12, p. 317]
If
$\varphi :\mathbb {D}\rightarrow \mathbb {D}$
is analytic and
$p>0$
, then
$$ \begin{align*}\int_{0}^{2\pi}|f(\varphi(e^{i\theta}))|^pd\theta\leq\frac{1+|\varphi(0)|}{1-|\varphi(0)|}\int_0^{2\pi}|f(e^{i\theta})|^pd\theta\end{align*} $$
for all
$f\in H^p$
.
3 The Hausdorff operators on weighted Dirichlet spaces
$\mathcal {D}^p_{\alpha }$
In this section, we will be concerned with the boundedness of Hausdorff operators on weighted Dirichlet spaces
$\mathcal {D}^p_{\alpha }$
. For the conditions in Lemma 2.1, we shall consider the case when
$X=\Omega =\mathbb {D},m=dA$
and
$\mu $
is positive Radon measure (the same case is discussed in the next two subsections). The main results read as follows.
Theorem 3.1 Let
$0<p<\infty $
and
$\alpha>-1$
. If the function K satisfies
$$ \begin{align*}\int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|)^{\frac{p+2+\alpha}{p}}}d\mu(w)<\infty\,,\end{align*} $$
then the operator
$\mathcal {H}_{K,\,\mu }$
is bounded on
$\mathcal {D}^p_{\alpha }(\mathbb {D})$
. Moreover,
-
(1) for
$p\leq \alpha +2$
,
$$ \begin{align*}\|\mathcal{H}_{K,\,\mu}\|_{\mathcal{D}^p_{\alpha}}\lesssim \int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|)^{\frac{p+2+\alpha}{p}}}d\mu(w)\,;\end{align*} $$
-
(2) for
$p>\alpha +2$
,
$$ \begin{align*}\|\mathcal{H}_{K,\,\mu}\|_{\mathcal{D}^p_{\alpha}}\leq \int_{\mathbb{D}}|K(w)|\left[ 1+\left( \frac{1+|w|}{1-|w|}\right) ^{p+\alpha+2}\right] ^{\frac{1}{p}}d\mu(w)\,.\end{align*} $$
Proof First, we need to show that all the conditions of Lemma 2.1 are satisfied for
$\mathcal {F}(X)=\mathcal {D}^p_{\alpha }$
and
$F(w,z)=K(w)f(\sigma _w(z))$
. To this end, we split the proof into three cases.
Case 1:
$p< \alpha +2$
.
Let
$f_n\in \mathcal {D}^p_{\alpha }$
and
$\lim _{n\rightarrow \infty }f_n=0$
in the norm of
$\mathcal {D}^p_{\alpha }$
. Then by Lemma 2.3, we have
$$ \begin{align*}|f_n(z)|\lesssim\frac{\|f_n\|_{\mathcal{D}^p_{\alpha}}}{(1-|z|^2)^{\frac{\alpha+2-p}{p}}}\rightarrow0\,,\end{align*} $$
as
$n\rightarrow \infty $
. Clearly, (i) in Lemma 2.1 holds.
By Lemmas 2.3 and 2.6, we obtain
$$ \begin{align*} \|f\circ\sigma_w\|^p_{\mathcal{D}^p_{\alpha}} &=|f\circ\sigma_w(0)|^p+\int_{\mathbb{D}}|f'(\sigma_w(z))|^p|\sigma^{\prime}_w(z)|^pdA_{\alpha}(z)\\ &=|f(w)|^p+\int_{\mathbb{D}}\left| f'(\sigma_w(z))\right| ^p\left| \frac{1-|w|^2}{(1-\overline{w}z)^2}\right| ^pdA_{\alpha}(z)\\ &\lesssim\frac{\|f\|^p_{\mathcal{D}^p_{\alpha}}}{(1-|w|^2)^{\alpha+2-p}}+\left(\frac{1+|w|}{1-|w|} \right) ^p\int_{\mathbb{D}}|f'(\sigma_w(z))|^pdA_{\alpha}(z)\\ &\leq\frac{\|f\|^p_{\mathcal{D}^p_{\alpha}}}{(1-|w|^2)^{\alpha+2-p}}+\left(\frac{1+|w|}{1-|w|} \right) ^{p+\alpha+2}\int_{\mathbb{D}}|f'(z)|^pdA_{\alpha}(z)\\ &\leq\left[\frac{1}{(1-|w|^2)^{\alpha+2-p}}+\left( \frac{1+|w|}{1-|w|}\right) ^{p+\alpha+2} \right] \|f\|^p_{\mathcal{D}^p_{\alpha}}\,, \end{align*} $$
which ensures that (ii) and (iii) in Lemma 2.1 hold true.
From Lemma 2.1, we know that for
$dA$
-
$a.e.$
$z\in \mathbb {D}$
$$ \begin{align} \mathcal{H}_{K,\,\mu}f(z)=(B)\int_{\mathbb{D}}K(w)f\circ\sigma_wd\mu(w)(z)\,, \end{align} $$
where the right-hand side is an analytic Bochner integral since f is analytic. Thus, we need to show that the left-hand side of (3.1) is continuous (and so
$\mathcal {H}_{K,\,\mu }f\in H(\mathbb {D})$
).
By Lemma 2.3, we have
$$ \begin{align*}|f(\sigma_{w}(z))|\lesssim\frac{\|f\|_{\mathcal{D}^p_{\alpha}}}{(1-|\sigma_{w}(z)|^2)^{\frac{\alpha+2-p}{p}}}.\end{align*} $$
Since
$$ \begin{align*}1-|\sigma_{w}(z)|^2=\frac{(1-|w|^2)(1-|z|^2)}{|1-\overline{w}z|^2}\gtrsim(1-|w|)(1-|z|^2)\,,\end{align*} $$
it follows that
$$ \begin{align*} |f(\sigma_{w}(z))|\lesssim\frac{\|f\|_{\mathcal{D}^p_{\alpha}}}{(1-|z|^2)^{\frac{\alpha+2-p}{p}}(1-|w|)^{\frac{\alpha+2-p}{p}}}. \end{align*} $$
Thus, by choosing an arbitrary point
$z_0\in \mathbb {D}$
and a compact neighborhood
$S\subset \mathbb {D}$
of
$z_0$
, we have
$$ \begin{align*}|K(w)||f(\sigma_{w}(z))|\lesssim \frac{|K(w)|}{(1-|w|)^{\frac{\alpha+2-p}{p}}}\|f\|_{\mathcal{D}^p_{\alpha}}\leq \frac{|K(w)|}{(1-|w|)^{\frac{\alpha+2+p}{p}}}\|f\|_{\mathcal{D}^p_{\alpha}}\end{align*} $$
for all
$z\in S$
. According to the hypothesis and Lebesgues’s dominated convergence theorem, it follows that the left-hand side of (3.1) is continuous; and therefore,
$\mathcal {H}_{K,\,\mu }f\in H(\mathbb {D})$
.
At last, we conclude that
$$ \begin{align*} \| \mathcal{H}_{K,\mu}f\|_{\mathcal{D}^p_{\alpha}}&\leq\int_{\mathbb{D}}|K(w)|\cdotp\|f\circ\sigma_w\|_{\mathcal{D}^p_{\alpha}}d\mu(w)\\ &\leq\int_{\mathbb{D}}|K(w)|\left[\frac{1}{(1-|w|^2)^{\alpha+2-p}}+\left( \frac{1+|w|}{1-|w|}\right) ^{p+\alpha+2} \right]^{\frac{1}{p}} d\mu(w)\|f\|_{\mathcal{D}^p_{\alpha}}\\ &\lesssim\int_{\mathbb{D}}|K(w)|\left[\frac{1}{(1-|w|)^{\alpha+2-p}}+ \frac{1}{(1-|w|)^{p+\alpha+2}} \right]^{\frac{1}{p}}d\mu(w) \|f\|_{\mathcal{D}^p_{\alpha}}\\ &\lesssim\int_{\mathbb{D}}|K(w)| \frac{1}{(1-|w|)^{\frac{p+\alpha+2}{p}}} dA(w)\|f\|_{\mathcal{D}^p_{\alpha}}\,, \end{align*} $$
which completes the proof of Case 1.
Case 2:
$p= \alpha +2$
.
The proof is almost identical to Case 1, with the main change being the utilization of the following inequality:
$$ \begin{align*}|f(z)|\lesssim\left( \log\frac{2}{1-|z|^2}\right) ^{\frac{p-1}{p}}\|f\|_{\mathcal{D}^p_{\alpha}}\lesssim\frac{\|f\|_{\mathcal{D}^p_{\alpha}}}{(1-|z|^2)^{(p-1)/p}}\lesssim\frac{\|f\|_{\mathcal{D}^p_{\alpha}}}{(1-|z|^2)^{(p+\alpha+2)/p}}\end{align*} $$
for any
$f\in \mathcal {D}^p_{\alpha }$
.
Case 3:
$p>\alpha +2$
.
The proof is also analogously to Case 1. Unlike the previous two cases, we can obtain a more precise estimate of the norm in this case. By Lemma 2.1, we have
$$ \begin{align*} \| \mathcal{H}_{K,\mu}f\|_{\mathcal{D}^p_{\alpha}}&\leq\int_{\mathbb{D}}|K(w)|\cdotp\|f\circ\sigma_w\|_{\mathcal{D}^p_{\alpha}}d\mu(w)\\ &\leq\int_{\mathbb{D}}|K(w)|\left[1+\left( \frac{1+|w|}{1-|w|}\right) ^{p+\alpha+2} \right]^{\frac{1}{p}} d\mu(w)\|f\|_{\mathcal{D}^p_{\alpha}}. \end{align*} $$
This finishes the whole proof.
A natural question comes to mind: how to characterize the boundedness of Hausdorff operators between different weighted Dirichlet spaces? To solve this problem, we need to use the following lemma, which shows the sufficient and necessary conditions for the boundedness of weighted composition operators between different weighted Bergman spaces.
Lemma 3.2 [Reference Čučković and Zhao6, Theorem 1]
Let u be an analytic function on
$\mathbb {D}$
, and let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
. Let
$0<p\leq q<\infty $
, and
$\alpha ,~\beta>-1$
. Then the weighted composition operator
$uC_{\varphi }$
is bounded from
$A^p_{\alpha }$
into
$A^q_{\beta }$
if and only if
$$ \begin{align*}\sup_{a\in \mathbb{D}}\int_{\mathbb{D}}\left(\frac{1-|a|^2}{|1-\overline{a}\varphi(w)|^2} \right)^{(2+\alpha)q/p}|u(w)|^qdA_{\beta}(w)<\infty.\end{align*} $$
Theorem 3.3 Let
$0< p\leq q<\infty $
,
$\alpha ,~\beta>-1$
. Assume that
$$ \begin{align*}\sup_{a\in \mathbb{D}}\int_{\mathbb{D}}|\sigma^{\prime}_w(z)|^q\left( \frac{1-|a|^{2}}{|1-\overline{a}\sigma_w(z)|^{2}}\right)^{\frac{(2+\alpha)q}{p}} dA_{\beta}(z)<\infty.\end{align*} $$
-
(1) For
$p<\alpha +2$
. If the function K satisfies
$\int _{\mathbb {D}}|K(w)|(1-|w|)^{-(\alpha +2-p)/p}d\mu (w)<\infty ,$
then the operator
$\mathcal {H}_{K,\,\mu }:\mathcal {D}^p_{\alpha }(\mathbb {D})\rightarrow \mathcal {D}^q_{\beta }(\mathbb {D})$
is bounded. -
(2) For
$p=\alpha +2$
. If the function K satisfies
$\int _{\mathbb {D}}|K(w)|\cdot |\log (1-|w|)|^{(p-1)/p}d\mu (w)<\infty ,$
then the operator
$\mathcal {H}_{K,\,\mu }:\mathcal {D}^p_{\alpha }(\mathbb {D})\rightarrow \mathcal {D}^q_{\beta }(\mathbb {D})$
is bounded. -
(3) For
$p>\alpha +2$
. If the function K satisfies
$\int _{\mathbb {D}}|K(w)|d\mu (w)<\infty $
, then the operator
$\mathcal {H}_{K,\,\mu }:\mathcal {D}^p_{\alpha }(\mathbb {D})\rightarrow \mathcal {D}^q_{\beta }(\mathbb {D})$
is bounded.
4 The Hausdorff operators on derivative Hardy spaces
$S^p(\mathbb {D})$
In this section, we obtain sufficient conditions for the boundedness of Hausdorff operators on derivative Hardy spaces.
Theorem 4.1 Let
$0<p<\infty $
. If the function K satisfies
$$ \begin{align*}\int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|)^{\frac{1+p}{p}}}d\mu(w)<\infty,\end{align*} $$
then the operator
$\mathcal {H}_{K,\,\mu }$
is bounded on
$S^p(\mathbb {D})$
. Moreover,
-
(1) for
$1\leq p<\infty $
,
$$ \begin{align*}\|\mathcal{H}_{K,\mu}\|_{S^p}\leq\int_{\mathbb{D}}\left(\left( \frac{1+|w|}{1-|w|}\right) ^{\frac{1+p}{p}}+\pi\right)|K(w)|d\mu(w);\end{align*} $$
-
(2) for
$0< p<1$
,
$$ \begin{align*}\|\mathcal{H}_{K,\mu}\|_{S^p}\lesssim\int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|)^{\frac{1+p}{p}}}d\mu(w).\end{align*} $$
Proof Since the proofs for cases
$1\leq p<\infty $
and
$0< p<1$
are similar, we only give the proof for case
$1\leq p<\infty $
.
First, we need to verify that (i) of Lemma 2.1 is satisfied for
$(X,m)=(\mathbb {D},dA)$
and
$(\Omega ,\mu )=(\mathbb {D},\mu )$
. Fix
$f_n\in S^p(\mathbb {D})$
and
$f_n\rightarrow 0$
strongly, then we see that for any
$z\in \mathbb {D}$
,
$$ \begin{align*}\lim_{n\rightarrow\infty}|f_n(z)|\leq\lim_{n\rightarrow\infty}\pi\|f_n\|_{S^p}=0\end{align*} $$
by Lemma 2.4, which implies that (i) holds.
Next, we need to show that (ii) and (iii) both hold. It is easy to see that
$|1-\overline {w}z|\geq 1-|w|$
for any
$z\in \mathbb {D}$
. By Lemmas 2.4 and 2.7, we obtain
$$ \begin{align*} \|f\circ\sigma_w\|_{S^p}&=|f\circ\sigma_{w}(0)|+\|(f\circ\sigma_{w})'\|_{H^p}\\ &=|f(w)|+\left( \frac{1}{2\pi}\int_0^{2\pi}|f'(\sigma_w(e^{i\theta}))|^p|\sigma^{\prime}_w(e^{i\theta})|^pd\theta\right) ^{1/p}\\ &\leq\pi\|f\|_{S^p}+\left( \frac{1}{2\pi}\int_0^{2\pi}|f'(\sigma_w(e^{i\theta}))|^p\left|\frac{1-|w|^2}{(1-\overline{w}e^{i\theta})^2} \right| ^pd\theta\right)^{1/p} \\ &\leq\pi\|f\|_{S^p}+\left(\frac{1+|w|}{1-|w|} \right) \left( \frac{1}{2\pi}\int_0^{2\pi}|f'(\sigma_w(e^{i\theta}))|^pd\theta\right)^{1/p}\\ &\leq\pi\|f\|_{S^p}+\left(\frac{1+|w|}{1-|w|} \right)^{\frac{p+1}{p}} \left( \frac{1}{2\pi}\int_0^{2\pi}|f'(e^{i\theta})|^pd\theta\right)^{1/p}\\ &\leq\left[\pi+ \left(\frac{1+|w|}{1-|w|} \right)^{\frac{p+1}{p}}\right] \|f\|_{S^p}. \end{align*} $$
This yields that (ii) and (iii) hold.
According to Lemma 2.1, it follows that for
$dA$
-
$a.e.$
$z\in \mathbb {D}$
,
$$ \begin{align} \mathcal{H}_{K,\,\mu}f(z)=\left( (B)\int_{\mathbb{D}}K(w)f\circ\sigma_wd\mu(w)\right)(z)\,, \end{align} $$
where the right-hand side is an analytic Bochner integral since f is analytic. Thus, to show that
$\mathcal {H}_{K,\,\mu }f$
is analytic, it suffices to prove that
$\mathcal {H}_{K,\,\mu }f$
is continuous.
Applying Lemma 2.4, we have
$$ \begin{align*}|f(\sigma_{w}(z))|\leq\pi\|f\|_{S^p},\end{align*} $$
which gives that for any
$z\in \mathbb {D}$
,
$$ \begin{align*}|K(w)||f(\sigma_{w}(z))|\leq\pi\|f\|_{S^p}|K(w)|.\end{align*} $$
Since
$$ \begin{align*}\int_{\mathbb{D}}|K(w)|d\mu(w)\leq\int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|)^{\frac{1+p}{p}}}d\mu(w) <\infty\,,\end{align*} $$
it follows that
$\mathcal {H}_{K,\,\mu }f$
is continuous.
By the definition of Hausdorff operators, we get that
$$ \begin{align*} \|\mathcal{H}_{K,\mu}f\|_{S^p}&\leq\int_{\mathbb{D}}|K(w)|\cdot\|f\circ\sigma_w\|_{S^p}d\mu(w)\\ &\leq\int_{\mathbb{D}}|K(w)|\left[\pi+ \left(\frac{1+|w|}{1-|w|} \right)^{\frac{p+1}{p}}\right]d\mu(w)\|f\|_{S^p}, \end{align*} $$
which is the desired result.
Moreover, we also give the sufficient conditions for the boundedness of Hausdorff operators between different derivative Hardy spaces. However, we need to use the following lemma to complete our proof.
Lemma 4.2 [Reference Čučković and Zhao6, Theorem 4]
Let u be an analytic function on
$\mathbb {D}$
, and let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
. Let
$0<p\leq q<\infty $
. Then the weighted composition operator
$uC_{\varphi }$
is bounded from
$H^p$
into
$H^q$
if and only if
$$ \begin{align*}\sup_{a\in \mathbb{D}}\int_{\partial\mathbb{D}}\left(\frac{1-|a|^2}{|1-\overline{a}\varphi(w)|^2} \right)^{q/p}|u(w)|^qd\sigma(w)<\infty,\end{align*} $$
where
$d\sigma $
is the normalized arc length measure on
$\partial \mathbb {D}$
.
Theorem 4.3 Let
$0< p\leq q<\infty $
and assume that
$$ \begin{align*}\sup_{a\in \mathbb{D}}\int_{\partial\mathbb{D}}|\sigma^{\prime}_w(z)|^q\left( \frac{1-|a|^{2}}{|1-\overline{a}\sigma_w(z)|^{2}}\right)^{q/p} d\sigma(w)<\infty.\end{align*} $$
-
(1) For
$1\leq p<\infty $
. If the function K satisfies
$\int _{\mathbb {D}}|K(w)|d\mu (w)<\infty ,$
then the operator
$\mathcal {H}_{K,\mu }:S^p(\mathbb {D})\rightarrow S^q(\mathbb {D})$
is bounded. -
(2) For
$0< p<1$
. If the function K satisfies
$\int _{\mathbb {D}}|K(w)|(1-|w|)^{1/p-1}d\mu (w)<\infty ,$
then the operator
$\mathcal {H}_{K,\mu }:S^p(\mathbb {D})\rightarrow S^q(\mathbb {D})$
is bounded.
5 The Hausdorff operators on Bloch type spaces
$\mathcal {B}^{\alpha }$
In this section, we investigate the Hausdorff operators on Bloch type spaces
$\mathcal {B}^{\alpha }$
. However, we only need to focus on two cases. For the case
$\alpha =1$
, this is given in [Reference Mirotin29, Theorem 1].
Theorem 5.1 Let
$0<\alpha <\infty $
. Then the following statements are true:
-
(1) If
$1<\alpha <\infty $
and the function K satisfies then the operator
$$ \begin{align*}\int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|)^{\alpha-1}}d\mu(w)<\infty\,,\end{align*} $$
$\mathcal {H}_{K,\mu }$
is bounded on
$\mathcal {B}^{\alpha }$
.
-
(2) If
$0<\alpha <1$
and the function K satisfies
$ \int _{\mathbb {D}}|K(w)|d\mu (w)<\infty ,$
then the operator
$\mathcal {H}_{K,\mu }$
is bounded on
$\mathcal {B}^{\alpha }$
.
Proof Since the proofs of (1) and (2) are similar, we only give the proof of (1). For any
$f_n\in \mathcal {B}^{\alpha }$
, if
$f_n$
strongly convergence to
$0$
, then by Lemma 2.5, we have
$$ \begin{align*}|f_n(z)|\lesssim\frac{\|f_n\|_{\mathcal{B}^{\alpha}}}{(1-|z|^2)^{\alpha-1}} \rightarrow0\end{align*} $$
as
$n\rightarrow \infty $
. This shows that the condition (i) in Lemma 2.1 holds for
$(X,m)=(\mathbb {D},dA)$
,
$\mathcal {F}(X)=\mathcal {B}^{\alpha }(\mathbb {D}),$
and
$F(w,z)=K(w)f(\sigma _w(z))$
. According to the definition of
$\mathcal {B}^{\alpha }$
, it follows from Lemma 2.5 that
$$ \begin{align*} \|f\circ\sigma_w\|_{\mathcal{B}^{\alpha}}=&|f(w)|+\sup_{z\in\mathbb{D}}(1-|z|^2)^{\alpha}|f'(\sigma_w(z))|\cdot|\sigma^{\prime}_w(z)|\\ \lesssim& \frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|w|^2)^{\alpha-1}}+\sup_{z\in\mathbb{D}}(1-|z|^2)^{\alpha}\frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|\sigma_w(z)|^2)^{\alpha}}\cdot|\sigma^{\prime}_w(z)|\\ \leq& \frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|w|^2)^{\alpha-1}}+\|f\|_{\mathcal{B}^{\alpha}}\frac{4^{\alpha-1}}{(1-|w|^2)^{\alpha-1}}\\ \lesssim&\frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|w|^2)^{\alpha-1}}. \end{align*} $$
This implies that the condition (ii) holds.
For (iii), by Lemma 2.5, we get that
$$ \begin{align*}|f(\sigma_w(z))|\lesssim\frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|\sigma_w(z)|^2)^{\alpha-1}}\lesssim \frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|z|^2)^{\alpha-1}(1-|w|)^{\alpha-1}}.\end{align*} $$
Hence, all conditions of Lemma 2.1 hold true.
Note that for
$dA$
-
$a.e.$
$z\in \mathbb {D}$
$$ \begin{align*}\mathcal{H}_{K,\mu}f(z)=\left( (B)\int_{\mathbb{D}}K(w)f\circ\sigma_wd\mu(w)\right)(z)\,, \end{align*} $$
where the right-hand side is an analytic Bochner integral since f is analytic. Thus, to show that
$\mathcal {H}_{K,\,\mu }f$
is analytic, it suffices to prove that
$\mathcal {H}_{K,\,\mu }f$
is continuous, but its proof is just similar to the previous ones and we leave it to the interested readers.
At last, we have
$$ \begin{align*} \|\mathcal{H}_{K,\mu}f\|_{\mathcal{B}^{\alpha}}\leq&\int_{\mathbb{D}}|K(w)|\cdot\|f\circ\sigma_w\|_{\mathcal{B}^{\alpha}}d\mu(w)\\ \lesssim&\|f\|_{\mathcal{B}^{\alpha}}\int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|^2)^{\alpha-1}} d\mu(w), \end{align*} $$
which completes the proof.
In the following, we show the sufficient conditions for the boundedness of Hausdorff operators between different Bloch type spaces.
Theorem 5.2 Let
$0<\alpha ,\beta <\infty $
. Suppose that for any
$w\in \mathbb {D}$
,
$$ \begin{align*}\sup_{z\in\mathbb{D}}\frac{|1-\overline{w}z|^{2\alpha-2}}{(1-|w|^2)^{\alpha-1}(1-|z|^2)^{\alpha-\beta}}<\infty.\end{align*} $$
-
(1) If
$\kern1pt1<\alpha <\infty $
and the function K satisfies then the operator
$$ \begin{align*}\int_{\mathbb{D}}\frac{|K(w)|}{(1-|w|)^{\alpha-1}}d\mu(w)<\infty,\end{align*} $$
$\mathcal {H}_{K,\mu }:\mathcal {B}^{\alpha }\rightarrow \mathcal {B}^{\beta }$
is bounded.
-
(2) If
$\alpha =1$
and the function K satisfies then the operator
$$ \begin{align*}\int_{\mathbb{D}}|K(w)|\log\frac{2}{1-|w|} d\mu(w)<\infty,\end{align*} $$
$\mathcal {H}_{K,\mu }:\mathcal {B}^{\alpha }\rightarrow \mathcal {B}^{\beta }$
is bounded.
-
(3) If
$0<\alpha <1$
and the function K satisfies
$ \int _{\mathbb {D}}|K(w)|d\mu (w)<\infty $
, then the operator
$\mathcal {H}_{K,\mu }:\mathcal {B}^{\alpha }\rightarrow \mathcal {B}^{\beta }$
is bounded.
Proof The idea of the proof is analogous to that in Theorem 5.1, so we only give some key steps. For any
$f\in \mathcal {B}^{\alpha }$
, if
$\alpha>1$
, by Lemma 2.5 and the assumptions,
$$ \begin{align*} \|f\circ\sigma_w\|_{\mathcal{B}^{\beta}}=&|f(w)|+\sup_{z\in\mathbb{D}}(1-|z|^2)^{\beta}|f'(\sigma_w(z))|\cdot|\sigma^{\prime}_w(z)|\\ \lesssim& \frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|w|^2)^{\alpha-1}}+\sup_{z\in\mathbb{D}}(1-|z|^2)^{\beta}\frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|\sigma_w(z)|^2)^{\alpha}}\cdot|\sigma^{\prime}_w(z)|\\ \leq& \frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|w|^2)^{\alpha-1}}+\|f\|_{\mathcal{B}^{\alpha}}\sup_{z\in\mathbb{D}}\frac{|1-\overline{w}z|^{2\alpha-2}}{(1-|w|^2)^{\alpha-1}(1-|z|^2)^{\alpha-\beta}}\\ \lesssim&\frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|w|^2)^{\alpha-1}}+\|f\|_{\mathcal{B}^{\alpha}}\\ \lesssim&\frac{\|f\|_{\mathcal{B}^{\alpha}}}{(1-|w|^2)^{\alpha-1}}. \end{align*} $$
For
$\alpha =1$
, Lemma 2.5 now gives
$$ \begin{align*}\|f\circ\sigma_w\|_{\mathcal{B}^{\beta}} \lesssim\|f\|_{\mathcal{B}^{\alpha}}\log\frac{2}{1-|w|^2}+\|f\|_{\mathcal{B}^{\alpha}} \lesssim\|f\|_{\mathcal{B}^{\alpha}}\log\frac{2}{1-|w|^2}. \end{align*} $$
When
$0<\alpha <1$
, we have
$$ \begin{align*}\|f\circ\sigma_w\|_{\mathcal{B}^{\beta}} \lesssim\|f\|_{\mathcal{B}^{\alpha}}+\|f\|_{\mathcal{B}^{\alpha}} \lesssim\|f\|_{\mathcal{B}^{\alpha}}. \end{align*} $$
Then the standard procedures, analogous to the previous ones, finish the proof.
