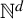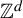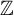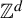1 Introduction
Bohr chaoticity is a topological invariant introduced in [Reference Fan, Fan, Ryzhikov and Shen9] for topological dynamical systems. For defining this invariant, we recall that a sequence
![]() $\boldsymbol w=(w_n)_{n\ge 0}\in \ell ^{\infty } (\mathbb {N},\mathbb {C})$
is a non-trivial weight sequence if
$\boldsymbol w=(w_n)_{n\ge 0}\in \ell ^{\infty } (\mathbb {N},\mathbb {C})$
is a non-trivial weight sequence if
 $$ \begin{align} \limsup_{N\to \infty} \frac{1}{N} \sum_{n=0}^{N-1}|w_n|>0. \end{align} $$
$$ \begin{align} \limsup_{N\to \infty} \frac{1}{N} \sum_{n=0}^{N-1}|w_n|>0. \end{align} $$
A non-trivial weight sequence
![]() $\boldsymbol {w}$
is orthogonal to a topological dynamical system
$\boldsymbol {w}$
is orthogonal to a topological dynamical system
![]() $(X,T)$
if
$(X,T)$
if
 $$ \begin{align} \lim_{N\to\infty} \frac 1N \sum_{n=0}^{N-1} w_n f(T^nx) =0 \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac 1N \sum_{n=0}^{N-1} w_n f(T^nx) =0 \end{align} $$
for every continuous function
![]() $f\in C(X)$
and every
$f\in C(X)$
and every
![]() $x\in X$
.
$x\in X$
.
Definition 1.1. [Reference Fan, Fan, Ryzhikov and Shen9]
A topological dynamical system
![]() $(X, T)$
is Bohr chaotic if it is non-orthogonal to every non-trivial weight sequence
$(X, T)$
is Bohr chaotic if it is non-orthogonal to every non-trivial weight sequence
![]() $\boldsymbol {w}\in \ell ^{\infty }(\mathbb {N},\mathbb {C})$
. In other words,
$\boldsymbol {w}\in \ell ^{\infty }(\mathbb {N},\mathbb {C})$
. In other words,
![]() $(X,T)$
is Bohr chaotic if we can find, for every non-trivial weight sequence
$(X,T)$
is Bohr chaotic if we can find, for every non-trivial weight sequence
![]() $\boldsymbol {w}\in \ell ^{\infty }(\mathbb {N},\mathbb {C})$
, a continuous function
$\boldsymbol {w}\in \ell ^{\infty }(\mathbb {N},\mathbb {C})$
, a continuous function
![]() $g\in C(X)$
and a point
$g\in C(X)$
and a point
![]() $x \in X$
such that
$x \in X$
such that
 $$ \begin{align} \limsup_{N\to \infty} \frac{1}{N} \bigg|\!\sum_{n=0}^{N-1}w_n g(T^n x)\bigg|>0. \end{align} $$
$$ \begin{align} \limsup_{N\to \infty} \frac{1}{N} \bigg|\!\sum_{n=0}^{N-1}w_n g(T^n x)\bigg|>0. \end{align} $$
Bohr chaotic systems must have positive entropy: for example, almost all
![]() $(\tfrac 12,\tfrac 12)$
Bernoulli sequences taking values
$(\tfrac 12,\tfrac 12)$
Bernoulli sequences taking values
![]() $-1$
and
$-1$
and
![]() $1$
are orthogonal to every topological dynamical system
$1$
are orthogonal to every topological dynamical system
![]() $(X,T)$
with zero entropy (see [Reference El Abdalaoui, Kułaga-Przymus, Lemańczyk and de la Rue5]). We list some further basic results on Bohr chaoticity, taken from [Reference Fan, Fan, Ryzhikov and Shen9]:
$(X,T)$
with zero entropy (see [Reference El Abdalaoui, Kułaga-Przymus, Lemańczyk and de la Rue5]). We list some further basic results on Bohr chaoticity, taken from [Reference Fan, Fan, Ryzhikov and Shen9]:
-
• any extension of a Bohr chaotic topological dynamical system is Bohr chaotic;
-
• if a topological dynamical system
 $(X,T)$
has a non-empty, closed, T-invariant subset
$(X,T)$
has a non-empty, closed, T-invariant subset
 $Y\subset X$
such that
$Y\subset X$
such that
 $(Y,T|_Y)$
is Bohr chaotic, then
$(Y,T|_Y)$
is Bohr chaotic, then
 $(X,T)$
is Bohr chaotic;
$(X,T)$
is Bohr chaotic; -
• no uniquely ergodic dynamical system is Bohr chaotic (this is generalized by Tal [Reference Tal31] to systems having at most countably many ergodic measures);
-
• all affine toral endomorphisms of positive entropy are Bohr chaotic;
-
• all systems having an m-order horseshoe,
 $m\ge 1$
, are Bohr chaotic. By an m-order horseshoe K of a system
$m\ge 1$
, are Bohr chaotic. By an m-order horseshoe K of a system
 $(X, T)$
, we mean a
$(X, T)$
, we mean a
 $T^m$
-invariant closed non-empty set
$T^m$
-invariant closed non-empty set
 $K\subset X$
such that the subsystem
$K\subset X$
such that the subsystem
 $(K, T^m)$
is conjugate either to the one-sided shift
$(K, T^m)$
is conjugate either to the one-sided shift
 $(\{0, 1\}^{\mathbb {N}}, \sigma )$
or to the two-sided shift
$(\{0, 1\}^{\mathbb {N}}, \sigma )$
or to the two-sided shift
 $(\{0,1\}^{\mathbb {Z}}, \sigma )$
;
$(\{0,1\}^{\mathbb {Z}}, \sigma )$
; -
• all subshifts of finite type with positive entropy are Bohr chaotic;
-
• all piecewise monotone
 $C^1$
interval maps of positive entropy are Bohr chaotic. For example, the
$C^1$
interval maps of positive entropy are Bohr chaotic. For example, the
 $\beta $
-shifts with
$\beta $
-shifts with
 $\beta>1$
;
$\beta>1$
; -
• every
 $C^{1+\delta }$
(
$C^{1+\delta }$
(
 $\delta>0$
) diffeomorphism of a compact smooth manifold admitting an ergodic non-atomic Borel probability invariant measure with non-zero Lyapunov exponents is Bohr chaotic.
$\delta>0$
) diffeomorphism of a compact smooth manifold admitting an ergodic non-atomic Borel probability invariant measure with non-zero Lyapunov exponents is Bohr chaotic.
The reason for the last two classes is that any such system admits a subsystem which is conjugate to a subshift of finite type of positive entropy [Reference Katok15, Reference Young32].
It is interesting to note that for the examples of Bohr chaotic systems constructed in [Reference Fan, Fan, Ryzhikov and Shen9], the sets of points
![]() $x\in X$
satisfying equation (1.3) are large in the sense that they are of full Hausdorff dimension. Actually, weighted ergodic averages on typical dynamical systems would be multifractal and a study on symbolic spaces is carried out in [Reference Fan7].
$x\in X$
satisfying equation (1.3) are large in the sense that they are of full Hausdorff dimension. Actually, weighted ergodic averages on typical dynamical systems would be multifractal and a study on symbolic spaces is carried out in [Reference Fan7].
In the present paper, we extend the notion of Bohr chaoticity from
![]() ${\mathbb Z}$
- to
${\mathbb Z}$
- to
![]() ${\mathbb Z}^d$
-actions and prove that a large class of algebraic dynamical systems—the so-called principal algebraic actions—are Bohr chaotic, provided they have positive entropy.
${\mathbb Z}^d$
-actions and prove that a large class of algebraic dynamical systems—the so-called principal algebraic actions—are Bohr chaotic, provided they have positive entropy.
By analogy with equation (1.1), we say that a complex sequence
![]() $\boldsymbol w=(w_{\boldsymbol n})_{\boldsymbol n \in \mathbb {N}^d}\in \ell ^{\infty }(\mathbb {N}^d,\mathbb C)$
is a non-trivial weight if
$\boldsymbol w=(w_{\boldsymbol n})_{\boldsymbol n \in \mathbb {N}^d}\in \ell ^{\infty }(\mathbb {N}^d,\mathbb C)$
is a non-trivial weight if
 $$ \begin{align*} \limsup_{N\to \infty} \frac{1}{N^d} \sum_{{\boldsymbol n} \in [0, N-1]^d} |w_{\boldsymbol n}|>0. \end{align*} $$
$$ \begin{align*} \limsup_{N\to \infty} \frac{1}{N^d} \sum_{{\boldsymbol n} \in [0, N-1]^d} |w_{\boldsymbol n}|>0. \end{align*} $$
Consider a continuous
![]() $\mathbb {N}^d$
- or
$\mathbb {N}^d$
- or
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $\alpha \colon \boldsymbol {n}\mapsto \alpha ^{\boldsymbol {n}}$
on some compact space X. As in equation (1.2), say that a (non-trivial) weight
$\alpha \colon \boldsymbol {n}\mapsto \alpha ^{\boldsymbol {n}}$
on some compact space X. As in equation (1.2), say that a (non-trivial) weight
![]() $(w_{\boldsymbol n})_{\boldsymbol n \in \mathbb {N}^d}$
is orthogonal to the dynamical system
$(w_{\boldsymbol n})_{\boldsymbol n \in \mathbb {N}^d}$
is orthogonal to the dynamical system
![]() $(X, \alpha )$
if
$(X, \alpha )$
if
 $$ \begin{align} \lim_{N\to \infty} \frac{1}{N^d} \sum_{{\boldsymbol n} \in [0, N-1]^d} w_{\boldsymbol n} g (\alpha ^{\boldsymbol n} x) =0 \end{align} $$
$$ \begin{align} \lim_{N\to \infty} \frac{1}{N^d} \sum_{{\boldsymbol n} \in [0, N-1]^d} w_{\boldsymbol n} g (\alpha ^{\boldsymbol n} x) =0 \end{align} $$
for every continuous function
![]() $g \in C(X)$
and every point
$g \in C(X)$
and every point
![]() $x\in X$
.
$x\in X$
.
Definition 1.2. If
![]() $\alpha $
is a continuous
$\alpha $
is a continuous
![]() $\mathbb {N}^d$
- or
$\mathbb {N}^d$
- or
![]() ${\mathbb Z}^d$
-action on a compact space X, we call
${\mathbb Z}^d$
-action on a compact space X, we call
![]() $(X, \alpha )$
Bohr chaotic if it is not orthogonal to any non-trivial weight, that is to say, if for any non-trivial weight
$(X, \alpha )$
Bohr chaotic if it is not orthogonal to any non-trivial weight, that is to say, if for any non-trivial weight
![]() $\boldsymbol w=(w_{\boldsymbol n})_{\boldsymbol n \in \mathbb {N}^d}$
, there exist
$\boldsymbol w=(w_{\boldsymbol n})_{\boldsymbol n \in \mathbb {N}^d}$
, there exist
![]() $g \in C(X)$
and
$g \in C(X)$
and
![]() $x\in X$
such that
$x\in X$
such that
 $$ \begin{align} \limsup_{N\to \infty} \frac{1}{N^d} \bigg|\!\sum_{{\boldsymbol n} \in [0, N-1]^d} w_{\boldsymbol n} g(\alpha ^{\boldsymbol n} x)\bigg|>0. \end{align} $$
$$ \begin{align} \limsup_{N\to \infty} \frac{1}{N^d} \bigg|\!\sum_{{\boldsymbol n} \in [0, N-1]^d} w_{\boldsymbol n} g(\alpha ^{\boldsymbol n} x)\bigg|>0. \end{align} $$
Note that if
![]() $\alpha $
is a continuous
$\alpha $
is a continuous
![]() $\mathbb {N}^d$
-action on X and if
$\mathbb {N}^d$
-action on X and if
![]() $(\bar {X},\bar {\alpha })$
is the natural extension of
$(\bar {X},\bar {\alpha })$
is the natural extension of
![]() $(X,\alpha )$
to a continuous
$(X,\alpha )$
to a continuous
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $\bar {\alpha }$
on a compact space
$\bar {\alpha }$
on a compact space
![]() $\bar {X}$
, then
$\bar {X}$
, then
![]() $(\bar {X},\bar {\alpha })$
is Bohr chaotic if and only if the same is true for
$(\bar {X},\bar {\alpha })$
is Bohr chaotic if and only if the same is true for
![]() $(X,\alpha )$
. Conversely, if a continuous
$(X,\alpha )$
. Conversely, if a continuous
![]() $\mathbb {Z}^d$
-action is Bohr chaotic, it is obviously also Bohr chaotic as an
$\mathbb {Z}^d$
-action is Bohr chaotic, it is obviously also Bohr chaotic as an
![]() $\mathbb {N}^d$
-action. In view of this last property, we focus our attention in much of this paper on Bohr chaoticity of
$\mathbb {N}^d$
-action. In view of this last property, we focus our attention in much of this paper on Bohr chaoticity of
![]() $\mathbb {Z}^d$
-actions, referring to
$\mathbb {Z}^d$
-actions, referring to
![]() $\mathbb {N}^d$
-actions only where necessary (like in Proposition 3.1 or Example 3.3).
$\mathbb {N}^d$
-actions only where necessary (like in Proposition 3.1 or Example 3.3).
As in the one-dimensional case, one can easily verify the following properties of continuous
![]() $\mathbb {Z}^d$
-actions
$\mathbb {Z}^d$
-actions
![]() $(X,\alpha )$
:
$(X,\alpha )$
:
-
(i) if X has a closed,
 $\alpha $
-invariant subset Y such that
$\alpha $
-invariant subset Y such that
 $(Y,\alpha |_Y)$
is Bohr chaotic, then
$(Y,\alpha |_Y)$
is Bohr chaotic, then
 $(X,\alpha )$
is Bohr chaotic;
$(X,\alpha )$
is Bohr chaotic; -
(ii) if
 $(X,\alpha )$
has a Bohr chaotic factor
$(X,\alpha )$
has a Bohr chaotic factor
 $(Y,\beta )$
(that is, if
$(Y,\beta )$
(that is, if
 $(Y,\beta )$
is a Bohr chaotic
$(Y,\beta )$
is a Bohr chaotic
 $\mathbb {Z}^d$
-action and there exists a continuous, surjective, equivariant map
$\mathbb {Z}^d$
-action and there exists a continuous, surjective, equivariant map
 $\phi \colon X\to Y$
), then
$\phi \colon X\to Y$
), then
 $(X,\alpha )$
is Bohr chaotic.
$(X,\alpha )$
is Bohr chaotic.
In particular, Bohr chaoticity is an invariant of topological conjugacy.
Our main results will be proved by using Riesz product measures borrowed from harmonic analysis and the main technical tool is the notion of m-goodness.
The paper is organized as follows. In §2, we present algebraic
![]() ${\mathbb Z}^d$
-actions and their basic properties, state our main results on Bohr chaoticity of principal algebraic
${\mathbb Z}^d$
-actions and their basic properties, state our main results on Bohr chaoticity of principal algebraic
![]() $\mathbb {Z}^d$
-actions (Theorems 2.1 and 2.3), and prove that Bohr chaotic algebraic
$\mathbb {Z}^d$
-actions (Theorems 2.1 and 2.3), and prove that Bohr chaotic algebraic
![]() $\mathbb {Z}^d$
-actions have to have completely positive entropy (Example 3.2). In §3, we show that zero-entropy
$\mathbb {Z}^d$
-actions have to have completely positive entropy (Example 3.2). In §3, we show that zero-entropy
![]() $\mathbb {Z}^d$
-actions are not Bohr chaotic. Our main tool, Riesz products, is presented in §4 where lacunarity of polynomials is discussed. In §5, we prove that any principal algebraic
$\mathbb {Z}^d$
-actions are not Bohr chaotic. Our main tool, Riesz products, is presented in §4 where lacunarity of polynomials is discussed. In §5, we prove that any principal algebraic
![]() ${\mathbb Z}^d$
-action defined by a so-called m-good polynomial is Bohr chaotic (Theorem 5.1). Section 6 is devoted to the proof of m-goodness for all irreducible polynomials
${\mathbb Z}^d$
-action defined by a so-called m-good polynomial is Bohr chaotic (Theorem 5.1). Section 6 is devoted to the proof of m-goodness for all irreducible polynomials
![]() $f\in R_1$
with positive Mahler measure, and Theorem 2.1 (for
$f\in R_1$
with positive Mahler measure, and Theorem 2.1 (for
![]() $d=1$
) is proved there. Theorem 2.3 (for
$d=1$
) is proved there. Theorem 2.3 (for
![]() $d \ge 2$
) is proved in §7, where we prove a gap theorem (Theorem 7.3) for irreducible polynomials which admit summable homoclinic points. This gap theorem is of independent interest. In §8, we speculate briefly on the necessity of our atorality assumptions for our main results and give some examples of Bohr chaotic principal actions arising from toral polynomials.
$d \ge 2$
) is proved in §7, where we prove a gap theorem (Theorem 7.3) for irreducible polynomials which admit summable homoclinic points. This gap theorem is of independent interest. In §8, we speculate briefly on the necessity of our atorality assumptions for our main results and give some examples of Bohr chaotic principal actions arising from toral polynomials.
2 Algebraic
 ${\mathbb Z}^d$
-actions
${\mathbb Z}^d$
-actions
In this section, we present the principal algebraic
![]() ${\mathbb Z}^d$
-actions which are our main objects of study and then state our main results (Theorems 2.1 and 2.3).
${\mathbb Z}^d$
-actions which are our main objects of study and then state our main results (Theorems 2.1 and 2.3).
An algebraic
![]() $\mathbb {Z}^d$
-action is an action of
$\mathbb {Z}^d$
-action is an action of
![]() $\mathbb {Z}^d$
by (continuous) automorphisms of a compact metrizable abelian group. Algebraic
$\mathbb {Z}^d$
by (continuous) automorphisms of a compact metrizable abelian group. Algebraic
![]() $\mathbb {Z}^d$
-actions provide a useful source of examples of continuous
$\mathbb {Z}^d$
-actions provide a useful source of examples of continuous
![]() $\mathbb {Z}^d$
-actions with a wide range of properties, both with zero and with positive entropy, and with or without Bohr chaoticity.
$\mathbb {Z}^d$
-actions with a wide range of properties, both with zero and with positive entropy, and with or without Bohr chaoticity.
We are interested in a particular family of algebraic
![]() $\mathbb {Z}^d$
-actions, the so-called cyclic actions. Denote by
$\mathbb {Z}^d$
-actions, the so-called cyclic actions. Denote by
![]() $\sigma $
the shift-action of
$\sigma $
the shift-action of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb {T}^{\mathbb {Z}^d}$
given by
$\mathbb {T}^{\mathbb {Z}^d}$
given by
for every
![]() $x=(x_{\boldsymbol {n}})_{\boldsymbol {n}\in \mathbb {Z}^d}\in \mathbb {T}^{\mathbb {Z}^d}$
. A cyclic algebraic
$x=(x_{\boldsymbol {n}})_{\boldsymbol {n}\in \mathbb {Z}^d}\in \mathbb {T}^{\mathbb {Z}^d}$
. A cyclic algebraic
![]() $\mathbb {Z}^d$
-action is a pair
$\mathbb {Z}^d$
-action is a pair
![]() $(X,\alpha _X)$
, where
$(X,\alpha _X)$
, where
![]() $X\subset \mathbb {T}^{\mathbb {Z}^d}$
is a closed, shift-invariant subgroup and
$X\subset \mathbb {T}^{\mathbb {Z}^d}$
is a closed, shift-invariant subgroup and
![]() $\alpha _X=\sigma |_X$
is the restriction to X of the shift-action
$\alpha _X=\sigma |_X$
is the restriction to X of the shift-action
![]() $\sigma $
in equation (2.1).
$\sigma $
in equation (2.1).
To describe these actions in more detail, we denote by
![]() $R_d = \mathbb {Z}[z_1^{\pm 1},\ldots ,z_d^{\pm 1}]$
the ring of Laurent polynomials in the variables
$R_d = \mathbb {Z}[z_1^{\pm 1},\ldots ,z_d^{\pm 1}]$
the ring of Laurent polynomials in the variables
![]() $z_1,\ldots ,z_d$
with coefficients in
$z_1,\ldots ,z_d$
with coefficients in
![]() $\mathbb {Z}$
. Every
$\mathbb {Z}$
. Every
![]() $f\in R_d$
will be written as
$f\in R_d$
will be written as
![]() $f=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}f_{\boldsymbol n} {{\boldsymbol z}}^{\boldsymbol n}$
with
$f=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}f_{\boldsymbol n} {{\boldsymbol z}}^{\boldsymbol n}$
with
![]() $f_{\boldsymbol n}\in \mathbb {Z}$
and
$f_{\boldsymbol n}\in \mathbb {Z}$
and
![]() $\boldsymbol {z}^{\boldsymbol n}=z_1^{n_1}\cdots z_d^{n_d}$
for every
$\boldsymbol {z}^{\boldsymbol n}=z_1^{n_1}\cdots z_d^{n_d}$
for every
![]() ${\boldsymbol n}=(n_1,\ldots ,n_d)\in \mathbb {Z}^d$
. The set
${\boldsymbol n}=(n_1,\ldots ,n_d)\in \mathbb {Z}^d$
. The set
![]() $\textsf {supp}(f) = \{{\boldsymbol n}\in \mathbb {Z}^d\mid f_{\boldsymbol n} \ne 0\}$
will be called the support of f, and we set
$\textsf {supp}(f) = \{{\boldsymbol n}\in \mathbb {Z}^d\mid f_{\boldsymbol n} \ne 0\}$
will be called the support of f, and we set
![]() $\|f\|_1=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}|f_{\boldsymbol n}|$
and
$\|f\|_1=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}|f_{\boldsymbol n}|$
and
![]() $\|f\|_\infty =\max _{{\boldsymbol n}\in \mathbb {Z}^d}|f_{\boldsymbol n}|$
. Following standard terminology, we call a non-zero element
$\|f\|_\infty =\max _{{\boldsymbol n}\in \mathbb {Z}^d}|f_{\boldsymbol n}|$
. Following standard terminology, we call a non-zero element
![]() $f\in R_d$
primitive if the greatest common divisor
$f\in R_d$
primitive if the greatest common divisor
![]() $\gcd (\{f_{\boldsymbol n}\mid {\boldsymbol n}\in \mathbb {Z}^d\})$
of its coefficients is equal to
$\gcd (\{f_{\boldsymbol n}\mid {\boldsymbol n}\in \mathbb {Z}^d\})$
of its coefficients is equal to
![]() $1$
, and irreducible if it is not a product of two non-units in
$1$
, and irreducible if it is not a product of two non-units in
![]() $R_d$
. For example,
$R_d$
. For example,
![]() $2{\boldsymbol z}^{\boldsymbol n}$
is irreducible, but not primitive, while
$2{\boldsymbol z}^{\boldsymbol n}$
is irreducible, but not primitive, while
![]() $2(1+{\boldsymbol z}^{\boldsymbol n})$
is neither primitive nor irreducible, for every
$2(1+{\boldsymbol z}^{\boldsymbol n})$
is neither primitive nor irreducible, for every
![]() ${\boldsymbol n}\in \mathbb {Z}^d$
.
${\boldsymbol n}\in \mathbb {Z}^d$
.
Every non-zero
![]() $f=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}f_{\boldsymbol n} {{\boldsymbol z}}^{\boldsymbol n}\in R_d$
defines a surjective group homomorphism
$f=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}f_{\boldsymbol n} {{\boldsymbol z}}^{\boldsymbol n}\in R_d$
defines a surjective group homomorphism
![]() $f(\sigma )=\sum _{\boldsymbol {m}\in \mathbb {Z}^d}f_{\boldsymbol {m}}\sigma ^{\boldsymbol {m}}\colon \mathbb {T}^{\mathbb {Z}^d} \to \mathbb {T}^{\mathbb {Z}^d}$
. Consider the closed, shift-invariant subgroup
$f(\sigma )=\sum _{\boldsymbol {m}\in \mathbb {Z}^d}f_{\boldsymbol {m}}\sigma ^{\boldsymbol {m}}\colon \mathbb {T}^{\mathbb {Z}^d} \to \mathbb {T}^{\mathbb {Z}^d}$
. Consider the closed, shift-invariant subgroup
 $$ \begin{align} X_f =\bigg\{ x\in{\mathbb T}^{\mathbb Z^d}\bigg| \sum_{{\boldsymbol m}\in{\mathbb Z}^d} x_{{\boldsymbol n}+{\boldsymbol m}} f_{{\boldsymbol m}} =0 \enspace (\text{mod}\;1)\enspace \text{for all}\enspace {\boldsymbol n}\in{\mathbb Z}^d\bigg\} = \ker(f(\sigma ))\subset \mathbb{T}^{\mathbb{Z}^d}, \end{align} $$
$$ \begin{align} X_f =\bigg\{ x\in{\mathbb T}^{\mathbb Z^d}\bigg| \sum_{{\boldsymbol m}\in{\mathbb Z}^d} x_{{\boldsymbol n}+{\boldsymbol m}} f_{{\boldsymbol m}} =0 \enspace (\text{mod}\;1)\enspace \text{for all}\enspace {\boldsymbol n}\in{\mathbb Z}^d\bigg\} = \ker(f(\sigma ))\subset \mathbb{T}^{\mathbb{Z}^d}, \end{align} $$
and denote by
the restriction to
![]() $X_f$
of the shift-action
$X_f$
of the shift-action
![]() $\sigma $
on
$\sigma $
on
![]() $\mathbb {T}^{\mathbb {Z}^d}$
. The dynamical system
$\mathbb {T}^{\mathbb {Z}^d}$
. The dynamical system
![]() $(X_f,\alpha _f)$
is called the principal algebraic action corresponding to
$(X_f,\alpha _f)$
is called the principal algebraic action corresponding to
![]() $f\in R_d$
.
$f\in R_d$
.
Formally we can extend this definition of a principal action
![]() $(X_f,\alpha _f)$
to include the case
$(X_f,\alpha _f)$
to include the case
![]() $f=0$
, the zero polynomial in
$f=0$
, the zero polynomial in
![]() $R_d$
. In this case, the definitions in equations (2.2) and (2.3) reduce to
$R_d$
. In this case, the definitions in equations (2.2) and (2.3) reduce to
![]() $X_f=\mathbb {T}^{\mathbb {Z}^d}$
and
$X_f=\mathbb {T}^{\mathbb {Z}^d}$
and
![]() $\alpha _f = \sigma $
, that is,
$\alpha _f = \sigma $
, that is,
![]() $(X_f,\alpha _f)$
is simply the shift action of
$(X_f,\alpha _f)$
is simply the shift action of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb {T}^{\mathbb {Z}^d}$
.
$\mathbb {T}^{\mathbb {Z}^d}$
.
For every cyclic algebraic action
![]() $(X,\alpha _X)$
with
$(X,\alpha _X)$
with
![]() $X\subsetneq \mathbb {T}^{\mathbb {Z}^d}$
, the set
$X\subsetneq \mathbb {T}^{\mathbb {Z}^d}$
, the set
is an ideal in
![]() $R_d$
(which is, of course, finitely generated since the ring
$R_d$
(which is, of course, finitely generated since the ring
![]() $R_d$
is Noetherian) and
$R_d$
is Noetherian) and
![]() $X= \bigcap _{f \in I_X} X_f$
. Conversely, if
$X= \bigcap _{f \in I_X} X_f$
. Conversely, if
![]() $I\subset R_d$
is an ideal, generated by
$I\subset R_d$
is an ideal, generated by
![]() $\{f^{(1)},\ldots ,f^{(r)}\}$
, say, we denote by
$\{f^{(1)},\ldots ,f^{(r)}\}$
, say, we denote by
![]() $(X_I,\alpha _I)$
the cyclic
$(X_I,\alpha _I)$
the cyclic
![]() $\mathbb {Z}^d$
-action defined by
$\mathbb {Z}^d$
-action defined by
 $$ \begin{align} X_I=\bigcap_{f\in I} X_f = \bigcap_{i=1}^r X_{f^{(i)}}\subset \mathbb{T}^{\mathbb{Z}^d}\quad \text{and}\quad \alpha _I=\sigma |_{X_I}, \end{align} $$
$$ \begin{align} X_I=\bigcap_{f\in I} X_f = \bigcap_{i=1}^r X_{f^{(i)}}\subset \mathbb{T}^{\mathbb{Z}^d}\quad \text{and}\quad \alpha _I=\sigma |_{X_I}, \end{align} $$
and write
![]() $\unicode{x3bb} _I$
for the normalized Haar measure of
$\unicode{x3bb} _I$
for the normalized Haar measure of
![]() $X_I$
. If the ideal
$X_I$
. If the ideal
![]() $I\subset R_d$
is principal,
$I\subset R_d$
is principal,
![]() $I=(f)$
, say, we write
$I=(f)$
, say, we write
![]() $(X_f,\alpha _f)$
instead of
$(X_f,\alpha _f)$
instead of
![]() $(X_{(f)},\alpha _{(f)})$
and denote by
$(X_{(f)},\alpha _{(f)})$
and denote by
![]() $\unicode{x3bb} _f$
the normalized Haar measure on
$\unicode{x3bb} _f$
the normalized Haar measure on
![]() $X_f$
.
$X_f$
.
2.1 Mahler measure
The topological entropy
![]() $h_{\text {top}}(\alpha _f)$
of a principal algebraic action
$h_{\text {top}}(\alpha _f)$
of a principal algebraic action
![]() $(X_f,\alpha _f)$
,
$(X_f,\alpha _f)$
,
![]() $f\in R_d\smallsetminus \{0\}$
, coincides with its measure-theoretic entropy
$f\in R_d\smallsetminus \{0\}$
, coincides with its measure-theoretic entropy
![]() $h_{\unicode{x3bb} _f}(\alpha _f)$
and is given by the (logarithmic) Mahler measure of its defining polynomial f:
$h_{\unicode{x3bb} _f}(\alpha _f)$
and is given by the (logarithmic) Mahler measure of its defining polynomial f:

For polynomials in a single variable (that is, for
![]() $f\in R_1$
), Mahler measure can be computed using Jensen’s formula: let
$f\in R_1$
), Mahler measure can be computed using Jensen’s formula: let
![]() $f(z)=f_0+f_1z +\cdots +f_k z^k$
with
$f(z)=f_0+f_1z +\cdots +f_k z^k$
with
![]() $f_0f_k\ne 0$
and (complex) roots
$f_0f_k\ne 0$
and (complex) roots
![]() $\unicode{x3bb} _1,\ldots , \unicode{x3bb} _k$
. Then
$\unicode{x3bb} _1,\ldots , \unicode{x3bb} _k$
. Then
 $$ \begin{align} \mathsf{m}(f)=\log|f_k| + \sum_{j:\ |\unicode{x3bb}_j|>1} \log|\unicode{x3bb}_j| \end{align} $$
$$ \begin{align} \mathsf{m}(f)=\log|f_k| + \sum_{j:\ |\unicode{x3bb}_j|>1} \log|\unicode{x3bb}_j| \end{align} $$
(cf. [Reference Lind, Schmidt and Ward21, p. 597], [Reference Schmidt29, equation (16.2)], or [Reference Young33]). The Kronecker lemma [Reference Kronecker17] states that if a polynomial
![]() $f\in R_1$
is irreducible, monic, and all its roots have absolute value at most
$f\in R_1$
is irreducible, monic, and all its roots have absolute value at most
![]() $1$
, then f is cyclotomic, that is, for some integer n,
$1$
, then f is cyclotomic, that is, for some integer n,
 $$ \begin{align} f(z)=\Phi_n(z) := \prod_{\substack{1\le \ell\le n \\ \textsf{gcd}(\ell,n)=1}} (z-e^{2 \pi i\ell/n}). \end{align} $$
$$ \begin{align} f(z)=\Phi_n(z) := \prod_{\substack{1\le \ell\le n \\ \textsf{gcd}(\ell,n)=1}} (z-e^{2 \pi i\ell/n}). \end{align} $$
Since Mahler measure is additive in the sense that
![]() $\mathsf {m}(f\cdot g)=\mathsf {m}(f)+\mathsf {m}(g)$
for all
$\mathsf {m}(f\cdot g)=\mathsf {m}(f)+\mathsf {m}(g)$
for all
![]() ${f,g\in R_d\smallsetminus \{0\}}$
, any
${f,g\in R_d\smallsetminus \{0\}}$
, any
![]() $f\in R_1\smallsetminus \{0\}$
with
$f\in R_1\smallsetminus \{0\}$
with
![]() $\mathsf {m}(f)=0$
must be a product of cyclotomic polynomials.
$\mathsf {m}(f)=0$
must be a product of cyclotomic polynomials.
A similar statement is true for multivariate polynomials as well: if
![]() $f\in R_d\smallsetminus \{0\}$
, then
$f\in R_d\smallsetminus \{0\}$
, then
![]() $\mathsf {m}(f)=0$
if and only if f is a product of so-called generalized cyclotomic polynomials
$\mathsf {m}(f)=0$
if and only if f is a product of so-called generalized cyclotomic polynomials
for some integers
![]() $m_1,\ldots , m_r$
and
$m_1,\ldots , m_r$
and
![]() ${\boldsymbol n}_0,{\boldsymbol n}_1,\ldots , {\boldsymbol n}_r\in {\mathbb Z}^d$
([Reference Boyd2], [Reference Schmidt29, Theorem 19.5], [Reference Smyth30]).
${\boldsymbol n}_0,{\boldsymbol n}_1,\ldots , {\boldsymbol n}_r\in {\mathbb Z}^d$
([Reference Boyd2], [Reference Schmidt29, Theorem 19.5], [Reference Smyth30]).
We recall the following properties of cyclic algebraic
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $(X_I,\alpha _I)$
(cf. [Reference Schmidt29, Ch. 6]).
$(X_I,\alpha _I)$
(cf. [Reference Schmidt29, Ch. 6]).
-
• The normalized Haar measure
 $\unicode{x3bb} _{X_I}$
of
$\unicode{x3bb} _{X_I}$
of
 $X_I$
is shift-invariant.
$X_I$
is shift-invariant. -
• If
 $I\subset R_d$
is non-zero and principal,
$I\subset R_d$
is non-zero and principal,
 $I=(f)$
, say, the topological entropy of
$I=(f)$
, say, the topological entropy of
 $(X_f,\alpha _f)$
is given by the Mahler measure in equation (2.6) of f; if
$(X_f,\alpha _f)$
is given by the Mahler measure in equation (2.6) of f; if
 $I\subset R_d$
contains at least two non-zero elements
$I\subset R_d$
contains at least two non-zero elements
 $f,g$
which are relatively prime to each other (that is, without a non-trivial common factor), then
$f,g$
which are relatively prime to each other (that is, without a non-trivial common factor), then
 $h_{\text {top}}(X_I,\alpha _I)=0$
.
$h_{\text {top}}(X_I,\alpha _I)=0$
. -
• If
 $d>1$
, every principal
$d>1$
, every principal
 $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
 $(X_f,\alpha _f)$
is ergodic (with respect to
$(X_f,\alpha _f)$
is ergodic (with respect to
 $\unicode{x3bb} _f$
); if
$\unicode{x3bb} _f$
); if
 $d=1$
, a principal
$d=1$
, a principal
 $\mathbb {Z}$
-action
$\mathbb {Z}$
-action
 $(X_f,\alpha _f)$
is ergodic if and only if f has no cyclotomic divisor.
$(X_f,\alpha _f)$
is ergodic if and only if f has no cyclotomic divisor. -
• For every non-zero and irreducible
 $f\in R_d$
, the following conditions are equivalent:
$f\in R_d$
, the following conditions are equivalent:-
–
 $\unicode{x3bb} _f$
is mixing under
$\unicode{x3bb} _f$
is mixing under
 $(X_f,\alpha _f)$
;
$(X_f,\alpha _f)$
; -
–
 $h_{\text {top}}(X_f,\alpha _f)>0$
.
$h_{\text {top}}(X_f,\alpha _f)>0$
.
-
2.2 Main results
Our main results are the following theorems which will be proved in §§6 and 7.
Theorem 2.1. Suppose
![]() $f\in R_1\smallsetminus \{0\}$
with
$f\in R_1\smallsetminus \{0\}$
with
![]() $\mathsf {m}(f)>0$
. Then the principal algebraic
$\mathsf {m}(f)>0$
. Then the principal algebraic
![]() ${\mathbb Z}$
-action
${\mathbb Z}$
-action
![]() $(X_f,\alpha _f)$
is Bohr chaotic.
$(X_f,\alpha _f)$
is Bohr chaotic.
For the higher dimensional case, we need an extra condition.
Definition 2.2. [Reference Lind, Schmidt and Verbitskiy20]
A non-zero Laurent polynomial
![]() $f\in R_d$
is atoral if it is not a unit in
$f\in R_d$
is atoral if it is not a unit in
![]() $R_d$
and its unitary variety
$R_d$
and its unitary variety
of f has dimension
![]() $\le d-2$
. This includes the possibility that
$\le d-2$
. This includes the possibility that
![]() $\mathsf U(f)=\varnothing $
, which is equivalent to expansivity of the
$\mathsf U(f)=\varnothing $
, which is equivalent to expansivity of the
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $\alpha _f$
. If
$\alpha _f$
. If
![]() $\mathsf U(f)$
has dimension
$\mathsf U(f)$
has dimension
![]() $d-1$
, f is called toral.
$d-1$
, f is called toral.
With this definition, the following is true.
Theorem 2.3. Suppose that
![]() $d\ge 2$
and that
$d\ge 2$
and that
![]() $f\in R_d$
is atoral. Then
$f\in R_d$
is atoral. Then
![]() $h_{\text {top}}(X_f,\alpha _f)>0$
and
$h_{\text {top}}(X_f,\alpha _f)>0$
and
![]() $(X_f,\alpha _f)$
is Bohr chaotic.
$(X_f,\alpha _f)$
is Bohr chaotic.
We illustrate these definitions with a few examples.
Example 2.4. (Toral automorphisms)
We start with a special case: let
![]() $f=f_0+\cdots +f_kz^k \in R_1$
with
$f=f_0+\cdots +f_kz^k \in R_1$
with
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $f_k=|f_0|=1$
. Then the principal
$f_k=|f_0|=1$
. Then the principal
![]() $\mathbb {Z}$
-action
$\mathbb {Z}$
-action
![]() $(X_f,\alpha _f)$
is conjugate to the toral automorphism
$(X_f,\alpha _f)$
is conjugate to the toral automorphism
![]() $(\mathbb {T}^k,A_f)$
, where
$(\mathbb {T}^k,A_f)$
, where

is the companion matrix of f. The map
![]() $\phi \colon X_f \to \mathbb {T}^k$
, defined by
$\phi \colon X_f \to \mathbb {T}^k$
, defined by
 $$ \begin{align*} \phi (x)= \left( \begin{smallmatrix} x_0 \\ \vdots \\ x_{k-1} \end{smallmatrix}\right) \end{align*} $$
$$ \begin{align*} \phi (x)= \left( \begin{smallmatrix} x_0 \\ \vdots \\ x_{k-1} \end{smallmatrix}\right) \end{align*} $$
for every
![]() $x=(x_n)_{n\in \mathbb {Z}}$
, implements this conjugacy. We conclude that
$x=(x_n)_{n\in \mathbb {Z}}$
, implements this conjugacy. We conclude that
![]() $(X_f,\alpha _f)$
and thus
$(X_f,\alpha _f)$
and thus
![]() $(\mathbb {T}^k,A_f)$
is Bohr chaotic if and only if
$(\mathbb {T}^k,A_f)$
is Bohr chaotic if and only if
![]() $\mathsf {m}(f)>0$
(cf. equation (2.6)).
$\mathsf {m}(f)>0$
(cf. equation (2.6)).
Consider now an irreducible toral automorphism
![]() $T_A\colon {\mathbb T}^k\to {\mathbb T}^k$
defined by a matrix
$T_A\colon {\mathbb T}^k\to {\mathbb T}^k$
defined by a matrix
![]() $A\in GL_k({\mathbb Z})$
. Then the characteristic polynomial
$A\in GL_k({\mathbb Z})$
. Then the characteristic polynomial
![]() $f(z)$
of A is irreducible, and the principal algebraic
$f(z)$
of A is irreducible, and the principal algebraic
![]() $\mathbb {Z}$
-action
$\mathbb {Z}$
-action
![]() $({\mathbb T}^k,A_f) \cong (X_f,\alpha _f)$
in equation (2.9) is a finite-to-one factor of
$({\mathbb T}^k,A_f) \cong (X_f,\alpha _f)$
in equation (2.9) is a finite-to-one factor of
![]() $({\mathbb T}^d,T_A)$
. Hence, if
$({\mathbb T}^d,T_A)$
. Hence, if
![]() $({\mathbb T}^k, A_f)$
is Bohr chaotic (which is the case if and only if
$({\mathbb T}^k, A_f)$
is Bohr chaotic (which is the case if and only if
![]() $\mathsf (m)(f)>0$
), then
$\mathsf (m)(f)>0$
), then
![]() $({\mathbb T}^k,T_A)$
is also Bohr chaotic (as an extension).
$({\mathbb T}^k,T_A)$
is also Bohr chaotic (as an extension).
If a toral automorphism
![]() $T_A\colon {\mathbb T}^k\to {\mathbb T}^k$
with
$T_A\colon {\mathbb T}^k\to {\mathbb T}^k$
with
![]() $A\in GL_k({\mathbb Z})$
is reducible (that is, has a proper invariant subtorus
$A\in GL_k({\mathbb Z})$
is reducible (that is, has a proper invariant subtorus
![]() $V\subsetneq \mathbb {T}^k$
), then the characteristic polynomial g of
$V\subsetneq \mathbb {T}^k$
), then the characteristic polynomial g of
![]() $T_A|_V$
will be a proper factor of f. If
$T_A|_V$
will be a proper factor of f. If
![]() $g'$
is one of the irreducible factors of g (and hence of f), then the system
$g'$
is one of the irreducible factors of g (and hence of f), then the system
![]() $(\mathbb {T}^{\text {deg}(g')},T_{A_{g'}})$
will be Bohr chaotic if and only if
$(\mathbb {T}^{\text {deg}(g')},T_{A_{g'}})$
will be Bohr chaotic if and only if
![]() $\mathsf {m}(g')>0$
, in which case both
$\mathsf {m}(g')>0$
, in which case both
![]() $(V,T_A|_V)$
and
$(V,T_A|_V)$
and
![]() $(\mathbb {T}^d,T_A)$
will be Bohr chaotic. By varying V over the A-invariant irreducible subtori of
$(\mathbb {T}^d,T_A)$
will be Bohr chaotic. By varying V over the A-invariant irreducible subtori of
![]() $\mathbb {T}^k$
, we see that
$\mathbb {T}^k$
, we see that
![]() $(\mathbb {T}^k,T_A)$
is Bohr chaotic if and only if
$(\mathbb {T}^k,T_A)$
is Bohr chaotic if and only if
![]() $h_{\text {top}}(T_A) = \mathsf {m}(f)>0$
.
$h_{\text {top}}(T_A) = \mathsf {m}(f)>0$
.
Example 2.5. (Constant polynomials)
Suppose that
![]() $f=p\in \mathbb {N}$
,
$f=p\in \mathbb {N}$
,
![]() $p>1$
, viewed as a constant polynomial in
$p>1$
, viewed as a constant polynomial in
![]() $R_d$
. Then the principal algebraic action
$R_d$
. Then the principal algebraic action
![]() $(X_f,\alpha _f)$
arising from this polynomial is the shift-action in equation (2.1) on
$(X_f,\alpha _f)$
arising from this polynomial is the shift-action in equation (2.1) on ![]() , which is certainly Bohr chaotic. If
, which is certainly Bohr chaotic. If
![]() $p=1$
(or, more generally, if f is a unit in
$p=1$
(or, more generally, if f is a unit in
![]() $R_d$
), then
$R_d$
), then
![]() $X_f$
reduces to a single point and the
$X_f$
reduces to a single point and the
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $\alpha _f$
becomes trivial. By default,
$\alpha _f$
becomes trivial. By default,
![]() $(X_f,\alpha _f)$
is not Bohr chaotic.
$(X_f,\alpha _f)$
is not Bohr chaotic.
Example 2.6. (The zero polynomial)
So far, we have always assumed that the polynomial
![]() $f\in R_d$
defining a principal algebraic action
$f\in R_d$
defining a principal algebraic action
![]() $(X_f,\alpha _f)$
is non-zero. If we deviate from this assumption and set
$(X_f,\alpha _f)$
is non-zero. If we deviate from this assumption and set
![]() $f=0$
(the zero polynomial in
$f=0$
(the zero polynomial in
![]() $R_d$
), then equation (2.2) reduces to
$R_d$
), then equation (2.2) reduces to
![]() $X_f=\mathbb {T}^{\mathbb {Z}^d}$
, and
$X_f=\mathbb {T}^{\mathbb {Z}^d}$
, and
![]() $\alpha _f$
becomes the shift action
$\alpha _f$
becomes the shift action
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb {T}^{\mathbb {Z}^d}$
. For every integer
$\mathbb {T}^{\mathbb {Z}^d}$
. For every integer
![]() $p>1$
,
$p>1$
,
![]() $\mathbb {T}^{\mathbb {Z}^d}$
contains the closed, shift invariant subset
$\mathbb {T}^{\mathbb {Z}^d}$
contains the closed, shift invariant subset ![]() in Example 2.5. Since
in Example 2.5. Since
![]() $(X_p,\sigma )$
is Bohr periodic, the same is true for
$(X_p,\sigma )$
is Bohr periodic, the same is true for
![]() $(X_f,\alpha _f) = (\mathbb {T}^{\mathbb {Z}^d},\sigma )$
.
$(X_f,\alpha _f) = (\mathbb {T}^{\mathbb {Z}^d},\sigma )$
.
Remark 2.7. To prove our Theorems 2.1 and 2.3, we may assume without loss of generality that the polynomial f in either of these theorems is primitive and irreducible.
Indeed, if f is not primitive, then
![]() $f = pg$
for some primitive polynomial
$f = pg$
for some primitive polynomial
![]() $g\in R_d$
, and
$g\in R_d$
, and
![]() $(X_f,\alpha _f)$
has the subsystem
$(X_f,\alpha _f)$
has the subsystem
![]() $(X_p,\alpha _p= \sigma |_{X_p})$
appearing in Example 2.5. Since
$(X_p,\alpha _p= \sigma |_{X_p})$
appearing in Example 2.5. Since
![]() $(X_p,\alpha _p)$
is Bohr chaotic, the same holds for
$(X_p,\alpha _p)$
is Bohr chaotic, the same holds for
![]() $(X_f,\alpha _f)$
.
$(X_f,\alpha _f)$
.
Similarly, if
![]() $f\in R_d$
is reducible and
$f\in R_d$
is reducible and
![]() $\mathsf {m}(f)>0$
, then at least one of the irreducible factors g of f has positive Mahler measure
$\mathsf {m}(f)>0$
, then at least one of the irreducible factors g of f has positive Mahler measure
![]() $\mathsf {m}(g)>0$
. If
$\mathsf {m}(g)>0$
. If
![]() $(X_g,\alpha _g)$
is Bohr chaotic, the Bohr chaoticity of
$(X_g,\alpha _g)$
is Bohr chaotic, the Bohr chaoticity of
![]() $(X_f,\alpha _f)$
follows immediately from Bohr chaoticity of the subsystem
$(X_f,\alpha _f)$
follows immediately from Bohr chaoticity of the subsystem
![]() $(X_g,\alpha _g)$
. For
$(X_g,\alpha _g)$
. For
![]() $d\ge 2$
in Theorem 2.3, we also note that atorality of a polynomial
$d\ge 2$
in Theorem 2.3, we also note that atorality of a polynomial
![]() $f\in R_d$
is inherited by all its irreducible factors.
$f\in R_d$
is inherited by all its irreducible factors.
3
 ${\mathbb Z}^d$
actions of zero entropy
${\mathbb Z}^d$
actions of zero entropy
Before going on to study our Bohr chaotic principal algebraic
![]() $\mathbb {Z}^d$
-actions, we would like to justify that any continuous
$\mathbb {Z}^d$
-actions, we would like to justify that any continuous
![]() ${\mathbb N}^d$
- or
${\mathbb N}^d$
- or
![]() ${\mathbb Z}^d$
-action with zero topological entropy is not Bohr chaotic (Proposition 3.1). This is an immediate consequence of the disjointness completely positive entropy systems and zero entropy systems. Also, we would like to point out that principal
${\mathbb Z}^d$
-action with zero topological entropy is not Bohr chaotic (Proposition 3.1). This is an immediate consequence of the disjointness completely positive entropy systems and zero entropy systems. Also, we would like to point out that principal
![]() ${\mathbb Z}$
-actions with zero topological entropy are disjoint from the Möbius function (Proposition 3.5).
${\mathbb Z}$
-actions with zero topological entropy are disjoint from the Möbius function (Proposition 3.5).
3.1 Zero entropy
 $\mathbb {Z}^d$
-actions are not Bohr chaotic
$\mathbb {Z}^d$
-actions are not Bohr chaotic
Consider a measure-preserving
![]() $\mathbb {N}^d$
- or
$\mathbb {N}^d$
- or
![]() ${\mathbb Z}^d$
-action
${\mathbb Z}^d$
-action
![]() $\gamma $
on a Lebesgue space
$\gamma $
on a Lebesgue space
![]() $(\Omega , \mu )$
, where
$(\Omega , \mu )$
, where
![]() $\Omega $
is a compact space equipped with its Borel field. We say that the measure-theoretic system
$\Omega $
is a compact space equipped with its Borel field. We say that the measure-theoretic system
![]() $(\Omega , \mu , \gamma )$
has completely positive entropy if any non-trivial factor of
$(\Omega , \mu , \gamma )$
has completely positive entropy if any non-trivial factor of
![]() $(\Omega , \mu , \gamma )$
has positive entropy. Bernoulli systems have complete positive entropy. For
$(\Omega , \mu , \gamma )$
has positive entropy. Bernoulli systems have complete positive entropy. For
![]() $d=1$
, the following result is folklore; for
$d=1$
, the following result is folklore; for
![]() $d\ge 1$
, we include a proof for completeness, based on a disjointness theorem due to Glasner, Thouvenot, and Weiss [Reference Glasner, Thouvenot and Weiss12, Theorem 1].
$d\ge 1$
, we include a proof for completeness, based on a disjointness theorem due to Glasner, Thouvenot, and Weiss [Reference Glasner, Thouvenot and Weiss12, Theorem 1].
Proposition 3.1. Suppose that
![]() $(\Omega , \mu , \gamma )$
has completely positive entropy,
$(\Omega , \mu , \gamma )$
has completely positive entropy,
![]() $\omega \in \Omega $
is a
$\omega \in \Omega $
is a
![]() $\mu $
-generic point, and
$\mu $
-generic point, and
![]() $\phi \in C(\Omega )$
is a continuous function having zero mean. Then
$\phi \in C(\Omega )$
is a continuous function having zero mean. Then
![]() $(\phi (\gamma ^{{\boldsymbol n}} \omega ))_{{\boldsymbol n} \in \mathbb {N}^d}$
is orthogonal to every zero entropy
$(\phi (\gamma ^{{\boldsymbol n}} \omega ))_{{\boldsymbol n} \in \mathbb {N}^d}$
is orthogonal to every zero entropy
![]() $\mathbb {N}^d$
- or
$\mathbb {N}^d$
- or
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $(X, \alpha )$
. That is to say, for every
$(X, \alpha )$
. That is to say, for every
![]() $f\in C(X)$
and every
$f\in C(X)$
and every
![]() $x\in X$
, we have
$x\in X$
, we have
 $$ \begin{align} \lim_{N\to\infty}\frac{1}{N^d}\sum_{{\boldsymbol n} \in [0, N-1]^d} \phi(\gamma ^{{\boldsymbol n}}\omega ) f(\alpha ^{\boldsymbol n} x)=0. \end{align} $$
$$ \begin{align} \lim_{N\to\infty}\frac{1}{N^d}\sum_{{\boldsymbol n} \in [0, N-1]^d} \phi(\gamma ^{{\boldsymbol n}}\omega ) f(\alpha ^{\boldsymbol n} x)=0. \end{align} $$
In particular, continuous
![]() ${\mathbb N}^d$
- or
${\mathbb N}^d$
- or
![]() ${\mathbb Z}^d$
-actions with zero topological entropy are not Bohr chaotic.
${\mathbb Z}^d$
-actions with zero topological entropy are not Bohr chaotic.
Proof. Suppose that for some f and some x, there exists a sequence
![]() $(N_j)$
tending to infinity such that
$(N_j)$
tending to infinity such that

We can assume that along this sequence
![]() $(N_j)$
, the following weak limits of measures exist:
$(N_j)$
, the following weak limits of measures exist:

where
![]() $\delta _\omega $
and
$\delta _\omega $
and
![]() $\delta _x$
denote the point masses at the points
$\delta _x$
denote the point masses at the points
![]() $\omega $
and x, respectively. Clearly, the measure
$\omega $
and x, respectively. Clearly, the measure
![]() $\unicode{x3bb} $
is
$\unicode{x3bb} $
is
![]() $\gamma \negthinspace \times \negthinspace \alpha $
-invariant, and the projection of
$\gamma \negthinspace \times \negthinspace \alpha $
-invariant, and the projection of
![]() $\unicode{x3bb} $
on X is equal to
$\unicode{x3bb} $
on X is equal to
![]() $\nu $
. Since
$\nu $
. Since
![]() $\omega $
is
$\omega $
is
![]() $\mu $
-generic, the projection of
$\mu $
-generic, the projection of
![]() $\unicode{x3bb} $
onto
$\unicode{x3bb} $
onto
![]() $\Omega $
is equal to
$\Omega $
is equal to
![]() $\mu $
. In other words,
$\mu $
. In other words,
![]() $\unicode{x3bb} $
is a joining of
$\unicode{x3bb} $
is a joining of
![]() $\mu $
and
$\mu $
and
![]() $\nu $
, where
$\nu $
, where
![]() $\nu $
has zero entropy. Since systems of completely positive entropy are disjoint from systems of zero entropy by [Reference Glasner, Thouvenot and Weiss12, Theorem 1], we obtain that
$\nu $
has zero entropy. Since systems of completely positive entropy are disjoint from systems of zero entropy by [Reference Glasner, Thouvenot and Weiss12, Theorem 1], we obtain that
![]() $\unicode{x3bb} =\mu \negthinspace \times \negthinspace \nu $
. Thus, by the definition of
$\unicode{x3bb} =\mu \negthinspace \times \negthinspace \nu $
. Thus, by the definition of
![]() $\unicode{x3bb} $
and the hypothesis that
$\unicode{x3bb} $
and the hypothesis that
![]() $\mathbb {E}_\mu \phi =0$
, we get that
$\mathbb {E}_\mu \phi =0$
, we get that
which is a contradiction.
Corollary 3.2. Let
![]() $(X,\alpha )$
be an algebraic
$(X,\alpha )$
be an algebraic
![]() $\mathbb {Z}^d$
-action which does not have completely positive entropy (with respect to the Haar measure
$\mathbb {Z}^d$
-action which does not have completely positive entropy (with respect to the Haar measure
![]() $\unicode{x3bb} _X$
). Then
$\unicode{x3bb} _X$
). Then
![]() $(X,\alpha )$
is not Bohr chaotic.
$(X,\alpha )$
is not Bohr chaotic.
Proof. If
![]() $(X,\alpha )$
does not have completely positive entropy, then [Reference Schmidt29, Theorem 20.8] implies that there exists a non-trivial closed,
$(X,\alpha )$
does not have completely positive entropy, then [Reference Schmidt29, Theorem 20.8] implies that there exists a non-trivial closed,
![]() $\alpha $
-invariant subgroup
$\alpha $
-invariant subgroup
![]() $Y\subset X$
such that the
$Y\subset X$
such that the
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $\alpha _{X/Y}$
induced by
$\alpha _{X/Y}$
induced by
![]() $\alpha $
on
$\alpha $
on
![]() $X/Y$
has zero entropy. Condition (ii) at the beginning of §3, combined with Proposition 3.1, shows that
$X/Y$
has zero entropy. Condition (ii) at the beginning of §3, combined with Proposition 3.1, shows that
![]() $(X,\alpha )$
cannot be Bohr chaotic.
$(X,\alpha )$
cannot be Bohr chaotic.
Example 3.3. (Furstenberg’s example)
Let
![]() $d=2$
and let
$d=2$
and let
![]() $I = (2-z_1, 3-z_2)\subset R_2$
. Then
$I = (2-z_1, 3-z_2)\subset R_2$
. Then
![]() $X_I=\{x\in \mathbb {T}^{\mathbb {Z}^2}\mid \sigma ^{(1,0)}x=2x,\,\sigma ^{(0,1)}x=3x\}$
, so that
$X_I=\{x\in \mathbb {T}^{\mathbb {Z}^2}\mid \sigma ^{(1,0)}x=2x,\,\sigma ^{(0,1)}x=3x\}$
, so that
![]() $x_{k,l}=2^k3^lx_{(0,0)}$
for every
$x_{k,l}=2^k3^lx_{(0,0)}$
for every
![]() $x\in X_I$
and
$x\in X_I$
and
![]() $(k,l)\in \mathbb {Z}^2$
. Since
$(k,l)\in \mathbb {Z}^2$
. Since
![]() $f^{(2)}=2-z_1$
and
$f^{(2)}=2-z_1$
and
![]() $f^{(3)}=3-z_2$
are irreducible and relatively prime to each other, I is a prime ideal, and hence
$f^{(3)}=3-z_2$
are irreducible and relatively prime to each other, I is a prime ideal, and hence
![]() $h_{\text {top}}(X_I,\alpha _I)=0$
[Reference Schmidt29, Proposition 17.5].
$h_{\text {top}}(X_I,\alpha _I)=0$
[Reference Schmidt29, Proposition 17.5].
If
![]() $\gamma $
is a continuous
$\gamma $
is a continuous
![]() $\mathbb {Z}^2$
-action on a compact space
$\mathbb {Z}^2$
-action on a compact space
![]() $\Omega $
,
$\Omega $
,
![]() $\mu $
is a probability measure on
$\mu $
is a probability measure on
![]() $\Omega $
with completely positive entropy under
$\Omega $
with completely positive entropy under
![]() $\gamma $
,
$\gamma $
,
![]() $\omega \in \Omega $
is a
$\omega \in \Omega $
is a
![]() $\mu $
-generic point, and
$\mu $
-generic point, and
![]() $\phi \in C(\Omega )$
has mean zero, Proposition 3.1 shows that
$\phi \in C(\Omega )$
has mean zero, Proposition 3.1 shows that
 $$ \begin{align*} \lim_{N\to\infty } \frac{1}{N^2} \sum_{(m,n)\in [0,N-1]^2} \phi (\gamma ^{(m,n)}\omega )h(2^m3^nt)=0 \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty } \frac{1}{N^2} \sum_{(m,n)\in [0,N-1]^2} \phi (\gamma ^{(m,n)}\omega )h(2^m3^nt)=0 \end{align*} $$
for every
![]() $h\in C(\mathbb {T})$
and
$h\in C(\mathbb {T})$
and
![]() $t\in \mathbb {T}$
.
$t\in \mathbb {T}$
.
In [Reference Furstenberg11], Furstenberg’s example was defined as the
![]() $\mathbb {N}^2$
-action
$\mathbb {N}^2$
-action
![]() $\alpha $
on
$\alpha $
on
![]() $X=\mathbb {T}$
given by
$X=\mathbb {T}$
given by
for every
![]() $(m,n)\in \mathbb {N}^2$
and
$(m,n)\in \mathbb {N}^2$
and
![]() $t\in \mathbb {T}$
.
$t\in \mathbb {T}$
.
We set
![]() $\Omega =\mathbb {T}^{\mathbb {N}^d}$
, write the coordinates of every
$\Omega =\mathbb {T}^{\mathbb {N}^d}$
, write the coordinates of every
![]() $\omega =(\omega _{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {N}^d}\in \Omega $
in the form
$\omega =(\omega _{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {N}^d}\in \Omega $
in the form
![]() $\omega _{\boldsymbol n} = (\omega _{\boldsymbol n}^{(1)},\ldots ,\omega _{\boldsymbol n}^{(d)})$
, and denote by
$\omega _{\boldsymbol n} = (\omega _{\boldsymbol n}^{(1)},\ldots ,\omega _{\boldsymbol n}^{(d)})$
, and denote by
![]() $\gamma $
the one-sided shift-action of
$\gamma $
the one-sided shift-action of
![]() $\mathbb {N}^d$
on
$\mathbb {N}^d$
on
![]() $\Omega $
(cf. equation (2.1)). According to Franklin [Reference Franklin10], for Lebesgue-almost everywhere (a.e.)
$\Omega $
(cf. equation (2.1)). According to Franklin [Reference Franklin10], for Lebesgue-almost everywhere (a.e.)
![]() $(\beta _1, \ldots , \beta _d)$
with
$(\beta _1, \ldots , \beta _d)$
with
![]() $\beta _1>1, \ldots , \beta _d>1$
, the point
$\beta _1>1, \ldots , \beta _d>1$
, the point
![]() $\beta =(\beta _{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {N}^d} \in \Omega $
with
$\beta =(\beta _{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {N}^d} \in \Omega $
with
![]() ${\beta _{\boldsymbol n} = (\beta _1^{n_1}\;(\text {mod}\,1), \ldots , \beta _d^{n_d}\;(\text {mod}\,1))}$
for every
${\beta _{\boldsymbol n} = (\beta _1^{n_1}\;(\text {mod}\,1), \ldots , \beta _d^{n_d}\;(\text {mod}\,1))}$
for every
![]() ${\boldsymbol n}\in \mathbb {N}^d$
is Lebesgue-generic for
${\boldsymbol n}\in \mathbb {N}^d$
is Lebesgue-generic for
![]() $\gamma $
on
$\gamma $
on
![]() $\Omega $
. If
$\Omega $
. If
![]() $\phi \colon \Omega \to \mathbb {C}$
is the map defined by
$\phi \colon \Omega \to \mathbb {C}$
is the map defined by
then
for every
![]() ${\boldsymbol n} = (n_1,\ldots ,n_d)\in \mathbb {N}^d$
. By Proposition 3.1, the sequence
${\boldsymbol n} = (n_1,\ldots ,n_d)\in \mathbb {N}^d$
. By Proposition 3.1, the sequence
![]() $(\phi (\gamma ^{{\boldsymbol n}}\beta ))_{{\boldsymbol n}\in \mathbb {N}^d}$
is almost surely orthogonal to all systems of zero entropy. Since Furstenberg’s example
$(\phi (\gamma ^{{\boldsymbol n}}\beta ))_{{\boldsymbol n}\in \mathbb {N}^d}$
is almost surely orthogonal to all systems of zero entropy. Since Furstenberg’s example
![]() $(\mathbb {T},\alpha )$
described in the preceding paragraph has zero entropy, we obtain the following corollary of Proposition 3.1.
$(\mathbb {T},\alpha )$
described in the preceding paragraph has zero entropy, we obtain the following corollary of Proposition 3.1.
Corollary 3.4. For almost all
![]() $(\beta _1, \beta _2)$
with
$(\beta _1, \beta _2)$
with
![]() $\beta _1>1$
and
$\beta _1>1$
and
![]() $\beta _2>1$
,
$\beta _2>1$
,
 $$ \begin{align*} \lim_{N\to\infty}\frac{1}{N^2}\sum_{0\le m, n<N} e^{2\pi i (\beta_1^m + \beta_2^n)} f(2^m 3^n t)=0 \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty}\frac{1}{N^2}\sum_{0\le m, n<N} e^{2\pi i (\beta_1^m + \beta_2^n)} f(2^m 3^n t)=0 \end{align*} $$
for every continuous function
![]() $f \in C(\mathbb {T})$
and every
$f \in C(\mathbb {T})$
and every
![]() $t\in \mathbb {T}$
.
$t\in \mathbb {T}$
.
3.2 Möbius disjointness and principal actions
We have just shown that zero entropy
![]() ${\mathbb Z}^d$
-actions are not Bohr chaotic. In fact, for principal actions, the result can be strengthened. We recall that a topological dynamical system
${\mathbb Z}^d$
-actions are not Bohr chaotic. In fact, for principal actions, the result can be strengthened. We recall that a topological dynamical system
![]() $(X,T)$
is Möbius disjoint if
$(X,T)$
is Möbius disjoint if
 $$ \begin{align} \lim_{n\to\infty} \frac 1n \sum_{k=1}^n \mu (k) f(T^kx) =0\quad \text{for every } f\in C(X) \text{ and every } x\in X. \end{align} $$
$$ \begin{align} \lim_{n\to\infty} \frac 1n \sum_{k=1}^n \mu (k) f(T^kx) =0\quad \text{for every } f\in C(X) \text{ and every } x\in X. \end{align} $$
Proposition 3.5. A zero entropy principal
![]() ${\mathbb Z}$
-algebraic action
${\mathbb Z}$
-algebraic action
![]() $(X_f,\alpha _f)$
,
$(X_f,\alpha _f)$
,
![]() $f\in R_1$
, is Möbius disjoint.
$f\in R_1$
, is Möbius disjoint.
Proof. Since
![]() $(X_f,\alpha _f)$
has zero entropy, that is,
$(X_f,\alpha _f)$
has zero entropy, that is,
![]() $\mathsf {m}(f)=0$
, the Kronecker lemma implies that f has the form
$\mathsf {m}(f)=0$
, the Kronecker lemma implies that f has the form
where
![]() $m_0\in {\mathbb Z}$
,
$m_0\in {\mathbb Z}$
,
![]() $n_j,m_j\in {\mathbb N}$
,
$n_j,m_j\in {\mathbb N}$
,
![]() $j=1,\ldots ,k$
, and
$j=1,\ldots ,k$
, and
![]() $\Phi _n$
is the nth cyclotomic polynomial defined in equation (2.8). One immediately concludes from equation (3.3) that
$\Phi _n$
is the nth cyclotomic polynomial defined in equation (2.8). One immediately concludes from equation (3.3) that
and hence
![]() $(X_f,\alpha _f)$
is topologically conjugate to the toral automorphism
$(X_f,\alpha _f)$
is topologically conjugate to the toral automorphism
![]() $({\mathbb T}^{N},T_A)$
, where
$({\mathbb T}^{N},T_A)$
, where
![]() $T_A:{\mathbb T}^{N}\to {\mathbb T}^{N}$
is a linear automorphism with the matrix
$T_A:{\mathbb T}^{N}\to {\mathbb T}^{N}$
is a linear automorphism with the matrix
![]() $A=A_{f}$
—the companion matrix of f, see Example 2.4. However, toral automorphisms with zero entropy are known to be Möbius disjoint [Reference Liu and Sarnak23, Theorem 1.1]. In fact, toral automorphisms, and more generally affine maps of compact abelian groups, are the primary examples motivating Sarnak’s (still unproven) conjecture that all topological dynamical systems with zero entropy are Möbius disjoint [Reference Sarnak28].
$A=A_{f}$
—the companion matrix of f, see Example 2.4. However, toral automorphisms with zero entropy are known to be Möbius disjoint [Reference Liu and Sarnak23, Theorem 1.1]. In fact, toral automorphisms, and more generally affine maps of compact abelian groups, are the primary examples motivating Sarnak’s (still unproven) conjecture that all topological dynamical systems with zero entropy are Möbius disjoint [Reference Sarnak28].
4 Riesz product measures on
 $X_f$
$X_f$
In this section, we start on the proofs of Theorems 2.1 and 2.3. As explained in Remark 2.7, we assume from now on—and without loss in generality—that the polynomial
![]() $f\in R_d$
defining our principal action
$f\in R_d$
defining our principal action
![]() $(X_f,\alpha _f)$
is primitive, irreducible, and has positive Mahler measure.
$(X_f,\alpha _f)$
is primitive, irreducible, and has positive Mahler measure.
For the proofs of these theorems, we shall use a class of measures called Riesz products. First, we will recall the general construction of Riesz product measures on arbitrary compact abelian groups. Second, we will construct Riesz products on
![]() $X_f$
based on lacunary polynomials in the dual group
$X_f$
based on lacunary polynomials in the dual group
![]() $\widehat {X}_f \subset R_d$
.
$\widehat {X}_f \subset R_d$
.
4.1 Riesz product measures
Let X be a compact abelian group with dual group
![]() $\widehat X$
.
$\widehat X$
.
Definition 4.1. [Reference Hewitt and Zuckerman13]
An infinite sequence of distinct characters
![]() $\Lambda =(\gamma _n)_{n\in \mathbb {N}}=\{\gamma _0, \gamma _1,\ldots \,\}\subset \widehat X$
is said to be dissociate if for every
$\Lambda =(\gamma _n)_{n\in \mathbb {N}}=\{\gamma _0, \gamma _1,\ldots \,\}\subset \widehat X$
is said to be dissociate if for every
![]() $k\ge 1$
and every k-tuple
$k\ge 1$
and every k-tuple
![]() $(n_1,n_2,\ldots , n_k)\in \mathbb {N}^k$
of distinct non-negative integers, the equality
$(n_1,n_2,\ldots , n_k)\in \mathbb {N}^k$
of distinct non-negative integers, the equality
with
![]() $\varepsilon _j\in \{-2,-1,0,1,2\}$
for every
$\varepsilon _j\in \{-2,-1,0,1,2\}$
for every
![]() $j=1,\ldots ,k$
, implies that
$j=1,\ldots ,k$
, implies that
Equivalently,
![]() $\Lambda $
is dissociate if any character in
$\Lambda $
is dissociate if any character in
![]() $\widehat X$
can be represented in at most one way as a finite product
$\widehat X$
can be represented in at most one way as a finite product
![]() $ \gamma _{n_1}^{\varepsilon _1}\gamma _{n_2}^{\varepsilon _2}\cdots \gamma _{n_k}^{\varepsilon _k} $
of elements of
$ \gamma _{n_1}^{\varepsilon _1}\gamma _{n_2}^{\varepsilon _2}\cdots \gamma _{n_k}^{\varepsilon _k} $
of elements of
![]() $\Lambda $
, where all
$\Lambda $
, where all
![]() $n_j$
are distinct and
$n_j$
are distinct and
![]() ${\varepsilon _j\in \{-1, 0,1\}}$
.
${\varepsilon _j\in \{-1, 0,1\}}$
.
Using dissociate sequences of characters, Hewitt and Zuckermann [Reference Hewitt and Zuckerman13] proposed a construction of interesting probability measures—the so-called Riesz products, generalizing Riesz products on
![]() ${\mathbb T}$
constructed by Riesz [Reference Riesz27] in 1918. More precisely, denote by
${\mathbb T}$
constructed by Riesz [Reference Riesz27] in 1918. More precisely, denote by
![]() $\unicode{x3bb} _X$
the Haar measure on X. Suppose that:
$\unicode{x3bb} _X$
the Haar measure on X. Suppose that:
-
(i)
 $\Lambda = (\gamma _n)_{n\ge 0}$
is a dissociate sequence of characters in
$\Lambda = (\gamma _n)_{n\ge 0}$
is a dissociate sequence of characters in
 $\widehat X$
;
$\widehat X$
; -
(ii)
 $a = (a_n)_{n\ge 0}$
is a sequence of complex numbers such that
$a = (a_n)_{n\ge 0}$
is a sequence of complex numbers such that
 $ |a_n|\le 1$
for all n.
$ |a_n|\le 1$
for all n.
For any
![]() $N\ge 0$
, denote by
$N\ge 0$
, denote by
![]() $\mu _a^{(N)}$
the measure on X which is absolutely continuous with respect to
$\mu _a^{(N)}$
the measure on X which is absolutely continuous with respect to
![]() $\unicode{x3bb} _X$
with density
$\unicode{x3bb} _X$
with density
 $$ \begin{align*} \frac {d\mu _a^{(N)}}{d\unicode{x3bb} _X}(x) = \prod_{n=0}^N(1 +{\mathsf{Re\, }} a_n\gamma _n(x)). \end{align*} $$
$$ \begin{align*} \frac {d\mu _a^{(N)}}{d\unicode{x3bb} _X}(x) = \prod_{n=0}^N(1 +{\mathsf{Re\, }} a_n\gamma _n(x)). \end{align*} $$
It is not very difficult to show that the sequence of measures
![]() $(\mu _{a}^{(N)})_{N\ge 0}$
converges weakly; the limiting measure
$(\mu _{a}^{(N)})_{N\ge 0}$
converges weakly; the limiting measure
![]() $\mu _a=\lim _N \mu _a^{(N)}$
is called the Riesz product, and we denote it as
$\mu _a=\lim _N \mu _a^{(N)}$
is called the Riesz product, and we denote it as
 $$ \begin{align} \mu _a=\prod_{n=0}^{\infty} (1 +{\mathsf{Re\, }} a_n\gamma _n(x)). \end{align} $$
$$ \begin{align} \mu _a=\prod_{n=0}^{\infty} (1 +{\mathsf{Re\, }} a_n\gamma _n(x)). \end{align} $$
The Riesz product
![]() $\mu _a$
is absolutely continuous with respect to the Haar measure
$\mu _a$
is absolutely continuous with respect to the Haar measure
![]() $\unicode{x3bb} _X$
if and only if
$\unicode{x3bb} _X$
if and only if
![]() $\sum _{n} |a_n|^2<\infty $
, and it is singular to the Haar measure
$\sum _{n} |a_n|^2<\infty $
, and it is singular to the Haar measure
![]() $\unicode{x3bb} _X$
if and only if
$\unicode{x3bb} _X$
if and only if
![]() ${\sum _{n} |a_n|^2=\infty }$
(see [Reference Peyrière25, Reference Zygmund34]). We will omit dependence of
${\sum _{n} |a_n|^2=\infty }$
(see [Reference Peyrière25, Reference Zygmund34]). We will omit dependence of
![]() $\mu _a$
on the sequence
$\mu _a$
on the sequence
![]() $\Lambda $
, since
$\Lambda $
, since
![]() $\Lambda $
will usually be fixed.
$\Lambda $
will usually be fixed.
Since
the Riesz product
![]() $\mu _a$
, associated to the sequences
$\mu _a$
, associated to the sequences
![]() $\Lambda $
and a, can be characterized by the Fourier coefficients
$\Lambda $
and a, can be characterized by the Fourier coefficients
![]() $ \widehat {\mu }_a(\gamma )=\int \overline {\gamma }(x)\,d\mu _a(x)$
,
$ \widehat {\mu }_a(\gamma )=\int \overline {\gamma }(x)\,d\mu _a(x)$
,
![]() $\gamma \in \widehat {X}$
, as follows.
$\gamma \in \widehat {X}$
, as follows.
-
(a) For any finite set of distinct characters
 $\{\gamma _{n_1},\gamma _{n_2},\ldots , \gamma _{n_k}\}\subset \Lambda $
and any
$\{\gamma _{n_1},\gamma _{n_2},\ldots , \gamma _{n_k}\}\subset \Lambda $
and any
 $(\varepsilon _1, \varepsilon _2, \ldots ,\varepsilon _k)\in \{-1,0,1\}^k$
, (4.2)where
$(\varepsilon _1, \varepsilon _2, \ldots ,\varepsilon _k)\in \{-1,0,1\}^k$
, (4.2)where $$ \begin{align} {\widehat\mu }_a(\gamma _{n_1}^{\varepsilon _1} \gamma _{n_2}^{\varepsilon _2}\cdots \gamma _{n_k}^{\varepsilon _k}) = a_{n_1}^{(\varepsilon _1)} a_{n_2}^{(\varepsilon _2)} \cdots a_{n_k}^{(\varepsilon _k)}, \end{align} $$
$$ \begin{align} {\widehat\mu }_a(\gamma _{n_1}^{\varepsilon _1} \gamma _{n_2}^{\varepsilon _2}\cdots \gamma _{n_k}^{\varepsilon _k}) = a_{n_1}^{(\varepsilon _1)} a_{n_2}^{(\varepsilon _2)} \cdots a_{n_k}^{(\varepsilon _k)}, \end{align} $$
 $a_n^{(\varepsilon )}= ({a_n}/{2}), 0,$
or
$a_n^{(\varepsilon )}= ({a_n}/{2}), 0,$
or
 ${\overline a_n}/{2}$
, depending on whether
${\overline a_n}/{2}$
, depending on whether
 $\varepsilon =1,0$
, or
$\varepsilon =1,0$
, or
 $-1$
.
$-1$
.
-
(b) For any character
 $\gamma \in \widehat {X}$
not of the form
$\gamma \in \widehat {X}$
not of the form
 $\gamma _{n_1}^{\varepsilon _1}\gamma _{n_2}^{\varepsilon _2}\cdots \gamma _{n_k}^{\varepsilon _k}$
with
$\gamma _{n_1}^{\varepsilon _1}\gamma _{n_2}^{\varepsilon _2}\cdots \gamma _{n_k}^{\varepsilon _k}$
with
 $\varepsilon _1,\varepsilon _2,\ldots ,\varepsilon _k\in \{-1,0,1\}$
as in case (a) above, one has (4.3)
$\varepsilon _1,\varepsilon _2,\ldots ,\varepsilon _k\in \{-1,0,1\}$
as in case (a) above, one has (4.3) $$ \begin{align} \widehat{\mu }_a(\gamma )=0. \end{align} $$
$$ \begin{align} \widehat{\mu }_a(\gamma )=0. \end{align} $$
For any two Riesz products
![]() $\mu _a$
and
$\mu _a$
and
![]() $\mu _b$
, it is proved in [Reference Peyrière25] that
$\mu _b$
, it is proved in [Reference Peyrière25] that
![]() $\mu _a$
and
$\mu _a$
and
![]() $\mu _b$
are mutually singular if
$\mu _b$
are mutually singular if
![]() $\sum |a_n-b_n|^2=\infty $
, and mutually equivalent if
$\sum |a_n-b_n|^2=\infty $
, and mutually equivalent if
![]() $\sum |a_n-b_n|^2<\infty $
and
$\sum |a_n-b_n|^2<\infty $
and
![]() $\sup _n|a_n|<1$
. For any Riesz product
$\sup _n|a_n|<1$
. For any Riesz product
![]() $\mu _a$
, it is proved in [Reference Fan6] that the orthogonal series
$\mu _a$
, it is proved in [Reference Fan6] that the orthogonal series
![]() $\sum c_n (\gamma _n(x)- a_n/2)$
(with
$\sum c_n (\gamma _n(x)- a_n/2)$
(with
![]() $c_n\in \mathbb {C}$
) converges
$c_n\in \mathbb {C}$
) converges
![]() $\mu _a$
-a.e. if and only if
$\mu _a$
-a.e. if and only if
![]() $\sum |c_n|^2<\infty $
. Such convergence results will be useful to us in the proofs of Theorems 2.1 and 2.3. Riesz products on
$\sum |c_n|^2<\infty $
. Such convergence results will be useful to us in the proofs of Theorems 2.1 and 2.3. Riesz products on
![]() $\mathbb {T}$
and some generalized Riesz products appear as spectral measures of some dynamical systems (see [Reference Bourgain1, Reference Ledrappier18, Reference Queffélec26]). Riesz products are tools in harmonic analysis (see [Reference Kahane14, Reference Katznelson16, Reference Zygmund34]).
$\mathbb {T}$
and some generalized Riesz products appear as spectral measures of some dynamical systems (see [Reference Bourgain1, Reference Ledrappier18, Reference Queffélec26]). Riesz products are tools in harmonic analysis (see [Reference Kahane14, Reference Katznelson16, Reference Zygmund34]).
4.2 The dual group
 $\widehat {X}_f$
$\widehat {X}_f$
Before constructing Riesz products on
![]() $X_f$
, let us describe the dual group of
$X_f$
, let us describe the dual group of
![]() $X_f$
(cf. [Reference Lind and Schmidt19, Reference Schmidt29]). Every Laurent polynomial with integer coefficients
$X_f$
(cf. [Reference Lind and Schmidt19, Reference Schmidt29]). Every Laurent polynomial with integer coefficients
defines a character
![]() $\gamma ^{(h)} \in \widehat {\mathbb {T}^{\mathbb {Z}^d}}$
, given by
$\gamma ^{(h)} \in \widehat {\mathbb {T}^{\mathbb {Z}^d}}$
, given by
where
for every
![]() $x\in \mathbb {T}^{\mathbb {Z}^d}$
. Conversely, every character of
$x\in \mathbb {T}^{\mathbb {Z}^d}$
. Conversely, every character of
![]() $\mathbb {T}^{\mathbb {Z}^d}$
is of the form
$\mathbb {T}^{\mathbb {Z}^d}$
is of the form
![]() $\gamma =\gamma ^{(h)}$
for some
$\gamma =\gamma ^{(h)}$
for some
![]() $h\in R_d$
, so that we may identify
$h\in R_d$
, so that we may identify
![]() $\widehat {\mathbb {T}^{\mathbb {Z}^d}}$
with
$\widehat {\mathbb {T}^{\mathbb {Z}^d}}$
with
![]() $R_d$
. Note, however, that the group operation in
$R_d$
. Note, however, that the group operation in
![]() $R_d$
is addition, whereas in
$R_d$
is addition, whereas in
![]() $\widehat {\mathbb {T}^{\mathbb {Z}^d}}$
, it is multiplication:
$\widehat {\mathbb {T}^{\mathbb {Z}^d}}$
, it is multiplication:
for all
![]() $h,h'\in R_d$
.
$h,h'\in R_d$
.
Since
![]() $X_f$
is a subgroup of
$X_f$
is a subgroup of
![]() $\mathbb {T}^{\mathbb {Z}^d}$
, every character
$\mathbb {T}^{\mathbb {Z}^d}$
, every character
![]() $\gamma ^{(h)}\in \widehat {\mathbb {T}^{\mathbb {Z}^d}}$
,
$\gamma ^{(h)}\in \widehat {\mathbb {T}^{\mathbb {Z}^d}}$
,
![]() $h\in R_d$
, restricts to a character
$h\in R_d$
, restricts to a character
![]() $\tilde {\gamma }^{(h)}\in \widehat {X}_f$
. From the definition of
$\tilde {\gamma }^{(h)}\in \widehat {X}_f$
. From the definition of
![]() $X_f$
in equation (2.2), it is clear that, for any two polynomials
$X_f$
in equation (2.2), it is clear that, for any two polynomials
![]() $h,h'\in R_d$
,
$h,h'\in R_d$
,
![]() $\tilde {\gamma }^{(h)} = \tilde {\gamma }^{(h')}$
if and only if
$\tilde {\gamma }^{(h)} = \tilde {\gamma }^{(h')}$
if and only if
![]() $h-h'$
is a multiple of f. This allows us to identify the dual group
$h-h'$
is a multiple of f. This allows us to identify the dual group
![]() $\widehat {X}_f$
with
$\widehat {X}_f$
with
![]() $R_d/(f)$
, where
$R_d/(f)$
, where
![]() $(f)=R_d\cdot f$
is the principal ideal in
$(f)=R_d\cdot f$
is the principal ideal in
![]() $R_d$
generated by f:
$R_d$
generated by f:
More generally, if
![]() $I\subset R_d$
is an ideal and
$I\subset R_d$
is an ideal and
![]() $X_I$
is given by equation (2.5), then
$X_I$
is given by equation (2.5), then
4.3 Lacunary polynomials
For the construction of Riesz product measures on
![]() $X_f$
, we have to take a closer look at dissociate families
$X_f$
, we have to take a closer look at dissociate families
![]() $\Lambda \subset \widehat {X}_f$
in the sense of Definition 4.1.
$\Lambda \subset \widehat {X}_f$
in the sense of Definition 4.1.
Definition 4.2. Given an integer
![]() $m\in \mathbb N$
, we say that a primitive irreducible polynomial
$m\in \mathbb N$
, we say that a primitive irreducible polynomial
![]() $f\in R_d$
is m-good if the following conditions hold.
$f\in R_d$
is m-good if the following conditions hold.
-
(C1) The collection of characters
is dissociate. Explicitly, this means that any non-zero polynomial of the form $$ \begin{align*} \{ \tilde{\gamma }^{(\boldsymbol{z}^{m{\boldsymbol n}})} \mid {\boldsymbol n}\in\mathbb{N}^d\}\subset \widehat{X}_f \end{align*} $$
$$ \begin{align*} \{ \tilde{\gamma }^{(\boldsymbol{z}^{m{\boldsymbol n}})} \mid {\boldsymbol n}\in\mathbb{N}^d\}\subset \widehat{X}_f \end{align*} $$
 $g({\boldsymbol z}^m)$
where with
$g({\boldsymbol z}^m)$
where with $$ \begin{align*} g({\boldsymbol z})=\sum_{{\boldsymbol n} \in \mathbb{Z}^d} \varepsilon _{\boldsymbol n} {\boldsymbol z}^{{\boldsymbol n}} \end{align*} $$
$$ \begin{align*} g({\boldsymbol z})=\sum_{{\boldsymbol n} \in \mathbb{Z}^d} \varepsilon _{\boldsymbol n} {\boldsymbol z}^{{\boldsymbol n}} \end{align*} $$
 $\varepsilon _{\boldsymbol n} \in \{-2,-1,0,1,2\}$
is not divisible by f.
$\varepsilon _{\boldsymbol n} \in \{-2,-1,0,1,2\}$
is not divisible by f.
-
(C2) For any
 ${\boldsymbol k} \in \mathbb {N}^d/ m\mathbb {N}^d$
, any two points
${\boldsymbol k} \in \mathbb {N}^d/ m\mathbb {N}^d$
, any two points
 ${\boldsymbol n} \ne {\boldsymbol n}'$
in
${\boldsymbol n} \ne {\boldsymbol n}'$
in
 $\mathbb {Z}^d$
, and any non-zero polynomial of the form
$\mathbb {Z}^d$
, and any non-zero polynomial of the form  with
with
 $\varepsilon _{\boldsymbol n} \in \{-1,0,1\}$
, the polynomial is not divisible by f.
$\varepsilon _{\boldsymbol n} \in \{-1,0,1\}$
, the polynomial is not divisible by f. $$ \begin{align*} {\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}}-{\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}} + g({\boldsymbol z}^{m}) \end{align*} $$
$$ \begin{align*} {\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}}-{\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}} + g({\boldsymbol z}^{m}) \end{align*} $$
For a given principal algebraic action
![]() $(X_f,\alpha _f)$
, where f is m-good, Riesz product measures
$(X_f,\alpha _f)$
, where f is m-good, Riesz product measures
![]() $\mu _a$
can be constructed using the countable dissociate collection of characters
$\mu _a$
can be constructed using the countable dissociate collection of characters
![]() $\Lambda =\{ \tilde {\gamma }^{({\boldsymbol z}^{m{\boldsymbol n}})}\mid \ {\boldsymbol n}\in \mathbb {N}^d\}$
(cf. condition (C1)). Condition (C2) ensures that any shifted family of characters
$\Lambda =\{ \tilde {\gamma }^{({\boldsymbol z}^{m{\boldsymbol n}})}\mid \ {\boldsymbol n}\in \mathbb {N}^d\}$
(cf. condition (C1)). Condition (C2) ensures that any shifted family of characters
![]() $\Lambda _{{\boldsymbol k}}=\{ \tilde {\gamma }^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}})}\mid \ {\boldsymbol n}\in \mathbb {N}^d \}$
(with
$\Lambda _{{\boldsymbol k}}=\{ \tilde {\gamma }^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}})}\mid \ {\boldsymbol n}\in \mathbb {N}^d \}$
(with
![]() ${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol {0}\}$
being fixed) is a
${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol {0}\}$
being fixed) is a
![]() $\mu _a$
-orthogonal system, as a direct consequence of equation (4.2) applied with
$\mu _a$
-orthogonal system, as a direct consequence of equation (4.2) applied with
![]() $k=2$
—a useful property which will help us control the behavior of weighted ergodic averages. As we will see, the coefficient sequence a will be chosen depending on the non-trivial weight sequence
$k=2$
—a useful property which will help us control the behavior of weighted ergodic averages. As we will see, the coefficient sequence a will be chosen depending on the non-trivial weight sequence
![]() $\boldsymbol w$
.
$\boldsymbol w$
.
5
 $(X_f, \alpha _f)$
is Bohr chaotic when f is m-good
$(X_f, \alpha _f)$
is Bohr chaotic when f is m-good
The following theorem will allow us to reduce the proof of Bohr chaoticity of
![]() $(X_f, \alpha _f)$
to checking the m-goodness of the polynomial f.
$(X_f, \alpha _f)$
to checking the m-goodness of the polynomial f.
Theorem 5.1. If a primitive irreducible polynomial
![]() $f\in R_d$
with positive Mahler measure is m-good, that is, if the conditions (C1) and (C2) hold for some positive integer m, then
$f\in R_d$
with positive Mahler measure is m-good, that is, if the conditions (C1) and (C2) hold for some positive integer m, then
![]() $(X_f,\alpha _f)$
is Bohr chaotic.
$(X_f,\alpha _f)$
is Bohr chaotic.
We begin with a simple auxiliary lemma.
Lemma 5.2. Let
![]() $\alpha $
be a continuous
$\alpha $
be a continuous
![]() ${\mathbb Z}^d$
-action on a compact metrizable space X, and let
${\mathbb Z}^d$
-action on a compact metrizable space X, and let
![]() ${\boldsymbol w} = (w_{\boldsymbol n})_{{\boldsymbol n} \in \mathbb {N}^d}$
be a non-trivial weight. Then
${\boldsymbol w} = (w_{\boldsymbol n})_{{\boldsymbol n} \in \mathbb {N}^d}$
be a non-trivial weight. Then
![]() $(X,\alpha )$
is not disjoint from
$(X,\alpha )$
is not disjoint from
![]() ${\boldsymbol w}=(w_{\boldsymbol n})$
if and only if for any
${\boldsymbol w}=(w_{\boldsymbol n})$
if and only if for any
![]() ${\boldsymbol k}\in \mathbb {N}^d$
,
${\boldsymbol k}\in \mathbb {N}^d$
,
![]() $(X,\alpha )$
is not disjoint from the weight
$(X,\alpha )$
is not disjoint from the weight
![]() $\widetilde {{\boldsymbol w}}=(\widetilde {w}_{\boldsymbol n})$
defined by
$\widetilde {{\boldsymbol w}}=(\widetilde {w}_{\boldsymbol n})$
defined by
![]() $\widetilde {w}_{\boldsymbol n}=w_{{\boldsymbol n}+{\boldsymbol k}}$
for all
$\widetilde {w}_{\boldsymbol n}=w_{{\boldsymbol n}+{\boldsymbol k}}$
for all
![]() ${\boldsymbol n}\in \mathbb {N}^d$
.
${\boldsymbol n}\in \mathbb {N}^d$
.
Proof. Introduce the following notation: for a continuous function
![]() $\phi $
on X, let
$\phi $
on X, let
 $$ \begin{align*} S_N^{{\boldsymbol w}}\phi(x)=\sum_{{\boldsymbol n} \in [0, N-1]^d} w_{\boldsymbol n} \phi(\alpha ^{\boldsymbol n} x). \end{align*} $$
$$ \begin{align*} S_N^{{\boldsymbol w}}\phi(x)=\sum_{{\boldsymbol n} \in [0, N-1]^d} w_{\boldsymbol n} \phi(\alpha ^{\boldsymbol n} x). \end{align*} $$
For any
![]() ${\boldsymbol k}\in \mathbb {N}^d$
and for any
${\boldsymbol k}\in \mathbb {N}^d$
and for any
![]() $x\in X$
, one has
$x\in X$
, one has
 $$ \begin{align*}\begin{aligned} |S_{N+\|{\boldsymbol k}\|_\infty}^{{\boldsymbol w}}\phi(x)-S^{\widetilde{{\boldsymbol w}}}_N\phi(\alpha ^{{\boldsymbol k}}x)|&=\bigg|\!\sum_{{\boldsymbol n} \in [0, N+\|{\boldsymbol k}\|_\infty-1]^d}\! w_{{\boldsymbol n}}\phi(\alpha ^{{\boldsymbol n}}x)-\!\!\sum_{{\boldsymbol n} \in [0, N-1]^d}\! {w}_{{\boldsymbol n}+{\boldsymbol k}}\phi(\alpha ^{{\boldsymbol n}+{\boldsymbol k}}x)\bigg|\\ &\le \|\phi\|_{\infty}\cdot | [0,N+\|{\boldsymbol k}\|_\infty-1]^d\triangle ({\boldsymbol k}+[0,N-1]^d)|. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} |S_{N+\|{\boldsymbol k}\|_\infty}^{{\boldsymbol w}}\phi(x)-S^{\widetilde{{\boldsymbol w}}}_N\phi(\alpha ^{{\boldsymbol k}}x)|&=\bigg|\!\sum_{{\boldsymbol n} \in [0, N+\|{\boldsymbol k}\|_\infty-1]^d}\! w_{{\boldsymbol n}}\phi(\alpha ^{{\boldsymbol n}}x)-\!\!\sum_{{\boldsymbol n} \in [0, N-1]^d}\! {w}_{{\boldsymbol n}+{\boldsymbol k}}\phi(\alpha ^{{\boldsymbol n}+{\boldsymbol k}}x)\bigg|\\ &\le \|\phi\|_{\infty}\cdot | [0,N+\|{\boldsymbol k}\|_\infty-1]^d\triangle ({\boldsymbol k}+[0,N-1]^d)|. \end{aligned} \end{align*} $$
To finish the proof, it suffices to notice that the cardinality of the symmetric difference is of order
![]() $O(N^{d-1})$
.
$O(N^{d-1})$
.
Proof of Theorem 5.1
Fix
![]() $m\in {\mathbb N}$
such that conditions (C1) and (C2) hold. Assume that
$m\in {\mathbb N}$
such that conditions (C1) and (C2) hold. Assume that
![]() ${\boldsymbol w}$
is a non-trivial weight (cf. equation (1.5)). Then for some
${\boldsymbol w}$
is a non-trivial weight (cf. equation (1.5)). Then for some
![]() ${\boldsymbol k}\in [0,\ldots ,m-1]^{d}$
, one has
${\boldsymbol k}\in [0,\ldots ,m-1]^{d}$
, one has
 $$ \begin{align} \limsup_{N\to \infty} \frac{1}{N^d} \sum_{{{\boldsymbol n}\mid m{\boldsymbol n}+{\boldsymbol k}} \in [0, N-1]^d} |w_{m{\boldsymbol n}+{\boldsymbol k}}|>0. \end{align} $$
$$ \begin{align} \limsup_{N\to \infty} \frac{1}{N^d} \sum_{{{\boldsymbol n}\mid m{\boldsymbol n}+{\boldsymbol k}} \in [0, N-1]^d} |w_{m{\boldsymbol n}+{\boldsymbol k}}|>0. \end{align} $$
Without loss of generality, we can assume
![]() ${\boldsymbol k}=\boldsymbol 0$
. Otherwise, consider the shifted weight
${\boldsymbol k}=\boldsymbol 0$
. Otherwise, consider the shifted weight
![]() $\widetilde {{\boldsymbol w}}=(\widetilde {w}_{\boldsymbol n})$
with
$\widetilde {{\boldsymbol w}}=(\widetilde {w}_{\boldsymbol n})$
with
![]() $\widetilde {w}_{\boldsymbol n}=w_{{\boldsymbol n}+{\boldsymbol k}}$
. By Lemma 5.2,
$\widetilde {w}_{\boldsymbol n}=w_{{\boldsymbol n}+{\boldsymbol k}}$
. By Lemma 5.2,
![]() $(X_f,\alpha _f)$
is not disjoint from
$(X_f,\alpha _f)$
is not disjoint from
![]() ${\boldsymbol w}$
if and only if
${\boldsymbol w}$
if and only if
![]() $(X_f,\alpha _f)$
is not disjoint from
$(X_f,\alpha _f)$
is not disjoint from
![]() $\widetilde {\boldsymbol w}$
. Thus, it is sufficient to consider the weight
$\widetilde {\boldsymbol w}$
. Thus, it is sufficient to consider the weight
![]() $\widetilde {{\boldsymbol w}}$
for which we can assume that equation (5.1) holds with
$\widetilde {{\boldsymbol w}}$
for which we can assume that equation (5.1) holds with
![]() ${\boldsymbol k}=0$
. In the following, we consider an arbitrary such weight.
${\boldsymbol k}=0$
. In the following, we consider an arbitrary such weight.
Step 1. Choice of the function
![]() $\phi $
and the point x. We are going to show that equation (1.5) holds for
$\phi $
and the point x. We are going to show that equation (1.5) holds for ![]() and for almost all
and for almost all
![]() $x\in X_f$
with respect to an appropriately chosen Riesz product measure. Note that for all
$x\in X_f$
with respect to an appropriately chosen Riesz product measure. Note that for all
![]() ${\boldsymbol n}\in \mathbb {N}^d$
,
${\boldsymbol n}\in \mathbb {N}^d$
,
Step 2. Choice of the measure. By condition (C1), the collection of characters
is dissociate. Consider now the following collection of coefficients:
Since
![]() $|a_{{\boldsymbol n}}|=1$
for all
$|a_{{\boldsymbol n}}|=1$
for all
![]() ${\boldsymbol n}$
, the Riesz product
${\boldsymbol n}$
, the Riesz product
![]() $\mu _a$
in equation (4.1) is well defined.
$\mu _a$
in equation (4.1) is well defined.
Step 3. Orthonormality. For each
![]() ${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol 0\}$
, consider the following collection of functions:
${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol 0\}$
, consider the following collection of functions:
We claim that for each
![]() ${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol 0\}$
,
${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol 0\}$
,
![]() $\mathcal F_{{\boldsymbol k}}$
is orthonormal in
$\mathcal F_{{\boldsymbol k}}$
is orthonormal in
![]() $L^2(X_f,\mu _a)$
. Indeed, for each
$L^2(X_f,\mu _a)$
. Indeed, for each
![]() ${\boldsymbol n}\ne {\boldsymbol n}'$
, condition (C2) means that the character corresponding to the polynomial
${\boldsymbol n}\ne {\boldsymbol n}'$
, condition (C2) means that the character corresponding to the polynomial
![]() ${\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}}-{\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}}$
:
${\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}}-{\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}}$
:
cannot be expressed as a product of characters in
![]() $\Lambda $
, and hence using equation (4.3) for the Fourier coefficients of Riesz products, one gets that
$\Lambda $
, and hence using equation (4.3) for the Fourier coefficients of Riesz products, one gets that
 $$ \begin{align*} \int_{X_f} \gamma ^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}})}(x) \overline{\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}})}(x)}\,d\mu _a(x) = \widehat{\mu _a}(\overline{\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}}-{\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}})}})=0. \end{align*} $$
$$ \begin{align*} \int_{X_f} \gamma ^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}})}(x) \overline{\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}})}(x)}\,d\mu _a(x) = \widehat{\mu _a}(\overline{\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}}-{\boldsymbol z}^{m{\boldsymbol n}'+{\boldsymbol k}})}})=0. \end{align*} $$
Since
![]() $|\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}})}(x)|^2=1$
for all x, the orthonormality of
$|\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}+{\boldsymbol k}})}(x)|^2=1$
for all x, the orthonormality of
![]() $\mathcal F_{{\boldsymbol k}}$
is thus proved.
$\mathcal F_{{\boldsymbol k}}$
is thus proved.
For
![]() ${\boldsymbol k}=0$
, we set
${\boldsymbol k}=0$
, we set

Direct application of equations (4.2) and (4.3) immediately gives that the collection of functions
![]() $\mathcal F_{\boldsymbol 0}$
is orthogonal in
$\mathcal F_{\boldsymbol 0}$
is orthogonal in
![]() $L^2(X_f,\mu _a)$
, and that
$L^2(X_f,\mu _a)$
, and that
 $$ \begin{align*} \int_{X_f} |\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}})}(x)|^2\,d\mu _a(x)=1-\frac{|a_{{\boldsymbol n}}|^2}{4}=\frac {3}{4}\quad \text{for all } {\boldsymbol n}\in\mathbb{N}^d. \end{align*} $$
$$ \begin{align*} \int_{X_f} |\gamma ^{({\boldsymbol z}^{m{\boldsymbol n}})}(x)|^2\,d\mu _a(x)=1-\frac{|a_{{\boldsymbol n}}|^2}{4}=\frac {3}{4}\quad \text{for all } {\boldsymbol n}\in\mathbb{N}^d. \end{align*} $$
Step 4. Almost everywhere convergence. Write
 $$ \begin{align*} S_N^{{\boldsymbol w}}\phi(x)= \sum_{{\boldsymbol n}\in [0,N-1]^d} w_{\boldsymbol n} \phi(\alpha _f^{\boldsymbol n} x) = \sum_{{\boldsymbol k}\in [0,m-1]^d}S_{N,{\boldsymbol k}}^{{\boldsymbol w}}\phi(x), \end{align*} $$
$$ \begin{align*} S_N^{{\boldsymbol w}}\phi(x)= \sum_{{\boldsymbol n}\in [0,N-1]^d} w_{\boldsymbol n} \phi(\alpha _f^{\boldsymbol n} x) = \sum_{{\boldsymbol k}\in [0,m-1]^d}S_{N,{\boldsymbol k}}^{{\boldsymbol w}}\phi(x), \end{align*} $$
where

We claim that for any
![]() ${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol 0\}$
, one has
${\boldsymbol k}\in [0,m-1]^d\smallsetminus \{\boldsymbol 0\}$
, one has
and for
![]() ${\boldsymbol k}=0$
, one has
${\boldsymbol k}=0$
, one has
 $$ \begin{align} \frac 1{N^d}\bigg( S_{N,{\boldsymbol 0}}^{{\boldsymbol w}}\phi(x)-\frac 12\sum_{\{{\boldsymbol n}\mid m{\boldsymbol n}\in[0,N-1]^d\}}|w_{\boldsymbol n}|\bigg)\to0 \quad\mu _a\!-\!a.e. \end{align} $$
$$ \begin{align} \frac 1{N^d}\bigg( S_{N,{\boldsymbol 0}}^{{\boldsymbol w}}\phi(x)-\frac 12\sum_{\{{\boldsymbol n}\mid m{\boldsymbol n}\in[0,N-1]^d\}}|w_{\boldsymbol n}|\bigg)\to0 \quad\mu _a\!-\!a.e. \end{align} $$
Now we write
 $$ \begin{align*} \frac {1}{N^d}S_N^{{\boldsymbol w}}\phi(x)=\frac {1}{N^d}\bigg(S_N^{{\boldsymbol w}}\phi(x) -\frac 12\sum_{\{{\boldsymbol n}\mid m{\boldsymbol n}\in[0,N-1]^d\}}|w_{\boldsymbol n}|\bigg)+\frac {1}{2N^d}\sum_{\{{\boldsymbol n}\mid m{\boldsymbol n}\in[0,N-1]^d\}}|w_{\boldsymbol n}|. \end{align*} $$
$$ \begin{align*} \frac {1}{N^d}S_N^{{\boldsymbol w}}\phi(x)=\frac {1}{N^d}\bigg(S_N^{{\boldsymbol w}}\phi(x) -\frac 12\sum_{\{{\boldsymbol n}\mid m{\boldsymbol n}\in[0,N-1]^d\}}|w_{\boldsymbol n}|\bigg)+\frac {1}{2N^d}\sum_{\{{\boldsymbol n}\mid m{\boldsymbol n}\in[0,N-1]^d\}}|w_{\boldsymbol n}|. \end{align*} $$
If equations (5.2) and (5.3) are indeed true, the first term in the brackets on the right-hand side converges to
![]() $0$
for
$0$
for
![]() $\mu _a$
-almost all
$\mu _a$
-almost all
![]() $x\in X_f$
, and the second term does not converge to
$x\in X_f$
, and the second term does not converge to
![]() $0$
by equation (5.1). Hence, we will be able to conclude that
$0$
by equation (5.1). Hence, we will be able to conclude that
and thus, that
![]() $(X_f,\alpha _f)$
is Bohr chaotic.
$(X_f,\alpha _f)$
is Bohr chaotic.
Finally, to establish equations (5.2) and (5.3), we will use the following multivariate generalization of the result of Davenport, Erdös, and LeVeque [Reference Davenport, Erdős and LeVeque3] due to Fan, Fan, and Qiu [Reference Fan, Fan and Qiu8, Theorem 6.1]: suppose that
![]() $\{\xi _{\boldsymbol \ell }\mid {\boldsymbol \ell }\in {\mathbb N}^d\}$
is a collection of measurable complex valued uniformly bounded functions on a probability space
$\{\xi _{\boldsymbol \ell }\mid {\boldsymbol \ell }\in {\mathbb N}^d\}$
is a collection of measurable complex valued uniformly bounded functions on a probability space
![]() $(\Omega ,\mathbb {P})$
such that
$(\Omega ,\mathbb {P})$
such that
 $$ \begin{align} \sum_{N=1}^{\infty} \frac 1{N}\int_{\Omega } |Z_{N}|^2\, d\mathbb{P}<\infty, \end{align} $$
$$ \begin{align} \sum_{N=1}^{\infty} \frac 1{N}\int_{\Omega } |Z_{N}|^2\, d\mathbb{P}<\infty, \end{align} $$
where
 $$ \begin{align*} Z_N=\frac {1}{N^d}\sum_{{\boldsymbol \ell}\in[0,N-1]^d} \xi_{{\boldsymbol \ell}} \quad (N\ge 1). \end{align*} $$
$$ \begin{align*} Z_N=\frac {1}{N^d}\sum_{{\boldsymbol \ell}\in[0,N-1]^d} \xi_{{\boldsymbol \ell}} \quad (N\ge 1). \end{align*} $$
Then
![]() $Z_N\to 0$
as
$Z_N\to 0$
as
![]() $N\to \infty \ \mathbb {P}$
-a.e. on
$N\to \infty \ \mathbb {P}$
-a.e. on
![]() $\Omega $
.
$\Omega $
.
In particular, if
![]() $\{\xi _{\boldsymbol \ell }\mid {\boldsymbol \ell }\in {\mathbb N}^d\}$
are uniformly bounded and orthogonal in
$\{\xi _{\boldsymbol \ell }\mid {\boldsymbol \ell }\in {\mathbb N}^d\}$
are uniformly bounded and orthogonal in
![]() $L^2(\Omega ,\mathbb {P})$
, then
$L^2(\Omega ,\mathbb {P})$
, then
 $$ \begin{align*} \frac 1{N}\int_{\Omega } |Z_{N}|^2\,d\mathbb{P} =\frac 1{N^{2d+1}}\sum_{{\boldsymbol \ell}\in[0,N-1]^d} \int_{X} |\xi_{{\boldsymbol \ell}}|^2\,d\mathbb{P} \le \frac{C}{N^{d+1}}, \end{align*} $$
$$ \begin{align*} \frac 1{N}\int_{\Omega } |Z_{N}|^2\,d\mathbb{P} =\frac 1{N^{2d+1}}\sum_{{\boldsymbol \ell}\in[0,N-1]^d} \int_{X} |\xi_{{\boldsymbol \ell}}|^2\,d\mathbb{P} \le \frac{C}{N^{d+1}}, \end{align*} $$
and hence equation (5.4) holds for any
![]() $d\ge 1$
.
$d\ge 1$
.
If we now apply this result to the orthogonal families of bounded functions
and
 $$ \begin{align*} \mathcal F_{\boldsymbol 0}^{\boldsymbol w}=\bigg\{ w_{m{\boldsymbol n}}\bigg(\psi\circ\alpha ^{m{\boldsymbol n}}(x)-\frac {a_{{\boldsymbol n}}}{2}\bigg) \mid {\boldsymbol n}\in{\mathbb N}^d \bigg\}, \end{align*} $$
$$ \begin{align*} \mathcal F_{\boldsymbol 0}^{\boldsymbol w}=\bigg\{ w_{m{\boldsymbol n}}\bigg(\psi\circ\alpha ^{m{\boldsymbol n}}(x)-\frac {a_{{\boldsymbol n}}}{2}\bigg) \mid {\boldsymbol n}\in{\mathbb N}^d \bigg\}, \end{align*} $$
we obtain equations (5.2) and (5.3), and hence, we complete the proof.
6 Bohr chaoticity of
 $(X_f, \alpha _f)$
: the case of
$(X_f, \alpha _f)$
: the case of
 $d=1$
$d=1$
In this section, we complete the proof of Theorem 2.1 in the case where
![]() $d=1$
: every principal algebraic
$d=1$
: every principal algebraic
![]() ${\mathbb Z}$
-action
${\mathbb Z}$
-action
![]() $(X_f,\alpha _f)$
with positive entropy is Bohr chaotic. Theorem 2.1 will follow from Remark 2.7, Theorem 5.1, and the following result.
$(X_f,\alpha _f)$
with positive entropy is Bohr chaotic. Theorem 2.1 will follow from Remark 2.7, Theorem 5.1, and the following result.
Theorem 6.1. Every primitive irreducible polynomial
![]() $f\in R_1$
with
$f\in R_1$
with
![]() $\mathsf {m}(f)>0$
is m-good for some positive integer m.
$\mathsf {m}(f)>0$
is m-good for some positive integer m.
The proof of Theorem 6.1 consists of the following three lemmas.
Lemma 6.2. (Preliminary lemma)
Let
![]() $f(z) = f_0 + f_1 z + \cdots + f_r z^r \in \mathbb {Z}[z]$
be an irreducible polynomial with
$f(z) = f_0 + f_1 z + \cdots + f_r z^r \in \mathbb {Z}[z]$
be an irreducible polynomial with
![]() $r\ge 1$
and
$r\ge 1$
and
![]() $f_0f_r\ne 0$
. If
$f_0f_r\ne 0$
. If
![]() $\mathsf {m}(f)>0$
, then at least one of the following statements is true:
$\mathsf {m}(f)>0$
, then at least one of the following statements is true:
-
(1) there exists a root of f in
 $\mathbb {C}$
which is not on the unit circle;
$\mathbb {C}$
which is not on the unit circle; -
(2) there exists a prime
 $p\ge 2$
such that f admits a root
$p\ge 2$
such that f admits a root
 $\unicode{x3bb} $
in the algebraic closure
$\unicode{x3bb} $
in the algebraic closure
 $\overline {\mathbb {Q}}_p$
of the field of p-adic numbers
$\overline {\mathbb {Q}}_p$
of the field of p-adic numbers
 $\mathbb {Q}_p$
such that
$\mathbb {Q}_p$
such that
 $|\unicode{x3bb} |_p>1$
.
$|\unicode{x3bb} |_p>1$
.
Proof. Suppose
![]() $r=1$
, that is,
$r=1$
, that is,
![]() $f(z)=f_0+f_1z$
. If the only root of f lies on the unit circle, then necessarily
$f(z)=f_0+f_1z$
. If the only root of f lies on the unit circle, then necessarily
![]() $|f_0|=|f_1|$
. The irreducibility of f implies that
$|f_0|=|f_1|$
. The irreducibility of f implies that
![]() $|f_0|=|f_1|=1$
, and thus
$|f_0|=|f_1|=1$
, and thus
![]() $\mathsf {m}(f)=0$
by equation (2.7). Therefore, assuming
$\mathsf {m}(f)=0$
by equation (2.7). Therefore, assuming
![]() $\mathsf {m}(f)>0$
for irreducible f with
$\mathsf {m}(f)>0$
for irreducible f with
![]() $\deg (f)=1$
, we conclude that
$\deg (f)=1$
, we conclude that
![]() $|f_0|\ne |f_1|$
, and hence condition (1) must hold.
$|f_0|\ne |f_1|$
, and hence condition (1) must hold.
Suppose
![]() $r\ge 2$
and the roots of f are all on the unit circle, that is, suppose that condition (1) does not hold. If
$r\ge 2$
and the roots of f are all on the unit circle, that is, suppose that condition (1) does not hold. If
![]() $|f_r|=1$
, then Kronecker’s theorem [Reference Kronecker17] implies that all roots of f are roots of unity, and equation (2.7) shows that
$|f_r|=1$
, then Kronecker’s theorem [Reference Kronecker17] implies that all roots of f are roots of unity, and equation (2.7) shows that
![]() $\mathsf {m}(f)=0$
, in contradiction to our hypothesis. However, if
$\mathsf {m}(f)=0$
, in contradiction to our hypothesis. However, if
![]() $|f_r|>1$
, then
$|f_r|>1$
, then
 $$ \begin{align*} f(z) =f_r \bigg( z^r +\frac{f_{r-1}}{f_r} z^{r-1}+\cdots +\frac{f_0}{f_r}\bigg), \end{align*} $$
$$ \begin{align*} f(z) =f_r \bigg( z^r +\frac{f_{r-1}}{f_r} z^{r-1}+\cdots +\frac{f_0}{f_r}\bigg), \end{align*} $$
and Vieta’s formula implies that
![]() $|{f_0}/{f_r}| = |\prod _{\zeta \in \mathbb {C}: f(\zeta )=0}\zeta | =1$
, that is, that
$|{f_0}/{f_r}| = |\prod _{\zeta \in \mathbb {C}: f(\zeta )=0}\zeta | =1$
, that is, that
![]() $|f_0|=|f_r|$
. Since f is irreducible,
$|f_0|=|f_r|$
. Since f is irreducible,
![]() $f_j/f_r$
is not integer for some
$f_j/f_r$
is not integer for some
![]() $1\le j\le r-1$
. Then there exists a rational prime p such that
$1\le j\le r-1$
. Then there exists a rational prime p such that
![]() $|f_j/f_r|_p>1$
. Let
$|f_j/f_r|_p>1$
. Let
![]() $\unicode{x3bb} _i,\; 1\le i \le r$
, be the roots of f in the algebraic closure
$\unicode{x3bb} _i,\; 1\le i \le r$
, be the roots of f in the algebraic closure
![]() $\overline {\mathbb {Q}}_p$
of
$\overline {\mathbb {Q}}_p$
of
![]() $\mathbb {Q}_p$
, the p-adic rationals. By considering the jth elementary symmetric polynomials of the roots and once again applying Vieta’s formulas, we get that
$\mathbb {Q}_p$
, the p-adic rationals. By considering the jth elementary symmetric polynomials of the roots and once again applying Vieta’s formulas, we get that
 $$ \begin{align*} 1<\bigg|\frac{f_j}{f_r}\bigg|_p = \bigg|\!\sum_{1\le i_1<i_2<\cdots <i_j \le r}\unicode{x3bb} _{i_1}\cdots \unicode{x3bb} _{i_j}\bigg|_p\le (\max_{1\le i\le r} |\unicode{x3bb} _i|_p)^j. \end{align*} $$
$$ \begin{align*} 1<\bigg|\frac{f_j}{f_r}\bigg|_p = \bigg|\!\sum_{1\le i_1<i_2<\cdots <i_j \le r}\unicode{x3bb} _{i_1}\cdots \unicode{x3bb} _{i_j}\bigg|_p\le (\max_{1\le i\le r} |\unicode{x3bb} _i|_p)^j. \end{align*} $$
Thus one has
![]() $|\unicode{x3bb} _i|_p>1$
for some
$|\unicode{x3bb} _i|_p>1$
for some
![]() $i\in \{1,\ldots ,r\}$
.
$i\in \{1,\ldots ,r\}$
.
The following key lemma will be used to show that for sufficiently large m, the sequence of polynomials
![]() $\{z^{nm}\}_{n\ge 0}$
gives a dissociate sequence of characters of
$\{z^{nm}\}_{n\ge 0}$
gives a dissociate sequence of characters of
![]() $X_f$
.
$X_f$
.
Lemma 6.3. (Condition (C1))
Suppose that
![]() $f=f_0+f_1z+\cdots +f_rz^r\in {\mathbb Z}[z]$
has a root in
$f=f_0+f_1z+\cdots +f_rz^r\in {\mathbb Z}[z]$
has a root in
![]() $\mathbb {C}$
or in
$\mathbb {C}$
or in
![]() $\overline {\mathbb {Q}}_p$
(for some p) of absolute value larger than
$\overline {\mathbb {Q}}_p$
(for some p) of absolute value larger than
![]() $1$
. Then for any sufficiently large m and any
$1$
. Then for any sufficiently large m and any
![]() $D\ge 0$
, the polynomials
$D\ge 0$
, the polynomials
 $$ \begin{align} P(z) =\sum_{j=0}^D \varepsilon _j z^{mj} \quad \text{with }\varepsilon _0,\varepsilon _1,\ldots,\varepsilon _D\in \{-2,-1,0,1,2\}, \end{align} $$
$$ \begin{align} P(z) =\sum_{j=0}^D \varepsilon _j z^{mj} \quad \text{with }\varepsilon _0,\varepsilon _1,\ldots,\varepsilon _D\in \{-2,-1,0,1,2\}, \end{align} $$
are not divisible by f unless
![]() $\epsilon _0=\epsilon _1=\cdots = \epsilon _D=0$
.
$\epsilon _0=\epsilon _1=\cdots = \epsilon _D=0$
.
Proof. First we consider the case that f has a root in
![]() $\mathbb {C}$
of modulus larger than
$\mathbb {C}$
of modulus larger than
![]() $1$
. For any polynomial g, we introduce the notation
$1$
. For any polynomial g, we introduce the notation
Without loss of generality, we may assume that
![]() $\varepsilon _D\ne 0$
and consider the reduced polynomial
$\varepsilon _D\ne 0$
and consider the reduced polynomial
 $$ \begin{align*} \widetilde{P}(z) =\sum_{j=0}^D \varepsilon _j z^{j}, \end{align*} $$
$$ \begin{align*} \widetilde{P}(z) =\sum_{j=0}^D \varepsilon _j z^{j}, \end{align*} $$
such that
![]() $ P(z)= \widetilde {P}(z^m)$
. Clearly,
$ P(z)= \widetilde {P}(z^m)$
. Clearly,
![]() $\rho _{\widetilde {P}} = \rho _P^m$
.
$\rho _{\widetilde {P}} = \rho _P^m$
.
However, using the Cauchy bound on the roots of polynomials, one gets that
 $$ \begin{align*} \rho_{\widetilde{P}}\le 1+\max_{j=0,\ldots,D-1} \bigg|\frac {\varepsilon _j}{\varepsilon _D}\bigg|\le 3, \end{align*} $$
$$ \begin{align*} \rho_{\widetilde{P}}\le 1+\max_{j=0,\ldots,D-1} \bigg|\frac {\varepsilon _j}{\varepsilon _D}\bigg|\le 3, \end{align*} $$
and hence
![]() $ \rho _P \le 3^{{1}/{m}}. $
Choose an integer
$ \rho _P \le 3^{{1}/{m}}. $
Choose an integer
![]() $M\ge 1$
large enough such that
$M\ge 1$
large enough such that
![]() $3^{{1}/{M}} <\rho _f$
(this is possible because
$3^{{1}/{M}} <\rho _f$
(this is possible because
![]() $\rho _f>1$
). Thus for all
$\rho _f>1$
). Thus for all
![]() $m\ge M$
, we have
$m\ge M$
, we have
![]() $\rho _P <\rho _f$
. However, if
$\rho _P <\rho _f$
. However, if
![]() $P(z)$
was divisible by f, we would have
$P(z)$
was divisible by f, we would have
![]() $\rho _f \le \rho _P$
, thus arriving to a contradiction.
$\rho _f \le \rho _P$
, thus arriving to a contradiction.
If f has a root in
![]() $\overline {\mathbb {Q}}_p$
(for some prime p) of absolute value larger than
$\overline {\mathbb {Q}}_p$
(for some prime p) of absolute value larger than
![]() $1$
, the same argument works with
$1$
, the same argument works with
![]() $|\cdot |$
replaced by
$|\cdot |$
replaced by
![]() $|\cdot |_p$
. Indeed, suppose
$|\cdot |_p$
. Indeed, suppose
![]() $\zeta $
is a root of f with
$\zeta $
is a root of f with
![]() $|\zeta |_p>1$
. If
$|\zeta |_p>1$
. If
![]() $f|P$
, then
$f|P$
, then
![]() $\zeta $
is also a root of P, so one has
$\zeta $
is also a root of P, so one has
 $$ \begin{align*} |\zeta|_{p}^{mD}\!=\!|\zeta^{mD}|_p\!=\!\bigg|\! \sum_{j=0}^{D-1} \frac{\varepsilon _j}{\varepsilon _D} \zeta^{mj}\bigg|_p \le \max_{j=0,\ldots, D-1}\bigg| \frac{\varepsilon _j}{\varepsilon _D} \zeta^{mj}\bigg|_p \le \bigg(\max_{j=0,\ldots, D-1} \bigg| \frac{\varepsilon _j}{\varepsilon _D}\bigg|_p\bigg) |\zeta|_{p}^{m(D-1)}. \end{align*} $$
$$ \begin{align*} |\zeta|_{p}^{mD}\!=\!|\zeta^{mD}|_p\!=\!\bigg|\! \sum_{j=0}^{D-1} \frac{\varepsilon _j}{\varepsilon _D} \zeta^{mj}\bigg|_p \le \max_{j=0,\ldots, D-1}\bigg| \frac{\varepsilon _j}{\varepsilon _D} \zeta^{mj}\bigg|_p \le \bigg(\max_{j=0,\ldots, D-1} \bigg| \frac{\varepsilon _j}{\varepsilon _D}\bigg|_p\bigg) |\zeta|_{p}^{m(D-1)}. \end{align*} $$
Thus arriving at a contradiction.
Lemma 6.4. (Condition (C2))
Suppose that
![]() $f(z)= f_rz^r+\cdots + f_1z+f_0 \in \mathbb {Z}[z]$
has a root in
$f(z)= f_rz^r+\cdots + f_1z+f_0 \in \mathbb {Z}[z]$
has a root in
![]() $\mathbb {C}$
or in
$\mathbb {C}$
or in
![]() $\overline {\mathbb {Q}}_p$
(for some prime p) of absolute value larger than
$\overline {\mathbb {Q}}_p$
(for some prime p) of absolute value larger than
![]() $1$
. Then for all sufficiently large integers m, any integer k with
$1$
. Then for all sufficiently large integers m, any integer k with
![]() $1\le k <m$
, every
$1\le k <m$
, every
![]() $D\ge 0$
, and all arbitrary
$D\ge 0$
, and all arbitrary
![]() $(D+1)$
-tuples
$(D+1)$
-tuples
![]() $\varepsilon =(\varepsilon _0,\ldots ,\varepsilon _D)$
and
$\varepsilon =(\varepsilon _0,\ldots ,\varepsilon _D)$
and
![]() $\delta =(\delta _0,\ldots ,\delta _D)$
in
$\delta =(\delta _0,\ldots ,\delta _D)$
in
![]() $\{-1,0,1\}^{D+1}$
, the polynomial
$\{-1,0,1\}^{D+1}$
, the polynomial
 $$ \begin{align} Q(z) = \sum_{j=0}^D \varepsilon _j z^{mj}-\sum_{j=0}^D \delta_j z^{mj+k} \end{align} $$
$$ \begin{align} Q(z) = \sum_{j=0}^D \varepsilon _j z^{mj}-\sum_{j=0}^D \delta_j z^{mj+k} \end{align} $$
is not divisible by f unless
![]() $Q(z)\equiv 0$
, that is, unless all
$Q(z)\equiv 0$
, that is, unless all
![]() $\epsilon _j$
and
$\epsilon _j$
and
![]() $\delta _j$
are equal to zero.
$\delta _j$
are equal to zero.
Proof. Assume Q is divisible by f. We treat the complex case first. Namely, assume
![]() $\zeta \in \mathbb {C}$
is such that
$\zeta \in \mathbb {C}$
is such that
![]() $f(\zeta )=0$
and
$f(\zeta )=0$
and ![]() . Without loss of generality, we may assume that
. Without loss of generality, we may assume that
![]() $|\varepsilon _D|+|\delta _D|>0$
. We distinguish two cases.
$|\varepsilon _D|+|\delta _D|>0$
. We distinguish two cases.
Case I.
![]() $\delta _D\ne 0$
. If the polynomial
$\delta _D\ne 0$
. If the polynomial
![]() $Q(z)$
, defined by equation (6.2), is divisible by f, then
$Q(z)$
, defined by equation (6.2), is divisible by f, then
![]() $Q(\zeta )=0$
, in other words,
$Q(\zeta )=0$
, in other words,
 $$ \begin{align} \smash[b]{\delta_D \zeta^{mD+k} =\sum_{j=0}^D \varepsilon _j \zeta^{mj}-\sum_{j=0}^{D-1} \delta_j \zeta^{mj+k}.} \end{align} $$
$$ \begin{align} \smash[b]{\delta_D \zeta^{mD+k} =\sum_{j=0}^D \varepsilon _j \zeta^{mj}-\sum_{j=0}^{D-1} \delta_j \zeta^{mj+k}.} \end{align} $$
It follows that
 $$ \begin{align*} \smash{R^{mD+k} \le \sum_{j=0}^D R^{mj}+\sum_{j=0}^{D-1} R^{mj+k}= \frac{R^{(D+1)m}-1}{R^m-1}+ \frac {R^{Dm}-1}{R^m-1}\cdot R^k,} \end{align*} $$
$$ \begin{align*} \smash{R^{mD+k} \le \sum_{j=0}^D R^{mj}+\sum_{j=0}^{D-1} R^{mj+k}= \frac{R^{(D+1)m}-1}{R^m-1}+ \frac {R^{Dm}-1}{R^m-1}\cdot R^k,} \end{align*} $$
and hence
As
![]() $m\to \infty $
, the right-hand side of this inequality converges to
$m\to \infty $
, the right-hand side of this inequality converges to
![]() $1$
, but the left-hand side remains equal to
$1$
, but the left-hand side remains equal to
![]() $R^k>1$
. If m is large enough, our assumption that Q is divisible by f leads to a contradiction.
$R^k>1$
. If m is large enough, our assumption that Q is divisible by f leads to a contradiction.
Case II.
![]() $\delta _D=0$
but
$\delta _D=0$
but
![]() $\varepsilon _D\ne 0$
. In this case, we have
$\varepsilon _D\ne 0$
. In this case, we have
 $$ \begin{align} \varepsilon _D \zeta^{mD} =-\sum_{j=0}^{D-1}\varepsilon _j \zeta^{jm}+\sum_{j=0}^{D-1}\delta_j \zeta^{jm+k}. \end{align} $$
$$ \begin{align} \varepsilon _D \zeta^{mD} =-\sum_{j=0}^{D-1}\varepsilon _j \zeta^{jm}+\sum_{j=0}^{D-1}\delta_j \zeta^{jm+k}. \end{align} $$
It follows that
Since
![]() $R>1$
, the last inequality is violated for all sufficiently large m, and we again arrive at a contradiction with our assumption that Q is divisible by f.
$R>1$
, the last inequality is violated for all sufficiently large m, and we again arrive at a contradiction with our assumption that Q is divisible by f.
In the p-adic case, the argument is simpler because of the non-archimedean triangle inequality
![]() $|\zeta +\xi |_p\le \max (|\zeta |_p,|\xi |_p)$
. Indeed, from equation (6.3), we get that
$|\zeta +\xi |_p\le \max (|\zeta |_p,|\xi |_p)$
. Indeed, from equation (6.3), we get that
![]() $|\zeta |_p^{mD+k}\le |\zeta |_p^{mD}$
(impossible), and from equation (6.4), we get that
$|\zeta |_p^{mD+k}\le |\zeta |_p^{mD}$
(impossible), and from equation (6.4), we get that
![]() $|\zeta |_p^{mD}\le |\zeta |_p^{m(D-1)+k}$
(equally impossible).
$|\zeta |_p^{mD}\le |\zeta |_p^{m(D-1)+k}$
(equally impossible).
Proof of Theorem 2.1
By Remark 2.7, we may assume that the polynomial
![]() $f(z) = f_0+\cdots +f_rz^r\in \mathbb {Z}[z]$
is primitive, irreducible, and has positive Mahler measure (cf. equation (2.7)). If f has a root in
$f(z) = f_0+\cdots +f_rz^r\in \mathbb {Z}[z]$
is primitive, irreducible, and has positive Mahler measure (cf. equation (2.7)). If f has a root in
![]() $\mathbb {C}$
of absolute value larger than 1, Lemmas 6.3 and 6.4 show that f is m-good for some
$\mathbb {C}$
of absolute value larger than 1, Lemmas 6.3 and 6.4 show that f is m-good for some
![]() $m\in {\mathbb N}$
(in fact, for all sufficiently large m). An application of Theorem 5.1 completes the proof of Theorem 2.1 in this case.
$m\in {\mathbb N}$
(in fact, for all sufficiently large m). An application of Theorem 5.1 completes the proof of Theorem 2.1 in this case.
If all complex roots of f have absolute value
![]() $\le 1$
, and if
$\le 1$
, and if
![]() $\zeta $
is a root of f, we denote by
$\zeta $
is a root of f, we denote by
![]() $\textbf {k}=\mathbb {Q}(\zeta )$
the algebraic number field generated by
$\textbf {k}=\mathbb {Q}(\zeta )$
the algebraic number field generated by
![]() $\zeta $
and write
$\zeta $
and write
![]() $P_{\textbf {k}}$
for the set of places (or valuations) of
$P_{\textbf {k}}$
for the set of places (or valuations) of
![]() $\textbf {k}$
. If
$\textbf {k}$
. If
![]() $|\zeta |_v$
is the absolute value of
$|\zeta |_v$
is the absolute value of
![]() $\zeta $
at a place
$\zeta $
at a place
![]() $v\in P_{\textbf {k}}$
, then our last assumption implies that
$v\in P_{\textbf {k}}$
, then our last assumption implies that
![]() $|\zeta |_v\le 1$
for every infinite place
$|\zeta |_v\le 1$
for every infinite place
![]() $v\in P_{\textbf {k}}$
. Since the product formula for algebraic number fields shows that
$v\in P_{\textbf {k}}$
. Since the product formula for algebraic number fields shows that
![]() $\prod _{v\in P_{\textbf {k}}}|\zeta |_v=1$
, we either have that
$\prod _{v\in P_{\textbf {k}}}|\zeta |_v=1$
, we either have that
![]() $|\zeta |_v=1$
for every
$|\zeta |_v=1$
for every
![]() $v\in P_{\textbf {k}}$
, or that there exists a finite place
$v\in P_{\textbf {k}}$
, or that there exists a finite place
![]() $v\in P_{\textbf {k}}$
with
$v\in P_{\textbf {k}}$
with
![]() $|\zeta |_v>1$
. In the first case,
$|\zeta |_v>1$
. In the first case,
![]() $\zeta $
is a root of unity, which makes f cyclotomic and
$\zeta $
is a root of unity, which makes f cyclotomic and
![]() $\mathsf {m}(f)=0$
, contrary to our hypothesis. In the second case, we can once again use the Lemmas 6.3 and 6.4 to show that f is m-good for all sufficiently large m, and Theorem 5.1 completes the proof of Theorem 2.1 as above.
$\mathsf {m}(f)=0$
, contrary to our hypothesis. In the second case, we can once again use the Lemmas 6.3 and 6.4 to show that f is m-good for all sufficiently large m, and Theorem 5.1 completes the proof of Theorem 2.1 as above.
7 Bohr chaoticity of
 $(X_f, \alpha _f)$
: the case of
$(X_f, \alpha _f)$
: the case of
 $d\ge 2$
$d\ge 2$
This section is devoted to the proof of Theorem 2.3 for
![]() $d\ge 2$
, which will again be based on Theorem 5.1. As before, we assume that the polynomial
$d\ge 2$
, which will again be based on Theorem 5.1. As before, we assume that the polynomial
![]() $f\in R_d$
is primitive and irreducible.
$f\in R_d$
is primitive and irreducible.
7.1 Homoclinic points of atoral polynomials in
 $R_d$
and the gap theorem
$R_d$
and the gap theorem
For every
![]() ${t\in \mathbb {T}}$
, we set
${t\in \mathbb {T}}$
, we set
Definition 7.1. A point
![]() $x\in X_f$
is homoclinic (or, more precisely, homoclinic to
$x\in X_f$
is homoclinic (or, more precisely, homoclinic to
![]() $0$
) if
$0$
) if
![]() $\lim _{{\boldsymbol n}\to \infty }\lVert x_{\boldsymbol n}\rVert =0$
. A homoclinic point
$\lim _{{\boldsymbol n}\to \infty }\lVert x_{\boldsymbol n}\rVert =0$
. A homoclinic point
![]() $x\in X_f$
is summable if
$x\in X_f$
is summable if
![]() $\sum _{{\boldsymbol n}\in \mathbb {Z}^d}\lVert x_{\boldsymbol n}\rVert <\infty $
.
$\sum _{{\boldsymbol n}\in \mathbb {Z}^d}\lVert x_{\boldsymbol n}\rVert <\infty $
.
The existence of non-zero summable homoclinic points of
![]() $(X_f,\alpha _f)$
is equivalent to atorality of the polynomial f.
$(X_f,\alpha _f)$
is equivalent to atorality of the polynomial f.
Theorem 7.2. [Reference Lind, Schmidt and Verbitskiy20]
If
![]() $0\ne f\in R_d$
, the following conditions are equivalent:
$0\ne f\in R_d$
, the following conditions are equivalent:
-
(1) the principal algebraic action
 $(X_f,\alpha _f)$
has a non-zero summable homoclinic point;
$(X_f,\alpha _f)$
has a non-zero summable homoclinic point; -
(2) the Laurent polynomial f is atoral in the sense of Definition 2.2.
For a principal algebraic
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $(X_f,\alpha _f)$
, the existence of summable homoclinic points has a number of important consequences (cf. [Reference Lind and Schmidt19]): it implies positivity of entropy and very strong specification properties of the action, and it guarantees the coincidence of entropy with the logarithmic growth rate of the number of periodic points of
$(X_f,\alpha _f)$
, the existence of summable homoclinic points has a number of important consequences (cf. [Reference Lind and Schmidt19]): it implies positivity of entropy and very strong specification properties of the action, and it guarantees the coincidence of entropy with the logarithmic growth rate of the number of periodic points of
![]() $\alpha _f$
(that is, of points in
$\alpha _f$
(that is, of points in
![]() $X_f$
with finite orbits under
$X_f$
with finite orbits under
![]() $\alpha _f$
—cf. [Reference Lind and Schmidt19, Reference Lind, Schmidt and Verbitskiy20]). Somewhat surprisingly, it also plays a role in the gap theorem stated below, which will imply conditions (C1) and (C2) in Definition 4.2.
$\alpha _f$
—cf. [Reference Lind and Schmidt19, Reference Lind, Schmidt and Verbitskiy20]). Somewhat surprisingly, it also plays a role in the gap theorem stated below, which will imply conditions (C1) and (C2) in Definition 4.2.
We remark in passing that some of these consequences of atorality also hold for toral polynomials, but with considerably harder proofs and/or weaker conclusions—cf. e.g., [Reference Dimitrov4] or [Reference Lind, Schmidt and Verbitskiy20]). However, it is not known if specification or gap properties hold in the toral case.
To state the gap theorem referred to above, we consider, for any non-empty subset
![]() ${{\mathcal S}\subset {\mathbb Z}^d}$
and any integer
${{\mathcal S}\subset {\mathbb Z}^d}$
and any integer
![]() $H\ge 1$
, the set
$H\ge 1$
, the set
![]() $\mathcal P({\mathcal S},H)\subset R_d$
of all Laurent polynomials with support in
$\mathcal P({\mathcal S},H)\subset R_d$
of all Laurent polynomials with support in
![]() ${\mathcal S}$
and coefficients bounded in absolute value by H:
${\mathcal S}$
and coefficients bounded in absolute value by H:
For every
![]() ${\boldsymbol n}=(n_1,\ldots ,n_d)\in \mathbb {Z}^d$
, we set
${\boldsymbol n}=(n_1,\ldots ,n_d)\in \mathbb {Z}^d$
, we set
![]() $\|{\boldsymbol n}\|=\max \{|n_1|,\ldots ,|n_d|\}$
. Then the following is true.
$\|{\boldsymbol n}\|=\max \{|n_1|,\ldots ,|n_d|\}$
. Then the following is true.
Theorem 7.3. (Gap theorem)
Suppose that
![]() $g\in R_d$
is primitive, irreducible, and atoral. For every
$g\in R_d$
is primitive, irreducible, and atoral. For every
![]() $H\ge 1$
, there exists an integer
$H\ge 1$
, there exists an integer
![]() $m\ge 1$
with the following property: for every pair of sets
$m\ge 1$
with the following property: for every pair of sets
![]() ${\mathcal S},{\mathcal S}'\subset \mathbb {Z}^d$
with distance
${\mathcal S},{\mathcal S}'\subset \mathbb {Z}^d$
with distance
and for every
![]() $v=\sum _{{\boldsymbol n}\in {\mathcal S}\cup {\mathcal S}'} v_{{\boldsymbol n}}{\boldsymbol z}^{{\boldsymbol n}} \in \mathcal {P}({\mathcal S}\cup {\mathcal S}',H)$
which is divisible by g, the restriction of v to
$v=\sum _{{\boldsymbol n}\in {\mathcal S}\cup {\mathcal S}'} v_{{\boldsymbol n}}{\boldsymbol z}^{{\boldsymbol n}} \in \mathcal {P}({\mathcal S}\cup {\mathcal S}',H)$
which is divisible by g, the restriction of v to
![]() ${\mathcal S}$
,
${\mathcal S}$
,
is also divisible by g.
For the proof of Theorem 7.3, we consider the algebra
![]() $\ell ^1(\mathbb {Z}^d,\mathbb {R})$
of all functions
$\ell ^1(\mathbb {Z}^d,\mathbb {R})$
of all functions
![]() $v\colon {\boldsymbol n} \mapsto v_{\boldsymbol n}$
from
$v\colon {\boldsymbol n} \mapsto v_{\boldsymbol n}$
from
![]() $\mathbb {Z}^d$
to
$\mathbb {Z}^d$
to
![]() $\mathbb {R}$
with
$\mathbb {R}$
with
![]() $\|v\|_1=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}|v_{\boldsymbol n}|<\infty $
, furnished with its usual multiplication (or convolution)
$\|v\|_1=\sum _{{\boldsymbol n}\in \mathbb {Z}^d}|v_{\boldsymbol n}|<\infty $
, furnished with its usual multiplication (or convolution)
![]() $(v,w)\mapsto v\cdot w$
and involution
$(v,w)\mapsto v\cdot w$
and involution
![]() $w\mapsto w^{*}$
, given by
$w\mapsto w^{*}$
, given by
and
for every
![]() $v,w\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
and
$v,w\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
and
![]() ${\boldsymbol m},{\boldsymbol n}\in \mathbb {Z}^d$
. If we denote by
${\boldsymbol m},{\boldsymbol n}\in \mathbb {Z}^d$
. If we denote by
![]() $\ell ^1(\mathbb {Z}^d,\mathbb {Z})\subset \ell ^1(\mathbb {Z}^d,\mathbb {R})$
the set of all integer-valued elements of
$\ell ^1(\mathbb {Z}^d,\mathbb {Z})\subset \ell ^1(\mathbb {Z}^d,\mathbb {R})$
the set of all integer-valued elements of
![]() $\ell ^1(\mathbb {Z}^d,\mathbb {R})$
and identify every
$\ell ^1(\mathbb {Z}^d,\mathbb {R})$
and identify every
![]() $h = \sum _{{\boldsymbol n}\in \mathbb {Z}^d}h_{\boldsymbol n}\boldsymbol {z}^{\boldsymbol n}\in R_d$
with the element
$h = \sum _{{\boldsymbol n}\in \mathbb {Z}^d}h_{\boldsymbol n}\boldsymbol {z}^{\boldsymbol n}\in R_d$
with the element
![]() $(h_{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {Z}^d}\in \ell ^1(\mathbb {Z}^d,\mathbb {Z})$
, we obtain an embedding
$(h_{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {Z}^d}\in \ell ^1(\mathbb {Z}^d,\mathbb {Z})$
, we obtain an embedding
in which the multiplication
![]() $(h,h')\mapsto h\cdot h'$
of Laurent polynomials extends to the composition in equation (7.2) in
$(h,h')\mapsto h\cdot h'$
of Laurent polynomials extends to the composition in equation (7.2) in
![]() $\ell ^1(\mathbb {Z}^d,\mathbb {R})$
. In fact, the multiplication
$\ell ^1(\mathbb {Z}^d,\mathbb {R})$
. In fact, the multiplication
![]() $(v,w)\mapsto v\cdot w$
in equation (7.2) is also well defined for
$(v,w)\mapsto v\cdot w$
in equation (7.2) is also well defined for
![]() $w\in \ell ^1 (\mathbb {Z}^d,\mathbb {R})$
and
$w\in \ell ^1 (\mathbb {Z}^d,\mathbb {R})$
and
![]() $v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, the space of all bounded sequences
$v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, the space of all bounded sequences
![]() $(v_{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {Z}^d}$
in the supremum norm
$(v_{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {Z}^d}$
in the supremum norm
![]() $\|v\|_\infty =\sup _{{\boldsymbol n}\in \mathbb {Z}^d}|v_{\boldsymbol n}|$
, and
$\|v\|_\infty =\sup _{{\boldsymbol n}\in \mathbb {Z}^d}|v_{\boldsymbol n}|$
, and
for all
![]() $w\in \ell ^1 (\mathbb {Z}^d,\mathbb {R})$
and
$w\in \ell ^1 (\mathbb {Z}^d,\mathbb {R})$
and
![]() $v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
.
$v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
.
The shift action
![]() $\bar \sigma $
of
$\bar \sigma $
of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, defined exactly as in equation (2.1) by
$\ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, defined exactly as in equation (2.1) by
for every
![]() ${\boldsymbol m}\in \mathbb {Z}^d$
and
${\boldsymbol m}\in \mathbb {Z}^d$
and
![]() $v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, extends to an action
$v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, extends to an action
![]() $w\mapsto w(\bar \sigma )$
of
$w\mapsto w(\bar \sigma )$
of
![]() $\ell ^1(\mathbb {Z}^d,\mathbb {R})$
on
$\ell ^1(\mathbb {Z}^d,\mathbb {R})$
on
![]() $\ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
by bounded linear operators with
$\ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
by bounded linear operators with
for every
![]() $w\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
. Equation (7.4) implies that
$w\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
. Equation (7.4) implies that
so that
for every
![]() $w\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
and
$w\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
and
![]() $v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
(cf. equation (7.3)).
$v\in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
(cf. equation (7.3)).
We define a surjective group homomorphism
![]() $\eta \colon \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R}) \to \mathbb {T}^{\mathbb {Z}^d}$
by setting
$\eta \colon \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R}) \to \mathbb {T}^{\mathbb {Z}^d}$
by setting
for every
![]() $v=(v_{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {Z}^d}$
and
$v=(v_{\boldsymbol n})_{{\boldsymbol n}\in \mathbb {Z}^d}$
and
![]() ${\boldsymbol n}\in \mathbb {Z}^d$
. Note that
${\boldsymbol n}\in \mathbb {Z}^d$
. Note that
![]() $\eta $
is shift-equivariant in the sense that
$\eta $
is shift-equivariant in the sense that
for every
![]() ${\boldsymbol n}\in \mathbb {Z}^d$
; more generally, if
${\boldsymbol n}\in \mathbb {Z}^d$
; more generally, if
![]() $w\in R_d=\ell ^1(\mathbb {Z}^d,\mathbb {Z})$
, then
$w\in R_d=\ell ^1(\mathbb {Z}^d,\mathbb {Z})$
, then
For every
![]() $x\in \mathbb {T}^{\mathbb {Z}^d}$
, there exists a unique point
$x\in \mathbb {T}^{\mathbb {Z}^d}$
, there exists a unique point
![]() $x^{\#} \in (-\tfrac 12,\tfrac 12]^{\mathbb {Z}^d}\subset \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, called the lift of x, such that
$x^{\#} \in (-\tfrac 12,\tfrac 12]^{\mathbb {Z}^d}\subset \ell ^{\infty } (\mathbb {Z}^d,\mathbb {R})$
, called the lift of x, such that
Let
![]() $g=\sum _{{\boldsymbol n}\in \mathbb {Z}^d} g_{\boldsymbol n} \boldsymbol {z}^{\boldsymbol n} \in R_d$
be the Laurent polynomial appearing in the statement of Theorem 7.3 and set
$g=\sum _{{\boldsymbol n}\in \mathbb {Z}^d} g_{\boldsymbol n} \boldsymbol {z}^{\boldsymbol n} \in R_d$
be the Laurent polynomial appearing in the statement of Theorem 7.3 and set
Since
![]() $U(f)= U(g)$
, f is again atoral and has non-trivial summable homoclinic points by Theorem 7.2.
$U(f)= U(g)$
, f is again atoral and has non-trivial summable homoclinic points by Theorem 7.2.
Lemma 7.4. For every
![]() $x\in \mathbb {T}^{\mathbb {Z}^d}$
, the following is true:
$x\in \mathbb {T}^{\mathbb {Z}^d}$
, the following is true:
-
(1)
 $x\in X_f$
if and only if
$x\in X_f$
if and only if
 $f(\bar {\sigma })x^{\#} \in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {Z}),\ that\ is, \ x^{\#}\cdot f^{*} \in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {Z}) $
(cf. equation (7.5));
$f(\bar {\sigma })x^{\#} \in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {Z}),\ that\ is, \ x^{\#}\cdot f^{*} \in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {Z}) $
(cf. equation (7.5)); -
(2) x is a non-trivial summable homoclinic point of
 $\alpha _f$
if and only if
$\alpha _f$
if and only if
 $x^{\#}\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
,
$x^{\#}\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
,  , and h is not divisible by
, and h is not divisible by
 $f^{*}$
in
$f^{*}$
in
 $R_d$
.
$R_d$
.
Proof. (1) Suppose that
![]() $x\in {\mathbb T}^{{\mathbb Z}^d}$
. By equation (7.7), we have
$x\in {\mathbb T}^{{\mathbb Z}^d}$
. By equation (7.7), we have
So,
![]() $x\in X_f$
, that is,
$x\in X_f$
, that is,
![]() $f(\sigma )x=0$
if and only if
$f(\sigma )x=0$
if and only if
![]() $f(\bar {\sigma })x^{\#} \in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {Z})$
.
$f(\bar {\sigma })x^{\#} \in \ell ^{\infty } (\mathbb {Z}^d,\mathbb {Z})$
.
(2) If x is a non-trivial summable homoclinic point of
![]() $\alpha _f$
, then
$\alpha _f$
, then
![]() $x^\# \in \ell ^1(\mathbb{Z}^d,\mathbb{R})$
, and part (1) of this proof implies that
$x^\# \in \ell ^1(\mathbb{Z}^d,\mathbb{R})$
, and part (1) of this proof implies that
![]() $h=x^\#\cdot f^*\in \ell^1(\mathbb{Z}^d,\mathbb{Z}) = R_d$
. If h were divisible by
$h=x^\#\cdot f^*\in \ell^1(\mathbb{Z}^d,\mathbb{Z}) = R_d$
. If h were divisible by
![]() $f^*$
, that is, if
$f^*$
, that is, if
![]() $x^\#\cdot f^* = h\cdot f^*$
for some
$x^\#\cdot f^* = h\cdot f^*$
for some
![]() $h\in R_d$
, then
$h\in R_d$
, then
![]() $(x^\#-h)\cdot f^*=0$
and [Reference Linnell and Puls22, Theorem 2.1] would imply that
$(x^\#-h)\cdot f^*=0$
and [Reference Linnell and Puls22, Theorem 2.1] would imply that
![]() $x^\#=h$
and
$x^\#=h$
and
![]() $x=\eta (x^\#)=\eta (h)=0$
. This violates our conditions on x. The converse is obvious.
$x=\eta (x^\#)=\eta (h)=0$
. This violates our conditions on x. The converse is obvious.
Proof of Theorem 7.3
Since
![]() $f=g^{*}$
is atoral, there exists a non-trivial summable homoclinic point
$f=g^{*}$
is atoral, there exists a non-trivial summable homoclinic point
![]() $x\in X_f$
. Let
$x\in X_f$
. Let
![]() $x^{\#}\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
be the lift of x (cf. equation (7.8)), and let
$x^{\#}\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
be the lift of x (cf. equation (7.8)), and let
![]() $h=f(\bar {\sigma })x^{\#}=x^{\#}\cdot f^{*} \in R_d$
(cf. Lemma 7.4). Since
$h=f(\bar {\sigma })x^{\#}=x^{\#}\cdot f^{*} \in R_d$
(cf. Lemma 7.4). Since
![]() $x^{\#}\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
, there exists an integer
$x^{\#}\in \ell ^1(\mathbb {Z}^d,\mathbb {R})$
, there exists an integer
![]() $R=R(x,f,H)$
such that
$R=R(x,f,H)$
such that
 $$ \begin{align*} \smash[t]{\sum_{\|{\boldsymbol n}\|\ge R} |x^{\#}_{{\boldsymbol n}}| <\frac 1{2H\|f\|_1}.} \end{align*} $$
$$ \begin{align*} \smash[t]{\sum_{\|{\boldsymbol n}\|\ge R} |x^{\#}_{{\boldsymbol n}}| <\frac 1{2H\|f\|_1}.} \end{align*} $$
For every non-empty subset
![]() ${\mathcal S}\subset \mathbb {Z}^d$
, we set
${\mathcal S}\subset \mathbb {Z}^d$
, we set
Let
![]() ${\mathcal S},{\mathcal S}'\subset \mathbb {Z}^d$
be two subsets of
${\mathcal S},{\mathcal S}'\subset \mathbb {Z}^d$
be two subsets of
![]() $\mathbb {Z}^d$
with distance
$\mathbb {Z}^d$
with distance
![]() $d({\mathcal S},{\mathcal S}')\ge 3R$
. Suppose that a Laurent polynomial
$d({\mathcal S},{\mathcal S}')\ge 3R$
. Suppose that a Laurent polynomial
![]() $v\in \mathcal P({\mathcal S}\cup {\mathcal S}', H)$
is divisible by
$v\in \mathcal P({\mathcal S}\cup {\mathcal S}', H)$
is divisible by
![]() $f^{*}$
, that is, that
$f^{*}$
, that is, that
![]() $v=\phi \cdot f^{*}$
for some
$v=\phi \cdot f^{*}$
for some
![]() $\phi \in R_d$
. Then:
$\phi \in R_d$
. Then:
-
(i)
 $v\cdot x^{\#}\in R_d$
;
$v\cdot x^{\#}\in R_d$
; -
(ii)
 $\textsf {supp}(v\cdot x^{\#})\subset B_R({\mathcal S})\cup B_R({\mathcal S}')$
.
$\textsf {supp}(v\cdot x^{\#})\subset B_R({\mathcal S})\cup B_R({\mathcal S}')$
.
Indeed, item (i) follows from Lemma 7.4(2):
because both
![]() $\phi $
and h belong to
$\phi $
and h belong to
![]() $R_d$
. For item (ii), we note that every
$R_d$
. For item (ii), we note that every
![]() ${\boldsymbol n} \notin B_R({\mathcal S})\cup B_R({\mathcal S}')$
satisfies that
${\boldsymbol n} \notin B_R({\mathcal S})\cup B_R({\mathcal S}')$
satisfies that
![]() $d({\boldsymbol n}, {\mathcal S}\cup {\mathcal S}')> R$
. Then
$d({\boldsymbol n}, {\mathcal S}\cup {\mathcal S}')> R$
. Then
![]() $v_{{\boldsymbol n}-{\boldsymbol m}}=0$
for all
$v_{{\boldsymbol n}-{\boldsymbol m}}=0$
for all
![]() ${\boldsymbol m}$
with
${\boldsymbol m}$
with
![]() $\|{\boldsymbol m}\|\le R$
, and hence
$\|{\boldsymbol m}\|\le R$
, and hence
 $$ \begin{align*} |(v\cdot x^{\#})_{{\boldsymbol n}}|=\bigg|\!\sum_{{\boldsymbol m}\in{\mathbb Z}^d} x^{\#}_{{\boldsymbol m}}v_{{\boldsymbol n}-{\boldsymbol m}}\bigg|\le \|v\|_\infty \sum_{\|{\boldsymbol m}\|>R}| x^{\#}_{{\boldsymbol m}}| < H\cdot \frac {1}{2H\|f\|_1}\le \frac 12. \end{align*} $$
$$ \begin{align*} |(v\cdot x^{\#})_{{\boldsymbol n}}|=\bigg|\!\sum_{{\boldsymbol m}\in{\mathbb Z}^d} x^{\#}_{{\boldsymbol m}}v_{{\boldsymbol n}-{\boldsymbol m}}\bigg|\le \|v\|_\infty \sum_{\|{\boldsymbol m}\|>R}| x^{\#}_{{\boldsymbol m}}| < H\cdot \frac {1}{2H\|f\|_1}\le \frac 12. \end{align*} $$
Since
![]() $(v\cdot x^{\#})_{{\boldsymbol n}} \in \mathbb {Z}$
by item (i), it follows that
$(v\cdot x^{\#})_{{\boldsymbol n}} \in \mathbb {Z}$
by item (i), it follows that
![]() $(v\cdot x^{\#})_{{\boldsymbol n}}=0$
.
$(v\cdot x^{\#})_{{\boldsymbol n}}=0$
.
Let
![]() $\psi $
be the restriction of
$\psi $
be the restriction of
![]() $v \cdot x^{\#}$
to
$v \cdot x^{\#}$
to
![]() $B_R({\mathcal S})$
, and let
$B_R({\mathcal S})$
, and let
![]() $v_{\mathcal S}$
and
$v_{\mathcal S}$
and
![]() $v_{{\mathcal S}'}$
be the restrictions of v to
$v_{{\mathcal S}'}$
be the restrictions of v to
![]() ${\mathcal S}$
and
${\mathcal S}$
and
![]() ${\mathcal S}'$
, respectively. Then
${\mathcal S}'$
, respectively. Then
![]() $\psi \in R_d$
by item (i), and we claim that
$\psi \in R_d$
by item (i), and we claim that
that is, that
Indeed, if
![]() ${\boldsymbol n} \in B_R({\mathcal S})$
, then
${\boldsymbol n} \in B_R({\mathcal S})$
, then
![]() $d({\boldsymbol n},B_R({\mathcal S}')) \ge R$
, and hence
$d({\boldsymbol n},B_R({\mathcal S}')) \ge R$
, and hence
 $$ \begin{align} |(v_{{\mathcal S}'}\cdot x^{\#})_{\boldsymbol n}| = \bigg|\!\sum_{{\boldsymbol m}\in {\mathcal S}'} v_{\boldsymbol m} x^{\#}_{{\boldsymbol n} -{\boldsymbol m}}\bigg|\le \|v\|_\infty \sum_{\|{\boldsymbol \ell}\|\ge R} |x^{\#}_{{\boldsymbol \ell}}|\le H\cdot \frac{1}{2 H \|f\|_1} = \frac{1}{2\|f\|_1}. \end{align} $$
$$ \begin{align} |(v_{{\mathcal S}'}\cdot x^{\#})_{\boldsymbol n}| = \bigg|\!\sum_{{\boldsymbol m}\in {\mathcal S}'} v_{\boldsymbol m} x^{\#}_{{\boldsymbol n} -{\boldsymbol m}}\bigg|\le \|v\|_\infty \sum_{\|{\boldsymbol \ell}\|\ge R} |x^{\#}_{{\boldsymbol \ell}}|\le H\cdot \frac{1}{2 H \|f\|_1} = \frac{1}{2\|f\|_1}. \end{align} $$
Since
![]() $\psi _{\boldsymbol n} = (v_{{\mathcal S}}\cdot x^{\#})_{\boldsymbol n} + (v_{{\mathcal S}'}\cdot x^{\#})_{\boldsymbol n}$
, it follows that
$\psi _{\boldsymbol n} = (v_{{\mathcal S}}\cdot x^{\#})_{\boldsymbol n} + (v_{{\mathcal S}'}\cdot x^{\#})_{\boldsymbol n}$
, it follows that
by equation (7.11). However, if
![]() ${\boldsymbol n}\notin B_R({\mathcal S})$
, then
${\boldsymbol n}\notin B_R({\mathcal S})$
, then
 $$ \begin{align*} |\psi _{\boldsymbol n} - (v_{\mathcal S} \cdot x^{\#})_{\boldsymbol n} |=|(v_{\mathcal S} \cdot x^{\#})_{\boldsymbol n} | = \bigg|\!\sum_{{\boldsymbol m}\in {\mathcal S}}(v_{\boldsymbol m} x^{\#}_{{\boldsymbol n}-{\boldsymbol m}})\bigg| \le H\cdot \frac{1}{2 H \|f\|_1} = \frac{1}{2\|f\|_1}. \end{align*} $$
$$ \begin{align*} |\psi _{\boldsymbol n} - (v_{\mathcal S} \cdot x^{\#})_{\boldsymbol n} |=|(v_{\mathcal S} \cdot x^{\#})_{\boldsymbol n} | = \bigg|\!\sum_{{\boldsymbol m}\in {\mathcal S}}(v_{\boldsymbol m} x^{\#}_{{\boldsymbol n}-{\boldsymbol m}})\bigg| \le H\cdot \frac{1}{2 H \|f\|_1} = \frac{1}{2\|f\|_1}. \end{align*} $$
This proves equation (7.10) for every
![]() ${\boldsymbol n}\in \mathbb {Z}^d$
.
${\boldsymbol n}\in \mathbb {Z}^d$
.
Since both
![]() $v_{\mathcal S}\cdot x^{\#}\cdot f^{*} = v_{\mathcal S}\cdot h$
and
$v_{\mathcal S}\cdot x^{\#}\cdot f^{*} = v_{\mathcal S}\cdot h$
and
![]() $\psi $
lie in
$\psi $
lie in
![]() $R_d$
, we have that
$R_d$
, we have that
![]() $(\psi -v_{\mathcal S}\cdot x^{\#})\cdot f^{*} \in R_d$
, but the smallness of the coordinates of
$(\psi -v_{\mathcal S}\cdot x^{\#})\cdot f^{*} \in R_d$
, but the smallness of the coordinates of
![]() $\psi -v_{\mathcal S}\cdot x^{\#}$
in equation (7.10) implies that
$\psi -v_{\mathcal S}\cdot x^{\#}$
in equation (7.10) implies that
![]() $(\psi -v_{\mathcal S}\cdot x^{\#})\cdot f^{*}=0$
. Thus, we have proved that
$(\psi -v_{\mathcal S}\cdot x^{\#})\cdot f^{*}=0$
. Thus, we have proved that
![]() $\psi \cdot f^{*}=v_{\mathcal S}\cdot x^{\#}\cdot f^{*}=v_{\mathcal S}\cdot h$
, where h is not divisible by
$\psi \cdot f^{*}=v_{\mathcal S}\cdot x^{\#}\cdot f^{*}=v_{\mathcal S}\cdot h$
, where h is not divisible by
![]() $f^{*}$
(cf. Lemma 7.4(2)). As
$f^{*}$
(cf. Lemma 7.4(2)). As
![]() $g=f^{*}$
is irreducible, we have proved that
$g=f^{*}$
is irreducible, we have proved that
![]() $v_{\mathcal S}$
is divisible by g, as claimed in the statement of this theorem.
$v_{\mathcal S}$
is divisible by g, as claimed in the statement of this theorem.
This completes the proof of Theorem 7.3 with
![]() $m\ge 3R$
.
$m\ge 3R$
.
7.2 The conditions (C1) and (C2): divisibility by f of lacunary polynomials
According to Theorem 5.1, to prove Theorem 2.3, it suffices to prove that any irreducible and atoral polynomial
![]() $f\in R_d$
is m-good for a sufficiently large
$f\in R_d$
is m-good for a sufficiently large
![]() $m\in {\mathbb N}$
. Now we are going to prove this and finish the proof of Theorem 2.3.
$m\in {\mathbb N}$
. Now we are going to prove this and finish the proof of Theorem 2.3.
Theorem 7.3 has an immediate corollary which implies that any atoral polynomial is m-good for sufficiently large m.
Corollary 7.5. Suppose that
![]() $f\in R_d$
is irreducible and atoral, and that
$f\in R_d$
is irreducible and atoral, and that
![]() $|\mathrm {supp}(f)|> 1$
. Then there exists, for every
$|\mathrm {supp}(f)|> 1$
. Then there exists, for every
![]() $H\ge 1$
, an integer
$H\ge 1$
, an integer
![]() $m\ge 1$
with the following property: for any set
$m\ge 1$
with the following property: for any set
![]() ${\mathcal S}\in {\mathbb Z}^d$
which is m-separated in the sense that
${\mathcal S}\in {\mathbb Z}^d$
which is m-separated in the sense that
no non-zero polynomial
![]() $g\in \mathcal P({\mathcal S},H)$
is divisible by f.
$g\in \mathcal P({\mathcal S},H)$
is divisible by f.
Proof. For
![]() $H\ge 1$
and f fixed, choose m as in the statement of Theorem 7.3 (that is,
$H\ge 1$
and f fixed, choose m as in the statement of Theorem 7.3 (that is,
![]() $m\ge 3R$
in the proof of that theorem). Consider an arbitrary m-separated set
$m\ge 3R$
in the proof of that theorem). Consider an arbitrary m-separated set
![]() ${\mathcal S}$
and any non-trivial polynomial
${\mathcal S}$
and any non-trivial polynomial
![]() $v = \sum _{{\boldsymbol n}\in {\mathcal S}}v_{\boldsymbol n}\boldsymbol {z}^{\boldsymbol n}\in \mathcal P({\mathcal S},H)$
.
$v = \sum _{{\boldsymbol n}\in {\mathcal S}}v_{\boldsymbol n}\boldsymbol {z}^{\boldsymbol n}\in \mathcal P({\mathcal S},H)$
.
If
![]() $|\textsf {supp}(v)|=1$
, then v cannot be divisible by f, since
$|\textsf {supp}(v)|=1$
, then v cannot be divisible by f, since
![]() $|\textsf {supp}(f)|>1$
by assumption. Assume therefore that
$|\textsf {supp}(f)|>1$
by assumption. Assume therefore that
![]() $|\textsf {supp}(v)|\ge 2$
, and that v is divisible by f. Since for any
$|\textsf {supp}(v)|\ge 2$
, and that v is divisible by f. Since for any
![]() ${\boldsymbol n}\in \textsf {supp}(v)$
, the sets
${\boldsymbol n}\in \textsf {supp}(v)$
, the sets
have distance at least m and hence, by Theorem 7.3, the restriction of v to
![]() $\mathcal {T}$
, that is,
$\mathcal {T}$
, that is,
![]() $v_{\mathcal {T}}=v_{{\boldsymbol n}}{\boldsymbol z}^{{\boldsymbol n}}$
must be divisible by f, which is impossible, v is not divisible by f.
$v_{\mathcal {T}}=v_{{\boldsymbol n}}{\boldsymbol z}^{{\boldsymbol n}}$
must be divisible by f, which is impossible, v is not divisible by f.
The condition that
![]() $|\textsf {supp}(f)|>1$
in Corollary 7.5 is obviously necessary: the polynomial
$|\textsf {supp}(f)|>1$
in Corollary 7.5 is obviously necessary: the polynomial
![]() $f=2$
is obviously irreducible and atoral, and divides
$f=2$
is obviously irreducible and atoral, and divides
![]() $2g$
for every
$2g$
for every
![]() $g\in R_d$
(irrespective of whether g is m-separated or not).
$g\in R_d$
(irrespective of whether g is m-separated or not).
Corollary 7.6. Suppose that
![]() $f\in R_d$
is irreducible and atoral, and that
$f\in R_d$
is irreducible and atoral, and that
![]() $|\mathrm {supp}(f)|>~1$
. For all sufficiently large
$|\mathrm {supp}(f)|>~1$
. For all sufficiently large
![]() $m\ge 1$
and every
$m\ge 1$
and every
![]() $\boldsymbol {k}\in [0,m-1]^d\smallsetminus \{{\boldsymbol 0}\}$
, no
$\boldsymbol {k}\in [0,m-1]^d\smallsetminus \{{\boldsymbol 0}\}$
, no
![]() $v\in \mathcal {P}(m\mathbb {Z}^d \cup (m\mathbb {Z}^d+{\boldsymbol k}),1)$
with
$v\in \mathcal {P}(m\mathbb {Z}^d \cup (m\mathbb {Z}^d+{\boldsymbol k}),1)$
with
![]() $v \ne 0$
is divisible by f.
$v \ne 0$
is divisible by f.
Proof. Put
![]() $H=1$
and let
$H=1$
and let
![]() $m\ge 6R$
, where R is the number appearing in the proof of Theorem 7.3. Suppose
$m\ge 6R$
, where R is the number appearing in the proof of Theorem 7.3. Suppose
![]() $v\in \mathcal {P}(m\mathbb {Z}^d \cup (m\mathbb {Z}^d+\boldsymbol {k}),1)$
is a non-trivial polynomial divisible by f. Consider the decomposition
$v\in \mathcal {P}(m\mathbb {Z}^d \cup (m\mathbb {Z}^d+\boldsymbol {k}),1)$
is a non-trivial polynomial divisible by f. Consider the decomposition
![]() $\textsf {supp}(v)={\mathcal S}_0\sqcup {\mathcal S}_1$
where
$\textsf {supp}(v)={\mathcal S}_0\sqcup {\mathcal S}_1$
where
Both sets
![]() ${\mathcal S}_0,{\mathcal S}_1$
are m-separated, as subsets of
${\mathcal S}_0,{\mathcal S}_1$
are m-separated, as subsets of
![]() $m{\mathbb Z}^d$
and
$m{\mathbb Z}^d$
and
![]() $m{\mathbb Z}^d+{\boldsymbol k}$
, respectively.
$m{\mathbb Z}^d+{\boldsymbol k}$
, respectively.
We claim that for any
![]() ${\boldsymbol n}\in {\mathcal S}_0$
, there exists
${\boldsymbol n}\in {\mathcal S}_0$
, there exists
![]() ${\boldsymbol n}'={\boldsymbol n}'({\boldsymbol n})\in {\mathcal S}_1$
such that
${\boldsymbol n}'={\boldsymbol n}'({\boldsymbol n})\in {\mathcal S}_1$
such that
![]() $d({\boldsymbol n},{\boldsymbol n}')<3R$
. Otherwise, there exists
$d({\boldsymbol n},{\boldsymbol n}')<3R$
. Otherwise, there exists
![]() ${\boldsymbol n}\in {\mathcal S}_0$
such that
${\boldsymbol n}\in {\mathcal S}_0$
such that
![]() $d({\boldsymbol n}, {\mathcal S}_1)\ge 3R$
so that
$d({\boldsymbol n}, {\mathcal S}_1)\ge 3R$
so that
![]() $d({\boldsymbol n}, \textsf {supp}(v)\smallsetminus \{{\boldsymbol n}\})\ge 3R$
. Then, by Theorem 7.3, the restriction of v to
$d({\boldsymbol n}, \textsf {supp}(v)\smallsetminus \{{\boldsymbol n}\})\ge 3R$
. Then, by Theorem 7.3, the restriction of v to
![]() $\{{\boldsymbol n}\}$
, that is,
$\{{\boldsymbol n}\}$
, that is,
![]() $\pm {\boldsymbol z}^{{\boldsymbol n}}$
, is divisible by f, which is impossible. Similarly, for any
$\pm {\boldsymbol z}^{{\boldsymbol n}}$
, is divisible by f, which is impossible. Similarly, for any
![]() ${\boldsymbol n}'\in {\mathcal S}_1$
, there exists
${\boldsymbol n}'\in {\mathcal S}_1$
, there exists
![]() ${\boldsymbol n}\in S_0$
such that
${\boldsymbol n}\in S_0$
such that
![]() $d({\boldsymbol n},{\boldsymbol n}')<3R$
. Thus, the support of v is a union of distinct pairs:
$d({\boldsymbol n},{\boldsymbol n}')<3R$
. Thus, the support of v is a union of distinct pairs:
 $$ \begin{align*} \textsf{supp}(v)=\bigcup_{{\boldsymbol n}\in{\mathcal S}_0}\{{\boldsymbol n},{\boldsymbol n}'\}, \end{align*} $$
$$ \begin{align*} \textsf{supp}(v)=\bigcup_{{\boldsymbol n}\in{\mathcal S}_0}\{{\boldsymbol n},{\boldsymbol n}'\}, \end{align*} $$
where the distance within each pair is at most
![]() $3R$
.
$3R$
.
Given a pair
![]() $\{{\boldsymbol n},{\boldsymbol n}'\}$
, consider the decomposition of
$\{{\boldsymbol n},{\boldsymbol n}'\}$
, consider the decomposition of
![]() $\textsf {supp}(v)$
:
$\textsf {supp}(v)$
:
The fact that
![]() $m\ge 6R$
implies
$m\ge 6R$
implies
![]() $d({\mathcal S}, {\mathcal S}')\ge 3R$
. Indeed,
$d({\mathcal S}, {\mathcal S}')\ge 3R$
. Indeed,
![]() $d({\boldsymbol n}, {\mathcal S}')= d({\boldsymbol n}, {\boldsymbol n}^{*})$
for some
$d({\boldsymbol n}, {\mathcal S}')= d({\boldsymbol n}, {\boldsymbol n}^{*})$
for some
![]() ${{\boldsymbol n}^{*}\in {\mathcal S}'}$
and
${{\boldsymbol n}^{*}\in {\mathcal S}'}$
and
 $$ \begin{align*} \begin{cases} d({\boldsymbol n}, {\boldsymbol n}^{*}) \ge m &\mbox{if}\ {\boldsymbol n}^{*}\in {\mathcal S}_0; \\ d({\boldsymbol n}, {\boldsymbol n}^{*})\ge d({\boldsymbol n}', {\boldsymbol n}^{*}) - d({\boldsymbol n}', {\boldsymbol n}) \ge m -3R &\mbox{if}\ {\boldsymbol n}^{*}\in {\mathcal S}_1. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} d({\boldsymbol n}, {\boldsymbol n}^{*}) \ge m &\mbox{if}\ {\boldsymbol n}^{*}\in {\mathcal S}_0; \\ d({\boldsymbol n}, {\boldsymbol n}^{*})\ge d({\boldsymbol n}', {\boldsymbol n}^{*}) - d({\boldsymbol n}', {\boldsymbol n}) \ge m -3R &\mbox{if}\ {\boldsymbol n}^{*}\in {\mathcal S}_1. \end{cases} \end{align*} $$
It follows that
![]() $d({\boldsymbol n}, {\mathcal S}')>3R$
. Similarly,
$d({\boldsymbol n}, {\mathcal S}')>3R$
. Similarly,
![]() $d({\boldsymbol n}', {\mathcal S}')>3R$
.
$d({\boldsymbol n}', {\mathcal S}')>3R$
.
Applying Theorem 7.3 to
![]() ${\mathcal S}$
and
${\mathcal S}$
and
![]() ${\mathcal S}'$
, we conclude that the restriction of v to
${\mathcal S}'$
, we conclude that the restriction of v to
![]() ${\mathcal S}=\{{\boldsymbol n},{\boldsymbol n}'\}$
, that is,
${\mathcal S}=\{{\boldsymbol n},{\boldsymbol n}'\}$
, that is,
must be divisible by f, which is impossible, since
![]() $v_{\mathcal S}$
is of the form
$v_{\mathcal S}$
is of the form
and hence is a product of a unit (
![]() $\pm {\boldsymbol z}^{{\boldsymbol m}}$
) and a generalized cyclotomic polynomial
$\pm {\boldsymbol z}^{{\boldsymbol m}}$
) and a generalized cyclotomic polynomial
![]() ${(1\pm {\boldsymbol z}^{{\boldsymbol \ell }})}$
, and thus must have zero Mahler measure
${(1\pm {\boldsymbol z}^{{\boldsymbol \ell }})}$
, and thus must have zero Mahler measure
![]() $m(v_S)=0$
. This implies that
$m(v_S)=0$
. This implies that
![]() $\mathsf {m}(f) =0$
, in violation of Theorem 7.2.
$\mathsf {m}(f) =0$
, in violation of Theorem 7.2.
Proof of Theorem 2.3
Since Remark 2.7 allows us to assume without loss in generality that the polynomial
![]() $f\in R_d$
is primitive and irreducible, the proof of Bohr chaoticity under the additional assumption of atorality of f is now complete.
$f\in R_d$
is primitive and irreducible, the proof of Bohr chaoticity under the additional assumption of atorality of f is now complete.
Indeed, if
![]() $|\textsf {supp}(f)|=1$
, atorality implies that we are in the situation of Example 2.5 with
$|\textsf {supp}(f)|=1$
, atorality implies that we are in the situation of Example 2.5 with
![]() $p>1$
, so that
$p>1$
, so that
![]() $(X_f,\alpha _f)$
is Bohr chaotic. If
$(X_f,\alpha _f)$
is Bohr chaotic. If
![]() $|\textsf {supp}(f)|\ge 2$
, Corollary 7.5 for
$|\textsf {supp}(f)|\ge 2$
, Corollary 7.5 for
![]() ${H=2}$
and Corollary 7.6 show that conditions (C1) and (C2) are satisfied. Therefore, Bohr chaoticity of
${H=2}$
and Corollary 7.6 show that conditions (C1) and (C2) are satisfied. Therefore, Bohr chaoticity of
![]() $(X_f,\alpha _f)$
for irreducible atoral polynomials
$(X_f,\alpha _f)$
for irreducible atoral polynomials
![]() $f\in R_d$
follows from Theorem 5.1.
$f\in R_d$
follows from Theorem 5.1.
8 Concluding remarks: toral polynomials
We have shown that a principal
![]() ${\mathbb Z}$
-action is Bohr chaotic if and only if it has positive entropy. A principal
${\mathbb Z}$
-action is Bohr chaotic if and only if it has positive entropy. A principal
![]() ${\mathbb Z}^d$
-action,
${\mathbb Z}^d$
-action,
![]() $d>1$
, is shown to be Bohr chaotic if it has positive entropy and is atoral. We believe that the atorality assumption (equivalently, existence of a non-trivial summable homoclinic point) can be removed.
$d>1$
, is shown to be Bohr chaotic if it has positive entropy and is atoral. We believe that the atorality assumption (equivalently, existence of a non-trivial summable homoclinic point) can be removed.
Irreducible toral polynomials come in two flavors: those for which
![]() $X_f$
has no non-trivial homoclinic points (cf. e.g., [Reference Lind and Schmidt19, Example 7.1]), and those for which
$X_f$
has no non-trivial homoclinic points (cf. e.g., [Reference Lind and Schmidt19, Example 7.1]), and those for which
![]() $X_f$
has no summable homoclinic points, but uncountably many non-zero homoclinic points
$X_f$
has no summable homoclinic points, but uncountably many non-zero homoclinic points
![]() $v\in X_f$
with the property that
$v\in X_f$
with the property that
![]() $v^{\#} \cdot f^{*} \in f^{*} R_d$
(cf. e.g., [Reference Lind and Schmidt19, Example 7.3]; for notation, we refer to equation (7.8)). Unfortunately, none of these latter homoclinic points can be used in our proof of the gap theorem (Theorem 7.3), since the key Lemma 7.4 is not valid in this case.
$v^{\#} \cdot f^{*} \in f^{*} R_d$
(cf. e.g., [Reference Lind and Schmidt19, Example 7.3]; for notation, we refer to equation (7.8)). Unfortunately, none of these latter homoclinic points can be used in our proof of the gap theorem (Theorem 7.3), since the key Lemma 7.4 is not valid in this case.
Remarkably, for toral examples of the kind illustrated in [Reference Lind and Schmidt19, Example 7.1], we can still prove Bohr chaoticity by using Theorems 5.1 and 6.1.
Theorem 8.1. Let
![]() $g\in R_1$
be an irreducible polynomial with positive Mahler measure and with all roots of absolute value
$g\in R_1$
be an irreducible polynomial with positive Mahler measure and with all roots of absolute value
![]() $1$
, and define
$1$
, and define
![]() $f\in R_d$
by
$f\in R_d$
by
![]() $f(z_1,\ldots ,z_d)=g(z_1)$
. Then
$f(z_1,\ldots ,z_d)=g(z_1)$
. Then
![]() $(X_f,\alpha _f)$
is Bohr chaotic.
$(X_f,\alpha _f)$
is Bohr chaotic.
Remark 8.2. There exist infinitely many distinct irreducible polynomials
![]() $g\in R_1$
with the properties required in Theorem 8.1. To see this, we follow a short note from math.stackexchange.com [24].
$g\in R_1$
with the properties required in Theorem 8.1. To see this, we follow a short note from math.stackexchange.com [24].
Let
![]() $\vartheta $
be a totally real algebraic number all of whose conjugates
$\vartheta $
be a totally real algebraic number all of whose conjugates
![]() $\vartheta _1=\vartheta ,\vartheta _2,\ldots ,\vartheta _r$
have absolute values strictly less than 2 (to find such a
$\vartheta _1=\vartheta ,\vartheta _2,\ldots ,\vartheta _r$
have absolute values strictly less than 2 (to find such a
![]() $\vartheta $
, take any totally real algebraic number and divide by a big integer). Assume also that
$\vartheta $
, take any totally real algebraic number and divide by a big integer). Assume also that
![]() $\vartheta $
is not itself an algebraic integer. Let
$\vartheta $
is not itself an algebraic integer. Let
![]() $\beta $
be a solution to the equation
$\beta $
be a solution to the equation
All the conjugates of
![]() $\vartheta $
are, by assumption, real numbers in the interval
$\vartheta $
are, by assumption, real numbers in the interval
![]() $(-2,2)$
. This forces all the conjugates of
$(-2,2)$
. This forces all the conjugates of
![]() $\beta $
to be complex numbers of absolute value one—which is what we want. Moreover,
$\beta $
to be complex numbers of absolute value one—which is what we want. Moreover,
![]() $\beta $
will not be a root of unity, since otherwise,
$\beta $
will not be a root of unity, since otherwise,
![]() $\vartheta $
would be an algebraic integer. Then
$\vartheta $
would be an algebraic integer. Then
![]() $\beta $
is a root of the polynomial
$\beta $
is a root of the polynomial
 $$ \begin{align*} h(x)=\prod _{i=1}^r (x^2 - \vartheta _ix + 1). \end{align*} $$
$$ \begin{align*} h(x)=\prod _{i=1}^r (x^2 - \vartheta _ix + 1). \end{align*} $$
Clearing denominators in h, one gets the desired polynomial g. It will be irreducible, because, by looking at infinite places,
![]() $[\mathbb {Q}(\beta ):\mathbb {Q}(\vartheta )]=2$
.
$[\mathbb {Q}(\beta ):\mathbb {Q}(\vartheta )]=2$
.
For example,
![]() $\vartheta =1/2$
yields
$\vartheta =1/2$
yields
![]() $g=2z^2-1+2$
,
$g=2z^2-1+2$
,
![]() $\vartheta = -6/5$
yields
$\vartheta = -6/5$
yields
![]() $g=5z^2-6z+5$
,
$g=5z^2-6z+5$
,
![]() $\vartheta = 1/\sqrt 2$
yields
$\vartheta = 1/\sqrt 2$
yields
![]() $g=2z^4+3z^2+2$
, etc.
$g=2z^4+3z^2+2$
, etc.
Proof of Theorem 8.1
Since g with
![]() $\mathsf m(g)>0$
is m-good for some sufficiently large m by Theorem 6.1,
$\mathsf m(g)>0$
is m-good for some sufficiently large m by Theorem 6.1,
![]() $f(z_1,\ldots ,z_d)=g(z_1)$
is also m-good, but now viewed as a polynomial in d-variables. Indeed, if
$f(z_1,\ldots ,z_d)=g(z_1)$
is also m-good, but now viewed as a polynomial in d-variables. Indeed, if
![]() $f({\boldsymbol z})=g(z_1)$
divides a non-trivial polynomial h of the form
$f({\boldsymbol z})=g(z_1)$
divides a non-trivial polynomial h of the form
with
![]() $\varepsilon _{\boldsymbol n}=\varepsilon _{(n_1,n_2,\ldots ,n_d)} \in \{-2,-1,0,1,2\}$
, then by rewriting h as
$\varepsilon _{\boldsymbol n}=\varepsilon _{(n_1,n_2,\ldots ,n_d)} \in \{-2,-1,0,1,2\}$
, then by rewriting h as
 $$ \begin{align*} h({\boldsymbol z}) &= \sum_{(n_2,\ldots,n_{d})\in {\mathbb Z}^{d-1}} \bigg( \sum_{n_1\in{\mathbb Z}} \varepsilon_{(n_1,n_2,\ldots,n_d)} z_1^{m n_1}\bigg) z_2^{m n_2}\cdots z_{d}^{m n_d} \\ &=: \sum_{(n_2,\ldots,n_{d})\in {\mathbb Z}^{d-1}} h_{n_2,\ldots,n_d}(z_1^m) z_2^{mn_2}\cdots z_{d}^{mn_d}, \end{align*} $$
$$ \begin{align*} h({\boldsymbol z}) &= \sum_{(n_2,\ldots,n_{d})\in {\mathbb Z}^{d-1}} \bigg( \sum_{n_1\in{\mathbb Z}} \varepsilon_{(n_1,n_2,\ldots,n_d)} z_1^{m n_1}\bigg) z_2^{m n_2}\cdots z_{d}^{m n_d} \\ &=: \sum_{(n_2,\ldots,n_{d})\in {\mathbb Z}^{d-1}} h_{n_2,\ldots,n_d}(z_1^m) z_2^{mn_2}\cdots z_{d}^{mn_d}, \end{align*} $$
we conclude that
![]() $g(z_1)$
must divide all polynomials
$g(z_1)$
must divide all polynomials
![]() $h_{n_2,\ldots ,n_d}(z_1^m)$
, some of which are non-zero. Since
$h_{n_2,\ldots ,n_d}(z_1^m)$
, some of which are non-zero. Since
![]() $g(z_1)$
is m-good, the resulting contradiction proves that condition (C1) is valid for f. For the proof of condition (C2), we can proceed similarly.
$g(z_1)$
is m-good, the resulting contradiction proves that condition (C1) is valid for f. For the proof of condition (C2), we can proceed similarly.
Theorem 8.1 obviously applies only to an extremely restricted class of toral polynomials. A more interesting example of an irreducible toral polynomial with positive entropy in [Reference Lind and Schmidt19, Example 7.3] is given by the polynomial
The unitary variety of f is a smooth real-analytic curve
 $$ \begin{align*} \mathsf U(f)=\bigg\{(e^{2\pi i s},e^{2\pi i t}): t=\pm \frac{1}{2 \pi} \cos ^{-1}\bigg(\frac{3}{2}-\cos 2 \pi s\bigg), - \frac{1}{6} \leq s \leq \frac{1}{6} \bigg\}. \end{align*} $$
$$ \begin{align*} \mathsf U(f)=\bigg\{(e^{2\pi i s},e^{2\pi i t}): t=\pm \frac{1}{2 \pi} \cos ^{-1}\bigg(\frac{3}{2}-\cos 2 \pi s\bigg), - \frac{1}{6} \leq s \leq \frac{1}{6} \bigg\}. \end{align*} $$
Moreover,
![]() $\mathsf U(f)$
is connected and has curvature bounded away from zero. As explained in [Reference Lind and Schmidt19, Example 7.3], one can use this fact to prove the existence of probability measures supported on
$\mathsf U(f)$
is connected and has curvature bounded away from zero. As explained in [Reference Lind and Schmidt19, Example 7.3], one can use this fact to prove the existence of probability measures supported on
![]() $\mathsf U(f)$
whose Fourier transforms (as functions on
$\mathsf U(f)$
whose Fourier transforms (as functions on
![]() $\widehat {\mathbb {S}^d}=\mathbb {Z}^d$
) vanish at infinity. By translating this information back to the system
$\widehat {\mathbb {S}^d}=\mathbb {Z}^d$
) vanish at infinity. By translating this information back to the system
![]() $(X_f,\alpha _f)$
, one obtains uncountably many homoclinic points
$(X_f,\alpha _f)$
, one obtains uncountably many homoclinic points
![]() $x\in X_f$
satisfying
$x\in X_f$
satisfying
 $$ \begin{align*} |x_{{\boldsymbol n}}| \le \frac {C}{1+\|{\boldsymbol n}\|^{\tfrac 12}}\quad \text{for all } {\boldsymbol n}\in {\mathbb Z}^2. \end{align*} $$
$$ \begin{align*} |x_{{\boldsymbol n}}| \le \frac {C}{1+\|{\boldsymbol n}\|^{\tfrac 12}}\quad \text{for all } {\boldsymbol n}\in {\mathbb Z}^2. \end{align*} $$
Unfortunately, none of these homoclinic points can be used in our proof of the gap theorem (Theorem 7.3), since they are not summable.
It would be interesting to see whether one can prove the gap theorem for
![]() $f=3-z_1- ({1}/{z_1})-z_2- ({1}/{z_2})$
directly, using some elementary methods, or establish Bohr chaoticity of
$f=3-z_1- ({1}/{z_1})-z_2- ({1}/{z_2})$
directly, using some elementary methods, or establish Bohr chaoticity of
![]() $X_f$
by some other means.
$X_f$
by some other means.
Acknowledgements
The authors would like to thank B. Weiss for valuable discussions and D. Lind for alerting them to an error in the submitted manuscript. K.S. and E.V. are grateful to Central China Normal University for their hospitality, where part of the work was done. A.H.F. was partly supported by NSF of China (Grant Nos. 11971192 and 12231013).