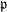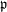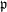1 Introduction
This work concerns the modular representation theory of finite groups and group schemes. A starting point for it is a duality theorem for finite groups due to Tate, that appears already in Cartan and Eilenberg [Reference Cartan and EilenbergCE56]. For our purposes it is useful to recast this theorem in terms of stable module categories. The stable module category of a finite group scheme
![]() $G$
over a field
$G$
over a field
![]() $k$
is the category obtained from the (abelian) category of finite-dimensional
$k$
is the category obtained from the (abelian) category of finite-dimensional
![]() $G$
-modules by annihilating morphisms that factor through a projective module; we denote it
$G$
-modules by annihilating morphisms that factor through a projective module; we denote it
![]() $\mathsf{stmod}\,G$
, and write
$\mathsf{stmod}\,G$
, and write
![]() $\text{}\underline{\operatorname{Hom}}_{G}(-,-)$
for the morphisms in this category. The category
$\text{}\underline{\operatorname{Hom}}_{G}(-,-)$
for the morphisms in this category. The category
![]() $\mathsf{stmod}\,G$
is triangulated with suspension
$\mathsf{stmod}\,G$
is triangulated with suspension
![]() $\unicode[STIX]{x1D6FA}^{-1}$
, and Tate duality translates to the statement that for all finite-dimensional
$\unicode[STIX]{x1D6FA}^{-1}$
, and Tate duality translates to the statement that for all finite-dimensional
![]() $G$
-modules
$G$
-modules
![]() $M$
and
$M$
and
![]() $N$
there are natural isomorphisms
$N$
there are natural isomorphisms
Here
![]() $\unicode[STIX]{x1D6FF}_{G}$
is the modular character of
$\unicode[STIX]{x1D6FF}_{G}$
is the modular character of
![]() $G$
, described in Jantzen [Reference JantzenJan03, § I.8.8]; it is isomorphic to the trivial representation
$G$
, described in Jantzen [Reference JantzenJan03, § I.8.8]; it is isomorphic to the trivial representation
![]() $k$
when
$k$
when
![]() $G$
is a finite group. Tate duality can be deduced from a formula of Auslander and Reiten [Reference AuslanderAus78] that applies to general associative algebras; see Theorem 4.2.
$G$
is a finite group. Tate duality can be deduced from a formula of Auslander and Reiten [Reference AuslanderAus78] that applies to general associative algebras; see Theorem 4.2.
In the language introduced by Bondal and Kapranov [Reference Bondal and KapranovBK89] the isomorphism above says that
![]() $\mathsf{stmod}\,G$
has Serre duality with Serre functor
$\mathsf{stmod}\,G$
has Serre duality with Serre functor
![]() $M\mapsto \unicode[STIX]{x1D6FA}\unicode[STIX]{x1D6FF}_{G}\otimes _{k}M$
. One of the main results of our work is that such a duality also holds locally.
$M\mapsto \unicode[STIX]{x1D6FA}\unicode[STIX]{x1D6FF}_{G}\otimes _{k}M$
. One of the main results of our work is that such a duality also holds locally.
The precise statement involves a natural action of the cohomology ring
![]() $H^{\ast }(G,k)$
of
$H^{\ast }(G,k)$
of
![]() $G$
on the graded abelian group
$G$
on the graded abelian group
The ring
![]() $H^{\ast }(G,k)$
is graded commutative, and also finitely generated as a
$H^{\ast }(G,k)$
is graded commutative, and also finitely generated as a
![]() $k$
-algebra, by a result of Friedlander and Suslin [Reference Friedlander and SuslinFS97]. Fix a homogeneous prime ideal
$k$
-algebra, by a result of Friedlander and Suslin [Reference Friedlander and SuslinFS97]. Fix a homogeneous prime ideal
![]() $\mathfrak{p}$
not containing
$\mathfrak{p}$
not containing
![]() $H^{{\geqslant}1}(G,k)$
and consider the triangulated category
$H^{{\geqslant}1}(G,k)$
and consider the triangulated category
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
that is obtained from
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
that is obtained from
![]() $\mathsf{stmod}\,G$
by localising the graded morphisms at
$\mathsf{stmod}\,G$
by localising the graded morphisms at
![]() $\mathfrak{p}$
and then taking the full subcategory of objects such that the graded endomorphisms are
$\mathfrak{p}$
and then taking the full subcategory of objects such that the graded endomorphisms are
![]() $\mathfrak{p}$
-torsion; see § 7 for details. Our interest in the subcategories
$\mathfrak{p}$
-torsion; see § 7 for details. Our interest in the subcategories
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
stems from the fact that they are the building blocks of
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
stems from the fact that they are the building blocks of
![]() $\mathsf{stmod}\,G$
and play a key role in the classification of its tensor ideal thick subcategories; see [Reference Benson, Iyengar and KrauseBIK15]. These subcategories may thus be viewed as analogues of the
$\mathsf{stmod}\,G$
and play a key role in the classification of its tensor ideal thick subcategories; see [Reference Benson, Iyengar and KrauseBIK15]. These subcategories may thus be viewed as analogues of the
![]() $K(n)$
-local spectra in stable homotopy theory that give the chromatic filtration of a spectrum; see [Reference RavenelRav92].
$K(n)$
-local spectra in stable homotopy theory that give the chromatic filtration of a spectrum; see [Reference RavenelRav92].
The following is our version of local Serre duality.
Theorem 1.1. Let
![]() $\mathsf{C}:=\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
and
$\mathsf{C}:=\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
and
![]() $d$
the Krull dimension of
$d$
the Krull dimension of
![]() $H^{\ast }(G,k)/\mathfrak{p}$
. For all
$H^{\ast }(G,k)/\mathfrak{p}$
. For all
![]() $M,N$
in
$M,N$
in
![]() $\mathsf{C}$
there are natural isomorphisms
$\mathsf{C}$
there are natural isomorphisms
where
![]() $I(\mathfrak{p})$
is the injective hull of the graded
$I(\mathfrak{p})$
is the injective hull of the graded
![]() $H^{\ast }(G,k)$
-module
$H^{\ast }(G,k)$
-module
![]() $H^{\ast }(G,k)/\mathfrak{p}$
.
$H^{\ast }(G,k)/\mathfrak{p}$
.
One corollary is that
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
has Auslander–Reiten (AR) triangles, so one can bring to bear the techniques of AR theory to the study of
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
has Auslander–Reiten (AR) triangles, so one can bring to bear the techniques of AR theory to the study of
![]() $G$
-modules. These results are contained in Theorem 7.10.
$G$
-modules. These results are contained in Theorem 7.10.
We deduce Theorem 1.1 from a more general result concerning
![]() $\mathsf{StMod}\,G$
, the stable category of all (including infinite dimensional)
$\mathsf{StMod}\,G$
, the stable category of all (including infinite dimensional)
![]() $G$
-modules. Consider its subcategory
$G$
-modules. Consider its subcategory
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
consisting of the
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
consisting of the
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $\mathfrak{p}$
-torsion modules; in other words, the
$\mathfrak{p}$
-torsion modules; in other words, the
![]() $G$
-modules whose support is contained in
$G$
-modules whose support is contained in
![]() $\{\mathfrak{p}\}$
. This is a compactly generated triangulated category and the full subcategory of compact objects is equivalent, up to direct summands, to
$\{\mathfrak{p}\}$
. This is a compactly generated triangulated category and the full subcategory of compact objects is equivalent, up to direct summands, to
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
; this is explained in Remark 7.2. There is an idempotent functor
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
; this is explained in Remark 7.2. There is an idempotent functor
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}:\mathsf{StMod}\,G\rightarrow \mathsf{StMod}\,G$
with image the
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}:\mathsf{StMod}\,G\rightarrow \mathsf{StMod}\,G$
with image the
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $\mathfrak{p}$
-torsion modules; see § 2 for details. The central result of this work is that
$\mathfrak{p}$
-torsion modules; see § 2 for details. The central result of this work is that
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G})$
is a dualising object for
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G})$
is a dualising object for
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
, in the following sense.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
, in the following sense.
Theorem 1.2. For any
![]() $G$
-module
$G$
-module
![]() $M$
and
$M$
and
![]() $i\in \mathbb{Z}$
there is a natural isomorphism
$i\in \mathbb{Z}$
there is a natural isomorphism
This result is proved in § 5. In the isomorphism, the vector space on the left is
![]() $\text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}^{-i}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G}))$
. The statement is in terms of
$\text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}^{-i}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G}))$
. The statement is in terms of
![]() $\widehat{\text{Ext}}$
to underscore its similarity to Serre duality on a nonsingular projective variety
$\widehat{\text{Ext}}$
to underscore its similarity to Serre duality on a nonsingular projective variety
![]() $X$
of dimension
$X$
of dimension
![]() $n$
:
$n$
:
for any coherent sheave
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() $X$
; see, for example, Hartshorne [Reference HartshorneHar77].
$X$
; see, for example, Hartshorne [Reference HartshorneHar77].
When
![]() $G$
is a finite group
$G$
is a finite group
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
is the Rickard idempotent module
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
is the Rickard idempotent module
![]() $\unicode[STIX]{x1D705}_{V}$
, introduced by Benson, Carlson and Rickard [Reference Benson, Carlson and RickardBCR96], that is associated to the irreducible subvariety
$\unicode[STIX]{x1D705}_{V}$
, introduced by Benson, Carlson and Rickard [Reference Benson, Carlson and RickardBCR96], that is associated to the irreducible subvariety
![]() $V$
of
$V$
of
![]() $\operatorname{Proj}H^{\ast }(G,k)$
defined by
$\operatorname{Proj}H^{\ast }(G,k)$
defined by
![]() $\mathfrak{p}$
. In this context, Theorem 1.2 was proved by Benson and Greenlees [Reference Benson and GreenleesBG08]; see the paragraph following Theorem 5.1 below for a detailed comparison with their work and that of Benson [Reference BensonBen08].
$\mathfrak{p}$
. In this context, Theorem 1.2 was proved by Benson and Greenlees [Reference Benson and GreenleesBG08]; see the paragraph following Theorem 5.1 below for a detailed comparison with their work and that of Benson [Reference BensonBen08].
Concerning
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
, the following consequences of Theorem 1.2 have been anticipated in [Reference BensonBen01] when
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
, the following consequences of Theorem 1.2 have been anticipated in [Reference BensonBen01] when
![]() $G$
is a finite group.
$G$
is a finite group.
Theorem 1.3. Assume
![]() $\unicode[STIX]{x1D6FF}_{G}\cong k$
. The
$\unicode[STIX]{x1D6FF}_{G}\cong k$
. The
![]() $H^{\ast }(G,k)$
-module
$H^{\ast }(G,k)$
-module
![]() $\widehat{\text{Ext}}_{G}^{\ast }(k,\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k))$
is injective and isomorphic to a twist of
$\widehat{\text{Ext}}_{G}^{\ast }(k,\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k))$
is injective and isomorphic to a twist of
![]() $I(\mathfrak{p})$
. Also, there is an isomorphism of
$I(\mathfrak{p})$
. Also, there is an isomorphism of
![]() $k$
-algebras
$k$
-algebras
where
![]() $(-)^{\wedge }$
denotes completion with respect to the
$(-)^{\wedge }$
denotes completion with respect to the
![]() $\mathfrak{p}$
-adic topology, and the
$\mathfrak{p}$
-adic topology, and the
![]() $G$
-module
$G$
-module
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
is pure injective.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
is pure injective.
Theorem 1.2 can be interpreted to mean that the category
![]() $\mathsf{StMod}\,G$
is Gorenstein, for it is analogous to Grothendieck’s result that a commutative noetherian ring
$\mathsf{StMod}\,G$
is Gorenstein, for it is analogous to Grothendieck’s result that a commutative noetherian ring
![]() $A$
is Gorenstein if, and only if,
$A$
is Gorenstein if, and only if,
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}A$
is the injective hull of
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}A$
is the injective hull of
![]() $A/\mathfrak{p}$
, up to suspension, for each
$A/\mathfrak{p}$
, up to suspension, for each
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Spec}A$
. In § 6 we propose a general notion of a Gorenstein triangulated category, in an attempt to place these results in a common framework.
$\operatorname{Spec}A$
. In § 6 we propose a general notion of a Gorenstein triangulated category, in an attempt to place these results in a common framework.
To prove Theorem 1.2 we use a technique from algebraic geometry in the tradition of Zariski and Weil; namely, the construction of generic points for algebraic varieties. Given a point
![]() $\mathfrak{p}\subseteq H^{\ast }(G,k)$
, there is a purely transcendental extension
$\mathfrak{p}\subseteq H^{\ast }(G,k)$
, there is a purely transcendental extension
![]() $K$
of
$K$
of
![]() $k$
and a closed point
$k$
and a closed point
![]() $\mathfrak{m}$
of
$\mathfrak{m}$
of
![]() $\operatorname{Proj}H^{\ast }(G_{K},K)$
lying above the point
$\operatorname{Proj}H^{\ast }(G_{K},K)$
lying above the point
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
. Here,
$\operatorname{Proj}H^{\ast }(G,k)$
. Here,
![]() $G_{K}$
denotes the group scheme that is obtained from
$G_{K}$
denotes the group scheme that is obtained from
![]() $G$
by extending the field to
$G$
by extending the field to
![]() $K$
. The crux is that one can choose
$K$
. The crux is that one can choose
![]() $\mathfrak{m}$
such that the following statement holds.
$\mathfrak{m}$
such that the following statement holds.
Theorem 1.4. Restriction of scalars induces an exact functor
that is surjective on objects, up to isomorphism.
This result is proved in § 3, building on our work in [Reference Benson, Iyengar, Krause and PevtsovaBIKP18]. It gives a remarkable description of the compact objects in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
: they are obtained from the finite-dimensional objects in
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
: they are obtained from the finite-dimensional objects in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
by restriction of scalars. This allows one to reduce the proof of Theorem 1.2 to the case of a closed point, where it is essentially equivalent to classical Tate duality. The theorem above has other consequences; for example, it implies that the compact objects in
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
by restriction of scalars. This allows one to reduce the proof of Theorem 1.2 to the case of a closed point, where it is essentially equivalent to classical Tate duality. The theorem above has other consequences; for example, it implies that the compact objects in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
are endofinite
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
are endofinite
![]() $G$
-modules in the sense of Crawley-Boevey [Reference Crawley-BoeveyCra92]; see § 3.
$G$
-modules in the sense of Crawley-Boevey [Reference Crawley-BoeveyCra92]; see § 3.
2 Cohomology and localisation
In this section we recall basic notions concerning certain localisation functors on triangulated categories with ring actions. The material is needed to state and prove the results in this work. The main triangulated category of interest is the stable module category of a finite group scheme, but the general framework is needed in §§ 6 and 7. Primary references for the material presented here are [Reference Benson, Iyengar and KrauseBIK08, Reference Benson, Iyengar and KrauseBIK11a]; see [Reference Benson, Iyengar, Krause and PevtsovaBIKP18] for the special case of the stable module category.
Triangulated categories with central action
Let
![]() $\mathsf{T}$
be a triangulated category with suspension
$\mathsf{T}$
be a triangulated category with suspension
![]() $\unicode[STIX]{x1D6F4}$
. For objects
$\unicode[STIX]{x1D6F4}$
. For objects
![]() $X$
and
$X$
and
![]() $Y$
in
$Y$
in
![]() $\mathsf{T}$
set
$\mathsf{T}$
set
Composition makes
![]() $\operatorname{End}_{\mathsf{T}}^{\ast }(X)$
a graded ring and
$\operatorname{End}_{\mathsf{T}}^{\ast }(X)$
a graded ring and
![]() $\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
a left-
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
a left-
![]() $\operatorname{End}_{\mathsf{T}}^{\ast }(Y)$
right-
$\operatorname{End}_{\mathsf{T}}^{\ast }(Y)$
right-
![]() $\operatorname{End}_{\mathsf{T}}^{\ast }(X)$
module.
$\operatorname{End}_{\mathsf{T}}^{\ast }(X)$
module.
Let
![]() $R$
be a graded commutative noetherian ring. In what follows we will only be concerned with homogeneous elements and ideals in
$R$
be a graded commutative noetherian ring. In what follows we will only be concerned with homogeneous elements and ideals in
![]() $R$
. In this spirit, ‘localisation’ will mean homogeneous localisation, and
$R$
. In this spirit, ‘localisation’ will mean homogeneous localisation, and
![]() $\operatorname{Spec}R$
will denote the set of homogeneous prime ideals in
$\operatorname{Spec}R$
will denote the set of homogeneous prime ideals in
![]() $R$
.
$R$
.
We say that a triangulated category
![]() $\mathsf{T}$
is
$\mathsf{T}$
is
![]() $R$
-linear if for each
$R$
-linear if for each
![]() $X$
in
$X$
in
![]() $\mathsf{T}$
there is a homomorphism of graded rings
$\mathsf{T}$
there is a homomorphism of graded rings
![]() $\unicode[STIX]{x1D719}_{X}:R\rightarrow \operatorname{End}_{\mathsf{T}}^{\ast }(X)$
such that the induced left and right actions of
$\unicode[STIX]{x1D719}_{X}:R\rightarrow \operatorname{End}_{\mathsf{T}}^{\ast }(X)$
such that the induced left and right actions of
![]() $R$
on
$R$
on
![]() $\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
are compatible in the following sense: for any
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
are compatible in the following sense: for any
![]() $r\in R$
and
$r\in R$
and
![]() $\unicode[STIX]{x1D6FC}\in \operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
, one has
$\unicode[STIX]{x1D6FC}\in \operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
, one has
An exact functor
![]() $F:\mathsf{T}\rightarrow \mathsf{U}$
between
$F:\mathsf{T}\rightarrow \mathsf{U}$
between
![]() $R$
-linear triangulated categories is
$R$
-linear triangulated categories is
![]() $R$
-linear if the induced map
$R$
-linear if the induced map
of graded abelian groups is
![]() $R$
-linear for all objects
$R$
-linear for all objects
![]() $X,Y$
in
$X,Y$
in
![]() $\mathsf{T}$
.
$\mathsf{T}$
.
In what follows, we fix a compactly generated
![]() $R$
-linear triangulated category
$R$
-linear triangulated category
![]() $\mathsf{T}$
and write
$\mathsf{T}$
and write
![]() $\mathsf{T}^{\mathsf{c}}$
for its full subcategory of compact objects.
$\mathsf{T}^{\mathsf{c}}$
for its full subcategory of compact objects.
Localisation
Fix an ideal
![]() $\mathfrak{a}$
in
$\mathfrak{a}$
in
![]() $R$
. An
$R$
. An
![]() $R$
-module
$R$
-module
![]() $M$
is
$M$
is
![]() $\mathfrak{a}$
-torsion if
$\mathfrak{a}$
-torsion if
![]() $M_{\mathfrak{q}}=0$
for all
$M_{\mathfrak{q}}=0$
for all
![]() $\mathfrak{q}$
in
$\mathfrak{q}$
in
![]() $\operatorname{Spec}R$
with
$\operatorname{Spec}R$
with
![]() $\mathfrak{a}\not \subseteq \mathfrak{q}$
. Analogously, an object
$\mathfrak{a}\not \subseteq \mathfrak{q}$
. Analogously, an object
![]() $X$
in
$X$
in
![]() $\mathsf{T}$
is
$\mathsf{T}$
is
![]() $\mathfrak{a}$
-torsion if the
$\mathfrak{a}$
-torsion if the
![]() $R$
-module
$R$
-module
![]() $\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X)$
is
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X)$
is
![]() $\mathfrak{a}$
-torsion for all
$\mathfrak{a}$
-torsion for all
![]() $C\in \mathsf{T}^{\mathsf{c}}$
. The full subcategory of
$C\in \mathsf{T}^{\mathsf{c}}$
. The full subcategory of
![]() $\mathfrak{a}$
-torsion objects
$\mathfrak{a}$
-torsion objects
is localising and the inclusion
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}\mathsf{T}\subseteq \mathsf{T}$
admits a right adjoint, denoted
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}\mathsf{T}\subseteq \mathsf{T}$
admits a right adjoint, denoted
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}$
.
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}$
.
Fix a
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Spec}R$
. An
$\operatorname{Spec}R$
. An
![]() $R$
-module
$R$
-module
![]() $M$
is
$M$
is
![]() $\mathfrak{p}$
-local if the localisation map
$\mathfrak{p}$
-local if the localisation map
![]() $M\rightarrow M_{\mathfrak{p}}$
is invertible, and an object
$M\rightarrow M_{\mathfrak{p}}$
is invertible, and an object
![]() $X$
in
$X$
in
![]() $\mathsf{T}$
is
$\mathsf{T}$
is
![]() $\mathfrak{p}$
-local if the
$\mathfrak{p}$
-local if the
![]() $R$
-module
$R$
-module
![]() $\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X)$
is
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X)$
is
![]() $\mathfrak{p}$
-local for all
$\mathfrak{p}$
-local for all
![]() $C\in \mathsf{T}^{\mathsf{c}}$
. Consider the full subcategory of
$C\in \mathsf{T}^{\mathsf{c}}$
. Consider the full subcategory of
![]() $\mathsf{T}$
of
$\mathsf{T}$
of
![]() $\mathfrak{p}$
-local objects
$\mathfrak{p}$
-local objects
and the full subcategory of
![]() $\mathfrak{p}$
-local and
$\mathfrak{p}$
-local and
![]() $\mathfrak{p}$
-torsion objects
$\mathfrak{p}$
-torsion objects
Note that
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}\subseteq \mathsf{T}_{\mathfrak{p}}\subseteq \mathsf{T}$
are localising subcategories. The inclusion
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}\subseteq \mathsf{T}_{\mathfrak{p}}\subseteq \mathsf{T}$
are localising subcategories. The inclusion
![]() $\mathsf{T}_{\mathfrak{p}}\rightarrow \mathsf{T}$
admits a left adjoint
$\mathsf{T}_{\mathfrak{p}}\rightarrow \mathsf{T}$
admits a left adjoint
![]() $X\mapsto X_{\mathfrak{p}}$
while the inclusion
$X\mapsto X_{\mathfrak{p}}$
while the inclusion
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}\rightarrow \mathsf{T}_{\mathfrak{p}}$
admits a right adjoint. We denote by
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}\rightarrow \mathsf{T}_{\mathfrak{p}}$
admits a right adjoint. We denote by
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}:\mathsf{T}\rightarrow \unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}$
the composition of those adjoints; it is the local cohomology functor with respect to
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}:\mathsf{T}\rightarrow \unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}$
the composition of those adjoints; it is the local cohomology functor with respect to
![]() $\mathfrak{p}$
; see [Reference Benson, Iyengar and KrauseBIK08, Reference Benson, Iyengar and KrauseBIK11a] for the construction of this functor.
$\mathfrak{p}$
; see [Reference Benson, Iyengar and KrauseBIK08, Reference Benson, Iyengar and KrauseBIK11a] for the construction of this functor.
The following observation is clear.
Lemma 2.1. For any element
![]() $r$
in
$r$
in
![]() $R\setminus \mathfrak{p}$
, say of degree
$R\setminus \mathfrak{p}$
, say of degree
![]() $n$
, and
$n$
, and
![]() $\mathfrak{p}$
-local object
$\mathfrak{p}$
-local object
![]() $X$
, the natural map
$X$
, the natural map
![]() $X\xrightarrow[{}]{r}\unicode[STIX]{x1D6F4}^{n}X$
is an isomorphism.
$X\xrightarrow[{}]{r}\unicode[STIX]{x1D6F4}^{n}X$
is an isomorphism.
The functor
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}$
commutes with exact functors preserving coproducts.
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}$
commutes with exact functors preserving coproducts.
Lemma 2.2. Let
![]() $F:\mathsf{T}\rightarrow \mathsf{U}$
be an exact functor between
$F:\mathsf{T}\rightarrow \mathsf{U}$
be an exact functor between
![]() $R$
-linear compactly generated triangulated categories such that
$R$
-linear compactly generated triangulated categories such that
![]() $F$
is
$F$
is
![]() $R$
-linear and preserves coproducts. Suppose that the action of
$R$
-linear and preserves coproducts. Suppose that the action of
![]() $R$
on
$R$
on
![]() $\mathsf{U}$
factors through a homomorphism
$\mathsf{U}$
factors through a homomorphism
![]() $f:R\rightarrow S$
of graded commutative rings. For any ideal
$f:R\rightarrow S$
of graded commutative rings. For any ideal
![]() $\mathfrak{a}$
of
$\mathfrak{a}$
of
![]() $R$
there is a natural isomorphism
$R$
there is a natural isomorphism
of functors
![]() $\mathsf{T}\rightarrow \mathsf{U}$
, where
$\mathsf{T}\rightarrow \mathsf{U}$
, where
![]() $\mathfrak{a}S$
denotes the ideal of
$\mathfrak{a}S$
denotes the ideal of
![]() $S$
that is generated by
$S$
that is generated by
![]() $f(\mathfrak{a})$
.
$f(\mathfrak{a})$
.
Proof. The statement follows from an explicit description of
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}$
in terms of homotopy colimits; see [Reference Benson, Iyengar and KrauseBIK11a, Proposition 2.9].◻
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}$
in terms of homotopy colimits; see [Reference Benson, Iyengar and KrauseBIK11a, Proposition 2.9].◻
Injective cohomology objects
Given an object
![]() $C$
in
$C$
in
![]() $\mathsf{T}^{\mathsf{c}}$
and an injective
$\mathsf{T}^{\mathsf{c}}$
and an injective
![]() $R$
-module
$R$
-module
![]() $I$
, Brown representability yields an object
$I$
, Brown representability yields an object
![]() $T(C,I)$
in
$T(C,I)$
in
![]() $\mathsf{T}$
such that
$\mathsf{T}$
such that
This yields a functor
For each
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Spec}R$
, we write
$\operatorname{Spec}R$
, we write
![]() $I(\mathfrak{p})$
for the injective hull of
$I(\mathfrak{p})$
for the injective hull of
![]() $R/\mathfrak{p}$
and set
$R/\mathfrak{p}$
and set
viewed as a functor
![]() $\mathsf{T}^{\mathsf{c}}\rightarrow \mathsf{T}$
.
$\mathsf{T}^{\mathsf{c}}\rightarrow \mathsf{T}$
.
Tensor triangulated categories
Let
![]() $\mathsf{T}=(\mathsf{T},\otimes ,\unicode[STIX]{x1D7D9})$
be a tensor triangulated category such that
$\mathsf{T}=(\mathsf{T},\otimes ,\unicode[STIX]{x1D7D9})$
be a tensor triangulated category such that
![]() $R$
acts on
$R$
acts on
![]() $\mathsf{T}$
via a homomorphism of graded rings
$\mathsf{T}$
via a homomorphism of graded rings
![]() $R\rightarrow \operatorname{End}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9})$
. Brown representability yields functions objects
$R\rightarrow \operatorname{End}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9})$
. Brown representability yields functions objects
![]() ${\mathcal{H}}om(X,Y)$
satisfying an adjunction isomorphism
${\mathcal{H}}om(X,Y)$
satisfying an adjunction isomorphism
Set
![]() $X^{\vee }:={\mathcal{H}}om(X,\unicode[STIX]{x1D7D9})$
for each
$X^{\vee }:={\mathcal{H}}om(X,\unicode[STIX]{x1D7D9})$
for each
![]() $X$
in
$X$
in
![]() $\mathsf{T}$
. It is part of our definition of a tensor triangulated category that the unit,
$\mathsf{T}$
. It is part of our definition of a tensor triangulated category that the unit,
![]() $\unicode[STIX]{x1D7D9}$
, is compact, and that compact objects are rigid: for all
$\unicode[STIX]{x1D7D9}$
, is compact, and that compact objects are rigid: for all
![]() $C,X$
in
$C,X$
in
![]() $\mathsf{T}$
with
$\mathsf{T}$
with
![]() $C$
compact the natural map
$C$
compact the natural map
is an isomorphism; see [Reference Benson, Iyengar and KrauseBIK08, § 8] for details.
The functors
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}$
and
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}$
and
![]() $T_{\mathfrak{p}}$
can be computed as follows:
$T_{\mathfrak{p}}$
can be computed as follows:
Indeed, the first isomorphism is from [Reference Benson, Iyengar and KrauseBIK08, Corollary 8.3], while the second one holds because for each
![]() $X\in \mathsf{T}$
and compact object
$X\in \mathsf{T}$
and compact object
![]() $C$
there are isomorphisms
$C$
there are isomorphisms
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\mathsf{T}}(X,T_{\mathfrak{p}}(\unicode[STIX]{x1D7D9})\otimes C) & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(X,{\mathcal{H}}om(C^{\vee },T_{\mathfrak{p}}(\unicode[STIX]{x1D7D9})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(X\otimes C^{\vee },T_{\mathfrak{p}}(\unicode[STIX]{x1D7D9}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9},X\otimes C^{\vee }),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9},{\mathcal{H}}om(C,X),I(\mathfrak{p})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X),I(\mathfrak{p})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\mathsf{T}}(X,T_{\mathfrak{p}}(\unicode[STIX]{x1D7D9})\otimes C) & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(X,{\mathcal{H}}om(C^{\vee },T_{\mathfrak{p}}(\unicode[STIX]{x1D7D9})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(X\otimes C^{\vee },T_{\mathfrak{p}}(\unicode[STIX]{x1D7D9}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9},X\otimes C^{\vee }),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9},{\mathcal{H}}om(C,X),I(\mathfrak{p})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X),I(\mathfrak{p})).\nonumber\end{eqnarray}$$
The first and the fourth isomorphisms above hold because
![]() $C$
is rigid; the second and the last one are adjunction isomorphisms; the third one is by the defining isomorphism (2.1).
$C$
is rigid; the second and the last one are adjunction isomorphisms; the third one is by the defining isomorphism (2.1).
We turn now to modules over finite group schemes, following the notation and terminology from [Reference Benson, Iyengar, Krause and PevtsovaBIKP18].
The stable module category
Let
![]() $G$
be a finite group scheme over a field
$G$
be a finite group scheme over a field
![]() $k$
of positive characteristic. The coordinate ring and the group algebra of
$k$
of positive characteristic. The coordinate ring and the group algebra of
![]() $G$
are denoted
$G$
are denoted
![]() $k[G]$
and
$k[G]$
and
![]() $kG$
, respectively. These are finite-dimensional Hopf algebras over
$kG$
, respectively. These are finite-dimensional Hopf algebras over
![]() $k$
that are dual to each other. We write
$k$
that are dual to each other. We write
![]() $\mathsf{Mod}\,G$
for the category of
$\mathsf{Mod}\,G$
for the category of
![]() $G$
-modules and
$G$
-modules and
![]() $\mathsf{mod}\,G$
for its full subcategory consisting of finite-dimensional
$\mathsf{mod}\,G$
for its full subcategory consisting of finite-dimensional
![]() $G$
-modules. We often identity
$G$
-modules. We often identity
![]() $\mathsf{Mod}\,G$
with the category of
$\mathsf{Mod}\,G$
with the category of
![]() $kG$
-modules, which is justified by [Reference JantzenJan03, I.8.6].
$kG$
-modules, which is justified by [Reference JantzenJan03, I.8.6].
We write
![]() $H^{\ast }(G,k)$
for the cohomology algebra,
$H^{\ast }(G,k)$
for the cohomology algebra,
![]() $\operatorname{Ext}_{G}^{\ast }(k,k)$
, of
$\operatorname{Ext}_{G}^{\ast }(k,k)$
, of
![]() $G$
. This is a graded commutative
$G$
. This is a graded commutative
![]() $k$
-algebra, because
$k$
-algebra, because
![]() $kG$
is a Hopf algebra, and acts on
$kG$
is a Hopf algebra, and acts on
![]() $\operatorname{Ext}_{G}^{\ast }(M,N)$
, for any
$\operatorname{Ext}_{G}^{\ast }(M,N)$
, for any
![]() $G$
-modules
$G$
-modules
![]() $M,N$
. Moreover, the
$M,N$
. Moreover, the
![]() $k$
-algebra
$k$
-algebra
![]() $H^{\ast }(G,k)$
is finitely generated, and, when
$H^{\ast }(G,k)$
is finitely generated, and, when
![]() $M,N$
are finite dimensional,
$M,N$
are finite dimensional,
![]() $\operatorname{Ext}_{G}^{\ast }(M,N)$
is finitely generated over it; this is by a theorem of Friedlander and Suslin [Reference Friedlander and SuslinFS97].
$\operatorname{Ext}_{G}^{\ast }(M,N)$
is finitely generated over it; this is by a theorem of Friedlander and Suslin [Reference Friedlander and SuslinFS97].
The stable module category
![]() $\mathsf{StMod}\,G$
is obtained from
$\mathsf{StMod}\,G$
is obtained from
![]() $\mathsf{Mod}\,G$
by identifying two morphisms between
$\mathsf{Mod}\,G$
by identifying two morphisms between
![]() $G$
-modules when they factor through a projective
$G$
-modules when they factor through a projective
![]() $G$
-module. An isomorphism in
$G$
-module. An isomorphism in
![]() $\mathsf{StMod}\,G$
will be called a stable isomorphism, to distinguish it from an isomorphism in
$\mathsf{StMod}\,G$
will be called a stable isomorphism, to distinguish it from an isomorphism in
![]() $\mathsf{Mod}\,G$
. In the same vein,
$\mathsf{Mod}\,G$
. In the same vein,
![]() $G$
-modules
$G$
-modules
![]() $M$
and
$M$
and
![]() $N$
are said to be stably isomorphic if they are isomorphic in
$N$
are said to be stably isomorphic if they are isomorphic in
![]() $\mathsf{StMod}\,G$
; this is equivalent to the condition that
$\mathsf{StMod}\,G$
; this is equivalent to the condition that
![]() $M$
are
$M$
are
![]() $N$
are isomorphic in
$N$
are isomorphic in
![]() $\mathsf{Mod}\,G$
, up to projective summands.
$\mathsf{Mod}\,G$
, up to projective summands.
The tensor product over
![]() $k$
of
$k$
of
![]() $G$
-modules passes to
$G$
-modules passes to
![]() $\mathsf{StMod}\,G$
and yields a tensor triangulated category with unit
$\mathsf{StMod}\,G$
and yields a tensor triangulated category with unit
![]() $k$
and suspension
$k$
and suspension
![]() $\unicode[STIX]{x1D6FA}^{-1}$
, the inverse of the syzygy functor. The category
$\unicode[STIX]{x1D6FA}^{-1}$
, the inverse of the syzygy functor. The category
![]() $\mathsf{StMod}\,G$
is compactly generated and the subcategory of compact objects identifies with
$\mathsf{StMod}\,G$
is compactly generated and the subcategory of compact objects identifies with
![]() $\mathsf{stmod}\,G$
, the stable module category of finite-dimensional
$\mathsf{stmod}\,G$
, the stable module category of finite-dimensional
![]() $G$
-modules. See Carlson [Reference CarlsonCar96, § 5] and Happel [Reference HappelHap88, ch. I] for details.
$G$
-modules. See Carlson [Reference CarlsonCar96, § 5] and Happel [Reference HappelHap88, ch. I] for details.
We use the notation
![]() $\text{}\underline{\operatorname{Hom}}_{G}(M,N)$
for the
$\text{}\underline{\operatorname{Hom}}_{G}(M,N)$
for the
![]() $\operatorname{Hom}$
-sets in
$\operatorname{Hom}$
-sets in
![]() $\mathsf{StMod}\,G$
. The cohomology algebra
$\mathsf{StMod}\,G$
. The cohomology algebra
![]() $H^{\ast }(G,k)$
acts on
$H^{\ast }(G,k)$
acts on
![]() $\mathsf{StMod}\,G$
via a homomorphism of
$\mathsf{StMod}\,G$
via a homomorphism of
![]() $k$
-algebras
$k$
-algebras
Thus, the preceding discussion on localisation functors on triangulated categories applies to the
![]() $H^{\ast }(G,k)$
-linear category
$H^{\ast }(G,k)$
-linear category
![]() $\mathsf{StMod}\,G$
.
$\mathsf{StMod}\,G$
.
Koszul objects
Each
![]() $b$
in
$b$
in
![]() $H^{d}(G,k)$
corresponds to a morphism
$H^{d}(G,k)$
corresponds to a morphism
![]() $k\rightarrow \unicode[STIX]{x1D6FA}^{-d}k$
in
$k\rightarrow \unicode[STIX]{x1D6FA}^{-d}k$
in
![]() $\mathsf{StMod}\,G$
; let
$\mathsf{StMod}\,G$
; let
![]() $k/\!\!/b$
denote its mapping cone. This gives a morphism
$k/\!\!/b$
denote its mapping cone. This gives a morphism
![]() $k\rightarrow \unicode[STIX]{x1D6FA}^{d}(k/\!\!/b)$
. For a sequence of elements
$k\rightarrow \unicode[STIX]{x1D6FA}^{d}(k/\!\!/b)$
. For a sequence of elements
![]() $\boldsymbol{b}:=b_{1},\ldots ,b_{n}$
in
$\boldsymbol{b}:=b_{1},\ldots ,b_{n}$
in
![]() $H^{\ast }(G,k)$
and a
$H^{\ast }(G,k)$
and a
![]() $G$
-module
$G$
-module
![]() $M$
, we set
$M$
, we set
It is easy to check that for a
![]() $G$
-module
$G$
-module
![]() $N$
and
$N$
and
![]() $s=\sum _{i}|b_{i}|$
, there is an isomorphism
$s=\sum _{i}|b_{i}|$
, there is an isomorphism
Let
![]() $\mathfrak{b}=(\boldsymbol{b})$
be the ideal of
$\mathfrak{b}=(\boldsymbol{b})$
be the ideal of
![]() $H^{\ast }(G,k)$
generated by
$H^{\ast }(G,k)$
generated by
![]() $\boldsymbol{b}$
. By abuse of notation we set
$\boldsymbol{b}$
. By abuse of notation we set
![]() $M/\!\!/\mathfrak{b}:=M/\!\!/\boldsymbol{b}$
. If
$M/\!\!/\mathfrak{b}:=M/\!\!/\boldsymbol{b}$
. If
![]() $\boldsymbol{b}^{\prime }$
is a finite set of elements in
$\boldsymbol{b}^{\prime }$
is a finite set of elements in
![]() $H^{\ast }(G,k)$
such that
$H^{\ast }(G,k)$
such that
![]() $\sqrt{(\boldsymbol{b}^{\prime })}=\sqrt{(\boldsymbol{b})}$
, then, by [Reference Benson, Iyengar and KrauseBIK15, Proposition 3.10], for any
$\sqrt{(\boldsymbol{b}^{\prime })}=\sqrt{(\boldsymbol{b})}$
, then, by [Reference Benson, Iyengar and KrauseBIK15, Proposition 3.10], for any
![]() $M$
in
$M$
in
![]() $\mathsf{StMod}\,G$
there is an equality
$\mathsf{StMod}\,G$
there is an equality
Fix
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Spec}H^{\ast }(G,k)$
. We will repeatedly use the fact that
$\operatorname{Spec}H^{\ast }(G,k)$
. We will repeatedly use the fact that
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)^{\mathsf{c}}$
is generated as a triangulated category by the family of objects
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)^{\mathsf{c}}$
is generated as a triangulated category by the family of objects
![]() $(M/\!\!/\mathfrak{p})_{\mathfrak{p}}$
with
$(M/\!\!/\mathfrak{p})_{\mathfrak{p}}$
with
![]() $M$
in
$M$
in
![]() $\mathsf{stmod}\,G$
; see [Reference Benson, Iyengar and KrauseBIK11a, Proposition 3.9]. In fact, if
$\mathsf{stmod}\,G$
; see [Reference Benson, Iyengar and KrauseBIK11a, Proposition 3.9]. In fact, if
![]() $S$
denotes the direct sum of a representative set of simple
$S$
denotes the direct sum of a representative set of simple
![]() $G$
-modules, then there is an equality
$G$
-modules, then there is an equality
It turns out that one has
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G)=\{0\}$
where
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G)=\{0\}$
where
![]() $\mathfrak{m}$
denotes
$\mathfrak{m}$
denotes
![]() $H^{{\geqslant}1}(G,k)$
, the ideal of elements of positive degree; see Lemma 2.5 below. For this reason, it is customary to focus on
$H^{{\geqslant}1}(G,k)$
, the ideal of elements of positive degree; see Lemma 2.5 below. For this reason, it is customary to focus on
![]() $\operatorname{Proj}H^{\ast }(G,k)$
, the set of homogeneous prime ideals not containing
$\operatorname{Proj}H^{\ast }(G,k)$
, the set of homogeneous prime ideals not containing
![]() $\mathfrak{m}$
, when dealing with
$\mathfrak{m}$
, when dealing with
![]() $\mathsf{StMod}\,G$
.
$\mathsf{StMod}\,G$
.
Tate cohomology
By construction, the action of
![]() $H^{\ast }(G,k)$
on
$H^{\ast }(G,k)$
on
![]() $\mathsf{StMod}\,G$
factors through
$\mathsf{StMod}\,G$
factors through
![]() $\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,k)$
, the graded ring of endomorphisms of the identity. The latter ring is not noetherian in general, which is one reason to work with
$\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,k)$
, the graded ring of endomorphisms of the identity. The latter ring is not noetherian in general, which is one reason to work with
![]() $H^{\ast }(G,k)$
. In any case, there is little difference, vis-à-vis their action on
$H^{\ast }(G,k)$
. In any case, there is little difference, vis-à-vis their action on
![]() $\mathsf{StMod}\,G$
, as the next remarks should make clear.
$\mathsf{StMod}\,G$
, as the next remarks should make clear.
Remark 2.3. Let
![]() $M$
and
$M$
and
![]() $N$
be
$N$
be
![]() $G$
-modules. The map
$G$
-modules. The map
![]() $\operatorname{Hom}_{G}(M,N)\rightarrow \text{}\underline{\operatorname{Hom}}_{G}(M,N)$
induces a map
$\operatorname{Hom}_{G}(M,N)\rightarrow \text{}\underline{\operatorname{Hom}}_{G}(M,N)$
induces a map
![]() $\operatorname{Ext}_{G}^{\ast }(M,N)\rightarrow \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(M,N)$
of
$\operatorname{Ext}_{G}^{\ast }(M,N)\rightarrow \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(M,N)$
of
![]() $H^{\ast }(G,k)$
-modules. This map is surjective in degree zero, with kernel
$H^{\ast }(G,k)$
-modules. This map is surjective in degree zero, with kernel
![]() $\operatorname{PHom}_{G}(M,N)$
, the maps from
$\operatorname{PHom}_{G}(M,N)$
, the maps from
![]() $M$
to
$M$
to
![]() $N$
that factor through a projective
$N$
that factor through a projective
![]() $G$
-module. It is bijective in positive degrees and hence one gets an exact sequence of graded
$G$
-module. It is bijective in positive degrees and hence one gets an exact sequence of graded
![]() $H^{\ast }(G,k)$
-modules
$H^{\ast }(G,k)$
-modules
with
![]() $X^{i}=0$
for
$X^{i}=0$
for
![]() $i\geqslant 0$
. For degree reasons, the
$i\geqslant 0$
. For degree reasons, the
![]() $H^{\ast }(G,k)$
-modules
$H^{\ast }(G,k)$
-modules
![]() $\operatorname{PHom}_{G}(M,N)$
and
$\operatorname{PHom}_{G}(M,N)$
and
![]() $X$
are
$X$
are
![]() $\mathfrak{m}$
-torsion. Consequently, for
$\mathfrak{m}$
-torsion. Consequently, for
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
the induced localised map is an isomorphism:
$\operatorname{Proj}H^{\ast }(G,k)$
the induced localised map is an isomorphism:
More generally, for each
![]() $r$
in
$r$
in
![]() $\mathfrak{m}$
localisation induces an isomorphism
$\mathfrak{m}$
localisation induces an isomorphism
of
![]() $H^{\ast }(G,k)_{r}$
-modules. This means that
$H^{\ast }(G,k)_{r}$
-modules. This means that
![]() $\operatorname{Proj}H^{\ast }(G,k)$
has a finite cover by affine open sets on which ordinary cohomology and stable cohomology agree.
$\operatorname{Proj}H^{\ast }(G,k)$
has a finite cover by affine open sets on which ordinary cohomology and stable cohomology agree.
Given the finite generation result due to Friedlander and Suslin mentioned earlier, the next remark can be deduced from the exact sequence (2.6).
Remark 2.4. When
![]() $M,N$
are finite-dimensional
$M,N$
are finite-dimensional
![]() $G$
-modules,
$G$
-modules,
![]() $\text{}\underline{\operatorname{Hom}}_{G}^{{\geqslant}s}(M,N)$
is a finitely generated
$\text{}\underline{\operatorname{Hom}}_{G}^{{\geqslant}s}(M,N)$
is a finitely generated
![]() $H^{\ast }(G,k)$
-module for any
$H^{\ast }(G,k)$
-module for any
![]() $s\in \mathbb{Z}$
. Moreover the
$s\in \mathbb{Z}$
. Moreover the
![]() $H^{\ast }(G,k)_{\mathfrak{p}}$
-module
$H^{\ast }(G,k)_{\mathfrak{p}}$
-module
is finitely generated for each
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
.
$\operatorname{Proj}H^{\ast }(G,k)$
.
Lemma 2.5. One has
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G)=\{0\}$
, where
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G)=\{0\}$
, where
![]() $\mathfrak{m}=H^{{\geqslant}1}(G,k)$
.
$\mathfrak{m}=H^{{\geqslant}1}(G,k)$
.
Proof. Given (2.5) it suffices to check that
![]() $S/\!\!/\mathfrak{m}=0$
in
$S/\!\!/\mathfrak{m}=0$
in
![]() $\mathsf{StMod}\,G$
, where
$\mathsf{StMod}\,G$
, where
![]() $S$
is the direct sum of representative set of simple
$S$
is the direct sum of representative set of simple
![]() $G$
-modules. For any
$G$
-modules. For any
![]() $G$
-module
$G$
-module
![]() $M$
, the
$M$
, the
![]() $H^{\ast }(G,k)$
-module
$H^{\ast }(G,k)$
-module
![]() $\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(M,S/\!\!/\mathfrak{m})$
is
$\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(M,S/\!\!/\mathfrak{m})$
is
![]() $\mathfrak{m}$
-torsion; see [Reference Benson, Iyengar and KrauseBIK08, Lemma 5.11(1)]. Thus, when
$\mathfrak{m}$
-torsion; see [Reference Benson, Iyengar and KrauseBIK08, Lemma 5.11(1)]. Thus, when
![]() $M$
is finite dimensional, the
$M$
is finite dimensional, the
![]() $H^{\ast }(G,k)$
-module
$H^{\ast }(G,k)$
-module
![]() $\text{}\underline{\operatorname{Hom}}_{G}^{{\geqslant}0}(M,S/\!\!/\mathfrak{m})$
is
$\text{}\underline{\operatorname{Hom}}_{G}^{{\geqslant}0}(M,S/\!\!/\mathfrak{m})$
is
![]() $\mathfrak{m}$
-torsion and finitely generated, so it follows that
$\mathfrak{m}$
-torsion and finitely generated, so it follows that
![]() $\text{}\underline{\operatorname{Hom}}_{G}^{i}(M,S/\!\!/\mathfrak{m})=0$
for
$\text{}\underline{\operatorname{Hom}}_{G}^{i}(M,S/\!\!/\mathfrak{m})=0$
for
![]() $i\gg 0$
, by Remark 2.4. This implies that
$i\gg 0$
, by Remark 2.4. This implies that
![]() $S/\!\!/\mathfrak{m}$
is projective, since
$S/\!\!/\mathfrak{m}$
is projective, since
![]() $kG$
is self-injective.◻
$kG$
is self-injective.◻
To gain a better understanding of the discussion above, it helps to consider the homotopy category of
![]() $\mathsf{Inj}\,G$
, the injective
$\mathsf{Inj}\,G$
, the injective
![]() $G$
-modules.
$G$
-modules.
The homotopy category of injectives
Let
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
and
$\mathsf{K}(\mathsf{Inj}\,G)$
and
![]() $\mathsf{D}(\mathsf{Mod}\,G)$
denote the homotopy category of
$\mathsf{D}(\mathsf{Mod}\,G)$
denote the homotopy category of
![]() $\mathsf{Inj}\,G$
and the derived category of
$\mathsf{Inj}\,G$
and the derived category of
![]() $\mathsf{Mod}\,G$
, respectively. These are also
$\mathsf{Mod}\,G$
, respectively. These are also
![]() $H^{\ast }(G,k)$
-linear compactly generated tensor triangulated categories, with the tensor product over
$H^{\ast }(G,k)$
-linear compactly generated tensor triangulated categories, with the tensor product over
![]() $k$
. The unit of the tensor product on
$k$
. The unit of the tensor product on
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
is an injective resolution of the trivial
$\mathsf{K}(\mathsf{Inj}\,G)$
is an injective resolution of the trivial
![]() $G$
-module
$G$
-module
![]() $k$
, while that of
$k$
, while that of
![]() $\mathsf{D}(\mathsf{Mod}\,G)$
is
$\mathsf{D}(\mathsf{Mod}\,G)$
is
![]() $k$
. The canonical quotient functor
$k$
. The canonical quotient functor
![]() $\mathsf{K}(\mathsf{Inj}\,G)\rightarrow \mathsf{D}(\mathsf{Mod}\,G)$
induces an equivalence of triangulated category
$\mathsf{K}(\mathsf{Inj}\,G)\rightarrow \mathsf{D}(\mathsf{Mod}\,G)$
induces an equivalence of triangulated category
![]() $\mathsf{K}(\mathsf{Inj}\,G)^{\mathsf{c}}\xrightarrow[{}]{{\sim}}\mathsf{D}^{b}(\mathsf{mod}\,G)$
, where the target is the bounded derived category of
$\mathsf{K}(\mathsf{Inj}\,G)^{\mathsf{c}}\xrightarrow[{}]{{\sim}}\mathsf{D}^{b}(\mathsf{mod}\,G)$
, where the target is the bounded derived category of
![]() $\mathsf{mod}\,G$
; see [Reference KrauseKra05, Proposition 2.3].
$\mathsf{mod}\,G$
; see [Reference KrauseKra05, Proposition 2.3].
Taking Tate resolutions identifies
![]() $\mathsf{StMod}\,G$
with
$\mathsf{StMod}\,G$
with
![]() $\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
, the full subcategory of acyclic complexes in
$\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
, the full subcategory of acyclic complexes in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
. In detail, let
$\mathsf{K}(\mathsf{Inj}\,G)$
. In detail, let
![]() $\mathsf{p}k$
and
$\mathsf{p}k$
and
![]() $\mathsf{i}k$
be a projective and an injective resolution of the trivial
$\mathsf{i}k$
be a projective and an injective resolution of the trivial
![]() $G$
-module
$G$
-module
![]() $k$
, respectively, and let
$k$
, respectively, and let
![]() $\mathsf{t}k$
be the mapping cone of the composed morphism
$\mathsf{t}k$
be the mapping cone of the composed morphism
![]() $\mathsf{p}k\rightarrow k\rightarrow \mathsf{i}k$
; this is a Tate resolution of
$\mathsf{p}k\rightarrow k\rightarrow \mathsf{i}k$
; this is a Tate resolution of
![]() $k$
. Since projective and injective
$k$
. Since projective and injective
![]() $G$
-modules coincide, one gets the exact triangle
$G$
-modules coincide, one gets the exact triangle
in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
. For a
$\mathsf{K}(\mathsf{Inj}\,G)$
. For a
![]() $G$
-module
$G$
-module
![]() $M$
, the complex
$M$
, the complex
![]() $M\otimes _{k}\mathsf{t}k$
is a Tate resolution of
$M\otimes _{k}\mathsf{t}k$
is a Tate resolution of
![]() $M$
and the assignment
$M$
and the assignment
![]() $M\mapsto M\otimes _{k}\mathsf{t}k$
induces an equivalence of categories
$M\mapsto M\otimes _{k}\mathsf{t}k$
induces an equivalence of categories
with quasi-inverse
![]() $X\mapsto Z^{0}(X)$
, the submodule of cycles in degree 0. Assigning
$X\mapsto Z^{0}(X)$
, the submodule of cycles in degree 0. Assigning
![]() $X$
in
$X$
in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
to
$\mathsf{K}(\mathsf{Inj}\,G)$
to
![]() $X\otimes _{k}\mathsf{t}k$
is a left adjoint of the inclusion
$X\otimes _{k}\mathsf{t}k$
is a left adjoint of the inclusion
![]() $\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)\rightarrow \mathsf{K}(\mathsf{Inj}\,G)$
. These results are contained in [Reference KrauseKra05, Theorem 8.2]. Consider the composed functor
$\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)\rightarrow \mathsf{K}(\mathsf{Inj}\,G)$
. These results are contained in [Reference KrauseKra05, Theorem 8.2]. Consider the composed functor
A straightforward verification yields that these functors are
![]() $H^{\ast }(G,k)$
-linear. The result below is the categorical underpinning of Remark 2.3 and Lemma 2.5.
$H^{\ast }(G,k)$
-linear. The result below is the categorical underpinning of Remark 2.3 and Lemma 2.5.
Lemma 2.6. There is a natural isomorphism
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}X\cong X\otimes _{k}\mathsf{p}k$
for
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}X\cong X\otimes _{k}\mathsf{p}k$
for
![]() $X\in \mathsf{K}(\mathsf{Inj}\,G)$
. For each
$X\in \mathsf{K}(\mathsf{Inj}\,G)$
. For each
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
, the functor
$\operatorname{Proj}H^{\ast }(G,k)$
, the functor
![]() $\unicode[STIX]{x1D70B}$
induces triangle equivalences
$\unicode[STIX]{x1D70B}$
induces triangle equivalences
Proof. We identify
![]() $\mathsf{StMod}\,G$
with
$\mathsf{StMod}\,G$
with
![]() $\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
. This entails
$\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
. This entails
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G))=\{0\}$
, by Lemma 2.5. It is easy to check that
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G))=\{0\}$
, by Lemma 2.5. It is easy to check that
![]() $kG$
is
$kG$
is
![]() $\mathfrak{m}$
-torsion, and hence so is
$\mathfrak{m}$
-torsion, and hence so is
![]() $\mathsf{p}k$
, for it is in the localising subcategory generated by
$\mathsf{p}k$
, for it is in the localising subcategory generated by
![]() $kG$
, and the class of
$kG$
, and the class of
![]() $\mathfrak{m}$
-torsion objects in
$\mathfrak{m}$
-torsion objects in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
is a tensor ideal localising subcategory; see, for instance, [Reference Benson, Iyengar and KrauseBIK08, § 8]. Thus, applying
$\mathsf{K}(\mathsf{Inj}\,G)$
is a tensor ideal localising subcategory; see, for instance, [Reference Benson, Iyengar and KrauseBIK08, § 8]. Thus, applying
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(-)$
to the exact triangle (2.8) yields
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(-)$
to the exact triangle (2.8) yields
![]() $\mathsf{p}k\cong \unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{i}k)$
. It then follows from (2.2) that
$\mathsf{p}k\cong \unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{i}k)$
. It then follows from (2.2) that
![]() $X\otimes _{k}\mathsf{p}k\cong \unicode[STIX]{x1D6E4}_{\mathfrak{m}}X$
for any
$X\otimes _{k}\mathsf{p}k\cong \unicode[STIX]{x1D6E4}_{\mathfrak{m}}X$
for any
![]() $X$
in
$X$
in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
.
$\mathsf{K}(\mathsf{Inj}\,G)$
.
From the construction of
![]() $\unicode[STIX]{x1D70B}$
and (2.8), the kernel of
$\unicode[STIX]{x1D70B}$
and (2.8), the kernel of
![]() $\unicode[STIX]{x1D70B}$
is the subcategory
$\unicode[STIX]{x1D70B}$
is the subcategory
These are precisely the
![]() $\mathfrak{m}$
-torsion objects in
$\mathfrak{m}$
-torsion objects in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
, by the already established part of the result. Said otherwise,
$\mathsf{K}(\mathsf{Inj}\,G)$
, by the already established part of the result. Said otherwise,
![]() $X\in \mathsf{K}(\mathsf{Inj}\,G)$
is acyclic if and only if
$X\in \mathsf{K}(\mathsf{Inj}\,G)$
is acyclic if and only if
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}X=0$
. It follows that
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}X=0$
. It follows that
![]() $\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
contains the subcategory
$\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
contains the subcategory
![]() $\mathsf{K}(\mathsf{Inj}\,G)_{\mathfrak{p}}$
of
$\mathsf{K}(\mathsf{Inj}\,G)_{\mathfrak{p}}$
of
![]() $\mathfrak{p}$
-local objects, for each
$\mathfrak{p}$
-local objects, for each
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
. On the other hand, the inclusion
$\operatorname{Proj}H^{\ast }(G,k)$
. On the other hand, the inclusion
![]() $\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)\subseteq \mathsf{K}(\mathsf{Inj}\,G)$
preserves coproducts, so its left adjoint
$\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)\subseteq \mathsf{K}(\mathsf{Inj}\,G)$
preserves coproducts, so its left adjoint
![]() $\unicode[STIX]{x1D70B}$
preserves compactness of objects and all compacts of
$\unicode[STIX]{x1D70B}$
preserves compactness of objects and all compacts of
![]() $\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
are in the image of
$\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)$
are in the image of
![]() $\unicode[STIX]{x1D70B}$
. Given this a simple calculation shows that
$\unicode[STIX]{x1D70B}$
. Given this a simple calculation shows that
![]() $\mathsf{K}(\mathsf{Inj}\,G)_{\mathfrak{p}}$
contains
$\mathsf{K}(\mathsf{Inj}\,G)_{\mathfrak{p}}$
contains
![]() ${\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)}_{\mathfrak{p}}$
. Thus
${\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)}_{\mathfrak{p}}$
. Thus
![]() ${\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)}_{\mathfrak{p}}=\mathsf{K}(\mathsf{Inj}\,G)_{\mathfrak{p}}$
.◻
${\mathsf{K}_{\text{ac}}(\mathsf{Inj}\,G)}_{\mathfrak{p}}=\mathsf{K}(\mathsf{Inj}\,G)_{\mathfrak{p}}$
.◻
3 Passage to closed points
Let
![]() $G$
be a finite group scheme over a field
$G$
be a finite group scheme over a field
![]() $k$
of positive characteristic. In this section we describe a technique that relates the
$k$
of positive characteristic. In this section we describe a technique that relates the
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $\mathfrak{p}$
-torsion objects in
$\mathfrak{p}$
-torsion objects in
![]() $\mathsf{StMod}\,G$
, for a point
$\mathsf{StMod}\,G$
, for a point
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
, to the corresponding modules at a closed point defined over a field extension of
$\operatorname{Proj}H^{\ast }(G,k)$
, to the corresponding modules at a closed point defined over a field extension of
![]() $k$
. Recall that a point
$k$
. Recall that a point
![]() $\mathfrak{m}$
is closed when it is maximal with respect to inclusion:
$\mathfrak{m}$
is closed when it is maximal with respect to inclusion:
![]() $\mathfrak{m}\subseteq \mathfrak{q}$
implies
$\mathfrak{m}\subseteq \mathfrak{q}$
implies
![]() $\mathfrak{m}=\mathfrak{q}$
for all
$\mathfrak{m}=\mathfrak{q}$
for all
![]() $\mathfrak{q}$
in
$\mathfrak{q}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
. In what follows,
$\operatorname{Proj}H^{\ast }(G,k)$
. In what follows,
![]() $k(\mathfrak{p})$
denotes the graded residue field of
$k(\mathfrak{p})$
denotes the graded residue field of
![]() $H^{\ast }(G,k)$
at
$H^{\ast }(G,k)$
at
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
For a field extension
![]() $K/k$
extension of scalars and restriction give exact functors
$K/k$
extension of scalars and restriction give exact functors
The functors form an adjoint pair, with the left adjoint
![]() $K\otimes _{k}(-)$
mapping
$K\otimes _{k}(-)$
mapping
![]() $k$
to
$k$
to
![]() $K$
and respecting tensor products, so one has a well-known projection formula:
$K$
and respecting tensor products, so one has a well-known projection formula:
for a
![]() $G$
-module
$G$
-module
![]() $M$
and
$M$
and
![]() $G_{K}$
-module
$G_{K}$
-module
![]() $N$
; see [Reference Balmer, Dell’Ambrogio and SandersBDS16, (2.16)] or [Reference Benson, Iyengar, Krause and PevtsovaBIKP17, Lemma 2.2].
$N$
; see [Reference Balmer, Dell’Ambrogio and SandersBDS16, (2.16)] or [Reference Benson, Iyengar, Krause and PevtsovaBIKP17, Lemma 2.2].
The functor
![]() $K\otimes _{k}(-)$
yields a homomorphism
$K\otimes _{k}(-)$
yields a homomorphism
![]() $H^{\ast }(G,k)\rightarrow H^{\ast }(G_{K},K)$
of rings. There is a natural isomorphism
$H^{\ast }(G,k)\rightarrow H^{\ast }(G_{K},K)$
of rings. There is a natural isomorphism
![]() $H^{\ast }(G_{K},K)\xrightarrow[{}]{{\sim}}K\otimes _{k}H^{\ast }(G,k)$
of
$H^{\ast }(G_{K},K)\xrightarrow[{}]{{\sim}}K\otimes _{k}H^{\ast }(G,k)$
of
![]() $K$
-algebras, so the preceding map above is just extension of scalars. There is an induced map
$K$
-algebras, so the preceding map above is just extension of scalars. There is an induced map
with
![]() $\mathfrak{q}$
mapping to
$\mathfrak{q}$
mapping to
![]() $\mathfrak{p}:=\mathfrak{q}\cap H^{\ast }(G,k)$
. We say that
$\mathfrak{p}:=\mathfrak{q}\cap H^{\ast }(G,k)$
. We say that
![]() $\mathfrak{q}$
lies over
$\mathfrak{q}$
lies over
![]() $\mathfrak{p}$
to indicate this.
$\mathfrak{p}$
to indicate this.
The main objective of this section is the proof of the following result. We say a functor is dense if it is surjective on objects, up to isomorphism.
Theorem 3.1. Fix
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
and
$\operatorname{Proj}H^{\ast }(G,k)$
and
![]() $K/k$
a purely transcendental extension of degree
$K/k$
a purely transcendental extension of degree
![]() $\dim (H^{\ast }(G,k)/\mathfrak{p})-1$
. There exists a closed point
$\dim (H^{\ast }(G,k)/\mathfrak{p})-1$
. There exists a closed point
![]() $\mathfrak{m}$
in
$\mathfrak{m}$
in
![]() $\operatorname{Proj}H^{\ast }(G_{K},K)$
lying over
$\operatorname{Proj}H^{\ast }(G_{K},K)$
lying over
![]() $\mathfrak{p}$
with
$\mathfrak{p}$
with
![]() $k(\mathfrak{m})\cong k(\mathfrak{p})$
such that the functor
$k(\mathfrak{m})\cong k(\mathfrak{p})$
such that the functor
![]() $(-)\downarrow _{G}$
restricts to functors
$(-)\downarrow _{G}$
restricts to functors
that are dense.
The proof of the theorem yields more: there is a subcategory of
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
on which
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
on which
![]() $(-)\downarrow _{G}$
is full and dense; ditto for the category of compact objects. However, the functor need not be full on all of
$(-)\downarrow _{G}$
is full and dense; ditto for the category of compact objects. However, the functor need not be full on all of
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})^{\mathsf{c}}$
; see Example 3.7.
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})^{\mathsf{c}}$
; see Example 3.7.
Here is one consequence of Theorem 3.1.
Corollary 3.2. The compact objects in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
are, up to isomorphism, the restrictions of finite-dimensional
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
are, up to isomorphism, the restrictions of finite-dimensional
![]() $G_{K}$
-modules in
$G_{K}$
-modules in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
.
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
.
Proof. By [Reference Benson, Iyengar and KrauseBIK08, Theorem 6.4], for any ideal
![]() $\mathfrak{a}$
in
$\mathfrak{a}$
in
![]() $H^{\ast }(G,k)$
, we have
$H^{\ast }(G,k)$
, we have
Applying this observation to the ideal
![]() $\mathfrak{m}$
of
$\mathfrak{m}$
of
![]() $H^{\ast }(G_{K},K)$
and noting that
$H^{\ast }(G_{K},K)$
and noting that
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}=\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{m})}$
, since
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}=\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{m})}$
, since
![]() $\mathfrak{m}$
is a closed point, the desired result follows from Theorem 3.1.◻
$\mathfrak{m}$
is a closed point, the desired result follows from Theorem 3.1.◻
The closed point in Theorem 3.1 depends on the choice of a Noether normalisation of
![]() $H^{\ast }(G,k)/\mathfrak{p}$
as is explained in the construction below, from [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, § 7].
$H^{\ast }(G,k)/\mathfrak{p}$
as is explained in the construction below, from [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, § 7].
Construction 3.3. Fix
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
; the following construction is relevant only when
$\operatorname{Proj}H^{\ast }(G,k)$
; the following construction is relevant only when
![]() $\mathfrak{p}$
is not a closed point. Choose elements
$\mathfrak{p}$
is not a closed point. Choose elements
![]() $\boldsymbol{a}:=a_{0},\ldots ,a_{d-1}$
in
$\boldsymbol{a}:=a_{0},\ldots ,a_{d-1}$
in
![]() $H^{\ast }(G,k)$
of the same degree such that their image in
$H^{\ast }(G,k)$
of the same degree such that their image in
![]() $H^{\ast }(G,k)/\mathfrak{p}$
is algebraically independent over
$H^{\ast }(G,k)/\mathfrak{p}$
is algebraically independent over
![]() $k$
and
$k$
and
![]() $H^{\ast }(G,k)/\mathfrak{p}$
is finitely generated as a module over the subalgebra
$H^{\ast }(G,k)/\mathfrak{p}$
is finitely generated as a module over the subalgebra
![]() $k[\boldsymbol{a}]$
. Thus the Krull dimension of
$k[\boldsymbol{a}]$
. Thus the Krull dimension of
![]() $H^{\ast }(G,k)/\mathfrak{p}$
is
$H^{\ast }(G,k)/\mathfrak{p}$
is
![]() $d$
. Set
$d$
. Set
![]() $K:=k(t_{1},\ldots ,t_{d-1})$
, the field of rational functions in indeterminates
$K:=k(t_{1},\ldots ,t_{d-1})$
, the field of rational functions in indeterminates
![]() $t_{1},\ldots ,t_{d-1}$
and
$t_{1},\ldots ,t_{d-1}$
and
viewed as elements in
![]() $H^{\ast }(G_{K},K)$
. Let
$H^{\ast }(G_{K},K)$
. Let
![]() $\mathfrak{p}^{\prime }$
be the extension of
$\mathfrak{p}^{\prime }$
be the extension of
![]() $\mathfrak{p}$
to
$\mathfrak{p}$
to
![]() $H^{\ast }(G_{K},K)$
and
$H^{\ast }(G_{K},K)$
and
It is proved as part of [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Theorem 7.7] that the ideal
![]() $\mathfrak{m}$
is a closed point in
$\mathfrak{m}$
is a closed point in
![]() $\operatorname{Proj}H^{\ast }(G_{K},K)$
with the property that
$\operatorname{Proj}H^{\ast }(G_{K},K)$
with the property that
![]() $\mathfrak{m}\cap H^{\ast }(G,k)=\mathfrak{p}$
. What is more, it follows from the construction (see in particular [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Lemmas 7.6, and (7.2)]) that the induced extension of fields is an isomorphism
$\mathfrak{m}\cap H^{\ast }(G,k)=\mathfrak{p}$
. What is more, it follows from the construction (see in particular [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Lemmas 7.6, and (7.2)]) that the induced extension of fields is an isomorphism
The sequence of elements
![]() $\boldsymbol{b}$
in
$\boldsymbol{b}$
in
![]() $H^{\ast }(G_{K},K)$
yields a morphism
$H^{\ast }(G_{K},K)$
yields a morphism
![]() $K\rightarrow \unicode[STIX]{x1D6FA}^{s}(K/\!\!/\boldsymbol{b})$
, where
$K\rightarrow \unicode[STIX]{x1D6FA}^{s}(K/\!\!/\boldsymbol{b})$
, where
![]() $s=\sum _{i}|b_{i}|$
, and composing its restriction to
$s=\sum _{i}|b_{i}|$
, and composing its restriction to
![]() $G$
with the canonical morphism
$G$
with the canonical morphism
![]() $k\rightarrow K\downarrow _{G}$
gives in
$k\rightarrow K\downarrow _{G}$
gives in
![]() $\mathsf{StMod}\,G$
a morphism
$\mathsf{StMod}\,G$
a morphism
Since the
![]() $a_{i}$
are not in
$a_{i}$
are not in
![]() $\mathfrak{p}$
, Lemma 2.1 yields a natural stable isomorphism
$\mathfrak{p}$
, Lemma 2.1 yields a natural stable isomorphism
for any
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $G$
-module
$G$
-module
![]() $M$
. This remark will be used often in the sequel.
$M$
. This remark will be used often in the sequel.
The result below extends [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Theorem 8.8]; the latter is the case
![]() $M=k/\!\!/\mathfrak{p}$
.
$M=k/\!\!/\mathfrak{p}$
.
Theorem 3.4. For any
![]() $G$
-module
$G$
-module
![]() $M$
, the morphism
$M$
, the morphism
![]() $M\otimes _{k}f$
induces a natural stable isomorphism of
$M\otimes _{k}f$
induces a natural stable isomorphism of
![]() $G$
-modules
$G$
-modules
When
![]() $M$
is
$M$
is
![]() $\mathfrak{p}$
-torsion, these induce natural stable isomorphisms
$\mathfrak{p}$
-torsion, these induce natural stable isomorphisms
Proof. We begin by verifying the second set of isomorphisms. As
![]() $M$
is
$M$
is
![]() $\mathfrak{p}$
-torsion so is
$\mathfrak{p}$
-torsion so is
![]() $M_{\mathfrak{p}}$
and then it is clear that the natural map
$M_{\mathfrak{p}}$
and then it is clear that the natural map
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}M=\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M_{\mathfrak{p}}\rightarrow M_{\mathfrak{p}}$
is an isomorphism. The third of the desired isomorphisms follows from (3.1). It thus remains to check that
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}M=\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M_{\mathfrak{p}}\rightarrow M_{\mathfrak{p}}$
is an isomorphism. The third of the desired isomorphisms follows from (3.1). It thus remains to check that
![]() $M\otimes _{k}f$
induces an isomorphism
$M\otimes _{k}f$
induces an isomorphism
It is easy to verify that the modules
![]() $M$
having this property form a tensor ideal localising subcategory of
$M$
having this property form a tensor ideal localising subcategory of
![]() $\mathsf{StMod}\,G$
. Keeping in mind (3.2), from [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Theorem 8.8] one obtains that this subcategory contains
$\mathsf{StMod}\,G$
. Keeping in mind (3.2), from [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Theorem 8.8] one obtains that this subcategory contains
![]() $k/\!\!/\mathfrak{p}$
. The desired assertion follows since the
$k/\!\!/\mathfrak{p}$
. The desired assertion follows since the
![]() $\mathfrak{p}$
-torsion modules form a tensor ideal localising subcategory of
$\mathfrak{p}$
-torsion modules form a tensor ideal localising subcategory of
![]() $\mathsf{StMod}\,G$
that is generated by
$\mathsf{StMod}\,G$
that is generated by
![]() $k/\!\!/\mathfrak{p}$
; see [Reference Benson, Iyengar and KrauseBIK11a, Proposition 2.7].
$k/\!\!/\mathfrak{p}$
; see [Reference Benson, Iyengar and KrauseBIK11a, Proposition 2.7].
Now we turn to the first set of isomorphisms. There the second one holds by (3.1), so we focus on the first. Let
![]() $M$
be an arbitrary
$M$
be an arbitrary
![]() $G$
-module, and let
$G$
-module, and let
![]() $\mathfrak{p}^{\prime }$
be as in Construction 3.3. Since
$\mathfrak{p}^{\prime }$
be as in Construction 3.3. Since
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M$
is
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M$
is
![]() $\mathfrak{p}$
-torsion, the already established isomorphism yields the second one below:
$\mathfrak{p}$
-torsion, the already established isomorphism yields the second one below:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{p}}M & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M)_{\mathfrak{p}}\nonumber\\ \displaystyle & \cong & \displaystyle ((\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M)_{K}\otimes _{K}K/\!\!/\boldsymbol{b})\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime })}(M_{K})\otimes _{K}K/\!\!/\boldsymbol{b})\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (M_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime })}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (M_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime }+(\boldsymbol{b}))}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (M_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(K/\!\!/\boldsymbol{b}))\downarrow _{G}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{p}}M & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M)_{\mathfrak{p}}\nonumber\\ \displaystyle & \cong & \displaystyle ((\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}M)_{K}\otimes _{K}K/\!\!/\boldsymbol{b})\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime })}(M_{K})\otimes _{K}K/\!\!/\boldsymbol{b})\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (M_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime })}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (M_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime }+(\boldsymbol{b}))}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (M_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(K/\!\!/\boldsymbol{b}))\downarrow _{G}.\nonumber\end{eqnarray}$$
The third one holds by Lemma 2.2, applied to the functor
![]() $K\otimes _{k}(-)$
from
$K\otimes _{k}(-)$
from
![]() $\mathsf{StMod}\,G$
to
$\mathsf{StMod}\,G$
to
![]() $\mathsf{StMod}\,G_{K}$
. The next one is standard, the penultimate one holds as
$\mathsf{StMod}\,G_{K}$
. The next one is standard, the penultimate one holds as
![]() $K/\!\!/\boldsymbol{b}$
is
$K/\!\!/\boldsymbol{b}$
is
![]() $(\boldsymbol{b})$
-torsion, and the last follows from
$(\boldsymbol{b})$
-torsion, and the last follows from
![]() $\sqrt{\mathfrak{p}^{\prime }+(\boldsymbol{b})}=\mathfrak{m}$
. This completes the proof.◻
$\sqrt{\mathfrak{p}^{\prime }+(\boldsymbol{b})}=\mathfrak{m}$
. This completes the proof.◻
In the next remark we recast part of Theorem 3.4.
Remark 3.5. Fix a point
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
, and let
$\operatorname{Proj}H^{\ast }(G,k)$
, and let
![]() $K$
,
$K$
,
![]() $\boldsymbol{b}$
and
$\boldsymbol{b}$
and
![]() $\mathfrak{m}$
be as in Construction 3.3. Consider the following adjoint pair of functors.
$\mathfrak{m}$
be as in Construction 3.3. Consider the following adjoint pair of functors.
It is easy to check that this induces an adjoint pair
Theorem 3.4 implies that
![]() $(\unicode[STIX]{x1D706}M)\downarrow _{G}\cong M$
for any
$(\unicode[STIX]{x1D706}M)\downarrow _{G}\cong M$
for any
![]() $M$
in
$M$
in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
.
Proof of Theorem 3.1.
Let
![]() $\mathfrak{m}$
,
$\mathfrak{m}$
,
![]() $\mathfrak{q}$
, and
$\mathfrak{q}$
, and
![]() $\boldsymbol{b}$
be as in Construction 3.3. As noted there,
$\boldsymbol{b}$
be as in Construction 3.3. As noted there,
![]() $\mathfrak{m}$
is a closed point in
$\mathfrak{m}$
is a closed point in
![]() $\operatorname{Proj}H^{\ast }(G_{K},K)$
lying over
$\operatorname{Proj}H^{\ast }(G_{K},K)$
lying over
![]() $\mathfrak{p}$
and
$\mathfrak{p}$
and
![]() $k(\mathfrak{m})\cong k(\mathfrak{p})$
. The modules in
$k(\mathfrak{m})\cong k(\mathfrak{p})$
. The modules in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
are precisely those with support contained in
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
are precisely those with support contained in
![]() $\{\mathfrak{p}\}$
. It then follows from [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Proposition 6.2] that
$\{\mathfrak{p}\}$
. It then follows from [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Proposition 6.2] that
![]() $(-)\downarrow _{G}$
restricts to a functor
$(-)\downarrow _{G}$
restricts to a functor
This functor is dense because for any
![]() $G$
-module
$G$
-module
![]() $M$
that is
$M$
that is
![]() $\mathfrak{p}$
-local and
$\mathfrak{p}$
-local and
![]() $\mathfrak{p}$
-torsion one has
$\mathfrak{p}$
-torsion one has
![]() $M\cong (\unicode[STIX]{x1D706}M)\downarrow _{G}$
where
$M\cong (\unicode[STIX]{x1D706}M)\downarrow _{G}$
where
![]() $\unicode[STIX]{x1D706}$
is the functor from Remark 3.5.
$\unicode[STIX]{x1D706}$
is the functor from Remark 3.5.
Consider the restriction of
![]() $(-)\downarrow _{G}$
to compact objects in
$(-)\downarrow _{G}$
to compact objects in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
. First we verify that its image is contained in the compact objects of
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
. First we verify that its image is contained in the compact objects of
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. To this end, it suffices to check that there exists a generator of
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. To this end, it suffices to check that there exists a generator of
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})^{\mathsf{c}}$
, as a thick subcategory, whose restriction is in
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})^{\mathsf{c}}$
, as a thick subcategory, whose restriction is in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)^{\mathsf{c}}$
.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)^{\mathsf{c}}$
.
Let
![]() $S$
be the direct sum of a representative set of simple
$S$
be the direct sum of a representative set of simple
![]() $G$
-modules. Each simple
$G$
-modules. Each simple
![]() $G_{K}$
-module is (isomorphic to) a direct summand of
$G_{K}$
-module is (isomorphic to) a direct summand of
![]() $S_{K}$
, so from (2.5) one gets the first equality below:
$S_{K}$
, so from (2.5) one gets the first equality below:
The second one holds by (2.4), since
![]() $\sqrt{\mathfrak{q}}=\mathfrak{m}$
. From Theorem 3.4 one gets isomorphisms of
$\sqrt{\mathfrak{q}}=\mathfrak{m}$
. From Theorem 3.4 one gets isomorphisms of
![]() $G$
-modules
$G$
-modules
It remains to note that
![]() $(S/\!\!/\mathfrak{p})_{\mathfrak{p}}$
is in
$(S/\!\!/\mathfrak{p})_{\mathfrak{p}}$
is in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)^{\mathsf{c}}$
, again by (2.5).
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)^{\mathsf{c}}$
, again by (2.5).
The last item to verify is that restriction is dense also on compacts. Since
![]() $K/\!\!/\boldsymbol{b}$
is compact, the functor
$K/\!\!/\boldsymbol{b}$
is compact, the functor
![]() $\unicode[STIX]{x1D70C}$
from Remark 3.5 preserves coproducts, and hence its left adjoint
$\unicode[STIX]{x1D70C}$
from Remark 3.5 preserves coproducts, and hence its left adjoint
![]() $\unicode[STIX]{x1D706}$
preserves compactness. Thus Theorem 3.4 gives the desired result.◻
$\unicode[STIX]{x1D706}$
preserves compactness. Thus Theorem 3.4 gives the desired result.◻
Theorem 3.4 yields that
![]() $f\cong (f_{K})\downarrow _{G}$
for any morphism
$f\cong (f_{K})\downarrow _{G}$
for any morphism
![]() $f$
in
$f$
in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
; in particular, the restriction functor is full and dense on the subcategory of
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
; in particular, the restriction functor is full and dense on the subcategory of
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
consisting of objects of the form
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,G_{K})$
consisting of objects of the form
![]() $\unicode[STIX]{x1D706}M$
, where
$\unicode[STIX]{x1D706}M$
, where
![]() $M$
is a
$M$
is a
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $\mathfrak{p}$
-torsion
$\mathfrak{p}$
-torsion
![]() $G$
-module. It need not be full on the entire category, or even on its subcategory of compact objects; see Example 3.7, modelled on the following example from commutative algebra.
$G$
-module. It need not be full on the entire category, or even on its subcategory of compact objects; see Example 3.7, modelled on the following example from commutative algebra.
Example 3.6. Let
![]() $k$
be a field and
$k$
be a field and
![]() $k[a]$
the polynomial ring in an indeterminate
$k[a]$
the polynomial ring in an indeterminate
![]() $a$
. Let
$a$
. Let
![]() $\mathsf{D}(k[a])$
denote its derived category; it is
$\mathsf{D}(k[a])$
denote its derived category; it is
![]() $k[a]$
-linear in an obvious way. For the prime
$k[a]$
-linear in an obvious way. For the prime
![]() $\mathfrak{p}:=(0)$
of
$\mathfrak{p}:=(0)$
of
![]() $k[a]$
the
$k[a]$
the
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $\mathfrak{p}$
-torsion subcategory
$\mathfrak{p}$
-torsion subcategory
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{D}(k[a]))$
is naturally identified with the derived category of
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{D}(k[a]))$
is naturally identified with the derived category of
![]() $k(a)$
, the field of rational functions in
$k(a)$
, the field of rational functions in
![]() $a$
.
$a$
.
With
![]() $k(t)$
denoting the field of rational functions in an indeterminate
$k(t)$
denoting the field of rational functions in an indeterminate
![]() $t$
, the maximal ideal
$t$
, the maximal ideal
![]() $\mathfrak{m}:=(a-t)$
of
$\mathfrak{m}:=(a-t)$
of
![]() $k(t)[a]$
lies over the prime ideal
$k(t)[a]$
lies over the prime ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $k[a]$
. The inclusion
$k[a]$
. The inclusion
![]() $k[a]\subset k(t)[a]$
induces an isomorphism
$k[a]\subset k(t)[a]$
induces an isomorphism
![]() $k(a)\cong k(t)[a]/\mathfrak{m}\cong k(t)$
. The analogue of Theorem 3.4 is that restriction of scalars along the inclusion
$k(a)\cong k(t)[a]/\mathfrak{m}\cong k(t)$
. The analogue of Theorem 3.4 is that restriction of scalars along the inclusion
![]() $k[a]\subset k(t)[a]$
induces a dense functor
$k[a]\subset k(t)[a]$
induces a dense functor
This property can be checked directly: the
![]() $\mathfrak{m}$
-torsion module
$\mathfrak{m}$
-torsion module
![]() $k(t)[a]/(a-t)$
restricts to
$k(t)[a]/(a-t)$
restricts to
![]() $k(a)$
, and each object in
$k(a)$
, and each object in
![]() $\mathsf{D}(k(a))$
is a direct sum of shifts of
$\mathsf{D}(k(a))$
is a direct sum of shifts of
![]() $k(a)$
. This functor is, however, not full: for
$k(a)$
. This functor is, however, not full: for
![]() $n\geqslant 1$
, the
$n\geqslant 1$
, the
![]() $k(t)[a]$
-module
$k(t)[a]$
-module
![]() $L:=k(t)[a]/(a-t)^{n}$
is
$L:=k(t)[a]/(a-t)^{n}$
is
![]() $\mathfrak{m}$
-torsion, and satisfies
$\mathfrak{m}$
-torsion, and satisfies
where
![]() $\mathsf{D}$
stands for the appropriate derived category. In particular, if
$\mathsf{D}$
stands for the appropriate derived category. In particular, if
![]() $n\geqslant 2$
, the canonical map
$n\geqslant 2$
, the canonical map
![]() $\operatorname{End}_{\mathsf{D}}(L)\rightarrow \operatorname{End}_{\mathsf{D}}(L\downarrow _{k[a]})$
is not surjective.
$\operatorname{End}_{\mathsf{D}}(L)\rightarrow \operatorname{End}_{\mathsf{D}}(L\downarrow _{k[a]})$
is not surjective.
Indeed, the module of endomorphisms of
![]() $L$
in
$L$
in
![]() $\mathsf{D}(k(t)[a])$
is
$\mathsf{D}(k(t)[a])$
is
In particular, it has rank
![]() $n$
as an
$n$
as an
![]() $k(a)$
-vector space. On the other hand, restricted to
$k(a)$
-vector space. On the other hand, restricted to
![]() $k[a]$
, the
$k[a]$
, the
![]() $k(t)[a]$
-module
$k(t)[a]$
-module
![]() $k(t)/(a-t)$
is isomorphic to
$k(t)/(a-t)$
is isomorphic to
![]() $k(a)$
. It then follows from the exact sequences
$k(a)$
. It then follows from the exact sequences
of
![]() $k(t)[a]$
-modules that
$k(t)[a]$
-modules that
![]() $L$
restricts to a direct sum of
$L$
restricts to a direct sum of
![]() $n$
copies of
$n$
copies of
![]() $k(a)$
, so that
$k(a)$
, so that
In particular, this has rank
![]() $n^{2}$
as a
$n^{2}$
as a
![]() $k(a)$
-vector space.
$k(a)$
-vector space.
Example 3.7. Let
![]() $V=\mathbb{Z}/2\times \mathbb{Z}/2$
and
$V=\mathbb{Z}/2\times \mathbb{Z}/2$
and
![]() $k$
a field of characteristic two. As
$k$
a field of characteristic two. As
![]() $k$
-algebras, one has
$k$
-algebras, one has
![]() $H^{\ast }(V,k)\cong k[a,b]$
, where
$H^{\ast }(V,k)\cong k[a,b]$
, where
![]() $a$
and
$a$
and
![]() $b$
are indeterminates of degree one. For the prime ideal
$b$
are indeterminates of degree one. For the prime ideal
![]() $\mathfrak{p}=(0)$
of
$\mathfrak{p}=(0)$
of
![]() $k[a,b]$
, Construction 3.3 leads to the field extension
$k[a,b]$
, Construction 3.3 leads to the field extension
![]() $K:=k(t)$
of
$K:=k(t)$
of
![]() $k$
, and the closed point
$k$
, and the closed point
![]() $\mathfrak{m}=(b-at)$
of
$\mathfrak{m}=(b-at)$
of
![]() $\operatorname{Proj}H^{\ast }(V_{K},K)$
.
$\operatorname{Proj}H^{\ast }(V_{K},K)$
.
Set
![]() $F:=\text{}\underline{\operatorname{End}}_{V}(k_{\mathfrak{p}})$
; this is the component in degree
$F:=\text{}\underline{\operatorname{End}}_{V}(k_{\mathfrak{p}})$
; this is the component in degree
![]() $0$
of the graded field
$0$
of the graded field
![]() $k[a,b]_{\mathfrak{p}}$
and can be identified with
$k[a,b]_{\mathfrak{p}}$
and can be identified with
![]() $K$
; see Construction 3.3.
$K$
; see Construction 3.3.
Fix an integer
![]() $n\geqslant 1$
and set
$n\geqslant 1$
and set
![]() $N:=K/\!\!/(b-at)^{n}$
. This is a finite-dimensional
$N:=K/\!\!/(b-at)^{n}$
. This is a finite-dimensional
![]() $\mathfrak{m}$
-torsion
$\mathfrak{m}$
-torsion
![]() $V_{K}$
-module and hence compact in
$V_{K}$
-module and hence compact in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,V_{K})$
. We claim that
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{StMod}\,V_{K})$
. We claim that
and hence that the map
![]() $\text{}\underline{\operatorname{End}}_{V_{K}}(N)\rightarrow \text{}\underline{\operatorname{End}}_{V}(N\downarrow _{V})$
is not surjective when
$\text{}\underline{\operatorname{End}}_{V_{K}}(N)\rightarrow \text{}\underline{\operatorname{End}}_{V}(N\downarrow _{V})$
is not surjective when
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
The claim can be checked as follows. Set
![]() $S:=\text{}\underline{\operatorname{End}}_{V_{K}}^{\ast }(K)_{\mathfrak{m}}\cong K[a,b]_{\mathfrak{m}}$
. Since
$S:=\text{}\underline{\operatorname{End}}_{V_{K}}^{\ast }(K)_{\mathfrak{m}}\cong K[a,b]_{\mathfrak{m}}$
. Since
![]() $(b-at)^{n}$
is not a zero divisor on
$(b-at)^{n}$
is not a zero divisor on
![]() $S$
, applying
$S$
, applying
![]() $\text{}\underline{\operatorname{Hom}}_{V_{K}}(K,-)$
to the exact triangle
$\text{}\underline{\operatorname{Hom}}_{V_{K}}(K,-)$
to the exact triangle
one gets that
![]() $\text{}\underline{\operatorname{Hom}}_{V_{K}}^{\ast }(K,N)$
is isomorphic to
$\text{}\underline{\operatorname{Hom}}_{V_{K}}^{\ast }(K,N)$
is isomorphic to
![]() $S/(b-at)^{n}$
, as an
$S/(b-at)^{n}$
, as an
![]() $S$
-module; in particular
$S$
-module; in particular
![]() $(b-at)^{n}$
annihilates it. Given this, applying
$(b-at)^{n}$
annihilates it. Given this, applying
![]() $\text{}\underline{\operatorname{Hom}}_{V_{K}}(-,N)$
to the exact triangle above yields that the rank of
$\text{}\underline{\operatorname{Hom}}_{V_{K}}(-,N)$
to the exact triangle above yields that the rank of
![]() $\text{}\underline{\operatorname{End}}_{V_{K}}(N)$
, as an
$\text{}\underline{\operatorname{End}}_{V_{K}}(N)$
, as an
![]() $F$
-vector space, is
$F$
-vector space, is
![]() $2n$
.
$2n$
.
As to the claim about
![]() $N\downarrow _{V}$
: the category
$N\downarrow _{V}$
: the category
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,V)$
is semi-simple for its generator
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,V)$
is semi-simple for its generator
![]() $k_{\mathfrak{p}}$
has the property that
$k_{\mathfrak{p}}$
has the property that
![]() $\text{}\underline{\operatorname{End}}_{V}^{\ast }(k_{\mathfrak{p}})$
is a graded field. It thus suffices to verify that
$\text{}\underline{\operatorname{End}}_{V}^{\ast }(k_{\mathfrak{p}})$
is a graded field. It thus suffices to verify that
![]() $N\downarrow _{V}\cong k_{\mathfrak{p}}^{n}$
; equivalently, that
$N\downarrow _{V}\cong k_{\mathfrak{p}}^{n}$
; equivalently, that
![]() $\operatorname{rank}_{F}\text{}\underline{\operatorname{Hom}}_{V}(k_{\mathfrak{p}},N\downarrow _{V})=n$
. This follows from the isomorphisms
$\operatorname{rank}_{F}\text{}\underline{\operatorname{Hom}}_{V}(k_{\mathfrak{p}},N\downarrow _{V})=n$
. This follows from the isomorphisms
The first isomorphism holds because
![]() $N\downarrow _{V}$
is
$N\downarrow _{V}$
is
![]() $\mathfrak{p}$
-local, the second one holds by adjunction.
$\mathfrak{p}$
-local, the second one holds by adjunction.
There is a close connection between this example and Example 3.6. Namely, the Bernstein–Gelfand–Gelfand (BGG) correspondence sets up an equivalence between
![]() $\mathsf{StMod}\,V$
and the derived category of dg modules over
$\mathsf{StMod}\,V$
and the derived category of dg modules over
![]() $R:=k[a,b]$
, viewed as a dg algebra with zero differential, modulo the subcategory of
$R:=k[a,b]$
, viewed as a dg algebra with zero differential, modulo the subcategory of
![]() $(a,b)$
-torsion dg modules; see [Reference Bernstein, Gelfand and GelfandBGG78] and also [Reference Benson, Iyengar and KrauseBIK12, § 5.2.2]. The BGG correspondence induces the equivalences in the following commutative diagram of categories:
$(a,b)$
-torsion dg modules; see [Reference Bernstein, Gelfand and GelfandBGG78] and also [Reference Benson, Iyengar and KrauseBIK12, § 5.2.2]. The BGG correspondence induces the equivalences in the following commutative diagram of categories:

where
![]() $\mathsf{D}(-)$
denotes the derived category of dg modules. The functor on the right is restriction of scalars along the homomorphism of rings
$\mathsf{D}(-)$
denotes the derived category of dg modules. The functor on the right is restriction of scalars along the homomorphism of rings
![]() $R_{\mathfrak{p}}\rightarrow S$
, which is induced by the inclusion
$R_{\mathfrak{p}}\rightarrow S$
, which is induced by the inclusion
![]() $R=k[a,b]\subset K[a,b]$
. Under the BGG equivalence, the
$R=k[a,b]\subset K[a,b]$
. Under the BGG equivalence, the
![]() $V_{K}$
-module
$V_{K}$
-module
![]() $N$
corresponds to
$N$
corresponds to
![]() $S/(b-at)^{n}$
, viewed as dg
$S/(b-at)^{n}$
, viewed as dg
![]() $S$
-module with zero differential. Since
$S$
-module with zero differential. Since
![]() $R_{\mathfrak{p}}$
is a graded field, isomorphic to
$R_{\mathfrak{p}}$
is a graded field, isomorphic to
![]() $K[a^{\pm 1}]$
, each dg
$K[a^{\pm 1}]$
, each dg
![]() $R_{\mathfrak{p}}$
-module is isomorphic to a direct sum of copies of
$R_{\mathfrak{p}}$
-module is isomorphic to a direct sum of copies of
![]() $R_{\mathfrak{p}}$
. Arguing as in Example 3.6 one can verify that the dg
$R_{\mathfrak{p}}$
. Arguing as in Example 3.6 one can verify that the dg
![]() $S$
-module
$S$
-module
![]() $S/(b-at)^{n}$
restricts to a direct sum of
$S/(b-at)^{n}$
restricts to a direct sum of
![]() $n$
copies of
$n$
copies of
![]() $R_{\mathfrak{p}}$
. This is another way to compute the endomorphism rings in question.
$R_{\mathfrak{p}}$
. This is another way to compute the endomorphism rings in question.
The remainder of this section is devoted to a further discussion of the compact objects in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. This is not needed subsequently.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. This is not needed subsequently.
Endofiniteness
Following Crawley-Boevey [Reference Crawley-BoeveyCra91, Reference Crawley-BoeveyCra92], a module
![]() $X$
over an associative ring
$X$
over an associative ring
![]() $A$
is endofinite if
$A$
is endofinite if
![]() $X$
has finite length as a module over
$X$
has finite length as a module over
![]() $\operatorname{End}_{A}(X)$
.
$\operatorname{End}_{A}(X)$
.
An object
![]() $X$
of a compactly generated triangulated category
$X$
of a compactly generated triangulated category
![]() $\mathsf{T}$
is endofinite if the
$\mathsf{T}$
is endofinite if the
![]() $\operatorname{End}_{\mathsf{T}}(X)$
-module
$\operatorname{End}_{\mathsf{T}}(X)$
-module
![]() $\operatorname{Hom}_{\mathsf{T}}(C,X)$
has finite length for all
$\operatorname{Hom}_{\mathsf{T}}(C,X)$
has finite length for all
![]() $C\in \mathsf{T}^{\mathsf{c}}$
; see [Reference Krause and ReichenbachKR00].
$C\in \mathsf{T}^{\mathsf{c}}$
; see [Reference Krause and ReichenbachKR00].
Let
![]() $A$
be a self-injective algebra, finite dimensional over some field. Then an
$A$
be a self-injective algebra, finite dimensional over some field. Then an
![]() $A$
-module is endofinite if and only if it is endofinite as an object of
$A$
-module is endofinite if and only if it is endofinite as an object of
![]() $\mathsf{StMod}\,A$
. This follows from the fact
$\mathsf{StMod}\,A$
. This follows from the fact
![]() $X$
is an endofinite
$X$
is an endofinite
![]() $A$
-module if and only if the
$A$
-module if and only if the
![]() $\operatorname{End}_{A}(X)$
-module
$\operatorname{End}_{A}(X)$
-module
![]() $\operatorname{Hom}_{A}(C,X)$
has finite length for every finite-dimensional
$\operatorname{Hom}_{A}(C,X)$
has finite length for every finite-dimensional
![]() $A$
-module
$A$
-module
![]() $C$
.
$C$
.
Lemma 3.8. Let
![]() $F:\mathsf{T}\rightarrow \mathsf{U}$
be a functor between compactly generated triangulated categories that preserves products and coproducts. Let
$F:\mathsf{T}\rightarrow \mathsf{U}$
be a functor between compactly generated triangulated categories that preserves products and coproducts. Let
![]() $X$
be an object in
$X$
be an object in
![]() $\mathsf{T}$
. If
$\mathsf{T}$
. If
![]() $X$
is endofinite, then so is
$X$
is endofinite, then so is
![]() $FX$
and the converse holds when
$FX$
and the converse holds when
![]() $F$
is fully faithful.
$F$
is fully faithful.
Proof. By Brown representability,
![]() $F$
has a left adjoint, say
$F$
has a left adjoint, say
![]() $F^{\prime }$
. It preserves compactness, as
$F^{\prime }$
. It preserves compactness, as
![]() $F$
preserves coproducts. For
$F$
preserves coproducts. For
![]() $X\in \mathsf{T}$
and
$X\in \mathsf{T}$
and
![]() $C\in \mathsf{U}^{\mathsf{c}}$
, there is an isomorphism
$C\in \mathsf{U}^{\mathsf{c}}$
, there is an isomorphism
of
![]() $\operatorname{End}_{\mathsf{T}}(X)$
-modules. Thus if
$\operatorname{End}_{\mathsf{T}}(X)$
-modules. Thus if
![]() $X$
is endofinite, then
$X$
is endofinite, then
![]() $\operatorname{Hom}_{\mathsf{U}}(C,FX)$
is a module of finite length over
$\operatorname{Hom}_{\mathsf{U}}(C,FX)$
is a module of finite length over
![]() $\operatorname{End}_{\mathsf{T}}(X)$
, and therefore also over
$\operatorname{End}_{\mathsf{T}}(X)$
, and therefore also over
![]() $\operatorname{End}_{\mathsf{U}}(FX)$
. For the converse, observe that each compact object in
$\operatorname{End}_{\mathsf{U}}(FX)$
. For the converse, observe that each compact object in
![]() $\mathsf{T}$
is isomorphic to a direct summand of an object of the form
$\mathsf{T}$
is isomorphic to a direct summand of an object of the form
![]() $F^{\prime }C$
for some
$F^{\prime }C$
for some
![]() $C\in \mathsf{U}^{\mathsf{c}}$
.◻
$C\in \mathsf{U}^{\mathsf{c}}$
.◻
Proposition 3.9. Let
![]() $\mathfrak{p}$
be a point in
$\mathfrak{p}$
be a point in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
and
$\operatorname{Proj}H^{\ast }(G,k)$
and
![]() $M$
a
$M$
a
![]() $G$
-module that is compact in
$G$
-module that is compact in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. Then
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. Then
![]() $M$
is endofinite both in
$M$
is endofinite both in
![]() $\mathsf{StMod}\,G$
and in
$\mathsf{StMod}\,G$
and in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
.
Proof. By Corollary 3.2, the module
![]() $M$
is of the form
$M$
is of the form
![]() $N\downarrow _{G}$
for a finite-dimensional
$N\downarrow _{G}$
for a finite-dimensional
![]() $G_{K}$
-module
$G_{K}$
-module
![]() $N$
. Clearly,
$N$
. Clearly,
![]() $N$
is endofinite in
$N$
is endofinite in
![]() $\mathsf{StMod}\,G_{K}$
and
$\mathsf{StMod}\,G_{K}$
and
![]() $(-)\downarrow _{G}$
preserves products and coproducts, so it follows by Lemma 3.8 that
$(-)\downarrow _{G}$
preserves products and coproducts, so it follows by Lemma 3.8 that
![]() $M$
is endofinite in
$M$
is endofinite in
![]() $\mathsf{StMod}\,G$
. By the same token, as the inclusion
$\mathsf{StMod}\,G$
. By the same token, as the inclusion
![]() $(\mathsf{StMod}\,G)_{\mathfrak{p}}\rightarrow \mathsf{StMod}\,G$
preserves products and coproducts,
$(\mathsf{StMod}\,G)_{\mathfrak{p}}\rightarrow \mathsf{StMod}\,G$
preserves products and coproducts,
![]() $M$
is endofinite in
$M$
is endofinite in
![]() $(\mathsf{StMod}\,G)_{\mathfrak{p}}$
as well. Finally, the functor
$(\mathsf{StMod}\,G)_{\mathfrak{p}}$
as well. Finally, the functor
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}$
is a right adjoint to the inclusion
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}$
is a right adjoint to the inclusion
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)\rightarrow (\mathsf{StMod}\,G)_{\mathfrak{p}}$
. It preserves products, being a right adjoint, and also coproducts. Thus
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)\rightarrow (\mathsf{StMod}\,G)_{\mathfrak{p}}$
. It preserves products, being a right adjoint, and also coproducts. Thus
![]() $M$
is endofinite in
$M$
is endofinite in
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
, again by Lemma 3.8.◻
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
, again by Lemma 3.8.◻
4
 $G$
-modules and Tate duality
$G$
-modules and Tate duality
Now we turn to various dualities for modules over finite group schemes. We begin by recalling the construction of the transpose and the dual of a module over a finite group scheme, and certain functors associated with them. Our basic reference for this material is Skowroński and Yamagata [Reference Skowroński and YamagataSY11, ch. III].
Throughout
![]() $G$
will be a finite group scheme over
$G$
will be a finite group scheme over
![]() $k$
. We write
$k$
. We write
![]() $(-)^{\vee }=\operatorname{Hom}_{k}(-,k)$
.
$(-)^{\vee }=\operatorname{Hom}_{k}(-,k)$
.
Transpose and dual
Let
![]() $G^{\text{op}}$
be the opposite group scheme of
$G^{\text{op}}$
be the opposite group scheme of
![]() $G$
; it can be realised as the group scheme associated to the cocommutative Hopf algebra
$G$
; it can be realised as the group scheme associated to the cocommutative Hopf algebra
![]() $(kG)^{\text{op}}$
. Since
$(kG)^{\text{op}}$
. Since
![]() $kG$
is a
$kG$
is a
![]() $G$
-bimodule, the assignment
$G$
-bimodule, the assignment
![]() $M\mapsto \operatorname{Hom}_{G}(M,kG)$
defines a functor
$M\mapsto \operatorname{Hom}_{G}(M,kG)$
defines a functor
Let
![]() $M$
be a finite-dimensional
$M$
be a finite-dimensional
![]() $G$
-module and
$G$
-module and
![]() $P_{1}\xrightarrow[{}]{f}P_{0}\rightarrow M$
a minimal projective presentation. The transpose of
$P_{1}\xrightarrow[{}]{f}P_{0}\rightarrow M$
a minimal projective presentation. The transpose of
![]() $M$
is the
$M$
is the
![]() $G^{\text{op}}$
-module
$G^{\text{op}}$
-module
![]() $\operatorname{Tr}M:=\operatorname{Coker}(f^{t})$
. By construction, there is an exact sequence of
$\operatorname{Tr}M:=\operatorname{Coker}(f^{t})$
. By construction, there is an exact sequence of
![]() $G^{\text{op}}$
-modules:
$G^{\text{op}}$
-modules:
The
![]() $P_{i}^{t}$
are projective
$P_{i}^{t}$
are projective
![]() $G^{\text{op}}$
-modules, so this yields an isomorphism of
$G^{\text{op}}$
-modules, so this yields an isomorphism of
![]() $G^{\text{op}}$
-modules
$G^{\text{op}}$
-modules
Given a
![]() $G^{\text{op}}$
-module
$G^{\text{op}}$
-module
![]() $N$
, the
$N$
, the
![]() $k$
-vector space
$k$
-vector space
![]() $\operatorname{Hom}_{k}(N,k)$
has a natural structure of a
$\operatorname{Hom}_{k}(N,k)$
has a natural structure of a
![]() $G$
-module, and the assignment
$G$
-module, and the assignment
![]() $N\mapsto \operatorname{Hom}_{k}(N,k)$
yields a functor
$N\mapsto \operatorname{Hom}_{k}(N,k)$
yields a functor
The Auslander–Reiten translate
In what follows we write
![]() $\unicode[STIX]{x1D70F}$
for the Auslander–Reiten translate of
$\unicode[STIX]{x1D70F}$
for the Auslander–Reiten translate of
![]() $G$
:
$G$
:
Given an extension of fields
![]() $K/k$
, for any finite-dimensional
$K/k$
, for any finite-dimensional
![]() $G$
-module
$G$
-module
![]() $M$
there is a stable isomorphism of
$M$
there is a stable isomorphism of
![]() $G_{K}$
-modules
$G_{K}$
-modules
Nakayama functor
The Nakayama functor
is given by the assignment
where
![]() $\unicode[STIX]{x1D6FF}_{G}=\unicode[STIX]{x1D708}(k)$
is the modular character of
$\unicode[STIX]{x1D6FF}_{G}=\unicode[STIX]{x1D708}(k)$
is the modular character of
![]() $G$
; see [Reference JantzenJan03, I.8.8]. Since the group of characters of
$G$
; see [Reference JantzenJan03, I.8.8]. Since the group of characters of
![]() $G$
is finite, by [Reference WaterhouseWat79, §§ 2.1 and 2.2], there exists a positive integer
$G$
is finite, by [Reference WaterhouseWat79, §§ 2.1 and 2.2], there exists a positive integer
![]() $d$
such that
$d$
such that
![]() $\unicode[STIX]{x1D6FF}_{G}^{\otimes d}\cong k$
and hence as functors on
$\unicode[STIX]{x1D6FF}_{G}^{\otimes d}\cong k$
and hence as functors on
![]() $\mathsf{Mod}\,G$
there is an equality
$\mathsf{Mod}\,G$
there is an equality
When
![]() $M$
is a finite-dimensional
$M$
is a finite-dimensional
![]() $G$
-module, there are natural stable isomorphisms
$G$
-module, there are natural stable isomorphisms
When in addition
![]() $M$
is projective, one has
$M$
is projective, one has
Let
![]() $K/k$
be an extension of fields. For any
$K/k$
be an extension of fields. For any
![]() $G$
-module
$G$
-module
![]() $M$
there is a natural isomorphism of
$M$
there is a natural isomorphism of
![]() $G_{K}$
-modules
$G_{K}$
-modules
This is clear for
![]() $M=kG$
since
$M=kG$
since
and the general case follows by taking a free presentation of
![]() $M$
.
$M$
.
Remark 4.1. A finite group scheme is unimodular if the character
![]() $\unicode[STIX]{x1D6FF}_{G}$
is trivial; equivalently, when
$\unicode[STIX]{x1D6FF}_{G}$
is trivial; equivalently, when
![]() $kG$
is symmetric. Examples include finite groups, unipotent groups schemes, and Frobenius kernels of reductive groups; see [Reference JantzenJan03, I.8.9, II.3.4(a)]. Group schemes that are not unimodular also abound.
$kG$
is symmetric. Examples include finite groups, unipotent groups schemes, and Frobenius kernels of reductive groups; see [Reference JantzenJan03, I.8.9, II.3.4(a)]. Group schemes that are not unimodular also abound.
Frobenius kernels of Borel subgroups of reductive groups are not unimodular for
![]() $p\geqslant 3$
; see [Reference JantzenJan03, II.3.4(c)]. The finite group scheme associated to a Lie algebra is unimodular if and only if
$p\geqslant 3$
; see [Reference JantzenJan03, II.3.4(c)]. The finite group scheme associated to a Lie algebra is unimodular if and only if
![]() $\text{tr}(\text{ad}\,x)=0$
for any
$\text{tr}(\text{ad}\,x)=0$
for any
![]() $x$
in the Lie algebra; see [Reference JantzenJan03, I.9.7]. This condition fails for the upper triangular matrices inside
$x$
in the Lie algebra; see [Reference JantzenJan03, I.9.7]. This condition fails for the upper triangular matrices inside
![]() $\text{sl}_{2}$
for
$\text{sl}_{2}$
for
![]() $p\geqslant 3$
.
$p\geqslant 3$
.
Tate duality
For finite groups, the duality theorem below is classical and due to Tate [Reference Cartan and EilenbergCE56, ch. XII, Theorem 6.4]. A proof of the extension to finite group schemes was sketched in [Reference Benson, Iyengar, Krause and PevtsovaBIKP17, § 2], and is reproduced here for readers convenience.
Theorem 4.2. Let
![]() $G$
be a finite group scheme over a field
$G$
be a finite group scheme over a field
![]() $k$
. For any
$k$
. For any
![]() $G$
-modules
$G$
-modules
![]() $M,N$
with
$M,N$
with
![]() $M$
finite dimensional, there are natural isomorphisms
$M$
finite dimensional, there are natural isomorphisms
Proof. A formula of Auslander and Reiten [Reference AuslanderAus78, Proposition I.3.4], see also [Reference KrauseKra03, Corollary p. 269], yields the first isomorphism below
The second isomorphism is standard. It remains to recall that
![]() $\unicode[STIX]{x1D70F}M\cong \unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D708}M$
.◻
$\unicode[STIX]{x1D70F}M\cong \unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D708}M$
.◻
Restricted to finite-dimensional
![]() $G$
-modules, Tate duality is the statement that the
$G$
-modules, Tate duality is the statement that the
![]() $k$
-linear category
$k$
-linear category
![]() $\mathsf{stmod}\,G$
has Serre duality, with Serre functor
$\mathsf{stmod}\,G$
has Serre duality, with Serre functor
![]() $\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}$
. A refinement of this Serre duality will be proved in § 7.
$\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}$
. A refinement of this Serre duality will be proved in § 7.
5 Local cohomology versus injective cohomology
Let
![]() $k$
be a field and
$k$
be a field and
![]() $G$
a finite group scheme over
$G$
a finite group scheme over
![]() $k$
. In this section we establish the main result of this work; it identifies for a prime ideal
$k$
. In this section we establish the main result of this work; it identifies for a prime ideal
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $H^{\ast }(G,k)$
, up to some twist and some suspension, the local cohomology object
$H^{\ast }(G,k)$
, up to some twist and some suspension, the local cohomology object
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
with the injective cohomology object
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)$
with the injective cohomology object
![]() $T_{\mathfrak{p}}(k)$
.
$T_{\mathfrak{p}}(k)$
.
Theorem 5.1. Fix a point
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
and let
$\operatorname{Proj}H^{\ast }(G,k)$
and let
![]() $d$
be the Krull dimension of
$d$
be the Krull dimension of
![]() $H^{\ast }(G,k)/\mathfrak{p}$
. There is a stable isomorphism of
$H^{\ast }(G,k)/\mathfrak{p}$
. There is a stable isomorphism of
![]() $G$
-modules
$G$
-modules
equivalently, for any
![]() $G$
-module
$G$
-module
![]() $M$
there is a natural isomorphism
$M$
there is a natural isomorphism
When
![]() $G$
is the group scheme arising from a finite group the modular character
$G$
is the group scheme arising from a finite group the modular character
![]() $\unicode[STIX]{x1D6FF}_{G}$
is trivial, and the result above was proved by Benson and Greenlees [Reference Benson and GreenleesBG08, Theorem 2.4] using Gorenstein duality for cochains on the classifying space of
$\unicode[STIX]{x1D6FF}_{G}$
is trivial, and the result above was proved by Benson and Greenlees [Reference Benson and GreenleesBG08, Theorem 2.4] using Gorenstein duality for cochains on the classifying space of
![]() $G$
. Benson [Reference BensonBen08, Theorem 2] gave a different proof by embedding
$G$
. Benson [Reference BensonBen08, Theorem 2] gave a different proof by embedding
![]() $G$
into a general linear group and exploiting the fact that its cohomology ring is a polynomial ring, as was proved by Quillen. These results have been extended to compact Lie groups; see [Reference Benson and GreenleesBG14, Theorem 6.10], and work of Barthel, Heard and Valenzuela [Reference Barthel, Heard and ValenzuelaBHV18, Proposition 4.33].
$G$
into a general linear group and exploiting the fact that its cohomology ring is a polynomial ring, as was proved by Quillen. These results have been extended to compact Lie groups; see [Reference Benson and GreenleesBG14, Theorem 6.10], and work of Barthel, Heard and Valenzuela [Reference Barthel, Heard and ValenzuelaBHV18, Proposition 4.33].
Theorem 5.1 is established using (by necessity) completely different arguments, thereby giving yet another proof in the case of finite groups that is, in a sense, more elementary than the other ones for it is based on classical Tate duality.
A caveat: in [Reference BensonBen08, Reference Benson and GreenleesBG08] it is asserted that
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)\cong \unicode[STIX]{x1D6FA}^{d}T_{\mathfrak{p}}(k)$
. However, this is incorrect and the correct shift is the one in the preceding theorem. We illustrate this by computing these modules directly for the quaternions.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)\cong \unicode[STIX]{x1D6FA}^{d}T_{\mathfrak{p}}(k)$
. However, this is incorrect and the correct shift is the one in the preceding theorem. We illustrate this by computing these modules directly for the quaternions.
Example 5.2. Let
![]() $G:=Q_{8}$
, the quaternions, viewed as a group scheme over a field
$G:=Q_{8}$
, the quaternions, viewed as a group scheme over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $2$
. In this case
$2$
. In this case
![]() $\unicode[STIX]{x1D6FF}_{G}=k$
, the trivial character. The cohomology algebra of
$\unicode[STIX]{x1D6FF}_{G}=k$
, the trivial character. The cohomology algebra of
![]() $G$
is
$G$
is
with
![]() $|x|=1=|y|$
and
$|x|=1=|y|$
and
![]() $|z|=4$
; see, for instance, [Reference BensonBen84, p. 186]. Thus
$|z|=4$
; see, for instance, [Reference BensonBen84, p. 186]. Thus
![]() $\operatorname{Proj}H^{\ast }(G,k)$
consists of a single point, namely
$\operatorname{Proj}H^{\ast }(G,k)$
consists of a single point, namely
![]() $\mathfrak{m}:=(x,y)$
. In particular,
$\mathfrak{m}:=(x,y)$
. In particular,
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}k=k$
, in
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}k=k$
, in
![]() $\mathsf{StMod}\,G$
.
$\mathsf{StMod}\,G$
.
Next we compute
![]() $I(\mathfrak{m})$
as a module over
$I(\mathfrak{m})$
as a module over
![]() $H^{\ast }(G,k)_{\mathfrak{m}}\cong k[z^{\pm 1}]\otimes _{k}B$
, using Lemma A.3. The extension
$H^{\ast }(G,k)_{\mathfrak{m}}\cong k[z^{\pm 1}]\otimes _{k}B$
, using Lemma A.3. The extension
![]() $k[z^{\pm 1}]\subseteq k[z^{\pm 1}]\otimes _{k}B$
is evidently finite (and hence also residually finite). Since
$k[z^{\pm 1}]\subseteq k[z^{\pm 1}]\otimes _{k}B$
is evidently finite (and hence also residually finite). Since
![]() $\mathfrak{m}\cap k[z^{\pm 1}]=(0)$
and
$\mathfrak{m}\cap k[z^{\pm 1}]=(0)$
and
![]() $k[z^{\pm 1}]$
is a graded field, from Lemma A.3 one gets an isomorphism of
$k[z^{\pm 1}]$
is a graded field, from Lemma A.3 one gets an isomorphism of
![]() $H^{\ast }(G,k)_{\mathfrak{m}}$
-modules,
$H^{\ast }(G,k)_{\mathfrak{m}}$
-modules,
 $$\begin{eqnarray}\displaystyle I(\mathfrak{m}) & \cong & \displaystyle \operatorname{Hom}_{k[z^{\pm 1}]}(k[z^{\pm 1}]\otimes _{k}B,k[z^{\pm 1}])\nonumber\\ \displaystyle & \cong & \displaystyle k[z^{\pm 1}]\otimes _{k}\operatorname{Hom}_{k}(B,k)\nonumber\\ \displaystyle & \cong & \displaystyle k[z^{\pm 1}]\otimes _{k}\unicode[STIX]{x1D6F4}^{3}B\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6F4}^{3}H^{\ast }(G,k)_{\mathfrak{m}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(\mathfrak{m}) & \cong & \displaystyle \operatorname{Hom}_{k[z^{\pm 1}]}(k[z^{\pm 1}]\otimes _{k}B,k[z^{\pm 1}])\nonumber\\ \displaystyle & \cong & \displaystyle k[z^{\pm 1}]\otimes _{k}\operatorname{Hom}_{k}(B,k)\nonumber\\ \displaystyle & \cong & \displaystyle k[z^{\pm 1}]\otimes _{k}\unicode[STIX]{x1D6F4}^{3}B\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6F4}^{3}H^{\ast }(G,k)_{\mathfrak{m}}.\nonumber\end{eqnarray}$$
This yields the first isomorphism below of
![]() $G$
-modules
$G$
-modules
and the second one holds because
![]() $\unicode[STIX]{x1D6FA}^{4}k\cong k$
in
$\unicode[STIX]{x1D6FA}^{4}k\cong k$
in
![]() $\mathsf{StMod}\,G$
.
$\mathsf{StMod}\,G$
.
In the proof of Theorem 5.1 the following simple observation will be used repeatedly; it is a direct consequence of Yoneda’s lemma.
Lemma 5.3. Let
![]() $X$
and
$X$
and
![]() $Y$
be
$Y$
be
![]() $G$
-modules that are
$G$
-modules that are
![]() $\mathfrak{p}$
-local and
$\mathfrak{p}$
-local and
![]() $\mathfrak{p}$
-torsion. There is an isomorphism
$\mathfrak{p}$
-torsion. There is an isomorphism
![]() $X\cong Y$
in
$X\cong Y$
in
![]() $\mathsf{StMod}\,G$
if and only if there is a natural isomorphism
$\mathsf{StMod}\,G$
if and only if there is a natural isomorphism
for all
![]() $\mathfrak{p}$
-local and
$\mathfrak{p}$
-local and
![]() $\mathfrak{p}$
-torsion (equivalently, for all)
$\mathfrak{p}$
-torsion (equivalently, for all)
![]() $G$
-modules
$G$
-modules
![]() $M$
.
$M$
.
Proof of Theorem 5.1.
The
![]() $G$
-module
$G$
-module
![]() $T_{\mathfrak{p}}(k)$
is
$T_{\mathfrak{p}}(k)$
is
![]() $\mathfrak{p}$
-local and
$\mathfrak{p}$
-local and
![]() $\mathfrak{p}$
-torsion; see, for example, [Reference Benson, Iyengar and KrauseBIK11b, Lemma 11.10]. This fact will be used in the sequel, without comment.
$\mathfrak{p}$
-torsion; see, for example, [Reference Benson, Iyengar and KrauseBIK11b, Lemma 11.10]. This fact will be used in the sequel, without comment.
The first isomorphism of the theorem is equivalent to the second: by (2.7) for any
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $H^{\ast }(G,k)$
-module
$H^{\ast }(G,k)$
-module
![]() $I$
there is an isomorphism
$I$
there is an isomorphism
Consequently, one can rephrase the defining isomorphism (2.1) for the object
![]() $T_{\mathfrak{p}}(k)$
as a natural isomorphism
$T_{\mathfrak{p}}(k)$
as a natural isomorphism
The desired equivalence is then a consequence of Lemma 5.3.
The main task is to prove that there is a stable isomorphism:
Recall that
![]() $\unicode[STIX]{x1D708}k=\unicode[STIX]{x1D6FF}_{G}$
.
$\unicode[STIX]{x1D708}k=\unicode[STIX]{x1D6FF}_{G}$
.
We first verify the isomorphism above for closed points of
![]() $\operatorname{Proj}H^{\ast }(G,k)$
and then use a reduction to closed points.
$\operatorname{Proj}H^{\ast }(G,k)$
and then use a reduction to closed points.
Claim.
The desired isomorphism holds when
![]() $\mathfrak{m}$
is a closed point of
$\mathfrak{m}$
is a closed point of
![]() $\operatorname{Proj}H^{\ast }(G,k)$
.
$\operatorname{Proj}H^{\ast }(G,k)$
.
Set
![]() $A:=H^{\ast }(G,k)$
and
$A:=H^{\ast }(G,k)$
and
![]() $R:=A_{\mathfrak{m}}$
. The injective hull,
$R:=A_{\mathfrak{m}}$
. The injective hull,
![]() $I(\mathfrak{m})$
, of the
$I(\mathfrak{m})$
, of the
![]() $A$
-module
$A$
-module
![]() $A/\mathfrak{m}$
is the same as that of the
$A/\mathfrak{m}$
is the same as that of the
![]() $R$
-module
$R$
-module
![]() $k(\mathfrak{m})$
, viewed as an
$k(\mathfrak{m})$
, viewed as an
![]() $A$
-module via restriction of scalars along the localisation map
$A$
-module via restriction of scalars along the localisation map
![]() $A\rightarrow R$
. Thus
$A\rightarrow R$
. Thus
![]() $I(\mathfrak{m})$
is the module
$I(\mathfrak{m})$
is the module
![]() $I$
described in Lemma A.2; this is where the fact that
$I$
described in Lemma A.2; this is where the fact that
![]() $\mathfrak{m}$
is closed is used.
$\mathfrak{m}$
is closed is used.
Let
![]() $M$
be a
$M$
be a
![]() $G$
-module that is
$G$
-module that is
![]() $\mathfrak{m}$
-local and
$\mathfrak{m}$
-local and
![]() $\mathfrak{m}$
-torsion. Given Lemma 5.3, the claim is a consequence of the following computation:
$\mathfrak{m}$
-torsion. Given Lemma 5.3, the claim is a consequence of the following computation:
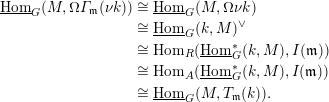 $$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\unicode[STIX]{x1D708}k)) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}k)\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(k,M)^{\vee }\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{A}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,T_{\mathfrak{m}}(k)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\unicode[STIX]{x1D708}k)) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D708}k)\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(k,M)^{\vee }\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{A}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,T_{\mathfrak{m}}(k)).\nonumber\end{eqnarray}$$
The first isomorphism holds because
![]() $M$
is
$M$
is
![]() $\mathfrak{m}$
-torsion; the second is Tate duality, Theorem 4.2, and the next one holds by Lemma A.2, which applies because
$\mathfrak{m}$
-torsion; the second is Tate duality, Theorem 4.2, and the next one holds by Lemma A.2, which applies because
![]() $\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M)$
is
$\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M)$
is
![]() $\mathfrak{m}$
-local and
$\mathfrak{m}$
-local and
![]() $\mathfrak{m}$
-torsion as an
$\mathfrak{m}$
-torsion as an
![]() $A$
-module. The penultimate one holds because the
$A$
-module. The penultimate one holds because the
![]() $A$
-module
$A$
-module
![]() $\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M)$
is
$\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M)$
is
![]() $\mathfrak{m}$
-local, and the last one is by definition (2.1).
$\mathfrak{m}$
-local, and the last one is by definition (2.1).
Let
![]() $\mathfrak{p}$
be a point in
$\mathfrak{p}$
be a point in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
that is not closed, and let
$\operatorname{Proj}H^{\ast }(G,k)$
that is not closed, and let
![]() $K$
,
$K$
,
![]() $\boldsymbol{b}$
, and
$\boldsymbol{b}$
, and
![]() $\mathfrak{m}$
be as in Construction 3.3. Recall that
$\mathfrak{m}$
be as in Construction 3.3. Recall that
![]() $\mathfrak{m}$
is a closed point in
$\mathfrak{m}$
is a closed point in
![]() $H^{\ast }(G_{K},K)$
lying over
$H^{\ast }(G_{K},K)$
lying over
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
Claim.
There is a stable isomorphism of
![]() $G$
-modules
$G$
-modules
where
![]() $d$
is the Krull dimension of
$d$
is the Krull dimension of
![]() $H^{\ast }(G,k)/\mathfrak{p}$
.
$H^{\ast }(G,k)/\mathfrak{p}$
.
Let
![]() $M$
be a
$M$
be a
![]() $G$
-module that is
$G$
-module that is
![]() $\mathfrak{p}$
-local and
$\mathfrak{p}$
-local and
![]() $\mathfrak{p}$
-torsion. Then Theorem 3.4 applies and yields isomorphisms of
$\mathfrak{p}$
-torsion. Then Theorem 3.4 applies and yields isomorphisms of
![]() $G$
-modules:
$G$
-modules:
This gives the sixth isomorphism below:
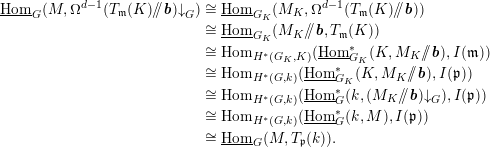 $$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}^{d-1}(T_{\mathfrak{m}}(K)/\!\!/\boldsymbol{b})\downarrow _{G}) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G_{K}}(M_{K},\unicode[STIX]{x1D6FA}^{d-1}(T_{\mathfrak{m}}(K)/\!\!/\boldsymbol{b}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G_{K}}(M_{K}/\!\!/\boldsymbol{b},T_{\mathfrak{m}}(K))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G_{K},K)}(\text{}\underline{\operatorname{Hom}}_{G_{K}}^{\ast }(K,M_{K}/\!\!/\boldsymbol{b}),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G,k)}(\text{}\underline{\operatorname{Hom}}_{G_{K}}^{\ast }(K,M_{K}/\!\!/\boldsymbol{b}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G,k)}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,(M_{K}/\!\!/\boldsymbol{b})\downarrow _{G}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G,k)}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,T_{\mathfrak{p}}(k)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,\unicode[STIX]{x1D6FA}^{d-1}(T_{\mathfrak{m}}(K)/\!\!/\boldsymbol{b})\downarrow _{G}) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G_{K}}(M_{K},\unicode[STIX]{x1D6FA}^{d-1}(T_{\mathfrak{m}}(K)/\!\!/\boldsymbol{b}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G_{K}}(M_{K}/\!\!/\boldsymbol{b},T_{\mathfrak{m}}(K))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G_{K},K)}(\text{}\underline{\operatorname{Hom}}_{G_{K}}^{\ast }(K,M_{K}/\!\!/\boldsymbol{b}),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G,k)}(\text{}\underline{\operatorname{Hom}}_{G_{K}}^{\ast }(K,M_{K}/\!\!/\boldsymbol{b}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G,k)}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,(M_{K}/\!\!/\boldsymbol{b})\downarrow _{G}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{H^{\ast }(G,k)}(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,M),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}(M,T_{\mathfrak{p}}(k)).\nonumber\end{eqnarray}$$
The first and the fifth isomorphisms are true by adjunction. The second isomorphism is easily verified by a direct computation using (2.3) and (3.2). The next isomorphism is by definition and the fourth one holds by Lemma A.3 applied to the canonical homomorphism
![]() $H^{\ast }(G,k)\rightarrow H^{\ast }(G_{K},K)$
; note that the
$H^{\ast }(G,k)\rightarrow H^{\ast }(G_{K},K)$
; note that the
![]() $H^{\ast }(G_{K},K)$
-module
$H^{\ast }(G_{K},K)$
-module
![]() $\text{}\underline{\operatorname{Hom}}_{G_{K}}^{\ast }(K,M_{K}/\!\!/\boldsymbol{b})$
is
$\text{}\underline{\operatorname{Hom}}_{G_{K}}^{\ast }(K,M_{K}/\!\!/\boldsymbol{b})$
is
![]() $\mathfrak{m}$
-torsion. The desired isomorphism (5.1) holds by Lemma 5.3, because both modules in question are
$\mathfrak{m}$
-torsion. The desired isomorphism (5.1) holds by Lemma 5.3, because both modules in question are
![]() $\mathfrak{p}$
-torsion; for the one on the left, see [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Proposition 6.2].
$\mathfrak{p}$
-torsion; for the one on the left, see [Reference Benson, Iyengar, Krause and PevtsovaBIKP18, Proposition 6.2].
We are now ready to wrap up the proof of the theorem. Since
![]() $\mathfrak{m}$
is a closed point in
$\mathfrak{m}$
is a closed point in
![]() $\operatorname{Proj}H^{\ast }(G_{K},K)$
, the first claim yields that the
$\operatorname{Proj}H^{\ast }(G_{K},K)$
, the first claim yields that the
![]() $G_{K}$
-modules
$G_{K}$
-modules
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\unicode[STIX]{x1D708}K)$
and
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\unicode[STIX]{x1D708}K)$
and
![]() $\unicode[STIX]{x1D6FA}^{-1}T_{\mathfrak{m}}(K)$
are isomorphic. This then gives an isomorphism of
$\unicode[STIX]{x1D6FA}^{-1}T_{\mathfrak{m}}(K)$
are isomorphic. This then gives an isomorphism of
![]() $G_{K}$
-modules:
$G_{K}$
-modules:
Restricting to
![]() $G$
and applying (5.1) gives the last of the following isomorphisms of
$G$
and applying (5.1) gives the last of the following isomorphisms of
![]() $G$
-modules:
$G$
-modules:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D708}k) & \cong & \displaystyle ((\unicode[STIX]{x1D708}k)_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D708}K\otimes _{K}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FA}^{-d}T_{\mathfrak{p}}(k).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D708}k) & \cong & \displaystyle ((\unicode[STIX]{x1D708}k)_{K}\otimes _{K}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D708}K\otimes _{K}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(K/\!\!/\boldsymbol{b}))\downarrow _{G}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FA}^{-d}T_{\mathfrak{p}}(k).\nonumber\end{eqnarray}$$
The first one holds by Theorem 3.4 and the second by (4.2). ◻
The following consequence of Theorem 5.1 was anticipated in [Reference BensonBen01, p. 203]. It concerns the Tate cohomology of a
![]() $G$
-module
$G$
-module
![]() $M$
, namely the
$M$
, namely the
![]() $H^{\ast }(G,k)$
-module
$H^{\ast }(G,k)$
-module
For a graded module
![]() $N=\bigoplus _{p\in \mathbb{Z}}N^{p}$
and
$N=\bigoplus _{p\in \mathbb{Z}}N^{p}$
and
![]() $i\in \mathbb{Z}$
the twist
$i\in \mathbb{Z}$
the twist
![]() $N(i)$
is the graded module with
$N(i)$
is the graded module with
![]() $N(i)^{p}=N^{p+i}$
.
$N(i)^{p}=N^{p+i}$
.
Corollary 5.4. Fix
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
. With
$\operatorname{Proj}H^{\ast }(G,k)$
. With
![]() $d$
the Krull dimension of
$d$
the Krull dimension of
![]() $H^{\ast }(G,k)/\mathfrak{p}$
there are isomorphisms of
$H^{\ast }(G,k)/\mathfrak{p}$
there are isomorphisms of
![]() $H^{\ast }(G,k)$
-modules
$H^{\ast }(G,k)$
-modules
and
where
![]() $(-)^{\wedge }$
denotes completion with respect to the
$(-)^{\wedge }$
denotes completion with respect to the
![]() $\mathfrak{p}$
-adic topology.
$\mathfrak{p}$
-adic topology.
Proof. Set
![]() $R=H^{\ast }(G,k)$
. The first of the stated isomorphisms is a composition of the following isomorphisms of
$R=H^{\ast }(G,k)$
. The first of the stated isomorphisms is a composition of the following isomorphisms of
![]() $R$
-modules:
$R$
-modules:
 $$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6FF}_{G},\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6FF}_{G},\unicode[STIX]{x1D6FA}^{-d}T_{\mathfrak{p}}(k))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6FF}_{G},T_{\mathfrak{p}}(k))(d)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}^{\ast }(H^{\ast }(G,\unicode[STIX]{x1D6FF}_{G}),I(\mathfrak{p}))(d).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k)) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6FF}_{G},\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6FF}_{G},\unicode[STIX]{x1D6FA}^{-d}T_{\mathfrak{p}}(k))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6FF}_{G},T_{\mathfrak{p}}(k))(d)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}^{\ast }(H^{\ast }(G,\unicode[STIX]{x1D6FF}_{G}),I(\mathfrak{p}))(d).\nonumber\end{eqnarray}$$
The second isomorphism holds by Theorem 5.1, the one after is standard, while the last one is by the definition of
![]() $T_{\mathfrak{p}}(k)$
.
$T_{\mathfrak{p}}(k)$
.
In the same vein, one has the following chain of isomorphisms:
 $$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,\operatorname{End}_{k}(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k))) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k),\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(T_{\mathfrak{p}}(k),T_{\mathfrak{p}}(k))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}^{\ast }(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,T_{\mathfrak{p}}(k)),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}^{\ast }(I(\mathfrak{p}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle (R_{\mathfrak{p}})^{\wedge }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,\operatorname{End}_{k}(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k))) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k),\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(k))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{G}^{\ast }(T_{\mathfrak{p}}(k),T_{\mathfrak{p}}(k))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}^{\ast }(\text{}\underline{\operatorname{Hom}}_{G}^{\ast }(k,T_{\mathfrak{p}}(k)),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}^{\ast }(I(\mathfrak{p}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle (R_{\mathfrak{p}})^{\wedge }.\nonumber\end{eqnarray}$$
The second isomorphism holds by Theorem 5.1 and the rest are standard. ◻
Remark 5.5. Another consequence of Theorem 5.1 is that
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G})$
, and hence also
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\unicode[STIX]{x1D6FF}_{G})$
, and hence also
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}k$
, is an indecomposable pure injective object in
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}k$
, is an indecomposable pure injective object in
![]() $\mathsf{StMod}\,G$
; see [Reference Benson and KrauseBK02, Theorem 5.1].
$\mathsf{StMod}\,G$
; see [Reference Benson and KrauseBK02, Theorem 5.1].
6 The Gorenstein property
In this section we introduce a notion of a Gorenstein triangulated category and reinterpret Theorem 5.1 to mean that
![]() $\mathsf{StMod}\,G$
has this property. The definition is justified by its consequences for modular representations; it yields duality results which will be discussed in the subsequent § 7.
$\mathsf{StMod}\,G$
has this property. The definition is justified by its consequences for modular representations; it yields duality results which will be discussed in the subsequent § 7.
Let
![]() $R$
be a graded commutative noetherian ring and
$R$
be a graded commutative noetherian ring and
![]() $\mathsf{T}$
a compactly generated
$\mathsf{T}$
a compactly generated
![]() $R$
-linear triangulated category. The support of
$R$
-linear triangulated category. The support of
![]() $\mathsf{T}$
is by definition the set
$\mathsf{T}$
is by definition the set
Definition 6.1. We say that
![]() $\mathsf{T}$
is
$\mathsf{T}$
is
![]() $R$
-Gorenstein (or simply Gorenstein when the action of
$R$
-Gorenstein (or simply Gorenstein when the action of
![]() $R$
is clear) if there is an
$R$
is clear) if there is an
![]() $R$
-linear triangle equivalence
$R$
-linear triangle equivalence
and for every
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{supp}_{R}(\mathsf{T})$
there is an integer
$\operatorname{supp}_{R}(\mathsf{T})$
there is an integer
![]() $d(\mathfrak{p})$
and a natural isomorphism
$d(\mathfrak{p})$
and a natural isomorphism
of functors
![]() $\mathsf{T}^{\mathsf{c}}\rightarrow \mathsf{T}$
.
$\mathsf{T}^{\mathsf{c}}\rightarrow \mathsf{T}$
.
In this context we call
![]() $F$
a global Serre functor, because in Proposition 7.3 we show that localising at
$F$
a global Serre functor, because in Proposition 7.3 we show that localising at
![]() $\mathfrak{p}$
induces a functor
$\mathfrak{p}$
induces a functor
![]() $\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}F_{\mathfrak{p}}$
which is an analogue of a Serre functor in the sense of Bondal and Kapranov [Reference Bondal and KapranovBK89].
$\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}F_{\mathfrak{p}}$
which is an analogue of a Serre functor in the sense of Bondal and Kapranov [Reference Bondal and KapranovBK89].
We have not as yet explored fully the dependence of the Gorenstein property of
![]() $\mathsf{T}$
on the ring
$\mathsf{T}$
on the ring
![]() $R$
; a beginning has been made in the work of Yuliawan [Reference YuliawanYul17].
$R$
; a beginning has been made in the work of Yuliawan [Reference YuliawanYul17].
Let
![]() $\mathsf{T}=(\mathsf{T},\otimes ,\unicode[STIX]{x1D7D9})$
be a tensor triangulated category such that
$\mathsf{T}=(\mathsf{T},\otimes ,\unicode[STIX]{x1D7D9})$
be a tensor triangulated category such that
![]() $R$
acts on
$R$
acts on
![]() $\mathsf{T}$
via a homomorphism of graded rings
$\mathsf{T}$
via a homomorphism of graded rings
![]() $R\rightarrow \operatorname{End}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9})$
. We assume that
$R\rightarrow \operatorname{End}_{\mathsf{T}}^{\ast }(\unicode[STIX]{x1D7D9})$
. We assume that
![]() $\unicode[STIX]{x1D7D9}$
is compact and that each compact object is rigid; see § 2 for details. The Gorenstein property is implied by the existence of a dualising object in
$\unicode[STIX]{x1D7D9}$
is compact and that each compact object is rigid; see § 2 for details. The Gorenstein property is implied by the existence of a dualising object in
![]() $\mathsf{T}$
, as explained below.
$\mathsf{T}$
, as explained below.
Lemma 6.2. Let
![]() $\mathsf{T}$
be a tensor triangulated category with an
$\mathsf{T}$
be a tensor triangulated category with an
![]() $R$
-action. Suppose that there exists a compact object
$R$
-action. Suppose that there exists a compact object
![]() $W$
with the following properties.
$W$
with the following properties.
(i) There is a compact object
 $W^{-1}$
such that
$W^{-1}$
such that
 $W\otimes W^{-1}\cong \unicode[STIX]{x1D7D9}$
.
$W\otimes W^{-1}\cong \unicode[STIX]{x1D7D9}$
.(ii) For each
 $\mathfrak{p}$
in
$\mathfrak{p}$
in
 $\operatorname{supp}_{R}(\mathsf{T})$
there exists an integer
$\operatorname{supp}_{R}(\mathsf{T})$
there exists an integer
 $d(\mathfrak{p})$
and an isomorphism
$d(\mathfrak{p})$
and an isomorphism  $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}W\cong \unicode[STIX]{x1D6F4}^{d(\mathfrak{p})}T_{\mathfrak{ p}}(\unicode[STIX]{x1D7D9}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}W\cong \unicode[STIX]{x1D6F4}^{d(\mathfrak{p})}T_{\mathfrak{ p}}(\unicode[STIX]{x1D7D9}).\end{eqnarray}$$
Then
![]() $\mathsf{T}$
is
$\mathsf{T}$
is
![]() $R$
-Gorenstein, with global Serre functor
$R$
-Gorenstein, with global Serre functor
![]() $F:=W\otimes -$
.
$F:=W\otimes -$
.
Proof. Since
![]() $W$
is compact, so is
$W$
is compact, so is
![]() $W\otimes C$
for any compact object
$W\otimes C$
for any compact object
![]() $C$
of
$C$
of
![]() $\mathsf{T}$
. Thus
$\mathsf{T}$
. Thus
![]() $F$
induces a functor on compact objects. It is an equivalence of categories with quasi-inverse
$F$
induces a functor on compact objects. It is an equivalence of categories with quasi-inverse
![]() $W^{-1}\otimes -$
, by condition (i). Moreover for any compact object
$W^{-1}\otimes -$
, by condition (i). Moreover for any compact object
![]() $C$
and
$C$
and
![]() $\mathfrak{p}\in \operatorname{supp}_{R}(\mathsf{T})$
one has isomorphisms
$\mathfrak{p}\in \operatorname{supp}_{R}(\mathsf{T})$
one has isomorphisms
where the first and the last one are consequences of (2.2), and the middle one is by (ii). ◻
The example below justifies the language of Gorenstein triangulated categories.
Example 6.3. Let
![]() $A$
be a commutative noetherian ring and
$A$
be a commutative noetherian ring and
![]() $\mathsf{D}$
the derived category of
$\mathsf{D}$
the derived category of
![]() $A$
-modules. This is an
$A$
-modules. This is an
![]() $A$
-linear compactly generated tensor triangulated category, with compact objects the perfect complexes of
$A$
-linear compactly generated tensor triangulated category, with compact objects the perfect complexes of
![]() $A$
-modules, that is to say, complexes quasi-isomorphic to bounded complexes of finitely generated projective
$A$
-modules, that is to say, complexes quasi-isomorphic to bounded complexes of finitely generated projective
![]() $A$
-modules.
$A$
-modules.
Recall that the ring
![]() $A$
is Gorenstein if for each
$A$
is Gorenstein if for each
![]() $\mathfrak{p}\in \operatorname{Spec}A$
the injective dimension of
$\mathfrak{p}\in \operatorname{Spec}A$
the injective dimension of
![]() $A_{\mathfrak{p}}$
, as a module over itself, is finite; see [Reference Bruns and HerzogBH98, 3.1]. By Grothendieck’s local duality theorem [Reference Bruns and HerzogBH98, § 3.5], this is equivalent to an isomorphism of
$A_{\mathfrak{p}}$
, as a module over itself, is finite; see [Reference Bruns and HerzogBH98, 3.1]. By Grothendieck’s local duality theorem [Reference Bruns and HerzogBH98, § 3.5], this is equivalent to an isomorphism of
![]() $A_{\mathfrak{p}}$
-modules
$A_{\mathfrak{p}}$
-modules
Thus
![]() $\mathsf{D}$
is Gorenstein with dualising object
$\mathsf{D}$
is Gorenstein with dualising object
![]() $A$
and
$A$
and
![]() $d(\mathfrak{p})=-\text{dim}\,A_{\mathfrak{p}}$
; see Lemma 6.2. Conversely, it is not difficult to check that
$d(\mathfrak{p})=-\text{dim}\,A_{\mathfrak{p}}$
; see Lemma 6.2. Conversely, it is not difficult to check that
![]() $\mathsf{D}$
is Gorenstein only if
$\mathsf{D}$
is Gorenstein only if
![]() $A$
is Gorenstein.
$A$
is Gorenstein.
For a finite group scheme
![]() $G$
over a field
$G$
over a field
![]() $k$
, the Gorenstein property for
$k$
, the Gorenstein property for
![]() $\mathsf{StMod}\,G$
is basically a reformulation of Theorem 5.1.
$\mathsf{StMod}\,G$
is basically a reformulation of Theorem 5.1.
Corollary 6.4. As an
![]() $H^{\ast }(G,k)$
-linear triangulated category,
$H^{\ast }(G,k)$
-linear triangulated category,
![]() $\mathsf{StMod}\,G$
is Gorenstein, with
$\mathsf{StMod}\,G$
is Gorenstein, with
![]() $F=\unicode[STIX]{x1D6FF}_{G}\otimes _{k}-$
the Nakayama functor and
$F=\unicode[STIX]{x1D6FF}_{G}\otimes _{k}-$
the Nakayama functor and
![]() $d(\mathfrak{p})=\dim H^{\ast }(G,k)/\mathfrak{p}$
for each
$d(\mathfrak{p})=\dim H^{\ast }(G,k)/\mathfrak{p}$
for each
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
.
$\operatorname{Proj}H^{\ast }(G,k)$
.
Next we discuss the Gorenstein property for
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
for a finite group scheme
$\mathsf{K}(\mathsf{Inj}\,G)$
for a finite group scheme
![]() $G$
. To this end observe that the assignment
$G$
. To this end observe that the assignment
![]() $X\mapsto \unicode[STIX]{x1D708}X$
induces triangle equivalences
$X\mapsto \unicode[STIX]{x1D708}X$
induces triangle equivalences
We are ready to establish the Gorenstein property for
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
.
$\mathsf{K}(\mathsf{Inj}\,G)$
.
Theorem 6.5. Let
![]() $G$
be a finite group scheme over a field
$G$
be a finite group scheme over a field
![]() $k$
. Then
$k$
. Then
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
is Gorenstein as an
$\mathsf{K}(\mathsf{Inj}\,G)$
is Gorenstein as an
![]() $H^{\ast }(G,k)$
-linear triangulated, with
$H^{\ast }(G,k)$
-linear triangulated, with
![]() $F$
induced by the Nakayama functor and
$F$
induced by the Nakayama functor and
![]() $d(\mathfrak{p})=\dim H^{\ast }(G,k)/\mathfrak{p}$
for each
$d(\mathfrak{p})=\dim H^{\ast }(G,k)/\mathfrak{p}$
for each
![]() $\mathfrak{p}\in \operatorname{Spec}H^{\ast }(G,k)$
.
$\mathfrak{p}\in \operatorname{Spec}H^{\ast }(G,k)$
.
Proof. Set
![]() $R:=H^{\ast }(G,k)$
and
$R:=H^{\ast }(G,k)$
and
![]() $\mathfrak{m}:=R^{{\geqslant}1}$
, the maximal ideal of
$\mathfrak{m}:=R^{{\geqslant}1}$
, the maximal ideal of
![]() $R$
. It is easy to verify that
$R$
. It is easy to verify that
![]() $I(\mathfrak{m}):=\operatorname{Hom}_{k}(R,k)$
is the injective hull of
$I(\mathfrak{m}):=\operatorname{Hom}_{k}(R,k)$
is the injective hull of
![]() $R/\mathfrak{m}$
as an
$R/\mathfrak{m}$
as an
![]() $R$
-module and hence that
$R$
-module and hence that
![]() $\operatorname{Hom}_{R}(-,I(\mathfrak{m}))=\operatorname{Hom}_{k}(-,k)$
on the category of graded
$\operatorname{Hom}_{R}(-,I(\mathfrak{m}))=\operatorname{Hom}_{k}(-,k)$
on the category of graded
![]() $R$
-modules; see [Reference Bruns and HerzogBH98, Proposition 3.6.16]. This observation is used in the first isomorphism below.
$R$
-modules; see [Reference Bruns and HerzogBH98, Proposition 3.6.16]. This observation is used in the first isomorphism below.
Let
![]() $\mathsf{p}k$
be a projective resolution of the trivial representation. For any
$\mathsf{p}k$
be a projective resolution of the trivial representation. For any
![]() $X$
in
$X$
in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
the complex
$\mathsf{K}(\mathsf{Inj}\,G)$
the complex
![]() $\mathsf{p}X:=\mathsf{p}k\otimes _{k}X$
is a projective resolution of
$\mathsf{p}X:=\mathsf{p}k\otimes _{k}X$
is a projective resolution of
![]() $X$
.
$X$
.
Suppose
![]() $X$
is compact in
$X$
is compact in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
; one may assume
$\mathsf{K}(\mathsf{Inj}\,G)$
; one may assume
![]() $X^{n}=0$
for
$X^{n}=0$
for
![]() $n\ll 0$
and that
$n\ll 0$
and that
![]() $H^{n}(X)$
is finitely generated for all
$H^{n}(X)$
is finitely generated for all
![]() $n$
and equal to
$n$
and equal to
![]() $0$
for
$0$
for
![]() $n\gg 0$
; see [Reference KrauseKra05, Proposition 2.3(2)]. Then, for each
$n\gg 0$
; see [Reference KrauseKra05, Proposition 2.3(2)]. Then, for each
![]() $Y$
in
$Y$
in
![]() $\mathsf{K}(\mathsf{Inj}\,G)$
from [Reference Krause and LeKL06, Theorem 3.4] one gets the first of the following natural isomorphisms:
$\mathsf{K}(\mathsf{Inj}\,G)$
from [Reference Krause and LeKL06, Theorem 3.4] one gets the first of the following natural isomorphisms:
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{K}}^{\ast }(X,Y),I(\mathfrak{m})) & \cong & \displaystyle \operatorname{Hom}_{\mathsf{K}}(Y,D(kG)\otimes _{kG}\mathsf{p}X)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{K}}(Y,\unicode[STIX]{x1D6FF}_{G}\otimes _{k}\mathsf{p}X)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{K}}(Y,\mathsf{p}(\unicode[STIX]{x1D6FF}_{G}\otimes _{k}X)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{K}}^{\ast }(X,Y),I(\mathfrak{m})) & \cong & \displaystyle \operatorname{Hom}_{\mathsf{K}}(Y,D(kG)\otimes _{kG}\mathsf{p}X)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{K}}(Y,\unicode[STIX]{x1D6FF}_{G}\otimes _{k}\mathsf{p}X)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{K}}(Y,\mathsf{p}(\unicode[STIX]{x1D6FF}_{G}\otimes _{k}X)).\nonumber\end{eqnarray}$$
The second one holds by the definition of the modular character, and the last one is immediate from the definition of
![]() $\mathsf{p}$
and the commutativity of tensor products. Since
$\mathsf{p}$
and the commutativity of tensor products. Since
![]() $\mathsf{p}(\unicode[STIX]{x1D6FF}_{G}\otimes _{k}X)=\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\unicode[STIX]{x1D6FF}_{G}\otimes _{k}X)$
, by Lemma 2.6, it follows that
$\mathsf{p}(\unicode[STIX]{x1D6FF}_{G}\otimes _{k}X)=\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\unicode[STIX]{x1D6FF}_{G}\otimes _{k}X)$
, by Lemma 2.6, it follows that
![]() $T_{\mathfrak{m}}\cong \unicode[STIX]{x1D6E4}_{\mathfrak{m}}\circ F$
.
$T_{\mathfrak{m}}\cong \unicode[STIX]{x1D6E4}_{\mathfrak{m}}\circ F$
.
For a prime ideal
![]() $\mathfrak{p}\neq \mathfrak{m}$
, the assertion follows from Theorem 5.1, for localisation at
$\mathfrak{p}\neq \mathfrak{m}$
, the assertion follows from Theorem 5.1, for localisation at
![]() $\mathfrak{p}$
yields a triangle equivalence
$\mathfrak{p}$
yields a triangle equivalence
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{K}(\mathsf{Inj}\,G))\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
by Lemma 2.6.◻
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{K}(\mathsf{Inj}\,G))\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
by Lemma 2.6.◻
Remark 6.6. There are extensions of the Gorenstein property to differential graded algebras, see [Reference Frankild, Iyengar and JørgensenFIJ03] and [Reference Dwyer, Greenlees and IyengarDGI06], for instance, and a natural question is how these relate to the Gorenstein property, in the sense of Definition 6.1, of the associated derived categories. We defer exploring these connections to another occasion.
Balmer, Dell’Ambrogio and Sanders [Reference Balmer, Dell’Ambrogio and SandersBDS16] have introduced a categorical framework extending the duality theory for schemes due to Grothendieck and Neeman. The relationship to our work might be explained thus: a commutative noetherian ring
![]() $R$
is Gorenstein precisely when it has an invertible dualising complex. The framework in [Reference Balmer, Dell’Ambrogio and SandersBDS16] captures the relative version (dealing with a morphism of rings, or schemes) of the Gorenstein property and its characterisation in terms of the relative dualising complex. We are interested in the characterisation of the Gorenstein property in terms of local cohomology, and in the fact that when
$R$
is Gorenstein precisely when it has an invertible dualising complex. The framework in [Reference Balmer, Dell’Ambrogio and SandersBDS16] captures the relative version (dealing with a morphism of rings, or schemes) of the Gorenstein property and its characterisation in terms of the relative dualising complex. We are interested in the characterisation of the Gorenstein property in terms of local cohomology, and in the fact that when
![]() $R$
is Gorenstein, so is
$R$
is Gorenstein, so is
![]() $R_{\mathfrak{p}}$
for each prime
$R_{\mathfrak{p}}$
for each prime
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Spec}R$
. Theorem 5.1 may be seen as an analogue of these results for modular representations.
$\operatorname{Spec}R$
. Theorem 5.1 may be seen as an analogue of these results for modular representations.
7 Local Serre duality
In this section we introduce a notion of local Serre duality for an essentially small
![]() $R$
-linear triangulated category and link it to the Gorenstein property from § 6. We use the concept of a Serre functor for a triangulated category which is due to Bondal and Kapranov [Reference Bondal and KapranovBK89]; this provides a conceptual way to formulate classical Serre duality and Grothendieck’s local duality in a triangulated setting.
$R$
-linear triangulated category and link it to the Gorenstein property from § 6. We use the concept of a Serre functor for a triangulated category which is due to Bondal and Kapranov [Reference Bondal and KapranovBK89]; this provides a conceptual way to formulate classical Serre duality and Grothendieck’s local duality in a triangulated setting.
In the second part of this section we discuss the existence of AR-triangles. These were introduced by Happel for derived categories of finite-dimensional algebras [Reference HappelHap88], and in [Reference HappelHap91] he established the connection with the Gorenstein property, while Reiten and Van den Bergh [Reference Reiten and Van den BerghRV02] discovered the connection between AR-triangles and the existence of a Serre functor.
Small triangulated categories with central action
Let
![]() $\mathsf{C}$
be an essentially small
$\mathsf{C}$
be an essentially small
![]() $R$
-linear triangulated category. Fix
$R$
-linear triangulated category. Fix
![]() $\mathfrak{p}\in \operatorname{Spec}R$
and let
$\mathfrak{p}\in \operatorname{Spec}R$
and let
![]() $\mathsf{C}_{\mathfrak{p}}$
denote the triangulated category obtained from
$\mathsf{C}_{\mathfrak{p}}$
denote the triangulated category obtained from
![]() $\mathsf{C}$
by keeping the objects of
$\mathsf{C}$
by keeping the objects of
![]() $\mathsf{C}$
and setting
$\mathsf{C}$
and setting
Then
![]() $\mathsf{C}_{\mathfrak{p}}$
is an
$\mathsf{C}_{\mathfrak{p}}$
is an
![]() $R_{\mathfrak{p}}$
-linear triangulated category and localising the morphisms induces an exact functor
$R_{\mathfrak{p}}$
-linear triangulated category and localising the morphisms induces an exact functor
![]() $\mathsf{C}\rightarrow \mathsf{C}_{\mathfrak{p}}$
; see [Reference BalmerBal10, Theorem 3.6] or [Reference Benson, Iyengar and KrauseBIK15, Lemma 3.5].
$\mathsf{C}\rightarrow \mathsf{C}_{\mathfrak{p}}$
; see [Reference BalmerBal10, Theorem 3.6] or [Reference Benson, Iyengar and KrauseBIK15, Lemma 3.5].
Let
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
be the full subcategory of
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
be the full subcategory of
![]() $\mathfrak{p}$
-torsion objects in
$\mathfrak{p}$
-torsion objects in
![]() $\mathsf{C}_{\mathfrak{p}}$
, namely
$\mathsf{C}_{\mathfrak{p}}$
, namely
This is a thick subcategory of
![]() $\mathsf{C}_{\mathfrak{p}}$
; see [Reference Benson, Iyengar and KrauseBIK15, p. 458f]. In [Reference Benson, Iyengar and KrauseBIK15] this category is denoted
$\mathsf{C}_{\mathfrak{p}}$
; see [Reference Benson, Iyengar and KrauseBIK15, p. 458f]. In [Reference Benson, Iyengar and KrauseBIK15] this category is denoted
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{C}$
. The notation has been changed to avoid confusion.
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{C}$
. The notation has been changed to avoid confusion.
Remark 7.1. Let
![]() $F:\mathsf{C}\rightarrow \mathsf{C}$
be an
$F:\mathsf{C}\rightarrow \mathsf{C}$
be an
![]() $R$
-linear equivalence. It is straightforward to check that this induces triangle equivalences
$R$
-linear equivalence. It is straightforward to check that this induces triangle equivalences
![]() $F_{\mathfrak{p}}:\mathsf{C}_{\mathfrak{p}}\xrightarrow[{}]{{\sim}}\mathsf{C}_{\mathfrak{p}}$
and
$F_{\mathfrak{p}}:\mathsf{C}_{\mathfrak{p}}\xrightarrow[{}]{{\sim}}\mathsf{C}_{\mathfrak{p}}$
and
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
making the following diagram commutative.
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
making the following diagram commutative.

Remark 7.2. Let
![]() $\mathsf{T}$
be a compactly generated
$\mathsf{T}$
be a compactly generated
![]() $R$
-linear triangulated category. Set
$R$
-linear triangulated category. Set
![]() $\mathsf{C}:=\mathsf{T}^{\mathsf{c}}$
and fix
$\mathsf{C}:=\mathsf{T}^{\mathsf{c}}$
and fix
![]() $\mathfrak{p}\in \operatorname{Spec}R$
. The triangulated categories
$\mathfrak{p}\in \operatorname{Spec}R$
. The triangulated categories
![]() $\mathsf{T}_{\mathfrak{p}}$
and
$\mathsf{T}_{\mathfrak{p}}$
and
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}$
are compactly generated. The left adjoint of the inclusion
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}$
are compactly generated. The left adjoint of the inclusion
![]() $\mathsf{T}_{\mathfrak{p}}\rightarrow \mathsf{T}$
induces (up to direct summands) a triangle equivalence
$\mathsf{T}_{\mathfrak{p}}\rightarrow \mathsf{T}$
induces (up to direct summands) a triangle equivalence
![]() $\mathsf{C}_{\mathfrak{p}}\xrightarrow[{}]{{\sim}}(\mathsf{T}_{\mathfrak{p}})^{\mathsf{c}}$
and restricts to a triangle equivalence
$\mathsf{C}_{\mathfrak{p}}\xrightarrow[{}]{{\sim}}(\mathsf{T}_{\mathfrak{p}})^{\mathsf{c}}$
and restricts to a triangle equivalence
This follows from the fact that the localisation functor
![]() $\mathsf{T}\rightarrow \mathsf{T}_{\mathfrak{p}}$
taking
$\mathsf{T}\rightarrow \mathsf{T}_{\mathfrak{p}}$
taking
![]() $X$
to
$X$
to
![]() $X_{\mathfrak{p}}$
preserves compactness and that for compact objects
$X_{\mathfrak{p}}$
preserves compactness and that for compact objects
![]() $X,Y$
in
$X,Y$
in
![]() $\mathsf{T}$
$\mathsf{T}$
For details we refer to [Reference Benson, Iyengar and KrauseBIK08].
Local Serre duality
Let
![]() $R$
be a graded commutative ring that is local; thus there is a unique homogeneous maximal ideal, say
$R$
be a graded commutative ring that is local; thus there is a unique homogeneous maximal ideal, say
![]() $\mathfrak{m}$
. Extrapolating from Bondal and Kapranov [Reference Bondal and KapranovBK89, § 3], we call an
$\mathfrak{m}$
. Extrapolating from Bondal and Kapranov [Reference Bondal and KapranovBK89, § 3], we call an
![]() $R$
-linear triangle equivalence
$R$
-linear triangle equivalence
![]() $F:\mathsf{C}\xrightarrow[{}]{{\sim}}\mathsf{C}$
a Serre functor if for all objects
$F:\mathsf{C}\xrightarrow[{}]{{\sim}}\mathsf{C}$
a Serre functor if for all objects
![]() $X,Y$
in
$X,Y$
in
![]() $\mathsf{C}$
there is a natural isomorphism
$\mathsf{C}$
there is a natural isomorphism
The situation when
![]() $R$
is a field was the one considered in [Reference Bondal and KapranovBK89]. For a general ring
$R$
is a field was the one considered in [Reference Bondal and KapranovBK89]. For a general ring
![]() $R$
, the appearance of
$R$
, the appearance of
![]() $\operatorname{Hom}_{R}^{\ast }(-,I(\mathfrak{m}))$
, which is the Matlis duality functor, is natural for it is an extension of vector-space duality; see also Lemma A.2. The definition proposed above is not the only possible extension to the general context, but it is well suited for our purposes.
$\operatorname{Hom}_{R}^{\ast }(-,I(\mathfrak{m}))$
, which is the Matlis duality functor, is natural for it is an extension of vector-space duality; see also Lemma A.2. The definition proposed above is not the only possible extension to the general context, but it is well suited for our purposes.
For an arbitrary graded commutative ring
![]() $R$
, we say that an
$R$
, we say that an
![]() $R$
-linear triangulated category
$R$
-linear triangulated category
![]() $\mathsf{C}$
satisfies local Serre duality if there exists an
$\mathsf{C}$
satisfies local Serre duality if there exists an
![]() $R$
-linear triangle equivalence
$R$
-linear triangle equivalence
![]() $F:\mathsf{C}\xrightarrow[{}]{{\sim}}\mathsf{C}$
such that for every
$F:\mathsf{C}\xrightarrow[{}]{{\sim}}\mathsf{C}$
such that for every
![]() $\mathfrak{p}\in \operatorname{Spec}R$
and some integer
$\mathfrak{p}\in \operatorname{Spec}R$
and some integer
![]() $d(\mathfrak{p})$
the induced functor
$d(\mathfrak{p})$
the induced functor
![]() $\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}F_{\mathfrak{p}}:\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
is a Serre functor for the
$\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}F_{\mathfrak{p}}:\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
is a Serre functor for the
![]() $R_{\mathfrak{p}}$
-linear category
$R_{\mathfrak{p}}$
-linear category
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
. Thus for all objects
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
. Thus for all objects
![]() $X,Y$
in
$X,Y$
in
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
there is a natural isomorphism
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
there is a natural isomorphism
For a compactly generated triangulated category, the Gorenstein property 6.1 is linked to local Serre duality for the subcategory of compact objects.
Proposition 7.3. Let
![]() $R$
be a graded commutative noetherian ring and
$R$
be a graded commutative noetherian ring and
![]() $\mathsf{T}$
a compactly generated
$\mathsf{T}$
a compactly generated
![]() $R$
-linear triangulated category. Suppose that
$R$
-linear triangulated category. Suppose that
![]() $\mathsf{T}$
is Gorenstein, with global Serre functor
$\mathsf{T}$
is Gorenstein, with global Serre functor
![]() $F$
and shifts
$F$
and shifts
![]() $\{d(\mathfrak{p})\}$
. Then for each
$\{d(\mathfrak{p})\}$
. Then for each
![]() $\mathfrak{p}\in \operatorname{supp}_{R}(\mathsf{T})$
, object
$\mathfrak{p}\in \operatorname{supp}_{R}(\mathsf{T})$
, object
![]() $X\in (\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T})^{\mathsf{c}}$
and
$X\in (\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T})^{\mathsf{c}}$
and
![]() $Y\in \mathsf{T}_{\mathfrak{p}}$
there is a natural isomorphism
$Y\in \mathsf{T}_{\mathfrak{p}}$
there is a natural isomorphism
Proof. Given Remark 7.2 we can assume
![]() $X=C_{\mathfrak{p}}$
for a
$X=C_{\mathfrak{p}}$
for a
![]() $\mathfrak{p}$
-torsion compact object
$\mathfrak{p}$
-torsion compact object
![]() $C$
in
$C$
in
![]() $\mathsf{T}$
. The desired isomorphism is a concatenation of the following natural ones:
$\mathsf{T}$
. The desired isomorphism is a concatenation of the following natural ones:
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C_{\mathfrak{p}},Y),I(\mathfrak{p})) & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,Y),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,T_{\mathfrak{p}}(C))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}F(C))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}F(C)_{\mathfrak{p}})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}F_{\mathfrak{p}}(C_{\mathfrak{p}}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}F_{\mathfrak{p}}(C_{\mathfrak{p}})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C_{\mathfrak{p}},Y),I(\mathfrak{p})) & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,Y),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,T_{\mathfrak{p}}(C))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}F(C))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}F(C)_{\mathfrak{p}})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}F_{\mathfrak{p}}(C_{\mathfrak{p}}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{T}}(Y,\unicode[STIX]{x1D6F4}^{-d(\mathfrak{p})}F_{\mathfrak{p}}(C_{\mathfrak{p}})).\nonumber\end{eqnarray}$$
In this chain, the first map is induced by the localisation
![]() $C\mapsto C_{\mathfrak{p}}$
and is an isomorphism because
$C\mapsto C_{\mathfrak{p}}$
and is an isomorphism because
![]() $Y$
is
$Y$
is
![]() $\mathfrak{p}$
-local. The second one is by the definition of
$\mathfrak{p}$
-local. The second one is by the definition of
![]() $T_{\mathfrak{p}}(C)$
; the third is by the Gorenstein property of
$T_{\mathfrak{p}}(C)$
; the third is by the Gorenstein property of
![]() $\mathsf{T}$
; the fourth is by the definition of
$\mathsf{T}$
; the fourth is by the definition of
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}$
; the last two are explained by Remark 7.2, where for the last one uses also the fact that
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}$
; the last two are explained by Remark 7.2, where for the last one uses also the fact that
![]() $C_{\mathfrak{p}}$
, and hence also
$C_{\mathfrak{p}}$
, and hence also
![]() $F_{\mathfrak{p}}(C_{\mathfrak{p}})$
, is
$F_{\mathfrak{p}}(C_{\mathfrak{p}})$
, is
![]() $\mathfrak{p}$
-torsion.◻
$\mathfrak{p}$
-torsion.◻
Corollary 7.4. Let
![]() $R$
be a graded commutative noetherian ring and
$R$
be a graded commutative noetherian ring and
![]() $\mathsf{T}$
a compactly generated
$\mathsf{T}$
a compactly generated
![]() $R$
-linear triangulated category. If
$R$
-linear triangulated category. If
![]() $\mathsf{T}$
is Gorenstein, then
$\mathsf{T}$
is Gorenstein, then
![]() $\mathsf{T}^{\mathsf{c}}$
satisfies local Serre duality.
$\mathsf{T}^{\mathsf{c}}$
satisfies local Serre duality.
Example 7.5. In the notation of Example 6.3, when
![]() $A$
is a (commutative noetherian) Gorenstein ring, local Serre duality reads: For each
$A$
is a (commutative noetherian) Gorenstein ring, local Serre duality reads: For each
![]() $\mathfrak{p}\in \operatorname{Spec}A$
and integer
$\mathfrak{p}\in \operatorname{Spec}A$
and integer
![]() $n$
there are natural isomorphisms
$n$
there are natural isomorphisms
where
![]() $X$
is a perfect complexes of
$X$
is a perfect complexes of
![]() $A_{\mathfrak{p}}$
-modules with finite length cohomology, and
$A_{\mathfrak{p}}$
-modules with finite length cohomology, and
![]() $Y$
is a complex of
$Y$
is a complex of
![]() $A_{\mathfrak{p}}$
-modules.
$A_{\mathfrak{p}}$
-modules.
Auslander–Reiten triangles
Let
![]() $\mathsf{C}$
be an essentially small triangulated category. Following Happel [Reference HappelHap88], an exact triangle
$\mathsf{C}$
be an essentially small triangulated category. Following Happel [Reference HappelHap88], an exact triangle
![]() $X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}Y\xrightarrow[{}]{\unicode[STIX]{x1D6FD}}Z\xrightarrow[{}]{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6F4}X$
in
$X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}Y\xrightarrow[{}]{\unicode[STIX]{x1D6FD}}Z\xrightarrow[{}]{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6F4}X$
in
![]() $\mathsf{C}$
is an Auslander–Reiten triangle if:
$\mathsf{C}$
is an Auslander–Reiten triangle if:
(i) any morphism
 $X\rightarrow X^{\prime }$
that is not a split monomorphism factors through
$X\rightarrow X^{\prime }$
that is not a split monomorphism factors through
 $\unicode[STIX]{x1D6FC}$
;
$\unicode[STIX]{x1D6FC}$
;(ii) any morphism
 $Z^{\prime }\rightarrow Z$
that is not a split epimorphism factors through
$Z^{\prime }\rightarrow Z$
that is not a split epimorphism factors through
 $\unicode[STIX]{x1D6FD}$
;
$\unicode[STIX]{x1D6FD}$
;(iii)
 $\unicode[STIX]{x1D6FE}\neq 0$
.
$\unicode[STIX]{x1D6FE}\neq 0$
.
In this case, the endomorphism rings of
![]() $X$
and
$X$
and
![]() $Z$
are local, and in particular the objects are indecomposable. Moreover, each of
$Z$
are local, and in particular the objects are indecomposable. Moreover, each of
![]() $X$
and
$X$
and
![]() $Z$
determines the AR-triangle up to isomorphism. Assuming conditions (ii) and (iii), the condition (i) is equivalent to the following.
$Z$
determines the AR-triangle up to isomorphism. Assuming conditions (ii) and (iii), the condition (i) is equivalent to the following.
(i′) The endomorphism ring of
 $X$
is local.
$X$
is local.
See [Reference KrauseKra00, § 2] for details.
Let
![]() $\mathsf{C}$
be a Krull–Schmidt category, that is, each object decomposes into a finite direct sum of objects with local endomorphism rings. We say that
$\mathsf{C}$
be a Krull–Schmidt category, that is, each object decomposes into a finite direct sum of objects with local endomorphism rings. We say that
![]() $\mathsf{C}$
has AR-triangles if for every indecomposable object
$\mathsf{C}$
has AR-triangles if for every indecomposable object
![]() $X$
there are AR-triangles
$X$
there are AR-triangles
The next proposition establishes the existence of AR-triangles; it is the analogue of a result of Reiten and Van den Bergh [Reference Reiten and Van den BerghRV02, I.2] for triangulated categories that are Hom-finite over a field.
Proposition 7.6. Let
![]() $R$
be a graded commutative ring that is local, and let
$R$
be a graded commutative ring that is local, and let
![]() $\mathsf{C}$
be an essentially small
$\mathsf{C}$
be an essentially small
![]() $R$
-linear triangulated category that is Krull–Schmidt. If
$R$
-linear triangulated category that is Krull–Schmidt. If
![]() $\mathsf{C}$
has a Serre functor, then it has AR-triangles.
$\mathsf{C}$
has a Serre functor, then it has AR-triangles.
Proof. Let
![]() $F$
be a Serre functor for
$F$
be a Serre functor for
![]() $\mathsf{C}$
and
$\mathsf{C}$
and
![]() $X$
an indecomposable object in
$X$
an indecomposable object in
![]() $\mathsf{C}$
. The ring
$\mathsf{C}$
. The ring
![]() $\operatorname{End}_{\mathsf{C}}(X)$
is thus local; let
$\operatorname{End}_{\mathsf{C}}(X)$
is thus local; let
![]() $J$
be its maximal ideal and
$J$
be its maximal ideal and
![]() $I$
the right ideal of
$I$
the right ideal of
![]() $\operatorname{End}_{\mathsf{C}}^{\ast }(X)$
that it generates. One has
$\operatorname{End}_{\mathsf{C}}^{\ast }(X)$
that it generates. One has
![]() $I^{0}=J$
, by Remark 7.7, so
$I^{0}=J$
, by Remark 7.7, so
![]() $\operatorname{End}_{\mathsf{C}}^{\ast }(X)/I$
is nonzero. Choose a nonzero morphism
$\operatorname{End}_{\mathsf{C}}^{\ast }(X)/I$
is nonzero. Choose a nonzero morphism
![]() $\operatorname{End}_{\mathsf{C}}^{\ast }(X)/I\rightarrow I(\mathfrak{m})$
and let
$\operatorname{End}_{\mathsf{C}}^{\ast }(X)/I\rightarrow I(\mathfrak{m})$
and let
![]() $\unicode[STIX]{x1D6FE}:X\rightarrow FX$
be the corresponding morphism in
$\unicode[STIX]{x1D6FE}:X\rightarrow FX$
be the corresponding morphism in
![]() $\mathsf{C}$
provided by Serre duality (7.1). We claim that the induced exact triangle
$\mathsf{C}$
provided by Serre duality (7.1). We claim that the induced exact triangle
is an AR-triangle. Indeed, by construction, if
![]() $X^{\prime }\rightarrow X$
is not a split epimorphism, then the composition
$X^{\prime }\rightarrow X$
is not a split epimorphism, then the composition
![]() $\operatorname{Hom}_{\mathsf{C}}^{\ast }(X,X^{\prime })\rightarrow \operatorname{End}_{\mathsf{C}}^{\ast }(X)/I\rightarrow I(\mathfrak{m})$
is zero, and therefore the naturality of (7.1) yields that the composition
$\operatorname{Hom}_{\mathsf{C}}^{\ast }(X,X^{\prime })\rightarrow \operatorname{End}_{\mathsf{C}}^{\ast }(X)/I\rightarrow I(\mathfrak{m})$
is zero, and therefore the naturality of (7.1) yields that the composition
![]() $X^{\prime }\rightarrow X\xrightarrow[{}]{\unicode[STIX]{x1D6FE}}FX$
is zero. Moreover as
$X^{\prime }\rightarrow X\xrightarrow[{}]{\unicode[STIX]{x1D6FE}}FX$
is zero. Moreover as
![]() $X$
is indecomposable so is
$X$
is indecomposable so is
![]() $FX$
.
$FX$
.
Applying this construction to
![]() $F^{-1}\unicode[STIX]{x1D6F4}X$
yields an AR-triangle starting at
$F^{-1}\unicode[STIX]{x1D6F4}X$
yields an AR-triangle starting at
![]() $X$
.◻
$X$
.◻
The following observations about graded rings has been, and will again be, used.
Remark 7.7. Let
![]() $E$
be a graded ring. For any
$E$
be a graded ring. For any
![]() $J$
a right ideal in
$J$
a right ideal in
![]() $E^{0}$
, the right ideal
$E^{0}$
, the right ideal
![]() $JE$
of
$JE$
of
![]() $E$
it generates satisfies
$E$
it generates satisfies
![]() $JE\cap E^{0}=J$
; this can be verified directly, or by noting that
$JE\cap E^{0}=J$
; this can be verified directly, or by noting that
![]() $E^{0}$
is a direct summand of
$E^{0}$
is a direct summand of
![]() $E$
, as right
$E$
, as right
![]() $E^{0}$
-modules. It follows that if
$E^{0}$
-modules. It follows that if
![]() $E$
is artinian than so is
$E$
is artinian than so is
![]() $E^{0}$
: any descending chain of ideals in
$E^{0}$
: any descending chain of ideals in
![]() $E^{0}$
stabilises, because the chain of ideals in
$E^{0}$
stabilises, because the chain of ideals in
![]() $E$
that they generate stabilises; cf. the proof of [Reference Bruns and HerzogBH98, Theorem 1.5.5].
$E$
that they generate stabilises; cf. the proof of [Reference Bruns and HerzogBH98, Theorem 1.5.5].
Let
![]() $R$
be a graded commutative ring. An
$R$
be a graded commutative ring. An
![]() $R$
-linear triangulated category
$R$
-linear triangulated category
![]() $\mathsf{C}$
is noetherian if the
$\mathsf{C}$
is noetherian if the
![]() $R$
-module
$R$
-module
![]() $\operatorname{Hom}_{\mathsf{C}}^{\ast }(X,Y)$
is noetherian for all
$\operatorname{Hom}_{\mathsf{C}}^{\ast }(X,Y)$
is noetherian for all
![]() $X,Y$
in
$X,Y$
in
![]() $\mathsf{C}$
.
$\mathsf{C}$
.
Lemma 7.8. Let
![]() $R$
be a graded commutative ring and
$R$
be a graded commutative ring and
![]() $\mathsf{C}$
an essentially small, noetherian,
$\mathsf{C}$
an essentially small, noetherian,
![]() $R$
-linear triangulated category. For each
$R$
-linear triangulated category. For each
![]() $\mathfrak{p}\in \operatorname{Spec}R$
, the idempotent completion of
$\mathfrak{p}\in \operatorname{Spec}R$
, the idempotent completion of
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
is a Krull–Schmidt category.
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
is a Krull–Schmidt category.
Proof. The noetherian property implies that for any object
![]() $X$
in
$X$
in
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
the
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
the
![]() $R_{\mathfrak{p}}$
-module
$R_{\mathfrak{p}}$
-module
![]() $E:=\operatorname{End}_{\unicode[STIX]{x1D6FE}_{\mathfrak{ p}}\mathsf{C}}^{\ast }(X)$
is of finite length. The graded ring
$E:=\operatorname{End}_{\unicode[STIX]{x1D6FE}_{\mathfrak{ p}}\mathsf{C}}^{\ast }(X)$
is of finite length. The graded ring
![]() $E$
is thus artinian, and then so is the ring
$E$
is thus artinian, and then so is the ring
![]() $E^{0}$
, by Remark 7.7. Artinian rings are semi-perfect, so the idempotent completion of
$E^{0}$
, by Remark 7.7. Artinian rings are semi-perfect, so the idempotent completion of
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
is a Krull–Schmidt category; see [Reference KrauseKra15, Corollary 4.4].◻
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{C}$
is a Krull–Schmidt category; see [Reference KrauseKra15, Corollary 4.4].◻
Corollary 7.9. Let
![]() $\mathsf{T}$
be a compactly generated
$\mathsf{T}$
be a compactly generated
![]() $R$
-linear triangulated category with
$R$
-linear triangulated category with
![]() $\mathsf{T}^{\mathsf{c}}$
noetherian. If
$\mathsf{T}^{\mathsf{c}}$
noetherian. If
![]() $\mathsf{T}$
is Gorenstein, then
$\mathsf{T}$
is Gorenstein, then
![]() $(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T})^{\mathsf{c}}$
has AR-triangles for
$(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T})^{\mathsf{c}}$
has AR-triangles for
![]() $\mathfrak{p}\in \operatorname{Spec}R$
.
$\mathfrak{p}\in \operatorname{Spec}R$
.
Proof. Set
![]() $\mathsf{S}:=(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T})^{\mathsf{c}}$
; this is an idempotent complete, essentially small,
$\mathsf{S}:=(\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T})^{\mathsf{c}}$
; this is an idempotent complete, essentially small,
![]() $R_{\mathfrak{p}}$
-linear triangulated category. Since
$R_{\mathfrak{p}}$
-linear triangulated category. Since
![]() $\mathsf{T}^{\mathsf{c}}$
is noetherian, it follows from Remark 7.2 and Lemma 7.8, that
$\mathsf{T}^{\mathsf{c}}$
is noetherian, it follows from Remark 7.2 and Lemma 7.8, that
![]() $\mathsf{S}$
is a Krull–Schmidt category. The Gorenstein hypothesis implies that the
$\mathsf{S}$
is a Krull–Schmidt category. The Gorenstein hypothesis implies that the
![]() $R_{\mathfrak{p}}$
-linear category
$R_{\mathfrak{p}}$
-linear category
![]() $\mathsf{S}$
has a Serre functor, by Proposition 7.3, and then Proposition 7.6 yields the existence of AR-triangles.◻
$\mathsf{S}$
has a Serre functor, by Proposition 7.3, and then Proposition 7.6 yields the existence of AR-triangles.◻
Next we consider local Serre duality for
![]() $\mathsf{D}^{b}(\mathsf{mod}\,G)$
and
$\mathsf{D}^{b}(\mathsf{mod}\,G)$
and
![]() $\mathsf{stmod}\,G$
. Recall from Lemma 2.6 that localisation at
$\mathsf{stmod}\,G$
. Recall from Lemma 2.6 that localisation at
![]() $\mathfrak{p}\in \operatorname{Proj}H^{\ast }(G,k)$
induces a triangle equivalence
$\mathfrak{p}\in \operatorname{Proj}H^{\ast }(G,k)$
induces a triangle equivalence
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{K}(\mathsf{Inj}\,G))\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. Using Remark 7.2, this yields (up to direct summands) triangle equivalences
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{K}(\mathsf{Inj}\,G))\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\mathsf{StMod}\,G)$
. Using Remark 7.2, this yields (up to direct summands) triangle equivalences
The result below contains Theorem 1.1 in the introduction.
Theorem 7.10. Let
![]() $G$
be a finite group scheme over a field
$G$
be a finite group scheme over a field
![]() $k$
. Then the
$k$
. Then the
![]() $H^{\ast }(G,k)$
-linear triangulated category
$H^{\ast }(G,k)$
-linear triangulated category
![]() $\mathsf{D}:=\mathsf{D}^{b}(\mathsf{mod}\,G)$
satisfies local Serre duality. Said otherwise, given
$\mathsf{D}:=\mathsf{D}^{b}(\mathsf{mod}\,G)$
satisfies local Serre duality. Said otherwise, given
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Spec}R$
and with
$\operatorname{Spec}R$
and with
![]() $d$
the Krull dimension of
$d$
the Krull dimension of
![]() $H^{\ast }(G,k)/\mathfrak{p}$
, for each
$H^{\ast }(G,k)/\mathfrak{p}$
, for each
![]() $M$
in
$M$
in
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{D}$
and
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{D}$
and
![]() $N$
in
$N$
in
![]() $\mathsf{D}_{\mathfrak{p}}$
, there are natural isomorphisms
$\mathsf{D}_{\mathfrak{p}}$
, there are natural isomorphisms
In particular,
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{D}$
has AR-triangles.
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}\mathsf{D}$
has AR-triangles.
AR-components and periodicity
The existence of AR-triangles for a triangulated category
![]() $\mathsf{C}$
gives rise to an AR-quiver; see for example [Reference Happel, Preiser and RingelHPR82, Reference LiuLiu10]. The vertices are given by the isomorphism classes of indecomposable objects in
$\mathsf{C}$
gives rise to an AR-quiver; see for example [Reference Happel, Preiser and RingelHPR82, Reference LiuLiu10]. The vertices are given by the isomorphism classes of indecomposable objects in
![]() $\mathsf{C}$
and an arrow
$\mathsf{C}$
and an arrow
![]() $[X]\rightarrow [Y]$
exists if there is an irreducible morphism
$[X]\rightarrow [Y]$
exists if there is an irreducible morphism
![]() $X\rightarrow Y$
.
$X\rightarrow Y$
.
In the context of
![]() $\mathsf{stmod}\,G$
, one can describe part of the structure of the AR-quiver of the
$\mathsf{stmod}\,G$
, one can describe part of the structure of the AR-quiver of the
![]() $\mathfrak{p}$
-local
$\mathfrak{p}$
-local
![]() $\mathfrak{p}$
-torsion objects as the Serre functor is periodic.
$\mathfrak{p}$
-torsion objects as the Serre functor is periodic.
Proposition 7.11. Let
![]() $G$
be a finite group scheme over a field
$G$
be a finite group scheme over a field
![]() $k$
. Fix a point
$k$
. Fix a point
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}H^{\ast }(G,k)$
and set
$\operatorname{Proj}H^{\ast }(G,k)$
and set
![]() $d=\dim H^{\ast }(G,k)/\mathfrak{p}$
. Then the Serre functor
$d=\dim H^{\ast }(G,k)/\mathfrak{p}$
. Then the Serre functor
is periodic, that is,
![]() $(\unicode[STIX]{x1D6FA}^{d}\unicode[STIX]{x1D708})^{r}=\operatorname{id}$
for some positive integer
$(\unicode[STIX]{x1D6FA}^{d}\unicode[STIX]{x1D708})^{r}=\operatorname{id}$
for some positive integer
![]() $r$
.
$r$
.
Proof. Lemma 2.1 and (4.1) provide an integer
![]() $r\geqslant 0$
such that
$r\geqslant 0$
such that
![]() $\unicode[STIX]{x1D708}^{r}M\cong M$
and
$\unicode[STIX]{x1D708}^{r}M\cong M$
and
![]() $\unicode[STIX]{x1D6FA}^{r}M\cong M$
for
$\unicode[STIX]{x1D6FA}^{r}M\cong M$
for
![]() $M$
in
$M$
in
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
. Thus
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
. Thus
![]() $(\unicode[STIX]{x1D6FA}^{d}\unicode[STIX]{x1D708})^{r}=\operatorname{id}$
, since
$(\unicode[STIX]{x1D6FA}^{d}\unicode[STIX]{x1D708})^{r}=\operatorname{id}$
, since
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\unicode[STIX]{x1D6FA}$
commute.◻
$\unicode[STIX]{x1D6FA}$
commute.◻
This has the following consequence.
Corollary 7.12. Every connected component of the AR-quiver of
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
is a stable tube in case it is infinite; and otherwise, it is of the form
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
is a stable tube in case it is infinite; and otherwise, it is of the form
![]() $\mathbb{Z}\unicode[STIX]{x1D6E5}/U$
, where
$\mathbb{Z}\unicode[STIX]{x1D6E5}/U$
, where
![]() $\unicode[STIX]{x1D6E5}$
is a quiver of Dynkin type and
$\unicode[STIX]{x1D6E5}$
is a quiver of Dynkin type and
![]() $U$
is a group of automorphisms of
$U$
is a group of automorphisms of
![]() $\mathbb{Z}\unicode[STIX]{x1D6E5}$
.
$\mathbb{Z}\unicode[STIX]{x1D6E5}$
.
Proof. Since the Serre functor on
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
is periodic, the desired result follows from [Reference LiuLiu10, Theorem 5.5]; see also [Reference Happel, Preiser and RingelHPR82].◻
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
is periodic, the desired result follows from [Reference LiuLiu10, Theorem 5.5]; see also [Reference Happel, Preiser and RingelHPR82].◻
The preceding result may be seen as a first step in the direction of extending the results of Farnsteiner’s [Reference FarnsteinerFar07, § 3] concerning
![]() $\mathsf{stmod}\,G$
to
$\mathsf{stmod}\,G$
to
![]() $\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
for a general (meaning, not necessarily closed) point
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{stmod}\,G)$
for a general (meaning, not necessarily closed) point
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $\operatorname{Proj}H^{\ast }(G,k)$
.
$\operatorname{Proj}H^{\ast }(G,k)$
.
Acknowledgements
It is a pleasure to thank Tobias Barthel, and a referee, for detailed comments on an earlier version of this manuscript.
Appendix A Injective modules at closed points
In this section we collect some remarks concerning injective hulls over graded rings, for use in § 5. Throughout
![]() $k$
will be a field and
$k$
will be a field and
![]() $A:=\bigoplus _{i\geqslant 0}A^{i}$
a finitely generated graded commutative
$A:=\bigoplus _{i\geqslant 0}A^{i}$
a finitely generated graded commutative
![]() $k$
-algebra with
$k$
-algebra with
![]() $A^{0}=k$
; we have in mind
$A^{0}=k$
; we have in mind
![]() $H^{\ast }(G,k)$
, for a finite group scheme
$H^{\ast }(G,k)$
, for a finite group scheme
![]() $G$
over
$G$
over
![]() $k$
.
$k$
.
As usual
![]() $\operatorname{Proj}A$
denotes the homogeneous prime ideals in
$\operatorname{Proj}A$
denotes the homogeneous prime ideals in
![]() $A$
that do not contain the ideal
$A$
that do not contain the ideal
![]() $A^{{\geqslant}1}$
. Given a point
$A^{{\geqslant}1}$
. Given a point
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Proj}A$
, we write
$\operatorname{Proj}A$
, we write
![]() $k(\mathfrak{p})$
for the graded residue field at
$k(\mathfrak{p})$
for the graded residue field at
![]() $\mathfrak{p}$
; this is the homogeneous field of fractions of the graded domain
$\mathfrak{p}$
; this is the homogeneous field of fractions of the graded domain
![]() $A/\mathfrak{p}$
. Observe that
$A/\mathfrak{p}$
. Observe that
![]() $k(\mathfrak{p})^{0}$
is a field extension of
$k(\mathfrak{p})^{0}$
is a field extension of
![]() $k$
and
$k$
and
![]() $k(\mathfrak{p})$
is of the form
$k(\mathfrak{p})$
is of the form
![]() $k(\mathfrak{p})^{0}[t^{\pm 1}]$
for some indeterminate
$k(\mathfrak{p})^{0}[t^{\pm 1}]$
for some indeterminate
![]() $t$
over
$t$
over
![]() $k(\mathfrak{p})^{0}$
; see, for example, [Reference Bruns and HerzogBH98, Lemma 1.5.7].
$k(\mathfrak{p})^{0}$
; see, for example, [Reference Bruns and HerzogBH98, Lemma 1.5.7].
Lemma A.1. The degree of
![]() $k(\mathfrak{m})^{0}/k$
is finite for any closed point
$k(\mathfrak{m})^{0}/k$
is finite for any closed point
![]() $\mathfrak{m}$
in
$\mathfrak{m}$
in
![]() $\operatorname{Proj}A$
.
$\operatorname{Proj}A$
.
Proof. One way to verify the lemma is as follows. The Krull dimension of
![]() $A/\mathfrak{m}$
is one so, by noetherian normalisation, there exists a subalgebra
$A/\mathfrak{m}$
is one so, by noetherian normalisation, there exists a subalgebra
![]() $k[t]$
of
$k[t]$
of
![]() $A/\mathfrak{m}$
where
$A/\mathfrak{m}$
where
![]() $t$
is an indeterminate over
$t$
is an indeterminate over
![]() $k$
and the
$k$
and the
![]() $A/\mathfrak{m}$
is finitely generated
$A/\mathfrak{m}$
is finitely generated
![]() $k[t]$
-module. Thus, inverting
$k[t]$
-module. Thus, inverting
![]() $t$
, one gets that
$t$
, one gets that
![]() $(A/\mathfrak{m})_{t}$
is a finitely generated module over the graded field
$(A/\mathfrak{m})_{t}$
is a finitely generated module over the graded field
![]() $k[t^{\pm 1}]$
, and hence isomorphic to
$k[t^{\pm 1}]$
, and hence isomorphic to
![]() $k(\mathfrak{m})$
. The finiteness of the extension
$k(\mathfrak{m})$
. The finiteness of the extension
![]() $k(\mathfrak{m})/k[t^{\pm 1}]$
implies that the extension
$k(\mathfrak{m})/k[t^{\pm 1}]$
implies that the extension
![]() $k(\mathfrak{m})^{0}/k$
of fields is finite.◻
$k(\mathfrak{m})^{0}/k$
of fields is finite.◻
The result below is familiar; cf. [Reference Bruns and HerzogBH98, Proposition 3.6.16].
Lemma A.2. Let
![]() $A$
be as above, let
$A$
be as above, let
![]() $\mathfrak{m}$
be a closed point in
$\mathfrak{m}$
be a closed point in
![]() $\operatorname{Proj}A$
and set
$\operatorname{Proj}A$
and set
![]() $R:=A_{\mathfrak{m}}$
. The
$R:=A_{\mathfrak{m}}$
. The
![]() $R$
-submodule
$R$
-submodule
![]() $I:=\bigcup _{i\geqslant 0}\operatorname{Hom}_{k}^{\ast }(R/\mathfrak{m}^{i},k)$
of
$I:=\bigcup _{i\geqslant 0}\operatorname{Hom}_{k}^{\ast }(R/\mathfrak{m}^{i},k)$
of
![]() $\operatorname{Hom}_{k}^{\ast }(R,k)$
is the injective hull of
$\operatorname{Hom}_{k}^{\ast }(R,k)$
is the injective hull of
![]() $k(\mathfrak{m})$
, and for any
$k(\mathfrak{m})$
, and for any
![]() $\mathfrak{m}$
-torsion
$\mathfrak{m}$
-torsion
![]() $R$
-module
$R$
-module
![]() $N$
, there is a natural isomorphism
$N$
, there is a natural isomorphism
Proof. Set
![]() $K=k(\mathfrak{m})^{0}$
and recall that
$K=k(\mathfrak{m})^{0}$
and recall that
![]() $k(\mathfrak{m})=K[t^{\pm 1}]$
, for some indeterminate
$k(\mathfrak{m})=K[t^{\pm 1}]$
, for some indeterminate
![]() $t$
over
$t$
over
![]() $K$
. Thus, one has isomorphisms of graded
$K$
. Thus, one has isomorphisms of graded
![]() $k(\mathfrak{m})$
-modules
$k(\mathfrak{m})$
-modules
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{k}^{\ast }(k(\mathfrak{m}),k) & \cong & \displaystyle \operatorname{Hom}_{K}^{\ast }(k(\mathfrak{m}),\operatorname{Hom}_{k}(K,k))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{K}^{\ast }(k(\mathfrak{m}),K)\nonumber\\ \displaystyle & \cong & \displaystyle k(\mathfrak{m}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{k}^{\ast }(k(\mathfrak{m}),k) & \cong & \displaystyle \operatorname{Hom}_{K}^{\ast }(k(\mathfrak{m}),\operatorname{Hom}_{k}(K,k))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{K}^{\ast }(k(\mathfrak{m}),K)\nonumber\\ \displaystyle & \cong & \displaystyle k(\mathfrak{m}).\end{eqnarray}$$
The first isomorphism is adjunction, the second holds because
![]() $\operatorname{rank}_{k}K$
is finite, by Lemma A.1, and the last one is a direct verification.
$\operatorname{rank}_{k}K$
is finite, by Lemma A.1, and the last one is a direct verification.
The
![]() $R$
-module
$R$
-module
![]() $\operatorname{Hom}_{k}^{\ast }(R,k)$
is injective and hence so is its
$\operatorname{Hom}_{k}^{\ast }(R,k)$
is injective and hence so is its
![]() $\mathfrak{m}$
-torsion submodule
$\mathfrak{m}$
-torsion submodule
This is precisely the
![]() $R$
-module
$R$
-module
![]() $I$
, by standard adjunction. Thus
$I$
, by standard adjunction. Thus
![]() $I$
must be a direct sum of shifts of injective hulls of
$I$
must be a direct sum of shifts of injective hulls of
![]() $k(\mathfrak{m})$
. It remains to verify that
$k(\mathfrak{m})$
. It remains to verify that
![]() $I$
is in fact just the injective hull of
$I$
is in fact just the injective hull of
![]() $k(\mathfrak{m})$
. To this end, note that for any
$k(\mathfrak{m})$
. To this end, note that for any
![]() $\mathfrak{m}$
-torsion
$\mathfrak{m}$
-torsion
![]() $R$
-module
$R$
-module
![]() $N$
, one has isomorphisms of graded
$N$
, one has isomorphisms of graded
![]() $k(\mathfrak{m})$
-modules
$k(\mathfrak{m})$
-modules
This settles the last assertion in the desired result and also yields the first isomorphism below of graded
![]() $k(\mathfrak{m})$
-modules:
$k(\mathfrak{m})$
-modules:
The second one holds by (A.1). It follows that
![]() $I$
is the injective hull of
$I$
is the injective hull of
![]() $k(\mathfrak{m})$
.◻
$k(\mathfrak{m})$
.◻
The next result, whose proof is rather similar to the one above, gives yet another way to get to the injective hull at a closed point of
![]() $\operatorname{Proj}$
.
$\operatorname{Proj}$
.
Recall that
![]() $I(\mathfrak{p})$
denotes the injective hull of
$I(\mathfrak{p})$
denotes the injective hull of
![]() $A/\mathfrak{p}$
for any
$A/\mathfrak{p}$
for any
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\operatorname{Spec}A$
.
$\operatorname{Spec}A$
.
Lemma A.3. Let
![]() $A\rightarrow B$
be a homomorphism of graded commutative algebras, let
$A\rightarrow B$
be a homomorphism of graded commutative algebras, let
![]() $\mathfrak{m}$
be a closed point in
$\mathfrak{m}$
be a closed point in
![]() $\operatorname{Proj}B$
, and set
$\operatorname{Proj}B$
, and set
![]() $\mathfrak{p}:=\mathfrak{m}\cap A$
. If the extension of residue fields
$\mathfrak{p}:=\mathfrak{m}\cap A$
. If the extension of residue fields
![]() $k(\mathfrak{p})\subseteq k(\mathfrak{m})$
is finite, then the
$k(\mathfrak{p})\subseteq k(\mathfrak{m})$
is finite, then the
![]() $B$
-module
$B$
-module
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{m})}\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p}))$
is the injective hull of
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{m})}\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p}))$
is the injective hull of
![]() $B/\mathfrak{m}$
, and, for any
$B/\mathfrak{m}$
, and, for any
![]() $\mathfrak{m}$
-torsion
$\mathfrak{m}$
-torsion
![]() $B$
-module
$B$
-module
![]() $N$
, adjunction induces an isomorphism
$N$
, adjunction induces an isomorphism
Proof. The
![]() $B$
-module
$B$
-module
![]() $I:=\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{m})}\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p}))$
is injective, for it is the
$I:=\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{m})}\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p}))$
is injective, for it is the
![]() $\mathfrak{m}$
-torsion submodule of the injective
$\mathfrak{m}$
-torsion submodule of the injective
![]() $B$
-module
$B$
-module
![]() $\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p}))$
. As
$\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p}))$
. As
![]() $\mathfrak{m}$
is a closed point,
$\mathfrak{m}$
is a closed point,
![]() $I$
is a direct sum of shifts of copies of
$I$
is a direct sum of shifts of copies of
![]() $I(\mathfrak{m})$
. It remains to make the computation below:
$I(\mathfrak{m})$
. It remains to make the computation below:
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{B}^{\ast }(k(\mathfrak{m}),I) & \cong & \displaystyle \operatorname{Hom}_{B}^{\ast }(k(\mathfrak{m}),\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{A}^{\ast }(k(\mathfrak{m}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{k(\mathfrak{p})}^{\ast }(k(\mathfrak{m}),\operatorname{Hom}_{A}^{\ast }(k(\mathfrak{p}),I(\mathfrak{p})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{k(\mathfrak{p})}^{\ast }(k(\mathfrak{m}),k(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle k(\mathfrak{m}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{B}^{\ast }(k(\mathfrak{m}),I) & \cong & \displaystyle \operatorname{Hom}_{B}^{\ast }(k(\mathfrak{m}),\operatorname{Hom}_{A}^{\ast }(B,I(\mathfrak{p})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{A}^{\ast }(k(\mathfrak{m}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{k(\mathfrak{p})}^{\ast }(k(\mathfrak{m}),\operatorname{Hom}_{A}^{\ast }(k(\mathfrak{p}),I(\mathfrak{p})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{k(\mathfrak{p})}^{\ast }(k(\mathfrak{m}),k(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle k(\mathfrak{m}).\nonumber\end{eqnarray}$$
These are all isomorphisms of
![]() $k(\mathfrak{m})$
-modules. The last one is where the hypothesis that
$k(\mathfrak{m})$
-modules. The last one is where the hypothesis that
![]() $k(\mathfrak{m})/k(\mathfrak{p})$
is finite is required. This implies that
$k(\mathfrak{m})/k(\mathfrak{p})$
is finite is required. This implies that
![]() $I\cong I(\mathfrak{m})$
. Given this, the last isomorphism follows by standard adjunction.◻
$I\cong I(\mathfrak{m})$
. Given this, the last isomorphism follows by standard adjunction.◻