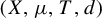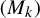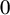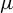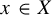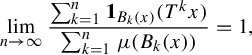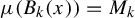1. Introduction
The Poincaré recurrence theorem is a fundamental result in dynamical systems. It states that if
![]() $(X, \mu , T)$
is a separable measure-preserving dynamical system with a Borel probability measure
$(X, \mu , T)$
is a separable measure-preserving dynamical system with a Borel probability measure
![]() $\mu $
, then
$\mu $
, then
![]() $\mu $
-almost every (a.e.) point
$\mu $
-almost every (a.e.) point
![]() $x \in X$
is recurrent, that is, there exists an increasing sequence
$x \in X$
is recurrent, that is, there exists an increasing sequence
![]() $n_i$
such that
$n_i$
such that
![]() $T^{n_i}x \to x$
. Equipping the system with a metric d such that
$T^{n_i}x \to x$
. Equipping the system with a metric d such that
![]() $(X,d)$
is separable and d-open sets are measurable, we may restate the result as
$(X,d)$
is separable and d-open sets are measurable, we may restate the result as
![]() $\liminf _{n \to \infty } d(T^{n}x,x) = 0$
. A natural question to ask is if anything can be said about the rate of convergence. In [Reference Boshernitzan5], Boshernitzan proved that if the Hausdorff measure
$\liminf _{n \to \infty } d(T^{n}x,x) = 0$
. A natural question to ask is if anything can be said about the rate of convergence. In [Reference Boshernitzan5], Boshernitzan proved that if the Hausdorff measure
![]() $\mathcal {H}_\alpha $
is
$\mathcal {H}_\alpha $
is
![]() $\sigma $
-finite on X for some
$\sigma $
-finite on X for some
![]() $\alpha> 0$
, then for
$\alpha> 0$
, then for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
,
$x \in X$
,
Moreover, if
![]() $H_{\alpha }(X) = 0$
, then for
$H_{\alpha }(X) = 0$
, then for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
,
$x\in X$
,
We may state Boshernitzan’s result in a different way: for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
, there exists a constant
$x\in X$
, there exists a constant
![]() $c> 0$
such that
$c> 0$
such that
 $$ \begin{align*} \sum_{k=1}^{\infty} \mathbf{1}_{B(x,ck^{-1/\alpha})}(T^{k}x) = \infty, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{\infty} \mathbf{1}_{B(x,ck^{-1/\alpha})}(T^{k}x) = \infty, \end{align*} $$
where
![]() $B(x,r)$
denotes the open ball with centre x and radius r. Such a sum resembles those that appear in dynamical Borel–Cantelli lemmas for shrinking targets,
$B(x,r)$
denotes the open ball with centre x and radius r. Such a sum resembles those that appear in dynamical Borel–Cantelli lemmas for shrinking targets,
![]() $B_k = B(y_k,r_k)$
, where the centres
$B_k = B(y_k,r_k)$
, where the centres
![]() $y_k$
do not depend on x. A dynamical Borel–Cantelli lemma is a zero-one law that gives conditions on the dynamical system and a sequence of sets
$y_k$
do not depend on x. A dynamical Borel–Cantelli lemma is a zero-one law that gives conditions on the dynamical system and a sequence of sets
![]() $A_k$
such that
$A_k$
such that
![]() $\sum _{k=1}^{\infty } \mathbf {1}_{A_k}(T^{k}x)$
converges or diverges for
$\sum _{k=1}^{\infty } \mathbf {1}_{A_k}(T^{k}x)$
converges or diverges for
![]() $\mu $
-a.e. x, depending on the convergence or divergence of
$\mu $
-a.e. x, depending on the convergence or divergence of
![]() $\sum _{k=1}^{\infty } \mu (A_k)$
. In some cases, it is possible to prove the stronger result, namely that if
$\sum _{k=1}^{\infty } \mu (A_k)$
. In some cases, it is possible to prove the stronger result, namely that if
![]() $\sum _{k=1}^{\infty } \mu (A_k) = \infty $
, then
$\sum _{k=1}^{\infty } \mu (A_k) = \infty $
, then
![]() $\sum _{k=1}^{\infty } \mathbf {1}_{A_k}(T^{k}x) \sim \sum _{k=1}^{\infty } \mu (A_k)$
. Such results are called strong dynamical Borel–Cantelli lemmas.
$\sum _{k=1}^{\infty } \mathbf {1}_{A_k}(T^{k}x) \sim \sum _{k=1}^{\infty } \mu (A_k)$
. Such results are called strong dynamical Borel–Cantelli lemmas.
Although the first dynamical Borel–Cantelli lemma for shrinking targets was proved in 1967 by Philipp [Reference Philipp24], recurrence versions have only recently been studied. The added difficulty arises because of the dependence on x that the sets
![]() $B_{k}(x)$
have. Persson proved in [Reference Persson23] that one can obtain a recurrence version of a strong dynamical Borel–Cantelli lemma for a class of mixing dynamical systems on the unit interval. Other recent recurrence results include those of Hussain et al. [Reference Hussain, Li, Simmons and Wang17], who obtained a zero-one law under the assumptions of mixing conformal maps and Ahlfors regular measures. Under similar assumptions, Kleinbock and Zheng [Reference Kleinbock and Zheng19] prove a zero-one law under Lipschitz twists, which combines recurrence and shrinking targets results. Both these papers put strong assumptions on the underlying measure of the dynamical system, assuming, for example, Ahlfors regularity. For other recent improvements of Boshernitzan’s result, see §6.1.
$B_{k}(x)$
have. Persson proved in [Reference Persson23] that one can obtain a recurrence version of a strong dynamical Borel–Cantelli lemma for a class of mixing dynamical systems on the unit interval. Other recent recurrence results include those of Hussain et al. [Reference Hussain, Li, Simmons and Wang17], who obtained a zero-one law under the assumptions of mixing conformal maps and Ahlfors regular measures. Under similar assumptions, Kleinbock and Zheng [Reference Kleinbock and Zheng19] prove a zero-one law under Lipschitz twists, which combines recurrence and shrinking targets results. Both these papers put strong assumptions on the underlying measure of the dynamical system, assuming, for example, Ahlfors regularity. For other recent improvements of Boshernitzan’s result, see §6.1.
The main result of the paper, Theorem 2.2, is a strong dynamical Borel–Cantelli result for recurrence for dynamical systems satisfying some general conditions. The theorem extends the main theorem of Persson [Reference Persson23], which is stated in Theorem 2.1, concerning a class of mixing dynamical systems on the unit interval to a more general class, that includes, for example, some mixing systems on compact smooth manifolds. Since we consider shrinking balls
![]() $B_k(x)$
for which the radii converge to
$B_k(x)$
for which the radii converge to
![]() $0$
at various rates, Theorem 2.2 is an improvement of Boshernitzan’s result for the systems considered. For now, we state the following result, which is the main application of Theorem 2.2. Equip a smooth manifold with the induced metric.
$0$
at various rates, Theorem 2.2 is an improvement of Boshernitzan’s result for the systems considered. For now, we state the following result, which is the main application of Theorem 2.2. Equip a smooth manifold with the induced metric.
Theorem 1.1. Consider a compact smooth N-dimensional manifold M. Suppose
![]() $f \colon M \to M$
is an Axiom A diffeomorphism that is topologically mixing on a basic set and
$f \colon M \to M$
is an Axiom A diffeomorphism that is topologically mixing on a basic set and
![]() $\mu $
is an equilibrium state corresponding to a Hölder continuous potential on the basic set. Suppose that there exist
$\mu $
is an equilibrium state corresponding to a Hölder continuous potential on the basic set. Suppose that there exist
![]() $c_1>0$
and
$c_1>0$
and
![]() $s> N - 1$
satisfying
$s> N - 1$
satisfying
for all
![]() $x \in M$
and
$x \in M$
and
![]() $r \geq 0$
. Assume further that
$r \geq 0$
. Assume further that
![]() $(M_n)$
is a sequence converging to
$(M_n)$
is a sequence converging to
![]() $0$
satisfying
$0$
satisfying
for some
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
 $$ \begin{align*} \lim_{\alpha \to 1^{+}}\limsup_{n\to \infty} \frac{M_n}{M_{\lfloor \alpha n\rfloor}} = 1. \end{align*} $$
$$ \begin{align*} \lim_{\alpha \to 1^{+}}\limsup_{n\to \infty} \frac{M_n}{M_{\lfloor \alpha n\rfloor}} = 1. \end{align*} $$
Define
![]() $B_n(x)$
to be the ball at x with
$B_n(x)$
to be the ball at x with
![]() $\mu (B_n(x)) = M_n$
. Then,
$\mu (B_n(x)) = M_n$
. Then,
 $$ \begin{align*} \lim_{n \to \infty}\frac{\sum^{n}_{k=1} \mathbf{1}_{B_k(x)}(f^{k}x)} {\sum^{n}_{k=1} \mu(B_k(x))} = 1 \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty}\frac{\sum^{n}_{k=1} \mathbf{1}_{B_k(x)}(f^{k}x)} {\sum^{n}_{k=1} \mu(B_k(x))} = 1 \end{align*} $$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in M$
.
$x \in M$
.
The above theorem applies to hyperbolic toral automorphisms with the Lebesgue measure as the equilibrium measure, which corresponds to the
![]() $0$
potential. It is clear that the Lebesgue measure satisfies the assumption. By perturbing the potential by a Hölder continuous function with small norm, we obtain a different equilibrium state for which the above assumption on the measure holds as well. Equilibrium states that are absolutely continuous with respect to the Lebesgue measure also satisfy the assumption.
$0$
potential. It is clear that the Lebesgue measure satisfies the assumption. By perturbing the potential by a Hölder continuous function with small norm, we obtain a different equilibrium state for which the above assumption on the measure holds as well. Equilibrium states that are absolutely continuous with respect to the Lebesgue measure also satisfy the assumption.
For shrinking targets (non-recurrence), Chernov and Kleinbock [Reference Chernov and Kleinbock9, Theorem 2.4] obtain a strong Borel–Cantelli lemma when T is an Anosov diffeomorphism,
![]() $\mu $
is an equilibrium state given by a Hölder continuous potential, and the targets are eventually quasi-round rectangles.
$\mu $
is an equilibrium state given by a Hölder continuous potential, and the targets are eventually quasi-round rectangles.
1.1. Paper structure
In §2, we state the main result of the paper, namely Theorem 2.2, and give examples of systems satisfying the assumptions. Applications to return times and pointwise dimension are also given. In §3, we prove a series of lemmas establishing properties of the measure
![]() $\mu $
and functions
$\mu $
and functions
![]() $r_n \colon X \to [0,\infty )$
defined as the radius of the balls
$r_n \colon X \to [0,\infty )$
defined as the radius of the balls
![]() $B_n(x)$
. In §4, we obtain estimates for the measure and correlations of the sets
$B_n(x)$
. In §4, we obtain estimates for the measure and correlations of the sets
![]() $E_n = \{x\in X : T^{n}x \in B_n(x)\}$
. This is done in Propositions 4.1 and 4.2 using indicator functions and decay of correlations. Finally, in §5, we use the previous propositions together with Theorem 2.1 to prove Theorem 2.2. Theorem 1.1 then follows once we show that the assumptions of Theorem 2.2 are satisfied. We conclude with final remarks (§6).
$E_n = \{x\in X : T^{n}x \in B_n(x)\}$
. This is done in Propositions 4.1 and 4.2 using indicator functions and decay of correlations. Finally, in §5, we use the previous propositions together with Theorem 2.1 to prove Theorem 2.2. Theorem 1.1 then follows once we show that the assumptions of Theorem 2.2 are satisfied. We conclude with final remarks (§6).
2. Results
2.1. Setting and notation
We say that T preserves the measure
![]() $\mu $
if
$\mu $
if
![]() ${\mu (T^{-1}A) = \mu (A)}$
for all
${\mu (T^{-1}A) = \mu (A)}$
for all
![]() $\mu $
-measurable sets A. From now on,
$\mu $
-measurable sets A. From now on,
![]() $(X,\mu ,T,d)$
will denote a metric measure-preserving system (m.m.p.s.) for which
$(X,\mu ,T,d)$
will denote a metric measure-preserving system (m.m.p.s.) for which
![]() $(X,d)$
is compact,
$(X,d)$
is compact,
![]() $\mu $
is a Borel probability measure and T is a measurable transformation. Given a sequence
$\mu $
is a Borel probability measure and T is a measurable transformation. Given a sequence
![]() $(M_n)$
in
$(M_n)$
in
![]() $[0,1]$
and ignoring issues for now, define the open ball
$[0,1]$
and ignoring issues for now, define the open ball
![]() $B_n(x)$
around x by
$B_n(x)$
around x by
![]() $\mu (B_n(x)) = M_n$
and define the functions
$\mu (B_n(x)) = M_n$
and define the functions
![]() $r_n \colon X \to [0,\infty )$
by
$r_n \colon X \to [0,\infty )$
by
![]() $B(x,r_n(x)) = B_n(x)$
. For each
$B(x,r_n(x)) = B_n(x)$
. For each
![]() $n \in \mathbb {N}$
, define
$n \in \mathbb {N}$
, define
For a set A, we denote the diameter, cardinality and closure of A by
![]() $\operatorname {\mathrm {diam}} A$
,
$\operatorname {\mathrm {diam}} A$
,
![]() $|A|$
and
$|A|$
and
![]() $\overline {A}$
, respectively. By the
$\overline {A}$
, respectively. By the
![]() $\delta $
-neighbourhood of A, we mean the set
$\delta $
-neighbourhood of A, we mean the set
![]() ${A(\delta )\hspace{-0.9pt} =\hspace{-0.9pt} \{x\hspace{-0.9pt} \in\hspace{-0.9pt} X\hspace{-0.9pt} :\hspace{-0.9pt} \operatorname {\mathrm {dist}}(x,A)\hspace{-0.9pt} <\hspace{-0.9pt} \delta \}}$
. For
${A(\delta )\hspace{-0.9pt} =\hspace{-0.9pt} \{x\hspace{-0.9pt} \in\hspace{-0.9pt} X\hspace{-0.9pt} :\hspace{-0.9pt} \operatorname {\mathrm {dist}}(x,A)\hspace{-0.9pt} <\hspace{-0.9pt} \delta \}}$
. For
![]() $a, b \in \mathbb {R}$
, we write
$a, b \in \mathbb {R}$
, we write
![]() $a \lesssim b$
to mean that there exists a constant
$a \lesssim b$
to mean that there exists a constant
![]() $c> 0$
depending only on
$c> 0$
depending only on
![]() $(X,\mu ,T,d)$
such that
$(X,\mu ,T,d)$
such that
![]() $a \leq cb$
. For
$a \leq cb$
. For
![]() $V\subset X$
and
$V\subset X$
and
![]() $\varepsilon> 0$
, let
$\varepsilon> 0$
, let
![]() $P_{\varepsilon }(V)$
denote the packing number of V by balls B of radius
$P_{\varepsilon }(V)$
denote the packing number of V by balls B of radius
![]() $\varepsilon $
. This is the maximum number of pairwise disjoint balls of radius
$\varepsilon $
. This is the maximum number of pairwise disjoint balls of radius
![]() $\varepsilon $
with centres in V. Since X is compact,
$\varepsilon $
with centres in V. Since X is compact,
![]() $P_{\varepsilon }(V)$
is finite for all
$P_{\varepsilon }(V)$
is finite for all
![]() $V\subset X$
and
$V\subset X$
and
![]() $\varepsilon> 0$
. For a compact smooth manifold M, let d denote the induced metric and let
$\varepsilon> 0$
. For a compact smooth manifold M, let d denote the induced metric and let
![]() $\operatorname {\mathrm {Vol}}$
denote the induced volume measure. The injectivity radius of M, which is the largest radius for which the exponential map at every point is a diffeomorphism, is denoted by
$\operatorname {\mathrm {Vol}}$
denote the induced volume measure. The injectivity radius of M, which is the largest radius for which the exponential map at every point is a diffeomorphism, is denoted by
![]() $\operatorname {\mathrm {inj}}_M$
. Since M is compact,
$\operatorname {\mathrm {inj}}_M$
. Since M is compact,
![]() $\operatorname {\mathrm {inj}}_M> 0$
(see for instance [Reference Chavel8]).
$\operatorname {\mathrm {inj}}_M> 0$
(see for instance [Reference Chavel8]).
Note that the open balls
![]() $B_n(x)$
and radii
$B_n(x)$
and radii
![]() $r_n(x)$
may not exist for some
$r_n(x)$
may not exist for some
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $x \in X$
. Sufficient conditions on
$x \in X$
. Sufficient conditions on
![]() $\mu $
, x and
$\mu $
, x and
![]() $(M_n)$
, for which
$(M_n)$
, for which
![]() $B_n(x)$
and
$B_n(x)$
and
![]() $r_n(x)$
exist, are given in Lemma 3.1. Notice that for a zero-one law, one would prove that
$r_n(x)$
exist, are given in Lemma 3.1. Notice that for a zero-one law, one would prove that
![]() $\limsup _{n\to \infty }E_n$
has either zero or full measure. Furthermore, in the shrinking target case, when one considers fixed targets
$\limsup _{n\to \infty }E_n$
has either zero or full measure. Furthermore, in the shrinking target case, when one considers fixed targets
![]() $B_n = B(y_n,r_n)$
, the corresponding sets are
$B_n = B(y_n,r_n)$
, the corresponding sets are
![]() $\tilde {E}_n = \{ x \in X : T^{n}x \in B_n\} = T^{-n} B_n$
and we can use the invariance of the measure
$\tilde {E}_n = \{ x \in X : T^{n}x \in B_n\} = T^{-n} B_n$
and we can use the invariance of the measure
![]() $\mu $
to conclude that
$\mu $
to conclude that
![]() $\mu (\tilde {E}_n) = M_n$
. However, in the recurrence case, when the targets depend on x, we instead settle for estimates on the measure and correlations of the sets
$\mu (\tilde {E}_n) = M_n$
. However, in the recurrence case, when the targets depend on x, we instead settle for estimates on the measure and correlations of the sets
![]() $E_n$
. We do so in Proposition 4.3 using decay of multiple correlations as our main tool. We state the definition of decay of multiple correlations for Hölder continuous observables as it is the form most commonly found in the literature; however, for our purposes, we only require decay of correlations for Lipschitz continuous observables.
$E_n$
. We do so in Proposition 4.3 using decay of multiple correlations as our main tool. We state the definition of decay of multiple correlations for Hölder continuous observables as it is the form most commonly found in the literature; however, for our purposes, we only require decay of correlations for Lipschitz continuous observables.
Definition 2.1. (r-Fold decay of correlations)
For an m.m.p.s
![]() $(X,\mu ,T,d)$
,
$(X,\mu ,T,d)$
,
![]() $r \in \mathbb {N}$
and
$r \in \mathbb {N}$
and
![]() $\theta \in (0,1]$
, we say that r-fold correlations decay exponentially for
$\theta \in (0,1]$
, we say that r-fold correlations decay exponentially for
![]() $\theta $
-Hölder continuous observables if there exist constants
$\theta $
-Hölder continuous observables if there exist constants
![]() $c_1>0$
and
$c_1>0$
and
![]() $\tau \in (0,1)$
such that for all
$\tau \in (0,1)$
such that for all
![]() $\theta $
-Hölder continuous functions
$\theta $
-Hölder continuous functions
![]() $\varphi _k : X \to \mathbb {R}$
,
$\varphi _k : X \to \mathbb {R}$
,
![]() $k=0,\dotsc ,r-1$
, and integers
$k=0,\dotsc ,r-1$
, and integers
![]() $0 = n_0 < n_1 < \cdots < n_{r-1}$
,
$0 = n_0 < n_1 < \cdots < n_{r-1}$
,
 $$ \begin{align*} \Bigl| \int \prod_{k=0}^{r-1} \varphi_k \circ T^{n_k} \mathop{}\!d\mu - \prod_{k=0}^{r-1} \int \varphi_k \mathop{}\!d\mu \Bigr| \leq c_1 e^{-\tau n} \prod_{k=0}^{r-1} \|\varphi_k\|_{\theta}, \end{align*} $$
$$ \begin{align*} \Bigl| \int \prod_{k=0}^{r-1} \varphi_k \circ T^{n_k} \mathop{}\!d\mu - \prod_{k=0}^{r-1} \int \varphi_k \mathop{}\!d\mu \Bigr| \leq c_1 e^{-\tau n} \prod_{k=0}^{r-1} \|\varphi_k\|_{\theta}, \end{align*} $$
where
![]() $n = \min \{n_{i+1} - n_{i}\}$
and
$n = \min \{n_{i+1} - n_{i}\}$
and
 $$ \begin{align*} \|\varphi\|_{\theta} = \sup_{x\neq y} \frac{|\varphi(x) - \varphi(y)|}{d(x,y)^{\theta}} + \|\varphi\|_{\infty}. \end{align*} $$
$$ \begin{align*} \|\varphi\|_{\theta} = \sup_{x\neq y} \frac{|\varphi(x) - \varphi(y)|}{d(x,y)^{\theta}} + \|\varphi\|_{\infty}. \end{align*} $$
It is well known that if M is a compact smooth manifold, f an Axiom A diffeomorphism that is topologically mixing when restricted to a basic set
![]() $\Omega $
, and
$\Omega $
, and
![]() $\varphi \colon \Omega \to \mathbb {R}$
Hölder continuous, then there exists a unique equilibrium state
$\varphi \colon \Omega \to \mathbb {R}$
Hölder continuous, then there exists a unique equilibrium state
![]() $\mu _\varphi $
for
$\mu _\varphi $
for
![]() $\varphi $
such that two-fold correlations decay exponentially for
$\varphi $
such that two-fold correlations decay exponentially for
![]() $\theta $
-Hölder continuous observables for all
$\theta $
-Hölder continuous observables for all
![]() $\theta \in (0,1]$
(see [Reference Bowen6]). In the same setting, Kotani and Sunada essentially prove in [Reference Kotani and Sunada20, Proposition 3.1] that, in fact, r-fold correlations decay exponentially for
$\theta \in (0,1]$
(see [Reference Bowen6]). In the same setting, Kotani and Sunada essentially prove in [Reference Kotani and Sunada20, Proposition 3.1] that, in fact, r-fold correlations decay exponentially for
![]() $\theta $
-Hölder continuous observables for all
$\theta $
-Hölder continuous observables for all
![]() $r \geq 1$
and
$r \geq 1$
and
![]() $\theta \in (0,1]$
. A similar result is proven in [Reference Chernov and Markarian10, Theorem 7.41] for billiards with bounded horizon and no corners, and for dynamically Hölder continuous functions – a class of functions that includes Hölder continuous functions. This result can be extended to billiards with no corners and unbounded horizon, and billiards with some corners and bounded horizon. Dolgopyat [Reference Dolgopyat12] proves that multiple correlations decay exponentially for partially hyperbolic systems that are ‘strongly u-transitive with exponential rate’. Dolgopyat lists systems in §6 of his paper for which this property holds: some time one maps of Anosov flows, quasi-hyperbolic toral automorphisms, some translations on homogeneous spaces and mostly contracting diffeomorphisms on three-dimensional manifolds. A similar property referred to as ‘Property
$\theta \in (0,1]$
. A similar result is proven in [Reference Chernov and Markarian10, Theorem 7.41] for billiards with bounded horizon and no corners, and for dynamically Hölder continuous functions – a class of functions that includes Hölder continuous functions. This result can be extended to billiards with no corners and unbounded horizon, and billiards with some corners and bounded horizon. Dolgopyat [Reference Dolgopyat12] proves that multiple correlations decay exponentially for partially hyperbolic systems that are ‘strongly u-transitive with exponential rate’. Dolgopyat lists systems in §6 of his paper for which this property holds: some time one maps of Anosov flows, quasi-hyperbolic toral automorphisms, some translations on homogeneous spaces and mostly contracting diffeomorphisms on three-dimensional manifolds. A similar property referred to as ‘Property
![]() $(\mathcal {P}_t)$
’ for real
$(\mathcal {P}_t)$
’ for real
![]() $t \geq 1$
is used by Pène in [Reference Pène22]. It is stated that when
$t \geq 1$
is used by Pène in [Reference Pène22]. It is stated that when
![]() $t> 1$
, property
$t> 1$
, property
![]() $(\mathcal {P}_t)$
holds for dynamical systems to which one can apply Young’s method in [Reference Young25].
$(\mathcal {P}_t)$
holds for dynamical systems to which one can apply Young’s method in [Reference Young25].
We state some assumptions on the system
![]() $(X,\mu ,T,d)$
and the sequence
$(X,\mu ,T,d)$
and the sequence
![]() $(M_n)$
that are used to obtain our result.
$(M_n)$
that are used to obtain our result.
Assumption 1. There exists
![]() $\varepsilon> 0$
such that
$\varepsilon> 0$
such that
and
 $$ \begin{align*} \lim_{\alpha \to 1^{+}}\limsup_{n \to \infty} \frac{M_n}{M_{\lfloor \alpha n \rfloor}} = 1. \end{align*} $$
$$ \begin{align*} \lim_{\alpha \to 1^{+}}\limsup_{n \to \infty} \frac{M_n}{M_{\lfloor \alpha n \rfloor}} = 1. \end{align*} $$
Assumption 2. There exists
![]() $s>0$
such that for all
$s>0$
such that for all
![]() $x \in X$
and
$x \in X$
and
![]() $r>0$
,
$r>0$
,
Assumption 3. There exists positive constants
![]() $\rho _0$
and
$\rho _0$
and
![]() $\alpha _0$
such that for all
$\alpha _0$
such that for all
![]() $x \in X$
and
$x \in X$
and
![]() ${0 < \varepsilon < \rho \leq \rho _0}$
,
${0 < \varepsilon < \rho \leq \rho _0}$
,
Assumption 4. There exists positive constants K and
![]() $\varepsilon _0$
such that for any
$\varepsilon _0$
such that for any
![]() $\varepsilon \in (0,\varepsilon _0)$
, the packing number of X satisfies
$\varepsilon \in (0,\varepsilon _0)$
, the packing number of X satisfies
Assumption 1 is needed for technical reasons that are explicit in [Reference Persson23, Lemma 2]. Assumption 2 is a standard assumption. Assumption 3 is more restrictive; however, in some cases, it can be deduced from Assumption 2. Assumption 4 holds for very general spaces, e.g. all compact smooth manifolds. As we will see in the proof of Theorem 1.1, Assumptions 3 and 4 hold when X is a compact smooth N-dimensional manifold and
![]() $s> N - 1$
. Assumption 3 is also used in [Reference Haydn, Nicol, Persson and Vaienti15], stated as Assumption B, in which the authors outline spaces that satisfy the assumption. For instance, the assumption is satisfied by dispersing billiard systems, compact group extensions of Anosov systems, a class of Lozi maps and one-dimensional non-uniformly expanding interval maps with invariant probability measure
$s> N - 1$
. Assumption 3 is also used in [Reference Haydn, Nicol, Persson and Vaienti15], stated as Assumption B, in which the authors outline spaces that satisfy the assumption. For instance, the assumption is satisfied by dispersing billiard systems, compact group extensions of Anosov systems, a class of Lozi maps and one-dimensional non-uniformly expanding interval maps with invariant probability measure
![]() $d\mu = h\mathop {}\!d\unicode{x3bb} $
, where
$d\mu = h\mathop {}\!d\unicode{x3bb} $
, where
![]() $\unicode{x3bb} $
is the Lebesgue measure and
$\unicode{x3bb} $
is the Lebesgue measure and
![]() $h \in L^{1+\delta }(\unicode{x3bb} )$
for some
$h \in L^{1+\delta }(\unicode{x3bb} )$
for some
![]() $\delta> 0$
.
$\delta> 0$
.
Assumption 4 is used in the following construction of a partition. Let
![]() $\varepsilon < \varepsilon _0$
and let
$\varepsilon < \varepsilon _0$
and let
![]() $\{B(x_k,\varepsilon )\}_{k=1}^{L}$
be a maximal
$\{B(x_k,\varepsilon )\}_{k=1}^{L}$
be a maximal
![]() $\varepsilon $
-packing of X, that is,
$\varepsilon $
-packing of X, that is,
![]() $L = P_{\varepsilon }(X)$
. Then,
$L = P_{\varepsilon }(X)$
. Then,
![]() $\{B(x_k,2\varepsilon )\}_{k=1}^{L}$
covers X. Indeed, for any
$\{B(x_k,2\varepsilon )\}_{k=1}^{L}$
covers X. Indeed, for any
![]() $x \in X$
, we must have that
$x \in X$
, we must have that
![]() $d(x,x_k) < 2\varepsilon $
for some k, for we could otherwise add
$d(x,x_k) < 2\varepsilon $
for some k, for we could otherwise add
![]() $B(x,\varepsilon )$
to the packing, which would contradict our maximality assumption. Now, let
$B(x,\varepsilon )$
to the packing, which would contradict our maximality assumption. Now, let
![]() $A_1 = B(x_1,2\varepsilon )$
and recursively define
$A_1 = B(x_1,2\varepsilon )$
and recursively define
 $$ \begin{align} A_k = B(x_k,2\varepsilon) \setminus \bigcup_{i=1}^{k-1} B(x_i,2\varepsilon) \end{align} $$
$$ \begin{align} A_k = B(x_k,2\varepsilon) \setminus \bigcup_{i=1}^{k-1} B(x_i,2\varepsilon) \end{align} $$
for
![]() $k = 2,\dotsc ,L$
. Then,
$k = 2,\dotsc ,L$
. Then,
![]() $\{A_k\}_{k=1}^{L}$
partitions X and satisfies
$\{A_k\}_{k=1}^{L}$
partitions X and satisfies
![]() $\operatorname {\mathrm {diam}} A_k < 4\varepsilon $
. By Assumption 4,
$\operatorname {\mathrm {diam}} A_k < 4\varepsilon $
. By Assumption 4,
![]() $L \lesssim \varepsilon ^{-K}$
.
$L \lesssim \varepsilon ^{-K}$
.
As previously mentioned, Theorem 2.2 extends Persson’s result in [Reference Persson23] by relaxing the conditions on
![]() $(X,\mu ,T,d)$
. In [Reference Persson23], it is assumed that
$(X,\mu ,T,d)$
. In [Reference Persson23], it is assumed that
![]() $X = [0,1]$
and that
$X = [0,1]$
and that
![]() $T \colon [0,1] \to [0,1]$
preserves a measure
$T \colon [0,1] \to [0,1]$
preserves a measure
![]() $\mu $
for which (two-fold) correlations decay exponentially for
$\mu $
for which (two-fold) correlations decay exponentially for
![]() $L_1$
against
$L_1$
against
![]() $BV$
functions. This is satisfied, for example, when T is a piecewise uniformly expanding map and
$BV$
functions. This is satisfied, for example, when T is a piecewise uniformly expanding map and
![]() $\mu $
is a Gibbs measure. That correlations decay exponentially for
$\mu $
is a Gibbs measure. That correlations decay exponentially for
![]() $L_1$
against
$L_1$
against
![]() $BV$
functions allows one to directly apply it to indicator functions. As established, when T is an Axiom A diffeomorphism defined on a manifold X, multiple correlations decay exponentially for Hölder continuous functions. Thus, we may not directly apply the result to indicator functions and must use an approximation argument, complicating the proof. That
$BV$
functions allows one to directly apply it to indicator functions. As established, when T is an Axiom A diffeomorphism defined on a manifold X, multiple correlations decay exponentially for Hölder continuous functions. Thus, we may not directly apply the result to indicator functions and must use an approximation argument, complicating the proof. That
![]() $\mu $
is non-atomic in [Reference Persson23] translates in Theorem 1.1 to
$\mu $
is non-atomic in [Reference Persson23] translates in Theorem 1.1 to
![]() $\mu $
satisfying Assumption 2 with
$\mu $
satisfying Assumption 2 with
![]() $s> \dim M - 1$
. Furthermore, Assumption 2 for
$s> \dim M - 1$
. Furthermore, Assumption 2 for
![]() $\mu $
and Assumption 1 for
$\mu $
and Assumption 1 for
![]() $(M_n)$
remain unchanged. As it will be of use later, we restate the main result of [Reference Persson23] by combining Proposition 1 and the main theorem. We do so to have a more general statement suitable for our use.
$(M_n)$
remain unchanged. As it will be of use later, we restate the main result of [Reference Persson23] by combining Proposition 1 and the main theorem. We do so to have a more general statement suitable for our use.
Theorem 2.1. (Persson [Reference Persson23])
Let
![]() $(X, \mu , T, d)$
be an m.m.p.s.,
$(X, \mu , T, d)$
be an m.m.p.s.,
![]() $(M_n)$
a sequence in
$(M_n)$
a sequence in
![]() $[0,1]$
satisfying Assumption 1 and
$[0,1]$
satisfying Assumption 1 and
![]() $\mu $
a measure satisfying Assumption 2. Define
$\mu $
a measure satisfying Assumption 2. Define
![]() $B_n(x)$
to be the ball around x such that
$B_n(x)$
to be the ball around x such that
![]() $\mu (B_n(x)) = M_n$
and let
$\mu (B_n(x)) = M_n$
and let
![]() $E_n = \{x \in X : T^{n}x \in B_n(x)\}$
. Suppose that there exists
$E_n = \{x \in X : T^{n}x \in B_n(x)\}$
. Suppose that there exists
![]() $C,\eta> 0$
such that for all
$C,\eta> 0$
such that for all
![]() $n,m \in \mathbb {N}$
,
$n,m \in \mathbb {N}$
,
and
Then,
 $$ \begin{align*} \lim_{n \to \infty}\frac{\sum^{n}_{k=1} \mathbf{1}_{B_k(x)}(T^{k}x)} {\sum^{n}_{k=1} \mu(B_k(x))} = 1 \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty}\frac{\sum^{n}_{k=1} \mathbf{1}_{B_k(x)}(T^{k}x)} {\sum^{n}_{k=1} \mu(B_k(x))} = 1 \end{align*} $$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
.
$x \in X$
.
In this paper, we establish inequalities in equations (2.2) and (2.3) for systems satisfying multiple decorrelation for Lipschitz continuous observables and conclude a strong Borel–Cantelli lemma for recurrence.
2.2. Main result
The main result of the paper is the following theorem.
Theorem 2.2. Let
![]() $(X,\mu ,T,d)$
be an m.m.p.s. for which three-fold correlations decay exponentially for Lipschitz continuous observables and such that Assumptions 2–4 hold. Suppose further that
$(X,\mu ,T,d)$
be an m.m.p.s. for which three-fold correlations decay exponentially for Lipschitz continuous observables and such that Assumptions 2–4 hold. Suppose further that
![]() $(M_n)$
is a sequence in
$(M_n)$
is a sequence in
![]() $[0,1]$
converging to
$[0,1]$
converging to
![]() $0$
and satisfying Assumption 1. Then,
$0$
and satisfying Assumption 1. Then,
 $$ \begin{align*} \lim_{n \to \infty}\frac{\sum^{n}_{k=1} \mathbf{1}_{B_k(x)}(T^{k}x)} {\sum^{n}_{k=1} \mu(B_k(x))} = 1 \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty}\frac{\sum^{n}_{k=1} \mathbf{1}_{B_k(x)}(T^{k}x)} {\sum^{n}_{k=1} \mu(B_k(x))} = 1 \end{align*} $$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
.
$x \in X$
.
Remark 2.3. Although we consider open balls
![]() $B_k(x)$
for our results, we only require control over the measure of
$B_k(x)$
for our results, we only require control over the measure of
![]() $B_k(x)$
and its
$B_k(x)$
and its
![]() $\delta $
-neighbourhoods. Thus, it is possible to substitute the open balls for closed balls or other neighbourhoods of x, as long as one retains similar control of the sets as stated in Assumptions 2 and 3. Furthermore, it is possible to relax the condition that
$\delta $
-neighbourhoods. Thus, it is possible to substitute the open balls for closed balls or other neighbourhoods of x, as long as one retains similar control of the sets as stated in Assumptions 2 and 3. Furthermore, it is possible to relax the condition that
![]() $(M_n)$
converges to
$(M_n)$
converges to
![]() $0$
as long as one can ensure that
$0$
as long as one can ensure that
![]() $r_n \leq \rho _0$
on
$r_n \leq \rho _0$
on
![]() $\operatorname {\mathrm {supp}}\mu $
for large n.
$\operatorname {\mathrm {supp}}\mu $
for large n.
After proving that Assumptions 3 and 4 hold when X is a compact smooth manifold and
![]() $\mu $
satisfies Assumption 2 for
$\mu $
satisfies Assumption 2 for
![]() $s> N - 1$
, we apply the above result to Axiom A diffeomorphisms and obtain Theorem 1.1. In §6.2, we list some systems that satisfy Assumptions 2–4, but it remains to show that some of these systems satisfy three-fold decay of correlations.
$s> N - 1$
, we apply the above result to Axiom A diffeomorphisms and obtain Theorem 1.1. In §6.2, we list some systems that satisfy Assumptions 2–4, but it remains to show that some of these systems satisfy three-fold decay of correlations.
2.3. Return times corollary
Define the hitting time of
![]() $x\in X$
into a set B by
$x\in X$
into a set B by
When
![]() $x \in B$
, we call
$x \in B$
, we call
![]() $\tau _{B}(x)$
the return time of x into B. In 2007, Galatolo and Kim [Reference Galatolo and Kim13] showed that if a system satisfies a strong Borel–Cantelli lemma for shrinking targets with any centre, then for every
$\tau _{B}(x)$
the return time of x into B. In 2007, Galatolo and Kim [Reference Galatolo and Kim13] showed that if a system satisfies a strong Borel–Cantelli lemma for shrinking targets with any centre, then for every
![]() $y\in X$
, the hitting times satisfy
$y\in X$
, the hitting times satisfy
 $$ \begin{align*} \lim_{r \to 0} \frac{\log \tau_{\overline{B}(y,r)}(x)} {-\log \mu(\overline{B}(y,r))} = 1 \end{align*} $$
$$ \begin{align*} \lim_{r \to 0} \frac{\log \tau_{\overline{B}(y,r)}(x)} {-\log \mu(\overline{B}(y,r))} = 1 \end{align*} $$
for
![]() $\mu $
-a.e. x. In our case, the proof translates directly to return times (see the corollary in [Reference Persson23] for a simplified proof).
$\mu $
-a.e. x. In our case, the proof translates directly to return times (see the corollary in [Reference Persson23] for a simplified proof).
Corollary 2.4. Under the assumptions of Theorem 2.2,
for
![]() $\mu $
-a.e. x.
$\mu $
-a.e. x.
The above corollary has an application to the pointwise dimension of
![]() $\mu $
. For each
$\mu $
. For each
![]() $x \in X$
, define the lower and upper pointwise dimensions of
$x \in X$
, define the lower and upper pointwise dimensions of
![]() $\mu $
at x by
$\mu $
at x by
and the lower and upper recurrence rates of x by
When T is a Borel measurable transformation that preserves a Borel probability measure
![]() $\mu $
and
$\mu $
and
![]() $X \subset \mathbb {R}^{N}$
is any measurable set, Barreira and Saussol [Reference Barreira and Saussol4, Theorem 1] proved that
$X \subset \mathbb {R}^{N}$
is any measurable set, Barreira and Saussol [Reference Barreira and Saussol4, Theorem 1] proved that
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
. Using Corollary 2.4, we obtain that for
$x\in X$
. Using Corollary 2.4, we obtain that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
,
$x\in X$
,
whenever the system satisfies a strong Borel-Cantelli lemma for recurrence. Contrast the above result with [Reference Barreira and Saussol4, Theorem 4], which states that equation (2.4) holds when
![]() $\mu $
has long return times, that is, for
$\mu $
has long return times, that is, for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
and sufficiently small
$x\in X$
and sufficiently small
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
 $$ \begin{align*} \liminf_{r \to 0} \frac{\log (\mu \{y\in B(x,r) : \tau_{B(x,r)}(y) \leq \mu(B(x,r))^{-1+\varepsilon}\})} {\log \mu(B(x,r))}> 1. \end{align*} $$
$$ \begin{align*} \liminf_{r \to 0} \frac{\log (\mu \{y\in B(x,r) : \tau_{B(x,r)}(y) \leq \mu(B(x,r))^{-1+\varepsilon}\})} {\log \mu(B(x,r))}> 1. \end{align*} $$
Furthermore, if X is a compact smooth manifold, then [Reference Barreira and Saussol4, Theorem 5] states that if the equilibrium measure
![]() $\mu $
is ergodic and supported on a locally maximum hyperbolic set of a
$\mu $
is ergodic and supported on a locally maximum hyperbolic set of a
![]() $C^{1+\alpha }$
diffeomorphism, then
$C^{1+\alpha }$
diffeomorphism, then
![]() $\mu $
has long return times and
$\mu $
has long return times and
![]() $\underline {R}(x) = \overline {R}(x) = \dim _{H}\mu $
for
$\underline {R}(x) = \overline {R}(x) = \dim _{H}\mu $
for
![]() $\mu $
-a.e. x. However, Barreira, Pesin and Schmeling [Reference Barreira, Pesin and Schmeling3] prove that if f is a
$\mu $
-a.e. x. However, Barreira, Pesin and Schmeling [Reference Barreira, Pesin and Schmeling3] prove that if f is a
![]() $C^{1+\alpha }$
diffeomorphism on a smooth compact manifold and
$C^{1+\alpha }$
diffeomorphism on a smooth compact manifold and
![]() $\mu $
a hyperbolic f-invariant compactly supported ergodic Borel probability measure, then
$\mu $
a hyperbolic f-invariant compactly supported ergodic Borel probability measure, then
![]() $\underline {d}_{\mu }(x) = \overline {d}_\mu (x) = \dim _H\mu $
for
$\underline {d}_{\mu }(x) = \overline {d}_\mu (x) = \dim _H\mu $
for
![]() $\mu $
-a.e. x.
$\mu $
-a.e. x.
3. Properties of
 $\mu $
and
$\mu $
and
 $r_n$
$r_n$
As previously mentioned, the functions
![]() $r_n \colon X \to [0,\infty )$
may not be well defined since it may be the case that the measure
$r_n \colon X \to [0,\infty )$
may not be well defined since it may be the case that the measure
![]() $\mu $
assigns positive measure to the boundary of an open ball. Lemma 3.1 gives sufficient conditions on x,
$\mu $
assigns positive measure to the boundary of an open ball. Lemma 3.1 gives sufficient conditions on x,
![]() $(M_n)$
and
$(M_n)$
and
![]() $\mu $
for
$\mu $
for
![]() $r_n(x)$
to be well defined. Lemma 3.2 gives conditions for which
$r_n(x)$
to be well defined. Lemma 3.2 gives conditions for which
![]() $r_n(x)$
converges uniformly to
$r_n(x)$
converges uniformly to
![]() $0$
, which allows us to use Assumption 3. Lemma 3.3 shows that we can use Assumption 3 to control the
$0$
, which allows us to use Assumption 3. Lemma 3.3 shows that we can use Assumption 3 to control the
![]() $\delta $
-neighbourhood of the sets
$\delta $
-neighbourhood of the sets
![]() $A_k$
in equation (2.1). Recall that
$A_k$
in equation (2.1). Recall that
![]() $(X,d)$
is a compact space and
$(X,d)$
is a compact space and
![]() $(M_n)$
is a sequence in
$(M_n)$
is a sequence in
![]() $[0,1]$
.
$[0,1]$
.
Lemma 3.1. If
![]() $\mu $
has no atoms and satisfies
$\mu $
has no atoms and satisfies
![]() $\mu (B) = \mu (\overline {B})$
for all open balls
$\mu (B) = \mu (\overline {B})$
for all open balls
![]() $B \subset X$
, then for each
$B \subset X$
, then for each
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $x \in X$
, there exists
$x \in X$
, there exists
![]() $r_n(x) \in [0,\infty )$
such that
$r_n(x) \in [0,\infty )$
such that
Moreover, for each
![]() $n \in \mathbb {N}$
, the function
$n \in \mathbb {N}$
, the function
![]() $r_n \colon X \to [0,\infty )$
is Lipschitz continuous with
$r_n \colon X \to [0,\infty )$
is Lipschitz continuous with
for all
![]() $x,y \in X$
.
$x,y \in X$
.
Proof. Let
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $x \in X$
. The infimum
$x \in X$
. The infimum
exists since the set contains
![]() $\operatorname {\mathrm {diam}} X \in (0,\infty )$
and has a lower bound. If
$\operatorname {\mathrm {diam}} X \in (0,\infty )$
and has a lower bound. If
![]() $r_n(x) = 0$
, then, since
$r_n(x) = 0$
, then, since
![]() $\mu $
is non-atomic, it must be that
$\mu $
is non-atomic, it must be that
![]() $M_n = 0$
, in which case
$M_n = 0$
, in which case
![]() $\mu (B(x,r_n(x))) = M_n$
. If
$\mu (B(x,r_n(x))) = M_n$
. If
![]() $r_n(x)> 0$
, then for all
$r_n(x)> 0$
, then for all
![]() $k> 0$
, we have that
$k> 0$
, we have that
![]() $\mu (B(x,r_n(x) + {1}/{k})) \geq M_n$
and thus
$\mu (B(x,r_n(x) + {1}/{k})) \geq M_n$
and thus
![]() $\mu (\overline {B(x,r_n(x))}) \geq M_n$
. Similarly,
$\mu (\overline {B(x,r_n(x))}) \geq M_n$
. Similarly,
![]() $\mu (B(x,r_n(x))) \leq M_n$
. Hence, by using our assumption, we obtain that
$\mu (B(x,r_n(x))) \leq M_n$
. Hence, by using our assumption, we obtain that
which proves equation (3.1).
To show that
![]() $r_n$
is Lipschitz continuous, let
$r_n$
is Lipschitz continuous, let
![]() $x, y \in X$
and let
$x, y \in X$
and let
![]() $\delta = d(x,y)$
. Then,
$\delta = d(x,y)$
. Then,
![]() $B(y,r_n(y)) \subset B(x,r_n(y) + \delta )$
and
$B(y,r_n(y)) \subset B(x,r_n(y) + \delta )$
and
Hence,
![]() $r_n(x) \leq r_n(y) + \delta $
. We conclude that
$r_n(x) \leq r_n(y) + \delta $
. We conclude that
![]() $|r_n(x) - r_n(y)| \leq \delta $
by symmetry.
$|r_n(x) - r_n(y)| \leq \delta $
by symmetry.
The assumption
![]() $\mu (B) = \mu (\overline {B})$
for sufficiently small radii follows from Assumption 3.
$\mu (B) = \mu (\overline {B})$
for sufficiently small radii follows from Assumption 3.
Lemma 3.2. If
![]() $\lim _{n \to \infty }M_n = 0$
, then
$\lim _{n \to \infty }M_n = 0$
, then
![]() $\lim _{n \to \infty }r_n = 0$
uniformly on
$\lim _{n \to \infty }r_n = 0$
uniformly on
![]() $\operatorname {\mathrm {supp}} \mu $
.
$\operatorname {\mathrm {supp}} \mu $
.
Proof. We first prove pointwise convergence on
![]() $\operatorname {\mathrm {supp}} \mu $
. Let
$\operatorname {\mathrm {supp}} \mu $
. Let
![]() $x\in X$
and suppose that
$x\in X$
and suppose that
![]() $r_n(x)$
does not converge to
$r_n(x)$
does not converge to
![]() $0$
as
$0$
as
![]() $n \to \infty $
for some
$n \to \infty $
for some
![]() $x \in X$
. Then there exists
$x \in X$
. Then there exists
![]() $\varepsilon> 0$
and an increasing sequence
$\varepsilon> 0$
and an increasing sequence
![]() $(n_i)$
such that
$(n_i)$
such that
![]() $r_{n_i}(x)> \varepsilon $
and
$r_{n_i}(x)> \varepsilon $
and
for all i. Taking the limit as
![]() $i \to \infty $
gives us
$i \to \infty $
gives us
![]() $\mu ( B(x,\varepsilon ) ) = 0$
. Hence,
$\mu ( B(x,\varepsilon ) ) = 0$
. Hence,
![]() $x \notin \operatorname {\mathrm {supp}} \mu $
.
$x \notin \operatorname {\mathrm {supp}} \mu $
.
Now suppose that
![]() $r_n$
does not converge to
$r_n$
does not converge to
![]() $0$
uniformly on
$0$
uniformly on
![]() $\operatorname {\mathrm {supp}} \mu $
. Then there exist
$\operatorname {\mathrm {supp}} \mu $
. Then there exist
![]() $\varepsilon> 0$
, an increasing sequence
$\varepsilon> 0$
, an increasing sequence
![]() $(n_i)$
and points
$(n_i)$
and points
![]() $x_i \in \operatorname {\mathrm {supp}} \mu $
such that
$x_i \in \operatorname {\mathrm {supp}} \mu $
such that
![]() $r_{n_i}(x_i)> \varepsilon $
for all
$r_{n_i}(x_i)> \varepsilon $
for all
![]() $i> 0$
. Since
$i> 0$
. Since
![]() $\operatorname {\mathrm {supp}} \mu $
is compact, we may assume that
$\operatorname {\mathrm {supp}} \mu $
is compact, we may assume that
![]() $x_i$
converges to some
$x_i$
converges to some
![]() $x \in \operatorname {\mathrm {supp}} \mu $
. By Lipschitz continuity,
$x \in \operatorname {\mathrm {supp}} \mu $
. By Lipschitz continuity,
Thus,
which contradicts the fact that we have pointwise convergence to
![]() $0$
on
$0$
on
![]() $\operatorname {\mathrm {supp}}\mu $
.
$\operatorname {\mathrm {supp}}\mu $
.
Lemma 3.3. Suppose that
![]() $\mu $
satisfies Assumption 3 and that
$\mu $
satisfies Assumption 3 and that
![]() $(X,d)$
satisfies Assumption 4. Let
$(X,d)$
satisfies Assumption 4. Let
![]() $\rho < \min \{\varepsilon _0, \rho _0\}$
and consider the partition
$\rho < \min \{\varepsilon _0, \rho _0\}$
and consider the partition
![]() $\{A_k\}_{k=1}^{L}$
given in equation (2.1) where
$\{A_k\}_{k=1}^{L}$
given in equation (2.1) where
![]() $\varepsilon = {\rho }/{2}$
. Then for each k and
$\varepsilon = {\rho }/{2}$
. Then for each k and
![]() $\delta < \rho $
,
$\delta < \rho $
,
Proof. Let
![]() $0 < \delta < \rho \leq \rho _0$
and fix k. It suffices to prove that
$0 < \delta < \rho \leq \rho _0$
and fix k. It suffices to prove that
![]() $A_k(\delta ) \setminus A_k$
is contained in
$A_k(\delta ) \setminus A_k$
is contained in
 $$ \begin{align*} (B(x_k,\rho+\delta) \setminus B(x_k,\rho)) \cup \bigcup_{i=1}^{k-1} (B(x_i,\rho) \setminus B(x_i,\rho - \delta)). \end{align*} $$
$$ \begin{align*} (B(x_k,\rho+\delta) \setminus B(x_k,\rho)) \cup \bigcup_{i=1}^{k-1} (B(x_i,\rho) \setminus B(x_i,\rho - \delta)). \end{align*} $$
Indeed, since
![]() $\delta < \rho \leq \rho _0$
, it then follows by Assumption 3 that
$\delta < \rho \leq \rho _0$
, it then follows by Assumption 3 that
Since
![]() $\rho < \varepsilon _0$
, we have that
$\rho < \varepsilon _0$
, we have that
![]() $L \lesssim \rho ^{-K}$
by Assumption 4 and we conclude. If
$L \lesssim \rho ^{-K}$
by Assumption 4 and we conclude. If
![]() $A_k(\delta ) \setminus A_k$
is empty, then there is nothing to prove. So suppose that
$A_k(\delta ) \setminus A_k$
is empty, then there is nothing to prove. So suppose that
![]() $A_k(\delta ) \setminus A_k$
is non-empty and contains a point x. Suppose
$A_k(\delta ) \setminus A_k$
is non-empty and contains a point x. Suppose
![]() $x \notin B(x_k,\rho + \delta ) \setminus B(x_k,\rho )$
. Since
$x \notin B(x_k,\rho + \delta ) \setminus B(x_k,\rho )$
. Since
![]() $x \in A_k(\delta ) \subset B(x_k,\rho +\delta )$
, we must have
$x \in A_k(\delta ) \subset B(x_k,\rho +\delta )$
, we must have
![]() $x\in B(x_k,\rho )$
. Furthermore, since
$x\in B(x_k,\rho )$
. Furthermore, since
![]() $x\notin A_k$
, by the construction of
$x\notin A_k$
, by the construction of
![]() $A_k$
, it must be that
$A_k$
, it must be that
![]() $x\in B(x_i,\rho )$
for some
$x\in B(x_i,\rho )$
for some
![]() $i < k$
. If
$i < k$
. If
![]() $x \in B(x_i,\rho -\delta )$
, then, since
$x \in B(x_i,\rho -\delta )$
, then, since
![]() $x \in A_k(\delta )$
, there exists
$x \in A_k(\delta )$
, there exists
![]() $y\in A_k$
such that
$y\in A_k$
such that
![]() $d(x,y) < \delta $
. Hence,
$d(x,y) < \delta $
. Hence,
![]() $y \in B(x_i,\rho )$
and
$y \in B(x_i,\rho )$
and
![]() $y\notin A_k$
, which is a contradiction. Thus,
$y\notin A_k$
, which is a contradiction. Thus,
![]() $x\in B(x_i,\rho ) \setminus B(x_i, \rho - \delta )$
, which concludes the proof.
$x\in B(x_i,\rho ) \setminus B(x_i, \rho - \delta )$
, which concludes the proof.
4. Measure and correlations of
 $E_n$
$E_n$
We give measure and correlations estimates of
![]() $E_n$
in Proposition 4.3, which will follow from Propositions 4.1 and 4.2. The proofs of those propositions are modifications of the proofs of [Reference Kirsebom, Kunde and Persson18, Lemmas 3.1 and 3.2]. The modifications account for the more difficult setting; that is, working with a general metric space
$E_n$
in Proposition 4.3, which will follow from Propositions 4.1 and 4.2. The proofs of those propositions are modifications of the proofs of [Reference Kirsebom, Kunde and Persson18, Lemmas 3.1 and 3.2]. The modifications account for the more difficult setting; that is, working with a general metric space
![]() $(X,d)$
, and for assuming decay of correlation for a smaller class of observables, that is, for Lipschitz continuous functions rather than
$(X,d)$
, and for assuming decay of correlation for a smaller class of observables, that is, for Lipschitz continuous functions rather than
![]() $L_1$
and
$L_1$
and
![]() $BV$
functions.
$BV$
functions.
Throughout the section,
![]() $(M_n)$
denotes a sequence in
$(M_n)$
denotes a sequence in
![]() $[0,1]$
that converges to
$[0,1]$
that converges to
![]() $0$
and satisfies Assumption 1. We also assume that the space
$0$
and satisfies Assumption 1. We also assume that the space
![]() $(X,\mu ,T,d)$
satisfies Assumptions 2–4. Hence, the functions
$(X,\mu ,T,d)$
satisfies Assumptions 2–4. Hence, the functions
![]() $r_n$
defined by
$r_n$
defined by
![]() $\mu (B(x,r_n(x))) = M_n$
are well defined for all n by Lemma 3.1 and converge uniformly to
$\mu (B(x,r_n(x))) = M_n$
are well defined for all n by Lemma 3.1 and converge uniformly to
![]() $0$
by Lemma 3.2. Thus, for large enough n, the functions
$0$
by Lemma 3.2. Thus, for large enough n, the functions
![]() $r_n$
are uniformly bounded by
$r_n$
are uniformly bounded by
![]() $\rho _0$
on
$\rho _0$
on
![]() $\operatorname {\mathrm {supp}}\mu $
. For notational convenience, C will denote an arbitrary positive constant depending solely on
$\operatorname {\mathrm {supp}}\mu $
. For notational convenience, C will denote an arbitrary positive constant depending solely on
![]() $(X,\mu ,T,d)$
and may vary from equation to equation.
$(X,\mu ,T,d)$
and may vary from equation to equation.
In the following propositions, it will be useful to partition the space into sets whose diameters are controlled. Since we wish to work with Lipschitz continuous functions to apply decay of correlations, we also approximate the indicator functions on the elements of the partition. Let
![]() $\rho < \min \{\varepsilon _0, \rho _0\}$
and recall the construction of the partition
$\rho < \min \{\varepsilon _0, \rho _0\}$
and recall the construction of the partition
![]() $\{A_k\}_{k=1}^{L}$
of X in equation (2.1), where
$\{A_k\}_{k=1}^{L}$
of X in equation (2.1), where
![]() $\varepsilon = {\rho }/{2}$
. For
$\varepsilon = {\rho }/{2}$
. For
![]() $\delta \in (0,\rho )$
, define the functions
$\delta \in (0,\rho )$
, define the functions
![]() $\{h_k \colon X \to [0,1]\}_{k=1}^{L}$
by
$\{h_k \colon X \to [0,1]\}_{k=1}^{L}$
by
Notice that the functions are Lipschitz continuous with Lipschitz constant
![]() $\delta ^{-1}$
.
$\delta ^{-1}$
.
Proposition 4.1. With the above assumptions on
![]() $(X,\mu ,T,d)$
and
$(X,\mu ,T,d)$
and
![]() $(M_n)$
, suppose additionally that two-fold correlations decay exponentially for Lipschitz continuous observables. Let
$(M_n)$
, suppose additionally that two-fold correlations decay exponentially for Lipschitz continuous observables. Let
![]() $n\in \mathbb {N}$
and consider the function
$n\in \mathbb {N}$
and consider the function
![]() $F \colon X \times X \to [0,1]$
given by
$F \colon X \times X \to [0,1]$
given by
 $$ \begin{align*} F(x,y) = \begin{cases} 1 & \text{if}\ x \in B(y, r_n(y)), \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} F(x,y) = \begin{cases} 1 & \text{if}\ x \in B(y, r_n(y)), \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
Then there exists constants
![]() $C,\eta> 0$
independent of n such that
$C,\eta> 0$
independent of n such that
Proof. We prove the upper bound part of equation (4.2) as the lower bound follows similarly.
Consider
![]() $Y = \{(x,y) : F(x,y) = 1\}$
. To establish an upper bound, define
$Y = \{(x,y) : F(x,y) = 1\}$
. To establish an upper bound, define
![]() $\hat {F} \colon X \times X \to [0, 1]$
as follows. Let
$\hat {F} \colon X \times X \to [0, 1]$
as follows. Let
![]() $\varepsilon _n \in (0,\rho _0]$
decay exponentially as
$\varepsilon _n \in (0,\rho _0]$
decay exponentially as
![]() $n\to \infty $
and define
$n\to \infty $
and define
Note that it suffices to prove the result for sufficiently large n. We also assume that
![]() $\varepsilon _0,\rho _0 < 1$
, as we may replace them by smaller values otherwise. Therefore, by Lemma 3.2, we may assume that
$\varepsilon _0,\rho _0 < 1$
, as we may replace them by smaller values otherwise. Therefore, by Lemma 3.2, we may assume that
![]() $r_n(x) \leq \rho _0$
for all
$r_n(x) \leq \rho _0$
for all
![]() $x\in \operatorname {\mathrm {supp}}\mu $
. If
$x\in \operatorname {\mathrm {supp}}\mu $
. If
![]() $M_n = 0$
, then
$M_n = 0$
, then
![]() $r_n = 0$
on
$r_n = 0$
on
![]() $\operatorname {\mathrm {supp}}\mu $
and we find that we do not have any further restrictions on
$\operatorname {\mathrm {supp}}\mu $
and we find that we do not have any further restrictions on
![]() $\varepsilon _n$
. If
$\varepsilon _n$
. If
![]() $M_n> 0$
, then by Assumption 2,
$M_n> 0$
, then by Assumption 2,
Thus, by using Assumption 1 and the exponential decay of
![]() $\varepsilon _n$
, we may assume that
$\varepsilon _n$
, we may assume that
![]() $3\varepsilon _n < r_n(x)$
for all
$3\varepsilon _n < r_n(x)$
for all
![]() $x\in X$
. We continue with assuming that
$x\in X$
. We continue with assuming that
![]() $M_n> 0$
since the arguments are significantly easier when
$M_n> 0$
since the arguments are significantly easier when
![]() $M_n = 0$
.
$M_n = 0$
.
Now,
![]() $\hat {F}$
is Lipschitz continuous with Lipschitz constant
$\hat {F}$
is Lipschitz continuous with Lipschitz constant
![]() $\varepsilon _n^{-1}$
. Furthermore,
$\varepsilon _n^{-1}$
. Furthermore,
This is because if
![]() $\hat {F}(x,y)> 0$
, then
$\hat {F}(x,y)> 0$
, then
![]() $d((x,y),(x',y')) < \varepsilon _n$
for some
$d((x,y),(x',y')) < \varepsilon _n$
for some
![]() $(x',y') \in Y$
, and so
$(x',y') \in Y$
, and so
 $$ \begin{align*} d(x,y) &\leq d(x',y') + d(x,x') + d(y',y) \\ &< r_n(y') + 2\varepsilon_n \\ &\leq r_n(y) + 3\varepsilon_n, \end{align*} $$
$$ \begin{align*} d(x,y) &\leq d(x',y') + d(x,x') + d(y',y) \\ &< r_n(y') + 2\varepsilon_n \\ &\leq r_n(y) + 3\varepsilon_n, \end{align*} $$
where the last inequality follows from the Lipschitz continuity of
![]() $r_n$
. Hence,
$r_n$
. Hence,
Using a partition of X, we construct an approximation H of
![]() $\hat {F}$
of the form
$\hat {F}$
of the form
where
![]() $h_{k}$
are Lipschitz continuous, for the purpose of leveraging two-fold decay of correlations. Let
$h_{k}$
are Lipschitz continuous, for the purpose of leveraging two-fold decay of correlations. Let
![]() $\rho _n < \min \{\varepsilon _0, \rho _0\}$
and consider the partition
$\rho _n < \min \{\varepsilon _0, \rho _0\}$
and consider the partition
![]() $\{A_k\}_{k=1}^{L_n}$
of X given in equation (2.1) for
$\{A_k\}_{k=1}^{L_n}$
of X given in equation (2.1) for
![]() $\varepsilon = \rho _n$
. Let
$\varepsilon = \rho _n$
. Let
![]() $\delta _n < \rho _n$
and obtain the functions
$\delta _n < \rho _n$
and obtain the functions
![]() $h_k$
as in equation (4.1) for
$h_k$
as in equation (4.1) for
![]() $\delta = \delta _n$
. Let
$\delta = \delta _n$
. Let
and
![]() $y_k \in A_k \cap \operatorname {\mathrm {supp}}\mu $
for
$y_k \in A_k \cap \operatorname {\mathrm {supp}}\mu $
for
![]() $k \in I$
. Note that
$k \in I$
. Note that
![]() $|I|\leq L_n \lesssim \rho _n^{-K}$
by Assumption 4, since
$|I|\leq L_n \lesssim \rho _n^{-K}$
by Assumption 4, since
![]() $\rho _n < \varepsilon _0$
. Define
$\rho _n < \varepsilon _0$
. Define
![]() $H \colon X \times X \to \mathbb {R}$
by
$H \colon X \times X \to \mathbb {R}$
by
For future reference, note that
which implies that
 $$ \begin{align*} \int \sum_{k \in I} h_k(x) \mathop{}\!d\mu(x) \leq 1 + \sum_{k \in I} \mu(A_k(\delta_n) \setminus A_k). \end{align*} $$
$$ \begin{align*} \int \sum_{k \in I} h_k(x) \mathop{}\!d\mu(x) \leq 1 + \sum_{k \in I} \mu(A_k(\delta_n) \setminus A_k). \end{align*} $$
Using Lemma 3.3, we obtain that
 $$ \begin{align} \int \sum_{k \in I} h_k(x) \mathop{}\!d\mu(x) \leq 1 + C \rho_n^{-2K}\delta_n^{\alpha_0}. \end{align} $$
$$ \begin{align} \int \sum_{k \in I} h_k(x) \mathop{}\!d\mu(x) \leq 1 + C \rho_n^{-2K}\delta_n^{\alpha_0}. \end{align} $$
Now,
 $$ \begin{align} \int \hat{F}(T^{n}x,x) \mathop{}\!d\mu(x) \leq &\int H(T^{n}x,x) \mathop{}\!d\mu(x) \nonumber\\ &+ \int |\hat{F}(T^{n}x,x) - H(T^{n}x,x)| \mathop{}\!d\mu(x). \end{align} $$
$$ \begin{align} \int \hat{F}(T^{n}x,x) \mathop{}\!d\mu(x) \leq &\int H(T^{n}x,x) \mathop{}\!d\mu(x) \nonumber\\ &+ \int |\hat{F}(T^{n}x,x) - H(T^{n}x,x)| \mathop{}\!d\mu(x). \end{align} $$
We use decay of correlations to bound the first integral from above:
 $$ \begin{align*} \int \hat{F}(T^{n}x,y_k)h_k(x) \mathop{}\!d\mu(x) \leq &\int \hat{F}(x,y_k)\mathop{}\!d\mu(x) \int h_k(x) \mathop{}\!d\mu(x) \\ &+ C\|\hat{F}\|_{\text{Lip}}\|h_k\|_{\text{Lip}}e^{-\tau n}. \end{align*} $$
$$ \begin{align*} \int \hat{F}(T^{n}x,y_k)h_k(x) \mathop{}\!d\mu(x) \leq &\int \hat{F}(x,y_k)\mathop{}\!d\mu(x) \int h_k(x) \mathop{}\!d\mu(x) \\ &+ C\|\hat{F}\|_{\text{Lip}}\|h_k\|_{\text{Lip}}e^{-\tau n}. \end{align*} $$
Notice that by equation (4.3),
Since
![]() $y_k \in \operatorname {\mathrm {supp}} \mu $
, we have that
$y_k \in \operatorname {\mathrm {supp}} \mu $
, we have that
![]() $3\varepsilon _n < r_n(y_k) \leq \rho _0$
. Hence, by Assumption 3,
$3\varepsilon _n < r_n(y_k) \leq \rho _0$
. Hence, by Assumption 3,
Furthermore,
![]() $\|\hat {F}\|_{\text {Lip}} \lesssim \varepsilon _n^{-1}$
and
$\|\hat {F}\|_{\text {Lip}} \lesssim \varepsilon _n^{-1}$
and
![]() $\|h_k\|_{\text {Lip}} \lesssim \delta _n^{-1}$
. Hence,
$\|h_k\|_{\text {Lip}} \lesssim \delta _n^{-1}$
. Hence,
and
 $$ \begin{align*} \int H(T^{n}x,x) \mathop{}\!d\mu(x) \leq (M_n + C\varepsilon_n^{\alpha_0})\sum_{k \in I} \int h_k(x)\mathop{}\!d\mu(x) + C \sum_{k\in I} \varepsilon_n^{-1} \delta_n^{-1}e^{-\tau n}. \end{align*} $$
$$ \begin{align*} \int H(T^{n}x,x) \mathop{}\!d\mu(x) \leq (M_n + C\varepsilon_n^{\alpha_0})\sum_{k \in I} \int h_k(x)\mathop{}\!d\mu(x) + C \sum_{k\in I} \varepsilon_n^{-1} \delta_n^{-1}e^{-\tau n}. \end{align*} $$
In combination with equation (4.4) and
![]() $|I| \lesssim \rho _n^{-K}$
, the former equation gives
$|I| \lesssim \rho _n^{-K}$
, the former equation gives
We now establish a bound on
in equation (4.5). By the triangle inequality,
is bounded above by
Now, if
![]() $x \in A_k$
, then by Lipschitz continuity,
$x \in A_k$
, then by Lipschitz continuity,
Also, using the fact that
![]() $\hat {F} \leq 1$
and
$\hat {F} \leq 1$
and
![]() $\mathbf {1}_{A_k} \leq h_k \leq \mathbf {1}_{A_k(\delta _n)}$
, we obtain
$\mathbf {1}_{A_k} \leq h_k \leq \mathbf {1}_{A_k(\delta _n)}$
, we obtain
Hence, since
![]() $\hat {F}(x,y) = \sum _{k \in I} \hat {F}(x,y)\mathbf {1}_{A_k}(y)$
for
$\hat {F}(x,y) = \sum _{k \in I} \hat {F}(x,y)\mathbf {1}_{A_k}(y)$
for
![]() $y \in \operatorname {\mathrm {supp}}\mu $
, we obtain that for
$y \in \operatorname {\mathrm {supp}}\mu $
, we obtain that for
![]() $x \in \operatorname {\mathrm {supp}}\mu $
,
$x \in \operatorname {\mathrm {supp}}\mu $
,
is bounded above by
 $$ \begin{align*} &\sum_{k \in I} | \hat{F}(T^{n}x,x) \mathbf{1}_{A_k}(x) - \hat{F}(T^{n}x,y_k) h_k(x) | \\ &\qquad \leq \sum_{k \in I} ( C \varepsilon_n^{-1} \rho_n \mathbf{1}_{A_k}(x) + \mathbf{1}_{A_k(\delta_n) \setminus A_k}(x) ). \end{align*} $$
$$ \begin{align*} &\sum_{k \in I} | \hat{F}(T^{n}x,x) \mathbf{1}_{A_k}(x) - \hat{F}(T^{n}x,y_k) h_k(x) | \\ &\qquad \leq \sum_{k \in I} ( C \varepsilon_n^{-1} \rho_n \mathbf{1}_{A_k}(x) + \mathbf{1}_{A_k(\delta_n) \setminus A_k}(x) ). \end{align*} $$
Now,
![]() $\sum _{k \in I} \mathbf {1}_{A_k} = 1$
on
$\sum _{k \in I} \mathbf {1}_{A_k} = 1$
on
![]() $\operatorname {\mathrm {supp}}\mu $
gives
$\operatorname {\mathrm {supp}}\mu $
gives
for
![]() $x\in \operatorname {\mathrm {supp}}\mu $
and thus
$x\in \operatorname {\mathrm {supp}}\mu $
and thus
 $$ \begin{align*} \int | \hat{F}(T^{n}x,x) - H(T^{n}x,x) | \mathop{}\!d\mu(x) \leq C \varepsilon_n^{-1} \rho_n + \sum_{k \in I} \mu(A_k(\delta_n) \setminus A_k). \end{align*} $$
$$ \begin{align*} \int | \hat{F}(T^{n}x,x) - H(T^{n}x,x) | \mathop{}\!d\mu(x) \leq C \varepsilon_n^{-1} \rho_n + \sum_{k \in I} \mu(A_k(\delta_n) \setminus A_k). \end{align*} $$
By Lemma 3.3,
By combining equations (4.5), (4.7) and (4.9), we obtain that
Now, let
 $$ \begin{align*} \varepsilon_n &= e^{-\gamma n}, \\ \rho_n &= \varepsilon_n^2, \\ \delta_n &= \varepsilon_n^{2 + 4K/\alpha_0}, \end{align*} $$
$$ \begin{align*} \varepsilon_n &= e^{-\gamma n}, \\ \rho_n &= \varepsilon_n^2, \\ \delta_n &= \varepsilon_n^{2 + 4K/\alpha_0}, \end{align*} $$
where
![]() $\gamma = \tfrac 12\bigl (3 + 4K + {4K}/{\alpha _0}\bigr )^{-1} \tau $
. Then,
$\gamma = \tfrac 12\bigl (3 + 4K + {4K}/{\alpha _0}\bigr )^{-1} \tau $
. Then,
![]() $\varepsilon _n$
decays exponentially as
$\varepsilon _n$
decays exponentially as
![]() $n \to \infty $
and
$n \to \infty $
and
![]() $\delta _n < \rho _n$
as required. For large enough n, we have
$\delta _n < \rho _n$
as required. For large enough n, we have
![]() $3\varepsilon _n < r_n(x)$
and
$3\varepsilon _n < r_n(x)$
and
![]() $\rho _n < \min \{\varepsilon _0, \rho _0\}$
as we assumed. Finally,
$\rho _n < \min \{\varepsilon _0, \rho _0\}$
as we assumed. Finally,
gives us an upper bound
Proposition 4.2. With the above assumptions on
![]() $(X,\mu ,T,d)$
and
$(X,\mu ,T,d)$
and
![]() $(M_n)$
, suppose additionally that three-fold correlations decay exponentially for Lipschitz continuous observables. Let
$(M_n)$
, suppose additionally that three-fold correlations decay exponentially for Lipschitz continuous observables. Let
![]() $m,n \in \mathbb {N}$
and consider the function
$m,n \in \mathbb {N}$
and consider the function
![]() $F\colon X\times X\times X \to [0,1]$
given by
$F\colon X\times X\times X \to [0,1]$
given by
 $$ \begin{align*} F(x,y,z) = \begin{cases} 1 & \text{if}\ x\in B(z, r_{n+m}(z))\ \text{and}\ y\in B(z, r_n(z)), \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} F(x,y,z) = \begin{cases} 1 & \text{if}\ x\in B(z, r_{n+m}(z))\ \text{and}\ y\in B(z, r_n(z)), \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
Then, there exists
![]() $C,\eta> 0$
independent of n and m such that
$C,\eta> 0$
independent of n and m such that
The proof of Proposition 4.2 follows roughly that of Proposition 4.1 by making some modifications to account for the added dimension.
Proof. Again, we assume, without loss of generality, that n is sufficiently large and that
![]() $\varepsilon _0,\rho _0 < 1$
and
$\varepsilon _0,\rho _0 < 1$
and
![]() $M_n> 0$
.
$M_n> 0$
.
Notice that
![]() $F(x,y,z) = G_1(x,z) G_2(y,z)$
for
$F(x,y,z) = G_1(x,z) G_2(y,z)$
for
 $$ \begin{align*} G_1(x,z) = \begin{cases} 1 & \text{if}\ x \in B(z, r_{n+m}(z)), \\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} G_1(x,z) = \begin{cases} 1 & \text{if}\ x \in B(z, r_{n+m}(z)), \\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
and
 $$ \begin{align*} G_2(y,z) = \begin{cases} 1 & \text{if}\ y \in B(z, r_{n}(z)), \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} G_2(y,z) = \begin{cases} 1 & \text{if}\ y \in B(z, r_{n}(z)), \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
Let
![]() $\varepsilon _{m,n} < \rho _0$
converge exponentially to
$\varepsilon _{m,n} < \rho _0$
converge exponentially to
![]() $0$
as
$0$
as
![]() $\min \{m,n\} \to \infty $
. Define the functions
$\min \{m,n\} \to \infty $
. Define the functions
![]() $\hat {G}_1, \hat {G}_2 \colon X \times X \to [0,1]$
similarly to how
$\hat {G}_1, \hat {G}_2 \colon X \times X \to [0,1]$
similarly to how
![]() $\hat {F}$
was defined in Proposition 4.1. That is,
$\hat {F}$
was defined in Proposition 4.1. That is,
![]() $\hat {G}_1$
and
$\hat {G}_1$
and
![]() $\hat {G}_2$
are Lipschitz continuous with Lipschitz constant
$\hat {G}_2$
are Lipschitz continuous with Lipschitz constant
![]() $\varepsilon _{m,n}^{-1}$
and satisfy
$\varepsilon _{m,n}^{-1}$
and satisfy
and
Thus,
Let
![]() $\rho _{m,n} < \min \{\varepsilon _0, \rho _0\}$
and consider the partition
$\rho _{m,n} < \min \{\varepsilon _0, \rho _0\}$
and consider the partition
![]() $\{A_k\}_{k=1}^{L_{m,n}}$
of X given in equation (2.1) for
$\{A_k\}_{k=1}^{L_{m,n}}$
of X given in equation (2.1) for
![]() $\varepsilon = {\rho _{m,n}}/{2}$
. Let
$\varepsilon = {\rho _{m,n}}/{2}$
. Let
![]() $\delta _{m,n} < \rho _{m,n}$
and obtain the functions
$\delta _{m,n} < \rho _{m,n}$
and obtain the functions
![]() $h_k$
as in equation (4.1) for
$h_k$
as in equation (4.1) for
![]() $\delta = \delta _{m,n}$
. Let
$\delta = \delta _{m,n}$
. Let
and
![]() $y_k \in A_k \cap \operatorname {\mathrm {supp}}\mu $
for
$y_k \in A_k \cap \operatorname {\mathrm {supp}}\mu $
for
![]() $k \in I$
. Define the functions
$k \in I$
. Define the functions
![]() $H_1, H_2 \colon X \times X \to \mathbb {R}$
by
$H_1, H_2 \colon X \times X \to \mathbb {R}$
by
for
![]() $i = 1,2$
. Using the triangle inequality, we bound the right-hand side of equation (4.10) by
$i = 1,2$
. Using the triangle inequality, we bound the right-hand side of equation (4.10) by
 $$ \begin{align} &\int |\hat{G}_1(T^{n+m}x,x) \hat{G}_2(T^{n}x,x) - H_1(T^{n+m}x,x) H_2(T^{n}x,x)| \mathop{}\!d\mu(x) \nonumber\\ &\qquad + \int H_1(T^{n+m}x,x) H_2(T^{n}x,x) \mathop{}\!d\mu(x). \end{align} $$
$$ \begin{align} &\int |\hat{G}_1(T^{n+m}x,x) \hat{G}_2(T^{n}x,x) - H_1(T^{n+m}x,x) H_2(T^{n}x,x)| \mathop{}\!d\mu(x) \nonumber\\ &\qquad + \int H_1(T^{n+m}x,x) H_2(T^{n}x,x) \mathop{}\!d\mu(x). \end{align} $$
We look to bound the first integral. Using the triangle inequality and the fact that
![]() $\hat {G}_1 \leq 1$
, we obtain that the integrand is bounded above by
$\hat {G}_1 \leq 1$
, we obtain that the integrand is bounded above by
As shown in equation (4.9),
and by equation (4.8),
and
Thus,
is bounded above by
 $$ \begin{align*} &C \varepsilon_{m,n}^{-1} \rho_{m,n} + C(1 + \varepsilon_{m,n}^{-1} \rho_{m,n}) \sum_{k \in I} \mathbf{1}_{A_k(\delta_{m,n}) \setminus A_k}(x) \\ &\qquad + \sum_{k \in I} \sum_{k' \in I} \mathbf{1}_{A_k(\delta_{m,n}) \setminus A_k}(x) \mathbf{1}_{A_{k'}(\delta_{m,n}) \setminus A_{k'}}(x). \end{align*} $$
$$ \begin{align*} &C \varepsilon_{m,n}^{-1} \rho_{m,n} + C(1 + \varepsilon_{m,n}^{-1} \rho_{m,n}) \sum_{k \in I} \mathbf{1}_{A_k(\delta_{m,n}) \setminus A_k}(x) \\ &\qquad + \sum_{k \in I} \sum_{k' \in I} \mathbf{1}_{A_k(\delta_{m,n}) \setminus A_k}(x) \mathbf{1}_{A_{k'}(\delta_{m,n}) \setminus A_{k'}}(x). \end{align*} $$
Integrating and using Lemma 3.3 together with the trivial estimate
![]() $\mu (A \cap B) \leq \mu (A)$
, we obtain that
$\mu (A \cap B) \leq \mu (A)$
, we obtain that
 $$ \begin{align} &\int H_2(T^{n}x,x) \bigl| \hat{G}_1(T^{n+m}x,x) - H_1(T^{n+m}x,x) \bigr| \mathop{}\!d\mu(x) \nonumber\\ &\qquad \lesssim \varepsilon_{m,n}^{-1} \rho_{m,n} + (1 + \varepsilon_{m,n}^{-1} \rho_{m,n}) \rho_{m,n}^{-2K} \delta_{m,n}^{\alpha_0} + \rho_{m,n}^{-3K} \delta_{m,n}^{\alpha_0}. \end{align} $$
$$ \begin{align} &\int H_2(T^{n}x,x) \bigl| \hat{G}_1(T^{n+m}x,x) - H_1(T^{n+m}x,x) \bigr| \mathop{}\!d\mu(x) \nonumber\\ &\qquad \lesssim \varepsilon_{m,n}^{-1} \rho_{m,n} + (1 + \varepsilon_{m,n}^{-1} \rho_{m,n}) \rho_{m,n}^{-2K} \delta_{m,n}^{\alpha_0} + \rho_{m,n}^{-3K} \delta_{m,n}^{\alpha_0}. \end{align} $$
We now estimate the second integral in equation (4.11) using decay of correlations:
is bounded above by
 $$ \begin{align} &\sum_{k \in I} \sum_{k' \in I} \|\hat{G}_1(\cdot, y_k)\|_{L^{1}} \|\hat{G}_2(\cdot, y_{k'})\|_{L^{1}} \|h_k h_{k'}\|_{L^{1}} \nonumber\\ &\qquad + \sum_{k \in I} \sum_{k' \in I} C \|\hat{G}_1\|_{\text{Lip}} \|\hat{G}_2\|_{\text{Lip}} \|h_k h_{k'}\|_{\text{Lip}} ( e^{-\tau n} + e^{-\tau m} ). \end{align} $$
$$ \begin{align} &\sum_{k \in I} \sum_{k' \in I} \|\hat{G}_1(\cdot, y_k)\|_{L^{1}} \|\hat{G}_2(\cdot, y_{k'})\|_{L^{1}} \|h_k h_{k'}\|_{L^{1}} \nonumber\\ &\qquad + \sum_{k \in I} \sum_{k' \in I} C \|\hat{G}_1\|_{\text{Lip}} \|\hat{G}_2\|_{\text{Lip}} \|h_k h_{k'}\|_{\text{Lip}} ( e^{-\tau n} + e^{-\tau m} ). \end{align} $$
Similarly to how equations (4.4) and (4.6) were established in Proposition 4.1, we obtain the bounds
 $$ \begin{align*} \|\hat{G}_1(\cdot,y_k)\|_{L^{1}} &\leq M_{n+m} + C\varepsilon_{m,n}^{\alpha_0}, \\ \|\hat{G}_2(\cdot,y_k)\|_{L^{1}} &\leq M_{n} + C\varepsilon_{m,n}^{\alpha_0} \end{align*} $$
$$ \begin{align*} \|\hat{G}_1(\cdot,y_k)\|_{L^{1}} &\leq M_{n+m} + C\varepsilon_{m,n}^{\alpha_0}, \\ \|\hat{G}_2(\cdot,y_k)\|_{L^{1}} &\leq M_{n} + C\varepsilon_{m,n}^{\alpha_0} \end{align*} $$
and
Also,
and
Combining the previous equations with equation (4.13), we obtain the upper bound
 $$ \begin{align} \int H_1(T^{n+m}x,x) H_2(T^{n}x,x) \mathop{}\!d\mu(x) &\leq M_{n+m}M_n + C\varepsilon_{m,n}^{\alpha_0} + C\rho_{m,n}^{-3K}\delta_{m,n} ^{\alpha_0} \nonumber\\ &\quad + C\rho_{m,n}^{-2K}\varepsilon_{m,n}^{-2}\delta_{m,n}^{-1} (e^{-\tau n} + e^{-\tau m}). \end{align} $$
$$ \begin{align} \int H_1(T^{n+m}x,x) H_2(T^{n}x,x) \mathop{}\!d\mu(x) &\leq M_{n+m}M_n + C\varepsilon_{m,n}^{\alpha_0} + C\rho_{m,n}^{-3K}\delta_{m,n} ^{\alpha_0} \nonumber\\ &\quad + C\rho_{m,n}^{-2K}\varepsilon_{m,n}^{-2}\delta_{m,n}^{-1} (e^{-\tau n} + e^{-\tau m}). \end{align} $$
Combining and simplifying equations (4.12) and (4.14), we obtain that
 $$ \begin{align*} &\int F(T^{n+m}x,T^{n}x,x) \mathop{}\!d\mu(x) - M_{n+m}M_n \lesssim \varepsilon_{m,n}^{-1} \rho_{m,n} + \varepsilon_{m,n}^{-1} \rho_{m,n}^{1-2K} \delta_{m,n}^{\alpha_0} \\ &\qquad+ \rho_{m,n}^{-3K} \delta_{m,n}^{\alpha_0} + \varepsilon_{m,n}^{\alpha_0} + \rho_{m,n}^{-2K}\varepsilon_{m,n}^{-2}\delta_{m,n}^{-1} (e^{-\tau n} + e^{-\tau m}). \end{align*} $$
$$ \begin{align*} &\int F(T^{n+m}x,T^{n}x,x) \mathop{}\!d\mu(x) - M_{n+m}M_n \lesssim \varepsilon_{m,n}^{-1} \rho_{m,n} + \varepsilon_{m,n}^{-1} \rho_{m,n}^{1-2K} \delta_{m,n}^{\alpha_0} \\ &\qquad+ \rho_{m,n}^{-3K} \delta_{m,n}^{\alpha_0} + \varepsilon_{m,n}^{\alpha_0} + \rho_{m,n}^{-2K}\varepsilon_{m,n}^{-2}\delta_{m,n}^{-1} (e^{-\tau n} + e^{-\tau m}). \end{align*} $$
Now, let
 $$ \begin{align*} \varepsilon_{m,n} &= e^{-\gamma \min \{m,n\}}, \\ \rho_{m,n} &= \varepsilon_{m,n}^2, \\ \delta_{m,n} &= \varepsilon_{m,n}^{2 + 6K/\alpha_0}, \end{align*} $$
$$ \begin{align*} \varepsilon_{m,n} &= e^{-\gamma \min \{m,n\}}, \\ \rho_{m,n} &= \varepsilon_{m,n}^2, \\ \delta_{m,n} &= \varepsilon_{m,n}^{2 + 6K/\alpha_0}, \end{align*} $$
where
![]() $\gamma = \tfrac 12\bigl (4 + 4K + {6K}/{\alpha _0}\bigr )^{-1} \tau $
. Then,
$\gamma = \tfrac 12\bigl (4 + 4K + {6K}/{\alpha _0}\bigr )^{-1} \tau $
. Then,
![]() $\varepsilon _{m,n}$
decays exponentially as
$\varepsilon _{m,n}$
decays exponentially as
![]() $n \to \infty $
and
$n \to \infty $
and
![]() ${\delta _{m,n} < \rho _{m,n}}$
as required. For large enough n, we have
${\delta _{m,n} < \rho _{m,n}}$
as required. For large enough n, we have
![]() $3\varepsilon _{m,n}< r_n(x)$
and
$3\varepsilon _{m,n}< r_n(x)$
and
![]() $\rho _{m,n} < \min \{\varepsilon _0, \rho _0\}$
as we assumed. Finally,
$\rho _{m,n} < \min \{\varepsilon _0, \rho _0\}$
as we assumed. Finally,
gives us the upper bound
Proposition 4.3. With the above assumptions on
![]() $(X,\mu ,T,d)$
and
$(X,\mu ,T,d)$
and
![]() $(M_n)$
, suppose additionally that three-fold correlations decay exponentially for Lipschitz continuous observables. There exists
$(M_n)$
, suppose additionally that three-fold correlations decay exponentially for Lipschitz continuous observables. There exists
![]() $C,\eta> 0$
such that for all
$C,\eta> 0$
such that for all
![]() $m,n \in \mathbb {N}$
,
$m,n \in \mathbb {N}$
,
and
Proof. The first inequality follows directly from Proposition 4.1 by noticing that
![]() $\mu (E_n) = \int F(T^{n}x,x)\mathop {}\!d\mu (x)$
and the second inequality follows from the first in combination with Proposition 4.2 by noticing that
$\mu (E_n) = \int F(T^{n}x,x)\mathop {}\!d\mu (x)$
and the second inequality follows from the first in combination with Proposition 4.2 by noticing that
![]() $\mu (E_{n+m} \cap E_{n}) = \int F(T^{n+m}x,T^{n}x,x)\mathop {}\!d\mu (x)$
.
$\mu (E_{n+m} \cap E_{n}) = \int F(T^{n+m}x,T^{n}x,x)\mathop {}\!d\mu (x)$
.
5. Proof of Theorems 1.1 and 2.2
We can now prove our main results.
Proof of Theorem 2.2
By Proposition 4.3, we see that the conditions of Theorem 2.1 are met and we conclude the proof.
Recall that M is a compact smooth N-dimensional manifold, and that d and
![]() $\operatorname {\mathrm {Vol}}$
are the induced metric and volume measure. The injectivity radius of M is denoted by
$\operatorname {\mathrm {Vol}}$
are the induced metric and volume measure. The injectivity radius of M is denoted by
![]() $\operatorname {\mathrm {inj}}_M$
and is positive.
$\operatorname {\mathrm {inj}}_M$
and is positive.
Proof of Theorem 1.1
By [Reference Kotani and Sunada20, Proposition 3.1], the system has three-fold decay of correlations for Lipschitz continuous observables. Thus, the theorem follows from Theorem 2.2 once we verify that Assumptions 3 and 4 hold.
For Assumption 4, let
![]() $\varepsilon \in (0,\operatorname {\mathrm {inj}}_M)$
and consider a maximal
$\varepsilon \in (0,\operatorname {\mathrm {inj}}_M)$
and consider a maximal
![]() $\varepsilon $
-packing
$\varepsilon $
-packing
![]() $\{B(x_k,\varepsilon )\}_{k=1}^{L}$
of M, that is,
$\{B(x_k,\varepsilon )\}_{k=1}^{L}$
of M, that is,
![]() $L = P_\varepsilon (M)$
. Now,
$L = P_\varepsilon (M)$
. Now,
 $$ \begin{align*} L \min_{k} \operatorname{\mathrm{Vol}}( B(x_k,\varepsilon) ) &\leq \sum_{k=1}^{L} \operatorname{\mathrm{Vol}}( B(x_k,\varepsilon) ) \\ &= \operatorname{\mathrm{Vol}}\Bigl( \bigcup_{k=1}^{L} B(x_k,\varepsilon) \Bigr) \\ &\leq \operatorname{\mathrm{Vol}}(M). \end{align*} $$
$$ \begin{align*} L \min_{k} \operatorname{\mathrm{Vol}}( B(x_k,\varepsilon) ) &\leq \sum_{k=1}^{L} \operatorname{\mathrm{Vol}}( B(x_k,\varepsilon) ) \\ &= \operatorname{\mathrm{Vol}}\Bigl( \bigcup_{k=1}^{L} B(x_k,\varepsilon) \Bigr) \\ &\leq \operatorname{\mathrm{Vol}}(M). \end{align*} $$
By [Reference Croke11, Proposition 14], there exists
![]() $C_1>0$
such that
$C_1>0$
such that
for all
![]() $y\in M$
. Hence,
$y\in M$
. Hence,
Thus, Assumption 4 holds for
![]() $K = N$
and
$K = N$
and
![]() $\varepsilon _0 = \operatorname {\mathrm {inj}}_M$
.
$\varepsilon _0 = \operatorname {\mathrm {inj}}_M$
.
For Assumption 3, let
![]() $x\in M$
and
$x\in M$
and
![]() $0 < \varepsilon < \rho \leq \operatorname {\mathrm {inj}}_M$
. For convenience, let
$0 < \varepsilon < \rho \leq \operatorname {\mathrm {inj}}_M$
. For convenience, let
![]() $\varepsilon ' = {\varepsilon }/{2}$
. Consider a maximal
$\varepsilon ' = {\varepsilon }/{2}$
. Consider a maximal
![]() $\varepsilon '$
-packing
$\varepsilon '$
-packing
![]() $\{B(x_k,\varepsilon ')\}_{k=1}^{L}$
of the annulus
$\{B(x_k,\varepsilon ')\}_{k=1}^{L}$
of the annulus
![]() $\{y : \rho \leq d(x,y) < \rho + \varepsilon \}$
. Then,
$\{y : \rho \leq d(x,y) < \rho + \varepsilon \}$
. Then,
![]() $\{B(x_k,\varepsilon ')\}_{k=1}^{L}$
is contained in the set
$\{B(x_k,\varepsilon ')\}_{k=1}^{L}$
is contained in the set
![]() $\{y : \rho - \varepsilon ' \leq d(x,y) < \rho + 3\varepsilon '\}$
. Thus,
$\{y : \rho - \varepsilon ' \leq d(x,y) < \rho + 3\varepsilon '\}$
. Thus,
 $$ \begin{align*} L\min_k \operatorname{\mathrm{Vol}}(B(x_k, \varepsilon')) &\leq \sum_{i=1}^{n} \operatorname{\mathrm{Vol}}(B(x_k, \varepsilon')) \\ &= \operatorname{\mathrm{Vol}} \Bigl( \bigcup_{i=1}^{n} B(x_k, \varepsilon') \Bigr) \\ &\leq \operatorname{\mathrm{Vol}} \{y \in M : \rho - \varepsilon' \leq d(x,y) < \rho + 3\varepsilon'\} \\ &= \operatorname{\mathrm{Vol}}(B(x, \rho + 3\varepsilon')) - \operatorname{\mathrm{Vol}}(B(x, \rho - \varepsilon')). \end{align*} $$
$$ \begin{align*} L\min_k \operatorname{\mathrm{Vol}}(B(x_k, \varepsilon')) &\leq \sum_{i=1}^{n} \operatorname{\mathrm{Vol}}(B(x_k, \varepsilon')) \\ &= \operatorname{\mathrm{Vol}} \Bigl( \bigcup_{i=1}^{n} B(x_k, \varepsilon') \Bigr) \\ &\leq \operatorname{\mathrm{Vol}} \{y \in M : \rho - \varepsilon' \leq d(x,y) < \rho + 3\varepsilon'\} \\ &= \operatorname{\mathrm{Vol}}(B(x, \rho + 3\varepsilon')) - \operatorname{\mathrm{Vol}}(B(x, \rho - \varepsilon')). \end{align*} $$
Since M is compact, there exists
![]() $C_2> 0$
such that for all
$C_2> 0$
such that for all
![]() $0 < s < r$
and
$0 < s < r$
and
![]() $y \in M$
,
$y \in M$
,
(see for instance [Reference Chavel8, p. 127]). Therefore,
Using equation (5.1) again and noting that
![]() $\varepsilon ' < \varepsilon < \operatorname {\mathrm {inj}}_M$
, we obtain that
$\varepsilon ' < \varepsilon < \operatorname {\mathrm {inj}}_M$
, we obtain that
Now,
![]() $\{B(x_k,\varepsilon )\}_{k=1}^{L}$
covers
$\{B(x_k,\varepsilon )\}_{k=1}^{L}$
covers
![]() $\{y \in M : \rho \leq d(x,y) < \rho + \varepsilon \}$
. Hence,
$\{y \in M : \rho \leq d(x,y) < \rho + \varepsilon \}$
. Hence,
 $$ \begin{align*} \mu \{y \in M : \rho \leq d(x,y) < \rho + \varepsilon\} &\leq \mu\Bigl(\bigcup_{k=1}^{L}B(x_k,\varepsilon)\Bigr) \\ &\leq L\max_{k} \mu(B(x_k,\varepsilon)) \\ &\lesssim \varepsilon^{1-N} \varepsilon^{s} \\ &= \varepsilon^{1+s-N}, \end{align*} $$
$$ \begin{align*} \mu \{y \in M : \rho \leq d(x,y) < \rho + \varepsilon\} &\leq \mu\Bigl(\bigcup_{k=1}^{L}B(x_k,\varepsilon)\Bigr) \\ &\leq L\max_{k} \mu(B(x_k,\varepsilon)) \\ &\lesssim \varepsilon^{1-N} \varepsilon^{s} \\ &= \varepsilon^{1+s-N}, \end{align*} $$
where in the third inequality, we have used that
![]() $\mu (B(x_k,\varepsilon )) \lesssim \varepsilon ^{s}$
. Thus, Assumption 3 holds for
$\mu (B(x_k,\varepsilon )) \lesssim \varepsilon ^{s}$
. Thus, Assumption 3 holds for
![]() $\rho _0 = \operatorname {\mathrm {inj}}_M$
and
$\rho _0 = \operatorname {\mathrm {inj}}_M$
and
![]() $\alpha _0 = 1 + s - N$
. Note that
$\alpha _0 = 1 + s - N$
. Note that
![]() $\alpha _0> 0$
as we assumed that
$\alpha _0> 0$
as we assumed that
![]() ${s> N - 1}$
.
${s> N - 1}$
.
6. Final remarks
6.1. Improvements of Boshernitzan’s result
By restricting the underlying system, one can improve Boshernitzan’s general result. Pawelec [Reference Pawelec21] proved that
for
![]() $\mu $
-a.e. x under the assumptions of exponential decay of correlations and some assumptions on
$\mu $
-a.e. x under the assumptions of exponential decay of correlations and some assumptions on
![]() $\mu $
related to
$\mu $
related to
![]() $\beta $
. For self-similar sets, Chang, Wu and Wu [Reference Chang, Wu and Wu7] and Baker and Farmer [Reference Baker and Farmer2] obtained a dichotomy result for the set
$\beta $
. For self-similar sets, Chang, Wu and Wu [Reference Chang, Wu and Wu7] and Baker and Farmer [Reference Baker and Farmer2] obtained a dichotomy result for the set
to have zero or full measure depending on the convergence or divergence of a series involving
![]() $(r_n)$
. For mixing systems on
$(r_n)$
. For mixing systems on
![]() $[0,1]$
, Kirsebom, Kunde and Persson [Reference Kirsebom, Kunde and Persson18] obtained several results, with varying conditions on
$[0,1]$
, Kirsebom, Kunde and Persson [Reference Kirsebom, Kunde and Persson18] obtained several results, with varying conditions on
![]() $(r_n)$
, on the measure of R and related sets. For integer matrices on the N-dimensional torus such that no eigenvalue is a root of unity, they obtain a condition for R to have zero or full measure, again depending on the convergence of a series involving
$(r_n)$
, on the measure of R and related sets. For integer matrices on the N-dimensional torus such that no eigenvalue is a root of unity, they obtain a condition for R to have zero or full measure, again depending on the convergence of a series involving
![]() $(r_n)$
. He and Liao [Reference He and Liao16] extend Kirsebom, Kunde and Persson’s results to non-integer matrices and to targets that are hyperrectangles or hyperboloids instead of open balls. Allen, Baker and Bárány [Reference Allen, Baker and Bárány1] give sufficient conditions for the set R, adapted to subshifts of finite type, to have measure
$(r_n)$
. He and Liao [Reference He and Liao16] extend Kirsebom, Kunde and Persson’s results to non-integer matrices and to targets that are hyperrectangles or hyperboloids instead of open balls. Allen, Baker and Bárány [Reference Allen, Baker and Bárány1] give sufficient conditions for the set R, adapted to subshifts of finite type, to have measure
![]() $1$
and sufficient conditions for the set to have measure
$1$
and sufficient conditions for the set to have measure
![]() $0$
. They also obtain a critical threshold for which the measure of R transitions from
$0$
. They also obtain a critical threshold for which the measure of R transitions from
![]() $0$
to
$0$
to
![]() $1$
.
$1$
.
6.2. Spaces satisfying the assumptions
If
![]() $\mu $
is absolutely continuous with respect to the Lebesgue measure
$\mu $
is absolutely continuous with respect to the Lebesgue measure
![]() $\unicode{x3bb} $
with density in
$\unicode{x3bb} $
with density in
![]() $L^{p}$
, then
$L^{p}$
, then
![]() $\mu $
satisfies Assumptions 2 and 3. Namely, if
$\mu $
satisfies Assumptions 2 and 3. Namely, if
![]() $\mathop {}\!d\mu = h \mathop {}\!d\unicode{x3bb} $
, then
$\mathop {}\!d\mu = h \mathop {}\!d\unicode{x3bb} $
, then
where q is the harmonic conjugate of p. Since
![]() $\unicode{x3bb} (B(x,\rho + \varepsilon ) \setminus B(x,\rho ) ) \leq \varepsilon ^{\alpha _0}$
and
$\unicode{x3bb} (B(x,\rho + \varepsilon ) \setminus B(x,\rho ) ) \leq \varepsilon ^{\alpha _0}$
and
![]() $\unicode{x3bb} (B(x,\rho )) \leq \rho ^{s}$
for some
$\unicode{x3bb} (B(x,\rho )) \leq \rho ^{s}$
for some
![]() $\alpha _0$
and s, we see that
$\alpha _0$
and s, we see that
![]() $\mu $
also satisfies the assumptions. Gupta, Holland and Nicol [Reference Gupta, Holland and Nicol14] consider planar dispersing billiards. These systems have an absolutely continuous invariant measure and so Assumptions 2 and 3 are satisfied. Furthermore, some of the systems have exponential decay of two-fold correlations for Hölder observables as shown by Young [Reference Young25] and exponential decay of multiple decorrelation as shown in [Reference Chernov and Markarian10, Theorem 7.41]. Thus, our results hold for such systems. The authors in [Reference Gupta, Holland and Nicol14] also consider Lozi maps, for which a broad class satisfies Assumption 3 and have exponential decay of two-fold correlations for Hölder observables. For our result to apply to these systems, one would have to show that three-fold correlations decay exponentially as well.
$\mu $
also satisfies the assumptions. Gupta, Holland and Nicol [Reference Gupta, Holland and Nicol14] consider planar dispersing billiards. These systems have an absolutely continuous invariant measure and so Assumptions 2 and 3 are satisfied. Furthermore, some of the systems have exponential decay of two-fold correlations for Hölder observables as shown by Young [Reference Young25] and exponential decay of multiple decorrelation as shown in [Reference Chernov and Markarian10, Theorem 7.41]. Thus, our results hold for such systems. The authors in [Reference Gupta, Holland and Nicol14] also consider Lozi maps, for which a broad class satisfies Assumption 3 and have exponential decay of two-fold correlations for Hölder observables. For our result to apply to these systems, one would have to show that three-fold correlations decay exponentially as well.
6.3. Improvements of the result
The main limitation of the method of proof is the reliance on Assumption 3, namely that we require control over the measure of
![]() $\delta $
-neighbourhoods of sets. It is reasonable to think that the result should hold for measures that do not satisfy this assumption; however, in that case, instead of considering open balls, one would need to consider other shrinking neighbourhoods. The reason for this is that for a general measure
$\delta $
-neighbourhoods of sets. It is reasonable to think that the result should hold for measures that do not satisfy this assumption; however, in that case, instead of considering open balls, one would need to consider other shrinking neighbourhoods. The reason for this is that for a general measure
![]() $\mu $
, there exists
$\mu $
, there exists
![]() $M_n \in [0,1]$
and
$M_n \in [0,1]$
and
![]() $x\in X$
such that there is no open ball
$x\in X$
such that there is no open ball
![]() $B_n(x)$
with
$B_n(x)$
with
![]() $\mu (B_n(x)) = M_n$
. Furthermore, one would like to improve the condition
$\mu (B_n(x)) = M_n$
. Furthermore, one would like to improve the condition
![]() $M_n \geq n^{-1} (\log n)^{4+\varepsilon }$
in Assumption 1 to one closer to the critical decay rate
$M_n \geq n^{-1} (\log n)^{4+\varepsilon }$
in Assumption 1 to one closer to the critical decay rate
![]() $M_n \geq n^{-1}$
.
$M_n \geq n^{-1}$
.
Acknowledgments
I wish to thank my supervisor, Tomas Persson, for helpful discussions and for his guidance in preparing this paper. I am grateful to Viviane Baladi for the reference [Reference Pène22] and to Nicholas Fleming-Vázquez for the reference [Reference Chernov and Markarian10, Theorem 7.41]. I am also grateful to the referee for their comments, which helped improve the presentation of the paper.