2.1 Airspace and traffic flow

Controlled airspace, a volume of earth’s atmosphere of defined geometry and size, accommodates flights with relevant ATC services according to its type (i.e. en-route sectors, airport control zones, and TMAs). TMAs are controlled airspaces founded at the confluence of air traffic service routes in the neighbourhood of one or more airports [55]. The monitoring, sequencing and separation management of flights within the TMAs are usually more complex than those of other airspaces because they contain a complex network of converging or intersecting routes around airports. Air traffic controllers should conventionally use vectoring techniques consisting of necessary heading, speed and altitude change instructions to aircraft to maintain safe and efficient air traffic flow. On the other hand, it is more difficult to provide an efficient traffic flow while ensuring the safe separation between aircraft especially at peak traffic hours when the airports have maximum demand. Air traffic controllers often implement higher time and distance separations than the necessary minima by delaying aircraft in the air or on the ground. These delays lead to decreased utilisation of runways and inefficient sequencing with extra flight times, distances and fuel. In this study, we focus on obtaining efficient sequences with minimum delay and fuel within the TMA during hours with high traffic demand.

In order to approach this problem, we adopted a generic TMA surrounding an airport with a single runway (Fig. 1). The runway serves for arrivals and departures. Arrivals are supposed to enter the TMA from a set of predefined entry points (EPs). Each arrival entering TMA from its associated EP at a known entry time, speed and altitude should follow a conflict-free trajectory to the merge point, called the final approach fix (FAF), using a vectoring manoeuvre.

Figure 1. A generic TMA configuration (top view).

As soon as the aircraft has arrived at its EP, it is directed to fly to FAF along the described descent profile in Fig. 2. The aircraft is required to perform level flight at its initial flight altitude and speed until it reaches the top of descent (TOD) point and then it commences continuous descent approach (CDA) until it arrives to the predefined final approach descent point (FDP). The CDA time and distance between TOD and FDP depend on the category and initial flight level of the aircraft. As the aircraft descends to FDP, it performs level flight and then fly-by-turn at FAF with a constant speed to align with FAP. As soon as the aircraft establishes the FAP, it performs level flight at FAF altitude and speed until it reaches the top of final approach point (TFA). This point depends on the aircraft category. Finally, the aircraft approaches along this common path and lands on the runway at the runway entry point (REP).

Figure 2. The descent profile of arrival within the TMA (side view).

Departures should wait for their take-off in the departure queue (DQ) at a designated area called the “holding point” located at the runway holding position. Here, they line up in the sequence determined by air traffic controllers and proceed towards the runway. The duration of waiting time at the holding point may vary depending on the density and traffic of the runway. Departure aircraft begin their take-offs from REP at their assigned operation time. If there is no delay requirement due to the wake turbulence separation, the departures enter the runway and take off. It is assumed that consecutive departures follow different flight paths rather than a common departure path therefore no crossing or overtaking conflicts occur between them within the TMA. It is also assumed that all arrival and departure routes are separated vertically to forbid crossing conflicts between them within the TMA. By these two assumptions, the safe separation is ensured between departure and departure or departure and arrival operations and no additional delay is required for the departures after take-off. Therefore, the flight time of departures within the TMA is not considered in the study, as it will not be affected by conflicts between any departure aircraft and others.

Estimated operation times of arrival and departure aircraft are known in advance. The operation times and sequences of each aircraft are determined based on these estimated times. Thus, estimated REP times of arrivals and departures, TMA entry point and altitude of arrivals, and aircraft performance category are the input parameters of the model. The output of the model consists of assigned operation times and sequences, total delay, total fuel consumption, VM variables to absorb the delay and fly-by-turn variables to align with the FAP. Additionally, the model calculates the CDA start time at the TOD point, fly-by-turn start and end time, and the start time of descent on the FAP to obtain the flight trajectory and profile of an arrival aircraft with necessary variables.

2.2 Separations

When the separation at the closest point between any aircraft pair is less than the specified safety minimum, a collision risk arises between them, which is referred to as conflict. Therefore, safe separation should be ensured for all aircraft within the TMA including runways, FAP and arrival/departure routes based on the required minima. Time separation minima between consecutive operation pairs on the runway and/or FAP are presented in Table 1 according to aircraft categories [Reference Balakrishnan and Chandran35]. These categories are set according to the maximum take-off mass of aircraft as heavy(H) (≥116,000kg), large(L) (19,000–116,000kg) and small(S) (≤19,000kg) [Reference De Neufville and Odoni56].

Table 1. Separation requirements (s) [Reference Balakrishnan and Chandran35]

Besides the wake turbulence separation minima on FAP and runway, aircraft should be separated on arrival and departure routes using minimum radar separation distance $(sep_{ij}^{radar})$ . This distance is specified as 3 nautical miles (nm) within the TMAs in the regulations. Two types of conflict can emerge between consecutive aircraft on arrival routes: (a) trailing conflict along the same route and (b) crossing conflict for converging routes (Fig. 3). The interarrival times between leading aircraft i and trailing aircraft j should be estimated at TOD, FDP and FAF points using aircraft speeds, entry times and distances at each route segment. At each point, the interarrival times should be greater or equal to the minimum radar separation time $(t_{ij}^{radar})$ so that $sep_{ij}^{radar}$ is not violated at any moment along same arrival routes. In case the trailing aircraft is faster than the leading aircraft, no overtaking is allowed but the trailing aircraft is delayed to ensure the required minimum separation.

Figure 3. Conflict geometries: (a) same route, (b) converging routes (top view).

Besides the trailing conflicts along the routes, the crossing conflicts are checked at FAF for each consecutive aircraft from different arrival routes. In this case, the value of $t_{ij}^{radar}$ depends not only on relative airspeeds $(\nu _i^{\,faf},\;\nu _j^{\,faf})$ of the aircraft pair and $sep_{ij}^{radar}$ but also the conflict geometry of routes intersecting with the angle ${\theta _{ij}}$ as shown in Fig. 3(b). Equation (1) estimates $t_{ij}^{radar}$ for two aircraft flying at constant speed along intersecting linear trajectories [Reference Vela, Solak, Singhose and Clarke57]:

(1) \begin{align}t_{ij}^{radar} = \frac{{sep_{ij}^{radar}}}{{\nu _i^{\,faf}\nu _j^{\,faf}\left| {\sin {\theta _{ij}}} \right|}}\sqrt {{{\left( {\nu _i^{\,faf}} \right)}^2} + {{\left( {\nu _j^{\,faf}} \right)}^2} - 2\nu _i^{\,faf}\nu _j^{\,faf}\cos {\theta _{ij}}} \;\;.\end{align}

2.3 VM and fly-by-turn to FAP

In order to ensure safe separation between operations, delayed aircraft are allowed to perform VMs in the horizontal plane at the EP level. The velocity of the aircraft $(\nu _i^{ep})$ is not changed during the VM. The VM is represented as vector deflection consisting of coordinated turns and level flight sections, as shown in Fig. 4 [Reference Cecen and Cetek54]. The deflection angle $\left(\psi _i^{vm}\right)$ from the original flight route, bank angle $\left(\phi _i^{vm}\right)$ , and manoeuver distance $\left(l_i^{vm}\right)$ are decision variables adjusted by the mathematical model to achieve required delay. The turning radius $\left(r_i^{vm}\right)$ , distance traveled along the arc $\left(a_i^{vm}\right)$ , projected arc distance on the original flight route $\left(b_i^{vm}\right)$ and level flight distance $\left(h_i^{vm}\right)$ are the other variables that are calculated based on angle and manoeuver distance variables.

Figure 4. VM (top view).

Aircraft perform a fly-by-turn consisting of only coordinated turn with constant speed to align with FAP (Fig. 5). The relative bearing $\left(\psi _i^{\,fb}\right)$ between the original flight route and FAP is constant, but it varies for different arrival routes. The fly-by-turn is performed at FAF altitude. Therefore, the velocity of the aircraft $\left(\nu _i^{\,fb}\right)$ during the turning does not change. The turning radius $\left(r_i^{\,fb}\right)$ , distance traveled along the arc $\left(a_i^{\,fb}\right)$ , and fly-by-turn distance $\left(l_i^{\,fb}\right)$ performed on the arrival route and FAP are calculated based on bank angle decision variable $\left(\phi _i^{\,fb}\right)$ .

Figure 5. Fly-by-turn to FAP (top view).

2.4 Fuel flow model

The Eurocontrol Base of Aircraft Data (BADA) performance model, providing the performance parameters for each aircraft type, was used to calculate the total fuel of aircraft during level flight, descent, VM and fly-by-turn. It was also used to estimate the required horizontal distance and time during CDA for given start and end flight levels [58].

2.4.1 Arrival fuel flow

The fuel flow rates per unit distance during level flight and descent for arrivals can be estimated using BADA performance parameters, such as aircraft mass (W), wing surface area (S), parasitic drag coefficient $({C_{D0}})$ , induced drag coefficient (dc), thrust specific fuel coefficients $({C_{f1}}$ and ${C_{f2}})$ , descent fuel flow coefficients $({C_{f3}}$ and ${C_{f4}})$ and cruise fuel flow correction coefficient $({C_{fcr}})$ . It is assumed that the airspeed of any aircraft does not change during level flight, and all aircraft perform CDA in the TMA [58].

In order to estimate fuel consumption, lift coefficient $({C_L})$ , drag coefficient $({C_D})$ and aerodynamic drag force (Drag) acting on aircraft at any altitude (alt) with density $(\rho )$ should be calculated as given in Equations (2), (3) and (4), respectively. It is assumed that the true airspeed $(\nu )$ of any aircraft does not change during level flight. However, the value of $\nu $ changes with altitude. In level flight, the bank angle $(\phi )$ is equal to zero.

(2) \begin{align}{C_L} = \frac{{2W/S}}{{\rho {\nu ^2}\cos \phi }},\end{align}

(3) \begin{align}{C_D} = {C_{D0}} + dcC_L^2,\end{align}

(4) \begin{align}Drag = \frac{{{C_D}\rho {\nu ^2}S}}{2},\end{align}

(5) \begin{align}Th = Drag,\end{align}

(6) \begin{align}\eta = {C_{f1}}\frac{\nu }{{{C_{f2}}}},\end{align}

(7) \begin{align}{f_{cr}} = \eta Th{C_{fcr}},\end{align}

(8) \begin{align}{f_{min}} = {C_{f3}}\left( {1 - \frac{{alt}}{{{C_{f4}}}}} \right).\end{align}

The total thrust (Th) required by the engines should be equal to the total Drag during level flight (Equation (5)). The thrust-specific fuel consumption $(\eta )$ required to produce unit thrust per unit time is calculated by Equation (6). The level flight fuel flow rate at any altitude can be estimated using ${C_{fcr}}$ as given in Equation (7). An aircraft performing CDA maintains its flight with idle thrust while the throttle is at its minimum level. Therefore, the fuel flow rate during CDA can be calculated by Equation (8).

2.4.3 Fuel flow for VM and fly-by-turn

The fuel in VM and fly-by-turn can be calculated with known fuel flow rates per unit distance for a given airspeed at any flight level. In these manoeuvres, aircraft perform a coordinated turn with the bank angle $(\phi )$ . An increase in the bank angle $(\phi )$ , which results in higher load factors, during the coordinated turn creates extra fuel. In the study, an aircraft type was determined for each aircraft category. For these aircraft types, the fuel flow rates were calculated with bank angles $(\phi )$ between 0° and 30° for altitudes at which the VM and fly-by-turn would be performed. To predict the value of the rate in terms of $(\phi )$ , we used the curve-fitting method using the calculated fuel flow rates and obtained a third-order polynomial function (9) with ${R^2} = 0.99$ .

(9) \begin{align}{f_i} = \alpha _i^3{\left( {{\phi _i}} \right)^3} + \alpha _i^2{\left( {{\phi _i}} \right)^2} + \alpha _i^1{\phi _i} + \alpha _i^0\end{align}

In (9), $\alpha _i^0$ , $\alpha _i^1$ , $\alpha _i^2$ and $\alpha _i^3$ are regression coefficients found in kg/nm for any aircraft type at a specified altitude. These coefficients correspond to the $\beta _i^0$ , $\beta _i^1$ , $\beta _i^2$ and $\beta _i^3$ in fuel calculation of fly-by-turn and level flight at FAF altitude.

3.1 Sets

U = $\left\{ {1,\;2,\; \ldots ,\;u} \right\}$ set of aircraft $i,j,k \in U$

O = $\{ {o_i}$ | $\;{o_i} = 1$ for arrival, ${o_i} = 2$ for departure, $i \in U\} $ operation type of aircraft

C = { ${c_i}$ | ${c_i} = 1$ for small, ${c_i} = 2$ for large, ${c_i} = 3$ for heavy, $i \in U\} $ aircraft categories

$N = \left\{ {1,\;2,\; \ldots ,n} \right\}$ set of TMA Eps

3.2 Parameters

u: Number of aircraft

$n:$ Number of TMA EPs

${o_i}$ : Operation type of aircraft i

${c_i}$ : Category of aircraft i

$e{p_i}$ : TMA EP of aircraft i

$t_i^{erep}$ : Estimated REP time of aircraft i

$t_i^{earliest}$ : Earliest REP time of aircraft i

$t_i^{latest}$ : Latest REP time of aircraft i

$t_i^{efaf}$ : Estimated FAF time of aircraft i. This time is calculated by considering estimated REP time, and time spent on FAP and during fly-by-turn as given in Equation (10).

(10) \begin{align}t_i^{efaf} = t_i^{erep} - d_i^{tfa - rep} - \left( {{l^{\,fap}} - l_i^{tfa - rep}} \right)/\nu _i^{\,faf}\forall \,i,\;{o_i} = 1\end{align}

$t_i^{ep}$ : Estimated TMA EP time of aircraft i

$sep_{ij}^{wake}$ : Wake turbulence time separation between aircraft i and j

$sep_{ij}^{radar}$ : Minimum radar separation distance between aircraft i and j in TMA

$l_i^{ep - faf}$ : Route length of aircraft i from EP to FAF

$l_i^{tod - faf}$ : Horizontal route length required for CDA from TOD to FAF altitude of aircraft i

$l_i^{tfa - rep}$ : Horizontal route length required for descent from TFA to REP of aircraft i

${l^{\,fap}}$ : FAP length equal to the distance between FAF and REP

$d_i^{tod - faf}$ : Required flight duration for CDA from TOD to FAF altitude of aircraft i

$d_i^{tfa - rep}$ : Required flight duration for descent from TFA to REP of aircraft i

$\nu _i^{ep}$ : Speed of aircraft i at EP level

$\nu _i^{\,faf}$ : Speed of aircraft i at FAF altitude

$f_i^{\,tfa - rep}$ : Fuel during descent from TFA to REP of aircraft i

$f_i^{\,tod - faf}$ : Fuel during CDA from TOD to FAF altitude of aircraft i

$f_i^{\,depunit}$ : Fuel per unit time of departure aircraft i

$\alpha _i^0,\;\alpha _i^1,\;\alpha _i^2,\;\alpha _i^3$ : Fuel coefficients for aircraft i at EP level during VM

$\beta _i^0,\;\beta _i^1,\;\beta _i^2,\;\beta _i^3$ : Fuel coefficients for aircraft i at FAF altitude during fly-by-turn

${\theta _{ij}}$ : Angle difference between arrival routes of aircraft i and j

$\psi _i^{\,fb}$ : Relative bearing of aircraft i performing fly-by-turn to FAP

M: Big enough positive number

p: Small enough positive number

g: Gravitational acceleration

3.3 Decision variables

${x_{ik}}$ : Binary variable that equals 1, if aircraft i is assigned to position k in the sequence; otherwise 0

${y_i}$ : Binary variable that equals 1, if aircraft i is delayed; otherwise 0

$t_i^{rep}$ : REP time of aircraft i

$t_i^{tfa}$ : TFA time of aircraft i

$t_i^{\,faf}$ : FAF time of aircraft i

$t_i^{tod}$ : TOD time of aircraft i

$d_i^{\,fblevel}$ : Total spent time during fly-by-turn and level flight at FAF altitude

$delay_i^{gnd}$ : Ground delay of aircraft i

$delay_i^{air}$ : Airborne delay of aircraft i

$l_i^{\,eplevel}$ : Level flight distance of aircraft i at EP level

$l_i^{\,faflevel}$ : Final approach level flight distance of aircraft i at FAF altitude

$r_i^{vm}$ : Turn radius of aircraft i in VM

$\phi _i^{vm}$ : Bank angle of aircraft i in VM

$\psi _i^{vm}$ : Deflection angle of aircraft i in VM

$a_i^{vm}$ : Arc distance traveled by aircraft i during VM

$b_i^{vm}$ : Total distance travelled by aircraft i projected on original flight route during VM

$h_i^{vm}$ : Distance traveled by aircraft i along the VM with no bank angle

$l_i^{vm}$ : VM distance of aircraft i

$r_i^{\,fb}$ : Turn radius of aircraft i in fly-by-turn

$\phi _i^{\,fb}$ : Bank angle of aircraft i in fly-by-turn

$a_i^{\,fb}$ : Arc distance traveled by aircraft i during fly-by-turn

$l_i^{\,fb}$ : Fly-by-turn distance of aircraft i performed on arrival route and FAP

$f_i^{\,vmturn}$ : Fuel of aircraft i during coordinated turn in VM

$f_i^{\,vmlevel}$ : Fuel of aircraft i during level flight with no bank angle in VM

$f_i^{\,fb}$ : Fuel of aircraft i during fly-by-turn

$f_i^{\,eplevel}$ : Fuel of aircraft i during level flight at EP level

$f_i^{\,faflevel}$ : Fuel of aircraft i during level flight at FAF altitude

$f_i^{\,arr}$ : Total fuel of arrival aircraft i

$f_i^{\,dep}$ : Total fuel of departure aircraft i

Quick Guide

3.4 Constraints

Time, duration, length calculation and aircraft assignment constraints:

(11) \begin{align} & t_i^{tfa} = t_i^{rep} - d_i^{tfa - rep}\,& \forall \,i,\;{o_i} = 1 \end{align}

(12) \begin{align} & t_i^{\,faf} \geqslant t_i^{tfa} - d_i^{\,fblevel}\,& \forall \,i,\;{o_i} = 1 \end{align}

(13) \begin{align} & t_i^{tod} = t_i^{\,faf} - d_i^{tod - faf} - l_i^{\,fb}/\nu _i^{\,faf}\,& \forall \,i,\;{o_i} = 1 \end{align}

(14) \begin{align} & d_i^{\,fblevel} = \left( {l_i^{\,faflevel} + l_i^{\,fb}} \right)/\nu _i^{\,faf}\, & \forall \,i,\;{o_i} = 1 \end{align}

(15) \begin{align} & l_i^{\,faflevel} = {l^{\,fap}} - l_i^{tfa - rep} - l_i^{\,fb}\,& \forall \,i,\;{o_i} = 1 \end{align}

(16) \begin{align} & l_i^{\,eplevel} = l_i^{ep - faf} - l_i^{tod - faf} - l_i^{vm} - l_i^{\,fb}\,& \forall \,i,\;{o_i} = 1 \end{align}

(17) \begin{align} & delay_i^{gnd} \geqslant t_i^{rep} - t_i^{erep}\,& \forall \,i \end{align}

(18) \begin{align} & delay_i^{air} \geqslant t_i^{\,faf} - t_i^{efaf} - delay_i^{gnd}\,& \forall \,i,\;{o_i} = 1 \end{align}

(19) \begin{align} & t_i^{earliest} \le t_i^{rep} \le t_i^{latest}\,& \forall \,i \end{align}

(20) \begin{align} & \mathop \sum \limits_i {x_{ik}} = 1\,& \forall \,k \end{align}

(21) \begin{align} & \mathop \sum \limits_k {x_{ik}} = 1\,& \forall \,i \end{align}

The TFA time calculated from runway entry time and time spent on FAP is formulated in Equation (11). The assigned FAF time calculated from TFA time and $d_i^{\,fblevel}$ is formulated in Equation (12). Equation (13) calculates the start time of CDA at the TOD point for each arrival. The calculation of $d_i^{\,fblevel}$ is formulated in Equation (14). Level flight distance of arrivals that varies with fly-by-turn distance at FAF altitude and level flight distance during the VM at TMA entry level are calculated in Equations (15) and (16), respectively. Equation (17) calculates the ground delay of each aircraft. Equation (18) calculates the airborne delay of each arrival. The time window (TW) of each aircraft is given in Equation (19), which shows the earliest and latest runway entry time that can be allocated to each aircraft. Equations (20) and (21) ensure that one aircraft is assigned to each position in the sequence and each aircraft is assigned to only one position, respectively.

Constraints of separation between consecutive aircraft:

(22) \begin{align} & t_j^{rep} \geqslant t_i^{rep} + sep_i^{wake} - M\left( {2 - {x_{ik - 1}} - {x_{jk}}} \right)\,\forall \,i \ne j,\;k \gt 1 \end{align}

(23) \begin{align} & t_j^{rep} \geqslant t_i^{rep} + sep_{ij}^{wake} - M\left( {2 - {x_{ik - 1}} - {x_{jk}}} \right)\,&\forall \,i \ne j,\;k \gt 1,\;{o_i} = {o_j} = 1,\;\nu _i^{\,faf} \le \nu _j^{\,faf} \end{align}

(24) \begin{align} & t_j^{rep} \geqslant t_i^{rep} + sep_{ij}^{wake} - M\left( {2 - {x_{ik - 1}} - {x_{jk}}} \right) + d_j^{tfa - rep} \nonumber \\ & \qquad - d_i^{tfa - rep} + d_j^{\,fblevel} - d_i^{\,fblevel}\,&\forall \,i \ne j,\;k \gt 1,\;{o_i} = {o_j} = 1,\;\nu _i^{\,faf} \gt \nu _j^{\,faf} \end{align}

(25) \begin{align} & t_j^{\,faf} \geqslant t_i^{\,faf} + sep_{ij}^{wake} - M\left( {2 - {x_{ik - 1}} - {x_{jk}}} \right)\,&\forall \,i \ne j,\;k \gt 1,\;{o_i} = {o_j} = 1,\;\nu _i^{\,faf} \gt \nu _j^{\,faf} \end{align}

(26) \begin{align} &t_j^{\,faf} \geqslant t_i^{\,faf} + sep_{ij}^{wake} - M\left( {2 - {x_{ik - 1}} - {x_{jk}}} \right) + d_i^{tfa - rep}\nonumber\\ & \qquad - d_j^{tfa - rep} + d_i^{\,fblevel} - d_j^{\,fblevel}\,&\forall \,i \ne j,\;k \gt 1,\;{o_i} = {o_j} = 1,\;\nu _i^{\,faf} \le \nu _j^{\,faf} \end{align}

(27) \begin{align} &t_j^{\,faf} \geqslant t_i^{\,faf} + \frac{{sep_{ij}^{radar}}}{{\nu _j^{\,faf}}} - M\left( {2 - {x_{ik - 1}} - {x_{jk}}} \right)\,&\forall \,i \ne j,\;k \gt 1,\;{o_i} = {o_j} = 1,\;e{p_i} = e{p_j} \end{align}

(28) \begin{align} & t_j^{\,faf} \geqslant t_i^{\,faf} + \frac{{sep_{ij}^{radar}}}{{\nu _i^{\,faf}\nu _j^{\,faf}\left| {\sin {\theta _{ij}}} \right|}}\sqrt {{{\left( {\nu _i^{\,faf}} \right)}^2} + {{\left( {\nu _j^{\,faf}} \right)}^2} - 2\nu _i^{\,faf}\nu _j^{\,faf}\cos {\theta _{ij}}} \nonumber \\ & \qquad - M\left( {2 - {x_{ik - 1}} - {x_{jk}}} \right)\,& \forall \,i \ne j,\;k \gt 1,\;\;{o_i}{ = _j} = 1,\; e{p_i} \ne e{p_j} \end{align}

In Equation (22), the necessary wake turbulence separation between the aircraft is provided while determining runway entry times. It is sufficient to ensure that separation between aircraft is provided on runway, which is the last point if $\nu _i^{\,faf} \gt \nu _j^{\,faf}$ (Equation (23)), and at FAF, which is the first point if $\nu _i^{\,faf} \le \nu _j^{\,faf}$ (Equation (25)). After assigning runway times for the first case, FAF time is determined by Equation (26). For the second case, REP times are calculated in Equation (24). At FAF, radar separation must be provided between aircraft arriving from the same route (Equation (27)), and converging routes (Equation (28)).

VM constraints of delayed arrivals:

(29) \begin{align} & delay_i^{air} + delay_i^{gnd} \geqslant p - M\left( {1 - {y_i}} \right)\,&\forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(30) \begin{align} & delay_i^{ar} + delay_i^{gnd} \le M{y_i}\,&\forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(31) \begin{align} &r_i^{vm} \geqslant \frac{{{{\left( {\nu _i^{ep}} \right)}^2}}}{{g\tan \phi _i^{vm}}} - M\left( {1 - {y_i}} \right)\,&\forall i,{\rm{\;}}{o_i} = 1 \end{align}

(32) \begin{align} & r_i^{vm} \le \frac{{{{\left( {\nu _i^{ep}} \right)}^2}}}{{g\tan \phi _i^{vm}}} + M\left( {1 - {y_i}} \right)\,&\forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(33) \begin{align} & r_i^{vm} \le M{y_i}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(34) \begin{align} & a_i^{vm} = 8\pi r_i^{vm}\frac{{\psi _i^{vm}}}{{2\pi }} \,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(35) \begin{align} & b_i^{vm} = 4r_i^{vm}\sin \psi _i^{vm}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(36) \begin{align} & h_i^{vm} \geqslant \frac{{l_i^{vm} - b_i^{vm}}}{{\cos \psi _i^{vm}{\rm{\;}}}} - M\left( {1 - {y_i}} \right)\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(37) \begin{align} & h_i^{vm} \le \frac{{l_i^{vm} - b_i^{vm}}}{{\cos \psi _i^{vm}}} + M\left( {1 - {y_i}} \right)\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(38) \begin{align} & h_i^{vm} \le M{y_i}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(39) \begin{align} & b_i^{vm} \le l_i^{vm}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(40) \begin{align} & a_i^{vm} + h_i^{vm} = l_i^{vm} + \left( {delay_i^{air} + delay_i^{gnd}} \right)\nu _i^{ep}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(41) \begin{align} & 0 \le \phi _i^{vm} \le {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 6}}\right.}\!\lower0.7ex\hbox{$6$}}\,& \forall i,{\rm{\;}}{o_i} = 1 \end{align}

(42) \begin{align} & 0 \le \psi _i^{vm} \le {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.}\!\lower0.7ex\hbox{$2$}}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(43) \begin{align} & 0 \le l_i^{vm} \le 20\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

By taking the value of decision variable ${y_i}$ in Equations (29) and (30), the model determines each delayed arrival aircraft i. Equations (31)–(33) calculate the turn radius in VM. The distance travelled along the arc and projected arc distance on the original flight route are calculated by Equations (34) and (35), respectively. Equations (36)–(38) calculate the distance travelled during level flight. Equation (39) ensures that the arc distance projected on the original flight route cannot be longer than the manoeuvre distance. Equation (40) guarantees that the distance travelled during VM satisfies the total delay. Equations (41)–(43) show bank angle, deflection angle and manoeuvre distance lower and upper bounds, respectively.

Constraints for fly-by-turn to FAP:

(44) \begin{align} & r_i^{\,fb} = \frac{{{{\left( {\nu _i^{\,faf}} \right)}^2}}}{{g\tan \phi _i^{\,fb}}}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(45) \begin{align} & a_i^{\,fb} = 2\pi r_i^{\,fb}\frac{{\psi _i^{\,fb}}}{{2\pi }}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(46) \begin{align} &l_i^{\,fb} = r_i^{\,fb}\tan \left( {\psi _i^{\,fb}/2} \right)\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(47) \begin{align} &0 \le \phi _i^{\,fb} \le {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 6}}\right.}\!\lower0.7ex\hbox{$6$}}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(48) \begin{align} & 0 \le l_i^{\,fb} \le 10\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

The decision variables of VM for turning onto FAP are calculated using Equations (44)–(48). Equations (44) and (45) calculate the turn radius and distance travelled along the arc, respectively. The projected arc distance on the arrival route and FAP are equal and they are calculated by Equation (46). Equations (47) and (48) show the bank angle and manoeuvre distance lower and upper bounds, respectively.

Constraints for calculating fuel in VM:

(49) \begin{align} & f_i^{\,vmturn} = \left( {\alpha _i^3{{\left( {\phi _i^{vm}} \right)}^3} + \alpha _i^2{{\left( {\phi _i^{vm}} \right)}^2} + \alpha _i^1\phi _i^{vm} + \alpha _i^0} \right)a_i^{vm}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(50) \begin{align} & f_i^{\,vmlevel} = \alpha _i^0h_i^{vm}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(51) \begin{align} &f_i^{\,fb} = \left( {\beta _i^3{{\left( {\phi _i^{\,fb}} \right)}^3} + \beta _i^2{{\left( {\phi _i^{\,fb}} \right)}^2} + {\rm{\;}}\beta _i^1\phi _i^{\,fb} + {\rm{\;}}\beta _i^0} \right)a_i^{\,fb}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(52) \begin{align} & f_i^{\,eplevel} = \alpha _i^0l_i^{\,eplevel}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(53) \begin{align} &f_i^{\,faflevel} = \beta _i^0l_i^{\,faflevel}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

Equations (49)–(53) show fuel calculation of arrival for different flight phases. The fuel along the arc and during the level flight of VM are calculated by Equations (49) and (50), respectively. Equation (51) shows fuel consumption depending on the bank angle when turning onto FAP. The fuel at TMA entry and FAF altitude until descent are calculated by Equations (52) and (53), respectively.

Constraints for calculating the total fuel:

(54) \begin{align} & f_i^{\,arr} \geqslant f_i^{\,vmturn} + f_i^{\,vmlevel} + f_i^{\,fb} + f_i^{\,eplevel} + f_i^{\,faflevel} + f_i^{\,tod - faf} + f_i^{\,tfa - rep} - M\left( {1 - {y_i}} \right)\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(55) \begin{align} & f_i^{\,arr} \le f_i^{\,vmturn} + f_i^{\,vmlevel} + f_i^{\,fb} + f_i^{\,eplevel} + f_i^{\,faflevel} + f_i^{\,tod - faf} + f_i^{\,tfa - rep} + M\left( {1 - {y_i}} \right)\, & \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(56) \begin{align} & f_i^{\,arr} \geqslant f_i^{\,fb} + f_i^{\,eplevel} + f_i^{\,faflevel} + f_i^{\,tod - faf} + f_i^{\,tfa - rep} - M{y_i}\,& \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(57) \begin{align} & f_i^{\,arr} \le f_i^{\,fb} + f_i^{\,eplevel} + f_i^{\,faflevel} + f_i^{\,tod - faf} + f_i^{\,tfa - rep} + M{y_i}\, & \forall \,i,{\rm{\;}}{o_i} = 1 \end{align}

(58) \begin{align} & f_i^{\,dep} = f_i^{\,depunit}delay_i^{gnd}\, & \forall \,i,{\rm{\;}}{o_i} = 2 \end{align}

(59) \begin{align} & {x_{ik}} \in \left\{ {0,{\rm{\;}}1} \right\}\, & \forall \,i,k \end{align}

(60) \begin{align} & {y_i} \in \left\{ {0,{\rm{\;}}1} \right\}\, & \forall \,i \end{align}

(61) \begin{align} & t_i^{rep},{\rm{\;}}t_i^{\,faf},{\rm{\;}}delay_i^{air},{\rm{\;}}delay_i^{gnd},{\rm{\;}}r_i^{vm},{\rm{\;}}a_i^{vm},{\rm{\;}}b_i^{vm},{\rm{\;}}h_i^{vm} \geqslant 0\, & \forall \,i \end{align}

(62) \begin{align} & r_i^{\,fb},{\rm{\;}}a_i^{\,fb},{\rm{\;}}f_i^{\,vmturn},{\rm{\;}}f_i^{\,vmlevel},{\rm{\;}}f_i^{\,fb},{\rm{\;}}f_i^{\,eplevel},{\rm{\;}}f_i^{\,faflevel},{\rm{\;}}f_i^{\,arr},{\rm{\;}}f_i^{\,dep} \geqslant 0\, & \forall \,i \end{align}

Equations (54)–(57) define fuel consumption for either delayed or not delayed arrivals. While Equations (54) and (55) give the total fuel of a delayed arrival, Equations (56) and (57) calculate the total fuel for a not delayed arrival. The total fuel calculation of departures depending on delays is given by Equation (58). Equations (59)–(62) show the sign equations of decision variables.

3.5 Objective functions

(63) \begin{align} min\;{z_1} &= \mathop \sum \limits_i delay_i^{air} + delay_i^{gnd} \end{align}

(64) \begin{align} min\;{z_2} &= \mathop \sum \limits_i f_i^{\,arr} + f_i^{\,de} \end{align}

The first objective (63) in this research is to minimise the total airborne and ground delays, and the second objective (64) is to minimise the total fuel.

We used the $\varepsilon$ -constraint method, one of the scalarisation techniques, to obtain solutions for the described problem. With this approach, one main objective is optimised, while the others are transformed into constraints. In this study, we convert the total delay objective function to an $\varepsilon$ -constraint and limited its value to $\varepsilon$ , while minimising total fuel. The $\varepsilon$ -constraint is given in Equation (65).

(65) \begin{align}\mathop \sum \limits_i delay_i^{air} + delay_i^{gnd} \le \varepsilon \end{align}

In a multi-objective problem, there are two or more conflicting objective functions to be optimised simultaneously. For this, multiple solutions exist, which can be categorised as Pareto optimal or non-dominated, in which there is a trade-off between objective functions. In these functions, f(x) corresponds to solution x of the model whose objective is minimisation. A solution x^* is called Pareto optimal, if a solution that satisfies f(x) ≤ f(x^* ) cannot be found [Reference Ehrgott53]. In the $\varepsilon$ -constraint method, the non-dominated solutions are obtained by parametrical variation of $\varepsilon$ .

4.1 Inputs and parameters

4.1.1 Airspace structure

The proposed model was tested for arrival and departure operations at LTFJ. LTFJ has a single runway 06/24 used for mixed operations within Istanbul TMA. By 2019, it accommodated more than 235,000 aircraft movements and 35.5 million passengers annually [60]. It is considered to be one of the busiest airports with a single runway and single terminal building [61]. Arrivals to LTFJ enter TMA from seven different EPs: ATVEP, GELBU, TURKO, ELVON, EVNOT, PAZAR and TESTA (Fig. 7). Because GELBU EP has a lower traffic flow rate compared to TURKO, they are both replaced by GTM01 as a new EP for simplification. All arriving flights, except ones from PAZAR, are assumed to follow a direct route from their EP to FAF at LTFJ whereas an indirect route is assumed for the entries from PAZAR due to its location. Both arrivals and departures use runway 06 direction [62].

The TMA entry levels of aircraft for all EP, the horizontal distance $(l_i^{ep - faf})$ of direct routes they will follow to reach FAF, the heading angle of routes, and relative bearings $(\psi _i^{\,fb})$ are given in Table 2 [62]. The angle ${\theta _{ij}}$ is equal to the acute angle between the converging routes. For example, the angle ${\theta _{ij}}$ between routes starting from EPs 1 and 2 is equal to 10°. For the arrivals from PAZAR, it is assumed that the aircraft make a fly-by-turn defined in Section 2.3 from heading 263° to 215° at FL130. The FAF altitude, FAP length $({l^{\,fap}})$ , and heading angle of aircraft on FAP are 5,000ft, 25nm, and 60°, respectively.

Table 2. TMA EP levels, horizontal distances of routes (nm), heading angles and relative bearings

Figure 7. İstanbul TMA and EPs to LTFJ.

4.1.3 Aircraft performance data

The selected aircraft types were the Cessna C550, Airbus A320 and Boeing B773 for small, large and heavy categories, respectively. For these aircraft types performing CDA in the TMA, the required fuel, horizontal distance and time values to descend from TMA EP level to FAF altitude without any wind condition for LTFJ are shown in Tables 3, 4 and 5, respectively. The extra fuel due to the VM at FL130 of aircraft coming from the PAZAR EP was included.

Table 3. Fuel for $\left(f_i^{\,tod - faf}\right)$ (kg)

Table 4. Horizontal distance for $\left(l_i^{tod - faf}\right)$ (nm)

Table 5. Times for $\left(d_i^{tod - faf}\right)$ (s)

The fuel, required horizontal distance and time to descend from the FAF altitude to the REP are given in Table 6 for three aircraft types.

Table 6. Fuel, required horizontal distance and time from TFA to REP

The fuel consumption of departures was calculated by the model as a linear function of delay and fuel flow rate. The engine characteristics of selected aircraft types and the amount of fuel consumed per unit of time while waiting at the runway holding position are given in Table 7 [59].

Table 7. Numbers, identifications, and fuel flow rates [59]

4.2 Test data

In order to evaluate the performance of the proposed mathematical model, we generated different problem scenarios that exhibit similar traffic characteristics to LTFJ data using the Monte Carlo simulation. We defined four traffic levels (TLs), consisting of 16, 18, 20 and 22 aircraft in different performance categories and produced six different problem scenarios for each TL. Each of these 24 problem scenarios covered a half-hour operational period. Additionally, we defined two different cases (C1 and C2) with different TWs to run scenarios as given in Table 8. For example, the earliest REP time of each aircraft was set to estimated REP time and the latest REP time of each aircraft was 180s after estimated REP time in C1. In C2, departure aircraft were allowed to perform their operations before estimated REP time. It is more difficult for controllers to perform operations of aircraft with optimum sequencing than for FCFS sequencing as there are significant differences in sequence. Therefore, TWs were limited to an acceptable level (i.e. equal to 180s).

Table 8. TWs for operations in cases C1 and C2

4.3 Results

The proposed mathematical model was tested with defined test data of scenarios. Initially, the ideal and nadir points, which are defined as the lower and upper bounds in non-dominated points, were calculated. After determining these points, we obtained the non-dominated solutions by using the $\varepsilon$ -constraint method. The parametrical variation in the value of $\varepsilon$ was made at 15-second intervals between lower and upper values of total delay at ideal and nadir points. Thus, the Pareto front was obtained by running the scenarios using GAMS solvers. In addition, all scenarios were run with the FCFS principle by using the proposed model as single-objective (FCFS-single) and multi-objective (FCFS-multi). The descriptions of the runs are shown in Table 9. A total of 760 runs were performed for the mathematical model in the study. The results of the proposed multi-objective approach were compared with the FCFS-single and FCFS-multi approach results.

Table 9. Description of runs

The graphs in Figs 8, 9, 10 and 11 show non-dominated points obtained by the model, and the result of FCFS-single and FCFS-multi for different scenarios with 16, 18, 20 and 22 TL, respectively. In graphs, showing the trade-offs between the objectives, the horizontal axis represents the total delay $({z_1})$ in seconds, while the vertical axis represents the total fuel $({z_2})$ in kilograms. The number of non-dominated solutions varies across scenarios for each TL. The number of non-dominated solutions differs for each scenario of the specified TL. The highest number of non-dominated solutions is 7, and this is obtained in the scenario presented in Fig. 10(a). In C1, the total number of non-dominated points for all scenarios is 27, 26, 25 and 27 for 16, 18, 20 and 22 TLs, respectively. In C2, these numbers are 16, 13, 15 and 16 for the same TLs.

Figure 8. Results for traffic level of 16 aircraft.

Figure 9. Results for traffic level of 18 aircraft.

Figure 10. Results for traffic level of 20 aircraft.

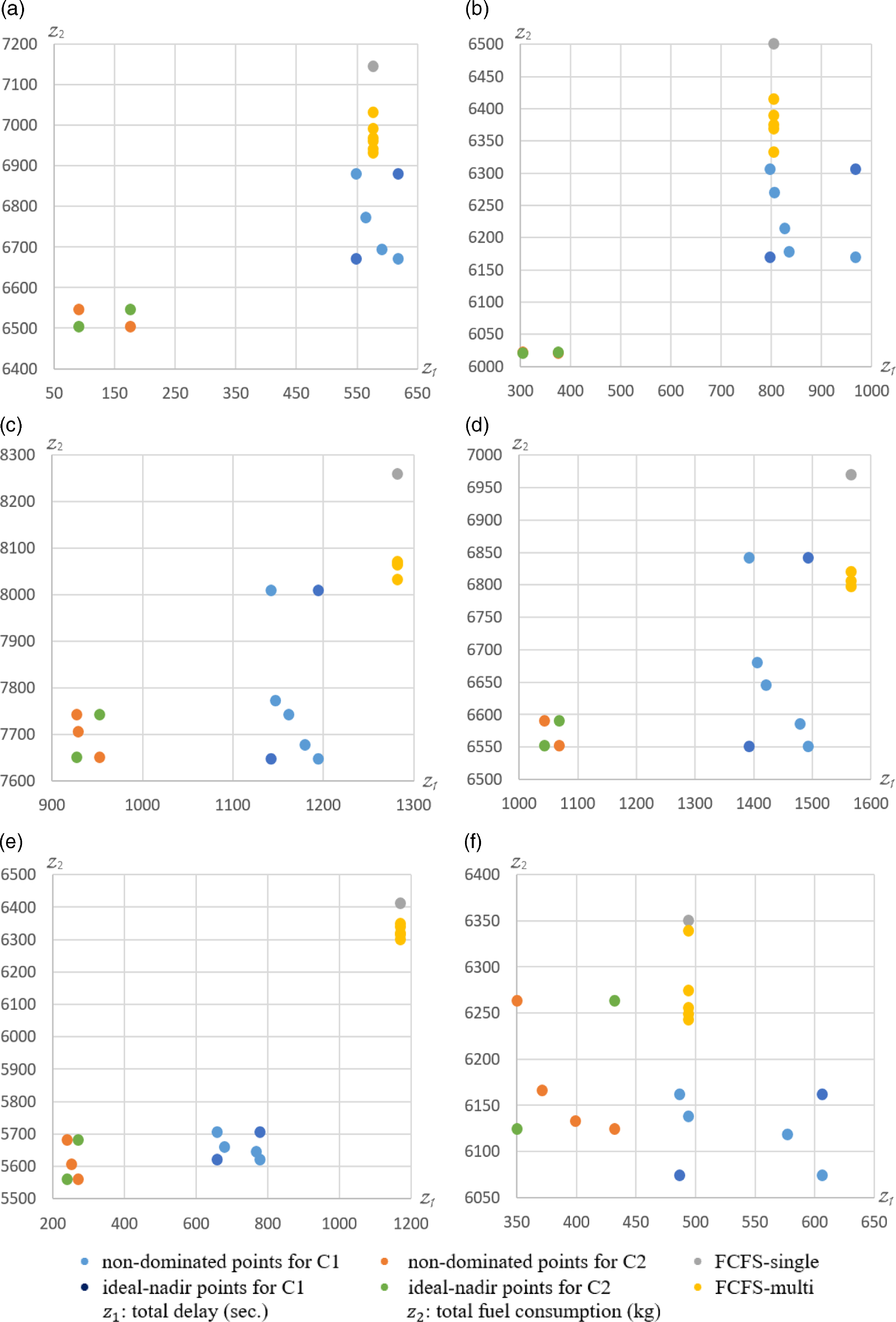
Figure 11. Results for traffic level of 22 aircraft.

All graphs show that the solution space narrows down in some scenarios for C2 compared to C1. However, almost all solutions obtained in C2 have lower total delay and fuel values when compared to solutions obtained in C1. Therefore, total delay and fuel are reduced when we allow departures to perform their operations before REP time. When we look at the non-dominated points compared to FCFS results, it is seen that total fuel is compromised in case of better total delay, while the total delay is compromised in case of better total fuel. There are also non-dominated solutions where both total fuel and total delay are better, according to FCFS results. When the primary objective was total fuel, the arrivals became the primary operations according to departures. In this case, the number of delayed departures increased while the number of delayed arrivals decreased. For example, in non-dominated results of C1 in Fig. 9(b), the number of delayed arrivals is 4, 3, 2 and 1 from left to right, while the number of delayed take-offs is 4, 5, 5 and 6. Therefore, the leftmost non-dominated solution point in graphs corresponds to minimum delay, while the rightmost non-dominated solution point corresponds to minimum fuel.

Figure 12 shows the average total delay of aircraft in all TL scenarios for C1 and C2. According to the figure, the average total delay in C2 was reduced by 23.2%, 49.6%, 35.9% and 43.9% compared with the C1 for 16, 18, 20 and 22 TL scenarios, respectively. This means that the number of delayed aircraft decreased when we allowed the departure aircraft to perform their operations before the REP time.

In order to compare the results of FCFS with non-dominated solutions of scenarios for C1 and C2, the percent improvement rates in total delay were calculated as given in Table 10. The percent improvement rates in total delay is equal to the percent ratio of the difference between the value of the objective in the FCFS approach and the value of the objective in obtained non-dominated solution to the FCFS approach. The values in the table show average, minimum and maximum improvement rates at each TL. Accordingly, the average total delay was reduced by 8.7% and 44% compared with FCFS for all TL runs in C1 and C2, respectively. These percentages correspond to an average of 73.7 and 372.6s for each run. In addition, when the maximum values are considered, it is seen that significant improvement in total delay have been achieved. The average values of maximum rates were 51% and 78.9% for all TL runs in C1 and C2, respectively. These percentages correspond to an average of 431.9 and 668.2s for each run.

The average total fuel of arrivals and departures in all TL scenarios for C1 and C2 is given in Fig. 13. According to the figure, the average total fuel of arrivals is close to each other in C1 and C2. There are small decreases in C2 except for 20 TL scenarios. When the total fuel of departures is compared, there has been a decrease in C2. This is a result of both a decrease in the number of delayed aircraft and a reduction in the delay duration of some individual aircraft. When the total fuel of the arrivals and departures is considered, it is lower in C2 than in C1.

We also compared the total fuels of non-dominated solutions with FCFS results and calculated average percent improvement rates in total fuel as given in Table 11. The values show average improvement rates compared to FCFS results of six different scenarios at each TL. The percent improvement rates in total fuel of non-dominated solutions compared to the FCFS-single approach are given as “FCFS-single”, while the improvement rates in total fuel of non-dominated solutions compared to the FCFS-multi approach are given as “FCFS-multi”. Accordingly, the percent improvements in total fuel of FCFS-single are higher than the FCFS-multi. The reason for this is that the model generates optimal trajectories using VMs while minimising both objective functions simultaneously. The model also generated optimal trajectories when it was run with the FCFS-multi approach. Therefore, the non-dominated solutions were compared with both FCFS-single and FCFS-multi results.

Table 10. The percent improvement rates in total delay for C1 and C2

Figure 12. Total delay (s).

As shown in Table 11, the average total fuel was reduced by 4.4% and 5.8% compared with the FCFS-multi for all TL runs in C1 and C2, respectively. These percentages correspond to an average of 268 and 353.3kg for each run. On the other hand, the average total fuel was reduced by 6% and 7.3% compared with FCFS-single for all TL runs in C1 and C2, respectively. These percentages correspond to an average of 372.5 and 453.2kg for each run. Note that these savings are only for a half-hour operational period on a single runway. These results indicate the importance of aircraft sequencing and scheduling considering the aircraft manoeuvres and flight profiles together at major airports within the TMA.

Table 11. Average percent improvement rates in total fuel

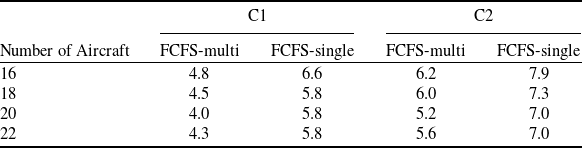
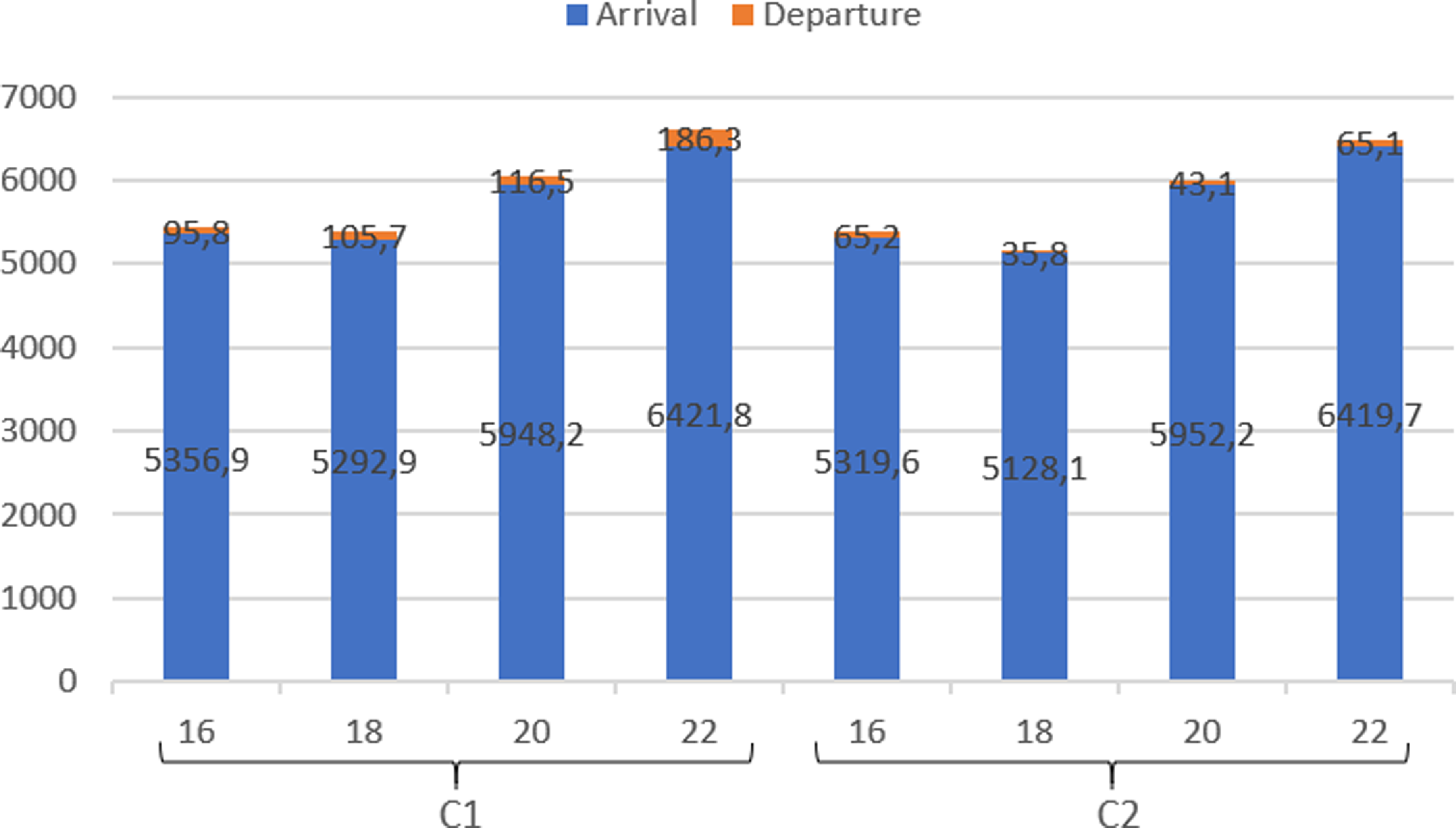
Figure 13. Total fuel (kg).

The runs with maximum improvement in total delay are determined for C1 and C2. The corresponding improvement in total fuel are also estimated for the same runs. In C1, the maximum decrease in total fuel for 16, 18, 20 and 22 TLs are 16.2%, 9.5%, 14.2% and 11.3%, respectively. In C2, the maximum decrease in total fuel for 16, 18, 20 and 22 TLs are 18.9%, 9.1%, 16.7% and 12.3%, respectively.

The runs with maximum improvement rates of non-dominated solutions can be seen in Fig. 8(e), 9(b), 10(e) and 11(e). We also selected these runs as an example to give more detailed information about the number of delayed aircraft and fuel of arrivals within the TMA. Table 12 shows the average number of delayed aircraft for non-dominated solutions in runs with maximum improvement rates. Accordingly, the total number of delayed aircraft in non-dominated solutions decreased according to FCFS. When we compared C1 and C2, there was a significant decrease in the number of delayed departures. Although there was an increase in the number of delayed arrivals in 16 and 18 TL scenarios, the total number of delayed aircraft decreased. This resulted in more decrease in the total fuel of aircraft in C2, as stated earlier.

Table 13 shows the total fuel of delayed arrivals during VM, while Table 14 shows fuel during level flight at EP level and FAF altitude in the same runs. The fuel given in Table 13 is directly proportional to the number of delayed aircraft given in Table 12. As the number of delayed aircraft decreased, the total fuel of VM decreased. The total fuel of aircraft during VM decreased significantly compared to FCFS in non-dominated solutions. According to the average values in the table, the percent improvement rate increased to 62% for 18 TL in C1 compared to FCFS-multi. The percent improvement rates were 48.1%, 27.2% and 35.2% for 16, 20 and 22 TLs, respectively. Accordingly, the total fuel of FCFS-single during VM is higher than FCFS-multi. The reason for this is that the proposed model generates optimal trajectories using VMs while minimising both objective functions simultaneously.

Table 12. The average number of delayed aircraft

Table 13. Fuel during the VM (kg)

Table 14. Fuel during level flights (kg)

When we examined total fuel during level flight given in Table 14, there was an increase in fuel at the TMA EP level according to FCFS, while a decrease in fuel at FAF altitude was observed. It is proof that this model allows aircraft to fly longer time at higher flight levels to achieve a fuel-optimal flight profile. Flying for less time at FAF altitude, it enabled the aircraft to make a fuel-optimal CDA approach.

In order to evaluate the effectiveness and practicality of the model in real-world situations, it was also tested with actual TMA operation data from LTFJ including 22 aircraft for a half-hour operational period. This data was selected from the 15:00–16:00 time zone with busy traffic on August 18 [63]. The calculated total delay and total fuel values for this reference day data are 555s and 7,446.1kg, respectively. These results are considered as the results of “baseline” scenario. Figure 14 shows the non-dominated solutions obtained with the proposed model for this scenario in C1 and C2. The solution times of the scenario for C1 and C2 are 227 and 98s, respectively. The results of baseline scenario are compared with the obtained non-dominated solutions for C1 and C2, and the percent improvement rates in the total delay and total fuel are given in Table 15. An improvement rate of up to 12.6% in total delay was achieved for C1, while up to 36.9% improvement was accomplished for C2. The improvement rates of total fuel range from 15.8% to 18.4% with an average of 17.4% for C1, whereas for C2, the rates range from 17.2% to 17.8% with an average of 17.5%. As the improvement rate in fuel consumption increases in non-dominated solutions, it results in an increase in total delay. The total delay is higher than the total delay in the baseline scenario in non-dominated solutions 3 and 4, where the total delay is shown with negative sign. The reason for this is that aircraft are kept on the ground for a longer duration to further improve the total fuel consumption of all operations.

Table 15. Percent improvement rates in the total delay and total fuel for real data

Table 16. Average computation times of non-dominated solutions (s)

Figure 14. Results for actual operation data.

The improvement rates in total fuel for baseline scenario based on the real operation data of LTFJ are greater than the improvement rates obtained in the test data results given in Section 4.3. The reason for this is that aircraft perform CDA in the study, while in the actual operation data they perform step-down approaches. Thus, in the study, they reach the runway with fewer level-offs (only at the FAF level) within the TMA. Compared to a step-down approach, CDA eliminates level segments by keeping aircraft at a higher altitude and reducing the need for additional thrust during descent. This results in lower fuel consumption.

4.4 Computation times

For each TL used in the study, the average computation times of solutions are given in Table 16. Accordingly, the computation time increases with the number of aircraft. In C1, the average solution time is almost 1 min. for 16 TL and less than 2, 3 and 5min. for 18, 20 and 22 TLs, respectively. In C2, the average solution time is less than 1min. for 16 TL, less than 2min for 18 TL, and less than 3min for 20 and 22 TLs.