No CrossRef data available.
Article contents
Theta functions, fourth moments of eigenforms, and the sup-norm problem I
Part of:
Discontinuous groups and automorphic forms
Partial differential equations on manifolds; differential operators
Published online by Cambridge University Press: 03 April 2025
Abstract
We give sharp point-wise bounds in the weight-aspect on fourth moments of modular forms on arithmetic hyperbolic surfaces associated to Eichler orders. Thereby, we strengthen a result of Xia and extend it to co-compact lattices. We realize this fourth moment by constructing a holomorphic theta kernel on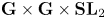 
$\mathbf {G} \times \mathbf {G} \times \mathbf {SL}_{2}$, for 
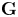$\mathbf {G}$ an indefinite inner form of 
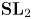$\mathbf {SL}_2$ over 
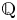$\mathbb {Q}$, based on the Bergman kernel, and considering its 
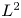$L^2$-norm in the Weil variable. The constructed theta kernel further gives rise to new elementary theta series for integral quadratic forms of signature 
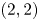$(2,2)$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
Atkin, A. O. L. and Lehner, J., Hecke operators on 
$\Gamma _{0}(m)$, Math. Ann. 185 (1970), 134–160.Google Scholar
$\Gamma _{0}(m)$, Math. Ann. 185 (1970), 134–160.Google ScholarAssing, E., On sup-norm bounds part I: ramified Maaß newforms over number fields, J. Eur. Math. Soc. (JEMS) 26 (2024), 1559–1609.Google Scholar
Blomer, V. and Holowinsky, R., Bounding sup-norms of cusp forms of large level, Invent. Math. 179 (2010), 645–681.CrossRefGoogle Scholar
Blomer, V., Harcos, G. and Milićević, D., Bounds for eigenforms on arithmetic hyperbolic 3-manifolds, Duke Math. J. 165 (2016), 625–659.CrossRefGoogle Scholar
Blomer, V., Harcos, G., Maga, P. and Milićević, D., The sup-norm problem for GL(2) over number fields, J. Eur. Math. Soc. (JEMS) 22 (2020), 1–53.Google Scholar
Blomer, V., Khan, R. and Young, M., Distribution of mass of holomorphic cusp forms, Duke Math. J. 162 (2013), 2609–2644.Google Scholar
Blomer, V. and Michel, P., Sup-norms of eigenfunctions on arithmetic ellipsoids, Int. Math. Res. Not. IMRN 2011 (2011), 4934–4966.Google Scholar
Blomer, V. and Michel, P., Hybrid bounds for automorphic forms on ellipsoids over number fields, J. Inst. Math. Jussieu 12 (2013), 727–758.Google Scholar
Blomer, V. and Maga, P., The sup-norm problem for PGL(4), Int. Math. Res. Not. IMRN 2015 (2015), 5311–5332.CrossRefGoogle Scholar
Blomer, V. and Maga, P., Subconvexity for sup-norms of cusp forms on ${\rm {PGL}}(n)$, Selecta Math. (N.S.) 22 (2016), 1269–1287.Google Scholar
${\rm {PGL}}(n)$, Selecta Math. (N.S.) 22 (2016), 1269–1287.Google ScholarBorel, A., Some finiteness properties of adele groups over number fields, Publ. Math. Inst. Hautes Études Sci. 16 (1963), 5–30.Google Scholar
Blomer, V. and Pohl, A., The sup-norm problem on the Siegel modular space of rank two, Amer. J. Math. 138 (2016), 999–1027.Google Scholar
Chinburg, T. and Friedman, E., An embedding theorem for quaternion algebras, J. Lond. Math. Soc. (2) 60 (1999), 33–44.Google Scholar
Chu, M. and Li, H., Small generators of cocompact arithmetic Fuchsian groups, Proc. Amer. Math. Soc. 144 (2016), 5121–5127.Google Scholar
Das, S. and Sengupta, J., $L^{\infty }$ norms of holomorphic modular forms in the case of compact quotient, Forum Math. 27 (2015), 1987–2001.CrossRefGoogle Scholar
$L^{\infty }$ norms of holomorphic modular forms in the case of compact quotient, Forum Math. 27 (2015), 1987–2001.CrossRefGoogle ScholarDas, S. and Sengupta, J., $L^\infty$ norms of holomorphic modular forms in the case of compact quotient, Preprint (2020), arXiv:1301.3677v3.Google Scholar
$L^\infty$ norms of holomorphic modular forms in the case of compact quotient, Preprint (2020), arXiv:1301.3677v3.Google ScholarGross, B. H. and Zagier, D. B., Heegner points and derivatives of $L$-series, Invent. Math. 84 (1986), 225–320.CrossRefGoogle Scholar
$L$-series, Invent. Math. 84 (1986), 225–320.CrossRefGoogle ScholarHoffstein, J. and Lockhart, P., Coefficients of Maass forms and the Siegel zero, Ann. of Math. (2) 140 (1994), 161–181; with an appendix by D. Goldfeld, J. Hoffstein and D. Lieman.CrossRefGoogle Scholar
Hu, Y., Nelson, P. D. and Saha, A., Some analytic aspects of automorphic forms on ${\rm {GL}}(2)$ of minimal type, Comment. Math. Helv. 94 (2019), 767–801.Google Scholar
${\rm {GL}}(2)$ of minimal type, Comment. Math. Helv. 94 (2019), 767–801.Google ScholarHu, Y. and Saha, A., Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity, Compos. Math. 156 (2020), 2368–2398.CrossRefGoogle Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level: II, Int. Math. Res. Not. IMRN 2012 (2012), 4764–4774.CrossRefGoogle Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level. III, Math. Ann. 356 (2013), 209–216.CrossRefGoogle Scholar
Ichino, A., Trilinear forms and the central values of triple product $L$-functions, Duke Math. J. 145 (2008), 281–307.Google Scholar
$L$-functions, Duke Math. J. 145 (2008), 281–307.Google ScholarIwaniec, H. and Sarnak, P., $L^{\infty }$ norms of eigenfunctions of arithmetic surfaces, Ann. of Math. (2) 141 (1995), 301–320.CrossRefGoogle Scholar
$L^{\infty }$ norms of eigenfunctions of arithmetic surfaces, Ann. of Math. (2) 141 (1995), 301–320.CrossRefGoogle ScholarJacquet, H. and Langlands, R. P., Automorphic forms on GL(2), Lecture Notes in Mathematics, vol. 114 (Springer, Berlin–New York, 1970).CrossRefGoogle Scholar
Khan, R., On the fourth moment of holomorphic Hecke cusp forms, Ramanujan J. 34 (2014), 83–107.CrossRefGoogle Scholar
Kıral, E. M., Bounds on sup-norms of half-integral weight modular forms, Acta Arith. 165 (2014), 385–399.CrossRefGoogle Scholar
Khayutin, I., Nelson, P. D. and Steiner, R. S., Theta functions, fourth moments of eigenforms, and the sup-norm problem II, Forum Math. Pi 12 (2024), e11.Google Scholar
Marshall, S., Upper bounds for Maass forms on semisimple groups, Preprint (2014), arXiv:1405.7033.Google Scholar
Nelson, P. D., Equidistribution of cusp forms in the level aspect, Duke Math. J. 160 (2011), 467–501.CrossRefGoogle Scholar
Nelson, P. D., Evaluating modular forms on Shimura curves, Math. Comp. 84 (2015), 2471–2503.CrossRefGoogle Scholar
Nelson, P. D., Quantum variance on quaternion algebras, I, Preprint (2016), arXiv:1601.02526.Google Scholar
Nelson, P. D., Quantum variance on quaternion algebras, II, Preprint (2017), arXiv:1702.02669.Google Scholar
Nelson, P. D., Quantum variance on quaternion algebras, III, Preprint (2019), arXiv:1903.08686.Google Scholar
Nelson, P. D., Bounds for twisted symmetric square $L$-functions via half-integral weight periods, Forum Math. Sigma 8 (2020), e44.CrossRefGoogle Scholar
$L$-functions via half-integral weight periods, Forum Math. Sigma 8 (2020), e44.CrossRefGoogle ScholarPetersson, H., Über eine Metrisierung der automorphen Formen und die Theorie der Poincaréschen Reihen, Math. Ann. 117 (1940), 453–537.CrossRefGoogle Scholar
Petersson, H., Einheitliche Begründung der Vollständigkeitssätze für die Poincaréschen Reihen von reeller Dimension bei beliebigen Grenzkreisgruppen von erster Art, Abh. Math. Semin. Hansischen Univ. 14 (1941), 22–60.Google Scholar
Ramacher, P. and Wakatsuki, S., Subconvex bounds for Hecke-Maass forms on compact arithmetic quotients of semisimple Lie groups, Math. Z. 298 (2021), 1383–1424.CrossRefGoogle Scholar
Saha, A., Hybrid sup-norm bounds for Maass newforms of powerful level, Algebra Number Theory 11 (2017), 1009–1045.CrossRefGoogle Scholar
Saha, A., On sup-norms of cusp forms of powerful level, J. Eur. Math. Soc. (JEMS) 19 (2017), 3549–3573.Google Scholar
Saha, A., Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, Math. Ann. 376 (2020), 609–644.CrossRefGoogle Scholar
Sarnak, P., Spectra of hyperbolic surfaces, Bull. Amer. Math. Soc. (N.S.) 40 (2003), 441–478.CrossRefGoogle Scholar
Selberg, A., On the zeros of Riemann's zeta-function, Skr. Norske Vid.-Akad. Oslo I 1942 (1942), 59.Google Scholar
Selberg, A., Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series, J. Indian Math. Soc. (N.S.) 20 (1956), 47–87.Google Scholar
Shimizu, H., Theta series and automorphic forms on ${\rm GL}_{2}$, J. Math. Soc. Japan 24 (1972), 638–683.CrossRefGoogle Scholar
${\rm GL}_{2}$, J. Math. Soc. Japan 24 (1972), 638–683.CrossRefGoogle ScholarSogge, C. D., Concerning the $L^p$ norm of spectral clusters for second-order elliptic operators on compact manifolds, J. Funct. Anal. 77 (1988), 123–138.CrossRefGoogle Scholar
$L^p$ norm of spectral clusters for second-order elliptic operators on compact manifolds, J. Funct. Anal. 77 (1988), 123–138.CrossRefGoogle ScholarSteiner, R. S., Uniform bounds on sup-norms of holomorphic forms of real weight, Int. J. Number Theory 12 (2016), 1163–1185.CrossRefGoogle Scholar
Steiner, R. S., Supnorm of modular forms of half-integral weight in the weight aspect, Acta Arith. 177 (2017), 201–218.CrossRefGoogle Scholar
Steiner, R. S., Sup-norm of Hecke–Laplace eigenforms on $S^3$, Math. Ann. 377 (2020), 543–553.CrossRefGoogle Scholar
$S^3$, Math. Ann. 377 (2020), 543–553.CrossRefGoogle ScholarSteiner, R. S., Small diameters and generators for arithmetic lattices in $\mathrm {SL}_2(\mathbb {R})$ and certain Ramanujan graphs, Ramanujan J. 62 (2023), 953–966.CrossRefGoogle Scholar
$\mathrm {SL}_2(\mathbb {R})$ and certain Ramanujan graphs, Ramanujan J. 62 (2023), 953–966.CrossRefGoogle ScholarStein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces. Princeton Mathematical Series, No. 32 (Princeton University Press, Princeton, NJ, 1971).Google Scholar
Sun, H. and Ye, Y., Double first moment for $L(\frac 12,{\rm Sym}^2f\times g)$ by applying Petersson's formula twice, J. Number Theory 202 (2019), 141–159.CrossRefGoogle Scholar
$L(\frac 12,{\rm Sym}^2f\times g)$ by applying Petersson's formula twice, J. Number Theory 202 (2019), 141–159.CrossRefGoogle ScholarTemplier, N., On the sup-norm of Maass cusp forms of large level, Selecta Math. (N.S.) 16 (2010), 501–531.CrossRefGoogle Scholar
Templier, N., Hybrid sup-norm bounds for Hecke–Maass cusp forms, J. Eur. Math. Soc. (JEMS) 17 (2015), 2069–2082.CrossRefGoogle Scholar
VanderKam, J. M., $L^\infty$ norms and quantum ergodicity on the sphere, Int. Math. Res. Not. IMRN 1997 (1997), 329–347.CrossRefGoogle Scholar
$L^\infty$ norms and quantum ergodicity on the sphere, Int. Math. Res. Not. IMRN 1997 (1997), 329–347.CrossRefGoogle ScholarVignéras, M.-F., Séries thêta des formes quadratiques indéfinies, in Séminaire Delange-Pisot-Poitou, 17e année (1975/76), Théorie des nombres: Fasc. 1, Exp. No. 20 (1977), 3, http://www.numdam.org/article/SDPP_1975-1976__17_1_A18_0.pdf.Google Scholar
Voight, J., Quaternion algebras, Graduate Texts in Mathematics, vol. 288 (Springer, Cham, 2021).CrossRefGoogle Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions $L$ automorphes en leur centre de symétrie, Compos. Math. 54 (1985), 173–242.Google Scholar
$L$ automorphes en leur centre de symétrie, Compos. Math. 54 (1985), 173–242.Google ScholarWatson, T. C., Rankin triple products and quantum chaos, PhD dissertation, Princeton University (2008), arXiv:0810.0425.Google Scholar
Weil, A., Sur certains groupes d'opérateurs unitaires, Acta Math. 111 (1964), 143–211.CrossRefGoogle Scholar
Xia, H., On $L^\infty$ norms of holomorphic cusp forms, J. Number Theory 124 (2007), 325–327.CrossRefGoogle Scholar
$L^\infty$ norms of holomorphic cusp forms, J. Number Theory 124 (2007), 325–327.CrossRefGoogle ScholarZagier, D., Appendix: The Eichler–Selberg trace formula on $\mathrm {SL}_2(\mathbb {Z})$, in Introduction to modular forms. Grundlehren der mathematischen Wissenschaften, vol. 222 (Springer, Berlin–New York, 1976), 44–55.Google Scholar
$\mathrm {SL}_2(\mathbb {Z})$, in Introduction to modular forms. Grundlehren der mathematischen Wissenschaften, vol. 222 (Springer, Berlin–New York, 1976), 44–55.Google ScholarZagier, D., Modular forms whose Fourier coefficients involve zeta-functions of quadratic fields, in Modular functions of one variable, VI (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976), Lecture Notes in Mathematics, vol. 627 (Springer, 1977), 105–169.Google Scholar