Introduction
The Hielos Patagónicos (Patagonian icefields), the largest temperate ice masses in the Southern Hemisphere, are located in a latitude zone of strong climatic gradients. Glacier/climate interactions in this region are of relevance for understanding the global climate pattern. In addition, the icefields and the periglacial areas hold valuable information on the Quaternary palaeoenvironments (Reference Warren and SugdenWarren and Sugden, 1993). For these reasons, interest in the glaciology of the Patagonian icefields has increased in recent years, although most of the field investigations so far have been quite limited in time and space. Reference Warren and AniyaWarren and Aniya (1999) point out the need for reliable climate data and detailed glaciological case studies to understand the response of the Patagonian icefields to climatic change. Initialization of more extensive measurements of glaciological and climate parameters has been urgently recommended (Casassa Reference Casassa, Rivera, Aniya, Naruse, Casassa, Sepuílveda and Sinclairand others, 2002).
The Patagonian icefields account for more than 60% of the Southern Hemisphere’s glacial area outside Antarctica. The largest ice mass is Hielo Patagonico Sur (HPS;southern Patagonia icefield), extending from 48.3 to 51.6° S and covering an area of approximately 13 000 km2 (Reference Aniya, Sato, Naruse, Skvarca and CasassaAniya and others, 1996). The average width of HPS is 30–40km, and the narrowest part at 50° S is only 17km wide (Fig. 1 inset with overview map). The main outlet glaciers, descending from firn plateaux, calve into Pacific fjords in the west or into lakes in the east. The low altitude of ablation areas, the vicinity of the sea and large mass turnovers are typical characteristics of these temperate glaciers. Field observations of frontal moraines, analyses of aerial photographs (with the oldest photographs dating back to the mid- 1940s) and satellite images showed the predominance of glacier retreat for HPS during the last 50 years (Reference Aniya, Sato, Naruse, Skvarca and CasassaAniya and others, 1996). Comparison of elevation data from the 2000 Shuttle Radar Topography Mission (SRTM) with earlier cartography revealed thinning of the ablation areas of the majority of Patagonian glaciers over the last 30 years (Reference Rignot, Rivera and CasassaRignot and others, 2003).

Fig. 1. Map of GPM with location of the stakes (profiles A, B, L and D), the automatic weather station, the GPS base and the campsites. The calving front is shown as a line with dashes. CT: Canal de los Témpanos; BR: Brazo Rico; BS: Brazo Sur; PM: Península Magallanes; CP: Cerro Pietrobelli. The insets show an overview map with locations of the northern (HPN) and southern (HPS) Patagonian icefields, and individual stake positions superimposed on a SPOT (Systeme Probatoire pour l’Observation de la Terre) image acquired on 23 August 1995; the dashed line in the zoom inset defines the border between the smooth glacier surface of the central ablation area (zone 1) and marginal and crevassed areas (zone 2).
Calving glaciers represent a large portion of the outlet glaciers of the Patagonian icefields. Although most of the HPS glaciers have retreated during the last 50 years, some of the large glaciers have behaved differently. Glaciar Brüggen, calving into a Pacific fjord, is thought to have reached its neoglacial maximum in the late 1990s (Reference Warren, Rivera and PostWarren and others, 1997), whereas Glaciar Perito Moreno (GPM) exhibited only minor fluctuations of the glacier front for about 80 years (Reference Aniya and SkvarcaAniya and Skvarca, 1992; Reference Skvarca and NaruseSkvarca and Naruse, 1997; Reference StueferStuefer, 1999).
In this paper, we describe the mass-balance components of GPM and their relations to climatic factors. The quasisteady-state assumption, confirmed by our field measurements, supports the estimation of mass fluxes over multi-year periods. The database for our study includes an 8 year time series of glaciological field observations, satellite images from various sensors and climate measurements near the glacier front. So far only small parts of these observations have been presented in the open literature, published after 2 years of fieldwork (Reference Rott, Stuefer, Siegel, Skvarca and EckstallerRott and others, 1998). GPM started to dam Brazo Rico and Brazo Sur, the southern arms of Lago Argentino, at the end of the 8 year field observation period.
This enabled us to document variations of glacier parameters preceding the damming event.
Characteristics of Glaciar Perito Moreno and fieldwork
GPM extends over a length of about 30 km from the continental divide eastwards to Lago (lake) Argentino (185ma.s.l.) (Fig. 1). The average height of the ice divide is about 2200 m, with the highest point at Cerro Pietrobelli (2950 m a.s.l.). Based on the digital elevation data of the SRTM (http://www2.jpl.nasa.gov/srtm/) and optical satellite data (Reference StueferStuefer, 1999), we determined the area of GPM as 254km2. This is a few square kilometres less than shown in previous publications, mainly due to a shift of the ice divide in the SRTM data compared to previous maps that were less accurate in the upper reaches of the glacier. The front terminates with calving cliffs rising 50–80 m above the water level in Canal de los Témpanos to the north and in the southern arm (Brazo Rico) of Lago Argentino (Reference Naruse and AniyaNaruse and others, 1992). The water of Brazo Rico discharges into the Canal de los Témpanos through a narrow channel or below the frontal ice near Península Magallanes.
Previous glaciological fieldwork on GPM has been carried out, mainly near the front and on the lower part of the terminus, with the first documented visit by Hauthal in 1899 (Reference HauthalHauthal, 1904). During the 1990s, surface motion, ice ablation, frontal position and meteorological data were measured during various field campaigns, usually in early summer, within the Japan–Argentina–Chile joint Glaciological Research Project in Patagonia (GRPP) (Reference Aniya and SkvarcaNaruse and Aniya, 1992). Two survey lines were set up, at a distance of about 5 km from the glacier front. Elevation measurements during the expeditions of 1990/91 and 1993/94 and repeat measurements in April 1996 showed no significant changes of ice thickness at any of the nine survey points (Reference Skvarca and NaruseSkvarca and Naruse, 1997). Later measurements showed average thickening of 1.4 m a–1 at eight points in the period 1999–2002 (Reference Skvarca, Naruse and De AngelisSkvarca and others, 2004).
We conducted ten field campaigns between November 1995 and October 2003, at the beginning and the end of the three summers 1995/96, 1996/97 and 1997/98 (November/December and March/April), and in March/ April of the years 1999–2002;the most recent campaign was in October 2003. An automatic weather station was installed in November 1995 on the shore of Brazo Rico, 360 m from the southern front of GPM (50°29’22.708” S, 73°02’48.002” W; 192ma.s.l.) (Fig. 1). The regular fieldwork focused on the establishment and maintenance of a stake network for measurements of ice ablation and ice motion. In addition, we measured ice thickness using seismic reflection, and conducted echo soundings of lake depth near the glacier fronts. Global positioning system (GPS) surveys were carried out in order to map glacier boundaries, lake shores and peaks.
Damming of Brazo Rico
GPM is noted for spectacular water outbursts after damming the Brazo Rico–Brazo Sur (BR-BS) by reaching the opposite shore at Península Magallanes. The first known oblique photograph of GPM showed the terminus in 1899 approximately 1 km above the present position (Reference HauthalHauthal, 1904). During the following years the glacier advanced, inhibiting the runoff from BR–BS in 1917, the first documented damming event (Reference LissLiss, 1970). About 22 damming episodes occurred between 1917 and the present (Reference HeinsheimerHeinsheimer, 1958; Reference Aniya and SkvarcaAniya and Skvarca, 1992; Reference Skvarca and NaruseSkvarca and Naruse, 1997). Reference LissLiss (1970) reported a maximum rise of BR– BS water level of 28.4 m during a damming period of more than 1.5 years from 1964 until 1965. This maximum was not confirmed by measurements of the elevation of lower boundaries of dense vegetation, which revealed an estimated maximum damming height of 23.5 m above the normal lake level (Reference StueferStuefer, 1999). Water drainage over the low land on the northeastern side of Brazo Rico would impede lake damming in excess of about 25 m. BR–BS was dammed typically every 2–4 years until 1988, when damming occurred for the last time before 2003. Since 1988 the glacier front has been in an advanced position and the glacier has repeatedly touched the opposite shore at Pen´nsula Magallanes during winter, but ice tunnels enabled runoff. Figure 2 shows the years when damming occurred. The maximum rise of BR–BS water level was reported for a few cases, as shown in Figure 2.

Fig. 2. Oblique frontal photograph of GPM, with diagram with the years of damming of BR–BS by the glacier terminus superimposed. The damming heights above a normal reference lake level are marked for years when lake level observations are available.
During 2003 the glacier front advanced ~100–120m in Canal de los Témpanos and by 150 m in Brazo Rico. In September 2003 the central part of the front of GPM blocked the outflow from BR–BS, which consequently caused flooding of pastureland and enlarged the normal lake surface area (~Ί50km2) by 22 km2 (Reference Casassa, Rivera, Aniya, Naruse, Casassa, Sepuílveda and SinclairChinni and Warren, 2004; Reference Rott, Stuefer, Nagler, Riedl, Lacoste and OuwehandRott and others, 2005). In early March 2004 the lake level of BR–BS had risen by ~9.35 m (Reference Skvarca and NaruseSkvarca and Naruse, 2005). On 11 March 2004 the water started to drain, first through englacial fissures and conduits, which subsequently evolved into an ice tunnel. Two days later a section of the ice front of 60 m height collapsed.
Most recently, in August 2005, the ice dam has formed again, impeding the drainage of water from BR–BS into the main body of Lago Argentino. The rupture of the ice dam occurred almost exactly 2 years after the 2004 event. The water from BR–BS started to drain on the morning of 10 March 2006, and the spectacular final collapse of the ice- tunnel roof took place 3 days later, around midnight of 13 March 2006.
Glacier Geometry
Cartography and SRTM topography
Digital elevation data of Patagonia, including the glaciers, are available from the SRTM conducted in February 2000 as a joint project of NASA, the US National Imagery and Mapping Agency (NIMA), the German Aerospace Research Center (DLR) and the Italian Space Agency (ASI) (http://www2.jpl.nasa.gov/srtm/). We used the SRTM standard digital elevation model (DEM) at 90 m resolution, with a nominal absolute vertical accuracy (90% linear error) of 16 m and a nominal absolute horizontal accuracy of 20 m. For geocoding satellite images we interpolated the SRTM to a 25 m grid. This DEM is based on single-pass interferometry of the spaceborne imaging radar-C synthetic aperture radar (SIR-C SAR) system, using the C-band channel. Two per cent of the GPM glacier area was not imaged by SRTM due to layover or radar shadow. We interpolated the elevation in these areas linearly. A possible error source for interferometric mapping over glaciers is radar penetration being of the order of several metres at C-band if snow is dry (Reference Rott, Siegel, Guyenne and DanesyRott and Siegel, 1997). However, in wet snow, as is the case for the SRTM campaign in Patagonia, the penetration depth amounts to only a few centimetres.
In order to obtain an independent estimate of accuracy, we compared SRTM elevation data to GPS measurements at reference points in the surroundings of our meteorological station (on land) and at ablation stakes on GPM, made 1 month afterwards. The mean elevation difference for reference points on land was 0.02 m;the difference at the stakes between GPS and SRTM was, on average, 0.4 m after correcting stake measurements by 2.1 m to account for 1 month’s ablation. The maximum absolute difference between any of the 16 GPS points and the SRTM DEM amounted to 6.5 m, where these differences can be partly attributed to the different horizontal scales (point measurements vs 90 m grid). This comparison implies high accuracy of the SRTM DEM on the glacier.
The accuracy of topography from previous sources is less reliable, as we found by comparing GPS measurements of control points outside the glaciers (e.g. at mountain peaks) with topographic maps, revealing elevation differences up to 100 m (Reference StueferStuefer, 1999). For comparison with SRTM, we derived a DEM by digitizing 1 : 100 000 scale cartographic maps, based on aerial photographs taken in March 1975 and published by the Instituto Geografico Militar of Argentina in 1982. A mean vertical random error of 49 m and a mean vertical bias of 9 m resulted from comparing SRTM and map topography over exposed rock near GPM. GPM topography derived from SRTM is consistently higher than the map topography over the glacier;taking into account the 9m bias, the topography comparison reveals an overall thickening of 1.4 ma–1 for the period 1975–2000, with a mean value of 1.9 m a–1 for the accumulation area and of 0.3 m a–1for the ablation area. These data agree with the near steady state of the glacier surface in the ablation area and with the observed balanced or slightly positive net mass balance over recent years. However, Rignot and others (Reference Rignot, Rivera and Casassa2003; online material at http://www.sciencemag.org/cgi/content/full/302/5644/434/DC1, table S1) used a different 1968 map source to derive a mean thinning of 0.42 m a–1 for 1975–2000 (total of 10.5 m) for the GPM glacier area below 1650 m. The different results and derived high vertical random errors indicate that inaccuracies of available maps are too high to enable a reliable quantitative comparison with SRTM for the GPM area.
Seismic measurements
The ice thickness of GPM was determined using the seismic reflection method along profiles A and B (Fig. 1) in November 1996. Large parts of the profiles are crevassed and very rugged, and water is abundant within the ice and at the surface. The seismic signals were recorded with a 24-channel Strataview seismograph, using two geophone strings, each with 12 geophones, at a spacing of 10 m along lines in the direction of the profiles. The P-wave velocity was estimated at 3700 ms–1 by analyzing travel times of the direct P-waves between the shot points and the geophones. This value is in agreement with measurements of wave speed in temperate ice of other glaciers (Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others, 1995; Reference Nolan and EchelmeyerNolan and Echelmeyer, 1999). The reflecting interface at the glacier bed was migrated using available routines from the DISCO2 software package under the assumption that the reflection originated in the plane of the profile.
The reflected seismic waves at profile A revealed a downward slope of the glacier bed from the margin towards the centre line, as expected. At a distance of 1650 m from the southern margin (almost halfway across the glacier), the farthest point reached, an ice thickness of 555 m was measured. Subtracting this value from the surface elevation of 360 m a.s.l. results in a depth of the glacier bed of 195 m below sea level, rising towards the calving terminus where the maximum depth of the glacier bed is ~20 m a.s.l.
Analysis of seismograms along profile B revealed a subglacial trough of approximately parabolic shape, with the deepest part shifted to the north of the centre (inset Fig. 3). The average surface altitude along this transect was 495 m a.s.l. The two-way travel time of the deepest reflected signal from the interface at the glacier bottom was 0.38s, corresponding to an ice thickness of 703 m (±35 m) and an elevation of 208 m below sea level. The greater steepness of the northern part of the glacier bed can possibly be explained by geological differences between the opposite sides of the valley. The dacitic-rhyolitic volcanic rocks, which build up Cerro Cervantes in the south, probably continue below the glacier towards the centre of the profile. The mountains north of the glacier are made up of black shale that is less resistant to erosion. A second reflector shows up clearly at two-way travel times between 0.03 and 0.15 s below the ice bottom. This reflector probably represents an interface between subglacial sediments and bedrock.

Fig. 3. Map of SIR-C/X-SAR-der¡ved magnitude of ice velocity on the terminus of GPM. Velocity is colour-coded in steps of 50cmd–1; the dashed lines indicate the direction of ice flow. The insets show cross-sections along seismic/stake profiles A and B; and along C1, C2 and C3, linear sections for calculating the calving flux; blue dashed lines show the lake water level (LWL).
Bathymetry
Bathymetric measurements were carried out close to the calving fronts in Canal de los Témpanos and Brazo Rico (Reference StueferStuefer, 1999). The lake depth was measured along lines oriented parallel to the glacier fronts at distances 40–100m from the calving cliffs. The maximum depth in Brazo Rico close to the front was 110m, and in Canal de los Témpanos the maximum depth was 164 m. The bottom depth at the front of section C2 in Figure 3 was estimated at 20 m below lake level by extrapolating the surface slope at Península Magallanes. The height of the ice front was obtained from Reference Naruse and AniyaNaruse and others (1992), who measured heights of 55–77 m above lake level, and from the analysis of digitized photographs. According to the water depth at the calving fronts and the height of the ice surface above the lake level, the glacier is grounded everywhere.
Surface Velocity
Stake measurements of velocities
We used a Trimble GPS Pathfinder Pro XL in differential mode for measuring 213 positions of ablation stakes between 1995 and 2003. The Trimble phase-processor software provided horizontal point measurement accuracies between 10 and 30 cm. For 19 stakes velocities were measured for two summer and one winter season, and for 8 stakes at profiles A and B for six additional annual periods. The lower transverse profile (profile A, Fig. 1) consisted of 5 stakes between the southern margin and the centre of the glacier;the distance to the calving front was 4.5 km and the mean elevation 360ma.s.l. A heavily crevassed zone prevented access to the northern part of the tongue. The upper transverse profile (profile B, Fig. 1), consisting of 11 stakes, spanned the whole glacier width of 4.4 km at a mean elevation of ~500ma.s.l., 7.5 km from the front. The 3 stakes of the longitudinal profile L (L01, L02, L03) were placed along the centre line; the maximum distance to profile B was 2.3 km (L01). The stakes were re-drilled at the initial positions during each field campaign to obtain comparable data for the different periods. All stakes were found again during the following campaigns. In March 1997 the stake net was reduced to 3 stakes at profile A (maintained until October 2003) and 5 stakes in the smooth central zone of profile B (until March 2002).
Figure 4 shows seasonal and mean annual deviations from the 6 year mean velocity profiles (1996/97–2001/02) along the transverse profiles. In the following discussion the terms summer and winter refer to the periods defined by the field campaigns that vary slightly from year to year (Table 1). Annual velocities and velocities measured during winter and summer periods are all similar. The mean annual velocity at A02, for example, varied between 1.05 and 1.14 md–1during the 7 years (Fig. 4a). In the centre of profile B (B05 and B06) the mean annual velocity varied between 1.72 and 1.84 md–1 over the 6 year measurement period, with the minimum in 1999/2000 (Fig. 4b). Our analysis suggests an uncertainty of about 0.005 md–1 in the seasonal velocities and 0.002 md–1 in the annual velocities.

Fig. 4. Seasonal and annual deviations of surface velocities from the 6 year (1996/97–2001/02) mean profiles as derived from the stakes of (a) profile A and (b) profile B. The insets show mean profiles and, for comparison, interferometric spaceborne imaging radar-C/X-band SAR velocities.
Table 1. Mean ice ablation (cm d–1) at stakes of profiles A and B for seasonal and annual measurement periods (dd/mm/yy), separated in the central part (zone 1) and in margin and crevasse zones (zone 2). Possible measurement errors are indicated in parentheses. From 2002 to 2003 the time lag between successive measurements was 18.5 months. Ablation values after March 1997 were measured with a reduced stake network. The temperature is the mean value at the weather station near the glacier front over the time period

The seasonal variations were also rather small, with an average increase of velocity of only 7% during the two summer periods 1995/96 and 1996/97 compared to the winter period 1996. The summer-to-winter velocity ratio showed a slight increase downstream, with the minimum difference observed in profile L (4%), followed by 7% in profile B and 8% in profile A. This ratio is contrary to the longitudinal trend in magnitude of the velocity. The maximum velocity, 2.39 md–1, was measured at L01 in summer 1996/97.
Considering the small average seasonal variability of the measured velocities and the rather stable glacier geometry, no surge-type characteristics are evident. Previous measurements of ice motion on GPM were carried out at stakes in proximity to profile A within the joint Japan-Argentina- Chile project during short periods in 1990, 1993 and 1994, as well as over an annual period from November 1993 to November 1994 (Reference Naruse and AniyaNaruse and others, 1992, Reference Naruse, Skvarca, Satow, Takeuchi and Nishida1995; Reference Skvarca and NaruseSkvarca and Naruse, 1997). The mean annual velocity in the centre of the glacier was 1.6 m d–1; velocities measured in Novem- ber/December 1993 were slightly larger than the annual mean 1993/94, in agreement with our observations.
Surface motion by means of SAR
Interferometric synthetic aperture radar (InSAR) and SAR amplitude cross-correlation were applied to map ice motion in the ablation area. These data contributed to retrieving mass fluxes and to studying the flow behaviour of the terminus. The multi-year field measurements at the stakes provide a baseline to determine the representativeness of the short-term velocities from satellite data. Because of the fast flow of GPM, SAR images of short time-spans (a few days maximum) are required for InSAR motion analysis to avoid phase decorrelation in shear zones (Reference Zebker and VillasenorZebker and Villasenor, 1992).
The best interferometric dataset of GPM so far available was acquired on 7, 9 and 10 October 1994 by the space- borne imaging radar-C/X-band SAR (SIR-C/X-SAR) that operated on board the space shuttle Endeavour (Reference StofanStofan and others, 1995). We used L-band (λ = 24.23 cm) repeat-pass images, with a resolution of 8.2 m in azimuth (along-track) and of 3.8 m in slant range (direction of the radar beam), and radar look angle from the vertical of 34.4° at the image centre. C- and X-band repeat-pass images decorrelated over the glacier due to surface melt. Close to the calving front, L-band images also decorrelated, even over the 1 day time- span because of chaotic displacement of seracs. In this section of the terminus, we applied amplitude correlation in the across-track and along-track directions to map the motion. This method is less accurate than InSAR, in particular if the repeat-pass time-span is short (Reference Gray, Mattar, Vachon and SteinGray and others, 1998; Reference Pattyn and DerauwPattyn and Derauw, 2002). Reference Michel and RignotMichel and Rignot (1999) calculated the motion field of the lowermost 4 km of the Moreno terminus in radar geometry, applying a combination of coherent and non-coherent image correlation using the L-band image pair from 9 and 10 October 1994.
An important step for interferometric retrieval of surface displacement is the separation of the topographic phase and the motion-related phase (Reference Mohr, Reeh and MadsenMohr and others, 2003). Because only one InSAR pair of good coherence (9/10 October 2004) was available, it was necessary to generate a synthetic topographic interferogram using a DEM and orbit parameters. At the given incidence angle and interferometric baseline of 29 m, one interferometric fringe (ΔΦ = 2π) corresponds to an altitude difference of 620m (the altitude of ambiguity, Ha) or to a displacement of 12.1 cm in line of sight (LOS) of the radar beam. Because of the high value of Ha and the gentle topography of the Moreno terminus, possible errors in the DEM have little impact on the retrieved interferometric velocity.
As InSAR provides only the LOS component of the velocity vector, assumptions about the flow direction are necessary in order to use the data for ice dynamic studies (Reference Joughin, Winebrenner, Fahnestock, Kwok and KrabillJoughin and others, 1996; Reference Reeh, Madsen and MohrReeh and others, 1999; Reference Mohr, Reeh and MadsenMohr and others, 2003). On the GPM terminus, surface topography was very close to steady state over annual intervals, as known from geodetic field measurements (Reference StueferStuefer, 1999). Also for the 1 day interval of 9–10 October 1995 a steady-state condition of the surface was closely fulfilled, as the 1 day ablation at the stake profile was estimated at 3–4cm, balancing the measured emergence velocity. In this case, surface-parallel flow can be assumed as an approximation to derive the velocity vector (Reference Joughin, Winebrenner, Fahnestock, Kwok and KrabillJoughin and others, 1996). However, according to the shallow-ice approximation (Reference PatersonPaterson 1994), this assumption requires surface flow to be uniform over an area extending over at least ten ice thicknesses. Because of the complex bedrock topography, this is not the case for GPM. Therefore we applied a two-step procedure to determine the velocity vector. The directional flow field was derived from flowlines in SAR images, Landsat images and aerial photography. The local verification with stake measurements showed good agreement. Using the LOS velocity field, the directional flow field and the surface slopes along the flowlines, the velocity vector was derived. Because of the small surface slope in the ablation area, the magnitude of the vertical velocity is typically of the order of 3–5% of the horizontal velocity. For the image section near the heavily crevassed calving front, we calculated displacement in azimuth and range by correlating L-band amplitude data from the 3 day repeat image pair of 7 and 10 October 1994.
Figure 3 shows a map of the SAR-derived motion field of the terminal 12 km of GPM. This map reveals some differences to the previously published velocity map (Reference Rott, Stuefer, Siegel, Skvarca and EckstallerRott and others, 1998) because more precise orbit data and a larger set of geodetic field data are now available, enabling more accurate geocoding. The main mass input to the ablation area is supplied through the southern ice stream, which drains an area ~Ί00km2 and is only 1.4 km wide near the equilibrium line. In this area, ~5 km southwest of stake L1 (Fig. 1), a velocity maximum of 3.5 md–1 was derived by means of cross-correlation. In this area the fractured surface is reminiscent of a surging glacier, though this is probably not the case. In the lower part of the terminus the velocity shows a minimum near profile A, and increases towards the front due to converging flow and a rising glacier bed.
Comparison of motion from InSAR, amplitude correlation and field data
The velocities from the two different SAR analysis techniques and from the geodetic field measurements show good agreement. Over the central part of the terminus a standard error estimate σest = 9cmd–1 in ground range was derived between motion from interferometry and from cross-correlation, based on linear regression of more than 3000 samples with a degree of coherence above 0.4 for the 1 day image pair. The main part of this error can be attributed to the cross-correlation analysis because the sensitivity of this method is related to range and azimuth resolution and is therefore lower than for InSAR.
For comparison of SAR-derived velocities with field data, the different observation periods have to be considered. SAR provides the motion for a 1 day or 3 day time interval in early summer 1994, whereas the field measurements were made over seasonal or annual periods, starting in summer 1995. The interannual velocity variations during the period 1995– 2003 and the seasonal variations amount to a few per cent variation. Because we use the SAR data for estimating annual mass fluxes, we compared the SAR motion fields with the mean annual velocities derived from the stake network (compare insets of Fig. 4). Excluding stakes at the glacier margins where the flow direction deviated more than 60° from ground range, a standard error σest = 5 cm d–1 was derived between the short-term interferometric and the annual velocities measured by differential GPS at the individual stakes after subtracting the mean bias of 3.6% between the SAR and GPS measurements. This bias, where the higher values correspond to SAR velocities, can be explained by slightly increased velocity in summer.
Ablation Measurements
Between November 1995 and October 2003, ice ablation was measured at the wooden stakes of profiles A–C. One additional stake (stake D) was drilled ~-500m from the ice front at Brazo Rico, 70 m from the southern glacier margin.
Ice may melt in any season because, even in winter, the lower terminus is often free of snow and the air temperature may stay above 0°C over extended periods. The ablation measurements revealed obvious differences between stakes located in marginal and crevassed zones (zone 2, containing the stakes A05, A01;B01, B02, B03, B09, B10) and stakes in the central part of the glacier (zone 1) that is rather smooth (Fig. 1). Zone 2, showing higher ablation, is characterized by slightly lower surface albedo and/or rather high crevasse density. Ablation measurements and their relative errors for the observation periods and ablation zones are summarized in Table 1. The relative errors for seasonal or annual periods are small due to high ablation sums. The mean ice ablation of the three summers in zone 1 amounted to 5.5cmd–1 at profile A, and 5.1 cmd–1 at profile B. The corresponding mean values of the two winter periods were 1.1 and 1.0cmd–1, and the mean values over the 6 year period March 1996–March 2002 were 2.7 and 2.4cmd–1. On average, in profile A the ablation in zone 2 was 11% higher than in zone 1, and in profile B it was 18% higher. The larger difference at profile B is probably an effect of the very rough glacier surface of zone 2, characterized by a maze of ice ridges and troughs with a typical vertical scale of ~Ί0m. The mean ablation of the five central stakes at profile B for the different observation periods is illustrated in Figure 5. In summer, the variability between the individual stakes, mainly caused by local variations of surface roughness, was slightly higher than the interannual variability. The inset of Figure 5 shows annual ice ablation for the different zones. The year 2000/01 had the lowest ablation, deviating by –21% from the 7 year average and coinciding with the comparatively low mean annual temperature of 5.6°C recorded at Moreno weather station. The variability between the three observed summer periods was rather small. This is in agreement with the small differences of mean summer temperatures and the slightly higher variability of mean annual temperatures (Table 1). Previous ablation measurements, carried out at four positions close to profile A in summer 1993/94 within the GRPP (Reference Naruse, Skvarca, Satow, Takeuchi and NishidaNaruse and others, 1995), show values similar to our 7 year measurements in that area.

Fig. 5. Winter, summer and annual ice ablation for four stakes of the central profile B from 1995 to 2002. Inset: Annual ablation values from April to March for zone 1 (profiles A and B) and zone 2 (profile A). The red line indicates mean temperatures for corresponding time periods.
Air-temperature data, shown in Table 1 and Figure 5, were measured at the weather station near the glacier terminus and used for modelling of ablation. A second temperature probe was installed in April 2002 close to the glacier margin, 400m above the main station, which recorded over a period of 18 months. A mean vertical lapse rate of temperature of 8°C km–1 was derived (comparable to Reference Takeuchi, Naruse and SkvarcaTakeuchi and others, 1996) for the calculation of positive degree-days for each stake elevation and measurement period. Figure 6 shows all seasonal and annual ablation measurements in relation to the corresponding positive degree-day sums; the lines illustrate the best linear fit for different seasons and surface zones. Mean degree-day factors during summer periods amount to 0.61 cm water equivalent per positive degree-day (cmw.e. °C–1 d–1) in zone 1 of profile A and to 0.64 cmw.e. °C–1 d–1 in zone 1 of profile B. The values for zone 2 are 0.68cm w.e. °C–1 d–1(profile A) and 0.76cm w.e. °C–1 d–1 (profile B). These values are comparable to those of other glaciers in maritime regions (Reference Braithwaite and ZhangBraithwaite and Zhang, 2000). For winter periods the degree-day factors shown in Figure 6 consider exclusively ice ablation and do not account for snow fallen and melted;the derived values vary between 0.27 and 0.43cmw.e.°C–1d–1. Annual values (Fig. 6a) result from field measurements in the years 1998/99 to 2001/02, when seasonal data were not available for this study. Ablation was measured at stake D at short intervals during summer 1995/ 96; the ablation data show a clear linear relation to temperature (Fig. 6b). The degree-day factor at stake D of 0.79 cm w.e. °C–1 d–1 is slightly higher than the long-term summer factors at zone 2, probably due to the closeness to the glacier margin (Reference StueferStuefer, 1999).

Fig. 6. (a) Seasonal and annual positive degree-days vs measured ablation. Note: The ablation data and degree-day factors (ddf) indicating the slope of the individual trend lines refer to ice ablation. Values have been converted to centimetres water equivalent (cm w.e.) in the text. (b) Ice ablation and corresponding degree- days at stake D measured for daily and short-term periods during 151 days in austral summer 1995/96.
Glacier Mass Fluxes
Field measurements and satellite data analysis were the basis for retrieving total net ablation and mass fluxes. Reference Rott, Stuefer, Siegel, Skvarca and EckstallerRott and others (1998) presented first estimates of mass-balance components under the assumption that GPM is close to equilibrium state, based on 2 years of field measurements. However, because of the longer response time of a glacier, the quasi-steady-state assumption should be applied over a multi-year period, so that interannual variations are filtered out. This was enabled by extension of the observation period.
Because of the size of the accumulation area, the difficult access, the high accumulation rate and the high spatial variability due to strong winds, it was not feasible to measure the total net accumulation, Bac, in the field. We therefore estimated Bac by the following relation, assuming conservation of mass,
B ab1 is the net ablation in the area between the equilibrium line and profile B, and M t is the mass flux through the glacier cross-section at profile B.
To retrieve Bac the total glacier area, S, was separated into the accumulation area, Sac, and the ablation area, Sab, using the average position of the equilibrium line inferred from positions of the snowline in late summer of the years 1986 and 1993–2005. The database includes one Landsat Thematic Mapper (TM) image of 1986, several ERS (European Remote-sensing Satellite) SAR images of 1993, 1995, 1996 and 1998, Envisat Advanced SAR (ASAR) images of 2003, 2004 and 2005, a RADARSAT image of 1997 and oblique photography from March 1994, 1999 and 2000. During the various field campaigns in late summer, which lasted up to 3 weeks, we observed little variability of snowline position. Reasons for this are probably the steepness of the glacier surface at the equilibrium line and frequent snowfalls, resulting in small interannual variability of the accumulation-area ratio (AAR). This suggests that the equilibrium line can be inferred with good accuracy from mean snowline positions at the end of several summers. We estimate the mean equilibrium-line altitude (ELA) as 1170ma.s.l., in close agreement with the ELA of 1150ma.s.l. derived by Reference Aniya, Sato, Naruse, Skvarca and CasassaAniya and others (1996). This results in an accumulation area of 177.5 km2, corresponding to an accumulation-area ratio (AAR = Sac/S) of 70.0%. The mean snowline altitude at the end of the 12 summers varied by ±70 m at maximum, which corresponds to a variation of the AAR between +2% and –2.5% of the mean value.
The surface ablation, Bab, was calculated by means of linear altitude gradients of net balance, separating the ablation area into a central region (zone 1) with an area Sab,1 = 35.6 km2 and the marginal and crevasse zones (zone 2) with S ab,2 = 40.9 km2. The zone extent was mapped from Landsat images, air photos and GPS measurements. The balance gradients, ß 1 = 11.47 kg m–2 a–1 m–1and ß2 = 14.39 kg m–2 a–1 m–1, derived from the measured mean annual ablation (Table 1), are characteristic for maritime glaciers and indicate high mass turnover (Oerle- mans and Fortuin, 1992). A mean surface balance bB;1 = –7688kgm–2a–1 was calculated for zone 1 and bB,2 = –9640 kg m–2 a–1 for zone 2, assuming p = 900kgm–3. For the crevassed area near the front we calculated a maximum ablation (bmax,2) of –14 245 kgm–2 a–1, corresponding to an ice ablation of 15.8 ma–1.A net balance Bab = –0.544Gta–1resulted for the total ablation area, and Bab1 = –0.243 Gta–1for the area between profile B and the equilibrium line.
The seismically derived cross-section and surface velocity measurements were the basis for calculating the ice discharge, Mt, through profile B:
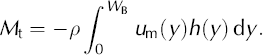
The y coordinate is aligned along the transverse profile, and u
m(y) is the mean horizontal velocity normal to the profile in a vertical column of ice; h(y) is the depth and W
B the profile width. Simple shear flow with the shear stress τxz
(τxz
= pfg(h — z) sin α) depending on the surface slope, α, and the weight of ice above (pg(h — z)) is assumed, following Reference PatersonPaterson (1994), for estimating the dependence of velocity on depth. We used α = 2.5°, the average slope over a distance of 5 km normal to the profile, and shape factor f = 0.75, valid for a parabolic channel and the measured ratio of ice depth to glacier width. For describing the ice flow, Glen’s flow law ![]() with parameters n = 3 and A = 3.8 × 10–24 Pa–3 s–1 was used, where A represents a mean of values reported for temperate glaciers by Reference GudmundssonGudmundsson (1994) and Reference PatersonPaterson (1994). Integration of the flow law from the surface (z = hc) to the bed (z = 0) yields (Reference PatersonPaterson, 1994)
with parameters n = 3 and A = 3.8 × 10–24 Pa–3 s–1 was used, where A represents a mean of values reported for temperate glaciers by Reference GudmundssonGudmundsson (1994) and Reference PatersonPaterson (1994). Integration of the flow law from the surface (z = hc) to the bed (z = 0) yields (Reference PatersonPaterson, 1994)

For ρ = 900kgm–3 and the measured depth in the centre, h c = 703 m, a mean velocity, u mc, amounting to 0.9 times the surface velocity, u sc, was derived. We used the same factor of 0.90 for the total cross-section, representing the mean between zero and full sliding. The resulting mass flow through the profile is M t = –0.727Gta–1. With the values for B ab1 and M t we estimate the net accumulation according to Equation (1) as B ac = 0.970Gta–1. This corresponds to a specific annual net accumulation b ac = 5465 mm w.e. a–1. With a conservatively estimated accuracy for Bab1 of 20% and for M t of 10%, the uncertainty of bac is ±480 mm w.e. a–1.
An estimate of the calving flux, B cv, provided an additional control for the assumption of a quasi-steady state of the glacier and for estimating errors of the various fluxes:
B ab2 is the surface melt loss in the area below profile B, and the residual, B r, accounts for errors of B ab2, B cv and M t, and/or deviations from the state of equilibrium.
For calculating the ice export due to calving, the front was separated into three linear sections, the section in Canal de los Témpanos (C1), the section in front of Península Magallanes (C2) and the section in Brazo Rico (C3) (Fig. 3). For each section we estimated B cv according to:
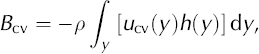
where u cv is the velocity normal to the calving front, h is the ice thickness at the front, and the y coordinate is aligned parallel to the front. The calving speed, u cv, was taken from the velocity map (Fig. 3), reducing the SAR velocities by 4% to represent the annual mean. The calving fluxes, B cv, the velocity magnitudes at the centre, u centre, and the mean calving velocities, u cv (Bcv divided by the profile crosssection) are specified in Table 2. The lowest calving speed is observed at profile C3, because this front is aligned oblique to the main ice flow upstream. For the profiles C1 (u cv/d = 6.4) and C3 (u cv/d = 6.5) the ratio of calving velocity to lake depth, d, is significantly higher than the average ratio of 2.5 reported for freshwater calving by Reference Funk and RöthlisbergerFunk and Rothlisberger (1989). Much higher ratios were also reported for the nearby Glaciar Upsala (Reference Skvarca, De Angelis, Naruse, Warren and AniyaSkvarca and others, 2002). A total calving flux of –0.361 Gta–1 was calculated assuming perfect sliding. This number includes the ice export and frontal melting. The main part (68%) of the calving flux is discharged through the frontal section, C1. These numbers differ slightly from Reference Rott, Stuefer, Siegel, Skvarca and EckstallerRott and others (1998) due to re-analysis of the velocity field and the slight shift of the calving profiles.
Table 2. Characteristics of the three sections of the calving front of GPM; h is the mean ice thickness, u centre the magnitude of the mean annual calving velocity in the centre of the profile, ucv the width- averaged calving rate and B cv the calving flux
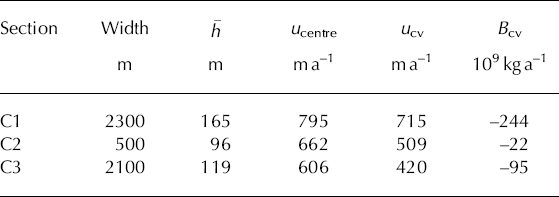
If we compare Mt with the independently calculated numbers for surface ablation below profile B (B ab2 = B ab – B ab1 = -0.301 Gta–1) and the calving flux Bcv (Equation (4)), a residual term, B r, of –0.065 Gta–1 results, that is within the estimated error bounds. Taking into account that some of the snow and rain deposited in the accumulation area is lost as runoff, in particular in the area close to the equilibrium line, it can be assumed that the average annual precipitation is significantly higher than the derived net accumulation of 5465 mm w.e. a–1. This conclusion is in agreement with the estimates of Reference SchwerdtfegerSchwerdtfeger (1958) and Reference Escobar, Vidal, Garin, Naruse, Naruse and AniyaEscobar and others (1992). Schwerdtfeger estimated the annual precipitation above 1500ma.s.l. to be at least 1.5-2 times the precipitation measured at the coastal weather stations, which would correspond to an annual precipitation sum of at least 7000 mm on the western side of HPS. Reference Escobar, Vidal, Garin, Naruse, Naruse and AniyaEscobar and others (1992) estimated the mean annual precipitation for the whole HPS at 7000mm and for the central plateau of the icefield at more than 8000 mm. These values were inferred from an estimation of the water balance. Reference Aristarain and DelmasAristarain and Delmas (1993), however, derived a mean annual water equivalent of 1200 mm from deuterium analysis and stratigraphy of a 13 m firn core that was drilled at 2680ma.s.l. near the ice divide of GPM. A possible explanation for this low value may be reduced accumulation due to wind drift near the continental divide.
Glacier Sensitivity to Climate
Seasonal sensitivity characteristics and monthly parameters for temperature sensitivity are estimated using a simple degree-day model (Reference Oerlemans and ReichertOerlemans and Reichert, 2000). Daily mean temperatures from Moreno base station serve as model input to reconstruct GPM mass balance. A linear relation of perturbations in precipitation and temperature to glacier mass balance is assumed and mutual interference of monthly perturbations is ignored. The main inaccuracies in modelling mass balance of Patagonian glaciers arise from the lack of knowledge of precipitation distribution. Precipitation measurements at two adjacent sites within 5 km of the Moreno terminus during summer 1996/97 showed significant differences, reflecting the influence of the strong winds on precipitation measurements with conventional methods (Reference StueferStuefer, 1999). Reference Carrasco, Casassa, Rivera, Casassa, Sepuílveda and SinclairCarrasco and others (2002) pointed out a homogeneous distribution of precipitation throughout the year at several weather stations on the west and east sides of HPS;precipitation occurs at some stations on the wind- exposed west side of HPS on ~90% of all days. For our model we assume precipitation to occur on every day of the year. Lacking other more accurate precipitation measurements in the glacier vicinity, we used a precipitation climatology (VASClimO) compiled by an initiative of the German Weather Service and the Johann Wolfgang Goethe University Frankfurt (Reference Beck, Grieser and RudolfBeck and others, 2005). The monthly precipitation dataset from 1951 to 2000 is based on quality- controlled station data. The grid data derived from the few precipitation records that are available in the vicinity of HPS do not resolve the detail of the strong precipitation gradients due to topographic effects of the Andes. In the absence of other long-term sources, we used monthly data from the closest gridpoint (50.5° S, 73.5° W) as proxy for the precipitation at Moreno base. The gridpoint data show maximum precipitation from May to July (between 104 and 98 mm monthly precipitation for the months May, June and July) and minimum precipitation (46 mm) in February;the annual mean precipitation sum from 1951 to 2000 was 838 mm (with a standard deviation, σ, of 102 mm).
In our model, snowfall is accumulated, while rain or water formed from melting is assumed to drain without balance effects. Melting of snow or ice is calculated with the positive- degree-day concept. As daily mean temperatures and daily sums of precipitation serve as source data, the model does not consider changes of state in the course of a day. We inversely derived a threshold of 2°C daily mean temperature to decide whether precipitation falls as snow or rain. Further model parameters are degree-day coefficients, for which we take into account the two roughness zones described previously and whether the surface is ice- or snow-covered. Degree-day factors over ice amount to 0.65 cm w.e. °C–1 d–1for zone 1 and to 0.74 cm w.e. °C–1 d–1 for zone 2 directly from the average of ablation stake measurements during summer periods. Degree-day coefficients over snow have been adjusted to get the best fit of observed to modelled data. In addition, parameters are adjusted to account for an approximate ELA of 1170 m. Using winter degree-day factors of 0.3 cm w.e. °C–1 d–1 for both surface zones and a linear precipitation increase with altitude of 15% per 100 m up to the ELA, a regression coefficient of R 2 = 0.86 is derived between modelled balance and all 103 observed stake measurements; the standard error of modelled ablation is 17%. As a first estimate the altitude increase of precipitation above the ELA was approximated as a parabola defined by the precipitation at the ELA and an assumed precipitation of 7600 mm w.e. at 2500 m with the same value up to the top of the Moreno catchment area (2950 m). This maximum precipitation was inversely determined to obtain a total net accumulation on GPM of about 0.970Gta–1, which was derived from mass flux considerations assuming a quasi-steady state of the glacier. The parabolic distribution of precipitation accounts for assumed large amounts of drifting snow, especially in the region below the main divide due to the prevailing strong westerly winds (Reference Woo and FitzharrisWoo and Fitzharris, 1992).
Figure 7 illustrates the annual specific balance for GPM for the example balance year 1999/2000. The maritime- like setting of GPM with high mass turnovers is expressed by the magnitude of balance ranging from about –18 to +7.6 m w.e. a–1. The almost linear balance gradients derived for the lower ablation area of GPM (below 1000ma.s.l.) amount to 1.65 m w.e. (a 100 mΓ1 for zone 1 and 1.88 m w.e. (a100m)”1 for zone 2. It is evident from the temperature record that at higher regions ablation plays a minor role, and that precipitation above the ELA falls predominantly as snow; the model shows almost no ablation above 2000 m. The strong increase of accumulation above the ELA reflects the precipitation pattern. A high sensitivity of changes in total mass balance to temperature and precipitation perturbations is derived using Oerlemans’ concept of seasonal sensitivity characteristic (SSC) parameters CT,k and C P ,k (Reference Oerlemans and ReichertOerlemans and Reichert, 2000). With the index k denoting a specific month, the balance, B, sensitivities for temperature, T, and precipitation, P, perturbations were defined as
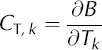
and
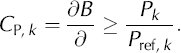
For the monthly sums of precipitation in the reference case (P ref, k ) we used the 1951–2000 average of the closest gridpoint of VASClimO data (Reference Beck, Grieser and RudolfBeck and others, 2005). The effects of 1°C temperature and 10% precipitation perturbations on the specific mass balance of GPM are shown in Figure 7. For the period 1996–2003 we observed differences in mean annual temperatures of 1 °C at Moreno base. High sensitivity to temperature persists throughout the ablation area. Temperature perturbations of ±1°C result in total mean mass-balance changes of 0.8mw.e. a–1, and at altitudes below 700m in changes of balance of more than ±3 m w.e. a–1. The hypsometry of GPM accounts for a small temperature influence on mass balance above the ELA. A reversed effect is derived for precipitation perturbations, with gradually increasing precipitation sensitivities from the ELA up to altitudes of 2000 m. The higher glacier regions experience balance changes almost directly proportional to changes in precipitation. Monthly perturbation sensitivities are illustrated in analogy with Oerlemans and Reichert’s figure 1 (2000) in Figure 8. Though the temperature sensitivity is slightly less pronounced, we found SSC for GPM similar to Franz Josef Glacier, New Zealand. Franz Josef Glacier is located in a maritime climate comparable to GPM, with annual precipitation values amounting to about 6m (Reference OerlemansOerlemans, 1997). Temperature effects dominate from September to April, with SSC values up to 0.12 m(monthΓ1for temperature perturbations of 1°C. There is still a significant temperature SSC in winter as melting and rain may occur throughout the year at the glacier terminus. GPM SSC values for precipitation increase towards winter, with maximum values of 0.045 m (monthΓ1 for 10% precipitation perturbation.

Fig. 7. Calculated mass-balance profile for the balance year 1999/2000 (black line). The dashed lines indicate profiles of temperature ablation and accumulation due to precipitation. The effects of uniform increases in temperature (+1°C) and precipitation (+10%) on the mass-balance profile are shown by the grey lines.

Fig. 8. SSCs for GPM for 1°C temperature and 10% precipitation perturbations as derived from degree-day model calculations.
Discussion of Mass-Balance Trends
Monthly balance sensitivities of GPM are used to estimate long-term trends of mass balance. A constant value for the calving flux is assumed, which can be justified by the observed long-term stability of the glacier front and the small annual variations of surface velocities. Various sources of meteorological data serve as input for the balance estimates. Homogeneous long-term climate observations are sparse in Patagonia, resulting in uncertainties for establishing relations between HPS glacier changes and possible climate trends. For GPM the closest weather station is Lago Argentino station located 60 km to the east of the glacier, operated by the Argentine Meteorological Service. Climatic records are available from 1937, although there are several gaps in the series. In 2001 the station was moved from El Calafate town to the newly built airport about 30km to the east. The warming trend south of 46° S during the 20th century, reported by Reference Hoffmann, Nunez and VargasHoffmann and others (1997), is not evident in the temperature data of Lago Argentino station. Reference Carrasco, Casassa, Rivera, Casassa, Sepuílveda and SinclairCarrasco and others (2002) also describe a general warming trend in the vicinity of HPS during the last 100 years, but point out considerable variability from station to station. They present examples of stations where the trend reversed in the 1980s with slightly decreasing air temperature and increasing precipitation.
For reconstruction of mass balance we used the SSC for GPM and monthly mean temperatures measured at Moreno base and Lago Argentino. Moreno base monthly temperatures were derived by linear regression from the Lago Argentino temperature series from 1941 with few gaps. The comparison of the mean temperatures for 60 months between January 1996 and December 2000 resulted in high linear regression (R 2 = 0.97) between the two stations. For the mass-balance dependence on precipitation we used the monthly data from the closest gridpoint of the 1951–2000 VASClimO precipitation climatology (Reference Beck, Grieser and RudolfBeck and others, 2005). The SSC method applies relative changes of precipitation δ(Pk/Pref,k) to derive monthly changes in glacier mass balance (δB). Therefore VASClimO precipitation data were used directly as an estimate for reconstructing the precipitation contribution to GPM balance changes.
Resulting specific annual balance (with the balance year from 1 April to 31 March of the following year) is plotted in Figure 9 for all available years of climate data, separately for temperature- and precipitation-controlled effects. For the years after 1973 the cumulative balance is shown for the two separate terms, as well as for their combined effect. Except for two extremely cold years (1951 and 1972), perturbations in temperature modulate the mass balance typically within a range ±0.5mw.e.a–1. For the precipitation effect, higher annual mass-balance variability is evident (Fig. 9b). The cumulative mass balance derived from temperature perturbations shows balanced or positive annual mass balance up to 1980. A slight but fairly consistent negative trend amounting to a total of about 2 m w.e. follows until the year 2000. From 2000 to 2004 the temperature effect triggers a positive or approximately balanced state of the glacier. The combined effects for the last 30 years result in negative balance from 1989 to 1998 (Fig. 9c). Later increased precipitation compensated for the partly negative balance trend from temperatures. Though precipitation estimates are less accurate than temperature measurements, and the absolute numbers of mass-balance variations should be considered with reservations, the SSC estimates clearly show that the mass-balance behaviour of GPM was determined similarly by temperature and precipitation. The simulations suggest that the repeated damming of BR–BS in 2003/04 and 2005/06 is the response to a few years of positive mass balance due to a combined effect of mass excess resulting from slightly colder temperatures and higher precipitation. No damming was observed during the 1990s (Fig. 2), as the minor precipitation excess could not compensate for the negative mass balance triggered by slightly increased temperatures. In general, the derived amplitudes of cumulative mass balance of GPM varied within a small range of 2mw.e. during the last 30 years, which agrees with the observed balanced state of the glacier.

Fig. 9. (a, b) Long-term specific balance derived from a degree-day model using the SSC and monthly temperature (a) and precipitation (b) perturbations. (c) Cumulative mass balance from 1973 to 2004 as calculated from monthly temperature and precipitation data separately, and the resulting combined cumulative mass balance.
Summary and Conclusions
Our investigations of GPM, based on measurements of climate parameters, ablation, ice motion, ice depth, bathymetry at the calving front and satellite data analysis, try to relieve the shortcomings in comprehensive multi-year glaciological studies of HPS glaciers. Whereas ablation and calving flux could be derived from field measurements and satellite data, the glacier size, high snowfall rates and limited access prohibited direct measurements of accumulation. However, as the GPM analysis indicates no significant net mass-balance trend over decades, the mean annual net accumulation could be deduced from other measurements. The annual net accumulation rate of 5465 ± 480mmw.e. a–1 is among the highest worldwide, comparable to glaciers in New Zealand and southeast Alaska, USA. A main reason for the stability of GPM is the geometry at the calving front where the ice flow is blocked in the central section by Península Magallanes. In the two other sections the lake bottom descending in front of the calving cliffs impedes further advance. This results in a comparatively high ratio of calving flux to total accumulation of 0.37 that clearly exceeds the typical ratio for freshwater calving of grounded glaciers (Reference Funk and RöthlisbergerFunk and Röthlisberger, 1989). Another reason for the stability is the area altitude distribution, as already pointed out by Reference Aniya, Sato, Naruse, Skvarca and CasassaAniya and others (1997). As the glacier surface is comparatively steep near the equilibrium line, a rise of 100 m in elevation of the line corresponds to a decrease of the accumulation area by only about 4%. During our investigation period the late-summer snowline remained within this range.
The altitude gradients of mass balance were calculated assuming steady state. Derived net balances range from –18 m w.e. a–1 at the terminus to +7.6 m w.e. a–1 in the upper section of the accumulation area. The ablation measurements revealed little interannual variability during the observed 7 years, with balance gradients between 1.65 and –1.88 m w.e. (a 100 mΓ1 for the ablation area. The high mass turnover is characteristic for maritime glaciers. Using the seasonal sensitivity characteristics defined by Reference Oerlemans and ReichertOerlemans and Reichert (2000) and a degree-day model, the sensitivity of glacier mass balance to variations in temperature and precipitation was studied and annual mass-balance changes were modelled for the last 50 years. Climate data from Moreno base, operating since December 1995, and from the nearest synoptic station, Lago Argentino, were used. The reconstruction of the mass balance suggests that over this period the deviations of the glacier from a quasi-steady state were rather small, in agreement with the lack of a homogeneous warming trend at Lago Argentino station. The model indicates that variability of precipitation has been slightly more relevant for year-to-year variations in mass balance than temperature. However, this conclusion is merely indicative, as uncertainties in the spatial distribution of precipitation are high in this region of strong orographic gradients.
The observations, carried out on GPM since 1995, provide hints on possible factors leading to the damming events in 2003/04 and 2005/06. Only small seasonal and annual variations in surface velocity of stakes were measured by means of GPS throughout the years 1995–2003, indicating that GPM is not a surge-type glacier. The mass- balance reconstruction reveals slightly negative cumulative mass balance during the years 1988–98 without damming, and a slightly positive trend since then. These data suggest that the damming events on GPM are triggered by minor mass-balance fluctuations of a near-steady-state glacier.
The balance gradients and their relations to climate variables determined in this study for GPM should also be a useful basis for estimating climate sensitivity of glaciers in the vicinity. As an example, for the main section of adjoining Glaciar Ameghino, covering 53 km2, we calculate a mean mass balance of –900kgm–2a–1 based on climate and satellite data of the last 8 years. The calving loss corresponds to about 12% of total surface ablation. A striking difference to GPM is the higher percentage of surface area below 1000 m altitude. The estimate of significantly negative mass balance agrees with a pronounced retreat of the Ameghino terminus since 1970 (Reference StueferStuefer, 1999). This behaviour coincides with the retreat of the majority of HPS glaciers (Reference Aniya, Sato, Naruse, Skvarca and CasassaAniya and others, 1997).
The main uncertainty for the mass balance of HPS glaciers is accumulation because of its strong spatial variability and the difficulties in measuring accumulation on large glaciers. Also long-term measurements of ablation and climate observations are very rare. Such measurements are essential for improving our knowledge of glacier response to climatic factors and can be carried out with modest resources, as in the case of the work reported here. In addition, accurate repeat measurements of surface topography are important to enable independent verification of mass balance derived from field observations and climate data. SRTM in February 2000 provided a good initial dataset of surface topography of HPS, whereas previous topographic maps are not sufficiently accurate everywhere for the reliable retrieval of mass changes, as experienced on GPM.
Acknowledgements
This work was supported by the Austrian Science Funds projects Nr. P10709 and P12923 GEO and by the Glacio- logical Research Project in Patagonia of Dirección Nacional del Antártico – Instituto Antártico Argentino. The Alfred Wegener Institute for Polar and Marine Research, Bremerhaven, Germany, was in charge of the seismic measurements; we thank A. Eckstaller for field support and data analysis. SIR-C and SRTM data were kindly made available by NASA, and ERS SAR and ENVISAT ASAR data by the European Space Agency. We thank Administración de Parques Nacionales – Intendencia Parque Nacional los Glaciares and Compañía Hielo y Aventura for logistic support in the field. Assistance of friends and colleagues of these organizations, as well as of Instituto Antártico Argentino and the University of Innsbruck was essential for successfully completing the numerous field campaigns under sometimes very challenging conditions. We thank M. Nolan, K. Echelmeyer and U. Bhatt for valuable remarks. Reviews by L. Copland, J. Bamber and Scientific Editor N. F. Glasser helped to substantially improve the paper.













