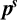 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODSPublished online by Cambridge University Press: 02 August 2023
We prove general Dwork-type congruences for constant terms attached to tuples of Laurent polynomials. We apply this result to establishing arithmetic and p-adic analytic properties of functions originating from polynomial solutions modulo 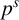 $p^s$ of hypergeometric and Knizhnik–Zamolodchikov (KZ) equations, solutions which come as coefficients of master polynomials and whose coefficients are integers. As an application, we show that the simplest example of a p-adic KZ connection has an invariant line subbundle while its complex analog has no nontrivial subbundles due to the irreducibility of its monodromy representation.
$p^s$ of hypergeometric and Knizhnik–Zamolodchikov (KZ) equations, solutions which come as coefficients of master polynomials and whose coefficients are integers. As an application, we show that the simplest example of a p-adic KZ connection has an invariant line subbundle while its complex analog has no nontrivial subbundles due to the irreducibility of its monodromy representation.
Communicated by Michael Coons