No CrossRef data available.
Article contents
On Markov chain approximations for computing boundary crossing probabilities of diffusion processes
Published online by Cambridge University Press: 11 May 2023
Abstract
We propose a discrete-time discrete-space Markov chain approximation with a Brownian bridge correction for computing curvilinear boundary crossing probabilities of a general diffusion process on a finite time interval. For broad classes of curvilinear boundaries and diffusion processes, we prove the convergence of the constructed approximations in the form of products of the respective substochastic matrices to the boundary crossing probabilities for the process as the time grid used to construct the Markov chains is getting finer. Numerical results indicate that the convergence rate for the proposed approximation with the Brownian bridge correction is 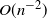 $O(n^{-2})$ in the case of
$O(n^{-2})$ in the case of 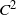 $C^2$ boundaries and a uniform time grid with n steps.
$C^2$ boundaries and a uniform time grid with n steps.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust



