Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T00:09:23.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Gravity currents: entrainment, stratification and self-similarity

Published online by Cambridge University Press:  30 October 2015

Diana Sher  and
Andrew W. Woods
Diana Sher
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present new experiments of the motion of a turbulent gravity current produced by the rapid release of a finite volume of dense aqueous solution from a lock of length 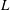$L$ into a channel 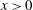$x>0$ filled with a finite depth, 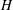$H$, of fresh water. Using light attenuation we measure the mixing and evolving density of the flow, and, using dye studies, we follow the motion of the current and the ambient fluid. After the fluid has slumped to the base of the tank, there are two phases of the flow. When the front of the current, 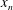$x_{n}$, is within the region 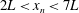$2L<x_{n}<7L$, the fluid in the head of the current retains its original density and the flow travels with a constant speed. We find that approximately 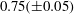$0.75(\pm 0.05)$ of the ambient fluid displaced by the head mixes with the fluid in the head. The mixture rises over the head and feeds a growing stratified tail region of the flow. Dye studies show that fluid with the original density continues to reach the front of the current, at a speed which we estimate to be approximately $1.35\pm 0.05$ times that of the front, consistent with data of Berson (Q. J. R. Meteorol. Soc., vol. 84, 1958, pp. 1–16) and Kneller et al. (J. Geophys. Res. Oceans, vol. 104, 1999, pp. 5281–5291). This speed is similar to that of the ‘bore’, the trailing edge of the original lock gate fluid, as described by Rottman & Simpson (J. Fluid Mech., vol. 135, 1983, pp. 95–110). The continual mixing at the front leads to a gradual decrease of the mass of unmixed original lock gate fluid. Eventually, when the nose extends beyond 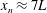$x_{n}\approx 7L$, the majority of the lock gate fluid has been diluted through the mixing. As the current continues, it adjusts to a second regime in which the position of the head increases with time as 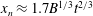$x_{n}\approx 1.7B^{1/3}t^{2/3}$, where 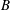$B$ is the total buoyancy of the flow per unit width across the channel, while the depth-averaged reduced gravity in the head decreases through mixing with the ambient fluid according to the relation 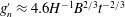$g_{n}^{\prime }\approx 4.6H^{-1}B^{2/3}t^{-2/3}$. Measurements also show that the depth of the head 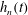$h_{n}(t)$ is approximately constant, 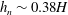$h_{n}\sim 0.38H$, and the reduced gravity decreases with height above the base of the current and with distance behind the front of the flow. Using the depth-averaged shallow-water equations, we derive a new class of self-similar solution which models the lateral structure of the flow by assuming the ambient fluid is entrained into the current in the head of the flow. By comparison with our data, we estimate that a fraction 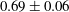$0.69\pm 0.06$ of the ambient fluid displaced by the head of the current is mixed into the flow in this approximately self-similar regime, and the front of the current has a Froude number $0.9\pm 0.05$. We discuss the implications of our results for the evolution of the buoyancy in a gravity current as a function of the distance from the source.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 130 - 162
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altinakar, M. S., Graf, W. H. & Hopfinger, E. J. 1996 Flow structure of turbidity currents. J. Hydraul. Res. 34, 713–718.Google Scholar
Berson, F. A. 1958 Some measurements on undercutting cold air. Q. J. R. Meteorol. Soc. 84, 1–16.CrossRefGoogle Scholar
Bonnecaze, R. T., Huppert, H. E. & Lister, J. R. 1993 Particle-driven gravity currents. J. Fluid Mech. 250, 339–369.Google Scholar
Brooke-Benjamin, T. B 1968 Gravity currents and related phenomenon. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Buckee, C. & Kneller, B 2000 The structure and fluid mechanics of turbidity currents. Sedimentology 47, 62–94.Google Scholar
Chen, J. C. 1980 Studies on gravitational spreading currents. Caltech 6077, 1–450.Google Scholar
Fragoso, A. T., Patterson, M. D. & Wettlaufer, J. S. 2013 Mixing in gravity currents. J. Fluid Mech. 734, 475–484.Google Scholar
Gill, A. E. 1981 Atmosphere–Ocean Dynamics. Academic.Google Scholar
Hacker, J., Linden, P. F. & Dalziel, S. B. 1996 Mixing in lock release gravity currents. Dyn. Atmos. Oceans 24, 183–195.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1993 Entrainment in turbulent gravity currents. Nature 362, 829–831.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment in two dimensional and axisymmetric gravity currents. J. Fluid Mech. 308, 289–311.Google Scholar
Hartel, C., Meiburg, E. & Necker, F. 2000 Analysis and direct numerical simulation of the flow at a gravity current head. Part I. Flow topology and front speed for slip and no slip boundaries. J. Fluid Mech. 418, 189–212.Google Scholar
Hogg, A. J. & Woods, A. W. 2001 The transition from inertia to bottom drag dominated motion of turbulent gravity currents. J. Fluid Mech. 449, 201–224.CrossRefGoogle Scholar
Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341.CrossRefGoogle Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.Google Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.Google Scholar
Johnson, C. & Hogg, A. 2013 Entraining gravity currents. J. Fluid Mech. 731, 477–801.CrossRefGoogle Scholar
von Karman, T. 1940 The engineer grapples with nonlinear problems. Bull. Am. Math. Soc. 46, 615–683.Google Scholar
Kneller, B., Bennett, S. J. & McCaffrey, W. D. 1999 Velocity structure turbulence and fluid stresses in experimental gravity currents. J. Geophys. Res. Oceans 104, 5281–5291.Google Scholar
Marino, B. M., Thomas, L. P. & Linden, P. F. 2005 The front condition for gravity currents. J. Fluid Mech. 536, 49–78.Google Scholar
McElwaine, J 2005 Rotational flow in gravity current heads. Phil. Trans. R. Soc. Lond. A 363, 1603–1623.Google Scholar
Morton, B., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection production by instantaneous and maintained point sources of buoyancy. Proc. R. Soc. Lond. A 231, 1–21.Google Scholar
Prandtl, L 1952 Essentials of Fluid Dynamics. Blackie.Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.Google Scholar
Samasiri, P. & Woods, A. W. 2015 Mixing in axisymmetric gravity currents. J. Fluid Mech. 782, R1.Google Scholar
Simpson, J. 1997 Gravity Currents, pp. 1–244. Cambridge University Press.Google Scholar
Simpson, J. & Britter, R. 1979 The dynamics of the head of a gravity current advancing over a horizontal surface. J. Fluid Mech. 94, 477–495.Google Scholar
van Sommeren, D. J. A., Caulfield, C. P. & Woods, A. W. 2012 Turbulent buoyant convection from a maintained source of buoyancy in a narrow vertical tank. J. Fluid Mech. 701, 278–303.Google Scholar
Sparks, R. S. J., Bursik, M. I., Carey, S. N., Gilbert, J. S., Glase, L. S., Sigurdsson, H. & Woods, A. W. 1997 Volcanic Plumes. Wiley–Blackwell.Google Scholar
Thomas, L., Dalziel, S. & Marino, B. 2003 The structure of the head of an inertial gravity current determined by particle tracking velocimetry. Exp. Fluids 34, 708–716.Google Scholar
Winters, K. B., Lombard, P. N., RiIey, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Yih, C. 1966 Stratified Flows, pp. 1–320. Wiley.Google Scholar