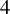1 Introduction
In this paper, we study Birkhoff billiards for centrally symmetric
$C^2$
-smooth strictly convex curves in the plane. We introduce the set
$\mathcal {M}_{\mathcal B}$
lying in the region
$\mathcal {B}$
between two invariant curves
$\alpha , \bar {\alpha }$
in the phase space (see Figure 1). The set
$\mathcal {M}_{\mathcal B}$
, by definition, consists of those orbits such that any finite sub-segment is locally maximizing, for the length functional
$\mathcal {L}$
associated to the billiard table. We assume that
$\alpha , \bar {\alpha }$
consist of
$4$
-periodic orbits of rotation numbers
$1/4$
and
$3/4$
, respectively. It then follows that the set
$\mathcal {M}_{\mathcal {B}}$
is a closed set which is invariant under the billiard map T. Our goal in this paper is to get an upper bound on the measure of the set
$\mathcal {M}_{\mathcal B}$
which is sharp, that is, the case when
$\mathcal {M}_{\mathcal B}$
occupies the whole of
$\mathcal {B}$
occurs if and only if the billiard table is circular. Thus, we show that the measure of the complement set
$\Delta _{\mathcal B}:=\mathcal B\setminus \mathcal M_{\mathcal B}$
can be estimated from below in terms of the isoperimetric defect of the billiard domain.
Figure 1 The region
$\mathcal B$
.
These bounds are of obvious importance for classical dynamics (and probably also for quantum properties), because all ‘rotational’ invariant curves, as well as Aubry–Mather sets, are filled by orbits which are locally length maximizing (we refer to the monographs [Reference Bangert, Kirchgraber and Walther3, Reference Kozlov and Treshchëv17–Reference Tabachnikov19] for background material).
Estimates of this type were obtained previously in [Reference Bialy6, Reference Bialy and Tsodikovich11], as an effective version of the so called the E. Hopf rigidity phenomenon for billiards.
The estimate presented here is related to the recent progress in the Birkhoff conjecture [Reference Bialy and Mironov9] for centrally symmetric billiard tables. Similarly to [Reference Bialy and Mironov9], we consider here the class of
$C^2$
-billiard tables having invariant curve consisting of
$4$
-periodic orbits and use its properties. We refer here to papers [Reference Arnold and Bialy1, Reference Avila, Kaloshin and De Simoi2, Reference Glutsyuk13–Reference Kaloshin and Sorrentino16] for other powerful recent approaches. However, the main novelty of the present paper is that the region
$\mathcal B$
lies away from the boundary of the phase cylinder.
It is an open question how to remove the restriction of central symmetry of the billiard table. It is also interesting if effective bounds can be found for a region between two arbitrary invariant curves in the phase space.
We now turn to the needed background and the formulation of the main result. Let
$\gamma $
be a
$C^2$
-smooth simple closed convex curve of positive curvature in
$\mathbb R^2$
. We fix the counterclockwise orientation on
$\gamma $
. We shall use the arclength parametrization s as well as the parametrization by the angle
$\psi $
formed by the outer unit normal n to
$\gamma $
with a fixed direction. These two parametrizations are related by
$d\psi =k(s)\,ds$
, where
$k(s)$
is the curvature at the point
$\gamma (s)$
.
The natural phase space of the Birkhoff billiard inside
$\gamma $
is the space
$\mathbf A$
of all oriented lines that intersect
$\gamma $
. This space is topologically a cylinder and we shall refer to it as the phase cylinder of T. The billiard map T acts on
$\mathbf A$
by the reflection law in
$\gamma $
. The phase cylinder carries a natural symplectic structure that can be described as follows.
Each oriented line is identified with the pair
$(\cos \delta ,s), \ \delta \in (0,\pi )$
, where
$\gamma (s)$
is the incoming point and
$\delta $
is the angle between the line and the tangent
$\gamma '(s)$
. In these coordinates, the symplectic form is
$d\unicode{x3bb} $
, where
$\unicode{x3bb} =\cos \delta \, ds$
and
$\cos \delta $
plays the role of momentum variable. We shall denote by
$\mu $
the corresponding invariant measure on the phase space
$\mathbf {A}$
. The billiard map T is a symplectic map and the chord length
$L(s,s_1)=|\gamma (s)-\gamma (s_1)|$
is a generating function of T (see Figure 2). Namely,
$$ \begin{align*} T^*\unicode{x3bb}-\unicode{x3bb}=\cos\delta_1\,ds_1-\cos\delta\, ds=dL. \end{align*} $$
Figure 2 Generating function L corresponding to the 1-form
$\unicode{x3bb} $
.
Moreover, one can check that T satisfies the twist condition:
$$ \begin{align} L_{12} (s,s_1)>0, \end{align} $$
meaning that T is a negative twist symplectic map (here and below, we use subindex
$1$
and/or
$2$
for the partial derivative with respect to the first or the second argument, respectively).
Remark. Traditionally, the generating function is the negative of ours, that is, the negative chord length. However, we prefer, for convenience, sign
$+$
for the generating function and hence the twist condition in equation (1) for the billiard map. Consequently, we deal with maximizing (and not minimizing) orbits.
For the generating function L, we can naturally define the variational principle as follows. For the configuration sequence
$\{s_n\}$
, we associate the formal sum
$$ \begin{align*}\mathcal L \{s_n\}=\sum_n L(s_n,s_{n+1}). \end{align*} $$
Configurations
$\{s_n\}$
, corresponding to billiard trajectories, are critical points of the functional
$\mathcal L$
.
We shall consider locally maximizing configurations, that is, those configurations which give local maximum for the functional between any two end-points. We shall call such configurations m-configurations, and the corresponding orbits on the phase cylinder
$\mathbf {A}$
, m-orbits. We denote by
$\mathcal M\subset \mathbf {A}$
the set swept by all m-orbits corresponding to the variational principle for the generating function L. We shall also use the following notation:
$$ \begin{align*} \mathcal M_{\mathcal B}:=\mathcal M \cap \mathcal B,\quad \Delta_{\mathcal B}:=\mathcal B\setminus\mathcal M_{\mathcal B}. \end{align*} $$
Let
$\gamma \subset \mathbb {R}^2$
be a
$C^2$
-smooth, centrally symmetric, convex closed curve of positive curvature. We shall assume that the billiard map corresponding to
$\gamma $
has a rotational (that is, winding once around the cylinder and simple) invariant curve
$\alpha \subset \mathbf {A}$
consisting of
$4$
-periodic orbits. We shall denote by
$\bar \alpha $
the corresponding invariant curve of rotation number
$\tfrac 34$
. This curve consists of the same billiard trajectories but with the reversed orientation of the lines. Our main result is the following.
Theorem 1.1. Suppose that the billiard ball map T of
$\gamma $
has a continuous rotational invariant curve
$\alpha \subset \mathbf A$
of rotation number
$1/4$
, consisting of
$4$
-periodic orbits. Let
$\bar \alpha $
be the corresponding invariant curve of rotation number
$\tfrac 34$
. Let
$\mathcal B\subset \mathbf A$
be the domain between the curves
$\alpha $
and
$\bar \alpha $
(see Figure 1). Then the following estimate holds:
$$ \begin{align} \frac{3\beta}{16}(P^2-4\pi A)\leq \mu(\Delta_{\mathcal B}), \end{align} $$
where
$P, A$
denote the perimeter and the area of
$\gamma $
, and
$\beta>0$
is the minimal curvature of
$\gamma $
.
Sharp estimates for
$\mathcal M$
were obtained first in [Reference Bialy6] and then in [Reference Bialy and Tsodikovich11] as a quantitative version of the so called E.Hopf rigidity phenomenon for billiards discovered in [Reference Bialy4] and then [Reference Bialy5, Reference Wojtkowski20]. In [Reference Bialy and Tsodikovich11], the region between the invariant curve
$\alpha $
and the boundary of the phase cylinder was considered, while in the present paper, the region
$\mathcal B$
lies away from the boundary. The significance of the invariant curve of 4-
$periodic$
orbits was first understood in [Reference Bialy and Mironov9], and we shall remember the properties of this curve here and use them below.
Here are some useful corollaries of Theorem 1.1.
Corollary 1.2. Set
$\mathcal M_{\mathcal B}$
of locally maximizing orbits occupies the whole region
$\mathcal B$
if and only if
$\gamma $
is a circle.
In fact, one can reformulate Corollary 1.2 in a dynamical way.
Corollary 1.3. Suppose that the restriction of billiard map T to
$\mathcal B$
has an invariant measurable field of non-vertical oriented lines, with the orientation chosen on the lines coherently by the condition
$ds>0$
. Then
$\gamma $
is a circle.
This is especially useful in establishing the following geometric fact.
Corollary 1.4. If
$\gamma $
is not a circle, then there always exist a point
$x\in \mathcal B$
and a vertical tangent vector
$v\in T_x\mathcal B$
such that for some positive integer n, the vector
$DT^n(v)$
is again vertical (this exactly means that the points x and
$T^n x$
are conjugate).
Corollary 1.3 follows immediately from Theorem 1.1 applying the criterion of local maximality in terms of Jacobi fields [Reference Bialy and Tsodikovich11, Theorem 1.1].
To deduce Corollary 1.4, one can argue analogously to [Reference Bialy4]. More precisely, suppose, by contradiction, that for any vertical vector
$v\in T_x\mathcal B$
and any positive integer n, the vector
$DT^n(v)$
is not vertical. This implies that any finite segment of a billiard trajectory
$\{\gamma (s_n), n\in [M,N]\}$
has a non-degenerate matrix of second variation
$\delta ^2\mathcal L_{MN}$
. Then, by a continuity argument, all the matrices
$\delta ^2\mathcal L_{MN}$
must be negative definite (because this holds true for orbits lying on the rotational invariant curve
$\alpha $
). Hence, all billiard configurations, corresponding to the orbits lying in
$\mathcal {B}$
, are locally maximizing. Therefore, Theorem 1.1 applies and the curve
$\gamma $
is a circle, which is a contradiction.
2 Important tools
2.1 Non-standard generating function
Another way to get the same symplectic form is to fix an origin in
$\mathbb R^2$
(we shall fix the origin at the center of
$\gamma $
) and to introduce the coordinates
$(p,\varphi )$
on the space of all oriented lines, so that
$\varphi $
is the angle between the right unit normal to the line and the horizontal, and p is the signed distance to the line (see Figure 3). In this way, the space of oriented lines is identified with
$T^*S^1$
. Moreover, the standard symplectic form
$d\beta $
with
$\beta =pd\varphi $
coincides with the symplectic form described before. In this description, p plays the role of momentum variable.
Figure 3 Generating function S corresponding to the 1-form
$\beta $
.
For the second choice of the coordinates
$(p,\varphi )$
, the generating function was found first in [Reference Bialy and Mironov8] for the two-dimensional case and then in [Reference Bialy7] for higher dimensions (see [Reference Bialy and Tabachnikov10] for further applications). This function S is determined by the formulas:
$$ \begin{align*} T^*\beta-\beta=p_1\,d \varphi_1-p\,d\varphi = dS, \quad S(\varphi ,\varphi _1 )=2h(\psi)\sin\delta, \end{align*} $$
where
$$ \begin{align*}\psi:=\frac{\varphi_1+\varphi}{2},\quad \delta:=\frac{\varphi_1-\varphi}{2}.\end{align*} $$
Here and throughout this paper, we denote by h the support function of
$\gamma $
with respect to
$0$
:
$$ \begin{align*} h(\psi):=\max_{\gamma} \left\langle\gamma,n_\psi \right\rangle\!{,} \end{align*} $$
where
$n_\psi $
is the unit outer normal to
$\gamma $
in the direction
$\psi $
. The fact that S is the generating function for T means that the line with coordinates
$(p,\varphi )$
is mapped into the line
$(p_1,\varphi _1)$
(see Figure 3) if and only if
$$ \begin{align} \begin{aligned} p&=-S_1(\varphi,\varphi_1) = h(\psi) \cos \delta-h'(\psi) \sin \delta,\\ p_1&=S_2(\varphi,\varphi_1) = h(\psi) \cos \delta+h'(\psi) \sin \delta. \end{aligned} \end{align} $$
It follows from the direct computation (see below Proposition 2.4) that the map T satisfies the twist condition with respect to the symplectic coordinates
$(p,\varphi )$
meaning that the cross-derivative satisfies
$ S_{12}=\tfrac 12\rho (\psi )\sin \delta>0$
, where
$\rho (\psi )=h"(\psi )+h(\psi )>0$
is the radius of curvature.
2.2 Two variational principles
One can associate variational principle
$\mathcal {S}$
also for the function S:
$$ \begin{align*} \mathcal S\{\varphi_n\}=\sum_n S(\varphi_{n}, \varphi_{n+1}). \end{align*} $$
In [Reference Bialy and Tsodikovich11], we gave a criterion for an orbit to be locally maximizing. It then follows from this criterion that the set
$\mathcal M$
does not depend on which generating function L or S is used for the map T. We shall use the function S to prove Theorem 1.1.
Remark. It appears that vertical vector in the statement of the Corollary 1.4 can be understood with respect to each of the vertical foliations
$\{s=\mathrm {const}\}$
or
$\{\varphi =\mathrm {const}\}$
. This follows from the proof of Corollary 1.4 and the fact, proven in [Reference Bialy and Tsodikovich11], that the classes of locally maximizing orbits corresponding to the generating functions
$L, S$
coincide.
In particular, the existence of conjugate points with respect to the vertical foliation
$\{\varphi =\mathrm {const}\}$
implies that one can find a beam of parallel lines such that after n reflections, the beam becomes parallel (infinitesimally) again.
2.3 Properties of the invariant curve of
$4$
-periodic orbits
If the billiard curve
$\gamma $
is an ellipse, then there exists a rotational invariant curve
$\alpha $
consisting of
$4$
-periodic orbits. The corresponding quadrilaterals inscribed in
$\gamma $
are called Poncelet
$4$
-gons. It is well known (see [Reference Connes and Zagier12] for several proofs) that all Poncelet 4-gons for an ellipse are parallelograms. This fact can be generalized from the case of an ellipse to any centrally symmetric billiard table. We now turn to state the results from [Reference Bialy and Mironov9] and refer to [Reference Bialy and Mironov9] for the proofs. The next theorem is illustrated in Figure 4.
Figure 4 Rectangle
$Q_0 Q_1 Q_2 Q_3$
corresponding to the
$4$
-periodic orbit forming parallelogram
$P_0 P_1 P_2 P_3$
.
Theorem 2.1. Let
$\gamma $
be a centrally symmetric billiard table. Assume that billiard ball map
$T:\mathbf A \rightarrow \mathbf A$
has a continuous rotational invariant curve
$\alpha =\{\delta =d(\psi )\}$
of rotation number
$\tfrac 14$
consisting of
$4$
-periodic orbits of T. Then the following properties hold.
-
(A) Function
$d(\psi )$
is
$\pi $
-periodic and the billiard quadrilaterals corresponding to the traces of the orbits contained in the invariant curve
$\alpha $
are parallelograms. -
(B) The tangent lines to
$\gamma $
at the vertices of the parallelogram form a rectangle. -
(C)
$0<d(\psi )<\pi /2,\quad d(\psi +{\pi }/{2})={\pi }/{2}-d(\psi ).$
-
(D) The functions d and h satisfy the identities
and
$$ \begin{align*}\tan d(\psi)=\frac{h(\psi)}{h(\psi+{\pi}/{2})}=-\frac{h'(\psi+{\pi}/{2})}{h'(\psi)}, \ \end{align*} $$
$$ \begin{align*}h^2(\psi)+h^2\bigg(\psi+\frac{\pi}{2}\bigg)=R^2=\mathrm{const}.\end{align*} $$
Remark. It follows from Theorem 2.1 item (D) that the orthoptic curve associated with
$\gamma $
is a circle of radius R (like in the case of an ellipse). Here the orthoptic curve of
$\gamma $
, by definition, is the locus of points Q, such that the two tangents to
$\gamma $
passing through Q form a right angle.
Corollary 2.2. Let
$\gamma $
be a convex centrally symmetric billiard table. Let
$\alpha =\{\delta =d(\psi )\}\subset \mathbf A$
be an invariant curve consisting of
$4$
-periodic orbits. It then follows from Theorem 2.1 item (D) that
$$ \begin{align*} h(\psi)= R\sin d(\psi) ,\quad h\bigg(\psi+\frac{\pi}{2}\bigg)=R\cos d(\psi), \end{align*} $$
for a positive constant R.
Corollary 2.3. The explicit formulas of item (D) show that the invariant curve
$\alpha $
is necessarily
$C^2$
-smooth, since the support function h is
$C^2$
-smooth by assumption.
2.4 Function
$\omega $
and an inequality
It turns out that one can introduce a measurable bounded function
$\omega $
on the set
$\mathcal M$
satisfying the inequality:
$$ \begin{align} \omega(p_1,\varphi_1)-\omega(p,\varphi) \geq S_{11}(\varphi,\varphi_1)+S_{22}(\varphi,\varphi_1) +2S_{12}(\varphi,\varphi_1). \end{align} $$
The construction of this function (see [Reference Bialy4]) was inspired by the celebrated E.Hopf theorem on tori with no conjugate points. Let us sketch this construction. Let
$\{(p_n,\varphi _n)\}$
be a locally maximizing orbit of the point
$z=(p_0,\varphi _0)$
. It then follows that there exists an invariant vector field
$\{(\delta p_n,\delta \varphi _n)\}$
along the orbit
$\{(p_n,\varphi _n)\}$
such that the corresponding field
$\delta \varphi _n$
is a Jacobi field along the billiard configuration
$\{\varphi _n\}$
(normalized by
$\delta \varphi _0=1$
) and is strictly positive. Remember, a Jacobi field along a configuration
$\{\varphi _n\}$
is a sequence
$\{\delta \varphi _n\}$
satisfying the discrete Jacobi equation:
$$ \begin{align} b_{n-1}\delta \varphi_{n-1}+a_n \delta \varphi_n+b_{n}\delta \varphi_{n+1}=0, \end{align} $$
where, as before,
$$ \begin{align*}a_n=S_{22}( \varphi_{n-1}, \varphi_n)+S_{11}( \varphi_n, \varphi_{n+1}),\ b_n=S_{12}( \varphi_n, \varphi_{n+1}).\end{align*} $$
Then the invariance of the field
$\{(\delta p_n,\delta \varphi _n)\}$
along the orbit implies (by differentiating the formula
$p_n=-S_1(\varphi _n,\varphi _{n+1})$
):
$$ \begin{align*} \delta p_n=-S_{11}(\varphi_n,\varphi_{n+1})\delta \varphi_n-S_{12}(\varphi_n,\varphi_{n+1})\delta \varphi_{n+1} ,\end{align*} $$
or equivalently, due to the Jacobi equation:
$$ \begin{align*} \delta p_n=S_{22}(\varphi_{n-1},\varphi_{n})\delta \varphi_n+S_{12}(\varphi_{n-1},\varphi_{n})\delta \varphi_{n-1}. \end{align*} $$
Then one defines
$\omega (p_n,\varphi _n):={\delta p_n}/{\delta \varphi _n}$
. One can prove that
$\omega $
is a measurable function and satisfies the relations:
$$ \begin{align} \begin{cases} \omega(T(p,\varphi))=S_{22}(\varphi,\varphi_1)+S_{12}(\varphi,\varphi_1)\delta \varphi_1(\varphi,p)^{-1},\\ \omega(p, \varphi)=-S_{11}(\varphi, \varphi_1)-S_{12}(\varphi,\varphi_1)\delta \varphi_{1}(\varphi,p). \end{cases} \end{align} $$
Subtracting the second equation from the first one and using
$S_{12}>0$
,
$ \delta \varphi _1>0$
, we get the inequality in equation (4).
Also notice that from equation (6), we have the inequality
$$ \begin{align*} S_{22}(\varphi_{-1},\varphi)<\omega(p,\varphi)<-S_{11}(\varphi,\varphi_1), \end{align*} $$
since in equation (6),
$S_{12},\delta \varphi _1, \delta \varphi _{-1}$
are positive. Using Proposition (2.4), it then follows that function
$\omega $
is bounded on
$\mathcal M_{\mathcal B}$
:
$$ \begin{align*} |\omega|<\max_{\mathcal B} \{|S_{11}|, |S_{22}|\}<K(\gamma), \end{align*} $$
where
$K(\gamma )$
depends only on
$\gamma $
(for example, one can set
$K(\gamma )=\max _{\gamma }\{\rho + h+ |h'|\}$
, using the formulas of Proposition (2.4)).
2.5 Derivatives of generating function S
The derivatives of the generating function S can be immediately computed.
Proposition 2.4. The second partial derivatives of
$S $
are
$$ \begin{align*} & S_{11}(\varphi,\varphi_1)=\tfrac{1}{2}(h"(\psi)-h(\psi))\sin \delta -h'(\psi)\cos \delta;&\\ &S_{22}(\varphi,\varphi_1)=\tfrac{1}{2}(h"(\psi)-h(\psi))\sin \delta +h'(\psi)\cos \delta;&\\ &S_{12}(\varphi,\varphi_1)=\tfrac{1}{2}(h"(\psi)+h(\psi))\sin \delta ,& \end{align*} $$
where
$\psi :=({\varphi _1+\varphi })/{2},\quad \delta :=({\varphi _1-\varphi })/{2}.$
3 Proof of Theorem 1.1
In the following, we shall work with the coordinates
$(p,\varphi )$
and the function
$\omega $
constructed above for the generating function S. We start the proof of Theorem 1.1 integrating equation (4) over
$\mathcal M_{\mathcal B}$
with respect to the invariant measure
$d\mu =dpd\varphi $
.
To perform the integration, we compute the invariant measure as follows.
The symplectic form
$dp \wedge d\varphi $
can be written using generating function in equation (3):
$$ \begin{align*} dp\wedge d\varphi=-d(S_1(\varphi,\varphi_1))\wedge d\varphi=S_{12}d\varphi\wedge d\varphi_1. \end{align*} $$
Since T is symplectic, the measure
$$ \begin{align*}d\mu= dp d\varphi=S_{12}d\varphi d\varphi_1\end{align*} $$
is invariant. Using the explicit formula for the second derivative (Proposition 2.4), we compute
$$ \begin{align*} d\mu &= S_{12}d\varphi d\varphi_1 =\big(\tfrac{1}{2}\rho(\psi)\sin\delta\big)d\varphi d\varphi_1=\rho(\psi)\sin\delta d\psi d\delta, \end{align*} $$
where (see Figure 3 showing all the notation)
$$ \begin{align*} \rho(\psi)=h"(\psi)+h(\psi) \end{align*} $$
is the radius of curvature of
$\gamma $
, and
$$ \begin{align*} \quad \psi:=\frac{\varphi_1+\varphi}{2},\quad \delta:=\frac{\varphi_1-\varphi}{2}. \end{align*} $$
Hence, integrating the inequality in equation (4) with respect to the invariant measure
$d\mu $
, we obtain
$$ \begin{align*} 0\geq \int_{\mathcal M_{\mathcal B}}[S_{11}(\varphi,\varphi_1)+2S_{12}(\varphi,\varphi_1)+S_{22}(\varphi,\varphi_1) ]d\mu. \end{align*} $$
Moreover, we get from Proposition 2.4, after obvious simplifications,
$$ \begin{align*} S_{11}(\varphi,\varphi_1)+2S_{12}(\varphi,\varphi_1)+S_{22}(\varphi,\varphi_1) =2h"(\psi)\sin\delta. \end{align*} $$
Thus, equation (4) yields the inequality:
$$ \begin{align} 0\geq \int_{\mathcal M_{\mathcal B}}[(h"(\psi)\sin\delta]d\mu. \end{align} $$
Since
$\mathcal M_{\mathcal B}=\mathcal B\setminus \Delta _{\mathcal B}$
, we get
$$ \begin{align} \int_{\mathcal B}[(h"(\psi)\sin\delta]\,d\mu\leq\int_{\Delta_{\mathcal B}}[(h"(\psi)\sin\delta]\,d\mu. \end{align} $$
Let us denote
$$ \begin{align} I:=\int_{\mathcal B}[(h"(\psi)\sin\delta]\,d\mu. \end{align} $$
We shall give an upper bound for the right-hand side of equation (8), and a lower bound on the left-hand side I, and together we get the required bound. For the right-hand side of equation (8), write
$$ \begin{align} \int\limits_{\Delta_{\mathcal B}} h"(\psi)\sin\delta d\mu &\leq \bigg| \int\limits_{\Delta_{\mathcal B}} h"(\psi)\sin\delta d\mu \bigg| \nonumber\\ &\leq \int\limits_{\Delta_{\mathcal B}}|h"(\psi)\sin\delta| d\mu \leq \mu(\Delta_{\mathcal B})\max\limits_{\Delta_{\mathcal B}} |h"|. \end{align} $$
Since
$h(\psi )+h"(\psi )=\rho (\psi )$
, where
$\rho (\psi )$
is the radius of curvature, then
$$ \begin{align*}|h"|\leq\rho+\max h.\end{align*} $$
Since
$\gamma $
is centrally symmetric, we have
$\max h\leq D/2$
, where D is the diameter. Also, the maximal radius of curvature of
$\gamma $
is
${1}/{\beta }$
, where
$\beta $
is the minimal curvature of
$\gamma $
. This gives us the estimate
$$ \begin{align}I\leq \int\limits_{\Delta_{\mathcal B}} h"(\psi)\sin\delta\,d\mu \leq \bigg(\frac{D}{2}+\frac{1}{\beta}\bigg)\mu(\Delta_{\mathcal B})\leq \frac{2}{\beta}\mu(\Delta_{\mathcal B}), \end{align} $$
where we used Blaschke’s rolling disk theorem, stating that
$\gamma $
is contained inside a disk with radius equal to the maximal radius of curvature of
$\gamma $
, and this means that
$D\leq {2}/{\beta }$
.
We now turn to estimate I from below. Namely, we shall prove in the next section the following.
Theorem 3.1. Integral I can be estimated from below:
$$ \begin{align*}I\geq \tfrac{3}{8}(P^2-4\pi A). \end{align*} $$
Proof of Theorem 1.1 follows immediately from equation (11) and Theorem 3.1.
4 Proof of Theorem 3.1
Substituting into the integral I the explicit expression
$d\mu =\rho (\psi )\sin \delta \,d\psi \,d\delta $
and integrating first with respect to
$\delta $
, we get from equation (9):
$$ \begin{align} I= \int_{0}^{2\pi}\,d\psi\ \ \bigg[ h"(h+h")\int_{d(\psi)}^{\pi -d(\psi)\,d\delta\ \sin^2\delta}\bigg]. \end{align} $$
Here we used the fact that in the coordinates
$(\psi ,\delta )$
, the domain of integration takes the form
$$ \begin{align*}\mathcal B=\{(\psi,\delta):\psi\in[0,2\pi],\ \delta\in[d(\psi), \pi-d(\psi)]\}.\end{align*} $$
Here and below,
$d(\psi )$
is the function described in §2.3.
Integrating in equation (12) with respect to
$\delta $
, we obtain
$$ \begin{align} I= \int_{0}^{2\pi} \big[h"(\psi)(h"(\psi)+h(\psi))\big]\bigg(\frac{\pi}{2}-d(\psi)+\frac{1}{2}\sin 2d(\psi)\bigg)\,d\psi. \end{align} $$
Now we substitute into equation (13) the expressions for
$h,h',h"$
via
$d(\psi )$
using Corollary 2.2 of Theorem 2.1:
$$ \begin{align} \begin{cases}h=R\sin d,\\ h'=R \cos d \ d', \\ h"=R\cos d\ d"-R\sin d\ ( d')^2,\\ d\bigg(\psi+\dfrac{\pi}{2}\bigg)=\dfrac{\pi}{2}-d(\psi). \end{cases} \end{align} $$
In what follows, we usually omit the arguments for the functions
$h,d$
and their derivatives.
Thus, we get from equation (11) the following equality on the function d:
$$ \begin{align}I&= {R^2}\int_{0}^{2\pi} (\sin d-\sin d\ d^{\prime 2}+\cos d\ d")(-\sin d\ d^{\prime 2}+\cos d\ d")\nonumber\\ &\quad\times\bigg(\frac{\pi}{2}-d+\frac{1}{2}\sin 2d\bigg)\,d\psi\nonumber\\&={R^2}\int_{0}^{2\pi}U\,d\psi, \end{align} $$
where we introduced U by the formula
$$ \begin{align*} U:= (\sin d-\sin d\ d^{\prime 2}+\cos d\ d")(-\sin d\ d^{\prime 2}+\cos d\ d")\\ \bigg(\frac{\pi}{2}-d+\frac{1}{2}\sin 2d\bigg). \end{align*} $$
The assumption of central symmetry implies that
$h(\psi ),d(\psi )$
are
$\pi $
-periodic. Hence,
$$ \begin{align*} \int_0^{2\pi}U(\psi)\,d\psi=2 \int_0^{\pi}U(\psi)\,d\psi. \end{align*} $$
We shall prove now the following estimate.
Theorem 4.1.
$$ \begin{align*} \int_0^{\pi}U(\psi)\,d\psi\geq \frac{3}{16R^2}(P^2-4\pi A). \end{align*} $$
Proof. The idea of the proof is to proceed in three steps: ‘symmetrization’, integration by parts, and Wirtinger inequality. Doing this, we pass to a new integrand,
$\tilde U$
, satisfying the inequality
$\tilde U\geq \mathrm {const}\ h^{\prime 2}$
. Moreover, integrating this inequality, we will be able to estimate the integral of
$\tilde U$
from below by isoperimetric defect.
We write
$$ \begin{align*} U=U_1+U_2+U_3+U_4+U_5, \end{align*} $$
where
$$ \begin{align*} &U_1=d^{\prime\prime 2}\cos^2 d\bigg(\frac{\pi}{2}-d+\frac{1}{2}\sin 2d\bigg),\\ &U_2=-2d"d^{\prime 2}\sin d\cos d \bigg(\frac{\pi}{2}-d+\frac{1}{2}\sin 2d\bigg),\\ &U_3=d"\sin d\cos d \bigg(\frac{\pi}{2}-d+\frac{1}{2}\sin 2d\bigg),\\ &U_4=d^{\prime 4}\sin^2 d\bigg(\frac{\pi}{2}-d+\frac{1}{2}\sin 2d\bigg),\\ &U_5=-d^{\prime 2}\sin^2 d\bigg(\frac{\pi}{2}-d+\frac{1}{2}\sin 2d\bigg). \end{align*} $$
Step 1. Symmetrization. We perform the change of the integration variable by the rule
$\psi \rightarrow \psi +{\pi }/{2}$
. By equation (14), which is the consequence of Theorem 2.1 and Corollary 2.2, this intertwines
$\sin (d)$
with
$\cos (d)$
and changes the sign of
$d"$
. Denote the changed integrand by
$\hat U_j$
.
Also denote the ‘symmetrized’ integrand by
$$ \begin{align*} V_j:=U_j+\hat U_j. \end{align*} $$
Then we have
$$ \begin{align*} \int_0^{\pi}U_j(\psi)\,d\psi=\int_0^{\pi}\hat U_j(\psi)\,d\psi=\frac{1}{2}\int_0^{\pi}V_j(\psi) \,d\psi, \end{align*} $$
where
$V_j$
can be written as
$$ \begin{align*} &V_1=d^{\prime\prime 2}\bigg(\frac{\pi}{4}+\bigg(\frac{\pi}{4}-d\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg),\\ &V_2=d"d^{\prime 2}\sin 2d\bigg(2d-\frac{\pi}{2}\bigg),\\ &V_3=d"\sin 2d\bigg(\frac{\pi}{4}-d\bigg),\\ &V_4=d^{\prime 4}\bigg(\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg),\\ &V_5=-d^{\prime 2}\bigg(\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg). \end{align*} $$
Step 2. Integration by parts. Terms
$V_2$
and
$V_3$
contain
$d"$
in the first power. Therefore, we apply integration by parts for
$V_2,V_3$
to get rid of the second derivative
$d"$
. Notice that thanks to the
$\pi $
-periodicity of the integrands, the off-integration terms vanish. Thus, we get new integrands
$W_i,i=1,\ldots ,5$
, where
$$ \begin{align*} &W_1=V_1=d^{\prime\prime 2}\bigg(\frac{\pi}{4}+\bigg(\frac{\pi}{4}-d\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg),\\ &W_2=d^{\prime 4}\bigg(-\frac{4}{3}\cos 2d\ \bigg(d-\frac{\pi}{4}\bigg)-\frac{2}{3}\sin 2d\bigg),\\ &W_3=d^{\prime 2}\bigg(2\cos 2d\ \bigg(d-\frac{\pi}{4}\bigg)+\sin 2d\bigg),\\ &W_4=V_4=d^{\prime 4}\bigg(\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg),\\ &W_5=V_5=-d^{\prime 2}\bigg(\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg). \end{align*} $$
Thus, we get for the integral of U:
$$ \begin{align} \int_{0}^{\pi}U \,d\psi=\int_{0}^{\pi}\sum_{i=1}^{5}U_i\,d\psi=\frac{1}{2} \int_{0}^{\pi}\sum_{i=1}^{5}V_i\,d\psi=\frac{1}{2} \int_{0}^{\pi}\sum_{i=1}^{5}W_i\,d\psi. \end{align} $$
Summing
$W_2+ W_4$
and
$W_3+ W_5$
, we rewrite using only three summands:
$$ \begin{align*} &X_1:=W_1=d^{\prime\prime 2}\bigg(\frac{\pi}{4}+\bigg(\frac{\pi}{4}-d\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg),\\ &X_2:=W_2+W_4=d^{\prime 4}\bigg(\frac{\pi}{4}-\frac{1}{3}\bigg(d-\frac{\pi}{4}\bigg)\cos 2d-\frac{1}{6}\sin 2d\bigg),\\ &X_3:=W_3+W_5=d^{\prime 2}\bigg(-\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg). \end{align*} $$
Thus, we have
$$ \begin{align} \int_{0}^{\pi}U \,d\psi=\frac{1}{2} \int_{0}^{\pi}(X_1+X_2+X_3)\,d\psi. \end{align} $$
Step 3. Use of the Wirtinger inequality. Let us introduce the function of d which is the multiplier in
$X_1$
:
$$ \begin{align*} f(d):=\frac{\pi}{4}+\bigg(\frac{\pi}{4}-d\bigg)\cos 2d+\frac{1}{2}\sin 2d. \end{align*} $$
This function is strictly positive since d varies in
$(0, \pi /2)$
. In fact, one can say more precisely
$$ \begin{align*}f\in \bigg[\frac{1}{2}+\frac{\pi}{4},\frac{\pi}{2}\bigg).\end{align*} $$
Also we can write
$$ \begin{align*} X_2=d^{\prime 4} f_2,\quad f_2:=\frac{\pi}{4}-\frac{1}{3}\bigg(d-\frac{\pi}{4}\bigg)\cos 2d-\frac{1}{6}\sin 2d, \end{align*} $$
and one can see that
$f_2$
is positive as well.
Similarly for
$X_3$
, we have
$$ \begin{align*} X_3= d^{\prime 2} f_3,\quad f_3:=-\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin 2d=(\sin 2d -f). \end{align*} $$
However, the function
$f_3$
is not necessarily positive. To bypass this difficulty, we shall use the Wirtinger inequality, which we apply to the function
$$ \begin{align*} Y:=d' \sqrt{f}. \end{align*} $$
Notice that Y is
$\pi $
-periodic and has zero average, since it can be written as a complete derivative. Hence,
$$ \begin{align*} \int_{0}^{\pi}(Y^{\prime 2}-4Y^2)\, d\psi\geq 0. \end{align*} $$
We have the following expressions:
$$ \begin{align*} Y'=\sqrt{f}d"+\frac{f'}{2\sqrt{f}}d^{\prime 2}\Rightarrow Y^{\prime 2}=f\ d^{\prime\prime 2}+f'\ d"d^{\prime 2}+\frac{f^{\prime 2}}{4f}d^{\prime 4}. \end{align*} $$
Therefore,
$$ \begin{align*} &\int_{0}^{\pi}(Y^{\prime 2}-4Y^2) \,d\psi=\int_{0}^{\pi}\bigg(f\ d^{\prime\prime 2}+f'\ d"d^{\prime 2}+\frac{f^{\prime 2}}{4f}d^{\prime 4} -4fd^{\prime 2}\bigg)\,d\psi\\ &\quad=\int_{0}^{\pi}\bigg(f\ d^{\prime\prime 2}-\frac{f"}{3}d^{\prime 4} +\frac{f^{\prime 2}}{4f}d^{\prime 4} - 4fd^{\prime 2}\bigg)\,d\psi=\int_{0}^{\pi}g\,d\psi\geq 0, \end{align*} $$
where
$g:=(f\ d^{\prime \prime 2}-{f"}{3}d^{\prime 4} +({f^{\prime 2}}/{4f})d^{\prime 4}-4fd^{\prime 2})$
and we performed integration by parts again.
Thus, finally we can write
$$ \begin{align*} X_1+X_2+X_3&=g+d^{\prime 4}\bigg(f_2+\frac{f"}{3}-\frac{f^{\prime 2}}{4f}\bigg)+(f_3+4f)\\ &=g+d^{\prime 4}\bigg(f_2+\frac{f"}{3}-\frac{f^{\prime 2}}{4f}\bigg)+d^{\prime 2}(\sin 2d+3f).\end{align*} $$
The following claim is crucial.
Lemma 4.2. Both expressions
$(\sin 2d+3f)$
and
$(f_2+{f"}/{3}-{f^{\prime 2}}/{4f})$
of the last formula are strictly positive.
Proof. (1) Since
$f\in [\tfrac 12+{\pi }/{4},{\pi }/{2}),$
then
$(3f+\sin 2d)\geq \tfrac 32+{3\pi }/{4}$
. Analyzing the behavior of the function f, one can claim more:
$$ \begin{align} (3f+\sin 2d)\geq 3f(0)=\frac{3\pi}{2}. \end{align} $$
(2) For the expression
$(f_2+{f"}/{3}-{f^{\prime 2}}/{4f})$
, we need to compute
$$ \begin{align*} f'=-2 \bigg(\frac{\pi}{4}-d\bigg)\sin 2d, \end{align*} $$
$$ \begin{align*} f"=-4\bigg(\frac{\pi}{4}-d\bigg)\cos 2d+2\sin 2d. \end{align*} $$
We substitute
$f_2$
and the second derivative of f:
$$ \begin{align*} &\bigg(f_2+\frac{f"}{3}-\frac{f^{\prime 2}}{4f}\bigg)=\frac{f"}{3}-\frac{f^{\prime 2}}{4f}+ \frac{\pi}{4}-\frac{1}{3}\bigg(d-\frac{\pi}{4}\bigg)\cos 2d-\frac{1}{6}\sin 2d\\ &\quad=-\frac{f^{\prime 2}}{4f}+\frac{1}{3}\bigg[-4\bigg(\frac{\pi}{4}-d\bigg)\cos 2d+2\sin 2d\bigg]+ \frac{\pi}{4}-\frac{1}{3}\bigg(d-\frac{\pi}{4}\bigg)\cos 2d-\frac{1}{6}\sin 2d\\ &\quad =-\frac{f^{\prime 2}}{4f}+\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin2d. \end{align*} $$
Thus, we need to check the sign of the expression:
$$ \begin{align*} &-\bigg(\frac{\pi}{4}-d\bigg)^2\sin^2 2d+\bigg(\frac{\pi}{4}+\bigg(\frac{\pi}{4}-d\bigg)\cos 2d+\frac{1}{2}\sin 2d\bigg) \\&\qquad\times\bigg(\frac{\pi}{4}+\bigg(d-\frac{\pi}{4}\bigg)\cos 2d+\frac{1}{2}\sin2d\bigg)\\&\quad= -\bigg(d-\frac{\pi}{4}\bigg)^2+\frac{\pi^2}{4^2}+\frac{1}{4}\sin^2 2d+ \frac{\pi}{4}\sin 2d\\&\quad=-\bigg(d-\frac{\pi}{4}\bigg)^2+\bigg( \frac{\pi}{4}+\frac{1}{2}\sin 2d\bigg)^2. \end{align*} $$
Notice that since
$d\in (0, {\pi }/{2})$
, then
$|d-{\pi }/{4}|<{\pi }/{4}$
and hence the last expression is strictly positive. This completes the proof of Lemma 4.2.
We are now in position to finish the proof of Theorem 4.1. Using Lemma 4.2, we can deduce from equation (17) with the help of equation (18),
$$ \begin{align} &2\int_{0}^{\pi}U \,d\psi\geq \int_{0}^{\pi}d^{\prime 2}(\sin 2d+3f)\,d\psi\geq\int_{0}^{\pi} \frac{3\pi}{2} d^{\prime 2}\,d\psi\nonumber\\ &\quad\geq \int_{0}^{\pi}\frac{3\pi}{2} \cos^2d\ d^{\prime 2}\,d\psi= \frac{3\pi}{2R^2} \int_{0}^{\pi} h^{\prime 2} \,d\psi, \end{align} $$
where we used
$h'=R\cos d\ d'$
of equation (14) in the last equality.
Now consider the isoperimetric defect
$P^2-4\pi A$
for the curve
$\gamma $
. We have the classical formulas:
$$ \begin{align*}P=\int_{0}^{2\pi} h \,d\psi,\quad A=\frac{1}{2}\int_{0}^{2\pi} (h^2-h^{\prime 2}) \,d\psi. \end{align*} $$
By Cauchy–Schwartz inequality, we have
$$ \begin{align*} P^2\leq 2\pi\int_{0}^{2\pi}h^2 \,d\psi=2\pi\bigg(2A+\int_{0}^{2\pi}h^{\prime 2} \,d\psi\bigg). \end{align*} $$
Hence, using equation (19), we get
$$ \begin{align*} P^2-4\pi A\leq 2\pi \int_{0}^{2\pi}h^{\prime 2} \,d\psi=4\pi \int_{0}^{\pi}h^{\prime 2} \,d\psi\leq \frac{16}{3}R^2\int_{0}^{\pi} U \,d\psi. \end{align*} $$
This completes the proof of Theorem 4.1.
5 Discussion
It is very natural to ask if one can reconstruct elliptic billiards by sharp inequalities containing the measures
$\mu (\Delta _{\mathcal {B}}),\mu (\mathcal {M}_{\mathcal {B}})$
(similarly to Theorem 1.1).
It would be very interesting to extend the ideas used in this paper to other Hamiltonian systems such as twist symplectic maps, as well as to continuous time systems.
An important goal in the study of Birkhoff billiards, as well as of general twist maps, in particular of standard-like maps, is to understand the dynamical behavior between two invariant curves. Our result can be considered as a step in this direction. It is not clear, however, how to approach this goal for arbitrary invariant curves and also how to remove the central-symmetry assumption.
Acknowledgements
MB was partially supported by ISF grant 580/20 and DFG grant MA-2565/7-1 within the Middle East Collaboration Program.
Open access
