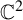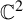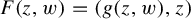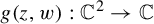Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saracco, Alberto
2022.
Dr. Strangelove: Or How I Learned to Stop Worrying and Love the Citations.
The Mathematical Intelligencer,
Vol. 44,
Issue. 4,
p.
326.
Beltrami, Veronica
Benini, Anna Miriam
and
Saracco, Alberto
2024.
Escaping Fatou components with disjoint hyperbolic limit sets.
Mathematische Zeitschrift,
Vol. 307,
Issue. 2,
Beltrami, Veronica
2025.
Automorphisms of ℂ2 with cycles of escaping Fatou components with hyperbolic limit sets.
International Journal of Mathematics,
Vol. 36,
Issue. 01,