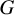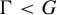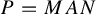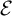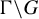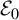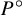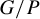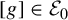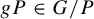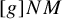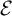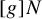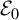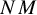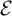1 Introduction
Let G be a connected semisimple real algebraic group. Let
![]() $(X, d)$
denote the associated Riemannian symmetric space. Let
$(X, d)$
denote the associated Riemannian symmetric space. Let
![]() $P=MAN$
be a minimal parabolic subgroup of G with fixed Langlands decomposition, where A is a maximal real split torus of G, M the maximal compact subgroup of P commuting with A, and N the unipotent radical of P. Note that N is a maximal horospherical subgroup of G, which is unique up to conjugations.
$P=MAN$
be a minimal parabolic subgroup of G with fixed Langlands decomposition, where A is a maximal real split torus of G, M the maximal compact subgroup of P commuting with A, and N the unipotent radical of P. Note that N is a maximal horospherical subgroup of G, which is unique up to conjugations.
Fix a positive Weyl chamber
![]() $\mathfrak a^+\subset \log A$
so that
$\mathfrak a^+\subset \log A$
so that
![]() $\log N$
consists of positive root subspaces, and we set
$\log N$
consists of positive root subspaces, and we set
![]() $A^+=\exp \mathfrak a^+$
. This means that N is a contracting horospherical subgroup in the sense that for any a in the interior of
$A^+=\exp \mathfrak a^+$
. This means that N is a contracting horospherical subgroup in the sense that for any a in the interior of
![]() $A^+$
,
$A^+$
,
Let
![]() $\Gamma $
be a Zariski dense discrete subgroup of G. In this paper, we are interested in the topological behavior of the action of the horospherical subgroup N on
$\Gamma $
be a Zariski dense discrete subgroup of G. In this paper, we are interested in the topological behavior of the action of the horospherical subgroup N on
![]() $\Gamma \backslash G$
via the right translations. When
$\Gamma \backslash G$
via the right translations. When
![]() $\Gamma <G$
is a cocompact lattice, every N-orbit is dense in
$\Gamma <G$
is a cocompact lattice, every N-orbit is dense in
![]() $\Gamma \backslash G$
, that is, the N-action on
$\Gamma \backslash G$
, that is, the N-action on
![]() $\Gamma \backslash G$
is minimal. This is due to Hedlund [Reference Hedlund11] for
$\Gamma \backslash G$
is minimal. This is due to Hedlund [Reference Hedlund11] for
![]() $G=\operatorname {PSL}_2(\mathbb R)$
and to Veech [Reference Veech19] in general. Dani gave a full classification of possible orbit closures of N-action for any lattice
$G=\operatorname {PSL}_2(\mathbb R)$
and to Veech [Reference Veech19] in general. Dani gave a full classification of possible orbit closures of N-action for any lattice
![]() $\Gamma <G$
[Reference Dani8].
$\Gamma <G$
[Reference Dani8].
For a general discrete subgroup
![]() $\Gamma <G$
, the quotient space
$\Gamma <G$
, the quotient space
![]() $\Gamma \backslash G$
does not necessarily admit a dense N-orbit, even a dense
$\Gamma \backslash G$
does not necessarily admit a dense N-orbit, even a dense
![]() $NM$
-orbit, for instance in the case where
$NM$
-orbit, for instance in the case where
![]() $\Gamma $
does not have a full limit set. Let
$\Gamma $
does not have a full limit set. Let
![]() $\mathcal F$
denote the Furstenberg boundary
$\mathcal F$
denote the Furstenberg boundary
![]() $G/P$
. We denote by
$G/P$
. We denote by
![]() $\Lambda =\Lambda _\Gamma $
the limit set of
$\Lambda =\Lambda _\Gamma $
the limit set of
![]() $\Gamma $
,
$\Gamma $
,
where
![]() $o\in X$
and the convergence is understood as in Definition 2.2. This definition is independent of the choice of
$o\in X$
and the convergence is understood as in Definition 2.2. This definition is independent of the choice of
![]() $o\in X$
. The limit set
$o\in X$
. The limit set
![]() $\Lambda $
is known to be the unique
$\Lambda $
is known to be the unique
![]() $\Gamma $
-minimal subset of
$\Gamma $
-minimal subset of
![]() $\mathcal F$
(see [Reference Benoist1, Reference Guivarc’h9, Reference Lee and Oh15]). Thus, the set
$\mathcal F$
(see [Reference Benoist1, Reference Guivarc’h9, Reference Lee and Oh15]). Thus, the set
is the unique P-minimal subset of
![]() $\Gamma \backslash G$
. For a given point
$\Gamma \backslash G$
. For a given point
![]() $[g]\in \mathcal E$
, the topological behavior of the horospherical orbit
$[g]\in \mathcal E$
, the topological behavior of the horospherical orbit
![]() $[g]N$
(or of
$[g]N$
(or of
![]() $[g]NM$
) is closely related to the ways in which the orbit
$[g]NM$
) is closely related to the ways in which the orbit
![]() $\Gamma (o)$
approaches
$\Gamma (o)$
approaches
![]() $gP$
along its limit cone. The limit cone
$gP$
along its limit cone. The limit cone
![]() $\mathcal L=\mathcal L_\Gamma $
of
$\mathcal L=\mathcal L_\Gamma $
of
![]() $\Gamma $
is defined as the smallest closed cone of
$\Gamma $
is defined as the smallest closed cone of
![]() $\mathfrak a^+$
containing the Jordan projection
$\mathfrak a^+$
containing the Jordan projection
![]() $\unicode{x3bb} (\Gamma )$
. It is a convex cone with non-empty interior:
$\unicode{x3bb} (\Gamma )$
. It is a convex cone with non-empty interior:
![]() $\operatorname {int} \mathcal L\ne \emptyset $
[Reference Benoist1]. If
$\operatorname {int} \mathcal L\ne \emptyset $
[Reference Benoist1]. If
![]() $\operatorname {rank } G=1$
, then
$\operatorname {rank } G=1$
, then
![]() $\mathcal L=\mathfrak a^+$
. In higher ranks, the limit cone of
$\mathcal L=\mathfrak a^+$
. In higher ranks, the limit cone of
![]() $\Gamma $
depends more subtly on
$\Gamma $
depends more subtly on
![]() $\Gamma $
.
$\Gamma $
.
1.1 Horospherical limit points
Recall that in the rank one case, a horoball in X based at
![]() $\xi \in \mathcal F$
is a subset of the form
$\xi \in \mathcal F$
is a subset of the form
![]() $gN (\exp \mathfrak a^+ )( o)$
, where
$gN (\exp \mathfrak a^+ )( o)$
, where
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $\xi =gP$
[Reference Dalbo5]. Our generalization to higher rank of the notion of a horospherical limit point involves the limit cone of
$\xi =gP$
[Reference Dalbo5]. Our generalization to higher rank of the notion of a horospherical limit point involves the limit cone of
![]() $\Gamma $
. By a
$\Gamma $
. By a
![]() $\Gamma $
-tight horoball based at
$\Gamma $
-tight horoball based at
![]() $\xi \in \mathcal F$
, we mean a subset of the form
$\xi \in \mathcal F$
, we mean a subset of the form
![]() $\mathcal H_{\xi }=g N (\exp \mathcal C) (o)$
, where
$\mathcal H_{\xi }=g N (\exp \mathcal C) (o)$
, where
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $\xi =gP$
and
$\xi =gP$
and
![]() $\mathcal C$
is a closed cone contained in
$\mathcal C$
is a closed cone contained in
![]() $\operatorname {int} \mathcal L\cup \{0\}$
. For
$\operatorname {int} \mathcal L\cup \{0\}$
. For
![]() $T>0$
, we write
$T>0$
, we write
where
![]() $\mathcal C_T=\{u\in \mathcal C: \|u\|<T\}$
for a Euclidean norm
$\mathcal C_T=\{u\in \mathcal C: \|u\|<T\}$
for a Euclidean norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathfrak a$
.
$\mathfrak a$
.
Definition 1.1. We call a limit point
![]() $\xi \in \Lambda $
a horospherical limit point of
$\xi \in \Lambda $
a horospherical limit point of
![]() $\Gamma $
if one of the following equivalent conditions holds:
$\Gamma $
if one of the following equivalent conditions holds:
-
• there exists a
 $\Gamma $
-tight horoball
$\Gamma $
-tight horoball
 $\mathcal H_\xi $
based at
$\mathcal H_\xi $
based at
 $\xi $
such that for any
$\xi $
such that for any
 $T>1$
,
$T>1$
,
 $\mathcal H_\xi (T)$
contains some point of
$\mathcal H_\xi (T)$
contains some point of
 $\Gamma (o)$
;
$\Gamma (o)$
; -
• there exist a closed cone
 $\mathcal C \subset {\operatorname {int} \mathcal L} \cup \{0\}$
and a sequence
$\mathcal C \subset {\operatorname {int} \mathcal L} \cup \{0\}$
and a sequence
 $ \gamma _j \in \Gamma $
satisfying that
$ \gamma _j \in \Gamma $
satisfying that
 $\beta _\xi (o,\gamma _jo) \in \mathcal C$
for all
$\beta _\xi (o,\gamma _jo) \in \mathcal C$
for all
 $j\ge 1$
and
$j\ge 1$
and
 $ \beta _\xi (o,\gamma _jo) \to \infty $
as
$ \beta _\xi (o,\gamma _jo) \to \infty $
as
 $j\to \infty $
, where
$j\to \infty $
, where
 $\beta $
denotes the
$\beta $
denotes the
 $\mathfrak a$
-valued Busemann map (Definition 2.3).
$\mathfrak a$
-valued Busemann map (Definition 2.3).
See Lemma 3.3 for the equivalence of the above two conditions. We denote by
the set of all horospherical limit points of
![]() $\Gamma $
. The attracting fixed point
$\Gamma $
. The attracting fixed point
![]() $y_\gamma $
of a loxodromic element
$y_\gamma $
of a loxodromic element
![]() $\gamma \in \Gamma $
whose Jordan projection
$\gamma \in \Gamma $
whose Jordan projection
![]() $\unicode{x3bb} (\gamma )$
belongs to
$\unicode{x3bb} (\gamma )$
belongs to
![]() $\operatorname {int} \mathcal L$
is always a horospherical limit point (Lemma 3.5). Moreover, for any
$\operatorname {int} \mathcal L$
is always a horospherical limit point (Lemma 3.5). Moreover, for any
![]() $u\in \operatorname {int} \mathcal L$
, any u-directional radial limit point
$u\in \operatorname {int} \mathcal L$
, any u-directional radial limit point
![]() $\xi $
(i.e.
$\xi $
(i.e.
![]() $\xi =gP$
for some
$\xi =gP$
for some
![]() $g\in G$
such that
$g\in G$
such that
![]() $\limsup _{t\to \infty } \Gamma g \exp (tu)\ne \emptyset $
) is also a horospherical limit point (Lemma 5.3).
$\limsup _{t\to \infty } \Gamma g \exp (tu)\ne \emptyset $
) is also a horospherical limit point (Lemma 5.3).
Remarks 1.2
-
(1) There exists a notion of horospherical limit points in the geometric boundary associated to a symmetric space, see [Reference Hattori10]. When
 $\operatorname {rank }G \geq 2 $
, this notion and the one considered here are different.
$\operatorname {rank }G \geq 2 $
, this notion and the one considered here are different. -
(2) Unlike the rank one case, a sequence
 $\gamma _i(o)\in \mathcal H_{\xi }(T_i)$
, with
$\gamma _i(o)\in \mathcal H_{\xi }(T_i)$
, with
 $T_i\to \infty $
, does not necessarily converge to
$T_i\to \infty $
, does not necessarily converge to
 $\xi $
for a
$\xi $
for a
 $\Gamma $
-tight horoball
$\Gamma $
-tight horoball
 $\mathcal H_\xi $
based at
$\mathcal H_\xi $
based at
 $\xi $
. It is hence plausible that a general discrete group
$\xi $
. It is hence plausible that a general discrete group
 $ \Gamma $
would support a horospherical limit point outside of its limit set.
$ \Gamma $
would support a horospherical limit point outside of its limit set.
1.2 Denseness of horospheres
The following theorem generalizes Dal’bo’s theorem [Reference Dalbo5] to discrete subgroups in higher rank semisimple Lie groups.
Theorem 1.3. Let
![]() $\Gamma <G$
be a Zariski dense discrete subgroup. For any
$\Gamma <G$
be a Zariski dense discrete subgroup. For any
![]() $[g]\in \mathcal E$
, the following are equivalent:
$[g]\in \mathcal E$
, the following are equivalent:
-
(1)
 $gP\in \Lambda _h$
;
$gP\in \Lambda _h$
; -
(2)
 $[g] NM$
is dense in
$[g] NM$
is dense in
 $\mathcal E$
.
$\mathcal E$
.
Remarks 1.4. Conze and Guivarc’h considered the notion of a horospherical limit point for Zariski dense discrete subgroups
![]() $\Gamma $
of
$\Gamma $
of
![]() $\operatorname {SL}_d(\mathbb R)$
using the description of
$\operatorname {SL}_d(\mathbb R)$
using the description of
![]() $\operatorname {SL}_d(\mathbb R)/P$
as the full flag variety and the standard linear action of
$\operatorname {SL}_d(\mathbb R)/P$
as the full flag variety and the standard linear action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbb R^d$
[Reference Conze, Guivarc’h, Burger and Iozzi4]. By duality, this notion coincides with ours and hence the special case of Theorem 1.3 for
$\mathbb R^d$
[Reference Conze, Guivarc’h, Burger and Iozzi4]. By duality, this notion coincides with ours and hence the special case of Theorem 1.3 for
![]() $G=\operatorname {SL}_d(\mathbb R)$
also follows from [Reference Conze, Guivarc’h, Burger and Iozzi4, Theorem 4.2]. (However the claim in [Reference Conze, Guivarc’h, Burger and Iozzi4, Theorem 6.3] is incorrect.)
$G=\operatorname {SL}_d(\mathbb R)$
also follows from [Reference Conze, Guivarc’h, Burger and Iozzi4, Theorem 4.2]. (However the claim in [Reference Conze, Guivarc’h, Burger and Iozzi4, Theorem 6.3] is incorrect.)
To extend Theorem 1.3 to N-orbits, we fix a
![]() $P^\circ $
-minimal subset
$P^\circ $
-minimal subset
![]() $\mathcal E_0$
of
$\mathcal E_0$
of
![]() $\Gamma \backslash G$
, where
$\Gamma \backslash G$
, where
![]() $P^\circ $
denotes the identity component of P. Clearly,
$P^\circ $
denotes the identity component of P. Clearly,
![]() $\mathcal E_0\subset \mathcal E$
. Since
$\mathcal E_0\subset \mathcal E$
. Since
![]() $P=P^\circ M$
, any
$P=P^\circ M$
, any
![]() $P^\circ $
-minimal subset is a translate of
$P^\circ $
-minimal subset is a translate of
![]() $\mathcal E_0$
by an element of the finite group
$\mathcal E_0$
by an element of the finite group
![]() $M^\circ \backslash M$
, where
$M^\circ \backslash M$
, where
![]() $ M^\circ $
is the identity component of
$ M^\circ $
is the identity component of
![]() $ M $
. Denote by
$ M $
. Denote by
![]() $ \mathfrak D_\Gamma = \{\mathcal E_0,\ldots , \mathcal E_p\} $
the finite collection of all
$ \mathfrak D_\Gamma = \{\mathcal E_0,\ldots , \mathcal E_p\} $
the finite collection of all
![]() $ P^\circ $
-minimal sets in
$ P^\circ $
-minimal sets in
![]() $ \mathcal E $
. To understand N-orbit closures, it is hence sufficient to restrict to
$ \mathcal E $
. To understand N-orbit closures, it is hence sufficient to restrict to
![]() $\mathcal E_0$
.
$\mathcal E_0$
.
The following is a refinement of Theorem 1.3.
Theorem 1.5. Let
![]() $\Gamma <G$
be a Zariski dense discrete subgroup. For any
$\Gamma <G$
be a Zariski dense discrete subgroup. For any
![]() $[g]\in \mathcal E_0$
, the following are equivalent:
$[g]\in \mathcal E_0$
, the following are equivalent:
-
(1)
 $gP\in \Lambda _h$
;
$gP\in \Lambda _h$
; -
(2)
 $[g] N$
is dense in
$[g] N$
is dense in
 $\mathcal E_0$
.
$\mathcal E_0$
.
Remark 1.6. We may consider horospherical limit points outside the context of
![]() $\Lambda $
. In this case, our proofs of Theorems 1.3 and 1.5 show that if
$\Lambda $
. In this case, our proofs of Theorems 1.3 and 1.5 show that if
![]() $gP\in \mathcal F$
is a horospherical limit point, then the closures of
$gP\in \mathcal F$
is a horospherical limit point, then the closures of
![]() $[g]MN$
and
$[g]MN$
and
![]() $[g]N$
contain
$[g]N$
contain
![]() $\mathcal E$
and
$\mathcal E$
and
![]() $\mathcal E_i $
for some
$\mathcal E_i $
for some
![]() $ \mathcal E_i \in \mathfrak D_\Gamma $
, respectively.
$ \mathcal E_i \in \mathfrak D_\Gamma $
, respectively.
For
![]() $G=\operatorname {SO}^\circ ({n,1})$
,
$G=\operatorname {SO}^\circ ({n,1})$
,
![]() $n\ge 2$
, Theorem 1.5 was proved in [Reference Maucourant and Schapira16]. When G has rank one and
$n\ge 2$
, Theorem 1.5 was proved in [Reference Maucourant and Schapira16]. When G has rank one and
![]() $\Gamma <G$
is convex cocompact, every limit point is horospherical and Winter’s mixing theorem [Reference Winter20] implies the N-minimality of
$\Gamma <G$
is convex cocompact, every limit point is horospherical and Winter’s mixing theorem [Reference Winter20] implies the N-minimality of
![]() $\mathcal E_0$
.
$\mathcal E_0$
.
1.3 Directional horospherical limit points
We also consider the following seemingly much stronger notion.
Definition 1.7. For
![]() $u\in \mathfrak a^+$
, a point
$u\in \mathfrak a^+$
, a point
![]() $ \xi \in \mathcal F$
is called
$ \xi \in \mathcal F$
is called
![]() $ u $
-horospherical if there exists a sequence
$ u $
-horospherical if there exists a sequence
![]() $ \gamma _j \in \Gamma $
such that
$ \gamma _j \in \Gamma $
such that
![]() $\sup _j \| \beta _\xi (o,\gamma _jo)- \mathbb R_+ u\|<\infty $
and
$\sup _j \| \beta _\xi (o,\gamma _jo)- \mathbb R_+ u\|<\infty $
and
![]() $ \beta _\xi (o,\gamma _jo)\to \infty $
as
$ \beta _\xi (o,\gamma _jo)\to \infty $
as
![]() $j\to ~\infty $
.
$j\to ~\infty $
.
Denote by
![]() $ \Lambda _h(u) $
the set of
$ \Lambda _h(u) $
the set of
![]() $ u $
-horospherical limit points. Surprisingly, it turns out that every horospherical limit point is u-horospherical for all
$ u $
-horospherical limit points. Surprisingly, it turns out that every horospherical limit point is u-horospherical for all
![]() $u\in \operatorname {int}\mathcal L$
.
$u\in \operatorname {int}\mathcal L$
.
Theorem 1.8. For all
![]() $u\in \operatorname {int} \mathcal L$
, we have
$u\in \operatorname {int} \mathcal L$
, we have
1.4 Existence of non-dense horospheres
A finitely generated subgroup
![]() $\Gamma <G$
is called an Anosov subgroup (with respect to P) if there exists
$\Gamma <G$
is called an Anosov subgroup (with respect to P) if there exists
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
![]() $\alpha (\mu (\gamma ))\ge C|\gamma | -C$
for all simple roots
$\alpha (\mu (\gamma ))\ge C|\gamma | -C$
for all simple roots
![]() $\alpha $
of
$\alpha $
of
![]() $(\mathfrak g, \mathfrak a^+)$
, where
$(\mathfrak g, \mathfrak a^+)$
, where
![]() $\mu (\gamma )\in \mathfrak a^+$
denotes the Cartan projection of
$\mu (\gamma )\in \mathfrak a^+$
denotes the Cartan projection of
![]() $\gamma $
and
$\gamma $
and
![]() $|\gamma |$
is the word length of
$|\gamma |$
is the word length of
![]() $\gamma $
with respect to a fixed finite generating set of
$\gamma $
with respect to a fixed finite generating set of
![]() $\Gamma $
.
$\Gamma $
.
For Zariski dense Anosov subgroups of G, almost all
![]() $NM$
-orbits are dense in
$NM$
-orbits are dense in
![]() $\mathcal E$
and almost all N-orbits are dense in
$\mathcal E$
and almost all N-orbits are dense in
![]() $\mathcal E_0$
with respect to any Patterson–Sullivan measure on
$\mathcal E_0$
with respect to any Patterson–Sullivan measure on
![]() $\Lambda $
[Reference Lee and Oh15, Reference Lee and Oh14]. In particular, the set of all horospherical limit points has full Patterson–Sullivan measures.
$\Lambda $
[Reference Lee and Oh15, Reference Lee and Oh14]. In particular, the set of all horospherical limit points has full Patterson–Sullivan measures.
However, as Anosov subgroups are regarded as higher rank generalizations of convex cocompact subgroups, it is a natural question whether the minimality of the
![]() $NM$
-action persists in the higher rank setting. It turns out that it is not the case. Our example is based on Thurston’s theorem [Reference Thurston18, Theorem 10.7] together with the following observation on the implication of the existence of a Jordan projection of an element of
$NM$
-action persists in the higher rank setting. It turns out that it is not the case. Our example is based on Thurston’s theorem [Reference Thurston18, Theorem 10.7] together with the following observation on the implication of the existence of a Jordan projection of an element of
![]() $\Gamma $
lying in the boundary
$\Gamma $
lying in the boundary
![]() $\partial \mathcal L$
of the limit cone.
$\partial \mathcal L$
of the limit cone.
Proposition 1.9. Let
![]() $\Gamma <G$
be a Zariski dense discrete subgroup. For any loxodromic element
$\Gamma <G$
be a Zariski dense discrete subgroup. For any loxodromic element
![]() $\gamma \in \Gamma $
, we have
$\gamma \in \Gamma $
, we have
where
![]() $y_\gamma $
and
$y_\gamma $
and
![]() $y_{\gamma ^{-1}}$
denote the attracting fixed points of
$y_{\gamma ^{-1}}$
denote the attracting fixed points of
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^{-1}$
, respectively.
$\gamma ^{-1}$
, respectively.
In particular, if
![]() $\unicode{x3bb} (\Gamma )\cap \partial \mathcal L\ne \emptyset $
, then
$\unicode{x3bb} (\Gamma )\cap \partial \mathcal L\ne \emptyset $
, then
![]() $\Lambda \ne \Lambda _h$
and hence there exists a non-dense
$\Lambda \ne \Lambda _h$
and hence there exists a non-dense
![]() $NM$
-orbit in
$NM$
-orbit in
![]() $\mathcal E$
.
$\mathcal E$
.
Thurston’s work [Reference Thurston18] provides many examples of Anosov subgroups satisfying that
![]() $\unicode{x3bb} (\Gamma )\cap \partial \mathcal L\ne \emptyset $
. To describe them, let
$\unicode{x3bb} (\Gamma )\cap \partial \mathcal L\ne \emptyset $
. To describe them, let
![]() $\Sigma $
be a a torsion-free cocompact lattice of
$\Sigma $
be a a torsion-free cocompact lattice of
![]() $\operatorname {PSL}_2(\mathbb R)$
and let
$\operatorname {PSL}_2(\mathbb R)$
and let
![]() $\pi \kern1.3pt{:}\kern1.3pt\Sigma \kern1.3pt{\to}\kern1.3pt \operatorname {PSL}_2(\mathbb R)$
be a discrete faithful representation. Let
$\pi \kern1.3pt{:}\kern1.3pt\Sigma \kern1.3pt{\to}\kern1.3pt \operatorname {PSL}_2(\mathbb R)$
be a discrete faithful representation. Let
![]() ${0\kern1.3pt{<}\kern1.3pt d_-(\pi ) \kern1.3pt{\le}\kern1.3pt d_+ (\pi ) \kern1.3pt{<}\kern1.3pt\infty }$
be the minimal and maximal geodesic stretching constants:
${0\kern1.3pt{<}\kern1.3pt d_-(\pi ) \kern1.3pt{\le}\kern1.3pt d_+ (\pi ) \kern1.3pt{<}\kern1.3pt\infty }$
be the minimal and maximal geodesic stretching constants:
 $$ \begin{align} d_+(\pi) =\sup_{\sigma\in \Sigma-\{e\} }\frac {\ell(\pi(\sigma))}{\ell(\sigma)} \quad \text{and} \quad d_-(\pi) =\inf_{\sigma\in \Sigma-\{e\}}\frac{\ell(\pi(\sigma))}{\ell(\sigma)}, \end{align} $$
$$ \begin{align} d_+(\pi) =\sup_{\sigma\in \Sigma-\{e\} }\frac {\ell(\pi(\sigma))}{\ell(\sigma)} \quad \text{and} \quad d_-(\pi) =\inf_{\sigma\in \Sigma-\{e\}}\frac{\ell(\pi(\sigma))}{\ell(\sigma)}, \end{align} $$
where
![]() $\ell (\sigma )$
denotes the length of the closed geodesic in the hyperbolic manifold
$\ell (\sigma )$
denotes the length of the closed geodesic in the hyperbolic manifold
![]() $\Sigma \backslash \mathbb H^2$
corresponding to
$\Sigma \backslash \mathbb H^2$
corresponding to
![]() $\sigma $
and
$\sigma $
and
![]() $\ell (\pi (\sigma ))$
is defined similarly.
$\ell (\pi (\sigma ))$
is defined similarly.
Consider the following self-joining subgroup:
It is easy to see that
![]() $\Gamma $
is an Anosov subgroup of
$\Gamma $
is an Anosov subgroup of
![]() $G=\operatorname {PSL}_2(\mathbb R) \times \operatorname {PSL}_2(\mathbb R)$
. Moreover, when
$G=\operatorname {PSL}_2(\mathbb R) \times \operatorname {PSL}_2(\mathbb R)$
. Moreover, when
![]() $\pi $
is not a conjugate by a Möbius tranformation,
$\pi $
is not a conjugate by a Möbius tranformation,
![]() $\Gamma _\pi $
is Zariski dense in G (cf. [Reference Kim and Oh12, Lemma 4.1]). Identifying
$\Gamma _\pi $
is Zariski dense in G (cf. [Reference Kim and Oh12, Lemma 4.1]). Identifying
![]() $\mathfrak a=\mathbb R^2$
, the Jordan projection
$\mathfrak a=\mathbb R^2$
, the Jordan projection
![]() $\unicode{x3bb} (\gamma _\pi )$
of
$\unicode{x3bb} (\gamma _\pi )$
of
![]() $\gamma _\pi =(\sigma , \pi (\sigma ))\in \Gamma _\pi $
is given by
$\gamma _\pi =(\sigma , \pi (\sigma ))\in \Gamma _\pi $
is given by
![]() $(\ell (\sigma ), \ell (\pi (\sigma )))\in \mathbb R^2$
. Hence, the limit cone
$(\ell (\sigma ), \ell (\pi (\sigma )))\in \mathbb R^2$
. Hence, the limit cone
![]() $\mathcal L$
of
$\mathcal L$
of
![]() $\Gamma _\pi $
is given by
$\Gamma _\pi $
is given by
Thurston [Reference Thurston18, Theorem 10.7] showed that
![]() $d_+(\pi )$
is realized by a simple closed geodesic of
$d_+(\pi )$
is realized by a simple closed geodesic of
![]() $\Sigma \backslash \mathbb H^2$
in most of the cases, which hence provides infinitely many examples of
$\Sigma \backslash \mathbb H^2$
in most of the cases, which hence provides infinitely many examples of
![]() $\Gamma _\pi $
which satisfy
$\Gamma _\pi $
which satisfy
![]() $\unicode{x3bb} (\Gamma _\pi )\cap \partial \mathcal L\ne \emptyset $
. Therefore, Proposition 1.9 implies (in this case, we have
$\unicode{x3bb} (\Gamma _\pi )\cap \partial \mathcal L\ne \emptyset $
. Therefore, Proposition 1.9 implies (in this case, we have
![]() $NM=N)$
the following corollary.
$NM=N)$
the following corollary.
Corollary 1.10. There are infinitely many non-conjuagte Zariski dense Anosov subgroups
![]() $\Gamma _{\pi }<\operatorname {PSL}_2(\mathbb R) \times \operatorname {PSL}_2(\mathbb R)$
with non-dense
$\Gamma _{\pi }<\operatorname {PSL}_2(\mathbb R) \times \operatorname {PSL}_2(\mathbb R)$
with non-dense
![]() $NM$
-orbits in
$NM$
-orbits in
![]() $\mathcal E$
.
$\mathcal E$
.
We close the introduction by the following question (cf. [Reference Kim13, Reference Quint17]).
Question 1.11. For a simple real algebraic group G with
![]() $\operatorname {rank} G\ge 2$
, is every discrete subgroup
$\operatorname {rank} G\ge 2$
, is every discrete subgroup
![]() $\Gamma <G$
with
$\Gamma <G$
with
![]() $\Lambda =\Lambda _h=\mathcal F$
necessarily a cocompact lattice in G?
$\Lambda =\Lambda _h=\mathcal F$
necessarily a cocompact lattice in G?
2 Preliminaries
Let G be a connected, semisimple real algebraic group. We fix, once and for all, a Cartan involution
![]() $\theta $
of the Lie algebra
$\theta $
of the Lie algebra
![]() $\mathfrak {g}$
of G, and decompose
$\mathfrak {g}$
of G, and decompose
![]() $\mathfrak {g}$
as
$\mathfrak {g}$
as
![]() $\mathfrak g=\mathfrak k\oplus \mathfrak {p}$
, where
$\mathfrak g=\mathfrak k\oplus \mathfrak {p}$
, where
![]() $\mathfrak {k}$
and
$\mathfrak {k}$
and
![]() $\mathfrak {p}$
are the
$\mathfrak {p}$
are the
![]() $+ 1$
and
$+ 1$
and
![]() $-1$
eigenspaces of
$-1$
eigenspaces of
![]() $\theta $
, respectively. We denote by K the maximal compact subgroup of G with Lie algebra
$\theta $
, respectively. We denote by K the maximal compact subgroup of G with Lie algebra
![]() $\mathfrak {k}$
.
$\mathfrak {k}$
.
Choose a maximal abelian subalgebra
![]() $\mathfrak a$
of
$\mathfrak a$
of
![]() $\mathfrak p$
. Choosing a closed positive Weyl chamber
$\mathfrak p$
. Choosing a closed positive Weyl chamber
![]() $\mathfrak a^+$
of
$\mathfrak a^+$
of
![]() $\mathfrak a$
, let
$\mathfrak a$
, let
![]() $A:=\exp \mathfrak a$
and
$A:=\exp \mathfrak a$
and
![]() $A^+=\exp \mathfrak a^+$
. The centralizer of A in K is denoted by M, and we set N to be the maximal contracting horospherical subgroup: for
$A^+=\exp \mathfrak a^+$
. The centralizer of A in K is denoted by M, and we set N to be the maximal contracting horospherical subgroup: for
![]() $a\in \operatorname {int} A^+$
,
$a\in \operatorname {int} A^+$
,
We set
![]() $P=MAN$
, which is the unique minimal parabolic subgroup of G, up to conjugation.
$P=MAN$
, which is the unique minimal parabolic subgroup of G, up to conjugation.
For
![]() $u\in \mathfrak a$
, we write
$u\in \mathfrak a$
, we write
![]() $a_u=\exp u\in A$
. We denote by
$a_u=\exp u\in A$
. We denote by
![]() $\|\cdot \|$
the norm on
$\|\cdot \|$
the norm on
![]() $\mathfrak g$
induced by the Killing form. Consider the Riemannian symmetric space
$\mathfrak g$
induced by the Killing form. Consider the Riemannian symmetric space
![]() $X:=G/K$
with the metric induced from the norm
$X:=G/K$
with the metric induced from the norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathfrak g$
and
$\mathfrak g$
and
![]() $o=K\in X$
.
$o=K\in X$
.
Let
![]() $\mathcal {F}=G/P$
denote the Furstenberg boundary. Since K acts transitively on
$\mathcal {F}=G/P$
denote the Furstenberg boundary. Since K acts transitively on
![]() $ \mathcal {F} $
and
$ \mathcal {F} $
and
![]() $K\cap P=M$
, we may identify
$K\cap P=M$
, we may identify
![]() $\mathcal {F}=K/M$
. We denote by
$\mathcal {F}=K/M$
. We denote by
![]() $\mathcal F^{(2)}$
the unique open G-orbit in
$\mathcal F^{(2)}$
the unique open G-orbit in
![]() $\mathcal {F} \times \mathcal {F}$
.
$\mathcal {F} \times \mathcal {F}$
.
Denote by
![]() $w_0\in K$
the unique element in the Weyl group such that
$w_0\in K$
the unique element in the Weyl group such that
![]() $\operatorname {Ad}_{w_0}\mathfrak a^+= -\mathfrak a^+$
; it is the longest Weyl element. We then have
$\operatorname {Ad}_{w_0}\mathfrak a^+= -\mathfrak a^+$
; it is the longest Weyl element. We then have
![]() $\check {P}:=w_0 P w_0^{-1}$
is an opposite parabolic subgroup of G, with
$\check {P}:=w_0 P w_0^{-1}$
is an opposite parabolic subgroup of G, with
![]() $ \check {N} $
its unipotent radical. The map
$ \check {N} $
its unipotent radical. The map
![]() $\operatorname {i}=-\operatorname {Ad}_{w_0}: \mathfrak a^+\to \mathfrak a^+$
is called the opposition involution.
$\operatorname {i}=-\operatorname {Ad}_{w_0}: \mathfrak a^+\to \mathfrak a^+$
is called the opposition involution.
For
![]() $g\in G$
, we consider the following visual maps:
$g\in G$
, we consider the following visual maps:
Then
![]() $\mathcal F^{(2)}=\{(g^+, g^-)\in \mathcal F\times \mathcal F: g\in G\}$
.
$\mathcal F^{(2)}=\{(g^+, g^-)\in \mathcal F\times \mathcal F: g\in G\}$
.
Any element
![]() $ g \in G $
can be uniquely decomposed as the commuting product
$ g \in G $
can be uniquely decomposed as the commuting product
![]() $ g_h,g_e,g_u $
, where
$ g_h,g_e,g_u $
, where
![]() $ g_h $
,
$ g_h $
,
![]() $ g_e $
, and
$ g_e $
, and
![]() $ g_u $
are hyperbolic, elliptic, and unipotent elements, respectively. The Jordan projection of g is defined as the element
$ g_u $
are hyperbolic, elliptic, and unipotent elements, respectively. The Jordan projection of g is defined as the element
![]() $\unicode{x3bb} (g) \in \mathfrak a^+ $
satisfying
$\unicode{x3bb} (g) \in \mathfrak a^+ $
satisfying
![]() $ g_h= \varphi \exp \unicode{x3bb} (g) \varphi ^{-1} $
for some
$ g_h= \varphi \exp \unicode{x3bb} (g) \varphi ^{-1} $
for some
![]() $\varphi \in G$
.
$\varphi \in G$
.
An element
![]() $g\in G$
is called loxodromic if
$g\in G$
is called loxodromic if
![]() $ \unicode{x3bb} (g) \in \operatorname {int} \mathfrak a^+ $
; in this case,
$ \unicode{x3bb} (g) \in \operatorname {int} \mathfrak a^+ $
; in this case,
![]() $g_u$
is necessarily trivial. For a loxodromic element
$g_u$
is necessarily trivial. For a loxodromic element
![]() $g\in G$
, the point
$g\in G$
, the point
![]() $\varphi ^+ \in \mathcal {F}$
is called the attracting fixed point of g, which we denote by
$\varphi ^+ \in \mathcal {F}$
is called the attracting fixed point of g, which we denote by
![]() $y_g$
. For any loxodromic element
$y_g$
. For any loxodromic element
![]() $g\in G$
and
$g\in G$
and
![]() $\xi \in \mathcal F$
with
$\xi \in \mathcal F$
with
![]() $(\xi , y_{g^{-1}})\in \mathcal F^{(2)}$
, we have
$(\xi , y_{g^{-1}})\in \mathcal F^{(2)}$
, we have
![]() $\lim _{k\to \infty } g^k \xi = y_{g}$
and the convergence is uniform on compact subsets.
$\lim _{k\to \infty } g^k \xi = y_{g}$
and the convergence is uniform on compact subsets.
Note that for any loxodromic element
![]() $g\in G$
,
$g\in G$
,
Let
![]() $\Gamma <G$
be a Zariski dense discrete subgroup of G. The limit cone
$\Gamma <G$
be a Zariski dense discrete subgroup of G. The limit cone
![]() $\mathcal L=\mathcal L_\Gamma $
of
$\mathcal L=\mathcal L_\Gamma $
of
![]() $\Gamma $
is the smallest closed cone of
$\Gamma $
is the smallest closed cone of
![]() $\mathfrak a^+$
containing
$\mathfrak a^+$
containing
![]() $\unicode{x3bb} (\Gamma )$
. It is a convex cone with non-empty interior [Reference Benoist1].
$\unicode{x3bb} (\Gamma )$
. It is a convex cone with non-empty interior [Reference Benoist1].
We will use the following simple lemma.
Lemma 2.1. For any
![]() $ v \in \unicode{x3bb} (\Gamma ) $
and
$ v \in \unicode{x3bb} (\Gamma ) $
and
![]() $ \zeta \in \mathcal {F} $
, there exists a loxodromic element
$ \zeta \in \mathcal {F} $
, there exists a loxodromic element
![]() $ \gamma \in \Gamma $
with
$ \gamma \in \Gamma $
with
![]() $ \unicode{x3bb} (\gamma )=v $
and a neighborhood
$ \unicode{x3bb} (\gamma )=v $
and a neighborhood
![]() $ U $
of
$ U $
of
![]() $ \zeta $
in
$ \zeta $
in
![]() $ \mathcal {F} $
such that
$ \mathcal {F} $
such that
![]() $ \{y_\gamma \}\times U $
is a relatively compact subset of
$ \{y_\gamma \}\times U $
is a relatively compact subset of
![]() $\mathcal {F}^{(2)} $
and as
$\mathcal {F}^{(2)} $
and as
![]() $k\to \infty $
,
$k\to \infty $
,
Proof. Let
![]() $\zeta \in \mathcal F$
. Choose
$\zeta \in \mathcal F$
. Choose
![]() $\gamma _1\in \Gamma $
such that
$\gamma _1\in \Gamma $
such that
![]() $\unicode{x3bb} (\gamma _1)=v$
. Since the set of all loxodromic elements of
$\unicode{x3bb} (\gamma _1)=v$
. Since the set of all loxodromic elements of
![]() $\Gamma $
is Zariski dense in G [Reference Benoist, Kobayashi, Kashiwara, Matsuki, Nishiyama and Oshima2] and
$\Gamma $
is Zariski dense in G [Reference Benoist, Kobayashi, Kashiwara, Matsuki, Nishiyama and Oshima2] and
![]() $\mathcal F^{(2)}$
is Zariski open in
$\mathcal F^{(2)}$
is Zariski open in
![]() $\mathcal F\times \mathcal F$
, there exists
$\mathcal F\times \mathcal F$
, there exists
![]() $\gamma _2\in \Gamma $
such that
$\gamma _2\in \Gamma $
such that
![]() $(\zeta , \gamma _2 y_{\gamma _1})\in \mathcal F^{(2)}$
. Let
$(\zeta , \gamma _2 y_{\gamma _1})\in \mathcal F^{(2)}$
. Let
![]() $\gamma =\gamma _2 \gamma _1\gamma _2^{-1}$
, so that
$\gamma =\gamma _2 \gamma _1\gamma _2^{-1}$
, so that
![]() $y_{\gamma }=\gamma _2y_{\gamma _1}$
. It now suffices to take any neighborhood U of
$y_{\gamma }=\gamma _2y_{\gamma _1}$
. It now suffices to take any neighborhood U of
![]() $\zeta $
such that
$\zeta $
such that
![]() $U\times \{ \gamma _2y_{\gamma _1}\}$
is a relatively compact subset of
$U\times \{ \gamma _2y_{\gamma _1}\}$
is a relatively compact subset of
![]() $\mathcal F^{(2)}$
.
$\mathcal F^{(2)}$
.
2.1 Convergence of a sequence in X to
 $\mathcal F$
$\mathcal F$
By the Cartan decomposition
![]() $G=KA^+K$
, for
$G=KA^+K$
, for
![]() $g\in G$
, we may write
$g\in G$
, we may write
where
![]() $\mu (g)\in \mathfrak a^+$
, called the Cartan projection of g, is uniquely determined, and
$\mu (g)\in \mathfrak a^+$
, called the Cartan projection of g, is uniquely determined, and
![]() $\kappa _1(g), \kappa _2(g)\in K$
. If
$\kappa _1(g), \kappa _2(g)\in K$
. If
![]() $\mu (g)\in \operatorname {int} \mathfrak a^+$
, then
$\mu (g)\in \operatorname {int} \mathfrak a^+$
, then
![]() $[\kappa _1(g)]\in K/M=\mathcal F$
is uniquely determined.
$[\kappa _1(g)]\in K/M=\mathcal F$
is uniquely determined.
Let
![]() $\Pi $
be the set of simple roots for
$\Pi $
be the set of simple roots for
![]() $(\mathfrak g, \mathfrak a)$
. For a sequence
$(\mathfrak g, \mathfrak a)$
. For a sequence
![]() $g_i\to G$
, we say
$g_i\to G$
, we say
![]() $g_i\to \infty $
regularly if
$g_i\to \infty $
regularly if
![]() $\alpha (\mu (g_i))\to \infty $
for all
$\alpha (\mu (g_i))\to \infty $
for all
![]() $\alpha \in \Pi $
. Note that if
$\alpha \in \Pi $
. Note that if
![]() $g_i\to \infty $
regularly, then for all sufficiently large i,
$g_i\to \infty $
regularly, then for all sufficiently large i,
![]() $\mu (g_i)\in \operatorname {int}\mathfrak a^+$
and hence
$\mu (g_i)\in \operatorname {int}\mathfrak a^+$
and hence
![]() $[\kappa _1(g_i)]$
is well defined.
$[\kappa _1(g_i)]$
is well defined.
Definition 2.2. A sequence
![]() $p_i \in X$
is said to converge to
$p_i \in X$
is said to converge to
![]() $\xi \in \mathcal F$
if there exists
$\xi \in \mathcal F$
if there exists
![]() $g_i\to \infty $
regularly in G with
$g_i\to \infty $
regularly in G with
![]() $p_i=g_i(o)$
and
$p_i=g_i(o)$
and
![]() $\lim _{i\to \infty }[\kappa _1(g_i)]=\xi $
.
$\lim _{i\to \infty }[\kappa _1(g_i)]=\xi $
.
2.2
 $P^\circ $
-minimal subsets
$P^\circ $
-minimal subsets
We denote by
![]() $\Lambda \subset \mathcal F$
the limit set of
$\Lambda \subset \mathcal F$
the limit set of
![]() $\Gamma $
, which is defined as
$\Gamma $
, which is defined as
For a non-Zariski dense subgroup,
![]() $\Lambda $
may be an empty set. For
$\Lambda $
may be an empty set. For
![]() $\Gamma <G$
Zariski dense, this is the unique
$\Gamma <G$
Zariski dense, this is the unique
![]() $\Gamma $
-minimal subset of
$\Gamma $
-minimal subset of
![]() $\mathcal F$
[Reference Benoist1, Reference Lee and Oh15].
$\mathcal F$
[Reference Benoist1, Reference Lee and Oh15].
It follows that the following set
![]() $\mathcal E$
is the unique P-minimal subset of
$\mathcal E$
is the unique P-minimal subset of
![]() $\Gamma \backslash G$
:
$\Gamma \backslash G$
:
Let
![]() $P^\circ $
denote the identity component of P. Then
$P^\circ $
denote the identity component of P. Then
![]() $\mathcal E$
is a disjoint union of at most
$\mathcal E$
is a disjoint union of at most
![]() $[P: P^{\circ }]$
-number of
$[P: P^{\circ }]$
-number of
![]() $P^\circ $
-minimal subsets. We fix one
$P^\circ $
-minimal subsets. We fix one
![]() $P^{\circ }$
-minimal subset
$P^{\circ }$
-minimal subset
![]() $\mathcal E_0$
once and for all. Note that any
$\mathcal E_0$
once and for all. Note that any
![]() $P^{\circ }$
-minimal subset is then of the form
$P^{\circ }$
-minimal subset is then of the form
![]() $\mathcal E_0 m$
for some
$\mathcal E_0 m$
for some
![]() $m\in M$
. We set
$m\in M$
. We set
2.3 Busemann map
The Iwasawa cocycle
![]() $\sigma : G\times \mathcal {F} \to \mathfrak a$
is defined as follows: for
$\sigma : G\times \mathcal {F} \to \mathfrak a$
is defined as follows: for
![]() $(g, \xi )\in G\times \mathcal {F} $
with
$(g, \xi )\in G\times \mathcal {F} $
with
![]() $\xi =[k]$
for
$\xi =[k]$
for
![]() $k\in K$
,
$k\in K$
,
![]() $\exp \sigma (g,\xi )$
is the A-component of
$\exp \sigma (g,\xi )$
is the A-component of
![]() $g k$
in the
$g k$
in the
![]() $KAN$
decomposition, that is,
$KAN$
decomposition, that is,
The
![]() $\mathfrak a$
-valued Busemann function
$\mathfrak a$
-valued Busemann function
![]() $\beta : \mathcal {F} \times X \times X \to \mathfrak a $
is defined as follows: for
$\beta : \mathcal {F} \times X \times X \to \mathfrak a $
is defined as follows: for
![]() $\xi \in \mathcal {F} $
and
$\xi \in \mathcal {F} $
and
![]() $g, h\in G$
,
$g, h\in G$
,
We note that for any
![]() $g\in G$
,
$g\in G$
,
![]() $\xi \in \mathcal F$
, and
$\xi \in \mathcal F$
, and
![]() $x,y, z\in X$
,
$x,y, z\in X$
,
In particular,
![]() $ \beta _\xi (o,go) \in \mathfrak a $
is defined by
$ \beta _\xi (o,go) \in \mathfrak a $
is defined by
and hence
![]() $\beta _P (o, a_u o)=u$
for any
$\beta _P (o, a_u o)=u$
for any
![]() $u\in \mathfrak a$
. For
$u\in \mathfrak a$
. For
![]() $h, g\in G$
, we set
$h, g\in G$
, we set
![]() $\beta _\xi (h, g):=\beta _{\xi }(ho, go)$
.
$\beta _\xi (h, g):=\beta _{\xi }(ho, go)$
.
2.4 Shadows
For
![]() $ q\in X$
and
$ q\in X$
and
![]() $r>0$
, we set
$r>0$
, we set
![]() $B(q,r)=\{x\in X: d(x, q)\le r\}$
. For
$B(q,r)=\{x\in X: d(x, q)\le r\}$
. For
![]() $p=g(o)\in X$
, the shadow of the ball
$p=g(o)\in X$
, the shadow of the ball
![]() $B(q,r)$
viewed from p is defined as
$B(q,r)$
viewed from p is defined as
Similarly, for
![]() $\xi \in \mathcal F$
, the shadow of the ball
$\xi \in \mathcal F$
, the shadow of the ball
![]() $B(q,r)$
as viewed from
$B(q,r)$
as viewed from
![]() $\xi $
is
$\xi $
is
Lemma 2.3. [Reference Lee and Oh15, Lemmas 5.6 and 5.7]
-
(1) There exists
 $\kappa>0$
such that for any
$\kappa>0$
such that for any
 $g\in G$
and
$g\in G$
and
 $r>0$
,
$r>0$
,  $$ \begin{align*}\sup_{\xi \in O_r(g(o),o)}\|\beta_{\xi}(g(o),o)-\mu(g^{-1})\|\le \kappa r .\end{align*} $$
$$ \begin{align*}\sup_{\xi \in O_r(g(o),o)}\|\beta_{\xi}(g(o),o)-\mu(g^{-1})\|\le \kappa r .\end{align*} $$
-
(2) If a sequence
 $p_i\in X$
converges to
$p_i\in X$
converges to
 $\xi \in \mathcal F$
, then for any
$\xi \in \mathcal F$
, then for any
 $0<\varepsilon <r$
, we have for all sufficiently large i.
$0<\varepsilon <r$
, we have for all sufficiently large i. $$ \begin{align*}O_{r-\varepsilon} (p_i, o)\subset O_r(\xi, o)\subset O_{r+\varepsilon} (p_i, o)\end{align*} $$
$$ \begin{align*}O_{r-\varepsilon} (p_i, o)\subset O_r(\xi, o)\subset O_{r+\varepsilon} (p_i, o)\end{align*} $$
3 Horospherical limit points
Let
![]() $\Gamma <G$
be a Zariski dense discrete subgroup. A
$\Gamma <G$
be a Zariski dense discrete subgroup. A
![]() $\Gamma $
-tight horoball based at
$\Gamma $
-tight horoball based at
![]() $\xi \in \mathcal F$
is a subset of the form
$\xi \in \mathcal F$
is a subset of the form
![]() $\mathcal H_{\xi }=g N (\exp \mathcal C) (o)$
, where
$\mathcal H_{\xi }=g N (\exp \mathcal C) (o)$
, where
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $\xi =gP$
and
$\xi =gP$
and
![]() $\mathcal C$
is a closed cone contained in
$\mathcal C$
is a closed cone contained in
![]() $\operatorname {int} \mathcal L\cup \{0\}$
. For
$\operatorname {int} \mathcal L\cup \{0\}$
. For
![]() $T>0$
, we write
$T>0$
, we write
![]() $\mathcal H_{\xi }(T)= gN (\exp (\mathcal C-\mathcal C_T))o$
. We recall the definition from the introduction.
$\mathcal H_{\xi }(T)= gN (\exp (\mathcal C-\mathcal C_T))o$
. We recall the definition from the introduction.
Definition 3.1. We say that
![]() $\xi \in \mathcal F$
is a horospherical limit point of
$\xi \in \mathcal F$
is a horospherical limit point of
![]() $\Gamma $
if there exists a
$\Gamma $
if there exists a
![]() $\Gamma $
-tight horoball
$\Gamma $
-tight horoball
![]() $\mathcal H_\xi $
based at
$\mathcal H_\xi $
based at
![]() $\xi $
such that
$\xi $
such that
![]() $\mathcal H_\xi (T)\cap \Gamma (o)\ne \emptyset $
for all
$\mathcal H_\xi (T)\cap \Gamma (o)\ne \emptyset $
for all
![]() $T>1$
.
$T>1$
.
In this section, we provide a mostly self-contained proof of the following theorem.
Theorem 3.2. Let
![]() $[g]\in \mathcal E$
. The following are equivalent:
$[g]\in \mathcal E$
. The following are equivalent:
-
(1)
 $g^+=gP\in \Lambda $
is a horospherical limit point;
$g^+=gP\in \Lambda $
is a horospherical limit point; -
(2)
 $[g]NM$
is dense in
$[g]NM$
is dense in
 $\mathcal E$
.
$\mathcal E$
.
The main external ingredient in our proof is the density of the group generated by the Jordan projection
![]() $ \unicode{x3bb} (\Gamma )$
, due to Benoist [Reference Benoist, Kobayashi, Kashiwara, Matsuki, Nishiyama and Oshima2], that is,
$ \unicode{x3bb} (\Gamma )$
, due to Benoist [Reference Benoist, Kobayashi, Kashiwara, Matsuki, Nishiyama and Oshima2], that is,
for every Zariski dense discrete subgroup
![]() $ \Gamma < G $
. In fact, for every cone
$ \Gamma < G $
. In fact, for every cone
![]() $ \mathcal C \subset \mathcal L $
with non-empty interior, there exists a Zariski dense subgroup
$ \mathcal C \subset \mathcal L $
with non-empty interior, there exists a Zariski dense subgroup
![]() $ \Gamma ' < \Gamma $
with
$ \Gamma ' < \Gamma $
with
![]() $ \mathcal L_{\Gamma '} \subset \mathcal C $
(see [Reference Benoist1]); therefore, we have
$ \mathcal L_{\Gamma '} \subset \mathcal C $
(see [Reference Benoist1]); therefore, we have
It is convenient to use a characterization of horospherical limit points in terms of the Busemann function.
Lemma 3.3. For
![]() $ \xi \in \Lambda $
, we have
$ \xi \in \Lambda $
, we have
![]() $\xi \in \Lambda _h$
if and only if there exists a closed cone
$\xi \in \Lambda _h$
if and only if there exists a closed cone
![]() ${\mathcal C \subset {\operatorname {int} \mathcal L} \cup \{0\}}$
and a sequence
${\mathcal C \subset {\operatorname {int} \mathcal L} \cup \{0\}}$
and a sequence
![]() $ \gamma _j \in \Gamma $
satisfying
$ \gamma _j \in \Gamma $
satisfying
Proof. Let
![]() $\xi =gP\in \Lambda _h$
be as defined in Definition 3.1. Then there exists
$\xi =gP\in \Lambda _h$
be as defined in Definition 3.1. Then there exists
![]() ${\gamma _j= gp n_j a_{u_j}k_j\in \Gamma }$
for some
${\gamma _j= gp n_j a_{u_j}k_j\in \Gamma }$
for some
![]() $p\in P$
,
$p\in P$
,
![]() $n_j\in N$
,
$n_j\in N$
,
![]() $k_j\in K$
, and
$k_j\in K$
, and
![]() $u_j\to \infty $
in some closed cone
$u_j\to \infty $
in some closed cone
![]() $\mathcal C$
contained in
$\mathcal C$
contained in
![]() $\operatorname {int}\mathcal L\cup \{0\}$
. Fix some closed cone
$\operatorname {int}\mathcal L\cup \{0\}$
. Fix some closed cone
![]() $\mathcal C'\subset \operatorname {int} \mathcal L\cup \{0\}$
whose interior contains
$\mathcal C'\subset \operatorname {int} \mathcal L\cup \{0\}$
whose interior contains
![]() $\mathcal C$
. Note that
$\mathcal C$
. Note that
 $$ \begin{align*} \beta_{\xi}(o, \gamma_j o) &= \beta_{gP}(e, g)+ \beta_{gP}(g, gpn_j a_{u_j})\\ &= \beta_P(g^{-1}, e)+ \beta_P(e,p)+ \beta_P(e, n_j)+\beta_P(e, a_{u_j})\\ & =\beta_{P}(g^{-1},p)+u_j. \end{align*} $$
$$ \begin{align*} \beta_{\xi}(o, \gamma_j o) &= \beta_{gP}(e, g)+ \beta_{gP}(g, gpn_j a_{u_j})\\ &= \beta_P(g^{-1}, e)+ \beta_P(e,p)+ \beta_P(e, n_j)+\beta_P(e, a_{u_j})\\ & =\beta_{P}(g^{-1},p)+u_j. \end{align*} $$
Therefore, the sequence
![]() $\beta _{\xi }(o, \gamma _j)-u_j$
is uniformly bounded. Since
$\beta _{\xi }(o, \gamma _j)-u_j$
is uniformly bounded. Since
![]() $u_j\in \mathcal C$
,
$u_j\in \mathcal C$
,
![]() $\beta _{\xi }(o,\gamma _j o)\in \mathcal C'$
for all large j. Therefore, equation (3.1) holds. For the other direction, let
$\beta _{\xi }(o,\gamma _j o)\in \mathcal C'$
for all large j. Therefore, equation (3.1) holds. For the other direction, let
![]() $\gamma _j$
and
$\gamma _j$
and
![]() $\mathcal C$
satisfy equation (3.1) for
$\mathcal C$
satisfy equation (3.1) for
![]() $\xi =gP$
for
$\xi =gP$
for
![]() $g\in G$
. Since
$g\in G$
. Since
![]() $G=gNAK$
, we may write
$G=gNAK$
, we may write
![]() $\gamma _j= gn_ja_{u_j} k_j $
for some
$\gamma _j= gn_ja_{u_j} k_j $
for some
![]() $n_j\in N, u_j\in \mathfrak a$
and
$n_j\in N, u_j\in \mathfrak a$
and
![]() $k_j\in K$
. By a similar computation as above, the sequence
$k_j\in K$
. By a similar computation as above, the sequence
![]() $\beta _\xi (o, \gamma _j o)-u_j$
is uniformly bounded. It follows that
$\beta _\xi (o, \gamma _j o)-u_j$
is uniformly bounded. It follows that
![]() $u_j\in \mathcal C'$
for all large j and
$u_j\in \mathcal C'$
for all large j and
![]() $u_j\to \infty $
. Therefore, for any
$u_j\to \infty $
. Therefore, for any
![]() $T>1$
, there exists
$T>1$
, there exists
![]() $j>1$
such that
$j>1$
such that
![]() $\gamma _j (o)\in g N \exp (\mathcal C'-\mathcal C^{\prime }_T)(o)$
. This proves
$\gamma _j (o)\in g N \exp (\mathcal C'-\mathcal C^{\prime }_T)(o)$
. This proves
![]() $\xi \in \Lambda _h$
.
$\xi \in \Lambda _h$
.
We note that the condition in equation (3.1) is independent of the choice of basepoint
![]() $ o $
. Indeed, for any
$ o $
. Indeed, for any
![]() $g\in G$
and
$g\in G$
and
![]() $\xi \in \mathcal F$
and for all
$\xi \in \mathcal F$
and for all
![]() $ \gamma \in \Gamma $
, we have
$ \gamma \in \Gamma $
, we have
and hence
 $$ \begin{align*} \|\beta_\xi(o, \gamma o)-\beta_\xi (go, \gamma go)\|&=\|\beta_\xi(o, go)+\beta_\xi (\gamma go, \gamma o)\|\\ &=\|\beta_\xi(o, go)-\beta_{\gamma^{-1}\xi} (o,go)\| \\ & \le 2 \cdot \max_{\eta \in \mathcal{F}} \|\beta_\eta (o, go)\|. \end{align*} $$
$$ \begin{align*} \|\beta_\xi(o, \gamma o)-\beta_\xi (go, \gamma go)\|&=\|\beta_\xi(o, go)+\beta_\xi (\gamma go, \gamma o)\|\\ &=\|\beta_\xi(o, go)-\beta_{\gamma^{-1}\xi} (o,go)\| \\ & \le 2 \cdot \max_{\eta \in \mathcal{F}} \|\beta_\eta (o, go)\|. \end{align*} $$
Since this bound is independent of
![]() $\gamma \in \Gamma $
, the condition in equation (3.1) implies that for any
$\gamma \in \Gamma $
, the condition in equation (3.1) implies that for any
![]() $p=go \in X$
,
$p=go \in X$
,
Let us now consider the following seemingly stronger condition for a limit point being horospherical.
Definition 3.4. For
![]() $u\in \mathfrak a^+$
, a point
$u\in \mathfrak a^+$
, a point
![]() $ \xi \in \mathcal F$
is called a
$ \xi \in \mathcal F$
is called a
![]() $ u $
-horospherical limit point if for some
$ u $
-horospherical limit point if for some
![]() $p\in X$
(and hence for any
$p\in X$
(and hence for any
![]() $p\in X$
), there exists a constant
$p\in X$
), there exists a constant
![]() $ R>0 $
and a sequence
$ R>0 $
and a sequence
![]() $ \gamma _j \in \Gamma $
satisfying
$ \gamma _j \in \Gamma $
satisfying
We denote the set of
![]() $ u $
-horospherical limit points by
$ u $
-horospherical limit points by
![]() $ \Lambda _h(u) $
.
$ \Lambda _h(u) $
.
By
![]() $ G $
-invariance of the Busemann map, the set of horospherical (respectively u-horospherical) limit points is
$ G $
-invariance of the Busemann map, the set of horospherical (respectively u-horospherical) limit points is
![]() $\Gamma $
-invariant. Therefore, for
$\Gamma $
-invariant. Therefore, for
![]() $x=[g]\in \Gamma \backslash G$
, we may say
$x=[g]\in \Gamma \backslash G$
, we may say
![]() $x^+:=\Gamma gP$
horospherical (respectively u-horospherical) if
$x^+:=\Gamma gP$
horospherical (respectively u-horospherical) if
![]() $g^+$
is.
$g^+$
is.
For
![]() $u\in \mathfrak a$
, we call
$u\in \mathfrak a$
, we call
![]() $x\in \Gamma \backslash G$
a u-periodic point if
$x\in \Gamma \backslash G$
a u-periodic point if
![]() $x a_u = xm_0$
for some
$x a_u = xm_0$
for some
![]() $m_0\in M$
; note that
$m_0\in M$
; note that
![]() $xa_{\mathbb R u} M_0$
is then compact. Note that for
$xa_{\mathbb R u} M_0$
is then compact. Note that for
![]() $u\in \operatorname {int}\mathfrak a^+$
, the existence of a u-periodic point is equivalent to the condition that
$u\in \operatorname {int}\mathfrak a^+$
, the existence of a u-periodic point is equivalent to the condition that
![]() $u\in \unicode{x3bb} (\Gamma )$
.
$u\in \unicode{x3bb} (\Gamma )$
.
Lemma 3.5. Let
![]() $u\in \mathfrak a^+$
. If
$u\in \mathfrak a^+$
. If
![]() $x\in \Gamma \backslash G$
is u-periodic, then
$x\in \Gamma \backslash G$
is u-periodic, then
![]() $x^+\in \mathcal F$
is a u-horospherical limit point.
$x^+\in \mathcal F$
is a u-horospherical limit point.
Proof. Since x is u-periodic, there exist
![]() $g\in G$
with
$g\in G$
with
![]() $x=[g]$
and
$x=[g]$
and
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $\gamma =g a_u m g^{-1}$
for some
$\gamma =g a_u m g^{-1}$
for some
![]() $m\in M$
, and
$m\in M$
, and
![]() $y_\gamma =g^+ \in \Lambda $
. Moreover, for any
$y_\gamma =g^+ \in \Lambda $
. Moreover, for any
![]() $k\ge 1$
,
$k\ge 1$
,
This implies
![]() $gP$
is u-horospherical.
$gP$
is u-horospherical.
Proposition 3.6. Let
![]() $x\in \Gamma \backslash G$
. If
$x\in \Gamma \backslash G$
. If
![]() $ x^+$
is u-horospherical for some
$ x^+$
is u-horospherical for some
![]() $u\in \unicode{x3bb} (\Gamma )$
, then the closure
$u\in \unicode{x3bb} (\Gamma )$
, then the closure
![]() $\overline {xN}$
contains a
$\overline {xN}$
contains a
![]() $ u $
-periodic point.
$ u $
-periodic point.
Proof. Choose
![]() $g\in G$
so that
$g\in G$
so that
![]() $x=[g]$
. We may assume without loss of generality that
$x=[g]$
. We may assume without loss of generality that
![]() $g=k\in K$
, since
$g=k\in K$
, since
![]() $kan N= k N a$
, and a translate of a u-periodic point by an element of A is again a u-periodic point. Since
$kan N= k N a$
, and a translate of a u-periodic point by an element of A is again a u-periodic point. Since
![]() $u\in \unicode{x3bb} (\Gamma )$
, there exists a u-periodic point, say,
$u\in \unicode{x3bb} (\Gamma )$
, there exists a u-periodic point, say,
![]() $x_0\in \Gamma \backslash G$
. It suffices to show that
$x_0\in \Gamma \backslash G$
. It suffices to show that
as every point in
![]() $x_0AM$
is u-periodic.
$x_0AM$
is u-periodic.
Since
![]() $k^+$
is
$k^+$
is
![]() $ u $
-horospherical and using equation (2.4), there exists
$ u $
-horospherical and using equation (2.4), there exists
![]() $ R>0 $
and sequences
$ R>0 $
and sequences
![]() $ \gamma _j \in \Gamma $
,
$ \gamma _j \in \Gamma $
,
![]() $ u_j \to \infty $
in
$ u_j \to \infty $
in
![]() $ \mathfrak a^+ $
and
$ \mathfrak a^+ $
and
![]() $ k_j \in K $
and
$ k_j \in K $
and
![]() $ n_j \in N $
satisfying
$ n_j \in N $
satisfying
![]() $\gamma _j^{-1} k = k_j a_{-u_j} n_j $
or
$\gamma _j^{-1} k = k_j a_{-u_j} n_j $
or
with
![]() $ \|\mathbb {R}_+u - u_j \| < R $
for all
$ \|\mathbb {R}_+u - u_j \| < R $
for all
![]() $ j $
. Let
$ j $
. Let
![]() $ \ell _j \to \infty $
be a sequence of integers satisfying
$ \ell _j \to \infty $
be a sequence of integers satisfying
By passing to a subsequence, we may assume without loss of generality that
![]() $ \gamma _j^{-1}kP$
converges to some
$ \gamma _j^{-1}kP$
converges to some
![]() $\xi _0 \in \mathcal {F} $
. Since
$\xi _0 \in \mathcal {F} $
. Since
![]() $\check {N}P$
is Zariski open and
$\check {N}P$
is Zariski open and
![]() $ \Gamma $
is Zariski dense, we may choose
$ \Gamma $
is Zariski dense, we may choose
![]() $g_0\in G$
such that
$g_0\in G$
such that
![]() $x_0=[g_0]$
and
$x_0=[g_0]$
and
![]() $g_0^{-1}\xi _0\in \check {N}P$
. Let
$g_0^{-1}\xi _0\in \check {N}P$
. Let
![]() $h_0\in \check {N}$
be such that
$h_0\in \check {N}$
be such that
![]() $ \xi _0=g_0 h_0 P $
. Since
$ \xi _0=g_0 h_0 P $
. Since
![]() $ g_0\check {N}P $
is open and
$ g_0\check {N}P $
is open and
![]() $\gamma _j^{-1}kP\to g_0h_0P$
, we may assume that for all j, there exists
$\gamma _j^{-1}kP\to g_0h_0P$
, we may assume that for all j, there exists
![]() $ h_j \in \check {N} $
satisfying
$ h_j \in \check {N} $
satisfying
![]() $ g_0 h_j P = \gamma _j^{-1}k P = k_j P $
with
$ g_0 h_j P = \gamma _j^{-1}k P = k_j P $
with
![]() $ h_j \to h_0 $
. Let
$ h_j \to h_0 $
. Let
![]() $p_j= a_{v_j}m_j \tilde n _j \in P=AMN$
be such that
$p_j= a_{v_j}m_j \tilde n _j \in P=AMN$
be such that
![]() $g_0 h_j p_j= k_j$
; since
$g_0 h_j p_j= k_j$
; since
![]() $h_j\to h_0$
and the product map
$h_j\to h_0$
and the product map
![]() $\check {N}\times P\to \check {N}P$
is a diffeomorphism, the sequence
$\check {N}\times P\to \check {N}P$
is a diffeomorphism, the sequence
![]() $p_j$
, as well as
$p_j$
, as well as
![]() ${v_j}\in \mathfrak a$
, are bounded.
${v_j}\in \mathfrak a$
, are bounded.
Therefore, by equation (3.4), we get for all j,
 $$ \begin{align*} g_0 &= k_j p_j^{-1}h_j^{-1} \\& =\gamma_j^{-1} kn^{-1}_j a_{u_j} ( \tilde n^{-1}_j m_j^{-1} a_{-v_j}) h_j^{-1} \\ &= \gamma_j^{-1} k n^{-1}_j (a_{u_j} \tilde n^{-1}_j a_{-u_j}) a_{u_j} m_j^{-1} a_{-v_j}h_j^{-1} \\ &= \gamma_j^{-1} k n^{-1}_j (a_{u_j} \tilde n^{-1}_j a_{-u_j}) m_j^{-1} (a_{u_j-v_j}h_j^{-1} a_{-u_j+v_j}) a_{u_j-v_j}. \end{align*} $$
$$ \begin{align*} g_0 &= k_j p_j^{-1}h_j^{-1} \\& =\gamma_j^{-1} kn^{-1}_j a_{u_j} ( \tilde n^{-1}_j m_j^{-1} a_{-v_j}) h_j^{-1} \\ &= \gamma_j^{-1} k n^{-1}_j (a_{u_j} \tilde n^{-1}_j a_{-u_j}) a_{u_j} m_j^{-1} a_{-v_j}h_j^{-1} \\ &= \gamma_j^{-1} k n^{-1}_j (a_{u_j} \tilde n^{-1}_j a_{-u_j}) m_j^{-1} (a_{u_j-v_j}h_j^{-1} a_{-u_j+v_j}) a_{u_j-v_j}. \end{align*} $$
Since
![]() $h_j^{-1} \in \check {N}$
and
$h_j^{-1} \in \check {N}$
and
![]() $ v_j \in \mathfrak a $
are uniformly bounded and since
$ v_j \in \mathfrak a $
are uniformly bounded and since
![]() $u_j\to \infty $
within a bounded neighborhood of the ray
$u_j\to \infty $
within a bounded neighborhood of the ray
![]() $\mathbb R_+ u\in \operatorname {int}\mathfrak a^+$
, we have
$\mathbb R_+ u\in \operatorname {int}\mathfrak a^+$
, we have
By setting
![]() $ n^{\prime }_j = n^{-1}_j (a_{u_j} \tilde n ^{-1}_j a_{-u_j}) \in N $
, we may now write
$ n^{\prime }_j = n^{-1}_j (a_{u_j} \tilde n ^{-1}_j a_{-u_j}) \in N $
, we may now write
Since
![]() $x_0$
is u-periodic, there exists
$x_0$
is u-periodic, there exists
![]() $ \gamma _0 \in \Gamma $
such that
$ \gamma _0 \in \Gamma $
such that
![]() $ \gamma _0 = g_0 a_u m_0 g_0^{-1} $
for some
$ \gamma _0 = g_0 a_u m_0 g_0^{-1} $
for some
![]() $ m_0 \in M $
. Hence, for all
$ m_0 \in M $
. Hence, for all
![]() $j\ge 1$
,
$j\ge 1$
,
In other words,
Since the sequence
![]() $ -u_j+\ell _j u+ v_j \in \mathfrak a $
is uniformly bounded by equation (3.5) and
$ -u_j+\ell _j u+ v_j \in \mathfrak a $
is uniformly bounded by equation (3.5) and
![]() $ {\tilde h}_j \to e $
in
$ {\tilde h}_j \to e $
in
![]() $ \check {N} $
, we conclude that the sequence
$ \check {N} $
, we conclude that the sequence
![]() $ \Gamma k n^{\prime }_j $
has an accumulation point in
$ \Gamma k n^{\prime }_j $
has an accumulation point in
![]() $ \Gamma g_0 AM $
. This proves equation (3.3).
$ \Gamma g_0 AM $
. This proves equation (3.3).
It turns out that a horospherical limit point is also
![]() $ u $
-horospherical for any
$ u $
-horospherical for any
![]() $u\in \operatorname {int} \mathcal L$
.
$u\in \operatorname {int} \mathcal L$
.
Proposition 3.7. For each
![]() $ u \in {\operatorname {int} \mathcal L} $
, we have
$ u \in {\operatorname {int} \mathcal L} $
, we have
![]() $ \Lambda _h=\Lambda _h(u) $
.
$ \Lambda _h=\Lambda _h(u) $
.
Proof. Let
![]() $ \xi \in \Lambda _h $
. By definition, there is a sequence
$ \xi \in \Lambda _h $
. By definition, there is a sequence
![]() $ \gamma _j \in \Gamma $
satisfying
$ \gamma _j \in \Gamma $
satisfying
![]() $v_j:=\beta _\xi (e,\gamma _j)\to \infty $
with the sequence
$v_j:=\beta _\xi (e,\gamma _j)\to \infty $
with the sequence
![]() $\|v_j\|^{-1}v_j$
converging to some point
$\|v_j\|^{-1}v_j$
converging to some point
![]() $v_0\in \operatorname {int} \mathcal L$
. By passing to a subsequence, we may assume that
$v_0\in \operatorname {int} \mathcal L$
. By passing to a subsequence, we may assume that
![]() $\gamma _j^{-1} \xi $
converges to some
$\gamma _j^{-1} \xi $
converges to some
![]() $\xi _0\in \mathcal F$
.
$\xi _0\in \mathcal F$
.
Let
![]() $u\in \operatorname {int}\mathcal L$
. We claim that
$u\in \operatorname {int}\mathcal L$
. We claim that
![]() $\xi \in \Lambda _h(u)$
. We first consider the case
$\xi \in \Lambda _h(u)$
. We first consider the case
![]() $u\not \in \mathbb R_+ v_0$
. Let
$u\not \in \mathbb R_+ v_0$
. Let
![]() $r:=\operatorname {rank} G-1\ge 0$
. Since
$r:=\operatorname {rank} G-1\ge 0$
. Since
![]() $\bigcup _{\gamma \in \Gamma }\mathbb R_+\unicode{x3bb} (\gamma )$
is dense in
$\bigcup _{\gamma \in \Gamma }\mathbb R_+\unicode{x3bb} (\gamma )$
is dense in
![]() $\mathcal L$
, there exist
$\mathcal L$
, there exist
![]() $w_1, \ldots , w_r\in \unicode{x3bb} (\Gamma )$
such that
$w_1, \ldots , w_r\in \unicode{x3bb} (\Gamma )$
such that
![]() $v_0$
belongs to the interior of the convex cone spanned by
$v_0$
belongs to the interior of the convex cone spanned by
![]() $u, w_1, \ldots , w_r$
, so that
$u, w_1, \ldots , w_r$
, so that
 $$ \begin{align*}v_0= c_0 u+ \sum_{\ell=1}^r c_\ell w_\ell \end{align*} $$
$$ \begin{align*}v_0= c_0 u+ \sum_{\ell=1}^r c_\ell w_\ell \end{align*} $$
for some positive constants
![]() $c_0,\ldots , c_\ell $
.
$c_0,\ldots , c_\ell $
.
Since
![]() $\|v_j\|^{-1}v_j \to v_0$
, we may assume, by passing to a subsequence, that for each
$\|v_j\|^{-1}v_j \to v_0$
, we may assume, by passing to a subsequence, that for each
![]() $j\ge 1$
, we have
$j\ge 1$
, we have
 $$ \begin{align} \|v_j\|^{-1} v_j = c_{0,j} u +\sum_{\ell =1}^r c_{\ell,j} w_\ell \end{align} $$
$$ \begin{align} \|v_j\|^{-1} v_j = c_{0,j} u +\sum_{\ell =1}^r c_{\ell,j} w_\ell \end{align} $$
for some positive
![]() $c_{\ell ,j}$
,
$c_{\ell ,j}$
,
![]() $\ell =0, \ldots , r$
. Note that for each
$\ell =0, \ldots , r$
. Note that for each
![]() $0\le \ell \le r$
,
$0\le \ell \le r$
,
![]() $c_{\ell ,j}\to c_\ell $
as
$c_{\ell ,j}\to c_\ell $
as
![]() $j\to \infty $
.
$j\to \infty $
.
By Lemma 2.1, we can find a loxodromic element
![]() $g_1\in \Gamma $
and a neighborhood
$g_1\in \Gamma $
and a neighborhood
![]() $U_1$
of
$U_1$
of
![]() $\xi _0$
such that
$\xi _0$
such that
![]() $\unicode{x3bb} (g_1^{-1})=w_1$
,
$\unicode{x3bb} (g_1^{-1})=w_1$
,
![]() $\{y_{g_1}\}\times U_1\subset \mathcal F^{(2)}$
and
$\{y_{g_1}\}\times U_1\subset \mathcal F^{(2)}$
and
![]() $g_1^{-k}U_1\to y_{g_1^{-1}}$
uniformly. Applying Lemma 2.1 once more, we can find
$g_1^{-k}U_1\to y_{g_1^{-1}}$
uniformly. Applying Lemma 2.1 once more, we can find
![]() $ g_2 \in \Gamma $
satisfying
$ g_2 \in \Gamma $
satisfying
![]() $ \unicode{x3bb} (g_2^{-1}) = w_2 $
and a neighborhood
$ \unicode{x3bb} (g_2^{-1}) = w_2 $
and a neighborhood
![]() $ U_2 \subset \mathcal {F} $
of
$ U_2 \subset \mathcal {F} $
of
![]() $ y_{g_1^{-1}} $
satisfying
$ y_{g_1^{-1}} $
satisfying
![]() $ \{y_{g_2} \}\times U_2 \subset \mathcal {F}^{(2)} $
and that
$ \{y_{g_2} \}\times U_2 \subset \mathcal {F}^{(2)} $
and that
![]() $ g_2^{-k}U_2 \to y_{g_2^{-1}} $
uniformly.
$ g_2^{-k}U_2 \to y_{g_2^{-1}} $
uniformly.
Continuing inductively, we get elements
![]() $ g_1,\ldots ,g_r \in \Gamma $
and open sets
$ g_1,\ldots ,g_r \in \Gamma $
and open sets
![]() $ U_1,\ldots ,U_r \subset \mathcal {F} $
satisfying that for all
$ U_1,\ldots ,U_r \subset \mathcal {F} $
satisfying that for all
![]() $ \ell = 1,\ldots ,r $
:
$ \ell = 1,\ldots ,r $
:
-
(1)
 $ {w}_\ell =\unicode{x3bb} (g_\ell ^{-1}) $
;
$ {w}_\ell =\unicode{x3bb} (g_\ell ^{-1}) $
; -
(2)
 $ y_{g_{\ell -1}^{-1}} \in U_{\ell } $
;
$ y_{g_{\ell -1}^{-1}} \in U_{\ell } $
; -
(3)
 $ g_\ell ^{-k}U_\ell \to y_{g_\ell ^{-1}} $
uniformly; and
$ g_\ell ^{-k}U_\ell \to y_{g_\ell ^{-1}} $
uniformly; and -
(4)
 $ \{ y_{g_\ell } \}\times U_\ell $
is a relatively compact subset of
$ \{ y_{g_\ell } \}\times U_\ell $
is a relatively compact subset of
 $ \mathcal {F}^{(2)} $
.
$ \mathcal {F}^{(2)} $
.
We set
![]() $\xi _\ell :=y_{g_\ell ^{-1}}$
for each
$\xi _\ell :=y_{g_\ell ^{-1}}$
for each
![]() $1\le \ell \le r$
; so
$1\le \ell \le r$
; so
![]() $U_{\ell }$
is a neighborhood of
$U_{\ell }$
is a neighborhood of
![]() $\xi _{\ell -1}$
for each
$\xi _{\ell -1}$
for each
![]() $1\le \ell \le r$
.
$1\le \ell \le r$
.
Since
![]() $\mathcal Q_{\eta _0}:=\{\eta \in \mathcal F: (\eta _0, \eta )\in \mathcal F^{(2)}\}=\bigcup _{R>0} O_R (\eta _0, o)$
for any
$\mathcal Q_{\eta _0}:=\{\eta \in \mathcal F: (\eta _0, \eta )\in \mathcal F^{(2)}\}=\bigcup _{R>0} O_R (\eta _0, o)$
for any
![]() $\eta _0\in \mathcal F$
and
$\eta _0\in \mathcal F$
and
![]() $U_\ell \subset \mathcal Q_{y_{g_\ell }}$
is a relatively compact subset of
$U_\ell \subset \mathcal Q_{y_{g_\ell }}$
is a relatively compact subset of
![]() $\mathcal {F}^{(2)} $
, there exists
$\mathcal {F}^{(2)} $
, there exists
![]() $ R_\ell>0 $
such that
$ R_\ell>0 $
such that
![]() $ U_\ell \subset O_{R_\ell }(y_{g_\ell },o) $
. Since
$ U_\ell \subset O_{R_\ell }(y_{g_\ell },o) $
. Since
![]() $g_\ell ^ko $
converges to
$g_\ell ^ko $
converges to
![]() $y_{g_\ell }$
as
$y_{g_\ell }$
as
![]() $k\to +\infty $
, by Lemma 2.3(2),
$k\to +\infty $
, by Lemma 2.3(2),
for all sufficiently large
![]() $k>1$
.
$k>1$
.
For each
![]() $1\le \ell \le r$
and
$1\le \ell \le r$
and
![]() $j\ge 1$
, let
$j\ge 1$
, let
![]() $k_{\ell ,j}$
be the largest integer smaller than
$k_{\ell ,j}$
be the largest integer smaller than
![]() $c_{\ell , j}\|v_j\|$
. As
$c_{\ell , j}\|v_j\|$
. As
![]() $\|v_j\|\to \infty $
and
$\|v_j\|\to \infty $
and
![]() $c_{\ell ,j}\to c_\ell $
, we have
$c_{\ell ,j}\to c_\ell $
, we have
![]() $k_{\ell , j}\to \infty $
as
$k_{\ell , j}\to \infty $
as
![]() $j\to \infty $
. By the uniform contraction
$j\to \infty $
. By the uniform contraction
![]() $ g_\ell ^{-k}U_i \to \xi _\ell $
, there exists
$ g_\ell ^{-k}U_i \to \xi _\ell $
, there exists
![]() $j_0>1$
such that for all
$j_0>1$
such that for all
![]() $j\ge j_0$
,
$j\ge j_0$
,
for all
![]() $ \ell =1,\ldots ,r $
.
$ \ell =1,\ldots ,r $
.
For each
![]() $j\ge j_0$
, we now set
$j\ge j_0$
, we now set
We claim that
![]() $\beta _\xi (e,\tilde {\gamma }_j)\to \infty $
as
$\beta _\xi (e,\tilde {\gamma }_j)\to \infty $
as
![]() $j\to \infty $
and that
$j\to \infty $
and that
this proves that
![]() $\xi $
is u-horospherical.
$\xi $
is u-horospherical.
Fix
![]() $ j\ge j_0 $
and for each
$ j\ge j_0 $
and for each
![]() $1\le \ell \le r$
, let
$1\le \ell \le r$
, let
![]() $ k_\ell :=k_{\ell ,j} $
,
$ k_\ell :=k_{\ell ,j} $
,
![]() $b_\ell :=c_{\ell ,j}\|v_j\|$
, and set
$b_\ell :=c_{\ell ,j}\|v_j\|$
, and set
and
![]() $ g_0=e $
. The cocycle property of the Busemann function gives that
$ g_0=e $
. The cocycle property of the Busemann function gives that
 $$ \begin{align} \beta_\xi(e,\tilde{\gamma}_j) =\beta_\xi(e,\gamma_j) -\sum_{\ell=1}^{r} \beta_{h_{\ell-1}^{-1}\gamma_j^{-1}\xi}(g^{k_\ell}_\ell, e). \end{align} $$
$$ \begin{align} \beta_\xi(e,\tilde{\gamma}_j) =\beta_\xi(e,\gamma_j) -\sum_{\ell=1}^{r} \beta_{h_{\ell-1}^{-1}\gamma_j^{-1}\xi}(g^{k_\ell}_\ell, e). \end{align} $$
By equation (3.8),
![]() $\gamma _j^{-1}\xi \in U_1$
and for each
$\gamma _j^{-1}\xi \in U_1$
and for each
![]() $1\le \ell \le r$
,
$1\le \ell \le r$
,
Hence, by Lemma 2.3(1), there exists
![]() $\kappa \ge 1$
such that for each
$\kappa \ge 1$
such that for each
![]() $1\le \ell \le r$
,
$1\le \ell \le r$
,
Note that for some
![]() $C_\ell>0$
,
$C_\ell>0$
,
![]() $\|\mu (g_\ell ^{-k}) -k \unicode{x3bb} (g_\ell ^{-1})\|\le C_\ell $
for all
$\|\mu (g_\ell ^{-k}) -k \unicode{x3bb} (g_\ell ^{-1})\|\le C_\ell $
for all
![]() $k\ge 1$
. Since
$k\ge 1$
. Since
![]() $\unicode{x3bb} (g_\ell ^{-1})=w_\ell $
, we get
$\unicode{x3bb} (g_\ell ^{-1})=w_\ell $
, we get
Therefore, by equation (3.10), we obtain
 $$ \begin{align*}\bigg\|\beta_\xi(e, \tilde \gamma_j) -\bigg(v_j -\sum_{\ell=1}^r k_\ell w_\ell \bigg) \bigg\| \le \kappa \sum_{\ell=1}^r (R_\ell + C_\ell+1) .\end{align*} $$
$$ \begin{align*}\bigg\|\beta_\xi(e, \tilde \gamma_j) -\bigg(v_j -\sum_{\ell=1}^r k_\ell w_\ell \bigg) \bigg\| \le \kappa \sum_{\ell=1}^r (R_\ell + C_\ell+1) .\end{align*} $$
By equation (3.6), we have
 $$ \begin{align*}c_{0,j} \|v_j\| u = v_j -\sum_{\ell=1}^{r} b_\ell w_\ell .\end{align*} $$
$$ \begin{align*}c_{0,j} \|v_j\| u = v_j -\sum_{\ell=1}^{r} b_\ell w_\ell .\end{align*} $$
Since
![]() $|b_\ell -k_\ell |\le 1$
and
$|b_\ell -k_\ell |\le 1$
and
![]() $c_{0,j}>0$
, we deduce that for all
$c_{0,j}>0$
, we deduce that for all
![]() $j\ge j_0$
,
$j\ge j_0$
,
 $$ \begin{align*} &\|\beta_\xi(e, \tilde \gamma_j)-\mathbb R_+ u\| \le \| \beta_\xi(e, \tilde \gamma_j)- c_{0,j} \|v_j\|\cdot u \| \\ &\quad\le \bigg\| \beta_\xi(e, \tilde \gamma_j)- \bigg(v_j -\sum_{\ell=1}^r k_\ell w_\ell \bigg) \bigg\| + \sum_{\ell=1}^r \| k_\ell w_\ell -b_\ell w_\ell \| \\&\quad\le \kappa \sum_{\ell=1}^r (R_\ell + C_\ell +\|w_\ell\| +1). \end{align*} $$
$$ \begin{align*} &\|\beta_\xi(e, \tilde \gamma_j)-\mathbb R_+ u\| \le \| \beta_\xi(e, \tilde \gamma_j)- c_{0,j} \|v_j\|\cdot u \| \\ &\quad\le \bigg\| \beta_\xi(e, \tilde \gamma_j)- \bigg(v_j -\sum_{\ell=1}^r k_\ell w_\ell \bigg) \bigg\| + \sum_{\ell=1}^r \| k_\ell w_\ell -b_\ell w_\ell \| \\&\quad\le \kappa \sum_{\ell=1}^r (R_\ell + C_\ell +\|w_\ell\| +1). \end{align*} $$
This proves equation (3.9) and, consequently,
![]() $\xi $
is u-horospherical for any
$\xi $
is u-horospherical for any
![]() $u\notin \mathbb R_+ v_0.$
To show that
$u\notin \mathbb R_+ v_0.$
To show that
![]() $\xi $
is
$\xi $
is
![]() $v_0$
-horospherical, fix any
$v_0$
-horospherical, fix any
![]() $u\notin \mathbb R_+v_0$
and
$u\notin \mathbb R_+v_0$
and
![]() $\tilde \gamma _j\in \Gamma $
be a sequence as in equation (3.9) associated to u. If we set
$\tilde \gamma _j\in \Gamma $
be a sequence as in equation (3.9) associated to u. If we set
![]() $\tilde v_j=\beta _\xi (e, \tilde \gamma _j)$
, then
$\tilde v_j=\beta _\xi (e, \tilde \gamma _j)$
, then
![]() $\|\tilde v_j\|^{-1} \tilde v_j$
converges to a unit vector in
$\|\tilde v_j\|^{-1} \tilde v_j$
converges to a unit vector in
![]() $\operatorname {int} \mathcal L$
proportional to u. Therefore, by repeating the same argument only now switching the roles of
$\operatorname {int} \mathcal L$
proportional to u. Therefore, by repeating the same argument only now switching the roles of
![]() $v_0$
and u, we prove that
$v_0$
and u, we prove that
![]() $\xi $
is
$\xi $
is
![]() $v_0$
-horospherical as well. This completes the proof.
$v_0$
-horospherical as well. This completes the proof.
We may now prove Theorem 3.2.
Proof of Theorem 3.2
Let
![]() $g\in G$
be such that
$g\in G$
be such that
![]() $\xi =g^+\in \Lambda $
is a horospherical limit point. Set
$\xi =g^+\in \Lambda $
is a horospherical limit point. Set
![]() $Y:=\overline {[g]NM}$
. We claim that
$Y:=\overline {[g]NM}$
. We claim that
![]() $Y=\mathcal E$
. By Benoist [Reference Benoist1], the group generated by
$Y=\mathcal E$
. By Benoist [Reference Benoist1], the group generated by
![]() $\unicode{x3bb} (\Gamma )\cap \operatorname {int} \mathcal L$
is dense in
$\unicode{x3bb} (\Gamma )\cap \operatorname {int} \mathcal L$
is dense in
![]() $\mathfrak a$
. Hence, for every
$\mathfrak a$
. Hence, for every
![]() $ \varepsilon> 0 $
, there exist loxodromic elements
$ \varepsilon> 0 $
, there exist loxodromic elements
![]() $ \gamma _1,\ldots ,\gamma _{q} \in \Gamma $
such that
$ \gamma _1,\ldots ,\gamma _{q} \in \Gamma $
such that
and the group
![]() $\mathbb Z\unicode{x3bb} (\gamma _1)+\cdots +\mathbb Z \unicode{x3bb} (\gamma _{q})$
is an
$\mathbb Z\unicode{x3bb} (\gamma _1)+\cdots +\mathbb Z \unicode{x3bb} (\gamma _{q})$
is an
![]() $\varepsilon $
-net in
$\varepsilon $
-net in
![]() $\mathfrak a$
, that is, its
$\mathfrak a$
, that is, its
![]() $\varepsilon $
-neighborhood covers all
$\varepsilon $
-neighborhood covers all
![]() $\mathfrak a$
. Denote
$\mathfrak a$
. Denote
![]() $u_i = \unicode{x3bb} (\gamma _i) $
for
$u_i = \unicode{x3bb} (\gamma _i) $
for
![]() $ i=1,\ldots ,q $
. By Proposition 3.7, the point
$ i=1,\ldots ,q $
. By Proposition 3.7, the point
![]() $ \xi $
is
$ \xi $
is
![]() $u_1 $
-horospherical. By Proposition 3.6, there exists a
$u_1 $
-horospherical. By Proposition 3.6, there exists a
![]() $ u_1 $
-periodic point
$ u_1 $
-periodic point
![]() $x_1 \in \mathcal E $
contained in
$x_1 \in \mathcal E $
contained in
![]() $ Y $
, set
$ Y $
, set
By Lemma 3.5,
![]() $x_1^+$
is
$x_1^+$
is
![]() $u_1$
-horospherical; in particular, it is a horospherical limit point. Therefore, we can inductively find a
$u_1$
-horospherical; in particular, it is a horospherical limit point. Therefore, we can inductively find a
![]() $u_i$
-periodic point
$u_i$
-periodic point
![]() $ x_i $
in
$ x_i $
in
![]() $ Y_{i-1}=\overline {x_{i-1} NM} $
for each
$ Y_{i-1}=\overline {x_{i-1} NM} $
for each
![]() $2\le i\le q$
. By periodicity,
$2\le i\le q$
. By periodicity,
![]() $x_i (\exp {u_i}) M=x_i M$
, and hence
$x_i (\exp {u_i}) M=x_i M$
, and hence
![]() $Y_i \exp {\mathbb Z u_i} = Y_i$
for each
$Y_i \exp {\mathbb Z u_i} = Y_i$
for each
![]() $1\le i\le q$
. Therefore, we obtain
$1\le i\le q$
. Therefore, we obtain
 $$ \begin{align*}Y\supset Y_1\, {\exp {\mathbb Z u_1}}\supset Y_2\, {\exp ({\mathbb Z u_1+\mathbb Z u_2})}\supset \cdots \supset Y_q\, {\exp {\bigg(\sum_{i=1}^q \mathbb Z u_i}\bigg)}.\end{align*} $$
$$ \begin{align*}Y\supset Y_1\, {\exp {\mathbb Z u_1}}\supset Y_2\, {\exp ({\mathbb Z u_1+\mathbb Z u_2})}\supset \cdots \supset Y_q\, {\exp {\bigg(\sum_{i=1}^q \mathbb Z u_i}\bigg)}.\end{align*} $$
Recalling the dependence of
![]() $Y_q$
and
$Y_q$
and
![]() $\sum _{i=1}^q \mathbb Z u_i$
on
$\sum _{i=1}^q \mathbb Z u_i$
on
![]() $\varepsilon $
, set
$\varepsilon $
, set
 $$ \begin{align*}Z_\varepsilon:= Y_q MN \exp \bigg(\sum_{i=1}^q \mathbb Z u_i\bigg) \subset Y.\end{align*} $$
$$ \begin{align*}Z_\varepsilon:= Y_q MN \exp \bigg(\sum_{i=1}^q \mathbb Z u_i\bigg) \subset Y.\end{align*} $$
Since
![]() $MN \exp (\sum _{i=1}^q \mathbb Z u_i)$
is an
$MN \exp (\sum _{i=1}^q \mathbb Z u_i)$
is an
![]() $\varepsilon $
-net of P and
$\varepsilon $
-net of P and
![]() $\mathcal E$
is P-minimal,
$\mathcal E$
is P-minimal,
![]() $Z_\varepsilon $
is a
$Z_\varepsilon $
is a
![]() $2\varepsilon $
-net of
$2\varepsilon $
-net of
![]() $\mathcal E$
for all
$\mathcal E$
for all
![]() $\varepsilon>0$
. Since Y contains a
$\varepsilon>0$
. Since Y contains a
![]() $2\varepsilon $
-net of
$2\varepsilon $
-net of
![]() $\mathcal E$
for all
$\mathcal E$
for all
![]() $\varepsilon>0$
and Y is closed, it follows that
$\varepsilon>0$
and Y is closed, it follows that
![]() $Y=\mathcal E$
.
$Y=\mathcal E$
.
For the other direction, suppose that
![]() $[g]NM$
is dense in
$[g]NM$
is dense in
![]() $\mathcal E$
for
$\mathcal E$
for
![]() $g\in G$
. Choose any
$g\in G$
. Choose any
![]() $u\in \operatorname {int} \mathcal L$
and a closed cone
$u\in \operatorname {int} \mathcal L$
and a closed cone
![]() $\mathcal C \subset \operatorname {int} \mathcal L\cup \{0\}$
which contains u. Then
$\mathcal C \subset \operatorname {int} \mathcal L\cup \{0\}$
which contains u. Then
![]() $\mathcal H_\xi =gN(\exp \mathcal C )(o)$
is a
$\mathcal H_\xi =gN(\exp \mathcal C )(o)$
is a
![]() $\Gamma $
-tight horoball. Let
$\Gamma $
-tight horoball. Let
![]() $t>1$
. Since
$t>1$
. Since
![]() $ga_{-2t u}\in \mathcal E$
, there exist
$ga_{-2t u}\in \mathcal E$
, there exist
![]() $\gamma _i\in \Gamma $
,
$\gamma _i\in \Gamma $
,
![]() $n_i\in N$
,
$n_i\in N$
,
![]() $m_i\in M$
, and
$m_i\in M$
, and
![]() $q_i\to e$
in G such that for all
$q_i\to e$
in G such that for all
![]() $i\ge 1$
,
$i\ge 1$
,
![]() $\gamma _i g n_i m_i q_i= g a_{-2t u}$
. Since
$\gamma _i g n_i m_i q_i= g a_{-2t u}$
. Since
![]() $d(\gamma _i^{-1}g, gn_i m_ia_{2t u})\le d(q_i a_{2t u},a_{2t u})\to 0 $
as
$d(\gamma _i^{-1}g, gn_i m_ia_{2t u})\le d(q_i a_{2t u},a_{2t u})\to 0 $
as
![]() $i\to \infty $
, it follows that for all sufficiently large
$i\to \infty $
, it follows that for all sufficiently large
![]() $i\ge 1$
,
$i\ge 1$
,
![]() $\gamma _i^{-1} go \in \mathcal H_\xi (t)$
. Hence,
$\gamma _i^{-1} go \in \mathcal H_\xi (t)$
. Hence,
![]() $g^+$
is a horospherical limit point by Definition 3.1.
$g^+$
is a horospherical limit point by Definition 3.1.
4 Topological mixing and directional limit points
There is a close connection between denseness of
![]() $ N $
-orbits and the topological mixing of one-parameter diagonal flows with direction in
$ N $
-orbits and the topological mixing of one-parameter diagonal flows with direction in
![]() $ \operatorname {int} \mathcal L $
. This connection allows us to make use of recent topological mixing results by Chow and Sarkar [Reference Chow and Sarkar3]: recall the notation
$ \operatorname {int} \mathcal L $
. This connection allows us to make use of recent topological mixing results by Chow and Sarkar [Reference Chow and Sarkar3]: recall the notation
![]() $\Omega _0$
from equation (2.2).
$\Omega _0$
from equation (2.2).
Theorem 4.1. [Reference Chow and Sarkar3]
For any
![]() $u\in \operatorname {int} \mathcal L$
,
$u\in \operatorname {int} \mathcal L$
,
![]() $\{a_{tu} : t\in \mathbb R\}$
is topologically mixing on
$\{a_{tu} : t\in \mathbb R\}$
is topologically mixing on
![]() $\Omega _0$
, that is, for any open subsets
$\Omega _0$
, that is, for any open subsets
![]() $\mathcal O_1, \mathcal O_2$
of
$\mathcal O_1, \mathcal O_2$
of
![]() $\Gamma \backslash G$
intersecting
$\Gamma \backslash G$
intersecting
![]() $\Omega _0$
,
$\Omega _0$
,
The above theorem was predated by a result of Dang [Reference Dang6] in the case where
![]() $ M $
is abelian.
$ M $
is abelian.
4.1
N-orbits based at directional limit points along
 $\operatorname {int} \mathcal L$
$\operatorname {int} \mathcal L$
Definition 4.2. For
![]() $u\in \operatorname {int} \mathfrak a^+$
, denote by
$u\in \operatorname {int} \mathfrak a^+$
, denote by
![]() $\Lambda _u$
the set of all u-directional limit points, that is,
$\Lambda _u$
the set of all u-directional limit points, that is,
![]() $\xi \in \Lambda _u$
if and only if
$\xi \in \Lambda _u$
if and only if
![]() $\limsup _{t\to +\infty } \Gamma g \exp (tu)\ne \emptyset $
for some (and hence any)
$\limsup _{t\to +\infty } \Gamma g \exp (tu)\ne \emptyset $
for some (and hence any)
![]() $g\in G$
with
$g\in G$
with
![]() $gP=\xi $
.
$gP=\xi $
.
It is easy to see that
![]() $\Lambda _u\subset \Lambda $
for
$\Lambda _u\subset \Lambda $
for
![]() $u\in \operatorname {int} \mathfrak a^+$
.
$u\in \operatorname {int} \mathfrak a^+$
.
Proposition 4.3. If
![]() $[g]\in \mathcal E_0$
satisfies
$[g]\in \mathcal E_0$
satisfies
![]() $g^+\in \Lambda _u$
for some
$g^+\in \Lambda _u$
for some
![]() $u\in \operatorname {int}\mathcal L$
, then
$u\in \operatorname {int}\mathcal L$
, then
Proof. Since
![]() $\Omega _0 N=\mathcal E_0$
, we may assume without loss of generality that
$\Omega _0 N=\mathcal E_0$
, we may assume without loss of generality that
![]() $x=[g]\in \Omega _0$
. There exist
$x=[g]\in \Omega _0$
. There exist
![]() $\gamma _i\in \Gamma $
and
$\gamma _i\in \Gamma $
and
![]() $t_i\to +\infty $
such that
$t_i\to +\infty $
such that
![]() $\gamma _i g a_{t_iu} $
converges to some
$\gamma _i g a_{t_iu} $
converges to some
![]() $h\in G$
. In particular,
$h\in G$
. In particular,
![]() $x \exp (t_i u)\to [h]$
. Since
$x \exp (t_i u)\to [h]$
. Since
![]() $x a_{t_iu}\in \Omega _0$
and
$x a_{t_iu}\in \Omega _0$
and
![]() $\Omega _0$
is
$\Omega _0$
is
![]() $ A $
-invariant and closed, we have
$ A $
-invariant and closed, we have
![]() $[h]\in \Omega _0$
. We write
$[h]\in \Omega _0$
. We write
![]() $\gamma _i g a_{t_iu}=hq_i$
, where
$\gamma _i g a_{t_iu}=hq_i$
, where
![]() $q_i\to e$
in G. Therefore,
$q_i\to e$
in G. Therefore,
![]() $xN=[h] q_i N a_{-t_iu}$
for all
$xN=[h] q_i N a_{-t_iu}$
for all
![]() $i\ge 1$
. Let
$i\ge 1$
. Let
![]() $\mathcal O\subset \Gamma \backslash G$
be any open subset intersecting
$\mathcal O\subset \Gamma \backslash G$
be any open subset intersecting
![]() $\Omega _0$
. It suffices to show that
$\Omega _0$
. It suffices to show that
![]() $xN\cap \mathcal O\ne \emptyset $
. Let
$xN\cap \mathcal O\ne \emptyset $
. Let
![]() $\mathcal O_1$
be an open subset intersecting
$\mathcal O_1$
be an open subset intersecting
![]() $\Omega _0$
and
$\Omega _0$
and
![]() $V\subset \check {P}$
be an open symmetric neighborhood of e such that
$V\subset \check {P}$
be an open symmetric neighborhood of e such that
![]() $\mathcal O_1 V\subset \mathcal O$
.
$\mathcal O_1 V\subset \mathcal O$
.
Since
![]() $q_i\to e$
and
$q_i\to e$
and
![]() $NV$
is an open neighborhood of e in G, there exists an open neighborhood, say, U of e in G and
$NV$
is an open neighborhood of e in G, there exists an open neighborhood, say, U of e in G and
![]() $i_0$
such that
$i_0$
such that
![]() $U\subset q_i NV$
for all
$U\subset q_i NV$
for all
![]() $i\ge i_0$
. By Theorem 4.1, we can choose
$i\ge i_0$
. By Theorem 4.1, we can choose
![]() $i>i_0$
such that
$i>i_0$
such that
![]() $[h] U\kern1.3pt{\cap}\kern1.3pt \mathcal O_1 a_{t_iu}\kern1.3pt{\ne}\kern1.3pt \emptyset $
. It follows that
$[h] U\kern1.3pt{\cap}\kern1.3pt \mathcal O_1 a_{t_iu}\kern1.3pt{\ne}\kern1.3pt \emptyset $
. It follows that
![]() ${[h] q_i NV a_{-t_iu} \kern1.3pt{\cap}\kern1.3pt \mathcal O_1\kern1.3pt{\ne}\kern1.3pt \emptyset }$
. Since
${[h] q_i NV a_{-t_iu} \kern1.3pt{\cap}\kern1.3pt \mathcal O_1\kern1.3pt{\ne}\kern1.3pt \emptyset }$
. Since
![]() $V\subset a_{-t_iu} V a_{t_iu}$
as
$V\subset a_{-t_iu} V a_{t_iu}$
as
![]() $u\in \mathfrak a^+$
, we have
$u\in \mathfrak a^+$
, we have
Since
![]() $V=V^{-1}$
, we get
$V=V^{-1}$
, we get
![]() $[h] q_i N a_{-t_iu} \cap \mathcal O_1 V \ne \emptyset $
. Therefore,
$[h] q_i N a_{-t_iu} \cap \mathcal O_1 V \ne \emptyset $
. Therefore,
![]() $xN\cap \mathcal O\ne \emptyset $
, as desired.
$xN\cap \mathcal O\ne \emptyset $
, as desired.
This immediately implies the following corollary.
Corollary 4.4. If
![]() $[g]\in \Omega _0$
is u-periodic for some
$[g]\in \Omega _0$
is u-periodic for some
![]() $u\in \operatorname {int}\mathcal L$
, then
$u\in \operatorname {int}\mathcal L$
, then
Proof. Since
![]() $ [g] (\exp ku) =[g]m_0^k$
for any integer k and M is compact, we have
$ [g] (\exp ku) =[g]m_0^k$
for any integer k and M is compact, we have
![]() $g^+\in \Lambda _u$
. Therefore, the claim follows from Proposition 4.3.
$g^+\in \Lambda _u$
. Therefore, the claim follows from Proposition 4.3.
We may now conclude our main theorem in its fullest form.
Theorem 4.5. Let
![]() $[g]\in \mathcal E_0$
. The following are equivalent:
$[g]\in \mathcal E_0$
. The following are equivalent:
-
(1)
 $g^+\in \Lambda $
is a horospherical limit point;
$g^+\in \Lambda $
is a horospherical limit point; -
(2)
 $[g]N$
is dense in
$[g]N$
is dense in
 $\mathcal E_0$
;
$\mathcal E_0$
; -
(3)
 $[g]NM$
is dense in
$[g]NM$
is dense in
 $\mathcal E$
.
$\mathcal E$
.
Proof. The implication
![]() $(2)\Rightarrow (3)$
is trivial and
$(2)\Rightarrow (3)$
is trivial and
![]() $ (3) \Rightarrow (1) $
was shown in Theorem 3.2. Hence, let us prove
$ (3) \Rightarrow (1) $
was shown in Theorem 3.2. Hence, let us prove
![]() $ (1)\Rightarrow (2) $
.
$ (1)\Rightarrow (2) $
.
Let
![]() $x=[g]\in \mathcal E_0$
. Suppose that
$x=[g]\in \mathcal E_0$
. Suppose that
![]() $g^+\in \Lambda _h$
. Fix any
$g^+\in \Lambda _h$
. Fix any
![]() $u\in \unicode{x3bb} (\Gamma )\cap \operatorname {int} \mathcal L_\Gamma $
. By Propositions 3.7 and 3.6,
$u\in \unicode{x3bb} (\Gamma )\cap \operatorname {int} \mathcal L_\Gamma $
. By Propositions 3.7 and 3.6,
![]() $xN$
contains a u-periodic point, say,
$xN$
contains a u-periodic point, say,
![]() $x_0$
. Hence, by Corollary 4.4,
$x_0$
. Hence, by Corollary 4.4,
![]() $\overline {xN}\supset \overline {x_0N}\supset \Omega _0 N=\mathcal E_0$
. This proves
$\overline {xN}\supset \overline {x_0N}\supset \Omega _0 N=\mathcal E_0$
. This proves
![]() $(1)\Rightarrow (2)$
.
$(1)\Rightarrow (2)$
.
5 Conical limit points, minimality, and Jordan projection
A point
![]() $\xi \in \mathcal F$
is called a conical limit point of
$\xi \in \mathcal F$
is called a conical limit point of
![]() $\Gamma $
if there exists a sequence
$\Gamma $
if there exists a sequence
![]() $ u_j \to \infty $
in
$ u_j \to \infty $
in
![]() $ \mathfrak a^+ $
such that for some (and hence every)
$ \mathfrak a^+ $
such that for some (and hence every)
![]() $ g \in G $
with
$ g \in G $
with
![]() $ \xi = gP $
,
$ \xi = gP $
,
A conical limit point of
![]() $\Gamma $
is indeed contained in
$\Gamma $
is indeed contained in
![]() $\Lambda $
. We consider the following restricted notion.
$\Lambda $
. We consider the following restricted notion.
Definition 5.1. We call
![]() $\xi \in \mathcal F$
a strongly conical limit point of
$\xi \in \mathcal F$
a strongly conical limit point of
![]() $\Gamma $
if there exists a closed cone
$\Gamma $
if there exists a closed cone
![]() $ \mathcal C \subset \operatorname {int} \mathcal L \cup \{0\} $
and a sequence
$ \mathcal C \subset \operatorname {int} \mathcal L \cup \{0\} $
and a sequence
![]() $ u_j \to \infty $
in
$ u_j \to \infty $
in
![]() $ \mathcal C $
such that for some (and hence every)
$ \mathcal C $
such that for some (and hence every)
![]() $ g \in G $
with
$ g \in G $
with
![]() $ \xi = gP $
,
$ \xi = gP $
,
Remarks 5.2. We mention that a conical limit point defined in [Reference Conze, Guivarc’h, Burger and Iozzi4] for
![]() $\Gamma <\operatorname {SL}_d(\mathbb R)$
coincides with our strongly conical limit point.
$\Gamma <\operatorname {SL}_d(\mathbb R)$
coincides with our strongly conical limit point.
Lemma 5.3. Any strongly conical limit point of
![]() $\Gamma $
is horospherical.
$\Gamma $
is horospherical.
Proof. Suppose that
![]() $ \xi = gP $
is strongly conical, that is, there exist
$ \xi = gP $
is strongly conical, that is, there exist
![]() $\gamma _j\in \Gamma $
and
$\gamma _j\in \Gamma $
and
![]() $ u_j \to \infty $
in some closed cone
$ u_j \to \infty $
in some closed cone
![]() $\mathcal C\subset \operatorname {int} \mathcal L \cup \{0\}$
such that
$\mathcal C\subset \operatorname {int} \mathcal L \cup \{0\}$
such that
![]() $\gamma _j g a_{u_j}$
converges to some
$\gamma _j g a_{u_j}$
converges to some
![]() $h\in G$
. Write
$h\in G$
. Write
![]() $\gamma _j g a_{u_j}=hq_j$
, where
$\gamma _j g a_{u_j}=hq_j$
, where
![]() $q_j\to e$
in G. Let
$q_j\to e$
in G. Let
![]() $\mathcal C'$
be a closed cone contained in
$\mathcal C'$
be a closed cone contained in
![]() $\operatorname {int} \mathcal L \cup \{0\}$
whose interior contains
$\operatorname {int} \mathcal L \cup \{0\}$
whose interior contains
![]() $\mathcal C \smallsetminus \{0\}$
.
$\mathcal C \smallsetminus \{0\}$
.
Then
![]() $\gamma _j^{-1}=g a_{u_j}q_j^{-1} h^{-1}$
and
$\gamma _j^{-1}=g a_{u_j}q_j^{-1} h^{-1}$
and
Since
![]() $\beta _P(e, a_{u_j})=u_j$
and
$\beta _P(e, a_{u_j})=u_j$
and
![]() $q_j^{-1}h^{-1}$
are uniformly bounded, the sequence
$q_j^{-1}h^{-1}$
are uniformly bounded, the sequence
is uniformly bounded. Since
![]() $u_j\in \mathcal C$
and
$u_j\in \mathcal C$
and
![]() $\mathcal C\subset \operatorname {int}\mathcal C'\cup \{0\}$
, it follows that
$\mathcal C\subset \operatorname {int}\mathcal C'\cup \{0\}$
, it follows that
for all sufficiently large j. This proves that
![]() $\xi \in \Lambda _h$
.
$\xi \in \Lambda _h$
.
Corollary 5.4. For any
![]() $g\in G$
with strongly conical
$g\in G$
with strongly conical
![]() $g^+\in \mathcal F$
, we have
$g^+\in \mathcal F$
, we have
5.1 Directionally conical limit points
If
![]() $v\in {\operatorname {int} \mathcal L}$
, then clearly
$v\in {\operatorname {int} \mathcal L}$
, then clearly
![]() $\Lambda _v$
is contained in the horospherical limit set of
$\Lambda _v$
is contained in the horospherical limit set of
![]() $\Gamma $
, and hence any
$\Gamma $
, and hence any
![]() $NM$
-orbit based at a point of
$NM$
-orbit based at a point of
![]() $\Lambda _v$
is dense in
$\Lambda _v$
is dense in
![]() $\mathcal E$
. However, we would like to show in this section that the existence of a point in
$\mathcal E$
. However, we would like to show in this section that the existence of a point in
![]() $\Lambda _v$
for
$\Lambda _v$
for
![]() $v\in \partial \mathcal L_\Gamma $
implies the existence of a non-dense
$v\in \partial \mathcal L_\Gamma $
implies the existence of a non-dense
![]() $NM$
-orbit in
$NM$
-orbit in
![]() $\mathcal E$
.
$\mathcal E$
.
The flow
![]() $\exp (\mathbb R u)$
is said to be topologically transitive on
$\exp (\mathbb R u)$
is said to be topologically transitive on
![]() $\Omega /M=\{\Gamma g M : g^{\pm }\in \Lambda \}$
if for any open subsets
$\Omega /M=\{\Gamma g M : g^{\pm }\in \Lambda \}$
if for any open subsets
![]() $\mathcal O_1, \mathcal O_2$
intersecting
$\mathcal O_1, \mathcal O_2$
intersecting
![]() $\Omega /M$
, there exists a sequence
$\Omega /M$
, there exists a sequence
![]() $t_n \to +\infty $
such that
$t_n \to +\infty $
such that
![]() $\mathcal O_1\cap \mathcal O_2 a_{t_n u}\ne \emptyset $
.
$\mathcal O_1\cap \mathcal O_2 a_{t_n u}\ne \emptyset $
.
We make the following simple observation.
Lemma 5.5. For
![]() $g\in \Omega $
, we have
$g\in \Omega $
, we have
Proof. We have
![]() $\check {N}=w_0 N w_0^{-1}$
. Note that
$\check {N}=w_0 N w_0^{-1}$
. Note that
![]() $[g]\in \Omega $
if and only if
$[g]\in \Omega $
if and only if
![]() $[gw_0]\in \Omega $
, since
$[gw_0]\in \Omega $
, since
![]() $(g w_0)^{\pm }=g^{\mp }$
. So
$(g w_0)^{\pm }=g^{\mp }$
. So
![]() $\Omega w_0=\Omega $
. Hence,
$\Omega w_0=\Omega $
. Hence,
![]() $gNM$
is dense in
$gNM$
is dense in
![]() $\Omega $
if and only if
$\Omega $
if and only if
![]() $gw_0 \check {N}M w_0^{-1} $
is dense in
$gw_0 \check {N}M w_0^{-1} $
is dense in
![]() $\Omega $
if and only if
$\Omega $
if and only if
![]() $[g]w_0\check {N}M$
is dense in
$[g]w_0\check {N}M$
is dense in
![]() $\Omega w_0=\Omega $
.
$\Omega w_0=\Omega $
.
Since the opposition involution preserves
![]() $\mathcal L$
and
$\mathcal L$
and
![]() $\unicode{x3bb} (g^{-1})=\operatorname {i}\unicode{x3bb} (g)$
for any loxodromic element, it follows that
$\unicode{x3bb} (g^{-1})=\operatorname {i}\unicode{x3bb} (g)$
for any loxodromic element, it follows that
![]() $\unicode{x3bb} (\gamma )\in \partial \mathcal L$
if and only if
$\unicode{x3bb} (\gamma )\in \partial \mathcal L$
if and only if
![]() $\unicode{x3bb} (\gamma ^{-1})\in \partial \mathcal L$
.
$\unicode{x3bb} (\gamma ^{-1})\in \partial \mathcal L$
.
Proposition 5.6
-
(1) If
 $\Lambda =\Lambda _h$
, then
$\Lambda =\Lambda _h$
, then
 $\exp (\mathbb R v)$
is topologically transitive on
$\exp (\mathbb R v)$
is topologically transitive on
 $\Omega /M$
for any
$\Omega /M$
for any
 $v\in \operatorname {int}\mathfrak a^+$
such that
$v\in \operatorname {int}\mathfrak a^+$
such that
 $\Lambda _v\ne \emptyset $
.
$\Lambda _v\ne \emptyset $
. -
(2) For any loxodromic element
 $\gamma \in \Gamma $
with
$\gamma \in \Gamma $
with
 $\{y_{\gamma }, y_{\gamma ^{-1}}\}\subset \Lambda _h$
, the flow
$\{y_{\gamma }, y_{\gamma ^{-1}}\}\subset \Lambda _h$
, the flow
 $\exp (\mathbb R \unicode{x3bb} (\gamma ))$
is topologically transitive on
$\exp (\mathbb R \unicode{x3bb} (\gamma ))$
is topologically transitive on
 $\Omega /M$
.
$\Omega /M$
.
Proof. Assume that
![]() $\Lambda =\Lambda _h$
; so the
$\Lambda =\Lambda _h$
; so the
![]() $NM$
-action on
$NM$
-action on
![]() $\mathcal E$
is minimal. Suppose that
$\mathcal E$
is minimal. Suppose that
![]() $ \Lambda _v\ne \emptyset $
for some
$ \Lambda _v\ne \emptyset $
for some
![]() $v\in \operatorname {int}\mathfrak a^+.$
We claim that for any
$v\in \operatorname {int}\mathfrak a^+.$
We claim that for any
![]() ${\mathcal O}_1, {\mathcal O}_2$
be two right M-invariant open subsets intersecting
${\mathcal O}_1, {\mathcal O}_2$
be two right M-invariant open subsets intersecting
![]() $\Omega $
,
$\Omega $
,
![]() ${\mathcal O}_1 \exp (t_iv) \cap {\mathcal O}_2\ne \emptyset $
for some sequence
${\mathcal O}_1 \exp (t_iv) \cap {\mathcal O}_2\ne \emptyset $
for some sequence
![]() $t_i \to +\infty $
. Choose
$t_i \to +\infty $
. Choose
![]() $x=[g]\in \Omega $
so that
$x=[g]\in \Omega $
so that
![]() $g^+\in \Lambda _v$
. Then there exists
$g^+\in \Lambda _v$
. Then there exists
![]() $\gamma _i\in \Gamma $
and
$\gamma _i\in \Gamma $
and
![]() $t_i\to +\infty $
such that
$t_i\to +\infty $
such that
![]() $\gamma _i g a_{t_i v}$
converges to some
$\gamma _i g a_{t_i v}$
converges to some
![]() $g_0$
. Note that
$g_0$
. Note that
![]() $x_0:=[g_0]\in \Omega $
. So write
$x_0:=[g_0]\in \Omega $
. So write
![]() $\gamma _i g a_{t_i v}= g_0 h_i$
with
$\gamma _i g a_{t_i v}= g_0 h_i$
with
![]() $h_i\to e$
. By the
$h_i\to e$
. By the
![]() $NM$
-minimality assumption,
$NM$
-minimality assumption,
![]() $x NM $
intersects every open subset of
$x NM $
intersects every open subset of
![]() $\Omega $
. Since
$\Omega $
. Since
![]() $v\in \operatorname {int} \mathfrak a^+$
and hence
$v\in \operatorname {int} \mathfrak a^+$
and hence
![]() $a_{-tv} n a_{tv}\to e$
as
$a_{-tv} n a_{tv}\to e$
as
![]() $t\to +\infty $
, we may assume without loss of generality that
$t\to +\infty $
, we may assume without loss of generality that
![]() $x \in {\mathcal O}_1$
. Choose an open neighborhood U of e in G so that
$x \in {\mathcal O}_1$
. Choose an open neighborhood U of e in G so that
![]() ${\mathcal O}_1\supset x U M$
. Note that there exists a sequence
${\mathcal O}_1\supset x U M$
. Note that there exists a sequence
![]() $T_i\to \infty $
as
$T_i\to \infty $
as
![]() $i\to \infty $
such that for all i,
$i\to \infty $
such that for all i,
where
![]() $ \check {N}_{R}=\check {N} \cap B_R^G $
is the set of elements of
$ \check {N}_{R}=\check {N} \cap B_R^G $
is the set of elements of
![]() $ \check {N} $
of norm
$ \check {N} $
of norm
![]() $ \leq R $
. So
$ \leq R $
. So
![]() ${\mathcal O}_1 a_{t_i v}\supset x_0h_i \check {N}_{T_i}$
.
${\mathcal O}_1 a_{t_i v}\supset x_0h_i \check {N}_{T_i}$
.
Choose an open neighborhood V of e in G and some open subset
![]() ${\mathcal O}_2'$
intersecting
${\mathcal O}_2'$
intersecting
![]() $\Omega $
so that
$\Omega $
so that
![]() ${\mathcal O}_2\supset {\mathcal O}_2' V$
. Since
${\mathcal O}_2\supset {\mathcal O}_2' V$
. Since
![]() $x_0\check {N}M$
is dense in
$x_0\check {N}M$
is dense in
![]() $\Omega $
,
$\Omega $
,
![]() $x_0 n\in {\mathcal O}_2'$
for some
$x_0 n\in {\mathcal O}_2'$
for some
![]() $n\in \check {N}$
. Hence,
$n\in \check {N}$
. Hence,
![]() $x_0 h_i n = x_0 n (n^{-1} h_i n)\in {\mathcal O}_2' V\subset {\mathcal O}_2 $
for all i large enough so that
$x_0 h_i n = x_0 n (n^{-1} h_i n)\in {\mathcal O}_2' V\subset {\mathcal O}_2 $
for all i large enough so that
![]() $n^{-1} h_i n\in V$
. Therefore, for all i such that
$n^{-1} h_i n\in V$
. Therefore, for all i such that
![]() $n\in \check {N}_{T_i}$
, we get
$n\in \check {N}_{T_i}$
, we get
This proves the first claim.
Now suppose that
![]() $\gamma \in \Gamma $
is a loxodromic element with
$\gamma \in \Gamma $
is a loxodromic element with
![]() $y_{\gamma }, y_{\gamma ^{-1}}\in \Lambda _h$
. Write
$y_{\gamma }, y_{\gamma ^{-1}}\in \Lambda _h$
. Write
![]() $\gamma =g m a_{ v} g^{-1} $
for some
$\gamma =g m a_{ v} g^{-1} $
for some
![]() $g\in G$
and
$g\in G$
and
![]() $m\in M$
. Since
$m\in M$
. Since
![]() $y_\gamma =g^+$
and
$y_\gamma =g^+$
and
![]() $y_{\gamma ^{-1}}=gw_0^+,$
we have each
$y_{\gamma ^{-1}}=gw_0^+,$
we have each
![]() $[g]NM$
and
$[g]NM$
and
![]() $[g]w_0 NM$
contains
$[g]w_0 NM$
contains
![]() $\Omega $
in its closure. Now in the notation of the proof of the first claim, note that
$\Omega $
in its closure. Now in the notation of the proof of the first claim, note that
![]() $x_0=[g_0]\in [g]M$
since
$x_0=[g_0]\in [g]M$
since
![]() $[g]\exp (\mathbb R v) M$
is closed. Therefore, each
$[g]\exp (\mathbb R v) M$
is closed. Therefore, each
![]() $\overline {x_0 NM}$
and
$\overline {x_0 NM}$
and
![]() $\overline {x_0 \check {N}M}$
contains
$\overline {x_0 \check {N}M}$
contains
![]() $ \Omega $
. Based on this, the same argument as above shows the topological transitivity of
$ \Omega $
. Based on this, the same argument as above shows the topological transitivity of
![]() $\exp \mathbb R v$
, which finishes the proof since
$\exp \mathbb R v$
, which finishes the proof since
![]() $v=\unicode{x3bb} (\gamma )$
.
$v=\unicode{x3bb} (\gamma )$
.
Since
![]() $\mathcal L$
is invariant under the opposition involution
$\mathcal L$
is invariant under the opposition involution
![]() $\operatorname {i}$
and
$\operatorname {i}$
and
![]() $\unicode{x3bb} (\gamma )=\operatorname {i} \unicode{x3bb} (\gamma ^{-1})$
for any loxodromic element
$\unicode{x3bb} (\gamma )=\operatorname {i} \unicode{x3bb} (\gamma ^{-1})$
for any loxodromic element
![]() $\gamma \in \Gamma $
, the Jordan projection
$\gamma \in \Gamma $
, the Jordan projection
![]() $\unicode{x3bb} (\gamma )$
belongs to
$\unicode{x3bb} (\gamma )$
belongs to
![]() $ \partial \mathcal L$
if and only if the Jordan projection
$ \partial \mathcal L$
if and only if the Jordan projection
![]() $\unicode{x3bb} (\gamma ^{-1})$
belongs to
$\unicode{x3bb} (\gamma ^{-1})$
belongs to
![]() $ \partial \mathcal L$
. Together with the result of Dang and Gloriuex [Reference Dang and Glorieux7, Proposition 4.7], which says that
$ \partial \mathcal L$
. Together with the result of Dang and Gloriuex [Reference Dang and Glorieux7, Proposition 4.7], which says that
![]() $\exp (\mathbb R u)$
is not topologically transitive on
$\exp (\mathbb R u)$
is not topologically transitive on
![]() $\Omega /M$
for any
$\Omega /M$
for any
![]() $u\in \partial \mathcal L\cap \operatorname {int} \mathfrak a^+$
, Proposition 5.6 implies the following corollary.
$u\in \partial \mathcal L\cap \operatorname {int} \mathfrak a^+$
, Proposition 5.6 implies the following corollary.
Corollary 5.7
-
(1) If
 $\Lambda _v\ne \emptyset $
for some
$\Lambda _v\ne \emptyset $
for some
 $v\in \partial \mathcal L\cap \operatorname {int} \mathfrak a^+$
, then
$v\in \partial \mathcal L\cap \operatorname {int} \mathfrak a^+$
, then  $$ \begin{align*}\Lambda\ne \Lambda_h.\end{align*} $$
$$ \begin{align*}\Lambda\ne \Lambda_h.\end{align*} $$
-
(2) For any loxodromic element
 $\gamma \in \Gamma $
, we have
$\gamma \in \Gamma $
, we have
 $\unicode{x3bb} (\gamma )\in \partial \mathcal L$
if and only if Hence, if
$\unicode{x3bb} (\gamma )\in \partial \mathcal L$
if and only if Hence, if $$ \begin{align*}\{y_\gamma, y_{\gamma^{-1}}\} \not\subset \Lambda_h .\end{align*} $$
$$ \begin{align*}\{y_\gamma, y_{\gamma^{-1}}\} \not\subset \Lambda_h .\end{align*} $$
 $\Lambda =\Lambda _h$
, then
$\Lambda =\Lambda _h$
, then
 $\unicode{x3bb} (\Gamma )\subset \operatorname {int} \mathcal L$
.
$\unicode{x3bb} (\Gamma )\subset \operatorname {int} \mathcal L$
.
Acknowledgements
We would like to thank Richard Canary and Pratyush Sarkar for helpful conversations regarding Corollary 1.10. O. Landesberg would also like to thank Subhadip Dey and Ido Grayevsky for helpful and enjoyable discussions. We thank the anonymous referee for pointing out to us the paper [Reference Conze, Guivarc’h, Burger and Iozzi4]. H. Oh is partially supported by NSF grant DMS-1900101