What do children learn when they learn to communicate?

Most theoretical accounts of human communication assume that languages comprise an inventory of elements and some procedures for combining them into messages. These elements are conceived of at various levels of description: phonemes, the acoustic/psychological equivalent of letters; morphemes, basic units of meaning that cannot be further decomposed (such that the word uni-corn-s comprises three morphemes); words, which can be either mono- or multi-morphemic; and sentences which comprise more complex combinations of words / morphemes. It is further assumed that the way meanings combine in these more complex structures follows the principle of compositionality, which holds that “the meaning of an expression is a function of the meanings of its parts and the way they are syntactically combined” (Partee, Reference Partee, Landman and Veltman1984).

Yet although human communication is almost universally assumed to be compositional, attempts to cash out this assumption have inevitably proven unsuccessful (Ramscar & Port, Reference Ramscar and Port2016). Phonemes fail to capture many of the acoustic properties that are essential to spoken communication, and although phonemes are assumed to ‘spell out’ speech signals, they are often impossible to identify from acoustic information alone (Port & Leary, Reference Port and Leary2005; Samuel, Reference Samuel2020). The idea that morphemes comprise basic sound-meaning units has been undermined by analyses of their functions (which are often meaningless), and the discovery of context effects that contradict the idea of them being elemental units of meaning (Blevins, Reference Blevins2016; Lieber, Reference Lieber2019). Meanwhile, centuries of dedicated research has failed to make theoretical sense of meaning units (with philosophers such as Wittgenstein, Reference Wittgenstein1953, and Quine, Reference Quine1960, concluding that meanings cannot possibly be atomic), while efforts to find psychological evidence for their existence have produced more questions than answers (Ramscar & Port, Reference Ramscar, Port, Dabrowska and Divjak2015). Since similar problems have arisen when theories have attempted to explain how smaller ‘elements of meaning’ are combined to form larger compositional elements (Culicover, Reference Culicover1999), it seems that viewed dispassionately, the results of the massive body of research seeking to explain language processing in terms of the composition and decomposition of basic elements of form and meaning do not so much support this view as indicate that human communication does not work that way at all.

This paper describes an alternative theory of language that begins with learning, a subject that ought to lie at the heart of any theory of language acquisition, and ends with an account of human communication that is in many ways the opposite of received wisdom. It describes how research on ‘associative’ learning has resulted in theories that are discriminative in processing terms, and explains how this further undermines the idea that languages comprise inventories of discrete form-meaning associations, or that human communication is a compositional process. Instead, because the best models of learning and communication are fundamentally systematic, fundamentally probabilistic, and fundamentally discriminative (such that the processes that underlie the use of language are also likely to be systematic, probabilistic, and discriminative), this account reframes human communication and its learning in these terms – so as to make it compatible with these processes. It also results in a number of concrete predictions about the kinds of problems that children will encounter in learning a language, and the kinds of properties we should expect human communicative codes to possess for children to learn them. In keeping with the spirit of this special issue, these predictions will be highlighted as this review seeks to explain why (theoretically) communication and children's learning to communicate are best characterized in discriminative terms.

How do children learn?

Accounts of communicative learning seek to answer two questions: what do children learn, and how do they learn it? Since starting from how they learn allows for the establishment of useful constraints on what children might be able to learn, it seems reasonable to begin by offering an account of learning. Beginning with learning also benefits from the fact that considerable agreement exists about the nature of many basic learning processes, which tend to be specified in greater detail than is the case in linguistics. There are two main reasons for this: first, humans share their basic learning mechanisms with other animals, allowing animal models to offer insight into the neural processes of learning (O'Doherty, Dayan, Friston, Critchley & Dolan, Reference O'Doherty, Dayan, Friston, Critchley and Dolan2003; Schultz, Reference Schultz2006); second, human and animal learning mechanisms appear to be error-driven, a learning method that has been subject to a large amount of computational research that provides considerable insight into the capabilities of – and constraints on – this kind of learning in real-world situations (Hinton, McClelland & Rumelhart, Reference Hinton, McClelland, Rumelhart, Rumelhart, McClelland and Research Group1986; Hinton, Deng, Yu, Dahl, Mohamed, Jaitly, Vanhoucke, Nguyen, Kingsbury & Sainath, Reference Hinton, Deng, Yu, Dahl, Mohamed, Jaitly, Vanhoucke, Nguyen, Kingsbury. and Sainath2012; Hannun, Case, Casper, Catanzaro, Diamos, Elsen, Prenger, Satheesh, Sengupta, Coates & Ng, Reference Hannun, Case, Casper, Catanzaro, Diamos, Elsen, Prenger, Satheesh, Sengupta, Coates and Ng2014; LeCun, Bengio & Hinton, Reference LeCun, Bengio and Hinton2015).

With regards to animal learning, it has long been known that simple association rates (the frequency at which a ‘stimulus’ – say the German article das – is associated with a ‘response,’ the noun Mädchen) are incapable of explaining basic conditioning (Ramscar, Dye & McCauley, Reference Ramscar, Dye and McCauley2013a). Two further factors are critical to predicting and explaining learning the predictive relationships between cues and events: cue background rates (Rescorla, Reference Rescorla1968; Ramscar, Dye & Klein, Reference Ramscar, Dye and Klein2013b; how often das occurs absent Mädchen), and blocking (Kamin, Reference Kamin, Campbell and Church1969; Arnon & Ramscar, Reference Arnon and Ramscar2012; the prior predictability of Mädchen in context). Learning is then a product of the interactions between these factors in experience, with association rates tending to promote learning, and blocking and background rates tending to inhibit it.

Formal models embodying these principles are adept at fitting and predicting learning effects. A classic example, the Rescorla and Wagner (Reference Rescorla, Wagner, Black and Prokasy1972) learning rule specifies how learning can be described in terms of the computation of discrepancies between a learner's expectations and reality, with the difference between the two serving to modify the values of a set of predictive cues in relation to a set of expected outcomes in trial-by-trial learning. Although it was originally proposed as part of an elemental model of learning couched in associative terms (see also Miller, Barnet & Grahame, Reference Miller, Barnet and Grahame1995; Siegel & Allan, Reference Siegel and Allan1996; Ellis, Reference Ellis2006), the error-driven learning mechanism described by the rule is best understood by re-conceptualizing learning as a discriminative process that reduces uncertainty about events in the world, such that learning only occurs when uncertainty is present (Ramscar, Yarlett, Dye, Denny & Thorpe, Reference Ramscar, Yarlett, Dye, Denny and Thorpe2010; Hoppe, Hendriks, Ramscar & van Rij, Reference Hoppe, Hendriks, Ramscar and van Rijin press). If an event (outcome) whose likelihood is underestimated occurs, the values of cues to it are strengthened, whereas if its likelihood is overestimated, the values of these cues are weakened. Because uncertainty is finite (learning can often result in certainty), cues compete for predictive value, leading to the discovery of reliable cues through competition, and the discriminatory weakening and elimination of others.

The Rescorla-Wagner learning rule is relatively simple, allowing processes such as error-driven learning and cue competition to be explained in relatively intuitive terms. However the algorithm it describes is simply the linear form of an earlier rule proposed by Widrow and Hoff (Reference Widrow and Hoff1960; see Stone, Reference Stone, Rumelhart and McClelland1986), that is in turn formally equivalent to the delta-rule used in connectionist networks (Sutton & Barto, Reference Sutton and Barto1981). In all of these variants, error-driven learning is a systematic process that produces a mapping that best discriminates the informative relationships in a set of inputs and a set of outputs given a training schedule. Because of this, Ramscar et al. (Reference Ramscar, Yarlett, Dye, Denny and Thorpe2010) suggest that from a computational perspective it is best understood as describing a discriminative learning mechanism (this point also applies to the error-driven learning algorithms found at the heart of most connectionist / neural network model; Ng & Jordan, Reference Ng and Jordan2002, and Bayesian models of learning, e.g., Daw, Courville & Dayan, Reference Daw, Courville and Dayan2008). Conceptually, the logic of discrimination enshrined in these models is far removed from the “blooming, buzzing confusion” assumed in many developmental theories.

For the sake of clarity, it is worth noting that ‘discrimination learning’ has been used in at least three ways in the literature (see Hoppe, van Rij, Hendriks & Ramscar, Reference Hoppe, van Rij, Hendriks and Ramscar2021 for discussion). The term discrimination learning was widely used in the animal learning literature in the early twentieth century, and, consistent with the behaviourist principles that dominated theory at this time, it was (and still is) used in a mechanism-neutral way to describe the fact that, objectively, both animals and humans are capable of learning different responses to different stimuli (Rescorla & Wagner, Reference Rescorla, Wagner, Black and Prokasy1972). The second area to use the term discrimination learning is machine learning, where the concept of a discriminative model was introduced to provide a mechanism neutral contrast to generative models. Whereas the latter learn the data that generates a set of labels, discriminative models simply learn to maximize the conditional probabilities of labels for a set of labels given an input representation (Ng & Jordan, Reference Ng and Jordan2002). Finally, discriminative learning can be used to describe the mechanism implemented in the error-driven learning models. Because in most learning situations this mechanism enforces cue competition – which serves to discriminate against or in favor of the units that serve as inputs by re-weighting the influence of individual units – it serves to re-represent an input representation so as to maximize its informativity about a set of outputs (Ramscar et al., Reference Ramscar, Yarlett, Dye, Denny and Thorpe2010).

From this latter perspective, the mind of a newborn learner can be thought of as an undifferentiated set of inputs that are connected to an undifferentiated set of output states. Starting from what is, in functional terms, a system containing a single entity, the learner's representation of the world will grow into a larger set of (more or less individuated) entities as the error resulting from perceptible variances and invariances in the environment produces differentiation, increasing the degree of discrimination between inputs and outputs (Ramscar et al., Reference Ramscar, Yarlett, Dye, Denny and Thorpe2010, Reference Ramscar, Dye and McCauley2013a; see also James, 1890).

Learning and morphology – where connectionism went wrong

To turn the second question posed above – what do children learn about language? – I will initially consider it in relation to linguistic morphology, and, in particular, English inflectional morphology. Although this is a relatively simple morphological system, its properties embody many characteristics of language as a whole: it is systematic (the formation of most but not all English plurals can be described as adding an allomorph of the morpheme –s to a singular noun form); it is productive (children can readily generate past tenses for novel forms such as rick-ricked); and yet the system is quasiregular in that irregular forms deviate by degrees from the regular pattern (e.g., knife-knives, mouse-mice, child-children; Seidenberg & Plaut, Reference Seidenberg and Plaut2014; Ramscar, Reference Ramscarin press).

These properties have led to morphological development being used as a test domain for theories of language acquisition, with the question of what children learn in acquiring a morphological system being the subject of considerable debate. For example, Pinker (Reference Pinker1998) claimed that compositional rules are explicitly represented components of morphological knowledge, and argued that the processes of inflectional morphology, which seemingly distinguish productive regular items from unproductive irregulars, provide evidence for this claim. This was in contrast to the classic connectionist model presented by Rumelhart and McClelland (Reference Rumelhart, McClelland, McClelland and Rumelhart1986), which took the phonological form of a verb's present tense as input, and generated the phonological form of its past tense as output, using a uniform procedure for the generation of both regular and irregular (and novel) forms (see Ramscar, Reference Ramscarin press, for a review).

For current purposes, what was notable about the famous ‘past tense’ debate is that both sides agreed that what children learn in the course of morphological development are ways of composing and decomposing morphemes (Ramscar, Reference Ramscarin press). In the case of English plurals, it is assumed that a child learns a morpheme that associates the concept mouse with the word ‘mouse,’ an association between the concept mice and ‘mice,’ an association between the concept rat and ‘rat,’ and an association between the concept for plurality (or sets of objects, excluding multiple mouses etc.) and a morpheme +s, etc. Yet the discrete system of associations between forms and meanings envisaged here is difficult to reconcile with the highly interconnected systems that associative learning actually produces. Moreover, this neat picture of form-meaning mapping is also inconsistent with the results of research into human categorization, which show that human performance on categorization tasks is best accounted for by models that treat categorization as a process in which discrete outcomes such as labels, responses, etc., are discriminated in context from a more continuous system of inputs (Love, Medin & Gureckis, Reference Love, Medin and Gureckis2004).

If we allow that morphological systems are not sets of discrete mappings between units of meaning and lexical forms, some of the limitations in the assumptions shared by both sides of this debate become apparent. The Rumelhart and McClelland (Reference Rumelhart, McClelland, McClelland and Rumelhart1986) model assumed children learn transformational rules that add a discrete English past tense morpheme +ed to a verb stem to generate a past tense form, or a discrete plural morpheme +s to a singular noun stem to generate a plural. In keeping with this, the model's training set is a list of uninflected stems that are transformed into past tense forms, as if the learning environment contained speakers producing repetitive bursts of singular-plural forms. Yet in reality, adults do not go around repeating, “go-went, walk-walks.” Instead children learn in context, from hearing sentences like, “shall we go walk the dog?” (Gleitman, Reference Gleitman1965). Thus not only is the learning scenario assumed implausible, but critically, Rumelhart and McClelland's theoretical account of inflection learning appears to be compositional, even though it is implemented in a discriminative learning model (in which compositionality seems to make little sense, Lake & Baroni, Reference Lake and Baroni2018). All of which raises a question: what might a discriminative theoretical account of morphological development actually look like?

A discriminative model of morphological development and processing

If we accept that children encounter morphological variations in contexts that offer no obvious evidence for transformation (they don't actually here numerous repetitions of “go-went, dog-dogs), the what of learning in morphological development can be straightforwardly recast in terms of their learning what it is about the environment that warrants the use of a given linguistic form in a given context (Ramscar, Reference Ramscarin press). To illustrate how this works, I will briefly describe how a discriminative model learning English noun morphology accounts for the patterns of over-regularization often observed in development (Seidenberg & Plaut, Reference Seidenberg and Plaut2014). The model uses essentially the same learning rule as the Rumelhart and McClelland (Reference Rumelhart, McClelland, McClelland and Rumelhart1986) model. Where it differs is how it represents the learning task, and the nature of linguistic knowledge itself (representations critical to the performance of learning models, Bröker & Ramscar, Reference Bröker and Ramscar2020).

Because of the nature of the input, English noun inflection is difficult to learn even in comparison to verb inflection. Whereas children encounter more inflected than uninflected verb forms, and more of these forms (by token) are irregular than regular, plurals are different. Children mainly encounter singular nouns, and most plural noun types and tokens are regular. Yet as with the past tense, children's irregular plural production follows a ‘U-shaped’ developmental trajectory. Children who have produced ‘mice’ in one context will still produce over-regularized forms like ‘mouses’ in others (Ramscar & Yarlett, Reference Ramscar and Yarlett2007).

The discriminative model of morphological development described here (Ramscar & Yarlett, Reference Ramscar and Yarlett2007; Ramscar & Dye, Reference Ramscar and Dye2009; Ramscar et al., Reference Ramscar, Dye and McCauley2013a) is based on results indicating that lexical learning involves discriminating the cues to word use (Ramscar, Thorpe & Denny, Reference Ramscar, Thorpe and Denny2007; Ramscar et al., Reference Ramscar, Yarlett, Dye, Denny and Thorpe2010; Ramscar et al., Reference Ramscar, Dye and Klein2013b), and that patterns of morphological variation reflect similar semantic and contextual factors (Ramscar, Reference Ramscar2002; Ramscar & Dye, Reference Ramscar and Dye2011; Ramscar, Dye & Hübner, Reference Ramscar, Dye and Hübner2013c). Accordingly, the model assumes that children encounter words and morphological variations in context, and are faced with the task of discriminating the cues that are informative about their use. Since initially any kind of stuff in the world is potentially informative about any lexical contrast, an important aspect of learning to discriminate the cues to noun forms involves discriminating the more specific cue dimensions in the objects associated with them from the other, less specific dimensions they also comprise (that mousiness is a better cue to ‘mice’ than stuff). Similarly, learning to discriminate singulars from plurals requires learning the dimensions of numerosity that best predict different forms (that multiple mouse objects best predicts ‘mice’).

Figure 1a depicts some of the environmental dimensions that reliably covary with the irregular plural ‘mice.’ Critically, while all these dimensions co-occur with ‘mice’ at the same rate, their covariance with other nouns differs, resulting in cue competition. Because generic cues like stuff are reinforced when ‘mice’ is encountered, learners will expect mice to occur whenever stuff is present, resulting in prediction-error in the contexts where stuff occurs and ‘mice’ is not heard. This process will cause the value of these generic cues to weaken over time, such that multiple mouse-items will be learned as the best cue to ‘mice.’

Figure 1. A: Some of the semantic dimensions that will be present whenever a child is exposed to the word ‘mice’ in the context of mice. B: A more abstract representation of the relative specificity of these dimensions as cues to plural forms. Although the less specific cues (stuff and mousiness) will be reinforced during early in learning, their ubiquity will ultimately cause them to produce more errors than the uniquely informative cues. As a result, the influence of these less specific cues will wane as experience grows.

Accordingly, the actual pattern of reinforcement and unlearning of the environmental cues to different forms will depend on their distribution in the learning environment. Figure 1b shows how the various potential semantic cues to ‘mice’ overlap relative to a simple set of idealized cues to different singular and plural forms – irregulars, regular stems, and the regular plural contrast +s – in learning. Broadly speaking, the plural forms classed as ‘regular’ in English are similar in that they all end in a final sibilant that discriminates plural from singular forms (they also differ slightly in that different forms use different allomorphs of this final sibilant). By contrast, irregulars discriminate singular from plural forms in various ways. It is thus important to note that in this model, ‘rats’ is not conceptualized as comprising a stem that is inflected for plurality by adding +s, but rather, ‘rat’ and ‘rats’ are different word forms. Children must learn to discriminate one from the other, and the contextual cues appropriate to the usage of each (see Hoppe et al., Reference Hoppe, Hendriks, Ramscar and van Rijin press, for a comprehensive tutorial on this kind of learning process).

At the same time, because ‘rat’ and ‘rats’ are very similar forms that appear in very similar ratty contexts, the specific cues to them are difficult to discriminate. Similarly, the fact that a final sibilant discriminates the plural and singular forms of a great many words means that it is difficult to discriminate the specific semantic cues to the final sibilant in ‘rats’ ‘cats’ and ‘bats’. Given the distribution of cues and forms – in which regulars are by far more frequent – a learner's language model will initially come to expect plural forms that end in sibilants whenever sets of objects are described. This over-general expectation causes interference when irregular plurals are produced, causing the production of over-regularized forms.

However, further exposure to the same distribution serves to eliminate this interference. This is because the same generic cues that lead to over-regularization must inevitably also produce expectations for irregular forms (‘mice’) in contexts where regular forms will be used. The prediction errors that result from this will cause the unlearning of these generic dimensions as cues to mice, increasing the relative strength of more specific cues, and reducing the likelihood of future over-regularization. Accordingly, this model makes a clear, unambiguous prediction: at an appropriate stage of development, exposing children to regular forms alone ought to serve to reduce over-regularization, in any morphological paradigm.Footnote ¹ To perform a test of this hypothesis in relation to English plurals, regular and irregular plural and singular forms were elicited from two groups of children, after which one performed a control task and the other a task that required them to access the regular forms from the elicitation test in memory. Whereas children in the control task over-regularized at the same rate in a posttest, the experimental manipulation – which involved processing only regular forms – produced a significant decrease in the rate at which irregular forms were over-regularized (Ramscar et al., Reference Ramscar, Dye and McCauley2013a).

Regularity, information and coding

The plural learning model described above offers an interesting perspective on the idea of regularity in language. From a generative/compositional perspective, regularity is often assumed to be a desirable or normative goal for morphological systems, such that irregular paradigms represent deviations from the norm. However this assumption is at odds with phenomena like suppletion, where the exponents of inflectional paradigms are more or less related allomorphs (e.g., ‘go’-‘went’ /‘mouse’-‘mice’) that serve to obscure the form-meaning relationship in the paradigm as a whole. Critically, although suppletive forms are often type infrequent, they tend to be highly frequent as tokens, raising the question of what ‘normative’ means when languages are viewed statistically. It is thus interesting to note that in the model described above, suppletive forms serve to accelerate the discrimination of the specific cues to individual forms in learning. From this perspective, suppletive irregular forms like ‘went’ and ‘feet’ can be seen to encode strong examples of the form contrasts that learning and communication ultimately rely upon. Given that these processes will be facilitated by strong contrasts – ‘one,’ ‘two,’ ‘three’ – and impaired by weak contrasts – ‘one,’ ‘john,’ ‘gone’ – when seen from the perspective of learning and communication it is not suppletion that needs explaining so much as regularity (Ramscar, Dye, Blevins & Baayen, Reference Ramscar, Dye, Blevins, Baayen, Bar On and Ravit2018): why do languages tolerate the less discriminative form contrasts that lead to over-regularization?

In answering to this question, it will help to imagine a world whose language is defined in an enormous codebook. The code comprises a set of sound-symbols (codewords), each of which serves to uniquely discriminate one of the many, specific messages a speaker might possibly wish to send from the other messages they might have sent, such that the task facing a learner is that of memorizing every codeword / message of what is a fully suppletive language. Using this language will prove problematic, and considering why can help highlight some problems – especially with regards to learning – that any actual language must solve.

First, given that people will want to communicate many different messages, the codebook will be have to be enormous (in fact, boundless). Second, in order to generate the enormous number of codewords this will require, many codewords will have to be long and/or complex. Third, since memorizing the whole book will be impossible, each individual will have learned only a fraction of it, restricting communication to only those codewords speakers share knowledge of. These factors will make the language massively inefficient, if not unusable.

How might one offset these problems? One way to simplify the code would be to employ combinatorics: codewords that discriminate different kinds of messages – questions, declarations, etc. – could be defined, and combined with other codewords in signals, enabling the number of unique words required to be reduced. The code could be further improved by analyzing the rate at which people use each message. Shorter signals could then be assigned to more frequent messages, making it easier for people to learn the signals they are more likely to use before less generally useful signals.

These latter modifications presuppose there is some consistency in the likelihood with which every person wants to send any given message. Yet how likely is it that this will always be the case? To address this, a further, less obvious modification could be made: an analysis could be made of the various kinds of signals people send, along with their probabilities. The code could then be redesigned so as to distribute the discriminatory power of different kinds of codewords more efficiently and more abstractly across signals. The idea would be to strike a balance, such that shared needs use less coding resources, and those that vary a lot require more, so that the code's overall structure was matched to the collective needs of the community.

Finally, the code could be modified so as to tolerate ambiguity. If the same codewords/signals could be used to communicate different (yet similar) messages, and if speakers were to use context to resolve any uncertainty about the different meanings intended, the code's impossibly vast vocabulary could be reduced dramatically (Piantadosi, Tily & Gibson, Reference Piantadosi, Tily and Gibson2012).

However, whereas learning the original code simply involved memorizing form-meaning pairings one-by-one, it is far from clear this strategy will be compatible with all of these modifications. While combinatorics is compatible with the memorization of form-meaning pairs, this strategy would become less plausible as the code began to get more complex, and as its level of abstraction grew. Finally, when ambiguity – and the requirement that context be used to resolve uncertainty about intended meanings – are introduced, the codebook and the memorization of form-meaning pairs become unworkable. If context is necessary to learn how signals are used, then either the codebook will have to describe context, which is impossible (the book would have to resemble the fabulous cartographers’ 1:1 scale map of the empire, Borges, Reference Borges, Borges and Hurley1946), or else the code will have to be learned in context, and its design will somehow have to facilitate this process.

Given this imaginary language was initially defined in a book, it made sense to talk about it through a process of top down analysis and modification modification. However, if we allow that human communicative codes have evolved in response to the selection pressures that arise out of people's desire to communicate more or less important things more or less successfully, we might allow that the ambiguous, highly abstract structure of the modified code might arise naturally, as codes are used, reused and changed by successive generations. In what follows, I will assume that it is exactly this kind of socially evolved code that children must learn in order to enter into a linguistic community. I will seek to elucidate how these codes work, describe in detail how some aspects of them are learned, and illustrate how in fact, rather their being unlearnable (as other characterizations of language suggest), it appears that the structures of human communicative codes have evolved (culturally) to support their learning.

Before doing so, it is worth noting that thinking in theoretical linguistics (Goldberg, Reference Goldberg2003; Partee, Reference Partee2007; Ellis & Ferreira-Junior, Reference Ellis and Ferreira-Junior2009) and computational linguistics (Bender & Koller, Reference Bender and Koller2020; Lake & Baroni, Reference Lake and Baroni2018) is still dominated by the assumption that languages revolve around inventories of form-meaning parings, such that language acquisition is usually thought to involve learning these pairings (Pinker, Reference Pinker1998; Bohn & Frank, Reference Bohn and Frank2019). This is despite the fact that, as noted earlier, centuries of study have failed to provide a detailed account of what form-meaning parings are, or how children learn them. By contrast, the plural model described above did not learn a set of individual form-meaning pairings. Rather, it learned the systematic relationships between a set of environmental cues and a set of forms based on their distribution in training. In this model (and in more sophisticated versions of it), prior learning serves to eliminate the majority of potential relationships between a given set of inputs and the totality of possible outputs, such that more or less ‘discrete’ form-meaning ‘pairings’ emerge dynamically (and probabilistically) as the model is run (as it processes the inputs present in a given context). Thus while the model learns comparatively discrete mapping between the form mice and its contextual cues, many of the cues it learns to regular plural forms (cats, rats) are generic, such that in most cases the model does not learn a simple pairing between a set of meaning cues and a form, but rather it learns to ‘pair’ various aspects of meaning with various sets of forms.

These generic mappings – which underpin the model's ability to infer the form of novel plurals – are often described as ‘distributed representations’ in the connectionist literature (Rumelhart, Hinton & McClelland, Reference Rumelhart, Hinton, McClelland, Rumelhart, Hinton and McClelland1986). However, the use of ‘representation’ here is somewhat misleading, because the outputs of error-driven learning models cannot be read from the ‘representations’ they learn (the weights between their input and output layers), because as the generic cues in the plural model described above serve to highlight, error-driven learning models do not learn discrete pathways from inputs to outputs. Rather it is the interaction between a specific set of inputs and the learned state of a model (that occurs as it is run) that serves to discriminate an output state (such that similar inputs can result in the same or different outputs, depending on training).

In practice – given an appropriately structured environment and an appropriate amount of training – these models settle into learned states which represent distributed, somewhat abstract relationships between their sets of inputs and outputs that are stable and predictable even in the absence of a discrete pathway from a given input to an output. This points to an interesting state of affairs: although these models don't learn form-meaning pairings, they are able to simulate combinatoric generalization without ever implementing a compositional system (as when the plural inflection model described above infers that a novel noun should end in a sibilant in a context where plurality is implied). Moreover, these models can also help explain the intuitions that people have about form-meaning pairings and compositionality, and why these intuitions are ultimately misleading, because they can explain how people can learn to discriminate specific form-meaning relationships in use (Wittgenstein, Reference Wittgenstein1953) without ever learning inventories of ‘form-meaning pairings’ (see also Ramscar, Reference Ramscarin press).

These considerations point in turn to a clear difference in the predictions that compositional accounts of language make about the way that linguistic forms are distributed, and the kind of distributive predictions made by the highly abstract communicative systems described here. If languages are compositional, we should expect the distribution of form-meaning pairings to reflect human habit and interest. That is, if people prefer red to green, then this preference, and its degree, ought to be reflected in the distribution of the words ‘red’ and ‘green,’ such that patterns of usage should reflect patterns of relevance.

By contrast, if human communicative codes are akin to the final iteration of the imaginary language described above – such that meanings and messages are distributed abstractly across the code – this predicts that any relationships between patterns of usage and patterns of human interest ought to be far more abstract. If languages are communication systems, the use of individual words and constructions ought to be determined by communicative constraints, and we should expect that patterns of usage reflect these constraints.

To offer a first test of these different hypotheses, Figure 2a plots the usage frequencies (in the Corpus of Contemporary American English, Davies, Reference Davies2009) for a set of common colour words taken from Wikipedia (red, orange, yellow, green, blue, purple, brown, magenta, tan, cyan, olive, maroon, navy, aquamarine, turquoise, silver, lime, teal, indigo, violet, pink, black, white, grey/gray). Figure 2b then shows how the distribution of these frequencies is geometric (the geometric being the discrete form of the exponential distribution).

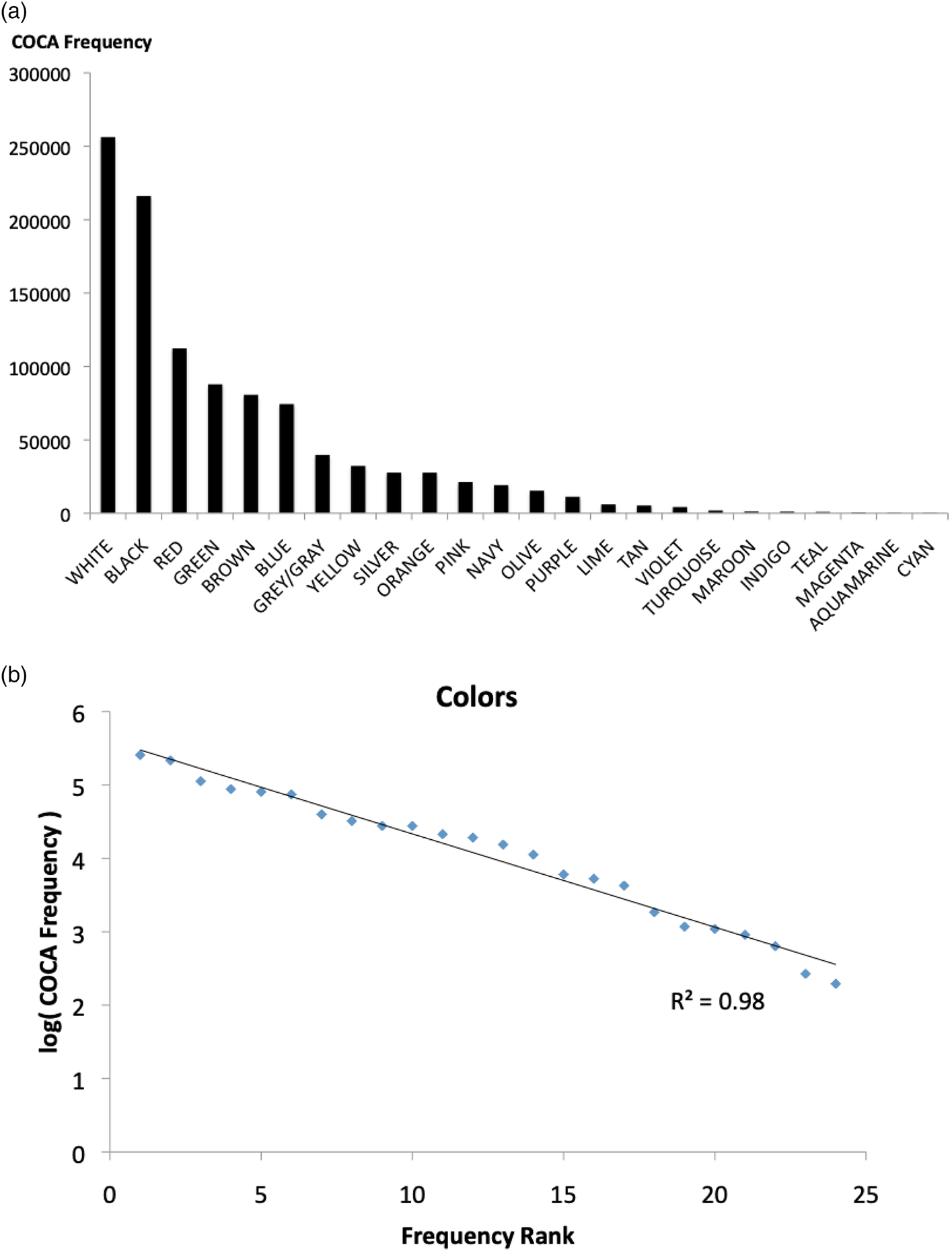
Figure 2. A: Corpus of Contemporary American English (COCA) frequencies of 24 color common English color words B: Log frequency x frequency rank plot of the same words (linear = exponential, R²=.98).

Empirically, it appears when people talk about colour in English, they use white exponentially more frequently than black, black exponentially more frequently than red, and red exponentially more frequently than green etc. Figure 3a then plots the COCA frequencies of a set of common kinship terms (mother, father, son, daughter, brother, sister, uncle, grandmother, aunt, grandfather, cousin, grandson, nephew, niece, granddaughter; taken from Kemp & Regier, Reference Kemp and Regier2012), and Figure 3b shows that the distribution of these words is also geometric.

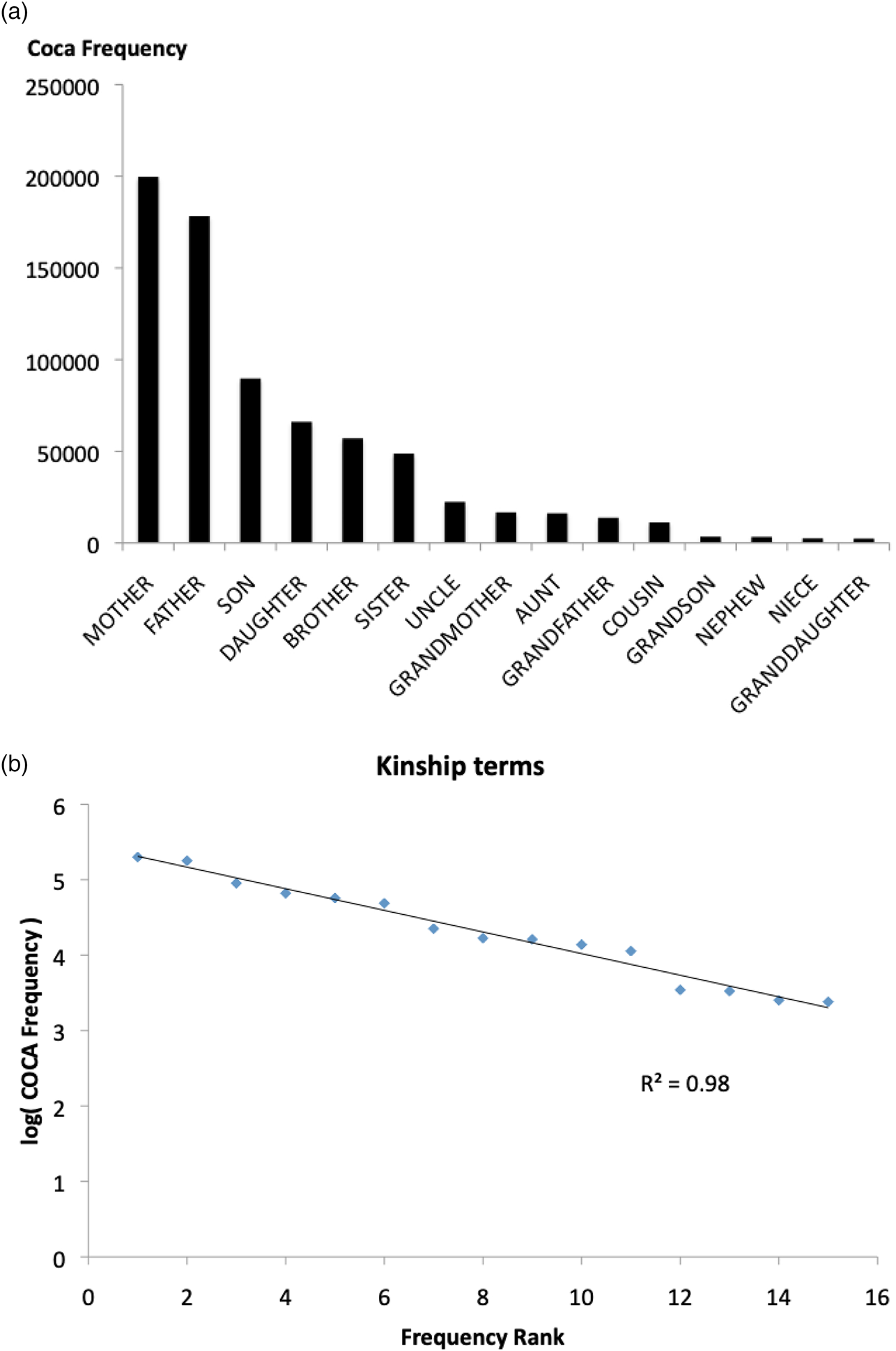
Figure 3. A: COCA frequencies of 15 common English kinship terms (Kemp & Regier, Reference Kemp and Regier2012) B: Log frequency x frequency rank plot of the same word frequencies (R²=.98).

Figure 4 plots the correlation between the distributions of colour and kin word (along with a replication using the 100 million-word British National Corpus), showing how the usage of what are supposed to be compositional items in these completely different domains follows exactly the same – highly abstract – pattern. Given sufficient time and effort, it is clear one could come up with plausible-sounding stories to account for these patterns of use. One might argue that colour word usage reflects biases on people's colour concepts, and that kinship usage reflects other biases, and that the suspicious similarities between their usage patters are coincidental, a consideration that points to a problem facing scientific studies of human communication: ‘language’ is such a complex and poorly defined construct that it is unclear that any of the many theories that compete to explain it can be falsified on the basis of a few failed predictions or contrary findings.

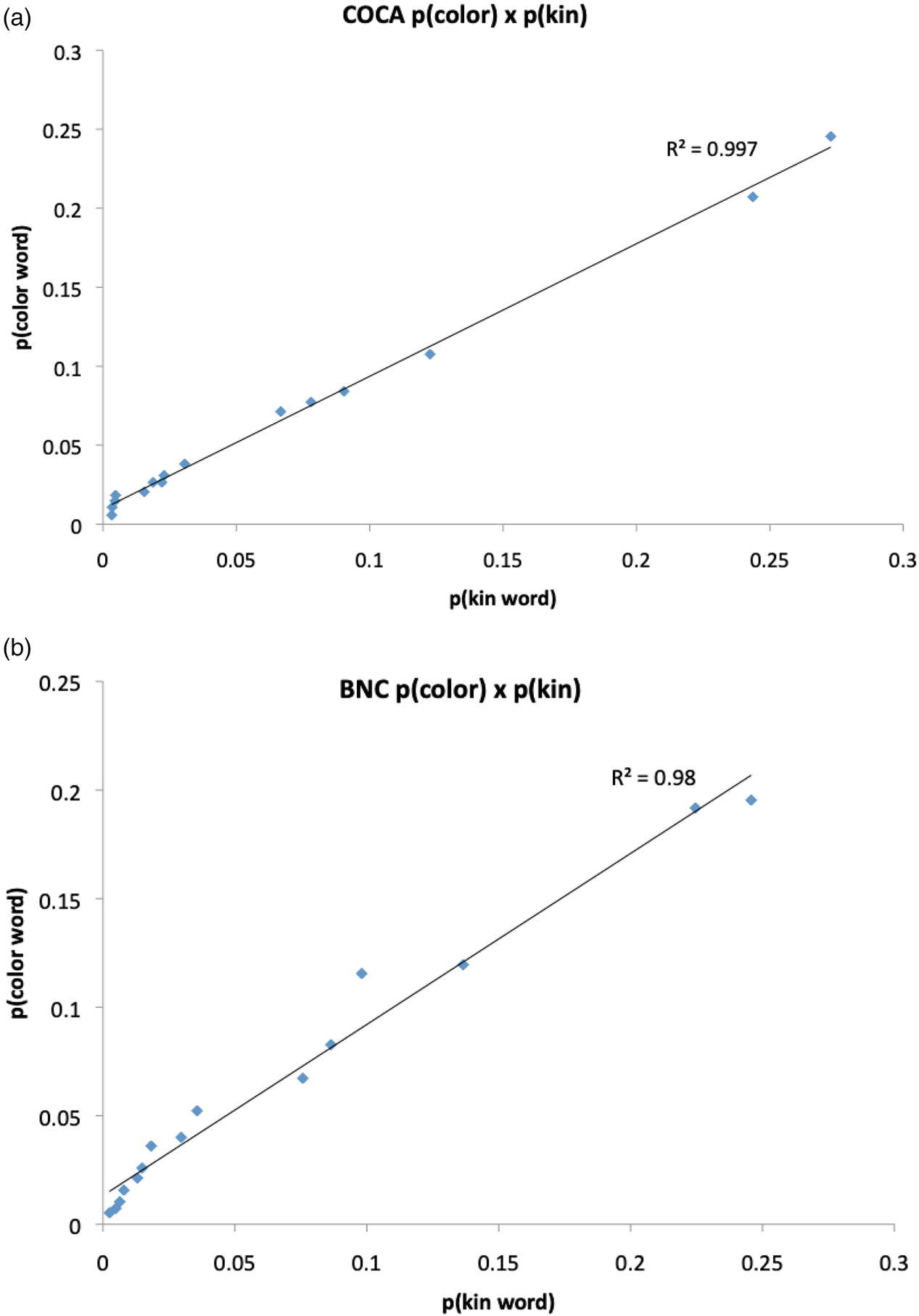
Figure 4. Point-wise comparisons of (A) the COCA probabilities of the 15 most frequent English colour words in Figure 1 (H=3.4 bits, calculated over all 24 items) and the probabilities of the English kin terms (3 bits) in Figure 3 (R²=.997), and (B) the same probabilities in the BNC (R²=.97; colour 3.4 bits; kin, 3 bits).

This should not surprise us, since this problem is not unique to the study of language. Indeed, despite the importance of falsification to science (Popper, Reference Popper1958), it is far from clear that theories themselves are actually falsifiable. Rather, it seems that whereas falsification allows for the rejection of specific hypotheses, it is explanatory adequacy that ultimately determines the fate of theories (Kuhn, Reference Kuhn1962). Thus, although the account of learning and communication presented here predicts these exact patterns, and predicts that they should be ubiquitous in communicative codes across different levels of description (Ramscar, Reference Ramscar2019, Reference Ramscar2020; Linke & Ramscar, Reference Linke and Ramscar2020) – such that the theory would be falsified if communicative codes were not structured in this wayFootnote ², the exact prediction and the exact findings that would falsify it are ultimately determined by the specific details of the various mechanisms proposed by different parts of the theory. Just like any other theory, the accuracy of the communicative account of language learning / use presented here will ultimately stand (or fall) on its ability to predict and explain linguistic phenomena more adequately and more accurately than other theories (Kuhn, Reference Kuhn1962; Cohen, Reference Cohen2017). Accordingly, the remainder of this article describes the mechanisms that predict these usage patterns in more detail, along with other predictions and explanations that can be derived from them, and findings in other domains that further support these analyses.

Information theory and human communication

One advantage of framing human communication in discriminative terms is that it enables linguistic theory to benefit from the insights gained from the study of discriminative codes in information theory. This work has shown, for example, how variable-length codes (in which codewords comprise a variable number of bits) enable the efficiency of communication to be maximized close to its theoretical limit (Shannon, Reference Shannon1948). The benefits of variable-length coding can be explained in intuitive terms: if one is easy to articulate, whereas five and twenty require successively more effort, then making one highly frequent and five and twenty successively less frequent will reduce the effort speakers must expend on number articulation. As the distribution and articulation of one, five and twenty suggests, the organization of natural languages do appear to reduce articulatory effort in this way (Lindblom, Reference Lindblom, Hardcastle and Marchal1990): word lengths and frequencies are reliably associated, with more frequent words (one) being shorter than less frequent words (nineteen, Piantadosi, Tily & Gibson, Reference Piantadosi, Tily and Gibson2011).

In recent years the development of massive speech and text corpora, and the tools to analyze and mine them has served to highlight these kinds of statistical regularities in linguistic codes. Studies of speech production have shown how words that are more predictable in context are more likely to undergo articulatory reduction (Bell, Brenier, Gregory, Girand & Jurafsky, Reference Bell, Brenier, Gregory, Girand and Jurafsky2009; Seyfarth, Reference Seyfarth2014; Linke & Ramscar, Reference Linke and Ramscar2020), whereas disfluencies and other difficulties in language processing are strongly associated with increases in lexical information (Howes, Reference Howes1957; van Rooij & Plomp, Reference van Rooij and Plomp1991; Westbury, Shaoul, Moroschan & Ramscar, Reference Westbury, Shaoul, Moroschan and Ramscar2016). The frequency distributions of words in natural languages have been shown to resemble variable length codes in that they are systematically skewed (Estoup, Reference Estoup1916), so that half the words in a corpus will reliably comprise tokens of around a hundred high-frequency types (‘and’, ‘the’), while the other half comprises very large numbers of low-frequency types (‘comprise’, ‘corpus’). The fact that word frequency distributions appear to have power law distributions has been taken as evidence that they have evolved (culturally) to optimize communication (Zipf, Reference Zipf1935, Reference Zipf1949), and many theories seek to explain how they help optimize linguistic communication (Mandelbrot, Reference Mandelbrot, Lazarsfield and Henry1966; Manin, Reference Manin2009; Piantadosi, Reference Piantadosi2014). These methods have also led to a resurgence of interest in the application of information theory to linguistics with many similarities between human and digital communication systems (and human behaviour and information theoretic predictions) being highlighted (Gibson et al., Reference Gibson, Futrell, Piantadosi, Dautriche, Mahowald, Bergen and Levy2019).

At the same time, however, some important properties of the communicative model described by information theory are difficult to reconcile with what is known about natural languages, and these differences become particularly salient when we consider how children learn to communicate, and what they must learn in doing so:

1. 1. Shannon's (Reference Shannon1948) theory of communication describes a system solution to the problem of signaling over a noisy channel (MacKay, Reference MacKay2003), based on predefined source and channel codes. Like the codebook of the imaginary language, source codes map messages onto source symbols (which are configured to optimize the use of bandwidth), while channel coding increases the reliability of transmission by adding redundancy to coded vectors of source symbols. These codes define a probabilistic model shared by every sender/receiver in a system. However the distributions of words in languages, and the fact that people learn them, guarantees no speaker / hearer ever learns an entire code (Ramscar, Hendrix, Love & Baayen, Reference Ramscar, Hendrix, Love and Baayen2013d).

2. 2. Individual samples of linguistic codes vary enormously (Ramscar et al., Reference Ramscar, Hendrix, Shaoul, Milin and Baayen2014; Ramscar, Sun, Hendrix & Baayen, Reference Ramscar, Sun, Hendrix and Baayen2017) suggesting that the probability models individuals learn may also vary considerably. By contrast, in information systems the provision of common codes ensures there is no difference between the individual probability models of each sender / receiver.

3. 3. The power law distributions observed in natural languages are not the most efficient distributions for variable length codes (Huffman, Reference Huffman1952; Gallager & Van Voorhis, Reference Gallager and Van Voorhis1975).

In other words, information theoretic models of communication are predicated on shared codes, whereas human communicative codes do not seem to be shared in anything like the same way. Further, while information theory describes a number of specific features that enable the development of optimized codes, these features do not appear to be present in linguistic codes. Finally, information theory describes a deductive process (Shannon, Reference Shannon1956) that serves to eliminate a receiver's uncertainty about the identity of a sender's message, using common codes that maximize the discriminability of messages while minimizing the cost of signaling. By contrast, most linguistic theories, even when they claim inspiration from information theory, adhere to compositional principles that make inductive assumptions about the way meanings are communicated.

These concerns differ in the degree to which they undermine the application of information theoretic concepts to human communication: however, they highlight two problems that appear to be critical. First, how do natural languages provide a degree of systematicity that is at least sufficient to support communication (how can they allow users to communicate despite their having partial access to a code)? Second, how do users of natural languages learn probability models that converge sufficiently for languages to be probabilistic systems (how can the common model that defines the information in a communication system be acquired and transmitted)? Unless these questions are answered, it would appear that the analogies researchers draw between language use and information theory, as well as any talk about languages as ‘probabilistic codes,’ can only be speculative at best

Learnability and the cost of naming

Personal names serve to discriminate individuals from their peers. Given that an obvious way of achieving this would be to give each individual a unique name, it seems that if any subsystem of language is going to be suppletive, it is names. It is thus notable that the world's languages do not take a suppletive approach to naming. Rather, somewhat strikingly, all languages adopt the same combinatoric solution to the problem of discriminating individuals, forming personal names from sequences of hierarchically structured name tokens that allow huge sets of identifiers to be constructed from relatively small sets of name types (Ramscar, Smith, Dye, Futrell, Hendrix, Baayen & Starr, Reference Ramscar, Smith, Dye, Futrell, Hendrix, Baayen, Starr, Knauff, Pauen, Sebanz and Wachsmuth2013e).

Name grammars

Formally, the information provided by a set of discrete codewords depends on their distribution (Shannon, Reference Shannon1948; see also Hartley, Reference Hartley1928; Nyquist, Reference Nyquist1924). Perhaps surprisingly, names offer a very intuitive explanation of this idea. Imagine that 33% of males are called John, and only 1% Cornelius. In this scenario, learning someone is named Cornelius is more informative than learning their name is John (Corneliuses are better discriminated by their names than Johns). On the other hand, Johns will be easier to remember (guessing ‘John’ will be correct 1/3 of the time). Further, although the memory advantage of John relies on its frequency, the memorability of Cornelius also benefits from this: Cornelius is easier to remember if the system contains fewer names (also, as discussed earlier, if John is easier to say than Cornelius, this will reduce the average effort of name articulation).

Finally, since John is so easy to remember and articulate, it may be possible to figure out a way of distributing names so that combining John with a high frequency word that serves as a name in context (Green, Smith etc.) can allow us to produce a combinatoric name that requires little/no more processing effort than Cornelius. That is, if the names John and Cornelius are distributed along the lines just described, one might possibly devise a system that balances the competing demands of discriminating individuals for communication purposes, while managing the processing and memory demands of using a code, in a near optimal way. Information theory offers formal proofs of these points, and shows that the most efficient way of distributing codewords (John, Cornelius) is by distributing their probabilities geometrically (Gallager & Van Voorhis, Reference Gallager and Van Voorhis1975; the geometric distribution being the discrete form of the exponential).Footnote ³

The actual name grammars of languages have been heavily impacted by name laws in the modern era, and the formal fixing of patronymic ‘family names’ for legal purposes in particular (in the Sinosphere, given names were legislated into patronyms, whereas in the West, bynames have become patronyms). While this has resulted in significant changes to the traditional, vernacular naming systems that existed before these laws were imposed (Ramscar, Reference Ramscar2019), it is still possible to discern a common structure in the name grammars of many languages. Perhaps surprisingly, the form of this structure is remarkably close to the John/Cornelius example above.

Names in modern Chinese (a family of Sino-Tibetan languages, Handel, Reference Handel2008) and modern Korean, a language isolate (Song, Reference Song2006) typically comprise two or three elements (Kiet, Baek, Kim & Jeong, Reference Kiet, Baek, Kim and Jeong2007). As a Korean name is encountered in speech, these comprise sequentially: first, one of a small number of family names (patronyms), second, a clan/generational name, and third, a given name. The size of the set of name tokens each is drawn from increases as names unfold, such that these names have a hierarchical structure in which each element simultaneously increases the degree to which an individual is identified, and reduces the number of alternatives that need to be discriminated between at each step.

Historically Sinosphere first names were drawn from a small set comprising around 100 or so name tokens (Baek, Kiet & Kim, Reference Baek, Kiet and Kim2007), and unlike family names in most of the world's languages (whose distributions appear to follow power laws) Chinese and Korean family names have been shown to be geometrically distributed (Yuan, Reference Yuan2002; Kiet et al., Reference Kiet, Baek, Kim and Jeong2007; Guo, Chen & Wang, Reference Guo, Chen and Wang2011). Since this suggests that the name grammars of Korean and Chinese may provide an optimal solution to some of the communicative problems posed by naming, Ramscar (Reference Ramscar2019) reconstructed a partial Vietnamese family name distribution from US census data (most Vietnamese Americans in the 2000 US census were named in Vietnam), and compared this to data from the 2000 South Korean census to examine whether this finding generalized to another, unrelated language (Vietnamese, which also employs patronyms as first names, is an Austroasiatic language, albeit with many lexical borrowings from Chinese; Sidwell & Blench, Reference Sidwell and Blench2011). As Figure 5 shows, the distribution of US Vietnamese and Korean first names is essentially identical.

Figure 5. A frequency normalized comparison of the distribution of the 60 most frequent first names in the 2000 South Korean Census to the 60 most frequent first names in a Vietnamese first name distribution constructed from the 2000 US Census (R²=.96; data from Ramscar, Reference Ramscar2019).

The distribution of English first names

The organization of Western and Sinosphere names suggests that Western given names and Sinosphere family names share a similar communicative function: given names come first as Western names are encountered in speech, and are drawn from a far smaller set than family names, which come last). However, analyses of U.S. census data show contemporary English first names to be Zipf distributed (Ramscar, Reference Ramscar2019). This is hardly surprising, first because the US population is over 325 million people (making it empirically impossible for individuals to sample the entire name distribution), and second because mixtures of exponentials often form produce power law distributions (Newman, Reference Newman2005). What is more relevant to actual communication – and critically, its development – are the distributions learners actually experience. In this regard, it is notable that analyses of the US social security records for the 50 US states and the District of Columbia across the 20^th Century (Ramscar, Reference Ramscar2020), show the average cumulative distributions of first names from 1910-2010 across the States to be geometric.

However, perhaps the most striking evidence for the communicative function of first names comes from comparing first name distributions in 18^th Century Scotland and England (Ramscar, Reference Ramscar2019) with those of China and Korea. Historically, first names in the latter comprised a stock of around 100 names (the colloquial Chinese expression for the common people – ‘Bǎijiāxìng’ – means ‘the hundred names’) and local name stocks for England and Scotland also comprised around 100 names, such that the distribution (r²=.96) and information entropy (Korea=4.7 bits; Scotland=4.8 bits) of historical Scottish / modern Korean first names share remarkably similar information structures (Ramscar, Reference Ramscar2019; Figure 6e)

Figure 6. A: Probabilities of the 100 most frequent given names (98% of population) by frequency rank in 4 Scottish parishes 1701–1800 plotted against an idealized exponential distribution. B: Pointwise comparison of the observed distribution to idealized exponential distribution. C: Pointwise comparison of the observed distribution to an idealized power-law distribution. D: Log (normalized) frequency x frequency rank plot comparing the distribution of first names in South Korea 2000 to that in Scotland 1701–1800 (Ramscar, Reference Ramscar2019).

How do name grammars work?

If we assume names encode identities (something neurotypical human brains seem to be adapted to discriminate, Kanwisher, McDermott & Chun, Reference Kanwisher, McDermott and Chun1997), it seems that the codes people use to communicate them employ exactly the kind of structures information theoretic accounts of human communication predict. Importantly, what should also be clear from the foregoing is that the function served by the name David is simply that of maximizing the likelihood that Davids (identities conditioned on David) will be discriminated from Marys etc. in communication (Figure 7).

Figure 7. Pictures discriminated by the search terms “David”, “David Bowie”, and “David Bowie Ziggy period” by Google image search (13/2/2019). “David” eliminates pictures not related to David, and “David Bowie” and “David Bowie Ziggy period” refine this discriminative process.

In some contexts, comprehenders may be able to discriminate a communicated message (identity) from a first name alone; in others, more information will have to be signaled. If we assume the contextual distributions of surnames are similar to those of first names, then empirical name grammars will tend to generate signals that minimize the average cost of name processing (Meylan & Griffiths, Reference Meylan and Griffiths2017), smooth the information communicated across signals (Aylett & Turk, Reference Aylett and Turk2004), and make names easier to access, use and recall (Dye, Johns, Jones & Ramscar, Reference Dye, Johns, Jones and Ramscar2016). It is thus important to note that from this perspective the name David Bowie is discriminative encoding, and its function can be explained without assuming that it is composed from the concepts DAVID and BOWIE.

Memorylessness and the alignment of communicative models

Thus far our discussion of geometric distributions has focused on their contribution to the efficiency of communication. However, these distributions have a further property that is particularly important to communicative learning. The geometric distribution is unique in being the only discrete memoryless distribution (just as the exponential distribution is unique in being the only continuous memoryless distribution). This property is important because it suggests a solution to a problem, raised above, of explaining how learners with very different experiences of a probability distribution nevertheless learn the same model of it, so that their communicative expectations are actually shared (a problem all probabilistic models of communication must face).

The memoryless property is best explained in terms of waiting times: if the probabilities of encountering people at any given point in time are distributed exponentially, then (because of the way these distributions interact with the laws of conditional probability) it can be proven that the probability of encountering someone at any specific point in time t_n is independent of the time that has elapsed since t₁, the time a person was last encountered. A counterintuitive result of this proof is that when the periods between encounters are exponentially distributed, the likelihood of encountering another individual in a minute is independent of the time that has elapsed since the last person was encountered, such that the likelihood is the same 30 minutes after the last encounter as it was 2 minutes after; and it will remain the same 2 hours later.

If we assume these probability laws apply to learning from lexical distributions, it follows that when words are geometrically distributed individuals will learn similar models of the words’ underlying probabilities, even if the size of two samples varies considerably (Townsend & Ashby, Reference Townsend and Ashby1983, pp. 38–45; Linke & Ramscar, Reference Linke and Ramscar2020). Accordingly, it is further worth noting that the human frontal cortex develops over a prolonged period, such that the control mechanisms that allow mature learners to more flexibly sample their environments take two to three decades to develop. From a communicative perspective this a hugely beneficial developmental trait, since restricting learners to a naïve sampling strategy will further increase the likelihood that typically developing children learn the same communicative models as their peers (Ramscar & Gitcho, Reference Ramscar and Gitcho2007; Thompson-Schill, Ramscar & Chrysikou, Reference Thompson-Schill, Ramscar and Chrysikou2009; Ramscar et al., Reference Ramscar, Dye and Klein2013b; Ramscar, Dye, Gustafson & Klein, Reference Ramscar, Dye, Gustafson and Klein2013f).

Whether these mathematical points about sampling and learning actually apply to human learners are empirical questions. This account makes clear predictions in regard to them: if learners are exposed to sets of geometrically distributed forms, they should acquire models of their probabilities that better approximate one another than when learning from other distributions. Conversely, if learning from geometric distributions does not produce convergence, it would suggest the probabilistic account of communication described here (indeed, any probabilistic account of communication) is false.Footnote ⁴

Semantics and the distributional structure of codes

As noted above, while almost all linguistic theories assume compositionality, no adequate account of what compositional meanings are, or how they are learned, actually exists (Ramscar & Port, Reference Ramscar, Port, Dabrowska and Divjak2015). While the many difficulties involved in defining meanings are acknowledged, the consensus is that these problems must be solvable. If children learn to use words like dog or red, this must be because they learn – or innately have – the concepts DOG and RED. The communicative account of names presented above offers a way out of this circular thinking. If we accept that the information contributed by Mary is not derived from the concept MARY, but rather is a function of Mary's role in a discriminative system of names, then providing a non-compositional account of how names are learned and used in context is a straightforward task. This line of reasoning points to an interesting conclusion: although the theoretical problems posed by compositionality seem particularly acute with regards to names (Gray, Reference Gray2014; Fara, Reference Fara2015), a series of analyses by Wittgenstein (Reference Wittgenstein1953) indicate that the problems involved in explaining the meanings of common nouns and names are ultimately the same. If Wittgenstein's analyses are right, then the use of nouns, verbs and adjectives etc., should be amenable to the same functional analysis.

A source of support for this suggestion comes from studies of colour and number words. Although infants can distinguish basic colour categories (Bornstein, Kessen & Weiskopf, Reference Bornstein, Kessen and Weiskopf1976), and despite their high frequencies in the input, children's use of colour words is haphazard for a surprisingly long period (Sandhofer & Smith, Reference Sandhofer and Smith1999). Children's learning of number words shows a very similar pattern of problems, and again, these do not stem from an inability to discriminate along the appropriate dimension (Ramscar, Dye, Popick & O'Donnell-McCarthy, Reference Ramscar, Dye, Popick and O'Donnell-McCarthy2011). Discriminatively, the obvious problem here is that while children might encounter ‘three apples’ or ‘red apples,’ three and red are never encountered independently. Rather, since these words inevitably occur in ambiguous contexts (Figure 8) children must learn to discriminate the cues to their use in context. As with the learning of the cues to mouse and mice described earlier, if language is used informatively, children will be able to solve this problem by discriminating a distributed representation of the environmental features that predict the use of various lexical contrasts in context in the code. However, because discriminative learning relies on cue competition and prediction error, the temporal structure of information is a critical factor in it.

Figure 8. An illustration of the challenge presented by colour and number learning. This picture contains: six circles, and three squares; white circles and black squares; and more circles than squares / less squares than circles; some of the circles and squares are larger and some are smaller. Somehow children must learn the cues that discriminate between the appropriate and inappropriate use of these words in context.

This point is best illustrated by comparing the effects of learning in contexts when complex (multi-feature) stimuli predict discrete linguistic forms (Labels), to its inverse. In the examples described so far in this paper, Features in the world have served as cues to Labels (FL-learning; Ramscar et al., Reference Ramscar, Yarlett, Dye, Denny and Thorpe2010), an information structure that naturally allows for features to compete as cues to labels. When this relationship is reversed (see Figure 9), such that labels serve as cues (LF-learning), cue competition becomes problematic, because the serial nature of speech means that only one label cue is present at any time. Since a single cue cannot compete with itself, learning ceases to be discriminative, and produces a representation of the probability of each feature given the label instead (Ramscar, Reference Ramscar2013; Hoppe et al., Reference Hoppe, van Rij, Hendriks and Ramscar2021, Vujović, Ramscar & Wonnacott, Reference Vujović, Ramscar and Wonnacott2021; see also Rische & Komarova, Reference Rische and Komarova2016; Ma & Komarova, Reference Ma and Komarova2017).

Figure 9. The possible predictive relationships labels (words or affixes) can enter into with the other features of the world (or a code). A feature-to-label relationship (left) will tend to facilitate cue competition between features, and the abstraction of the informative dimensions that predict labels in learning, whereas a label-tofeature relationship (right) will facilitate learning of the probabilities of the features given the label.

With regards to colours and numbers, although discourse factors may make these temporal relationships rather more complicated in the real world, this analysis predicts that post-nominal constructions will be more likely to facilitate the discrimination of the appropriate system of cues to set of these words than pre-nominal constructions. Empirical results support this prediction, showing that training with post-nominal constructions significantly improves the accuracy and consistency of two-year olds’ number and colour word use, whereas pre-nominal training has no effect on their performance. These results also help explain why children struggle to learn colour and number words despite their frequency in the input: in English, where these problems have mostly been studied, children overwhelmingly encounter colour and number words in pre-nominal constructions (Ramscar et al., Reference Ramscar, Yarlett, Dye, Denny and Thorpe2010, Reference Ramscar and Dye2011).

However, this analysis raises a question: if sentences like “red ball” are unhelpful to learners, why do people use them so often? The answer appears to lie in the specific problems nouns pose in communication. Because humankind has a propensity for inventing things that need names, in most languages nouns comprise a very large set of types. Analyses show that, by splitting them into classes, the German grammatical gender system serves to reduce the uncertainty associated with nouns in context, a function that English (a largely non-gendered language), achieves through its distribution of pre-nominal adjectives (which are more frequent, and more informative about nouns than German pre-nominal adjectives; Dye, Milin, Futrell & Ramscar, Reference Dye, Milin, Futrell, Ramscar, Kiefer, Blevins and Bartos2017; Dye, Milin, Futrell & Ramscar, Reference Dye, Milin, Futrell and Ramscar2018).

These findings indicate that gender systems may communicate more information about content than is often supposed (and that English pre-nominal adjectives communicate more grammatical information than is often supposed), but more importantly, they also indicate that content information may be far more distributed than compositional theories assume.

Meaning, function, and the distributional structure of codes

The distinction between function and content words that is assumed in many linguistic theories appears to be further complicated by findings showing that measures derived from the distributional patterns of words can accurately predict human behaviour in tasks normally associated with ‘semantic processing’ (Landauer & Dumais, Reference Landauer and Dumais1997; McDonald & Ramscar, Reference McDonald and Ramscar2001; Ramscar, Reference Ramscar2002; Ramscar & Yarlett, Reference Ramscar and Yarlett2003; Johns & Jones, Reference Johns and Jones2010). These models are typically described at a lexical level, as capturing distributional aspects of the ‘meaning’ of individual lexical items. However, for present purposes, what is important to understand about these models is that they simply measure the conditioning history of a word in relation to the other words in a sample. When two words have the same conditioning histories (if their co-occurrence patterns are identical), then although learning will discriminate them from words that don't share their history, it will not result in their being discriminated from one another. Further, because learning is probabilistic, when a subset of words share conditioning histories that only slightly vary from one another, a learner's expectations about the behaviour of the words within this subset will be far less discriminated from each other than they will be from the rest of the lexical system. The members of this subset will thus form a probabilistic cluster within this system, and a learner's expectations will tend to relate as much to this subset as any individual item within it.

These considerations suggest that, because semantically similar words covary systematically in the lexicon, they will cluster together when they are learned in context. From this perspective, co-occurrence patterns can be seen to discriminate a level of coarse semantic similarities that is at a higher level than content words, and yet informative about them (again, blurring distinctions between ‘content’ and ‘function’ words). Which further suggests that all meaningful linguistic communication – including communication about seemingly concrete things like nouns – might be discriminative, based on the same process of incremental uncertainty reduction as names. This hypothesis makes clear, falsifiable predictions: If grammar works discriminatively, then for the same functional reasons that name distributions are geometrically distributed, it predicts any other class of words that is systematically encoded in distributional patterns should also be geometrically distributed. Moreover, the theory further predicts that children should be able to learn these classes along with their native language.Footnote ⁵ Initial support for this prediction comes from analyses showing how a set of relatively unambiguous semantic clusters that can be reliably extracted from child-directed speech using a range of co-occurrence model (Asr, Willits & Jones, Reference Asr, Willits and Jones2016; see Table 1) are geometrically distributed (Ramscar, 2109; Figure 10). Assuming these findings generalize to the other lexical subcategories discriminated by co-occurrence patterns in speech (see Figure 5), they can begin to explain how adult and child speakers are able to align their communicative expectations.

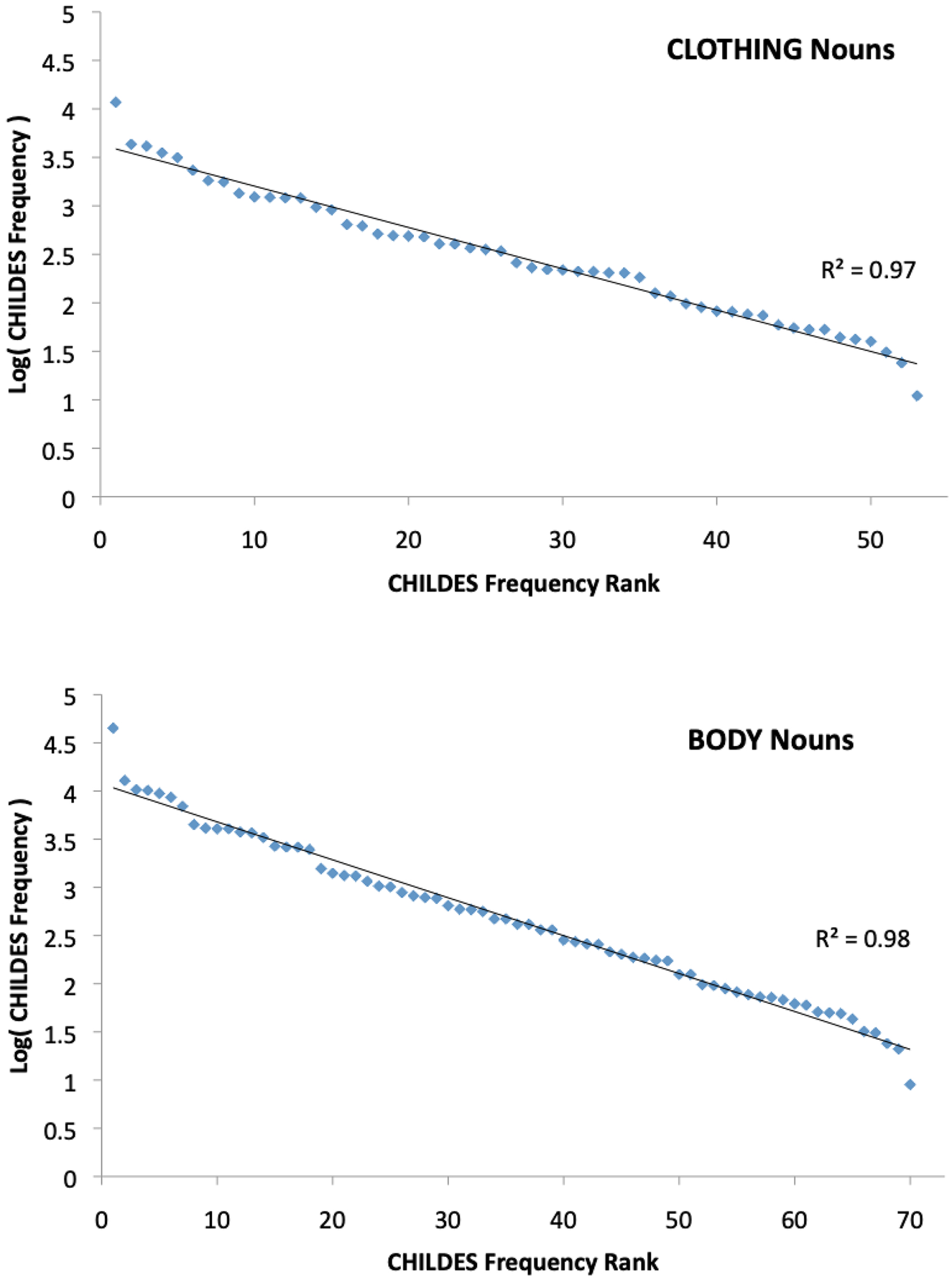
Figure 10. Log frequency x frequency rank plots of the two noun categories extracted from by CHILDES (Asr et al, Reference Asr, Willits and Jones2016). As can be seen, both of these categories, which are discriminated by the contexts in which they occur, have a geometric distribution.

Table 1: Nouns in two categories defined by context in CHILDES (Asr et al., Reference Asr, Willits and Jones2016).

Learning verbs and arguments

So far this article focused on the learning of systems of lexical items and morphological contrasts, albeit that it has sought to emphasize the importance of context in defining these classes, and the way that the learning of classes of items depends on shared patterns of variance and invariance in relation to other items. From this perspective, a long-studied feature of verbs is particularly notable: namely, that verbs inevitably take arguments, the structure of which often differs systematically across verb classes. Thus unlike nouns and names, which can be characterized as being learned as classes of lexical items, verbs are different. Verb learning seems to be best characterized in terms of the acquisition of classes of arguments (patterns of relations between lexical items), because an aspect of verbs that is relatively invariant across contexts is their relationship to the arguments they occur in.

The idea that distributional patterns might systematically discriminate verbs into coherent subcategories has a long history (Levin, Reference Levin1993), and numerous theories have been put forward to explain the relationship between the semantic properties of verb subcategories and their different argument structures (Fillmore, Reference Fillmore, Bach and Harms1968; Jackendoff, Reference Jackendoff1972; Goldberg, Reference Goldberg1995), and the way children learn corrects patterns of generalization within them (Gropen, Pinker, Hollander & Goldberg, Reference Gropen, Pinker, Hollander and Goldberg1991; Brooks & Zizak, Reference Brooks and Zizak2002; Ambridge et al., Reference Ambridge, Pine, Rowland, Chang and Bidgood2013, Reference Ambridge, Pine, Rowland, Freudenthal and Chang2014). For example, constructionist accounts of argument learning propose that a child's knowledge of a language is initially a set of initial fixed patterns, which then develop into semi-productive item-based constructions, before adult competence (in which the scope of some constructions remains limited, while the scope of others seems more open-ended) is achieved.

At a broad level these theories account well for the patterns of behaviour associated with verb argument learning (Goldberg, Reference Goldberg1995; Cameron-Faulkner, Lieven & Tomasello, Reference Cameron-Faulkner, Lieven and Tomasello2003; Tomasello, Reference Tomasello2006; Ambridge & Lieven, Reference Ambridge and Lieven2011; Ambridge et al., Reference Ambridge, Pine, Rowland, Freudenthal and Chang2014). However, the mechanisms that they use to explain the developmental progression described above – schematization and analogy – tend to be poorly specified (Beekhuizen, Bod & Verhagen, Reference Beekhuizen, Bod and Verhagen2014), as is the relationship between traditional and constructionist ideas about the basic functions of language, such as compositionality (Kay & Michaelis, Reference Kay, Michaelis, Maienborn, von Heusinger and Portner2012). By contrast, the processes of ‘schematization’ and ‘analogy’ (or at least their discriminative analogues) are clearly specified in learning models. Cue competition leads to abstraction, while overgeneralization / analogy simply represent the probabilistic output of a system given its current state of learning (Ramscar et al., Reference Ramscar, Dye and McCauley2013a).

To date, however, there have been very few investigations of verb argument learning from an explicitly discriminative perspective, such that when it comes to accounting for their acquisition, only promissory notes and predictions can be offered in this article (though see Bidgood et al., Reference Bidgood, Pine, Rowland, Sala, Freudenthal and Ambridge2021; Ambridge et al., Reference Ambridge, Maitreyee, Tatsumi, Doherty, Zicherman, Pedro, Bannard, Samanta, McCauley, Arnon and Bekman2020, for encouraging signs in this direction). Accordingly, what is notable for current purposes is the degree of compatibility between constructionist accounts of verb argument acquisition and a discriminative learning perspective. One aspect of children's early grammars emphasized by the former is that they appear to comprise a mixture of words, holophrases and ‘unanalyzed expressions’ (Pine & Lieven, Reference Pine and Lieven1997; Tomasello, Reference Tomasello2003), such that when language use initially becomes productive, utterances tend to be organized around particular words (Tomasello, Reference Tomasello2000). These early constructions typically comprise what Braine (Reference Braine1976) describes as ‘pivot words’ (specific relational terms, which are typically verbs), and ‘open slots,’ that are filled in turn by a wider range of words or expressions (typically semantically appropriate nouns). Initially, only the items that are related by pivot words tend to vary, with variance in other words only emerging later, as children's experience grows.

This pattern of learning is highly compatible with the behaviour of discriminative learning models, in which the initial process of association is always maximal: when a child hears a string comprised of a series of novel acoustic contrasts for the very first time, all and any available contextual / semantic cues in the environment will be associated to that string (Arnon & Ramscar, Reference Arnon and Ramscar2012). The discrimination of the more or less discrete ‘components’ in a system then depends on experience and error; such that the degree to which different aspects of form and meaning are associated in context will be a function of the distribution of the forms and a learner's experience of it (Ramscar et al., Reference Ramscar, Dye and McCauley2013a). Moreover, explicitly treating the learning of argument structure as a discriminative process also highlights the way that communicative systems have evolved to support learning: analyses of the empirical distribution of a set of English verb subcategories defined by the shared alternation patterns of their members (Levin, Reference Levin1993) reveal that like nouns and names, verb arguments are geometrically distributed (Ramscar, Reference Ramscar2019, Reference Ramscar2020; see Figure 11 for an example).

Figure 11. Table 2 shows the verbs in the Build subcategory (Levin, Reference Levin1993). The top panel plots their frequencies in CHILDES, and the bottom panel shows the fit of these frequencies to a geometric distribution. A comparison of 40 sets of verb alternation patterns to the sets of verbs beginning with the 20 most frequent English letters showed that although the frequency distributions of verbs following letters are Zipf distributed, the frequency distributions of the verbs defined by their alternation patterns are all geometric (Ramscar, Reference Ramscar2020).

In the light of this discussion of the discriminability and learnability of forms in morphological paradigms, it is worth highlighting a further aspect of the distribution of verb alternation subcategories: that the most frequent arguments in each distribution tend to involve irregular verbs (strongly marking at least some of the semantic contrasts in the argument), whereas the less frequent arguments are regular, a pattern that will appear to support the appropriate generalization of lower frequency items across the full set of alternations warranted by each subcategory. Given that the account of verb learning put forward here assumes that learning to produce a plural or use an argument differ only in their degrees of complexity, it follows that this discriminative account of the acquisition of verb arguments predicts that the incorrect use of arguments (*don't giggle me) is not merely the product of a child's failure to adequately learn the specific cues to a particular argument, but also their failure to unlearn the generic cues that lead to over-generalization. The theory thus predicts that, at an appropriate stage of development, training children on correct arguments (don't tickle me) should result in a decrease in over-generalization errors (*don't giggle me). Failure to find evidence for this would not only falsify this prediction (and the assumptions that inform it), it would also raise serious questions about the account of morphological development described earlier.Footnote ⁶

Table 2: The ‘Build’ verb alternation class (Levin, Reference Levin1993).

Models of learning and representation

It is clear that modeling the acquisition and processing of verbs is a more complicated task than modeling inflectional morphology or number and colour word learning. While the semantic dimensions of the morphological models described earlier were crude, they succeeded in capturing many of the more important features of the discriminative puzzle solved by a child learning to use plural forms in a useful, informative way (and as Box, Reference Box1979, pointed out, usefulness is all scientific models can aspire to). Moreover, the fact that the representations employed in the various models described earlier were actually sufficient for their purpose highlights a commonality in all of them: that seemingly different learning tasks such as inflectional morphology and colour word learning both involve the discrimination of relationships between relatively straightforward perceptual/contextual dimensions and relatively simple forms. The simplicity of this approach came with clear theoretical benefits, in that it is amenable to modeling using simple two-layer networks. In these, the discriminative nature of error-driven learning, the contribution of the input and output representation, and any theoretical insights that might be gleaned from interactions between them, can be made fairly transparent.

By contrast, given what they communicate – causality, agency, manner, etc., often all at once – learning to use verb arguments involves the task of discriminating semantic relationships that are multidimensional, that are distributed across different items that arguments comprise, and that are likely far more semantically abstract than anything considered earlier. Meanwhile, the distributions described above guarantee that learners encounter some argument structures at very high rates, and others hardly at all. It thus follows that in any individual, the degree to which learning will have discriminated any given argument structure along its various semantic / form dimensions is likely to vary considerably at any given time. For example, in the 460+ million word COCA corpus, make, the most frequent of the build verbs described above, occurs 130,000 times; embroider, the least frequent, occurs 5 times. Learners will thus encounter make across a wide range of contexts, in which a wide variety of forms will fill its arguments. This will lead them to discriminate very abstract representations of the relationship between make arguments and the cues to the forms they comprise. By contrast, embroider will be encountered in a far more restrictive set of contexts in which a small set of forms comprise its arguments. Accordingly, learners will acquire representations that are less abstract, such that at the form level embroider will be associated more with specific items and less with abstract classes, while, at the semantic level, the cues to embroider arguments will be more associated with the whole structure, and less with specific parts of it (in both cases, this is a consequence of the fact that learners will have had less opportunity to discriminate more abstract relationships at the form and semantic level; Ramscar et al., Reference Ramscar, Dye and McCauley2013a). In other words, not only must learners discriminate their representations of the cues to make and embroider arguments across multiple dimensions (e.g., between forms and forms, and semantics and forms) at multiple levels of abstraction at the same time, but since their experiences of the two different arguments will differ greatly, their representations of them will likely differ greatly as well.

Since the two-layer networks described earlier are ill-suited to modeling interactions at multiple layers of abstraction in learning, it follows that accounting for verb argument learning in children will involve the addressing of some difficult methodological and theoretical challenges. For example, at first blush, multi-layer, deep learning networks appear ideally suited to capturing this kind of complex multidimensional learning (LeCun et al., Reference LeCun, Bengio and Hinton2015). They develop representations at multiple layers of abstraction (Kozma, Ilin & Siegelmann, Reference Kozma, Ilin and Siegelmann2018), and appear – at least in principle – to be capable of learning many of the complex relational patterns that characterize human communicative codes (Graves, Reference Graves2012; Hannun et al., Reference Hannun, Case, Casper, Catanzaro, Diamos, Elsen, Prenger, Satheesh, Sengupta, Coates and Ng2014; Sutskever, Vinyals & Le, Reference Sutskever, Vinyals and Le2014; Jozefowicz, Vinyals, Schuster, Shazeer & Wu, Reference Jozefowicz, Vinyals, Schuster, Shazeer and Wu2016). However, although multi-layer networks are theoretically capable of the kind of complex, multi-level learning that appears to characterize this domain, this kind of modeling often leads to Bonini's problem (Bonini, Reference Bonini1963), in that understanding exactly how these models actually learn their functions can be as challenging as understanding children's learning itself.

Given this problem, recent attempts to understand the performance of multi-layer networks in language processing tasks by treating them as experimental subjects (McCloskey, Reference McCloskey1991) are interesting (see e.g., Futrell, Wilcox, Morita, Qian, Ballesteros & Levy, Reference Futrell, Wilcox, Morita, Qian, Ballesteros and Levy2019; Linzen, Dupoux & Goldberg, Reference Linzen, Dupoux and Goldberg2016; Wilcox, Levy, Morita & Futrell, Reference Wilcox, Levy, Morita, Futrell, Linzen, Chrupała and Alishahi2018), first because these approaches underline the difficulties involved in actually translating the complexities of learning at multiple levels of abstraction into theoretical insight (Bonini's paradox), and secondly because they suggest that the study of communicative development may be maturing away from straw-man arguments about learnability, and towards the development of accounts of what human communication actually comprises and what learning to communicate actually entails.

As well as requiring the kind of reappraisal of the processes involved in human communication outlined here, it seems inevitable that explaining how children learn to communicate will also involve a reappraisal of what we might expect from theories and models themselves. For example, just as there seems little use in asking whether multi-layer network models of language processing are capable of compositionality if it turns out that human communication is not compositional, the complex architecture of the human brain seems to rule out the idea that human learning can be reduced to a single set of representations that are processed in a uniform fashion within a single model.

Whereas for the purposes of exposition this article has treated ‘error-driven learning’ as a somewhat monolithic, abstract concept, it seems clear that the brain contains a range of different circuits that are capable of learning from prediction error depending upon the complexity of the stimuli and the temporal dynamics of the learning ‘episode’Footnote ⁷ involved (Freedberg, Toader, Wassermann & Voss, Reference Freedberg, Toader, Wassermann and Voss2020). For example, dissociable neurobiological circuits implementing error sensitive learning mechanisms have been identified in the striatum (Schultz, Dayan & Montague, Reference Schultz, Dayan and Montague1997; Daw, Niv & Dayan, Reference Daw, Niv and Dayan2005) and the medial temporal lobe (MTL; Delgado & Dickerson, Reference Delgado and Dickerson2012; Shohamy & Daw, Reference Shohamy, Daw, Gazzaniga and Mangun2014), yet they appear to differ in their temporal sensitivity to prediction error. In tasks that tap people's ability to learn probabilistic associations, the performance of amnesic patients with MTL damage is impaired when response-contingent feedback is delayed, but not when feedback is provided immediately. By contrast, patients with Parkinson's disease (which involves the progressive degeneration of substantia nigra dopaminergic neurons and their projections into the striatum) show the opposite pattern (Foerde, Race, Verfaellie & Shohamy, Reference Foerde, Race, Verfaellie and Shohamy2013). These findings suggest that changes in trial durations on the ‘same’ task can elicit responses from different learning circuits in the brain, resulting in concomitant differences in what is learned.

In a similar vein, the fact that learners simultaneously appear sensitive to both the specifics of individual experiences and abstractions from them indicates that the brain's multiple learning mechanisms produce multiple representations at multiple levels of abstraction (Squire, Reference Squire2004), suggesting that no single ‘language learning model’ will suffice to account for the full range of linguistic behaviour observed in individuals. Thus although many theories have suggested that the ‘end state’ of language learning can be characterized by the acquisition of a particular set of abstract linguistic representations (Gold, Reference Gold1967; Pinker, Reference Pinker1998) or that abstractions are barely learned at all (Ambridge, Reference Ambridge2020), it seems far more likely to be the case that language learning has no end state, and that explaining an individual's communicative capacities requires more than a single model operating on one level of representation.

Rather, in the same way that linguistic units are better thought of as descriptive idealizations as opposed to psychological elements (Ramscar & Port, Reference Ramscar and Port2016; Samuel, Reference Samuel2020), we should accept that the linguistic representations posited by all theories of communicative development are wrong, yet some will prove more theoretically useful than others. Accordingly, it is to be hoped the focus of the field of language development can move away from vague questions about ‘learnability’ to more specific questions about what children learn and how they learn it. To return to an earlier example, the what and how of Rumelhart and McClelland's (Reference Rumelhart, McClelland, McClelland and Rumelhart1986) past tense model are easily stated: it assumed that morphological learning involves mastering the transformation of root forms into past tense forms using phonetic information alone. Given a set of phonological cues representing root forms, it used error-driven learning in order to try to discriminate the set of values that best predicted a corresponding set of phonological representations representing past tense forms. From the perspective of the discriminative models of inflection described earlier, the Rumelhart and McClelland model used the wrong input-output representations (sound-to-sound) and attempted to learn the wrong function (transforming root forms into past tense forms, rather than trying to use context to predict the forms of words, Ramscar, Reference Ramscarin press). However, the important point here is not so much which of these models is ‘right’ and which is ‘wrong’ (though there are numerous reasons to believe that Rumelhart & McClelland's approach was misguided from the outset, Ramscar, Reference Ramscarin press), but rather what is important is that although these models all use the same basic learning algorithm, they embody very different theoretical models, and these differences matter (Bröker & Ramscar, Reference Bröker and Ramscar2020).

From the perspective outlined here, a child learning to communicate must master a systematic set of mappings between their experiences of ‘the world’ and a highly structured, resolutely probabilistic system of forms. Since any model of this process is likely to be complex and ‘incomplete,’ understanding how a specific model contributes to theory must necessarily involve a discussion of its limitations as well as its capabilities. For example, when it comes to word learning and what it means for a child to ‘know a word,’ there is a vast difference between learning about yellow from lexical co-occurrence data and learning about yellow as most children eventually do (as ‘embodied’ sensory agents, in contexts where objects of various hues are experienced along with various form contrasts). However, it is likely that, for a child, learning that yellow serves as a cue to just a subset of words can still be useful in language processing even before the child knows what yellow ‘means’, because pronominal adjectives can provide statistical information about upcoming nouns even before one understands their semantic relationship to the world (Dye et al., Reference Dye, Milin, Futrell, Ramscar, Kiefer, Blevins and Bartos2017). However to conflate knowledge of the former with knowledge of the latter is a theoretical failure. Rather, when it comes to understanding how language is used and processed in communication, it seems clear that what is required are more subtle and more detailed theoretical approaches that break these different senses of a child's ‘knowing’ a word down into their component parts. In this review, I have tried to show how information theory and learning theory can offer important tools for the development of these kinds of more subtle and detailed kinds of theoretical description.

Conclusion: learning, communication and discrimination

One of the most important ideas contributed by information theory is the proposal that codewords do not contribute information in isolation, but rather as part of a system. The information value of any given codeword is a function of the set of codewords it belongs to – i.e., the codewords that might be expected to occur in a given context – and it contributes information as a function of the expectancies provided by the system, in an eliminative rather than compositional manner. Similarly, one of the most important ideas contributed by learning theory is the proposal that what is learned is not just a function of events that occur together, but also of events that might have been expected to occur but do not. And again, this process works in an eliminative manner, discriminating against and eliminating potential associations that result in error so as to positively weight informative cues and negatively weight uninformative cues. In reality, learning is as much about learning to ignore as it is about learning to associate.

To date it seems fair to say that the literature on human communication and its development has not covered itself in glory when it comes to grasping either of these ideas. However there seems to be no principled reason to suppose that progress towards better models of these processes is impossible. What I have sought to outline here is how, when seen through the lens of learning and information theory, much of the structure of natural communications systems begin to make sense, and many of the mysteries of communicative development begin to seem a lot less puzzling. Clearly a more complete discriminative theory of human communication will require more flesh on its bones than this short review can provide. A better alignment between linguistic theory and the appropriate formal models of communication, computation and learning can only help in this regard.