Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-20T10:32:42.340Z Has data issue: false hasContentIssue false
  • English
  • Français

MAXIMAL SUBSEMIGROUPS OF INFINITE SYMMETRIC GROUPS

Part of: Semigroups Basic linear algebra

Published online by Cambridge University Press:  29 January 2024

SUZANA MENDES-GONÇALVES Open the ORCID record for SUZANA MENDES-GONÇALVES [Opens in a new window]  and
R. P. SULLIVAN
SUZANA MENDES-GONÇALVES*
Affiliation:
Centro de Matemática, Universidade do Minho, 4710 Braga, Portugal
R. P. SULLIVAN
Affiliation:
School of Mathematics and Statistics, University of Western Australia, Nedlands, Western Australia 6009, Australia e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Brazil et al. [‘Maximal subgroups of infinite symmetric groups’, Proc. Lond. Math. Soc. (3) 68(1) (1994), 77–111] provided a new family of maximal subgroups of the symmetric group 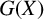$G(X)$ defined on an infinite set X. It is easy to see that, in this case, 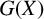$G(X)$ contains subsemigroups that are not groups, but nothing is known about nongroup maximal subsemigroups of 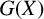$G(X)$. We provide infinitely many examples of such semigroups.

Keywords

maximal subsemigroupsinfinite symmetric groupinfinite general linear group

MSC classification

Primary: 20M20: Semigroups of transformations, etc.
Secondary: 15A04: Linear transformations, semilinear transformations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 2 , October 2024 , pp. 324 - 337
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

To the memory of Eckehart Hotzel, with respect and gratitude

Research by the first author was partially financed by Portuguese Funds through FCT (Fundação para a Ciência e a Tecnologia) within the Projects UIDB/00013/2020 and UIDP/00013/2020.

References

Brazil, M., Covington, J., Penttila, T., Praeger, C. E. and Woods, A. R., ‘Maximal subgroups of infinite symmetric groups’, Proc. Lond. Math. Soc. (3) 68(1) (1994), 77–111.10.1112/plms/s3-68.1.77CrossRefGoogle Scholar
Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, Volumes 1 and 2, Mathematical Surveys, 7 (American Mathematical Society, Providence, RI, 1961 and 1967).Google Scholar
East, J., Mitchell, J. D. and Péresse, Y., ‘Maximal subsemigroups of the semigroup of all mappings on an infinite set’, Trans. Amer. Math. Soc. 367(3) (2015), 1911–1944.10.1090/S0002-9947-2014-06110-2CrossRefGoogle Scholar
Hotzel, E., ‘Maximality properties of some subsemigroups of Baer–Levi semigroups’, Semigroup Forum 51 (1995), 153–190.10.1007/BF02573628CrossRefGoogle Scholar
Howie, J. M., An Introduction to Semigroup Theory (Academic Press, London, 1976).Google Scholar
Hungerford, T. W., Algebra (Springer-Verlag, New York, 1974).Google Scholar
Jacobson, N., Lectures on Abstract Algebra, 3 volumes (van Nostrand, Amsterdam, 1953).10.1007/978-1-4684-7053-6CrossRefGoogle Scholar
Mendes Araújo, C. and Mendes-Gonçalves, S., ‘Injective linear transformations with equal gap and defect’, Bull. Aust. Math. Soc. 105 (2022), 106–116.10.1017/S0004972721000344CrossRefGoogle Scholar
Mendes-Gonçalves, S. and Sullivan, R. P., ‘Baer–Levi semigroups of linear transformations’, Proc. Roy. Soc. Edinburgh Sect. A 134(3) (2004), 477–499.10.1017/S0308210500003309CrossRefGoogle Scholar
Mendes-Gonçalves, S. and Sullivan, R. P., ‘Maximal inverse subsemigroups of the symmetric inverse semigroup on a finite-dimensional vector space’, Comm. Algebra 34(3) (2006), 1055–1069.10.1080/00927870500442013CrossRefGoogle Scholar
Sanwong, J. and Sullivan, R. P., ‘Injective transformations with equal gap and defect’, Bull. Aust. Math. Soc. 79 (2009), 327–336.10.1017/S0004972708001330CrossRefGoogle Scholar