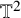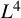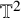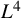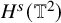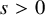1 Introduction
In the seminal work [Reference Bourgain1], Bourgain proved Strichartz estimates for the Schrödinger equation on (rational) tori
![]() $\mathbb {T}^{d}:=(\mathbf {\mathbb {R}}/2\pi \mathbf {\mathbb {Z}})^{d}$
. More precisely, in dimension
$\mathbb {T}^{d}:=(\mathbf {\mathbb {R}}/2\pi \mathbf {\mathbb {Z}})^{d}$
. More precisely, in dimension
![]() $d=2$
, the endpoint estimate in [Reference Bourgain1] states that there exists
$d=2$
, the endpoint estimate in [Reference Bourgain1] states that there exists
![]() $c>0$
such that for all
$c>0$
such that for all
![]() $\phi \in L^2(\mathbb {T}^2)$
and
$\phi \in L^2(\mathbb {T}^2)$
and
![]() $N \in \mathbf {\mathbb {N}}$
,
$N \in \mathbf {\mathbb {N}}$
,
The proof in [Reference Bourgain1] is based on the circle method and can be reduced to an estimate for the number of divisors function, which necessitates the above constant
![]() $C_N$
. However, in the example
$C_N$
. However, in the example
![]() $\widehat {\phi }=\chi _{[-N,N]^2\cap \mathbf {\mathbb {Z}}^2}$
, we have
$\widehat {\phi }=\chi _{[-N,N]^2\cap \mathbf {\mathbb {Z}}^2}$
, we have
see [Reference Bourgain1, Reference Takaoka and Tzvetkov15, Reference Kishimoto11].
More recently, the breakthrough result of Bourgain–Demeter on Fourier decoupling [Reference Bourgain and Demeter2] provided a more robust approach which has significantly extended the range of available Strichartz estimates on rational and irrational tori. However, the above endpoint
![]() $L^4$
estimate has not been improved by this method. Here, we will consider dimension
$L^4$
estimate has not been improved by this method. Here, we will consider dimension
![]() $d=2$
only, but let us remark that in dimension
$d=2$
only, but let us remark that in dimension
![]() $d=1$
, there is a similar problem concerning the
$d=1$
, there is a similar problem concerning the
![]() $L^6$
estimate, where it is known from [Reference Bourgain1] that the best constant is between
$L^6$
estimate, where it is known from [Reference Bourgain1] that the best constant is between
![]() $c (\log N)^{1/6}$
and
$c (\log N)^{1/6}$
and
![]() $C_N$
, with recent improvements of the upper bound to
$C_N$
, with recent improvements of the upper bound to
![]() $c(\log N)^{2+\varepsilon }$
[Reference Guth, Maldague and Wang7, Reference Guo, Li and Yung6] by Fourier decoupling techniques.
$c(\log N)^{2+\varepsilon }$
[Reference Guth, Maldague and Wang7, Reference Guo, Li and Yung6] by Fourier decoupling techniques.
In this paper, we obtain the sharp
![]() $L^4$
estimate in dimension
$L^4$
estimate in dimension
![]() $d=2$
by using methods of incidence geometry. Set
$d=2$
by using methods of incidence geometry. Set
![]() $\log x:=\max \{1,\log _e x\}$
for
$\log x:=\max \{1,\log _e x\}$
for
![]() $x>0$
.
$x>0$
.
Theorem 1.1. There exists
![]() $c>0$
, such that for all bounded sets
$c>0$
, such that for all bounded sets
![]() $S\subset \mathbf {\mathbb {Z}}^{2}$
and all
$S\subset \mathbf {\mathbb {Z}}^{2}$
and all
![]() $\phi \in L^{2}(\mathbb {T}^{2})$
, we have
$\phi \in L^{2}(\mathbb {T}^{2})$
, we have
In fact, we prove a stronger result.
Theorem 1.2. There exists
![]() $c>0$
, such that for all bounded sets
$c>0$
, such that for all bounded sets
![]() $S\subset \mathbf {\mathbb {Z}}^{2}$
and all
$S\subset \mathbf {\mathbb {Z}}^{2}$
and all
![]() $\phi \in L^{2}(\mathbb {T}^{2})$
, we have
$\phi \in L^{2}(\mathbb {T}^{2})$
, we have
Remark 1.3. Theorem 1.2 implies Theorem 1.1: Applying (1.3) to each interval
![]() $[2\pi \frac {k-1}{m},2\pi \frac {k}{m}]$
,
$[2\pi \frac {k-1}{m},2\pi \frac {k}{m}]$
,
![]() $k=1,\ldots ,m$
, for
$k=1,\ldots ,m$
, for
![]() $m\approx \log \#S$
, we obtain (1.2). In particular, (1.1) implies the sharpness of Theorem 1.2 as well.
$m\approx \log \#S$
, we obtain (1.2). In particular, (1.1) implies the sharpness of Theorem 1.2 as well.
For the proof of Theorem 1.2, we develop a new method based on a counting argument for parallelograms with vertices in given sets, which relies on the Szemerédi-Trotter Theorem. We remark that the Szemerédi-Trotter Theorem was previously used to bound the number of right triangles with vertices in a given set [Reference Pach and Sharir13], and it has also been introduced in [Reference Bourgain and Demeter2] in connection to Fourier decoupling and discrete Fourier restriction theory. More precisely, if
![]() $\widehat {\phi }=\chi _S$
, estimate (1.2) is a corollary of the Pach-Sharir bound in [Reference Pach and Sharir13]. We point out that in our proof of Theorem 1.2, we also make use of the fourth vertex.
$\widehat {\phi }=\chi _S$
, estimate (1.2) is a corollary of the Pach-Sharir bound in [Reference Pach and Sharir13]. We point out that in our proof of Theorem 1.2, we also make use of the fourth vertex.
Theorems 1.1 and 1.2 apply to functions with Fourier support in arbitrary sets. Although we make use of the lattice structure, we only use an elementary number theoretic argument in the proof of Theorem 1.2: in the parallelogram
![]() $(\xi _1,\xi _2,\xi _3,\xi _4)\in (\mathbf {\mathbb {Z}}^2)^4$
the quantity
$(\xi _1,\xi _2,\xi _3,\xi _4)\in (\mathbf {\mathbb {Z}}^2)^4$
the quantity
![]() $\tau =2(\xi _1-\xi _2)\cdot (\xi _1-\xi _4)$
must be a multiple of the greatest common divisor of the two coordinates of
$\tau =2(\xi _1-\xi _2)\cdot (\xi _1-\xi _4)$
must be a multiple of the greatest common divisor of the two coordinates of
![]() $\xi _1-\xi _4$
, which is used to avoid a logarithmic loss in Theorem 1.2.
$\xi _1-\xi _4$
, which is used to avoid a logarithmic loss in Theorem 1.2.
The
![]() $L^4$
-Strichartz estimate plays a distinguished role in the analysis of the cubic nonlinear Schrödinger equation (cubic NLS)
$L^4$
-Strichartz estimate plays a distinguished role in the analysis of the cubic nonlinear Schrödinger equation (cubic NLS)
which is
![]() $L^2(\mathbb {T}^2)$
-critical. (NLS) is known to be locally well-posed in Sobolev spaces
$L^2(\mathbb {T}^2)$
-critical. (NLS) is known to be locally well-posed in Sobolev spaces
![]() $H^s(\mathbb {T}^2)$
for
$H^s(\mathbb {T}^2)$
for
![]() $s>0$
due to [Reference Bourgain1]. It is also known [Reference Kishimoto11, Cor. 1.3] that the Cauchy problem is not perturbatively well-posed in
$s>0$
due to [Reference Bourgain1]. It is also known [Reference Kishimoto11, Cor. 1.3] that the Cauchy problem is not perturbatively well-posed in
![]() $L^2(\mathbb {T}^2)$
, which is closely related to the example (1.1) discussed above.
$L^2(\mathbb {T}^2)$
, which is closely related to the example (1.1) discussed above.
By the conservation of energy, local well-posedness in
![]() $H^1(\mathbb {T}^2)$
implies global well-posedness for small enough data [Reference Bourgain1, Theorem 2]. In the defocusing case, this has been refined to global well-posedness in
$H^1(\mathbb {T}^2)$
implies global well-posedness for small enough data [Reference Bourgain1, Theorem 2]. In the defocusing case, this has been refined to global well-posedness in
![]() $H^s(\mathbb {T}^2)$
for
$H^s(\mathbb {T}^2)$
for
![]() $s>3/5$
; see [Reference De Silva, Pavlović, Staffilani and Tzirakis4, Reference Fan, Staffilani, Wang and Wilson5, Reference Schippa14]. Additionally, the result in [Reference Colliander, Keel, Staffilani, Takaoka and Tao3] shows that energy is transferred from small to higher frequencies and therefore causing growth of Sobolev norms
$s>3/5$
; see [Reference De Silva, Pavlović, Staffilani and Tzirakis4, Reference Fan, Staffilani, Wang and Wilson5, Reference Schippa14]. Additionally, the result in [Reference Colliander, Keel, Staffilani, Takaoka and Tao3] shows that energy is transferred from small to higher frequencies and therefore causing growth of Sobolev norms
![]() $\|u(t)\|_{H^s}$
for
$\|u(t)\|_{H^s}$
for
![]() $s>1$
.
$s>1$
.
Theorem 1.2 has the following consequence:
Theorem 1.4. There exists
![]() $\delta>0$
such that for
$\delta>0$
such that for
![]() $s>0$
and initial data
$s>0$
and initial data
![]() $u_{0}\in H^{s}(\mathbb {T}^2)$
with
$u_{0}\in H^{s}(\mathbb {T}^2)$
with
![]() $\|u_{0}\|_{L^{2}(\mathbb {T}^2)}\leq \delta $
, the Cauchy problem (NLS) is globally well-posed.
$\|u_{0}\|_{L^{2}(\mathbb {T}^2)}\leq \delta $
, the Cauchy problem (NLS) is globally well-posed.
The proof is based on an estimate showing that
![]() $\|u(t)\|_{H^s(\mathbb {T}^2)}$
can grow only by a fixed multiplicative constant on a logarithmic time scale and because of
$\|u(t)\|_{H^s(\mathbb {T}^2)}$
can grow only by a fixed multiplicative constant on a logarithmic time scale and because of
![]() $\sum _{N\in 2^{\mathbf {\mathbb {N}}}} 1/\log N=\infty $
, any finite time interval can be covered. This argument crucially relies on the sharpness of the estimate in Theorem 1.2. Indeed, if the time interval in Theorem 1.2 were
$\sum _{N\in 2^{\mathbf {\mathbb {N}}}} 1/\log N=\infty $
, any finite time interval can be covered. This argument crucially relies on the sharpness of the estimate in Theorem 1.2. Indeed, if the time interval in Theorem 1.2 were
![]() $[0,(\log \#S)^{-\alpha }]$
for
$[0,(\log \#S)^{-\alpha }]$
for
![]() $\alpha>1$
instead, the sum would be
$\alpha>1$
instead, the sum would be
![]() $\sum _{N\in 2^{\mathbf {\mathbb {N}}}}1/(\log N)^\alpha <\infty $
, which would not yield a global result.
$\sum _{N\in 2^{\mathbf {\mathbb {N}}}}1/(\log N)^\alpha <\infty $
, which would not yield a global result.
2 Preliminaries
We write
![]() $A\lesssim B$
if
$A\lesssim B$
if
![]() $A\le CB$
for some universal constant
$A\le CB$
for some universal constant
![]() $C>0$
, and
$C>0$
, and
![]() $A\approx B$
if both
$A\approx B$
if both
![]() $A\lesssim B$
and
$A\lesssim B$
and
![]() $B\lesssim A$
. Given a set E, we denote
$B\lesssim A$
. Given a set E, we denote
![]() $\chi _{E}$
as the sharp cutoff at E.
$\chi _{E}$
as the sharp cutoff at E.
For proposition P, denote by
![]() $1_{P}$
the indicator function
$1_{P}$
the indicator function
 $$ \begin{align*}1_{P}:=\begin{cases} 1, & {P}\ \text{is true}\\ 0, & \text{otherwise} \end{cases}.\end{align*} $$
$$ \begin{align*}1_{P}:=\begin{cases} 1, & {P}\ \text{is true}\\ 0, & \text{otherwise} \end{cases}.\end{align*} $$
For a function
![]() $f:\mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$
,
$f:\mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$
,
![]() ${\mathcal {F}}f=\widehat {f}$
denotes the Fourier series of f. For
${\mathcal {F}}f=\widehat {f}$
denotes the Fourier series of f. For
![]() $S\subset \mathbf {\mathbb {Z}}^{2}$
, we denote by
$S\subset \mathbf {\mathbb {Z}}^{2}$
, we denote by
![]() $P_{S}$
the Fourier multiplier
$P_{S}$
the Fourier multiplier
![]() $\widehat {P_{S}f}:=\chi _{S}\cdot \widehat {f}$
.
$\widehat {P_{S}f}:=\chi _{S}\cdot \widehat {f}$
.
![]() $2^{\mathbf {\mathbb {N}}}$
denotes the set of dyadic numbers. For dyadic number
$2^{\mathbf {\mathbb {N}}}$
denotes the set of dyadic numbers. For dyadic number
![]() $N\in 2^{\mathbf {\mathbb {N}}}$
, we denote by
$N\in 2^{\mathbf {\mathbb {N}}}$
, we denote by
![]() $P_{\le N}$
the sharp Littlewood-Paley cutoff
$P_{\le N}$
the sharp Littlewood-Paley cutoff
![]() $P_{\le N}f:=P_{[-N,N]^{2}}f$
. We denote
$P_{\le N}f:=P_{[-N,N]^{2}}f$
. We denote
![]() $P_{N}:=P_{\le N}-P_{\le N/2}$
, where we set
$P_{N}:=P_{\le N}-P_{\le N/2}$
, where we set
![]() $P_{\le 1/2}:=0$
. For function
$P_{\le 1/2}:=0$
. For function
![]() $\phi :\mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$
and time
$\phi :\mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$
and time
![]() $t\in \mathbf {\mathbb {R}}$
, we define
$t\in \mathbf {\mathbb {R}}$
, we define
![]() $e^{it\Delta }\phi $
as the function such that
$e^{it\Delta }\phi $
as the function such that
For simplicity, we denote
![]() $u_{N}=P_{N}u$
and
$u_{N}=P_{N}u$
and
![]() $u_{\le N}=P_{\le N}u$
, for
$u_{\le N}=P_{\le N}u$
, for
![]() $u:\mathbb {T}^2\rightarrow \mathbf {\mathbb {C}}$
.
$u:\mathbb {T}^2\rightarrow \mathbf {\mathbb {C}}$
.
Geometric notations on
 $\mathbf {\mathbb {Z}}^{2}$
$\mathbf {\mathbb {Z}}^{2}$
For integer point
![]() $(a,b)\in \mathbf {\mathbb {Z}}^{2}$
,
$(a,b)\in \mathbf {\mathbb {Z}}^{2}$
,
![]() ${(a,b)}^{\perp }$
denotes
${(a,b)}^{\perp }$
denotes
![]() $(-b,a)$
.
$(-b,a)$
.
For integer point
![]() $(a,b)\in \mathbf {\mathbb {Z}}^{2}\setminus \left \{ 0\right \} $
,
$(a,b)\in \mathbf {\mathbb {Z}}^{2}\setminus \left \{ 0\right \} $
,
![]() $\gcd \left ((a,b)\right )$
denotes
$\gcd \left ((a,b)\right )$
denotes
![]() $\gcd (a,b)$
.
$\gcd (a,b)$
.
Given two integer points
![]() $\xi _1,\xi _2\in \mathbf {\mathbb {Z}}^2$
,
$\xi _1,\xi _2\in \mathbf {\mathbb {Z}}^2$
,
![]() $\overleftrightarrow {\xi _1\xi _2}$
denotes the line through
$\overleftrightarrow {\xi _1\xi _2}$
denotes the line through
![]() $\xi _1$
and
$\xi _1$
and
![]() $\xi _2$
.
$\xi _2$
.

Figure 2.1 Parallelogram Q.
A parallelogram is a quadruple
![]() $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in (\mathbf {\mathbb {Z}}^{2})^{4}$
such that
$Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in (\mathbf {\mathbb {Z}}^{2})^{4}$
such that
![]() $\xi _{1}+\xi _{3}=\xi _{2}+\xi _{4}$
. The set of all parallelograms is denoted by
$\xi _{1}+\xi _{3}=\xi _{2}+\xi _{4}$
. The set of all parallelograms is denoted by
![]() ${\mathcal {Q}}$
. Segments and points are two-element pairs and elements of
${\mathcal {Q}}$
. Segments and points are two-element pairs and elements of
![]() $\mathbf {\mathbb {Z}}^{2}$
, respectively. We call by the edges of Q either the segments
$\mathbf {\mathbb {Z}}^{2}$
, respectively. We call by the edges of Q either the segments
![]() $(\xi _{1},\xi _{2}),(\xi _{2},\xi _{3}),(\xi _{3},\xi _{4}),(\xi _{4},\xi _{1})$
, or the vectors
$(\xi _{1},\xi _{2}),(\xi _{2},\xi _{3}),(\xi _{3},\xi _{4}),(\xi _{4},\xi _{1})$
, or the vectors
![]() $\pm \left (\xi _{1}-\xi _{2}\right ),\pm \left (\xi _{1}-\xi _{4}\right )$
.
$\pm \left (\xi _{1}-\xi _{2}\right ),\pm \left (\xi _{1}-\xi _{4}\right )$
.
For a parallelogram
![]() $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}$
(see Fig. 2.1), we denote by
$Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}$
(see Fig. 2.1), we denote by
![]() $\tau _{Q}$
the number
$\tau _{Q}$
the number
For
![]() $\tau \in \mathbf {\mathbb {N}}$
, we denote by
$\tau \in \mathbf {\mathbb {N}}$
, we denote by
![]() ${\mathcal {Q}}^{\tau }$
the set of parallelograms
${\mathcal {Q}}^{\tau }$
the set of parallelograms
![]() $Q\in {\mathcal {Q}}$
such that
$Q\in {\mathcal {Q}}$
such that
![]() $\tau _{Q}=\tau $
. Thus, in particular,
$\tau _{Q}=\tau $
. Thus, in particular,
![]() ${\mathcal {Q}}^{0}$
is the set of rectangles.
${\mathcal {Q}}^{0}$
is the set of rectangles.
Szemerédi-Trotter
The following is a consequence of Szemerédi-Trotter theorem of incidence geometry.
Proposition 2.1 [Reference Tao and Vu16, Corollary 8.5].
Let
![]() $S\subset \mathbf {\mathbb {R}}^{2}$
be a set of n points, where
$S\subset \mathbf {\mathbb {R}}^{2}$
be a set of n points, where
![]() $n\in \mathbf {\mathbb {N}}$
. Let
$n\in \mathbf {\mathbb {N}}$
. Let
![]() $k\ge 2$
be an integer. The number m of lines in
$k\ge 2$
be an integer. The number m of lines in
![]() $\mathbf {\mathbb {R}}^{2}$
passing through at least k points of S is bounded by
$\mathbf {\mathbb {R}}^{2}$
passing through at least k points of S is bounded by
Remark 2.2. An optimizer S for (2.1) is a lattice
![]() $S=\mathbf {\mathbb {Z}}^{2}\cap [-N,N]^{2},N\in \mathbf {\mathbb {N}}$
.
$S=\mathbf {\mathbb {Z}}^{2}\cap [-N,N]^{2},N\in \mathbf {\mathbb {N}}$
.
3 Proof of Theorem 1.2
In this section, we prove Theorem 1.2. We will first reduce Theorem 1.2 to Proposition 3.1, then to showing Lemma 3.3. Then we will finish the proof by showing Lemma 3.3.
The proof of Theorem 1.2 will be reduced to the following proposition.
Proposition 3.1. Let
![]() $f:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$
be a function of the form
$f:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$
be a function of the form
 $$\begin{align*}f=\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}}, \end{align*}$$
$$\begin{align*}f=\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}}, \end{align*}$$
where
![]() $S_{0},\ldots ,S_{m},m\ge 1$
are disjoint subsets of
$S_{0},\ldots ,S_{m},m\ge 1$
are disjoint subsets of
![]() $\mathbf {\mathbb {Z}}^{2}$
such that
$\mathbf {\mathbb {Z}}^{2}$
such that
![]() $\#S_{j}\le 2^{j}$
, and
$\#S_{j}\le 2^{j}$
, and
![]() $\lambda _{0},\ldots ,\lambda _{m}\ge 0$
. Suppose that for each
$\lambda _{0},\ldots ,\lambda _{m}\ge 0$
. Suppose that for each
![]() $j=0,\ldots ,m$
and
$j=0,\ldots ,m$
and
![]() $\xi \in S_{j}$
, there exists at most one line
$\xi \in S_{j}$
, there exists at most one line
![]() $\ell \ni \xi $
such that
$\ell \ni \xi $
such that
![]() $\#(\ell \cap S_{j})\ge 2^{j/2+C}$
. Then, we have
$\#(\ell \cap S_{j})\ge 2^{j/2+C}$
. Then, we have
 $$ \begin{align} \sum_{Q\in{\mathcal{Q}}^{0}}f(Q)\lesssim m\cdot\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4} \end{align} $$
$$ \begin{align} \sum_{Q\in{\mathcal{Q}}^{0}}f(Q)\lesssim m\cdot\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4} \end{align} $$
and
 $$ \begin{align} \sup_{M\in2^{\mathbf{\mathbb{N}}}}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$
$$ \begin{align} \sup_{M\in2^{\mathbf{\mathbb{N}}}}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$
Here,
![]() $C>0$
is a uniform constant to be specified shortly, and
$C>0$
is a uniform constant to be specified shortly, and
![]() $f(Q)$
denotes
$f(Q)$
denotes
![]() $f(\xi _{1})f(\xi _{2})f(\xi _{3})f(\xi _{4})$
for parallelogram
$f(\xi _{1})f(\xi _{2})f(\xi _{3})f(\xi _{4})$
for parallelogram
![]() $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})$
.
$Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})$
.
Proof of Theorem 1.2 (assuming Proposition 3.1).
Let
![]() $S\subset \mathbf {\mathbb {Z}}^{2}$
be a bounded set. Let m be the least integer greater than
$S\subset \mathbf {\mathbb {Z}}^{2}$
be a bounded set. Let m be the least integer greater than
![]() $\log _{2}\#S$
. Since
$\log _{2}\#S$
. Since
![]() $\frac {1}{\log \#S}\lesssim \frac {1}{m}$
, to prove Theorem 1.2, we only need to show for
$\frac {1}{\log \#S}\lesssim \frac {1}{m}$
, to prove Theorem 1.2, we only need to show for
![]() $\phi \in L^{2}(\mathbb {T}^{2})$
that
$\phi \in L^{2}(\mathbb {T}^{2})$
that
Decomposing
![]() $\widehat {\phi }=\sum _{k=0}^{3}i^{k}\widehat {\phi }_{k}$
,
$\widehat {\phi }=\sum _{k=0}^{3}i^{k}\widehat {\phi }_{k}$
,
![]() $\widehat {\phi }_{k}\ge 0$
, it suffices to show that for
$\widehat {\phi }_{k}\ge 0$
, it suffices to show that for
![]() $f:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$
supported in S,
$f:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$
supported in S,
We define a sequence
![]() $\left \{ f_{n}\right \} $
of functions
$\left \{ f_{n}\right \} $
of functions
![]() $f_{n}:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty ),\mathrm {supp}(f_{n})\subset S$
inductively. Let
$f_{n}:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty ),\mathrm {supp}(f_{n})\subset S$
inductively. Let
![]() $f_{0}:=f$
. Given
$f_{0}:=f$
. Given
![]() $n\in \mathbf {\mathbb {N}}$
and a function
$n\in \mathbf {\mathbb {N}}$
and a function
![]() $f_{n}$
, we choose an enumeration
$f_{n}$
, we choose an enumeration
![]() $\xi _{1},\xi _{2},\ldots $
of
$\xi _{1},\xi _{2},\ldots $
of
![]() $\mathbf {\mathbb {Z}}^{2}$
(which may depend on n) such that
$\mathbf {\mathbb {Z}}^{2}$
(which may depend on n) such that
![]() $f_{n}(\xi _{1})\ge f_{n}(\xi _{2})\ge \ldots $
. Let
$f_{n}(\xi _{1})\ge f_{n}(\xi _{2})\ge \ldots $
. Let
![]() $S_{j}^{0}:=\left \{ \xi _{2^{j}},\ldots ,\xi _{2^{j+1}-1}\right \} $
and
$S_{j}^{0}:=\left \{ \xi _{2^{j}},\ldots ,\xi _{2^{j+1}-1}\right \} $
and
![]() $\lambda _{j}:=2^{j/2}f_n(\xi _{2^{j}})$
for
$\lambda _{j}:=2^{j/2}f_n(\xi _{2^{j}})$
for
![]() $j=0,\ldots ,m$
. We have
$j=0,\ldots ,m$
. We have
and
 $$ \begin{align} \|\lambda_{j}\|_{\ell_{j\le m}^{2}}&=\|2^{j/2}f_{n}(\xi_{2^{j}})\|_{\ell_{j\le m}^{2}}\\& \lesssim f_{n}(\xi_{1})+\|\sum_{j=1}^{m}f_{n}(\xi_{2^{j}})\chi_{\left\{ \xi_{2^{j-1}+1},\ldots,\xi_{2^{j}}\right\} }\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\nonumber \\& \lesssim\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}.\nonumber \end{align} $$
$$ \begin{align} \|\lambda_{j}\|_{\ell_{j\le m}^{2}}&=\|2^{j/2}f_{n}(\xi_{2^{j}})\|_{\ell_{j\le m}^{2}}\\& \lesssim f_{n}(\xi_{1})+\|\sum_{j=1}^{m}f_{n}(\xi_{2^{j}})\chi_{\left\{ \xi_{2^{j-1}+1},\ldots,\xi_{2^{j}}\right\} }\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\nonumber \\& \lesssim\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}.\nonumber \end{align} $$
For
![]() $j=0,\ldots ,m$
, we define
$j=0,\ldots ,m$
, we define
![]() $E_{j}\subset S_{j}^{0}$
as the set of intersections
$E_{j}\subset S_{j}^{0}$
as the set of intersections
![]() $\xi \in S_{j}^{0}$
of two lines
$\xi \in S_{j}^{0}$
of two lines
![]() $\ell _{1},\ell _{2}$
such that
$\ell _{1},\ell _{2}$
such that
By the Szemerédi-Trotter bound (2.1) and (3.5), we have
 $$ \begin{align} \sqrt{\#E_{j}} & \le\#\left\{ \ell\subset\mathbf{\mathbb{R}}^{2}:\ell\text{ is a line and }\#\left(\ell\cap S_{j}^{0}\right)\ge2^{j/2+C}\right\} \\ & \lesssim(\#S_{j}^{0})^{2}/(2^{j/2+C})^3+\#S_{j}^{0}/2^{j/2+C}\nonumber \\ & \lesssim2^{j/2-C}.\nonumber \end{align} $$
$$ \begin{align} \sqrt{\#E_{j}} & \le\#\left\{ \ell\subset\mathbf{\mathbb{R}}^{2}:\ell\text{ is a line and }\#\left(\ell\cap S_{j}^{0}\right)\ge2^{j/2+C}\right\} \\ & \lesssim(\#S_{j}^{0})^{2}/(2^{j/2+C})^3+\#S_{j}^{0}/2^{j/2+C}\nonumber \\ & \lesssim2^{j/2-C}.\nonumber \end{align} $$
Let
![]() $f_{n+1}:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$
be the function
$f_{n+1}:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$
be the function
 $$\begin{align*}f_{n+1}:=f_{n}\chi_{E}, \quad E:=\bigcup_{j=0}^{m}E_{j}. \end{align*}$$
$$\begin{align*}f_{n+1}:=f_{n}\chi_{E}, \quad E:=\bigcup_{j=0}^{m}E_{j}. \end{align*}$$
Since
![]() $f_{n}(\xi )\le f_{n}(\xi _{2^{j}})=\lambda _{j}2^{-j/2}$
holds for
$f_{n}(\xi )\le f_{n}(\xi _{2^{j}})=\lambda _{j}2^{-j/2}$
holds for
![]() $\xi \in E_{j}\subset S_{j}^{0}$
, by (3.7) and (3.6), we have
$\xi \in E_{j}\subset S_{j}^{0}$
, by (3.7) and (3.6), we have
Fixing
![]() $C\in \mathbf {\mathbb {N}}$
as a big number gives
$C\in \mathbf {\mathbb {N}}$
as a big number gives
which implies
Let
![]() $S_{j}:=S_{j}^{0}\setminus E_{j}$
. By the definition of
$S_{j}:=S_{j}^{0}\setminus E_{j}$
. By the definition of
![]() $E_{j}$
, the function
$E_{j}$
, the function
 $$\begin{align*}g_{n}:=\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}} \end{align*}$$
$$\begin{align*}g_{n}:=\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}} \end{align*}$$
satisfies the conditions for Proposition 3.1. Since
![]() $f_n(\xi )\le f_n(\xi _{2^{j}})=\lambda _{j}2^{-j/2}$
holds for
$f_n(\xi )\le f_n(\xi _{2^{j}})=\lambda _{j}2^{-j/2}$
holds for
![]() $\xi \in S_{j}\subset S_{j}^{0}=\left \{ \xi _{2^{j}},\ldots ,\xi _{2^{j+1}-1}\right \} $
, we have
$\xi \in S_{j}\subset S_{j}^{0}=\left \{ \xi _{2^{j}},\ldots ,\xi _{2^{j+1}-1}\right \} $
, we have
 $$ \begin{align} h_{n}:=f_{n}-f_{n+1}=\sum_{j=0}^{m}f_{n}\chi_{S_{j}}\le\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}}=g_{n}. \end{align} $$
$$ \begin{align} h_{n}:=f_{n}-f_{n+1}=\sum_{j=0}^{m}f_{n}\chi_{S_{j}}\le\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}}=g_{n}. \end{align} $$
Denoting
![]() $T_{0}:=\frac {1}{m}$
, by (3.9), we have
$T_{0}:=\frac {1}{m}$
, by (3.9), we have
 $$ \begin{align*} \int_{0}^{T_{0}}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdt & \le\frac{1}{T_{0}}\int_{0}^{2T_{0}}\int_{0}^{T}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdtdT\\ & \approx\frac{1}{T_{0}}\int_{0}^{2T_{0}}\int_{0}^{T}{\mathcal{F}}\left(\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}\right)(0)dtdT\\ & \approx\frac{1}{T_{0}}\sum_{Q\in{\mathcal{Q}}}h_{n}\left(Q\right)\cdot\mathrm{Re}\int_{0}^{2T_{0}}\int_{0}^{T}e^{it\tau_{Q}}dtdT\\ & \approx\sum_{Q\in{\mathcal{Q}}}h_{n}\left(Q\right)\cdot\frac{1-\cos\left(2T_{0}\tau_{Q}\right)}{T_{0}\tau_{Q}^{2}}\\ & \lesssim T_{0}\sum_{Q\in{\mathcal{Q}}^{0}}h_{n}(Q)+\sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}h_{n}(Q)\\ & \lesssim T_{0}\sum_{Q\in{\mathcal{Q}}^{0}}g_{n}(Q)+\sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q) \end{align*} $$
$$ \begin{align*} \int_{0}^{T_{0}}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdt & \le\frac{1}{T_{0}}\int_{0}^{2T_{0}}\int_{0}^{T}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdtdT\\ & \approx\frac{1}{T_{0}}\int_{0}^{2T_{0}}\int_{0}^{T}{\mathcal{F}}\left(\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}\right)(0)dtdT\\ & \approx\frac{1}{T_{0}}\sum_{Q\in{\mathcal{Q}}}h_{n}\left(Q\right)\cdot\mathrm{Re}\int_{0}^{2T_{0}}\int_{0}^{T}e^{it\tau_{Q}}dtdT\\ & \approx\sum_{Q\in{\mathcal{Q}}}h_{n}\left(Q\right)\cdot\frac{1-\cos\left(2T_{0}\tau_{Q}\right)}{T_{0}\tau_{Q}^{2}}\\ & \lesssim T_{0}\sum_{Q\in{\mathcal{Q}}^{0}}h_{n}(Q)+\sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}h_{n}(Q)\\ & \lesssim T_{0}\sum_{Q\in{\mathcal{Q}}^{0}}g_{n}(Q)+\sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q) \end{align*} $$
and
 $$ \begin{align*} & \sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q)\\ \lesssim{}&\sum_{M\in2^{\mathbf{\mathbb{N}}}}\min\left\{ T_{0}M,\frac{1}{T_{0}M}\right\} \frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q)\\ \lesssim{}&\sup_{M\in2^{\mathbf{\mathbb{N}}}}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q), \end{align*} $$
$$ \begin{align*} & \sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q)\\ \lesssim{}&\sum_{M\in2^{\mathbf{\mathbb{N}}}}\min\left\{ T_{0}M,\frac{1}{T_{0}M}\right\} \frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q)\\ \lesssim{}&\sup_{M\in2^{\mathbf{\mathbb{N}}}}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q), \end{align*} $$
concluding by (3.1), (3.2) and (3.6) that
 $$ \begin{align} \|e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\|_{L^{4}([0,T_{0}]\times\mathbb{T}^{2})}&=\left(\int_{0}^{T_{0}}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdt\right)^{1/4}\\ &\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}\lesssim\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}.\nonumber \end{align} $$
$$ \begin{align} \|e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\|_{L^{4}([0,T_{0}]\times\mathbb{T}^{2})}&=\left(\int_{0}^{T_{0}}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdt\right)^{1/4}\\ &\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}\lesssim\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}.\nonumber \end{align} $$
Writing
![]() $f=\sum _{n=0}^{\infty }(f_{n}-f_{n+1})=\sum _{n=0}^{\infty }h_{n}$
, by (3.10) and (3.8), we have
$f=\sum _{n=0}^{\infty }(f_{n}-f_{n+1})=\sum _{n=0}^{\infty }h_{n}$
, by (3.10) and (3.8), we have
 $$ \begin{align*} \|e^{it\Delta}{\mathcal{F}}^{-1}f\|_{L_{t,x}^{4}\left([0,T_{0}]\times\mathbb{T}^{2}\right)} & \le\sum_{n=0}^{\infty}\|e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\|_{L_{t,x}^{4}\left([0,T_{0}]\times\mathbb{T}^{2}\right)}\\ & \lesssim\sum_{n=0}^{\infty}\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\\ & \lesssim\sum_{n=0}^{\infty}2^{-n}\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\lesssim\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}, \end{align*} $$
$$ \begin{align*} \|e^{it\Delta}{\mathcal{F}}^{-1}f\|_{L_{t,x}^{4}\left([0,T_{0}]\times\mathbb{T}^{2}\right)} & \le\sum_{n=0}^{\infty}\|e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\|_{L_{t,x}^{4}\left([0,T_{0}]\times\mathbb{T}^{2}\right)}\\ & \lesssim\sum_{n=0}^{\infty}\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\\ & \lesssim\sum_{n=0}^{\infty}2^{-n}\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\lesssim\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}, \end{align*} $$
which is (3.4) and therefore completes the proof of Theorem 1.2.
A cross is a triple
![]() $(\xi ,\ell _{1},\ell _{2})$
of two mutually orthogonal lines
$(\xi ,\ell _{1},\ell _{2})$
of two mutually orthogonal lines
![]() $\ell _{1},\ell _{2}$
and their intersection
$\ell _{1},\ell _{2}$
and their intersection
![]() $\xi $
. For
$\xi $
. For
![]() $\{S_j\}_{j=0}^m$
as in Proposition 3.1, we categorize crosses
$\{S_j\}_{j=0}^m$
as in Proposition 3.1, we categorize crosses
![]() $\left (\xi ,\ell _{1},\ell _{2}\right ),\xi \in \cup _{j=0}^m S_j$
into three types:
$\left (\xi ,\ell _{1},\ell _{2}\right ),\xi \in \cup _{j=0}^m S_j$
into three types:
 $$\begin{align*}\begin{cases} \text{Type 1} & \text{ if } a\ge j/2+C\\ \text{Type 2} & \text{ if } 1\le a<j/2+C\\ \text{Type 3} & \text{ if }a=0, \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} \text{Type 1} & \text{ if } a\ge j/2+C\\ \text{Type 2} & \text{ if } 1\le a<j/2+C\\ \text{Type 3} & \text{ if }a=0, \end{cases} \end{align*}$$
where j is the index such that
![]() $\xi \in S_j$
, and a is the number
$\xi \in S_j$
, and a is the number
Note that
![]() $a\in \{0\}\cup [1,\infty )$
since
$a\in \{0\}\cup [1,\infty )$
since
![]() $\ell _1\cap S_j$
is nonempty.
$\ell _1\cap S_j$
is nonempty.
Given a rectangle
![]() $\left (\xi _{1},\xi _{2},\xi _{3},\xi _{4}\right )$
of four distinct vertices, its vertex
$\left (\xi _{1},\xi _{2},\xi _{3},\xi _{4}\right )$
of four distinct vertices, its vertex
![]() $\xi _{1}$
is called a vertex of type
$\xi _{1}$
is called a vertex of type
![]() $\alpha $
,
$\alpha $
,
![]() $\alpha =1,2,3$
if the cross
$\alpha =1,2,3$
if the cross
![]() $(\xi _{1},\overleftrightarrow {\xi _{1}\xi _{2}},\overleftrightarrow {\xi _{1}\xi _{4}})$
is of type
$(\xi _{1},\overleftrightarrow {\xi _{1}\xi _{2}},\overleftrightarrow {\xi _{1}\xi _{4}})$
is of type
![]() $\alpha $
.
$\alpha $
.
For
![]() $\alpha ,\beta =1,2,3$
, we denote by
$\alpha ,\beta =1,2,3$
, we denote by
![]() ${\mathcal {Q}}_{\alpha ,\beta }^{0}$
the set of rectangles
${\mathcal {Q}}_{\alpha ,\beta }^{0}$
the set of rectangles
![]() $\left (\xi _{1},\xi _{2},\xi _{3},\xi _{4}\right )\in {\mathcal {Q}}^{0}$
of four distinct vertices
$\left (\xi _{1},\xi _{2},\xi _{3},\xi _{4}\right )\in {\mathcal {Q}}^{0}$
of four distinct vertices
![]() $\xi _1,\xi _2,\xi _3,\xi _4\in \cup _{j=0}^m S_j$
such that
$\xi _1,\xi _2,\xi _3,\xi _4\in \cup _{j=0}^m S_j$
such that
![]() $\xi _{1},\xi _{2}$
are type
$\xi _{1},\xi _{2}$
are type
![]() $\alpha $
-vertices and
$\alpha $
-vertices and
![]() $\xi _{3},\xi _{4}$
are type
$\xi _{3},\xi _{4}$
are type
![]() $\beta $
-vertices. Although the union of
$\beta $
-vertices. Although the union of
![]() ${\mathcal {Q}}_{\alpha ,\beta }^{0}$
is only a proper subcollection of
${\mathcal {Q}}_{\alpha ,\beta }^{0}$
is only a proper subcollection of
![]() ${\mathcal {Q}}^{0}$
, the following lemma provides a reduction to counting rectangles in
${\mathcal {Q}}^{0}$
, the following lemma provides a reduction to counting rectangles in
![]() ${\mathcal {Q}}_{\alpha ,\beta }^{0}$
.
${\mathcal {Q}}_{\alpha ,\beta }^{0}$
.
Lemma 3.2. Let f and
![]() $\left \{ S_{j}\right \}_{j=0}^m$
be as in Proposition 3.1. Let
$\left \{ S_{j}\right \}_{j=0}^m$
be as in Proposition 3.1. Let
![]() $\tau \ge 0$
be an integer. We have
$\tau \ge 0$
be an integer. We have
 $$ \begin{align} \sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}. \end{align} $$
$$ \begin{align} \sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}. \end{align} $$
Proof. For
![]() $\xi \in \mathbf {\mathbb {Z}}^{2}\setminus \left \{ 0\right \} $
and
$\xi \in \mathbf {\mathbb {Z}}^{2}\setminus \left \{ 0\right \} $
and
![]() $\sigma \in \mathbf {\mathbb {Z}}$
, we denote by
$\sigma \in \mathbf {\mathbb {Z}}$
, we denote by
![]() ${\mathcal {E}}_{\xi }^{\sigma }$
the set of segments
${\mathcal {E}}_{\xi }^{\sigma }$
the set of segments
![]() $(\xi _{1},\xi _{4})\in (\mathbf {\mathbb {Z}}^{2})^{2}$
such that
$(\xi _{1},\xi _{4})\in (\mathbf {\mathbb {Z}}^{2})^{2}$
such that
![]() $\xi _{1}-\xi _{4}=\xi $
and
$\xi _{1}-\xi _{4}=\xi $
and
![]() $\xi _{1}\cdot \xi =\sigma $
.
$\xi _{1}\cdot \xi =\sigma $
.
Since
![]() $\tau _{Q}=2\left \vert (\xi _{1}-\xi _{2})\cdot (\xi _{1}-\xi _{4})\right \vert $
is a multiple of
$\tau _{Q}=2\left \vert (\xi _{1}-\xi _{2})\cdot (\xi _{1}-\xi _{4})\right \vert $
is a multiple of
![]() $\gcd (\xi _{1}-\xi _{4})$
for any parallelogram
$\gcd (\xi _{1}-\xi _{4})$
for any parallelogram
![]() $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})$
such that
$Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})$
such that
![]() $\xi _{1}-\xi _{4}\neq 0$
, we have
$\xi _{1}-\xi _{4}\neq 0$
, we have
 $$ \begin{align*} \sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q) & \lesssim\sum_{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\sum_{\xi_{1},\xi_{2}\in\mathbf{\mathbb{Z}}^{2}}f(\xi_{1})^{2}f(\xi_{2})^{2}\\ & \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*} $$
$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q) & \lesssim\sum_{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\sum_{\xi_{1},\xi_{2}\in\mathbf{\mathbb{Z}}^{2}}f(\xi_{1})^{2}f(\xi_{2})^{2}\\ & \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*} $$
and by Cauchy-Schwarz inequality,
 $$ \begin{align*} & \sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)\\& \quad \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{\sigma_{1},\sigma_{2}\in\mathbf{\mathbb{Z}}\\ \sigma_{1}-\sigma_{2}=\pm\tau/2 } }\sum_{\substack{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma_{1}}\\ (\xi_{2},\xi_{3})\in{\mathcal{E}}_{\xi}^{\sigma_{2}} } }f(\xi_{1})f(\xi_{4})f(\xi_{2})f(\xi_{3})\\& \quad \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\left(\sum_{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma}}f(\xi_{1})f(\xi_{4})\right)^{2}\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\left(\sum_{\substack{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma}\\ (\xi_1,\xi_1+\xi \mathbf{\mathbb{R}},\xi_1+\xi^\perp \mathbf{\mathbb{R}})\text{ is a cross of type }\alpha\\ (\xi_4,\xi_4+\xi \mathbf{\mathbb{R}},\xi_4+\xi^\perp \mathbf{\mathbb{R}})\text{ is a cross of type }\beta } }f(\xi_{1})f(\xi_{4})\right)^{2}\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\sum_{\substack{ (\xi_1,\xi_4)\in{\mathcal{E}}^\sigma_\xi\\(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\text{ or }(\xi_2,\xi_3)=(\xi_1,\xi_4) } }f(\xi_1)f(\xi_4)f(\xi_2)f(\xi_3)\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\left(\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\sum_{\xi_{1}-\xi_{4}=\xi}f(\xi_{1})^{2}f(\xi_{4})^{2}\right)\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*} $$
$$ \begin{align*} & \sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)\\& \quad \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{\sigma_{1},\sigma_{2}\in\mathbf{\mathbb{Z}}\\ \sigma_{1}-\sigma_{2}=\pm\tau/2 } }\sum_{\substack{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma_{1}}\\ (\xi_{2},\xi_{3})\in{\mathcal{E}}_{\xi}^{\sigma_{2}} } }f(\xi_{1})f(\xi_{4})f(\xi_{2})f(\xi_{3})\\& \quad \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\left(\sum_{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma}}f(\xi_{1})f(\xi_{4})\right)^{2}\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\left(\sum_{\substack{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma}\\ (\xi_1,\xi_1+\xi \mathbf{\mathbb{R}},\xi_1+\xi^\perp \mathbf{\mathbb{R}})\text{ is a cross of type }\alpha\\ (\xi_4,\xi_4+\xi \mathbf{\mathbb{R}},\xi_4+\xi^\perp \mathbf{\mathbb{R}})\text{ is a cross of type }\beta } }f(\xi_{1})f(\xi_{4})\right)^{2}\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\sum_{\substack{ (\xi_1,\xi_4)\in{\mathcal{E}}^\sigma_\xi\\(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\text{ or }(\xi_2,\xi_3)=(\xi_1,\xi_4) } }f(\xi_1)f(\xi_4)f(\xi_2)f(\xi_3)\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\left(\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\sum_{\xi_{1}-\xi_{4}=\xi}f(\xi_{1})^{2}f(\xi_{4})^{2}\right)\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*} $$
finishing the proof.
There are three main inequalities to be shown.
Lemma 3.3. Let f and
![]() $\{\lambda _j\}_{j=0}^m$
be as in Proposition 3.1.
$\{\lambda _j\}_{j=0}^m$
be as in Proposition 3.1.
In the cases
![]() $(\alpha ,\beta )\neq (2,2)$
, we have
$(\alpha ,\beta )\neq (2,2)$
, we have
 $$ \begin{align} \sum_{Q\in{\mathcal{Q}}_{\alpha,\beta}^{0}}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$
$$ \begin{align} \sum_{Q\in{\mathcal{Q}}_{\alpha,\beta}^{0}}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$
In case
![]() $(\alpha ,\beta )=(2,2)$
, we have
$(\alpha ,\beta )=(2,2)$
, we have
 $$ \begin{align} \sum_{Q\in{\mathcal{Q}}_{2,2}^{0}}f(Q)\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4} \end{align} $$
$$ \begin{align} \sum_{Q\in{\mathcal{Q}}_{2,2}^{0}}f(Q)\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4} \end{align} $$
and
 $$ \begin{align} \sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{2,2}^{0}}\frac{1}{\gcd(\xi_{1}-\xi_{4})}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$
$$ \begin{align} \sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{2,2}^{0}}\frac{1}{\gcd(\xi_{1}-\xi_{4})}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$
Proof of Proposition 3.1 assuming Lemma 3.3.
We first prove (3.1), which concerns the case
![]() $\tau =0$
. By (3.11), (3.12) and (3.13), we have
$\tau =0$
. By (3.11), (3.12) and (3.13), we have
 $$\begin{align*}\sum_{Q\in{\mathcal{Q}}^{0}}f(Q)\lesssim\max_{\alpha,\beta=1,2,3}\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*}$$
$$\begin{align*}\sum_{Q\in{\mathcal{Q}}^{0}}f(Q)\lesssim\max_{\alpha,\beta=1,2,3}\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*}$$
which is just (3.1).
Now we prove (3.2), which is for
![]() $\tau \neq 0$
. By (3.11), for
$\tau \neq 0$
. By (3.11), for
![]() $M\in 2^{\mathbf {\mathbb {N}}}$
, we have
$M\in 2^{\mathbf {\mathbb {N}}}$
, we have
 $$\begin{align*}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\frac{1}{M}\max_{\alpha,\beta=1,2,3}\sum_{\tau\approx M}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*}$$
$$\begin{align*}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\frac{1}{M}\max_{\alpha,\beta=1,2,3}\sum_{\tau\approx M}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*}$$
and for
![]() $\alpha ,\beta =1,2,3$
, we have
$\alpha ,\beta =1,2,3$
, we have
 $$ \begin{align*} & \frac{1}{M}\sum_{\tau\approx M}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)\\& =\frac{1}{M}\sum_{\tau\approx M}\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}1_{\gcd(\xi_{1}-\xi_{4})\mid\tau}\cdot f(Q)\\& =\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}\left(\frac{1}{M}\sum_{\tau\approx M}1_{\gcd(\xi_{1}-\xi_{4})\mid\tau}\right)\cdot f(Q)\\& \lesssim\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}\frac{1}{\gcd(\xi_{1}-\xi_{4})}\cdot f(Q), \end{align*} $$
$$ \begin{align*} & \frac{1}{M}\sum_{\tau\approx M}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)\\& =\frac{1}{M}\sum_{\tau\approx M}\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}1_{\gcd(\xi_{1}-\xi_{4})\mid\tau}\cdot f(Q)\\& =\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}\left(\frac{1}{M}\sum_{\tau\approx M}1_{\gcd(\xi_{1}-\xi_{4})\mid\tau}\right)\cdot f(Q)\\& \lesssim\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}\frac{1}{\gcd(\xi_{1}-\xi_{4})}\cdot f(Q), \end{align*} $$
which is
![]() $O(\|\lambda _{j}\|_{\ell ^{2}_{j\le m}}^{4})$
by (3.12) and (3.14), and finishes the proof of (3.2).
$O(\|\lambda _{j}\|_{\ell ^{2}_{j\le m}}^{4})$
by (3.12) and (3.14), and finishes the proof of (3.2).
Before turning to the proof of Lemma 3.3, we consider two preparatory lemmas, where we use the following notation:
For vectors
![]() $\overrightarrow {j}=(j_1,j_2,j_3,j_4)\in \mathbf {\mathbb {N}}^4$
and
$\overrightarrow {j}=(j_1,j_2,j_3,j_4)\in \mathbf {\mathbb {N}}^4$
and
![]() $\overrightarrow {a}=(a_1,a_2,a_3,a_4)\in \mathbf {\mathbb {N}}^4$
, we denote by
$\overrightarrow {a}=(a_1,a_2,a_3,a_4)\in \mathbf {\mathbb {N}}^4$
, we denote by
![]() ${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a})$
the set of rectangles
${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a})$
the set of rectangles
![]() $(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}^{0}\cap \left (S_{j_{1}}\times S_{j_{2}}\times S_{j_{3}}\times S_{j_{4}}\right )$
of four distinct vertices such that
$(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}^{0}\cap \left (S_{j_{1}}\times S_{j_{2}}\times S_{j_{3}}\times S_{j_{4}}\right )$
of four distinct vertices such that
where the cyclic convention on index
![]() $\xi _{4l+k}=\xi _{k},l\in \mathbf {\mathbb {Z}}$
is used (see Fig. 3.1).
$\xi _{4l+k}=\xi _{k},l\in \mathbf {\mathbb {Z}}$
is used (see Fig. 3.1).

Figure 3.1 Rectangle
![]() $(\xi _1,\xi _2,\xi _3,\xi _4)\in {\mathcal {Q}}^{0}( \overrightarrow{j}, \overrightarrow{a})$
.
$(\xi _1,\xi _2,\xi _3,\xi _4)\in {\mathcal {Q}}^{0}( \overrightarrow{j}, \overrightarrow{a})$
.
Lemma 3.4. Let
![]() $\left \{ S_{j}\right \} _{j=0}^{m},m\ge 1$
be as in Proposition 3.1. Let
$\left \{ S_{j}\right \} _{j=0}^{m},m\ge 1$
be as in Proposition 3.1. Let
![]() $j_{1},j_{2},j_{3},j_{4},a_{3}\ge 0$
be integers. Then, the number of rectangles
$j_{1},j_{2},j_{3},j_{4},a_{3}\ge 0$
be integers. Then, the number of rectangles
![]() $(\xi _1,\xi _2,\xi _3,\xi _4)\in {\mathcal {Q}}^0\cap (S_{j_1}\times S_{j_2}\times S_{j_3}\times S_{j_4})$
of four distinct vertices such that
$(\xi _1,\xi _2,\xi _3,\xi _4)\in {\mathcal {Q}}^0\cap (S_{j_1}\times S_{j_2}\times S_{j_3}\times S_{j_4})$
of four distinct vertices such that
is
![]() $O(2^{j_{1}+j_{2}+a_{3}})$
.
$O(2^{j_{1}+j_{2}+a_{3}})$
.
Proof. There are at most
![]() $\#S_{j_1}\cdot \#S_{j_2}=O(2^{j_{1}+j_{2}})$
possible choices of
$\#S_{j_1}\cdot \#S_{j_2}=O(2^{j_{1}+j_{2}})$
possible choices of
![]() $(\xi _{1},\xi _{2})\in S_{j_{1}}\times S_{j_{2}}$
. Once the pair of two vertices
$(\xi _{1},\xi _{2})\in S_{j_{1}}\times S_{j_{2}}$
. Once the pair of two vertices
![]() $(\xi _{1,}\xi _{2})\in S_{j_{1}}\times S_{j_{2}}$
is fixed, the third vertex
$(\xi _{1,}\xi _{2})\in S_{j_{1}}\times S_{j_{2}}$
is fixed, the third vertex
![]() $\xi _{3}$
should lie on the line
$\xi _{3}$
should lie on the line
![]() $\ell _{23}\ni \xi _{2}$
orthogonal to
$\ell _{23}\ni \xi _{2}$
orthogonal to
![]() $\overleftrightarrow {\xi _{1}\xi _{2}}$
(see Fig. 3.2), and we require
$\overleftrightarrow {\xi _{1}\xi _{2}}$
(see Fig. 3.2), and we require
so there are only
![]() $O(2^{a_{3}})$
possible choices of
$O(2^{a_{3}})$
possible choices of
![]() $\xi _{3}\in \ell _{23}$
, which then uniquely determines a rectangle. Therefore, we have
$\xi _{3}\in \ell _{23}$
, which then uniquely determines a rectangle. Therefore, we have
![]() $O(2^{j_{1}+j_{2}}\cdot 2^{a_{3}})=O(2^{j_{1}+j_{2}+a_{3}})$
such rectangles.
$O(2^{j_{1}+j_{2}}\cdot 2^{a_{3}})=O(2^{j_{1}+j_{2}+a_{3}})$
such rectangles.
The following lemma is useful in the case that
![]() $\xi _{1}$
is a vertex of type
$\xi _{1}$
is a vertex of type
![]() $2$
.
$2$
.

Figure 3.2 Choice of
![]() $\xi _1,\xi _2,\xi _3$
in the proof of Lemma 3.4.
$\xi _1,\xi _2,\xi _3$
in the proof of Lemma 3.4.
Lemma 3.5. Let
![]() $\left \{ S_{j}\right \} _{j=0}^{m},m\ge 1$
be as in Proposition 3.1. Let
$\left \{ S_{j}\right \} _{j=0}^{m},m\ge 1$
be as in Proposition 3.1. Let
![]() $j_{1},j_{2},j_{3},j_{4}$
,
$j_{1},j_{2},j_{3},j_{4}$
,
![]() $a_{1},a_{2},a_{3},a_{4}\ge 0$
be integers. Assume that
$a_{1},a_{2},a_{3},a_{4}\ge 0$
be integers. Assume that
We have
and
 $$ \begin{align} \sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim 2^{2j_{1}-2a_{1}+a_{2}+a_{4}/2}. \end{align} $$
$$ \begin{align} \sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim 2^{2j_{1}-2a_{1}+a_{2}+a_{4}/2}. \end{align} $$
We note that the assumption (3.16) is a priori necessary if
![]() $\xi _{1}$
is a vertex of type
$\xi _{1}$
is a vertex of type
![]() $2$
.
$2$
.
Proof. By (2.1), the number of lines
![]() $\ell $
such that
$\ell $
such that
![]() $2^{a_{1}}\le \#(\ell \cap S_{j_{1}})<2^{a_1+1}$
is
$2^{a_{1}}\le \#(\ell \cap S_{j_{1}})<2^{a_1+1}$
is
![]() $O(2^{2j_{1}}\cdot 2^{-3a_{1}}+2^{j_{1}}\cdot 2^{-a_{1}})=O(2^{2j_{1}-3a_{1}})$
, and for each such
$O(2^{2j_{1}}\cdot 2^{-3a_{1}}+2^{j_{1}}\cdot 2^{-a_{1}})=O(2^{2j_{1}-3a_{1}})$
, and for each such
![]() $\ell $
, we have
$\ell $
, we have
![]() $O(2^{a_1})$
number of points
$O(2^{a_1})$
number of points
![]() $\xi _1\in \ell \cap S_{j_1}$
. Thus, there exist at most
$\xi _1\in \ell \cap S_{j_1}$
. Thus, there exist at most
![]() $O(2^{2j_{1}-2a_{1}})$
crosses
$O(2^{2j_{1}-2a_{1}})$
crosses
![]() $(\xi _{1},\ell _{12},\ell _{14})$
such that
$(\xi _{1},\ell _{12},\ell _{14})$
such that
For such a cross
![]() $(\xi _{1},\ell _{12},\ell _{14})$
to be a corner of a rectangle in
$(\xi _{1},\ell _{12},\ell _{14})$
to be a corner of a rectangle in
![]() ${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a}) $
, for (3.15), we require further that
${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a}) $
, for (3.15), we require further that
and
By (3.20), there exist at most
![]() $O(2^{a_{2}})$
choices of vertices
$O(2^{a_{2}})$
choices of vertices
![]() $\xi _{2}\in \ell _{12}\cap S_{j_{2}}$
.
$\xi _{2}\in \ell _{12}\cap S_{j_{2}}$
.

Figure 3.3 Choice of
![]() $\xi _1$
and
$\xi _1$
and
![]() $\xi _2$
in the proof of Lemma 3.5.
$\xi _2$
in the proof of Lemma 3.5.
Having fixed
![]() $\xi _{1}$
and
$\xi _{1}$
and
![]() $\xi _{2}$
, we choose either
$\xi _{2}$
, we choose either
![]() $\xi _{3}$
or
$\xi _{3}$
or
![]() $\xi _{4}$
as follows, which then uniquely determines a rectangle
$\xi _{4}$
as follows, which then uniquely determines a rectangle
![]() $(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}^{0}$
.
$(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}^{0}$
.
-
• Choice of
 $\xi _{4}$
. Since the choice of
$\xi _{4}$
. Since the choice of
 $\xi _{4}\in \ell _{14}\cap S_{j_{4}}$
in advance uniquely determines a rectangle, by (3.21), we have (3.17). Also, labeling
$\xi _{4}\in \ell _{14}\cap S_{j_{4}}$
in advance uniquely determines a rectangle, by (3.21), we have (3.17). Also, labeling
 $\ell _{14}\cap S_{j_{4}}\setminus \left \{ \xi _{1}\right \} =:\left \{ \xi _{4}^{1},\ldots ,\xi _{4}^{l}\right \} ,l<2^{a_{4}+1}$
, we have which implies (3.19).
$\ell _{14}\cap S_{j_{4}}\setminus \left \{ \xi _{1}\right \} =:\left \{ \xi _{4}^{1},\ldots ,\xi _{4}^{l}\right \} ,l<2^{a_{4}+1}$
, we have which implies (3.19). $$\begin{align*}\sum_{r=1}^{l}\frac{1}{\gcd(\xi_{1}-\xi_{4}^{r})}\lesssim\frac{1}{1}+\cdots+\frac{1}{l}\lesssim\log l\lesssim2^{a_{4}/2}, \end{align*}$$
$$\begin{align*}\sum_{r=1}^{l}\frac{1}{\gcd(\xi_{1}-\xi_{4}^{r})}\lesssim\frac{1}{1}+\cdots+\frac{1}{l}\lesssim\log l\lesssim2^{a_{4}/2}, \end{align*}$$
-
• Choice of
 $\xi _{3}$
. We can also determine a rectangle by choosing
$\xi _{3}$
. We can also determine a rectangle by choosing
 $\xi _{3}\in \ell _{23}\cap S_{j_{3}}$
, where
$\xi _{3}\in \ell _{23}\cap S_{j_{3}}$
, where
 $\ell _{23}\ni \xi _{2}$
is the line parallel with
$\ell _{23}\ni \xi _{2}$
is the line parallel with
 $\ell _{14}$
(see Fig. 3.3). To form a rectangle in
$\ell _{14}$
(see Fig. 3.3). To form a rectangle in
 ${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a}) $
, we require so there are at most
${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a}) $
, we require so there are at most $$\begin{align*}\#(\ell_{23}\cap S_{j_{3}})=\#(\overleftrightarrow{\xi_{2}\xi_{3}}\cap S_{j_{3}})<2^{a_{3}+1}, \end{align*}$$
$$\begin{align*}\#(\ell_{23}\cap S_{j_{3}})=\#(\overleftrightarrow{\xi_{2}\xi_{3}}\cap S_{j_{3}})<2^{a_{3}+1}, \end{align*}$$
 $O(2^{a_{3}})$
choices of such vertices
$O(2^{a_{3}})$
choices of such vertices
 $\xi _{3}$
. Thus, we have (3.18).
$\xi _{3}$
. Thus, we have (3.18).
We can now lay the last brick of the proof of Proposition 3.1.
Proof of Lemma 3.3.
We split the proof into the cases (i)
![]() $\alpha =1$
(or
$\alpha =1$
(or
![]() $\beta =1$
), (ii)
$\beta =1$
), (ii)
![]() $(\alpha ,\beta )=(2,2)$
, (iii)
$(\alpha ,\beta )=(2,2)$
, (iii)
![]() $(\alpha ,\beta )=(3,3)$
and (iv)
$(\alpha ,\beta )=(3,3)$
and (iv)
![]() $(\alpha ,\beta )=(2,3)$
(or
$(\alpha ,\beta )=(2,3)$
(or
![]() $(3,2)$
).
$(3,2)$
).
Case I:
![]() $\alpha =1$
(or
$\alpha =1$
(or
![]() $\beta =1$
).
$\beta =1$
).
For
![]() $\xi _{1}\in S_{j_{1}},j_{1}\in \mathbf {\mathbb {N}}$
, by the assumption of Proposition 3.1, there exists at most one line
$\xi _{1}\in S_{j_{1}},j_{1}\in \mathbf {\mathbb {N}}$
, by the assumption of Proposition 3.1, there exists at most one line
![]() $\ell _{\xi _{1}}\ni \xi _1$
such that
$\ell _{\xi _{1}}\ni \xi _1$
such that
![]() $\#(\ell _{\xi _{1}}\cap S_{j_{1}})\ge 2^{j_1/2+C}$
. Thus, for any rectangle
$\#(\ell _{\xi _{1}}\cap S_{j_{1}})\ge 2^{j_1/2+C}$
. Thus, for any rectangle
![]() $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}_{1,\beta }^{0}$
, to which the inequality
$Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}_{1,\beta }^{0}$
, to which the inequality
applies since
![]() $\xi _{1}$
is of type
$\xi _{1}$
is of type
![]() $\alpha =1$
, we have either
$\alpha =1$
, we have either
![]() $\xi _{2}\in \ell _{\xi _{1}}$
or
$\xi _{2}\in \ell _{\xi _{1}}$
or
![]() $\xi _{4}\in \ell _{\xi _{1}}$
. We conclude that for each pair of points
$\xi _{4}\in \ell _{\xi _{1}}$
. We conclude that for each pair of points
![]() $(\xi _{1},\xi _{3})\in (\mathbf {\mathbb {Z}}^{2})^{2}$
such that
$(\xi _{1},\xi _{3})\in (\mathbf {\mathbb {Z}}^{2})^{2}$
such that
![]() $\xi _{1}\neq \xi _{3}$
, there is only one possible choice of the other two vertices
$\xi _{1}\neq \xi _{3}$
, there is only one possible choice of the other two vertices
![]() $\left \{ \xi _{2},\xi _{4}\right \} $
such that
$\left \{ \xi _{2},\xi _{4}\right \} $
such that
![]() $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}_{1,\beta }^{0}$
, and similar for
$Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}_{1,\beta }^{0}$
, and similar for
![]() $(\xi _{2},\xi _{4})$
. By Cauchy-Schwarz inequality, we have
$(\xi _{2},\xi _{4})$
. By Cauchy-Schwarz inequality, we have
 $$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{1,\beta}^{0}}f(Q) & =\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{1,\beta}^{0}}f(\xi_{1})f(\xi_{3})\cdot f(\xi_{2})f(\xi_{4})\\ & \lesssim\sum_{\xi_{1},\xi_{3}\in\mathbf{\mathbb{Z}}^{2}}\left(f(\xi_{1})f(\xi_{3})\right)^{2}\\ & \lesssim\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{1,\beta}^{0}}f(Q) & =\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{1,\beta}^{0}}f(\xi_{1})f(\xi_{3})\cdot f(\xi_{2})f(\xi_{4})\\ & \lesssim\sum_{\xi_{1},\xi_{3}\in\mathbf{\mathbb{Z}}^{2}}\left(f(\xi_{1})f(\xi_{3})\right)^{2}\\ & \lesssim\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
which is just (3.12) for the case.

Figure 3.4 Determination of a rectangle from given
![]() $\xi _1,\xi _3\in \mathbb {Z}^2$
.
$\xi _1,\xi _3\in \mathbb {Z}^2$
.
Case II:
![]() $(\alpha ,\beta )=(2,2)$
.
$(\alpha ,\beta )=(2,2)$
.
Let
![]() $j_{1},\ldots ,j_{4},a_{1},\ldots ,a_{4}$
be integers such that
$j_{1},\ldots ,j_{4},a_{1},\ldots ,a_{4}$
be integers such that
![]() $0\le j_{k}\le m$
and
$0\le j_{k}\le m$
and
![]() $1\le a_{k}<j_{k}/2+C$
for
$1\le a_{k}<j_{k}/2+C$
for
![]() $k=1,\ldots ,4$
. By (3.17), (3.18) and their cyclic relabels of indices
$k=1,\ldots ,4$
. By (3.17), (3.18) and their cyclic relabels of indices
![]() $1,2,3,4$
, for non-negative tuple
$1,2,3,4$
, for non-negative tuple
![]() $\left (c_{k,l}\right )_{k\le 4,l\le 2}$
such that
$\left (c_{k,l}\right )_{k\le 4,l\le 2}$
such that
![]() $\sum _{k=1}^4\sum _{l=1}^2 c_{k,l}=1$
, we have
$\sum _{k=1}^4\sum _{l=1}^2 c_{k,l}=1$
, we have
The choices
![]() $(c_{k,l})_{k\le 4,l\le 2}=\frac {1}{24}\cdot ((2,3),(3,4),(0,6),(3,3))$
and
$(c_{k,l})_{k\le 4,l\le 2}=\frac {1}{24}\cdot ((2,3),(3,4),(0,6),(3,3))$
and
![]() $\frac {1}{12}\cdot ((1,2),(1,2),(3,0),(1,2))$
give
$\frac {1}{12}\cdot ((1,2),(1,2),(3,0),(1,2))$
give
respectively. Interpolating (3.22), (3.23) and their dihedral relabelings of indices
![]() $1,2,3,4$
, for
$1,2,3,4$
, for
![]() $\delta =\frac {1}{10000}$
, we have
$\delta =\frac {1}{10000}$
, we have
from which we conclude by
 $$\begin{align*}{\mathcal{Q}}^0_{2,2}\subset\bigcup_{\substack{0\le j_k \le m \\ 1\le a_k\le j_k/2+C \\ k=1,2,3,4}}{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \end{align*}$$
$$\begin{align*}{\mathcal{Q}}^0_{2,2}\subset\bigcup_{\substack{0\le j_k \le m \\ 1\le a_k\le j_k/2+C \\ k=1,2,3,4}}{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \end{align*}$$
that (using that
![]() $f(\xi )=2^{-j/2}\lambda _j$
for
$f(\xi )=2^{-j/2}\lambda _j$
for
![]() $\xi \in S_j$
)
$\xi \in S_j$
)
 $$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{2,2}^{0}}f(Q) & \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a})\cdot 2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }2^{-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert a_{k}-a_{k+1}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \lesssim\sum_{\substack{0\le j_{k}\le m\\ k=1,2,3,4 } }\left(2^{-\delta\left\vert j_{1}-j_{2}\right\vert /2}\lambda_{j_{1}}\lambda_{j_{2}}\cdot2^{-\delta\left\vert j_{3}-j_{4}\right\vert }\lambda_{j_{3}}\lambda_{j_{4}}\right)\\& \quad \cdot\sum_{\substack{{1\le a_{k}\le m/2} +C\\ k=1,2,3,4 } }2^{-\delta\left(\left\vert a_{1}-a_{2}\right\vert +\left\vert a_{2}-a_{3}\right\vert +\left\vert a_{3}-a_{4}\right\vert \right)}\\& \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}\cdot\sum_{1\le a_{4}\le m/2+C}1\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{2,2}^{0}}f(Q) & \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a})\cdot 2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }2^{-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert a_{k}-a_{k+1}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \lesssim\sum_{\substack{0\le j_{k}\le m\\ k=1,2,3,4 } }\left(2^{-\delta\left\vert j_{1}-j_{2}\right\vert /2}\lambda_{j_{1}}\lambda_{j_{2}}\cdot2^{-\delta\left\vert j_{3}-j_{4}\right\vert }\lambda_{j_{3}}\lambda_{j_{4}}\right)\\& \quad \cdot\sum_{\substack{{1\le a_{k}\le m/2} +C\\ k=1,2,3,4 } }2^{-\delta\left(\left\vert a_{1}-a_{2}\right\vert +\left\vert a_{2}-a_{3}\right\vert +\left\vert a_{3}-a_{4}\right\vert \right)}\\& \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}\cdot\sum_{1\le a_{4}\le m/2+C}1\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
which is just (3.13).
We pass to showing (3.14), which is just a repeat of the preceding proof. By (3.17), (3.18), (3.19) and their cyclic relabels, for non-negative tuple
![]() $\left (c_{k,l}\right )_{k\le 4,l\le 2}$
such that
$\left (c_{k,l}\right )_{k\le 4,l\le 2}$
such that
![]() $\sum _{k,l}c_{k,l}=1$
, we have
$\sum _{k,l}c_{k,l}=1$
, we have
 $$\begin{align*}\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim2^{\sum_{k=1}^{4}\sum_{l=1}^{2}c_{k,l}\left(2j_{k}-2a_{k}+a_{k+1}+a_{k+1+l}\right)}\cdot2^{-c_{1,2}\cdot a_{4}/2}. \end{align*}$$
$$\begin{align*}\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim2^{\sum_{k=1}^{4}\sum_{l=1}^{2}c_{k,l}\left(2j_{k}-2a_{k}+a_{k+1}+a_{k+1+l}\right)}\cdot2^{-c_{1,2}\cdot a_{4}/2}. \end{align*}$$
Plugging the same choices of
![]() $\left (c_{k,l}\right )_{k\le 4,l\le 2}$
, we obtain
$\left (c_{k,l}\right )_{k\le 4,l\le 2}$
, we obtain
 $$\begin{align*}\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim2^{\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert \alpha_{k}-\alpha_{k+1}\right\vert \right)}\cdot2^{-\delta a_{4}}, \end{align*}$$
$$\begin{align*}\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim2^{\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert \alpha_{k}-\alpha_{k+1}\right\vert \right)}\cdot2^{-\delta a_{4}}, \end{align*}$$
concluding that
 $$ \begin{align*} &\sum_{Q=(\xi_1,\xi_2,\xi_3,\xi_4)\in{\mathcal{Q}}_{2,2}^{0}}\frac{1}{\gcd(\xi_1-\xi_4)}f(Q)\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }2^{-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert a_{k}-a_{k+1}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\cdot2^{-\delta a_{4}}\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ k=1,2,3,4 } }\left(2^{-\delta\left\vert j_{1}-j_{2}\right\vert /2}\lambda_{j_{1}}\lambda_{j_{2}}\cdot2^{-\delta\left\vert j_{3}-j_{4}\right\vert }\lambda_{j_{3}}\lambda_{j_{4}}\right)\\& \qquad \cdot\sum_{\substack{{1\le a_{k}\le m/2} +C\\ k=1,2,3,4 } }2^{-\delta\left(\left\vert a_{1}-a_{2}\right\vert +\left\vert a_{2}-a_{3}\right\vert +\left\vert a_{3}-a_{4}\right\vert \right)}\cdot2^{-\delta a_{4}}\\& \quad \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
$$ \begin{align*} &\sum_{Q=(\xi_1,\xi_2,\xi_3,\xi_4)\in{\mathcal{Q}}_{2,2}^{0}}\frac{1}{\gcd(\xi_1-\xi_4)}f(Q)\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }2^{-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert a_{k}-a_{k+1}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\cdot2^{-\delta a_{4}}\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ k=1,2,3,4 } }\left(2^{-\delta\left\vert j_{1}-j_{2}\right\vert /2}\lambda_{j_{1}}\lambda_{j_{2}}\cdot2^{-\delta\left\vert j_{3}-j_{4}\right\vert }\lambda_{j_{3}}\lambda_{j_{4}}\right)\\& \qquad \cdot\sum_{\substack{{1\le a_{k}\le m/2} +C\\ k=1,2,3,4 } }2^{-\delta\left(\left\vert a_{1}-a_{2}\right\vert +\left\vert a_{2}-a_{3}\right\vert +\left\vert a_{3}-a_{4}\right\vert \right)}\cdot2^{-\delta a_{4}}\\& \quad \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
which is just (3.14).
Case III:
![]() $(\alpha ,\beta )=(3,3)$
.
$(\alpha ,\beta )=(3,3)$
.
For
![]() $j_{1},j_{2},j_{3},j_{4}\in \mathbf {\mathbb {N}}$
, by Lemma 3.4, we have
$j_{1},j_{2},j_{3},j_{4}\in \mathbf {\mathbb {N}}$
, by Lemma 3.4, we have
One can check
and so
 $$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{3,3}^{0}}f(Q) & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}q_{j_{1},j_{2},j_{3},j_{4}}2^{-\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{3}\ge0}2^{-\frac{1}{100}\left\vert j_{1}-j_{3}\right\vert }\lambda_{j_{1}}\lambda_{j_{3}}\cdot\sum_{j_{2},j_{4}\ge0}2^{-\frac{1}{100}\left\vert j_{2}-j_{4}\right\vert }\lambda_{j_{2}}\lambda_{j_{4}}\\ & \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{3,3}^{0}}f(Q) & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}q_{j_{1},j_{2},j_{3},j_{4}}2^{-\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{3}\ge0}2^{-\frac{1}{100}\left\vert j_{1}-j_{3}\right\vert }\lambda_{j_{1}}\lambda_{j_{3}}\cdot\sum_{j_{2},j_{4}\ge0}2^{-\frac{1}{100}\left\vert j_{2}-j_{4}\right\vert }\lambda_{j_{2}}\lambda_{j_{4}}\\ & \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
which is just (3.12) for the case.
Case IV:
![]() $(\alpha ,\beta )=(2,3)$
(or
$(\alpha ,\beta )=(2,3)$
(or
![]() $(3,2)$
).
$(3,2)$
).
For
![]() $j_{1},j_{2},j_{3},j_{4}\in \mathbf {\mathbb {N}}$
, by Lemma 3.4, we have
$j_{1},j_{2},j_{3},j_{4}\in \mathbf {\mathbb {N}}$
, by Lemma 3.4, we have
For
![]() $\overrightarrow {a}=(a_1,a_2,0,0)$
with integers
$\overrightarrow {a}=(a_1,a_2,0,0)$
with integers
![]() $a_{1},a_{2}$
such that
$a_{1},a_{2}$
such that
![]() $1\le a_{1}<j_{1}/2+C$
and
$1\le a_{1}<j_{1}/2+C$
and
![]() $1\le a_{2}<j_{2}/2+C$
, by Lemma 3.4 and (3.18), we also have
$1\le a_{2}<j_{2}/2+C$
, by Lemma 3.4 and (3.18), we also have
and
 $$ \begin{align} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) & \lesssim\min\left\{ 2^{2j_{1}-2a_{1}},2^{2j_{2}-2a_{2}}\right\} \\ & \lesssim2^{j_{1}+j_{2}-(a_{1}+a_{2})}.\nonumber \end{align} $$
$$ \begin{align} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) & \lesssim\min\left\{ 2^{2j_{1}-2a_{1}},2^{2j_{2}-2a_{2}}\right\} \\ & \lesssim2^{j_{1}+j_{2}-(a_{1}+a_{2})}.\nonumber \end{align} $$
Interpolating (3.25) and (3.26), we have
 $$ \begin{align*} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) & \lesssim2^{\frac{3}{5}\left(j_{3}+j_{4}+\frac{1}{2}(a_{1}+a_{2})\right)+\frac{2}{5}\left(j_{1}+j_{2}-(a_{1}+a_{2})\right)}\\ &=2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)-\frac{1}{10}\left(a_{1}+a_{2}\right)}, \end{align*} $$
$$ \begin{align*} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) & \lesssim2^{\frac{3}{5}\left(j_{3}+j_{4}+\frac{1}{2}(a_{1}+a_{2})\right)+\frac{2}{5}\left(j_{1}+j_{2}-(a_{1}+a_{2})\right)}\\ &=2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)-\frac{1}{10}\left(a_{1}+a_{2}\right)}, \end{align*} $$
which implies
 $$ \begin{align} q_{j_{1},j_{2},j_{3},j_{4}} & \le\sum_{\substack{1\le a_{1}<j_{1}/2+C\\ 1\le a_{2}<j_{2}/2+C } }\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \\ & \lesssim\sum_{a_{1},a_{2}\in\mathbf{\mathbb{N}}}2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)-\frac{1}{10}\left(a_{1}+a_{2}\right)}\nonumber \\ & \lesssim2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)}.\nonumber \end{align} $$
$$ \begin{align} q_{j_{1},j_{2},j_{3},j_{4}} & \le\sum_{\substack{1\le a_{1}<j_{1}/2+C\\ 1\le a_{2}<j_{2}/2+C } }\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \\ & \lesssim\sum_{a_{1},a_{2}\in\mathbf{\mathbb{N}}}2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)-\frac{1}{10}\left(a_{1}+a_{2}\right)}\nonumber \\ & \lesssim2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)}.\nonumber \end{align} $$
By (3.24), (3.27) and the inequality
 $$ \begin{align*} & \min\left\{ j_{1}+j_{4},j_{2}+j_{3},j_{1}+j_{2},\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)\right\} -(j_{1}+j_{2}+j_{3}+j_{4})/2\\& \quad \le-\frac{1}{100}\left(\left\vert j_{1}-j_{3}\right\vert +\left\vert j_{2}-j_{4}\right\vert \right), \end{align*} $$
$$ \begin{align*} & \min\left\{ j_{1}+j_{4},j_{2}+j_{3},j_{1}+j_{2},\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)\right\} -(j_{1}+j_{2}+j_{3}+j_{4})/2\\& \quad \le-\frac{1}{100}\left(\left\vert j_{1}-j_{3}\right\vert +\left\vert j_{2}-j_{4}\right\vert \right), \end{align*} $$
we conclude
 $$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{2,3}^{0}}f(Q) & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}q_{j_{1},j_{2},j_{3},j_{4}}2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}2^{-\frac{1}{100}\left(\left\vert j_{1}-j_{3}\right\vert +\left\vert j_{2}-j_{4}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{3}\ge0}2^{-\frac{1}{100}\left\vert j_{1}-j_{3}\right\vert }\lambda_{j_{1}}\lambda_{j_{3}}\cdot\sum_{j_{2},j_{4}\ge0}2^{-\frac{1}{100}\left\vert j_{2}-j_{4}\right\vert }\lambda_{j_{2}}\lambda_{j_{4}}\\ & \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{2,3}^{0}}f(Q) & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}q_{j_{1},j_{2},j_{3},j_{4}}2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}2^{-\frac{1}{100}\left(\left\vert j_{1}-j_{3}\right\vert +\left\vert j_{2}-j_{4}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{3}\ge0}2^{-\frac{1}{100}\left\vert j_{1}-j_{3}\right\vert }\lambda_{j_{1}}\lambda_{j_{3}}\cdot\sum_{j_{2},j_{4}\ge0}2^{-\frac{1}{100}\left\vert j_{2}-j_{4}\right\vert }\lambda_{j_{2}}\lambda_{j_{4}}\\ & \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$
which is just (3.12) for the case.
Remark 3.6. We thank Po-Lam Yung for the following more conceptional explanation of above interpolation type arguments. For example, in Case IV,
![]() $(\frac 12,\frac 12,\frac 12,\frac 12)$
is in the interior of the convex hull C of
$(\frac 12,\frac 12,\frac 12,\frac 12)$
is in the interior of the convex hull C of
![]() $(1,0,0,1)$
,
$(1,0,0,1)$
,
![]() $(0,1,1,0)$
,
$(0,1,1,0)$
,
![]() $(1,1,0,0)$
and
$(1,1,0,0)$
and
![]() $(\frac 25,\frac 25,\frac 35,\frac 35)$
. More precisely,
$(\frac 25,\frac 25,\frac 35,\frac 35)$
. More precisely,
All these points lie in the plane
![]() $P=\{x_1+x_3 = 1 \text { and } x_2+x_4 = 1\}$
. Hence, for small
$P=\{x_1+x_3 = 1 \text { and } x_2+x_4 = 1\}$
. Hence, for small
![]() $\delta> 0$
, the four points
$\delta> 0$
, the four points
are all in
![]() $P\cap C$
. Therefore, regardless of the signs of
$P\cap C$
. Therefore, regardless of the signs of
![]() $j_1-j_3$
and
$j_1-j_3$
and
![]() $j_2-j_4$
, there exist
$j_2-j_4$
, there exist
![]() $c_j\geq 0$
satisfying
$c_j\geq 0$
satisfying
![]() $c_1+c_2+c_3+c_4 = 1$
so that
$c_1+c_2+c_3+c_4 = 1$
so that
 $$ \begin{align*} &c_1(j_1+j_4) + c_2(j_2+j_3) + c_3(j_1+j_2) + c_4( \tfrac35(j_3+j_4)+\tfrac25(j_1+j_2) ) \\ & \quad = \tfrac12(j_1+j_2+j_3+j_4) - \delta (|j_1-j_3| + |j_2-j_4|), \end{align*} $$
$$ \begin{align*} &c_1(j_1+j_4) + c_2(j_2+j_3) + c_3(j_1+j_2) + c_4( \tfrac35(j_3+j_4)+\tfrac25(j_1+j_2) ) \\ & \quad = \tfrac12(j_1+j_2+j_3+j_4) - \delta (|j_1-j_3| + |j_2-j_4|), \end{align*} $$
and in the argument in Case IV above, we have chosen
![]() $\delta = \tfrac 1{100}$
.
$\delta = \tfrac 1{100}$
.
This completes the overall proof of Theorem 1.2.
4 Proof of Theorem 1.4
We only carry out the proof on the relevant case
![]() $0<s\le 1$
, which is most convenient with adapted function spaces. For this purpose, we recall the definition of the function space
$0<s\le 1$
, which is most convenient with adapted function spaces. For this purpose, we recall the definition of the function space
![]() $Y^{s}$
from [Reference Herr, Tataru and Tzvetkov10] and relevant facts. For a general theory, we refer to [Reference Koch, Tataru and Vişan12, Reference Herr, Tataru and Tzvetkov10, Reference Hadac, Herr and Koch8, Reference Hadac, Herr and Koch9].
$Y^{s}$
from [Reference Herr, Tataru and Tzvetkov10] and relevant facts. For a general theory, we refer to [Reference Koch, Tataru and Vişan12, Reference Herr, Tataru and Tzvetkov10, Reference Hadac, Herr and Koch8, Reference Hadac, Herr and Koch9].
Definition 4.1. Let
![]() $\mathcal {Z}$
be the collection of finite non-decreasing sequences
$\mathcal {Z}$
be the collection of finite non-decreasing sequences
![]() $\left \{ t_{k}\right \} _{k=0}^{K}$
in
$\left \{ t_{k}\right \} _{k=0}^{K}$
in
![]() $\mathbf {\mathbb {R}}$
. We define
$\mathbf {\mathbb {R}}$
. We define
![]() $V^{2}$
as the space of all right-continuous functions
$V^{2}$
as the space of all right-continuous functions
![]() $u:\mathbf {\mathbb {R}}\rightarrow \mathbf {\mathbb {C}}$
with
$u:\mathbf {\mathbb {R}}\rightarrow \mathbf {\mathbb {C}}$
with
![]() $\lim _{t\rightarrow -\infty }u(t)=0$
and
$\lim _{t\rightarrow -\infty }u(t)=0$
and
 $$\begin{align*}\|u\|_{V^{2}}:=\left(\sup_{\left\{ t_{k}\right\} _{k=0}^{K}\in{\mathcal{Z}}}\sum_{k=1}^{K}\left\vert u(t_{k})-u(t_{k-1})\right\vert ^{2}\right)^{1/2}<\infty. \end{align*}$$
$$\begin{align*}\|u\|_{V^{2}}:=\left(\sup_{\left\{ t_{k}\right\} _{k=0}^{K}\in{\mathcal{Z}}}\sum_{k=1}^{K}\left\vert u(t_{k})-u(t_{k-1})\right\vert ^{2}\right)^{1/2}<\infty. \end{align*}$$
For
![]() $s\in \mathbf {\mathbb {R}}$
, we define
$s\in \mathbf {\mathbb {R}}$
, we define
![]() $Y^{s}$
as the space of
$Y^{s}$
as the space of
![]() $u:\mathbf {\mathbb {R}}\times \mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$
such that
$u:\mathbf {\mathbb {R}}\times \mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$
such that
![]() $e^{it|\xi |^2}\widehat {u(t)}(\xi )$
lies in
$e^{it|\xi |^2}\widehat {u(t)}(\xi )$
lies in
![]() $V^{2}$
for each
$V^{2}$
for each
![]() $\xi \in \mathbf {\mathbb {Z}}^{2}$
and
$\xi \in \mathbf {\mathbb {Z}}^{2}$
and
 $$\begin{align*}\|u\|_{Y^{s}}\:=\left(\sum_{\xi\in\mathbf{\mathbb{Z}}^{2}}\left(1+\left\vert \xi\right\vert ^{2}\right)^{s}\|e^{it|\xi|^{2}}\widehat{u(t)}(\xi)\|_{V^{2}}^{2}\right)^{1/2}<\infty. \end{align*}$$
$$\begin{align*}\|u\|_{Y^{s}}\:=\left(\sum_{\xi\in\mathbf{\mathbb{Z}}^{2}}\left(1+\left\vert \xi\right\vert ^{2}\right)^{s}\|e^{it|\xi|^{2}}\widehat{u(t)}(\xi)\|_{V^{2}}^{2}\right)^{1/2}<\infty. \end{align*}$$
For time interval
![]() $I\subset \mathbf {\mathbb {R}}$
, we also consider the restriction space
$I\subset \mathbf {\mathbb {R}}$
, we also consider the restriction space
![]() $Y^s(I)$
of
$Y^s(I)$
of
![]() $Y^s$
.
$Y^s$
.
The space
![]() $Y^{s}$
is used in [Reference Herr, Tataru and Tzvetkov10] and later works on critical regularity theory of Schrödinger equations on periodic domains. Some well-known properties are the following.
$Y^{s}$
is used in [Reference Herr, Tataru and Tzvetkov10] and later works on critical regularity theory of Schrödinger equations on periodic domains. Some well-known properties are the following.
Proposition 4.2 [Reference Herr, Tataru and Tzvetkov10, Section 2].
![]() $Y^{s}$
-norms have the following properties.
$Y^{s}$
-norms have the following properties.
-
• Let
 $A,B$
be disjoint subsets of
$A,B$
be disjoint subsets of
 $\mathbf {\mathbb {Z}}^{2}$
. For
$\mathbf {\mathbb {Z}}^{2}$
. For
 $s\in \mathbf {\mathbb {R}}$
, we have (4.1)
$s\in \mathbf {\mathbb {R}}$
, we have (4.1) $$ \begin{align} \|P_{A\cup B}u\|_{Y^{s}}^{2}=\|P_{A}u\|_{Y^{s}}^{2}+\|P_{B}u\|_{Y^{s}}^{2}. \end{align} $$
$$ \begin{align} \|P_{A\cup B}u\|_{Y^{s}}^{2}=\|P_{A}u\|_{Y^{s}}^{2}+\|P_{B}u\|_{Y^{s}}^{2}. \end{align} $$
-
• For
 $s\in \mathbf {\mathbb {R}}$
, time
$s\in \mathbf {\mathbb {R}}$
, time
 $T>0$
and a function
$T>0$
and a function
 $f\in L^{1}H^{s}$
, denoting we have
$f\in L^{1}H^{s}$
, denoting we have $$\begin{align*}{\mathcal{I}}(f)(t):=\int_{0}^{t}e^{i(t-t')\Delta}f(t')dt', \end{align*}$$
(4.2)
$$\begin{align*}{\mathcal{I}}(f)(t):=\int_{0}^{t}e^{i(t-t')\Delta}f(t')dt', \end{align*}$$
(4.2) $$ \begin{align} \|\chi_{[0,T)}\cdot{\mathcal{I}}(f)\|_{Y^{s}}\lesssim\sup_{v\in Y^{-s}:\|v\|_{Y^{-s}}\le1}\left\vert \int_0^T\int_{\mathbb{T}^{2}}f\overline{v}dxdt\right\vert. \end{align} $$
$$ \begin{align} \|\chi_{[0,T)}\cdot{\mathcal{I}}(f)\|_{Y^{s}}\lesssim\sup_{v\in Y^{-s}:\|v\|_{Y^{-s}}\le1}\left\vert \int_0^T\int_{\mathbb{T}^{2}}f\overline{v}dxdt\right\vert. \end{align} $$
-
• For time
 $T>0$
and a function
$T>0$
and a function
 $\phi \in H^s(\mathbb {T}^2)$
, we have (4.3)and for function
$\phi \in H^s(\mathbb {T}^2)$
, we have (4.3)and for function $$ \begin{align} \|\chi_{[0,T)}\cdot e^{it\Delta}\phi\|_{Y^s}\approx\|\phi\|_{H^s} \end{align} $$
$$ \begin{align} \|\chi_{[0,T)}\cdot e^{it\Delta}\phi\|_{Y^s}\approx\|\phi\|_{H^s} \end{align} $$
 $u\in Y^s$
,
$u\in Y^s$
,
 $u\in L^\infty H^s$
and (4.4)
$u\in L^\infty H^s$
and (4.4) $$ \begin{align} \|\chi_{[0,T)}u\|_{Y^s}\gtrsim\|u\|_{L^\infty([0,T);H^s)}. \end{align} $$
$$ \begin{align} \|\chi_{[0,T)}u\|_{Y^s}\gtrsim\|u\|_{L^\infty([0,T);H^s)}. \end{align} $$
For
![]() $N\in 2^{\mathbf {\mathbb {N}}}$
, denote by
$N\in 2^{\mathbf {\mathbb {N}}}$
, denote by
![]() ${\mathcal {C}}_{N}$
the set of cubes of size N
${\mathcal {C}}_{N}$
the set of cubes of size N
We transfer (1.3) to the following estimate.
Lemma 4.3. For all
![]() $N\in 2^{\mathbf {\mathbb {N}}}$
, intervals
$N\in 2^{\mathbf {\mathbb {N}}}$
, intervals
![]() $I\subset \mathbf {\mathbb {R}}$
such that
$I\subset \mathbf {\mathbb {R}}$
such that
![]() $\left \vert I\right \vert \le \frac {1}{\log N}$
, cubes
$\left \vert I\right \vert \le \frac {1}{\log N}$
, cubes
![]() $C\in {\mathcal {C}}_{N}$
, and
$C\in {\mathcal {C}}_{N}$
, and
![]() $u\in Y^{0}$
, we have
$u\in Y^{0}$
, we have
Proof. We follow the notations in [Reference Herr, Tataru and Tzvetkov10, Section 2]. Let u be a
![]() $U_{\Delta }^{4}L^2$
-atom; that is,
$U_{\Delta }^{4}L^2$
-atom; that is,
 $$\begin{align*}u(t)=\sum_{j=1}^{J}1_{[t_{j-1},t_{j})}e^{it\Delta}\phi_{j} \end{align*}$$
$$\begin{align*}u(t)=\sum_{j=1}^{J}1_{[t_{j-1},t_{j})}e^{it\Delta}\phi_{j} \end{align*}$$
for
![]() $\phi _{1},\ldots ,\phi _{J}\in L^{2}(\mathbb {T}^{2})$
,
$\phi _{1},\ldots ,\phi _{J}\in L^{2}(\mathbb {T}^{2})$
,
![]() $t_0\le ...\le t_J$
,
$t_0\le ...\le t_J$
,
![]() $\sum _{j=1}^{J}\|\phi _{j}\|_{L^{2}}^{4}=1$
. By (1.3), we have
$\sum _{j=1}^{J}\|\phi _{j}\|_{L^{2}}^{4}=1$
. By (1.3), we have
 $$ \begin{align} \|P_{C}u\|_{L^{4}_{t,x}(I\times\mathbb{T}^{2})}^{4}\lesssim\sum_{j=1}^{J}\|P_{C}e^{it\Delta}\phi_{j}\|_{L^{4}_{t,x}(I\times\mathbb{T}^{2})}^{4}\lesssim\sum_{j=1}^{J}\|\phi_{j}\|_{L^{2}}^{4}\lesssim 1. \end{align} $$
$$ \begin{align} \|P_{C}u\|_{L^{4}_{t,x}(I\times\mathbb{T}^{2})}^{4}\lesssim\sum_{j=1}^{J}\|P_{C}e^{it\Delta}\phi_{j}\|_{L^{4}_{t,x}(I\times\mathbb{T}^{2})}^{4}\lesssim\sum_{j=1}^{J}\|\phi_{j}\|_{L^{2}}^{4}\lesssim 1. \end{align} $$
By [Reference Herr, Tataru and Tzvetkov10, Proposition 2.3] and (4.6), for
![]() $u\in Y^{0}$
, we conclude
$u\in Y^{0}$
, we conclude
Since we only rely on the
![]() $L^4$
estimate, Lemma 4.3 explains why we can work with the
$L^4$
estimate, Lemma 4.3 explains why we can work with the
![]() $Y^s$
-norm instead of the
$Y^s$
-norm instead of the
![]() $U^2$
-based space as was used in [Reference Herr, Tataru and Tzvetkov10].
$U^2$
-based space as was used in [Reference Herr, Tataru and Tzvetkov10].
For
![]() $N\in 2^{\mathbf {\mathbb {N}}}$
, we set the interval
$N\in 2^{\mathbf {\mathbb {N}}}$
, we set the interval
![]() $I_N:=[0,1/\log N)$
. Let
$I_N:=[0,1/\log N)$
. Let
![]() $Z_N$
be the norm
$Z_N$
be the norm
We show our main trilinear estimate:
Lemma 4.4. For
![]() $0<s\le 1$
and
$0<s\le 1$
and
![]() $N\gg 2^{1/s}$
, we have
$N\gg 2^{1/s}$
, we have
where each
![]() $u_j$
could also be replaced by its complex conjugate. The implicit constant is independent from s.
$u_j$
could also be replaced by its complex conjugate. The implicit constant is independent from s.
Proof. Let
![]() $k_s=\lfloor 1/s \rfloor $
. In this proof, we use
$k_s=\lfloor 1/s \rfloor $
. In this proof, we use
![]() $2^{k_s}$
-adic cutoffs: for
$2^{k_s}$
-adic cutoffs: for
![]() $N\in 2^{k_s\mathbf {\mathbb {N}}}$
, we denote
$N\in 2^{k_s\mathbf {\mathbb {N}}}$
, we denote
Since
![]() $\|\chi _{I_N}\cdot u\|_{Z_{\widetilde {N}}}\approx \|u\|_{Z_N}$
holds for
$\|\chi _{I_N}\cdot u\|_{Z_{\widetilde {N}}}\approx \|u\|_{Z_N}$
holds for
![]() $\widetilde {N}\in [2^{-k_s}N,N]$
, we assume further that
$\widetilde {N}\in [2^{-k_s}N,N]$
, we assume further that
![]() $N\in 2^{k_s\mathbf {\mathbb {N}}}$
. (4.7) is reduced to showing
$N\in 2^{k_s\mathbf {\mathbb {N}}}$
. (4.7) is reduced to showing
 $$ \begin{align} \left\vert \int_{I_N\times\mathbb{T}^2}u_1u_2u_3\cdot v_{<N}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|u_3\|_{Z_N}\|v\|_{Y^{0}} \end{align} $$
$$ \begin{align} \left\vert \int_{I_N\times\mathbb{T}^2}u_1u_2u_3\cdot v_{<N}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|u_3\|_{Z_N}\|v\|_{Y^{0}} \end{align} $$
and
 $$ \begin{align} \left\vert \int_{I_N\times\mathbb{T}^2}u_1u_2u_3\cdot v_{\ge N}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|u_3\|_{Z_N}\cdot N^{s}\|v\|_{Y^{-s}} \end{align} $$
$$ \begin{align} \left\vert \int_{I_N\times\mathbb{T}^2}u_1u_2u_3\cdot v_{\ge N}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|u_3\|_{Z_N}\cdot N^{s}\|v\|_{Y^{-s}} \end{align} $$
with implicit constants in (4.8) and (4.9) independent from s.
We prove (4.8) and (4.9). For
![]() $M\ge N$
in
$M\ge N$
in
![]() $2^{k_s\mathbf {\mathbb {N}}}$
and
$2^{k_s\mathbf {\mathbb {N}}}$
and
![]() $C\in {\mathcal {C}}_M$
, partitioning
$C\in {\mathcal {C}}_M$
, partitioning
![]() $I_N$
to intervals of length comparable to
$I_N$
to intervals of length comparable to
![]() $\frac {1}{\log M}$
and applying (4.5) to each, we have
$\frac {1}{\log M}$
and applying (4.5) to each, we have
 $$ \begin{align} \|\chi_{I_N}\cdot P_C u\|_{L_{t,x}^{4}}\lesssim\left(\frac{\log M}{\log N}\right)^{1/4}\|u\|_{Y^{0}}. \end{align} $$
$$ \begin{align} \|\chi_{I_N}\cdot P_C u\|_{L_{t,x}^{4}}\lesssim\left(\frac{\log M}{\log N}\right)^{1/4}\|u\|_{Y^{0}}. \end{align} $$
By (4.10), for
![]() $u\in Y^{s}$
, we have
$u\in Y^{s}$
, we have
 $$ \begin{align} \|\chi_{I_N}\cdot u\|_{L_{t,x}^{4}} & \lesssim\|u_{<N}\|_{Y^{0}}+\sum_{M\ge N}\left(\frac{\log M}{\log N}\right)^{1/4}\|u_{\sim M}\|_{Y^{0}}\\ & \lesssim\|u\|_{Y^{0}}+\sum_{M\ge N}\left(\frac{\log M}{\log N}\right)^{1/4}\frac{N^{s}}{M^{s}}\cdot N^{-s}\|u\|_{Y^{s}}\nonumber\\ & \lesssim\|u\|_{Y^{0}}+N^{-s}\|u\|_{Y^{s}}\lesssim\|u\|_{Z_N},\nonumber \end{align} $$
$$ \begin{align} \|\chi_{I_N}\cdot u\|_{L_{t,x}^{4}} & \lesssim\|u_{<N}\|_{Y^{0}}+\sum_{M\ge N}\left(\frac{\log M}{\log N}\right)^{1/4}\|u_{\sim M}\|_{Y^{0}}\\ & \lesssim\|u\|_{Y^{0}}+\sum_{M\ge N}\left(\frac{\log M}{\log N}\right)^{1/4}\frac{N^{s}}{M^{s}}\cdot N^{-s}\|u\|_{Y^{s}}\nonumber\\ & \lesssim\|u\|_{Y^{0}}+N^{-s}\|u\|_{Y^{s}}\lesssim\|u\|_{Z_N},\nonumber \end{align} $$
which implies (4.8).
We prove (4.9) by partitioning the frequency domain
![]() $\mathbf {\mathbb {Z}}^{2}$
into congruent cubes. By (4.10) and (4.1), for
$\mathbf {\mathbb {Z}}^{2}$
into congruent cubes. By (4.10) and (4.1), for
![]() $M\in 2^{k_s\mathbf {\mathbb {N}}}$
and
$M\in 2^{k_s\mathbf {\mathbb {N}}}$
and
![]() $u,v\in Y^{0}$
, we have
$u,v\in Y^{0}$
, we have
 $$ \begin{align} &\|\chi_{I_N} \cdot P_{\le M}\left(uv\right)\|_{L_{t,x}^{2}}\\&\quad \lesssim\sum_{\substack{C_{1},C_{2}\in{\mathcal{C}}_{M}\\ \operatorname{\mathrm{dist}}(C_{1},C_{2})\le M } }\|\chi_{I_N}\cdot P_{C_{1}}u\cdot P_{C_{2}}v\|_{L_{t,x}^{2}}\nonumber \\&\quad \lesssim\sum_{\substack{C_{1},C_{2}\in{\mathcal{C}}_{M}\\ \operatorname{\mathrm{dist}}(C_{1},C_{2})\le M } }\|\chi_{I_N}\cdot P_{C_{1}}u\|_{L_{t,x}^{4}}\|\chi_{I_N}\cdot P_{C_{2}}v\|_{L_{t,x}^{4}}\nonumber \\&\quad \lesssim\left(1+\frac{\log M}{\log N}\right)^{1/2}\left(\sum_{C\in{\mathcal{C}}_{M}}\|P_{C}u\|_{Y^{0}}^2\sum_{C\in{\mathcal{C}}_{M}}\|P_{C}v\|_{Y^{0}}^2\right)^{1/2}\nonumber \\&\quad \lesssim\left(1+\frac{\log M}{\log N}\right)^{1/2}\|u\|_{Y^{0}}\|v\|_{Y^{0}}.\nonumber \end{align} $$
$$ \begin{align} &\|\chi_{I_N} \cdot P_{\le M}\left(uv\right)\|_{L_{t,x}^{2}}\\&\quad \lesssim\sum_{\substack{C_{1},C_{2}\in{\mathcal{C}}_{M}\\ \operatorname{\mathrm{dist}}(C_{1},C_{2})\le M } }\|\chi_{I_N}\cdot P_{C_{1}}u\cdot P_{C_{2}}v\|_{L_{t,x}^{2}}\nonumber \\&\quad \lesssim\sum_{\substack{C_{1},C_{2}\in{\mathcal{C}}_{M}\\ \operatorname{\mathrm{dist}}(C_{1},C_{2})\le M } }\|\chi_{I_N}\cdot P_{C_{1}}u\|_{L_{t,x}^{4}}\|\chi_{I_N}\cdot P_{C_{2}}v\|_{L_{t,x}^{4}}\nonumber \\&\quad \lesssim\left(1+\frac{\log M}{\log N}\right)^{1/2}\left(\sum_{C\in{\mathcal{C}}_{M}}\|P_{C}u\|_{Y^{0}}^2\sum_{C\in{\mathcal{C}}_{M}}\|P_{C}v\|_{Y^{0}}^2\right)^{1/2}\nonumber \\&\quad \lesssim\left(1+\frac{\log M}{\log N}\right)^{1/2}\|u\|_{Y^{0}}\|v\|_{Y^{0}}.\nonumber \end{align} $$
We conclude quadrilinear estimates. By (4.12) and Young’s convolution inequality on
![]() $(L,K)$
using that
$(L,K)$
using that
![]() $\sum _{R\in 2^{k_s\mathbf {\mathbb {N}}}}R^{-s}\lesssim 1$
, we have
$\sum _{R\in 2^{k_s\mathbf {\mathbb {N}}}}R^{-s}\lesssim 1$
, we have
 $$ \begin{align} & \sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<N}(u_1u_2)P_{<N}(w_{\sim L}v_{\sim K})dxdt\right\vert \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}}\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}}\sum_{K\ge N}\sum_{L\gtrsim K}(L/K)^{-s}\|w_{\sim L}\|_{Y^{s}}\|v_{\sim K}\|_{Y^{-s}}\nonumber \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}} \|w\|_{Y^{s}} \|v\|_{Y^{-s}}\nonumber \end{align} $$
$$ \begin{align} & \sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<N}(u_1u_2)P_{<N}(w_{\sim L}v_{\sim K})dxdt\right\vert \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}}\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}}\sum_{K\ge N}\sum_{L\gtrsim K}(L/K)^{-s}\|w_{\sim L}\|_{Y^{s}}\|v_{\sim K}\|_{Y^{-s}}\nonumber \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}} \|w\|_{Y^{s}} \|v\|_{Y^{-s}}\nonumber \end{align} $$
and
 $$ \begin{align} & \sum_{M\ge N}\sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I\times\mathbb{T}^{2}}P_{\sim M}\left(u_1u_2\right)P_{\sim M}\left(w_{\sim L}v_{\sim K}\right)dxdt\right\vert \\&\quad \lesssim\sum_{M\ge N}\frac{\log M}{\log N}(\|P_{\ge M/4}u_1\|_{Y^0}\|u_2\|_{Y^0}+\|u_1\|_{Y^0}\|P_{\ge M/4}u_2\|_{Y^0})\nonumber \\&\qquad \cdot\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\sum_{M\ge N}\frac{\log M}{\log N}\frac{N^s}{M^s}\|u_1\|_{Z_N} \|u_2\|_{Z_N}\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\|u_1\|_{Z_N} \|u_2\|_{Z_N}\sum_{K\ge N}\sum_{L\gtrsim K}(L/K)^{-s}\|w_{\sim L}\|_{Y^s}\|v_{\sim K}\|_{Y^{-s}}\nonumber \\&\quad \lesssim \|u_1\|_{Z_N} \|u_2\|_{Z_N} \|w\|_{Y^s} \|v\|_{Y^{-s}}.\nonumber \end{align} $$
$$ \begin{align} & \sum_{M\ge N}\sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I\times\mathbb{T}^{2}}P_{\sim M}\left(u_1u_2\right)P_{\sim M}\left(w_{\sim L}v_{\sim K}\right)dxdt\right\vert \\&\quad \lesssim\sum_{M\ge N}\frac{\log M}{\log N}(\|P_{\ge M/4}u_1\|_{Y^0}\|u_2\|_{Y^0}+\|u_1\|_{Y^0}\|P_{\ge M/4}u_2\|_{Y^0})\nonumber \\&\qquad \cdot\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\sum_{M\ge N}\frac{\log M}{\log N}\frac{N^s}{M^s}\|u_1\|_{Z_N} \|u_2\|_{Z_N}\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\|u_1\|_{Z_N} \|u_2\|_{Z_N}\sum_{K\ge N}\sum_{L\gtrsim K}(L/K)^{-s}\|w_{\sim L}\|_{Y^s}\|v_{\sim K}\|_{Y^{-s}}\nonumber \\&\quad \lesssim \|u_1\|_{Z_N} \|u_2\|_{Z_N} \|w\|_{Y^s} \|v\|_{Y^{-s}}.\nonumber \end{align} $$
Combining (4.13) and (4.14), we have
 $$ \begin{align} \sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I_N\times\mathbb{T}^{2}}(u_1u_2)w_{\sim L}v_{\sim K}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|w\|_{Z_N}N^{s}\|v\|_{Y^{-s}}. \end{align} $$
$$ \begin{align} \sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I_N\times\mathbb{T}^{2}}(u_1u_2)w_{\sim L}v_{\sim K}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|w\|_{Z_N}N^{s}\|v\|_{Y^{-s}}. \end{align} $$
Note that in (4.12), (4.13), (4.14), (4.15) each function on the left-hand side could be replaced by its complex conjugate. We bound
 $$ \begin{align*} & \left\vert \int_{I_N\times\mathbb{T}^{2}}u_1u_2u_3v_{\ge N}dxdt\right\vert \\&\quad \le\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{\ge K/4}u_1\cdot u_2\cdot u_3\cdot v_{\sim K}dxdt\right\vert \\&\qquad +\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<K/4}u_1\cdot P_{\ge K/4}u_2\cdot u_3\cdot v_{\sim K}dxdt\right\vert \\&\qquad +\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<K/4}u_1\cdot P_{<K/4}u_2\cdot P_{\ge K/4}u_3\cdot v_{\sim K}dxdt\right\vert. \end{align*} $$
$$ \begin{align*} & \left\vert \int_{I_N\times\mathbb{T}^{2}}u_1u_2u_3v_{\ge N}dxdt\right\vert \\&\quad \le\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{\ge K/4}u_1\cdot u_2\cdot u_3\cdot v_{\sim K}dxdt\right\vert \\&\qquad +\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<K/4}u_1\cdot P_{\ge K/4}u_2\cdot u_3\cdot v_{\sim K}dxdt\right\vert \\&\qquad +\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<K/4}u_1\cdot P_{<K/4}u_2\cdot P_{\ge K/4}u_3\cdot v_{\sim K}dxdt\right\vert. \end{align*} $$
Proof of Theorem 1.4.
Let
![]() $s>0$
and
$s>0$
and
![]() $N\gg 2^{1/s}$
. By (4.7), (4.2) and the expansion
$N\gg 2^{1/s}$
. By (4.7), (4.2) and the expansion
![]() $|u|^2u-|v|^2v=(|u|^2+\overline {u}v)(u-v)+v^2\overline {(u-v)}$
, we have
$|u|^2u-|v|^2v=(|u|^2+\overline {u}v)(u-v)+v^2\overline {(u-v)}$
, we have
Based on (4.16), we use the contraction mapping principle. Let
![]() $B_N\subset H^s$
be the ball
$B_N\subset H^s$
be the ball
and
![]() $X_N$
be the complete metric space
$X_N$
be the complete metric space
equipped with the norm
![]() $Z_N$
, where
$Z_N$
, where
![]() $\delta ,\eta>0$
are universal constants to be fixed shortly.
$\delta ,\eta>0$
are universal constants to be fixed shortly.
By (4.16), there exists
![]() $\eta>0$
such that the map
$\eta>0$
such that the map
is a contraction map on
![]() $X_N$
of Lipschitz constant
$X_N$
of Lipschitz constant
![]() $1/2$
, which fixes
$1/2$
, which fixes
![]() $0$
.
$0$
.
By (4.3), there exists
![]() $\delta>0$
such that
$\delta>0$
such that
holds for every
![]() $\phi \in B_N$
, so that the map
$\phi \in B_N$
, so that the map
is a contraction mapping on
![]() $X_N$
. Thus, for
$X_N$
. Thus, for
![]() $u_0\in B_N$
, there exists a solution u to (NLS) in
$u_0\in B_N$
, there exists a solution u to (NLS) in
![]() $X_N$
on time interval
$X_N$
on time interval
![]() $I_N$
. Moreover, since the map
$I_N$
. Moreover, since the map
![]() $u\mapsto {\mathcal {I}}(|u|^2u)$
is a contraction map of Lipschitz constant
$u\mapsto {\mathcal {I}}(|u|^2u)$
is a contraction map of Lipschitz constant
![]() $1/2$
, given solutions
$1/2$
, given solutions
![]() $u,v\in X_N$
to
$u,v\in X_N$
to
![]() $u_0,v_0\in B_N$
, we have
$u_0,v_0\in B_N$
, we have
 $$ \begin{align*} \|u-v\|_{Z_N}&\le\|e^{it\Delta}(u_0-v_0)\|_{Z_N}+\|{\mathcal{I}}(|u|^2u)-{\mathcal{I}}(|v|^2v)\|_{Z_N}\\ &\le\|e^{it\Delta}(u_0-v_0)\|_{Z_N}+\frac12\|u-v\|_{Z_N}, \end{align*} $$
$$ \begin{align*} \|u-v\|_{Z_N}&\le\|e^{it\Delta}(u_0-v_0)\|_{Z_N}+\|{\mathcal{I}}(|u|^2u)-{\mathcal{I}}(|v|^2v)\|_{Z_N}\\ &\le\|e^{it\Delta}(u_0-v_0)\|_{Z_N}+\frac12\|u-v\|_{Z_N}, \end{align*} $$
which implies that the flow map
![]() $u_0\mapsto u\in X_N$
is Lipschitz continuous by (4.3).
$u_0\mapsto u\in X_N$
is Lipschitz continuous by (4.3).
We then check uniqueness. Let
![]() $u,v\in Y^s\cap C^0H^s$
be solutions to (NLS) on a time interval
$u,v\in Y^s\cap C^0H^s$
be solutions to (NLS) on a time interval
![]() $[0,T),T>0$
, with common initial data
$[0,T),T>0$
, with common initial data
![]() $u_0$
such that
$u_0$
such that
![]() $\|u_0\|_{L^2}\le \delta $
. There exists
$\|u_0\|_{L^2}\le \delta $
. There exists
![]() $N_0\gg 2^{1/s}$
such that
$N_0\gg 2^{1/s}$
such that
![]() $I_{N_0}\subset [0,T)$
and
$I_{N_0}\subset [0,T)$
and
We have
 $$ \begin{align*} \|P_{\le N_0}(u-e^{it\Delta}u_0)\|_{Y^0(I_N)}&\lesssim\|P_{\le N_0}(|u|^2u)\|_{L^1(I_N;L^2)}\\ &\lesssim N_0\||u|^2u\|_{L^1(I_N;L^1)}\lesssim N_0\|u\|_{L^4(I_N;L^4)}^3, \end{align*} $$
$$ \begin{align*} \|P_{\le N_0}(u-e^{it\Delta}u_0)\|_{Y^0(I_N)}&\lesssim\|P_{\le N_0}(|u|^2u)\|_{L^1(I_N;L^2)}\\ &\lesssim N_0\||u|^2u\|_{L^1(I_N;L^1)}\lesssim N_0\|u\|_{L^4(I_N;L^4)}^3, \end{align*} $$
which shrinks to zero as
![]() $N\rightarrow \infty $
since
$N\rightarrow \infty $
since
![]() $u\in L^4_{t,x}$
on
$u\in L^4_{t,x}$
on
![]() $I_{N_0}$
by (4.11). Thus, applying the same argument to v, by (4.17), there exists
$I_{N_0}$
by (4.11). Thus, applying the same argument to v, by (4.17), there exists
![]() $N\ge N_0$
such that
$N\ge N_0$
such that
which implies
![]() $u=v$
on
$u=v$
on
![]() $I_N$
. Therefore, the maximal time
$I_N$
. Therefore, the maximal time
![]() $t_*\ge 0$
that
$t_*\ge 0$
that
![]() $u= v$
on
$u= v$
on
![]() $[0,t_*]$
cannot be less than T, implying the uniqueness of solution to (NLS).
$[0,t_*]$
cannot be less than T, implying the uniqueness of solution to (NLS).
In summary, we proved uniform Lipschitz local well-posedness of (NLS) mapping
![]() $B_N$
to
$B_N$
to
![]() $X_N$
. It remains to extend the lifespan over arbitrarily large time interval. For
$X_N$
. It remains to extend the lifespan over arbitrarily large time interval. For
![]() $N\gg 2^{1/s},t_0\in \mathbf {\mathbb {R}}$
, and a solution
$N\gg 2^{1/s},t_0\in \mathbf {\mathbb {R}}$
, and a solution
![]() $u\in Y^s$
to (NLS) such that
$u\in Y^s$
to (NLS) such that
![]() $u(t_0)\in B_N$
and
$u(t_0)\in B_N$
and
![]() $\|u(t_0)\|_{L^2}\le \delta $
, by (4.4), we have
$\|u(t_0)\|_{L^2}\le \delta $
, by (4.4), we have
Moreover, since
![]() $u(t_0)$
is a limit of smooth data in
$u(t_0)$
is a limit of smooth data in
![]() $B_N$
and solutions to (NLS) in
$B_N$
and solutions to (NLS) in
![]() $C^0H^2$
conserve their
$C^0H^2$
conserve their
![]() $L^2$
-norms, we have
$L^2$
-norms, we have
Thus, there exists a constant
![]() $K\in 2^{\mathbf {\mathbb {N}}}$
such that
$K\in 2^{\mathbf {\mathbb {N}}}$
such that
![]() $u(t_0+\frac {1}{2\log N})\in B_{KN}$
.
$u(t_0+\frac {1}{2\log N})\in B_{KN}$
.
Let
![]() $u_0\in H^s$
be any function that
$u_0\in H^s$
be any function that
![]() $\|u_0\|_{L^2}\le \delta $
. Let
$\|u_0\|_{L^2}\le \delta $
. Let
![]() $N_0\gg 2^{1/s}$
be a dyadic number such that
$N_0\gg 2^{1/s}$
be a dyadic number such that
![]() $u_0\in B_{N_0}$
. For
$u_0\in B_{N_0}$
. For
![]() $j\in \mathbf {\mathbb {N}}$
, let
$j\in \mathbf {\mathbb {N}}$
, let
 $$\begin{align*}N_j:=K^jN_0\text{ and }T_j:=\sum_{k=0}^{j-1}\frac{1}{2\log N_k}. \end{align*}$$
$$\begin{align*}N_j:=K^jN_0\text{ and }T_j:=\sum_{k=0}^{j-1}\frac{1}{2\log N_k}. \end{align*}$$
We extend the solution inductively. For
![]() $j\in \mathbf {\mathbb {N}}$
, we can extend the solution
$j\in \mathbf {\mathbb {N}}$
, we can extend the solution
![]() $u\in Y^s$
to (NLS) on
$u\in Y^s$
to (NLS) on
![]() $[0,T_j]$
to
$[0,T_j]$
to
![]() $[0,T_{j+1}]$
with
$[0,T_{j+1}]$
with
![]() $u(T_{j+1})\in B_{N_{j+1}}$
. Since
$u(T_{j+1})\in B_{N_{j+1}}$
. Since
![]() $\lim _{j\rightarrow \infty }T_j=\infty $
, the lifespan of u is infinite.
$\lim _{j\rightarrow \infty }T_j=\infty $
, the lifespan of u is infinite.
Acknowledgements
The authors are grateful to Ciprian Demeter for kindly pointing out an error in the first preprint version of this paper. In addition, the authors thank Ciprian Demeter and Po-Lam Yung for carefully reading Sections 1–3 and for a number of remarks that helped us to improve the exposition. Also, we thank the anonymous referees – in particular, for their detailed suggestions concerning the exposition in Section 4.
Competing interests
The authors have no competing interest to declare.
Financial Support
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – IRTG 2235 – Project-ID 282638148.