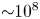1. Introduction
Pair plasmas are composed of positively and negatively charged particles with equal mass. This symmetry is predicted to quell many of the unstable dynamics that are common to conventional ion–electron plasmas (Helander Reference Helander2014). Extreme astrophysical environments that generate intense gamma radiation are abundant throughout the universe, and many likely produce electron–positron pairs at sufficient density and scale to form a plasma (Uso Reference Uso1992; Wardle et al. Reference Wardle, Homan, Ojha and Roberts1998; Ruffini, Vereshchagin & Xue Reference Ruffini, Vereshchagin and Xue2010; Uzdensky Reference Uzdensky2011). Accordingly, electron–positron plasma research is well motivated by its astrophysical relevance and unique characteristics. Experimental efforts, however, are hampered by the difficulty of amassing positrons (Greaves & Surko Reference Greaves and Surko1995; Pedersen et al. Reference Pedersen, Danielson, Hugenschmidt, Marx, Sarasola, Schauer, Schweikhard, Surko and Winkler2012; Higaki et al. Reference Higaki, Kaga, Fukushima, Okamoto, Nagata, Kanai and Yamazaki2017). Impressive advances have been made in creating relativistic pair plasmas using powerful pulsed lasers (Chen et al. Reference Chen, Wilks, Bonlie, Liang, Myatt, Price, Meyerhofer and Beiersdorfer2009; Sarri et al. Reference Sarri2015; Warwick et al. Reference Warwick, Dzelzainis, Dieckmann, Schumaker, Doria, Romagnani, Poder, Cole, Alejo, Yeung, Krushelnick, Mangles, Najmudin, Reville, Samarin, Symes, Thomas, Borghesi and Sarri2017; von der Linden et al. Reference von der Linden, Fiksel, Peebles, Edwards, Willingale, Link, Mastrosimone and Chen2021; Chen & Fiuza Reference Chen and Fiuza2023). Nevertheless, the MeV particle energies and surplus radiation associated with these techniques are not conducive to observing collective effects over long time scales.
The APEX (A Positron Electron eXperiment) project aims to produce and study neutral ($n_{-} = n_{+}$
), low-temperature ($k_B T \sim 1$
eV) electron–positron plasma (Stoneking et al. Reference Stoneking, Pedersen, Helander, Chen, Hergenhahn, Stenson, Fiksel, von der Linden, Saitoh and Surko2020). Magnetic fields will be used to confine the positrons and electrons for times ranging from $1$
to 1000 s. Two devices are being developed: (i) a magnetically levitated superconducting dipole (Saitoh, Stoneking & Pedersen Reference Saitoh, Stoneking and Pedersen2020) and (ii) a compact, optimized stellarator (EPOS). Both will have a confinement volume of ${\sim }10$
litres. To obtain a neutral, 1 eV plasma with a millimetre-scale Debye length (Stenson et al. Reference Stenson, Horn-Stanja, Stoneking and Pedersen2017),
(where $\epsilon _0$
is the permittivity of free space, $k_B$
is the Boltzmann constant, $e$
is the elementary charge and $n = n_{-} + n_{+} \approx 2 n_e$
is the total number density of the electrons and positrons), therefore requires $N > 10^{10} e^+$
. Positron beams typically utilize $\beta ^+$
decay of $^{22}$
Na and solid-neon moderators (Mills & Gullikson Reference Mills and Gullikson1986); commercially available sources can produce ${\sim }5 \times 10^6$
slow-$e^+$
s$^{-1}$
(Krause-Rehberg et al. Reference Krause-Rehberg, van der Walt, Büttner and Börner2004; Danielson et al. Reference Danielson, Dubin, Greaves and Surko2015). If the positrons could be captured with an efficiency of $\epsilon \sim 10$
% and then confined without loss, it would take approximately $6$
hours to accumulate $10^{10}$
. To operate at a significantly higher rate, APEX will utilize the high-intensity NEPOMUC beam (NEutron induced POsitron source MUniCh; Hugenschmidt et al. Reference Hugenschmidt, Piochacz, Reiner and Schreckenbach2012), which can deliver positrons with a comparable energy distribution but an order of magnitude more flux. The NEPOMUC is located at the FRM II neutron source in Garching, Germany. Thermal neutron capture in cadmium generates high-energy gamma rays that induce pair production of electrons and positrons in platinum foils (Hugenschmidt et al. Reference Hugenschmidt, Kögel, Repper, Schreckenbach, Sperr and Triftshäuser2002). Approximately $10^9 e^{+}~\mathrm {s}^{-1}$
are electrostatically extracted and then magnetically guided at 1 keV with an energy spread of the order of 10 eV. Brightness enhancement of the primary beam is achieved by focusing it on an annealed tungsten surface, from which a remoderated 20 eV, 2 mm beam is emitted with an energy spread of ${\sim }1$
eV (Piochacz et al. Reference Piochacz, Kögel, Egger, Hugenschmidt, Mayer, Schreckenbach, Sperr, Stadlbauer and Dollinger2008; Hugenschmidt et al. Reference Hugenschmidt, Ceeh, Gigl, Lippert, Piochacz, Reiner, Schreckenbach, Vohburger, Weber and Zimnik2014; Stanja et al. Reference Stanja, Hergenhahn, Niemann, Paschkowski, Sunn Pedersen, Saitoh, Stenson, Stoneking, Hugenschmidt and Piochacz2016; Dickmann et al. Reference Dickmann, Egger, Kögel, Vohburger and Hugenschmidt2020).
The large number of positrons required for APEX will be accumulated from the NEPOMUC remoderated beam using a buffer-gas trap (BGT) (Surko, Leventhal & Passner Reference Surko, Leventhal and Passner1989) operating at between 1 and 10 Hz. The maximum attainable number is limited by the trapping efficiency and the lifetime to approximately $10^6 e^+$
(Cassidy et al. Reference Cassidy, Greaves, Meligne and Mills2010). Bunches of positrons will be transferred from the BGT to an adjacent Penning–Malmberg trap (the accumulator), wherein better vacuum conditions allow for longer confinement times and pulse stacking to produce a non-neutral plasma of $N = 10^8 e^+$
in ${\sim }30$
s. Even if positron transfer and confinement were perfect, it is not feasible to trap sufficient positrons in the accumulator due to the space-charge potential of the non-neutral plasma. Ultimately, $N > 10^{10} e^+$
will require the development of a multicell trap with ultrahigh-vacuum conditions, a high magnetic field (${>}3$
T) and kilovolt confinement potentials (Surko & Greaves Reference Surko and Greaves2003; Hurst et al. Reference Hurst, Danielson, Baker and Surko2019; Singer et al. Reference Singer, König, Stoneking, Steinbrunner, Danielson, Schweikhard and Pedersen2021).
In this article, we focus on the optimization of the BGT. BGTs can be tuned to produce bunches of positrons with very low energy spreads ($\Delta E < 100$
mV) or short pulse widths ($\Delta t <100$
ns), and have typical capture efficiencies of ${\gtrsim }10$
% (Danielson et al. Reference Danielson, Dubin, Greaves and Surko2015; Baker et al. Reference Baker, Isaac, Edwards, Evans, Clayton, van der Werf and Charlton2020). Trap-based positron beams have been instrumental in advancing high-resolution studies of matter–antimatter interactions, antihydrogen research and positronium laser spectroscopy (Cassidy Reference Cassidy2018; Fajans & Surko Reference Fajans and Surko2020). Although BGTs are traditionally used with rare-gas-moderated radioisotope sources (Greaves & Surko Reference Greaves and Surko1996), they have more recently been adapted for LINAC-based positron beams (Higaki et al. Reference Higaki, Michishio, Hashidate, Ishida and Oshima2020; Blumer et al. Reference Blumer2022). However, BGTs have not previously been used to accumulate positrons from a reactor-based positron source. We aim to address some of the important considerations for this novel application. Due to a long maintenance shutdown of FRM II, the commissioning of the BGT has been performed using electrons. We present the results of this study and discuss the important similarities and differences that pertain to trapping positrons at the NEPOMUC facility.
2. Buffer-gas trap system
2.1. Overview
The BGT system is based on a commercial device manufactured by First Point Scientific. It consists of two separate Penning–Malmberg traps (Malmberg & deGrassie Reference Malmberg and deGrassie1975; Danielson et al. Reference Danielson, Dubin, Greaves and Surko2015) interconnected by an evacuated beam guide. The BGT is designed to efficiently capture positrons from a continuous beam (Surko et al. Reference Surko, Leventhal and Passner1989; Wysocki et al. Reference Wysocki, Leventhal, Passner and Surko1989; Murphy & Surko Reference Murphy and Surko1992). Bunches of ${\sim }10^6$
particles from the BGT can be stacked in the accumulator to produce a non-neutral plasma of $N \sim 10^8$
. Cryopumps are mounted to each of the three vacuum pump boxes (PBs) to provide a base pressure of ${\sim }10^{-7}$
Pa. Both traps employ water-cooled solenoids that create a uniform magnetic field to radially confine charged particles. Axial confinement is achieved by biasing a set of cylindrical electrodes. The electrode voltages are generated by a software-timed analogue-output device and $+20$
dB amplifiers (${\pm }100$
V) with a bandwidth of ${\sim }100$
kHz. An overview of the BGT system and axial magnetic field is shown in figure 1. An electron emitter, two Faraday cups (FCs) and a phosphor screen (PS) were used to commission the traps and optimize their performance. Boost coils (BCs) were used to increase the magnetic field at the emitter and PS. With appropriate biasing to account for the opposite charge, the traps and diagnostics are expected to perform comparably – but not identically – with either electrons or positrons (Stenson et al. Reference Stenson, Hergenhahn, Stoneking and Pedersen2018; Machacek et al. Reference Machacek, Gay, Buckman and Hodgman2022).
Figure 1. Schematic of the BGT system configured for $e^{-}$
trapping (top view) and the on-axis magnetic field strength. Key: vacuum system, grey; electromagnets, black; emitter, red; trap electrodes, orange; FCs, green; PS, cyan.
2.2. Buffer-gas trap
The BGT will be used to capture positrons from the NEPOMUC beam. The magnetic field inside the solenoid is approximately $B_z = 55$
mT. The electrodes are grouped into three stages of increasing internal diameter (7, 14 and 25 mm). A manual high-precision valve controls the flow of nitrogen gas into stage 1. Incoming positrons (or electrons) that undergo inelastic scattering from the N$_2$
molecules can be confined by the electric potential minimum. Differential pumping and the asymmetric electrode structure result in a pressure reduction of roughly an order of magnitude from one stage to the next. The pressure gradient is designed to maximize particle capture in stage 1 (inelastic scattering) and minimize losses in stage 3 (radial diffusion, direct annihilation and positronium formation) (Marler & Surko Reference Marler and Surko2005a). Additional cooling gas (CF$_4$
or CO$_2$
) can be added to increase the cooling rate in the final stage (Natisin, Danielson & Surko Reference Natisin, Danielson and Surko2014).
The on-axis electric potential for trapping electrons (figure 2a) is very similar to an inversion of the traditional positron-trapping potential (Murphy & Surko Reference Murphy and Surko1992; Machacek et al. Reference Machacek, Gay, Buckman and Hodgman2022). The bias applied to the stage-1 electrode is chosen to maximize the inelastic scattering cross-section for the DC beam (Sullivan et al. Reference Sullivan, Marler, Gilbert, Buckman and Surko2001; Chaudhuri et al. Reference Chaudhuri, do N. Varella, de Carvalho and Lima2004). The bottom of the electric potential is located in stage 3, which consists of two, 25 mm long electrodes. The first (RQ) has been cut into eight sectors, which are used to apply a rotating quadrupole electric field that compresses the plasma to a diameter of ${\sim }1$
mm (Greaves & Surko Reference Greaves and Surko2000; Cassidy et al. Reference Cassidy, Deng, Greaves and Mills2006, Reference Cassidy, Greaves, Meligne and Mills2010; Deller et al. Reference Deller, Mortensen, Isaac, van der Werf and Charlton2014). The small beam size makes it possible to install a pumping restriction in the low-field region between the BGT and accumulator to further improve the vacuum in the latter without overly degrading the transfer efficiency – although pumping restrictions were not used for this work. The trap can be emptied by switching the gate electrode to ground with a nominal slew rate of 42 V $\mathrm {\mu }$
s$^{-1}$
.
Figure 2. The electrodes (above) and on-axis electric potentials of (a) the BGT during electron trapping; and (b) the accumulator with a non-neutral plasma of $10^8 e^-$
. The dotted lines represent the potentials with the BGT gate/accumulator inlet open; the dashed line represents the space-charge potential of the plasma in the accumulator.
2.3. Accumulator
Bunches of particles ejected from the BGT can be recaptured and stacked in the accumulator (Jørgensen et al. Reference Jørgensen2005). The bunches are caught dynamically: the inlet potential is lowered by 4 V to allow the particles to enter the trap and then raised again to prevent their escape (rise time of ${\sim }5$
ns). The particles cool to the bottom of the well before the next bunch arrives via collisions with 300 K gas molecules (CF$_4$
). The relatively low pressure (${\lesssim }10^{-5}$
Pa) allows for longer positron lifetimes than would be possible inside the BGT. The solenoid nominally produces a uniform magnetic field of $B_{z} = 70$
mT. Extra windings at the ends of the coil flatten the field at the centre (figure 1). The 100 mm long electric potential well produced by the electrodes facilitates the accumulation of a non-neutral plasma containing up to $10^8$
positrons (or electrons).
The accumulator contains 19 cylindrical electrodes with an internal diameter of $25$
mm. The inner surfaces are coated in a thin layer of colloidal graphite (Planocarbon N650) to minimize electrostatic asymmetries. The middle 15 electrodes are each 6.5 mm long and the other four – two at either end – are 25 mm long. The centre electrode (RD) is cut into four azimuthal sectors. This allows a rotating dipole electric field to be applied to compress the plasma (Greaves & Surko Reference Greaves and Surko2000). Two resistor chains connect the seven electrodes located on either side of RD to create an axial harmonic minimum in the vacuum electric potential (figure 2b). This provides good confinement (Mohamed, Mohri & Yamazaki Reference Mohamed, Mohri and Yamazaki2013) and reduces the number of voltages that need to be supplied. The depth of the well is increased by ${\sim }100$
mV after each pulse from the BGT is recaptured to accommodate the increase in the space-charge potential of the plasma.
3. Results
3.1. Electron beam
An yttria-coated iridium disc cathode (Kimball Physics) was used to create an electron beam for testing the BGT system. The heating current and filament bias supplied to the cathode were adjusted to set the emission current (pA to $\mathrm {\mu }$
A) and beam energy (5–100 eV), respectively. The electron work function of the emitter is $2.6$
eV. After a stabilization period of ${\sim }1$
hour, the cathode provided consistent and reproducible thermionic emission of electrons. Additional stabilization time was required whenever the ambient vacuum conditions changed significantly (e.g. due to adjustment of the BGT gas pressure).
The electron beam properties that are most relevant to trapping are compared with those of the NEPOMUC primary and remoderated beams in table 1. The energy distribution is separated into the components associated with motion either parallel or perpendicular to the guiding magnetic field. During adiabatic transport (Ghosh, Danielson & Surko Reference Ghosh, Danielson and Surko2020), parallel and perpendicular energy are exchanged to simultaneously conserve the total energy,
and the magnetic moment,
Similarly, the electron beam expands and compresses with the magnetic field lines. The area of the beam in the plane perpendicular to the magnetic field is inversely proportional to the magnetic flux density. Accordingly, the radius of the beam is given by
where $|\boldsymbol{B_{0}}|$
and $r_{0}$
refer to the magnetic field strength and radius of the beam at the location of the source.
Table 1. Typical parameters of the NEPOMUC primary and remoderated positron beams (Hugenschmidt et al. Reference Hugenschmidt, Ceeh, Gigl, Lippert, Piochacz, Reiner, Schreckenbach, Vohburger, Weber and Zimnik2014; Stanja et al. Reference Stanja, Hergenhahn, Niemann, Paschkowski, Sunn Pedersen, Saitoh, Stenson, Stoneking, Hugenschmidt and Piochacz2016) and the electron beam from the $\mathrm {Y}_2\mathrm {O}_3$
emitter in $|\boldsymbol{B}|\sim 5$
mT.
The parallel energy distribution was measured using retarding potential analysis: a negative bias supplied to an electrode along the beamline was increased until the electrons were reflected. Figure 3 shows the current collected at FC-1 as a function of the voltage applied to the stage-1 electrode. The emitter was biased to $-\,30$
V. The high magnetic field inside the trap undesirably broadens the incoming parallel energy distribution. However, the mirror ratio was significantly reduced by energizing BC-1 located behind the emitter to increase the field at the source from approximately $4$
to 16 mT. A Gaussian distribution was fitted to the $B_0 = 16$
mT data in figure 3(b) to determine the mean parallel energy $\langle E_\parallel \rangle \approx 26.6$
eV and full width at half maximum spread $\Delta E_\parallel \approx 1.0$
eV of the electron beam in the 55 mT trap.
Figure 3. Parallel energy distribution of a 1 nA electron beam in the BGT ($|\boldsymbol{B}| = 55$
mT). (a) Cut-off curve of the current collected at FC-1 as a function of the voltage applied to the stage-1 electrode. (b) The collected current differentiated by the retarding potential. The measurements were performed with the magnetic field strength at the electron source approximately equal to 4 mT (dashed lines) or 16 mT (solid lines).
The radial distribution of the DC beam was measured using a conductive-glass-mounted PS. The electrons were magnetically guided through both traps and then accelerated into the positively biased screen to create an image that was reflected from a 45$^\circ$
mirror and recorded by a CCD camera. An example is shown in figure 4. A two-dimensional Gaussian fit to the data indicates the diameter of the DC electron beam was ${\sim }1.5$
mm (at the screen).
Figure 4. Image of a 1 nA electron beam at the PS ($|B| \sim 4$
mT). The dashed line indicates the half-maximum contour of a two-dimensional Gaussian fit to the data ($r = 0.75$
mm).
In this section, we have demonstrated that the electron beam emitted from the yttria-coated iridium cathode can be tuned to broadly reproduce the characteristics of the remoderated NEPOMUC beam. In the following section, we present the results of using the electron beam to test the BGT. Unless stated otherwise, the emitter was biased to $-30$
V and the magnetic fields were as shown in figure 1 (i.e. with both BCs energized).
3.2. Buffer gas trap
3.2.1. Nitrogen pressure
Capturing an electron from the DC beam requires at least one scattering event that reduces the parallel energy below the inlet potential of the BGT (Itikawa Reference Itikawa2005). This will predominately happen in the high-pressure region inside the 370 mm long stage-1 electrode. If scattering does not occur in the first pass, there is a second opportunity after the particle is reflected from the electric potential of the gate electrode.
The stage-1 electrode was biased to $-17$
V, resulting in a mean parallel energy of the electron beam of ${\sim }9.6$
eV. This exceeds the threshold for exciting the electronic states of N$_2$
that are conventionally exploited for positron trapping (Murphy & Surko Reference Murphy and Surko1992; Marler & Surko Reference Marler and Surko2005a). Figure 5 shows retarding potential analysis measurements that were made with the DC beam and the gate electrode of the BGT as the flow of nitrogen into stage 1 was increased. The pressure inside stage 1 was estimated – based on the pumping speed of the cryopump and the conductance of the electrodes and the vacuum chamber – to be $630$
times higher than the pressure measured by an ion gauge located in PB-1. The cut-off curves in figure 5 have been normalized to the maximum measured electron current for each pressure ($I \sim 200$
pA). With an estimated pressure of 0.11 Pa in stage 1, ${\sim }50$
% of the transmitted DC beam loses ${>}5$
eV of parallel energy; as discussed in § 3.2.3, the fraction of the total DC beam will be smaller than this due to back-scattering. The parallel energy loss is due to a combination of inelastic scattering as well as elastic scattering that mixes energy between the parallel and perpendicular directions (Shyn, Stolarski & Carignan Reference Shyn, Stolarski and Carignan1972). Although elastic scattering can temporarily trap particles, energy dissipation is required to achieve substantial confinement times.
Figure 5. The normalized DC electron current (${\sim }200$
pA) collected at FC-1 with a retarding potential applied to the BGT gate electrode. The emitter and BGT stage-1 electrode were biased to $-30$
and $-17$
V, respectively. The legend indicates the estimated pressure inside stage 1.
3.2.2. Trapping potential
The DC electron current was set to $\sim$
20 pA, the nitrogen pressure inside of stage 1 was stabilized at $0.1$
Pa and the electrode biases were configured to trap electrons in stage 3. The trap was emptied at a rate of 5 Hz by grounding the gate electrode for 20 ms. The total charge in each ejected bunch was measured using a FC connected to a charge-sensitive preamplifier (Cremat CR-111) and 1 MHz pulse-shaping amplifier with an estimated systematic uncertainty of $\pm 20$
%. A ring electrode was mounted directly in front of the grounded FC and biased to $-$
5 V to suppress the emission of low-energy secondary electrons. The electrode voltages were fine-tuned using a multi-parameter genetic optimizer (Holland Reference Holland1975) to maximize the number of captured electrons. The voltage range of the stage-1 electrode was constrained to target inelastic scattering via electronic excitation – as opposed to vibrational excitation of the N$_2$
molecules, which have an unusually large cross-section for electron impact (Schulz Reference Schulz1959).
After the optimum potential well was determined, single-parameter scans were performed with each electrode in turn. The relative number of electrons trapped in 200 ms is shown in figure 6. The results reveal that stage 1 should ideally be ${\sim }9.2$
V below the parallel energy of the DC beam and that the drop between stages 1 and 2 should be 1.7 V. The trap output was maximized with a 3.1 V step from stage 2 to stage 3. However, the optimal value of the stage-3 bias was observed to vary with the incident electron current and filling time, indicating that the space-charge potential can fill a significant fraction of the electrostatic well.
Figure 6. The number of electrons trapped in stage 3 of the BGT at 5 Hz with each electrode bias individually scanned around the established optimum (dashed lines: $-22.0$
(inlet), $-17.4$
(stage 1), $-15.7$
(stage 2) and $-12.6$
V (stage 3)). The emitter was biased to $-30$
V and the N$_2$
pressure inside of stage 1 was ${\sim }0.1$
Pa.
Ionization makes it conceivable for the trapping efficiency of electrons to exceed 100 % (Machacek et al. Reference Machacek, Gay, Buckman and Hodgman2022). Tuning the trap electrodes to maximize the production of secondary electrons is not relevant to the ultimate goal of trapping positrons. However, the mean energy of the DC electron beam inside the trap was kept below the ionization threshold of N$_2$
(15.6 eV; Trickl et al. Reference Trickl, Cromwell, Lee and Kung1989), and the trapped electrons likely cooled rapidly to ${\sim }1$
eV (Schulz Reference Schulz1962). There are more nuanced differences between electron and positron impact that should also be considered, and we do not imagine that an inversion of the optimized electron-trapping potential will be perfect for trapping positrons. For example, the optimized step from stage 1 to 2 is probably determined by vibrational scattering interactions that are much stronger for electrons. Nonetheless, by following a similar process with the NEPOMUC positron beam, we expect to arrive at a similar set of optimized voltages. See § 4 for further discussion.
3.2.3. Cooling and compression
Penning traps can confine charged particles almost indefinitely (Dubin & O'Neil Reference Dubin and O'Neil1999). In the relatively poor vacuum of the BGT ($10^{-3}$
Pa), however, collisions with neutral gas molecules drive transport to the walls within ${\sim }1$
s. Even with positrons, losses due to expansion can exceed the annihilation rate (Baker et al. Reference Baker, Isaac, Edwards, Evans, Clayton, van der Werf and Charlton2020). Fortunately, radial transport can be almost eliminated by the ‘rotating-wall’ (RW) technique (Greaves & Surko Reference Greaves and Surko2000), which involves using an azimuthally segmented electrode to create a rotating electric field that radially compresses the distribution of trapped particles. This has been demonstrated to be effective in the single-particle (Greaves & Moxom Reference Greaves and Moxom2008; Isaac et al. Reference Isaac, Baker, Mortensen, van der Werf and Charlton2011) and plasma (Danielson & Surko Reference Danielson and Surko2005) regimes. In both cases, either cyclotron cooling (in a high magnetic field; $|\boldsymbol{B}| > 1$
T) or gas cooling is required to counter the heating of the particles caused by the rotating electric field. For positrons, the vibrational inelastic cross-section with N$_2$
is small; therefore, an additional cooling gas is typically used (e.g. CO$_2$
, CF$_4$
or SF$_6$
) (Greaves & Surko Reference Greaves and Surko2001; Cassidy et al. Reference Cassidy, Greaves, Meligne and Mills2010; Deller et al. Reference Deller, Mortensen, Isaac, van der Werf and Charlton2014; Natisin et al. Reference Natisin, Danielson and Surko2014; Blumer et al. Reference Blumer2022).
Electron trapping was performed in the BGT using 0.1 Pa of N$_2$
in stage 1 and the optimized voltage set identified in § 3.2.2. The number of trapped electrons measured at the FC for a range of fill times is shown in figure 7(a) (squares). To estimate the capture efficiency, the trapping rate was compared with the incident current. The latter could not be measured directly because the emitter and the electron beam are both affected by the presence of nitrogen. Instead, the current that transitioned the trap with nitrogen in stage 1 and the electrode biased to $-17$
V was measured. Assuming that 25 % of the 10 eV beam was back-scattered and not observed (Shyn & Carignan Reference Shyn and Carignan1980; Khandker et al. Reference Khandker, Arony, Haque, Maaza, Billah and Uddin2020), we estimate that the total incident electron current was ${\sim }24$
pA. The trapping rate was found from a linear fit to the data (figure 7a) for fill times shorter than 100 ms. Accordingly, without the RW technique and with no additional cooling gas (only N$_2$
), the electron trapping efficiency was estimated to be $\epsilon \approx 17$
%. For fill times longer than 200 ms, the trapping and loss rates reached an equilibrium and the output saturated at $N = 2.5 \times 10^6 e^-$
. The loss rate was independently measured by filling the trap for 200 ms and then holding the electrons for a range of times before ejecting them. Fitting an exponential decay function to the N$_2$
data shown in figure 7(b) (squares) indicates that the mean confinement time was $\tau = 400 \pm 64$
ms.
Figure 7. Number of electrons trapped in the BGT for a range of (a) fill (${\rm hold} = 20$
ms) and (b) hold (${\rm fill} = 200$
ms) times. The incident electron current was estimated to be 24 pA. The three datasets represent trapping with only N$_2$
(squares); trapping with N$_2$
and CF$_4$
(triangles); and trapping with N$_2$
, CF$_4$
and RW compression (6.55 MHz, 2.0 V$_{\mathrm {pp}}$
) (circles). The solid lines in (b) are fits of a single exponential decay to the data (see text).
Excitation of the $\nu _3$
vibrational mode of CF$_4$
(0.159 eV) can provide a strong cooling mechanism for electrons or positrons (Marler & Surko Reference Marler and Surko2005b); the ionization threshold of CF$_4$
is 16.2 eV (Nishimura et al. Reference Nishimura, Huo, Ali and Kim1999). Figure 7 also shows data from fill-and-hold measurements that were made with a small amount of CF$_4$
injected into stage 3 of the trap (${\sim }10^{-4}$
Pa) (triangles). The additional gas more than doubled the capture efficiency to $\epsilon \approx 36$
%. The notable improvement is attributed to the electrons cooling more rapidly to the bottom of the electric potential. Although CF$_4$
increased the trapping rate, it reduced the mean confinement to $\tau = 336 \pm 37$
ms. The final set of data in figure 7 (circles) was obtained from fill-and-hold measurements made using the same N$_2$
and CF$_4$
pressures as described above but with the RW technique applied using the segmented electrode (RQ) in stage 3 of the trap (6.55 MHz and 2.0 V$_{\mathrm {pp}}$
).Footnote 1 The voltages produced a rotating quadrupole electric field that compressed the non-neutral electron plasma and further increased the capture efficiency to $\epsilon \approx 56$
%. The RW technique had an even more significant effect on the electron confinement time, which was measured from the data shown in figure 7(b) (circles) to be $\tau = 99 \pm 2$
s. Despite the good confinement, the BGT output saturated at $N \approx 2.5 \times 10^7 e^-$
for fill times exceeding 0.5 s (not shown) because of the limited amount of space charge that could be held in the electrostatic well.
3.3. Accumulator
3.3.1. Pulse stacking
The space-charge limitation in the BGT could be addressed by adapting the electric potential to the increasing number of particles in the non-neutral plasma. However, this approach is less viable for trapping positrons because the annihilation lifetime in stage 3 of the BGT will likely be much shorter than the ${\sim }30$
s that will be needed to reach $N = 10^8 e^+$
. Instead, our strategy is to operate the BGT with short fill times and to stack bunches in the accumulator to obtain a larger non-neutral plasma.
A simple stacking scheme was performed using bunches of $N \sim 1.7 \times 10^6 e^-$
ejected from the BGT at a rate of 15 Hz. A bias of $-14$
V was applied to the accumulator inlet electrode to block the electron bunches. The blocking potential was momentarily lowered by 4 V for 300 ns with a variable delay after ejection. The number of electrons detected at FC-2 is shown in figure 8(a). With a delay of $1.2\ \mathrm {\mu }$
s, the lowering of the blocking potential coincided with the electron ejection and flight time, and allowed the bunch to pass unhindered through the accumulator and reach the FC. The later peaks are the result of electrons reflecting back and forth between the BGT and the accumulator before being transmitted (Evans & Isaac Reference Evans and Isaac2021).
Figure 8. (a) Number of electrons detected at FC-2 for a single bunch of electrons ejected from the BGT with a 300 ns long, 4 V square pulse added to a blocking potential on the accumulator inlet electrode. (b) The number of electrons collected by stacking multiple bunches from the BGT in the accumulator.
The optimal delay was used with the accumulator electrodes biased to create a confining electric potential (see figure 2b). Multiple BGT bunches were stacked in the accumulator by repeatedly lowering the inlet potential and progressively increasing the depth of the well by $160$
mV per pulse. The number of electrons collected for a given number of stacks is shown in figure 8(b). The capture efficiency for a single bunch is estimated to be ${\sim }95$
%. For more than 30 stacks, the transfer efficiency steadily dropped. The output reached $N = 1.25 \times 10^8 e^-$
for 100 stacks. The RW technique was applied continuously during the stacking process (0.5 V$_{\mathrm {pp}}$
; 4.5 MHz). Cooling was provided by the gases that diffused from the BGT to the accumulator, and the pressure in the latter was approximately $10^{-5}$
Pa. Trap-and-hold measurements indicate that the average lifetime of electrons in the accumulator was $\tau \sim 600$
s. This is far longer than the total fill time (${\sim }6$
s), and further refinement of the trapping scheme might enable considerably more electrons to be accrued in this device. For example, the RW parameters could be periodically adjusted during the fill (Fitzakerley et al. Reference Fitzakerley, George, Hessels, Skinner, Storry, Weel, Gabrielse, Hamley, Jones, Marable, Tardiff, Grzonka, Oelert and Zielinski2016).
4. Discussion
A BGT and accumulator have been constructed for operation with the NEPOMUC positron beam at FRM II. The traps have been commissioned and tested using non-neutral electron plasma. The electron beam emitted by a yttrium-oxide-coated iridium cathode was tuned to broadly reproduce the characteristics of the NEPOMUC remoderated positron beam. It was necessary to boost the magnetic field at the cathode to achieve efficient electron trapping in the BGT. This reduced the mirror ratio and resulted in a narrower parallel energy spread of the beam entering the trap. Similar tuning of the magnetic field at the NEPOMUC remoderator will likely be required to minimize the parallel energy spread of the positron beam and thereby maximize the trapping efficiency (Sullivan et al. Reference Sullivan, Jones, Caradonna, Makochekanwa and Buckman2008).
There are several important caveats to consider when using the electron trapping results to forecast performance with positrons. Positron impact can excite N$_2$
from the singlet ground state ($X^{1}\varSigma ^{+}_{g}$
) to the singlet excited states, but spin-flipping transitions are suppressed (Sullivan et al. Reference Sullivan, Marler, Gilbert, Buckman and Surko2001). By contrast, electrons can excite the triplet states via exchange interactions (Su et al. Reference Su, Cheng, Zhang and Tennyson2021). In addition, electron attachment in the region of $2.3$
eV significantly enhances the cross-section for exciting the low-energy vibrational states (Schulz Reference Schulz1962). The electronic and vibrational inelastic scattering cross-sections are consequently smaller for positrons, and higher gas pressures will be needed to trap and cool. More significantly, unlike electrons, positrons will be lost to positronium formation and annihilation (Marler & Surko Reference Marler and Surko2005a). We estimate the capture efficiency of the BGT to be ${\sim }50$
% for electrons (comparable to the BGT described by Machacek et al. (Reference Machacek, Gay, Buckman and Hodgman2022)). To reiterate, the trapping rate strongly depends on the energy spread of the incoming beam. Even if the energy distribution of the remoderated NEPOMUC beam were identical to that of the electron beam, the trapping efficiency would likely be halved because of the proximity of the positronium-formation threshold for N$_2$
(8.8 eV) to the $X^{1}\varSigma ^{+}_{g}$
to $a^1\varPi$
transition (8.6 eV) (Murphy & Surko Reference Murphy and Surko1992). If future refinements of the NEPOMUC remoderator can achieve much narrower energy spreads (${<}0.3$
eV) (Mills Reference Mills1989; Zecca et al. Reference Zecca, Chiari, Sarkar, Chattopadhyay and Brunger2010), it might be possible to more efficiently trap positrons using the vibrational states of CF$_4$
(Murtagh Reference Murtagh2014; Marjanović et al. Reference Marjanović, Banković, Cassidy, Cooper, Deller, Dujko and Petrović2016). Although only 0.159 eV would be extracted from the beam per inelastic collision (hence the small-energy-spread requirement), losses due to positronium formation could be mitigated.
The RW technique enabled very good confinement of electrons in the BGT. The long lifetime could be exploited to realize non-neutral plasma with an appreciable amount of space charge (Surko et al. Reference Surko, Leventhal and Passner1989). However, we do not expect such long lifetimes for positrons due to annihilation with the buffer and cooling gases (Clarke et al. Reference Clarke, van der Werf, Griffiths, Beddows, Charlton, Telle and Watkeys2006; Cooper et al. Reference Cooper, Alonso, Deller, Wall and Cassidy2015). To produce bunches containing significantly more than $N = 10^6 e^+$
, therefore, requires a trap with better vacuum conditions. The performance of the accumulator is expected to be similar for positrons and electrons, as the capture and trapping dynamics only weakly depend on inelastic scattering cross-sections. The limits of this device are principally associated with transport losses due to field asymmetries and space-charge constraints (Kabantsev & Driscoll Reference Kabantsev and Driscoll2002). As long as the vacuum is not contaminated with molecules with very large positron-annihilation cross-sections, such as hydrocarbons (Barnes et al. Reference Barnes, Marler, Sullivan and Surko2004; Danielson, Ghosh & Surko Reference Danielson, Ghosh and Surko2022), the lifetime of positrons in the accumulator should surpass the required filling time of ${\sim }30$
s. Based on the preliminary tests with electrons, we are optimistic about achieving our goal of accumulating non-neutral plasma of $N = 10^8 e^+$
from the NEPOMUC positron beam. However, as already discussed, APEX requires $N > 10^{10} e^+$
to create an electron–positron pair plasma (Stoneking et al. Reference Stoneking, Pedersen, Helander, Chen, Hergenhahn, Stenson, Fiksel, von der Linden, Saitoh and Surko2020), which far exceeds the capacity of the accumulator. Consequently, bunches of positrons produced by the BGT system will ultimately be used to fill a multicell trap (Surko & Greaves Reference Surko and Greaves2003; Hurst et al. Reference Hurst, Danielson, Baker and Surko2019) that is currently being developed (Singer et al. Reference Singer, König, Stoneking, Steinbrunner, Danielson, Schweikhard and Pedersen2021).
5. Summary and outlook
In this work, we have described the APEX BGT system and demonstrated its capability to reliably produce single-component electron plasmas. Based on the performance with electrons and recent measurements of the energy spread of the remoderated NEPOMUC beam, we expect to be able to trap positrons with an efficiency of ${\sim }10\,\%$
. The primary goal of the experiments presented in § 3 was to optimize the traps and refine our control and diagnostic techniques. However, a nearly identical source of either positrons or electrons has obvious benefits for performing systematic comparisons between matter and antimatter (Kurz et al. Reference Kurz, Gilbert, Greaves and Surko1998; Marler & Surko Reference Marler and Surko2005b; Stenson et al. Reference Stenson, Hergenhahn, Stoneking and Pedersen2018). Moreover, the BGT system is a crucial component of the APEX and EPOS pair plasma experiments (Stoneking et al. Reference Stoneking, Pedersen, Helander, Chen, Hergenhahn, Stenson, Fiksel, von der Linden, Saitoh and Surko2020), where electrons and positrons must be combined in equal quantities.
In general, the ability to use the BGT to produce bunches of positrons with narrow energy spreads will extend the capabilities of the NEPOMUC facility. Anticipated applications include almost background-free positron-annihilation-induced Auger electron spectroscopy (Weiss et al. Reference Weiss, Yang, Kim, Nangia and Fazleev1996; Hugenschmidt Reference Hugenschmidt2016) and the production of a dense positronium gas (Cassidy Reference Cassidy2018; Mills Reference Mills2019). The continuing advancement of positron research and the manifest benefits of trap-based beams have driven demand for ever-increasing rates of positron trapping. To this end, it is feasible to adapt the BGT system described in this work to take advantage of the very high flux of the NEPOMUC primary beam (see table 1) by exploiting in situ remoderation with SiC (Störmer et al. Reference Störmer, Goodyear, Anwand, Brauer, Coleman and Triftshäuser1996; Leite et al. Reference Leite, Debu, Pérez, Reymond, Sacquin, Vallage and Liszkay2017; Michishio et al. Reference Michishio, Higaki, Ishida and Oshima2022).
Acknowledgements
The authors wish to express their gratitude to all members of the APEX collaboration for supporting this work. We acknowledge valuable discussions with R. Greaves, and thank A. Card, C.L. Manson, D. Witteman and S. Ghosh for contributing to the design of experimental components.
Editor Francesco Califano thanks the referees for their advice in evaluating this article.
Funding
This work received financial support from the US DOE (DE-SC0019271) and the University of California San Diego Foundation. The work has also received funding from the European Research Council (741322), the Deutsche Forschungsgemeinschaft (HU 978/20-1, STE 2614/2-1) and the Helmholtz Association.
Declaration of interest
The authors report no conflict of interest.
Open access
