A) Embedding process

The embedding process produces a watermarked signal by taking a host signal and a watermark as its inputs, and one watermark bit will be embedded into one frame. There are six steps in the speech embedding process, as shown in Fig. 1 (left), which are detailed as follows.

1. 1. Segmentation. A host signal is segmented into M non-overlapping frames of length N, where M is the total number of watermark bits. Let F denote a segment of length N, i.e. F = [f ₀ f ₁ … f _N−1]^T, where f _i for i=0 to N − 1 are N samples of a segment

2. 2. Matrix Formation. We map a segment F to a matrix X with the following equation.

   (1)$${\bf X} = \left[ \matrix{f_0 & f_1 & f_2 & \cdots & f_{K-1} \cr f_1 & f_2 & f_3 & \cdots & f_{K} \cr f_2 & f_3 & f_4 & \cdots & f_{K+1} \cr \vdots & \vdots & \vdots & \ddots & \vdots \cr f_{L-1} & f_L & f_{L+1} & \cdots & f_{N-1}} \right],$$
   where L, which is called a “window length” of the matrix transformation, is not less than 2 and is not greater than N. The size of X is L × K, where K=N−L+1.

3. 3. Singular Value Decomposition (SVD). We factorize the real matrix X by using SVD, i.e.

   (2)$$ {\bf X} = {\bf U}{\bf \Sigma}{\bf V}^{\rm T}, $$
   where the columns of U and those of V are the orthonormal eigenvectors of XX^T and of X^TX, respectively, and Σ is a diagonal matrix whose elements are the square roots of the eigenvalues of X^TX.

   Let $\sqrt {\lambda _{i}}$ for i=1 to q denote the elements of Σ in descending order, where $\sqrt {\lambda_{q}}$ is the smallest non-zero eigen value. We call $\sqrt {\lambda _{i}}$ a “singular value” and call $\{\sqrt {\lambda _0},\, \sqrt {\lambda _1},\, {\ldots },\, \sqrt {\lambda _{q}}\}$ a “singular spectrum.”

4. 4. Singular Value Modification. A singular spectrum is modified according to the watermark bit to be embedded and requires the properties of the watermarking scheme. It is shown in our previous work that modifying high-order singular values distorts the host signal less but is sensitive to noise or attacks. Contrarily, modifying low-order singular values can improve robustness but causes sound quality to be poor [Reference Karnjana, Galajit, Aimmanee, Wutiwiwatchai and Unoki9,Reference Karnjana, Unoki, Aimmanee and Wutiwiwatchai14]. Thus, there is the trade-off between robustness and sound quality. In this work, we aim for semi-fragility. Therefore, we propose the following embedding rule.

   Given a singular spectrum $\{\sqrt {\lambda _0},\, \sqrt {\lambda _1},\, {\ldots },\, \sqrt {\lambda _{q}}\}$, a specific part of this singular spectrum, which is $\{\sqrt {\lambda _p},\, \sqrt {\lambda _{p+1}},\,{\ldots },\, \sqrt {\lambda _{q}}\}$, is modified according to the embedded-watermark bit w with

   (3)$$ \sqrt{\lambda_{i}^{\ast}} = \left\{ \matrix{\sqrt{\lambda_{i}} + \alpha_i\cdot \left(\sqrt{\lambda_{p}} - \sqrt{\lambda_{i}}\right), & {\rm if } w = 1,\cr \sqrt{\lambda_{i}} \quad {\rm (i.e. unchanged)}, & {\rm if } w = 0,} \right.$$
   where $\sqrt{\lambda_{i}^{\ast}}$ is the modified singular values for i=p to q, $\sqrt{\lambda_p}$ is the largest singular value that is less than $\gamma \cdot \sqrt{\lambda_0}$, and α_i, which is called the “embedding strength,” is normally distributed over the interval [p,  q] and has a maximum value of 1. Note that α_i is a positive real value that is less than 1. Specifically, α_i for i=p to q is determined by
   (4)$$\alpha_i = e^{-{(i-\mu)^2}/{2{\sigma^2}}},$$
   where μ and σ² are the mean and the variance of the Gaussian distribution, respectively.

   Hence, our embedding rule requires three parameters, which are γ, μ, and σ. We have shown that by appropriately adjusting these parameters regarding the host signal, we can achieve a good balance between robustness and sound quality [Reference Karnjana, Galajit, Aimmanee, Wutiwiwatchai and Unoki9].

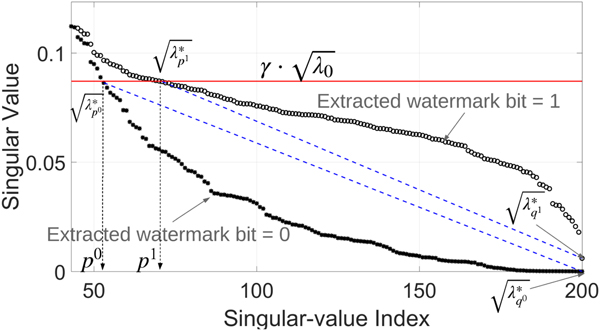
   As shown in Fig. 1 (left), these parameters are provided by the CNN-based parameter estimation, which is to be discussed in detail in the next section. An example of the part $\{\sqrt{\lambda_p},\, \sqrt{\lambda _{p+1}},\,{\ldots },\, \sqrt {\lambda _{q}}\}$ of a singular spectrum is shown in Fig. 2.

5. 5. Hankelization. Let Σ* be a diagonal matrix defined by

   (5)$$ {\bf \Sigma}^{\ast} = \left[\matrix{\sqrt{\lambda_{0}}&\cdots & 0 & 0 & \cdots & 0 \cr \vdots &\ddots & \vdots & \vdots & \vdots \cr 0 & \cdots & \sqrt{\lambda_{p-1}} & 0 &\cdots & 0 \cr 0 & \cdots & 0 & \sqrt{\lambda_{p}^{\ast}} &\cdots & 0 \cr \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \cr 0 & 0 & 0 & 0 &\cdots & \sqrt{\lambda_{q}^{\ast}}} \right].$$
   We compute a watermarked matrix X* (the matrix into which the watermark bit is embedded) from the product UΣ*V^T. Then, we hankelize the matrix X* to obtain the signal F*, which is the watermarked segment. The hankelization is the average of the anti-diagonal i + j = k + 1, where i and j are the row index and the column index, respectively, of an element of X*, and k (for k=0 to N−1) is the index of element F*.

6. 6. Segment Reconstruction. The watermarked signal is finally produced by sequentially concatenating all watermark segments.

Fig. 2. Example of the part $$\{\sqrt{\lambda_p},\, \sqrt{\lambda_{p+1}},\, {\ldots},\, \sqrt{\lambda_{q}}\}$ of a singular spectrum: (a) selected interval of singular spectrum without embedding, (b) embedding watermark bit 1, and (c) embedding watermark bit 0. The red line indicates the threshold level $\gamma \cdot \sqrt{\lambda_{0}}$, and the blue dashed line connects $\sqrt{\lambda_{p}}$ and $\sqrt{\lambda_{q}}$.

B) Extraction process

The extraction process takes a watermarked signal as an input for extracting an embedded watermark. The extraction process consists of four steps, as shown in the dashed box of Fig. 1 (right). The first three steps are the same as those of the embedding process, which are segmentation, matrix formation, and singular value decomposition. The fourth step is watermark-bit extraction. Watermark bits are extracted in this step by decoding singular spectra, and how the spectra are decoded depends on how they are modified in the embedding process. To understand the idea behind this step, let us consider the two singular spectra in Fig. 3. This figure shows two extracted singular spectra of one watermarked frame: $\{ \sqrt{\lambda_{0^0}^{\ast}},\,{\ldots },\,\sqrt{\lambda _{p^0}^{\ast}},\,{\ldots},\,\sqrt{\lambda_{q^0}^{\ast}}\}$ and $\{ \sqrt {\lambda _{0^1}^{\ast}},\,{\ldots },\,\sqrt {\lambda _{p^1}^{\ast}},\,{\ldots },\,\sqrt {\lambda _{q^1}^{\ast}}\}$. The superscripts 0 and 1 of the indices of singular values denote the embedded watermark bits. It can be seen that most singular values (circles) under the red line are above the blue dashed line connecting $\sqrt {\lambda_p}$ and $\sqrt {\lambda_q}$, when the embedded watermark bit is 1, but most of the singular values (asterisks) under the red line are under the blue dashed line when the embedded watermark bit is 0. Therefore, we can use the following condition to determine the hidden watermark bit w*.

(6)$$ {w}^{\ast} = \left\{ \matrix{0, & {\rm if } \displaystyle \sum_{i=p}^{q}\left(\sqrt{\lambda_i^{\ast}}-l (i)\right) \lt 0,\cr 1, & {\rm if } \displaystyle \sum_{i=p}^{q}\left(\sqrt{\lambda_i^{\ast}}-l (i)\right) \geq 0,} \right. $$

where l(i) is the corresponding values on the blue dashed line, which is defined by

(7)$$ l(i) = \left(\displaystyle{\sqrt{\lambda_p^{\ast}}-\sqrt{\lambda_q^{\ast}} \over p-q} \right) \cdot (i-q)+\sqrt{\lambda_q^{\ast}}.$$

The output of the fourth step is the extracted watermark bit w* (j) for j=1 to M.

Fig. 3. Decoding hidden watermark bit: if most of the singular values (circle) that are under threshold level $\gamma \cdot \sqrt{\lambda_{0}}$ are above blue dashed line, extracted watermark bit is 1, but if most of the singular values (asterisks) that are under threshold level $\gamma \cdot \sqrt{\lambda_{0}}$ are under blue dashed line, extracted watermark bit is 0.

C) Tampering detection

To check whether watermarked signals have been tampered with or not, extracted-watermark bits w* (j) are to be compared with embedded-watermark bits w(j) for j=1 to M. To detect tampering, embedded-watermark bits w(j) are assumed to be known by the owner or an authorized person. Theoretically, when there is tampering, watermark bits that are embedded into the location of the tampering are destroyed. Tampering could be detected by mismatches between w* (j) and w(j). Since we embed one watermark bit into one frame of the host signal, each mismatch can be used to indicate the corresponding frame that has possibly been tampered with.

A) Training CNN

The CNN is a feedforward neural network and a supervised learning scheme that is trained by a training dataset consisting of many different pairs of input and target. In other words, these pairs are used to find a deterministic function that maps an input to an output, and the trained CNN performs this function [Reference LeCun and Bengio18].

In this work, the CNN is used to find the parameters γ, μ, and σ for each speech segment. The reason we choose the CNN in this work is because we know that there is a relationship between singular values and signal frequencies [Reference Karnjana, Unoki, Aimmanee and Wutiwiwatchai15,Reference Karnjana, Unoki, Aimmanee and Wutiwiwatchai16], for instance, high-order singular values are associated with a high-frequency band, and, contrarily, low-order singular values are associated with a low-frequency band. Therefore, we hypothesize that a CNN trained with inputs represented in both time and frequency domains can perform better compared with either a CNN trained with time-domain input or that trained with frequency-domain input only. Thus, we choose to use spectrograms of the input segments as the inputs in the training dataset. Since a spectrogram is two-dimensional (2D) and the CNN can extract patterns in 2D data more efficiently than other neural networks, we therefore designed our novel parameter estimation on the basis of the CNN.

As mentioned in the previous section, there are three parameters, γ, μ, and σ, to be optimized. Two of these parameters, μ and σ, relate to the embedding strength α_i. Thus, they contribute to the robustness of the proposed scheme. The parameter γ directly defines the number of modified singular values. Thus, it contributes more to the sound quality aspect of the proposed scheme. Accordingly, we implement two CNNs, one for μ and σ and the other for γ. The input of both CNNs is a spectrogram of size 13 × 67. The CNNs are composed of two convolutional layers, two pooling layers, and two normalization layers. The first convolution layer convolutes an input spectrogram with 128 kernels of size 3 × 3 and a stride of size 2 × 2, and the other convolutes with 64 kernels of size 3 × 3. A rectified linear unit function is used as the activation function. A kernel size of 2 × 2 is applied for all pooling layers. The flattened output is combined with a fully connected layer with 256 units. The outputs of the first CNN and the second CNN are the vector $[\mu \ \sigma ]^{\rm T}$ and the parameter γ, respectively. The structure of both CNNs is shown in Fig. 4.

Fig. 4. Structure of CNNs in this work: (a) CNN used to determine embedded strength parameters and (b) CNN used to determine the parameter of γ.

B) Generating high-quality dataset

Since DE proved its effectiveness in finding the optimum parameters in our previous work [Reference Karnjana, Unoki, Aimmanee and Wutiwiwatchai14], we therefore deploy it to generate a dataset for training our CNNs. The definition of a high-quality dataset in this proposed method is a dataset in which a good sample of input–output pairs is used in CNN training so that the CNN can map from the input and specific output with high-precision estimation. DE works as follows.

Let x be a D-dimensional vector that we want to find concerning a cost function C(x), i.e. we are searching for x such that C(x) is minimized. The DE algorithm consists of four steps: initialization, mutation, crossover, and selection [Reference Storn and Price19].

First, we initialize vectors x_i,G, for i = 1 to NP, where NP is the size of the population in the generation G. For the initialization step, G=1.

Second, each x_i,G is mutated to a vector v_i,G+1 by ${\bf v}_{i,G+1} = \displaystyle {\bf x}_{r_1,G}+F\cdot ({\bf x}_{r_2,G}-{\bf x}_{r_3,G})$, where i,  r ₁,  r ₂, and r ₃ are distinct and random from {1,  2,  …,  N P}. The predefined constant F determines the convergence rate of DE and is in the interval [0,  2].

Third, each pair of x_i,G and v_i,G+1 is used to generate another vector u_i,G+1 by using the following formula. Given that

(8)$${\bf u}_{i,G+1} = \left[\matrix{u_{1i,G+1} & u_{2i,G+1} &{\ldots} & u_{Di,G+1}}\right]^{\rm T},$$

(9)$${\bf u}_{ji,G+1} = \left\{\matrix{{\bf v}_{ji,G+1}, \hfill & {\rm if} \Xi{(j)} \les C R{\rm or} j= \upsilon, \hfill \cr {\bf x}_{ji,G}, \hfill & {\rm otherwise},\hfill}\right.$$

$\Xi {(j)}$ is a random real number in the interval [0,  1], CR is a predefined constant in [0,  1], and υ is random from {1,  2,  …,  D}.

In the last step, we compare C(x_i,G) with C(u_i,G+1). If C(x_i,G) < C(u_i,G+1), x_i,G+1 = x_i,G; otherwise, x_i,G+1 = u_i,G+1. Once obtaining all members of the generation G+1, we iteratively repeat the mutation step, the crossover step, and the selection step until a specific condition is satisfied. Then, the DE algorithm gives x_i, which yields the lowest cost in the last generation as the answer.

A DE optimizer used for generating the dataset is shown in Fig. 5. Note that we include a few compression algorithms, as well as coding algorithms, in our DE optimizer because we want to ensure that the proposed scheme is robust against these operations. Note also that the extraction processes in Fig. 5 are a bit different from the extraction process described in Section II-B. The difference is that all extraction processes in the DE optimizer know the parameter γ used in the embedding process, whereas the extraction process in Section II-B is entirely blind.

Fig. 5. DE optimizer used to generate dataset.

The cost function C developed in this work is defined as follows.

(10)$$\eqalign{{C} &= \beta_1 {\rm BER}_{{\rm NA}} + \beta_2 {\rm BER}_{{\rm MP3}} + \beta_3 {\rm BER}_{{\rm MP4}} \cr & \quad+ \beta_4 {\rm BER}_{{\rm G711}} + \beta_5 {\rm BER}_{{\rm G726}},}$$

where β_i for i=1 to 5 are constants and $\sum_{\forall_i} \beta_i = 1$, and BER is the bit-error rate. The BER can be used to represent the extraction precision and is defined as

(11)$${\rm BER} = \displaystyle{1 \over M}{\sum_{j=1}^{M} w(j)\oplus {w}^{\ast} (j)},$$

where w(j) and w* (j) are the embedded-watermark bits and the extracted-watermark bits, respectively, and the symbol ⊕ is a bitwise XOR operator. Hence, the terms BER_NA, BER_MP3, BER_MP4, BER_G711, and BER_G726 denote the average BER values when there is no attack, when MP3 compression is performed, when MP4 compression is performed, when G.711 speech companding is performed, and when G.726 companding is performed on watermarked signals, respectively.

Note that, although our cost function is a function of only BERs, we can set the upper bound of the parameter γ in the DE algorithm to control the sound quality of watermarked signals. Issues regarding the cost function are to be discussed at length in Section V after we have shown our evaluation results.

The framework used to generate the training dataset is shown in Fig. 6.

Fig. 6. Framework for generating training dataset.

A) Sound quality evaluation

Three objective measurements were used to evaluate the speech quality of watermarked signals: the log-spectral distance (LSD), the perceptual evaluation of speech quality (PESQ), and the signal-to-distortion ratio (SDR). The LSD is a distance measure (expressed in dB) between two spectra, which are the spectra of the original signal and the watermarked signal. The LSD is defined by

(12)$${\rm LSD} = \sqrt{\displaystyle{1 \over 2\pi}\int\limits_{-\pi}^{\pi} \left[10\log_{} \displaystyle{P(\omega) \over {P}^{\ast} (\omega)}\right]^2d\omega},$$

where P(ω) and P* (ω) are the spectra of the original signal and the watermarking signal, respectively.

The PESQ measures the degradation of a watermarked signal compared with the original signal [Reference Beerends, Hekstra, Rix and Hollier22]. The PESQ score ranges from very annoying (− 0.5) to imperceptible (4.5). Note that we used the PESQ software recommended by the International Telecommunication Union (ITU) [Reference Recommendation23].

The SDR is the power ratio (expressed in dB) between the signal and the distortion, which is defined by

(13)$${\rm SDR} = 10 \log \displaystyle{\sum_{n} [A(n)]^2 \over \sum_{n} [A(n)-{A}^{\ast} (n)]^2},$$

where A(n) and A* (n) are the amplitudes of the original and watermarked signals, respectively.

In this work, we set the criteria for good sound quality as follows. The LSD should be less than 1 dB, a PESQ score of 3.0 was set as the acceptable quality, and the SDR should be greater than 30 dB [Reference Wang, Miyauchi, Unoki and Kim24].

The results of the sound quality evaluation are shown in Table 1. All methods satisfied the criteria for good sound quality. Besides the LSB-based method, our proposed one outperformed the others. The proposed scheme was improved considerably in terms of sound quality in comparison with the previously proposed one.

Table 1. Sound-quality evaluations: proposed scheme versus other methods.

B) Semi-fragility evaluation

To detect tampering, a watermarking scheme should be robust against non-malicious speech processing, e.g.compression and speech codecs, and fragile to malicious attacks, e.g. pitch shifting and bandpass filtering. Robustness can be indicated by the bit-error rate (BER), as defined in (11). In this work, we chose a BER of 10% as our threshold. A robust scheme should have a BER of less than 10%. If the BER is higher than 20%, the speech signal is considered to have been tampered with. The speech signal is presumably unintentionally modified or tampered with at a low degree if its BER is between 10 and 20% [Reference Karnjana, Galajit, Aimmanee, Wutiwiwatchai and Unoki9].

We evaluated the semi-fragility of the proposed scheme by performing 10 signal processing operations on the watermarked signals as follows. Four were non-malicious operations: G.711 speech companding, G.726 companding, MP3 compression with 128 kbps, and MP4 compression with 96 kbps. Six were possible malicious operations: band-pass filtering (BPF) with 100–6000 Hz and − 12 dB/octave, Gaussian-noise addition (AWGN) with 15 and 40 dB signal-to-noise ratios (SNR), pitch shifting (PSH) by ± 4, ± 10, and ± 20%, single-echo addition with − 6 dB and delay times of 20 and 100 ms, replacing 1/3 and 1/2 of the watermarked signals with an un-watermarked segment, and ± 4% speed changing (SCH).

The results are shown in Table 2. The LSB-based method was excellent in robustness when there was no attack, but it was too fragile to all other operations (except for G.711). The other methods were semi-fragile and could be used for detecting tampering. However, the FE-based method was too robust against echo addition. Thus, it cannot be used to detect tampering when a watermarked signal has been tampered with by this attack. The proposed method was robust in the cases of no attack and the G.711 codec and was fragile to other attacks. However, it was too fragile to MP4 compression. Compared with our previously proposed method, it was more robust against the G.726 codec. Thus, it can be used to detect tampering in speech signals. Also, the BERs of the proposed method can be associated with the degree of tampering. For example, when the degree of pitch shifting increases, the BER increases. This can be used to indicate the degree of attacks.

Table 2. BER (%): proposed scheme versus other methods.

C) Tampering detection ability

As described in Section II-C, tampering can be detected by checking the mismatch between extracted-watermark bits w* (j) and embedded-watermark bits w(j) for j=1 to M. In this section, we demonstrate how it can be done in two experiments.

In the first experiment, a 29 × 131 bitmap image of the word “APSIPA,” as shown in Fig. 7 (a), was used as the watermark. To embed this image, which composed 3799 bits of information, the first 320 frames of all 12 speech signals were connected to construct a new 95 s host signal. Note that the duration was 95 s because our embedding capacity was 40 bps, and there were 3799 bits in total. After embedding the image into the host signal, we divided it into three segments, and the middle segment of the watermarked signal was tampered with by performing the operations listed in Table 2. The reasons we can consider some of these operations to be tampering are as follows. Adding white noise can be considered as channel distortion. Replacing watermarked speech with un-watermarked speech can be considered as content modification. Speeding up or slowing down a watermarked signal can be considered as modifying the duration and tempo of speech. Pitch shifting can be considered as manipulating the individuality of the speaker. Filtering with a low-pass filter is regarded as removing specific frequency information of the speech.

Fig. 7. Comparison of watermark image between original image (a) and reconstructed images after performing following signal-processing operations: (b) no attacks, (c) MP3, (d) G.711, (e) G.726, (f) MP4, (g) PSH −20%, (h) PSH +20%, (i) SCH +4%, (j) SCH −4%, (k) BPF, (l) PSH −10%, (m) PSH +10%, (n) AWGN (40 dB), (o) echo (100 ms), (p) replace (1/3), (q) PSH −4%, (r) PSH +4%, (s) AWGN (15 dB), (t) echo (20 ms, and (u) replace (1/2).

The results are shown in Fig. 7. The hidden image could be correctly extracted when there was no tampering with the watermarked signal, as shown in Fig. 7 (b). The extracted images from other tampered-watermarked signals are shown in Figs 7 (c)–7 (u). It can be seen that the watermark bits in the tampered segment were destroyed, and the destroyed area of the extracted image was associated with the tampered speech segment. In our experiment, this destroyed area was the middle two characters of the word “APSIPA.” Moreover, the degree of tampering could be observed from the extracted image. For example, the middle segments of the watermarked speech signals whose extracted images are shown in Figs 7 (n) and 7 (s) were attacked by adding white Gaussian noise (AWGN). It can be seen that the middle part of the extracted image of Fig. 7 (s) was more severely damaged because the speech signal of Fig. 7 (s) was added with stronger noise. Similarly, Figs 7 (g), 7 (l), 7 (q),7 (h), 7 (m), and 7 (r) (all of which were attacked by pitch shifting with different degrees) showed the same tendency. The part of the extracted image was more severely damaged when the degree of the attack increased. Therefore, we can use the destroyed areas to identify the tampered segments of the watermarked signals, as well as the degree of tampering.

In addition to the tampered location and the tampering degree, we could roughly predict the tampering type by analyzing the destroyed area of the extracted image. According to our embedding rule, a singular spectrum is unchanged when the embedding watermark bit was 0. Therefore, if the destroyed area is dark, such as those in Figs 7 (p) and 7 (u), it is likely that such an area would be extracted from an un-watermarked segment. That is because a singular spectrum is typically convex, and singular values between $\sqrt{\lambda_{p}}$ and $\sqrt{\lambda_{q}}$ are therefore under the straight line that connects $\sqrt {\lambda _{p}}$ and $\sqrt {\lambda _{q}}$. Hence the extracted bit is 0, i.e. the black pixel.

As mentioned in Section III-A, removing high-frequency components from a signal can result in reducing the values of its high-order singular values. Therefore, removing high-frequency components increases the chance of obtaining 0 as the extracted watermark bit. Consequently, the damaged area of the extracted image got darker, as evidenced in Figs 7 (l) and 7 (g), when the pitches of the middle speech segments were decreased by 10 and 20%, respectively. In contrast, adding high-frequency components can cause high-order singular values to increase in value.

In the second experiment, we simulated attacks by using STRAIGHT [Reference Kawahara and Morise1]. For example, we can use STRAIGHT to modify the sentence “No, I did not” to“Yes, I did” by replacing “No” with “Yes” and the removing “not” from the sentence. The steps of the simulation are as follows. First, a watermark, which is a 166 × 23 bitmap image of the word “STRAIGHT,” was embedded into a host signal that was 96 slong. An extracted image with no attack on the watermarked signal is shown in Fig. 8 (a). Second, the watermarked signal was read by STRAIGHT to get specific features, which were the fundamental frequency (F0), aperiodic information, and an F0 adaptively smoothed spectrogram. Third, these specific features were used to synthesize another speech signal, and the synthesized speech signal replaced the watermarked signal on the second half. A replaced part can change important information in the host signal and mislead the listeners. Fourth, the signal obtained from the previous step was inputted into the extraction process to get the watermark. The extracted watermark is shown in Fig. 8 (b). It can be seen that the extracted watermark of the replaced segment was destroyed. Similar to the results from the first experiment, our scheme could be used to identify a tampered segment in a speech signal. Note that replacing some part of a speech signal with a synthesized signal is different from replacing it with an un-watermarked signal since the synthesized signal has distortion. For example, in this experiment, the SDR of the synthesized speech signal was − 27.81 dB, which is quite low. Therefore, a synthesized signal can be roughly considered as a noisy speech signal. Hence, the destroyed area in Fig. 8 (b) looks similar to that shown in Fig. 7 (s).

Fig. 8. Comparison of extracted watermark-image: (a) no tampering and (b) second half of speech signal replaced by synthesized speech signal.

D) Computational time

The computational time of DE-based parameter estimation is considerably high because the DE optimizer has to simulate the embedding process, the extraction process, and many attacks. As a consequence, it performs SVD many times for each input segment, and SVD is time-consuming. Also, the search space of DE is large. The computational time is reduced considerably when CNN-based parameter estimation replaces DE-based estimation in the watermarking scheme. A 10-fold cross-validation was conducted to ensure model stability. All of the simulations were conducted on a personal computer with Windows 10 (Home Edition). The CPU was an Intel^® Core™ i5 with a clock speed of 2.3 GHz and a memory size of 8 GB with a speed of 2,133 MHz. A comparison of computational times is shown in Table 3. It can be seen that the CNN-based method was approximately 2 million times faster.

Table 3. Comparison of computational times for determining parameters of host signal when automatic parameterization is based on differential evolution and when it is based on CNN.

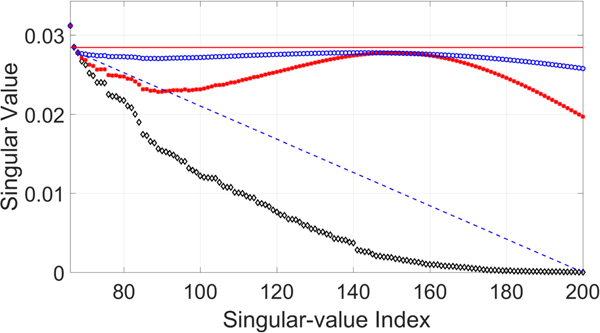
Although the CNN-based parameter estimation can successfully reduce the computational time, we have to trade the accuracy of the parameter estimation for it. A comparison of parameters obtained from the DE-based method and those obtained from the CNN-based method are shown in Fig. 9. The root-mean-square error (RMSE) of the estimated parameter γ was 0.0022, the RMSE of the estimated parameter μ was 32.1956, and the average RMSE of estimated parameter σ was 40.2616. The RMSE values of the parameters μ and σ may be quite large. However, the robustness and inaudibility of the scheme when both methods were used to determine the parameters were comparable, as shown in Table 4. An example of a singular spectrum of a frame that is embedded with parameters obtained with the DE-based method and those obtained with the CNN-based method is shown in Fig. 10. In this example, the error (or difference) between the two parameter vectors $[\mu _{{\rm {DE}}}\ \sigma _{{\rm {DE}}}]^{\rm T}$ and $[\mu _{{\rm {CNN}}}\ \sigma _{{\rm {CNN}}}]^{\rm T}$ was $\sqrt {(\mu _{{\rm {DE}}} - \mu _{{\rm {CNN}}})^2 + (\sigma _{{\rm {DE}}} - \sigma _{{\rm {CNN}}})^2} = 90.56$, which is quite large compared with the RMSE. However, the modified singular spectra do not look much different.

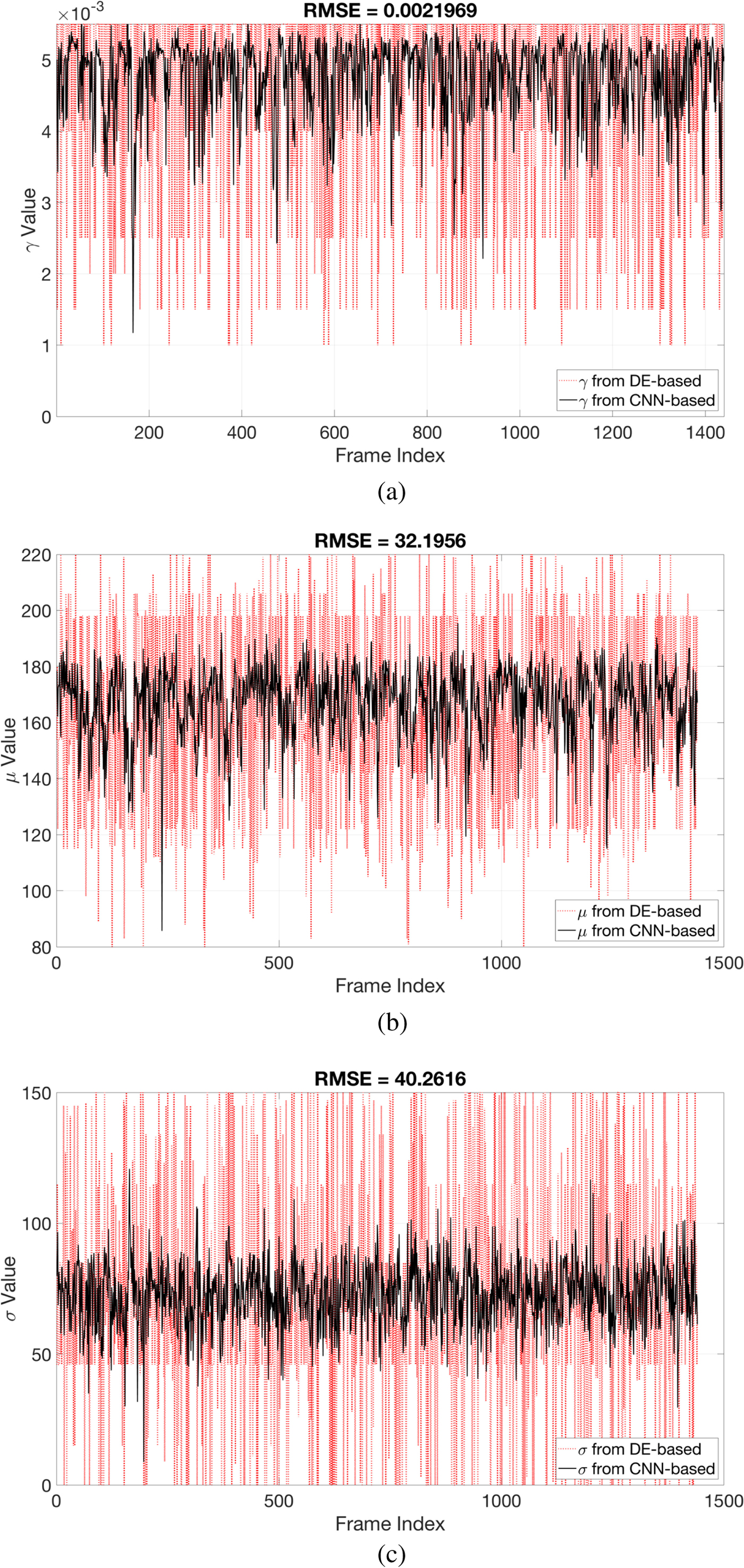
Fig. 9. RMSE of γ, μ, and σ from DE-based parameter estimation and CNN-based parameter estimation.

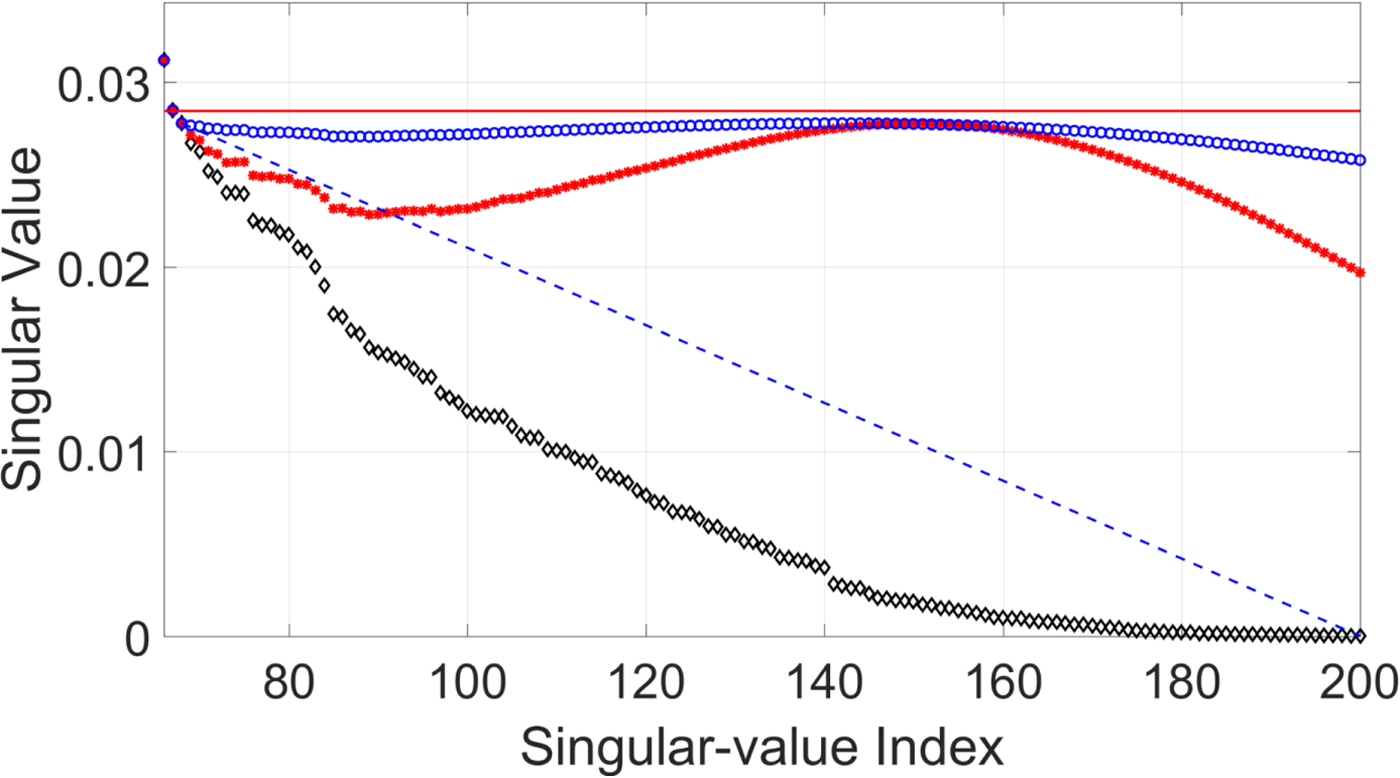
Fig. 10. Example of singular spectrum of embedded frame. “◇” denotes original singular spectrum, “*” denotes modified singular spectrum where parameters are obtained from CNN-based method, and “°” denotes singular spectrum where parameters are obtained from DE-based method.

Table 4. Comparison of robustness and inaudibility of scheme when automatic parameterization is based on differential evolution and when it is based on CNN.