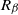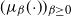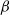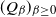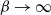1. Introduction
We consider a family of nearest-neighbor matrices
![]() $(Q_\beta)_{\beta \geq 0}$
on
$(Q_\beta)_{\beta \geq 0}$
on
![]() $\mathbb{Z}_+=\{0,1,\ldots\}$
with coefficients
$\mathbb{Z}_+=\{0,1,\ldots\}$
with coefficients
 \begin{equation} Q_\beta(x,y)= \begin{cases}\exp\!(\!-\!\beta \phi(x,y)) > 0 & \hbox{if } |x-y|=1 , \\[5pt] Q_\beta(x,y) = 0 & \hbox{if }|x-y|\neq 1,\end{cases} \qquad x \geq 0, y \geq 0.\end{equation}
\begin{equation} Q_\beta(x,y)= \begin{cases}\exp\!(\!-\!\beta \phi(x,y)) > 0 & \hbox{if } |x-y|=1 , \\[5pt] Q_\beta(x,y) = 0 & \hbox{if }|x-y|\neq 1,\end{cases} \qquad x \geq 0, y \geq 0.\end{equation}
Here,
![]() $\phi(x,y)$
is a function depending on the two values x, y, commonly known as the potential of a physical system. By calling
$\phi(x,y)$
is a function depending on the two values x, y, commonly known as the potential of a physical system. By calling
![]() $Q_{\beta}^{(m)}$
to the mth power of the matrix
$Q_{\beta}^{(m)}$
to the mth power of the matrix
![]() $Q_\beta$
, from irreducibility we get that
$Q_\beta$
, from irreducibility we get that
![]() $R_\beta\;:\!=\;R(Q_\beta)=(\limsup_{n\to\infty} (Q_{\beta}^{(2n)}(x,x))^{1/2n})^{-1}$
is a common convergence radius, i.e. it is independent of
$R_\beta\;:\!=\;R(Q_\beta)=(\limsup_{n\to\infty} (Q_{\beta}^{(2n)}(x,x))^{1/2n})^{-1}$
is a common convergence radius, i.e. it is independent of
![]() $x\in \mathbb{Z}_+$
(see [Reference Seneta17, Theorem 6.1]). For each fixed
$x\in \mathbb{Z}_+$
(see [Reference Seneta17, Theorem 6.1]). For each fixed
![]() $\beta \geq 0$
, we say that the matrix
$\beta \geq 0$
, we say that the matrix
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-recurrent if
$R_\beta$
-recurrent if
![]() $\sum_{n=0}^{\infty}R_\beta^{2n}Q_{\beta}^{(2n)}(x,x)=\infty$
for some (equivalently for all)
$\sum_{n=0}^{\infty}R_\beta^{2n}Q_{\beta}^{(2n)}(x,x)=\infty$
for some (equivalently for all)
![]() $x\in \mathbb{Z}_+$
, and
$x\in \mathbb{Z}_+$
, and
![]() $R_\beta$
-transient when the series converges. If
$R_\beta$
-transient when the series converges. If
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-recurrent, we say that it is
$R_\beta$
-recurrent, we say that it is
![]() $R_\beta$
-null recurrent if
$R_\beta$
-null recurrent if
![]() $\lim_{n \to \infty}Q_{\beta}^{(2n)}(x,x)R_\beta^{2n}= 0$
, and
$\lim_{n \to \infty}Q_{\beta}^{(2n)}(x,x)R_\beta^{2n}= 0$
, and
![]() $R_\beta$
-positive recurrent if the limit is non-zero ([Reference Seneta17, Reference Vere-Jones18] are recommended for more details on the definitions and classification of non-negative matrices).
$R_\beta$
-positive recurrent if the limit is non-zero ([Reference Seneta17, Reference Vere-Jones18] are recommended for more details on the definitions and classification of non-negative matrices).
For each fixed
![]() $\beta \geq 0$
, the matrix
$\beta \geq 0$
, the matrix
![]() $Q_\beta$
induces a Markov chain, say
$Q_\beta$
induces a Markov chain, say
![]() $X^\beta=(X^\beta_n\;:\; n\ge 0)$
, which inherits the same recurrence properties as
$X^\beta=(X^\beta_n\;:\; n\ge 0)$
, which inherits the same recurrence properties as
![]() $Q_\beta$
. Two questions arise from this setting: (i) Does the
$Q_\beta$
. Two questions arise from this setting: (i) Does the
![]() $R_\beta$
classification depend on
$R_\beta$
classification depend on
![]() $\beta$
? (ii) Does there exist a Markov chain
$\beta$
? (ii) Does there exist a Markov chain
![]() $X^\infty$
such that
$X^\infty$
such that
![]() $ \lim_{\beta \to \infty} X^{\beta} =X^{\infty}$
in the finite-distributional sense?
$ \lim_{\beta \to \infty} X^{\beta} =X^{\infty}$
in the finite-distributional sense?
The existence of weak limits as
![]() $\beta \to \infty$
(also called zero-temperature limits) has been widely studied under different settings: [Reference Bissacot, Garibaldi and Thieullen5–Reference Chazottes, Gambaudo and Ugalde7, Reference Leplaideur15] in the finite space state, and [Reference Freire and Vargas9, Reference Jenkinson, Mauldin and Urbński11, Reference Kempton13] in the countable case. We also recommend [Reference Bissacot and Garibaldi4] for results on ergodic optimal problems using weak KAM methods, and [Reference Baraviera and Lopes2] for results on large deviations. The aforementioned references deal with the problem of zero-temperature limits under sufficient conditions over either the potential or the space of trajectories. In this article, we prove the existence of zero-temperature limits for our model through a probabilistic approach rather than the dynamical system point of view. More precisely, we study the
$\beta \to \infty$
(also called zero-temperature limits) has been widely studied under different settings: [Reference Bissacot, Garibaldi and Thieullen5–Reference Chazottes, Gambaudo and Ugalde7, Reference Leplaideur15] in the finite space state, and [Reference Freire and Vargas9, Reference Jenkinson, Mauldin and Urbński11, Reference Kempton13] in the countable case. We also recommend [Reference Bissacot and Garibaldi4] for results on ergodic optimal problems using weak KAM methods, and [Reference Baraviera and Lopes2] for results on large deviations. The aforementioned references deal with the problem of zero-temperature limits under sufficient conditions over either the potential or the space of trajectories. In this article, we prove the existence of zero-temperature limits for our model through a probabilistic approach rather than the dynamical system point of view. More precisely, we study the
![]() $R_\beta$
-positivity dependence on
$R_\beta$
-positivity dependence on
![]() $\beta \geq 0$
under different conditions on the potential. Provided that the weak limit exists, a precise characterization of the typical configurations of the limiting measure are described. The rest of this article is organized as follows: In Section 2 we review known results related to the existence of an infinite-volume Gibbs measure for a Hamiltonian defined on the set of nearest-neighbor trajectories reflected at the origin. In Section 3 we provide some conditions for the existence of equilibrium measures for finite values of
$\beta \geq 0$
under different conditions on the potential. Provided that the weak limit exists, a precise characterization of the typical configurations of the limiting measure are described. The rest of this article is organized as follows: In Section 2 we review known results related to the existence of an infinite-volume Gibbs measure for a Hamiltonian defined on the set of nearest-neighbor trajectories reflected at the origin. In Section 3 we provide some conditions for the existence of equilibrium measures for finite values of
![]() $\beta$
. In Section 4 we analyze the existence of weak limits (i.e. in the sense of finite-dimensional distributions) as
$\beta$
. In Section 4 we analyze the existence of weak limits (i.e. in the sense of finite-dimensional distributions) as
![]() $\beta \to \infty$
. Finally, in Section 5 we analyze some application examples to contextualize our main theorems.
$\beta \to \infty$
. Finally, in Section 5 we analyze some application examples to contextualize our main theorems.
2. Markov chains on non-negative matrices
Observe that in the case of nearest-neighbor matrices (1.1), for each fixed
![]() $\beta \geq 0$
there exists a strictly positive solution to the problem
$\beta \geq 0$
there exists a strictly positive solution to the problem
For general irreducible non-negative matrices, the existence of a strictly positive solution to (2.1) is only guaranteed for
![]() $R_\beta$
-recurrent matrices (see [Reference Vere-Jones18, Corollary 2]). Note that the matrix
$R_\beta$
-recurrent matrices (see [Reference Vere-Jones18, Corollary 2]). Note that the matrix
![]() $P_\beta=(p_\beta(x,y)\;:\; x,y\in \mathbb{Z}_+)$
defined by
$P_\beta=(p_\beta(x,y)\;:\; x,y\in \mathbb{Z}_+)$
defined by
is the stochastic matrix of an irreducible birth-and-death chain
![]() $X^\beta=(X^\beta_n\;:\; n\ge 0)$
reflected at 0. The matrix
$X^\beta=(X^\beta_n\;:\; n\ge 0)$
reflected at 0. The matrix
![]() $Q_\beta$
turns out to be
$Q_\beta$
turns out to be
![]() $R_\beta$
-positive recurrent (respectively
$R_\beta$
-positive recurrent (respectively
![]() $R_\beta$
-null recurrent or
$R_\beta$
-null recurrent or
![]() $R_\beta$
-transient) if and only if
$R_\beta$
-transient) if and only if
![]() $X^\beta$
is positive recurrent (respectively null recurrent or transient). Also, we say that the matrix
$X^\beta$
is positive recurrent (respectively null recurrent or transient). Also, we say that the matrix
![]() $Q_\beta$
is geometrically ergodic if the stopping time
$Q_\beta$
is geometrically ergodic if the stopping time
![]() $\tau_y=\inf\{n>0\;:\; X^{\beta}_n=y\}$
has exponential moment, i.e.
$\tau_y=\inf\{n>0\;:\; X^{\beta}_n=y\}$
has exponential moment, i.e.
![]() $\mathbb{E}_{x}(\theta^{\tau_{y}})\;:\!=\;\mathbb{E}(\theta^{\tau_{y}}\mid X_0=x)<\infty$
for some
$\mathbb{E}_{x}(\theta^{\tau_{y}})\;:\!=\;\mathbb{E}(\theta^{\tau_{y}}\mid X_0=x)<\infty$
for some
![]() $\theta>1$
. In a similar way to [Reference Littin and Martnez16], we need to introduce the sequence of truncated matrices
$\theta>1$
. In a similar way to [Reference Littin and Martnez16], we need to introduce the sequence of truncated matrices
![]() $Q_\beta^{[m]}=(Q_{\beta}(x,y), x \geq m, y \geq m )$
and the sequence
$Q_\beta^{[m]}=(Q_{\beta}(x,y), x \geq m, y \geq m )$
and the sequence
![]() $R_{\beta,m}\;:\!=\;R_\beta(Q_\beta^{[m]})$
,
$R_{\beta,m}\;:\!=\;R_\beta(Q_\beta^{[m]})$
,
![]() $m \geq 0$
, of their corresponding convergence radius. The Markov chain related to
$m \geq 0$
, of their corresponding convergence radius. The Markov chain related to
![]() $Q_\beta^{[m]}$
will be denoted by
$Q_\beta^{[m]}$
will be denoted by
![]() $X^{\beta,[m]}$
. Clearly,
$X^{\beta,[m]}$
. Clearly,
![]() $R_{\beta,0}=R_\beta$
and
$R_{\beta,0}=R_\beta$
and
![]() $X^{\beta,[0]}=X^{\beta}$
. Note that for each fixed
$X^{\beta,[0]}=X^{\beta}$
. Note that for each fixed
![]() $\beta \geq 0$
, the sequence
$\beta \geq 0$
, the sequence
![]() $(R_{\beta,m})_{m \geq 0}$
is non-decreasing, i.e.
$(R_{\beta,m})_{m \geq 0}$
is non-decreasing, i.e.
![]() $R_{\beta,m} \leq R_{\beta,m+1}$
for all
$R_{\beta,m} \leq R_{\beta,m+1}$
for all
![]() $m \geq 0$
.
$m \geq 0$
.
Theorem 2.1 ([Reference Littin and Martnez16].) Let
![]() $Q_\beta$
be a nearest-neighbor matrix as in (1.1). Assume
$Q_\beta$
be a nearest-neighbor matrix as in (1.1). Assume
![]() $R(Q_{\beta})>0$
. Then
$R(Q_{\beta})>0$
. Then
![]() $R_{\beta,m} < R_{\beta,m+1}$
for some
$R_{\beta,m} < R_{\beta,m+1}$
for some
![]() $m \geq 0$
if and only if the matrix
$m \geq 0$
if and only if the matrix
![]() $Q_\beta$
is geometrically ergodic and consequently is
$Q_\beta$
is geometrically ergodic and consequently is
![]() $R_\beta$
-positive recurrent. Conversely, if
$R_\beta$
-positive recurrent. Conversely, if
![]() $R_{\beta,m} = R_{\beta,m+1}$
for all
$R_{\beta,m} = R_{\beta,m+1}$
for all
![]() $m \geq 0$
, the matrix
$m \geq 0$
, the matrix
![]() $Q^{[1]}_\beta$
is
$Q^{[1]}_\beta$
is
![]() $R_\beta$
-transient and
$R_\beta$
-transient and
![]() $Q_\beta$
cannot be geometrically ergodic.
$Q_\beta$
cannot be geometrically ergodic.
From (2.1) and (2.2) we observe that, for all
![]() $x \geq 1$
, the transition probabilities defined in (2.2) satisfy the recurrence formula
$x \geq 1$
, the transition probabilities defined in (2.2) satisfy the recurrence formula
where
![]() $\psi(x)=\phi(x,x+1)+\phi(x+1,x)$
. In order to simplify our presentation we set
$\psi(x)=\phi(x,x+1)+\phi(x+1,x)$
. In order to simplify our presentation we set
![]() $u_\beta(x)=p_\beta(x,x+1)$
. From the obvious relation
$u_\beta(x)=p_\beta(x,x+1)$
. From the obvious relation
![]() $p_\beta(x+1,x)=1-u_\beta(x+1)$
we have
$p_\beta(x+1,x)=1-u_\beta(x+1)$
we have
with the reflecting condition
![]() $u_\beta(0)=p_\beta(0,1)=1$
. By iterating the formula in (2.4) we deduce that
$u_\beta(0)=p_\beta(0,1)=1$
. By iterating the formula in (2.4) we deduce that
![]() $u_\beta(x)$
can be written as the continued fraction
$u_\beta(x)$
can be written as the continued fraction
 \begin{equation} u_\beta(x)=\cfrac{R_\beta^2 \exp\!(\!-\!\beta\psi(x))}{1-\cfrac{R_\beta^2 \exp\!(\!-\!\beta\psi(x+1))}{1-\cfrac{R_\beta^2 \exp\!(\!-\!\beta\psi(x+2))}{1-\cdots}}}, \qquad x \geq 1.\end{equation}
\begin{equation} u_\beta(x)=\cfrac{R_\beta^2 \exp\!(\!-\!\beta\psi(x))}{1-\cfrac{R_\beta^2 \exp\!(\!-\!\beta\psi(x+1))}{1-\cfrac{R_\beta^2 \exp\!(\!-\!\beta\psi(x+2))}{1-\cdots}}}, \qquad x \geq 1.\end{equation}
2.1. Hamiltonians and existence of Gibbs measures
In a similar way to [Reference Ferrari and Martnez8, Reference Littin and Martnez16], we introduce a brief presentation concerning the existence of Gibbs measures. Let
![]() $\Omega$
be the space of trajectories of nearest neighbors reflected at the origin, i.e.
$\Omega$
be the space of trajectories of nearest neighbors reflected at the origin, i.e.
![]() $\Omega= \{x \in \mathbb{N}_0^\mathbb{Z}\;:\; |x_k -x_{k+1}|=1 \text{ for all } k \in \mathbb{Z}\}$
. Given a discrete interval
$\Omega= \{x \in \mathbb{N}_0^\mathbb{Z}\;:\; |x_k -x_{k+1}|=1 \text{ for all } k \in \mathbb{Z}\}$
. Given a discrete interval
![]() $[i,j] \subset \mathbb{Z}$
,
$[i,j] \subset \mathbb{Z}$
,
![]() $i \leq j$
, and
$i \leq j$
, and
![]() $x \in \Omega$
, we denote by
$x \in \Omega$
, we denote by
![]() $x[i,j]=(x_i,x_{i+1},\ldots ,x_{j-1},x_j)$
the coordinates of x in the interval [i, j], and
$x[i,j]=(x_i,x_{i+1},\ldots ,x_{j-1},x_j)$
the coordinates of x in the interval [i, j], and
![]() $\Omega[i,j]=\{x[i,j]\;:\; x \in \Omega\}$
the restriction of
$\Omega[i,j]=\{x[i,j]\;:\; x \in \Omega\}$
the restriction of
![]() $\Omega$
into the interval [i, j]. For each
$\Omega$
into the interval [i, j]. For each
![]() $x[i,j] \in \Omega[i,j]$
we consider the Hamiltonian
$x[i,j] \in \Omega[i,j]$
we consider the Hamiltonian
 \begin{equation} \mathcal{H}_{[i,j]}(x)=\sum_{k=i}^{j-1}\phi(x_k,x_{k+1}).\end{equation}
\begin{equation} \mathcal{H}_{[i,j]}(x)=\sum_{k=i}^{j-1}\phi(x_k,x_{k+1}).\end{equation}
By keeping fixed the states u, v at sites
![]() $i-1$
and
$i-1$
and
![]() $j+1$
respectively, we now define, for
$j+1$
respectively, we now define, for
![]() $x[i,j] \sim (u,v)$
,
$x[i,j] \sim (u,v)$
,
![]() $\mathcal{H}^{u,v}_{[i,j]}(x)= \mathcal{H}_{[i,j]}(x)+\phi(u, x_{i})+\phi(x_{j}, v)$
, where
$\mathcal{H}^{u,v}_{[i,j]}(x)= \mathcal{H}_{[i,j]}(x)+\phi(u, x_{i})+\phi(x_{j}, v)$
, where
![]() $x[i,j] \sim (u,v)$
is used to denote the restriction
$x[i,j] \sim (u,v)$
is used to denote the restriction
![]() $|x_i-u|=|x_j-v|=1$
. The Gibbs measure over the finite interval [i, j] at inverse temperature
$|x_i-u|=|x_j-v|=1$
. The Gibbs measure over the finite interval [i, j] at inverse temperature
![]() $\beta$
and boundary conditions (u, v) is
$\beta$
and boundary conditions (u, v) is
where
 \begin{equation*} \mathcal{Z}_{[i,j], \beta}^{u,v}=\sum_{\substack{x \in \Omega[i,j]: \\ x[i,j] \sim (u,v)}} \exp \big({-}\beta \mathcal{H}^{u,v}_{[i,j]}(x)\big)\end{equation*}
\begin{equation*} \mathcal{Z}_{[i,j], \beta}^{u,v}=\sum_{\substack{x \in \Omega[i,j]: \\ x[i,j] \sim (u,v)}} \exp \big({-}\beta \mathcal{H}^{u,v}_{[i,j]}(x)\big)\end{equation*}
is the partition function associated to the Hamiltonian
![]() $\mathcal{H}^{u,v}_{[i,j]}$
in the interval [i, j]. For any
$\mathcal{H}^{u,v}_{[i,j]}$
in the interval [i, j]. For any
![]() $[\ell,m] \subset [i,j]$
and
$[\ell,m] \subset [i,j]$
and
![]() $\tilde{x} \in \Omega[\ell,m]$
, we notice that
$\tilde{x} \in \Omega[\ell,m]$
, we notice that
 \begin{equation*} \mu_{[i,j], \beta}^{u,v}(\tilde x)=\frac{1}{\mathcal{Z}_{[i,j],\beta}^{u,v}} \sum_{\substack{x \in \Omega[i,j]: \\ x[\ell,m] = \tilde{x}}}\exp \big({-}\beta \mathcal{H}^{u,v}_{[i,j]}(x)\big).\end{equation*}
\begin{equation*} \mu_{[i,j], \beta}^{u,v}(\tilde x)=\frac{1}{\mathcal{Z}_{[i,j],\beta}^{u,v}} \sum_{\substack{x \in \Omega[i,j]: \\ x[\ell,m] = \tilde{x}}}\exp \big({-}\beta \mathcal{H}^{u,v}_{[i,j]}(x)\big).\end{equation*}
From a direct calculation, we get, for
![]() $\tilde{x} \in \Omega[\ell,m]$
,
$\tilde{x} \in \Omega[\ell,m]$
,
where
![]() $\mathcal{Z}_{[i,\ell-1],\beta}^{u,x_{\ell}}$
and
$\mathcal{Z}_{[i,\ell-1],\beta}^{u,x_{\ell}}$
and
![]() $\mathcal{Z}_{[m+1,j],\beta}^{x_{m},v}$
are the partition functions over the intervals
$\mathcal{Z}_{[m+1,j],\beta}^{x_{m},v}$
are the partition functions over the intervals
![]() $[i,\ell-1]$
and
$[i,\ell-1]$
and
![]() $[m+1,j]$
respectively. Recalling the definition in (1.1), the following equalities are valid:
$[m+1,j]$
respectively. Recalling the definition in (1.1), the following equalities are valid:
and therefore, for
![]() $\tilde{x} \in \Omega[\ell,m]$
,
$\tilde{x} \in \Omega[\ell,m]$
,
 \begin{equation*} \mu_{[i,j], \beta}^{u,v}(\tilde x)=\frac{Q_{\beta}^{(\ell-i+1)}(u,x_\ell)Q_{\beta}^{(j-m+1)}(x_m,v)}{Q_{\beta}^{(j-i+2)}(u,v)} \exp\!(\!-\!\beta \mathcal{H}_{[\ell,m]}(\tilde x)).\end{equation*}
\begin{equation*} \mu_{[i,j], \beta}^{u,v}(\tilde x)=\frac{Q_{\beta}^{(\ell-i+1)}(u,x_\ell)Q_{\beta}^{(j-m+1)}(x_m,v)}{Q_{\beta}^{(j-i+2)}(u,v)} \exp\!(\!-\!\beta \mathcal{H}_{[\ell,m]}(\tilde x)).\end{equation*}
[Reference Gurevich10, Theorem C] states that in the thermodynamic limit
![]() $[i,j] \nearrow \mathbb{Z}$
there exists a unique equilibrium measure
$[i,j] \nearrow \mathbb{Z}$
there exists a unique equilibrium measure
![]() $\mu_{\beta}(\!\cdot\!)$
associated to the Hamiltonian
$\mu_{\beta}(\!\cdot\!)$
associated to the Hamiltonian
![]() $\mathcal{H}^{u,v}_{[i,j]}(\!\cdot\!)$
at inverse temperature
$\mathcal{H}^{u,v}_{[i,j]}(\!\cdot\!)$
at inverse temperature
![]() $\beta>0$
if and only if the matrix
$\beta>0$
if and only if the matrix
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-positive recurrent. In this latter case, there exist
$R_\beta$
-positive recurrent. In this latter case, there exist
![]() $\lambda_\beta=1/R_\beta>0$
, an eigenvector
$\lambda_\beta=1/R_\beta>0$
, an eigenvector
![]() $h_\beta>0$
, and an eigenmeasure
$h_\beta>0$
, and an eigenmeasure
![]() $\nu_\beta>0$
with strictly positive components such that
$\nu_\beta>0$
with strictly positive components such that
 \begin{equation*} \sum_{y=0}^{\infty} \exp\!(\!-\!\beta \phi(x,y))h_\beta(y)=\lambda_\beta h_\beta (x), \qquad \sum_{x=0}^{\infty} \exp\!(\!-\!\beta \phi(x,y))\nu_\beta(x)=\lambda_\beta \nu_\beta (y),\end{equation*}
\begin{equation*} \sum_{y=0}^{\infty} \exp\!(\!-\!\beta \phi(x,y))h_\beta(y)=\lambda_\beta h_\beta (x), \qquad \sum_{x=0}^{\infty} \exp\!(\!-\!\beta \phi(x,y))\nu_\beta(x)=\lambda_\beta \nu_\beta (y),\end{equation*}
and
![]() $h_\beta$
,
$h_\beta$
,
![]() $\nu_\beta$
can be chosen satisfying
$\nu_\beta$
can be chosen satisfying
![]() $\sum_{x=0}^{\infty}h_\beta(x)\nu_\beta(x)=1$
. Moreover,
$\sum_{x=0}^{\infty}h_\beta(x)\nu_\beta(x)=1$
. Moreover,
since
![]() $\Delta(x,y) =x-y\ (\mathrm{mod}\ 2)$
. The equilibrium measure
$\Delta(x,y) =x-y\ (\mathrm{mod}\ 2)$
. The equilibrium measure
![]() $\mu_{ \beta}(\!\cdot\!)$
(which is independent of the boundary conditions u, v) is a Markov chain with stationary distribution
$\mu_{ \beta}(\!\cdot\!)$
(which is independent of the boundary conditions u, v) is a Markov chain with stationary distribution
![]() $\pi_\beta(x)=h_\beta(x) \nu_\beta(x)$
,
$\pi_\beta(x)=h_\beta(x) \nu_\beta(x)$
,
![]() $x \geq 0$
, and transition probabilities given by (2.2), so that, for all
$x \geq 0$
, and transition probabilities given by (2.2), so that, for all
![]() $\tilde x \in \Omega[l,m]$
,
$\tilde x \in \Omega[l,m]$
,
 \begin{equation} \mu_{ \beta}(\tilde x)=\frac{\pi_\beta(\tilde{x}_{\ell})h_\beta(\tilde x_{m})}{\lambda_\beta^{m-\ell}h_\beta(\tilde x_{\ell})}\exp \left(\!-\!\beta \mathcal{H}_{[\ell,m]}(\tilde{x})\right)=\pi_\beta(\tilde{x}_{\ell})\prod_{k=\ell}^{m-1} \frac{h_\beta(\tilde{x}_{k+1})}{\lambda_\beta h_\beta(\tilde{x}_{k})} \exp\!(\!-\!\beta \phi(\tilde{x}_k,\tilde{x}_{k+1})) .\end{equation}
\begin{equation} \mu_{ \beta}(\tilde x)=\frac{\pi_\beta(\tilde{x}_{\ell})h_\beta(\tilde x_{m})}{\lambda_\beta^{m-\ell}h_\beta(\tilde x_{\ell})}\exp \left(\!-\!\beta \mathcal{H}_{[\ell,m]}(\tilde{x})\right)=\pi_\beta(\tilde{x}_{\ell})\prod_{k=\ell}^{m-1} \frac{h_\beta(\tilde{x}_{k+1})}{\lambda_\beta h_\beta(\tilde{x}_{k})} \exp\!(\!-\!\beta \phi(\tilde{x}_k,\tilde{x}_{k+1})) .\end{equation}
Remark 2.1. The Hamiltonian defined in (2.6) can be written in terms of
![]() $\psi(\!\cdot\!)$
. We first set
$\psi(\!\cdot\!)$
. We first set
![]() $\mathcal{N}_{[i,j]}(x;\; a,b)=\sum_{k=i}^{j-1} \textbf{1}_{\{x_k=a,x_{k+1}=b\}}$
, the number of transitions from a to b. It is not difficult to notice that
$\mathcal{N}_{[i,j]}(x;\; a,b)=\sum_{k=i}^{j-1} \textbf{1}_{\{x_k=a,x_{k+1}=b\}}$
, the number of transitions from a to b. It is not difficult to notice that
In the particular case
![]() $x_i=x_j$
,
$x_i=x_j$
,
![]() $j \equiv i\ (\mathrm{mod}\;2)$
, we necessarily have
$j \equiv i\ (\mathrm{mod}\;2)$
, we necessarily have
![]() $\mathcal{N}_{[i,j]}( x;\; a,a+1)=\mathcal{N}_{[i,j]}( x;\; a+1,a)$
. Since
$\mathcal{N}_{[i,j]}( x;\; a,a+1)=\mathcal{N}_{[i,j]}( x;\; a+1,a)$
. Since
![]() $\psi(a)=\phi(a,a+1)+\phi(a+1,a)$
, we now get
$\psi(a)=\phi(a,a+1)+\phi(a+1,a)$
, we now get
![]() $\mathcal{H}_{[i,j]}(x)=\sum_{a=0}^{\infty} \psi(a)\mathcal{N}_{[i,j]}( x;\; a+1,a)$
.
$\mathcal{H}_{[i,j]}(x)=\sum_{a=0}^{\infty} \psi(a)\mathcal{N}_{[i,j]}( x;\; a+1,a)$
.
To conclude this section, we present some useful bounds for the sequence
![]() $R_{\beta,m}$
,
$R_{\beta,m}$
,
![]() $m \geq 0$
. Let us define
$m \geq 0$
. Let us define
 \begin{equation} \mathcal{Z}^{[m]}_{2n,\beta}= \big(Q_\beta^{[m]}\big)^{(2n)}(m,m)=\sum_{\substack{x \in \Omega^{[m]}[0,2n]:\\ x_{0}=x_{2 n}=m}} \exp (\!-\!\beta \mathcal{H}_{2n}(x)),\end{equation}
\begin{equation} \mathcal{Z}^{[m]}_{2n,\beta}= \big(Q_\beta^{[m]}\big)^{(2n)}(m,m)=\sum_{\substack{x \in \Omega^{[m]}[0,2n]:\\ x_{0}=x_{2 n}=m}} \exp (\!-\!\beta \mathcal{H}_{2n}(x)),\end{equation}
where
![]() $\Omega^{[m]}=\{ x \in \Omega \;:\; x_{k} \geq m \text{ for all } k \in \mathbb{Z}\}$
and
$\Omega^{[m]}=\{ x \in \Omega \;:\; x_{k} \geq m \text{ for all } k \in \mathbb{Z}\}$
and
![]() $\mathcal{H}_{2n}(x)=\mathcal{H}_{[0,2n]}(x)$
. Similarly, for
$\mathcal{H}_{2n}(x)=\mathcal{H}_{[0,2n]}(x)$
. Similarly, for
![]() $m<m^\prime$
we consider the finite matrices
$m<m^\prime$
we consider the finite matrices
![]() $Q_\beta^{[m,m^\prime]}$
with coordinates
$Q_\beta^{[m,m^\prime]}$
with coordinates
![]() $m \leq x \leq m^\prime$
and
$m \leq x \leq m^\prime$
and
![]() $m \leq y \leq m^\prime$
. In this case we write
$m \leq y \leq m^\prime$
. In this case we write
 \begin{equation*} \mathcal{Z}^{[m,m^\prime]}_{2n,\beta}= \big(Q_\beta^{[m,m^\prime]}\big)^{(2n)}(m,m)=\sum_{\substack{x \in \Omega^{[m,m^\prime ]}[0,2n]:\\ x_{0}=x_{2 n}=m}} \exp (\!-\!\beta \mathcal{H}_{2n}(x)),\end{equation*}
\begin{equation*} \mathcal{Z}^{[m,m^\prime]}_{2n,\beta}= \big(Q_\beta^{[m,m^\prime]}\big)^{(2n)}(m,m)=\sum_{\substack{x \in \Omega^{[m,m^\prime ]}[0,2n]:\\ x_{0}=x_{2 n}=m}} \exp (\!-\!\beta \mathcal{H}_{2n}(x)),\end{equation*}
where
![]() $\Omega^{[m,m^\prime]}=\{ x \in \Omega\;:\; m\leq x_{k} \leq m^\prime\text{ for all } k \in \mathbb{Z}\}$
. We now define the power series
$\Omega^{[m,m^\prime]}=\{ x \in \Omega\;:\; m\leq x_{k} \leq m^\prime\text{ for all } k \in \mathbb{Z}\}$
. We now define the power series
and similarly, for
![]() $m < m^\prime$
,
$m < m^\prime$
,
![]() $\mathcal{Z}_{\beta}^{[m,m^\prime]}(r)=\sum_{n=0}^{\infty} r^{2 n}\mathcal{Z}^{[m,m^\prime]}_{2n,\beta}$
. From the monotone convergence theorem we get
$\mathcal{Z}_{\beta}^{[m,m^\prime]}(r)=\sum_{n=0}^{\infty} r^{2 n}\mathcal{Z}^{[m,m^\prime]}_{2n,\beta}$
. From the monotone convergence theorem we get
![]() $\lim_{m^\prime \to \infty} \mathcal{Z}^{[m,m^\prime]}_{2n,\beta}(r)= \mathcal{Z}^{[m]}_{2n,\beta}(r)$
for each
$\lim_{m^\prime \to \infty} \mathcal{Z}^{[m,m^\prime]}_{2n,\beta}(r)= \mathcal{Z}^{[m]}_{2n,\beta}(r)$
for each
![]() $0<r<R_{\beta,m}$
fixed. Let us deduce now some general bounds for
$0<r<R_{\beta,m}$
fixed. Let us deduce now some general bounds for
![]() $R_{\beta,m}$
and
$R_{\beta,m}$
and
![]() $R_{\beta,[m,m^\prime]}\;:\!=\;R\big(Q_{\beta}^{[m,m^\prime]}\big)$
,
$R_{\beta,[m,m^\prime]}\;:\!=\;R\big(Q_{\beta}^{[m,m^\prime]}\big)$
,
![]() $0 \leq m < m^\prime$
. First, we set
$0 \leq m < m^\prime$
. First, we set
![]() $\alpha_m=\inf_{x \geq m}\psi(x)$
,
$\alpha_m=\inf_{x \geq m}\psi(x)$
,
![]() $ \alpha_{m,m^\prime}=\min_{m \leq x < m^\prime}\psi(x)$
. For each
$ \alpha_{m,m^\prime}=\min_{m \leq x < m^\prime}\psi(x)$
. For each
![]() $x \in \Omega^{[m]}$
such that
$x \in \Omega^{[m]}$
such that
![]() $x_0=x_{2n}$
, the Hamiltonian satisfies
$x_0=x_{2n}$
, the Hamiltonian satisfies
![]() $\mathcal{H}_{2n}(x) \geq n \alpha_m$
(see Remark 2.1). From (2.8) we get
$\mathcal{H}_{2n}(x) \geq n \alpha_m$
(see Remark 2.1). From (2.8) we get
![]() $\mathcal{Z}^{[m]}_{2n,\beta} \leq \mathcal{Z}^{[m]}_{2n,0} \exp\!(\!-\!n\beta \alpha_m)$
. Since
$\mathcal{Z}^{[m]}_{2n,\beta} \leq \mathcal{Z}^{[m]}_{2n,0} \exp\!(\!-\!n\beta \alpha_m)$
. Since
![]() $\mathcal{Z}^{[m]}_{2n,0}=\textrm{Card} (\Omega^{[m]}[0,2n]\;:\; x_0=x_{2n}=m)$
, from (2.9) it follows that
$\mathcal{Z}^{[m]}_{2n,0}=\textrm{Card} (\Omega^{[m]}[0,2n]\;:\; x_0=x_{2n}=m)$
, from (2.9) it follows that
![]() $\mathcal{Z}_{\beta}^{[m]}(r) \leq \mathcal{Z}_{0}^{[m]}(r \exp \left(\!-\!\beta \alpha_m/2\right)) $
, and thus
$\mathcal{Z}_{\beta}^{[m]}(r) \leq \mathcal{Z}_{0}^{[m]}(r \exp \left(\!-\!\beta \alpha_m/2\right)) $
, and thus
Following the same ideas, from the inequality
![]() $\mathcal{Z}^{[m,m^\prime]}_{2n,\beta} \leq \mathcal{Z}^{[m,m^\prime]}_{2n,0} \exp (\!-\!n\beta \alpha_{m,m^\prime})$
we get
$\mathcal{Z}^{[m,m^\prime]}_{2n,\beta} \leq \mathcal{Z}^{[m,m^\prime]}_{2n,0} \exp (\!-\!n\beta \alpha_{m,m^\prime})$
we get
![]() $\mathcal{Z}_{\beta}^{[m,m^\prime]}(r) \leq \mathcal{Z}_{0}^{[m,m^\prime]}(r \exp (\!-\!\beta \alpha_{m,m^\prime}/2))$
and hence we obtain the preliminary bound
$\mathcal{Z}_{\beta}^{[m,m^\prime]}(r) \leq \mathcal{Z}_{0}^{[m,m^\prime]}(r \exp (\!-\!\beta \alpha_{m,m^\prime}/2))$
and hence we obtain the preliminary bound
![]() ${R_{\beta,[m,m^\prime]}} \geq \exp \left(\beta \alpha_{m,m^\prime}/2\right){R_{0,[m,m^\prime]}} $
. When
${R_{\beta,[m,m^\prime]}} \geq \exp \left(\beta \alpha_{m,m^\prime}/2\right){R_{0,[m,m^\prime]}} $
. When
![]() $\beta=0$
, the values of
$\beta=0$
, the values of
![]() ${R_{0,[m,m^\prime]}} $
and
${R_{0,[m,m^\prime]}} $
and
![]() $R_{0,m}$
can be computed explicitly. Since
$R_{0,m}$
can be computed explicitly. Since
![]() $Q_0^{[m,m^\prime]}$
is a tridiagonal matrix with constant coefficients, from the Perron–Frobenius theorem we have that the convergence radius is strictly positive and it is the inverse of the spectral radius. [Reference Kulkarni, Schmidt and Tsui14, Theorem 2.2] states the main eigenvalue is
$Q_0^{[m,m^\prime]}$
is a tridiagonal matrix with constant coefficients, from the Perron–Frobenius theorem we have that the convergence radius is strictly positive and it is the inverse of the spectral radius. [Reference Kulkarni, Schmidt and Tsui14, Theorem 2.2] states the main eigenvalue is
![]() $\lambda_{0}^{[m,m^\prime]}=2 \cos ({\pi}/({m^\prime-m+2}))$
, so
$\lambda_{0}^{[m,m^\prime]}=2 \cos ({\pi}/({m^\prime-m+2}))$
, so
![]() ${R_{0,[m,m^\prime]}} =1/\lambda_{0}^{[m,m^\prime]}$
. From [Reference Seneta17, Theorem 6.8] and by taking the limit
${R_{0,[m,m^\prime]}} =1/\lambda_{0}^{[m,m^\prime]}$
. From [Reference Seneta17, Theorem 6.8] and by taking the limit
![]() $m^\prime \to \infty$
we actually get
$m^\prime \to \infty$
we actually get
![]() $R_0={ R_{0,m} }=1/2$
for all
$R_0={ R_{0,m} }=1/2$
for all
![]() $m \geq 0$
, which implies that
$m \geq 0$
, which implies that
![]() $Q^{[1]}_0$
is
$Q^{[1]}_0$
is
![]() $1/2$
-transient. The sequence of truncated matrices
$1/2$
-transient. The sequence of truncated matrices
![]() $Q_0^{[m]}$
remains constant, in particular
$Q_0^{[m]}$
remains constant, in particular
![]() $Q_0^{[1]}=Q_0$
, and therefore the matrix
$Q_0^{[1]}=Q_0$
, and therefore the matrix
![]() $Q_0$
is always
$Q_0$
is always
![]() $1/2$
-transient.
$1/2$
-transient.
3. Existence of equilibrium measures
The behavior of
![]() $(\psi(x))_{x \geq 0}$
plays a crucial role in the recurrence properties of
$(\psi(x))_{x \geq 0}$
plays a crucial role in the recurrence properties of
![]() $Q_\beta$
. Keeping this in mind, we review in more detail the main assumptions of this work.
$Q_\beta$
. Keeping this in mind, we review in more detail the main assumptions of this work.
-
(C0) The function
 $\psi(x)$
has a minimum, denoted here by
$\psi(x)$
has a minimum, denoted here by
 $\alpha(\phi)\;:\!=\;\min_{x \geq 0} \psi(x)>-\infty$
. We also assume that there exists a subset
$\alpha(\phi)\;:\!=\;\min_{x \geq 0} \psi(x)>-\infty$
. We also assume that there exists a subset
 $\mathcal{M} \subseteq \mathbb{Z}_+$
such that
$\mathcal{M} \subseteq \mathbb{Z}_+$
such that
 $\psi(x)=\alpha(\phi)$
for all
$\psi(x)=\alpha(\phi)$
for all
 $x \in \mathcal{M}$
and
$x \in \mathcal{M}$
and
 $\inf_{x \in \mathbb{Z}_+\setminus \mathcal{M}} \psi(x) \geq \alpha(\phi)+\Delta$
for some
$\inf_{x \in \mathbb{Z}_+\setminus \mathcal{M}} \psi(x) \geq \alpha(\phi)+\Delta$
for some
 $\Delta>0$
.
$\Delta>0$
.
Provided that (1) holds, we have one of the following:
-
(C1)
 $\mathcal{M}$
is finite, i.e. the minimum is attained in a finite number of indices.
$\mathcal{M}$
is finite, i.e. the minimum is attained in a finite number of indices. -
(C2)
 $\mathcal{M}$
is a sub-sequence
$\mathcal{M}$
is a sub-sequence
 $\{x_k\}_{k \geq 0}$
satisfying
$\{x_k\}_{k \geq 0}$
satisfying
 $\lim_{k\to \infty}x_k=\infty$
.
$\lim_{k\to \infty}x_k=\infty$
.
Without loss of generality we can assume
![]() $\alpha(\phi)=0$
, since in any other case we only need to take
$\alpha(\phi)=0$
, since in any other case we only need to take
![]() $\widetilde{\psi}(x)=\psi(x)-\alpha(\phi)$
and the argument does not vary. Observe that when (C0) and (C1) hold,
$\widetilde{\psi}(x)=\psi(x)-\alpha(\phi)$
and the argument does not vary. Observe that when (C0) and (C1) hold,
![]() $\liminf_{x \to \infty}\psi(x) \geq \alpha(\phi)+\Delta$
. Hence, there exists
$\liminf_{x \to \infty}\psi(x) \geq \alpha(\phi)+\Delta$
. Hence, there exists
![]() $N_0 \geq 0$
and
$N_0 \geq 0$
and
![]() $\varepsilon \geq \Delta$
such that
$\varepsilon \geq \Delta$
such that
![]() $\alpha_m \geq \alpha(\phi)+\varepsilon$
for all
$\alpha_m \geq \alpha(\phi)+\varepsilon$
for all
![]() $m>N_0$
and
$m>N_0$
and
![]() $\alpha_{N_0}=\alpha(\phi)$
. We now state our main results of this section.
$\alpha_{N_0}=\alpha(\phi)$
. We now state our main results of this section.
Theorem 3.1. Assume that (C0) and (C1) hold. Then there exists
![]() $0 \leq \beta_\mathrm{c}<\infty$
such that, for all
$0 \leq \beta_\mathrm{c}<\infty$
such that, for all
![]() $\beta>\beta_\mathrm{c}$
, the matrix
$\beta>\beta_\mathrm{c}$
, the matrix
![]() $Q_\beta$
is geometrically ergodic.
$Q_\beta$
is geometrically ergodic.
The following corollary establishes a similar result when
![]() $\psi$
diverges to infinity.
$\psi$
diverges to infinity.
Corollary 3.1. Assume that (C0) holds and that
![]() $\lim_{x \to \infty}\psi(x)=\infty$
. Then, for all
$\lim_{x \to \infty}\psi(x)=\infty$
. Then, for all
![]() $\beta>0$
, the matrix
$\beta>0$
, the matrix
![]() $Q_{\beta}$
is geometrically ergodic.
$Q_{\beta}$
is geometrically ergodic.
The proof of these results will be derived at the end of this section. The case (C2) has more complex behavior depending on the local (and global) configurations of those values where
![]() $\psi(x)=\alpha(\phi)$
. To describe it in more detail the next definition is required.
$\psi(x)=\alpha(\phi)$
. To describe it in more detail the next definition is required.
Definition 3.1. We say that the discrete interval
![]() $I_{x_0,\ell}=[x_0,x_0+\ell-1]$
is a run of size
$I_{x_0,\ell}=[x_0,x_0+\ell-1]$
is a run of size
![]() $\ell \geq 2$
(the value
$\ell \geq 2$
(the value
![]() $\ell=\infty$
is permitted) for the matrix
$\ell=\infty$
is permitted) for the matrix
![]() $Q_\beta^{[m]}$
if
$Q_\beta^{[m]}$
if
![]() $\psi(x)=\alpha(\phi)$
for
$\psi(x)=\alpha(\phi)$
for
![]() $x\in [x_0, x_0+\ell-1)$
,
$x\in [x_0, x_0+\ell-1)$
,
![]() $\psi({x_0+\ell-1})>\alpha(\phi)$
, and
$\psi({x_0+\ell-1})>\alpha(\phi)$
, and
![]() $\psi({x_0-1})>\alpha(\phi)$
if
$\psi({x_0-1})>\alpha(\phi)$
if
![]() $x_0 \geq m+1$
.
$x_0 \geq m+1$
.
Let
![]() $\mathcal{R}$
be all those values of
$\mathcal{R}$
be all those values of
![]() $x \in \mathbb{Z}_+$
in some run of
$x \in \mathbb{Z}_+$
in some run of
![]() $Q_\beta$
. Each
$Q_\beta$
. Each
![]() $x \in \mathcal{R}$
belongs to a unique run of size
$x \in \mathcal{R}$
belongs to a unique run of size
![]() $2 \leq \ell \leq \infty$
, so that
$2 \leq \ell \leq \infty$
, so that
![]() $\mathcal{R}$
can be partitioned into the form
$\mathcal{R}$
can be partitioned into the form
![]() $\mathcal{R}=\bigcup_{\ell={2}}^{\infty}\mathcal{R}_{\ell}$
, where
$\mathcal{R}=\bigcup_{\ell={2}}^{\infty}\mathcal{R}_{\ell}$
, where
![]() $\mathcal{R}_{\ell}$
is used to indicate the collection of runs of size
$\mathcal{R}_{\ell}$
is used to indicate the collection of runs of size
![]() $\ell$
. If
$\ell$
. If
![]() $\psi$
has no runs of size
$\psi$
has no runs of size
![]() $\ell$
we write
$\ell$
we write
![]() $\mathcal{R}_{\ell}=\emptyset$
. For each non-empty
$\mathcal{R}_{\ell}=\emptyset$
. For each non-empty
![]() $\mathcal{R}_{\ell}$
, we can find
$\mathcal{R}_{\ell}$
, we can find
![]() $\{x_k\}_{1 \leq k \leq |\mathcal{R}_\ell|}$
(possibly an infinite sequence) such that
$\{x_k\}_{1 \leq k \leq |\mathcal{R}_\ell|}$
(possibly an infinite sequence) such that
![]() $\mathcal{R}_{\ell}=\bigcup_{k={1}}^{|R_\ell|}I_{x_k,\ell}$
. From the construction, we notice that
$\mathcal{R}_{\ell}=\bigcup_{k={1}}^{|R_\ell|}I_{x_k,\ell}$
. From the construction, we notice that
![]() $I_{x_k,\ell} \cap I_{x_{k^\prime},\ell^\prime}=\emptyset$
if either
$I_{x_k,\ell} \cap I_{x_{k^\prime},\ell^\prime}=\emptyset$
if either
![]() $k\neq k^\prime$
or
$k\neq k^\prime$
or
![]() $\ell \neq \ell^\prime$
. We now define
$\ell \neq \ell^\prime$
. We now define
which is allowed to be infinite (the value of
![]() $\beta$
has no influence in the definition of
$\beta$
has no influence in the definition of
![]() $\ell_{\max}$
). The following lemma establishes a preliminary bound on the convergence radius in terms of
$\ell_{\max}$
). The following lemma establishes a preliminary bound on the convergence radius in terms of
![]() $\ell_{\max}$
.
$\ell_{\max}$
.
Lemma 3.1. Assume that (C0) holds with
![]() $\alpha(\phi)=0$
. For every
$\alpha(\phi)=0$
. For every
![]() $m \geq 0$
,
$m \geq 0$
,
![]() $\beta > 0$
we have
$\beta > 0$
we have
where
![]() $\ell^{[m]}_{\max}=\ell_{\max}(Q_\beta^{[m]})$
. In particular, if
$\ell^{[m]}_{\max}=\ell_{\max}(Q_\beta^{[m]})$
. In particular, if
![]() $\ell_{\max}^{[m]}=\infty$
, then
$\ell_{\max}^{[m]}=\infty$
, then
![]() $R_{\beta,m}^2=\frac14$
is constant.
$R_{\beta,m}^2=\frac14$
is constant.
Proof. Suppose first that
![]() $\ell_{\max}^{[m]}<\infty$
. Observe that, for each fixed
$\ell_{\max}^{[m]}<\infty$
. Observe that, for each fixed
![]() $m \geq 0$
, the inequality
$m \geq 0$
, the inequality
![]() $\frac14 = R_{0,m}^2 \leq R_{\beta,m}^2$
applies when
$\frac14 = R_{0,m}^2 \leq R_{\beta,m}^2$
applies when
![]() $\psi(x) \geq 0$
. Now, if
$\psi(x) \geq 0$
. Now, if
![]() $I_{x_0,\ell}$
is a run of
$I_{x_0,\ell}$
is a run of
![]() $Q_{\beta}^{[m]}$
, with
$Q_{\beta}^{[m]}$
, with
![]() $2 \leq \ell \leq \ell_{\max}^{[m]}$
and
$2 \leq \ell \leq \ell_{\max}^{[m]}$
and
![]() $x_0 \geq m$
, then
$x_0 \geq m$
, then
![]() $R_{\beta,m} \leq R(Q_\beta^{I_{x_0,\ell}})$
, where
$R_{\beta,m} \leq R(Q_\beta^{I_{x_0,\ell}})$
, where
![]() $Q_\beta^{I_{x_0,\ell}}\;:\!=\;(Q_{\beta}(x,y);\; x, y \in I_{x_0,\ell})$
. From [Reference Kulkarni, Schmidt and Tsui14, Theorem 2.2] we know that
$Q_\beta^{I_{x_0,\ell}}\;:\!=\;(Q_{\beta}(x,y);\; x, y \in I_{x_0,\ell})$
. From [Reference Kulkarni, Schmidt and Tsui14, Theorem 2.2] we know that
(the inverse of its largest eigenvalue). The inequality (3.2) is obtained by taking
![]() $\ell = \ell_{\max}^{[m]}$
.
$\ell = \ell_{\max}^{[m]}$
.
Now observe that
![]() $\ell_{\max}=\infty$
implies
$\ell_{\max}=\infty$
implies
![]() $\ell_{\max}^{[m]}=\infty$
for all
$\ell_{\max}^{[m]}=\infty$
for all
![]() $m \geq 0$
. From its definition in (3.1), we can find a sub-sequence
$m \geq 0$
. From its definition in (3.1), we can find a sub-sequence
![]() $\{\ell_{k}^{[m]}\}_{k \geq 1}$
satisfying
$\{\ell_{k}^{[m]}\}_{k \geq 1}$
satisfying
![]() $\lim_{k \to \infty}\ell_{k}^{[m]}=\infty$
such that
$\lim_{k \to \infty}\ell_{k}^{[m]}=\infty$
such that
holds for every
![]() $k \geq 1$
(this is possible by taking the convergence radius of the truncated matrix
$k \geq 1$
(this is possible by taking the convergence radius of the truncated matrix
![]() $Q_{\beta}^{I_{x_0,\ell_k^{[m]}}}$
, where
$Q_{\beta}^{I_{x_0,\ell_k^{[m]}}}$
, where
![]() $I_{x_0,\ell_k^{[m]}}$
is a discrete interval contained in some run of
$I_{x_0,\ell_k^{[m]}}$
is a discrete interval contained in some run of
![]() $Q_{\beta}^{[m]}$
). The proof finishes by letting
$Q_{\beta}^{[m]}$
). The proof finishes by letting
![]() $k \to \infty$
.
$k \to \infty$
.
Remark 3.1. The matrix
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-recurrent if and only if
$R_\beta$
-recurrent if and only if
![]() $\mathbb{P}_0(\tau_0<\infty)=1$
. From [Reference Ferrari and Martnez8] we know that this is equivalent to the condition
$\mathbb{P}_0(\tau_0<\infty)=1$
. From [Reference Ferrari and Martnez8] we know that this is equivalent to the condition
![]() $\mathcal F_{0}(R_\beta)=1$
, where
$\mathcal F_{0}(R_\beta)=1$
, where
![]() $\{\mathcal F_{x}(R_\beta)\}_{x \geq 0}$
is defined recursively as
$\{\mathcal F_{x}(R_\beta)\}_{x \geq 0}$
is defined recursively as
If (C0) holds with
![]() $\ell_{\max}=\infty$
and
$\ell_{\max}=\infty$
and
![]() $\alpha(\phi)=0$
, from Lemma 3.1 we get that
$\alpha(\phi)=0$
, from Lemma 3.1 we get that
![]() $R_{\beta,m}=\frac12$
for all
$R_{\beta,m}=\frac12$
for all
![]() $m \geq 0$
,
$m \geq 0$
,
![]() $\beta \geq 0$
. This implies that
$\beta \geq 0$
. This implies that
![]() $R_{\beta}^2 \exp\!(\!-\!\beta \psi(x)) \leq \frac14$
for each
$R_{\beta}^2 \exp\!(\!-\!\beta \psi(x)) \leq \frac14$
for each
![]() $x \geq 0$
, and thus
$x \geq 0$
, and thus
 \begin{equation}\mathcal F_{x}(R_\beta) \leq \cfrac{1/4}{1-\cfrac{1/4}{1-\cfrac{1/4}{1-\cdots}}}=\frac12. \end{equation}
\begin{equation}\mathcal F_{x}(R_\beta) \leq \cfrac{1/4}{1-\cfrac{1/4}{1-\cfrac{1/4}{1-\cdots}}}=\frac12. \end{equation}
In particular,
![]() $\mathcal F_{0}(R_\beta) \leq \frac12<1$
, so that
$\mathcal F_{0}(R_\beta) \leq \frac12<1$
, so that
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $\frac12$
-transient for all
$\frac12$
-transient for all
![]() $\beta \geq 0$
. The same occurs if the limit
$\beta \geq 0$
. The same occurs if the limit
![]() $\lim_{x \to \infty}\psi(x)=\alpha(\phi)=0$
exists. From (2.10), and recalling that
$\lim_{x \to \infty}\psi(x)=\alpha(\phi)=0$
exists. From (2.10), and recalling that
![]() $R_{0,m}=\frac12$
,
$R_{0,m}=\frac12$
,
By letting
![]() $m \to \infty$
, since
$m \to \infty$
, since
![]() $\lim_{x \to \infty}\psi(x)=0$
the only option is
$\lim_{x \to \infty}\psi(x)=0$
the only option is
![]() $\lim_{m \to \infty}R_{\beta,m}=\frac12$
, and consequently
$\lim_{m \to \infty}R_{\beta,m}=\frac12$
, and consequently
![]() $R_{\beta,m}=\frac12$
for all
$R_{\beta,m}=\frac12$
for all
![]() $m \geq 0$
. Hence, (3.3) applies in this case and we conclude that
$m \geq 0$
. Hence, (3.3) applies in this case and we conclude that
![]() $Q_{\beta}$
is
$Q_{\beta}$
is
![]() $\frac12$
-transient for all
$\frac12$
-transient for all
![]() $\beta \geq 0$
.
$\beta \geq 0$
.
The next theorem establishes the behavior of
![]() $Q_\beta$
for finite
$Q_\beta$
for finite
![]() $\ell_{\max}$
.
$\ell_{\max}$
.
Theorem 3.2. Assume that (C0) and (C2) hold, and assume that
![]() $\ell_{\max}<\infty$
. If the number of runs of size
$\ell_{\max}<\infty$
. If the number of runs of size
![]() $\ell_{\max}$
is finite, i.e.
$\ell_{\max}$
is finite, i.e.
![]() $|\mathcal{R}_{\ell_{\max}}|<\infty$
, there exists
$|\mathcal{R}_{\ell_{\max}}|<\infty$
, there exists
![]() $\beta_\mathrm{c}<\infty$
such that, for all
$\beta_\mathrm{c}<\infty$
such that, for all
![]() $\beta>\beta_\mathrm{c}$
, the matrix
$\beta>\beta_\mathrm{c}$
, the matrix
![]() $Q_{\beta}$
is geometrically ergodic.
$Q_{\beta}$
is geometrically ergodic.
The proof relies on Proposition 3.1, so is given at the end of this section.
Proposition 3.1. If (C0) and (C1) hold with
![]() $\ell_{\max}^{[m]}<\infty$
and
$\ell_{\max}^{[m]}<\infty$
and
![]() $\alpha(\phi)=0$
, for all
$\alpha(\phi)=0$
, for all
![]() $m \geq 0$
we have
$m \geq 0$
we have
Proof. Since
![]() $R_{\beta,m}^2$
is a non-decreasing function of
$R_{\beta,m}^2$
is a non-decreasing function of
![]() $\beta$
and it takes values in the interval
$\beta$
and it takes values in the interval
![]() $\big[\frac{1}{4},1\big]$
, the limit exists. Moreover, from (3.2), we deduce that
$\big[\frac{1}{4},1\big]$
, the limit exists. Moreover, from (3.2), we deduce that
![]() $\lim_{\beta \to \infty} R^2_{\beta,m} \leq c_\infty(\ell_{\max}^{[m]})$
. To prove the converse, let us first introduce the random variable
$\lim_{\beta \to \infty} R^2_{\beta,m} \leq c_\infty(\ell_{\max}^{[m]})$
. To prove the converse, let us first introduce the random variable
We also recall the identity
To simplify the proof, let us assume that the initial state is
![]() $X_0^{\beta,[m]}=x_0$
, since
$X_0^{\beta,[m]}=x_0$
, since
![]() $I_{x_0,\ell_{\max}^{[m]}}$
is a run of size
$I_{x_0,\ell_{\max}^{[m]}}$
is a run of size
![]() $\ell_{\max}^{[m]}$
. Observe that
$\ell_{\max}^{[m]}$
. Observe that
We now fix
![]() $N_{\textrm{out}}\big(n,X^{\beta,[m]}\big)=t$
, with
$N_{\textrm{out}}\big(n,X^{\beta,[m]}\big)=t$
, with
![]() $t \geq 0$
. For any sequence
$t \geq 0$
. For any sequence
![]() $\widetilde{x}[0,2n]=(\widetilde{x}_0,\widetilde{x}_{1},\ldots$
,
$\widetilde{x}[0,2n]=(\widetilde{x}_0,\widetilde{x}_{1},\ldots$
,
![]() $\widetilde{x}_{2n-1},\widetilde{x}_{2n}) \in \Omega^{[m]}[0,2n]$
, let us define
$\widetilde{x}_{2n-1},\widetilde{x}_{2n}) \in \Omega^{[m]}[0,2n]$
, let us define
 \begin{align*}\textrm{T}_{\textrm{in}}(\widetilde{x}[0,2n])& \;:\!=\; \{k \in [0,2n)\;:\;\widetilde{x}_k \textrm{ and }\widetilde{x}_{k+1} \textrm{ belong to the same run} \}, \\[5pt] \textrm{T}_{\textrm{out}}(\widetilde{x}[0,2n])& \;:\!=\; [0,2n)\setminus \textrm{T}_{\textrm{in}}(\widetilde{x}[0,2n]). \end{align*}
\begin{align*}\textrm{T}_{\textrm{in}}(\widetilde{x}[0,2n])& \;:\!=\; \{k \in [0,2n)\;:\;\widetilde{x}_k \textrm{ and }\widetilde{x}_{k+1} \textrm{ belong to the same run} \}, \\[5pt] \textrm{T}_{\textrm{out}}(\widetilde{x}[0,2n])& \;:\!=\; [0,2n)\setminus \textrm{T}_{\textrm{in}}(\widetilde{x}[0,2n]). \end{align*}
We emphasize that only sequences satisfying
![]() $\widetilde{x}_{0}=\widetilde{x}_{2n}=x_0$
are considered. For any subset
$\widetilde{x}_{0}=\widetilde{x}_{2n}=x_0$
are considered. For any subset
![]() $\widetilde{\mathcal{I}} \subseteq [0,2n)$
, we write
$\widetilde{\mathcal{I}} \subseteq [0,2n)$
, we write
![]() $\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}$
to denote that
$\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}$
to denote that
![]() $\textrm{T}_{\textrm{in}}(\widetilde{x}[0,2n])=\widetilde{\mathcal{I}}$
. From the identity
$\textrm{T}_{\textrm{in}}(\widetilde{x}[0,2n])=\widetilde{\mathcal{I}}$
. From the identity
![]() $\textrm{Card}(\widetilde{\mathcal{I}} )=2n-2N_{\textrm{out}}(n,X^{\beta,[m]})=2n-2t$
, we have
$\textrm{Card}(\widetilde{\mathcal{I}} )=2n-2N_{\textrm{out}}(n,X^{\beta,[m]})=2n-2t$
, we have
 \begin{equation}\mathbb{P}_{x_0}\big(X_{2n}^{\beta,[m]}=x_0,N_{\textrm{out}}(n,X^{\beta,[m]})=t\big) =\sum_{\substack{\widetilde{\mathcal{I}} \subseteq [0,2n):\\ \textrm{Card}({\widetilde{\mathcal I}})=2n-2t}}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}}\mathbb{P}_{x_0}\big( X_{k}^{\beta,[m]} = \widetilde{x}_k;\; 1 \leq k \leq 2n\big). \end{equation}
\begin{equation}\mathbb{P}_{x_0}\big(X_{2n}^{\beta,[m]}=x_0,N_{\textrm{out}}(n,X^{\beta,[m]})=t\big) =\sum_{\substack{\widetilde{\mathcal{I}} \subseteq [0,2n):\\ \textrm{Card}({\widetilde{\mathcal I}})=2n-2t}}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}}\mathbb{P}_{x_0}\big( X_{k}^{\beta,[m]} = \widetilde{x}_k;\; 1 \leq k \leq 2n\big). \end{equation}
Given a fixed
![]() $\widetilde{\mathcal{I}} \subseteq [0,2n)$
, from either (2.2) or (2.7) we have
$\widetilde{\mathcal{I}} \subseteq [0,2n)$
, from either (2.2) or (2.7) we have
 \begin{align*}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \mathbb{P}_{x_0}\big( X_{k}^{\beta,[m]}& = \widetilde{x}_k;\; 1 \leq k \leq 2n\big) \\[5pt] & = R_{\beta,m}^{2n}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \exp\!\Bigg({-}\beta \sum_{k=0}^{2n-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg) \\[5pt] & = R_{\beta,m}^{2n}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}}\exp\!\Bigg({-}\beta \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})-\beta\sum_{k \in \widetilde{\mathcal{O}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg), \end{align*}
\begin{align*}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \mathbb{P}_{x_0}\big( X_{k}^{\beta,[m]}& = \widetilde{x}_k;\; 1 \leq k \leq 2n\big) \\[5pt] & = R_{\beta,m}^{2n}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \exp\!\Bigg({-}\beta \sum_{k=0}^{2n-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg) \\[5pt] & = R_{\beta,m}^{2n}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}}\exp\!\Bigg({-}\beta \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})-\beta\sum_{k \in \widetilde{\mathcal{O}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg), \end{align*}
where
![]() $\widetilde{\mathcal O}=[0,2n)\setminus \widetilde{\mathcal I}$
. For every
$\widetilde{\mathcal O}=[0,2n)\setminus \widetilde{\mathcal I}$
. For every
![]() $k \in \widetilde{\mathcal O}$
we know that
$k \in \widetilde{\mathcal O}$
we know that
![]() $\widetilde{x}_k$
and
$\widetilde{x}_k$
and
![]() $\widetilde{x}_{k+1}$
are not in the same run. On the other hand, since
$\widetilde{x}_{k+1}$
are not in the same run. On the other hand, since
![]() $Q_\beta^{[m]}$
is a nearest-neighbor matrix, the number of visits coincides:
$Q_\beta^{[m]}$
is a nearest-neighbor matrix, the number of visits coincides:
Recalling that
![]() $\textrm{Card}(\widetilde{\mathcal O})=2t$
, since
$\textrm{Card}(\widetilde{\mathcal O})=2t$
, since
![]() $\phi(\tilde{x}_k,\tilde{x}_{k+1})+\phi(\tilde{x}_{k+1},\tilde{x}_{k}) \geq \Delta$
we have
$\phi(\tilde{x}_k,\tilde{x}_{k+1})+\phi(\tilde{x}_{k+1},\tilde{x}_{k}) \geq \Delta$
we have
![]() $\sum_{k \in \widetilde{\mathcal{O}}}\phi(\tilde{x}_k,\tilde{x}_{k+1}) \geq t \Delta$
, leading to the inequality
$\sum_{k \in \widetilde{\mathcal{O}}}\phi(\tilde{x}_k,\tilde{x}_{k+1}) \geq t \Delta$
, leading to the inequality
 \begin{equation}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \mathbb{P}_{x_0}(X_{k}^{\beta,[m]} = \widetilde{x}_k;\; 1 \leq k \leq 2n) \leq R_{\beta,m}^{2n}{\mathrm{e}}^{-\beta \Delta t}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \exp\!\Bigg({-}\beta \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg). \end{equation}
\begin{equation}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \mathbb{P}_{x_0}(X_{k}^{\beta,[m]} = \widetilde{x}_k;\; 1 \leq k \leq 2n) \leq R_{\beta,m}^{2n}{\mathrm{e}}^{-\beta \Delta t}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}} \exp\!\Bigg({-}\beta \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg). \end{equation}
In the rest of the proof, the runs of
![]() $Q_{\beta}^{[m]}$
will be labeled as
$Q_{\beta}^{[m]}$
will be labeled as
![]() $\{I_{x_{i,m},\ell_{i,m}}\}_{i \geq -n_{m}}$
, with the convention that
$\{I_{x_{i,m},\ell_{i,m}}\}_{i \geq -n_{m}}$
, with the convention that
![]() $x_{i,m}<x_{i^{\prime},m}$
for
$x_{i,m}<x_{i^{\prime},m}$
for
![]() $i<i^\prime$
and
$i<i^\prime$
and
![]() $x_{0,m}=x_0$
, since
$x_{0,m}=x_0$
, since
![]() $I_{x_0,\ell_{\max}^{[m]}}$
is the first run of length
$I_{x_0,\ell_{\max}^{[m]}}$
is the first run of length
![]() $\ell_{\max}^{[m]}$
(i.e. for
$\ell_{\max}^{[m]}$
(i.e. for
![]() $-n_m \leq i<0$
the run
$-n_m \leq i<0$
the run
![]() $I_{x_{i,m},\ell_{i,m}}$
has size at most
$I_{x_{i,m},\ell_{i,m}}$
has size at most
![]() $\ell_{\max}^{[m]}-1$
). For any
$\ell_{\max}^{[m]}-1$
). For any
![]() $\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}$
, we now set
$\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}$
, we now set
Observe that
![]() $\widetilde{\mathcal{I}}_{i,m} \cap\widetilde{\mathcal{I}}_{i^\prime,m}=\emptyset$
when
$\widetilde{\mathcal{I}}_{i,m} \cap\widetilde{\mathcal{I}}_{i^\prime,m}=\emptyset$
when
![]() $i \neq i^\prime$
. Since
$i \neq i^\prime$
. Since
![]() $\textrm{Card} (\widetilde{\mathcal{I}}_{i,m})\;:\!=\;2t_i$
for some
$\textrm{Card} (\widetilde{\mathcal{I}}_{i,m})\;:\!=\;2t_i$
for some
![]() $t_i \geq 1$
if
$t_i \geq 1$
if
![]() $\widetilde{\mathcal{I}}_{i,m} \neq \emptyset$
, it follows that the number of non-empty subsets
$\widetilde{\mathcal{I}}_{i,m} \neq \emptyset$
, it follows that the number of non-empty subsets
![]() $\{\widetilde{\mathcal{I}}_{i,m}\}_{i \geq -n_m}$
is bounded by t. Hence, there exists a finite value, say
$\{\widetilde{\mathcal{I}}_{i,m}\}_{i \geq -n_m}$
is bounded by t. Hence, there exists a finite value, say
![]() $i_{\max}$
, such that
$i_{\max}$
, such that
![]() $\widetilde{\mathcal{I}}=\cup_{i=-n_m}^{i_{\max}}\widetilde{\mathcal{I}}_{i,m}$
, so
$\widetilde{\mathcal{I}}=\cup_{i=-n_m}^{i_{\max}}\widetilde{\mathcal{I}}_{i,m}$
, so
 \begin{equation*} \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1}) =\sum_{i=-n_m}^{i_{\max}}\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1}). \end{equation*}
\begin{equation*} \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1}) =\sum_{i=-n_m}^{i_{\max}}\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1}). \end{equation*}
Notice that
![]() $2 t_i=\textrm{Card} (\widetilde{\mathcal{I}}_{i,m})$
,
$2 t_i=\textrm{Card} (\widetilde{\mathcal{I}}_{i,m})$
,
![]() $i \geq -n_m$
, is the total time that
$i \geq -n_m$
, is the total time that
![]() $X^{\beta,[m]}$
stays in
$X^{\beta,[m]}$
stays in
![]() $I_{x_{i,m},\ell_{i,m}}$
up to the instant 2n. Also, for
$I_{x_{i,m},\ell_{i,m}}$
up to the instant 2n. Also, for
![]() $i \geq 0$
, observe that
$i \geq 0$
, observe that
![]() $\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1})$
is the contribution of a path of nearest neighbors with
$\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1})$
is the contribution of a path of nearest neighbors with
![]() $2t_i$
transitions that starts and ends on
$2t_i$
transitions that starts and ends on
![]() $x_{i,m}$
, restricted to not leave
$x_{i,m}$
, restricted to not leave
![]() $I_{x_{i,m},\ell_{i,m}}$
. For
$I_{x_{i,m},\ell_{i,m}}$
. For
![]() $i<0$
, the same argument applies, with the only difference that the path starts and ends in
$i<0$
, the same argument applies, with the only difference that the path starts and ends in
![]() $x_{i,m}+\ell_{i,m}-1$
. Let
$x_{i,m}+\ell_{i,m}-1$
. Let
![]() $\widetilde {x}[\widetilde{\mathcal{O}}]\;:\!=\;(\widetilde{x}_{k})_{k \in \widetilde{\mathcal{O}}}$
be the restriction of
$\widetilde {x}[\widetilde{\mathcal{O}}]\;:\!=\;(\widetilde{x}_{k})_{k \in \widetilde{\mathcal{O}}}$
be the restriction of
![]() $\widetilde{x}[0,2n]$
onto
$\widetilde{x}[0,2n]$
onto
![]() $\widetilde{\mathcal{O}}$
. For any sequence
$\widetilde{\mathcal{O}}$
. For any sequence
![]() $\widetilde{x}[0,2n]$
such that
$\widetilde{x}[0,2n]$
such that
![]() $\widetilde {x}[\widetilde{\mathcal{O}}]=x_{\widetilde{\mathcal{O}}}$
is fixed, the subsets
$\widetilde {x}[\widetilde{\mathcal{O}}]=x_{\widetilde{\mathcal{O}}}$
is fixed, the subsets
![]() $\widetilde{\mathcal{I}}_{i,m}$
defined in (3.9) are kept fixed too. Therefore,
$\widetilde{\mathcal{I}}_{i,m}$
defined in (3.9) are kept fixed too. Therefore,
 \begin{align}\sum_{\substack{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}:\\ \widetilde{x}[\widetilde{\mathcal O}]=x_{\widetilde{\mathcal O}}}}& \exp\!\Bigg({-}\beta \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg) \nonumber \\[5pt] & = \sum_{\substack{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}:\\ \widetilde{x}[\widetilde{\mathcal O}]=x_{\widetilde{\mathcal O}}}}\exp\!\Bigg({-}\beta\sum_{i=-n_m}^{i_{\max}}\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg)\nonumber \\[5pt] & = \sum_{\substack{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}:\\ \widetilde{x}[\widetilde{\mathcal O}]=x_{\widetilde{\mathcal O}}}}\prod_{i=-n_m}^{i_{\max}}\exp\!\Bigg({-}\beta\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg)\nonumber \\[5pt] & \leq \prod_{i=-n_m}^{i_{\max}}\Bigg(\max_{x \in I_{x_{i,m},\ell_{i,m}}} \sum_{\substack{\widetilde{x}[0,2t_i] \sim [0,2t_i] :\\ \widetilde{x}_0=\widetilde{x}_{2t_i}=x}}\exp\!\Bigg({-}\beta\sum_{k =0}^{2t_i-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg)\Bigg). \end{align}
\begin{align}\sum_{\substack{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}:\\ \widetilde{x}[\widetilde{\mathcal O}]=x_{\widetilde{\mathcal O}}}}& \exp\!\Bigg({-}\beta \sum_{k \in \widetilde{\mathcal{I}}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg) \nonumber \\[5pt] & = \sum_{\substack{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}:\\ \widetilde{x}[\widetilde{\mathcal O}]=x_{\widetilde{\mathcal O}}}}\exp\!\Bigg({-}\beta\sum_{i=-n_m}^{i_{\max}}\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg)\nonumber \\[5pt] & = \sum_{\substack{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}:\\ \widetilde{x}[\widetilde{\mathcal O}]=x_{\widetilde{\mathcal O}}}}\prod_{i=-n_m}^{i_{\max}}\exp\!\Bigg({-}\beta\sum_{k \in \widetilde{\mathcal{I}}_{i,m}}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg)\nonumber \\[5pt] & \leq \prod_{i=-n_m}^{i_{\max}}\Bigg(\max_{x \in I_{x_{i,m},\ell_{i,m}}} \sum_{\substack{\widetilde{x}[0,2t_i] \sim [0,2t_i] :\\ \widetilde{x}_0=\widetilde{x}_{2t_i}=x}}\exp\!\Bigg({-}\beta\sum_{k =0}^{2t_i-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg)\Bigg). \end{align}
Now, for each typical path considered on the right-hand side of (3.10), we know that
![]() $\tilde{x}_k$
and
$\tilde{x}_k$
and
![]() $\tilde{x}_{k+1}$
are in the same run, and from (3.7) we deduce that
$\tilde{x}_{k+1}$
are in the same run, and from (3.7) we deduce that
![]() $\sum_{k =0}^{2t_i-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})=0$
. Also, the maximum in (3.10) is over the paths with
$\sum_{k =0}^{2t_i-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})=0$
. Also, the maximum in (3.10) is over the paths with
![]() $2t_i$
transitions restricted to not leave
$2t_i$
transitions restricted to not leave
![]() $I_{x_{i,m},\ell_{i,m}}$
. This can be computed by taking the
$I_{x_{i,m},\ell_{i,m}}$
. This can be computed by taking the
![]() $2t_i$
-power of the truncated and finite matrix
$2t_i$
-power of the truncated and finite matrix
![]() $Q_0^{[x_{i,m},x_{i,m}+\ell_{i,m}-1]}$
. By using the Perron–Frobenius theorem, it can be shown that
$Q_0^{[x_{i,m},x_{i,m}+\ell_{i,m}-1]}$
. By using the Perron–Frobenius theorem, it can be shown that
where the limit only depends on x and
![]() $\ell_{i,m}$
(see [Reference Kulkarni, Schmidt and Tsui14, p. 65] for a more precise characterization of
$\ell_{i,m}$
(see [Reference Kulkarni, Schmidt and Tsui14, p. 65] for a more precise characterization of
![]() $C(x,\ell_{i,m})$
in terms of Chebyshev polynomials). Hence, for
$C(x,\ell_{i,m})$
in terms of Chebyshev polynomials). Hence, for
![]() $i \geq -n_m$
,
$i \geq -n_m$
,
 \begin{align}&\max_{x \in I_{x_{i,m},\ell_{i,m}}}\sum_{\substack{\widetilde{x}[0,2t_i] \sim [0,2t_i] :\\ \widetilde{x}_0=\widetilde{x}_{2t_i}=x}}\exp\!\Bigg({-}\beta\sum_{k=0}^{2t_i-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg) \\[5pt] & \qquad \qquad \qquad \qquad \qquad \qquad = \max_{{x \in I_{x_{i,m},\ell_{i,m}}}}\big(Q_0^{[x_0,x_0+\ell_{i,m}-1]}\big)^{(2t_i)}(x,x)\leq \frac{D_0(\ell_{i,m})}{(c_\infty(\ell_{i,m}))^{t_i}},\end{align}
\begin{align}&\max_{x \in I_{x_{i,m},\ell_{i,m}}}\sum_{\substack{\widetilde{x}[0,2t_i] \sim [0,2t_i] :\\ \widetilde{x}_0=\widetilde{x}_{2t_i}=x}}\exp\!\Bigg({-}\beta\sum_{k=0}^{2t_i-1}\phi(\tilde{x}_k,\tilde{x}_{k+1})\Bigg) \\[5pt] & \qquad \qquad \qquad \qquad \qquad \qquad = \max_{{x \in I_{x_{i,m},\ell_{i,m}}}}\big(Q_0^{[x_0,x_0+\ell_{i,m}-1]}\big)^{(2t_i)}(x,x)\leq \frac{D_0(\ell_{i,m})}{(c_\infty(\ell_{i,m}))^{t_i}},\end{align}
where
![]() $D_0(\ell_{i,m})$
is a finite constant depending only on
$D_0(\ell_{i,m})$
is a finite constant depending only on
![]() $\ell_{i,m}$
and
$\ell_{i,m}$
and
![]() $c_\infty(\ell_{i,m}) \geq c_\infty(\ell_{\max}^{[m]})$
. Since the number of different configurations in
$c_\infty(\ell_{i,m}) \geq c_\infty(\ell_{\max}^{[m]})$
. Since the number of different configurations in
![]() $\widetilde{\mathcal{O}}$
is bounded by
$\widetilde{\mathcal{O}}$
is bounded by
![]() $\binom{2t}{t} \leq 4^{t}$
, the number of different runs visited is at most t, and
$\binom{2t}{t} \leq 4^{t}$
, the number of different runs visited is at most t, and
![]() $\sum_{i = -n_m}^{i_{\max}}2t_i=2n-2t$
, from (3.8), (3.10), and (3.11) it follows that
$\sum_{i = -n_m}^{i_{\max}}2t_i=2n-2t$
, from (3.8), (3.10), and (3.11) it follows that
 \begin{align}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}}\mathbb{P}_{x_0}\big(X_{k}^{\beta,[m]} \in \widetilde{x}_k;\; 1 \leq k \leq 2n\big)& \leq R_{\beta,m}^{2n}(4{\mathrm{e}}^{-\beta\Delta})^t\prod_{i=-n_m}^{i_{\max}} \frac{D\big(\ell_{\max}^{[m]}\big)}{\big(c_\infty\big(\ell_{\max}^{[m]}\big)\big)^{t_i}} \nonumber \\[5pt] & \leq \big(4{\mathrm{e}}^{-\beta\Delta}D_{2}\big(\ell_{\max}^{[m]}\big)R_{\beta,m}^2\big)^{t} \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n-2t}, \end{align}
\begin{align}\sum_{\widetilde{x}[0,2n] \sim \widetilde{\mathcal{I}}}\mathbb{P}_{x_0}\big(X_{k}^{\beta,[m]} \in \widetilde{x}_k;\; 1 \leq k \leq 2n\big)& \leq R_{\beta,m}^{2n}(4{\mathrm{e}}^{-\beta\Delta})^t\prod_{i=-n_m}^{i_{\max}} \frac{D\big(\ell_{\max}^{[m]}\big)}{\big(c_\infty\big(\ell_{\max}^{[m]}\big)\big)^{t_i}} \nonumber \\[5pt] & \leq \big(4{\mathrm{e}}^{-\beta\Delta}D_{2}\big(\ell_{\max}^{[m]}\big)R_{\beta,m}^2\big)^{t} \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n-2t}, \end{align}
where
![]() $D\big(\ell_{\max}^{[m]}\big)=\max_{2 \leq \ell_{i,m} \leq \ell_{\max}^{[m]}}D_0(\ell_{i,m})$
and
$D\big(\ell_{\max}^{[m]}\big)=\max_{2 \leq \ell_{i,m} \leq \ell_{\max}^{[m]}}D_0(\ell_{i,m})$
and
![]() $D_{2}\big(\ell_{\max}^{[m]}\big)=\max\big(1,D\big(\ell_{\max}^{[m]}\big)\big)$
. For fixed
$D_{2}\big(\ell_{\max}^{[m]}\big)=\max\big(1,D\big(\ell_{\max}^{[m]}\big)\big)$
. For fixed
![]() $t \geq 0$
, we can find at most
$t \geq 0$
, we can find at most
![]() $\binom{2n}{2t}$
different forms to choose
$\binom{2n}{2t}$
different forms to choose
![]() $\widetilde{\mathcal{I}}$
. Combining (3.6) with (3.12), and setting
$\widetilde{\mathcal{I}}$
. Combining (3.6) with (3.12), and setting
we now get
 \begin{align} \sum_{t=0}^{n}\mathbb{P}_{x_0}\big(X_{2n}^{\beta,[m]}=x_0, N_{\textrm{out}}(n,X^{\beta,[m]})=t\big)& \leq \sum_{t=0}^{n} \binom{2n}{2t}\theta_\beta^{2t} \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n-2t} \nonumber \\[5pt] & \leq \sum_{t=0}^{2n} \binom{2n}{t}\theta_\beta^{t} \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n-t} \nonumber \\[5pt] & = \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n} \Bigg(1 + \frac{\theta_\beta\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}}{R_{\beta,m}}\Bigg)^{2n}. \end{align}
\begin{align} \sum_{t=0}^{n}\mathbb{P}_{x_0}\big(X_{2n}^{\beta,[m]}=x_0, N_{\textrm{out}}(n,X^{\beta,[m]})=t\big)& \leq \sum_{t=0}^{n} \binom{2n}{2t}\theta_\beta^{2t} \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n-2t} \nonumber \\[5pt] & \leq \sum_{t=0}^{2n} \binom{2n}{t}\theta_\beta^{t} \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n-t} \nonumber \\[5pt] & = \Bigg(\frac{R_{\beta,m}}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,}\Bigg)^{2n} \Bigg(1 + \frac{\theta_\beta\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}}{R_{\beta,m}}\Bigg)^{2n}. \end{align}
From (3.4), (3.5), and (3.14),
 \begin{align} R_{\beta,m}^{-1}=\limsup_{n \to \infty}\big(\big(Q_\beta^{[m]}\big)^{(2n)}(x_0,x_0)\big)^{{1}/{2n}}& = \limsup_{n \to \infty}R_{\beta,m}^{-1}\mathbb{P}_{x_0}\big(X_{2n}^{\beta,[m]}=x_0\big)^{{1}/{2n}} \nonumber \\[5pt] & \leq \frac{1}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,} \Bigg(1 + \frac{\theta_\beta\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}}{R_{\beta,m}}\Bigg). \end{align}
\begin{align} R_{\beta,m}^{-1}=\limsup_{n \to \infty}\big(\big(Q_\beta^{[m]}\big)^{(2n)}(x_0,x_0)\big)^{{1}/{2n}}& = \limsup_{n \to \infty}R_{\beta,m}^{-1}\mathbb{P}_{x_0}\big(X_{2n}^{\beta,[m]}=x_0\big)^{{1}/{2n}} \nonumber \\[5pt] & \leq \frac{1}{\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}\,} \Bigg(1 + \frac{\theta_\beta\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}}{R_{\beta,m}}\Bigg). \end{align}
Finally, seeing that
![]() $c_\infty\big(\ell_{\max}^{[m]}\big)\leq 1$
, from (3.13) we get
$c_\infty\big(\ell_{\max}^{[m]}\big)\leq 1$
, from (3.13) we get
 \begin{equation*}0 \leq \lim_{\beta \to \infty}\frac{\theta_\beta\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}}{R_{\beta,m}} \leq2\sqrt{D\big(\ell_{\max}^{[m]}\big)}\lim_{\beta \to \infty}\exp\!(\!-\!\beta\Delta/2) =0, \end{equation*}
\begin{equation*}0 \leq \lim_{\beta \to \infty}\frac{\theta_\beta\sqrt{c_\infty\big(\ell_{\max}^{[m]}\big)}}{R_{\beta,m}} \leq2\sqrt{D\big(\ell_{\max}^{[m]}\big)}\lim_{\beta \to \infty}\exp\!(\!-\!\beta\Delta/2) =0, \end{equation*}
and the proof finishes by letting
![]() $\beta \to \infty$
in (3.15).
$\beta \to \infty$
in (3.15).
We now provide an analog result under the hypotheses (C0) and (C1).
Proposition 3.2. Assume that (C0) and (C1) hold with
![]() $\alpha(\phi)=0$
. Then
$\alpha(\phi)=0$
. Then
![]() $\lim_{\beta \to \infty}R_{\beta}^2=c_\infty(\ell_{\max})$
.
$\lim_{\beta \to \infty}R_{\beta}^2=c_\infty(\ell_{\max})$
.
Proof. As mentioned in the proof of Proposition 3.1, the limit exists and satisfies
![]() $\lim_{\beta \to \infty} R_{\beta}^2 \leq c_{\infty}(\ell_{\max})$
. Now, if (C0) and (C1) hold with
$\lim_{\beta \to \infty} R_{\beta}^2 \leq c_{\infty}(\ell_{\max})$
. Now, if (C0) and (C1) hold with
![]() $\alpha(\phi)=0$
, there exist
$\alpha(\phi)=0$
, there exist
![]() $N_0 \geq 0$
and
$N_0 \geq 0$
and
![]() $\Delta>0$
such that
$\Delta>0$
such that
![]() $\psi(N_0)=0$
and
$\psi(N_0)=0$
and
![]() $\psi(x) \geq \Delta$
for all
$\psi(x) \geq \Delta$
for all
![]() $x \geq N_0+1$
. Given fixed
$x \geq N_0+1$
. Given fixed
![]() $M \geq 10$
, we now consider a matrix
$M \geq 10$
, we now consider a matrix
![]() $Q_{\beta}^{\prime}$
such that
$Q_{\beta}^{\prime}$
such that
![]() $\psi^{\prime}(x)=0$
if
$\psi^{\prime}(x)=0$
if
![]() $x=N_0+kM$
for some
$x=N_0+kM$
for some
![]() $k \geq 1$
, and
$k \geq 1$
, and
![]() $\psi^{\prime}(x)=\psi(x)$
in all the other cases. Observe that
$\psi^{\prime}(x)=\psi(x)$
in all the other cases. Observe that
![]() $Q_{\beta}^{\prime}$
fulfills (C0) and (C2) with
$Q_{\beta}^{\prime}$
fulfills (C0) and (C2) with
![]() $\ell_{\max}(Q_\beta^\prime)=\ell_{\max}(Q_\beta)=\ell_{\max} <\infty$
and
$\ell_{\max}(Q_\beta^\prime)=\ell_{\max}(Q_\beta)=\ell_{\max} <\infty$
and
![]() $\alpha(\phi)=0$
. By applying Proposition 3.1 to the matrix
$\alpha(\phi)=0$
. By applying Proposition 3.1 to the matrix
![]() $Q_{\beta}^{\prime}$
for
$Q_{\beta}^{\prime}$
for
![]() $m=0$
we have
$m=0$
we have
![]() $\lim_{\beta \to \infty}R^2(Q_\beta^\prime)=c_\infty(\ell_{\max}(Q_\beta^\prime))=c_\infty(\ell_{\max})$
. Since
$\lim_{\beta \to \infty}R^2(Q_\beta^\prime)=c_\infty(\ell_{\max}(Q_\beta^\prime))=c_\infty(\ell_{\max})$
. Since
![]() $0 \leq \psi^{\prime}(x) \leq \psi(x)$
for all
$0 \leq \psi^{\prime}(x) \leq \psi(x)$
for all
![]() $x \geq 0$
, it follows that
$x \geq 0$
, it follows that
![]() $R^2(Q_\beta) \geq R^2(Q_\beta^\prime)$
for all
$R^2(Q_\beta) \geq R^2(Q_\beta^\prime)$
for all
![]() $\beta \geq 0$
, therefore
$\beta \geq 0$
, therefore
![]() $c_\infty(\ell_{\max}) \geq \lim_{\beta \to \infty}R^2(Q_{\beta}) \geq \lim_{\beta \to \infty}R^2(Q_\beta^\prime)=c_\infty(\ell_{\max})$
, and the proof is done.
$c_\infty(\ell_{\max}) \geq \lim_{\beta \to \infty}R^2(Q_{\beta}) \geq \lim_{\beta \to \infty}R^2(Q_\beta^\prime)=c_\infty(\ell_{\max})$
, and the proof is done.
3.1. Proofs of the main theorems
We can assume
![]() $\alpha(\phi)=0$
without loss of generality. In fact, if
$\alpha(\phi)=0$
without loss of generality. In fact, if
![]() $\widetilde{Q}_{\beta}$
is a matrix such that
$\widetilde{Q}_{\beta}$
is a matrix such that
![]() $\widetilde{\psi}(x)=\psi(x)-\alpha(\phi)$
for all
$\widetilde{\psi}(x)=\psi(x)-\alpha(\phi)$
for all
![]() $x \geq 0$
, from the definition of the convergence radius we have
$x \geq 0$
, from the definition of the convergence radius we have
where
![]() ${R}^2_{\beta,m}=R^2\big({Q}_{\beta}^{[m]}\big)$
,
${R}^2_{\beta,m}=R^2\big({Q}_{\beta}^{[m]}\big)$
,
![]() $\widetilde{R}^2_{\beta,m}=R^2\big(\widetilde{Q}_{\beta}^{[m]}\big)$
. Note that
$\widetilde{R}^2_{\beta,m}=R^2\big(\widetilde{Q}_{\beta}^{[m]}\big)$
. Note that
![]() $\widetilde{R}_{\beta,m}^2$
is the value obtained by letting
$\widetilde{R}_{\beta,m}^2$
is the value obtained by letting
![]() $\alpha(\phi)=0$
. Since the multiplicative term
$\alpha(\phi)=0$
. Since the multiplicative term
![]() $\exp (\beta \alpha(\phi))$
has no influence in the
$\exp (\beta \alpha(\phi))$
has no influence in the
![]() $R_{\beta}$
-classification, for every fixed
$R_{\beta}$
-classification, for every fixed
![]() $\beta \geq 0$
, the matrices
$\beta \geq 0$
, the matrices
![]() $Q_{\beta}$
and
$Q_{\beta}$
and
![]() $\widetilde{Q}_{\beta}$
have the same recurrence properties. Moreover, for every
$\widetilde{Q}_{\beta}$
have the same recurrence properties. Moreover, for every
![]() $m \geq 0$
, the value of the quotient
$m \geq 0$
, the value of the quotient
is independent of
![]() $\alpha(\phi)$
, and therefore the use of Theorem 2.1 does not depend on its value.
$\alpha(\phi)$
, and therefore the use of Theorem 2.1 does not depend on its value.
Proof of Theorem
3.1. Assume
![]() $\alpha(\phi)=0$
for simplicity. From Theorem 2.1, we only need to prove that, for some
$\alpha(\phi)=0$
for simplicity. From Theorem 2.1, we only need to prove that, for some
![]() $m \geq 0$
, we have
$m \geq 0$
, we have
![]() $R_{\beta,m}<R_{\beta,m+1}$
for each
$R_{\beta,m}<R_{\beta,m+1}$
for each
![]() $\beta>\beta_\mathrm{c}$
. From assumption (C1), there exists
$\beta>\beta_\mathrm{c}$
. From assumption (C1), there exists
![]() $N_0$
and
$N_0$
and
![]() $\varepsilon \geq \Delta$
such that
$\varepsilon \geq \Delta$
such that
![]() $\psi(x) \geq \alpha(\phi)+\varepsilon$
when
$\psi(x) \geq \alpha(\phi)+\varepsilon$
when
![]() $x \geq m>N_0$
.
$x \geq m>N_0$
.
Since
![]() ${R_{0,m}}=\frac12$
, from (2.10) we obtain
${R_{0,m}}=\frac12$
, from (2.10) we obtain
![]() $R_{\beta,m}\geq \frac{1}{2}\exp \left(\beta \varepsilon/2\right)$
. On the other hand, if (C0) and (C1) apply, the function
$R_{\beta,m}\geq \frac{1}{2}\exp \left(\beta \varepsilon/2\right)$
. On the other hand, if (C0) and (C1) apply, the function
![]() $\psi$
has a run of size at most
$\psi$
has a run of size at most
![]() $\ell_{\max}\leq N_0+2$
and therefore
$\ell_{\max}\leq N_0+2$
and therefore
![]() $\sqrt{c_{\infty}(\ell_{\max})} $
is an upper bound for
$\sqrt{c_{\infty}(\ell_{\max})} $
is an upper bound for
![]() $R_\beta$
. A sufficient condition to get
$R_\beta$
. A sufficient condition to get
![]() $R_\beta<R_{\beta,m}$
for some
$R_\beta<R_{\beta,m}$
for some
![]() $m>N_0$
is
$m>N_0$
is
By choosing
![]() $\beta_\mathrm{c}=-({2}/{\varepsilon})\ln(\cos({\pi}/({\ell_{\max}+1})))>0$
, we have
$\beta_\mathrm{c}=-({2}/{\varepsilon})\ln(\cos({\pi}/({\ell_{\max}+1})))>0$
, we have
 \begin{align*}\exp\!\Bigg(\frac{\beta \varepsilon}{2}\bigg) > \frac{1}{\cos({\pi}/({\ell_{\max}+1}))}\end{align*}
\begin{align*}\exp\!\Bigg(\frac{\beta \varepsilon}{2}\bigg) > \frac{1}{\cos({\pi}/({\ell_{\max}+1}))}\end{align*}
for all
![]() $\beta >\beta_\mathrm{c}$
, finishing the proof.
$\beta >\beta_\mathrm{c}$
, finishing the proof.
Remark 3.2. Corollary 3.1 follows by using the same argument as in the proof of Theorem 3.1, using the fact that, for all
![]() $L>0$
large enough, we can find
$L>0$
large enough, we can find
![]() $N_L<\infty$
such that
$N_L<\infty$
such that
![]() $\inf_{x > N_L}\psi(x)>L$
. This implies that, for all
$\inf_{x > N_L}\psi(x)>L$
. This implies that, for all
![]() $\beta>-({2}/{L})\ln(\cos({\pi}/({\ell_{\max}+1})))>0$
, the matrix
$\beta>-({2}/{L})\ln(\cos({\pi}/({\ell_{\max}+1})))>0$
, the matrix
![]() $Q_\beta$
is geometrically ergodic. The proof finishes by letting
$Q_\beta$
is geometrically ergodic. The proof finishes by letting
![]() $L \to \infty$
.
$L \to \infty$
.
Proof of Theorem
3.2. We follow a similar approach to Theorem 3.1 with
![]() $\alpha(\phi)=0$
. Under the main assumptions, there exists
$\alpha(\phi)=0$
. Under the main assumptions, there exists
![]() $N_0 \geq 1$
such that the function
$N_0 \geq 1$
such that the function
![]() $\psi(\!\cdot\!)$
restricted to
$\psi(\!\cdot\!)$
restricted to
![]() $[N_0+1,\infty)$
has a run of size at most
$[N_0+1,\infty)$
has a run of size at most
![]() $\ell_{\max}-1$
. By applying Proposition 3.1 to the matrices
$\ell_{\max}-1$
. By applying Proposition 3.1 to the matrices
![]() $Q_\beta^{[N_0+1]}$
and
$Q_\beta^{[N_0+1]}$
and
![]() $Q_\beta$
we get
$Q_\beta$
we get
![]() $c_\infty\big(\ell_{\max}^{[N_0+1]}\big) = \lim_{\beta \to \infty}R^2_{\beta,N_0+1}$
and
$c_\infty\big(\ell_{\max}^{[N_0+1]}\big) = \lim_{\beta \to \infty}R^2_{\beta,N_0+1}$
and
![]() $c_\infty(\ell_{\max}) = \lim_{\beta \to \infty}R^2_{\beta}$
. Clearly,
$c_\infty(\ell_{\max}) = \lim_{\beta \to \infty}R^2_{\beta}$
. Clearly,
![]() $c_\infty(\ell_{\max}) < c_{\infty}\big(\ell_{\max}^{[N_0+1]}\big)$
and thus, for all
$c_\infty(\ell_{\max}) < c_{\infty}\big(\ell_{\max}^{[N_0+1]}\big)$
and thus, for all
![]() $\beta$
large enough,
$\beta$
large enough,
![]() $R^2_{\beta} \leq c_\infty(\ell_{\max}) < R^2_{\beta,N_0+1} \leq c_{\infty}\big(\ell_{\max}^{[N_0+1]}\big)$
because
$R^2_{\beta} \leq c_\infty(\ell_{\max}) < R^2_{\beta,N_0+1} \leq c_{\infty}\big(\ell_{\max}^{[N_0+1]}\big)$
because
![]() $R_{\beta}$
and
$R_{\beta}$
and
![]() $R_{\beta,N_0+1}$
are non-decreasing on
$R_{\beta,N_0+1}$
are non-decreasing on
![]() $\beta$
.
$\beta$
.
4. The existence of zero-temperature limits
This section is devoted to studying the existence of a weak limit for the family of equilibrium measures
![]() $(\mu_{ \beta}(\!\cdot\!))_{\beta>\beta_\mathrm{c}}$
as
$(\mu_{ \beta}(\!\cdot\!))_{\beta>\beta_\mathrm{c}}$
as
![]() $\beta \to \infty$
, which is equivalent to the convergence of the finite-dimensional distributions. In the countable case, this is reduced to the existence of a measure, say
$\beta \to \infty$
, which is equivalent to the convergence of the finite-dimensional distributions. In the countable case, this is reduced to the existence of a measure, say
![]() $\mu_{\infty}(\!\cdot\!)$
, such that
$\mu_{\infty}(\!\cdot\!)$
, such that
![]() $\mu_{\infty}(\tilde{x})=\lim_{\beta \to \infty}\mu_{\beta}(\tilde{x})$
for each
$\mu_{\infty}(\tilde{x})=\lim_{\beta \to \infty}\mu_{\beta}(\tilde{x})$
for each
![]() $\tilde{x} \in \Omega[i,j]$
,
$\tilde{x} \in \Omega[i,j]$
,
![]() $i<j$
(more details related to the convergence on probability measures can be found in [Reference Billingsley3]). Since
$i<j$
(more details related to the convergence on probability measures can be found in [Reference Billingsley3]). Since
![]() $p_\beta(x,y) = 0$
if
$p_\beta(x,y) = 0$
if
![]() $|x-y|\neq 1$
, we only need to show the existence of a limit for the stationary measure
$|x-y|\neq 1$
, we only need to show the existence of a limit for the stationary measure
![]() $\pi_\beta(\!\cdot\!)$
and the transition probabilities given the recursive formula (2.3). The following proposition shows the convergence of
$\pi_\beta(\!\cdot\!)$
and the transition probabilities given the recursive formula (2.3). The following proposition shows the convergence of
![]() $u_\beta(x)=p_{\beta}(x,x+1)$
,
$u_\beta(x)=p_{\beta}(x,x+1)$
,
![]() $x \geq 0$
.
$x \geq 0$
.
Proposition 4.1. Assume that (C0) and (C1) hold, or that (C0) and (C1) hold with
![]() $\ell_{\max}<\infty$
. For all
$\ell_{\max}<\infty$
. For all
![]() $x \geq 1$
,
$x \geq 1$
,
 \begin{equation*}\lim_{\beta \to \infty} u_\beta(x)(1-u_\beta(x+1)) =\begin{cases} 0 & \psi(x)>\alpha(\phi), \\[5pt] c_\infty(\ell_{\max}) & \psi(x)=\alpha(\phi).\end{cases} \end{equation*}
\begin{equation*}\lim_{\beta \to \infty} u_\beta(x)(1-u_\beta(x+1)) =\begin{cases} 0 & \psi(x)>\alpha(\phi), \\[5pt] c_\infty(\ell_{\max}) & \psi(x)=\alpha(\phi).\end{cases} \end{equation*}
Proof. From (3.16) we know that
![]() $\widetilde{R}_{\beta}^2={R}^2_{\beta}\exp\!(\!-\!\beta\alpha(\phi))$
, where
$\widetilde{R}_{\beta}^2={R}^2_{\beta}\exp\!(\!-\!\beta\alpha(\phi))$
, where
![]() $\widetilde{R}^2_{\beta}$
is the convergence radius obtained with
$\widetilde{R}^2_{\beta}$
is the convergence radius obtained with
![]() $\alpha(\phi)=0$
. By using Proposition 3.1 or 3.2 respectively,
$\alpha(\phi)=0$
. By using Proposition 3.1 or 3.2 respectively,
![]() $\lim_{\beta\to\infty}R_{\beta}^2 \exp\!(\!-\!\beta\alpha(\phi))=\lim_{\beta\to\infty}\widetilde{R}_{\beta}^2 = c_{\infty}(\ell_{\max})$
. If
$\lim_{\beta\to\infty}R_{\beta}^2 \exp\!(\!-\!\beta\alpha(\phi))=\lim_{\beta\to\infty}\widetilde{R}_{\beta}^2 = c_{\infty}(\ell_{\max})$
. If
![]() $\psi(x)=\alpha(\phi)$
, from (2.4) we deduce that
$\psi(x)=\alpha(\phi)$
, from (2.4) we deduce that
Similarly, if
![]() $\psi(x) \geq \alpha(\phi)+\Delta$
,
$\psi(x) \geq \alpha(\phi)+\Delta$
,
concluding the proof.
Remark 4.1. If (C0) and (C1) hold, then
Since
![]() $\psi(x) \geq \alpha(\phi)+\Delta$
, from (3.16) and Lemma 3.1 we have
$\psi(x) \geq \alpha(\phi)+\Delta$
, from (3.16) and Lemma 3.1 we have
Combining this with (2.4) we get
We now choose
![]() $\beta \geq \widetilde{\beta}$
, with
$\beta \geq \widetilde{\beta}$
, with
![]() $\widetilde{\beta}=-({1}/{\Delta})\ln({1}/{4c_{\infty}(\ell_{\max})})>0$
, so that
$\widetilde{\beta}=-({1}/{\Delta})\ln({1}/{4c_{\infty}(\ell_{\max})})>0$
, so that
![]() $c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)\leq \frac14$
. By using the above inequality iteratively we have, for
$c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)\leq \frac14$
. By using the above inequality iteratively we have, for
![]() $x \geq N_0+1$
,
$x \geq N_0+1$
,
![]() $\beta \geq \widetilde{\beta}$
,
$\beta \geq \widetilde{\beta}$
,
 \begin{equation*} 0 \leq u_\beta(x)\leq\cfrac{c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{1-\cfrac{ c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{1-\cfrac{ c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{1-\cfrac{ c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{\cdots}}}} \leq \cfrac{1/4}{1-\cfrac{ 1/4}{1-\cfrac{ 1/4}{1-\cfrac{ 1/4}{\cdots}}}}=\frac12. \end{equation*}
\begin{equation*} 0 \leq u_\beta(x)\leq\cfrac{c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{1-\cfrac{ c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{1-\cfrac{ c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{1-\cfrac{ c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)}{\cdots}}}} \leq \cfrac{1/4}{1-\cfrac{ 1/4}{1-\cfrac{ 1/4}{1-\cfrac{ 1/4}{\cdots}}}}=\frac12. \end{equation*}
In particular,
![]() $0 \leq u_{\beta}(x+1) \leq \frac12$
for all
$0 \leq u_{\beta}(x+1) \leq \frac12$
for all
![]() $x \geq N_0+1$
. From (4.2), it follows that
$x \geq N_0+1$
. From (4.2), it follows that
![]() $0 \leq u_{\beta}(x) \leq 2 c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)$
uniformly on
$0 \leq u_{\beta}(x) \leq 2 c_{\infty}(\ell_{\max}) \exp\!(\!-\!\beta \Delta)$
uniformly on
![]() $x \geq N_0+1$
,
$x \geq N_0+1$
,
![]() $\beta \geq \widetilde{\beta}$
. By letting
$\beta \geq \widetilde{\beta}$
. By letting
![]() $\beta \to \infty$
, we get (4.1) as desired.
$\beta \to \infty$
, we get (4.1) as desired.
From (2.7), when
![]() $\alpha(\phi)=0$
we see that, for each
$\alpha(\phi)=0$
we see that, for each
![]() $\tilde{x} \in \Omega[0,2n]$
,
$\tilde{x} \in \Omega[0,2n]$
,
![]() $n \geq 1$
, such that
$n \geq 1$
, such that
![]() $x_0=x_{2n}$
, the equilibrium measure has the upper bound
$x_0=x_{2n}$
, the equilibrium measure has the upper bound
so that
![]() $\lim_{\beta \to \infty }\mu_{ \beta}(\tilde x)=0$
if
$\lim_{\beta \to \infty }\mu_{ \beta}(\tilde x)=0$
if
![]() $\psi(x_k)>0$
for some
$\psi(x_k)>0$
for some
![]() $0 \leq k \leq 2n$
. Observe that when the conditions of Proposition 3.1 or 3.2 are satisfied, if
$0 \leq k \leq 2n$
. Observe that when the conditions of Proposition 3.1 or 3.2 are satisfied, if
![]() $x_k \in I_{x_0,\ell}$
for all
$x_k \in I_{x_0,\ell}$
for all
![]() $1 \leq k \leq 2n$
, since
$1 \leq k \leq 2n$
, since
![]() $I_{x_0,\ell}$
is a run of size
$I_{x_0,\ell}$
is a run of size
![]() $\ell$
we have
$\ell$
we have
![]() $\mu_{ \beta}(\tilde x)=\pi_\beta (x_0)R_{\beta}^{2n}$
, so that
$\mu_{ \beta}(\tilde x)=\pi_\beta (x_0)R_{\beta}^{2n}$
, so that
![]() $\lim_{\beta \to \infty }\mu_{ \beta}(\tilde x)=\pi_\infty(x_0)(c_{\infty}(\ell_{\max}))^{n}$
provided that the limit
$\lim_{\beta \to \infty }\mu_{ \beta}(\tilde x)=\pi_\infty(x_0)(c_{\infty}(\ell_{\max}))^{n}$
provided that the limit
![]() $\pi_\infty(\!\cdot\!)$
exists. This means that the candidates to have strictly positive probability mass are those trajectories restricted to
$\pi_\infty(\!\cdot\!)$
exists. This means that the candidates to have strictly positive probability mass are those trajectories restricted to
![]() $\mathcal{R}$
. The following theorem proves the tightness of the family of stationary measures
$\mathcal{R}$
. The following theorem proves the tightness of the family of stationary measures
![]() $(\pi_{\beta}(\!\cdot\!))_{\beta>\beta_\mathrm{c}}$
under our main assumptions.
$(\pi_{\beta}(\!\cdot\!))_{\beta>\beta_\mathrm{c}}$
under our main assumptions.
Theorem 4.1. Assume that the number of runs of size
![]() $\ell_{\max}<\infty$
is finite. Let
$\ell_{\max}<\infty$
is finite. Let
![]() $\pi_\beta(\!\cdot\!)$
be the stationary measure associated to
$\pi_\beta(\!\cdot\!)$
be the stationary measure associated to
![]() $X^\beta$
,
$X^\beta$
,
![]() $\beta>\beta_\mathrm{c}$
. Then, there exists a limiting probability measure
$\beta>\beta_\mathrm{c}$
. Then, there exists a limiting probability measure
![]() $\pi_\infty(\!\cdot\!)$
satisfying
$\pi_\infty(\!\cdot\!)$
satisfying
![]() $\lim_{\beta\to\infty}\sum_{x=N_0+2}^{\infty}\pi_\beta(x)=0$
for some
$\lim_{\beta\to\infty}\sum_{x=N_0+2}^{\infty}\pi_\beta(x)=0$
for some
![]() $N_0 \geq 0$
. In particular,
$N_0 \geq 0$
. In particular,
![]() $\pi_\infty(x)=0$
for all
$\pi_\infty(x)=0$
for all
![]() $x \geq N_0+2$
.
$x \geq N_0+2$
.
Proof. Let us recall first that, up to a constant (see, for instance, [Reference Asmussen1, Theorem 3.2]), the stationary measure
![]() $\pi_\beta(\!\cdot\!)$
can be represented in the form
$\pi_\beta(\!\cdot\!)$
can be represented in the form
 \begin{equation}\pi_\beta(b)=\mathbb{E}_a\Bigg(\sum_{k=0}^{\tau_a^{}-1}\textbf{1}_{\{X_k^\beta=b\}}\Bigg) =\sum_{k=0}^{\infty}\mathbb{P}_a( X^\beta_k=b,\tau_a^{}>k). \end{equation}
\begin{equation}\pi_\beta(b)=\mathbb{E}_a\Bigg(\sum_{k=0}^{\tau_a^{}-1}\textbf{1}_{\{X_k^\beta=b\}}\Bigg) =\sum_{k=0}^{\infty}\mathbb{P}_a( X^\beta_k=b,\tau_a^{}>k). \end{equation}
We denote by
![]() $N_0+1$
the largest non-negative integer belonging to a run of size
$N_0+1$
the largest non-negative integer belonging to a run of size
![]() $\ell_{\max}$
, which is well defined since
$\ell_{\max}$
, which is well defined since
![]() $\psi$
has a finite number of runs with size
$\psi$
has a finite number of runs with size
![]() $\ell_{\max}<\infty$
. We necessarily have
$\ell_{\max}<\infty$
. We necessarily have
![]() $\psi(N_0)=0$
and
$\psi(N_0)=0$
and
![]() $\psi(N_0+1)>0$
. From (4.3), by using
$\psi(N_0+1)>0$
. From (4.3), by using
![]() $a=N_0+1$
and by taking the sum over
$a=N_0+1$
and by taking the sum over
![]() $b \geq N_0+2$
it follows that
$b \geq N_0+2$
it follows that
 \begin{equation*}\pi_\beta([N_0+2,\infty))=\mathbb{E}_{N_0+1}\Bigg(\sum_{k=0}^{\tau_{N_0+1}^{}-1}\textbf{1}_{\{X^\beta_k\geq N_0+2\}}\Bigg). \end{equation*}
\begin{equation*}\pi_\beta([N_0+2,\infty))=\mathbb{E}_{N_0+1}\Bigg(\sum_{k=0}^{\tau_{N_0+1}^{}-1}\textbf{1}_{\{X^\beta_k\geq N_0+2\}}\Bigg). \end{equation*}
Clearly,
![]() $\pi_\beta(N_0+1)=1$
for all
$\pi_\beta(N_0+1)=1$
for all
![]() $\beta > \beta_\mathrm{c}$
. We remark that
$\beta > \beta_\mathrm{c}$
. We remark that
![]() $\tau_{N_0+1}^{}$
can take only even values. Now, if
$\tau_{N_0+1}^{}$
can take only even values. Now, if
![]() $\tau_{N_0+1}^{}=2n$
for some
$\tau_{N_0+1}^{}=2n$
for some
![]() $n \geq 1$
, in order to get at least one visit to the interval
$n \geq 1$
, in order to get at least one visit to the interval
![]() $[N_0+2,\infty)$
we need
$[N_0+2,\infty)$
we need
![]() $X^\beta_0=X^\beta_{2n}=N_0+1$
and
$X^\beta_0=X^\beta_{2n}=N_0+1$
and
![]() $X^\beta_k \geq N_0+2$
for all
$X^\beta_k \geq N_0+2$
for all
![]() $1 \leq k \leq 2n-1$
, so that, for each fixed
$1 \leq k \leq 2n-1$
, so that, for each fixed
![]() $n \geq 1$
,
$n \geq 1$
,
 \begin{equation*}\mathbb{E}_{N_0+1}\Bigg(\sum_{k=0}^{2n-1}\textbf{1}_{\{X^\beta_k\geq N_0+2, \tau_{N_0+1}^{}=2n\}}\Bigg) =\exp\!(\!-\!\beta \psi (N_0+1))R_{\beta}^{2n}\mathcal{Z}_{2n-2,\beta}^{[N_0+2]}, \end{equation*}
\begin{equation*}\mathbb{E}_{N_0+1}\Bigg(\sum_{k=0}^{2n-1}\textbf{1}_{\{X^\beta_k\geq N_0+2, \tau_{N_0+1}^{}=2n\}}\Bigg) =\exp\!(\!-\!\beta \psi (N_0+1))R_{\beta}^{2n}\mathcal{Z}_{2n-2,\beta}^{[N_0+2]}, \end{equation*}
where
![]() $\mathcal{Z}_{2n-2,\beta}^{[N_0+2]}$
was defined in (2.8). Therefore,
$\mathcal{Z}_{2n-2,\beta}^{[N_0+2]}$
was defined in (2.8). Therefore,
By noticing that
![]() $\mathcal{Z}^{[N_0+2]}_{2n,\beta} = R_{\beta,N_0+2}^{-2n}\mathbb{P}_{N_0+2}\big(X^{\beta,[N_0+2]}_{2n}=N_0+2\big)$
, where
$\mathcal{Z}^{[N_0+2]}_{2n,\beta} = R_{\beta,N_0+2}^{-2n}\mathbb{P}_{N_0+2}\big(X^{\beta,[N_0+2]}_{2n}=N_0+2\big)$
, where
![]() $X^{\beta,[N_0+2]}$
is the Markov chain associated to
$X^{\beta,[N_0+2]}$
is the Markov chain associated to
![]() $Q_{\beta}^{[N_0+2]}$
, we now get the inequality
$Q_{\beta}^{[N_0+2]}$
, we now get the inequality
We claim that
![]() $R_{\beta}/R_{\beta,N_0+2} \leq \kappa $
for some
$R_{\beta}/R_{\beta,N_0+2} \leq \kappa $
for some
![]() $\kappa<1$
and
$\kappa<1$
and
![]() $\beta$
large enough. If (C2) holds, from Proposition 3.1 we have
$\beta$
large enough. If (C2) holds, from Proposition 3.1 we have
 \begin{equation}\lim_{\beta \to \infty}\frac{R_{\beta}^2}{R^2_{\beta,N_0+2}} =\frac{c_\infty(\ell_{\max})}{c_{\infty}\big(\ell_{\max}^{[N_0+2]}\big)}<1. \end{equation}
\begin{equation}\lim_{\beta \to \infty}\frac{R_{\beta}^2}{R^2_{\beta,N_0+2}} =\frac{c_\infty(\ell_{\max})}{c_{\infty}\big(\ell_{\max}^{[N_0+2]}\big)}<1. \end{equation}
If (C1) holds, we use the inequality
![]() $R_{\beta,N_0+2} \geq \frac{1}{2}\exp\!(\beta\Delta/2)$
and Lemma 3.1 to deduce that
$R_{\beta,N_0+2} \geq \frac{1}{2}\exp\!(\beta\Delta/2)$
and Lemma 3.1 to deduce that
![]() $R^2_{\beta}/R_{\beta,N_0+2}^2 \leq 4 c_{\infty}(\ell_{\max})\exp\!(\!-\!\beta \Delta)$
. In both cases, there exists
$R^2_{\beta}/R_{\beta,N_0+2}^2 \leq 4 c_{\infty}(\ell_{\max})\exp\!(\!-\!\beta \Delta)$
. In both cases, there exists
![]() $\tilde{\beta}<\infty$
such that
$\tilde{\beta}<\infty$
such that
 \begin{equation*}\kappa^2\;:\!=\;\sup_{\beta > \tilde{\beta}}\frac{R_{\beta}^2}{R^2_{\beta,N_0+2}} <1. \end{equation*}
\begin{equation*}\kappa^2\;:\!=\;\sup_{\beta > \tilde{\beta}}\frac{R_{\beta}^2}{R^2_{\beta,N_0+2}} <1. \end{equation*}
By taking the limit
![]() $\beta \to \infty$
in (4.4) we get
$\beta \to \infty$
in (4.4) we get
concluding the proof.
From Prokhorov’s theorem the existence of accumulation points for the sequence
![]() $(\pi_\beta(\!\cdot\!))_{\beta>\beta_\mathrm{c}}$
is guaranteed. On the other hand, our theorem implies that
$(\pi_\beta(\!\cdot\!))_{\beta>\beta_\mathrm{c}}$
is guaranteed. On the other hand, our theorem implies that
![]() $\pi_{\infty}(I_{x_0,\ell})=0$
for each run of size
$\pi_{\infty}(I_{x_0,\ell})=0$
for each run of size
![]() $\ell<\ell_{\max}$
. In fact, if we consider the finite and strictly sub-stochastic matrix
$\ell<\ell_{\max}$
. In fact, if we consider the finite and strictly sub-stochastic matrix
![]() $\tilde{P}_\beta=(p_\beta(x,y)\;:\; x,y\in I_{x_0,\ell})$
with coefficients as in (2.2) and the stopping time
$\tilde{P}_\beta=(p_\beta(x,y)\;:\; x,y\in I_{x_0,\ell})$
with coefficients as in (2.2) and the stopping time
![]() $\tau_{x_0,x_0+\ell}=\min\{\tau_{x_0-1},\tau_{x_0+\ell}\}$
, we have, for
$\tau_{x_0,x_0+\ell}=\min\{\tau_{x_0-1},\tau_{x_0+\ell}\}$
, we have, for
![]() $y \in I_{x_0,\ell}$
,
$y \in I_{x_0,\ell}$
,
![]() $\mathbb{P}_{x_0}\big(X_n^{\beta}=y,\tau_{x_0,x_0+\ell}>n\big) = \tilde{P}^{(n)}_\beta(x_0,y)$
. From the Perron–Frobenius theorem, there exists an eigenvector
$\mathbb{P}_{x_0}\big(X_n^{\beta}=y,\tau_{x_0,x_0+\ell}>n\big) = \tilde{P}^{(n)}_\beta(x_0,y)$
. From the Perron–Frobenius theorem, there exists an eigenvector
![]() $\tilde{h}_\beta>0$
and an eigenmeasure
$\tilde{h}_\beta>0$
and an eigenmeasure
![]() $\tilde{\nu}_\beta>0$
such that, for each
$\tilde{\nu}_\beta>0$
such that, for each
![]() $y \in I_{x_0,\ell}$
, we get
$y \in I_{x_0,\ell}$
, we get
![]() $\lim_{n \to \infty}\tilde{\theta}_\beta^{2n} \tilde{P}^{(2n+\Delta(x_0,y))}_\beta(x_0,y)=\tilde{h}_\beta(x_0) \tilde{\nu}_\beta(y)$
for some
$\lim_{n \to \infty}\tilde{\theta}_\beta^{2n} \tilde{P}^{(2n+\Delta(x_0,y))}_\beta(x_0,y)=\tilde{h}_\beta(x_0) \tilde{\nu}_\beta(y)$
for some
![]() $\tilde{\theta}_\beta<1$
(we recall that
$\tilde{\theta}_\beta<1$
(we recall that
![]() $\Delta(x_0,y)=x_0-y \ (\mathrm{mod}\;2)$
). If we choose
$\Delta(x_0,y)=x_0-y \ (\mathrm{mod}\;2)$
). If we choose
![]() $\tilde{\nu}_\beta$
satisfying
$\tilde{\nu}_\beta$
satisfying
![]() $\sum_{y }^{}\tilde{\nu}_{\beta}(y)=1$
we also get
$\sum_{y }^{}\tilde{\nu}_{\beta}(y)=1$
we also get
Here, the parameter
![]() $\tilde{\theta}_\beta={R_{\beta}}/{\sqrt{c_\infty(\ell)}}$
is the survival rate of the killed process
$\tilde{\theta}_\beta={R_{\beta}}/{\sqrt{c_\infty(\ell)}}$
is the survival rate of the killed process
![]() $\tilde{X}^{\beta}=\big(X_{n \wedge \tau_{x_0,x_0+\ell}}^{\beta}\;:\; n \geq 0\big)$
. This means that, for large of values of
$\tilde{X}^{\beta}=\big(X_{n \wedge \tau_{x_0,x_0+\ell}}^{\beta}\;:\; n \geq 0\big)$
. This means that, for large of values of
![]() $\beta$
, the killed process
$\beta$
, the killed process
![]() $\tilde{X}_{\beta}$
has a quasi-stationary distribution
$\tilde{X}_{\beta}$
has a quasi-stationary distribution
![]() $\tilde{\nu}_\beta$
with survival rate
$\tilde{\nu}_\beta$
with survival rate
![]() $\tilde{\theta}_{\beta}$
. We know that if the assumptions of Proposition 3.1 or 3.2 are fulfilled, then
$\tilde{\theta}_{\beta}$
. We know that if the assumptions of Proposition 3.1 or 3.2 are fulfilled, then
![]() $\lim_{\beta \to \infty} R^2_{\beta}=c_{\infty}(\ell_{\max})$
and consequently
$\lim_{\beta \to \infty} R^2_{\beta}=c_{\infty}(\ell_{\max})$
and consequently
![]() $\lim_{\beta \to \infty} \tilde{\theta}_\beta=\sqrt{{c_{\infty}(\ell_{\max})}/{c_{\infty}(\ell)}}<1$
when
$\lim_{\beta \to \infty} \tilde{\theta}_\beta=\sqrt{{c_{\infty}(\ell_{\max})}/{c_{\infty}(\ell)}}<1$
when
![]() $\ell<\ell_{\max}$
. From the same analysis, we obtain, for a run of size
$\ell<\ell_{\max}$
. From the same analysis, we obtain, for a run of size
![]() $\ell_{\max}$
, that its survival rate satisfies
$\ell_{\max}$
, that its survival rate satisfies
![]() $\lim_{\beta \to \infty} \tilde{\theta}^{\star}_\beta=1$
. Intuitively, for large values of
$\lim_{\beta \to \infty} \tilde{\theta}^{\star}_\beta=1$
. Intuitively, for large values of
![]() $\beta$
, once the Markov chain is attracted for a run of
$\beta$
, once the Markov chain is attracted for a run of
![]() $\ell_{\max}$
, it will remain trapped there for a long time. The same occurs for each run of size
$\ell_{\max}$
, it will remain trapped there for a long time. The same occurs for each run of size
![]() $\ell_{\max}$
and this explains why
$\ell_{\max}$
and this explains why
![]() $\pi_{\infty}(\!\cdot\!)$
gives strictly positive mass to each of these runs of size
$\pi_{\infty}(\!\cdot\!)$
gives strictly positive mass to each of these runs of size
![]() $\ell_{\max}$
.
$\ell_{\max}$
.
5. Examples
In this section we review in more detail some particular examples that can be analyzed more explicitly. Let us introduce first, for all
![]() $x \geq 0$
,
$x \geq 0$
,
For each fixed
![]() $0 \leq r<R_{\beta}$
, the sequence
$0 \leq r<R_{\beta}$
, the sequence
![]() $(\mathcal F_{x}(r))_{x \geq 0}$
satisfies the recurrence formula
$(\mathcal F_{x}(r))_{x \geq 0}$
satisfies the recurrence formula
Defining
From (5.1) we have
5.1. Example 1: Ultimately constant potential, case 1
We first consider the case
![]() $\psi(0)=\alpha$
,
$\psi(0)=\alpha$
,
![]() $\psi(x)=\alpha+\Delta$
,
$\psi(x)=\alpha+\Delta$
,
![]() $x \geq 1$
, for a pair of real values
$x \geq 1$
, for a pair of real values
![]() $\alpha,\Delta \in \mathbb R$
. This is a particular example of an ultimately constant potential, previously introduced in [Reference Ferrari and Martnez8]. Note that, for
$\alpha,\Delta \in \mathbb R$
. This is a particular example of an ultimately constant potential, previously introduced in [Reference Ferrari and Martnez8]. Note that, for
![]() $x \geq 2$
, we get the continued fraction
$x \geq 2$
, we get the continued fraction
 \begin{equation} \mathcal G_{x}(r)=\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\mathcal G_{x+1}(r)} \quad \Rightarrow \quad \mathcal G_{x}(r)=\frac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{\cdots}}}} .\end{equation}
\begin{equation} \mathcal G_{x}(r)=\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\mathcal G_{x+1}(r)} \quad \Rightarrow \quad \mathcal G_{x}(r)=\frac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{r^2 {\mathrm{e}}^{-\beta (\alpha+\Delta)}}{\cdots}}}} .\end{equation}
In particular,
![]() $\mathcal G_{x}(r)=\mathcal G(r)$
is constant for all
$\mathcal G_{x}(r)=\mathcal G(r)$
is constant for all
![]() $x \geq 2$
, and this can be deduced by solving the equation
$x \geq 2$
, and this can be deduced by solving the equation
because from (5.6) we know that
![]() $\lim_{r\to 0^+}\mathcal G(r)=0$
. Recalling that
$\lim_{r\to 0^+}\mathcal G(r)=0$
. Recalling that
![]() $ \psi(0)=\alpha$
, from (5.4) we now deduce that
$ \psi(0)=\alpha$
, from (5.4) we now deduce that
 \begin{equation*} \mathcal F_0(r)=\dfrac{r^2{\mathrm{e}}^{-\beta \alpha }}{1-\dfrac{1 - \sqrt{1-4r^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} }}{2}} = {\mathrm{e}}^{\beta \Delta}\bigg(\dfrac{1 - \sqrt{1-4r^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} }}{2}\bigg).\end{equation*}
\begin{equation*} \mathcal F_0(r)=\dfrac{r^2{\mathrm{e}}^{-\beta \alpha }}{1-\dfrac{1 - \sqrt{1-4r^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} }}{2}} = {\mathrm{e}}^{\beta \Delta}\bigg(\dfrac{1 - \sqrt{1-4r^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} }}{2}\bigg).\end{equation*}
Clearly, if
![]() $\Delta \leq 0$
, then
$\Delta \leq 0$
, then
![]() $\mathcal F_0(r)\leq \frac12{\mathrm{e}}^{\beta \Delta} \leq \frac{1}{2}$
for all
$\mathcal F_0(r)\leq \frac12{\mathrm{e}}^{\beta \Delta} \leq \frac{1}{2}$
for all
![]() $0 \leq r \leq R_{\beta}$
. Therefore, the matrix
$0 \leq r \leq R_{\beta}$
. Therefore, the matrix
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-transient for all
$R_\beta$
-transient for all
![]() $\beta \geq 0$
. When
$\beta \geq 0$
. When
![]() $\Delta>0$
, the critical value
$\Delta>0$
, the critical value
![]() $\beta_\mathrm{c}={\ln(2)}/{\Delta}$
is such that
$\beta_\mathrm{c}={\ln(2)}/{\Delta}$
is such that
 \begin{equation*} Q_\beta \text{ is } \begin{cases}R_\beta\text{-transient} & \text{if } \beta
< \beta_\mathrm{c}, \\[5pt] \text{geometrically ergodic} & \text{if } \beta > \beta_\mathrm{c}, \\[5pt] R_\beta\text{-null recurrent} & \text{if } \beta = \beta_\mathrm{c}. \end{cases}\end{equation*}
\begin{equation*} Q_\beta \text{ is } \begin{cases}R_\beta\text{-transient} & \text{if } \beta
< \beta_\mathrm{c}, \\[5pt] \text{geometrically ergodic} & \text{if } \beta > \beta_\mathrm{c}, \\[5pt] R_\beta\text{-null recurrent} & \text{if } \beta = \beta_\mathrm{c}. \end{cases}\end{equation*}
To prove this, we first remark that the convergence radius of
![]() $Q_\beta^{[m]}$
is
$Q_\beta^{[m]}$
is
![]() $R_{\beta,m}=\frac{1}{2}{\mathrm{e}}^{({\beta}/{2})(\alpha+\Delta)}$
for all
$R_{\beta,m}=\frac{1}{2}{\mathrm{e}}^{({\beta}/{2})(\alpha+\Delta)}$
for all
![]() $m \geq 1$
. Since
$m \geq 1$
. Since
![]() $R_\beta \leq R_{\beta,1}$
, we automatically have
$R_\beta \leq R_{\beta,1}$
, we automatically have
![]() $\mathcal F_0(R_{\beta})\leq \mathcal F_0(R_{\beta,1})=\frac12{\mathrm{e}}^{\beta \Delta}<1$
for
$\mathcal F_0(R_{\beta})\leq \mathcal F_0(R_{\beta,1})=\frac12{\mathrm{e}}^{\beta \Delta}<1$
for
![]() $0 \leq \beta<\beta_\mathrm{c}$
, so that
$0 \leq \beta<\beta_\mathrm{c}$
, so that
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-transient. Similarly, for
$R_\beta$
-transient. Similarly, for
![]() $\beta=\beta_\mathrm{c}$
, we have
$\beta=\beta_\mathrm{c}$
, we have
![]() $\mathcal F_0(R_{\beta,1})=1$
and thus
$\mathcal F_0(R_{\beta,1})=1$
and thus
![]() $R_{\beta}=R_{\beta,1}$
, giving
$R_{\beta}=R_{\beta,1}$
, giving
![]() $\mathcal F_0(R_{\beta})=1$
and consequently that
$\mathcal F_0(R_{\beta})=1$
and consequently that
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-recurrent. Recalling that
$R_\beta$
-recurrent. Recalling that
![]() $\lim_{r \to R_{\beta}^-}\mathcal F^{\prime}_0(r)=\mathbb{E}_0(\tau_0)$
, the null recurrence is deduced by taking the derivative
$\lim_{r \to R_{\beta}^-}\mathcal F^{\prime}_0(r)=\mathbb{E}_0(\tau_0)$
, the null recurrence is deduced by taking the derivative
Finally, for
![]() $\beta>\beta_\mathrm{c}$
, we have
$\beta>\beta_\mathrm{c}$
, we have
![]() $\mathcal F_0(R_{\beta,1})>1$
. The only option is
$\mathcal F_0(R_{\beta,1})>1$
. The only option is
![]() $R_{\beta}<R_{\beta,1}$
, therefore
$R_{\beta}<R_{\beta,1}$
, therefore
![]() $Q_\beta$
is geometrically ergodic. The value of
$Q_\beta$
is geometrically ergodic. The value of
![]() $R_{\beta}$
is the solution to the equation
$R_{\beta}$
is the solution to the equation
 \begin{equation} {\mathrm{e}}^{\beta \Delta}\Bigg(\frac{1 - \sqrt{1-4R_{\beta}^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} }}{2}\Bigg)=1 ,\end{equation}
\begin{equation} {\mathrm{e}}^{\beta \Delta}\Bigg(\frac{1 - \sqrt{1-4R_{\beta}^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} }}{2}\Bigg)=1 ,\end{equation}
giving
![]() $R^2_{\beta}={\mathrm{e}}^{\beta \alpha}(1-{\mathrm{e}}^{-\beta \Delta})$
. Since
$R^2_{\beta}={\mathrm{e}}^{\beta \alpha}(1-{\mathrm{e}}^{-\beta \Delta})$
. Since
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-positive recurrent, for
$R_\beta$
-positive recurrent, for
![]() $\beta>\beta_\mathrm{c}$
the main eigenvalue is
$\beta>\beta_\mathrm{c}$
the main eigenvalue is
![]() $\lambda_\beta=R_{\beta}^{-1}=\sqrt{{{\mathrm{e}}^{-\beta \alpha}}/({1-{\mathrm{e}}^{-\beta \Delta}})}$
.
$\lambda_\beta=R_{\beta}^{-1}=\sqrt{{{\mathrm{e}}^{-\beta \alpha}}/({1-{\mathrm{e}}^{-\beta \Delta}})}$
.
Let us compute now the transition probabilities and the stationary measure of
![]() $X^{\beta}$
when
$X^{\beta}$
when
![]() $\Delta>0$
and
$\Delta>0$
and
![]() $\beta>\beta_\mathrm{c}$
. Since
$\beta>\beta_\mathrm{c}$
. Since
![]() $X^\beta$
is reflected at the origin,
$X^\beta$
is reflected at the origin,
![]() $p_{\beta}(0,1)=1$
for all
$p_{\beta}(0,1)=1$
for all
![]() $\beta \geq 0$
. To compute
$\beta \geq 0$
. To compute
![]() $u_\beta(x)$
for
$u_\beta(x)$
for
![]() $x \geq 1$
we use the recurrence formula (2.5):
$x \geq 1$
we use the recurrence formula (2.5):
 \begin{equation} u_\beta(x) = \frac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-u_\beta(x+1)} = \cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{\cdots}}}} , \qquad x \geq 1.\end{equation}
\begin{equation} u_\beta(x) = \frac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-u_\beta(x+1)} = \cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{1-\cfrac{R_{\beta}^{2}{\mathrm{e}}^{-\beta (\alpha+\Delta)}}{\cdots}}}} , \qquad x \geq 1.\end{equation}
From (5.9), we observe that
![]() $p_\beta<\frac12$
is a solution to the equation
$p_\beta<\frac12$
is a solution to the equation
![]() $p_\beta(1-p_\beta)=R_\beta^2{\mathrm{e}}^{-\beta (\alpha+\Delta)}$
, so
$p_\beta(1-p_\beta)=R_\beta^2{\mathrm{e}}^{-\beta (\alpha+\Delta)}$
, so
The last equality is deduced directly from (5.8). Obviously,
![]() $p_{\beta}(x,x-1)=1-{\mathrm{e}}^{-\beta \Delta}$
. The stationary measure
$p_{\beta}(x,x-1)=1-{\mathrm{e}}^{-\beta \Delta}$
. The stationary measure
![]() $\pi_\beta(x)$
is the solution to the recurrence formula
$\pi_\beta(x)$
is the solution to the recurrence formula
 \begin{align*} \pi_\beta(0) & = (1-{\mathrm{e}}^{-\beta \Delta})\pi_\beta(1), \\[5pt] \pi_\beta(1) & = \pi_\beta(0)+(1-{\mathrm{e}}^{-\beta \Delta})\pi_\beta(2), \\[5pt] \pi_\beta (x) & = {\mathrm{e}}^{-\beta \Delta}\pi_\beta (x-1)+(1-{\mathrm{e}}^{-\beta \Delta}) \pi_\beta (x+1), \qquad x \geq 2.\end{align*}
\begin{align*} \pi_\beta(0) & = (1-{\mathrm{e}}^{-\beta \Delta})\pi_\beta(1), \\[5pt] \pi_\beta(1) & = \pi_\beta(0)+(1-{\mathrm{e}}^{-\beta \Delta})\pi_\beta(2), \\[5pt] \pi_\beta (x) & = {\mathrm{e}}^{-\beta \Delta}\pi_\beta (x-1)+(1-{\mathrm{e}}^{-\beta \Delta}) \pi_\beta (x+1), \qquad x \geq 2.\end{align*}
A direct computation shows that
 \begin{align*} \pi_\beta(0) & = \frac{1}{2}\bigg(1-\frac{{\mathrm{e}}^{-\beta \Delta}}{1-{\mathrm{e}}^{-\beta \Delta}}\bigg), \\[5pt] \pi_\beta(1) & = \frac{1}{2(1-{\mathrm{e}}^{-\beta \Delta})}\bigg(1-\frac{{\mathrm{e}}^{-\beta \Delta}}{1-{\mathrm{e}}^{-\beta \Delta}}\bigg), \\[5pt] \pi_\beta(x) & = \frac{1-2e^{-\beta \Delta}}{2e^{-\beta \Delta}(1-e^{-\beta \Delta})}\bigg(\frac{{\mathrm{e}}^{-\beta \Delta}}{1-{\mathrm{e}}^{-\beta \Delta}}\bigg)^{x}, \qquad x \geq 2.\end{align*}
\begin{align*} \pi_\beta(0) & = \frac{1}{2}\bigg(1-\frac{{\mathrm{e}}^{-\beta \Delta}}{1-{\mathrm{e}}^{-\beta \Delta}}\bigg), \\[5pt] \pi_\beta(1) & = \frac{1}{2(1-{\mathrm{e}}^{-\beta \Delta})}\bigg(1-\frac{{\mathrm{e}}^{-\beta \Delta}}{1-{\mathrm{e}}^{-\beta \Delta}}\bigg), \\[5pt] \pi_\beta(x) & = \frac{1-2e^{-\beta \Delta}}{2e^{-\beta \Delta}(1-e^{-\beta \Delta})}\bigg(\frac{{\mathrm{e}}^{-\beta \Delta}}{1-{\mathrm{e}}^{-\beta \Delta}}\bigg)^{x}, \qquad x \geq 2.\end{align*}
By taking the limit
![]() $\beta \to \infty$
we notice that
$\beta \to \infty$
we notice that
In the limit
![]() $\beta \to \infty$
, the transition probabilities are
$\beta \to \infty$
, the transition probabilities are
![]() $p_{\infty}(0,1)=1$
and
$p_{\infty}(0,1)=1$
and
![]() $p_{\infty}(x,x-1)=1$
,
$p_{\infty}(x,x-1)=1$
,
![]() $x \geq 1$
. This means that the limiting behavior of
$x \geq 1$
. This means that the limiting behavior of
![]() $X^\beta$
, denoted by
$X^\beta$
, denoted by
![]() $X^\infty$
, is deterministic as
$X^\infty$
, is deterministic as
![]() $\beta \to \infty$
. If the initial state is
$\beta \to \infty$
. If the initial state is
![]() $x \geq 2$
,
$x \geq 2$
,
![]() $X^\infty$
attains the value 1 after
$X^\infty$
attains the value 1 after
![]() $x-1$
steps and then oscillates between 0 and 1. This explains why the limiting stationary measure is
$x-1$
steps and then oscillates between 0 and 1. This explains why the limiting stationary measure is
![]() $\pi_\infty(0)=\pi_\infty(1)=\frac12$
.
$\pi_\infty(0)=\pi_\infty(1)=\frac12$
.
5.2. Example 2: Ultimately constant potential, case 2
Related to the previous case, we now consider a potential such that
![]() $\psi(x)=\alpha$
,
$\psi(x)=\alpha$
,
![]() $0 \leq x \leq N_0$
, and
$0 \leq x \leq N_0$
, and
![]() $\alpha(x)=\alpha+\Delta$
for
$\alpha(x)=\alpha+\Delta$
for
![]() $x \geq N_0+1$
for some
$x \geq N_0+1$
for some
![]() $N_0 \geq 1$
(case 1 is recovered by letting
$N_0 \geq 1$
(case 1 is recovered by letting
![]() $N_0=0$
). From similar arguments, for
$N_0=0$
). From similar arguments, for
![]() $x \geq N_0+2$
we find that
$x \geq N_0+2$
we find that
![]() $\mathcal G_{x}(r)=\mathcal G(r)$
is constant and takes the same form as (5.7).
$\mathcal G_{x}(r)=\mathcal G(r)$
is constant and takes the same form as (5.7).
Since
![]() $\psi(N_0)=\alpha$
, from (5.5) we also get
$\psi(N_0)=\alpha$
, from (5.5) we also get
From (5.7) we know that
![]() $\mathcal G_{N_0+2}(r) \leq \frac12$
, so
$\mathcal G_{N_0+2}(r) \leq \frac12$
, so
![]() $\mathcal G_{N_0+1}(r)\leq 2r^2 {\mathrm{e}}^{-\beta \alpha} \leq \frac12{\mathrm{e}}^{\beta \Delta}$
, because
$\mathcal G_{N_0+1}(r)\leq 2r^2 {\mathrm{e}}^{-\beta \alpha} \leq \frac12{\mathrm{e}}^{\beta \Delta}$
, because
![]() $4r^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} \leq 1$
. When
$4r^2{\mathrm{e}}^{-\beta (\alpha+\Delta)} \leq 1$
. When
![]() $\Delta \leq 0$
, from (5.5) it follows that
$\Delta \leq 0$
, from (5.5) it follows that
![]() $\mathcal G_{x}(r) \leq \frac12$
for all
$\mathcal G_{x}(r) \leq \frac12$
for all
![]() $x \geq 2$
and consequently, from (5.4), we deduce that
$x \geq 2$
and consequently, from (5.4), we deduce that
![]() $\mathcal F_0(r) \leq \frac12$
for all
$\mathcal F_0(r) \leq \frac12$
for all
![]() $0 \leq r \leq R_\beta$
. This implies that
$0 \leq r \leq R_\beta$
. This implies that
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_\beta$
-transient for all
$R_\beta$
-transient for all
![]() $\beta>0$
. If
$\beta>0$
. If
![]() $\Delta>0$
, from Theorem 3.1 we know that there exists
$\Delta>0$
, from Theorem 3.1 we know that there exists
![]() $0<\beta_\mathrm{c}<\infty$
such that
$0<\beta_\mathrm{c}<\infty$
such that
![]() $Q_\beta$
is geometrically ergodic for all
$Q_\beta$
is geometrically ergodic for all
![]() $\beta>\beta_\mathrm{c}$
. In fact, by introducing the function
$\beta>\beta_\mathrm{c}$
. In fact, by introducing the function
![]() $g_\beta(r,z)={r^2{\mathrm{e}}^{-\beta \alpha}}/({1-z})$
and
$g_\beta(r,z)={r^2{\mathrm{e}}^{-\beta \alpha}}/({1-z})$
and
![]() $g_\beta^{(n)}(r,z)=g_\beta(r,g_\beta^{(n-1)}(r,z))$
for
$g_\beta^{(n)}(r,z)=g_\beta(r,g_\beta^{(n-1)}(r,z))$
for
![]() $n \geq 1$
, with the convention
$n \geq 1$
, with the convention
![]() $g_\beta^{(0)} (r,z)=z$
, we have, for
$g_\beta^{(0)} (r,z)=z$
, we have, for
![]() $\beta \geq 0$
,
$\beta \geq 0$
,
Given
![]() $\beta>0$
, note that
$\beta>0$
, note that
![]() $R^{2}_{\beta,x}=\frac{1}{4}{\mathrm{e}}^{\beta (\alpha+\Delta)}$
for
$R^{2}_{\beta,x}=\frac{1}{4}{\mathrm{e}}^{\beta (\alpha+\Delta)}$
for
![]() $x \geq N_0+1$
and
$x \geq N_0+1$
and
![]() $\mathcal G\big(\frac{1}{2}{\mathrm{e}}^{{\beta(\alpha+\Delta)}/{2}} \big)=\frac{1}{2}$
. The critical value
$\mathcal G\big(\frac{1}{2}{\mathrm{e}}^{{\beta(\alpha+\Delta)}/{2}} \big)=\frac{1}{2}$
. The critical value
![]() $\beta_\mathrm{c}$
can be specified through the equation
$\beta_\mathrm{c}$
can be specified through the equation
For
![]() $0 \leq \beta<\beta_\mathrm{c}$
we have
$0 \leq \beta<\beta_\mathrm{c}$
we have
This means that
![]() $R_\beta^2=\frac{1}{4}{\mathrm{e}}^{\beta (\alpha+\Delta)}$
for
$R_\beta^2=\frac{1}{4}{\mathrm{e}}^{\beta (\alpha+\Delta)}$
for
![]() $\beta \leq \beta_\mathrm{c}$
, and hence
$\beta \leq \beta_\mathrm{c}$
, and hence
![]() $Q_\beta$
cannot be geometrically ergodic. More precisely,
$Q_\beta$
cannot be geometrically ergodic. More precisely,
![]() $Q_\beta$
is
$Q_\beta$
is
![]() $R_{\beta}$
-transient for
$R_{\beta}$
-transient for
![]() $0 \leq \beta<\beta_\mathrm{c}$
and
$0 \leq \beta<\beta_\mathrm{c}$
and
![]() $R_{\beta_\mathrm{c}}$
-null recurrent for
$R_{\beta_\mathrm{c}}$
-null recurrent for
![]() $\beta=\beta_\mathrm{c}$
because
$\beta=\beta_\mathrm{c}$
because
![]() $u_{\beta_\mathrm{c}}(x)=\frac12$
for
$u_{\beta_\mathrm{c}}(x)=\frac12$
for
![]() $x \geq N_0+1$
(see (5.12)). For
$x \geq N_0+1$
(see (5.12)). For
![]() $\beta>\beta_\mathrm{c}$
,
$\beta>\beta_\mathrm{c}$
,
![]() $Q_\beta$
is geometrically ergodic. This can verified assuming that
$Q_\beta$
is geometrically ergodic. This can verified assuming that
![]() $R^2_{\beta,1}=\frac{1}{4}{\mathrm{e}}^{\beta (\alpha+\Delta)}$
(otherwise is deduced in an obvious manner); from (5.11) we have
$R^2_{\beta,1}=\frac{1}{4}{\mathrm{e}}^{\beta (\alpha+\Delta)}$
(otherwise is deduced in an obvious manner); from (5.11) we have
![]() $g_{\beta}^{(N_0+1)}\big(\frac{1}{2}{\mathrm{e}}^{{\beta(\alpha+\Delta)}/{2}},\frac{1}{2}\big)>1$
and (5.10) implies
$g_{\beta}^{(N_0+1)}\big(\frac{1}{2}{\mathrm{e}}^{{\beta(\alpha+\Delta)}/{2}},\frac{1}{2}\big)>1$
and (5.10) implies
![]() $R_\beta<R_{\beta,1}$
because
$R_\beta<R_{\beta,1}$
because
![]() $\mathcal F_0(R_\beta) \leq 1$
.
$\mathcal F_0(R_\beta) \leq 1$
.
To analyze the asymptotic behavior as
![]() $\beta \to \infty$
, note that (5.9) applies for
$\beta \to \infty$
, note that (5.9) applies for
![]() $x \geq N_0+1$
and
$x \geq N_0+1$
and
![]() $\beta >0$
, and thus
$\beta >0$
, and thus
![]() $u_{\beta}(x)$
is a solution to the equation
$u_{\beta}(x)$
is a solution to the equation
Since
![]() $X^\beta$
is geometrically ergodic for
$X^\beta$
is geometrically ergodic for
![]() $\beta>\beta_\mathrm{c}$
, we get
$\beta>\beta_\mathrm{c}$
, we get
In addition,
and
![]() $u_{\beta}(0)=1$
. The stationary distribution
$u_{\beta}(0)=1$
. The stationary distribution
![]() $\pi_\beta(\!\cdot\!)$
can be computed from the well-known formula for
$\pi_\beta(\!\cdot\!)$
can be computed from the well-known formula for
![]() $x \geq 1$
(see [Reference Karlin and McGregor12, p. 78]):
$x \geq 1$
(see [Reference Karlin and McGregor12, p. 78]):
 \begin{equation} \pi_\beta(x)=\Bigg(\prod_{k=1}^{x}\frac{p_{\beta}(k-1,k)}{p_{\beta}(k,k-1)}\Bigg)\pi_\beta(0) = \Bigg(\prod_{k=1}^{x} \frac{u_\beta(k-1)}{1-u_\beta(k)}\Bigg)\pi_\beta(0),\end{equation}
\begin{equation} \pi_\beta(x)=\Bigg(\prod_{k=1}^{x}\frac{p_{\beta}(k-1,k)}{p_{\beta}(k,k-1)}\Bigg)\pi_\beta(0) = \Bigg(\prod_{k=1}^{x} \frac{u_\beta(k-1)}{1-u_\beta(k)}\Bigg)\pi_\beta(0),\end{equation}
where
![]() $\pi_{\beta}(0)=1-\sum_{x=1}^{\infty}\pi_{\beta}(x)$
. We now set
$\pi_{\beta}(0)=1-\sum_{x=1}^{\infty}\pi_{\beta}(x)$
. We now set
![]() $u_{\infty}(x)=\lim_{\beta \to \infty} u_{\beta}(x)$
. If
$u_{\infty}(x)=\lim_{\beta \to \infty} u_{\beta}(x)$
. If
![]() $\widetilde{Q}_\beta$
is the matrix obtained for
$\widetilde{Q}_\beta$
is the matrix obtained for
![]() $\alpha=0$
, then
$\alpha=0$
, then
![]() $R^2({Q}_\beta)={\mathrm{e}}^{\beta \alpha}R^2(\widetilde{Q}_\beta)$
(see (3.16)). From Proposition 3.2 we have
$R^2({Q}_\beta)={\mathrm{e}}^{\beta \alpha}R^2(\widetilde{Q}_\beta)$
(see (3.16)). From Proposition 3.2 we have
![]() $\lim_{\beta \to \infty}R^2(\widetilde{Q}_{\beta})=c_{\infty}(N_0+2)$
, so
$\lim_{\beta \to \infty}R^2(\widetilde{Q}_{\beta})=c_{\infty}(N_0+2)$
, so
From (5.13) and (5.16) we get
![]() $u_{\infty}(x)=0$
for
$u_{\infty}(x)=0$
for
![]() $x \geq N_0+1$
(this was also shown in a more general context in Remark 4.1). On the other hand, when
$x \geq N_0+1$
(this was also shown in a more general context in Remark 4.1). On the other hand, when
![]() $1 \leq x \leq N_0$
, by letting
$1 \leq x \leq N_0$
, by letting
![]() $\beta \to \infty$
in (5.14) we deduce the recurrence formula
$\beta \to \infty$
in (5.14) we deduce the recurrence formula
with
![]() $u_{\infty}(N_0+1)=0$
. Finally, from (5.15) note that
$u_{\infty}(N_0+1)=0$
. Finally, from (5.15) note that
 \begin{equation*} \pi_\beta(N_0+j)= \Bigg(\prod_{k=N_0+2}^{N_0+j}\frac{u_\beta(k-1)}{1-u_\beta(k)}\Bigg)\pi_\beta(N_0+1), \qquad j \geq 2,\end{equation*}
\begin{equation*} \pi_\beta(N_0+j)= \Bigg(\prod_{k=N_0+2}^{N_0+j}\frac{u_\beta(k-1)}{1-u_\beta(k)}\Bigg)\pi_\beta(N_0+1), \qquad j \geq 2,\end{equation*}
but
![]() $u_{\beta}(N_0+j)=p_{\beta}$
for all
$u_{\beta}(N_0+j)=p_{\beta}$
for all
![]() $j \geq 1$
, hence
$j \geq 1$
, hence
Thus,
 \begin{equation*} \pi_\beta([N_0+2,\infty)) = \pi_{\beta}(N_0+1)\sum_{j=2}^{\infty}\bigg(\frac{p_\beta}{1-p_\beta}\bigg)^{j-1} = \pi_{\beta}(N_0+1)\frac{p_\beta}{1-2p_{\beta}}.\end{equation*}
\begin{equation*} \pi_\beta([N_0+2,\infty)) = \pi_{\beta}(N_0+1)\sum_{j=2}^{\infty}\bigg(\frac{p_\beta}{1-p_\beta}\bigg)^{j-1} = \pi_{\beta}(N_0+1)\frac{p_\beta}{1-2p_{\beta}}.\end{equation*}
Since
![]() $\pi_{\beta}(N_0+1) \leq 1$
and
$\pi_{\beta}(N_0+1) \leq 1$
and
![]() $\lim_{\beta \to \infty}p_\beta=0$
, we conclude that
$\lim_{\beta \to \infty}p_\beta=0$
, we conclude that
![]() $\lim_{\beta \to \infty}\pi_\beta([N_0+2,\infty))=0$
(this is guaranteed by Theorem 4.1). For
$\lim_{\beta \to \infty}\pi_\beta([N_0+2,\infty))=0$
(this is guaranteed by Theorem 4.1). For
![]() $0 \leq x \leq N_0+1$
the value of
$0 \leq x \leq N_0+1$
the value of
![]() $\pi_\infty(x)$
can be obtained by direct computation combining (5.15) and (5.17) with the additional conditions
$\pi_\infty(x)$
can be obtained by direct computation combining (5.15) and (5.17) with the additional conditions
![]() $u_{\infty}(0)=1$
,
$u_{\infty}(0)=1$
,
![]() $u_{\infty}(N_0+1)=0$
, and
$u_{\infty}(N_0+1)=0$
, and
![]() $\sum_{x=0}^{N_0+1}\pi_{\infty}(x)=1$
.
$\sum_{x=0}^{N_0+1}\pi_{\infty}(x)=1$
.
5.3. Example 3: The periodical case
We assume
![]() $\psi(x)=\psi(x+L)$
,
$\psi(x)=\psi(x+L)$
,
![]() $x \in \mathbb{Z}_+$
, for some
$x \in \mathbb{Z}_+$
, for some
![]() $L \geq 2$
, i.e. the function
$L \geq 2$
, i.e. the function
![]() $\psi(x)$
is periodic with period
$\psi(x)$
is periodic with period
![]() $L \geq 2$
. Here, the interesting case is
$L \geq 2$
. Here, the interesting case is
![]() $\ell_{\max}<L$
, because
$\ell_{\max}<L$
, because
![]() $\ell_{\max}=L$
implies that
$\ell_{\max}=L$
implies that
![]() $\psi(x)$
is constant. Since
$\psi(x)$
is constant. Since
![]() $Q_\beta^{[x]}=Q_\beta^{[x+L]}$
for all
$Q_\beta^{[x]}=Q_\beta^{[x+L]}$
for all
![]() $x \geq 0$
, from the definition of the convergence radius we have
$x \geq 0$
, from the definition of the convergence radius we have
![]() $R_{\beta,x}=R_{\beta,x+L}$
for all
$R_{\beta,x}=R_{\beta,x+L}$
for all
![]() $x \in \mathbb{Z}^{+}$
. Recalling that the sequence
$x \in \mathbb{Z}^{+}$
. Recalling that the sequence
![]() $R_{\beta,x}$
is non-decreasing in x, we have deduced that
$R_{\beta,x}$
is non-decreasing in x, we have deduced that
![]() $R_{\beta,x}=R_{\beta}$
is constant for all
$R_{\beta,x}=R_{\beta}$
is constant for all
![]() $x \geq 0$
. This means that the sequence of matrices
$x \geq 0$
. This means that the sequence of matrices
![]() $Q_{\beta}^{[x]}$
is
$Q_{\beta}^{[x]}$
is
![]() $R_\beta$
-transient for all
$R_\beta$
-transient for all
![]() $x \geq 1$
. Since
$x \geq 1$
. Since
![]() $Q_{\beta}^{[L]}=Q_{\beta}$
,
$Q_{\beta}^{[L]}=Q_{\beta}$
,
![]() $Q_{\beta}$
is
$Q_{\beta}$
is
![]() $R_\beta$
-transient for all
$R_\beta$
-transient for all
![]() $\beta \geq 0$
. Note that in the periodical case, if
$\beta \geq 0$
. Note that in the periodical case, if
![]() $\ell_{\max}<L$
, we automatically get an infinite number of runs with size
$\ell_{\max}<L$
, we automatically get an infinite number of runs with size
![]() $\ell_{\max}$
. The existence of an equilibrium measure is discarded for all
$\ell_{\max}$
. The existence of an equilibrium measure is discarded for all
![]() $\beta>0$
and hence
$\beta>0$
and hence
![]() $\pi_\infty(\!\cdot\!)$
cannot exist.
$\pi_\infty(\!\cdot\!)$
cannot exist.
Acknowledgements
The authors would like to thank the anonymous referee for his comments, suggestions, and corrections, which have helped us to improve this paper.
Funding information
J.L. would like to thank the ‘Núcleo de Investigación No. 2 Sistemas Complejos en Ciencia e Ingeniería-UCN-VRIDT 042/2020’. G.C. acknowledges the fellow program ANID BECAS/DOCTORADO NACIONAL No. 21200620.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.