Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-16T17:14:19.783Z Has data issue: false hasContentIssue false
  • English
  • Français

OHNO–ZAGIER TYPE RELATIONS FOR MULTIPLE t-VALUES

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  11 November 2022

ZHONGHUA LI Open the ORCID record for ZHONGHUA LI [Opens in a new window]  and
YUTONG SONG Open the ORCID record for YUTONG SONG [Opens in a new window]
ZHONGHUA LI*
Affiliation:
School of Mathematical Sciences, Tongji University, No. 1239 Siping Road, Shanghai 200092, PR China
YUTONG SONG
Affiliation:
School of Mathematical Sciences, Tongji University, No. 1239 Siping Road, Shanghai 200092, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study Ohno–Zagier type relations for multiple t-values and multiple t-star values. We represent the generating function of sums of multiple t-(star) values with fixed weight, depth and height in terms of the generalised hypergeometric function 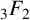$\,_3F_2$ . As applications, we get a formula for the generating function of sums of multiple t-(star) values of maximal height and a weighted sum formula for sums of multiple t-(star) values with fixed weight and depth.

Keywords

multiple t-valuemultiple zeta valuegeneralised hypergeometric function

MSC classification

Primary: 11M32: Multiple Dirichlet series and zeta functions and multizeta values
Secondary: 33C20: Generalized hypergeometric series, $_pF_q$
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 2 , April 2023 , pp. 215 - 226
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Fundamental Research Funds for the Central Universities (grant number 22120210552).

References

Aoki, T., Kombu, Y. and Ohno, Y., ‘A generating function for sums of multiple zeta values and its applications’, Proc. Amer. Math. Soc. 136(2) (2008), 387–395.CrossRefGoogle Scholar
Hoffman, M. E., ‘Multiple harmonic series’, Pacific J. Math. 152(2) (1992), 275–290.CrossRefGoogle Scholar
Hoffman, M. E., ‘An odd variant of multiple zeta values’, Commun. Number Theory Phys. 13(3) (2019), 529–567.CrossRefGoogle Scholar
Ihara, K., Kajikawa, J., Ohno, Y. and Okuda, J., ‘Multiple zeta values vs. multiple zeta-star values’, J. Algebra 332 (2011), 187–208.CrossRefGoogle Scholar
Ihara, K., Kaneko, M. and Zagier, D., ‘Derivation and double shuffle relations for multiple zeta values’, Compos. Math. 142(2) (2006), 307–338.CrossRefGoogle Scholar
Kaneko, M. and Tsumura, H., ‘Zeta functions connecting multiple zeta values and poly-Bernoulli numbers’, in: Various Aspects of Multiple Zeta Functions—In Honour of Professor Kohji Matsumoto’s 60th Birthday, Advanced Studies in Pure Mathematics, 84 (eds. Mishou, H., Nakamura, T., Suzuki, M. and Umegaki, Y.) (Mathematical Society of Japan, Tokyo, 2020), 181–204.CrossRefGoogle Scholar
Ohno, Y. and Zagier, D., ‘Multiple zeta values of fixed weight, depth and height’, Indag. Math. (N.S.) 12(4) (2001), 483–487.CrossRefGoogle Scholar
Prudnikov, A. P., Brychkov, Y. A. and Marichev, O. I., Integrals and Series, Volume 3: More Special Functions (Gordon and Breach Science Publishers, New York, 1990).Google Scholar
Takeyama, Y., ‘On a weighted sum of multiple $T$ -values of fixed weight and depth’, Bull. Aust. Math. Soc. 104 (2021), 398–405.CrossRefGoogle Scholar
Zagier, D., ‘Values of zeta functions and their applications’, in: First European Congress of Mathematics, Vol. II (Paris, 1992), (eds. Joseph, A., Mignot, F., Murat, F., Prum, B. and Rentschler, R.), Progress in Mathematics, 120 (Birkhäuser, Basel, 1994), 497–512.CrossRefGoogle Scholar
Zhao, J., Multiple Zeta Functions, Multiple Polylogarithms and Their Special Values, Series on Number Theory and Its Applications, 12 (World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2016).CrossRefGoogle Scholar